复杂网络9讲-加权网络
复杂网络的基础知识
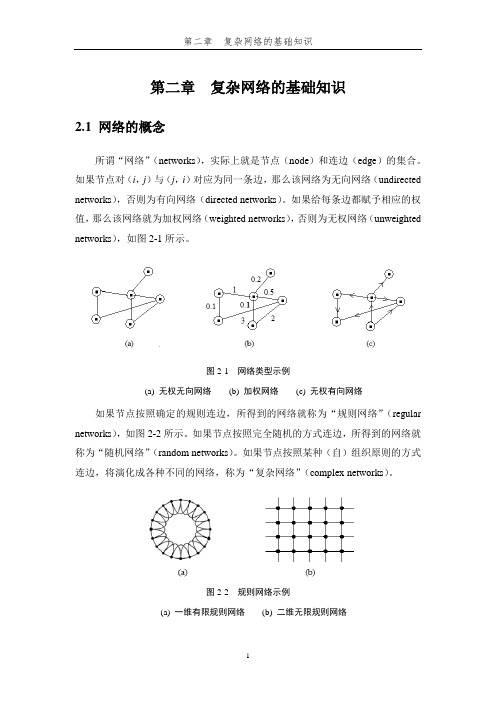
第二章复杂网络的基础知识2.1 网络的概念所谓“网络”(networks),实际上就是节点(node)和连边(edge)的集合。
如果节点对(i,j)与(j,i)对应为同一条边,那么该网络为无向网络(undirected networks),否则为有向网络(directed networks)。
如果给每条边都赋予相应的权值,那么该网络就为加权网络(weighted networks),否则为无权网络(unweighted networks),如图2-1所示。
图2-1 网络类型示例(a) 无权无向网络(b) 加权网络(c) 无权有向网络如果节点按照确定的规则连边,所得到的网络就称为“规则网络”(regular networks),如图2-2所示。
如果节点按照完全随机的方式连边,所得到的网络就称为“随机网络”(random networks)。
如果节点按照某种(自)组织原则的方式连边,将演化成各种不同的网络,称为“复杂网络”(complex networks)。
图2-2 规则网络示例(a) 一维有限规则网络(b) 二维无限规则网络2.2 复杂网络的基本特征量描述复杂网络的基本特征量主要有:平均路径长度(average path length )、簇系数(clustering efficient )、度分布(degree distribution )、介数(betweenness )等,下面介绍它们的定义。
2.2.1 平均路径长度(average path length )定义网络中任何两个节点i 和j 之间的距离l ij 为从其中一个节点出发到达另一个节点所要经过的连边的最少数目。
定义网络的直径(diameter )为网络中任意两个节点之间距离的最大值。
即}{max ,ij ji l D = (2-1) 定义网络的平均路径长度L 为网络中所有节点对之间距离的平均值。
即∑∑-=+=-=111)1(2N i N i j ij lN N L (2-2)其中N 为网络节点数,不考虑节点自身的距离。
复杂网络

复杂网络的意味着这个节点在
某种意义上越“重要”(“能力大”)。 网络的平均度:网络中所有节点的度和的平均值 ,记作<k>。事实上,<k>=2q/p
度(degree):节点 i 的度 ki 定义为与该节点连接的其 他节点的数目。
节点的聚类系数(簇系数):在简单图中,设节点v的邻集 为N(v), |N(v)|=ki,则节点v的聚类系数定义为这ki个节点之间 存在边数Ei与总的可能边数ki(ki-1)/2之比,即:Ci=2Ei/ki(ki-1) ★ 节点v的邻点间关系的密切程度
也就是说,幂律分布函数是唯一满足“无标度 条件”的概率分布函数。
复杂网络应用
电力系统复杂网络的应用:
电力系统复杂网络受到随意攻击
细胞复杂网络的应用:
肺部细胞形成一个复杂网络
因特网复杂网络的应用:
因特网形成的复杂网络
交通运输复杂网络的应用:
航 空 网
道 路 交 通 网
城 市 公 共 交 通 网
无标度网络模型
研究发现许多复杂网络的连接度分布函数具有幂律形式, 由于这类网络的节点的连接度没有明显的特征长度,故 称为无标度网络。 Barabasi 和Albert 提出了一个无标度网络模型,称 为BA模型。该模型考虑到了实际网络的两个重要特性: ①增长特性;②优先连接特性。 基于这两个特性,BA无标度网络模型构造算法如下: ①增长:从一个具有m0个节点的网络开始,每次引入一 个新的节点,并且连到m个已存在的节点上,这 里 。 ②优先连接:一个新节点与一个已经存在的节点i相连 接的概率 与节点i的度ki,节点j的度kj之间满足如下 ki 关系:
具有较短的平均路径长度又具有较高的聚类系数的网络就称为小世界 网络。 Newman和Watts提出了NW小世界模型,用“随机化加边”取代WS小 世界模型构造中的“随机化重连”。算法如下: ①从规则图开始:含有N 个节点的最近邻耦合网络。 ②随机化加边:以概率P在随机选取的一对节点之间加上一条边。 NW小世界模型中,p=0对应于原来的最近邻耦合网络,p=1对应于全 局耦合网络。
复杂网络 PPT课件

二十一世纪(二十世纪末),系统成为主要的研 究对象,整合成为主要方法;
整合的方法在于了解细部以后,研究“如何组合”的
问题,这导致复杂网络结构的研究; 如:普列高津的耗散结构理论、哈肯的协同学、混沌 和复杂系统理论、系统生物学、…
复杂系统与复杂网络
复杂系统与复杂网络的概念
系统:集合(具体元素)+ 系统的结构是什么?
统失控等一系列不同网络间的连锁反应。
(4)网络分层结构的复杂性
行政管理网络是具有层结构的,多数网络都有节点的
分层结构,只是在许多网络中没有意识到是一种造成 复杂性的重要结构。
对复杂网络的理解
复杂网络是二十一世纪科学研究的思想和理念, 它启发我们用什么观点理解这个世界:整个世界 以及组成世界的任何细部都是由网络及其变化形 成的; 复杂网络也是研究复杂系统的一种技术和方法, 它关注系统中个体相互作用的拓扑结构,是理解 复杂系统性质和功能的基本方法。
复杂网络 Complex Network
为什么研究复杂网络?
二十一世纪涌现的新现象
互联网是怎样“链”接的? 从一个页面到另一个页面,
平均需要点击多少次鼠标?
美国航空网
城市公共交通网
为什么两者结构差异如此之大? 这种差异是必然还是偶然的? 城市交通涌堵的原因是什么?
• 非典发现在广州,为什么却 在北京爆发呢? • 传染病是怎样扩散和消失的?
互联网 病毒传播网
计算机病毒是怎样传播的? 为什么“好事不出门,坏事 行千里”呢?……
神经网络
生态网络
社交网络
电力网络
电信网络航空网络Biblioteka Facebook 全球友谊图
复杂网络的分析及优化

复杂网络的分析及优化随着互联网的迅速发展,越来越多的数据在网络中传输,网络结构也越来越复杂。
如何分析和优化这些复杂的网络成为一个关键问题。
本文将介绍复杂网络的分析及优化方法,包括网络拓扑结构分析、网络连通性研究、网络优化算法等。
一、网络拓扑结构分析网络的拓扑结构是指网络中节点和边的分布规律。
通过对网络拓扑结构的分析可以了解网络的整体特征和局部特征,从而深刻地认识网络内部的相互关系。
1.1 度分布度是指一个节点的直接连接数,度分布是指网络中节点度数的频率分布。
通常情况下,度分布呈现长尾分布,即有少数节点的度数非常大,而大多数节点的度数较小。
度分布的形态对网络的性质和行为有很大影响,因此度分布是复杂网络拓扑结构分析的重要指标。
1.2 聚集系数聚集系数是指网络中三角形的数量与所有可能的三角形数量的比值。
聚集系数可以用来描述网络的密集程度和连通性。
在社交网络和生物网络中,聚集系数通常比较高,而在物理和技术网络中,聚集系数较低。
1.3 特征路径长度特征路径长度是指网络中任意两个节点之间的最短路径的平均数。
网络的特征路径长度反映了网络内部连接的紧密程度,对于描述物理网络和社交网络的距离关系非常有用。
二、网络连通性研究网络连通性是指在网络结构中通过节点和边互相连接所形成的整体连通性。
网络连通性是复杂网络中最重要和最基本的特性之一。
2.1 连通性分析连通性分析是指通过对网络中节点和边的连接性进行分析,确定网络的连通性。
在无向网络中,如果任意两个节点都可以通过路径相互连接,则该网络是连通的。
在有向网络中,如果所有节点都可以到达任意另一个节点,则该网络是强连通的。
2.2 最大连通子图最大连通子图是指网络中最大的连通子集,其中任意两个节点都可以通过路径相互连接。
最大连通子图是分析网络组成和功能的关键。
2.3 非连通子图非连通子图是指网络中不属于任何连通子图的节点或边。
非连通子图可以通过增加新的节点或边,改变网络的拓扑结构,从而使网络成为连通的。
网络科学中的复杂网络理论

网络科学中的复杂网络理论网络科学是一门涵盖计算机科学、数学、物理学等多个学科的交叉学科,其研究的对象是网络,包括社交网络、物流网络、电力网络、金融网络等。
在网络科学的研究中,复杂网络理论是一个重要的分支,它能够帮助我们理解网络的特性和行为。
本文将从复杂网络的概念、网络拓扑结构、网络动力学、网络优化等方面介绍复杂网络理论。
一、复杂网络的概念复杂网络是由许多节点和边组成的网络,节点和边之间的关系可以是同性的或异性的,也可以是有向的或无向的。
复杂网络中的节点可以是人、公司、电力系统中的发电站等,边可以表示这些节点之间的联系,如社交网络中的朋友关系、电力系统中的输电线路等。
由于网络中的节点和边是多种多样的,所以复杂网络具有超过简单网络的复杂性和多样性。
复杂网络理论研究的是网络的结构和行为,通过分析网络节点和边之间的关系,可以揭示网络中的规律和特性。
复杂网络理论已被应用于许多领域,如社交网络分析、流行病模型、交通优化、生物信息学等。
二、网络拓扑结构网络的拓扑结构是指节点和边之间关系的模式,包括邻接矩阵、度分布、聚类系数、路径长度等几个方面。
1. 邻接矩阵邻接矩阵是一个方阵,其中的行和列分别对应网络的节点,矩阵中的元素为1表示对应节点之间有一条边,为0则表示没有边相连。
邻接矩阵是表示网络拓扑结构最简单的方式,但对于大规模网络,其密集的矩阵往往需要大量的存储空间,使得计算和分析变得困难。
2. 度分布节点的度是指该节点连接的边数。
度分布是一个度数与节点数量或概率的关系图,可以揭示网络节点之间关系的多样性。
常见的度分布包括泊松分布、幂律分布等。
幂律分布是指在一个网络中存在很少的高度连接的节点,多数节点的度数较低,这称为“无标度网络”。
无标度网络中的少数节点有着重要的作用,称为“超级节点”,它们是网络中的枢纽或关键节点。
3. 聚类系数聚类系数是指一个节点的邻居之间相互之间已经连接的比例。
聚类系数越高表示该节点的邻居之间越紧密。
复杂网络的基础知识

第二章复杂网络的基础知识2.1 网络的概念所谓“网络”(networks),实际上就是节点(node)和连边(edge)的集合。
如果节点对(i,j)与(j,i)对应为同一条边,那么该网络为无向网络(undirected networks),否则为有向网络(directed networks)。
如果给每条边都赋予相应的权值,那么该网络就为加权网络(weighted networks),否则为无权网络(unweighted networks),如图2-1所示。
图2-1 网络类型示例(a) 无权无向网络(b) 加权网络(c) 无权有向网络如果节点按照确定的规则连边,所得到的网络就称为“规则网络”(regular networks),如图2-2所示。
如果节点按照完全随机的方式连边,所得到的网络就称为“随机网络”(random networks)。
如果节点按照某种(自)组织原则的方式连边,将演化成各种不同的网络,称为“复杂网络”(complex networks)。
图2-2 规则网络示例(a) 一维有限规则网络(b) 二维无限规则网络2.2 复杂网络的基本特征量描述复杂网络的基本特征量主要有:平均路径长度(average path length )、簇系数(clustering efficient )、度分布(degree distribution )、介数(betweenness )等,下面介绍它们的定义。
2.2.1 平均路径长度(average path length )定义网络中任何两个节点i 和j 之间的距离l ij 为从其中一个节点出发到达另一个节点所要经过的连边的最少数目。
定义网络的直径(diameter )为网络中任意两个节点之间距离的最大值。
即}{max ,ij ji l D = (2-1) 定义网络的平均路径长度L 为网络中所有节点对之间距离的平均值。
即∑∑-=+=-=111)1(2N i N i j ij lN N L (2-2)其中N 为网络节点数,不考虑节点自身的距离。
复杂网络的名词解释

复杂网络的名词解释随着互联网的迅猛发展,我们的世界正变得越来越复杂。
在数字时代,网络已经成为了人们日常生活和工作中不可或缺的一部分。
然而,网络的本质是什么,它是如何运作的?这些问题引发了学者们对复杂网络的研究和解释。
复杂网络是网络科学中的一个重要概念,用来描述由许多相互连接的节点组成的系统。
在复杂网络中,节点可以表示个体、物体或者观察对象,而边则表示节点之间的连接或关系。
这些连接可以是社交媒体中的关注关系,互联网中的网页链接,或者是生物体内蛋白质之间的相互作用。
复杂网络的一个显著特征是其非均匀分布的拓扑结构。
相比于简单网络,如正则网络或随机网络,复杂网络的拓扑结构更加复杂多样。
大规模复杂网络常常呈现出具有高度聚集性和短平均路径长度的特点。
也就是说,网络中的节点倾向于组成局部紧密相连的群组,而通过少数边连接的节点之间的距离则很短。
在复杂网络中,节点的连接方式和模式对网络的功能和行为起着决定性的影响。
例如,一些节点连接非常多的其他节点,被称为“中心节点”或“关键节点”,它们在信息传播、网络稳定性和攻击扩散等方面起到至关重要的作用。
此外,复杂网络还具有小世界特性,即任何两个节点之间可以通过少量的中间节点快速建立联系。
这种性质使得复杂网络具有高效的信息传递能力和鲁棒性。
研究复杂网络有助于我们更好地理解和解释真实世界中许多复杂系统的行为。
它在社会学、生物学、物理学、经济学以及信息科学等领域中都有广泛的应用。
例如,在社交网络中,可以利用复杂网络的分析方法来揭示人们之间的社会关系、信息传播的路径和影响力;在生物网络中,通过研究蛋白质相互作用网络可以了解生命体系中蛋白质调控的机制和疾病的发生;在经济学中,分析金融市场网络可以评估系统的脆弱性和风险传播。
此外,复杂网络的研究不仅限于静态结构的探索,还包括网络动力学的研究。
网络动力学研究网络中节点的状态或行为随时间变化的规律。
例如,在传染病传播的研究中,网络动力学的分析可以帮助我们理解疾病传播的机制和采取相应的干预措施。
复杂网络简要介绍

复杂网络简要介绍复杂网络是一种用于描述复杂系统中各种元素(节点)之间相互关系和连接模式的数学和图论模型。
复杂网络的研究领域涵盖了多种学科,包括物理学、计算机科学、社会学、生物学等,它们用于分析和理解各种真实世界复杂系统,如社交网络、生物网络、大气环流系统、互联网、蛋白质相互作用网络等。
复杂网络的特征和性质通常包括以下几个方面:节点和边:复杂网络由一组节点(或顶点)和连接这些节点的边(或链接)组成。
节点代表系统中的个体、元素或实体,边表示节点之间的相互关系、连接或交互。
度分布:复杂网络中的节点通常具有不同数量的连接,这被称为节点的度。
度分布描述了网络中不同节点的度数分布模式,例如是否存在高度连接的节点(所谓的“中心节点”)。
小世界性质:复杂网络中的节点通常以较短的路径相互连接,这被称为“小世界性质”,研究表明即使在大型网络中,节点之间的通信路径也相对较短。
社区结构:复杂网络中的节点通常会自发地形成一些具有内部紧密连接的子群,被称为社区。
社区结构有助于理解网络中的模块化和集团性质。
无标度性:复杂网络的度分布通常呈现无标度性质,这意味着只有少数节点具有极高的度数,而大多数节点具有较低的度数。
自组织性:复杂网络通常表现出自组织性,即它们的全局结构和性质是由局部节点之间的局部规则和相互作用自发形成的。
鲁棒性:复杂网络通常具有一定的鲁棒性,即它们能够在一定程度上抵抗节点故障或攻击而保持功能完整性。
复杂网络的研究旨在揭示各种系统之间的共性和特殊性质,并通过网络模型和分析方法来探讨这些系统的结构、功能和演化。
这种研究对于理解真实世界中的复杂系统行为、信息传播、社交动态、生物互动等方面具有广泛的应用。
2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)网络结构拓扑演化同WSF网络
(2)赋边权:设定一参数p 以概率p按公式
w ji ki k i
i
赋边权
以概率1-p按公式
w ji
i i
i
赋边权
当p=1时, ZTZH模型=WSF模型
当p=1时,边权的赋予完全由节点的适应度决定. ZTZH模型的点强度分布也符合幂律分布 p(s) s r 数p,随着p的增加, s 从3连续下降。
2.加权网络上的统计量
权相关性 最短路径 集聚系数
权相关性
1.基本概念: 点权:无权网中节点度的自然推广
点权 Si 的近邻集合)
S ki
wij ,即与节点 i i关联的边权之和。( 其中 N
jNi
i
是节点i
单位权: U i i, 顶点连接的平均权重.
Yi 权重分布的差异性:
p i
p
• 3.技术网络 在一些基础设施网络中,例如Internet,铁路网和航空网中, 运输过程中的流量可以转化为权重,Barrat等人分析了全 球航空网络,把两机场i和j之间的航班的有效座位数作为 ij 机场间的权重 ,而李炜等人在研究中国航空网时, 把两机场间的航班数作为机场间的权重。在对不同数据进 行研究时,发现这些网络具有小世界网络和无标度网络的 特征。特别是度分布表现为如下形式: p(k ) k f (k / k x ) ,其中 2.0 ,且 f (k / k ) 是指数截 断函数。与一个机场能够运作的最大航线数有关。点强度 分布呈现出幂律尾,并且边权和度具有一定的相关性:平 均来讲,边权与边的两端顶点的度值的函数关系为 ij ~ ( k i k j ) 其中 0.5 。点强度和度之间的关系服从 幂律函数关系 s(k ) Ak ,其中 1.5 ,这说明机场越大, 处理交通流量的能力就越强。
对于相似权:l i k
1 1 wi j 1 w jk
2.最短路径:两点之间所有连通的路径中距离之和最小的一条或几条路径。
无权网:边数最少的路径
最短路径
加权网:因为距离不满足三角不等式,所以两边距离之和不一定大于第三边பைடு நூலகம் 边数最少的路径 最短路径
网络的其他全局统计量,如介数,可以在加权最短路径的基础上进行计算
k nn (k )
knn,i
1 ki
1 kj ki jN i
a k
jV ij
j
k nn,i
在加权网络中:
k
定义节点的加权平均近邻度 考虑权与度的相关性
当
w k nn ,i k nn ,i
w knn ,i knn ,i
w nn ,i
1 Si
jN j
a
ij
wij k j
x
• 经济物理学科学家合作网络的建立和统计分析 科学家之间的合作有多个层次,若希望通过网络分析挖掘 科学家在科学研究上的内在关联就必须考虑不同层次的相 互作用的贡献,而网络连接权重就就需要综合考虑层次和 强度两个方面。考虑科学家交流的三个层次:合著,引用 和致谢,记录为 ( S1 , S 2 , x, y, z ) ,作者 S1 与S 2 合作x次, S2 S1 引用作者 的文章 y次,并且在 的文章致谢里感谢 S2 z次。事实上,可以把整个数据看做三个不同的网络,合 著网络,引用网络和致谢网络,把这三种关系综合在一起 考虑,看做一个网络,采用以下赋权方式: 可以取{1,2,3} 分别对应合著, wij wij ,其中 引用和致谢关系, wi 是三种关系所对应的权重,定义 j 为:wij tanh( Tij )
无标度加权网络模型特点:
3 p ( k ) k 拓扑结构与BA模型相同,故度分布
rs p ( s ) s 点权分布符合幂律分布: 其中指数与参数
m有关。 边权分布
ZTZH模型
在WSF模型的基础上进行推广,赋边权时综合考虑节点的度和适应度。 适应度 i :反应节点i本身的性质,假设其服从[0,1]上的均匀分布.(当不知道随机变 量取值的特点时,假设其服从某一区间上的均匀分布)
这时必须考虑赋边权,表示相联系的强度.
另外,我们希望在同一个网络中研究这三个层次的相互作用,还应该考虑 加权的方式.
当系统中包含同一属性的不同层次的关系的时候,必须仔细研究加权方 式.
加权的方式:
根据相关的物理量(例如:电阻网络边上的权值代表电 阻值,邮递员问题中的距离) 根据相互作用的某种属性(例如:科学家通过文献相互 作用,把引文的次数作为权重) 边权按照意义划分: 相异权: 权值越大,两点之间的距离越大,关系越疏 远.(例:邮递员问题中的距离) 相似权: 权值越大,两点之间的距离越小,关系越亲 密.(例:科学家合作网中,把次数作为权重,得到相似 权) 注意: 在计算两点间的距离和聚类系数时,边权的意 义不同,计算方式也不同.
• 边权固定模型
1.无标度加权网络模型(WSF) 2001年,Yook和Barabasi提出了类似于BA模型的加权网络生成模型。
其定义如下:
(1)网络拓扑结构的演化(同BA模型) 增长:初始时有n0个节点,每个时间间隔加入一个新节点j,并使新节点j 与m个已经存在的点连接(m≤ n0 ) 择优连接:新加入的点与网络中已经存在的点的连接不是等概率的,而是 以一种择优的方式选择与自己连接的点。新节点j与节点i连接的概率:
时,具有较大权重的边倾向于连接具有较大度值的点
当 时,具有较大权重的边倾向于连接具有较小度值的点 w 所以,对于相互作用强度(权重)给定的边, knn ,i 表明它与具有不同度值的顶 点之间的亲和力。
• 最短路径
1.加权网络中两点之间的距离与权重的关系: 距离是权重的某种函数,这时需要看权重是相似权还是相异权。 相异权:定义两点之间的距离 lij wij 1 l 相似权:令 ij wij 假设顶点i和k分别通过两条权重分别为 wij 和 w jk 的边相连,现求i与k之 间的距离。 对于相异权: lik wij w jk
j i
ki kl
l
(2)赋边权(基于两个假设:权重Wij正比于节点i的度;所有新节点有相同的点权) 新节点与已存在节点之间的每一条连接j i, 被赋予一定的权重 wij ,权 重的多少取决于被连接节点i的度 w k i ji k i
i
{i‘}代表新节点j所要连接的点的集合。这时新节点j的点权为1
jN i
[
wij Si
] 2 表示与i相连的边权分布的离散程度。
拥有相同点权与单位权的两个节点相比,差异性越大,离散程度越大。 点强度分布P(s)与度分布的作用类似,主要是考察节点具有点强度s的 概率。
边权分布P(w)代表一条边具有权重w的概率。
结论2:差异性 Y i 与度 k的关系
如果与顶点i关联的边的权重值差别不大,则 Y i 与
Watts-Strogatz 定义的聚类系数:
C (i )
a
j ,k j ,k
ij
a jk a ki
ij
a
a ki
加权网的聚类系数:
w CH
w
j ,k
ij
w jk wki
j ,k
maxij wij wij wik
一些加权网络的实证结果
• 1.生物网络 Almaas等人将酵母中的新陈代谢反应看作加权网络进行 研究,把从代谢物i到j的流量看作边权 ,观察到流量具有 高度非均匀性,在理想的培养下条件下,边权的分布符合 幂律分布 p()(0 ) 其中 0.0003, 1.5 此外还发现给定两端度值的边的权重平均值和两个端点的 ~ ( k k ) 度值的关系为 ij ,其中 0.5。除了全局流量 i j 分布的非均匀性外,计算边权差异性 Yi 还可以观察到在 单个代谢物的层面上边权分布的非均匀性。在此网络上对 出度和入度相同的顶点计算边权差异性,发现它们都服从 Yi ~ k 0.27 这是一种介于Y (k ) const 和 Y (k ) ~ k 1 之间的中间 状态,说明一个代谢物参与的化学反应越多,其中的某一 个化学反应携带主要流量的可能性就越高。??
8.2 加权网络的演化模型
研究的意义是什么?
• 边权固定模型 • 边权演化模型 • 应用
例:某一新思想的在一个学术领域 的产生传播过程中,随着时间的 推移,可能会有更多的科学家介入 (增长),同时随着新思想影响程 度的加深,已有交流的科学家之 间的相互作用强度也会发生变化 (权值改变)。静态网络显然已经 不能揭示加权网络的演化行为, 因此在这里研究网络拓扑结构和 权重分布的耦合演化机制,来描 述新思想传播过程。
1 ki
成正比。
Yi
jN i
[
wij Si
]2 [
wij w ki
]2 k i
wij
2
2 2
w ki
1 ki
如果权值相差较大,那么只有一条边的权重起主要作用,则
Yi 1
2.相关性分析 加权网络需要进行 度相关性分析 点权相关性分析 权与度相关性分析 度相关性分析:因为对网络加权不改变节点的度的性质,所以度相关性 分析与无权网络中分析相同。 在无权网络中: 定义节点i的近邻平均度 k nn,i ,得到度为 k 的所有节点的近邻平均度 显然 Knn(k) 是 k 的函数。那么度相关性可以通过函数 Knn(k) 的单调性得到: 如果 Knn(k) 是无单调性,那么该网络没有度相关性。 如果 Knn(k)是增函数,那么该网络是同向匹配网络。(度大的节点倾 向于与度大的节点相连) 如果 Knn(k) 是减函数,那么该网络是负向匹配网络。
0
• 2.社会网络 以科学家合作网为例,Newman定义了科学家合 p p 作网的权重 ij p i j /(n p 1) ,其中p包括数据 库中的所有文章,如果i是文章p的作者之一, p 1 则 ,否则 i 0 , n 表示文章p中作者 的数目。从平均效果来看,合作者较少时作者之 间的相互关系更加紧密。
