特殊四边形有关的创新题
特殊平行四边形难题综合训练(含答案)

特殊平⾏四边形难题综合训练(含答案)第五章特殊平⾏四边形难题综合训练1、正⽅形ABCD ,正⽅形BEFG 和正⽅形RKPF 的位置如图所⽰,点G 在线段DK 上,且G 为BC 的三等分点,R 为EF 中点,正⽅形BEFG 的边长为4,则△DEK 的⾯积为() A .10B .12C .14D .162、如图,在正⽅形ABCD 内有⼀折线段,其中AE ⊥EF ,EF ⊥FC ,并且AE =6,EF =8,FC =10,则正⽅形的边长为 .第1题第2题第3题第4题 3、如图,平⾯内4条直线l 1、l 2、l 3、l 4是⼀组平⾏线,相邻2条平⾏线的距离都是1个单位长度,正⽅形ABCD 的4个顶点A 、B 、C 、D 都在这些平⾏线上,其中点A 、C 分别在直线l 1、l 4上,该正⽅形的⾯积是平⽅单位. 4、如图,在菱形ABCD 中,边长为10,∠A =60°.顺次连结菱形 ABCD 各边中点,可得四边形A 1B 1C 1D 1;顺次连结四边形 A 1B 1C 1D 1各边中点,可得四边形A 2B 2C 2D 2;顺次连结四边形A 2B 2C 2D 2各边中点,可得四边形A 3B 3C 3D 3;按此规律继续下去…….则四边形A 2B 2C 2D 2的周长是;四边形A 2013B 2013C 2013D 2013的周长是 . 5、如图,四边形ABCD 是矩形,点E 在线段CB 的延长线上,连接DE 交AB 于点F ,∠AED =2∠CED ,点G 是DF 的中点,若BE =1,AG =4,则AB 的长为 .6、如图,四边形ABCD 中,AB =BC ,∠ABC =∠CDA =90°,BE ⊥AD 于点E ,且四边形ABCD 的⾯积为8,则BE =() A .2 B .3 C .22 D .32第5题第6题第7题第8题7、如图,菱形OABC 的顶点O 在坐标原点,顶点A 在x 轴上,∠B =120°,OA =2,将菱形OABC 绕原点顺时针旋转105°⾄OA ′B ′C ′的位置,则点B ′的坐标为()A 、(2,2-)B 、(2,2-)C 、(3,3-)D 、(2,2--)8、如图,正⽅形ABCD 中,AB =3,点E 在边CD 上,且CD =3DE .将△ADE 沿AE 对折⾄△AFE ,延长EF 交边BC 于A .①②B .①③C .②③D .①②③ 9、如图,在正⽅形ABCD 中,点O 为对⾓线AC 的中点,过点0作射线OM 、ON 分别交AB 、BC 于点E 、F ,且∠EOF =90°,BO 、EF 交于点P .则下列结论中:(1)图形中全等的三⾓形只有两对;(2)正⽅形ABCD 的⾯积等于四边形OEBF ⾯积的4倍;(3)BE +BF =20A ;(4)AE 2+CF 2=20POB .正确的结论有()个. A .1B .2C .3D .410、如图,在矩形ABCD 中,由8个⾯积均为1的⼩正⽅形组成的L 型模板如图放置,则矩形ABCD 的周长为 .11、在边长为6的菱形ABCD 中,动点M 从点A 出发,沿A →B →C 向终点C 运动,连接DM 交AC 于点N .(1)如图11-1,当点M 在AB 边上时,连接BN .求证:ABN ADN △≌△;(2)如图11-2,若∠ABC = 90°,记点M 运动所经过的路程为x (6≤x ≤12).试问:x 为何值时,△ADN 为等腰三⾓形.12、如图所⽰,正⽅形ABCD 的边CD 在正⽅形ECGF 的边CE 上,连接BE DG ,. (1)求证:BE DG .(2)图中是否存在通过旋转能够互相重合的两个三⾓形若存在,说出旋转过程;若不存在,请说明理由. CMBNAD(图11-2)CB M AND(图11-1)13、请阅读,完成证明和填空.数学兴趣⼩组在学校的“数学长廊”中兴奋地展⽰了他们⼩组探究发现的结果,内容如下:(1)如图13-1,正三⾓形ABC 中,在AB AC 、边上分别取点M N 、,使BM AN =,连接BN CM 、,发现BN CM =,且60NOC ∠=°.请证明:60NOC ∠=°.(2)如图13-2,正⽅形ABCD 中,在AB BC 、边上分别取点M N 、,使AM BN =,连接AN DM 、,那么AN = ,且DON ∠=度.(3)如图13-3,正五边形ABCDE 中,在AB BC 、边上分别取点M N 、,使AM BN =,连接AN EM 、,那么AN = ,且EON ∠= 度.(4)在正n 边形中,对相邻的三边实施同样的操作过程,也会有类似的结论.请⼤胆猜测,⽤⼀句话概括你的发现:. 14、ABC △是等边三⾓形,点D 是射线BC 上的⼀个动点(点D 不与点B C 、重合),ADE △是以AD 为边的等边三⾓形,过点E 作BC 的平⾏线,分别交射线AB AC 、于点F G 、,连接BE . (1)如图(a )所⽰,当点D 在线段BC 上时.A A A BBB CCC DDO OOM M M NNN E图13-1图13-2图13-3…(3)在(2)的情况下,当点D 运动到什么位置时,四边形BCGE 是菱形并说明理由.15、如图,ABC △中,点O 是边AC 上⼀个动点,过O 作直线MN BC ∥,设MN 交BCA ∠的平分线于点E ,交BCA ∠的外⾓平分线于点F .(1)探究:线段OE 与OF 的数量关系并加以证明;(2)当点O 在边AC 上运动时,四边形BCFE 会是菱形吗若是,请证明,若不是,则说明理由; (3)当点O 运动到何处,且ABC △满⾜什么条件时,四边形AECF 是正⽅形16、如图,已知直线128:33l y x =+与直线2:216l y x =-+相交于点C l l 12,、分别交x 轴于A B 、两点.矩形DEFG 的顶点D E 、分别在直线12l l 、上,顶点F G、都在x 轴上,且点G 与点B 重合.(1)求ABC △的⾯积;AG CD BF E 图(a )ADCBFEG图(b )AF N DC B M EO17、在ABC △中,2120AB BC ABC ==∠=,°,将ABC △绕点B 顺时针旋转⾓α(0<°α90)<°得A BC A B 111△,交AC 于点E ,11A C 分别交AC BC 、于D F 、两点.(1)如图1,观察并猜想,在旋转过程中,线段1EA 与FC 有怎样的数量关系并证明你的结论; (2)如图2,当α30=°时,试判断四边形1BC DA 的形状,并说明理由18、在菱形ABCD 中,对⾓线AC 与BD 相交于点O ,56AB AC ==,.过点D 作DE AC ∥交BC 的延长线于点E .(1)求BDE △的周长;(2)点P 为线段BC 上的点,连接PO 并延长交AD 于点Q .求证:BP DQ =.ADBECF 1AADBECF 1A 1C19、如图,在平⾯直⾓坐标系中,矩形AOBC在第⼀象限内,E是边OB上的动点(不包括端点),作∠AEF = 90,使EF交矩形的外⾓平分线BF于点F,设C(m,n).(1)若m = n时,如图,求证:EF = AE;(2)若m≠n时,如图,试问边OB上是否还存在点E,使得EF = AE若存在,请求出点E的坐标;若不存在,请说明理由.(3)若m = tn(t>1)时,试探究点E在边OB 的何处时,使得EF =(t + 1)AE成⽴并求出点E的坐标.20、如图,将正⽅形沿图中虚线(其中x<y)剪成①②③④四块图形,⽤这四块图形恰.能拼成⼀个.....矩形(⾮正⽅形).(1)画出拼成的矩形的简图;(2)求x的值.A Q DEB P COxO E BAyCFxO E BAyCFO E BAyCF21、如图所⽰,在矩形ABCD 中,1220AB AC ==,,两条对⾓线相交于点O .以OB 、OC 为邻边作第1个平⾏四边形1OBBC ;对⾓线相交于点1A ;再以11A B 、1A C 为邻边作第2个平⾏四边形111A B C C ,对⾓线相交于点1O ;再以11O B 、11O C 为邻边作第3个平⾏四边形1121O B B C ……依次类推. (1)求矩形ABCD 的⾯积;(2)求第1个平⾏四边形11OBB C 、第2个平⾏四边形111A B C C 和第6个平⾏四边形的⾯积.22、如图(22),直线l 的解析式为4y x =-+,它与x 轴、y 轴分别相交于A B 、两点.平⾏于直线l 的直线m 从原点O 出发,沿x 轴的正⽅形以每秒1个单位长度的速度运动,它与x 轴、y 轴分别相交于M N 、两点,设运动时间为t 秒(04t <≤). (1)求A B 、两点的坐标;(2)⽤含t 的代数式表⽰MON △的⾯积1S ;A 1 A 2B 2C 2C 1 B 1O 1 DABC O①当2t ≤4时,试探究2S 与t 之间的函数关系式;②在直线m 的运动过程中,当t 为何值时,2S 为OAB △⾯积的51623、如图15,在四边形ABCD 中,E 为AB 上⼀点,△ADE 和△BCE 都是等边三⾓形,AB 、BC 、CD 、DA 的中点分别为P 、Q 、M 、N ,试判断四边形PQMN 为怎样的四边形,并证明你的结论. OMAP N y l mx BO MAP N y l mxBE PF 图2224、数学课上,张⽼师出⽰了问题:如图1,四边形ABCD 是正⽅形,点E 是边BC 的中点.90AEF ∠=,且EF交正⽅形外⾓DCG ∠的平⾏线CF 于点F ,求证:AE =EF .经过思考,⼩明展⽰了⼀种正确的解题思路:取AB 的中点M ,连接ME ,则AM =EC ,易证AME ECF △≌△,所以AE EF =.在此基础上,同学们作了进⼀步的研究:(1)⼩颖提出:如图2,如果把“点E 是边BC 的中点”改为“点E 是边BC 上(除B ,C 外)的任意⼀点”,其它条件不变,那么结论“AE =EF ”仍然成⽴,你认为⼩颖的观点正确吗如果正确,写出证明过程;如果不正确,请说明理由;(2)⼩华提出:如图3,点E 是BC 的延长线上(除C 点外)的任意⼀点,其他条件不变,结论“AE =EF ”仍然成⽴.你认为⼩华的观点正确吗如果正确,写出证明过程;如果不正确,请说明理由.25、如图,ABCD 是正⽅形,点G 是BC 上的任意⼀点,DE AG ⊥于E ,BF DE ∥,交AG 于F .求证:AF BF EF =+. ADF CGE B图1 ADF C GE B 图2 ADFC GE B图3DCBA EF G参考答案1、D2、1043、5或94、2010052355 5、15 6、C 7、A 8、B 9、C 10、5811、(1)证明:∵四边形ABCD 是菱形∴AB = AD ,∠1 =∠2⼜∵AN = AN ∴△ABN ≌△ADN (2)解:∵∠ABC =90°,∴菱形ABCD 是正⽅形此时,∠CAD =45°.下⾯分三种情形:Ⅰ)若ND =NA ,则∠ADN =∠NAD =45°.此时,点M 恰好与点B 重合,得x =6;∴∠3=∠4,从⽽CM =CN ,易求AC =62,∴CM =CN =AC -AN =62-6,故x = 12-CM =12-(62-6)=18-62综上所述:当x = 6或12 或18-62时,△ADN 是等腰三⾓形12、(1)因为ABCD 是正⽅形,所以BC =CD 。
特殊四边形培优习题精选及答案
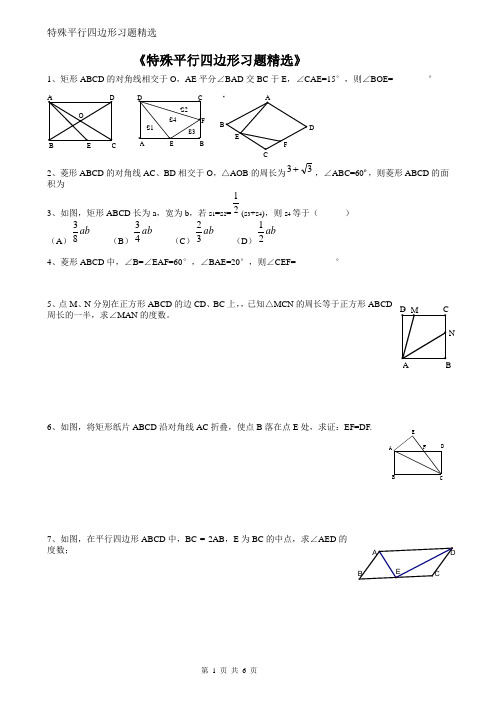
《特殊平行四边形习题精选》1、矩形ABCD 的对角线相交于O ,AE 平分∠BAD 交BC 于E ,∠CAE=15°,则∠BOE=________°2、菱形ABCD 的对角线AC 、BD 相交于O ,△AOB 的周长为33 ,∠ABC=60º,则菱形ABCD 的面积为__________3、如图,矩形ABCD 长为a ,宽为b ,若s 1=s 2=21(s 3+s 4),则s 4等于( )(A )ab 83 (B )ab 43 (C )ab 32 (D )ab214、菱形ABCD 中,∠B=∠EAF=60°,∠BAE=20°,则∠CEF=_________°5、点M 、N 分别在正方形ABCD 的边CD 、BC 上,,已知△MCN 的周长等于正方形ABCD周长的一半,求∠MAN 的度数。
6、如图,将矩形纸片ABCD 沿对角线AC 折叠,使点B 落在点E 处,求证:EF=DF.7、如图,在平行四边形ABCD 中,BC = 2AB ,E 为BC 的中点,求∠AED 的度数;D C BA MNA B CDOE A B C D E FS1S2S4S3A B C DEF FEDCB A8、如图,以正方形ABCD 的对角线AC 为一边,延长AB 到E ,使AE = AC ,以AE 为一边作菱形AEFC ,若菱形的面积为29,求正方形边长;9、如图AD 是⊿ABC 边BC 边上的高线,E 、F 、G 分别是AB 、BC 、AC 的中点,求证:四边形EDGF 是等腰梯形;10、如图1,正方形ABCD 边长为1,G 为CD 边上的一个动点(点G 与C 、D 不重合),以CG 为一边向正方形ABCD 外作正方形GCEF ,连接DE 交BG 的延长线于点H 。
(1)求证:①△BCG ≌△DCE ;②BH ⊥DE 。
(2)当点G 运动到什么位置时,BH 垂直平分DE ?请说明理由。
特殊平行四边形的经典题型

特殊平行四边形的经典题型特殊平行四边形包括矩形、菱形和正方形,那这几种图形在各种经典题型里可是各有各的“戏码”呢。
矩形嘛,经常会在面积和对角线相关的题目里出现。
比如说,已知一个矩形的长是8,对角线长是10,让你求宽是多少。
这时候就可以用到勾股定理啦,因为矩形的对角线把矩形分成了两个直角三角形,对角线就是斜边,长和宽就是两条直角边。
根据勾股定理a² + b² = c²(这里的a和b就是长和宽,c就是对角线),已知a = 8,c = 10,那宽b就等于6。
这类型的题目就像是给你一把钥匙,只要你知道用勾股定理这个“开锁方法”,就能轻松解决。
菱形呢,它的对角线互相垂直且平分这个性质可是出题的热门点。
像有一道题说菱形的对角线分别是6和8,问菱形的面积是多少。
很多人可能会先求边长再用底乘高来算面积,其实完全不用这么麻烦,直接根据菱形面积等于对角线乘积的一半这个公式,就能得出面积是24啦。
还有就是菱形四边相等这个性质,有时候会在证明题里出现,比如证明四个点构成的四边形是菱形,就需要通过证明四条边相等来得出结论。
正方形就更有趣了,它是集矩形和菱形的性质于一身的特殊平行四边形。
有这样一道题,正方形ABCD中,E是AB的中点,连接CE,CE的垂直平分线交AD于F,让你证明AF = 1/4 AD。
这题就要用到正方形的性质,它的角是直角,边相等,再结合一些三角形全等的知识。
首先设正方形边长为a,通过相似三角形或者勾股定理求出AF的长度,最后就能得出AF = 1/4 AD的结论。
在做特殊平行四边形的经典题型时,还有一些小技巧。
如果是证明题,一定要仔细分析已知条件,看这些条件能推出什么性质或者结论,然后再往要证明的结论上靠。
如果是计算面积或者边长的题目,一定要牢记各种图形的面积公式和特殊性质。
而且啊,多画图绝对是个好办法,有时候看着图形,思路一下子就清晰了呢。
不要觉得这些题型很难,只要多做几道,就会发现其实它们都是有规律可循的。
(完整版)特殊的平行四边形(压轴题)

特殊平行四边形1、如图,四边形OABC 与四边形ODEF 都是正方形。
(1)当正方形ODEF 绕点O 在平面内旋转时,AD 与CF 有怎样的数量和位置关系?证明你的结论;(2)若ODEF 绕点O 旋转,当点D 转到直线OA 上时,DCO 恰好是30°,当点D 转到直线OA或直线OC 上时,求AD 的长。
(本小题只写出结论,不必写出过程)FEDCBAO2、如图,在正方形ABCD 中,点P 是射线BC 上的任意一点(点B 与点C 除外),连接DP ,分别过点C 、A 作直线DP 的垂线,垂足为点E 、F.(1)当点P 在BC 的延长线上时,那么线段AF 、CE 、EF 之间有怎样的数量关系?请证明你的结论; (2)当点P 在BC 边上时,正方形的边长为2,AF 、CE 之间有怎样的数量关系?请证明你的结论; (3)在(2)的条件下,当CE=1时,求EF 的长.P FEDCB A DCBA3、菱形ABCD 中,点E 、F 分别在BC 、CD 边上,且B EAF ∠=∠。
(1)如果B ∠=60°,求证:AE=AF ; (2)如果)(︒<<︒=∠900ααB ,(1)中的结论:AE=AF 是否依然成立,请说明理由。
(3)如果AB 长为5,菱形ABCD 面积为20,BE=a ,求AF 的长。
(用含a 的式子表示)FED CBA4、如图,在正方形ABCD 中,点E 在边AB 上(点E 与点A 、B 不重合).过点E 作FG ⊥DE ,FG 与边BC 相交于点F ,与边DA 的延长线相交于点G 。
(1)BF 、AG 、AE 的数量之间具有怎样的关系?证明你的结论.(2)连接DF ,如果正方形的边长为2,设AE=a ,求△DFG 的面积。
(用含a 的式子表示)(3)如果正方形的边长为2,FG 的长为25,求点C 到直线DE 的距离。
GFEDCBA5、已知,在矩形ABCD 中,AB=10,BC=20,四边形EFGH 的三个顶点E 、F 、H 分别在矩形ABCD 边AB 、BC 、DA 上,AE=2。
特殊四边形的计算与证明问题(真题10道+模拟30道)-中考数学重难题型押题培优导练案【原卷版】

专题14特殊四边形的计算与证明问题(北京真题10道+模拟30道)【方法归纳】题型概述,方法小结,有的放矢考点考查年份考查频率十年8考特殊四边形的计算与证明(大题)2013.2014.2015.2016.2017.2020.2021.2022以四边形为载体的计算与证明是北京市中考数学常考的一类解答题,要求学生理解和掌握平行四边形、矩形、菱形、正方形的性质定理和判定定理,会画出四边形全等变换后的图形,并会结合其他知识解答一些有探索性、开放性的问题,提高解决问题的能力.解决此类问题的关键是要牢牢把握四边形的性质与特征,挖掘相关图形之间的联系,利用所给图形及图形之间形状、大小、位置关系,进行观察、实验、比较、联想、类比、分析、综合等.常用到的矩形、菱形、正方形的解题策略有:(1)对于矩形:①判定四边形是矩形,一般先判定是平行四边形,然后再判定是矩形;②矩形的内角是直角和对角线相等,相对于平行四边形来说是矩形特殊的性质;③利用矩形的性质计算或证明时,常常运用勾股定理,锐角三角函数或相似三角形求解.(2)对于菱形:①判定四边形是菱形,一般先判定是平行四边形,然后再判定是菱形;②菱形的邻边相等和对角线垂直,相对于平行四边形来说是菱形特殊的性质;③利用菱形的性质计算或证明时,常常运用勾股定理,锐角三角函数或相似三角形求解;④求线段和的最小值时,往往运用菱形的轴对称的性质转化为求线段的长度.(3)对于正方形:①判定四边形是正方形,一般先判定是平行四边形,然后再判定是矩形或菱形,最后判定这个四边形是正方形;②正方形是最特殊的四边形,在正方形的计算或证明时,要特别注意线段或角的等量转化.【典例剖析】典例精讲,方法提炼,精准提分【例1】(2021·北京·中考真题)如图,在四边形ABCD中,∠ACB=∠CAD=90°,点E在BC上,AE//DC,EF⊥AB,垂足为F.(1)求证:四边形AECD是平行四边形;,求BF和AD的长.(2)若AE平分∠BAC,BE=5,cosB=45【例2】(2022·北京·中考真题)如图,在▱ABCD中,AC,BD交于点O,点E,F在AC上,AE=CF.(1)求证:四边形EBFD是平行四边形;(2)若∠BAC=∠DAC,求证:四边形EBFD是菱形.【真题再现】必刷真题,关注素养,把握核心1.(2014·北京·中考真题)如图,在平行四边形ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD.(1)求证:四边形ABEF是菱形;(2)若AB=4,AD=6,∠ABC=60°,求tan∠ADP的值.2.(2016·北京·中考真题)如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.(1)求证:BM=MN;(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.3.(2017·北京·中考真题)如图,在四边形ABCD中,BD为一条对角线,AD∥BC,AD=2BC,∠ABD=90°,E为AD的中点,连接BE.(1)求证:四边形BCDE为菱形;(2)连接AC,若AC平分∠BAD,BC=1,求AC的长.4.(2017·北京·中考真题)数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证.,(以上材料来源于《古证复原的原理》、《吴文俊与中国数学》和《古代世界数学泰斗刘徽》)请根据上图完成这个推论的证明过程.证明:S矩形NFGD=S△ADC-(S△ANF+S△FGC),S矩形EBMF=S△ABC-(____________+____________).易知,S△ADC=S△ABC,_____________=______________,______________=_____________.可得S矩形NFGD= S矩形EBMF.5.(2013·北京·中考真题)如图,在▱ABCD中,F是AD的中点,延长BC到点E,使CE=1BC,连结DE,2CF.(1)求证:四边形CEDF是平行四边形;(2)若AB=4,AD=6,∠B=60°,求DE的长.6.(2015·北京·中考真题)在▱ABCD,过点D作DE∠AB于点E,点F在边CD上,DF=BE,连接AF,BF.(1)求证:四边形BFDE是矩形;(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.7.(2020·北京·中考真题)如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,EF∠AB,OG∠EF.(1)求证:四边形OEFG是矩形;(2)若AD=10,EF=4,求OE和BG的长.8.(2016·北京·中考真题)如图,四边形ABCD是平行四边形,AE平分∠BAD,交DC的延长线于点E.求证:DA=DE.【模拟精练】押题必刷,巅峰冲刺,提分培优一、解答题1.(2022·北京房山·二模)已知:如图,在四边形ABCD中,AB∥DC,AC⊥BD,垂足为M,过点A作AE⊥AC,交CD的延长线于点E.(1)求证:四边形ABDE是平行四边形;(2)若AC=8,sin∠ABD=4,求BD的长.52.(2022·北京西城·二模)如图,菱形ABCD的对角线AC,BD交于点O,点E,F分别在DA,BC的延长线上,且BE∠ED,CF=AE.(1)求证:四边形EBFD是矩形;(2)若AB=5,cos∠OBC=4,求BF的长.53.(2022·北京朝阳·二模)如图,在菱形ABCD中,O为AC,BD的交点,P,M,N分别为CD,OD,OC 的中点.(1)求证:四边形OMPN是矩形;(2)连接AP,若AB=4,∠BAD=60∘,求AP的长.4.(2022·北京东城·二模)如图,在平行四边形ABCD中,DB=DA,点F是AB的中点,连接DF并延长,交CB的延长线于点E,连接AE.(1)求证:四边形AEBD是菱形;(2)若DC=√10,tan∠DCB=3,求菱形AEBD的边长.5.(2022·北京平谷·二模)如图,在□ABCD中,连接AC,点E是AB中点,点F是AC的中点,连接EF,过E作EG∥AF,交DA的延长线于点G.(1)求证:四边形AGEF是平行四边形;(2)若sin∠G=3,AC=10,BC=12,连接GF,求GF的长.56.(2022·北京北京·二模)如图,在等边△ABC中,D是BC的中点,过点A作AE∥BC,且AE=DC,连接CE.(1)求证:四边形ADCE是矩形;(2)连接BE交AD于点F,连接CF.若AB=4,求CF的长.7.(2022·北京丰台·二模)如图,在∠ABC中,∠BAC=90∘,AD∠BC,垂足为D,AE∠BC,CE∠DA.(1)求证:四边形AECD是矩形;(2)若AB=5,cosB=3,求AE的长.58.(2022·北京密云·二模)如图,在平行四边形ABCD中,AC平分∠BAD,点E为AD边中点,过点E作AC的垂线交AB于点M,交CB延长线于点F.(1)求证:平行四边形ABCD是菱形;(2)若FB=2,sinF=3,求AC的长.59.(2022·北京市十一学校模拟预测)如图,在四边形ABCD中,AD=CD,BD⊥AC于点O,点E是DB延长线上一点,OE=OD,BF⊥AE于点F.(1)求证:四边形AECD是菱形;(2)若AB平分∠EAC,OB=3,tan∠CED=3,求EF和AD的长.410.(2022·北京昌平·二模)如图,在矩形ABCD中,对角线AC,BD交于点O,分别过点C,D作BD,AC的平行线交于点E,连接OE交AD于点F.(1)求证:四边形OCED是菱形;(2)若AC=8,∠DOC=60°,求菱形OCED的面积.11.(2022·北京海淀·二模)如图,在Rt∠ABC中,∠A =90°,点D,E,F分别为AB,AC,BC的中点,连接DF,EF.(1)求证:四边形AEFD是矩形;(2)连接BE,若AB = 2,tan C =1,求BE的长.212.(2022·北京东城·一模)如图,在正方形ABCD中,E为对角线AC上一点(AE>CE),连接BE,DE.(1)求证:BE=DE;(2)过点E作EF⊥AC交BC于点F,延长BC至点G,使得CG=BF,连接DG.∠依题意补全图形;∠用等式表示BE与DG的数量关系,并证明.13.(2022·北京东城·一模)如图,在四边形ABCD中,AC与BD相交于点O,且AO=CO,点E在BD上,∠EAO=∠DCO.(1)求证:四边形AECD是平行四边形;(2)若AB=BC,CD=5,AC=8,tan∠ABD=2,求BE的长.314.(2022·北京市十一学校二模)如图,在平行四边形ABCD中,CE⊥AD于点E,延长DA至点F,使得AF=DE,连接BF,CF.(1)求证:四边形BCEF是矩形;(2)若AB=6,CF=8,DF=10,求EF的长.15.(2022·北京石景山·一模)如图所示,△ABC中,∠ACB=90°,D,E分别为AB,BC的中点,连接DE 并延长到点F,使得EF=DE,连接CD,CF,BF.(1)求证:四边形BFCD是菱形;(2)若cos A=5,DE=5,求菱形BFCD的面积.1316.(2022·北京大兴·一模)如图,在平面四边形ABCD中,点E,F分别是AB,CD上的点,CF=BE.(1)求证:四边形AEFD是平行四边形;(2)若∠A=60°,AD=2,AB=4,求BD的长.17.(2022·北京丰台·一模)如图,在四边形ABCD中,∠DCB=90°,AD∥BC,点E在BC上,AB∥DE,AE 平分∠BAD.(1)求证:四边形ABED为菱形;(2)连接BD,交AE于点O.若AE=6,sin∠DBE=3,求CD的长.518.(2022·北京市师达中学模拟预测)如图,四边形ABCD是平行四边形,AE∠BC,AF∠CD,垂足分别为E,F,且BE=DF.(1)求证:四边形ABCD是菱形;(2)连接EF并延长,交AD的延长线于点G,若∠CEG=30°,AE =2,求EG的长.19.(2022·北京四中模拟预测)如图,在四边形ABCD中,AD=CD,BD∠AC于点O,点E是DB延长线上一点,OE=OD,BF∠AE于点F.(1)求证:四边形AECD是菱形;(2)若AB平分∠EAC,OB=3,BE=5,求EF和AD的长.20.(2021·北京丰台·一模)如图,在菱形ABCD中,对角线AC、BD交于点O,过点A作AE∠BC于E,延长BC到点F,使CF=BE,连接DF.(1)求证:四边形AEFD是矩形;(2)连接OE,若AD=10,EC=4,求OE的长度.21.(2022·北京市燕山教研中心一模)如图,在菱形ABCD中,对角线AC与BD相交于点O,过点D作DE⊥BD 交BC的延长线于点E.(1)求证:四边形ACED是平行四边形;(2)若BD=4,AC=3,求sin∠CDE的值.22.(2022·北京平谷·一模)如图,∠ABC中,∠ACB=90°,点D为AB边中点,过D点作AB的垂线交BC 于点E,在直线DE上截取DF,使DF=ED,连接AE、AF、BF.(1)求证:四边形AEBF是菱形;(2)若cos∠EBF=3,BF=5,连接CD,求CD的长.523.(2022·北京市第一六一中学分校一模)在矩形ABCD中,AC,BD相交于点O,过点C作CE∠BD交AD的延长线于点E.(1)求证:∠ACD=∠ECD;(2)连接OE,若AB=2,tan∠ACD=2,求OE的长.24.(2022·北京房山·一模)如图,在平行四边形ABCD中,过点B作BE∠CD交CD的延长线于点E,过点C作CF∥EB交AB的延长线于点F.(1)求证:四边形BFCE是矩形;(2)连接AC,若AB=BE=2,tan∠FBC=1,求AC的长225.(2022·北京朝阳·一模)如图,在矩形ABCD中,AC,BD相交于点O,AE//BD,BE//AC.(1)求证:四边形AEBO是菱形;(2)若AB=OB=2,求四边形AEBO的面积.26.(2022·北京·中国人民大学附属中学分校一模)如图,正方形ABCD中,P为BD上一动点,过点P作PQ⊥AP 交CD边于点Q.(1)求证:PA=PQ;(2)用等式表示PB、PD、AQ之间的数量关系,并证明;(3)点P从点B出发,沿BD方向移动,若移动的路径长为4,则AQ的中点M移动的路径长为(直接写出答案).BC,27.(2022·北京市三帆中学模拟预测)已知:△ABC中,AB=AC,AD⊥BC于点D,过点A作AE,且AE=12连结DE.(1)求证:四边形ABDE是平行四边形;(2)作FG⊥AB于点G,AG=4,cos∠GAF=4,求FG和FD的长.528.(2022·北京西城·一模)如图,在∠ABC中,BA=BC,BD平分∠ABC交AC于点D,点E在线段BD上,点F在BD的延长线上,且DE=DF,连接AE,CE,AF,CF.(1)求证:四边形AECF是菱形;(2)若BA∠AF,AD=4,BC=4√5,求BD和AE的长.29.(2022·北京顺义·一模)如图,在四边形ABCD中,AD∥BC,AC⊥BD,垂足为O,过点D作BD的垂线交BC的延长线于点E.(1)求证:四边形ACED是平行四边形;(2)若AC=4,AD=2,cos∠ACB=4,求BC的长.530.(2022·北京通州·一模)如图.在∠ABC中,AB=BC,BD平分∠ABC交AC于点D.点E为AB的中点,连接DE,过点E作EF∥BD交CB的延长线于点F.(1)求证:四边形DEFB是平行四边形;(2)当AD=4,BD=3时,求CF的长.。
特殊四边形的经典题型

特殊四边形的经典题型特殊四边形的经典题型是“四边形概念,包括特殊四边形”。
这类问题主要考核学生对特殊四边形的概念、特征、种类、构图方法、性质等的认知能力和依据这些概念分析处理问题的能力。
首先,考生需要理解四边形的特性。
四边形是由四条直线组成的闭合多边形,一般来说,有四个内角,它们两两相等,这使得四个内角总和为360°。
此外,四边形也可以分为等边四边形和不等边四边形。
对于等边四边形,每条边相等,而不等边四边形的每条边的长度是不同的。
其次,考生还需要熟悉特殊四边形的概念。
特殊四边形是指具有特殊属性的四边形,这些特殊的四边形通常具有特殊的角度、边长或两者特性结合在一起。
其中,最常见的是正方形、长方形、菱形、梯形、平行四边形、直角三角形、等腰三角形、梯形和矩形。
此外,考生还应熟悉不同特殊四边形的性质。
例如,正方形和长方形的内角相等,每个角都是90°,而菱形的内角都是相等的,每个角都是60°;梯形的两个角是相反的,即有两个内角为90°,另两个为120°。
另外,平行四边形的内角分别是两个相等的角和两个相反的角,其中两个角都是90°;直角三角形的内角分别是一个90°,其余两个都是60°;等腰三角形的内角分别是60°,其余两个都是60°。
最后,考生根据这些概念,可以灵活处理类似问题,如根据特殊四边形的特性,求外角之和,求泰勒斯边长,求内角之和,求特殊四边形的外接圆等。
熟练处理这些题型,可以帮助学生更好地掌握特殊四边形的概念,并加深对此的理解和掌握。
中考数学题型二 创新作图题

结论,观察新图形的对称性,找出新图形的对称中心或对称轴,再对比
题图,从而解决问题.
3.涉及面积问题时,常用到的结论有过对角线的交点的任意一条直线
将特殊四边形的面积平分、等底等高的两个三角形的面积相等等.
前往
方法
高分
方法 类型3 利用正多边形的性质作图 (5年1考)
例3 如图,已知正六边形ABCDEF,请仅用无刻度的直尺,分别按下列 要求画图. (1)在图(1)中,画出一个以BC为边的矩形; (2)在图(2)中,在AF上画出点M,使得AM=14AF.
答图(2)
前往
方法
高分
方法 类型3 利用正多边形的性质作图 (5年1考)
解题通法
正多边形中作图的关键点
在正多边形中作图,要充分利用正多边形的对称性.
(1)当边数为偶数时,以正六边形为例,如图(1).
①正六边形的对称轴的一种作法如图(1)所示,直线MN即为其对称轴.依
此可类推其他边数为偶数的正多边形的对称轴的作法.
高分
方法 类型2 利用特殊四边形的性质作图 (5年1考)
1.理解题意
2.问题分析 (1)
前往
方法
高分
方法 类型2 利用特殊四边形的性质作图 (5年1考)
(2)
3.参考答案 (1)如答图(1),点F即为所求. (2)如答图(2),点P即为所求(作法不唯一).
答图(1)
前往
方法
高分
答图(2)
方法 类型2 利用特殊四边形的性质作图 (5年1考)
题型
题型二 创新作图题
内容一览 题型概述
方法
类型1 利用三角形的性质作图 类型2 利用特殊四边形的性质作图 类型3 利用正多边形的性质作图 类型4 利用圆的性质作图 类型5 利用网格的性质作图
人教版八年级数学下册-难点探究专题(选做):特殊四边形中的综合性问题

难点探究专题(选做):特殊四边形中的综合性问题◆类型一特殊平行四边形的动态探究问题一、动点问题1.(2016·枣庄中考)如图,把△EFP放置在菱形ABCD中,使得顶点E,F,P分别在线段AB,AD,AC上,已知EP=FP=6,EF=63,∠BAD=60°,且AB>6 3.(1)求∠EPF的大小;(2)若AP=10,求AE+AF的值;(3)若△EFP的三个顶点E,F,P分别在线段AB,AD,AC上运动,请直接写出AP的最大值和最小值.二、图形的变换问题2.如图①,点O是正方形ABCD两条对角线的交点.分别延长OD到点G,OC到点E,使OG=2OD,OE=2OC,然后以OG,OE为邻边作正方形OEFG,连接AG,DE.(1)求证:DE⊥AG;(2)正方形ABCD固定,将正方形OEFG绕点O逆时针旋转α角(0°<α<360°)得到正方形OE′F′G′,如图②.①在旋转过程中,当∠OAG′是直角时,求α的度数;②若正方形ABCD的边长为1,在旋转过程中,求AF′的最大值和此时α的度数,直接写出结果不必说明理由.◆类型二四边形间的综合性问题3.(2016·德州中考)我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.(1)如图①,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.求证:中点四边形EFGH是平行四边形;(2)如图②,点P是四边形ABCD内一点,且满足P A=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)参考答案与解析1.解:(1)如图①,过点P 作PG ⊥EF 于点G ,H 为PE 的中点,连接GH ,∴∠PGE=90°,GH =PH =HE =12PE =3.∵PF =PE ,∴∠FPG =∠EPG ,FG =GE =12EF =3 3.在Rt △PGE 中,由勾股定理得PG =PE 2-GE 2=62-(33)2=3.∴PG =GH =PH ,即△GPH 为等边三角形,∴∠GPH =60°,∴∠FPE =∠FPG +∠GPE =2∠GPE =2×60°=120°.(2)如图①,过点P 作PM ⊥AB 于点M ,作PN ⊥AD 于点N ,∴∠ANP =∠AMP =90°.∵AC为菱形ABCD 的对角线,∴∠DAC =∠BAC =12∠DAB =30°,PM =PN .在Rt △PME 和Rt △PNF 中,PM =PN ,PE =PF ,∴Rt △PME ≌Rt △PNF ,∴ME =NF .∵∠P AM =30°,AP=10,∴PM =12AP =5.由勾股定理得AM =P A 2-PM 2=5 3.在△ANP 和△AMP 中,⎩⎪⎨⎪⎧∠NAP =∠MAP ,∠ANP =∠AMP =90°,AP =AP ,∴△ANP ≌△AMP ,∴AN =AM =5 3.∴AE +AF =(AM +ME )+(AN -NF )=AM +AN +ME -NF =10 3.(3)如图②,△EFP 的三个顶点分别在AB ,AD ,AC 上运动,点P 在P 1,P 之间运动.P 1O =PO =12PE =3,AE =EF =63,AO =AE 2-EO 2=9.∴AP 的最大值为AO +OP =12,AP 的最小值为AO -OP 1=6.2.(1)证明:如图,延长ED 交AG 于点H .∵四边形ABCD 与OEFG 均为正方形,∴OA =OD ,OG =OE ,∠AOG =∠DOE =90°,∴Rt △AOG ≌Rt △DOE ,∴∠AGO =∠DEO .∵∠AGO +∠GAO =90°,∴∠DEO +∠GAO =90°,∴∠AHE =90°,即DE ⊥AG ;(2)解:①在旋转过程中,∠OAG ′成为直角有以下两种情况:a .α由0°增大到90°过程中,当∠OAG ′为直角时,∵OA =OD =12OG =12OG ′,∴∠AG ′O =30°,∠AOG ′=60°.∵OA ⊥OD ,∴∠DOG ′=90°-∠AOG ′=30°,即α=30°;b .α由90°增大到180°过程中,当∠OAG ′为直角时,同理可求的∠AOG ′=60°,∴α=90°+∠AOG ′=150°.综上,当∠OAG ′为直角时,α=30°或150°;②AF ′长的最大值是2+22,此时α=315°. 3.(1)证明:如图①中,连接BD .∵点E ,H 分别为边AB ,DA 的中点,∴EH ∥BD ,EH =12BD .∵点F ,G 分别为边BC ,CD 的中点,∴FG ∥BD ,FG =12BD ,∴EH ∥FG ,EH =GF ,∴中点四边形EFGH 是平行四边形.(2)解:四边形EFGH 是菱形.理由如下:如图②中,连接AC ,BD .∵∠APB =∠CPD ,∴∠APB +∠APD =∠CPD +∠APD ,即∠APC =∠BPD .在△APC 和△BPD 中,⎩⎪⎨⎪⎧AP =PB ,∠APC =∠BPD ,PC =PD ,∴△APC ≌△BPD ,∴AC =BD .∵点E ,F ,G 分别为边AB ,BC ,CD 的中点,∴EF =12AC ,FG =12BD ,∴EF =FG .∵四边形EFGH 是平行四边形,∴四边形EFGH 是菱形.(3)解:四边形EFGH 是正方形.理由如下:如图②中,设AC 与BD 交于点O .AC 与PD 交于点M ,AC 与EH 交于点N .∵△APC ≌△BPD ,∴∠ACP =∠BDP .∵∠DMO =∠CMP ,∴∠COD =∠CPD =90°.∵EH ∥BD ,AC ∥HG ,∴∠EHG =∠ENO =∠BOC =∠DOC =90°.∵四边形EFGH 是菱形,∴四边形EFGH 是正方形.19.2.3 一次函数与方程、不等式一.选择题(共8小题)1.一次函数y=kx+b的图象如图所示,则方程kx+b=0的解为()A.x=2B.y=2C.x=﹣1D.y=﹣12.一次函数y=kx+b(k,b为常数,且k≠0)的图象如图所示,根据图象信息可求得关于x 的方程kx+b=0的解为()A.x=﹣1B.x=2C.x=0D.x=33.一元一次方程ax﹣b=0的解x=3,函数y=ax﹣b的图象与x轴的交点坐标为()A.(3,0)B.(﹣3,0)C.(a,0)D.(﹣b,0)4.已知方程kx+b=0的解是x=3,则函数y=kx+b的图象可能是()A.B.C.D.5.若方程x﹣3=0的解也是直线y=(4k+1)x﹣15与x轴的交点的横坐标,则k的值为()A.﹣1B.0C.1D.±16.如图,直线y1=x+b与y2=kx﹣1相交于点P,点P的横坐标为﹣1,则关于x的不等式x+b>kx﹣1的解集在数轴上表示正确的是()A.B.C.D.7.如图,直线y=﹣x+m与y=nx+4n(n≠0)的交点的横坐标为﹣2,则关于x的不等式﹣x+m >nx+4n>0的整数解为()A.﹣1B.﹣5 C.﹣4D.﹣38.如图,一次函数y=kx+b的图象经过A、B两点,则不等式kx+b<0的解集是()A.x<0B.0<x<1C.x<1 D.x>1二.填空题(共10小题)9.若直线y=2x+b与x轴交于点(﹣3,0),则方程2x+b=0的解是_________.10.如图是一次函数y=kx+b的图象,则方程kx+b=0的解为_________.11.一次函数y=kx+b(k,b为常数,且k≠0)的图象如图所示,根据图象信息可求得关于x的方程kx+b=0的解为_________.12.如图,已知直线y=ax﹣b,则关于x的方程ax﹣1=b的解x=_________.13.如图,直线y=kx+b分别交x轴和y轴于点A、B,则关于x的方程kx+b=0的解为_________.14.如图,已知函数y=2x+b和y=ax﹣3的图象交于点P(﹣2,﹣5),根据图象可得方程2x+b=ax﹣3的解是_________.15.如图,已知函数y=2x+b与函数y=kx﹣3的图象交于点P,则不等式kx﹣3>2x+b的解集是_________.16.如图,直线y=kx+b过A(﹣1,2)、B(﹣2,0)两点,则0≤kx+b≤﹣2x的解集为_________.17.一次函数y1=kx+b与y2=x+a的图象如图,则kx+b>x+a的解集是_________.18.如图,函数y=kx和的图象相交于A (a,2),则不等式的解集为_________.三.解答题(共4小题)19.如图,根据函数y=kx+b(k,b是常数,且k≠0)的图象,求:(1)方程kx+b=0的解;(2)式子k+b的值;(3)方程kx+b=﹣3的解.20.如图,直线l1:y=2x与直线l2:y=kx+3在同一平面直角坐标系内交于点P.(1)写出不等式2x>kx+3的解集:_________;(2)设直线l2与x轴交于点A,求△OAP的面积.21.在平面直角坐标系x0y中,直线y=kx+b(k≠0)过(1,3)和(3,1)两点,且与x轴、y轴分别交于A、B两点,求不等式kx+b≤0的解.22.在直角坐标系xOy中,直线y=kx+b(k≠0)经过(﹣2,1)和(2,3)两点,且与x 轴、y轴分别交于A、B两点,求不等式kx+b≥0的解集.19.2.3 一次函数与方程、不等式一.选择题(共8小题)1.一次函数y=kx+b的图象如图所示,则方程kx+b=0的解为()A.x=2B.y=2C.x=﹣1D.y=﹣12.一次函数y=kx+b(k,b为常数,且k≠0)的图象如图所示,根据图象信息可求得关于x 的方程kx+b=0的解为()A.x=﹣1B.x=2C.x=0D.x=33.一元一次方程ax﹣b=0的解x=3,函数y=ax﹣b的图象与x轴的交点坐标为()A.(3,0)B.(﹣3,0)C.(a,0)D.(﹣b,0)4.已知方程kx+b=0的解是x=3,则函数y=kx+b的图象可能是()A.B.C.D.5.若方程x﹣3=0的解也是直线y=(4k+1)x﹣15与x轴的交点的横坐标,则k的值为()A.﹣1B.0C.1D.±16.如图,直线y1=x+b与y2=kx﹣1相交于点P,点P的横坐标为﹣1,则关于x的不等式x+b>kx﹣1的解集在数轴上表示正确的是()A.B.C.D.7.如图,直线y=﹣x+m与y=nx+4n(n≠0)的交点的横坐标为﹣2,则关于x的不等式﹣x+m >nx+4n>0的整数解为()A.﹣1B.﹣5 C.﹣4D.﹣38.如图,一次函数y=kx+b的图象经过A、B两点,则不等式kx+b<0的解集是()A.x<0B.0<x<1C.x<1 D.x>1二.填空题(共10小题)9.若直线y=2x+b与x轴交于点(﹣3,0),则方程2x+b=0的解是_________.10.如图是一次函数y=kx+b的图象,则方程kx+b=0的解为_________.11.一次函数y=kx+b(k,b为常数,且k≠0)的图象如图所示,根据图象信息可求得关于x的方程kx+b=0的解为_________.12.如图,已知直线y=ax﹣b,则关于x的方程ax﹣1=b的解x=_________.13.如图,直线y=kx+b分别交x轴和y轴于点A、B,则关于x的方程kx+b=0的解为_________.14.如图,已知函数y=2x+b和y=ax﹣3的图象交于点P(﹣2,﹣5),根据图象可得方程2x+b=ax﹣3的解是_________.15.如图,已知函数y=2x+b与函数y=kx﹣3的图象交于点P,则不等式kx﹣3>2x+b的解集是_________.16.如图,直线y=kx+b过A(﹣1,2)、B(﹣2,0)两点,则0≤kx+b≤﹣2x的解集为_________.17.一次函数y1=kx+b与y2=x+a的图象如图,则kx+b>x+a的解集是_________.18.如图,函数y=kx和的图象相交于A (a,2),则不等式的解集为_________.三.解答题(共4小题)19.如图,根据函数y=kx+b(k,b是常数,且k≠0)的图象,求:(1)方程kx+b=0的解;(2)式子k+b的值;(3)方程kx+b=﹣3的解.20.如图,直线l1:y=2x与直线l2:y=kx+3在同一平面直角坐标系内交于点P.(1)写出不等式2x>kx+3的解集:_________;(2)设直线l2与x轴交于点A,求△OAP的面积.21.在平面直角坐标系x0y中,直线y=kx+b(k≠0)过(1,3)和(3,1)两点,且与x轴、y轴分别交于A、B两点,求不等式kx+b≤0的解.22.在直角坐标系xOy中,直线y=kx+b(k≠0)经过(﹣2,1)和(2,3)两点,且与x 轴、y轴分别交于A、B两点,求不等式kx+b≥0的解集.。
中考数学压轴题重难点突破七 与特殊四边形有关的证明与计算(动态探究问题)

(2)在 AB 上取 AF=EC,连接 EF, 由(1)同理可得∠CEP=∠FAE, ∵AF=EC,AE=EP, ∴△FAE≌△CEP(SAS),∴∠ECP=∠AFE, ∵AF=EC,AB=BC,∴BF=BE, ∴∠BEF=∠BFE=45°,∴∠AFE=135°, ∴∠ECP=135°,∴∠DCP=45°.
【模型应用】 (2)如图②,F 是 DE 延长线上一点,FB⊥BE,EF 交 AB 于点 G. Ⅰ)判断△FBG 的形状并说明理由; Ⅱ)若 G 为 AB 的中点,且 AB=4,求 AF 的长;
(2)解:Ⅰ)△FBG 为等腰三角形,理由: ∵四边形 ABCD 是正方形,∴∠GAD=90°, ∴∠AGD+∠ADG=90°,由(1)知△ABE≌△ADE, ∴∠ADG=∠EBG,∴∠AGD+∠EBG=90°, ∵FB⊥BE,∴∠FBG+∠EBG=90°, ∴∠AGD=∠FBG,∵∠AGD=∠FGB, ∴∠FBG=∠FGB,∴FG=FB, ∴△FBG 是等腰三角形.
FH AD ∴GH=AG=2,∴FH=2GH=2, 在 Rt△AHF 中,AF= AH2+FH2= 13.
【模型迁移】 (3)如图③,F 是 DE 延长线上一点,FB⊥BE,EF 交 AB 于点 G,BE=BF. 求证:GE=( 2-1)DE.
(3)证明:∵FB⊥BE,∴∠FBE=90°, 在 Rt△EBF 中,BE=BF,∴EF= 2BE, 由(1)知 BE=DE,由(2)知 FG=BF, ∴GE=EF-FG= 2BE-BE= 2DE-DE=( 2-1)DE.
类型二:与特殊四边形有关的证明与计算(动态探究问题) (省卷 2021T27,2019T27,2015T27,2014T27;兰州 2021T27)
(2022·兰州)综合与实践 【问题情境】数学活动课上,老师出示了一个问题:如图①,在正方形 ABCD 中,E 是 BC 的中点,AE⊥EP,EP 与正方形的外角∠DCG 的平分线交 于 P 点.试猜想 AE 与 EP 的数量关系,并加以证明; 【思考尝试】(1)同学们发现,取 AB 的中点 F,连接 EF 可以解决这个问 题.请在图①中补全图形,解答老师提出的问题;
竞赛讲义:四边形创新题(含答案).

第 1页,共 5页四边形综合创新题1. 直角三角形通过剪切可以拼成一个与该直角三角形面积相等的矩形.方法如下:请你根据上面的作图原理,并用上面的图示方法,解答下列问题:(1对任意三角形,设计一种方案,将它分成若干块,再拼成一个与原三角形面积相等的矩形.(2对任意四边形,设计一种方案,将它分成若干块,再拼成一个与原四边形面积相等的矩形.2. 已知等边三角形纸片 ABC 的边长为 8, D 为 AB 边上的点,过点 D 作 DG BC ∥交 AC 于点 G . DE BC ⊥于点 E ,过点 G 作 GF BC ⊥于点 F ,把三角形纸片 ABC 分别沿 DG DE GF , , 按图 1所示方式折叠, 点 A B C , , 分别落在点 A ', B ', C '处. 若点 A ', B ', C '在矩形 DEFG 内或其边上,且互不重合,此时我们称 A B C '''△ (即图中阴影部分为“重叠三角形” .(1若把三角形纸片 ABC 放在等边三角形网格中(图中每个小三角形都是边长为1的等边三角形 ,点 A B C D , , , 恰好落在网格图中的格点上.如图 2所示,请直接写出此时重叠三角形 A B C '''的面积;(2实验探究:设 AD 的长为 m ,若重叠三角形 A B C '''存在.试用含 m 的代数式表示重叠三角形 A B C '''的面积,并写出 m 的取值范围(直接写出结果,备用图供实验,探究使用 . 解:(1重叠三角形 A B C '''的面积为 ; (2 用含 m 的代数式表示重叠三角形 A B C '''的面积为 ; m 的取值范围为 .中点中点②①②图 1图 2B 备用图B备用图B D3. 我们给出如下定义:若一个四边形的两条对角线相等,则称这个四边形为等对角线四边形.请解答下列问题:(1 写出你所学过的特殊四边形中是等对角线四边形的两种图形的名称、 ;(2探究:当等对角线四边形中两条对角线所夹锐角为 60 时,这对 60 角所对的两边之和与其中一条对角线的大小关系,并证明你的结论.4. 梯形 ABCD 中, AD ∥ BC ,∠ B =90°, AB =14cm, AD =18cm, BC =21cm,点 P 从点 A 开始沿 AD 边向点 D 以 1cm/s的速度移动,点 Q 从点 C 开始沿 CB 向点 B 以 2cm/s的速度移动,如果 P 、 Q 分别从 A 、 C 同时出发,设移动时间为 t .(1当 t 为何值时,四边形 PDCQ 是平行四边形?(2四边形 PDCQ 可以是菱形吗?如果可以,求出 t 的值;如果不可以,说明理由 .(3四边形 PDCQ 可以是等腰梯形吗?如果可以,直接写出 t 的值;如果不可以,说明理由 .第 2页,共 5页第 3页,共 5页ABD C 图 15. (1探究新知:如图 1,已知△ ABC 与△ ABD 的面积相等,试判断 AB 与 CD 的位置关系,并说明理由.(2结论应用:①如图 2,点 M , N 在反比例函数 xky =(k >0的图象上,过点 M 作ME ⊥ y 轴,过点 N 作 NF ⊥ x 轴,垂足分别为 E , F .试证明:MN ∥ EF .②若①中的其他条件不变,只改变点 M , N 的位置如图 3所示,请判断 MN 与EF 是否平行?请说明理由 .6. 已知:点 1, 2(-A , 1, 2(-B , 正比例函数 ax y = 0(>a 与反比例函数 xky = 0(>k 的图像交于 D C , 两点,(1求证:四边形 ACBD 是平行四边形. (2 当 2, 21==k a 时, 判定四边形 ACBD 的形状. (3 当 2, 2==k a 时, 判定四边形 ACBD 的形状.(4 当 6, 2==k a 时, 判定四边形 ACBD 的形状.图 3第 4页,共 5页2解:(1重叠三角形 A B C '''(2用含 m 的代数式表示重叠三角形 A B C '''2 m -;m 的取值范围为 843m <≤ .3.解:(1略.写对一种图形的名称给 1分 , 最多给 2分 . (2 结论:等对角线四边形中两条对角线所夹锐角为 60°时 , 这对 60°角所对的两边之和大于或等于一条对角线的长. ………………………………… 3分方法一:如图 1, 已知:四边形 ABCD ,对角线 AC 、 BD 交于点 O , AC = BD , 且∠ AOD = 60°.求证:BC +AD ≥ AC .证明:过点 D 作 DF ∥ AC ,在 DF 上截取 DE ,使 DE =AC .连结 CE 、BE . ………………………………… 4分故∠ EDO = 60°,且四边形 ACED 是平行四边形.所以△ BDE 是等边三角形, CE =AD . …………… 6分所以 DE =BE =AC . ①当 BC 与 CE 不在同一条直线上时(如图 1 , 在△ BCE 中,有 BC +CE >BE .所以BC +AD >AC . ……………………… 7分②当 BC 与 CE 在同一条直线上时(如图 2 , 则 BC +CE =BE .因此 BC +AD =AC . ………………………………………………… 8分综合①、②,得BC +AD ≥ AC .即等对角线四边形中两条对角线所夹锐角为 60°时,这对 60°角所对的两边之和大于或等于其中一条对角线的长.4. 解 :(1因为 AD ∥ BC ,当 DP =CQ 时,四边形 PDCQ 是平行四边形, ∵ DP=18-t , CQ =2t 即 18-t =2t , ∴ t =6.∴当 t =6s时,四边形 PDCQ 是平行四边形 .(2若四边形 PDCQ 是菱形,则四边形 PDCQ 首先是平行四边形∴ t =6,当 t =6时, DP =18-6=12,过 D 作 DM ⊥ BC 交 BC 于 M , ∵∠ B =90°, AD ∥ BC ,∴四边形ABMD 是矩形 . ∴ CM =BC -BM = BC -AD =21-18 =3cm 又 DM = AB=14cm,E AB F图 1A DF B图 2第 5页,共 5页∴ Rt △ CDM 中,由勾股定理1219622≠=+=+=DM CM CD 即CD ≠ DP ,四边形PDCQ 的邻边不相等,∴四边形 PDCQ 不可以是菱形 .(3过 P 作 PN ⊥ BC 交 BC 于 N ,若四边形 PDCQ 是等腰梯形,则 QN =CM=3cm ∴ DP = CQ -CM -QN = CQ -6 ∴ 18-t =2t -6 ∴ t =8∴当 t =8s时,四边形 PDCQ 是等腰梯形 .5. 解:(1证明:分别过点 C , D ,作 CG ⊥ AB , DH ⊥垂足为 G , H ,则∠ CGA =∠ DHB =90°. ∴ CG ∥ DH . ∵△ ABC 与△ ABD 的面积相等, ∴ CG =DH . ∴四边形 CGHD 为平行四边形. ∴ AB ∥ CD .(2①证明:连结 MF , NE .设点 M 的坐标为(x 1, y 1 ,点 N 的坐标为(x 2, y 2 .∵点 M , N 在反比例函数 xky =(k >0的图象上, ∴ k y x =11, k y x =22. ∵ ME ⊥ y 轴, NF ⊥ x 轴, ∴ OE =y 1, OF =x 2. ∴ S △ EFM =k y x 212111=⋅, S △ EFN =k y x 212122=⋅. ∴ S △ EFM =S △ EFN .由(1中的结论可知:MN ∥ EF . ② MN ∥ EF .证明与①类似,略.。
专题44 特殊的四边形 初中数学学科素养能力培优竞赛试题精选专练含解析卷

专题44特殊的四边形一、三角形的中位线【典例】如图在△ABC中,D、E分别为AB、AC上的点,且BD=CE,M、N分别是BE、CD的中点.过MN的直线交AB于P,交AC于Q,线段AP、AQ相等吗?为什么?【解答】解:AP=AQ.理由如下:如图,取BC的中点H,连接MH,NH.∵M,H为BE,BC的中点,∴MH∥EC,且MH=12EC.∵N,H为CD,BC的中点,∴NH∥BD,且NH=12BD.∵BD=CE,∴MH=NH.∴∠HMN=∠HNM;∵MH∥EC,∴∠HMN=∠PQA,同理∠HNM=∠QPA.∴△APQ为等腰三角形,∴AP=AQ.【巩固】如图,在▱ABCD中,对角线AC,BD相交于点O,AB=OB,点E,F分别是OA,OD的中点,连接EF,EM⊥BC于点M,EM交BD于点N,若∠CEF=45°,FN=5,求线段BC的长.二、矩形中的折叠【典例】如图,折叠矩形纸片ABCD ,使点B 的对应点E 落在CD 边上,GH 为折痕,已知AB =6,BC =10.当折痕GH 最长时,线段BH 的长为 .【解答】解:由题知,当E 点与D 点重合时GH 最长, 设BH =x ,则CH =10﹣x ,HE =BH =x , 由勾股定理得,HC 2+CE 2=HE 2, 即(10﹣x )2+62=x 2, 解得x =6.8, 故答案为:6.8.【巩固】如图,点E 是矩形ABCD 的边CD 上一点,(1)如图1,将△ADE 沿AE 翻折,使点D 的对应点M 恰好在BC 边的中点,求AD AB的值;(2)如图2,若点E 为CD 的中点,过点A 作AF ⊥BE 于F ,连接DF ,求证DF =BC .三、直角三角形斜边上的中线【典例】如图,在△ABC 中,AB =3,AC =4,BC =5,P 为边BC 上一动点,PE ⊥AB 于E ,PF ⊥AC 于F ,M 为EF 中点,则AM 的最小值为( )A .1B .1.3C .1.2D .1.5【解答】解:∵AB =3,AC =4,BC =5, ∴∠EAF =90°,∵PE ⊥AB 于E ,PF ⊥AC 于F , ∴四边形AEPF 是矩形,∴EF ,AP 互相平分.且EF =AP , ∴EF ,AP 的交点就是M 点.∵当AP 的值最小时,AM 的值就最小,∴当AP ⊥BC 时,AP 的值最小,即AM 的值最小. ∵12AP •BC =12AB •AC ,∴AP •BC =AB •AC . ∵AB =3,AC =4,BC =5, ∴5AP =3×4, ∴AP =2.4, ∴AM =1.2; 故选:C . 【巩固】如图,∠BAC =∠BDC =90°,四边形ABDE 为平行四边形,若AD =6,BC =8,则CE 的长为 .四、菱形中最值问题【典例】如图,边长为4的菱形ABCD中,∠ABC=30°,P为BC上方一点,且S△PBC=1 4S菱形ABCD,则PB+PC的最小值为.【解答】解:过A作AE⊥BC于E,∵∠ABC=30°,AB=4,∴AE=12AB=2,∴S△PBC=14S菱形ABCD=14×4×2=2,设点P到BC的距离为h,∴h=1,即点P在平行于BC且到BC的距离为1的直线上,作点B关于直线l的对称点G,连接CG交直线l于点P,则此时,PB+PC的值最小,PB+PC的最小值=CG,∵BG⊥l,∴BG⊥BC,∴∠CBG=90°,BG=2h=2,∴CG=√22+42=2√5,【巩固】如图,菱形ABCD中,AB=2,∠A=120°,点P是直线BD上一动点,连接PC,当PC+PB 2的值最小时,线段PD长是.巩固练习1.如图,在矩形ABCD中,AB=4,AD=5,点E,F分别是边AB,BC上的动点,点E 不与A,B重合,且EF=AB,G是五边形AEFCD内满足GE=GF且∠EGF=90°的点.现给出以下结论.其中错误的是()A.∠GEB与∠GFB一定互补B.点G到边AB,BC的距离一定相等C.点G到边AD,DC的距离可能相等D.点G到边AB的距离的最大值为2√22.如图,分别以R t△ABC的直角边AC及斜边AB为边向外作等边△ACD、等边△ABE,EF⊥AB,垂足为F,连接DF,当ACAB=时,四边形ADFE是平行四边形.3.如图,矩形ABCD,AB=1,BC=2,点A在x轴正半轴上,点D在y轴正半轴上.当点A在x轴上运动时,点D也随之在y轴上运动,在这个运动过程中,点C到原点O的最大距离为.4.如图,菱形ABCD的边长为4,∠BAD=120°,点E是AB的中点,点F是AC上的一动点,则EF+BF的最小值是.5.如图,在矩形ABCD中,AD=√3AB,对角线相交于点O,动点M从点B向点A运动(到点A即停止),点N是AD上一动点,且满足∠MON=90°,连结MN.在点M、N 运动过程中,则以下结论正确的是.(写出所有正确结论的序号)①点M、N的运动速度不相等;②存在某一时刻使S△AMN=S△MON;③S△AMN逐渐减小;④MN2=BM2+DN2.6.如图,菱形ABCD,AB=5,E在BC上,BE=4,过点E作EG⊥AD于G,交BD于F,连接DE,若∠A=4∠DEG,则EF的长为.7.如图,在矩形ABCD中,AB=2,AD=4,E为AD的中点,F为线段EC上一动点,P 为BF中点,连接PD,则线段PD长的取值范围是.8.如图,在△ABC中,∠ABC=90°,BD为△ABC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.(1)求证:四边形BDFG是菱形:(2)若∠BAC=30°,BC=2,求四边形BDFG的面积.9.已知四边形ABCD是矩形.(1)如图1,E、F分别是AB、AD上的点,CE垂直平分BF,垂足为G,连接DG.①求证:DG=CG;②若BC=2AB,求∠DGC的大小;(2)如图2,AB=BC=6,M、N、P分别是AB、CD、AD上的点,MN垂直平分BP,点Q是CD的中点,连接MP,PQ,若PQ⊥MP,直接写出CN的长.10.已知:如图,把矩形纸片OABC放入直角坐标系x O y中,使OA、OC分别落在x轴、y轴的正半轴上,连接AC,将△ABC沿AC翻折,点B落在该坐标平面内,设这个落点为D,CD交x轴于点E.如果CE=5,OC、OE的长是关于x的方程x2+(m﹣1)x+12=0的两个根,并且OC>OE.(1)求点D的坐标;(2)如果点F是AC的中点,判断点(8,﹣20)是否在过D、F两点的直线上,并说明现由.11.如图1,在菱形ABCD中,对角线AC与BD相交于点O,AB=13,BD=24,在菱形ABCD的外部以AB为边作等边三角形ABE.点F是对角线BD上一动点(点F不与点B重合),将线段AF绕点A顺时针方向旋转60°得到线段AM,连接FM.(1)线段AO的长为;(2)如图2,当点F在线段BO上,且点M,F,C三点在同一条直线上时,求证:AM=√33AC;(3)连接EM.若△AFM的周长为3√29,请直接写出△AEM的面积.12.在菱形ABCD中,∠BAD=60°.(1)如图1,点E为线段AB的中点,连接DE、CE、若AB=4,求线段EC的长;(2)如图2,M为线段AC上一点(不与A、C重合),以AM为边向上构造等边三角形AMN,线段MN与AD交于点G,连接NC、DM,Q为线段NC的中点,连接DQ、MQ,判断DM与DQ的数量关系,并证明你的结论;(3)在(2)的条件下,若AC=√3,请你直接写出DM+CN的最小值.专题44特殊的四边形一、三角形的中位线【典例】如图在△ABC中,D、E分别为AB、AC上的点,且BD=CE,M、N分别是BE、CD的中点.过MN的直线交AB于P,交AC于Q,线段AP、AQ相等吗?为什么?【解答】解:AP=AQ.理由如下:如图,取BC的中点H,连接MH,NH.∵M,H为BE,BC的中点,∴MH∥EC,且MH=12EC.∵N,H为CD,BC的中点,∴NH∥BD,且NH=12BD.∵BD=CE,∴MH=NH.∴∠HMN=∠HNM;∵MH∥EC,∴∠HMN=∠PQA,同理∠HNM=∠QPA.∴△APQ为等腰三角形,∴AP=AQ.【巩固】如图,在▱ABCD中,对角线AC,BD相交于点O,AB=OB,点E,F分别是OA,OD的中点,连接EF,EM⊥BC于点M,EM交BD于点N,若∠CEF=45°,FN=5,求线段BC的长.【解答】解:设EF=x,∵点E、点F分别是OA、OD的中点,∴EF是△OAD的中位线,∴AD =2x ,AD ∥EF ,∴∠CAD =∠CEF =45°,∵四边形ABCD 是平行四边形,∴AD ∥BC ,AD =BC =2x ,∴∠ACB =∠CAD =45°,∵EM ⊥BC ,∴∠EMC =90°,∴△EMC 是等腰直角三角形,∴∠CEM =45°,连接BE ,∵AB =OB ,AE =OE∴BE ⊥AO∴∠BEM =45°,∴BM =EM =MC =x ,∴BM =FE ,易得△ENF ≌△MNB ,∴EN =MN =12x ,BN =FN =5,R t △BNM 中,由勾股定理得:BN 2=BM 2+MN 2,即52=x 2+(12x )2, 解得,x =2√5,∴BC =2x =4√5.答:线段BC 的长为4√5.二、矩形中的折叠【典例】如图,折叠矩形纸片ABCD ,使点B 的对应点E 落在CD 边上,GH 为折痕,已知AB =6,BC =10.当折痕GH 最长时,线段BH 的长为 .【解答】解:由题知,当E 点与D 点重合时GH 最长,设BH =x ,则CH =10﹣x ,HE =BH =x ,由勾股定理得,HC 2+CE 2=HE 2,即(10﹣x )2+62=x 2,解得x =6.8,故答案为:6.8.【巩固】如图,点E 是矩形ABCD 的边CD 上一点,(1)如图1,将△ADE 沿AE 翻折,使点D 的对应点M 恰好在BC 边的中点,求AD AB 的值;(2)如图2,若点E 为CD 的中点,过点A 作AF ⊥BE 于F ,连接DF ,求证DF =BC .【解答】(1)解:如图1,∵四边形ABCD 是矩形,∴AD =BC ,由折叠可得AD =AM ,∴BC =AM ,又∵M 是BC 的中点,∴BM =12BC =12AM ,又∵∠B =90°,∴R t △ABM 中∠BAM =30°,∴BM =12AM ,AB =√3BM ,∴AM AB =√3BM =23√3,即AD AB =23√3;(2)证明:如图2所示,延长BE ,AD ,交于点G ,则∠BEC =∠GED ,∵AG ∥BC ,∴∠G =∠CBE ,∵E 是CD 的中点,∴DE =CE ,在△BCE 和△GDE 中,{∠BEC =∠GED ∠CBE =∠G CE =DE ,∴△BCE ≌△GDE (AAS ),∴DG =BC =AD ,即D 是AG 的中点,又∵AF ⊥BG ,∴R t △AFG 中,DF =12AG =AD ,又∵矩形ABCD 中,AD =BC ,∴DF =BC .三、直角三角形斜边上的中线【典例】如图,在△ABC 中,AB =3,AC =4,BC =5,P 为边BC 上一动点,PE ⊥AB 于E ,PF ⊥AC 于F ,M 为EF 中点,则AM 的最小值为( )A .1B .1.3C .1.2D .1.5【解答】解:∵AB =3,AC =4,BC =5,∴∠EAF =90°,∵PE ⊥AB 于E ,PF ⊥AC 于F ,∴四边形AEPF 是矩形,∴EF ,AP 互相平分.且EF =AP ,∴EF ,AP 的交点就是M 点.∵当AP 的值最小时,AM 的值就最小,∴当AP ⊥BC 时,AP 的值最小,即AM 的值最小.∵12AP •BC =12AB •AC , ∴AP •BC =AB •AC .∵AB =3,AC =4,BC =5,∴5AP =3×4,∴AP =2.4,∴AM =1.2;故选:C .【巩固】如图,∠BAC =∠BDC =90°,四边形ABDE 为平行四边形,若AD =6,BC =8,则CE 的长为 .【解答】解:如图,过点B 作BF ∥CD ,且BF =CD ,连接DF ,CF ,AF ,∵BF ∥CD ,DC =BF ,∴四边形BDCF 是平行四边形,且∠BDC =90°,∴四边形BDCF 是矩形,∴BC=DF=8,CF∥BD,CF=BD,∵四边形ABDE是平行四边形,∴BD∥AE,BD=AE,∴AE∥CF,AE=CF,∴四边形AECF是平行四边形,∴AF=CE,∵∠BAC=∠BDC=90°,∴点A,点B,点C,点D四点共圆,∴∠CAD=∠CBD,∵四边形BDCF是矩形,∴∠DBC=∠DFC,∠FCD=90°,∴∠DFC=∠DAC,∴点A,点F,点C,点D四点共圆,∴∠FAD+∠FCD=180°,∴∠FAD=90°,∴AF=√DF2−AD2=√82−62=2√7,∴EC=2√7,故答案为:2√7.四、菱形中最值问题【典例】如图,边长为4的菱形ABCD中,∠ABC=30°,P为BC上方一点,且S△PBC=1 4S菱形ABCD,则PB+PC的最小值为.【解答】解:过A作AE⊥BC于E,∵∠ABC=30°,AB=4,∴AE=12AB=2,∴S△PBC=14S菱形ABCD=14×4×2=2,设点P到BC的距离为h,∴h=1,即点P在平行于BC且到BC的距离为1的直线上,作点B关于直线l的对称点G,连接CG交直线l于点P,则此时,PB +PC 的值最小,PB +PC 的最小值=CG ,∵BG ⊥l ,∴BG ⊥BC ,∴∠CBG =90°,BG =2h =2,∴CG =√22+42=2√5,【巩固】如图,菱形ABCD 中,AB =2,∠A =120°,点P 是直线BD 上一动点,连接PC ,当PC +PB 2的值最小时,线段PD 长是 .【解答】解:如图,过P 作PE ⊥BC 于E ,连接AP ,由菱形ABCD ,可得AB =CB ,∠ABP =∠CBP =∠ADP =30°,∴△ABP ≌△CBP ,BP =2PE ,∴AP =CP ,∴PC +PB 2=AP +PE , ∵当点A ,P ,E 在同一直线上时,AP +PE 最短, ∴此时,PC +PB 2的值最小,AP ⊥AD ,∵R t △ABE 中,AB =2,∴BE =1,AE =√3,∴R t △BEP 中,PE =13√3, ∴AP =23√3, ∵∠ADP =30°,∴R t △ADP 中,PD =2AP =43√3,故答案为:43√3.巩固练习1.如图,在矩形ABCD 中,AB =4,AD =5,点E ,F 分别是边AB ,BC 上的动点,点E 不与A ,B 重合,且EF =AB ,G 是五边形AEFCD 内满足GE =GF 且∠EGF =90°的点.现给出以下结论.其中错误的是( )A .∠GEB 与∠GFB 一定互补B .点G 到边AB ,BC 的距离一定相等C .点G 到边AD ,DC 的距离可能相等D .点G 到边AB 的距离的最大值为2√2【解答】解:A 、∵四边形ABCD 是矩形,∴∠B =90°,又∵∠EGF =90°,四边形内角和是360°,∴∠GEB +∠GFB =180°,故A 正确;B 、过G 作GM ⊥AB ,GN ⊥BC ,分别交AB 于M ,交BC 于N ,∵GE =GF 且∠EGF =90°,∴∠GEF =∠GFE =45°,又∵∠B =90°,∴∠BEF +∠EFB =90°,即∠BEF =90°﹣∠EFB ,∵∠GEM =180°﹣∠BEF ﹣∠GEF =180°﹣45°﹣(90°﹣∠EFB )=45°+∠EFB , ∠GFN =∠EFB +∠GFE =∠EFB +45°,∴∠GEM =∠GFN ,在△GEM 和△GFN 中,{∠GME =∠GNF∠GEM =∠GFN GE =GF ,∴△GEM≌△GFN(AAS),∴GM=GN,故B正确;C、∵AB=4,AD=5,并由B知,点G到边AD,DC的距离不相等,故C错误:D、在直角三角形EMG中,MG≤EG,当点E、M重合时EG最大,∵EF=AB=4,∴GE=EB=BF=FG=4×√22=2√2,故D正确.故选:C.2.如图,分别以R t△ABC的直角边AC及斜边AB为边向外作等边△ACD、等边△ABE,EF⊥AB,垂足为F,连接DF,当ACAB=时,四边形ADFE是平行四边形.【解答】解:当ACAB =√32时,四边形ADFE是平行四边形.理由:∵ACAB =√32,∴∠CAB=30°,∵△ABE为等边三角形,EF⊥AB,∴EF为∠BEA的平分线,∠AEB=60°,AE=AB,∴∠FEA=30°,又∠BAC=30°,∴∠FEA=∠BAC,在△ABC和△EAF中,{∠ACB =∠EFA∠BAC =∠AEF AB =AE,∴△ABC ≌△EAF (AAS );∵∠BAC =30°,∠DAC =60°,∴∠DAB =90°,即DA ⊥AB ,∵EF ⊥AB ,∴AD ∥EF ,∵△ABC ≌△EAF ,∴EF =AC =AD ,∴四边形ADFE 是平行四边形.故答案为:√32.3.如图,矩形ABCD ,AB =1,BC =2,点A 在x 轴正半轴上,点D 在y 轴正半轴上.当点A 在x 轴上运动时,点D 也随之在y 轴上运动,在这个运动过程中,点C 到原点O 的最大距离为 .【解答】解:如图,取AD 的中点H ,连接CH ,OH ,∵矩形ABCD,AB=1,BC=2,∴CD=AB=1,AD=BC=2,∵点H是AD的中点,∴AH=DH=1,∴CH=√DH2+CD2=√1+1=√2,∵∠AOD=90°,点H是AD的中点,∴OH=12AD=1,在△OCH中,CO<OH+CH,当点H在OC上时,CO=OH+CH,∴CO的最大值为OH+CH=√2+1,故答案为:√2+1.4.如图,菱形ABCD的边长为4,∠BAD=120°,点E是AB的中点,点F是AC上的一动点,则EF+BF的最小值是.【解答】解:连接DB,DE,设DE交AC于M,连接MB,DF,延长BA,DH⊥BA于H,∵四边形ABCD是菱形,∴AC,BD互相垂直平分,∴点B关于AC的对称点为D,∴FD=FB,∴FE+FB=FE+FD≥DE.只有当点F运动到点M时,取等号(两点之间线段最短),△ABD中,AD=AB,∠DAB=120°,∴∠HAD=60°,∵DH⊥AB,∴AH=12AD,DH=√32AD,∵菱形ABCD的边长为4,E为AB的中点,∴AE=2,AH=2,∴EH=4,DH=2√3,在R t△EHD中,DE=√EH2+DH2=√42+(2√3)2=2√7,∴EF+BF的最小值为2√7.故答案为:2√7.5.如图,在矩形ABCD中,AD=√3AB,对角线相交于点O,动点M从点B向点A运动(到点A即停止),点N是AD上一动点,且满足∠MON=90°,连结MN.在点M、N 运动过程中,则以下结论正确的是.(写出所有正确结论的序号)①点M、N的运动速度不相等;②存在某一时刻使S△AMN=S△MON;③S△AMN逐渐减小;④MN2=BM2+DN2.【解答】解:如图,当M与B点重合时,此时NO⊥BD,∵在矩形ABCD中,AD=√3AB,∴∠ADB=∠DAC=30°,∴∠AOD=180°﹣30°﹣30°=120°,∴∠NAO=∠AOD﹣∠NOD=120°﹣90°=30°,∴∠DAO=∠NOA=30°,∴AN=ON=DN•sin30°=12DN,∵AN+DN=AD,∴AN=13AD,当M点运动到M'位置时,此时OM'⊥AB,N点运动到了N',∵AC和BD是矩形ABCD的对角线,∴M点运动的距离是MM'=12AB,N点运动的距离是NN'=12AD−AN=12AD−13AD=16AD,又∵AD=√3AB,∴NN'=16×√3AB=√36AB=√33MM',∴N 点的运动速度是M 点的√33, 故①正确,当M 在M '位置时, ∵∠OM 'A =90°,∠N 'AB =90°,∠M 'ON '=90°,∴四边形AM 'ON '是矩形,∴此时S △AMN =S △MON ,故②正确,令AB =1,则AD =√3,设BM =x ,则N 点运动的距离为√33x , ∴AN =13AD +√33x =√33+√33x ,∴S △AMN =12AM •AN =12(AB ﹣BM )•AN =12(1﹣x )(√33+√33x )=√36−√36x 2, ∵0≤x ≤1,在x 的取值范围内函数√36−√36x 2的图象随x 增加而减小, ∴S △AMN 逐渐减小,故③正确,∵MN 2=(AB ﹣BM )2+(AD ﹣DN )2=AB 2﹣2AB •BM +BM 2+AD 2﹣2AD •DN +DN 2=(AB 2﹣2AB •BM +3AB 2﹣2√3AB •DN )+BM 2+DN 2=(4AB 2﹣2AB •BM ﹣2√3AB •DN )+BM 2+DN 2, ∵AN =13AD +√33BM =√33AB +√33BM ,∴DN =AD ﹣AN =√3AB ﹣(√33AB +√33BM )=2√33AB −√33BM , ∵2√3AB •DN =2√3AB ×(2√33AB −√33BM )=4AB 2﹣2AB •BM , ∴MN 2=(4AB 2﹣2AB •BM ﹣2√3AB •DN )+BM 2+DN 2=BM 2+DN 2,故④正确,方法二判定④:如图2,延长MO 交CD 于M ',∵∠MOB =∠M 'OD ,OB =OD ,∠DBA =∠BDC ,∴△OMB ≌△OM 'D (ASA ),∴BM =DM ',OM =OM ',连接NM ',∵NO ⊥MM ',则MN =NM ',∵NM '2=DN 2+DM '2,故④正确,故答案为:①②③④.6.如图,菱形ABCD,AB=5,E在BC上,BE=4,过点E作EG⊥AD于G,交BD于F,连接DE,若∠A=4∠DEG,则EF的长为.【解答】解:如图,过点D作DM⊥BD,交BC的延长线于点M,设∠DEG=α,则∠A=4α,∵四边形ABCD是菱形,∴∠ABC=180°﹣∠A=180°﹣4α,∠ABD=∠CBD=∠BDC,∴∠ABD=∠CBD=∠BDC=90°﹣2α,∴∠M=90°﹣∠CBD=90°﹣(90°﹣2α)=2α,∠CDM=90°﹣∠BDC=90°﹣(90°﹣2α)=2α,∴∠M=∠CDM,∴CD=CM=5,∵EG⊥AD,∴∠BEG=90°,∴∠DEM=180°﹣∠BEG﹣∠DEG=180°﹣90°﹣α=90°﹣α,∴∠EDM=180°﹣∠DEM﹣∠M=180°﹣(90°﹣α)﹣2α=90°﹣α,∴DM=EM=EC+CM=1+5=6,∴BM=BC+CM=5+5=10,∴BD=√BM2−DM2=√102−62=8,∵∠BEF=∠BDM=90°,∠FBE=∠MBD,∴△FBE∽△MBD,∴EFDM =BEBD,即EF6=48,∴EF=3.故答案为:3.7.如图,在矩形ABCD中,AB=2,AD=4,E为AD的中点,F为线段EC上一动点,P 为BF中点,连接PD,则线段PD长的取值范围是.【解答】解:如图:当点F与点C重合时,点P在点P1处,CP1=BP1,当点F与点E重合时,点P在点P2处,EP2=BP2,∴P1P2∥EC且P1P2=12CE,当点F在EC上除点C、E的位置处时,有BP=FP,由中位线定理可知:P1P∥CF且P1P=12CF,∴点P的运动轨迹是线段P1P2,∵矩形ABCD中,AB=2,AD=4,E为AD的中点,∴△ABE,△BEC、△DCP1为等腰直角三角形,∴∠ECB=45°,∠DP1C=45°,∵P1P2∥EC,∴∠P2P1B=∠ECB=45°,∴∠P2P1D=90°,∴DP的长DP1最小,DP2最大,∵CD=CP1=DE=2,∴DP1=2√2,CE=2√2,∴P1P2=√2,∴DP2=√(2√2)2+(√2)2=√10,故答案为:2√2≤PD≤√10.8.如图,在△ABC中,∠ABC=90°,BD为△ABC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.(1)求证:四边形BDFG是菱形:(2)若∠BAC=30°,BC=2,求四边形BDFG的面积.【解答】(1)证明:∵∠ABC=90°,BD为AC的中线,∴BD=12AC,∵AG∥BD,BD=FG,∴四边形BDFG是平行四边形,∵CF⊥BD,∴CF⊥AG,又∵点D是AC中点,∴DF=12AC,∴BD=DF;∴平行四边形BDFG是菱形;(2)解:作DH⊥AG于H,如图所示:∵四边形BDFG是菱形,∴GF=BD,∵∠ABC=90°,∠BAC=30°,BC=2,∴AC=2BC=4,∵点D是AC中点,∴GF=BD=12AC=AD=2,∴∠DBA=∠BAC=30°,又∵AG∥BD,∴∠BAF=∠DBA=30°,∴∠DAF=60°,∵DH⊥AG,∴∠ADH=30°,∴AH=12AD=1,DH=√3AH=√3,∴S菱形BDFG=GF•DH=2×√3=2√3.9.已知四边形ABCD是矩形.(1)如图1,E、F分别是AB、AD上的点,CE垂直平分BF,垂足为G,连接DG.①求证:DG=CG;②若BC=2AB,求∠DGC的大小;(2)如图2,AB=BC=6,M、N、P分别是AB、CD、AD上的点,MN垂直平分BP,点Q是CD的中点,连接MP,PQ,若PQ⊥MP,直接写出CN的长.【解答】解:(1)①如图1,过G作MN⊥CD于N,与AB交于点M,则MN∥AD,∵CE垂直平分BF,∴GB=GF,∴AM=BM,∵四边形ABCD是矩形,∴∠A=∠ADN=∠MND=90°,∴四边形ADNM是矩形,∴DN=AM=12AB=12CD,∵MN垂直平分CD,∴DG=CG;②连接CF,如图1,∵CE垂直平分BF,∴CF=CB.∴∠BCG=∠FCG=12∠BCF,∵四边形ABCD是矩形,∴AB=CD,∠CDF=∠BCD=90°,AD∥BC,∵BC=2AB,∴CF=2CG,延长CD至H,使得DH=CD,连接FH,则CF=CH,∴AD垂直平分CH,∴FH=FC=CH,∴∠FCD=60°,∴∠BCF=90°﹣∠FCD=30°,∴∠BCG=∠FCG=15°,∴∠GDC=∠GCD=∠BCD﹣∠BCG=75°,∴∠CGD=180°﹣75°×2=30°;(3)∵MN垂直平分BP,∴MB=MP,∴∠MBP=∠MPB,∵MP⊥PQ,∴∠MPQ=∠A=90°,∴∠ABP+∠APB=∠BPM+∠BPQ=90°,∴∠BPA=∠BPQ,作BS⊥PQ于S,连接BQ,如图2,∴BA=BS,∵BP=BP,∴R t△PBA≌R t△PBS(HL),∴AP=PS,∵AB=BC,∴BS=BC,∵BQ=BQ,∴R t△QBS≌R t△QBC(HL),∴QS=QC=3,∴PQ=AP+CQ,设AP=x,PD=6﹣x,PQ=3+x,在R t△PQD中,DQ=3,由勾股定理得,(3+x)2﹣(6﹣x)2=32,解得,x=2,∴AP=2,设BM=MP=y,AM=6﹣y,在R t△AMP中由勾股定理得,y2﹣(6﹣y)2=22,解得,y=10 3,作NK ⊥AB 于K ,如图2,得四边形AKND 是矩形,∴AB =AD =KN ,∠A =∠MKN =90°,∵MN ⊥BP ,∴∠ABP +∠KMN =∠KMN +∠KNM =90°,∴∠ABP =∠KNM ,∴△ABP ≌△KNM (ASA ),∴AP =KM =2,∴CN =BK =BM ﹣MK =103−2=43;另一解法:过N 点作NK ⊥AB 于点K ,得四边形AKND 是矩形,∴AB =AD =MN ,∠A =∠MKN =90°,∵MN ⊥BP ,∴∠ABP +∠KMN =∠KMN +∠KNM =90°,∴∠ABP =∠KNM ,∴△ABP ≌△KNM (ASA ),∴AP =KM ,∵MN 垂直平分BP ,∴MB =MP ,不妨设BM =MP =x ,则AM =6﹣x ,∴AP =√x 2−(6−x)2=√12x −36,∴DP =6−√12x −36,∵Q 是CD 的中点,∴DQ =3,∵PQ ⊥MP ,∠A =∠D =90°,∴∠APM +∠AMP =∠APM +∠DPQ =90°,∴∠AMP =∠DPQ ,∴△APM ∽△DQP ,∴AP DQ =AM DP ,即√12x−363=6−√12x−36, 解得,x =6或103,∴CN =BK =AB ﹣AM ﹣MK =6﹣(6﹣x )−√12x −36=x −√12x −36=0或43.舍去CN =0,10.已知:如图,把矩形纸片OABC放入直角坐标系x O y中,使OA、OC分别落在x轴、y轴的正半轴上,连接AC,将△ABC沿AC翻折,点B落在该坐标平面内,设这个落点为D,CD交x轴于点E.如果CE=5,OC、OE的长是关于x的方程x2+(m﹣1)x+12=0的两个根,并且OC>OE.(1)求点D的坐标;(2)如果点F是AC的中点,判断点(8,﹣20)是否在过D、F两点的直线上,并说明现由.【解答】解:(1)∵OC、OE的长是关于x的方程x2+(m﹣1)x+12=0的两个根,设OC=x1,OE=x2,x1>x2.∴x1+x2=﹣(m﹣1).x1•x2=12.在R t△COE中,∵OC2+OE2=CE2,CE=5.∴x12+x22=52,即(x1+x2)2﹣2x1x2=25.∴[﹣(m﹣1)]2﹣2×12=25,解这个方程,得m1=﹣6,m2=8.∵OC+OE=x1+x2=﹣(m﹣1)>0,∴m=8不符合题意,舍去.∴m=﹣6.解方程x2﹣7x+12=0,得x1=4,x2=3.∴OC=4,OE=3.△ABC沿AC翻折后,点B的落点为点D.过D点作DG⊥x轴于G.DH⊥y轴于H.∴∠BCA=∠ACD.∵矩形OABC中,CB∥OA.∴∠BCA=∠CAE.∴∠CAE=∠ACD.∴EC=EA.在R t△COE与R t△ADE中,∵{OC =AD EC =EA∴R t △COE ≌R t △ADE .∴ED =3,AD =4,EA =5.在R t △ADE 中,DG •AE =ED •AD ,∴DG =ED⋅AD AE=125, 在△CHD 中,OE ∥HD , ∴CE CD =CE HD,55+3=3HD , ∴HD =245,由已知条件可知D 是第四象限的点,∴点D 的坐标是(245,−125);(2)∵F 是AC 的中点,∴点F 的坐标是(4,2),设过D 、F 两点的直线的解析式为y =kx +b .∴{4k +b =2245k +b =−125,解得{k =−112b =24, ∴过点D 、F 两点的直线的解析式为y =−112x +24,∵x =8,y =﹣20满足上述解析式,∴点(8,﹣20)在过D 、F 两点的直线上.11.如图1,在菱形ABCD 中,对角线AC 与BD 相交于点O ,AB =13,BD =24,在菱形ABCD 的外部以AB 为边作等边三角形ABE .点F 是对角线BD 上一动点(点F 不与点B 重合),将线段AF 绕点A 顺时针方向旋转60°得到线段AM ,连接FM .(1)线段AO 的长为 ;(2)如图2,当点F在线段BO上,且点M,F,C三点在同一条直线上时,求证:AM=√33AC;(3)连接EM.若△AFM的周长为3√29,请直接写出△AEM的面积.【解答】解:(1)∵四边形ABCD是菱形,∴AC⊥BD,OB=12BD=12,在R t△AOB中,AB=13,根据勾股定理得,AO=√AB2−OB2=√132−122=5,故答案为5;(2)由旋转知,AM=AF,∠MAF=60°,∴△AMF是等边三角形,∴∠AFM=60°,∵点M,F,C三点在同一条直线上,∴∠AFC=180°﹣∠AFM=120°,∵菱形ABCD的对角线AC与BD相交于O,∴OA=OC=12AC,在△AOF和△COF中,{OA=OC∠AOF=∠COF=90°OF=OF,∴△AOF≌△COF(SAS),∴∠AFO=12∠AFC=60°,在R t△AOF中,sin∠AFO=OA AF,AF=OAsin∠AFO=OAsin60°=2√33OA=√33AC,∴AM=√33AC;(3)①当点F在线段OB上时,如图,由(2)知,△AMF是等边三角形,∵△AFM的周长为3√29,∴AF=√29,在R t△AOF中,根据勾股定理得,OF=√AF2−AO2=2,∴BF=OB﹣OF=12﹣2=10,连接EM ,∵△ABE 是等边三角形,∴AE =AB =13,∠BAE =60°,由(1)知,AM =AF ,∠FAM =60°,∴∠BAE =∠EAM ,∴∠EAM =∠BAF ,∴△AEM ≌△ABF (SAS ),∴EM =BF =10,∠AEM =∠ABF ,过点M 作MN ⊥AE 于N ,∴∠MNE =∠AOB =90°,∴△MNE ∽△AOB ,∴MN AO =EM AB , ∴MN 5=1013,∴MN =5013,∴S △AEM =12AE •MN =12×13×5013=25, ②当点F 在OD 上时,同①的方法得,MN =7013, S △AEM =12AE •MN =12×13×7013=35,即:△AEM 的面积为25或35.12.在菱形ABCD 中,∠BAD =60°.(1)如图1,点E 为线段AB 的中点,连接DE 、CE 、若AB =4,求线段EC 的长;(2)如图2,M 为线段AC 上一点(不与A 、C 重合),以AM 为边向上构造等边三角形AMN ,线段MN 与AD 交于点G ,连接NC 、DM ,Q 为线段NC 的中点,连接DQ 、MQ ,判断DM 与DQ 的数量关系,并证明你的结论;(3)在(2)的条件下,若AC=√3,请你直接写出DM+CN的最小值.【解答】解:(1)如图1,连接BD,则BD平分∠ABC,∵四边形ABCD是菱形,∴AD∥BC,∴∠A+∠ABC=180°,∵∠A=60°,∴∠ABC=120°,∴∠ABD=12∠ABC=60°,∴△ABD是等边三角形,∴BD=AD=4,∵E是AB的中点,∴DE⊥AB,由勾股定理得:DE=√42−22=2√3,∵DC∥AB,∴∠EDC=∠DEA=90°,在R t△DEC中,DC=4,EC=√DC2+DE2=√42+(2√3)2=2√7;(2)如图2,延长CD至H,使DH=CD,连接NH、AH,∵AD =CD ,∴AD =DH ,∵CD ∥AB ,∴∠HDA =∠BAD =60°,∴△ADH 是等边三角形,∴AH =AD ,∠HAD =60°,∵△AMN 是等边三角形,∴AM =AN ,∠NAM =60°,∴∠HAN +∠NAG =∠NAG +∠DAM ,∴∠HAN =∠DAM ,在△ANH 和△AMD 中,∵{AH =AD∠HAN =∠DAM AN =AM,∴△ANH ≌△AMD (SAS ),∴HN =DM ,∵D 是CH 的中点,Q 是NC 的中点,∴DQ 是△CHN 的中位线,∴HN =2DQ ,∴DM =2DQ .(3)如图2,由(2)知,HN =DM ,∴要CN +DM 最小,便是CN +HN 最小,即:点C ,H ,N 在同一条线上时,CN +DM 最小, 此时,点D 和点Q 重合,即:CN +DM 的最小值为CH ,如图3,由(2)知,△ADH 是等边三角形,∴∠H=60°.∵AC是菱形ABCD的对角线,∴∠ACD=12∠BCD=12∠BAD=30°,∴∠CAH=180°﹣30°﹣60°=90°,在R t△ACH中,CH=ACcos30°=2,∴DM+CN的最小值为2.。
初三特殊平行四边形练习题

初三特殊平行四边形练习题题一:已知平行四边形ABCD,AB=10cm,BC=8cm,BD垂直于BC,求BD的长度。
解:由于ABCD为平行四边形,所以AB ∥ CD 且 AD ∥ BC。
根据垂直平行四边形定理可知,垂直于平行边的连线所对应的边长相等。
因此,BD = AC = AB = 10cm。
答案:BD的长度为10cm。
题二:已知平行四边形EFGH,EH=12cm,HF=6cm,EF垂直于HF,求EF的长度。
解:由于EFGH为平行四边形,所以EF ∥ GH 且 EG ∥ FH。
根据垂直平行四边形定理可知,垂直于平行边的连线所对应的边长相等。
因此,EF = GH = HF = 6cm。
答案:EF的长度为6cm。
题三:在平行四边形IJKL中,LJ=12cm,IK=16cm,LK垂直于LJ,求LK的长度。
解:由于IJKL为平行四边形,所以IJ ∥ LK 且 IL ∥ KJ。
根据垂直平行四边形定理可知,垂直于平行边的连线所对应的边长相等。
因此,LK = IJ = LK = 12cm。
答案:LK的长度为12cm。
题四:在平行四边形MNOP中,MN=8cm,NO=6cm,MP垂直于MN,求MP的长度。
解:由于MNOP为平行四边形,所以MN ∥ OP 且 MP ∥ NO。
根据垂直平行四边形定理可知,垂直于平行边的连线所对应的边长相等。
因此,MP = NO = 6cm。
答案:MP的长度为6cm。
题五:已知平行四边形QRST,QT=14cm,RS=10cm,符合B呼W=QW,求QW的长度。
解:在平行四边形QRST中,根据B呼W=QW的性质可知,比例相等的边与对角线共线。
因此,BW ∥ TR 且 BQ ∥ ST。
与TR平行的边的长度为QS。
根据比例B呼W = QW,可以得到QS/QW = TR/BW= QT/QS。
解方程得到QS^2= QW^2,即QS = QW。
由QS = QT - TS 可知,QS = 14cm - 10cm = 4cm。
九年级上册数学特殊的四边形试题

AGEBCF D 特殊的四边形试题1.如图,四边形ABCD 是菱形,点G 是BC 延长线上一点,连接AG ,分别交BD 、CD 于点E 、F ,连接CE .(1)求证:∠DAE =∠DCE ;(2)当AE =2EF 时,判断FG 与EF 有何等量关系并证明你的结论2.如图,在△ABC 中,D 是BC 边的中点,E 、F 分别在AD 及其延长线上, CE ∥BF ,连接BE 、CF .(1)求证:△BDF≌△CDE;(2)若AB=AC ,求证:四边形BFCE 是菱形. 3.(10分)如图,在□ABCD 中,E 、F 分别是边AB 、CD的中点,AG ∥BD 交CB 的延长线于点G . (1)求证:△ADE ∽≌△CBF ;(2)若四边形BEDF 是菱形,则四边形AGBD 是什么特殊四边形?请说明你的理由.4.已知:如图14,E 是正方形ABCD 的对角线BD 上一点,EF ⊥BC , EG ⊥CD ,垂足分别是F 、G 。
求证:AE = FG .5.如图11,四边形ABCD 中,点M ,N 分别在AB ,BC 上, 将△BMN 沿MN 翻折,得△FMN ,若MF ∥AD ,FN ∥DC , 则∠B = °.6.如图,矩形ABCD 中,AB=1,E 、F 分别为AD 、CD 的中点,沿BE 将△ABE 折叠,若点A 恰好落在BF 上,则AD= .7.如图,矩形ABCD 中,AB=3,BC=4,点E 是BC 边上一点,连接AE ,把∠B 沿AE 折叠,使点B 落在点B′处.当△CEB′为直角三角形时,BE 的长为 .8.探究:如图①, 在四边形ABCD 中,∠BAD =∠BCD =90°,AB =AD ,AE ⊥CD 于点E .若AE =10,求四边形ABCD 的面积.应用:如图②,在四边形ABCD 中,∠ABC +∠ADC =180°,AB =AD ,AE ⊥BC 于点E .若AE =19,BC =10,CD =6,则四边形ABCD 的面积为 .9.如图,在矩形ABCD 中,E 、F 分别是AB 、CD 上的点,AE =CF ,连接EF 、BF ,EF 与对角线AC 交于点O ,且BE =BF ,∠BEF =2∠BAC 。
创新作图题-在特殊四边形中作图-中考数学第二轮总复习课件(全国通用)

①找点:两__点__确__定__一__条__直__线__________________________
;
根据图形的判定方法构造三角形、四边形等
②画线:________________________________________
知识点
01 利用常用技巧作图 02 利用性质作位置关系 03 利用性质作数量关系 04 按要求构造图形
当堂训练
利用性质作数量关系
知识点三
1.如图1、图2,四边形ABCD是正方形,DE=CE.请仅用无刻度的直尺按要求完成 下列画图. (1)在图1中,画出CD边的中点;(2)在图2中,画出AD边的中点.
E
E
E
利用平行四边
D
F CD
F CD
F C 形的对角线互
相平分作图
O
N MO
NM
O
A 图1 B A 图2 B A 图2 B 点F即为所求 点N即为所求
按要求构造图形
知识点四
【例4】如图,在菱形ABCD中,∠A=120º,P为AB上一点,请仅用无刻度的直尺
作图.
(1)在图1中,画一个以BP为边的等边三角形;
(2)在图2中,画一个以BP为一边的平行四边形.
A
D
A
D
P
P
B
QC
图1
如图1,△BPQ即为所求;
Q
B
C
图2
如图2,四边形BPDQ即为所求.
强化训练
当堂训练
利用常用技巧作图
1.在菱形ABCD中,AE⊥BC于E,请仅用无刻度的直尺作图.
(1)过点C在图1中画出AB边上的高;
(2)过点C在图2中画出AD边上的高.
A
特殊的四边形练习题
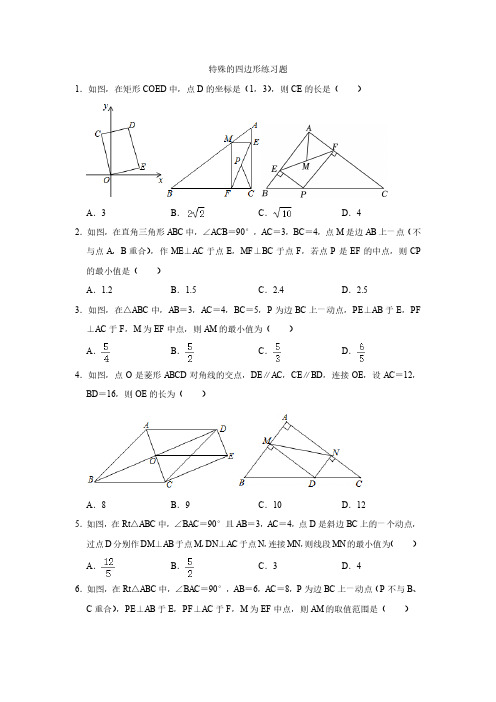
特殊的四边形练习题1.如图,在矩形COED中,点D的坐标是(1,3),则CE的长是()A.3B.C.D.42.如图,在直角三角形ABC中,∠ACB=90°,AC=3,BC=4,点M是边AB上一点(不与点A,B重合),作ME⊥AC于点E,MF⊥BC于点F,若点P是EF的中点,则CP 的最小值是()A.1.2B.1.5C.2.4D.2.53.如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF ⊥AC于F,M为EF中点,则AM的最小值为()A.B.C.D.4.如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE,设AC=12,BD=16,则OE的长为()A.8B.9C.10D.125.如图,在Rt△ABC中,∠BAC=90°且AB=3,AC=4,点D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连接MN,则线段MN的最小值为()A.B.C.3D.46.如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,P为边BC上一动点(P不与B、C重合),PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的取值范围是()A.≤AM<4B.6≤AM<8C.≤AM<8D.3≤AM<47.如图,在∠MON的两边上分别截取OA、OB,使OA=OB;分别以点A、B为圆心,OA 长为半径作弧,两弧交于点C;连接AC、BC、AB、OC.若AB=2cm,四边形OACB的面积为4cm2.则OC的长为()cm.A.2B.3C.4D.58.如图,剪两张对边平行且宽度相同的纸条随意交叉叠放在一起,转动其中一张,重合部分构成一个四边形,则下列结论中不一定成立的是()A.∠ABC=∠ADC,∠BAD=∠BCD B.AB=BCC.AB=CD,AD=BC D.∠DAB+∠BCD=180°9.如图,平行四边形ABCD中,∠A=110°,AD=DC.E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠PEF=()A.35°B.45°C.50°D.55°10.如图,两张等宽的纸条交叉叠放在一起,若重合部分构成的四边形ABCD中,AB=3,AC=2,则四边形ABCD的面积为()A.B.C.D.511.如图,两张等宽的纸条交叉重叠在一起,重叠的部分为四边形ABCD,若测得A,C之间的距离为6cm,点B,D之间的距离为8cm,则线段AB的长为()A.5 cm B.4.8 cm C.4.6 cm D.4 cm12.如图,分别以Rt△ABC的斜边AB,直角边AC为边向外作等边△ABD和△ACE,F为AB的中点,DE,AB相交于点G.连接EF,若∠BAC=30°,下列结论:①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④△DBF≌△EF A.则正确结论的序号是()A.①③B.②④C.①③④D.②③④13.如图,菱形ABCD中,∠BAD=60°,AC与BD交于点O,E为CD延长线上一点,且CD=DE,连结BE,分别交AC,AD于点F、G,连结OG,则下列结论:①OG=AB;②S四边形ODGF>S△ABF;③由点A、B、D、E构成的四边形是菱形;④S△ACD=4S△BOG.其中正确的结论是()A.①②B.①②③C.①③④D.②③④14.如图,菱形ABCD中,AC与BD交于点O,CD=2OB,E为CD延长线上一点,使得DE=CD,连结BE,分别交AC、AD于点F、G,连结OG,AE,则下列结论:①∠ABC =120°;②;③四边形ODEG与四边形OBAG的面积相等;④由点A、B、D、E构成的四边形是菱形.其中正确的结论个数是()A.4B.3C.2D.115.如图,正方形ABCD的边长为2,E为AB边的中点,点F在BC边上,点B关于直线EF的对称点记为B',连接B'D,B'E,B'F.当点F在BC边上移动使得四边形BEB'F成为正方形时,B'D的长为()A.B.C.2D.316.如图,AD是△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,连接EF交AD于G.有以下四个结论:①GA=GD;②AD⊥EF;③当∠BAC=90°时,四边形AEDF是正方形;④AE2+DF2=AF2+DE2.其中正确的是()A.②③B.②④C.①③④D.②③④17.如图,已知四边形ABCD为正方形AB=2,点E为对角线AC上一点,连接DE,过点E作EF⊥DE,交BC延长线于点F,以DE、EF为邻边作矩形DEFG,连接CG.在下列结论中:①矩形DEFG是正方形;②2CE+CG=AD;③CG平分∠DCF;④CE =CF.其中正确的结论有()A.①③B.②④C.①②③D.①②③④18.如图,在正方形ABCD中,点O是对角线AC,BD的交点,过点O作射线OM,ON 分别交BC,CD于点E,F,且∠EOF=90°,OC,EF交于点G.给出下列结论:①△COE≌△DOF;②CF=BE;③四边形CEOF的面积为正方形ABCD面积的;④DF2+CF2=2OE2,其中正确的是()A.①②③④B.①②③C.①②④D.③④19.如图,将两条宽度都为3的纸条重叠在一起,使∠ABC=60°,则四边形ABCD的面积为.20.如图,在△ABC中,∠ABC=90°,BD为AC边上的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若AG=13,BG=5,则CF的长为.21.如图所示,四边形ABCD中,AC⊥BD于点O,AO=CO=4,BO=DO=3,点P为线段AC上的一个动点.过点P分别作PM⊥AD于点M,作PN⊥DC于点N.连接PB,在点P运动过程中,PM+PN+PB的最小值等于.22.如图所示,四边形ABCD中,AC⊥BD于点O,AO=CO=8,BO=DO=6,点P为线段AC上的一个动点.(1)填空:AD=CD=.(2)过点P分别作PM⊥AD于M点,作PH⊥DC于H点.连接PB,在点P运动过程中,PM+PH+PB的最小值为.23.如图,∠EOD=90°,点A、B分别在OE,OD上,∠EAB与∠ABD的角平分线交于点P,PC⊥AB于C,若PC=2,则OP=.24.如图,在四边形ABCD中,∠BAD=45°,∠BCD=90°,连接BD、CA,且CA平分∠BCD,若AC=45,BC=15,则BD=.25.如图,AD是△ABC的高,∠BAC=45°,若AD=18,DC=6,则△ABC的面积是.26.如图,以△ABC的两边AB,AC为边向形外作正方形ABEF,ACGH,则称这两个正方形为外展双叶正方形.有以下5个结论:①△ABC面积与△AFH面积相等.②过点A作边BC的垂线交FH于点D,则FD=HD.③O为边BC的中点,OA延长线与HF交于点P,则AP⊥HF且HF=2AO.④连接FC、HB相交于点R,则FC=HB且FC⊥HB.⑤连结EG,S为EG的中点,则SB=SC且SB⊥SC.其中正确的结论是(填序号).27.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.(1)求证:四边形ABCD是菱形;(2)若AB=,BD=2,求OE的长.28.如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.(1)求证:BD=DF;(2)求证:四边形BDFG为菱形;(3)若AG=13,CF=6,求四边形BDFG的周长.29.如图,已知四边形ABCD为正方形,AB=4,点E为对角线AC上一动点,连接DE、过点E作EF⊥DE.交BC点F,以DE、EF为邻边作矩形DEFG,连接CG.(1)求证:矩形DEFG是正方形;(2)探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.30.四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.(1)如图,求证:矩形DEFG是正方形;(2)若AB=2,CE=2,求CG的长;(3)当线段DE与正方形ABCD的某条边的夹角是40°时,直接写出∠EFC的度数.31.如图,已知:在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF∥AE.(1)求证:四边形BECF是菱形;(2)当∠A=°时,四边形BECF是正方形;(3)在(2)的条件下,若AC=4,则四边形ABFC的面积为.32.如图,在矩形ABCD中,AB=8cm,BC=16cm,点P从点D出发向点A运动,运动到点A停止,同时,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是1cm/s.连接PQ、AQ、CP.设点P、Q运动的时间为t s.(1)当t为何值时,四边形ABQP是矩形;(2)当t为何值时,四边形AQCP是菱形;(3)分别求出(2)中菱形AQCP的周长和面积.。
与特殊四边形有关的创新题

与特殊四边形有关的创新题山东 于秀坤探索型试题是各地中考试题中的重要类型,特别是涉及到特殊四边形有关探索型试题非常多,比较常见的有探索四边形的形状、探索线段之间的关系等问题.一、探索四边形的形状例1(2006年贵阳)如图1,在平行四边形ABCD 中,对角线AC\BD 相交于点O ,AF ⊥BD ,CE ⊥BD ,垂足分别为E 、F ;(1)连结AE 、CF ,得四边形AFCE ,试判断四边形AFCE 是下列图形中的哪一种? ①平行四边形;②菱形;③矩形;(2)请证明你的结论;分析:要判别四边形AFCE 是①平行四边形;②菱形;③矩形哪一种,首先要判断这个四边形是否是平行四边形,如果是平行四边形,然后再判断是否邻边相等或对角线垂直,若成立,则是菱形;若不是菱形,再判断对角线是否相等或是否有一个角是直角,若成立,则该四边形是矩形. 解:(1)画图连结AE 、CF ,四边形AFCE 为平行四边形(2)证明:∵AF ⊥BD ,CE ⊥BD ,∴∠AFO =∠CEO ,又∵∠AOF =∠COE ,∴OA = OC ,∴⊿AOF ≌⊿COE ,∴ OF = OE .又∵OA = OC ,∴四边形AFCE 是平行四边形评注:当四边形中涉及对角线时,一般根据“两条对角线互相平分的四边形是平行四边形”证明平行四边形.例2(2006年湛江)如图2,点E F G H ,,,分别为四边形ABCD 的边AB BC CDDA ,,,的中点,试判断四边形EFGH 的形状,并证明你的结论.分析:因为点E 、F 、G 、H 分别是四边形ABCD 的各边中点,中点联想中位线,所以连接AC ,可利用三角形的中位线的性质,证明HG//EF ,HG=EF ,从而根据一组对边平行且相等的四边形是平行三边形说明四边形HEFG 是平行四边形.解:四边形EFGH 是平行四边形 证明:连结AC ,如图2. 因为E 、F 分别是AB 、BC 的中点, 所以EF 是ABC △的中位线, 所以EF//AC ,且12EF AC =. 同理:GH AC ∥,且12GH AC =, A BC GD H FE 图2∥.所以EF GH所以四边形EFGH是平行四边形.评注:当已知四边形各边的中点时,一般需要连接四边形的对角线,将四边形转化为两个三角形,然后利用三角形中位线的性质解决问题.二、猜想数量关系例3 (2006年大连)如图3,E、F分别是平行四边形ABCD对角线BD所在直线上两点,DE = BF.请你以F为一个端点,和图中已标有字母的某一点连成一条新的线段,猜想并证明它和图中已有的某一条线段相等(只须研究一组线段相等即可).⑴连结_______________;⑵猜想:_______________;⑶证明:(说明:写出证明过程中的重要依据)分析:本题是一道条件和结论开放性问题,正确给出条件,是猜想结论的关键.由四边形ABCD是平行四边形,可以得到AD=BC,再根据已知条件DE=BF,所以可连接CF,通过证明BFCDEA来得到结论CF=AE.所以猜想的结论可以是CF=AE.解:(1)CF .(2)CF=AE.(3)证明:∵四边形ABCD是平行四边形,图3∴AD∥BC,AD=BC (平行四边形对边平行且相等),∴∠ADB=∠CBD(两直线平行内错角相等),∴∠ADE=∠CBF(等角的补角相等)∵ DE=BF,∴△ADE≌△CBF(SAS),∴CF =AE(全等三角形的对应边相等).评注:添加条件,猜想结论是一类重要的题目,解决问题的关键是依据已知条件并结合已知图形的性质,进行添加和猜想.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
与特殊四边形有关的创新题
一、探索四边形的形状
例1(贵阳)如图1,在平行四边形ABCD 中,对角线AC\BD 相交于点O ,AF ⊥BD ,CE ⊥BD ,垂足分别为E 、F ;
(1)连结AE 、CF ,得四边形AFCE ,试判断四边形AFCE 是下列图形中的哪一种? ①平行四边形;②菱形;③矩形;
(2)请证明你的结论;
分析:要判别四边形AFCE 是①平行四边形;②菱形;③矩形哪一种,首先要判断这个四边形是否是平行四边形,如果是平行四边形,然后再判断是否邻边相等或对角线垂直,若成立,则是菱形;若不是菱形,再判断对角线是否相等或是否有一个角是直角,若成立,则该四边形是矩形.
解:(1)画图连结AE 、CF ,四边形AFCE 为平行四边形
(2)证明:∵AF ⊥BD ,CE ⊥BD ,
∴∠AFO =∠CEO ,
又∵∠AOF =∠COE ,
∴OA = OC ,
∴⊿AOF ≌⊿COE ,
∴ OF = OE .
又∵OA = OC ,
∴四边形AFCE 是平行四边形
评注:当四边形中涉及对角线时,一般根据“两条对角线互相平分的四边形是平行四边形”证明平行四边形.
例2(湛江)如图2,点E F G H ,
,,分别为四边形A B C D 的边AB BC CD DA ,,,的中点,试判断四边形E F G H 的形状,并证明你的结论.
分析:因为点E 、F 、G 、H 分别是四边形ABCD 的各边中点,中点联想中位线,所以连接AC ,可利用三角形的中位线的性质,证明HG//EF ,HG=EF ,从而根据一组对边平行且相等的四边形是平行三边形说明四边形HEFG 是平行四边形.
解:四边形E F G H 是平行四边形
证明:连结A C ,如图2.
因为E 、F 分别是AB 、BC 的中点,
所以EF 是A B C △的中位线,
所以EF//AC ,且1
2E F A C =.
同理:G H A C ∥,且1
2G H A C =
, 所以EF G H ∴ ∥. 所以四边形E F G H 是平行四边形.
A B
C G
D H F
E 图2
评注:当已知四边形各边的中点时,一般需要连接四边形的对角线,将四边形转化为两个三角形,然后利用三角形中位线的性质解决问题.
二、猜想数量关系
例3 (大连)如图3,E、F分别是平行四边形ABCD对角线BD所在直线上两点,DE = BF. 请你以F为一个端点,和图中已标有字母的某一点连成一条新的线段,猜想并
证明它和图中已有的某一条线段相等(只须研究一组线段相等即可).
⑴连结_______________;⑵猜想:_______________;
⑶证明:(说明:写出证明过程中的重要依据)
分析:本题是一道条件和结论开放性问题,正确给出条件,是猜想结论的关键.由四边形ABCD是平行四边形,可以得到AD=BC,再根据已知条件DE=BF,所以可连接CF,通过证明BFCDEA来得到结论CF=AE.所以猜想的结论可以是CF=AE.
解:(1)CF .
(2)CF=AE.
(3)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC (平行四边形对边平行且相等),
∴∠ADB=∠CBD(两直线平行内错角相等),
∴∠ADE=∠CBF(等角的补角相等)
∵ DE=BF,
∴△ADE≌△CBF(SAS),
∴CF =AE(全等三角形的对应边相等).
评注:添加条件,猜想结论是一类重要的题目,解决问题的关键是依据已知条件并结合已知图形的性质,进行添加和猜想.。
