第02章 流体的PVT5
合集下载
化工热力学第二章 流体的p-V-T关系和状态方程
第二章 内 容
§2.1 纯流体的p-V-T相图 §2.2 气体状态方程（EOS） §2.3 对应态原理和普遍化关联式 §2.4 液体的p-V-T性质 §2.5 真实气体混合物p-V-T关系
§2.6 状态方程的比较和选用
§2.1 纯流体的p-V-T相图
§2.1.1 T –V 图 §2.1.2 p-V 图 §2.1.3 p-T 图 §2.1.4 p-V-T 立体相图 §2.1.5 纯流体p-V-T关系的应用及思考
§2.1.4 P-V-T立体相图
P-V-T立体相图
§2.1.4 P-V-T立体相图
水的P-V-T立体相图
【例2-1】 将下列纯物质经历的过程表 示在p-V图上：
1）过热蒸汽等温冷凝为过冷液体； 2）过冷液体等压加热成过热蒸汽； 3）饱和液体恒容加热； 4）在临界点进行的恒温膨胀
P
C
1）过热蒸汽等温冷凝为过冷液体； 2）过冷液体等压加热成过热蒸汽； 3）饱和蒸汽可逆绝热膨胀； 4）饱和液体恒容加热； 5）在临界点进行的恒温膨胀
• 1）由于刚性容器体积保持不变， 因此加热过程在等容线上变化，到 达B1时，汽液共存相变为液相单相； 继续加热，当T>Tc，则最终单相为 超临界流体，即C1点。
• 2）当水慢慢加热后，则状态从位 于汽液共存区的A2，变为汽相单相 B2，继续加热，当T>Tc，则最终单 相为临界流体C2。
§2.1 纯流体的P-V-T相图
P-T图
液相区
8atm下变成液体
气相区
1atm下变成气体
液化气的p-T 图
-82.62 ℃
室温10~40℃
乙烯、丙烯、 丁烯能做液化 气吗？
96.59℃
TC = 196.46 Tb =36.05 ℃
chap2 流体的P-V-T关系化工热力学
Z
(1) (2)
Z(0)
h(0)
h
3.注意点
（1）单位要一致，且采用国际单位制;
（2）R的取值取决于PVT的单位. 0.08205 1.987 8314 m3 · atm/kmol· K, cal/mol· K, l· atm/mol· K kcal/kmol· K
m3 · Pa/kmol· (J/kmol· ) K K
（2）便于计算机应用的形式
1 A h Z 1 h B 1 h b B h V Z ( 2 22 ) ( 2 22 a)
式中 A=ap/R2T2.5
B=bp/RT
0.08664 RTc P 0.08664 (P/Pc ) 0.08664 Pr B RTPc (T/Tc ) Tr
力减小。压力减小的数值与撞击器壁的分子成正比；与吸引其 分子数成正比，即与气体比容的平方成反比。
b —
体积校正项。
分子本身占有体积，分子自由活动空间减小由V变成V-b。
在临界点处
P 0 V T Tc 微分 2 P 2 0 V T Tc RTc 2a 27 R 2 Tc2 (Vc b)2 Vc 3 0 a 联立 64Pc 2RTc 6a b RTc (Vc b)3 Vc 4 0 8Pc
第二章 流体的P-V-T关系
2.1 纯物质的P-V-T关系
一.P-T图
超临界流体区 （T>Tc和P>Pc） 液固平衡线
液体区
临界点
固体区 气体区
汽液平衡线
一.P-T图
P
密 流 区
第2章_流体的pVT关系
18
2.2.1.5 Patel-Teja方程 方程 方程形式： 方程形式：
RT a (T ) − p= V − b V (V + b) + c(V − b)
方程常数： 方程常数： 常数
R 2Tc2 a(T ) = Ω a ⋅ α (Tr ) Pc
RTc b = Ωb Pc
0.5
a(Tr )
0.5
= 1 + F (1 − Tr )
23
2.2.1.7 立方型状态方程求解 立方型状态方程求解 工程计算通常采用迭代法进行计算 已知p 已知 、T，计算 的过程。 ，计算V 的过程。
现以PR方程为例，经恒等变形后可得 现以 方程为例，经恒等变形后可得： 方程为例
( k +1 )
V
=b+
p+ V
RT a
( k )2
+ 2bV ( k ) − b 2
7
2.2.1 立方型状态方程
的三次方形式 是指方程可展开为V的三次方形式 。 指方程可展开为 的三
方程形式简单，能够用解析法求解，精确度较高， 方程形式简单，能够用解析法求解，精确度较高， 给工程应用带来方便。 给工程应用带来方便。
2.2.1.1 Van de Waals 方程 方程形式： 方程形式：
4
p-T 图的特征、相关概念 图的特征、
单相区 两相平衡线(饱和曲线) 两相平衡线(饱和曲线) 汽化曲线 熔化曲线 升华曲线 三相点t(T 三相点 t， Pt) 临界点C(TC , PC , VC ) 临界点 图2-2 纯物质的p-T图 纯物质的 图 临界等容线 V=VC V>VC 气相区 V<VC 液相区
d1 , d 2 , d 3为关联常数 Ω a ,Ω b ,Ω c为与临界性质有关的常数
化工热力学第二章 流体的pVT关系
化工热力学
第二章 流体的PVT关系
第2章 流体的p-V-T关系
流体指除固体以外的流动相的总称。均 匀流体一般分为液体和气体两类。
南阳理工学院 生化学院
化工热力学
第二章 流体的PVT关系
重点内容
纯物质的p-V-T关系
状态方程 立方型状态方程 多参数状态方程 对应态原理及其应用 流体的蒸气压、蒸发焓和蒸发熵
方程形式： p RT a(T )
V b V (V b)
Soave 是把R-K 方程中的常数a 看作是温度的函数，在SRK 方程中，a 不仅是物性的函数，而且还是温度的函数，只有在特 定的温度下，对于某一物质而言， a 才能为定值。
方程常数：
a(T
)
ac
(Tr
,)
0.42748
混合规则与混合物的p-V-T关系 液体的p-V-T关系
南阳理工学院 生化学院
化工热力学
第二章 流体的PVT关系
本章要求：
1.了解纯物质的P-T图和P-V图 2.正确、熟练地应用R-K方程、两项维里方程计 算单组分气体的P-V-T关系 3.正确、熟练地应用三参数普遍化方法计算单组 分气体的P-V-T关系 4.了解计算真实气体混合物P-V-T关系的方法， 并会进行计算。
化工热力学
第二章 流体的PVT关系
V T
p
V
V V p T
dV dT dp V
对于液体，由于其具有不可压缩性，体积膨胀系数和等温 压缩系数是温度和压力的弱函数，其数值可以从文献或工具书 中查到。因此，在液体的温度和压力变化不大时，可以将体积 膨胀系数和等温压缩系数当作常数，则
第二章 流体的PVT关系
第2章 流体的p-V-T关系
流体指除固体以外的流动相的总称。均 匀流体一般分为液体和气体两类。
南阳理工学院 生化学院
化工热力学
第二章 流体的PVT关系
重点内容
纯物质的p-V-T关系
状态方程 立方型状态方程 多参数状态方程 对应态原理及其应用 流体的蒸气压、蒸发焓和蒸发熵
方程形式： p RT a(T )
V b V (V b)
Soave 是把R-K 方程中的常数a 看作是温度的函数，在SRK 方程中，a 不仅是物性的函数，而且还是温度的函数，只有在特 定的温度下，对于某一物质而言， a 才能为定值。
方程常数：
a(T
)
ac
(Tr
,)
0.42748
混合规则与混合物的p-V-T关系 液体的p-V-T关系
南阳理工学院 生化学院
化工热力学
第二章 流体的PVT关系
本章要求：
1.了解纯物质的P-T图和P-V图 2.正确、熟练地应用R-K方程、两项维里方程计 算单组分气体的P-V-T关系 3.正确、熟练地应用三参数普遍化方法计算单组 分气体的P-V-T关系 4.了解计算真实气体混合物P-V-T关系的方法， 并会进行计算。
化工热力学
第二章 流体的PVT关系
V T
p
V
V V p T
dV dT dp V
对于液体，由于其具有不可压缩性，体积膨胀系数和等温 压缩系数是温度和压力的弱函数，其数值可以从文献或工具书 中查到。因此，在液体的温度和压力变化不大时，可以将体积 膨胀系数和等温压缩系数当作常数，则
化工热力学讲义-1-第二章-流体的p-V-T关系
pVT性质实验装置简介
装置组成
高压容器、温度计、压力计、体积测量系统等。
工作原理
通过改变流体的压力、体积和温度，测量相应 的物理量变化。
适用范围
适用于气体、液体等多种流体的pVT性质测定。
实验步骤和数据处理
02
01
03
实验步骤 1. 准备实验装置，检查各部件完好。 2. 将待测流体注入高压容器中，密封容器。
p-v-t关系
p-v-t关系是指流体的压力、体积和温度之间的关系。对于理想气体， 其p-v-t关系符合理想气体状态方程，即pV=nRT，其中p为压力，V 为体积，T为温度，n为摩尔数，R为气体常数。对于实际气体，其 p-v-t关系需要考虑分子间的相互作用力和分子本身的体积等因素， 因此需要使用更复杂的状态方程来描述。
THANK YOU
感谢聆听
02
流体的压缩性与膨胀性
压缩因子及计算方法
01
压缩因子的定义
表示实际气体与理想气体偏差程 度的物理量，用Z表示。
02
压缩因子的计算方 法
通过实验测定不同温度、压力下 的气体体积，利用状态方程计算 得到。
03
压缩因子与气体性 质的关系
不同气体的压缩因子不同，与气 体的分子结构、相互作用力等因 素有关。
行提供依据。
管道压力损失计算
在管道输送过程中，流体的 压力和体积会发生变化，通 过流体的p-v-t关系可以计算 出管道的压力损失，以便优
化管道设计和运行参数。
管道泄漏检测
利用流体的p-v-t关系，可以 实时监测管道内流体的状态 变化，从而及时发现管道泄 漏等异常情况。
化学反应过程中的体积变化问题
反应体积变化预测
反应器压力控制
第2章_流体的p-V-T(x)关系
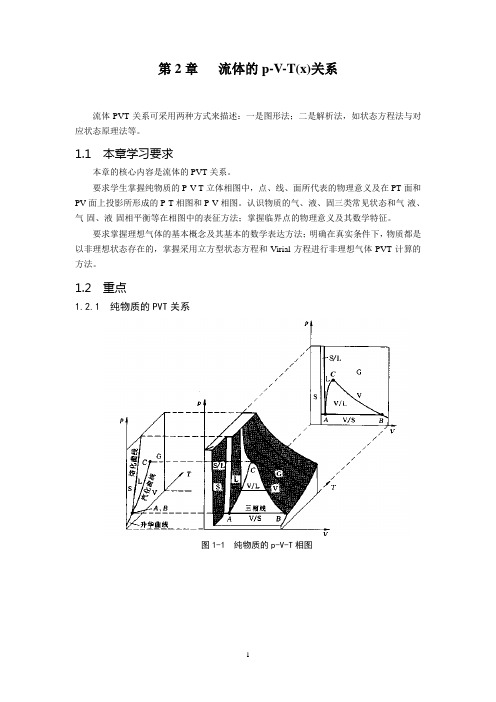
第2章流体的p-V-T(x)关系流体PVT关系可采用两种方式来描述：一是图形法；二是解析法，如状态方程法与对应状态原理法等。
1.1 本章学习要求本章的核心内容是流体的PVT关系。
要求学生掌握纯物质的P-V-T立体相图中，点、线、面所代表的物理意义及在PT面和PV面上投影所形成的P-T相图和P-V相图。
认识物质的气、液、固三类常见状态和气-液、气-固、液-固相平衡等在相图中的表征方法；掌握临界点的物理意义及其数学特征。
要求掌握理想气体的基本概念及其基本的数学表达方法；明确在真实条件下，物质都是以非理想状态存在的，掌握采用立方型状态方程和Virial方程进行非理想气体PVT计算的方法。
1.2 重点1.2.1 纯物质的PVT关系图1-1 纯物质的p-V-T相图图1-2 纯物质的p-T图图1-3 纯物质的p-V图临界点C在图上表现为拐点，数学上的可表述为：CT TPV=⎛⎫∂=⎪∂⎝⎭(1-1)C22T TPV=⎛⎫∂=⎪∂⎝⎭(1-2)1.2.2 状态方程(Equations of State，EOS)状态方程是物质P-V-T关系的解析式，可表达为函数关系：f(P,V,T)0=(1-3) 状态方程的重要价值在于：(1) 用状态方程可精确地代表相当广泛范围内的P-V-T数据，大大减小实验测定的工作量；(2) 用状态方程可计算不能直接从实验测定的其它热力学性质；(3) 用状态方程可进行相平衡计算，如计算饱和蒸气压、混合物气液相平衡、液-液平衡等，尤其是在计算高压气液平衡时的简捷、准确、方便，为其它方法不能与之相比的。
1.2.3 理想气体状态方程理想气体状态方程是流体状态方程中最简单的一种，理想气体的概念是一种假想的状态，实际上并不存在，它是极低压力或极高温度下各种真实气体的极限情况。
数学表达式为：P0(V)lim(PV)RT→→∞=或PV RT=(1-4)1.2.4 真实气体状态方程大体上分为三类：第一类是立方型状态方程，如Van der Waals、RK、SRK、PR、PT等；第二类是多项级数展开式的状态方程，如Virial、BWR、MH等；第三类是理论型状态方程。
第2章流体的pVT关系PPT课件
V2
TTc
0
12
p VTTc
VcRTcb2
2a Vc2 0
2p
V2
Hale Waihona Puke TTcV2cRTbc3
V6ca4 0
解得：
a
9 8
R TcVc
b Vc 3
13
将Van der Waals方程应用于临界点得
p cV R cT cbV a c2V c R T V c c/39 R T V c c V 2 c/88 3R V T cc
饱和线
➢ 饱和液体线
➢ 饱和蒸汽线
等温线：三种情况
T=Tc、T>Tc、T<Tc
临界点数学特征
p
V TTc
0
2 p
V2
TTc
70
第二节 流体的状态方程(EOS)
定义：描述流体p-V-T关系的函数表达式
f(p,V,T)0
重要价值： ⑴精确地表达相当广泛范围内的pVT数据； ⑵推算不能直接测量的其它热力学性质。 状态方程的分类：
a 1 R2Tc2.5 0.42748R2Tc2.5
9(3 21) pc
pc
b 3 21 RTc 0.08664RTc
3 pc
pc
Zc1/30.333
RK 方程的特点：
RK方程的计算准确度有较大的提高；
用以预测气相pVT计算，效果较好，但对液相效果较差。
改进方法：把a/T 0.5改为温度函数 a(T), 得SRK方程。
方程常数：
a(T )a c(T r,)0 .4 5 7 2 3 5R 2 p T cc2(T r,)
0.51F(1Tr0.5)
b0.077796 RTc pc
化工热力学02流体的pVT关系
• 应用范围：
(1)可用于气相、液湘的p-V-T 性质计算。
• (2) 计算烃类及其混合物效 果较好。
•应用注意事项：
•
• 同一物质的BWR 常数要取自同一文献，
不能用不同文献的常数 进行拼凑。
PPT文档演模板
化工热力学02流体的pVT关系
2.2.4.2 Martin-Hou(MH)方程
•(1) 通式：
• 超临界CO2最为常用。
PPT文档演模板
化工热力学02流体的pVT关系
•例 题：
•1. 判断并说明理由
•（1） 纯物质由蒸汽变为液体必须经过冷凝的相变化过 程。 •（2） 纯物质的三相点随所处压力或温度的不同而改变。 •（3） 指定温度下的纯物质，当压力低于该温度下的饱 和蒸汽压时，气体状态为过热蒸汽。 •（4） T温度下的过热蒸汽，压力P < PS(T) •（5） 纯物质的饱和液体的摩尔体积随着温度升高而增 大，饱和蒸汽的摩尔体积随着温度的升高而减小
(1) vdW 方程是后续立方型方程的基础
•其中 ：压力修正项, a表示气体分子间的相互作用，
•
单位为Pa.m6.mol-2
• b: 体积修正项：表示每摩尔实际气体分子因分子本
•
身占据体积而使分子自由活动空间减小的数值。
•
单位：m3.mol-1
•
• 不同物质具有不同的a,b值。
PPT文档演模板
化工热力学02流体的pVT关系
（教学重点） （3）用状态方程计算不能直接从实验测定的其它热力学性质； （4）用状态方程进行相平衡和化学反应平衡计算。
（教学难点）
PPT文档演模板
化工热力学02流体的pVT关系
2.2.1 理想气体状态方程
第2章_流体的pVT关系
14
2.2.1.3 Soave-Redlich-Kwong (SRK)方程 方程形式：
RT a(T ) p V b V (V b)
方程常数：
R 2Tc 2 a (T ) ac (Tr , ) 0.42748 (Tr , ) pc
(Tr )
0.5
2 2
7.6816 102 (Pa m3 mol-1 ) RTC 8.314 126.2 b 0.08664 0.08664 2.6784 105 (m3 mol-1 ) 28 8 pC 3.394 106
代入式(2-15)
RT a(T ) 8.314 273.15 p V b V (V b) 4.636 2.6784 105 7.6816 102 9.3355 107 (Pa) 4.636 (4.636 2.6784) 10 10
12
2.2.1.2 Redlich-Kwong (RK) 方程 方程形式：
RT a p 0.5 V b T V (V b)
重点对压力项进行改进； 方程常数用类似于Van der Waals方程的方法得到。
13
方程常数a, b及ZC ：
a
3
2 1 R Tc 3 pc
1 F (1 Tr )
0.5
RTc b 0.08664 8 pc
2
15
F 0.48 1.57 0.176
SRK方程的特点:
计算常数需要Tc , pc和，a是温度的函数；
在计算纯物质汽液平衡时较为有利，但预测液相体 积的精度不够； 为了改善计算液相体积的精度，Peng-Robinson提出 了PR方程。
2.2.1.3 Soave-Redlich-Kwong (SRK)方程 方程形式：
RT a(T ) p V b V (V b)
方程常数：
R 2Tc 2 a (T ) ac (Tr , ) 0.42748 (Tr , ) pc
(Tr )
0.5
2 2
7.6816 102 (Pa m3 mol-1 ) RTC 8.314 126.2 b 0.08664 0.08664 2.6784 105 (m3 mol-1 ) 28 8 pC 3.394 106
代入式(2-15)
RT a(T ) 8.314 273.15 p V b V (V b) 4.636 2.6784 105 7.6816 102 9.3355 107 (Pa) 4.636 (4.636 2.6784) 10 10
12
2.2.1.2 Redlich-Kwong (RK) 方程 方程形式：
RT a p 0.5 V b T V (V b)
重点对压力项进行改进； 方程常数用类似于Van der Waals方程的方法得到。
13
方程常数a, b及ZC ：
a
3
2 1 R Tc 3 pc
1 F (1 Tr )
0.5
RTc b 0.08664 8 pc
2
15
F 0.48 1.57 0.176
SRK方程的特点:
计算常数需要Tc , pc和，a是温度的函数；
在计算纯物质汽液平衡时较为有利，但预测液相体 积的精度不够； 为了改善计算液相体积的精度，Peng-Robinson提出 了PR方程。
天津大学化工热力学第2章流体pVT关系
a
12
要求：
形式简单 计算方便 适用于不同极性及分子形状的化合物 计算各种热力学性质时均有较高的精确度
分类： （1）理想气体状态方程；
（2）virial（维里）方程； （3）立方型状态方程； （4）多参数状态方程
a
13
理想气体状态方程
假设：
分子的大小如同几何点
分子间不存在相互作用力 极低的压力下真实气体非常接近理想气体
不同于气体，它的密度接近于液体，而传递性质 则接近于气体，可作为特殊的萃取溶剂和反应介 质。
超临界分离技术和反应技术成为研究热点
a
10
2.2 流体的状态方程
a
11
定义： 描述流体p –V -T关系的函数式为
fp,V,T0
称为状态方程（Equation of Satate，EOS） 它用来联系在平衡态下纯流体的压力、摩尔体积、温度之间 的关系。 作用： 状态方程具有非常重要的价值 （1）表示较广泛范围内p、V、T之间的函数关系； （2）可通过它计算不能直接从实验测得的其他热力学性质。
（2）一般适用于气体p V T 性质计算；
（3）可以较准确地用于非极性和弱极性化合物，误差在2％ 左右
（4）但对于强极性及含有氢键的化合物仍会产生较大的偏 差。误差达10～20％。
（5）很少用于液体p V T 性质计算；
（6）为了进一步提高RK方程的精度，扩大其使用范围，便 提出了更多的立方型状态方程。
nn1
意义：引入h后，使迭代过程简单，便于直接三次方程求解。但需要注意的是
该迭代方法不能用于饱和液相摩尔体积根的计算。
a
33
Z
(1)
Z(0)
h(0)
a
(2)
第2章 流体的PVT关系和状态方程
36
§2.2.1 理想气体状态方程
例: 将1kmol甲烷压缩储存于容积为0.125m3,温度 为323.16K的钢瓶内。问此时甲烷产生的压力多大? 其实验值为1.875x107Pa。 解: nRT 1000 8.314 323.16
V 0.125 （2.150 1.875 ） 107 误差 100% 14.67% 7 1.875 10 P 2.150 107 Pa
2
P V 2
T
0
在C点
超临界流体（T>Tc和P>Pc）
17
2.1.3 p-T图
临界等容线
液固平衡线
超临界流体区 液体区
（T>Tc和P>Pc）
临界点 固体区
汽液平衡线
气体区
三相点F=C-P+2=0
18
汽固平衡线
水的三相点：0.0098℃
p-T图的特征、相关概念
单相区 两相平衡线（饱和曲线）
0℃～ 50℃ )能保留产品的天然有效活性。 溶解能力 强。
惰性（不污染产品） 、价廉易得、选择性良好和产
物易从反应混合物中分离出来。
25
超临界萃取技术的工业应用
大规模超临界流体萃取的兴起于
用超临界CO2成功地从咖啡中提取咖啡因。 用超临界戊烷流体从石油中分离重油组分 。
现在用于提取油脂、香精、色素、药物、酶
TB
，℃
燃烧值，kJ/g
甲烷
乙烷 丙烷
-82.62
32.18 96.59
45.36
48.08 41.98
-161.45
-88.65 -42.15
55.6
§2.2.1 理想气体状态方程
例: 将1kmol甲烷压缩储存于容积为0.125m3,温度 为323.16K的钢瓶内。问此时甲烷产生的压力多大? 其实验值为1.875x107Pa。 解: nRT 1000 8.314 323.16
V 0.125 （2.150 1.875 ） 107 误差 100% 14.67% 7 1.875 10 P 2.150 107 Pa
2
P V 2
T
0
在C点
超临界流体（T>Tc和P>Pc）
17
2.1.3 p-T图
临界等容线
液固平衡线
超临界流体区 液体区
（T>Tc和P>Pc）
临界点 固体区
汽液平衡线
气体区
三相点F=C-P+2=0
18
汽固平衡线
水的三相点：0.0098℃
p-T图的特征、相关概念
单相区 两相平衡线（饱和曲线）
0℃～ 50℃ )能保留产品的天然有效活性。 溶解能力 强。
惰性（不污染产品） 、价廉易得、选择性良好和产
物易从反应混合物中分离出来。
25
超临界萃取技术的工业应用
大规模超临界流体萃取的兴起于
用超临界CO2成功地从咖啡中提取咖啡因。 用超临界戊烷流体从石油中分离重油组分 。
现在用于提取油脂、香精、色素、药物、酶
TB
，℃
燃烧值，kJ/g
甲烷
乙烷 丙烷
-82.62
32.18 96.59
45.36
48.08 41.98
-161.45
-88.65 -42.15
55.6
第二章__流体的P-V-T关系
简单对比态原理 使用情况 由简单对比态原理知，只有在各种气体的临界 压缩因子Zc相等的条件下，才能严格成立。而实际 上，大部分物质的临界压缩因子Zc在0.2～0.3范围内 变动，并不是一个常数。可见，范德华提出的简单 对比态原理只是一个近似的关系，只适用于球形非 极性的简单分子。拓宽对比态原理的应用范围和提 高计算精度的有效方法是在简单对比态原理（二参 数对比态原理）的关系式中引入第三参数。
s r r
Pitzer用在 T r = 0.7的流体与氩、氪、氙（简单球形
log p 1 . 00 ( T 0 . 7 )
因此，任何流体 值均可由该流体的临界温度、 临界压力值及Tr = 0.7时的饱和蒸气压来确定。
26
三参数对比态原理
以偏心因子作为第三参数的对比态原理
p r 的函数 ，可分别由相应的图或 Z (1) 都是 T r 、 式中：Z (0) 、
表查出具体的数值。
27
三参数对比态原理
以偏心因子作为第三参数的对比态原理
使用情况
Pitzer关系式对于非极性或弱极性的气体能够提
供可靠的结果，误差在3%以内，应用于极性气体时， 误差要增大到5％～10%，而对于缔合气体和量子气体
但pitzer发现简单流体氩氪氙的所有蒸气压数据落在了同一条直线上而且该直线通过07这一点如右图pitzer用在07的流体与氩氪氙简单球形分子的值之差来定义偏心因子因此任何流体的值均可由该流体的临界温度临界压力值及07时的饱和蒸气压来确定
2.1纯物质的p-V-T关系
固液
C
液
汽液
汽固
纯物质的p-V-T图
17
二、立方型状态方程
（5）立方型状态方程的通用形式
第2章_流体的p-V-T关系-合肥工业大学-化工热力学
2
2
RTc b 8 pc
虽然van der Waals 方程准确度不高，无 很大实用价值，但建立方程的理论和方法对以 后立方型方程的发展产生了重大影响。目前工 程上广泛采用的立方型方程基本上都是从van der Waals方程衍生出来的。
上一内容 下一内容 回主目录
2.2.2
24
其中有代表性的有：
上一内容 下一内容
液相 固相 气相
图2-2
回主目录
2.1
6
流体p-V-T关系，还可以用以T为参变量的p-V图表 示，见图2-3。图中高于临界温度的等温线T1、T2，曲线 平滑且不与相界线相交。
近于双曲线，即 pV=RT=常数。 （相当于理想气 体的情形）。 小于临界温度的 等温线T3 、T4有 三个不同部分组 成。 图2-3
2.1
10
随着温度变化，饱和液体和饱和气体的密度 迅速改变，但两者改变的总和变化甚微。 Cailleter和Mathias注
意到，当以饱和液体和
饱和蒸汽密度的算术平 均值对温度作图时，得 一近似的直线，如图2-4 所示。这结果称为直线 直径定律，常用于临界 密度的实验测定。
上一内容 下一内容
图2-4
(2-1)
(2-2)
图2-3
上一内容 下一内容 回主目录
2.1
9
式 (2-1) 和 式 （ 2-2 ） 提 供 了 经 典的临界点定义。 Martin 和 侯 虞 钧 在研究气体状态方 程时发现，在临界 点P对V的三阶和 四阶导数也是零或 是很小的数值。 图2-3
上一内容 下一内容 回主目录
26
上一内容
下一内容
回主目录
（2）Soave-Ridlich-Kwang方程（1972年）
化工热力学 第二章 流体的压力,体积,温度的关系：状态方程式
化工热力学
第二章 流体的PVT关系
PR方程可以表示成压缩因子Z的三次方表达式：
Z 3 1 BZ 2 A 2B 3B2 Z AB B2 B3 0
A ap 0.45724 Pr T
R2T 2
T2 r
B bP 0.07780 Pr
RT
Tr
化工热力学
第二章 流体的PVT关系
三.多常数状态方程
a 27R2TC 2 64PC
PC
RTC VC b
a VC 2
R 3b b
8a 27bR
a 9b2
a 27b2
b RTC 8PC
化工热力学
第二章 流体的PVT关系
2、RK方程
P
a
1 V b RT 或
V V bT 2
P
RT V b
T
1
2V
a
V
b
a、b： 正值常数，与流体的特性有关，
将有关的已知值代入式（2—13）和式（2—14）可求出饱和 液体的摩尔体积，
化工热力学
第二章 流体的PVT关系
Vi1
Vi3
2.01294 Vi2 2.79573 0.530405
10 2
将迭代初值 Vi V0 b 0.044891 m3 kmol1 代入上式，
反复迭代至收敛，其结果为
当有PVT实验数据，可采用最小二乘法求a、b值，步骤：
1）、将实验的 Ti 、Vi 值代入方程（2—10）求出相应的 Pi ，
所得的 Pi 为a、b的函数。
2）、利用最小二乘法求a、b
n
2
Pi 计算 Pi 实测 Fa、b
i 1
令
F
0
a b
第2章流体的p-V-T关系和状态方程.docx
第2章流体的p-V-T关系和状态方程重点难点：纯物质的p-V-T关系及应用，状态方程及状态方程的选用。
1）纯物质的p-V-T关系及应用工程上所用的水蒸气多是由锅炉、蒸汽发生器等在压力近似不变的情况下产生的，可视为定压加热过程。
水在定压下加热变为水蒸气的过程可以概扌舌为：三个阶段，五种状态。
①水的定压预热阶段：水在定压下从未饱和状态加热到饱和状态，即为预热阶段，相当于锅炉中省煤器内水的定压预热过程。
②饱和水定压汽化阶段：对达到饱和温度的水继续加热，饱和水开始汽化产生蒸汽而形成饱和液体与饱和蒸汽的混合物，即湿饱和蒸汽（简称湿蒸汽），湿蒸汽中含饱和蒸汽的质量分数称为干度庆这时饱和压力不变，饱和温度也不变。
随着加热过程的继续进行，水逐渐减少，汽逐渐增多，直至最后一滴水变为蒸汽，这时的蒸汽称为干饱和蒸汽或饱和蒸汽（即不含饱和水的饱和蒸汽）。
把饱和水定压加热为干饱和蒸汽的过程称为汽化阶段，相当于锅炉汽锅内的吸热过程。
③干饱和蒸汽定压过热阶段：继续定压加热，蒸汽温度升高，比容增大，这相当于蒸汽在锅炉的过热器中定压加热过程。
由于这时蒸汽的温度已超过相应压力下的饱和温度，故称为过热蒸汽。
过热蒸汽温度与饱和温度之差，称为过热度。
上述三个过程包含了未饱和水到过热蒸汽的定压加热全过程。
过程中水及水蒸气经历了五种状态，即未饱和水（过冷水）1、饱和水2、湿饱和蒸汽3、干饱和蒸汽4和过热蒸汽5。
可得水在定压下受热过程的厂7图。
相图，给出了气、液、固三者Z间的平衡关系，能表达"、卩变化所引起的相态变化。
图中三条曲线分别表示两相共存的p和T条件，也是单相区的边界条件。
九三条线相交于三相点2,表示三相共存并处于平衡状态。
飞按相律，三相点处自由度等于零，三条曲线上自由度为出1，每一单相区自由度为2。
汽化曲线终止于临界点C,临界点C是纯物质汽、液两相可以共存的最高温度或最高压力点，是流体p-V-T 曲面上一个重要的点，该点的温度、压力和摩尔体积分别称为临界温度几、图2・4纯物质的/>-7•图临界压力仇和临界体积人。
第二章 流体的P-V-T关系
（ 1） VanDer Waals方程
常数a , b值的确定：在临界点处，函数的一阶导数和二 阶导数都为零,
P 0 V TC 2P 0 V 2 TC
可得
27R Tc a 64Pc RTc b 8Pc
2
2
2.2.2 立方型状态方程
1 A h Z ( ) 1 h B 1 h b BP h V Z
其中：B=b/RT ， A/B=a/bRT1.5 即Z=f1(h), h=f2(Z)，通过试差即可计算出V
2.2.2 立方型状态方程
（ 2） R-K方程 Redlich-Kwon R-K方程的解法： ① 已知T，V，求P， 显压型，直接计算，很方便。 （P9，例2-1），在计算时，一定要注意单位， 1atm=0.101325×106Pa=0.101325MPa ② 已知P，T，求V，用上式试差求解，工程上最常 用的情况，P，T易测 ③ 已知P，V，求T，如求操作温度，试差求解
2.2.2 立方型状态方程
（ 2） R-K方程 Redlich-Kwon
R-K方程的应用范围 ⑴适用于气体PVT性质的计算； ⑵非极性、弱极性物质误差在2%左 右，对于强极性物质误差在1020%。
2.2.2 立方型状态方程
（ （ （ （ 1） 2） 3） 4） Van Der Waals方程 R-K方程Redlich-Kwong S-R-K方程 Peng-Robinson方程
2.2.3 多常数状态方程
（1） 维里方程 Virial Equation
（1）方程的提出 （2）两项维里方程 （3）应用范围与条件
2.2.3 多常数状态方程
（1） 维里方程
（1）方程的提出
Virial
常数a , b值的确定：在临界点处，函数的一阶导数和二 阶导数都为零,
P 0 V TC 2P 0 V 2 TC
可得
27R Tc a 64Pc RTc b 8Pc
2
2
2.2.2 立方型状态方程
1 A h Z ( ) 1 h B 1 h b BP h V Z
其中：B=b/RT ， A/B=a/bRT1.5 即Z=f1(h), h=f2(Z)，通过试差即可计算出V
2.2.2 立方型状态方程
（ 2） R-K方程 Redlich-Kwon R-K方程的解法： ① 已知T，V，求P， 显压型，直接计算，很方便。 （P9，例2-1），在计算时，一定要注意单位， 1atm=0.101325×106Pa=0.101325MPa ② 已知P，T，求V，用上式试差求解，工程上最常 用的情况，P，T易测 ③ 已知P，V，求T，如求操作温度，试差求解
2.2.2 立方型状态方程
（ 2） R-K方程 Redlich-Kwon
R-K方程的应用范围 ⑴适用于气体PVT性质的计算； ⑵非极性、弱极性物质误差在2%左 右，对于强极性物质误差在1020%。
2.2.2 立方型状态方程
（ （ （ （ 1） 2） 3） 4） Van Der Waals方程 R-K方程Redlich-Kwong S-R-K方程 Peng-Robinson方程
2.2.3 多常数状态方程
（1） 维里方程 Virial Equation
（1）方程的提出 （2）两项维里方程 （3）应用范围与条件
2.2.3 多常数状态方程
（1） 维里方程
（1）方程的提出
Virial
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
能双分子效应的加和。
Bm = ∑∑ y i y j Bij
i j
2.4.2 状态方程法
1）混合物的维里方程 ①混合物的维里系数与组成间的关系
对于二元混合物，混合物的第二维里系数为
Bm = y1 y1 B11 + y1 y 2 B12 + y 2 y1 B21 + y 2 y 2 B22
B11 , B22 -纯组分维里系数，查文献或手册； B12 , B21 -交叉维里系数，要计算
2.4.2 状态方程法
1）混合物的维里方程
①混合物的维里系数与组成间的关系 由于交叉维里系数是考虑分子1与分 子2之间的相互作用力的，从文献上查不 到，既然查不到，就要考虑是否可以通 过式子计算得到。美国Prausnitz提出了 交叉维里系数的计算法
2.4.2 状态方程法
1）混合物的维里方程 ②交叉维里系数的计算 对于纯组分气体 对于混合气体
zi Pi = y i P ⋅ zm
2.4
真实气体混合物的PVT关系
2.4.1 普遍化关系式法
2）道尔顿定律+z图
不管是求PVT性质中的那一个参数，纯组 分 i 的压力 Pi 都是未知的，因而必须采 取特殊的数学手段进行求取。
0 根据混合物温度假设Pi , T 查或计算 → z i ∑ → z m →V zm = yi zi V= z m nRT P zi ni RT V
2.4.2 状态方程法
1）混合物的维里方程
2）混合物的R-K方程
2.4.2 状态方程法
1）混合物的维里方程
①混合物的维里系数与组成间的关系
对单组分气体
BP z = 1+ 对气体混合物 RT
Bm P zm = 1 + RT
2.4.2 状态方程法
1）混合物的维里方程 ①混合物的维里系数与组成间的关系 B m 是混合物的第二维里系数，它表示所有可
RTc 0 B= B + ωB ' Pc
RTc ij Pcij
(
)
)
Bij =
(B
0
ij
+ ω ij B 'ij
2.4.2 状态方程法
1）混合物的维里方程
②交叉维里系数的计算 由Prausnitz提出的经验式计算， P21 （2-53）-（2-57）五个式子计算
2.4.2 状态方程法
1）混合物的维里方程 ③混合物的两项维里方程
2.4.1 普遍化关系式法
3）阿玛格定律+z图
⑵注意点：
① z i是由查 Tri , Pri两参数压缩因子图得到
2.4
真实气体混合物的PVT关系
2.4.1 普遍化关系式法
3）阿玛格定律+z图 与D-定律的区别主要表现在对
D-定律：z i 是由 Pi、T混 决定，一般要试差 或迭代，可用于低于5Mpa一下的体系 A-定律：z i 是由 P混、T混 决定，不需要试差或 迭代，可用于高压体系，30Mpa以上
道尔顿定律关键在于组分 i 的压缩因子 z i的计算，而组分 i 的压缩因子的计算 关键又在于 Pi 的计算，应用道尔顿定律 时要注意以下几点：
2.4
真实气体混合物的PVT关系
2.4.1 普遍化关系式法
2）道尔顿定律+z图
① z i 是由Tr，Pr查两参数压缩因子图得来的 ② Pi 是纯组分的分压，不能称为分压； 对理想气体混合物，分压力为 Pi = yi P 对真实气体混合物，纯组分的压力为
2.4.2 状态方程法
2）混合物的R-K方程 ①R-K方程中参数a，b的计算
当R-K方程用于混合物时，也要把R-K方程中的 参数a，b用混合物a，b来代替
b = ∑ y i bi
a = ∑∑ y i y j a ij
i j
bi = 0.0867 RTci Pci
aij = 0.4287 R 2Tcij
2.4.2 状态方程法
1）混合物的维里方程
2）混合物的R-K方程
2.4.2 状态方程法
2）混合物的R-K方程 一般形式 RT
变形
a P= − 0 .5 V − b T V (V + b )
1 a z= − 1 + h bRT 1.5 bP = h zRT
h 1+ h
2.4.1 普遍化关系式法
1）虚拟临界常数法 2）道尔顿定律+z图 3）阿玛格定律+z图 4）三参数普遍化关系式法 5）应用举例
2.4
真实气体混合物的PVT关系
2.4.1 普遍化关系式法
1）虚拟临界常数法
该法是由W.B.Kay提出的，其思想是把混合 物人为地看作是一种纯物质，由于世界上的每 一种纯物质，都具有相应的临界点，那么把混 合物看作一种纯物质，就要找出它的临界常数， 这些常数是通过一些混合规则将混合物中各组 分的临界参数联系在一起，由于它不是客观上 真实存在的，所以称其为虚拟临界常数
2.4
真实气体混合物的PVT关系
2.4.1 普遍化关系式法
3）阿玛格定律+z图 阿玛格定律与压缩因子相结合，也可以计算真 实气体混合物的PVT性质 ⑴要点：
V = ∑ Vi z i ni RT Vi = P z m = ∑ yi z i
2.4
真实气体混合物的PVT关系
2.4
真实气体混合物的PVT关系
2.4.1 普遍化关系式法
5）应用举例
（P21-23，例2-6，2-7自看） D+z图法、A+z图法、虚拟临界常数 法和普压法，关键在于求出混合物的压 缩因子 Z m
2.4
真实气体混合物的PVT关系
2.4.1 普遍化关系式法 2.4.2 状态方程法
2.4
真实气体混合物的PVT关系
2.4.2 状态方程法
2）混合物的R-K方程
③应用举例 (P33,例2-10 ）
2.4
真实气体混合物的PVT关系
2.4.2 状态方程法 1）混合物的维里方程
2）混合物的R-K方程
2.4
真实气体混合物的PVT关系
2.4.1 普遍化关系式法
1）虚拟临界常数法
Kay规则： T = y Tc + y Tc + LL = y Tc ∑ i i cm 1 1 2 2
Pcm = y1 Pc1 + y2 Pc2 + LL = ∑ yi Pci
虚拟对比参数
T Trm = Tcm
P Prm = Pcm
→ Pi
Pi =
(1)
→ Pi
(1)
− Pi = ∆ → 若∆小于所给精度, 则终止迭代; 否则继续进行.
0
2.4
真实气体混合物的PVT关系
2.4.1 普遍化关系式法
1）虚拟临界常数法 2）道尔顿定律+z图 3）阿玛格定律+z图 4）三参数普遍化关系式法 5）应用举例
2.4
真实气体混合物的PVT关系
2.4.1 普遍化关系式法 2.4.2 状态方程法
2.4
真实气体混合物的PVT关系
2.4.1 普遍化关系式法
1）虚拟临界常数法 2）道尔顿定律+z图 3）阿玛格定律+z图 4）三参数普遍化关系式法 5）应用举例
2.4
真实气体混合物的PVT关系
2 .5
Pcij
2.4.2 状态方程法
2）混合物的R-K方程 ②一般解题步骤
查Tci P Pci ( 2 −55 ) → (2−58 )−(2−59 ) a R − K方程 → →V Vci (2−53)−(2−57 ) ( 2 −58 )( 2 −60 ) → Tcij , Pcij → aij b T zci ωi
第二章 流体的P-V-T关系
2.1 2.2 2.3 2.4 2.5
纯物质的P-V-T性质 气体的状态方程式 对比态原理及其应用 真实气体混合物的PVT关系 液体的PVT关系
2.4
真实气体混合物的PVT关系
真实气体混合物的非理想性，可看成 是由两方面的原因造成的: ①由纯气体的非理想性 ②由于混合作用所引起的非理想性。
z i 的求取不同
2.4
真实气体混合物的PVT关系
2.4.1 普遍化关系式法
1）虚拟临界常数法 2）道尔顿定律+z图 3）阿玛格定律+z图 4）三参数普遍化关系式法 5）应用举例
2.4
真实气体混合物的PVT关系
2.4.1 普遍化关系式法
4）三参数普遍化关系式法
Pitzer提出的三参数普遍化关系式
z = f (Tr , Pr, ω )
普维法---用于压力较低情况下的 普压法---用于较高压力下的
具体一个状态用普变化关系式法的那一种，要根 据图2-9判断
2.4
真实气体混合物的PVT关系
2.4.1 普遍化关系式法
4）三参数普遍化关系式法
2.4
真实气体混合物的PVT关系
2.4.1 普遍化关系式法
2.4
真实气体混合物的PVT关系
真实气体混合物PVT性质的计算方法， 与纯组分PVT性质的计算方法是相同的， 也有两种： ①状态方程法 ②普遍化关系式法 但由于混合物组分数的增加，使它的 计算又具有特殊性。
Bm = ∑∑ y i y j Bij
i j
2.4.2 状态方程法
1）混合物的维里方程 ①混合物的维里系数与组成间的关系
对于二元混合物，混合物的第二维里系数为
Bm = y1 y1 B11 + y1 y 2 B12 + y 2 y1 B21 + y 2 y 2 B22
B11 , B22 -纯组分维里系数，查文献或手册； B12 , B21 -交叉维里系数，要计算
2.4.2 状态方程法
1）混合物的维里方程
①混合物的维里系数与组成间的关系 由于交叉维里系数是考虑分子1与分 子2之间的相互作用力的，从文献上查不 到，既然查不到，就要考虑是否可以通 过式子计算得到。美国Prausnitz提出了 交叉维里系数的计算法
2.4.2 状态方程法
1）混合物的维里方程 ②交叉维里系数的计算 对于纯组分气体 对于混合气体
zi Pi = y i P ⋅ zm
2.4
真实气体混合物的PVT关系
2.4.1 普遍化关系式法
2）道尔顿定律+z图
不管是求PVT性质中的那一个参数，纯组 分 i 的压力 Pi 都是未知的，因而必须采 取特殊的数学手段进行求取。
0 根据混合物温度假设Pi , T 查或计算 → z i ∑ → z m →V zm = yi zi V= z m nRT P zi ni RT V
2.4.2 状态方程法
1）混合物的维里方程
2）混合物的R-K方程
2.4.2 状态方程法
1）混合物的维里方程
①混合物的维里系数与组成间的关系
对单组分气体
BP z = 1+ 对气体混合物 RT
Bm P zm = 1 + RT
2.4.2 状态方程法
1）混合物的维里方程 ①混合物的维里系数与组成间的关系 B m 是混合物的第二维里系数，它表示所有可
RTc 0 B= B + ωB ' Pc
RTc ij Pcij
(
)
)
Bij =
(B
0
ij
+ ω ij B 'ij
2.4.2 状态方程法
1）混合物的维里方程
②交叉维里系数的计算 由Prausnitz提出的经验式计算， P21 （2-53）-（2-57）五个式子计算
2.4.2 状态方程法
1）混合物的维里方程 ③混合物的两项维里方程
2.4.1 普遍化关系式法
3）阿玛格定律+z图
⑵注意点：
① z i是由查 Tri , Pri两参数压缩因子图得到
2.4
真实气体混合物的PVT关系
2.4.1 普遍化关系式法
3）阿玛格定律+z图 与D-定律的区别主要表现在对
D-定律：z i 是由 Pi、T混 决定，一般要试差 或迭代，可用于低于5Mpa一下的体系 A-定律：z i 是由 P混、T混 决定，不需要试差或 迭代，可用于高压体系，30Mpa以上
道尔顿定律关键在于组分 i 的压缩因子 z i的计算，而组分 i 的压缩因子的计算 关键又在于 Pi 的计算，应用道尔顿定律 时要注意以下几点：
2.4
真实气体混合物的PVT关系
2.4.1 普遍化关系式法
2）道尔顿定律+z图
① z i 是由Tr，Pr查两参数压缩因子图得来的 ② Pi 是纯组分的分压，不能称为分压； 对理想气体混合物，分压力为 Pi = yi P 对真实气体混合物，纯组分的压力为
2.4.2 状态方程法
2）混合物的R-K方程 ①R-K方程中参数a，b的计算
当R-K方程用于混合物时，也要把R-K方程中的 参数a，b用混合物a，b来代替
b = ∑ y i bi
a = ∑∑ y i y j a ij
i j
bi = 0.0867 RTci Pci
aij = 0.4287 R 2Tcij
2.4.2 状态方程法
1）混合物的维里方程
2）混合物的R-K方程
2.4.2 状态方程法
2）混合物的R-K方程 一般形式 RT
变形
a P= − 0 .5 V − b T V (V + b )
1 a z= − 1 + h bRT 1.5 bP = h zRT
h 1+ h
2.4.1 普遍化关系式法
1）虚拟临界常数法 2）道尔顿定律+z图 3）阿玛格定律+z图 4）三参数普遍化关系式法 5）应用举例
2.4
真实气体混合物的PVT关系
2.4.1 普遍化关系式法
1）虚拟临界常数法
该法是由W.B.Kay提出的，其思想是把混合 物人为地看作是一种纯物质，由于世界上的每 一种纯物质，都具有相应的临界点，那么把混 合物看作一种纯物质，就要找出它的临界常数， 这些常数是通过一些混合规则将混合物中各组 分的临界参数联系在一起，由于它不是客观上 真实存在的，所以称其为虚拟临界常数
2.4
真实气体混合物的PVT关系
2.4.1 普遍化关系式法
3）阿玛格定律+z图 阿玛格定律与压缩因子相结合，也可以计算真 实气体混合物的PVT性质 ⑴要点：
V = ∑ Vi z i ni RT Vi = P z m = ∑ yi z i
2.4
真实气体混合物的PVT关系
2.4
真实气体混合物的PVT关系
2.4.1 普遍化关系式法
5）应用举例
（P21-23，例2-6，2-7自看） D+z图法、A+z图法、虚拟临界常数 法和普压法，关键在于求出混合物的压 缩因子 Z m
2.4
真实气体混合物的PVT关系
2.4.1 普遍化关系式法 2.4.2 状态方程法
2.4
真实气体混合物的PVT关系
2.4.2 状态方程法
2）混合物的R-K方程
③应用举例 (P33,例2-10 ）
2.4
真实气体混合物的PVT关系
2.4.2 状态方程法 1）混合物的维里方程
2）混合物的R-K方程
2.4
真实气体混合物的PVT关系
2.4.1 普遍化关系式法
1）虚拟临界常数法
Kay规则： T = y Tc + y Tc + LL = y Tc ∑ i i cm 1 1 2 2
Pcm = y1 Pc1 + y2 Pc2 + LL = ∑ yi Pci
虚拟对比参数
T Trm = Tcm
P Prm = Pcm
→ Pi
Pi =
(1)
→ Pi
(1)
− Pi = ∆ → 若∆小于所给精度, 则终止迭代; 否则继续进行.
0
2.4
真实气体混合物的PVT关系
2.4.1 普遍化关系式法
1）虚拟临界常数法 2）道尔顿定律+z图 3）阿玛格定律+z图 4）三参数普遍化关系式法 5）应用举例
2.4
真实气体混合物的PVT关系
2.4.1 普遍化关系式法 2.4.2 状态方程法
2.4
真实气体混合物的PVT关系
2.4.1 普遍化关系式法
1）虚拟临界常数法 2）道尔顿定律+z图 3）阿玛格定律+z图 4）三参数普遍化关系式法 5）应用举例
2.4
真实气体混合物的PVT关系
2 .5
Pcij
2.4.2 状态方程法
2）混合物的R-K方程 ②一般解题步骤
查Tci P Pci ( 2 −55 ) → (2−58 )−(2−59 ) a R − K方程 → →V Vci (2−53)−(2−57 ) ( 2 −58 )( 2 −60 ) → Tcij , Pcij → aij b T zci ωi
第二章 流体的P-V-T关系
2.1 2.2 2.3 2.4 2.5
纯物质的P-V-T性质 气体的状态方程式 对比态原理及其应用 真实气体混合物的PVT关系 液体的PVT关系
2.4
真实气体混合物的PVT关系
真实气体混合物的非理想性，可看成 是由两方面的原因造成的: ①由纯气体的非理想性 ②由于混合作用所引起的非理想性。
z i 的求取不同
2.4
真实气体混合物的PVT关系
2.4.1 普遍化关系式法
1）虚拟临界常数法 2）道尔顿定律+z图 3）阿玛格定律+z图 4）三参数普遍化关系式法 5）应用举例
2.4
真实气体混合物的PVT关系
2.4.1 普遍化关系式法
4）三参数普遍化关系式法
Pitzer提出的三参数普遍化关系式
z = f (Tr , Pr, ω )
普维法---用于压力较低情况下的 普压法---用于较高压力下的
具体一个状态用普变化关系式法的那一种，要根 据图2-9判断
2.4
真实气体混合物的PVT关系
2.4.1 普遍化关系式法
4）三参数普遍化关系式法
2.4
真实气体混合物的PVT关系
2.4.1 普遍化关系式法
2.4
真实气体混合物的PVT关系
真实气体混合物PVT性质的计算方法， 与纯组分PVT性质的计算方法是相同的， 也有两种： ①状态方程法 ②普遍化关系式法 但由于混合物组分数的增加，使它的 计算又具有特殊性。