自动控制原理-夏超英-第2章+习题解答
自动控制原理课后习题答案

第1章控制系统概述【课后自测】1-1 试列举几个日常生活中的开环控制和闭环控制系统,说明它们的工作原理并比较开环控制和闭环控制的优缺点。
解:开环控制——半自动、全自动洗衣机的洗衣过程。
工作原理:被控制量为衣服的干净度。
洗衣人先观察衣服的脏污程度,根据自己的经验,设定洗涤、漂洗时间,洗衣机按照设定程序完成洗涤漂洗任务。
系统输出量(即衣服的干净度)的信息没有通过任何装置反馈到输入端,对系统的控制不起作用,因此为开环控制。
闭环控制——卫生间蓄水箱的蓄水量控制系统和空调、冰箱的温度控制系统。
工作原理:以卫生间蓄水箱蓄水量控制为例,系统的被控制量(输出量)为蓄水箱水位(反应蓄水量)。
水位由浮子测量,并通过杠杆作用于供水阀门(即反馈至输入端),控制供水量,形成闭环控制。
当水位达到蓄水量上限高度时,阀门全关(按要求事先设计好杠杆比例),系统处于平衡状态。
一旦用水,水位降低,浮子随之下沉,通过杠杆打开供水阀门,下沉越深,阀门开度越大,供水量越大,直到水位升至蓄水量上限高度,阀门全关,系统再次处于平衡状态。
开环控制和闭环控制的优缺点如下表1-2 自动控制系统通常有哪些环节组成各个环节分别的作用是什么解:自动控制系统包括被控对象、给定元件、检测反馈元件、比较元件、放大元件和执行元件。
各个基本单元的功能如下:(1)被控对象—又称受控对象或对象,指在控制过程中受到操纵控制的机器设备或过程。
(2)给定元件—可以设置系统控制指令的装置,可用于给出与期望输出量相对应的系统输入量。
(3)检测反馈元件—测量被控量的实际值并将其转换为与输入信号同类的物理量,再反馈到系统输入端作比较,一般为各类传感器。
(4)比较元件—把测量元件检测的被控量实际值与给定元件给出的给定值进行比较,分析计算并产生反应两者差值的偏差信号。
常用的比较元件有差动放大器、机械差动装置和电桥等。
(5)放大元件—当比较元件产生的偏差信号比较微弱不足以驱动执行元件动作时,可通过放大元件将微弱信号作线性放大。
自动控制原理课后习题答案

• 20世纪40年代,Evans提出并完善了根轨迹法。
• 20世纪50年代末,最优控制系统设计。
• 20世纪50年代末,基于时域分析的现代控制理 论。
• 60年代~80年代:最优控制、随机系统的最优控 制、复杂系统的自适应控制和学习控制得到了研 究。
5. 干扰量(Disturbance):引起被控量偏离预定运 行规律的量。除给定值之外,凡能引起被控量变 化的因素,都是干扰。干扰又称扰动
6.反馈(Feedback):将系统输出量引回输入端,并 与参考输入进行比较的过程。
7.前向通路 (Forward Channel):从给定量到被控 量的通道。
缺点: 闭环控制系统的参数如果匹配得不好,会造成被控量的 较大摆动,甚至系统无法正常工作。
例: 飞机自动驾驶控制
被控对象: 飞机
被控量: 飞机的俯仰角 θ
控制任务:系统在任何扰动作用下,保持飞机俯仰角不变。
仰俯角控制系统方块图
IV 复合控制
开环控制和闭环控制相结合的一种控制。实质上,它是在 闭环控制回路的基础上,附加了一个输入信号或扰动作用 的顺馈通路,来提高系统的控制精度。
an
d
n n
c(t
)
dt n
+
an-1
d n-1n-1c(t ) dt n-1
+"+
a1
dc(t) dt
+
a0c(t )
=
bm
d m m r (t ) dt m
+ bm-1
d m-1m-1r (t ) dt m-1
+" + b1
自动控制原理课后习题答案

第1章控制系统概述【课后自测】1-1 试列举几个日常生活中的开环控制和闭环控制系统,说明它们的工作原理并比较开环控制和闭环控制的优缺点。
解:开环控制——半自动、全自动洗衣机的洗衣过程。
工作原理:被控制量为衣服的干净度。
洗衣人先观察衣服的脏污程度,根据自己的经验,设定洗涤、漂洗时间,洗衣机按照设定程序完成洗涤漂洗任务。
系统输出量(即衣服的干净度)的信息没有通过任何装置反馈到输入端,对系统的控制不起作用,因此为开环控制。
闭环控制——卫生间蓄水箱的蓄水量控制系统和空调、冰箱的温度控制系统。
工作原理:以卫生间蓄水箱蓄水量控制为例,系统的被控制量(输出量)为蓄水箱水位(反应蓄水量)。
水位由浮子测量,并通过杠杆作用于供水阀门(即反馈至输入端),控制供水量,形成闭环控制。
当水位达到蓄水量上限高度时,阀门全关(按要求事先设计好杠杆比例),系统处于平衡状态。
一旦用水,水位降低,浮子随之下沉,通过杠杆打开供水阀门,下沉越深,阀门开度越大,供水量越大,直到水位升至蓄水量上限高度,阀门全关,系统再次处于平衡状态。
开环控制和闭环控制的优缺点如下表1-2 自动控制系统通常有哪些环节组成?各个环节分别的作用是什么?解:自动控制系统包括被控对象、给定元件、检测反馈元件、比较元件、放大元件和执行元件。
各个基本单元的功能如下:(1)被控对象—又称受控对象或对象,指在控制过程中受到操纵控制的机器设备或过程。
(2)给定元件—可以设置系统控制指令的装置,可用于给出与期望输出量相对应的系统输入量。
(3)检测反馈元件—测量被控量的实际值并将其转换为与输入信号同类的物理量,再反馈到系统输入端作比较,一般为各类传感器。
(4)比较元件—把测量元件检测的被控量实际值与给定元件给出的给定值进行比较,分析计算并产生反应两者差值的偏差信号。
常用的比较元件有差动放大器、机械差动装置和电桥等。
(5)放大元件—当比较元件产生的偏差信号比较微弱不足以驱动执行元件动作时,可通过放大元件将微弱信号作线性放大。
夏超英自动控制原理12345章答案

自动控制原理习题详解(上册夏超英主编科学出版社)第一章习题解答1-1什么是开环控制系统?什么是闭环控制系统?比较开环控制系统和闭环控制系统的不同,说明各自的优缺点。
答:在开环控制系统中,信号从控制器到执行机构再到被控对象单方向传递,输出量不对控制作用产生影响。
开环控制系统结构简单,成本低,但无法克服被控对象变化和扰动对输出的影响。
在闭环控制系统中,被控对象的输出反方向被引到控制系统的输入端,信号沿前向通路和反馈通路闭路传输,控制量不仅与参考输入有关,还与输出有关,即根据参考输入和系统输出之间的偏差进行控制。
闭环控制系统需要对输出量进行测量,存在稳定性设计问题,较开环控制系统复杂,但可以有效地克服被控对象变化和扰动对输出的影响。
1-2日常生活中反馈无处不在。
人的眼、耳、鼻和各种感觉、触觉器官都是起反馈作用的器官。
试以驾车行驶和伸手取物过程为例,说明人的眼、脑在其中所起的反馈和控制作用。
答:在驾车行驶和伸手取物过程的过程中,人眼和人脑的作用分别如同控制系统中的测量反馈装置和控制器。
在车辆在行驶过程中,司机需要观察道路和行人情况的变化,经大脑处理后,不断对驾驶动作进行调整,才能安全地到达目的地。
同样,人在取物的过程中,需要根据观察到的人手和所取物体间相对位置的变化,调整手的动作姿势,最终拿到物体。
可以想象蒙上双眼取物的困难程度,即使物体的方位已知。
1-3 水箱水位控制系统的原理图如图1-12所示,图中浮子杠杆机构的设计使得水位达到设定高度时,电位器中间抽头的电压输出为零。
描述图1-12所示水位调节系统的工作原理,指出系统中的被控对象、输出量、执行机构、测量装置、给定装置等。
出水进水阀门进水2Q图1-12 水箱水位控制系统原理图答:当实际水位和设定水位不相等时,电位器滑动端的电压不为零,假设实际水位比设定水位低,则电位器滑动端的电压大于零,误差信号大于零(0e >),经功率放大器放大后驱动电动机M 旋转,使进水阀门开度加大,当进水量大于出水量时(12Q Q >),水位开始上升,误差信号逐渐减小,直至实际水位与设定水位相等时,误差信号等于零,电机停止转动,此时,因为阀门开度仍较大,进水量大于出水量,水位会继续上升,导致实际水位比设定水位高,误差信号小于零,使电机反方向旋转,减小进水阀开度。
自动控制原理第二章习题答案详解
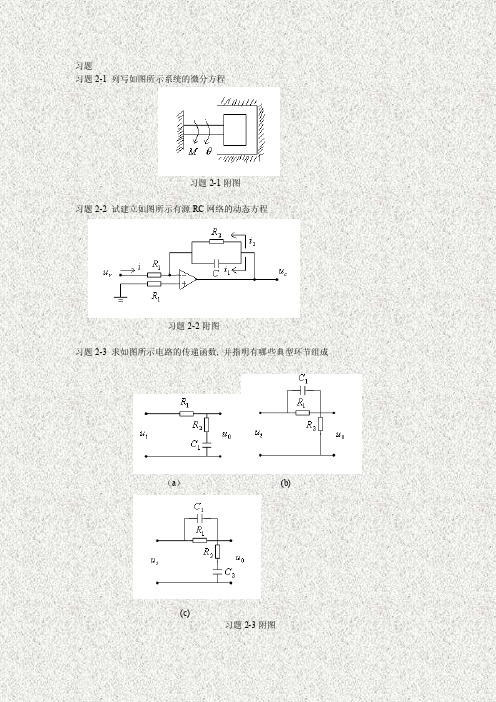
习题习题2-1 列写如图所示系统的微分方程习题2-1附图习题2-2 试建立如图所示有源RC网络的动态方程习题2-2附图习题2-3 求如图所示电路的传递函数, 并指明有哪些典型环节组成(a)(b)(c)习题2-3附图习题2-4 简化如图所示方块图, 并求出系统传递函数习题2-4附图习题2-5 绘制如下方块图的等效信号流图, 并求传递函数图(a)图(b)习题2-5附图习题2-6 系统微分方程组如下, 试建立对应信号流图, 并求传递函数。
),(d )(d )(),(d )(d ),()()()(),()(),(d )(d )(),()()(54435553422311121t y tt y T t x k t x k tt x t y k t x t x t x t x k t x t x k tt x t x t y t r t x +==--==+=-=τ习题2-7 利用梅逊公式直接求传递函数。
习题2-7附图习题2-8 求如图所示闭环传递函数, 并求(b)中)(s H x 的表达式, 使其与(a)等效。
图(a )图(b)习题2-8附图习题2-9 求如下各图的传递函数(a)(b)(c)习题2-9附图习题2-10 已知某些系统信号流图如图所示, 求对应方块图(a )(b)(c)(d)习题2-10附图习题答案习题2-1答案:解:设外加转矩M 为输入量,转角θ为输出量,转动惯量J 代表惯性负载,根据牛顿定律可得:θθθ1122d d d d k t f M tJ --=式中,1,1,k f 分别为粘性阻尼系数和扭转弹性系数,整理得:M k t f tJ =++θθθ1122d d d d习题2-2答案:解: 设r u 为输入量,c u 为输出量,,,,21i i i 为中间变量,根据运算放大器原理可得:1221d d R u i R u i t u c i r c c ===消去中间变量可得: r c c u R Ru t u C R 122d d -=+ 习题2-3答案: 解: (a)11111111221212211121121120++=+++=+++=+++=Ts Ts s R R R C R s C R R sC R sC R sC sC R R sC R u u i β其中:221121,R R R C R T +==β, 一阶微分环节,惯性环节.(b)21121212111221122011//1R R s C R R R s C R R R sC R R R sC R R u u i+++=++=+= 11111111212121221121111++=+∙++∙+=+++=Ts Ts s C R R R R s C R R R R R R s C R R s C R αα其中 α=+=21211,R R R T C R , 一阶微分环节,惯性环节.(c)s C R s C R s C R s C R s C R sC R R sC sC R u u i 21221122112211220)1)(1()1)(1(1//11+++++=+++= 由微分环节,二阶振荡环节组成。
自动控制原理 第二章习题答案
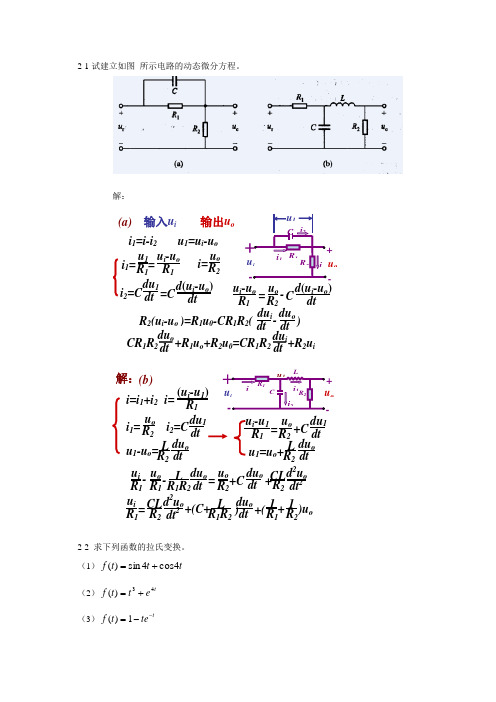
2-1试建立如图 所示电路的动态微分方程。
解:输入u i 输出u ou 1=u i -u oi 2=C du 1 dt )- R 2(u i -u o )=R 1u 0-CR 1R 2( du i dt dt du oC + - u i o R 1R 2 i 1 i i 2u 1i 1=i-i 2 u o i= R 2u 1 i 1= R 1 = u i -u o R 1 dt d (u i -u o ) =C C d (u i -u o ) dtu o - R 2 = u i -u o R 1 CR 1R 2 du o dt du idt +R 1u o +R 2u 0=CR 1R 2 +R 2u i(a)i=i 1+i 2 i 2=C du 1 dtu o i 1= R 2 u 1-u o = L R 2 du o dt R1i= (u i -u 1) (b)C+-iu o R 1R 2i 1 ii 2Lu 1 = R 1 u i -u 1 u o +C R 2 du 1 dtu 1=u o + L R 2 du o dtdu o dt R 1R 2 L du o dt + CL R 2 d 2u o dt 2 = - - u i R 1 u o R 1 u o R 2 +C )u o R 1R 2 L du o dt ) CL R 2 d 2u o dt 2 = + +( u i R 1 1 R 11 R 2+(C+ 解:2-2 求下列函数的拉氏变换。
(1)t t t f 4cos 4sin )(+= (2)te t tf 43)(+= (3)t te t f --=1)((4)te t tf 22)1()(-= 解:(1) f(t)=sin4t+cos4tL [sin ωt ]= ωω2+s 2=s s+42+16L [sin4t+cos4t ]= 4s 2+16s s 2+16+s ω2+s 2L [cos ωt ]=解:(2) f(t)=t 3+e 4t 解:L [t 3+e 4t ]= 3!s 41s-4+ 6s+24+s 4s 4(s+4)=(3) f(t)=t n e atL [t n e at ]=n!(s-a)n+1(4) f(t)=(t-1)2e 2tL [(t-1)2e 2t ]=e -(s-2)2(s-2)3解:解:2-3求下列函数的拉氏反变换。
自动控制原理课后习题答案第二章

解:由图可得
联立上式消去中间变量U1与U2,可得:
2-8某位置随动系统原理方块图如图2-7所示。已知电位器最大工作角度,功率放大级放大系数为K3,要求:
(1) 分别求出电位器传递系数K0、第一级与第二级放大器得比例系数K1与K2;
(2) 画出系统结构图;
(3) 简化结构图,求系统传递函数。
证明:(a)根据复阻抗概念可得:
即 取A、B两点进行受力分析,可得:
整理可得:
经比较可以瞧出,电网络(a)与机械系统(b)两者参数得相似关系为
2-5 设初始条件均为零,试用拉氏变换法求解下列微分方程式,并概略绘制x(t)曲线,指出各方程式得模态。
(1)
(2)
2-7由运算放大器组成得控制系统模拟电路如图2-6所示,试求闭环传递函数Uc(s)/Ur(s)。
2-10试简化图2-9中得系统结构图,并求传递函数C(s)/R(s )与C(s)/N(s)。
图2-9 题2-10系统结构图
分析:分别假定R(s)=0与N(s)=0,画出各自得结构图,然后对系统结构图进行等效ቤተ መጻሕፍቲ ባይዱ换,将其化成最简单得形式,从而求解系统得传递函数。
解:(a)令N(s)=0,简化结构图如图所示:
可求出:
令R(s)=0,简化结构图如图所示:
所以:
(b)令N(s)=0,简化结构图如下图所示:
所以:
令R(s)=0,简化结构图如下图所示:
2-12 试用梅逊增益公式求图2-8中各系统信号流图得传递函 数C(s)/R(s)。
图2-11 题2-12系统信号流图
解:
(a)存在三个回路:
存在两条前向通路:
所以:
(3)简化后可得系统得传递函数为
自动控制原理第2章课后习题及解答
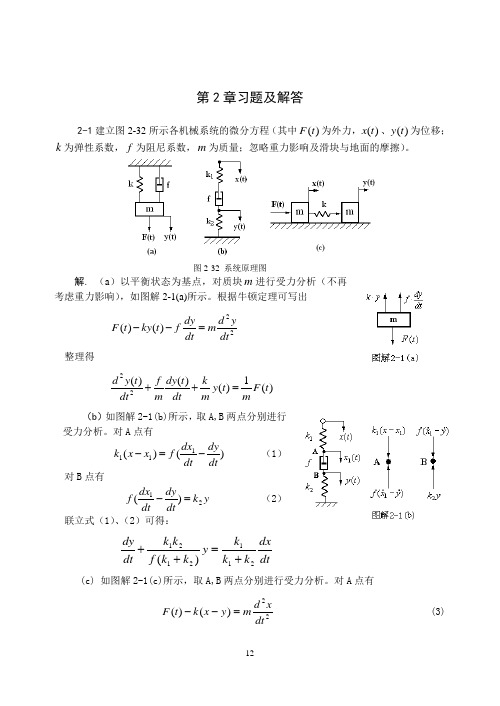
2-3 证明图 2-34 (a) 所示的力学系统和图 2-34 (b) 所示的电路系统是相似系统 (即 有相同形式的数学模型) 。
图 2-34 系统原理图
解 (a) 取A、B两点分别进行受力分析,如图解2-3(a)所示。对A点有
−y ) = f1 ( y −y 1 ) k 2 ( x − y) + f 2 ( x
比较两系统的传递函数,如果设 R1 = 1 k1 , R2 = 1 k 2 , C1 = f 1 , C 2 = f 2 ,则两系统 的传递函数相同,所以两系统是相似的。 2-4 如图 2-35 所示,二极管是一个非线性元件,其电流 id 和电压 ud 之间的关系为
= id 10−14 ( e 0.026 − 1) ,假设电路在工作点 u(0) = 2.39V , i= (0) 2.19 × 10−3 A 处做微小变
(c) 由图解 2-2(c)可写出
Ur ( = s ) R1 [ I1 ( s ) + I 2 ( s )] + ( Ls + R2 ) I 2 ( s ) 1 I 1 ( s ) = ( Ls + R2 ) I 2 ( s ) Cs U c ( s ) = R2 I 2 ( s )
(6) (7) (8)
F (t ) − k ( x − y ) = m
d 2x dt 2
(3)
- 12 -
对 B 点有
k ( x − y) = m
d2y dt 2
(4)
联立式(3) 、 (4)消去中间变量 x 可得
d 4 y 2K d 2 y K + = F (t ) dt 4 m dt 2 m 2
2-2 应用复数阻抗方法求图 2-33 所示各无源网络的传递函数。
自动控制原理-课后习题答案

第1章控制系统概述【课后自测】1-1 试列举几个日常生活中的开环控制和闭环控制系统,说明它们的工作原理并比较开环控制和闭环控制的优缺点。
解:开环控制——半自动、全自动洗衣机的洗衣过程。
工作原理:被控制量为衣服的干净度。
洗衣人先观察衣服的脏污程度,根据自己的经验,设定洗涤、漂洗时间,洗衣机按照设定程序完成洗涤漂洗任务。
系统输出量(即衣服的干净度)的信息没有通过任何装置反馈到输入端,对系统的控制不起作用,因此为开环控制。
闭环控制——卫生间蓄水箱的蓄水量控制系统和空调、冰箱的温度控制系统。
工作原理:以卫生间蓄水箱蓄水量控制为例,系统的被控制量(输出量)为蓄水箱水位(反应蓄水量)。
水位由浮子测量,并通过杠杆作用于供水阀门(即反馈至输入端),控制供水量,形成闭环控制。
当水位达到蓄水量上限高度时,阀门全关(按要求事先设计好杠杆比例),系统处于平衡状态。
一旦用水,水位降低,浮子随之下沉,通过杠杆打开供水阀门,下沉越深,阀门开度越大,供水量越大,直到水位升至蓄水量上限高度,阀门全关,系统再次处于平衡状态。
开环控制和闭环控制的优缺点如下表1-2 自动控制系统通常有哪些环节组成各个环节分别的作用是什么解:自动控制系统包括被控对象、给定元件、检测反馈元件、比较元件、放大元件和执行元件。
各个基本单元的功能如下:(1)被控对象—又称受控对象或对象,指在控制过程中受到操纵控制的机器设备或过程。
(2)给定元件—可以设置系统控制指令的装置,可用于给出与期望输出量相对应的系统输入量。
(3)检测反馈元件—测量被控量的实际值并将其转换为与输入信号同类的物理量,再反馈到系统输入端作比较,一般为各类传感器。
(4)比较元件—把测量元件检测的被控量实际值与给定元件给出的给定值进行比较,分析计算并产生反应两者差值的偏差信号。
常用的比较元件有差动放大器、机械差动装置和电桥等。
(5)放大元件—当比较元件产生的偏差信号比较微弱不足以驱动执行元件动作时,可通过放大元件将微弱信号作线性放大。
自动控制原理第二章课后习题答案(免费)

自动控制原理第二章课后习题答案(免费)离散系统作业注明:*为选做题2-1 试求下列函数的Z 变换 (1)()E z L =();n e t a = 解:01()[()]1k k k z E z L e t a z z z aa∞-=====--∑ (2) ();at e t e -= 解:12211()[()][]1...1atakT k aT aT aTaT k z E z L e t L ee z e z e z z e e z∞----------=====+++==--∑2-2 试求下列函数的终值:(1)112();(1)Tz E z z --=-解: 11111()(1)()1lim lim lim t z z Tz f t z E z z---→∞→→=-==∞- (2)2()(0.8)(0.1)z E z z z =--。
解:211(1)()(1)()0(0.8)(0.1)lim lim limt z z z z f t z E z z z →∞→→-=-==-- 2-3* 已知()(())E z L e t =,试证明下列关系成立:(1)[()][];n z L a e t E a =证明:0()()nn E z e nT z∞-==∑00()()()()[()]n n n n n n z z E e nT e nT a z L a e t a a ∞∞--=====∑∑ (2)()[()];dE z L te t TzT dz=-为采样周期。
证明:11100[()]()()()()()()()()()nn n n n n n n n n L te t nT e nT zTz ne nT z dE z de nT z dz dz e nT n zne nT z ∞∞---==∞-=∞∞----======-=-∑∑∑∑∑所以:()[()]dE z L te t Tzdz=- 2-4 试求下图闭环离散系统的脉冲传递函数()z Φ或输出z 变换()C z 。
自动控制原理第二版课后答案第二章精选全文完整版

x kx ,简记为
y kx 。
若非线性函数有两个自变量,如 z f (x, y) ,则在
平衡点处可展成(忽略高次项)
f
f
z xv
|( x0 , y0 )
x y |(x0 , y0 )
y
经过上述线性化后,就把非线性关系变成了线性 关系,从而使问题大大简化。但对于如图(d)所示的 强非线性,只能采用第七章的非线性理论来分析。对于 线性系统,可采用叠加原理来分析系统。
Eb (s) Kbsm (s)
Js2 m(s) Mm fsm(s)
c
(s)
1
i
m
(s)
45
系统各元部件的动态结构图
传递函数是在零初始条件下建立的,因此,它只 是系统的零状态模型,有一定的局限性,但它有现 实意义,而且容易实现。
26
三、典型元器件的传递函数
1. 电位器
1 2
max
E
Θs
U s
K
U
K E
max
27
2. 电位器电桥
1
2
E
K1p1
K1 p 2
U
Θ 1
s
Θ
K1 p
Θ 2
s
U s
28
3.齿轮
传动比 i N2 N1
G2(s)
两个或两个以上的方框,具有同一个输入信号,并 以各方框输出信号的代数和作为输出信号,这种形
式的连接称为并联连接。
41
3. 反馈连接
R(s)
-
C(s) G(s)
H(s)
一个方框的输出信号输入到另一个方框后,得 到的输出再返回到这个方框的输入端,构成输 入信号的一部分。这种连接形式称为反馈连接。
自动控制原理第2章 习题及解析

第二章 习题解析2-4 当系统处于零初始条件下时,给系统输入单位阶跃响应信号,其输出响应为2()1t t y t e e --=-+试求该系统的传递函数。
参考解答:2111421()()21(2)(1)s s Y s R s s s s s s s s++=-+==++++ 22()42()()32Y s s s G s R s s s ++==++2-5 某可控硅整流器的输出电压d 2cos U KU αΦ=式中,K 为常数;2U Φ为整流变压器副边相电压有效值;α为可控硅的控制角。
设α在0α附近作微小变化,试将d U 与α的关系式线性化。
参考解答:将非线性微分方程d 2cos U KU αΦ=进行线性化,即在平衡点α0 附近将其展为泰勒级数取一次近似,线性化后用变量增量的线性方程ΔU d = C Δα 代替原来的非线性方程,式中常数2020sin sin dd dU C KU U KU d ααααααΦΦ===-→∆=-∆略去增加量符号“Δ”,上式可简写为20sin d U KU ααΦ=- 2-6 试求图2-70所示电路的传递函数()/()y r U s U s 。
参考解答:图 a)可作出该无源电路的动态结构图(图a-1)亦可作成图(图a-2)所示由结构图等效变换可求得传递函数212()11()()11c r U s R Cs bTs U s R R Cs Ts ++==+++式中21212(),1R T R R C b R R =+=<+ ,该网络称为滞后网络。
图 b)由图(b )网络可作出其动态结构图(b-1),简化为(b-2)即可得传递函数:112221122112212()(1)(1)()()1y r U s R C s R C s U s R C R C s R C R C R C s ++=++++该网络称为滞后-超前网络(滞后-超前电路)。
2-7 试求图2-71所示有源电路的传递函数y r ()/()U s U s 。
自动控制原理习题及答案
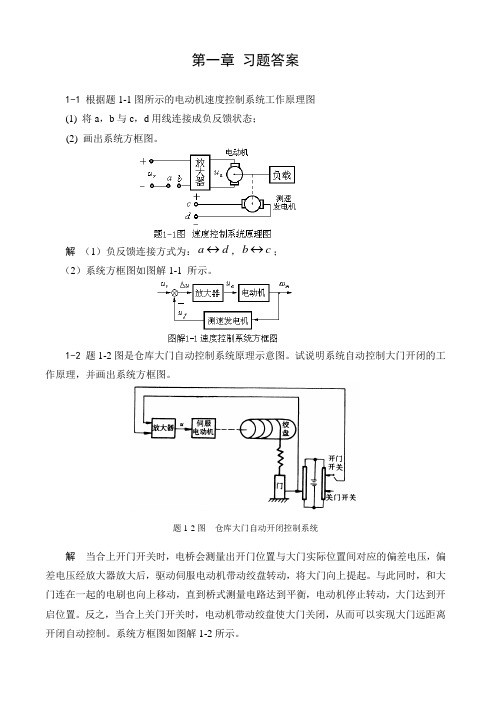
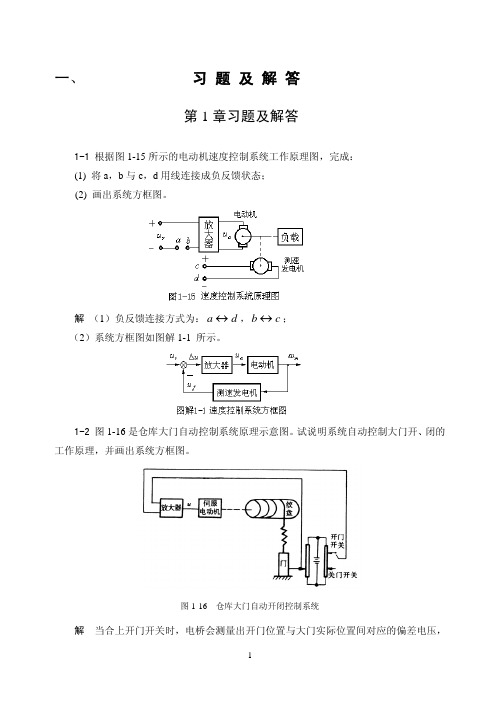
第一章 习题答案1-1 根据题1-1图所示的电动机速度控制系统工作原理图(1) 将a ,b 与c ,d 用线连接成负反馈状态;(2) 画出系统方框图。
解 (1)负反馈连接方式为:d a ↔,c b ↔;(2)系统方框图如图解1-1 所示。
1-2 题1-2图是仓库大门自动控制系统原理示意图。
试说明系统自动控制大门开闭的工作原理,并画出系统方框图。
题1-2图 仓库大门自动开闭控制系统解 当合上开门开关时,电桥会测量出开门位置与大门实际位置间对应的偏差电压,偏差电压经放大器放大后,驱动伺服电动机带动绞盘转动,将大门向上提起。
与此同时,和大门连在一起的电刷也向上移动,直到桥式测量电路达到平衡,电动机停止转动,大门达到开启位置。
反之,当合上关门开关时,电动机带动绞盘使大门关闭,从而可以实现大门远距离开闭自动控制。
系统方框图如图解1-2所示。
1-3 题1-3图为工业炉温自动控制系统的工作原理图。
分析系统的工作原理,指出被控对象、被控量和给定量,画出系统方框图。
题1-3图 炉温自动控制系统原理图解 加热炉采用电加热方式运行,加热器所产生的热量与调压器电压c u 的平方成正比,c u 增高,炉温就上升,c u 的高低由调压器滑动触点的位置所控制,该触点由可逆转的直流电动机驱动。
炉子的实际温度用热电偶测量,输出电压f u 。
f u 作为系统的反馈电压与给定电压r u 进行比较,得出偏差电压e u ,经电压放大器、功率放大器放大成a u 后,作为控制电动机的电枢电压。
在正常情况下,炉温等于某个期望值T °C ,热电偶的输出电压f u 正好等于给定电压r u 。
此时,0=-=f r e u u u ,故01==a u u ,可逆电动机不转动,调压器的滑动触点停留在某个合适的位置上,使c u 保持一定的数值。
这时,炉子散失的热量正好等于从加热器吸取的热量,形成稳定的热平衡状态,温度保持恒定。
当炉膛温度T °C 由于某种原因突然下降(例如炉门打开造成的热量流失),则出现以下的控制过程:控制的结果是使炉膛温度回升,直至T °C 的实际值等于期望值为止。
自动控制原理_课后习题答案
系统方框图如图解 1-5 所示。 1-6 摄像机角位置自动跟踪系统如图 1-20 所示。当光点显示器对准某个方向时,摄像 机会自动跟踪并对准这个方向。试分析系统的工作原理,指出被控对象、被控量及给定量, 画出系统方框图。
图 1-20 摄像机角位置随动系统原理图
解 控制系统的任务是使摄像机自动跟踪光点显示器指示的方向。
器吸取的热量,形成稳定的热平衡状态,温度保持恒定。
当炉膛温度T °C 由于某种原因突然下降(例如炉门打开造成的热量流失),则出现以
2
下的控制过程:
控制的结果是使炉膛温度回升,直至T °C 的实际值等于期望值为止。 → T ° C ↓ → u f ↓ → ue ↑ → u1 ↑ → ua ↑ →θ ↑ → uc ↑ → T ° C ↑
图(a)系统,当 u 低于给定电压时,其偏差电压经放大器 K 放大后,驱动电机 D 转动, 经减速器带动电刷,使发电机 F 的激磁电流 I j 增大,发电机的输出电压会升高,从而使偏
差电压减小,直至偏差电压为零时,电机才停止转动。因此,图(a)系统能保持 110 伏不变。
图(b)系统,当 u 低于给定电压时,其偏差电压经放大器 K 后,直接使发电机激磁电流
图 2-33 系统原理图
解. (a)以平衡状态为基点,对质块 m 进行受力分析(不再
自动控制原理课后习题答案第二章资料讲解

第 二 章2-3试证明图2-5(a)的电网络与(b)的机械系统有相同的数学模型。
分析 首先需要对两个不同的系统分别求解各自的微分表达式,然后两者进行对比,找出两者之间系数的对应关系。
对于电网络,在求微分方程时,关键就是将元件利用复阻抗表示,然后利用电压、电阻和电流之间的关系推导系统的传递函数,然后变换成微分方程的形式,对于机械系统,关键就是系统的力学分析,然后利用牛顿定律列出系统的方程,最后联立求微分方程。
证明:(a)根据复阻抗概念可得:2221212112212211212112212122111()1()111oiR u C s R R C C s R C R C R C s R u R R C C s R C R C R C C sR C s R C s+++++==+++++++即220012121122121212112222()()i i o id u du d u duR R C C R C R C R C u R R C C R C R C u dt dt dt dt++++=+++取A 、B 两点进行受力分析,可得:o 112()()()i o i o dx dx dx dx f K x x f dt dt dt dt -+-=- o 22()dx dxf K x dt dt -= 整理可得:2212111221121212211222()()o o i i o id x dx d x dx f f f K f K f K K K x f f f K f K K K x dt dt dt dt ++++=+++经比较可以看出,电网络(a )和机械系统(b )两者参数的相似关系为1112221211,,,K f R K f R C C ::::2-5 设初始条件均为零,试用拉氏变换法求解下列微分方程式,并概略绘制x(t)曲线,指出各方程式的模态。
(1) ;)()(2t t x t x =+&(2))。
自动控制原理习题及答案.doc

第一章 习题答案1-1 根据题1-1图所示的电动机速度控制系统工作原理图(1) 将a ,b 与c ,d 用线连接成负反馈状态;(2) 画出系统方框图。
解 (1)负反馈连接方式为:d a ↔,c b ↔;(2)系统方框图如图解1-1 所示。
1-2 题1-2图是仓库大门自动控制系统原理示意图。
试说明系统自动控制大门开闭的工作原理,并画出系统方框图。
题1-2图仓库大门自动开闭控制系统解当合上开门开关时,电桥会测量出开门位置与大门实际位置间对应的偏差电压,偏差电压经放大器放大后,驱动伺服电动机带动绞盘转动,将大门向上提起。
与此同时,和大门连在一起的电刷也向上移动,直到桥式测量电路达到平衡,电动机停止转动,大门达到开启位置。
反之,当合上关门开关时,电动机带动绞盘使大门关闭,从而可以实现大门远距离开闭自动控制。
系统方框图如图解1-2所示。
1-3 题1-3图为工业炉温自动控制系统的工作原理图。
分析系统的工作原理,指出被控对象、被控量和给定量,画出系统方框图。
题1-3图炉温自动控制系统原理图解加热炉采用电加热方式运行,加热器所产生的热量与调压器电压c u的平方成正比,c u增高,炉温就上升,c u的高低由调压器滑动触点的位置所控制,该触点由可逆转的直流电动机驱动。
炉子的实际温度用热电偶测量,输出电压f u。
f u作为系统的反馈电压与给定电压u进行比较,得出偏差电压e u,经电压放大器、功率放大器放大成a u r后,作为控制电动机的电枢电压。
在正常情况下,炉温等于某个期望值T°C,热电偶的输出电压f u正好等于给定电压r u 。
此时,0=-=f r e u u u ,故01==a u u ,可逆电动机不转动,调压器的滑动触点停留在某个合适的位置上,使c u 保持一定的数值。
这时,炉子散失的热量正好等于从加热器吸取的热量,形成稳定的热平衡状态,温度保持恒定。
当炉膛温度T °C 由于某种原因突然下降(例如炉门打开造成的热量流失),则出现以下的控制过程:控制的结果是使炉膛温度回升,直至T °C 的实际值等于期望值为止。
自动控制原理参考答案-第2章

La ⎧ ⎪Tl = R a ⎪ JRa ⎪ ⎪Tm = C C e m ⎪ ⎨ ⎪ K = 2k1 H 0 ⎪ 1 k2 ⎪ 2F H 0 ⎪ ⎪T1 = k2 ⎩
题 2-8:试用动态结构图简化方法求解题 2-8 图所示两系统的传递函数。
u2
L R ia
+
u i(t)
+
u d (t)
+
Ea
M m(t)
J1
f1 r 1 f2
-
-
-
ω1 r2
M c(t)
+ if 题 2-5 图
ω2
J2
电枢控制直流电动机拖动开环系统
(1) ud (t ) = 2.34U 2 {0.82 − 0.57[ K1ui (t ) − 35o ]} = 2.34U 2 {1.168 − 0.57 K1ui (t )} (2) 参照教材 38 页图 2-24 (3) 参照教材式(2-4)、(2-5)、(2-6)、(2-17) 2.73U 2 ⎧ ′ ( s) = M c ( s) / i ⎧M c − 1.34 K1U 2U i ( s) ⎪U d ( s ) = s ⎪ ⎪ ⎪i = r2 / r1 ⎪ LsI ( s ) + RI ( s ) + C Ω ( s ) = U ( s ) 其中, ⎨ a e 1 d ⎨ a 2 ⎪ J = J1 + J 2 / i ⎪ M ( s ) = Cm I a ( s ) ⎪ f = f + f / i2 ⎪ 1 2 ⎩ ′ ( s) ⎪ ⎩ JsΩ1 ( s ) + f Ω1 ( s ) = M ( s ) − M c
⇒
[iJLs 3 + (iJR + ifL) s 2 + (ifR + iCmCe ) s ]Ω1 ( s ) = 2.73CmU 2 − 1.34 K1CmU 2 sU i ( s ) − ( Ls + R ) M c ( s )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 习题解答2-1试求下列各函数的拉氏变换。
(a )()12f t t =+,(b )2()37()f t t t t δ=+++,(c )23()2ttt f t e ete ---=++,(d )2()(1)f t t =+,(e )()sin 22cos 2sin 2tf t t t e t -=++,(f )()2cos tf t te t t -=+,(g )()sin32cos f t t t t t =-,(h )()1()2cos 2f t t t t =+ 解:(a )212()F s s s =+(b )23372()1F s s s s=+++(c )2121()12(3)F s s s s =+++++ (d )2()21f t t t =++,3221()F s s s s=++(e )222222()44(1)4s F s s s s =++++++ (f )2222211621()11(1)s d s s F s s ds s s ⎛⎫ ⎪++⎝⎭=+=++++ (g )2222222223262231()(3)(1)s d d s s s s F s ds ds s s ⎛⎫⎛⎫ ⎪ ⎪+++⎝⎭⎝⎭=-+=-++(h )2222211684()(4)s d s s F s s ds s s ⎛⎫ ⎪++⎝⎭=+=++2-2试求图2.54所示各信号的拉氏变换。
(a ) (b ) (c ) (d )图2.54 习题2-2图解:(a )021()t s e X s s s -=+(b )000221()t s t se e X s t s s s--=-+- (c )33112212()()t s t st s t s t s t s t s t s a ae be be ce ce a b a c b ce X s e e s s s s s s s s s s----------=-+-+-=++-(d )11()1()1()1()()1()1()11()1()(2)1(2)1(2)1111()21()2()1()(2)1(2)1(2)x t t t T t t t T t T t T T Tt T t T t T t T t T T Tt t T t t T t T t T t T t T T T T=--+--------+--+-=-⨯-+---+--+-所以22222222211111111()222Ts Ts TsTsTs Ts s s s e e e e T T T X s e e s s T s T s T s s s s s------+++=-+-++=-+2-3运用部分分式展开,求下列各像函数的原函数。
(a )2()(2)F s s s =+,(b )10()(1)(10)F s s s s =++,(c )232()420s F s s s +=++,(d )22(2)()(1)(4)s F s s s +=++,(e )21()s F s s+=,(f )22()s e F s s -=解:(a )部分分式分解有211()(2)2F s s s s s -==+++查表得2()1t f t e -=-(b )部分分式分解有101 1.11110.1111()(1)(10)110F s s s s s s s -==++++++查表得10()1 1.11110.1111t t f t e e --=-+(c )部分分式分解有222223224()3420(2)4(2)4s s F s s s s s ++==-++++++⎫=查表得2222()3cos 4sin 4 3.162(0.949cos 40.3162sin 4)3.162sin(4108.38)t t t tf t e t e t e t t et ----=-=-=+o(d )部分分式分解有222222222222(2)0.6670.667 2.667()(1)(4)120.66720.66720.66720.2980.4470.894122122s s F s s s s s s s s s s s s s +-+==+++++⎛⎫⎛⎫=--=-- ⎪ ⎪++++++⎝⎭⎝⎭查表得()()0.6670.2980.447cos20.894sin 20.6670.298(sin 2153.4)t t f t e t t e t --=--=-+o(e )部分分式分解有22111()s F s s s s+==+ 查表得()1f t t =+(f )根据位移定理有()(2)1(2)f t t t =-⋅-2-4用拉氏变换求解下面的常微分方程。
(a )30,(0)1,(0)2y y y y y ++===&&&&(b )245,(0)1,(0)1y y y t y y ++===&&&& (c )sin ,(0)1,(0)2y y t y y +===&&&&(d )243,(0)1,(0)4ty y y te y y -++===-&&&&解:(a )根据微分定理,微分方程两边拉氏变换得2()2()13()0s Y s s sY s Y s --+-+=即23()3s Y s s s +=++部分分式分解有2222230.5 1.658() 1.50763(0.5) 1.658(0.5) 1.658s s Y s s s s s ++==+++++++ 拉氏反变换得到0.50.5()cos1.658 1.5076sin1.658t t y t e t e t --=+(b )根据微分定理,微分方程两边拉氏变换得232()24()45()s Y s s sY s Y s s--+-+=即432362()(45)s s Y s s s s ++=++部分分式分解有4323322262282210324961()(45)525125125(2)1125(2)1s s s Y s s s s s s s s s +++==-+++++++++ 拉氏反变换得到2221822103496()cos sin 525125125125t ty t t t e t e t --=-+++(c )根据微分定理,微分方程两边拉氏变换得221()2()11s Y s s sY s s --+-=+ 即322234()()(1)s s s Y s s s s +++=++部分分式分解有322222234 2.50.50.5()()(1)111s s s s Y s s s s s s s s +++==-+++++++ 拉氏反变换得到()4 2.50.5cos 0.5sin t y t e t t -=-++(d )根据微分定理,微分方程两边拉氏变换得221()44()43()(2)s Y s s sY s Y s s -++-+=+即3222441()(43)(2)s s s Y s s s s +++=+++部分分式分解有32222224413111()(43)(2)(3)(2)3(2)s s s s s Y s s s s s s s s +++++===-+++++++拉氏反变换得到32()t t y t e te --=-注:可利用Matlab 命令来求解微分方程。
例如对本题的(a ),键入Matlab 命令('23*0','(0)1,(0)2')y dsolve D y Dy y y Dy =++=== 回车后得到exp(-1/2*)*cos(1/2*11^(1/2)*)5/11*exp(-1/2*)*11^(1/2)*sin(1/2*11^(1/2)*)y t t t t =+2-5设质量、弹簧、阻尼器系统如图2.55(a )、(b )、(c )所示,图中i x 是输入位移,0x 是输出位移。
试分别列写各系统的输入输出微分方程描述。
i x0x 0x ixx ix f(a ) (b ) (c )图2.55 习题2-5图解:(a )对于图2.55(a )所示的质量、弹簧、阻尼器系统,有01020()i mx f x x f x =--&&&&& 即01201()i mx f f x f x ++=&&&&(b )对于图2.55(b )所示的质量、弹簧、阻尼器系统,设弹簧1K 下端位置为y ,则有10020()()()i K x y f y x f y x K x -=--=&&&& 即有120()i K x y K x -=&&&消去中间变量y 得到1212001()i K K K K x x K x f++=&&(c )对于图2.55(c )所示的质量、弹簧、阻尼器系统,有20010()()i i K x f x x K x x =-+-&&即01201()i i f x K K x f x K x ++=+&&2-6车轮的减震器模型如图2.56所示,图中y 为减振系统支撑点向上的位移,单位为m ;2375m kg =为去掉四个车轮质量后的整车质量的四分之一;130000s k N m =为减震器的弹性系数;9800f N s m =⋅为减震器的阻尼系数;120m kg =kg 为单个车轮的质量;1000000w k N m =为轮胎的弹性系数。
图中所示为重力作用下,车辆在水平路面匀速行驶时减振系统所处于的平衡位置。
考虑由于路面不平引起的轮胎变形r ∆,减振系统支撑点的增量运动y ∆,求二者间的输入输出微分方程并求传递函数。
图2.56 习题2-6图解:根据牛顿力学知识,有12()()()()()w w w s w w s w w m y k r y k y y f y y m y k y y f y y =-----=-+-&&&&&&&& 对上面的第2式微分,将w y &&表示成w y &、y 、y&、y &&、y &&&的函数有 2s s w w k k m y y y y y f f f =++-&&&&&&&&&将结果代入上面的第1式,消去w y &&得1212222211111()s w w s w w s s s s s fk fk f k k m m fm y y y y y r y m k f m k f m k f m k f m k f+=++--+-----&&&&&&& 将结果代入上面的第2式,消去w y &得 2221212112222222221111()s s w w s w s w s w s wm m f m m k m k f k fm m y y y y r m k f k m k f k m k f k m k f k +-=--++++++&&&&& 将上述w y 的结果及其微分代入到上面的第2式,消去w y 和w y &,整理得1212122()()s s w w s w w s w m m y f m m y k m k m k m y fk y k k y fk r k k r +++++++=+&&&&&&&&&&&根据上面的结果得到传递函数为4321212122()()()()w s w s s w w s wfk s k k Y s R s m m s f m m s k m k m k m s fk s k k +=+++++++ 将各个参数的数值代入得到432()130666617333333()51656846130666617333333Y s s R s s s s s +=++++2-7用一根弹簧连接两个摆,如图2.57所示,系统在下平衡位置时弹簧刚好不受力。
