浙教版九年级数学下册第三章《 3.2简单几何体的三视图(1)》公开课课件
合集下载
2018年秋九年级数学下册第三章投影与三视图3.2简单几何体的三视图第1课时a课件新版浙教版

3.2简单几何体的三视图(1)
(2)画出长方体与水平投影面上的正 投影(棱A,A在水平投影面上的正投 影为A’),得到的正投影是什么图形? 它与长方体的底面有什么关系?
想一想:长方体按下图摆放,在平行光
线下,它分别在水平投影面、侧投影面、 正投影面三个相互垂直的平面上的正投 影是什么图形?
返回
错误的三视图 —长未对正1
错误的三视图 —长未对正2
错误的三视图 —高不平齐1
错误的三视图 —高不平齐2
错误的三视图 —宽不相等1
错误的三视图 —宽不相等1
错误的三视图
错误的三视图
俯视图
主视图
左视图
主视图
Hale Waihona Puke 左视图俯视图从上面看 到的图形
从左面看 到的图形
主视图
左视图
俯视图
例1:一个长方体的立体图如图所示,长为4,宽为2, 高为3,请画它的三视图.
3cm
4cm
2cm
主视方面
线段DG
线段IH
线段EF 线段DE 矩形DIHG
长方体和立方体都是直四棱柱。
想一想:长方体按下图摆放,在平行光
线下,它分别在水平投影面、侧投影面、 正投影面三个相互垂直的平面上的正投 影是什么图形?
※我们把物体的正投影称为视图.
物体在正投影面、侧投影面和水平投影面上得 到的视图分别称为主视图、左视图和俯视图,它 们统称为三视图.
※
产生主视图的投射线方向 叫做主视方向
想一想:三视图的大小与物体的大 小有怎样的联系? 宽 高 长
宽
长
高
※三视图中的“三等规则”.
长对正. 高平齐. 宽相等. ※三视图中的位置.
在主视图、俯视 图中都体现形体的长 度,且长度在竖直方 向上是对正的,我们 称之为长对正。
(2)画出长方体与水平投影面上的正 投影(棱A,A在水平投影面上的正投 影为A’),得到的正投影是什么图形? 它与长方体的底面有什么关系?
想一想:长方体按下图摆放,在平行光
线下,它分别在水平投影面、侧投影面、 正投影面三个相互垂直的平面上的正投 影是什么图形?
返回
错误的三视图 —长未对正1
错误的三视图 —长未对正2
错误的三视图 —高不平齐1
错误的三视图 —高不平齐2
错误的三视图 —宽不相等1
错误的三视图 —宽不相等1
错误的三视图
错误的三视图
俯视图
主视图
左视图
主视图
Hale Waihona Puke 左视图俯视图从上面看 到的图形
从左面看 到的图形
主视图
左视图
俯视图
例1:一个长方体的立体图如图所示,长为4,宽为2, 高为3,请画它的三视图.
3cm
4cm
2cm
主视方面
线段DG
线段IH
线段EF 线段DE 矩形DIHG
长方体和立方体都是直四棱柱。
想一想:长方体按下图摆放,在平行光
线下,它分别在水平投影面、侧投影面、 正投影面三个相互垂直的平面上的正投 影是什么图形?
※我们把物体的正投影称为视图.
物体在正投影面、侧投影面和水平投影面上得 到的视图分别称为主视图、左视图和俯视图,它 们统称为三视图.
※
产生主视图的投射线方向 叫做主视方向
想一想:三视图的大小与物体的大 小有怎样的联系? 宽 高 长
宽
长
高
※三视图中的“三等规则”.
长对正. 高平齐. 宽相等. ※三视图中的位置.
在主视图、俯视 图中都体现形体的长 度,且长度在竖直方 向上是对正的,我们 称之为长对正。
浙教版 九年级数学 下册 第三章 3.2 简单几何体的三视图 课件(共18张PPT)

请观察下面三个投影,它们有什么 相同与不同的地方?你能试着给正投
影下定义吗?
中心投影 投影
斜投影
正投影
平行投影
简单几何体的三视图(1)
看一看
从左面看到的图形: 左视图
从正面看到的图形: 主视图 从正上方往下看到的 图形:俯视图
主视图、左视图、俯视图合称三视图。
从上面看
主视图
左视图
从左面看
从正面看
甲
乙
2、小明的爸爸送给小明一个礼物,小明打开包装后画出它 的主视图与俯视图如图所示,根据小明画的视图,请你猜礼
物是( B )
A、钢笔 B、生日蛋糕 C、光盘 D、一套衣服
3、一个长方体木块上的正中位置搁一个乒乓球,已知它的主视 图与俯视图,小明补画的左视图正确吗?为什么?如果错了,怎
主 视 图
5cm
高 平 齐
5cm
左 视 图
5cm
4cm 3cm
长对正
3cm
4cm
画图原则:
俯 视 图
4cm
主、俯视图长对正,主、左视图高平齐, 俯、左视图宽相等.
练一练:
课堂训练
1、图甲,乙都是由小立方体组成的几何体,则图甲,图乙的
视图一样的是( C )
A、主视图、左视图 B、主视图、俯视图 C、左视图、俯视图 D、以上都不对
• 位置:主视图 左视图
•
俯视图
• 大小:长对正,高平齐,宽相等.
横看成岭侧成峰,远近高低各不同。 不识庐山真面目,只缘身在此山中。
——苏轼
•不习惯读书进修的人,常会自满于现状,觉得再没有什么事情需要学习,于是他们不进则退。经验丰富的人读书用两只眼睛,一只眼睛看到纸面上的话,另 一眼睛看到纸的背面。2022年4月11日星期一2022/4/112022/4/112022/4/11 •书籍是屹立在时间的汪洋大海中的灯塔。2022年4月2022/4/112022/4/112022/4/114/11/2022 •正确的略读可使人用很少的时间接触大量的文献,并挑选出有意义的部分。2022/4/112022/4/11April 11, 2022 •书籍是屹立在时间的汪洋大海中的灯塔。
影下定义吗?
中心投影 投影
斜投影
正投影
平行投影
简单几何体的三视图(1)
看一看
从左面看到的图形: 左视图
从正面看到的图形: 主视图 从正上方往下看到的 图形:俯视图
主视图、左视图、俯视图合称三视图。
从上面看
主视图
左视图
从左面看
从正面看
甲
乙
2、小明的爸爸送给小明一个礼物,小明打开包装后画出它 的主视图与俯视图如图所示,根据小明画的视图,请你猜礼
物是( B )
A、钢笔 B、生日蛋糕 C、光盘 D、一套衣服
3、一个长方体木块上的正中位置搁一个乒乓球,已知它的主视 图与俯视图,小明补画的左视图正确吗?为什么?如果错了,怎
主 视 图
5cm
高 平 齐
5cm
左 视 图
5cm
4cm 3cm
长对正
3cm
4cm
画图原则:
俯 视 图
4cm
主、俯视图长对正,主、左视图高平齐, 俯、左视图宽相等.
练一练:
课堂训练
1、图甲,乙都是由小立方体组成的几何体,则图甲,图乙的
视图一样的是( C )
A、主视图、左视图 B、主视图、俯视图 C、左视图、俯视图 D、以上都不对
• 位置:主视图 左视图
•
俯视图
• 大小:长对正,高平齐,宽相等.
横看成岭侧成峰,远近高低各不同。 不识庐山真面目,只缘身在此山中。
——苏轼
•不习惯读书进修的人,常会自满于现状,觉得再没有什么事情需要学习,于是他们不进则退。经验丰富的人读书用两只眼睛,一只眼睛看到纸面上的话,另 一眼睛看到纸的背面。2022年4月11日星期一2022/4/112022/4/112022/4/11 •书籍是屹立在时间的汪洋大海中的灯塔。2022年4月2022/4/112022/4/112022/4/114/11/2022 •正确的略读可使人用很少的时间接触大量的文献,并挑选出有意义的部分。2022/4/112022/4/11April 11, 2022 •书籍是屹立在时间的汪洋大海中的灯塔。
新浙教版九年级数学下册第三章《3.2简单几何体的三视图(1)》优质课课件

探究 二、你能说出这三个视图分别是从哪个 方向观察这本书得到的吗?
从正面看 从左面看 从上面看 这些图形的投影面分别在什么位置?
新授 一、把物体放在三个互相垂直的平面的 空间:
从投影的角度 认识三视图
主视图
正面
左视图
俯视图
侧面 水平面ຫໍສະໝຸດ 授 二、用投影的方法画三视图:左视图、右视图 各是什么形状?
主视图
左视图 高
长
宽
宽 俯视图
(1)确定主视图的位置,画出主视图;
(2)在主视图的下方画出俯视图,注意 与主视图“长对正”; (3)在主视图的右方画出左视图,注意 与主视图“高齐平”,与俯视图“宽相
巩固
1、找出与图中的几何体对应的三视图, 在三视图下面的括号内填上对应数码:
(1)
(2)
(3)
(4)
3.2简单几何体的三视图(第1课时)
导入
※下图表示从不同方向看到一架飞机的 图形:
主视图
左视图
俯视图
探究
一、请你从前、后、左、右、上、下六 个面观察同一本字典,画出得到的正投 影,你有什么发现?
1、正面和背面正投影 的形状、大小一致;
2、顶面和底面正投影 的形状、大小一致; 3、左面和右面正投影 的形状、大小一致;
•
新授 三、将三视图结合起来:
主视图
左视图
主视图
俯视图
正面
左视图
俯视图
侧面 水平面
归纳 基本几何体三视图的位置规定:
主视图在左上边,它的下方应是 俯视图,左视图坐落在主视图的右边。
新授 四、观察三视图,比较长、宽、高:
主视图
高 高齐 高
左视图
平
新浙教版九年级数学下册第三章《3.3由三视图描述几何体》公开课课件.ppt
量出三视图的有关尺寸,并根据已知的比例求 出它的侧面积.
E
OM
L
4.5 cm
F 3 cm G N
K
C H D 比例 1:2
2 cm
2.5 cm
BA
1.5cm
R 6cm
4cm
Q
P 5 cmS
9cm
XU
T
3cm
巩固练习:
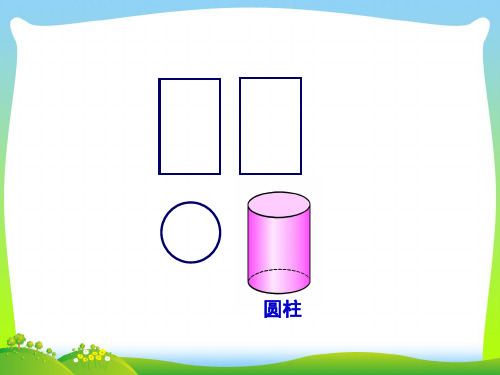
已知一个几何体的三视图如图所示,描述该几何体的形状,
请依据三视图中所给的尺寸求出它的侧面积。
主视图 左视图
俯视图
圆柱
机器零件的三视图
3.3由三视图描述几何体
主视图 左视图
主视图 左视图
俯视图
直长三方棱体柱
俯视图 三四圆棱棱锥锥锥
你能从下面所给的三视图中推断出它们分别表示什么 几何体吗?
例 :已知一个几何体的三视图如图所示,描述该 几何体的形状.
E
HM
L
F
GN
C
D
BA
K
答:这个几何体是 底面为直角梯形的 直四棱柱。
主视图 左视图
311
1 俯视图
9、春去春又回,新桃换旧符。在那桃花盛开的地方,在这醉人芬芳的季节,愿你生活像春天一样阳光,心情像桃花一样美丽,日子像桃子一样甜蜜。 2020/12/192020/12/19Saturday, December 19, 2020
10、人的志向通常和他们的能力成正比例。2020/12/192020/12/192020/12/1912/19/2020 11:34:21 AM 11、夫学须志也,才须学也,非学无以广才,非志无以成学。2020/12/192020/12/192020/12/19Dec-2019-Dec-20 12、越是无能的人,越喜欢挑剔别人的错儿。2020/12/192020/12/192020/12/19Saturday, December 19, 2020 13、志不立,天下无可成之事。2020/12/192020/12/192020/12/192020/12/1912/19/2020
九年级数学下册 3.2 简单几何体的三视图课件3 (新版)浙教版

解: (1)从三个方向看立体图形,图象都是矩形,可以想象 (xiǎngxiàng)出:整体是长方体,如图所示.
第五页,共15页。
(2)从正面、侧面看立体图形(túxíng),图象都是等腰三角形;从上面看,图 象是圆;可以想象出:整体是圆锥,如图所示
第六页,共15页。
例5 根据物体(wùtǐ)的三视图摸索物体(wùtǐ)的现状.
第一页,共15页。
根据如图右 边(yòu bian)的 椅子的视图,工 人就能制造出 符合设计要求 的椅子.
由于三视图不仅反映了物体的形状,而且反映了各个方 向的尺寸大小,设计(shèjì)人员可以把自己构思的创造物用 三视图表示出来,再由工人制造出符合各种要求的机器、工 具、生活用品等,因此三视图在许多行业有着广泛的应用.
注意:根据“长对正,高平齐,宽相等” 画 三视图必须遵循的法则作图。
第十四页,共15页。
辨一辨,说一说:
1、一个几何体的视图是唯一的,但从 视图反过来考虑几何体时,它有多种可 能性。请你举一些(yīxiē)例子加以说明.
提示:例如(lìrú)正方体的主视图是一个正 方形,但主视图是正方形的几何体就有很 多,如四棱柱,长方体,圆柱等.
第十五页,共15页。
第十二页,共15页。
【反思(fǎn sī)】
1、你能画出一个几何体的三视图吗?
2、你能由三视图得到(dé dào)该几何 体吗?
3、你会由“给出数字(shùzì)的俯视图” 画出几何体的主视图、左视图吗?
第十三页,共15页。
动手(dòng shǒu)设计
请画出下面立体(lìtǐ)图形的三视图。
俯视(fǔshì)方向
第十页,共15页。
【探究探(t究ànjiū)】 (tànjiū)
第五页,共15页。
(2)从正面、侧面看立体图形(túxíng),图象都是等腰三角形;从上面看,图 象是圆;可以想象出:整体是圆锥,如图所示
第六页,共15页。
例5 根据物体(wùtǐ)的三视图摸索物体(wùtǐ)的现状.
第一页,共15页。
根据如图右 边(yòu bian)的 椅子的视图,工 人就能制造出 符合设计要求 的椅子.
由于三视图不仅反映了物体的形状,而且反映了各个方 向的尺寸大小,设计(shèjì)人员可以把自己构思的创造物用 三视图表示出来,再由工人制造出符合各种要求的机器、工 具、生活用品等,因此三视图在许多行业有着广泛的应用.
注意:根据“长对正,高平齐,宽相等” 画 三视图必须遵循的法则作图。
第十四页,共15页。
辨一辨,说一说:
1、一个几何体的视图是唯一的,但从 视图反过来考虑几何体时,它有多种可 能性。请你举一些(yīxiē)例子加以说明.
提示:例如(lìrú)正方体的主视图是一个正 方形,但主视图是正方形的几何体就有很 多,如四棱柱,长方体,圆柱等.
第十五页,共15页。
第十二页,共15页。
【反思(fǎn sī)】
1、你能画出一个几何体的三视图吗?
2、你能由三视图得到(dé dào)该几何 体吗?
3、你会由“给出数字(shùzì)的俯视图” 画出几何体的主视图、左视图吗?
第十三页,共15页。
动手(dòng shǒu)设计
请画出下面立体(lìtǐ)图形的三视图。
俯视(fǔshì)方向
第十页,共15页。
【探究探(t究ànjiū)】 (tànjiū)
《3.2 简单几何体的三视图》第一课时 课件 浙教版数学九年级下册

请观察下面三个投影,它们有什么相同与不同的地方?你能试着给正投影下 定义吗?
在平行投影中,如果投射线垂直于投影面,那么这种投影就称为正投影.
中心投影
斜投影
正投影
平行投影
投影
例 画出如图摆放的正方体在投影面P上的正投影. (1)正方体的一个面ABCD平行于投影面P; (2)正方体的一个面ABCD倾斜于投影面P,上底面ADEF垂直于投影面P.
正方体: 1、六个面都是相同的正方形; 2、12条棱都相等.
请说明立方体、长方体、直四棱柱、四棱柱、和棱柱的相互关系.
例2 观察如图所示的首饰盒,它是一个怎样的多面体?这个多面 体与直四棱柱有什么关系?
单位:cm 3
3 3
6 6
主视方向
棱
你发现规律了吗 ?? 侧棱(条) 侧面(个) 面(个) 顶点(个)棱 (条)
柱
三
的
棱
顶
柱
3
3Hale Waihona Puke 569点、 棱 、 侧
四 棱 柱
4
46
8 12
棱
、
五
侧
棱
面
柱
的
数
六
量
棱
关 系
柱
5
5
7 10 15
6
6 8 12 18
n棱柱
n
n n+2 2n 3n
向的正投影.正投影面
上的正投影就是主视
图,水平投影面上的
正投影就是俯视图,
左视图
侧投影面上的正投影
就是左视图
三视图的对应规律
主视图和俯视图 ----长对正
主视图和左视图 ----高平齐
俯视图和左视图 ----宽相等
在平行投影中,如果投射线垂直于投影面,那么这种投影就称为正投影.
中心投影
斜投影
正投影
平行投影
投影
例 画出如图摆放的正方体在投影面P上的正投影. (1)正方体的一个面ABCD平行于投影面P; (2)正方体的一个面ABCD倾斜于投影面P,上底面ADEF垂直于投影面P.
正方体: 1、六个面都是相同的正方形; 2、12条棱都相等.
请说明立方体、长方体、直四棱柱、四棱柱、和棱柱的相互关系.
例2 观察如图所示的首饰盒,它是一个怎样的多面体?这个多面 体与直四棱柱有什么关系?
单位:cm 3
3 3
6 6
主视方向
棱
你发现规律了吗 ?? 侧棱(条) 侧面(个) 面(个) 顶点(个)棱 (条)
柱
三
的
棱
顶
柱
3
3Hale Waihona Puke 569点、 棱 、 侧
四 棱 柱
4
46
8 12
棱
、
五
侧
棱
面
柱
的
数
六
量
棱
关 系
柱
5
5
7 10 15
6
6 8 12 18
n棱柱
n
n n+2 2n 3n
向的正投影.正投影面
上的正投影就是主视
图,水平投影面上的
正投影就是俯视图,
左视图
侧投影面上的正投影
就是左视图
三视图的对应规律
主视图和俯视图 ----长对正
主视图和左视图 ----高平齐
俯视图和左视图 ----宽相等
浙教版九年级数学下册第三章《3.2简单几何体的三视图(1)》精品课件

长对正、高平齐、宽相等
“长对正、高平齐、宽相等”是画三视图必须 遵循的法则. 在画三视图时,我们一般先选择 主视方向,画出主视图,再把左视图画在主 视图的右边,把俯视图画在主视图的下方.
例1 一个长方体如图,它的 底面是一个正方形. 请按立 体图的尺寸大小和指定的主 视方向画出三视图.
解:所求三视图如图.
解:按1 颐2的比例,画出三视图如图.
练一练
完成课内练习1,2,3
小结
什么是三视图 三视图的画法是…… ……
作业布置
见配套作业本
物体在正投影面上的正 投影叫做主视图;在水 平投影面上的正投影叫 做俯视图;在侧投影面 上的正投影叫做左视图.
主视图、左视图和俯视 图合称三视图.
产生主视图的投影线方 向也叫做主视方向.
从图可以看出,在三视图中,主视图和俯视 图共同反映了物体左右方向的尺寸,通常称 之为“长对正”;主视图和左视图共同反映 了物体上下方向的尺寸,通常称之为“高平 齐”;俯视图和左视图共同反映了物体前后 方向的尺寸,通常称之为“宽相等”.
10、阅读一切好书如同和过去最杰出的人谈话。2021/7/302021/7/302021/7/307/30/2021 9:12:01 AM
11、一个好的教师,是一个懂得心理学和教育学的人。2021/7/302021/7/302021/7/30Jul-2130-Jul-21
12、要记住,你不仅是教课的教师,也是学生的教育者,生活的导师和道德的引路人。2021/7/302021/7/302021/7/30Friday, July 30, 2021
棱柱是特殊的几何体, 分为直棱柱和斜棱柱,
现阶段我们只讨论直 棱柱.直棱柱的上下底 面可以是三角形、四 边形、五边形……侧 面都是矩形,上、下 底面是全等多边形. 根 据底面图形的边数,
浙教版九年级下3.2简单几何体的三视图(1)课件(共28张PPT)

谢谢观赏
You made my day!
我们,还在路上……
3.2简单几何体的三视图(1)
(2)画出长方体与水平投影面上的正 投影(棱A,A在水平投影面上的正投 影为A’),得到的正投影是什么图形? 它与长方体的底面有什么关系?
想一想:长方体按下图摆放,在平行光
线下,它分别在水平投影面、侧投影面、 正投影面三个相互垂直的平面上的正投 影是什么图形?
想一想:长方体按下图摆放,在平行光
俯视图
例1:一个长方体的立体图如图所示,长为4,宽为2, 高为3,请画它的三视图.
3cm
4cm
2cm
主视方面
线段DG 线段IH
线段EF
线段DE 矩形DIHG
长方体和立方体都是直四棱柱。
•1、书籍是朋友,虽然没有热情,但是非常忠实。2022年3月2日星期三2022/3/22022/3/22022/3/2 •2、科学的灵感,决不是坐等可以等来的。如果说,科学上的发现有什么偶然的机遇的话,那么这种‘偶然的机遇’只能给那些学有素养的人,给那些善于独 立思考的人,给那些具有锲而不舍的人。2022年3月2022/3/22022/3/22022/3/23/2/2022 •3、书籍—通过心灵观察世界的窗口.住宅里没有书,犹如房间里没有窗户。2022/3/22022/3/2March 2, 2022 •4、享受阅读快乐,提高生活质量。2022/3/22022/3/22022/3/22022/3/2
线下,它分别在水平投影面、侧投影面、 正投影面三个相互垂直的平面上的正投 影是什么图形?
※我们把物体的正投影称为视图. ※物体在正投影面、侧投影面和水平投影面上得 到的视图分别称为主视图、左视图和俯视图,它 们统称为三视图.
产生主视图的投射线方向 叫做主视方向
You made my day!
我们,还在路上……
3.2简单几何体的三视图(1)
(2)画出长方体与水平投影面上的正 投影(棱A,A在水平投影面上的正投 影为A’),得到的正投影是什么图形? 它与长方体的底面有什么关系?
想一想:长方体按下图摆放,在平行光
线下,它分别在水平投影面、侧投影面、 正投影面三个相互垂直的平面上的正投 影是什么图形?
想一想:长方体按下图摆放,在平行光
俯视图
例1:一个长方体的立体图如图所示,长为4,宽为2, 高为3,请画它的三视图.
3cm
4cm
2cm
主视方面
线段DG 线段IH
线段EF
线段DE 矩形DIHG
长方体和立方体都是直四棱柱。
•1、书籍是朋友,虽然没有热情,但是非常忠实。2022年3月2日星期三2022/3/22022/3/22022/3/2 •2、科学的灵感,决不是坐等可以等来的。如果说,科学上的发现有什么偶然的机遇的话,那么这种‘偶然的机遇’只能给那些学有素养的人,给那些善于独 立思考的人,给那些具有锲而不舍的人。2022年3月2022/3/22022/3/22022/3/23/2/2022 •3、书籍—通过心灵观察世界的窗口.住宅里没有书,犹如房间里没有窗户。2022/3/22022/3/2March 2, 2022 •4、享受阅读快乐,提高生活质量。2022/3/22022/3/22022/3/22022/3/2
线下,它分别在水平投影面、侧投影面、 正投影面三个相互垂直的平面上的正投 影是什么图形?
※我们把物体的正投影称为视图. ※物体在正投影面、侧投影面和水平投影面上得 到的视图分别称为主视图、左视图和俯视图,它 们统称为三视图.
产生主视图的投射线方向 叫做主视方向
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
( 第1题 )
圆锥,
球的三视图.
主视图 左视图
主 视 图
左 视 图
俯视图
俯视图
立方体的三视图都是正方形。
主视图
左视图
俯视图
例1:一个长方体的立体图如图所示,长为4,宽为2, 高为3,请画它的三视图. 主视图 左视图
高 平 齐
1cm 长对正 3cm
2cm
宽相等
主视方向 俯视图 主视图和俯视图共同反映左右方向的尺寸, 常称为“长对正”; 主视图和左视图共同反映上下方向的尺寸,常称为“高平齐”; 俯视图和左视图共同反映前后方向的尺寸,常称为“宽相等”
宽 相 等
俯视图
拓展练习:
1、若干个相同的小正方体搭成的 几何体的俯视图如图,各小方格内 的数字表示叠在该层位置的小正方 体的个数,则这个几何体的左视图 是( A ),主视图是( B )
A. B. C. D.
3
2
1
2、下列是由一些相同的小正方体构 成的几何体的三视图,这些相同小正 方体的个数是( B ) A.3个 B.4个 C.5个 D.6个
猜 猜 他 们 是 什 么 关 系 ?
看 事 物 不 能 只 看 单 方 面
从不同的方向观察同一物体时,可能看到不同的图形。
主视图
左视图
从上面看
从左面看 从 正 面 看 主视图:从正面看到的图形
俯视图 左视图:从左面看到的图形 俯视图:从上面看到的图形
主视图
左视图
俯视图
主视图
左视图
俯视图
1.说出圆锥、球的三视图各是什么图形.
例2:由5个相同的小立方块搭成的几何体如图所 示,请画出它的三视图:
主视图
高平齐
左视图
长对正 宽相等
俯视图
1、下图是由几个小立方块所搭出的俯视 图,小正方形中的数字表示该位置小立方 块 的个数,你能画出这个几何体的主视 图和左视图吗? 1 1 2 3
2
主视图
高 平 齐 长 对 正
左视图
主视方向
主视图
左视图
俯视图
本节课你的收获是什么?
