最新浙教版九年级数学下册1.3解直角三角形公开课优质PPT课件(12)
合集下载
浙教版数学九年级下册1.3《解直角三角形》课件(共34张PPT)

3 3
0 1 0
2 2
3 2
1
0
不存在
2 2
1 2
1
3
互余两角三角函数关系: sin(90°-A)=cosA tanAtanB=1 同角三角函数关系: sin2A+cos2A=1 cos(90°-A)=sinA
sin A tan A cos A
引例:山坡上种树,要求株距(相临两树间的水平距离)
500 3 250 3 m 2
北
C
B 500
300 东 O
在Rt△BOC中, ∠BOC=45°,
BC OC 250 3 m
250 1 3 3 60 14000 m h 14 km h
∴AB=AC+BC
250 250 3 250 1 3 m
2 2
tan
h 3.5 0.7, l 5 2
35
答:斜面钢条a的长度约为6.1米,坡角约为35°.
例2、如图,在Rt△ABC中,∠C=90°,∠A=50°, AB=3,求∠B和a,b(边长保留2个有效数字) 解:Rt△ABC中 ∠B=90°-∠A=40° A 3
a sin A AB
答:船的航速约为14km/h.
例.如图,两建筑物的水平距离BC为24米,从点A测得点D 的俯角α=30°,测得点C 的俯角β=60°,求AB 和CD 两座 建筑物的高.(结果保留根号) 分析: 过D作DE∥BC, 问题可化归为解Rt△ABC 和Rt△AED. C E A β α
D
B
已知:BC=24m, ∠α=30°, ∠β=60°. 求:AB,CD的高.
0 1 0
2 2
3 2
1
0
不存在
2 2
1 2
1
3
互余两角三角函数关系: sin(90°-A)=cosA tanAtanB=1 同角三角函数关系: sin2A+cos2A=1 cos(90°-A)=sinA
sin A tan A cos A
引例:山坡上种树,要求株距(相临两树间的水平距离)
500 3 250 3 m 2
北
C
B 500
300 东 O
在Rt△BOC中, ∠BOC=45°,
BC OC 250 3 m
250 1 3 3 60 14000 m h 14 km h
∴AB=AC+BC
250 250 3 250 1 3 m
2 2
tan
h 3.5 0.7, l 5 2
35
答:斜面钢条a的长度约为6.1米,坡角约为35°.
例2、如图,在Rt△ABC中,∠C=90°,∠A=50°, AB=3,求∠B和a,b(边长保留2个有效数字) 解:Rt△ABC中 ∠B=90°-∠A=40° A 3
a sin A AB
答:船的航速约为14km/h.
例.如图,两建筑物的水平距离BC为24米,从点A测得点D 的俯角α=30°,测得点C 的俯角β=60°,求AB 和CD 两座 建筑物的高.(结果保留根号) 分析: 过D作DE∥BC, 问题可化归为解Rt△ABC 和Rt△AED. C E A β α
D
B
已知:BC=24m, ∠α=30°, ∠β=60°. 求:AB,CD的高.
浙教版数学九年级下册1.3.3解直角三角形 课件(共15张PPT)

那什么是仰角?什么是俯角呢?
导入新知
如图, 在进行测量时,从 下向上看,视线与水平线 的夹角叫做仰角;
仰角 俯角
从上往下看,视线与水平线的夹角叫做俯角. 【分析】(1)C观测D的仰角应为CD与水平面的较小的夹 角,即∠DCE;C观测B的俯角应为CB与水平线的较小的夹 角,即为∠BCE,不难得出∠BCD=∠DCE+∠BCE;(2) 易得CE=AB,则由直角三角形的锐角函数值即可分别求得 BE和DE,求和即可.
拓展延伸 1.如图,物华大厦离小伟家60m,小伟 从自家的窗中眺望大厦,并测得大厦顶 部仰角是450,而大厦底部的俯角是370, 求该大厦的的高度 (结果精确到0.1m).
分析:结合仰角与俯角理解图形,先过点A作AE⊥CD于 E,可得四边形ABCE是矩形,可得BC=AE,然后分别解 两个直角三角形,可得大厦的高度.
新知讲解
问题2:如图,学校的实验楼对面是一幢教学楼,小敏在实验 楼的窗口C测得教学楼顶总D的仰角为18°,教学楼底部B的俯 角为20°,量得实验楼与教学楼之间的距离AB=30m. (结果精确到0.1m.参考数据: tan20°≈0.36,tan18°≈0.32) (2)求教学楼的高BD .
解:(2)由已知得CE=AB=30(m), 在Rt△CBE中,BE=CE×tan20°≈30×0.36=10.80(m), 在Rt△CDE中,DE=CE×tan18°≈30×0.32=9.60(m), ∴教学楼的高BD=BE+DE=10.80+9.60≈20.4(m). 答:教学楼的高为20.4m.
1.3 解直角三角形(3)
—— 仰角与俯角
浙教版
九年级下
导入新知
复习回顾: 堤坝横断面的问题实质是解有关梯形的计算问题,利 用坡度可以把有关线段分别与梯形的高建立联系,从 而求解. 某人沿着坡角为45 °的斜坡走了310 2 m,则此人的垂 直高度增加了____________m . 310
浙教版九年级数学下册第一章《 解直角三角形》公开课课件

3.选择合适的边角关系式,使计算尽可能简单,且 不易出错.
4.按照题中的精确度进行计算,并按照题目中要求的 精确度确定答案以及注明单位.
你会了吗?
问题:一人在塔底A处测 得塔顶C的仰角为45°, 此人向塔前100米到B处, 又测得塔顶的仰角为60°, 已知测角器的高度为2米, 求塔高.
45° A 100
• 17、儿童是中心,教育的措施便围绕他们而组织起来。2021/7/302021/7/302021/7/302021/7/30
• 2、Our destiny offers not only the cup of despair, but the chalice of opportunity. (Richard Nixon, American President )命运给予我们的不是失望之酒,而是机会之杯。二〇二一年六月十七日2021年6月17日星期四 • 3、Patience is bitter, but its fruit is sweet. (Jean Jacques Rousseau , French thinker)忍耐是痛苦的,但它的果实是甜蜜的。10:516.17.202110:516.17.202110:5110:51:196.17.202110:516.17.2021 • 4、All that you do, do with your might; things done by halves are never done right. ----R.H. Stoddard, American poet做一切事都应尽力而为,半途而废永远不行6.17.20216.17.202110:5110:5110:51:1910:51:19 • 5、You have to believe in yourself. That's the secret of success. ----Charles Chaplin人必须相信自己,这是成功的秘诀。-Thursday, June 17, 2021June 21Thursday, June 17, 20216/17/2021
4.按照题中的精确度进行计算,并按照题目中要求的 精确度确定答案以及注明单位.
你会了吗?
问题:一人在塔底A处测 得塔顶C的仰角为45°, 此人向塔前100米到B处, 又测得塔顶的仰角为60°, 已知测角器的高度为2米, 求塔高.
45° A 100
• 17、儿童是中心,教育的措施便围绕他们而组织起来。2021/7/302021/7/302021/7/302021/7/30
• 2、Our destiny offers not only the cup of despair, but the chalice of opportunity. (Richard Nixon, American President )命运给予我们的不是失望之酒,而是机会之杯。二〇二一年六月十七日2021年6月17日星期四 • 3、Patience is bitter, but its fruit is sweet. (Jean Jacques Rousseau , French thinker)忍耐是痛苦的,但它的果实是甜蜜的。10:516.17.202110:516.17.202110:5110:51:196.17.202110:516.17.2021 • 4、All that you do, do with your might; things done by halves are never done right. ----R.H. Stoddard, American poet做一切事都应尽力而为,半途而废永远不行6.17.20216.17.202110:5110:5110:51:1910:51:19 • 5、You have to believe in yourself. That's the secret of success. ----Charles Chaplin人必须相信自己,这是成功的秘诀。-Thursday, June 17, 2021June 21Thursday, June 17, 20216/17/2021
浙教版九年级下1.3.1解直角三角形课件(共16张PPT)

谢谢观赏
You made my day!
我们,还在路上……
(来自《点拨》)
知1-讲
例1 在Rt△ABC中,∠C=90°,c=2 3 ,a=3,解这
个直角三角形. 解析:已知斜边和一条直角边的长,可以先利用勾股定理
求出另一条直角边的长,再利用正弦或余弦求角的 度数.
(来自《点拨》)
解: 在Rt△ABC中,c= 2 3 , a=3, ∴ bc2a21293
∴b=AB·cosA=3cos50°≈1.9.
总结
知2-讲
已知斜边c和一锐角∠A,解直角三角形的一般步骤是:
(1)根据∠A+∠B=90°求出∠B;
(2)根据sin
A=
a c
(3)根据cos A= b c
求出a; 求出b或根据勾股定理求出b.
(来自《点拨》)
知2-练
1 在Rt△ABC中,∠C=90°. (1)若∠B=60°, BC= 2 , 则∠A=_______,AC= ________,AB=________; (2)若∠A=45°,AB=2,则∠B=________,AC= ________,BC=________.
知两边解直角 三角形
形 添设辅助线解
直角三角形
知斜边一锐角解直 角三角形
知一直角边一锐角 解直角三角形
知两直角边解直 角三角形
知一斜边一直角 解直角三角形
实际 应用
直接抽象出直 角三角形
抽象出图形,再 添设辅助线求解
1.必做:完成教材P19作业题A组T1-T4 2.补充: 请完成《典中点》剩余部分习题
(来自《典中点》)
知1-练
2 在Rt△ABC中,∠C=90°. (1)若c= 6 2 , a=6,则b=________,∠B=______, ∠A=________; (2)若a= 4 3 , b=4,则∠A=______,∠B=______, c=________.
You made my day!
我们,还在路上……
(来自《点拨》)
知1-讲
例1 在Rt△ABC中,∠C=90°,c=2 3 ,a=3,解这
个直角三角形. 解析:已知斜边和一条直角边的长,可以先利用勾股定理
求出另一条直角边的长,再利用正弦或余弦求角的 度数.
(来自《点拨》)
解: 在Rt△ABC中,c= 2 3 , a=3, ∴ bc2a21293
∴b=AB·cosA=3cos50°≈1.9.
总结
知2-讲
已知斜边c和一锐角∠A,解直角三角形的一般步骤是:
(1)根据∠A+∠B=90°求出∠B;
(2)根据sin
A=
a c
(3)根据cos A= b c
求出a; 求出b或根据勾股定理求出b.
(来自《点拨》)
知2-练
1 在Rt△ABC中,∠C=90°. (1)若∠B=60°, BC= 2 , 则∠A=_______,AC= ________,AB=________; (2)若∠A=45°,AB=2,则∠B=________,AC= ________,BC=________.
知两边解直角 三角形
形 添设辅助线解
直角三角形
知斜边一锐角解直 角三角形
知一直角边一锐角 解直角三角形
知两直角边解直 角三角形
知一斜边一直角 解直角三角形
实际 应用
直接抽象出直 角三角形
抽象出图形,再 添设辅助线求解
1.必做:完成教材P19作业题A组T1-T4 2.补充: 请完成《典中点》剩余部分习题
(来自《典中点》)
知1-练
2 在Rt△ABC中,∠C=90°. (1)若c= 6 2 , a=6,则b=________,∠B=______, ∠A=________; (2)若a= 4 3 , b=4,则∠A=______,∠B=______, c=________.
九年级数学下册 第一章 解直角三角形 1.3 解直角三角形①课件 (新版)浙教版

精品课件
5
2020/1/1
精品课件
6
5. 一个住宅区的配电房示意图如图所示, 它是一个轴对称图形援 求配电房房顶离地 面的高度(精确到 0.1m).
2020/1/1
精品课件
7
6. 如图,在一张长方形纸片ABCD中,AD=25cm,AB=20cm, 点 E,F分别是CD和AB的中点.现将这张纸片按图示方式折叠,求 ∠DAH的大小及EG的长(精确到0.1cm).
●本节教学的重点是运用三角函数解直角三角形的方法.
●解直角三角形的过程中,由已知条件求某条边或某个角的方 法,以及求这些边、角的顺序往往不唯一,如何让学生学会选 择较优的方法和求解顺序,是本节教学的难点.
2020/1/1
精品课件
2
2020/1/1
精品课件
3
2020/1/1
精品课件
4
2020/1/1
1.3 解直角三角形①
2020/1/1
精品课件
1
教学目标:
1. 经历运用锐角三角函数、勾股定理等知识解决在直角三角 形中, 由已知的一些边、角,求出另一些边角的问题的过 程.了解解直角三角形的概念.
2. 会运用锐角三角函数、勾股定理等知识解直角三角形,以 及解决与直角三角形有关的简单实际问题.
重难点:
∠DAH =60°,
EG 25 10 3 7.(7 cm).
2020/1/1
精品课件
8
编后语
折叠课件作用 ①向学习者提示的各种教学信息; ②用于对学习过程进行诊断、评价、处方和学习引导的各种信息和信息处理; ③为了提高学习积极性,制造学习动机,用于强化学习刺激的学习评价信息; ④用于更新学习数据、实现学习过程控制的教学策略和学习过程的控制方法。 对于课件理论、技术上都刚起步的老师来说,POWERPOINT是个最佳的选择。因为操作上非常简单,大部分人半天就可以基本掌握。所以,就可以花心思
浙教版九下 1.3解直角三角形 课件

的关系
正切函数:tan
A
A的对边 A的邻边
余切函数:cot
A
A的邻边 A的对边
解直角三角形:(如图)
B
例1.在⊿ABC中,∠C=900,
C
A
1.已知a,b.解直角三角形
(即求:∠A,∠B及C边)
知∠A,b. 解直角三角形
4. 已知∠A,c. 解直角三角形
A
A的对边 A的邻边
余切函数:cot
A
A的邻边 A的对边
特殊角的三角函数值: 00 300 450 600 900
sinA 0 1 2 3 1
2
2
2
cosA 1 3 2 1 0
2
2
2
tanA 0
3 3
1
3∝
cotA ∝
31
30
3
互余两角三角函数关系:
Sin(900-A)=cosA cos(900-A)=sinA tan(900-A)=cotA cot(900-A)=tanA
解直角三角形
三角函数定义
锐角三
特殊角的三角函数值
解 角函数
互余两角三角函数关系
直
同角三角函数关系
角
三
角
两锐角之间的关系
形 解直角 三边之间的关系
三角形
边角之间的关系
定义 函数值 互余关系 函数关系
正弦函数:sin
A
A的对边 斜边
三 角 函 数
余弦函数:cos
A
A的邻边 斜边
定 义
正切函数:tan
同角三角函数关系:
1. sin2A+cos2A=1
浙教版 九年级数学 下册 第一章 1.3 解直角三角形 课件(共18张PPT)

坡角: tan i h l
重要结论
SABC12absinC 1
SABC2bcsinA
1 SABC2acsinB
A
c
b
B
a
C
如图, 在进行测量时,从下向上看,
视线与水平线的夹角叫做仰角;从上往下 看,视线与水平线的夹角叫做俯角.
视线
铅
仰角
垂
线
俯角
水平线
视线
例1.海防哨所0发现,在它的北偏西300,距离哨所 500m的A处有一艘船向正东方向,经过3分时间后到 达哨所东北方向的B处.问船从A处到B处的航速是 多少km/h(精确到1km/h)?
C
600
B
4m
合作探究
(2)若王同学分别在点C、点D处将旗杆
上绳子分别拉成仰角为600、300,如图
A
量出CD=8米,你能求出旗杆AB的长吗?
D
300
8m
600
C
B
合作探究
(3)若王同学分别在点C、点D处将旗杆
上绳子分别拉成仰角为600、450,如图
A
量出CD=8米,你能求出旗杆AB的长吗?
D
450
北
A
B
300
O
东
解: 在Rt△AOC中,
北
OA=500m, ∠AOC=300,A
C
B
∴AC=OAsin∠AOC
=500sin300
500
=500×0.5=250(m)
300
∴OC=OAcos∠AOC
=500× 在Rt△BOC中,
3 2
=250
3 (m).
∠BOC=450,
O
核心:构造含
重要结论
SABC12absinC 1
SABC2bcsinA
1 SABC2acsinB
A
c
b
B
a
C
如图, 在进行测量时,从下向上看,
视线与水平线的夹角叫做仰角;从上往下 看,视线与水平线的夹角叫做俯角.
视线
铅
仰角
垂
线
俯角
水平线
视线
例1.海防哨所0发现,在它的北偏西300,距离哨所 500m的A处有一艘船向正东方向,经过3分时间后到 达哨所东北方向的B处.问船从A处到B处的航速是 多少km/h(精确到1km/h)?
C
600
B
4m
合作探究
(2)若王同学分别在点C、点D处将旗杆
上绳子分别拉成仰角为600、300,如图
A
量出CD=8米,你能求出旗杆AB的长吗?
D
300
8m
600
C
B
合作探究
(3)若王同学分别在点C、点D处将旗杆
上绳子分别拉成仰角为600、450,如图
A
量出CD=8米,你能求出旗杆AB的长吗?
D
450
北
A
B
300
O
东
解: 在Rt△AOC中,
北
OA=500m, ∠AOC=300,A
C
B
∴AC=OAsin∠AOC
=500sin300
500
=500×0.5=250(m)
300
∴OC=OAcos∠AOC
=500× 在Rt△BOC中,
3 2
=250
3 (m).
∠BOC=450,
O
核心:构造含
浙教版九年级下册 1.3解直角三角形 课件

正切函数:tan
A
A的对边 A的邻边
余切函数:cot
A
A的邻边 A的对边
解直角三角形:(如图)
B
例1.在⊿ABC中,∠C=900,
C
A
1.已知a,b.解直角三角形(
即求:∠A,∠B及C边)
2. 已知∠A,a.解直角三角形
3.已知∠A,b. 解直角三角形 4. 已知∠A,c. 解直角三角形
1.计算: 1 2-
解直角三角形
三角函数定义
锐角三
特殊角的三角函数值
解 角函数
互余两角三角函数关系
直
同角三角函数关系
角
三
角
两锐角之间的关系
形 解直角
三边之间的关系
三角形
边角之间的关系
定义 函数值 互余关系 函数关系
正弦函数:sin
A
A的对边 斜边
三 角 函 数 定
余弦函数:cos A
A的邻边 斜边
义
正切函数:tan
同角三角函数关系:
1. sin2A+cos2A=1
2.tan A sin A cos A
3. tanA·cotA=1
1.两锐角之间的关系:
B
A+B=900
解
a +b =c 直
2.三2边之间的关2系: 2
C
A
角
三
角 形
3.边角之间的 关系
正弦函数:sin
A
A的对边 斜边
余弦函数:cos
A
A的邻边 斜边
A
A的对边 A的邻边
余切函数:cot
A
A的邻边 A的对边
特殊角的三角函数值: 00 300 450 600 900
新浙教版九年级数学下册第一章《解直角三角形复习》公开课课件.ppt

B
┌ C D
C
再见
• 9、春去春又回,新桃换旧符。在那桃花盛开的地方,在这醉人芬芳的季节,愿你生活像春天一样阳光,心情像桃花一样美丽,日子像桃子一样甜蜜。 2020/12/192020/12/19Saturday, December 19, 2020
• 10、人的志向通常和他们的能力成正比例。2020/12/192020/12/192020/12/1912/19/2020 11:29:39 AM • 11、夫学须志也,才须学也,非学无以广才,非志无以成学。2020/12/192020/12/192020/12/19Dec-2019-Dec-20 • 12、越是无能的人,越喜欢挑剔别人的错儿。2020/12/192020/12/192020/12/19Saturday, December 19, 2020 • 13、志不立,天下无可成之事。2020/12/192020/12/192020/12/192020/12/1912/19/2020
礁的危险吗?
北
A
w要解决这个问题,我们可以将其数
东
学化,如图:
w请与同伴交流你是怎么想的? 怎么去做?
B
CD
钢缆长几何
w如图,一灯柱AB被一钢缆CD固定.CD与地面成 40°夹角,且DB5m.现再在CD上方2m处加固另 一根钢缆ED,那么,钢缆ED的长度为多少 (结果 精确到0.01m)?
w怎么 做?
A
⌒
D 60°
A
D
45° 75°
B
C
┓
B
E
C
[达标练习三]
1、 我军某部在一次野外训练中,有一辆坦克 准备通过一座和山顶的水平距离为1000米,山 高为565米,如果这辆坦克能够爬30°的斜坡, 试问:它能不能通过这座小山?
新浙教版九年级数学下册第一章《解直角三角形复习1》公开课课件.ppt

⑶已知∠A、 a,则b=_a___c__o__At__;c=___s_in__A___。斜边
已知一锐角、对边,求邻边,用锐角的余切;
c
求斜边,用锐角的正弦。
⑷已知a、b,则c=___a__2___b_2_。
⑸已知a、c,则b=___c_2___a_2__ 。
A 邻边b
B
对边
a
┏ C
[达标练习一]
1.在下列直角三角形中,不能解的是(B )
B
c
a
┏
A
b
Байду номын сангаас
C
第19章解直角三角形
一.知识结构
二.概括 1. 了解勾股定理的历史,经历勾股定理的探索过程; 2. 理解并掌握直角三角形中边角之间的关系; 3. 能应用直角三角形的边角关系解决有关实际问题.
直的
第 角边 解三 一 三角 直角 章 角关 角形
形系
实际应用
知一边一锐角 解直角三角形
知两边解直角 三角形
知斜边一锐角解 直角三角形
知一直角边一锐 角解直角三角形
〖 达 标
知两直角边解
一
直角三角形
〗
知一斜边一直角
添设辅助线解
边解直角三角形
直角三角形 〖达标二〗
直接抽象出直角 三角形
〖 达
抽象出图形,再 添设辅助线求解
标 三 〗
在Rt△ABC中,∠C为直角,∠A、∠B为锐角,
c a c 它们所对的边分别为 、 、b ,其中除直角 外,
求证: 2. ABCD的面积S=AB ·BC ·sinB
A
(∠B为锐角)。
⌒
D 60°
A
D
450
75°
九年级数学下册1.3解直角三角形课件3(新版)浙教版

3.选择合适的边角关系式,使计算尽可 精确度确定答案以及注明单位.
一人在塔底A处测得塔顶C 的仰角为45°,此人向塔 前100米到B处,又测得塔 顶的仰角为60°,已知测 角器的高度为2米,求塔高
.
45° A 100
60° B
C
第1章 解直角三角形
1.两锐角之间的关系
A: +B=90°
B
解 2.三边之间的关系:
直 角 三
a2+b2=c2 C 正弦函数:sin
A
=
A的对边 斜边
A
角 形
3.边角之间
余弦函数:cos
A
=
A的邻边 斜边
的关系
正切函数:tan
A
=
A的对边 A的邻边
余切函数:cot
A
=
A的邻边 A的对边
30°
a
A 1200米
B C
2.仰角:在视线与水平线所形成的角中,视线在
水平线上方的角. 俯角:在视线与水平线所形成的角中,视线
在水平线下方的角.
如图,某飞机于空中A处探测到目标C,此时飞行 高度AC=1200米,从飞机上看地平面控制点B的俯 角α=30°,求飞机A到控制点B距离 .
铅
仰角
垂
俯角
线
D
2米
边分别为a、b,这组邻边所夹的锐角为r时,则它
的面积能否用这三个已知量来表示呢?
1.弄清俯角、仰角、方位角等概念的意义,明确各
术语与示意图中的什么元素对应,只有明确这些概念, 才能恰当地把实际问题转化为数学问题
2.认真分析题意、画图并找出要求的直角三角形, 或通过添加辅助线构造直角三角形来解决问题.
A
α
一人在塔底A处测得塔顶C 的仰角为45°,此人向塔 前100米到B处,又测得塔 顶的仰角为60°,已知测 角器的高度为2米,求塔高
.
45° A 100
60° B
C
第1章 解直角三角形
1.两锐角之间的关系
A: +B=90°
B
解 2.三边之间的关系:
直 角 三
a2+b2=c2 C 正弦函数:sin
A
=
A的对边 斜边
A
角 形
3.边角之间
余弦函数:cos
A
=
A的邻边 斜边
的关系
正切函数:tan
A
=
A的对边 A的邻边
余切函数:cot
A
=
A的邻边 A的对边
30°
a
A 1200米
B C
2.仰角:在视线与水平线所形成的角中,视线在
水平线上方的角. 俯角:在视线与水平线所形成的角中,视线
在水平线下方的角.
如图,某飞机于空中A处探测到目标C,此时飞行 高度AC=1200米,从飞机上看地平面控制点B的俯 角α=30°,求飞机A到控制点B距离 .
铅
仰角
垂
俯角
线
D
2米
边分别为a、b,这组邻边所夹的锐角为r时,则它
的面积能否用这三个已知量来表示呢?
1.弄清俯角、仰角、方位角等概念的意义,明确各
术语与示意图中的什么元素对应,只有明确这些概念, 才能恰当地把实际问题转化为数学问题
2.认真分析题意、画图并找出要求的直角三角形, 或通过添加辅助线构造直角三角形来解决问题.
A
α
新浙教版九年级数学下册第一章《解直角三角形3》公开课课件
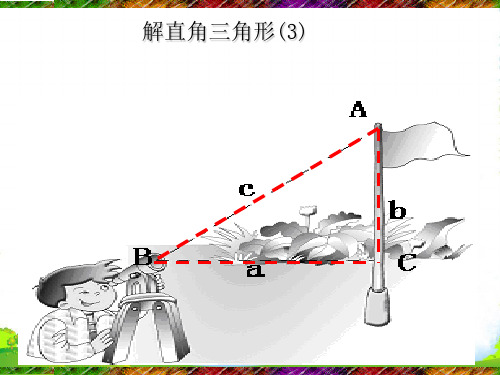
船 的 航 速 : 2 5 ( 0 1 3 ) 3 1 3 6 6 0 m /h 1 4 ( k m /h ) 6 0
答船从A处到B处的航速是每时约为14km
例3.为测甲,乙两楼的高度,测得两楼之间的距离为36m,从甲楼顶点A观测到乙楼顶D 的俯角为30°,观测到乙楼底C的俯角为45° 求这两楼的高度(精确到0.1m)
30°
60°
解设AB x米
在 R t A B D 中 , D 3 0 0 BD
AB
3x
tan 300
在 R t A B C 中 , A C B 6 0 0 BC
AB tan 600
3 x
3
CD BD BC 3x 3 x 8
AB x 4 3(米)
3
4 3 答:旗杆AB的长为 米.
从A处 下 水B到 时 间3: 002
2
45°
=150221( 2 秒)
A
C
从 A 跑C 到 下水 B 时 到 3 间 03 0 : 0 = 2 0( 10秒)
62
210<212
某海滨浴场的沿岸可以看作直线AC,如图所示,1号救生员在岸 边的A点看到海中的B点有人求救,便立即向前跑300米到离B点最 近的地点C再跳入海中游到B点救助;若每位救生员在岸上 跑步 的速度都是6米/秒,在水中游泳的速度都是2米/秒。
解直角三角形(3)
如图, 在进行测量时,从下向上看,
视线与水平线的夹角叫做仰角;从上往下 看,视线与水平线的夹角叫做俯角.
如图,为了测量电线杆的高度AB,在离 电线杆24米的C处,用高1.20米的测角仪CD 测得电线杆顶端B的仰角a=30°,求电线杆 AB的高.(精确到0.1米)
你会解吗?
2022年浙教初中数学九下《解直角三角形》PPT课件12

2.若 x1 xy0,则 x2006y2007 的
值为: ( ) A 、0 B、1 C、 -1 D、 2
3、求下列二次根式中字母x的取值范围:
⑴ 2x 1 ⑵ x2 3 ⑶ 2x 2x
⑷2
x5
⑸ x1 x 1
第一章 二次根式复习
4.若2<x<5化简 (x1)2 (x5)2
4 9
18 6
4
3
在直角坐标系内,点P(-2,2 )到原点的距离
为=
5.计算: (1) (1 2)2 ( 2 1)2( 6)2
(2) (2 23)3(2 2)
(3) ( 32)2006 ( 32)2007
(4) ( 27 1)( 12 1 4)5
3
5
人生就是慢慢成长, 每天取得进步
E作EF∥BC交CD于点F。已知
AB=4,BC=6,∠B=60°。
(1)求点E到BC的距离。
(2)点P为线段EF上的一个动
点,过点P作PM⊥EF交BC于
点M,过点M作MN∥AB交折线
ADC于点N,连接PN,设EP=x
①当点N在线段AD上时(如图
.
乙),△PMN的形状是否发生
改变?若不变,求出△PMN的
( 6 )2 ( 3 ) 2 (3 2 )3 (2 ) ;
第一章 二次根式复习
(7) a2b22a(b ab);
(8)a a2 (a0).
二次根式化简结果的要求: (1)根号内不含有开的尽方的因式; (2)根号内不含有分母.
例5
第一章 二次根式复习
设a、b、c为△ABC的三边,试化简:
( a b c ) 2 ( a b c ) 2 ( b a c ) 2 ( c a b ) 2
浙教版数学九下课件1.3解直角三角形2.1ppt

初中数学课件
灿若寒星*****整理制作
1. 解直角三角形.
在直角三角形中,由已知元素求出未知元素 的过程,叫做解直角三角形.
2.两种情况: 解直角三角形,只有下面两种情况: (1)已知两条边; (2)已知一条边和一个锐角
如图,在进行测量时,从下向上看,视线 与水平线的夹角叫做仰角;从上往下看, 视线与水平线的夹角叫做俯角.
A
35°12′
F
43°24′
D E
B
32.6
C
如图,在地面上的A点测得树顶C的仰角为 30°,沿着向树的方向前进6米到达B处, 测得树顶端C的仰角为45°.请画出测量示 意图,求出树高CD(精确到0.1米)
C
A
BD
小结: 1.找到实际问题与“解直角三角形”间 的 联系点; 2.分析题意后能画出准确的示意图
经过3分时间后到达哨所东北方向的B处。问船
从A处到B处的航速是每时多少KM(精确到
1KM/h)
北
A
C
B
30
45
o
东
例4.为知道甲,乙两楼间的距离,测得两楼
之间的距离为32.6m,从甲楼顶点A观测 到乙楼顶D的俯角为35°12′,观测到乙 楼底C的俯角为43°24′.求这两楼的高 度(精确到0.1m)
高.(=DE×tana
=AC×tana
∴AB=BE+AE
=
AC×tana+CD
=9.17+1.20≈10.4(米)
答:电线杆的高度约为10.4米.
如图,某飞机于空中A处探
测到目标C,此时飞行高度
AC=1200米,从飞机上看地 面控制点B的俯角a=16゜31′, 求飞机A到控制点B的距离. (精确到1米)
灿若寒星*****整理制作
1. 解直角三角形.
在直角三角形中,由已知元素求出未知元素 的过程,叫做解直角三角形.
2.两种情况: 解直角三角形,只有下面两种情况: (1)已知两条边; (2)已知一条边和一个锐角
如图,在进行测量时,从下向上看,视线 与水平线的夹角叫做仰角;从上往下看, 视线与水平线的夹角叫做俯角.
A
35°12′
F
43°24′
D E
B
32.6
C
如图,在地面上的A点测得树顶C的仰角为 30°,沿着向树的方向前进6米到达B处, 测得树顶端C的仰角为45°.请画出测量示 意图,求出树高CD(精确到0.1米)
C
A
BD
小结: 1.找到实际问题与“解直角三角形”间 的 联系点; 2.分析题意后能画出准确的示意图
经过3分时间后到达哨所东北方向的B处。问船
从A处到B处的航速是每时多少KM(精确到
1KM/h)
北
A
C
B
30
45
o
东
例4.为知道甲,乙两楼间的距离,测得两楼
之间的距离为32.6m,从甲楼顶点A观测 到乙楼顶D的俯角为35°12′,观测到乙 楼底C的俯角为43°24′.求这两楼的高 度(精确到0.1m)
高.(=DE×tana
=AC×tana
∴AB=BE+AE
=
AC×tana+CD
=9.17+1.20≈10.4(米)
答:电线杆的高度约为10.4米.
如图,某飞机于空中A处探
测到目标C,此时飞行高度
AC=1200米,从飞机上看地 面控制点B的俯角a=16゜31′, 求飞机A到控制点B的距离. (精确到1米)
新浙教版九年级数学下册第一章《解直角三角形(复习)》公开课课件
B
D
旋转
A
45o 60o
B
D
C
45o 60o
oooooo66666660000000
o
平移
BDDDDDD
45o
D
45o
C
A
问题1:楼房BC的高度是多少?
问题2:楼房AD的高度是多少?
B 45º
M
30º
D
E
45o
C 50m A
5.如图,为了求河的宽度,在河对岸岸边任 意取一点A,再在河这边沿河边取两点B、C,使 得∠ABC=60°,∠ACB=45°,量得BC长为100米, 求河的宽度(. 即求BC边上的高)
3.某海滨浴场的沿岸可以看作直线AC,如图所示,1
号救生员在D点发现在他的北偏东30°方向的海中的点
B处有人求救,便立即沿海岸线向前跑60米到离B点最
近的点C再跳入海中游到点B救助;若救生员在岸上跑
步的速度都是6米/秒, 在水中游泳的速度是2米/秒。
而在同一时间2号救生员在点A处发现求救目标在他
的东北方向。
(1)若将坡道倾斜角改建
为30°(即∠CAO=30),
那么建筑物DE是否会被拆除? C
为什么?
建筑物
(2)如果你是当地 D
长官,你有什么好
E
AB
O
主意?
B
(1)请问1号救生员到达B处需要多长时
间?他的做法是否合理?
(2)请问2号救生员赶到B处最短
需要多长时间?
A
D
C
4. 如图已知铁塔塔基距楼房水平距离BD为50米,由楼顶A 望塔顶的仰角为45 º,由楼顶望塔底的俯角为30º,塔高DC为 ( )米
A
新浙教版九年级数学下册第一章《解直角三角形2》优质公开课课件.ppt

解:
tanatan5.20AC0.091
C
AB
A
α
B
ACABtan5.2
Dd
d
200.0911.82cm
l
d D 2 A C 6 .4 cm
例4
体育项目400M栏比赛中,规定相邻两栏架的路程为45M。 在弯道处,以跑道离内侧0.3M处的弧线(图1-19中的虚 线)的长度作为相邻两栏架之间的间隔路程。已知跑道的 内侧线半径为36M,问在设定A栏架后,B栏架离A栏架的 距离是多少( π 取3。14,结果精确到0。1M)。
A
D
B
C
• 9、春去春又回,新桃换旧符。在那桃花盛开的地方,在这醉人芬芳的季节,愿你生活像春天一样阳光,心情像桃花一样美丽,日子像桃子一样甜蜜。 2020/12/192020/12/19Saturday, December 19, 2020
• 10、人的志向通常和他们的能力成正比例。2020/12/192020/12/192020/12/1912/19/2020 11:28:08 AM • 11、夫学须志也,才须学也,非学无以广才,非志无以成学。2020/12/192020/12/192020/12/19Dec-2019-Dec-20 • 12、越是无能的人,越喜欢挑剔别人的错儿。2020/12/192020/12/192020/12/19Saturday, December 19, 2020 • 13、志不立,天下无可成之事。2020/12/192020/12/192020/12/192020/12/1912/19/2020
• 14、Thank you very much for taking me with you on that splendid outing to London. It was the first time that I had seen the Tower or any of the other famous sights. If I'd gone alone, I couldn't have seen nearly as much, because I wouldn't have known my way about.
