第七章 光的量子性 习题及答案
第七章 光的量子性

Vg应与光强有关,实际却与光的频率有关。 Vg应与光强有关,实际却与光的频率有关。矛盾 应与光强有关
3.照射时间长,积累能量多,只要照射足够长时间,总会有 照射时间长,积累能量多,只要照射足够长时间,
电子逸出,有电流。实际却是若入射光频率ν 电子逸出,有电流。实际却是若入射光频率ν <ν0 ,无论照 入射光频率 射多长时间,无光电流产生。 射多长时间,无光电流产生。 矛盾 光很弱,必须要照射长时间 才能积累足够的能量, 长时间, 积累足够的能量 4.光很弱,必须要照射长时间,才能积累足够的能量,使电 子从金属表面逸出。但实际却只要 不管I 多弱, 子从金属表面逸出。但实际却只要 ν >ν0,不管I0多弱,一 照上去,就有光电流产生。 矛盾 照上去,就有光电流产生。
普适常数就是黑体的单色幅出度。 普适常数就是黑体的单色幅出度。
∴基尔霍夫定律
M(ν ,T ) = Mb (ν ,T ) A(ν ,T )
T=5000k T=3000k
讨论:
1.同样温度下,黑体的辐射最大。 1.同样温度下,黑体的辐射最大。 同样温度下 2.绝对黑体不存在,黑体模型。 2.绝对黑体不存在,黑体模型。 绝对黑体不存在 3.黑体是否一定是黑的? 黑色物体是否就是黑体? 3.黑体是否一定是黑的? 黑色物体是否就是黑体? 黑体是否一定是黑的
一、黑体
黑体—在任何温度状态下全部吸收任何波长的电磁波. 黑体 在任何温度状态下全部吸收任何波长的电磁波. 在任何温度状态下全部吸收任何波长的电磁波 由
∴
Mb (ν ,T ) = f (ν ,T ) Ab (ν ,T )
黑体
Ab (ν , T ) = 1
Mb (ν ,T )
可见光 T=6000k
光的量子性作业.ppt

1 121.5107
R
9.德计物差布算质为U罗物波的意质公电h指波式场出波是中实长加物 的m速h粒 公0v后子 式,,与 是其初光 物速一hp质为样波零也的。的具公低电有式速子波是粒在动子电性的势
2m0eU 10.电子显微镜中的电子从静止开始通过电势差为
U则的约静为电9场38加V速后 ,1其.2U2德5 布nm罗意0.波04n长m是0.04nm
最小能量值的整数倍,对于频率为 的谐振子
来说,最小能量为 h
5.按其照 动爱量因大斯小坦= 光h子学说;,动如能果=光子h波c长为 ,则
6.在康普顿散射实验中,当光子与散射物质中的自 由电子或束缚较弱的电子发生碰撞时,光子能量 减少 ,波长 变长;当光子与原子内束缚较紧 的电子碰撞是,光子能量 不变 ,波长 不变
由此估算普朗克常量h的数值。
解:
hv
1 2
mm2
Wm
h
c
1
1 2
m12
Wm
c h
2
1 2
m22
Wm
h
1 2
mv1
2
1 2
mv2
2
(1.85 0.82) 1.60 1019
6.6 1034 J s
c( 1 1 )
3108 ( 1 1 ) 109
1 2
300 400
5.在康普顿效应中,已知入射光波长为1nm,求 在900方向上所散射的X射线波长。
5.67 10 8 J s2 m 2 K4 )
解:
P E0 4R 2 T 4 4R 2
5.67 10 8 34 4 3.14 (6371 10 3 )2
2.34 10 9 W
3.已知金属锂的功函数为2.13eV (1)用波长为410nm的光照射锂,计算所发出
第七章光的量子性习题及答案

1第七章 光的量子性1. 在深度远大于表面波波长的液体中,表面波的传播速度满足如下规律:v =224()2Fg l p p l r +式中g 为重力加速度,r 为液体密度,F为表面波的波长.试计算表面波的群速度.解:u = v - l vd dl = v-l dv d l =224()2g l p p l r + -l 224(()2d g d r lp p l l +=3422g F g F l p p lrl p p lr ++ 2. 测量二硫化碳的折射率实验数据为:当=589 nm .n ¢ = 1.629:当"l =656nm 时,n ¢¢=1.620 试求波长589nm 的光在二氧化硫的相速度、群速度和群折射率。
解:由v = c n 得 v 1 =2997924581.629= 1.840×108 m /s.v 2 =2997924581.620=1.8506×108 m /s所以△v = v 2 – v 1 = 1.057×106 m /s由一般瑞利公式由一般瑞利公式 u = v - l vl ¶¶=1.840×108 - 589 ×1.507×1.507×10106 /(656 – 589) = 1.747 ×108 m /sn = c /v = 299792458 /1.747×108 = 1.7163. 在测定光速的迈克尔逊旋转棱镜法中,设所用棱镜为正n 面棱柱体。
试导出:根据棱镜的转速、反射镜距离等数据计算光速公式。
解:设反射镜间距离为L 转速V 0 则n 面棱柱每转过面棱柱每转过 一个面,一个面,光往返一个来回。
所用时间光往返一个来回。
所用时间t = 1n /V 0 = 01nV 所以所以c = 2L /t = 021LnV = 2LnV 04.试用光的相速度v 和dvd l 来表示群速度u= d dk w,再用v 和dnd l 表示群速度u = d dk w解:(1) 由u = d dk w= v - l v l ¶¶ (2) 由 u = v - l vl¶¶<1 v = c /n <2>→ dvd l =()cd n d l = -223,(1)c dnn d c dn v dn v dv v v v dn n d n d n d ll l l l l l<>=+=+=+把〈把〈33〉代入〈〉代入〈11〉得dv u =v -d5.计算在下列各种色散介质中的传播的各种不同性质的波的群速度:(1)v = 常量 (2)v = al , ( a 为常量) (3)v = a /l (在水面上的表面张力波) (4)v = a /l (5)222v c b l =+(电离层的电磁波,其中c 是真空中的光速,l 是介质中的波长) (6)222c v c a ww em =-(在充满色散介质的直波导管中的电磁波,式中c 为真空中的光速,a 是与波导管有关的常量,()e e w =是介质的介电常数,()m m w =是介质的磁导率)解:(1)l ld dvv u -= ,0,==dv v 常量 所以常量==v u (2)l ld dv v u -=, l l l d a dv a v 2,==,所以222v a a a u ==-=l l l l (3)l l l2/32,ad dv av -==,所以v av u 2322/3=+=l l(4)dv uv d l l =-=()2ad a ad l l l l l -=v 2= (5)dv u v d ll =-=2222222222()d c b c c b d c b l l l l l ++-=+v c 2= (6)kv dk d u ==w w,,)1(11w ww d dvv v d dk u -== 而)(),(,222w m m w e e em w w==-=ac c v2/3222)(])(2[a c d d v v d dv -+-=em w w em w em w w w所以])(21[1w em em w em d d v cu +=6.利用维恩公式求:辐射的最概然频率v m ,辐射的最大光谱密度()m l e 辐射出射度M0(T)与温度的关系. 解: 由维恩位移定律T T b b T m m m 1×Þ=Þ=l l l 由斯沁藩公式()()44T T M T T M ×Þ=s7.太阳光谱非常接近于480m nm l =的绝对黑体的光谱.试求在1 s 内太阳由于辐射而损失的质量,并估算太阳的质量减少1% (由于热辐射)所经历的时间(太阳的质量m 0为2.0×1030千克,太阳的半径r 是7.0×108m) 解:由维恩位移公式解:由维恩位移公式m m bT b T l l =Þ=:由斯沁藩公式由斯沁藩公式34484()92.897810() 5.6705110()48010b b M T m s s l ---´===´´´=7.35×107瓦()()()瓦总262872106357.4100.714.341053.74´=´´´´´==×=r T M S T M P b b p由方程由方程P 总t =m 0×1%×c 221800.01 3.8810m c t sP ´´Þ==´总所以在1s 内kg 1015.5109106357.41916262´=´´=×=D c s P m 总损 8.地球表面每平方厘米每分钟由于辐射而损失的能量平均值为0.546J.如有有一黑体,它在辐射相同的能量时,温度应为多少? 解:解:4()0.546109160bM=´=()s m W ×/由斯沁藩公式由斯沁藩公式11()444()891()()()200.145.670510b bM M T T T Ks s-=Þ===´9.若有一黑体的辐出度等于5.70W /cm 2,试求该辐射最大光谱强度相对应的波长。
《光纤通信基础》习题及答案

光栅技术
第二章部分
2.1、光纤的结构由哪几部分组成?各有什么作用? 答:光纤(Optical Fiber)是由中心的纤芯和外围的包层同轴组成的圆柱形细丝。纤芯的 折射率比包层稍高,损耗比包层更低,光能量主要在纤芯内传输。包层为光的传输提供反射 面和光隔离,并起一定的机械保护作用。 2.2、简述光纤的类型包括哪几种以及各自特点? 解:实用光纤主要有三种基本类型: 1)、突变型多模光纤(Step Index Fiber, SIF), 纤芯折射率为 n1 保持不变,到包层突然 变为 n2。这种光纤一般纤芯直径 2a=50~80 μm,光线以折线形状沿纤芯中心轴线方向传播, 特点是信号畸变大。 2)、渐变型多模光纤(Graded Index Fiber, GIF), 在纤芯中心折射率最大为 n1,沿径向 r 向外围逐渐变小,直到包层变为 n2。这种光纤一般纤芯直径 2a 为 50μm,光线以正弦形 状沿纤芯中心轴线方向传播,特点是信号畸变小。 3)、单模光纤(Single Mode Fiber, SMF),折射率分布和突变型光 纤相似,纤芯直径只有 8~10 μm,光线以直线形状沿纤芯中心轴线方向传播。因为这种光 纤只能传输一个模式(两个偏振态简并),所以称为单模光纤,其信号畸变很小。 2.3、色散的产生以及危害? 答:由于光纤中所传信号的不同频率成分, 或信号能量的各种模式成分,在传输过程中, 因群速度不同互相散开,引起传输信号波形失真,脉冲展宽的物理现象称为色散;光纤色散 的存在使传输的信号脉冲畸变,从而限制了光纤的传输容量和传输带宽。 2.4、光缆的结构分类? 答:(1) 层绞式结构:层绞式光缆的结构类似于传统的电缆结构方式,故又称为古典式光缆。 (2) 骨架式结构:架式光缆中的光纤置放于塑料骨架的槽中,槽的横截面可以是 V 形、U 形 或其他合理的形状,槽的纵向呈螺旋形或正弦形,一个空槽可放置 5~10 根一次涂覆光纤。 (3) 束管式结构:束管式结构的光缆近年来得到了较快的发展。它相当于把松套管扩大为整 个纤芯,成为一个管腔,将光纤集中松放在其中。 (4) 带状式结构:带状式结构的光缆首先将一次涂覆的光纤放入塑料带内做成光纤带,然后 将几层光纤带叠放在一起构成光缆芯。 2.5、光缆的种类? 答:根据光缆的传输性能、距离和用途,光缆可以分为市话光缆、长途光缆、海底光缆和用
量子习题解答
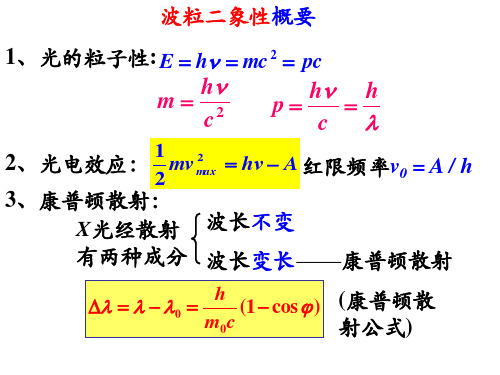
n 0,1,2,3...
8、氢原子: 氢原子能级:
me4 1 1 En 2 13.6 2 (e V) 2 2 2 (4 0 ) n n
轨道角动量
L l (l 1)
轨道角动量沿磁场方向分量:Lz m 主量子数 轨道量子数 轨道磁量子数
n=1,2,3…
l=0,1,2,3…,n-1 ml=-l,-(l-1),…,0,1,..,l
h 0 ( 1 cos ) m0 c
4、不确定关系(1927):
h 2
x p x (或, 或h) 位臵动量不确定关系: 2
能量时间不确定关系:Et / 2
5、氢原子光谱(1913) 谱线的波数
1 1 R ( 2 2 ) T ( m) T ( n) m n
玻尔磁子
电子自旋磁矩在磁场中的能量 Es B B
e B 9.27 10 24 J / T 2me
10、多电子原子的电子组态 电子的状态用4 个量子数n,l,ml,ms确定。n相同 的状态组成一壳层,可容纳2n2个电子;l相同 的状态组成一次壳层,可容纳2(2l+1)个电子。 基态原子电子组态遵循两个规律: (1)能量最低原理,即电子总处于可能最 低的能级。一般n越大,l越大,能量就越高。 (2)泡利不相容原理(1921),不可能有两个 或两个以上的电子处在同一量子状态。即不 能有两个电子具有相同的n, l, ml , ms。
解: 光子的散射角 θ π 时电子获得的能量最大, v 电子的反冲速度沿入射光子的运动方向.设 为入 pe 射光的频率,为散射光的频率, 为反冲电子的动 v 量。 1 由能量守恒有: h(v v) Ek
由动量守恒有: 2 式得 由1 、
2023年大学_光学教程第三版(姚启钧著)课后题答案下载

2023年光学教程第三版(姚启钧著)课后题答案下载2023年光学教程第三版(姚启钧著)课后题答案下载本教程以物理光学和应用光学为主体内容。
第1章到第3章为应用光学部分,介绍了几何光学基础知识和光在光学系统中的传播和成像特性,注意介绍了激光系统和红外系统;第4~8章为物理光学部分,讨论了光在各向同性介质、各向异性介质中的传播规律,光的干涉、衍射、偏振特性及光与物质的相互作用,并结合介绍了DWDM、双光子吸收、Raman放大、光学孤子等相关领域的应用和进展。
第9章则专门介绍航天光学遥感、自适应光学、红外与微光成像、瞬态光学、光学信息处理、微光学、单片光电集成等光学新技术。
光学教程第三版(姚启钧著):内容简介绪论0.1 光学的研究内容和方法0.2 光学发展简史第1章光的干涉1.1 波动的独立性、叠加性和相干性1.2 由单色波叠加所形成的干涉图样1.3 分波面双光束干涉1.4 干涉条纹的可见度光波的时间相干性和空间相干性 1.5 菲涅耳公式1.6 分振幅薄膜干涉(一)——等倾干涉1.7 分振幅薄膜干涉(二)——等厚干涉视窗与链接昆虫翅膀上的彩色1.8 迈克耳孙干涉仪1.9 法布里一珀罗干涉仪多光束干涉1.10 光的干涉应用举例牛顿环视窗与链接增透膜与高反射膜附录1.1 振动叠加的三种计算方法附录1.2 简谐波的表达式复振幅附录1.3 菲涅耳公式的推导附录1.4 额外光程差附录1.5 有关法布里一珀罗干涉仪的(1-38)式的推导附录1.6 有同一相位差的多光束叠加习题第2章光的衍射2.1 惠更斯一菲涅耳原理2.2 菲涅耳半波带菲涅耳衍射视窗与链接透镜与波带片的比较2.3 夫琅禾费单缝衍射2.4 夫琅禾费圆孔衍射2.5 平面衍射光栅视窗与链接光碟是一种反射光栅2.6 晶体对X射线的'衍射视窗与链接与X射线衍射有关的诺贝尔奖附录2.1 夫琅禾费单缝衍射公式的推导附录2.2 夫琅禾费圆孔衍射公式的推导附录2.3 平面光栅衍射公式的推导习题第3章几何光学的基本原理3.1 几个基本概念和定律费马原理3.2 光在平面界面上的反射和折射光导纤维视窗与链接光导纤维及其应用3.3 光在球面上的反射和折射3.4 光连续在几个球面界面上的折射虚物的概念 3.5 薄透镜3.6 近轴物近轴光线成像的条件3.7 共轴理想光具组的基点和基面视窗与链接集成光学简介附录3.1 图3-6中P1和JP1点坐标的计算附录3.2 棱镜最小偏向角的计算附录3.3 近轴物在球面反射时物像之间光程的计算附录3.4 空气中的厚透镜物像公式的推导习题第4章光学仪器的基本原理4.1 人的眼睛4.2 助视仪器的放大本领4.3 目镜4.4 显微镜的放大本领4.5 望远镜的放大本领视窗与链接太空实验室——哈勃太空望远镜4.6 光阑光瞳4.7 光度学概要——光能量的传播视窗与链接三原色原理4.8 物镜的聚光本领视窗与链接数码相机4.9 像差概述视窗与链接现代投影装置4.10 助视仪器的像分辨本领视窗与链接扫描隧显微镜4.11 分光仪器的色分辨本领习题第5章光的偏振5.1 自然光与偏振光5.2 线偏振光与部分偏振光视窗与链接人造偏振片与立体电影 5.3 光通过单轴晶体时的双折射现象 5.4 光在晶体中的波面5.5 光在晶体中的传播方向5.6 偏振器件5.7 椭圆偏振光和圆偏振光5.8 偏振态的实验检验5.9 偏振光的干涉5.10 场致双折射现象及其应用视窗与链接液晶的电光效应及其应用5.11 旋光效应5.12 偏振态的矩阵表述琼斯矢量和琼斯矩阵附录5.1 从沃拉斯顿棱镜出射的两束线偏振光夹角公式(5-15)的推导习题第6章光的吸收、散射和色散6.1 电偶极辐射对反射和折射现象的解释6.2 光的吸收6.3 光的散射视窗与链接光的散射与环境污染监测6.4 光的色散6.5 色散的经典理论习题第7章光的量子性7.1 光速“米”的定义视窗与链接光频梳7.2 经典辐射定律7.3 普朗克辐射公式视窗与链接诺贝尔物理学奖7.4 光电效应7.5 爱因斯坦的量子解释视窗与链接双激光束光捕获7.6 康普顿效应7.7 德布罗意波7.8 波粒二象性附录7.1 从普朗克公式推导斯忒藩一玻耳兹曼定律附录7.2 从普朗克公式推导维恩位移定律习题第8章现代光学基础8.1 光与物质相互作用8.2 激光原理8.3 激光的特性8.4 激光器的种类视窗与链接激光产生106T强磁场8.5 非线性光学8.6 信息存储技术8.7 激光在生物学中的应用视窗与链接王淦昌与惯性的束核聚变习题主要参考书目基本物理常量表光学教程第三版(姚启钧著):目录点击此处下载光学教程第三版(姚启钧著)课后题答案。
第七章光的量子性光电效应爱因斯坦的量子解释

34
在整个电磁波谱中,射线的波长在0.01nm一下, 14 所以该光子在电子波谱中属于射线。
六. 光压
1
一. 光子
普朗克把能量子的概念只局限于谐振子及其发射 或吸收的机制上,对于辐射场,仍然认为只是一 种电磁波。 爱因斯坦指出,光不仅具有波动性,也具有粒子性。 光是一粒一粒以光速c运动的粒子流,这些光粒子称 光量子,简称光子。每个光子的能量为:
h
不同频率的光其光子能量不同,光子只能整个地被 吸收或发射。
因此,光电倍增管的灵敏度比普通光电管高几百万倍, 微弱的光照就可产生很大的电流。
11
五. 光子的质量和动量
光子不仅具有能量,也具有动量和质量。但光子又是 以光速运动,牛顿力学便不适用。按照狭义相对论的 观点,质量和能量具有如下关系: 2
E mc
因此,光子的质量为:
E h m 2 2 c c
从光子具有动量这一假设出发,还可以解释光压的 作用。即当光子流遇到任何障碍物时,在障碍物上 施加压力,就好像气体分子在容器壁上的碰撞形成 气压的一样。 光压就是光子流产生的压强。 俄罗斯科学家门捷列夫首先 于1900年做了光压的实验, 证实了光压的存在。 光压的存在的事实说明,光不但有能量,而且确实有动 量。这有力地证明了光的物质性,证明了光和电子、原 子、分子等实物一样,是物质的不同形式。
8
阴极可用多种材料制成, 常用的阴极材料有银氧铯 光电阴极、锑铯光电阴极、 铋银氧铯光电阴极等。不 同的阴极材料用于不同波 长范围的光。
为了提高真空光电管的灵敏度,通常在玻璃泡内充入 某种低压惰性气体,光电子在飞向阳极的过程中与气 体分子碰撞,使气体电离,这样可增大光电流,使灵 敏度增加。
题解1 - 光的量子性(已修改)

3、(D)
Ek
hc
入
hc
散
hc 散 入
散
入
hc 1.2入 入 1 hc 1 E 散 入 5 散 5
E / Ek 5 : 1
4、(C)
A铍 3.9 1.6 10 0铍 34 h 6.63 10 14 14 9.4 10 ( Hz ) 7.5 10 ( Hz )
2.897 103 4 1.0 10 (K) 6 0.29 10
3
对天狼星: T3
b
m
3
2、 铝的逸出功为4.2eV,今用波长为200nm的紫外光照 射到铝表面上,发射的光电子的最大初动能为多少?遏 止电势差为多少?铝的红限波长是多少? 解:发射的光电子的最大初动能为:
6.63 1034 3 108 19 Ek max A 4.2 1.6 10 200 109 3.225 1019 ( J ) 2.01(eV ) 遏止电势差为: U Ek max 2.01eV 2.01V a e e hc
5、(C)
hv Ek max A Ek max hv A
h就是图中直线PQ的斜率OP/OQ 6、(C) hv1 e U a hv0 ( 1 ) 1
hv2 e U a2 hv0 (2) u 2 2 u1 (3)
(1)~(3)式联立求解,得:
v2 2v1 v0
7、 (B)
0 0 hc ( Ek) 0 0 hc 0.1 Ek /( Ek) 0.25 0 0 0.5 0.1
8 、 ( D)
光电效应是吸收光子的过程,而康普顿效应则相当于 光子和电子的弹性碰撞过程。
第七章光的量子性普朗克公式 能量子

15
4. 在光电效应驰豫时间问题上,用波动论解释也 陷入困境。 按照波动论,光波能量是连续传递的,金属中的 电子从入射光中获得足够的能量总需要一定的时 间,并且光越弱,需要积累的时间越长。
可见,光的波动理论不能解释光电效应的实验规 律,说明光的波动论在光电效应问题上又陷入了 困境,需要理论创新。
16
J. Jeans 1877-1946
上式称为瑞利-金斯公式,c为光速,k为波耳兹曼常 数,k=1.38×10-23J/K.
3
理论曲线和实验曲线的比较:
由图可以看出,维恩公式在波长 较短时与实验结果符合的较好, 在长波段与实验结果产生了明显 的偏离。 而瑞利-金斯公式在波长很长时与 实验结果符合较好,在短波部分与 实验结果完全不符。
3
或
M B ( , T )
2hc2
1 e
hc kT
5
1
——称为普朗克黑体辐射公式 普朗克公式与黑体辐射的实验曲线符合的很好。
7
普朗克的假设和公式,不仅从理论上解决了黑体辐射 问题,而且他的能量量子化的新思想对近代物理学的 发展具有深远的影响。从此开创了一个物理学新领域 -量子理论。
可以证明,维恩公式和瑞利-金斯公式分别是普朗克 公式在短波和长波段的极限情况,也可由它导出斯特 藩-玻耳兹曼定律和维恩位移定律。 可见普朗克的能量子假设说在黑体辐射中取得了巨大 的成功。因而获得了1918年诺贝尔物理学奖。
当0时,由瑞利-金斯公式 可得: kT WB (T ) M B ( , T )d 2c 4 d 0 0 这显然是错误的。经典理论与实验结果在短波部分的严 重偏离,在物理学史上,被称为“紫外灾难”。
4
二. 普朗克公式 能量子
光的量子性习题及答案

第七章光的量子性1.在深度远大于表面波波长的液体中,表面波的传播速度满足如下规律:v = 式中g 为重力加速度,ρ为液体密度,F为表面波的波长.试计算表面波的群速度.解:由任何脉动的一般瑞利公式u = v - λvδδλ= v-λdvdλ-λ3g F λπ+2. 测量二硫化碳的折射率实验数据为:当λ=589 nm .n' = 1.629:当"λ=656nm时,n''=1.620 试求波长589nm的光在二氧化硫的相速度、群速度和群折射率。
解:由v = cn得v1=2997924581.629= 1.840×108 m/s.v2 =2997924581.620=1.8506×108 m/s所以△v = v2– v1 = 1.057×106 m/s由一般瑞利公式u = v - λvλ∂∂=1.840×108- 589 ×1.507×106/(656 –589) = 1.747×108 m/sn = c/v = 299792458 /1.747×108 = 1.7163. 在测定光速的迈克尔逊旋转棱镜法中,设所用棱镜为正n 面棱柱体。
试导出:根据棱镜的转速、反射镜距离等数据计算光速公式。
解:设反射镜间距离为L 转速V0则n 面棱柱每转过一个面,光往返一个来回。
所用时间t = 1n/V= 01nV所以c = 2L /t = 021LnV= 2LnV04.试用光的相速度v 和dvdλ来表示群速度u=ddkω,再用v 和dndλ表示群速度u =ddkω解:(1) 由 u = d dk ω= v - λv λ∂∂(2) 由 u = v - λvλ∂∂<1> v = c /n <2>→ dv d λ= ()c d nd λ = -223,(1)c dnn d c dn v dn v dvv v v dn n d n d n d λλλλλλλ<>=+=+=+把〈3〉代入〈1〉得dv u =v -d5.计算在下列各种色散介质中的传播的各种不同性质的波的群速度:(1)v = 常量 (2)v = , ( a 为常量) (3)v = a(在水面上的表面张力波) (4)v = a /λ(5)v =(电离层的电磁波,其中c 是真空中的光速,λ是介质中的波长) (6)v =(在充满色散介质的直波导管中的电磁波,式中c 为真空中的光速,a 是与波导管有关的常量,()εεω=是介质的介电常数,()μμω=是介质的磁导率)解:(1)λλd dvv u -= ,0,==dv v 常量 所以常量==v u(2)λλd dv v u -=, λλλd a dv a v 2,==,所以222v a a a u ==-=λλλλ (3)λλλ2/32,ad dv av -==,所以va v u 2322/3=+=λλ(4)dv u v d λλ=-=()2ad aa d λλλλλ-=v 2=(5)dv u v d λλ=-=2d d λλ=v c 2= (6)kv dk d u ==ωω,,)1(11ωωωd dvv vd dk u -== 而)(),(,222ωμμωεεεμωω==-=ac c v2/3222)(])(2[a c d d v v d dv -+-=εμωωεμωεμωωω所以])(21[1ωεμεμωεμd d v cu +=6.利用维恩公式求:辐射的最概然频率v m ,辐射的最大光谱密度()mλε辐射出射度M 0(T)与温度的关系.解: 由维恩位移定律T T b b T m m m 1⋅⇒=⇒=λλλ由斯沁藩公式()()4040T T M T T M ⋅⇒=σ7.太阳光谱非常接近于480m nm λ=的绝对黑体的光谱.试求在1 s 内太阳由于辐射而损失的质量,并估算太阳的质量减少1% (由于热辐射)所经历的时间(太阳的质量m 0为2.0×1030千克,太阳的半径r 是7.0×108m) 解:由维恩位移公式m m bT b T λλ=⇒=:由斯沁藩公式34484()92.897810() 5.6705110()48010b b M T m σσλ---⨯===⨯⨯⨯=7.35×107瓦()()()瓦总262872106357.4100.714.341053.74⨯=⨯⨯⨯⨯⨯==⋅=r T M S T M P b b π由方程 P 总t =m 0×1%×c 221800.01 3.8810m c t sP ⨯⨯⇒==⨯总所以在1s 内kg 1015.5109106357.41916262⨯=⨯⨯=⋅=∆c s P m 总损8.地球表面每平方厘米每分钟由于辐射而损失的能量平均值为0.546J.如有有一黑体,它在辐射相同的能量时,温度应为多少? 解:4()0.546109160b M =⨯=()s m W ⋅/ 由斯沁藩公式11()444()891()()()200.145.670510b b M M T T T K σσ-=⇒===⨯9.若有一黑体的辐出度等于5.70W /cm 2,试求该辐射最大光谱强度相对应的波长。
《大学物理AII》作业 No.07 光的量子理论 参考解答

级上的原子数大于低能级上的原子数,这种分布称为(粒子数反转分布) 。 11、 激光器的结构包括: (1)具有(亚稳态)能级,能实现粒子数反转分布的(激 活介质) ; (2)具有“抽运”作用的能量输入系统,即(激励能源) ; (3)具有光 放大作用的(光学谐振腔) 。 12、 某金属在一束绿光的照射下有光电效应产生。当用更强的绿光照射时光电效 应发生的变化是(饱和光电流增大) ;当用强度相同的紫光照射时光电效应发生 的变化是(光电子动能增加或者反向截止电压增加) 。
13、相比较于普通光源,激光的优异特性表现为: (方向性好、单色性好、相干 性好、偏振性好等) 。 二、简答题 1、炼钢工人凭观察炼钢炉内的颜色就可以估计炉内的温度,这是根据什么原 理? 答:将被加热的钢铁视为黑体,根据黑体辐射的维恩位移定律 mT 常数 ,可以 看出随着温度升高,加热的钢体发出光的波长要变短,即可以由暗红变为赤红、 橙色,而最后变白。如果掌握了颜色变化与对应温度变化之间的联系规律,就可 以凭钢炉内的颜色估计出炉内的温度。
3、当康普顿散射角为 90 度时, 试计算下列波长的光子被散射时,损失的能量与 散射前光子的能量的比值。 (1)波长 3cm(微波范围) ; (2)波长 500nm (可见光范围) ; (3)波长 0.1nm (X 射线范围) ; (4)波长 0.001nm ( 射线范围) ; 通过以上计算,对入射光波长与散射的关系能得出什么结论? 解:设入射光波长 、频率 ,散射光波长 、频率 ;则光子散射时损失的能 量与入射光子能量之比为:
0.0024 nm 2.4 10 12 m 2
由以上计算结果可以看出,入射光的波长愈短,散射时能量损失愈大,则入 射光与散射光的波长差别就愈明显,康普顿效应也就愈明显。
最新-高三物理复习光的波动性、量子论初步例题及练习题含答案 精品

高三物理复习光的波动性 量子论初步例题及练习题典型例题例1.能产生干涉现象的两束光是( )A .频率相同、振幅相同的两束光B .频率相同、相位差恒定的两束光C .两只完全相同的灯光发出的光D .同一光源的两个发光部分发出的光分析:比例考察的是对“相干条件”的了解解答:只有频率相同、相差恒定、振动方向相同的光波,在它们相遇的空间里能够产生稳定的干涉,观察到稳定的干涉图样,但是,光波并不是一列连续波,它是由一段段不连续的具有有限长度的所谓“波列”组合而成的,并且波动间的间歇也是不规则的。
两个独立光源发出的光,即使是“频率相同的单色光(实际上严格的单色光并不存在),也不能保持有恒定的相差。
因此,为了得到相干光波,通常是把同一光源发出的一束光分成两束。
杨氏双缝干涉实验中,所以在光源和双缝间设置一个狭缝,就是让点光源发出的一束光,先经第一个缝产生衍射,使得由双缝得到的两束光成为相干光波。
光源发光是以原子为发光单位的,由前面分析可知,我们无法使两只完全相同的灯泡、同一光源的两个发光部分发出频率相同、相差恒定的光。
这样的光源不会产生稳定的干涉现象,无法观察到干涉图样。
所以应选B 。
例2.在真空中频率为4×1014Hz 的是红光,频率为6×1014Hz 的是绿光,现在有一束单色光,它在n=1.5的玻璃中,波长为5000Å,它在这种玻璃中的频率是多少?是什么颜色?在真空中的频率是多少?又是什么颜色?分析:光的频率决定于光的颜色,光从一种介质传到另一种介质时,由于频率不变,故颜色不变,因此,本题关键是求频率。
由n=υc 得,光在玻璃中的速度为 υ=n c =5.11038⨯m/s=2×m/s 它在玻璃中的频率为ν=λυ=108105000102-⨯⨯Hz=4×1014H z 由此可知,该单色光在真空中的频率也为4×1014Hz ,故为红光。
在真空中与玻璃中均为红颜色。
2019年光量子学习题答案.doc

《光量子学基础》习题答案(沈建其提供,2009年6月)说明:习题难度非常低,大多习题均可以在ppt 中直接找到答案。
第一次习题:1.计算(1):de Broglie 波长均为5埃(Å)的电子、中子与光子的动量与能量各为多少?答:这三种粒子的动量都是3424106.6310 1.3310510p h λ---⨯===⨯⨯Kg ·m/s (或241.310-⨯ Kg ·m/s)。
电子的动能 ()224218300 1.33100.96510220.91110k pE m ---⨯===⨯⨯⨯J 6.03=eV (或6eV ) (1电子伏特=191.6010-⨯焦耳)中子的动能 ()224221270 1.33100.5261022 1.6710k p E m ---⨯===⨯⨯⨯J 20.33010-=⨯eV 以上使用牛顿力学的动能公式(6.03eV 远比电子的静止能量20m c 约0.5MeV 小,0.0033eV 远比中子的静止能量20m c 约990MeV 小,说明没有必要使用相对论来计算) 但光子是相对论性粒子,必须用相对论来计算:光子动能(总能)2481.3310 3.0010k E pc -==⨯⨯⨯J =4.001610-⨯J=2.50310⨯eV 。
说明:虽然以上问题中,牛顿力学的动能公式是非常良好的近似,但使用相对论亦可。
有的学生计算了动能部分,有的学生计算了总能量2E mc =,答案是开明的,都属对,但要知道2E mc =与动能22p m 之间如下关系:粒子总能量2E mc =,动质量m =2E mc =可以用泰勒展开:2246001...2E m c m v av bv =++++,其中20m c 为静止能量(rest energy ), 2012m v 为牛顿动能(它只是2E mc =的一部分)。
只有当低速的时候,220012m c m v +才重要,其中2012m v更重要。
几何光学和光学仪器

几何光学和光学仪器一、几何光学基本概念与原理1.1 光线:光线是用来表示光的传播方向的直线,通常用一个小箭头表示。
1.2 光的反射:光在传播过程中遇到障碍物,一部分光会被反射回来,例如平面镜成像、球面镜成像等。
1.3 光的折射:光从一种介质进入另一种介质时,传播方向会发生改变,称为折射现象,如透镜、棱镜等。
1.4 透镜:透镜是一种光学元件,能够使光线发生折射,分为凸透镜和凹透镜。
1.5 焦点:凸透镜对光有会聚作用,能使平行光线汇聚于一点,该点称为焦点。
1.6 光路:光在传播过程中的路径,可以通过光线的实际路径或反向延长线来表示。
二、光学仪器的基本原理与结构2.1 望远镜:望远镜是一种利用透镜或反射镜收集和放大远处物体光线的仪器,主要由物镜、目镜等组成。
2.2 显微镜:显微镜是一种利用透镜放大微小物体光线的仪器,主要由物镜、目镜等组成。
2.3 照相机:照相机是一种利用透镜成像的原理,将景物记录在底片或数字传感器上的设备。
2.4 投影仪:投影仪是一种将图像投射到屏幕上的设备,主要利用透镜和光源将图像放大后投射出来。
2.5 眼镜:眼镜是一种用于纠正视力问题的光学仪器,根据个人的视力情况选择不同类型的透镜。
2.6 光学仪器的设计与制作:光学仪器的设计与制作需要考虑光线的传播、折射、聚焦等原理,以及各种光学元件的性能和组合方式。
三、光学仪器的应用与拓展3.1 光学仪器在科研领域的应用:如望远镜在天文观测、显微镜在生物研究等方面的应用。
3.2 光学仪器在生活中的应用:如照相机记录生活瞬间、眼镜改善视力等。
3.3 光学仪器的发展与创新:随着科技的发展,光学仪器不断更新换代,如数码相机、激光技术等。
3.4 光学仪器在我国的发展:我国光学仪器产业经过多年的发展,已经取得了一定的成绩,部分产品在国际市场上具有竞争力。
四、光学知识在现代科技领域的应用4.1 光纤通信:利用光在光纤中传输的特性,实现高速、大容量的数据传输。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第七章光的量子性1.在深度远大于表面波波长的液体中,表面波的传播速度满足如下规律:v = 式中g 为重力加速度,ρ为液体密度,F为表面波的波长.试计算表面波的群速度.解:u = v - λvδδλ= v-λdvdλ-λ3g F λπ+2. 测量二硫化碳的折射率实验数据为:当=589 nm .n' = 1.629:当"λ=656nm时,n''=1.620 试求波长589nm的光在二氧化硫的相速度、群速度和群折射率。
解:由v = cn得v1=2997924581.629= 1.840×108 m/s.v2 =2997924581.620=1.8506×108 m/s所以△v = v2– v1 = 1.057×106 m/s由一般瑞利公式u = v - λvλ∂∂=1.840×108- 589 ×1.507×106/(656 –589) = 1.747×108 m/sn = c/v = 299792458 /1.747×108 = 1.7163. 在测定光速的迈克尔逊旋转棱镜法中,设所用棱镜为正n 面棱柱体。
试导出:根据棱镜的转速、反射镜距离等数据计算光速公式。
解:设反射镜间距离为L 转速V0则n 面棱柱每转过一个面,光往返一个来回。
所用时间t = 1n/V= 01nV所以c = 2L /t = 021LnV= 2LnV04.试用光的相速度v 和dvdλ来表示群速度u=ddkω,再用v 和dndλ表示群速度u =ddkω解:(1) 由 u = d dk ω= v - λvλ∂∂(2) 由 u = v - λvλ∂∂<1 v = c /n <2>→ dv d λ= ()c d nd λ = -223,(1)c dnn d c dn v dn v dvv v v dn n d n d n d λλλλλλλ<>=+=+=+把〈3〉代入〈1〉得dv u =v -d5.计算在下列各种色散介质中的传播的各种不同性质的波的群速度:(1)v = 常量 (2)v = 为常量) (3)v = a(在水面上的表面张力波) (4)v = a /λ(5)v =电离层的电磁波,其中c 是真空中的光速,λ是介质中的波长) (6)v =(在充满色散介质的直波导管中的电磁波,式中c 为真空中的光速,a 是与波导管有关的常量,()εεω=是介质的介电常数,()μμω=是介质的磁导率)解:(1)λλd dvv u -= ,0,==dv v 常量 所以常量==v u(2)λλd dv v u -=, λλλd a dv a v 2,==,所以222v a a a u ==-=λλλλ (3)λλλ2/32,ad dv av -==,所以va v u 2322/3=+=λλ(4)dv u v d λλ=-=()2ad a a d λλλλλ-=v 2=(5)dv u v d λλ=-=2d d λλ=v c 2= (6)kv dk d u ==ωω,,)1(11ωωωd dvv vd dk u -== 而)(),(,222ωμμωεεεμωω==-=ac c v2/3222)(])(2[a c d d v v d dv -+-=εμωωεμωεμωωω所以]21[1ωεμεμωεμd v cu +=6.利用维恩公式求:辐射的最概然频率v m ,辐射的最大光谱密度()m λε辐射出射度M 0(T)与温度的关系.解: 由维恩位移定律T T b b T m m m 1⋅⇒=⇒=λλλ由斯沁藩公式()()4040T T M T T M ⋅⇒=σ7.太阳光谱非常接近于480m nm λ=的绝对黑体的光谱.试求在1 s 内太阳由于辐射而损失的质量,并估算太阳的质量减少1% (由于热辐射)所经历的时间(太阳的质量m 0为2.0×1030千克,太阳的半径r 是7.0×108m) 解:由维恩位移公式m m bT b T λλ=⇒=:由斯沁藩公式34484()92.897810() 5.6705110()48010b b M T m σσλ---⨯===⨯⨯⨯=7.35×107瓦()()()瓦总262872106357.4100.714.341053.74⨯=⨯⨯⨯⨯⨯==⋅=r T M S T M P b b π由方程 P 总t =m 0×1%×c 221800.01 3.8810m c t sP ⨯⨯⇒==⨯总所以在1s 内kg 1015.5109106357.41916262⨯=⨯⨯=⋅=∆c s P m 总损8.地球表面每平方厘米每分钟由于辐射而损失的能量平均值为0.546J.如有有一黑体,它在辐射相同的能量时,温度应为多少? 解:4()0.546109160b M =⨯=()s m W ⋅/ 由斯沁藩公式11()444()891()()()200.145.670510b b M M T T T K σσ-=⇒===⨯9.若有一黑体的辐出度等于5.70W /cm 2,试求该辐射最大光谱强度相对应的波长。
解:斯沁藩公式4()()b M T T σ=114()4485.7010()()1001.2985.6705110b M T K σ-⨯⇒===⨯由维恩位移公式362.897810 2.89410289.41001.298m m b T b m nmT λλ--⨯=⇒===⨯=10.用交流供电的灯丝温度是变动的。
一电灯钨丝白炽时的平均温度为2300K ,其中最高和最低温度的差约为80K 。
问热辐射的总功率的最大和最小值之比为多少?钨丝的辐射可当作黑体。
解:斯沁藩公式4()()b M T T σ=所以()()ST M p b ⋅= ()()ST M p b ⋅=11 ()()ST M p b ⋅=2211.若将恒星表面的辐射近似的看作是黑体辐射,则可以用测量max λ的办法来估计恒星表面的温度。
现测得太阳的max λ为510nm ,北极星的max λ为350nm ,试求它们的表面温度。
解:由维恩位移公式m m bT b T λλ=⇒=()()K568210510108978.293max =⨯⨯==--太阳太阳λbT()()K 4.827910350108978.293max =⨯⨯==--北极星北极星λbT12.小灯泡所消耗的功率为1W ,均匀的向各个方向辐射能量。
设辐射的平均波长为500nm ,试求在10km 处每秒钟落在垂直于光线方向上每平方厘米面积上的光子数。
解:由149299792458 5.9961050010cv λ-===⨯⨯由题意列方程得 pt =42r nhv π92234141121044 3.1410000 6.62610 5.99610pt n r hv π-⨯⇒===⨯⨯⨯⨯⨯⨯⨯()每平方厘米面积上的光子数 95121021010000n =⨯⨯=⨯,个13.已知铯的逸出功为1.88eV 。
现用波长为300nm 的紫外光照射,试求光子的初动能和初速。
解:由爱因斯坦光电效应方程2234199191129979245816.62610 1.88 2.258 3.6134102230010 1.6010hv mv W mv hv W eV J ----=+⇒=-=⨯⨯⨯-==⨯⨯⨯58.910v ===⨯m /s14.用波长为253nm 的光照射钨丝的表面时,在光电管的电路中产生的光电流,由于外加1V的遏止电压而截止。
已知钨的逸出功为4.5eV ,试求接触电势差。
解:由22112122m g a K m mv eV W W hv mv W =+-<>=+<>由爱因斯坦光电效应方程联立<1> 和〈2〉得a k gW W hv w eV -=--所以接触电势差348919, 6.626101310 4.5125310 1.610g a k e eV eV hv W eV W W U e e e ---⨯⨯⨯⨯-----⨯⨯====-0.593V15.波长为320nm 的紫外光入射到逸出功为2.2eV 的金属表面上,求光电子从金属表面逸出时的最大速度。
若入射光的波长为原来的一半,初涉光电子的最大动能是否增至两倍?解:由爱因斯坦光电效应方程212hv mv W =+57.6910v ⇒==⨯m /s若入射光波长减半,则82'34919131016.62610 2.2 5.565216010 1.610mv hv W eV ---⨯=-=⨯⨯⨯-=⨯⨯(≠1.628eV )所以最大动能不会增至两倍。
16.波长为0.1nm 的X 射线被碳块散射,在散射角为 90°的方向上进行观察。
试求(1)康普顿位移 △λ(2)反冲电子的动能解:△λ=λ-λ0=21222sin ()2 2.426308910sin (45)0.002412k nmθ-=⨯⨯⨯=反冲电子动能34817'991111() 6.62610310() 4.678100.1100.1024110k E hc J λλ----=-=⨯⨯⨯⨯-=⨯⨯⨯17.已知入射光子的波长为0.003nm ,而反冲电子的速度为光速的β 倍( β = 0.6 ),试确定康普顿位移△λ解:由康普顿效应能量守恒22'2'000.25hv m c hv m c hv v h-+=+⇒=196.609910⨯所以8'12'19310 4.34106.909910c v λ-⨯===⨯⨯△λ='1212(4.3413)10 1.3410m λλ---=-⨯=⨯ 18.在电子显微镜中,电子受到90kV 的电压加速,如果观察到物质的分子结构(其大小为 910-cm 数量级),问显微镜的孔径应为多大? 解:由瑞利判据△y =0.610sin sin n u n u λ⇒=0.6101y λ<>∆由已知△y =10-11m由 德布罗意波长公式2h h p mv λ==<>由能量守恒2132mv eU =<>联立<1>,<2>,<3>得34sin 0.24970.25n u m-===≈19.(1)一只100W 灯泡,5%的功率辐射是可见光,假定可见光平均波长为500nm ,则每秒可辐射的可见光子数为多少?(2)假定灯泡为点光源,可以向各个方向发光,求在距离2m 处每秒垂直通过单位面积的光子数。
解:(1)依题意列方程191110257.105.0%5⨯==⇒⋅=⨯hc p N t chN p λλ(2)由172222105.2405.04%5⨯==⇒⋅=⨯hc r tp N chN r t p πλλπ个20.人在黑暗中,眼睛的视网膜如能接收到波长为550nm 的最大有效辐射 18210J -⨯,就能感知这一光源。
