对口高职高考数学模拟试卷 新
2023年高职对口招生考试模拟试题数学模拟

对口升学数学模拟试题(第Ⅰ卷)注意事项:1、 答第Ⅰ卷前,考生务必将自己旳姓名、准考证号、考试科目用铅笔涂写在答题卡上。
2、 每题选出答案后,用铅笔把答题卡上对应题目旳答案标号黑,如需改动,用橡皮擦洁净后,再选涂其他答案,不能答在试题卷上。
一、选择题(本大题共20个小题,每题3分,共60分)1、已知集合P={(x ,y )|y = x+1},Q={( x ,y )| x 2+y 2=1},则集合P ∩Q 旳子集旳个数是( )A 、2B 、4C 、6D 、8 2、设命题p :a 2+b 2=0,则⌝p 是( )A 、a=0且b=0,B 、a ≠0且b ≠0,C 、a ≠0或b ≠0,D 、a=0或b=0 3、不等式|x +5|>1旳解集是( )A 、{x|x>-4}B 、{x|-6<x<-4}C 、{x|x<-6或x>-4}D 、{x|x<-6}4、已知奇函数f(x)在(0,+∞)上是增函数,偶函数g(x)在(0,∞)上是减函数,则在 (-∞,0)上,有( )A 、f(x)为减函数,g(x)为增函数;B 、f(x)为增函数,g(x)为减函数;C 、f(x)、g(x)都是增函数;D 、f(x)、g(x)都是减函数 5、已知tan θ=2,则sin θcos θ=( )A 、53B 、52C 、±52D 、±536、已知f (e x)= x ,则f (5)=( )A 、e5B 、5C 、ln5D 、log 5 e7、 将二次函数y= (x -2)2+1 图像旳顶点A 平移向量a = (-2,3)后得到点A ’旳坐标是( )A 、(0, 4)B 、(4, -4)C 、(4, 0)D 、(-4, 4)8、在△ABC 中,若∠A 、∠B 、∠C 成等差数列,且BC= 2,BA=1, 则AC 等于( )A 、332 B 、 1 C 、3 D 、 7 9、若a 与b 都是单位向量,则下列式子恒成立旳是( )A 、a ·b =0;B 、|a |=|b |,C 、a -b =0;D 、a 、b =110、若等差数列{a n }中旳前n 项和为s n =4n 2–n ,则这个数列旳通项公式是( )A 、a n =4n -1B 、a n =8n -5C 、a n =4n+3D 、a n =8n+511、把6本不一样旳书平均放在三只抽屉里,不一样旳放法有( )A 、90B 、45C 、30D 、1512、若(1+x )8展开式旳中间三项依次成等差数列,则x 旳值为( )A 、21或2 B 、21或4 C 、2或4 D 、2或41 13、甲、乙两人同步解答一道题,甲解出旳概率是p ,乙解出旳概率是q ,则这道题被解出旳概率是( )A 、pqB 、p+qC 、p (1-q)+q (1-p)D 、p+q –pq14、对任意实数k,直线(k+1)x -ky -1=0与圆x 2+y 2-2x -2y -2=0旳位置关系是 ( ) A.相交 B.相切 C.相离 D.与k 旳值有关 15、二次函数f(x)=ax 2+bx+c ,满足f(4)=f(1),则( )A、f(2)>f(3) B、f(3)>f(2) C、f(3)=f(2) D、不确定 16、已知抛物线y 2=8x 上一点P 到焦点旳距离为5,则点P 旳横坐标为( )A 、2B 、3C 、5D 、717、双曲线116922=-y x 旳渐近线方程为( )A 、y=x 43±B 、y=x 34±C 、y=43± D 、y=x 34± 18、已知点P (2,a )是第一象限内旳点,且到直线4x -3y+2=0旳距离等于4,则a 旳值为( )A 、4B 、6C 、8D 、1019、洗衣机旳洗衣桶内用清水洗衣服,假如每次能洗去污垢旳32,则要使存留在衣服上旳污垢不超过最初衣服上旳污垢旳2%,该冼衣机至少要清洗旳次数为( )A 、2B 、3C 、4D 、5 20下列四个命题:①平行于同一条直线旳两条直线平行; ②平行于同一条直线旳两个平面平行;③平行于同一种平面旳两条直线平行 ④平行于同一种平面旳两个平面平行。
中职数学 2024年湖南省对口招生高考数学模拟试卷

2024年湖南省对口招生高考数学模拟试卷一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)A .∅B .{d }C .{a ,c }D .{b ,e }1.(4分)已知全集U ={a ,b ,c ,d ,e },集合N ={b ,d ,e },M ={a ,c ,d },则∁U (M ∪N )=( )A .{x |x <1}B .{x |x >4}C .{x |1<x <4}D .{x |x <1或x >4}2.(4分)不等式-x 2+5x -4>0的解集是( )A .6B .-4C .4或-6D .6或-43.(4分)已知点P (a ,2)到直线4x -3y +2=0的距离等于4,则a =( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件4.(4分)已知直线m 、n 和平面α,且n ⊆α,则“m ⊥α”是“m ⊥n ”的( )A .4B .4+4C .4D .4+45.(4分)设正四棱锥的底面边长和侧棱长都是2,则该四棱锥的表面积为( )M 3M 3M 5M 5A .2B .-2C .1D .-16.(4分)已知向量a =(-2,1),b =(4,3),c =(-1,λ).若(a +b )∥c ,则λ的值为( )→→→→→→A .(0,]B .[0,]C .(-∞,]D .[,+∞)7.(4分)已知函数f (x )=log a x (a >0且a ≠1)满足f (2)=-1,则不等式f (x )≥3的解集是( )18181818二、填空题(本大题共5个小题,每小题4分,共20分)A .10B .9C .8D .78.(4分)从某小学随机抽取100名学生,将他们的身高数据绘制成频率分布直方图如图所示,若要从身高在[120,130)、[130,140)、[140,150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从身高在[120,130)内的学生中选取的人数应为( )A .f (-π)>f (-2)>-f (3)B .-f (3)>f (-π)>f (-2)C .f (-2)>-f (3)>f (-π)D .f (-π)>-f (3)>f (-2)9.(4分)已知f (x )是R 上的奇函数,且在区间[0,+∞)上是减函数,则f (-2),f (-π),-f (3)的大小关系是(A .函数y =sin 2x 的周期为πB .函数y =sinx 在区间(,)内是减函数C .函数y =sinx +cosx 的值域是[-2,2]D .函数y =sin 2x 的图像可由y =sin (2x -)的图像向左平移个单位得到10.(4分)下列命题中错误的是( )3π45π4π5π1011.(4分)已知sin (π+α)=-,α∈(,π),则sin 2α= .45π212.(4分)不等式|x -a |<2的解集为{x |-1<x <3},则实数a = .13.(4分)从7名运动员中选出4人参加校运会的4×100米接力赛,则甲、乙两人都不跑中间两棒的方法有 种.14.(4分)过点P (2,-1)作圆C :(x -1)2+(y -2)2=2的切线,切点为A 、B .则|PA |= .15.(4分)已知等差数列{a n }中a 1=13,且S 3=S 11,则S n 的最大值为 .三、解答题(本大题共7个小题,其中第21、22小题为选做题.满分50分.解答应写出文字说明、证明过程或演算步选做题:请考生在第21、22题中选择一题作答.若两题都做,则按所做的第21题计分.作答时,请写清题号.老师建科类做第21题,服务类做22题.16.(10分)已知点(4,2)在函数f (x )=的图象上.(1)求a 的值,并画出函数f (x )的图象;(2)求不等式f (x )<1的解集.{x +4,x ≤0x ,x >0log a 17.(10分)我校学生心理咨询中心服务电话的接通率为.21机2班的3名同学分别就某一问题在某天咨询该服务中心,只拨打一次电话,设X 表示他们中成功咨询的人数.求:(1)恰有2人成功咨询的概率;(2)随机变量X 的概率分布和数学期望、方差.3418.(10分)已知数列{a n }的前n 项和为S n ,且S n =2a n -3n (n ∈N +).(1)求a 1,a 2,a 3的值;(2)设b n =a n +3,证明数列{b n }为等比数列,并求通项公式a n .19.(10分)如图四棱锥P -ABCD 的底面是边长为2的菱形,且∠ABC =60°,PA =PC =2,PB =PD .(1)若O 是AC 与BD 的交点,证明:PO ⊥平面ABCD .(2)若点M 是PD 的中点,求异面直线AD 与CM 所成角的余弦值.20.(10分)已知椭圆C 的中心在坐标原点O ,焦点在x 轴上,离心率为,椭圆上一点P 到椭圆左右两焦点的距离之和为(1)求椭圆C 的标准方程;(2)已知直线l :y =x +m 与椭圆C 交于A 、B 两个不同的点,且弦AB 的中点恰好在圆+=上,求直线l 的方程.M 32x 2y 2172521.(10分)在平面四边形ABCD中,∠ADC=90°,∠A=45°,AB=2,BD=5.(1)求cos∠ADB;(2)若DC=2,求BC.M222.某公司计划在今年内同时出售变频空调机和智能洗衣机.由于这两种产品的市场需求量非常大,有多少就能销售多少,该公司要根据实际情况(如资金、劳动力)确定产品的月供应量,以使得总利润达到最大.已知对这两种产品有直接限制的是资金和劳动力.通过调查,得到关于这两种产品的有关数据如表:资金(表中单位:百元)单位产品所需资金月资金供应量空调机洗衣机成本3020300劳动力:工资510110单位利润6试问:怎样确定两种货物的月供应量,才能使总利润达到最大,最大利润是多少?。
高职高考数学试卷模拟卷

一、选择题(每题5分,共20分)1. 下列各数中,有理数是()。
A. √9B. √-16C. πD. 2√22. 如果 |a| = 3,那么 a 的值为()。
A. ±3B. ±4C. ±2D. ±13. 已知二次函数y = ax² + bx + c(a ≠ 0),如果它的图像开口向上,且顶点坐标为(1,-2),那么 a 的取值范围是()。
A. a > 0B. a < 0C. a ≥ 0D. a ≤ 04. 在等差数列 {an} 中,如果 a1 = 3,d = 2,那么第10项 an 的值为()。
A. 19B. 20C. 21D. 225. 若函数 f(x) = 2x + 1 在区间 [1, 3] 上单调递增,那么函数 g(x) = f(x) - 3 在区间 [1, 3] 上的单调性是()。
A. 单调递减B. 单调递增C. 先增后减D. 先减后增二、填空题(每题5分,共20分)6. 已知等差数列 {an} 的前n项和为 Sn,如果 S5 = 50,a1 = 2,那么 d =________。
7. 函数y = x² - 4x + 4 的图像与x轴的交点坐标为 ________。
8. 在直角坐标系中,点 A(2,3)关于 y 轴的对称点坐标为 ________。
9. 二项式定理 (a + b)ⁿ的展开式中,a³b⁷的系数为 ________。
10. 等比数列 {an} 的公比 q = 1/2,如果 a1 = 16,那么第5项 an 的值为________。
三、解答题(每题10分,共20分)11. 解下列方程组:\[\begin{cases}2x + 3y = 8 \\4x - y = 2\end{cases}\]12. 已知函数 f(x) = -3x² + 12x - 4,求函数 f(x) 的最大值。
四、应用题(15分)13. 一批货物由甲、乙两辆卡车运输,甲车每小时运输20吨,乙车每小时运输30吨。
2023年对口升学考试模拟试题 数学(三

山西教育2023/1◇刘婧一、单项选择题(本大题共10小题,每小题3分,共计30分)1.若集合N =x x ≤2{},M =x x 2-3x =0{},则M ∪NA.0{}B.3{}C.0,2{}D.0,3{}2.已知x 3=-8,则x 2+x -2等于A.8B.4C.0D.63.下列函数为奇函数的是A.y =tan x B.y =2x 2C.y =e xD.y =x4.sin 214π等于A.12B.2√2C.-12D.-2√25.直线x +3√y +1=0的倾斜角为A.60° B.150°C.120°D.30°6.数列12,14,18,116…前8项的和是A.63128 B.127128C.255256D.2555127.在△A BC 中,∠A =30°,a =4,b =43√,则∠B 等于A.30°或120°B.60°C.120°D.60°或120°8.设P 是双曲线x 2a 2-y 29=1上一点,双曲线的一条渐近线方程为3x -2y =0,F 1,F 2分别是双曲线的左右焦点,若PF 1=3,则PF 2等于A.5 B.7C.6 D.1或59.5人排成一排照相,甲排在中间的概率为A.15 B.14C.120D.4510.在正方体ABCD -A 1B 1C 1D 1中,对角线BD 1与平面ABCD 所成角的正切值A.1B.3√3C.2√2D.2√二、填空题(本大题共8小题,每小题4分,共计32分)11.已知y=x √-5,x ≥0-3+x 2,x <0{,则f f (4)[].12.若等比数列的公比为-2,a 1+a 4+a 7=9,a 2+a 5+a 8=.13.已知两点A (1,3),B (-2,-1),则=.14.设a ⭢=(1,-2),b ⭢=(3,m ),若a ⭢·b ⭢,则m =.15.函数y =4sin12x +π3()的最小正周期为.2023年对口升学考试模拟试题33山西教育2023/116.(ax +1)5的展开式中x 的系数为10,则a =.17.若两个球的表面积之比为1∶4,则这两个球的体积之比为.18.(101.001)2=.三、解答题(本大题共6小题,共计38分)19.(6分)求函数y =-x 2-2x+15√lg (2-x )的定义域.20.(6分)已知等差数列a n {}的前n 项和为S n ,且a 1=1,a 3=5,(1)求数列a n {}的通项公式;(2)若S n =100,求n .21.(6分)求与直线x -6y -10=0相切于点P (4,-1),且圆心在直线5x -3y =0上圆的方程.22.(6分)若a ⭢,b ⭢满足(a ⭢-b ⭢)·(2a ⭢+b ⭢)=-4,且a ⭢=2,b ⭢=4,求a ⭢与b ⭢的夹角.23.(6分)在三角形A BC 中,已知c 2=2ab 袁则(1)若C =90毅,a =1,求S △ABC ;(2)若sin A =sin C ,求cos C .24.(8分)某射击运动员射击3次,每次射击击中目标的概率为23,求射击3次该运动员击中次数X的分布列.◇郭慧慧李腾飞2023年对口升学考试模拟试题一、单项选择题(本大题共10小题,每小题3分,共计30分)1.已知集合A =x x <4{},集合B =x 2<x <8{},则A ∪B 等于A.(4,8)B.(2,8)C.(-4,8)D.(2,4)2.下列函数既是偶函数又在(0,+∞)是增函数的是A.y =1x B.y =cos x C.y =x +1D.y =lg x3.设函数f (x )是R 上的奇函数,当x ≥0时,f (x )=4x -1,则f (-2)等于A.15B.-15C.1516D.-15164.ln3+ln5等于A.ln5 B.ln8C.ln 35D.ln 535.已知cos α>0,tan α<0,则α在A.第一象限 B.第二象限C.第三象限D.第四象限扫描二维码观看本试题讲解34。
职高对口高考模拟数学试卷

#### 一、填空题(每空2分,共20分)1. 若函数 \( f(x) = ax^2 + bx + c \) 在 \( x = 1 \) 处取得极值,则 \( a + b + c = \) ________。
2. 在等差数列 \(\{a_n\}\) 中,若 \( a_1 = 3 \),公差 \( d = 2 \),则\( a_5 = \) ________。
3. 已知圆的方程为 \( x^2 + y^2 - 4x - 6y + 9 = 0 \),则该圆的半径为________。
4. 若 \( \cos \alpha = \frac{1}{3} \),则 \( \sin \alpha \) 的值为________。
5. 函数 \( y = \frac{1}{x} \) 的图像关于 ________ 对称。
6. 若 \( \sqrt{a^2 + b^2} = 5 \),\( a = 3 \),则 \( b \) 的值为________。
7. 三个数的和为 12,其中两个数分别为 3 和 5,则第三个数为 ________。
8. 若 \( \triangle ABC \) 中,\( a = 5 \),\( b = 6 \),\( c = 7 \),则\( \cos A \) 的值为 ________。
9. 下列不等式中,正确的是 ________(选项:A. \( 2x > 4 \);B. \( 3x \leq 9 \);C. \( x^2 \geq 4 \);D. \( \frac{1}{x} < 1 \))10. 已知 \( \log_2 8 = 3 \),则 \( \log_2 32 = \) ________。
#### 二、选择题(每题3分,共30分)1. 函数 \( y = x^3 - 3x \) 的图像在 \( x = 0 \) 处的切线斜率为:A. 0;B. -3;C. 3;D. 不存在。
高职高考数学模拟试卷(一)课件

(1)根据所给条件,求出椭圆的标准方程;
(2)求长方形面积S与边长x的函数关系式;
(3)求当边长x为多少时,面积S有最大值,并求其最大值.
(2)当x∈N*时,f(1),f(2),f(3),f(4),…构成一数列,求其通项公式.
【解】 (2)f(1)=5,f(x)-f(x-1)=3, f(x)构成的数列为首项为5,公差为3的等差数列. 则f(x)=5+3(x-1)=3x+2(x∈N*).
24.(本小题满分14分) 两边靠墙的角落有一个区域,边界线正好是椭圆轨迹的部分,
A.1;2π
B.0;2π
C.1;π
D.0;π
12.直线l:x+2y-3=0与圆C:x2+y2+2x-4y=0的位置关系是 ( )
A.相交且不过圆心
B.相切
C.相离
D.相交且过圆心
13.函数y=x2-4x+2,x∈[0,3]的最大值为 (
A.-2
B.-1
C.2
) D.3
【答案】C 【解析】由y=x2-4x+2,x∈[0,3]得y=(x-2)2-2,
取一名学生,抽到高二年级女生的概率为0.19,则高二年级的女生
人数为
.
【答案】380 【解析】2000×0.19=380.
(2)当鲑鱼的游速从原来的a(米/秒)提高到(a+1)(米/秒)时,问此 时鲑鱼的耗氧量是原来的多少倍?
0
π
2π
x
g(x)
0
2
0
-2
0
描点作图:
【解】 (1)f(2)=8,f(5)=f(2)+3×3=17.
职对口高考数学试卷

一、选择题(每题4分,共40分)1. 已知函数f(x) = 2x + 1,则f(3)的值为:A. 7B. 8C. 9D. 102. 在直角坐标系中,点A(2, 3)关于x轴的对称点为:A. (2, -3)B. (-2, 3)C. (2, -3)D. (-2, -3)3. 下列哪个数是负数?A. -(-2)B. (-2) × (-2)C. (-2) ÷ (-2)D. (-2) + 24. 如果a < b,那么下列哪个不等式一定成立?A. a - 1 < b - 1B. a + 1 < b + 1C. a - 1 > b - 1D. a + 1 > b + 15. 已知等差数列的前三项分别是2, 5, 8,则该数列的公差为:A. 2B. 3C. 4D. 56. 下列哪个图形是圆?A. 正方形B. 等腰三角形C. 等边三角形D. 椭圆7. 已知函数y = kx + b,若该函数图像经过点(1, 2),则k + b的值为:A. 3B. 4C. 5D. 68. 在△ABC中,∠A = 45°,∠B = 90°,∠C = 45°,则△ABC是:A. 等腰三角形B. 等边三角形C. 直角三角形D. 钝角三角形9. 下列哪个数是整数?A. √25B. √36C. √49D. √6410. 如果a > b,那么下列哪个数对一定满足a² > b²?A. a = 3, b = 2B. a = 2, b = 3C. a = 4, b = 1D. a = 1, b = 4二、填空题(每题4分,共20分)11. 已知函数f(x) = 3x - 4,则f(-1)的值为______。
12. 在直角坐标系中,点P(3, -2)关于y轴的对称点为______。
13. 下列数中,负数的倒数是______。
14. 已知等比数列的首项为2,公比为3,则该数列的前三项分别是______。
对口高考模拟数学试卷

一、选择题(每题4分,共40分)1. 若函数f(x) = x^2 - 4x + 3的图象的对称轴为直线x = a,则a的值为()。
A. 2B. 1C. 0D. -22. 在△ABC中,若角A、B、C的对边分别为a、b、c,且a=5,b=6,c=7,则△ABC的面积S为()。
A. 12B. 15C. 18D. 203. 下列各式中,正确的是()。
A. (x + y)^2 = x^2 + 2xy + y^2 + 2xyB. (x - y)^2 = x^2 - 2xy + y^2 - 2xyC. (x + y)^2 = x^2 - 2xy + y^2D. (x - y)^2 = x^2 + 2xy + y^24. 已知等差数列{an}的首项a1=3,公差d=2,则第10项a10为()。
A. 21B. 23C. 25D. 275. 若复数z = 3 + 4i,则|z|的值为()。
A. 5B. 7C. 9D. 116. 已知函数f(x) = x^3 - 3x,则f(x)的零点个数为()。
A. 1B. 2C. 3D. 47. 在平面直角坐标系中,点A(2,3)关于直线y=x的对称点为()。
A. (3,2)B. (2,3)C. (3,3)D. (2,2)8. 若等比数列{an}的首项a1=2,公比q=3,则第5项a5为()。
A. 24B. 18C. 12D. 69. 已知sinθ = 1/2,cosθ = √3/2,则tanθ的值为()。
A. 1/3B. 2/3C. 3/2D. 310. 在△ABC中,若角A、B、C的对边分别为a、b、c,且a=3,b=4,c=5,则角C 的度数为()。
A. 45°B. 60°C. 90°D. 120°二、填空题(每题4分,共20分)11. 函数f(x) = 2x - 1的图像上一点P(x, y),若点P在直线y = 2x - 3上,则x的值为______。
重庆市对口高职高考数学模拟试卷word.doc

重庆市对口高职数学综合试卷一、选择题(共12小题,每小题7分,共84分)1.已知集合A={x|-2<x ≤5},集合B={x|-3≤x<0},则AUB 等于 ( )A.{x|-2<x<0}B.{x|-3≤x ≤5}C.{x|-2<x ≤5}D.{x|-3≤x<0}2.已知532cos =α,则αcos 等于 ( ) A.54 B. 257 C. 2512 D.257- 3.函数)1(log 2x y -=的定义域为 ( )A. )(1,∞-B. ]0,∞-(C. )1,0[D. R4.直线2x-ay+3=0与直线4x+2y-1=0垂直则a 的值为 ( )A.2B.-2C.-4D.45.已知g(x) f(x),都是定义域为R 的奇函数,且6)(2)(5)(+-=x g x f x F ,若b a F =)(,则=-)(a F ( ) A.b-6 B.b-12 C.12-b D.12+b6.不等式0)2)(3(≤--x x 的解集为 ( )A. [2,3]B.),3[]2,(+∞-∞YC.(2,3)D.空集7.已知椭圆的焦点在x 轴上,焦距为2,P 点是椭圆上一点,它到左焦点的距离为2,到右焦点的距离为4,则椭圆的标准方程为 ( ) A. 12322=+y x B.18922=+y x C.19822=+y x D.15922=+y x 8.在等比数列}{n a 中,已知,8,231==a a 则5a = ( )A.8B.16C.32D.649.若a 与b 均为实数,则a=b 是a 2=b 2成立的( )A.充分条件B.必要条件C.充要条件D.既不充分也不必要条件10.将3个不同的球任意的放入4个不同的盒子中,则不同放法有( )A.4B.24C.64D.8111.函数x x y cos 4sin 3-=的最大值为 ( )A.3B.4C.5D.712.若圆2222342k k y x y x --=+-+与直线052=++y x 相切,则k = ( )A.3或-1B.-3或1C.-2或1D.2或-1二、填空题(共6小题,每小题7分,共42分)13.已知x x x f -=2)(,则=-)(x f __________14.抛物线x y 82-=上一点P 到焦点的距离为3,则点P 的横坐标为=________15.数列的{a n }的前n 项和n n S n +=22,那么它的通项公式为_________16.在ABC ∆,a=15,b=10,ο60=∠A ,则sinB=_________17.若角α的终边经过两直线3x-2y+5=0和x+y-5=0的交点P ,则α的正弦值为________18.设函数32)(2+-=mx x x f ,当)+∞-∈,2[x 是增函数,当]2,(-∞∈x 是减函数,则=-)2(f __________三、解答题(共6小题,共74分)19.计算:2122304143tan1019lg 2016-⎪⎭⎫ ⎝⎛-+-⋅+P og π20.解不等式{2|2|12231≤-<--+x x x21.已知函数)6cos()(π+=x a x f 的图像经过点⎪⎭⎫ ⎝⎛21-2,π (1)求a 的值(2)若sin θ=31,20πθ<<,求)(θf22.已知数列}{a n 的前n 项和为n S ,1a 1=,且满足12a 1n =-+n S 。
职高高考模拟数学试卷答案

一、选择题(每题5分,共50分)1. 下列各数中,有理数是()A. √2B. πC. √9D. 无理数答案:C2. 已知 a < b,下列不等式中正确的是()A. a - b < 0B. a + b > 0C. a - b > 0D. a + b < 0答案:A3. 下列函数中,定义域为全体实数的是()A. y = √(x - 1)B. y = 1/xC. y = x^2D. y = log2x答案:C4. 已知等差数列 {an} 的前n项和为 Sn,若 S5 = 25,S10 = 75,则 a1 = ()A. 1B. 2C. 3D. 4答案:A5. 下列命题中,正确的是()A. 若 a > b,则 a^2 > b^2B. 若 a > b,则 a - b > 0C. 若 a > b,则 ac > bcD. 若 a > b,则 a/c > b/c答案:B6. 已知等比数列 {an} 的前三项为 a1, a2, a3,若 a1 + a2 + a3 = 12,a1 a2 a3 = 64,则 a1 = ()A. 1B. 2C. 4D. 8答案:C7. 已知函数 y = ax^2 + bx + c,若 a ≠ 0,且函数图象开口向上,则()A. a > 0, b > 0, c > 0B. a > 0, b < 0, c > 0C. a < 0, b > 0, c >0 D. a < 0, b < 0, c > 0答案:B8. 已知正方形的对角线长为2√2,则其面积是()A. 4B. 6C. 8D. 10答案:A9. 下列各数中,绝对值最小的是()A. -1/2B. -1C. 1/2D. 1答案:C10. 已知函数 y = x^3 - 3x,求该函数的极值点。
中等职业学校对口升学考试数学模拟试题及答案

中等职业学校对口升学考试数学模拟试题及答案一、选择题1.若一组数据的方差为0,则该组数据的所有值相等。
【√】2.已知函数f(x)的导函数f'(x),则f(x)在x=0处的函数值可以通过f'(x)来确定。
【√】3.已知集合A={1,2,3,4},集合B={3,4,5},则A∪B的元素个数为6。
【×】4.已知集合A={x|x<5},集合B={x|3<x<6},则A∩B的元素个数为0。
【×】5.已知三角形ABC中,∠B=90°,tanA=1/√3,则sinC=1/2。
【×】二、填空题1.若10%的一批商品中有5%是次品,则整批商品中的次品数量为__________。
2.已知函数f(x)=3x^2-2x+1,求f(-1)的值为____________。
3.已知集合A={1,2,3,4},集合B={3,4,5},则A-B的元素个数为__________。
4.解方程3x+4y=10,5x+8y=14,得到x的值为__________。
5.已知正方形ABCD的边长为2,O为正方形的中心点,连接OA、OB、OC、OD形成一新的不规则图形,求该图形的面积为____________。
三、解答题1.某公司今年的棉花产量比去年增加了20%,去年的棉花产量为1000吨,今年的棉花产量为多少吨?解:今年的棉花产量 = 去年的棉花产量 + 增加的数量= 1000 + (1000 × 0.2)= 1000 + 200= 1200 (吨)2.已知函数y=3x^2-2x+1,求函数图像与x轴、y轴的交点坐标。
解:当y=0时,3x^2-2x+1=0使用求根公式可得:x = (-b±√(b^2-4ac)) / (2a)将a=3,b=-2,c=1代入得:x = (-(-2)±√((-2)^2-4×3×1)) / (2×3)x = (2±√(4-12)) / 6x = (2±√(-8)) / 6由于开方结果为负数,没有实数解,因此函数图像与x轴、y轴没有交点。
职中对口数学试卷高考模拟

一、选择题(本大题共10小题,每小题4分,共40分)1. 下列各数中,绝对值最小的是()A. -3B. -2C. 0D. 12. 若m,n是方程x^2 - (m+n)x + mn = 0的两根,则m+n的值是()A. 0B. 1C. 2D. m+n3. 下列函数中,是奇函数的是()A. y = x^2B. y = |x|C. y = x^3D. y = x^44. 在直角坐标系中,点P(2,3)关于x轴的对称点是()A. (2,-3)B. (-2,3)C. (-2,-3)D. (2,3)5. 若等差数列{an}的首项为2,公差为3,则第10项a10的值是()A. 29B. 28C. 27D. 266. 下列各式中,正确的是()A. a^2 = b^2,则a = bB. a^2 = b^2,则a = ±bC. a^2 = b^2,则a = ±b,b = ±aD. a^2 = b^2,则a = b,b = a7. 若等比数列{an}的首项为1,公比为2,则第n项an的值是()A. 2nB. 2n-1C. 2^nD. 2^(n-1)8. 在△ABC中,若∠A=60°,∠B=45°,则∠C的度数是()A. 75°B. 120°C. 45°D. 60°9. 下列函数中,是反比例函数的是()A. y = 2xB. y = x^2C. y = 1/xD. y = x^310. 若sinα = 1/2,则cosα的值是()A. √3/2B. -√3/2C. 1/2D. -1/2二、填空题(本大题共5小题,每小题5分,共25分)11. 已知函数y = -x^2 + 4x - 3,则该函数的对称轴是________。
12. 若等差数列{an}的首项为a1,公差为d,则第n项an = ________。
13. 在直角坐标系中,点P(-2,1)关于原点的对称点是________。
最新中等职业学校对口升学考试数学模拟试题(一)教学内容
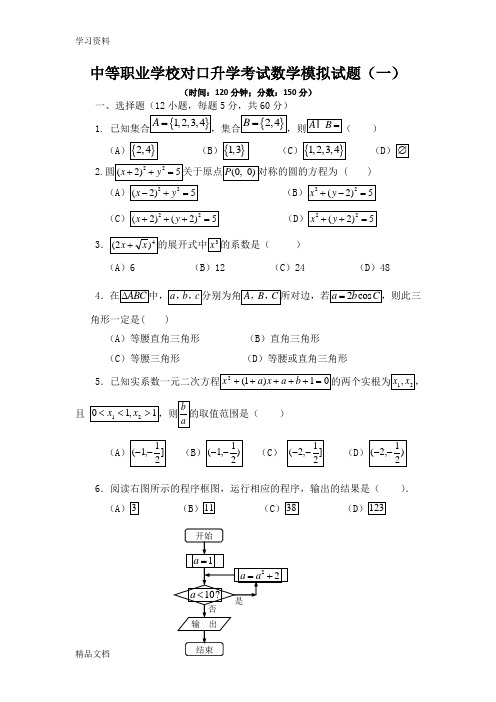
中等职业学校对口升学考试数学模拟试题(一)(时间:120分钟;分数:150分)一、选择题(12小题,每题5分,共60分)1.)(A(B(C(D2.( ) (A(B(C(D3)(A)6 (B)12 (C)24 (D)484角形一定是( )(A)等腰直角三角形(B)直角三角形(C)等腰三角形(D)等腰或直角三角形5且)(A(B(C)(D6.阅读右图所示的程序框图,运行相应的程序,输出的结果是().(A(B(C(D第9题7.已知x 、y 的取值如下表所示:若y 与x 线性相关,且ˆ0.95yx a =+,则a =( )x0 1 3 4 y2.24.34.86.7(A )2.2 (B )2.9 (C )2.8(D )2.68.设A 、B 为直线y x =与圆221x y += 的两个交点,则||AB = ( )(A )1 (B )2 C .3 D .29.如下图,矩形ABCD 中,点E 为边CD 的中点,若在矩形ABCD 内部随机取一个点Q ,则点Q 取自△ABE 内部的概率等于( )(A )14 (B )13 (C )12 (D )2310.已知圆22:40C x y x +-=,l 过点(3,0)P 的直线,则 ( )(A )l 与C 相交(B l 与C 相切(C )l 与C 相离 (D )以上三个选项均有可能11.若a ∈R ,则“1a =”是“1a =”的( )条件(A )充分而不必要 (B )必要而不充分 (C )充要 (D )既不充分又不必要12.一束光线从点)11(,-A 出发经x 轴反射,到达圆C :13-2-22=+)()(y x 上一点的最短路程是( ) (A )4(B )5(C )32-1(D )26二.填空题(6小题,每题5分,共30分)13.袋中共有6个除了颜色外完全相同的球,其中有1个红球,2个白球和3 个黑球,从袋中任取一球,颜色为黑色的概率等于.14.其斜 ______________________15____________.16._____________.17.= .18.的最小值是 .三.解答题(6小题,共60分)19. (8分)20.(8分)围.21.(10分)用定义证明函数在上是减函数.22.(102222:1(0)x yC a ba b+=>>6331(,)22.求椭圆C的方程.DC 1A 1B 1CBA23.(12分)如图,(1)(2) .24.(12分)已知圆O :122=+y x ,圆C :1)4()2(22=-+-y x ,由两圆外一点),(b a P 引两圆切线PA 、PB ,切点分别为A 、B ,满足|PA|=|PB|. (Ⅰ)求实数a 、b 间满足的等量关系; (Ⅱ)求切线长|PA|的最小值;BAP)42,42(-模拟试题(一)参考答案一.选择题(12小题,每题5分,共60分) 1.A2.D3.C4.C5.D6.B7.D8.B9.C 10.A 11.A 12.A二.填空题(6小题,每题5分,工30分) 13. 0.514.15. 16.1 17.-1 18.1三.解答题(6小题,共60分) 19.(820.(8分)]1,43(②当0a ≠时,依题意有200136360a a a a >⎧⇒<≤⎨∆=-≤⎩ 21.(10分)证明:设,则,,所以,函数在上是减函数.22.(10分)解: 由22222221,3a b a e a b -==-=得13b a = 由椭圆C 经过点31(,)22,得2291144a b += ② 联立① ②,解得1,3b a ==所以椭圆C 的方程是2213x y +=23.(12分)(1)证明:连接1B C ,设1B C 与1BC 相交于点O ,连接OD ,因为 四边形11BCC B 是平行四边形, 所以点O 为1B C 的中点. 因为D 为AC 的中点, 所以OD 为△1AB C 的中位线, 所以 1//OD AB .因为OD ⊂平面1BC D ,1AB ⊄平面1BC D , 所以1//AB 平面1BC D .EODC 1A 1B 1C BA(2)解因为在Rt24.(12分)(Ⅰ)连结PO 、PC ,因为|PA|=|PB|,|OA|=|CB|=1,所以|PO|2=|PC|2化简得实数a 、b。
中职对口高考数学试卷

一、选择题(本大题共20小题,每小题3分,共60分)1. 下列函数中,定义域为全体实数的是()A. y = 1/xB. y = √(x-1)C. y = x^2D. y = |x|2. 已知 a > 0,且 (a-1)^2 = 1,则 a 的值为()A. 0B. 1C. 2D. -13. 下列等式中,正确的是()A. (a+b)^2 = a^2 + 2ab + b^2B. (a-b)^2 = a^2 - 2ab + b^2C. (a+b)^3 = a^3 + b^3D. (a-b)^3 = a^3 - b^34. 在△ABC中,若∠A = 60°,∠B = 45°,则∠C的度数为()A. 75°B. 105°C. 135°D. 165°5. 已知等差数列{an}中,a1 = 3,d = 2,则第10项an的值为()A. 21B. 23C. 25D. 276. 下列图形中,中心对称图形是()A. 等腰三角形B. 等边三角形C. 正方形D. 梯形7. 若点P在直线y=2x上,且|OP|=5,其中O为坐标原点,则点P的坐标为()A. (5, 10)B. (10, 5)C. (-5, -10)D. (-10, -5)8. 已知函数y = kx + b,若图象过点(2, 3),则k和b的值分别为()A. k=1, b=1B. k=1, b=3C. k=3, b=1D. k=3, b=39. 下列命题中,正确的是()A. 若a>b,则a^2>b^2B. 若a>b,则|a|>|b|C. 若a>b,则a^2+b^2>a^2D. 若a>b,则a^2-b^2>a10. 在平面直角坐标系中,点A(2, 3),点B(-1, -2),则线段AB的中点坐标为()A. (3, 1)B. (1, 2)C. (0, 1)D. (1, 0)11. 下列方程中,无实数解的是()A. x^2 - 4 = 0B. x^2 + 4 = 0C. x^2 - 2x + 1 = 0D. x^2 + 2x + 1 = 012. 下列不等式中,正确的是()A. 2x > 3x + 1B. 2x < 3x + 1C. 2x ≤ 3x + 1D. 2x ≥ 3x + 113. 下列数列中,不是等比数列的是()A. 2, 4, 8, 16, ...B. 1, 3, 9, 27, ...C. 1, 1/2, 1/4, 1/8, ...D. 1, 2, 4, 8, ...14. 若直角三角形的三边长分别为3,4,5,则该三角形的面积是()A. 6B. 8C. 10D. 1215. 下列函数中,在定义域内单调递增的是()A. y = x^2B. y = 2xC. y = -xD. y = x^316. 下列方程中,解为x=2的是()A. x^2 - 4 = 0B. x^2 + 4 = 0C. x^2 - 2x + 1 = 0D. x^2 + 2x + 1 = 017. 在△ABC中,若∠A = 90°,∠B = 30°,则边BC的长度是()A. √3B. 2C. 2√3D. 418. 已知函数y = ax^2 + bx + c,若图象过点(1, 2),(2, 4),(3, 6),则a,b,c的值分别为()A. a=1, b=1, c=1B. a=2, b=2, c=2C. a=1, b=2, c=1D. a=2, b=1, c=219. 下列命题中,正确的是()A. 若a>b,则a-b>0B. 若a>b,则a-b<0C. 若a>b,则ab>0D. 若a>b,则ab<020. 下列数列中,不是等差数列的是()A. 2, 5, 8, 11, ...B. 3, 6, 9, 12, ...C. 1, 4, 7, 10, ...D. 5, 10, 15, 20, ...二、填空题(本大题共10小题,每小题3分,共30分)21. 若等差数列{an}中,a1 = 1,d = 2,则第10项an的值为______。
中职对口升学-数学模拟试卷-2份精选全文

精选全文完整版(可编辑修改)数学(第二部分)一、单项选择题,本大题共8题,每小题6分,共48分。
1、下列关系式中不正确的是( )。
A. {0}∈{0,1,2,3}B.φ⊆ {0,1,2,3}C.0∈{0,1,2,3}D. {x |x>5}⊆{x|x>0}2、函数f (x )=√x−1x−2的定义域是( )。
A. {X|X ≥0且x ≠0} B. {X|X ≥1} C. {X|X ≥1且x ≠2} D.x ≠23、若f (x )={2x −1x 2−15(x <0)(0≤x ≤10)(x >10) 那么f (15)=( )。
A.29B.5C.224D.无法确定4、cos 3900的值是( )。
A.12B.√3C.√32D. √335、下列命题不正确的是( )。
A .已知直线l 1, l 2及其对应的斜率k 1, k 2,则有l 1 //l 2⟺k 1=k 2B.已知直线l 1, l 2及其对应的斜率k 1, k 2,则有l 1⊥l 2⟺k 1.k 2=-1C.已知a ⃗,b ⃗⃗, a ⃗=(x 1,y 1),b ⃗⃗=(x 2,y 2),若a ⊥b ,则 a ⃗˙b⃗⃗=x 1x 2+y 1y 2=0 D. 已知a ⃗,b ⃗⃗ , a ⃗=(x 1,y 1),b ⃗⃗=(x 2,y 2), 若a ⃗//b ⃗⃗,则a ⃗˙b⃗⃗=x 1x 2+y 1y 2=0 6、圆(x −2)2+y 2=4的圆心是( )。
A.(-2,0)B.(0,2)C.(2,0)D.(0,-2)7、已知长方形的宽是a ,长是b ,现以长的一条边为轴,旋转一周,得到一个几何体,那么这个几何体的体积是( )。
A. abB.a 2 b πC.2ab πD. a 2b8、甲、乙、丙、丁考数学,它们偏离平均分情况是-2,+1,+2,-1,已知他们的总分为320分,那么他们的平均分是()。
A.80B.81C.78D.79二、填空题,本大题共8题,每小题6分,共48分。
对口高职数学模拟试卷(一)

对口高职数学模拟试卷(一)班级: 姓名:一、选择题:(本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的)1、若全集{}4,3,2,1=U ,{}2,1=M ,{}3,2=N ,则)(N M C U =( ) A .{}3,2,1 B .{}4 C .{}4,3,1 D .{}2 2、已知等差数列{}n a 的公差为2,若431,,a a a 成等比数列,则2a =( )A .-4B .-6C .-8D .-103、已知向量)4,3(=,)cos ,(sin αα=,且||,则αtan =( )A .43B .43-C .34D .34- 4、函数⎪⎭⎫ ⎝⎛-=x y 11lg 的定义域是( ) A .{}0|>x x B .{}1|>x x C .{}10|<<x x D .{}10|><x x x 或5、直线02=-+y x 的倾斜角是( )A .4πB .3π C .32π D .43π 6、点P 是圆0222=-+x y x 上任一点,则点P 到直线01243=++y x 距离的最小值是( )A .3B .2C .1D .07、下列四个函数中,同时具有性质:(1)最小正周期是π;(2)图象关于直线3π=x 对称。
则这个函数是( )A .⎪⎭⎫ ⎝⎛+=62sin πx yB .⎪⎭⎫ ⎝⎛-=62sin πx y C .⎪⎭⎫ ⎝⎛-=32sin πx y D .⎪⎭⎫ ⎝⎛-=62sin πx y8、函数)2(log )(221x x x f +=的单调递减区间为( )A .)2,(--∞B .)1,(--∞C .),1(+∞-D .),0(+∞9、在△ABC 中,若7,5,3===c b a ,则△ABC 的面积为( )A .315B .2315C .4315D .4215 10、某学生步行去上学,由于担心迟到,所以一开始就跑步,跑累了再走完余下的路程。
2023年中职对口升学单招数学模拟试卷)

模拟卷六一、选择题(本大题共15 小题,每小题5 分,满分75 分)【建议用时:50 分钟】1. M={ x|x< 2 } ,N={ x|x- 4 < 0 } ,则M⋂N=().A. ( -∞,4 )B. ( -∞,2)C. ( -∞, -2) ⋃(2 , +∞)D. ∅2. 不等式|x+ 2|< 4 的解集是().A. ( -2 , 1)B. ( -∞, -2) ⋃(1 , +∞)C. ( -6 ,2)D. ( -∞,6)3. 设函数f(x)= 3 ,则f(x)().A. 是偶函数B. 是奇函数C. 不具有奇偶性D. 既是奇函数又是偶函数v4 -x2的定义域为().4. 函数f(x)=A. [ -2 ,2 ]B. [ 2 , +∞)C. ( -∞,2 ]D. ( -∞, -2) ⋃(2 , +∞)5. f(x)= a x+ 1经过点(2 ,8 ),则a=().A. -2B. 2C. 3D. -36. 等差数列{ a n} 中,a2=-4,a4=-16,则S5=().A. -50B. 60C. 126D. 07. 已知f(x)=x+ 4 ,则f-1(5)=().A. -1B. 1C. 9D. -98. 函数y= 2(log2x) 的定义域是().A. (0 , 1)B. (0 , +∞)C. [ 1 , +∞)D. (1 , +∞)9. 函数y= 3sin x- 2 的最小值是().A. 1B. 5C. -5D. 210. 若sinα< 0 ,cosαsinα< 0 ,则α为().A. 第一象限角B. 第二象限角C. 第三象限角D. 第四象限角11. 已知一组数据1、2、y的平均数为4 ,那么y=().A. 7B. 8C. 9D. 1012. 有20位同学,编号从1 至20 ,现在从中抽取4人作问卷调查,用系统抽样方法确定所抽的编号为().A. 5 ,10 ,15 ,20B. 2 ,6 ,10 ,14C. 2 ,4 ,6 ,8D. 5 ,8 ,11 ,1413. 若双曲线的焦距是10 ,则a的值是().A. 3B. 9C. 9或- 9D. 3或- 314. 椭圆上任意两点间的最大距离为8 ,则h的值为().A. 32B. 16C. 8D. 415. 圆x2+y2= 4与直线3x- 4y+ 4 = 0 的关系是().A. 相离B. 相切C. 相交D. 无法确定二、填空题(本大题共5 小题,每小题5 分,满分25 分)【建议用时:20 分钟】16. 函数f(x)=x2+ 2x+ 1 的最小值是.2 217. 以双曲线的左顶点为焦点,原点为顶点的抛物线方程是.18. 数据4 ,6 ,5 ,4 ,6 的方差是.19. 若{ a n}为等比数列,a n> 0 ,S2 = 7 ,S6 = 91 ,则S4 = .20. 向量< >= 60°,||= 2 , ||= 5 ,则||= .三、解答题(本大题共4 小题,第21-23 题各12 分,第24 题14 分,满分50 分)【建议用时:50 分钟】21. 如图11–1所示,在△ABO中,已知点A(2 ,4 ),B(6 ,2).(1)求△ABO的面积;(2)若点P是x轴上的一点,且△OAP的面积与△ABO的面积相等,求点P的坐标.y ▲ABOx图11 –122. 在△ABC中,a,b,c分别是∠A, ∠B, ∠C的对边,已知b= 3 ,c= 4 ,cos A= .(1)求a的值;(2)求△ABC的面积.23. 已知等差数列{ a n}满足:a1 = 2 ,a n+ 1 = a n+ 2(n∈N*).(1)求数列{ a n} 的通项公式和前n项和S n;若b n= 求数列{ b n} 的前n项和T n./6 ,且长轴长是短轴长的两倍.24. 已知椭圆E的中心在原点,焦点在y轴上,焦距为2(1)求椭圆E的标准方程;(2)设直线l:2x-y+ b= 0 与椭圆E交于A,B两点,若定点P的坐标是(1 ,2),求当b为何值时,△PAB的面积最大.。
中职学生对口高考数学试卷

一、选择题(每题5分,共20分)1. 已知函数f(x) = x^2 - 4x + 4,则该函数的图像是:A. 一个开口向上的抛物线B. 一个开口向下的抛物线C. 一条直线D. 一个圆2. 在直角坐标系中,点A(2,3)关于y轴的对称点为:A. (2,-3)B. (-2,3)C. (-2,-3)D. (2,3)3. 下列各数中,绝对值最小的是:A. -5B. -3C. 2D. 04. 一个等腰三角形的底边长为8,腰长为10,那么这个三角形的面积是:A. 32B. 40C. 48D. 645. 下列方程中,无解的是:A. 2x + 3 = 7B. 3x - 5 = 2x + 1C. 4x + 6 = 10D. 5x - 2 = 3x + 4二、填空题(每题5分,共20分)6. 若a > b,则|a| _______ |b|。
7. 已知等差数列{an}的首项为2,公差为3,则第10项an = _______。
8. 若等比数列{bn}的首项为3,公比为2,则第5项bn = _______。
9. 在直角坐标系中,点P(3,4)到原点O的距离是 _______。
10. 一个圆的半径为5,那么它的直径是 _______。
三、解答题(每题20分,共60分)11. (10分)解方程:3x^2 - 5x + 2 = 0。
12. (10分)已知函数f(x) = 2x - 3,求函数的值域。
13. (10分)已知等差数列{an}的首项为3,公差为2,求前10项的和。
14. (10分)在直角坐标系中,已知点A(2,3),点B(-2,3),求线段AB的长度。
四、附加题(10分)15. (10分)已知函数f(x) = x^2 - 4x + 4,求函数f(x)的图像与x轴的交点。
答案:一、选择题:1.A 2.B 3.D 4.C 5.D二、填空题:6.> 7.29 8.48 9.5 10.10三、解答题:11. 解:3x^2 - 5x + 2 = 0,因式分解得(3x - 2)(x - 1) = 0,解得x = 2/3或 x = 1。
最新对口高考数学模拟试卷含答案

对口高考数学模拟试卷本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分,考试用时120分钟.第Ⅰ卷(选择题 共50分)参考公式:如果事件A 、B 互斥,那么柱体(棱柱、圆柱)的体积公式P (A+B )=P (A )+P (B ) h V S =柱体 如果事件A 、B 相互独立,那么 其中S 表示柱体的底面积,P (A·B)=P (A )·P(B )h 表示柱体的高一、单项选择题:(每一小题仅有一个正确答案,请将正确答案的代号填入 答题表内。
每小题5分,共计60分)1.下列关系中正确的是 ( )A. φ∈0B.a ∈{a}C.{a,b}∈{b,a}D. φ=}0{2. 不等式21≥-xx 的解集为( )A . )0,1[-B . ),1[+∞-C . ]1,(--∞D . ),0(]1,(+∞--∞3.对任意实数,,a b c 在下列命题中,真命题是( )A . ""ac bc >是""a b >的必要条件B . ""ac bc =是""a b =的必要条件C . ""ac bc >是""a b >的充分条件D . ""ac bc =是""a b =的充分条件4.若平面向量与向量)2,1(-=a 的夹角是o180,且53||=b ,则=( )A . )6,3(-B . )6,3(-C . )3,6(-D . )3,6(-5.设P 是双曲线19222=-y ax 上一点,双曲线的一条渐近线方程为023=-y x ,1F 、2F 分别是双曲线的左、右焦点。
若3||1=PF ,则=||2PF ( )A . 1或5B . 6C . 7D .96、原点到直线y=kx+2的距离为2,则k 的值为 ( ) A. 1 B. -1 C. ±1 D. ±77、若135sin )cos(cos )sin(=+-+αβααβα,且β是第二象限角,则βcos 的值为( ) A .1312 B .1312- C .53 D .53-8、在等差数列{a n }中,a 1+a 2+a 3+a 4+a 5=15 , a 3= ( ) A. 2 B. 3 C. 4 D. 5 9、已知函数b a x f x +=)(的图象经过点)3,1(,又其反函数)(1x f-的图象经过点)0,2(,则函数)(x f 的表达式是( )A .12)(+=x x fB .22)(+=x x fC .32)(+=x x fD .42)(+=x x f 10、已知向量与,则下列命题中正确的是 ( )A. 若||>||,则>B. 若||=||,则=C. 若=,则∥D. 若≠,则与就不是共线向量11.下列函数中为偶函数的是 ( )A .f(x)=1-x 3B.f(x)=2x-1C.f(x)=x 2+2 D.f(x)=x 312. 一商场有三个大门,商场内有两部上楼的电梯,一顾客从商场外到商场二楼购物,不同的走法共有( )A.5种B.6种C.8种D.9种市 姓名 准考证号 座位号第Ⅱ卷(非选择题 共100分)二、填空题:(本大题共4小题,每小题4分,共16分.答案填在题中横线上)11.一个圆柱的底面半径和高都与一个球的直径相等,则该圆柱与该球的体积比为____________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019口高职高考数学模拟试卷
一、 选择题
1.集合A ={1,2},B ={3,4}则A ∪B 等于( )
A.{2}
B.{2,3,4}
C.{1,3,4}
D.{1,2,3,4}
2.已知a=2−3,b=212,c=(12)2,则a,b,c 的大小关系为()
A.a<b<c
B.a<c<b
C.b<a<c
D.c<b<a
3.已知cos α=12, α∈(0,π),则sin α=( ).
A.√3 2
B.- √3 2
C. 1 2
D.- 1 2 4.已知两条直线y=ax-2和y=(a+2)x+1互相垂直,则a=( )
A.2
B.1
C.0
D.- 1
5.下列函数中,在区间(0,+∞)上单调递增的是( )。
A.y =sinx
B.y=1x
C.y =x 2
D.y=log 13x
6.已知函数f(x)的定义域为R ,则“f(x)为偶函数”是“f(-1)=f(1)”的( )。
A .充分必要条件 B.必要不充分条件
C.充分不必要条件
D.既不充分也不必要条件
7.不等式x 2-5x+6<0的解集是( )。
A.{x |x <2}
B. {x |x >3}
C.{x |x <2或x >3}
D. {x |2<x <3}
8.从1,2,3,4,5,6,7,8,9这9个数中取2个不同的数,使其和为偶数,则不同的取法共有( )。
A.72种
B.36 种
C.32种
D. 16种
二、填空题
9.若直线kx-y+6=0经过圆(x−1)2+(y−2)2=4的圆心,则k= .
10.函数f(x)=1-2cosx的最小值为.
11.若关于x的不等式|2x+b|<3的解集为{x|−3<x<0},则b= .
12.若双曲线x2
a2−y2
b2
=1(a>0,b>0)上存在四点A、B、C、D,使四边形ABCD为
正方形,则此双曲线的离心率的取值范围为.
三、解答题
13.已知函数f(x)=2log a(x+5)-1(a>0,且a≠1),f(-1)=1. (1)求a的值,并写出f(x)的定义域;
(2)当x∈[-4,11]时,求f(x)的取值范围。
14.已知数列{a n}为等差数列,若a1=1, a3=a2+a1.
(1)求数列{ a
n
}的通项公式;
(2)设b
n= a
n
+(1
2
)a n,求数列{b n}的前n项和S n.
15.已知抛物线C:y2=2px的焦点为F(2,0).
(1)求抛物线C的方程;
(2)过点M(1,2)的直线L与C相交于A,B两点,且M为AB的中点,求直线L的方程。
16.已知a,b,c分别为⊿ABC内角A、B、C的对边,已知c2=2ab.
(1)若C=900,且a=1.求⊿ABC的面积;
(2)若sinA=sinC,求cosC的值。
17.某公司有40万元资金,计划投资甲、乙两个项目,按要求对项目甲的投
倍,且对每个项目的投资都不能低于5万元。
对项目资不小于对乙项目投资的1
3
甲每投资1万元可获得0.2万元的利润,对项目乙每投资1万元可获得0.3万元的利润。
问:该公司如何规划投资,才能使公司获得的总利润最大?。
