江苏省南通、泰州、扬州、连云港、淮安五市2013届高三第三次模拟考试数学试卷
2013届江苏省南通、泰州、扬州、连云港、淮安五市高三第三次模拟考试数学试卷 数学讲评建议

江苏省南通、泰州、扬州、连云港、淮安五市2013届高三第三次模拟考试数学试卷数学Ⅰ讲评建议1. 考查集合的运算,源于《必修1》习题1.3感受·理解第3题. 2. 考查复数的四则运算.3. 考查算法的流程图,源于《必修3》1.2.3循环结构的引例.4. 考查充分必要条件,源于《选修2—1》习题1.1思考·运用第4题(3). 5. 考查统计中的总体分布的估计,应注意组距是20. 6. 考查抛物线的标准方程与简单性质,注意p 的含义. 7. 考查古典概型.符合条件的有(1,3),(2,6),(3,9)三个.8. 考查圆与直线的位置关系.找出点Q 在直线260x y --=上,转化为圆上的点到直线的距离求解.9. 考查sin()y A x ωϕ=+的图象性质,周期性,诱导公式.由图知5A =,12T =,从而ωπ=6,6ϕπ=,则(2013)(9)f f ==.源于《必修4》复习题感受·理解第13题.10.考查等比数列和基本不等式,由2213a a a =,211a a -=及0n a >得()2131111124a a a a a +==++≥(当且仅当11a =时取等号),此时22a =,则12n n a -=.本题也可以利用基本量思想求解.11.考查函数的图象与基本性质.由偶函数的性质,得到1 2 1a b c ===-,,.由题意知3 2 D C C D x x x x =⎧⎨+=⎩,,所以12C x =,则()211721224t =-⨯-=-. 12.考查导数与归纳推理.设111( e )x T x ,,则111e e 1x x x =+,解得10x =,所以01(0 e )T ,;设222( e )x T x ,,则222e e x x x =,解得21x =,所以2(1 e)T ,;设232( e )x T x ,,则331e e 1x x x =-, 解得32x =,所以23(2 e )T ,;…,通过归纳可猜想:1( e ) n n T n n +∈N ,,.讲评时提醒学生本题可推导出{}n x 是等差数列用于求解.13.考查平面向量的数量积.由2EF AB DC =+ ,平方并整理得2AB DC ⋅=,即()AB AC AD ⋅- 2AB AC AB AD =⋅-⋅=①, 由15AD BC ⋅= ,得()15AD AC AB AD AC AD AB ⋅-=⋅-⋅=②,②-①得AC BD ⋅ ()AC AD AB =⋅-13=.本题亦可用解析法求解.本题源于《必修4》习题2. 2.感受·理解第7题和《选修2—1》空间向量的应用的一道题.讲评时可回顾复习课本原题,提醒学生后期复习应重视回归课本. 14.考查一元二次方程,不等式等相关知识.方法一:因为123123 0a a a a a a >>⎧⎨++=⎩,,所以10a >,30a <,消去2a 得31122aa -<<-,且21413413()0a a a a a a a -+++=,两边同除以1a 得()2334411110a aa a a a -+++=,解得31a a 2441a a =-1-,所以24412112a a -<<---4a << 方法二:由123123 0a a a a a a >>⎧⎨++=⎩,得321132111 10 a a a a a a a a ⎧>>⎪⎪⎨⎪++=⎪⎩,,令2131 a x a a y a ⎧=⎪⎪⎨⎪=⎪⎩,,则1 10 y x x y <<⎧⎨++=⎩,,利用线性规划知识求出21a a 的取值范围,再结合242411a a a a =-,求出4a 的取值范围. 方法三:可以用求根公式求出4a ,再结合21a a 的取值范围,利用单调性求解. 15.考查直线与平面平行,平面与平面垂直的判定,提醒学生要规范书写.16.考查正,余弦定理,两角和与差的三角函数.强调学生对于各种形式有敏锐的观察力.原条件利用“化边为角”或“化角为边”两种思路均可求解,若对等式两边同时加1,再进行转化,更为便捷;第二问中可利用均值代换,不妨设A απ=-3,C απ=+3,π03α<≤求解,可简化求解过程.17.考查函数模型及其应用.学生对于题意的正确理解较为关键,运算中若未能使用分式的合比性质,也可以利用消去1T ',2T '求解.本题源于生活,结论与欧盟现行标准完全吻合.18.考查椭圆的标准方程,直线的斜率,直线与椭圆的位置关系.在第(2)问的运算上要注意先化简再代入.本题的几何背景是:在如图所示的圆中,因为1234567∠+∠=∠=∠=∠=∠+∠,且27∠=∠,所以16∠=∠.19.考查等差和等比数列.作为C 级要求知识点的考查,有一定的思维量及运算量. 其问题本质是:“几何级数增长”快于“代数级数增长”,即1q >且x →+∞时,x q mx n >+.答案提供的方法中,对于不等关系,实际是利用公比大于1的正项等比数列单调递增的性质,结合两个等式项数相同进行变形.对此,学生如有思维障碍,可利用特殊数值探索,找到求解方法.方法二:(注意到数列的函数特征,运用函数性质求解) 1(1)1n n n b a q n d --=---(易知0d >),令()1x f x q dx =--,有(0)(1)0f f k =-=,()ln x f x q q d '=-, 令()ln 0x f x q q d '=-=,则log ln q d x q =.记0log ln q d x q=.若00x ≤,则在[0)+∞,上()0f x '>,函数()f x 在[0 )+∞,上为单调增函数,则(0)(1)f f k <-,这与(0)(1)0f f k =-=相矛盾;若01x k -≥,则在0[0 ]x ,上()0f x '<,函数()f x 在0[0 ]x ,上为单调减函数,则(0)(1)f f k >-,这与(0)(1)0f f k =-=相矛盾; 所以,001x k <<-.故在0[0 )x ,上()0f x '<,函数()f x 在0[0 ]x ,上为单调减函数, 在0( )x +∞,上()0f x '>,函数()f x 在0[ )x +∞,上为单调增函数. 因为(0)(1)0f f k =-=,所以,当01x k <<-时,()0f x <,当1x k >-时,()0f x >, 所以,当n k >时,(1)0f n ->,即n n a b <, 当1n k <<时,(1)0f n -<,即n n a b >,综上所述,当1n k <<时,n n a b <;当n k >时,n n a b >;当1 n k =,时,n n a b =. 20.考查函数的图象与性质.本题第(2)问原准备考查“n 阶”,但最终定为思路及方法完全一致的“2阶”进行考查.本题关键在于判断()n f x mx > 在0m >时无上界,再用单调性即可证出结论.。
2013年江苏省五市高考数学三模试卷(南通、泰州、扬州、连云港、淮安)

2013年江苏省五市高考数学三模试卷(南通、泰州、扬州、连云港、淮安)学校:___________姓名:___________班级:___________考号:___________一、填空题(本大题共14小题,共70.0分)1.已知集合A=(-2,1],B=[-1,2),则A∪B= .【答案】(-2,2)【解析】试题分析:已知集合A=(-2,1],B=[-1,2),根据并集的定义进行求解.∵集合A=(-2,1],B=[-1,2),A∪B=(-2,2),故答案为:(-2,2).2.设复数z满足(3+4i)z+5=0(i是虚数单位),则复数z的模为.【答案】1【解析】试题分析:直接移项已知方程,两边求模,化简即可.因为复数z满足(3+4i)z+5=0,所以(3+4i)z=-5,两边求模可得:|(3+4i)||z|=5,所以|z|=1.故答案为:1.3.如图是一个算法流程图,则输出的S的值是.【答案】2400【解析】试题分析:按照程序框图的流程写出前几次循环的结果,并判断每一次得到的结果是否满足判断框中的条件,直到满足条件,执行输出.经过第一次循环得到结果为s=400,此时满足判断框的条件,经过第二次循环得到结果为s=2×400,此时满足判断框的条件,经过第二次循环得到结果为s=3×400,此时满足判断框的条件,经过第二次循环得到结果为s=4×400,此时满足判断框的条件,经过第二次循环得到结果为s=5×400,此时满足判断框的条件,经过第二次循环得到结果为s=6×400,此时不满足判断框的条件,执行输出s,即输出2400.故答案为:2400.4.“M>N”是“log2M>log2N”成立的条件.【答案】必要不充分【解析】试题分析:当M>N时,不确定两个数字的正负,不一定得到log2M>log2N,即前者不一定推出后者;当log2M>log2N时,根据对数函数的单调性知有M>N,即后者可以推出前者,得到结论.∵当M>N时,不确定两个数字的正负,不一定得到log2M>log2N,即前者不一定推出后者;当log2M>log2N时,根据对数函数的单调性知有M>N,即后者可以推出前者,∴“M>N”是“log2M>log2N”成立的必要不充分条件,故答案为:必要不充分5.根据某固定测速点测得的某时段内过往的100辆机动车的行驶速度(单位:km/h)绘制的频率分布直方图如图所示.该路段限速标志牌提示机动车辆正常行驶速度为60km/h~120km/h,则该时段内非正常行驶的机动车辆数为.【答案】15【解析】试题分析:利用频率等于纵坐标乘以组距求出正常行驶的频率;利用所有的频率和为1,求出非正常行驶的频率;利用频数等于频率乘以样本容量求出这100辆汽车中非正常行驶的汽车的辆数.正常行驶在60km/h~120km/h的频率为20×(0.0100+0.0150+0.0175)=0.85,非正常行驶的频率有1-0.85=0.15;所以这100辆汽车中非正常行驶的汽车有100×0.15=15.故答案为:15.6.在平面直角坐标系x O y中,抛物线x2=2py(p>0)上纵坐标为1的一点到焦点的距离为3,则焦点到准线的距离为.【答案】4【解析】试题分析:先根据抛物线的方程求得准线的方程,进而利用点A的纵坐标求得点A到准线的距离,进而根据抛物线的定义求得答案.依题意可知抛物线的准线方程为y=点A与抛物线焦点的距离为3,∴纵坐标为1,点A到准线的距离为+1=3,解得p=4.抛物线焦点(0,2),准线方程为y=-2,∴焦点到准线的距离为:4.故答案为:4.7.从集合{1,2,3,4,5,6,7,8,9}中任取两个不同的数,则其中一个数恰是另一个数的3倍的概率为.【答案】【解析】试题分析:所有的取法共有=36种方法,用列举法求得其中,满足条件的取法共有三种方法,由此求得所求事件的概率.从集合{1,2,3,4,5,6,7,8,9}中任取两个不同的数a和b,所有的取法共有=36种方法,其中,满足个数恰是另一个数的3倍的取法有1和3,2和6,3和9,共三种方法,故其中一个数恰是另一个数的3倍的概率为=,故答案为.8.在平面直角坐标系x O y中,设点P为圆C:(x-1)2+y2=4上的任意一点,点Q(2a,a-3)(a∈R),则线段PQ长度的最小值为.【答案】【解析】试题分析:根据点Q的坐标可得点Q在直线x-2y-6=0上,求出圆心(1,0)到直线x-2y-6=0的距离,再将此距离减去半径,即得所求.设点Q(x,y),则x=2a,y=a-3,∴x-2y-6=0,故点Q在直线x-2y-6=0上.由于圆心(1,0)到直线x-2y-6=0的距离为d==,故则线段PQ长度的最小值为-2,故答案为-2.9.函数f(x)=A sin(ωx+φ)(A>0,ω>0,0≤φ<2π)在R上的部分图象如图所示,则f(2013)的值为.【答案】【解析】试题分析:由函数的最值求出A,由周期求出ω,由五点法作图求出φ的值,球的函数的解析式,再利用诱导公式求得f(2013)的值为.由函数的图象可得A=5,周期T==11-(-1)=12,∴ω=.再由五点法作图可得(-1)+φ=0,∴φ=,故函数f(x)=5sin(x+).故f(2013)=5sin(+)=5sin=5sin(336π-)=5sin(-)=-5sin=,故答案为.10.各项均为正数的等比数列{a n}中,a2-a1=1.当a3取最小值时,数列{a n}的通项公式a n= .【答案】2n-1【解析】试题分析:设出等比数列的公比,代入a2-a1=1后求出首项和公比的关系,把a3用公比表示,利用二次函数求最值求出使a3最小的q的值,则通项公式可求.设等比数列的公比为q(q>0),由a2-a1=1,得a1(q-1)=1,所以.=(q>0),而,当q=2时有最大值,所以当q=2时a3有最小值4.此时.所以数列{a n}的通项公式a n=2n-1.故答案为2n-1.11.已知函数是偶函数,直线y=t与函数y=f(x)的图象自左向右依次交于四个不同点A,B,C,D.若AB=BC,则实数t的值为.【答案】【解析】试题分析:由f(x)是偶函数可得x>0时恒有f(-x)=f(x),根据该恒等式即可求得a,b,c的值,从而得到f(x),令t=f(x),可解得A,B,C三点的横坐标,根据AB=BC可列关于t的方程,解出即可.因为f(x)是偶函数,所以x>0时恒有f(-x)=f(x),即x2-bx+c=ax2-2x-1,所以(a-1)x2+(b-2)x-c-1=0,所以,解得a=1,b=2,c=-1,所以f(x)=,由t=x2+2x-1,即x2+2x-1-t=0,解得x=-1±,故x A=-1-,x B=-1+,由t=x2-2x-1,即x2-2x-1-t=0,解得x=1±,故x C=1-,因为AB=BC,所以x B-x A=x C-x B,即2=2-2,解得t=-,故答案为:-.12.过点P(-1,0)作曲线C:y=e x的切线,切点为T1,设T1在x轴上的投影是点H1,过点H1再作曲线C的切线,切点为T2,设T2在x轴上的投影是点H2,…,依次下去,得到第n+1(n∈N)个切点T n+1.则点T n+1的坐标为.【答案】(n,e n)【解析】试题分析:设T1(x1,),可得切线方程代入点P坐标,可解得x1=0,即T1(0,1),可得H1(0,0),在写切线方程代入点H1(0,0),可得T2(1,e),H2(1,0),…由此可得推得规律,从而可得结论.设T1(x1,),此处的导数值为,故切线方程为y-=(x-x1),代入点P(-1,0)可得0-=(-1-x1),解得x1=0,即T1(0,1),H1(0,0),同理可得过点H1再作曲线C的切线方程为y-=(x-x2),代入点H1(0,0),可得0-=(0-x2),可解得x2=1,故T2(1,e),H2(1,0),…依次下去,可得T n+1的坐标为(n,e n)故答案为:(n,e n)13.在平面四边形ABCD中,点E,F分别是边AD,BC的中点,且AB=1,,CD=.若,则的值为.【答案】13【解析】试题分析:由题意求得,=①,=②,把①、②相加求得2=,由此可得=2.由求得+=15+ +,把它代入的表达式可得的值.如图所示:∵==+,∴=①;∵==+,∴=②.把①、②相加求得2=,由AB=1,,CD=,平方可得2×4=1+2+3,∴=2.设AB和CD相较于点O,∵=()•(-)=--+,∴+=15++.∴=()•()=+--=15++--=15+•()+•()=15++=15+=15+=15-=15-2=13,故答案为13.14.已知实数a1,a2,a3,a4满足a1+a2+a3=0,a1a42+a2a4-a2=0,且a1>a2>a3,则a4的取值范围是.【答案】【解析】试题分析:先根据题意a1+a2+a3=0得a1≥0a3≤0a1≥|a2|-a3≥|a2|.对于方程a1a42+a2a4-a2=0,将a4看成未知数,解二次方程得a4=-•±•,设=x,由a1≥|a2|知-1≤x≤1,利用a4=-x±的单调性结合x的取值范围,即可得出a4的取值范围.a1+a2+a3=0得a1≥0,a3≤0,a1≥|a2|-a3≥|a2|.a4==-•±•,设=x,由a1≥|a2|.知-1≤x≤1,a4=-x±,由x2+4x≥0,得0≤x≤1,当a4=-x+时,有当x=1,a4取最大,最大值a4=-+;当a4=-x-时,有当x=1,a4取最小,最小值a4=--;则a4的取值范围是.故答案为:.二、解答题(本大题共12小题,共80.0分)15.如图,在四棱锥P-ABCD中,底面ABCD是矩形,四条侧棱长均相等.(1)求证:AB∥平面PCD;(2)求证:平面PAC⊥平面ABCD.【答案】证明:(1)在矩形ABCD中,AB∥CD,又AB⊄平面PCD,CD⊂平面PCD,所以AB∥平面PCD.(2)如图,连结BD,交AC于点O,连结PO,在矩形ABCD中,点O为AC,BD的中点,又PA=PB=PC=PD,故PO⊥AC,PO⊥BD又AC∩BD=O,AC,BD⊂平面ABCD,所以PO⊥平面ABCD又PO⊂平面PAC,所以平面PAC⊥平面ABCD.【解析】(1)由矩形ABCD,对边平行得到AB∥CD,结合线面平行的判定定理得到AB∥平面PCD;(2)连结BD,交AC于点O,连结PO,由在矩形ABCD中,点O为AC,BD的中点,可得PO⊥AC,PO⊥BD,进而由线面垂直的判定定理得到PO⊥平面ABCD,进而由面面垂直的判定定理得到平面平面PAC⊥平面ABCD.16.在△ABC中,角A,B,C所对的边分别为a,b,c.已知.(1)求角B的大小;(2)设T=sin2A+sin2B+sin2C,求T的取值范围.【答案】解:(1)∵在△ABC中,b2=a2+c2-2accos B,∴b2-a2-c2=-2accos B,同理可得c2-a2-b2=-2abcos C∵∴,∵sin C≠0,可得sin B cos C=2sin A cos B-sin C cos B,∴2sin A cos B=sin B cos C+sin C cos B=sin(B+C)=sin A,∵sin A≠0,∴等式两边约去sin A,可得,∵0<B<π,∴角B的大小.(2)∵B=,sin2A=(1-cos2A),sin2C=(1-cos2C)T=sin2A+sin2B+sin2C=∵A+C=,可得2C=-2A,∴cos2A+cos2C=cos2A+cos(-2A)=cos2A-sin2A=sin(-2A)因此,=-sin(-2A)∵,可得-<-2A<,∴-1≤sin(-2A),可得<-sin(-A)≤因此,T=sin2A+sin2B+sin2C的取值范围为(,]【解析】(1)根据余弦定理,将题中等式化简整理,可得sin B cos C=2sin A cos B-sin C cos B,称项化简得2sin A cos B=sin(B+C)=sin A,在两边约去sin A得,结合三角形内角取值范围即可得到角B的大小;(2)根据B=代入,结合二倍角的余弦公式降次,再用辅助角公式合并可得T=sin2A+sin2B+sin2C=-sin(-2A).最后根据角A的取值范围,结合正弦函数的图象与性质,即可得到T的取值范围.17.某单位设计的两种密封玻璃窗如图所示:图1是单层玻璃,厚度为8mm;图2是双层中空玻璃,厚度均为4mm,中间留有厚度为x的空气隔层.根据热传导知识,对于厚度为d的均匀介质,两侧的温度差为△T,单位时间内,在单位面积上通过的热量,其中k为热传导系数.假定单位时间内,在单位面积上通过每一层玻璃及空气隔层的热量相等.(注:玻璃的热传导系数为4×10-3J•mm/°C,空气的热传导系数为2.5×10-4J•mm/°C.)(1)设室内,室外温度均分别为T1,T2,内层玻璃外侧温度为,外层玻璃内侧温度为,且.试分别求出单层玻璃和双层中空玻璃单位时间内,在单位面积上通过的热量(结果用T1,T2及x表示);(2)为使双层中空玻璃单位时间内,在单位面积上通过的热量只有单层玻璃的4%,应如何设计x的大小?【答案】解:(1)设单层玻璃和双层中空玻璃单位时间内,在单位面积上通过的热量分别为Q1,Q2,则,===.(2)由(1)知,当=4%时,解得x=12(mm).答:当x=12mm时,双层中空玻璃通过的热量只有单层玻璃的4%.【解析】(1)直接由单位面积上通过的热量公式求得单层玻璃在单位面积上通过的热量.分别求出双层玻璃在单位面积上经过玻璃及空气隔层的热量,利用合比定理转化为含有T1,T2的关于x的表达式;(2)利用在单位面积上经过两种玻璃的热量的比值等于4%求取x的值.18.如图,在平面直角坐标系x O y中,椭圆的右焦点为F(1,0),离心率为.分别过O,F的两条弦AB,CD相交于点E(异于A,C两点),且OE=EF.(1)求椭圆的方程;(2)求证:直线AC,BD的斜率之和为定值.【答案】解:(1)由题意,得c=1,,故,可得b2=a2-c2=1,∴椭圆的方程为.①(2)证明:设直线AB的方程为y=kx,②直线CD的方程为y=-k(x-1),③由①②联解,得点A的横坐标为,点B的横坐标为,同理,联解①③,得点C的横坐标为,D的横坐标为记A(x1,kx1),B(x2,kx2),C(x3,k(1-x3)),D(x4,k(1-x4)),因此,直线AC,BD的斜率之和为====0.即直线AC,BD的斜率之和为0(定值)【解析】(1)根据题意,建立关于a、c的方程组,解之可得且c=1,再用平方关系算出b2=1,即可得到椭圆的方程;(2)设直线AB的方程为y=kx,与椭圆方程联解可得A的横坐标为,点B的横坐标为,同理得到点C、D的横坐标关于k的式子,由此结合直线的斜率公式化简整理,即可算出直线AC,BD的斜率之和为0,从而证出所求证的命题是真命题.19.已知数列{a n}是首项为1,公差为d的等差数列,数列{b n}是首项为1,公比为q(q>1)的等比数列.(1)若a5=b5,q=3,求数列{a n•b n}的前n项和;(2)若存在正整数k(k≥2),使得a k=b k.试比较a n与b n的大小,并说明理由.【答案】解:(1)依题意,,故,所以a n=1+20(n-1)=20n-19,令,①则,②①-②得,==(29-20n)•3n-29,所以.(2)因为a k=b k,所以1+(k-1)d=q k-1,即,故,又,所以==,(ⅰ)当1<n<k时,由q>1知,=<0;(ⅱ)当n>k时,由q>1知,=(q-1)2q k-2(n-k)>0,综上所述,当1<n<k时,a n>b n;当n>k时,a n<b n;当n=1时,a n=b n.【解析】(1)由q=3,b1=1可求得b5,从而得到a5,由a1=1及通项公式可求得a n,利用错位相减法即可求得数列{a n•b n}的前n项和;(2)由a k=b k,即1+(k-1)d=q k-1,得,,作差b n-a n变形,然后分1<n<k时,当n>k时,n=1三种情况讨论讨论差的符号即可作出大小比较;20.设f(x)是定义在(0,+∞)的可导函数,且不恒为0,记.若对定义域内的每一个x,总有g n(x)<0,则称f(x)为“n阶负函数”;若对定义域内的每一个x,总有,则称f(x)为“n阶不减函数”(为函数g n(x)的导函数).(1)若既是“1阶负函数”,又是“1阶不减函数”,求实数a的取值范围;(2)对任给的“2阶不减函数”f(x),如果存在常数c,使得f(x)<c恒成立,试判断f(x)是否为“2阶负函数”?并说明理由.【答案】解:(1)依题意,在(0,+∞)上单调递增,故恒成立,得,因为x>0,所以a≤0.而当a≤0时,显然在(0,+∞)恒成立,所以a≤0.(2)①先证f(x)≤0:若不存在正实数x0,使得g2(x0)>0,则g2(x)≤0恒成立.假设存在正实数x0,使得g2(x0)>0,则有f(x0)>0,由题意,当x>0时,,可得g2(x)在(0,+∞)上单调递增,当x>x0时,恒成立,即恒成立,故必存在x1>x0,使得(其中m为任意常数),这与f(x)<c恒成立(即f(x)有上界)矛盾,故假设不成立,所以当x>0时,g2(x)≤0,即f(x)≤0;②再证f(x)=0无解:假设存在正实数x2,使得f(x2)=0,则对于任意x3>x2>0,有,即有f(x3)>0,这与①矛盾,故假设不成立,所以f(x)=0无解,综上得f(x)<0,即g2(x)<0,故所有满足题设的f(x)都是“2阶负函数”.【解析】(1)根据“n阶不减函数”的定义,设=,将[g1(x)] ≥0化简整理,可得在(0,+∞)上恒成立,因此a≤0.再将a≤0代入g1(x)表达式,可得g1(x)<0在(0,+∞)上恒成立,由此可得满足条件的实数a的取值范围为(-∞,0];(2)分两步:①根据“存在常数c,使得f(x)<c恒成立”,结合反证法证出g2(x)≤0对任意x∈(0,+∞)成立,从而得到f(x)≤0任意x∈(0,+∞)恒成立;②根据“2阶不减函数”的性质,结合函数的单调性和不等式的性质证出方程f(x)=0无解.由以上两条,即可得到所有满足题设的f(x)都是“2阶负函数”.21.选修4-1:几何证明选讲如图,⊙O的半径为3,两条弦AB,CD交于点P,且AP=1,CP=3,.求证:△APC≌△DPB.【答案】证明:延长OP交⊙O与点E,F,由相交弦定理得,又AP=1,CP=3,∴DP=1,BP=3,∴AP=DP,BP=CP,而∠APC=∠DPB,∴△APC≌△DPB.【解析】利用相交弦定理即可得出DP,BP,再利用三角形全等.的判定方法即可证明22.选修4-2:矩阵与变换已知矩阵M=不存在逆矩阵,求实数x的值及矩阵M的特征值.【答案】解:由题意,矩阵M的行列式=0,解得x=5,矩阵M=的特征多项式=(λ-5)(λ-6)-(-5)×(-6),令f(λ)=0并化简得λ2-11λ=0,解得λ=0或λ=11,所以矩阵M的特征值为0和11.【解析】先根据矩阵M=不存在逆矩阵得出对应的行列式等于0求出x,再根据特征值的定义列出特征多项式,令f(λ)=0解方程可得特征值即可.23.选修4-4:坐标系与参数方程在平面直角坐标系x O y中,已知A(0,1),B(0,-1),C(t,0),,其中t≠0.设直线AC与BD的交点为P,求动点P的轨迹的参数方程(以t为参数)及普通方程.【答案】解:直线AC的方程为,①直线BD的方程为,②由①②解得,动点P的轨迹的参数方程为(t为参数,且t≠0),将平方得,③将平方得,④由③④得,.(注:普通方程由①②直接消参可得.漏写“x≠0”扣(1分).)【解析】因为动点P为动直线直线AC、BD的交点,所以可用消参法求P的轨迹方程.先利用A,B,C,D四点坐标,则可得到含参数的直线AC、BD方程,再消去参数,即可得到求动点P的轨迹的参数方程,最后消去参数t化成普通方程即可.24.选修4-5:不等式选讲已知a>0,b>0,n∈N*.求证:.【答案】证明:先证,只要证2(a n+1+b n+1)≥(a+b)(a n+b n),即要证a n+1+b n+1-a n b-ab n≥0,即要证(a-b)(a n-b n)≥0,若a≥b,则a-b≥0,a n-b n≥0,所以,(a-b)(a n-b n)≥0.若a<b,则a-b<0,a n-b n<0,所以(a-b)(a n-b n)>0,综上,可得(a-b)(a n-b n)≥0,从而.因为,所以.【解析】先用分析法证明,再利用基本不等式,即可证得成立.25.设n∈N*且n≥2,证明:+2[a1(a2+a3+…+a n)+a2(a3+a4+…+a n)+…+a n-1a n].【答案】证明:(1)当n=2时,有,命题成立.(2)假设当n=k(k≥2)时,命题成立,即+2[a1(a2+a3+…+a k)+a2(a3+a4+…+a k)+…+a k-1a k]成立,那么,当n=k+1时,有==+2[a1(a2+a3+…+a k)+a2(a3+a4+…+a k)+…+a k-1a k]+2(a1+a2+…=+2[a1(a2+a3+…+a k+a k+1)+a2(a3+a4+…+a k+a k+1)+…+a k a k+1].所以当n=k+1时,命题也成立.根据(1)和(2),可知结论对任意的n∈N*且n≥2都成立.【解析】直接利用数学归纳法的证明步骤证明不等式,(1)验证n=2时不等式成立;(2)假设当n=k(k≥2)时成立,利用上假设证明n=k+1时,不等式也成立.26.如图是某游戏中使用的材质均匀的圆形转盘,其中Ⅰ,Ⅱ,Ⅲ,Ⅳ部分的面积各占转盘面积的,,,.游戏规则如下:①当指针指到Ⅰ,Ⅱ,Ⅲ,Ⅳ部分时,分别获得积分100分,40分,10分,0分;②(ⅰ)若参加该游戏转一次转盘获得的积分不是40分,则按①获得相应的积分,游戏结束;(ⅱ)若参加该游戏转一次获得的积分是40分,则用抛一枚质地均匀的硬币的方法来决定是否继续游戏.正面向上时,游戏结束;反面向上时,再转一次转盘,若再转一次的积分不高于40分,则最终积分为0分,否则最终积分为100分,游戏结束.设某人参加该游戏一次所获积分为ξ.(1)求ξ=0的概率;(2)求ξ的概率分布及数学期望.【答案】解:(1)事件“ξ=0”包含:“首次积分为0分”事件A和“首次积分为40分后再转一次的积分不高于40分”事件B,且A与B两者互斥,∵P(A)=,又∵由题意参加该游戏转一次获得的积分是40分,则用抛一枚质地均匀的硬币的方法来决定是否继续游戏.反面向上时,再转一次转盘,若再转一次的积分不高于40分,则最终积分为0分,∴P(B)=.∴;(2)ξ的所有可能取值为0,10,40,100,由(1)知,又,,,所以ξ的概率分布为:因此,(分).【解析】(1)事件“ξ=0”包含:“首次积分为0分”和“首次积分为40分后再转一次的积分不高于40分”,且两者互斥,利用互斥事件的概率计算公式和相互独立事件的概率计算公式即可得出;(2)ξ的所有可能取值为0,10,40,100,利用互斥事件的概率计算公式和相互独立事件的概率计算公式和数学期望计算公式即可得出.。
江苏省(南通、泰州、扬州、连云港、淮安)五市2013届高三第三次调研(5月)测试化学试题.pdf

南通市2013届高三第三次模拟 化 学 说明:本试卷分为第一卷(选择题)和第二卷(非选择题)两部分,总分:120分,答题时间:100分钟。
可能用到的相对原子质量:H 1 C 12 N 14 O 16 Si 28 S 32 选择题(共40分) 单项选择题:本题包括10小题,每小题2分,共计20分。
每小题只有一个选项符合题意。
1.化学家认为石油、煤作为能源使用时,燃烧了“未来的原始材料”。
下列对上述观点理解正确的是 A.大力提倡使用廉价化石燃料作为能源 B.应更多地利用石油和煤生产基本化工原料 C.化石燃料属于可再生能源,不影响可持续发展 D.研发新型催化剂,提高石油和煤各组分的燃烧热 2.下列有关化学用语表示正确的是 A.氢氧化钠的电子式: B. Cl-的结构示意图: C.2-丁醇的结构简式: D.碳酸的电离方程式:H2CO32H++CO32- 3.常温下,下列各组离子在指定溶液中一定能大量共存的是 A.0.1 mol·L-1 KNO3溶液:Mg2+、Fe2+、Cl-、SO42- B.无色透明的溶液:Cu2+、NH4+、NO3-、CO32- C.使pH试纸变红的溶液:K+、Ca2+、Cl-、ClO- D.水电离出的c(H+)=10-12 mol·L-1的溶液:Na+、NH4+、SO42-、NO3- 4.下表为六种短周期元素的部分性质。
元素代号XYZQRT原子半径/10-10m0.370.740.750.820.991.10主要化合价+1-2+5、-3+3+7、-1+5、-3下列有关说法正确的是 A.元素X、Y、Z形成的化合物一定是离子化合物 B.元素R的氧化物对应水化物一定为强酸 C.化合物QR3分子中各原子均满足8电子稳定结构 D.元素Z的简单气态氢化物的热稳定性比元素T的稳定 5.下列有关物质的性质与应用相对应的是 A.炭具有强还原性,常用于冶炼镁、等金属 B.铝的金属性较强,可用作飞机、火箭的结构材料 C.碳酸钠溶液碱性,可用于洗去铁屑表面的油污 D.浓硫酸具有强氧化性,可用于与亚硫酸钠反应制取二氧化硫 6.用下列实验装置进行相应实验,能达到实验目的的是 图Ⅰ 图Ⅱ 图Ⅲ 图Ⅳ A.用图Ⅰ所示装置吸收尾气中的二氧化硫 B.用图Ⅱ所示装置配制100 mL 0.100 mol·L-1稀硫酸 C.用图Ⅲ所示装置除去溴苯中少量的溴 D.用图Ⅳ所示装置制取并收集氨气 7.硫酸亚铁是一种重要的化工原料,可以制备一系列物质(如下图所示)。
13大市2013年高三历次考试数学试题分类汇编2:函数

【推荐】江苏省13大市2013年高三历次考试数学试题分类汇编2:函数一、填空题1 .(江苏省泰州、南通、扬州、宿迁、淮安五市2013届高三第三次调研测试数学试卷)已知函数2221 0 () 0ax x x f x x bx c x ⎧--⎪=⎨++<⎪⎩,≥,,是偶函数,直线y t =与函数()y f x =的图象自左向右依次交于四个不同点A ,B ,C ,D .若AB BC =,则实数t 的值为______. 【答案】74- 2 .(江苏省盐城市2013届高三年级第二次模拟考试数学试卷)设函数)(x f y =满足对任意的R x ∈,0)(≥x f 且9)()1(22=++x f x f .已知当]1,0[∈x 时,有242)(--=x x f ,则⎪⎭⎫ ⎝⎛62013f 的值为________. 【答案】53 .(常州市2013届高三教学期末调研测试数学试题)已知函数f (x )=32,2,(1),02x x x x ⎧⎪⎨⎪-<<⎩≥,若关于x 的方程f (x )=kx 有两个不同的实根,则实数k 的取值范围是______. 【答案】10,2⎛⎫ ⎪⎝⎭4 .(苏北三市(徐州、淮安、宿迁)2013届高三第二次调研考试数学试卷)已知函数⎪⎩⎪⎨⎧∈-∈=]3,1(,2329]1,0[,3)(x x x x f x ,当]1,0[∈t 时,]1,0[))((∈t f f ,则实数t 的取值范围是_____. 【答案】37[log ,1]35 .(江苏省苏锡常镇四市2013届高三教学情况调研(一)数学试题)设函数()ln f x x =的定义域为(),M +∞,且0M >,对于任意a ,b ,(,)c M ∈+∞,若a ,b ,c 是直角三角形的三条边长,且()f a ,()f b ,()f c 也能成为三角形的三条边长,那么M 的最小值为________. 【答案】26 .(徐州、宿迁市2013届高三年级第三次模拟考试数学试卷)已知函数2,01,()12, 1.2x x x f x x +<⎧⎪=⎨+⎪⎩≤≥若0a b >≥,且()()f a f b =,则()bf a 的取值范围是__. 【答案】5[,3)4;7 .(扬州、南通、泰州、宿迁四市2013届高三第二次调研测试数学试卷)设f (x )是定义在R 上的奇函数,当x < 0时,f (x )=x + e x(e 为自然对数的底数),则()ln6f 的值为____. 【答案】1ln 66- 8 .(江苏省泰州市2012-2013学年度第一学期期末考试高三数学试题)设函数f(x)是定义在R上的奇函数,且f(a)>f(b), 则f(-a)_________ f(-b)(填“>”或:“<”)【答案】<9 .(江苏省苏锡常镇四市2013届高三教学情况调研(一)数学试题)已知函数123()1234x x x x f x x x x x +++=+++++++,则55(2)(2)22f f -++--=_____. 【答案】810.(常州市2013届高三教学期末调研测试数学试题)函数22()log (4)f x x =-的值域为______.【答案】(,2]-∞11.(江苏省无锡市2013届高三上学期期末考试数学试卷)已知关于x 的函数y=2(1)t x t x-+(f∈R)的定义域为D,存在区间[a,b]⊆D,f(x)的值域也是[a,b].当t 变化时,b-a 的最大值=______________. 【答案】23312.(扬州市2012-2013学年度第一学期期末检测高三数学试题)已知函数2log ()3x x f x ⎧=⎨⎩(0)(0)x x >≤,则=)]0([f f ____. 【答案】013.(南通市2013届高三第一次调研测试数学试卷)定义在R 上的函数()f x ,对任意x ∈R 都有(2)()f x f x +=,当(2,0)x ∈- 时,()4x f x =,则(2013)f =________.【答案】答案:14. 本题考查一般函数的性质——周期性在解题中的应用.14.(镇江市2013届高三上学期期末考试数学试题)方程lg(2)1x x +=有______个不同的实数根.【答案】2;15.(南京市、盐城市2013届高三年级第一次模拟考试数学试题)已知函数21(1),02,()(2),2x x f x f x x ⎧⎪--≤<=⎨-≥⎪⎩, 若关于x 的方程()f x kx =(0)k >有且仅有四个根, 其最大根为, 则函数225()6724g t t t =-+的值域为 . 【答案】41[,1)25--16.(连云港市2012-2013学年度第一学期高三期末考试数学试卷)已知函数f (x )=⎩⎨⎧2,x ∈[0,1]x ,x ∉[0,1].则使f [f (x )]=2成立的实数x 的集合为________. 【答案】{x |0≤x ≤1,或x =2};二、填空题17.(南京市、盐城市2013届高三年级第一次模拟考试数学试题)对于定义在区间D 上的函数()f x , 若任给0x D ∈, 均有0()f x D ∈, 则称函数()f x 在区间D 上封闭.试判断()1f x x =-在区间[2,1]-上是否封闭, 并说明理由; 若函数3()1x a g x x +=+在区间[3,10]上封闭, 求实数a 的取值范围;若函数3()3h x x x =-在区间[,](,)a b a b Z ∈上封闭, 求,a b 的值. 【答案】解: (1)()1f x x =-在区间[2,1]-上单调递增,所以()f x 的值域为[-3,0] 而[-1,0][2,1]⊄-,所以()f x 在区间[2,1]-上不是封闭的(2)因为33()311x a a g x x x +-==+++,①当3a =时,函数()g x 的值域为{}3[3,10]⊆,适合题意②当3a >时,函数()g x 在区间[3,10]上单调递减,故它的值域为309[,]114a a ++, 由309[,]114a a ++[3,10]⊆,得303119104a a +⎧≥⎪⎪⎨+⎪≤⎪⎩,解得331a ≤≤,故331a <≤③当3a <时,在区间[3,10]上有33()3311x a a g x x x +-==+<++,显然不合题意 综上所述, 实数a 的取值范围是331a ≤≤(3)因为3()3h x x x =-,所以2()333(1)(1)h x x x x '=-=+-,所以()h x 在(,1)-∞-上单调递减,在(1,1)-上递增,在(1,)+∞上递增. ①当1a b <≤-时,()h x 在区间[,]a b 上递增,所以()()h a a h b b ≥⎧⎨≤⎩,此时无解 ②当111a b ≤--<≤且时,因max ()(1)2h x h b =-=>,矛盾,不合题意③当11a b ≤->且时,因为(1)2,(1)2h h -==-都在函数的值域内,故22a b ≤-⎧⎨≥⎩, 又33()3()3a h a a a b h b b b ⎧≤=-⎨≥=-⎩,解得202202a a b b -≤≤≥⎧⎨≤≤≤⎩或或,从而22a b =-⎧⎨=⎩④当11a b -≤<≤时,()h x 在区间[,]a b 上递减,()()h b a h a b ≥⎧⎨≤⎩(*), 而,a b Z ∈,经检验,均不合(*)式⑤当111a b -<≤≥且时,因min ()(1)2h x h a ==-<,矛盾,不合题意⑥当1b a >≥时,()h x 在区间[,]a b 上递增,所以()()h a a h b b ≥⎧⎨≤⎩,此时无解 综上所述,所求整数,a b 的值为2,2a b =-=。
2013届南通、泰州、扬州、连云港、淮安五市高三第三次模含答案
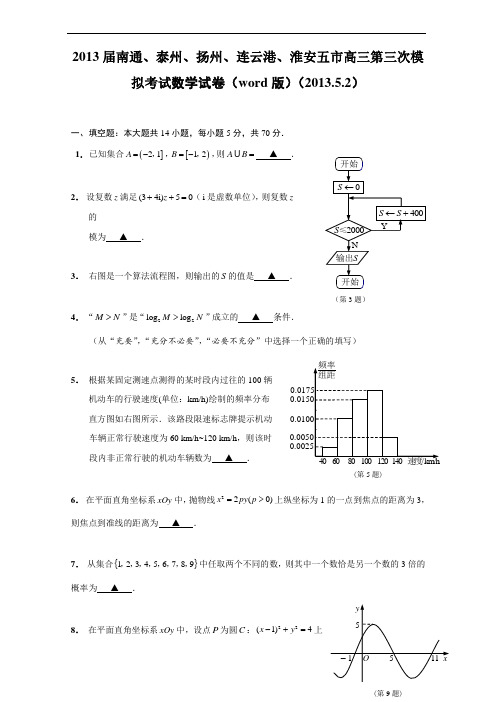
(第3题)(第5题)2013届南通、泰州、扬州、连云港、淮安五市高三第三次模拟考试数学试卷(word 版)(2013.5.2)一、填空题:本大题共14小题,每小题5分,共70分. 1. 已知集合(]2 1A =-,,[)1 2B =-,,则A B = ▲ .2. 设复数z 满足(34i)50z ++=(i 是虚数单位),则复数z的模为 ▲ .3. 右图是一个算法流程图,则输出的S 的值是 ▲ .4. “M N >”是“22log log M N >”成立的 ▲ 条件.(从“充要”,“充分不必要”,“必要不充分”中选择一个正确的填写)5. 根据某固定测速点测得的某时段内过往的100辆 机动车的行驶速度(单位:km/h)绘制的频率分布 直方图如右图所示.该路段限速标志牌提示机动车辆正常行驶速度为60 km/h~120 km/h ,则该时 段内非正常行驶的机动车辆数为 ▲ .6. 在平面直角坐标系xOy 中,抛物线22(0)x py p =>上纵坐标为1的一点到焦点的距离为3,则焦点到准线的距离为 ▲ .7. 从集合{}1 2 3 4 5 6 7 8 9,,,,,,,,中任取两个不同的数,则其中一个数恰是另一个数的3倍的概率为 ▲ .8. 在平面直角坐标系xOy 中,设点P 为圆C :22(1)4x y -+=上的任意一点,点Q (2a ,3a -)(a ∈R ),则线段PQ 长度的最小值为 ▲ .9. 函数()sin()f x A x ωϕ=+(0A >,0ω>,02)ϕ<π≤在R 上的部分图象如图所示,则(2013)f 的值为 ▲ .10.各项均为正数的等比数列{}n a 中,211a a -=.当3a 取最小值时,数列{}n a 的通项公式a n = ▲ .11.已知函数2221 0 () 0ax x x f x x bx c x ⎧--⎪=⎨++<⎪⎩,≥,,是偶函数,直线y t =与函数()y f x =的图象自左向右依次交于四个不同点A ,B ,C ,D .若AB BC =,则实数t 的值为 ▲ .12.过点(1 0)P -,作曲线C :e x y =的切线,切点为1T ,设1T 在x 轴上的投影是点1H ,过点1H 再作曲线C 的切线,切点为2T ,设2T 在x 轴上的投影是点2H ,…,依次下去,得到第1n +()n ∈N 个切点1n T +.则点1n T +的坐标为 ▲ .13.在平面四边形ABCD 中,点E ,F 分别是边AD ,BC 的中点,且AB 1=,EF CD =若15AD BC ⋅=,则AC BD ⋅的值为 ▲ .14.已知实数a 1,a 2,a 3,a 4满足a 1+a 2+a 30=,a 1a 42+a 2a 4-a 20=,且a 1>a 2>a 3,则a 4的取值范围是 ▲ . 二、解答题15.如图,在四棱锥P ABCD -中,底面ABCD 是矩形,四条侧棱长均相等. (1)求证:AB //平面PCD ; (2)求证:平面PAC ⊥平面ABCD .16.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c .已知222222sin C b a c c a b--=--. (1)求角B 的大小;(2)设222sin sin sin T A B C =++,求T 的取值范围.17.某单位设计的两种密封玻璃窗如图所示:图1是单层玻璃,厚度为8 mm ;图2是双层中空玻璃,厚度均为4 mm ,中间留有厚度为x 的空气隔层.根据热传导知识,对于厚度为d 的均匀介质,两侧的温度差为T ∆,单位时间内,在单位面积上通过的热量T Q k d ∆=⋅,其中k 为热传导系数.假定单位时间内,在单位面积上通过每一层玻璃及空气隔层的热量相等.(注:玻璃的热传导系数为3410 J mm/C -⨯⋅,空气的热传导系数为42.510 J mm/C -⨯⋅.)(1)设室内,室外温度均分别为1T ,2T ,内层玻璃外侧温度为1T ',外层玻璃内侧温度为2T ',且1122T T T T ''>>>.试分别求出单层玻璃和双层中空玻璃单位时间内,在单位面积上通过的热量(结果用1T ,2T 及x 表示);(2)为使双层中空玻璃单位时间内,在单位面积上通过的热量只有单层玻璃的4%,应如何设计x 的大小?ABC(第15题)PDO(第18题)18.如图,在平面直角坐标系xOy 中,椭圆22221(0)y x a b a b+=>>的右焦点为(1 0)F ,,离心率O ,F 的两条弦AB ,CD 相交于点E (异于A ,C 两点),且OE EF =.(1)求椭圆的方程;(2)求证:直线AC ,BD 的斜率之和为定值.19.已知数列{}n a 是首项为1,公差为d 的等差数列,数列{}n b 是首项为1,公比为(1)q q >的等比数列.(1)若55a b =,3q =,求数列{}n n a b ⋅的前n 项和;(2)若存在正整数(2)k k ≥,使得k k a b =.试比较n a 与n b 的大小,并说明理由.(第21—A 题)20.设()f x 是定义在(0 )+∞,的可导函数,且不恒为0,记()()()n nf xg x n x =∈*N .若对定义域内的每一个x ,总有()0n g x <,则称()f x 为“n 阶负函数”;若对定义域内的每一个x ,总有[]()0n g x '≥,则称()f x 为“n 阶不减函数”([]()n g x '为函数()n g x 的导函数). (1)若31()(0)a f x x x x x =-->既是“1阶负函数”,又是“1阶不减函数”,求实数a 的取值范围;(2)对任给的“2阶不减函数”()f x ,如果存在常数c ,使得()f x c <恒成立,试判断()f x 是否为“2阶负函数”?并说明理由.数学附加题21.【选做题】A .选修4—1:几何证明选讲如图,⊙O 的半径为3,两条弦AB ,CD 交于点P ,且1AP =, 3CP =,OP = 求证:△APC ≌△DPB .B .选修4—2:矩阵与变换已知矩阵M 566x ⎡⎤=⎢⎥⎣⎦不存在逆矩阵,求实数x 的值及矩阵M 的特征值.C .选修4—4:坐标系与参数方程在平面直角坐标系xOy 中,已知(0 1)A ,,(0 1)B -,,( 0)C t ,,()3 0D t,,其中0t ≠.设直线AC 与BD 的交点为P ,求动点P 的轨迹的参数方程(以t 为参数)及普通方程.D .选修4—5:不等式选讲已知0a >,0b >,n ∈*N.求证:11n n n na b a b ++++22.【必做题】设n ∈*N 且2n ≥,证明:()22221212n n a a a a a a ++⋅⋅⋅+=++⋅⋅⋅+()1232n a a a a ⎡+++⋅⋅⋅+⎣()234n a a a a +++⋅⋅⋅++⋅⋅⋅]1n n a a -+.23.【必做题】下图是某游戏中使用的材质均匀的圆形转盘,其中Ⅰ,Ⅱ,Ⅲ,Ⅳ部分的面积各占转盘面积的112,16,14,12.游戏规则如下:① 当指针指到Ⅰ,Ⅱ, Ⅲ,Ⅳ部分时,分别获得积分100分,40分,10分,0分; ② (ⅰ)若参加该游戏转一次转盘获得的积分不是40分,则按①获得相应的积分,游戏结束;(ⅱ)若参加该游戏转一次获得的积分是40分,则用抛一枚质地均匀的硬币的方法来决定是否继续游戏.正面向上时,游戏结束;反面向上时,再转一次转盘,若再转一次的积分不高于40分,则最终积分为0分,否则最终积分为100分,游戏结束.设某人参加该游戏一次所获积分为ξ.(1)求0ξ=的概率;(2)求ξ的概率分布及数学期望.南通市2013届高三第三次调研测试数学参考答案及评分建议(第23题)(第3题)(第5题)一、填空题:本大题共14小题,每小题5分,共70分. 1. 已知集合(]2 1A =-,,[)1 2B =-,,则A B =▲ .【答案】(2 2)-,2. 设复数z 满足(34i)50z ++=(i 是虚数单位),则复数z 的模为 ▲ . 【答案】13. 右图是一个算法流程图,则输出的S 的值是 ▲ . 【答案】24004. “M N >”是“22log log M N >”成立的 ▲ 条件.(从“充要”,“充分不必要”,“必要不充分”中选择一个正确的填写) 【答案】必要不充分5. 根据某固定测速点测得的某时段内过往的100辆 机动车的行驶速度(单位:km/h)绘制的频率分布 直方图如右图所示.该路段限速标志牌提示机动车辆正常行驶速度为60 km/h~120 km/h ,则该时 段内非正常行驶的机动车辆数为 ▲ . 【答案】156. 在平面直角坐标系xOy 中,抛物线22(0)x py p =>上纵坐标为1的一点到焦点的距离为3,则焦点到准线的距离为 ▲ .【答案】47. 从集合{}1 2 3 4 5 6 7 8 9,,,,,,,,中任取两个不同的数,则其中一个数恰是另一个数的3倍的概率为 ▲ .【答案】1128. 在平面直角坐标系xOy 中,设点P 为圆C :22(1)4x y -+=上的任意一点,点Q (2a ,3a -)(a ∈R ),则线段PQ 长度的最小值为 ▲ .【答案29. 函数()sin()f x A x ωϕ=+(0A >,0ω>,02)ϕ<π≤在R 上的部分图象如图所示,则(2013)f 的值为 ▲ .【答案】10.各项均为正数的等比数列{}n a 中,211a a -=.当3a 取最小值时,数列{}n a 的通项公式a n = ▲ .【答案】12n -11.已知函数2221 0 () 0ax x x f x x bx c x ⎧--⎪=⎨++<⎪⎩,≥,,是偶函数,直线y t =与函数()y f x =的图象自左向右依次交于四个不同点A ,B ,C ,D .若AB BC =,则实数t 的值为 ▲ . 【答案】7- 12.过点(1 0)P -,作曲线C :e x y =的切线,切点为1T ,设1T 在x 轴上的投影是点1H ,过点1H 再作曲线C 的切线,切点为2T ,设2T 在x 轴上的投影是点2H ,…,依次下去,得到第1n +()n ∈N 个切点1n T +.则点1n T +的坐标为 ▲ . 【答案】()e n n ,13.在平面四边形ABCD 中,点E ,F 分别是边AD ,BC 的中点,且AB 1=,EF CD =若15AD BC ⋅=,则AC BD ⋅的值为 ▲ . 【答案】1314.已知实数a 1,a 2,a 3,a 4满足a 1+a 2+a 30=,a 1a 42+a 2a 4-a 20=,且a 1>a 2>a 3,则a 4的取值范围是 ▲ .【答案】二、解答题15.如图,在四棱锥P ABCD -中,底面ABCD 是矩形,四条侧棱长均相等. (1)求证:AB //平面PCD ; (2)求证:平面PAC ⊥平面ABCD . 证明:(1)在矩形ABCD 中,//AB CD , 又AB ⊄平面PCD , CD ⊂平面PCD ,所以AB //平面PCD . ………6分 (2)如图,连结BD ,交AC 于点O ,连结PO , 在矩形ABCD 中,点O 为 AC BD ,的中点, 又PA PB PC PD ===, 故PO AC⊥,PO BD ⊥, ………9分又AC BD O =,AC BD ,⊂平面ABCD , 所以PO ⊥平面A, ………12分又PO ⊂平面PAC , 所以平面PAC ⊥平面A. ………14分16.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c .已知222222sin 2sin sin C b a c A C c a b --=---. (1)求角B 的大小;(2)设222sin sin sin T A B C =++,求T 的取值范围. 解:(1)在△ABC 中,222222sin 2cos cosB sin cos 2sin sin 2cos cos sin cos C b a c ac B c C B A C ab C b C B Cc a b ---====----, ………3分 因为sin 0C ≠,所以sin cos 2sin cos sin cos B C A B C B =-, 所以2AB=+, ………5分 因为sin 0A ≠,所以1cos 2B =,ABC(第15题)PDO因为0πB <<,所以π3B =. ………7分(2)222131sin sin sin (1cos2)(1cos2)242T A B C A C =++=-++-()71714π(cos2cos2)cos2cos 2A C A A -⎡⎤=⎢⎥⎣+=--⎦+()()71171πcos22cos 2422423A A A =-=-+ ………11分因为2π03A <<,所以4π023A <<,故ππ5π2333A <+<,因此()π11cos 232A -+<≤,所以3924T <≤. ………14分17.某单位设计的两种密封玻璃窗如图所示:图1是单层玻璃,厚度为8 mm ;图2是双层中空玻璃,厚度均为4 mm ,中间留有厚度为x 的空气隔层.根据热传导知识,对于厚度为d 的均匀介质,两侧的温度差为T ∆,单位时间内,在单位面积上通过的热量T Q k d ∆=⋅,其中k 为热传导系数.假定单位时间内,在单位面积上通过每一层玻璃及空气隔层的热量相等.(注:玻璃的热传导系数为3410 J mm/C -⨯⋅,空气的热传导系数为42.510 J mm/C -⨯⋅.)(1)设室内,室外温度均分别为1T ,2T ,内层玻璃外侧温度为1T ',外层玻璃内侧温度为2T ',且1122T T T T ''>>>.试分别求出单层玻璃和双层中空玻璃单位时间内,在单位面积上通过的热量(结果用1T ,2T 及x 表示);(2)为使双层中空玻璃单位时间内,在单位面积上通过的热量只有单层玻璃的4%,应如何设计x 的大小?解:(1)设单层玻璃和双层中空玻璃单位时间内,在单位面积上通过的热量分别为1Q ,2Q , 则3121214108 2 000T T T T Q ---=⨯⋅=, ………2分 3431112222410 2.510410T T T T T T Q ---''''---=⨯⋅=⨯⋅=⨯⋅ ………6分 11122244410 2.510410T T T T T T x ''''---===⨯⨯⨯ 11122234344410 2.510410T T T T T T x ---''''-+-+-=++⨯⨯⨯124 000 2 000T T x -=+. ………9分(2)由(1)知21121Q Q x =+, 当121x =+4%时,解得12x =(mm ). 答:当12x =mm 时,双层中空玻璃通过的热量只有单层玻璃的4%. ………14分18.如图,在平面直角坐标系xOy 中,椭圆22221(y x a b a b+=>右焦点为(1 0)F ,. 分别过O ,F 的两条弦AB ,CD相交于点E (异于A 图1图2(第17题)C 两点),且OE EF =.(1)求椭圆的方程;(2)求证:直线AC ,BD 的斜率之和为定值.(1)解:由题意,得1c =,c e a ==,故a从而2221b a c =-=,所以椭圆的方程为221x y +=. ①………5分(2)证明:设直线AB 的方程为y kx =,② 直线CD的方程为(y kx =--,③ ………7分 由①②得,点A ,B的横坐标为由①③得,点C ,D, ………9分记11( )A x kx ,,22( )B x kx ,,33( (1))C x k x -,,44( (1))D x k x -,, 则直线AC ,BD 的斜率之和为13241324(1)(1)kx k x kx k x x x x x ----+-- 132413241324(1)()()(1)()()x x x x x x x x k x x x x +--+-+-=⋅--1234123413242()()()()()x x x x x x x x k x x x x --+++=⋅-- ………13分2222124232(1)4222201121()()k k k k k x x x k x ⎛⎫---+ ⎪+++⎝-⎭=⋅--0=. ………16分19.已知数列{}n a 是首项为1,公差为d 的等差数列,数列{}n b 是首项为1,公比为(1)q q >的等比数列.(1)若55a b =,3q =,求数列{}n n a b ⋅的前n 项和;(2)若存在正整数(2)k k ≥,使得k k a b =.试比较n a 与n b 的大小,并说明理由. 解:(1)依题意,5145511381a b b q -===⨯=, 故5181120514a a d --===-, 所以1n a n =+, ………3分令2111213413(2019)3n n S n -=⨯+⨯+⨯+⋅⋅⋅+-⋅, ① 则213 13213(2039)3(2019)3n n n S n n -=⨯+⨯+⋅⋅⋅+-⋅+-⋅, ② ①-②得,()2121+20333(2019)3n n n S n --=⨯++⋅⋅⋅+--⋅,13(13)1+20(2019)313n n n --=⨯--⋅-(2920)329n n =-⋅-, 所以(22nn n S -⋅=. ………7分(2)因为k k a b =, 所以11(1)k k d q-+-=,即111k q d k --=-,故111(1)1k n q a n k --=+--,又1n n b q -=, ………9分所以1111(1)1k n n n q b a qn k --⎡⎤--=-+-⎢⎥-⎣⎦()()111(1)1(1)11n k k q n q k --⎡⎤=-----⎣⎦- ()()23231(1)1(1)11n n k k q k q q q n q q q k -----⎡⎤=-++⋅⋅⋅++--++⋅⋅⋅++⎣⎦- ………11分(ⅰ)当1n k <<时,由1q >知()()232311()1(1)n n k k n n n q b a k n q q q n q q q ------⎡⎤-=-++⋅⋅⋅++--++⋅⋅⋅+⎣⎦ 211()(1)(1)()1n n q k n n q n k n q k ---⎡⎤<-----⎣⎦- 22(1)()(1)1n q q k n n k ----=--0<, ………13分(ⅱ)当n k >时,由1q >知()()231231(1)()11n n k k k n n q b a k q q q n k q q q k ------⎡⎤-=-++⋅⋅⋅+--++⋅⋅⋅++⎣⎦- 121(1)()()(1)1k k q k n k q n k k q k ---⎡⎤>-----⎣⎦- 22(1)()k q q n k -=-- 0>,综上所述,当1n k <<时,n n a b >;当n k >时,n n a b <;当1 n k =,时,n n a b =.………16分(注:仅给出“1n k <<时,n n a b >;n k >时,n n a b <”得2分.)20.设()f x 是定义在(0 )+∞,的可导函数,且不恒为0,记()()()n n f x g x n x=∈*N .若对定义域内的每一个x ,总有()0n g x <,则称()f x 为“n 阶负函数”;若对定义域内的每一个x ,总有[]()0n g x '≥,则称()f x 为“n 阶不减函数”([]()n g x '为函数()n g x 的导函数).(1)若31()(0)a f x x x x x =-->既是“1阶负函数”,又是“1阶不减函数”,求实数a 的取值范围;(2)对任给的“2阶不减函数”()f x ,如果存在常数c ,使得()f x c <恒成立,试判断()f x 是否为“2阶负函数”?并说明理由. 解:(1)依题意,142()1()1f x a g x x x x ==--在(0 )+∞,上单调递增, 故15342[()]0a g x x x '=-+≥恒成立,得212a x ≤, ………2分因为x >,所以0a ≤. ………4分而当0a ≤时,1421()10a g x x x=--<显然在(0 )+∞,恒成立, 所以0a ≤. ………6分(2)①先证()0f x ≤:若不存在正实数0x ,使得20()0g x >,则2()0g x ≤恒成立. ………8分假设存在正实数0x ,使得20()0g x >,则有0()0f x >,由题意,当0x >时,2()0g x '≥,可得2()g x 在(0 )+∞,上单调递增, 当0x x >时,0220()()f x f x x x >恒成立,即2020()()f x f x x x >⋅恒成立, 故必存在10x x >,使得201120()()f x f x x m x >⋅>(其中m 为任意常数), 这与()f x c <恒成立(即()f x 有上界)矛盾,故假设不成立,所以当0x >时,2()0g x ≤,即()0f x ≤; (13)分②再证()0f x =无解:假设存在正实数2x ,使得2()0f x =, 则对于任意320x x >>,有322232()()0f x f x x x >=,即有3()0f x >, 这与①矛盾,故假设不成立, 所以()0f x =无解,综上得()0f x <,即2()0g x <,(第21—A 题)故所有满足题设的()f x 都是“2阶负函数”. ………16分南通市2013届高三第三次调研测试 数学附加题参考答案及评分建议21.【选做题】A .选修4—1:几何证明选讲如图,⊙O 的半径为3,两条弦AB ,CD 交于点P ,且1AP =, 3CP =,OP = 求证:△APC ≌△DPB .证明:延长OP 交⊙O 与点E ,F , ………2分由相交弦定理得((333CP DP AP BP FP EP ⋅=⋅=⋅=⨯+=,………6分 又1AP =,3CP =, 故1DP =,3BP =, ………8分所以AP DP =,BP CP =, 而APC DPB ∠=∠, 所以△APC≌△D. ………10分B .选修4—2:矩阵与变换已知矩阵M 566x ⎡⎤=⎢⎥⎣⎦不存在逆矩阵,求实数x 的值及矩阵M 的特征值. 解:由题意,矩阵M 的行列式5066x =,解得5x =, ………4分矩阵M 5566⎡⎤=⎢⎥⎣⎦的特征多项式 55()(5)(6)(5)(6)66f λλλλλ--==----⨯---, ………8分 令()0f λ=并化简得2110λλ-=,解得0λ=或11λ=, 所以矩阵M 的特征值为0和11. ………10分C .选修4—4:坐标系与参数方程在平面直角坐标系xOy 中,已知(0 1)A ,,(0 1)B -,,( 0)C t ,,()3 0D t,,其中0t ≠.设直线AC 与BD 的交点为P ,求动点P 的轨迹的参数方程(以t 为参数)及普通方程. 解:直线AC 的方程为1x y +=,①直线BD 的方程为13x y t -=,② ………2分由①②解得,动点P 的轨迹的参数方程为2226 333t x t t y t ⎧=⎪+⎨-⎪=+⎩,(t 为参数,且0t ≠), ………6分将263t x t =+平方得222236(3)t x t =+, ③将2233t y t -=+平方得()()2222233t y t-=+,④ ………8分 由③④得,221(0)3x y x +=≠. ………10分 (注:普通方程由①②直接消参可得.漏写“0x ≠”扣1分.)D .选修4—5:不等式选讲已知0a >,0b >,n ∈*N .求证:11n n n na b a b++++ 证明:先证112n n n n a b a ba b +++++≥, 只要证112()()()n n n n a b a b a b +++++≥, 即要证11n n n n a b a b ab +++--≥0,即要证(n n a b a b --)≥0, ………5分若a b ≥,则a b -≥0,n n a b -≥0,所以()(n n a b a b --)≥0, 若a b <,则0a b -<,0n n a b -<,所以()()0n n a b a b -->, 综上,得()(n n a b a b --)≥0. 从而112n n n n a b a ba b +++++≥, ………8分因为2a b+所以11n nn na b a b ++++ ………10分22.【必做题】设n ∈*N 且2n ≥,证明:()22221212n n a a a a a a ++⋅⋅⋅+=++⋅⋅⋅+()1232n a a a a ⎡+++⋅⋅⋅+⎣()234n a a a a +++⋅⋅⋅++⋅⋅⋅]1n n a a -+.证明:(1)当2n =时,有()2221212122a a a a a a +=++,命题成立. ………2分(2)假设当(2)n k k =≥时,命题成立, 即()22221212k k a a a a a a ++⋅⋅⋅+=++⋅⋅⋅+()1232k a a a a ⎡+++⋅⋅⋅+⎣()234k a a a a +++⋅⋅⋅++⋅⋅⋅]1k k a a -+成立, ………4分 那么,当1n k =+时,有()2121k k a a a a +++⋅⋅⋅++ ()()221212112k k k k a a a a a a a a ++=++⋅⋅⋅++++⋅⋅⋅++22212k a a a =++⋅⋅⋅+()1232k a a a a ⎡+++⋅⋅⋅+⎣()234k a a a a +++⋅⋅⋅++⋅⋅⋅]1k k a a -+ (12a +2a ++⋅⋅⋅)211k k k a a a ++++.2222121k k a a a a +=++⋅⋅⋅++()12312k k a a a a a +⎡+++⋅⋅⋅++⎣+(234a a a ++⋅⋅⋅k a +)1k a ++ +⋅⋅⋅ ]1k k a a ++. 所以当1n k =+时,命题也成立. ………8分根据(1)和(2),可知结论对任意的n ∈*N 且2n ≥都成立. ………10分23.【必做题】下图是某游戏中使用的材质均匀的圆形转盘,其中Ⅰ,Ⅱ,Ⅲ,Ⅳ部分的面积各占转盘面积的1,16,14,12.游戏规则如下:① 当指针指到Ⅰ,Ⅱ, Ⅲ,Ⅳ部分时,分别获得积分100分,40分,10分,0分; ② (ⅰ)若参加该游戏转一次转盘获得的积分不是40分,则按①获得相应的积分,游戏结束;(ⅱ)若参加该游戏转一次获得的积分是40分,则用抛一枚质地均匀的硬币的方法来决定是否继续游戏.正面向上时,游戏结束;反面向上时,再转一次转盘,若再转一次的积分不高于40分,则最终积分为0分,否则最终积分为100分,游戏结束.设某人参加该游戏一次所获积分为ξ.(1)求0ξ=的概率;(2)求ξ的概率分布及数学期望.解:(1)事件“0ξ=”包含:“首次积分为0分”和“首次积分为40分后再转一次的积分不高于40分”,且两者互斥, 所以11(026P ξ==; ………4分(2)ξ的所有可能取值为0,10,40,100, 由(1)知83(0)144P ξ==,又1(10)4P ξ==,111(40)6212P ξ==⨯=,111113(100)126212144P ξ==+⨯⨯=,所以ξ的概率分布为:………7分因此,831113535()0104010014441214436E ξ=⨯+⨯+⨯+⨯=(分). ………10分(第23题)。
13大市2013年高三历次考试数学试题分类汇编1:集合

【推荐】江苏省13大市2013年高三历次考试数学试题分类汇编1:集合一、填空题1 .(徐州、宿迁市2013届高三年级第三次模拟考试数学试卷)若集合{}1,0,1A =-,{}|cos(),B y y x x A ==π∈,则A B = ____.【答案】{1,1}-;2 .(扬州市2012-2013学年度第一学期期末检测高三数学试题)若集合}11|{≤≤-=x x M ,2{|20}N x x x =-≤,则M∩N=____.【答案】[0,1]3 .(苏北三市(徐州、淮安、宿迁)2013届高三第二次调研考试数学试卷)已知全集},3,2,1,0{=U 集合},3,2,1{},1,0{==B A 则=B A C U )(_____.【答案】{2,3}4 .(苏州市2012-2013学年度第一学期高三期末考试数学试卷)已知集合{}1,1,2,4A =-,{}1,0,2B =-,则A B = _____________.【答案】{}1,2-5 .(连云港市2012-2013学年度第一学期高三期末考试数学试卷)集合A ={1,2,3},B ={2,4,6},则A B =_________.【答案】{2};6 .(常州市2013届高三教学期末调研测试数学试题)设集合{}1,A a =,{}B a =,若B A ⊆,则实数a 的值为______.【答案】07 .(江苏省无锡市2013届高三上学期期末考试数学试卷)设全集U=R,集合A={}{}2|20,|1x x x B x x -<=>,则集U A B = ð___________. 【答案】{}|01x x <≤8 .(南通市2013届高三第一次调研测试数学试卷)已知全集U =R,集合{}10A x x =+>,则U A =ð________.【答案】 答案:(,1]-∞-.考查集合运算.注意集合的规范表示法,重视集合的交并补的运算.9 .(江苏省泰州市2012-2013学年度第一学期期末考试高三数学试题)已知集合{}1,2,3A =,{}1,2,5B =,则A B ⋂=___________【答案】{}2,110.(江苏省泰州、南通、扬州、宿迁、淮安五市2013届高三第三次调研测试数学试卷)已知集合(]2 1A =-,,[)1 2B =-,,则A B =U ______.【答案】(2 2)-,11.(南京市、盐城市2013届高三第三次模拟考试数学试卷)记函数f (x )=3-x 的定义域为A ,函数g (x )=lg(x -1)的定义域为B ,则A ∩B =________.【答案】(1,3]12.(南京市、淮安市2013届高三第二次模拟考试数学试卷)已知集合A={2a,3},B={2,3}.若A B={1,2,3},则实数a 的值为____.【答案】013.(江苏省苏锡常镇四市2013届高三教学情况调研(一)数学试题)已知全集{}1,2,3,4,5,6U =,{}1,3,5A =,{}1,2,3,5B =,则()U A B = ð______.【答案】{}2,4,614.(2012-2013学年度苏锡常镇四市高三教学情况调研(二)数学试题)设全集U R =,集合{}|13A x x =-≤≤,{}|1B x x =>,则U A B = ð______.【答案】[1,1]-15.(扬州、南通、泰州、宿迁四市2013届高三第二次调研测试数学试卷)设集合{}{}2223050A x x x B x x x =--=-≤,≥,则()A B =R I ð____.【答案】(]03,16.(江苏省盐城市2013届高三年级第二次模拟考试数学试卷)若集合}2,1{-=m A ,且}2{=B A ,则实数m 的值为________.【答案】417.(南京市、盐城市2013届高三年级第一次模拟考试数学试题)已知集合{}2,1,0,1-=U ,{}1,1-=A , 则U A ð= .【答案】{}0,218.(镇江市2013届高三上学期期末考试数学试题)已知集合M ={1 ,2,3, 4,5},N ={2,4,6,8,10},则M ∩N =______.【答案】{}4,2;。
2013江苏高考数学模拟试卷3-参考答案

犛 0 1 1 犪 2 0 1 1 =2 1+ 烄 烅 犪 犪 0 0 7 犱=7 1 0 0 8= 1 +1 烆
{
{
2 0 1 3×2 0 1 2 2 0 1 3×2 0 1 2 ) vw , ×犱=2 ×4=6 0 3 9. 犛 0 1 3 犪 0 1 3× ( -4 0 2 1 + 2 0 1 3 =2 1+ 2 2 , 】 (÷ø# 4 + ±2, vw ω= , ! 狓) 犃=2, 【 1~^w3ö 犳( π (2狓+ 4π) 2 1 1 3 π, , 1Ùùt®^3 1 × π + y φ=3 vw 犳( 狓) =2 s i n( 狓+ =π, 狓) =2 s i n( 狓+ π) . 犳( φ) 4 2 2 2 φ 2 4 8. 狓) =2 s i n 犳( 1 3 1
3 2 ( 3 2 + =2 犿+3 狀) + 犿 狀 犿 狀
(
)
· y + (# 2 +1 2=2 4, 4. 犿 狀 犿 狀 槡
→ = → → 】 1 3. 5 【 犆= 犆- 犈犎 λ犈 λ犃
λ → , λ→ → =犃 → → =1- → 犃 犅 犃犎 犈+犈犎 犃 犅+ 犆, λ犃 3 3
2 0 1 3 !"#$%&'()*+,-./ · 0&12/35
】 !¾789# 狓=-2. 1. 狓=-2 【 2 狆=8, 狆=4, ) } } , } , ) 】 ! 犃∩犅= [ 2.[ 0, 1 狓 1-狓>0 ={ 狓 狓<1 犅= { 狓 狓≥0 0, 1 . 【 犃= { | | | ) 】 !êëCgì(´;# 3. 1 1 2 5 【 0. 0 0 5 0+0. 0 0 4 3+0. 0 0 3 2 ×2 0×1 5 0 0=3 7 5, êëgì(´;+ ( 1 5 0 0-3 7 5=1 1 2 5. 4. 5. 1 【 1 1 1 1 1 1- i ! 犪- =0, 犪= . + + ií(t< 狓 = , 狕= 犪 i = 犪 i = + 犪- 】 1+ i 2 2 2 2 2 2
江苏省南通、泰州、扬州、连云港、淮安五市高三第三次模拟考试数学试卷
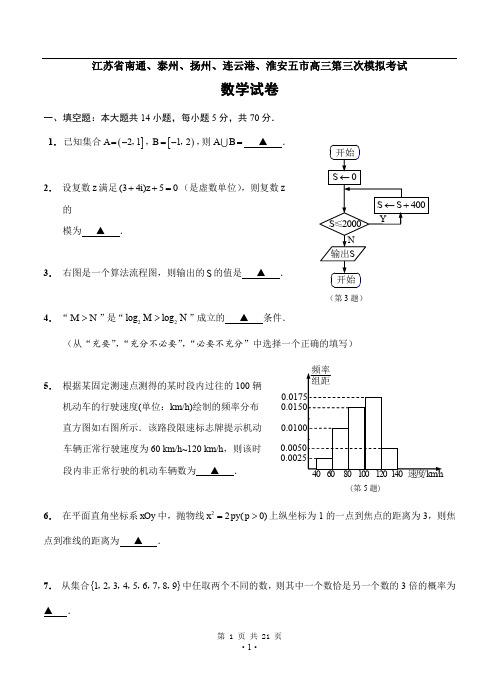
(第3题)(第5题)江苏省南通、泰州、扬州、连云港、淮安五市高三第三次模拟考试数学试卷一、填空题:本大题共14小题,每小题5分,共70分.1. 已知集合(]2 1A =-,,[)1 2B =-,,则A B = ▲ .2. 设复数z 满足(34i)50z ++=(是虚数单位),则复数z的模为 ▲ .3. 右图是一个算法流程图,则输出的S 的值是 ▲ .4. “M N >”是“22log log M N >”成立的 ▲ 条件.(从“充要”,“充分不必要”,“必要不充分”中选择一个正确的填写)5. 根据某固定测速点测得的某时段内过往的100辆 机动车的行驶速度(单位:km/h)绘制的频率分布 直方图如右图所示.该路段限速标志牌提示机动车辆正常行驶速度为60 km/h~120 km/h ,则该时 段内非正常行驶的机动车辆数为 ▲ .6. 在平面直角坐标系xOy 中,抛物线22(0)x py p =>上纵坐标为1的一点到焦点的距离为3,则焦点到准线的距离为 ▲ .7. 从集合{}1 2 3 4 5 6 7 8 9,,,,,,,,中任取两个不同的数,则其中一个数恰是另一个数的3倍的概率为 ▲ .(第9题)8. 在平面直角坐标系xOy 中,设点P 为圆C :22(1)4x y -+=上的任意一点,点Q (2a ,3a -) (a ∈R ),则线段PQ 长度的最小值为 ▲ .9. 函数()sin()f x A x ωϕ=+(0A >,0ω>,02)ϕ<π≤在R 上的部分图象如图所示,则(2013)f 的值为 ▲ .10.各项均为正数的等比数列{}n a 中,211a a -=.当3a 取最小值时,数列{}n a 的通项公式a n = ▲ .11.已知函数2221 0 () 0ax x x f x x bx c x ⎧--⎪=⎨++<⎪⎩,≥,,是偶函数,直线y t =与函数()y f x =的图象自左向右依次交于四个不同点A ,B ,C ,D .若AB BC =,则实数的值为 ▲ .12.过点(1 0)P -,作曲线C :e x y =的切线,切点为1T ,设1T 在x 轴上的投影是点1H ,过点1H 再作曲线C 的切线,切点为2T ,设2T 在x 轴上的投影是点2H ,…,依次下去,得到第1n +()n ∈N 个切点1n T +.则点1n T +的坐标为 ▲ .13.在平面四边形ABCD中,点E ,F 分别是边AD ,BC 的中点,且AB 1=,EF ,CD =.若15AD BC ⋅=,则AC BD ⋅的值为 ▲ .14.已知实数a 1,a 2,a 3,a 4满足a 1+a 2+a 30=,a 1a 42+a 2a 4-a 20=,且a 1>a 2>a 3,则a 4的取值范围是 ▲ .二、解答题15.如图,在四棱锥P ABCD -中,底面ABCD 是矩形,四条侧棱长均相等. (1)求证:AB //平面PCD ; (2)求证:平面PAC ⊥平面ABCD .16.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c .已知222222sin 2sin sin C b a c A C c a b --=---. (1)求角B 的大小;(2)设222sin sin sin T A B C =++,求T 的取值范围.17.某单位设计的两种密封玻璃窗如图所示:图1是单层玻璃,厚度为8 mm ;图2是双层中空玻璃,厚度均为4 mm ,中间留有厚度为x 的空气隔层.根据热传导知识,对于厚度为d 的均匀介质,两侧的温度差为T ∆,单位时间内,在单位面积上通过的热量T Q k d∆=⋅,其中k 为热传导系数.假定单位时间内,在单位面积上通过每一层玻璃及空气隔层的热量相等.(注:玻璃的热传导系数为3410 J mm/C -⨯⋅,空气的热传导系数为42.510 J mm/C -⨯⋅.)(1)设室内,室外温度均分别为1T ,2T ,内层玻璃外侧温度为1T ',外层玻璃内侧温度为2T ',且1122T T T T ''>>>.试分别求出单层玻璃和双层中空玻璃单位时间内,在单位面积上通过的热量(结ABC(第15题)PDO(第18题)果用1T ,2T 及x 表示);(2)为使双层中空玻璃单位时间内,在单位面积上通过的热量只有单层玻璃的4%,应如何设计x 的大小?18.如图,在平面直角坐标系xOy 中,椭圆22221(0)y x a b a b+=>>的右焦点为(1 0)F ,,.分别过O ,F 的两条弦AB ,CD 相交于点E (异于A ,C 两点),且OE EF =.(1)求椭圆的方程;(2)求证:直线AC ,BD 的斜率之和为定值.图1图2(第17题)19.已知数列{}n a 是首项为1,公差为d 的等差数列,数列{}n b 是首项为1,公比为(1)q q >的等比数列.(1)若55a b =,3q =,求数列{}n n a b ⋅的前n 项和;(2)若存在正整数(2)k k ≥,使得k k a b =.试比较n a 与n b 的大小,并说明理由.20.设()f x 是定义在(0 )+∞,的可导函数,且不恒为0,记()()()n n f x g x n x=∈*N .若对定义域内的每一个x ,总有()0n g x <,则称()f x 为“n 阶负函数”;若对定义域内的每一个x ,总有[]()0n g x '≥,则称()f x 为“n 阶不减函数”([]()n g x '为函数()n g x 的导函数).(1)若31()(0)a f x x x x x =-->既是“1阶负函数”,又是“1阶不减函数”,求实数a 的取值范围;(2)对任给的“2阶不减函数”()f x ,如果存在常数c ,使得()f x c <恒成立,试判断()f x 是否为“2阶负函数”?并说明理由.数学附加题21.【选做题】A .选修4—1:几何证明选讲如图,⊙O 的半径为3,两条弦AB ,CD 交于点P ,且1AP =, 3CP =,OP = 求证:△APC ≌△DPB .B .选修4—2:矩阵与变换已知矩阵M 566x ⎡⎤=⎢⎥⎣⎦不存在逆矩阵,求实数x 的值及矩阵M 的特征值.C .选修4—4:坐标系与参数方程在平面直角坐标系xOy 中,已知(0 1)A ,,(0 1)B -,,( 0)C t ,,()3 0D t,,其中0t ≠.设直线AC 与BD 的交点为P ,求动点P 的轨迹的参数方程(以为参数)及普通方程.D .选修4—5:不等式选讲已知0a >,0b >,n ∈*N .求证:11n n n na b a b++++22.【必做题】设n ∈*N 且2n ≥,证明:()22221212n n a a a a a a ++⋅⋅⋅+=++⋅⋅⋅+()1232n a a a a ⎡+++⋅⋅⋅+⎣()234n a a a a +++⋅⋅⋅++⋅⋅⋅]1n n a a -+.23.【必做题】下图是某游戏中使用的材质均匀的圆形转盘,其中Ⅰ,Ⅱ,Ⅲ,Ⅳ部分的面积各占转盘面积的112,(第3题)16,14,12.游戏规则如下: ① 当指针指到Ⅰ,Ⅱ, Ⅲ,Ⅳ部分时,分别获得积分100分,40分,10分,0分; ② (ⅰ)若参加该游戏转一次转盘获得的积分不是40分,则按①获得相应的积分,游戏结束; (ⅱ)若参加该游戏转一次获得的积分是40分,则用抛一枚质地均匀的硬币的方法来决定是否继续游戏.正面向上时,游戏结束;反面向上时,再转一次转盘,若再转一次的积分不高于40分,则最终积分为0分,否则最终积分为100分,游戏结束.设某人参加该游戏一次所获积分为ξ.(1)求0ξ=的概率;(2)求ξ的概率分布及数学期望.南通市2013届高三第三次调研测试数学参考答案及评分建议一、填空题:本大题共14小题,每小题5分,共70分.1. 已知集合(]2 1A =-,,[)1 2B =-,,则A B = ▲ .【答案】(2 2)-,2. 设复数z 满足(34i)50z ++=(是虚数单位),则复数z 的 模为 ▲ . 【答案】3. 右图是一个算法流程图,则输出的S 的值是 ▲ . 【答案】24004. “M N >”是“22log log M N >”成立的 ▲ 条件.(从“充要”,“充分不必要”,“必要不充分”中选择一个正确的填写)(第23题)(第9题)(第5题)【答案】必要不充分5. 根据某固定测速点测得的某时段内过往的100辆 机动车的行驶速度(单位:km/h)绘制的频率分布 直方图如右图所示.该路段限速标志牌提示机动车辆正常行驶速度为60 km/h~120 km/h ,则该时 段内非正常行驶的机动车辆数为 ▲ . 【答案】156. 在平面直角坐标系xOy 中,抛物线22(0)x py p =>上纵坐标为1的一点到焦点的距离为3,则焦 点到准线的距离为 ▲ .【答案】47. 从集合{}1 2 3 4 5 6 7 8 9,,,,,,,,中任取两个不同的数,则其中一个数恰是另一个数的3倍的概率为 ▲ .【答案】1128. 在平面直角坐标系xOy 中,设点P 为圆C :22(1)4x y -+=上的任意一点,点Q (2a ,3a -) (a ∈R ),则线段PQ 长度的最小值为 ▲ .【答案2-9. 函数()sin()f x A x ωϕ=+(0A >,0ω>,02)ϕ<π≤在R 上的部分图象如图所示,则(2013)f 的值为 ▲ . 【答案】 10.各项均为正数的等比数列{}n a 中,211a a -=.当3a 取最小值时,数列{}n a 的通项公式a n = ▲ .【答案】12n -11.已知函数2221 0 () 0ax x x f x x bx c x ⎧--⎪=⎨++<⎪⎩,≥,,是偶函数,直线y t =与函数()y f x =的图象自左向右依次交于四个不同点A ,B ,C ,D .若AB BC =,则实数的值为 ▲ . 【答案】74-12.过点(1 0)P -,作曲线C :e x y =的切线,切点为1T ,设1T 在x 轴上的投影是点1H ,过点1H 再作曲线C 的切线,切点为2T ,设2T 在x 轴上的投影是点2H ,…,依次下去,得到第1n +()n ∈N 个 切点1n T +.则点1n T +的坐标为 ▲ . 【答案】()e n n ,13.在平面四边形ABCD 中,点E ,F 分别是边AD ,BC 的中点,且AB 1=,EF ,CD =.若15AD BC ⋅=,则AC BD ⋅的值为 ▲ . 【答案】1314.已知实数a 1,a 2,a 3,a 4满足a 1+a 2+a 30=,a 1a 42+a 2a 4-a 20=,且a 1>a 2>a 3,则a 4的取值范围是 ▲ .【答案】二、解答题15.如图,在四棱锥P ABCD -中,底面ABCD 是矩形,四条侧棱长均相等. (1)求证:AB //平面PCD ; (2)求证:平面PAC ⊥平面ABCD . 证明:(1)在矩形ABCD 中,//AB CD , 又AB ⊄平面PCD , CD ⊂平面PCD ,所以AB //平面PCD . ………6分 (2)如图,连结BD ,交AC 于点O ,连结PO , 在矩形ABCD 中,点O 为 AC BD ,的中点, 又PA PB PC PD ===,故PO AC ⊥,PO BD ⊥, ………9分ABC(第15题)PDO又AC BD O =,AC BD ,⊂平面ABCD ,所以PO ⊥平面ABCD , ………12分又PO ⊂平面PAC ,所以平面PAC ⊥平面ABCD . ………14分16.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c .已知222222sin 2sin sin C b a c A C c a b --=---. (1)求角B 的大小;(2)设222sin sin sin T A B C =++,求T 的取值范围. 解:(1)在△ABC 中,222222sin 2cos cosB sin cos 2sin sin 2cos cos sin cos C b a c ac B c C B A C ab C b C B Cc a b ---====----, ………3分因为sin 0C ≠,所以sin cos 2sin cos sin cos B C A B C B =-,所以2sin cos sin cos sin cos sin()sin A B B C C B B C A =+=+=, ………5分因为sin 0A ≠,所以1cos 2B =,因为0πB <<,所以π3B =. ………7分(2)222131sin sin sin (1cos 2)(1cos 2)242T A B C A C =++=-++-()71714π(cos 2cos 2)cos 2cos 242423A C A A -⎡⎤=⎢⎥⎣+=--⎦+()()71171πcos22cos 2422423A A A =-=-+ (11)分因为2π03A <<,所以4π023A <<,故ππ5π2333A <+<,因此()π11cos 232A -+<≤,所以3924T <≤. ………14分17.某单位设计的两种密封玻璃窗如图所示:图1是单层玻璃,厚度为8 mm ;图2是双层中空玻璃,厚度均为4 mm ,中间留有厚度为x 的空气隔层.根据热传导知识,对于厚度为d 的均匀介质, 两侧的温度差为T ∆,单位时间内,在单位面积上通过的热量T Q k d ∆=⋅,其中k 为热传导系数.假定单位时间内,在单位面积上通过每一层玻璃及空气隔层的热量相等.(注:玻璃的热传导系 数为3410 J mm/C -⨯⋅,空气的热传导系数为42.510 J mm/C -⨯⋅.)(1)设室内,室外温度均分别为1T ,2T ,内层玻璃外侧温度为1T ',外层玻璃内侧温度为2T ', 且1122T T T T ''>>>.试分别求出单层玻璃和双层中空玻璃单位时间内,在单位面积上通过 的热量(结果用1T ,2T 及x 表示);(2)为使双层中空玻璃单位时间内,在单位面积上通过的热量只有单层玻璃的4%,应如何设计x 的大小?解:(1)设单层玻璃和双层中空玻璃单位时间内,在单位面积上通过的热量分别为1Q ,2Q , 则3121214108 2 000T T T T Q ---=⨯⋅=, ………2图1图2(第17题)(第18题)3431112222410 2.51041044T T T T T T Q x ---''''---=⨯⋅=⨯⋅=⨯⋅………6分11122234344410 2.510410T T T T T T x ---''''---===⨯⨯⨯ 11122234344410 2.510410T T T T T T x ---''''-+-+-=++⨯⨯⨯124 000 2 000T T x -=+. ………9分(2)由(1)知21121Q Q x =+, 当121x =+4%时,解得12x =(mm ). 答:当12x =mm 时,双层中空玻璃通过的热量只有单层玻璃的4%. ………14分18.如图,在平面直角坐标系xOy 中,椭圆22221(0)y x a b a b+=>>的右焦点为(1 0)F ,.分别过O ,F 的两条弦AB ,CD 相交于点E (异于A ,C 两点),且OE EF =. (1)求椭圆的方程;(2)求证:直线AC ,BD 的斜率之和为定值.(1)解:由题意,得1c =,c e a ==,故a =从而2221b a c =-=,所以椭圆的方程为2212x y +=. ① (5)分(2)证明:设直线AB 的方程为y kx =,②直线CD 的方程为(1)y k x =--, ③ (7)由①②得,点A ,B的横坐标为由①③得,点C ,D………9分记11( )A x kx ,,22( )B x kx ,,33( (1))C x k x -,,44( (1))D x k x -,, 则直线AC ,BD 的斜率之和为13241324(1)(1)kx k x kx k x x x x x ----+-- 132413241324(1)()()(1)()()x x x x x x x x k x x x x +--+-+-=⋅--1234123413242()()()()()x x x x x x x x k x x x x --+++=⋅-- (13)分2222124232(1)4222201121()()k k k k k x x x k x ⎛⎫---+ ⎪+++⎝-⎭=⋅-- 0=. ………16分19.已知数列{}n a 是首项为1,公差为d 的等差数列,数列{}n b 是首项为1,公比为(1)q q >的等比数列.(1)若55a b =,3q =,求数列{}n n a b ⋅的前n 项和;(2)若存在正整数(2)k k ≥,使得k k a b =.试比较n a 与n b 的大小,并说明理由. 解:(1)依题意,5145511381a b b q -===⨯=, 故5181120514a a d --===-, 所以120(1)2019n a n n =+-=-, ………3分令2111213413(2019)3n n S n -=⨯+⨯+⨯+⋅⋅⋅+-⋅, ①则213 13213(2039)3(2019)3n n n S n n -=⨯+⨯+⋅⋅⋅+-⋅+-⋅, ② ①-②得,()2121+20333(2019)3n n n S n --=⨯++⋅⋅⋅+--⋅,13(13)1+20(2019)313n n n --=⨯--⋅-(2920)329n n =-⋅-,所以(2029)3292n n n S -⋅+=. ………7分(2)因为k k a b =, 所以11(1)k k d q-+-=,即111k q d k --=-,故111(1)1k n q a n k --=+--,又1n n b q -=, ………9分所以1111(1)1k n n n q b a qn k --⎡⎤--=-+-⎢⎥-⎣⎦()()111(1)1(1)11n k k q n q k --⎡⎤=-----⎣⎦- ()()23231(1)1(1)11n n k k q k q q q n q q q k -----⎡⎤=-++⋅⋅⋅++--++⋅⋅⋅++⎣⎦- ………11分(ⅰ)当1n k <<时,由1q >知()()232311()1(1)1n n k k n n n q b a k n q q q n q q q k ------⎡⎤-=-++⋅⋅⋅++--++⋅⋅⋅+⎣⎦- 211()(1)(1)()1n n q k n n q n k n q k ---⎡⎤<-----⎣⎦- 22(1)()(1)1n q q k n n k ----=--0<, ………13分(ⅱ)当n k >时,由1q >知()()231231(1)()11n n k k k n n q b a k q q q n k q q q k ------⎡⎤-=-++⋅⋅⋅+--++⋅⋅⋅++⎣⎦- 121(1)()()(1)1k k q k n k q n k k q k ---⎡⎤>-----⎣⎦- 22(1)()k q q n k -=-- 0>,综上所述,当1n k <<时,n n a b >;当n k >时,n n a b <;当1 n k =,时,n n a b =. ………16分(注:仅给出“1n k <<时,n n a b >;n k >时,n n a b <”得2分.)20.设()f x 是定义在(0 )+∞,的可导函数,且不恒为0,记()()()n n f x g x n x=∈*N .若对定义域内的每 一个x ,总有()0n g x <,则称()f x 为“n 阶负函数”;若对定义域内的每一个x ,总有[]()0n g x '≥, 则称()f x 为“n 阶不减函数”([]()n g x '为函数()n g x 的导函数).(1)若31()(0)a f x x x x x =-->既是“1阶负函数”,又是“1阶不减函数”,求实数a 的取值范围;(2)对任给的“2阶不减函数”()f x ,如果存在常数c ,使得()f x c <恒成立,试判断()f x 是 否为“2阶负函数”?并说明理由. 解:(1)依题意,142()1()1f x ag x x x x==--在(0 )+∞,上单调递增, 故15342[()]0a g x x x '=-+≥ 恒成立,得212a x ≤, ………2分 因为0x >,所以0a ≤. ………4分 而当0a ≤时,1421()10a g x x x=--<显然在(0 )+∞,恒成立,所以0a ≤. ………6分(2)①先证()0f x ≤:若不存在正实数0x ,使得20()0g x >,则2()0g x ≤恒成立. ………8分假设存在正实数0x ,使得20()0g x >,则有0()0f x >,由题意,当0x >时,2()0g x '≥,可得2()g x 在(0 )+∞,上单调递增, 当0x x >时,0220()()f x f x x x >恒成立,即2020()()f x f x x x >⋅恒成立,故必存在10x x >,使得201120()()f x f x x m x >⋅>(其中m 为任意常数), 这与()f x c <恒成立(即()f x 有上界)矛盾,故假设不成立,所以当0x >时,2()0g x ≤,即()0f x ≤; ………13分 ②再证()0f x =无解:假设存在正实数2x ,使得2()0f x =, 则对于任意320x x >>,有322232()()0f x f x x x >=,即有3()0f x >, 这与①矛盾,故假设不成立, 所以()0f x =无解,综上得()0f x <,即2()0g x <,故所有满足题设的()f x 都是“2阶负函数”. ………16分南通市2013届高三第三次调研测试 数学附加题参考答案及评分建议21.【选做题】A .选修4—1:几何证明选讲(第21—A 题)如图,⊙O 的半径为3,两条弦AB ,CD 交于点P ,且1AP =, 3CP =,OP = 求证:△APC ≌△DPB .证明:延长OP 交⊙O 与点E ,F , ………2分由相交弦定理得((333CP DP AP BP FP EP ⋅=⋅=⋅=-⨯=,………6分 又1AP =,3CP =,故1DP =,3BP =, ………8分所以AP DP =,BP CP =, 而APC DPB ∠=∠,所以△APC ≌△DPB . ………10分B .选修4—2:矩阵与变换已知矩阵M 566x ⎡⎤=⎢⎥⎣⎦不存在逆矩阵,求实数x 的值及矩阵M 的特征值. 解:由题意,矩阵M 的行列式5066x =,解得5x =, ………4分 矩阵M 5566⎡⎤=⎢⎥⎣⎦的特征多项式 55()(5)(6)(5)(6)66f λλλλλ--==----⨯---, ………8分 令()0f λ=并化简得2110λλ-=,解得0λ=或11λ=,所以矩阵M 的特征值为0和11. (10)分C .选修4—4:坐标系与参数方程在平面直角坐标系xOy 中,已知(0 1)A ,,(0 1)B -,,( 0)C t ,,()3 0D t,,其中0t ≠.设直线AC 与BD 的交点为P ,求动点P 的轨迹的参数方程(以为参数)及普通方程. 解:直线AC 的方程为1x y t +=,①直线BD 的方程为13x y t -=,② (2)分由①②解得,动点P 的轨迹的参数方程为2226 33 3t x t t y t ⎧=⎪+⎨-⎪=+⎩,(为参数,且0t ≠), ………6分 将263t x t =+平方得222236(3)t x t =+, ③将2233t y t -=+平方得()()2222233t y t -=+, ④ ………8分由③④得,221(0)3x y x +=≠. ………10分 (注:普通方程由①②直接消参可得.漏写“0x ≠”扣1分.)D .选修4—5:不等式选讲已知0a >,0b >,n ∈*N.求证:11n n n na b a b ++++证明:先证112n n n n a b a ba b +++++≥, 只要证112()()()n n n n a b a b a b +++++≥, 即要证11n n n n a b a b ab +++--≥0,即要证()(n n a b a b --)≥0, ………5分若a b ≥,则a b -≥0,n n a b -≥0,所以()(n n a b a b --)≥0, 若a b <,则0a b -<,0n n a b -<,所以()()0n n a b a b -->, 综上,得()(n n a b a b --)≥0.从而112n n n n a b a ba b +++++≥, ………8分因为2a b+,所以11n n n na b a b ++++ ………10分 22.【必做题】设n ∈*N 且2n ≥,证明:()22221212n n a a a a a a ++⋅⋅⋅+=++⋅⋅⋅+()1232n a a a a ⎡+++⋅⋅⋅+⎣()234n a a a a +++⋅⋅⋅++⋅⋅⋅]1n n a a -+.证明:(1)当2n =时,有()2221212122a a a a a a +=++,命题成立. ………2分 (2)假设当(2)n k k =≥时,命题成立, 即()22221212k k a a a a a a ++⋅⋅⋅+=++⋅⋅⋅+()1232k a a a a ⎡+++⋅⋅⋅+⎣()234k a a a a +++⋅⋅⋅++⋅⋅⋅]1k k a a -+成立, ………4分那么,当1n k =+时,有()2121k k a a a a +++⋅⋅⋅++ ()()221212112k k k k a a a a a a a a ++=++⋅⋅⋅++++⋅⋅⋅++22212k a a a =++⋅⋅⋅+()1232k a a a a ⎡+++⋅⋅⋅+⎣()234k a a a a +++⋅⋅⋅++⋅⋅⋅]1k k a a -+(12a +2a ++⋅⋅⋅)211k k k a a a ++++.2222121k k a a a a +=++⋅⋅⋅++()12312k k a a a a a +⎡+++⋅⋅⋅++⎣+(234a a a ++⋅⋅⋅k a +)1k a ++ +⋅⋅⋅ ]1k k a a ++.所以当1n k =+时,命题也成立. ………8分根据(1)和(2),可知结论对任意的n ∈*N 且2n ≥都成立. ………10分23.【必做题】下图是某游戏中使用的材质均匀的圆形转盘,其中Ⅰ,Ⅱ,Ⅲ,Ⅳ部分的面积各占转盘面积的112,16,14,12.游戏规则如下: ① 当指针指到Ⅰ,Ⅱ, Ⅲ,Ⅳ部分时,分别获得积分100分,40分,10分,0分; ② (ⅰ)若参加该游戏转一次转盘获得的积分不是40分,则按①获得相应的积分,游戏结束; (ⅱ)若参加该游戏转一次获得的积分是40分,则用抛一枚质地均匀的硬币的方法来决定是否继续游戏.正面向上时,游戏结束;反面向上时,再转一次转盘,若再转一次的积 分不高于40分,则最终积分为0分,否则最终积分为100分,游戏结束. 设某人参加该游戏一次所获积分为ξ.(1)求0ξ=的概率;(2)求ξ的概率分布及数学期望.解:(1)事件“0ξ=”包含:“首次积分为0分”和“首次积分为40分后再转一次的积分不高于40分”,且两者互斥,所以111183(0)(1)26212144P ξ==+⨯⨯-=; ………4分(2)ξ的所有可能取值为0,10,40,100,(第23题)第 21 页 共 21 页·21· 由(1)知83(0)144P ξ==,又1(10)4P ξ==,111(40)6212P ξ==⨯=,111113(100)126212144P ξ==+⨯⨯=,所以ξ的概率分布为:………7分因此,831113535()0104010014441214436E ξ=⨯+⨯+⨯+⨯=(分).…10分。
南京市、盐城市2013届高三第三次模拟考试数学参考答案及评分标准(定稿)

南京市、盐城市2013届高三第三次模拟考试数学参考答案及评分标准 2013.05说明:1.本解答给出的解法供参考.如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.2.对计算题,当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数. 4.只给整数分数,填空题不给中间分数.一、填空题:本大题共14小题,每小题5分,共70分.1.(1,3] 2.5 3.8 4.127 5. 23 6.710 7.2 8.①④ 9.562 10.2 11.2 12.2x +y -2=0 13.(12,17) 14.332二、解答题:本大题共6小题,共90分.解答时应写出文字说明、证明过程或演算步骤. 15.解(1)方法一:因为tan α=2,所以sin αcos α=2,即sin α=2cos α. ………………………… 2分 又sin 2α+cos 2α=1,解得sin 2α=45,cos 2α=15. ………………………… 4分 所以cos2α=cos 2α-sin 2α=-35. ………………………… 6分 方法二:因为cos2α=cos 2α-sin 2α ………………………… 2分=cos 2α-sin 2αsin 2α+cos 2α =1-tan 2αtan 2α+1, ………………………… 4分 又tan α=2,所以cos2α=1-2222+1=-35. ………………………… 6分(2)方法一:因为α∈(0,π),且tan α=2,所以α∈(0,π2).又cos2α=-35<0,故2α∈(π2,π) ,sin2α=45. ………………………… 8分所以sin(2α-β)=sin2αcos β-cos2αsin β=45×(-7210)-(-35)×210=-22. ………… 12分 又2α-β∈(-π2,π2),所以2α-β=-π4. ………………………… 14分 方法二:因为α∈(0,π),且tan α=2,所以α∈(0,π2),tan2α=2tan α1-tan 2α=-43. 从而2α∈(π2,π). ………………………… 8分 由cos β=-7210,β∈(0,π),得sin β=210,β∈(π2,π),因此tan β=-17. ………………………… 10分 所以tan(2α-β)=tan2α-tan β1+tan2αtan β=-43+171+(-43)×(-17)=-1. ………………………… 12分 又2α-β∈(-π2,π2),所以2α-β=-π4. ………………………… 14分16.证明(1)如图,取BC 的中点G ,连结AG ,FG .因为F 为C 1B 的中点,所以FG =∥12C 1C . 在三棱柱ABC -A 1B 1C 1中,A 1A =∥C 1C ,且E 为A 1A 的中点, 所以FG =∥EA . 所以四边形AEFG 是平行四边形. 所以EF ∥AG . ………………………… 4分 因为EF ⊄平面ABC ,AG ⊂平面ABC ,所以EF ∥平面ABC . ………………………… 6分 (2)因为在正三棱柱ABC -A 1B 1C 1中,A 1A ⊥平面ABC ,BD ⊂平面ABC ,所以A 1A ⊥BD .因为D 为AC 的中点,BA =BC ,所以BD ⊥AC .因为A 1A ∩AC =A ,A 1A ⊂平面A 1ACC 1,AC ⊂平面A 1ACC 1,所以BD ⊥平面A 1ACC 1. 因为C 1E ⊂平面A 1ACC 1,所以BD ⊥C 1E . ………………………… 9分(第16题)ABC D EC 1A 1B 1FG所以EB 2+C 1E 2=C 1B 2.从而∠C 1EB =90°,即C 1E ⊥EB .……………………… 12分 因为BD ∩EB =B ,BD ⊂平面BDE , EB ⊂平面BDE ,所以C 1E ⊥平面BDE . ………………………… 14分17.解(1)由题意知,f (x )=-2x +3+ln x ,所以f ′(x )=-2+1x =-2x +1x (x >0). ……………………… 2分 由f ′(x )>0得x ∈(0,12) .所以函数f (x )的单调增区间为(0,12). ……………………… 4分 (2)由f ′(x )=mx -m -2+1x ,得f ′(1)=-1,所以曲线y =f (x )在点P (1,1)处的切线l 的方程为y =-x +2.…………………… 6分 由题意得,关于x 的方程f (x )=-x +2有且只有一个解, 即关于x 的方程12m (x -1)2-x +1+ln x =0有且只有一个解. 令g (x )=12m (x -1)2-x +1+ln x (x >0).则g ′(x )=m (x -1)-1+1x =mx 2-(m +1)x +1x =(x -1)(mx -1)x (x >0). …………… 8分 ①当0<m <1时,由g ′(x )>0得0<x <1或x >1m ,由g ′(x )<0得1<x <1m , 所以函数g (x )在(0,1)为增函数,在(1,1m )上为减函数,在(1m ,+∞)上为增函数. 又g (1)=0,且当x →∞时,g (x )→∞,此时曲线y =g (x )与x 轴有两个交点.故0<m <1不合题意. ……………………… 10分 ②当m =1时,g ′(x )≥0,g (x )在(0,+∞)上为增函数,且g (1)=0,故m =1符合题意. ③当m >1时,由g ′(x )>0得0<x <1m 或x >1,由g ′(x )<0得1m <x <1,所以函数g (x )在(0,1m ) 为增函数,在(1m ,1)上为减函数,在(1,+∞)上为增函数. 又g (1)=0,且当x →0时,g (x )→-∞,此时曲线y =g (x )与x 轴有两个交点. 故m >1不合题意.综上,实数m 的值为m =1. ……………………… 14分18.解 如图所示,不妨设纸片为长方形ABCD ,AB =8cm ,AD =6cm ,其中点A 在面积为S 1的部分内.折痕有下列三种情形:①折痕的端点M ,N 分别在边AB ,AD 上; ②折痕的端点M ,N 分别在边AB ,CD 上; ③折痕的端点M ,N 分别在边AD ,BC 上.(1)在情形②、③中MN ≥6,故当l =4时,折痕必定是情形①.设AM =x cm ,AN =y cm ,则x 2+y 2=16. ……………………… 2分 因为x 2+y 2≥2xy ,当且仅当x =y 时取等号, 所以S 1=12xy ≤4,当且仅当x =y =22时取等号.即S 1的最大值为4. ……………………… 5分 (2)由题意知,长方形的面积为S =6×8=48.因为S 1∶S 2=1∶2,S 1≤S 2,所以S 1=16,S 2=32.当折痕是情形①时,设AM =x cm ,AN =y cm ,则12xy =16,即y =32x .由⎩⎪⎨⎪⎧0≤x ≤8,0≤32x ≤6,得163≤x ≤8.所以l =x 2+y 2=x 2+322x 2,163≤x ≤8. ……………………… 8分设f (x )=x 2+322x 2,x >0,则f ′(x )=2x -2×322x 3=2(x 2+32)(x +42)(x -42)3,x >0.故 所以f (x )的取值范围为[64,80],从而l 的范围是[8,45]; ……………… 11分 当折痕是情形②时,设AM =x cm ,DN =y cm ,则12(x +y )×6=16,即y =163-x .ABCD (情形①)MNABCD (情形②)MNABCD (情形③)MN由⎩⎪⎨⎪⎧0≤x ≤8,0≤163-x ≤8,得0≤x ≤163.所以l =62+(x -y )2=62+4(x -83)2,0≤x ≤163.所以l 的范围为[6,21453]; ……………………… 13分 当折痕是情形③时,设BN =x cm ,AM =y cm ,则12(x +y )×8=16,即y =4-x .由⎩⎨⎧0≤x ≤6,0≤4-x ≤6,得0≤x ≤4. 所以l =82+(x -y )2=82+4(x -2)2,0≤x ≤4. 所以l 的取值范围为[8,45].综上,l 的取值范围为[6,45]. ……………………… 16分19.解(1)由题意得,m >8-m >0,解得4<m <8.即实数m 的取值范围是(4,8). ……………………… 2分 (2)因为m =6,所以椭圆C 的方程为x 26+y 22=1.①设点P 坐标为(x ,y ),则x 26+y 22=1. 因为点M 的坐标为(1,0),所以PM 2=(x -1)2+y 2=x 2-2x +1+2-x 23=2x 23-2x +3=23(x -32)2+32,x ∈[-6,6]. ……………………… 4分所以当x =32时,PM 的最小值为62,此时对应的点P 坐标为(32,±52).……………………… 6分②由a 2=6,b 2=2,得c 2=4,即c =2,从而椭圆C 的右焦点F 的坐标为(2,0),右准线方程为x =3,离心率e =63. 设A (x 1,y 1),B (x 2,y 2),AB 的中点H (x 0,y 0),则x 126+y 122=1,x 226+y 222=1,所以x 12-x 226+y 12-y 222=0,即k AB =y 1-y 2x 1-x 2=-x 03y 0. ……………………… 9分令k =k AB ,则线段AB 的垂直平分线l 的方程为y -y 0=-1k (x -x 0).令y =0,则x N =ky 0+x 0=23x 0.因为F (2,0),所以FN =|x N -2|=23|x 0-3|. ……………………… 12分 因为AB =AF +BF =e (3-x 1)+e (3-x 2)=263|x 0-3|. 故AB FN =263×32=6.即ABFN 为定值6. ……………………… 16分20.解(1)设等差数列{a n }的公差为d ,则S n =na 1+n (n -1)2d ,从而S nn =a 1+n -12d .所以当n ≥2时,S n n -S n -1n -1=(a 1+n -12d )-(a 1+n -22d )=d2.即数列{S nn }是等差数列. ……………………… 2分 (2)因为对任意正整数n ,k (n >k ),都有S n +k +S n -k =2S n 成立,所以S n +1+S n -1=2S n ,即数列{S n }是等差数列. ……………………… 4分 设数列{S n }的公差为d 1,则S n =S 1+(n -1)d 1=1+(n -1)d 1, 所以S n =[1+(n -1)d 1]2,所以当n ≥2时,a n =S n -S n -1=[1+(n -1)d 1]2-[1+(n -2)d 1]2=2d 21n -3d 21+2d 1,因为{a n }是等差数列,所以a 2-a 1=a 3-a 2,即(4d 21-3d 21+2d 1)-1=(6d 21-3d 21+2d 1)-(4d 21-3d 21+2d 1),所以d 1=1,即a n =2n -1.又当a n =2n -1时,S n =n 2,S n +k +S n -k =2S n 对任意正整数n ,k (n >k )都成立, 因此a n =2n -1. ……………………… 7分 (3)设等差数列{a n }的公差为d ,则a n =a 1+(n -1)d ,b n =a a n ,所以b n b n -1=a a n -a n -1=a d ,即数列{b n }是公比大于0,首项大于0的等比数列. ……………………… 9分 记公比为q (q >0).以下证明:b 1+b n ≥b p +b k ,其中p ,k 为正整数,且p +k =1+n . 因为(b 1+b n )-(b p +b k )=b 1+b 1q n -1-b 1q p -1-b 1q k -1=b 1(q p -1-1)( q k -1-1). 当q >1时,因为y =q x 为增函数,p -1≥0,k -1≥0, 所以q p -1-1≥0,q k -1-1≥0,所以b 1+b n ≥b p +b k .当q =1时,b 1+b n =b p +b k .当0<q <1时,因为y =q x 为减函数,p -1≥0,k -1≥0, 所以q p -1-1≤0,q k -1-1≤0,所以b 1+b n ≥b p +b k .综上,b 1+b n ≥b p +b k ,其中p ,k 为正整数,且p +k =1+n .………………… 14分 所以n (b 1+b n )=(b 1+b n )+(b 1+b n )+…+(b 1+b n )≥(b 1+b n )+(b 2+b n -1)+(b 3+b n -2)+…+(b n +b 1)=(b 1+b 2+…+b n )+(b n +b n -1+…+b 1), 即b 1+b 2+…+b n n≤b 1+b n2. …………………… 16分 南京市、盐城市2013届高三第三次模拟考试数学附加题参考答案及评分标准 2013.0521.【选做题】在A 、B 、C 、D 四小题中只能选做2题,每小题10分,共20分. A .选修4—1:几何证明选讲证明 如图,延长PO 交⊙O 于D ,连结AO ,BO .AB 交OP 于点E .因为PA 与⊙O 相切, 所以PA 2=PC ·PD .设⊙O 的半径为R ,因为PA =12,PC =6,所以122=6(2R +6),解得R =9. …………………… 4分 因为PA ,PB 与⊙O 均相切,所以PA =PB .又OA =OB ,所以OP 是线段AB 的垂直平分线. …………………… 7分 即AB ⊥OP ,且AB =2AE . 在Rt △OAP 中,AE =OA ·PA OP =365.所以AB =725. …………………… 10分 B .选修4—2:矩阵与变换 解 (1)由题知,⎣⎢⎡⎦⎥⎤1 a b 1 ⎣⎢⎡⎦⎥⎤11=⎣⎢⎡⎦⎥⎤02,即⎩⎨⎧1+a =0,b +1=2,解得⎩⎨⎧a =-1,b =1.…………………… 4分(2)设P' (x ,y )是曲线C'上任意一点,P' 由曲线C 上的点P (x 0,y 0) 经矩阵M 所表示的变换得到,ABOC (第21题A )DE所以⎣⎢⎡⎦⎥⎤1 -11 1 ⎣⎢⎡⎦⎥⎤x 0y 0=⎣⎢⎡⎦⎥⎤x y ,即⎩⎨⎧x 0-y 0=x ,x 0+y 0=y ,解得⎩⎨⎧x 0=y +x 2,y 0=y -x 2.…………………… 7分 因为x 0y 0=1,所以y +x 2·y -x 2=1,即y 24-x 24=1.即曲线C' 的方程为y 24-x 24=1. …………………… 10分 C .选修4—4:坐标系与参数方程解 以极点为原点,极轴为x 轴正半轴建立平面直角坐标系,则圆C 的直角坐标方程为(x -3)2+(y -1)2=4,点M 的直角坐标为(33,3). …………………… 3分 当直线l 的斜率不存在时,不合题意. 设直线l 的方程为y -3=k (x -33), 由圆心C (3,1)到直线l 的距离等于半径2.故|23k -2|k 2+1=2. …………………… 6分解得k =0或k =3.所以所求的直线l 的直角坐标方程为y =3或3x -y -6=0. ………………… 8分 所以所求直线l 的极坐标方程为ρsin θ=3或ρsin(π3-θ)=3. …………………… 10分 D .选修4—5:不等式选讲解 原不等式等价于 ⎩⎨⎧x ≥4,x 2-4x -3<0,或⎩⎨⎧x <4,-x 2+4x -3<0. …………………… 5分解得⎩⎨⎧x ≥4,2-7<x <2+7,或⎩⎨⎧x <4,x <1或x >3.即4≤x <2+7或3<x <4或x <1.综上,原不等式的解集为{x | x <1或3<x <2+7}. …………………… 10分 【必做题】第22题、第23题,每题10分,共20分.22.解(1)如图,取AC 的中点F ,连接BF ,则BF ⊥AC .以A 为坐标原点,过A 且与FB 平行的直线为x轴,AC 为y 轴,AP 为z 轴,建立空间直角坐标系. 则A (0,0,0),B (3,1,0), C (0,2,0),P (0,0,2),E (0,1,1), 从而→PB =(3,1,-2), →AE =(0,1,1).设直线AE 与PB 所成角为θ, 则cos θ=|→PB ·→AE|→PB |×|→AE ||=14.即直线AE 与PB 所成角的余弦值为14 . …………………… 4分 (2)设PA 的长为a ,则P (0,0,a ),从而→PB =(3,1,-a ),→PC =(0,2,-a ).设平面PBC 的法向量为n 1=(x ,y ,z ),则n 1·→PB =0,n 1·→PC =0, 所以3x +y -az =0,2y -az =0. 令z =2,则y =a ,x =33a .所以n 1=(33a ,a ,2)是平面PBC 的一个法向量.因为D ,E 分别为PB ,PC 中点,所以D (32,12,a 2),E (0,1,a2), 则→AD =(32,12,a 2),→AE =(0,1,a 2).设平面ADE 的法向量为n 2=(x ,y ,z ),则n 2·→AD =0,n 2·→AE =0. 所以32x +12y +a 2z =0,y +a2z =0. 令z =2,则y =-a ,x =-33a .所以n 2=(-33a ,-a ,2)是平面ADE 的一个法向量. …………………… 8分 因为面ADE ⊥面PBC ,所以n 1⊥n 2,即n 1·n 2=(33a ,a ,2)·(- 33a ,-a ,2)=-13a 2-a 2+4=0,解得a =3,即PA 的长为3. …………………… 10分 23.解(1)p 1=23,p 2=23×23+13×(1-23)=59. …………………… 2分 (2)因为移了n 次后棋子落在上底面顶点的概率为p n ,故落在下底面顶点的概率为1-p n .于是移了n +1次后棋子落在上底面顶点的概率为p n +1=23p n +13(1-p n )=13p n +13.…………………… 4分从而p n +1-12=13(p n -12).所以数列{p n -12}是等比数列,其首项为16,公比为13.所以p n -12=16×(13)n -1.即p n =12+12×13n . …………………… 6分 用数学归纳法证明:①当n =1时,左式=14×23-1=35,右式=12,因为35>12,所以不等式成立.当n =2时,左式=14×23-1+14×59-1=7855,右式=43,因为7855>43,所以不等式成立.②假设n =k (k ≥2)时,不等式成立,即i =1∑k14P i -1>k 2k +1.则n =k +1时,左式=i =1∑k14P i -1+14P k +1-1>k 2k +1+14(12+12×13k +1)-1=k 2k +1+3k +13k +1+2.要证k 2k +1+3k +13k +1+2≥(k +1)2k +2,只要证3k +1 3k +1+2≥(k +1)2k +2-k 2k +1.只要证3k +13k +1+2≥k 2+3k +1 k 2+3k +2.只要证2 3k +1≤1k 2+3k +1.只要证3k +1≥2k 2+6k +2. 因为k ≥2,所以3k +1=3(1+2)k ≥3(1+2k +4C 2k )=6k 2+3=2k 2+6k +2+2k (2k -3)+1>2k 2+6k +2,所以k 2k +1+3k +1 3k +1+2≥(k +1)2k +2.即n =k +1时,不等式也成立.由①②可知,不等式i =1∑n14P i -1>n 2n +1对任意的n ∈N *都成立. ……………………10分。
江苏省南通泰州扬州连云港淮安五市2013届高三第三次模拟考试数学试题

4 22
2
42
3
0 A 2π
0 2 A 4π
因为
3 ,所以
3,
π 2A π 5π
1≤ cos 2 A π 1
故3
3 3 ,因此
3 2,
3 T≤9
所以 2
4.
17. 【解析】( 1)设单层玻璃和双层中空玻璃单位时间内,在单位面积上通过的热量分别为
Q1 , Q2 ,则 Q1
4 10 3 T1 T2 8
T1 T2 2 000 ,
2EF AB DC ,平方并整理得
AB DC 2 ,
AB AC AD 即
AB AC AB AD 2 ①,由 AD BC 15 ,得
AD AC AB
AD AC AD AB 15 ②,②
①得 AC BD AC AD AB
13 .
14.【答案】
1 5, 1 5
2
2 【解析】方法一:因为
a1 a2 a1 a2
(2)①先证 f (x )≤0 :
若不存在正实数 x0 ,使得 g2 ( x0 ) 0 ,则 g2 (x)≤0 恒成立.
假设存在正实数 x0 ,使得 g2 ( x0 ) 0 ,则有 f (x0 ) 0,
由题意,当 x 0 时, g2 ( x)≥0 ,可得 g 2( x ) 在 (0, ) 上单调递增,
1 2
5 a4
15 2.
方法二:由
1 a2 a1
a1 a2 a3,
1 a2
a1 a2 a3 0 得
a1
a3 ,
x
a1
a3 0,
y
a1
令
a2 , a1
a3 ,
y
a1 则 x
13大市2013年高三历次考试数学试题分类汇编6:数列

曲线 C 的切线,切点为 T2 ,设 T2 在 x 轴上的投影是点 H 2 ,,依次下去,得到第 n 1 (n N) 个切点 Tn 1 .则点 Tn 1 的坐标为______.
【答案】 n, en
2
9 . (江苏省泰州、南通、扬州、宿迁、淮安五市 2013 届高三第三次调研测试数学试卷)已知
(1) n (n 15) bn = n 16 an
(ii)当 n<16 时,
当 n 为偶数时
1 bn (n 15) = =-1n 16 n 16 an
n=14 时(
1 b 13 bn )max=- ( n )min=2 an 14 an 1 1 14 bn n 15 b = =1+ , n=1 , ( n )max=1= , n 16 15 15 an n 16 an
14( .江苏省无锡市 2013 届高三上学期期末考试数学试卷) 等差数列{an}的公差为-2,且 a1,a3,a4
成等比数列,则 a20=_______________.
【答案】 30 15( .南京市、 盐城市 2013 届高三第三次模拟考试数学试卷) 已知数列{an}的通项公式为 an=-n+p,
an 满 足
a1 1, an 1 1 an (an 1) , (n N ) ,且
____.
【答案】 二、解答题
1 1 1 =2,则 a2013 4a1 的最小值为 a1 a2 a2012
7 2
25. (江苏省苏锡常镇四市 2013 届高三教学情况调研(一)数学试题)设数列
an 的各项均为正
数,其前 n 项的和为 S n ,对于任意正整数 m , n , S m n (1)若 a1 1 ,求 a2 , a3 , a4 及数列 an 的通项公式; (2)若 a4 a2 (a1 a2 1) ,求证:数列 an 成等比数列.
南京市、盐城市2013届高三第三次模拟考试数学参考答案及评分标准(定稿).pptx

所以 C1E⊥平面 BDE.
………………………… 14 分
17.解(1)由题意知,f(x)=-2x+3+lnx, 1 -2x+1
所以 f′(x)=-2+x= x (x>0). 由 f′(x)>0 得 x∈(0,21) . 所以函数 f(x)的单调增区间为(0,21). (2)由 f′(x)=mx-m-2+1x,得 f′(1)=-1,
故FANB=23 6×23= 6.
即FANB为定值 6.
学海无 涯
……………………… 16 分
20.解(1)设等差数列{an}的公差为
d,则
S n=na
1+n(n2-1)d,从而Snn=
n-1 a1+ 2 d.
所以当 n≥2 时,Snn-nS-n-11 =(a1+n-2 1d)-(a1+n-2 2d)=d2.
得 0≤x≤136.
8
16
所以 l= 62+(x-y)2= 62+4(x-3)2,0≤x≤ 3 .
2 145 所以 l 的范围为[6, 3 ]; ……………………… 13 分
学海无 涯
当折痕是情形③时,设 BN=xcm,AM=ycm,则21(x+y)×8=16,即 y=4-x. 由00≤ ≤x4≤-6x,≤6,得 0≤x≤4. 所 以 l= 82+(x-y)2= 82+4(x-2)2,0≤x≤4. 所以 l 的取值范围为[8,4 5].
学海无 涯
②折痕的端点 M,N 分别在边 AB,CD 上;
③折痕的端点 M,N 分别在边 AD,BC 上.
D
C
DN
C
D
C
N
A
M
B
(情形①)
A
Mபைடு நூலகம்
B
(情形②)
江苏省南京、盐城市2013届高三第三次模拟考试数学试题 Word版含答案.pdf

南京市2013届高三第次模拟考试 数学:1..参考公式: 样本数据x1,x2,…,xn的方差s2=(xi-)2,其中=xi. 一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题卡相应位置上. 函数f(x)=的定义域为A,函数g(x)=lg(x-1)的定义域为B,则A∩B=2.已知复数z满足(z+)i=+= 4.右图是7位评委给某作品打出的分数的茎叶图,那么 这组数据的方差是 ▲ . 5.已知函数f (x)=ωx+()((>0)的部分图象如图所示,则ω==(3,1),=(0,).若·=0,=λ,则λ的为 8.已知m,n是直线,α,β是 ①若mα,m⊥β,则α⊥β;②若m(α,α∩β=n,α⊥β,则m⊥n; ③若mα,nβ,α∥β则m∥n;④若m∥α,m(β,α∩β=n,则m∥n. 中为真命题的是. °,D是BC边上一点,AD=5, AC=7,DC=3,则AB的长为 ▲ . 10.记定义函数=f′(x).如果x0[a,b],使得-f′(x0)(b-)成立,则称x0为函数区间上的中值点.=x-在区间-上中值点为 11.双曲线-=1(a>b>0)的焦点过作一条渐近线的垂线,垂足为,延长与另一条渐近线交于点若=,则双曲线的离心率为12.已知圆x2+y2-(-2m)x-my+m2-m=0直线l点(,0)直线l圆截得的弦长为定,则直线l的方程为 13.bn=2n-cn=若在数列{cn}中,c8>cn(n∈N*,n≠8),则实数p的取值范围是 ▲ . 14.设点P是曲线y=x2上的一个动点,曲线y=x2在点P处的切线为l,过点P且与直线l垂直的直线与曲线y=x2的另一交点为Q,则PQ的最小值为 ▲ . 二、解答题:本大题共6小题,共90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤. 15.(本小题满分14分) α,β(0,π),α=2,cosβ=-求α的值求α-β的值.16.(本小题满分14分) -AC,D,E,F分别为线段AC,A1A,C1B的中点. (1)F∥平面A; ⊥平面BDE. 17.(本小题满分1分) m(x-)2-++∈R. (1)当m=0时,求函数f(x)的单调增区间; (2)当m>0时,若曲线y=(1,1)处的切线l与曲线y=18.(本小题满分1分) 19.(本小题满分16分) 椭圆+=1. 若椭圆x轴上,求实数m的取值范围; 若是椭圆上点的坐标为的A,B两点,线段AB的垂直平分线l交x轴于点N,证明: 是定值,并求出这个定值. 20.(本小题满分16分) an}的前n项和为Sn. (1)求证:数列{}是等差数列; (2)若a1=1,且对任意正整数n,k(n>k),都有+=2成立,求数列{an}的通项公式; (3)记bn=a (a>0),求证:≤. 南京市2013届高三第次模拟考试 数学附加题: ... 21.【选做题】在A、B、C、D四小题中只能选做2题,每小题10分,共20分.请在答题卡指定区域内作答.解答应写出文字说明、证明过程或演算步骤. A.选修4—1:几何证明选讲 如图,PA,PB是⊙O的切线,切点分别为A,B,线段OP交⊙O于点C.若PA=12,PC=6,求AB的长. C.选修4—4:坐标系与参数方程 已知圆C的极坐标方程为ρ=cos(θ-),点M的极坐标为(6,),直线l过点M,且与圆C相切,求l的极坐标方程. D.选修4—5:不等式选讲 解不等式x|x-4|-3<0. 答题卡指定区域内作答.解答应写出文字说明、证明过程或演算步骤. 22.(本小题满分10分) 如图,三棱锥P-ABC中,已知PA⊥面ABC,△ABC正三角形,DE分别为PBPC中点. 若PA=2,求直线A与B所成角的弦值;若ADE⊥平面PBC,求PA的长. 23.(本小题满分10分) 如图,一颗棋子从三棱柱的一个顶点沿棱移到相邻的另一个顶点的概率均为,刚开始时,棋子在上底面点A处,若移了n次后,棋子落在上底面顶点的概率记为pn. (1)求p1,p2的值; (2)求证:>. 南京市2013届高三第次模拟考试 数学参考及评分标准2013.05 说明: 1.本解答给出的解法供参考如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则. 对计算题,当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分. 解答右端所注分数,表示考生正确做到这一步应得的累加分数. 只给整数分数,填空题不给中间分数.、填空题:本大题共14小题,每小题5分,共70分. 1.(1,3 2.5 3. 4. 5. 6. 7. 8.①④ 9. 10.11. 12.+-= 13. 14. 二、解答题:本大题共6小题,共90分.解答时应写出文字说明、证明过程或演算步骤. 15.α=2,所以=2,即sinα=2cosα.………………………… 2分α+cos2α=1,解得sin2α=,cos2α=. ………………………… 4分α=cos2α-sin2α=-.………………………… 6分α=cos2α-sin2α………………………… 2分 =, ………………………… 4分α=2,所以cos2α==-.………………………… 6分α(0,π),α=2,所以α(0,). 又cos2α=-α(,π) ,sin2α=. ………………………… 8分β=-β(0,π),β=,β(,π). ………………………… 10分α-β)=sin2αcosβ-αsinβ=×(-)-(-)×-………… 12分α-β(-),所以2α-β=-. ………………………… 14分α(0,π),α=2,所以α(0,),tan2α==-. 从而2α(,π). ………………………… 8分β=-β(0,π),β=,β(,π), 因此tanβ=-………………………… 10分α-β)===-………………………… 12分α-β(-),所以2α-β=-. ………………………… 14分16.C1C. 在三棱柱ABC-C1C,且E为A1A的中点, 所以FGEA. 所以四边形AEFG是平行四边形. 所以EF∥AG. ………………………… 4分 因为EF(平面ABC,AG(平面ABC, 所以EF∥平面A………………………… 6分 (2)因为在正三棱柱ABC-⊥平面ABC,BD(平面ABC, 所以A1A⊥BD. 因为D为AC的中点,⊥AC. 因为A1A∩AC=A,A1A(平面A1ACC1,AC(平面A1ACC1,所以BD⊥平面A1ACC1. 因为C1E(平面A1ACC1,所以BD⊥C1E. ………………………… 9分 根据题意,可得EB=C1E=AB,C1B=AB, 所以C1E⊥平面BDE. ………………………… 14分 17.解-++′(x)=-+=……………………… 2分 由f′(x)>0得x∈(0,) . 所以函数f(x)的单调增区间为(0,). ……………………… 4分 (2)由f′(x)=--+′(1)=-=(1,1)处的切线l的方程为y=-+…………………… 6分 由题意得,关于x的方程f(x)=-+m(x-)2-++=g(x)=(x-)2-++(x>0). 则g′(x)=(x-)-+==(). …………… 8分 ①当0<<′(x)>0得0<<,由g′(x)<<<g(x)在(0,1)为增函数,在(1,)上为减函数,在(,+)上为增函数. 又g(1)=→∞时,g(x)→∞,此时曲线y=g(x)<<……………………… 10分 ②当m=′(x)≥0,g(x)在(0,+)上为增函数,且g(1)==③当m>1时,由g′(x)>0得0<<′(x)<<<g(x)在(0,) 为增函数,在(,1)上为减函数,在(1,+)上为增函数. 又g(1)=→0时,g(x)→-∞=g(x)=……………………… 14分 18.解③中MN≥6,故当l=4时,折痕必定是情形①. 设AM=xcm,AN=ycm,则x2+y=……………………… 2分 因为x2+y≥2xy,当且仅当x=y时取等号, 所以S1=xy≤4,当且仅当x=y=2时取等号. 即S1的最大值为4. ……………………… 5分 (2)由题意知,长方形的面积为S=6×8=48. 因为S1∶S2=1∶2,S1≤S2,所以S1=16,S2=32. 当折痕是情形①时,设AM=xcm,AN=ycm,则xy==得≤x≤8. 所以l==≤x≤8. ……………………… 8分 设f(x)=x+f ′(x)=x-,x>0.故 x(,4)4(4,8)8f ′(x)-0+f(x)646480所以f(x)的取值范围为[64,80],从而l的范围是[8,4];……………… 11分 当折痕是情形②时,设AM=xcm,DN=ycm,则(x+==得0≤x≤. 所以l==. 所以l的范围为[6,]; ……………………… 13分 当折痕是情形③时,设BN=xcm,AM=ycm,则(x+==得0≤x≤4. 所以l==]. 综上,l的取值范围为[6,4]. ……………………… 16分 19.解……………………… 2分 (2)因为m=6,所以椭圆C+=1. ①设点P坐标为(x,y),则+=1. 因为点M的坐标为x-1)2+y2=x2-2x+1+2-=-2x+3 =(x-)2+,x∈[-,]. ……………………… 4分 所以当x=时,PM的最小值为,此时对应的点P坐标为(,±). ……………………… 6分 ②由a2=6,b2=2,得c2=4,即c=2, 从而椭圆C的右焦点F的坐标为(2,0),右准线方程为x=3,离心率e=. 设A(x1,y1),B(x2,y2),AB的中点H(x0,y0),则 +=1,+=1, 所以+=0,即kAB==-. ……………………… 9分 令k=kAB,则线段AB的垂直平分线l的方程为y-y0=-(x-x0). 令y=0,则xN=ky0+x0=x0. 因为F(2,0),所以FN=|xN-|x0-3|. ……………………… 12分 因为AB=+=x1)+e(3-x2)=|x0-3|. 故=×=.……………………… 2分 (2)因为对任意正整数n,k(n>k),都有+=2成立, 所以+=2,即数列{}是等差数列. ……………………… 4分 设数列{}的公差为d1,则=+(n-)d1=+(-)d1, 所以Sn=+(-)d1]2,所以当n≥2时, an=-+(-)d1]2-+(-)d1]2=n-+an}是等差数列,所以a2-=-(4d-+)-=(-+)-(-+), 所以d1=an=-an=-+=2对任意正整数n,k(n>k)都成立, 因此an=-……………………… 7分 (3)设等差数列{an}的公差为d,则an=+(-)d,bn=a, 所以=a-=ad, 即数列{bn}是公比大于0,首项大于0的等比数列. ……………………… 9分 记公比为q(q>0). 以下证明:b1+n≥bp+bk,其中p,k为正整数,且p+k=1+n. 因为(b1+n)-(bp+bk)=b1+b1qn-1-b1qp-1-b1qk-1=b1(qp-1-)( qk-1-). 当q>1时,因为y=----+n≥bp+bk. 当q=1时,b1+n=bp+bk. 当0<<=----+n≥bp+bk. 综上,b1+n≥bp+bk,其中p,k为正整数,且p+k=1+n.………………… 14分 所以n(b1+n)=(+n)+(+n)++(+n) ≥(b1+n)+(+n-1)+(+n-2)++(+) =(+++n)+(+-++), 即≤. …………………… 16分 南京市2013届高三第次模拟考试 数学参考及评分标准2013.05 21.【选做题】在A、B、C、D四小题中只能选做2题,每小题10分,共20分. A.选修4—1:几何证明选讲 证明 如图,延长PO交⊙O于D,连结AO,BO.AB交OP于点E. 因为PA与⊙O 相切, 所以PA2=PC·PD. 设⊙O的半径为R,因为PA=12,PC=6, 所以122=6(2R+6),解得R=9. …………………… 4分 因为PA,PB与⊙O均相切,所以PA=PB. 又OA=OB,所以OP是线段AB的垂直平分线. …………………… 7分 即AB⊥OP,且AB=2AE. 在Rt△OAP中,AE==. 所以AB=. …………………… 10分 B.选修4—2:矩阵与变换 解 (1) =,即 解得 …………………… 4分 (2)设P' (x,y)是曲线C'上任意一点,P' 由曲线C上的点P (x0,y0) 经矩阵M所表示的变换得到, 所以 = ,即解得 …………………… 7分 因为x0y0=1,所以·=1,即-=1. 即曲线C' 的方程为-=1. …………………… 10分 C.选修4—4:坐标系与参数方程 解则圆C的直角坐标方程为x-)2+y-2=,3). …………………… 3分 当直线l的斜率不存在时,不合题意. 设l的方程为y-3=k(x-3),1)到直线l的距离等于半径2. 故=.. 解得或 即4≤x<2+或3<x<4或x<1. 综上,原不等式的解集为{x| x<1或3<x<2+}. …………………… 10分 【必做题】第22题、第23题,每题10分,共20分. 22.解则A(0,0,0),B(,1,0),C(0,2,0),P(0,0,),(0,,), =(,1,-), =(0,,). 设直线A与B所成角为θ,则θ=|=. 直线A与B所成角的弦值. (2)设PA的长为a,则P(0,0,),=(,1,-),=(0,2,-). 设平面PBC的法向量为n1=(x,y,z),则n1·=0,n1·=0, 所以x+y-z=0,2y-z=0. 令z=,则y=,x=. 所以n1=(,,)是平面PBC的一个法向量. 因为DE分别为PBPC中点,所以D(,,),E(0,1,), 则=(,,),=(0,1,)设平面ADE的法向量为n2=(x,y,z),则n2·=0,n2·=0. 所以x+y+z=0,y+z=0. 令z=2,则y=-,x=-. 所以n2=(-,-,2)是平面ADE的一个法向量. 因为面ADE⊥面PBC所以n1⊥n2,n1·n2=(,,)·(- ,-,2)a2-a2+4=0,,即PA的长.…………………… 10分 23.解, p2=×+×(1-. …………………… 2分 (2)因为移了n次后棋子落在上底面顶点的概率为pn,故落在下底面顶点的概率为1-pn. 于是移了n+1次后棋子落在上底面顶点的概率为pn+1=pn+(1-pn)=pn+. …………………… 4分 从而pn+1-=(pn-). pn-,公比为. 所以pn-=×()n-1pn=×. …………………… 6分 用数学归纳法证明: ①当n=1时,左式==,右式=,因为>,所以不等式成立. 当n=2时,左式=+=,右式=,因为>,所以不等式成立. ②假设n=k(k≥2)时,不等式成立,即>. 则n=k+1时,+>+=+. 要证+≥, 只要证≥-. 只要证≥. 只要证≤. 只要证3k+1≥2k2+k+2 因为≥2, 所以3k+1=3(1+2)k≥3(1+2k+4C)=6k2+2k2+k+22k(2k-+1>2k2+k+2+≥. 即n=k+1时,不等式也成立. 由①②可知,不等式>对任意的n∈N*都成立. ……………………10分 A (第16题) F B1 A1 C1 (第9题) C D B A (第5题) -2 - y O x (第4题) 8 8 9 9 9 0 1 1 2 (第题) Read x If x≤0 Then ←x+2 Else y←log2x End If Print y P O C (第21题A) A BB CB EB DB PB (第22题) A B C D E F (第23题) (第16题) A B C D G A B C D (情形②) M N A B C D (情形③) M N A B C D (情形①) M N A B P O C (第21题A) D E A BB CB EB DB PB (第22题) y x z F。
南京市、盐城市2013届高三第三次模拟考试数学参考答案及评分标准(定稿)-(5744)

南京市、盐城市2013届高三第三次模拟考试数学参考答案及评分标准2013.05说明:1.本解答给出的解法供参考.如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.2.对计算题,当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.4.只给整数分数,填空题不给中间分数.一、填空题:本大题共14小题,每小题5分,共70分.1.(1,3] 2.5 3.8 4.1275.236.7107.2 8.①④9.56210.211.2 12.2x+y-2=0 13.(12,17) 14.33 2二、解答题:本大题共6小题,共90分.解答时应写出文字说明、证明过程或演算步骤.15.解(1)方法一:因为tanα=2,所以sinαcosα=2,即sinα=2cosα.…………………………2分又sin2α+cos2α=1,解得sin2α=45,cos2α=15.…………………………4分所以cos2α=cos2α-sin2α=-35.…………………………6分方法二:因为cos2α=cos2α-sin2α…………………………2分=cos2α-sin2αsin2α+cos2α=1-tan2αtan2α+1,…………………………4分又tanα=2,所以cos2α=1-2222+1=-35.…………………………6分(2)方法一:因为α∈(0,π),且tanα=2,所以α∈(0,π2 ).又cos2α=-35<0,故2α∈(π2,π),sin2α=45.…………………………8分由cos β=-7210,β∈(0,π),得sin β=210,β∈(π2,π).…………………………10分所以sin(2α-β)=sin2αcos β-cos2αsin β=45×(-7210)-(-35)×210=-22.…………12分又2α-β∈(-π2,π2),所以2α-β=-π4.…………………………14分方法二:因为α∈(0,π),且tan α=2,所以α∈(0,π2),tan2α=2tan α1-tan 2α=-43.从而2α∈(π2,π).…………………………8分由cos β=-7210,β∈(0,π),得sin β=210,β∈(π2,π),因此tan β=-17.…………………………10分所以tan(2α-β)=tan2α-tan β1+tan2αtan β=-43+171+(-43)×(-17)=-1.………………………… 12分又2α-β∈(-π2,π2),所以2α-β=-π4.…………………………14分16.证明(1)如图,取BC 的中点G ,连结AG ,FG .因为F 为C 1B 的中点,所以FG =∥12C 1C .在三棱柱ABC -A 1B 1C 1中,A 1A =∥C 1C ,且E 为A 1A 的中点,所以FG =∥EA .所以四边形AEFG 是平行四边形.所以EF ∥AG .…………………………4分因为EF 平面ABC ,AG 平面ABC ,所以EF ∥平面ABC .…………………………6分(2)因为在正三棱柱ABC -A 1B 1C 1中,A 1A ⊥平面ABC ,BD 平面ABC ,所以A 1A ⊥BD .因为D 为AC 的中点,BA =BC ,所以BD ⊥AC .因为A 1A ∩AC =A ,A 1A 平面A 1ACC 1,AC 平面A 1ACC 1,所以BD ⊥平面A 1ACC 1.因为C 1E 平面A 1ACC 1,所以BD ⊥C 1E .…………………………9分(第16题)A BCDEC 1A 1B 1FG根据题意,可得EB=C1E=62AB,C1B=3AB,所以EB2+C1E2=C1B2.从而∠C1EB=90°,即C1E⊥EB.………………………12分因为BD∩EB=B,BD 平面BDE,EB平面BDE,所以C1E⊥平面BDE.…………………………14分17.解(1)由题意知,f(x)=-2x+3+lnx,所以f′(x)=-2+1x=-2x+1x(x>0).………………………2分由f′(x)>0得x∈(0,12) .所以函数f(x)的单调增区间为(0,12).………………………4分(2)由f′(x)=mx-m-2+1x,得f′(1)=-1,所以曲线y=f(x)在点P(1,1)处的切线l的方程为y=-x+2.……………………6分由题意得,关于x的方程f(x)=-x+2有且只有一个解,即关于x的方程12m(x-1)2-x+1+ln x=0有且只有一个解.令g(x)=12m(x-1)2-x+1+lnx(x>0).则g′(x)=m(x-1)-1+1x=mx2-(m+1)x+1x=(x-1)(mx-1)x(x>0).……………8分①当0<m<1时,由g′(x)>0得0<x<1或x>1m,由g′(x)<0得1<x<1m,所以函数g(x)在(0,1)为增函数,在(1,1m)上为减函数,在(1m,+∞)上为增函数.又g(1)=0,且当x→∞时,g(x)→∞,此时曲线y=g(x)与x轴有两个交点.故0<m<1不合题意.………………………10分②当m=1时,g′(x)≥0,g(x)在(0,+∞)上为增函数,且g(1)=0,故m=1符合题意.③当m>1时,由g′(x)>0得0<x<1m或x>1,由g′(x)<0得1m<x<1,所以函数g(x)在(0,1m) 为增函数,在(1m,1)上为减函数,在(1,+∞)上为增函数.又g(1)=0,且当x→0时,g(x)→-∞,此时曲线y=g(x)与x轴有两个交点.故m>1不合题意.综上,实数m的值为m=1.………………………14分18.解如图所示,不妨设纸片为长方形ABCD ,AB =8cm ,AD =6cm ,其中点A 在面积为S 1的部分内.折痕有下列三种情形:①折痕的端点M ,N 分别在边AB ,AD 上;②折痕的端点M ,N 分别在边AB ,CD 上;③折痕的端点M ,N 分别在边AD ,BC 上.(1)在情形②、③中MN ≥6,故当l =4时,折痕必定是情形①.设AM =xcm ,AN =ycm ,则x 2+y 2=16.………………………2分因为x 2+y 2≥2xy ,当且仅当x =y 时取等号,所以S 1=12xy ≤4,当且仅当x =y =22时取等号.即S 1的最大值为4.………………………5分(2)由题意知,长方形的面积为S =6×8=48.因为S 1∶S 2=1∶2,S 1≤S 2,所以S 1=16,S 2=32.当折痕是情形①时,设AM =xcm ,AN =ycm ,则12xy =16,即y =32x.由0≤x ≤8,0≤32x ≤6,得163≤x ≤8.所以l =x 2+y 2=x 2+322x 2,163≤x ≤8.………………………8分设f(x)=x 2+322x 2,x >0,则f ′(x)=2x -2×322x 3=2(x 2+32)(x +42)(x -42)x3,x >0.故x 163(163,42)4 2 (42,8)8f ′(x) -0 +f(x)6449↘64↗80 所以f(x)的取值范围为[64,80],从而l 的范围是[8,45];………………11分当折痕是情形②时,设AM =xcm ,DN =ycm ,则12(x +y)×6=16,即y =163-x .由0≤x ≤8,0≤163-x ≤8,得0≤x ≤163.ABCD(情形①)MNABCD (情形②)MNABCD(情形③)MN所以l=62+(x-y)2=62+4(x-83)2,0≤x≤163.所以l的范围为[6,21453];………………………13分当折痕是情形③时,设BN=xcm,AM=ycm,则12(x+y)×8=16,即y=4-x.由0≤x≤6,0≤4-x≤6,得0≤x≤4.所以l=82+(x-y)2=82+4(x-2)2,0≤x≤4.所以l的取值范围为[8,45].综上,l的取值范围为[6,45].………………………16分19.解(1)由题意得,m>8-m>0,解得4<m<8.即实数m的取值范围是(4,8).………………………2分(2)因为m=6,所以椭圆C的方程为x 26+y22=1.①设点P坐标为(x,y),则x26+y22=1.因为点M的坐标为(1,0),所以PM2=(x-1)2+y2=x2-2x+1+2-x23=2x23-2x+3=23(x-32)2+32,x∈[-6,6].………………………4分所以当x=32时,PM的最小值为62,此时对应的点P坐标为(32,±52).………………………6分②由a2=6,b2=2,得c2=4,即c=2,从而椭圆C的右焦点F的坐标为(2,0),右准线方程为x=3,离心率e=6 3.设A(x1,y1),B(x2,y2),AB的中点H(x0,y0),则x12 6+y122=1,x226+y222=1,所以x12-x226+y12-y222=0,即k AB=y1-y2x1-x2=-x03y0.………………………9分令k=k AB,则线段AB的垂直平分线l的方程为y-y0=-1k(x-x0).令y=0,则x N=ky0+x0=23x0.因为F(2,0),所以FN=|x N-2|=23|x0-3|.………………………12分因为AB=AF+BF=e(3-x1)+e(3-x2)=263|x0-3|.故ABFN=263×32=6.即ABFN为定值6.………………………16分20.解(1)设等差数列{a n}的公差为d,则S n=na1+n(n-1)2d,从而S nn=a1+n-12d.所以当n≥2时,S nn-S n-1n-1=(a1+n-12d)-(a1+n-22d)=d2.即数列{S nn}是等差数列.………………………2分(2)因为对任意正整数n,k(n>k),都有S n+k+S n-k=2S n成立,所以S n+1+S n-1=2S n,即数列{S n}是等差数列.………………………4分设数列{S n}的公差为d1,则S n=S1+(n-1)d1=1+(n-1)d1,所以S n=[1+(n-1)d1]2,所以当n≥2时,a n=S n-S n-1=[1+(n-1)d1]2-[1+(n-2)d1]2=2d21n-3d21+2d1,因为{a n}是等差数列,所以a2-a1=a3-a2,即(4d21-3d21+2d1)-1=(6d21-3d21+2d1)-(4d21-3d21+2d1),所以d1=1,即a n=2n-1.又当a n=2n-1时,S n=n2,S n+k+S n-k=2S n对任意正整数n,k(n>k)都成立,因此a n=2n-1.………………………7分(3)设等差数列{a n}的公差为d,则a n=a1+(n-1)d,b n=a a n,所以b nb n-1=a a n-a n-1=a d,即数列{b n}是公比大于0,首项大于0的等比数列.………………………9分记公比为q(q>0).以下证明:b1+b n≥b p+b k,其中p,k为正整数,且p+k=1+n.因为(b1+b n)-(b p+b k)=b1+b1q n-1-b1q p-1-b1q k-1=b1(q p-1-1)( q k-1-1).当q>1时,因为y=q x为增函数,p-1≥0,k-1≥0,所以q p-1-1≥0,q k-1-1≥0,所以b1+b n≥b p+b k.当q=1时,b1+b n=b p+b k.当0<q<1时,因为y=q x为减函数,p-1≥0,k-1≥0,所以q p-1-1≤0,q k-1-1≤0,所以b1+b n≥b p+b k.综上,b1+b n≥b p+b k,其中p,k为正整数,且p+k=1+n.…………………14分所以n(b1+b n)=(b1+b n)+(b1+b n)+…+(b1+b n)≥(b1+b n)+(b2+b n-1)+(b3+b n-2)+…+(b n+b1)=(b1+b2+…+b n)+(b n+b n-1+…+b1),即b1+b2+…+b nn≤b1+b n2.……………………16分南京市、盐城市2013届高三第三次模拟考试数学附加题参考答案及评分标准2013.0521.【选做题】在A、B、C、D四小题中只能选做2题,每小题10分,共20分.A.选修4—1:几何证明选讲证明如图,延长PO交⊙O于D,连结AO,BO.AB交OP于点E.因为PA与⊙O相切,所以PA2=PC・PD.设⊙O的半径为R,因为P A=12,PC=6,所以122=6(2R+6),解得R=9.……………………4分因为PA,PB与⊙O均相切,所以PA=PB.又OA=OB,所以OP是线段AB的垂直平分线.……………………7分即AB⊥OP,且AB=2AE.在Rt△OAP中,AE=OA・P AOP=365.所以AB=725.……………………10分B.选修4—2:矩阵与变换解(1)由题知,1 ab111=2,即1+a=0,b+1=2,解得a=-1,b=1.……………………4分(2)设P' (x,y)是曲线C'上任意一点,P'由曲线C上的点P(x0,y0)经矩阵M所表示的变换得到,所以1 -11 1x0y0=xy,即x0-y0=x,x0+y0=y,解得x0=y+x2,y0=y-x2.……………………7分ABPO C(第21题A)D E因为x 0y 0=1,所以y +x 2・y -x 2=1,即y 24-x24=1.即曲线C'的方程为y 24-x24=1.……………………10分C .选修4—4:坐标系与参数方程解以极点为原点,极轴为x 轴正半轴建立平面直角坐标系,则圆C 的直角坐标方程为(x -3)2+(y -1)2=4,点M 的直角坐标为(33,3).……………………3分当直线l 的斜率不存在时,不合题意.设直线l 的方程为y -3=k(x -33),由圆心C(3,1)到直线l 的距离等于半径2.故|23k -2|k 2+1=2.……………………6分解得k =0或k =3.所以所求的直线l 的直角坐标方程为y =3或3x -y -6=0.…………………8分所以所求直线l 的极坐标方程为ρsin θ=3或ρsin(π3-θ)=3.……………………10分D .选修4—5:不等式选讲解原不等式等价于x ≥4,x 2-4x -3<0,或x <4,-x 2+4x -3<0.……………………5分解得x ≥4,2-7<x <2+7,或x <4,x <1或x >3.即4≤x <2+7或3<x <4或x <1.综上,原不等式的解集为{x| x <1或3<x <2+7}.……………………10分【必做题】第22题、第23题,每题10分,共20分.22.解(1)如图,取AC 的中点F ,连接BF ,则BF ⊥AC .以A 为坐标原点,过A 且与FB 平行的直线为x 轴,AC 为y 轴,AP 为z 轴,建立空间直角坐标系.则A(0,0,0),B(3,1,0),C(0,2,0),P(0,0,2),E(0,1,1),从而→PB =(3,1,-2),→AE =(0,1,1).设直线AE 与PB 所成角为θ,则cos θ=|→PB ・→AE|→PB|×|→AE||=14.AB C EDP(第22题)yxz F即直线AE 与PB 所成角的余弦值为14.……………………4分(2)设P A 的长为a ,则P(0,0,a),从而→PB =(3,1,-a),→PC =(0,2,-a).设平面PBC 的法向量为n 1=(x ,y ,z),则n 1・→PB =0,n 1・→PC =0,所以3x +y -az =0,2y -az =0.令z =2,则y =a ,x =33a .所以n 1=(33a ,a ,2)是平面PBC 的一个法向量.因为D ,E 分别为PB ,PC 中点,所以D(32,12,a 2),E(0,1,a2),则→AD =(32,12,a 2),→AE =(0,1,a 2).设平面ADE 的法向量为n 2=(x ,y ,z),则n 2・→AD =0,n 2・→AE =0.所以32x +12y +a 2z =0,y +a 2z =0.令z =2,则y =-a ,x =-33a .所以n 2=(-33a ,-a ,2)是平面ADE 的一个法向量.……………………8分因为面ADE ⊥面PBC ,所以n 1⊥n 2,即n 1・n 2=(33a ,a ,2)・(-33a ,-a ,2)=-13a 2-a 2+4=0,解得a =3,即PA 的长为3.……………………10分23.解(1)p 1=23,p 2=23×23+13×(1-23)=59.……………………2分(2)因为移了n 次后棋子落在上底面顶点的概率为p n ,故落在下底面顶点的概率为1-p n .于是移了n +1次后棋子落在上底面顶点的概率为p n+1=23p n +13(1-p n )=13p n +13.……………………4分从而p n+1-12=13(p n -12).所以数列{p n -12}是等比数列,其首项为16,公比为13.所以p n -12=16×(13)n -1.即p n =12+12×13n .……………………6分用数学归纳法证明:①当n =1时,左式=14×23-1=35,右式=12,因为35>12,所以不等式成立.当n =2时,左式=14×23-1+14×59-1=7855,右式=43,因为7855>43,所以不等式成立.②假设n =k(k ≥2)时,不等式成立,即i =1∑k14P i -1>k2k +1.则n =k +1时,左式=i =1∑k14P i -1+14P k+1-1>k2k +1+14(12+12×13k+1)-1=k 2k +1+3k+13k+1+2.要证k 2k +1+3k+13k+1+2≥(k +1)2k +2,只要证3k+13k+1+2≥(k +1)2k +2-k2k +1.只要证3k+13k+1+2≥k 2+3k +1k2+3k +2.只要证23k+1≤1k 2+3k +1.只要证3k+1≥2k 2+6k +2.因为k ≥2,所以3k+1=3(1+2)k ≥3(1+2k +4C 2k )=6k2+3=2k 2+6k +2+2k(2k -3)+1>2k 2+6k +2,所以k 2k +1+3k+13k+1+2≥(k +1)2k +2.即n =k +1时,不等式也成立.由①②可知,不等式i =1∑n14P i -1>n2n +1对任意的n ∈N *都成立.……………………10分。
数列周练三

2014届一轮复习数学试题选编:等差与等比数列综合填空题1 .(江苏省扬州市2013届高三下学期5月考前适应性考试数学(理)试题)数列{}n a 中,12a =,1n n a a cn +=+(c 是常数,123n =,,,),且123a a a ,,成公比不为1的等比数列,则{}n a 的通项公式是______.2 .(常州市2013届高三教学期末调研测试数学试题)已知数列{}n a 满足143a =,()*11226n n a n N a +-=∈+,则11ni ia =∑=______. 3 .(江苏省徐州市2013届高三上学期模底考试数学试题)已知各项均为正数的等比数列{a n }的前n 项和为S n ,若a 3=18,S 3=26,则{a n }的公比q =________.4 .(扬州、南通、泰州、宿迁四市2013届高三第二次调研测试数学试卷)设数列{a n }满足:()()*3118220()n n n n a a a a a n ++=---=∈N ,,则a 1的值大于20的概率为____.5 .(苏北老四所县中2013届高三新学期调研考试)已知数列}{na 满足122n n aqa q +=+-(q 为常数,||1q <),若3456,,,a a a a ∈}{18,6,2,6,30---,则1a = ▲ .6 .(镇江市2013届高三上学期期末考试数学试题)观察下列等式:31×2×12=1-122, 31×2×12+42×3×12=1-13×2, 31×2×12+42×3×12+53×4×12=1-14×2,,由以上等式推测到一个一般的结论:对于n ∈N *, 31×2×12+42×3×122++n +2n n +×12n =______. 7 .(江苏省扬州市2013届高三上学期期中调研测试数学试题)已知等比数列{}n a 的首项是1,公比为2,等差数列{}n b 的首项是1,公差为1,把{}n b 中的各项按照如下规则依次插入到{}n a 的每相邻两项之间,构成新数列}{n c :1122334,,,,,,,a b a b b a b 564,,b b a ,,即在n a 和1n a +两项之间依次插入{}n b 中n 个项,则2013c =____.8 .(江苏省淮安市2013届高三上学期第一次调研测试数学试题)若数列{}n a 是各项均为正数的等比数列,则当n b =时,数列{}n b 也是等比数列;类比上述性质,若数列{}n c 是等差数列,则当n d =_______时,数列{}n d 也是等差数列.9 .(江苏省无锡市2013届高三上学期期中考试数学试题)已知等差数列{}n a 满足:21-=a ,02=a .若将1a ,4a ,5a 都加上同一个数,所得的三个数依次成等比数列,则所加的这个数为___________.10.(江苏省泰州、南通、扬州、宿迁、淮安五市2013届高三第三次调研测试数学试卷)过点(1 0)P -,作曲线C :e x y =的切线,切点为1T ,设1T 在x 轴上的投影是点1H ,过点1H 再作曲线C 的切线,切点为2T ,设2T 在x 轴上的投影是点2H ,,依次下去,得到第1n +()n ∈N 个切点1n T +.则点1n T +的坐标为______.11.(江苏省2013届高三高考模拟卷(二)(数学) )已知数列{a n }满足3a n +1+a n =4(n ∈N*),且a 1=9,其前n 项之和为S n ,则满足不等式|S n -n -6|<1125的最小整数n 是______. 解答题12.(江苏省无锡市2013届高三上学期期中考试数学试题)数列{}n a 是公比大于1的等比数列,62=a ,263=S . (1)求数列{}n a 的通项公式;(2)在n a 与1+n a 之间插入n 个数,使这2+n 个数组成公差为n d 的等差数列.设第n 个等差数列的前n 项和是n A .求关于n 的多项式)(n g ,使得n n d n g A )(=对任意+∈N n 恒成立;(3)对于(2)中的数列1d ,2d ,3d ,⋅⋅⋅,n d ,⋅⋅⋅,这个数列中是否存在不同的三项m d ,k d ,p d (其中正整数m ,k ,p 成等差数列)成等比数列?若存在,求出这样的三项;若不存在,说明理由.13.(江苏省南京市四区县2013届高三12月联考数学试题 )设等差数列}{n a 的公差0≠d ,数列}{n b 为等比数列,若a b a ==11,33b a =,57b a = (1)求数列}{n b 的公比q ;(2)若*,,N m n b a m n ∈=,求n 与m 之间的关系;(3)将数列}{n a ,}{n b 中的公共项按由小到大的顺序排列组成一个新的数列}{n c ,是否存在正整数r q p ,,)(r q p <<使得r q p ,,和r c q c p c r q p +++,,均成等差数列?说明理由.14.(江苏省盐城市2013届高三10月摸底考试数学试题)已知数列{}n a 的前n 项和为n S , 且1517a a +=.(1)若{}n a 为等差数列, 且856S =.①求该等差数列的公差d ;②设数列{}n b 满足3nn n b a =⋅,则当n 为何值时,n b 最大?请说明理由; (2)若{}n a 还同时满足: ①{}n a 为等比数列;②2416a a =;③对任意的正整数k ,存在自然数m ,使得2k S +、k S 、m S 依次成等差数列,试求数列{}n a 的通项公式.15.(常州市2013届高三教学期末调研测试数学试题)已知数列{}n a 是等差数列,12315a a a ++=,数列{}n b 是等比数列,12327b b b =.(1)若1243,a b a b ==.求数列{}n a 和{}n b 的通项公式;(2)若112233,,a b a b a b +++是正整数且成等比数列,求3a 的最大值.16.(江苏省连云港市2013届高三上学期摸底考试(数学)(选修历史))已知数列*122{}:1,(0),{}()n n n n n a a a a a b b a a n N +==>=∈满足数列满足 (1)若{}n a 是等差数列,且345,{}n b a a =求的值及的通项公式; (2)若{}n a 的等比数列,求{}n b 的前n 项和.n S17.(南京市、盐城市2013届高三年级第一次模拟考试数学试题)若数列{}n a 是首项为612t -,公差为6的等差数列;数列{}n b 的前n 项和为3n n S t =-.(1)求数列{}n a 和{}n b 的通项公式;(2)若数列{}n b 是等比数列, 试证明: 对于任意的(,1)n n N n ∈≥, 均存在正整数n c , 使得1n n c b a +=, 并求数列{}n c 的前n 项和n T ;(3)设数列{}n d 满足n n n d a b =⋅, 且{}n d 中不存在这样的项k d , 使得“1k k d d -<与1k k d d +<”同时成立(其中2≥k , *∈N k ), 试求实数的取值范围.18.(江苏省徐州市2013届高三上学期模底考试数学试题)设()2012()k k k f n c c n c n c n k =+++⋅⋅⋅+∈N ,其中012,,,,k c c c c ⋅⋅⋅为非零常数, 数列{a n }的首项a 1=1,前n 项和为S n ,对于任意的正整数n ,a n +S n =()k f n . (1)若k =0,求证:数列{a n }是等比数列;(2)试确定所有的自然数k ,使得数列{a n }能成等差数列.19.(江苏省徐州市2013届高三考前模拟数学试题)已知数列{}n a ,其前n 项和为n S .⑴若对任意的n *∈N ,2-12+12,,n n n a a a 组成公差为4的等差数列,且1=1a ,220132nS n=,求n 的值;⑵若数列{+}nnS a a 是公比为(1)q q ≠-的等比数列,a 为常数,求证:数列{}n a 为等比数列的充要条件为1=1+q a.20.(江苏省淮安市2013届高三上学期第一次调研测试数学试题)已知各项均为正数的数列{}n a 前n 项的和为n S ,数列{}2n a 的前n 项的和为n T ,且()2*234,n n S T n N -+=∈.⑴证明数列{}n a 是等比数列,并写出通项公式; ⑵若20n n S T λ-<对*n N ∈恒成立,求λ的最小值; ⑶若12,2,2x y n n n a a a ++成等差数列,求正整数,x y 的值.21.(江苏省泰兴市2013届高三上学期期中调研考试数学试题)已知数列{}n a 中,12a =,23a =,其前n 项和n S 满足1121n n n S S S +-+=+,其中2n ≥,*n ∈N . (1)求证;数列{}n a 为等差数列,并求其通项公式;(2)设n n n a b -⋅=2,n T 为数列{}n b 的前n 项和,求使n T >2的n 的取值范围.(3)设λλ(2)1(41n an n n c ⋅-+=-为非零整数,*n ∈N ),试确定λ的值,使得对任意*n ∈N ,都有n n c c >+1成立.22.(江苏省2013届高三高考压轴数学试题)已知等差数列{a n }的首项a 1为a (,0)a R a ∈≠.设数列的前n 项和为S n ,且对任意正整数n 都有24121n n a n a n -=-. (1) 求数列{a n }的通项公式及S n ;(2) 是否存在正整数n 和k ,使得S n , S n +1 , S n +k 成等比数列?若存在,求出n 和k 的值;若不存在,请说明理由.23.(2013江苏高考数学)本小题满分16分.设}{n a 是首项为a ,公差为d 的等差数列)0(≠d ,n S 是其前n 项和.记cn nS b n n +=2,*N n ∈,其中c 为实数.(1)若0=c ,且421b b b ,,成等比数列,证明:k nk S n S 2=(*,N n k ∈);(2)若}{n b 是等差数列,证明:0=c .24.(江苏省南京市四校2013届高三上学期期中联考数学试题)已知等差数列{}n a 的前n 项和为n S ,公差,50,053=+≠S S d 且1341,,a a a 成等比数列. (Ⅰ)求数列{}n a 的通项公式; (Ⅱ)设⎭⎬⎫⎩⎨⎧n n a b 是首项为1,公比为3的等比数列,求数列{}n b 的前n 项和n T .25.(扬州市2012-2013学年度第一学期期末检测高三数学试题)已知数列{}n a 的前n 项和为n S .(Ⅰ)若数列{}n a 是等比数列,满足23132a a a =+, 23+a 是2a ,4a 的等差中项,求数列{}n a 的通项公式;(Ⅱ)是否存在等差数列{}n a ,使对任意*n N ∈都有22(1)n n a S n n ⋅=+?若存在,请求出所有满足条件的等差数列;若不存在,请说明理由.26.(苏州市2012-2013学年度第一学期高三期末考试数学试卷)设数列{}n a 的前n 项和为n S ,满足21n n a S An Bn +=++(0A ≠).(1)若132a =,294a =,求证数列{}n a n -是等比数列,并求数列{}n a 的通项公式; (2)已知数列{}n a 是等差数列,求1B A-的值.27.(2012年江苏理)已知各项均为正数的两个数列{}n a 和{}n b 满足:221nn n n n b a b a a ++=+,*N n ∈,(1)设n n n a b b +=+11,*N n ∈,求证:数列2n n b a ⎧⎫⎛⎫⎪⎪⎨⎬ ⎪⎝⎭⎪⎪⎩⎭是等差数列; (2)设nnn a b b ∙=+21,*N n ∈,且{}n a 是等比数列,求1a 和1b 的值.。
南京市、盐城市2013届高三第三次模拟考试数学参考答案及评分标准(定稿)

南京市、盐城市2013届高三第三次模拟考试数学参考答案及评分标准 2013.05说明:1.本解答给出的解法供参考.如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.2.对计算题,当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数. 4.只给整数分数,填空题不给中间分数.一、填空题:本大题共14小题,每小题5分,共70分.1.(1,3] 2.5 3.8 4.127 5. 236.710 7.2 8.①④ 9.56210.2 11.2 12.2x +y -2=0 13.(12,17) 14.332二、解答题:本大题共6小题,共90分.解答时应写出文字说明、证明过程或演算步骤. 15.解(1)方法一:因为tan α=2,所以sin αcos α=2,即sin α=2cos α. ………………………… 2分又sin 2α+cos 2α=1,解得sin 2α=45,cos 2α=15. ………………………… 4分所以cos2α=cos 2α-sin 2α=-35. ………………………… 6分方法二:因为cos2α=cos 2α-sin 2α ………………………… 2分=cos 2α-sin 2αsin 2α+cos 2α =1-tan 2αtan 2α+1, ………………………… 4分 又tan α=2,所以cos2α=1-2222+1=-35. ………………………… 6分(2)方法一:因为α∈(0,π),且tan α=2,所以α∈(0,π2).又cos2α=-35<0,故2α∈(π2,π) ,sin2α=45. ………………………… 8分由cos β=-7210,β∈(0,π),得sin β=210,β∈(π2,π). ………………………… 10分所以sin(2α-β)=sin2αcos β-cos2αsin β=45×(-7210)-(-35)×210=-22. ………… 12分又2α-β∈(-π2,π2),所以2α-β=-π4. ………………………… 14分方法二:因为α∈(0,π),且tan α=2,所以α∈(0,π2),tan2α=2tan α1-tan 2α=-43.从而2α∈(π2,π). ………………………… 8分由cos β=-7210,β∈(0,π),得sin β=210,β∈(π2,π),因此tan β=-17. ………………………… 10分所以tan(2α-β)=tan2α-tan β1+tan2αtan β=-43+171+(-43)×(-17)=-1. ………………………… 12分又2α-β∈(-π2,π2),所以2α-β=-π4. ………………………… 14分16.证明(1)如图,取BC 的中点G ,连结AG ,FG .因为F 为C 1B 的中点,所以FG =∥12C 1C . 在三棱柱ABC -A 1B 1C 1中,A 1A =∥C 1C ,且E 为A 1A 的中点, 所以FG =∥EA . 所以四边形AEFG 是平行四边形. 所以EF ∥AG . ………………………… 4分 因为EF ⊄平面ABC ,AG ⊂平面ABC ,所以EF ∥平面ABC . ………………………… 6分 (2)因为在正三棱柱ABC -A 1B 1C 1中,A 1A ⊥平面ABC ,BD ⊂平面ABC ,所以A 1A ⊥BD .因为D 为AC 的中点,BA =BC ,所以BD ⊥AC .因为A 1A ∩AC =A ,A 1A ⊂平面A 1ACC 1,AC ⊂平面A 1ACC 1,所以BD ⊥平面A 1ACC 1. 因为C 1E ⊂平面A 1ACC 1,所以BD ⊥C 1E . ………………………… 9分根据题意,可得EB =C 1E =62AB ,C 1B =3AB , 所以EB 2+C 1E 2=C 1B 2.从而∠C 1EB =90°,即C 1E ⊥EB .……………………… 12分 因为BD ∩EB =B ,BD ⊂平面BDE , EB ⊂平面BDE ,(第16题)ABC D EC 1A 1B 1FG所以C 1E ⊥平面BDE . ………………………… 14分17.解(1)由题意知,f (x )=-2x +3+ln x ,所以f ′(x )=-2+1x =-2x +1x (x >0). ……………………… 2分由f ′(x )>0得x ∈(0,12) .所以函数f (x )的单调增区间为(0,12). ……………………… 4分(2)由f ′(x )=mx -m -2+1x,得f ′(1)=-1,所以曲线y =f (x )在点P (1,1)处的切线l 的方程为y =-x +2.…………………… 6分 由题意得,关于x 的方程f (x )=-x +2有且只有一个解, 即关于x 的方程12m (x -1)2-x +1+ln x =0有且只有一个解.令g (x )=12m (x -1)2-x +1+ln x (x >0).则g ′(x )=m (x -1)-1+1x =mx 2-(m +1)x +1x =(x -1)(mx -1)x(x >0). …………… 8分①当0<m <1时,由g ′(x )>0得0<x <1或x >1m ,由g ′(x )<0得1<x <1m ,所以函数g (x )在(0,1)为增函数,在(1,1m )上为减函数,在(1m ,+∞)上为增函数.又g (1)=0,且当x →∞时,g (x )→∞,此时曲线y =g (x )与x 轴有两个交点.故0<m <1不合题意. ……………………… 10分 ②当m =1时,g ′(x )≥0,g (x )在(0,+∞)上为增函数,且g (1)=0,故m =1符合题意. ③当m >1时,由g ′(x )>0得0<x <1m 或x >1,由g ′(x )<0得1m<x <1,所以函数g (x )在(0,1m ) 为增函数,在(1m ,1)上为减函数,在(1,+∞)上为增函数.又g (1)=0,且当x →0时,g (x )→-∞,此时曲线y =g (x )与x 轴有两个交点. 故m >1不合题意.综上,实数m 的值为m =1. ……………………… 14分18.解 如图所示,不妨设纸片为长方形ABCD ,AB =8cm ,AD =6cm ,其中点A 在面积为S 1的部分内.折痕有下列三种情形:①折痕的端点M ,N 分别在边AB ,AD 上; ②折痕的端点M ,N 分别在边AB ,CD 上;③折痕的端点M ,N 分别在边AD ,BC 上.(1)在情形②、③中MN ≥6,故当l =4时,折痕必定是情形①.设AM =x cm ,AN =y cm ,则x 2+y 2=16. ……………………… 2分 因为x 2+y 2≥2xy ,当且仅当x =y 时取等号, 所以S 1=12xy ≤4,当且仅当x =y =22时取等号.即S 1的最大值为4. ……………………… 5分 (2)由题意知,长方形的面积为S =6×8=48.因为S 1∶S 2=1∶2,S 1≤S 2,所以S 1=16,S 2=32.当折痕是情形①时,设AM =x cm ,AN =y cm ,则12xy =16,即y =32x.由⎩⎪⎨⎪⎧0≤x ≤8,0≤32x ≤6,得163≤x ≤8.所以l =x 2+y 2=x 2+322x 2,163≤x ≤8. ……………………… 8分设f (x )=x 2+322x 2,x >0,则f ′(x )=2x -2×322x 3=2(x 2+32)(x +42)(x -42)x 3,x >0.故所以f (x )的取值范围为[64,80],从而l 的范围是[8,45]; ……………… 11分 当折痕是情形②时,设AM =x cm ,DN =y cm ,则12(x +y )×6=16,即y =163-x .由⎩⎪⎨⎪⎧0≤x ≤8,0≤163-x ≤8,得0≤x ≤163.所以l =62+(x -y )2=62+4(x -83)2,0≤x ≤163.所以l 的范围为[6,21453]; ……………………… 13分当折痕是情形③时,设BN =x cm ,AM =y cm ,则12(x +y )×8=16,即y =4-x .ABCD (情形①)MNABCD (情形②)MNABCD (情形③)MN由⎩⎨⎧0≤x ≤6,0≤4-x ≤6,得0≤x ≤4. 所以l =82+(x -y )2=82+4(x -2)2,0≤x ≤4. 所以l 的取值范围为[8,45].综上,l 的取值范围为[6,45]. ……………………… 16分19.解(1)由题意得,m >8-m >0,解得4<m <8.即实数m 的取值范围是(4,8). ……………………… 2分 (2)因为m =6,所以椭圆C 的方程为x 26+y 22=1.①设点P 坐标为(x ,y ),则x 26+y 22=1.因为点M 的坐标为(1,0),所以PM 2=(x -1)2+y 2=x 2-2x +1+2-x 23=2x 23-2x +3=23(x -32)2+32,x ∈[-6,6]. ……………………… 4分 所以当x =32时,PM 的最小值为62,此时对应的点P 坐标为(32,±52).……………………… 6分②由a 2=6,b 2=2,得c 2=4,即c =2,从而椭圆C 的右焦点F 的坐标为(2,0),右准线方程为x =3,离心率e =63. 设A (x 1,y 1),B (x 2,y 2),AB 的中点H (x 0,y 0),则x 126+y 122=1,x 226+y 222=1, 所以x 12-x 226+y 12-y 222=0,即k AB =y 1-y 2x 1-x 2=-x 03y 0. ……………………… 9分令k =k AB ,则线段AB 的垂直平分线l 的方程为y -y 0=-1k (x -x 0).令y =0,则x N =ky 0+x 0=23x 0.因为F (2,0),所以FN =|x N -2|=23|x 0-3|. ……………………… 12分因为AB =AF +BF =e (3-x 1)+e (3-x 2)=263|x 0-3|.故AB FN =263×32=6. 即ABFN为定值6. ……………………… 16分20.解(1)设等差数列{a n }的公差为d ,则S n =na 1+n (n -1)2d ,从而S nn =a 1+n -12d . 所以当n ≥2时,S n n -S n -1n -1=(a 1+n -12d )-(a 1+n -22d )=d2.即数列{S nn }是等差数列. ……………………… 2分(2)因为对任意正整数n ,k (n >k ),都有S n +k +S n -k =2S n 成立,所以S n +1+S n -1=2S n ,即数列{S n }是等差数列. ……………………… 4分 设数列{S n }的公差为d 1,则S n =S 1+(n -1)d 1=1+(n -1)d 1, 所以S n =[1+(n -1)d 1]2,所以当n ≥2时,a n =S n -S n -1=[1+(n -1)d 1]2-[1+(n -2)d 1]2=2d 21n -3d 21+2d 1,因为{a n }是等差数列,所以a 2-a 1=a 3-a 2,即(4d 21-3d 21+2d 1)-1=(6d 21-3d 21+2d 1)-(4d 21-3d 21+2d 1),所以d 1=1,即a n =2n -1.又当a n =2n -1时,S n =n 2,S n +k +S n -k =2S n 对任意正整数n ,k (n >k )都成立, 因此a n =2n -1. ……………………… 7分 (3)设等差数列{a n }的公差为d ,则a n =a 1+(n -1)d ,b n =a a n ,所以b n b n -1=a a n -a n -1=a d ,即数列{b n }是公比大于0,首项大于0的等比数列. ……………………… 9分 记公比为q (q >0).以下证明:b 1+b n ≥b p +b k ,其中p ,k 为正整数,且p +k =1+n . 因为(b 1+b n )-(b p +b k )=b 1+b 1q n -1-b 1q p -1-b 1q k -1=b 1(q p -1-1)( q k -1-1).当q >1时,因为y =q x 为增函数,p -1≥0,k -1≥0, 所以q p -1-1≥0,q k -1-1≥0,所以b 1+b n ≥b p +b k .当q =1时,b 1+b n =b p +b k .当0<q <1时,因为y =q x 为减函数,p -1≥0,k -1≥0, 所以q p -1-1≤0,q k -1-1≤0,所以b 1+b n ≥b p +b k .综上,b 1+b n ≥b p +b k ,其中p ,k 为正整数,且p +k =1+n .………………… 14分 所以n (b 1+b n )=(b 1+b n )+(b 1+b n )+…+(b 1+b n )≥(b 1+b n )+(b 2+b n -1)+(b 3+b n -2)+…+(b n +b 1)=(b 1+b 2+…+b n )+(b n +b n -1+…+b 1), 即b 1+b 2+…+b n n ≤b 1+b n2. …………………… 16分南京市、盐城市2013届高三第三次模拟考试数学附加题参考答案及评分标准 2013.0521.【选做题】在A 、B 、C 、D 四小题中只能选做2题,每小题10分,共20分. A .选修4—1:几何证明选讲证明 如图,延长PO 交⊙O 于D ,连结AO ,BO .AB 交OP 于点E .因为P A 与⊙O 相切, 所以P A 2=PC ·PD .设⊙O 的半径为R ,因为P A =12,PC =6,所以122=6(2R +6),解得R =9. …………………… 4分 因为P A ,PB 与⊙O 均相切,所以P A =PB .又OA =OB ,所以OP 是线段AB 的垂直平分线. …………………… 7分 即AB ⊥OP ,且AB =2AE . 在Rt △OAP 中,AE =OA ·P A OP =365.所以AB =725. …………………… 10分B .选修4—2:矩阵与变换解 (1)由题知,⎣⎢⎡⎦⎥⎤1 a b 1 ⎣⎡⎦⎤11=⎣⎡⎦⎤02,即⎩⎨⎧1+a =0,b +1=2, 解得⎩⎨⎧a =-1,b =1.…………………… 4分(2)设P' (x ,y )是曲线C'上任意一点,P' 由曲线C 上的点P (x 0,y 0) 经矩阵M 所表示的变换得到,所以⎣⎢⎡⎦⎥⎤1 -11 1 ⎣⎢⎡⎦⎥⎤x 0y 0=⎣⎢⎡⎦⎥⎤x y ,即⎩⎨⎧x 0-y 0=x ,x 0+y 0=y ,解得⎩⎨⎧x 0=y +x 2,y 0=y -x 2.…………………… 7分 因为x 0y 0=1,所以y +x 2·y -x 2=1,即y 24-x 24=1.即曲线C' 的方程为y 24-x 24=1. …………………… 10分C .选修4—4:坐标系与参数方程解 以极点为原点,极轴为x 轴正半轴建立平面直角坐标系,则圆C 的直角坐标方程为(x -3)2+(y -1)2=4,点M 的直角坐标为(33,3). …………………… 3分ABOC (第21题A )DE当直线l 的斜率不存在时,不合题意. 设直线l 的方程为y -3=k (x -33),由圆心C (3,1)到直线l 的距离等于半径2.故|23k -2|k 2+1=2. …………………… 6分解得k =0或k =3.所以所求的直线l 的直角坐标方程为y =3或3x -y -6=0. ………………… 8分所以所求直线l 的极坐标方程为ρsin θ=3或ρsin(π3-θ)=3. …………………… 10分D .选修4—5:不等式选讲解 原不等式等价于 ⎩⎨⎧x ≥4,x 2-4x -3<0,或⎩⎨⎧x <4,-x 2+4x -3<0. …………………… 5分解得⎩⎨⎧x ≥4,2-7<x <2+7,或⎩⎨⎧x <4,x <1或x >3.即4≤x <2+7或3<x <4或x <1.综上,原不等式的解集为{x | x <1或3<x <2+7}. …………………… 10分【必做题】第22题、第23题,每题10分,共20分.22.解(1)如图,取AC 的中点F ,连接BF ,则BF ⊥AC .以A 为坐标原点,过A 且与FB 平行的直线为x 轴,AC 为y 轴,AP 为z 轴,建立空间直角坐标系. 则A (0,0,0),B (3,1,0), C (0,2,0),P (0,0,2),E (0,1,1),从而→PB =(3,1,-2), →AE =(0,1,1). 设直线AE 与PB 所成角为θ, 则cos θ=|→PB ·→AE|→PB |×|→AE ||=14.即直线AE 与PB 所成角的余弦值为14 . …………………… 4分(2)设P A 的长为a ,则P (0,0,a ),从而→PB =(3,1,-a ),→PC =(0,2,-a ).设平面PBC 的法向量为n 1=(x ,y ,z ),则n 1·→PB =0,n 1·→PC =0, 所以3x +y -az =0,2y -az =0. 令z =2,则y =a ,x =33a . 所以n 1=(33a ,a ,2)是平面PBC 的一个法向量.(第22题)因为D ,E 分别为PB ,PC 中点,所以D (32,12,a 2),E (0,1,a2), 则→AD =(32,12,a 2),→AE =(0,1,a2). 设平面ADE 的法向量为n 2=(x ,y ,z ),则n 2·→AD =0,n 2·→AE =0. 所以32x +12y +a 2z =0,y +a2z =0. 令z =2,则y =-a ,x =-33a . 所以n 2=(-33a ,-a ,2)是平面ADE 的一个法向量. …………………… 8分 因为面ADE ⊥面PBC , 所以n 1⊥n 2,即n 1·n 2=(33a ,a ,2)·(- 33a ,-a ,2)=-13a 2-a 2+4=0, 解得a =3,即P A 的长为3. …………………… 10分 23.解(1)p 1=23,p 2=23×23+13×(1-23)=59. …………………… 2分(2)因为移了n 次后棋子落在上底面顶点的概率为p n ,故落在下底面顶点的概率为1-p n .于是移了n +1次后棋子落在上底面顶点的概率为p n +1=23p n +13(1-p n )=13p n +13.…………………… 4分从而p n +1-12=13(p n -12).所以数列{p n -12}是等比数列,其首项为16,公比为13.所以p n -12=16×(13)n -1.即p n =12+12×13n . …………………… 6分用数学归纳法证明:①当n =1时,左式=14×23-1=35,右式=12,因为35>12,所以不等式成立.当n =2时,左式=14×23-1+14×59-1=7855,右式=43,因为7855>43,所以不等式成立.②假设n =k (k ≥2)时,不等式成立,即i =1∑k14P i -1>k 2k +1.则n =k +1时,左式=i =1∑k14P i -1+14P k +1-1>k 2k +1+14(12+12×13k +1)-1=k 2k +1+3k +13k +1+2.要证k 2k +1+3k +13k +1+2≥(k +1)2k +2,只要证3k +1 3k +1+2≥(k +1)2k +2-k 2k +1.只要证3k +13k +1+2≥k 2+3k +1 k 2+3k +2.只要证2 3k +1≤1k 2+3k +1.只要证3k +1≥2k 2+6k +2. 因为k ≥2,所以3k +1=3(1+2)k ≥3(1+2k +4C 2k )=6k 2+3=2k 2+6k +2+2k (2k -3)+1>2k 2+6k +2,所以k 2k +1+3k +1 3k +1+2≥(k +1)2k +2.即n =k +1时,不等式也成立.由①②可知,不等式i =1∑n14P i -1>n 2n +1对任意的n ∈N *都成立. ……………………10分。
江苏省南通、泰州、扬州、连云港、淮安五市2013届高三第三次模拟考试数学试卷

(第3题)(第5题)江苏省南通、泰州、扬州、连云港、淮安五市2013届高三第三次模拟考试数学试卷一、填空题:本大题共14小题,每小题5分,共70分.1. 已知集合(]2 1A =-,,[)1 2B =-,,则A B = ▲ .2. 设复数z 满足(34i)50z ++=(是虚数单位),则复数z的模为 ▲ .3. 右图是一个算法流程图,则输出的S 的值是 ▲ .4. “M N >”是“22log log M N >”成立的 ▲ 条件.(从“充要”,“充分不必要”,“必要不充分”中选择一个正确的填写)5. 根据某固定测速点测得的某时段内过往的100辆 机动车的行驶速度(单位:km/h)绘制的频率分布 直方图如右图所示.该路段限速标志牌提示机动车辆正常行驶速度为60 km/h~120 km/h ,则该时 段内非正常行驶的机动车辆数为 ▲ .6. 在平面直角坐标系xOy 中,抛物线22(0)x py p =>上纵坐标为1的一点到焦点的距离为3,则焦点到准线的距离为 ▲ .7. 从集合{}1 2 3 4 5 6 7 8 9,,,,,,,,中任取两个不同的数,则其中一个数恰是另一个数的3倍的概率为 ▲ .(第9题)8. 在平面直角坐标系xOy 中,设点P 为圆C :22(1)4x y -+=上的任意一点,点Q (2a ,3a -) (a ∈R ),则线段PQ 长度的最小值为 ▲ .9. 函数()sin()f x A x ωϕ=+(0A >,0ω>,02)ϕ<π≤在R 上的部分图象如图所示,则(2013)f 的值为 ▲ .10.各项均为正数的等比数列{}n a 中,211a a -=.当3a 取最小值时,数列{}n a 的通项公式a n = ▲ .11.已知函数2221 0 () 0ax x x f x x bx c x ⎧--⎪=⎨++<⎪⎩,≥,,是偶函数,直线y t =与函数()y f x =的图象自左向右依次交于四个不同点A ,B ,C ,D .若AB BC =,则实数的值为 ▲ .12.过点(1 0)P -,作曲线C :e x y =的切线,切点为1T ,设1T 在x 轴上的投影是点1H ,过点1H 再作曲线C 的切线,切点为2T ,设2T 在x 轴上的投影是点2H ,…,依次下去,得到第1n +()n ∈N 个切点1n T +.则点1n T +的坐标为 ▲ .13.在平面四边形ABCD中,点E ,F 分别是边AD ,BC 的中点,且AB1=,EF CD =.若15AD BC ⋅=,则AC BD ⋅的值为 ▲ .14.已知实数a 1,a 2,a 3,a 4满足a 1+a 2+a 30=,a 1a 42+a 2a 4-a 20=,且a 1>a 2>a 3,则a 4的取值范围是 ▲ . 二、解答题15.如图,在四棱锥P ABCD -中,底面ABCD 是矩形,四条侧棱长均相等. (1)求证:AB //平面PCD ; (2)求证:平面PAC ⊥平面ABCD .16.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c .已知222222sin 2sin sin C b a c A C c a b --=---. (1)求角B 的大小;(2)设222sin sin sin T A B C =++,求T 的取值范围.17.某单位设计的两种密封玻璃窗如图所示:图1是单层玻璃,厚度为8 mm ;图2是双层中空玻璃,厚度均为4 mm ,中间留有厚度为x 的空气隔层.根据热传导知识,对于厚度为d 的均匀介质,两侧的温度差为T ∆,单位时间内,在单位面积上通过的热量T Q k d∆=⋅,其中k 为热传导系数.假定单位时间内,在单位面积上通过每一层玻璃及空气隔层的热量相等.(注:玻璃的热传导系数为3410 J mm/C -⨯⋅,空气的热传导系数为42.510 J mm/C -⨯⋅.)(1)设室内,室外温度均分别为1T ,2T ,内层玻璃外侧温度为1T ',外层玻璃内侧温度为2T ',且1122T T T T ''>>>.试分别求出单层玻璃和双层中空玻璃单位时间内,在单位面积上通过的热量(结果用1T ,2T 及x 表示);(2)为使双层中空玻璃单位时间内,在单位面积上通过的热量只有单层玻璃的4%,应如何设ABC(第15题)PDO(第18题)计x 的大小?18.如图,在平面直角坐标系xOy 中,椭圆22221(0)y x a b a b+=>>的右焦点为(1 0)F ,,分别过O ,F 的两条弦AB ,CD 相交于点E (异于A ,C 两点),且OE EF =.(1)求椭圆的方程;(2)求证:直线AC ,BD 的斜率之和为定值.19.已知数列{}n a 是首项为1,公差为d 的等差数列,数列{}n b 是首项为1,公比为(1)qq >的等比数列.图1图2(第17题)(第21—A 题)(1)若55a b =,3q =,求数列{}n n a b ⋅的前n 项和;(2)若存在正整数(2)k k ≥,使得k k a b =.试比较n a 与n b 的大小,并说明理由.20.设()f x 是定义在(0 )+∞,的可导函数,且不恒为0,记()()()n n f x g x n x=∈*N .若对定义域内的每一个x ,总有()0n g x <,则称()f x 为“n 阶负函数”;若对定义域内的每一个x ,总有[]()0n g x '≥,则称()f x 为“n 阶不减函数”([]()n g x '为函数()n g x 的导函数).(1)若31()(0)a f x x x x x =-->既是“1阶负函数”,又是“1阶不减函数”,求实数a 的取值范围;(2)对任给的“2阶不减函数”()f x ,如果存在常数c ,使得()f x c <恒成立,试判断()f x 是否为“2阶负函数”?并说明理由.数学附加题21.【选做题】A .选修4—1:几何证明选讲如图,⊙O 的半径为3,两条弦AB ,CD 交于点P ,且1AP =, 3CP =,OP = 求证:△APC ≌△DPB .B .选修4—2:矩阵与变换已知矩阵M 566x ⎡⎤=⎢⎥⎣⎦不存在逆矩阵,求实数x 的值及矩阵M 的特征值.C .选修4—4:坐标系与参数方程在平面直角坐标系xOy 中,已知(0 1)A ,,(0 1)B -,,( 0)C t ,,()3 0D ,,其中0t ≠.设直线AC与BD 的交点为P ,求动点P 的轨迹的参数方程(以为参数)及普通方程.D .选修4—5:不等式选讲已知0a >,0b >,n ∈*N .求证:11n n n na b a b ++++22.【必做题】设n ∈*N 且2n ≥,证明:()22221212n n a a a a a a ++⋅⋅⋅+=++⋅⋅⋅+()1232n a a a a ⎡+++⋅⋅⋅+⎣()234n a a a a +++⋅⋅⋅++⋅⋅⋅]1n n a a -+.23.【必做题】下图是某游戏中使用的材质均匀的圆形转盘,其中Ⅰ,Ⅱ,Ⅲ,Ⅳ部分的面积各占转盘面积的112,16,14,12.游戏规则如下:① 当指针指到Ⅰ,Ⅱ, Ⅲ,Ⅳ部分时,分别获得积分100分,40分,10分,0分; ② (ⅰ)若参加该游戏转一次转盘获得的积分不是40分,则按①获得相应的积分,游戏结束; (ⅱ)若参加该游戏转一次获得的积分是40分,则用抛一枚质地均匀的硬币的方法来决定是否继续游戏.正面向上时,游戏结束;反面向上时,再转一次转盘,若再转一次的积分不高于40(第3题)分,则最终积分为0分,否则最终积分为100分,游戏结束.设某人参加该游戏一次所获积分为ξ.(1)求0ξ=的概率;(2)求ξ的概率分布及数学期望.南通市2013届高三第三次调研测试数学参考答案及评分建议一、填空题:本大题共14小题,每小题5分,共70分.1. 已知集合(]2 1A =-,,[)1 2B =-,,则A B = ▲ .【答案】(2 2)-,2. 设复数z 满足(34i)50z ++=(是虚数单位),则复数z 的 模为 ▲ . 【答案】3. 右图是一个算法流程图,则输出的S 的值是 ▲ . 【答案】24004. “M N >”是“22log log M N >”成立的 ▲ 条件.(从“充要”,“充分不必要”,“必要不充分”中选择一个正确的填写) 【答案】必要不充分5. 根据某固定测速点测得的某时段内过往的100辆 机动车的行驶速度(单位:km/h)绘制的频率分布 直方图如右图所示.该路段限速标志牌提示机动车辆正常行驶速度为60 km/h~120 km/h ,则该时 段内非正常行驶的机动车辆数为 ▲ .(第23题)(第9题)【答案】156. 在平面直角坐标系xOy 中,抛物线22(0)x py p =>上纵坐标为1的一点到焦点的距离为3,则焦 点到准线的距离为 ▲ .【答案】47. 从集合{}1 2 3 4 5 6 7 8 9,,,,,,,,中任取两个不同的数,则其中一个数恰是另一个数的3倍的概率为 ▲ .【答案】1128. 在平面直角坐标系xOy 中,设点P 为圆C :22(1)4x y -+=上的任意一点,点Q (2a ,3a -) (a ∈R),则线段PQ 长度的最小值为 ▲ .【答案29. 函数()sin()f x A x ωϕ=+(0A >,0ω>,02)ϕ<π≤在R 上的部分图象如图所示,则(2013)f 的值为 ▲ . 【答案】10.各项均为正数的等比数列{}n a 中,211a a -=.当3a 取最小值时,数列{}n a 的通项公式a n = ▲ .【答案】12n -11.已知函数2221 0 () 0ax x x f x x bx c x ⎧--⎪=⎨++<⎪⎩,≥,,是偶函数,直线y t =与函数()y f x =的图象自左向右依次交于四个不同点A ,B ,C ,D .若AB BC =,则实数的值为 ▲ . 【答案】74- 12.过点(1 0)P -,作曲线C :e x y =的切线,切点为1T ,设1T 在x 轴上的投影是点1H ,过点1H 再作 曲线C 的切线,切点为2T ,设2T 在x 轴上的投影是点2H ,…,依次下去,得到第1n +()n ∈N 个 切点1n T +.则点1n T +的坐标为 ▲ . 【答案】()e n n ,13.在平面四边形ABCD 中,点E ,F 分别是边AD ,BC 的中点,且AB 1=,EFCD =.若15AD BC ⋅=,则AC BD ⋅的值为 ▲ . 【答案】1314.已知实数a 1,a 2,a 3,a 4满足a 1+a 2+a 30=,a 1a 42+a 2a 4-a 20=,且a 1>a 2>a 3,则a 4的取值范围是 ▲ .【答案】二、解答题15.如图,在四棱锥P ABCD -中,底面ABCD 是矩形,四条侧棱长均相等. (1)求证:AB //平面PCD ; (2)求证:平面PAC ⊥平面ABCD . 证明:(1)在矩形ABCD 中,//AB CD , 又AB ⊄平面PCD , CD ⊂平面PCD ,所以AB //平面PCD . ………6分 (2)如图,连结BD ,交AC 于点O ,连结PO ,在矩形ABCD 中,点O 为 AC BD ,的中点, 又PA PB PC PD ===,故PO AC ⊥,PO BD ⊥, ………9分 又ACBD O =,AC BD ,⊂平面ABCD , 所以PO ⊥平面ABCD , ………12分又PO ⊂平面PAC ,所以平面PAC ⊥平面ABCD . ………14分ABC(第15题)PDO16.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c .已知222222sin 2sin sin C b a c A C c a b --=---. (1)求角B 的大小;(2)设222sin sin sin T A B C =++,求T 的取值范围. 解:(1)在△ABC 中,222222sin 2cos cosB sin cos 2sin sin 2cos cos sin cos C b a c ac B c C B A C ab C b C B Cc a b ---====----, ………3分因为sin 0C ≠,所以sin cos 2sin cos sin cos B C A B C B =-,所以2sin cos sin cossin cos sin()sin A B B C C B B C A =+=+=, ………5分因为sin 0A ≠,所以1cos 2B =,因为0πB <<,所以π3B =. ………7分(2)222131sin sin sin (1cos2)(1cos2)242T A B C A C =++=-++-()71714π(cos2cos2)cos2cos 2A C A A -⎡⎤=⎢⎥⎣+=--⎦+()()71171πcos22cos 2422423A A A =-=-+ (11)分因为2π03A <<,所以4π023A <<,故ππ5π2333A <+<,因此()π11cos 232A -+<≤,所以3924T <≤. ………14分17.某单位设计的两种密封玻璃窗如图所示:图1是单层玻璃,厚度为8 mm ;图2是双层中空玻璃,厚度均为4 mm ,中间留有厚度为x 的空气隔层.根据热传导知识,对于厚度为d 的均匀介质, 两侧的温度差为T ∆,单位时间内,在单位面积上通过的热量T Q k d ∆=⋅,其中k 为热传导系数.假定单位时间内,在单位面积上通过每一层玻璃及空气隔层的热量相等.(注:玻璃的热传导系 数为3410 J mm/C -⨯⋅,空气的热传导系数为42.510 J mm/C -⨯⋅.)(1)设室内,室外温度均分别为1T ,2T ,内层玻璃外侧温度为1T ',外层玻璃内侧温度为2T ', 且1122T T T T ''>>>.试分别求出单层玻璃和双层中空玻璃单位时间内,在单位面积上通过 的热量(结果用1T ,2T 及x 表示);(2)为使双层中空玻璃单位时间内,在单位面积上通过的热量只有单层玻璃的4%,应如何设计x 的大小?解:(1)设单层玻璃和双层中空玻璃单位时间内,在单位面积上通过的热量分别为1Q ,2Q , 则3121214108 2 000T T T T Q ---=⨯⋅=, ………2分3431112222410 2.51041044T T T T T T Q x ---''''---=⨯⋅=⨯⋅=⨯⋅ ………6分11122234344410 2.510410T T T T T T x ---''''---===⨯⨯⨯ 11122234344410 2.510410T T T T T T x ---''''-+-+-=++⨯⨯⨯124 000 2 000T T x -=+. ………9分(2)由(1)知21121Q Q x =+, 图1图2(第17题)(第18题)当121x =+4%时,解得12x =(mm ). 答:当12x =mm 时,双层中空玻璃通过的热量只有单层玻璃的4%. ………14分18.如图,在平面直角坐标系xOy 中,椭圆22221(0)y x a b a b+=>>的右焦点为(1 0)F ,.分别过O ,F 的两条弦AB ,CD 相交于点E (异于A ,C 两点),且OE EF =. (1)求椭圆的方程;(2)求证:直线AC ,BD 的斜率之和为定值.(1)解:由题意,得1c =,c e ==,故a =从而2221b a c =-=,所以椭圆的方程为221x y +=. ① (5)分(2)证明:设直线AB 的方程为y kx =,②直线CD 的方程为(1)y k x =--, ③ (7)分由①②得,点A ,B 的横坐标为由①③得,点C ,D , ………9分记11( )A x kx ,,22( )B x kx ,,33( (1))C x k x -,,44( (1))D x k x -,, 则直线AC ,BD 的斜率之和为13241324(1)(1)kx k x kx k x ----+132413241324(1)()()(1)()()x x x x x x x x k x x x x +--+-+-=⋅--1234123413242()()()()()x x x x x x x x k x x x x --+++=⋅-- (13)分2222124232(1)4222201121()()k k k k k x x x k x ⎛⎫---+ ⎪+++⎝-⎭=⋅-- 0=. ………16分19.已知数列{}n a 是首项为1,公差为d 的等差数列,数列{}n b 是首项为1,公比为(1)q q >的等比数列.(1)若55a b =,3q =,求数列{}n n a b ⋅的前n 项和;(2)若存在正整数(2)k k ≥,使得k k a b =.试比较n a 与n b 的大小,并说明理由. 解:(1)依题意,5145511381a b b q -===⨯=, 故5181120514a a d --===-, 所以120(1)2019n a n n =+-=-, ………3分令2111213413(2019)3n n S n -=⨯+⨯+⨯+⋅⋅⋅+-⋅, ① 则213 13213(2039)3(2019)3n n n S n n -=⨯+⨯+⋅⋅⋅+-⋅+-⋅, ② ①-②得,()2121+20333(2019)3n n n S n --=⨯++⋅⋅⋅+--⋅,13(13)1+20(2019)313n n n --=⨯--⋅-(2920)329n n =-⋅-,所以(2029)3292n n n S -⋅+=. ………7分(2)因为k k a b =, 所以11(1)k k d q-+-=,即111k q d k --=-,故111(1)1k n q a n k --=+--,又1n n b q -=, (9)分所以1111(1)1k n n n q b a qn k --⎡⎤--=-+-⎢⎥-⎣⎦()()111(1)1(1)11n k k q n q k --⎡⎤=-----⎣⎦- ()()23231(1)1(1)1n n k k q k q q q n q q q -----⎡⎤=-++⋅⋅⋅++--++⋅⋅⋅++⎣⎦ ………11分(ⅰ)当1n k <<时,由1q >知()()232311()1(1)n n k k n n n q b a k n q q q n q q q ------⎡⎤-=-++⋅⋅⋅++--++⋅⋅⋅+⎣⎦ 211()(1)(1)()1n n q k n n q n k n q k ---⎡⎤<-----⎣⎦- 22(1)()(1)1n q q k n n k ----=--0<, ………13分(ⅱ)当n k >时,由1q >知()()231231(1)()11n n k k k n n q b a k q q q n k q q q k ------⎡⎤-=-++⋅⋅⋅+--++⋅⋅⋅++⎣⎦- 121(1)()()(1)1k k q k n k q n k k q k ---⎡⎤>-----⎣⎦- 22(1)()k q q n k -=-- 0>,综上所述,当1n k <<时,n n a b >;当n k >时,n n a b <;当1 n k =,时,n n a b =. ………16分(注:仅给出“1n k <<时,n n a b >;n k >时,n n a b <”得2分.)20.设()f x 是定义在(0 )+∞,的可导函数,且不恒为0,记()()()n n f x g x n x=∈*N .若对定义域内的每一个x ,总有()0n g x <,则称()f x 为“n 阶负函数”;若对定义域内的每一个x ,总有[]()0n g x '≥, 则称()f x 为“n 阶不减函数”([]()n g x '为函数()n g x 的导函数).(1)若31()(0)a f x x x x x =-->既是“1阶负函数”,又是“1阶不减函数”,求实数a 的取值范围;(2)对任给的“2阶不减函数”()f x ,如果存在常数c ,使得()f x c <恒成立,试判断()f x 是 否为“2阶负函数”?并说明理由. 解:(1)依题意,142()1()1f x a g x x x==--在(0 )+∞,上单调递增, 故15342[()]0a g x x x '=-+≥ 恒成立,得212a x ≤, ………2分 因为0x >,所以0a ≤. ………4分 而当0a ≤时,1421()10a g x x x=--<显然在(0 )+∞,恒成立, 所以0a ≤. ………6分(2)①先证()0f x ≤:若不存在正实数0x ,使得20()0g x >,则2()0g x ≤恒成立. ………8分假设存在正实数0x ,使得20()0g x >,则有0()0f x >,由题意,当0x >时,2()0g x '≥,可得2()g x 在(0 )+∞,上单调递增, 当0x x >时,0220()()f x f x x x >恒成立,即2020()()f x f x x x >⋅恒成立, 故必存在10x x >,使得201120()()f x f x x m x >⋅>(其中m 为任意常数), 这与()f x c <恒成立(即()f x 有上界)矛盾,故假设不成立,所以当0x >时,2()0g x ≤,即()0f x ≤; ………13分 ②再证()0f x =无解:假设存在正实数2x ,使得2()0f x =,(第21—A 题)则对于任意320x x >>,有322232()()0f x f x x x >=,即有3()0f x >, 这与①矛盾,故假设不成立, 所以()0f x =无解,综上得()0f x <,即2()0g x <,故所有满足题设的()f x 都是“2阶负函数”. ………16分南通市2013届高三第三次调研测试 数学附加题参考答案及评分建议21.【选做题】A .选修4—1:几何证明选讲如图,⊙O 的半径为3,两条弦AB ,CD 交于点P ,且1AP =, 3CP =,OP = 求证:△APC ≌△DPB .证明:延长OP 交⊙O 与点E ,F , ………2分由相交弦定理得((333CP DP AP BP FP EP ⋅=⋅=⋅=⨯+=,………6分 又1AP =,3CP =,故1DP =,3BP =, ………8分所以AP DP =,BP CP =, 而APC DPB ∠=∠,所以△APC ≌△DPB . ………10分B .选修4—2:矩阵与变换已知矩阵M 566x ⎡⎤=⎢⎥⎣⎦不存在逆矩阵,求实数x 的值及矩阵M 的特征值. 解:由题意,矩阵M 的行列式5066x =,解得5x =, ………4分 矩阵M 5566⎡⎤=⎢⎥⎣⎦的特征多项式 55()(5)(6)(5)(6)66f λλλλλ--==----⨯---, ………8分 令()0f λ=并化简得2110λλ-=,解得0λ=或11λ=,所以矩阵M 的特征值为0和11. ………10分C .选修4—4:坐标系与参数方程在平面直角坐标系xOy 中,已知(0 1)A ,,(0 1)B -,,( 0)C t ,,()3 0D t,,其中0t ≠.设直线AC与BD 的交点为P ,求动点P 的轨迹的参数方程(以为参数)及普通方程. 解:直线AC 的方程为1x y t +=,①直线BD 的方程为13x y -=,② (2)分由①②解得,动点P 的轨迹的参数方程为2226 333t x t t y t ⎧=⎪+⎨-⎪=+⎩,(为参数,且0t ≠), ………6分 将263t x t =+平方得222236(3)t x t =+,③将2233t y t -=+平方得()()2222233t y t -=+, ④ ………8分由③④得,221(0)3x y x +=≠. ………10分(注:普通方程由①②直接消参可得.漏写“0x ≠”扣1分.)D .选修4—5:不等式选讲已知0a >,0b >,n ∈*N.求证:11n n n na b a b ++++证明:先证112n n n na b a ba b +++++≥, 只要证112()()()n n n n a b a b a b +++++≥, 即要证11n n n n a b a b ab +++--≥0,即要证()(n n a b a b --)≥0, ………5分若a b ≥,则a b -≥0,n n a b -≥0,所以()(n n a b a b --)≥0, 若a b <,则0a b -<,0n n a b -<,所以()()0n n a b a b -->, 综上,得()(n n a b a b --)≥0.从而112n n n n a b a ba b +++++≥, ………8分因为2a b+所以11n n n na b a b ++++ ………10分 22.【必做题】设n ∈*N 且2n ≥,证明:()22221212n n a a a a a a ++⋅⋅⋅+=++⋅⋅⋅+()1232n a a a a ⎡+++⋅⋅⋅+⎣()234n a a a a +++⋅⋅⋅++⋅⋅⋅]1n n a a -+.证明:(1)当2n =时,有()2221212122a a a a a a +=++,命题成立. ………2分 (2)假设当(2)n k k =≥时,命题成立, 即()22221212k k a a a a a a ++⋅⋅⋅+=++⋅⋅⋅+()1232k a a a a ⎡+++⋅⋅⋅+⎣()234k a a a a +++⋅⋅⋅++⋅⋅⋅]1k k a a -+成立, ………4分那么,当1n k =+时,有()2121k k a a a a +++⋅⋅⋅++ ()()221212112k k k k a a a a a a a a ++=++⋅⋅⋅++++⋅⋅⋅++22212k a a a =++⋅⋅⋅+()1232k a a a a ⎡+++⋅⋅⋅+⎣()234k a a a a +++⋅⋅⋅++⋅⋅⋅]1k k a a -+ (12a +2a ++⋅⋅⋅)211k k k a a a ++++.2222121k k a a a a +=++⋅⋅⋅++()12312k k a a a a a +⎡+++⋅⋅⋅++⎣+(234a a a ++⋅⋅⋅k a +)1k a ++ +⋅⋅⋅ ]1k k a a ++.所以当1n k =+时,命题也成立. ………8分根据(1)和(2),可知结论对任意的n ∈*N 且2n ≥都成立. ………10分23.【必做题】下图是某游戏中使用的材质均匀的圆形转盘,其中Ⅰ,Ⅱ,Ⅲ,Ⅳ部分的面积各占转盘面积的112,16,14,12.游戏规则如下:① 当指针指到Ⅰ,Ⅱ, Ⅲ,Ⅳ部分时,分别获得积分100分,40分,10分,0分; ② (ⅰ)若参加该游戏转一次转盘获得的积分不是40分,则按①获得相应的积分,游戏结束; (ⅱ)若参加该游戏转一次获得的积分是40分,则用抛一枚质地均匀的硬币的方法来决定是否继续游戏.正面向上时,游戏结束;反面向上时,再转一次转盘,若再转一次的积分不高于40分,则最终积分为0分,否则最终积分为100分,游戏结束. 设某人参加该游戏一次所获积分为ξ.(1)求0ξ=的概率;(2)求ξ的概率分布及数学期望.解:(1)事件“0ξ=”包含:“首次积分为0分”和“首次积分为40分后再转一次的积分不高于40分”,且两者互斥,所以111183(0)(1)P ξ==+⨯⨯-=; ………4分(2)ξ的所有可能取值为0,10,40,100, 由(1)知83(0)144P ξ==,又1(10)4P ξ==,111(40)6212P ξ==⨯=,111113(100)126212144P ξ==+⨯⨯=,所以ξ的概率分布为:………7分因此,831113535()0104010014441214436E ξ=⨯+⨯+⨯+⨯=(分). …10分 (第23题)。
江苏省南通、泰州、扬州、连云港、淮安五市2013届高三第三次模拟考试数学试题(扫描版)

1. 【答案】(2 2)-,【解析】考查集合的运算,(]2 1A =-,,[)1 2B =-,,则A B =U (2 2)-,. 2.【答案】1 【解析】考查复数的四则运算.由(34i)50z ++=得34, 1.5iz z -+==3.【答案】2400 【解析】考查算法的流程图,40080012002400.++=4.【答案】必要不充分【解析】考查充分必要条件。
5.【答案】15【解析】考查统计中的总体分布的估计,应注意组距是20. 6.【答案】4【解析】考查抛物线的标准方程与简单性质,注意p 的含义.7.【答案】1【解析】考查古典概型.符合条件的有(1,3),(2,6),(3,9)三个. 8.2【解析】考查圆与直线的位置关系.找出点Q 在直线260x y --=上,转化为圆上的点到直线的距离求解.9.【答案】【解析】 考查sin()y A x ωϕ=+的图象性质,周期性,诱导公式.由图知5A =,12T =,从而ωπ=6,6ϕπ=,则(2013)(9)f f ==10.【答案】12n -【解析】考查等比数列和基本不等式,由2213a a a =,211a a -=及0n a >得()2131111124a a a a a +==++≥(当且仅当11a =时取等号),此时22a =,则12n n a -=.本题也可以利用基本量思想求解.11.【答案】7-【解析】考查函数的图象与基本性质.由偶函数的性质,得到1 2 1a b c ===-,,.由题意知3 2 D C C D x x x x =⎧⎨+=⎩,,所以12C x =,则()211721224t =-⨯-=-.12.【答案】() e n n ,【解析】考查导数与归纳推理.设111( e )x T x ,,则111e e 1x x x =+,解得10x =,所以01(0 e )T ,;设222( e )x T x ,,则222e e x x x =,解得21x =,所以2(1 e)T ,;设232( e )x T x ,,则331e e 1x x x =-,解得32x =,所以23(2 e )T ,;…,通过归纳可猜想:1( e ) nn T n n +∈N ,,.讲评时提醒学生本题可推导出{}n x 是等差数列用于求解.13.【答案】13【解析】考查平面向量的数量积.由2EF AB DC =+ ,平方并整理得2AB DC ⋅= ,即()AB AC AD⋅- 2AB AC AB AD =⋅-⋅= ①,由15AD BC ⋅= ,得()15AD AC AB AD AC AD AB ⋅-=⋅-⋅= ②,②-①得AC BD⋅ ()AC AD AB=⋅- 13=. 14.【答案】【解析】方法一:因为123123 0a a a a a a >>⎧⎨++=⎩,,所以10a >,30a <,消去2a 得31122a a -<<-,且21413413()0a a a a a a a -+++=,两边同除以1a 得()2334411110a a a a a a -+++=,解得31a a 2441a a =-1-,所以24412112a a -<<---,解得4a <.方法二:由123123 0a a a a a a >>⎧⎨++=⎩,得321132111 10 a a a a a a a a ⎧>>⎪⎪⎨⎪++=⎪⎩,,令2131 a x a a y a ⎧=⎪⎪⎨⎪=⎪⎩,,则1 10 y x x y <<⎧⎨++=⎩,,利用线性规划知识求出21a a 的取值范围,再结合242411a a a a =-,求出4a 的取值范围.方法三:可以用求根公式求出4a ,再结合21a 的取值范围,利用单调性求解.15.【解析】(1)在矩形ABCD 中,//AB CD , 又AB ⊄平面PCD ,CD ⊂平面PCD ,所以AB //平面PCD .(2)如图,连结BD ,交AC 于点O ,连结PO ,在矩形ABCD 中,点O 为 AC BD ,的中点, 又PA PB PC PD ===, 故PO AC ⊥,PO BD ⊥, 又AC BD O =I ,AC BD ,⊂平面ABCD , 所以PO ⊥平面ABCD , 又PO ⊂平面PAC ,所以平面PAC ⊥平面ABCD . 16.【解析】(1)在△ABC 中,ABC(第15题)PDO222222sin 2cos cosB sin cos 2sin sin 2cos cos sin cos C b a c ac B c C B A C ab C b C B C c a b ---====----,因为sin 0C ≠,所以sin cos 2sin cos sin cos B C A B C B =-,所以2sin cos sin cos sin cos sin()sin A B B C C B B C A =+=+=, 因为sin 0A ≠,所以1cos 2B =, 因为0πB <<,所以π3B =. (2)222131sin sin sin (1cos 2)(1cos 2)242T A B C A C =++=-++-()71714π(cos2cos2)cos2cos 242423A C A A -⎡⎤=⎢⎥⎣+=--⎦+()()71171πcos22cos 2422423A A A =-=-+ 因为2π03A <<,所以4π023A <<, 故ππ5π2333A <+<,因此()π11cos 232A -+<≤, 所以3924T <≤. 17. 【解析】(1)设单层玻璃和双层中空玻璃单位时间内,在单位面积上通过的热量分别为1Q ,2Q ,则3121214108 2 000T T T T Q ---=⨯⋅=,3431112222410 2.51041044T T T T T T Q x ---''''---=⨯⋅=⨯⋅=⨯⋅11122234344410 2.510410T T T T T T x ---''''---===⨯⨯⨯11122234344410 2.510410T T T T T T x ---''''-+-+-=++⨯⨯⨯124 000 2 000T T x -=+. (2)由(1)知21121Q Q x =+,当1=4%时,解得12x =(mm ).答:当12x =mm 时,双层中空玻璃通过的热量只有单层玻璃的4%. 18.【解析】(1)解:由题意,得1c =,c e a =,故a = 从而2221b a c =-=,所以椭圆的方程为2212x y +=.①(2)证明:设直线AB 的方程为y kx =, ②直线CD 的方程为(1)y k x =--,③ 由①②得,点A ,B的横坐标为由①③得,点C ,D的横坐标为,记11( )A x kx ,,22( )B x kx ,,33( (1))C x k x -,,44( (1))D x k x -,, 则直线AC ,BD 的斜率之和为 13241324(1)(1)kx k x kx k x x x x x ----+-- 132413241324(1)()()(1)()()x x x x x x x x k x x x x +--+-+-=⋅-- 1234123413242()()()()()x x x x x x x x k x x x x --+++=⋅--2222213242(1)2420212121()()k k k k k k x x x x -⎛⎫---+ ⎪+++⎝⎭=⋅--0=.19.【解析】(1)依题意,5145511381a b b q -===⨯=, 故5181120514a a d --===-,所以120(1)2019n a n n =+-=-,令2111213413(2019)3n n S n -=⨯+⨯+⨯+⋅⋅⋅+-⋅, ①则213 13213(2039)3(2019)3n nn S n n -=⨯+⨯+⋅⋅⋅+-⋅+-⋅, ②①-②得,()2121+20333(2019)3n nn S n --=⨯++⋅⋅⋅+--⋅,13(13)1+20(2019)313n nn --=⨯--⋅- (2920)329n n =-⋅-,所以(2029)329n n n S -⋅+=. (2)因为k k a b =,所以11(1)k k d q -+-=,即111k q d k --=-, 故111(1)1k n q a n k --=+--, 又1n n b q -=,所以1111(1)1k n n n q b a qn k --⎡⎤--=-+-⎢⎥-⎣⎦()()111(1)1(1)11n k k q n q k --⎡⎤=-----⎣⎦-()()23231(1)1(1)11n n k k q k q q q n q q q k -----⎡⎤=-++⋅⋅⋅++--++⋅⋅⋅++⎣⎦- (ⅰ)当1n k <<时,由1q >知()()232311()1(1)1n n k k n n n q b a k n q q q n q q q k ------⎡⎤-=-++⋅⋅⋅++--++⋅⋅⋅+⎣⎦- 211()(1)(1)()1n n q k n n q n k n q k ---⎡⎤<-----⎣⎦-22(1)()(1)1n q q k n n k ----=--0<,(ⅱ)当n k >时,由1q >知()()231231(1)()11n n k k k n n q b a k q q q n k q q q k ------⎡⎤-=-++⋅⋅⋅+--++⋅⋅⋅++⎣⎦- 121(1)()()(1)1k k q k n k q n k k q k ---⎡⎤>-----⎣⎦-22(1)()k q q n k -=--0>,综上所述,当1n k <<时,n n a b >;当n k >时,n n a b <;当1 n k =,时,n n a b =. (注:仅给出“1n k <<时,n n a b >;n k >时,n n a b <”得2分.) 20.【解析】(1)依题意,142()1()1f x ag x x x x ==--在(0 )+∞,上单调递增, 故15342[()]0a g x x x '=-+≥ 恒成立,得212a x ≤, 因为0x >,所以0a ≤.而当0a ≤时,1421()10a g x x x =--<显然在(0 )+∞,恒成立, 所以0a ≤. (2)①先证()0f x ≤:若不存在正实数0x ,使得20()0g x >,则2()0g x ≤恒成立. 假设存在正实数0x ,使得20()0g x >,则有0()0f x >,由题意,当0x >时,2()0g x '≥,可得2()g x 在(0 )+∞,上单调递增, 当0x x >时,0220()()f x f x x x >恒成立,即2020()()f x f x x x >⋅恒成立,故必存在10x x >,使得201120()()f x f x x m x >⋅>(其中m 为任意常数),这与()f x c <恒成立(即()f x 有上界)矛盾,故假设不成立, 所以当0x >时,2()0g x ≤,即()0f x ≤; ②再证()0f x =无解:假设存在正实数2x ,使得2()0f x =,则对于任意320x x >>,有322232()()0f x f x x x >=,即有3()0f x >,这与①矛盾,故假设不成立, 所以()0f x =无解,综上得()0f x <,即2()0g x <,故所有满足题设的()f x 都是“2阶负函数”.更多2013届各地最新模拟下载只需复制网址下载,绝对安全无毒江苏省南京、盐城市2013届高三第三次模拟考试数学试卷(WORD 版).doc:/file/20316351江苏省南京市四星级高级中学2013届高三联考调研考试数学试卷2013.3.doc:/file/20316354 江苏省南通、泰州、扬州、连云港、淮安五市2013届高三第三次模拟考试数学试题(扫描版).doc:/file/20316355江苏省苏、锡、常、镇四市2013届高三教学情况调查(二)数学试题(word版).doc:/file/20316358江苏省苏、锡、常、镇四市2013届高三教学情况调研(二)数学试题(扫描版)有答案.doc:/file/20316361江西省2013届高三九校第二次联考数学(文)试题.doc: /file/20316365 江西省2013届高三九校第二次联考数学(理)试题.doc: /file/20316363 江西省南昌市2013届高三第二次模拟测试(word解析版)数学文.doc: /file/20316371江西省南昌市2013届高三第二次模拟测试(word解析版)数学理.doc: /file/20316368河南省商丘市2013届高三第三次模拟考试数学(理)试题.doc: /file/20316208河南省商丘市2013届高三第三次模拟考试试题(worc版)数学文.doc: /file/20316206河南省平顶山、许昌、新乡2013届高三第三次调研考试(word版)数学理].doc:/file/20316205河南省郑州市2013届高三第三次测验预测试题(word版)数学文.doc: /file/20316218河南省郑州市2013届高三第三次测验预测试题(word版)数学理.doc: /file/20316213贵州黔东南州2013年高三年级第二次模拟考试试卷数学文.doc: /file/20316203山东省泰安市2013届高三第二次模拟考试(word版)数学文.doc: /file/20316424山东省泰安市2013届高三第二次模拟考试(word版)数学理.doc: /file/20316421山东省莱芜市2013届高三第二次模拟考试数学理.doc: /file/20316418山东省菏泽市2013届高三第二次模拟考试数学(文)试题.doc: /file/20316414山东省菏泽市2013届高三第二次模拟考试数学(理)试题.doc: /file/20316410江苏省南京、盐城市2013届高三第三次模拟考试数学试卷(WORD版).doc:/file/20316351江苏省南京市四星级高级中学2013届高三联考调研考试数学试卷2013.3.doc:/file/20316354江苏省南通、泰州、扬州、连云港、淮安五市2013届高三第三次模拟考试数学试题(扫描版).doc: /file/20316355江苏省苏、锡、常、镇四市2013届高三教学情况调查(二)数学试题(word版).doc:/file/20316358江苏省苏、锡、常、镇四市2013届高三教学情况调研(二)数学试题(扫描版)有答案.doc:/file/20316361江西省2013届高三九校第二次联考数学(文)试题.doc: /file/20316365 江西省2013届高三九校第二次联考数学(理)试题.doc: /file/20316363 江西省南昌市2013届高三第二次模拟测试(word解析版)数学文.doc: /file/20316371江西省南昌市2013届高三第二次模拟测试(word解析版)数学理.doc: /file/20316368河南省郑州市2013届高三第三次测验预测试题(word版)数学文.doc: /file/20316218广东省东莞市2013届高三模拟试题(一)数学文试题.doc: /file/20316197 广东省东莞市2013届高三模拟试题(一)数学理试题.doc: /file/20316194 河南省商丘市2013届高三第三次模拟考试数学(理)试题.doc: /file/20316208河南省商丘市2013届高三第三次模拟考试试题(worc版)数学文.doc: /file/20316206河南省平顶山、许昌、新乡2013届高三第三次调研考试(word版)数学理].doc:/file/20316205河南省郑州市2013届高三第三次测验预测试题(word版)数学理.doc: /file/20316213湖北省黄冈市2013届高三4月调研考试【数学(理)试题】(含答案).doc: /file/20316188湖北省黄冈市2013届高三4月调研考试数学文试题__扫描版含答案.doc: /file/20316192福建省龙岩市2013届高三临考适应性检测理科数学卷 1.doc: /file/20316185贵州黔东南州2013年高三年级第二次模拟考试试卷数学文.doc: /file/20316203贵州黔东南州2013年高三年级第二次模拟考试试卷数学理[.doc: /file/203162012013年5月4日福建宁德市普通高中毕业班质量检查数学文(扫描版).doc:/file/203156672013年5月4日福建宁德市普通高中毕业班质量检查数学理(扫描版).doc:/file/203156632013年长春市三摸理科数学试题及答案[学优高考网].doc: /file/20193637【2013邯郸二模】河北省邯郸市2013届高三第二次模拟考试数学文Word版.doc:/file/20246716【2013邯郸二模】河北省邯郸市2013届高三第二次模拟考试数学理Word版含答案.doc:/file/20246714东北三省四市教研协作体2013年高三等值诊断联合考试(长春三模)(word解析版)数学文[学优高考网].doc: /file/20315673东北三省四市教研协作体2013年高三等值诊断联合考试(长春三模)(word解析版)数学理[学优高考网].doc: /file/20315670安徽省2013届高三4月高考模拟数学(文)试题(1.doc: /file/20315680 安徽省2013届高三4月高考模拟数学(文)试题(2).doc: /file/20315744 安徽省安庆市示范中学2013届高三4月联考数学文试题(纯WORD版).doc:/file/20315678安徽省安庆市示范中学2013届高三4月联考数学理试题(纯WORD版).doc:/file/20315676河南省濮阳市2013届高三第二次二模拟考试数学文扫描版含答案.doc: /file/20246808河南省濮阳市2013届高三第二次二模拟考试数学理扫描版含答案.doc: /file/20246787河南省豫东、豫北十所名校2013届高中毕业班阶段性测试(四)word版数学文.doc:/file/20246811河南省豫东、豫北十所名校2013届高中毕业班阶段性测试(四)word版数学理.doc:/file/202468172013揭阳二模数学试题(文科)与答案(精美WORD).doc: /file/20060564 2013揭阳二模数学试题(理科)与答案(精美WORD).doc: /file/20060521太原市2013年高考二模数学文试题及答案.doc: /file/20185651太原市2013年高考二模数学理试题及答案.doc: /file/20185561安徽省安庆市示范高中2013届高三4月联考数学文试题(扫描版).doc: /file/20058824安徽省皖南八校2013届高三第三次联考理科数学试题(word版).doc: /file/20058941山东省济宁市2013届高三4月联考_文科数学_Word版含答案.doc: /file/20060437山东省济宁市2013届高三4月联考_理科数学_Word版含答案.doc: /file/20060401新建文件夹(2).rar: /file/20186103河南省中原名校2013届高三下学期第二次联考数学(文)试题.doc: /file/20185164河南省中原名校2013届高三下学期第二次联考数学(理)试题.doc: /file/20185100河南省郑州市2013年高中毕业年级第二次质量预测数学(文)试题.doc: /file/20184991河南省郑州市2013年高中毕业年级第二次质量预测理科数学试卷.doc: /file/20184930浙江省金华十校2013届高三模拟考试数学(文)试题2013.4.doc: /file/20060458浙江省金华十校2013届高三模拟考试数学(理)试题2013.4.doc: /file/200604762013届安徽省高三四月联考数学试卷(理科).doc: /file/20058813宁夏银川一中2013届高三第一次月考试卷(数学文).doc: /file/19990031开封市2013届高三第一次模拟考试数学试题(文).doc: /file/19990593武汉市2013届高三四月调考理科数学试卷及答案.doc: /file/20013551河南省2013年新课程高考适应性考试(一)数学(文)试题.doc: /file/19944534河南省开封市2013届高三第一次模拟考试数学(理)试题.doc: /file/19990427河南省开封市2013届高三第二次模拟考试数学(文)试题.doc: /file/19990847河南省开封市2013届高三第二次质量检测数学(理)试题_Word版含答案.doc:/file/19990853河南省普通高中2013年新课程高考适应性考试数学(理)试卷.doc: /file/19944526湖北省武汉市2013届毕业生四月调考数学文试题(word版).doc: /file/20013545银川一中2013届高三年级第二次月考数学(文).doc: /file/19990035。
江苏省南京、盐城市2013届高三第三次模拟考试数学试卷(WORD版)

(1)求证:数列{}是等差数列;
(2)若a1=1,且对任意正整数n,k(n>k),都有+=2成立,求数列{an}的通项公式;
(3)记bn=a(a>0),求证:≤.
南京市、盐城市2013届高三第三次模拟考试
数学附加题
注意事项:
1.附加题供选考物理的考生使用.
2.本试卷共40分,考试时间30分钟.
南京市、盐城市2013届高三第三次模拟考试
数学参考答案及评分标准2013.05
说明:
1.本解答给出的解法供参考.如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.
2.对计算题,当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分.
3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.
4.只给整数分数,填空题不给中间分数.
一、填空题:本大题共14小题,每小题5分,共70分.
1.(1,3]2.53.84.5.
6.7.28.①④9.10.2
11.212.2x+y-2=013.(12,17)14.
二、解答题:本大题共6小题,共90分.解答时应写出文字说明、证明过程或演算步骤.
又g(1)=0,且当x→0时,g(x)→-∞,此时曲线y=g(x)与x轴有两个交点.
故m>1不合题意.
综上,实数m的值为m=1.………………………14分
18.解如图所示,不妨设纸片为长方形ABCD,AB=8cm,AD=6cm,其中点A在面积为S1的部分内.
折痕有下列三种情形:
①折痕的端点M,N分别在边AB,AD上;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2000S ≤
N 400S S ←+
Y
0S ←
S 输出 (第3题)
开始
开始
(第5题)
0.0100 0.0175 0.0025
0.0050 0.0150 频率
组距
40 60 80 100 120 140 速度/ km/h
江苏省南通、泰州、扬州、连云港、淮安五市2013届高三第三次模拟考试
数学试卷
一、填空题:本大题共14小题,每小题5分,共70分.
1. 已知集合(]2 1A =-,
,[)1 2B =-,,则A B =U ▲ .
2. 设复数z 满足(34i)50z ++=(是虚数单位),则
复数z 的 模为 ▲ .
3. 右图是一个算法流程图,则输出的S 的值是 ▲ .
4. “M N >”是“22log log M N >”成立的 ▲ 条件.
(从“充要”,“充分不必要”,“必要不充分”中选择一个正确的填写)
5. 根据某固定测速点测得的某时段内过往的100辆
机动车的行驶速度(单位:km/h)绘制的频率分布
直方图如右图所示.该路段限速标志牌提示机动
O 11 5 -1 5
x
(第9题)
y 车辆正常行驶速度为60 km/h~120 km/h ,则该时 段内非正常行驶的机动车辆数为 ▲ .
6. 在平面直角坐标系xOy 中,抛物线22(0)x py p =>上纵坐标为1的一点到焦点的距离为3,则焦点到准线的距离为 ▲ .
7. 从集合{}1 2 3 4 5 6 7 8 9,,,,,,,,
中任取两个不同的数,则其中一个数恰是另一个数的3倍的概率为 ▲ .
8. 在平面直角坐标系xOy 中,设点P 为圆C :22(1)4x y -+=上的任意一点,点Q (2a ,
3a -)
(a ∈R ),则线段PQ 长度的最小值为 ▲ . 9. 函数()sin()f x A x ωϕ=+(0A >,0ω>,02)ϕ<π≤在R 上
的部分图象如图所示,则(2013)f 的值为 ▲ . 10.各项均为正数的等比数列{}n a 中,211a a -=.当3a 取最小值时,数列{}n a 的通项公式a n = ▲ .
11.已知函数2
221 0 () 0ax x x f x x bx c x ⎧--⎪=⎨++<⎪⎩
,≥
,,是偶函数,直线y t =与函数()y f x =的图象自左向
右依次交于四个不同点A ,B ,C ,D .若AB BC =,则实数的值为 ▲ . 12.过点(1 0)P -,作曲线C :e x y =的切线,切点为1T ,设1T 在x 轴上的投影是点1H ,过点1H 再作曲线C 的切线,切点为2T ,设2T 在x 轴上的投影是点2H ,…,依次下去,得到第1n +()n ∈N 个切点1n T +.则点1n T +的坐标为 ▲ .
13.在平面四边形ABCD 中,点E ,F 分别是边AD ,BC 的中点,且AB 1=,2EF =,
CD 3=.
若15AD BC ⋅=u u u r u u u r ,则AC BD ⋅u u u r u u u r
的值为 ▲ .
14.已知实数a 1,a 2,a 3,a 4满足a 1+a 2+a 30=,a 1a 42+a 2a 4-a 20=,且a 1>a 2>a 3,则a 4的取值范围是 ▲ . 二、解答题
15.如图,在四棱锥P ABCD -中,底面ABCD 是矩形,四条侧棱长均相等. (1)求证:AB //平面PCD ; (2)求证:平面PAC ⊥平面ABCD .
16.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,
c .已知222
222
sin 2sin sin C b a c A C c a b --=---. (1)求角B 的大小;
(2)设222sin sin sin T A B C =++,求T 的取值范围.
17.某单位设计的两种密封玻璃窗如图所示:图1是单层玻璃,厚度为8 mm ;图2是双层中空玻璃,厚度均为4 mm ,中间留有厚度为x 的空气隔层.根据热传导知识,对于厚度为d 的均匀介质,两侧的温度差为T ∆,单位时间内,在单位面积上通过的热量
T Q k d
∆=⋅,其中k 为热传导系数.
假定单位时间内,在单位面积上通过每一层玻璃及空气隔层的热量相等.(注:玻璃
A
B
C
(第15题)
P
D
O。
