-拉弯和压弯构件

合集下载

第6章-拉弯和压弯构件

第6章拉弯与压弯构件
压弯（拉弯）构件——同时承受轴向力和弯矩的构件
弯矩的产生
轴向力的偏心作用端弯矩作用横向荷载作用
压弯构件
拉弯构件
拉弯构件:
应用：屋架下弦截面形式：受拉为主，和一般轴心拉杆一样。受弯为主，采用在弯矩作用平面内有较大抗弯刚度的截面。破坏形式：强度破坏，即截面出现塑性铰。
6.2.1 压弯构件在弯矩作用平面内的失稳现象
（a）
在确定压弯构件弯矩作用平面内极限承载力时，可用两种方法。一种是边缘屈服准则的计算方法
通过建立平衡方程，引入等效弯矩系数m=Mmax /M，其中
1 1 N / NE
N E 2 EI / l 2
mM N fy x A Wx (1 x N / N E )
第6章拉弯与压弯构件

拉弯与压弯构件实际上就是轴力与弯矩共同作用的构件，也就是为轴心受力构件与受弯构件的组合，典型的三种拉、压弯构件如下图所示。同其他构件一样，拉、压弯构件也需同时满足正常使用及承载能力两种极限状态的要求。正常使用极限状态：满足刚度要求。承载能力极限状态：需满足强度、整体稳定、局部稳定三方面要求。截面形式：同轴心受力构件，分实腹式截面与格构式截面实腹式：型钢截面与组合截面格构式：缀条式与缀板式
mx M x
N 1xW1x 1 0.8 ' N Ex
f
y
y1
x
f
y
x
y2
N A
mx M x
N 2 xW2 x 1 1.25 ' N Ex
W1x — 受压区边缘的毛截面抵抗矩，W1x I x y1 ； W2 x — 受拉区边缘的毛截面抵抗矩，W2 x I x y2 ；

拉弯和压弯构件(第一讲)

N
Mx
x A
Wpx 1 0.8
N N Ex
fy
3.规范规定的实腹式压弯构件整体稳定计算式
N
mxM x
f
x A
xW1x
1
0.8
RN
N Ex
N 轴向压力；
M x 所计算构件段范围内的最大弯矩；
x 轴心受压构件的稳定系数；
W1x 受压最大纤维的毛截面抵抗矩；
NEx 欧拉临界力，NEx 2EA/ 2x； R 抗力分项系数, Q235: R 1.087, 其它1.111; mx 等效弯矩系数，详见规范取值。
2
0
以Nz/NEy的不同值代入上式得N/NEy和Mx/Mcrx相关曲线:
如偏安全地取Nz/NEy＝1，则上式成为：
Mx M crx
2
1
N N Ey
2
即
N Mx 1 N Ey M crx
用NEy=yAfy，Mcrx=bW1xfy代入上式得规范公式
N tx M x f y A bW1x
v0
1 (
x
1)1 x
Afy N Ex
W1x A
代入上式整理得：
N
x A
Mx
W1x 1x
N N Ex
fy
2.最大强度准则
实腹式压弯构件当受压最大边缘刚开始屈服时尚有较大的强度储备，即容许截面塑性深入。因此若要反映构件的实际受力情况，宜采用最大强度准则，即以具有各种初始缺陷的构件为计算模型，求解其极限承载力。规范考虑截面塑性发展和二介弯矩，对初弯曲和残余应力用综合等效弯矩系数v0，最后提出一近似相关公式：
拉弯构件需要计算：强度、刚度(限制长细比)。
压弯构件需要计算：强度、整体稳定(弯矩作用平面内稳定和弯矩作用平面外稳定)、局部稳定、刚度(限制长细比)。

钢结构——拉弯构件和压弯构件

钢结构——拉弯构件和压弯构件钢结构是指采用钢材作为主要构造材料的建筑结构。

在钢结构中，常见的构件有拉弯构件和压弯构件。

拉弯构件主要承受拉力，而压弯构件则主要承受压力。

本文将分别介绍拉弯构件和压弯构件的特点、设计和应用。

拉弯构件是指同时承受拉力和弯矩的构件。

它们常常用于桥梁、塔架等需要抵抗拉力的结构中。

拉弯构件受力时，在受拉面上会产生拉应变，而在另一侧会产生压应变。

拉弯构件的设计目标是在满足强度和刚度的要求下，最大程度地减小构件重量。

为了实现这一目标，拉弯构件通常采用I型、H型或者箱型截面，这些截面具有较大的截面面积和惯性矩，能够提供足够的强度和刚度。

拉弯构件的设计需要考虑以下几个因素：首先是受力情况。

拉弯构件在受力时，应根据实际情况确定构件的截面形状和尺寸，以满足承受拉力和弯矩的要求。

其次是构件的材料选择。

常见的拉弯构件材料有普通碳素钢和高强度钢。

高强度钢具有较高的强度和刚度，能够减小构件的截面尺寸和重量。

最后是构件的连接方式。

拉弯构件的连接方式有焊接、螺栓连接和铆接等，设计时需要选择适合的连接方式以满足受力要求。

压弯构件是指同时受到压力和弯矩作用的构件。

它们通常用于承担压力的柱子和梁等结构中。

压弯构件在受力时，产生的主要应力是压应力和弯曲应力。

与拉弯构件相比，压弯构件的设计更加复杂，需要考虑稳定性问题。

在设计过程中，需要根据实际情况确定构件的截面形状和尺寸，以满足承受压力和弯矩的要求，并保证构件的稳定性。

常见的压弯构件截面有角钢、工字钢和管材等。

与拉弯构件相比，压弯构件的设计更注重稳定性。

在设计压弯构件时，需要考虑构件的临界压弯强度，即其能够承受的最大弯矩和压力。

为了提高构件的稳定性，常见的设计方法有增大截面尺寸、采用合适的截面形状、设置剪力加强构件等。

此外，还需要考虑构件的支撑条件和边界约束等因素，以保证压弯构件在受力过程中不发生屈曲或失稳。

拉弯构件和压弯构件在钢结构设计和应用中都起着重要的作用。

第六章拉弯和压弯构件10.22

15:55
6
二、强度计算公式
将受压区应力图形分解成有斜线和无斜线的两部分，使受压区有斜线腹板的面积与受拉区的应力图形面积相等，则两者的合力组成一力偶组成一力偶，其值等于截面上的弯矩弯矩，而受压区组成一力偶弯矩中无斜线部分的合力合力则代表截面上的轴心压力合力轴心压力
Mx = 1 1 1 2 f y bh 2 f y b (α h ) = f y bh 2 (1 α 2 ) 4 4 4
N M + =1 N Ey M cr
N N M 1 1 Ey =0 N N M Nω cr Ey Ey
N N Ey
N Ey = y Af y
M cr = bW1x f y
该相关公式是由弹性理论推导得出，但通过计算分析比较可知，构件在弹塑范围工作在弹塑范围工作时 N / NEy + M / Mcr 都大于1，而且大得不多，故仍可以偏安全可以偏安全地采用上面的相关公式。地采用上面的相关公式
x f y A W1x e0 = (1 x ) 1 N Ex x A
将e0值代入，整理得
N + x A
Mx N W1x 1 x N Ex
ym
= fy
上式为压弯构件按边缘屈服准则导出的相关公式屈服准则导出的相关公式。屈服准则导出的相关公式
N
e
15:55
13
2.最大强度准则
15:55 15
所计算构件段范围内的最大弯矩
N + x A
β mx M x γ xW1x 1 0.8
N ′ N Ex
≤f
等效弯矩系数的取值：等效弯矩系数的取值：
分类框架柱和两端支承的构件无横向荷载作用时

【土木建筑】第6章拉弯与压弯构件

15鏈?----灏忕
櫧榧犲拰ERP.files/cio.gif
冩??=/ERP鏂噡1/2001
15
Z0 l~@ 慶琶 5艭危??內? g??a? J ?χ??$ゥ孅?0lH ` ?' R?;N?囏a杸) G????t$撈0??c+ 僿??v胐顑o 2 ??? ??刻' N稍嶀?寃??泲? ?a碍鹄YZF猏虓 [贋用` 拷T,V3B励 =桽\= •?ST傄u烶輤腙€鲳0_儖?絅= 计裌巹4 ~{飪秞 ?• 塀'墕銒 t[隿+ 废榰N 82 )撅 ~ ?uG?
4/ERP鏂噡1/2001
15鏈?----
灏忕櫧榧犲拰ERP.files/ </ERP
鏂噡1/2001
15鏈?----灏忕
櫧榧犲拰ERP.files/0830.gif 冪╒
阇?/ERP鏂噡1/2001
15鏈?-
---灏忕櫧榧犲拰
ERP.files/biaoshi.gif 冭賏?;/ERP
鏂噡1/2001
如果M=0，则构件变为轴心压杆，则有N Nx Afyx
代入上式便有：

Af yx
A

Af yxv0
W1x (1 Af yx
NEx )
f y (b)
联立1、2两式，消去v0 则有：
N
Mx
x A W1x (1x N
NEx )
fy
N
mxM x
x A W1x (1x N
同其他构件一样，拉、压弯构件也需同时满足正常使用及承载能力两种极限状态的要求。
正常使用极限状态：满足刚度要求。承载能力极限状态：需满足强度、整体稳定、局部稳
定三方面要求。截面形式：同轴心受力构件，

钢结构设计原理---拉弯压弯构件

max maxx,y []
[]取值同轴压构件。
第六章拉弯、压弯构件
§6.2 拉弯、压弯构件的强度
对拉弯构件、截面有削弱或构件端部弯矩大于跨间弯矩的压弯构件，需要进行强度计算。
hw h
h (1-2)h h
Af=bt y
x Mx x Aw=hwtw
y
fy
fy
fy
fy H
N
H
fy
fy
(a) (b) (c
第六章拉弯、压弯构件
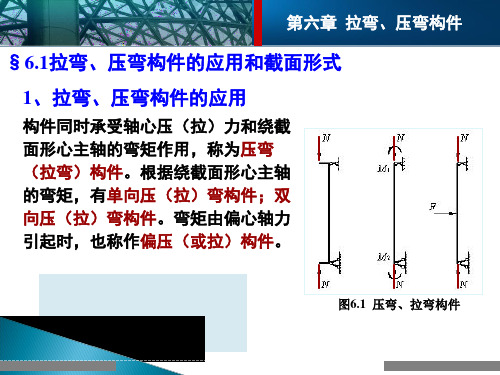
§6.1拉弯、压弯构件的应用和截面形式 1、拉弯、压弯构件的应用
构件同时承受轴心压（拉）力和绕截面形心主轴的弯矩作用，称为压弯（拉弯）构件。根据绕截面形心主轴的弯矩，有单向压（拉）弯构件；双向压（拉）弯构件。弯矩由偏心轴力引起时，也称作偏压（或拉）构件。
图6.1 压弯、拉弯构件
2. 箱形截面的腹板
考虑到两块腹板可能受力不均，因而箱形截面高厚比值取为共字
型截面腹板的0.8倍。但不应小于
40 235/ fy
第六章拉弯、压弯构件
3.T形截面的腹板
当弯矩作用在T形截面对称轴内并使腹板自由边受压时：
当0≤1.0时
h0 15 tw
235/ fy
（6.26a）
当0＞1.0时
h0 18 tw
（6.4）
第六章拉弯、压弯构件
1.单向拉弯、压弯构件强度计算公式
N Mx f
An xWnx
（6.5a）
第六章拉弯、压弯构件
2.双向拉弯、压弯构件强度计算公式
N Mx My f
An xWnx yWny
（6.5b）
N——轴心压力设计值
An——验算截面净截面面积

钢结构设计原理-第6章-拉弯和压弯构件概要

(6.2.2)
第6.3节压弯构件的稳定
本目录
1. 弯矩作用平面内的稳定性 2. 弯矩作用平面外的稳定 3. 双向弯曲实腹式压弯构件的整体稳定 4. 压弯构件的局部稳定
基本要求
1. 理解实腹式压弯构件的整体稳定性的概念 2. 2. 了解在弯矩作用平面内与弯矩作用平面外失
稳破坏的情况与验算方法
6.3.1 弯矩作用平面内的稳定性
本章目录
6.1 概述 6.2 拉弯和压弯构件的强度 6.3 压弯构件的稳定 6.4 压弯构件（框架柱）的设计 6.5 框架柱的柱脚
基本要求
1．了解拉弯和压弯构件的构造特点和构造要求。 2．掌握拉弯和压弯构件的破坏形式和计算方法。
第6.1节概述
本节目录
1. 拉弯构件 2. 压弯构件
基本要求
1 . 建立拉弯构件与压弯构件的概念 2 . 了解设计计算的内容
加挠度将使各截面的弯矩增大，如果假定构件的挠曲
线与正弦曲线的半个波段相一致，则中央截面的最大
弯矩为：
Mmax1NM/NE
(6.3.3)
在式中
NE，为2E 欧拉/Il2 临界力。
称为1弯矩放大系数。 1 N / NE
2.允许截面发展一定的塑性
如前所述，以点A'（图6.3.2）作为承载力极限状态时，该点对应的极限弯矩为：
压弯构件整体破坏的形式有以下三种：（1）因端部弯矩很大或有较大削弱而发生强度破坏，（2）在弯矩作用平面内发生弯曲屈曲，（3）在弯矩作用平面外发生弯扭屈曲。
组成截面的板件在压应力作用下也可能发生局部屈曲。
第6.2节拉弯和压弯构件的强度
本节目录
1.拉弯和压弯构件的强度和刚度计算
基本要求

第七章拉弯和压弯构件

例7.1 如下图所示拉弯构件，承受的荷载的设计值为：轴向拉力800kN，横向均布荷载7kN/m。试选择其截面，设截面无削弱，材料为Q235钢。
解：
试采用普通工字钢I28a，截面面积A＝55.37cm2，自重0.43kN/m，Wx＝508cm3，ix＝11.34cm，iy＝2.49cm。构件截面最大弯距Mx＝（7+0.43×1.2）×62/8＝
Af＝aAW a＝Af/AW
（7.4）
工字形截面绕强轴受弯的压弯构件轴力弯距相关曲线：式（7.3）、式（7.4）曲线
规范采用直线式相关公式代替曲线公式：
（7.5）
曲线与直线相差不大直线考虑附加挠度的不利影响直线代替曲线偏安全
式（7.3）和（7.4）曲线
式（7.5）直线
考虑截面塑性部分发展
➢ W1x－按受压最大纤维确定的毛截面的模量
较适用于格构式构件，
对短粗实腹杆偏于安全，对细长实腹杆偏于不安全
❖ 7.3.1.2 最大强度准则
容许截面塑性深入，以具有各种初始缺陷的构件为计算模型，求解其极限承载能力
考虑一定初弯曲和实测残余应力数值计算得到200 条相关曲线
考虑截面的塑性发展，借用边缘纤维屈服准则公式（7.10）根据极限承载力曲线，得出近似相关公式：
压弯构件
拉弯构件
拉弯和压弯构件也可按其截面形式分为实腹式构件和格构式构件两种
➢ 当受力较小时，可选用热轧型钢或冷弯薄壁型钢截面
➢ 当受力较大时，可选用钢板焊接组合截面或型钢与型钢、型钢与钢板的组合截面
➢ 当构件计算长度较大且受力较大时，为提高截面的抗弯刚度，采用格构式截面
➢ 对称截面一般适用于所受弯矩值不大或正负弯矩值相差不大的情况

钢结构设计原理6拉弯和压弯构件

N
mxM x
tyM y f
x A
xWx
1
0.8
N N 'Ex
byW1x
N
myM y
txM x f
yA
yWy
1
0.8
N
N
' Ey
bxWx
6.4 实腹式压弯构件的局部稳定为保证压弯构件中板件的局部稳定，限制翼缘和腹板的宽厚比及高厚比。 6.4.1 受压翼缘的宽厚比压弯构件受压翼缘应力情况与梁受压翼缘基本相同，因此自由外伸宽度与厚度之比以及箱形截面翼缘在腹板之间的宽厚比均与梁受压翼缘的宽厚比限值相同。 6.4.2 腹板的高厚比 1.工字形截面平均剪应力和不均匀正应力共同作用下，临界条件
N p Af y (2 1) Aw f y
M px W px f y (Awh 0.25 Awh) f y ( 0.25) Awhf y
(2 1)2 4 1
N2
N
2 p
Mx M px
1
(2)中和轴在翼缘范围内
N Aw f y
4 1 M x N 1 2(2 1) M px N p
根据内外力平衡条件，由一对水平力H所组成的力偶与外
力矩M平衡，合力N应与外轴力平衡，为了简化，取
h hw A f Aw A (2 1) Aw
内力的计算分为两种情况：
(1)中和轴在腹板范围内
N Aw f y
N (1 2)htw f y (1 2) Aw f y
M x Af hf y Aw f y (1)h Awhf y ( 2 )
1.边缘屈服准则
横向荷载产生的跨中挠度为vm 。当荷载对称时，假定挠曲线为正弦曲线。轴心力作用后，挠度增加，在弹性

拉弯压弯构件

6.5.2 框架柱的计算长度
在钢结构中，多数压弯构件都是框架结构的组成部分，两端受到其它构件的各种约束，这时，压弯构件即框架柱的稳定应由框架的整体稳定决定。因此，不能单独研究压弯构件，必须取整个框架或框架的一部分进行分析。
第6章拉弯构件和压弯构件
关于框架柱的稳定设计，目前有两种方法:
一种是采用一阶理论，不考虑框架变形的二阶影响，计算框架由各种荷载设计值产生的内力，把框架柱作为单独的压弯构件来设计，将框架整体稳定问题简化为柱的稳定计算问题。
min N
M min
max N
M max
应力梯度
0 ( max min ) / max
第6章拉弯构件和压弯构件
第6章拉弯构件和压弯构件
第6章拉弯构件和压弯构件
第6章拉弯构件和压弯构件
第6章拉弯构件和压弯构件
第6章拉弯构件和压弯构件
第6章拉弯构件和压弯构件
第6章拉弯构件和压弯构件
第6章拉弯构件和压弯构件
第6章拉弯构件和压弯构件
第6章拉弯构件和压弯构件
第6章拉弯构件和压弯构件
6.3.3 双向弯曲实腹式压弯构件的整体稳定
弯矩作用在两个主轴平面内的压弯构件为双向弯曲压弯构件，在实际工程中应用较少。双向弯曲压弯构件丧失整体稳定性属于空间失稳，理论计算非常繁杂，目前多采用数值分析法求解。为便于应用，并与单向弯曲压弯构件计算相衔接，多采用相关公式形式计算。 <规范>规定：弯矩作用在两个主轴平面内的双轴对称实腹式工字形（含H形）和箱形（闭口）截面的压弯构件的稳定性计算按下列相关公式进行：
第6章拉弯构件和压弯构件
6.4.1压弯构件翼缘的宽厚比限值

第6章拉弯和压弯构件

N N Ey
1
N N Ey
N Ey N
Mx M crx
2
0
N / NEy
1.0
0.0
1 0.5
N / NEy 5 2
0.2
M x / Mcrx
1.0
大多数工程构件
N /NEy 1
即 N Mx 1
NEy M crx
可视为压弯杆件平面外稳定的下限值
第6章拉弯和压弯构件
压弯杆件平面外稳定工程计算公式的表达
Mx
N
y
v
Mx zN
稳定问题要采用二阶分析——在荷载产生变形的基础上建立平衡方程构件的侧向变形与轴力N 产生附加的弯矩——称P－δ效应(二阶效应) 构件的挠度比仅因弯矩产生的挠度增大——放大效应
弯矩等效
第6章拉弯和压弯构件
压弯构件考虑轴压力作用的弹性弯曲平衡方程
Mx
N
y6章拉弯和压弯构件
例如工业厂房的变截面柱为压弯构件 eN
MN
截面类型
第6章拉弯和压弯构件
截面选择
受力状态 -轴压为主，弯矩为辅 -单向弯矩为主 -双向压弯
截面类型与选择
双轴对称,两主轴长细比接近( λx = λy ) 双轴对称或单轴对称
第6章拉弯和压弯构件
拉、压弯构件的计算内容
拉弯构件
轴力—弯曲挠度变形曲线
第6章拉弯和压弯构件
部分考虑塑性发展的弹塑性设计方法：
N / Np 1.0
N / Np 1.0
20 40
偏心率0y =1
80 120
vmax /
0 20
截面承载力
80
轴力—弯曲挠度变形曲线
(以长细比为参数)

第六章拉弯和压弯构件

三、截面形式当弯矩较小和正负弯矩绝对值大致相等或使用上有特殊要求时，常采用双轴对称截面。当构件的正负弯矩绝对值相差较大时，为了节省钢材，常采用单轴对称截面。
四.拉弯构件的设计要求需进行强度和刚度计算。五、压弯构件的设计要求 1．压弯构件的破坏方式：（1）强度破坏。
（2）为弯矩作用平面内丧失整体稳定当N<Nux时，构件内、外力矩的平衡是稳定的。当N达到Nux后，在减小荷载情况下v 仍不断增大，截面内力矩已不能与外力矩保持稳定的平衡。称这种现象为压弯构件丧失弯矩作用平面内的整体稳定，它属于弯曲失稳（屈曲）。（3）弯矩作用平面外丧失整体稳定当荷载达某一值Nuy ，构件将突然发生弯矩作用平面外的弯曲变形，并伴随绕纵向剪切中心轴的扭转，而发生破坏。称这种现象为压弯构件丧失弯矩作用平面外的整体稳定，它属于弯扭失稳（屈曲）。（4）局部失稳（屈曲）将导致压弯构件整体稳定承载力降低。 2. 设计要求应进行强度、刚度、整体稳定性和局部稳定性计算。
第六章拉弯和压弯构件第一节概述一、定义同时承受弯矩和轴心拉力或轴心压力的构件称为拉弯构件或压弯构件。压弯构件也称为梁—柱。二、应用单层厂房的柱、多层或高层房屋的框架柱、承受不对称荷载的工作平台柱、以及支架柱、塔架、桅杆塔等常是压弯构件；桁架中承受节间内荷载的杆件则是压弯或拉弯构件。
2.箱形截面的腹板箱形截面的腹板箱形截面腹板边缘的嵌固程度比工字形截面弱，且两块腹板的受力情况也可能有差别，腹板的 h0/tw不应超过上式右侧乘以0.8后的值，当此值小于 40 235 / f 时，应采用 40 235 / f 。
y y
3. T形截面的腹板形截面的腹板当α0 ≤1时，应力分布不均的影响小，限值取 h 与翼缘相同， / t ≤ 15 235 / f 。当α0>1时，应力分布不均的有利影响较大,限值提高20%，取为：

拉弯和压弯构件

算例3图
截面几何特征计算
[解] 一、截面几何特征
A = 2 × 35 × 1.4 + 57 × 0.8 = 143.6cm 2
0.8 × 57 Ix = + 2 × 35 × 1.4 × 29.2 2 = 95900cm 4 12
3
1.4 × 353 = 10000cm 4 Iy = 2× 12
Mx N 980 × 10 3 675 × 10 6 + = + 2 An γ W x 143 . 6 × 10 1 . 0 × 3207 × 10 3
= 68 .2 + 210 .5 = 278 . N/mm
= 315 N/mm 2 ( 满足 )
2
< f
验算截面： λ、φ、N计算
2. 在弯矩作用平面内稳定
i、W的计算
ix =
Ix = A
95900 = 25 .8 cm 143 . 6
iy =
Iy A
=
10000 = 8 . 35 cm 143 .6
W1 x
95900 = = 3207 cm 3 29 . 9
验算截面：强度
二、验算截面 1. 强度
1 1 M x = PL = × 18 ×15 = 675kN ⋅ m 4 4
λ — 构件在弯矩作用平面内长细比，λ< 30时，取λ=30，λ >100时，取λ=100。
腹板宽厚比限值：箱、T形
2. 箱形 A、取工字形截面结果的0.8倍
h0 235 h0 235 时，取 = 40 。 B、 ≤ 40 tw fy tw fy
3. T形
α 0 ≤ 1.0时， α 0 > 1.0时，
2

钢结构—— 拉弯构件和压弯构件

N
N
N
N
P
N
N
图6.1 压弯构件
N
N
6.2 拉弯和压弯构件的强度
双向拉弯和压弯构件
N An

Mx xWnx
yWny f
My
（6.7）
An --- 净截面面积 Mx、My --- 绕x轴和y轴的弯矩 Wnx、Wny --- 对x轴和y轴的净截面模量 γx、γy --- 截面塑性发展系数,
2
f
M2 N
x — 平面内轴心受压构件的稳定系数；
M x — 压弯构件的最大弯距设计值；
— 参数； N Ex
W1x— 平面内对较大受压纤维的毛截面抵抗矩
mx— 等效弯距系数；
M1
N
二、弯矩作用平面外的稳定
tx M x N f y A bW1x
y
——弯距作用平面外轴心受压构件的稳定系数；
第六章拉弯和压弯构件
本章内容: (1)拉弯和压弯构件的强度和刚度 (2)压弯构件的稳定本章重点：压弯构件的稳定本章难点：压弯构件的稳定本章要求：了解压弯和拉弯构件的强度计算了解压弯构件的稳定计算
6.1 概述
压弯(拉弯)构件：同时承受轴心力和弯矩的构件。产生原因：偏心荷载、横向荷载、弯距作用
6.3 、刚度

拉弯和压弯构件的允许长细比[λ]同轴心受力构件
6.4
压弯构件的稳定
一、弯矩作用平面内的稳定
y
X
y
X
X y M.13）
N x A

mx M x ) xW1 x (1 0.8 N / N Ex
EA N Ex 2 1.1x
M x ——所计算构件段范围内的最大弯距设计； η ——截面影响系数，箱形截面取0.7，其他截面取1.0