第九章统计热力学初步
第九章统计热力学初步学习指导

第九章统计热力学初步8+2学时本章从最可几分布引出配分函数的概念,得出配分函数与热力学函数的关系。
由配分函数的分离与计算可求得简单分子的热力学函数与理想气体简单反应的平衡常数。
使学生了解系统的热力学宏观性质可以通过微观性质计算出来。
基本要求:1、理解统计热力学中涉及的一些基本概念如(定域子系统与非定位系统、独立粒子系统与相依粒子系统、微观状态、分布、最可几分布与平衡分布、配分函数)2、理解统计力学的三个基本假定。
理解麦克斯韦–玻尔兹曼分布公式的不同表示形式及其适用条件。
3、理解粒子配分函数的物理意义和析因子性质。
4、明确配分函数与热力学函数间的关系5、了解平动、转动、振动对热力学函数的贡献,了解公式的推导过程。
6、学会利用物质的吉布斯自由能函数、焓函数计算化学反应的平衡常数与热效应。
7、学会由配分函数直接求平衡常数的方法重点:1.平衡分布和玻耳兹曼分布公式;2.粒子配分函数的定义、物理意义及析因子性质;3.双原子分子的平动、转动和振动配分函数的计算;4.热力学能与配分函数的关系式;5.熵与配分函数的关系式;玻耳兹曼熵定理。
难点:1. 粒子配分函数的定义、物理意义及析因子性质;2. 双原子分子的平动、转动和振动配分函数的计算。
第九章统计热力学初步主要公式及其适用条件1. 分子能级为各种独立运动能级之和2. 粒子各运动形式的能级及能级的简并度(1)三维平动子简并度:当a = b = c时有简并,()相等的能级为简并的。
(2)刚性转子(双原子分子):其中。
简并度为:g r,J = 2J +1。
(3)一维谐振子其中分子振动基频为,k为力常数,μ为分子折合质量。
简并度为1,即g v,ν = 1。
(4)电子及原子核全部粒子的电子运动及核运动均处于基态。
电子运动及核运动基态的简并度为常数。
3.能级分布微态数定域子系统:离域子系统:温度不太低时(即时):一般情况下:系统总微态数:4. 等概率定理在N,V,U确定的情况下,系统各微态出现的概率相等。
物理化学复习二

,其中 A=0.509(mol-1·kg)1/2 ,I = (1/2) S bBZB2 2. 原电池 (1) 热力学
D G= -zFE D S= -(G/ T)p = zF ( E/ T)p D H =D G + T D S = -zFE +zFT( E/ T)p Qir = T D S =zFT( E/ T)p (2) 能斯特方程 D rGmq = -zFEq = -RTlnKq
(2) 可以将煤的燃烧反应 C(石墨) + O2 CO2设计成电池。 已知 25℃、pq 时,C(石墨)的燃烧焓为 -393.51kJ·mol-1;C(石墨)、CO2(g)、
O2(g)的标准摩尔熵分别为5.69、213.64和205.03J·mol-1·K-1。 (a) 求该电池的标准电动势E q;
(1) 氧分子的平动配分函数。 (2) 氧分子的转动配分函数(已知转动惯量I为1.935×10-46 kg·m2)。
(3) 氧分子的振动配分函数 qv0 (已知其振动频率为4.648×1013s-1)。 (4) 氧分子的电子配分函数(已知电子基态的简并度为3,电子激发态 可忽略)。 (5) 忽略振动和电子的影响,估算氧分子的恒容摩尔热容。 已知阿伏加德罗常数L=6.022×1023mol-1,普朗克常数h=6.626×10-34J·s, 光速k=1.381×10-23J·K-1。 解:(1) V=nRT/p = 1mol×8.3145J.mol-1.K-1×298.15K/100000Pa = 0.02479 m3 qt =
统计热力学基础

统计热力学基础教学目的与要求:通过本章的教学使学生初步了解统计热力学的基本研究方法,各种独立子系统的微观状态数的求法,不同系统的统计规律,系统的各热力学函数的表示式,配分函数的计算,固体的热容理论导出的基本思路。
重点与难点:统计热力学的基本研究方法,不同系统的微观状态数的计算,玻尔兹曼分布律的含义,系统的热力学函数的表示式,配分函数的计算,不同的固体热容理论的基本方法。
概论统计热力学的研究任务和目的统计力学的研究对象是大量微观粒子所构成的宏观系统。
从这一点来说,统计热力学和热力学的研究对象都是一样的。
但热力学是根据从经验归纳得到的四条基本定律,通过演绎推理的方法,确定系统变化的方向和达到平衡时的状态。
由于热力学不管物质的微观结构和微观运动形态,因此只能得到联系各种宏观性质的一般规律,而不能给出微观性质与宏观性质之间的联系。
而统计热力学则是从物质的微观结构和基本运动特性出发,运用统计的方法,推导出系统的宏观性质,和变化的可能方向。
统计力学的研究方法是微观的方法,它根据统计单位(微粒)的力学性质如速度、动量、位置、振动、转动等,用统计的方法来推求系统的热力学性质,例如压力、热容、熵等热力学函数。
统计力学建立了体系的微观性质和宏观性质之间的联系。
从这个意义上,统计力学又可称为统计热力学。
相对于热力学,统计力学对系统的认识更深刻,它不但可以确定系统的性质,变化的方向和限度,而且还能确定系统的性质的微观根源,这一点要比热力学要深刻。
对于简单系统,应用统计热力学的方法进行处理,其结果是令人满意的。
当然统计热力学也有自身的局限性,由于统计力学要从微观粒子的基本运动特性出发,确定系统的状态,这就有一个对微观粒子的运动行为的认识问题。
由于人们对于物质结构的认识不断深化,不断地修改充实物质结构的模型,所对统计理论和统计方法也要随之修改,所以统计理论是一种不断发展和完善的。
同时模型本身也有近似性,所以由此得到的结论也有近似性。
统计热力学基础第九章2
l l al e 3 h
e
N Z1
Z1 V (
2m 3 / 2 ) 2 h
al
V
dxdydzdp x dpy dpz h
1
3
e
l
N 2m 3 / 2 V( 2 ) h
2 2 ( p2 1 x p y pz ) 3/ 2 N( ) e 2 mkT dpx dpy dpz 2mkT
配分函数的分离
根据配分函数的定义,将 i 和 i 的表达式代入,得:
q i exp(
i
i
kBT
)
i ,ti ,ri ,vi ,ei ,n exp(
i
i ,t i ,r i ,v i,e i,n
kBT
)
从数学上可以证明,几个独立变数乘积之和等于
f (v) m 3/ 2 [4 N ( ) e v v 2 kT [e v
mv 2 2 kT
mv2 2 kT
v2 ] 0
v2] 0
e
mv m 2 2 kT
mvm 2 [( )vm 2v m ] 0 kT
2kT m 2 RT M
vm
用分布函数计算与速率有关的物理量 在速率 0 ~ 区间内的平均值
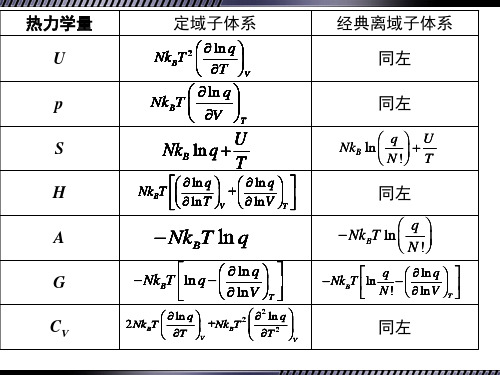
SV Nk B ln qV Nk BT
d ln qV dT
d ln qe Se Nk B ln qe Nk BT dT d ln qn Sn Nk B ln qn Nk BT dT
的不可分辨性是与平动相联 系的。
§9.4 平动配分函数
1. 一维平动子:
0
2
大学物理第九章热力学讲解

i C R
V2
单 i 3 双 i 5 多 i 6
i 气体分子的自由度
ν摩尔理想气体在等体过程中, 温度从T1升高到 T2(或降低) ,吸收的热量为
Q V
E - E
2
1
i RT - T
2
2
1
CV T2 - T1
2
1
2
2
1
V
Q E - E + pV V
p
2
1
2
1
C DT + RDT V
定压摩尔热容: 1mol 理想气体在等压过程中吸
收的热量dQp ,温度升高 dT,其定压摩尔热容为
dQ C p
dT p ,m
dQ C dT
p
p ,m
定压摩尔热容另一表述: 1mol 理想气体在等压
p
等 p2 体
升 压
p1
o
2 ( p2,V ,T2 )
1 ( p1,V ,T1)
V
V
T1 T2 Q 0 DE 0
QV
E1
E2
p
等 p1
体
降 压
p2
o
Q E - E i RT - T
V
2
1
2
2
1
1( p1,V ,T1)
2( p2,V ,T2 )
V
V
T1 T2 Q 0 DE 0
2 公式适用条件 气体压强不太大,温度不太低,密度不太高
例1 一容器内贮有氧气 0.10kg,压强为10atm, 温度为 470C。因容器漏气,过一段时间后,压强 减到原来的 5/8,温度降到 270C。问: (1)容器体积为多大? (2)漏去了多少氧气?
09章_统计热力学基础(2)

Ni i
t non −local
g =Π Ni!
由此可见,定位 体系与非定位体 系,最概然的分 布公式是相同的。
Ni i
∂ ln t + α + βε i = 0 ∂N i
−εi / kT * i
gi e N =N −εi / kT ∑gi e
i
上一内容 下一内容 回主目录
返回
上一内容 下一内容 回主目录
返回
根据
•根据对物质结构的某些基本假定 •实验所得的光谱数据 求得 •物质结构的一些基本常数 计算 •分子配分函数 计算 热力学性质
上一内容 下一内容 回主目录
返回
9.3 配分函数
配分函数的定义 配分函数的分离 非定位体系配分函数与热力学函数的关系 定位体系配分函数与热力学函数的关系
上一内容
下一内容
回主目录
返回
简并度(degeneration)
能量是量子化的,但每一个能级上可能有若 干个不同的量子状态存在,反映在光谱上就是代 表某一能级的谱线常常是由好几条非常接近的精 细谱线所构成。 量子力学中把能级可能有的微观状态数称为 该能级的简并度,用符号 gi 表示。
上一内容
下一内容
A,B,C
A B C BC AC AB BC AC AB A B C ABC 0 0 ABC
23=8 or
giN1,
上一内容
下一内容
回主目录
返回
有简并度时定位体系的微态数
先从N个分子中选出N1个粒子放在 1 1 能极 εε
N 上,有 C N 1 种取法;
但 ε1 能极上有 g1个不同状态,每个分子在ε1
求和的限制条件仍为:
第9章_统计热力学初步-wfz-1

§9.2 能级分布的微观状态数及系统的总微态数
1. 能级分布
平衡系统中, 粒子各能级的能量值只与粒子的性质及 V有关,所 以平衡系统中各能级的能量也完全确定
任何一种能级分布均应服从 粒子数及能量守恒关系:
ì U = ï ï ï í ï N = ni
å
i
由于粒子的不停运动并彼此交换 能量 , 使 N 、 U 、 V 确定的系统并非 只有一种能级分布。
h2 et = 8m
2 骣 2 2 ny nx nz 琪 琪 + + 琪 2 2 琪 a b c2 桫
(n x , n y , n z
势箱边长
= 1, 2, L
量子数
)
m 为分子质量 a、b、c 为容器边长 h 为Planck常数
yn
x ,n y ,n z
对应于量子数
n x , n y , n z的量子态
3
量子态: 系统中粒子所处的各种不同的微观状态. 能级: 粒子能量相同的一组量子态组成一个能级.不同能级的 能量 i值是不连续的, 即量子化的. 在一定宏观状态的独立子系统中, 系统的总粒子数N 和总能量U 是不变的, 若处于能级i的粒子数目为 ni ,必然有 N ni U ni i
11.622
10-
40
J
e t, 1 - e t, 0 = (11.622 - 5.811 )? 10-
40
J
5.811
10-
40
J
由以上计算知:平动子相邻能级的能量差Δ 非常小,所以平动子 很容易受激发而处于各能级。在常温下,平动子的量子化效应不突出, 可近似用经典力学方法处理。
10
2. 分子转动 双原子分子可近似看作原子间距 d 保持不变的刚性转子 . 转子的转动惯量 I :
物理化学 天津大学第四版 课后答案 第九章 统计热力学初步

0
0
2
4
6
8
10
12
c QuantumNumber J
差 ∆ε = 0.426 ×10−23 J ,试求 300
. K
时
I2
分子的 Θv
、 qv
、
q
0 v
及
f
0 v
。
hν ∆ε
w ∆ε
解:分子的振动特征温度为
=
hν , Θv
=
k
=
k
= 308.5 K
a 分子的振动配分函数为
d 1
1
q = e − e = e − e v
. nj+1 w nj
= exp(− ∆ε
kT
)
=
⎧5.409 ⎨
×
10 −7
for
⎩0.3553 for I 2
HCl
课 后 答 案 网
a 12.试证明离域子系统的平衡分布与定域子系统同样符合波尔兹曼分布,即
d ni =
N q
gi
exp {-
ei
kT }
h 略。
k 14.2 mol N2 置于一容器中,T = 400 K, p = 50 kPa ,试求容器中 N2 分子的平动 . 配分函数。
能级上粒子的分布数 n 与基态能级的分布数 n0 之比。
解:根据 Boltzma nn 分布
n n0
=
g g0
exp{− (ε
− ε0)
kT} =
g g0
exp{− 11× 0.1kT
kT}
g = 0.3329
g0
( ) 基态的统计权重 g0 = 1,能级
nx2
第九章 统计热力学

一、统计热力学在物理化学中的地位
大量微观粒子构成的宏观系统
宏观性质 →宏观性质
微观结构和运动 →宏观性质
宏观现象是微观运动的结果
宏观现象与微观现象有差别
研究 对象
以由大量微观粒子构成的宏观系统
研究方法
从物质的微观结构和微观运动形态出发,利用统计 平均的方法来获得物质的各种宏观性质
研究作用
统计热力学是联系物质宏观特性与微观性质的桥梁,它 弥补了热力学的不足,两者彼此联系,互相补充。 利用统计热力学方法不需要低温下的量热实验,就能求 得熵函数,其结果甚至比热力学第三定律所得的熵值更准确。
宏观系统是由大量微观粒子构成的。 对于总粒子数为N,总能量为U,体积为V的独 立子系统,每个粒子的能量是不完全相同的,并
且随着粒子之间的能量交换,每个粒子能量也是
变化的。但系统中总粒子数不变和系统总能量是 不变的,应遵循下面的关系式
一、独立子系统中粒子数和能量守衡关系式
N nj
状态分布
j
三、粒子各运动形式的能级及简并度
1. 三维平动子
能级公式:
讨论:
2 n 2 n 2 nz h x y t 2 2 8m a 2 b c 2
(9.1.1a)
1)式中:h 6.626 10
34
J s ,称为普郎克常数
2)式中(nx,ny,nz)是表示三维平动子每个量子状态的一组平动 量子数,分别说明三个互相垂直方向平动能的分量,其值只能
0 1
g0
2
g2
… … … · · ·
j
gj
· · ·
能级简并度 粒子分布数
g1
· · ·
物理化学第九章 统计热力学初步

统计热力学的基本任务
根据对物质结构的某些基本假定,以及实 验所得的光谱数据,求得物质结构的一些基本常 数,如核间距、键角、振动频率等,从而计算分 子配分函数。再根据配分函数求出物质的热力学 性质,这就是统计热力学的基本任务。
定域子系统和离域子系统
粒子(子)(particles) ——聚集在气体、液体、固 体中的分子、原子、离子等。
t r v e n
同时,其简并度等于各独立运动形式的简并度之 积:
g gt gr gv ge gn
运动自由度
对于一个具有n个原子的分子,通常有3n个自 由度,分别为: 3个平动自由度(xyz轴方向的平动) 3个转动自由度(围绕三个轴的旋转) 3n-6个振动自由度 对于线型分子,转动自由度为2(围绕线轴的 旋转可忽略),振动自由度为3n-5
系统的可能的能级分布方式有:
能级分布数
能级分布 n0
n1
n2 n3
Σni
Σniεi =9hν/2
Ⅰ 0 3 0 0 3 3×3 hν/2=9hν/2
Ⅱ 2 0 0 1 3 2×hν/2+1×7hν/2=9hν/2
Ⅲ 1 1 1 0 3 1×hν/2+1×3hν/2 +1×5hν/2=9hν/2
2.状态分布
1.分子的平动
t
h2 8m
(
nx2 a2
n2y b2
nz2 c2
)
对立方容器a=b=c,V=a3
t
h2 8mV 3 / 2
( nx2
n2y
nz2
)
量子力学中把能级可能有的微观状态数称为该 能级的简并度(degeneration),用符号g表示。 简并度亦称为退化度或统计权重。
热力学与统计物理第九章系综理论

§微正则系综 (Microcanonical Ensemble)
一. 等概率假设
孤立系是与外界既无能量交换又无粒子交换的系统。 由于绝对的孤立系是没有的。所以精确的说,孤立 系是指能量在E~E+∆E之间,且∆E<<E的系统。尽 管∆E很小,但在此范围内,系统可能具有的微观状
(q, p) 是系统的某一微观态出现在Г空间中
(q, p) 处的概率。
说明:(1)推论:具有同一能量和同一粒子数的全 部微观状态都是可以经历的;因为只有它们 是可以经历的,才谈得上是等概率的
(2)微正则分布是平衡态统计系综理论中的唯一基 本假设,其正确性由它的推论与实际结果符合而 得到肯定 二.系统的微观态数
当粒子之间有很强的相互作用时,粒子除具有独 立的动能外。还有相互作用的势能,这样任何一个 微观粒子状态发生变化,都会影响其它粒子的运动 状态。这时某个粒子具有确定的能量和动量这句话 的意义已经含糊不清,因为它随时间变化。结果是 粒子不能从整个系统中分离出来。
处理粒子间有强相互作用这类问题,不能用粒 子相空间,而要用系统相空间,即把整个系统所对 应的每个可能的微观态集合起来进行考虑,直接从 整个系统的状态出发,不必过问个别粒子的状态。
令 : (N, E,V ) CV N
由: p ln N
kT V V
比较由实验得到的理想气体的物态方程:
pV nRT k R N0
即为玻尔兹曼常量。
四、应用 微正则分布求热力学函数的程序:
1.求出微观状态数Ω(N,E,V) 2.求熵S=ln Ω
3.从S(N,E,V) →E(S,N,V)
因此时刻t,系统的运动状态处于dΩ内的概率可
热力学统计物理-统计热力学课件第九章

d
dt t i
[ q i q& i p i p & i]
2020/4/4
7
考虑相空间中一个固定的体积元:
d d q 1Ld qfd p 1Ld pf
体积元边界: qi,qidqi;pi,pidpi i1,2,L, f
t时刻代表点数: t+dt时刻代表点数: 增加代表点数:
d
( dt)d
t dtd t
间中运动,其邻域的代表点密度是不随时间改变的常数。
2020/4/4
11
•表达式交换 t t 保持不变,说明刘维尔定理是可逆的。
•刘维尔定理完全是力学规律的结果,其中并未引入任何统 计的概念。
2020/4/4
12
§9.2 微正则系综
统计物理学研究系统在给定宏观条件下的宏观性质. 这就 是说,所研究的系统是处在某种宏观条件之下的,如果研究的 是一个孤立系统,给定的宏观条件就是系统具有确定的粒子
s (t) 1
s
2020/4/4
16
B(t) s(t)Bs
s
上式给出了宏观量与微观量的关系,是在系综理论中求 宏观量的基本公式。而确定系综分布函数是系综理论的根本 问题。
二、平衡状态的孤立系统经典及量子分布
1.微正则分布
平衡孤立系统的能量具有确定值,能量在 EEE范围内。
B (t)B (q ,p )(q ,p ,t)d
热力学中类似的两个系统达到热平衡的条件:
US11
N1,V1
US22
N2,V2
比较可得:
1 kT
Skln
S U
N ,V
1 T
——熵与微观状态数的关系—玻耳兹曼关系。
•不仅适用于近独立粒子系统,也适用于粒子间存在相互
大学物理2-1第九章(热力学基础)习题答案

大学物理2-1第九章(热力学基础)习题答案习 题 九9-1 一系统由图示的状态a 经acd 到达状态b ,系统吸收了320J 热量,系统对外作功126J 。
(1)若adb 过程系统对外作功 42J ,问有多少热量传入系统? (2)当系统由b 沿曲线ba 返回状态a ,外界对系统作功84 J ,试问系统是吸热还是放热? 热量是多少?[解] 由热力学第一定律A E Q +∆= 得AQ E -=∆在a <b 过程中,E E E a b∆=-JA Q 19412632011=-=-= 在adb 过程中 JA E Q 236421942=+=+∆=在ba 过程中 JA E A E E Q b a 27884194333-=--=+∆-=+-=本过程中系统放热。
9-2 2mol 氮气由温度为 300K ,压强为510013.1⨯Pa(1atm)的初态等温地压缩到 510026.2⨯Pa(2atm)。
求气体放出的热量。
[解] 在等温过程中气体吸收的热量等于气体对外做的功,所以J P P RT M m A Q mol T 3211046.321ln 30031.82ln ⨯-=⨯⨯⨯===即气体放热为J 31046.3⨯。
9-3 一定质量的理想气体的内能E 随体积的变化关系为E - V 图上的一条过原点的直线,如图所示。
试证此直线表示等压过程。
[证明] 设此直线斜率为k ,则此直线方程为kvE =又E 随温度的关系变化式为Tk T C M M E v mol'=⋅=所以T k kV '=因此C kk T V ='=(C 为恒量) 又由理想气体的状态方程知,C TpV '= (C '为恒量)所以 p 为恒量 即此过程为等压过程。
9-4 2mol 氧气由状态1变化到状态2所经历的过程如图所示:(1)沿l →m →2路径。
(2)1→2直线。
试分别求出两过程中氧气对外作的功、吸收的热量及内能的变化。
第九章统计热力学教材

2019/6/14
粒子的微观性质
M,I,ε等
物质结构
导论
统计热力学 系统的宏观性质
U、H、S等
桥 梁 宏观物理化学
粒子:聚集在气体、液体、固体中的分子、原子、 离子等,简称为子。
系统的分类
(1)由运动情况分类
离域子系统(即全同粒子系统):其粒子处于混乱运动状态, 各粒子没有固定位置,彼此无法分辨。(如气体、液体)
§9.4 玻尔兹曼分布及配分函数
平衡分布~最概然分布 =玻尔兹曼分布
1. 玻尔兹曼分布
若能级i的简并度为gi,则系统的N个粒子中,在该能
级上的粒子数ni:
n j
N q
eεj/ k T
ni
N
q
ε / k T
ge i
i
其中q 定义为粒子的配分函数:
q
eεj/ k T
j
q
g eεi/ k T i
2 N
N!
m 2
N
N 2
m
!
N 2
m !
1 2N
0.99993
而2 10 12 与5 10 23 相比可忽略不计,宏观上 几乎不能察觉。
因此,对宏观体系来讲,粒子分布方式几乎总 在最概然分布附近。
结论:平衡分布即为最概然分布所能代表的那些 分布。
换言之,最概然分布~平衡分布。
例如N=10时,M=4、5、6三种分布数学几率之和 为0. 656 ;而N=20时,M=8、9 、10 、11 、12 五种分 布数学几率之和为0.737。
作图见课本 图9. 3. 1 ,PD / PB曲线随N增大而变 狭窄,可以想象,当N变得足够大时,曲线就变为在 最概然分布(M/N=0. 5)处的一条线。
《大学物理》第九章 热力学基础 (2)

吸收热量
m M mol
CV T
m M mol
C p T
m RT ln V2
M mol
V1
或 m RT ln p1
M mol
p2
对外作功
0
pV
或 m RT M mol
m RT ln V2
M mol
V1
或 m RT ln p1
M mol
p2
内能增量
m M mol
CV T
m M mol
CV T
0
pV 常量
返回 退出
例9-2 设有氧气 8 g,体积为0.4110-3 m3 ,温度为 300 K。如氧气做绝热膨胀,膨胀后的体积为4.110-3 m3 。问:气体做功多少?氧气做等温膨胀,膨胀后 的体积也是4.110-3 m3 ,问这时气体做功多少?
解: m=0.008 kg M =0.032 kg T1=300 K
941 (J)
等温膨胀做功:
A
m M
RT1 ln
V2 V1
1 8.31 300 ln 10 4
1.44 103 (J)
返回 退出
作业 Page70 9-1 9-6
返回 退出
理想气体热力学过程的主要公式
过程 特征 过程方程
等体 V=常量 p 常量 T
等压 p=常量 V 常量 T
等温 T=常量 pV 常量
C
(3)比较各过程吸热多少?
D
解:(1) A A B A A C A A D
(2)等压过程 E A B 0
O V1
V2 V
等温过程 E A C 0 绝热过程 E A D A A D 0
(3) Q A B Q A C Q A D
物理化学(考研重点)(精品)91能级及简并度2011518(改).ppt

00-7-23
9
nx2 +ny2 +nz2 = 6
00-7-23
10
2. 双原子分子的转动
例1 双原子分子可近似看作原子间距 R0 保持不变的刚性转子 。
刚性转子的转动
R0 即为分子的平衡键长
设两原子的质量分别为m1, m2, 由分子的折合质量 为
= m1m2 /(m1+m2)
转子的转动惯量 I 可由下式计算: I = R02 分子的转动惯量与分子结构有关, 数值可由光谱数据获得。
按粒子的 相互作用
独立子系统 粒子间相互作用可以忽略的 系统, 如理想气体;
相依子系统 粒子间相互作用不能忽略的 系统, 如真实气体、液体等.
本章只讨论独立子系统, 包括独立离域子系统(如理想气体) 和独立定域子系统 (如作独立简谐振动的晶体). 00-7-23 3
系统中粒子处于各种不同的微观状态, 量子学说把这些微观 状态称为量子态。 粒子能量相同的一组量子态组成一个能级。 若将不同能级 i 分别计为 1, 2, …, i , …,若处于能级 i 的粒 子数目为 ni , 对于N,U,V 确定的独立子系统,必然有:
N n i
i
U n i i
i
若以量子态 j 为计量单元, 能量为 j量子态有nj粒子,同样有
N n j
j
U n j j
j
用上式来求系统的总能量, 必须知道系统有哪些量子态, 各 量子态上的粒子数及能量大小。 解决这一问题要应用量子统 计方法。本书介绍一种修正的玻尔兹曼统计方法。
00-7-23 2
统计热力学将聚集在气体, 液体, 固体中的分子, 原子和 离子等统称为粒子, 简称为子.
大学物理-热力学基础必考知识点

第九章 热力学基础主要内容一.准静态过程(理想过程,在P-V 图中代表一条线) 系统从一个平衡态到另一个平衡态,中间经历的每一状态都可以近似看成平衡态(平衡态在P-V 图中代表一个点)过程。
二.理想气体状态方程:112212PV PV PV C T T T =→=; m PV RT M'=; P nkT = 8.31J R k mol =;231.3810J k k -=⨯;2316.02210A N mol -=⨯;A R N k =三.热力学第一定律Q E W =∆+;dQ dE dW =+…1.气体做功 21V V W Pdv =⎰ (规定气体对外做功>0 )2.Q (规定气体从外界吸收热量>0,过程量,只有在某个过程中才有意义)3.2121()V m V m m m dE C dT E E C T T M M ''=-=- 或 (状态量,理想气体内能只取决于温度,内能变化公式适用于任意的过程。
),2V m i C R =,=,P +22m i C R (i 为自由度,单原子分子自由度为3,双原子分子为5,多原子分子为6), =+,P ,m V m C C R ,气体比热容比:γ=>,,1P m V m C C四.热力学第一定律在理想气体的等值过程和绝热过程中的应用1. 等体过程-2(V m T 2. 等压过程⎧=⋅-=-⎪⎪⎪=∆+=-=⋅∆⎨⎪⎪∆=-∆⎪⎩21212121()()+2()2()=2p m V m m W P V V R TT M m i Q E W C T T P VM mi E C T T P V M;3.等温过程212211T T E E m V m p Q W RTln RTlnM V M p -=⎧⎪''⎨===⎪⎩1. 绝热过程210()V m Q W E C T T ν=⎧⎪⎨=-∆=--⎪⎩绝热方程1PV C γ=, -12V T C γ= ,13P T C γγ--= 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
若以量子态 j 为计量单元, 同样有
N =
∑n
j
j
U =
∑n ε
j j
j
用上式来求系统的总能量, 必须知道系统有哪些量子态, 各 量子态上的粒子数及能量大小. 解决这一问题要应用量子统计 方法. 本书介绍一种修正的玻尔兹曼统计方法. 该方法运用于大 多数粒子间相互作用可忽略的系统 , 得到的结果比较满意 11-02-14 5 .
i i
i
=
∑
i
1⎞ 9 ⎛ n i ⎜ i + ⎟h ν = h ν 2⎠ 2 ⎝
16
11-02-14
上述方程组简化为
∑ in
i
i
=3
此外,由于系统的总能量为 9hν /2,故 i < 4。从而
0n 0 + n 1 + 2n 2 + 3n 3 = 3
该方程只存在下列 3 组解:
能级分布D I II III
11-02-14
6
¾ 对单原子分子, n = 1, 转动自由度为 0, 振动自由度也为 0. ¾ 对双原子分子, n = 2, 转动自由度为 2, 振动自由度为 1. ¾ 对非线型多原子分子, 转动自由度为 3, 振动自由度为3n-6.
(绕分子轴转动 能量近似为零) • 双原子分子转动
• 双原子分子的振动
• • • •
基态能级: 各运动形式能量最低的能级称为各自的基态能级. 非简并能级: 只包含一种量子态的能级. 简并能级: 包含有多种不同量子态的能级. 统计权重(简并度 ) g : 某简并能级所包含的不同量子态的数目.
11-02-14 7
1. 分子的平动 根据量子理论, 质量为m 的粒子在边长为a, b, c的矩形箱 中平动时, 其能级公式为 2 2 2 2 ⎛ ⎞ n n h ⎜ nx y z ⎟ εt = + 2 + 2 2 ⎜ 8m ⎝ a b c ⎟ ⎠ 式中 h = 6.626 ×10-34J ⋅s, 为普朗克常数. nx, ny, nz = 1, 2, 3, …, 表示三维平动子每个量子态的一组量子数, 分别描述 三个互相垂直方向上平动能的分量. 若粒子在立方容器 (体积为V ) 中平动, 则能级公式简化为
11-02-14 11
2. 双原子分子的转动 双原子分子可近似看作原子间距 d 保持不变的刚性转子 . 转子的转动惯量 I :
2 II= =μ μd d2
• 刚性转子的转动
式中μ 为分子的折合质量, μ = m1m2 /(m1+m2). 分子的转动惯 量与分子结构有关, 数值可由光谱数据获得. (设转动角速度为ω, 则转动角动量为 Iω, 转动能为 (1/2)I ω2 ) 刚性转子的能级公式: ε r = J ( J + 1)
3. 双原子分子的振动 作一维简谐振动的粒子即一维谐振子. 双原子分子中原子 沿化学键方向的振动可近似为一维简谐运动; 原子晶体中各原 子在点阵附近的振动, 可近似为在空间互相垂直方向上三个独 立的一维简谐运动. 一维谐振子能级公式:
1 ε v = (υ + )hν 2
式中 υ = 0, 1, 2, …, 振动量子数. ν 是谐振子振动频率, 与分子结构有关, 可由光谱数据获得. 可见一维谐振子各能级的能值取决于粒子的结构性质. 一维谐振子的任何振动能级的简并度 非简并 ). 一维谐振子的任何振动能级的简并度g g v, vv= =1 1(( 非简并 ). v, 一维谐振子基态 ε v, 0 = hν/2 . 相邻能级的能量差Δε = hν. 在通常温度时振动能级 Δε /kT 值约在 10 左右, 量子化效应很 明显 , 通常不能将振动能级视为连续变化. 11-02-14 13
= 0.02462m 3
H2 的质量 m 为
M 2.0158 × 10-3 kg ⋅ mol −1 = m= 6.022 × 10 23 mol −1 L = 3.347 × 10 − 27 kg
11-02-14 10
基态能量:
ε t,0
3 × 6.626 × 10 J ⋅ s h = ×3 = 2/ 3 8mV 8 × 3.347 × 10 − 27 kg × 0.02462m 3
11-02-14 4
引 言
量子态: 系统中粒子所处的各种不同的微观状态. 能级: 粒子能量相同的一组量子态组成一个能级. 不同能级的 能量ε i 值是不连续的, 即量子化的. 在一定宏观状态的独立子系统中, 系统的总粒子数 N 和总 能量 U 是不变的, 若处于能级 i 的粒子数目为 ni , 必然有 N = ∑ ni U = ∑ ni ε i
2
(
− 34
(
)
2
)
2/ 3
= 5.812 × 10-40 J
第一激பைடு நூலகம்态能量:
ε t,1
h2 - 40 = × 6 = 1 1 . 624 × 10 J 2/ 3 8mV
第一激发态与基态的能量差:
ε t,1 − ε t,0 = (11.624 − 5.812) × 10-40 J = 5.812 × 10-40 J
h2 8π 2 I
式中 J = 0, 1, 2, …, 是转动量子数. 能级简并度gr ,J = 2J + 1. 刚性转子基态转动能为零. 相邻能级的能量差Δε 也很小. 在温度不太低时转子的 Δε /kT 值约在 10-2数量级, 量子化效应 不很明显 , 在某些数学处理中可将转动能级视为连续变化. 12 11-02-14
( n x , n y , nz = 1,2,......)
ε = 12h 2 8ma 2 g = 1 ε = 11h 2 8ma 2 g = 3 ε = 9h 2 8ma 2 ε = 6h 2 8ma 2 ε = 3h 2 8ma 2 g =3 g =3 g =1
g:简并度(统计权重)
11-02-14 9
ε = εt + εr + ε v + εe + εn
若不考虑电子及核子运动, 则分子运动可分解为平动, 转 动和振动. 对 n 个原子组成的分子, 这三种运动的自由度为: • 总自由度为 3n (一个原子在三维空间运动的自由度为3); • 平动自由度为 3 (分子质心在三维空间的平动); • 转动和振动自由度共为(3n-3) .
h2 2 2 2 εt = n x + n y + nz 2/ 3 8mV
(
)
立方容器中基态能级: (nx, ny, nz) = (1, 1, 1), gt, 0 = 1, 非简并能级; 第一激发态能级: (nx, ny, nz) = (1, 1, 2), (1, 2, 1), (2, 1, 1), gt,1 = 3; 第二激发态能级 : (nx, ny, nz) = (1, 2, 2), (2, 2, 1), (2, 1, 2), gt,2 = 8 3. 11-02-14
• 微观世界
引 言
• 热力学研究大量粒子的平衡系统. 它以三个定律和基础热数 据为基础, 预示过程的方向和限度. • 统计热力学从粒子的微观性质及结构数据出发, 以粒子遵循 的力学定律为基础, 用统计的方法推求大量粒子运动的统计 平均结果, 以得出平衡系统各种宏观性质的数值. m , de , ν, Δε, …… U , S , p , KΘ, ……. 统计热力学研究的主题是为宏观系统的平衡性质提供分 子的理论或解释,它起到联系微观与宏观性质的桥梁作用。
11-02-14 3
引 言
系统分类: 离域子系统(全同粒 子系统)
(无固定位置,各粒子无 法彼此分辨)
独立子系统
(粒子间无相互作用,或 粒子间相互作用可忽略)
系统 定域子系统(可辨粒 子系统)
(粒子运动定域化,可通 过其位置加以分辨)
相依子系统
(粒子间相互作用不能 忽略)
本章只讨论独立子系统, 包括独立离域子系统(如理想气体) 和独立定域子系统(如作独立简谐振动的晶体).
例 300 , 101.325 1 例9.1.1 9.1.1 在 在 300K K , 101.325kPa kPa条件下,将 条件下,将 1mol mol H H 22置于立方 置于立方 形容器中,试求单个分子平动的基态能级的能量值 ε ,以及 形容器中,试求单个分子平动的基态能级的能量值 ε t,0 t,0 ,以及 第一激发态与基态的能量差。 第一激发态与基态的能量差。 解:300 K,101.325 kPa 条件下的 H2 可看作理想气 体,1mol H2 的体积为 nRT 1mol × 8.314J ⋅ mol −1 ⋅ K −1 × 300K = V= 101.325 × 10 3 Pa p
• 一维谐振子的振动
4. 电子及核运动 电子运动及核运动的能级差一般都很大, 系统中各粒子的 这两种运动一般均处于基态. 例外情况是有的, 如NO分子中 的电子能级间隔很小, 常温下部分电子处于激发态. 本章仅讨论最简单的情况, 即认为系统中全部粒子的电子 运动与核运动均处于基态. 对大多数物质来说, 这种处理是符合 实际情况的. 对指定的物质而言, 电子运动基态简并度 = 常数 电子运动基态简并度g g e,0 e,0 = 常数 核运动基态简并度 = 常数 核运动基态简并度g g n,0 n,0 = 常数
§9-1 §9-1 粒子各种运动形式的能级及能级的简并度 粒子各种运动形式的能级及能级的简并度
粒子运动形式包括:平动(t); 核运动; 电子运动(e)及核子运动(n). • 分子作为整体的平动和核子运动可被分离出来. • 核运动和电子运动可根据玻恩-奥本海默近似加以分离. • 若忽略分子转动和振动的耦合, 核运动又可分离为转动 ( r )及振动( v ). 这样, 粒子的能级等于各独立运动形式的能级量之和, 即
11-02-14 15
例:下面以三个在定点A,B,C 做独立振动的一维谐振子构 成的系统,总能量为
