第4章习题与解答
第4章课后习题及答案

返 回
第 4 章 供 电 与 用 电
练习题解答
4.1.1 某三相同步发电机,三相绕组联结成星形时的线电压为 10.5kV,若将它联结成三角形,则线电压是多少?若联结成星形 时,L2相绕组的首末端接反了,则三个线电压的有效值U12 , U23 和U31各是多少? · · · · U31= U3 -U1 · -U2 解: 星形联结时UlY = 10.5kV U3 · U 3 UlY 10.5 = kV = 6.06kV ∴UpY = · · U 1=U23 √ 3 √3 · ·-U =U 三角形联结时相电压不变, 2 3 · UlY = UpY =6.06kV L2首末端接反的相量图如图所示:
· · · 0 0 0 IL2 = I2 - I1 ( 8 . 8 30 8 . 8 0 ) A 4 . 56 105 A · · · 0 0 0 IL3 = I3 - I2 ( 8 . 8 30 8 . 8 30 ) A 8 . 8 90 A
XL= Z sin = 77.1×0.6 Ω = 46.3 Ω
返 回 上一题 下一题
第 4 章 供 电 与 用 电
4.3.2 某三相负载,额定相电压为220V,每相负载的电阻为4Ω,感 抗为3Ω,接于线电压为380V的对称三相电源上,试问该负载应
采用什么联结方式?负载的有功功率、无功功率和视在功率?
· I
l2
· I
l3
· I
2
· I
3
-jXC
解: 负载为不对称三相负载
· · 0 U U 220 120 2 23 · 0 I2 = Z = -jX = 8 . 8 30 A -j25 2 C
返 回 上一题 下一题
第4章 电路的暂态分析-习题解答

4.7 在题 4.7 图所示电路中,开关 S 闭合前电路已处于稳态,试确定 S 闭合后电
4
压 uL 和电流 iL、i1、i2 的初始值和稳态值。 【解】由于 i L (0 ) i L (0 )
uS 6 3A ,则 R1 2
i1 (0 )
R2 4 iL (0 ) 3 2A 24 R1 R2
6
【解】该电容电压的初始值为 20000V,放电的起始瞬间的冲击电流达到最 大值,冲击电流的峰值大小为 流。 这种情况下不会造成触电事故是由于放电时间极短,等效电路的时间常数为
20000 V 200 A ,远远超过了人体允许的致命电 100
RC 100 50 1012 5 109 s 5ns
u c (0 ) u c (0 ) R1i1 (0 ) 6V i1 (0 )
u c (0 ) 1A R1
i2 (0 ) 0 ic (0 ) I S i1 (0 ) 3 1 2A
1
②
) 。
① 立即亮 ③ 由亮逐渐变为不亮
② 逐渐变亮 ④ 由不亮逐渐变亮,再逐渐变为不亮 ① )。
(7)R、C 电路在零状态条件下,时间常数的意义是( ① 响应由零值增长到稳态值的 0.632 倍时所需时间 ② 响应由零值增长到稳态值的 0.368 倍时所需时间 ③ 过渡过程所需的时间 ④ 响应由稳态值下降到零值的 0.632 倍时所需时间 (8)一阶线性电路时间常数的数值取决于( ① 电路的结构形式 ③ )。
因此该电容的初始电压将在 5 25ns 时间内释放完毕,虽然冲击电流很大,但 是作用时间极短,对人体而言最多感觉到颤抖,不会造成致命伤害。
光学第四章习题解答

′ s1 = d − s1 = 22 − 2 = 20cm
1 1 1 1 1 1 又∵ − = 即: = − s s f′ s s′ f ′
' 1 1 1 1 1 1
1 1 1 39 ∴ = − =− s1 20 0.5 20
− 20 s′ = − = −0.51 (cm). ɺ 39 ′
1
s′ 20 又∵ β = = − = −39. 0.51 s
∴ Φ= 1 1 1 = − f ′ s′ s 1 1 = − − 1.0 − 0.25 100 = −1 + 25 = +3.0 ( D) = +300 度
需配戴300度的远视眼镜 度的远视眼镜 需配戴
4.3 一照相机对准远物时,底片距物镜 一照相机对准远物时,底片距物镜18cm,当 , 镜头拉至最大长度时,底片与物镜相距20cm ,求目 镜头拉至最大长度时,底片与物镜相距 的物在镜头前的最近距离? 的物在镜头前的最近距离? 解: ∵ 1 − 1 = 1 s′ s f ′
解:(1)将 s = −20cm,f ′ = 15cm 代入高斯公式
s1 f ′ (−20) ×′ −20 + 15
′ s1 60 × 0.5 = −1.5cm (2) y1′ = β1 y1 = y1 = −20 s1
EO 2 (3) u = arctg = arctg = 7°35′40′′ PO 15
(4)将 s2 = −5cm,f ′ = 15cm 代入高斯公式
s2 f ′ ( −5) × 15 ′ s2 = = = −7.5cm s2 + f ′ −5 + 15 ′ s2 −7.5 ′ × 2 = 3cm 出射光瞳的半径 E ′O′ = y2 = y2 = −5 s2
第4章 多组份系统热力学习题及解答

ln
1) 22
2436 (3.337 3.091) 2436 (6.428) 15660J mol1
(答:-8.13×103 J)
4-5 333.15 K 时甲醇的饱和蒸气压是 83.40 kPa,乙醇的饱和蒸气压是 47.00 kPa。 二者可形成理想液态混合物。若混合物的组成为二者的质量分数各为 50%,求 333.15 K 时平衡蒸气组成,以摩尔分数表示。 解:在 333.15K 时,设甲醇气体的摩尔分数为 yA ,则:
(2) pB pB* xB 2.93 0.4588 1.344kPa
(3) p pA pB 5.369 1.344 6.713kPa
(4) yA
pA p
5.369 6.713
0.7998 0.80 , yB
1 yA
1 0.80 0.20
(答:(1)5.36 kPa;(2)1.35 kPa;(3)6.71 kPa;(4)0.80,0.20)
解:1mol
气体
NH3 的化学势: (g)
(g,T)
RT
ln
p p
,(
p
p )
(NH3, g,T ) (NH3, g,T ) RT ln
pNH3 p
,( pNH3
p )
溶液中,溶质 NH3 的化学势:
(NH3, l,T )
(NH3, g,T )
NH3
x
A
p
* A
x
A
pB* (1 xA )
193.3 0.274
193.3 0.2740 66.6 0.726
《土力学》第四章习题集及详细解答

《土力学》第四章习题集及详细解答第4章土中应力一填空题1。
土中应力按成因可分为和 .2。
土中应力按土骨架和土中孔隙的分担作用可分为和。
3.地下水位下降则原水位出处的有效自重应力。
4。
计算土的自重应力应从算起。
5。
计算土的自重应力时,地下水位以下的重度应取。
二选择题1.建筑物基础作用于地基表面的压力,称为( A ).(A)基底压力;(B)基底附加压力;(C)基底净反力;(D)附加应力2.在隔水层中计算土的自重应力c时,存在如下关系( B ).(A) =静水压力(B) =总应力,且静水压力为零(C) =总应力,但静水压力大于零(D)=总应力—静水压力,且静水压力大于零3.当各土层中仅存在潜水而不存在毛细水和承压水时,在潜水位以下的土中自重应力为( C ).(A)静水压力(B)总应力(C)有效应力,但不等于总应力(D)有效应力,但等于总应力4.地下水位长时间下降,会使( A )。
(A)地基中原水位以下的自重应力增加(B)地基中原水位以上的自重应力增加(C)地基土的抗剪强度减小(D)土中孔隙水压力增大5.通过土粒承受和传递的应力称为( A ).(A)有效应力;(B)总应力;(C)附加应力;(D)孔隙水压力6.某场地表层为4m厚的粉质黏土,天然重度=18kN/m3,其下为饱和重度sat=19 kN/m3的很厚的黏土层,地下水位在地表下4m处,经计算地表以下2m处土的竖向自重应力为( B )。
(A)72kPa ; (B)36kPa ;(C)16kPa ;(D)38kPa7.同上题,地表以下5m处土的竖向自重应力为( A ).(A)91kPa ; (B)81kPa ;(C)72kPa ;(D)41kPa8.某柱作用于基础顶面的荷载为800kN,从室外地面算起的基础深度为1。
5m,室内地面比室外地面高0.3m,基础底面积为4m2,地基土的重度为17kN/m3,则基底压力为( C ).(A)229.7kPa ;(B)230 kPa ; (C)233 kPa ;(D)236 kPa9.由建筑物的荷载在地基内产生的应力称为( B ).(A)自重应力;(B)附加应力;(C)有效应力;(D)附加压力10.已知地基中某点的竖向自重应力为100 kPa,静水压力为20 kPa,土的静止侧压力系数为0。
计算机系统结构 第四章(习题解答)
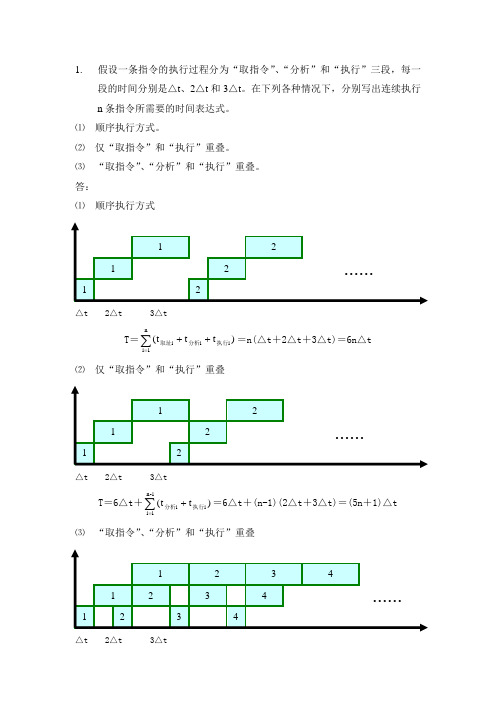
1. 假设一条指令的执行过程分为“取指令”、“分析”和“执行”三段,每一段的时间分别是△t 、2△t 和3△t 。
在下列各种情况下,分别写出连续执行n 条指令所需要的时间表达式。
⑴ 顺序执行方式。
⑵ 仅“取指令”和“执行”重叠。
⑶ “取指令”、“分析”和“执行”重叠。
答:⑴ 顺序执行方式12 ......1 2 12T =∑=++n1i i i i )t t t (执行分析取址=n(△t +2△t +3△t)=6n △t⑵ 仅“取指令”和“执行”重叠12 ......1 212T =6△t +∑=+1-n 1i i i )t t (执行分析=6△t +(n-1)(2△t +3△t)=(5n +1)△t⑶ “取指令”、“分析”和“执行”重叠12 34 ......1 2 3 41234△t2△t3△t△t2△t3△t△t2△t3△tT =6△t +∑=1-n 1i i )t (执行=6△t +(n-1)(3△t)=(3n +3)△t2. 一条线性流水线有4个功能段组成,每个功能段的延迟时间都相等,都为△t 。
开始5个任务,每间隔一个△t 向流水线输入一个任务,然后停顿2个△t ,如此重复。
求流水线的实际吞吐率、加速比和效率。
答:1 2 3 4 5 6 7 8 9 10 11 12 13 14 15...1 2 3 4 5 6 7 8 9 10 11 12 13 14 151 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1 2 3 4 56 7 8 9 10 11 12 13 14 151 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23我们可以看出,在(7n+1)Δt 的时间内,可以输出5n 个结果,如果指令的序列足够长(n →∞),并且指令间不存在相关,那么,吞吐率可以认为满足:)n (t75t )n /17(5t )1n 7(n 5TP ∞→∆=∆+=∆+=加速比为:)n (720n /17201n 7n 20t )1n 7(t 4n 5S ∞→=+=+=∆+∆⨯=从上面的时空图很容易看出,效率为:)n (75n /1751n 7n 5t )1n 7(4t 4n 5E ∞→=+=+=∆+⨯∆⨯=3. 用一条5个功能段的浮点加法器流水线计算∑==101i i A F 。
第4章_组合逻辑电路习题解答
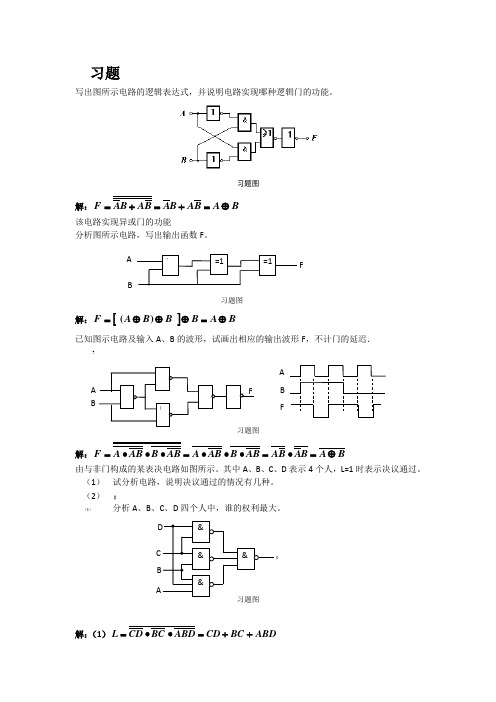
习题写出图所示电路的逻辑表达式,并说明电路实现哪种逻辑门的功能。
习题图解:B A B A B A B A B A F ⊕=+=+= 该电路实现异或门的功能分析图所示电路,写出输出函数F 。
习题图 解:[]B A B BB A F ⊕=⊕⊕⊕=)(已知图示电路及输入A 、B 的波形,试画出相应的输出波形F ,不计门的延迟.?解:B A B A B A AB B AB A AB B AB A F ⊕=•=•••=•••=由与非门构成的某表决电路如图所示。
其中A 、B 、C 、D 表示4个人,L=1时表示决议通过。
(1) 试分析电路,说明决议通过的情况有几种。
(2) 【 (3) 分析A 、B 、C 、D 四个人中,谁的权利最大。
习题图解:(1)ABD BC CD ABD BC CD L ++=••=C & && & D $ L B A " =1=1 =1FFA B[FB A(2)(3)根据真值表可知,四个人当中C 的权利最大。
分析图所示逻辑电路,已知S 1﹑S 0为功能控制输入,A ﹑B 为输入信号,L 为输出,求电路所具有的功能。
&习题图解:(1)011011)(S S B S A S S B S A L ⊕⊕+⊕=⊕⊕•⊕= (2)(3)当S 1S 0=00和S 1S 0=11时,该电路实现两输入或门,当S 1S 0=01时,该电路实现两输入或非门,当S 1S 0=10时,该电路实现两输入与非门。
(2)1¥电路逻辑功能为:“判输入ABC 是否相同”电路。
已知某组合电路的输入A 、B 、C 和输出F 的波形如下图所示,试写出F 的最简与或表达式。
习题图:解:(1)根据波形图得到真值表:,(2)由真值表得到逻辑表达式为C AB BC A C B A F ++=、设∑=)14,12,10,9,8,4,2(),,,(m D C B A F ,要求用最简单的方法,实现的电路最简单。
第4章集成运算放大器习题解答

页脚 .第四章习题参考答案4-1 什么叫“虚短”和“虚断”?答 虚短:由于理想集成运放的开环电压放大倍数无穷大,使得两输入端之间的电压近似相等,即-+≈u u 。
虚断:由于理想集成运放的开环输入电阻无穷大,流入理想集成运放的两个输入端的电流近似等于零,即0≈=-+i i 。
4-2 理想运放工作在线性区和非线性区时各有什么特点?分析方法有何不同?答 理想运放工作在线性区,通常输出与输入之间引入深度负反馈,输入电压与输出电压成线性关系,且这种线性关系只取决于外部电路的连接,而与运放本身的参数没有直接关系。
此时,利用运放“虚短”和“虚断”的特点分析电路。
理想运放工作在非线性去(饱和区),放大器通常处于开环状态,两个输入端之间只要有很小的差值电压,输出电压就接近正、负电压饱和值,此时,运放仍具有“虚断”的特点。
4-3 要使运算放大器工作在线性区,为什么通常要引入负反馈?答 由于理想运放开环电压放大倍数∞=uo A ,只有引入深度负反馈,才能使闭环电压放大倍数FA 1u =,保证输出电压与输入电压成线性关系,即运放工作在线性区。
4-4 已知F007运算放大器的开环放大倍数dB A uo 100=,差模输入电阻Ω=M r id 2,最大输出电压V U sat o 12)(±=。
为了保证工作在线性区,试求:(1)+u 和-u 的最大允许值;(2)输入端电流的最大允许值。
解 (1)由运放的传输特性5o uo 1012===++u u u A 则V 102.1101245--+⨯===u u(2)输入端电流的最大允许值为A 106102102.11164id --+⨯=⨯⨯==r u I 4-5 图4-29所示电路,设集成运放为理想元件。
试计算电路的输出电压o u 和平衡电阻R 的值。
解 由图根据“虚地”特点可得0==+-u u图中各电流为601.01--=u i 305.02---=u i 180o f u u i -=- 由“虚断”得f 21i i i =+以上几式联立,可得V 7.2o =u平衡电阻为 Ω==k R 18180//60//30图4-29 题4-5图4-6 图4-30所示是一个电压放大倍数连续可调的电路,试问电压放大倍数uf A 的可调围是多少?图4-30 题4-6图解 设滑线变阻器P R 被分为x R 和x P R R -上下两部分。
电工学课后习题-第4章-供电与用电习题及答案

电源相电流 IpS = IlS = 22 A
返 回 上一题 下一题
第 4 章
供 电 与 用 电
4.2.2 有一电源和负载都是三角形联结的对称三相电路, 已知 电源相电压为 220 V,负载每相阻抗模 Z 为 10Ω,试求负 载的 相电流和线电流,电源的相电流和相电流。 [解] 电源三角形联结, 线电压 UlS = UpS = 220 V 负载线电压 UlL = UlS = 220 V 负载相电压 UpL = UlL = 220 V UpL 220 = 10 A = 22 A 负载相电流 IpL = Z 负载线电流 IlL = √3 IpL = 38 A 电源线电流 IlS = IlL = 38 A
N M Za Za Za
Zb
L2
L3 (题4.3.4图)
Zb (题4.3.5图)
4.3.5 在如图所示三相电路中,已知 Za = (3+j4) Ω, Zb = (8-j6) Ω,电源线电压为 380 V,求电路的总有功功率、无功功率和视在 功率以及从电源取用的电流。
返 回 上一页 下一页
第 4 章
负载的线电流和有功功率。
[解]: ⑴星形联结 UpL = UlL /√ 3 =380/√ 3 V = 220 V Up Ip= R = 220 A = 15.7 A 14 Il = Ip = 15.7 A P = 3Up Ip λ=3×220 × 15.7 × 1W = 10 362 W ⑵三角形联结 Up = Ul = 380 V Up Ip = R = 380 A = 27.1 A 14 Il =√ 3 Ip =√ 3 ×27.1A = 47 A P = 3Up Ipλ= 3×380 × 21.7 × 1 W= 30 894 W
第4章习题及答案

第四章习题及解答4-3 什么是进程?进程与程序的主要区别是什么?答:进程是一个具有一定独立功能的程序关于某个数据集合的一次活动。
进程与程序的主要区别是:(1) 程序是指令的有序集合,是一个静态概念。
进程是程序在处理机的一次执行过程,是一个动态概念。
进程是有生命期的,因创建而产生,因调度而执行,因得到资源而暂停,因撤消而消亡;(2) 进程是一个独立的运行单元,是系统进行资源分配和调度的独立单元,而程序则不是。
(3) 进程与程序之间无一一对应关系。
一个程序可以对应多个进程,一个进程至少包含一个程序。
4-4 图4.2标明程序段执行的先后次序。
其中:I表示输入操作,C表示计算操作,P 表示打印操作,下角标说明是对哪个程序进行上述操作。
请指明:(1)哪些操作必须有先后次序? 其原因是什么?(2)哪些操作可以并发执行? 其原因又是什么?答:(1) ①I n、C n和P n之间有先后顺序要求,这是由于程序本身的逻辑要求。
②使用同一设备的不同的程序段,如C1…C n,I1…I n,P1…P n,之间有先后顺序要求,这是由于设备某一时刻只能为一个程序服务。
(2) 不同程序使用不同设备时,占用不同设备,无逻辑关系,可以并发执行,如I2和C1;I3、C2和P1。
4-9 某系统进程调度状态变迁图如图4.31(1) 什么原因会导致发生变迁2、变迁3、变迁4 ?答:发生变迁2的原因:时间片到发生变迁3的原因:请求I/O或其他系统调用发生变迁4的原因:I/O完成或其他系统调用完成(2) 在什么情况下,一个进程的变迁3 能立即引起另一个进程发生变迁1 ?答:一个进程的变迁3 能立即引起另一个进程发生变迁的条件是,就绪队列非空。
(3) 下列因果变迁是否可能发生?若可能,需要什么条件?a. 2→1;b. 3→2;c. 4→1答:a. 2→1 不需要条件,一定会发生。
b. 3→2 不可能发生。
c. 4→1 可能发生,条件:就绪队列为空,或在可剥夺调度方式下,转变为就绪状态的进程优先级最高。
计算机系统结构第四章(习题解答)

1. 假设一条指令的执行过程分为“取指令”、“分析”和“执行”三段,每一段的时间分别是△t 、2△t 和3△t 。
在下列各种情况下,分别写出连续执行n 条指令所需要的时间表达式。
⑴ 顺序执行方式。
⑵ 仅“取指令”和“执行”重叠。
⑶ “取指令”、“分析”和“执行”重叠。
答:⑴ 顺序执行方式12 ......1 2 12T =∑=++n1i i i i )t t t (执行分析取址=n(△t +2△t +3△t)=6n △t⑵ 仅“取指令”和“执行”重叠12 ......1 212T =6△t +∑=+1-n 1i i i )t t (执行分析=6△t +(n-1)(2△t +3△t)=(5n +1)△t⑶ “取指令”、“分析”和“执行”重叠12 34 ......1 2 3 41234△t2△t3△t△t2△t3△t△t2△t3△tT =6△t +∑=1-n 1i i )t (执行=6△t +(n-1)(3△t)=(3n +3)△t2. 一条线性流水线有4个功能段组成,每个功能段的延迟时间都相等,都为△t 。
开始5个任务,每间隔一个△t 向流水线输入一个任务,然后停顿2个△t ,如此重复。
求流水线的实际吞吐率、加速比和效率。
答:1 2 3 4 5 6 7 8 9 10 11 12 13 14 15...1 2 3 4 5 6 7 8 9 10 11 12 13 14 151 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1 2 3 4 56 7 8 9 10 11 12 13 14 151 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23我们可以看出,在(7n+1)Δt 的时间内,可以输出5n 个结果,如果指令的序列足够长(n →∞),并且指令间不存在相关,那么,吞吐率可以认为满足:)n (t75t )n /17(5t )1n 7(n 5TP ∞→∆=∆+=∆+=加速比为:)n (720n /17201n 7n 20t )1n 7(t 4n 5S ∞→=+=+=∆+∆⨯=从上面的时空图很容易看出,效率为:)n (75n /1751n 7n 5t )1n 7(4t 4n 5E ∞→=+=+=∆+⨯∆⨯=3. 用一条5个功能段的浮点加法器流水线计算∑==101i i A F 。
线性代数课后习题解答第四章习题详解

第四章 向量组的线性相关性1.设T T T v v v )0,4,3(,)1,1,0(,)0,1,1(321===, 求21v v -及32123v v v -+. 解 21v v -T T )1,1,0()0,1,1(-=T )10,11,01(---=T )1,0,1(-=32123v v v -+T T T )0,4,3()1,1,0(2)0,1,1(3-+=T )01203,41213,30213(-⨯+⨯-⨯+⨯-⨯+⨯= T )2,1,0(=2.设)(5)(2)(3321a a a a a a +=++-其中T a )3,1,5,2(1=, T a )10,5,1,10(2=,T a )1,1,1,4(3-=,求a . 解 由)(5)(2)(3321a a a a a a +=++-整理得)523(61321a a a a -+=])1,1,1,4(5)10,5,1,10(2)3,1,5,2(3[61T T T --+=T)4,3,2,1(=3. 已知向量组A : a 1=(0, 1, 2, 3)T , a 2=(3, 0, 1, 2)T , a 3=(2, 3, 0, 1)T ;B : b 1=(2, 1, 1, 2)T , b 2=(0, -2, 1, 1)T , b 3=(4, 4, 1, 3)T , 证明B 组能由A 组线性表示, 但A 组不能由B 组线性表示. 证明 由 ⎪⎪⎪⎭⎫⎝⎛-=312123111012421301402230) ,(B A ⎪⎪⎪⎭⎫ ⎝⎛-------971820751610402230421301~r ⎪⎪⎪⎭⎫⎝⎛------531400251552000751610421301 ~r ⎪⎪⎪⎭⎫⎝⎛-----000000531400751610421301~r 知R (A )=R (A , B )=3, 所以B 组能由A 组线性表示. 由⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫⎝⎛-=000000110201110110220201312111421402~~r r B 知R (B )=2. 因为R (B )≠R (B , A ), 所以A 组不能由B 组线性表示.4. 已知向量组A : a 1=(0, 1, 1)T , a 2=(1, 1, 0)T ;B : b 1=(-1, 0, 1)T , b 2=(1, 2, 1)T , b 3=(3, 2, -1)T , 证明A 组与B 组等价. 证明 由⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛--=000001122010311112201122010311011111122010311) ,(~~r r A B ,知R (B )=R (B , A )=2. 显然在A 中有二阶非零子式, 故R (A )≥2, 又R (A )≤R (B , A )=2, 所以R (A )=2, 从而R (A )=R (B )=R (A , B ). 因此A 组与B 组等价.5. 已知R (a 1, a 2, a 3)=2, R (a 2, a 3, a 4)=3, 证明 (1) a 1能由a 2, a 3线性表示; (2) a 4不能由a 1, a 2, a 3线性表示.证明 (1)由R (a 2, a 3, a 4)=3知a 2, a 3, a 4线性无关, 故a 2, a 3也线性无关. 又由R (a 1, a 2, a 3)=2知a 1, a 2, a 3线性相关, 故a 1能由a 2, a 3线性表示. (2)假如a 4能由a 1, a 2, a 3线性表示, 则因为a 1能由a 2, a 3线性表示, 故a 4能由a 2, a 3线性表示, 从而a 2, a 3, a 4线性相关, 矛盾. 因此a 4不能由a 1, a 2, a 3线性表示.6. 判定下列向量组是线性相关还是线性无关: (1) (-1, 3, 1)T , (2, 1, 0)T , (1, 4, 1)T ; (2) (2, 3, 0)T , (-1, 4, 0)T , (0, 0, 2)T .解 (1)以所给向量为列向量的矩阵记为A . 因为⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-=000110121220770121101413121~~r r A ,所以R (A )=2小于向量的个数, 从而所给向量组线性相关. (2)以所给向量为列向量的矩阵记为B . 因为022200043012||≠=-=B ,所以R (B )=3等于向量的个数, 从而所给向量组线性相无关.7. 问a 取什么值时下列向量组线性相关? a 1=(a , 1, 1)T , a 2=(1, a , -1)T , a 3=(1, -1, a )T . 解 以所给向量为列向量的矩阵记为A . 由)1)(1(111111||+-=--=a a a aa a A知, 当a =-1、0、1时, R (A )<3, 此时向量组线性相关.8. 设a 1, a 2线性无关, a 1+b , a 2+b 线性相关, 求向量b 用a 1, a 2线性表示的表示式.解 因为a 1+b , a 2+b 线性相关, 故存在不全为零的数λ1, λ2使 λ1(a 1+b )+λ2(a 2+b )=0,由此得 2211121122121211)1(a a a a b λλλλλλλλλλλλ+--+-=+-+-=, 设211λλλ+-=c , 则 b =c a 1-(1+c )a 2, c ∈R .9. 设a 1, a 2线性相关, b 1, b 2也线性相关, 问a 1+b 1, a 2+b 2是否一定线性相关?试举例说明之. 解 不一定.例如, 当a 1=(1, 2)T , a 2=(2, 4)T , b 1=(-1, -1)T , b 2=(0, 0)T 时, 有 a 1+b 1=(1, 2)T +b 1=(0, 1)T , a 2+b 2=(2, 4)T +(0, 0)T =(2, 4)T , 而a 1+b 1, a 2+b 2的对应分量不成比例, 是线性无关的.10.举例说明下列各命题是错误的:(1) 若向量组m a a a ,,,21 是线性相关的,则1a 可由,,2m a a 线性表示.(2) 若有不全为0的数m λλλ,,,21 使 01111=+++++m m m m b b a a λλλλ 成立, 则m a a ,,1线性相关, m b b ,,1 亦线性相关. (3) 若只有当m λλλ,,,21 全为0时,等式01111=+++++m m m m b b a a λλλλ 才能成立,则m a a ,,1 线性无关, m b b ,,1 亦线性无关.(4) 若m a a ,,1 线性相关, m b b ,,1 亦线性相关,则有不全为0的数, m λλλ,,,21 使.0 ,01111=++=++m m m m b b a a λλλλ 同时成立.解 (1) 设)0,,0,0,1(11 ==e a , 032====m a a a满足m a a a ,,,21 线性相关, 但1a 不能由,,,2m a a 线性表示.(2) 有不全为零的数m λλλ,,,21 使 01111=+++++m m m m b b a a λλλλ原式可化为 0)()(111=++++m m m b a b a λλ取 m m m b e a b e a b e a -==-==-==,,,222111 . 其中m e e ,,1 为单位向量,则上式成立,而m a a ,,1 ,m b b ,,1 均线性相关.(3) 由01111=+++++m m m m b b a a λλλλ (仅当01===m λλ )m m b a b a b a +++⇒,,,2211 线性无关取021====m ααα , 取m b b ,,1 为线性无关组. 满足以上条件,但不能说是m ααα,,,21 线性无关的.(4) Ta )0,1(1= Ta )0,2(2= Tb )3,0(1= Tb )4,0(2=⎪⎭⎪⎬⎫-=⇒=+-=⇒=+21221121221143020λλλλλλλλb b a a 021==⇒λλ与题设矛盾.11.设144433322211,,,a a b a a b a a b a a b +=+=+=+=,证明向量组4321,,,b b b b 线性相关. 证明 设有4321,,,x x x x 使得044332211=+++b x b x b x b x 则0)()()()(144433322211=+++++++a a x a a x a a x a a x 0)()()()(443332221141=+++++++a x x a x x a x x a x x(1) 若4321,,,a a a a 线性相关,则存在不全为零的数4321,,,k k k k ,411x x k +=; 212x x k +=; 323x x k +=; 434x x k +=;由4321,,,k k k k 不全为零,知4321,,,x x x x 不全为零,即4321,,,b b b b 线性相关. (2) 若4321,,,a a a a 线性无关, 则⎪⎪⎩⎪⎪⎨⎧=+=+=+=+000043322141x x x x x x x x 011000110001110014321=⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎭⎫⎝⎛⇒x x x x 由01100011000111001= 知此齐次方程存在非零解. 则4321,,,b b b b 线性相关. 综合得证.12.设r r a a a b a a b a b +++=+== 2121211,,,,且向量组r a a a ,,,21 线性无关,证明向量组r b b b ,,,21 线性无关.证明 设02211=+++r r b k b k b k 则++++++++++p r p r r a k k a k k a k k )()()(2211 0=+r r a k因向量组r a a a ,,,21 线性无关,故⎪⎩⎪⎨⎧==++=+++000221r r r k k k k k k ⇔⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎭⎫ ⎝⎛0001001101121 r k k k因为0110011011≠= 故方程组只有零解. 则021====r k k k . 所以r b b b ,,,21 线性无关13.求下列向量组的秩,并求一个最大无关组:(1) ⎪⎪⎪⎪⎭⎫ ⎝⎛-=41211a ,⎪⎪⎪⎪⎭⎫ ⎝⎛=41010092a ,⎪⎪⎪⎪⎭⎫⎝⎛---=82423a ; (2) )3,1,2,1(1=T a ,)6,5,1,4(2---=T a ,)7,4,3,1(3---=Ta .解 (1) 3131,2a a a a ⇒=-线性相关.由⎪⎪⎪⎭⎫ ⎝⎛----=⎪⎪⎪⎭⎫ ⎝⎛824241010094121321T T Ta a a ⎪⎪⎪⎭⎫⎝⎛--000032198204121~秩为2,一组最大线性无关组为21,a a .(2) ⎪⎪⎪⎭⎫ ⎝⎛------=⎪⎪⎪⎭⎫ ⎝⎛743165143121321T T T a a a ⎪⎪⎪⎭⎫⎝⎛------10550189903121~⎪⎪⎪⎭⎫⎝⎛---0000189903121~ 秩为2,最大线性无关组为TT a a 21,.14.利用初等行变换求下列矩阵的列向量组的一个最大无关组,并把其余列向量用最大无关组线性表示:(1) ⎪⎪⎪⎪⎭⎫⎝⎛4820322513454947513253947543173125; (2) ⎪⎪⎪⎪⎭⎫ ⎝⎛---14011313021512012211.解 (1) ⎪⎪⎪⎪⎭⎫⎝⎛482032251345494751325394754317312514131233~r r r r r r ---⎪⎪⎪⎪⎭⎫⎝⎛531053103210431731252334~r r r r --⎪⎪⎪⎪⎭⎫ ⎝⎛0003100321043173125 所以第1、2、3列构成一个最大无关组.(2) ⎪⎪⎪⎪⎭⎫⎝⎛---1401131302151201221114132~r r r r --⎪⎪⎪⎪⎭⎫⎝⎛------222001512015120122114323~rr r r ↔+⎪⎪⎪⎪⎭⎫⎝⎛---00000222001512012211,所以第1、2、3列构成一个最大无关组.15. 设向量组(a , 3, 1)T , (2, b , 3)T , (1, 2, 1)T , (2, 3, 1)T的秩为2, 求a , b .解 设a 1=(a , 3, 1)T , a 2=(2, b , 3)T , a 3=(1, 2, 1)T , a 4=(2, 3, 1)T . 因为⎪⎪⎭⎫ ⎝⎛----⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛=5200111031116110111031113111332221) , , ,(~~2143b a a b a b a r r a a a a ,而R (a 1, a 2, a 3, a 4)=2, 所以a =2, b =5.16.设n a a a ,,,21 是一组n 维向量,已知n 维单位坐标向量n e e e ,,,21 能由它们线性表示,证明n a a a ,,,21 线性无关.证明 n 维单位向量n e e e ,,,21 线性无关. 不妨设:nnn n n n nn n n a k a k a k e a k a k a k e a k a k a k e +++=+++=+++= 22112222121212121111所以 ⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎭⎫ ⎝⎛T n T Tnn n n n n T n T T a a a k k k k k k k k k e ee 2121222211121121两边取行列式,得T n T T nn n n n nTnTTa a a k k k k k k k k k e e e2121222211121121= 由 002121≠⇒≠T nT T T n T T a a a e e e 即n 维向量组n a a a ,,,21 所构成矩阵的秩为n . 故n a a a ,,,21 线性无关.17.设n a a a ,,,21 是一组n 维向量,证明它们线性无关的充分必要条件是:任一n 维向量都可由它们线性表示.证明 设n εεε,,,21 为一组n 维单位向量,对于任意n 维向量T n k k k a ),,,(21 =则有n n k k k a εεε+++= 2211即任一n 维向量都可由单位向量线性表示.必要性⇒n a a a ,,,21 线性无关,且n a a a ,,,21 能由单位向量线性表示,即nnn n n n nn n n k k k k k k k k k εεεαεεεαεεεα+++=+++=+++= 22112222121212121111故 ⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎭⎫ ⎝⎛n T T T nn n n n n T n T T k k k k k k k k k a aa εεε2121222211121121 两边取行列式,得 TnTTnn n n n n TnTTk k k k k k k k k a a a εεε2121222211121121=由 0021222211121121≠⇒≠nnn n nn T n T T k k k k k k k k k a a a令 ⎪⎪⎪⎪⎭⎫ ⎝⎛=⨯nn n n n n n n k k k k k k k k k A212222111211 . 由⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎭⎫ ⎝⎛⇒⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎭⎫⎝⎛-T n T T T n T TT n T T T n T Ta a a A A a a a εεεεεε 212112121即n εεε,,,21 都能由n a a a ,,,21 线性表示,因为任一n 维向量能由单位向量线性表示,故任一 n 维向量都可以由n a a a ,,,21 线性表示.充分性⇐已知任一n 维向量都可由n a a a ,,,21 线性表示,则单位向量组:n εεε,,,21 可由n a a a ,,,21 线性表示,由16题知n a a a ,,,21 线性无关.18. 设向量组a 1, a 2, ⋅ ⋅ ⋅, a m 线性相关, 且a 1≠0, 证明存在某个向量a k (2≤k ≤m ), 使a k 能由a 1, a 2, ⋅ ⋅ ⋅, a k -1线性表示.证明 因为a 1, a 2, ⋅ ⋅ ⋅, a m 线性相关, 所以存在不全为零的数λ1, λ2, ⋅ ⋅ ⋅,λm , 使λ1a 1+λ2a 2+ ⋅ ⋅ ⋅ +λm a m =0,而且λ2, λ3,⋅ ⋅ ⋅, λm 不全为零. 这是因为, 如若不然, 则λ1a 1=0, 由a 1≠0知λ1=0, 矛盾. 因此存在k (2≤k ≤m ), 使λk ≠0, λk +1=λk +2= ⋅ ⋅ ⋅ =λm =0,于是λ1a 1+λ2a 2+ ⋅ ⋅ ⋅ +λk a k =0,a k =-(1/λk )(λ1a 1+λ2a 2+ ⋅ ⋅ ⋅ +λk -1a k -1),即a k 能由a 1, a 2, ⋅ ⋅ ⋅, a k -1线性表示.19.设向量组:B r b b ,,1 能由向量组:A s a a ,,1 线性表示为K a a b b s r ),,(),,(11 =,其中K 为r s ⨯矩阵,且A 组线性无关。
发电厂电气部分第四章习题解答

第四章电气主接线4—1 对电气主接线的基本要求是什么?答:对电气主接线的基本要求是:可靠性、灵活性和经济性.其中保证供电可靠是电气主接线最基本的要求。
灵活性包括:操作、调度、扩建的方便性。
经济性包括:节省一次投资,占地面积小,电能损耗少。
4-2 隔离开关与断路器的区别何在?对它们的操作程序应遵循哪些重要原则?答:断路器具有专用灭弧装置,可以开断或闭合负荷电流和开断短路电流,故用来作为接通和切断电路的控制电器.而隔离开关没有灭弧装置,其开合电流极小,只能用来做设备停用后退出工作时断开电路。
4—3 防止隔离开关误操作通常采用哪些措施?答:为了防止隔离开关误操作,除严格按照规章实行操作票制度外,还应在隔离开关和相应的断路器之间加装电磁闭锁和机械闭锁装置或电脑钥匙。
4-4 主母线和旁路母线各起什么作用?设置专用旁路断路器和以母联断路器或者分段断路器兼作旁路断路器,各有什么特点?检修出线断路器时,如何操作?答:主母线主要用来汇集电能和分配电能。
旁路母线主要用与配电装置检修短路器时不致中断回路而设计的。
设置旁路短路器极大的提高了可靠性。
而分段短路器兼旁路短路器的连接和母联短路器兼旁路断路器的接线,可以减少设备,节省投资。
当出线和短路器需要检修时,先合上旁路短路器,检查旁路母线是否完好,如果旁路母线有故障,旁路断路器在合上后会自动断开,就不能使用旁路母线。
如果旁路母线完好,旁路断路器在合上就不会断开,先合上出线的旁路隔离开关,然后断开出线的断路器,再断开两侧的隔离开关,有旁路短路器代替断路器工作,便可对短路器进行检修。
4-5 发电机—变压器单元接线中,在发电机和双绕作变压器之间通常不装设断路器,有何利弊?答:发电机和双绕组变压器之间通常不装设断路器,避免了由于额定电流或短路电流过大,使得在选择出口断路器时,受到制造条件或价格等原因造成的困难。
但是,变压器或者厂用变压器发生故障时,除了跳主变压器高压侧出口断路器外,还需跳发电机磁场开关,若磁场开关拒跳,则会出现严重的后果,而当发电机定子绕组本身发生故障时,若变压吕高压侧失灵跳闸,则造成发电机和主变压器严重损坏.并且发电机一旦故障跳闸,机组将面临厂用电中断的威胁。
[分享]第四章刚体的转动问题与习题解答
![[分享]第四章刚体的转动问题与习题解答](https://img.taocdn.com/s3/m/c9e3663ccec789eb172ded630b1c59eef8c79aab.png)
第四章 刚体的转动 问题与习题解答问题:4-2、4-5、4-94-2如果一个刚体所受合外力为零,其合力矩是否也一定为零?如果刚体所受合外力矩为零,其合外力是否也一定为零?答:一个刚体所受合外力为零,其合力矩不一定为零,如图a 所示。
刚体所受合外力矩为零,其合外力不一定为零,例如图b 所示情形。
4-5为什么质点系动能的改变不仅与外力有关,而且也与内力有关,而刚体绕定轴转动动能的改变只与外力矩有关,而与内力矩无关?答:因为合外力对质点所作的功,等于质点动能的增量;而质点系中内力一般也做功,故内力对质点系的动能的增量有贡献。
而在刚体作定轴转动时,任何一对内力对转轴的力矩皆为一对大小相等、方向相反的力矩,且因定轴转动时刚体转过的角度d θ都一样,故其一对内力矩所作的功()0inij ij ji ij ji W M d M d M M d θθθ=+=+=,其内力功总和也为零,因而根据刚体定轴转动的动能定理可知:内力矩对其转动动能的增量无贡献。
4-9一人坐在角速度为0ω的转台上,手持一个旋转的飞轮,其转轴垂直地面,角速度为ω'。
如果突然使飞轮的转轴倒转,将会发生什么情况?设转台和人的转动惯量为J ,飞轮的转动惯量为J '。
答:(假设人坐在转台中央,且飞轮的转轴与转台的转轴重合)视转台、人和飞轮为同一系统。
(1)如开始时飞轮的转向与转台相同,则系统相对于中心轴的角动量为:10L J J ωω''=+飞轮转轴快速倒转后,飞轮的角速度大小还是ω',但方向与原来相反;如设转台此时的角速度为1ω,则系统的角动量为:21L J J ωω''=-在以上过程中,外力矩为零,系统的角动量守恒,所以有:10J J J J ωωωω''''-=+即 102J Jωωω''=+,转台的转速变大了。
(2)如开始时飞轮的转向与转台相反,则系统相对于中心轴的角动量为:10L J J ωω''=-飞轮转轴快速倒转后,飞轮的角速度大小还是ω',但方向与原来相反;如设转台此时的角速度为1ω,则系统的F 1F 3ab角动量为:21L J J ωω''=+在以上过程中,外力矩为零,系统的角动量守恒,所以有:10J J J J ωωωω''''+=-即 102J Jωωω''=-,转台的转速变慢了。
机械原理总复习题及解答第四章
机械原理总复习题及解答第四章第4章凸轮机构及其设计4.1填空题4.1.1.设计滚⼦从动件盘形凸轮机构时,滚⼦中⼼的轨迹称为凸轮的廓线;与滚⼦相包络的凸轮廓线称为廓线。
4.1.2.盘形凸轮的基圆半径是上距凸轮转动中⼼的最⼩向径。
4.1.3.根据图4.1的??22d d s 运动线图,可判断从动件的推程运动是_____________,从动件的回程运动是______________。
图4.1题4.1.9图4.1.4.在设计滚⼦从动件盘形凸轮轮廓曲线中,若出现时,会发⽣从动件运动失真现象。
此时,可采⽤⽅法避免从动件的运动失真。
4.2判断题4.2.1..偏置直动尖顶从动件盘形凸轮机构中,其推程运动⾓等于凸轮对应推程廓线所对中⼼⾓;其回程运动⾓等于凸轮对应回程廓线所对中⼼⾓。
( )4.2.2.在直动从动件盘形凸轮机构中进⾏合理的偏置,是为了同时减⼩推程压⼒⾓和回程压⼒⾓。
( )4.2.3.当凸轮机构的压⼒⾓的最⼤值超过许⽤值时,就必然出现⾃琐现象。
()4.2.4.凸轮机构中,滚⼦从动件使⽤最多,因为它是三种从动件中的最基本形式。
()4.2.5.直动平底从动件盘形凸轮机构⼯作中,其压⼒⾓始终不变。
()4.2.6.滚⼦从动件盘形凸轮机构中,基圆半径和压⼒⾓应在凸轮的实际廓线上来度量。
()4.2.7.滚⼦从动件盘形凸轮的实际轮廓曲线是理论轮廓曲线的等距曲线。
因此,只要将理论廓线上各点的向径减去滚⼦半径,便可得到实际轮廓曲线上相应点的向径。
()4.2.8.从动件按等加速等减速运动规律运动时,推程的始点、中点及终点存在柔性冲击。
因此,这种运动规律只适⽤于中速重载的凸轮机构中。
()4.2.9.从动件按等加速等减速运动规律运动是指从动件在推程中按等加速运动,⽽在回程中则按等减速运动,且它们的绝对值相等。
()4.2.10.从动件按等速运动规律运动时,推程起始点存在刚性冲击,因此常⽤于低速的凸轮机构中。
()4.2.11.在对⼼直动尖顶从动件盘形凸轮机构中,当从动件按等速运动规律运动时,对应的凸轮廓线是⼀条阿⽶德螺旋线。
第四章习题及解答
第四章习题及解答4.1 数字电路设计的基本步骤有哪些?每一步完成的目标任务是什么?见书P48。
4.2 组合逻辑电路的设计为什么可以从卡诺图直接进入?因为逻辑函数可以有多种有表达形式,卡诺图就是其中的一种,因此,直接从卡诺图直接进入设计就是最直接、最有效的一种方式,它简化了设计,更便于化简。
4.3 某车间有A 、B 、C 、D 四台电动机,今要求:(1)A 必须开机;(2)其他三台电动机中至少有两台开机,如不满足上述要求,则指示灯熄灭。
设指示灯亮为“1”,熄灭为“0”,电机开机为“1”,停机为“0”,试用与非门组成指示灯控制电路。
根据题意,用卡诺图表示电机运行的状态,求出输出表达式:F= ABC+ABD+ACD用与非门实现逻辑:4.4 试设计一个供4组使用的智力抢答器电路。
设4组变量分别为:A 、B 、C 、D 。
输出用4个发光二极管,表示抢答结果,灯亮答表达式: F ABCD ABCD ABCD =+++4.5 电话室需对4种电话编码控制,按紧急次序排列优先权由高到底依次为火警电话、急救电话、工作电话、生活电话,其编码为11,10,01,00,试设计该编码电路。
设火警电话、急救电话、工作电话、生活电话为变量A 、B 、C 、D ,编码输出量为X 、Y 。
AB CD01001110000000000001111000 01 11 10 F ABC ABD ACDABC ABD ACD =++=AB C D题4.3图列出编码真值表:4.6 试用3线-8线译码器和门电路实现以下函数:4.7 试用四选一多路选择器实现函数Y ABC AC BC =++。
1. 求出最小项、及最小项反函数非表达式:2. 对比四选一多路选择器表达式:0123Y ABD ABD ABD ABD =+++我们发现用原函数无法用一个四选一选择器实现,但反函数只有三个最小项,因为实际的数据选择器,它们都有两个互补的变量输出,因此从反变量输出端(~W)就可以达到要求了。
(完整版)第4章应变式传感器习题及解答

(完整版)第4章应变式传感器习题及解答第4章应变式传感器⼀、单项选择题1、为减⼩或消除⾮线性误差的⽅法可采⽤()。
A. 提⾼供电电压B. 提⾼桥臂⽐C. 提⾼桥臂电阻值D. 提⾼电压灵敏度2、全桥差动电路的电压灵敏度是单臂⼯作时的()。
A. 不变B. 2倍C. 4倍D. 6倍3、电阻应变⽚配⽤的测量电路中,为了克服分布电容的影响,多采⽤( )。
A.直流平衡电桥 B.直流不平衡电桥C.交流平衡电桥 D.交流不平衡电桥4、通常⽤应变式传感器测量( )。
A. 温度 B.密度C.加速度 D.电阻5、影响⾦属导电材料应变灵敏系数K的主要因素是()。
A.导电材料电阻率的变化 B.导电材料⼏何尺⼨的变化C.导电材料物理性质的变化 D.导电材料化学性质的变化6、产⽣应变⽚温度误差的主要原因有()。
A.电阻丝有温度系数 B.试件与电阻丝的线膨胀系数相同C.电阻丝承受应⼒⽅向不同 D.电阻丝与试件材料不同7、电阻应变⽚的线路温度补偿⽅法有()。
A.差动电桥补偿法 B.补偿块粘贴补偿应变⽚电桥补偿法C.补偿线圈补偿法 D.恒流源温度补偿电路法8、当应变⽚的主轴线⽅向与试件轴线⽅向⼀致,且试件轴线上受⼀维应⼒作⽤时,应变⽚灵敏系数K的定义是()。
A.应变⽚电阻变化率与试件主应⼒之⽐B.应变⽚电阻与试件主应⼒⽅向的应变之⽐C.应变⽚电阻变化率与试件主应⼒⽅向的应变之⽐D.应变⽚电阻变化率与试件作⽤⼒之⽐9、制作应变⽚敏感栅的材料中,⽤的最多的⾦属材料是()。
10、利⽤相邻双臂桥检测的应变式传感器,为使其灵敏度⾼、⾮线性误差⼩()。
A.两个桥臂都应当⽤⼤电阻值⼯作应变⽚B.两个桥臂都应当⽤两个⼯作应变⽚串联C.两个桥臂应当分别⽤应变量变化相反的⼯作应变⽚D.两个桥臂应当分别⽤应变量变化相同的⼯作应变⽚11、在⾦属箔式应变⽚单臂单桥测⼒实验中不需要的实验设备是()。
A.直流稳压电源 B.低通滤波器C.差动放⼤器 D.电压表12、关于电阻应变⽚,下列说法中正确的是()A.应变⽚的轴向应变⼩于径向应变B.⾦属电阻应变⽚以压阻效应为主C.半导体应变⽚以应变效应为主D.⾦属应变⽚的灵敏度主要取决于受⼒后材料⼏何尺⼨的变化13、⾦属丝的电阻随着它所受的机械变形(拉伸或压缩)的⼤⼩⽽发⽣相应的变化的现象称为⾦属的()。
概率论与数理统计习题解答(第4章)

第4章习题答案三、解答题1. 设随机变量X求)(X E ,)(2X E ,)53(+X E .解:E (X ) =∑∞=1i ixp= ()2-4.0⨯+03.0⨯+23.0⨯= -0.2E (X 2) =∑∞=12i i p x= 44.0⨯+ 03.0⨯+ 43.0⨯= 2.8E (3 X +5) =3 E (X ) +5 =3()2.0-⨯+5 = 4.42. 同时掷八颗骰子,求八颗骰子所掷出的点数和的数学期望. 解:记掷1颗骰子所掷出的点数为X i ,则X i 的分布律为6,,2,1,6/1}{ ===i i X P记掷8颗骰子所掷出的点数为X ,同时掷8颗骰子,相当于作了8次独立重复的试验, E (X i ) =1/6×(1+2+3+4+5+6)=21/6 E (X ) =8×21/3=283. 某图书馆的读者借阅甲种图书的概率为p 1,借阅乙种图书的概率为p 2,设每人借阅甲乙图书的行为相互独立,读者之间的行为也是相互独立的. (1) 某天恰有n 个读者,求借阅甲种图书的人数的数学期望.(2) 某天恰有n 个读者,求甲乙两种图书至少借阅一种的人数的数学期望. 解:(1) 设借阅甲种图书的人数为X ,则X~B (n , p 1),所以E (X )= n p 1 (2) 设甲乙两种图书至少借阅一种的人数为Y , 则Y ~B (n , p ),记A ={借甲种图书}, B ={借乙种图书},则p ={A ∪ B }= p 1+ p 2 - p 1 p 2 所以E (Y )= n (p 1+ p 2 - p 1 p 2 )4. 将n 个考生的的录取通知书分别装入n 个信封,在每个信封上任意写上一个考生的姓名、地址发出,用X 表示n 个考生中收到自己通知书的人数,求E (X ).解:依题意,X~B (n ,1/n ),所以E (X ) =1.5. 设)(~λP X ,且}6{}5{===X P X P ,求E (X ).解:由题意知X ~P (λ),则X 的分布律P{}k X ==λλ-e k k!,k = 1,2,...又P {}5=X =P {}6=X , 所以λλλλ--=e e!6!565解得 6=λ,所以E (X ) = 6.6. 设随机变量X 的分布律为,,4,3,2,1,6}{22 --===k kk X P π问X 的数学期望是否存在?解:因为级数∑∑∑∞=+∞=+∞=+-=-=⨯-11212112211)1(6)6)1(()6)1((k k k k k k kk k k πππ, 而 ∑∞=11k k 发散,所以X 的数学期望不存在.7. 某城市一天的用电量X (十万度计)是一个随机变量,其概率密度为⎪⎩⎪⎨⎧>=-.0,0,91)(3/其它x xe x f x 求一天的平均耗电量.解:E (X ) =⎰⎰⎰∞-∞-∞∞-==03/203/9191)(dx e x dx xe xdx x f x x x =6.8. 设某种家电的寿命X (以年计)是一个随机变量,其分布函数为⎪⎩⎪⎨⎧>-=.0,5,251)(2其它x x x F求这种家电的平均寿命E (X ).解:由题意知,随机变量X 的概率密度为)()(x F x f '=当x >5时,=)(x f 3350252xx =⨯--,当x ≤5时,=)(x f 0. E (X ) =10|5050)(5-53=-==∞++∞∞+∞⎰⎰xdx x x dx x xf 所以这种家电的平均寿命E (X )=10年.9. 在制作某种食品时,面粉所占的比例X 的概率密度为⎩⎨⎧<<-=.0,10,)1(42)(5其它x x x x f 求X 的数学期望E (X ).解:E (X ) =dx x x dx x xf ⎰⎰+∞∞-=-152)1(42)(=1/410. 设随机变量X 的概率密度如下,求E (X ).⎪⎪⎪⎩⎪⎪⎪⎨⎧≤<-≤≤-+=.010,)1(2301)1(23)(22其它,,,,x x x x x f解:0)1(1023)1(0123)()(22=-++-=+∞∞-=⎰⎰⎰dx x x dx x x dx x xf X E .111. 设),4(~p B X ,求数学期望)2(sinX E π. 解:X 的分布律为k n kk n p p C k X P --==)1(}{, k = 0,1,2,3,4,X 取值为0,1,2,3,4时,2sinX π相应的取值为0,1,0,-1,0,所以)21)(1(4)1(1)1(1)2(sin13343114p p p p p C p p C XE --=-⨯--⨯=π12. 设风速V 在(0,a )上服从均匀分布,飞机机翼受到的正压力W 是V 的函数:2kV W =,(k > 0,常数),求W 的数学期望.解:V 的分布律为⎪⎩⎪⎨⎧<<=其它 ,00 ,1)(a v a v f ,所以 ===+∞∞-=⎰⎰aa v a k dv a kv dx v f kv W E 03022|)31(1)()(231ka13. 设随机变量(X ,求E (X ),E (Y ),E (X – Y ).解:E (X )=0×(3/28+9/28+3/28)+1×(3/14+3/14+0)+ 2×(1/28+0+0)= 7/14=1/2 E (Y )=0×(3/28+3/14+1/28)+1×(9/28+3/14+0)+ 2×(3/28+0+0)=21/28=3/4 E (X -Y ) = E (X )- E (Y )=1/2-3/4= -1/4.14. 设随机变量(X ,Y )具有概率密度⎩⎨⎧≤+≤≤≤≤=其它,01,10,10,24),(y x y x xy y x f ,求E (X ),E (Y ),E (XY )解:E (X )=⎰⎰⎰⎰-=⋅11022424xDydydx x xydxdy x dx x x ⎰-⋅=1022)1(2124dx x x x ⎰+-=10432)2412(52)51264(1543=+-=x x x.152)34524638()1(31242424)(5/22424)(1654311010322210102=-+-=-⋅==⋅===⋅=⎰⎰⎰⎰⎰⎰⎰⎰⎰--x x x x dx x x dydx y xxydxdy xy XY E xdxdy y xydxdy y Y E DxDy15.所得利润(以元计)为)12(1000X Y -=,求E (Y ),D (Y ).解: E (Y) = E [1000(12-X )]=1000E [(12-X )]=1000×[(12-10)×0.2+(12-11)]×0.3+(12-12)×0.3+(12-13)×0.1+(12-14)×0.1] = 400E (Y 2) = E [10002(12-X )2]=10002E [(12-X )2]=10002[(12-10)2×0.2+(12-11)2×0.3+(12-12)2×0.3+(12-13)2×0.1 +(12-14)2×0.1]=1.6×106D (Y )=E (Y 2)-[E (Y )]2=1.6×106- 4002=1.44×10616. 设随机变量X 服从几何分布 ,其分布律为,,2,1,)1(}{1 =-==-k p p k X P k 其中0 < p < 1是常数,求E (X ),D (X ).解:令q=1- p ,则∑∑∑∑∞=∞=-∞=-∞==⨯=⨯==⨯=111111)()}{()(k kk k k k k dqdq p qk p p qk k X P k X Ep q dq d p q dq d p k k /1)11(0∑∞==-==∑∑∑∑∞=-∞=-∞=-∞=⨯+⨯-=⨯==⨯=1111112122])1([)()}{()(k k k k k k k q k qk k p p qk k X P k X Ep qk k pq k k /1)1(12+⨯-=∑∞=-p qdq d pq p q dqd pq k k kk /1)(/1012222∑∑∞=∞=+=+=p p q p q pq p q dq d pq /1/2/1)1(2/1)11(2322+=+-=+-= D (X ) = E (X 2)- E (X ) =2q /p 2+1/p -1/p 2 = (1-p )/p 217. 设随机变量X 的概率密度为⎪⎩⎪⎨⎧<-=其它,01||,11)(2x x x f π,试求E (X ),D (X ).解:E (X )=011)(112=-=⎰⎰-∞∞-dx xxdx x f x πD (X )=E (X 2)=⎰⎰⎰--∈-∞∞-=-=2/2/2]2/,2/[11222cos sin sin 11)(ππππππdt tt tx dx xxdx x f x t2122cos 122/0=-=⎰ππdt t 18. 设随机变量(X ,Y )具有D (X ) = 9,D (Y ) = 4,6/1-=XY ρ,求)(Y X D +,)43(+-Y X D . 解:因为)()(),(Y D X D Y X Cov XY =ρ,所以)()(),(Y D X D Y X Cov XY ρ==-1/6×3×2=-1,11249),(2)()()(=-+=++=+Y X Cov Y D X D Y X D51)1(6369)3,(2)(9)()43(=--+=-++=+-Y X Cov Y D X D Y X D19. 在题13中求Cov (X ,Y ),ρXY . 解:E (X ) =1/2, E (Y ) =3/4, E (XY )=0×(3/28+9/28+3/28+3/14+1/28)+1×3/14+2×0+4×0=3/14, E (X 2)= 02×(3/28+9/28+3/28)+12×(3/14+3/14+0)+ 22×(1/28+0+0)=4/7, E (Y 2)= 02×(3/28+3/14+1/28)+12×(9/28+3/14+0)+ 22×(3/28+0+0)=27/28, D (X )= E (X 2) -[E (X )]2 = 4/7-(1/2)2= 9/28, D (Y )= E (Y 2)- [E (Y )]2=27/28-(3/4)2= 45/112, Cov (X ,Y )= E (XY )- E (X ) E (Y ) =3/14- (1/2) ×(3/4)= -9/56, ρXY = Cov (X ,Y ) /()(X D )(Y D )=-9/56 ÷ (28/9112/45)= -5/520. 在题14中求Cov (X ,Y ),ρXY ,D (X + Y ).解:52)()(==Y E X E ,,)(152=XY E 752)()()(),(-=-=Y E X E XY E Y X Cov )(5124)(2101032Y E dydx y x X E x ===⎰⎰-[])(25125451)()()(22Y D X E X E X D ==-=-= 752),(2)()()(32)()(),(=++=+-==Y X Cov Y D X D Y X D Y D X D Y X Cov XYρ21. 设二维随机变量(X , Y )的概率密度为⎪⎩⎪⎨⎧≤+=.0,1,1),(22其它y x y x f π试验证X 和Y 是不相关的,但X 和Y 不是相互独立的.解:0/12/)(112111122=-==⎰⎰⎰-----dx x x dydx x X E x xππOx2x20/)(111122==⎰⎰----x x dydx y Y E π 0/)(111122==⎰⎰----x x dydx xy XY E π,所以Cov (X ,Y )=0,ρXY =0,即X 和Y 是不相关.⎪⎩⎪⎨⎧<<--=⎪⎩⎪⎨⎧<<-==⎰⎰---∞+∞-其他,,其他,01112011,/1),()(21122x x x dy dy y x f x f x x X ππ ⎪⎩⎪⎨⎧<<--=⎪⎩⎪⎨⎧<<-==⎰⎰---∞+∞-其他,,其他,01112011,/1),()(21122y y y dx dx y x f y f y y Y ππ 当x 2 + y 2≤1时,f ( x,y )≠f X ( x ) f Y (y ),所以X 和Y 不是相互独立的22. 设随机变量(X , Y )的概率密度为⎩⎨⎧<<<=.010,2||,2/1),(其它x x y y x f 验证X 和Y 是不相关的,但X 和Y 不是相互独立的.解:由于f ( x,y )的非零区域为D : 0 < x < 1, | y |< 2x32221102212====⎰⎰⎰⎰⎰-dx x xdydx dxdy y x xf X E xx D ),()(,0211022⎰⎰⎰⎰-===xx Dydydx dxdy y x yf Y E ),()(,0211022⎰⎰⎰⎰-===xx Dxydydx dxdy y x xyf XY E ),()(,所以Cov (X ,Y )=0,从而0)()(),(==y D x D y x Cov xy ρ,因此X 与Y 不相关 .⎪⎩⎪⎨⎧<<===⎰⎰-∞∞-其他,010,221),()(22Xx x dy dy y x f x x x f⎪⎪⎪⎩⎪⎪⎪⎨⎧<≤-=<<-+===⎰⎰⎰-∞+∞-其他,020,421202,42121),()(1212Y y y dx y y dx dx y x f y y y f所以,当0<x <1, -2<y<2时,)()(),(y f x f y x f Y X ≠,所以X 和Y 不是相互独立的 .⎪⎩⎪⎨⎧≤>>=⎩⎨⎧≥<<--==-0,00,0,1)(,0),()(y y e y f Y x Y mx xY Y x n mY Y Q Q y Y θθθ的密度函数为[]()()()取最大值时,当又则令)(n ln 0n m )(d n ln,n 0)(1)()(d )()()()(1.1.)()(.)()( 20000000Q E n m x e dx Q E n m x n m e n e n m n e n m dx Q E nxn m e n m m xenx nxe e n m xe n m m xe nxe dy n m e ye n m m xde de nx yde n m dye m x dy e y x n m y dy Yf Y Q Q E x xxx x x x x y x xyx y x y x y x y x y y x x y x y Y +-=∴<+-=+-=∴+==-+=-⎪⎭⎫ ⎝⎛-+-=-+++-=+-++-+-=-+⎥⎥⎦⎤⎢⎢⎣⎡+-+=-++-=+--==---------∞+----∞+---∞+--∞∞-⎰⎰⎰⎰⎰⎰⎰θθθθθθθθθθθθθθθθθθθθθθθθθθθ四、应用题.1. 某公司计划开发一种新产品市场,并试图确定该产品的产量,他们估计出售一件产品可获利m 元,而积压一件产品导致n 元的损失,再者,他们预测销售量Y (件)服从参数θ的解:设生产x 件产品时,获利Q 为销售量Y 的函数2. 设卖报人每日的潜在卖报数为X 服从参数为λ的泊松分布,如果每日卖出一份报可获报酬m 元,卖不掉而退回则每日赔偿n 元,若每日卖报人买进r 份报,求其期望所得及最佳卖报数。
《电路原理导论》第四章习题解答

习题四4-1用叠加定理求图示电路中的电流I 。
答:A 2=I解:(1)电流源单独作用时如图4-1′A 12131621224//42=⨯⨯=⨯++='sI I(2)电压源单独作用时如图4-1″A 12144//412=⨯+=''I(3)当两电源同时作用时A 2=''+'=I I I4-2用叠加定理求图示电路中的I 1、U 4 。
答:V 3;A 5.141-==U I解:(1)当电压源单独作用时如图4-2′()A 166//24311==++='R R R R U I sA 5.02114=⨯='I ;V 14='U (2)当电流源单独作用时如图4-2″A 5.0//212432141=+⨯++⨯=''R R R R R R RR I I s()[]()[]V 432//24//4////43214-=⨯+=+=''s I R R R R U 图4-1 习题4-1题图图4-2 习题4-2题图2Ω图2Ω图图4-2′图4-2″(3)当两电源同时作用时A 5.15.01111=+=''+'=I I I V 341444-=-=''+'=U U U 4-3利用叠加定理求图4-3电路中的电压U 。
答:V 6=U解:(1)当电压源单独作用时如图4-3′V 11516=+⋅='U (2)当电流源单独作用时如图4-3″A 51556=+⨯=''I ,V 551=⨯=''U (3)当两电源同时作用时V 651=+=''+'=U U U4-4利用叠加定理求图示电路的电压U ab 。
答:V 9=ab U解:(1)当电流源单独作用时如图4-4′V 5.46241866186A 3-=⨯-=Ω⨯+⨯-='abU (2)当电压源单独作用时如图4-4″A 875.12.1936181218121236==+⨯+=''us IV 5.1312875.15312181218=⨯⨯=Ω⨯''+=''usabI U (3)当两电源同时作用时V 95.135.4=+-=''+'=ab abab U U U 4-5图4-5电路中已知Ω=11R ,Ω=22R ,Ω=33RΩ=44R ,Ω=55R ,V 6=s U ,A 7=s I ,试用叠加定理求电路中的I 。
计算机组成原理第四章课后习题和答案解析[完整版]
![计算机组成原理第四章课后习题和答案解析[完整版]](https://img.taocdn.com/s3/m/08bc56dd551810a6f52486ec.png)
第4章存储器1. 解释概念:主存、辅存、Cache、RAM、SRAM、DRAM、ROM、PROM、EPROM、EEPROM、CDROM、Flash Memory。
答:主存:主存储器,用于存放正在执行的程序和数据。
CPU可以直接进行随机读写,访问速度较高。
辅存:辅助存储器,用于存放当前暂不执行的程序和数据,以及一些需要永久保存的信息。
Cache:高速缓冲存储器,介于CPU和主存之间,用于解决CPU和主存之间速度不匹配问题。
RAM:半导体随机存取存储器,主要用作计算机中的主存。
SRAM:静态半导体随机存取存储器。
DRAM:动态半导体随机存取存储器。
ROM:掩膜式半导体只读存储器。
由芯片制造商在制造时写入内容,以后只能读出而不能写入。
PROM:可编程只读存储器,由用户根据需要确定写入内容,只能写入一次。
EPROM:紫外线擦写可编程只读存储器。
需要修改内容时,现将其全部内容擦除,然后再编程。
擦除依靠紫外线使浮动栅极上的电荷泄露而实现。
EEPROM:电擦写可编程只读存储器。
CDROM:只读型光盘。
Flash Memory:闪速存储器。
或称快擦型存储器。
2. 计算机中哪些部件可以用于存储信息?按速度、容量和价格/位排序说明。
答:计算机中寄存器、Cache、主存、硬盘可以用于存储信息。
按速度由高至低排序为:寄存器、Cache、主存、硬盘;按容量由小至大排序为:寄存器、Cache、主存、硬盘;按价格/位由高至低排序为:寄存器、Cache、主存、硬盘。
3. 存储器的层次结构主要体现在什么地方?为什么要分这些层次?计算机如何管理这些层次?答:存储器的层次结构主要体现在Cache-主存和主存-辅存这两个存储层次上。
Cache-主存层次在存储系统中主要对CPU访存起加速作用,即从整体运行的效果分析,CPU访存速度加快,接近于Cache的速度,而寻址空间和位价却接近于主存。
主存-辅存层次在存储系统中主要起扩容作用,即从程序员的角度看,他所使用的存储器其容量和位价接近于辅存,而速度接近于主存。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第4章数据库和数据仓库4.1本章知识框架与学习要求数据库技术是数据管理的最新技术,是计算机科学的重要分支。
它已经成为先进信息技术的重要组成部分,是现代计算机信息系统和计算机应用系统的基础和核心。
数据库已经成为人们存储数据、管理信息、共享资源的最先进最常用的技术。
认识和掌握有关的数据库技术对学好本课程具有重要作用。
本章主要介绍了数据库技术的相关概念包括数据的组织层次、数据模型、信息模型、关系规范化等,以及数据库的设计方法,数据库仓库和数据挖掘的概念。
4.1.1 知识框架与学习要求一、数据的描述与组织(掌握)(一)三个世界1.现实世界2.信息世界3.计算机世界(二)数据组织的层次1.数据项(字段)2.记录3.数据文件4.数据库二、数据库管理技术(一)数据管理的发展(了解)1.简单应用阶段2.文件系统阶段3.数据库系统阶段(二)数据库管理系统(掌握)1.数据库系统(DBS)2.数据库管理系统(DBMS)(1)数据库的定义功能(2)数据库的操作功能(3)数据库的保护功能(4)数据库的维护功能(5)数据的存储管理三、数据模型(掌握)(一)信息模型(概念模型)1.信息模型的要素2.两个实体集之间联系的分类3.实体联系模型(E-R模型)(二)数据模型1.数据模型的三要素2.数据模型与信息模型的关系3.三种主要的数据模型(1)层次模型(Hierarchical Model)(2)网状模型(Network Model)(3)关系模型(Relational Model)(三)概念模型向关系模型的转换(四)关系的规范化1.第一范式(1NF)2.第二范式(2NF)3.第三范式(3NF)五、数据库设计(掌握)(一)数据库设计方法简述(二)数据库设计步骤六、数据仓库和数据挖掘(了解)(一)数据仓库1.数据仓库的概念2.数据仓库和数据库的区别3.数据仓库的特性4.数据仓库的基本结构5.数据仓库工具的组成(二)数据挖掘1.数据挖掘的概念2.数据仓库与数据挖掘的关系4.1.2 学习重点本章重点掌握以下几方面的内容:1.三个世界即现实世界、信息世界、计算机世界的特点及区别与联系;2.人工管理阶段、文件系统阶段及数据库系统阶段应用程序与数据关系的区别;3.数据库管理系统功能4.信息(概念)模型的要素、E-R模型的绘制方法;5.数据模型的三要素、数据模型与信息模型的关系、关系模型;6.概念模型向关系模型的转换;7.数据库设计方法和步骤4.2 教材习题与解答4.2.1 习题一、名词解释1.数据库2.记录3.DBMS4.DBS5.概念模式6.数据模型7.概念模型8.键或码9.数据操作10.1NF 11. 2NF 12.3NF 13.关系14.关系模式15.数据仓库16.数据挖掘二、简答题1. 数据库系统组织数据的特点是什么?2. 数据库系统与文件系统的区别是什么?3. 数据管理经历了哪几个阶段?各个阶段的特点是什么?4. 数据模型的三要素是什么?5. 数据库管理系统的主要功能是什么?6. 信息模型的要素有哪些?7. 试述概念模式在数据库中的重要地位。
8.举出实例,要求实体型之间具有一对一、一对多和多对多的联系。
9.实体之间的联系方式有几种?不同的联系方式在转换为关系模型时的处理方式有什么不同?10.什么是E-R图?构成E-R图的基本要素是什么?如何将E-R模型转换为关系模型?11.某工厂生产多种产品,每种产品又要使用多种零件,一种零件可能装在多种产品上。
每种零件由一种材料制造,每种材料可用于不同零件的制作。
有关产品、零件、材料的数据字段如下:产品:产品号(GNO),产品名(GNA),产品单价(GUP)零件:零件号(PNO),零件名(PNA),单重(UW),单价(UP)材料:材料号(MNO),材料名(MNA),计量单位(CU),单价(MUP)以各产品需要各种零件数为GQTY,各零件需要的材料数为PQTY(1)请画出产品、零件、材料的E-R图。
(2)请将该E-R图转换为关系数据模型12. 教学管理涉及的实体有:教员:职工号、姓名、年龄、职称学生:学号、姓名、年龄、性别课程:课程号、课程名、学时数这些实体间的联系如下:一个教员只讲授一门课程,一门课程可由多个教员讲授;一个学生学习多门课程,每门课程有多个学生学习。
请画出教员、学生、课程的E-R图,并构造其关系数据模型。
三、单选题1. DBMS对数据库的保护主要通过四个方面实现,因而在DBMS中应该包括这四个子系统:数据库的并发控制、数据库的恢复、数据完整性控制和()。
A.数据的检索B.数据的更新C.数据安全性控制D.数据的存储2. 在数据库系统的三级模式结构中,外模式通常还称为()。
A.用户模式B.内模式C.物理模式D.概念模式3. 实体与实体间的联系方式有( )种。
A.1 B.2 C.3 D.44.若联系为M:N,则关系的码为所连接的()。
A.N端和M端的码的组合B.N端的码C.M端的码D.都不是5. 数据仓库有四个重要的特点:面向主题、相对稳定的、反映历史变化和()。
A.分散的B.合并的C.集中的D.集成的4.2.2 习题解答一、名词解释1.数据库是存储起来的相关数据的集合。
2.记录是具有一定关系的数据项的有序集合。
3.DBMS即数据库管理系统,是位于用户与操作系统之间的一层数据管理软件。
他的主要功能包括:数据定义功能、数据操纵功能、数据库的运行管理功能、数据库的建立和维护功能。
4.DBS即数据库系统,是指在计算机系统中引入数据库后的系统,这类系统由五部分组成:硬件系统、数据库集合、数据库管理系统(DBMS)及相关软件、数据库管理员(Data Base Administrator,简记为DBA)和用户。
5.概念模式也称模式是数据库中全体数据的逻辑结构和特征的描述,是所有用户的公共数据视图。
它是数据库系统模式结构的中间层,既不涉及数据的物理存储细节和硬件环境,也与具体的应用、所使用的应用开发工具及高级程序设计语言无关。
6.数据模型是数据库中用来对现实世界进行抽象的工具,是数据库系统中用于提供信息表示和操作手段的形式构架。
7.概念模型也称信息模型, 它是按用户的观点来对数据和信息建模,是现实世界到机器世界的中间层次。
它主要用于数据库设计。
8.键或码指能唯一标识每个实体的属性或属性集,有时也称为实体标识符。
例如学生的学号可以作为学生实体的键。
9.数据操作是指对数据库中各种对象(型)的实例(值)允许执行的操作的集合,包括操作及有关的操作规则。
操作主要包括数据库检索和更新(包括插入、删除、修改)两大类操作。
10.满足下述要求的关系,叫做关系的第一范式(1NF),否则称为非规范形式。
(1)关系中每个数据项(元组中每个分量)必须是一个不可分的数据项,即此项所表达的实体属性必是原子属性,且要求数据项没有重复组。
(2)列是同质的,即每一列中所有数据项类型相同。
各列指定一个相异的名字,列的次序任意。
(3)各行相异,不允许有重复的行,行的次序任意。
11.在满足第一范式的关系上消去非主属性对主关键字的不完全依赖性,所得的关系叫第二范式的关系。
12.在满足第二范式的关系上消去非主属性对主关键字的传递依赖性,称为第三范式。
13.关系即指二维表。
14.关系模式即对关系的描述,用关系名(属性1,属性2,……,属性n)来表示。
15.数据仓库是一个面向主题的、集成的、非易失的且随时间变化的数据集合,用来支持经营管理中的决策制定过程。
16.数据挖掘,又称为数据库中的知识发现,就是从大量数据中获取有效的、新颖的、潜在有用的、最终可理解的模式的非平凡过程。
二、简答题1. 数据库系统组织数据的特点是:(1)面向全组织的复杂数据结构。
数据库中的数据结构不仅描述了数据自身,而且描述了整个组织数据之间的联系,实现了整个组织数据的结构化。
(2)数据冗余度小,易于扩充。
由于数据库从组织的整体来看待数据,数据不再是面向某一特定的应用,而是面向整个系统,减少了数据冗余和数据之间的不一致现象。
在数据库系统下,可以根据不同的应用需求选择相应的数据加以使用,使系统易于扩充。
(3)数据与程序独立。
数据库系统提供了数据存储与逻辑结构之间的映射功能及总体逻辑结构与局部逻辑结构之间的映射功能,从而使得当数据的存储结构改变时,逻辑结构保持不变,或者当总体逻辑结构改变时,局部逻辑结构可以保持不变,从而实现了数据的物理独立性和逻辑独立性,把数据的定义和描述与应用程序完全分离开。
(4)统一的数据控制功能。
数据库系统提供了专门的管理软件即数据库管理系统对数据实施统一的管理和控制,这些控制包括数据的安全性控制(Security)、完整性控制(Integrity)和并发控制即允许多个用户同时使用数据库资源等。
2. 数据库系统与文件系统的区别是:(1)数据库系统的数据是面向组织,而文件系统是面向局部应用的。
(2)数据库系统数据共享性高、冗余度小,文件系统数据共享性差、冗余度大。
(3)数据库系统的数据与程序独立,文件系统的数据与程序不完全独立。
(4)数据库系统具有统一的数据控制功能,文件系统没有。
3. 数据管理经历了简单应用阶段、文件系统阶段、数据库系统阶段。
简单应用阶段(20世纪50年代以前)。
这个阶段最基本的特征是无数据管理及完全分散的手工方式。
其表现在:(1)无外存或只有磁带外存,输入输出设备简单。
(2)无操作系统,无文件管理系统,无管理数据的软件。
(3)数据是程序的组成部分,数据不独立。
(4)文件系统尚未出现,程序员必须自行设计数据的组织方式。
文件系统阶段(20世纪50年代后期到60年代中期)。
这个阶段的基本特征是有了面向应用的数据管理功能,工作方式是分散的非手工的。
其表现为:(1)外存有了很大的发展,除磁带机外,还出现了大容量的硬盘和灵活软磁盘。
数据可以长期保存,数据以独立数据文件的形式长期存储在外存储器上,可以被应用程序随时访问。
(2)系统软件方面出现了操作系统、文件管理系统和多用户的分时系统,出现了专用于商业事务管理的高级语言COBOL。
它主要用于文件处理,也可以进行非数值处理。
(3)数据管理方面,实现了数据对程序的一定的独立性,数据不再是程序的组成部分,修改数据不必修改程序,数据有结构,被组织到文件内,存储在磁带、磁盘上,可以反复使用和保存。
(4)文件类型已经多样化。
(5)数据存取以记录为单位。
数据库系统阶段的特点参考第1题。
4. 数据模型的三要素是数据结构、数据操作和完整性约束三部分。
5. 数据库管理系统的主要功能是:(1)数据库的定义功能(2)数据库的操作功能(3)数据库的保护功能(4)数据库的维护功能(5)数据的存储管理6. 信息模型的要素有:(1)实体(Entity):客观存在,可以相互区别的事物称为实体。
