希望杯第1试试题
第十五届“希望杯”数学竞赛第一试试题及答案整理

A. log3 x -1
-x
B. 2 - 3
C. 3-2+x
D. 2 - log3 x
A
4பைடு நூலகம்
40
二、 组填空题(每题 分,共 分) 11 . 已 知 函 数
f (x)
=
ì í
1,
x为有理数,
g(
x)
=
ì í
0,
x为有理数,
当
xÎR 时 ,
î0,x为无理数.
î1,x为无理数.
f (g (x)) = _______, g ( f( )x) = _ _ _ _ _ _ _ .
B. 减法 D. 除法
{ } 9.等比数列
an
中,“
a 1
<
a 3
”是“
a 7
<
a 9
”的(
)
A. 充分而不必要条件 B. 必要而不充分条件 C. 充要条件
D. 既不充分又不必要条件
10.已知函数 f (x) 的图象与函数 g(x) = 3x 的图象关于点 (0,1) 对称,则 f (x) =( )
4. 等差数列
{an
}
、
{bn}
的前
n
项的和分别为
Sn
、
Tn
,且
Sn Tn
=
3n - 3 ,则 a6 2n + 3 b6
=(
)
A. 3 2
B. 1
6
C.
5
27
D.
23
5. 如图,EF 是梯形 ABCD 的中位线,则在向量 1 ( AD + BC) 、
2
A
1 ( AC + BD) 、 1 (2AD - AB - CD) 中,与 EF 相等的向量的个 E
希望杯一试试题及答案

希望杯一试试题及答案一、选择题(每题2分,共10分)1. 以下哪个选项是正确的数学公式?A. \(a^2 + b^2 = c^2\)B. \(a^2 - b^2 = c^2\)C. \(a^2 + 2ab + b^2 = c^2\)D. \(a^2 - 2ab + b^2 = c^2\)答案:A2. 地球的自转周期是多久?A. 24小时B. 12小时C. 48小时D. 36小时答案:A3. 世界上最长的河流是?A. 尼罗河B. 亚马逊河C. 黄河D. 长江答案:B4. 以下哪个元素是人体必需的微量元素?A. 铁B. 钠C. 钙D. 钾答案:A5. 光的三原色是哪三种颜色?A. 红、黄、蓝B. 红、绿、蓝C. 红、白、蓝D. 绿、蓝、紫答案:B二、填空题(每题2分,共10分)1. 圆的周长公式是 \(C = \pi \times \) ________。
答案:直径2. 化学元素周期表中,氢的原子序数是 ________。
答案:13. 牛顿第一运动定律也被称为 ________。
答案:惯性定律4. 世界上最大的哺乳动物是 ________。
答案:蓝鲸5. 光合作用的主要产物是 ________ 和 ________。
答案:氧气;葡萄糖三、简答题(每题5分,共20分)1. 请简述什么是相对论。
答案:相对论是物理学中的一种理论,由阿尔伯特·爱因斯坦提出,主要包括狭义相对论和广义相对论。
狭义相对论主要研究在没有引力作用的惯性系中物理现象的规律,广义相对论则是在狭义相对论的基础上引入引力作用,研究引力对时空的影响。
2. 解释什么是生态系统。
答案:生态系统是指在一定区域内生物群落与其生存环境相互作用形成的一个统一整体。
它包括生物部分(如植物、动物、微生物等)和非生物部分(如气候、土壤、水等),这些部分相互作用、相互依赖,共同维持生态系统的平衡。
3. 描述一下什么是基因突变。
答案:基因突变是指DNA分子中的碱基序列发生改变,这种改变可能是单个碱基的替换、插入、缺失或重复。
历届(第1-23届)希望杯数学竞赛初一七年级真题及答案

“希望杯”全国数学竞赛(第1-23届)初一年级/七年级第一/二试题目录1.希望杯第一届(1990年)初中一年级第一试试题......................003-0052.希望杯第一届(1990年)初中一年级第二试试题......................010-0123.希望杯第二届(1991年)初中一年级第一试试题...... 0错误!未定义书签。
-0204.希望杯第二届(1991年)初中一年级第二试试题...... 0错误!未定义书签。
-0265.希望杯第三届(1992年)初中一年级第一试试题...... 0错误!未定义书签。
-0326.希望杯第三届(1992年)初中一年级第二试试题...... 0错误!未定义书签。
-0407.希望杯第四届(1993年)初中一年级第一试试题...... 0错误!未定义书签。
-0508.希望杯第四届(1993年)初中一年级第二试试题...... 0错误!未定义书签。
-0589.希望杯第五届(1994年)初中一年级第一试试题...... 0错误!未定义书签。
-06610.希望杯第五届(1994年)初中一年级第二试试题..... 0错误!未定义书签。
-07311.希望杯第六届(1995年)初中一年级第一试试题..... 0错误!未定义书签。
-080 12希望杯第六届(1995年)初中一年级第二试试题..... 0错误!未定义书签。
-08713.希望杯第七届(1996年)初中一年级第一试试题..... 0错误!未定义书签。
-09814.希望杯第七届(1996年)初中一年级第二试试题....... 错误!未定义书签。
-10515.希望杯第八届(1997年)初中一年级第一试试题....... 错误!未定义书签。
-11316.希望杯第八届(1997年)初中一年级第二试试题....... 错误!未定义书签。
-12017.希望杯第九届(1998年)初中一年级第一试试题....... 错误!未定义书签。
希望杯第1-8届五年级数学试题及答案(WORD版)

第一届小学“希望杯”全国数学邀请赛五年级第1试一、填空题1.计算=_______ .2.将1、2、3、4、5、6分别填在图中的每个方格内,使折叠成的正方体中对面数字的和相等。
3.在纸上画5条直线,最多可有_______ 个交点.4.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是______ ,温差最大的景区是______ 。
5.,各表示一个两位数,若+=139,则=_______ 。
6.三位数和它的反序数的差被99除,商等于_______ 与_______ 的差。
7.右图是半个正方形,它被分成一个一个小的等腰三角形,图2中,正方形有_______ 个,三角形有_______ 个。
8.一次智力测验,主持人亮出四块三角形的牌子:在第(4)块牌子中,?表示的数是_______ 。
9.正方形的一条对角线长13厘米,这个正方形的面积是平方厘米。
10.六位自然数1082□□能被12整除,末两位数有种情况。
11.右边的除法算式中,商数是。
12.比大,比小的分数有无穷多个,请写出三个:。
13.A、B、C、D、E五位同学进行乒乓球循环赛(即每2人赛一场),比赛进行了一段时间后,A赛了4场,B赛了3场,C赛了2场,D赛了1场,这时,E 赛了场.14.观察5*2=5+55=60,7*4=7+77+777+7777=8638,推知9*5的值是。
15.警察查找一辆肇事汽车的车牌号(四位数),一位目击者对数字很敏感,他提供情况说:“第一位数字最小,最后两位数是最大的两位偶数,前两位数字的乘积的4倍刚好比后两位数少2”。
警察由此判断该车牌号可能是。
16.一个小方木块的六个面上分别写有数字2,3,5,6,7,9。
小光,小亮二人随意往桌上扔放这个木块。
规定:当小光扔时,如果朝上的一面写的是偶数,得1分。
当小亮扔时,如果朝上的一面写的是奇数,得1分。
每人扔100次,得分高的可能性最大。
17.从1,2,3,4,5,6,7,8,9。
第十四届小学四年级“希望杯”全国数学邀请赛试题及答案

第十四届小学“希望杯”全国数学邀请赛四年级第1试试题以下每题6分,共120分。
1、计算:25×259÷(37÷8)= .2、若9个连续偶数的和是2016,则这些数中,最小的是.3、有110张相同得长方形纸片,长比宽多10厘米,将这些纸片如图1无重合摆放,可以摆成长是2750厘米的长方形,将这些纸片如图2无重合摆放,可以摆成长是厘米的长方形。
4、甲、乙、丙3人一起购买学习用品,已知甲和乙共支付了67元,乙和丙共支付了64元,甲和丙共支付了63元,那么,甲支付了元。
5、图3由5×4个边长为1的小正方形组成,其中阴影部分的面积是。
6、一个工厂电表的示数是52222千瓦,若干天后,电表的示数(五位数)又出现4个相同的数码,那么该工厂在这些天内至少又用了千瓦的电.7、已知碳素笔每支1元8角,笔记本每个3元5角,文具盒每个4元2角,晶晶买这三种文具刚好用了20元,则她买了个笔记本。
8、一个除法算式,若被除数比除数大2016,商是15,余数是0,则被除数是。
9、若一个长方形的长减少3厘米、宽增加2厘米,得到一个和原长方形面积相等的正方形,则长方形的周长是厘米。
10、已知a,b,c都是质数,若a×b+b×c=119,则a+b+c= .11、王华每星期二、六学书法,已知2016年的元旦是星期五,那么在2016年8月,王华学书法的天数是。
12、一个四位数A,将四位数的各位上的数字(均不为0)重新排列得到的最大数比A大7668,得到的最小数比A小594,则A= 。
a2016能被12整除,则这样的六位数有个。
13、若六位数b14、3堆桃子的个数分别是93,70,63,一只猴子在3堆桃子间搬运,已知猴子每次最多可以搬5个桃子,并且在从一堆搬到另一堆的途中会吃掉1个,当3堆桃子个数相等时,猴子至少吃掉了个桃子。
15、在1到100这100个数中,被2,3,5除都有非零的余数,且余数彼此不等的数有个。
七年级数学第3届“希望杯”第1试试题

山东省滨州市无棣县埕口中学七年级数学第3届“希望杯”第1试试题一、选择题(每小题6分,共60分)以下每题的四个结论中,仅有一个是正确的,请将表示正确答案的英文字母填在表格内和每题后面的圆括号内。
1.有理数1a-的值一定不是( ) (A )正整数 (B )负整数 (C )负分数 (D )0 2.下面给出的四对单项式中,是同类项的一对是( )(A )213x y 与23x z - (B )233.22m n 与3211992n m (C )20.2a b 与20.2ab (D )11abc 与111ab 3.(1)(1)(1)x x x ---++等于( )(A )33x - (B )1x - (C )31x - (D )3x - 4.两个10次多项式的和是( )(A )20次多项式 (B )10次多项式(C )100次多项式 (D )不高于10次的多项式5.若10a +<,则在下列每组四个数中,按从小到大的顺序排列的一组是( ) (A ),1,1,a a -- (B ),1,1,a a --(C )1,,,1a a -- (D )1,,1,a a --6.123.4(123.5),123.4123.5,123.4(123.5)a b c =---=-=--,则(A )c b a >> (B )c a b >> (C )a b c >> (D )b c a >>7.若00a b <,>,且||||a b <,那么下列式子中结果是正数的是( )(A )()()a b ab a -+ (B )()()a b a b +-(C )()()a b ab a ++ (D )()()ab b a b -+8.从25a b +减去44a b -的一半,应当得到( ) (A )4a b - (B )b a - (C )9a b - (D )7b9. ,,,a b c m 都是有理数,并且23,2a b c m a b c m ++=++=,那么b 与c(A )互为相反数 (B )互为倒数 (C )互为负倒数 (D )相等10.张梅写出了五个有理数,前三个有理数的平均值为15,后两个有理数的平均值是10,那么张梅写出的五个有理数的平均值是( ) (A )5 (B )183 (C )1122(D )13 二、填空题(每小题6分,共60分)11.2(3)(4)56(7)(8)910(11)(12)131415+-+-+++-+-+++-+-+++=12. (-2)×5×(-8)×(-12)(-3)×4×(-15)= 。
小学四年级希望杯历年数学竞赛试题与答案1-14届(最新全套完整版)

第一届小学“希望杯”全国数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
5.如果规定a※b =13×a-b÷8,那么17※24的最后结果是。
6.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是,温差最大的景区是。
7.AOB是三角形的纸,OA=OB,图中的虚线是折痕,至少折次就可以得到8个相同的三角形。
8.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有,它们的和等于。
9.甲、乙、丙、丁四个学习小组共有图书280本,班主任老师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10.幼儿园老师给几组小朋友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小朋友共组。
11.在 a=20032003×2002和 b=20022003×2003中,较大的数是,它比较小的数大。
12.小明的家离学校2千米,小光的家离学校3千米,小明和小光的家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是。
14.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。
希望杯第1-8届五年级数学试题及答案(WORD版)

第一届小学“希望杯"全国数学邀请赛五年级第1试一、填空题1.计算=_______ 。
2.将1、2、3、4、5、6分别填在图中的每个方格内,使折叠成的正方体中对面数字的和相等。
3.在纸上画5条直线,最多可有_______ 个交点。
4.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是______ ,温差最大的景区是______ .5.,各表示一个两位数,若+=139,则=_______ 。
6.三位数和它的反序数的差被99除,商等于_______ 与_______ 的差。
7.右图是半个正方形,它被分成一个一个小的等腰三角形,图2中,正方形有_______ 个,三角形有_______ 个。
8.一次智力测验,主持人亮出四块三角形的牌子:在第(4)块牌子中,?表示的数是_______ 。
9.正方形的一条对角线长13厘米,这个正方形的面积是平方厘米.10.六位自然数1082□□能被12整除,末两位数有种情况.11.右边的除法算式中,商数是。
12.比大,比小的分数有无穷多个,请写出三个:。
13.A、B、C、D、E五位同学进行乒乓球循环赛(即每2人赛一场),比赛进行了一段时间后,A赛了4场,B赛了3场,C赛了2场,D赛了1场,这时,E 赛了场.14.观察5*2=5+55=60,7*4=7+77+777+7777=8638,推知9*5的值是。
15.警察查找一辆肇事汽车的车牌号(四位数),一位目击者对数字很敏感,他提供情况说:“第一位数字最小,最后两位数是最大的两位偶数,前两位数字的乘积的4倍刚好比后两位数少2"。
警察由此判断该车牌号可能是.16.一个小方木块的六个面上分别写有数字2,3,5,6,7,9.小光,小亮二人随意往桌上扔放这个木块.规定:当小光扔时,如果朝上的一面写的是偶数,得1分。
当小亮扔时,如果朝上的一面写的是奇数,得1分。
每人扔100次,得分高的可能性最大。
17.从1,2,3,4,5,6,7,8,9.中随意取出两个数字,一个作分子,一个作分母,组成一个分数,所有分数中,最大的是,循环小数有个。
【奥数真题】第十三届小学四年级希望杯全国数学邀请赛试题(第一试)

【奥数真题】第十三届小学四年级希望杯全国数学邀请赛试题(第一试)学校:___________姓名:___________班级:___________考号:___________一、填空题1.计算:2468×629÷(1234×37)=_________。
2.有一个除法算式,被除数和除数的和是136,商是7,则除数是___________。
3.定义:a⊕b=a+b+ab,则(2⊕3)⊕4的值为_________。
4.买一支水彩笔需要1元7角,用15元钱最多可以买这样的水彩笔_________支。
5.王雷是国庆节那天出生的,若他年龄的3倍减去8刚好是他出生那月的总天数,则王雷今年_________岁。
6.数一数,图1中共有_________个三角形。
7.某班30人参加跳绳比赛,开始时有4人迟到没有参加比赛,这时平均成绩为20个。
后来这4位同学赶到了比赛场地,分别跳了26,27,28,29个。
这时全班同学的平均成绩是_________个。
8.明明临摹一本字帖练习毛笔字,临摹第一遍时,他每天写25个字,临摹第二遍时,他每天多写3个字,结果恰好比第一遍少用了3天,则这本字帖共有_________字。
9.图2有16个1×1的小正方形组成,图中△ABC的面积是_________。
10.乌龟和兔子在全长为1000米的赛道上比赛,兔子的速度是乌龟速度的15倍.但兔子在比赛的过程中休息了一会儿,醒来时发现乌龟刚好到达终点,而此时兔子还差100米才到终点.则在兔子休息期间乌龟爬行了________米.11.从1至9这九个数中任取一个奇数和一个偶数相乘,不同的乘积有________个。
12.一个长方形的相框长为40厘米,宽为32厘米,放入一张长为32厘米宽为28厘米的相片,则相框中没有被照片覆盖的部分的面积是_________平方厘米.13.一个长方形的长和宽都增加3厘米后,面积增加了90平方厘米,则原长方形的周长是________厘米.14.王蕾和姐姐从家步行去体育馆打羽毛球,已知姐姐每分钟比王蕾多走20米,25分钟后姐姐到体育馆,这时姐姐发现没有带球拍,于是立即按原路返回取球拍,在离体育馆300米的地方遇到了王蕾.则王蕾家到体育馆的路程是_________米.15.如图3,用小正方形摆成下列图形,按摆放规律,第25个图形需要小正方形_________个.16.若1069+=,则这样的abc有_________个.abc cba二、解答题17.爷爷,爸爸,小明今年的年龄分别是60岁,35岁,11岁,则再过_________年爷爷的年龄等于小明和爸爸年龄的和.18.甲筐和乙筐内原来分别放有54个和63个鸡蛋,若要使甲筐内的鸡蛋的个数变为乙筐内鸡蛋个数的两倍.那么应从乙筐内取出________个鸡蛋放入甲筐.19.某地希望杯组委会给当地参加希望杯考试的考生安排考场,若每个考场安排30名考生,则会有一个考场有26名考生;若每个考场安排26名考生,则会有一个考场有20名考生,并且要比前一种方案多用9个考场.则该地区参加考试的考生有_________名.20.图4由3个边长是6的正方形组成,则图中阴影部分的面积是________.参考答案1.34【解析】观察题中的数据,2468与1234,629与37分别成倍数关系,先根据除法的性质去括号,再利用数据之间的倍数关系,采用合适的简便方法进行计算。
小学四年级希望杯历年数学竞赛试题和答案解析1_14届[最新[全套](完整版)]
]](https://img.taocdn.com/s3/m/f473ed0e0912a21614792942.png)
第一届小学“希望杯”全国数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
5.如果规定a※b =13×a-b÷8,那么17※24的最后结果是。
6.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是,温差最大的景区是。
7.AOB是三角形的纸,OA=OB,图中的虚线是折痕,至少折次就可以得到8个相同的三角形。
8.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有,它们的和等于。
9.甲、乙、丙、丁四个学习小组共有图书280本,班主任老师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10.幼儿园老师给几组小朋友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小朋友共组。
11.在 a=20032003×2002和 b=20022003×2003中,较大的数是,它比较小的数大。
12.小明的家离学校2千米,小光的家离学校3千米,小明和小光的家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是。
14.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。
希望杯第1试试题
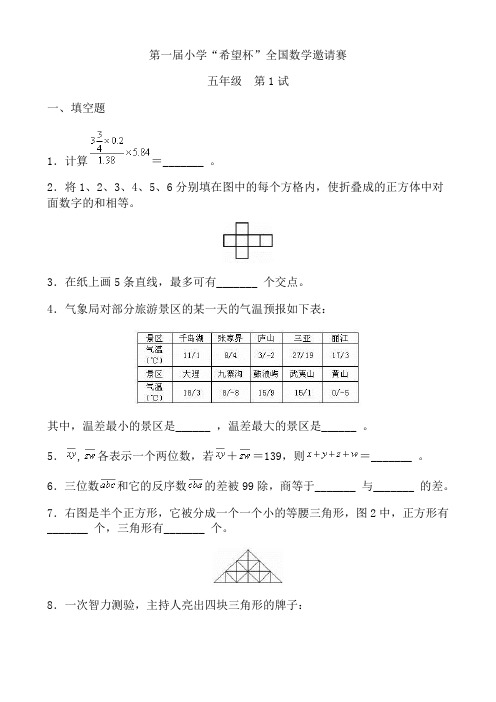
第一届小学“希望杯”全国数学邀请赛五年级第1试一、填空题1.计算=_______ 。
2.将1、2、3、4、5、6分别填在图中的每个方格内,使折叠成的正方体中对面数字的和相等。
3.在纸上画5条直线,最多可有_______ 个交点。
4.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是______ ,温差最大的景区是______ 。
5.,各表示一个两位数,若+=139,则=_______ 。
6.三位数和它的反序数的差被99除,商等于_______ 与_______ 的差。
7.右图是半个正方形,它被分成一个一个小的等腰三角形,图2中,正方形有_______ 个,三角形有_______ 个。
8.一次智力测验,主持人亮出四块三角形的牌子:在第(4)块牌子中,?表示的数是_______ 。
9.正方形的一条对角线长13厘米,这个正方形的面积是平方厘米。
10.六位自然数1082□□能被12整除,末两位数有种情况。
11.右边的除法算式中,商数是。
12.比大,比小的分数有无穷多个,请写出三个:。
13.A、B、C、D、E五位同学进行乒乓球循环赛(即每2人赛一场),比赛进行了一段时间后,A赛了4场,B赛了3场,C赛了2场,D赛了1场,这时,E赛了场。
14.观察5*2=5+55=60,7*4=7+77+777+7777=8638,推知9*5的值是。
15.警察查找一辆肇事汽车的车牌号(四位数),一位目击者对数字很敏感,他提供情况说:“第一位数字最小,最后两位数是最大的两位偶数,前两位数字的乘积的4倍刚好比后两位数少2”。
警察由此判断该车牌号可能是。
16.一个小方木块的六个面上分别写有数字2,3,5,6,7,9。
小光,小亮二人随意往桌上扔放这个木块。
规定:当小光扔时,如果朝上的一面写的是偶数,得1分。
当小亮扔时,如果朝上的一面写的是奇数,得1分。
每人扔100次,得分高的可能性最大。
17.从1,2,3,4,5,6,7,8,9。
希望杯数学竞赛第一届至十历届四年级全部试题与答案(打印版)

目录1.第一届小学“希望杯”全国数学邀请赛(第1试) (2)2. 第一届小学“希望杯”全国数学邀请赛(第2试) (5)3. 第二届小学“希望杯”全国数学邀请赛(第1试) (7)4. 第二届小学“希望杯”全国数学邀请赛(第2试) (10)5. 第三届小学“希望杯”全国数学邀请赛(第1试) (13)6. 第三届小学“希望杯”全国数学邀请赛(第2试) (16)7. 第四届小学“希望杯”全国数学邀请赛(第1试) (18)8. 第四届小学“希望杯”全国数学邀请赛(第2试) (21)9. 第五届小学“希望杯”全国数学邀请赛(第1试) (23)10. 第五届小学“希望杯”全国数学邀请赛(第2试) (26)11. 第六届小学“希望杯”全国数学邀请赛(第1试) (28)12. 第六届小学“希望杯”全国数学邀请赛(第2试) (30)13. 第七届小学“希望杯”全国数学邀请赛(第1试) (32)14. 第七届小学“希望杯”全国数学邀请赛(第2试) (36)15. 第八届小学“希望杯”全国数学邀请赛(第1试) (39)16. 第八届小学“希望杯”全国数学邀请赛(第2试) (41)17. 第九届小学“希望杯”全国数学邀请赛(第1试) (44)18. 第九届小学“希望杯”全国数学邀请赛(第2试) (46)19. 第十届小学“希望杯”全国数学邀请赛(第1试) (48)20. 第十届小学“希望杯”全国数学邀请赛(第2试) (50)21.第一届---第八届“希望杯”全国数学邀请赛参考答案 (53)第一届小学“希望杯”全国数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
第十三届小学“希望杯”全国数学邀请赛 六年级 第1试试题解析

第十三届小学“希望杯”全国数学邀请赛六年级第1试试题吴乃华1、计算:12+14+18+116+132=?_____________。
解:观察这这五个分数的分数值,刚好后一个是前一个的一半,现在,要求五个分数的分数的和,如右图,减去最后一个分数,不就是这五个分数的和了吗?所以,12+14+18+116+132=1-132=31322、将13999化成小数,小数部分在第2015位上的数字是_______________。
解:13999=0.013013013…循环节为“013”,2015÷3=671 (2)即2015位上的数字,是在此循环小数循环671次后的第二个数字,所以1.3、若四位数27AB能被13整除,则两位数AB的最大值是_____________。
解:根据能被13整除的特征,一个整数的末三位数与末三位以前的数字所组成的数之差(以大减小)能被13整除,这个数就能被13整除。
因为,AB7-2=AB5,这个三位数的个位是5,能被5整除,可知5AB是13与某数5的倍数的积。
由于AB5=75×13=975所以,两位数AB的最大值是97。
4、若一个分数的分子减少20%,并且分母增加28%,则新分数比原来的分数减少了______%。
解:本题旨在探讨新分数比原来的分数减少的百分数,与原分数是多少无关。
设原分数为37。
根据题意则新分数为:37+%⨯⨯(1-20%)(128)=58×37因此新分数比原来的分数减少了1-58=0.375=37.5%。
5、若111111++++20112012201320142015<a +1,则自然数a =______________。
解:假设111111++++20112012201320142015的分母部分是5个12015, 则1÷(12015×5)=403; 假设是分母部分是5个12011,则1÷(12011×5)=402.2; 可知,402.2<12011+12012+12013+12014+12015<403 可得a ≤4.02.2+1≥403所以,a =4026、定义:符号{x}表示x 的小数部分,如{3.14}=0.14,{0.5}=0.5,那么,2015315412++345⎧⎫⎧⎫⎧⎫⎨⎬⎨⎬⎨⎬⎩⎭⎩⎭⎩⎭=_______________。
第一届希望杯-四年级-第一试试卷及解析

第一届小学"希望杯"全国数学邀请赛四年级第1试
一、以下每题4分,共100分1.右边三个图中,都有一些三角形,在图A中,有______个;在图B中,有______个;中图C中,有______ 个. 2.写出下面
等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+……=2002÷______ .
3.观察1、2、3、6、12、23、44、x 、164的规律,可知x =______ .
4.如图2,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍.
5.如果规定a※b =13×a -b ÷8,那么17※24的最后结果是______.
6.气象局对部分旅游景区的某一天的气温预报如下表:
景区千岛湖张家界庐山三亚丽江大理九寨沟鼓浪屿武夷山黄山
气温(℃)11/18/43/-227/1917/318/38/-815/915/10/-5。
第11届“希望杯”数学邀请赛(高一 第1试)

第十一届“希望杯”数学邀请赛高一第1试2000年3月26日上午8:00至9:30一、选择题(每小题6分,共60分)以下每题的四个结论中,仅有一个是正确的,请将表示正确答案的英文字母填在每题后面的圆括号内。
1、以下四个判断中,正确的是()。
(A)若,则;(B)若,则或;(C)若,则;(D)若,则。
2、已知,则由小到大排列的顺序是()。
(A);(B);(C);(D)。
3、函数的单调递增区间是()。
(A);(B);(C);(D)。
4、下面给出的每一组数分别表示三条线段的长,将每组数表示的三条线段首尾相连,其中恰能构成三角形的是()。
(A);(B);(C);(D)。
5、设定义域为R的函数都有反函数,并且函数的图象关于直线对称,若,那么()。
(A)1999;(B)2000;(C)2001;(D)2002。
6、将长为dm,宽为dm的长方形纸片围成一个容器(不考虑底面,也不考虑粘接处),立放于桌面上,下面四种方案中,容积最大的是()。
(A)直三棱柱;(B)直四棱柱;(C)高为dm的圆柱;(D)高为dm的圆柱。
7、周期函数的图象大致如下,当时,,则在上的解析式是()。
(A);(B);(C);(D)。
8、The root(根) of the equation is in the interval(区间) of ()。
(A)(3,4);(B)(4,5);(C)(5,6);(D)(6,7)。
9、函数的图象与轴、轴有三个交点,有一个圆恰好通过这三个点,则此圆与坐标轴的另一个交点是()。
(A);(B);(C);(D)。
10、无盖的圆柱形容器的底面半径为1,母线长为3,现在将盛满水的该容器平稳地慢慢倾斜,当水剩到原来的时,圆柱的母线与水平面所成的角()。
(A)等于60°;(B)等于45°;(C)等于30°;(D)在45°和60°之间。
二、A组填空题(每题6分,共60分)11、 We want to cut one orange into eight equal pieces, at least ________ times we have to cut it.12、已知集合M满足,则不同的M的个数是________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一届小学“希望杯”全国数学邀请赛五年级第1试一、填空题1.计算=_______ 。
2.将1、2、3、4、5、6分别填在图中的每个方格内,使折叠成的正方体中对面数字的和相等。
3.在纸上画5条直线,最多可有_______ 个交点。
4.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是______ ,温差最大的景区是______ 。
5.,各表示一个两位数,若+=139,则=_______ 。
6.三位数和它的反序数的差被99除,商等于_______ 与_______ 的差。
7.右图是半个正方形,它被分成一个一个小的等腰三角形,图2中,正方形有_______ 个,三角形有_______ 个。
8.一次智力测验,主持人亮出四块三角形的牌子:在第(4)块牌子中,?表示的数是_______ 。
9.正方形的一条对角线长13厘米,这个正方形的面积是平方厘米。
10.六位自然数1082□□能被12整除,末两位数有种情况。
11.右边的除法算式中,商数是。
12.比大,比小的分数有无穷多个,请写出三个:。
13.A、B、C、D、E五位同学进行乒乓球循环赛(即每2人赛一场),比赛进行了一段时间后,A赛了4场,B赛了3场,C赛了2场,D赛了1场,这时,E赛了场。
14.观察5*2=5+55=60,7*4=7+77+777+7777=8638,推知9*5的值是。
15.警察查找一辆肇事汽车的车牌号(四位数),一位目击者对数字很敏感,他提供情况说:“第一位数字最小,最后两位数是最大的两位偶数,前两位数字的乘积的4倍刚好比后两位数少2”。
警察由此判断该车牌号可能是。
16.一个小方木块的六个面上分别写有数字2,3,5,6,7,9。
小光,小亮二人随意往桌上扔放这个木块。
规定:当小光扔时,如果朝上的一面写的是偶数,得1分。
当小亮扔时,如果朝上的一面写的是奇数,得1分。
每人扔100次,得分高的可能性最大。
17.从1,2,3,4,5,6,7,8,9。
中随意取出两个数字,一个作分子,一个作分母,组成一个分数,所有分数中,最大的是,循环小数有个。
18.如图所示的四边形的面积等于。
19.一艘轮船往返于A、B码头之间,它在静水中航速不变,当河水流速增加时,该船往返一次所用时间比河水流速增加前所用时间(填“多”或“少”)。
20.新来的教学楼管理员拿15把不同的钥匙去开15个教室的门,但是不知哪一把钥匙开哪一个门,他最多试开次,就可将钥匙与教室门锁配对。
21.一个分数,分子加分母等于168;分子,分母都减去6,分数变成,原来的分数是。
22.一只甲虫从画有方格的木板上的A点出发,沿着一段一段的横线,竖线爬行到B点,图(1)中的路线对应下面的算式1-2+1+2+2-1+2+1=6请在图(2)中用粗线画出对应于算式-2-1+2+2+2+1+1+1的路线。
23.新年晚会上,老师让每位同学从一个装有许多玻璃球的口袋中摸两个球,这些球给人的手感相同,只有红、黄、白、蓝、绿五色之分(摸时,看不到颜色),结果发现总有两个人取的球相同,由此可知,参加取球的至少有人。
24.A、B、C、D、E五人参加围棋赛,四位观战者预测了结果。
甲说:“E第3,A第4。
”乙说:“A第3,B第1。
”丙说:“B第4,E第2。
”丁说:“D第1,C第3。
”实际结果是每人只猜对了一个,参赛5人也没有并列名次,所以一定是第1,第2,第3。
25.下图是一所小学的科技楼,它有4层,正面每层的三个圆形窗户由左向右表示一个三位数,这些三位数是:837,571,206,439。
但是不知道这四个数和哪一层的窗户对应。
请你观察一下,然后画出表示2003的四个窗户。
第二届小学“希望杯”全国数学邀请赛五年级第1试一、填空题1.0.4×[]×26=。
2.根据规律填空:0.987654,0.98765,0.9877,0.988,,1.0。
3.一个数被7除,余数是3,该数的3倍7除,余数是。
考点:有余数的除法.分析:可以把这个数看成两个数的和,即“7的倍数”和余数3.这个数字乘3之后,根据乘法分配律,可以得到两个数的和,也就是“7的倍数”的3倍和“余数3”的3倍,由此可以解决问题.解答:解:可以把这个数写成“7的倍数+3”;这个数的3倍即:(7的倍数+3)×3=“7的倍数的”×3+3×3,“7的倍数的”×3仍能被7整除,余数3×3=9,除以7后余数为2.答:一个数被7除,余数是3,该数的3倍被7除,余数是2.故答案为:2.点评:此题考查了有余数的除法各部分间的关系.4.2004的约数中,比100大且比200小的约数是。
5.下边的加法算式中,每个“□”内有一个数字,所有“□”内的数字之和最大可达到。
和最大可达到60.解答:解:由于三个三位数的和为2004,所以:末尾和最大24,十位和最大18,百位和最大18,24+18+18=60,即所有“□”内的数字之和最大可达到60.故答案为:60.点评:根据整数加法的计算法则及三个三位数的和为2004,推出每个数位上的数相加和的最大值是完成本题的关键.6.甲、乙、丙三人掷骰子,每人掷三次,他们掷出的点数的积都是24。
将每人掷出的点数的和由大到小排列,依次是甲、乙、丙,则点数3是掷出的。
(点数:向上的一面上的数字。
骰子的六个面上的点数分别是1至6)考点:孙子定理(中国剩余定理);找一个数的因数的方法.分析:根据题意甲乙丙每次掷出的点数既是1至6中的数字,也得是24的因数,所以掷出的点数是1、2、3、4、6,3次掷的点数之积分别都是24,只有这3种可能1,4,6;2,3,4;2,2,6;3次掷的点数之和从大到小的顺序为1,4,6;2,2,6;2,3,4.由此可以解决问题.解答:解:3次掷的点数之积分别都是24,只有这3种可能1,4,6;2,3,4;2,2,6;3次掷的点数之和从大到小的顺序为1,4,6;2,2,6;2,3,4.故答案为:丙.点评:此题主要利用一个数的因数解决实际问题,进一步利用讨论排除法得出结论.7.在一个四位数的某位数字的前面添上一个小数点,再和原来的四位数相减,差是1803.6,则原来的四位数是。
考点:整数、小数复合应用题;小数点位置的移动与小数大小的变化规律.分析:因为相减后的差,小数位数为1位,可知在此四位数上添的小数点,必在十位和个位之间,使其形成了一位小数.换句话说,这个四位数缩小到它的十分之一,,原数与新数的差等于1083.6.解答:解:设这个四位数原数为x,x-0.1x=1803.6,x=2004;答:原来的四位数是2004.故答案为:2004.点评:此题应认真分析,通过观察数字得出:小数点,必在十位和个位之间,然后列方程进行解答.8.,,都是质数,并且+=33,+=44,+=66,那么=,考点:整数的裂项与拆分.专题:整数的分解与分拆.分析:因为a+b=33的和为奇数,b+c=44,c+d=66,这两个的和是偶数,所以a=2,b=31;进而可以得出:c=13;d=53;那么cd=53×13=689.解答:解:因为在所有的质数中只有一个偶质数2,所以a+b=33的和为奇数,b+c=44,c+d=66,这两个的和是偶数,所以a=2,则,b=33-2=31;c=44-31=13;d=66-13=53;所以cd=53×13=689.故答案为:689.点评:本题同学们不要急于解方程组,要善于从数的特点去思索,要打破思维定势,利用:奇数+偶数=奇数,奇数+奇数=偶数,以及在所有的质数中只有一个偶质数2,这个特例去解决问题,就容易多了.9.如果A◆B=,那么1◆2-2◆3-3◆4-…-2002◆2003-2003◆2004=。
10.用1-8这八个自然数中的四个组成四位数,从个位到千位的的数字依次增大,且任意两个数字的差都不是1,这样的四位数共有个。
考点:简单的排列、组合.分析:先确定千位数,从个位到千位的数字依次增大,所以千位上的数字最小是4,任意两个数字的差都不是1,若个位数字是1,那么千位上的数字最小就是1+2×3=7,所以千位的数字只能是7或8,分情况讨论.解答:解:当千位上的数是8时,有:8642,8531,8631,8641,共4个;当千位上的数字是7时,有7531,1个;共有:4+1=5(个)故答案为:5.点评:本题首先根据题干所限制的条件找出千位或个位上的数字,再用列举法写出这些数字.11.甲、乙、丙三个网站定期更新,甲网站每隔一天更新1次,乙网站每隔两天更新1次,丙网站每隔三天更新1次。
在一个星期内,三个网站最少更新网站次。
考点:最大与最小.分析:甲网站每隔一天更新1次,即每两天一次,一周最少3次;乙网站每隔两天更新1次,即每三天一次,一周最少2次;丙网站每隔三天更新1次,即每四天一次,一周最少1次;由此可以解决问题.解答:解:甲网站每隔一天更新1次,即每两天一次,一周最少3次;乙网站每隔两天更新1次,即每三天一次,一周最少2次;丙网站每隔三天更新1次,即每四天一次,一周最少1次;3+2+1=6(次),答:三个网站最少更新网站6次.故答案为6.点评:此题在分析时要注意每周最少更新的次数,分别从第二天,第三天、第四天开始更新,由此可以解决问题.12.下图中共有个正方形。
13.如图,每个小格的边长都是1个单位长度,一只甲虫在水平方向上每爬行1个单位长度需要5秒,在竖直方向上每爬行1个单位长度需要6秒,每拐弯一次需要1秒。
它从A点爬到B点,最少需要秒。
14.将长15厘米,宽9厘米的长方形的长和宽都分成三等份,长方形内任意一点与分点及顶点连结,如图3,则阴影部分的面积是平方厘米。
15.沿图中的虚线折叠,可以围成一个长方体,它的体积是立方厘米。
16.小永的三门功课的成绩,如果不算语文,平均分是98分;如果不算数学,平均分是93分;如果不算英语,平均分是91分。
小永三门功课的平均成绩是分。
17.A、B、C、D四支球队进行循环赛(即每两队赛1场),比赛进行一段时间后,A赛了3场,B赛了2场,C赛了1场,这时,D赛了场。
18.一只皮箱的密码是一个三位数。
小光说:“它是954。
”小明说:“它是358。
”小亮说:“它是214。
”小强说:“你们每人都只猜对了位置不同的一个数字。
这只皮箱的密码是。
19.一次校友聚会有50人参加,在参加聚会的同学中,每个女生认识的男生人数各不相同,而且恰好构成一串连续的自然数,最多的全认识,最少的也认识15人。
这次聚会是个女生参加。
20.2003年10月28日,“神舟”五号载人飞船发射试验队队长许达哲透露:我国将在2004年下半年发射“神舟”六号载人飞船,共3人乘“神六”遨游太空7天。
