天津市南开中学2011届高三第三次月考(数学理)扫描版
天津市高三数学第三次月考试题 理 新人教A版
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分,在每小题的4个选项中,只有一项是符合题目要求的。
1. 复数=++-ii i 111 A. i - B.C. i -1D. i +12. 条件甲:⎩⎨⎧<<<+<3042xy y x ;条件乙:⎩⎨⎧<<<<3210y x ,则甲是乙的A. 充要条件B. 充分而不必要条件C. 必要而不充分条件D. 既不充分也不必要条件3. 设x ,y 满足⎪⎩⎪⎨⎧≤--≥-≥+22142y x y x y x ,则y x z +=A. 有最小值2,最大值3B. 有最小值2,无最大值C. 有最大值3,无最小值D. 既无最小值,也无最大值4. 某程序框图如图所示,该程序运行后输出的k 的值是A. 4B. 5C. 6D. 75. 已知等比数列{a n }的首项为1,若4a 1,2a 2,a 3成等差数列,则数列⎭⎬⎫⎩⎨⎧n a 1的前5项和为A.1631 B. 2 C.1633 D.3316 6. 将函数⎪⎭⎫⎝⎛+=42sin 2)(πx x f 的图像向右平移)0(>ϕϕ个单位,再将图像上每一点横坐标缩短到原来的21倍,所得图像关于直线4π=x 对称,则ϕ的最小正值为 A.8πB. 83πC. 43πD. 2π7. 设F 是抛物线)0(2:21>=p px y C 的焦点,点A 是抛物线与双曲线22222:by a x C -=1)0,0(>>b a 的一条渐近线的一个公共点,且x AF ⊥轴,则双曲线的离心率为A. 2B. 3C.25D. 58. 若直角坐标平面内的两点P 、Q 满足条件:①P 、Q 都在函数)(x f y =的图像上;②P 、Q 关于原点对称,则称点对[P,Q]是函数)(x f y =的一对“友好点对”(注:点对[P,Q]与[Q,P]看作同一对“友好点对”)。
2011届高三年级第三次月考数学试卷

2011届高三年级第三次月考数学试卷一、选择题(10×5=50分) 1、0sin(330)-的值为( ) A .12B .-12CD .2、若34sin ,cos 55θθ==-,则2θ所在象限是( ) A .一B .二C .三D .四3、如图中的图象所表示的函数的解析式为( )A .3|1|(02)2y x x =-≤≤B .33|1|(02)22y x x =--≤≤C .3|1|(02)2y x x =--≤≤D .1|1|(02)y x x =--≤≤4、函数()y f x =图象如图所示,则函数12log ()y f x = 图象大致是( )5、函数32()ln 2f x xπ=-的零点一定位于区间( ) A .(1,2)B .(2,3)C .(3,4) D .(4,5)6、直线1ln()y x y x a =+=+与曲线相切,则a 的值为( ) A .1B .2C .-1D .-27、已知1sin 2sin ,'2y x x y =+则是( ) A .仅有最小值的奇函数 B .既有最大值又有最小值的偶函数 C .仅有最大值的偶函数D .既不是奇函数也不是偶函数8、函数3()1f x ax x =++有极值的充要条件是( ) A .0a >B .0a ≥C .0a <D .0a ≤AB C D9、函数32()6f x ax ax b =-+在[-1,2]上最大值为3,最小值为-29(a>0),则( ) A .a=2,b=-29B .a-3, b=2C .a=2, b=3D .以上都不对10、函数21()ln 22f x x ax x =--存在单调递减区间,则a 的取值范围是( ) A .(1,)-+∞ B .[0,1) C .(-1,0]D .(,)-∞+∞二、填空题(6×4=24分)11、设230.311331log ,log ,(),,,2a b c a b c ===则大小关系为 。
2011届高三数学月考、联考、模拟试题汇编 直线和圆

直线和圆题组一一、选择题1.(北京龙门育才学校2011届高三上学期第三次月考)直线x-y+1=0与圆(x+1)2+y 2=1的位置关系是( ) A .相切 B .直线过圆心 C .直线不过圆心但与圆相交 D .相离 答案 B.2.(北京五中2011届高三上学期期中考试试题理)若过定点)0,1(-M 且斜率为k 的直线与圆05422=-++y x x 在第一象限内的部分有交点,则k 的取值范围是( ))(A 50<<k )(B 05<<-k )(C 130<<k )(D 50<<k答案 A.3、(福建省三明一中2011届高三上学期第三次月考理)两圆042222=-+++a ax y x 和0414222=+--+b by y x 恰有三条公切线,若R b R a ∈∈,,且0≠ab ,则2211b a +的最小值为 ( )A .91B .94C .1D .3答案 C.3.(福建省厦门双十中学2011届高三12月月考题理)已知点P 是曲线C:321y x x =++上的一点,过点P 与此曲线相切的直线l 平行于直线23y x =-,则切线l 的方程是( ) A .12+=x y B .y=121+-xC .2y x =D .21y x =+或2y x =答案 A.4. (福建省厦门双十中学2011届高三12月月考题理)设斜率为1的直线l 与椭圆124:22=+y x C 相交于不同的两点A 、B ,则使||AB 为整数的直线l 共有( ) A .4条 B .5条 C .6条 D .7条 答案 C.5.(福建省厦门外国语学校2011届高三11月月考理) 已知圆22670x y x +--=与抛物线22(0)y px p =>的准线相切,则p = ( ▲ )A 、1B 、2C 、3D 、4答案 B.6.(甘肃省天水一中2011届高三上学期第三次月考试题理)过点M(1,5)-作圆22(1)(2)4x y -+-=的切线,则切线方程为( ) A .1x =-B .512550x y +-=C .1512550x x y =-+-=或D .15550x x y =-+-=或12答案 C.7.(甘肃省天水一中2011届高三上学期第三次月考试题理)已知圆222410x y x y ++-+=关于直线220ax by -+=41(0,0),a b a b>>+对称则的最小值是( )A .4B .6C .8D .9答案 D.8.(广东省惠州三中2011届高三上学期第三次考试理)已知直线x y a +=与圆224x y +=交于A 、B 两点,O 是坐标原点,向量OA 、OB满足||||OA OB OA OB +=-,则实数a 的值是( )(A )2 (B )2- (C 或 (D )2或2- 答案 D.9. (广东省清远市清城区2011届高三第一次模拟考试理)曲线321y x x x =-=-在处的切线方程为( A .20x y -+= B .20x y +-= C . 20x y ++= D .20x y --=答案 C.10.(贵州省遵义四中2011届高三第四次月考理)若直线02=+-c y x 按向量)1,1(-=a 平移后与圆522=+y x 相切,则c 的值为( )A .8或-2B .6或-4C .4或-6D .2或-8邪恶少女漫画/wuyiniao/ 奀莒哂答案 A.11.(黑龙江大庆实验中学2011届高三上学期期中考试理) 若直线y x =是曲线322y x x ax =-+的切线,则a =( ).1A .2B .1C - .1D 或2 答案 D.邪恶少女漫画/wuyiniao/ 奀莒哂12.(黑龙江哈九中2011届高三12月月考理)“3=a ”是“直线012=--y ax ”与“直线046=+-c y x 平行”的 ( )A .充分不必要条件 C .必要不充分条件D .充要条件D .既不充分也不必要条件答案 B.13.(湖北省南漳县一中2010年高三第四次月考文)已知α∥β,a ⊂α,B ∈β,则在β内过点B 的所有直线中A .不一定存在与a 平行的直线B .只有两条与a 平行的直线C .存在无数条与a 平行的直线D .存在唯一一条与a 平行的直线 答案 D.14.(重庆市南开中学2011届高三12月月考文)已知圆C 与直线040x y x y -=--=及都相切,圆心在直线0x y +=上,则圆C 的方程为( )A .22(1)(1)2x y ++-=B .22(1)(1)2x y -++=C .22(1)(1)2x y -+-=D .22(1)(1)2x y +++=答案 B. 二、填空题14.(湖北省南漳县一中2010年高三第四次月考文)已知两点(4,9)(2,3)P Q --,,则直线PQ 与y 轴的交点分有向线段PQ的比为 .答案 2.15. (福建省厦门外国语学校2011届高三11月月考理)已知椭圆的中心为坐标原点O ,焦点在x 轴上,斜率为1且过椭圆右焦点的直线交椭圆于A 、B 两点,)1,3(-=+与共线,求椭圆的离心率▲▲.答案 36=e . 16.(甘肃省天水一中2011届高三上学期第三次月考试题理)设直线30ax y -+=与圆22(1)(2)4x y -+-=相交于A 、B 两点,且弦AB 的长为a = 答案 0.17. (广东省中山市桂山中学2011届高三第二次模拟考试文) 在极坐标中,圆4cos ρθ=的圆心C 到直线sin()4πρθ+=的距离为 .18.(河南省郑州市四十七中2011届高三第三次月考文)如下图,直线PC 与圆O 相切于点C ,割线PAB 经过圆心O ,弦CD ⊥AB 于点E , 4PC =,8PB =,则CE = .答案12519.(黑龙江省哈尔滨市第162中学2011届高三第三次模拟理)已知函数()x f 的图象关于直线2=x 和4=x 都对称,且当10≤≤x 时,()x x f =.求()5.19f =_____________。
2019届天津市南开区南开中学高三下学期第三次月考数学(理)试题(解析版)

2019届天津市南开区南开中学高三下学期第三次月考数学(理)试题一、单选题1.已知集合2{|340}M x x x =--≤,集合{|ln 0}N x x =≥,则M N ⋂=( ) A .{|14}x x ≤≤ B .{|1}x x ≥ C .{|14}x x -≤≤ D .{|1}x x ≥- 【答案】A【解析】{|14},{|1}M x x N x x =-≤≤=≥,所以{|14}M N x x ⋂=≤≤,故选A.2.已知,x y 满足约束条件20,20,1,x y x y y +-≥⎧⎪--≤⎨⎪≥⎩则2z x y =+的最小值为( )A .2B .3C .4D .5【答案】B【解析】做出可行域,根据图像,即可求解. 【详解】做出可行域,如下图所示(阴影部分):由12y x y =⎧⎨+=⎩,解得11x y =⎧⎨=⎩,(1,1)A 由图像可得,当目标函数2z x y =+过点A 时, 取得最小值为3. 故选:B.【点睛】本题考查二元一次不等式表示平面区域,考查线性目标函数的最值,属于基础题. 3.如图是一个算法流程图,则输出k 的值是( )A .3B .4C .5D .6【答案】D【解析】根据循环体的运算定义,直到满足条件,退出循环体,输出k ,即可求出结论. 【详解】38,2S k ==;34,3S k ==;26,4S k ==; 10,5S k ==;22,6S k =-=,输出6.故选:D 【点睛】本题考查循环结构运行结果,属于基础题.4.已知等比数列{}n a 的前n 项和为n S ,则“10a >”是“20190S >”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件【答案】C【解析】根据充分条件和必要条件的定义,结合等比数列的前n 项和公式进行判断即可. 【详解】若公比q =1,则当a 1>0时,则S 2019>0成立, 若q ≠1,则S 2019()2019111a q q-=-,∵1﹣q 与1﹣q 2019符号相同, ∴a 1与S 2019的符号相同, 则“a 1>0”⇔“S 2019>0”, 即“a 1>0”是“S 2019>0”充要条件, 故选:C . 【点睛】本题主要考查充分条件和必要条件的判断,根据等比数列前n 项和公式是解决本题的关键.5.要得到函数y =的图象,只需将函数24y x π=+⎛⎫ ⎪⎝⎭的图象上所有的点的( )A .横坐标缩短到原来的12倍(纵坐标不变),再向左平行移动6π个单位长度B .横坐标缩短到原来的12倍(纵坐标不变),再向右平行移动4π个单位长度 C .横坐标伸长到原来的2倍(纵坐标不变),再向左平行移动4π个单位长度 D .横坐标伸长到原来的2倍(纵坐标不变),再向右平行移动6π个单位长度 【答案】C【解析】将y =化为)2y x π=+根据三角函数伸缩、平移关系,即可求解. 【详解】将函数24y x π=+⎛⎫ ⎪⎝⎭的图象横坐标伸长到原来的2倍(纵坐标不变),得到函数4y x π=+⎛⎫ ⎪⎝⎭的图像,再向左平移4π个长度单位,得到函数)2y x y x π=+==. 故选:C. 【点睛】本题考查诱导公式的应用,三角函数图像变换关系,属于基础题.6.已知()f x 是定义在R 上的偶函数,且在(],0-∞上是增函数,设()4log 7a f =,,()0.60.2c f =,则,,a b c 的大小关系是( )A .c b a <<B .b c a <<C .b a c <<D .a b c <<【答案】C【解析】试题分析:函数()f x 是偶函数,在上是增函数,所以在(]0,+∞上是减函数,0.6420.2log 7log 3<<Q ()()()0.6420.2log 7log 3f f f b a c ∴>>∴<<【考点】函数奇偶性单调性7.设直线0)30(x y m m -+=≠与双曲线()222210,0x y a b a b-=>>的两条渐近线分别交于点,A B ,若(),0,P m PA PB =,则双曲线的离心率等于( )A .32B 5C 5D .2【答案】B【解析】将直线0)30(x y m m -+=≠与双曲线的渐近线方程22220x y a b-=联立,结合韦达定理,求出AB 中点M 坐标,由(),0,P m PA PB =,得出直线PM 斜率为-3,求出,a b 关系,即可求解. 【详解】双曲线()222210,0x y a b a b -=>>的两条渐近线方程为22220x y a b-=,联立2222030x y a b x y m ⎧-=⎪⎨⎪-+=⎩消去x 得222222(9)60b a y mb b m --+=,当2222290,0,40b a m m a b -≠≠∆=>,设AB 中点为00(,)M x y ,则202239mb y b a =-, 2002239ma x y m b a =-=-,2222223(,)99ma mb M b a b a∴--, (),0,P m PA PB =,2222222223393299MPmb b b a k ma a b mb a -===----,解得2222222154,,144b b a b e a a =∴==+=,e ∴=. 故选:B【点睛】本题考查双曲线的离心率,考查直线与双曲线的渐近线的位置关系,合理设出渐近线方程是解题的关键,考查计算能力,属于中档题.8.()()21,02,41,0x x f x x x g x xx x ⎧+>⎪=--=⎨⎪+≤⎩,若方程[()]0g f x a -=的实数根个数有4个,则a 的取值范围是( )A .51,4⎡⎫⎪⎢⎣⎭B .(]0,1C .51,2⎡⎫⎪⎢⎣⎭D .()1,2【答案】A【解析】设2()(1)11t f x x ==-++≤,方程[()]0g f x a -=的实数根个数有4个,根据已知条件,()g t a =有两不大于1的解,结合()y g t =图像与直线y a =关系,即可求出a 的范围. 【详解】设2()(1)11t f x x ==-++≤,()g t a = 方程[()]0g f x a -=的实数根个数有4个,()g t a =有两不大于1的解,由已知得,当0t ≤,()1g t ≤ 当0t >,1()14g t t t =+≥,当且仅当12t =时,等号成立, 做出()y g t =的图像如下图所示:5(1)4g =,所以54a ≤ 当54a =时,5()4g t =,则0t >,有1544t t +=解得1t =或14t =此时()t f x =只有三个解,不合题意, 根据图像可得514a ≤<. 故选:A.【点睛】本题考查复合函数根的个数求参数,换元结合函数图像是解题的关键,属于中档题.二、填空题9.已知i 为虚数单位,则13ii+=-__________. 【答案】1255i + 【解析】由复数的除法运算法则,即可求解. 【详解】1(1)(3)24123(3)(3)1055i i i i i i i i ++++===+--+. 故答案为:1255i + 【点睛】本题考查复数的代数运算,属于基础题.10.123x x ⎛⎝展开式中的常数项为__________. 【答案】220-【解析】写出123x x ⎛⎝展开式的通项,令x 的指数为零,即得常数项. 【详解】12x ⎛ ⎝展开式中第1k +项为 41212311212((1),0,1,2,12k k k k k kk T C xC x k --+==-=L ,令4120,93k k -==,所以常数项为931212220C C -=-=-. 故答案为:-220 【点睛】本题考查二项展开式中特定的项,掌握二项展开式的通项是解题的关键,属于基础题.11.设三棱锥的三条侧棱两两互相垂直,且长度分别为2,4,则其外接球的表面积为__________. 【答案】32π【解析】将三棱锥补成长方体,转化为求长方体外接球的问题,利用长方体的对角线为外接球的直径,即可求解. 【详解】三棱锥的三条侧棱两两互相垂直,以三棱锥的侧棱为边补成长方体,则长方体相邻的三边长为2,4,且长方体的外接球即为所求,=所以所求的外接球的表面积为2432ππ⨯=. 故答案为:32π. 【点睛】本题考查球与锥的接切问题,将问题转化为熟悉几何体的外接球,可提高解题效率,减少计算量,属于基础题.12.在直角坐标系xOy 中,以原点O 为极点,x 轴正半轴为极轴建立极坐标系,已知曲线M ()14cos πθ+=,曲线N 的参数方程为244x t y t ⎧=⎨=⎩(t 为参数).若曲线M 与N 相交于,A B 两点,则线段AB 的长等于__________. 【答案】8()14cos πθ+=化为直角坐标方程,244x t y t ⎧=⎨=⎩消去参数化为普通方程,联立方程,由韦达定理结合弦长公式,即可得出结论.【详解】()214cos πρθ+=展开得sin 1cos ρθρθ-=,得到10x y --=为曲线M 的直角坐标方程,244x t y t⎧=⎨=⎩消去参数得24y x =, 联立2104x y y x--=⎧⎨=⎩,消去x ,得2440y y --=, 1616320∆=+=>,设1122(,),(,)A x y B x y ,12124,4y y y y +==-,2121212||11||2()48AB y y y y y y =+-=+-=.故答案为:8. 【点睛】本题考查极坐标方程与直线坐标方程互化,参数方程与普通方程互化,考查直线与圆锥曲线的位置关系,要熟练掌握相交弦长公式,属于基础题.13.如图在平行四边形ABCD 中,已知8AB =,5AD =,3CP PD =u u u v u u u v ,2AP BP ⋅=u u u r u u u r,则AB AD ⋅u u u v u u u v的值是______________.【答案】22【解析】根据基底,AB AD u u u r u u u r 表示,,AP BP u u u v u u u v 再根据向量数量积化简2AP BP ⋅=u u u r u u u r,即得结果. 【详解】13()()()()44AP BP AD DP BC CP AD AB AD AB ⋅=+⋅+=+⋅-u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v u u u v2231162AD AB AB AD=--⋅u u u v u u u v u u u v u u u v 311256413222.1622AB AD AB AD AB AD =-⨯-⋅=-⋅=∴⋅=u u u v u u u v u u uv u u u v u u u v u u u v【点睛】用向量基本定理解决问题的一般思路是先选择一组基底,并运用该基底将条件和结论表示成向量的形式,再通过向量的运算来解决. 14.已知()2f x x bx c =++,且()12f x ≤在[]3,5x ∈恒成立,则b c +的值为__________. 【答案】152【解析】()12f x ≤等价于()1122f x -≤≤,在[]3,5x ∈恒成立,只需()()max min 1212f x f x ⎧≤⎪⎪⎨⎪≥-⎪⎩,根据()2f x x bx c =++的对称轴分类讨论,求出()f x 在[]3,5x ∈的最大值和最小值,结合不等式的性质,即可求解. 【详解】()222()24b b f x x bxc x c =++=+-+,对称轴方程为2b x =-,()12f x ≤在[]3,5x ∈恒成立,需()()max min 1212f x f x ⎧≤⎪⎪⎨⎪≥-⎪⎩,当3,62b b -≤≥-时,()max min1=(5)52521()(3)392f x f b c f x f b c ⎧=++≤⎪⎪⎨⎪==++≥-⎪⎩①②,(1)-⨯①+②得152b ≤-,不合题意舍去; 当5,102b b -≥≤-时,()max min1=(3)3921()(5)5252f x f b c f x f b c ⎧=++≤⎪⎪⎨⎪==++≥-⎪⎩③④,(1)-⨯③+④得172b ≥-,不合题意舍去; 当max max 35,106,(){(3),(5)}2bb f x f f <-<-<<-=2min1(3)3921(5)52521()()242f b c f b c b b f x f c ⎧=++≤⎪⎪⎪=++≤⎨⎪⎪=-=-+≥-⎪⎩⑤⑥⑦⑤+⑥(2)+-⨯⑦得228320,(8)02b b b ++≤+≤,2(8)0,8b b ∴+==-,代入⑤⑦得312312c c ⎧≤⎪⎪⎨⎪≥⎪⎩,3115,22c b c ∴=+=. 故答案为:152.【点睛】本题考查二次函数的最值以及不等式的性质,考查分类讨论思想,属于较难题.三、解答题15.已知函数()226f x cos x sin x π⎛⎪⎭+⎫⎝=-. (1)求函数()f x 的最小正周期;(2)在ABC V 中,角,,A B C 所对的边分别为,,a b c ,且满足()2a c cosB bcosC -=,求2f A ⎛⎫⎪⎝⎭的取值范围. 【答案】(1)π;(2)2⎛⎝ 【解析】(1)用两角差余弦公式、辅助角公式,化简()fx 2(6)x π=+,即可求出周期;(2)用正弦定理将条件等式化为角,结合三角形内角和关系,可求出3B π=,求出A的范围,整体替换结合正弦函数的值域,即可求解. 【详解】(1)由()226f x cos x sin x π⎛⎪⎭+⎫⎝=-22266cos xcossin xsinsin x ππ=++32222sin x x =+2(6)x π=+,则()f x 的最小正周期2T ππω==;(2)由正弦定理:2sin sin sin a b cR A B C=== 则2,2,2a RsinA b RsinB c RsinC ===, 由()2a c cosB bcosC -=,则()2sinA sinC cosB sinBcosC -=,则()2sinAcosB sin B C =+, 由()() 0sin B C sin A sinA π+=-=>, 所以12cosB =, 由0B π<<,则3B π=22266A A f A ππ⎛⎫⎛⎫⎛⎫=⨯+=+≤ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭由203A π<<,则5666A πππ<+<,所以1126sin A π⎛⎫ ⎪⎝⎭<+≤(6)A π<+≤所以2A f ⎛⎫∈ ⎪⎝⎭⎝. 【点睛】本题考查三角函数恒等变换以及图像与性质,考查正弦定理边角互化,考查计算能力,属于中档题.16.甲、乙两队参加听歌猜歌名游戏,每队3人.随机播放一首歌曲, 参赛者开始抢答,每人只有一次抢答机会,答对者为本队赢得一分,答错得零分, 假设甲队中每人答对的概率均为23,乙队中3人答对的概率分别为211,,332,且各人回答正确与否相互之间没有影响.(1)若比赛前随机从两队的6个选手中抽取两名选手进行示范,求抽到的两名选手在同一个队的概率;(2)用ξ表示甲队的总得分,求随机变量ξ的分布列和数学期望; (3)求两队得分之和大于4的概率. 【答案】(1)25;(2)分布列见解析,()2E ξ=;(3)48243【解析】(1)用求组合数的方法,求出从6人中抽取2人的抽法个数,再求出2人来自同一组的抽法个数,按求古典概型概率的方法,即可求解; (2)甲队中每人答对的概率均为23,且每人答题时相互独立,答对者为本队赢得一分,甲队的总得分ξ服从二项分布,23,3~B ξ⎛⎫⎪⎝⎭,即可求出分布列和期望; (3)两队得分之和大于4按互斥事件分为:总分和为5分包括甲队2分乙队3分和甲队3分乙队2分,总分和为6分甲乙各3分.分别求出以上各互斥事件的概率,然后相加,即可求出结果. 【详解】(1)6个选手中抽取两名选手共有2615C =种结果,抽到的两名选手在同一个队包括同在甲队或乙队,共有:2326C =种结果用A 表示事件:“从两队的6个选手中抽取两名选手, 求抽到的两名选手在同一个队.”()62155P A == 故从两队的6个选手中抽取两名选手进行示范, 抽到的两名选手在同一个队的概率为25(2)由题意知,ξ的可能取值为0,1,2,3,且23,3~B ξ⎛⎫ ⎪⎝⎭()303110327P C ξ⎛⎫=== ⎪⎝⎭ ()21321613327P C ξ⎛⎫⎛⎫===⎪⎪⎝⎭⎝⎭ ()223211223327P C ξ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭()333283327P C ξ⎛⎫===⎪⎝⎭ξ∴的分布列为:ξ123P1272949827ξ的数学期望12480123227992)7(E ξ=⨯+⨯+⨯+⨯=. (3)用B 表示事件:“两队得分之和大于4”, 包括:两队得分之和为5,两队得分之和为6, 用1A 表示事件:“两队得分之和为5”, 包括甲队3分乙队2分和乙队3分甲队2分.()3121212121113332323323P A ⎛⎫⎛⎫=⨯⨯+⨯⨯+⨯⨯ ⎪ ⎪⎝⎭⎝⎭4211409323243⎛⎫+⨯⨯= ⎪⎝⎭用2A 表示事件:“两队得分之和为6”,甲队3分乙队3分,()32221183332243P A ⎛⎫=⨯⨯=⎪⎝⎭ ()()()1240848243243243P P A P A B =+=+=【点睛】本题考古典概型概率以及互斥事件概率,考查离散型随机变量的分布列和期望,解题的关键要把问题转化为二项分布,属于中档题.17.如图,四边形ABCD 是正方形,EA ⊥平面ABCD ,//EA PD ,22AD PD EA ===,F ,G ,H 分别为PB ,EB ,PC 的中点.(1)求证://FG 平面PED ;(2)求平面FGH 与平面PBC 所成锐二面角的大小;(3)在线段PC 上是否存在一点M ,使直线FM 与直线PA 所成的角为3π?若存在,求出线段PM 的长;若不存在,请说明理由. 【答案】(1)见解析(2)4π(3)见解析 【解析】试题分析: 1? \*?GB2?=⑴建立平面直角坐标系,由11,0,2GF ⎛⎫=- ⎪⎝⎭u u u v ,()0,2,0DC =u u u v ,GF DC ⊥u u u v u u u v证得//FG 平面PED2?\*?GB2?=⑵建立空间直角坐标系,根据两个平面的法向量所成的角与二面角相等或互补,由两个平面法向量所成的角求解二面角的大小;⑶假设存在点M ,由共线向量基本定理得到M 点的坐标,其中含有一个未知量,然后利用直线FM 与直线PA 所成角为3π转化为两向量所成的角为3π,由两向量的夹角公式求出M 点的坐标,得到的M 点的坐标符合题意,说明假设成立,最后得到结论. 解析:(1)∵EA ⊥平面ABCD ,//EA PD ,∴PD ⊥平面ABCD , ∴PD AD ⊥,PD CD ⊥,又四边形ABCD 是正方形, ∴AD CD ⊥,故PD ,AD ,CD 两两垂直, 如图,建立空间直角坐标系,∵22AD PD EA ===, ∴()0,0,0D ,()0,0,2P ,()2,0,0A ,()0,2,0C ,()2,2,0B ,()2,0,1E ,∵F ,G ,H 分别为PB ,EB ,PC 的中点, ∴()1,1,1F ,12,1,2G ⎛⎫⎪⎝⎭,()0,1,1H , 11,0,2GF ⎛⎫=- ⎪⎝⎭u u u v ,平面PED 的一个法向量为()0,2,0DC =u u u v ,又∵11002002GF DC ⋅=-⨯+⨯+⨯=u u u v u u u v ,∴GF DC ⊥u u u v u u u v,又∵FG ⊄平面PED ,∴//FG 平面PED .(2)11,0,2GF ⎛⎫=- ⎪⎝⎭u u u v ,12,0,2GH ⎛⎫=- ⎪⎝⎭u u u v ,设()1111,,n x y z =u v为平面FGH 的一个法向量,则1100n GF n GH ⎧⋅=⎪⎨⋅=⎪⎩u v u u u v u v u u u v ,即11111021202x z x z ⎧-+=⎪⎪⎨⎪-+=⎪⎩,取11y =,得()10,1,0n =u v ,()2,2,2PB =-u u u v ,()0,2,2PC =-u u u v,设()2222,,n x y z u u v =为平面PBC 的一个法向量,则220n PB n PC ⎧⋅=⎪⎨⋅=⎪⎩u u v u u u vu u v u u u v , 即222222220220x y z y z +-=⎧⎨-=⎩,取21z =得()20,1,1n u u v =,∴12cos ,n n = 12122n n n n ⋅=⋅u v u u v u v u u v ,∴平面FGH 与平面PBC 所成锐二面角的大小为4π. (3)假设在线段PC 上存在一点M ,使直线FM 与直线PA 所成角为3π, 设PM PC λ=u u u u v u u u v,其中01λ≤≤,由()0,2,2PC =-u u u v ,则()0,2,2PM λλ=-u u u u v , 又∵FM FP PM =+u u u u v u u u v u u u u v ,()1,1,1FP =--u u uv ,∴()1,21,12FM λλ=---u u u u v , ∵直线FM 与直线PA 所成角为3π,()2,0,2PA u uu v =-,∴1cos ,2FM PA =u u u u v u u u v ,即()222412221221λλ--+=⋅+-,解得58λ=, ∴550,,44PM ⎛⎫=- ⎪⎝⎭u u u u v ,524PM =u u u u v ,∴在线段PC 上存在一点M ,使直线FM 与直线PA 所成角为3π,此时4PM =. 18.已知数列{}n a 中,11a =,且()2212121,3kk k k k k a a a a -+=+-=+,其中*k N ∈. (1)求234,,a a a 的值; (2)求数列{}n a 通项公式; (3)求数列{}n a 的前2n 项和. 【答案】(1)20a =,33a =,44a =;(2)()()1122221311,(21311,(2n n n n n n a n +-⎧⎡⎤+--⎪⎢⎥⎪⎣⎦=⎨⎡⎤⎪+--⎢⎥⎪⎣⎦⎩为奇数)为偶数);(3)+1233222n n S n =-- 【解析】(1)用1k =代入递推公式分别求出23,a a ,再将2k =,代入前一个递推公式,求出4a ;(2)由递推公式可得()212113kk k k a a +-=+-+,用累加法求出奇数项的通项公式,再由递推关系,求出偶数项的通项公式,即可求解;(3)根据通项公式将前2n 项和分成奇数项和与偶数项分别求和,转化为求等比数列和常数列的和. 【详解】(1)211110a a =-=-=,323033,a a =+=+=431314;a a =+=+= (2)()21221313,kk k k k k a a a +-=+=+-+ 所以()212113kk k k a a +--=-+, 所以()131113a a -=-+,()225313a a -=-+,·······()212113kk k k a a +--=-+累加,得()()()121221111...1)33.(..3k kk a a +=+-+-++-+++⎦+⎡⎤⎣()()()()11131311113kk ⎡⎤-⋅--⋅-⎣⎦=++---()11133122kk +---=++()13112kk ++-=-令21k n +=,则12n k -=,112n k ++=所以()212113112(n n n a n -+⎡⎤⎢-⎥⎦=-⎣+为奇数)()()12213131313122k kk k k kk k a a +++-+-=-=--=-令2k n =,则2n k =所以()22(13121,nn n a n ⎡⎤-⎢⎥⎣⎦=+-为偶数);所以()()1122221311,(21311,(2n n n n n n a n +-⎧⎡⎤+--⎪⎢⎥⎪⎣⎦=⎨⎡⎤⎪+--⎢⎥⎪⎣⎦⎩为奇数)为偶数) (3)1321n a a a -++⋅⋅⋅+()()()113121111312112222221133311122n n n ++-+----⎛⎫⎡⎤=++⋅⋅⋅⋅⋅⋅++-+-+⋅⋅⋅⋅⋅⋅+-- ⎪⎢⎥⎣⎦⎝⎭()()()()021111133112231n n n -⎡⎤=+++-+⋅⋅⋅⋅⋅⋅+⋅⋅⋅-+-⎣⋅+-⎦⋅⋅ ()()()()12121133112312nn n ⎡⎤=++--+-+⋅⋅⋅⋅⋅⋅+⋅⋅⋅⋅⋅⋅+--⎣⎦()()()2422422222222421133311122n n n a a a n⎛⎫⎡⎤++⋅⋅⋅⋅⋅⋅+=++⋅⋅⋅⋅⋅⋅++-+-+⋅⋅⋅⋅⋅⋅+-- ⎪⎢⎥⎣⎦⎝⎭()()()()12121133311122n nn ⎡⎤=++⋅⋅⋅⋅⋅⋅++-+-+⋅⋅⋅⋅⋅⋅+--⎣⎦ 所以()+11223133333 (322213)22n n nnSn n n ⋅-=+++-=-=---【点睛】本题考查求数列的通项公式,关键要寻找项之间的关系,考查用分组求和等价转化为求等比数列的和,考查计算能力,属于中档题.19.如图,在平面直角坐标系0x y 中,已知椭圆()2222:10x yE a b a b+=>>的离心率3e =,12,A A分别是椭圆E 的左、右两个顶点,圆2A 的半径为a ,过点1A 作圆2A 的切线,切点为P ,在x 轴的上方交椭圆E 于点Q .(1)求直线OP 的方程; (2)求1PQ QA 的值;(3)设a 为常数,过点O 作两条互相垂直的直线,分别交椭圆于点,B C ,分别交圆2A 于点,M N ,记三角形OBC 和三角OMN 的面积分别为12,S S .求12S S ⋅的最大值.【答案】(1)3y x =;(2)34;(3)45a 【解析】(1)连接2A P ,根据已知条件由21A P A P ⊥,212|||||A P OA OA a ===,可得||OP a =,从而有2OA P ∆为等边三角形,可得出直线OP 倾斜角为3π,即可求解; (2)由32e =,椭圆方程化为222241x y a a +=,由(1)知2||,3OP a POA π=∠=,求出P 点坐标,进而求出直线1A P 方程,与椭圆方程联立,求出点Q 坐标,即可求解; (3)设OM 的方程为()0y kx k =>,与椭圆方程联立求出B 点坐标,进而求出||OB ,同理求出||,||,||OC OM ON ,求出12S S ⋅以k 为自变量的目标函数,应用基本不等式,求出其最大值. 【详解】(1)连接2A P ,则21A P A P ⊥,且2||A P a =,又12||2A A a =,所以1260A A P ∠=o.又22||||A P A O =,所以2OPA V 为正三角形,所以260POA ∠=o,所以直线OP的方程为y =.(2)由(1)知,由(1)知2||,3OP a POA π=∠=,P点坐标为(,)22a ,1(,0)A a -, 1A P的方程为)3y x a =+,因为e =c a =所以222231,44c a b a ==, 故椭圆E 的方程为222241x y a a+=由()2222341y x a x y a a ⎧=+⎪⎪⎨⎪+=⎪⎩,消去y ,得22780x ax a ++=, x a =-或7a x =-,7Q ax ∴=- 所以()1||327||47a a PQ a QA a⎛⎫-- ⎪⎝⎭==--- (3)不妨设OM 的方程为()0y kx k =>,联立方程组222241y kx x y aa =⎧⎪⎨+=⎪⎩整理得222(14),k x a x +==0,k B >在第一象限,得B ⎛⎫所以||OB =用1k -代替上面的k,得||OC =圆2A 方程为2220x y ax +-=,联立2220y kx x y ax =⎧⎨+-=⎩整理得22(1)20k x ax +-=, 0x =或221a k +,得2222(,)11a ak M k k ++,所以||OM = 用1k -代替上面的k,得||ON = 所以4121||||||||4S S OB OC OM ON a ⋅=⋅⋅⋅⋅=15=≤当且仅当1k =时等号成立,所以12,S S 的最大值为45a . 【点睛】本题考椭圆的性质应用,考查直线与圆锥曲线的位置关系、直线方程及圆的性质,考查计算能力和综合运用知识分析问题解决问题的能力,属于较难题.20.已知函数f (x )=(x +b )(x e -a ),(b >0),在(-1,f (-1))处的切线方程为(e -1)x +ey +e -1=0. (Ⅰ)求a ,b ;(Ⅱ)若方程f (x )=m 有两个实数根x 1,x 2,且x 1<x 2,证明:x 2-x 1≤1+(12)1m e e--.【答案】(Ⅰ)1a =,1b =(Ⅱ)见解析【解析】(Ⅰ)由题意利用导函数研究函数的切线方程,得到关于a ,b 的方程组,求解方程组并检验可得1a =,1b =.(Ⅱ)由(Ⅰ)可知()()()11x f x x e =+-,则()f x 在(-1,0)处的切线方程为()()111h x x e ⎛⎫=-+ ⎪⎝⎭,构造函数()()()F x f x h x =-,结合新构造函数的性质分类讨论即可证得题中的不等式.【详解】 (Ⅰ)由题意()10f -=,所以()()1110f b a e ⎛⎫-=-+-=⎪⎝⎭, 又()()1x f x x b e a '=++-,所以()111b f a e e-=-=-+', 若1a e=,则20b e =-<,与0b >矛盾, 故1a =,1b =.(Ⅱ)由(Ⅰ)可知()()()11x f x x e =+-, ()()00,10f f =-=, 设在(-1,0)处的切线方程为,易得,()()111h x x e ⎛⎫=-+ ⎪⎝⎭, 令()()()F x f x h x =-即()()()()11111x F x x e x e ⎛⎫=+---+ ⎪⎝⎭,()()12x F x x e e'=+-, 当2x ≤-时,()()1120xF x x e e e=+-<-<', 当2x >-时,设()()()12x G x F x x e e =+'=-, ()()30x G x x e =+>', 故函数()F x '在()2,-+∞上单调递增,又()10F '-=,所以当(),1x ∈-∞-时,()0F x '<,当()1,x ∈-+∞时,()0F x '>,所以函数()F x 在区间(),1-∞-上单调递减,在区间()1,-+∞上单调递增, 故.()()11f x h x ≥,设()h x m =的根为'1x ,则'111me x e =-+-又函数()h x 单调递减, 故()()()'111h x f x h x =≥,故'11x x ≤, 设()y f x =在(0,0)处的切线方程为()y t x =,易得()t x x =令()()()()()11x T x f x t x x e x =-=+--,()()22x T x x e =+-', 当2x ≤-时,()()2220xT x x e =+-<-<',当2x >-时,故函数()T x '在()2,-+∞上单调递增,又()00T '=,所以当(),0x ∈-∞时,()0T x '<,当()0,x ∈+∞时,()0T x '>,所以函数()T x 在区间(),0-∞上单调递减,在区间()0,+∞上单调递增,,()()22f x t x ≥设()t x m =的根为'2x ,则'2x m =又函数()t x 单调递增,故()()()'222t x f x t x =≥,故'22x x ≥, 又'11x x ≤,()''2121121111m e me x x x x m e e -⎛⎫-≤-=--+=+ ⎪--⎝⎭. 【点睛】导数是研究函数的单调性、极值(最值)最有效的工具,而函数是高中数学中重要的知识点,所以在历届高考中,对导数的应用的考查都非常突出 ,本专题在高考中的命题方向及命题角度 从高考来看,对导数的应用的考查主要从以下几个角度进行: (1)考查导数的几何意义,往往与解析几何、微积分相联系. (2)利用导数求函数的单调区间,判断单调性;已知单调性,求参数. (3)利用导数求函数的最值(极值),解决生活中的优化问题. (4)考查数形结合思想的应用.。
南开中学高2011级10-11学年(下)3月月考——数学文

南开中学高2011级高三月考试卷(3月)数 学(文科)本试题分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分,考试时间120分钟.第Ⅰ卷(选择题,共50分)注意事项:1.答题前,考生务必将自己的姓名、考号、考试科目填涂在机读卡上.2.每小题选出答案后,用铅笔把机读卡上对应题目的答案标号涂黑,如需改动,用橡皮擦擦干净后,再选涂其它答案,不能答在试题上.3.考试结束,监考人员将机读卡和答题卷一并收回.一、选择题:(本大题10个小题,每小题5分,共50分)各题答案必须答在机读卡 1.已知集合},5,4,3,2,1{=M },6,5,4{=N 则集合MN 中的元素的个数是( )A. 1B. 2C. 3D. 42.给定空间中的直线l 及平面a ,条件“直线l 与平面a 内无数条直线都垂直”是“直线l 与a 平面垂直”的( )条件A .充要B .充分非必要C .必要非充分D .既非充分又非必要3.以抛物线x y 42=的焦点为圆心,且过坐标原点的圆的方程为( )22A.20x y x +-= 22B.0x y x ++= 22C.0x y x +-= 22D.20x y x ++=4.等差数列{}n a 的前n 项和为n S ,若142,20,a S ==则6S =( ) A .16 B .24 C .36 D .42 5.已知a ,b 为正实数,且,12=+b a 则ba 11+的最小值为() B.6C.3+D.3-b .为了得到函数sin(2)3y x π=-的图像,只需把函数)62sin(π+=x y 的图像( )A .向左平移4π个长度单位 B .向右平移4π个长度单位 C .向左平移2π个长度单位 D .向右平移2π个长度单位7.若函数812 (,1]()log (1,)x x f x x x -⎧∈-∞=⎨∈+∞⎩,则使01()4f x >的0x 的取值范围为 ( )A .(,1](3,)-∞+∞B .(,2](4,)-∞+∞C .(,2)(3,)-∞+∞ D .(,3)(4,)-∞+∞8.函数()f x 在定义域R 内可导,若()(2),(1)()0f x f x x f x '=--<,设(0)a f =,1()2b f = ,(3)c f =,则( )A .a b c <<B .c a b <<C .c b a <<D .b c a << 9.函数,,)(3R x x x x f ∈+=当02≤<-θπ时,0)1()cos (>-+m f m f θ恒成立,则实数m 的取值范围是( )A.(0,1) 1B.(,)2-∞ C.(,0)-∞ D.(,1]-∞10.如图所示,⊥PA 平面ABCD ,底面ABCD 为正方形O AB PA ,2==为四棱锥ABCD P -内一点,,1=AO若DO 与平面PBC 成角中最大角为α,则α= ( )A.15B.30C.45D.60第Ⅱ卷(非选择题,共100分)二、填空题:(本大题5个小题,每小题5分,共25分)各题答案必须填写在答题卡Ⅱ(只填结果,不要过程).11.已知向量(1,),(1,),a n b n ==-若,a b ⊥则||_______a =⋅12.在等比数列}{n a 中,12341,2,a a a a +=+=,则5678a a a a +++= ; 13.在锐角MBC 的三内角A ,B ,C 的对边边长分别为a ,b ,c ,若5sin ,2b a B =则cos _______A =⋅14.在体积43π的球的表面上有,,A B C 三点,1,2,,AB BC A C ==两点的球面距离为3π,则球心到平面ABC 的距离为 ; 15.已知双曲线)0,0(12222>>=-b a by a x 的左、右焦点分别为,,21F F 着在双曲线的右支上存在一点P ,使得|,|3||21PF PF =则双曲线的离心率e 的取值范围为_____.三、解答题:(本大题6个小题,共75分)各题解答必须答在答题卡Ⅱ上(必须写出必要的文字说明、演算步骤或推理过程) 16.(本小题13分)已知函数2()sin(2)cos .6f x x x π=-+(1)若()1,f θ=求sin cos θθ的值; (2)求函数()f x 的单调区间.17.(本小题13分)己知21(1,),(1,)a x m b m x=-+=+,当0m >时,求使不等式0a b >成立的x 的取值范围.18.(本小题13分)如图所示, PA ⊥平面ABCD ,底面ABCD 为菱形,60,2,ABC PA AB N ∠===为PC 的中点.(1)求证:BD ⊥平面PAC . (2)求二面角B AN C --的正切值.19.(本小题12分)已知1x =为函数32()1f x x x ax =--+的一个极值点. (1)求a 及函数)(x f 的单调区间;(2)若对于任意2[1,2],[1,2],)22x t fx t mt ∈-∈≥-+恒成立,求m 取值范围.20.(本小题12分)已知椭圆2222:1(0)x y C a b a b+=>>的离心率为3e =,且过点,,A B 分别是椭圆的左右两个顶点,P 为椭圆C 上的动点.(1)求椭圆的标准方程;(2)若P 与,A B 均不重合,设直线PA PB 与的斜率分别为12,k k ,求12k k 的值; (3)M 为过P 且垂直于x 轴的直线上的点,若(0)OPOMλλ=>,求点M 的轨迹方程.21.(本小题12分)已知数列}{n a 的前以项和为,n S 且对于任意的*,N n ∈恒有2,n n S a n =-设⋅+=)1(log 2n n a b(1)求证:数列}1{+n a 是等比数列; (2)求数列}{},{n n b a 的通项公式n a 和;n b(3)若12,nb n n nc a a +=证明:1243n c c c +++<⋅重庆南开中学高2011级高三月考(3月)数学参考答案 (文科)一、选择题:BCADC BCADB 二、填空题:11.2 12.12 55.13 23.14 ]2,1(15⋅ 三、解答题:16.解:(1)1cos 2()sin 2coscos 2sin662xf x x x ππ+=-+1222x =+ ………………………………………………5分由,1)(=θf 可得sin 23θ=所以1sin cos sin 262θθθ==. …………9分(2)当222,,22k x k k Z ππππ-+≤≤+∈即[,],44x k k k Z ππππ∈-++∈时,)(x f 单调递增.所以,函数)(x f 的单调增区间是[,],.44k k k Z ππππ-++∈ (13)分17.解:22(1)(1)()(1)0x m x m x m x x m a b m x x x+-++--=-++==> ………………4分∴当0<m <l 时,(0,)(1,)x m ∈+∞;…………………………7分当m =l 时,(0,1)(1,)x ∈+∞; ………………………………10分当m >l 时,(0,1)(,)x m ∈+∞⋅ ………………………………13分18.解:(1) ABCD BD AC PA ABCD BD PA BD PAC BD ABCD PA AC A ⇒⊥⎫⎪⊥⎫⎪⇒⊥⇒⊥⎬⎬⊂⎭⎪⎪=⎭是菱形平面平面平面 ………5分(2)由(l)可知,BO ⊥平面P AC ,故在平面P AC 内,作OM ⊥A , 连结BM (如图),则∠BMO 为二面角B AN C --的平 面角.在Rt BMO ∆中,易知22,3==OM AO tan 6,BMO ∴∠=即二面角B AN C --的正切值为 6. ………………13分19.解:(1)2()32,f x x x a '=-- ……………………………………2分由(1)0f '=得:1,a = (3)分()(31)(1),f x x x '∴=+- ………………………………………4分1()(,)(1,)3f x ∴-∞-+∞在和上增函数,)(x f 在1(,1)3-上减函数 (6)分(2)(1,2)x ∈-时,)(x f 最小值为0 ………………………………8分2220t mt ∴-+≤对]2,1[∈t 恒成立,分离参数得:tt m 12+≥易知:]2,1[∈t 时,2312≤+t t 23≥∴m ………………………12分 20.解:(1)由题意可得,2=b …………………………………………………………1分又3,3c e a==即2223,,a c a b c ==+得,1,3==c a ……………2分 所以椭圆方程为.12322=+y x ………………………………………………3分(2)设),0)(,(000=/y y x P ),0,3(),0,3(B A -则,1232020=+y x 即,3222020x y -=则1k =2k =即22200012222000222(3)233.3333x x y k k x x x --====---- 12k k ∴的值为2.3- ………………………………………………8分(3)设(,)M x y ,其中[x ∈由已知222||||λ=OM OP 及点P 在椭圆C 上可得,)(3632222222222λ=++=+-+y x x yx x x 整理得,63)13(2222=+-y x λλ其中[x ∈ ………………12分21.解: (1)当n =l 时,1121,S a =-得1 1.2,n n a s a n ==-∴当2n ≥时,112(1),n n S a n --=--两式相减得:1221,n n n a a a -=--12 1.n n a a -∴=+111222(1),n n n a a a --∴+=+=+{1}n a ∴+是以112a +=为首项,2为公比的等比数列.……………………4分(2)由(1)得11222,n n n a +==-*21,.n n a n N ∴=-∈*22log (1)log 2,.n n n b a n n N ∴=+==∈……………………………………8分1111222(3),,n n n n n n n C c a a a a +++-+==由{}n a 为正项数列,所以{}n c 也为正项数列,从而122222(21)2(21)1,21242n n n n n n n n c a c a ++++--==<=--所以数列{}n c 递减, 所以21121111111()()222n n c c c c c c c -+++<++++111()421312nc -=<⋅- ………12分另证:由11211,(21)(21)2121n n nn n n c ++==----- 所以12n c c c +++12231111111()()212121212121n n +=-+-++-------。
南开中学高三理科3月考试题.docx

重庆南开中学高2016级(下)3月月考数学试题(理科)本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分,满分150分,考试时间120分钟.第I 卷(选择题,共60分)一、选择题:本大题共12小题,每小题5分。
在每小题给出的四个选项中。
只有一项是符合题目要求的。
1.若集合A= {1,2,345},集合B={xk (4 — x )<°},则图中阴影部分表示() A. {1,234} B. {1,2,3} C. {4,5}D. {1,4} 22. 等比数列{a"}满足a 3-a 7,贝ijcosa 5 =()1 B.一 2A.1 C. ±- 23. 设z •为虚数单位且Z 的共辗复数是Z,若z + z=4,Z • Z=8,则Z 的虚部为()A. ±2B. ±2zC. 2D. -24.现有4种不同的颜色为公民基本道德规范四个主题词(如 图)涂色,要求相邻的词语涂色不同,则不同的涂法种 数为() A. 27B. 54C. 108D. 1445. 执行右图所示的程序框图,输出的x 值为()A. 5B. 6C. 7D. 86. 在AABC 中AC=6, AC 的垂直平分线交AB 边所在直线于N 点, 则痛•应的值为() A. -6A /3 B. -15A /^" C. -9D. -187. 某几何体的三视图及其尺寸如图所示,则该几何体的各侧面中 最大|洞蜒|幡|瀚c. 2V2 D. 2>/6俯视图D.2的最大值为.在AA3C 中,AB=AC, E 为AC 边上的点,且AC=3AE, 最大值为•8.已知圆C : x 2 + y 2 =1,在线段A3: x-y + 2 = 0(-2<x<3)±任取一点M ,过点M 作圆C 的切线,则“点M 与切点的距离不大于3”的概率P%().1 3 2 A ・一 B. — C.—3 5 34D.—59.如图,将绘有函数/(%) = 2sin((ZK + (pi a )>0,<(p<7i j 部分图象的纸片沿x 轴折成直二面角,若A3之间的空间距离为而,则f(—1) = () A. — 2 B. 2 C. - V3 D. V310.直三棱柱ABC-A l B,C l 的各顶点均在同一个球面上, 则此球的表面积为() 11. A. 20“B. 16/r广 v 2已知双曲线C :。
天津市高三数学上学期第三次月考试题 理(含解析)新人教A版

天津一中2012—2013学年高三数学三月考试卷(理科)一、选择题:1.复数2i2i -=+ A .34i 55- B .34i 55+ C .41i 5- D .31i 5+【答案】A 【解析】2(2)(2)34342(2)(2)555i i i i i i i i ----===-++-,选A. 2.“1m =-”是“直线(21)10mx m y +-+=和直线330x my ++=垂直”的 A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件【答案】A【解析】若0m =,两直线方程为1y =和1x =-,此时两直线垂直。
若12m =,两直线方程为2x =-和13302x y ++=,此时两直线相交。
当0m ≠且12m ≠时,两直线方程为11212m y x m m =+--和33y x m m =--,两直线的斜率为12m m -和3m-。
若两直线垂直,则有3()112m m m⨯-=--,解得1m =-,所以直线(21)10mx m y +-+=和直线330x my ++=垂直时的条件为1m =-或0m =。
所以1m =-是直线(21)10mx m y +-+=和直线330x my ++=垂直的充分不必要条件,选A.3.执行右图所示的程序框图,则输出的S 的值是A .-1B .23C .32D .4【答案】D【解析】第一次循环,21,224S i ==-=-;第二次循环,22,32(1)3S i ===--;第三次循环,23,42223S i ===-;第四次循环,24,5322S i ===-;所以该循环是周期为4的周期循环,所以当9i =时,和第四次循环的结果相同,所以4S =.选D. 4.函数x x x f 2log 12)(+-=的零点所在的一个区间是 A .⎪⎭⎫ ⎝⎛41,81 B .⎪⎭⎫ ⎝⎛21,41C .⎪⎭⎫⎝⎛1,21 D .)2,1( 【答案】C【解析】因为2(1)21log 110f =-+=>,2011()21log 10222f =⨯-+=-<,所以根据根的存在性定理可知函数x x x f 2log 12)(+-=的零点所在的区间为1(,1)2,选C.5.91x ⎫⎪⎭展开式中的常数项是A .36-B .36C .84-D .84【答案】C【解析】展开式的通项公式为93921991()(1)kkkk k kk T C C x x --+=-=-,令9302k -=得3k =。
天津市南开中学高三数学下学期第三次月考试卷 理(含解析)

2014-2015学年天津市南开中学高三(下)第三次月考数学试卷(理科)一、选择题(每小题有且只有1个选项符合题意,将正确的选项涂在答题卡上,每小题5分,共40分.)1.某空间几何体的三视图如图所示,则该几何体的表面积为()A. 180 B. 240 C. 276 D. 3002.已知m,n是两条不同直线,α,β是两个不同平面,给出四个命题:①若α∩β=m,n⊂α,n⊥m,则α⊥β②若m⊥α,m⊥β,则α∥β③若m⊥α,n⊥β,m⊥n,则α⊥β④若m∥α,n∥β,m∥n,则α∥β其中正确的命题是()A.①②B.②③C.①④D.②④3.已知三棱柱ABC﹣A1B1C1的侧棱与底面垂直,体积为,底面是边长为的正三角形,若P为底面A1B1C1的中心,则PA与平面ABC所成角的大小为()A.B.C.D.4.在平面直角坐标系xOy中,M为不等式组所表示的区域上一动点,则直线OM斜率的最小值为()A. 2 B. 1 C.D.5.已知F1和F2分别是双曲线(a>0,b>0)的两个焦点,A和B是以O为圆心,以|OF1|为半径的圆与该双曲线左支的两个交点,且△F2AB是等边三角形,则该双曲线的离心率为()A.B.C.D. 26.已知双曲线C1:=1(a>0,b>0)的焦距是实轴长的2倍.若抛物线C2:x2=2py (p>0)的焦点到双曲线C1的渐近线的距离为2,则抛物线C2的方程为()A. x2=y B. x2=y C. x2=8y D. x2=16y7.抛物线C1:的焦点与双曲线C2:的右焦点的连线交C1于第一象限的点M.若C1在点M处的切线平行于C2的一条渐近线,则p=()A.B.C.D.8.已知椭圆E:的右焦点为F(3,0),过点F的直线交椭圆E于A、B两点.若AB的中点坐标为(1,﹣1),则E的方程为()A.B.C.D.二、填空题:(每小题0分,共30分.)015春•天津校级月考)已知数列{a n}的前n项和S n满足S n=2a n+1(n∈N*),且a1=1,则通项公式a n= .1015春•天津校级月考)圆心在直线x﹣2y+7=0上的圆C与x轴交于两点A(﹣2,0)、B(﹣4,0),则圆C的方程为.1015春•天津校级月考)在边长为2的菱形ABCD中,∠BAD=60°,E为CD的中点,则•= .1015春•天津校级月考)已知cos(x﹣)=﹣,则cosx+cos(x﹣)= .1015春•天津校级月考)已知函数y=x3﹣3x+c的图象与x轴恰有三个公共点,则实数c的取值范围是.1015春•天津校级月考)点F是椭圆E:的左焦点,过点F且倾斜角是锐角的直线l与椭圆E交于A、B两点,若△AOB的面积为,则直线l的斜率是.三、解答题:(15-18每小题0分,19-20每小题0分,共80分.)1015春•天津校级月考)一个袋子中装有大小形状完全相同的编号分别为1,2,3,4,5的5个红球与编号为1,2,3,4的4个白球,从中任意取出3个球.(Ⅰ)求取出的3个球颜色相同且编号是三个连续整数的概率;(Ⅱ)记X为取出的3个球中编号的最大值,求X的分布列与数学期望.1013•铁岭模拟)在△ABC中,角A,B,C的对边分别为a,b,c,且acosC,bcosB,ccosA 成等差数列,(Ⅰ)求B的值;(Ⅱ)求2sin2A+cos(A﹣C)的范围.1014•东莞二模)如图,在四棱锥P﹣ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且PA=PD=AD,E、F分别为PC、BD的中点.(Ⅰ)求证:EF∥平面PAD;(Ⅱ)求证:面PAB⊥平面PDC;(Ⅲ)在线段AB上是否存在点G,使得二面角C﹣PD﹣G的余弦值为?说明理由.1014•河北区三模)已知函数f(x)=.(Ⅰ)若a=2,求f(x)在(1,f(1))处的切线方程;(Ⅱ)求f(x)在区间[1,e]上的最小值;(Ⅲ)若f(x)在区间(1,e)上恰有两个零点,求a的取值范围.1014•天津三模)已知数列{a n}的前n项和S n=﹣a n﹣+2(n∈N*),数列{b n}满足b n=2n a n.(1)求证数列{b n}是等差数列,并求数列{a n}的通项公式;(2)设数列{a n}的前n项和为T n,证明:n∈N*且n≥3时,T n>;(3)设数列{c n}满足a n(c n﹣3n)=(﹣1)n﹣1λn(λ为非零常数,n∈N*),问是否存在整数λ,使得对任意n∈N*,都有c n+1>c n.2013•和平区一模)已知椭圆C的中心在坐标原点,焦点在x轴上,离心率为,它的一个顶点恰好是抛物线x2=4的焦点.(I)求椭圆C的标准方程;(II)若A、B是椭圆C上关x轴对称的任意两点,设P(﹣4,0),连接PA交椭圆C于另一点E,求证:直线BE与x轴相交于定点M;(III)设O为坐标原点,在(II)的条件下,过点M的直线交椭圆C于S、T两点,求•的取值范围.2014-2015学年天津市南开中学高三(下)第三次月考数学试卷(理科)参考答案与试题解析一、选择题(每小题有且只有1个选项符合题意,将正确的选项涂在答题卡上,每小题5分,共40分.)1.某空间几何体的三视图如图所示,则该几何体的表面积为()A. 180 B. 240 C. 276 D. 300考点:由三视图求面积、体积.专题:计算题.分析:由三视图可知几何体复原后,上部是四棱锥,下部是正方体,利用三视图的数据,求出几何体的表面积即可.解答:解:由题意可知几何体复原后,上部是四棱锥,下部是正方体,四棱锥的底面是边长为6的正方形,侧面斜高为5;下部是棱长为6的正方体,所以几何体的表面积为:5个正方形的面积加上棱锥的侧面积,即:5×6×6+4××4=240.故选B.点评:本题考查几何体与三视图的关系,几何体的表面积的求法,考查计算能力.2.已知m,n是两条不同直线,α,β是两个不同平面,给出四个命题:①若α∩β=m,n⊂α,n⊥m,则α⊥β②若m⊥α,m⊥β,则α∥β③若m⊥α,n⊥β,m⊥n,则α⊥β④若m∥α,n∥β,m∥n,则α∥β其中正确的命题是()A.①②B.②③C.①④D.②④考点:命题的真假判断与应用;平面与平面之间的位置关系.专题:空间位置关系与距离.分析:由面面垂直的判定定理,可判断①的真假;由面面平行的判定定理及线面垂直的几何特征,可以判断②的真假;由面面垂直的判定定理,及线面垂直的几何特征,可以判断③的真假;根据线面平行的几何特征及面面平行的判定方法,可以判断④的真假.解答:解:①若α∩β=m,n⊂α,n⊥m,如图,则α与β不一定垂直,故①为假命题;②若m⊥α,m⊥β,根据垂直于同一条直线的两个平面平行,则α∥β;故②为真命题;③若m⊥α,n⊥β,m⊥n,则α⊥β,故③为真命题;④若m∥α,n∥β,m∥n,如图,则α与β可能相交,故④为假命题.故选B.点评:本题考查的知识点是平面与平面之间的位置关系,熟练掌握空间直线与平面平行及垂直的判定定理、性质定义、几何特征是解答的关键.3.已知三棱柱ABC﹣A1B1C1的侧棱与底面垂直,体积为,底面是边长为的正三角形,若P为底面A1B1C1的中心,则PA与平面ABC所成角的大小为()A.B.C.D.考点:直线与平面所成的角.专题:空间位置关系与距离;空间角.分析:利用三棱柱ABC﹣A1B1C1的侧棱与底面垂直和线面角的定义可知,∠APA1为PA与平面A1B1C1所成角,即为∠APA1为PA与平面ABC所成角.利用三棱锥的体积计算公式可得AA1,再利用正三角形的性质可得A1P,在Rt△AA1P中,利用tan∠APA1=即可得出.解答:解:如图所示,∵AA1⊥底面A1B1C1,∴∠APA1为PA与平面A1B1C1所成角,∵平面ABC∥平面A1B1C1,∴∠APA1为PA与平面ABC所成角.∵==.∴V 三棱柱ABC﹣A1B1C1==,解得.又P为底面正三角形A1B1C1的中心,∴==1,在Rt△AA1P中,,∴.故选B.点评:熟练掌握三棱柱的性质、体积计算公式、正三角形的性质、线面角的定义是解题的关键.4.在平面直角坐标系xOy中,M为不等式组所表示的区域上一动点,则直线OM斜率的最小值为()A. 2 B. 1 C.D.考点:简单线性规划.专题:不等式的解法及应用.分析:本题属于线性规划中的延伸题,对于可行域不要求线性目标函数的最值,而是求可行域内的点与原点(0,0)构成的直线的斜率的最小值即可.解答:解:不等式组表示的区域如图,当M取得点A(3,﹣1)时,z直线OM斜率取得最小,最小值为k==﹣.故选C.点评:本题利用直线斜率的几何意义,求可行域中的点与原点的斜率.本题主要考查了用平面区域二元一次不等式组,以及简单的转化思想和数形结合的思想,属中档题.5.已知F1和F2分别是双曲线(a>0,b>0)的两个焦点,A和B是以O为圆心,以|OF1|为半径的圆与该双曲线左支的两个交点,且△F2AB是等边三角形,则该双曲线的离心率为()A.B.C.D. 2考点:双曲线的简单性质.专题:计算题;圆锥曲线的定义、性质与方程.分析:连接AF1,可得∠AF2F1=30°,∠F1AF2=90°,F2F1=2c,AF1=c,AF2=c,由双曲线的定义可知:AF2﹣AF1=c﹣c=2a,变形可得离心率的值.解答:解:连接AF1,可得∠AF2F1=30°,∠F1AF2=90°,由焦距的意义可知F2F1=2c,AF1=c,由勾股定理可知AF2=c,由双曲线的定义可知:AF2﹣AF1=2a,即c﹣c=2a,变形可得双曲线的离心率==+1故选:C.点评:本题考查双曲线的性质,涉及直角三角形的性质,属中档题.6.已知双曲线C1:=1(a>0,b>0)的焦距是实轴长的2倍.若抛物线C2:x2=2py (p>0)的焦点到双曲线C1的渐近线的距离为2,则抛物线C2的方程为()A. x2=y B. x2=y C. x2=8y D. x2=16y考点:抛物线的简单性质.专题:计算题;圆锥曲线的定义、性质与方程.分析:利用双曲线C1:=1(a>0,b>0)的焦距是实轴长的2倍,推出a,b的关系,求出抛物线的焦点坐标,通过点到直线的距离求出p,即可得到抛物线的方程.解答:解:∵双曲线C1:=1(a>0,b>0)的焦距是实轴长的2倍,∴c=2a,即=4,∴,双曲线的一条渐近线方程为:.抛物线C2:x2=2py(p>0)的焦点(0,)到双曲线C1的渐近线的距离为2,∴2=,∵,∴p=8.∴抛物线C2的方程为x2=16y.故选:D.点评:本题考查抛物线的简单性质,点到直线的距离公式,双曲线的简单性质,考查计算能力.7.抛物线C1:的焦点与双曲线C2:的右焦点的连线交C1于第一象限的点M.若C1在点M处的切线平行于C2的一条渐近线,则p=()A.B.C.D.考点:利用导数研究曲线上某点切线方程;双曲线的简单性质.专题:圆锥曲线的定义、性质与方程.分析:由曲线方程求出抛物线与双曲线的焦点坐标,由两点式写出过两个焦点的直线方程,求出函数在x取直线与抛物线交点M的横坐标时的导数值,由其等于双曲线渐近线的斜率得到交点横坐标与p的关系,把M点的坐标代入直线方程即可求得p的值.解答:解:由,得x2=2py(p>0),所以抛物线的焦点坐标为F().由,得,.所以双曲线的右焦点为(2,0).则抛物线的焦点与双曲线的右焦点的连线所在直线方程为,即①.设该直线交抛物线于M(),则C1在点M处的切线的斜率为.由题意可知,得,代入M点得M()把M点代入①得:.解得p=.故选:D.点评:本题考查了双曲线的简单几何性质,考查了利用导数研究曲线上某点的切线方程,函数在曲线上某点处的切线的斜率等于函数在该点处的导数,是中档题.8.已知椭圆E:的右焦点为F(3,0),过点F的直线交椭圆E于A、B两点.若AB的中点坐标为(1,﹣1),则E的方程为()A.B.C.D.考点:椭圆的标准方程.专题:圆锥曲线的定义、性质与方程.分析:设A(x1,y1),B(x2,y2),代入椭圆方程得,利用“点差法”可得.利用中点坐标公式可得x1+x2=2,y1+y2=﹣2,利用斜率计算公式可得==.于是得到,化为a2=2b2,再利用c=3=,即可解得a2,b2.进而得到椭圆的方程.解答:解:设A(x1,y1),B(x2,y2),代入椭圆方程得,相减得,∴.∵x1+x2=2,y1+y2=﹣2,==.∴,化为a2=2b2,又c=3=,解得a2=18,b2=9.∴椭圆E的方程为.故选D.点评:熟练掌握“点差法”和中点坐标公式、斜率的计算公式是解题的关键.二、填空题:(每小题0分,共30分.)015春•天津校级月考)已知数列{a n}的前n项和S n满足S n=2a n+1(n∈N*),且a1=1,则通项公式a n= .考点:数列递推式.专题:等差数列与等比数列.分析:通过a n+1=S n+1﹣S n,可得该数列从第2项起的公比为,进而可得结论.解答:解:∵S n=2a n+1(n∈N*),∴S n+1=2a n+2,两式相减得:a n+1=2a n+2﹣2a n+1,整理得:=,又∵a1=1,∴a1+a2=2a2,即a2=,∴,故答案为:.点评:本题考查求数列的通项,注意解题方法的积累,属于基础题.1015春•天津校级月考)圆心在直线x﹣2y+7=0上的圆C与x轴交于两点A(﹣2,0)、B(﹣4,0),则圆C的方程为(x+3)2+(y﹣2)2=5 .考点:圆的标准方程.专题:计算题;直线与圆.分析:由条件求得圆心的坐标为C(﹣3,2),半径r=|AC|=,从而得到圆C的方程.解答:解析:直线AB的中垂线方程为x=﹣3,代入直线x﹣2y+7=0,得y=2,故圆心的坐标为C(﹣3,2),再由两点间的距离公式求得半径r=|AC|=,∴圆C的方程为(x+3)2+(y﹣2)2=5.故答案为:(x+3)2+(y﹣2)2=5点评:本题主要考查圆的标准方程,直线和圆的位置关系的应用,属于中档题.1015春•天津校级月考)在边长为2的菱形ABCD中,∠BAD=60°,E为CD的中点,则•= 1 .考点:平面向量数量积的运算.专题:平面向量及应用.分析:由题意可得||=||=2,且与的夹角∠BAD=60°,用与作基底表示要求的向量,由数量积的运算可得.解答:解:由题意可得||=||=2,且与的夹角∠BAD=60°,由向量的运算可得=+=+,=﹣,∴•=(+)•(﹣)=﹣﹣=22﹣×2×2×﹣×22=1故答案为:1点评:本题考查平面向量的数量积,涉及平面向量基本定理,属基础题.1015春•天津校级月考)已知cos(x﹣)=﹣,则cosx+cos(x﹣)= ﹣1 .考点:两角和与差的余弦函数.专题:三角函数的求值.分析:由和差角的三角函数公式可得cosx+cos(x﹣)=cosx+cosx+sinx=cos(x﹣),代入已知数据可得.解答:解:∵cos(x﹣)=﹣,∴cosx+cos(x﹣)=cosx+cosx+sinx=cosx+sinx=(cosx+sinx)=cos(x﹣)=﹣1故答案为:﹣1点评:本题考查两角和与差的三角函数公式,属基础题.1015春•天津校级月考)已知函数y=x3﹣3x+c的图象与x轴恰有三个公共点,则实数c的取值范围是(﹣2,2).考点:利用导数研究函数的极值.专题:导数的概念及应用.分析:由题意,根据根的存在性定理知,只需使函数f(x)的极大值与极小值符号相反即可.解答:解:令f′(x)=3x2﹣3=0解得,x=1或x=﹣1,∵函数f(x)=x3﹣3x+c的图象与x轴恰好有三个不同的公共点,∴f(1)f(﹣1)<0,即(c﹣2)(c+2)<0,则﹣2<c<2,故答案为:(﹣2,2).点评:本题考查了函数的图象与性质,利用导数求极值及根的存在性定理.1015春•天津校级月考)点F是椭圆E:的左焦点,过点F且倾斜角是锐角的直线l与椭圆E交于A、B两点,若△AOB的面积为,则直线l的斜率是.考点:椭圆的简单性质.专题:直线与圆;圆锥曲线的定义、性质与方程.分析:求出椭圆的a,b,c,求得F的坐标,设直线AB:x=my﹣4,(m>0),代入椭圆方程,可得(25+9m2)y2﹣72my﹣81=0,运用韦达定理,由△AOB的面积为S=|OF|•|y1﹣y2|=,两边平方,化简整理,解方程即可得到m,进而得到直线l的斜率.解答:解:椭圆E:的a=5,b=3,c=4,则F(﹣4,0),设直线AB:x=my﹣4,(m>0),代入椭圆方程,可得(25+9m2)y2﹣72my﹣81=0,设A(x1,y1),B(x2,y2),y1+y2=,y1y2=,则|y1﹣y2|2=(y1+y2)2﹣4y1y2=()2﹣4•=,则△AOB的面积为S=|OF|•|y1﹣y2|=,两边平方可得,16•=81,解得m=,即有直线l的斜率为,故答案为:.点评:本题考查椭圆的方程和性质,主要考查椭圆的方程的运用,联立直线方程,运用韦达定理,考查化简运算能力,属于中档题.三、解答题:(15-18每小题0分,19-20每小题0分,共80分.)1015春•天津校级月考)一个袋子中装有大小形状完全相同的编号分别为1,2,3,4,5的5个红球与编号为1,2,3,4的4个白球,从中任意取出3个球.(Ⅰ)求取出的3个球颜色相同且编号是三个连续整数的概率;(Ⅱ)记X为取出的3个球中编号的最大值,求X的分布列与数学期望.考点:离散型随机变量的期望与方差;离散型随机变量及其分布列.专题:概率与统计.分析:(Ⅰ)设“取出的3个球颜色相同且编号是三个连续整数”为事件A,利用古典概型的概率公式求解即可.(Ⅱ)X的取值可能是2,3,4,5,分别分别求出概率得到分布列,然后求解期望即可.解答:解:(Ⅰ)设“取出的3个球颜色相同且编号是三个连续整数”为事件A,则P(A)==.(Ⅱ)X的取值为2,3,4,5.=,=,=,=.所以X的分布列为X 2 3 4 5PX的数学期望EX=2×+3×+4×=.点评:本题考查离散型随机变量的分布列以及期望的求法,考查古典概型概率的求法,考查计算能力.1013•铁岭模拟)在△ABC中,角A,B,C的对边分别为a,b,c,且acosC,bcosB,ccosA 成等差数列,(Ⅰ)求B的值;(Ⅱ)求2sin2A+cos(A﹣C)的范围.考点:正弦定理;等差数列;三角函数的定义域.专题:计算题.分析:(Ⅰ)根据等差数列的性质可知acosC+ccosA=2bcosB,利用正弦定理把边转化成角的正弦,化简整理得sinB=2sinBcosB,求得cosB,进而求得B.(Ⅱ)先利用二倍角公式对原式进行化简整理,进而根据A的范围和正弦函数的单调性求得2sin2A+cos(A﹣C)的范围.解答:解:(Ⅰ)∵acosC,bcosB,ccosA成等差数列,∴acosC+ccosA=2bcosB,由正弦定理得,a=2RsinA,b=2RsinB,c=2RsinC,代入得:2RsinAcosC+2RcosAsinC=4RsinBcosB,即:sin(A+C)=sinB,∴sinB=2sinBcosB,又在△ABC中,sinB≠0,∴,∵0<B<π,∴;(Ⅱ)∵,∴∴==,∵,∴∴2sin2A+cos(A﹣C)的范围是.点评:本题主要考查了正弦定理的应用.解题的关键就是利用了正弦定理把边的问题转化成了角的问题,利用三角函数的特殊性质求得答案.1014•东莞二模)如图,在四棱锥P﹣ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且PA=PD=AD,E、F分别为PC、BD的中点.(Ⅰ)求证:EF∥平面PAD;(Ⅱ)求证:面PAB⊥平面PDC;(Ⅲ)在线段AB上是否存在点G,使得二面角C﹣PD﹣G的余弦值为?说明理由.考点:平面与平面垂直的判定;直线与平面平行的判定;二面角的平面角及求法.专题:空间位置关系与距离;空间角.分析:(I)证明:连接AC,则F是AC的中点,E为PC 的中点,证明EF∥PA,留言在线与平面平行的判定定理证明EF∥平面PAD;(II)先证明CD⊥PA,然后证明PA⊥PD.利用直线与平面垂直的判定定理证明PA⊥平面PCD,最后根据面面垂直的判定定理即可得到面PAB⊥面PDC.(III)假设在线段AB上,存在点G,使得二面角C﹣PD﹣G的余弦值为,然后以O为原点,直线OA,OF,OP分别为x,y,z轴建立空间直角坐标系,设G(1,a,0)(0≤a≤2).利用空间向量的坐标运算求出a值,即可得出结论.解答:证明:(Ⅰ)连结AC∩BD=F,ABCD为正方形,F为AC中点,E为PC中点.∴在△CPA中,EF∥PA…(2分)且PA⊂平面PAD,EF⊄平面PAD∴EF∥平面PAD…(4分)(Ⅱ)因为平面PAD⊥平面ABCD,平面PAD∩面ABCD=ADABCD为正方形,CD⊥AD,CD⊂平面ABCD所以CD⊥平面PAD.∴CD⊥PA…(6分)又PA=PD=AD,所以△PAD是等腰直角三角形,且∠APD=90°即PA⊥PDCD∩PD=D,且CD、PD⊂面PDC∴PA⊥面PDC又PA⊂面PAB,∴面PAB⊥面PDC.…..(9分)(Ⅲ)如图,取AD的中点O,连结OP,OF.∵PA=PD,∴PO⊥AD.∵侧面PAD⊥底面ABCD,面PAD⊥面ABCD,∴PO⊥面ABCD,而O,F分别为AD,BD的中点,∴OF∥AB,又ABCD是正方形,故OF⊥AD.∵PA=PD=AD,∴PA⊥PD,OP=OA=1.以O为原点,直线OA,OF,OP分别为x,y,z轴建立空间直角坐标系,则有A(1,0,0),F(0,1,0),D(﹣1,0,0),P(0,0,1).若在AB上存在点G,使得二面角C﹣PD﹣G的余弦值为,连结PG,DG设G(1,a,0)(0≤a≤2).由(Ⅱ)知平面PDC的法向量为=(1,0,﹣1).设平面PGD的法向量为=(x,y,z).∵=(1,0,1),=(﹣2,﹣a,0),∴由,=0可得,令x=1,则y=﹣,z=﹣1,故=(1,﹣,﹣1),∴cos==,解得,a=.所以,在线段AB上存在点G(1,,0),使得二面角C﹣PD﹣G的余弦值为.…(14分)点评:本题考查直线与平面垂直的判定,直线与平面平行的判定的应用及二面角的平面角及求法,考查逻辑推理能力.1014•河北区三模)已知函数f(x)=.(Ⅰ)若a=2,求f(x)在(1,f(1))处的切线方程;(Ⅱ)求f(x)在区间[1,e]上的最小值;(Ⅲ)若f(x)在区间(1,e)上恰有两个零点,求a的取值范围.考点:利用导数研究曲线上某点切线方程;函数的零点;利用导数求闭区间上函数的最值.专题:导数的综合应用.分析:(Ⅰ)把a=2代入可得f′(1)=﹣1,f(1)=,进而可得方程,化为一般式即可;(Ⅱ)可得x=为函数的临界点,分≤1,1<<e,,三种情形来讨论,可得最值;(Ⅲ)由(Ⅱ)可知当0<a≤1或a≥e2时,不合题意,当1<a<e2时,需,解之可得a的范围.解答:解:(I)当a=2时,f(x)=,f′(x)=x﹣,∴f′(1)=﹣1,f(1)=,故f(x)在(1,f(1))处的切线方程为:y﹣=﹣(x﹣1)化为一般式可得2x+2y﹣3=0…..(3分)(Ⅱ)求导数可得f′(x)=x﹣=由a>0及定义域为(0,+∞),令f′(x)=0,解得x=,①若≤1,即0<a≤1,在(1,e)上,f′(x)>0,f(x)在[1,e]上单调递增,因此,f(x)在区间[1,e]的最小值为f(1)=.②若1<<e,即1<a<e2,在(1,)上,f′(x)<0,f(x)单调递减;在(,e)上,f′(x)>0,f(x)单调递增,因此f(x)在区间[1,e]上的最小值为f()=,③若,即a≥e2在(1,e上,f′(x)<0,f(x)在[1,e]上单调递减,因此,f(x)在区间[1,e]上的最小值为f(e)=.综上,当0<a≤1时,f min(x)=;当1<a<e2时,f min(x)=;当a≥e2时,f min(x)=.….(9分)(Ⅲ)由(Ⅱ)可知当0<a≤1或a≥e2时,f(x)在(1,e)上是单调递增或递减函数,不可能存在两个零点.当1<a<e2时,要使f(x)在区间(1,e)上恰有两个零点,则即,此时,e<a<.所以,a的取值范围为(e,)…..(13分)点评:本题考查利用导数研究函数的切线,涉及函数的零点和闭区间的最值,属中档题.1014•天津三模)已知数列{a n}的前n项和S n=﹣a n﹣+2(n∈N*),数列{b n}满足b n=2n a n.(1)求证数列{b n}是等差数列,并求数列{a n}的通项公式;(2)设数列{a n}的前n项和为T n,证明:n∈N*且n≥3时,T n>;(3)设数列{c n}满足a n(c n﹣3n)=(﹣1)n﹣1λn(λ为非零常数,n∈N*),问是否存在整数λ,使得对任意n∈N*,都有c n+1>c n.考点:等差数列的性质;数列与不等式的综合.专题:等差数列与等比数列.分析:(1)由已知条件推导出2n a n=2n﹣1a n﹣1+1.由此能证明{数列b n}是首项和公差均为1的等差数列.从而求出a n=.(2)由(1)知=(n+1)•()n,利用错位相减法能求出T n=3﹣.再用数学归纳法能证明n∈N*且n≥3时,T n>.(3)由a n(c n﹣3n)=(﹣1)n﹣1λn可求得c n,对任意n∈N+,都有c n+1>c n即c n+1﹣c n>0恒成立,整理可得(﹣1)n﹣1•λ<()n﹣1,分n为奇数、偶数两种情况讨论,分离出参数λ后转化为函数最值即可解决.解答:(1)证明:在S n=﹣a n﹣+2(n∈N*)中,令n=1,得S1=﹣a1﹣1+2=a1,解得a1=,当n≥2时,S n﹣1=﹣a n﹣1﹣()n﹣2+2,∴a n=S n﹣S n﹣1=﹣a n+a n﹣1+()n﹣1,∴2a n=a n﹣1+()n﹣1,即2n a n=2n﹣1a n﹣1+1.∵b n=2n a n,∴b n=b n﹣1+1,即当n≥2时,b n﹣b n﹣1=1,又b1=2a1=1,∴{数列b n}是首项和公差均为1的等差数列.于是b n=1+(n﹣1)•1=n=2n a n,∴a n=.(2)证明:∵,∴=(n+1)•()n,∴T n=2×+3×()2+…+(n+1)×()n,①=2×()2+3×()3+…+(n+1)×()n+1,②①﹣②,得:=1+=1+﹣(n+1)•()n+1=,∴T n=3﹣.∴T n﹣=3﹣=,∴确定T n与的大小关系等价于比较2n与2n+1的大小.下面用数学归纳法证明n∈N*且n≥3时,T n>.①当n=3时,23>2×3+1,成立②假设当n=k(k≥3)时,2k>2k+1成立,则当n=k+1时,2k+1=2•2k>2(2k+1)=4k+2=2(k+1)+1+(2k﹣1)>2(k+1)+1,∴当n=k+1时,也成立.于是,当n≥3,n∈N*时,2n>2n+1成立∴n∈N*且n≥3时,T n>.(3)由,得=3n+(﹣1)n﹣1•λ•2n,∴c n+1﹣c n=[3n+1+(﹣1)n•λ•2n+1]﹣[3n+(﹣1)n﹣1•λ•2n]=2•3n﹣3λ(﹣1)n﹣1•2n>0,∴,①当n=2k﹣1,k=1,2,3,…时,①式即为λ<,②依题意,②式对k=1,2,3…都成立,∴λ<1,当n=2k,k=1,2,3,…时,①式即为③,依题意,③式对k=1,2,3…都成立,∴,∴,又λ≠0,∴存在整数λ=﹣1,使得对任意n∈N*有c n+1>c n.点评:本题考查数列递推式、等差数列的通项公式、数列求和等知识,考查恒成立问题,考查转化思想,错位相减法对数列求和是高考考查的重点内容,要熟练掌握.2013•和平区一模)已知椭圆C的中心在坐标原点,焦点在x轴上,离心率为,它的一个顶点恰好是抛物线x2=4的焦点.(I)求椭圆C的标准方程;(II)若A、B是椭圆C上关x轴对称的任意两点,设P(﹣4,0),连接PA交椭圆C于另一点E,求证:直线BE与x轴相交于定点M;(III)设O为坐标原点,在(II)的条件下,过点M的直线交椭圆C于S、T两点,求•的取值范围.考点:直线与圆锥曲线的综合问题;椭圆的标准方程.专题:圆锥曲线中的最值与范围问题.分析:(1)由抛物线x2=4得焦点.设椭圆方程为.由题意可得,再利用及a2=b2+c2即可得出;(2)由题意可知直线PA的斜率存在,设直线PA的方程为y=k(x+4),与椭圆的方程联立即可得到根与系数的关系.设点A(x1,y1),E(x2,y2),则B(x1,﹣y1).直线BE的方程为.把y1,y2分别用x1,x2表示,在代入直线BE的方程即可得出;(3)当过点M的直线斜率存在时,设直线ST的方程为y=m(x+1),且S(x3,y3),T(x4,y4)在椭圆C上,与椭圆的方程联立得到根与系数的关系及判别式,再利用向量的数量积,即可得出其其中范围.当过点M的直线斜率不存在时,比较简单.解答:(1)解:由抛物线x2=4得焦点.设椭圆方程为.由题意可得,解得,∴椭圆的方程为.(2)证明:由题意可知直线PA的斜率存在,设直线PA的方程为y=k(x+4),联立,消去y得到(4k2+3)x2+32k2x+64k2﹣12=0 ①设点A(x1,y1),E(x2,y2),则B(x1,﹣y1).直线BE的方程为.令y=0,则,把y1=k(x1+4),y2=k(x2+4)代入上式并整理得.②由①得,,将其代入②并整理得.∴直线BE与x轴相交于定点M(﹣1,0).(3)当过点M的直线斜率存在时,设直线ST的方程为y=m(x+1),且S(x3,y3),T(x4,y4)在椭圆C上,联立得(4m2+3)x2+8m2x+4m2﹣12=0,则△=(8m2)2﹣4(4m2+3)(4m2﹣12)=144(m2+1)>0.∴,,∴=m2(x3x4+x3+x4+1)=﹣.∴=x3x4+y3y4==﹣.由m2≥0得.当过点M的直线斜率不存在时,直线ST的方程为x=﹣1,,,此时,,∴•的取值范围为.点评:本题综合考查了椭圆、抛物线的标准方程及其性质、直线与圆锥曲线相交问题转化为一元二次方程得根与系数的关系、直线过定点问题、向量相等及其数量积等基础知识及基本技能,考查了分类讨论的思想方法、推理能力和计算能力.。
天津市高三数学第三次月考试题 理 新人教A版

天津市新华中学2013届高三第三次月考数学试题 理一、选择题:(本大题共8小题,每小题6分,共48分.)在每小题给出的四个选项中,只有一项是符合题目要求的.1. 倾斜角为135︒,在y 轴上的截距为1-的直线方程是( )A. 01=+-y xB. 01=--y xC. 01=-+y xD. 01=++y x2. 已知实数x y ,满足2203x y x y y +≥⎧⎪-≤⎨⎪≤≤⎩,,,则2z x y =-的最小值是( )A. 7B. -5C. 4D. -73. 如图,E 、F 分别是三棱锥P-ABC 的棱AP 、BC 的中点,PC=10,AB=6,EF=7,则异面直线AB 与PC 所成的角为( )A. 90°B. 60°C. 45°D. 30°4. 设n S 是等差数列{a n }的前n 项和,5283()S a a =+,则53a a 的值为( ) A. 16 B. 13 C. 35 D. 565. 设b a ,是两条直线,βα,是两个平面,则b a ⊥的一个充分条件是 ( ) A. βαβα⊥⊥,//,b a B. βαβα//,,⊥⊥b a C. βαβα//,,⊥⊂b a D. βαβα⊥⊂,//,b a6. 若直线1l :280ax y +-=与直线2l :(1)40x a y +++=平行 ,则a 的值为( )A. 1B. 1或2C. -2D. 1或-27. 已知正项等比数列{}n a 满足:7652a a a =+,若存在两项,m n a a 使得14m n a a a =,则14m n+的最小值为( ) A. 32 B. 53 C. 256D. 不存在8. 已知三棱锥S ABC -的所有顶点都在球O 的球面上,ABC ∆是边长为1的正三角形,SC 为球O 的直径,且2SC =,则此棱锥的体积为( )A. 26B. 36C. 23D. 22二、填空题:(本大题共6小题,每小题6分,共36分.)把答案填在题中横线上.9. 已知一个几何体的三视图如下图所示(单位:cm),其中正视图是直角梯形,侧视图和俯视图都是矩形,则这个几何体的体积是________cm 3.10. 已知向量,a b r r 夹角为45︒,且 1,210a a b =-=r r r ;则b =r ___ ___. 11. 若1111335(21)(21)S n n =++⋅⋅⋅+⨯⨯-+,则S = . 12. 设数列{a n }满足132nn n a a +=+,(n ∈N ﹡),且11a =,则数列{a n }的通项公式为 .13. 在数列{a n }中,(1)()8nn a n =+,则数列{a n }中的最大项是第 项。
天津市高三数学第三次月考 理 新人教A版

(理科)一、选择题:(本大题共8小题,每小题6分,共48分.)在每小题给出的四个选项中,只有一项是符合题目要求的.1. 倾斜角为135︒,在y 轴上的截距为1-的直线方程是( )A. 01=+-y xB. 01=--y xC. 01=-+y xD. 01=++y x【答案】D【解析】直线的斜率为tan1351k ==-,所以满足条件的直线方程为1y x =--,即10x y ++=,选D.2. 已知实数x y ,满足2203x y x y y +≥⎧⎪-≤⎨⎪≤≤⎩,,,则2z x y =-的最小值是( )A. 7B. -5C. 4D. -7【答案】B【解析】由2z x y =-得,2y x z =-,做直线2y x =,平移直线2y x z =-,由图象 可知当直线2y x z =-经过点B 时,直线的截距最大,此时2z x y =-最小,由23x y y +=⎧⎨=⎩得,13x y =-⎧⎨=⎩,代入2z x y =-得最小值2235z x y =-=--=-,所以选B.3. 如图,E 、F 分别是三棱锥P-ABC 的棱AP 、BC 的中点,PC=10,AB=6,EF=7,则异面直线AB 与PC 所成的角为( )A. 90°B. 60°C. 45°D. 30°【答案】B【解析】,取AC 的中点M,连结EM,MF ,因为E,F 是中点,所以16//,322MF AB MF AB ===,110//,522ME PC ME PC ===,所以MF 与ME 所成的角即为AB 与PC 所成的角。
在三角形MEF 中,222537151cos 253302EMF +--===-⨯⨯,所以120EMF ∠=,所以直线AB 与PC 所成的角为为60,选B.4. 设n S 是等差数列{a n }的前n 项和,5283()S a a =+,则53a a 的值为( ) A. 16 B. 13 C. 35 D. 56【答案】D【解析】由5283()S a a =+得,1555()322a a a +=⨯,即3556a a =,所以5356a a =,选D.5. 设b a ,是两条直线,βα,是两个平面,则b a ⊥的一个充分条件是 ( ) A. βαβα⊥⊥,//,b a B. βαβα//,,⊥⊥b a C. βαβα//,,⊥⊂b a D. βαβα⊥⊂,//,b a【答案】C【解析】若b β⊥,//αβ,所以b α⊥,又a α⊂,所以b a ⊥,即a b ⊥,所以选C. 6. 若直线1l :280ax y +-=与直线2l :(1)40x a y +++=平行 ,则a 的值为( ) A. 1 B. 1或2C. -2D. 1或-2【答案】A【解析】直线1l 的方程为42ay x =-+,若1a =-,则两直线不平行,所以1a ≠-,要使两直线平行,则有282114a a -=≠=-+,由211a a =+,解得1a =或2a =-。
天津市南开区高三数学(理)第三次月考

天津市南开区高三数学(理)第三次月考第一卷(50分)一. 选择题:(本大题共10小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
)1. 已知M={y|y = x 2 , x ∈R} N={y|x 2+y 2=2} 则M ⋂N=( )A. {(1,1)(-1,1)}B. {1}C. [0,1]D. [0,2] 2. 已知f (x )是定义在R 上的偶函数,它在),0[+∞上递减,那么一定有( )A.)1()43(2+->-a a f fB. )1()43(2+-≥-a a f fC. )1()43(2+-<-a a f fD.23()(1)4f f a a -≤-+3. 已知函数()21x f x =+的反函数为1()f x -,则1()0f x -<的解集为( )A. (,2)-∞B. (1,2)C. (2,)∞D. (,1)-∞4. 如果0<a<1,那么下列不等式中正确的是( )A. 2131)1()1(a a ->-B. log (1-a )(1+a )>0C. (1-a )3>(1+a )2D.(1-a )1+a>15. 一个等差数列的项数为奇数,所有奇数项的和为72,所有偶数项的和为66,则这个等差数列共有( )A. 11项B. 21项C. 23项D. 25项6. 已知Rt△ABC 中,∠C=900,∠A, ∠B, ∠C 所对的边分别是a , b , c ,且a , b , c 成等差数列,求tanA+tanB 的值( )A. 2512B. 43C. 137D. 27. 已知函数,0),35sin()(≠+=k kx x f 其中π使得自变量x 在任意两个整数之间(包括正整数本身)变化时,函数)(x f 至少有一个最大值和一个最小最小值。
则最小自然数k为 ( )A. 15B. 16C. 31D. 32 8. 若-2<a <7,1<b <2,则ab的取值范围是( ) A. (-1,7) B.(-2,7) C.(-7,1) D.(-7,2)9. 在全体实数中引进一种新的运算*,其规定如下: (1)对任意a ,b 有()()1a b a b b *=+- (2)对任意实数a 有2a a a *=*当2x =时,()2321x x *⎡⎤*-*+⎣⎦的值为( )A. 18B. 16C. 12D. 6 10. 已知奇函数()f x 满足:()(2)f x f x =-,且当x ∈(0,1)时,()21x f x =-,则12(log 35)f 的值为( )A. -3529B. -1916C. -2935D. 以上答案均不对第二卷(共100分)二. 填空题(本大题共6小题,每小题4分)11. ()(,),{()}n n f n i i i n Z f n -=+∈为虚数单位则集合元素个数为________。
天津市高三数学第三次月考试题 理(含解析)新人教A版

天津耀华中学2013届高三年级第三次月考 理科数学试卷本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟.第Ⅰ卷(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分,在每小题的4个选项中,只有一项是符合题目要求的. 1. 复数=++-ii i 111 A. i -B.C. i -1D. i +1【答案】D 【解析】2211(1)1221(1)(1)12ii i i i i i i i i i i ++-++-++====+-+-,选D. 2. 条件甲:⎩⎨⎧<<<+<3042xy y x ;条件乙:⎩⎨⎧<<<<3210y x ,则甲是乙的A. 充要条件B. 充分而不必要条件C. 必要而不充分条件D. 既不充分也不必要条件【答案】C 【解析】当⎩⎨⎧<<<<3210y x 能得到⎩⎨⎧<<<+<3042xy y x ,但当⎩⎨⎧<<<+<3042xy y x 时,不妨取21x y ==,满足⎩⎨⎧<<<+<3042xy y x ,但⎩⎨⎧<<<<3210y x 不满足,所以甲是乙的必要而不充分条件 选C.3. 设x ,y 满足⎪⎩⎪⎨⎧≤--≥-≥+22142y x y x y x ,则y x z +=A. 有最小值2,最大值3B. 有最小值2,无最大值C. 有最大值3,无最小值D. 既无最小值,也无最大值【答案】B【解析】由y x z +=得y x z =-+.做出不等式对应的平面区域阴影部分,平移直线y x z =-+,由图象可知当直线y x z =-+经过点C (2,0)时,直线的截距最小,此时z 最小,为202z x y =+=+=,无最大值,选B.4. 某程序框图如图所示,该程序运行后输出的k 的值是A. 4B. 5C. 6D. 7【答案】A【解析】第一次循环为00,021,1S S k ==+==;第二次循环为11,123,2S S k ==+==;第三次循环为33,3211,3S S k ==+==;第四次循环为1111,112100,4S S k ==+>=;第五次循环,不满足条件,输出4k =.选A.5. 已知等比数列{a n }的首项为1,若1234,2,a a a 成等差数列,则数列⎭⎬⎫⎩⎨⎧n a 1的前5项和为 A.1631B. 2C.1633 D.3316 【答案】A【解析】因为1234,2,a a a 成等差数列,所以13244a a a +=,即211144a a q a q +=,所以2440q q -+=,即2(2)02q q -==,,所以1112n n n a a q --==,所以111()2n n a -=,所以⎭⎬⎫⎩⎨⎧n a 1的前5项和55511(1())13122[1()]121612S -==-=-,选A. 6. 将函数⎪⎭⎫ ⎝⎛+=42sin 2)(πx x f 的图像向右平移)0(>ϕϕ个单位,再将图像上每一点横坐标缩短到原来的21倍,所得图像关于直线4π=x 对称,则ϕ的最小正值为 A.8πB.83π C.43π D.2π【答案】B【解析】函数⎪⎭⎫⎝⎛+=42sin 2)(πx x f 的图像向右平移)0(>ϕϕ个单位得到2sin[2()]2sin(22)44y x x ππϕϕ=-+=+-,再将图像上每一点横坐标缩短到原来的21倍得到2sin(42)4y x πϕ=+-,此时 关于直线4π=x 对,即当4π=x 时,4242,4442x k k Zππππϕϕπ+-=⨯+-=+∈,所以324k πϕπ=+,3,82k k Z ππϕ=+∈,所以当0k =时,ϕ的最小正值为38πϕ=,选B. 7. 设F 是抛物线)0(2:21>=p px y C 的焦点,点A 是抛物线与双曲线22222:by a x C -=1)0,0(>>b a 的一条渐近线的一个公共点,且x AF ⊥轴,则双曲线的离心率为A. 2B. 3C.25D. 5【答案】D【解析】由题意知(,0)2p F ,不妨取双曲线的渐近线为b y x a =,由22b y x a y px⎧=⎪⎨⎪=⎩得222pa x b =.因为x AF ⊥,所以2A p x =,即2222pa p x b ==,解得224b a =,即22224b a c a ==-,所以225c a =,即25e =,所以离心率e = D.8. 若直角坐标平面内的两点P 、Q 满足条件:①P 、Q 都在函数)(x f y =的图像上;②P 、Q关于原点对称,则称点对[P,Q]是函数)(x f y =的一对“友好点对”(注:点对[P,Q]与[Q,P]看作同一对“友好点对”).已知函数⎩⎨⎧≤-->=)0(4)0(log )(22x x x x x x f ,则此函数的“友好点对”有A. 0对B. 1对C. 2对D. 3对【答案】C【解析】解:根据题意:当0x >时,0x -<,则22()()4()4f x x x x x -=---=-+, 若P 、Q 关于原点对称,可知,函数为奇函数,可有2()4()f x x x f x -=-+=-,即2()4,(0)f x x x x =->,则函数24,(0)y x x x =--≤的图象关于原点对称的函数是2()4,(0)f x x x x =->,由题意知,作出函数2()4,(0)f x x x x =->的图象,看它与函数2()log ,(0)f x x x =>交点个数即可得到友好点对的个数.由图象可知它们的图象交点个数为2个,所以此函数的“友好点对”有2对,选C.第Ⅱ卷(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分.9. 某单位共有老、中、青职工430人,其中青年职工160人,中年职工人数是老年职工人数的2倍.为了解职工身体状况,现采用分层抽样方法进行调查,在抽取的样本中有青年职工32人,则该样本中的老年职工人数为_______; 【答案】18【解析】由题意知,中年职工和老年职工共有270人,则老年职工人数为90人.则抽出老年职工人数为x ,则3290160x =,解得18x =. 10. 一个几何体的三视图如图所示,则该几何体的体积为____________;【答案】8011. 若⊙1与⊙2相交于A 、B 两点,且两圆在点A 处的切线互相垂直,则线段AB 的长度是____________________; 【答案】4【解析】由题知)0,(),0,0(21m O O ,且53||5<<m ,又21AO A O ⊥,所以有525)52()5(222±=⇒=+=m m ,所以452052=⋅⋅=AB . 12. 已知函数d cx bx x x f +++=23)(在区间[1,2]-上是减函数,那么b c +的最大值为________________; 【答案】215-【解析】函数的导数为2'()32f x x bx c =++,因为函数d cx bx x x f +++=23)(在区间[1,2]-上是减函数,所以2'()320f x x bx c =++≤在[1,2]-上横成立.则有'(1)0'(2)0f f -≤⎧⎨≤⎩,即3201240b c b c -+≤⎧⎨++≤⎩,设z b c =+,则c b z =-+.做出不等式对应的平面区域BCD,如图,平移直线c b z =-+,由图象平移可知当直线c b z =-+经过点B 时,直线c b z =-+的截距最大,此时z 最大.由3201240b c b c -+=⎧⎨++=⎩,解得326b c ⎧=-⎪⎨⎪=-⎩,即3(,6)2B --,代入z b c =+得315(6)22z =-+-=-,即b c +的最大值为215-.13. 如图所示,在平行四边形ABCD 中,BD AP ⊥,垂足为P ,且3=AP ,则⋅=_______;【答案】18 【解析】设ACBD O =,则2()AC AB BO =+,AP AC = 2()AP AB BO +=22AP AB AP BO +222()2AP AB AP AP PB AP ==+=18=.14. 设{a n }是等比数列,公比2=q ,S n 为{a n }的前n 项和.记1217+-=n nn n a S S T ,*N n ∈,设0n T 为数列{T n }的最大项,则n 0=__________; 【答案】4【解析】设首项为1a,则n S =,2n S =11n n a a +=,所以1217+-=n nn n a S ST =2(2)17(n -=[(2)17](n =+-,因为8n≥=,当且仅当n =,即4n=,4n =时取等号,此时[(2)17](817)(n n T =+-≤-=有最大值,所以04n =.三、解答题:本大题共6小题,共80分.解答应写出必要的文字说明、证明过程或演算步骤. 15. (本小题满分13分)已知函数)(1cos 2)62sin()(2R x x x x f ∈-+-=π(1)求)(x f 的单调递增区间;(2)在△ABC 中,三内角A,B,C 的对边分别为a,b,c ,已知21)(=A f ,b,a,c 成等差数列,且9=⋅AC AB ,求a 的值.16. (本小题满分13分)甲、乙、丙三人进行象棋比赛,每两人比赛一场,共赛三场.每场比赛胜者得3分,负者得0分,没有平局,在每一场比赛中,甲胜乙的概率为32,甲胜丙的概率为41,乙胜丙的概率为51. (1)求甲获第一名且丙获第二名的概率;(2)设在该次比赛中,甲得分为ξ,求ξ的分布列和数学期望.17. (本小题满分13分)在四棱锥P -ABCD 中,底面ABCD 是直角梯形,AB//CD ,︒90=ABC ∠,AB=PB=PC=BC=2CD ,平面PBC ⊥平面ABCD.(1)求证:AB ⊥平面PBC ;(2)求平面ADP 与平面BCP 所成的锐二面角的大小; (3)在棱PB 上是否存在点M 使得CM//平面PAD ?若存在,求PBPM的值;若不存在,请说明理由.18. (本小题满分13分)如图F 1、F 2为椭圆1:2222=+by a x C 的左、右焦点,D 、E 是椭圆的两个顶点,椭圆的离心率23=e ,2312-=∆DEF S .若点),(00y x M 在椭圆C 上,则点),(00by a x N 称为点M 的一个“椭点”,直线l 与椭圆交于A 、B 两点,A 、B 两点的“椭点”分别为P 、Q.(1)求椭圆C 的标准方程;(2)问是否存在过左焦点F 1的直线l ,使得以PQ 为直径的圆经过坐标原点?若存在,求出该直线的方程;若不存在,请说明理由.19. (本小题满分14分)已知函数x x ppx x f ln )(--=,)21(ln )(22p e e x p x x g -+-=,其中无理数e=2.71828….(1)若p=0,求证:x x f -≥1)(;(2)若)(x f 在其定义域内是单调函数,求p 的取值范围;(3)对于在区间(1,2)中的任意常数p ,是否存在00>x 使得)()(00x g x f ≤成立?若存在,求出符合条件的一个x 0;若不存在,请说明理由.20. (本小题满分14分)已知数列{a n }的前n 项和)(2)21(*1N n a S n n n ∈+--=-,数列{b n }满足n n n a b 2=.(1)求证数列{b n }是等差数列,并求数列{a n }的通项公式; (2)设数列⎭⎬⎫⎩⎨⎧+n a n n 1的前n 项和为T n ,证明:*N n ∈且3≥n 时,125+>n n T n ; (3)设数列{c n }满足n c a n n n n λ1)1()3(--=-(λ为非零常数,*N n ∈),问是否存在整数λ,使得对任意*N n ∈,都有n n c c >+1.数学发展性试题(理科):(15分)1. 若0,,>c b a 且324)(-=+++bc c b a a ,则c b a ++2的最小值为( )A. 13-B. 13+C. 232+D. 232-2. 对于各数互不相等的整数数组),,,,(321n i i i i ⋯(n 是不小于3的正整数),若对任意的p ,},,3,2,1{n q ⋯∈,当q p <时有q p i i >,则称q p i i ,是该数组的一个“逆序”.一个数组中所有“逆序”的个数称为该数组的“逆序数”,如数组(2,3,1)的逆序数等于2.若数组),,,,(321n i i i i ⋯的逆序数为n ,则数组),,,(11i i i n n ⋯-的逆序数为_________;3. 定义在)1,1(-上的函数⎪⎪⎭⎫⎝⎛--=-xy y x f y f x f 1)()(,当)0,1(-∈x 时0)(>x f .若)0(,21,11151f R f Q f f P =⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛=,则P,Q,R 的大小关系为_____________.【试题答案】一、选择题:本大题共8小题,每小题5分,共40分.题号 1 2 3 4 5 6 7 8 答案DCBA ABDC二、填空题:本大题共6小题,每小题5分,共30分. 9. 18 10. 8011. 4 12. 215-13. 18 14. 4三、解答题:本大题共6小题,共80分. 15. 解:(1)x x x x x x f 2cos 2cos 212sin 231cos 2)62sin()(2+-=-+-=π)62sin(2cos 212sin 23π+=+=x x x 令)(226222Z k k x k ∈+≤+≤-πππππ )(x f 的单调递增区间为)](6,3[Z k k k ∈+-ππππ(2)由21)(=A f ,得21)62sin(=+πA ∵62626ππππ+<+<A ,∴6562ππ=+A ,∴3π=A 由b,a,c 成等差数列得2a=b+c∵9=⋅AC AB ,∴9cos =A bc ,∴18=bc由余弦定理,得bc c b A bc c b a 3)(cos 22222-+=-+= ∴183422⨯-=a a ,∴23=a16. 解:(1)甲获第一,则甲胜乙且甲胜丙,所以甲获第一的概率为614132=⨯ 丙获第二,则丙胜乙,其概率为54511=-, 所以甲获第一名且丙获第二名的概率为1525461=⨯ (2)ξ可能取的值为0,3,6.41)411)(321()0(=--==ξP127)321(41)411(32)3(=-+-==ξP 614132)6(=⨯==ξP 所以ξ的分布列为ξ0 3 6P41 127 61 E ξ=4116161273410=⨯+⨯+⨯17. 解:(1)证明:因为o 90=∠ABC ,所以AB ⊥BC因为平面PBC ⊥平面ABCD ,平面PBC ∩平面ABCD=BC ,AB ⊂平面ABCD , 所以AB ⊥平面PBC. (2)如图,取BC 的中点O ,连接PO ,因为PB=PC ,所以PO ⊥BC.因为PB=PC ,所以PO ⊥BC ,因为平面PBC ⊥平面ABCD ,所以PO ⊥平面ABCD.以O 为原点,OB 所在的直线为x 轴,在平面ABCD 内过O 垂直于BC 的直线为y 轴,OP 所在直线为z 轴建立空间直角坐标系O -xyz.不妨设BC=2.由AB=PB=PC=BC=2CD 得,)0,2,1(),0,1,1(),3,0,0(A D P -.所以)0,1,2(),3,1,1(=-=DA DP , 设平面PAD 的法向量为),,(z y x =.因为⎪⎩⎪⎨⎧=⋅=⋅0DA m ,所以⎩⎨⎧=+=+-0203y x z y x令1-=x ,则3,2==z y .所以)3,2,1(-=m .取平面BCP 的一个法向量)0,1,0(=, 所以22,cos =>=<n m 所以平面ADP 与平面BCP 所成的锐二面角的大小为4π (3)在棱PB 上存在点M 使得CM//平面PAD ,此时21=PB PM .取AB 的中点N ,连接CM ,CN ,MN ,则MN//PA ,AN=21AB.因为AB=2CD ,所以AN=CD ,因为AB//CD ,所以四边形ANCD 是平行四边形,所以CN//AD.因为MN ∩CN=N ,PA ∩AD=A ,所以平面MNC//平面PAD. 因为CM ⊂平面MNC ,所以CM//平面PAD. 18. 解:(1)由题意得23==a c e ,故ab ac 21,23==,231)231(412)23(21)(2122-=-⨯=⨯-=⨯-⨯=∆a a a a b c a S DEF , 故42=a ,即a=2,所以b=1,c=3,故椭圆C 的标准方程为1422=+y x . (2)①当直线l 的斜率不存在时,直线l 的方程为3-=x联立⎪⎩⎪⎨⎧=+-=14322y x x 解得⎪⎩⎪⎨⎧=-=213y x 或⎪⎩⎪⎨⎧-=-=213y x ,不妨令)21,3(),21,3(---B A ,所以对应的“椭点”坐标)21,23(),21,23(---Q P .而021≠=⋅. 所以此时以PQ 为直径的圆不过坐标原点.②当直线l 的斜率存在时,设直线l 的方程为)3(+=x k y联立⎪⎩⎪⎨⎧=++=14)3(22y x x k y ,消去y 得:041238)14(2222=-+++k x k x k设),(),,(2211y x B y x A ,则这两点的“椭点”坐标分别为),2(),,2(2211y xQ y x P ,由根与系数的关系可得:14382221+-=+k k x x ,144122221+-=k k x x 若使得以PQ 为直径的圆经过坐标原点,则OP ⊥OQ , 而),2(),,2(2211y xOQ y x OP ==,因此0=⋅, 即042221212121=+=+⨯y y x x y y x x 即141222+-k k =0,解得22±=k所以直线方程为2622+=x y 或2622--=x y 19. 解:(1)证明:当p=0时,x x f ln )(-=.令)0(1ln )(>+-=x x x x m ,则xxx x m -=-='111)( 若10<<x ,则0)(>'x m ,)(x m 在区间)1,0(上单调递增; 若1>x ,则0)(<'x m ,)(x m 在区间),1(+∞上单调递减. 易知,当x=1时,)(x m 取得极大值,也是最大值.于是0)1()(=≤m x m ,即01ln ≤+-x x ,即x x -≥-1ln 故若p=0,有x x f -≥1)((2)2221)(xp x px x x p p x f +-=-+=',令)0()(2>+-=x p x px x h ①当p=0,01)(<-='xx f ,则)(x f 在),0(+∞上单调递减,故当p=0时符合题意; ②若p>0,pp p p p x p p x px x h 4141)21()(22-≥-+-=+-= 则当041≥-p p ,即21≥p 时,0)(≥'x f 在x>0上恒成立,故当21≥p 时,)(x f 在),0(+∞上单调递增;③若p<0,p p p x p p x px x h 41)21()(22-+-=+-=的图像的对称轴为021<=px ,0)0(<=p h ,则0)(<'x f 在x>0上恒成立,故当p<0时,)(x f 在),0(+∞上单调递减.综上所述,),21[]0,(+∞-∞∈U p(3)令pxee x px x g xf x F 2ln 2)()()(2-+-=-=,则原问题等价于是否存在x 0>0使得0)(0≤x F 成立,故只需满足0)]([min ≤x F 即可.因为)2)(()2)((22)(2222p ex p e x xp px e px e px px e e x p x F ---=+--=---=' 而21,0<<>p x ,故02,0<->pep e , 故当p e x <<0时,0)(<'x F ,则)(x F 在),0(p e 上单调递减;当pex >时,0)(>'x F ,则)(x F 在),(+∞pe上单调递增. 易知04ln 222ln 22)()(min >-+=-++-==p e e p e pe F x F 与上述要求的0)]([min ≤x F 相矛盾,故不存在00>x 使得)()(00x g x f ≤成立.20. 解:(1)在2)21(1+--=-n n n a S 中,令n=1,可得1121a a S n =+--=,即211=a 当2≥n 时,2)21(211+--=---n n n a S ,∴111)21(---++-=-=n n n n n n a a S S a , ∴11)21(2--+=n n n a a ,即12211+=--n n n n a a .∵n n n a b 2=,∴11+=-n n b b ,即当2≥n 时,11=--n n b b . 又1211==a b ,∴数列{b n }是首项和公差均为1的等差数列. 于是n n n a n n b 21)1(1==⋅-+=,∴nn n a 2=. (2)由(1)得n n n n a n n c )21)(1(1+=+=,所以 n n n T )21)(1()21(4)21(321232++⋯+⨯+⨯+⨯= ①1432)21)(1()21(4)21(3)21(221+++⋯+⨯+⨯+⨯=n n n T ② 由①-②得132)21)(1()21()21()21(121++-+⋯+++=n n n n T1112323)21)(1(211])21(1[411++-+-=+---+=n n n n n∴nn n T 233+-= )12(2)122)(3(125233125+--+=+-+-=+-n n n n n n n n T n n n n 于是确定T n 与125+n n 的大小关系等价于比较n2与2n+1的大小 由⋯⨯<+⨯<+⨯<+⨯<+⨯<;522;1422;1322;1222;11225432可猜想当3≥n 时,122+>n n .证明如下: 证法1:①当n=3时,由上验算显示成立. ②假设n=k+1时1)1(2)12(1)1(224)12(22221++>-+++=+=+>=+k k k k k g k k所以当n=k+1时猜想也成立综合①②可知,对一切3≥n 的正整数,都有122+>n n . 证法2:当3≥n 时1222)11(21101210+>+=+++≥++⋯+++=+=--n n C C C C C C C C C nn n n n n n n n n n n n n n 综上所述,当n=1,2时125+<n n T n ,当3≥n 时125+>n nT n(3)∵n n nnn nn a n c 2)1(3)1(311⋅-+⋅-+=--λλ∴]2)1(3[]2)1(3[1111n n n n n n n n c c ⋅-+-⋅-+=--+++λλ02)1(3321>⋅--⋅=-n n n λ∴1123)1(--⎪⎭⎫⎝⎛<⋅-n n λ ①当n=2k -1,k=1,2,3,……时,①式即为2223-⎪⎭⎫⎝⎛<k λ ②依题意,②式对k=1,2,3……都成立,∴1<λ当n=2k,k=1,2,3,……时,①式即为1223-⎪⎭⎫⎝⎛->k λ ③依题意,③式对k=1,2,3……都成立, ∴23->λ ∴123<<-λ,又0≠λ ∴存在整数1-=λ,使得对任意*N n ∈有n n c c >+1.数学发展性试题1. D2. 232nn - 3. Q R P >>。
2021届天津市南开区南开中学高三下学期第三次月考数学(理)试题
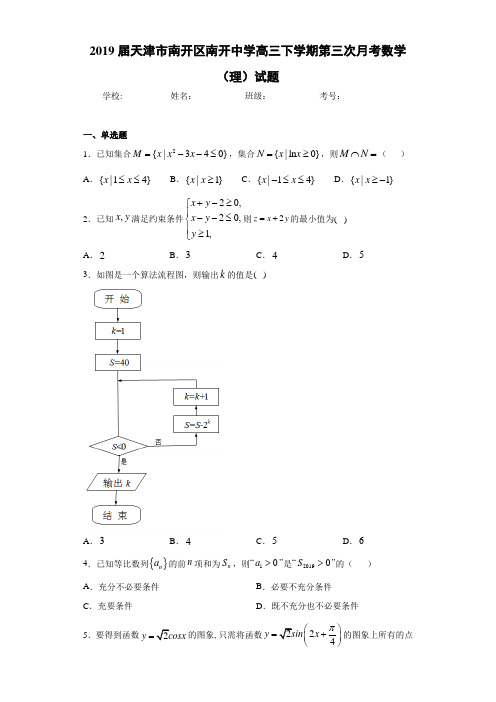
(2)用 表示甲队的总得分,求随机变量 的分布列和数学期望;
(3)求两队得分之和大于4的概率.
17.如图,四边形 是正方形, 平面 , , , , , 分别为 , , 的中点.
(1)求证: 平面 ;
(2)求平面 与平面 所成锐二面角的大小;
B.横坐标缩短到原来的 倍(纵坐标不变),再向右平行移动 个单位长度
C.横坐标伸长到原来的 倍(纵坐标不变),再向左平行移动 个单位长度
D.横坐标伸长到原来的 倍(纵坐标不变),再向右平行移动 个单位长度
6.已知 是定义在 上的偶函数,且在 上是增函数,设 , , ,则 的大小关系是()
A. B. C. D.
5.C
【分析】
将 化为 根据三角函数伸缩、平移关系,即可求解.
【详解】
将函数 的图象横坐标伸长到原来的 倍(纵坐标不变),
得到函数 的图像,再向左平移 个长度单位,
得到函数 .
故选:C.
【点睛】
本题考查诱导公式的应用,三角函数图像变换关系,属于基础题.
6.C
【解析】
试题分析:函数 是偶函数,在上是增函数,所以在 上是减函数,
本题考查二元一次不等式表示平面区域,考查线性目标函数的最值,属于基础题.
3.D
【分析】
根据循环体的运算定义,直到满足条件,退出循环体,输出 ,即可求出结论.
【详解】
; ; ;
; ,输出6.
故选:D
【点睛】
本题考查循环结构运行结果,属于基础题.
4.C
【分析】
根据充分条件和必要条件的定义,结合等比数列的前n项和公式进行判断即可.
