第02章-正弦交流电路(2)
合集下载
大学物理学第2章正弦交流电路_02

解法2: 利用相量图分析求解
设 U AB为参考相量,
I1 10A
I2 100 5 5
2 2
j10Ω
I
I1
A
A
I 1 超前 U AB 90
10 2A,
I2
C1
B
5Ω j5Ω
V
画相量图如下:
I 2滞后UAB 45°
由相量图可求得: I =10 A
UL= I XL =100V U L超前I 90°
I1 Z2 j400 I 0.5 33 A Z1 Z 2 100 j200 j400
0.89 - 59.6 A
同理:
I
I2
Z1 I Z1 Z 2
100 j200 0.5 33 A 100 j200 j400 0.5 93.8 A
UL
I1 100 10
U
由相量图可求得: V =141V
45° I 45°
I2
U AB
10 2
2.5 正弦稳态电路的功率
2.5.1 功率
一、瞬时功率
I +
i = Im sinωt U u = Umsin (ωt + ) - p = u i = UmImsin(ωt + ) sinωt = U I cos + U I cos ( 2ωt + )
S =√P2 + Q2 = 190 V· A
例2 如图所示是测量电感线圈参数R和L的实验电路,已知电 压表的读数为50V,电流表的读数为1A,功率表的读数为30W, 电源的频率f=50Hz。试求R和L的值。 ﹡ I 解:根据图中3个仪表的读数, A W ﹡ + 可先求得线圈的阻抗 电 R 感 Z | Z | R jL V U 线 圈 L U | Z | 50 I 功率表读数表示线圈吸收的有功功率,故有 P UI cos 30W 30 arctan( ) 53.130 UI 从而求得
电工电子技术-第2章 正弦交流电路
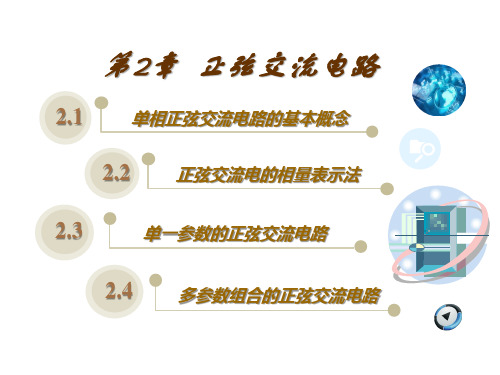
区别与一般复数,相量的头顶上一般加符号“·”。 例:正弦量i=14.1sin(ωt+36.9°)A的最大值相量表示为:
•
I m = 14.1∠36.9°A
其有效值相量为:I• = 10∠36.9°A
由于一个电路中各正弦量都是同频率的,所以相量只需 对应正弦量的两要素即可。即模值对应正弦量的最大值或 有效值,幅角对应正弦量的初相。
i u u、i 即时对应! R
电流、电压的瞬时值表达式
设 i Im sin t u、i 同相!
则 u ImR sin t Um sin t
u、i最大值或有效值之间符
合欧姆定律的数量关系。
Um ImR
或
U IR
•
相量关系式
•
I
U
U0
U
0 I0
RRR
相量图
U
I
(2)电阻元件上的功率关系
3
C -4
D
D 3 j4 第四象限 D 5 arctan 4
3
上式中的j 称为旋转因子,一个复数乘以j相当于在复
平面上逆时针旋转90°;除以j相当于在复平面上顺时针
旋转90°。
※数学课程中旋转因子是用i表示的,电学中为了区别 于电流而改为j。
正弦量的相量表示法
与正弦量相对应的复数形式的电压和电流称为相量。为
乘、除时用极坐标形式比较方便。
在复数运算当中,一定要根据复数所在象
限正确写出幅角的值。如:
+j
B4
A
A 3 j4 第一象限 A 553.1arctan 4 3
B 3 j4 第二象限 B 5180 arctan 4
-3 0
3
+1
3
•
I m = 14.1∠36.9°A
其有效值相量为:I• = 10∠36.9°A
由于一个电路中各正弦量都是同频率的,所以相量只需 对应正弦量的两要素即可。即模值对应正弦量的最大值或 有效值,幅角对应正弦量的初相。
i u u、i 即时对应! R
电流、电压的瞬时值表达式
设 i Im sin t u、i 同相!
则 u ImR sin t Um sin t
u、i最大值或有效值之间符
合欧姆定律的数量关系。
Um ImR
或
U IR
•
相量关系式
•
I
U
U0
U
0 I0
RRR
相量图
U
I
(2)电阻元件上的功率关系
3
C -4
D
D 3 j4 第四象限 D 5 arctan 4
3
上式中的j 称为旋转因子,一个复数乘以j相当于在复
平面上逆时针旋转90°;除以j相当于在复平面上顺时针
旋转90°。
※数学课程中旋转因子是用i表示的,电学中为了区别 于电流而改为j。
正弦量的相量表示法
与正弦量相对应的复数形式的电压和电流称为相量。为
乘、除时用极坐标形式比较方便。
在复数运算当中,一定要根据复数所在象
限正确写出幅角的值。如:
+j
B4
A
A 3 j4 第一象限 A 553.1arctan 4 3
B 3 j4 第二象限 B 5180 arctan 4
-3 0
3
+1
3
电工电子技术第2章

第2章 正弦交流电路
在交流电路中,因各电流和电压多 +j A 为同一频率的正弦量,故可用有向线段 b r 来表示正弦量的最大值(有效值) Im 、 ψ Um(I、U)和初相ψ ,称为正弦量的相量。 O a +1 在正弦量的大写字母上打“•”表示,如 图2-5 有向线段的表示正弦量 幅值电流、电压相量用 I m、 m表示,有 U • U 效值电流、电压相量用 I 、 表示。将电 U • 路中各电压、电流的相量画在同一坐标 φ I ψ 中,这样的图形称为相量图。 ψ 同频率的u和i可用图2-6相量图表示。 图2-6 u和i的相量图 即 超前 Iφ°,I或 U滞后φ°。 U
第2章 正弦交流电路
2.1
正弦交流电的基本概念
正弦交流电压和电流的大小和方向都按正弦规律 作周期性变化,波形如图2-1a。
u U m s in ( t u ) i I m s in ( t i )
(2-1)
为便于分析,在电路中电压参考方向用“+”、“–” 标出,电流参考方向用实线箭头表示;电压、电流实 际方向用虚线箭头表示如图2-1b、c所示
第2章 正弦交流电路
u Im O φ Ψu Ψi i Um
u
i
t
T
图2-2 u和i相位不等的正弦量波形图
当φ=0º 时,称u、I同相;当φ=180º 时,称u比i反相; 当φ=±90º 时,称u与i正交 。 u i u i
u i
ui
u
i
t
u
i
O a) 同相
t O
b) 反相
O c)正交
t
图2-3 正弦量的同相、反相和正交
第2章 正弦交流电路
第2章正弦交流电-2.2单一元件正弦交流电路

③由于电压的初相为45°,而电流的初相为−45º,故电压和电流的 相量图如图所示。 1 U I =— 1 ×100×10=500(var) ④Q=UI=— m m 2 2
相量图
2.2单一元件正弦交流电路电阻 Nhomakorabea路电感电路
电容电路
1 电容元件
(1)电容参数C
q q=Cu 或 C=— u 电容量的单位是F(法[拉])。 具有参数C的电路元件称电容元件,简称电容。
相量图
③电压、电流的相量图如图所示。
2.2单一元件正弦交流电路
电阻电路
电感电路
电容电路
1 电感元件
(1) 电感参数L
Ψ Ψ=LI 或 L=— I
电感元件
式中,磁链与电流的比值L叫做线圈的电感量,电感量的单位为H(亨[利])。 具有L参数的电路元件称电感元件,简称电感。 空心线圈的电感量是一个常数,与通过的电流大小无关,这种电感叫做线性电感。线性 电感的大小只与线圈的形状、尺寸、匝数有关。一般而言,线圈直径的截面积越大,匝数越 密,电感量越大。
p>0,吸收能量
p<0,释放能量
2.2单一元件正弦交流电路
电阻电路
电感电路
电容电路
2 电感交流电路
例题:已知加在L=10mH电感线圈两端的正弦交流电压u=100sin(1000t+45º)V,求:①感抗XL; ②线圈中的电流最大值Im和线圈中的电流i;③作电路中电压与电流的相量图;④无功功率Q。 解:①感抗XL=ωL=1000×10×10−3=10Ω Um 100V ②Im=—= ———=10(A) XL 10Ω φi=φu−90º=45º−90º=−45º i=10sin(1000t−45º)(A)
电工第2章 正弦交流电路

函数(cos)。 1.正弦量数学表达式
图2-2 正弦交流电波形图
2.1 正弦交流电量及基本概念
(1)最大值 又称为幅值,是正弦量的最大值,用带右下标m的大写 字母表示,如Im、Um、Em分别表示正弦电流、正弦电压、正弦电动 势的最大值。 (2)角频率ω 在单位时间内正弦量所经历的电角度,用ω表示,其单 位为弧度每秒(rad/s)。正弦交流电变化一次所需的时间,称为周期T, 其单位为秒(s),正弦量在单位时间内变化的次数,称为频率f, 其单位为赫[兹](Hz)。
图2-9 纯电阻电路
2.3 单一参数元件的正弦交流电路
(2) 有效值关系 由电流与电压的幅值关系Im= Um /R,两端同除 以 ,可得它们的有效值关系为U=IR (3) 相量关系 因为电流i和电压u均为同频率的正弦量。 相量形式为 2.电阻元件的功率 (1) 瞬时功率 在关联参考方向下,电阻元件的 瞬时功率(用小写字母p表示):
图2-4 两正弦量的同相与反相
2.1 正弦交流电量及基本概念
例2.1 已知正弦量u=220sin(314t + 30°)V, 试求正弦量的三要素、有效值及变化周期。 解:对照式(2-1),可知三要素:
2.1 正弦交流电量及基本概念
例2.2 已知正弦电压u和正弦电流i1、i2的瞬时表达式为u = 310sin(ωt -45°)V,,i2=28.2sin(ωt +45°)A,试以电压u为参考量重新写出u和 电流i1、i2的瞬时值表达式。 解:以电压u为参考量, 则电压u的表达式为 由于i1、i2与u的相位差为
2.2 正弦交流电的相量表示方法
2.2.2 正弦量的相量表示法 正弦量和相量是一一对应关系(注意:正弦量和相量不是相等
关系!)。在复平面中,例如相量可用长度为 ,与实轴正向的夹 角为ψ的矢量表示。这种表示相量的图形称为相量图。如图2-7所示
图2-2 正弦交流电波形图
2.1 正弦交流电量及基本概念
(1)最大值 又称为幅值,是正弦量的最大值,用带右下标m的大写 字母表示,如Im、Um、Em分别表示正弦电流、正弦电压、正弦电动 势的最大值。 (2)角频率ω 在单位时间内正弦量所经历的电角度,用ω表示,其单 位为弧度每秒(rad/s)。正弦交流电变化一次所需的时间,称为周期T, 其单位为秒(s),正弦量在单位时间内变化的次数,称为频率f, 其单位为赫[兹](Hz)。
图2-9 纯电阻电路
2.3 单一参数元件的正弦交流电路
(2) 有效值关系 由电流与电压的幅值关系Im= Um /R,两端同除 以 ,可得它们的有效值关系为U=IR (3) 相量关系 因为电流i和电压u均为同频率的正弦量。 相量形式为 2.电阻元件的功率 (1) 瞬时功率 在关联参考方向下,电阻元件的 瞬时功率(用小写字母p表示):
图2-4 两正弦量的同相与反相
2.1 正弦交流电量及基本概念
例2.1 已知正弦量u=220sin(314t + 30°)V, 试求正弦量的三要素、有效值及变化周期。 解:对照式(2-1),可知三要素:
2.1 正弦交流电量及基本概念
例2.2 已知正弦电压u和正弦电流i1、i2的瞬时表达式为u = 310sin(ωt -45°)V,,i2=28.2sin(ωt +45°)A,试以电压u为参考量重新写出u和 电流i1、i2的瞬时值表达式。 解:以电压u为参考量, 则电压u的表达式为 由于i1、i2与u的相位差为
2.2 正弦交流电的相量表示方法
2.2.2 正弦量的相量表示法 正弦量和相量是一一对应关系(注意:正弦量和相量不是相等
关系!)。在复平面中,例如相量可用长度为 ,与实轴正向的夹 角为ψ的矢量表示。这种表示相量的图形称为相量图。如图2-7所示
第2章(正弦交流电路)

i u
P>0
充电 储存 能量
i
u
放电
i u
p
放电
P<0
释放 能量
充电
(1-41)
无功功率Q:电容瞬时功率所能达到的最大值。用
以衡量电容电路中能量交换的规模。
因为:
p = i u = -2UI sinwt· coswt =-UI· sin2wt
所以:
Q =-UI=-I2 XC =-U2/XC
Q
的单位: 乏、千乏(var、kvar) 电容性无功功率取负值 电感性无功功率取正值
t
i1 i1
j1 = j 2
i1 与 i2 同相
Dj=j1-j20
t
j1
j2
i1
i1 超前于 i2
i2
j1 j2
t
Dj=j1-j20
i1 滞后于 i2
(1-9)
3、正弦量的有效值
最大值 瞬时值
i = Im sin (wt + j )
但是,在工程应用中常用有效值表示交流电
的大小。常用交流电表指示的电压、电流读数,
i
u
P
i
u
释放 能量
i
u
i
u
+
P >0
储存 能量
P <0
+
P >0
P <0
wt
(1-35)
无功功率Q:电感瞬时功率所能达到的最大值。用 以衡量电感电路中能量交换的规模。
因为:
p = i u = 2UI sinwt· coswt =UI· sin2wt
所以:
Q =UI=I2 XL =U2/XL
第2章_正弦交流电路

ψ
+
90
°
- jA
- jA = 1 - 90° × r ψ = r ψ − 90°
三. 正弦量的相量表示法 相量:表示正弦量的复数。 相量:表示正弦量的复数。
相量表示方法: 相量表示方法: 设正弦量: 设正弦量: i = I msin( ω t + ψi )
大写字母上打点, 大写字母上打点,表示相量 模 =正弦量的最大值 & 最大值相量 Im = Imejψi = Im ψi 辐角= 辐角=正弦量的初相角 有效值相量
i1 i3 i2
i2 =
2 I 2 sin ( ω t + ψ 2 ), 求 i3 = i1 + i2
结论: 同频正弦量运算后仍得到同频的正弦量。 结论:●同频正弦量运算后仍得到同频的正弦量。 直接进行正弦量的运算很繁琐。 ●直接进行正弦量的运算很繁琐。 解决办法:把正弦量用相量(复数)表示, 解决办法:把正弦量用相量(复数)表示,先进行复数 运算,求出相量解, 运算,求出相量解,再根据相量解写出正弦量瞬时值表 达式。这种分析方法称为相量法。 达式。这种分析方法称为相量法 相量法。
正弦量的波形
i
Im
ψ
ωt
i = I m sin(ω t + ψ )
幅值(最大值) I m : 幅值(最大值) 角频率(弧度/ ω : 角频率(弧度/秒)
特征量: 特征量:
ψ : 初相角
2.1.1 正弦量的三要素
1. 幅度(最大值): 幅度(最大值) 最大的瞬时值,对确定的正弦量而言是一个常 最大的瞬时值, 量。最大值必须用带下标m的大写字母表示。 最大值必须用带下标m的大写字母表示。 如:Um、Im。
超前i (1)ϕ >0, u超前 , 超前 滞后u 或i滞后 滞后
04电工(第2章交流2RLC串联电路,交流电路分析,功率因数提高)

消耗有功功率为: P PR UI cos
当U、P 一定时 cos
I
供电线路功耗
希望将cos 提高
供电局一般要求用户的cos >0.85 ,否则受处罚
常用电路的功率因数
纯电阻电路
纯电感电路或 纯电容电路
cos 1 ( 0) cos 0 ( 90)
R-L-C串联电路
电动机 空载 满载
0 cos 1
第4讲
第2章 正弦交流电路
2.4 正弦交流电路的分析计算 2.5 正弦交流电路的功率
清华大学电机系电工学教研室 唐庆玉编
海南风光
本课内容
第2章 正弦交流电路
2.1 正弦电压与电流 2.1.1正弦量的参考方向和电源模型 2.1.1 周期、频率和角频率 2.1.2 相位、初相位和相位差 2.1.3 最大值和有效值
例3(教材例2.20)
已知: R1 、R2、R3 、R4 、L、C、u、i、,求支路电流i1、 i2 、i3 。
A
A
R1 i1 R2 i2 R3 i3 R4
R1
I1 R2
I2 R3
I3 R4
u
+
L
+ C uS
相量模型
i
-
U
-
+
+
jX L
jX
US
C-
I
B
B
结点电位法
U I
VA 1
R1 1
1
R1 R2 jX L R3 jX C
i 2I sint
u 2U sin(t )
UIZ
Z
R2
X
2 L
i
+
+
第2章 正弦交流电路

同相反相的概念
同相:相位相同,相位差为零。 反相:相位相反,相位差为180°。 下面图中是三个正弦电流波形。 i1与 i2 同相, i1与 i3反相。
i
i1 i2
O
i3
ωt
总 结
描述正弦量的三个特征量:
幅值、频率、初相位
9
电气与自动化工程学院
2.2 正弦量的相量表示法
正弦量的表示方法:
★ 三角函数式: i
相位 表示正弦量的变化进程,也称相位角。 初相位 t =0时的相位。
i I m sint 相位: t 初相位: 0
i I m sin t
相位:
i
O
t
i
t
说 明
初相位:
ψ
t
初相位给出了观察正弦波的起点或参考点。
7
电气与自动化工程学院
相位差
两个同频率的正弦量的相位之差或初相位之差称为相位差。 正弦交流电路中电压和电流的频率是相同的,但初相不 一定相同,设电路中电压和电流为:
26
电气与自动化工程学院
2.3.3 电容元件的交流电路 电压电流关系
对于电容电路:
dq du i C dt dt
i
+
如果电容两端加正弦电压:
u
_
C
u Um sin t
则:
注意u 和i的参考方向!
dU m sint i C CUm cost CUm sin t 90 I m sin t 90 dt
2.1.1 频率和周期
正弦量变化一次所需要的时间(秒)称为周期(T)。 每秒内变化的次数称为频率( f ),单位是赫兹(Hz)。
u i
频率是周期的倒数:
正弦交流电路_单一参数的正弦交流电路

电压超前于电流90°
iL
+
uL
L
−
u 波 形 图0
i
U•
相
t
量 图
I• 0°
第二章 正弦交流电路
2.2 单一参数的正弦交流电路
(2)大小关系
uL L Im sin( t 90 ) U m sin( t 90 )
最大值: U m L I m 有效值: U ω L I
定义: X L L ——感抗
第二章 正弦交流电路
2.2 单一参数的正弦交流电路
(3)相量关系 I I 0 U U 9 0 X L I 90 0 X L 90 I 0 jX L I
U jX L I j L I
u
i
0
t
第二章 正弦交流电路
2.功率 (1)瞬时功率
p ui
U m I m s in t s in t 90
(能量的吞吐)。
0
t
p
第二章 正弦交流电路
2.2 单一参数的正弦交流电路
(3)无功功率 为了同电感的无功功率相
p u i UI sin 2t
比较,设电流 i I m s in t
u
i
为参考量,则: u U m sin( t 90 )
p uHale Waihona Puke U I sin 2 t0
t
储放 储放储放 能能 能能能能
p
0
t
u
i
第二章 正弦交流电路
2.2 单一参数的正弦交流电路
2. 功率
平均功率(有功功率) P 1 T pdt U I I 2 R U 2
T0
R
平均功率衡量电路 中所消耗的电能, 也称有功功率。
iL
+
uL
L
−
u 波 形 图0
i
U•
相
t
量 图
I• 0°
第二章 正弦交流电路
2.2 单一参数的正弦交流电路
(2)大小关系
uL L Im sin( t 90 ) U m sin( t 90 )
最大值: U m L I m 有效值: U ω L I
定义: X L L ——感抗
第二章 正弦交流电路
2.2 单一参数的正弦交流电路
(3)相量关系 I I 0 U U 9 0 X L I 90 0 X L 90 I 0 jX L I
U jX L I j L I
u
i
0
t
第二章 正弦交流电路
2.功率 (1)瞬时功率
p ui
U m I m s in t s in t 90
(能量的吞吐)。
0
t
p
第二章 正弦交流电路
2.2 单一参数的正弦交流电路
(3)无功功率 为了同电感的无功功率相
p u i UI sin 2t
比较,设电流 i I m s in t
u
i
为参考量,则: u U m sin( t 90 )
p uHale Waihona Puke U I sin 2 t0
t
储放 储放储放 能能 能能能能
p
0
t
u
i
第二章 正弦交流电路
2.2 单一参数的正弦交流电路
2. 功率
平均功率(有功功率) P 1 T pdt U I I 2 R U 2
T0
R
平均功率衡量电路 中所消耗的电能, 也称有功功率。
《电工学》教案02正弦交流电路

7. 掌握三相四线制供电系统中单相及三相负载的正确联接方法,理解中线的作用;
8. 掌握对称三相电路电压、电流及功率的计算。
2.1 正弦电压与电流
1. 正弦电流及其三要素
随时间按正弦规律变化的电流称为正弦电流,同样地有正弦电压等。这些按正弦规律变
化的物理量统称为正弦量。
设图 2.1 中通过元件的电流 i 是正弦电流,其参考方向如图所示。正弦电流的一般表达
式为:
i (t)= I m sin(ωt+ψ)
图 2.1 电路元件
图 2.2 正弦电流波形图
它表示电流 i 是时间 t 的正弦函数,不同的时间有不同的量值,称为瞬时值,用小写字
母表示。电流 i 的时间函数曲线如图 2.2 所示,称为波形图。
I m 为正弦电流的最大值(幅值),即正弦量的振幅,用大写字母加下标 m 表示正弦量 的最大值,例如 I m 、U m 、 Em 等,它反映了正弦量变化的幅度。( t +ψ)随时间变化,称
少角度或时间,以角度表示时为ψ1-ψ2,若以时间表示,则为(ψ1-ψ2)/ω。如果两个正弦 电流的相位差为 12 = ,则称这两个正弦量为反相。如果 12 = 2 ,则称这两个正弦量为正
交。
图 2.4 正弦量的相位关系
3. 有效值
周期电流 i 流过电阻 R 在一个周期所产生的能量与直流电流 I 流过电阻 R 在时间 T 内所
从以上分析可知:
(1) 电感两端的电压与电流同频率;
(2) 电感两端的电压在相位上超前电流 90°;
(3) 电感两端的电压与电流有效值(或最大值)之比为 L。
令
X L = L =2 f L
X L 称为感抗,它用来表示电感元件对电流阻碍作用的一个物理量。它与角频率成正比。
电工电子技术及应用第2章

需要强调的是,相量只表示正弦量,并不等于正
弦量;只有同频率的正弦量其相量才能相互运算,
才能画在同一个复平面上。
画在同一个复平面上表示相量的图称为相量图。
相量与正弦量的关系
U U
对应关系
Umsin( t )
不相等!!
例2-9
已知正弦电压、电流为 u 220 2 sin(t π )V,
i
+ +
R
i
us
u
π
2π
o
t
T
a)
b)
图2-1
Байду номын сангаас 一、正弦量的三要素
1.振幅值(最大值) 正弦量在任一时刻的值称为瞬 时值,用小写字母表示, 如
u
i、 u
, 分别表示电流及
u1 u2
电压的瞬时值。正弦量瞬时值
中的最大值称为振幅值也叫最 大值或峰值,用大写字母加下
o
Um2
Um1
t
图2-2
标m表示,如Im、Um , 分别表
6.55 j2.45 6.99 159.5
A B 685 11 130 0.52 j5.98 (7.07 j8.43)
7.59 j14.41 16.2962.2
例2-8
已知复数 A 4 j3 B 3 j4 ,求AB和A/B。
起点不同,正弦量的初相不同,因此初相与计时
起点的选择有关。我们规定初相|ψ |不超过π 弧 度,即-π ≤ψ ≤π 。图2-3所示是不同初相时的 几种正弦电流的波形图。
在选定参考方向下,已知正弦量的解析 式为 i 10sin( 314t 240 )A 。试求正弦量的 振幅、频率、周期、角频率和初相。
弦量;只有同频率的正弦量其相量才能相互运算,
才能画在同一个复平面上。
画在同一个复平面上表示相量的图称为相量图。
相量与正弦量的关系
U U
对应关系
Umsin( t )
不相等!!
例2-9
已知正弦电压、电流为 u 220 2 sin(t π )V,
i
+ +
R
i
us
u
π
2π
o
t
T
a)
b)
图2-1
Байду номын сангаас 一、正弦量的三要素
1.振幅值(最大值) 正弦量在任一时刻的值称为瞬 时值,用小写字母表示, 如
u
i、 u
, 分别表示电流及
u1 u2
电压的瞬时值。正弦量瞬时值
中的最大值称为振幅值也叫最 大值或峰值,用大写字母加下
o
Um2
Um1
t
图2-2
标m表示,如Im、Um , 分别表
6.55 j2.45 6.99 159.5
A B 685 11 130 0.52 j5.98 (7.07 j8.43)
7.59 j14.41 16.2962.2
例2-8
已知复数 A 4 j3 B 3 j4 ,求AB和A/B。
起点不同,正弦量的初相不同,因此初相与计时
起点的选择有关。我们规定初相|ψ |不超过π 弧 度,即-π ≤ψ ≤π 。图2-3所示是不同初相时的 几种正弦电流的波形图。
在选定参考方向下,已知正弦量的解析 式为 i 10sin( 314t 240 )A 。试求正弦量的 振幅、频率、周期、角频率和初相。
第二章 正弦交流电路

如:
u1 u2
2U1 sin t 1
2U 2 sin t 2
u u1 u2
2U1 sin t 1 2U 2 sin t 2 2U sin t
幅度、相位变化 频率不变
结论:因角频率()不变,所以以下讨论同 频率正弦波时, 可不考虑,主要研究幅度 与初相位的变化。
电容的相量欧姆定律
总结:R、L、C相量形式的欧姆定律
、I 表示, 在正弦交流电路中,若正弦量用相量 U
电路参数用复数阻抗( R R、L jX L、C jX C ) 表示,则复数形式的欧姆定律和直流电路中的形式相 似。
RI U R jLI jX I U L L 1 j jX I U I C C C
R、L、C正弦交流电路的分析计算小结
电路 电路图 基本 参数 (正方向) 关系
i 复数 阻抗 设 电压、电流关系 瞬时值 有效值 相量图 相量式 功率 有功功率 无功功率
u 2U sin t
I
U IR
U
R
u
u iR
R
则
I R U
UI
0
i 2I sin t
设
u、 i 同相
du iC dt
2U sin t
du iC 2UC cos t dt 2U C sin(t 90 )
特点:
1. 频率相同
2. 相位相差 90°(u 落后 i 90° )
u
i
I
UC
90
t
U
U
u 2U sin t
i 2U C sin(t 90 )
U I XL
u1 u2
2U1 sin t 1
2U 2 sin t 2
u u1 u2
2U1 sin t 1 2U 2 sin t 2 2U sin t
幅度、相位变化 频率不变
结论:因角频率()不变,所以以下讨论同 频率正弦波时, 可不考虑,主要研究幅度 与初相位的变化。
电容的相量欧姆定律
总结:R、L、C相量形式的欧姆定律
、I 表示, 在正弦交流电路中,若正弦量用相量 U
电路参数用复数阻抗( R R、L jX L、C jX C ) 表示,则复数形式的欧姆定律和直流电路中的形式相 似。
RI U R jLI jX I U L L 1 j jX I U I C C C
R、L、C正弦交流电路的分析计算小结
电路 电路图 基本 参数 (正方向) 关系
i 复数 阻抗 设 电压、电流关系 瞬时值 有效值 相量图 相量式 功率 有功功率 无功功率
u 2U sin t
I
U IR
U
R
u
u iR
R
则
I R U
UI
0
i 2I sin t
设
u、 i 同相
du iC dt
2U sin t
du iC 2UC cos t dt 2U C sin(t 90 )
特点:
1. 频率相同
2. 相位相差 90°(u 落后 i 90° )
u
i
I
UC
90
t
U
U
u 2U sin t
i 2U C sin(t 90 )
U I XL
电工学第2章正弦交流电路PPT课件

p=ui=Um sin(ωt+90°) Imsinωt
=UmIm cosωtsinωt =UIsin2ωt
电感元件的功率波形
上式表明, 电感元件的瞬时功率是一个幅值为UI 并以2ω的角频率随时间而变化的正弦量。瞬时功率 的变化曲线如右图所示。
26
当p>0时,表明电感元件吸收能量并作负载 使用,即将电能转换成磁场能量储存起来;
1. 相位角(或相位)——(ωt +ψi) 2. 初相位——t=0时的相位角,即ωt +ψi|t=0=ψi
初相位不同,正弦波的起始点不同,如下图所 示。
(a)ψi=0
(b)ψi>0
(c)ψi<0
由于正弦量是周期性变化量,其值经2π后又重复,所
以一般取主值,| ψi |≤π。
8
2.1.3 初相位
在一个正弦交流电路中, 电压u和电流i的频率是相同的, 但初相位却可以不同。设:
19
在电阻元件的交流电路中,电压u与电流i 相 位相同、频率相同。其波形图、相量图如下所示:
根据 i=Imsinωt ;u=iR=ImRsinωt
可知电压幅值: Um=Im R;
U=I R
如果用相量来表 示电压与电流的
•
•
U
•
Um
•
R
或
••
U IR
关系,则有: I I m
20
瞬时功率:p=ui= Umsinωt Imsinωt=UmImsin²ωt
③指数形式可改写为极坐标形式:
A=r
三种复数式可以互相转换。复数的加减运 算可用直角坐标式;复数的乘除运算用指数形 式或极坐标形式则比较方便。
13
e e 例如: 设A1= a1+jb1 =r1 j 1 ;A2= a2+jb2 =r2 j 2
电路 第二章 正弦交流电路2

归纳上述的讨论可知;由于任一瞬时电感元件上的电压u 正比于电流的变化率△i/△t,因此在相位上电感电压超前 电流900,即u比i早1/4周期达到最大值或零值。
电感元件上u、i的波形,如图 (b)所示。显然,电感元 件上的电压和电流为同频率的正弦量。
(二)大小关系
将式(2—13)的正弦电流代入式(2—14),经过数学 运算可得到电感电压的表达式为 u=ωLImcosωt =Umsin(ωt+900)
U =U R+UL十U C=I R+j IXL-jIXC
=I [(R+j(XL-XC )= Z
上RL式C称串为联相电量路形对式正的弦欧电姆流定的阻律碍。作式用中。的它Z=概R括+j了(X前L-述X电c)反阻映、了感 抗及容抗的性质。它是一个复数,故称为复阻抗。
为X为超见LU前,电>了X电L阻方c与,U流端便便c电反作9可0相压图0画;,相,U出它量在cR为们,L串电C的它联串容相与电联端量电路电电和流中路压为I同的一相U相相量般x=;量,选UU图它电LL为+,滞流U电如后I作c感称图电为端为流(b参电电)。9考压抗0图0相相端。中量量电由,,,压图U设它相可1R6
流容则上它的元式表Xωc表件中示1=cω达上,1电ωc=1式电U容c =称m为压元1/I为/m与(件=i=容电2U对πω抗/流If交CC,之U)流用m间电c符o的的s号ω大阻tX小=碍c表关I作m示系s用in,为(。ω即ωt若+C9频U0m0率)=由Ifm的此单可位得为出赫电,
电容C的单位为法,则容抗Xc的单位为欧。
Xc=U/I 这就是电容元件上电压和电流之间的有效值关系。 容抗Xc的大小与电容C和频率f成反比。频率f越高,电容C
电工学第二章 正弦交流电
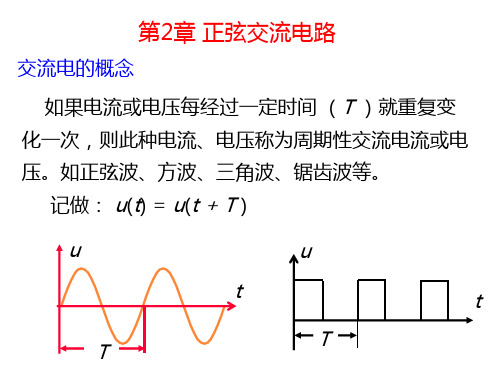
电流超前电压 90 u i u i ωt O 90°
O
ωt
电压与电流同相 u i u i O
ψ1 ψ 2 0
ψ 1 ψ 2 180
电压与电流反相 u i u i O
ωt
ωt
注意: ① 两同频率的正弦量之间的相位差为常数, 与计时的选择起点无关,仅取决于两者的初相位。
i
O
i1
i2
t
② 不同频率的正弦量比较无意义。
例1
已知:
幅度:
i sin 1000 t 30 A
I 1 2 0 . 707 A
I m 1A
频率:
1000 rad/s
f
2
1000 2
159 Hz
初相位:
30
例2:
i1 I m1 sin t 90 i2 I m2 sin t 90
小写
u i O p
2
i u
ωt p
p ui
U m I m sin ω t
1 2 U m I m (1 cos 2 ω t )
O
ω t
结论: p 0
(耗能元件),且随时间变化。
(2) 平均功率(有功功率)P 瞬时功率在一个周期内的平均值
P
大写
i
+
1 T 1
0
T 0
p dt
I 2 11 60 A
I I1 I 2 12.7 30A 11 60A
12.7( cos 30 j sin 30 )A 11( cos 60 j sin 60 )A
O
ωt
电压与电流同相 u i u i O
ψ1 ψ 2 0
ψ 1 ψ 2 180
电压与电流反相 u i u i O
ωt
ωt
注意: ① 两同频率的正弦量之间的相位差为常数, 与计时的选择起点无关,仅取决于两者的初相位。
i
O
i1
i2
t
② 不同频率的正弦量比较无意义。
例1
已知:
幅度:
i sin 1000 t 30 A
I 1 2 0 . 707 A
I m 1A
频率:
1000 rad/s
f
2
1000 2
159 Hz
初相位:
30
例2:
i1 I m1 sin t 90 i2 I m2 sin t 90
小写
u i O p
2
i u
ωt p
p ui
U m I m sin ω t
1 2 U m I m (1 cos 2 ω t )
O
ω t
结论: p 0
(耗能元件),且随时间变化。
(2) 平均功率(有功功率)P 瞬时功率在一个周期内的平均值
P
大写
i
+
1 T 1
0
T 0
p dt
I 2 11 60 A
I I1 I 2 12.7 30A 11 60A
12.7( cos 30 j sin 30 )A 11( cos 60 j sin 60 )A
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
设 u U m sinω t
u U m sinω t i R R
2U sinω t R
i
+ u _ R
① 频率相同 ②大小关系: I U R ③相位关系 : u、i 同相
相量式:
I
I I 0o
相量图
U
U U 0 IR 0 I R
相量模型
2. 功率关系 (1) 瞬时功率 p:瞬时电压与瞬时电流的乘积
U jX L I
I
U
di jX L jω L u L dt
1 jX C j ωC
U
I
C
du i C U jX C I dt
I
U
正误判断
问在电阻电路中:
瞬时值 有效值
U I R
?
U i R
?
u ? i R
在电感电路中:
正误判断
i
+
u
L
可得相量式: I I 0
-
U U 90 Iω L 90
I j L I (jX L )
电感电路相量形式的欧姆定律
U
相量模型
相量图
I
2. 功率关系 (1) 瞬时功率
i 2 I sinω t u 2 I ω L sin ( ω t 90 )
2.3 单一参数的交流电路 2.3.1 电阻元件的交流电路
1. 电压与电流的关系 根据欧姆定律: u iR 设 u U m sinω t
+ u _
i
R
u U m sinω t 2U i sinω t R R R I msin ω t 2 I sin ω t
U I ③相位关系 :u、i 同相 ① 频率相同 ②大小关系: R
i 2 I sin ω t u 2 U sin ω t
u i
i u ωt p
p ui
O
p
U m I m sin ω t
2
1 U m I m (1 cos 2 ω t ) 2 结论: p 0 (耗能元件)
O
ωt
(2) 平均功率(有功功率)P 瞬时功率在一个周期内的平均值
UI sin2 ω t (2) 平均功率
p i u U m I m sinω t sin( ω t 90) Um Im U m I m sinω t cos ω t sin2 ω t 2 L是非耗
能元件
1 T P p dt T o 1 T UI sin (2ω t ) dt 0 T o
Z 的模表示 u、i 的大小关系,辐角(阻抗角) 为 u、i 的相位差。
Z 是一个复数,不是相量,上面不能加点。
Z Z R j X L X C
U Z R 2 ( X L X C )2 阻抗模: I X L XC ω L 1 / C arctan 阻抗角: ψu ψi arctan R R
i
+ u _ p R
1 P T
T
0
1 p dt T
T
0
u i dt
p
1 T1 U m I m (1 cos 2 ω t ) dt T 0 2
1 T
T 0
P
ωt
UI (1 cos2ω t )dt UI O
2
P UI I R
U R
2
单位:瓦(W)
注意:通常铭牌数据或测量的功率均指有功功率。
定义:
I U ω C
或
1 U I ωC
1 1 XC 容抗(Ω ) U I X C ωC 2 π f C
直流: C X 交流:f
,电容C视为开路
XC
容抗XC是频率的函数
所以电容C具有隔直通交的作用
由: u
i
2Usinω t 2Uω C sin( ω t 90)
P Q
2
2
S PQ
P、Q、S 都不是正弦量,不能用相量表示。
阻抗三角形、电压三角形、功率三角形
将电压三角形的有效值同除I得到阻抗三角形 将电压三角形的有效值同乘I得到功率三角形 S
U U R (U L U C )
2 2
U R U cos U X U sin
Z R 2 ( X L X C )2
2.3.3 电容元件的交流电路
1.电流与电压的关系
i
+
C 设: 2 U sin ω t u du 则: i C 2 UC ω cos ω t ① 频率相同 dt 2 U ω C sin(ω t 90) ② I =UC
u _
I
u i u i
ωt
③电流超前电压90
90
有效值
求(1)感抗XL;(2)线圈两端的电压u; (3)有功功率和无功功率。
解: X L L 6.28
U m I m jX L (5 2 30) j 6.28 31.4 260(V ) u 31.4 2 sin(314 t 60)V PL 0W QL UI 5 31.4 157Var
p 瞬时功率 : i u UI sin2 ω t
u,i o i u
i u p + +
i u -
u
+
i
u
+
i
结论: 纯电容不消 ωt 耗能量,只和 电源进行能量 交换(能量的 吞吐)。 所以电容C是储 能元件。
+ p <0
o
+ p <0
p >0
p >0
ωt
充电 放电 充电 放电
(3) 无功功率 Q 为了同电感电路的无功功率相比较,这里也设
Z
U
R
S P 2 Q2 P S cos Q S sin
X L XC U L U C
Q
R Z cos X Z sin
UR
P
例2.5
R、L、C串联交流电路如图所示。已知R=30、L= 127mH、C=40F,电源电压u=220 2 sin(314 t+45)V 求:1. 感抗、容抗及复阻抗;
i 2 I sinω t 则:u 2Usin ( ω t 90 )
所以p UI sin2ω t
同理,无功功率等于瞬时功率达到的最大值。
Q UI I X C
2
U XC
2
单位:var
单一参数电路中的基本关系
参数
阻抗
基本关系
相量式
相量图
R L
R
u iR
U IR
u i L
u i XL
?
U I L
?
?
U jL I
?
U
XL
?
I
2.4 电阻、电感与电容串联的交流电路
1.电压电流关系 根据KVL (1) 瞬时值表达式 i
+
uR – + uL u – + uc – –
+
R
设 i= I msin t
u= uR + uL + uC =Ri + L di + 1∫ idt dt C
可得相量式 则:
U U 0 I I 90 jUω C
1 U j I I ( j X C ) ωC
相量模型
I
电容电路中复数形式的欧姆定律 相量图
U
2.功率关系 由
i
u 2Usinω t i 2Uω C sin( ω t 90)
+
u _ C
根据电压三角形可得:
Q UI sin
单位:var
电感和电容与电源 之间的能量互换
(4) 视在功率 S 电路中总电压与总电流有效值的乘积。
S UI Z I
2
单位:V· A
注: SN=UN IN 称为发电机、变压器 等供电设备的容量, 可用来衡量发电机、变压器可能提供的最大有功功率。
S
所以:
P UI cos
因数,用来衡 量对电源的利 用程度。
根据电压三角形可得: Ucos =UR=RI
U
P UI cos U R I I R
2
UX
(3) 无功功率Q
电阻消耗的电能
2
UR
Q U L I U C I (U L U C ) I I ( X L X C )
UR
U U R (U L U C )
2
2
阻抗三角形
Z
由阻抗三角形:
R
X X L XC
R Z cos X Z sin
X L XC R ( X L X C ) , arctan R
2 2
Z
2.功率关系
(1) 瞬时功率 设:i I m sinω t
(3) 无功功率 Q 用以衡量电感电路中能量交换的规模。用瞬时功率 达到的最大值表征,即
p 瞬时功率 : i u UI sin2 ω t
Q U I I XL U
2 2
XL
单位:var
练习题: 1.一只L=20mH的电感线圈,通以 i 5 2sin(314 30)A的电流 t
