第四章(III)
第四章 船舶稳性
第二节 船舶稳性的计算
(2)影响初稳性高度的因素及计算
①GMf计算:
GM f
ix
式中:——液体密度(g/cm3);
ix——自由液面对其横倾轴的面积惯性距(m4)
ix值可查取“液舱自由液面惯性矩ix表”或用下式近似计算:
ix klb1 b2 (b12 b22 )
其中:l — 舱长(m); b1、b2 — 前、后边宽(m)。
2020/4/8
第一节 稳性的基本概念
3.按外力性质 静稳性:在静态力矩作用下,不计及倾斜角加速度 和惯性矩的稳性。 动稳性;在动态力矩作用下,计及倾斜角加速度和 惯性矩的稳性。
2020/4/8
第一节 稳性的基本概念
4.按船舱是否进水分 完整稳性:船体在完整状态时的稳性。 破舱稳性;船体破舱进水后所具有的稳性。
思考:在动态外力矩的作用下,什么时候船舶第一次达 到横倾角速度为零?
2020/4/8
第二节 船舶稳性的计算
1.动稳性与静稳性的区别
静稳性
动稳性
受力性质 静态外力作用
动态外力作用
基本标志 平衡条件
复原力矩MR(力臂GZ) MR = GZ 当MR = Mh时,船舶平衡于静倾角s
MR所作功AR(力臂ld) Md=AR = ld 当AR = Ah时,船舶平衡于动倾角d
第二节 船舶稳性的计算
(3)初稳心点法
GZ MS GM sin (m)
式中: MS —— 形状稳性力臂(m),MS= f(,) 。 GMsin —— 重量稳性力臂
初稳性点M随船舶吃水(或排水量)而改变,故其参考 点不像基点K、假定重心GA那样固定不变
2020/4/8
第二节 船舶稳性的计算
GM Pi (KG ZPi )
马原第四章(自己总结的)

第四章4-11.社会制度的改变原因:生产力与生产关系的、经济基础与上层建筑矛盾发展的必然结果。
2.资本主义萌芽(资本主义生产关系的产生):1)时间:14世纪末—15世纪初2)地点:地中海沿岸的一些城市3)途径:a)从小商品经济中分化出来b)从商人和高利贷者转换而来4)资本主义萌芽的形式(两种,对应上面两种途径):课本P139—1403.资本主义原始积累1)资本主义社会化生产(能够实现要求商品更大规模生产,满足世界市场扩大的需要)。
2)利用暴力手段进行原始积累,为资本主义迅速发展创造条件。
3)资本原始积累定义:生产者与生产资料相分离,货币资本迅速集中到少数人的手中的过程。
P1414)资本主义原始积累时间:西欧:15世纪后30年——16世纪高潮——19世纪初结束5)资本主义原始积累途径:P141-142a)暴力手段剥夺农民土地(资本主义原始积累过程的基础)b)暴力手段掠夺货币财富4.资本主义生产方式的形成P142劳动价值论5.以私有制为基础的商品经济1)自然经济:P1432)商品经济:以交换为目的而进行生产的经济形式,他是一定历史条件下的产物。
3)商品经济产生的历史条件:a)社会分工的出现b)生产资料和劳动产品属于不同的所有者4)商品经济的基本矛盾:私人劳动和社会劳动的矛盾6.商品的二因素1)商品的定义:用来交换的能够满足人们某种需要的劳动产品,具有使用价值和价值两个因素,是两者的矛盾统一体。
2)二因素:a)使用价值:商品能够满足人们某种需要的属性,即商品的有用性,反应的是人与自然之间的物质关系,是商品的自然属性,是一切劳动产品所共有的属性。
适用价值构成社会财富的物质内容。
b)价值:凝结在商品中的无差别的一般人类劳动,即人类脑力和体力的耗费价值所持有的是商品的社会属性。
商品价值在本质上体现了生产者之间的一定的社会关系。
c)两者关系:对立统一。
p144-1457.生产商品的劳动的二重性1)生产商品的劳动分为:a)具体劳动:生产一定使用价值的具体形式的劳动(有用劳动)。
民法 第四章 III 无权利能力社团

【案例】
商人甲与2008年12月1日委托诚信律师事务所 (特殊普通合伙)律师乙提起诉讼,请求法院判 决其债务人丙支付拖欠货款50万元。甲将相关资 料交给乙。从资料中乙发现甲的债权到年底将经 过诉讼时效。由于工作忙碌,乙忘记了此事,直 到2009年3月才向法院提起诉讼。在诉讼中丙提 出诉讼时效抗辩,甲因此败诉。
3、责任能力:不具有完全的民事责任能力, 不能独立承担民事责任。
二、合伙
(一)定义 合伙是两个以上的人(自然人或法人)根据
合伙协议,共同出资、共享利益、共担风险的 非法人组织。 (二)法律特征 1. 人格相对独立 2. 财产相对独立 3. 利益相对独立 竞业禁止 4. 民事责任相对独立
(三)种类
A.甲、乙、丁分担5万元
B.甲、乙、丙、丁分担5万元
C.甲、乙、丙分担5万元
D.甲、乙、丙承担大部分,丁承担小部分
(2)退伙
指合伙人脱离合伙企业,丧失合伙人的资格。包 括法定退伙、强制退伙和自愿退伙。
合伙人退伙的,其他合伙人应当与他按照退伙时 合伙企业的财产状况进行结算,退还退伙人的财 产份额。
【案例】
甲、乙二人每人出资5万元合伙经营一家饭 店,因经营不善,对丙负债7万元,而合伙 所剩净资产仅为4万元。同时甲欠丁个人债 务1万元,丙、丁同时起诉要求甲偿还债务, 而甲个人资产为3万元。试分析甲应该如何 偿还债务?
6.入伙和退伙
(1)入伙 第三人入伙应当取得全体合伙人的一致同
意。 在普通合伙企业,新合伙人对入伙前合伙
(三)种类
1. 非法人企业:如合伙企业、个人独资企 业等;
2. 非法人经营体:如领取了营业执照的个 人合伙、领取了营业执照的企业法人的分 支机构、筹建中的法人等;
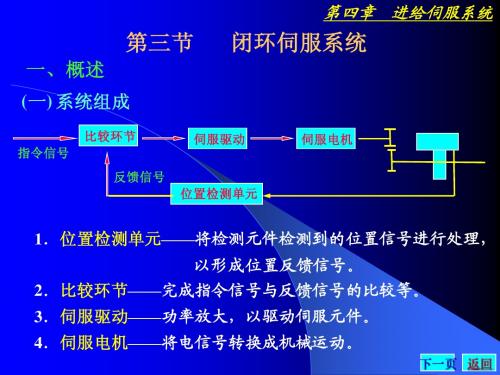
第四章闭环伺服系统
U = U 0 sin (ω t+ 2 π x /λ )
上一页 下一页 返回
第四章 进给伺服系统
脉冲编码器
脉冲编码器是一种旋转式角位移检测装置,能 将机械转角变换成电脉冲,是数空机床上使用 最光的检测装置。
光电式
脉 冲 编 码 器 的 分 类 增量式脉冲编码器 接触式
磁
磁
检测 电路
伺服系统 数字显示
尺
磁尺位置检测装置
上一页 下一页 返回
第四章 进给伺服系统
磁尺位置检测装置
表面录有相等节距(一般为0.05,0.1, 磁性标尺:
0.2,1mm)周期变化的磁信号。
磁 尺 按 基 N 本 形 状 分 为 平面实体形 磁尺 一般长度为600mm
磁尺
带 状 磁 尺 基体厚0.2mm,宽70mm
① 20mm
② 10mm
③ 0.35mm
④ 2.85mm
答: ① 设有一光栅的条纹密度是10条/mm,要利用它测 出1的位移,应采用___套光电转换装置。 ①1 答: ② ②2 ③3 ④4
上一页 下一页 返回
第四章 进给伺服系统
磁尺位置检测装置 磁尺: 是一种精度较高的位置检测装置。它 由磁性标尺、磁头、和检测电路组成。
W、ω、θ之间的关系
ω
ω
θ
BC=ABsin(θ/2) 其中
ω
光栅 节距
标尺光栅 θ
BC=ω/2 , AB=W/2 ,
指示光栅 B
因此
W=ω/sin(θ/2)
C θ /2 W /2
由于θ很小,θ单位为rad时, Sin(θ/2) ≈ θ 故 W ≈ ω/ θ
第四章 褶皱 § 3 褶皱的分类级组合形式

第三节 褶皱的分类及褶皱组合
褶皱位态分类简表
类 型 轴面倾角 80—90 80—90 80—90 10—80 10—80 10—80 0—10 枢纽倾伏角 0—10 10—80 80—90 0—10 10—80
10—80(侧伏角)
直立水平褶皱 直立倾伏褶皱 倾 竖 褶 皱 斜歪水平褶皱 斜歪倾伏褶皱 斜 卧 褶 皱 平 卧 褶 皱
第三节
褶皱的分类及褶皱组合
第三节 褶皱的分类及褶皱组合
一、褶皱的位态分类
里卡德(Rickard)在总结前人研究褶皱产状分类
的基础上, 根据褶皱轴面倾角、枢纽倾伏角和侧伏角
这三个变量, 绘制了一个三角网图, 对褶皱产状作三 维的定量研究。
轴面等倾角线:AB边与BC边等度数连线 枢纽等侧伏角线:AC边各度数与B点的连线 枢纽等倾伏角线:AC边与BC边等度数相连的曲
侏罗山式褶皱
ቤተ መጻሕፍቲ ባይዱ
侏罗山式褶皱在剖面上的形态
隔档隔槽式褶皱
第三节 褶皱的分类及褶皱组合
第三节 褶皱的分类及褶皱组合
(四)复背斜和复向斜(阿尔卑斯式褶皱 )
1、基本特征:
(1)一系列线状褶皱平行排列,走向与构
造带的走向一致
(2)背斜、向斜相间连续排列,同等发育
(3)不同级别的褶皱组成复背斜或复向斜
地面上的 表现
第三节 褶皱的分类及褶皱组合
平面图、图切剖面图上表示方法
贵州乌江电站某处小褶皱(自然剖面)
第三节 褶皱的分类及褶皱组合
雁列式褶皱-平面表示
第三节 褶皱的分类及褶皱组合
(二)隔档式褶皱和隔槽式褶皱(侏罗山式褶皱) 1. 基本特征: (1)一系列线状褶皱平行排列,走向与 构造带的走向一致 (2)紧密的褶皱与开阔的褶皱相间排列 (3)沉积盖层沿刚性基底上软层滑脱形 成的薄皮褶皱 2. 隔档式褶皱、隔槽式褶皱 (1)隔档式褶皱:背斜紧闭,向斜宽缓 的线状褶皱 (2)隔槽式褶皱:向斜紧闭,背斜宽缓 的线状褶皱
理论力学第四章

同理求解得
F1min
G tan tanjf 1 tanjf tan
G tan(
jf
)
y
F1
x
Fmax
FN G
4、几何法求F1的最小值F1min,受力分析如图。
F1min
画力三角形如图。
由力三角形可得 F1min Gtan( jf )
物块平衡时,F1的大小应满足
FR2
-jf
jf
FR2
G
G F1min
对多数材料,通常情况下
f fs
理论力学
中南大学土木工程学院
3
第4页/共46页
§4-2 摩擦角与自锁现象
一、摩擦角 ①全约束力 即FR= FN + FS ,它与接触面的公法线成一偏 角j ,当物体处于临界平衡状态,即静摩擦力达到最大值 Fmax时,偏角j达到最大值jf,全约束力与法线夹角的最大 值jf叫做摩擦角。
fs2P 1 fs2
代入(3)
得
tan min
1 fs2 2 fs
1 tan2jf 2tanjf
cot 2jf
tan(
2
2jf
)
理论力学
中南大学土木工程学院
18
第19页/共46页
FNB
B
FSB Pmin A FSA
几何法求解
当梯子处于向下滑动的临界平衡状态
时,受力如图,显然 FRA FRB ,于是
G tan jf F1 G tan jf
理论力学
中南大学土木工程学院
17
第18页/共46页
[例] 梯子长AB=l,重为P,若梯子与墙和地面的静摩擦因数均为 f s=0.5,
求 多大时,梯子能处于平衡?
第四章习题答案: - 精品课程建设网 湖州师范学院

第五章聚合方法一、名称解释1. 自由基聚合实施方法(Process of Radical Polymerization):主要有本体聚合,溶液聚合,乳液聚合,悬浮聚合四种。
2. 离子聚合实施方法:主要有溶液聚合,淤浆聚合。
3. 逐步聚合实施方法:主要有熔融聚合,溶液聚合,界面聚合。
4. 本体聚合:本体聚合是单体本身、加入少量引发剂(或不加)的聚合。
5. 悬浮聚合:悬浮聚合一般是单体以液滴状悬浮在水中的聚合,体系主要由单体、水、油溶性引发剂、分散剂四部分组成。
6. 悬浮作用:某些物质对单体有保护作用,能降低水的表面张力,能使水和单体的分散体系变为比较稳定的分散体系,这种作用称为悬浮作用。
7. 本体聚合:本体聚合是单体本身、加入少量引发剂(或不加)的聚合。
8. 溶液聚合:是指单体和引发剂溶于适当溶剂的聚合。
9. 乳液聚合:是单体在水中分散成乳液状而进行的聚合,体系由单体、水、水溶性引发剂、水溶性乳化剂组成。
10. 分散剂:分散剂大致可分为两类,(1)水溶性有机高分子物,作用机理主要是吸咐在液滴表面,形成一层保护膜,起着保护人用,同时还使表面(或界面)张力降低,有利于液滴分散。
(2)不溶于水的无机粉末,作用机理是细粉吸咐在液滴表面,起着机械隔离的作用。
11. 乳化剂:常用的乳化剂是水溶性阴离子表面活性剂,其作用有:(1)降低表面张力,使单体乳化成微小液滴,(2)在液滴表面形成保护层,防止凝聚,使乳液稳定,(3)更为重要的作用是超过某一临界浓度之后,乳化剂分子聚集成胶束,成为引发聚合的场所。
12. 胶束:当乳化剂浓度超过临界浓度(CMC)以后,一部分乳化剂分子聚集在一起,乳化剂的疏水基团伸身胶束回部,亲水基伸向水层的一种状态。
13. 临界胶束浓度:乳化剂开始形成胶束时的浓度称为临界胶束浓度,简称CMC。
14. 亲水亲油平衡值(HLB):该值用来衡量表面活性剂中亲水部分和亲油部分对水溶性的贡献,该值的大小表表亲水性的大小。
模糊数学 第四章---模糊关系

2.模糊自反关系(fuzzy reflexive relations)
定义 R F ( X X ), 若x X , R( x, x) 1,
则称R为模糊自反关系.
X有限时,R (rij )nn , rii R( xi , xi ) 1 根据主对角线元素是否为1判定R 是否自反
2. 运算
设R, S F ( X Y )
R S ( x, y ) X Y , R( x, y ) S ( x, y ); R S ( x, y ) X Y , R( x, y ) S ( x, y );
( R S )( x, y ) R( x, y ) S ( x, y ) ( R S )( x, y ) R( x, y ) S ( x, y )
设R (rij )nm , S ( sij )nm ,
即R( xi , y j ) rij , S ( xi , y j ) sij
则(R S )( xi , y j ) R( xi , y j ) S ( xi , y j ) rij sij 所以,R S (rij sij )nm .
1
X 有限时,
根据矩阵是否为对称阵判定R 是否对称关系
0.3 0.1 为对称关系. 0.1 0.3
命题3.3 R对称 [0, 1], R 是普通对称关系.
证明: 设R对称,且( x, y) R , 则R( x, y)
故R( y, x) R( x, y) ( y, x) R
类似可得: R S (rij sij ) nm . R c (1 rij )nm .
R 1 ( yi , x j ) R( x j , yi ) rji R S i, j, rij sij
【学生卷】初中数学高中化学必修一第四章《物质结构元素周期律》经典练习(培优)(3)

一、选择题1.W、X、Y、Z为原子序数依次增大的短周期元素,四种元素的核外电子数满足X+Y=W+Z;化合物XW3与 WZ相遇会产生白烟。
下列叙述正确的是A.原子半径:Z>Y>XB.电负性:Z>W>YC.两元素含氧酸酸性:Z>XD.XW3分子内键角为109°28'2.X、Y、Z、M、W为原子序数依次增大的5种短周期元素。
X的质子总数与电子层数相同,Y是农作物生长必需的三大营养元素之一,W的单质可用于自来水消毒,Z与M同主族且二者可形成常见气体甲,X、Y、Z三种元素可形成化合物乙。
下列说法不正确的是A.气体甲可以与Z的某种氢化物反应生成强酸B.化合物乙中可能含有离子键C.Y简单氢化物的沸点大于Z简单氢化物的沸点D.X分别与Y、Z、M形成的简单化合物中,X与Z形成的化合物稳定性最高3.短周期元素A和B,其中A元素的原子最外层电子数是a,次外层电子数是b; B元素的原子M层电子数是(a- b),L层电子数是(a+b),则A、B两种元素形成的化合物的化学式可能表示为A.B3A2B.AB2C.A3B2D.BA24.根据中学化学教材所附元素周期表判断,下列叙述错误的是A.K层电子数为奇数的所有元素所在族的序数与该元素原子的K层电子数相等B.L层电子数为奇数的所有主族元素所在族的序数与该元素原子的L层电子数相等C.L层电子数为偶数的所有元素所在族的序数与该元素原子的L层电子数相等D.M层电子数为奇数的所有主族元素所在族的序数与该元素原子的M层电子数相等5.利用某分子筛作催化剂,NH3可脱除废气中的NO和NO2,生成两种无毒物质,其反应历程如下图所示,下列说法正确的是A.X是N2B.上述历程的总反应为:2NH3+NO+NO2催化剂2N2+ 3H2OC.+4NH中含有非极性共价键D.NH3、+4NH、H2O中的质子数、电子数均相同6.镓(Ga)常以极少量分散于铝土矿(Al2O3)中。
普通生态学第四章种群生态学总结

普通生态学第四章种群生态学总结第四章生物种群:在一定的时间内,占据特定空间的同种生物个体的总和。
种群特征:数量特征:种群具有的密度、出生率、死亡率、迁入率和迁出率;空间分布特征:种群有一定的分布区域和分布方式;遗传特征:具有一定的遗传组成-进化、适应能力种群生态学:就以生物种群及其环境为研究对象,研究这些群体属性,包括种群的基本特征、种群的统计特征、数量动态及调节规律、种群内个体分布及种内、种间关系。
生物种群的基本特征:1.种群大小(Size):一个种群的全体数目多少。
密度(Density):单位面积或单位容积内某个种群的个体数目;相对密度公式:D=n/a·t 粗密度(Crude Density):是指单位空间内的个体数(或生物量);生态密度(Ecological Density):是指单位栖息空间(种群实际所占据的有用面积或空间)内的个体数(或生物量)。
密度的测定:绝对密度:(1)普查法:如人口普查2)取样调查法:木本:n/10m2;草本及农作物:n/1m2;水体:n/15ml;动物:标记重捕;相对密度:盖度,频度,丰度…影响种群密度的因素:(1)环境中可利用的物质和能量的多少;(2)种群对物质和能量利用效率的高低;(3)生物种群营养级的高低;(4)种群本身的生物学特性(如同化能力的高低等)“饱和点”和最适密度:当环境中拥有可利用的物质和能量最丰富、环境条件最适应时,某种群可达到该环境下的最大密度,这个密度称为“饱和点”。
维持种群最佳状况的密度,称为最适密度。
拥挤效应:在这个拥挤的环境里,虽然食物、饮水和筑巢材料很丰富,但动物的行为发生了异常。
引起拥挤效应。
2.年龄结构:各个年龄或年龄组在整个种群中都占有一定的比例,形成一定的年龄结构;研究种群的年龄结构对分析种群动态和进行预测预报具有重要价值从生态学的角度,种群的年龄结构可以分为三种类型:增长型种群、稳定型种群和衰退型种群。
(1)增长型:种群的年龄结构含有大量的幼年个体和较少的老年个体,幼中年个体除了补充死亡的老年个体外还有剩余,所以这类种群的数量呈上升趋势。
第四章烯烃-3

较好的醇的实 验室制备方法
烯烃的羟汞化——还原反应的可能机理 烯烃的羟汞化——还原反应的可能机理
羟汞化(亲电加成机理) 羟汞化(亲电加成机理)
H2O
δ
H HO −H
+
HO R CH CH2 Hg OAc
R CH
CH2 Hg OAc OAc
R CH
CH2 Hg
δ
R CH
CH2 Hg OAc
OAc
NaBH4
HO R CH CH2 Hg H HO
HO R CH CH2 + Hg H
R CH
CH2 + H
Hg
还原脱汞(经过自由基中间体) 还原脱汞(经过自由基中间体)
烯烃的羟汞化——还原反应 例:烯烃的羟汞化——还原反应
Hg(OAc)2 H2O NaBH4
CH3(CH2)3
CH
CH2
CH3(CH2)3
CH OH
烯丙位溴代的实验室常用方法
Br NBS
NBS:
O N O Br
(PhCOO)2
N-bromosuccinimide romos N-溴代丁二酰亚胺
NBS 溴代机理(自由基取代机理) 溴代机理(自由基取代机理)
O N O Br + HBr O N H O ∆ Br Br + Br2
NBS 持续提 供低浓度 Br2
反式加成
A R2 R4 R1 R3 A A R1 R3 C A C R4 R3 R2 R1 C A A C C A R2 R4 R3 A R2 R1 A C R4 R2 R4 R2 R3 A R1 A R4
A R1 C R3 A
A R2 C R4 A
R1 R3
线性代数第四章答案

线性代数第四章答案第四章向量组的线性相关性1 设v1(1 1 0)T v2(0 1 1)T v3(3 4 0)T求v1v2及3v12v2v3解v1v2(1 1 0)T(0 1 1)T(10 11 01)T(1 0 1)T3v12v2v33(1 1 0)T 2(0 1 1)T (3 4 0)T(31203 31214 30210)T(0 1 2)T2 设3(a1a)2(a2a)5(a3a) 求a其中a1(2 5 1 3)Ta2(10 1 5 10)T a3(4 1 1 1)T解由3(a1a)2(a2a)5(a3a)整理得(1 2 3 4)T3 已知向量组A a1(0 1 2 3)T a2(3 0 1 2)T a3(2 3 0 1)TB b1(2 1 1 2)T b2(0 2 1 1)T b3(4 4 1 3)T证明B组能由A组线性表示但A组不能由B组线性表示证明由知R(A)R(A B)3 所以B组能由A组线性表示由知R(B)2 因为R(B)R(B A) 所以A组不能由B组线性表示4 已知向量组A a1(0 1 1)T a2(1 1 0)TB b1(1 0 1)T b2(1 2 1)T b3(3 2 1)T证明A组与B组等价证明由知R(B)R(B A)2 显然在A中有二阶非零子式故R(A)2 又R(A)R(BA)2 所以R(A)2 从而R(A)R(B)R(A B) 因此A组与B组等价5 已知R(a1a2a3)2 R(a2a3a4)3 证明(1) a1能由a2a3线性表示(2) a4不能由a1a2a3线性表示证明 (1)由R(a2a3a4)3知a2a3a4线性无关故a2a3也线性无关又由R(a1 a2a3)2知a1a2a3线性相关故a1能由a2a3线性表示(2)假如a4能由a1a2a3线性表示则因为a1能由a2a3线性表示故a4能由a2a3线性表示从而a2a3a4线性相关矛盾因此a4不能由a1a2a3线性表示6 判定下列向量组是线性相关还是线性无关(1) (1 3 1)T (2 1 0)T (1 4 1)T(2) (2 3 0)T (1 4 0)T (0 0 2)T解 (1)以所给向量为列向量的矩阵记为A因为所以R(A)2小于向量的个数从而所给向量组线性相关(2)以所给向量为列向量的矩阵记为B因为所以R(B)3等于向量的个数从而所给向量组线性相无关7 问a取什么值时下列向量组线性相关?a1(a 1 1)T a2(1 a 1)T a3(1 1 a)T解以所给向量为列向量的矩阵记为A由如能使行列式等于0,则此时向量组线性相关(具体看书后相应答案)8 设a1a2线性无关a1b a2b线性相关求向量b用a1a2线性表示的表示式解因为a1b a2b线性相关故存在不全为零的数12使(a1b)2(a2b)01由此得设则b c a1(1c)a2c R9 设a1a2线性相关b1b2也线性相关问a1b1a2b2是否一定线性相关?试举例说明之(也可看书后答案)解不一定例如当a1(1 2)T, a2(2 4)T, b1(1 1)T, b2(0 0)T时有a1b1(1 2)T b1(0 1)T, a2b2(2 4)T(0 0)T(2 4)T而a1b1a2b2的对应分量不成比例是线性无关的10 举例说明下列各命题是错误的(1)若向量组a1a2a m是线性相关的则a1可由a2a m线性表示解设a1e1(1 0 0 0) a2a3a m0则a1a2a m线性相关但a1不能由a2a m线性表示(2)若有不全为0的数12m使a1m a m1b1m b m01成立则a1a2a m线性相关, b1b2b m亦线性相关解有不全为零的数12m使a1m a m 1b1m b m01原式可化为(a1b1) m(a m b m)01取a1e1b1a2e2b2a m e m b m其中e1e2e m为单位坐标向量则上式成立而a1 a2a m和b1b2b m均线性无关(3)若只有当12m全为0时等式a1m a m1b1m b m01才能成立则a1a2a m线性无关, b1b2b m亦线性无关解由于只有当12m全为0时等式由1a1m a m1b1m b m0成立所以只有当12m全为0时等式(a1b1)2(a2b2) m(a m b m)01成立因此a1b1a2b2a m b m线性无关取a1a2a m0取b1b m为线性无关组则它们满足以上条件但a1a2a m线性相关(4)若a1a2a m线性相关, b1b2b m亦线性相关则有不全为0的数12m使a1m a m0 1b1m b m01同时成立解a1(1 0)T a2(2 0)T b1(0 3)T b2(0 4)Ta12a2 01221b12b2 01(3/4)210 与题设矛盾1211 设b1a1a2b2a2a3 b3a3a4 b4a4a1证明向量组b1b2b3b4线性相关证明由已知条件得a1b1a2a2b2a3 a3b3a4 a4b4a1于是a1 b1b2a3b1b2b3a4b1b2b3b4a1从而b1b2b3b40这说明向量组b1b2b3b4线性相关12 设b1a1b2a1a2b r a1a2 a r且向量组a1a2a r线性无关证明向量组b1b2b r线性无关证明已知的r个等式可以写成上式记为BAK因为|K|10 K可逆所以R(B)R(A)r从而向量组b1b2b r线性无关13 求下列向量组的秩, 并求一个最大无关组(1)a1(1 2 1 4)T a2(9 100 10 4)T a3(2 4 2 8)T解由知R(a1a2a3)2 因为向量a1与a2的分量不成比例故a1a2线性无关所以a1 a2是一个最大无关组(2)a1T(1 2 1 3) a2T(4 1 5 6) a3T(1 3 4 7)解由知R(a1T a2T a3T)R(a1a2 a3)2 因为向量a1T与a2T的分量不成比例故a1T a2T 线性无关所以a1T a2T是一个最大无关组14 利用初等行变换求下列矩阵的列向量组的一个最大无关组(1)解因为所以第1、2、3列构成一个最大无关组.(2)解因为所以第1、2、3列构成一个最大无关组(关于14的说明:14题和书上的14题有些不同,答案看书后的那个)15 设向量组(a 3 1)T (2 b 3)T(1 2 1)T (2 3 1)T的秩为2 求a b解设a1(a 3 1)T a2(2 b 3)T a3(1 2 1)T a4(2 3 1)T因为而R(a1a2a3a4)2 所以a2 b516 设a1a2a n是一组n维向量已知n维单位坐标向量e1e2e n 能由它们线性表示证明a1a2a n线性无关证法一记A(a1a2a n) E(e1e2e n) 由已知条件知存在矩阵K使EAK两边取行列式得|E||A||K|可见|A|0 所以R(A)n从而a1a2a n线性无关证法二因为e1e2e n能由a1a2a n线性表示所以R(e1e2e n)R(a1a2a n)而R(e1e2e n)n R(a1a2a n)n所以R(a1a2a n)n从而a1a2a n线性无关17 设a1a2a n是一组n维向量, 证明它们线性无关的充分必要条件是任一n维向量都可由它们线性表示证明必要性设a为任一n维向量因为a1a2a n线性无关而a1a2a n a 是n1个n维向量是线性相关的所以a能由a1a2a n线性表示且表示式是唯一的充分性已知任一n维向量都可由a1a2a n线性表示故单位坐标向量组e1 e2e n能由a1a2a n线性表示于是有nR(e1e2e n)R(a1a2a n)n即R(a1a2a n)n所以a1a2a n线性无关18 设向量组a1a2a m线性相关且a10证明存在某个向量a k (2km) 使a k能由a1a2a k1线性表示证明因为a1a2a m线性相关所以存在不全为零的数12m使a12a2m a m01而且23m不全为零这是因为如若不然则1a10由a10知10 矛盾因此存在k(2km) 使0 k1k2m0k于是a12a2k a k01a k(1/k)(1a12a2k1a k1)即a k能由a1a2a k1线性表示19 设向量组B b1b r能由向量组A a1a s线性表示为(b1b r)(a1a s)K其中K为sr矩阵且A组线性无关证明B组线性无关的充分必要条件是矩阵K的秩R(K)r证明令B(b1b r) A(a1a s) 则有BAK必要性设向量组B线性无关由向量组B线性无关及矩阵秩的性质有rR(B)R(AK)min{R(A) R(K)}R(K)及R(K)min{r s}r因此R(K)r充分性因为R(K)r所以存在可逆矩阵C使为K的标准形于是(b1b r)C( a1a s)KC(a1a r)因为C可逆所以R(b1b r)R(a1a r)r从而b1b r线性无关20 设证明向量组12n与向量组12n等价证明将已知关系写成将上式记为BAK因为所以K可逆故有ABK1由BAK和ABK1可知向量组12n与向量组12n可相互线性表示因此向量组12n与向量组12n等价21 已知3阶矩阵A与3维列向量x满足A3x3A x A2x且向量组x A x A2x线性无关(1)记P(x A x A2x) 求3阶矩阵B使APPB解因为APA(x A x A2x)(A x A2x A3x)(A x A2x 3A x A2x)所以(2)求|A|解由A3x3A x A2x得A(3x A x A2x)0因为x A x A2x线性无关故3x A x A2x0即方程A x0有非零解所以R(A)3 |A|0(从22题开始,凡涉及到基础解系问题的,答案都不是唯一的,可以参考本文答案,也可以看书后的答案,不过以书后的答案为主。
高等数学 线性代数 习题答案第四章

习题 4-11.验证函数f (x )=lnsin x 在[π5π,66]上满足罗尔定理的条件,并求出相应的ξ,使f ′(ξ)=0.解: 显然()ln sin f x x =在5π,66x ⎡⎤⎢⎥⎣⎦上连续,在π5π,66⎛⎫⎪⎝⎭内可导,且π5π()()ln 266f f ==-,满足罗尓定理的条件. 令cos ()cot 0sin x f x x x '===,则π2x = 即存在ππ5π(,)66ξα=∈,使()0f ξ'=成立.2. 下列函数在指定区间上是否满足罗尔定理的三个条件?有没有满足定理结论中的ξ ?[][][]2(1)()1,;(2)(),;1,10,21sin ,0π(3)()0,π1,0e x f x f x x x x f x x =-=--<≤⎧=⎨=⎩解: (1) 2()1e x f x =-在[]1,1-上连续,在()1,1-内可导,且(1)1,(1)1,e e f f -=-=- 即 (1)(1)f f -= () f x ∴在[]1,1-上满足罗尓定理的三个条件. 令 2()20ex f x x '==得 0x =,即存在0(1,1)ξ=∈-,使()0f ξ'=.(2) 101()1112x x f x x x x -≤<⎧==-⎨-≤≤⎩显然()f x 在(0,1),(1,2)内连续,又1111(10)lim ()lim(1)0,(10)lim ()lim(1)0,(10)(10)(1)0,即x x x x f f x x f f x x f f f --++→→→→-==-=+==-=-=+==所以()f x 在1x =处连续,而且22(00)lim ()lim(1)1(0),(20)lim ()lim(1)1(2),x x x x f f x x f f f x x f ++--→→→→+==-==-==-==即()f x 在0x =处右连续,在2x =处左连续,所以()f x 在[]0,2 上连续.又1111()(1)1(1)lim lim 1,11()(1)1(1)lim lim 111x x x x f x f xf x x f x f xf x x --++-→→+→→--'===-----'===--(1)(1)()f f f x -+''∴≠∴在1x =处不可导,从而()f x 在(0,2)内不可导.又 (0)(2)1f f == 又由 101()112x f x x -<<⎧'=⎨<<⎩知 ()0f x '≠综上所述,函数()f x 满足罗尓定理的条件(1),(3)不满足条件(2),没有满足定理结论的ξ.(3) 由0(00)lim sin 0(0)1x f x f +→+==≠=知()f x 在0x =不右连续, () f x ∴在[]0,π上不连续, 显然()f x 在()0,π上可导,又(0)1,(π)0f f ==,即(0)(π)f f ≠,且()cos (0,π) f x x x '=∈,取π(0,π)2ξ=∈,有π()cos cos 02f ξξ'===. 综上所述,函数()f x 满足罗尓定理的条件(2),不满足条件(1),(3),有满足定理结论的ξ,ξ=π2.3. 不用求出函数()(1)(2)(3)f x x x x =---的导数,说明方程()0f x '=有几个实根,并指出它们所在的区间.解: 显然()f x 在[]1,2上连续,在()1,2内可导,且(1)(2)0f f ==,由罗尓定理知,在()1,2内至少存在一点1ξ,使1()0f ξ'=,即()0f x '=在()1,2内至少有一个实根.同理 ()0f x '=在()2,3内也至少有一个实根2ξ.又()0f x '=是二次方程,最多有两个实根,故()0f x '=有两个实根,分别在区间()1,2和()2,3内.4. 验证拉格朗日中值定理对函数3()2f x x x =+在区间[0,1]上的正确性.解: 显然3()2f x x x =+在[0,1]上连续,在()0,1内可导,满足拉格朗日中值定理的条件.若令2(1)(0)()32310f ff x x -'=+==-则x =,取ξ=,即存在(0,1)3ξ=∈,使得(1)(0)()10f f f ξ-=-成立. 从而拉格朗日中值定理对函数3()2f x x x =+在[0,1]上成立.5. 已知函数f (x )在[a ,b ]上连续,在(a ,b )内可导,且f (a )=f (b )=0,试证:在(a ,b )内至少存在一点ξ,使得f (ξ)+f ′(ξ) = 0,ξ∈(a ,b ). 证: 令()()e xF x f x =,则()()()e e xxF x f x f x ''=+由e x 在(),-∞+∞上连续,可导,()f x 在[],a b 上连续,在(),a b 内可导,知()F x 在[],a b 上连续,在(),a b 内可导,而且()()0,()()0,()()e e 即abF a f a F b f b F a F b =====,由罗尓定理至少存在一点(,)a b ξ∈使()0F ξ'=. 即 ()()0e e f f ξξξξ'+= 而0e ξ≠ 故 ()()0f f ξξ'+=即在(),a b 内至少存在一点ξ,使得()()0f f ξξ'+=. 6.若方程10110n n n a x a x a x --+++= 有一个正根x 0,证明方程12011(1)0n n n a nx a n x a ---+-++=必有一个小于0x 的正根. 证: 令1011()…nn n f x a x a xa x --=+++,显然()f x 在[]00,x 连续,在()00,x 内可导,且(0)0f =,依题意知0()0f x =.即有0(0)()f f x =.由罗尓定理,至少存在一点0(0,)x ξ∈,使得()0f ξ'=成立,即12011(1)0…n n n a n a n a ξξ---+-++=成立,这就说明ξ是方程12011(1)0n n n a nx a n x a ---+-++= 的一个小于0x 的正根.7. 设f (a ) = f (c ) = f (b ),且a <c <b , f ″(x )在[a ,b ]上存在,证明在(a ,b )内至少存在一点ξ,使f ″(ξ)= 0.证: 显然()f x 分别在[],a c 和[],c b 上满足罗尓定理的条件,从而至少存在1(,)a c ξ∈,2(,)c b ξ∈,使得12()()0f f ξξ''==.又由题意知()f x '在[]12,ξξ上满足罗尓定理的条件,从而至少存在一点12(,)(,)a b ξξξ∈⊂,使得()0f ξ''=.即在(,)a b 内至少存在一点ξ,使()0f ξ''=.习题4-21.利用洛必达法则求下列极限:(1) sin3lim tan5x xxπ→; (2) 0e 1lim (e 1)x x x x x →---;(3)lim m m n n x a x a x a →--; (4) 20()lim x xx a x a x →+-,(a >0); (5) 0ln lim cot x xx+→; (6) 0lim sin ln x x x +→; (7) 1ln(1)lim arccot x x x →+∞+; (8) 0e 1lim()e 1x x x x →--; (9) 10lim(1sin )xx x →+; (10) 2lim (arctan )πx x x →+∞(11) c s c 03e lim()2x x x x →-+ ; (12) 2120lim e x x x →;(13) lim )x x →+∞; (14) 1101lim (1)e xxx x →⎡⎤+⎢⎥⎣⎦.解:222000011sin 33cos33(1)limlim lim cos3cos 5tan 55sec 5533(1)(1)5511(2)lim lim lim (1)111lim 22(3)lim lim lim πππe e e e e e e e e x x x x x xx x x x x xx x x x m m m n n n x a x a x a x x x x x x x x x x x x a mx x a nx →→→→→→→--→→→==⋅=⋅-⋅-=----==--+++==+-==-.m n m nm m x a n n --=2002220()ln ln()()(4)lim lim 21()()()ln ln()()lim2x xxxx x x x x x x a x a a a x a x a a x x xa x a x a x a a a x a x a x a x →→→⎡⎤+-++⎢⎥+-+⎣⎦=⎡⎤++++-++⎢⎥+++⎣⎦=[]200021()ln ln 012 aa a a aa a a a ++-⋅+==2200000000001ln sin 2sin cos (5)lim lim lim lim cot csc 12sin 0cos 001ln sin (6)lim sin ln lim lim lim tan csc csc cot sin lim lim tan 100x x x x x x x x x x x x x x x x x x x x x x x xx x x xxx x ++++++++++→→→→→→→→→→==-=--=-⋅====-⋅-=-⋅=-⨯=222221111ln(1)111(7)lim lim lim lim 111cot 11arc x x x x xx x x x x x x x x →+∞→+∞→+∞→+∞-++++====+-++ 20002200001(1)(8)lim()lim lim 1(1)21443limlim 12022e e e e e e e e e e e e e e e e e e e x x x x x x x x x x x xxxxx x x x x x x xx x x x x x →→→→→-----==-------====+-++0002cos 11ln(1sin )cos 1sin ln(1sin )lim limlim 11sin 12112ln(arctan )arctan 1limlim 112ln(arctan )(9)lim(1sin )lim 2(10)lim (arctan )lim πππee =e ee ee eeπx x x x x xx xx x xxxxx x x x x x x x xxx x x x →→→→+∞→+∞++++→→⋅⋅+-→+∞→+∞+========221lim12lim(1)arctan (1)arctan πeeex x x xx xx→+∞→+∞--+-+===020033lnln322csc ln lim csc 2sin sin 0002(2)(3)33(2)limlim 1(3)(2)cos cos 3(11)lim()lim lim 21e e e e e e e e eee ee exxxx x x x x x x x e e e x x x x xxxxx x x x x x x x xxx →→→---+++→→→+-+--⋅----+--+-===+====2221111220000221()(12)lim lim lim lim 11()e e ee x xx x x x x x x x x x→→→→'⋅====∞'202211ln(1)1ln(1)1limlim lim 0(13)lim )lim1111lim31(14)lim (1) eeee x x x x x x x x xx xxx x x x x →→→+∞→+∞+-+-→=++===⎡⎤===+⎢⎥⎣⎦00111211lim2(1)2eex x xx →→-+--+==2.设 21lim 1x x mx nx →++-=5,求常数m ,n 的值.解: 1lim(1)0, x x →-= 而21lim 51x x mx n x →++=-21lim()0 x x mx n →∴++= 且21()lim 5(1)x x mx n x →'++='-即 10m n ++= 且 1l i m (2)5x x m →+= 即 1m n +=- 且 25m += 于是得 3,4m n ==-. 3.验证极限sin lim x x xx→∞+存在,但不能由洛必达法则得出.解: sin 1limlim(1sin )1x x x x x x x→∞→∞+=+=,极限存在,但若用洛必达法则,有sin lim lim(1cos )x x x xx x→∞→∞+=+因lim cos x x →∞不存在,所以不能用洛必达法则得出.4.设f (x )二阶可导,求2()2()()limh f x h f x f x h h →+-+-.解: 这是型未定式,利用洛必达法则有 [][]200000()2()()()()limlim2()()()()1lim 21()()1()()11lim lim ()()2222().h h h h h f x h f x f x h f x h f x h h hf x h f x f x h f x hf x h f x f x h f x f x f x h h f x →→→→→''+-+-+--=''''-+---=''''+---''''=+=+-''=5.设f (x )具有二阶连续导数,且f (0) = 0,试证g (x ) = (),0'(0),0f x x x f x ⎧≠⎪⎨⎪=⎩可导,且导函数连续. 证: 当0x ≠时,2()()()()()f x xf x f x g x x x '-''==当0x =时,由200000()(0)()(0)()(0)lim lim lim 00()(0)1()(0)1lim lim (0)2202x x x x x f x f g x g f x xf x x x x f x f f x f f x x →→→→→'-'--==--''''--''===- 即 1(0)(0)2g f '''=所以 2()(),0()1(0),02xf x f x x xg x f x '-⎧≠⎪⎪'=⎨⎪''=⎪⎩由(),()f x f x '的连续性知()g x '在0x ≠处连续,又20000()()()()()lim ()limlim211lim ()(0)(0)22x x x x xf x f x f x xf x f x g x x xf x fg →→→→'''''-+-'=='''''===故()g x '在0x =处连续,所以()g x '在(),-∞+∞内处处连续.综上所述,(),0()(0),0f x xg x x f x ⎧≠⎪=⎨⎪'=⎩可导,且导函数连续.习题4-31.求函数f (x ) =e x x 的n 阶马克劳林公式.解:()()(1),()(1)(2),()()…x x x x x x k x f x e xe e x f x e x e e x f x e k x '=+=+''=++=+=+()()(0)1(0),(1,2,3,)!!(1)!k k f k fk k k k k ∴====-又 (0)0f =321(1)()(01)2!(1)!(1)!n x n x x e n x f x x x x n n θθθ+++∴=+++++<<-+2.当01x =-时,求函数f (x ) = 1x的n 阶泰勒公式. 解:()()[]23()2341()1()112212!3!!()(1),()(1),()(1),,()(1)!(1)(1)!(1)(1)!1,(0,1,2,)!!(1)()(1)1(1)111(1) … n n n n n n n n n nn n f x f x f x f x x x x x n f n f n n n n x f x x x x x θ-++++''''''=-=-=-=-∴-=-⋅=----==-=+∴=-+-⎡⎤+++++++⎣⎦-++ (01)θ<<3.按(4)x -的乘幂展开多项式432()53 4.f x x x x x =-+-+解: 函数432()534f x x x x x =-+-+,根据泰勒公式按(4)x -的幂的展开式是2(4)34(4)()(4)(4)(4)(4)2!(4)(4)(4)(4)3!4! f f x f f x x f f x x '''=+-+-'''+-+- 而[][][]432324244(4)(4)454434456,(4)21,41523(4)137,123022!2(4)111,24303!3!(4)12414!4!x x x f f x x x f x x f x f ====-⨯+-⨯+=-'==-+-''==-+'''==-=⨯=所以,234()5621(4)37(4)11((4)(4)f x x x x x =-+-+-+-+-.4.利用泰勒公式求下列极限:(1) 30sin limx x x x →-; (2) 21lim ln(1)x x x x →+∞⎡⎤-+⎢⎥⎣⎦. 解: (1) 利用泰勒公式,有34sin ()3!x x x o x =-+所以 343300430()sin 3!lim lim 1()1lim()66x x x x o x x x x x o x x →→→--==-= (2) 利用泰勒公式,有221111ln(1)()2o x x x x+=-+,所以222222221111lim lim ln(1)(())21()1111lim lim .()1222x x x x x x x x o x x x x o x x o x x →+∞→+∞→+∞→+∞⎡⎤⎡⎤=-+--+⎢⎥⎢⎥⎣⎦⎣⎦⎡⎤⎢⎥⎡⎤==-=-⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦ 习题4-41. 求下面函数的单调区间与极值:(1)32()26187f x x x x =---; (2)()ln f x x x =-; (3)23()1(2)f x x =--; (4)()(4)f x x x =-. 解: (1) 2()612186(1)(3),f x x x x x '=--=+-令()0f x '=得驻点121,3,x x =-=-在()(),,13,-∞-+∞上,()0f x '>,在()1,3-上()0f x '< ∴ ()f x 在(,1],[3,)-∞-+∞上单调增加,在[]1,3-上单调减少.当 1x =-时, ()f x 有极大值,极大值为(1)3f -=, 当 3x =时, ()f x 有极小值,极小值为(3)61f =-.(2) 11()1x f x x x-'=-=,令()0f x '=得驻点1x = 在()0,1上,()0f x '<;在()1,+∞上,()0f x '> ∴ ()f x 在(0,1]上单调递减;在[1,)+∞上单调递增. 当1x =时,()f x 有极小值,极小值为(1)1f =. (3)()()0f x f x ''=≠ 但当2x =时,()f x '不存在, 在(,2)-∞上,()0f x '>;在(2,)+∞上,()0f x '<, ∴ ()f x 在(,2]-∞上单调递增;在[2,)+∞上单调递减. 当2x =时, ()f x 有极大值,极大值为(2)1f =.(4) 2240()40x xx f x x xx ⎧-≥=⎨-+<⎩ ,则 240()240x x f x x x ->⎧'=⎨-+<⎩且当 0x =时,()f x '不存在,又令()0f x '=得2x = 在(,0),(2,)-∞+∞上,()0f x '>,在(0,2)上()0f x '< ∴ ()f x 在(,0],[2,)-∞+∞上单调递增;在[0,2]上单调递减; 当0x =时,()f x 有极大值,极大值为(0)0f =; 当2x =时, ()f x 有极小值,极小值为(2)4f =-. 2. 试证方程sin x = x 只有一个根.证: 显然0x =是方程sin x x =得一个根(亦可将()sin f x x x =-运用零点定理).令()sin f x x x =-,则()cos 10f x x '=-≤,而()0f x '=的点不是单调区间的分界点,故()f x 在(,)-∞+∞内单调下降,所以()f x 在(,)-∞+∞内只有一个零点,即方程sin x x =只有0x =一个根.3. 已知()([0,))f x C ∈+∞,若f (0) = 0, f ′(x )在[0,)+∞内存在且单调增加,证明()f x x在[0,+∞)内也单调增加.解: 0 x ∀>,由题意知()f x 在[]0,x 上满足拉格朗日中值定理的条件,利用拉格朗日中值定理得,(0,) x ξ∃∈,使()(0)()f x f xf ξ'-=, 因 ()f x '在[0,)+∞单调增加,且(0)0f =,所以()()()f x xf xf x ξ''=≤ 即 ()()0xf x f x '-≥令 ()()(0) f x F x x x=>,则 2()()()0xf x f x F x x '-'=≥ 所以()F x 单调递增,即 ()f x x在(0,)+∞内单调增加.4. 证明下列不等式:(1) 1+12x x >0; (2)2ln(1)(0)2 x x x x x -<+<>.证: (1) 令 1()12f x x =+则1()(12f x '=, 当 0x >时1,()0f x '<>即()f x 单调递增,从而()(0)0f x f >=,故112x +>. (2) 令 2()ln(1)2x f x x x =+-+,则 21()111x f x x x x'=-+=++当 0x >时,有()0f x '>,即()f x 单调递增,从而()(0)0f x f >= ,即2ln(1)2x x x +>-又令 ()ln(1)g x x x =-+,则1()111xg x x x'=-=++ 当 0x >时,()0g x '>,即 ()g x 单调递增,从而()(0)0g x g >=,即ln(1)x x >+.综上所述,当0x >时有2ln(1)2x x x x -<+<. 5. 试问a 为何值时,f (x ) = a sin x +13sin 3x 在x =3π处取得极值?是极大值还是极小值?并求出此极值.解: ()cos cos3f x a x x '=+若3πx =为极值点,则cos cos 03ππa +=,所以2a =.又()2sin 3sin 3,()03πf x x x f ''''=--=<故函数在3πx =处取得极大值,极大值为()3πf =习题4 - 51. 某个体户以每条10元的价格购进一批牛仔裤,设此批牛仔裤的需求函数为402Q P =-,问该个体户应将销售价定为多少时,才能获得最大利润? 解: 利润2()10260400L P PQ Q P P =-=-+-, ()460L P P '=-+,令 ()0L P '=得 P =15所以应将销售价定为每条15元,才能获得最大利润.2.设 f (x ) = cx α (c >0,0<α<1)为一生产函数,其中c 为效率因子,x 为投入量,产品的价格P 与原料价格Q 均为常量,问:投入量为多少时可使利润最大? 解: 依题意,总利润()()()L x Pf x Q x P cx Qx α=-=⋅- 则 1()L x Pc xQ αα-'=- 令 ()0L x '=得 11Q x Pc αα-⎛⎫=⎪⎝⎭所以,投入量为11Q Pc αα-⎛⎫⎪⎝⎭时利润最大.3. 某产品的成本函数为23()156C Q Q Q Q =-+,(1) 生产数量为多少时,可使平均成本最小?(2) 求出边际成本,并验证边际成本等于平均成本时平均成本最小. 解: (1) 2()()156C Q C Q Q Q Q==-+ 令 260()Q C Q '=-=⎡⎤⎣⎦得Q =3 故 生产数量3Q =时,可使平均成本最小. (2) 2()15123MC C Q Q Q '==-+当 3Q =时,15123396MC =-⨯+⨯= 2()156336C Q =-⨯+=即边际成本等于平均成本时平均成本最小. 4. 已知某厂生产Q 件产品的成本为C =25000+2000Q +1402Q (元). 问:(1) 要使平均成本最小,应生产多少件产品?(2) 若产品以每件5000元售出,要使利润最大,应生产多少件产品? 解: (1) 平均成本 250001()200040C Q Q Q =++ 边际成本1()200020C Q Q '=+. 当()()C Q C Q '=时,平均成本最小,由()()C Q C Q '=即2500011200020004020Q Q Q ++=+ 得1000Q =(负值不合题意已舍去). 所以要使平均成本最小,应生产1000件产品.(2)221()5000()500025000200040130002500040L Q Q C Q Q Q Q Q Q =-=---=-+-令 1()3000020L Q Q '=-+=, 得60000Q =(件) 所以应生产60000件产品.5. 某厂全年消耗(需求)某种钢材5170吨,每次订购费用为5700元,每吨钢材单价为2400元,每吨钢材一年的库存维护费用为钢材单价的13.2%,求: (1) 最优订购批量; (2) 最优批次; (3) 最优进货周期; (4) 最小总费用.解: 由题意 215170,5700,1,240013.2%316.8 R C T C ====⨯= 则(1)最优订购批量70*431.325q === (2)最优批次 5170*12*431.325R n q ==≈(次)(3)最优进货周期 36530.452*12T t n ===(天) (4)最小总费用*136643.9E ==≈(元)6. 用一块半径为R 的圆形铁皮,剪去一圆心角为α的扇形后,做成一个漏斗形容器,问α为何值时,容器的容积最大?解: 设漏斗的底面半径为r ,高为h ,为了计算方便令2ϕπα=-,则2,,2ππR r R r h ϕϕ====漏斗的容积2322123(83)πππV hr V ϕϕ==<<'=-令 0V '=得10ϕ=(舍之),2ϕ=,34222237),40,9πππV V ϕϕϕ''=-+-⎫''=-<⎪⎭故当ϕ=时漏斗得容积最大.由2πϕα=-得2π2πα==, 所以,当2πα=-时,容积最大. 7. 工厂生产出的酒可即刻卖出,售价为k ;也可窖藏一个时期后再以较高的价格卖出.设售价V 为时间t 的函数V = k (k >0)为常数.若贮存成本为零,年利率为r ,则应何时将酒售出方获得最大利润(按连续复利计算). 解: ()e rtrtA t k k -=⋅=令()0rt r A t k ⎫'-==⎪⎭得214t r = 所以,应窖藏214r 时以后售出可获得最大利润. 8. 若火车每小时所耗燃料费用与火车速度的三次方成正比,已知速度为20km/h ,每小时的燃料费用40元,其他费用每小时200元,求最经济的行驶速度. 解: 设火车每小时所耗燃料费为Q ,则 3Q k v = (k 为比例常数) 依题意得 34020k =⋅, 解得 1200k =, 又设火车行驶()km s 后,所耗费用为, 32200(200)()s E kv kv s v v=+⋅=+ 令 2200()0100v E s v'=-=, 得27.14v =≈ (km/h), 所以,最经济得行驶速度为27.14 km/h.习题 4-61. 讨论下列函数的凸性,并求曲线的拐点:(1) y =2x -3x ; (2) y = ln(1+2x ); (3) y = x e x; (4) y = 4(1)x ++e x; (5) y =2(3)x x +; (6) y=arctan e x. 解: (1)223,126,0.3令 得 y x x y x y x '=-''''=-==当13x <时,0y ''>; 当13x >时,0y ''<,且12()327f = 所以,曲线23y x x =-在1(,)3-∞内是下凸的,在1(,)3+∞内是上凸的,点12(,)327是曲线的拐点.(2) 222222222(1)222(1),1(1)(1)x x x x x y y x x x +-⋅--'''===+++, 令0y ''=得,121,1x x =-=,这两点将定义域(,)-∞+∞分成三个部分区间,列表考察各部分区间上二阶导数得符号.所以,曲线2l n (1)y x =+在(,1)-∞-及(1,)+∞内是上凸的,在(1,1)-内是下凸的,点(1,ln 2)±是曲线的拐点.(3) 324(1),12(1)0xxy x e y x e '''=++=++> 所以,曲线在定义域(,)-∞+∞内处处下凸,没有拐点.(4) 343212,(3)(3)x x y y x x --'''==++,令 0y ''=得6x = 当 6x <时,0y ''<,当6x >时,0y ''>;又2(6)27f =,函数的定义域为(,3)(3,)-∞--+∞ ;所以曲线在(,3),(3,6)-∞--内上凸,在(6,)+∞内下凸,点2(6,)27是拐点. (6)arctan 2arctan arctan arctan 2222221112(12)(1)(1)(1)x x x x y e x x x ey e e x x x '=⋅+-''=⋅-⋅=+++令 0y ''= 得 12x =当 12x <时,0y ''>,当12x >时,0y ''<,且 1arctan 21()2e f =,所以曲线在1(,)2-∞内向下凸,在1(,)2+∞内向上凸,点1arctan 21(,)2e是拐点. 2. 利用函数的凸性证明下列不等式:(1) e e 2x y +>2e x y+, x ≠y ;(2) x ln x +y ln y >(x +y )ln2x y +,x >0,y >0,x ≠y .证: (1) 令()e x f x =,则()e x f x '=,()0e xf x ''=>,所以函数()f x 的曲线在定义域(,)-∞+∞内是严格下凸的,由曲线下凸的定义有: ()(),()()22x y f x f y x y f x y ++∀≠<≠ 即 22e e ex y x y ++< 即2()2e e e x yx y x y ++>≠.(2) 令()ln f x x x =,则1()1ln ,()f x x f x x'''=+=当 0x >时,恒有()0f x >,所以()f x 的曲线在(0,)+∞内是严格下凸的,由曲线下凸的定义有, 0,0,,x y x y ∀>>≠有()()()22f x f y x y f ++>即ln ln ()ln222x x y x y x y+++> 即 ln ln ()ln 2x yx x y y x y ++>+.3. 当a ,b 为何值时,点(1,3)为曲线y =a 3x +b 2x 的拐点. 解: 因为32y ax bx =+是二阶可导的,所以在拐点处0y ''=,而232,62y a x b x y a x b'''=+=+ 所以 620a b += 又拐点(1,3)应是曲线上的点,所以3a b +=解方程6203a b a b +=⎧⎨+=⎩ 得 39,22a b =-=所以当39,22a b =-=时,点(1,3)为曲线32y ax bx =+的拐点. 4. 求下列曲线的渐近线:(1) y = ln x ; (2)y =22x -; (3) y = 23xx -; (4) y = 221x x -.解: (1) 0lim lim ln x x y x ++→→==-∞,所以ln y x =有垂直渐近线 0x =. 又 lim x y →+∞=+∞,但1ln lim lim lim 01x x x y xx y x x→+∞→+∞→+∞====,lim (0)x y x →+∞-⋅=∞,所以不存在水平或斜渐近线.(2) 220x x -=,所以有水平渐近线0y =,又2lim 0x x x y x -→∞→∞== ,所以没有斜渐近线,又函数22x y -=没有间断点,因而也没有垂直渐近线. (3) 221limlim 0331x x xxx x →∞→∞==--,所以有水平渐近线0y =,又函数23x y x ==-有两个间断点x x ==,且22,,3x x x xx x=∞=∞--所以有两条垂直渐近线x =x =又 21lim lim 3x x y x x →∞→∞==∞-,所以没有斜渐近线.(4) 2lim lim 21x x x y x →∞→∞==∞- ,所以没有水平渐近线,又 函数221x y x =-有间断点12x =,且212lim 21x x x →=∞-,所以有垂直渐近线12x =. 又 1limlim 212x x y x x x →∞→∞==- 2111l i m ()l i m ()l i m 22122(21)4x x x x x y x x x x →∞→∞→∞-=-==-- 所以有斜渐近线1124y x =+. 5.作出下列函数的图形: (1) f (x ) =21xx+; (2) ()2arctan f x x x =- (3) ()2,(0,)e xf x x x -=∈+∞. 解: (1) (i) 定义域为(,)-∞+∞.()()f x f x -=- ,故曲线关于原点对称.(ii) 21lim limlim 012x x x x y x x→∞→∞→∞===+ ,故曲线有渐近线0y =.(iii) 222222121,(1)(1)x x x x y x x +-⋅-'==++ 22223322423232(1)(1)2(1)222442(3)(1)(1)(1)x x x x x x x x x x x y x x x -+--⋅+⋅---+-''===+++,令0y '=即210x -=得驻点1x =±,又使0y ''=的点为0,x =.图4-1(2) (i) 定义域为(,)-∞+∞.又 ()arctan y x x x y -=-+=-,故为奇函数.(ii) 2arctan lim ,limlim (1)1,x x x y x y x x→±∞→±∞→±∞=∞=-=πlim ()lim (2arctan )(2)()π2x x y x x →±∞→±∞-=-=-±= 所以有渐近线πy x = .(iii) 222211,11x y x x -'=-=++ 2222222(1)(1)24,(1)(1)x x x x x y x x +--⋅''==++令 0y '=得驻点1x =±,又使0y ''=的点为0x =. 列表如下:图4-2(3) (i) 定义域为(,)-∞+∞,且()((,))f x C ∈-∞+∞. (ii) ()2(1),()2(2),e e xxf x x f x x --'''=-=-由()0f x '=得1x =,由()0f x ''=得2x =,把定义域分为三个区间 (,1),(1,2),(2,);-∞+∞(iv) lim ()0x f x →+∞=,故曲线()y f x =有渐近线0y =,lim ()x f x →+∞=-∞.(v) 补充点(0,0)并连点绘图,如图所示:图4-3。
第四章 扩展原理

扩展原理 II
f ( A )
f ( A) ~
[0,1]
扩展原理 I
f ( A) f (
~
[0,1]
H A( ))
第四章
扩展原理
(2)
设
B
~
F
(Y
),
B
•
HB()
B
f 1(B ) f 1(HB ( )) f 1(B )
•
f 1(B ) f 1( HB ( )) f 1(B ), [0,1]
O
A
x
f ( A) { yY x A, 使得f ( x) y}
称f ( A)为A的像.
第四章
扩展原理
B P(Y ),令 f 1(B) {x X y B, 使得y f ( x)}
称f 1(B)是B的逆像. y
f
B
O
x
f 1(B)
第四章
扩展原理
二、扩展原理
集合套的观点
设映射f : X Y , x f ( x). A F ( X ). ~ [0,1], A P( X ), f ( A ) P(Y ).
扩展原理
扩展原理 III
设映射f : X Y , x f ( x)
(1)若 A F ( X ), A H A( ) A , [0,1],则
~
•
f ( A)
~
[0,1]
f (H A( ))
(2)若 B F (Y ), B HB ( ) B , [0,1],则
~
•
f 1(B)
~
f
1 ( B ) ~
f
[0,1]
1 (B
)
第四章
扩展原理
定理1 设映射f : X Y , x f ( x)
高等教育自学考试高等数学(一)第 四 章 微分中值定理和导数的应用

第四章微分中值定理和导数的应用一、考核要求Ⅰ 知道罗尔定理成立的条件和结论,知道拉格朗日中值定理成立的条件和结论。
Ⅱ 能识别各种类型的未定式,并会用洛必达法则求它们的极限。
Ⅲ 会判别函数的单调性,会用单调性求函数的单调区间,并会利用函数的单调性证明简单的不等式。
Ⅳ 会求函数的极值。
Ⅴ 会求出数在闭区间上的最值,并会求简单应用问题的最值。
Ⅵ 会判断曲线的凹凸性,会求曲线的凹凸区间和拐点。
Ⅶ 会求曲线的水平渐近线和垂直渐近线。
二、基本概念、主要定理和公式、典型例题Ⅰ 微分中值定理今后,如果函数f(x)在某一点x0处的导数值=0,就说这一点是驻点,因此罗尔中值定理的结论也可以说f(x)在(a,b)内至少有一个驻点。
从y=f(x)的几何图形(见下图)可以看出,若y=f(x)满足罗尔中值的条件,则它在(a,b)内至少有一点,其切线是水平的,根据导数的几何意义知道,该点的斜率=k=0。
从函数y= f(x)的图形看(见下图),连接y= f(x)在[a,b]上的图形的端点A与B,则线段AB的斜率为:将AB平行移动至某处,当AB的平行线与曲线y=f(x)相切时,若切点为x=c,则根据导数的几何意义知:或写作故从几何图形看,拉格朗日定理是成立的。
典型例题例一:(单选)下列函数在相应区间上满足罗尔中值定理的条件的函数是()① ,[-1,1];② ,[-1,1];③ ,[1, 2];④ ,[-1,1]。
解:①在[-1,1]上处处有意义,没有无意义的点,因为他没有分母,所以在b区间[-1,1]上处处连续满足第一个条件。
又f(-1)=1,f(1)=1,所以在端点上函数值相等,满足第三个条件因此这函数在开间内不是处处可导,只少在0这一点不可导的,因此不满足第二个条件。
② 在x=o处不可导,∴也不满足第二个条件。
③ f(1)=1,f(2)=4,∴在[1,2]上满足第三个条件。
④ ,处处可导且处处连续,f(-1)=1, f(1)=1。
2021年高中化学必修一第四章《物质结构元素周期律》经典练习题(答案解析)(3)

一、选择题1.下列有关化学用语表达正确的是A.CH2=C(CH3)CH=CH2系统命名为:2-甲基-1,4-丁二烯B.二氧化碳的结构式:O=C=OUC.中子数为146、质子数为92的铀(U)原子:14692D.氟原子的结构示意图:2.下列不能用于鉴别亚硝酸钠和食盐的试剂是A.酸化的碘化钾溶液和淀粉B.酸化的FeCl2溶液C.酸性高锰酸钾溶液D.硝酸银溶液3.五种主族元素X、Y、Z、M和N在周期表中的位置如图所示。
下列说法正确的是XYZ M N……A.M的原子半径比N小B.Y和Z既可形成Z2Y,也可形成Z2Y2 C.X2M的热稳定性比X2Y强D.M和N的氧化物的水化物均为强酸4.某种化合物的结构如图所示,其中 X、Y、Z、Q、W 为原子序数依次增大的五种短周期元素,Q 核外最外层电子数与 Y 核外电子总数相同,X 的原子半径是元素周期表中最小的。
下列叙述正确的是A.该化合物中与 Y 单键相连的 Q 满足 8 电子稳定结构B.WX 的水溶液呈中性C.元素非金属性的顺序为 Y>Z>QD.Z 的最高价氧化物对应的水化物是一元弱酸5.短周期主族元素A、B、C、D、E的原子序数依次增大,其中A、D同主族,B、C、E 分处三个连续的主族,且最外层电子数依次增加。
C是地壳中含量最多的元素,C和D可形成两种化合物(阳离子与阴离子个数比均为2:1),A和D也可以形成离子化合物。
下列说法错误的是A.原子半径:D>E>B>CB.A与其他四种元素形成的二元化合物中其化合价均为+1C.最高价含氧酸的酸性:E>BD .化合物DCA 、DEC 的水溶液均显碱性 6.下列离子方程式书写正确的是A .向碳酸氢钠溶液中加入足量氢氧化钡溶液:2+-332HCO + Ba + OH = BaCO +H O -↓B .过量二氧化碳通入次氯酸钠溶液中:-2-223CO +H O+2ClO =2HClO+COC .向硫酸铝溶液中加入过量氨水:3+-+32242Al +4NH H O=AlO +4NH +2H OD .向2FeI 溶液中通入足量氯气:2+-3+-222Fe +2I +2Cl =I +2Fe +4Cl7.过氧化钠常用作供氧剂:2Na 2O 2+2H 2O=4NaOH+O 2↑。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
被动站、从设备
第四章 常见的工业控制网络技术 (3) PROFIBUS
PROFIBUS - DP 的基本功能 1
PROFIBUS_DP 用于设备级的高速数据传送,中央 控制器通过高速串行通信线同分散的现场设备(如 I/O、 驱动器、阀门等)进行通信,多数数据交换是周期性的,除 此之外,智能化现场设备还需要非周期通信,以进行配置、 诊断和报警处理。 中央控制器周期性地读取从设备的输入信息并周期地向 从设备发送输出信息,总线循环时间必须要比中央控制器的 程序循环时间短。除周期性用户数据传输外, PROFIBUS_DP 还提供了强有力的诊断、配置功能,数 据通信是由主机和从机进行监控的。
第四章 常见的工业控制网络技术 (3) PROFIBUS
总线存取协议
混合总线访问协议 主站间的逻辑令牌环 主从站间的主从协议 主站 主动站在一个限定时间内 (Token Hold Time) 对总线有控制权 从站 从站只是响应一个主站的请求, 它们对总线没有控制权
主动站、主设备
PC
PROFIBUS
第四章 常见的工业控制网络技术 (3) PROFIBUS
引
言
适用于:
车间级数据通讯
PROCESS FIELD BUS
现场级设备通讯
PROCESS FIELD BUS
第四章 常见的工业控制网络技术 (3) PROFIBUS
PROFIBUS 三层协议
EN 50170 Volume 2
通用目的自动化 制造业自动化 过程自动化
第四章 常见的工业控制网络技术 (3) PROFIBUS
物
总线连接:
理
层(3)
PROFIBUS_DP 规定电缆接口采用 9 针 D 型连接器(DB9),连 接器的机械和电气特性 引脚 RS-485 信号名称 含 义 符合 IEC 807-3 的规 1 屏 蔽 屏蔽,保护地 定,DB9 连接器的插 2 - 24 V 输出电压 N24V 座与设备相连接,插头 3 B / B’ RXD/TXD-P 数据 P (收 / 发) 与总线电缆相连接。连 4 CNTR - P 控制 P 接器引脚分配如右表所 5 C / C’ DGND 数据地 示: 6 VP 正电源电压 7 + 24 V 输出电压 P24V 8 A / A’ RXD/TXD-N 数据 N (收 / 发) 9 CNTR - N 控制 N
第四章 常见的工业控制网络技术 (3) PROFIBUS
PROFIBUS – DP 的传输特点
高速(H2), RS 485 屏蔽双绞线,或光缆 依据 RS 485,异步 NRZ 传输 波特率从 9.6 kBit/s 到 12 Mbps,可选。 采用光纤技术的情况下可实现 100 Mbps 的环网。 双绞屏蔽电缆 每段 32 个站,最多允许 127 个站; 有中继器距离可延长到 90 公里。 总线存取 主站间令牌传递,主站与从站间数据传递; 支持单主站或多主站系统。 数据帧长度 短帧 1 字节,普通帧 3 ~ 255 字节。 数据传输服务 循环的和非循环的数据传输。
而且可传送事件。 PROFIBUS_FMS 的应用层包括两个
部分:现场总线信息规范(FMS)描述通信对象和服务; 低层接口(LLI)用于将 FMS 适配到第 2 层。
第四章 常见的工业控制网络技术 (3) PROFIBUS
PROFIBUS_FMS (2)
PROFIBUS_FMS 行规:
PROFIBUS_FMS 提供了广泛的功能以满足普遍的应用。 FMS 行规作了如下定义,括号中的数字为 PROFIBUS 用户组织提 供的文件号: 控制器间通信(3.002):
这一行规定义了用于 PLC 控制之间通信的 FMS 服务。根据控制器 的等级对每个PLC 必须支持的服务、参数和数据类型作了规定。
楼宇自动化行规(3.011 ):
此行规用于提供特定的分类和服务作为楼宇自动化的公共基础。行规 描述了使用 FMS 的楼宇自动化系统如何进行监控、开环和闭环控制、操 作员控制、报警处理和档案管理。
PROFIBUS_PA
低速 (H1), IEC 61158-2
同步 Manchester 编码, 31.25 kBit/s
本质安全 (可选) 和总线供电 (可选)
屏蔽或非屏蔽的双绞电缆
每段距离达 1900 米,用中继器可延长到 10 公里
最多 127 个站, 每站 10 - 32 个设备(依赖于 EX - 类型和供电消耗)
PROFIBUS-FMS
RS 485 / FO 通用
-大范围的应用 -多主通信
PROFIBUS-DP PROFIBUS-PA
RS 485 / FO 快速
-即插即用 - 高 效、廉 价
IEC 61158-2 面向应用
-总线供电 -本质安全
第四章 常见的工业控制网络技术 (3) PROFIBUS
基 本 特 征(1)
第四章 常见的工业控制网络技术 (3) PROFIBUS
PROFIBUS_PA
第四章 常见的工业控制网络技术 (3) PROFIBUS
PROFIBUS_FMS (1)
PROFIBUS_FMS 的设计旨在解决车间一级的数据
通信问题,在这一级可编程控制器主要是互相通信。在此 领域内,高级通信功能比快速系统反应时间更重要。 PROFIBUS_FMS 的应用层提供用户可用的通信服 务,有了这些服务才可能存取变量、传送程序并控制执行,
第四章 常见的工业控制网络技术 (3) PROFIBUS
PROFIBUS - DP 的扩展功能
PROFIBUS_DP 扩展功能允许非循环的读写功能并能中断并行于
循环数据传输的应答。另外,对从站参数和测量值的非循环存取可用于某 些诊断或操作员控制站(第二类主站,DPM2)。有了这些扩展功能,
PROFIBUS_DP 可满足某些复杂设备的要求,例如过程自动化的现场
注: 两根 PROFIBUS 数据通信线也常称为 A 线、B 线: A RXD/TXD-N B RXD/TXD-P
第四章 常见的工业控制网络技术 (3) PROFIBUS
物
总线导线:
理
层(2)
PROFIBUS_DP 的物理层支持屏蔽双绞线和光纤两种传输介质。 这里只介绍应用最为广泛的以屏蔽双绞线为传输介质的物理层规范,此 时的物理层规范与 EIA RS-485 兼容。 选择屏蔽双绞线电缆时,可以参照 EIA RS-485 标准。另外,在 干扰不严重的情况下,也可以使用非屏蔽的双绞线电缆。 PROFIBUS_DP 最大允许的总线长度(在采用PROFIBUS 标 准电缆类型 A 时),称为段长度,其值取决于传输速率。 速率(kbps) 段长度(米) 9.6 1200 19.2 1200 93.75 1200 187.5 1000 500 400 1500 200 12000 100
第四章 常见的工业控制网络技术 (3) PROFIBUS
工业网络
第四章 常见的工业网络技术(3)
PROFIBUS
第四章 常见的工业控制网络技术 (3) PROFIBUS
第三部分 PROFIBUS
一、PROFIBUS 概述 概述 二、PROFIBUS 通信协议 三、PROFIBUS 实现的可能性 四、PROFIBUS 产品的开发 本 章 小 结
第四章 常见的工业控制网络技术 (3) PROFIBUS
PROFIBUS - DP 的基本功能 3
设备类型:
第二类 DP 主站(DPM2):
可编程、可组态、可诊断的设备 第一类 DP 主站(DPM1): 中央可编程控制器,如 PLC、PC 等 DP 从站:
带二进制或模拟输入输出的驱动器、阀门、传感器等
第四章 常见的工业控制网络技术 (3) PROFIBUS
PROFIBUS 与 OSI 参考模型
DP 设备行规 用户层 DP 基本功能和扩展功能
DP 用户接口 (直接数据链路映射程序 DDLM)
第3 ~ 7 层 第2层 数据链路层 第1层 物理层 空
现场总线数据链路层 FDL
物理层 PHY FMA 1/2
第四章 常见的工业控制网络技术 (3) PROFIBUS
PROFIBUS - DP 的基本功能 5
运行模式:
PROFIBUS_DP 规范了对系统行为的详细描述以保证设备的互换
性,系统行为主要取决于 DPM1 的操作状态,这些状态由本地或总体的 配置设备所控制,主要有以下四种状态: 运行:第一类主站与指定的 DP 从站进行用户数据交换。 清除:第一类主站可对 DP 从站设置参数,检查通信接口配置并读取 这些 DP 从站用户的数据。 停止:只能进行主-主数据传送,主站不能轮询 DP 从站。 离线:停止与所有主站和从站的通信,FDL 从令牌环中退出。用户 接口等待一个启动信号。
低压开关设备(3.032 ):
这是一个以行业为主的 FMS 应用行规,规定了通过 FMS 通信过程 中的低压开关设备的应用行为。
第四章 常见的工业控制网络技术 (3) PROFIBUS
第三部分 PROFIBUS
一、PROFIBUS 概述 二、PROFIBUS 通信协议 三、PROFIBUS 实现的可能性 四、PROFIBUS 产品的开发 本 章 小 结 通信协议
第四章 常见的工业控制网络技术 (3) PROFIBUS
