求数轴表示的不等式(组)的解集
在数轴上表示一元一次不等式的解集

解
解得
y-1 ≤ 0 y≤1
-1 0 1 2 3 4 5
(4) y与5的差大于-2;
解
y-5 > -2
解得 y > 3
-1 0 1 2 3 4 5
求不等式
2+ x 2
≥
2x +1 3
的正整数解.
分析 首先求出不等式的解集.然后求出正整数解.
解 去分母,得 6+3x≥4x+2. 移项,合并同类项,得 x≤4. 正整数解为 1,2,3,4.
当
-1 0 1 x2 3 x 4 5 6
+
≤
由图可知,满足条2件的正整6数有 1,2,3,4,5,6.
≥
时
0
,
代
练习
1. 解下列不等式,并把它们的解集在数轴上表 示出来:
(1) 4x -3 < 2x+7 ;
(2)
x
2
33 x 45
.
解 (1) 原不等式为 4x -3 < 2x+7
移项,得 4x-2x < 3+7
解不等式
2x -1
≥
10x+1 ,并把解集在数轴上表示出来.
6
解 去分母,得 6(2x-1)≥10x+1.
去括号,移项,合并同类项得 2x≥7.
解得
x7
2
这个不等式的解集在数轴上表示如下图:
-2 -1 0 1 2 3 7 4
2
4.3 一元一次不等式的解法 第2课时 在数轴上表示 一元一次不等式的解集
学习目标
1 掌握用数轴表示一元一次不等式的解集的方法。 2会求不等式的特殊解。
一个不等式的解集常常可以借助数
不等式组及其解集

专题19 不等式组及其解集1.一元一次不等式组:把几个含有相同未知数的一元一次不等式合起来,组成一个一元一次不等式组.2.不等式组的解集:一般地,几个不等式的解集的公共部分,叫作由它们所组成的不 等式组的解集,解不等式组就是求它的解集. 不等式组(a <b )数轴表示 解集 口诀 同大取大 同小取小 大小小大 中间找 无解 大大小小 无解了当不等式带有“≤”或“≥”时,上面的口诀依然适用,如不等式组的解集为.4.解决和不等式组解集有关的问题时,注意利用数轴这一数学工具,过程直观明了.典例精析例1 解不等式组 并将解集在数轴上表示出来.【分析】解一元一次不等式组,先求出每个不等式的解集,然后利用数轴求出这些解集的公共部分即为不等式组的解集.【解】解不等式①,得x>-2解不等式②,得x≤2把不等式①和②的解集在数轴上表示出来,如图19-1所示.∴不等式的解集为-2<x ≤2【点评】熟练解出不等式,并准确地在数轴上表示出来,从而在数轴上找到不等式解集的公共部分即为不等式组的解集.拓展与变式1 解不等式组并写出它所有的整数解.,x a x b<⎧⎨>⎩x b >,x a x b <⎧⎨<⎩x a <,x a x b >⎧⎨<⎩a xb <<,x a x b <⎧⎨>⎩23x x ≤⎧⎨<⎩2x ≤22,11,39x x x x >-⎧⎪-+⎨≤⎪⎩①②()41710,85,3x x x x +≤+⎧⎪⎨--<⎪⎩①②拓展与变式2 不等式组的所有整数解的和是 . 拓展与变式3 若|x+1|=x+1,|2x-7|=7-2x ,则满足条件的所有非负整数x 有 .【反思】根据题意列出不等式(组),解出不等式组从而找出符合条件的解,注意非负整数即自然数,也就是0和正整数.例2 如果a>2,那么不等式组的解集为 ,的解集为 . 【分析】把每个不等式的解集表示在数轴上(或用口诀),结合数轴找不等式组的解集.【解】把不等式的解集表示在数轴上,不等式组表示在数轴上如图19-2所示,可知解集为x >a .不等式组表示在数轴上如图19-3所示, 可知解集为2<x ≤a .【点评】利用数轴上的数越往右越大,在数轴上找好数约位置,结合数轴找到不拓展与变式4 (1)已知关于x 的不等式组的解集为x ≥2,则a 的取值范围是 .(2)已知关于x 的不等式组有解,则a 的取值范围是 . 拓展与变式5 已知关于x 的不等式组的解集为0<x <2,求m -n 的值.拓展与变式6 解关于x 的不等式组34125x +-≤<,2x a x >⎧⎨>⎩,2x a x ≤⎧⎨>⎩,2x a x >⎧⎨>⎩,2x a x ≤⎧⎨>⎩,2x a x >⎧⎨≥⎩,2x a x <⎧⎨>⎩2,11x m n x m +>+⎧⎨-<-⎩①②0,12.23x a x x x -≥⎧⎪-+⎨+>⎪⎩①②拓展与变式7 已知关于x 的不等式组的整数共有3个,求a 的取值范围.拓展与变式8 定义新运算:对干任意实数a ,b 都有a #b =ab -a -b +1,等式右边是通常的加法减法及乘法运算.例如:2#4=2×4-2-4+1=3.请根据上述知识解决问题:若3#x 的值大于4而不大于m 时,恰有两个整数解,求m 的取值范围.【反思】解决含参数的不等式组问题,数形结合必不可少,同时要注意等号能否取到,可将取等号的值代入原题中检验.专题突破1.不等式组的整数解有( ). A. 1个 B. 2个 C. 3个 D. 4个0,321x a x -≥⎧⎨-≥-⎩①②24,241x x x x ≤+⎧⎨+<-⎩2.不等式组的解集是x>1,则m 的取值范围是 .3.解不等式组并将不等式组的解集在数轴上表示出来.4.某旅行社某天有空房10间,当天接待了一个旅行团,当每个房间只住3人时,有一个房间的住宿情况是不满也不空.若旅行团的人数为偶数,问:旅行团共有多少人?5.关于x 的不等式组有2个整数解,求a 的取值范围.551,1x x x m +<+⎧⎨-≥⎩()5623,3513,44x x x x -≤+⎧⎪⎨-<-⎪⎩①②()2331,324x x x x a <-+⎧⎪⎨+>+⎪⎩①②。
一元一次不等式组的解法经典例题透析
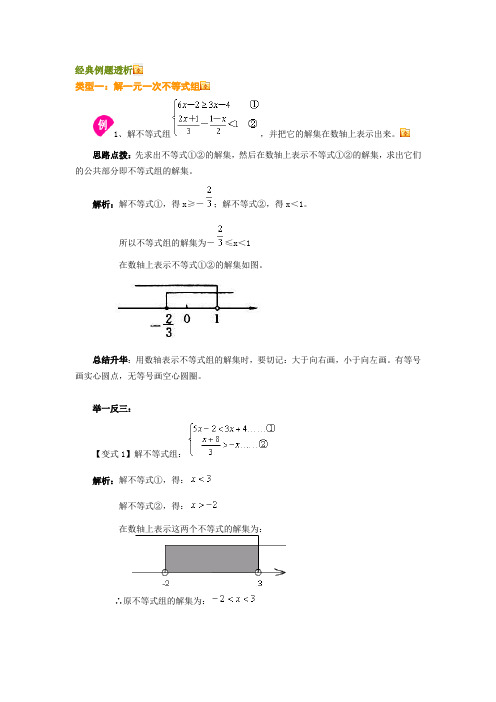
经典例题透析类型一:解一元一次不等式组1、解不等式组,并把它的解集在数轴上表示出来。
思路点拨:先求出不等式①②的解集,然后在数轴上表示不等式①②的解集,求出它们的公共部分即不等式组的解集。
解析:解不等式①,得x≥-;解不等式②,得x<1。
所以不等式组的解集为-≤x<1在数轴上表示不等式①②的解集如图。
总结升华:用数轴表示不等式组的解集时,要切记:大于向右画,小于向左画。
有等号画实心圆点,无等号画空心圆圈。
举一反三:【变式1】解不等式组:解析:解不等式①,得:解不等式②,得:在数轴上表示这两个不等式的解集为:∴原不等式组的解集为:【变式2】解不等式组:思路点拨:在理解一元一次不等式组时要注意以下两点:(1)不等式组里不等式的个数并未规定;(2)在同一不等式组里的未知数必须是同一个.(3)注意在数轴表示解集时“空心点”与“实心点”的区别解法一:解不等式①,得:解不等式②,得:解不等式③,得:在数轴上表示这三个不等式的解集为:∴原不等式组的解集为:解法二:解不等式②,得:解不等式③,得:由与得:再与求公共解集得:.【变式3】解不等式组:解析:解不等式①得:x>-2解不等式②得:x<-7∴不等式组的解集为无解【变式4】解不等式:-1<≤5思路点拨:(1)把连写不等式转化为不等式组求解;(2)根据不等式的性质,直接求出连写不等式的解集。
解法1:原不等式可化为下面的不等式组解不等式①,得x>-1,解不等式②,得x≤8所以不等式组的解集为-1<x≤8。
即原不等式的解集为-1<x≤8 解法2:-1<≤5,-3<2x-1≤15,-2<2x≤16,-1<x≤8。
所以原不等式的解集为-1<x≤8总结升华:对于连写形式的不等式可以化成不等式组来求解,而对于只有中间部分含有未知数的连写形式的不等式也可以按照解不等式的步骤求解,如解法2.【变式5】求不等式组的整数解。
思路点拨:按照不等式组的解法,先求出每个不等式的解集,在数轴上表示出各个不等式的解集,取其公共部分得到不等式的解集,再在不等式组的解集内求出符合要求的整数解。
如何确定不等式组的解集
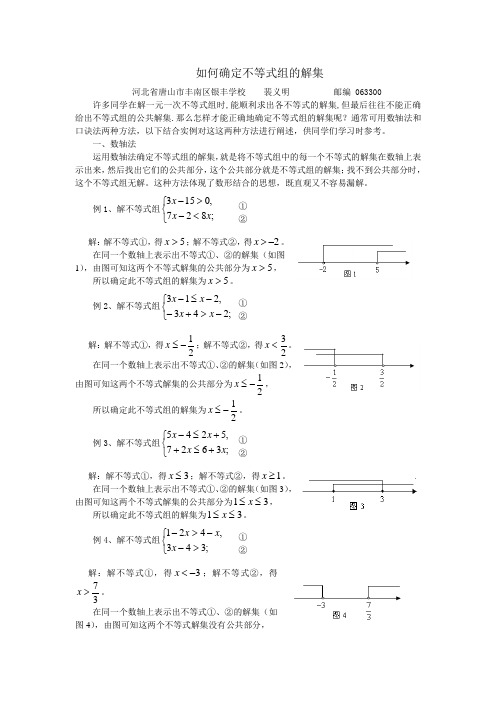
如何确定不等式组的解集河北省唐山市丰南区银丰学校 裴义明 邮编 063300许多同学在解一元一次不等式组时,能顺利求出各不等式的解集,但最后往往不能正确给出不等式组的公共解集.那么怎样才能正确地确定不等式组的解集呢?通常可用数轴法和口诀法两种方法,以下结合实例对这这两种方法进行阐述,供同学们学习时参考。
一、数轴法运用数轴法确定不等式组的解集,就是将不等式组中的每一个不等式的解集在数轴上表示出来,然后找出它们的公共部分,这个公共部分就是不等式组的解集;找不到公共部分时,这个不等式组无解。
这种方法体现了数形结合的思想,既直观又不容易漏解。
例1、解不等式组⎩⎨⎧<->-;827,0153x x x 解:解不等式①,得5>x ;解不等式②,得2->x 。
在同一个数轴上表示出不等式①、②的解集(如图1),由图可知这两个不等式解集的公共部分为5>x ,所以确定此不等式组的解集为5>x 。
例2、解不等式组⎩⎨⎧->+--≤-;243,213x x x x 解:解不等式①,得21-≤x ;解不等式②,得23<x 。
在同一个数轴上表示出不等式①、②的解集(如图2),由图可知这两个不等式解集的公共部分为21-≤x , 所以确定此不等式组的解集为21-≤x 。
例3、解不等式组⎩⎨⎧+≤++≤-;3627,5245x x x x解:解不等式①,得3≤x ;解不等式②,得1≥x 。
在同一个数轴上表示出不等式①、②的解集(如图3),由图可知这两个不等式解集的公共部分为31≤≤x ,所以确定此不等式组的解集为31≤≤x 。
例4、解不等式组⎩⎨⎧>-->-;343,421x x x解:解不等式①,得3-<x ;解不等式②,得37>x 。
在同一个数轴上表示出不等式①、②的解集(如图4),由图可知这两个不等式解集没有公共部分,① ②①②① ②①②所以确定此不等式组无解。
中考数学在数轴上表示不等式(组)的解集专题练习(含解析)

2019中考数学-在数轴上表示不等式(组)的解集专题练习(含解析)一、单选题1.把不等式组的解集表示在数轴上,下列选项正确的是()A.B.C. D.2.以数轴上的原点O为圆心,3为半径的扇形中,圆心角∠AOB=90°,另一个扇形是以点P为圆心,5为半径,圆心角∠CPD=60°,点P在数轴上表示实数a,如图.如果两个扇形的圆弧部分((AB和CD))相交,那么实数a的取值范围是()A. -5≤a≤-1B. -4≤a≤-2C. -3≤a≤-3D. -2≤a≤-53.一次函数y=ax+3与y=bx﹣1的图象如图所示,其交点B(﹣3,m),则不等式ax﹣bx+3>﹣1的解集表示在数轴上正确的是()A. B.C. D.4.下列哪个不等式组的解集在数轴上的表示如图所示( )A.B.C.D.5.2x﹣4≥0的解集在数轴上表示正确的是().A.B.C.D.6.用不等式表示图中的解集,其中正确的是( )A. x≥-2B. x>-2C. x<-2D. x≤-27.不等式2x+3≥1的解集在数轴上表示为()A.B.C.D.8.不等式组中的两个不等式的解集在同一个数轴上表示正确的是()A.B.C.D.9.不等式组的解集在数轴上表示正确的是()A.B.C. D.10.如图,天平右盘中的每个砝码的质量都是1克,则物体A的质量m克的取值范围表示在数轴上为()A.B.C.D.11.不等式组的解集在数轴上表示正确的是()A.B.C.D.12.不等式的解集在数轴上表示如右图,则其解集是()A. x≥2B. x>-2C. x≥-2D. x≤-2二、填空题13.若关于x的不等式组的解表示在数轴上如图所示,则这个不等式组的解________14.数轴上所表示的关于x的不等式组的解集为________15.若关于x的一元一次不等式组有2个负整数解,则a的取值范围是________.16.解不等式组:,并把解集在数轴上表示出来________.三、计算题17.解不等式组:,并把解集在数轴上表示出来.18.解下列不等式组;并把解集在数轴上表示.四、综合题19.综合题。
在数轴上表示不等式的解

索罗学院
在数轴上表示不等式的解
疑惑:不等式的解在数轴上的表示方法
解析:不等式的解集指的是一个范围,题目经常要求我们在数轴上表示不等式的解集,在数轴上表示时需要注意:如果带有等号,也就是取到了端点,此时在端点处需标上实心圆,反之不带等号则在端点处标记空心圆。
几种常见情况如下:1、不等式解集表示单方向时,在数轴上的表示方法(1)x>3 (2)x≤-1 2、不等式解集表示一个公共区域或多个区域时,在数轴上表示方法 (1)-1≤x<3 (2)x>2 且x≤-2
结论:当不等式的解集取到端点时,需要在端点处标记实心圆,反之没有取到端点,则标记空心圆。
本文由索罗学院整理索罗学院是一个免费的中小学生学习网,上面有大量免费学习视频,欢迎大家前往观看!。
第8讲用数轴表示不等式的解集及一元一次不等式组(教师版)

第8讲用数轴表示不等式的解集及一元一次不等式组知识精要一、不等式的解集1、不等式解的全体叫做不等式的解集。
(注:一般情况下一元一次方程的解只有一个,一元一次不等式的解可以有无数个。
)2、不等式的解集可以再数轴上直观的表示出来。
如:在数轴上表示大于3的数的点应该数3所对应点的左边还是右边?(右边)因此我们可以在数轴上把x>3直观地表示出来.画图时要注意方向(向右)和端点(不包括数3,在对应点画空心圆圈).如图所示:同样,如果某个不等式的解集为x≤-2,那么它表示x取那些数?此时在作x≤-2的数轴表示时,要包括-2的对应点,因而在该点处应画实心圆点.如图所示:引导学生总结出在数轴上表示不等式解集的要点:小于向左画,大于向右画;无等号画空心圆圈,有等号画实心圆点。
2、一元一次不等式组1、有几个含有同一个未知数的一次不等式组成的不等式组,叫做一元一次不等式组。
2、不等式组中所有不等式的解集的公共部分叫做这个不等式组的解集。
3、求不等式组的解集的过程叫做解不等式组。
4、解一元一次不等式组的一般步骤是:(1)求出不等式组中各个不等式的解集;(2)在数轴上表示各个不等式的解集;(3)确定各个不等式解集的公共部分,就得到这个不等式组的解集。
【典型例题】例1. 解不等式3(1)5182x x x +-+>-【思路点拨】不等式中含有分母,应先根据不等式的基本性质2去掉分母,再作其他变形.去分母时,不要忘记给分子加括号.【答案与解析】解:去分母,得8x+3(x+1)>8-4(x -5), 去括号,得8x+3x+3>8-4x+20, 移项,得8x+3x+4x >8+20-3,合并同类项,得15x >25,系数化为1.得.53x >∴不等式的解集为.53x >【总结升华】解一元一次不等式与解一元一次方程的步骤异同见下表:ax =bax >bax <b解:当a ≠0时,;b x a=当a =0,b ≠0时,无解;当a =0,b =0时,x为任意有理数.解:当a >0时,;b x a>当a <0时,;b x a<当a =0,b ≥0时,无解;当a =0,b <0时,x 为任意有理数.解:当a >0时,;b x a<当a <0时,;b xa>当a =0,b ≤0时,无解;当a =0,b >0时,x 为任意有理数.【变式】(湖南益阳)解不等式,并把解集在数轴上表示出来.5113x x -->解:去分母得5x -1-3x >3,移项、合并同类项,得2x >4, 系数化为1,得x >2,解集在数轴上的表示如图所示.例2.某市居民用电的电价实行阶梯收费,收费标准如下表:一户居民每月用电量x (单位:度)电费价格(单位:元/度)0<x≤200a 200<x≤400b x >4000.92(1)已知李叔家四月份用电286度,缴纳电费178.76元;五月份用电316度,缴纳电费198.56元,请你根据以上数据,求出表格中a ,b 的值.(2)六月份是用电高峰期,李叔计划六月份电费支出不超过300元,那么李叔家六月份最多可用电多少度?【思路点拨】(1)根据题意即可得到方程组,然后解此方程组即可求得答案;(2)根据题意列不等式,解不等式.【答案与解析】解:(1)根据题意得:,解得:.(2)设李叔家六月份最多可用电x 度,根据题意得:200×0.61+200×0.66+0.92(x﹣400)≤300,解得:x≤450.答:李叔家六月份最多可用电450度.【总结升华】考查了一元一次方程组与一元一次不等式的应用.注意根据题意得到等量关系是关键.例3. 解不等式组: ,并求出正整数解。
不等式的解集

第三节不等式的解集—目标导引1.理解不等式的解与解集的意义.2.掌握不等式的解集的数轴表示.不等式的解集—内容全解1、不等式的解能使不等式成立的未知数的值叫做不等式的解.[例1]x=3,6,9中,哪一个是不等式2x-2.5≥15的解?解:把x=3代入不等式2x-2.5≥15中2×3-2.5≥15,6-2.5≥15,3.5≥15显然不成立.∴x=3就不是此不等式的解.把x=6代入得,2×6-2.5≥15,12-2.5≥15,9.5≥15 不成立.∴x=6也不是此不等式的解.把x=9代入得2×9-2.5≥15,18-2.5≥15,15.5≥15∴x=9是不等式2x-2.5≥15的一个解,就此问题继续探索一下,2x-2.5≥15的解是不是就是这一个x=9呢?答案显然不是,由此我们得到:2.不等式的解集定义一个含有未知数的不等式的所有解,组成这个不等式的解集.3.不等式的解与解集的区别解是一个或几个未知数的值,解集是所有的解组成的.第三课时●课题§1.3 不等式的解集●教学目标(一)教学知识点1.能够根据具体问题中的大小关系了解不等式的意义.2.理解不等式的解、不等式的解集、解不等式这些概念的含义.3.会在数轴上表示不等式的解集.(二)能力训练要求1.培养学生从现实生活中发现并提出简单的数学问题的能力.2.经历求不等式的解集的过程,发展学生的创新意识.(三)情感与价值观要求从实际问题抽象为数学模型,让学生认识数学与人类生活的密切联系及对人类历史发展的作用,通过探索求不等式的解集的过程,体验数学活动充满着探索与创造.●教学重点1.理解不等式中的有关概念.2.探索不等式的解集并能在数轴上表示出来.●教学难点探索不等式的解集并能在数轴上表示出来.●教学方法引导学生探索学习法.●教具准备投影片一张记作(§1.3 A)●教学过程Ⅰ.创设问题情境,引入新课[师]上节课,我们对照等式的性质类比地推导出了不等式的基本性质,并且讨论了它们的异同点.下面我找一位同学简单地回顾一下不等式的基本性质.[生]不等式的基本性质1:不等式的两边都加上(或减去)同一个整式,不等号的方向不变.不等式的基本性质2:不等式的两边都乘以(或除以)同一个正数,不等号的方向不变.不等式的基本性质3:不等式的两边都乘以(或除以)同一个负数,不等号的方向改变.[师]很好.在学习了等式的基本性质后,我们利用等式的基本性质学习了一元一次方程,知道了方程的解、解方程等概念,大家还记得这些概念吗?[生]记得.能够使方程两边的值相等的未知数的值就是方程的解.求方程的解的过程,叫做解方程.[师]非常好.上节课我们用类推的方法,仿照等式的基本性质推导出了不等式的基本性质,能不能按此方法推导出不等式的解和解不等式呢?本节课我们就来试一试.Ⅱ.新课讲授1.现实生活中的不等式.燃放某种礼花弹时,为了确保安全,人在点燃导火线后要在燃放前转移到10 m以外的安全区域.已知导火线的燃烧速度为以0.02 m/s,人离开的速度为4 m/s,那么导火线的长度应为多少厘米?[师]分析:人转移到安全区域需要的时间最少为410秒,导火线燃烧的时间为10002.0⨯x 秒,要使人转移到安全地带,必须有:10002.0⨯x >410.解:设导火线的长度应为x cm ,根据题意,得10002.0⨯x >410∴x >5. 2.想一想(1)x =5,6,8能使不等式x >5成立吗?(2)你还能找出一些使不等式x >5成立的x 的值吗? [生](1)x =5不能使x >5成立,x =6,8能使不等式x >5成立. (2)x =9,10,11…等比5大的数都能使不等式x >5成立.[师]由此看来,6,7,8,9,10…都能使不等式成立,那么大家能否根据方程的解来类推出不等式的解呢?不等式的解唯一吗?[生]可以.能使不等式成立的未知数的值,叫做不等式的解.如6、7、8都是x >5的解.所以不等式的解不唯一,有无数个解.[师]正因为不等式的解不唯一,因此把所有满足不等式的解集合在一起,构成不等式的解集(solution set ).请大家再类推出解不等式的概念.[生]求不等式解集的过程叫解不等式. 3.议一议.请你用自己的方式将不等式x >5的解集和不等式x -5≤-1的解集分别表示在数轴上,并与同伴交流.[生]不等式x >5的解集可以用数轴上表示5的点的右边部分来表示(图1-3),在数轴上表示5的点的位置上画空心圆圈,表示5不在这个解集内.图1-3不等式x -5≤-1的解集x ≤4可以用数轴上表示4的点及其左边部分来表示(图1-4),在数轴上表示4的点的位置上画实心圆点,表示4在这个解集内.图1-4[师]请大家讨论一下,如何把不等式的解集在数轴上表示出来呢?请举例说明. [生]如x >3, 即为数轴上表示3的点的右边部分,在数轴上表示3的点的位置上画空心圆圈,表示不包括这一点.x <3,可以用数轴上表示3的点的左边部分来表示,在这一点上画空心圆圈.x ≥3,可以用数轴上表示3的点和它的右边部分来表示,在表示3的点的位置上画实心圆点,表示包括这一点.x ≤3,可以用数轴上表示3的点和它的左边部分来表示,在表示3的点的位置上画实心圆点.4.例题讲解投影片(§1.3 A )根据不等式的基本性质求不等式的解集,并把解集在数轴上表示出来. (1)x -2≥-4;(2)2x ≤8 (3)-2x -2>-10 解:(1)根据不等式的基本性质1,两边都加上2,得x ≥-2 在数轴上表示为:图1-5(2)根据不等式的基本性质2,两边都除以2,得x ≤4 在数轴上表示为:图1-6(3)根据不等式的基本性质1,两边都加上2,得-2x >-8 根据不等式的基本性质3,两边都除以-2,得x <4 在数轴上表示为:图1-7Ⅲ.课堂练习 1.判断正误:(1)不等式x -1>0有无数个解; (2)不等式2x -3≤0的解集为x ≥32. 2.将下列不等式的解集分别表示在数轴上: (1)x >4;(2)x ≤-1; (3)x ≥-2;(4)x ≤6. 1.解:(1)∵x -1>0,∴x >1 ∴x -1>0有无数个解.∴正确. (2)∵2x -3≤0,∴2x ≤3, ∴x ≤23,∴结论错误. 2.解:图1-8Ⅳ.课时小结本节课学习了以下内容1.理解不等式的解,不等式的解集,解不等式的概念.2.会根据不等式的基本性质解不等式,并把解集在数轴上表示出来.Ⅴ.课后作业习题1.3Ⅵ.活动与探究小于2的每一个数都是不等式x+3<6的解,所以这个不等式的解集是x<2.这种解答正确吗?解:不正确.从解不等式的过程来看,根据不等式的基本性质1,两边都减去3,得x<3.所以不等式x+3<6的解集为x<3,而不是x<2.当然小于2的值都在x<3这个范围内,它只是解集中的一部分,不是全部,所以不能以部分来代替全部.因此说x<2是不等式x+3<6的解是错误的.●板书设计§1.3 不等式的解集一、1.现实生活中的不等式(水费问题);2.想一想(类推不等式中的有关概念);3.议一议(如何把不等式的解集在数轴上表示出来);4.例题讲解.二、课堂练习三、课时小结四、课后作业●备课资料参考练习1.用不等式表示:(1)x的3倍大于或等于1;(2)x与5的和不小于0;(3)y与1的差不大于6;(4)x 的41小于或等于2. 2.不等式的解集x <3与x ≤3有什么不同?在数轴上表示它们时怎样区别?分别在数轴上把这两个解集表示出来.3.不等式x +3≥6的解集是什么? 参考答案1.(1)3x ≥1;(2)x +5≥0;(3)y -1≤6;(4)41x ≤2. 2.x <3指小于3的所有数,x ≤3指小于3的所有数和3;在数轴上表示它们时,x <3不包括3,只是3左边的部分,x ≤3不仅包括3左边的部分,而且还包括3.在数轴上表示略. 3.x ≥3.●迁移发散 迁移1.根据下列数量关系列出不等式:(1)x 的3倍大于1;(2)x 与5的和是负数; (3)y 与1的差是正数;(4)x 的一半不大于8.解:(1)3x >1;(2)x +5<0;(3)y -1>0;(4)21x ≤8. 2.在-4,-2,-1,0,1,2,3中找出使不等式成立的x 的值. (1)2x +5>3;(2)5-x ≥3;(3)6≤3x +3. 解:(1)0,1,2,3;(2)-4,-2,-1,0,1; (3)1,2,3.3.在数轴上表示下列不等式的解集: (1)x >3;(2)x ≥0;(3)x <-4. 解:(1)图1-9(2)图1-10(3)图1-114.不等式x ≤5有多少个解?有多少个正整数解. 答:有无数个解.正整数解只有1、2、3、4、5.5.某种商品的进价为150元,出售时标价为225元,由于销售情况不好,商店准备降价出售,但要保证利润不低于10%.那么商店要降多少元出售此商品?请列出不等式.点拨:利润率=进价进价售价-.解:设要降价x 元. 由题意列出不等式得:150150225--x ≥10%.发散本节我们用到了以前学过的数轴.你还记得这些吗?1.数轴定义:规定了正方向、原点、单位长度的直线叫做数轴.2.数轴上的点与实数的关系:一一对应.3.数轴上数的特点:右边的总比左边的大. ●方法点拨[例2]写出不等式x -5<-1的3个解,并写出这个不等式的解集. 解:3个解x =0,x =-1,x =1. 解集是x <4.4.求不等式解集的过程叫做解不等式.5.不等式的解集在数轴上的表示.①当不等式的解集是x >a 时.(如图1-1)图1-1在数轴上把表示a 的这个点用空心圆圈(表示不等于a )向右画一折线.表示数轴上a 右边的数字,都比a 大.②不等式的解集是x ≥a 时.(如图1-2)图1-2在数轴上把表示a 的这个点用实心圆点向右画一折线. ③当不等式的解集是x <a 时.(如图1-3)图1-3在数轴上把表示a的这个点用空心圆圈向左画一条折线.④当不等式的解集是x≤a时.(如图1-4)图1-4在数轴上把表示a的点用实心圆点向左画一折线.[例3]用数轴表示下列不等式的解集.(1)x≥-3 (2)x<-3.5解:(1)如图1-5图1-5(2)如图1-6图1-6[例4]根据数轴判断不等式的解集.(1)图1-7(2)图1-8解:(1)不等式的解集为x>-1.(2)不等式的解集为x≤2.3.不等式的解集作业导航理解不等式的解和不等式的解集的含义,会在数轴上表示不等式的解集.一、选择题1.下列说法中,正确的是( ) A.x =2是不等式3x >5的一个解 B.x =2是不等式3x >5的唯一解 C.x =2是不等式3x >5的解集 D.x =2不是不等式3x >5的解2.不等式-4≤x <2的所有整数解的和是( ) A.-4 B.-6 C.-8 D.-93.用不等式表示图中的解集,其中正确的是( )图1A.x >-3B.x <-3C.x ≥-3D.x ≤-34.若不等式(a +1)x <a +1的解集为x <1,那么a 必须满足( ) A.a <0 B.a ≤-1 C.a >-1 D.a <-15.已知ax <2a (a ≠0)是关于x 的不等式,那么它的解集是( ) A.x <2 B.x >-2C.当a >0时,x <2D.当a >0时,x <2;当a <0时,x >2 二、填空题6.当a ________时,x >ab表示ax >b 的解集. 7.不等式2x -1≥5的最小整数解为________. 8.如图2,表示的不等式的解集是________.图29.大于________的每一个数都是不等式5x >15的解. 10.如果不等式(a -3)x <b 的解集是x <3a b,那么a 的取值范围是________. 三、解答题11.在数轴上表示下列不等式的解集: (1)x >3 (2)x ≥-2 (3)x ≤4(4)x <-21 12.利用不等式的性质求出下列不等式的解集,并把它们的解集在数轴上表示出来: (1)-2x ≥3 (2)-4x +12<013.不等式的解集中是否一定有无限多个数?不等式|x |≤0、x 2<0的解集是什么?不等式x 2>0和x 2+4>0的解集分别又是什么? 14.已知-4是不等式ax >9的解集中的一个值,试求a 的取值范围. 15.已知不等式2x-1>x 与ax -6>5x 同解,试求a 的值.参考答案一、1.A 2.D 3.C 4.C 5.D二、6.>0 7.3 8.x <2 9.3 10.a >3 三、11.略 12.(1)x ≤-23(2)x >3 13.不等式的解集中不一定有无数多个数. |x |≤0的解集是x =0,x 2<0无解.x 2>0的解集为x >0或x <0,x 2+4>0的解集为一切实数. 14.a <-4915.2●作业指导 随堂练习1.解:(1)√ (2)×2.解:(1)x >4图1-12(2)x ≤-1图1-13(3)x ≥-2图1-14(4)x≤6图1-15习题1.31.解:有无数个解.如x=15,14,13,…,0,-1.都是它的解2.解:(1)x≤0图1-16(2)x>-2.5图1-172(3)x<3图1-18(4)x≥4图1-19§1.3 不等式的解集●温故知新想一想,做一做填空1.不等式的两边都加上(或减去)同一个整式,不等号的__________.2.不等式的两边都乘以(或除以)同一个正数,不等号的方向__________.3.不等式的两边都乘以(或除以)同一个负数,不等号的方向__________.4.规定了__________、__________、__________的直线叫做数轴.5.数轴上的点与实数之间是__________的关系.你做对了吗?我们一起来对对答案:1.方向不变2.不变3.变向4.正方向原点单位长度5.一一对应看看书,动动脑1.x=3能满足2x-1.5≥15吗?2.填空①__________叫做不等式的解.②__________组成不等式的解集.③__________叫做解不等式.§1.3 不等式的解集班级:_______ 姓名:_______一、认真选一选1.下列说法错误的是()A.-3x>9的解集为x<-3B.不等式2x>-1的整数解有无数多个C.-2是不等式3x<-4的解D.不等式x>-5的负整数解有无数多个2.如图1—3—1表示的是以下哪个不等式的解集()图1—3—1A.x>-1B.x<-1C.x≥-1D.x≤-13.把不等式x>2的解集表示在数轴上,以下表示正确的是()4.不等式-3≤x<2的整数解的个数是()A.4个B.5个C.6个D.无数个二、请你填一填1.如果3+2x 是正数,则x 的取值范围是________,如果3+2x 是非负数,则x 的取值范围是________.2.不等式|x |<37的整数解是________. 3.x 的3倍不大于-8,用不等式表示为________,其解集是________. 4.使不等式x >-47且x <2同时成立的整数x 的值是________ .三、请在数轴上表示下列不等式的解集(1)x ≥0 (2)x <-2.5 (3)-2<x ≤3四、请写出满足下列条件的一个不等式(1)0是这个不等式的一个解.(2)-2,-1,0,1都是不等式的解.(3)0不是这个不等式的解.(4)与x ≤-1的解集相同的不等式. (5)不等式的整数解只有-1,0,1,2.参 考 答 案一、1.D 2.D 3.C 4.B 二、1.x >-23 x ≥-23 2.-2,-1,0,1,2 3.3x ≤-8 x ≤-384.-1,0,1 三、(1)(2)(3)四、(1)x >-1(或x ≥0,x >-2等都可以)(2)x <2(或x ≤1,x ≥-2,x >-5等均可) (3)x >1(或x <-1等均可)(4)2x ≤-2(或x +1≤0,2x +2≤0等均可) (5)-1≤x ≤2(或-1.5<x <2.1等)。
一元一次不等式组解集数轴表示

一元一次不等式组解集数轴表示全文共四篇示例,供读者参考第一篇示例:一元一次不等式组是数学中常见的问题,通过解不等式组可以得到一个或多个解集,这些解集常常用数轴表示。
本文将介绍一元一次不等式组的概念、解的求法以及如何用数轴来表示解集。
一、一元一次不等式组的概念一元一次不等式组是由若干个一元一次不等式组成的集合,形式如下:ax + b < cdx + e <= fgx + h > i其中a、b、c、d、e、f、g、h、i为实数,且a、d、g不全为0。
不等式组的解是使得所有不等式同时成立的实数的集合。
1. 逐个不等式求解法:首先分别解每一个不等式,得到它们的解集,然后取所有解集的交集即为不等式组的解。
2. 图像法:将每个不等式表示在坐标系中,然后考虑它们的交集部分即为不等式组的解。
3. 系数比较法:通过比较不等式的系数大小关系,消去变量,从而得到更简单的一元一次不等式。
再通过解这个简单的不等式来得到原不等式组的解。
三、数轴表示解集数轴是一种用于表示数值大小和相对位置的图形工具,一维数轴上通常有一个原点和正、负两个方向。
我们可以使用数轴来表示一元一次不等式组的解集,具体步骤如下:1. 首先解出不等式组的解,得到形如[x1, x2]或(x1, x2)的解集。
2. 画出一条水平的数轴,数轴上标出各个解的值。
如果解是开区间,则在对应的点上画一个空心圆;如果解是闭区间,则在对应的点上画一个实心圆。
3. 根据解的相对位置,在相应的区间上用短线段连接起来,形成解集的表示。
4. 最后检查数轴上的解集是否符合原不等式组中每个不等式,如果符合则表示正确。
通过这种方法,我们可以直观地看到不等式组的解集在数轴上的位置关系,更容易理解和分析解的性质。
四、例题和解析解不等式组:x+1 < 32x-5 > 1我们首先通过逐个不等式求解的方法得到x的取值范围分别是(-∞, 2)和(3, +∞),则不等式组的解集为(-∞, 2)∪(3, +∞)。
用数轴法确定不等式组的解集

21i2 02 - 月 f
J i 用囝∞
黄 永 秋
确定不等式组的解集
⑩广 西 浦 北 县 第 六 中学
不 等 式 组 是 中学 数 学 中 一 个 非 常 重 要 的学 习 内 容 , 是 中 也 考 数 学 中 的 一 个 常 考 点 , 时 也 是 不 少 学 生 的 失 分 点 . 教 学 同 在 条 虚
㈩ 2 <3, c r% x+ x 2 2 x
一
:
() ‘ 1l≤ , 一
2x -2≥ — +4;
( ) x 3 r2+‘
【x 2 -2≤ — +4:
( )一 4 f ≤2- , X
【 0 x- ≤ 一l <3 - 4
中 , 不 少 教 师 教 会 学 生 巧 记 口诀 进 行 解 答 , 用 口诀 时 必 须 有 利 判 定 好 不 等式 组 的 情 形 然 后 依 据 相 应 的 口诀 解 答 , 求 学 生 必 要 须 熟 练 记 忆 和 应 用 口诀 , 时 它 只 适 用 于较 为简 单 的 不 等 式 组 同 情 形 的解 集 确 定 , 广 度 不 高 ; 推 当然 常 传 授 的 还 是 数 轴 法 , 用 利 数 轴 法 解 答 时 要 求 学 生 会 在 数 轴 上 表 达 出每 一 不 等 式 的 解 集 , 并准确地找出公共部分 , 同时 准 确 地 将 它 表 达 成 不 等 式 . 而不 然 少 学 生 并 不 能 较 好 地 利 用 数 轴 法 进 行 有 效 解 答 , 了 帮 助 学 生 为 熟 练 利 用 数 轴 法 进 行 解 答 , 者建 议 同 学 们 依 据 数 轴 的箭 头 始 笔 终 指 向 右 边 的 特 点 , 成 良好 的 数 轴 观 察 与 表 达 习 惯 ; 时 用 养 同 虚 线 在 数 轴 上 对 每 一 个 不 等 式 的解 集 进 行 标 记 , 而更 直 观 地 从
2022中考真题分类11——不等式(参考答案)

2022中考真题分类11——不等式一、解不等式1. (2022·辽宁阜新)不等式组120.510.5x x −−≤⎧⎨−<⎩的解集,在数轴上表示正确的是( )A .B .C .D .【答案】A【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集. 【详解】解:由−x −1≤2,得:x ≥−3, 由0.5x −1<0.5,得:x <3, 则不等式组的解集为−3≤x <3, 故选:A .【点睛】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键. 2. (2022·江苏镇江)如图,数轴上的点A 和点B 分别在原点的左侧和右侧,点A 、B 对应的实数分别是a 、b ,下列结论一定成立的是( )A .0a b +<B .0b a −<C .22a b >D .22a b +<+0b a −>,∴B 选项的结论不成立;22a b <,∴C选项的结论不成立; 22a b +<+,∴D 选项的结论成立.故选:D .【点睛】本题主要考查了不等式的性质,有理数大小的比较法则,利用点在数轴上的位置确定出a ,b 的取值范围是解题的关键.3. (2022·山东临沂)满足1m 的整数m 的值可能是( ) A .3 B .2 C .1 D .0【详解】310<<13−<,10110−=−3m ∴≥,故选:A .【点睛】本题考查了绝对值的化简,无理数的估算和不等式的求解,熟练掌握知识点是解题的关键.4.(2022·浙江衢州)不等式组3221112x x x −+⎧⎪⎨−⎪⎩<(),>的解集是( )A .3x <B .无解C .24x <<D .3<<4x键.5. (2022·广西河池)如果点P (m ,1+2m )在第三象限内,那么m 的取值范围是( ) A .102m −<<B .12m >−C .0m <D .12m <−6. (2022·山东滨州)把不等式组321132x xx x −<⎧⎪+−⎨≥⎪⎩中每个不等式的解集在同一条数轴上表示出来,正确的为( )A .B .C .D .∴不等式组的解集为35x−<≤,在数轴上表示为:,故选:C.【点睛】本题考查了解一元一次不等式组及在数轴上表示解集,熟练掌握知识点是解题的关键.7.(2022·辽宁锦州·中考真题)不等式131722x x−≤−的解集在数轴上表示为()A.B.C.D.故选C.二、含参不等式8.(2022·山东济宁)若关于x的不等式组>0,72>5x ax−⎧⎨−⎩仅有3个整数解,则a的取值范围是()A.-4≤a<-2B.-3<a≤-2C.-3≤a≤-2D.-3≤a<-2【答案】D【分析】先求出每个不等式的解集,再求出不等式组的解集,即可解答.【详解】解:>072>5x a x −⎧⎨−⎩①②由①得,x a > 由②得,1x <因不等式组有3个整数解1x a ∴<<32a ∴−≤<−故选:D .【点睛】本题考查解一元一次不等式组、一元一次不等式组的整数解,掌握相关知识是解题关键.9. (2022·湖南邵阳)关于x 的不等式组()1233111222x x x a ⎧−>−⎪⎪⎨⎪−<−⎪⎩有且只有三个整数解,则a 的最大值是( ) A .3 B .4C .5D .610. (2022·山东聊城)关于x ,y 的方程组2232x y k x y k −=−⎧⎨−=⎩的解中x 与y 的和不小于5,则k 的取值范围为( )A .8k ≥B .8k >C .8k ≤D .8k <【答案】A【分析】由两式相减,得到3x y k +=−,再根据x 与 y 的和不小于5列出不等式即可求解.【详解】解:把两个方程相减,可得3x y k +=−, 根据题意得:35k −≥, 解得:8k ≥.所以k 的取值范围是8k ≥. 故选:A .【点睛】本题考查二元一次方程组、不等式,将两式相减得到x 与y 的和是解题的关键. 11. (2022·四川达州)关于x 的不等式组23112x a x x −+<⎧⎪⎨−+⎪⎩恰有3个整数解,则a 的取值范围是_______. 【答案】23a ≤<【分析】首先确定不等式组的解集,先利用含a 的式子表示,根据整数解的个数就可以确定有哪些整数解,根据解的情况可以得到关于a 的不等式,从而求出a 的范围11x+②2a−,3,不等式组有解∴不等式组的解集为:2a−不等式组211x+恰有3<.【点睛】考查不等式组的解法及整数解的确定.求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.本题要根据整数解的取值情12.(2022·内蒙古·中考真题)已知关于x的不等式组531xa x−≥−⎧⎨−<⎩无解,则a的取值范围是_____.【答案】a≥2【分析】先把a当作已知条件求出各不等式的解集,再根据不等式组无解求出a的取值范围即可.【详解】解:531xa x−≥−⎧⎨−<⎩①②,由①得:x≤2,由②得:x>a,∵不等式组无解,∴a≥2,故答案为a≥2.【点睛】本题主要考查了解一元一次不等式组,解题的关键关键是掌握解集的规律:同大取大;同小取小;大小小大中间找;大大小小无处找.13. (2022·四川绵阳)已知关于x 的不等式组2325323x x mx x +≥+⎧⎪+⎨−<−⎪⎩无解,则1m 的取值范围是_________.14. (2022·四川攀枝花)如果一元一次方程的解是一元一次不等式组的解.则称该一元一次方程为该一元一次不等式组的关联方程.若方程1103x −=是关于x 的不等式组2220x nn x −≤⎧⎨−<⎩的关联方程,则n 的取值范围是 ___________.即n 的取值范围为:13n ≤<, 故答案为:13n ≤<.【点睛】本题主要考查解一元一次不等式组和一元一次方程,解题的关键是理解并掌握“关联方程”的定义和解一元一次不等式组、一元一次方程的能力.三、不等式实际应用15. (2022·四川绵阳)某水果经营户从水果批发市场批发水果进行零售,部分水果批发价格与零售价格如下表:请解答下列问题:(1)第一天,该经营户用1700元批发了菠萝和苹果共300kg ,当日全部售出,求这两种水果获得的总利润?(2)第二天,该经营户依然用1700元批发了菠萝和苹果,当日销售结束清点盘存时发现进货单丢失,只记得这两种水果的批发量均为正整数且菠萝的进货量不低于88kg ,这两种水果已全部售出且总利润高于第一天这两种水果的总利润,请通过计算说明该经营户第二天批发这两种水果可能的方案有哪些?16.(2022·黑龙江牡丹江)某工厂准备生产A和B两种防疫用品,已知A种防疫用品每箱成本比B种防疫用品每箱成本多500元.经计算,用6000元生产A种防疫用品的箱数与用4500元生产B种防疫用品的箱数相等.请解答下列问题:(1)求A,B两种防疫用品每箱的成本;(2)该工厂计划用不超过90000元同时生产A和B两种防疫用品共50箱,且B种防疫用品不超过25箱,该工厂有几种生产方案?(3)为扩大生产,厂家欲拿出与(2)中最低成本相同的费用全部用于购进甲和乙两种设备(两种都买).若甲种设备每台2500元,乙种设备每台3500元,则有几种购买方案?最多可购买甲,乙两种设备共多少台?(请直接写出答案即可)【答案】(1)A种防疫用品2000元/箱,B种防疫用品1500元/箱(2)共有6种方案17.(2022·内蒙古呼和浩特)今年我市某公司分两次采购了一批土豆,第一次花费30万元,第二次花费50万元,已知第一次采购时每吨土豆的价格比去年的平均价格上涨了200元,第二次采购时每吨土豆的价格比去年的平均价格下降了200元,第二次的采购数量是第一次采购数量的2倍.(1)问去年每吨土豆的平均价格是多少元?(2)该公司可将土豆加工成薯片或淀粉,因设备原因,两种产品不能同时加工,若单独加工成薯片,每天可加工5吨土豆,每吨土豆获利700元;若单独加工成淀粉,每天可加工8吨土豆,每吨土豆获利400元.由于出口需要,所有采购的土豆必须全部加工完且用时不超过60天,其中加工成薯片的土豆数量不少于加工成淀粉的土豆数量的23,为获得最大利润,应将多少吨土豆加工成薯片?最大利润是多少?【答案】(1)去年每吨土豆的平均价格是2200元(2)应将175吨土豆加工成薯片,最大利润为202500元【分析】(1)设去年每吨土豆的平均价格是x元,则第一次采购的平均价格为(x+200)元,第二次采购的平均价格为(x-200)元,根据第二次的采购数量是第一次采购数量的两倍,据此列方程求解;(2)先求出今年所采购的土豆枣数,根据所有采购的土豆必须全部加工完且用时不超过18. (2022·广西·中考真题)金鷹酒店有140间客房需安装空调,承包给甲、乙两个工程队合作安装,每间客房都安装同一品牌同样规格的一台空调,已知甲工程队每天比乙工程队多安装5台,甲工程队的安装任务有80台,两队同时安装.问: (1)甲,乙两个工程队每天各安装多少台空调,才能同时完成任务?(2)金鹰酒店响应“縁色环保”要求,空调的最低温度设定不低于26℃,每台空调每小时耗电1.5度:据预估,每天至少有100间客房有旅客住宿,旅客住宿时平均每天开空调约8小时,若电费0.8元/度,请你估计该酒店每天所有客房空调所用电费 W (单位:元)的范围?【答案】(1)甲工程队每天安装20台空调,乙工程队每天安装15台空调,才能同时完成任务(2)9601344W ≤≤,9.60>,的增大而增大,100m ≤≤140m 时,1344.【点睛】本题考查了列分式方程解决实际问题,列函数解析式,不等式的应用,准确理解题意,熟练掌握知识点是解题的关键.19. (2022·黑龙江)学校开展大课间活动,某班需要购买A 、B 两种跳绳.已知购进10根A 种跳绳和5根B 种跳绳共需175元:购进15根A 种跳绳和10根B 种跳绳共需300元.(1)求购进一根A 种跳绳和一根B 种跳绳各需多少元?(2)设购买A 种跳绳m 根,若班级计划购买A 、B 两种跳绳共45根,所花费用不少于548元且不多于560元,则有哪几种购买方案?(3)在(2)的条件下,哪种购买方案需要的总费用最少?最少费用是多少元? 【答案】(1)购进一根A 种跳绳需10元,购进一根B 种跳绳需15元(2)有三种方案:方案一:购买A 种跳绳23根,B 种跳绳22根;方案二:购买A 种跳绳24根,B 种跳绳21根;方案三:购买A 种跳绳25根,B 种跳绳20根 (3)方案三需要费用最少,最少费用是550元【分析】(1)设购进一根A 种跳绳需x 元,购进一根B 种跳绳需y 元,可列方程组1051751510300x y x y +=⎧⎨+=⎩,解方程组即可求得结果; (2)根据题意可列出不等式组()()101545560101545548m m m m ⎧+−≤⎪⎨+−≥⎪⎩,解不等式组得到解集再结合m 为正整数即可确定方案;(3)设购买跳绳所需费用为w 元,根据题意,得5675w m =−+,结合函数的性质,可知w 随m 的增大而减小,由此即可求得答案.【详解】(1)解:设购进一根A 种跳绳需x 元,购进一根B 种跳绳需y 元,根据题意,得1051751510300x y x y +=⎧⎨+=⎩,解得1015x y =⎧⎨=⎩,答:购进一根A 种跳绳需10元,购进一根B 种跳绳需15元;(2)根据题意,得()()101545560101545548m m m m ⎧+−≤⎪⎨+−≥⎪⎩,解得2325.4m ≤≤,∵m 为整数,∴m 可取23,24,25.∴有三种方案:方案一:购买A 种跳绳23根,B 种跳绳22根; 方案二:购买A 种跳绳24根,B 种跳绳21根; 方案三:购买A 种跳绳25根,B 种跳绳20根;(3)设购买跳绳所需费用为w 元,根据题意,得()1015455675w m m m =+−=−+ ∵50−<,∴w 随m 的增大而减小,∴当25m =时,w 有最小值,即w 525675550=−⨯+=(元) 答:方案三需要费用最少,最少费用是550元.【点睛】本题主要考查的是不等式应用题、二元一次方程组应用题、一次函数相关应用题,根据题意列出对应的方程是解题的关键.20. (2022·贵州黔东南)某快递公司为了加强疫情防控需求,提高工作效率,计划购买A 、B 两种型号的机器人来搬运货物,已知每台A 型机器人比每台B 型机器人每天少搬运10吨,且A型机器人每天搬运540吨货物与B型机器人每天搬运600吨货物所需台数相同.(1)求每台A型机器人和每台B型机器人每天分别搬运货物多少吨?(2)每台A型机器人售价1.2万元,每台B型机器人售价2万元,该公司计划采购A、B两种型号的机器人共30台,必须满足每天搬运的货物不低于2830吨,购买金额不超过48万元.请根据以上要求,完成如下问题:①设购买A型机器人m台,购买总金额为w万元,请写出w与m的函数关系式;②请你求出最节省的采购方案,购买总金额最低是多少万元?【答案】(1)每台A型机器人每天搬运货物90吨,每台B型机器人每天搬运货物为100 w m m m;1.22300.860②由题意得:()901003028300.86048m m m ⎧+−≥⎨−+≤⎩,解得:1517m ≤≤, ∵-0.8<0,∴w 随m 的增大而减小,∴当m =17时,w 有最小值,即为0.8176046.4w =−⨯+=,答:当购买A 型机器人17台,B 型机器人13台时,购买总金额最少,最少金额为46.4万元.【点睛】本题主要考查分式方程的应用、一元一次不等式组的应用及一次函数的应用,熟练掌握分式方程的应用、一元一次不等式组的应用及一次函数的应用是解题的关键. 21. (2022·广西玉林)我市某乡村振兴果蔬加工公司先后两次购买龙眼共21吨,第一次购买龙眼的价格为0.4万元/吨:因龙眼大量上市,价格下跌,第二次购买龙眼的价格为0.3万元/吨,两次购买龙眼共用了7万元. (1)求两次购买龙眼各是多少吨?(2)公司把两次购买的龙眼加工成桂圆肉和龙眼干,1吨龙眼可加工成桂圆肉0.2吨或龙眼干0.5吨,桂圆肉和龙眼干的销售价格分别是10万元/吨和3万元/吨,若全部的销售额不少于39万元,则至少需要把多少吨龙眼加工成桂圆肉? 【答案】(1)第一次购买了7吨龙眼,第二次购买了14吨龙眼 (2)至少要把15吨龙眼加工成桂圆肉【分析】(1)设第一次购买龙眼x 吨,第二次购买龙眼y 吨,根据题意列出二元一次方程组即可求解;(2)设将a 吨龙眼加工成桂圆肉,则(21-a )吨龙眼加工成龙眼干,则总的销售额为:31.50.5a +,则根据题意有不等式31.50.539a +≥,解该不等式即可求解.【详解】(1)设第一次购买龙眼x 吨,第二次购买龙眼y 吨, 根据题意有:210.40.37x y x y +=⎧⎨+=⎩,解得:714x y =⎧⎨=⎩, 即第一次购买龙眼7吨,第二次购买龙眼14吨;(2)设将a 吨龙眼加工成桂圆肉,则(21-a )吨龙眼加工成龙眼干,则总的销售额为:0.210(21)0.5331.50.5a a a ⨯⨯+−⨯⨯=+, 则根据题意有:31.50.539a +≥, 解得:15a ≥,即至少要把15吨龙眼加工成桂圆肉.【点睛】本题考查了二元一次方程组即一元一次不等式的应用,明确题意列出二元一次方程组即一元一次不等式是解答本题的关键.22. (2022·河南)近日,教育部印发《义务教育课程方案》和课程标准(2022年版),将劳动从原来的综合实践活动课程中独立出来.某中学为了让学生体验农耕劳动,开辟了一处耕种园,需要采购一批菜苗开展种植活动.据了解,市场上每捆A 种菜苗的价格是菜苗基地的54倍,用300元在市场上购买的A 种菜苗比在菜苗基地购买的少3捆.(1)求菜苗基地每捆A 种菜苗的价格.(2)菜苗基地每捆B 种菜苗的价格是30元.学校决定在菜苗基地购买A ,B 两种菜苗共100捆,且A 种菜苗的捆数不超过B 种菜苗的捆数.菜苗基地为支持该校活动,对A ,B 两种菜苗均提供九折优惠.求本次购买最少花费多少钱.20xx代入检验:将20x是原方程的解,20∴菜苗基地每捆A种菜苗的价格为)解:设:购买Am≤由题意可知:100m≤,解得5023.(2022·江苏苏州)某水果店经销甲、乙两种水果,两次购进水果的情况如下表所示:(1)求甲、乙两种水果的进价;(2)销售完前两次购进的水果后,该水果店决定回馈顾客,开展促销活动.第三次购进甲、乙两种水果共200千克,且投入的资金不超过3360元.将其中的m千克甲种水果和3m千克乙种水果按进价销售,剩余的甲种水果以每千克17元、乙种水果以每千克30元的价格销售.若第三次购进的200千克水果全部售出后,获得的最大..利润不低于800元,求正整数m的最大值.【答案】(1)甲种水果的进价为每千克12元,乙种水果的进价为每千克20元24.(2022·四川遂宁)某中学为落实《教育部办公厅关于进一步加强中小学生体质管理的通知》文件要求,决定增设篮球、足球两门选修课程,需要购进一批篮球和足球.已知购买2个篮球和3个足球共需费用510元;购买3个篮球和5个足球共需费用810元.(1)求篮球和足球的单价分别是多少元;(2)学校计划采购篮球、足球共50个,并要求篮球不少于30个,且总费用不超过5500元.那么有哪几种购买方案?方案四:采购篮球33个,采购足球17个.【点睛】本题考查二元一次方程组的应用、一元一次不等式组的应用,解答本题的关键是明确题意,列出相应的方程组和不等式组.25.(2022·四川达州)某商场进货员预测一种应季T恤衫能畅销市场,就用4000元购进一批这种T恤衫,面市后果然供不应求.商场又用8800元购进了第二批这种T恤衫,所购数量是第一批购进量的2倍,但每件的进价贵了4元.(1)该商场购进第一批、第二批T恤衫每件的进价分别是多少元?(2)如果两批T恤衫按相同的标价销售,最后缺码的40件T恤衫按七折优惠售出,要使两批T恤衫全部售完后利润率不低于80%(不考虑其他因素),那么每件T恤衫的标价至少是多少元?【点睛】本题考查了列分式方程解决实际问题,列不等式解决实际问题,准确理解题意,找准数量关系是解题的关键.26. (2022·四川德阳)习近平总书记对实施乡村振兴战略作出重要指示强调:实施乡村振兴战略,是党的十九大作出的重大决策部署,是新时代做好“三农”工作的总抓手.为了发展特色产业,红旗村花费4000元集中采购了A 种树苗500株,B 种树苗400株,已知B 种树苗单价是A 种树苗单价的1.25倍. (1)求A 、B 两种树苗的单价分别是多少元?(2)红旗村决定再购买同样的树苗100株用于补充栽种,其中A 种树苗不多于25株,在单价不变,总费用不超过480元的情况下,共有几种购买方案?哪种方案费用最低?最低费用是多少元?【答案】(1)A 种树苗的单价是4元,则B 种树苗的单价是5元(2)有6种购买方案,购买A 种树苗,25棵,购买B 种树苗75棵费用最低,最低费用是475元.【分析】(1)设A 种树苗的单价是x 元,则B 种树苗的单价是1.25x 元,根据“花费4000元集中采购了A 种树苗500株,B 种树苗400株,”列出方程,即可求解;(2)设购买A 种树苗a 棵,则购买B 种树苗(100-a )棵,其中a 为正整数,根据题意,列出不等式组,可得2025a ≤≤,从而得到有6种购买方案,然后设总费用为w 元,根据题意列出函数关系式,即可求解.【详解】(1)解:设A 种树苗的单价是x 元,则B 种树苗的单价是1.25x 元,根据题意得:500400 1.254000x x +⨯=,解得:4x =, ∴1.25x =5,答:A 种树苗的单价是4元,则B 种树苗的单价是5元;(2)解:设购买A 种树苗a 棵,则购买B 种树苗(100-a )棵,其中a 为正整数,根据题意得:()02545100480a a a <≤⎧⎨+−≤⎩, 解得:2025a ≤≤,∵a 为正整数,∴a 取20,21,22,23,24,25, ∴有6种购买方案, 设总费用为w 元,∴()45100500w a a a =+−=−+, ∵-1<0,∴w 随a 的增大而减小,∴当a =25时,w 最小,最小值为475, 此时100-a =75,答:有6种购买方案,购买A 种树苗,25棵,购买B 种树苗75棵费用最低,最低费用是475元.【点睛】本题主要考查了一元一次方程的应用,一元一次不等式组的应用,一次函数的应用,明确题意,准确得到数量关系是解题的关键.27. (2022·黑龙江牡丹江)为了迎接“十•一”小长假的购物高峰.某运动品牌专卖店准备购进甲、乙两种运动鞋.其中甲、乙两种运动鞋的进价和售价如下表:已知:用3000元购进甲种运动鞋的数量与用2400元购进乙种运动鞋的数量相同. (1)求m 的值;(2)要使购进的甲、乙两种运动鞋共200双的总利润(利润=售价−进价)不少于21700元,且不超过22300元,问该专卖店有几种进货方案?(3)在(2)的条件下,专卖店准备对甲种运动鞋进行优惠促销活动,决定对甲种运动鞋每双优惠a (50<a <70)元出售,乙种运动鞋价格不变.那么该专卖店要获得最大利润应如何进货?【答案】(1)m =10;(2)11种;(3)购进甲种运动鞋95双,购进乙种运动鞋105双,可获得最大利润28.(2022·内蒙古·中考真题)某商店决定购进A、B两种北京冬奥会纪念品.若购进A种纪念品10件,B种纪念品5件,需要1000元;若购进A种纪念品5件,B种纪念品3件,需要550元.(1)求购进A、B两种纪念品的单价;(2)若该商店决定拿出1万元全部用来购进这两种纪念品,考虑市场需求,要求购进A种纪念品的数量不少于B种纪念品数量的6倍,且购进B种纪念品数量不少于20件,那么该商店共有几种进货方案?(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在第(2)问的各种进货方案中,哪一种方案获利最大?求出最大利润.2⎩x150x160150160xy均为正整数可取的正整数值是相对应的y可取的正整数值是∴共有6种进货方案)设总利润为∵50>∴W 随x 的增大而增大∴当160x =时,W 有最大值:516030003800⨯+=(元)∴当购进A 种纪念品160件,B 种纪念品20件时,可获得最大利润,最大利润是3800元.【点睛】本题考查二元一次方程组、一元一次不等式组和一次函数的实际应用.根据题意正确的列出二元一次方程组,一元一次不等式组,根据一次函数的性质进行求解,是解题的关键.29. (2022·辽宁阜新)某公司引入一条新生产线生产A ,B 两种产品,其中A 产品每件成本为100元,销售价格为120元,B 产品每件成本为75元,销售价格为100元,A ,B 两种产品均能在生产当月全部售出.(1)第一个月该公司生产的A ,B 两种产品的总成本为8250元,销售总利润为2350元,求这个月生产A ,B 两种产品各多少件?(2)下个月该公司计划生产A ,B 两种产品共180件,且使总利润不低于4300元,则B 产品至少要生产多少件?【答案】(1)这个月生产A 产品30件,B 产品70件 (2)140件【分析】(1)设生产A 产品x 件,B 产品y 件,根据题意列出方程组,求出即可; (2)设B 产品生产m 件,则A 产品生产()180m −件,根据题意列出不等式组,求出即可.【详解】(1)解:设生产A 产品x 件,B 产品y 件,根据题意,得()()100758250,120100100752350x y x y +=⎧⎨−+−=⎩ 解得3070x y =⎧⎨=⎩,∴这个月生产A 产品30件,B 产品70件, 答:这个月生产A 产品30件,B 产品70件;(2)解:设B 产品生产m 件,则A 产品生产()180m −件,根据题意,得()()()100751201001804300m m −+−−≥, 解这个不等式,得140m ≥. ∴B 产品至少生产140件, 答:B 产品至少生产140件.【点睛】本题考查了二元一次方程组和一元一次不等式的应用,能根据题意列出方程组和不等式是解此题的关键.30. (2022·湖北黄石)某校为配合疫情防控需要,每星期组织学生进行核酸抽样检测;防疫部门为了解学生错峰进入操场进行核酸检测情况,调查了某天上午学生进入操场的累计人数y (单位:人)与时间x (单位:分钟)的变化情况,发现其变化规律符合函数关系式:2(08),640,(810)ax bx c x y x ⎧++≤≤=⎨<≤⎩数据如下表. 10x640(1)求a ,b ,c 的值;(2)如果学生一进入操场就开始排队进行核酸检测,检测点有4个,每个检测点每分钟检测5人,求排队人数的最大值(排队人数-累计人数-已检测人数);(3)在(2)的条件下,全部学生都完成核酸检测需要多少时间?如果要在不超过20分钟让全部学生完成核酸检测,从一开始就应该至少增加几个检测点? 【答案】(1)10a =−,160b =,0c(2)490人(3)从一开始应该至少增加3个检测点【分析】(1)根据题意列方程,待定系数法求解析式即可求解;(2)根据排队人数=累计人数-已检测人数,首先找到排队人数和时间的关系,再根据二次函数和一次函数的性质,找到排队人数最多时有多少人;8分钟后入校园人数不再增加,检测完所有排队同学即完成所有同学体温检测;(3)设从一开始就应该增加m 个检测点,根据不等关系“要在20分钟内让全部学生完成c;,由(1)知y=。
用数轴表示不等式解集的步骤

用数轴表示不等式解集的步骤
咱先得把数轴画出来。
这数轴呢,就像一条长长的线,有原点,原点就是0啦,然后两边分别是正数和负数。
就像在马路上有个中心点,两边是不同的方向一样有趣。
画好数轴后呢,就要看不等式的符号啦。
如果是大于号或者大于等于号,那解集在数轴上的表示就很有特点哦。
比如说x > 3,那就在数轴上找到3这个点,然后呢,因为是大于3,所以要把3这个点画成空心的小圆圈,就像这个点说“我不包括我自己哦”,然后向3的右边画一条线,表示所有大于3的数都是这个不等式的解。
要是x ≥ 3呢,3这个点就画成实心的小圆点啦,意思是3也在这个解集里面,然后同样向右边画一条线。
要是不等式是小于号或者小于等于号呢,那也是类似的操作。
像x < -2,就在数轴上找到 - 2这个点,画个空心圆圈,因为不包括 - 2本身嘛,然后向 - 2的左边画条线,表示所有小于 - 2的数都是解。
要是x ≤ - 2呢, - 2那个点就画实心,再向左画线。
还有一种情况哦,如果不等式是像 - 1 < x < 2这种,那就在数轴上找到 - 1和2这两个点, - 1这个点画空心,2这个点也画空心,然后在 - 1和2之间画条线,表示这个区间里的数才是不等式的解。
宝子们,用数轴表示不等式解集是不是还挺好玩的呀?就像在数轴这个小世界里给解找到了它们的家一样。
只要按照这些步骤来,就不会出错啦。
多做几道题练练手,就会越来越熟练的哦。
加油呀,宝子们!。
用数轴表示不等式的解集

用数轴表示不等式的解集不等式是数学中常见的概念,它描述了一种关系,即一个数与另一个数之间的大小关系。
而要表示不等式的解集,我们可以使用数轴来进行图示,以便更直观地理解和表示解集。
让我们从最简单的不等式开始。
考虑一个简单的一元线性不等式:x > 2。
这个不等式表示了x大于2的所有实数解。
我们可以在数轴上找到2这个点,并在其右侧用一个箭头表示所有大于2的数。
这样,我们就用数轴清晰地表示了不等式的解集。
接下来,我们考虑一个稍微复杂一些的不等式:-3 < x ≤ 5。
这个不等式表示了x大于-3且小于等于5的所有实数解。
我们可以在数轴上找到-3和5这两个点,并用一个空心圆点表示-3,用一个实心圆点表示5。
然后,在这两个点之间画一条实线,表示所有满足不等式的数。
注意到我们使用的是实线而非虚线,因为不等式中包含了等于的条件。
这样,我们就用数轴清晰地表示了不等式的解集。
当不等式中包含绝对值时,我们需要将数轴分成正负两部分来表示解集。
例如,考虑不等式|2x - 3| < 4。
首先,我们将2x - 3分成两个部分:2x - 3 > 0和2x - 3 < 0。
对于2x - 3 > 0,我们解得x > 3/2。
对于2x - 3 < 0,我们解得x < 3/2。
然后,我们在数轴上找到3/2这个点,并在其左右两侧用箭头表示解集。
注意到我们使用的是开区间而非闭区间,因为不等式中不包含等于的条件。
这样,我们就用数轴清晰地表示了不等式的解集。
除了一元不等式外,我们还可以用数轴表示多元不等式的解集。
例如,考虑一个简单的二元不等式系统:x + y > 3和x - y < 1。
我们可以将这两个不等式分别表示在x轴和y轴上,并找到它们的交集区域。
这个交集区域即为整个不等式系统的解集。
通过使用数轴,我们可以直观地看到这个解集所对应的数对。
数轴是表示不等式解集的一种非常直观且易于理解的方法。
29 在数轴上表示不等式的解集(解析版)初中数学

专题29 在数轴上表示不等式的解集一、单选题1.一个不等式组的解集在数轴上的表示如图,则这个不等式组的解集是()A.-1≤x<3B.-1<x≤3C.-1<x<3D.-1≤x≤3【答案】A【分析】根据在数轴上表示不等式解集的方法进行解答即可.【详解】解:∵-1处是实心圆点且折线向右,3处是空心圆点且折线向左,∵-1≤x<3.故选:A.【点睛】本题考查的是在数轴上表示不等式的解集,熟知“小于向左,大于向右”是解答此题的关键.2.不等式组24020xx-⎧⎨+>⎩的解集在数轴上表示正确的是()A.B.C.D.【答案】C【分析】先求出不等式组的解集,再在数轴上表示出来即可.【详解】解:24020xx-⎧⎨+>⎩①②,解不等式∵,得2x,解不等式∵,得2x>-,∴不等式组的解集是22x-<,在数轴上表示为:,故选:C.【点睛】本题考查了一元一次不等式组和在数轴上表示不等式组的解集,能求出不等式组的解集是解题的关键.3.不等式组5031xx+⎧⎨->⎩的解集在数轴上表示为()A.B.C.D.【答案】C【分析】先将每一个不等式解出来,然后根据求解的口诀即可解答.【详解】解:50,1xx+≥⎧⎨⎩3-②>,①,解不等式∵得:x≥﹣5,解不等式∵得:x<2,由大于向右画,小于向左画,有等号画实点,无等号画空心,∵不等式50,1xx+≥⎧⎨⎩3->,的解集在数轴上表示为:故选:C.【点睛】本题考查了不等式组的解集在数轴上表示,不等式组解集的表示方法:大小小大中间找,大大小小无处找,同大取大,同小取小.4.不等式3x﹣1>5的解集在数轴上表示正确的是()A.B.C.D.【答案】A【分析】依次移项、合并同类项、系数化为1即可得.【详解】解:3x ﹣1>5,3x >5+1,3x >6,x >2,故选A .【点睛】本题主要考查解一元一次不等式,解题的关键是掌握解一元一次不等式的基本步骤.5.不等式3x -2>4的解集在数轴上表示正确的是∵ ∵A .B .C .D .【答案】B【解析】不等式移项得:3x >6∵解得:x >2∵表示在数轴上得:∵故选B∵6.把不等式组12239x x +≥⎧⎨--≥-⎩的解用数轴上的点表示出来,则其解集构成的图形为( )A .射线B .线段C .直线D .长方形【答案】B【分析】先求出不等式组的解集,并在数轴上表示出来,观察数轴即可得出结论【详解】解:12239x x +≥⎧⎨--≥-⎩①②解不等式∵得:1≥x解不等式∵得:3x ≤不等式组的解集是:13x ≤≤其解集构成的图形为:线段故选:B【点睛】本题考查了不等式组的解法,用数轴表示不等式的解集时,要注意“两定”:一是定界点,一般在数轴上只标出原点和界点即可.定边界点时要注意,点是实心还是空心,若边界点含于解集为实心点,不含于解集即为空心点;二是定方向,定方向的原则是:“小于向左,大于向右”.7.如图,是关于x 的不等式2x -m< -1的解集,则m 的值为( )A .2m ≤-B .1m ≤-C .2m =-D .1m =- 【答案】D【分析】根据不等式的解集,可得关于m 的方程,根据解方程,可得答案.【详解】解不等式2x -m< -1得:12m x -< , 因为由图可得不等式的解集为1x <-, 所以112m -=-, 所以m=-1.故选:D .【点睛】考查了不等式的解集,解题关键是当题中有两个未知字母时,应把关于某个字母的不等式中的字母当成未知数,求得解集,再根据数轴上的解集进行判断,求得另一个字母的值.8.把不等式2x ﹣1>﹣5的解集在数轴上表示,正确的是( )A .B .C .D .【答案】C【分析】 按照移项,合并,系数化为1的方法计算即可.【详解】移项得:2x >1﹣5,合并得:2x >﹣4,解得:x >﹣2,故选:C .【点睛】本题考查解不等式,熟练掌握解不等式的一般步骤是解决本题的关键.9.如图,数轴上表示一个不等式的解集是( )A .2x ≥-B .2x -≤C .2x >-D .2x <-【答案】C【分析】根据在数轴上表示不等式解集的方法解答即可.【详解】∵-2处是空心圆圈,且折线向右,∵这个不等式的解集是x >-2.故选C .【点睛】考查的是在数轴上表示不等式的解集.在数轴上实心圆点包括该点,空心圆圈不包括该点,大于向右小于向左.10.不等式213x +≥的解集在数轴上表示正确的是( )A .B .C .D .【答案】D【分析】 解不等式求得不等式的解集,然后根据数轴上表示出的不等式的解集,再对各选项进行逐一分析即可.【详解】解:不等式213x +≥的解集为:1≥x ,故选:D .【点睛】本题考查的解一元一次不等式以及在数轴上表示不等式解集,熟知实心圆点与空心圆点的区别是解答此题的关键.11.用不等式表示如图所示的解集正确的是( )A .x >2B .x ≥2C .x <2D .x ≤2【答案】C【分析】根据不等式组解集在数轴上的表示方法可知不等式的解集.【详解】解:观察数轴可知:向左画又是空心圆,即表示小于2的数.故选:C .【点睛】本题考查了不等式解集的数轴表示法,明确“>”、“<”、“实心圆点”、“空心圆”的含义是解答本题的关键. 12.不等式组21512x x ->⎧⎪⎨+⎪⎩①②中,不等式∵和∵的解集在数轴上表示正确的是( ) A . B .C .D . 【答案】C【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解,确定不等式组的解集.【详解】解:解不等式∵,得:1x <,解不等式∵,得:3x -,则不等式组的解集为31x -<≦,将两不等式解集表示在数轴上如下:故选:C .【点睛】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.13.不等式x +2≥3的解集在数轴上表示正确的是( )A .B .C .D .【答案】C【分析】根据解一元一次不等式基本步骤:移项、合并同类项可得.【详解】解:∵23x +≥,∵32x ≥-,∵1x ≥,故选:C .【点睛】本题主要考查了解一元一次不等式的基本能力,严格遵循解不等式的基本步骤是关键,尤其需要注意不等式两边都乘以或除以同一个负数不等号方向要改变.14.不等式组()2160.510.5x x ⎧+<⎨+≥⎩的解集在数轴上表示正确的是( )A .B .C .D .【答案】A【分析】准确求解不等式组,在进行判断即可.【详解】()2160.510.5x x ⎧+<⎨+≥⎩①②解不等式∵得:x <2,解不等式∵得:x≥﹣1,则不等式组的解集为﹣1≤x <2,在数轴上表示为:故选:A .【点睛】本题主要考查解一元一次不等式组,熟练掌握一元一次不等式组的解法是解题的关键.15.在数轴上表示不等式240x -的解集,正确的是( )A .B .C .D .【答案】B【分析】先根据不等式的解法求出解,然后在数轴上表示,选出正确答案即可.【详解】x-,解:240x,24x2x,∵不等式的解集为:2在数轴上表示为:,故选:B.【点睛】本题考查求一元一次不等式解集及在数轴上表示不等式的解集,熟练掌握不等式的解法及在数轴上表示解集是解题关键.x-≤的解集在数轴上表示正确的是()16.不等式2A.B.C.D.【答案】C【分析】先求出不等式的解集,再在数轴上表示出来即可.【详解】把x的系数化为1得,x≥−2.在数轴上表示为:故选:C.【点睛】本题考查的是在数轴上表示不等式的解集,熟知实心圆点与空心圆点的区别是解答此题的关键.17.不等式x-1>0的解集在数轴上表示正确的是( )A .B .C .D .【答案】A【分析】 先求出不等式的解集,然后在数轴上表示即可.【详解】∵x -1>0,∵x>1,在数轴上表示为:故选A.【点睛】此题主要考查了在数轴上表示不等式的解集,关键是用数轴表示不等式的解集时,要注意“两定”:一是定界点,一般在数轴上只标出原点和界点即可.定界点时要注意,点是实心还是空心,若边界点含于解集为实心点,不含于解集即为空心点;二是定方向,定方向的原则是:“小于向左,大于向右”.18.在数轴上表示不等式组20260x x +>⎧⎨-⎩的解集,正确的是( ) A .B .C .D .【答案】A【解析】 20260x x +>⎧⎨-≤⎩①② 解∵得,2x >- ;解∵得,3x ≤ ;∵不等式组的解集是:23x -<≤ .故选A.点睛:不等式组的解法是,先分别解两个不等式,求出它们的解集,再求两个不等式解集的公共部分.不等式组解集的确定方法是:同大取大,同小取小,大小小大取中间,大大小小无解.在数轴上的表示时注意, 空心圈表示不包含该点,实心点表示包含该点.19.若关于x 的不等式(1)1a x a -+>-的解集如图所示,则a 必满足( )A .0a <B .1a >C .1a <-D .1a <【答案】B【分析】由不等式的解集可知1-a <0,由此得a 的范围.【详解】解:由图可知:不等式(1)1a x a -+>-的解集为:x <-1,即()11a x a ->-,则1-a <0,∵a >1,故选B .【点睛】本题考查了运用数轴表示不等式的解集.关键是由不等式解集的结果得出不等式,求字母a 的值. 20.不等式组1021x x +≥⎧⎨-≤⎩的解集在数轴上表示正确的( )A .B .C .D .【答案】D【分析】先分别求出各不等式的解集,再求其公共解集即可.【详解】解:1021x x +≥⎧⎨-≤⎩①②由∵得x ≥﹣1,由∵得x ≤3,根据“小大大小中间找”的原则可知不等式组的解集为﹣1≤x ≤3.故选:D .【点睛】把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.求不等式组的解集应遵循“同大取较大,同小取较小,小大大小中间找,大大小小解不了”的原则.21.下列不等式组的解集,在数轴上表示为如图所示的是( )A .1020x x ->⎧⎨+≤⎩B .1020x x +>⎧⎨+≤⎩C .1020x x +>⎧⎨-≤⎩D .1020x x -≤⎧⎨+<⎩ 【答案】C【分析】由数轴可得表示的解集为12x -<≤,把各个选项求出解集,即可解答.【详解】数轴表示的解集为12x -<≤.解不等式组1020x x ->⎧⎨+≤⎩,得:12x x >⎧⎨≤-⎩,解集为空集,故A 不符合题意. 解不等式组1020x x +>⎧⎨+≤⎩,得:12x x >-⎧⎨≤-⎩,解集为空集,故B 不符合题意.解不等式组1020xx+>⎧⎨-≤⎩,得:12xx>-⎧⎨≤⎩,解集为12x-<≤,故C符合题意.解不等式组1020xx-≤⎧⎨+<⎩,得:12xx≤⎧⎨<-⎩,解集为2x<-,故D不符合题意.故选C.【点睛】本题考查在数轴上表示不等式的解集以及解不等式组,解决本题的关键是求出不等式组的解集.22.不等式组10840xx-⎧⎨-≤⎩>的解集在数轴上表示为().A.B.C.D.【答案】A【分析】解不等式组,看解集表示是否正确即可.【详解】解:10 840 xx-⎧⎨-≤⎩>①②解不等式∵得,1x>,解不等式∵得,2x≥,不等式组的解集为:2x≥.故选:A.【点睛】本题考查了一元一次不等式组的解法及在数轴上表示解集,解题关键是熟练的运用解不等式组的方法进行计算.23.不等式325132x x++≤-的解集表示在数轴上是()A.B.C.D.【答案】B【分析】根据一元一次不等式的解法,去分母,去括号,移项,合并同类项,系数化为1即可得解.【详解】解:去分母,得,2(3x+2)≤3(x+5)﹣6,去括号,得6x+4≤3x+15﹣6,移项、合并同类项,得3x≤5,系数化为1,得,x≤53,在数轴上表示为:故选:B.【点睛】本题考查了解一元一次不等式,以及在数轴上表示不等式的解集,>向右画,<向左画,≤与≥用实心圆点,<与>用空心圆圈.24.不等式-3<a≤1的解集在数轴上表示正确的是()A.B.C.D.【答案】A【分析】根据在数轴上表示不等式解集的方法求解即可.【详解】解:∵-3<a≤1,∵1处是实心原点,且折线向左.故选:A .【点睛】本题考查了在数轴上表示不等式的解集,掌握“小于向左,大于向右”是解题的关键.25.不等式组111x x -<⎧⎨≥-⎩的解集在数轴上表示正确的是( ) A .B .C .D . 【答案】B【分析】先根据不等式组求出解集,然后在数轴上准确的表示出来即可.【详解】111x x -<⎧⎨-⎩①② 由不等式∵组得,x<2∵不等式组的解集为:21x x ⎧⎨≥-⎩< 其解集表示在数轴上为, 故选B .【点睛】此题主要考查不等式组的解法及在数轴上表示不等式组的解集.不等式组的解集在数轴上表示的方法:把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.26.不等式x <2的解集在数轴上表示为( )A.B.C.D.【答案】B【分析】根据不等式组解集在数轴上的表示方法就可得到.【详解】解:x<2的解集表示在数轴上2左边的数构成的集合,在数轴上表示为:故选:B【点睛】不等式组解集在数轴上的表示方法:把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.27.不等式2x+1≤5的解集,在数轴上表示正确的是()A.B.C.D.【答案】C【分析】先移项得到2x≤4,再把系数化为1得到不等式的解集,然后利用数轴表示出解集即可得答案.【详解】2x+1≤5移项得:2x≤5﹣1,系数化为1得:x≤2.故选:C.【点睛】本题考查了一元一次不等式的解法和在数轴上表示不等式的解集,熟知“小于向左,大于向右,在表示解集时≥、≤要用实心圆点表示;<,>要用空心圆点表示”是解答此题的关键.28.已知两个不等式的解集在数轴上如右图表示,那么这个解集为()A .≥-1B .>1C .-3<≤-1D .>-3【答案】A【解析】>-3 ,≥-1,大大取大,所以选A29.在平面直角坐标系中,点P (2x+4,x ﹣3)在第四象限,则x 的取值范围表示在数轴上,正确的是( ) A . B .C .D .【答案】A【解析】根据题意,得:24030x x +>⎧⎨-<⎩①②∵解不等式∵,得:x>−2∵解不等式∵,得:x<3∵则不等式组的解集为−2<x<3∵故选A.二、填空题30.不等式0ax b +>的解集在数轴上表示如图所示,则该不等式的解集为 ___________________.【答案】x >-3【分析】根据不等式解集的数轴表示法可以得到解答.【详解】解:阅读数轴,折线向右且表示3的点为空心,所以不等式的解集为x>-3.故答案为x>-3.【点睛】本题考查不等式的解集,熟练掌握解集的数轴表示法是解题关键.31.一个一元一次不等式组的解集在数轴上的表示如图,则该不等式组的解集是_______.【答案】13x -≤<【分析】根据一元一次不等式的解集在数轴上的表示方法即可得.【详解】由数轴图可知,该不等式组的解集是13x -≤<,故答案为:13x -≤<.【点睛】本题考查了一元一次不等式的解集在数轴上的表示,掌握理解不等式的解集在数轴上的表示方法是解题关键.32.某个关于x 的不等式的解集在数轴上的表示如图所示,这个不等式的解集是_____.【答案】x ≥﹣2【分析】根据不等式的解集在数轴上的表示方法解答即可.【详解】解:∵﹣2处是实心圆点,且折线向右,∵x ≥﹣2.故答案为:x ≥﹣2.【点睛】本题考查了不等式的解集在数轴上的表示方法,一般的,不等式的解集在数轴上遵循“小于向左,大于向右;边界含于解集为实心点,不含于解集为空心点”.33.若关于x 的不等式的解集在数轴上表示如图,请写出此解集为______.【答案】21x -<≤【分析】根据不等式的解集与数轴的关系即可解答.【详解】由数轴知,此不等式的解集为21x -<,故答案为:21x -<.【点睛】本题考查了在数轴上表示不等式的解集,熟练掌握不等式的解集与数轴的关系是解答的关键.34.如图,张小雨把不等式3x >2x -3的解集表示在数轴上,则阴影部分盖住的数字是____.【答案】-3【分析】先求出不等式的解,即可求出答案.【详解】由3x >2x -3∵解得:x∵-3∵∵阴影部分盖住的数字是:-3.故答案是:-3.【点睛】本题主要考查解一元一次不等式以及不等式的解在数轴上的表示,掌握一元一次不等式的解在数轴上的表示方法,是解题的关键.35.关于x 的某个不等式组的解集在数轴上表示如图所示,则这个不等式组的解集为______________.【答案】﹣1≤x ≤4【解析】【分析】∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵【详解】∵∵∵−1∵∵∵∵∵∵∵∵∵∵∵∵∵∵x1≥﹣∵∵4∵∵∵∵∵∵∵∵∵∵∵∵x4≤∵∵∵∵∵∵∵∵∵∵1x4-≤≤∵∵∵∵∵∵1x4-≤≤∵∵【点睛】∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵∵36.如图∵∵,表示的不等式的解集是________.【答案】x∵2【解析】由数轴得不等式的解集是x∵2∵故答案为x∵2.37.关于x的不等式﹣2x+a≥4的解集如图所示,则a的值是__.【答案】2.【分析】由不等式﹣2x+a≥4可得x≤42a-,然后由数轴可得x≤﹣1,进而问题可求解.【详解】解:∵﹣2x+a≥4,∵x≤42a-,∵x≤﹣1,∵41 2a-=-,∵a=2,故答案为2.【点睛】本题主要考查含参数的不等式的解法,熟练掌握一元一次不等式的解法是解题的关键.38.根据如图所示,用不等式表示公共部分x 的范围______.【答案】32x -≤<【分析】根据实心圆点包括该点,空心圆圈不包括该点,大于向右小于向左,公共部分即是解集;【详解】由图示可以看出,从-3出发向右画出的折线且表示-3的点是实心圆,表示3x ≥-;从2出发向左画出的折线且表示2的点是空心圆,表示2x <,∵这个不等式组的解集为:32x -≤<.故答案是32x -≤<.【点睛】本题主要考查了数轴上不等式的解集,准确分析判断是解题的关键.39.一个关于 x 的一元一次不等式组的解在数轴上的表示如图所示,则该不等式组的解是__________.【答案】3x >【分析】数轴的某一段上面,表示解集的线的条数,与不等式的个数一样,那么这段就是不等式组的解集.实心圆点包括该点,空心圆圈不包括该点,大于向右小于向左.两个不等式的公共部分就是不等式组的解集.【详解】解:由图示可看出,从1出发向右画出的线且1处是实心圆,表示x ≥1;从3出发向右画出的线且3处是空心圆,表示x >3,不等式组的解集是指它们的公共部分,所以这个不等式组的解为:3x >,故答案为: 3x >.【点睛】等式的解集在数轴上表示的方法:把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.40.不等式3x+2>2(x-1)的解集为_____,在数轴上表示为.【答案】x>-4,数轴上表示见解析【解析】【分析】利用不等式的基本性质,把不等号右边的x移到左边,合并同类项即可求得原不等式的解集.【详解】3x+2>2(x-1),3x-2x>-2-2,x>-4,把解集表示在数轴上为.故答案是:x>-4,数轴上表示见解析.【点睛】考查了解简单不等式的能力,解答这类题学生往往在解题时不注意移项要改变符号这一点而出错.解不等式要依据不等式的基本性质:(1)不等式的两边同时加上或减去同一个数或整式不等号的方向不变;(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变;(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变.41.如果关于x的不等式x≥12a-的解集在数轴上表示如图所示,那么a的值为_____.【答案】-3【分析】根据不等式的解集及其在数轴上的表示得出关于a的方程,解之可得答案.【详解】解:根据题意知:12a-=﹣2,∵a﹣1=﹣4,则a=﹣3,故答案为:﹣3.【点睛】本题主要考查解一元一次不等式及不等式解集在数轴上的表示,解题的关键是根据解集在数轴上的表示得出关于a的方程.42.关于x的不等式2x﹣a≤﹣1的解集如图所示,则a的值是_____.【答案】-1【分析】首先解不等式2x﹣a≤﹣1可得x≤12a-,根据数轴可得x≤﹣1,进而得到12a-=﹣1,再解方程即可.【详解】∵2x﹣a≤﹣1,∵x≤1 2a-,∵x≤﹣1,∵12a-=﹣1,解得:a=﹣1,故答案为:﹣1.【点睛】此题主要考查了在数轴上表示不等式的解集,关键是正确解出不等式的解集.43.将数轴上x的范围用不等式表示:__________.【答案】x>2【解析】【分析】根据在数轴上表示不等式解集的方法得出该不等式的解集即可.【详解】解:数轴上表示不等式解集的方法可知,该不等式的解集为:x>2.故答案为:x>2.【点睛】本题考查了在数轴上表示不等式的解集,熟知实心圆点与空心原点的区别是解题的关键.44.若不等式(a -3)x <3-a 的解集在数轴上表示如图所示,则a 的取值范围是______.【答案】a <3【解析】【分析】由图示可知:不等式的解集为:x >-1,根据不等式的性质可知:a -3<0,解之即可.【详解】解:由图示可知:不等式的解集为:x >-1,根据题意得:a -3<0,解得:a <3,故答案为:a <3.【点睛】本题考查解一元一次不等式和在数轴上表示不等式的解集,正确掌握不等式的性质是解题的关键.三、解答题45.解不等式,并把解集表示在数轴上:23x->72x+.【答案】x <-33,数轴表示见解析【分析】先根据不等式的解法求解不等式,然后在数轴上表示出解集.【详解】 解:23x->72x+,去分母得:2x -12>21+3x ,移项得:2x -3x >12+21,合并同类项得:-x >33系数化为1得:x <-33,在数轴上表示为:【点睛】本题考查了解一元一次不等式,解答本题的关键是掌握不等式的解法以及在数轴上表示不等式的解集.46.解不等式并把不等式的解集在数轴上表示出来.5(x-2)+8<6(x-1)+7【答案】3x>-【分析】利用不等式的基本性质,把不等号右边的x移到左边,合并同类项即可求得原不等式的解集.【详解】解:5(x−2)+8<6(x−1)+7,5x−10+8<6x−6+7,整理得:−x<3,解得:x>−3,画图如下:【点睛】此题考查了解一元一次不等式,掌握不等式的性质是本题的关键,解答这类题学生往往在解题时不注意移项要改变符号这一点而出错.47.解不等式:11126x x-+<-,并把它的解集表示在数轴上.【答案】2x<,表示在数轴上见解析【分析】先去分母,再去括号,移项、合并同类项,把x 的系数化为1即可.【详解】去分母,得:()()3161x x -<-+,去括号,得:3361x x -<--,移项,得:3613x x +<-+,合并同类项,得:48x <,系数化为1,得:2x <,将不等式的解集表示在数轴上如下:【点睛】本题考查了解一元一次不等式,熟知解一元一次不等式的基本步骤是解答此题的关键.48.解不等式,并把解集表示在数轴上21132x x -+-< 【答案】x >-1,图详见解析【分析】先根据解一元一次不等式基本步骤:去分母、去括号、移项、合并同类项、系数化为1得解集,再将解集表示在数轴上.【详解】 解:21132x x -+-< 6-2(2-x)<3(x+1)6-4+2x<3x+32x -3x<3+4-6-x<1x>-1故不等式的解集为x>-1表示在数轴上如下:【点睛】本题主要考查解一元一次不等式的基本能力,严格遵循解不等式的基本步骤是关键,尤其需要注意不等式两边都乘以或除以同一个负数不等号方向要改变.49.解不等式,并在数轴上表示解集:231232x x --≥-. 【答案】117x ≤,图详见解析 【分析】先去分母、移项合并,然后把系数化为1得到不等式的解集,然后用数轴表示其解集.【详解】去分母,得:()()2233112x x -≥--去括号,得:249312x x -≥--,移项,得:293124x x -≥--+,合并同类项,得:711x -≥-,系数化为1,得:117x ≤, 将解集表示在数轴上如下:【点睛】本题主要考查了解一元一次不等式,严格遵循解不等式的基本步骤是关键,尤其需要注意不等式两边都乘以或除以同一个负数不等号方向要改变.50.解不等式3185315x x +-->,并把解集在数轴上表示出来.【答案】3x <,见解析【分析】根据解一元一次不等式基本步骤:去分母、去括号、移项、合并同类项、系数化为1可得.【详解】解: 3185315x x +--> ()()33518x x +-->.39558x x +-+>3 5895x x ->--26x ->-.3x <.它在数轴上的表示如图所示:【点睛】本题主要考查解一元一次不等式的基本能力,严格遵循解不等式的基本步骤是关键,尤其需要注意不等式两边都乘以或除以同一个负数不等号方向要改变.51.解不等式组()453142? 3x x x x ⎧-<-⎪⎨+-≥⎪⎩,并将解集在数轴上表示出来. 【答案】12x ≤,数轴上表示见解析 【分析】先求出每个不等式的解集,再根据找不等式组解集的规律找出不等式组的解集,最后在数轴上表示出来即可.【详解】 ()453142?3x x x x ⎧-<-⎪⎨+-≥⎪⎩①②, 解不等式∵得:2x <,解∵得:12x ≤, ∵不等式组的解集为1 2x ≤在数轴上表示不等式组的解集为:【点睛】本题考查了解一元一次不等式(组),在数轴上表示不等式组的解集的应用,解此题的关键是能根据不等式的解集找出不等式组的解集.52.(1)解方程:(x +1)2=214; (2)解不等式:3136x x ->-,并把不等式的解集在数轴上表示出来. 【答案】(1)1215,22x x ==-;(2)3x >,数轴见解析. 【分析】(1)利用平方根定义进行求解可得答案;(2)根据解一元一次不等式基本步骤:去分母、移项、合并同类项、系数化为1可得.【详解】解:(1)∵(x +1)2=94, ∵x +1=±32, 则x =﹣1±32, ∵x 1=12,x 2=﹣52; (2)∵3136x x ->-, ∵2x >6﹣x +3,2x +x >6+3,3x >9,∵x >3,将解集表示在数轴上如下:【点睛】本题考查了利用平方根解方程、解一元一次不等式等知识,是重要考点,难度较易,掌握相关知识是解题关键.53.解不等式组:2(21)3(1)1132x x x x x -+⎧⎪+-⎨<-⎪⎩,并把不等式组的解集表示在数轴上.【答案】不等式组的的解集为15x -<,数轴见解析【分析】先分别求解不等式,再根据数轴表示不等式解集的方法准确画出图形即可.【详解】解:()()221311122x x x x x ⎧-+⎪⎨+-<-⎪⎩①②, 由∵得:5x ,由∵得:1x >-,∴不等式组的的解集为15x -<.【点睛】本题考查解不等式组及在数轴上表示不等式组的解集,准确求解不等式组并理解数轴表示解集的细节是解题关键.54.解不等式,并把不等式(2)的解集在数轴上表示出来.(1)46715x x -≥-;(2)235324x x +≥⎧⎨-≤⎩【答案】(1)3x ≤;(2)1≤x≤2,数轴表示见解析【分析】。
初一数学在数轴上表示不等式(组)的解集(含答案)

初一数学在数轴上表示不等式(组)的解集一选择题1.如图,表示的不等式组的解集为()A.1<x≤2 B.x≤2 C.x<1 D.空集2.下列在数轴上表示x<﹣2的解集,正确的是()A.B.C.D.3.如图,数轴上表示的解集为()A.﹣3<x≤2 B.x≤2 C.x>﹣3 D.﹣3≤x<24.如图,该数轴表示的不等式的解集为()A.x<2 B.x>1 C.0<x<2 D.1<x<25.不等式组的解集在数轴上表示正确的是()A.B.C.D.6.不等式x≥﹣2的解集在数轴上表示正确的是()A.B.C.D.7.不等式x﹣2<0的解集在数轴上表示出来正确的是()A.B.C.D.8.不等式组的解集在数轴上表示正确的是()A.B.C.D.9.不等式组的解集在数轴上表示正确的是()A.B.C.D.10.一个不等式组中两个不等式的解集在同一数轴上的表示如图所示,这个不等式组的解集为()A.x<﹣1 B.x≤1 C.﹣1<x≤1 D.x≥111.不等式x<1的解集在数轴上的表示,正确的是()A.B.C.D.12.已知不等式的解集在数轴上表示如图所示,则此不等式的解集是()A.B.C.D.13.把不等式x≥﹣1的解集表示在数轴上正确的是()A.B.C.D.14.在数轴上表示﹣2≤x<1正确的是()A. B.C. D.15.把不等式组的解集表示在数轴上,下列选项正确的是()A.B.C.D.16.将不等式组的解集在数轴上表示,正确的是()A. B. C. D.17.交通法规人人遵守,文明城市处处安全.在通过桥洞时,我们往往会看到如图所示的标志,这是限制车高的标志.则通过该桥洞的车高x(m)的范围在数轴上可表示为()A. B.C. D.二填空题18.如图,数轴上表示关于x的不等式组的解集是.19.关于x的一元一次不等式组的解集在数轴上的表示如图,则该不等式组的解集是.20.现规定一种新运算,a※b=2a﹣b,其中a、b为常数.已知关于x的不等式k※x≤3的解集在数轴上表示如图,则k的值为.21.世界杯正如火如荼地进行着,其小组赛赛制为:每队胜一场得3分,平一场得1分,负一场得0分.若某强队想要在小组赛中确保出线,就必须在3场中保持不败并且积分不少于7分,则该队至少胜多少场?设该队胜x场,则列出的不等式为.22.关于x的不等式组恰有3个整数解,则实数a的取值范围是.23.清明将至,前去扫墓的人逐渐增多.某花店购进白菊,白百合,马蹄莲共计m捆.白菊每捆20支,白百合每捆12支,马蹄莲每捆10支.现取出白菊的,白百合的,马蹄莲的,全部用于扎成A、B两款花束销售.其中A款花束白菊2支,白百合3支,马蹄莲1支,B款花束白菊5支,马蹄莲2支.如此取出后剩下的白百合支数不多于马蹄莲支数,则购进的白菊捆数与白百合捆数之比至少为.24.已知关于x的一元一次不等式(m+2)x>4的解集是,如图,数轴上的A,B,C,D四个点中,实数m对应的点可能是.25.某公司决定采购整箱的苹果、脐橙和柚子来奖励员工以及回馈客户.其中每箱苹果40元,每箱脐橙120元,每箱柚子80元:公司采购的所有水果的箱数之和不超过120箱,购买的苹果不低于28箱,且购买脐橙的费用是购买苹果费用的4倍,购买柚子的费用是购买苹果费用的3倍.公司把采购的所有水果均用于奖励员工和回馈客户,最后发现奖励给员工与回馈给客户的同种类型的水果的数量之差不超过3箱,且奖励给员工的所有水果的总费用与回馈给客户的所有水果的总费用相同,则公司奖励员工的所有水果的箱数总和最多为箱.初一数学在数轴上表示不等式(组)的解集参考答案与解析1.分析:数轴的某一段上面,表示解集的线的条数,与不等式的个数一样,那么这段就是不等式组的解集.实心圆点包括该点,空心圆圈不包括该点,大于向右小于向左.两个不等式的公共部分就是不等式组的解集.解:不等式组公共部分在1的左边.因而解集为:x<1.故选:C.2.分析:根据不等式的解集在数轴上表示出来的方法画数轴即可.解:在数轴上表示不等式x<2的解集,故选:B.3.分析:根据求不等式组的解集的表示方法,可得答案.解:由图可得,x>﹣3且x≤2,∴在数轴上表示的解集是﹣3<x≤2,故选:A.4.分析:根据“大小小大中间取”和不等式的解集在数轴上表示方法即可求出不等式的解集.解:该数轴表示的不等式的解集为1<x<2.故选:D.5.分析:先求出每一个不等式的解集,在数轴上表示出来,其公共部分即为不等式组的解集.解:由(1)得,x>﹣1,由(2)得,x≤2,故原不等式组的解集为:﹣1<x≤2.故选:D.6.分析:将已知解集表示在数轴上即可.解:不等式x≥﹣2的解集在数轴上表示正确的是.故选:D.7.分析:先解不等式,再在数轴上表示出不等式的解集.解:不等式x﹣2<0的解集为x<2,在数轴上表示为:故选:B.8.分析:分别求出各不等式的解集,再求出其公共解集,并在数轴上表示出来即可.解:,由①得,x>1;由②得,x<2,故此不等式组的解集为:1<x<2,在数轴上表示为:,故选:C.9.分析:先求出不等式组中每一个不等式的解集,再求出它们的公共部分,然后把不等式的解集表示在数轴上即可.解:不等式组的解集为x<1,在数轴上表示为.故选:C.10.分析:本题可根据数轴的性质,实心圆点包括该点用“≥”,“≤”表示,空心圆圈不包括该点用“<”,“>”表示,大于向右,小于向左.观察相交的部分即为不等式的解集.解:数轴上表示解集的线的条数与不等式的个数一样的部分是﹣1左边的部分,则不等式解集为:x<﹣1.故选:A.11.分析:将已知解集表示在数轴上即可.解:不等式x<1的解集在数轴上表示为,故选:C.12.分析:根据数轴上不等式解集的表示方法进行解答即可.解:∵表示﹣的数上的点是空心圆点,且曲线向右折,∴此不等式的解集是:x>﹣.故选:C.13.分析:根据比﹣1大的数在﹣1的右边,x≥﹣1包括界点﹣1,据此求解即可.解:把不等式x≥﹣1的解集表示在数轴上,正确的是,故选:B.14.分析:根据﹣2是实心点,方向向右,1是空心点,方向向左画出图形即可得到答案.解:﹣2是实心点,方向向右,1是空心点,方向向左,如图所示:,故选:D.15.分析:先求出不等式组中每一个不等式的解集,再求出它们的公共部分,然后把不等式的解集表示在数轴上即可.解:由﹣x≤﹣1解得x≥1,由x+1>0解得x>﹣1,不等式的解集是x≥1,在数轴上表示如图,故选:A.16.分析:先求出不等式组的解集并在数轴上表示出来,找出符合条件的选项即可.解:由x≤1得x≤3,所以不等式组的解集为1<x≤3,在数轴上的表示为:,故选:A.17.分析:利用已知图表直接得出该桥洞的车高x(m)的取值范围.解:由题意可得:通过该桥洞的车高x(m)的取值范围是:0<x≤4.5.在数轴上表示如图:,故选:D.18.分析:从数轴可得不等式组的解集为﹣1<x≤3.解:从图可知,不等式组的解集为﹣1<x≤3,故答案为﹣1<x≤3.19.分析:根据数轴得出不等式组的解集即可.解:根据数轴可知:不等式组的解集是﹣1≤x<3,故答案为:﹣1≤x<3.20.分析:根据k※x≤3得出2k﹣x≤3,求出不等式的解集是x≥﹣3+2k,根据数轴得出﹣3+2k =﹣1,再求出k即可.解:∵k※x≤3,∴2k﹣x≤3,∴﹣x≤3﹣2k,∴x≥﹣3+2k,从数轴可知:﹣3+2k=﹣1,解得:k=1,故答案为:1.21.分析:由该队胜x场,可得出该队平(3﹣x)场,利用积分=3×胜的场数+1×平的场数,结合积分不少于7分,即可得出关于x的一元一次不等式,此题得解.解:设该队胜x场,则平(3﹣x)场,根据题意得:3x+3﹣x≥7.故答案为:3x+3﹣x≥7.22.分析:先解出不等式组的解集,然后根据不等式组恰有3个整数解,即可得到a的取值范围.解:,解不等式①得:x>3.5,解不等式②,得:x≤a,∵关于x的不等式组恰有3个整数解,∴这三个整数解是4,5,6,∴6≤a<7,故答案为:6≤a<7.23.分析:根据题意线设出白菊和白百合的捆数,然后根据题中条件分别写出取去的白菊、白百合、马蹄莲的支数,再根据题意设出A款花束和B款花束的数量,根据花束中每个花的支数可列出方程组,解出方程组,再根据取出后剩下的白百合支数不多于马蹄莲支数列出不等式,解出不等式即可.解:设购进白菊有x捆,白百何有y捆,则马蹄莲有(m﹣x﹣y)捆,∵白菊每捆20支,白百合每捆12支,马蹄莲每捆10支,∴白菊有20x支,白百合有12y支,马蹄莲有10(m﹣x ﹣y)支,∵现取出白菊的,白百合的,马蹄莲的,全部用于扎成A、B两款花束销售,∴取出的白菊有10x支,白百合有4y支,马蹄莲有(m﹣x﹣y)支,设A款花束有a束,B款花束有b束,根据A款花束白菊2支,白百合3支,马蹄莲1支,B款花束白菊5支,马蹄莲2支可列方程组得:,由②得:a=④,把④代入①得:b=2x﹣y⑤,把④和⑤代入③得:m=,∵取出后剩下的白百合支数不多于马蹄莲支数,∴12y﹣4y≤10(m﹣x﹣y)﹣(m﹣x﹣y),即8y≤(﹣x﹣y),整理得:5x≥3y,∴,故答案为:3:5.24.分析:根据已知得出关于m的不等式,求出不等式的解集即可.解:(m+2)x>4,∵关于x的一元一次不等式(m+2)x>4的解集是,∴m+2<0,∴m的取值范围是m<﹣2,∵数轴上的A,B,C,D四个点中,只有点A表示的数小于﹣2,∴实数m对应的点可能是点A.故答案为:点A.25.分析:设该公司购买苹果x箱,脐橙y箱,柚子z箱,根据题意可知,,解得28≤x≤31,且y=x,z=x.由x是6的倍数可知,x=30,y=40,z=45.设回馈给客户的苹果a箱,脐橙b箱,柚子c箱,则奖励给员工的苹果(30﹣a)箱,脐橙(40﹣b)箱,柚子(45﹣z)箱,列出方程,整理得a+3b+2c=120.由同种类型的水果的数量之差不超过3箱,得出a,b,c的范围,再结合想要奖励给员工的水果箱数最多,可得出a,b,c的值,进而可得出结论.解:设该公司购买苹果x箱,脐橙y箱,柚子z箱,根据题意可知,,解得28≤x≤31,且y=x,z=x.∵y,z是整数,∴x一定为6的倍数.∴x=30,y=40,z=45.设回馈给客户的苹果a箱,脐橙b箱,柚子c箱,则奖励给员工的苹果(30﹣a)箱,脐橙(40﹣b)箱,柚子(45﹣z)箱,∴40a+120b+80c=40(30﹣a)+120(40﹣b)+80(45﹣c),整理得a+3b+2c=120.∵同种类型的水果的数量之差不超过3箱,∴,解得.∵a,b,c为整数,∴a=14或15或16,b=19或20或21,c=21或22或23或24.∵a+3b+2c=120,解得a=14,b=20,c=23.或a=16,b=20,c=22或a=15,b=c=21或a=15,b=19,c=24,若想奖励给员工最多,则回馈用户最少,∴a+b+c的最小值为:57.∴奖励给员工最多的为:30+40+45﹣57=58(箱).故答案为:58.。
