八年级数学上册提优练习
初二提优测试卷答案数学

一、选择题(每题5分,共25分)1. 下列数中,是偶数的是()A. -3B. 5C. 8D. 10答案:C解析:偶数是指能够被2整除的整数,因此8是偶数。
2. 下列图形中,是轴对称图形的是()A. 矩形B. 三角形C. 圆D. 正方形答案:C解析:轴对称图形是指图形中存在一条直线,使得图形在这条直线的两侧完全重合。
圆具有无数条对称轴,因此是轴对称图形。
3. 下列等式中,正确的是()A. 3x + 5 = 2x + 8B. 4x - 2 = 3x + 6C. 2x + 3 = 5x - 7D. 5x + 2 = 3x + 9答案:D解析:将等式两边的同类项合并,可得5x - 3x = 9 - 2,即2x = 7,所以x =3.5。
将x的值代入原等式,等式成立。
4. 下列函数中,是正比例函数的是()A. y = 2x + 3B. y = 3x - 5C. y = 2xD. y = 3x^2答案:C解析:正比例函数是指当x变化时,y也按照相同的比例变化。
在选项中,只有C中的函数y = 2x满足这一条件。
5. 下列方程中,有唯一解的是()A. 2x + 3 = 7B. 2x + 3 = 2xC. 2x + 3 = 5xD. 2x + 3 = 7x答案:A解析:将方程中的同类项合并,可得2x = 4,即x = 2。
将x的值代入原方程,方程成立,因此方程有唯一解。
二、填空题(每题5分,共25分)1. 若a = -3,则a^2的值为__________。
答案:9解析:a^2表示a的平方,即a乘以自己。
将a = -3代入,可得(-3)^2 = 9。
2. 下列图形中,周长最大的是__________。
答案:圆解析:周长是指图形边界上所有线段长度的总和。
在所有图形中,圆的周长最大,因为圆的周长与半径成正比。
3. 若x = 2,则2x + 3的值为__________。
答案:7解析:将x = 2代入2x + 3,可得2×2 + 3 = 7。
苏教版8年级上学期数学综合提优练习(附答案)

苏教版8年级上学期数学综合提优练习一、综合题1.在平面直角坐标系中.抛物线y=ax2+2ax−3a(a≠0)与x轴交于A.B两点(点A在点B的左侧).与y轴交于点C.该抛物线的顶点为D.(1)求该抛物线的对称轴及点A、B的坐标;(2)当a>0时.如图1.连接AD.BD.是否存在实数a.使△ABD为等边三角形?若存在.求出实数a的值.若不存在.请说明理由;(3)当a=1时.如图2.点P是该抛物线上一动点.且位于第三象限.连接AP.直线PO交AC于点Q. △APQ和△OCQ的面积分别为S1和S2.当S1−S2的值最大时.求直线PO的解析式.2.综合题:提出问题(1)问题如图1.点A为线段BC外一动点.且BC=a.AB=b.填空:当点A位于时.线段AC的长取得最大值.且最大值为(用含a.b的式子表示)(2)应用点A为线段BC外一动点.且BC=3.AB=1.如图2所示.分别以AB.AC为边.作等边三角形ABD和等边三角形ACE.连接CD.BE.①请找出图中与BE相等的线段.并说明理由;②直接写出线段BE长的最大值.(3)拓展:如图3.在平面直角坐标系中.点A的坐标为(2.0).点B的坐标为(5.0).点P为线段AB外一动点.且PA=2.PM=PB.∠BPM=90.请直接写出线段AM长的最大值及此时点P的坐标.3.操作:在∠ABC中.AC=BC=2.∠C=90°.将一块等腰三角形板的直角顶点放在斜边AB的中点P 处.将三角板绕点P旋转.三角板的两直角边分别交射线AC、CB于D、E两点。
图①.②.③是旋转三角板得到的图形中的3种情况。
研究:(1)三角板ABC绕点P旋转.观察线段PD和PE之间有什么数量关系?并结合图②加以证明。
(2)三角板ABC绕点P旋转.∠PBE是否能为等腰三角形?若能.指出所有情况(即写出∠PBE为等腰三角形时CE的长);若不能.请说明理由。
(图④不用)4.如图.将矩形ABCD沿AF折叠.使点D落在BC边的点E处.过点E作EG∠CD交AF于点G.连接DG.(1)求证:四边形EFDG是菱形;(2)求证:EG2= 12GF •AF;(3)若AB=4.BC=5.求GF的长.5.已知:直线y=−x+1与x轴、y轴分别交于A、B两点.点C为直线AB上一动点.连接OC. ∠AOC为锐角.在OC上方以OC为边作正方形OCDE.连接BE.设BE=t.(1)如图1.当点C在线段AB上时.判断BE与AB的位置关系.并说明理由;(2)真接写出点E的坐标(用含t的式子表示);(3)若tan∠AOC=k.经过点A的抛物线y=ax2+bx+c(a>0)顶点为P.且有6a+3b+ 2c=0. △POA的面积为12k.当t=√2时.求抛物线的解析式.26.如图. 四边形ABCD内接于⊙O.BD平分∠ABC. 过点D作DE∥AB. 交BC于点E. 连结AE交BD于点F. 已知∠AFD=∠ADB+∠CDE.(1)①假设∠ABD=α. 则∠AFD=.②证明:AB=AE;(2)若AB2=BF⋅BD,AD=2. 求CB的长;(3)若CE=2,AB=8.求DE的长.7.在等腰∠ABC中.AB=AC=2. ∠BAC=120°.AD∠BC于D.点O、点P分别在射线AD、BA上的运动.且保证∠OCP=60°.连接OP.(1)当点O运动到D点时.如图一.此时AP=1.∠OPC是什么三角形。
新苏科版八年级数学上册提优

八年级数学提优训练21、在平面直角坐标系中,点P(2,2)点Q在y轴上,△POQ为等腰三角形,那么符合条件的Q点有()。
A.5个B.4个C.3 个D.2个2、在平面直角坐标系中,点P的坐标为(-2,2a+1),则点P所在的象限是()A、第一象限B、第二象限C、第三象限D、第四象限3、如图,一个质点在第一象限及x轴、y轴上运动,一秒钟后,它从原点运动到(0,1),然后接着按图中箭头所示方向运动[即(0,0)→(0,1)→(1,1)→(1,0)→…],且每秒运动一个单位长度,那么第2011秒后质点所在位置的坐标是()A、(13,44)B、(44,13)C、(45,14)D、(13,45)第3题图第4题图第5题图4、已知:如图在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E 三点在同一条直线上,连接BD,BE.以下四个结论:①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;其中结论正确的个数是()A、1B、2C、3D、05、附图为八个全等的正六边形紧密排列在同一平面上的情形.根据图中标示的各点位置,判断△ACD与下列哪一个三角形全等?()A .△ACFB .△ADEC .△ABCD .△BCF6、线段CD 是由线段AB 平移得到的.点A (–1,4)的对应点为C (4,7),则点B (– 4, – 1)的对应点D 的坐标为( )A.(2,9)B.(5,3)C.(1,2)D.(– 9,– 4)7、若点A (x ,y )在第三象限,则点B (-x ,-y )关于x 轴的对称点在( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限 8、已知P (0,a )在y 轴的负半轴上,则Q (1,12+---a a )在( )A. y 轴的左边,x 轴的上方B. y 轴的右边,x 轴的上方C. y 轴的左边,x 轴的下方D. y 轴的右边,x 轴的下方9、数学在我们的生活中无处不在,就连小小的台球桌上都有数学问题,如图所示,∠1=∠2,若∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证∠1为( )A.60°B.30°C.45°D.50°10、如图所示,在2×2的方格纸中有一个以格点为顶点的△ABC ,则与△ABC 成轴对称且以格点为顶点的三角形共有( )A.3个B.4个C.5个D.6个第10题图第13题图第15题图11、在平面直角坐标系内,点P (2x -6,x -5)在第四象限,则x 的取值范围是_________ 12、在平面直角坐标系中,点A 的坐标为(14),,将线段OA 绕点O 顺时针旋转90︒得到线段OA ',则点A '的坐标是 .13、如图,在平面直角坐标系上有点A (1,0),点A 第一次跳动至点A1(-1,1),第四次向右跳动5个单位至点A4(3,2),…,依此规律跳动下去,点A 第100次跳动至点A100的坐标是______14、如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0)(4,0)根据这个规律探索可得,第100个点的坐标为____________15、如图,动点P 在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2011次运动后,动点P 的坐标是____________.16、在△ABC 中,如果A (1,1)B (-1,-1)C (2,-1)则△ABC 的面积是 。
提优试卷八年级上册数学

一、选择题(每题4分,共20分)1. 若a、b是方程x^2 - 5x + 6 = 0的两根,则a + b的值为()A. 2B. 3C. 4D. 52. 在直角坐标系中,点A(2,3)关于y轴的对称点坐标为()A.(2,-3)B.(-2,3)C.(-2,-3)D.(2,-3)3. 若a^2 + b^2 = 1,则a + b的取值范围是()A. -√2 < a + b < √2B. -√2 ≤ a + b ≤ √2C. -√2 < a + b ≤ √2D. -√2 ≤ a + b < √24. 下列函数中,y = kx + b(k ≠ 0)为一次函数的是()A. y = x^2 + 1B. y = 2x + 3C. y = √xD. y = log2x5. 若一个三角形的三边长分别为3,4,5,则这个三角形是()A. 直角三角形B. 等腰三角形C. 等边三角形D. 梯形二、填空题(每题4分,共20分)6. 若x + y = 3,则x^2 + y^2 = _______。
7. 若a^2 - 2a + 1 = 0,则a的值为_______。
8. 在直角坐标系中,点P(-3,4)关于x轴的对称点坐标为_______。
9. 若a,b是方程x^2 - 4x + 3 = 0的两根,则a + b的值为_______。
10. 下列函数中,y = kx + b(k ≠ 0)为反比例函数的是_______。
三、解答题(每题10分,共30分)11. (1)已知a、b是方程x^2 - 3x + 2 = 0的两根,求a^2 + b^2的值。
(2)已知函数y = kx + b(k ≠ 0)为一次函数,若点A(2,3)在该函数图象上,求k和b的值。
12. (1)已知等腰三角形ABC中,AB = AC,∠B = 50°,求∠C的度数。
(2)已知三角形ABC中,AB = 3,BC = 4,AC = 5,求三角形ABC的面积。
第2章+轴对称图形+综合提优练习2024-2025学年苏科版八年级数学上册+

第2章《轴对称图形》综合提优练习一、选择题1.△ABC中,BC=10,AB的垂直平分线与AC的垂直平分线分别交BC于点D,E,且DE =4,则AD+AE的值为()A.6B.14C.6或14D.8或122.如图,在△ABC中,∠BAC>90°,D为BC的中点,点E在AC上,将△CDE沿DE 折叠,使得点C恰好落在BA的延长线上的点F处,连接AD、CF,则图中所有的等腰三角形的个数为()A.1B.2C.3D.43.如图,AD∥BC,点E是线段AB的中点,DE平分∠ADC,BC=AD+2,CD=7,则BC2﹣AD2的值等于()A.14B.9C.8D.54.如图,四边形ABCD中,AB=AD,BC=BD,若∠ABD=∠BAC=α,则∠BDC的度数为()A.2αB.45°+αC.90°﹣αD.180°﹣3α5.如图,∠BAC=30°,AP平分∠BAC,GF垂直平分AP,交AC于F,Q为射线AB上一动点,若PQ的最小值为3,则AF的长为()A.3B.6C.3D.96.如图,等腰直角三角形ABC中,∠BAC=90°,D、E分别为AB、AC边上点,AD=AE,AF⊥BE交BC于点F,过点F作FG⊥CD交BE的延长线于点G,交AC于点M.以下四个结论:①△ADC≌△AEB;②∠AEG=∠CDB;③△EGM是等腰三角形;④BG=AF+FG;恒成立的结论有()A.①②③④B.①③C.②③④D.①②④二、填空题7.如图,AE是∠CAM的角平分线,点B在射线AM上,DE是线段BC的中垂线交AE于E,过点E作AM的垂线交AM于点F.若∠ACB=28°,∠EBD=25°,则∠AED =°.8.如图,在△ABC中,∠C=60°,AC=5,BC=4,点D为CB延长线上一点.当点D 在CB延长线上运动时,AD﹣BD的最小值为.9.如图,线段OM⊥ON,O为垂足,一把角尺的直角顶点A在线段OM上,端点B在线段ON上,已知ON=AB=4,AC=2,当点B在从点O运动到点N的过程中,点C也随着运动,当线段OC最长时,∠BAO的度数为.10.如图,在Rt△ABC中,∠ACB=90°,点D为斜边AB上的一点,连接CD,将△BCD 沿CD翻折,使点B落在点E处,点F为直角边AC上一点,连接DF,将△ADF沿DF 翻折,点A恰好与点E重合,则∠CEF的度数为.11.如图,∠ABC=60°,AB=4,动点P从点B出发,以每秒1个单位长度的速度沿射线BC运动,设点P的运动时间为t秒(t>0),当△ABP为锐角三角形时,t的取值范围是.12.如图,AD是△ABC的中线,∠ADC=60°,BC=6,把△ADC沿直线AD折叠后,点C落在点E的位置上,连接BE,则BE的长是.13.如图,△ABC的边AB、AC的垂直平分线m、n相交于点D,连接CD,若∠1=39°,则∠BCD的大小是度.14.如图,在△ABC中,∠ACB=90°,S△ABC=14,BC=4,P是AB边上的动点(不与点B重合),将△BCP沿CP所在的直线翻折,得到△B′CP,连接B′A,则B′A长度的最小值是.三、解答题15.如图,已知线段a、b,请用无刻度的直尺和圆规作出特定的三角形:(1)求作一个等腰三角形,使得它的腰长为b,底边上的高为a.(2)求作一个三角形,使得它的两边长分别为a、b,第三边上的中线为c.16.如图,在等边三角形ABC中,D是AB上的一点,E是CB延长线上一点,连接CD、DE,已知∠EDB=∠ACD.(1)求证:△DEC是等腰三角形.(2)当∠BDC=5∠EDB,EC=8时,求△EDC的面积.17.已知:A、B两点在直线l的同侧,试分别画出符合条件的点M.(不用写作法)(1)如图①,在l上求作一点M,使得AM+BM最小;(2)如图②,在l上求作一点M,使得|AM﹣BM|最小;(3)如图②,在l上求作一点M,使得|AM﹣BM|最大.18.如图钢架中,∠A=20°,焊上等长的钢条来加固钢架,若AP1=P1P2,问这样的钢条至多需要多少根?(1)请补充完整如下解答:解:由题意可知,P1P2=P2P3=P3P4=P4P5=…∵∠A=20°,AP1=P1P2,∴∠AP2P1=.∴∠P2P1P3=∠P1P3P2=40°,同理可得,∠P3P2P4=∠P2P4P3=60°,∠P4P3P5=∠P4P5P3=.∴∠P5P4B=100°>90°,∴对于直线P4B上任意一点P6(点P4除外),P4P5<P5P6,∴这样的钢条至多需要根.(2)继续探究:当∠A=15°时,这样的钢条至多需要多少根?19.在探索三角形全等的条件时,老师给出了定长线段a,b,且长度为b的边所对的角为n°(0<n<90°)小明和小亮按照所给条件分别画出了图1中的三角形,他们把两个三角形重合在一起(如图2),其中AB=a,BD=BC=b,发现它们不全等,但他们对该图形产生了浓厚兴趣,并进行了进一步的探究:(1)当n=45时(如图2),小明测得∠ABC=65°,请根据小明的测量结果,求∠ABD 的大小;(2)当n≠45时,将△ABD沿AB翻折,得到△ABD′(如图3),小明和小亮发现∠D′BC的大小与角度n有关,请找出它们的关系,并说明理由;(3)如图4,在(2)问的基础上,过点B作AD′的垂线,垂足为点E,延长AE到点F,使得EF=(AD+AC),连接BF,请判断△ABF的形状,并说明理由.20.定义:如果1条线段将一个三角形分割成2个等腰三角形,我们把这条线段叫做这个三角形的“双等腰线”.如果2条线段将一个三角形分成3个等腰三角形,我们把这2条线段叫做这个三角形的“三等腰线”.如图1,BE是△ABD的“双等腰线”,AD、BE是△ABC的“三等腰线”.(1)请在图2三个图中,分别画出△ABC的“双等腰线”,并做必要的标注或说明.(2)如果一个等腰三角形有“双等腰线”,那么它的底角度数是.(3)如图3,△ABC中,∠C=∠B,∠B<45°.画出△ABC所有可能的“三等腰线”,使得对∠B取值范围内的任意值都成立,并做必要的标注或说明.(每种可能用一个图单独表示,如果图不够用可以自己补充)。
(精选)人教版八年级数学上期中复习提优试题精选附答案

人教版八年级数学上学期(全卷总分120分)系描11题1AOB12 13 14 6 cm第3题1514题 M 第4题15题须添16 第5题16题第7题N18题第9题20正四边形和正六四边形按如图所示的规律拼图案即从第D C C AC, 第8题点P,BC -和过和 4QPA9.如佟 /ABC AOC 和BCD 如图摆放A. C. 2.如[A.3.如I边AB70。
, A.;、AC 上的点 则 / 1 + /2= 110°P 至I BC 的距离佛山电视台的台徽,其中为轴对称图形的是RtAABC 中, 戋段PQ=AB D. 22.5 B = 42°, AABC 的外角 / DAC已知 / AOB =60B. 17.5 且与AB 垂直 A. 84.小明不小心把一块三角形形状的玻璃打碎成了三块,如性 ①②③,他想要到玻璃店去配一块大小形状完全一样的玻璃19. (12分)问题引入A. 15 10.用正三角形B. 140 D. 700,则/AEC= ___________/C = 90°, AC = 12 cm 将^ ABC 沿着DE 折叠压平,A 与A'重合 18. (6分)如图所示A 且垂直于AC 的射线AX 上运动,要使△ ABC率.则AP=.A. BD = CE C. /BAD = /CAE 6.下列图形分别是桂林、湖南B. /ABD =/ACE D. /BAC = /DAE若 AD = 8,B. 6 ABC 中,AB r B. 115° C, 110° D 在折纸活动中,小明制作了一张△ N 在边 OB 上,PM = PN,若 MN=2,贝U OM = ___________如图所示,顶角 A 为120°的等腰△ ABC 中,DE 垂直平7.如图,在^ ABC 中,AC =4 cm,线段AB 的垂直平分线交AC△ BCN 的周长是7 cm,则BC 的长为( ) A , 1 cm B. 2 cm C. 3 cm D , 4 cm 8.如图,AB//CD, BP 和CP 分别平分/ABC 和/DCB, AD 过,则/ DFE 等于(105° ABC 纸片,点D 、E 分 分 AB 于 D,若 DE= 2,则 EC= ____________ .三、解答题(共72分)/ X —17. (6分)如图是由三个阴影的小正方形组成的图形,请你在三个网格图中,各补画出一个有阴影的小正方形,使补画后的图形为轴对称图形AS B.② C.③ D.①和②5.如图,已知 AB=AC, AD=AE,若要得到 AABD^AACE 加一个条件,则下列所添条件不成立的是()第12题13题4 D. 2 /ABC =75°, E 为BC 延长线上 第一个图案第二个图案第三个图案A. 2n+1B. 3n+2C. 4n+2二、填空题(每小题3分,共18分) 一、选择题(每小题3分,共30分)1.如图,直线a 、b 、c 、d 互不平行,对它们截出的一些角的数量关述错误的是()(用a 表示),并说明理由;第19题1 _____(3)BO 、CO 分别是△ ABC 的外角/ DBC 、/ECB 的n 等分线,它们父于点O, / CBO :、/DBC , , 1 , 、…,一,/BCO = n/ECB, /A=a,请猜想/ BOC = ___________________________ . 第20题(2)问题解决:如图2,在4ABC 中,D 是BC 边上的中点,DELDF 于点D, DE 交 AB 于点E,DF 交AC 于点F,连接EF,求证BE + CF>EF.第23题24. (9分)如图,在等边△ ABC 中,点E 为边AB 上任意一点,点D 在边CB / 的延长线上,且ED = EC.(1)当点E 为AB 的中点时(如图1),则白 以 有AE _________ DB (填知" 或匚") 图।(2)猜想AE 与DB 的数量关系,并证明你的猜想.(1)如图1,在4ABC 中,点。
八年级数学上学期提优训练试题试题

八年级数学提优训练
制卷人:歐陽文化、歐陽理複;制卷時間:二O 二二年二月七日
1.在平面直角坐标系xOy 中,点A 1,A 2,A 3,…和B 1,B 2,B 3,…分别在直线y kx b =+和x 轴上.△OA 1B 1,△B 1A 2B 2,△B 2A 3B 3,…都是等腰直角三角形,假如A 1〔1,1〕,A 2〔23,27〕,那么点A n 的纵坐标是_ _____.
2.如图,在平面直角坐标系中,直线AB 交x 轴于点A 〔-4,0〕,交y 轴于点B 〔0,2〕,P 为线段OA 上一个动点,Q 为第二象限的一个动点,且满足PQ =PA ,OQ =OB .〔1〕求直线AB 的函数关系式;
〔2〕假设 △OPQ 为直角三角形,试求点P 的坐标,并判断点Q 是否在直线AB 上.
y
x y=kx+b O B 3 B 2 B 1 A 3 A 2 A 1
〔第1题〕
初二数学提优训练〔二〕
1.如图,点M 是直线32+=x y 上的动点,过点M 作MN 垂直于x 轴于点N ,y 轴上是否存在点P ,使△MNP 为等腰直角三角形,请写出符合条件的点P 的坐标 .
2.(此题10分)如图,在平面直角坐标系中,OA=OB=OC=6,过点A 的直线AD 交BC 于点D ,
交y 轴与点G ,△ABD 的面积为△ABC 面积的
3
1. (1)求点D 的坐标;
(2)过点C 作CE⊥AD,交AB 交于F ,垂足为E .
①求证:OF=OG ;
②求点F 的坐标.
(3)在(2)的条件下,在第一象限内是否存在点P ,使△CFP
为等腰直角三角形,假设存在,直接写出点P 坐标;
假设不存在,请说明理由. 制卷人:歐陽文化、歐陽理複;制卷時間:二O 二二年二月七日
〔第1题图〕。
八年级上册数学提优试卷

一、选择题(每题3分,共30分)1. 下列数中,有理数是()A. √3B. √4C. √-1D. √02. 已知a,b是实数,且a+b=0,则()A. a和b都是正数B. a和b都是负数C. a和b互为相反数D. a和b相等3. 下列各式中,正确的是()A. 3a+b=3a+2bB. 2a+b=2a-2bC. 3a+2b=3a+bD. 3a+b=3a-b4. 已知m=2,n=3,则下列各式中正确的是()A. m+n=5B. m-n=1C. mn=6D. m/n=2/35. 下列各式中,错误的是()A. a²+b²=(a+b)²B. a²-b²=(a+b)(a-b)C. (a+b)²=a²+2ab+b²D. (a-b)²=a²-2ab+b²6. 已知m=5,n=3,则下列各式中正确的是()A. m+n=8B. m-n=2C. mn=15D. m/n=5/37. 下列各式中,正确的是()A. 2a+b=2a+2bB. 3a+b=3a-2bC. 4a+b=4a+2bD. 5a+b=5a-2b8. 已知m=4,n=2,则下列各式中正确的是()A. m+n=6B. m-n=2C. mn=8D. m/n=2/49. 下列各式中,错误的是()A. a²+b²=(a+b)²B. a²-b²=(a+b)(a-b)C. (a+b)²=a²+2ab+b²D. (a-b)²=a²-2ab+b²10. 已知m=3,n=2,则下列各式中正确的是()A. m+n=5B. m-n=1C. mn=6D. m/n=3/2二、填空题(每题5分,共25分)11. 有理数a,b满足a+b=0,则a=________,b=________。
初二数学提优试卷

一、选择题(每题3分,共30分)1. 若a > b,则下列不等式中正确的是()A. a + 1 > b + 1B. a - 1 < b - 1C. a^2 > b^2D. a^2 < b^22. 下列各组数中,有理数集S中能构成等差数列的是()A. S = {1, 3, 5, 7, 9}B. S = {1, 4, 9, 16, 25}C. S = {1, 2, 4, 8, 16}D. S = {1, 2, 3, 5, 8}3. 若函数f(x) = 2x + 1在x = 3时的值为7,则下列函数值正确的是()A. f(2) = 5B. f(4) = 9C. f(5) = 11D. f(6) = 134. 已知等腰三角形ABC中,AB = AC,若∠BAC = 60°,则∠B = ()A. 60°B. 45°C. 30°D. 75°5. 若一个正方形的边长为a,则其对角线长为()A. √2aB. 2aC. a√2D. a6. 已知一元二次方程x^2 - 4x + 3 = 0,下列选项中,正确的是()A. 该方程有两个不相等的实数根B. 该方程有两个相等的实数根C. 该方程没有实数根D. 无法确定7. 若a、b、c是等差数列的连续三项,且a + b + c = 12,则a = ()A. 4B. 6C. 8D. 108. 下列图形中,不是平行四边形的是()A. 矩形B. 正方形C. 菱形D. 梯形9. 若x + y = 5,x - y = 1,则x^2 + y^2 = ()A. 25B. 21C. 16D. 1010. 若函数f(x) = -x^2 + 4x + 3在x = 2时的值为3,则下列函数值正确的是()A. f(1) = 2B. f(3) = 2C. f(4) = 1D. f(5) = 0二、填空题(每题4分,共20分)11. 已知等差数列{an}中,a1 = 2,d = 3,则第10项an = _______。
八年级提优测试卷数学答案

一、选择题1. 答案:D。
解析:选项A、B、C都是一次函数,而选项D是反比例函数,其图像是双曲线。
2. 答案:B。
解析:三角形内角和定理指出,任何三角形的内角和等于180度,故选B。
3. 答案:A。
解析:正方形的四条边相等,对角线互相垂直,故选A。
4. 答案:C。
解析:平行四边形的对边平行且相等,故选C。
5. 答案:D。
解析:一元二次方程ax^2 + bx + c = 0的解可以用公式x = (-b± √(b^2 - 4ac)) / 2a求得,故选D。
二、填空题6. 答案:x^2 - 4x + 4。
解析:将x = 2代入方程x^2 - 4x + c = 0,得c = 4,所以原方程可化为x^2 - 4x + 4 = 0。
7. 答案:-1/3。
解析:将x = -1代入方程x + 2 = 0,得-1 + 2 = 0,所以x = -1是方程的解。
8. 答案:π。
解析:圆的周长公式是C = 2πr,其中r是圆的半径,所以圆的周长是π。
9. 答案:8。
解析:长方体的体积公式是V = 长×宽×高,所以体积是8。
10. 答案:-5。
解析:由题意知,-5是方程x^2 - 4x - 5 = 0的解,所以-5是方程的根。
三、解答题11. 答案:(1)设甲的速度为x千米/小时,则乙的速度为x - 4千米/小时。
根据题意,列方程:x + (x - 4) = 12解得:x = 8答:甲的速度为8千米/小时。
(2)设甲走的路程为y千米,则乙走的路程为y + 3千米。
根据题意,列方程:y + (y + 3) = 15解得:y = 6答:甲走了6千米。
12. 答案:(1)由题意得,直角三角形的斜边长为5,一条直角边长为3,根据勾股定理得另一条直角边长为4。
(2)设另一条直角边为x,则根据勾股定理得:x^2 + 4^2 = 5^2解得:x = 3答:另一条直角边长为3。
13. 答案:(1)设甲乙两人相向而行,设甲的速度为v1千米/小时,乙的速度为v2千米/小时。
第十一章三角形提优测试卷 2024-2025学年人教版八年级数学上册

第十一章三角形提优测试卷(时间:90分钟满分:100分)一、选择题(每小题4分,共32分)1. 下列图形具有稳定性的是 ( )2. 下列说法不正确的是 ( )A.三角形的三条高线交于一点B.直角三角形的高交于三角形的一个顶点C.三角形的三条角平分线交于一点D.三角形的三条中线交于一点3.如图,△ABC中,点D为AB边上的一点,点 F为BC延长线上一点,DF交AC于点 E.下列结论中不正确的是( )A.∠F+∠ACF=∠A+∠ADFB.∠B+∠ACB<180°C.∠DEC>∠BD.∠A>∠ACF4.已知△ABC的三边分别为a,b,c,且a>b>c,若b=5,c=4,则周长l的取值范围是 ( )A.1<l<9B.10<l<18C.14<l<18D.0<l<185.一个多边形的边数增加1,则内角和与外角和增加的度数之和是 ( )A.60°B.90°C.180°D.360°6.在△ABC中,AD 是 BC边上的中线,△ADC的周长比△ABD的周长多3,AB与AC的和为13,则AC的长为( )A.7B.8C.9D. 107.如图,在△ABC中,∠ABC,∠ACB 的平分线交于点O,D 是∠ACF与∠ABC的平分线的交点,若∠BOC=120°,则∠D 的度数为 ( )A.15°B.20°C.25°D.30°8.如图,四边形纸片ABCD中,已知∠A=160°,∠B=30°,∠C=60°,四边形纸片 ABCD 分别沿EF,MN,OP,GH折叠,使A 与A',B 与 B',C 与 C',D 与 D'重合,则∠1+∠2+∠3+∠4+∠5+∠6+∠7-∠8的值是( )A.600°B.700°C.720°D.800°二、填空题(每小题4分,共24分)9.已知a,b,c是△ABC的三边长,a,b满足|a−7|+(b−1)²=0,c为奇数,则c= .10.如图,∠CBE,∠BCF 的平分线相交于点 D,∠A=50°,则∠D= .11.如图,在△ABC中,E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF,△BEF的面积分别为S△ABC,.S△ADF,S△BEF,且S ABC=12,,则 S△ADF- S BEF=¯12.在△ABC中,AD是高,∠BAD=60°,∠CAD=20°,AE平分∠BAC,则∠EAD的度数为 .13.若一个n边形的所有内角与某个外角的和等于1350°,则n等于 .14.如图,图中∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I的值为 .三、解答题(共44分)15.(6分)如图,已知△ABC.(1)画中线AD;(2)画△ABD的高 BE及△ACD的高CF;(3)量一量,比较BE和CF的大小:BE CF.(填“>”“<”或“=”)16.(6分)如图,CE平分∠ACD,F为CA 延长线上一点,FG∥CE交AB 于点G,∠ACD=100°,∠AGF=20°,求∠B 的度数.17.(11分)小刚准备用一段长50米的篱笆围成一个三角形形状的场地,用于饲养鸡,已知第一条边长为m米,由于条件限制,第二条边长只能比第一条边长的3倍少2米.(1)第二条边长为米,第三条边长为米.(用含m的式子表示)(2)第一条边长能否为10米? 为什么?(3)求m的取值范围.18.(8分)如图所示,∠A=10°,∠ABC=90°,∠ACB=∠DCE,∠ADC=∠EDF,∠CED=∠FEG.求∠F 的度数.19.(13分)如图,四边形ABCD中,AB∥CD,∠B=∠D,点E为BC延长线上一点,连接AE.(1)如图①,求证:AD∥BC.(2)①如图②,∠DAE 和∠DCE 的平分线相交于点F,连接AC.若∠BAE=70°,求∠F的度数;②如图③,∠DCE的平分线交 AE 于点 G,连接AC,若∠BAC=∠DAE,∠AGC=2∠CAE,求∠CAE的度数.第十一章提优测试卷1. A2. A3. D4. C5. C6. B7. D8. A 解析:∵ 四边形ABCD 中,∠A=160°,∠B=30°,∠C=60°, ∴∠D =360°−160°−30°−60°=110°,∴∴∠1+∠2=360°−(180°− 160°)×2=320°,∠3+∠4=360°−(180°−110°)×2=220°,∠5+ ∠6=360°−(180°−60°)×2=120°,∠7−∠8=−(∠B +∠B ′)=-60°,∴∠1+∠2+∠3+∠4+∠5+∠6+∠7-∠8=320°+220°+ 120°−60°=600°. 9.7 10.65° 11.2 12.20°或40° 解析:如图①,当∠C 为锐角时,∠BAC=∠BAD+∠CAD=80°,∴∠BAE=40°,∴∠EAD=∠BAD-∠BAE=20°.如图②,当∠ACB 为钝角时,∠BAC =∠BAD--∠CAD = 40°.∴∠CAE=20°,则∠EAD=∠DAC+∠EAC=40°. 13.9 解析:设这个外角度数为x,根据题意,得(n-2)×180+x=1350,解得x=1710-180n.由于0<x<180,即0<1710-180n<180,解得8.5<n<9.5,所以n=9.14.540° 解析:设AI 与BC,CD 分别交于点J,K,DE 与 GH 交于点N,则∠A+∠B=∠AJC,∠AJC+∠C=∠IKD,: ∠A+∠B+∠C=∠IKD.同理∠E+∠F+∠G=∠HND.∴∠A+∠B+∠C+∠D+∠E+∠. F+∠G+∠H+∠I=∠IKD+∠D+∠HND+∠I+∠H=540°.15.(1)(2)如图所示.C (3)=16.∵ CE 平分. ∠ACD,∴∠ACE =12∠ACD =12×100∘=50∘.:FC CE,∴∠AFG=∠ACE=50°,∴ ∠BAC=∠AFG+∠AGF =50°+20°=70°.又∠ACB=180°-∠ACD=180°-100°=80°,∴ ∠B=180°-∠BAC-∠ACB=180°-70°-80°=30°.17.(1)(3m-2) (52-4m)(2)不能.理由如下:若第一条边长为10米,则第二条边长为28米,第三条边长为12米,而10+12<28,不符合三角形两边之和大于第三边,∴不能构成三角形…第一条边长不能为10米.(3)由题意,知三角形的三边长分别为m 米,(3m-2)米,(52-4m)米.则 {m >0,3m −2>0,52−4m >0,解得 23<m <13.由三角形两边之和大于第三边,得 {m +3m −2>52−4m,m +52−4m >3m −2,3m −2+52−4m >m,解得 274<m <9.故 m 的取值范围是 274<m <9.18.在△ABC 中,∠A=10°,∠ABC=90°,.∠ACB=80°,∴∠DCE=∠ACB=80°.在△ACD 中,∠DCE 是它的一个外角,. ∠DC E=∠A+∠ADC,∴∠ADC=70°,∴∠EDF=∠ADC=70°.在△ADE 中,∠EDF 是它的一个外角,. ∠EDF=∠A+∠AED,..∠AED=60°,..∠FEG=∠AED=60°。
人教八年级上册数学第十四章提优测试卷(含答案)

八年级上册数学第十四章提优测试卷 一、选择题(本题共10小题,每小題3分,计30分) 1.下列运算正确的是( ) A.a 2·a 3=a 6 B.(a 2)3=a 5 C.(-2a 2b)3=-8a 6b 3 D.(2a+1)2=4a 2+2a+1 2.若(2a-1)°=1,则 ( )A.a=21B.a=0C.a≠21D.a≠03.下列各式成立的是 ( ) A.a-b+c=a-(b+c) B. a+b-c=a-(b-c) C.a-b-c=a-(b+c) D.a-b+c-d=(a+c)-(b-d)4.已知x 2+16x+k 是完全平方式,则常数k 等于 ( )A.64B.48C.32D.16 5.如果a m ÷a n+2=a ,那么m 等于 ( ) A.n+3 B.n+2 C.n+1 D. n 6.计算(x-y+z)(x+y-z)的正确结果为( ) A x 2-y 2+2yz-z 2 B. x 2-2xy+y 2-z 2C .x 2 +2xy+y 2-z 2 D.x 2+y 2-2yz+z 27.将下列多项式因式分解,结果中不含有因式a+1的是( ) A.a 2-1 B. a 2 +a C.a 2+a-2 D.(a+2)2-2(a+2)+18.已知x =3,y=-23,则代数式[(x-y)2+(x+y)·(x-y)]÷2x 的值为 ( ) A.3 B.27 C.4 D.299.把多项式x 2+ax+b 分解因式,得(x+1)(x-3),则a ,b 的值分别是 ( ) A.a=2,b=3 B.a=-2,b=-3 C.a=-2,b=3 D.a=2,b=-3 10.已知a ,b ,c 为三角形三边,则式子a 2-b 2+2bc-c 2的值( ) A.大于0 B.小于0C.大于或等于0D.不能确定二、填空题(本题共5小题,每小题3分,计15分)1.()0132-⨯π= ,(a-1)0= (a≠1).12.已知:a+b =3,ab =2,则(a-b)2= . 13.若m 2-n 2=6,且m-n =2,则m+n = .14.若x 2-21x+k =(x-a)2成立,则a ·k= .15.若多项式6x4y2+A 的各项的公因式是2x 3y 2 ,写出一个符合条件的单项式A 为 .三、解答题(本题共8小题,计75分) 16.计算:(1)(-ab 2)3・(21a 3bc)3÷(-31a 2b 9); (2)x(x-2y)-(x-y)2;(3)(2m-n)2-(m+2n)(m-2n); (4)(3a+b-c)(3a-b+c).17.分解因式:(1)18a 3-2a; (2)xy(xy-12)+36;(3)(x 2-5)2+8(5-x 2)+1618.当a =3,b =-1时,求下列代数式的值. (1)(a+b)(a-b); (2)a 2+2ab+b 2.19.已知23a ×8a ÷42a-1的值为64,求a 的值.20.已知4x =3y ,求代数式(x-2y)2-(x-y)(x+y)-2y 2的值.21.试说明(2n-3)+(41m 3+2n)(41m 3-2n)+12n 的值与n 的值无关.22.给你多个长方形和正方形卡片,其三种形状如图所示,请你运用拼图的方法,选取相应种类和数量的卡片,拼成一个长方形,使它的面积等于2a 2+5ab+2b 2,并根据你拼成的图形分解多项式2a 2+5ab+2b 2.23.根据多项式的乘法可得(x+p)(x+q)=x 2+(p+q)x+pq ,反过来,x 2+(p+q)x+pq =(x+p)(x+q).这就是说,对于二次项系数为1的二次三项式x 2+ax+b ,如果常数项b 可以分解为pq 的积,并且有p+q =a ,那么x 2+ax+b =(x+p)(x+q),这就是用十字相乘法分解因式.如分解因式x 2-x-56,因为-56=(-8)×7且(-8)+7=-1,所以x 2-x-56=(x-8)(x+7). 试用十字相乘法分解下列因式:(1)x 2-5x+6 (2)x 2+7x+12 (3)a 2+3a-10 (4)m 2-7m-60参考答案一、1. C 2.C 3 .C 4. A5.A [解析]∵a m ÷a n+2=a m-(n+2)=a m-n-2,∴m-n-2=1,即m =n+3.6.A7.C8.D[解析][(x-y)2+(x+y)(x-y)÷2x =(x 2-2xy+y 2+x 2-y 2)÷2x =(2x 2-2xy)÷2x =x-y ,当x =3,y =-23时,原式=3-(-23)=29,故选D.9.B[解析]∵(x+1)(x-3)=x ・x-x ・3+1・x-1×3=x 2-3x+x-3=x 2-2x-3,∴x 2+ax+b =x 2-2x-3,∴a =-2,b =-3.故选B.10.A[解析]a 2-b 2+2bc-c 2=a 2-(b-c)2=(a+b-c)(a-b+c),∵a ,b ,c 为三角形三边,∴a+b-c ˃0,a-b+c =a+c-b >0,∴式子的值大于0.二、11.321 12. 113.3[解析]由m 2-n 2=6得(m-n)(m+n)=6,把m-n =2代入得2(m+n)=6,解得m+n =3.14.641[解析]∵x 2-21x+k=(x-a)2=x 2-2ax+a 2成立, -21=-2a, a=41∴ k=a 2, 解得 k=161∴ a ·k=41×161=64115.4x 3y 3(不唯一)三、16.解:(1)原式=-a 3b 6・(81a 9b 3c 3)÷(-31a 2b 9)=83a 10c 3(2)原式=x 2-2xy-(x 2-2xy+y 2)=x 2-2xy-x 2+2xy-y 2=-y 2.(3)原式=4m 2-4mn+n 2-(m 2-4n 2)=4m 2-4mn+n 2-m 2+4n 2=3m 2-4mn+5n 2 (4)原式=[3a+(b-c)][3a-(b-c)]=(3a)2-(b-c)2=9a 2-(b 2-2bc+c 2)=9a 2-b 2+2bc-c 2. 17.解:(1)原式=2a(9a 2-1)=2a(3a+1)(3a-1)(2)原式=(xy)2-12xy+36=(xy-6)2(3)原式=(x 2-5)2-8(x 2-5)+16=(x 2-5-4)2=(x-9)2=(x+3)2(x-3)2. 18.解:(1)原式=a 2-b 2=32-12=8. (2)原式=(a+b)2=(3-1)2=4. 19.解:由题意,得23a ×8a ÷42a-1=64,∴23a ×(23)a ÷(22)2a-1=26,23a ×23a ÷24a-2=26,∴23a+3a-(4a-2)=26,22a+2=26,∴2a+2=6,∴a=2. 20.解:(x-2y)2-(x-y)(x+y)-2y 2=x 2-4xy+4y 2-(x 2-y 2)-2y 2=-4xy+3y 2=-y(4x-3y).∵4x =3y ,∴原式=0.21.解(2n-3)2+(41m 3+2n)(41m 3-2n)+12n=4n 2-12n+9+161m 6-4n 2+12n=9+161m 6,因为结果中不含字母n ,所以原式的值与n 的值无关.22.解:用题图中所示的卡片2张图①,5张图②,2张图③就可以拼成一个长为2a+b 宽为a+2b 的长方形,如图所示,且这个长方形的面积为(2a+b)(a+2b)因此,2a 2+5ab+2b 2=(2a+b)(a+2b).23. 解:(1)原式(x-2)(x-3). (2)原式=(x+3)(x+4). (3)原式=(a+5)(a-2). (4)原式=(m-12)(m+5)。
数学提优测试卷八年级上册

一、选择题(每题3分,共15分)1. 已知等差数列{an}中,a1=2,d=3,则第10项a10=()A. 28B. 31C. 34D. 372. 在直角坐标系中,点A(1,-2),B(-3,4),C(5,6)构成一个三角形,则三角形ABC的面积是()A. 15B. 20C. 25D. 303. 若x=2是方程2x²-3x+1=0的解,则方程的另一个解是()A. 1B. 1/2C. -1D. -1/24. 已知函数f(x)=3x-2,若f(2x+1)=9,则x的值为()A. 2B. 3C. 4D. 55. 在等腰三角形ABC中,AB=AC,BC=10,底边BC上的高AD垂直于BC,则AD的长度是()A. 5B. 10C. 5√2D. 10√2二、填空题(每题5分,共25分)6. 若x²-4x+3=0,则x²+4x的值为______。
7. 在直角坐标系中,点P(-2,3),点Q(2,-3),则线段PQ的中点坐标是______。
8. 已知函数f(x)=2x+1,若f(3)=7,则f(-1)的值为______。
9. 在等边三角形ABC中,AB=AC=BC,则角A的度数是______。
10. 若x=√2是方程x²-3x+2=0的解,则方程的另一个解是______。
三、解答题(每题10分,共40分)11. (10分)已知数列{an}的前n项和为Sn,且S1=1,S2=3,S3=6,求通项公式an。
12. (10分)在平面直角坐标系中,已知点A(1,2),B(3,4),C(5,6),求三角形ABC的面积。
13. (10分)解方程组:$$\begin{cases}2x+y=5 \\x-3y=-1\end{cases}$$14. (10分)已知等腰三角形ABC中,AB=AC,BC=10,底边BC上的高AD垂直于BC,求AD的长度。
答案:一、1.B 2.A 3.A 4.A 5.A二、6. 5 7.(0,0) 8. -1 9. 60° 10. 2三、11. an=2n-112. S△ABC=613. 解:将第一个方程乘以3,得:$$\begin{cases}6x+3y=15 \\x-3y=-1\end{cases}$$将两个方程相加,得:$$7x=14$$解得:x=2,将x=2代入第一个方程,得:$$2+y=5$$解得:y=3,所以方程组的解为:$$\begin{cases}x=2 \\y=3\end{cases}$$14. 解:由等腰三角形的性质,得:$$AD=BD=\frac{BC}{2}=5$$在直角三角形ABD中,由勾股定理得:$$AB=\sqrt{AD^2+BD^2}=\sqrt{5^2+5^2}=5\sqrt{2} $$所以AD的长度为5√2。
人教八年级上册数学 第十四章 提优测试卷(含答案)

八年级上册数学第十四章提优测试卷时间:60分钟 满分:100分一、选择题(每小题4分,共32分) 1.下列运算中,正确的是( )A. 2a-a=2B.(a 2)3=a 5C. a ·a 3=a 4D.(a+b)2=a 2+b 2 2.长方形的面积为9a 2-6ab+3a ,它的一边长为3a ,则另一边长为( ) A. 3a-2b+1 B. 2a-3b C.2a-3b+1 D.3a -2b 3.计算(-a)5·a 3-a 8的结果是( )A.0B.-2a 16 C-a 16 D.-2a 8 4.下列多项式的因式分解中,正确的是( ) A.x 3-4x=x(x+2)(x-2) B.x 2+2x-1=(x-1)2C.-x 2+(-2)2=(x+2)(x-2)D.(2x-1)2=4x 2-4x+15.小明的作业本撕掉了一角,留下一道残缺不全的题目,如图所示,请你帮他推测出被除式等于( )A.x 2-8x+6B.5x 3-15x 2+30xC.5x 3-15x 2+6 D.x 2+2x+66.若4x 2+(a-1)xy+9y 2是完全平方式,则a 的值是( ) A.7或-5 B.13或11 C.-13或14 D.-7或-57.若a+b =-2,则(2a+2b-1)(1-a-b)的值为( ) A.-8 B.10 C.12 D.-158.若am-bn =5,an+bm =8,则(a 2+b 2)(m 2+n 2)的值为( ) A.13 B.39 C.75 D.89 二、填空题(每小题4分,共16分)9.已知(a+b)2=1,(a-b)2=49,则ab = .10.如图,两个正方形的边长分别为a 、b ,如果a+b =7,ab =13,则阴影部分的面积为 .11.一个长方形的长减少3cm ,同时宽增加2cm ,就成为一个正方形,并且这两个图形的面积相等,则原长方形的长是 ,宽是 .12.新定义一种运算:a @b =2(a+b)2-2(a-b)2,下面给出关于这种运算的几个结论:①a @b=8ab;②(a+1)@(b+1)=(b+1)@(a+1)③若a@b=0,则a一定为0;④若a-b=0,则(a@a)+(b@b)=16a2,其中正确结论的序号是.(把所有正确结论的序号都填在横线上)三、解答题(本大题共6小题,共52分)13.(6分)计算:(1)4(a-b)2-(2a+b)(-b+2a); (2)(m-2n+3)(m+2n-3)14.(8分)甲、乙两人共同计算一道整式乘法题:(2x+a)(3x+b),甲由于把第一个多项式中的“+a”看成了“-a”,得到的结果为6x2+11x-10,乙由于漏抄了第二个多项式中x的系数,得到的结果为2x2-9x+10.(1)求a、b正确的值;(2)计算这道乘法题的正确结果.15.(8分)已知(x3+mx+n)(x2-x+1)的展开式中不含x3和x2项.(1)求m、n的值;(2)当m、n取第(1)小题的值时,求(m+n)(m2-mn+n2)的值.16.(8分)已知21=2,22=4,23=8,…(1)你能据此推测22020的个位数字是多少吗?(2)根据规律,计算(2+1)(22+1)(24+1)…(232+1)+2的个位数字.17.(10分)仔细阅读下面例题:例题:已知二次三项式x2+5x+m有一个因式是x+2,求另一个因式以及m的值.解:设另一个因式为x+n,得x2+5x+m=(x+2)(x+n)则x2+5x+m=x2+(n+2)x+2n,∴n+2=5,m=2n,解得n=3,m=6∴另一个因式为x+3,m的值为6.依照以上方法解答下列问题:(1)若二次三项式x2-7x+12可分解为(x-3)(x+a),则a的值为,(2)若二次三项式2x2+bx-6可分解为(2x+3)(x-2),则b的值为,(3)已知二次三项式2x2+9x-k有一个因式是2x-1,求另一个因式以及k的值.18.(12分)定义:如果一个数的平方等于-1,记为i2=-1,这个数叫作虚数单位.那么和我们所学的实数对应起来就叫作复数,表示为a+bi(a、b为实数),a叫作这个复数的实部,b叫作这个复数的虚部,它的加、减、乘法运算与整式的加、减、乘法运算类似.例如:计算:(2+i)(3-2i)=6-4i+3i-2i2=6-i+2=8-i(1)填空:计算:i3= ,i4= ,i5= .(2)计算:①(4+i)(4-i); ②(4+i) .(3)试一试:请利用分数的基本性质(分子和分母同乗一个不为0的数,分数的大小不变),将ii-+33化简成a+bi的形式.参考答案一、1.C 2.A 3.D 4.A 5.B 6.B 7.D 8..D8.D【解析】∵am-bn=5,an+bm=8 ∴(am-bn)2=25, 即a2m2-2abmn+b2n2=25①,(an+bm)2=64,即a2n2+2abmn+b2m2=64②,①+②,得a2m2+b2n2+a2n2+b2m2=89, ∴a2(m2+n2)+b2(m2+n2)=89,∴(a2+b2)(m2+n2)=89.二、9.-12 10.5 11.9cm 4cm12.①②④【解析】①a@b=2a2+4ab+2b2-(2a2-4ab+2b2)=8ab,正确.②(a+1)@(b+1)=2(a+b+2)2-2(a-b)2,(b+1)@(a+1)=2(a+b+2)2-2(b-a)2,所以(a+1)@(b+1)=(b+1)@(a+1),正确;③若a@b=8ab=0,则ab至少一个为0,故不正确.④若a-b=0,即a=b,那么(a@a)+(b@b)=8a2+8a2=16a2,正确.三、13.解:(1)原式=4(a2-2ab+b2)-(4a2-b2)=4a2-8ab+4b2-4a2+b2= 5b2-8ab (3分)(2)原式=[m-(2n-3)][m+(2n-3)]=m2-(2n-3)2=m2-4n2+12n-9. (6分)14.解:(1)(2x-a)(3x+b)=6x2+2bx-3ax-ab=6x2+(2b-3a)x-ab=6x2+11x-10. (2分) (2x+a)(x+b)=2x2+2bx+ax+ab=2x2+(2b+a)x+ab=2x2-9x+10. (3分) 2b-3a=11,2b+a=-9 b=-2 (5分)(2)(2x-5)(3x-2)=6x2-4x-15x+10=6x2-19x+10 (8分)15.解:1)原式=x5-x4+x3+mx3+mx2+mx+nx2-nx+n=x5-x4+x3+(1+m)x3+(n-m)x2+(m-n)x+n. (3分)∴根据题意,得1+m=0,n-m=0,解得m=-1,n=-1. (5分)(2)(m+n)(m2-mn+n2)=m3-m2n+mn2+m2n-mn2+n3=m3+n3当m=-1,n=-1时,原式=(-1)3+(-1)3=-2 (8分)16.解(1)∵21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,...,∴2n的个位数在2,4,8,6这四个数中循环,(2分)∵2020÷4=505,∴22020的个位数字为6;(4分)(2)(2+1)(22+1)(24+1)…(232+1)+2=(2-1)(2+1)(22+1)(24+1)…(232+1)+2=264-1+2=264+1 (7分)∵64÷4=16,∴264的个位数字为6,∴264+1的个位数字为7. (8分)17.解:(1)-4. (2分)(2)-1 (4分)(3)设另一个因式为x+n,得2x2+9x-k=(2x-1)(x+n), (6分)则2x2+9x-k=2x2+(2n-1)x-n,∴2n-1=9 ,-k=-n, (8分)解得n=5,k=5.∴另一个因式为x+5,k的值为5. (10分) 18.解:(1)-i 1 i (3分)(2)①原式=42-i2=16+1=17 (5分)②原式=42+8i+i2=16+8i-1=15+8i(7分)(3)ii-+33=()()()iiiiiiii53541068969333222+=+=-++=+-+(12分)。
八年级数学上学期1-3单元提优练习
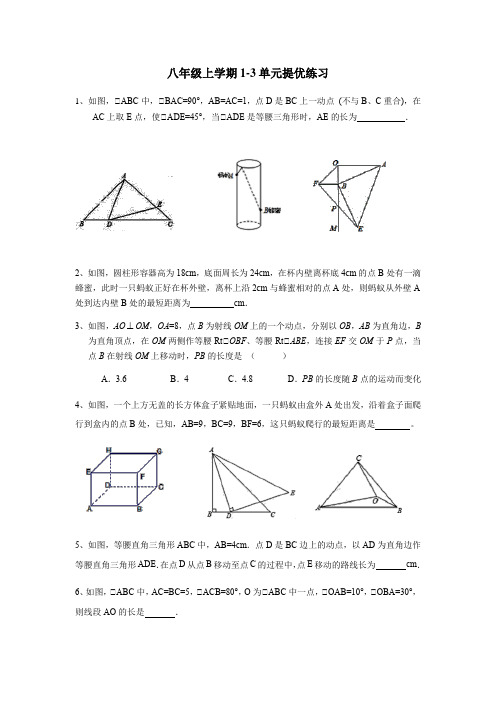
八年级上学期1-3单元提优练习1、如图,△ABC中,△BAC=90°,AB=AC=1,点D是BC上一动点(不与B、C重合),在AC上取E点,使△ADE=45°,当△ADE是等腰三角形时,AE的长为.2、如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A 处到达内壁B处的最短距离为__________cm.3、如图,AO OM,OA=8,点B为射线OM上的一个动点,分别以OB,AB为直角边,B为直角顶点,在OM两侧作等腰Rt△OBF、等腰Rt△ABE,连接EF交OM于P点,当点B在射线OM上移动时,PB的长度是()A.3.6 B.4 C.4.8 D.PB的长度随B点的运动而变化4、如图,一个上方无盖的长方体盒子紧贴地面,一只蚂蚁由盒外A处出发,沿着盒子面爬行到盒内的点B处,已知,AB=9,BC=9,BF=6,这只蚂蚁爬行的最短距离是。
5、如图,等腰直角三角形ABC中,AB=4cm.点D是BC边上的动点,以AD为直角边作等腰直角三角形ADE.在点D从点B移动至点C的过程中,点E移动的路线长为cm.6、如图,△ABC中,AC=BC=5,△ACB=80°,O为△ABC中一点,△OAB=10°,△OBA=30°,则线段AO的长是.7、如图,甲、乙到河中游泳,当乙在离河岸50米的C处游泳时,甲正在河岸上离B点10米的A处.突然,乙感到身体不适,需要回到岸上,于是他沿最短路径向岸边的B处游去;同时,岸上的甲带上备用救生衣从A处入水,以相同速度去迎乙,两人在D处相遇,一起平安回到岸边.求乙拿到救生衣之前的游泳距离CD的长.8、勾股定理是人类早期发现并证明的重要数学定理,目前发现的证明方法约有400多种。
其中的“面积法”给了小华灵感,他发现,当两个全等的直角三角形如图摆放时,也可以用“面积法”来证明勾股定理,下面是小华证明过程的开始,请你结合图形把后面的证明过程写出来.将两个全等的直角三角形按上图所示摆放,其中△DAB=90°,求证:a2+b2=c2证明:连结DB,过点D作BC边上的高DF,则DF=EC=b﹣a.9、如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE(1)填空:△△AEB的度数为;△线段AD、BE之间的数量关系是;(2)拓展探究如图2,△ACB和△DCE均为等腰直角三角形,△ACB=△DCE=900, 点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE。
初二上册数学提优试卷

一、选择题(每题3分,共30分)1. 下列数中,不是整数的是()A. 0.5B. -2C. 3D. -52. 下列各数中,有最小正整数的是()A. 0.5B. -2C. 3D. -53. 在下列各数中,绝对值最大的是()A. 3B. -2C. 0D. -34. 下列各数中,能被3整除的是()A. 12B. 15C. 18D. 215. 下列各数中,能被5整除的是()A. 20B. 25C. 30D. 356. 下列各数中,有最大负整数的是()A. -2B. -3C. -4D. -57. 下列各数中,有最大正整数的是()A. 1B. 2C. 3D. 48. 下列各数中,能被2整除的是()A. 10B. 12C. 14D. 169. 下列各数中,有最小正整数的是()A. 0.5B. 1C. 2D. 310. 下列各数中,有最小负整数的是()A. -1B. -2C. -3D. -4二、填空题(每题3分,共30分)11. 5的倒数是______,-3的倒数是______。
12. 下列数中,有最大正整数的是______,有最小负整数的是______。
13. 下列各数中,能被3整除的是______,能被5整除的是______。
14. 下列各数中,有最大正整数的是______,有最小负整数的是______。
15. 下列各数中,能被2整除的是______,能被3整除的是______。
16. 下列各数中,有最大正整数的是______,有最小负整数的是______。
17. 下列各数中,能被2整除的是______,能被3整除的是______。
18. 下列各数中,有最大正整数的是______,有最小负整数的是______。
三、解答题(每题10分,共30分)19. (1)求下列各数的倒数:$\frac{2}{3}$,$\frac{5}{7}$,$\frac{8}{9}$。
(2)判断下列各数是否能被2、3、5整除:18,27,45。
八年级上册数学提优测试卷

一、选择题(每题3分,共30分)1. 下列各数中,无理数是()A. 3.14B. √2C. 0.1010010001……D. 2/32. 若x²=1,则x的值为()A. 1B. -1C. 1或-1D. 03. 下列图形中,属于平行四边形的是()A. 矩形B. 正方形C. 菱形D. 以上都是4. 已知三角形ABC中,∠A=90°,∠B=45°,则∠C的度数是()A. 45°B. 90°C. 135°D. 180°5. 下列函数中,是反比例函数的是()A. y=x+1B. y=2xC. y=1/xD. y=3x²6. 已知一次函数y=kx+b的图象经过点(1,2)和点(-1,-2),则k和b的值分别为()A. k=2,b=0B. k=0,b=2C. k=-2,b=0D. k=0,b=-27. 在△ABC中,若∠A=60°,∠B=30°,则∠C的度数是()A. 60°B. 90°C. 120°D. 150°8. 已知等腰三角形ABC中,AB=AC,若底边BC的长度为6cm,则腰长AB的长度为()A. 6cmB. 8cmC. 10cmD. 12cm9. 下列关于圆的性质中,正确的是()A. 圆的直径等于圆的半径的两倍B. 圆的周长等于圆的半径的π倍C. 圆的面积等于圆的半径的平方乘以πD. 以上都是10. 若等边三角形的三边长分别为a,则其面积S为()A. S=(√3/4)a²B. S=(√3/2)a²C. S=(√3/3)a²D. S=(√3/6)a²二、填空题(每题5分,共25分)11. 若x²-5x+6=0,则x的值为______。
12. 已知等腰三角形ABC中,AB=AC,若底边BC的长度为10cm,则腰长AB的长度为______cm。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
提优练习2
1、如图:已知∠PAQ=60°,AB=8cm,点C从点A开始以每秒2cm的速度沿射线AP运动,
则经过秒以A、B、C三点为顶点的三角形是直角三角形.
2、如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=6,若点P是边AB上的一个动点,以每秒3个单位的速度按照从A→B→A运动,同时点Q从B→C以每秒1个单位的速度运动,当一个动点到达终点时,另一个动点也随之停止运动.在运动过程中,设运动时间为t,若△BPQ为直角三角形,则t的值为_________.
3、如图,点P、Q是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A出发,沿线段AB 运动,点Q从顶点B出发,沿线段BC运动,且它们的速度都为1cm/s,连接AQ、CP交于点M,在P、Q运动的过程中,假设运动时间为t秒,问当t的值为时,△PBQ为直角三角形.
4、如图,在Rt△ABC中,∠ABC=90°,AB=16,BC=12,点D为AC边上的动点,点D从点C出发,沿边CA往A运动,当运动到点A时停止,若设点D运动的时间为t秒,点D运动的速度为每秒2个单位长度.
(1)当t=2时,CD=________,AD= ________;(请直接写出答案)
(2)当t为何值时,△CBD是直角三角形?
(3)求当t为何值时,△CBD是等腰三角形?并说明理由.
8
60
Q
A
P
C
第3题
5.请阅读下列材料:
已知:如图1在Rt△ABC中,∠BAC=90°,AB=AC,点D、E分别为线段BC上两动点,若∠DAE=45度.探究线段BD、DE、EC三条线段之间的数量关系.
小明的思路是:把△AEC绕点A顺时针旋转90°,得到△ABE′,连接E′D,使问题得到解决.请你参考小明的思路探究并解决下列问题:
(1)猜想BD、DE、EC三条线段之间存在的数量关系式,并对你的猜想给予证明;
(2)当动点E在线段BC上,动点D运动在线段CB延长线上时,如图2,其它条件不变,(1)中探究的结论是否发生改变?请说明你的猜想并给予证明.
6、如图,已知△ABC中,BC=AC=8厘米,∠C=90°,如果点P在线段AC上以1厘米/秒的速度由A点
向C点运动,同时,点Q在线段BC上由C点向B点运动,运动速度与点P的运动速度相等,点M 是AB的中点.
(1)在点P和点Q运动过程中,△APM与△CQM是否保持全等,请说明理由;
(2)在点P和点Q运动过程中,四边形PMQC的面积是否变化?若变化说明理由;若不变,求出这
个四边形的面积;
(3)线段AP、PQ、BQ之间存在什么数量关系,写出这个关系,并加以证明.。
