双向板等效均布荷载计算程序

汽车等效均布荷载的计算复习进程

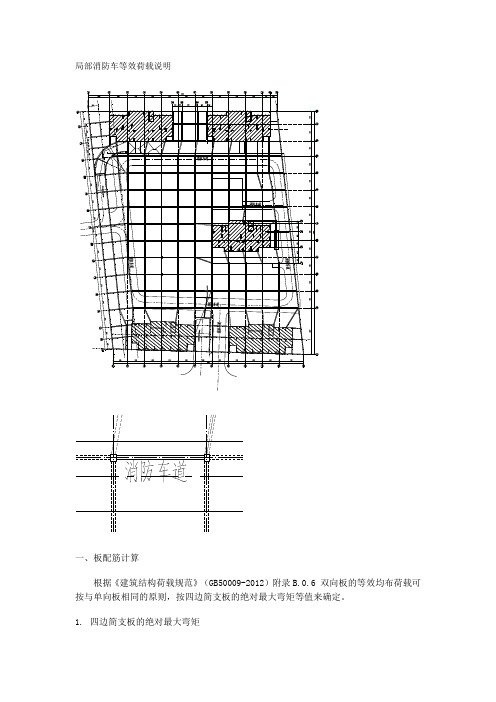
汽车等效均布荷载的计算汽车等效均布荷载的计算本工程最小板跨为2.4m×2.5m，板厚180mm，汽车最大轮压为100KN（根据《城市桥梁设计荷载标准》第4.1.3条城—A级车辆荷载）,汽车轮压着地面积为0.6m×0.2m（参考《建筑结构荷载规范》规范说明中4.1.1条“对于20~30T的消防车，可按最大轮压为60kN 作用在0.6m×0.2m的局部面积上的条件决定；”），动力系数为1.3，板顶填土S=0.9m。

平面简图详见附图一。

计算过程如下：一、X方向计算1.填土中扩散角取30°，tan30°=0.52.a x=0.6+2×0.5×0.9=1.5ma y=0.2+2×0.5×0.9=1.1ma x/l x=1.5/2.4=0.625 a y/l x=1.1/2.4=0.458l y/l x=2.5/2.4=1.042考虑动力系数后q=1.3P/(a x a y)=78.785kN/m2简支双向板的绝对最大弯矩：Mx max=0.0843×157.57×1.5×1.1=10.96Kn×mMy max=0.0962×157.57×1.5×1.1=12.51Kn×mMe max=0.0368×qe×l2qe=Me max/0.212=59Kn/m2二、Y方向计算1.填土中扩散角取30°，tan30°=0.5仅供学习与交流，如有侵权请联系网站删除谢谢22. a×=0.2+2×0.5×0.9=1.1ma y=0.6+2×0.5×0.9=1.5ma×/l×=1.5/2.4=0.458 a y/l×=1.1/2.4=0.625 l y/l×=2.4/2.5=0.96考虑动力系数后q=1.3P/(a×a y)=78.785kN/m2简支双向板的绝对最大弯矩：Mx max=0.0962×157.57×1.5×1.1=12.50Kn×m My max=0.0843×157.57×1.5×1.1=10.96Kn×m Me max=0.0368×qe×l2qe=Me max/0.23=54.37Kn/m2附图一仅供学习与交流，如有侵权请联系网站删除谢谢3。

双向板等效均布荷载计算分析

双向板等效均布荷载计算分析摘要：本文根据《建筑结构荷载规范》（GB50009-2012）第5.1~5.2条及相应条文说明、附录C中对双向板等效荷载计算的介绍，针对工程设计中遇到的板跨小于等于3m×3m时，消防车荷载及飞机牵引车荷载作用下双向板等效均布荷载如何取值进行了计算分析，为类似工程进行受力分析提供了参考。

关键词：双向板板跨等效均布荷载计算分析前言双向板为四边支承的矩形板，其长边和短边长度之比一般不大于2。

双向楼板在房屋建筑中应用非常广泛，在一些构筑物中也普遍使用。

《建筑结构荷载规范》（GB50009-2012）5.1.4条规定，楼面结构上的局部荷载可按附录C得规定，换算为等效均布荷载。

而附录C中仅对局部荷载作用下，如何计算等效均布荷载仅对单向板情况做了详细介绍，等效均布荷载的计算公式也仅适用于单向板的情况。

对双向板等效均布荷载计算，附录C第C.0.6条指出，双向板的等效均布荷载可按与单向板相同的原则，按四边简支板的绝对最大弯矩值来确定。

规范第5.1.1条第8项已经规定板跨不小于3mx3m时相应的消防车（满载总重为300kN）楼面均布活荷载标准值，按等效均布活荷载确定，并已确定相应取值。

本文将分析板跨小于3mx3m时，消防车荷载作用下双向板等效均布荷载如何合理取值；并进一步分析机场工程中经常遇到的板跨小于等于3mx3m电缆井、消防井等构筑物在飞机牵引车荷载作用下等效均布荷载如何合理取值。

对单向板等效均布荷载取值问题，本文不再进行讨论。

1消防车荷载作用下双向板等效均布荷载取值（板跨小于等于3mx3m）消防车荷载计算参数和《建筑结构荷载规范》（GB50009-2012）相同，不考虑覆土厚度影响。

消防车全车总重300kN，前轴重为60kN，后轴重为2×120kN，有两个前轮和四个后轮，轮压作用尺寸均为0.2m×0.6m。

由于板跨小于3m×3m，板上只能放置一辆消防车，当消防车后轮某个轮压位于双向板中心位置时，局部荷载作用引起的绝对弯矩值最大。

等效荷载

局部消防车等效荷载说明一、板配筋计算根据《建筑结构荷载规范》（GB50009-2012）附录B.0.6 双向板的等效均布荷载可按与单向板相同的原则，按四边简支板的绝对最大弯矩等值来确定。

1.四边简支板的绝对最大弯矩板8.1*8.1，局部荷载为18.4kN/m2，分布宽度B=1.4m，这里仅考虑局部荷载产生的绝对最大弯矩。

采用PKPM提供的《钢筋砼基本构件计算GJ》之“板结构设计计算”模块，应用有限元法计算出，绝对最大弯矩Mmax=10.9kN*m。

2.等效均布荷载q e根据计算条件，应用建筑结构静力计算手册中均布荷载作用下的弯矩系数表查出弯矩系数如下：泊松比μ=0；X方向表中系数=0.0368,Y方向表中系数=0.0368；计算跨中弯矩：Mx=表中系数×q e×Lx2=0.0368×q e×8.12 My=表中系数×q e×Lx2=0.0368×q e×8.12，调整为钢筋混凝土泊松比，重新计算跨中弯矩，μ=1/6,带入局部荷载作用下的最大弯矩得：Mx(μ)=Mx+μMy=0.0368×q e×8.12+0.0368×q e×8.12/6=4.0 （1）My(μ)=My+μMx=0.0368×q e×8.12+0.0368×q e×8.12/6=10.9 （2）由（1）得：q e=1.42 kN/m2由（2）得：q e=3.87 kN/m2等效均布荷载q e按3.87 kN/m2。

2）等效荷载值序号l01(mm) l02(mm) l01/l02m1m2M max(kN·m) M max方向q e(kN/m2)修正q e(kN/m2)1 7300 8100 0.90 0.0456 0.0358 11.1 同m1 4.04 7.92 6500 8100 0.80 0.0561 0.0334 10.8 同m1 4.15 8.03 4050 8100 0.50 0.0965 0.0174 10.8 同m1 6.62 9.8注：采用消防荷载产生的弯矩绝对最大值与顶板种植荷载产生的弯矩绝对最大值之和进行等效。

双向板等效均布荷载计算方法的探究

双向板等效均布荷载计算方法的探究作者：刘媛媛来源：《装饰装修天地》2017年第06期摘要：通过计算实例分析得出：四边简支的双向板弯矩系数与板跨比大致成线性比例关系，如果利用一元线性回归分析法近似计算，得到弯矩计算公式，计算集中荷载作用下的等效均布荷载大小，计算出的配筋结果符合实际情况。

此方法可作为双向板等效均布荷载的简答计算方法，可以供工程类设计人员参考使用。

关键词：双向板；等效均布荷载；集中荷载；一元线性回归分析法；弯矩计算1 绪言在工程中我们经常会遇到局部荷载作用在双向板上的情况，在计算过程中，一种用电算，计算方法是把集中荷载转换成分布荷载加入荷载中。

这种方法计算出的结果不准备。

另一种就是手算，根据荷载规范中对双向板等效均布荷载的计算方法介绍，也不能精确的计算出配筋结果，只有“按四边简支板的绝对最大弯矩等值来确定”这一条来计算，并且双向板在局部荷载作用下手算很困难，《建筑结构荷载设计手册第二版》中给出了一个表格，正确性有待考证。

本文通过实际例子计算，对计算结果进行探究分析得出：如果按照一元线性回归分析方法计算双向板上的局部荷载，把局部荷载转换成等效均布荷载，得出的板最大弯矩符合实际情况，配筋结果安全经济。

此方法为双向板等效均布荷载计算提供了一种简便的计算方法。

2 双向板支承板的内力计算（1）荷载情况：长边方向梁——梯形荷载短边方向梁——三角形荷载；（2）内力计算：一般按连续板计算，可按下内力分布计算。

3 有元线性回归分析法的原理如果在回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。

如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。

假设预测目标因变量为y，影响他变化的一个自变量为x，因双向板弯矩系数与板跨比大致成线性比例关系，所有，因变量与自变量的变化大致呈线性关系，如此可采用一条直线来近似表示两者的关系，其中任意一条直线方程可写成（3-1）形式，因此自变量xi，ki（i=1，2，3，4，…….，n）用直线方程[y-]=a0+a1x来替代ki，得出的误差由公式（2-2）所示。

(整理)(一)双向板按弹性理论的计算方法.

(一)双向板按弹性理论的计算方法1．单跨双向板的弯矩计算为便于应用，单跨双向板按弹性理论计算，已编制成弯矩系数表，供设计者查用。

在教材的附表中，列出了均布荷载作用下，六种不同支承情况的双向板弯矩系数表。

板的弯矩可按下列公式计算：M = 弯矩系数×(g+p)l x2式中M 为跨中或支座单位板宽内的弯矩(kN·m/m)；g、p为板上恒载及活载设计值(kN/m2)；l x为板的跨度(m)。

显示更多隐藏2．多跨连续双向板的弯矩计算(1)跨中弯矩双向板跨中弯矩的最不利活载位置图多跨连续双向板也需要考虑活载的最不利位置。

当求某跨跨中最大弯矩时，应在该跨布置活载，并在其前后左右每隔一区格布置活载，形成如上图(a)所示棋盘格式布置。

图(b)为A-A剖面中第2、第4区格板跨中弯矩的最不利活载位置。

为了能利用单跨双向板的弯矩系数表，可将图(b)的活载分解为图(c)的对称荷载情况和图(d)的反对称荷载情况，将图(c)与(d)叠加即为与图(b)等效的活载分布。

在对称荷载作用下，板在中间支座处的转角很小，可近似地认为转角为零，中间支座均可视为固定支座。

因此，所有中间区格均可按四边固定的单跨双向板计算；如边支座为简支，则边区格按三边固定、一边简支的单跨双向板计算；角区格按两邻边固定、两邻边简支的单跨双向板计算。

在反对称荷载作用下，板在中间支座处转角方向一致，大小相等接近于简支板的转角，所有中间支座均可视为简支支座。

因此，每个区格均可按四边简支的单跨双向板计算。

将上述两种荷载作用下求得的弯矩叠加，即为在棋盘式活载不利位置下板的跨中最大弯矩。

(2)支座弯矩支座弯矩的活载不利位置，应在该支座两侧区格内布置活载，然后再隔跨布置，考虑到隔跨活载的影响很小，可假定板上所有区格均满布荷载(g+p)时得出的支座弯矩，即为支座的最大弯矩。

这样，所有中间支座均可视为固定支座，边支座则按实际情况考虑，因此可直接由单跨双向板的弯矩系数表查得弯矩系数，计算支座弯距。

双向板 - 计算步骤

双向板 - 计算步骤双向板计算LB-1矩形板计算一、构件编号: LB-1 二、示意图三、依据规范《建筑结构荷载规范》 GB50009-2001 《混凝土结构设计规范》 GB50010-2021 四、计算信息 1.几何参数计算跨度: Lx = 3000 mm; Ly = 4600 mm 板厚: h = 120 mm 2.材料信息混凝土等级: C25 fc=11.9N/mm2 ft=1.27N/mm2 ftk=1.78N/mm2 钢筋种类: HRB400 fy = 360 N/mm2 Es = 2.0×105 N/mm2最小配筋率: ρ= 0.200%纵向受拉钢筋合力点至近边距离: as = 40mm 保护层厚度: c = 20mm 3.荷载信息(均布荷载)永久荷载分项系数: γG = 1.200 可变荷载分项系数: γQ = 1.400 准永久值系数: ψq = 1.000永久荷载标准值: ｑgk = 4.100kN/m2可变荷载标准值: ｑqk = 2.000kN/m24.计算方法:弹性板5.边界条件(上端/下端/左端/右端):固定/简支/简支/简支6.设计参数结构重要性系数: γo = 1.00 泊松比:μ = 0.200 五、计算参数:1.计算板的跨度: Lo = 3000 mmEc=2.80×104N/mm2第1页，共6页双向板计算2.计算板的有效高度: ho = h-as=120-40=80 mm六、配筋计算(lx/ly=3000/4600=0.652<2.000 所以按双向板计算): 1.X向底板钢筋1) 确定X向板底弯矩Mx = 表中系数(γG*ｑgk+γQ*ｑqk)*Lo2= (0.0634+0.0307*0.200)*(1.200*4.100+1.400*2.000)*32= 4.829 kN*m 2) 确定计算系数αs = γo*Mx/(α1*fc*b*ho*ho)= 1.00*4.829×106/(1.00*11.9*1000*80*80) = 0.0633) 计算相对受压区高度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2*0.063) = 0.066 4) 计算受拉钢筋面积As = α1*fc*b*ho*ξ/fy = 1.000*11.9*1000*80*0.066/360= 173mm25) 验算最小配筋率ρ = As/(b*h) = 173/(1000*120) = 0.144% ρ所以取面积为As = ρmin*b*h = 0.200%*1000*120 = 240 mm2采取方案?8@200, 实配面积251 mm2 2.Y向底板钢筋1) 确定Y向板底弯矩My = 表中系数(γG*ｑgk+γQ*ｑqk)*Lo2= (0.0307+0.0634*0.200)*(1.200*4.100+1.400*2.000)*32= 3.012 kN*m 2) 确定计算系数αs = γo*My/(α1*fc*b*ho*ho)= 1.00*3.012×106/(1.00*11.9*1000*80*80) = 0.0403) 计算相对受压区高度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2*0.040) = 0.040 4) 计算受拉钢筋面积As = α1*fc*b*ho*ξ/fy = 1.000*11.9*1000*80*0.040/360= 107mm25) 验算最小配筋率ρ = As/(b*h) = 107/(1000*120) = 0.089% ρ所以取面积为As = ρmin*b*h = 0.200%*1000*120 = 240 mm2采取方案?8@200, 实配面积251 mm2 3.Y向上边支座钢筋 1) 确定上边支座弯矩Moy = 表中系数(γG*ｑgk+γQ*ｑqk)*Lo2= 0.1131*(1.200*4.100+1.400*2.000)*32第2页，共6页双向板计算= 7.861 kN*m 2) 确定计算系数αs = γo*Moy/(α1*fc*b*ho*ho)= 1.00*7.861×106/(1.00*11.9*1000*80*80) = 0.1033) 计算相对受压区高度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2*0.103) = 0.109 4) 计算受拉钢筋面积As = α1*fc*b*ho*ξ/fy = 1.000*11.9*1000*80*0.109/360= 289mm25) 验算最小配筋率ρ = As/(b*h) = 289/(1000*120) = 0.241% ρ≥ρmin = 0.200% 满足最小配筋要求采取方案?8@160, 实配面积314 mm2 七、跨中挠度计算：Mk -------- 按荷载效应的标准组合计算的弯矩值 Mq -------- 按荷载效应的准永久组合计算的弯矩值 1.计算荷载效应 Mk = Mgk + Mqk= (0.0634+0.0307*0.200)*(4.100+2.000)*32= 3.816 kN*m Mq = Mgk+ψq*Mqk= (0.0634+0.0307*0.200)*(4.100+1.0*2.000)*32= 3.816 kN*m 2.计算受弯构件的短期刚度 Bs1) 计算按荷载荷载效应的两种组合作用下，构件纵向受拉钢筋应力σsk = Mk/(0.87*ho*As) 混规(7.1.4-3)= 3.816×106/(0.87*80*251) = 218.438 N/mm σsq = Mq/(0.87*ho*As) 混规(7.1.4-3)= 3.816×106/(0.87*80*251) = 218.438 N/mm2) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积: Ate = 0.5*b*h = 0.5*1000*120= 60000mm2ρte = As/Ate 混规(7.1.2-4) = 251/60000 = 0.418%3) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψk = 1.1-0.65*ftk/(ρte*σsk) 混规(7.1.2-2) = 1.1-0.65*1.78/(0.418%*218.438) = -0.166 因为ψ不能小于最小值0.2，所以取ψk = 0.2ψq = 1.1-0.65*ftk/(ρte*σsq) 混规(7.1.2-2) = 1.1-0.65*1.78/(0.418%*218.438) = -0.166 因为ψ不能小于最小值0.2，所以取ψq = 0.2 4) 计算钢筋弹性模量与混凝土模量的比值αEαE = Es/Ec = 2.0×105/2.80×104= 7.143 5) 计算受压翼缘面积与腹板有效面积的比值γf 矩形截面，γf=06) 计算纵向受拉钢筋配筋率ρ第3页，共6页双向板计算ρ = As/(b*ho)= 251/(1000*80) = 0.314% 7) 计算受弯构件的短期刚度 Bs2Bsk = Es*As*ho/[1.15ψk+0.2+6*αE*ρ/(1+ 3.5γf')](混规(7.2.3-1))52= 2.0×10*251*80/[1.15*-0.166+0.2+6*7.143*0.314%/(1+3.5*0.0)]22= 5.692×10 kN*m2Bsq = Es*As*ho/[1.15ψq+0.2+6*αE*ρ/(1+ 3.5γf')](混规(7.2.3-1))52= 2.0×10*251*80/[1.15*-0.166+0.2+6*7.143*0.314%/(1+3.5*0.0)]= 5.692×102 kN*m23.计算受弯构件的长期刚度B1) 确定考虑荷载长期效应组合对挠度影响增大影响系数θ当ρ'=0时，θ=2.0 混规(7.2.5) 2) 计算受弯构件的长期刚度 BBk = Mk/(Mq*(θ-1)+Mk)*Bs (混规(7.2.2-1))= 3.816/(3.816*(2.0-1)+3.816)*5.692×102= 2.846×102 kN*m2Bq = Bsq/θ (混规(7.2.2-2))= 5.692×102/2.0= 2.846×102 kN*m2B = min(Bk,Bq)= min(284.588,284.588) = 284.588 4.计算受弯构件挠度f = f*(q4maxgk+qqk)*Lo/B= 0.00677*(4.100+2.000)*34/2.846×102= 11.749mm 5.验算挠度挠度限值fo=Lo/200=3000/200=15.000mmfmax=11.749mm≤fo=15.000mm，满足规范要求! 八、裂缝宽度验算: 1.跨中X方向裂缝 1) 计算荷载效应Mx = 表中系数(ｑgk+ψｑqk)*Lo2= (0.0634+0.0307*0.200)*(4.100+1.00*2.000)*32= 3.816 kN*m2) 光面钢筋,所以取值vi=0.7 3) 因为C > 65，所以取C = 654) 计算按荷载效应的准永久组合作用下，构件纵向受拉钢筋应力σsq=Mq/(0.87*ho*As) 混规(7.1.4-3)=3.816×106/(0.87*80*251) =218.438N/mm5) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积，Ate=0.5*b*h=0.5*1000*120=60000 mm2ρte=As/Ate 混规(7.1.2-4) =251/60000 = 0.0042第4页，共6页双向板计算因为ρte=0.0042 < 0.01,所以让ρte=0.01 6) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ=1.1-0.65*ftk/(ρte*σsq) 混规(7.1.2-2) =1.1-0.65*1.780/(0.0100*218.438) =0.5707) 计算单位面积钢筋根数n n=1000/dist = 1000/200 =58) 计算受拉区纵向钢筋的等效直径deqd2eq= (∑ni*di)/(∑ni*vi*di) =5*8*8/(5*0.7*8)=11 9) 计算最大裂缝宽度ωmax=αcr*ψ*σsq/Es*(1.9*C+0.08*Deq/ρte) (混规(7.1.2-1)=1.9*0.570*218.438/2.0×105*(1.9*20+0.08*11/0.0100) =0.1532mm ≤ 0.30, 满足规范要求2.跨中Y方向裂缝 1) 计算荷载效应My = 表中系数(ｑgk+ψｑqk)*Lo2= (0.0307+0.0634*0.200)*(4.100+1.00*2.000)*32= 2.380 kN*m2) 光面钢筋,所以取值vi=0.7 3) 因为C > 65，所以取C = 654) 计算按荷载效应的准永久组合作用下，构件纵向受拉钢筋应力σsq=Mq/(0.87*ho*As) 混规(7.1.4-3)=2.380×106/(0.87*80*251) =136.228N/mm5) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积，Ate=0.5*b*h=0.5*1000*120=60000 mm2ρte=As/Ate 混规(7.1.2-4) =251/60000 = 0.0042因为ρte=0.0042 < 0.01,所以让ρte=0.01 6) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ=1.1-0.65*ft k/(ρte*σsq) 混规(7.1.2-2) =1.1-0.65*1.780/(0.0100*136.228) =0.2517) 计算单位面积钢筋根数n n=1000/dist = 1000/200 =58) 计算受拉区纵向钢筋的等效直径deqd= (∑n2eqi*di)/(∑ni*vi*di) =5*8*8/(5*0.7*8)=11 9) 计算最大裂缝宽度ωmax=αcr*ψ*σsq/Es*(1.9*C+0.08*Deq/ρte) (混规(7.1.2-1)=1.9*0.251*136.228/2.0×105*(1.9*20+0.08*11/0.0100)第5页，共6页双向板计算=0.0420mm ≤ 0.30, 满足规范要求 3.支座上方向裂缝 1) 计算荷载效应Moy = 表中系数((ｑgk+ψｑqk)*Lo2)= 0.1131*(4.100+1.00*2.000)*32= 6.211 kN*m2) 光面钢筋,所以取值vi=0.7 3) 因为C > 65，所以取C = 654) 计算按荷载效应的准永久组合作用下，构件纵向受拉钢筋应力σsq=Mq/(0.87*ho*As) 混规(7.1.4-3)=6.211×106/(0.87*80*314) =284.215N/mm5) 计算按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率矩形截面积，Ate=0.5*b*h=0.5*1000*120=60000 mm2ρte=As/Ate 混规(7.1.2-4) =314/60000 = 0.0052因为ρte=0.0052 < 0.01,所以让ρte=0.01 6) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ=1.1-0.65*ftk/(ρte*σsq) 混规(7.1.2-2) =1.1-0.65*1.780/(0.0100*284.215) =0.6937) 计算单位面积钢筋根数n n=1000/dist = 1000/160 =68) 计算受拉区纵向钢筋的等效直径deqd*d2eq= (∑nii)/(∑ni*vi*di) =6*8*8/(6*0.7*8)=11 9) 计算最大裂缝宽度ωmax=αcr*ψ*σsq/Es*(1.9*C+0.08*Deq/ρte) (混规(7.1.2-1)=1.9*0.693*284.215/2.0×105*(1.9*20+0.08*11/0.0100) =0.2421mm ≤ 0.30, 满足规范要求第6页，共6页感谢您的阅读，祝您生活愉快。

楼面等效均布活荷载的计算方法

楼面等效均布活荷载的计算方法建筑结构荷载规范关于双向板楼面等效荷载计算方法的表达比较含糊，引起了对规范说明不同的理解，本文根据对规范的理解提出两种不同的计算方式，经过比较分析提出正确的计算方式根据《建筑结构荷载规范》GB50009-2012附录B“楼面等效均布活荷载的确定方法”的规定，对于单向板的计算已经有比较明确的公式和规定，本文不进行叙述，对于双向板的等效均布荷载计算方法，规范仅指出可按与单向板相同的原则，按四边简支板的绝对最大弯矩等值来确定。

这样对规范的表述就有了不同理解，第一种理解为：按与单向板相同的计算方式进行计算；第二种理解：按四边简支板绝对最大弯矩等值的原则进行计算。

两种方法计算比较如下：1 按与单向板相同的计算原则进行计算计算简图 11.1 基本资料周边支承的双向板，板的跨度Lx＝2800mm，板的跨度Ly＝3500mm，板的厚度h ＝150mm；局部集中荷载N＝42kN，荷载作用面的宽度btx＝1000mm，荷载作用面的宽度bty ＝1000mm；垫层厚度s＝100mm ；荷载作用面中心至板左边的距离x＝1400mm，最左端至板左边的距离x1＝900mm，最右端至板右边的距离x2＝900mm荷载作用面中心至板下边的距离y＝1750mm，最下端至板下边的距离y1＝1250mm，最上端至板上边的距离y2＝1250mm1.2 计算结果1.2.1 荷载作用面的计算宽度bcx＝btx+2*s+h＝1000+2*100+150＝1350mmbcy＝bty+2*s+h＝1000+2*100+150＝1350mm1.2.2 局部荷载的有效分布宽度按上下支承考虑时局部荷载的有效分布宽度当bcy≥bcx，bcx≤0.6Ly 时，取bx＝bcx+0.7Ly＝1350+0.7*3500＝3800mm按左右支承考虑时局部荷载的有效分布宽度当bcx≥bcy，bcy≤0.6Lx 时，取by＝bcy+0.7Lx＝1350+0.7*2800＝3310mm1.2.3 绝对最大弯矩1.2.3.1 按两端简支计算Y 方向绝对最大弯矩将局部集中荷载转换为Y 向线荷载qy＝N*btx/(btx*bty)＝42*1/(1*1)＝42kN/m根据静力计算手册得出简支梁局部均布荷载作用下的弯矩：MmaxY＝qy*bty*Ly(2-bty/Ly)/8=42*1*3.5*(2-1/3.5)/8=31.5kN·m1.2.3.2 按两端简支计算X 方向绝对最大弯矩，将局部集中荷载转换为X 向线荷载qx＝N*bty/(btx*bty)＝42*1/(1*1)＝42kN/m根据静力计算手册得出简支梁局部均布荷载作用下的弯矩：MmaxX＝qx*btx*Lx(2-btx/Lx)/8=42*1*2.8*(2-1/2.8)/8=24.15kN·m1.2.4 由绝对最大弯矩等值确定的等效均布荷载按上下支承考虑时的等效均布荷载qey＝8MmaxY/(bx*Ly^2)＝8*31.5/(3.8*3.5^2)＝5.41kN/m.按左右支承考虑时的等效均布荷载qex＝8MmaxX/(by*Lx^2)＝8*24.15/(3.31*2.8^2)＝7.44kN/m.等效均布荷载qe＝Max{qex,qey}＝Max{5.41,7.44}＝7.44kN/m.2 按四边简支板绝对最大弯矩等值的原则进行计算2.1 按四边简支计算跨中最大弯矩，计算条件同第一种计算方式2.1.1 根据计算条件，应用建筑结构静力计算手册(p227)中局部均布荷载作用下的弯矩系数表查出弯矩系数如下：泊松比μ=0；X 方向表中系数=0.1268,Y 方向表中系数=0.1017；计算跨中弯矩：Mx=表中系数×q×btx×bty=0.1268×42×1×1=5.33kN/m.My=表中系数×q×btx×bty=0.1017×42×1×1=4.27kN/m.调整为钢筋混凝土泊松比，重新计算跨中弯矩，μ=1/6Mx(μ)=Mx+μMy=5.33+4.27/6=6.04kN/m.My(μ)=My+μMx=4.27+5.33/6=5.16kN/m.2.2 根据跨中弯矩相等原则用查表法反算等效均布荷载2.2.1 根据计算条件，应用建筑结构静力计算手册(p216 页)中均布荷载作用下的弯矩系数表查出弯矩系数如下：泊松比μ=0；X 方向表中系数=0.0561,Y 方向表中系数=0.0334；计算跨中弯矩：(据公式M=表中系数×qL2，L 为Lx 与Ly 中较小者)Mx=表中系数×q×L2=0.0561×q×2.82My=表中系数×q×L2=0.0334×q×2.82调整为钢筋混凝土泊松比，重新计算跨中弯矩，μ=1/6,带入局部荷载作用下的最大弯矩得：Mx(μ)=Mx+μMy=0.0561×q×2.82+0.0334×q×2.82/6=6.04(1)My(μ)=My+μMx=0.0334×q×2.82+0.0561×q×2.82/6=5.16(2)由（1）式得q=12.49kN/m.；由（2）式得q=15.39kN/m.；取大值，等效均布荷载q=15.39kN/m.3 结果比较及结语由计算结果可以明显看出，第一种计算方法得出的计算结果比第二种小很多，根据内力等值的原则，第二种计算方法应该是合理的，应该选用第二种计算方法。

[整理](一)双向板按弹性理论的计算方法

(一)双向板按弹性理论的计算方法1．单跨双向板的弯矩计算为便于应用，单跨双向板按弹性理论计算，已编制成弯矩系数表，供设计者查用。

在教材的附表中，列出了均布荷载作用下，六种不同支承情况的双向板弯矩系数表。

板的弯矩可按下列公式计算：M = 弯矩系数×(g+p)l x2式中M 为跨中或支座单位板宽内的弯矩(kN·m/m)；g、p为板上恒载及活载设计值(kN/m2)；l x为板的跨度(m)。

2．多跨连续双向板的弯矩计算(1)跨中弯矩双向板跨中弯矩的最不利活载位置图多跨连续双向板也需要考虑活载的最不利位置。

当求某跨跨中最大弯矩时，应在该跨布置活载，并在其前后左右每隔一区格布置活载，形成如上图(a)所示棋盘格式布置。

图(b)为A-A剖面中第2、第4区格板跨中弯矩的最不利活载位置。

为了能利用单跨双向板的弯矩系数表，可将图(b)的活载分解为图(c)的对称荷载情况和图(d)的反对称荷载情况，将图(c)与(d)叠加即为与图(b)等效的活载分布。

在对称荷载作用下，板在中间支座处的转角很小，可近似地认为转角为零，中间支座均可视为固定支座。

因此，所有中间区格均可按四边固定的单跨双向板计算；如边支座为简支，则边区格按三边固定、一边简支的单跨双向板计算；角区格按两邻边固定、两邻边简支的单跨双向板计算。

在反对称荷载作用下，板在中间支座处转角方向一致，大小相等接近于简支板的转角，所有中间支座均可视为简支支座。

因此，每个区格均可按四边简支的单跨双向板计算。

将上述两种荷载作用下求得的弯矩叠加，即为在棋盘式活载不利位置下板的跨中最大弯矩。

(2)支座弯矩支座弯矩的活载不利位置，应在该支座两侧区格内布置活载，然后再隔跨布置，考虑到隔跨活载的影响很小，可假定板上所有区格均满布荷载(g+p)时得出的支座弯矩，即为支座的最大弯矩。

这样，所有中间支座均可视为固定支座，边支座则按实际情况考虑，因此可直接由单跨双向板的弯矩系数表查得弯矩系数，计算支座弯距。

集中荷载作用下双向板等效荷载的简捷计算方法

ｔＭ＝［（０．０３８６ｘ＋０．０００９）＋ｌ，（一０．１２０３ｘ＋０．１５４１）］ｇｚ
（０．５≤ ≤ １）（７）
１
＝一２ ∑（。一６。＋ｂＸ ቤተ መጻሕፍቲ ባይዱ）一（）＝０（４）
ｂ０，ｂｌ有：
＾
（２）
的散点（表１、表２的弯矩系数）分别落在一元线性回归方程
的两侧且随着的增加保持相同的增减性，又有相关系数最大的为０．９９２３，最小的为０．９３０８，所以认为这四条回归方程是合适的。因此，均布荷载作用于四边简支双向板的跨中弯矩方程
例分析表明可得到满意的结果，此方法可供类似工程设计参考。
【关键词】双向板；弯矩系数；线性回归；等效均布荷载【中图分类号】ＴＵ３１１．４
在建筑设计中双向板楼面经常会遇到板上有设备等其
他集中荷载作用于板面的情况，为方便此种情况的楼面设计，可将此集中荷载按照《建筑结构荷载设计规范》（ＧＢ
们之间的平均变化数量的关系，据此进行预测或控制。
假设预测目标因变量为Ｋ，影响它变化的一个自变量为
，
当集中荷载作用于板跨中时：Ｍ＝（系数）Ｐ，Ｍ＝（系数）Ｐ（钢筋混凝土板＝Ｏ，
１为双向板的短边）；
∑Ｘ一（ ∑Ｘ）
ｌ＝ｌｉ＝ｌ

(一)双向板按弹性理论的计算方法

(一)双向板按弹性理论的计算方法1．单跨双向板的弯矩计算为便于应用，单跨双向板按弹性理论计算，已编制成弯矩系数表，供设计者查用。

在教材的附表中，列出了均布荷载作用下，六种不同支承情况的双向板弯矩系数表。

板的弯矩可按下列公式计算：M = 弯矩系数×(g+p)l x2式中M 为跨中或支座单位板宽内的弯矩(kN·m/m)；g、p为板上恒载及活载设计值(kN/m2)；l x为板的跨度(m)。

显示更多隐藏2．多跨连续双向板的弯矩计算(1)跨中弯矩双向板跨中弯矩的最不利活载位置图多跨连续双向板也需要考虑活载的最不利位置。

当求某跨跨中最大弯矩时，应在该跨布置活载，并在其前后左右每隔一区格布置活载，形成如上图(a)所示棋盘格式布置。

图(b)为A-A剖面中第2、第4区格板跨中弯矩的最不利活载位置。

为了能利用单跨双向板的弯矩系数表，可将图(b)的活载分解为图(c)的对称荷载情况和图(d)的反对称荷载情况，将图(c)与(d)叠加即为与图(b)等效的活载分布。

在对称荷载作用下，板在中间支座处的转角很小，可近似地认为转角为零，中间支座均可视为固定支座。

因此，所有中间区格均可按四边固定的单跨双向板计算；如边支座为简支，则边区格按三边固定、一边简支的单跨双向板计算；角区格按两邻边固定、两邻边简支的单跨双向板计算。

在反对称荷载作用下，板在中间支座处转角方向一致，大小相等接近于简支板的转角，所有中间支座均可视为简支支座。

因此，每个区格均可按四边简支的单跨双向板计算。

将上述两种荷载作用下求得的弯矩叠加，即为在棋盘式活载不利位置下板的跨中最大弯矩。

(2)支座弯矩支座弯矩的活载不利位置，应在该支座两侧区格内布置活载，然后再隔跨布置，考虑到隔跨活载的影响很小，可假定板上所有区格均满布荷载(g+p)时得出的支座弯矩，即为支座的最大弯矩。

这样，所有中间支座均可视为固定支座，边支座则按实际情况考虑，因此可直接由单跨双向板的弯矩系数表查得弯矩系数，计算支座弯距。

双向板楼等效活荷载的计算

浅谈双向板等效均布活荷载的计算摘要：本文根据《建筑结构荷载规范》（GB50009-2001）（2006版）附录B中对双向板等效荷载计算的概述，介绍了工程设计中双向板上等效均布活荷载的计算方法，为后续使用电算软件对结构整体进行受力分析提供了计算数据。

关键词：双向板等效均布活荷载计算0 前言双向楼板由于其经济、美观等优势而被广泛应用于建筑中。

本人在设计某污水处理厂脱水机房时，遇到了设备搁置于二层楼面的情况，由于脱水机房内设备较多以及工艺的要求，无法将所有设备布置于梁上，需要将布置于楼板上的设备重量进行等效均布活荷载的换算。

根据《建筑结构荷载规范》（GB50009-2001）（2006版）第4.1.3条规定，楼面板上的局部线荷载、面荷载等可按附录B的规定，换算为等效均布活荷载。

而附录B中仅对局部荷载作用下，如何计算等效均布荷载做了粗略的规定，所提供的计算公式也仅适用于单向板情况。

对于双向板的等效均布活荷载计算，本文基于对规范的规定理解提出一种计算方法。

《建筑结构荷载规范》（GB50009-2001）（2006版）第B.0.1条指出：楼面（板、次梁及主梁）的等效均布活荷载应在其设计控制部位上，根据需要按内力（如弯矩、剪力等）、变形裂缝的等值要求来确定在一般情况下，可仅按内力的等值来确定；第B.0.6条指出，双向板的等效均布荷载可按与单向板相同的原则，按四边简支板的绝对最大弯矩等值来确定。

这里通过一块楼板及其上部的设备荷载来介绍一下《建筑结构荷载规范》（GB50009-2001）第B.0.6条所述的双向板（这里所指的双向板一般指长边与短边长度之比小于或等于2.0的板，长边与短边长度之比大于2.0的板可按沿短边受力的单向板考虑）如何按四边简支的绝对最大弯矩等值确定其等效均布荷载。

而对于单向板上局部荷载的等效，《建筑结构荷载规范》（GB50009-2001）第B.0.4条、第B.0.5条已有详细说明，这里不再进行讨论。

楼面双向板等效均布活荷载的计算方法

楼面双向板等效均布活荷载的计算方法这个题目来自于《建筑结构荷载规范GB50009-2001》的附录B，要弄清它需要先知道楼面等效均布活荷载。

规范中虽然介绍了计算的原则，但究其本源，其实就是为了方便地统一处理各种类型的局部活荷载，也就是说寻找一个均布面荷载值，使它对结构产生的效果与局部活荷载产生的效果相同（也就是等效的含义），这样我们对结构荷载问题的处理就比较统一，因为我们进行结构分析时，已习惯输入KN/m2这样的荷载方式，甚至有时候对某些楼面（比如地下室顶板）进行荷载值限定时，会写下该处的荷载不能超过多少KN/m2这样的说明文字。

所谓“等效”，主要是指内力的等值，而且对于连续跨也常常是按单跨简支来考虑。

在处理单向板和悬臂板时，很容易理解，规范中也给出了计算的原则。

但是对于双向板而言，规范中仅给出一条简单的说明：“按四边简支板的绝对最大弯矩等值来确定”，让很多人望而却步。

有些耐心的结构工程师在针对具体的工程项目时，还是可以得到一些关于这个问题的结果的。

他可以近似地让局部荷载作用于双向板的跨中，因为这种荷载布置以及均布荷载下的四边简支双向板的绝对最大弯矩都可以在《建筑结构静力计算手册》中查表得到。

有多些耐心的结构工作者还可以通过有限元分析来得到结果，这些结构人士以高校老师诸多。

其实学过《板壳理论》的力学专业出身的人可能会有这样的印象，那就是薄板理论中首先推导的就是双向板局部荷载下的挠曲面方程，对其偏导就可以得到弯矩方程，结果是一个级数方程式。

我们可以在程序中取前面几项，就可以得到足够近似的值。

你可以通过访问的在线计算部分得到结果。

这里有两个问题需要特别强调一下，有些程序处理双向板时，可能是因为规范的嘎然而止，导致其武断地用两个方向的单向板来分别计算，取其中大者作为结果，这是偏不安全的。

（Morgain好像是这样计算的）。

还有个问题是关于绝对最大弯矩的问题，这是针对当局部荷载不是作用在板的正中间的情况。

双向板计算

7
0.95。 (2)钢筋分带布置问题
当按弹性理论计算求得的最大弯矩配筋时，考虑到近支座处弯矩比计算的最大弯矩小得多，为了节约钢材，可将两个方向的跨中正弯矩配筋在距支座 lx/4 宽度内减少一半(见上图)。但支座处的负弯矩配筋应按计算值均匀布置。支座负弯矩钢筋可在距支座不小于 lx/6 处截断一半，其余的一半可在距支座不小于 lx/4 处截断，或弯下作为跨中正弯矩配筋。
(二)双向板按塑性理论的计算方法
1．双向板的塑性铰线及破坏机构 (1)四边简支双向板的塑性铰线及破坏机构
(a)简支双向板的裂缝分布图
(b)简支双向板的塑性铰线及破坏机构图
均布荷载作用的四边简支双向板，板中不仅作用有两个方向的弯矩和剪力，同时还作用有扭矩。由于短跨方向弯矩较大，故第一批裂缝出现在短跨跨中的板底，且与长跨平行(上图 a)。近四角处，弯矩减小，而扭矩增大，弯矩和扭矩组合成斜向主弯矩。随荷载增大，由于主弯矩的作用，跨中裂缝向四角发展。继续加大荷载，短跨跨中钢筋应力将首先到达屈服，弯矩不再增加，变形可继续增大，裂缝开展，使与裂缝相交的钢筋陆续屈服，形成如上
当按塑性理论计算时，钢筋布置已反映在所选用的弯矩计算公式中，跨中钢筋的配筋数量不分中间带及边带。当边支座为简支时，边区格及角区格与楼板边缘垂直的跨中钢筋一般不宜截断，或通过计算确定截断钢筋的数量及位置。支座上负弯矩钢筋可在伸入板内不少于 lx/4 处截断。
(3)边支座构造钢筋及角部附加钢筋
简支板角部裂缝图无论按弹性或塑性理论计算，边支座一般按简支支座考虑，计算上取 M=0。但实际上由于砖墙或边梁的约束作用，仍存在有一定的负弯矩，故需在简支支座的顶部设置构造钢筋，其数量与单向板的要求相同。角区格的角部受荷后有翘起的趋势(见上图)，如支座处有砖墙压住，限制了板的翘起，角部板的顶面将出现见如上图所示斜裂缝。为了控制这种裂缝的发展，需在简支板的角部 lx/4 范围内配置顶部附加钢筋(参见本章第四节板中构造钢筋图)。

再谈楼面双向板等效均布活荷载的计算

再谈楼面双向板等效均布活荷载的计算为什么要再谈，因为这一段时间以来，陆陆续续不断有网上朋友与我讨论这个问题，而且经常是间隔一段时间，这样造成的后果是逼得我不断地温习这个命题。

在这些有益的讨论中，我们也发现了很多有用的东西，所以有必要再进行一次梳理。

在叙述之前，有必要再强调一下命题的意义，那就是我们要找到一个满布的均布荷载值，该值对楼板产生的影响与我们已知的集中荷载（或局部分布荷载）的影响等效，而且我们已认可这里的等效是产生的弯矩值相等。

当已知荷载的位置不确定时，我们处理时很方便，我们会假定它作用在楼板平面的中心位置。

让很多人感到困惑的是已知荷载的位置偏离楼板平面的中心位置很多时的情况。

我们知道等效是指弯矩值相等，但是，什么位置的弯矩是我们这次要讨论的重点，《建筑结构荷载规范GB50009-2001》的附录B说的是，“按四边简支板的绝对最大弯矩等值来确定”，上一篇文章我们认为取局部荷载作用处的弯矩作为对象比较合适。

也就是说，让满布等效荷载作用下，在已知局部荷载作用的位置处产生的弯矩与已知局部荷载作用下该点的弯矩值相等。

我们不妨称这种等效为“荷载作用处等效”。

另一种理解是“中心位置处等效”，就是说，让满布等效荷载作用下，在楼板平面中心位置处产生的弯矩与已知局部荷载作用下楼板平面的中心位置处的弯矩值相等。

《建筑结构荷载设计手册? 第二版》的附录四，给出了双向板楼面等效均布荷载计算表（有227页之多，占了该手册近一半，而且因为是表，所以数据覆盖不全面），是按“中心位置处等效”理解来考虑的。

还有一种理解，作者认为与“绝对最大弯矩等效”比较靠，那就是，让满布等效荷载作用下，在楼板平面的中心位置处产生的弯矩，与已知局部荷载作用下局部荷载作用的位置处产生的弯矩值相等。

为了看看这几种不同的理解到底有多大差别，我们举一个例子说明：如图所示双向板，板两边的边长lx=ly=5m；已知荷载P=10kN；作用的区域边长btx=bty=0.5m；荷载中心位置距板边的距离dx=dy=1.5m。

双向板等效均布荷载计算公式

双向板等效均布荷载计算公式英文回答：Calculation of Equivalent Uniform Load for Two-Way Slabs.The design of two-way slabs requires the calculation of the equivalent uniform load (EUL) that represents the actual distributed loading on the slab. The EUL is used in the design of the slab reinforcement and can be calculated using one of several methods.Method 1: Strip Method.The strip method is a simplified approach that divides the slab into a series of parallel strips and assumes that the load is uniformly distributed along each strip. The EUL for each strip is then calculated as follows:w = (L/2) q.where:w is the EUL (in lb/ft or kN/m)。

L is the length of the strip (in ft or m)。

q is the uniformly distributed load (in lb/ft² orkN/m²)。

The EUL for the entire slab is then calculated by summing the EULs for all the strips.Method 2: Finite Element Method.The finite element method (FEM) is a more accurate method that uses computer software to analyze the behavior of the slab under various loading conditions. The FEM can account for the effects of boundary conditions, concentrated loads, and other factors that may affect the distribution of the load on the slab.The FEM is a complex method that requires specialized software and expertise to use. However, it can provide more accurate results than the strip method, especially for slabs with irregular shapes or complex loading conditions.Choice of Method.The choice of method for calculating the EUL depends on the complexity of the slab and the desired level of accuracy. The strip method is a simple and straightforward approach that is suitable for most regular slabs with uniformly distributed loads. The FEM is a more accurate method that should be used for slabs with irregular shapes or complex loading conditions.中文回答：双向板等效均布荷载计算公式。

双向板等效均布荷载折减系数

双向板等效均布荷载折减系数你知道吗，咱们说到“双向板”等效均布荷载折减系数这事儿，首先得告诉你，这可不是啥高深的理论，虽然听起来有点儿学术。

其实它的意思挺简单的，就是一种用来简化计算的方法。

你想啊，建筑结构这么复杂，一块板子上的荷载其实不是均匀分布的，哪儿可能，中心那块重，边上轻，差别大得很！但我们为了计算方便，就得用一种“折减”的方式，按照某种比例，把这些荷载换成均匀的。

说白了，就是把不均匀的荷载“缩水”成一个大家伙，这样计算起来就能省不少事。

那咱们怎么折减呢？这就得讲讲这个“折减系数”了。

你想，这个系数就像是给荷载穿上了一件“降温服”，让它看起来不那么沉重了。

因为，双向板是承受着两方向的力，既有纵向的荷载，也有横向的荷载。

传统计算方法把这些荷载当作是均匀分布的，可实际上，荷载的分布哪里会这么简单？所以，折减系数就像是一个魔法，帮我们把这些复杂的分布压缩成一个简单的数字，方便后续的分析和设计。

你别看这只是个“系数”，其实它可有很大的作用。

要是没有了它，估计不少建筑的设计都会像“过山车”一样危险，谁敢住呀！因为如果不折减，板子上实际承受的荷载比我们计算出来的要大，结构就可能出问题。

所以啊，这个折减系数不仅是个数字，它还是我们安全设计的保障。

这玩意儿到底怎么计算呢？其实也没那么神秘，通常得根据板的跨度、荷载的类型、以及板的支撑条件来推算。

其实呢，最关键的一点就是“双向板”的特点，它不像单向板那样简简单单地就受一个方向的力，它可得两个方向的力同时来，麻烦了不是？所以，计算时得考虑这两个方向的力是怎么共同作用的，这可不是随便套个公式就能搞定的。

比如说，如果板的跨度比较大，那折减系数就得适当调大，因为跨度越大，板子承担的荷载差异就越明显，咱不能小看这个“差异”哦。

可是，别光盯着跨度不放，支撑条件也很重要。

如果支撑条件比较好，板子就能更均匀地分担荷载，折减系数也可以适当减小点。

反过来说，如果支撑条件差，那板子可能得“拼命”地分担荷载，折减系数就得加大，免得它太累了。

双向板-计算步骤

双向板-计算步骤⼀、构件编号: LB-1⼆、⽰意图三、依据规范《建筑结构荷载规范》 GB50009-2001《混凝⼟结构设计规范》 GB50010-2010四、计算信息1.⼏何参数计算跨度: Lx = 3000 mm; Ly = 4600 mm板厚: h = 120 mm2.材料信息混凝⼟等级: C25 fc=mm2 ft=mm2 ftk=mm2Ec=×104N/mm2钢筋种类: HRB400 fy = 360 N/mm2Es = ×105 N/mm2最⼩配筋率: ρ= %纵向受拉钢筋合⼒点⾄近边距离: as = 40mm保护层厚度: c = 20mm3.荷载信息(均布荷载)永久荷载分项系数: γG =可变荷载分项系数: γQ =准永久值系数: ψq =永久荷载标准值: ｑgk = m2可变荷载标准值: ｑqk = m24.计算⽅法:弹性板5.边界条件(上端/下端/左端/右端):固定/简⽀/简⽀/简⽀6.设计参数结构重要性系数: γo =泊松⽐:µ =五、计算参数:1.计算板的跨度: Lo = 3000 mm2.计算板的有效⾼度: ho = h-as=120-40=80 mm六、配筋计算(lx/ly=3000/4600=< 所以按双向板计算):向底板钢筋1) 确定X向板底弯矩Mx = 表中系数(γG*ｑgk+γQ*ｑqk)*Lo2= +***+**32= kN*m2) 确定计算系数αs = γo*Mx/(α1*fc*b*ho*ho)= *×106/**1000*80*80)=3) 计算相对受压区⾼度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2* =4) 计算受拉钢筋⾯积As = α1*fc*b*ho*ξ/fy = **1000*80*360= 173mm25) 验算最⼩配筋率ρ = As/(b*h) = 173/(1000*120) = %ρ<ρmin = % 不满⾜最⼩配筋要求所以取⾯积为As = ρmin*b*h = %*1000*120 = 240 mm2采取⽅案?8@200, 实配⾯积251 mm2向底板钢筋1) 确定Y向板底弯矩My = 表中系数(γG*ｑgk+γQ*ｑqk)*Lo2= +***+**32= kN*m2) 确定计算系数αs = γo*My/(α1*fc*b*ho*ho)= *×106/**1000*80*80)=3) 计算相对受压区⾼度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2* =4) 计算受拉钢筋⾯积As = α1*fc*b*ho*ξ/fy = **1000*80*360= 107mm25) 验算最⼩配筋率ρ = As/(b*h) = 107/(1000*120) = %ρ<ρmin = % 不满⾜最⼩配筋要求所以取⾯积为As = ρmin*b*h = %*1000*120 = 240 mm2采取⽅案?8@200, 实配⾯积251 mm2向上边⽀座钢筋1) 确定上边⽀座弯矩M o y = 表中系数(γG*ｑgk+γQ*ｑqk)*Lo2= **+**32= kN*m2) 确定计算系数αs = γo*M o y/(α1*fc*b*ho*ho)= *×106/**1000*80*80)=3) 计算相对受压区⾼度ξ = 1-sqrt(1-2*αs) = 1-sqrt(1-2* =4) 计算受拉钢筋⾯积As = α1*fc*b*ho*ξ/fy = **1000*80*360= 289mm25) 验算最⼩配筋率ρ = A s/(b*h) = 289/(1000*120) = %ρ≥ρmin = % 满⾜最⼩配筋要求采取⽅案?8@160, 实配⾯积314 mm2七、跨中挠度计算：Mk -------- 按荷载效应的标准组合计算的弯矩值Mq -------- 按荷载效应的准永久组合计算的弯矩值1.计算荷载效应Mk = Mgk + Mqk= +**+*32 = kN*mMq = Mgk+ψq*Mqk= +**+**32 = kN*m2.计算受弯构件的短期刚度 Bs1) 计算按荷载荷载效应的两种组合作⽤下，构件纵向受拉钢筋应⼒σsk = Mk/*ho*As) 混规= ×106/*80*251) = N/mmσsq = Mq/*ho*As) 混规= ×106/*80*251) = N/mm 2) 计算按有效受拉混凝⼟截⾯⾯积计算的纵向受拉钢筋配筋率矩形截⾯积: Ate = *b*h = *1000*120= 60000mm2ρte = As/Ate 混规 = 251/60000 = %3) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψk = 混规 = =因为ψ不能⼩于最⼩值，所以取ψk =ψq = 混规 = =因为ψ不能⼩于最⼩值，所以取ψq =4) 计算钢筋弹性模量与混凝⼟模量的⽐值αEαE = Es/Ec = ×105/×104 =5) 计算受压翼缘⾯积与腹板有效⾯积的⽐值γf矩形截⾯，γf=06) 计算纵向受拉钢筋配筋率ρρ = As/(b*ho)= 251/(1000*80) = %7) 计算受弯构件的短期刚度 BsBsk = Es*As*ho2/[ψk++6*αE*ρ/(1+ γf')](混规 = ×105*251*802/[*++6**%/(1+*] = ×102 kN*m2Bsq = Es*As*ho2/[ψq++6*αE*ρ/(1+ γf')](混规 = ×105*251*802/[*++6**%/(1+*] = ×102 kN*m23.计算受弯构件的长期刚度B1) 确定考虑荷载长期效应组合对挠度影响增⼤影响系数θ当ρ'=0时，θ= 混规 2) 计算受弯构件的长期刚度 BBk = Mk/(Mq*(θ-1)+Mk)*Bs (混规= *+*×102= ×102 kN*m2Bq = Bsq/θ (混规= ×102/= ×102 kN*m2B = min(Bk,Bq)= min,=4.计算受弯构件挠度f max = f*(q gk+q qk)*Lo4/B= *+*34/×102=5.验算挠度挠度限值fo=Lo/200=3000/200=fmax=≤fo=，满⾜规范要求!⼋、裂缝宽度验算:1.跨中X⽅向裂缝1) 计算荷载效应Mx = 表中系数(ｑgk+ψｑqk)*Lo2= +**+**32= kN*m2) 光⾯钢筋,所以取值v i=3) 因为C > 65，所以取C = 654) 计算按荷载效应的准永久组合作⽤下，构件纵向受拉钢筋应⼒σsq=Mq/*ho*As) 混规=×106/*80*251)=mm5) 计算按有效受拉混凝⼟截⾯⾯积计算的纵向受拉钢筋配筋率矩形截⾯积，Ate=*b*h=*1000*120=60000 mm2ρte=As/Ate 混规 =251/60000 =因为ρte= < ,所以让ρte=6) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ= 混规 = =7) 计算单位⾯积钢筋根数nn=1000/dist = 1000/200=58) 计算受拉区纵向钢筋的等效直径d eqd eq= (∑n i*d i2)/(∑n i*v i*d i)=5*8*8/(5**8)=119) 计算最⼤裂缝宽度ωmax=αcr*ψ*σsq/Es**C+*Deq/ρte) (混规=**×105**20+*11/ = ≤ , 满⾜规范要求2.跨中Y⽅向裂缝1) 计算荷载效应My = 表中系数(ｑgk+ψｑqk)*Lo2= +**+**32= kN*m2) 光⾯钢筋,所以取值v i=3) 因为C > 65，所以取C = 654) 计算按荷载效应的准永久组合作⽤下，构件纵向受拉钢筋应⼒σsq=Mq/*ho*As) 混规=×106/*80*251)=mm5) 计算按有效受拉混凝⼟截⾯⾯积计算的纵向受拉钢筋配筋率矩形截⾯积，Ate=*b*h=*1000*120=60000 mm2ρte=As/Ate 混规 =251/60000 =因为ρte= < ,所以让ρte=6) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ= 混规 = =7) 计算单位⾯积钢筋根数nn=1000/dist = 1000/200=58) 计算受拉区纵向钢筋的等效直径d eqd eq= (∑n i*d i2)/(∑n i*v i*d i)=5*8*8/(5**8)=119) 计算最⼤裂缝宽度ωmax=αcr*ψ*σsq/Es**C+*Deq/ρte) (混规=**×105**20+*11/ = ≤ , 满⾜规范要求3.⽀座上⽅向裂缝1) 计算荷载效应M o y = 表中系数((ｑgk+ψｑqk)*Lo2)= *+**32= kN*m2) 光⾯钢筋,所以取值v i=3) 因为C > 65，所以取C = 654) 计算按荷载效应的准永久组合作⽤下，构件纵向受拉钢筋应⼒σsq=Mq/*ho*As) 混规=×106/*80*314)=mm5) 计算按有效受拉混凝⼟截⾯⾯积计算的纵向受拉钢筋配筋率矩形截⾯积，Ate=*b*h=*1000*120=60000 mm2ρte=As/Ate 混规 =314/60000 =因为ρte= < ,所以让ρte=6) 计算裂缝间纵向受拉钢筋应变不均匀系数ψψ= 混规 = =7) 计算单位⾯积钢筋根数nn=1000/dist = 1000/160=68) 计算受拉区纵向钢筋的等效直径d eqd eq= (∑n i*d i2)/(∑n i*v i*d i)=6*8*8/(6**8)=119) 计算最⼤裂缝宽度ωmax=αcr*ψ*σsq/Es**C+*Deq/ρte) (混规=**×105**20+*11/ = ≤ , 满⾜规范要求。