数字信号处理-基于计算机的方法(第四版)第九章答案
数字信号处理(第四版)第9章数字信号处理的实现

第9章 数字信号处理的实现
2. 极点位置敏感度 下面分析系数量化误差对极零点位置的影响。如果 极零点位置改变了,严重时不仅IIR系统的频率响应会 发 生变化,还会影响系统的稳定性。因此研究极点位置 的 改变更加重要。为了表示系数量化对极点位置的影响,引 入极点位置灵敏度的概念,所谓极点灵敏度, 是指每 个极 点对系数偏差的敏感程度。相应的还有零点位置灵 敏度 ,分析方法相同。下面讨论系数量化对极点位置的 影响 。
就是量化后的数值。x可以是标量、向量和矩阵。将数取
整的方法有四舍五入取整、向上取整、向下取整、向零
取整,对应的MATLAB取整函数分别为 round(x)、
ceil(x)、floor(x)、fix(x)。round最常用,对应的MATLAB
量化语句为xq=q*round(x/q)。
第9章 数字信号处理的实现
解 求解本例的系数量化与绘图程序为ep911.m。
第9章 数字信号处理的实现
%ep911.m: 例题9.1.1 系数量化与图9.1.3绘图程序 B=1; A=[1, -0.17, 0.965];%量化前系统函数系数向量
b=4; Aq=quant(A, b);
进行b位量化
%量化2进制位数 %对系统函数分母系数向量A
p=roots(A) pq=roots(Aq) ap=abs(p) a pq=abs(pq) %以下为绘图部分省略
%计算量化前的极点 %计算量化后的极点 %计算量化前极点的模 %计算量化后极点的模
第9章 数字信号处理的实现
运行程序,得到量化后的系统函数
为
并求出H(z)和
的极点分别为
显然,因为系数的量化,使极点位置发生变化,算出极点
的模为: |p1, 2|=0.9823,
数字信号处理第9章答案

滤波器? 为什么?
(该题21分, (1)15分, (2)6分) (自测时间2.5~3小时, 满分100分)
第 9 章
自
测
题
题9图
第 9 章
自
测
题
9.4 自 测 题 (四)
1. 设
0.19 X ( z) (1 0.9 z )(1 0.9 z 1 )
试求与X(z)对应的所有可能的序列x(n)。 (该题12分) 2. 假设x(n)=R8(n), h(n)=R4(n)。 (1)令y(n)=x(n)*h(n), 求y(n)。 要求写出y(n)的表达式, 并画出y(n)的波形。
ˆ (1) 写出 x (t ) 的表达式;
(2) 求出理想低通滤波器的输出信号y(t)。
(该题14分 , (1)6分, (2)8分) 4. 假设线性非时变系统的单位脉冲响应h(n)和输入信号
x(n)分别用下式表示:
h(n)=R8(n), x(n)=0.5nR8(n) (1) 计算并图示该系统的输出信号y(n);
y1(n)=IDFT[Y(k)]
(FFT计算作为一个框图), 并注明FFT的最小计算区间N
等于多少。 (该题22分, (1) 7分, (2) 7分, (3) 8分)
第 9 章
自
测
题
5. 二阶归一化低通巴特沃斯模拟滤波器的系统函数为
H a (s) 1 s 2 2s 1
采样间隔T=2 s, 为简单起见, 令3 dB截止频率Ωc=1 rad/s, 用 双线性变换法将该模拟滤波器转换成数字滤波器H(z), 要求: (1) 求出H(z); (2) 计算数字滤波器的3 dB截止频率; (3) 画出数字滤波器的直接型结构图。 (该题15分, (1) 5分, (2) 5分, (3) 5分)
数字信号处理—基于计算机的方法答案(精品)
sin kπ kπ d
d
cos
kω
st
⎤ ⎥
⎦
v1 (t ) = ws (t ) cos nωst
∑ =
w(t
)[d
cos
nωst
+
2d
∞ k =1
sin kπ kπ d
d
cos
kωst
cos
nωst
n≠k
+
2d
sin nπ nπ d
d
cos2
nωst]
cos2
nωst
=
1 2
+
1 2
cos
2nωst
Solution:
( ) ∑ ∑ s t
=
∞ k =−∞
Π
⎡t ⎢⎣
− kTs τ
⎤ ⎥⎦
=
∞ k =−∞
ck e−
jkωst
∑ ∑ =
∞
d
k =−∞
sin kπ d kπ d
e− jkωst
=
d
+ 2d
∞ k =1
sin kπ d kπ d
cos kωst
∑ ws
(t)
=
w(t)
⎡⎢⎣d
+
2d
∞ k =1
is obtained with this demodulation technique , where w(t) is the oriqinal waveform and Cw(t) is the recovered waveform. Note that C is a function of n ,where the oscillator frequency is nfs.
数字信号处理教程课后习题及答案

6.试判断:
是否是线性系统?并判断(2),(3)是否是移不变系统?
分析:利用定义来证明线性:满足可加性和比例性, T [a1 x1 (n ) + a 2 x2 (n )] = a1T [ x1 (n )] + a2T [ x2 (n )] 移不变性:输入与输出的移位应相同 T[x(n-m)]=y(n-m)。
,
(2)x(n) = R3(n)
,
(3)x(n) = δ (n − 2) ,
(4)x(n) = 2n u(−n − 1) ,
h(n) = R5(n) h(n) = R4 (n) h(n) = 0.5n R3(n) h(n) = 0.5n u(n)
分析:
①如果是因果序列 y (n ) 可表示成 y (n ) ={ y (0) , y(1) , y(2) ……},例如小题(2)为
y1 (1) = ay1 (0) + x1 (1) = 0 y1 (2) = ay1 (1) + x1 (2) = 0
┇
8
y1(n) = ay1(n − 1) + x1(n) = 0 ∴ y1 (n) = 0 , n ≥ 0 ii) 向 n < 0 处递推,将原方程加以变换
y1(n + 1) = ay1(n) + x1(n + 1)
结果 y (n ) 中变量是 n ,
∞
∞
∑ ∑ y (n ) =
x ( m )h (n − m ) =
h(m)x(n − m) ;
m = −∞
m = −∞
②分为四步 (1)翻褶( -m ),(2)移位( n ),(3)相乘,
(NEW)程佩青《数字信号处理教程》(第4版)笔记和课后习题(含考研真题)详解

目 录第1章 离散时间信号与系统1.1 复习笔记1.2 课后习题详解1.3 名校考研真题详解第2章 Z变换与离散时间傅里叶变换(DTFT)2.1 复习笔记2.2 课后习题详解2.3 名校考研真题详解第3章 离散傅里叶变换(DFT)3.1 复习笔记3.2 课后习题详解3.3 名校考研真题详解第4章 快速傅里叶变换(FFT)4.1 复习笔记4.2 课后习题详解4.3 名校考研真题详解第5章 数字滤波器的基本结构5.1 复习笔记5.2 课后习题详解5.3 名校考研真题详解第6章 几种特殊滤波器及简单一、二阶数字滤波器设计6.1 复习笔记6.2 课后习题详解6.3 名校考研真题详解第7章 无限长单位冲激响应(IIR)7.1 复习笔记7.2 课后习题详解7.3 名校考研真题详解第8章 有限长单位冲激响应(FIR)数字滤波器设计方法8.1复习笔记8.2 课后习题详解8.3 名校考研真题详解第9章 序列的抽取与插值——多抽样率数字信号处理基础9.1 复习笔记9.2 课后习题详解9.3 名校考研真题详解第10章 数字信号处理中的有限字长效应10.1 复习笔记10.2 课后习题详解10.3 名校考研真题详解第1章 离散时间信号与系统1.1 复习笔记一、离散时间信号——序列1.序列序列可以有三种表示法。
(1)函数表示法。
例如x(n)=a n u(n)。
(2)数列的表示法。
例如x(n)={...,-5,-3,-l,0,2,7,9,…)本书中,凡用数列表示序列时,都将n=0时x(o)的值用下划线(_)标注,这个例子中有z(-1)=-3,x(0)=-l,x(1)=0,…(3)用图形表示,如图l-1所示。
图1-1 离散时间信号的图形表示2.序列的运算(1)基于对序列幅度x(n)的运算序列的简单运算有①加法;②乘法;③累加;④序列绝对和;⑤序列的能量;⑥平均功率。
(2)基于对n的运算①移位,某序列为x(n)则x(n-m)就是x(n)的移位序列,当m=正数时,表示序列x(n)逐项依次右移(延时)m位;当m=负数时,表示序列 x(n)逐项依次左移(超前)m位;②翻褶,若序列为x(n),则x(-n)是以n=0为对称轴将x(n)序列加以翻褶;③时间尺度变换。
《数字信号处理》课后答案

数字信号处理课后答案 1.2 教材第一章习题解答1. 用单位脉冲序列()n δ及其加权和表示题1图所示的序列。
解:()(4)2(2)(1)2()(1)2(2)4(3) 0.5(4)2(6)x n n n n n n n n n n δδδδδδδδδ=+++-+++-+-+-+-+-2. 给定信号:25,41()6,040,n n x n n +-≤≤-⎧⎪=≤≤⎨⎪⎩其它(1)画出()x n 序列的波形,标上各序列的值; (2)试用延迟单位脉冲序列及其加权和表示()x n 序列; (3)令1()2(2)x n x n =-,试画出1()x n 波形; (4)令2()2(2)x n x n =+,试画出2()x n 波形; (5)令3()2(2)x n x n =-,试画出3()x n 波形。
解:(1)x(n)的波形如题2解图(一)所示。
(2)()3(4)(3)(2)3(1)6() 6(1)6(2)6(3)6(4)x n n n n n n n n n n δδδδδδδδδ=-+-+++++++-+-+-+-(3)1()x n 的波形是x(n)的波形右移2位,在乘以2,画出图形如题2解图(二)所示。
(4)2()x n 的波形是x(n)的波形左移2位,在乘以2,画出图形如题2解图(三)所示。
(5)画3()x n 时,先画x(-n)的波形,然后再右移2位,3()x n 波形如题2解图(四)所示。
3. 判断下面的序列是否是周期的,若是周期的,确定其周期。
(1)3()cos()78x n A n ππ=-,A 是常数;(2)1()8()j n x n e π-=。
解:(1)3214,73w w ππ==,这是有理数,因此是周期序列,周期是T=14; (2)12,168w wππ==,这是无理数,因此是非周期序列。
5. 设系统分别用下面的差分方程描述,()x n 与()y n 分别表示系统输入和输出,判断系统是否是线性非时变的。
智慧树知道网课《数字信号处理》课后章节测试满分答案

绪论单元测试1【单选题】(2分)确定性信号和随机信号的区别是什么?A.能否用计算机处理B.能否用有限个参量进行唯一描述2【单选题】(3分)如何由连续时间信号获得离散时间信号?A.在信号幅度上进行量化B.在时域上对连续时间信号进行采样第一章测试1【单选题】(2分)以下那个说法是正确的?A.在对连续时间信号进行采样得到离散时间信号的过程中,只要实现了等间隔采样,采样间隔T怎样选择都不会影响采样后离散时间信号的频谱特征。
B.在对连续时间信号进行采样得到离散时间信号的过程中,采样间隔T的选择非常关键,如果选择不当,采样后的离散时间信号将存在频域混叠失真现象。
2【单选题】(2分)A.B.C.D.3【判断题】(2分)A.错B.对4【单选题】(2分)下面哪段语句不会报错?A.x=ones(1,5);n h=0:2;h=(nh+1).*ones(1,3);n=0:6;y=conv(x,h);stem(n,y);B.x=[123];h=ones(1,5);n=0:7;y=conv(x,h);stem(n,y);C.x=ones(1,4);n h=0:2;h=(nh+1)*ones(1,3); n=0:5;y=conv(x,h);stem(n,y);5【单选题】(2分)A.B.C.D.6【单选题】(2分)请问以下哪个说法是正确的?A.连续时间正弦信号采样后不一定为周期序列。
B.连续时间正弦信号采样后一定为周期序列。
7【单选题】(2分)A.B.C.D.8【单选题】(2分)A.3B.C.8D.8/39【单选题】(2分)A.5B.40C.20D.1010【单选题】(2分)A.非线性移不变系统B.非线性移变系统C.线性移不变系统D.线性移变系统11【单选题】(2分)A.非线性移变系统B.线性移不变系统C.非线性移不变系统D.线性移变系统12【单选题】(2分)A.B.13【单选题】(2分)A.B.C.D.14【单选题】(2分)A.非因果、稳定系统B.因果、稳定系统C.因果、非稳定系统D.非因果、非稳定系统15【单选题】(2分)A.系统是因果、非稳定系统B.系统是非因果、非稳定系统C.系统是非因果、稳定系统D.系统是因果、稳定系统16【单选题】(2分)A.b=[11];a=[1-0.90.81];x=ones(1,100);y=filter(b,a,x);B.b=[11];a=[10.9-0.81];x=ones(1,100);y=filter(b,a,x);17【单选题】(2分)A.10msB.150msC.2msD.200ms18【单选题】(2分)A.采样间隔T的取值是不唯一的。
数字信号处理课后答案课件

傅里叶变换的性质
线性性质
若离散信号x(n)和y(n)的 傅里叶变换分别为 X(e^jωn)和Y(e^jωn), 则对于任意实数a和b,有 aX(e^jωn) + bY(e^jωn) 的傅里叶变换等于 aX(e^jωn)和bY(e^jωn) 的傅里叶变换之和。
从而实现信号的分离、抑制或提 取。
滤波器分类
根据不同的特性,滤波器可分为 低通、高通、带通和带阻滤波器,
每种滤波器都有各自的应用场景 和特点。
滤波器原理
滤波器的原理是基于频率响应, 即不同频率的信号经过滤波器后, 其幅度和相位会发生不同的变化。
IIR滤波器设计
IIR滤波器概述
IIR滤波器设计方法
IIR滤波器稳定性
在设计IIR滤波器时,需要考虑其稳定 性。如果系统函数的极点位于单位圆 外,则系统不稳定,可能会导致无穷 大的输出。因此,在设计过程中需要 进行稳定性分析。
FIR滤波器设计
FIR滤波器概述
FIR(Finite Impulse Response)滤 波器是一种具有有限冲击响应的数字 滤波器,其系统函数可以表示为有限 项之和。
插值法
对于非周期性的连续时间信号,可以通过插值法得到离散时间信号。常用的插值方法包括 线性插值、多项式插值、样条插值等。
傅里叶变换法
对于任何连续时间信号,可以通过傅里叶变换将其转换为频域表示形式,然后对频域表示 形式进行采样,得到离散时间信号。再通过逆傅里叶变换将其转换回时域表示形式。
05 第五章 信号的分 析与合成
抽样定理的充分性
对于任何连续时间信号,如果其最高频率分量小于等于fmax,则可 以通过其抽样信号无失真地重建出原信号。
数字信号处理习题集及答案

第一章 数字信号处理概述判断说明题:1.模拟信号也可以与数字信号一样在计算机上进行数字信号处理,自己要增加一道采样的工序就可以了。
( ) 答:错。
需要增加采样和量化两道工序。
2.一个模拟信号处理系统总可以转换成功能相同的数字系统,然后基于数字信号处理理论,对信号进行等效的数字处理。
( )答:错。
受采样频率、有限字长效应的约束,与模拟信号处理系统完全等效的数字系统未必一定能找到。
因此数字信号处理系统的分析方法是先对抽样信号及系统进行分析,再考虑幅度量化及实现过程中有限字长所造成的影响。
故离散时间信号和系统理论是数字信号处理的理论基础。
第二章 离散时间信号与系统分析基础一、离散时间信号与系统频域分析 计算题:1.设序列)(n x 的傅氏变换为)(ωj e X ,试求序列)2(n x 的傅里叶变换。
解: 由序列傅氏变换公式 DTFT ∑∞-∞=-==nnj j e n x e X n x ωω)()()]([可以得到DTFT 2)()2()]2([n j n n jn en x en x n x '-∞-∞='-∑∑'==ωω为偶数)()(21)(21)(21)(21)(21)]()1()([2122)2(2)2(22ωωπωωπωωωj j j j n j n n jn n j nn e X e X e X e X e n x e n x e n x n x -+=+=+=-+=++-∞-∞=∞-∞=--∞-∞=∑∑∑2.计算下列各信号的傅里叶变换。
(a )][2n u n- (b )]2[)41(+n u n(c )]24[n -δ 解:(a )∑∑-∞=--∞-∞==-=2][2)(n nj n nj n ne en u X ωωωωωj nn j e e 2111)21(0-==∑∞= (b )∑∑∞-=--∞-∞==+=2)41(]2[41)(n n j n n j n n e e n u X ωωω)( ωωωj j m m j m e e e -∞=---==∑41116)41(20)2(2 (c )ωωωδω2]24[][)(j n n j nj n e e n en x X -∞-∞=--∞-∞==-==∑∑ 7.计算下列各信号的傅立叶变换。
《数字信号处理(第四版)》部分课后习题解答

《数字信号处理(第四版)》部分课后习题解答一、简答题1. 什么是数字信号处理?数字信号处理(DSP)是指对数字信号进行处理和分析的一种技术。
它使用数学和算法处理模拟信号,从而实现信号的采样、量化、编码、存储和重构等过程。
DSP广泛应用于通信、音频处理、图像处理和控制系统中。
2. 数字信号处理的主要特点有哪些?•数字信号处理能够处理和分析具有广泛频谱范围的信号。
•数字信号处理能够实现高精度的信号处理和复杂的算法运算。
•数字信号处理能够实现信号的存储、传输和复原等功能。
•数字信号处理可以利用计算机等处理硬件进行实时处理和系统集成。
3. 数字信号处理的基本原理是什么?数字信号处理的基本原理是将连续时间的模拟信号转换成离散时间的数字信号,然后通过一系列的算法对数字信号进行处理和分析。
该过程主要涉及信号的采样、量化和编码等环节。
4. 什么是离散时间信号?离散时间信号是指信号的取样点在时间上呈现离散的情况。
在离散时间信号中,只能在离散时间点上获取信号的取样值,而无法观测到连续时间上的信号变化。
5. 描述离散时间信号的功率和能量的计算方法。
对于离散时间信号,其功率和能量的计算方法如下:•功率:对于离散时间信号x(n),其功率可以通过求平方和的平均值来计算,即功率P = lim(T->∞) [1/T *∑|x(n)|^2],其中T表示信号x(n)的观测时间。
•能量:对于离散时间信号x(n),其能量可以通过求平方和来计算,即能量E = ∑|x(n)|^2。
二、计算题1. 设有一个离散时间周期序列x(n) = [2, 3, -1, 4, 0, -2],求其周期N。
由于x(n)是一个周期序列,我们可以通过观察序列来确定其周期。
根据观察x(n)的取值,我们可以发现序列在n=1和n=5两个位置上取得了相同的数值。
因此,序列x(n)的周期为N = 5 - 1 = 4。
2. 设有一个信号x(t) = 2sin(3t + π/4),请将其离散化为离散时间信号x(n)。
数字信号处理课后习题答案全章

(1)y(n)=x(n)+2x(n-1)+3x(n-2) (2)y(n)=2x(n)+3 (3)y(n)=x(n-n0) n0 (4)y(n)=x(-n)
团结 信赖 创造 挑战
(5)y(n)=x2(n)
因此系统是非时变系统。
团结 信赖 创造 挑战
(5) y(n)=x2(n)
令输入为
输出为
x(n-n0)
y′(n)=x2(n-n0)
y(n-n0)=x2(n-n0)=y′(n)
故系统是非时变系统。 由于
T[ax1(n)+bx2(n)]=[ax1(n)+bx2(n)]2 ≠aT[x1(n)]+bT[x2(n) =ax21(n)+bx22(n)
x(n)=-δ(n+2)+δ(n-1)+2δ(n-3)
h(n)=2δ(n)+δ(n-1)+ δ(n-12)
由于
2
x(n)*δ(n)=x(n)
x(n)*Aδ(n-k)=Ax(n-k)
故
团结 信赖 创造 挑战
y(n)=x(n)*h(n)
=x(n)*[2δ(n)+δ(n-1)+ δ(n-21 ) 2
=2x(n)+x(n-1)+ x1 (n-2) 将x(n)的表示式代入上式, 得到2
解: (1) y(n)=x(n)*h(n)=
R4(m)R5(n-m)
先确定求和域。 由R4(m)和R5(n-mm)确定y(n)对于m的
间如下:
0≤m≤3
-4≤m≤n
计算机科学导论(第4版)习题答案-第9、10章

第9章网络计算习题(答案)一.选择题1.C 2.B 3.A 4.C 5.C6.A 7.ABCD 8.ABCD 9.ABCD 10.ABC 11.A 12.D 13.B 14.C 15.B16.B 17.A 18.B二.简答题1.什么叫信息、数据、信号?答:信息(Information)是客观事物的属性和相互联系特性的表现,它反映了客观事物的存在形式和运动状态。
计算机中的信息—般是字母、数字、符号的组合,而将这些信息进行传输的载体可以是文字、声音、图形、图像等。
数据(Data)是信息的数字化形式或数字化的信息形式。
信号(Signal)是携带信息的传输介质,在通信系统中常用电信号、光信号、载波信号、脉冲信号、调制信号等描述。
2.什么是串行通信和并行通信?答:在数据通信中,将待传送的每个字符的二进制代码按由低位到高位的顺序依次发送,每次由发送端传送到接收端的数据只有一位,这种方式称为串行通信。
至少有8位二进制数据同时通过多位数据线从一个设备传送到另一个设备,每次发送一个字符代码,这种工作方式称为并行通信。
3.什么是同步通信和异步通信?答:同步是每次发送多个字节或信息块,要求通信的收、发双方在时间基准上保持一致,系统需要一个同步时钟,用于传输大量的信息。
异步每次发送和接收一个字符的数据,同步在字符的基础上进行,起始时刻是任意的,字符与字符之间的间隔也是任意的,即各个字符之间是异步的。
4.简述计算机网络的定义。
答:计算机网络就是利用通信设备和线路将地理位置分散的、具有独立功能的多个计算机系统连接起来,按照以功能完善的网络软件(即网络通信协议、信息交换方式和网络操作系统(Network Operating System:NOS)等)进行数据通信,以实现网络中资源共享和信息传递的系统。
5.简述资源子网和通信子网的组成。
答:资源子网由主机系统、终端、终端控制器、连网外设、各种软件资源与信息资源织成。
资源子网负责全网的数据处理业务,向网络用户提供各种网络资源与网络服务。
数字信号处理习题集(附答案)

第一章数字信号处理概述简答题:1.在A/D变换之前和D/A变换之后都要让信号通过一个低通滤波器,它们分别起什么作用?答:在A/D变化之前为了限制信号的最高频率,使其满足当采样频率一定时,采样频率应大于等于信号最高频率2倍的条件。
此滤波器亦称为“抗混叠”滤波器。
在D/A变换之后为了滤除高频延拓谱,以便把抽样保持的阶梯形输出波平滑化,故又称之为“平滑”滤波器。
判断说明题:2.模拟信号也可以与数字信号一样在计算机上进行数字信号处理,自己要增加一道采样的工序就可以了。
()答:错。
需要增加采样和量化两道工序。
3.一个模拟信号处理系统总可以转换成功能相同的数字系统,然后基于数字信号处理理论,对信号进行等效的数字处理。
()答:受采样频率、有限字长效应的约束,与模拟信号处理系统完全等效的数字系统未必一定能找到。
因此数字信号处理系统的分析方法是先对抽样信号及系统进行分析,再考虑幅度量化及实现过程中有限字长所造成的影响。
故离散时间信号和系统理论是数字信号处理的理论基础。
第二章 离散时间信号与系统分析基础一、连续时间信号取样与取样定理计算题:1.过滤限带的模拟数据时,常采用数字滤波器,如图所示,图中T 表示采样周期(假设T 足够小,足以防止混叠效应),把从)()(t y t x 到的整个系统等效为一个模拟滤波器。
(a ) 如果kHz rad n h 101,8)(=π截止于,求整个系统的截止频率。
(b ) 对于kHz T 201=,重复(a )的计算。
解 (a )因为当0)(8=≥ωπωj e H rad 时,在数 — 模变换中)(1)(1)(Tj X T j X T e Y a a j ωω=Ω= 所以)(n h 得截止频率8πω=c 对应于模拟信号的角频率c Ω为8π=ΩT c因此 Hz Tf c c 6251612==Ω=π 由于最后一级的低通滤波器的截止频率为T π,因此对T 8π没有影响,故整个系统的截止频率由)(ωj e H 决定,是625Hz 。
数字信号处理第四版高西全课后答案

0≤m≤3
-4≤m≤n
非零区间如下:
第 1 章 时域离散信号和时域离散系统
根据非零区间, 将n分成四种情况求解: ① n<0时, y(n)=0
② 0≤n≤3时, y(n)= ③ 4≤n≤7时, y(n)= ④ n>7时, y(n)=0
1=n+1
n
1=8-m n0
3
mn4
第 1 章 时域离散信号和时域离散系统
最后结果为 0
n<0或n>7
y(n)= n+1 0≤n≤3 8-n 4≤n≤7
y(n)的波形如题8解图(一)所示。 (2) y(n) =2R4(n)*[δ(n)-δ(n-2)]=2R4(n)-2R4(n-2)
=2[δ(n)+δ(n-1)-δ(n+4)-δ(n+5) y(n)的波形如题8解图(二)所示
(5) 画x3(n)时, 先画x(-n)的波形(即将x(n)的波形以纵轴为中心翻转180°), 然后再右移2位, x3(n)波形如题2解图(四)所示。
第 1 章 时域离散信号和时域离散系统
题2解图(一)
第 1 章 时域离散信号和时域离散系统
题2解图(二)
第 1 章 时域离散信号和时域离散系统
题2解图(三)
5. 设系统分别用下面的差分方程描述, x(n)与y(n)分别表示系统输入和输 出, 判断系统是否是线性非时变的。
(1)y(n)=x(n)+2x(n-1)+3x(n-2) (2)y(n)=2x(n)+3 (3)y(n)=x(n-n0) n0 (4)y(n)=x(-n)
第 1 章 时域离散信号和时域离散系统
T[ax1(n)+bx2(n)]=ax1(n) sin(ωn)+bx2(n) sin(ωn) =aT[x1(n)]+bT[x2(n)]
数字信号处理第四版高西全课后答案

=aT[x1(n)]+mbT0[x2(n)]
故系统是线性系统。
n
m0
第 1 章 时域离散信号和时域离散系统
(8) y(n)=x(n) sin(ωn)
令输入为
输出为
x(n-n0)
y′(n)=x(n-n0) sin(ωn) y(n-n0)=x(n-n0) sin[ω(n-n0)]≠y′(n) 故系统不是非时变系统。 由于
x(m)h(n-m)
m
第 1 章 时域离散信号和时域离散系统
题7图
第 1 章 时域离散信号和时域离散系统
y(n)={-2,-1,-0.5, 2, 1, 4.5, 2, 1; n=-2, -1, 0, 1, 2, 3, 4, 5}
第 1 章 时域离散信号和时域离散系统
解法(二) 采用解析法。 按照题7图写出x(n)和h(n)的表达式分别为
+6δ(n-1)+6δ(n-2)+6δ(n-3)+6δ(n-4)
1
4
(2m 5) (n m) 6 (n m)
m4
m0
第 1 章 时域离散信号和时域离散系统
(3) x1(n)的波形是x(n)的波形右移2位, 再乘以2, 画出图形如题2解图 (二)所示。
(4) x2(n)的波形是x(n)的波形左移2位, 再乘以2, 画出图形如题2解图(三) 所示。
因此系统是非线性系统。
第 1 章 时域离散信号和时域离散系统
(6) y(n)=x(n2)
令输入为
输出为
x(n-n0)
y′(n)=x((n-n0)2) y(n-n0)=x((n-n0)2)=y′(n) 故系统是非时变系统。 由于
T[ax1(n)+bx2(n)]=ax1(n2)+bx2(n2) =aT[x1(n)]+bT[x2(n)]
数字信号处理—基于计算机的方法答案
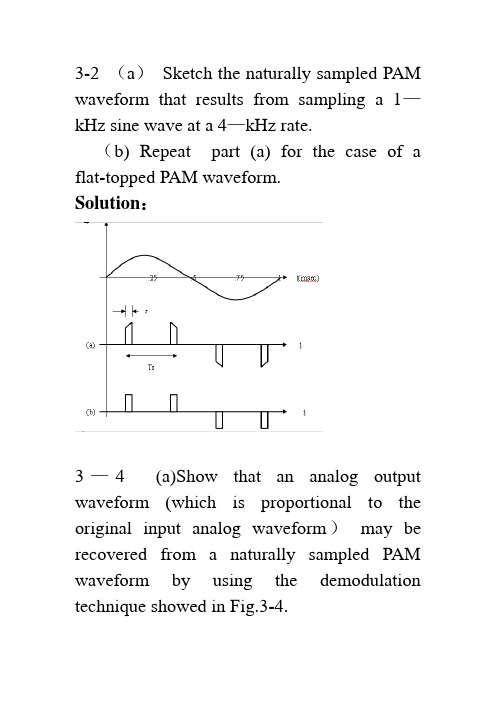
3-2 (a)Sketch the naturally sampled PAM waveform that results from sampling a 1—kHz sine wave at a 4—kHz rate.(b) Repeat part (a) for the case of a flat-topped PAM waveform.Solution:3—4 (a)Show that an analog output waveform (which is proportional to the original input analog waveform)may be recovered from a naturally sampled PAM waveform by using the demodulation technique showed in Fig.3-4.(b) Find the constant of proportionality C, that is obtained with this demodulation technique , where w (t) is the oriqinal waveform and Cw(t) is the recovered waveform. Note that C is a function of n ,where the oscillator frequency is nfs.Solution :()()()()()()1111sin sin 2cos sin 2cos cos sin [cos 2cos cos sin 2cos s s jk ts k k k jk t s k k s sk s s s s s k n kt kT s t c ek d k d d e d d k tk d k dk d w t w t d d k t k d v t w t n tk dw t d n t n dd d k t n tn k d d ωωτππωπππωπωππωππωω∞∞-=-∞=-∞∞∞-=-∞=∞=∞=≠-⎡⎤=∏=⎢⎥⎣⎦==+⎡⎤=+⎢⎥⎣⎦==++∑∑∑∑∑∑2]s n t ω211cos cos 222s s n t n t ωω=+ after LPF: ()()()sin sin o w t w t n d d n d n d d n dcw t c ππππ==∴= 3-7 In a binary PCM system, if the quantizing noise is not to exceed P ± percent of the peak-to-peak analog level, show that the number of bits in each PCM word needs to be⎪⎭⎫ ⎝⎛=⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛≥P p n 50log 32.350log 10] [log 10102(Hint : Look at Fig. 3-8c.)Solution:Binary PCM M=n2levelsfor PP q V P n 100||≤We need)50(log )10(log 50log 5025011002 size step 1022p P n PM P M V P M V n PP PP ≥⎪⎭⎫ ⎝⎛≥≥=≤≤==δ)(log )(log )(log )(log )(log x b a x x b a b b a ==3—8 The information in an analog voltage waveform is to be transmitted over a PCM system with a ±0。
数字信号处理 第九章答案

9.2、对于下面各组峰波纹值p δ和s δ,求出相应的峰值通带波纹p α和最小阻带衰减s α。
(a ),08.0,04.0==s p δδ(b ),04.0,015.0==s p δδ解:)lg(20)1lg(20s s p p δαδα-=--=(a )dB dB dBdB s p 94.21)08.0lg(2035.0)04.01lg(20=-==--=αα(b ) dB dB dBdB s p 96.27)04.0lg(2031.1)015.01lg(20=-==--=αα9.11、下面的因果IIR 数字传输函数式用式(9.14)的双线性变换法在T=0.4时设计得到,求出它们各自的原因过模拟传输函数。
(a ),6410)2(4)(22++-+=z z z z z G a (b ))8412)(13(8122218)(223+-++++=z z z z z z z G b 解:S S S T S T z 2.012.012121-+=-+= 222.012.0112.04508.02.1)()(s s s s z G s G s s z a a ++-==-+= 324.624.2192.0304792.0)()(2322.012.01+-+++==-+=s s s s s z G s G ssz b b 9.13、一个IIR 低通数字滤波器具有归一化的通带边界频率πω45.0=。
在T=0.4ms 时,若利用冲激不变发来设计数字滤波器,则原型模拟低通滤波器的通带边界频率是多少赫兹?在T=0.4ms 时,若利用双线性变换法来设计数字滤波器,则模拟低通原型滤波器的通带边界频率是多少赫兹?解: ○2利用双线性变换法来设计数字滤波器,则模拟低通原型滤波器的通带边界频率Hz F F TF p p p P 5.562104.0245.023=⨯⨯==-πππω。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
−α p / 20
9.2 We obtain the solutions by using Eqs. (9.3) and (9.4). € (a) α p = −20log10 1 − δ p = −20log10 (1 − 0.04) = 0.3546dB, €
(
)
α s = −20log10 (δ s ) = −20log10 (0.08) = 21.9382 dB.
are mapped onto a single point in the z -plane as z €in the figure below mapping is illustrated €
jΩ
3π T π T
⎛ 2 πk ⎞ j ⎜Ω o ± ⎟T T ⎠ = eσ oT e ⎝
= eσ oT e jΩ oT . The
HLP (e jω )
€
€ €
9.4 €
€
€
HHP (e jω )
€
1 + δp 1 – δp
1 – δp
1 + δp
δs –π – ωs – ωp 0 ωp ωs π
δs
ω
–π –(π – ω p ) –(π – ω s )
0
ω π π − ωs π − ω p
Therefore, the passband edge and the stopband edge of the highpass filter are given by ω p,HP = π − ω p , and ω s,HP = π − ω s , respectively. 9.5 Note that G( z) is a complex bandpass filter with a passband in the range 0 ≤ ω ≤ π . Its passband edges are at ω p,BP = ω o ± ω p ,and stopband edges at ω s,BP = ω o ± ω s . A real € coefficient bandpass transfer function can be generated according to GBP ( z) = H LP (e jω o z) + H LP (e – jω o z) which will have a passband € in the range 0 ≤ ω ≤ π €
Not for sale
1
Chapter 9
9.1 We obtain the solutions by using Eq. (9.3) and Eq. (9.4). (a) δ p = 1 − 10 (b) δ p = 1 − 10
−α p / 20
= 1 − 10−0.24 / 20 = 0.0273, δ s = 10−α s / 20 = 10−49 / 20 = 0.0035. = 1 − 10−0.14 / 20 = 0.016,δ s = 10−α s / 20 = 10−68 / 20 = 0.000398.
∑δ (t − nT ). Thus, h p (t ) = ∑ ha (nT )δ (t − nT )..
n =−∞
∞
Now, H a ( s) =
€
∫ ha (t)e−st dt and
€ € ∞ ∞ ∞ − st − st H p ( s) = ∫ h p ( t )e dt = ∑ ∫ ha ( nT )δ ( t − nT )e dt = ∑ ha ( nT )e− snT . € −∞ n =−∞ −∞ n =−∞ € ∞ ∞ Comparing the above expression with G( z) = ∑ g[ n ]z− n = ∑ h ( nT ) z− n , we
HLP (e
jω
)
€
1 + δp 1 – δp
G(e ) 1 + δp
jω
1 – δp
δs –π – ωs – ωp 0 ωp ωs π
δs
ω
–π
ω 0 ωo π ωo − ωs ω − ω ω + ω ωo + ωs o p o p
∞
∞ n =−∞
9.6 (a) h p ( t ) = ha ( t )⋅ p( t ) where p( t ) = We also have, g[ n ] = ha ( nT ).
∞
∑
k =−∞ ∞
⎛ 2πkt ⎞ H a ⎜ s + j ⎟. As a result, we have ⎝ T ⎠
€
G( z) =
€
1 T
∑
k =−∞
⎛ 2πkt ⎞ H a ⎜ s + j ⎟ ⎝ T ⎠
ln z.
1 s= T
(7-1)
€
sT (b) The transformation from the s -plane to z -plane is given by z = e . If we express jω σ oT jΩ oT
k =−∞
∞ ∞ ⎛ ⎞ 1 1 − j (2 πkt /T ) ⎟ h p ( t ) = ⎜ e h ( t ) = ∑ ha (t)e− j (2 πkt /T ) . ⎜ T ∑ ⎟ a T ⎝ k =−∞ ⎠ k =−∞
. 1 ln z T
Hence,
€
1 H p ( s) = T
€ 9.3
€
G(e jω ) = H 2 (e jω ) = H (e jω ) .
2
Let δ p and δ s denote the passband and stopband ripples of H (e jω ) , respectively. Also, let
jω δ p,2 = 2 δ p, and δ s,2 denote the passband and stopband ripples of G(e ) , respectively. € Then δ p,2 = 1 − (1 − δ p ) 2 , and δ s,2 = ( δ s ) 2 . For a cascade of sections, € € M δ p,M = 1 − (1 − δ p ) M , and δ s,M = ( δ s ) . € €
∞ n =−∞ n =−∞
−∞
€
conclude that G( z) = H p ( s)
s=
We can also show that a Fourier series expansion of p(t) is given by € ∞ 1 − j (2 πkt /T ) p( t ) = . Therefore, ∑e € T
(d) For z = e jω = e jΩT , or equivalently, ω = ΩT . € € € 9.7 Assume ha ( t ) is causal. Now, ha ( t ) = ∫ H a ( s)e st ds. Hence, € € snT g[ n ] = ha ( nT ) = ∫ H a ( s) e ds. Therefore,
SOLUTIONS MANUAL
to accompany
Digital Signal Processing: A Computer-Based Approach
Fourth Edition
Sanjit K. Mitra
Prepared by Chowdary Adsumilli, John Berger, Marco Carli, Hsin-Han Ho, Rajeev Gandhi, Martin Gawecki, Chin Kaye Koh, Luca Lucchese, Mylene Queiroz de Farias, and Travis Smith
€
€
€
€
Not for sale
€
2
and another passband in the range – π ≤ ω ≤ 0. However because of the overlap of the two spectra a simple formula for the bandedges cannot be derived.
€
€
€
€
Not for sale
Im z
€
€
σ –π T
π – 3T
−1
1
Re z
s -plane
z -plane
Note that the strip of width 2π / T in the s-plane for values of s in the range π π − ≤ Ω ≤ is mapped into the entire z -plane, and so are the adjacent strips of width T T
s = σo + jΩo , then we can write z = re
€
=e
e
. Therefore,
€
Not for sale
€
3
€
€
€
⎧ < 1, for σo < 1, ⎪ z = ⎨ = 1, for σo = 1, Or in other words, a point in the left-half -plane is mapped onto ⎪ ⎩ > 1, for σo > 1. a point inside the unit circle in the z -plane, a point in the right-half -plane is mapped onto a point outside the unit circle in the z -plane, and a point on the jω -axis in the splane is mapped onto a point on the unit circle in the z -plane. As a result, the mapping has the desirable properties enumerated in Section 9.1.3. € € 2πk € (c) However, all points in the s -plane defined by s = σ + j Ω ± j , k = 0, 1, 2, …, , a o o € T
