2019版优化探究理数(苏教版)练习：第四章第四节两角和与差的正弦、余弦、正切公式含解析

合集下载

2019版一轮优化探究理数(苏教版)：第四章第二节三角函数的图象与性质 Word版含解析

一、填空题1．函数y ＝|sin x |的最小正周期为________．解析：由图象知T ＝π.答案：π2．函数y ＝lg(sin x －cos x )的定义域为________．解析：由已知得sin x －cos x >0，即sin x >cos x .在[0,2π]内满足sin x >cos x 的x 的集合为(π4，54π)．又正弦、余弦函数的周期为2π，∴所求定义域为{x |π4＋2k π<x <54π＋2k π，k ∈Z}．答案：{x |π4＋2k π<x <54π＋2k π，k ∈Z}3．函数y ＝sin x (－π4≤x ≤3π4)的值域是________．答案：[－22，1]4．函数f (x )＝sin 2x ＋3sin x cos x 在区间[π4，π2]上的最大值是________．解析：f (x )＝1－cos 2x 2＋32sin 2x ＝32sin 2x －12cos 2x ＋12＝sin(2x －π6)＋12， ∵π4≤x ≤π2，∴π3≤2x －π6≤56π. 从而可得f (x )max ＝1＋12＝32. 答案：325．M ，N 是曲线y ＝πsin x 与曲线y ＝πcos x 的两个不同的交点，则|MN |的最小值为________．解析：当|MN |最小时，点M ，N 必为两曲线的相邻的两个交点，所以可设为M (π4，2π2)，N (5π4，－2π2)，根据两点间距离公式得|MN |＝π2＋(2π)2＝3π.答案：3π6．定义在R 上的函数f (x )既是偶函数又是周期函数，若f (x )的最小正周期是π，且当x ∈[0，π2]时，f (x )＝sin x ，则f (5π3)的值为________．解析：f (5π3)＝f (－π3)＝f (π3)＝sin π3＝32.答案：327．已知函数f (x )＝3sin ωx ＋cos ωx (ω>0)，y ＝f (x )的图象与直线y ＝2的两个相邻交点的距离π则f (x )的单调递增区间是________．解析：f (x )＝3sin ωx ＋cos ωx ＝2sin(ωx ＋π6)(ω>0)．∵f (x )图象与直线y ＝2的两个相邻交点的距离等于π，恰好是f (x )的一个周期， ∴2πω＝π，ω＝2.f (x )＝2sin(2x ＋π6)．故其单调增区间应满足2k π－π2≤2x ＋π6≤2k π＋π2(k ∈Z)．k π－π3≤x ≤k π＋π6(k ∈Z)．答案：[k π－π3，k π＋π6]，k ∈Z8．已知函数f (x )＝3sin(ωx －π6)(ω>0)和g (x )＝3cos(2x ＋φ)的图象的对称中心完全相同，若x ∈[0，π2]，则f (x )的取值范围是________．解析：由3sin(ωx －π6)＝0，得ωx ＝k π＋π6(k ∈Z)， ∴x ＝k πω＋π6ω，即对称中心为(k πω＋π6ω，0)(k ∈Z)．由3cos(2x ＋φ)＝0得2x ＝k π＋π2－φ(k ∈Z)，∴x ＝k π2＋π4－φ2，即对称中心为(k π2＋π4－φ2，0)(k ∈Z)．∴k πω＝k π2得ω＝2，故f (x )＝3sin(2x －π6)，∵x ∈[0，π2]，∴－12≤sin(2x －π6)≤1，故－32≤f (x )≤3.答案：[－32，3] 9．某学生对函数f (x )＝2x ·cos x 的性质进行研究，得出如下的结论： ①函数f (x )在[－π，0]上单调递增，在[0，π]上单调递减；②点(π2，0)是函数y ＝f (x )图象的一个对称中心；③函数y ＝f (x )图象关于直线x ＝π对称；④存在常数M >0，使|f (x )|≤M |x |对一切实数x 均成立．其中正确的结论是________．(填写所有你认为正确的结论序号)解析：对于①，f (－2π3)＝2π3>－π3＝f (－π3)，不正确；对于②，f (0)＝0，f (π)＝－2π，不正确；对于③，f (0)＝0，f (2π)＝4π，不正确．答案：④二、解答题10．已知函数f (x )＝sin x ＋cos x ，x ∈R.(1)求f (π12)的值；(2)试写出一个函数g (x )，使得g (x )f (x )＝cos 2x ，并求g (x )的单调区间．解析：(1)因为f (x )＝2sin(x ＋π4)，。

2019版一轮优化探究理数(苏教版)练习：第四章第四节两角和与差的正弦、余弦、正切公式 Word版含解析

一、填空题1、若sin α＝35，α∈(－π2，π2)，则cos(α＋5π4)＝________.解析：∵α∈(－π2，π2)，sin α＝35，∴cos α＝45，∴cos(α＋5π4)＝－22(cos α－sin α)＝－210.答案：－2 102、已知1－cos 2αsin αcos α＝1，tan(β－α)＝－13，则tan(β－2α)＝________.解析：依题意由1－cos 2αsin αcos α＝1得2sin2αsin αcos α＝1，则tan α＝1 2，从而tan(β－2α)＝tan[(β－α)－α]＝tan(β－α)－tan α1＋tan(β－α)·tan α＝－－13－121＋(－13)×12＝－1.答案：－13、已知tan(α－π6)＝37，tan(π6＋β)＝25，则tan(α＋β)的值为________、解析：tan(α＋β)＝tan [(α－π6)＋(π6＋β)]＝tan(α－π6)＋tan(π6＋β)1－tan(α－π6)·tan(π6＋β)＝37＋251－37×25＝1.答案：14、在等式cos(*)(1＋3tan 10°)＝1的括号中，填写一个锐角，使得等式成立，这个锐角的度数是________、解析：1＋3tan 10°＝1＋3sin 10°cos 10°＝cos 10°＋3sin 10°cos 10°＝2sin (30°＋10°)cos 10°＝2sin 40°cos 10°，所以填40°. 答案：40°5、设a ＝sin 14°＋cos 14°，b ＝sin 16°＋cos 16°，c ＝62，则a 、b 、c 的大小关系是________、解析：∵a 2＝1＋2sin 14°cos 14°＝1＋sin 28°∈(1，32)，b 2＝1＋2sin 16°cos 16°＝1＋sin 32°∈(32，2)，c 2＝32，且a >0，b >0，c >0，∴a <c <b .答案：a <c <b6、已知A 、B 均为钝角，且sin A ＝55，sin B ＝1010，则A ＋B 等于________、解析：由已知可得cos A ＝－255，cos B ＝－31010，∴cos(A ＋B )＝cos A cos B －sin A sin B ＝22，又∵π2<A <π，π2<B <π，∴π<A ＋B <2π，∴A ＋B ＝7π4.答案：7π47、若tan(α＋β)＝25， tan(β－π4)＝14，则tan (α＋π4)＝______.解析：tan(α＋π4)＝tan [(α＋β)－(β－π4)]＝tan (α＋β)－tan (β－π4)1＋tan (α＋β)tan (β－π4)＝25－141＋25×14＝322.答案：3228、已知α，β∈(3π4，π)，sin(α＋β)＝－35，sin(β－π4)＝1213，则cos(α＋π4)＝________.解析：由于α，β∈(3π4，π)，所以3π2<α＋β<2π，π2<β－π4<3π4，故cos(α＋β)＝45，cos(β－π4)＝－513，cos(α＋π4)＝cos[(α＋β)－(β－π4)]＝45×(－513)＋(－35)×1213 ＝－5665.答案：－56659、非零向量a ＝(sin θ，2)，b ＝(cos θ，1)，若a 与b 共线，则tan(θ－π4)＝________.解析：因为非零向量a ，b 共线，所以a ＝λb ，即(sin θ，2)＝λ(cos θ，1)，所以λ＝2，sin θ＝2cos θ，得tan θ＝2，所以tan(θ－π4)＝tan θ－11＋tan θ＝13. 答案：13二、解答题10、已知α为锐角，且tan(π4＋α)＝2.(1)求tan α的值；(2)求sin 2αcos α－sin αcos 2α的值、解析：(1)tan(π4＋α)＝1＋tan α1－tan α，所以1＋tan α1－tan α＝2， 1＋tan α＝2－2tan α，所以tan α＝13.(2)sin 2αcos α－sin αcos 2α＝2sin αcos 2α－sin αcos 2α＝sin α(2cos 2α－1)cos 2α＝sin αcos 2αcos 2α＝sin α. 因为tan α＝13，所以cos α＝3sin α，又sin 2α＋cos 2α＝1，所以sin 2 α＝110，又α为锐角，所以sin α＝1010，所以sin 2αcos α－sin αcos 2α＝1010.11、如图所示，在平面直角坐标系xOy 中，以Ox 轴为始边作两个锐角α，β，它们的终边分别与单位圆交于A 、B 两点，已知A 、B 的横坐标分别为210、255.(1)求tan(α＋β)的值；(2)求α＋2β的值、解析：由已知条件得cos α＝210，cos β＝255. ∵α、β为锐角，∴sin α＝1－cos 2α＝7210，sin β＝1－cos 2β＝55，因此tan α＝7，tan β＝12.(1)tan(α＋β)＝tan α＋tan β1－tan α·tan β＝7＋121－7×12＝－3.(2)∵tan 2β＝2tan β1－tan 2β＝2×121－(12)2＝43， ∴tan(α＋2β)＝7＋431－7×43＝－1.∵α，β为锐角，∴0<α＋2β<3π2，∴α＋2β＝3π4.12、已知向量OA →＝(cos α，sin α)(α∈[－π，0])、向量m ＝(2,1)，n ＝(0，－5)，且m ⊥(OA →－n )、(1)求tan α的值；(2)若cos(β－π)＝210，且0<β<π，求cos(2α－β)、解析：(1)∵OA →＝(cos α，sin α)，∴OA →－n ＝(cos α，sin α＋5)，∵m ⊥(OA →－n )，∴m ·(OA →－n )＝0，即2cos α＋(sin α＋5)＝0，① 又sin 2α＋cos 2α＝1，②由①②联立方程组解得，cos α＝－255，sin α＝－55.∴tan α＝sin αcos α＝12.(2)∵cos(β－π)＝210，即cos β＝－210，0<β<π，∴sin β＝7210，π2<β<π，又∵sin 2α＝2sin αcos α＝2×(－55)×(－255)＝45，cos 2α＝2cos 2α－1＝2×45－1＝35， ∴cos(2α－β)＝cos 2αcos β＋sin 2αsin β ＝35×(－210)＋45×7210＝22.。

苏教版数学高一苏教版必修4两角和与差的正弦

互动课堂疏导引导 1.两角和与差的正弦公式 sin （α-β）=cos(2π-α+β)=cos ［(2π-α)+β］ =cos(2π-α)cosβ-sin(2π-α)sinβ =sinαcosβ-cosαsinβ，即sin （α-β）=sinαcosβ-cosαsinβ.在上式中，以-β代β可得sin （α+β）=sinαcosβ+cosαsinβ.2.正确理解和差角的正弦公式（1）公式对于任意的角α、β都成立.(2)搞清sin （α±β）的意义，例如sin （α+β）是两角α与β的和的正弦，它表示角α+β终边上任意一点的纵坐标与原点到这点的距离之比，在一般情况下，sin （α+β）≠sinα+sinβ, 如α=3π，β=6π时，sin （3π+6π）=sin 2π=1， sin 3π+sin 6π=23+21=213+≠1, ∴sin(3π+6π)≠sin 3π+sin 6π. 只有在某些特殊情况下，sin （α+β）=sinα+sinβ.例如，当α=0，β=6π时，sin （0+6π）=sin 6π=21， sin0+sin 6π=0+21=21，sin （0+6π）=sin0+sin 6π. 在学习时一定要注意:不能把sin （α+β）按分配律展开.(3)牢记公式并能熟练左、右两边互化.例如化简sin20°cos50°-sin70°cos40°,能观察出此式等于sin （20°-50°）=-sin30°=-21. （4）灵活运用和（差）角公式，例如化简sin （α+β）cosβ-cos(α+β)sinβ,不要将sin （α+β）,cos(α+β)展开，而应就整个式子，直接运用公式sin ［（α+β）-β］=sinα,这也是公式的逆用.3.有关点（向量）的一组旋转公式已知点P （x,y ）,与原点距离保持不变绕原点旋转θ角到点P′(x′,y′),则⎩⎨⎧+=-=,cos sin ',sin cos 'θθθθy x y y x x 公式推导如下：如下图所示：设∠xOP=α,则cosα=r x ,sinα=ry . ∴x′=rcos(α+θ)=r(cosαcosθ-sinαsinθ)=xcosθ-ysinθ，y′=rsin(α+θ)=r(sinαcosθ+cosαsinθ)=xsinθ+ycosθ.即⎩⎨⎧+=-=.cos sin ',sin cos 'θθθθy x y y x x 4.形如asinx+bcosx(a,b 不同时为零)的三角函数式可化为一个角的一个三角函数式. 记住以下重要结论： asinx+bcosx=22b a +sin(x+θ)其中sinθ=22b a b+,cosθ=22b a a +,推导如下：考察以（a,b ）为坐标的点P （a,b ）,设以OP 为终边的一个角为θ，则cosθ=22ba a+,sinθ=22b a b +. 于是asinx+bcosx=22b a +(22b a a +sinx+22b a b +cosx)=a 2+b 2(cosθsinx+sinθcosx)=22b a +sin(x+-θ). 其中sinθ=22b a b +,cosθ=22b a a+.活学巧用【例1】化简下列各式（1）cos （80°+3α）cos(35°+3α)+sin(80°+3α)cos(55°-3α)； (2)sin(x+3π)+2sin(x-3π)-3cos(32π-x)； (3))cos(cos cos 2sin cos 2)sin βαβαβαβα+--+(. 解析：（1）原式=cos （80°+3α）cos(35°+3α)+sin(80°+3α)sin(35°+3α)=cos ［(80°+3α)-(35°+3α)］=cos45°=22. (2)原式=sin （x+3π）+2sin(x-3π)-3cos ［π-(x+3π)］ =［sin(x+3π)+3cos(x+3π)］+2sin(x-3π)=2［sin(x+3π)·21+cos(x+3π)·23］+2sin(x-3π) =2［sin(x+3π)cos 3π+cos(x+3π)sin 3π］+2sin(x-3π) =2sin ［(x+3π)+3π］+2sin(x-3π) =2sin(x+32π)+2sin(x -3π) =2sin ［π-(3π-x)］+2sin(x-3π) =2sin(3π-x)+2sin(x-3π)=0. (3)原式=βαβαβαβαβαβαβαβαβαβαsin sin cos cos sin cos cos sin sin sin cos cos cos cos 2sin cos 2sin cos cos sin +-=+--+ =)cos()sin(βαβα--=tan(α-β). 【例2】已知cos （α+β）=31-,cos2α=-135,α、β均为钝角，求sin （α-β）. ∵α、β∈(90°,180°),∴α+β,2α∈(180°,360°).∵cos(α+β)=-31＜0,cos2α=-135＜0. ∴α+β,2α∈(180°,270°). ∴sin(α+β)=322)31(1)(cos 122-=---=+--βα, sin2α=1312)135(12cos 122-=---=--α. ∴sin(α-β)=sin ［2α-(α+β)］=sin2αcos(α+β)-cos2α·sin(α+β) =(-1312)×(-31)-(-135)(322-)=3921012-. 【例3】已知向量=(3,4),绕原点旋转30°到OP 的位置，求点P′(x′,y′)的坐标. 解析：x′=xcosθ-ysinθ=3cos30°-4sin30°=3×23-4×243321-=, y′=xsinθ+ycosθ=3sin30°+4cos30°=3×.234323421+=⨯+∴P′的坐标(2433-,2343+). 【例4】将下列各式化成Asin(x+φ)的形式.(1)sinx+cosx; (2)2(sinx-cosx); (3)42sin(4π-x)+46cos(4π-x). 解析：(1)sinx+cosx=2(sinx·22+cosx·22) =2(sinxcos 4π+cosxsin 4π)=2sin(x+4π). (2)2(sinx-cosx)=2·2(sinx·22-cosx·22) =2(sinxcos 4π-cosxsin 4π)=2sin(x-4π). (3)42sin(4π-x)+46cos(4π-x) =42［sin(4π-x)+3cos(4π-x)］ =42×2［sin(4π-x)·21+cos(π4-x)·23］ =22［sin(4π-x)cos 3π+cos(4π-x)sin 3π］ =22sin(4π-x+32)=22sin(127π-x).。

2019版一轮优化探究理数(苏教版)练习第四章第六节正、余弦定理和应用举例 Word版含解析

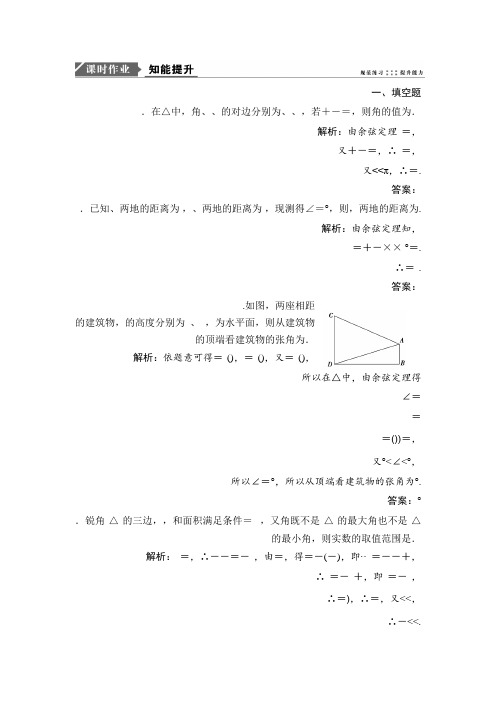
一、填空题．在△中，角、、的对边分别为、、，若＋－＝，则角的值为．解析：由余弦定理＝，又＋－＝，∴＝，又<<π，∴＝.答案：．已知、两地的距离为，、两地的距离为，现测得∠＝°，则，两地的距离为.解析：由余弦定理知，＝＋－×× °＝.∴＝ .答案：.如图，两座相距的建筑物，的高度分别为、，为水平面，则从建筑物的顶端看建筑物的张角为．解析：依题意可得＝()，＝()，又＝()，所以在△中，由余弦定理得∠＝＝＝())＝，又°<∠<°，所以∠＝°，所以从顶端看建筑物的张角为°.答案：°．锐角△的三边，，和面积满足条件＝，又角既不是△的最大角也不是△的最小角，则实数的取值范围是．解析：＝，∴－－＝－，由＝，得＝－(－)，即··＝－－＋，∴＝－＋，即＝－，∴＝)，∴＝，又<<，∴－<<.答案：(－)．在△中，＝(，，分别为角，，的对边)，则△的形状为．解析：∵＝，∴＋)＝，∴＝，∴＝，∴＋－＝，即＋＝，∴△为直角三角形．答案：直角三角形．在△中，角，，的对边分别为，，，若＝＋，则角的取值范围是．解析：∵＝＝＝＝－≥－＝，即∈[，)，∴∈(，]．答案：(，]．若△的周长等于，面积是，＝°，则边的长是．解析：依题意及面积公式＝，得＝°，得＝.又周长为，故＋＋＝，＋＝－，由余弦定理得：＝＋－＝＋－°＝＋－＝(＋)－，故＝(－)－，解得＝.答案：．在△中，＝°，＝，面积为，则＋＋)＝.解析：＝·＝×·· °＝，∴＝，∴＝＋－·＝＋－××× °＝＋－××＝，∴＝.∴＋＋)＝)＝°)＝.答案：。

近年高考数学一轮复习第四章三角函数、解三角形课时训练(二十)两角和与差的正弦、余弦和正切公式文(2

（江苏专版）2019版高考数学一轮复习第四章三角函数、解三角形课时跟踪检测（二十）两角和与差的正弦、余弦和正切公式文编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（（江苏专版）2019版高考数学一轮复习第四章三角函数、解三角形课时跟踪检测（二十）两角和与差的正弦、余弦和正切公式文）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为（江苏专版）2019版高考数学一轮复习第四章三角函数、解三角形课时跟踪检测（二十）两角和与差的正弦、余弦和正切公式文的全部内容。

课时跟踪检测(二十）两角和与差的正弦、余弦和正切公式一抓基础,多练小题做到眼疾手快1．（2018·苏北四市调研)sin 45°cos 15°＋cos 225°sin 165°＝________.解析:sin 45°cos 15°＋cos 225°sin 165°＝sin 45°cos 15°＋(－cos 45°)sin 15°＝sin（45°－15°）＝sin 30°＝错误!。

答案:错误!2．若2sin错误!＝3sin(π－θ），则tan θ＝________.解析:由已知得sin θ＋错误!cos θ＝3sin θ，即2sin θ＝错误!cos θ，所以tan θ＝错误!。

答案:错误!3．(2018·苏锡常镇调研)若tan α＝错误!，tan(α－β）＝－错误!，则tan（β－2α）＝________。

解析:tan(β－2α）＝－tan(2α－β）＝－tan(α＋α－β）＝－错误!＝－错误!＝－错误!。

2019版一轮优化探究理数(苏教版)练习：选修4-4 第二节参数方程

1．已知曲线C 的参数方程为⎩⎪⎨⎪⎧ x ＝t －1t ，y ＝3(t ＋1t )(t 为参数，t >0)．求曲线C 的普通方程．解析：由x ＝t －1t平方得x 2＝t ＋1t －2，又y ＝3(t ＋1t )，则t ＋1t ＝y 3，代入x 2＝t ＋1t －2，得x 2＝y 3－2.∴3x 2－y ＋6＝0(y ≥6)．故曲线C 的普通方程为3x 2－y ＋6＝0(y ≥6)．2．已知直线l ：3x ＋4y －12＝0与圆C ：⎩⎨⎧ x ＝－1＋2cos θ，y ＝2＋2sin θ(θ为参数)，试判断它们的公共点个数．解析：圆的方程可化为(x ＋1) 2＋(y －2)2＝4，其圆心为C (－1,2)，半径为2.由于圆心到直线l 的距离d ＝|3×(－1)＋4×2－12|32＋42＝75<2，所以直线l 与圆C 相交．故直线l 与圆C 的公共点的个数为2.3．已知点P (x ，y )是椭圆x 24＋y 2＝1上的动点．(1)求z ＝x 2＋y 2的最大值和最小值；(2)求t ＝2x ＋y 的最大值和最小值．解析：椭圆的参数方程为⎩⎨⎧x ＝2cos θ，y ＝sin θ，(θ为参数)，则 (1)∵z ＝x 2＋y 2＝4cos 2θ＋sin 2θ＝1＋3cos 2θ，∴当cos θ＝±1，即x ＝±2时，z 的最大值为4；当cos θ＝0，即x ＝0时，z 的最小值为1.(2)∵t ＝2x ＋y ＝4cos θ＋sin θ＝17sin(θ＋φ)，其中tan φ＝4，当sin(θ＋φ)＝1时，t 的最大值为17；当sin(θ＋φ)＝－1时，t 的最小值为－17.4．已知直线l 的参数方程：⎩⎨⎧x ＝t ，y ＝1＋2t (t 为参数)和圆C 的极坐标方程：ρ＝22sin(θ＋π4)(θ为参数)．(1)将直线l 的参数方程和圆C 的极坐标方程化为直角坐标方程；(2)判断直线l 和圆C 的位置关系．解析：(1)消去参数t ，得直线l 的直角坐标方程为y ＝2x ＋1；ρ＝22sin(θ＋π4)，即ρ＝2(sin θ＋cos θ)，两边同乘以ρ得ρ2＝2(ρsin θ＋ρcos θ)，消去参数θ，得圆C 的直角坐标方程为：(x －1)2＋(y －1)2＝2.(2)圆心C 到直线l 的距离d ＝|2－1＋1|22＋(－1)2＝255<2，所以直线l 和圆C 相交．。

2019版一轮优化探究理数(苏教版)练习：第四章第四节两角和与差的正弦、余弦、

一、填空题1．若sin α＝35，α∈(－π2，π2)，则cos(α＋5π4)＝________. 解析：∵α∈(－π2，π2)，sin α＝35，∴cos α＝45， ∴cos(α＋5π4)＝－22(cos α－sin α)＝－210. 答案：－2102．已知1－cos 2αsin αcos α＝1，tan(β－α)＝－13，则tan(β－2α)＝________. 解析：依题意由1－cos 2αsin αcos α＝1 得2sin 2 αsin αcos α＝1，则tan α＝12，从而tan(β－2α)＝tan[(β－α)－α] ＝tan (β－α)－tan α1＋tan (β－α)·tan α＝－－13－121＋(－13)×12＝－1. 答案：－13．已知tan(α－π6)＝37，tan(π6＋β)＝25，则tan(α＋β)的值为________．解析：tan(α＋β)＝tan [(α－π6)＋(π6＋β)] ＝tan (α－π6)＋tan (π6＋β)1－tan (α－π6)·tan (π6＋β)＝37＋251－37×25＝1.答案：14．在等式cos(*)(1＋3tan 10°)＝1的括号中，填写一个锐角，使得等式成立，这个锐角的度数是________．解析：1＋3tan 10°＝1＋3sin 10°cos 10°＝cos 10°＋3sin 10°cos 10°＝2sin (30°＋10°)cos 10°＝2sin 40°cos 10°，所以填40°.答案：40°5．设a ＝sin 14°＋cos 14°，b ＝sin 16°＋cos 16°，c ＝62，则a 、b 、c 的大小关系是________．解析：∵a 2＝1＋2sin 14°cos 14°＝1＋sin 28°∈(1，32)，b 2＝1＋2sin 16°cos 16°＝1＋sin 32°∈(32，2)，c 2＝32，且a >0，b >0，c >0，∴a <c <b . 答案：a <c <b6．已知A 、B 均为钝角，且sin A ＝55，sin B ＝1010，则A ＋B 等于________．解析：由已知可得cos A ＝－255，cos B ＝－31010， ∴cos(A ＋B )＝cos A cos B －sin A sin B ＝22，又∵π2<A <π，π2<B <π， ∴π<A ＋B <2π，∴A ＋B ＝7π4. 答案：7π47．若tan(α＋β)＝25， tan(β－π4)＝14，则tan (α＋π4)＝______. 解析：tan(α＋π4)＝tan [(α＋β)－(β－π4)] ＝tan (α＋β)－tan (β－π4)1＋tan (α＋β)tan (β－π4)＝25－141＋25×14＝322.答案：3228．已知α，β∈(3π4，π)，sin(α＋β)＝－35，sin(β－π4)＝1213，则cos(α＋π4)＝________.解析：由于α，β∈(3π4，π)，所以3π2<α＋β<2π，π2<β－π4<3π4，故cos(α＋β)＝45，cos(β－π4)＝－513，cos(α＋π4)＝cos[(α＋β)－(β－π4)]＝45×(－513)＋(－35)×1213 ＝－5665. 答案：－56659．非零向量a ＝(sin θ，2)，b ＝(cos θ，1)，若a 与b 共线，则tan(θ－π4)＝________. 解析：因为非零向量a ，b 共线，所以a ＝λb ，即(sin θ，2)＝λ(cos θ，1)，所以λ＝2，sin θ＝2cos θ，得tan θ＝2，所以tan(θ－π4)＝tan θ－11＋tan θ＝13.答案：13 二、解答题10．已知α为锐角，且tan(π4＋α)＝2. (1)求tan α的值； (2)求sin 2αcos α－sin αcos 2α的值．解析：(1)tan(π4＋α)＝1＋tan α1－tan α，所以1＋tan α1－tan α＝2，1＋tan α＝2－2tan α，所以tan α＝13.(2)sin 2αcos α－sin αcos 2α＝2sin αcos 2α－sin αcos 2α＝sin α(2cos 2α－1)cos 2α＝sin αcos 2αcos 2α＝sin α.因为tan α＝13，所以cos α＝3sin α，又sin 2α＋cos 2α＝1，所以sin 2 α＝110，又α为锐角，所以sin α＝1010，11．如图所示，在平面直角坐标系xOy 中，以Ox 轴为始边作两个锐角α，β，它们的终边分别与单位圆交于A 、B 两点，已知A 、B 的横坐标分别为210、255. (1)求tan(α＋β)的值； (2)求α＋2β的值．解析：由已知条件得cos α＝210，cos β＝255. ∵α、β为锐角，∴sin α＝1－cos 2α＝7210， sin β＝1－cos 2β＝55，因此tan α＝7，tan β＝12.(1)tan(α＋β)＝tan α＋tan β1－tan α·tan β＝7＋121－7×12＝－3.(2)∵tan 2β＝2tan β1－tan 2β＝2×121－(12)2＝43， ∴tan(α＋2β)＝7＋431－7×43＝－1.∵α，β为锐角，∴0<α＋2β<3π2， ∴α＋2β＝3π4.12．已知向量OA →＝(cos α，sin α)(α∈[－π，0])．向量m ＝(2,1)，n ＝(0，－5)，且m ⊥(OA →－n )． (1)求tan α的值；(2)若cos(β－π)＝210，且0<β<π，求cos(2α－β)．解析：(1)∵OA →＝(cos α，sin α)， ∴OA →－n ＝(cos α，sin α＋5)， ∵m ⊥(OA →－n )，∴m ·(OA →－n )＝0，即2cos α＋(sin α＋5)＝0，① 又sin 2α＋cos 2α＝1，② 由①②联立方程组解得， cos α＝－255，sin α＝－55. ∴tan α＝sin αcos α＝12. (2)∵cos(β－π)＝210，即cos β＝－210，0<β<π， ∴sin β＝7210，π2<β<π，又∵sin 2α＝2sin αcos α＝2×(－55)×(－255)＝45， cos 2α＝2cos 2α－1＝2×45－1＝35，∴cos(2α－β)＝cos 2αcos β＋sin 2αsin β ＝35×(－210)＋45×7210＝22.。

两角和与差的正弦余弦正切公式练习题(答案)

两角和差的正弦余弦正切公式练习题之邯郸勺丸创作知识梳理1．两角和与差的正弦、余弦和正切公式sin(α±β)＝sin_αcos_β±cos_αsin_β.cos(α∓β)＝cos_αcos_β±sin_αsin_β..tan α±tan β1∓tan αtan β＝tan(α±β) 2．二倍角的正弦、余弦、正切公式sin 2α＝2sin_αcos_α.cos 2α＝cos2α－sin2α＝2cos2α－1＝1－2sin2α..2tan α1－tan2α＝tan 2α 3．有关公式的逆用、变形等(1)tan α±tan β＝tan(α±β)(1∓tan_αtan_β)．.1－cos 2α2＝sin2α，1＋cos 2α2＝(2)cos2α(3)1＋sin 2α＝(sin α＋cos α)2，1－sin 2α＝(sin α－cos.⎝⎛⎭⎪⎫α±π4sin 2＝sin α±cos α，α)24．函数f(α)＝a sin α＋bcos α(a，b 为常数)，可以化为f(α)＝a2＋b2sin(α＋φ)，其中tan φ＝ba一、选择题1．给出如下四个命题①对于任意的实数α和β，等式恒成立；②存在实数α，β，使等式能成立；③公式成立的条件是且；④不存在无穷多个α和β，使；其中假命题是（）A．①②B．②③C．③④D．②③④2．函数的最大值是（）A．B．C．D． 23．当时，函数的（）A．最大值为1，最小值为－1 B．最大值为1，最小值为C．最大值为2，最小值为－2 D．最大值为2，最小值为－14．已知的值（）A．B．C．D．5．已知（）A．B．－C．D．－6．的值等于（）A．B．C．D．7．函数其中为相同函数的是（）A．B．C．D．8．α、β、都是锐角，等于（）A．B．C．D．9．设的两个根，则p、q之间的关系是（）A．p+q+1=0 B．p－q+1=0 C．p+q－1=0 D．p－q－1=010．已知的值是（）A．B．－C．D．11．在△ABC中，，则与1的关系为（）A．B．C．D．不克不及确定12．的值是（）A．B．C．D．二、填空题（每小题4分，共16分，将答案填在横线上）13．已知，则的值为.14．在△ABC中，，则∠B= .15．若则=.16．若的取值范围是.三、解答题（本大题共74分，17—21题每题12分，22题14分）17．化简求值：．18．已知是方程的两根，求的值.19．求证：．20．已知α，β∈（0，π）且，求的值. 21．证明：.22．已知△ABC的三个内角满足：A+C=2B，求的值.两角和差的正弦余弦正切公式练习题参考答案一、1．C 2．A 3．D 4．D 5．B 6．C 7．C 8．B 9．B10．D11．B 12．A二、13．m 14．15．16．三、17．原式==．18．，．19．证：右．20．21．左=右．22．由题设B=60°，A+C=120°，设知A=60°+α，C=60°－α，故．。

2019版一轮优化探究理数(苏教版)练习：第四章第六节正、余弦定理和应用举例

一、填空题1．在△ABC 中，角A 、B 、C 的对边分别为a 、b 、c ，若a 2＋c 2－b 2＝3ac ，则角B 的值为________．解析：由余弦定理cos B ＝a 2＋c 2－b 22ac ，又a 2＋c 2－b 2＝3ac ，∴cos B ＝32，又0<B <π，∴B ＝π6. 答案：π62．已知A 、B 两地的距离为10 km ，B 、C 两地的距离为20 km ，现测得∠ABC ＝120°，则A ，C 两地的距离为________km.解析：由余弦定理知，AC 2＝102＋202－2×10×20cos 120°＝700.∴AC ＝107 km. 答案：1073.如图，两座相距60 m 的建筑物AB ，CD 的高度分别为20 m 、50 m ，BD 为水平面，则从建筑物AB 的顶端A看建筑物CD 的张角为________．解析：依题意可得AD ＝2010 (m)，AC ＝30 5 (m)，又CD ＝50 (m)，所以在△ACD 中，由余弦定理得cos ∠CAD ＝AC 2＋AD 2－CD 22AC ·AD＝(305)2＋(2010)2－5022×305×2010＝ 6 0006 0002＝22，又0°<∠CAD <180°，所以∠CAD ＝45°，所以从顶端A 看建筑物CD 的张角为45°.答案：45°4．锐角△ABC 的三边a ，b ，c 和面积S 满足条件S ＝c 2－(a －b )24k，又角C 既不是△ABC 的最大角也不是△ABC 的最小角，则实数k 的取值范围是________．解析：cos C ＝a 2＋b 2－c 22ab ，∴c 2－a 2－b 2＝－2ab cos C ，由S ＝c 2－(a －b )24k，得4kS ＝c 2－(a －b )2，即4k ·12·ab sin C ＝c 2－a 2－b 2＋2ab ， ∴2kab sin C ＝－2ab cos C ＋2ab ，即k sin C ＝1－cos C ，∴k ＝1－cos C sin C ，∴k ＝tan C 2，又π4<C <π2， ∴2－1<k <1.答案：(2－1,1)5．在△ABC 中，cos 2B 2＝a ＋c 2c (a ，b ，c 分别为角A ，B ，C 的对边)，则△ABC 的形状为________．解析：∵cos 2B 2＝a ＋c 2c ，∴cos B ＋12＝a ＋c 2c ， ∴cos B ＝a c ，∴a 2＋c 2－b 22ac ＝a c ，∴a 2＋c 2－b 2＝2a 2，即a 2＋b 2＝c 2，∴△ABC 为直角三角形．答案：直角三角形6．在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，若2b ＝a ＋c ，则角B 的取值范围是________．解析：∵cos B ＝a 2＋c 2－b 22ac ＝a 2＋c 2－(a ＋c )242ac＝3(a 2＋c 2)－2ac 8ac＝3(a 2＋c 2)8ac －14≥34－14＝12，即cos B ∈[12，1)，∴B ∈(0，π3]．答案：(0，π3]7．若△ABC 的周长等于20，面积是103，A ＝60°，则BC 边的长是________．解析：依题意及面积公式S ＝12bc sin A ，得103＝12bc sin 60°，得bc ＝40.又周长为20，故a ＋b ＋c ＝20，b ＋c ＝20－a ，由余弦定理得：a 2＝b 2＋c 2－2bc cos A ＝b 2＋c 2－2bc cos 60°＝b 2＋c 2－bc ＝(b ＋c )2－3bc ，故a 2＝(20－a )2－120，解得a ＝7.答案：78．在△ABC 中，A ＝60°，b ＝1，面积为3，则a ＋b ＋c sin A ＋sin B ＋sin C＝________. 解析：S ＝12bc ·sin A ＝12×1·c ·sin 60°＝3，∴c ＝4，∴a 2＝b 2＋c 2－2bc ·cos A＝1＋42－2×1×4×cos 60°＝1＋16－2×4×12＝13，∴a ＝13.∴a ＋b ＋c sin A ＋sin B ＋sin C＝a sin A ＝13sin 60°＝2393. 答案：23939．如图，一船在海上由西向东航行，在A 处测得某岛M 的方位角为北偏东α角，前进m km 后在B 处测得该岛的方位角为北偏东β角，已知该岛周围n km 范围内(包括边界)有暗礁，现该船继续东行．当α与β满足条件________时，该船没有触礁危险．解析：由题可知，在△ABM 中，根据正弦定理得BM sin (90°－α)＝m sin (α－β)，解得BM ＝m cos αsin (α－β)，要使船没有触礁危险需要BM sin(90°－β)＝m cos αcos βsin (α－β)>n ，所以α与β的关系满足m cos αcos β>n sin(α－β)时船没有触礁危险．答案：m cos αcos β>n sin(α－β)二、解答题10．在△ABC 中，角A ，B ，C 所对的边长分别为a ，b ，c ，已知2sin A ＝3cos A .(1)若a 2－c 2＝b 2－mbc ，求实数m 的值；(2)若a ＝3，求△ABC 的面积的最大值．解析：(1)∵2sin A ＝3cos A ，∴2sin 2A ＝3cos A ，即2cos 2A ＋3cos A －2＝0，解得cos A ＝12或－2(舍去)，又0<A <π，∴A ＝π3.由余弦定理，知b 2＋c 2－a 2＝2bc cosA ．又a 2－c 2＝b 2－mbc ，可得cos A ＝m 2，∴m ＝1.(2)由余弦定理及a ＝3，A ＝π3，可得3＝b 2＋c 2－bc ，再由基本不等式b 2＋c 2≥2bc ，∴bc ≤3，∴S △ABC ＝12bc sin A ＝12bc sin π3＝34bc ≤334，故△ABC 的面积的最大值为334.11．设锐角△ABC 的内角A ，B ，C 所对的边长分别为a ，b ，c ，a ＝2b sin A .(1)求B 的大小；(2)求cos A ＋sin C 的取值范围．解析：(1)由a ＝2b sin A 及正弦定理a sin A ＝b sin B ＝2R ，得sin A ·2R ＝2sin B ·2R ·sin A ，即sin B ＝12，∵△ABC 是锐角三角形，∴B ＝π6.(2)由(1)，知C ＝π－A －B ＝5π6－A ，∴cos A ＋sin C＝cos A ＋sin(5π6－A )＝32cos A ＋32sin A＝3(32cos A ＋12sin A )＝3sin(A ＋π3)．∵△ABC 是锐角三角形，∴⎩⎪⎨⎪⎧ 0<A <π2，0<C <π2，即⎩⎪⎨⎪⎧ 0<A <π2，0<5π6－A <π2，则π3<A <π2.∴2π3<A ＋π3<5π6. 则12<sin(A ＋π3)<32. ∴32<3sin(A ＋π3)<32.∴cos A ＋sin C 的取值范围为(32，32)．12．如图，当甲船位于A 处时获悉，在其正东方向相距20海里的B 处有一艘渔船遇险等待营救．甲船立即前往救援，同时把消息告知在甲船的南偏西30°，相距10海里C 处的乙船．(1)求处于C 处的乙船和遇险渔船间的距离；(2)设乙船沿直线CB 方向前往B 处救援，其方向与CA →成θ角，求f (x )＝sin 2θsin x＋cos 2θcos x (x ∈R)的值域．解析：(1)连结BC ，在△ABC 中，由余弦定理得BC 2＝202＋102－2×20×10cos 120°＝700，BC ＝107.即处于C 处和乙船和遇险渔船间的距离为107海里．(2)∵sin θ20＝sin 120°107，∴sin θ＝37，∵θ是锐角，∴cos θ＝47，∴f (x )＝sin 2θsin x ＋cos 2θcos x ＝37sin x ＋47cos x＝57sin(x ＋φ)，∴f (x )的值域为[－57，57]．。

数学苏教版4优化训练：3.1.1两角和与差的余弦含解析

第3章三角恒等变换3。

1 两角和与差的三角函数3.1.1 两角和与差的余弦5分钟训练（预习类训练，可用于课前）1.若sin （2π+α）=-54，α∈（2π,π),则cos(3π—α)=_______________。

思路解析：由诱导公式得sin （2π+α）=cos α=—54,又α∈(2π，π）,所以sin α=53。

所以cos （3π-α）=cos 3πcos α+sin 3πsin α=21×（-54）+23×53=10433-. 答案：10433- 2。

计算cos （α—35°)cos （25°+α）+sin （α-35°)sin （25°+α）=____________。

思路解析：逆用两角差的余弦公式可得到结果。

原式=cos(α-35°-25°—α)=cos （—60°）=21. 答案:21 10分钟训练（强化类训练,可用于课中）1。

已知sin α=53，cos β=1312，求cos （α-β)的值。

解：∵sin α=53＞0，cos β=1312＞0， ∴α可能在一、二象限，β在一、四象限。

若α、β均在第一象限，则cos α=54，sin β=135，cos(α—β）=54·1312+53·135=6563。

若α在第一象限,β在第四象限，则cos α=54,sin β=-135，cos(α-β）=54·1312+53·（-135)=6533。

若α在第二象限，β在第一象限,则cos α=—54,sin β=135，cos （α-β）=(—54）·1312+53·135=-6533。

若α在第二象限，β在第四象限,则cos α=—54，sin β=-135， cos （α-β)=（-54）·1312+53·（-135）=-6563. 2。

2019版一轮优化探究文数(苏教版)练习第四章第四节两角和与差的正弦、余弦、正切公式 Word版含解析

一、填空题．若α＝，α∈(－，)，则(α＋)＝.解析：∵α∈(－，)，α＝，∴α＝，∴(α＋)＝－( α－α)＝－.答案：－．已知α α α)＝，(β－α)＝－，则 (β－α)＝.解析：依题意由α α α)＝得α α)＝，则α＝，从而(β－α)＝[(β－α)－α]＝α＋(β－α(· α)＝－＝－.答案：－．已知(α－)＝，(＋β)＝，则(α＋β)的值为．解析：(α＋β)＝[(α－)＋(＋β)]＝＝＝.答案：．在等式(*)(＋°)＝的括号中，填写一个锐角，使得等式成立，这个锐角的度数是．解析：＋°＝＋° °)＝°＋() ° °)＝°)＝° °)，所以填°.答案：°．设＝ °＋ °，＝ °＋ °，＝，则、、的大小关系是．解析：∵＝＋° °＝＋°∈(，)，＝＋° °＝＋°∈(，)，＝，且>，>，>，∴<<.答案：<<．已知、均为钝角，且＝，＝，则＋等于．解析：由已知可得＝－，＝－，∴(＋)＝－＝，又∵<<π，<<π，∴π<＋<π，∴＋＝.答案：．若(α＋β)＝，(β－)＝，则 (α＋)＝.解析：(α＋)＝[(α＋β)－(β－)]＝＝＝.答案：．已知α，β∈(，π)，(α＋β)＝－，(β－)＝，则(α＋)＝.解析：由于α，β∈(，π)，所以<α＋β<π，<β－<，故(α＋β)＝，(β－)＝－，(α＋)＝[(α＋β)－(β－)]＝×(－)＋(－)×＝－.答案：－．非零向量＝( θ，)，＝( θ，)，若与共线，则(θ－)＝.解析：因为非零向量，共线，所以＝λ，即( θ，)＝λ( θ，)，所以λ＝，θ＝θ，得θ＝，所以(θ－)＝θ－＋θ)＝.答案：二、解答题．已知α为锐角，且(＋α)＝.()求α的值；()求α α－α α)的值．解析：()(＋α)＝α－α)，所以α－α)＝，＋α＝－α，所以α＝.()α α－α α)＝αα－α α)＝α(α－( α)＝α α α)＝α.因为α＝，所以α＝α，又α＋α＝，所以α＝，又α为锐角，所以α＝，所以α α－α α)＝.。

2020年一轮优化探究文数(苏教版)练习：第四章第四节两角和与差的正弦、余弦、正切公式Word版含解

=1.卜知能提升、填空题卄3nn 5 n1 .若 Sin a= 5， at ( — 2，2)，贝Ucos(a+；4)= n n 3 4解析：T at ( — 2， 2)， sin a= 5，- cos a=5,••• cos(a+ 劭=—-^^(cos a — sin a =-嚅.答案：-冷 -1 —cos 2a1 (2).已知sin aos a=1, tan(3a = — 3,则 tan (32o) =解析：依题意由\ cos 2a= 1 sin a cosa2 2sin a1 得 =1，贝U tan a=sin a cos a从而 tan( B — 2 0)= tan[( B — a)— oc] tan 3— a — tan a 1 + tan3- a tan a1 —3—1 1 + 叶3 1 2 ==x2 -1. 答案：—1 3.已知tan( na — 6)= 3 n27，tan (6+ 3 = 5,贝U tan(a+ 3的值为n n解析：tan(a+3 =tan [(a — 6)+(6 + 3]n n 3 2tan a — 6 + tan 6+ 3 7+ 5n n 3 2 1 — tan a — 6 tan g + 3 1 — 7 x5答案：14.在等式cos(*)(1 + 3tan 10°)= 1的括号中，填写一个锐角，使得等式成立, 这个锐角的度数是答案：40°5 .设 a = sin 14 丰 cos 14 b = sin 16 + cos 16 ； c =¥，贝a 、b 、c 的大小关系是 ________ .3解析：T a 2= 1 + 2sin 14 cos 14 丄 1 + sin 28 E (1, ?), b 2= 1 + 2sin 16 cos 16 丄 13 3+ sin 32 E (°, 2), c 2= 2，且 a>0, b>0, c>0,： a<c<b. 答案：a<c<b6.已知A 、B 均为钝角，且sin A ^f, sin B =〒0°，贝U A + B 等于解析：由已知可得cos A 二一铲，cos B 二一诽， ••• cos(A + B) = cos Acos B — sin As in B = ~2，□ nn又••• 2<A < n 2<B < n7n• n <A + B<2 n, •- A + B = 4 . 答案：7n2n 1 r 「 n7.若 tan(a+ ® = 5, tan(B —4)= 4,则 tan (a+ 4)= ________ 解析：tan(a+ 4) = tan [(a+ B — ( B — Q]n 21 tan a+ B — tan 0— 45 431 + tan a+ B tan 0-才 1+ |x 4 答案：223 n 3 n 12^^ n8.已知 a, BE (匸,n, sin(a+ 0 = — 5, sin(B — 4)=后，则 cos(a+ 4)=解析：1 + 3- 10, 1 + 拆=込矇匚器 10 = 12 3^^ =o所以填40°2sin 40 cos 10n1 + tan a 十、、r 1 + tan (1)tan(4+ a a 1—an a 所以 1—an1所以 tan a_ 3.1 、 ■ ・22 因为 tan a= 3, 所以 cos a= 3sin o, 又 sin a+ cos a 1 ,所以 sin 2 a_ 10 , 又a 为锐角，所以sin a_^0-0 ,3 n 3 nn n解析：由于 a,氏(才,n,所以"2< a+ f<2 n, 2< 4<~4，故 cos(a+ 3 = 5, cos(B5 / n —4)a — 13 , cos(a+4) a cos[( a+ n4)3 12 +(—5)x n56 65. 答案：-Hn9.非零向量 a = (sin 9, 2), b = (cos 9, 1),若 a 与 b 共线，则 tan(9-》= 解析: 因为非零向量a , b 共线,所以a _ 2b ,即(sin 9, 2)_ 2(cos 9, 1),所以入n tan 9— 1 1sin 9_2cos 9,得 tan 9_ 2,所以 tan(9—;)_ _-.4 1 + tan 9 3答案: 、解答题n10.已知a 为锐角，且tanq + a = 2. ⑴求tan a 的值;⑵求 sin 2 a cos a — sin a 的值. COS 2a解析: 1 + tan a= 2 — 2tan a,sin 2ocos a — sin a 2sin a coS 2 a — sina ⑵cos 2asin a 2co$ a — 1 COS 2aCOS 2a sin a os 2a a sin a_ cos 2 asin 2a cos a — sin a _ 10 所以——- =而. COS2a11 •如图所示，在平面直角坐标系xOy 中，以Ox 轴为始边作两个锐角 a B,它们的终边分别与单位圆交于 A 、B 两点, B 的横坐标分别为请、255 ⑴求tan(a+®的值; ⑵求a+ 2B的值. 解析：由已知条件得cos 汗探cos A 響 a B为锐角，二 sin a —寸 1 — Cos 2a — ^2 10，____ yj5 sin ,；1 — cos2 3="5，因此 tan a 7, 1 tan 2. 17 +2 1 — tan a ta n B1H 1—7Xtan a+ tan B(1)ta n( a+ B = = =—3. —、.. c 2ta n B⑵•tan 2 A 1 - tan 2 312X£ = 4 12 = 3, 21- 4 7+4 --tan(a+ 2 f)— 4= 1 — 7X41.、 3冗 •' a B 为锐角，二 0< a+2， • •• a+ 2p=眾 4 12.已知向量 OA — (cos a, sin 认 a€ [ — n ，0])•向量 m — (2,1)， n — (0，—(5)，且 m l(OA — n). (1)求 tan a的值； yj 2 ⑵若 cos( p — n — 10，且 0<B <n 求 cos(2 a — B .解析：(1)： OA= (cos a sin a, ■ - OA — n = (cos a, sin a+ 5), ■/ m ±(OA — n),••• m (OA — n) = 0, 即 2cos a+ (sin a+ 5) = 0,① 又 sin 2 a+ cos 2 a= 1，② 由①②联立方程组解得，(2)v cos(B — n 弄皤，即 cos B= — 12, 0< n, • sin A32a5X (—而+ 4X 座—返 5X 10 — 2 .cos a=—2*55 ,sin a= — • tansin a 1cos 厂 2.又sin 2a= 2sin a cos a 2X (-詐4- 5 - \72cos 2a=2cos2 a-仁 2X 5- i a5。

数学苏教必修优化训练：两角和与差的正弦含解析

3.1.2 两角和与差的正弦5分钟训练（预习类训练，可用于课前）1.sin13°cos17°+cos13°sin17°的值.思路解析：由sin αcos β+cos αsin β=sin(α+β)可得结果.解：原式=sin （13°+17°）=sin30°=21. 2.化简sin 1225πcos 611π-cos 1211πsin 65π的值是( ) A.-22 B.22 C.-sin 12π D.sin 12π 思路解析：先用诱导公式将角转化一下,再逆用公式即得.原式=-sin12πcos 65π+cos 12πsin 65π =sin(65π-12π) =sin 43π =22. 答案:B10分钟训练（强化类训练,可用于课中）1.（2005 湖北）若sin α+cos α=tan α(0<α<2π)，则α属于( ) A.(0,6π) B.(6π,4π) C.(4π,3π) D.(3π,2π) 思路解析：tan α=sin α+cos α=2sin(α+4π). ∵0<α<2π, ∴4π<α+4π<43π. ∴22<sin(α+4π)≤1. ∴1<tan α≤2<3. ∴4π<α<3π. 答案:C2.函数f(x)=cos2x-3sin2x(x ∈R )的最小正周期为_________________.思路解析：f(x)=cos2x-3sin2x=2(21cos2x-23sin2x) =2(sin6πcos2x-cos 6πsin2x) =2sin(6π-2x). ∴T=22π=π. 答案:π3.求sin 187πcos 92π-sin 9πsin 92π的值. 思路解析：观察分析这些角的联系，会发现9π=2π-187π. 解:sin 187πcos 92π-sin 9πsin 92π =sin 187πcos 92π-sin （2π-187π）sin 92π =sin 187πcos 92π-cos 187πsin 92π =sin （187π-92π） =sin 6π =21. 4.要使得sin α-3cos α=mm --464有意义，则m 的取值范围是( ) A.（-∞，37] B.［1，+∞) C.［-1，37］ D.（-∞，-1）∪［37，+∞］思路解析：这道题主要考查对两角和与差的三角函数公式的逆用与化简、证明方法的掌握. 由已知化简得sin α-3cos α=2（21sin α-23cos α）=2sin （α-3π），所以2sin （α-3π）=m m --464，即sin （α-3π）=m m --432. ∵-1≤sin （α-3π）≤1， ∴-1≤mm --432≤1. 解不等式，可得到-1≤m ≤37.答案:C志鸿教育乐园和你的关系一个新生去学校报到。

苏教版数学高一必修四练习两角和与差的正弦

双基达标 (限时15分钟)1．计算：sin 75°＝________.解析 sin 75°＝sin(45°＋30°)＝sin 45°cos 30°＋cos 45°sin 30°＝22×32＋22×12＝6＋24.答案 6＋242．cos 44°sin 14°－sin 44°cos 14°的值是________．解析原式＝sin(14°－44°)＝sin(－30°)＝－12.答案－12 3．已知sin α＝－35，α是第四象限角，则sin ⎝ ⎛⎭⎪⎫π4－α＝ ________.解析由sin α＝－35，α是第四象限角，得cos α＝1－sin 2α＝ 1－⎝ ⎛⎭⎪⎫－352＝45， sin ⎝ ⎛⎭⎪⎫π4－α＝sin π4cos α－cos π4sin α ＝22×45－22×⎝ ⎛⎭⎪⎫－35＝7210. 答案 7210 4．函数f (x )＝(1＋3tan x )cos x 的最小正周期为________．解析 f (x )＝(1＋3tan x )cos x ＝cos x ＋3sin x＝2sin ⎝ ⎛⎭⎪⎫x ＋π6，T ＝2π|ω|＝2π. 答案 2π5．化简sin π6＋α＋cos π3＋α的结果是________．解析原式＝sin π6cos α＋cos π6sin α＋cos π3cos α－sin π3·sin α＝cos α.答案 cos α6．已知α∈0，π2，β∈－π2，0，且cos(α－β)＝35，sin β＝－210，求α.解 ∵α∈⎝ ⎛⎭⎪⎫0，π2，β∈⎝ ⎛⎭⎪⎫－π2，0，∴α－β∈(0，π)． ∵cos(α－β)＝35，∴sin(α－β)＝45. ∵β∈⎝ ⎛⎭⎪⎫－π2，0，sin β＝－210，∴cos β＝7210. ∴sin α＝sin ＝sin(α－β)cos β＋cos(α－β)sin β＝45×7210＋35×⎝ ⎛⎭⎪⎫－210＝22. ∴α＝π4.综合提高 (限时30分钟)7．已知sin(45°－α)＝－23，且45°＜α＜90°，则sin α＝________.解析 ∵45°＜α＜90°，∴－45°＜45°－α＜0°，∴cos(45°－α)＝53，∴sin α＝sin＝sin 45°cos(45°－α)－cos 45°sin(45°－α) ＝22×53－22×⎝ ⎛⎭⎪⎫－23＝10＋226. 答案 10＋2268．(tan 10°－3)cos 10°sin 50°＝________.解析原式＝(tan 10°－tan 60°)cos 10°sin 50°＝⎝ ⎛⎭⎪⎫sin 10°cos 10°－sin 60°cos 60°cos 10°sin 50°＝sin (－50°)cos 10°cos 60°·cos 10°sin 50° ＝－1cos 60°＝－2.答案－29．若15sin x ＋5cos x ＝10，则锐角x 的值为________．(用弧度表示) 解析 15sin x ＋5cos x ＝25⎝ ⎛⎭⎪⎫32sin x ＋12cos x ＝25sin ⎝ ⎛⎭⎪⎫x ＋π6 即25sin ⎝ ⎛⎭⎪⎫x ＋π6＝10，∴sin ⎝ ⎛⎭⎪⎫x ＋π6＝22∵x ∈⎝ ⎛⎭⎪⎫0，π2，∴x ＋π6∈⎝ ⎛⎭⎪⎫0，2π3， ∴x ＋π6＝π4，∴x ＝π12答案 π1210．函数y ＝cos x ＋cos ⎝ ⎛⎭⎪⎫x ＋π3的最大值是________．解析 y ＝cos x ＋cos ⎝ ⎛⎭⎪⎫x ＋π3 ＝cos x ＋cos x cos π3－sin x sin π3＝32cos x －32sin x＝3⎝ ⎛⎭⎪⎫32cos x －12sin x ＝3cos ⎝ ⎛⎭⎪⎫x ＋π6. 当cos ⎝ ⎛⎭⎪⎫x ＋π6＝1时y max ＝ 3. 答案 311．已知3sin β＝sin(2α＋β)，求证tan(α＋β)＝2tan α.证明由已知得3sin ＝sin ，即3＝sin(α＋β)cos α＋cos(α＋β)sin α，即2sin(α＋β)cos α＝4cos(α＋β)sin α，∴tan(α＋β)＝2tan α.12．若sin(α＋β)＝12，sin(α－β)＝13，求tan αtan β的值．解 ∵sin(α＋β)＝12，sin(α－β)＝13，∴sin αcos β＋cos αsin β＝12，sin αcos β－cos αsin β＝13，∴sin αcos β＝512，cos αsin β＝112，tan αtan β＝sin αcos βcos αsin β＝5.13．(创新拓展)已知sin α＋cos β＝34，cos α＋sin β＝－54，求sin(α＋β)的值；解已知sin α＋cos β＝34 ①，cos α＋sin β＝－54②，①2＋②2得sin 2α＋2sin αcos β＋cos 2β＋cos 2α＋2cos αsin β＋sin 2 β＝⎝ ⎛⎭⎪⎫342＋⎝ ⎛⎭⎪⎫－542. ∵sin 2α＋cos 2α＝1，sin 2 β＋cos 2 β＝1，sin αcos β＋cos αsin β＝sin(α＋β)，∴2＋2sin(α＋β)＝3416，即sin(α＋β)＝116.。

数学苏教必修优化训练：两角和与差的余弦含解析

第3章三角恒等变换3.1 两角和与差的三角函数3.1.1 两角和与差的余弦5分钟训练（预习类训练，可用于课前）1.若sin （2π+α）=-54，α∈（2π，π），则cos （3π-α）=_______________. 思路解析：由诱导公式得sin （2π+α）=cos α=-54，又α∈（2π，π），所以sin α=53. 所以cos （3π-α）=cos 3πcos α+sin 3πsin α=21×（-54）+23×53=10433-. 答案:10433- 2.计算cos （α-35°）cos （25°+α）+sin （α-35°）sin （25°+α）=____________. 思路解析：逆用两角差的余弦公式可得到结果.原式=cos(α-35°-25°-α)=cos(-60°)=21. 答案:21 10分钟训练（强化类训练,可用于课中）1.已知sin α=53，cos β=1312，求cos （α-β）的值. 解：∵sin α=53＞0，cos β=1312＞0， ∴α可能在一、二象限，β在一、四象限.若α、β均在第一象限，则cos α=54，sin β=135，cos （α-β）=54·1312+53·135=6563. 若α在第一象限，β在第四象限，则cos α=54，sin β=-135，cos （α-β）=54·1312+53·(-135)=6533. 若α在第二象限，β在第一象限，则cos α=-54，sin β=135， cos （α-β）=（-54）·1312+53·135=-6533. 若α在第二象限，β在第四象限，则cos α=-54，sin β=-135， cos （α-β）=（-54）·1312+53·（-135）=-6563. 2.计算sin33°cos27°+sin57°cos63°的值.思路解析：从整体出发，对局部进行三角变换，出现特殊值是求值常用的方法.题目中都是非特殊角，不能直接计算，可将sin33°化为cos57°,cos63°化为sin27°，再逆用两角和的余弦公式，则迎刃而解.解：原式=cos57°cos27°+sin57°sin27°=cos(57°-27°)=cos30°=23. 3.已知cos α=71，cos （α+β）=-1411，且α、β∈（0，2π），求cos β的值. 思路解析：本题的解法要求观察并分析出角和角之间的关系β=（α+β）-α，再利用两角差的余弦公式展开，求出结果.这种“变角”的技巧在三角函数求值以及证明中常用，因为变角后可充分利用已知条件中的三角函数值来计算或证明.要注意，避免出现将cos （α+β）展开，通过解方程54cos β-53sin β=53求cos β这种复杂方法. 解:由于α，β∈（0，2π），cos α=71，cos （α+β）=-1411，则sin α=α2cos 1-=2)71(1-=734, sin （α+β）=22)1411(1)(cos 1--=+-βα=1435. 所以cos β=cos ［（α+β）-α］=cos （α+β）cos α+sin （α+β）sin α=-1411×71+1435×734=21. 4.已知sin α+sin β=53，cos α+cos β=54，求cos （α-β）的值. 思路解析：本题是一道综合题，由于cos （α-β）=cos αcos β+sin αsin β，欲求cos （α-β）的值，只需求出cos αcos β+sin αsin β的值，而要得到两组同名三角函数乘积，需将条件两式平方，再相加即得cos αcos β+sin αsin β的结果.解：①sin α+sin β=53， ②cos α+cos β=54. ①式平方得sin 2α+2sin αsin β+sin 2β=259， ②式平方得cos 2α+2cos αcos β+cos 2β=2516. 以上两式相加，得2+2（cos αcos β+sin αsin β）=1,即2+2cos （α-β）=1，得到cos （α-β）=-21. 5.求cos80°cos35°+cos10°cos55°的值.解： cos80°cos35°+cos10°cos55°=cos80°cos35°+cos （90°-80°）cos （90°-35°）=cos80°cos35°+sin80°sin35°=cos （80°-35°）=cos45°=22. 6.已知cos （α-β）=-54，cos （α+β）=54，且（α-β）∈（2π，π），（α+β）∈（23π，2π），求cos2β的值.思路解析：此题主要考查灵活“变角”的技巧.由分析可知2β=（α+β）-（α-β）. 解：由于cos （α-β）=-54，cos （α+β）=54，且（α-β）∈（2π，π），（α+β）∈（23π，2π），可得sin （α-β）=53，sin （α+β）=-53，所以cos2β=cos ［（α+β）-（α-β）］=cos （α+β）·cos （α-β）+sin （α+β）·sin （α-β）=54·（-54）+（-53）·53=-1. 志鸿教育乐园过路费甲同学要回坐位，但被乙同学挡着路，乙同学向甲同学说：“此路是我开，此树是我栽，我想从此过，留下买路财！”这时老师站在门外说：“刷卡可以吗？”30分钟训练（巩固类训练,可用于课后）1.(2005 上海)若cos α=71,α∈(0,2π),则cos(α+3π)=_________________. 思路解析：∵α∈(0,2π), ∴sin α=4911-=734, cos(α+3π)=cos αcos 3π-sin αsin 3π=71×21-734×23=-1411. 答案:-1411 2.设α∈(0,2π),若sin α=53,则2cos(α+4π)等于( ) A.57 B.51 C.-57 D.-51 思路解析：∵α∈(0,2π),若sin α=53，∴cos α=54. ∴2cos(α+4π)=2(cos αcos 4π-sin αsin 4π)=51. 答案:B3.sin163°sin223°+sin253°sin313°等于( )A.-21B.21C.-23D. 23 思路解析：sin163°sin223°+sin253°sin313°＝sin163°sin223°+cos(90°-253°)cos(90°-313°)＝cos163°cos223°+ sin163°sin223°＝cos(223°-163°)＝cos60°=21. 答案:B4.（2005 广东）化简f(x)=cos(316+k π+2x)+cos(316-k π-2x)+23sin(3π+2x)(x ∈R ,k ∈Z ),并求函数f(x)的值域和最小正周期.解:f(x)=cos(2k π+3π+2x)+cos(2k π-3π-2x)+23sin(3π+2x) =cos(3π+2x)+cos(3π+2x)+23sin(3π+2x) =2cos(3π+2x)+23sin(3π+2x) =4［cos(3π+2x)cos 3π+sin(3π+2x)sin 3π］ =4cos2x.∴f(x)∈［-4,4］,T=22π=π. ∴f(x)的值域是［-4,4］，最小正周期是π.5.化简315sinx+35cosx.解：原式=65（23sinx+21cosx ） =65（sin60°sinx+cos60°cosx ） =65cos （60°-x ）.6.已知sin α+sin β+sin γ=0，且cos α+cos β+cos γ=0.求证：cos （α-β）=-21. 证明：由已知可得sin α+sin β=-sin γ，cos α+cos β=-cos γ.两式平方相加得到2+2cos （α-β）=1.所以cos （α-β）=-21.得证. 7.如图3-1-1，平面直角坐标系中，已知OA =（cos80°，sin80°），OB =（cos20°，sin20°），求|AB |.若AB 中点是C ，那么|OC |呢？图3-1-1思路解析：这道题属于向量和三角函数的综合问题.解:AB =（cos20°-cos80°，sin20°-sin80°）, |AB |=2)80sin 20(sin )80cos 20(cos ︒-︒+︒-︒ =2222280sin 80sin 20sin 80cos 20cos 220cos ︒+︒︒+︒+︒-︒=)80sin 20sin 80cos 20(cos 211︒︒+︒︒-+ =)2080cos(22︒-︒- =︒-60cos 22=1.可知△AOB 是等边三角形，可求得|OC |=23. 8.已知sin α+sin β=22，求cos α+cos β的取值范围. 思路解析：本题用到了平方关系：sin 2α+cos 2α=1，这一关系在三角函数运算中经常用到. 解：由于sin α+sin β=22，等式两边平方可知，sin 2α+2sin αsin β+sin 2β=21. ① 设cos α+cos β=m,平方可知，cos 2α+2cos αcos β+cos 2β=m 2. ② ①+②得sin 2α+2sin αsin β+sin 2β+cos 2α+2cos αcos β+cos 2β=m 2+21, 整理，有m 2=23+2cos （α-β）. 又由于cos （α-β）∈［-1，1］，所以m 2∈［-21，27］，即得0≤m 2≤27. 解得-214≤m ≤214. 所以-214≤cos α+cos β≤214. 9.已知0<β<4π,4π<α<43π,cos(4π-α)=53,sin(43π+β)=135,求sin(α+β)的值. 思路解析：注意到(43π+β)-(4π-α)=2π+(α+β)，可先求cos ［2π+(α+β)］. 对给值求值问题，要认真观察分析题目中的条件和结论中各个角度之间的关系，实现由已知到未知的代换. 解：∵4π<α<43π,∴-2π<4π-α<0. ∴sin(4π-α)=-54. 又∵0<β<4π, ∴43π<43π+β<π. ∴cos(43π+β)=-1312. ∴sin(α+β)=cos ［2π-(α+β)］ =-cos ［2π+(α+β)］ =-cos ［(43π+β)-(4π-α)］ =-［(-1312)×53+135(-54)］ =6556.。

苏教版高中数学必修四两角和与差的正弦

两角和与差的正、余弦（2）一、课题：两角和与差的正、余弦（2）二、教学目标：1.进一步熟悉两角和与差的正（余）弦公式，能对公式进行灵活运用；2.能将sin cos a x b x +化为一个角的一个三角函数式；3.能灵活运用公式在三角形内求角的三角函数。

三、教学重、难点：公式的灵活运用。

四、教学过程：（一）复习：1．()C αβ±及()S αβ±公式； 2．练习：（1）已知4cos 5α=，3cos()5αβ+=，且,αβ均为锐角，求cos β的值；（2）已知sin α=，cos β=,αβ均为锐角，求αβ+的值。

（二）新课讲解：例1：求证cos αα2sin()6πα=+．证明（法一）：右边2(sin cos cos sin )66ππαα=+12(cos )2αα=+=左边。

证明（法二）：左边12(cos )2αα=+2(sin cos cos sin )66ππαα=+=右边。

说明：一般地，式子sin cos a x b x +可以化为一个角的一个三角函数式。

sin cos a x b x +Q )x x =，221+=Q ，则令cos sin ϕϕ⎧=⎪⎪⎨⎪=⎪⎩ 所以，sin cos a x b x+sin sin cos )x x ϕϕ=+)x ϕ=+．例2：已知3cos sin 54sin cos 5αβαβ⎧+=⎪⎪⎨⎪+=⎪⎩，求sin()αβ+的值。

解：3cos sin (1)54sin cos (2)5αβαβ⎧+=⎪⎪⎨⎪+=⎪⎩Q 22(1)(2)+得：22(sin cos cos sin )1βαβα++=， ∴1sin()2αβ+=-．【变题】已知sin sin sin 0αβγ++=，且cos cos cos 0αβγ++=，求cos()αβ-．（答案1cos()2αβ-=-）例3：在ABC ∆中，若5tan tan 1B C =，求cos cos()A B C -的值。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2019版优化探究理数(苏教版)练习：第四章 第四节 两角和与差的正弦、余弦、正切公式含解析

2019版一轮优化探究理数(苏教版)：第四章 第二节 三角函数的图象与性质 Word版含解析

2019版一轮优化探究理数(苏教版)练习：第四章 第四节 两角和与差的正弦、余弦、正切公式 Word版含解析