16[1].3.1分式方程导学案(2课时)

合集下载

16.3.1分式方程教案

初中数学集体备课教案
第十六单元集体备课导学教案题 16.3.1 分式的方程
1.使学生理解分式方程的意义．
主备人
日期
课
学目
习标
2.使学生掌握可化为一元一次方程的分式方程的一般解法．了解解分式方程解的检验方法． 3.通过学习分式方程的解法，使学生理解解分式方程的基本思想是把分式方程转化成整式方程，把未知问题转化成已知问题，从而渗透数学的转化思想．解分式方程的基本思路和解法。理解解分式方程时可能无解的原因。
2 3 = x−3 x
例 2 解方程
x 3 −1 = x −1 ( x − 1)( x + 2)
归纳：归纳：解分式方程的一般步骤： 1．在方程的两边都乘最简公分母，约去分母，化成整式方程； 2．解这个整式方程； 3．把整式方程的根代入最简公分母，看结果是不是零，使最简公分母为零的根是原方程的增根，必须舍去。 4. 随堂练习（1）若方程＝__________. （2）解关于 x 的方程 ( ) A. －2 B. －1 （3）解分式方程
100 60 = . 20 + v 20 − v
总结：像这样分母中含未知数的方程叫做分式方程. 注意：分母是否含有末知数是区别分式方程与整式方程的关键。
找朋友
分式方程整式方程
B C F
A (1)
A D E
B x− ）
x−2 x = 2 3
1 =2 x
C (4)
x( x −1) = −1 x
4 3 + = 7 x y
x m −2= 会产生增根，则增根 x＝_____，此时 m x−3 x−3 x−3 m = 会产生增根，则常数 m 的值等于 x −1 x −1

数学学习指南16.3分式方程导学案2

数学学习指南课题：16.3分式方程备：3.12 授：3. 课时数：学习目标：1．会分析题意找出等量关系.2．会列出可化为一元一次方程的分式方程解决实际问题.（一）独立自主学习（自学课本29-31页内容，并完成下列问题）1．如何解分式方程（1）解分式方程的基本思想——，即把分式方程的分母去掉，使分式方程化成整式方程，就可以利用整式方程的解法求解了。

（2）解分式方程的步骤：①：在方程的两边都乘最简公分母，约去分母，化成整式方程；②这个整式方程；③：把整式方程的根代入最简公分母，看结果是不是零，使最简公分母为零的根是原方程的增根，必须舍去。

（二）小组合作探究例1．两个工程队共同参加一项筑路工程，甲队单独施工1个月完成总工程的三分之一，这时增加了乙队，两队又共同工作了半个月，总工程全部完成。

哪个队的施工速度快？分析：甲队一个月完成总工程的（），设乙队如果单独施工1个月能完成总工程的（），那么甲队半个月完成总工程的（），乙队半个月完成总工程的（），两队半个月完成总工程的（）。

等量关系为：（）＝（）则有（）＝1解：方程两边同乘_______，得___________________解得 ___________检验：例2：从2004年5月起某列列车平均提速v千米/时。

用相同的时间，列车提速前行驶s千米，提速后比提速前多行驶50千米，提速前列车的平均速度是多少？分析：这里的字母v，s表示已知数据，设提速前的平均速度为x千米/时，则提速前列车行驶s千米所用的时间为小时，提速后列车的平均速度为千米/时，提速后列车行驶（s＋50）千米所用的时间为小时。

等量关系：提速前行驶50千米所用的时间＝提速后行驶（s＋50）千米所用的时间列方程得：方程两边同乘 ___________，得 _________________去括号，得 _____________移项、合并，得 ______________解得 ___________检验：（三）课堂小结总结用分式方程解实际问题的一般步骤：（1）审：分析题意,找出数量关系和相等关系.（2）设：选择恰当的未知数,注意单位和语言完整.（3）列：根据数量和相等关系,正确列出方程.（4）解：认真仔细解这个分式方程.（5）验：检验.（是否是分式方程的根，是否符合题意）（6）答：注意单位和语言完整.（四）知识达标检验1、王军同学准备在课外活动时间组织部分同学参加电脑网络培训，按原定的人数估计共需费用300元.后因人数增加到原定人数的2倍，费用享受了优惠，一共只需要480元，参加活动的每个同学平均分摊的费用比原计划少4元.原定的人数是多少？2、一艘轮船在静水中的最大航速为20千米/时，它沿江以最大航速顺流航行100千米所用的时间，与以最大航速逆流航行60千米所用时间相等，江水的流速为多少？课后作业：学校要举行跳绳比赛，同学们都积极练习.甲同学跳180个所用的时间，乙同学可以跳240个；又已知甲每分钟比乙少跳5个，求每人每分钟各跳多少个。

八年级数学分式方程导学案(二)

八年级数学分式方程导学案（二）（二）总体说明本节是分式的第4小节，这是第二课时，本课时主要研究分式方程的解法，只要求会解可化为一元一次方程的分式方程（方程中的分式不超过两个）、解分式方程的关键是把分式方程转化为整式方程，在引导学生探索分式方程的解法时，要注意体现这种转化的思想、一、学生知识状况分析学生的技能基础：在上一节课的基础上，学生基本了解分式方程的概念，熟悉等式的性质并能利用等式的性质解一元一次方程中，了解一般一元一次方程的解法,去分母,去括号,移项,合并同类项,化系数为1,并理解每一步的根据是什么,从而能通过观察类比的方法，探索分式方程的解法并能理解解题步骤的根据、学生活动经验基础：本节课主要采用观察、类比的方法、讨论的形式，学生比较熟悉，能在二元一次方程转化为一元一次方程的基础上，再次体会数学转化思想、二、教学任务分析在上一节课中，学生通过对实际问题的分析，已经感受到分式方程是刻画现实世界的有效模型，本节课安排《分式方程》第二课时，旨在学会解分式方程，能从中体会数学转化思想的深刻含义，为此，本课时的教学目标是：知识与技能：（1）体会分式方程到整式方程的转化思想、（2）掌握分式方程的解法、数学能力：（1）培养学生的数学转化思想、（2）培养学生的观察、类比、探索的能力、情感与态度：鼓励学生独立思考，认真观察，大胆猜想，积极动手，提高分析问题与解决问题能力、—反馈练习、预习教案：旧知回顾1、等式性质有哪些？2、解下列一元一次方程（1）（2）第二环节：教材助读活动内容：解下列分式方程：第三环节：探究点一活动内容：解下列分式方程第四环节：探究点二活动内容：解分式方程时，小明的解为，他的答案正确吗？第五环节：当堂检测活动内容：解下列分程（1）（2）第六环节：我的知识网络在今天的学习活动中，你学会了哪些知识？掌握了哪些数学方法？注意事项：学生在解方程过程中易犯的错误：1、解方程时忘记检验；2、去分母时忘记加括号；3、去分母时漏乘不含分母的项、第七环节：反馈练习活动内容：1、方程的解为（）A、1B、 -1C、D、 02、方程的解为___________、3、解方程4、若关于的方程有增根,则的值为_______、课后练习：请完成课后作业解下列方程1、2、。

八年级数学下册 16.3.1 分式方程导学案新人教版

八年级数学下册 16.3.1 分式方程导学案新人教版一、课题16、3、1 分式方程（1）编写备课组二、本课学习目标与任务：1、了解分式方程的概念；2、掌握分式方程的解法，会运用转化思想将分式方程转化为整式方程。

三、知识链接：1、问题：一艘轮船在静水中的速度为20千米/时，它顺水航行100千米所用时间和逆水航行60千米所用时间相等，江水的速度是多少？若设轮船在静水中的速度为x千米/时,则:（1）轮船顺流航行速度为千米/时，逆流航行速度为千米/时；（2）顺流航行100千米所用时间为 _______小时；（3）逆流航行60千米所用时间为 __________小时；（4）根据题意可列方程为___________________、2、以上方程是一元一次方程吗？它的特点是分母中含有______________、四、自学任务（分层）与方法指导：一、熟读课文，理解定义1、归纳分式方程的定义：___________________________________的方程叫分式方程。

2、巩固练习：下列方程中是分式方程的有____________________(填序号)①2x=1 ② ③ ④⑤⑥ ⑦ ⑧3、如何将分式方程①转化为整式方程？方程两边同时乘以最简公分母约去分母得解这个整式方程得检验：、归纳：上述解方程的实质是将分式方程转化为整式方程来解，通常是在分式方程两边同时乘以最简公分母、二、看懂例题，尝试练习1、解方程①＝; ②＝、2、归纳解分式方程的一般步骤：、3、完成课后“练习”（先自己独立思考，然后对学或小组合作探究）五、小组合作探究问题与拓展：讨论：上面两个分式方程中，为什么方程①去分母后所得整式方程的解就是①的解，而方程②=去分母后所得整式方程的解却不是方程②的解呢？归纳：（1）将分式方程变形为整式方程时，方程两边同乘以一个含有未知数的整式，并约去分母，有可能产生不适合原方程的解(或根)，这种根通常称为增根、（2）解分式方程时，去分母后所得整式方程的解有可能使原方程中分母为0，因此应检验：将整式方程的解代入最简公分母，如果最简公分母的值不为0，则整式方程的解是原分式方程的解；否则，这个解不是原分式方程的解、值、六、自学与合作学习中产生的问题及记录当堂检测题一、基础演练1、下列方程:①＝5; ② ; ③x+3=; ④=中是分式方程的有、2、分式方程=的解是、3、当x= 时，分式的值是1、4、设A＝，B＝+1,当x= 时，A与B的值相等、5、解方程：① ＝＋1 ②－＝0二、能力提升6、当a取什么值时，方程的解是负数？八年级数学分层教学导学稿学案一、课题16、3、1 分式方程（2）编写备课组二、本课学习目标与任务：1、了解分式方程增根的意义；2、会解决较简单的有关分式方程的解的问题三、知识链接：1、、解方程2、解上述方程中得到的使分式方程的最简公分母为_________，称为此分式方程的--------四、自学任务（分层）与方法指导：一、熟读课文，理解性质为什么会产生增根？二、看懂例题，尝试练习例1 已知关于x的分式方程（1）若此方程有增根x=1,求k的值；（2）若此方程有增根x= -1,求k的值；（3）若此方程有增根,求k的值；（4）若此方程无解，求k的值。

分式方程(第2课时)

徐闻县和安中学数学教研组 ◆八年级数学导学案 ◆◆我们的约定：我的课堂我作主！执笔：林朝清第周星期第节本学期学案累计: 15 课时姓名：________课题：16.3 分式方程（第2课时）学习目标我的目标我实现1．会分析题意找出等量关系.2．会列出可化为一元一次方程的分式方程解决实际问题.学习过程我的学习我作主导学活动1：知识回顾解下列方程1．01522=--+x x x x 2．xx x -=+--23123解分式方程的步骤：。

导学活动2：知识引入 1．引导说出列方程解应用题的步骤 .2．相关背景：工作量=工作效率⨯时间；时间工作量工作效率=；工作效率工作量时间=. 一般把工作量看成13．针对性练习：一项工程甲工程队单独做需要a 天完成，则甲工程队的工作效率为；乙工程队单独做需要b 天完成，则乙工程队的工作效率为；甲、乙合作的工作效率为；导学活动3：知识转化例3：两个工程队共同参与一项筑路工程，甲队单独做需要3个月完成，当甲队单独施工1个月后，乙队加入共同施工，又工作了半个月，总工程全部完成，求乙队单独施工需要多少个月能完成全部工程？练习：1．甲做180个零件与乙做240个零件所用的时间相同，已知两人每小时共做140个零件，求甲、乙两人每小时各做多少个零件？徐闻县和安中学数学教研组 ◆八年级数学导学案 ◆◆我们的约定：我的课堂我作主！学习评价我的评价我自信当堂检测（限时：12分钟）我自信我进取1、解方程： 1625222-=-++x x x x x2．A 、B 两种机器人都被用来搬运化工原料，A 型机器人比B 型机器人每小时多搬运30千克. A 型机器人搬运900千克所用时间与B 型机器人搬运600千克所用时间相等，求两种机器人每小时分别搬运多少化工原料？3．甲、乙两个工程队合作一项工程，10天可以完成，如果单独做甲队需要的天数是乙队的一半，求两队单独做各需多少天完成？自我小结：列方程解应用题的步骤自我评价：我完成本节导学案的情况为（）. A. 很好 B. 较好 C. 一般 D. 较差课后作业我的作业我承担课本（P32）习题16.3 第3、4题。

新人教版八年级数学上册《分式方程》导学案

《分式方程》导学案学习目标：1．使学生理解分式方程的意义．2．使学生掌握可化为一元一次方程的分式方程的一般解法．3．了解解分式方程解的检验方法．学习重点：(1)可化为一元一次方程的分式方程的解法．(2)分式方程转化为整式方程的方法及其中的转化思想学习难点：检验分式方程解的原因学习过程：一、自主学习：1.概念：分式方程：分母中含有的方程叫分式方程。

2.练习：判断下列各式哪个是分式方程．（1）5x y += （2）2253x y z +-= （3）1x （4）05y x =+ 3. 看课本例题回答问题：轮船顺流航行的速度为千米/时；逆流航行的速度为千米/时，顺流航行 100千米所用的时间为小时，逆流航行 60 千米所用的时间为小时。

由两次航行所用时间相等，可列方程100602020v v =+- 二、合作探究1、观察课本生解题过程，思考：方程100602020v v=+-和()()100206020v v -=+中 V 的取值范围相同吗？所以对上题中的解 v=5 必须检验。

检验：将 v=5 代入原方程中，左边= 4，右边=4 ，左边 =右边，因此 v=5 是原方程的解。

注意：分式方程必须检验2、解方程：2110525x x =--小结：一般地，解分式方程时，去分母后所得整式方程的解有可能使原方程中分母为0，因此检验时常将整式方程的解代入最简公分母，如果最简公分母的值不为0，则整式方程的解是原分式方程的解，否则，这个解不是原分式方程的解，是原分式方程的增根三、学以致用1、解方程：（1）1223x x =+ （2）21133x x x x =+++（3）22411x x =-- （4）22510x x x x -=+-（5）572x x =- （6）11322xx x -=---四、能力提升：1、若关于 x 的分式方程1011m xx x --=--有增根，则m 的取值是?点拨：把分式方程进行转化，然后找到有可能的增根，代入。

16[1]3_分式方程(2)导学案

16.3 分式方程（2）导学案时间：姓名：班级：一.明确目标，预习交流【学习目标】1、列分式方程解应用题的一般步骤；2、学会用等量关系列分式方程解应用题；【重、难点】重点：学会用等量关系列分式方程解应用题难点：用等量关系列分式方程解应用题【预习作业】：2.解方程(1)3222xxx-=--（2）21321--=+-xxx3.行程问题等量关系，工程问题等量关系。

4.一件工作，甲单独做a小时完成，乙单独做b小时完成，则甲的工效为，乙的工效为。

则甲、乙合作小时完成。

二.合作探究，生成总结探讨1.两个工程队共同参与一项筑路工程，甲队单独施工完成总工程的三分之一，这时增加了乙队，两队又共同工作了半个月，总工程全部完成。

求乙队单独完成需要的时间。

归纳：解工程问题的基本思路是（1）。

（2）。

（3）。

练一练：1.甲、乙两个工程队共同完成一项工程，乙队先单独做1天后，再由两队合作2天就完成了全部工程。

已知甲队单独完成工程所需的天数是乙队单独完成所需天数的23，求甲、乙两队单独完成各需多少天？2.要在规定的日期内加工一批机器零件，如果甲单独做，刚好在规定日期内完成，乙单独做则要超过3天。

现在甲、乙两人合作2天后，再由乙单独做，正好按期完成。

问规定日期是多少天？3.一个工厂接了一个订单，加工生产720 t产品，预计每天生产48 t，就能按期交货，后来，由于市场行情变化，订货方要求提前5天完成，问：工厂应每天生产多少吨？4.甲、乙两班同学参加“绿化祖国”活动，已知乙班每小时比甲班多种2棵树，甲班种60棵所用的时间与乙班种66棵树所用的时间相等，求甲、乙两班每小时各种多少棵树？探讨2.如图，小明家、王老师家、学校在同一条路上。

小明家到王老师家的路程为3km，王老师家到学校的路程为0.5km。

由于小明的父亲战斗在抗击“非典”第一线，为了使小明能按时到校，王老师每天骑自行车接他上学。

已知王老师骑自行车的速度是步行速度的3倍，每天比平时步行上班多用20min。

新人教版八年级上《15.3.1分式方程(二)》导学案

15.3.1 分式方程(二)【学习目标】1.进一步了解分式方程的概念, 和产生增根的原因.2．掌握分式方程的解法，会解可化为一元一次方程的分式方程，会检验一个数是不是原方程的根.3．理解“增根”和“无解”不是一回事.【学习重点】：会解可化为一元一次方程的分式方程，会检验一个数是不是原方程的根.【学习难点】：掌握“增根”和“无解”不是一回事【知识准备】：【自主探究文】【探究一】解分式方程 .⑴11122x x =-- ⑵ 214111x x x +-=--【探究二】X 为何值时，代数式xx x x 231392---++的值等于2？【探究三】利用增根的性质解题。

若分式方程424-+=-x a x x 有增根，求a 的值【探究四】理解“增根”和“无解”.（一）已知分式方程有增根，确定字母系数的值。

例1.当a 为何值时，关于x 的方式方程349332+=-+-x x ax x 有增根？归纳:解决此类问题的一般步骤是：（1）把分式方程化为方程；（2）求出使最简公分母为的x 的值；（3）把x 的值分别代入整式方程，求出字母系数的值。

（二）已知分式方程无解，确定字母系数的值。

例2 若关于X 的分式方程132323-=-++--xmx x x 无解，求出m 的值。

【自测自结】1、方程2332x x =--的解是， 2、若x =2是关于x 的分式方程2372a x x +=的解，则a 的值为 3、解方程①2373226x x +=++ ②2512552x x x +=+-③3233x x x =--- ④ 2211566x x x x =+-++4.如果关于x 的方程7766x m x x --=--有增根，则增根为， 5.分式方程()2933x x x x x =+--出现增根，那么增根一定是( ) A ．0 B ．3 C ．0或3 D ．1通过本节课的学习，你有哪些收获？还有哪些困惑呢？。

人教版八年级数学上册《分式》导学案：分式方程(第二课时)

人教版八年级数学上册《分式》导学案分式方程（第二课时）【学习目标】1.了解分式方程增根的含义和产生增根的原因，并会检验分式方程的根；2.掌握分式方程的一般步骤，会解可化为一元一次方程的分式方程.【知识梳理】1.分式方程：分母中含有的方程叫分式方程.2.解分式方程的一般步骤：（1）去分母，即将分式方程的两边都乘，把分式方程转化为整式方程.（2）解这个 .（3）检验：将整式方程的根代入分式方程中分式的分母中，使分式方程中有的分母为零时，得到的是原方程的增根，应当舍去.（4）写出分式方程的根.3.分式方程的增根及产生增根的原因.因为解分式方程，所以解分式方程必须检验.口诀记忆法：同乘最简公分母，化成整式写清楚，求得解后需验根，原（解）留增（根）舍别含糊。

【典型例题】知识点一分式方程的解法1.解方程xx x x x x x 22222222--=-+-+2.x x 3251=-）（ 231322--=--xx x ）（知识点二分式方程的增根3.若关于x 的方程xx x k --=+-3423有增根，试求k 的值.4.若方程132323-=-++--xmx x x 无解，求m 的值.5.已知关于x 的分式方程（1）若分式方程有增根，求m 的值；（2）若分式方程的解是正数，求m 的取值范围．【巩固训练】1.分式方程21221933x x x -=--+的解为（） A.3 B.-3 C.无解 D.3或-32.下列关于分式方程增根的说法正确的是( )A.使所有的分母的值都为零的解是增根B.分式方程的解为零就是增根C.使分子的值为零的解就是增根D.使最简公分母的值为零的解是增根3.解分式方程4223=-+-xx x 时，去分母后得（） A.)2(43-=-x x B.)2(43-=+x x C.4)2()2(3=-+-x x x D.43=-x4.如果关于x 的方程无解，则m 的值等于（）A ．﹣3B ．﹣2C ．﹣1D ．35.若关于x 的分式方程的解为非负数，则m 的取值范围是（）A ．m ≤5B ．m ＜5且m ≠3C ．m ≠3D ．m ≤5且m ≠36.解分式方程：（1）23611y y -=+- （2）28142x x x +=-- （3）3215122=-+-xx x7.已知关于x 的方程+＝3 （1）当m 取何值时，此方程的解为x ＝3；（2）当m 取何值时，此方程会产生增根；（3）当此方程的解是正数时，求m 的取值范围．。

新人教版八年下《16.3分式方程》word导学案2篇

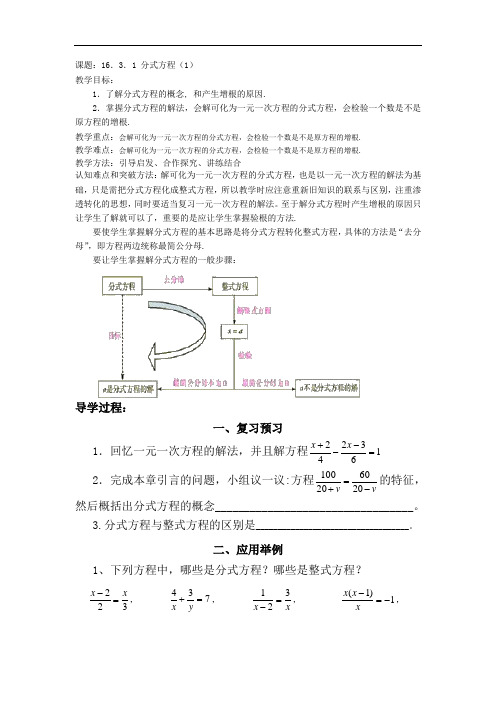
课题：16．3．1 分式方程（1）教学目标：1．了解分式方程的概念, 和产生增根的原因.2．掌握分式方程的解法，会解可化为一元一次方程的分式方程，会检验一个数是不是原方程的增根.教学重点：会解可化为一元一次方程的分式方程，会检验一个数是不是原方程的增根.教学难点：会解可化为一元一次方程的分式方程，会检验一个数是不是原方程的增根.教学方法：引导启发、合作探究、讲练结合认知难点和突破方法：解可化为一元一次方程的分式方程，也是以一元一次方程的解法为基础，只是需把分式方程化成整式方程，所以教学时应注意重新旧知识的联系与区别，注重渗透转化的思想，同时要适当复习一元一次方程的解法。

至于解分式方程时产生增根的原因只让学生了解就可以了，重要的是应让学生掌握验根的方法.要使学生掌握解分式方程的基本思路是将分式方程转化整式方程，具体的方法是“去分母”，即方程两边统称最简公分母.要让学生掌握解分式方程的一般步骤：导学过程：一、复习预习1．回忆一元一次方程的解法，并且解方程163242=--+x x 2．完成本章引言的问题，小组议一议:方程v v -=+206020100的特征，然后概括出分式方程的概念__________________________________。

3.分式方程与整式方程的区别是___________________________________。

二、应用举例1、下列方程中，哪些是分式方程？哪些是整式方程？322x x =-， 734=+yx ， x x 321=-， 1)1(-=-x x x ，23x x=-π， 10512=-+x x ， 21=-x x ， 1312=++x xx 2、探究：如何解方程v v -=+206020100 (1)、小组内讨论交流解法；（2）、在教师的引导下，师生共同探析。

方程两边同时乘以（20+v ）（20-v ）得100（20-v ）=60（20+v ）解得：v=5检验：将v=5代入分式方程，左边=4=右边【此步应强调，学生容易漏掉此步。

新人教版八年级数学上册《分式方程(2)》导学案

新人教版八年级数学上册《分式方程(2)》导学案最新人教版八年级数学上册《分式方程（2）》导学案
一、学习和教学目标：
1．进一步了解分式方程的概念,和产生增根的原因.
2.掌握分数阶方程的解法，能够解出可以转化为一维方程的分数阶方程，能够测试一个数
是不是原方程的根.
二、方程的关键点可以一次学习，
会检验一个数是不是原方程的根.
三、学习和教学难点：能够解可转化为一维一阶方程的分数阶方程，
会检验一个数是不是原方程的根.
四、知识回顾：
1、前面我们已经学习了哪些方程
2、整式方程与分式方程的区别在哪里？
__________________________________________________________.3、解分式方程的步骤是什么？
(1)____________________; (2)_____________________
(3)__________________________________. 4.求解分数阶方程（1）
五、例题讲解：1、解方程
[来源：科技网z | x | x | k]
x2?3xx2?4x?42、当x=时代数式2与的值互为倒数。

十、4x2？9.课堂练习：1
3、
3x3x？1x？1.2.22、x？2倍？236127536?? 2.4、 x？1x？1x？1x？1x？11? x2。

八年级数学下册 16.3.2 分式方程的应用导学案新人教版

八年级数学下册 16.3.2 分式方程的应用导学案新人教版一、课题16、3、2 分式方程的应用（1）编写备课组二、本课学习目标与任务：1、进一步熟悉分式方程的解法；2、会列分式方程解决实际问题。

三、知识链接：1、列方程（组）的关键是寻找问题中的____________________、2、八年级学生去距学校10千米的博物馆参观，一部分同学骑自行车先走，过了20分钟后，其余同学乘汽车出发，结果他们同时到达。

已知汽车的速度是骑车同学速度的2倍，求骑车同学的速度。

（1）此题中所包含的相等关系是：①____________________________________________________;②_____________________________________________________（2）若设骑车同学的速度为x千米/时，则汽车所用的时间为__________________小时，骑车同学所用的时间为______________________小时。

（3）列出方程，并解方程解答这一问题。

四、自学任务（分层）与方法指导：一、熟读课文，理解法则列分式方程解应用题的步骤及注意的问题二、看懂例题，尝试练习要在规定的日期内加工一批机器零件，如果甲单独做，恰好在规定的时间内完成；如果乙单独做，则要超过规定日期3天才能完成、现甲、乙两人合做2天后，再由乙单独做，正好按期完成，问规定日期是多少天？五、小组合作探究问题与拓展：为了方便广大游客到昆明参加浏览“世博会”，铁道部临时增开了一列南宁到昆明的直达快车、已知南宁到昆明铁路全长828km，一列普通列车与一列直达快车都由南宁开往昆明，直达快车的平均速度是普通列车平均速度的1、5倍，直达快车比普通列车晚出发2h，比普通列车早4h 到达昆明，求两车的平均速度、六、自学与合作学习中产生的问题及记录当堂检测题1、某化肥厂原计划每天生产化肥x吨，由于采取了新技术，每天多生产化肥3吨，实际生产180吨与原计划生产120吨的时间相等，那么适合x的方程是（）、A、B、C、D、2、一轮船先顺顺航行46千米再逆流航行了34千米,所用的时间恰好等于该船在静水中航行80千米所用的时间、已知水流速度是每小时3千米，设该船在静水中的速度是每小时x千米，则可列方程为（）、A、B、C、D、3、某工地调来72人挖土和运土，已知3人挖出的土1人恰好能全部运走，怎样调配劳动力才能使挖出的土能及时运走且不误工，解决此问题，可设派x人挖土，其他人运土、列方程：①；②③x+3x=72 ④、上述所列方程正确的有（）、A、1个B、2个C、3个D、4个4、部分学生自行组织春游，预计费用120元，后来又有2名学生参加，总费用不变，这样每人可少交3元，若设原来这部分学生的人数是x人，则可列方程为、5、从甲地到乙地有两条公路：一条是全长600km的普通公路，另一条是全长480km的高速公路，某客车在高速公路上行驶的平均速度比在普通公路上快45km/h。

八年级数学下册 16.3.1 分式方程导学案新人教版(2)

二、导
1、通过自学，能谈你对解分式方程的步骤了解吗？
2、教师补充点评。
三、探
下面分小组研究下怎么样来解分式方程：
1 ，怎样将分式方程化成整式方程？
2，能否解这个整式方程？
3，将解代入方程检验，能得到什么结果？
小组合作，完成后进行展示，班级交流归纳：
老师指导归纳内容；（特别强调培根，和格式要求）
四、当堂检测（老师进行个别指导）
五、评
1、小组总结并上黑板上展示
2、教师评价激励。
六、补Байду номын сангаас
1、学生针对本节内容自己纠错
2、学生在帮扶人过关检测。
3、拓展训练：
教学反思：
二次备课
（学生纠错）
16.3.1分式方程
上节作业反馈：
1．教学目标：分式方程的概念。解的一般步骤。分式方程验根的必要性。
2 .教学重难点：解分式方程的一般步骤，熟练掌握分式方程的解法
3.学法指导：分式方程化成整式方程解，特点是对根进行检验
导学过程：
1、学：
分式方程的定义：
分式方程的特征是什么：
练习：下列方程中哪些是分式方程？哪些是整式方程？

八年级数学下册 16.3 分式方程(第2课时)导学案新人教版

八年级数学下册 16.3 分式方程（第2课时）导学案新人教版【学习目标】1、掌握含有字母系数的分式方程的解法。

2、进一步了解分式方程产生增根的原因，理解分式方程若有增根，则增根一定是使分式的分母为0时的未知数的值。

3、能应用分式方程的解法进行简单的公式变形。

【重点难点】重点：含有字母系数的分式方程的解法。

难点：正确运用题设条件解含有字母系数的分式方程。

【导学指导】复习旧知：1、什么叫分式方程？2、解分式方程的一般步骤是什么？3、什么叫做分式方程的增根？为什么会产生增根？学习新知：1、从xx年9月起某列车平均提速v千米/时，用相同的时间，列车提速前行驶s千米，提速后比提速前多行驶50千米，提速前列车的平均速度为多少？分析：这里的v,s表示已知数据，设提速前列车的平均速度为x千米/时，则提速前列车行驶s千米所用的时间为小时，提速后列车的平均速度为千米/时，提速后列车运行s+50千米所用的时间为小时。

根据行驶时间的等量关系可以列出方程。

这里，x是未知数，字母s,v是已知数，上述方程是含有字母系数的分式方程。

2、如何解含有字母系数的分式方程呢？解分式方程；类似的，只把x当成未知数，s像300，v像10是已知数,我们可以解下面的含有字母系数的分式方程：300/x=300+50/x+10s/x=s+50/x+v【课堂练习】1、教材P32习题16、3第2题。

2、照相机成像应用了一个重要的光学原理，即1/f=1/u+1/v (f≠v)。

其中f表示照相机镜头的焦距，u表示物体到镜头的距离，v表示胶片（像）到镜头的距离。

如果一架照相机f已固定，那么就要依靠调整u,v来使成像清晰，问在f,v已知的情况下，怎样确定物体到镜头的距离u?【要点归纳】今天我们学习了哪些知识？你有什么收获？与同伴交流一下。

【拓展训练】1、当a为何值时，分式方程x/x-3=2 + a/x-3会产生增根？2、若1/2y+3y+7的值为1/8，求1/4y+6y-9的值。