第二章(8)2011.5.17
医生工作量统计(2011年5-12月)
一对一手法 一对一手法 马燕茹
第二周 工作量 工作量收入
姓名
马燕茹 马燕茹 李月萍 许幸妹
测评
一对一 手法
早综
合计 3000 3000 4350 4850
Hale Waihona Puke 300 100第二周 工作量 工作量收入
姓名
赵冬梅 赵冬梅 李月萍 许幸妹
650 1050 300 100
600 600
100 200
其它
0 0
其它
早综
合计 1700 2200 100 100 0 0
第一周 工作量 工作量收入
姓名
赵冬梅 赵冬梅 李月萍 许幸妹 刘启亮
500 700 100 100
900 900
300 600
其它
其它
第二周(2011.5.9—2011.5.15)
马燕茹
日期 2011.5.7 儿童姓名 李贞熹 内容 上门 分类 上门 操作人 马燕茹 费用 主管医生 备注 1000 马燕茹
2700 3000 300 0 0 0
1550 5000 2650 5000 0 0 0 0 0 0 0 0
魏汝强
内容 早综 早综 发育商 早综 早综 早综 早综 早综 早综 早综 早综 发育商 早综 一对一手法 指导 发育商 发育商 早综 发育商 分类 早综 早综 测评 早综 早综 早综 早综 早综 早综 早综 早综 测评 早综 一对一手 法 测评 测评 早综 测评 操作人 赵冬梅 赵冬梅 许幸妹 赵冬梅 赵冬梅 赵冬梅 赵冬梅 赵冬梅 赵冬梅 魏汝强 赵冬梅 赵冬梅 赵冬梅 赵冬梅 许幸妹 李月萍 刘启亮 许幸妹 费用 主管医生 备注 日期 2011.5.3 2011.5.3 2011.5.3 2011.5.5 2011.5.5 2011.5.5 2011.5.5 2011.5.7 2011.5.7 2011.5.7 2011.5.7 2011.5.7 2011.5.7 2011.5.7 2011.5.7 儿童姓名 许智涵 许博涵 许博涵 魏钰麒 马博文 张晨曦 彭可心 张振 尤嘉 张嘉懿 王艾糖 顾乐涵 孙瑞辰 孙瑞辰 孙瑞辰 内容 发育商 发育商 一对一手法指导 一对一手法指导 发育商 早综 早综 一对一手法指导 早综 发育商 发育商 早综 发育商 家庭环境 气质
高数(高等教育出版社)第一版,第二章习题详解参考

第二章习题解答参考习题2-11.设f (x )=8 x,试按定义求 f (1) .解2.设f1xf 1lim8 1x 8.f (1)= lim8x 0x x0x2bx c ,其中 a, b, c 为常数.按定义求 f (x ) .f (x )= ax解f xf x x f x= limxx022a x xb x xc ax cbx limxx02 ax x a x2 b x2 ax b .limxx03.证明(sin x ) = cos x .证设 f x sin x ,则 f x x f x sin x x sin x 2 cosx x x sin222 cos xsinxf x x f x x2f x lim 2limx x x0x0sin xx2lim cos x cos x,2x2x0所以(sin x ) = cos x .4.下列说法可否作为 f ( x )在 x 0可导的定义?f (x0 h ) f ( x 0h )( 1)limh 存在;h 0解不能.因为从极限式中不能判断 f x0存在,也不能判断lim f ( xh ) f (x)存在.h0h例如 f x x 在x0 点不可导,但lim f (0h ) f (0 h)h hlim0h 0h h0h却存在.( 2)lim f (x 0h)f (x)和lim f (x0h )f(x)存在且相等;h0h h 0h解可以.因为 lim f (x0h ) f ( x0 )f x0,hh0lim f ( x0h ) f ( x0 ) f ( x0h ) f ( x0)f x0,根据导数存在的充要h lim hh 0h0条件,可知 f x存在.5.求下列函数的导数:( 1)y x 5;(2)y1;(3)x232( 4)y log1x;(5)y x x;(6)3x 5解(1)y 5 x 5 1 5 x 4;y x37x ;y lg x .(2)(3)(4)1131y x 22;x2 2 x x221522 x2 7x;y x 722x 777y11;1x ln 3x ln3(5)(6)2511512y x 32x66x 66;56x 1y.x ln 106.已知物体的运动规律为s t 3(米),求这物体在 t2 (秒)时的速度.解因为 s t3, v ds3t 2,所以 t 2 时,v 2 3 2212 .dt7.如果 f ( x )为偶函数,且 f (0)存在,证明 f (0)=0.证因为 f(0)=lim f x f 0,而 f ( x ) 为偶函数,故 f (x ) f ( x) ,x0x所以 f (0)limf x f0f xf 0,0lim f (0)x x x 0x所以 f (0)=0.8.抛物线y x 2在哪一点的切线平行于直线y 4 x 5 ?在哪一点的切线垂直于直线 2 x 6 y50 ?解由 y x2,可得 y 2 x ,若切点为x0 , x 02,则依题设 2 x 0 4 ,即 x0 2时,切线平行于直线11 ,即 x03y 4 x 5 ; 2 x0时,切线垂直于直线322 x 6 y 50;所以抛物线切线垂直于直线y x2 在点 2 , 4 的切线平行于直线y 4 x 5 ?在点3,9的242 x 6 y 50 .9.在抛物线y x 2上取横坐标为x1 1 及 x2 3 的两点,作过这两点的割线,问该抛物线上哪一点的切线平行于这条割线?解由题设可知 y 2 x,所取的两点为 1,1, 3, 9 ,连接两点的直线斜率为 k 4 ,依题设,应有 2 x 4 ,即 x 2 ,所以所求点为2, 4.10. 如果y f x在点4, 3处的切线过点0, 2 ,求 f4.解依题设,曲线在点4, 3处的切线为 y3f4x 4 ,满足 2 3 f404,从而f 41.411.讨论下列函数在x0 处的连续性与可导性:x21x0,(1)y3 x ;(2)ysin,x0 ,x0.解( 1)因为lim 3 x0y0 ,所以 y 3 x在 x0 点连续,x03x1,所以 y3 x 在 x0 点不可导;而 limx lim2x 0xx 321(2)因为 limx 2 s in 1y 0 ,所以 yx sin x,x0, 在 x0 点连续,xx0 ,x0.211x sin12,x 0,又 limx0 ,所以 yx sinx 在 x0 点可导.lim x sinx 0 xxx0 ,x 0.12.设 f (x )=sin x , x 0在 x0 处可导,求 a, b 的值.axb , x 0解因为 f (x )=sin x , x0 处可导, axb , x在 x所以 lim f ( x)f0 ,且 ff,x 0又 limf ( x )0 , limf ( x )b , fb ,故 b0 , f0 ,x 0x从而 f 0lim fxf 0 lim sin x1 ,xxxx 0flimf xf 0limaxa ,所以 a1 .xxx 0x 0213.已知 f ( x)x , x 0,求 f (0), f(0) 和 f (0).x, x2f ( x)f 0x 2解因为 f ( x) x , x ,所以 f (0)limlim0 ,x, xxxx 0x 0f (0)f ( x)f 0 limx 1 ,所以 f(0) 不存在.limxxxx14.设函数 f ( x)=x 3 ,x 0 ,求 f (x ) .3xx ,解 当 x 0 时, f ( x )3 x 2 ,当 x 0 时, f ( x)3 x 2 ,当 x0 时, f (0)limf xf 0limx 3 0 ,xxxx 0f (0)lim f xf 0limx 3 0 ,所以 f(0)0 ,xxxx 02 所以 f(x )=3 x , x 0 .3 x 2 , x 015.设所给的函数可导,证明:(1)奇函数的导函数是偶函数;偶函数的导函数是奇函数;(2)周期函数的导函数仍是周期函数.证 (1)设 f x 为奇函数,则 fxfx ,而 ff xh f x,xlimhh 0fxlim fx hfxf x hf xhlimhhhf xhf xf x hfxx,limhlimhfhh 0所以 fx为偶函数;相似地,若 f x 为偶函数,则 fx f x,于是f xlimfxh fxfxhf xhlimhhh0lim f xhf xfx,所以 fx为奇函数.hh0(2)设 fx为周期函数,则存在 T ,使 f x Tf x,则fx Tf x Thf x Tf x hf xfx ,limhlimhhh所以 fx也是以 T 为周期的周期函数.16.设有一根细棒,取棒的一端作为原点,棒上任意点的坐标为x .于是分布在区间 [0, x ] 上细棒的质量 m 是 x 的函数 mm ( x ) .应怎样确定细棒在点 x 0 处的线密度(对于均匀细棒来说,单位长度细棒的质量叫这细棒的线密度)?解 设在 x 0 处的线密度为 x 0,给 x 0 以 x 的增量,则在区间 [ x 0 , x 0x ] 上细棒的平均线密度为m x 0x m x 0,x故x 0m x 0x m x 0mx 0 .limxx 017.证明: 双曲线 xy a 2 上任一点处的切线与两坐标轴构成的三角形的面积都等于 2 a 2 .222证由 xya 2可得 y a , x 0 ,于是 ya2 , x 0 ,若切点为x 0 ,a ,x 0xx则该点处的切线为ya 2a 2 xx 0 ,它与两坐标轴的交点分别为2 x 0 , 0,x 0x 02220, 2 a,所以所求三角形的面积为 S 12 x 02a2 a 2 .x 02x 018.设函数 f (x ) 在 x 0 处可导,试讨论函数 | f (x ) | 在 x 0 处的可导性.解因为函数 f(x ) 在 x0 处可导,所以 limf ( x)f 0f0 存在,xx而 fx 0 limf ( x)fxx,故x(1)若f ( 0 )f ( x)f 0f0 可知:f ( x ) f,其中xxxl i mx f,x,从而 f ( x )此时 fxlim x flimx f,x 0xxxx 0因此 | f ( x) | 在 x 0 点的左导数为f 0,右导数为 f,所以 |f ( x) | 在 x0 处可导的充要条件是 f 00 ;( 2)若 f (0)0 ,设 f (0)0 ,则 lim f ( x)f 00 ,由保号性定理,0 ,x当 x U 0,时, f x0 ,此时有 ff ( x)f 0f ( x )f 0x x 0limxlimxf,相似地,x 0x若 f (0)0 ,则 limf ( x)f 00 ,由保号性定理,0 ,当 xU 0,时,xf ( x)f 0f ( x )f 0f x0 ,此时有 fxx 0limxlimxf;xx 0总之,若 f ( x) 在 x 0处可导,则当 f (0)0 时, | f (x ) | 在 x 0 处可导;当f (0) 0时,| f (x ) | 在 x 0处可导的充要条件是 f 00 .习题2-21.求下列函数的导数:(1) (3) (5)(7)y 3cos2 x ;( 2) y 3 x4cos2 x ; (4) 2e y 3e4 x1 ;( 6) y1;( 8)xln xy4sin(3 t1) ;y( x 1) 5 ;yx;21x y(x 2x1)( x 1) 3 ;2ln x x 3(9) yx 3 e x sin x ;( 10) y 2 .3ln x x解( 1) y3 sin 2 x 2 x3 sin2 x 2 6 sin2 x;( 2) y 4 cos(3 t1) 3t 1 12 cos(3 t1) ;( 3)( 4)y 2e 3 x 3 x4 sin 2 x 2 x 6e 3 x 8 sin 2 x ;y5( x 1) 4 x1 5( x1)4 ;( 5) ( 6)( 7)y3e 4 x 4 x12e 4 x ;1 2x2 xxx 21y2 1;221 x1 21 xxln x1xln xxlnx 1yx;222xln xxln xxln x( 8) y32x 1) 3( x 2222 x 2;2 x 1 ( x 1)( x1)( x 1) 5 x( 9) y2x3 x3x 2xx sin xx cos x;3 x e sin x x e sin xx e cos x x e3sin x2 23ln x233 2 xx 3 xx2ln x xx x 9 x 4 ln x x42 ( 10)y3 x2 xx 2 223ln x3ln xx 22.证明:( 1) (cot x)csc 2 x;( ) (csc x )csc xcot x.2证(1)(cot x )cos x sin x sin x2cos x cos x csc2x ;sin x sin x(2)(csc x)1cos x1cos xcsc x cot x .2sin x sin xsin x sin x3.证明:( 1)(arccos x )1;(2)(arccot x)1.221x1 x证(1)设y arccos x ,则其反函数为 x cos y , y2,2,由于 x sin y ,由反函数求导法则,arccos x111;sin y12y12cos x(2)设y arc cot x ,则其反函数为 x cot y , y0,,由于 x csc 2y ,由反函数求导法则,arccos x111.csc212y12y cot x4.求下列函数在给定点处的导数:2(1)y 2 cos x 3 sin x ,求y xπ ;(2)y32x,求 f (2) .4x3解(1)因为y 2 sin x 3 cos x ,所以y xπ4ππ522 sin3 cos;442212 x22 x,所以 y2 2 210 .(2)因为y232x 223x3x33233 5.写出曲线y 2 x1与 x 轴交点处的切线方程.2 x解令 y0 ,得曲线 y 2 x1与 x 轴交点为1, 0和1, 0,2 x22而 y21,所以 y1 4 ,222 x所以所求切线有两条,方程分别为y 4 x 2 , y 4 x2.6.求下列函数的导数:( 1)y(2 x 23) 5;(2)y sin (5 2 x 2 ) ;( 3) ( 5) ( 7)( 9)y e 3 x 22 x 1 ;(4) y sin ( x 2 ) ;y cos 2 x ; (6) y a 2x 2 ;y arctane x ;(8) y ( arccos x ) 2 ; yln sin x ;(10) ylog a (x 31) .解 (1) y5 (2 x 23) 4 (2 x 2 3)20 x (2 x 2 3)4;( 2) ycos(5 2 x 2 ) (52 x 2 )4 x cos(5 2 x 2 ) ;( 3) y e 3 x 23 x 26 x 2 e 3 x22 x 12 x 12 x 1;( 4) y cos( x 2 ) ( x 2 ) 2 x cos( x2) ;( 5) y 2 cos x cos x2 cos x sin xsin 2 x;( 6) y1222 xx;2 a 2x 2a x2 a 2 x 2a 2x 21x( 7) y2exe2 x;e x11 e( 8)( 9)y2(arccos x)(arccos x)2(arccos x)12 arccos x ;122x1 xy1 cos x cot x ;sin xxsin xsin12( 10) y33 x.3 1) ln a ( x 1)( x 31) ln a ( x7.求下列函数的导数:(1)(3)(5)(7)(9)yarccos (1 2 x) ; ( 2) y y1ln x ; (4) y1ln xysin n x cos nx ; ( 6) yy e arctan x;(8) yy1 x 1 x ; (10)1 x1 xarcsin 1 ;x ln (xx 2a 2 ) ;1 sin2 x ; 1 sin 2 xln ln ( ln x) ;y arccot1 tan x .2 2解( 1) y121;(1 2 x )221 (12 x)x 1 x1 (12 x )( 2)( 3)y1 1 x 1x ;1x2x 222111xxx2x1 1ln x 1 lnx1x x2y22;1 ln xx 1 ln x12 x122122( 4) yx2 x a ;2 2xa2xx22 2xaxaxa( 5) yn sin n1xsin xcos nxsin n xsin nx nxn1cos x cos nxsin x sin nxn sin n 1 x cos n 1x;n sin x( 6) y11 sin2 x1sin 2 x1 sin2 x2sin 2 x112 cos 2 x 1sin 2 x1 sin2 x 2 cos 2 x1 sin2 x1sin 2 x 22sin 2 x112 cos 2 x2 cos 2 x; 1 sin 2 x 1sin 2 x 1 sin 2 xcos 2 x 1sin 2 x( 7) ( 8)( 9)arctan xarctan xarctanx1 y ee1 xx1 ln ( ln x)1 1y x ) ln ( ln x) ln xln ( lnln xarctanxe;2 1 xx1;x ln x ln ( ln x)111 x1x1x112 1 x 2 1 x1 x2 1 x 2 1 xy21 x1x1 x 1 x21 x1 x 121x2;221 x 1 x1 x 1 x1 x 1 x( 10)y11x41 2 x x1x2tan22sec2 122x2 tan24tan222xsec21.2x4tanx1223 cos28.设f ( x )1cos x ,x0,求 f x.ln (1 x )x cos x ,x0sin x,x0解当 x0 时, f (x )1cos x x sin x ,x0,1x2x x当 x 0 时,f(0)1cos x0lim 2 sin2lim sin x sin20 ,lim x x2xx0x0x02ln1x x cos x01f (0)lim ln1x cos x ln e 10 ,lim x xx0x0sin x ,x0所以 f00,从而 f(x )1cos x x sin x, x .1x0 9.求函数y( sin x ) cos x 的导函数.解法 1因为y( sin x ) cos x e cos x ln sin x ,所以 y e cos x lnsin x cos x ln sin x sin xcos xsin x ln sin x cos xcosxsin xsin x sin x ln sin x2x .cos xcossin x解法 2对数求导法,由 y( sin x) cos x,得 ln y cos x ln ( sin x ) ,两边同时对 x 求导,得ysin x ln sin x cos xcos x,y sin x所以 y sin x sin x ln sin x cos2x.cos xsin x10.设f(x )sin x , (x )x3,求 f [(x )] , f[(x )] , { f [(x )]}.解 因为 f (x )sin x , ( x) x 3 ,所以 f ( x)cos x ,(x ) 3 x2,所以 f [( x)] f 3 x 2 sin 3 x 2 ,f [( x )]cos( x )cos x 3,{ f [ ( x)]} sin x 3 cos x 3 x 3 3 x 2 cos x 3 .11.设 f ( x) 存在,求下列函数的导数:( 1) f n (cos x ) ; ( 2) cos n [ f ( x)] .解(1) nn 1(cos x)f (cos x )n 1f (cos x)nf nf(cos x ) f (cos x) cos xn sin xfn 1(cos x ) f (cos x ) ;(2) cos n [ f (x)]n cos n 1 [ f ( x)] cos [ f (x )]n cos n 1 [ f (x)] sin [ f ( x)] f xn 1[ f (x )] fx .n sin [ f ( x)] cos12. 求曲线 f x 2 sin x sin2所有具有水平切线的点.x解 因为 fx2 cos x 2 sin x cos x ,令 fx0 ,得 cos x 1sin x0 ,于是 cos x 0 ,或 sin x1 ,推得 x k, k Z ,或 x 2k3Z ,2, k2所以所求的点为2 k, 3 ,2k3 1 ,其中 k Z .,22习题2-31.求下列函数的二阶导数:(1)(3)ye3 x 5;(2) y 2x ln x ;(4) sinye t sin t;y tan x ;(5) yln( x4 x 2 ) ;( ) y (1 x 2 ) arctan x.6解 ( 1) y 3e 3 x 5 , y9e 3 x 5 ;(2) yetsin t e t cos t e t cos t sin t,yetsin te tsin t cos t2etcos tcos t ;2(3) y2 sin x cos x ln xsin 2 x 1ln xsin 2 xsin x ,xxsin 2 x2sin x cos xx sin2y ln x 2 cos 2 x xxx22 sin 2 x22 x ln xsin x ;x 2 cosx 2(4)(5)22 sec x sec x tan x2ysec x , y2 sec x tan x ;112 x1y,x4 22 4x 24 2xx13xy4x 222 x;2423x(6) y2 x arctan x1 , y2 arctan xx.21x2. y x 3 e x,求 y ( 5 )(0).解设 u x 3 , v e x,则 u3 x 2 , u 6 x , u6 , u n 0, n 4 ; v ne x , n N ,代入莱布尼兹公式,得y ( 5 )u 5 v5 u 4 v 10 u v10 u v5u v 4uv 510 6e x10 6 xe x5 3 x 2e xx 3 e x ,所以(5 )60.y (0)3. yx 2 e 2 x ,求 y ( 20 ) .解 设 ux 2 , v e 2 x , 则 u2 x , u2 , u n0,n 3 ; v n2 n e 2 x , n N,20181920代入莱布尼兹公式,得y ( 20 )C 20k u nkv kC 202C 201 C 200 u vu vuvk 0190 2 218 e 2 x C 201 2 x 219 e 2 x C 200 x 2 2 20 e 2 x2 20 e 2 x95 20 xx 2 .4.试从dx1导出:( 1)d 2 xy3;(2)d 3 x3( y ) 2y y.2( y ) d y 35dy yd y( y )解因为d x1,所以 d 2 x d 1 d 1 dx y 1y 3,d yy2dy ydx ydyy2yd yy3dydy dxd x3dyy 3dx3dydyy322yy y 3 yy13 yy y.6y5yy5.证明:函数 y C 1e xC 2 ex( ,C 1 , C 2 是常数)满足关系式 y2y 0 .解 因为 y C 1 e xC 2 ex,所以所以xxxx2x2xyC 1 eC 2eC 1eC 2 e, yC 1 e C 2 e,y2y2C 1e x 2C 2 ex2C 1 e x C 2 ex0 .6. 求常数 的值,使得函数 ye x 满足方程 y5 y6 y.解 因为 ye x ,所以 y ex, y2ex,代入方程 y5 y6 y 0 , 得256 e x0 ,因为 e x0,xR ,所以256,解得 1 6 , 21 .7. 设 fxsin xa , g xb sin xc cos x ,求常数 b, c 的值,使得f 0g 0,且 f 0g0 .解 因为 fxsin x a, g xb sin xc cos x ,所以 f x cos x a, g xb cos xc sin x ,所以由 f 0g 0, f 0g 0,可得 c sin a ,且 bcos a .8.求下列函数的 n 阶导数.(1) y x na 1 x n 1 a 2 x n 2a n 1 x a n ( a 1 , a 2 , a n 是常数);(2) y xe x ;(3) ysin 2 x ; (4) yx 2 16.5 x解(1) yn 1n 1 a 1 xn 2n 3a n 1 ,nxn 2 a 2 xn 2n 3n 4a ,根据幂函数的导数公式特点:每求导一次,幂函数降一次幂,故y n n ! .(2)y e x xe x e x x 1 , y e x x 1 e x e x x 2,yxx2x xx 3 ,由此可见,每求一次导数,增加一个e x,e e e所以n xx n, n N;y e(3)y sin 2 x1cos 2 x11cos 2 x,222y 2 sin x cos x sin 2 x cos 2 x2,y 2 cos 2 x 2 cos 2 x22,y 2 2sin 2 x 2 2cos 2 x32,42 3cos 2 x23 cos 2 x4,y2所以n2n1 cos 2 x n, n N .y2(4)因为y111,x 2 5 x6x3x2而1x32112x3,x3,x331123x34x3,1n可见,123n x n 11nx3n1x33n !,1n同理,123n x n11nx2n1x22n !,所以n n n1n1n 11.y 1 n ! x 3x 2 1 n !x3n 1xn 12习题2-41.求由下列方程所确定的隐函数的导数d y :d x(1) x y e xy0 ; (2) 2 x 2 y xy 2 y 30 ;(3) e xyy ln xsin 2 x ;( ) xya( a 0 的常数).4解( 1)将方程两边同时对 x 求导,得dydydy ye xyxy,变形得:1;1ey x0 dx1xydx dxxe(2)将方程两边同时对 x 求导,得2dyy2dy2dy 0,2 2 xy xx 2 y3 ydxdx dx变形整理得:dy224 xy y 2;dx2 x 2 xy3 y(3)将方程两边同时对 x 求导,得e xyy xdydyln xy 2 cos 2 x ,dxdxx变形整理得:dy2 x cos 2 xyxy exy;dxx ln x 2xyx e(4)将方程两边同时对 x 求导,得11dy ,2 x2y dx变形整理得:dyy, x.dxx2.求曲线 x 2 y 52 xy0 在点 (1,1) 处的切线方程.解将方程两边同时对 x 求导,得: 2 x5 y 4 dy2 yx dy0 ,dx dx将 x1 , y 1 代入,解得:dy1,10 ,dx所以曲线在点 (1,1) 处的切线方程为: y1 .3.已知 y sinx cos( xy )0 ,求隐函数 yy x 在点 0, π的导数值.2解将方程两边同时对 x 求导,得:dyy cos xsin( x y ) dy ,sin x1dxdx将 x0 , y2 代入,解得: dy1.dx0,222 4.求下列方程所确定的隐函数的二阶导数 d y .dx 2(1) y tan( x y ) ; (2) y 1x e y ;(3) y lny xy ;(4) arctany ln x 2 y 2 .x解(1)将方程两边同时对 x 求导,得:dysec 2 ( xy ) 1dy,dxdx解得dycsc 2 ( xy ) ,dxd 2dy再求导,得:y2 csc( xy)csc( xy ) cot xy,21dxdx将 dy2csc 2( xy) 代入,整理得:d y2 csc 2 ( x y) cot3 xy ;dxdx 2(2)将方程两边同时对 x 求导,得:dye yx e y dy,dxdxe y dy1 xe ye ye yx e y dy解得:dyy,再求导,得: d 2 y dxdxe y 2y2,dx1xedx1xedy y22 y2 xe y2 y3 y将 e代入,整理化简得:d yeey2y 33;dx1 xedx12 yxe(3)将方程两边同时对 x 求导,得:dyln ydy 1 dy , dxdxdx1 dy解得:dy1d 2 yy dx 2 ,,再求导,得: 2dxln y dxln y将 dyd 2 y13;1代入,整理化简得:2ydx ln ydx ln ydyxy2 x 2 ydy(4)将方程两边同时对 x 求导,得:1dx1 dx,y 2222y 21xxx1dy x yx y 1dy解得:dy x y,再求导,得:d 2 ydxdx,dxx ydx 22x y222将 dyx y代入,整理化简得:dy 2 xy.3dxxydx 2xy5.用对数求导法求下列函数的导数:(1) y(sinx) cos x ;(2) y(tan 2 x ) x;x x(3) y;(4) y (2 x 1) x (3 x 1) x 1 .1 x解 ( 1)两边取自然对数,得: ln ycos x ln(sin x ) ,两边同时对 x 求导,得:1 dysin x ln sin xcos x cos x ,y dxsin x整理化简得:dy(sin x) cos xsin x ln sin xcos x cot x ;dx(2)两边取自然对数,得: ln y x ln(tan2 x ) ,两边同时对 x 求导,得:1dy ln(tan 2 x )xsec 2 2 x2tan 2 x ,y dx整理化简得:dy(tan 2 x) xln(tan 2 x)4 x ;dxsin 4 x(3)两边取自然对数,得: lny x lnx x ln xln1 x,1x两边同时对 x 求导,得:1dy ln x ln 1 xx 1 1 1 y dxxxx整理化简得:dyx ln x x1 1;dx1 x1 x(4)两边取自然对数, 得: ln yln(2 x1)1x1ln(3 x1)1 x1 ,ln 4 ln28两边同时对 x 求导,得:1 dy2 1 131)81, y dx 2 x 2 x 4(3 x x 1整理化简得:dy(2 x1) x(3 x1) x 12 1 1 31) 8 11dx2 x 2 x 4(3 x x 6.求下列参数方程所确定的函数的导数d y : d x2 atxa cos btb sin atxt21 ( a 为常数).(1)( a , b 为常数); (2)2ya sin btb cos ata (1 )ty1t2解(1)因为dxab sinbtab cosat ,dyab cosbtab sinat,dtdt所以d yab cos btab sin atcos btsin at;d xab sin btab cos atsinbtcos at2 a 1 t22 at 2t2(2)因为dx2 a 1 t,22dt1212ttdy2at 1 2a (1 2) 2 t4 atttdt221 t 21 2t所以dy1 2 t 2 t .dxt 2 t 2 17.求曲线x tet1 在 t0 处的切线方程与法线方程.t 2 )ey (2 t t解 因为 dxe tte t , dy2 2 t e t(2 t t 2 )e t ,dtdt所以dy2 t 2 , dyt 02 ,又 x t 0 1, y t 0dx1 tdx故所求切线为: y2 x 1,法线为:y1 x 1 . 28 . 已 知曲 线 x2n在 ttm t0 时过原点,且在该点处的切线与ype t2e2 x3 y5 0 平行,求常数 m , n, p .解 因为 dxm ,dyp e t ,故dyt2 tp e ,dtdtdx2t m由题设可知: x tn0 , yt 0p2e0 ,dyt 0p 2 ,dxm3所以所求常数为: n0 , p2e, m3e .注:此题的书后答案有误.29.求下列参数方程所确定的函数的二阶导数 dy :d x 2(1)x1 t 2;(2)xe t cos t ;y tt 3yte sin tx ln 12xf ( t )t;(4)( f(t ) 存在且不为零).(3)y tf ( t )f (t )yt arctan t( 1)因为dx2 t ,dy,所以dy13 t 21 3t , 解13t 2dt dtdx2 t2t221 322于是 d yd13t dt2t 21 3t;2dt2 t2dx2 t3dx4t(2)因为dxe tcos te tsin t ,dye t sin t e t cos t ,dtdt所以dye t sin te t cos tsin t cos t ,于是dxt cos t tsin tcos tsin te ed 2 yd sin tcos tdt cos tsin 2sin t2 1tcos t2dtcos tsin tdxcos tsin 2tcos ttsin tdxte e2;e tcos tsin t 311dx2tdy1dy12t1,1t(3)因为 dtt 2dt1t 2 ,所以dx2 t2 ,1 t 221221于是 d yt;22 t4 tdx1 t 2(4)因为dxf( t ) ,dyf ( t ) tf ( t )f (t ) tf (t ),所以dyt ,dtdtdx于是 d 2 y1.2f (t )dx10.将水注入深 8 米、上顶直径 8 米的正圆锥形容器中,注水速率为4 吨/分钟.当水深为 5 米时,其表面上升的速率为多少?解 如图所示,设在 t 时刻容器中水面的高度为h t(米),此时水面的半径为 rt(米),则依题意应有1 r 2t h t4 t ,而h tr t , 384所以 1h 3 t4t ,两边同时对时间 t 求导,12可得1h2t dh4 ,当 h t5 时,可求得dh16 , 4dt dt2516 所以当水深为 5 米时,其表面上升的速率为m m in .2511.汽车 A 以 50 公里 / 小时的速度向西行驶,汽车 B 以 6 0 公里 / 小时的速度向北行驶,两辆车都朝着两条路的交叉口行驶. 当汽车 A 距离交叉路口 0.3 公里,汽车 B 距离交叉路口 0.4 公里时,两辆车以什么速率接近?解 如图所示,设在 t 时刻,汽车 A 距离交叉路口x t ,汽车 B 距离交叉路口 y t ,则两车之间的直线距离为 st x 2y 2t t ,两边同时对时间 t 求导,可得x tdxy dytdxdydsdtdt60 ,,依题意可知 50 ,dt2y 2dtdtx t t故当 x t0.3 , y t0.4 时,ds 0.350 0.4 6078 ,即当汽车 A 距离交叉dt0.32 20.4路口 0.3 公里,汽车 B 距离交叉路口 0.4 公里时,两辆车以78 km / h 的速率接近.12.一个路灯安装在 1 5 英尺高的柱子上, 一个身高为6 英尺的人从柱子下以5 英尺/秒的速度沿直线走离柱子,当他距离柱子4 0 英尺时,他身影的顶端以多快的速率移动?解 如图所示,设在 t 时刻,此人离灯柱的水平距离为x t,身影的顶端离灯柱的水平距离为y t,则依题意有:dx,6y tx t5,515,可见y tx tdt y t3两边同时对时间 t 求导,得dy5dx25 ,dt3dt3所以他身影的顶端以25 feet / s 的速率移动,与他离灯柱的水平3距离无关,只与他的前进速度、身高、灯柱高有关.习题2-51.函数y x2,求当 x 1 ,而 x0.1 , 0.01 时,y 与 d y 之差是多少?解当 x 1 , x0.1 时,y20.21, d y 2 x x0.2 ,1.11所以y dy0.01;当x 1 ,x0.01时, y 1.01 210.0201, d y 2 x x0.02 ,所以y dy0.0001;2.求函数y x2x 在 x 3 处, x等于 0.1 , 0.01时的增量与微分.解因为 y x 2x ,所以dy 2 x1x ,当 x 3 , x0.1 时,2 3.1230.71, dy0.7;y 3.13当 x 3 , x0.01 时,y 3.012 3.0120.0701, dy0.07 .333.函数y x 3x ,求自变量x由 2变到 1.99时在 x 2 处的微分.解因为y3x ,所以 dy21x ,x 3 x当 x2, x0.01 时, dy3210.010.11 .24.求下列函数的微分(1)(3)(5)y x 2 x 2 1 x3x 4;( 2)3yx;( 4)1 x2y3ln cos x;( 6)y xe x2;y tan 2 (1x 2 ) ;y e ax sin bx .23解(1)dy 1 4 x x 4 x dx ;x 2x 22x 2x 2x 2 2;( 2) dy e dx xe dxe dx xe2 x dx e1 2 x dx22221 x dx xd 1 x1 x dx x2 x dx( 3) dy1 xdx ;2221 2121 2xxx( 4) dy2 tan(12) d tan(1 x22 tan(1x 222) d (12x )) sec (1x x )4 x tan(12) sec 22;x (1 x ) dx( 5) dy 3 ln cos x ln 3dln cos x3 ln cos x ln 31 d cos xcos xln cos x3ln 3 tan xdx ;( 6) dyaxax sin bxaxcos bx d bxaxa sin bxb cos bxdx .e d e e5.将适当的函数填入下列括号内,使等式成立:(1) d( ) sintd t ;( 2) d()(3) d ( )x;( 4) d ( )d x1 x2(5) d ( ) x 2( 6) d ()xe d x ;23 xd x ;secd x;x 2a 2ln xd x .x解(1)1 cost;( )1tan 3 x ;( ) 1x 2;233(4) 1arctanx ;(5) 1e x ;(6) 1l n 2 x .2aa 226.某扩音器的插头为圆柱形,其截面半径r 为 0.15 厘米,长度 L 为 4 厘米,为了提高它的导电性能,要在圆柱的侧面镀一层厚度为 0.001 厘米的铜,问每个插头约需要多少克纯铜?(铜的密度为8.9 克/ 立方厘米,3.1416 )解因为圆柱形的扩音器插头的体积为Vr2L ,侧面镀层的体积约为VdV2 rLr ,当 r 0.15 , r 0.001L4时, V32 3.1416 0.15 4 0.0013.7699210 ,,故所需铜的重量约为 m3.769921030.03355克.8.97.设有一凸透镜,镜面是半径为R 的球面,镜面的口径为 2h ,若 h 比 R 小h 2 得多,试证明透镜的厚度 D.2 R解如下图所示,镜面半径 R 、镜面口径 2h 、透镜厚度 D 之间有关系:h 222,化简得: h22RDD20 ,R DR2R4R 2 4 h 2h 得: DR R 12R2 2,若 h 比 R 小得多,则1 h 21h 2,22 R 2R222故DRR1hR R 1h h .R 22 R 22 R8.利用微分求下列函数值的近似值(1);(2);(3); ( 4) e 1.01 ;( )26 ;( ) 3 .996cos 59tan 46lg 1156解 (1) cos 59coscoscossin6013 18033180130.5151 ;2 2180( 2) tan 46 tan 0tantan245141804sec18041 21801.0349;( 3) lg 11 lg 10 1lg 10111.0434;10 ln 10( 4) e1.01e1 0.01ee 0.01 2.7455;( 5) 2625 1251 15.1 ;22512(6) 3 996310004310001000349.9867 .39.当 | x | 较小时,证明下列近似公式:( 1) sin x x ; (2) (1x )1x ; ( 3) ln(1 x ) x .解 (1)设 fx sin x ,则 fxcos x ,当 | x | 较小时, fxsin xsin 0 cos 0 xx ,所以 sin x x ;( 2)设 f x(1 x) ,则 fx1(1 x )当 | x | 较小时, f x(1 x ) f 1f 1 x1x ,所以 (1x )1x ;(3)设 f x ln(1 x) ,则 fx1,1x当 | x | 较小时, f xln(1 x ) f 1 f 1 x x ,所以 ln(1x )x .习题2-61. 一飞机在离地面 2000 米的高度,以 200 公里 / 小时的速度飞临某目标之上空,以便进行航空摄影.试求飞机飞至该目标上方时摄影机转动的速度.解 如右图示意,A 为摄影目标,B 为其正上方的点,设 t 时刻飞机离 B 点的水平距离为 x t ,摄影机镜头 C 与 A 点连线与飞机的水平飞行方向成夹角,则co tx t , xtx200000t ,两边同时对时间20003600t 求 导 , 可 得 csc 2d1 dx t1, 即dt 2000 dt36d 1,当飞机飞至该目标上方时,,dtsin2362代入解得:d1 360 5rad / s .dt36 22. 一架飞机着陆的路径如图 2-11 所示,并且满足下列条件:(ⅰ)降落点为原点, 飞机开始降落时水平距离为 l ,飞行高度为h .(ⅱ)在整个降落过程中, 飞行员必须使飞机保持恒定的水平速度 v .(ⅲ)垂直方向的加速度的绝对值不能超过常数 k (必须比重力加速度小很多) .3图 2-11( 1) 求一个三次多项式 P x2ax bxcx d ,通过在开始降落和着陆的点对P x 和 P x施加一定的条件限制,使它满足条件。
概率论与数理统计第二章课后习题答案

概率论与数理统计课后习题答案第二章1.一袋中有5 只乒乓球,编号为1,2,3,4,5,在其中同时取3只,以X 表示取出的3只球中的最 大号码,写出随机变量X 的分布律. 【解】353524353,4,51(3)0.1C 3(4)0.3C C (5)0.6C X P X P X P X ==========2.设在15只同 类型零件中有2只为次品,在其中取3次,每次任取1只,作不放回抽样,以X 表示取出 的次品个数,求: (1) X 的分 布律;(2) X 的分 布函数并作图; (3)133{},{1},{1},{12}222P X P X P X P X ≤<≤≤≤<<.【解】313315122133151133150,1,2.C 22(0).C 35C C 12(1).C 35C 1(2).C 35X P X P X P X ========== 故X 的分布律为(2) 当x <0时, F (x )=P (X ≤x )=0当0≤x <1时 ,F (x )=P (X ≤x )=P (X =0)=2235当1≤x <2时 ,F (x )=P (X ≤x )=P (X =0)+P (X =1)=3435当x ≥2时, F (x )=P (X ≤x )=1 故X 的分布函 数0,022,0135()34,12351,2x x F x x x <⎧⎪⎪≤<⎪=⎨⎪≤<⎪⎪≥⎩(3)3.射手向目标独立 地进行了3次射击,每次击中率为0.8,求3次射击中击中目标的次数的分布律及分布函 数,并求3次射击中至少击中2次的概率. 【解】设X 表示击中目标的次数.则X =0,1,2,3.31232233(0)(0.2)0.008(1)C 0.8(0.2)0.096(2)C (0.8)0.20.384(3)(0.8)0.512P X P X P X P X ============故X 的 分布律为分布函数0,00.008,01()0.104,120.488,231,3x x F x x x x <⎧⎪≤<⎪⎪=≤<⎨⎪≤<⎪≥⎪⎩(2)(2)(3)0.896P X P X P X ≥==+==4.(1) 设随机变量X 的分布律为P {X =k }=!k akλ,其中k =0,1,2,…,λ>0为常数,试确定常数a .(2) 设随机变量X 的分布律为P {X =k }=a/N , k =1,2,…,N ,试确定常数a . 【解】(1) 由分布律的性质知1()e !kk k P X k a a k λλ∞∞======∑∑故 e a λ-=(2) 由分布律的性质知111()NNk k aP X k a N======∑∑即 1a =.5.甲、乙两人投篮,投中的概率分别为0.6,0.7,今各投3次,求: (1) 两人投中次数相等的概率; (2) 甲比乙投中次数多的概率.【解】分别令X 、Y 表示甲、乙投中次数,则X~b (3,0.6),Y~b (3,0.7)(1)(3,3)P X Y ==33121233(0.4)(0.3)C 0.6(0.4)C 0.7(0.3)=++22223333C (0.6)0.4C (0.7)0.3(0.6)(0.7)+0.32076=(2)=0.2436.设某机场每天有200架飞机在此降落,任一飞机在某一时刻降落的概率设为0.02,且设各飞机降落是相互独立的.试问该机场需配备多少条跑道,才能保证某一时刻飞机需立即降 落而没有空闲跑道的概率小于0.01(每条跑道只能允许一架飞机降落)?【 解】设X 为某一时刻需立即降落的飞机数,则X ~b (200,0.02),设机场需配备N 条跑道,则有()0.01P X N ><即 2002002001C (0.02)(0.98)0.01k k kk N -=+<∑利用泊松近似2000.02 4.np λ==⨯=41e 4()0.01!kk N P X N k -∞=+≥<∑ 查表得N ≥9.故机场至少应配备9条跑道.7.有 一繁忙的汽车站,每天有大量汽车通过,设每辆车在一天的某时段出事故的概率为0.000 1,在某天的该时段内有1000辆汽车通过,问出事故的次数不小于2的概率是多少(利用泊 松定理)? 【解】设X 表示出事故的次数,则X ~b (1000,0.0 001)8.已知在五重贝努里试验中成功的次数X 满足P {X = 1}=P {X =2},求概率P {X =4}. 【解】设在每次试验中成功的概率为p ,则故所以 4451210(4)C ()33243P X ===. 9.设事件A 在每一次试验中发生的概率为0.3,当A 发生不少于3次时,指示灯发出信号, (1) 进行了5次独立试验,试求指示灯发出信号的概率; (2) 进行了7次独立试验,试求指示灯发出信号的概率. 【解】(1) 设X 表示5次独立试验中A 发生的次数,则X ~6(5,0.3)5553(3)C (0.3)(0.7)0.16308kk k k P X -=≥==∑(2) 令Y 表示7次独立试验中A 发生的次数,则Y~b (7,0.3)7773(3)C (0.3)(0.7)0.35293k k k k P Y -=≥==∑10.某公安局在长度为t 的时间间隔内收到的紧急呼救的次数X 服从参数为(1/2)t 的泊松分布,而与时间间隔起点无关(时间以小时计).(1) 求某一天中午12时至下午3时没收到呼救的概率; ( 2) 求某一天中午12时至下午5时至少收到1次呼救的概率. 【解】(1 )32(0)eP X -== (2) 52(1)1(0)1e P X P X -≥=-==-11.设P { X =k }=kkkp p --22)1(C , k =0,1,2P {Y =m }=mm m p p --44)1(C , m =0,1,2,3,4 分别为随机变量X ,Y 的概率分布,如果已知P {X ≥1}=59,试求P {Y ≥1}. 【解】因为5(1)9P X ≥=,故4(1)9P X <=. 而 2(1)(0)(1)P X P X p <===-故得 24(1),9p -= 即 1.3p =从而 465(1)1(0)1(1)0.8024781P Y P Y p ≥=-==--=≈ 12.某教科书出版了2000册,因装订等原因造成错误的概率为0.001,试求在这2000册书中恰有5册错误的概率.【解】令X 为2000册书中错误的册数,则X~b (2000,0.001).利用泊松近似计算,20000.0012np λ==⨯=得 25e 2(5)0.00185!P X -=≈= 13.进行某种试验,成功的概率为34,失败的概率为14.以X 表示试验首次成功所需试验的次数,试写出X 的分布律,并计算X 取偶数的概率. 【解】1,2,,,X k =113()()44k P X k -==(2)(4)(2)P X P X P X k =+=++=+321131313()()444444k -=++++213141451()4==- 14.有2500名同一年龄和同社会阶层的人参加了保险公司的人寿保险.在一年中每个人死亡的概率为0.002,每个参加保险的人在1月1日须交12元保险费,而在死亡时家属可从保险公司领取2000元赔偿金.求: (1) 保险公司亏本的概率;(2) 保险公司获利分别不少于10000元、20000元的概率. 【解】以“年”为单位来考虑.(1) 在1月1日,保险公司总收入为2500×12=30000元. 设1年中死亡人数为X ,则X~b (2500,0.002),则所求概率为(200030000)(15)1(14)P X P X P X >=>=-≤由于n 很大,p 很小,λ=np =5,故用泊松近似,有514e 5(15)10.000069!kk P X k -=>≈-≈∑(2) P (保险公司获利不少于10000)(30000200010000)(10)P X P X =-≥=≤510e 50.986305!kk k -=≈≈∑ 即保险公司获利不少于10000元的概率在98%以上P (保险公司获利不少于20000)(30000200020000)(5)P X P X =-≥=≤55e 50.615961!kk k -=≈≈∑ 即保险公司获利不少于20000元的概率约为62%15.已知随机变量X 的密度函数为f (x )=A e -|x |, -∞<x <+∞,求:(1)A 值;(2)P {0<X <1}; (3) F (x ). 【解】(1) 由()d 1f x x ∞-∞=⎰得||01e d 2e d 2x x A x A x A ∞∞---∞===⎰⎰故 12A =. (2) 11011(01)e d (1e )22x p X x --<<==-⎰(3) 当x <0时,11()e d e 22x x x F x x -∞==⎰当x ≥0时,0||0111()e d e d e d 222x x x x x F x x x x ---∞-∞==+⎰⎰⎰11e 2x -=-故 1e ,02()11e 02xx x F x x -⎧<⎪⎪=⎨⎪-≥⎪⎩16.设某种仪器内装有三只同样的电子管,电子管使用寿命X 的密度函数为f (x )=⎪⎩⎪⎨⎧<≥.100,0,100,1002x x x求:(1) 在开始150小时内没有电子管损坏的概率; (2) 在这段时间内有一只电子管损坏的概率; (3) F (x ). 【解】(1) 15021001001(150)d .3P X x x ≤==⎰33128[(150)]()327p P X =>==(2) 1223124C ()339p == (3) 当x <100时F (x )=0当x ≥100时()()d xF x f t t -∞=⎰100100()d ()d x f t t f t t -∞=+⎰⎰2100100100d 1xt t x==-⎰ 故 1001,100()0,0x F x xx ⎧-≥⎪=⎨⎪<⎩ 17.在区间[0,a ]上任意投掷一个质点,以X 表示这质点的坐标,设这质点落在[0,a ]中任意小区间内的概率与这小区间长度成正比例,试求X 的分布函数. 【解】 由题意知X ~∪[0,a ],密度函数为1,0()0,x af x a⎧≤≤⎪=⎨⎪⎩其他 故当x <0时F (x )=0 当0≤x ≤a 时01()()d ()d d xx xx F x f t t f t t t a a-∞====⎰⎰⎰当x >a 时,F (x )=1即分布函数0,0(),01,x x F x x a a x a<⎧⎪⎪=≤≤⎨⎪>⎪⎩ 18.设随机变量X 在[2,5]上服从均匀分布.现对X 进行三次独立观测,求至少有两次的观测值大于3的概率. 【解】X ~U [2,5],即1,25()30,x f x ⎧≤≤⎪=⎨⎪⎩其他 5312(3)d 33P X x >==⎰故所求概率为22333321220C ()C ()33327p =+=19.设顾客在某银行的窗口等待服务的时间X (以分钟计)服从指数分布1()5E .某顾客在窗口等待服务,若超过10分钟他就离开.他一个月要到银行5次,以Y 表示一个月内他未等到服务而离开窗口的次数,试写出Y 的分布律,并求P {Y ≥1}. 【解】依题意知1~()5X E ,即其密度函数为51e ,0()50,xx f x -⎧>⎪=⎨⎪≤⎩x 0 该顾客未等到服务而离开的概率为25101(10)e d e 5x P X x -∞->==⎰2~(5,e )Y b -,即其分布律为225525()C (e )(1e ),0,1,2,3,4,5(1)1(0)1(1e )0.5167kk k P Y k k P Y P Y ----==-=≥=-==--=20.某人乘汽车去火车站乘火车,有两条路可走.第一条路程较短但交通拥挤,所需时间X 服从N (40,102);第二条路程较长,但阻塞少,所需时间X 服从N (50,42). (1) 若动身时离火车开车只有1小时,问应走哪条路能乘上火车的把握大些? (2) 又若离火车开车时间只有45分钟,问应走哪条路赶上火车把握大些? 【解】(1) 若走第一条路,X~N (40,102),则406040(60)(2)0.977271010x P X P Φ--⎛⎫<=<== ⎪⎝⎭若走第二条路,X~N (50,42),则506050(60)(2.5)0.993844X P X P Φ--⎛⎫<=<== ⎪⎝⎭++故走第二条路乘上火车的把握大些.(2) 若X~N (40,102),则404540(45)(0.5)0.69151010X P X P Φ--⎛⎫<=<== ⎪⎝⎭若X~N (50,42),则504550(45)( 1.25)44X P X P Φ--⎛⎫<=<=- ⎪⎝⎭1(1.25)0.1056Φ=-= 故走第一条路乘上火车的把握大些.21.设X ~N (3,22),(1)求P{2<X≤5},P{-4<X≤10},P{|X|>2},P{X>3}; (2)确定c使P{X>c}=P{X≤c}.【解】(1)23353(25)222XP X P---⎛⎫<≤=<≤⎪⎝⎭11(1)(1)1220.841310.69150.5328ΦΦΦΦ⎛⎫⎛⎫=--=-+⎪ ⎪⎝⎭⎝⎭=-+=433103(410)222XP X P----⎛⎫-<≤=<≤⎪⎝⎭770.999622ΦΦ⎛⎫⎛⎫=--=⎪ ⎪⎝⎭⎝⎭(||2)(2)(2)P X P X P X>=>+<-323323222215151122220.691510.99380.6977X XP PΦΦΦΦ-----⎛⎫⎛⎫=>+<⎪ ⎪⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫⎛⎫=--+-=+-⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭=+-=333(3)()1(0)0.522XP X PΦ->=>=-=-(2) c=322.由某机器生产的螺栓长度(cm)X~N(10.05,0.062),规定长度在10.05±0.12内为合格品,求一螺栓为不合格品的概率.【解】10.050.12(|10.05|0.12)0.060.06XP X P⎛-⎫->=>⎪⎝⎭1(2)(2)2[1(2)]0.0456ΦΦΦ=-+-=-=23.一工厂生产的电子管寿命X(小时)服从正态分布N(160,σ2),若要求P{120<X≤200}≥0.8,允许σ最大不超过多少?【解】120160160200160 (120200)XP X Pσσσ---⎛⎫<≤=<≤⎪⎝⎭404040210.8ΦΦΦσσσ-⎛⎫⎛⎫⎛⎫=-=-≥⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭故4031.251.29σ≤=24.设随机变量X 分布函数为F (x )=e ,0,(0),00.xt A B x ,x λ-⎧+≥>⎨<⎩ (1) 求常数A ,B ;(2) 求P {X ≤2},P {X >3}; (3) 求分布密度f (x ).【解】(1)由00lim ()1lim ()lim ()x x x F x F x F x →+∞→+→-=⎧⎪⎨=⎪⎩得11A B =⎧⎨=-⎩(2) 2(2)(2)1eP X F λ-≤==-33(3)1(3)1(1e)e P X F λλ-->=-=--=(3) e ,0()()0,0x x f x F x x λλ-⎧≥'==⎨<⎩25.设随机变量X 的概率密度为f (x )=⎪⎩⎪⎨⎧<≤-<≤.,0,21,2,10,其他x x x x 求X 的分布函数F (x ),并画出f (x )及F (x ).【解】当x <0时F (x )=0当0≤x <1时0()()d ()d ()d xxF x f t t f t t f t t -∞-∞==+⎰⎰⎰20d 2xx t t ==⎰当1≤x<2时()()d x F x f t t -∞=⎰111122()d ()d ()d d (2)d 132222212xx f t t f t t f t tt t t tx x x x -∞==+=+-=+--=-+-⎰⎰⎰⎰⎰当x ≥2时()()d 1xF x f t t -∞==⎰故 220,0,012()21,1221,2x x x F x x x x x <⎧⎪⎪≤<⎪=⎨⎪-+-≤<⎪⎪≥⎩26.设随机变量X 的密度函数为(1) f (x )=a e -|x |,λ>0;(2) f (x )=⎪⎩⎪⎨⎧<≤<<.,0,21,1,10,2其他x x x bx 试确定常数a ,b ,并求其分布函数F (x ). 【解】(1) 由()d 1f x x ∞-∞=⎰知||021e d 2e d x x aa x a x λλλ∞∞---∞===⎰⎰故 2a λ=即密度函数为 e ,02()e 02xx x f x x λλλλ-⎧>⎪⎪=⎨⎪≤⎪⎩当x ≤0时1()()d e d e 22xxx x F x f x x x λλλ-∞-∞===⎰⎰当x >0时0()()d e d e d 22xxx x F x f x x x x λλλλ--∞-∞==+⎰⎰⎰11e 2xλ-=-故其分布函数11e ,02()1e ,02xx x F x x λλ-⎧->⎪⎪=⎨⎪≤⎪⎩(2) 由12201111()d d d 22b f x x bx x x x ∞-∞==+=+⎰⎰⎰得 b =1即X 的密度函数为2,011(),120,x x f x x x<<⎧⎪⎪=≤<⎨⎪⎪⎩其他当x ≤0时F (x )=0 当0<x <1时0()()d ()d ()d xxF x f x x f x x f x x -∞-∞==+⎰⎰⎰2d 2xx x x ==⎰当1≤x <2时01211()()d 0d d d x xF x f x x x x x x x -∞-∞==++⎰⎰⎰⎰312x=- 当x ≥2时F (x )=1 故其分布函数为20,0,012()31,1221,2x x x F x x x x ≤⎧⎪⎪<<⎪=⎨⎪-≤<⎪⎪≥⎩27.求标准正态分布的上α分位点, (1)α=0.01,求z α; (2)α=0.003,求z α,/2z α. 【解】(1) ()0.01P X z α>=即 1()0.01z αΦ-= 即 ()0.09z αΦ= 故 2.33z α= (2) 由()0.003P X z α>=得1()0.003z αΦ-=即 ()0.997z αΦ= 查表得 2.75z α= 由/2()0.0015P X z α>=得/21()0.0015z α-Φ=即 /2()0.9985z αΦ= 查表得 /2 2.96z α=求Y =X 的分布律.【解】Y 可取的值为0,1,4,91(0)(0)5117(1)(1)(1)615301(4)(2)511(9)(3)30P Y P X P Y P X P X P Y P X P Y P X =======-+==+====-=====29.设P {X =k }=(2)k, k =1,2,…,令 1,1,.X Y X ⎧=⎨-⎩当取偶数时当取奇数时求随机变量X 的函数Y 的分布律. 【解】(1)(2)(4)(2)P Y P X P X P X k ===+=++=+242111()()()222111()/(1)443k =++++=-=2(1)1(1)3P Y P Y =-=-==30.设X ~N (0,1).(1) 求Y =e X 的概率密度; (2) 求Y =2X 2+1的概率密度; (3) 求Y =|X |的概率密度.【解】(1) 当y ≤0时,()()0Y F y P Y y =≤=当y >0时,()()(e )(ln )xY F y P Y y P y P X y =≤=≤=≤ln ()d yX f x x -∞=⎰故 2/2ln d ()1()(ln ),0d y Y Y x F y f y f y y y y -===> (2)2(211)1P Y X =+≥=当y ≤1时()()0Y F y P Y y =≤=当y >1时2()()(21)Y F y P Y y P X y =≤=+≤212y P X P X ⎛-⎛⎫=≤=≤≤ ⎪ ⎝⎭⎝()d X f x x =故 d ()()d Y Y XX f y F y f f y ⎤⎛==+⎥ ⎥⎝⎦(1)/4,1y y --=>(3) (0)1P Y ≥=当y ≤0时()()0Y F y P Y y =≤=当y >0时()(||)()Y F y P X y P y X y =≤=-≤≤ ()d yX yf x x -=⎰故d()()()()d Y Y X X f y F y f y f y y==+- 2/2,0y y -=> 31.设随机变量X ~U (0,1),试求:(1) Y =e X 的分布函数及密度函数; (2) Z =-2ln X 的分布函数及密度函数. 【解】(1) (01)1P X <<=故 (1e e)1XP Y <=<= 当1y ≤时()()0Y F y P Y y =≤=当1<y <e 时()(e )(ln )XY F y P y P X y =≤=≤ln 0d ln yx y ==⎰当y ≥e 时()(e )1XY F y P y =≤=即分布函数0,1()ln ,1e 1,e Y y F y y y y ≤⎧⎪=<<⎨⎪≥⎩故Y 的密度函数为11e ,()0,Y y y f y ⎧<<⎪=⎨⎪⎩其他 (2) 由P (0<X <1)=1知(0)1P Z >=当z ≤0时,()()0Z F z P Z z =≤=当z >0时,()()(2ln )Z F z P Z z P X z =≤=-≤/2(ln )(e )2z z P X P X -=≤-=≥ /21/2ed 1e z z x --==-⎰即分布函数-/20,0()1-e ,Z z z F z z ≤⎧=⎨>⎩0故Z 的密度函数为/21e ,0()20,z Z z f z z -⎧>⎪=⎨⎪≤⎩032.设随机变量X 的密度函数为f (x )=22,0π,π0,.xx ⎧<<⎪⎨⎪⎩其他试求Y =sin X 的密度函数. 【解】(01)1P Y <<=当y ≤0时,()()0Y F y P Y y =≤=当0<y <1时,()()(sin )Y F y P Y y P X y =≤=≤(0arcsin )(πarcsin π)P X y P y X =<≤+-≤<arcsin π220πarcsin 22d d ππyy x xx x -=+⎰⎰ 222211arcsin 1πarcsin ππy y =+--()()2arcsin πy =当y ≥1时,()1Y F y = 故Y 的密度函数为221,01π()10,Y y f y y⎧<<⎪=-⎨⎪⎩其他 33.设随机变量X 的分布函数如下:⎪⎩⎪⎨⎧≥<+=.)3(,)2(,)1(,11)(2x x x x F试填上(1),(2),(3)项.【解】由lim ()1x F x →∞=知②填1。
一榀框架结构荷载计算书

⼀榀框架结构荷载计算书毕业设计题⽬⼀榀框架计算书班级⼟⽊⼯程2006级⾼本学⽣姓名孟凡龙指导⽼师2011.5摘要本⼯程为济南某综合教学楼楼,主体三层,钢筋混凝⼟框架结构。
梁板柱均为现浇,建筑⾯积约为3000m2,宽35⽶,长为60⽶,建筑⽅案确定。
建筑分类为⼄类公共类建筑,⼆类场地,抗震等级三级。
.⽬录第⼀章框架结构设计任务书 (1)1.1⼯程概况 (1)1.2设计资料 (2)1.3设计内容 (2)第⼆章框架结构布置及结构计算图确定 (2)2.1梁柱界⾯确定 (2)2.2结构计算简图 (2)第三章荷载计算 (5)3.1恒荷载计算: (5)3.1.1屋⾯框架梁线荷载标准值 (5)3.1.2楼⾯框架梁线荷载标准值 (5)3.1.3屋⾯框架节点集中荷载标准值 (6)3.1.4楼⾯框架节点集中荷载标准值 (7)3.1.5恒荷载作⽤下结构计算简图 (8)3.2活荷载标准值计算 (9)3.2.1屋⾯框架梁线荷载标准值 (9)3.2.2楼⾯框架梁线荷载标准值 (9)3.2.3屋⾯框架节点集中荷载标准值 (9)3.2.4楼⾯框架节点集中荷载标准值 (10)3.2.5活荷载作⽤下的结构计算简图 (10)3.3风荷载计算 (11)第四章结构内⼒计算 (15)4.1恒荷载作⽤下的内⼒计算 (15)4.2活荷载作⽤下的内⼒计算 (25)4.3风荷载作⽤下内⼒计算 (33)第五章内⼒组合 (34)5.1框架横梁内⼒组合 (38)5.2柱内⼒组合 (46)第六章配筋计算 (60)6.1梁配筋计算 (60)6.2 柱配筋计算 (75)6.3楼梯配筋计算 (80)6.4基础配筋计算 (84)第七章电算结果 (80)7.1结构电算步骤 (86)7.2结构电算结果 (87)参考⽂献 (112)⼀框架结构设计任务书1.1 ⼯程概况:本⼯程为济南某综合教学楼楼,主体三层,钢筋混凝⼟框架结构。
梁板柱均为现浇,建筑⾯积约为3000m2,宽35⽶,长为60⽶,建筑⽅案确定。
《中学数学教学设计》课程教学大纲
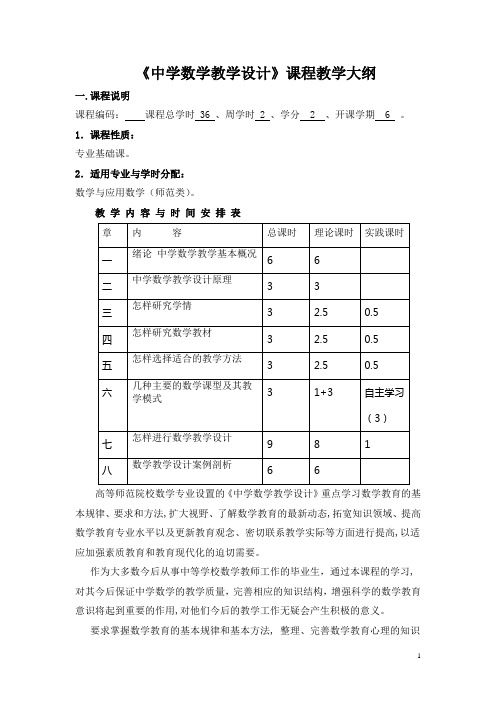
《中学数学教学设计》课程教学大纲一.课程说明课程编码:课程总学时 36 、周学时 2 、学分 2 、开课学期 6 。
1.课程性质:专业基础课。
2.适用专业与学时分配:数学与应用数学(师范类)。
教学内容与时间安排表高等师范院校数学专业设置的《中学数学教学设计》重点学习数学教育的基本规律、要求和方法,扩大视野、了解数学教育的最新动态,拓宽知识领域、提高数学教育专业水平以及更新教育观念、密切联系教学实际等方面进行提高,以适应加强素质教育和教育现代化的迫切需要。
作为大多数今后从事中等学校数学教师工作的毕业生,通过本课程的学习,对其今后保证中学数学的教学质量,完善相应的知识结构,增强科学的数学教育意识将起到重要的作用,对他们今后的教学工作无疑会产生积极的意义。
要求掌握数学教育的基本规律和基本方法, 整理、完善数学教育心理的知识结构;全面吸收数学教育前沿的思想观点, 更新数学教育观念;学习数学教学方法、手段和技能;提高数学教学的实际运作能力和教学水平。
4.本门课程与其它课程关系:与《数学史》、《初等数学研究》、《教育学》、《心理学》等课程联系密切。
5.推荐教材及参考书:自编讲义《中学数学教学设计》推荐教材:叶立军主编,《数学课程与教学论》,浙江大学出版社,2011.5.李善良主编,《初中数学教学实践与反思》,东北师范大学出版社,2011.参考书:何小亚,姚静主编,《中学数学教学设计》,科学出版社,2011.叶立军主编,《新课标中学数学实用教学80法》,广东教育出版社,2004.叶立军等著,《现代数学教学论》,浙江大学出版社 2006.6.课程教学方法与手段:教学中,结合课堂教学案例,采用案例教学法、探究式、讲解式、讨论式、启发式以及问题引导式等多种教学方法相结合的方式展开,以提高学生参与度,从而提高教学效果。
7.课程考试方法与要求:1.考试类型:考试课2.考试方式:以教学设计、试卷考核、课外作业及平时情况综合评定8.实践教学内容安排:到实验学校见习、撰写教学设计二、教学内容纲要第一章绪论中学数学教学基本概况(2学时)1.基本教学内容:第一节基础教育改革现状及其对数学教师素质的要求第二节现代数学教育的基本概况第三节几次课程改革的启示第四节数学课程标准解读2.基本要求(1)了解数学课程与教学论的历史发展,了解历史上几次重要的数学课程改革事件;(2)了解我国数学教育改革的历程及其特征(3)掌握数学课程标准的基本理念及其数学课程标准对中学数学教学的要求,为教学设计打下坚实的基础。
毛中特第二章选择题

第二章新民主主义革命理论【真题在线】一、单项选择题1.(2007.9)国民革命失败后,毛泽东在八七会议上提出的著名论断是A. 须知政权是由枪杆子中取得的B. 兵民是胜利之本C. 一切反动派都是纸老虎D. 星星之火,可以燎原2.(2009.8)1925年毛泽东在《中国社会各阶级的分析》中指出,中国过去一切革命斗争成效甚少的主要原因A.没有找到革命的新道路B.没有扩大民主主义宣传C.没有到群众中做实际的调查D.没有团结真正的朋友以攻击真正的敌人3.(2009.13)马克思主义中国化理论成果的精髓是A.理论联系实际B.解放思想C.实事求是D.与时俱进4.(2011.5)1927年大革命失败后,党的工作重心开始转向农村,在农村建立革命根据地。
农村革命根据地能够在中国长期存在和发展的根本原因是A.中国是一个政治、经济、文化发展极不平衡的半殖民地半封建的大国B.良好的群众基础和革命形势的继续向前发展C.相当力量正式红军的存在D.党的领导及正确的政策5.(2012.10)毛泽东在《中国革命和中国共产党》中论述了民主革命和社会主义革命的关系。
他指出:“民主革命是社会主义革命的必要准备,社会主义革命是民主革命的必然趋势。
”这两个革命阶段能够有机连接的原因是A.资本主义道路在中国走不通B.俄国十月革命为中国提供了经验C.民主革命中包含了社会主义因素D.中国国情决定中国革命必须分两步走二、多项选择题1.(2007.25)新民主主义革命时期,以国共合作为基础所建立的统一战线有A. 国民革命联合战线B. 工农民主统一战线C. 抗日民族统一战线D. 人民民主统一战线2.(2008.26)关于民主革命时期富农身份的界定,下列选项中正确的有A.剥削雇农的剩余劳动,是农村中的资产阶级B.既是劳动者,又是剥削者C.自身不劳动,出租土地并放高利贷D.对雇农的剥削带有浓厚的半封建性3.(2009.26)新民主主义的文化,是民族的科学的大众的文化。
概率论与数理统计习题及答案第二章.doc

习题 2-21. 设 A 为任一随机事件 , 且 P ( A )= p (0< p <1). 定义随机变量1, 发生 ,XA0, 不发生 .A写出随机变量 X 的分布律 .解 { =1}= ,{ =0}=1- p .P X p P X或者X 0 1P1- pp2. 已知随机变量X 只能取 -1,0,1,2 四个值 , 且取这四个值的相应概率依次为1 , 3 , 5 , 7. 试确定常数 c ,并计算条件概率 P{ X1 | X0} .2c 4c 8c 16c解 由离散型随机变量的分布律的性质知,1 3 571,2c4c8c 16c37所以 c .161P{ X1}8所求概率为{ <1|X0 }=2c.P XP{ X 0}1 5 7252c 8c 16c3. 设随机变量 X 服从参数为 2, p 的二项分布 , 随机变量 Y 服从参数为 3, p 的二项分布 ,若P{X ≥1}5, 求P{Y ≥1}.9解 注意 p{x=k}=C n k p k q n k , 由题设 5P{ X ≥1}1 P{ X0} 1 q 2 ,9故 q1 p2 从而.3P{Y ≥1} 1 P{ Y 0}1 (2 )3 19 .3 274. 在三次独立 的重复试验中 , 每次试验成功的概率相同 , 已知至少成功一次的概率19为, 求每次试验成功的概率 .27解设每次试验成功的概率为p , 由题意知至少成功一次的概率是19,那么一次都27没有成功的概率是8 . 即 (1 p)38 ,故p = 1 .272735. 若 X 服从参数为的泊松分布 ,且P{X1} P{ X 3}, 求参数 .解 由泊松分布的分布律可知 6 .6. 一袋中装有 5 只球 , 编号为 1,2,3,4,5.在袋中同时取 3 只球, 以 X 表示取出的 3 只球中的最大号码 , 写出随机变量 X 的分布律 .解 从 1,2,3,4,5 中随机取 3 个,以 X 表示 3 个数中的最大值, X 的可能取值是 3,4,5,在 5 个数中取 3 个共有C 5310 种取法 .{ =3} 表示取出的 3 个数以 3 为最大值, P{=3}=C 22= 1;C 53 10{ =4} 表示取出的 3 个数以 4 为最大值, P{=4}=C 323 ;C 53 10 { =5} 表示取出的 3 个数以 5 为最大值, P{=5}=C 423 .5 C 53X 的分布律是X 3 45P13310105习题 2-31. 设 X 的分布律为X -11P求分布函数( ), 并计算概率 { <0},{ <2},{-2 ≤ <1}.F xPXPXPX0, x 1, 解 (1)0.15, 1≤ x 0,F ( x )=0≤ x 1,0.35, 1,x ≥1.(2) P { X <0}= P { X =-1}=; (3) P { X <2}= P { X =-1}+ P { X =0}+P { X =1}=1; (4) P {-2 ≤ x <1}= P { X =-1}+ P { X =0}=.2. 设随机变量 X 的分布 函数为( ) = + arctan x - ∞< <+∞.F xA Bx试求 : (1) 常数 A 与 B ; (2)X 落在 (-1, 1] 内的概率 .解 (1) 由于 (- ∞)=0,(+∞)=1, 可知F FA B()1 12A, B.A B( )122于是F ( x) 1 1arctan x, x .2(2) P{ 1X ≤1} F (1) F ( 1)1 1 1 1arctan( 1))( arctan1) (2 21 1 1 1 () 1 .2424 23. 设随机变量 X 的分布函数为F ( x )=0,x 0, x,0≤x 1,1,x ≥1,求 P { X ≤ -1}, P { < X <}, P {0< X ≤ 2}.解 P {X ≤ 1} F( 1) 0,P {< X <}= F - F {}- P { X =}=, P {0< X ≤2}= F (2)- F (0)=1.5.X 的绝对值不大于1;P{ X1}1 1}1 假设随机变量 ,P{X; 在事件{ 1 X 1} 出现的条件下 ,84X 在 (-1,1) 内任一子区间上取值的条件概率与该区间的长度成正比 . (1) 求 X 的分布函数 F ( x) P{ X ≤ x }; (2)求 X 取负值的概率 p .解 (1) 由条件可知 ,当 x1时,F ( x) 0 ;当 x 1 时 , F ( 1) 1;当 x 1时 , 8F (1)= P { X ≤ 1}= P ( S )=1.所以P{ 1 X1} F (1) F ( 1)P{X 1}1 1 514.88易见 , 在 X 的值属于 (1,1) 的条件下 , 事件 { 1 X x} 的条件概率为P{ 1 X ≤ x | 1X 1} k[ x( 1)],取 x =1 得到 1= k (1+1),所以 k = 1.2x 1 . 因此P{ 1 X ≤x | 1 X 1}于是 , 对于1 x 1 ,有2P{ 1X ≤ x} P{ 1X ≤ x, 1 X 1}P{ 1 X 1} P{ 1 X ≤ x | 1 X 1}5 x 1 5x 5 . 对于 x ≥1,8 2 16有 F ( x) 1. 从而0, x 1, F ( x)5x 7 , 1x 1,161, ≥x1.(2) X 取负值的概率p P{ X0} F(0) P{ X0} F (0) [F(0)F (0 )] F (0 )7 . 习题 2-4161. 选择题设 f ( x)2x, x [0, c],则 f ( x) 是某一随机变量的概率(1)0,x如果 c =(),[0, c].密度函数 .(A)1(B)1.(C) 1.(D)3.2.3c2f ( x)dx 11 ,于是 c 1解 由概率密度函数的性质可得2xdx, 故本题应选 (C ).(2) 设 X ~ N (0,1), 又常数 c 满足 P{ X ≥ c} P{ X c} , 则 c 等于 ( ).(A) 1.(B) 0.(C)1 (D) -1..2解因为P{ X ≥ c} P{ X c} ,所以 1 P{ X c} P{ X c} , 即2P{ Xc} 1, 从而 P{X c} 0.5 , 即 ( c) 0.5 , 得 c =0. 因此本题应选 (B).(3) 下列函数中可以作为某一随机变量的概率密度的是( ).cos x, x [0, ],1x2,(A)f (x)(B)f (x),0,其它 .20,其它 .1( x) 2x≥22e,≥ 0,e , x0, (C)f (x) (D)f ( x)20, x0.0,x 0.解 由概率密度函数的性质f ( x)dx 1 可知本题应选 (D).(4) 设随机变量X ~ N(,42) , Y~N(,52), P 1P{X ≤4 },P 2 PY ≥ 5 }, 则( ).(A) 对任意的实数 , P 1P 2 . (B) 对任意的实数 , P 1 P 2 .(C) 只对实数的个别值 ,有P 1 P 2 . (D) 对任意的实数 , P P .12解 由正态分布函数的性质可知对任意的实数, 有P 1( 1) 1 (1) P 2 .因此本题应选 (A).Xf xf (x)f ( x)F x(5) 设随机变量 的概率密度为 , 且 , 又( )为分布函数 , 则对任意实数 a , 有 ( ).a(A)F ( a) 1∫0 f (x)dx .(B)F ( a)(C) F ( a)F ( a) . (D) Fa解由分布函数的几何意义及概率密度的性质知答案为1 a2 ∫0f ( x)dx.2F ( a) 1 .(B).(6) 设随机变量X 服从正态分布N (1, 12 ) , Y 服从正态分布 N ( 2, 22) ,且P{ X11} P{ Y21},则下式中成立的是 (). (A) σ1 < σ2 .(B)σ 1 > σ 2 .(C)μ1 <μ2 .(D)μ1 >μ2 .解 答案是 (A). XN(0 1)u 满足(7) 设随机变量 服从正态分布对给定的正数, 数(0,1),P{ X u }, 若P{X x}, 则 x 等于 ().(A)u .(B)u.(C)u 1-.(D)u 1.2122解 答案是 (C).2. 设连续型随机变量 X 服从参数为的指数分布 ,要使P{ kX 2k}1成立 ,4应当怎样选择数 k ?解 因为随机变量 X 服从参数为的指数分布 , 其分布函数为F ( x)1 e x , x 0,0,x ≤ 0.由题意可知1 P{ k X 2k} F(2k) F ( k) (1 e2 k )(1 e k ) e k e 2 k .4于是kln 2.3. 设随机变量 X 有概率密度f ( x) 4 x 3 , 0 x 1, 0,其它 ,要使 P{ X ≥ a}P{ Xa} ( 其中 a >0) 成立 , 应当怎样选择数 a ?解由条件变形 , 得到 1P{ Xa} P{ Xa},可知P{ X a} 0.5 ,于是a3dx 0.5,因此 a14x.424. 设连续型随机变量 X 的分布函数为0,x 0,F ( x)x 2 , 0≤x ≤1,1,x 1,求: (1)X 的概率密度 ; (2) P{0.3 X 0.7} .解 (1)根据分布函数与概率密度的关系F ( x)f ( x) ,可得f (x)2x, 0 x 1,0, 其它 .(2)P{0.3 X0.7}F (0.7) F (0.3) 0.720.320.4 .5. 设随机变量 X 的概率密度为2x,0≤ x ≤1,f ( x ) =其它 ,0,求P {X ≤ 1}与P {1< X ≤2}.241}11 1解P{X ≤ 22xdx x 22 ;24P{ 1 X ≤2}1 2 xdx x 2 1 15 .1444 166. 设连续型随机变量 X 具有概率密度函数x,0 x ≤1,f ( x) Ax,1x ≤2,0,其它 .求 : (1) 常数 A ; (2) X 的分布函数 F ( x ).解 (1) 由概率密度的性质可得11 2( A x)dx1 x2xdx12于是A 2;(2) 由公式 F ( x) xf ( x)dx可得当 x ≤0 时 , F ( x) 0 ; 当 0x ≤1时 ,F( x)x1 x2 ;xdx2当 1x ≤2时 ,F ( x)1x(2xdx1当 x >2 时,F ( x) 1.0,1 x2 , 所以F ( x)2 x 22x1,2112[ Ax x 2]A 1,21x 2 x)dx 2x1;2x ≤ 0,0 x ≤ 1,1 x ≤ 2,1,x2.7. 设随机变量 X 的概率密度为1f ( x) 4( x 1), 0 x 2,0, 其它 ,对 X 独立观察 3 次, 求至少有 2 次的结果大于 1 的概率 . 解根据概率密度与分布函数的关系式P{ a X ≤ b} F (b) F ( a)b f ( x)dx ,a可得P{ X 1} 21 ( x 1)dx 54.1 8 所以 , 3 次观察中至少有2 次的结果大于 1 的概率为C 2(5)2(3) C 3 ( 5)3 175 .8 8 2568 4x 2 8. 设 X ~U(0,5) , 求关于 x 的方程 4 Xx 2 0 有实根的概率 .解 随机变量 X 的概率密度为1, ≤ x 5,f ( x)50, 其它 ,若方程有实根 , 则16 X 232≥0, 于是 X 2 ≥ 2. 故方程有实根的概率为P { X 2 ≥2}= 1P{ X 2 2}1 P{2 X2}1 21dx0 512 .59. 设随机变量 X ~ N(3,22) .(1)计算 P{2 X ≤5} , P{ 4 X ≤10}, P{| X | 2}, P{X 3};(2)确定 c 使得P{ X c} P{ X ≤ c}; (3) 设 d 满足 P{ X d}≥0.9 , 问 d 至多为多少?解 (1) 由 P { a <x ≤ b }= P { a3 X 3 ≤ b 3 } Φ( b 3 ) Φ( a 3)公式,得到2 2 2 22XΦ(1) Φ( 0.5) 0.5328P,{2< ≤5}=P {-4< X ≤10}= Φ(3.5) Φ( 3.5) 0.9996,P{|X|2}=P{X2} +P{X2}=1 2 32 3Φ() +Φ(2 ) =,2P{ X 3} =1 P{ X ≤3} 1Φ( 3 3 ) 1 Φ(0) = .2(2) 若P{Xc}P{ X ≤ c} , 得 1P{ X ≤ c}P{ x ≤ c} ,所以P{ X ≤ c} 0.5由 Φ(0) =0 推得c3 0, 于是 c =3.2 Φ(d3(3)P{ X d}≥ 0.9 即1)≥ 0.9 , 也就是2Φ( d 3 )≥ 0.9 Φ(1.282) ,2因分布函数是一个不减函数, 故(d 3)≥ 1.282,2解得d ≤ 3 2 ( 1.282) 0.436 .10. 设随机变量 X ~ N (2, 2) , 若 P{0 X4} 0.3 , 求 P{X 0} .解 因为X ~ N2,所以 ZX~ N(0,1). 由条件 P{0 X4} 0.3可知0.3 P{0 X4}0 2X 24 22(2P{}( )) ,于是 222 ( )10.3从而 ( )0.65 .,P{X 0}P{X202}(22 所以) 1( ) 0.35.习题 2-5 1. 选择题(1) 设 X 的分布函数为 F ( x ), 则 Y 3 X 1 的分布函数 G y 为( ).(A) F (1 1 (B)F (3 y 1) .y) .3311(C)3F ( y) 1.(D)F ( y).3 3解 由随机变量函数的分布可得 , 本题应选 (A).(2) 设X~N 01 ,令YX 2, 则Y ~().(A)N( 2, 1). (B)N(0,1) . (C) N( 2,1) . (D)N (2,1) .解 由正态分布函数的性质可知本题应选 (C).2. 设 X ~ N(1,2), Z 2X 3 , 求 Z 所服从的分布及概率密度 . 解 若随机变量 X ~ N(,2) , 则 X 的线性函数 YaX b 也服从正态分布 , 即Y aX b ~ N( a b,( a ) 2). 这里 1,2 , 所以 Z ~ N(5,8) .概率密度为1 ( x 5) 2f (z)16,x.e43. 已知随机变量 X 的分布律为X -1137P(1) 求 =2- X 的分布律; (2) 求 =3+ 2分布律 .YYX解 (1)2-X-5-1123P(2)3+X 23 41252P4. 已知随机变量 X 的概率密度为1, 1 x 4,f X ( x)=2 x ln 20,其它,且 Y =2- X , 试求 Y 的概率密度 .解 先求Y的分布函数F Y ( y):F Y ( y) = P{ Y ≤ y}P{2X ≤ y}P{X ≥2 y}2 y1 P{ X 2y} =1-f X ( x)dx.于是可得 Y 的概率密度为1, 1 2 y4,f Y ( y)f X (2y)(2 y)=2(2 y) ln 20,其它 .1, 2 y1,f Y ( y)即2(2 y) ln 20,其它 .5. 设随机变量 X 服从区间 (-2,2) 上的均匀分 布, 求随机变量 YX 2 的概率密度 .解 由题意可知随机变量 X 的概率密度为f X ( x)1 ,2 x2,40, 其它 .因为对于 0<y <4,F Y ( y) P{ Y ≤ y} P{ X 2 ≤ y} P{y ≤ X ≤ y }F X ( y ) F X ( y ) .于是随机变量YX 2 的概率密度函数为f Y ( y)1 f X ( y )11 , 0 y 4.f X ( y )y4 2 y2 yf ( y)1 , 0 y 4,即4 y0,其它 .总习题二1. 一批产品中有 20%的次品 , 现进行有放回抽样 , 共抽取 5 件样品 . 分别计算这 5 件样品中恰好有 3 件次品及至多有 3 件次品的概率 .解 以 X 表示抽取的 5 件样品中含有的次品数 . 依题意知 X ~ B(5,0.2) .(1) 恰好有 3 件次品的概率是 P X C 5 0.2 3 0.8 .{ =3}= 3 23(2) 至多有 3 件次品的概率是C 5k 0.2k 0.85 k .k 02. 一办公楼装有 5 个同类型的供水设备 . 调查表明 , 在任一时刻 t 每个设备被使用 的概率为 . 问在同一时刻(1) 恰有两个设备被使用的概率是多少? (2) 至少有 1 个设备被使用的概率是多少? (3) 至多有 3 个设备被使用的概率是多少?(4) 至少有 3 个设备被使用的概率是多少?解 以 X 表示同一时刻被使用的设备的个数,则X ~B (5,,{ = }=k k5 kP X kC 50.1 0.9, k =0,1, ,5.(1) 所求的概率是 P XC 50.1 0.90.0729 ;{ =2}=223(2)所求的概率是 P X(1 0.1)5 0.40951 ;{ ≥ 1}=1(3)所求的概率是{ ≤ 3}=1-P{ =4}- { =5}=;P XXP X(4) 所求的概率是 P { X ≥ 3}= P { X =3}+ P { X =4}+ P { X =5}=.3. 设随机变量 X 的概率密度为xkf ( x)e , x ≥0,0, x0,1且已知k θ, 求常数.,2k x解由概率密度的性质可知dx1得到 k =1.e1x1由已知条件1, 得.1 e dx2ln 24. 某产品的某一质量指标 X ~ N(160, 2 ) , 若要求 P{120 ≤X ≤ 200} ≥, 问允许最大是多少 ?解 由P{120 ≤ ≤ 200} P{ 120 160 X160 200 160X≤ ≤ }= ( 404040) (1( ))2 ( ) 1≥,( 40 ) ≥ , 40最大值为 .得到 查表得 ≥ , 由此可得允许5.设随机变量 X 的概率密度为( x ) = e -| x | , - ∞< <+∞.φX A x试求 : (1) 常数 ; (2) {0< <1}; (3)的分布函数 .AP X解 (1)由于(x)dxAe |x|dx 1, 即2 Ae x dx 1故 2A = 1, 得1到A = .2所以φ( x ) =1 e -|x |.2(2) P {0< X <1} = 11 xdx1 ( e x 11 e 10.316.e2 ) 220 (3)因为 F ( x)x1 e |x| 得到2 dx,11当 x <0 时 , F ( x)x x x ,2 e dx 2e当 x ≥0 时,F ( x)1 0x1 xe x1 x,2e dx2dx 1 e21e x ,x0,所以 X 的分布函数为F ( x)21 ex,1 x ≥ 0.2。
蓄电池核对性放电试验1

变电检修桥西工区交直流班 培训课件
引言
蓄电池是将所获得的电能以化学能的形式贮存并可将化 学能转化为电能的一种电学装置。 蓄电池组是直流系统的重要组成部分,发电厂、变电站中 的蓄电池组为保护、控制等直流设备提供可靠的后备直流电 源,保证发电厂、变电站在交流全停情况下一段时间内的直 流设备的供电,在系统事故情况下具有特殊重要的作用。但 运行中的蓄电池本身出现的落后电池、开路等情况会造成蓄 电池容量不足,不能保证事故时的放电容量。 运行中的蓄电池组的容量检测是目前直流系统运行维护中 的一个难题。目前普遍采用的方式是蓄电池组定期核对性放 电与每日(或每周)的巡视检查相结合。
第三章 工作前准备
工 作 前 检 查 试 验 用 的 相 关 仪 器
第四章 蓄电池核对性放电试验
试验中的危险点
1、连接电池注意极性,防止电池短路、接地
2、工作过程中,与带电设备做好隔离措施,用措施布明 显标志区分 3、低压带电工作,防止低压触电。使用电气工具做好绝缘, 戴线手套
4、电池正负极做好标记,接线正确。防止电池短路放炮
5、严禁直流短路、接地
6、与带电设备保持安全距离
蓄电池核对性放电 试验每隔一小时测量 一次,测量时填写检 查记录表。
所有工作 完成后填入蓄电 池核对性放电试 验完成统计表。
谢谢各位 请多提宝贵意见
容量试验
2005.6
2011.5.10
4天
合格
2011.5.5-2011.5.8
6
联盟
蓄电池
GFM/G-200
容量试验
2005.12
2011.5.13
4天
合格
2011.5.12-2011.5.15
7
中华
高等代数第二章课后习题

第二章 行列式
第二章 行列式
第二章 行列式
第二章 行列式
第二章 行列式
x1-m
x2
…
xn
x1
x2-m … xn
3)
.
.
.
.
. .
.
.
.
x1
x2
…
xn-m
第二章 行列式
第 章 行列式
2
1
第二章 行列式
5x1+6x2=1 x1+5x2+6x3=0 4) x2+5x3+6x4=0 x3+5x4+6x5=0
x4+5x5=1
2
第 章 行列式 3
ห้องสมุดไป่ตู้
a a ...a 2
n-1
n-1
n-1 n-1
其中 a1,a2,...,an-1 是互不相同的数. 1) 由行列式定义说明,p(x)是一个 n-1 次多项式;
2)由行列式性质,求 p(x)的根 .
4
1.计算下面的行列式:
第二章 行列式
246 427 327
1)
1014 543 443 ;
-342 721 621
1
第 章 行列式 2
第二章 行列式
6.由行列式定义计算
2x x 1 2
f(x)= 1 3
x 1 -1 2x 1
1 11 x
中 x4 与 x3 的系数,并说明理由.
3
第二章 行列式
证明奇偶排列各半.
8.设
1
P(x)=
1 .
.
.
1
x
x2...xn-1
a1 a12 ...a1n-1 . .. . .. . ..
《公共场所卫生管理条例实施细则》解读

二、明确公共场所卫生管理档案主要内容
(一)卫生管理部门、人员设置情况及卫生管理制度; (二)空气、微小气候(湿度、温度、风速)、水质、采光、照明、
噪声的检测情况; (三)顾客用品用具的清洗、消毒、更换及检测情况; (四)卫生设施的使用、维护、检查情况;
二、明确公共场所卫生管理档案主要内容
(五)集中空调通风系统的清洗、消毒情况; (六)安排从业人员健康检查和培训考核情况; (七)公共卫生用品进货索证管理情况; (八)公共场所危害健康事故应急预案或者方案; (九)省、自治区、直辖市卫生行政部门要求记录的其他情况。
7.预防性卫生监督:公共场所的选址、设计、装修应当符合国家相关标准和规范 的要求。
公共场所室内装饰装修期间不得营业。进行局部装饰装修的,经营者 应当采取有效措施,保证营业的非装饰装修区域室内空气质量合格。
8.禁烟:室内公共场所禁止吸烟。应当设置醒目的禁止吸烟警语和标志。 室外公共场所设置的吸烟区不得位于行人必经的通道上。 公共场所不得设置自动售烟机。 应当开展吸烟危害健康的宣传,并配备专(兼)职人员对吸烟者进行
(一)未按照规定建立卫生管理制度、设立卫生管理部门或者配备专(兼) 职卫生管理人员,或者未建立卫生管理档案的;
第四章 法律责任
(二)未按照规定组织从业人员进行相关卫生法律知识和公共场所卫生知识培训,或者安排未经相关卫生法 律知识和公共场所卫生知识培训考核的从业人员上岗的;
(三)未按照规定设置与其经营规模、项目相适应的清洗、消毒、保洁、盥洗等设施设备和公共卫生间,或 者擅自停止使用、拆除上述设施设备,或者挪作他用的;
劝阻。(无处罚条款)
9.场所自测:应当按照卫生标准、规范的要求对公共场所的空气、微小气候、水 质、采光、照明、噪声、顾客用品用具等进行卫生检测,检测每年不得少于一 次;检测结果不符合卫生标准、规范要求的应当及时整改。
毛中特第二章选择题

第二章新民主主义革命理论【真题在线】一、单项选择题1.(2007.9)国民革命失败后,毛泽东在八七会议上提出的著名论断是A. 须知政权是由枪杆子中取得的B. 兵民是胜利之本C. 一切反动派都是纸老虎D. 星星之火,可以燎原2.(2009.8)1925年毛泽东在《中国社会各阶级的分析》中指出,中国过去一切革命斗争成效甚少的主要原因A.没有找到革命的新道路B.没有扩大民主主义宣传C.没有到群众中做实际的调查D.没有团结真正的朋友以攻击真正的敌人3.(2009.13)马克思主义中国化理论成果的精髓是A.理论联系实际B.解放思想C.实事求是D.与时俱进4.(2011.5)1927年大革命失败后,党的工作重心开始转向农村,在农村建立革命根据地。
农村革命根据地能够在中国长期存在和发展的根本原因是A.中国是一个政治、经济、文化发展极不平衡的半殖民地半封建的大国B.良好的群众基础和革命形势的继续向前发展C.相当力量正式红军的存在D.党的领导及正确的政策5.(2012.10)毛泽东在《中国革命和中国共产党》中论述了民主革命和社会主义革命的关系。
他指出:“民主革命是社会主义革命的必要准备,社会主义革命是民主革命的必然趋势。
”这两个革命阶段能够有机连接的原因是A.资本主义道路在中国走不通B.俄国十月革命为中国提供了经验C.民主革命中包含了社会主义因素D.中国国情决定中国革命必须分两步走二、多项选择题1.(2007.25)新民主主义革命时期,以国共合作为基础所建立的统一战线有A. 国民革命联合战线B. 工农民主统一战线C. 抗日民族统一战线D. 人民民主统一战线2.(2008.26)关于民主革命时期富农身份的界定,下列选项中正确的有A.剥削雇农的剩余劳动,是农村中的资产阶级B.既是劳动者,又是剥削者C.自身不劳动,出租土地并放高利贷D.对雇农的剥削带有浓厚的半封建性3.(2009.26)新民主主义的文化,是民族的科学的大众的文化。
概率论与数理统计第二章答案

第二章 随机变量及其分布1、解:设公司赔付金额为X ,则X 的可能值为; 投保一年内因意外死亡:20万,概率为投保一年内因其他原因死亡:5万,概率为投保一年内没有死亡:02、一袋中有55,在其中同时取三只,以X 表示取出的三只球中的最大号码,写出随机变量X 的分布律解:X 可以取值3,4,5,分布律为1061)4,3,2,1,5()5(1031)3,2,1,4()4(1011)2,1,3()3(352435233522=⨯====⨯====⨯===C C P X P C C P X P C C P X P 中任取两球再在号一球为中任取两球再在号一球为号两球为号一球为也可列为下表 X : 3, 4,5P :106,103,101 ;3、设在15只同类型零件中有2只是次品,在其中取三次,每次任取一只,作不放回抽样,以X 表示取出次品的只数,(1)求X 的分布律,(2)画出分布律的图形。
解:任取三只,其中新含次品个数X 可能为0,1,2个。
3522)0(315313===C C X P3512)1(31521312=⨯==C C C X P 351)2(31511322=⨯==C C C X P .再列为下表X : 0, 1, 2P : 351,3512,3522 4、进行重复独立实验,设每次成功的概率为p ,失败的概率为q =1-p (0<p <1) (1)将实验进行到出现一次成功为止,以X 表示所需的试验次数,求X 的分布律。
(此时称X 服从以p 为参数的几何分布。
)(2)将实验进行到出现r 次成功为止,以Y 表示所需的试验次数,求Y的分布律。
(此时称Y 服从以r, p 为参数的巴斯卡分布。
)(3)一篮球运动员的投篮命中率为45%,以X 表示他首次投中时累计已投篮的次数,写出X 的分布律,并计算X 取偶数的概率。
解:(1)P (X=k )=q k -1p k=1,2,……(2)Y=r+n={最后一次实验前r+n -1次有n 次失败,且最后一次成功},,2,1,0,)(111 ===+=-+--+n p q C p p q C n r Y P r n n n r r n n n r 其中 q=1-p ,【或记r+n=k ,则 P {Y=k }= ,1,,)1(11+=----r r k p p C rk r r k (3)P (X=k ) = k - k=1,2…P (X 取偶数)=311145.0)55.0()2(1121===∑∑∞=-∞=k k k k X P 5、 一房间有3扇同样大小的窗子,其中只有一扇是打开的。
(新版)供应链管理复习资料2011.5

供应链管理复习资料第一章供应链基本架构一、供应链是围绕企业,通过对信息流、物流、资金流的控制,从采购原材料开始,制成中间产品和最终产品,最后由销售网络把产品运送到消费者手中,将供应商、制造商、分销商直到最终用户连接成一个整体的功能网链结构模式二、供应链的基本特征;供应链具有以下特征:1)复杂性 2)动态性 3)面向用户需求 4)交叉性三、供应链的基本类型可分为以下四种:(1)根据供应链存在的稳定性强弱划分,分为稳定的供应链和动态的供应链(2)根据供应链容量与用户需求的关系,分为平衡的供应链和倾斜的供应链(3)根据供应链的功能模式,分为有效性供应链和反应性供应链(4)根据商品的库存情况,分为推动式供应链和拉动是供应链。
四、拉式模式的优势:(1)支持产品的不断变化;(2)缩短交货周期;(3)改进质量,降低单位成本;(4)提高经营效率;(5)能够全面衡量业绩,更易于实施控制。
五、有效地供应链管理对企业提出了很高的要求,它们必须:(1)迅速准确地了解顾客需求;(2)选择最佳方式,以最低的成本满足顾客需求;(3)制定明智的供应链决策,包括从原料采购决策到产品制造在内的所有供应链决策;(4)将产成品分销给消费者,收取货款。
六、供应链设计过程包含下列步骤:(1)建立供应链目标(2)指定供应链策略(3)决定供应链结构的候选方案(4)评价供应链结构的候选方案(5)选择供应链结构(6)决定单个供应链成员的候选企业(7)评价并选择单个供应链成员(8)衡量和评价供应链的绩效(9)当绩效目标未达到或有新的具有吸引力的选择存在时,评价供应链的候选方案七、供应链设计的考虑事项:1市场覆盖范围目标:(1)顾客购买行为;(2)分销类型。
2产品特性八、功能性产品和革新性产品的需求特征比较功能性产品和革新性产品的需求特征比较需求特征功能性产品革新性产品产品寿命周期(年) >2 1-2个边界贡献(%) 5-20 20-60产品多样性低(每一目录10到20个)高(每一目录上千个)预测的平均边际错误率(%) 10 40-100平均缺货率 1-2 10-40季末降价率(%) 0 10-25按订单生产的提前期天-2周九、设计策略功能性产品革新性产品有效性供应链反应性供应链十、供应链管理形成动因(1)供应链管理是管理指导思想的转变(2)由于全球化市场竞争越来越激烈,企业面临的风险也越来越大,企业仅靠自身已不能取得竞争优势,不得不联合起来,形成各种虚拟组织,以取得在市场中的领先优势(3)供应链管理产生的第三个动因来自于一个经济学原理,那就是交易可以使每个人或每个企业的状况变得更好。
实验一迈克尔逊干涉仪实验报告_2011.5.17

实验一迈克尔逊干涉仪实验报告_2011.5.17英文回答:Introduction。
The Michelson interferometer is a device that uses interference to measure the speed of light and the index of refraction of materials. It was invented by Albert Michelson in 1881, and it has since become one of the most important tools in optics.Theory。
The Michelson interferometer works by splitting a beam of light into two beams, which are then reflected back to the original source. The two beams interfere with each other, and the resulting interference pattern can be used to measure the speed of light or the index of refraction of a material.Experimental Procedure。
In this experiment, we used a Michelson interferometer to measure the speed of light. We set up the interferometer on a vibration-isolated table, and we used a helium-neon laser as the light source. We aligned the mirrors so that the two beams interfered with each other, and we measured the distance between the bright fringes in the interference pattern.Results。
第二章 §2

第2课时 奇偶性、对称性与周期性题型一 函数奇偶性的判定例1 判断下列函数的奇偶性:(1)f (x )=3-x 2+x 2-3;(2)f (x )=lg (1-x 2)|x -2|-2; (3)f (x )=⎩⎪⎨⎪⎧x 2+x ,x <0,-x 2+x ,x >0; (4)f (x )=log 2(x +x 2+1).解 (1)由⎩⎪⎨⎪⎧3-x 2≥0,x 2-3≥0,得x 2=3,解得x =±3, 即函数f (x )的定义域为{-3,3},关于原点对称.从而f (x )=3-x 2+x 2-3=0.因此f (-x )=-f (x )且f (-x )=f (x ),所以函数f (x )既是奇函数又是偶函数.(2)由⎩⎪⎨⎪⎧1-x 2>0,|x -2|≠2,得定义域为(-1,0)∪(0,1),关于原点对称. ∴x -2<0,∴|x -2|-2=-x ,∴f (x )=lg (1-x 2)-x. 又∵f (-x )=lg[1-(-x )2]x =-lg (1-x 2)-x=-f (x ), ∴函数f (x )为奇函数.(3)显然函数f (x )的定义域为(-∞,0)∪(0,+∞),关于原点对称.∵当x <0时,-x >0,则f (-x )=-(-x )2-x =-x 2-x =-f (x );当x >0时,-x <0,则f(-x)=(-x)2-x=x2-x=-f(x);综上可知,对于定义域内的任意x,总有f(-x)=-f(x)成立,∴函数f(x)为奇函数.(4)显然函数f(x)的定义域为R,f(-x)=log2[-x+(-x)2+1]=log2(x2+1-x)=log2(x2+1+x)-1=-log2(x2+1+x)=-f(x),故f(x)为奇函数.思维升华判断函数的奇偶性,其中包括两个必备条件(1)定义域关于原点对称,这是函数具有奇偶性的必要不充分条件,所以首先考虑定义域;(2)判断f(x)与f(-x)是否具有等量关系,在判断奇偶性的运算中,可以转化为判断奇偶性的等价等量关系式(f(x)+f(-x)=0(奇函数)或f(x)-f(-x)=0(偶函数))是否成立.跟踪训练1 (1)下列函数是偶函数的是()A.f(x)=x3-sin xB.f(x)=3x-13xC.f(x)=x2+tan xD.f(x)=x·ln(x2+1-x)答案 D解析由函数奇偶性定义知,A中函数为奇函数,B中函数为奇函数,C中函数为非奇非偶函数,D中函数为偶函数.(2)设函数f(x),g(x)的定义域为R,且f(x)是奇函数,g(x)是偶函数,则下列结论正确的是() A.f(x)g(x)是偶函数B.|f(x)g(x)|是奇函数C.|f(x)|g(x)是偶函数D.f(|x|)g(x)是奇函数答案 C解析令F1(x)=f(x)g(x),∴F1(-x)=f(-x)g(-x)=-f(x)g(x)=-F1(x),∴F 1(x )为奇函数,故A 错误;令F 2(x )=|f (x )g (x )|,∴F 2(x )=|f (-x )g (-x )|=|-f (x )g (x )|=|f (x )g (x )|=F 2(x ),故F 2(x )为偶函数,故B 错误;令F 3(x )=|f (x )|g (x ),∴F 3(-x )=|f (-x )|g (-x )=|f (x )|g (x )=F 3(x ),∴F 3(x )为偶函数,故C 正确;令F 4(x )=f (|x |)g (x ),∴F 4(-x )=f (|-x |)g (-x )=f (|x |)g (x )=F 4(x ),∴F 4(x )为偶函数,故D 错误.题型二 函数奇偶性的应用命题点1 利用奇偶性求参数的值例2 若函数f (x )=x 3⎝⎛⎭⎫12x -1+a 为偶函数,则a 的值为________. 答案 12解析 方法一 (定义法)∵f (x )为偶函数,∴f (-x )=f (x ),∴(-x )3⎝ ⎛⎭⎪⎫12-x -1+a =x 3·⎝ ⎛⎭⎪⎫12x -1+a , ∴2a =-⎝ ⎛⎭⎪⎫12-x -1+12x -1=1, ∴a =12. 方法二 (特值法)f (x )为偶函数,∴f (-1)=f (1),又f (-1)=-a +2,f (1)=a +1,∴-a +2=a +1,∴a =12.命题点2 利用奇偶性求解析式例3 (2019·全国Ⅱ)设f (x )为奇函数,且当x ≥0时,f (x )=e x -1,则当x <0时,f (x )等于( )A .e -x -1B .e -x +1 C .-e -x -1D .-e -x +1 答案 D解析 当x <0时,-x >0,∵当x ≥0时,f (x )=e x -1,∴f (-x )=e -x -1.又∵f (x )为奇函数,∴f (x )=-f (-x )=-e -x +1.命题点3 利用奇偶性求函数值例4 已知函数f (x )=ax 3+bx 5+2.若f (x )在区间[-t ,t ]上的最大值为M ,最小值为m ,则M +m =________.答案 4解析 令g (x )=ax 3+bx 5,则g (x )为奇函数,当x ∈[-t ,t ]时,g (x )max +g (x )min =0,又f (x )=g (x )+2,∴M =g (x )max +2,m =g (x )min +2,∴M +m =g (x )max +2+g (x )min +2=4.思维升华 利用函数奇偶性可以解决以下问题(1)求函数值:将待求值利用奇偶性转化为求已知解析式的区间上的函数值.(2)求解析式:将待求区间上的自变量转化到已知解析式的区间上,再利用奇偶性的定义求出.(3)求解析式中的参数:利用待定系数法求解,根据f (x )±f (-x )=0得到关于参数的恒等式,由系数的对等性得方程(组),进而得出参数的值.(4)画函数图象:利用函数的奇偶性可画出函数在其对称区间上的图象.(5)求特殊值:利用奇函数的最大值与最小值之和为零可求一些特殊结构的函数值.跟踪训练2 (1)已知函数f (x )是定义在R 上的奇函数,且当x ≥0时,f (x )=2x +x +b ,则f (-1)的值为( )A .b +3B .-b -3C .-2D .2答案 C解析 ∵f (x )为R 上的奇函数,∴f (0)=0,即20+0+b =0,∴b =-1,∴f (-1)=-f (1)=-(21+1+b )=-2.(2)已知函数f (x )=a sin x +b tan x +1,若f (a )=-2,则f (-a )=________.答案 4解析 令g (x )=a sin x +b tan x ,则g (x )为奇函数,且f (x )=g (x )+1,∵f (a )=g (a )+1=-2,∴g (a )=-3,∴f (-a )=g (-a )+1=-g (a )+1=4.题型三 函数的周期性、对称性命题点1 函数的周期性例5 (1)已知函数f (x )对任意x ∈R ,都有f (x +2π)=f (x ),当x ∈(0,π)时,f (x )=2sin x 2,则f ⎝⎛⎭⎫2 023π3等于( )A.12B.32C .1 D. 3 答案 C解析 因为f (x +2π)=f (x ),所以f (x )的周期为2π.所以f ⎝⎛⎭⎫2 023π3=f ⎝⎛⎭⎫674π+π3=f ⎝⎛⎭⎫337×2π+π3 =f ⎝⎛⎭⎫π3,又因为当x ∈(0,π)时,f (x )=2sin x 2,所以f ⎝⎛⎭⎫π3=2sin π6=1. (2)(2020·西安模拟)已知定义在R 上的函数f (x )满足f (x )=-f (x +2),当x ∈(0,2]时,f (x )=2x +log 2x ,则f (2 020)等于( )A .5 B.12C .2D .-5 答案 D解析 ∵f (x )=-f (x +2),∴f (x )的周期为4,f (2 020)=f (0)=-f (2)=-(22+log 22)=-5.思维升华 函数周期性常用结论对f (x )定义域内任一自变量的值x :(1)若f (x +a )=-f (x ),则T =2a (a >0).(2)若f (x +a )=1f (x ),则T =2a (a >0). (3)若f (x +a )=-1f (x ),则T =2a (a >0). (4)若f (x +a )+f (x )=c ,则T =2a (a >0,c 为常数).命题点2 函数的对称性例6 (多选)已知函数f (x )的定义域为R ,对任意x 都有f (2+x )=f (2-x ),且f (-x )=f (x ),则下列结论正确的是( )A .f (x )的图象关于x =2对称B .f (x )的图象关于(2,0)对称C .f (x )的最小正周期为4D .y =f (x +4)为偶函数答案 ACD解析 ∵f (2+x )=f (2-x ),则f (x )的图象关于x =2对称,故A 正确,B 错误;∵函数f (x )的图象关于x =2对称,则f (-x )=f (x +4),又f (-x )=f (x ),∴f (x +4)=f (x ),∴T =4,故C 正确;∵T =4且f (x )为偶函数,故y =f (x +4)为偶函数,故D 正确.思维升华 对称性的三个常用结论(1)若函数f (x )满足f (a +x )=f (b -x ),则y =f (x )的图象关于直线x =a +b 2对称. (2)若函数f (x )满足f (a +x )=-f (b -x ),则y =f (x )的图象关于点⎝ ⎛⎭⎪⎫a +b 2,0对称. (3)若函数f (x )满足f (a +x )+f (b -x )=c ,则函数f (x )的图象关于点⎝⎛⎭⎪⎫a +b 2,c 2对称. 跟踪训练3 (1)设定义在R 上的函数f (x )满足f (x +3)=f (x ),且当x ∈[0,3)时,f (x )=2x -x 2+1,则f (0)+f (1)+f (2)+…+f (2 021)=________.答案 2 696解析 ∵f (x +3)=f (x ),∴T =3,又x ∈[0,3)时,f (x )=2x -x 2+1,∴f (0)=1,f (1)=2,f (2)=1,∴f (0)+f (1)+f (2)=1+2+1=4,∴f (0)+f (1)+f (2)+…+f (2 021)=674×4=2 696.(2)已知函数f (x )的定义域为R ,且f (x )为奇函数,其图象关于直线x =2对称.当x ∈[0,4]时,f (x )=x 2-4x ,则f (2 022)=________.答案 4解析 ∵f (x )的图象关于直线x =2对称,∴f (-x )=f (x +4),又f (x )为奇函数,∴f (-x )=-f (x ),故f (x +4)=-f (x ),∴T =8,又∵2 022=252×8+6,∴f (2 022)=f (6)=f (-2)=-f (2)=-(4-8)=4.我们把不给出具体解析式,只给出函数的特殊条件或特征的函数称为抽象函数,一般用y =f (x )表示,抽象函数问题可以全面考查函数的概念和性质,将函数定义域、值域、单调性、奇偶性、周期性、图象集于一身,是考查函数的良好载体.例1 若函数f (2x )的定义域是[-1,1],则f (log 2x )的定义域为________.答案 [2,4]解析 对于函数y =f (2x ),-1≤x ≤1,∴2-1≤2x ≤2.则对于函数y =f (log 2x ),2-1≤log 2x ≤2, ∴2≤x ≤4.故y =f (log 2x )的定义域为[2,4].例2 已知函数f (x )对任意正实数a ,b ,都有f (ab )=f (a )+f (b )成立.(1)求f (1),f (-1)的值;(2)求证:f ⎝⎛⎭⎫1x =-f (x );(3)若f (2)=p ,f (3)=q (p ,q 均为常数),求f (36)的值.(1)解 令a =1,b =1,得f (1)=f (1)+f (1),解得f (1)=0,令a =b =-1,∴f (1)=f (-1)+f (-1),∴f (-1)=0.(2)证明 令a =1x,b =x , 得f (1)=f ⎝⎛⎭⎫1x +f (x )=0,∴f ⎝⎛⎭⎫1x =-f (x ).(3)解 令a =b =2,得f (4)=f (2)+f (2)=2p ,令a =b =3,得f (9)=f (3)+f (3)=2q ,令a =4,b =9,得f (36)=f (4)+f (9)=2p +2q .例3 已知函数y =f (x )的定义域为R ,并且满足f (x +y )=f (x )+f (y ),f ⎝⎛⎭⎫13=1,且当x >0时,f (x )>0. (1)求f (0)的值;(2)判断函数的奇偶性并证明;(3)判断函数的单调性,并解不等式f (x )+f (2+x )<2.解 (1)令x =y =0,则f (0)=f (0)+f (0),∴f (0)=0.(2)f (x )是奇函数,证明如下:令y =-x ,得f (0)=f (x )+f (-x )=0,∴f (-x )=-f (x ),故函数f (x )是R 上的奇函数.(3)f (x )是R 上的增函数,证明如下:任取x 1,x 2∈R ,x 1<x 2,则x 2-x 1>0,∴f (x 2)-f (x 1)=f (x 2-x 1+x 1)-f (x 1)=f (x 2-x 1)+f (x 1)-f (x 1)=f (x 2-x 1)>0,∴f (x 1)<f (x 2),故f (x )是R 上的增函数,∵f ⎝⎛⎭⎫13=1,∴f ⎝⎛⎭⎫23=f ⎝⎛⎭⎫13+13=f ⎝⎛⎭⎫13+f ⎝⎛⎭⎫13=2,∴f (x )+f (2+x )=f (x +(2+x ))=f (2x +2)<f ⎝⎛⎭⎫23,又由y =f (x )是定义在R 上的增函数,得2x +2<23,解得x <-23,故x ∈⎝⎛⎭⎫-∞,-23.课时精练1.(2021·重庆一中月考)下列函数中,既是偶函数又在(0,+∞)上单调递增的是() A .y =x -1 B .y =|x |+1C .y =cos x xD .y =-x 2 答案 B2.若函数f (x )=k -2x1+k ·2x在定义域上为奇函数,则实数k 的值为( ) A .-2 B .0 C .1或-1 D .2答案 C解析 因为f (x )在定义域上为奇函数,所以f (-x )=-f (x ),即k -2-x 1+k ·2-x =2x -k 1+k ·2x, 即k ·2x -12x +k =2x -k k ·2x +1, 根据等式恒成立可得,k =±1.3.(2021·南昌联考)函数f (x )=9x +13x 的图象( ) A .关于x 轴对称B .关于y 轴对称C .关于坐标原点对称D .关于直线y =x 对称 答案 B解析 f (x )=32x +13x =3x +3-x ,f (-x )=3-x +3x , ∴f (-x )=f (x ),故f (x )为偶函数,其图象关于y 轴对称.4.已知函数f (x )是定义在R 上的周期为2的奇函数,当0<x <1时,f (x )=4x ,则f ⎝⎛⎭⎫-52+f (1)等于( )A .-2B .0C .2D .1答案 A解析 ∵函数f (x )为定义在R 上的奇函数,且周期为2,∴f (1)=-f (-1)=-f (-1+2)=-f (1),∴f (1)=0,f ⎝⎛⎭⎫-52=f ⎝⎛⎭⎫-12=-f ⎝⎛⎭⎫12=124-=-2, ∴f ⎝⎛⎭⎫-52+f (1)=-2.5.(多选)已知y =f (x )是定义在R 上的奇函数,则下列函数中为奇函数的是( )A .y =f (|x |)B .y =f (-x )C .y =xf (x )D .y =f (x )+x答案 BD解析 由奇函数的定义f (-x )=-f (x )验证,A 项,f (|-x |)=f (|x |),为偶函数;B 项,f [-(-x )]=f (x )=-f (-x ),为奇函数;C 项,-xf (-x )=-x ·[-f (x )]=xf (x ),为偶函数;D 项,f (-x )+(-x )=-[ f (x )+x ],为奇函数.可知BD 正确.6.(多选)若定义域为R 的函数f (x )在(4,+∞)上单调递减,且函数y =f (x +4)为偶函数,则() A .f (2)>f (3) B .f (2)=f (6)C .f (3)=f (5)D .f (3)>f (6)答案 BCD解析 ∵y =f (x +4)为偶函数,∴f (-x +4)=f (x +4),∴y =f (x )的图象关于直线x =4对称,∴f (2)=f (6),f (3)=f (5).又y =f (x )在(4,+∞)上单调递减,∴f (5)>f (6),∴f (3)>f (6).7.已知f (x )=ax 2+bx 是定义在[a -1,2a ]上的偶函数,那么a +b 的值是________. 答案 13解析 f (x )=ax 2+bx 为偶函数,则b =0,又定义域[a -1,2a ]关于原点对称,则a -1+2a =0,∴a =13,∴a +b =13.8.(2021·咸阳模拟)已知函数f (x )=⎩⎪⎨⎪⎧x 2-ax ,x ≤0,ax 2+x ,x >0为奇函数,则a =________. 答案 -1解析 由题意,得f (-x )=-f (x ),则f (-1)=-f (1),即1+a =-a -1,得a =-1(经检验符合题意).9.已知函数f (x )对∀x ∈R 满足f (1-x )=f (1+x ),f (x +2)=-f (x ),且f (0)=1,则f (26)=________. 答案 1解析 ∵f (x +2)=-f (x ),∴f (x )的周期为4,∴f (26)=f (2).∵对∀x ∈R 有f (1-x )=f (1+x ),∴f (x )的图象关于直线x =1对称,∴f (2)=f (0)=1,即f (26)=1.10.已知函数f (x )=x 3+x ,对任意的m ∈[-2,2],f (mx -2)+f (x )<0恒成立,则x 的取值范围为________.答案 ⎝⎛⎭⎫-2,23 解析 易知原函数在R 上单调递增,且为奇函数,故f (mx -2)+f (x )<0⇒f (mx -2)<-f (x )=f (-x ),此时应有mx -2<-x ⇒mx +x -2<0对所有m ∈[-2,2]恒成立.令g (m )=xm +x -2,此时只需⎩⎨⎧ g (-2)<0,g (2)<0即可, 解得-2<x <23. 11.已知函数f (x )=⎩⎪⎨⎪⎧ -x 2+2x ,x >0,0,x =0,x 2+mx ,x <0是奇函数.(1)求实数m 的值;(2)若函数f (x )在区间[-1,a -2]上单调递增,求实数a 的取值范围.解 (1)设x <0,则-x >0,所以f (-x )=-(-x )2+2(-x )=-x 2-2x .又f (x )为奇函数,所以f (-x )=-f (x ),于是x <0时,f (x )=x 2+2x =x 2+mx ,所以m =2.(2)要使f (x )在[-1,a -2]上单调递增,结合f (x )的图象(如图所示)知⎩⎪⎨⎪⎧a -2>-1,a -2≤1,所以1<a ≤3,故实数a 的取值范围是(1,3].12.设f (x )是定义在R 上的奇函数,且对任意实数x ,恒有f (x +2)=-f (x ).当x ∈[0,2]时,f (x )=2x -x 2.(1)求证:f (x )是周期函数;(2)当x ∈[2,4]时,求f (x )的解析式.(1)证明 ∵f (x +2)=-f (x ),∴f (x +4)=-f (x +2)=f (x ).∴f (x )是周期为4的周期函数.(2)解 ∵x ∈[2,4],∴-x ∈[-4,-2],∴4-x ∈[0,2],∴f (4-x )=2(4-x )-(4-x )2=-x 2+6x -8.∵f (4-x )=f (-x )=-f (x ),∴-f (x )=-x 2+6x -8,即当x ∈[2,4]时,f (x )=x 2-6x +8.13.若f (x )=e x -a e -x 为奇函数,则满足f (x -1)>1e 2-e 2的x 的取值范围是( ) A .(-2,+∞) B .(-1,+∞)C.(2,+∞) D.(3,+∞)答案 B解析∵f(x)是定义域为R的奇函数,∴f(0)=1-a=0,∴a=1,∴f(x)=e x-e-x,∴f(x)为R上的增函数,-e2,又f(-2)=e-2-e2=1e2∴原不等式可化为f(x-1)>f(-2),∴x-1>-2,即x>-1.14.已知函数f(x)对任意实数x满足f(-x)+f(x)=2,若函数y=f(x)的图象与y=x+1有三个交点(x1,y1),(x2,y2),(x3,y3),则y1+y2+y3=________.答案 3解析因为f(-x)+f(x)=2,则f(x)的图象关于点(0,1)对称,又直线y=x+1也关于点(0,1)对称,因为y=f(x)与y=x+1有三个交点,则(0,1)是一个交点,另两个交点关于(0,1)对称,则y1+y2+y3=2+1=3.15.(多选)已知f(x)是定义域为R的奇函数,且函数f(x+2)为偶函数,则下列结论正确的是()A.函数y=f(x)的图象关于直线x=1对称B.f(4)=0C.f(x+8)=f(x)D.若f(5)=-1,则f(2 021)=-1答案BCD解析根据题意,f(x)是定义域为R的奇函数,则f(-x)=-f(x),又由函数f(x+2)为偶函数,则函数f(x)的图象关于直线x=2对称,则有f(-x)=f(4+x),则有f(x+4)=-f(x),即f(x+8)=-f(x+4)=f(x),则函数f(x)是周期为8的周期函数;据此分析选项:对于A,函数f(x)的图象关于直线x=2对称,A错误;对于B,f(x)是定义域为R的奇函数,则f(0)=0,又由函数f(x)的图象关于直线x=2对称,则f(4)=0,B正确;对于C,函数f(x)是周期为8的周期函数,即f(x+8)=f(x),C正确;对于D,若f(5)=-1,则f(2 021)=f(5+2 016)=f(5)=-1,D正确.16.函数f(x)的定义域为D={x|x≠0},且满足对于任意x1,x2∈D,有f(x1·x2)=f(x1)+f(x2).(1)求f(1)的值;(2)判断f(x)的奇偶性并证明你的结论;(3)如果f(4)=1,f(x-1)<2,且f(x)在(0,+∞)上单调递增,求x的取值范围.解(1)因为对于任意x1,x2∈D,有f(x1·x2)=f(x1)+f(x2),所以令x1=x2=1,得f(1)=2f(1),所以f(1)=0.(2)f(x)为偶函数,证明如下:f(x)的定义域关于原点对称,令x1=x2=-1,有f(1)=f(-1)+f(-1),所以f(-1)=12f(1)=0.令x1=-1,x2=x,得f(-x)=f(-1)+f(x),所以f(-x)=f(x),所以f(x)为偶函数.(3)依题设有f(4×4)=f(4)+f(4)=2,由(2)知f(x)是偶函数,所以f(x-1)<2等价于f(|x-1|)<f(16).又f(x)在(0,+∞)上单调递增,所以0<|x-1|<16,解得-15<x<17且x≠1,所以x的取值范围是(-15,1)∪(1,17).。
介绍他人入职注意事项2011.5.17

介绍他人入职的注意事项亲爱的眉州同事们:首先感谢大家对眉州的信任,介绍亲戚、朋友到眉州工作,我们也会对他们进行无微不至的关怀。
为了您介绍的新员工能够尽快入职,请注意以下几点入职要求:1、首先您须对您介绍的新员工如实介绍企业的情况(包括员工食宿、工作时间、劳动强度等);2、新员工持有正式身份证(户籍证明、临时、过期身份证均不能入职);3、新员工来京前办理好健康证(县级以上医院出具的食品卫生健康证或乙肝表面抗原(HBsAg)结果为阴性),并携带一张彩色一寸照片;4、年龄:女16周岁—45周岁,男16周岁---50周岁;5、符合应聘岗位的录用要求(不明之处可咨询当店经理或行政专员);6、认识并能够书写汉字,可以用普通话与他人进行简单的沟通;7、接受人力资源部安排的入职培训(培训报到时间在每周三和周日下午2:00—4:00之间,因此介绍员工时尽量安排周三或周日上午到人力资源部报到,报到当天请携带好本人身份证、健康证原件、一寸彩色照片,如证件齐全,下午便可以安排培训,培训注意事项详见附件);8、能够服从企业统一分配;9、新员工填写入职登记表时,请写清楚介绍人所在分店和姓名。
附件:培训注意事项为了便于培训期间做笔记,请提前准备好练习本、笔;培训期间,不提供洗漱用品(提供洗脸盆、迷彩服),请参加培训人员自行携带洗漱用品以及个人换洗衣物。
(培训结束分配到各分店后,在店内领取洗漱用品)报到前,请整理好自己的仪容仪表,要求:①男员工头发长度保持不盖耳部、不触衣领,不得留胡须;②女员工发长超过肩部的必须用发圈扎起,刘海不得过眉;③所有人员不得将头发染成除黑色外的其它颜色,不得留长指甲。
培训期间,公司提供免费食宿;培训为封闭式培训,期间不允许请假,请参加培训人员在报到之前处理好个人事务;培训期间将安排一次体能训练,请参加培训人员穿舒适的平底鞋;不能完成体能训练的,公司有权不予录用。
培训期间,所有学员需遵守集团培训基地规章制度,违反规定的,公司有权不予录用。
第二章第1节

级数学导学案(第二章)2.1平方差公式执笔人:田星 审稿人:张树宏一、学习目标:会推导平方差公式,了解公式的几何解释,并能运用公式计算。
二、学习重点:掌握公式的结构特征和字母表示的广泛含义,正确运用公式进行计算。
三、学法指导:通过对平方差公式的推导、公式特征的分析及典型例题的练习,掌握公式及应用。
四、学习过程:【课前准备及预习感悟】1.学习本节内容需要熟悉“多项式乘多项式”、“幂的乘方”和“积的乘方”的运算法则,学习前可先检查自己是否熟悉这几个法则;2.同学们在利用多项式乘法方则进行多项式乘多项式的运算时,是否感到有些繁琐?是否渴望有一个公式能很快得出运算结果?学完本节内容后你的这一愿望就基本会如愿以赏了!依据预习提纲预习并完成相关的问题预习教材34-35页“练习”以上内容,完成下列问题:1、 用多项式乘法计算()()a b a b +-=_______________________=_______________。
由此可得平方差公式____________________,即两个数的____与这两个数的_____的_____,等于这两个数的__________。
2、 自主探究平方差公式的几何意义做一做:在一块边长为a 厘米的正方形纸板上,因为工作的需要,中间挖去一块边长为b 厘米的小正方形,请问剩下的面积有多少?还能通过剪纸拼图的方法来计算出这个图形的面积吗?”思考:平方差公式有何结构特征?(1)左边:(2)右边:想一想:(1)你能否推导该公式?推导的依据是什么?(2)为什么取名叫“平方差公式”,而不叫“两数和乘两数差公式”?(3)平方差公式的结构和特点是什么?预习疑难摘要【课堂学习研讨交流】1、小组研讨预习中碰到的疑难问题,不会的要向其他同学或老师请教哦!2、说说平方差公式的特征,和你的伙伴交流认识。
【知识应用与能力形成】例1、(教科书35页例1)(学生尝试独立解题,2个学生板演)(1).(32)(32)x y x y +- 22(2).(72)(72)m m -+--例2(教科书35页例2)(学生尝试独立解题,2个学生板演)803×797例题反思:【课内训练巩固】1、下列各式能用平方差公式计算的是( )A 、(2a-3b)(3b-2a)B 、(-2a+3b)(-2a-3b)C 、(2a-3b)(-3b+2a)D 、(2a-3b)(3a+2b)2、教科书35页练习第1 、2题【学习体会】1、本节课你有何收获?把你认为重点的内容划在书上。
组合数学第二章课后习题答案

A(x)= +
A +A =1, A r + A r =0
解得:A =1,A =
a =A cos +A sin = cos + sin
a, 的母函数为(1-x)
证明:
当m=0时,命题成立。
假设对于m-1,命题成立,即 =(1-x) ,
= (1+x+ x +…x +…)(1+2 x+3 x +…+n x + (n+1) x +…)
=
=
G=
G= 即为序列{ a }的母函数。
求解完毕。
2.13题(高亮)
解:
B(x)=1 +2 x+3 x +……
1: a =1 b =1
x: a =1 +2 b =2
x : a =1 +2 +3 b =3
2.24题(李拂晓)
设 -2 + =5, =1, =2,求解这个递推关系。
解:
由题意可知,特征方程为: -2x+1=(x-1)(x-1)=0,所以1是二重特征根,令特解为,
=k ,代入递推关系得,
k -2k +k =5
解得,2k=5, k=5/2
故非齐次方程特解是: =5/2 ,
一般解: =5/2 +An+B
即: 解的k=4
故非其次方程特解是:
一般解: ,系数A由初始条件确定。
(5)
则
相减得:
特征方程是:
两个特征根是:
因为 则(*)的解:
(*)的解可表示为:
农民收入影响因素的回归分析

农民收入影响因素的回归分析摘要:随之社会经济的发展和时代环境的改变,近几年来虽然我国农民居民的纯收入水平明显有所改变,居民收入的绝对量在不断增长,但增长的幅度在不断下滑,农民的内部收入出现了严重的失衡。
因此,本文通过对农民收入变动的多因素,以农作物总播种面积、农产品生产价格总指数、第一产业就业人数占全社会就业人数的比重、农村用电量、财政支出对农业的投入等影响因素为自变量,建立多元线性回归分析模型并进行研究分析,这对将来农民提高收入水平起着至关重要的意义。
关键字:回归分析、农民收入、影响因素、eviews操作本文所研究的是农民收入的影响因素,考虑到获取数据的方便程度和建立模型的合理性,综合选择了五项指标作为影响农民纯收入的因素:农作物总播种面积、农产品生产价格总指数、第一产业就业人数占全社会就业人数的比重、农村用电量、财政支出对农业的投入为影响变量。
相关数据从1986—2009如下表所示,通过建立回归分析模型来说明农民收入的影响原因。
(数据来源: 2010年中国农业统计年鉴)对问题中的各变量给出以下假设:农村居民家庭人均纯收入y (元)、农作物总播种面积1x (千公顷)、农产品生产价格总指数2x (%)、第一产业就业人数占全社会就业人数的比重3x (%)、农村用电量4x (亿千瓦时)、财政支出对农业的投入5x (亿元)。
从而有因变量y 与多个自变量54321,,,,x x x x x 相关,故我们可以采用多元线性回归对问题进行分析。
第三章 模型假定多元线性回归分析的基本形式:设随机变量y 与一般变量n x x x x ,...,,,321的理论线性回归分析模型为:=y εβββ++++n n x x ...110,其中n ββββ,...,,,210是1+n 个未知数,0β为回归常数,n ββββ,...,,,321为回归系数,ε 为随机误差。
对随机误差假定()0=εE ,()2σε=Var ,则有()=y E εβββ++++n n x x ...110。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
LOGO
p87: 4、7、9、10、11
LOGO
LOGO
§2.6 两组分系统相图
——固液平衡相图
p~xCH3OH
pH2O*
液相线
pCH3OH*
气相线
p~yCH3OH
H2O CH3OH
LOGO
xCH3OH→
p~x图与T~x图的比较
液相区
气相区
气液两相区
气液两相区
气相区
液相区
可把两个图形近似地看成关于x轴的对称图形
LOGO
LOGO
3.完全不互溶双液系统
物系 蒸气压曲线 沸点 溴苯 QM 429K 水 QN 373.15K 水+溴苯 QO 368.15K
LOGO
在实验室和工业上,常用水蒸气蒸馏提纯与水不 互溶的高沸点物质。 条件:该物质与水不互溶 方法:以鼓泡方式使水蒸气通过有机液体,带 出气体冷凝后,分层,可得纯有机物。 特点:沸点一定低于100℃
LOGO
第二章多相多组分系统热力学(8)
主讲:李平
主要内容
1 2 3 4 5
§2.1 均相多组分系统热力学
√ §2.3 液体热力学 √ §2.4 Gibbs相律 √
§2.2 气体热力学 §2.5 单组分系统的相图 §2.6 两组分系统的相图
√
√
6
7
§2.7 三组分系统的相平衡
T
LOGO
重点知识回顾
3. 纯物质两相平衡时温度与压力的关系
dp H m dT T Vm
g
Clapeyron 方程
p2 H m 1 1 ln p1 R T1 T2 Clausius-Clapeyron
g p2 H m (T2 T1 ) ln p1 RTT2 1
LOGO
馏出物组成(了解内容)
nA p py A p nA nB
A
nB p pyB p nA nB
B
两式相除,得:
mA M B p nA mA / M A mB M A p nB mB / M B
A B
mA p M A A mB pB M B
T T’ E E’ T
F
F’
若指定温度T,两个相的 组成必为E点和F点确定;
A XB→
B
若指定液相的组成为E',体系的温度必为T', 平衡时气相的组成必为F'。
LOGO
§2.6
气液平衡相图
二组分系统相图
固液平衡相图
完全互 溶双液 系统
部分互 溶双液 系统
LOGO
ii)精馏原理 精馏是多次简 单蒸馏的组合。 将一定组成的 溶液加热到T2, 此时物系点为O, 气相相点G2(组成 为y2),液相相点 L2(组成为x2)。
LOGO
精馏塔示意图
精馏塔底部是加热区,温度最高,塔顶温度最低。 精馏结果,塔顶冷凝收集的是纯低沸点组分,纯 高沸点组分则留在塔底。
完全不 互溶双 液系统
简单低共 熔混合物 系统
热 分 析 法 绘 制 相 图 溶 解 度 法 绘 制 相 图
形成化 合物系 统 形 成 不 稳 定 化 合 物
形成固 态溶液 系统
理 想 液 体 混 合 物
实 际 液 体 混 合 物
形 成 稳 定 化 合 物
完 全 互 溶 固 熔 体
部 分 互 溶 固 熔 体
LOGO
2.部分互溶双液系统
Al1C线:是不同温度下苯酚 在水中的溶解度曲线; Bl2C线:是不同温度下水在 苯酚中的溶解度曲线; C点:是两曲线的汇合点, 叫临界会溶点,其对应的温 度称会溶温度。 会溶温度的高低反映了一对液体间相互溶解能力的 强弱。会溶温度越低,两液体间的互溶性越好。
E O1 A x XB→
O2
杠杆规则
nl EO ng OF
ng EO nl OF n 'g EO ' n 'l O ' F
B
LOGO
重点知识回顾
(4)相律分析 在液相区或气相区: C=2,P=1,f*=2-1+1=2 在气液两相平衡区: C=2,P=2,f*=2-2+1=1
p
* A
气相线
A
XB→
B
LOGO
重点知识回顾
(2)p~x图与T~x图的比较
p
* pB
T TA 气相线 l+g 液相线 TB
p
* A
l+g
A
XB
B
A
XB
B
LOGO
(3) 物系点与相点
重点知识回顾
物系点:是整个体系总的状态点。 相点:是表示平衡体系中每一个相的状态点。 在单相区,物系点与相点合 T 二为一,如图中的O1 和O2 。 在两相平衡区,物系点O位 于两个相点E、F的连接线 T EF上。 O'O F
LOGO
(2)实际液体混合物的相图 正偏差与负偏差
2
正偏差 负偏差 一般说来,当A组分发生正偏差时,B组分也发 生正偏差;反之亦然。
LOGO
最大正偏差与最大负偏差
最大正偏差
最大负偏差
LOGO
实际液体混合物的相图 p
LOGO
2.部分互溶双液系统
黄色区域是单相区,水和苯酚 可以完全互溶。 f *=2-1+1=2 白色帽形区域是两相区,水层和 苯酚层两相共存。 f *=2-2+1=1 物系点为O时,共存的两相为组 成l1 的水层和组成l2 的苯酚层,二 者互称为共轭溶液。两液层的相对 量由杠杆规则计算。
LOGO
重点知识回顾
1. 水的相图
p
C
Tc
l g O
g
T
s l
点、线、面的含义 自由度 f
D
B s A
LOGO
重点知识回顾
2. 一般物质单组分系统相图
p
C
D
p
C
D
B A
O
B A
T
O
一般单组分相图
水的相图
LOGO
3.完全不互溶双液系统
完全不互溶:绝对不互溶的液体不存在,当两种 液体之间的相互溶解度非常小时,就称为完全不 互溶。因不互溶,故没有浓度变量,相图用p~T 绘制。
两种不互溶的液体A和B共存时,各组分的蒸气 压与单独存在时一样,总蒸气压 p=p*A+p*B,即 系统的总蒸气压恒高于任一纯组分的蒸气压。因 此,不互溶双液系的沸点恒低于组成它的任一纯 组分的沸点。
w酚层 Ol1 w水层 Ol2
LOGO
2.部分互溶双液系统
下临界会溶温度
同时具有上下临界会溶温度
LOGO
2. 部分互溶双液系统
不具有会溶温度
LOGO
气-液平衡相图
图中水平线段(eEf)是三相平衡线,当物系点 处于该线段上时,系统呈三相平衡:l1 (组成为e) 、 l2 (组成为f) 、g (组成为E)。
水在苯酚中形成的饱和溶液,组成为b
苯酚在水中形成的饱和溶液,组成为a
T~ a ~b
LOGO
2. 部分互溶双液系统 T
T3
a3
b3
T2
a2
b2
b1
T1 a1 H 2O
w WC6H5OH→
C6H5OH
a1a2a3:是不同温度下苯酚在水中的溶解度 b1b2b3:是不同温度下水在苯酚中的溶解度
方程的定积分式
LOGO
重点知识回顾
1. 完全互溶双液系统相图 (1)理想液态混合物的p-x相图 p
p ( p p ) xB p
* B * A
* A * B * B
* A
液相线
l+g
* pB
p p p * pB ( p p* ) yB A
实际混合物的 p~ X图与T~ X图
正偏差
负偏差
最大正偏差
最大负偏差
LOGO
最低恒沸点
T2 T1
最大正偏差
O点对应的温度:最低恒沸点 O点对应的组成:恒沸混合物
LOGO
蒸馏和精馏原理 蒸馏与精馏是分离液体混合物常用的方法,在 实验室和工厂应用很广。 i)简单蒸馏
LOGO
(2)实际液体混合物的相图 正偏差与负偏差 pCH3OH~XCH3OH
p~XCH3OH
pCH3OH*
pCH3OH=pCH3OH*XCH3OH pH2O* pH2O~XH2O pH2O=pH2O*XH2O
H2O
CH3OH
LOGO
具有最低恒沸点的相图可以看作由两个简单 的T-x图的组合。对具有最高、低恒沸点的实际溶 液精馏时,不能将两组分完全分离,其精馏结果 可得到一个纯物质,另一个是恒沸混合物。
组成为X1时:塔顶为恒沸混合物 塔底为纯B 组成为X2时:塔顶为恒沸混合物 塔底为纯A
LOGO
一、气液平衡相图
2.部分互溶双液系统 部分互溶:是指一定温度下某液体在另一液体中只能 有限地溶解。超过一定范围时,就要分成两个液层。 液-液平衡相图 实验数据的获得:以水-苯酚体系为例
一定温度T时,将一定量的水和苯酚(苯 酚的质量百分数为W%)混合,充分震荡使 之达到平衡。
