第二章习题4 (1)

合集下载

传感器技术第3版课后部分习题解答

光勇 0909111621 物联网1102班《传感器技术》作业第一章习题一1-1衡量传感器静态特性的主要指标。

说明含义。

1、线性度——表征传感器输出-输入校准曲线与所选定的拟合直线之间的吻合（或偏离）程度的指标。

2、回差（滞后）—反应传感器在正（输入量增大）反（输入量减小）行程过程中输出-输入曲线的不重合程度。

3、重复性——衡量传感器在同一工作条件下，输入量按同一方向作全量程连续多次变动时，所得特性曲线间一致程度。

各条特性曲线越靠近，重复性越好。

4、灵敏度——传感器输出量增量与被测输入量增量之比。

5、分辨力——传感器在规定测量围所能检测出的被测输入量的最小变化量。

6、阀值——使传感器输出端产生可测变化量的最小被测输入量值，即零位附近的分辨力。

7、稳定性——即传感器在相当长时间仍保持其性能的能力。

8、漂移——在一定时间间隔，传感器输出量存在着与被测输入量无关的、不需要的变化。

9、静态误差（精度）——传感器在满量程任一点输出值相对理论值的可能偏离（逼近）程度。

1-2计算传感器线性度的方法，差别。

1、理论直线法：以传感器的理论特性线作为拟合直线，与实际测试值无关。

2、端点直线法：以传感器校准曲线两端点间的连线作为拟合直线。

3、“最佳直线”法：以“最佳直线”作为拟合直线，该直线能保证传感器正反行程校准曲线对它的正负偏差相等并且最小。

这种方法的拟合精度最高。

4、最小二乘法：按最小二乘原理求取拟合直线，该直线能保证传感器校准数据的残差平方和最小。

1—4 传感器有哪些组成部分？在检测过程中各起什么作用？答：传感器通常由敏感元件、传感元件及测量转换电路三部分组成。

各部分在检测过程中所起作用是：敏感元件是在传感器中直接感受被测量，并输出与被测量成一定联系的另一物理量的元件，如电阻式传感器中的弹性敏感元件可将力转换为位移。

传感元件是能将敏感元件的输出量转换为适于传输和测量的电参量的元件，如应变片可将应变转换为电阻量。

第二章习题及练习答案

第2章第二章习题及练习答案2.1 选择题A,B,C,C,A2.2 填空题1.在Python中，字典和集合都是用一对__大括号___作为定界符，字典的每个元素有两部分组成，即_键_和值，其中__键___不允许重复。

2.假设有列表a = ['name','age','sex']和b = ['Dong',38,'Male']，请使用一个语句将这两个列表的内容转换为字典，并且以列表a中的元素为键，以列表b中的元素为值，这个语句可以写为__c = dict(zip(a,b))__。

3.假设有一个列表a，现要求从列表a中每3个元素取1个，并且将取到的元素组成新的列表b，可以使用语句___b = a[::3]__。

4.使用列表推导式生成包含10个数字5的列表，语句可以写为__[5 for i in range(10)]_。

5. ___不可以________（可以、不可以）使用del命令来删除元组中的部分元素。

2.3 简答题1.为什么应尽量从列表的尾部进行元素的增加与删除操作？答：当列表增加或删除元素时，列表对象自动进行内存扩展或收缩，从而保证元素之间没有缝隙，但这涉及到列表元素的移动，效率较低，应尽量从列表尾部进行元素的增加与删除操作以提高处理速度。

2.简单解释Python的字符串驻留机制。

答：Python支持字符串驻留机制，即：对于短字符串，将其赋值给多个不同的对象时，内存中只有一个副本，多个对象共享该副本。

这一点不适用于长字符串，即长字符串不遵守驻留机制。

2.4 编程题1.编写程序，生成包含1000个0到100之间的随机整数，并统计每个元素的出现次数。

（提示：使用集合。

）答：import randomx = [random.randint(0,100) for i in range(1000)]d = set(x)for v in d:print(v, ':', x.count(v))2.假设有一段英文，其中有单独的字母“I”误写为“i”，请编写程序进行纠正。

第二章汉字习题及参考答案

第二章汉字习题及参考答案第一节现代汉字概述（P76—P77）练习题一、填空。

1. 汉字是世界上历史最悠久的一种独立发展的文字。

2. 除中国外，现在使用汉字的国家还有日本、韩国、新加坡和马来西亚等。

3. 现代世界各国所用的文字可分为表意文字和表音文字两种性质不同的文字，汉字属于表意性质的文字，日文的假名属于表音性质的文字。

4. 大多数拼音文字是线性文字，汉字是平面性文字。

5. 先进的电脑与古老的汉字正在有机地结合起来。

这种结合使汉字不再仅仅是人与人之间交流信息的工具，而且成为人与机器沟通信息的纽带。

1.现代汉字有哪五个特点？这些特点对汉字的学习和使用有什么影响？现代汉字有五大特点：（1）汉字基本上是一种表意文字。

（2）汉字基本上是一种语素文字。

（3）汉字在形体上表现为方块形。

（4）汉字在语音上代表一个音节。

（5）汉字在书面上不实行分词连写。

总之，现代汉字是一种表意性质的语素文字。

这是它区别于纯粹表音的音素文字或音节文字的基本特点。

从这个基本观点出发，汉字教学应正确估价并充分利用汉字的表意作用，同时要加强汉字的字音教学，以弥补汉字表音功能薄弱的缺点。

2. “森”表示树多貌，“淼”表示大水貌，运用同样的造字法所造的汉字，你还能举出4—5个例字来吗？磊品晶焱犇众卉鑫3. 新造字的造字方法有哪几种跟传统的方法不同的？请举例说明。

新造字是指现代新造的汉字。

新造字除了大量使用形声法和少量使用会意法外，还有一些新的造字法，例如：（1）切音合形造字法，就是两个字合成一个字，意义也合，但是读音则利用切音方法，前字取声母，后字取韵母和声调。

例如方言字“甭”（béng）,是“不”和“用”的切音；字义是“不用”，是“不”和“用”的合义。

（2）省形的切音合形造字法，语音和意义跟上面的方法相同，只是字形也各取一半。

例如科技用字“巯”（qiú），是“氢”和“硫”的切音，字义是：有机化合物中含“氢”和“硫”的基。

《逻辑学基础教程》习题和答案

第二章练习题一、根据语言的有关知识，回答下列问题1．分析下列对话中B的话语中的预设：A：你怎么迟到了？B：因为我的自行车给偷走了。

2．从语用学的角度看，“战争就是战争”和“孩子就是孩子”这类同义反复的语句是否违反了交际的合作准则？如果违反了，那么，它们的语用含义是什么？3．根据语境分析下列对话是否违反了交际的合作准则？如果违反了，那么，它们的语用隐涵是什么？（1）“妈妈，我出去和同学玩一会儿，好吗？”“你的作业做完了吗？”（2）甲：“五一节我们去北京旅游，好吗？”乙：“我们初中的老同学要一起聚会呢。

”二、运用语义上行和加下标的方法，分析下列划横线的语词表达的概念是否相同？1．甲：“认识的源泉是客观事物。

”乙：“认识的源泉是人类的社会实践。

”2．在电影院里，几个年轻人旁若无人地议论着影片的内容，声音越来越大，旁边一位老年人小声提醒他们“你们别再说话了，好吗？”有个年轻人却反问道“你不是也在说话吗？”3．在一次文化界人士的聚会上，著名画家张大千举杯向著名京剧演员梅兰芳说：“梅先生，你是君子，我是小人，我敬你一杯！”此语一出，举座皆惊。

张大千笑道：“因为君子动口，小人动手嘛！”此言一出，笑声哄堂。

4．奴隶到底有没有哲学？甲、乙两人提出了不同的观点并且展开了讨论。

甲说：奴隶有哲学。

因为哲学是关于世界观的学问，而世界观是人人都有的，奴隶也不例外。

如果奴隶没有哲学，就等于说劳动人民没有世界观，这是不符合实际的。

乙说：奴隶不可能有哲学。

因为在奴隶社会，奴隶不过是会说话的工具。

他们尽管有世界观，但是由于被剥夺了从事精神创作活动的权利，所以他们根本不可能把自己的世界观系统化、理论化，上升为一个哲学体系。

而且，他们又不识字，不能把有关世界观的哲学体系记录下来，流传下去。

三、下列各段文字中，哪些语词表达的是标有横线的词项的内涵和外延？1．公司是依法设立的，由法定数额的股东所组成的以盈利为目的的企业法人。

可以分为有限责任公司和无限责任公司。

高数(高等教育出版社)第一版,第二章习题详解参考

第二章习题解答参考习题 2-11．设()=8f x x ，试按定义求(1)f '．解 ()()()0011818(1)=limlim 8x x f x f x f x x∆→∆→+∆-+∆-'==∆∆． 2．设2()=f x ax bx c ++，其中,,a b c 为常数.按定义求()f x '．解 ()()()0=limx f x x f x f x x∆→+∆-'∆()()()220limx a x x b x x c ax bx c x∆→+∆++∆+-++=∆()202lim 2x ax x a x b x ax b x∆→∆+∆+∆==+∆． 3．证明 (sin )=cos x x '．证设()sin f x x =，则()()()sin sin 2cos sin 22x x f x x f x x x x x ∆∆⎛⎫+∆-=+∆-=+ ⎪⎝⎭ ()()()002cos sin 22lim lim x x x x x f x x f x f x x x∆→∆→∆∆⎛⎫+ ⎪+∆-⎝⎭'==∆∆0sin2lim cos cos 22x xx x x x ∆→∆∆⎛⎫=+⋅= ⎪∆⎝⎭，所以 (sin )=cos x x '．4．下列说法可否作为()f x 在0x 可导的定义（1）000()()limh f x h f x h h→+--存在；解不能．因为从极限式中不能判断()0f x 存在，也不能判断000()()limh f x h f x h→+-存在．例如()f x x =在0x =点不可导，但00(0)(0)limlim 0h h h h f h f h h h→→--+--==却存在．（2）000()()lim h f x h f x h +→+-和000()()lim h f x h f x h+→---存在且相等；解可以．因为()0000()()lim h f x h f x f x h++→+-'=，()0000000()()()()lim lim h h f x h f x f x h f x f x h h+--→-→----'==--，根据导数存在的充要条件，可知()0f x '存在．5．求下列函数的导数：（1）5y x =；（2）y =；（3）y x =；（4）13log y x = ；（5）y =（6）lg y x =．解（1）51455y x x -'==；（2）132212y x x --'⎛⎫'==-= ⎪⎝⎭（3）221577222277y x x x '⎛⎫'=== ⎪⎝⎭（4）111ln 3ln3y x x '==-；（5）25152326616y x x x +--''⎛⎫⎛⎫'==== ⎪ ⎪⎝⎭⎝⎭；（6）1ln10y x '=． 6．已知物体的运动规律为3s t =(米)，求这物体在2t =(秒)时的速度．解因为3s t =，23dsv t dt==，所以2t =时，()223212v =⨯=． 7．如果()f x 为偶函数，且(0)f '存在，证明(0)=0f '．证因为()()0(0)=lim x f x f f x∆→∆-'∆，而()f x 为偶函数，故()()f x f x -∆=∆，所以()()()()000(0)limlim (0)x x f x f f x f f f x x∆→∆→-∆--∆-''==-=-∆-∆，所以(0)=0f '．8．抛物线2y x =在哪一点的切线平行于直线45y x =-在哪一点的切线垂直于直线2650x y -+=解由2y x =，可得2y x '=，若切点为()200,x x ，则依题设024x =，即02x =时，切线平行于直线45y x =-；01213x ⋅=-，即032x =-时，切线垂直于直线2650x y -+=；所以抛物线2y x =在点()2,4的切线平行于直线45y x =-在点39,24⎛⎫- ⎪⎝⎭的切线垂直于直线2650x y -+=．9．在抛物线2y x =上取横坐标为11x =及23x =的两点，作过这两点的割线，问该抛物线上哪一点的切线平行于这条割线解由题设可知2y x '=，所取的两点为()1,1，()3,9，连接两点的直线斜率为4k =，依题设，应有24x =，即2x =，所以所求点为()2,4．10.如果()y f x =在点()4,3处的切线过点()0,2，求()4f '．解依题设，曲线在点()4,3处的切线为()()344y f x '-=-，满足()()23404f '-=-，从而()144f '=．11．讨论下列函数在0x =处的连续性与可导性：（1）y = （2）21sin ,0,0,0.x x y xx ⎧≠⎪=⎨⎪=⎩ 解（1）因为()000x y →==，所以y =0x =点连续，而20031lim x x x →→==+∞，所以y =0x =点不可导；（2）因为()201lim sin 00x x y x →==，所以21sin ,0,0,0.x x y x x ⎧≠⎪=⎨⎪=⎩在0x =点连续，又 2001sin1limlim sin 0x x x x x x x →→==，所以21sin ,0,0,0.x x y x x ⎧≠⎪=⎨⎪=⎩在0x =点可导． 12．设sin ,0()=,0x x f x ax b x <⎧⎨+≥⎩在0x =处可导，求,a b 的值．解因为sin ,0()=,0x x f x ax b x <⎧⎨+≥⎩在0x =处可导，所以()0lim ()0x f x f →=，且()()00f f -+''=，又0lim ()0x f x -→=，0lim ()x f x b +→=，()0f b =，故0b =，()00f =，从而()()()000sin 0lim lim 1x x f x f xf x x---→→-'===， ()()()0000lim lim x x f x f ax f a xx +++→→-'===，所以1a =． 13．已知2,0(),0x x f x x x ⎧≥=⎨-<⎩，求(0)f +'，(0)f -'和(0)f '．解因为2,0(),0x x f x x x ⎧≥=⎨-<⎩，所以()200()0(0)lim lim 0x x f x f x f x x +++→→-'===， ()00()0(0)lim lim 1x x f x f xf x x---→→--'===-，所以(0)f '不存在． 14．设函数33,0()=,0x x f x x x ⎧≥⎨-<⎩，求()f x '．解当0x >时，2()3f x x '=，当0x <时，2()3f x x '=-，当0x =时，()()3000(0)limlim 0x x f x f x f xx +++→→-'===， ()()3000(0)lim lim 0x x f x f x f xx ---→→--'===，所以(0)0f '=，所以 223,0()=3,0x x f x x x ⎧≥'⎨-<⎩．15．设所给的函数可导，证明：（1）奇函数的导函数是偶函数；偶函数的导函数是奇函数；（2）周期函数的导函数仍是周期函数．证（1）设()f x 为奇函数，则()()f x f x -=-，而()()()limh f x h f x f x h→+-'=，()()()()()0limlim h h f x h f x f x h f x f x h h→→-+----+'-== ()()0lim h f x h f x h →--=-()()()0lim h f x h f x f x h→--'==-，所以()f x '为偶函数；相似地，若()f x 为偶函数，则()()f x f x -=，于是()()()()()0limlim h h f x h f x f x h f x f x h h→→-+----'-== ()()()0limh f x h f x f x h→--'=-=--，所以()f x '为奇函数．（2）设()f x 为周期函数，则存在T ，使()()f x T f x +=，则()()()0limh f x T h f x T f x T h →++-+'+=()()()0lim h f x h f x f x h→+-'==，所以()f x '也是以T 为周期的周期函数．16．设有一根细棒，取棒的一端作为原点，棒上任意点的坐标为x ．于是分布在区间[0,]x 上细棒的质量m 是x 的函数()m m x =．应怎样确定细棒在点0x 处的线密度（对于均匀细棒来说，单位长度细棒的质量叫这细棒的线密度）解设在0x 处的线密度为()0x ρ，给0x 以x ∆的增量，则在区间00[,]x x x +∆上细棒的平均线密度为()()00m x x m x x+∆-∆，故()()()()00000limx m x x m x x m x xρ∆→+∆-'==∆．17．证明：双曲线2xy a =上任一点处的切线与两坐标轴构成的三角形的面积都等于22a ．证由2xy a =可得2,0a y x x =≠，于是22,0a y x x '=-≠，若切点为200,a x x ⎛⎫ ⎪⎝⎭，则该点处的切线为()220200a a y x x x x -=--，它与两坐标轴的交点分别为()02,0x ，2020,a x ⎛⎫ ⎪⎝⎭，所以所求三角形的面积为220012222a S x a x =⨯⨯=． 18．设函数()f x 在0x =处可导，试讨论函数|()|f x 在0x =处的可导性．解因为函数()f x 在0x =处可导，所以()()0()0lim0x f x f f x→-'=存在，而()()()0limx x f x f f x x=→-'=，故（1）若(0)0f =，由()()0()0lim 0x f x f f x →-'=可知：()()0f x f xα'=+，其中lim 0x α→=，从而()()0f x x f α'=+⎡⎤⎣⎦，此时()()()000limlim 0x x x x f xf x f xxαα=→→'+⎡⎤⎣⎦''==⋅+，因此|()|f x 在0x =点的左导数为()0f '-，右导数为()0f '，所以|()|f x 在0x =处可导的充要条件是()00f '=；（2）若(0)0f ≠，设(0)0f >，则()0lim ()00x f x f →=>，由保号性定理，0δ∃>，当()0,x U δ∈时，()0f x >，此时有()()()()0()0()0limlim0x x x f x f f x f f x f xx=→→--''===，相似地，若(0)0f <，则()0lim ()00x f x f →=<，由保号性定理，0δ∃>，当()0,x U δ∈时，()0f x <，此时有()()()()00()0()0limlim 0x x x f x f f x f f x f x x=→→---⎡⎤⎣⎦''===-；总之，若()f x 在0x =处可导，则当(0)0f ≠时，|()|f x 在0x =处可导；当(0)0f =时，|()|f x 在0x =处可导的充要条件是()00f '=．习题 2-21．求下列函数的导数：（1）3cos2y x =；（2）4sin(31)y t =-；（3）32e 4cos2x y x =+；（4）5(1)y x =+；（5）43e 1x y -=+；（6）y =（7）1ln y x x=；（8）23(1)(1)y x x x =++-；（9）3e sin xy x x =；（10）322ln 3ln x x y x x +=+．解（1）()()()()3sin 223sin 226sin 2y x x x x ''=⋅-=-⋅=-；（2）()4cos(31)3112cos(31)y t t t ''=-⋅-=-；（3）()()()()332e 34sin 226e 8sin 2x x y x x x x '''=+-=-；（4）()445(1)15(1)y x x x ''=++=+；（5）()443e 4012e x x y x --''=-+=-；（6）y '==（7）()()()()2221ln ln ln 1ln ln ln x x x x x x y x x x x x x +⋅'+'=-=-=-；（8）()()3222221(1)(1)3(1)(1)522y x x x x x x x x '=+-+++⋅-=-++；（9）()23323e sin e sin e cos e 3sin sin cos x x x x y x x x x x x x x x x x x '=++=++；（10）()()()()()2234222222333ln 2ln 294ln 323ln 3ln x x x x x x x x x x x xx x y x x x x ⎛⎫⎛⎫++-++ ⎪ ⎪-+-+⎝⎭⎝⎭'==++2．证明：（1）2(cot )csc x x '=-；（2） (csc )csc cot x x x '=- ．证（1）22cos sin sin cos cos (cot )csc sin sin x x x x x x x x x '-⋅-⋅⎛⎫'===- ⎪⎝⎭；（2）21cos 1cos (csc )csc cot sin sin sin sin x x x x x x x x x '⎛⎫'==-=-⋅=- ⎪⎝⎭． 3．证明：（1）(arccos )x '= （2）21(arccot )1x x '=-+．证（1）设arccos y x =，则其反函数为cos x y =，,22y ππ⎡⎤∈-⎢⎥⎣⎦，由于sin x y '=-，由反函数求导法则，()1arccos sin x y '=-== （2）设arccot y x =，则其反函数为cot x y =，()0,y π∈，由于2csc x y '=-，由反函数求导法则，()222111arccos csc 1cot 1x y y x'=-=-=-++． 4．求下列函数在给定点处的导数：（1）2cos 3sin y x x =-，求π4x y ='；（2）2233x y x =+-，求(2)f '．解（1）因为2sin 3cos y x x '=--，所以π4ππ2sin3cos 442x y ='=--=-；（2）因为()()()22212223333x xy x x ⋅-'=-+=+--，所以()22222103332x y =⋅'=+=-．5．写出曲线122y x x=-与x 轴交点处的切线方程．解令0y =，得曲线122y x x =-与x 轴交点为1,02⎛⎫ ⎪⎝⎭和1,02⎛⎫- ⎪⎝⎭，而2122y x '=+，所以142y ⎛⎫'±= ⎪⎝⎭，所以所求切线有两条，方程分别为42y x =+，42y x =-．6．求下列函数的导数：（1）25(23)y x =+；（2）2sin (52)y x =-；（3）2321e xx y -++=；（4）2sin ()y x =；（5）2cos y x =；（6）y =（7）()arctan x y e =；（8）2(arccos )y x =；（9）lnsin y x =；（10）3log (1)a y x =+．解（1）242245(23)(23)20(23)y x x x x ''=⋅+⋅+=+；（2）222cos(52)(52)4cos(52)y x x x x ''=-⋅-=--；（3）()()223212321e 32162e xx x x y x x x -++-++''=⋅-++=-+；（4）222cos()()2cos()y x x x x ''=⋅=；（5）()()2cos cos 2cos sin sin 2y x x x x x ''==-=-；（6）()22y a x ''=-==（7）()()221e e 1e 1e xxxx y ''==++；（8）2(arccos )(arccos )2(arccos )y x x x ⎛⎫''=== ⎝ （9）()1cos sin cot sin sin xy x x x x''===；（10）233313(1)(1)ln (1)ln x y x x a x a''=+=++．7．求下列函数的导数：（1）arccos(12)y x =-；（2）1arcsin y x=；（3）1ln 1ln xy x-=+；（4）ln (y x =；（5）sin cos n y x nx =⋅；（6）y =（7）e y =；（8）[]ln ln(ln )y x =；（9）y =（10）1arccot tan 22x y ⎛⎫= ⎪⎝⎭．解（1）2)y x ''=-==；（2）211y x x '⎫⎫'==-=⎪⎪⎭⎭；（3）()()()()22111ln 1ln 21ln 1ln x x x x y x x x -+--'==-++；（4）y x ''=+==；（5）()()()1sin sin cos sin sin n n y n x x nx x nx nx -'''=⋅+-()1sin cos cos sin sin n n x x nx x nx -=⋅-()1sin cos 1n n x n x -=+⎡⎤⎣⎦；（6）1sin 21sin 2x y x '-⎛⎫'=⎪+⎝⎭()()()22cos 21sin 21sin 22cos 21sin 2x x x x x -+--=+2cos 21sin 2xx-=+()2cos 2cos 21sin 2x x x =-+；（7）(1ee1y x'''===+ （8）()()()1111ln (ln )ln ln (ln )ln (ln )ln ln ln (ln )y x x x x x x x x '''==⋅=；（9）y'====；（10）211tan 2211tan 22x y x '⎛⎫'=- ⎪⎝⎭⎛⎫+ ⎪⎝⎭2241sec 2224tan 2x x x '⎛⎫=- ⎪⎝⎭⎛⎫+ ⎪⎝⎭ 222sec 1213cos 4tan 22xx x =-=-⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭． 8．设1cos ,0()ln (1)cos ,0x x f x x x x x -<⎧=⎨+-≥⎩，求()f x '．解当0x ≠时，sin ,0()1cos sin ,01x x f x x x x x x<⎧⎪'=⎨-+>⎪+⎩，当0x =时，20002sin sin1cos 022(0)lim limlim sin 022x x x x xx x f xxx ----→→→--'===⋅=，()()100ln 1cos 0(0)lim lim ln 1cos ln 10x x x x x x f x x e x +++→→+--⎡⎤'==+-=-=⎢⎥⎣⎦，所以()00f '=，从而sin ,0()1cos sin ,01x x f x x x x x x <⎧⎪'=⎨-+≥⎪+⎩．9．求函数cos (sin )x y x =的导函数．解法1 因为cos cos lnsin (sin )x x x y x e ==，所以()()cos cos lnsin cos cos ln sin sin sin ln sin cos sin x x x x y e x x x x x x x ⎛⎫''=⋅=-+ ⎪⎝⎭()2cos cos sin sin ln sin sin xx x x x x ⎛⎫=-+ ⎪⎝⎭．解法2 对数求导法，由cos (sin )x y x =，得ln cos ln (sin )y x x =，两边同时对x 求导，得cos sin ln sin cos sin y x x x x y x'=-+，所以()2cos cos sin sin ln sin sin xx y x x x x ⎛⎫'=-+ ⎪⎝⎭．10．设()sin f x x =，3()x x ϕ=，求[()]f x ϕ'，[()]f x ϕ'，{[()]}f x ϕ'．解因为()sin f x x =，3()x x ϕ=，所以()cos f x x '=，2()3x x ϕ'=，所以()()22[()]3sin 3f x f x x ϕ'==，[]()3[()]cos ()cos f x x x ϕϕ'==，()()()()33323{[()]}sin cos 3cos f x x x x x x ϕ''⎡⎤'===⎣⎦. 11．设()f x '存在，求下列函数的导数：（1）(cos )n f x ；（2）cos [()]n f x ．解（1）[]()11(cos )(cos )(cos )(cos )(cos )cos nn n f x nf x f x nf x f x x --''''⎡⎤==⎣⎦1sin (cos )(cos )n n xf x f x -'=-；（2）{}{}{}()11cos [()]cos [()]cos[()]cos [()]sin[()]n n n f x n f x f x n f x f x f x --'''==-()1sin[()]cos [()]n n f x f x f x -'=-⋅⋅．12. 求曲线()22sin sin f x x x =+所有具有水平切线的点．解因为()2cos 2sin cos f x x x x '=+，令()0f x '=，得()cos 1sin 0x x +=，于是cos 0x =，或sin 1x =-，推得 ,2x k k Z ππ=+∈，或32,2x k k Z ππ=+∈，所以所求的点为2,32k ππ⎛⎫+ ⎪⎝⎭，32,12k ππ⎛⎫+- ⎪⎝⎭，其中k Z ∈．习题 2-31．求下列函数的二阶导数：（1）35e x y -= ；（2）e sin t y t -= ；（3）2sin ln y x x = ；（4）tan y x = ；（5）ln(y x = ；（6）2(1)arctan y x x =+ ．解（1）353e x y -'=，359e x y -''=；（2）()e sin e cos e cos sin t t t y t t t t ---'=-+=- ，()()e cos sin e sin cos 2e cos t t t y t t t t t ---''=--+--=-；（3）()221sin 2sin cos ln sin ln sin 2xy x x x x x x x x'=+⋅=⋅+，()()22sin 22sin cos sin ln 2cos 2x x x x xy x x x x ⋅-''=+⋅+ ()()222sin 2sin 2cos 2ln x xx x x x=+⋅-；（4）2sec y x '=，22sec sec tan 2sec tan y x x x x x ''=⋅⋅=⋅；（5）1y ⎛⎫'=+= ⎝ ()3221422y x x -''=-+⋅=；（6）2arctan 1y x x '=+，22arctan 1x y x x ⎛⎫''=+ ⎪+⎝⎭． 2．3e x y x = ，求(5)(0)y ．解设3u x =，x v e =，则23u x '=，6u x ''=，6u '''=，()0,4n u n =∀≥；(),nx v e n N +=∀∈，代入莱布尼兹公式，得 ()()()()5445(5)510105y u v u v u v u v u v uv ''''''''''''=+++++2310610653x x x x e xe x e x e =⋅+⋅+⋅+，所以 (5)(0)60y =．3．22e x y x =，求(20)y ．解设2u x =，2x v e =，则2u x '=，2u ''=，()0,3n u n =∀≥；()22,nn x v e n N +=∀∈，代入莱布尼兹公式，得 ()()20(20)200n k k k k yC u v -==∑()()()181920210202020C u v C u v C uv '''=++ 182119202202202019022222x x x e C x e C x e =⋅⋅+⋅+⋅()202229520x e x x =++．4．试从d 1d x y y='导出：（1）223d d ()x y y y ''=-'；（2）3235d 3()d ()x y y y y y ''''''-='．解因为d 1d x y y ='，所以()()2232d 111d x d d dx y y y dy y dx y dy y y y ''''⎛⎫⎛⎫==⋅=-⋅=- ⎪ ⎪'''''⎝⎭⎝⎭， ()()3333d d x d y d y dx y dy dx dyy y ⎛⎫⎛⎫''''=-=-⋅ ⎪ ⎪ ⎪ ⎪''⎝⎭⎝⎭ ()()()()()32265331y y y y y y y y y y y '''''''''''''''-⋅-=-⋅='''． 5．证明：函数12e e x x y C C λλ-=+（12,,C C λ是常数）满足关系式20y y λ''-=．解因为12e e x x y C C λλ-=+，所以()1212e e e e x x x x y C C C C λλλλλλλλ--'=+-=-，2212e e x x y C C λλλλ-''=+，所以()22221212e e e e 0x x x x y y C C C C λλλλλλλλ--''-=+-+=． 6. 求常数λ的值，使得函数x y e λ=满足方程560y y y '''+-=．解因为x y e λ=，所以x y e λλ'=，2x y e λλ''=，代入方程560y y y '''+-=，得()2560x e λλλ+-=，因为0,x e x R λ≠∀∈，所以2560λλ+-=，解得16λ=-，21λ=．7. 设()()sin f x x a =+，()sin cos g x b x c x =+，求常数,b c 的值，使得()()00f g =，且()()00f g ''=.解因为()()sin f x x a =+，()sin cos g x b x c x =+，所以()()cos f x x a '=+，()cos sin g x b x c x '=-,所以由()()00f g =，()()00f g ''=，可得sin c a =，且cos b a =． 8．求下列函数的n 阶导数．（1）12121n n n n n y x a x a x a x a ---=+++++L （12,,n a a a L 是常数）；（2）e x y x =；（3）2sin y x =；（4）2156y x x =-+．解（1）()()12312112n n n n y nx n a x n a x a ----'=+-+-++L ，()()()()()23412211223n n n n y n n x n n a x n n a x a ----''=-+--+--++L ，根据幂函数的导数公式特点：每求导一次，幂函数降一次幂，故()!ny n =．（2）()e e e 1x x x y x x '=+=+，()()e 1e e 2x x x y x x ''=++=+，()()e 2e e 3x x x y x x '''=++=+，由此可见，每求一次导数，增加一个e x ，所以()()e n x y x n =+，n N +∀∈；（3）()()21cos 211sin cos 2222x y x x -===-， ()2sin cos sin 2cos 22y x x x x π⎛⎫'===-+ ⎪⎝⎭，()2cos 22cos 222y x x π⎛⎫''==-+⋅ ⎪⎝⎭，()222sin 22cos 232y x x π⎛⎫'''=-=-+⋅⎡⎤ ⎪⎣⎦⎝⎭， ()()4332cos 22cos 242y x x π⎛⎫=-=-+⋅⎡⎤ ⎪⎣⎦⎝⎭，所以()12cos 22nn y x n π-⎛⎫=-+⋅ ⎪⎝⎭，n N +∀∈．（4）因为 21115632y x x x x ==--+--，而()2133x x -'⎛⎫=-- ⎪-⎝⎭，()()()311233x x -''⎛⎫=--- ⎪-⎝⎭， ()()()()4112333x x -'''⎛⎫=---- ⎪-⎝⎭，可见，()()()()()()1112333n n n x x --⎛⎫=----- ⎪-⎝⎭L ()()11!3n n n x --=--，同理，()()()()()()()()11112321!22n n nn n x n x x ----⎛⎫=-----=-- ⎪-⎝⎭L ，所以()()()()()()()1111111!321!32nn n nn n n y n x x n x x ----++⎛⎫⎡⎤=----=-- ⎪⎣⎦ ⎪--⎝⎭．习题 2-41．求由下列方程所确定的隐函数的导数d d y x：（1）e 0xy x y +-=；（2）22320x y xy y -+=；（3）e ln sin 2xy y x x +=；（4= （0a >的常数）．解（1）将方程两边同时对x 求导，得1e 0xy dy dy y x dx dx ⎛⎫+-+= ⎪⎝⎭，变形得：e 11e xy xydy y dx x -=-；（2）将方程两边同时对x 求导，得22222230dy dy dy xy x y x y y dx dx dx ⎛⎫⎛⎫+-+⋅+= ⎪ ⎪⎝⎭⎝⎭，变形整理得：2224223dy xy y dx x xy y -+=-+；（3）将方程两边同时对x 求导，得 e ln 2cos 2xy dy dy y y x x x dx dx x ⎛⎫⎛⎫+++= ⎪ ⎪⎝⎭⎝⎭，变形整理得：22cos 2e ln exyxy dy x x y xy dx x x x --=+；（4）将方程两边同时对x 求导，得0+=，变形整理得：()0dy x dx =>． 2．求曲线2520x y xy +-=在点(1,1)处的切线方程．解将方程两边同时对x 求导，得：42520dy dy x y y x dx dx ⎛⎫+-+= ⎪⎝⎭，将1x =，1y =代入，解得：()1,10dydx=，所以曲线在点(1,1)处的切线方程为：1y =．3．已知sin cos()0y x x y -+=，求隐函数()y y x =在点π0,2⎛⎫⎪⎝⎭的导数值．解将方程两边同时对x 求导，得：sin cos sin()10dy dy x y x x y dx dx ⎛⎫⎛⎫++++= ⎪ ⎪⎝⎭⎝⎭，将0x =，2y π=代入，解得：0,212dydxππ⎛⎫ ⎪⎝⎭=--．4．求下列方程所确定的隐函数的二阶导数22d d yx．（1）tan()y x y =+；（2）1e y y x =+；（3）ln y y x y =+；（4）arctan yx=. 解（1）将方程两边同时对x 求导，得：2sec ()1dy dy x y dx dx ⎛⎫=++ ⎪⎝⎭，解得2csc ()dyx y dx=-+，再求导，得：()222csc()csc()cot 1d y dy x y x y x y dx dx ⎛⎫=-+-+++⎡⎤ ⎪⎣⎦⎝⎭，将2csc ()dy x y dx=-+代入，整理得：()22322csc ()cot d y x y x y dx =-++；（2）将方程两边同时对x 求导，得：e e y ydy dyx dx dx=+，解得：e 1e y y dy dx x =-，再求导，得：()()222e 1e e e e 1e yy y y y y dy dy x x dx dx d ydxx ⎡⎤⎛⎫---+ ⎪⎢⎥⎝⎭⎣⎦=-，将e 1e y y dy dx x =-代入，整理化简得：()()()()222332e 2e e 321e yyyy x y d y dx y x --==--；（3）将方程两边同时对x 求导，得：ln 1dy dy dyy dx dx dx+=+，解得：1ln dy dx y =，再求导，得：()2221ln dyd yy dxdx y =-，将1ln dy dx y =代入，整理化简得：()2321ln d y dx y y =-；（4）将方程两边同时对x 求导，得：2222221121dy dy x y x ydx dx x x y y x -+⋅=⋅+⎛⎫+ ⎪⎝⎭，解得：dy x y dx x y +=-，再求导，得：()()()22211dy dy x y x y d y dx dx dx x y ⎛⎫⎛⎫+--+- ⎪ ⎪⎝⎭⎝⎭=-，将dy x ydx x y +=-代入，整理化简得：()()222322x y d y dx x y +=-. 5．用对数求导法求下列函数的导数：（1）cos (sin )x y x =；（2）(tan 2)x y x =；（3）1xx y x ⎛⎫= ⎪+⎝⎭；（4）(2y x =-解（1）两边取自然对数，得：ln cos ln(sin )y x x =，两边同时对x 求导，得：()1cos sin ln sin cos sin dy xx x x y dx x=-+⋅, 整理化简得：()cos (sin )sin ln sin cos cot x dyx x x x x dx=-+⋅⎡⎤⎣⎦；（2）两边取自然对数，得：ln ln(tan 2)y x x =，两边同时对x 求导，得：()2sec 221ln(tan 2)tan 2x dyx x y dx x ⋅=+⋅，整理化简得：4(tan 2)ln(tan 2)sin 4x dy x x x dx x ⎡⎤=+⎢⎥⎣⎦；（3）两边取自然对数，得：()ln ln ln ln 11x y x x x x x ⎛⎫==-+⎡⎤ ⎪⎣⎦+⎝⎭，两边同时对x 求导，得：()111ln ln 11dy x x x y dx x x ⎛⎫=-++-⎡⎤ ⎪⎣⎦+⎝⎭整理化简得：1ln 111xdy x x dx x x x ⎛⎫⎡⎤=+ ⎪⎢⎥+++⎝⎭⎣⎦；（4）两边取自然对数，得：()111ln ln(21)ln ln(31)ln 1248y x x x x =-++++-，两边同时对x 求导，得：()121312124(31)81dy y dx x x x x =+++-+-，整理化简得：()2131(22124(31)81dy x dx x x x x ⎤=-+++⎢⎥-+-⎦6．求下列参数方程所确定的函数的导数d d yx：（1）cos sin sin cos x a bt b at y a bt b at =+⎧⎨=-⎩（,a b 为常数）；（2）22221(1)1at x t a t y t ⎧=⎪⎪+⎨-⎪=⎪+⎩（a 为常数）．解（1）因为()()sin cos dx ab bt ab at dt =-+，()()cos sin dyab bt ab at dt=+，所以()()()()()()()()cos sin cos sin d d sin cos sin cos ab bt ab at bt at y x ab bt ab at bt at ++==-+-+；（2）因为()()()()22222221222111a t at t a t dx dt t t +-⋅-==++， ()()()22222221(1)2411at t a t t dy atdt t t -+--⋅-==++ 所以22d 22d 11y t tx t t =-=--． 7．求曲线2e 1(2)ettx t y t t --⎧=+⎪⎨=-⎪⎩在0t =处的切线方程与法线方程．解因为e e t t dx t dt --=-，()222e (2)e t t dy t t t dt--=---，所以221dy t dx t +=-，02t dy dx==，又01,0t t xy====故所求切线为：()21y x =-，法线为：()112y x =--． 8．已知曲线2e 2e tx t mt n y p ⎧=++⎪⎨=-⎪⎩在0t =时过原点，且在该点处的切线与2350x y +-=平行，求常数,,m n p ．解因为2dx t m dt =+，e tdy p dt=，故e 2t dy p dx t m =+，由题设可知：00t xn ===，02e 0t yp ==-=，23t dy p dxm ===-，所以所求常数为：0n =，2e p =，3e m =-．注：此题的书后答案有误．9．求下列参数方程所确定的函数的二阶导数22d d yx：（1）231x t y t t⎧=-⎪⎨=-⎪⎩；（2）e cos e sin t t x t y t ⎧=⎨=⎩；（3）()2ln 1arctan x t y t t⎧=+⎪⎨=-⎪⎩；（4）()()()x f t y tf t f t '=⎧⎨'=-⎩（()f t ''存在且不为零）．解（1）因为2dx t dt =-，213dy t dt=-，所以21313222dy t t dx t t -==-+-，于是 22223131313222224d y d t dt t t dx dt t dx t t ++⎛⎫=-+⋅==- ⎪-⎝⎭；（2）因为e cos e sin t t dx t t dt =-，e sin e cos t t dyt t dt=+，所以e sin e cos sin cos e cos e sin cos sin t t t tdy t t t t dx t t t t++==--，于是 ()()()22222cos sin sin cos sin cos 1cos sin e cos e sin cos sin t tt t t t d y d t t dt dx dt t t dx t t t t -+++⎛⎫==⋅ ⎪--⎝⎭- ()32e cos sin tt t =-；（3）因为221dx t dt t =+，2111dy dt t =-+，所以22111221dy t t t dx t -+==+，于是2222112241d y t t dx t t+==+；（4）因为()dx f t dt ''=，()()()()dy f t tf t f t tf t dt ''''''=+-=，所以dy t dx=，于是221()d y dx f t =''．10．将水注入深8米、上顶直径8米的正圆锥形容器中，注水速率为4吨/分钟．当水深为5米时，其表面上升的速率为多少解如图所示，设在t 时刻容器中水面的高度为()h t （米），此时水面的半径为()r t （米），则依题意应有()()2143r t h t t π=，而()()84h t r t =，所以()31412h t t π=，两边同时对时间t 求导，可得()2144dh h t dt π=，当()5h t =时，可求得1625dh dt π=，所以当水深为5米时，其表面上升的速率为16min 25m π． 11．汽车A 以50公里/小时的速度向西行驶，汽车B 以60公里/小时的速度向北行驶，两辆车都朝着两条路的交叉口行驶．当汽车A 距离交叉路口0.3公里，汽车B 距离交叉路口0.4公里时，两辆车以什么速率接近解如图所示，设在t 时刻，汽车A 距离交叉路口()x t ，汽车B 距离交叉路口()y t ，则两车之间的直线距离为()()()22s t x t y t =+t 求导，可得()()()()22dx dy x t y t ds dt dt dtx t y t +=+50dx dt =，60dy dt =，故当()0.3x t =，()0.4y t =时，22780.30.4ds dt ==+，即当汽车A 距离交叉路口0.3公里，汽车B 距离交叉路口0.4公里时，两辆车以78/km h 的速率接近．12．一个路灯安装在15英尺高的柱子上，一个身高为6英尺的人从柱子下以5英尺/秒的速度沿直线走离柱子，当他距离柱子40英尺时，他身影的顶端以多快的速率移动解如图所示，设在t 时刻，此人离灯柱的水平距离为()x t ，身影的顶端离灯柱的水平距离为()y t ，则依题意有：5dx dt =，()()()615y t x t y t -=，可见()()53y t x t =，两边同时对时间t 求导，得52533dy dx dt dt ==，所以他身影的顶端以25feet /3s 的速率移动，与他离灯柱的水平距离无关，只与他的前进速度、身高、灯柱高有关．习题 2-51．函数2y x =，求当1x =，而0.1x ∆=，0.01时，y ∆与d y 之差是多少解当1x =，0.1x ∆=时，21.110.21y ∆=-=，d 20.2y x x =∆=，所以 0.01y dy ∆-=；当1x =，0.01x ∆=时，21.0110.0201y ∆=-=，d 20.02y x x =∆=，所以 0.0001y dy ∆-=；2．求函数2y x x =+在3x =处，x ∆等于0.1，0.01时的增量与微分．解因为2y x x =+，所以()21dy x x =+∆，当3x =，0.1x ∆=时，223.1 3.1330.71y ∆=+--=，0.7dy =；当3x =，0.01x ∆=时，223.01 3.01330.0701y ∆=+--=，0.07dy =．3．函数3y x x =-，求自变量x 由2变到1.99时在2x =处的微分．解因为3y x x =-，所以()231dy x x =-∆，当2x =，0.01x ∆=-时，()()23210.010.11dy =⨯-⨯-=-．4．求下列函数的微分（1）234123y x x x x =+-+；（2）2e x y x -=；（3）21xy x =- ；（4）22tan (1)y x =+；（5）ln cos 3x y = ；（6）e sin ax y bx =．解（1）()23144dy x x x dx =+-+；（2）()()()2222222e e e e 2e 12x x x x x dy dx x d x dx x x dx x dx -----=+-=+-=-；（3）()()()()()()()222222222211121111x dx xd x x dx x x dx xdy dx x x x ------+===---；（4）2222222tan(1)tan(1)2tan(1)sec (1)(1)dy x d x x x d x =++=+++2224tan(1)sec (1)x x x dx =++；（5）()()ln cos ln cos 13ln 3ln cos 3ln 3cos cos x x dy d x d x x==⋅lncos 3ln 3tan x xdx =-⋅；（6）()()()()()()e sin e cos e sin cos ax ax ax dy d ax bx bx d bx a bx b bx dx =+=+⎡⎤⎣⎦． 5．将适当的函数填入下列括号内，使等式成立：（1）d()sin d t t ω=；（2）2d()sec 3d x x =；（3）d()x =；（4）22d d()xx a =+；（5）2d()e d x x x =；（6）ln d()d xx x=. 解（1）()1cos t ωω-；（2）()1tan 33x ；（3；（4）1arctan x a a ；（5）21e 2x ；（6）21ln 2x ．6．某扩音器的插头为圆柱形，其截面半径r 为0.15厘米，长度L 为4厘米，为了提高它的导电性能，要在圆柱的侧面镀一层厚度为0.001厘米的铜，问每个插头约需要多少克纯铜（铜的密度为8.9克/立方厘米， 3.1416π≈）解因为圆柱形的扩音器插头的体积为2V r L π=，侧面镀层的体积约为2V dV rL r π∆≈=∆，当0.15r =，0.001r ∆=，4L =时，32 3.14160.1540.001 3.7699210V -∆≈⨯⨯⨯⨯≈⨯，故所需铜的重量约为33.76992108.90.03355m -≈⨯⨯≈克．7．设有一凸透镜，镜面是半径为R 的球面，镜面的口径为2h ，若h 比R 小得多，试证明透镜的厚度22h D R≈．解如下图所示，镜面半径R 、镜面口径2h 、透镜厚度D 之间有关系：()222h R D R +-=，化简得：2220h RD D -+=，得：22222441R R h h D R R --==--若h 比R 小得多，则2222112h h R R-≈-，故222221122h h h D R R R R R R R⎛⎫=--≈--= ⎪⎝⎭．8．利用微分求下列函数值的近似值（1）cos59o ；（2）tan 46o ；（3）lg11；（4） 1.01e ；（526；（63996解（1）()00cos59cos 601cos cos sin 318033180πππππ⎛⎫⎛⎫⎛⎫⎛⎫=-=-≈-- ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭o130.51512180π⎫=-≈⎪⎝⎭；（2）()002tan 46tan 451tan tan sec 418044180πππππ⎛⎫⎛⎫⎛⎫=+=+≈+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭o 12 1.0349180π=+⨯≈；（3）()1lg11lg 101lg101 1.043410ln10=+≈+⨯≈；（4） 1.0110.010.01 2.7455e e e e +=≈+⨯≈；（526251251 5.1225=+≈=；（6()233331996100041000100049.98673-=-≈⨯⨯-≈．9．当||x 较小时，证明下列近似公式：（1）sin x x ≈；（2）(1)1x x αα+≈+；（3）ln(1)x x +≈．解（1）设()sin f x x =，则()cos f x x '=，当||x 较小时，()sin sin0cos0f x x x x =≈+⋅=，所以sin x x ≈；（2）设()(1)f x x α=+，则()1(1)f x x αα-'=+图2-11当||x 较小时，()()()(1)111f x x f f x x αα'=+≈+=+，所以(1)1x x αα+≈+；（3）设()ln(1)f x x =+，则()11f x x'=+，当||x 较小时，()()()ln(1)11f x x f f x x '=+≈+=，所以ln(1)x x +≈．习题 2-61.一飞机在离地面2000米的高度，以200公里/小时的速度飞临某目标之上空，以便进行航空摄影．试求飞机飞至该目标上方时摄影机转动的速度．解如右图示意，A 为摄影目标，B 为其正上方的点，设t 时刻飞机离B 点的水平距离为()x t ，摄影机镜头C 与A 点连线与飞机的水平飞行方向成θ夹角，则()cot 2000x t θ=，()()20000003600x t x t =-，两边同时对时间t求导，可得()211csc 200036dx t d dt dt θθ-==-，即21sin 36d dt θθ=，当飞机飞至该目标上方时，2πθ=，代入解得：()13605/362d rad s dt θππ=⨯=． 2.一架飞机着陆的路径如图2-11所示，并且满足下列条件：（ⅰ）降落点为原点，飞机开始降落时水平距离为l ，飞行高度为h ．（ⅱ）在整个降落过程中，飞行员必须使飞机保持恒定的水平速度v ．（ⅲ）垂直方向的加速度的绝对值不能超过常数k （必须比重力加速度小很多）．（1）求一个三次多项式()32P x ax bx cx d =+++，通过在开始降落和着陆的点对()P x 和()P x '施加一定的条件限制，使它满足条件（ⅰ）；（2）根据条件（ⅱ）和（ⅲ），试证明：226hv k l≤；（3）假设一条航线不允许飞机的垂直加速度超过2860k =哩小时．如果一架飞机的飞行高度为35000呎，速度为300哩小时，飞机应从距离飞机场多远处开始降落（4）画出满足问题（3）中条件的航线图．解假设从飞机开始着陆时计时，飞行时间为t ，飞机位置为(),x y ．（1）如要满足条件（ⅰ），应有0t =时，,x l y h ==，0t dy dt==；t T =（T 为着陆时刻）时，0x y ==，0t Tdydt==，因为()32y P x ax bx cx d ==+++，于是()()232dy dx dxP x ax bx c dt dt dt'==++，所以应有 32h al bl cl d =+++，2320al bl c ++=，0d =，0c =，解得3223,,0h h a b c d l l =-===，所以()323223h h P x x x l l=-+；（2）由条件（ⅱ）和（ⅲ）可知：dxv dt =，22d y k dt ≤，由()323223h h y P x x x l l==-+，可得：23266dy h h dx x x dt l l dt ⎛⎫=-+ ⎪⎝⎭， 222223232212666d y h h dx h h d xx x x dt ll dt l l dt ⎛⎫⎛⎫⎛⎫=-++-+ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭，所以[]0,x l ∀∈，应有232126hh x v k ll ⎛⎫-+≤ ⎪⎝⎭，故226hv k l ≤；（3）当2860k =哩，0.62135000350000.305 6.62921000h ==⨯⨯≈呎哩，300v =哩小时，由226hv k l ≤，可解得64.52l ≥≈（哩），即飞机应从距离飞机场约64.52哩的水平距离处开始降落．（4）满足条件（3）的航线为()3232322350003350000.260625.223264.5264.52P x x x x x ⨯⨯=-+≈-+（呎）（注：式中x 的单位哩，图略）．本章复习题A1、填空题（1）()f x 在点0x 可导是()f x 在点0x 连续的_____条件，()f x 在点0x 连续是()f x 在点0x 可导的______条件．解因为()f x 在点0x 可导，则()f x 在点0x 连续，故第一个空应填“充分”，第二个空应填“必要”．（2）()f x 在点0x 可导是()f x 在点0x 可微的______条件．解应填“充分必要”．（3）若假定0()f x '存在，则000()()limh f x h f x h h→+--=______．解因为()()00000000()()()()limlim h h f x h f x f x f x h f x h f x h h h→→+-+--+--= ()()00000()()lim h f x h f x f x h f x h h →+---⎡⎤=+⎢⎥-⎣⎦()02f x '=，所以应填“()02f x '”．（4）若()(1)(2)f x x x x =++，则(0)_______f '=．解因为()(1)(2)(2)(1)f x x x x x x x '=++++++，故(0)2f '=，应填“2”．（5）曲线231x t y t⎧=+⎨=⎩在2t =处的切线方程为________．解因为23322t t y dy t t dx x t '==='，所以2t =时，23t dy dx ==，5x =，8y =，切线方程为()835y x -=-，即370x y --=，所以应填“370x y --=”．2、选择题（1）()f x 在点0x 的左导数0()f x -'及右导数0()f x +'都存在且相等是()f x 在点0x 可导的（）．A ．充分条件B ．充分必要条件C ．必要条件D ．既非充分条件也非必要条件解选B ．（2）设101()n n n f x a x a x a -=+++L ，则()(0)n f =（）．A ．n aB ．0aC ．0!n aD ．0 解选C ．因为()0()!n f x n a =．（3）设函数()y f x =二阶可导，(ln )y f x =，则22d d yx等于（）．A ．1(ln )f x x 'B ．21[(ln )(ln )]f x f x x '''- C ．21[(ln )(ln )]xf x f x x '''- D ．21(ln )f x x' 解选B ．因为1(ln )(ln )f x y f x x x'''=⋅=，则221(ln )(ln )(ln )(ln )f x x f x f x f x x y x x '''⋅⋅-'''-''==．（4）若函数()y f x =有01()2f x '=，则当0x ∆→时，该函数在0x x =处的微分d y 是（）．A ．与x ∆等价的无穷小B ．与x ∆同阶的无穷小C ．比x ∆低阶的无穷小D ．比x ∆高阶的无穷小解选B ．因为()0012x x dyy x x x ='=∆=∆，所以001lim 2x x x dy x =∆→=∆．（5）已知方程222x y R +=确定了函数()y y x =，则22d d yx 等于（）．A ．xy- B ．23R y C ．33R y - D ．23R y -解选D ．由222x y R +=可得220x y y '+⋅=，。

线性代数第二章习题答案

习题 2-11．由6名选手参加乒乓球比赛，成绩如下：选手1胜选手2、4、5、6而负于选手3；选手2胜选手4、5、6而负于选手1、3；选手3胜选手1、2、4而负于选手5、6；选手4胜选手5、6而负于选手1、2、3；选手5胜选手3、6而负于选手1、2、4；选手6胜选手2而负于选手1、3、4、5．若胜一场得1分，负一场得0分，使用矩阵表示输赢状况，并排序．解： ⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛000010100100110000001011111000111010654321654321，选手按胜多负少排序为：6,5,4,3,2,1． 2．设矩阵⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫⎝⎛+-=2521,03231z x y x B A ，已知B A =，求z y x ,,．解：由于B A =得⎪⎩⎪⎨⎧=-=+=-0253223z x y x ，解得：⎪⎩⎪⎨⎧===211z y x 。

习题 2-21．设⎪⎪⎭⎫⎝⎛=0112A ，⎪⎪⎭⎫ ⎝⎛-=4021B ，求（1）B A 52-；（2）BA AB -；（3）22B A -．解：（1）⎪⎪⎭⎫⎝⎛--=⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛=-202892001050224402150112252B A ；（2）⎪⎪⎭⎫⎝⎛--=⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛=-2592041021820112402140210112BA AB ；（3）⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=-152441606112254021402101120112B A 22．2．已知⎪⎪⎪⎭⎫ ⎝⎛--=230412301321A ，⎪⎪⎪⎭⎫ ⎝⎛---=052110351234B ，求B A 23-．解：⎪⎪⎪⎭⎫ ⎝⎛----⎪⎪⎪⎭⎫ ⎝⎛--=0521103512342230412301321323B -A ⎪⎪⎪⎭⎫ ⎝⎛----=⎪⎪⎪⎭⎫ ⎝⎛----⎪⎪⎪⎭⎫ ⎝⎛--=61941016151055011010422061024686901236903963 3．设⎪⎪⎪⎭⎫ ⎝⎛----=⎪⎪⎪⎭⎫ ⎝⎛=101012121234,432112122121B A ，求（1）B A -3；（2）B A 32+；（3）若X 满足B X A =-，求X ；（4）若Y 满足()()O Y B Y A =-+-22，求Y ．解：（1）⎪⎪⎪⎭⎫⎝⎛-----⎪⎪⎪⎭⎫ ⎝⎛=-10101212123443211212212133B A ⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛-----⎪⎪⎪⎭⎫ ⎝⎛=13973282851311010121212341296336366363；（2）⎪⎪⎪⎭⎫⎝⎛----+⎪⎪⎪⎭⎫ ⎝⎛=+1010121212343432112122121232B A ⎪⎪⎪⎭⎫⎝⎛--=⎪⎪⎪⎭⎫⎝⎛----+⎪⎪⎪⎭⎫ ⎝⎛=561252527813143030363636912864224244242；（3）由B X A =-得，⎪⎪⎪⎭⎫ ⎝⎛---=⎪⎪⎪⎭⎫⎝⎛-----⎪⎪⎪⎭⎫ ⎝⎛=-=533104041113101012121234432112122121B A X ；（4）由()()O Y B Y A =-+-22得，⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=+=223232340342231031033112020335532)(32B A Y 。

课后习题-Ubuntu Linux 操作系统与实验教程(第2版)-微课-马丽梅-清华大学出版社

Ubuntu linux 操作系统与实验教程（第2版）课后习题第一章习题一1、判断题（1）在一台主机上只能安装一个虚拟机。

（2）在一个虚拟机下只能安装一个操作系统。

（3）格式化虚拟机下的操作系统就是格式化主机的操作系统。

（4）虚拟机的安装有三种安装类型。

（5）VMware Workstation 15 默认分配的推荐虚拟机的存是1G。

（6）Ubuntu 有两种安装方式：即Ubuntu和安装Ubuntu。

（7）解压vmware-install.pl文件安装VM tools。

（8）VMtools安装完成后可以在主机和虚拟机之间任意拖动和复制文件。

2、简答题（1）请简述在虚拟机的安装过程中，四种网络类型的特点？（2）简述.vmdk 和.vmx 文件的不同点？（3）Ubuntu应该建立几个分区？每个分区的大小是多少？（4）虚拟机捕获屏幕有什么作用？3、实验题（1）安装VMware Workstation Pro 15。

（2）为安装ubuntukylin-16.04.06创建虚拟机。

（3）在虚拟机中安装ubuntukylin-16.04.06。

（4）在Ubuntu下安装VM tools。

（5）上述实验完成后创建快照，如果使用Ubuntu过程中出现问题，可以恢复快照。

（6）更改虚拟机的内存、添加硬盘。

第二章习题二1、判断题（1）Linux操作系统诞生于1991 年8月。

（2）Linux是一个开放源的操作系统。

（3）Linux是一个类unix操作系统。

（4）Linux是一个多用户系统，也是一个多任务操作系统。

（5）Ubuntu Linux 16.04默认的桌面环境是Gnome。

（6）Ubuntu每一年发布一个新版本。

（7）ubuntu Linux 16.04包含LibreOffice套件。

2、简答题（1）什么是Linux？（2）简述Linux系统的产生过程？（3）简述Linux系统的组成？（4）什么是Linux 内核版本？举例说明版本号的格式。

酒店管理概论第二章习题答案[4页]

第二章习题答案案例分析预订处理的得与失小张是上海国际大酒店的前厅接待员。

去年国庆节期间，上海几乎所有酒店客房都已爆满，而且房价飙升。

10月1日11:30左右，小张在繁忙的工作中接到一位李先生预订客房的电话。

李先生是该酒店某协议公司的老总，也是酒店的常客，所以小张格外小心。

当时刚好还剩下一间标准间，小张就把它留给了李先生，并与他约好抵店时间是当晚23 : 00。

但一直等到23 : 40，李总还未抵店。

在这半个多小时里，有许多电话或客人亲自到酒店来问是否还有客房，小张都一一婉言谢绝了。

之后小张心想:也许李先生不会来了，因为经常有客人订了房间后不来住，如果再不卖掉，24 : 00以后就很难卖出去了。

为了酒店的利益，不能白白空一间房，到23 :45，小张将这最后一间标准间卖给了一位正急需客房的熟客。

24 : 00左右李总出现在前台，并说因车子抛锚、手机无电，故未事先来电说明。

一听说房间已卖掉，他顿时恼羞成怒，立即要求酒店赔偿损失，并声称将取消与酒店的协议。

阅读完上面的材料，请回答以下问题:1.从本次预订事件的处理来看，你认为作为前厅预订员应该具备怎样的素质?2.如果你是大堂经理的话，会怎样处理这件事?参考答案;1.作为一个优秀的前厅预订员，工作不仅仅要符合操作程序，还必须具有应变能力。

小张的做法动机是好的，但处理的方式欠妥，没有把酒店的长期商业利益考虑进去，很可能就因这一次事件李总以后再也不会来酒店消费，甚至还会向亲朋好友做反面广告，使酒店失去了一个重要的客户和一个商务公司的长期消费的收入。

2.首先向客人道歉，并立即打电话联系其他酒店，为李总重新预订一间同档次的客房;并派车把李总送去新的酒店，协助他办好入住手续，欢迎他再次光临酒店。

评析：此办法较好。

气愤的客人看到大堂副理忙个不停地打电话到别的酒店为他找房间，从心理上得到安慰。

大堂副理联系好酒店，又派车把李总送去新的同档次酒店入住，平息了李总的气愤，用优质的服务赢回了客人对酒店的忠诚度。

人教A版高中数学必修4第二章平面向量2.1 平面向量的实际背景及基本概念习题(4)

2.1平面向量的实际背景及基本概念一、选择题1.【题文】下列各量中不是向量的是（） A ．浮力 B ．风速 C ．位移D ．密度2．【题文】在下列判断中，正确的是( )①长度为的向量都是零向量；②零向量的方向都是相同的；③单位向量的长度都相等； ④单位向量都是同方向；⑤任意向量与零向量都共线． A ．①②③ B ．②③④ C ．①②⑤ D ．①③⑤3．【题文】若AB AD =且BA CD =，则四边形ABCD 的形状为（） A ．平行四边形 B ．矩形 C ．菱形 D ．等腰梯形4．【题文】已知：如图，D ，E ，F 依次是等边三角形ABC 的边AB ，BC ，CA 的中点，在以A ，B ，C ，D ，E ，F 为起点或终点的向量中，与向量AD 共线的向量有（）A ．个B ．个C ．个D ．个5．【题文】下列说法正确的有( )①方向相同的向量叫相等向量；②零向量的长度为；③共线向量是在同一条直线上的向量；④零向量是没有方向的向量；⑤共线向量不一定相等；⑥平行向量方向相同． A ．个 B ．个 C ．个 D ．个6．【题文】给出下列说法：①AB 和BA 的模相等；②方向不同的两个向量一定不平行；③向量就是有向线段；④0=0；⑤AB CD >，其中正确说法的个数是( )A. B. C. D.7．【题文】若四边形ABCD 是矩形，则下列说法中不正确的是（） A ．AB 与CD 共线B ．AC 与BD 共线C ．AD 与CB 是相反向量 D ．AB 与CD 的模相等8.【题文】下列说法正确的是( )A ．有向线段AB 与BA 表示同一向量 B ．两个有公共终点的向量是平行向量C ．零向量与单位向量是平行向量D ．对任一向量，aa是一个单位向量二、填空题9．【题文】如图，正六边形ABCDEF 中，点O 为中心，以,,,,,,A B C D E F O 为起点与终点的向量中，与向量AB 平行的向量有个（含AB ）．10.【题文】给出下列四个条件：①=a b ；②=a b ；③与的方向相反；④0=a 或0=b ，其中能使a b 成立的条件有________．11．【题文】下列说法中，正确的是． ①向量AB 的长度与BA 的长度相等；②向量a与向量b平行，则a与b的方向相同或相反；③两个有共同起点的单位向量，其终点必相同；④向量AB与向量CD是相等向量，则A、B、C、D能构成平行四边形．三、解答题12．【题文】如图，D，E，F分别是△ABC的边AB，BC，CA的中点，在以A，B，C，D，E，F为起点和终点的向量中：（1）找出与向量EF相等的向量；（2）找出与向量DF相等的向量．13．【题文】如图，在△ABC中，D，E分别是边AB，AC的中点，F，G分别是DB，EC 的中点，求证：向量DE与FG共线．14．【题文】如图，EF是△ABC的中位线，AD是BC边上的中线，在以A，B，C，D，E，F为端点的有向线段表示的向量中请分别写出：（1）与向量CD共线的向量；（2）与向量DF的模相等的向量；（3）与向量DE相等的向量.2.1平面向量的实际背景及基本概念参考答案与解析一、选择题1.【答案】D【解析】根据向量的定义，从大小和方向两个方面考虑，可知密度不是向量．考点：平面向量的概念.【题型】选择题【难度】较易2．【答案】D【解析】由零向量与单位向量的概念知①③⑤正确．考点：零向量与单位向量.【题型】选择题【难度】较易3．【答案】C【解析】四边形ABCD中，∵BA CD=，∴BA CD，且BA CD=，∴四边形ABCD是平行四边形.又AB AD=，∴平行四边形ABCD是菱形.考点：相等向量.【题型】选择题【难度】较易4．【答案】C【解析】∵D，E，F分别为AB，BC，CA的中点，∴AD∥EF ，∴与向量AD共线的向量有AB，FE，EF，DA，BA，BD，DB，共7个．考点：共线向量.【题型】选择题【难度】较易5．【答案】A【解析】长度相等且方向相同的向量叫做相等向量，故①错误；长度为的向量叫零向量，故②正确；通过平移能够移到同一条直线上的向量叫共线向量，故③错误；零向量的方向是任意的，故④错误；共线向量方向相同或相反，⑤正确；平行向量方向相同或相反，故⑥错误，因此②与⑤正确，其余都是错误的，故选C.考点：相等向量，共线向量.【题型】选择题【难度】一般6．【答案】B【解析】①正确，AB与BA是方向相反、模相等的两个向量；②错误，方向不同包括共线反向的向量；③错误，向量用有向线段表示，但二者并不等同；④错误，是一个向量，而为一数量，应为0=0；⑤错误，向量不能比较大小.只有①正确，故选B.考点：向量的有关概念.【题型】选择题【难度】一般7．【答案】B【解析】∵四边形ABCD是矩形，∴AB CD且AB CD=，AD CB，∴AB 与CD共线，且模相等，AD与CB是相反向量，∵AC与BD相交，∴AC与BD不共线，故B错误.考点：共线向量，相等向量.【题型】选择题【难度】一般 8. 【答案】C【解析】向量AB 与BA 方向相反，不是同一向量；有公共终点的向量的方向不一定相同或相反；当=0a 时，aa无意义，故A 、B 、D 错误．零向量与任何向量都是平行向量，C 正确．考点：平行向量;单位向量. 【题型】选择题【难度】较难二、填空题 9．【答案】10【解析】正六边形ABCDEF 中，点O 为中心，以,,,,,,A B C D E F O 为起点与终点的向量中，与向量AB 平行的向量有,,,,,,,,,AB BA OC CO OF FO CF FC DE ED ，共10个．考点：平行向量. 【题型】填空题【难度】较易 10.【答案】①③④【解析】因为与为相等向量，所以a b ，即①能够使a b 成立；=a b 并没有确定与的方向，即②不能够使ab 成立；与方向相反时，a b ，即③能够使a b 成立；因为零向量与任意向量共线，所以0=a 或0=b 时，a b 能够成立．故使a b 成立的条件是①③④.考点：平行向量. 【题型】填空题【难度】一般11．【答案】①【解析】对于①，向量AB 与BA 互为相反向量，长度相等，正确；对于②，因为零向量与任何向量平行，但零向量的方向是任意的，不能说方向相同或相反，所以②错误；对于③，两个有共同起点的单位向量，其终点不一定相同，因为方向不一定相同，所以③错误；对于④，向量AB 与向量CD 是相等向量，则A 、B 、C 、D 可能在同一直线上，则A 、B 、C 、D 四点不一定能构成平行四边形，所以④错误．综上，正确的是①．考点：平面向量的概念. 【题型】填空题【难度】一般三、解答题 12．【答案】（1）,BD DA （2）,BE EC【解析】（1）∵E ，F 分别为BC ，AC 的中点， ∴EFBA ，且12EF BA =，又D 是BA 的中点， ∴EF BD DA ==，∴与向量EF 相等的向量是,BD DA .（2）∵D ，F 分别为BA ，AC 的中点， ∴DFBC ，且12DF BC =，又E 是BC 的中点，∴DF BE EC ==， ∴与向量DF 相等的向量是,BE EC ．考点：共线向量.【题型】解答题【难度】较易13．【答案】详见解析【解析】证明：∵D，E分别是边AB，AC的中点，∴DE是△ABC的中位线，∴DE BC，∴四边形DBCE是梯形．又∵F，G分别是DB，EC的中点，∴FG是梯形DBCE的中位线，∴FG DE.∴向量DE与FG共线．考点：向量共线.【题型】解答题【难度】一般14．【答案】（1）,,,,,,BD BC EF DB CB FE DC（2）,,,,FD AE EA EB BE（3）,CF FA【解析】根据三角形中位线的性质及共线向量及相等向量的概念即可得到：（1）与向量CD共线的向量为,,,,,,BD BC EF DB CB FE DC．（2）与向量DF的模相等的向量为,,,,FD AE EA EB BE．（3）与向量DE相等的向量为,CF FA．考点：相等向量，平行向量. 【题型】解答题【难度】一般。

软件体系结构课后习题第二章作业

习题1：选择一个规模合适的系统为其建立“4+1”模型。

解：一个ATM系统的“4+1”模型:
1.首先是场景：
2.然后是逻辑视图：
3.开发视图如下：
4.进程视图如下：
5.物理视图如下:
习题2：引入了软件体系结构以后，传统软件过程发生了哪些变化？这些变化有什么好处？
答：软件体系结构的引入使传统软件设计开发更加具体和形象，使得软件过程变得更加方便和多样化。

其好处在于：包括程序员在内的绝大多数系统的利益相关人员都可借助软件体系结构来进行彼此理解、协商、达成共识或者相互沟通；软件体系结构的模型可以应用到具有相似质量属性和功能需求的系统中，并能够促进大规模软件的系统级复用；在很多方面使得软件开发更加易于维护和理解。

习题3：软件体系结构的生命周期模型与软件生命周期模型有什么关系？
答：软件体系结构在系统开发的全过程中起着基础的作用，是设计的起点和依据，同时也是装配和维护的指南。

软件体系结构是贯穿于软件研发的整个软件生命周期的系统开发、运行、维护所实施的全部工作和任务的结构框架，给出了软件开发活动各阶段之间的关系。

软件体系结构的生命周期模型为软件生命周期模型提供了很好的结构依据和参考，也为其构建了很好的开发方式。

2019版《安全生产管理》第二章练习题4

A.信号装置
B.防尘装置
C.急救室
D.安全教育室
C
P88，安全技术措施-卫生技术措施-辅助措施-安全宣传教育措施
22.我国规定的禁止标志共有（）个。
A.40
B.39
C.16
D.8
A
P92
禁止标志：禁止40-禁止吸烟--黑白红
警告标志：提醒39-注意安全，当心火灾--黑黑黄
指令标志：强制16-必须戴防毒面具--蓝白
D．安全操作规程----设备
D
9.不得认定为工伤的是（）
A.故意犯罪
B.违反规章制度和操作规程
C.醉酒
D.自残
B
P105
10.以下不属于“三同时”制度实施的范围是（）。
A.项目施工
B.项目设计
C.项目资金审批
D.项目的投入使用
C
11.单元综合抵消因子的值愈（），说明单元现实危险性与单元固有危险性比值愈（），即单元内危险性的可控程度愈（）
减少与消除事故影响设施6类
13.重大危险源评价以（）作为评价对象
A.危险单元
B.危险因素
C.机械设备
D.危险指数
A
P69
14.重大危险源级别中最危险的是（）
A.一级重大危险源
B.二级重大危险源
C.三级重大危险源
D.四级重大危险源
A
15.重大危险源的安全生产监督管理工作主要由（）安全生产监督管理部门进行
A．15
B．30
C．60
D．90
B
P64
3．取得特种作业操作许可证的人员，每（）几年复审一次?
A、一年 B．二年 C．三年 D.四年
C
4.建筑施工企业安全管理人员安全资格培训时间不少于（）学时。

初中数学湘教版七年级上册第二章代数式2.2 列代数式-章节测试习题(4)

章节测试题1.【答题】已知a是两位数，b是一位数，把b接在a的后面，就成了一个三位数，这个三位数可以表示为（）A. a+bB. 100b+aC. 100a+bD. 10a+b【答案】D【分析】本题主要考查了三位数的表示方法，该题的易错点是忘了a是个两位数，错写成（100a+b）．【解答】解：两位数的表示方法：十位数字×10+个位数字；三位数字的表示方法：百位数字×100+十位数字×10+个位数字．a是两位数，b是一位数，依据题意可得a扩大了10倍，所以这个三位数可表示成10a+b．选D.2.【答题】某商店进了一批商品，每件商品的进价为a元，若要获利20%，则每件商品的零售价应为（）A. 20%a元B. (1＋20%)a元C. 元D. (1－20%)a元【答案】B【分析】此题的等量关系：零售价-进价=获利．获利20%，即实际获利=20%a，设未知数，列方程求解即可．【解答】解：设每件售价为x元，则x-a=20%a，解得x=（1+20%）a．选D.方法总结：解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程组，再求解．3.【答题】用含字母的式子表示下列数量关系．（1）小雪买单价为a元的笔记本4本，共花______元；（2）三角形的底为a，高为h，则三角形的面积是______；（3）m是一个两位数，n是一个一位数，将m写到n的左边成为一个三位数，用代数式表示这个三位数为______．（4）某微商平台有一商品，标价为a元，按标价5折再降价30元销售，则该商品售价为______元．【答案】4a；ah；10m+n；（0.5a–30）【分析】本题考查列代数式.列式子表示数量关系，一定要弄清“和”“差”“积”“倍”等关系．【解答】（1）笔记本4本共花4a元；（2）三角形的面积是ah；（3）由题意知m是一个两位数，n是一个一位数，将m写到n的左边成为一个三位数，即m扩大了10倍，n不变，可得这个三位数为10m+n．故答案为10m+n；（4）由题意可得，该商品的售价为a×0.5–30=（0.5a–30）元，故答案为（0.5a–30）．4.【答题】某种水果的售价是a千克b元，那么表示的实际意义是______．【答案】每元买千克【分析】本题考查代数式的意义.【解答】表示的实际意义是每元买千克，故答案为每元买千克．5.【题文】某商场的一种彩电标价为m元/台，节日期间，商场按九折的优惠价出售，则商场销售n台彩电共得多少元？你所得到的单项式的系数和次数分别是多少？【答案】0.9mn元，0.9mn的系数是0.9，次数是2．【分析】本题考查列代数式以及单项式的相关概念.【解答】销售n台彩电共得0.9mn元，0.9mn的系数是0.9，次数是2．6.【答题】原价为a元的书包，现按8折出售，则售价为______元．【答案】a【分析】本题考查列代数式.【解答】依题意可得，售价为a=a，故答案为a．7.【答题】某商店进了一批商品，每件商品的进价为a元，若要获利20%，则每件商品的零售价应为（）A. 20%a元B. （1＋20%）a元C. 元D. （1-20%）a元【答案】B【分析】本题考查列代数式.【解答】设每件售价为x元，则x–a=20%a，解得x=（1+20%）a．选D．8.【答题】下面由小木棒拼出的系列图形中，第个图形由个正方形组成，请写出第个图形中小木棒的根数与的关系式______．【答案】S=3n+1【分析】本题考查图形的规律.【解答】当时，；当时，；当时，；当时，；当时，，∴第个图形中小木棒的根数与的关系式为S=3n+1，故答案为S=3n+1．9.【题文】如图，将边长为m的正方形纸板沿虚线剪成两个小正方形和两个矩形，拿掉边长为n的小正方形纸板后，将剩下的三块拼成新的矩形．（1）用含m或n的代数式表示拼成矩形的周长；（2）m=7，n=4，求拼成矩形的面积．【答案】（1）4m；（2）33．【分析】本题考查列代数式以及求代数式的值.【解答】（1）矩形的宽为m–n，矩形的长为m+n，矩形的周长为2[（m–n）+（m+n）]=4m；（2）当m=7，n=4时，矩形的长为m+n=7+4=11，矩形的宽为m–n=7–4=3，∴矩形的面积为S=11×3=33．10.【题文】张华发现某月的日历中一个有趣的问题，他用笔在上面画如图所示的十字框，若设任意一个十字框里的五个数为a、b、c、d、k．设中间的一个数为k，如图，试回答下列问题：（1）此日历中能画出______个十字框；（2）若a+b+c+d=84，求k的值；（3）是否存在k的值，使得a+b+c+d=108，请说明理由．【答案】（1）12；（2）k=21；（3）不存在，理由见解答.【分析】本题考查数字的规律.【解答】（1）由题意可得：十字框顶端分别在：1，2，5，6，7，8，9，12，13，14，15，16一共有12个位置；（2）由题意可得：设最上面为a，最左边为b，最右边为c，最下面为d，则b=a+6，c=a+8，d=a+14，k=a+7，故a+a+6+a+8+a+14=84，解得a=14，则k=21；（3）不存在k的值，使得a+b+c+d=108，理由：当a+b+c+d=108，则a+a+6+a+8+a+14=108，解得a=20，故d=34＞31（不合题意），故不存在k的值，使得a+b+c+d=108．11.【答题】在下列各式中，不是代数式的是（）A. 5x–yB.C. x=1D. 1【答案】C【分析】本题考查代数式的定义.【解答】A.5x–y是代数式，故不符合题意；B.是代数式，故不符合题意；C.x=1是方程，不是代数式，故符合题意；D.1是代数式，故不符合题意；选C．12.【答题】用代数式表示“m的一半与n的3倍的和”是（）A. B. C. D.【答案】D【分析】本题考查列代数式.【解答】“m的一半与n的3倍的和”可以表示为，选D．13.【答题】一个两位数，用x表示十位数字，个位数字比十位数字大3，则这个两位数为（）A. 11x+3B. 11x–3C. 2x+3D. 2x–3【答案】A【分析】本题考查列代数式.【解答】由题意可得，这个两位数为10x+（x+3）=10x+x+3=11x+3，选A．14.【答题】某超市一商品的进价为m元，将其价格提高50%作为零售价，半年后又以6折的价格促销，则此时这一商品的价格为（）A. m元B. 0.9m元C. 0.92m元D. 1.04m元【答案】B【分析】本题考查列代数式.【解答】由题意可得，这一商品的价格为m（1+50%）×0.6=0.9m（元），选B．15.【答题】“比a的2倍大1的数”用代数式表示是（）A. 2（a+1）B. 2（a﹣1）C. 2a+1D. 2a﹣1【答案】C【分析】本题考查列代数式.【解答】∵该数比a的2倍大，故是在2a的基础上加上1，因此，答案是2a＋1，选C.16.【答题】元旦期间，某服装店为了让利给顾客，一款羊绒毛衣原售价为b元，现降价20%后，再次降价a元，则现售价为（）A. 元B. 元C. 元D. 元【答案】A【分析】解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程，再求解．根据原售价下调了20%后又降价a元为现价列出方程，即可解答．【解答】设原售价是b元，则现价=（1-20%）b-a=，选A．17.【答题】用棋子摆出下列一组“口”字，按照这种方法摆下去，则第n个“口”字需要用棋子（）A. （4n﹣4）枚B. 4n枚C. （4n+4）枚D. n2枚【答案】B【分析】本题考查图形的规律.观察图形可知，构成每个“口”字的棋子数量，等于构成边长为（n+1）的正方形所需要的棋子数量减去构成边长为（n+1-2）的正方形所需要的棋子数量．【解答】由图可知第n个“口”字需要用棋子的数量为（n+1）2-（n+1-2）2=4n，选B．18.【答题】某养殖场2016年底的生猪出栏价格是每千克a元．受市场影响，2017年第一季度末的出栏价格平均每千克下降了15%，到了第二季度末平均每千克比第一季度末又上升了20%，则第三季度初这家养殖场的生猪出栏价格是每千克（）A. （1-15%）（1+20%）a元B. （1-15%）20%a元C. （1+15%）（1-20%）a元D. （1+20%）15%a元【答案】A【分析】本题考查列代数式，注意题目蕴含的数量关系，找准关系是解决问题的关键．由题意可知：2014年第一季度出栏价格为2013年底的生猪出栏价格的（1﹣15%），第二季度平均价格每千克是第一季度的（1+20%），由此列出代数式即可．【解答】第三季度初这家养殖场的生猪出栏价格是每千克（1﹣15%）（1+20%）a元．选A．19.【答题】某商店进了一批商品，每件商品的进价为a元，若想获利，则每件商品的零售价定为（）A. 元B. 元C. 元D. 元【答案】D【分析】本题考查一元一次方程的应用，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程组，再求解．根据等量关系：零售价-进价=获利获利，即实际获利=，设未知数，列方程求解即可．【解答】设每件售价为x元，则x-a=，解得x=（1+．选D．20.【答题】体育委员小金带了500元钱去买体育用品，已知一个足球x元，一个篮球y元．则代数式500﹣2x﹣3y表示的实际意义为______．【答案】体育委员买了3个足球和2个篮球后剩余的经费【分析】本题考查列代数式.【解答】∵买一个足球a元，一个篮球b元，∴3a表示委员买了3个足球，2b表示买了2个篮球，∴代数式500﹣3a﹣2b表示体育委员买了3个足球、2个篮球，剩余的钱．。

微观经济学第二章习题

第二章：需求、供给与均衡价格（习题）一、名词解释：需求供给均衡价格需求的变动供给的变动需求量的变动供给量的变动需求弹性供给弹性替代品互补品需求的交叉弹性需求的收入弹性恩格尔定律二、填空题1.需求函数Q d=?(P)表示一种商品的（需求量）和（价格）之间存在着一一对应关系。

2.对于一个家庭或国家来说，富裕程度越高，恩格尔系数越( 小)；反之，则越( 大)。

3.供给函数Q s=?(P)表示一种商品的（供给量）和（价格）之间存在着一一对应关系。

4.需求表或需求曲线表示（需求量）和（价格）之间的函数关系。

5.在供给不变的情况下，需求增加，会使需求曲线向（右）平移，从而使得均衡价格和均衡数量（都增加）；需求减少，会使需求曲线向（左）平移，从而使得均衡价格和均衡数量（都减少）。

6.蛛网定理说明（背离均衡点的）商品的供求数量和价格的变化。

7.对于富有弹性的商品来说，降低价格会（增加）厂商的销售收入；对于缺乏弹性的商品来说，降低价格会（减少）厂商的销售收入。

8.在需求的价格弹性小于l的条件下，卖者适当（提高）价格能增加总收益。

9价格弹性是指（需求量相对）变动对（价格相对）变动的反应程度。

10. 在需求不变的情况下，供给增加，会使供给曲线向（右）平移，从而使得均衡价格（下降），均衡数量（增加）；供给减少，会使供给曲线向（左）平移，从而使得均衡价格（上升），均衡数量（减少）。

11.蛛网形状取决于商品的弹性：如果需求弹性小于供给弹性，则蛛网是( 发散的)；如果商品的需求弹性大于供给弹性，则蛛网是（收敛的）。

因此，农产品的蛛网形状是（发散的）。

12.化纤产品是棉布的（代替品），化纤产品价格下降时，要使棉布的需求量不变，棉布的价格会相应（下降）。

而汽车是汽油的（互补品），要是汽油的需求量不变，汽车涨价时，汽油的价格（下跌）。

13.要保持原有需求量，替代商品价格成（同方向）变动，而互补商品的价格成（反方向）变动。

三、单项选择题1.需求曲线一条向（）倾斜的曲线。

庞皓计量经济学第二章练习题及参考解答(第四版)

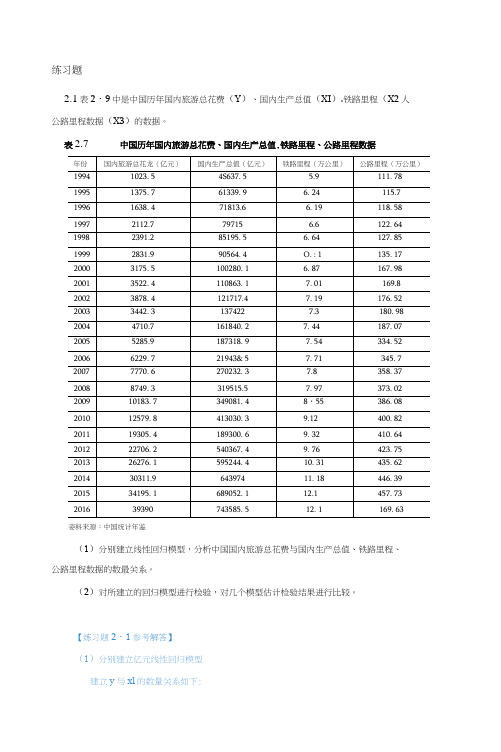
练习题2.1表2・9中是中国历年国内旅游总花费（Y）、国内生产总值（XI）.铁路里程（X2人公路里程数据（X3）的数据。

表2.7 中国历年国内旅游总花费、国内生产总值.铁路里程、公路里程数据姿料来源：中国统计年鉴（1）分别建立线性回归模型，分析中国国内旅游总花费与国内生产总值、铁路里程、公路里程数据的数最关系。

（2）对所建立的回归模型进行检验，对几个模型估计检验结果进行比较。

【练习题2・1参考解答】（1）分别建立亿元线性回归模型建立y与xl的数量关系如下:Y t= -3228.02 + 0.05X nDependent Variable: Y Method: Least Squares Date: 03/12/18 Time: 22:32Sample: 1994 2016 Included observatio ns: 23Variable Coe 帀dent Std. Error t-Statistic Prob.C ・3228.021 834.3232 -3.869043 0.0009X10.0501310.002312 21.67981 0.0000R-squared 0.957231 Mean dependentvar 11003.76Adjusted R-squared 0.955195 S.D. dependentvar11666.83S.E. of regression 2469.548 Akaike rfo criterion 18.54440Sum squared resid 1.28E*08 Schwarz criterion 18.64314Log likelihood ・211.2606 Hannan-Quinn criter.18.56923F-statistic 470.0140 Durbin-Watson stat 0.215776Prob(F-statistic) 0.030000建立y与x2的数量关系如卜I£ = -39438.73 + 6165・25乂力Dependent Variable:/ Method: Least Squares Date: 03/12/18 Time: 22:35 Sample: 1994 2016 Included observations:23Variable Coefficient Std. Error t-Statistic Prob.C •39433.731950.462 ・20.22020 0.0000X2 6165253 232.6620 26.49647 0.0000R-squared 0.970957 Mean dependent var11003.76Adjusted R-squared 0.969574 S.D. dependentvar 11666.83S.E. of regression 2035056 Akaike irfo criterion 18.15738sum squared resia 86970504 scnwarz criterion18.25611Log likelihood -206.8098 HannarvQuinn criter.18.18221F-statistic702.0629 Durbin-V/atson stat 0.699706Prob(F-statistic)o.oocooo建立y与x3的数量关系如卜：Y t = -9106.17 + 71.64X1{Dependent Variable: Y Method: Least Squares Date: 03/12/18 Time: 22:35 Sample: 1994 2016Indudod obcorvations: 23Variable Coefficient Std. Error t-Statistic Prob.C -9106.166 3170.972 -2.871727 0.0091X3 71.63938 10.20302 7.021388 0.0000R-squared 0 701280 Mzn d^pend^nt var11003 76Adjusted R-squared 0687055 SD. dependentvar 11666.83S.E. of regression 6526.601 AKaike irfo criterion 20.43810Sum squared resid 8 95E+08 Schwarz criterion 20.58684Log likelihood-233.6132 Hannan-Quinn enter20.51293F-AtatiAtic49 29989Oirbin-WAtAon Atat O 219452Prob(F-stdtistic)0000001（2）对所建立的回归模型进行检验，对几个模型估计检验结果进行比较。

微积分上第二章习题参考答案

2 2 dy sin x 2. (1 x 2 )sin x 2 x[cos x 2 ln(1 x 2 ) ] ; 2 dx 1 x
微积分第二章习题参考答案
16
x e x sin e x cos 0 x 三.解: , 2 3 2 0 y
1 S | 2 x0 | | 2 y0 | 2a 2为常数,与切点无关. 2
微积分第二章习题参考答案 6
§2.2求导法则(21-22)
一.1. 2cos x sec x, 3cos x 2sec x; x e sin 2. cos e , ; 2x 1 e
2 2
x 2 x cos2 x sin2 x 1 2 3. , e ( cos3 x 3sin3 x ); 2 x 2
微积分第二章习题参考答案 26

(n)
2
n 1

2. y xe .
x x x x y e xe e ( x 1),
y e x ( x 1) e x e x ( x 2),
t2 2 t2
3. y
1 1 x
2
, y
x (1 x )
2 3 2
;
4. y ( n ) n ! 2n e 2 x 1 ;
5. y e (sin cos ) 2e sin(

4
);
微积分第二章习题参考答案

20
2 dy d y 2 2 2 2 6. 2tf ( t ) , 2 2 f ( t ) 4t f ( t ) ; dt dx
lim f (cos x )( sin x )
x 0

(完整版)第二章习题答案

1050元），故不应购买该债券。
甲企业计划利用一笔长期资金投资购买股票。现有 m 公司股票 n 公司股票可供选
，甲企业只准备投资一家公司股票，已知 m 公司股票现行市价为每股 9 元，上年每股股
0.15 元，预计以后每年以 6% 的增长率增长。n 公司股票现行市价为每股 7 元，上年
0.60 元，股利分配政策将一贯坚持固定股利政策，甲企业所要求的投资必要报
1 000元？
＝（P/A，i，n）
＝（P/A，i，8）
（P/A，i，8）
，当利率为3%时，系数是7.0197；当利率为4%时，系数
6.4632。因此判断利率应在3%～4%之间，设利率为x，则用内插法计算x值。
利率年金现值系数
i＝3%+0.0354%≈3.04%
＝10.78%
某公司在2004年1月1日平价发行新债券，每张面值1000元，票面利率为10％，5
12月31日付息。（计算过程中至少保留小数点后4位，计算结果取整）。
要求：
1）2004年1月1日到期收益率是多少?
2）假定2008年1月1日的市场利率下降到8％，那么此时债券的价值是多少?
1）保持第2年的净利润水平；（2）保持第2年的净利润增长率水平；（3）第三年的净利
6％，第四、五年的股利和第三年相同，从第六年开始保持5％的净利润增长率。
10％，计算上述三种情形下该股票的价值。
答案]
/净利润，由于股利支付率不变，普通股股数不变，则净利润增
1年的每股股利＝1×（1＋4％）＝1.04（元）
n 股票股票现行市价为 7 元，低于其投资价值 7.50 元，故值得投资购买。甲企业
n 公司股票。

会计基础第二章习题

第二章会计要素与会计科目一、判断题1.()按照我国的会计准则，负债不仅指现实已经存在的债务责任，还包括某些将来可能发生的、偶然事项形成的债务责任。

2.()对会计要素的具体内容进行分类核算的项目称为“会计科目”。

3.()对于明细科目较多的总账科目，可在总分类科目与明细分类科目之间设置二级或多级科目。

4.()对于某一项财产，要成为企业的资产，其所有权必须属于企业。

5.()多栏式明细账一般适用于资产类账户。

6.()二级科目(子目)不属于明细分类科目。

7.()会计档案的保管期限分为永久和定期两类。

其中定期保管又分为3年、5年、l0年、l5年和25年。

8.()会计科目的基本结构包括账户、增减金额、余额等。

9.()会计科目的设置原则包括合法性原则、相关性原则和实用性原则。

10.()会计科目和会计账户的口径一致．性质相同，都具有一定的格式或结构．所以在实际工作中，对会计科目和账户不加严格区分。

11.()会计科目和账户的设置、复式记账、填制会计凭证、登记会计账簿、进行成本计算、财产清查和编制财务会计报告等．国家有统一的会计制度的要求。

12.()会计科目和账户都是对会计对象具体内容的科学分类，两者口径一致，性质相同。

13.()会计科目是账户的名称，账户是会计科目的载体和具体运用。

14.()会计要素中既有反映财务状况的要素，又有反映经营成果的要素。

15.()记账凭证可以作为登记账簿的直接依据，原始凭证则不能作为登记账簿直接依据。

16.()借贷记账法下账户的基本结构是：每一个账户的增加计入借方，减少计入贷方。

17.()流动负债是指需要在一年或超过一年的一个营业周期内偿还的债务。

18.()明细分类科目对总分类科目起着补充说明和统驭控制的作用。

19.()某项财产物资要成为企业的资产，只要该企业拥有其所有权就能将其确认为资产。

20.()企业的收入一定会导致经济利益流入。

21.()企业只能使用国家统一的会计制度规定的会计科目，不得自行增减或合并。

矩阵理论第2章习题解答

第二章习题答案1．设a 1，a 2，…，a n 均为正数，nC x ∈，且Tn x x x x ),,,(21 =. 证明函数2/112][)(∑==ni i i x a x f在C n 上定义了一个向量范数.证明：(1) 正定性：对0≠∀x ，有f (x )>0，当x =0时，f (x )=0. (2) 奇次性：)(][][)(2/1122/112x f x a x a x f ni i i ni i i ⋅=⋅==∑∑==λλλλ.(3) 三角不等式：])([][)(122122∑∑==+++=+=+ni i i i i i i i ni i i iy x y x y x a y x ay x f)2()()()2()()(122122∑∑==⋅++≤⋅++≤ni i i i ni i i i y x a y f x f y x a y f x f∑∑∑===⋅++≤⋅++≤ni i i ni i i ni i i i i y a x a y f x f y a x a y f x f 12/1212/1222122)()(2)()()2()()( 222)]()([)()(2)()(y f x f y f x f y f x f +=⋅++=. 所以函数f (x )是一个向量范数.2. 证明：在R 1中任何向量范数x ，一定有x x λ= 0>λ.证明：对任意向量范数x ，根据向量范数的定义和性质，又因为1R x ∈，有 x x x x λ=⋅=⋅=11，其中01>=λ.3. 设x 是P n 中的向量范数，nn P A ⨯∈，则Ax 也是P n 中的向量范数的充要条件为A是可逆矩阵.证明：必要性：如果矩阵A 不可逆，则存在0≠x ，使得0=Ax ，即0=Ax ，这与向量范数的正定性矛盾，所以矩阵A 可逆.充分性：矩阵A 可逆，对0≠∀x ，则0≠Ax ，所以0>Ax ，正定性满足；Ax Ax ⋅=λλ，奇次性满足；Ay Ax Ay Ax y x A +≤+=+)(，三角不等式也满足，故Ax 是向量范数.4. 证明(1) 2/1)]([2A A tr A H m =;(2) 2m A与2x 是相容的；(3) a A 与1x 、2x 均相容； (4) {}22222min ,m m m m ABABAB≤⋅.证明：(1) 设nn PA ⨯∈，令),,(1n A αα =. 根据定义有∑∑===ni nj ijm a A 11222，∑==ni ijja 1222α，n j ,,1 =，所以有∑==nj mjA 1222α，同时有，⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=n Hn H n n H H n H n H HA A αααααααααααα111111)( ，所以有212)(m n j j H j H A A A tr ==∑=αα.(2) 见课本61页下.(3) 令()Tn x x x x ,,,21 =，nn ij Pa A ⨯∈=)(. 因为j n i nj ijji n i n j jijx ax a Ax ⋅≤=∑∑∑∑====11,111max11,11,}{max max x A x a n x a a ij ji nj j ni ij ji ⋅=⋅⋅≤⋅≤∑∑==. 所以，a A 与1x 相容;因为∑∑∑∑∑∑∑=======⋅=⋅≤+++=n i nj j nj ij n i nj j nj ij ni n in i i x a x a x a x a x a Ax112121121212221122)()(22222}{max }{max x a n x a n ij ijij ij⋅⋅=⋅⋅≤. 所以，a A 与2x 相容.(4) 令),,,,(1n j B βββ =，因为222j jA A ββ≤，n j ,,1 =，同时有222222212222221212222)(),,(m n nm n m BA A A A A AB =++≤++==ββββββ有上述结果有2222222)(m m HHm HH m Hm A BA B A B AB AB=≤==，所以(4)成立.5. 若rm PA ⨯∈，且r HE A A =，则12=A ，r A m =2.证明：根据定义1)()(2===E r A A r A H ；r E tr A A tr A H m ===)()(2.6. 设x ，Ax 的向量范数为2∙，证明：它对应的算子范数是{}n xAx A σσσ,,,m ax m ax 212122===.证明：对任意矩阵A ，存在酉矩阵U ，V ，得到矩阵A 的奇异值分解A =UDV . 其中n σσ,,1 是矩阵A 的奇异值，D =diag(n σσσ,,,21 ). 根据定义，有)()())(()(222D r V D V r UDV UDV r A A r A H H H =====max{n σσσ,,,21 }.7. 若∙是算子范数，则 (1) 1=E ; (2) 11--≥A A;(3) xAxAx 011min≠--=. 证明：根据算子范数定义xAxA x 0max≠=， (1) 1max max00===≠≠x xxEx E x x ; (2) 111--≤==A A AA E ，11--≥A A ；(3) xx A Ax 101max-≠-=，令x A y 1-=，则Ay x =，得AyyAy 01max≠-=，从而xAxy Ay Ayy A x y y 00011minminmax 1≠≠≠--===. 8. 设v A ，μA 是对应于两个向量范数v x ，v Bx x=μ的算子范数，B 可逆，则νμ1-=BAB A .证明：根据定义，有μμμxAx Ax 0max≠=，把νμBx x=代入上式，得到ννμBx BAx A x 0max≠=，令y =Bx ，则y B x 1-=，则νννμ110max--≠==BAB y y BAB Ay .9. 设a x ，b x 是C n 上的两个向量范数，a 1，a 2是两个正实数，证明 (1) c b a x x x =},max{; (2) d b ax x a xa =+21都是C n 上的向量范数.证明：需要证明(1)和(2)满足范数定义中的三个条件即可.(1) (正定性) 当0≠x 时，0>ax ，0>b x ，则0>c x ；当x =0时，0=a x ，0=b x ，则0=cx. 奇次性显然成立. (三角不等式)},m a x {},m a x {b b a a b a cy x y x y x y x yx ++≤++=+c c b a b a y x y y x x +=+≤},max{},max{. (1)证毕.(2) 正定性和奇次性同(1)，容易得到. 下面证明三角不等式：d d b b a a b a d y x y x a y x a y x a y x a y x +=+++≤+++=+)()(2121. 证毕.10. 证明F F A A A n≤≤21. 证明：因为22122)()()(F Hn HA A A tr A A r A ==+++≤=λλλ ，即F A A ≤2，其中i λ为半正定矩阵A H A 的特征值. 又由于22212)()(A n A A r n A H n F ⋅=⋅≤+++=λλλ ，即21A A nF ≤. 证毕. 11．设a A 是nn C⨯上的相容矩阵范数，B ，C 都是n 阶可逆矩阵，且aB1-及aC1-都是小于或等于1，证明对任何nn CA ⨯∈a b BAC A =定义了nn C⨯上的一个相容矩阵范数.证明：首先证明a b BAC A =是一个矩阵范数。

计算机财务管理答案

计算机财务管理答案篇一：终稿第一章习题习题1【答案】：答案略习题2【答案】：答案略习题3【答案】：答案略习题4【答案】：答案略习题5【答案】：单元地址主要指出在Excel工作表格中，一个单元或一组单元的位置，以便Excel可以由此“参考”辨识目标单元，以进行数据分析处理。

在工作表格中所使用的“地址”基本有如下两种形式：相对地址和绝对地址。

相对地址是以某一特定单元为基准对其他单元进行定位。

绝对地址是直接指出某些单元在工作表格中的确切位置。

习题6【答案】：单元区域是指由若干个单元组成的区域。

单元区域的表示方法有三种：连续区域、合集区域和交集区域。

连续区域第一个和最后一个单元引用中间用冒号“：”连接，表示由若干个连续单元组成的区域；合集区域单元引用间用逗号“，”连接，表示互不相连的单元组成的区域；交集区域两个单元引用间用空格“”连接，表示两个单元引用的公共单元区域。

习题7【答案】：答案略习题8【答案】：答案略习题9【答案】：答案略习题10【答案】：答案略习题11【答案】：答案略第二章习题习题1【答案】：答案略习题2【答案】：答案略习题3【答案】：答案略习题4【答案】：答案略第三章习题习题1【答案】：见附件习题2【答案】：答案略习题3【答案】：答案略习题4【答案】：答案略习题5【答案】：答案略习题6【答案】：答案略附件：见CWGL03-XT.XLS第四章习题习题1【答案】：答案略习题2【答案】：答案略习题3【答案】：答案略习题4【答案】：答案略习题5【答案】：答案略习题6【答案】：见附件习题7【答案】：答案略习题8【答案】：答案略附件：见CWGL04-XT.XLS第五章习题习题1【答案】：答案略习题2【答案】：答案略习题3【答案】：见附件决策变量：xi 表示对各方案的投资情况，i?1,2,3,4 表示A,B,C,D 四个方案，xi?0 表示不投资，xi?1表示投资目标函数：组合净现值SUM（NPV）=21.4x1?16.07x2?11.94x3?13.22x4 约束条件：xi?二进制，表示xi只能取0或1；?10x1?5x2?5x3?0x4??10 ，表示第0期满足资本限额；30x1?5x2?5x3?40x4??10 ，表示第1期满足资本限额；5x1?20x2?15x3?60x4??10 ，表示第2期满足资本限额。