float转化成二进制

合集下载

浮点数与二进制数的转换

浮点数与二进制数的转换一、引言浮点数与二进制数的转换是计算机科学中的基础知识之一。

浮点数是用来表示实数的一种数学模型，而二进制数是计算机中常用的数值表示方式。

了解浮点数与二进制数的转换原理与方法，对于理解计算机内部的运算过程以及编程中的数值处理具有重要意义。

二、浮点数的表示方式浮点数的表示方式通常采用IEEE 754标准，其中包括单精度浮点数和双精度浮点数两种形式。

单精度浮点数由32个bit位表示，双精度浮点数由64个bit位表示。

浮点数的表示方式由三部分组成：符号位、指数位和尾数位。

1. 符号位浮点数的符号位用来表示数值的正负，0表示正数，1表示负数。

2. 指数位浮点数的指数位用来表示数值的数量级。

指数位采用偏移码表示，即将真实的指数值加上一个固定的偏移值，以便能够表示负数的指数。

3. 尾数位浮点数的尾数位用来表示数值的精度。

尾数位是一个二进制小数，其范围为[1, 2)之间。

三、二进制数与浮点数的转换方法1. 二进制数转换为浮点数将二进制数的符号位、指数位和尾数位分别转换为浮点数的符号位、指数位和尾数位。

其中，符号位直接转换，指数位需要减去偏移值，尾数位需要转换为浮点数形式。

2. 浮点数转换为二进制数将浮点数的符号位、指数位和尾数位分别转换为二进制数的符号位、指数位和尾数位。

其中，符号位直接转换，指数位需要加上偏移值，尾数位需要转换为二进制数形式。

四、举例说明以单精度浮点数为例，假设要将二进制数1011.001转换为浮点数。

1. 二进制数转换为浮点数数值的符号位为0，表示正数。

数值的指数位为100，偏移值为127，所以真实的指数值为100 - 127 = -27。

数值的尾数位为1.001，转换为浮点数形式为1.001 * 2^(-27)。

因此，将二进制数1011.001转换为浮点数的结果为0 10000101 00100000000000000000000。

2. 浮点数转换为二进制数浮点数的符号位为0，表示正数。

float转换二进制 -回复

float转换二进制-回复如何将一个浮点数（float）转换为二进制（binary）形式。

第一步：理解浮点数和二进制数的基本概念在计算机中，浮点数是一种表示实数的数据类型，它可用于存储任意大小的数值，包括整数和小数。

浮点数通常由两部分组成：符号位（表示正负）和尾数（表示数值的大小）。

而二进制数则是一种由0和1组成的数制系统。

它由位（bit）组成，每个位表示一个数值，可以是0或1。

二进制数用于计算机中的所有数据存储和处理，因为计算机的内部电路只能处理二进制数。

第二步：将浮点数拆分为符号位、阶码和尾数在浮点数的二进制转换中，我们首先需要将浮点数拆分为符号位、阶码与尾数。

符号位表示浮点数的正负，通常用一个位来表示，0表示正数，1表示负数。

阶码表示浮点数的指数部分，它确定了浮点数在二进制中小数点的位置。

尾数表示浮点数的小数部分，它确定了浮点数数值的大小。

例如，考虑一个浮点数-3.14。

它的符号位为1，表示为负数。

为了将浮点数转换为二进制数，我们需要对其进行规范化，使其成为一个小于2但大于等于1的数。

在这个例子中，我们可以将-3.14转换为-1.57乘以2的1次方。

因此，-1.57的符号位为1，阶码为1，尾数为0.57。

第三步：将整数部分和小数部分分别转换为二进制对于整数部分，我们可以使用十进制到二进制的转换方法，将其转换为二进制数。

对于小数部分，我们需要使用乘2取整法将其转换为二进制数。

乘2取整法是将小数乘以2，并取整数部分的方法，重复进行直到小数部分为0或达到所需的精度。

对于整数部分-1，可以将其直接转换为二进制，即1。

对于小数部分0.57，将其乘以2得到1.14，取整得到1，然后再将小数部分0.14乘以2得到0.28，取整得到0，以此类推。

重复这个过程，直到小数部分为0或达到所需的精度。

最后，我们将整数部分和小数部分的二进制数合并得到浮点数的二进制表示形式。

对于本例中的-3.14，整数部分的二进制为1，小数部分的二进制为1001 1001 1001（循环）。

float转换成二进制

float转换成二进制
float是一种浮点数类型，它在计算机内部存储时需要转换成二进制。

在转换过程中，需要将浮点数分为三个部分：符号位、指数位和尾数位。

符号位表示数值的正负性，指数位表示数值的大小，尾数位表示数值的精度。

转换过程需要根据浮点数的类型和计算机的体系结构来确定。

在IEEE 754标准中，单精度浮点数使用32位二进制表示，其中第一位为符号位，接下来的8位为指数位，最后的23位为尾数位。

双精度浮点数使用64位二进制表示，其中第一位为符号位，接下来的11位为指数位，最后的52位为尾数位。

在进行float转换成二进制时，可以使用以下步骤：
1. 判断浮点数的符号位，如果为正数，则符号位为0，否则为1。

2. 将浮点数的绝对值转换成二进制，并找到小数点位置。

对于单精度浮点数，最多可以表示7位十进制数字，因此需要进行四舍五入。

3. 将小数点移动到尾数位的最左边。

移动的步数为指数位的值减去偏移量（偏移量为2^(n-1)-1，其中n为指数位的位数）。

对于单精度浮点数，偏移量为127，因此需要将小数点移动到第23位。

4. 将指数位转换成二进制，并将其与偏移量相加。

对于单精度浮点数，偏移量为127，因此需要将指数位的值加上127。

5. 将符号位、指数位和尾数位组合在一起，得到浮点数的二进制表示。

需要注意的是，在进行浮点数运算时，可能会出现舍入误差。

因此，在对浮点数进行比较时，应该使用误差范围来判断是否相等，而不是直接比较二进制值。

c语言float转二进制

c语言float转二进制要将浮点数转化为二进制，可以按照以下步骤进行：1. 将浮点数分解为符号、阶码和尾数。

浮点数的表示一般采用科学计数法，即一个实数可以表示为±m×10^n 的形式，其中m 称为尾数或者有效数字，n 称为阶码。

例如，对于浮点数-3.14159，尾数为3.14159，而阶码为-1。

2. 将符号位转为二进制。

浮点数的符号位为0 表示正数，为1 表示负数。

对于正数，符号位为0；对于负数，符号位为1。

3. 将阶码进行偏移。

在IEEE 754 标准中，浮点数的阶码需要进行偏移，以便更好地表示阶码的范围。

32 位的单精度浮点数的阶码偏移量为127，64 位的双精度浮点数的阶码偏移量为1023。

对于上面的例子，-1 的偏移后的阶码为126。

4. 将偏移后的阶码转为二进制。

阶码是一个整数段，需要将其转化为二进制数。

对于偏移后的阶码126，二进制表示为01111110。

5. 处理尾数部分。

尾数部分是浮点数的小数部分，需要将其转化为二进制数。

常用的方法是乘2 取整，将小数部分乘以2，取整数部分作为二进制中的一位，然后再乘2 取整，直到小数部分变为0 或者已经达到了所需的精度。

对于尾数部分3.14159，可以采用以下方式转化为二进制数：尾数部分2x 取整二进制0.14159 0.28318 00.28318 0.56636 00.56636 1.13272 10.13272 0.26544 00.26544 0.53088 00.53088 1.06176 10.06176 0.12352 00.12352 0.24704 00.24704 0.49408 00.49408 0.98816 00.98816 1.97632 10.97632 1.95264 10.95264 1.90528 10.90528 1.81056 10.81056 1.62112 10.62112 1.24224 1由于尾数部分已经达到了所需的精度，即小数部分为零时停止。

numpy float数组转二进制

一、介绍numpy是一个功能强大的数学库，用于处理大型多维数组和矩阵，它提供了大量的数学函数和方法，方便用户进行科学计算和数据分析。

在numpy中，数组是一个重要的数据结构，而对于数组中的元素类型，常见的有整数、浮点数、字符串等。

本文将重点介绍如何将numpy中的浮点数数组转换为二进制格式。

二、numpy float数组转二进制方法1. 使用tofile()方法numpy中的数组对象有一个tofile()方法，可以将数组以二进制格式写入文件。

对于浮点数数组，可以设置参数为'b'，表示写入二进制格式。

例如：```pythonimport numpy as nparr = np.array([1.23, 4.56, 7.89], dtype=np.float64)arr.tofile('float_array.bin')```这样就将浮点数数组arr以二进制格式写入了文件float_array.bin中。

2. 使用astype()方法和tobytes()方法另一种方法是先将浮点数数组转换为指定类型的数组，再使用tobytes()方法将数组转换为bytes对象。

例如：```pythonarr = np.array([1.23, 4.56, 7.89])arr_bytes = arr.astype(np.float64).tobytes()```这样就得到了浮点数数组arr的二进制表示arr_bytes。

3. 使用struct.pack()方法除了numpy自带的方法，还可以使用Python标准库中的struct模块来实现。

struct.pack()方法可以将数据按照指定格式转换为bytes对象。

例如：```pythonimport structarr = np.array([1.23, 4.56, 7.89])arr_bytes = b''.join(struct.pack('d', x) for x in arr)```这样就用struct.pack()方法将浮点数数组arr转换为二进制表示arr_bytes。

float的二进制

float的二进制表示方式float是一种浮点数类型，使用32个bit位来存储。

它的二进制表示方式有三个部分：符号位、指数位和尾数位。

1. 符号位：1 bit，表示数值的正负，0代表正数，1代表负数。

2. 指数位：8 bits，用于表示数值的大小和范围，可以表示2^8=256个不同的值。

它的取值范围是-127至128，但是有一个偏移量127，所以真实的指数范围是-126至127。

具体地，指数位上的数值加上127就是实际的指数。

如，假设指数位为10000000，代表的实际指数就是10000000+127=100000000，也就是-1的二进制表示方式。

3. 尾数位：23 bits，用于表示数值的精度，可以表示2^23=8388608个不同的值。

举个例子：假设一个float数值的二进制表示方式为1 10000000 10100000000000000000000，我们可以解读出以下信息：1. 符号位为1，代表这个数值为负数。

2. 指数位为10000000，代表的实际指数是10000000+127=100000000，也就是-1的二进制表示方式。

3. 尾数位为10100000000000000000000，代表的数值是1.65625。

所以，这个float数值的真实值为-1.65625。

小数的二进制表示方式总体来说，将十进制小数转化为二进制小数的实现方式如下：- 将小数部分乘以2，记录整数部分，并将小数部分取出，若为1放到结果中，否则为0；- 对新获得的小数部分重复第一步操作，直至小数部分为0或达到要求的小数位数。

- 合并小数部分和整数部分，得到该小数的二进制表示方式。

例如：将0.625的十进制表示方式转化为二进制表示方式，可以按照以下步骤完成：1. 0.625*2=1.25，整数部分为1，剩余小数部分为0.25；2. 0.25*2=0.5，整数部分为0，剩余小数部分为0.5；3. 0.5*2=1.0，整数部分为1，剩余小数部分为0；4. 将记录下来的整数部分连接起来，得到该小数的二进制表示方式为0.101。

float 0 二进制

float 0 二进制float 0 二进制是一个关于浮点数0的二进制表示的话题。

在计算机科学中，浮点数是一种用来表示实数的近似值的数据类型。

浮点数在计算机科学和工程中得到了广泛应用，尤其是在科学计算、图形处理和人工智能等领域。

浮点数的二进制表示是通过将实数转换为二进制来实现的。

在浮点数的二进制表示中，通常使用一定的位数来表示整数部分和小数部分。

而浮点数0的二进制表示则是一种特殊的情况，它可以简化为一个全为0的二进制数。

浮点数的二进制表示使用了科学计数法，其中包括了一个指数和一个尾数。

指数部分用于表示小数点的位置，而尾数部分用于表示具体的数值。

浮点数的二进制表示允许表示非常大或非常小的数值，并且具有一定的精度损失。

浮点数的二进制表示需要考虑数值的精度和范围限制。

在计算机中，浮点数的表示是有限的，即存在精度损失和溢出的情况。

在进行浮点数计算时，需要注意这些限制，并进行适当的处理，以避免出现错误结果。

浮点数的二进制表示在计算机科学中也存在一些常见问题。

例如，浮点数的比较和相等性判断需要考虑精度损失的问题。

此外，浮点数的舍入和舍入误差也是一个重要的问题，需要进行适当的处理。

在实际应用中，浮点数的二进制表示通常是透明的，用户无需关心具体的实现细节。

然而，在某些特定的场景下，了解浮点数的二进制表示可以帮助我们更好地理解浮点数的计算和运算规则。

浮点数的二进制表示是计算机科学中一个重要而复杂的话题。

了解浮点数的二进制表示对于进行科学计算、图形处理和人工智能等领域的开发和研究都具有重要意义。

在实际应用中，我们需要充分理解浮点数的二进制表示，并注意其中存在的精度损失和溢出问题，以确保计算结果的准确性和可靠性。

c语言float二进制写法

c语言float二进制写法
C语言中，float类型的数据是用32位来表示的，其中包括1
位符号位，8位指数位和23位尾数位。

float类型的数据采用IEEE 754标准来表示，其二进制写法如下：
1. 符号位，第1位表示符号位，0表示正数，1表示负数。

2. 指数位，接下来的8位用来表示指数部分，采用偏移码表示，即实际指数值加上127，得到偏移码值。

因此，偏移码范围为0到255，实际指数范围为-126到+127。

3. 尾数位，最后的23位用来表示尾数部分，尾数部分采用二
进制小数表示，范围为0到1。

因此，一个float类型的数的二进制表示即为，符号位 + 指数
位 + 尾数位。

举个例子，如果我们要表示3.14这个float类型的数，首先确
定符号位为0（正数），然后将3.14转换为二进制小数，得到尾数
部分，最后确定指数部分，将所有部分组合起来就得到了3.14的
float类型的二进制表示。

需要注意的是，由于浮点数的精度问题，有些十进制小数无法完全精确地用二进制表示，因此在实际编程中需要注意浮点数运算可能产生的精度损失。

IEEE 754标准float类型数据信息丢失的原因剖析

IEEE 754标准float类型数据信息丢失的原因剖析——楚得允。

本人对单精度浮点数的数据信息的丢失有一些疑惑，但是并未找到相关的资料，以下是本人的一点研究心得，仅供参考。

在阅读之前，应该先了解IEEE 754 格式的单精度浮点数的存储格式以及有效范围。

可以参考：百度百科- IEEE 754。

一．存储过程：首先看一个简单的float 数据的存储过程。

⑴．float数据存储时，先把它转化成二进制表示的数据。

比如：float f1 = 4.75f;这样把4.75用二进制表示为：100.11⑵．然后通过小数点移位，把数据表示成类似科学计数法的形式，也就是整数部分就只有一个“1”。

这样100.11 转化成： 1.0011 * 2^2. *************************************格式Ⅰ⑶．获取float 数据存储的指数和尾数以及符号位。

明显：符号位S = 0；（0表示正数，1表示负数）指数exp = 2；尾数fraction = 0011 *************************************格式Ⅱ⑷．这样通过偏差修正获得指数的二进制形式：01111111 + 10 = 10000001最终得到单精度浮点数存储的详细值：0 10000001 0011000000000000000000000S | -→exp←- | ----------→fraction ←-----------|可以通过以下的程序验证存储结果：#include <iostream.h>void main(void){float f1 = 4.75f;int *p1 = (int*)&f1;cout << "f1 = " << f1 << endl<< hex << "内存数据为：" << *p1 << endl;}把f1的内存数据取出之后，可以看到结果是：40980000 ，用二进制可以表示为：0100 0000 1001 1000 0000 0000 0000 0000，可以看到数据和上面的第4）的存储数据是一样的。

float转换二进制

float转换二进制float是一种非常常见的数据类型，在编程中经常用到。

它用来表示带有小数位的实数，即浮点数。

而二进制是一种计算机内部所使用的数字系统，它只有0和1两个数字。

在编程中，我们经常需要将float类型的数据转换为二进制数，这样可以更方便地进行计算和存储。

接下来，我将一步步为大家解释如何将float类型转换为二进制数。

首先，我们需要了解float类型的特点。

在大多数现代计算机中，float 类型一般占用32位（4字节）或64位（8字节）的存储空间。

其中，32位的float类型被称为单精度浮点数，64位的float类型被称为双精度浮点数。

在这篇文章中，我们将以32位的单精度浮点数为例进行讲解。

接下来，我们需要知道float类型的内部存储结构。

在IEEE 754浮点计算标准中，32位的float类型被分为三个部分：符号位、指数位和尾数位。

其中，符号位用来表示浮点数的正负，指数位用来表示浮点数的指数，尾数位用来表示浮点数的小数部分。

具体的存储结构如下图所示：[图1：float内部存储结构]在图1中，我们可以看到，float类型的符号位占用1位，指数位占用8位，尾数位占用23位。

根据这个存储结构，我们可以将float类型转换为二进制数，具体的步骤如下：1. 首先，确定符号位：根据float类型的正负，确定符号位的值。

如果float类型为正数，则符号位为0；如果float类型为负数，则符号位为1。

2. 确定指数位：浮点数的指数部分需要进行偏移码的处理。

偏移码是为了将指数的正负转换为二进制数。

在32位的float类型中，指数位占用了8位，其中7位用来表示指数的大小，第8位用来表示指数的正负。

因此，我们需要将指数位加上127，以得到偏移码。

然后，将得到的偏移码转换为二进制数，作为指数位的值。

3. 确定尾数位：尾数位是float类型的小数部分，在转换前需要将小数部分进行规格化。

规格化是将小数部分的最高位设置为1，并去掉前导零。

c语言 float 二进制

c语言float 二进制摘要：1.C 语言中的float 类型2.float 类型的内存存储方式3.float 类型的二进制表示4.浮点数运算与精度问题正文：1.C 语言中的float 类型在C 语言中，float 是一种用于表示实数的数据类型。

它可以用来存储带有小数部分的数字，相比于整型数据类型，float 类型可以表示更大的数值范围。

float 类型的大小为4 字节（32 位），它的取值范围约为-3.4E38 到3.4E38，精度为6-7 位小数。

2.float 类型的内存存储方式float 类型的内存存储方式采用IEEE 754 标准，这种标准将实数表示为一个符号位、一个指数位和一个尾数位。

其中，符号位表示正负，指数位表示浮点数的阶码，尾数位表示浮点数的小数部分。

3.float 类型的二进制表示float 类型的二进制表示形式为：符号位（1 位）+ 指数位（11 位）+ 尾数位（23 位）。

- 符号位：用1 位二进制表示，0 表示正数，1 表示负数。

- 指数位：用11 位二进制表示，其中偏置量为127（即二进制的1111111111），因此，实际的指数值等于二进制表示减去偏置量。

- 尾数位：用23 位二进制表示，表示浮点数的小数部分。

4.浮点数运算与精度问题由于float 类型的存储方式和计算原理，浮点数运算可能会产生精度问题。

例如，当两个不同的float 数相加时，由于它们的表示形式可能不同，直接相加可能导致精度丢失。

为了解决这个问题，C 语言提供了一些特殊的函数，如round、ceil、floor 等，用于对浮点数进行四舍五入或向上取整等操作。

总之，C 语言中的float 类型是一种用于表示实数的数据类型，其内存存储方式采用IEEE 754 标准，二进制表示形式包括符号位、指数位和尾数位。

c++ float double序列化二进制

在C++中，序列化（serialization）是将对象的状态信息转换为可以存储或传输的形式的过程。

反序列化（deserialization）则是反向操作，从序列化的数据中提取对象的状态信息。

要将`float`或`double`类型的变量序列化为二进制，你可以将它们转换为`std::vector<char>`或`std::array<char, N>`的形式，其中N是所需的字节数。

然后你可以将这个二进制数据保存到文件中，或者通过网络发送。

以下是一个简单的例子，展示了如何将一个`float`变量序列化为二进制，然后反序列化回原始的`float`变量。

```cpp#include <fstream>#include <vector>#include <cmath>// 序列化std::vector<char> serializeFloat(float value) {std::vector<char> buffer(sizeof(float));std::memcpy(buffer.data(), &value, sizeof(float));return buffer;}// 反序列化float deserializeFloat(const std::vector<char>& buffer) {float value;std::memcpy(&value, buffer.data(), sizeof(float));return value;}int main() {float value = 3.14159f;auto serialized = serializeFloat(value);// 现在你可以将serialized数据保存到文件中，或者通过网络发送...// 反序列化数据回到原始的float值float deserialized = deserializeFloat(serialized);std::cout << "Deserialized value: " << deserialized << std::endl;return 0;}```这个例子使用了C++标准库中的`std::memcpy`函数来执行低级别的内存操作。

matlab浮点数转换为二进制

在MATLAB中，你可以使用dec2bin 函数将浮点数转换为二进制表示形式。

这个函数可以将一个十进制的非负整数或小数转换成一个二进制字符串。

下面是一个简单的示例，演示如何将浮点数转换为二进制：
matlabCopy Code
定义一个浮点数
x = 3.14;
将浮点数转换为二进制字符串
binaryString = dec2bin(typecast(single(x), 'uint32'), 32);
disp(binaryString);
在这个示例中，我们使用了typecast 函数将浮点数转换为单精度浮点数的二进制表示形式，然后使用dec2bin 函数将其转换为二进制字符串。

最终的二进制字符串将会以字符数组的形式显示出来。

需要注意的是，浮点数的二进制表示形式可能会比较复杂，并且受到浮点数表示精度的影响。

因此，在实际使用中，你可能需要对结果进行进一步的处理和理解。

lua float转换为 byte数组

lua float转换为byte数组在Lua中，将一个浮点数（float）转换为字节数组（byte array）通常涉及对浮点数的二进制表示进行分解。

由于Lua标准库并没有直接提供这样的功能，你需要手动实现这个过程。

下面是一个简单的示例，展示如何将一个单精度浮点数（32位）转换为字节数组：lua复制代码function floatToByteArray(f)-- 将浮点数转换为二进制字符串local binstr = string.format("%c%c%c%c", f, f*256, f*256*256, f*256*256*256)-- 将二进制字符串转换为字节数组local bytes = {}for i = 1, #binstr dolocal byte = string.byte(binstr, i)table.insert(bytes, byte)end-- 因为Lua中的浮点数可能存在精度问题，上面的方法并不总是可靠的-- 更好的方法是直接使用Lua的位操作来提取浮点数的各个字节-- 注意：这可能需要Lua 5.3或更高版本，因为较旧的版本可能不支持所有的位操作函数local bits = string.dump(function()return f end):sub(6,9) -- 获取浮点数的二进制表示for i = 1, 4dolocal byte = bit32.band(bit32.rshift(bits, (3 - i) * 8), 0xFF)table.insert(bytes, byte)endreturn bytesend-- 使用示例local f = 123.456local bytes = floatToByteArray(f)for _, byte in ipairs(bytes) doprint(byte)end这个示例中的floatT oByteArray函数接受一个浮点数作为输入，并返回一个包含该浮点数字节表示的表。

float类型在内存中的表示

float类型在内存中的表示先说一下计算机中二进制的算法：∙整数整数的二进制算法大家应该很熟悉，就是不断的除以2取余数，然后将余数倒序排列。

∙小数小数的二进制算法和整数的大致相反，就是不断的拿小数部分乘以2取积的整数部分，然后正序排列。

比如求0.9的二进制：0.9*2=1.8 取 10.8*2=1.6 取 10.6*2=1.2 取 10.2*2=0.4 取00.4*2=0.8 取00.8*2=1.6 取 1… …如此循环下去。

因此我么得到的二进制小数也是无限循环的：0.11100110011...从小数的二进制算法中我们可以知道，如果想让这种算法停止，只有在小数部分是0.5的时候才可以，但是很不幸，这类的小数很少。

所以大部分小数是很难用二进制来精确表示的。

------------------------我是分割线------------------------------OK，有了上面的知识，我们进入正题：看看float类型在内存中是如何表示的。

float类型又称为单精度浮点类型，在IEEE 754-2008中是这样定义它的结构的：S EEEEEEEE FFFFFFFFFFFFFFFFFFFFFFF31 30 23 22 0float类型总共4个字节——32位：1.符号位其中最左边的为符号位，0为正，1为负。

2.指数接下来的E是指数，一共8位，也用二进制来表示。

3.尾数最后的F是小数部分，尾数正是由这23位的小数部分+1位组成的。

（这个稍后解释）。

这里我们需要多说一下指数。

虽然指数也是用8位二进制来表示的，但是IEEE在定义它的时候做了些手脚，使用了偏移来计算指数。

IEEE规定，在float类型中，用来计算指数的偏移量为127。

也就是说，如果你的指数实际是0，那么在内存中存的就是0+127=127的二进制。

稍后我们来看这个到底如何使用。

好了，看了这么多，我们该演示一下计算机如何将一个十进制的实数转换为二进制的。

float浮点数的二进制存储方式及转换

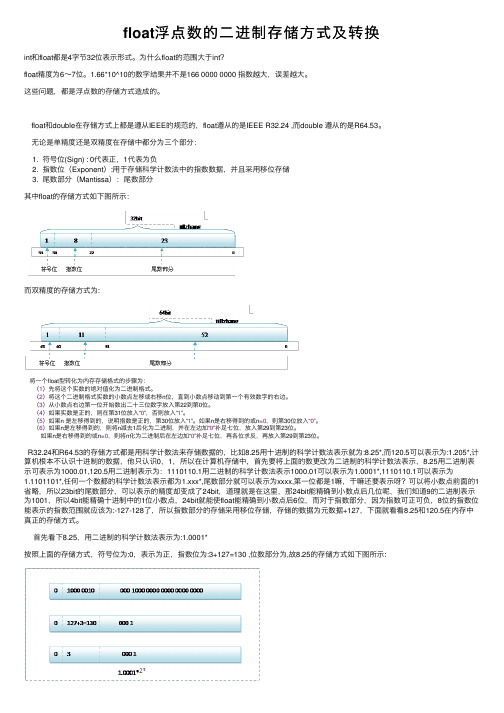
float浮点数的⼆进制存储⽅式及转换int和float都是4字节32位表⽰形式。

为什么float的范围⼤于int？float精度为6～7位。

1.66*10^10的数字结果并不是166 **** **** 指数越⼤，误差越⼤。

这些问题，都是浮点数的存储⽅式造成的。

float和double在存储⽅式上都是遵从IEEE的规范的，float遵从的是IEEE R32.24 ,⽽double 遵从的是R64.53。

⽆论是单精度还是双精度在存储中都分为三个部分：1. 符号位(Sign) : 0代表正，1代表为负2. 指数位（Exponent）:⽤于存储科学计数法中的指数数据，并且采⽤移位存储3. 尾数部分（Mantissa）：尾数部分其中float的存储⽅式如下图所⽰：⽽双精度的存储⽅式为:将⼀个float型转化为内存存储格式的步骤为：（1）先将这个实数的绝对值化为⼆进制格式。

（2）将这个⼆进制格式实数的⼩数点左移或右移n位，直到⼩数点移动到第⼀个有效数字的右边。

（3）从⼩数点右边第⼀位开始数出⼆⼗三位数字放⼊第22到第0位。

（4）如果实数是正的，则在第31位放⼊“0”，否则放⼊“1”。

（5）如果n 是左移得到的，说明指数是正的，第30位放⼊“1”。

如果n是右移得到的或n=0，则第30位放⼊“0”。

（6）如果n是左移得到的，则将n减去1后化为⼆进制，并在左边加“0”补⾜七位，放⼊第29到第23位。

如果n是右移得到的或n=0，则将n化为⼆进制后在左边加“0”补⾜七位，再各位求反，再放⼊第29到第23位。

R32.24和R64.53的存储⽅式都是⽤科学计数法来存储数据的，⽐如8.25⽤⼗进制的科学计数法表⽰就为:8.25*,⽽120.5可以表⽰为:1.205*,计算机根本不认识⼗进制的数据，他只认识0，1，所以在计算机存储中，⾸先要将上⾯的数更改为⼆进制的科学计数法表⽰，8.25⽤⼆进制表⽰可表⽰为1000.01,120.5⽤⼆进制表⽰为：1110110.1⽤⼆进制的科学计数法表⽰1000.01可以表⽰为1.0001*,1110110.1可以表⽰为1.1101101*,任何⼀个数都的科学计数法表⽰都为1.xxx*,尾数部分就可以表⽰为xxxx,第⼀位都是1嘛，⼲嘛还要表⽰呀？可以将⼩数点前⾯的1省略，所以23bit的尾数部分，可以表⽰的精度却变成了24bit，道理就是在这⾥，那24bit能精确到⼩数点后⼏位呢，我们知道9的⼆进制表⽰为1001，所以4bit能精确⼗进制中的1位⼩数点，24bit就能使float能精确到⼩数点后6位，⽽对于指数部分，因为指数可正可负，8位的指数位能表⽰的指数范围就应该为:-127-128了，所以指数部分的存储采⽤移位存储，存储的数据为元数据+127，下⾯就看看8.25和120.5在内存中真正的存储⽅式。

浮点数系列之：把float转成double

浮点数系列之：把float转成double⼤多数语⾔都提供从float到double的转换，⽐如C语⾔，你可以直接通过⼀个赋值语句来实现把⼀个float的数字转成 double。

⽽某些蛋疼的语⾔⾥⾯，对⼆进制的⽀持实在是少的可怜，我们还是不得不处理这样蛋疼的问题。

MQL4 这种语⾔⼤家可能没有这么听说过，是⼀种写⾦融交易策略的语⾔。

我的⼀个同事在⽤这种语⾔写策略的时候，遇到了⼀个问题，要从⽹络中接收float的⼆进制数据，然后进⾏计算，⽽这种语⾔只⽀持double，没有float的。

于是，我这个救⽕队员上马了。

说句实话，我⾮常喜欢这样蛋疼的问题。

当然，对⼆进制，底层⾮常熟悉的⼈，这基本上不是问题。

⽽我⼯作了这样多年，说句实话，我还真不知道 float 和 double的内部是什么样的⼀个结构。

于是我查找了很多资料，终于基本上搞懂了浮点数，于是我准备把我所学的写成博客，⽅便后⾯的⼈查看资料。

⾸先就从我解决的这个问题开始吧。

⾯对⼀个问题，⾸先就要从了解“敌⼈”开始。

我⾸先要知道 float 和 double 是怎么表⽰⼀个数字的。

有了这些知识，我想就能有办法把⼀个float转成 double。

幸好有google。

我找到了著名的阮⼀峰⽼师的⼀篇博客。

详细的可以看⽼师的博客：简单的说，⼀个浮点数，不管是 float 和 double 由三部分组成。

1. 符号2. ⼩数点的位置3. 有效数字这符合我们的常识认识，⼀个⼩数就是由这三部分组成的。

⼩数点的位置，有时候可以⽤“科学计数法”来表⽰，⽽有效数字可以简单的认为是⼀个整数，根据IEEE 754的标准，在⼀个 float 4个字节，32个位中，这是三个部分分配如下：（图⽚来⾃阮⼀峰的博客）符号位是1位，还有 8 位表⽰⼩数点的位置，后⾯的表⽰有效数字。

为了证明⼀下，上⾯结构的数字是 0.15625，我⽤PHP写可⼀段脚本来验证了⼀下：C:\Users\cykzl>php -aInteractive mode enabled<?php$bin = "00111110001000000000000000000000";$dec = bindec($bin);$float = unpack("f", pack("L", $dec));echo $float[1];>^Z0.15625C:\Users\cykzl>果然没有错。

浮点数与16进制的转换

浮点数与16进制的转换1 前⾔我们在学习 C 语⾔时，通常认为浮点数和⼩数是等价的，并没有严格区分它们的概念，这也并没有影响到我们的学习，原因就是浮点数和⼩数是绑定在⼀起的，只有⼩数才使⽤浮点格式来存储。

其实，整数和⼩数可以都使⽤定点格式来存储，也可以都使⽤浮点格式来存储，但实际情况却是，C 语⾔使⽤定点格式存储整数，使⽤浮点格式存储⼩数，这是在 “数值范围” 和 “数值精度” 两项重要指标之间追求平衡的结果。

2 什么是浮点数？浮点型简单讲就是实数的意思。

浮点数在计算机中⽤以近似表⽰任意某个实数。

具体的说，这个实数由⼀个整数或定点数(即尾数)乘以某个基数(计算机中通常是 2)的整数次幂得到，这种表⽰⽅法类似于基数为 10 的科学记数法。

3 浮点数在内存中的存储⾸先明确⼀点，⽆论是整型、浮点型还是字符等等数据类型在计算机底层都是以⼆进制的⽅式存储的。

浮点数在内存中的存储和整数不同，因为整数都可以转换为⼀⼀对应的⼆进制数据。

⽽浮点数的存储是由符号位 (sign) + 指数位 (exponent) + ⼩数位 (fraction) 组成。

类型符号位指数尾数Float1位(第31位)8位(第23~30位)23位(第0~22位)Double1位(第63位)11位(第52~62位)52位(第0~51位)int 和 float 同样占据四个字节的内存，但是 float 所能表⽰的最⼤值⽐ int ⼤得多，其根本原因是浮点数在内存中是以指数的⽅式存储。

浮点数转换到内存中存储的步骤分为如下三步：将浮点数转换成⼆进制⽤科学计数法表⽰⼆进制浮点数计算指数偏移后的值对于第3点：计算指数时需要加上偏移量(后⾯有介绍为什么使⽤偏移量)，⽽偏移量的值与浮点数的类型有关( float 偏移量值为 127，double 偏移量值为 1023)。

⽐⽅对于指数 6，float 与 double 类型偏移后的值分别为：float : 127 + 6 = 133double：1023 + 6 = 10294 实例浮点数19.625⽤float是如何存储的：将浮点数转换成⼆进制：10011.101(将 19.625 整数部分采⽤除 2 取余，⼩数部分采⽤乘 2 取整法)；⽤科学计数法表⽰⼆进制浮点数：1.0011101*2^4；计算指数偏移后的值：127 + 4 = 131 (10000011)；拼接综上所述，float 类型的 19.625 在内存中的值为：0 - 10000011 - 001 1101 0000 0000 0000 0000。

浮点数的二进制表示

浮点数的二进制表示基础知识：十进制转十六进制；十六进制转二进制；了解：目前C/C++编译器标准都遵照IEEE制定的浮点数表示法来进行float,double 运算。

这种结构是一种科学计数法，用符号、指数和尾数来表示，底数定为2——即把一个浮点数表示为尾数乘以2的指数次方再添上符号。

下面是具体的规格：符号位阶码尾数xxfloat182332double1115264以下通过几个例子讲解浮点数如何转换为二进制数例一：已知：double类型384144。

求：其对应的二进制表示。

分析：double类型共计64位，折合8字节。

由最高到最低位分别是63、2、1、……、0位：最高位63位是符号位，1表示该数为负，0表示该数为正；62-52位，一共11位是指数位；51-0位，一共52位是尾数位。

步骤：按照IEEE 浮点数表示法，下面先把38414.4转换为十六进制数。

把整数部和小数部分开处理:整数部直接化十六进制：960E。

小数的处理:0.4=0.5*0+0.25*1+0.125*1+0.0625*0+……实际上这永远算不完！这就是著名的浮点数精度问题。

所以直到加上前面的整数部分算够53位就行了。

隐藏位技术：最高位的1不写入内存（最终保留下来的还是52位）。

如果你够耐心，手工算到53位那xx因该是：38414.4(10)=1001011000001110.0110101010101010101010101010101010101(2)科学记数法为：1.0010110000011100110101010101010101010101010101010101，右移了15位，所以指数15。

或者可以如下理解：1.00101100000111001101010101010101010101010101010101012×215于是来看阶码，按IEEE标准一共11位，可以表示范围是-1024 ~1023。

因为指数可以为负，为了便于计算，规定都先加上1023(2^10-1)，在这里，阶码：15+10231038。

32位浮点数转二进制

32位浮点数转二进制
将32位浮点数转换为二进制可以分为以下几个步骤：
1. 取出符号位：首先需要确定浮点数的符号位，符号位位于32位中的第31位。

如果符号位为0，则浮点数为正数；如果符号位为1，则浮点数为负数。

2. 取出指数部分：接下来需要确定浮点数的指数部分。

在32位浮点数中，第23位到第30位表示指数部分。

3. 取出尾数部分：最后需要确定浮点数的尾数部分。

在32位浮点数中，第0位到第22位表示尾数部分。

4. 转换为二进制：根据符号位、指数部分和尾数部分，可以将32位浮点数转换为二进制数。

具体来说，32位浮点数的格式如下：
符号位(1位) + 指数部分(8位) + 尾数部分(23位)
转换为二进制时，首先将符号位转换为二进制数，然后将指数部分和尾数部分分别转换为二进制数。

最后将这三个部分拼接在一起，即可得到完整的32位浮点数。

例如，将32位浮点数 01000001 10010000 00001100 10000001 转换
为二进制数为：
符号位为 0，指数部分为 10010000，尾数部分为 0.11001001 11111111 11110111 11110001
因此，该32位浮点数转换为二进制数为：3.875。