2011走向高考,贾凤山,高中总复习,化学,1-2-2_57
2011走向高考,贾凤山,高中总复习,第6篇1-1

A
首页
上页
下页
末页
第六篇
第1章
③确定起始个体编号.在第1段用简单随机抽样确定 起始的个体编号S. ④按照事先确定的规则抽取样本.通常是将S加上间 隔k,得到第2个个体编号S+k,再将(S+k)加上k,得到第 3 3个个体编号S+2k,这样继续下去,获得容量为n的样 S 2k n 本.其样本编号依次是:S,S+k,S+2k,…,S+(n- 1)k.
末页
《走 向 高 考 》 高 考 总 复 习 A
分层 抽样
首页
上页
下页
第六篇
第1章
误区警示 1.抽样时不能抽取方便样本. 2.用随机数表抽样时,由于编号时位数不一致,导 致抽样的不均匀. 3 3.系统抽样时,当总体个数N不能被样本容量整除 N 时,剔除多余个体,必须随机抽样,剔除多余个体后要重 新编号.
[例4]
某初级中学有学生270人,其中一年级108人,
》 高 考 总 复 习
二、三年级各81人,现要利用抽样方法抽取10人参加某项 调查,考虑选用简单随机抽样、分层抽样和系统抽样三种 方案.使用简单随机抽样和分层抽样时,将学生按一、二、 三年级依次统一编号为1,2,…,270;使用系统抽样时, 将学生统一随机编号为1,2,…,270,并将整个编号依次 分为10段.如果抽得号码有下列四种情况:
》 高 考 总 复 习 A
首页
上页
下页
末页
第六篇
第1章
《走 向 高 考
[例2]
某商场通过检查发票及销售记录的2%来快
》 高 考 总 复 习
速估计每月的销售总额.采取如下方法:从某本发票的存 根中随机抽一张,如15号,然后按序往后将65号,115号, 15 65 115 165号,…,发票上的销售额组成一个调查样本.这种抽 取样本的方法是 A.抽签法 C.系统抽样法 ( ) B.随机数表法 D.其他方式的抽样
2011走向高考,贾凤山,高中总复习,英语,必修2-2

必修二Module 2Ⅰ.单词拼写1.The town has changed so much that you couldn't ________ (认出) it.2.I ________ (不同意) with Tom—he said the picture was good and I said it was bad.3.It is ________ (不合法) for a person under 17 to drive a car in Britain.4.Ten of the world's most ________ (强大的) states met to discuss trade barriers.5.Do you know there is ________ (联系) between taking drugs and being addicted?6.She felt a sharp p________ in her knee.7.Do you like Li Ning, a great g________ in China?8.Beating thieves is a kind of c________.9.She is now under medical t________,because she is seriously ill.10.The noise outside drove me d________ and I felt bored.答案:1.recognize 2.disagreed 3.illegal 4.powerful 5.connection 6.pain7.gymnast 8.crime9.treatment10.distractedⅡ.根据句意,用所给单词的适当形式填空1.Swimming is ________ in this river because there is a dangerous fish in it.2.He ________ his uncle at first sight though they last met ten years ago.3.The man who was ________ with the burglary was tried and sentenced ten years in prison.4.I was against the project; that is, I ________ to the project.5.Taking exercise has a positive ________ on our health.6.It is quite ________ to drive when you get drunk.7.Users will become ________ to crack cocaine if they smoke it.8.Y ou shouldn't take the drug because it can increase your heart rate and blood ________.9.Many people die from accidents ________ to careless driving.10.The government should make smoking ________ in order to save lives.答案:1.banned 2.recognised 3.connected 4.disagreed 5.effect 6.dangerous 7.addicted8.pressure9.related10.illegalⅢ.完成句子1.报告可以归纳为3个要点。
2011走向高考,贾凤山,高中总复习,英语,必修2-3

必修二Module 3Ⅰ.单词拼写1.We know the husband of actress Chen Hong is a famous ________ (导演).2.He likes to play different ________ (音乐的) instruments in his spare time.3.Joseph Haydn was an Austrian ________ (作曲家).4.His brother-in-law is a ________ (讲师) of history in a famous university.5.Einstein is a great scientific ________ (天才).6.This is a highly c________ matter.7.His t________ and experience qualified him to handle the company's foreign business very well.8.The a________ at a play, concert, film or public meeting is the group of people watching or listening to it.9.To r________,press both buttons.10.I prefer pop music to c________ music.答案:1.director 2.musical poser 4.lecturer 5.genius plex7.talent 8.audience9.record10.classicalⅡ.根据句意,用所给单词或短语的适当形式填空1.This is the most successful movie ________.2.The ship was ________ at sea.3.At last he became an orchestra ________ and served in a famous TV station.4.The play written by him was a________ of tragedy and comedy.5.The town survives mainly through ________.6.Human beings ________ other animals.7.Though the film was ________,he seemed to be absorbed in something else.8.You should do right things by yourself, and never be ______ by bad examples.9.Mozart was a great ________ remembered by the whole world.10.Everyone wants to be a noble ________.答案:1.of all time 2.lost 3.conductor 4.mixture 5.tourism 6.are different from 7.catchy8.influenced9.musician10.princeⅢ.翻译句子1.他们本来是要来帮忙的,但未能及时赶到。
2011走向高考,贾凤山,高中总复习,第1篇1-2ppt

《 走 向 高 考 》 高 考 总 复 习 人 教 A 版 数 学
形式上接近但采用的方法却不同
首页
上页
下页
末页
15
要 点 自 主 归 纳 思 想 方 法 点 拨 课 堂 典 例 讲 练 课 堂 巩 固 训 练 课 后 强 化 作 业
域的关系,通过求反函数的定义域,得到原函数的值 cx+d 域.形如y= (a≠0)的函数的值域,均可使用反函数 ax+b 法.此外,这种类型的函数值域也可使用“分离常数法”求解.
首页 上页 下页 末页
《 走 向 高 考 》 高 考 总 复 习 人 教 A 版 11 数 学
要 点 自 主 归 纳 思 想 方 法 点 拨 课 堂 典 例 讲 练 课 堂 巩 固 训 练 课 后 强 化 作 业
首页 上页 下页 末页
《 走 向 高 考 》 高 考 总 复 习 人 教 A 版 9 数 学
要 点 自 主 归 纳 思 想 方 法 点 拨 课 堂 典 例 讲 练 课 堂 巩 固 训 练 课 后 强 化 作 业
(3)基本初等函数的值域
①y=kx+b(k≠0)的值域为R. ②y=ax2+bx+c(a≠0)的值域是:当a>0时,值域为 4ac-b2 4ac-b2 . ,+∞ ;当a<0时,值域为 -∞, 4a 4a k (k≠0)的值域是{y|y∈R且y≠0}. ③y= x ④y=ax(a>0,且a≠1)的值域是(0,+∞).
知识归纳 1.映射 (1)映射的概念:设A、B是两个集合,如果按照某种对
应法则f,对于集合A中的 任何 一个元素,在集合B中都有 惟一确定 的元素与它对应,这样的对应关系叫做从集合A 到集合B的映射,记作f:A→B.
2011走向高考,贾凤山,高中总复习,阶段性测试题4-推荐下载
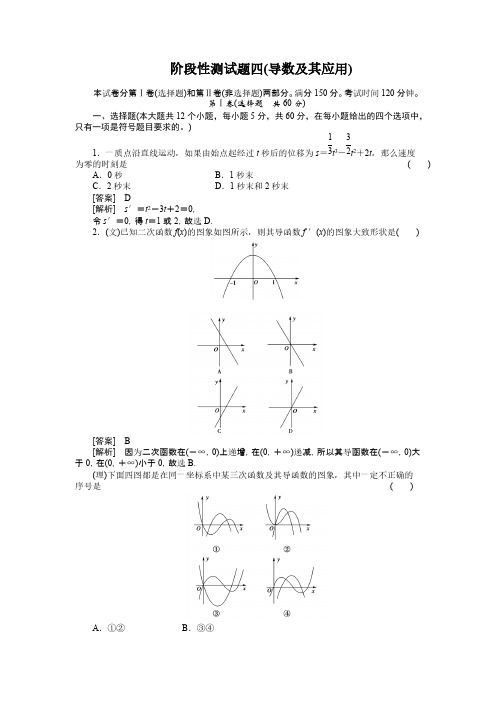
[答案] B [解析] 令 f(x)=x3-3x2-9x+2,则 f′(x)=3x2-6x-9,
令 f′(x)=0 得 x=-1 或 x=3(舍去).
∵f(-1)=7,f(-2)=0,f(2)=-20.
∴f(x)的最小值为 f(2)=-20, 故 m≤-20,综上可知应选 B. (理)已知实数 a,b,c,d 成等比数列,且曲线 y=3x-x3 的极大值点坐标为(b,c),则
3
27
27
分别将 t=0 和 t=2代入①式,得 k=-a 和 k= 4 -a,由它们互为相反数得,a= 8 . 4.(文)若关于 x 的不等式 x3-3x2-9x+2≥m 对任意 x∈[-2,2]恒成立,则 m 的取值
范围是
( )
A.(-∞,7]
B.(-∞,-20]
C.(-∞,0]
D.[-12,7]
( )
( )
C.①③
D.②④
[答案] B
[解析] 因为三次函数的导函数为二次函数,其图象为抛物线,观察四图,由导函数与
原函数的关系可知,当导函数大于 0 时,其函数为增函数,当导函数小于 0 时,其函数为减
函数,由此规律可判定③④不正确.
3.已知曲线 C:f(x)=x3-ax+a,若过曲线 C 外一点 A(1,0)引曲线 C 的两条切线,它
4
1
=3t3-t2+3, 1
令 S′=4t2-2t=0,∵0<t<1,∴t=2,
1
1
1
B.3
D.3
t
∫
1
2
易知当 t=2时,Smin=4. 8.已知函数 f(x)=x3+ax2+bx+c,x∈[-2,2]表示的曲线过原点,且在 x=±1 处的切
2011走向高考贾凤山高中总复习第1篇21ppt

要
(3)分数指数幂
点
自
主
归
纳
n>1)
思
想
方 法
(4)分数指数幂的运算性质
点
拨
ar·as=ar+s,(ar)s=ar·s,
《
走
.(a>0 , m , n∈N , 且
向 高 考
》
高
考
总
复
习
人 教
·A
课 堂
(a·b)r=ar·br.(a>0,b>0,r,s∈Q)
典
版
数 学
例
讲
练
课 堂 巩 固 训 练
首页
上页
(理)(09·山东文)函数y=
要 点 自 主 归 纳
思 想 方 法 点 拨
的图象大致为(
) 《 走 向 高 考 》
高 考 总 复 习
人 教
·A
课 堂 典
版
解析:函数有意义,需ex-e-x≠0,即x∈{x|x≠0},排
数 学
例
讲 练
除答案C、D;又y=
,当
课 x>0时为减函数,排除B,故选A.
堂
巩 固
课 堂 典
版
因此其最值在x∈[0,1]的两个端点得到,于是必有1+a=3,
数 学
例
讲 练
∴a=2.
课
点评:指数函数的最值问题一般都是用单调性解决.
堂
巩
固
训
练
首页
上页
下页
末页
第一篇 第2章 基本初等函数(Ⅰ)
三、解题技巧
要 点 自
《
1.比较一组幂式、对数式形式的数的大小时,一般
走 向
2011走向高考,贾凤山,高中总复习,第9篇1-2
《 走 向 高 考 》 高 考 总 复 习 · 人 教 版 数 学
∵∠BFC=∠BCA,∠CBD为公共角,
∴△BCF∽△BDC, 又∵AD=CD,
A
首页
上页
下页
末页
第九篇
要 点 自 主 归 纳 课 堂 典 例 讲 练 课 堂 巩 固 训 练 课 后 强 化 作 业
第1章
[例3]
如图,已知AP是⊙O的切线,P为切点,AC是
《 走 向 高 考 》 高 考 总 复 习 · A 人 教 版 数 学
证明:连结AD,则∠BPD=∠BAD+∠PDA= ( 的度数+ 的度数).
首页
上页
下页
末页
第九篇
要 点 自 主 归 纳 课 堂 典 例 讲 练 课 堂 巩 固 训 练 课 后 强 化 作 业
第1章
点评:特别地,①当弦AB与CD的交点为圆心时, ∠BPD的度数等于 的度数,即圆心角定理. ②当弦AB与CD的交点落在圆周上时,此时A、P、C
《 走 向 高 考 》 高 考 总 复 习 · 人 教 版 数 学
推论1 经过圆心且垂直于切线的直线必过切点.
推论2 经过切点垂直于切线的直线必经过圆心. (3)弦切角定理 弦切角等于它所夹弧对的圆周角.
A
首页
上页
下页
末页
第九篇
要 点 自 主 归 纳 课 堂 典 例 讲 练 课 堂 巩 固 训 练 课 后 强 化 作 业
从圆外一点引圆的两条切线,它们
A
线长是这点到割线与圆的交点的两条线段长的比例中项. 的切线长相等,圆心和这一点连线平分两切线夹角.
首页
上页
下页
末页
第九篇
要 点 自 主 归 纳 课 堂 典 例 讲 练 课 堂 巩 固 训 练 课 后 强 化 作 业
2011走向高考-贾凤山-高中总复习-第7篇1-2

2011走向高考-贾凤山-高中总复习-第7篇1-2第七篇 第1章 第二讲一、选择题1.如图所示的程序框图输出的结果是( )A.34B.45C.56D.67[答案] C[解析] i =1≤4满足,执行第一次循环后,A =23,i =2;i =2≤4满足,执行第二次循环后,[答案] C3.如图甲、乙,它们都表示的是输出所有立方不大于1000的正整数的程序框图,那么应分别补充的条件为()A.(1)n3≥1000,(2)n3<1000B.(1)n3≤1000,(2)n3≥1000C.(1)n3≤1000,(2)n3>1000D.(1)n3≤1000,(2)n3<1000[答案] C[解析]框图(1)中,条件满足时输出n,由题设n3≤1000时就应输出n,故条件为n3≤1000;框图(2)中,条件不满足则返回继续循环过程,条件满足则跳出循环,由题设只有当n3>1000时,才跳出循环结束程序.4.用秦九韶算法求多项式f(x)=12+35x-8x2+79x3+6x4+5x5+3x6在x=-4的值时,v4的值为()A.-57B.220C.-845D.3392[答案] B[解析]v0=3,v1=v0x+5=-7,v2=v1x +6=34,v3=v2x+79=-57,v4=v3x-8=220. 5.如果下边的程序执行后输出的结果是990,那么在程序UNTIL后面的“条件”应为()A.i>10 B.i>=10C.i<=9 D.i<9[答案] C[解析]∵输出结果为990,990=11×10×9,∴需执行3次,故条件应为i ≤9.6.(09·福建)阅读如图所示的程序框图,运行相应的程序,输出的结果是 ( )A .1B .2C .3D .4[答案] D[解析] 初值S =2,n =1执行第一次后S =-1,n =2执行第二次后S =12,n =3执行第三次后S =2,n =4此时符合条件,输出n =4.7.以下程序运行后的输出结果为( )i =1WHILE i <8i=i+2s=2]A.17B.19C.21D.23[答案] C[解析]这是一个循环语句程序,控制循环的条件i<8,当i≥8时,跳出循环,输出S的值.从程序可见只输出最后一次循环中S的值,到i=7时,i<8,则赋值后i=9,S=2×9+3=21,i重新赋值后i=8.再判断后跳出循环,输出S=21.8.(09·海南、宁夏)如果执行下边的程序框图,输入x=-2,h=0.5,那么输出的各个数的和等于()A.3B.3.5C.4D.4.5[答案] B[解析]当x<0时,输出y恒为0,当x=0时,输出y=0.当x=0.5时,输出y=x=0.5.当1≤x≤2时输出y恒为1,而h=0.5,故x 依次取值:-2,-1.5,-1,-0.5,0,0.5、1、1.5、2.故输出的各个数依次为:0,0,0,0,0,0.5,1,1,1.其和为3.5.故选B.9.下图是把二进制数11111(2)化成十进制数的一个程序框图,判断框内应填入的条件是() A.i>5 B.i≤4C.i>4 D.i≤5[答案] C[解析]s=1×24+1×23+1×22+1×21+1=(((2×1+1)×2+1)×2+1)×2+1(秦九韶算法).循环体需执行4次后跳出,故选C.10.以下程序运行后输出结果为()INPUT“输入正整数a,b=”;a,bt=a*bWHILE a< >bIF a>=b THEN a=a-bELSE b=b-aEND IFWENDm=t/aPRINT mEND程序运行时,从键盘输入a=18,b=30.A.6 B.90C.540 D.15[答案] B[解析]这是求从键盘输入的两个正整数a,b的最小公倍数的程序,程序先求a与b的积t 和用等值算法求a,b的最大公约数,最后用t与最大公约数的商即m表示两数的最小公倍数并输出,选B.二、填空题11.(08·广东)阅读下面程序框图,若输入m =4,n=3,则输出a=________,i=________.[答案]12 3[解析]要结束程序的运行,就必须通过“n 整除a”的条件,而同时m也整除a,那么a的最小值应为m和n的最小公倍数12,此时i=3.12.(09·山东)执行下边的程序框图,输出的T=______.[答案] 30[解析] 初值S =0,n =0,T =0, 执行第一次后:S =5,n =2,T =2, 执行第二次后:S =10,n =4,T =6, 执行第三次后:S =15,n =6,T =12, 执行第四次后:S =20,n =8,T =20, 执行第五次后:S =25,n =10,T =30, ∵T >S ,∴输出T =30.13.某算法的程序如右图所示,如果输出的y 值是4,那么输出的x 的所有可能的值是________.[答案] -12或4 [解析] ①若x <0,则有1x2=4, ∴x =-12. ②若x >0,则有x 2-3x =4,∴(x -4)(x +1)=0.∴x =4.综上,x =-12或4. 14.将六进制数113(6)化为二进制数为________.[答案] 101101(2)[解析]113(6)=1×62+1×6+3=45.∴45=101101(2),∴113(6)=101101(2).三、解答题15.某城市现有人口总数为100万人,如果年自然增长率为1.2%,试解答下列问题:(1)写出该城市人口数y(万人)与年份x(年)的函数关系式;(2)写出计算10年以后该城市人口总数的算法;(3)写出计算大约多少年以后该城市人口将达到120万人的算法.[解析](1)y=100(1+1.2%)x(x∈N)(2)y=100i=1WHILE i<=10y=y*1.012i=i+1WENDPRINT yEND(3)y=100i=0WHILE y<120y=y*1.012i=i+1 WEND PRINT i END16.已知数列{a n}满足a1=1,a n+1=2a na n+1,写出求a n的算法语句.[解析]INPUT“n=”;ni=2A=1B=(2]17.画出求S=1-323+533-743+953-1163+…+197 993-1991003的程序框图.[解析]。
2011走向高考,贾凤山,高中总复习,英语,必修1-1
《 走 向 高 考 》 高 考 总 复 习 外 研 版
考 点 详 解
考 点 自 查
考 点 详 解
注意: 注意:作“说明书”讲时,用instruction的复数形式instru ctions。 即学即用 Always read the ________ on the bottle carefully and take the right amount of medicine. A.explanations B.instructions C.descriptions D.introductions 答案:B
向 高 考 》 高 考 总 复 习 外 研 版
考 点 详 解
首页
上页
下页
末页
考 点 自 查
考 点 详 解
8.________ adj. 学术的________n. 学术 9.________ n. 记述,描述________ v. 记述,描述 10.________ n. 系统________ adj. 有系统的 11.________ n.指示,说明________ v. 指示,指导 12.______ adj. 吃惊的______adj. 令人吃惊的_______ _ v. 使惊奇 13.________ adj. 尴尬的,难堪的________ adj. 令人 尴尬的,令人难堪的 14.________ adj. 失望的______adj. 令人失望的 ________n.失望 15.________ v. 使印象深刻________ n. 印象
向 高 考 》 高 考 总 复 习 外 研 版
首页
上页
下页
末页
考 点 自 查
考 点 详 解
Ⅱ.短语 短语 1.nothing ________ 毫不相似,完全不像 2.be ________ to 与……相似 3.look forward ________期待;盼望 4.________ other words 换句话说 5.divide... ________... 把……分成…… 6.be ________ with 对……感到厌烦 7.make great ________ 取得很大进步 8.at the start ________ 在……开始的时候 9.one's attitude ________ ... 某人对……的看法 10.be ________ by 对……有印象 答案:1.like 2.similar 3.to 4.in 5.into 6.bored 7.progress 8.of 9.to/towards 10.impressed
2011走向高考,贾凤山,高中总复习,英语,必修1-2

英语必修1—2课后强化作业Ⅰ.单词拼写1.To our great joy, the poor girl was ________ (接收) into Peking University.2.She screamed as ________ (大声地) as she could.3.He remembered our names from ten years ago—isn't that just ________ (令人惊讶的)?4.I'm very ________ (严格的) about things like homework.5.He likes ________ (文学) so much that he wants to be a great writer in the future.6.He took a very s________ approach to management.7.We're busy doing some r________ for the coming exam.8.Can you say that dolphins are much more i________ than other animals?9.I'm n________ about talking of exam.10.We enjoy Mr. Wang's class for his teaching is well o________.答案:1.admitted 2.loudly 3.amazing 4.strict 5.literature6.anisedⅡ.句型转换1.I'd rather do translation than revision.I like doing translation ________ ________ revision.2.If you don't work harder from now on, you'll fail in the English exam.You ________ ________ the English exam ________ you ________ harder from now on.3.He couldn't take part in the school sports meeting because he has hurt in playing football.He was hurt in playing football, and ________ ________ ________,he couldn't take part in the school sports meeting.4.They prefer listening to pop music to watching TV.They ________ ________ listen to pop music ________ ________ TV.5.She was too excited about the good news to know what to say.She was ________ excited about the good news ________ she ________ know what to say.6.After she had bought all the things she needed, she went home happily.________ all the things she needed ________,she went home happily.答案:1.more than 2.won't pass; unless; work 3.as a result4.would rather; than watch 5.so; that; didn't 6.With; boughtⅢ.翻译句子1.你离开的时候要确定把灯关了。
2011走向高考,贾凤山,高中总复习,英语,必修1-1

英语必修1—1课后强化作业Ⅰ.单词拼写1.Their ________ (态度) towards me show that they don't like me.2.His lecture makes a strong ________ (印象) on all the students.3.After arriving in New York, he ________ (告诉) his mother of his safe arrival. 4.To our ________ (惊奇), he was still alive.5.I watched him until he ________ (消失) from sight in the distance.6.I want to c________ 100 miles by dark.7.Let's d________ the apple into two and share it.8.When I began to sing, he laughed and made me e______.9.We have just received i________ that we must hand in all our baggage in no time. 10.She was chosen as an a________ to help Mr. Brown finish his research.答案:1.attitudes 2.impression rmed 4.amazement5.disappeared 6.cover7.divide8.embarrassed9.instructions10.assistant Ⅱ.根据句意,用所给单词或短语的适当形式填空1.We were ________ to hear the news of Shen Dianxia's death.2.His latest book will ________ soon.3.She ________ me as a woman of great kindness.4.We all know that lies can not ________ facts.5.Ten ________ by five is two.6.There is ________ swimming for exercise.7.The girl dare not go out at night ________.8.The boss asked him to leave. ________,he was fired.9.We're really ________ seeing you again.10.Your hairstyle ________ mine.答案:1.amazed 2.appear 3.impressed 4.cover5.divided 6.nothing like7.by herself8.In other words9.looking forward to10.is similar toⅢ.完成句子1.我们相信她是不会来的。
2011走向高考,贾凤山,高中总复习,第1篇2-2doc

第一篇 第2章 第二讲一、选择题1.设f (x )=⎩⎪⎨⎪⎧2e x -1x <2log 3(x 2-1) x ≥2,则f (f (2))的值为 ( )A .0B .1C .2D .3[答案] C[解析] f (2)=log 3(22-1)=log 33=1,则f (f (2))=f (1)=2e 0=2.2.(文)已知函数y =f (x )的图象与函数y =2-x -1的图象关于直线y =x 对称,则f (3)的值为( )A .1B .-1C .2D .-2 [答案] D[解析] 由反函数对称性知,y =f (x )的反函数为y =2-x -1,则设f (3)=x , 则f -1(x )=3,即2-x -1=3,得x =-2.故选D.(理)在同一平面直角坐标系中,函数f (x )=2x +1与g (x )=21-x 的图象关于 ( )A .原点对称B .x 轴对称C .y 轴对称D .直线y =x 对称 [答案] C[解析] y =2x +1的图象关于y 轴对称的曲线对应函数为y =21-x ,故选C.3.已知函数f (x )=⎩⎪⎨⎪⎧log 2x (x >0)2x (x ≤0),若f (a )=12,则实数a =( )A .-1B. 2C .-1或 2D .1或- 2[答案] C[解析] 当a >0时,log 2a =12,∴a =2;当a <0时,2a =12,∴a =-1,选C.4.若关于x 的方程9x +(4+a )·3x +4=0有解,则实数a 的取值范围是 ( ) A .(-∞,-8)∪[0,+∞) B .(-∞,-4) C .[-8,4)D .(-∞,-8] [答案] D[解析] ∵-(4+a )=3x +43x ≥4,∴a ≤-8.5.(文)设a =log 0.70.8,b =log 1.10.9,c =1.10.9,则a 、b 、c 的大小顺序是 ( ) A .a <b <c B .b <c <a C .b <a <c D .c <b <a [答案] C[解析] 因为0<a =log 0.70.8<log 0.70.7=1,b =log 1.10.9<log 1.11=0,c =1.10.9>1.10=1,所以选C.(理)设a >1,且m =log a (a 2+1),n =log a (a -1),p =log a (2a ),则m ,n ,p 的大小关系为( )A .n >m >pB .m >p >nC .m >n >pD .p >m >n [答案] B[解析] 由a >1得a 2+1>2a >a -1>0,log a (a 2+1)>log a (2a )>log a (a -1). 6.(文)函数f (x )=ln|x -1|的图象大致是( )[答案] B[解析] f (x )=ln|x -1|=⎩⎪⎨⎪⎧ln(x -1) x >1ln(1-x ) x <1,∵x ≠1排除A ,又x >1时,f (x )为增函数,排除C 、D.(理)已知函数f (x )=log m (x +1),且m >1,a >b >c >0,则f (a )a ,f (b )b ,f (c )c的大小关系是( )A.f (a )a >f (b )b >f (c )cB.f (c )c >f (b )b >f (a )aC.f (b )b >f (c )c >f (a )aD.f (a )a >f (c )c >f (b )b [答案] B[解析] 本题考查数形结合思想,f (x )x可以转化成f (x )上的点与原点连线的斜率,据函数y =log 2(x +1)的图象,设A (a ,f (a )),B (b ,f (b )),C (c ,f (c )),显然k OA <k OB <k OC , ∴f (a )a <f (b )b <f (c )c,故选B 7.(文)已知函数f (x )是以2为周期的偶函数,且当x ∈(0,1)时,f (x )=2x -1,则f (log 210)的值为 ( )A.35B.85 C .-58 D .-53 [答案] A[解析] f (log 210)=====①f (log 210-4)=f (log 258)=====②f (log 285)=2log 285-1=85-1=35.注:①处用周期为2,②处用f (x )为偶函数.(理)已知函数f (x )=2x 的反函数f -1(x )满足f -1(a )+f -1(b )=4,则1a +1b的最小值为( )A .1 B.13 C.12 D.14[答案] C[解析] f (x )=2x 的反函数解析式为f -1(x )=log 2x , ∴f -1(a )+f -1(b )=log 2a +log 2b =log 2(ab )=4,∴ab =16,∴1a +1b =a +b ab ≥2ab =12,选C.8.设0<a <b <1,且a +b =1,给出下列结论: ①log 2(b -a )<0;②log 2a +log 2b >-2;③log 2a >1;④log 2⎝⎛⎭⎫b a +a b <1. 其中正确结论的个数是 ( )A .1B .2C .3D .4 [答案] A[解析] 由已知可得0<a <12<b <1,∴0<b -a <1,∴log 2(b -a )<0,①对;log 2a +log 2b =log 2(ab )=log 2[-(a -12)2+14],∵0<a <12,∴-⎝⎛⎭⎫a -122+14<14, ∴log 2⎣⎡⎤-⎝⎛⎭⎫a -122+14<-2,②错; log 2a <0,∴③错;因为b a +a b >2b a ·ab=2(a ,b 不相等取不到等号),故log 2⎝⎛⎭⎫a b +b a >log 22=1.∴④错. [点评] 可用特值法,取a =14,b =34,则log 234-14=-1,log 214+log 234=log 2316<log 2416=-2;log 214=-2;log 2⎝⎛⎭⎫3+13=log 2103>log 22=1,故②③④错,选A. 9.设a >1,函数f (x )=log a x 在区间[a,2a ]上的最大值与最小值之差为12,则a 等于( )A. 2 B .2 C .2 2 D .4 [答案] D[解析] ∵a >1,∴f (x )=log a x 在[a,2a ]上为增函数,∴log a 2a -log a a =12,解得a =4,故选D.10.(文)已知f (x )=log 3x +2(x ∈[1,9]),则函数y =[f (x )]2+f (x 2)的最大值是 ( )A .13B .16C .18D .22 [答案] A[解析] y =[f (x )]2+f (x 2)的定义域为⎩⎪⎨⎪⎧1≤x ≤91≤x 2≤9,即x ∈[1,3]. 若令t =log 3x ,则t ∈[0,1], ∴y =(t +2)2+2t +2=(t +3)2-3,∴当t =1时,y 取得最大值13,故选A.(理)已知函数y =f (x )(x ∈R )满足f (x +2)=f (x ),且当x ∈[-1,1]时,f (x )=x 2,则y =f (x )与y =log 7x 的图象的交点个数为 ( )A .3B .4C .5D .6 [答案] D[解析] ∵f (x +2)=f (x ), ∴f (x )是以2为周期的周期函数,又∵x ∈[-1,1]时,f (x )=x 2分别作出y =f (x )与y =log 7x 的图象可知有6个交点,故选D.二、填空题 11.若0<a <1,x >y >1,给出下列命题:①a x >a y ②x a >y a ③log a x >log a y ④log x a >log y a ,其中真命题的序号是________.[答案] ②④[解析] ∵0<a <1,x >y >1,∴y =a x 递减,故①不正确;y =x a 递增,故②正确.y =log a x 递减,故③不正确. ∵log x a <0,log y a <0,∴log x a >log y a ⇔log a x <log a y ,正确.综上知,②④正确.12.若正整数m 满足10m -1<2512<10m ,则m =________.(lg2=0.3010) [答案] 155[解析] 由10m -1<2512<10m ,两边取以10为底的对数,则有lg10m -1<lg2512<lg10m ,于是m -1<512lg2<m ,又因lg2=0.3010,所以m -1<154.112<m ,又m 为整数,故m =155.13.设函数f (x )=⎩⎪⎨⎪⎧log 2(x -1) x ≥2⎝⎛⎭⎫12x -1 x <2,若f (x 0)>1,则x 0的取值范围是________.[答案] (-∞,-1)∪(3,+∞)[解析] 若x 0≥2,则log 2(x 0-1)>1,∴x 0>3; 若x 0<2,则⎝⎛⎭⎫12x 0-1>1,∴x 0<-1. 因此x 0取值范围是(-∞,-1)∪(3,+∞).15.已知函数f (x )=log122-axx -1(a 是常数且a <2). (1)求f (x )的定义域;(2)若f (x )在区间(2,4)上是增函数,求a 的取值范围.[解析] (1)∵2-axx -1>0,∴(ax -2)(x -1)<0,①当a <0时,函数的定义域为 ⎝⎛⎭⎫-∞,2a ∪(1,+∞); ②当a =0时,函数的定义域为(1,+∞);③当0<a <2时,函数的定义域为⎝⎛⎭⎫1,2a . (2)∵f (x )在(2,4)上是增函数,∴只要使2-axx -1在(2,4)上是减函数且恒为正即可.令g (x )=2-axx -1,1°当a =0时,g (x )=2x -1在(2,4)递减,且g (4)>0满足题意;2°当a ≠0时,显然a ≠2,解法一:g ′(x )=-a (x -1)-(2-ax )(x -1)2=a -2(x -1)2, ∴当a -2<0,即a <2时,g ′(x )≤0. ①a <0时,g (4)>0满足题意;②0<a <2时,必有2a ≥4,∴0<a ≤12.综上所述,a ∈⎝⎛⎦⎤-∞,12. 解法二:∵g (x )=2-ax x -1=-a +2-ax -1,∴要使g (x )=-a +2-ax +1在(2,4)上是减函数,只需2-a >0,∴a <2,以下步骤同解法一.16.已知函数f (x )=⎝⎛⎭⎫13x ,x ∈[-1,1],函数g (x )=f 2(x )-2af (x )+3的最小值为h (a ). (1)求h (a );(2)是否存在实数m 、n ,同时满足以下条件: ①m >n >3;②当h (a )的定义域为[n ,m ]时,值域为[n 2,m 2].若存在,求出m ,n 的值;若不存在,说明理由.[分析] (1)由f (x )=⎝⎛⎭⎫13x的单调性可求出f (x )的值域,g (x )是以f (x )为变元的二次函数,令t =⎝⎛⎭⎫13x,可求关于t 的二次函数的最小值h (a ).(2)由(1)知当m >n >3时h (a )的表达式,考察h (a )在[n ,m ]上的单调性,结合其值域[n 2,m 2],可列出关于m ,n 的方程组求解m ,n ,如果有解则所求实数m ,n 存在,否则不存在.[解析] (1)因为x ∈[-1,1],所以⎝⎛⎭⎫13x ∈⎣⎡⎦⎤13,3. 设⎝⎛⎭⎫13x=t ,t ∈⎣⎡⎦⎤13,3,则g (x )=φ(t )=t 2-2at +3=(t -a )2+3-a 2. 当a <13时,h (a )=φ⎝⎛⎭⎫13=289-2a 3; 当13≤a ≤3时,h (a )=φ(a )=3-a 2; 当a >3时,h (a )=φ(3)=12-6a .所以h (a )=⎩⎪⎨⎪⎧289-2a 3⎝⎛⎭⎫a <133-a 2⎝⎛⎭⎫13≤a ≤312-6a (a >3).(2)因为m >n >3,a ∈[n ,m ],所以h (a )=12-6a .因为h (a )的定义域为[n ,m ],值域为[n 2,m 2],且h (a )为减函数,所以⎩⎪⎨⎪⎧12-6m =n 212-6n =m2,两式相减得6(m -n )=(m -n )(m +n ),因为m >n ,所以m -n ≠0,得m +n =6,但这与“m >n >3”矛盾,故满足条件的实数m ,n 不存在.[点评] 解题关键在于利用换元的思想方法,将问题转化为二次函数在闭区间上的最值问题,然后通过分类讨论求出函数的最值.对于存在性问题,往往是首先假设符合条件的参数存在,然后根据给出的条件进行推理求解,若不能推出矛盾,则说明符合要求的参数存在,否则说明符合要求的参数不存在.17.(文)已知函数f (x )=|log 2(x +1)|,实数m ,n 在其定义域内,并且m <n ,f (m )=f (n ). (1)求证:m +n >0;(2)试比较f ⎝ ⎛⎭⎪⎫m +n m -n 与f ⎝ ⎛⎭⎪⎫m +n n -m 的大小,并说明理由.[解析] (1)证明:法1:由f (m )=f (n )得 |log 2(m +1)|=|log 2(n +1)|, ∴[log 2(m +1)]2-[log 2(n +1)]2=0,∴[log 2(m +1)+log 2(n +1)]·[log 2(m +1)-log 2(n +1)]=0. ∵m <n ,∴m +1<n +1, ∴log 2(m +1)-log 2(n +1)≠0,∴必有log 2[(m +1)(n +1)]=0,∴(m +1)(n +1)=1,① 又0<m +1<n +1,∴0<m +1<1<n +1, ∴m <0<n ,∴mn <0.由①得mn +m +n =0,∴m +n =-mn >0. 法2:同法1得(m +1)(n +1)=1, 而0<m +1<n +1,∴(m +1)+(n +1)2>(m +1)·(n +1)=1,∴m +n +2>2,∴m +n >0.(2)解:法1:f ⎝ ⎛⎭⎪⎫m +n m -n =⎪⎪⎪⎪⎪⎪log 2⎝⎛⎭⎪⎫m +n m -n +1 =⎪⎪⎪⎪⎪⎪log 22m m -n =⎪⎪⎪⎪⎪⎪log 2-2m n -m . 由(1)知n >-m >0,∴2n >n -m >-2m >0, ∴0<-2m n -m <1且2n n -m>1,∴f ⎝ ⎛⎭⎪⎫m +n m -n =-log 2-2m n -m =log 2n -m -2m . f ⎝ ⎛⎭⎪⎫m +n n -m =⎪⎪⎪⎪⎪⎪log 2⎝⎛⎭⎪⎫m +n n -m +1 =⎪⎪⎪⎪⎪⎪log 22n n -m =log 22n n -m. ∵n -m -2m -2n n -m =(n -m )2+4mn -2m (n -m )=(n +m )2-2m (n -m )>0, ∴n -m -2m >2nn -m ,∴f ⎝ ⎛⎭⎪⎫m +n m -n >f ⎝ ⎛⎭⎪⎫m +n n -m .法2:由(1)知n >0,m <0, ∴n -m >n +m >0,0<m +nn -m<1,f ⎝ ⎛⎭⎪⎫m +n m -n =⎪⎪⎪⎪⎪⎪log 2⎝ ⎛⎭⎪⎫-m +n n -m +1 =-log 2⎝ ⎛⎭⎪⎫-m +n n -m +1=log 211-m +n n -m, 而f ⎝ ⎛⎭⎪⎫m +n n -m =⎪⎪⎪⎪⎪⎪log 2⎝ ⎛⎭⎪⎫m +n n -m +1=log 2⎝ ⎛⎭⎪⎫1+m +n n -m .∵1>1-⎝ ⎛⎭⎪⎫m +n n -m 2,两边同除以1-m +nn -m,得11-m +n n -m>1+m +n n -m ,∴log 211-m +n n -m>log 2⎝ ⎛⎭⎪⎫1+m +n n -m ,∴f ⎝ ⎛⎭⎪⎫m +n m -n >f ⎝ ⎛⎭⎪⎫m +n n -m .(理)函数f (x )对任意的a ,b ∈R ,都有f (a +b )=f (a )+f (b )-1,并且当x >0时,f (x )>1. (1)求证:f (x )是R 上的增函数;(2)若f (4)=5,解不等式f (3m 2-m -2)<3.[分析] 欲证f (x )为增函数,即证x 2>x 1时,f (x 2)>f (x 1).由已知x >0时,f (x )>1,∴x 2-x 1>0时,f (x 2-x 1)>1,再结合条件.f (a +b )=f (a )+f (b )-1,有f (x 2)-f (x 1)=f (x 2-x 1+x 1)-f (x 1)=f (x 2-x 1)+f (x 1)-1-f (x 1)=f (x 2-x 1)-1>0. [解析] (1)证明:设x 1、x 2∈R ,且x 1<x 2, 则x 2-x 1>0,∴f (x 2-x 1)>1. f (x 2)-f (x 1)=f [(x 2-x 1)+x 1]-f (x 1) =f (x 2-x 1)+f (x 1)-1-f (x 1) =f (x 2-x 1)-1>0,∴f (x 1)<f (x 2),即f (x )是R 上的增函数. (2)解:f (4)=f (2+2)=f (2)+f (2)-1=5, ∴f (2)=3.∴不等式即为f (3m 2-m -2)<f (2). ∵f (x )是增函数,于是有3m 2-m -2<2,解得-1<m <43.因此不等式的解集为⎝⎛⎭⎫-1,43. 18.已知函数f (x )=log 4(4x +1)+kx (k ∈R )是偶函数. (1)求k 的值;(2)设g (x )=log 4⎝⎛⎭⎫a ·2x -43a ,若函数f (x )与g (x )的图象有且只有一个公共点,求实数a 的取值范围.[解析] (1)由函数f (x )是偶函数可知:f (x )=f (-x ), ∴log 4(4x +1)+kx =log 4(4-x +1)-kx , ∴log 44x +14-x +1=-2kx ,即x =-2kx 对一切x ∈R 恒成立,∴k =-12.(2)函数f (x )与g (x )的图象有且只有一个公共点,即方程log 4(4x +1)-12x =log 4⎝⎛⎭⎫a ·2x -43a 有且只有一个实根, 即方程2x +12x =a ·2x -43a 有且只有一个实根,令t =2x >0,则方程(a -1)t 2-43at -1=0有且只有一个正根,①a =1时,t =-34,不合题意;②a ≠1时,由Δ=0得a =34或-3,若a =34,则t =-2不合题意;若a =-3,则t =12满足要求;若Δ>0,则此时方程应有一个正根与一个负根, ∴-1a -1<0,∴a >1,由Δ>0得,a <-3或a >34,∴a >1.综上,实数a 的取值范围是{-3}∪(1,+∞).[点评] 函数与方程思想是高中数学中一种重要的思想方法,也是高考考查的热点.利用这种思想可以将函数与方程的问题相互转化.本例中,将两个函数图象只有一个公共点转化为相应的方程只有一个实数根进行求解,使问题的解决变得简单易行.。
2011走向高考,贾凤山,高中总复习,第3篇2-3

第三篇 第2章 第三讲一、选择题1.(文)抛物线y =x 2的准线方程是 ( ) A .4y +1=0 B .4x +1=0 C .2y +1=0 D .2x +1=0 [答案] A[解析] x 2=y 中2p =1,∴p 2=14,∴准线y =-14,即4y +1=0.(理)抛物线y =ax 2的准线方程为y +1=0,则a = ( ) A.14 B.12C .-14D .-12[答案] A[解析] ∵y =ax 2 ∴x 2=1a y ,∴准线方程为y =-14a ∴-14a =-1,∴a =14,故选A.2.已知抛物线C 1:y =2x 2与抛物线C 2关于直线y =-x 对称,则C 2的准线方程是( )A .x =-18B .x =12C .x =18D .x =-12[答案] C[解析] 抛物线C 1:y =2x 2的准线方程为y =-18,其关于直线y =-x 对称的抛物线C 2:y 2=-12x 的准线方程为x =18.故应选C.3.(文)抛物线x 2=4y 上一点A 的纵坐标为4,则点A 与抛物线焦点的距离为 ( ) A .2 B .3 C .4 D .5 [答案] D[解析] 由x 2=4y 知其准线方程为y =-1,据抛物线的定义,点A 与焦点的距离等于点A 与准线的距离,显然A 的纵坐标为4.其距离为5.(理)抛物线y 2=8x 上的点(x 0,y 0)到抛物线焦点的距离为3,则|y 0|=( )A. 2 B .2 2 C .2 D .4 [答案] B[解析] 设点A (x 0,y 0),过点A 作AA 1⊥l (l 为准线),则|AF |=|AA 1|=x 0+2=3即x 0=1,代入抛物线方程得|y 0|=8x 0=22,故选B.4.(09·山东)设斜率为2的直线l 过抛物线y 2=ax (a ≠0)的焦点F ,且和y 轴交于点A .若△OAF (O 为坐标原点)的面积为4,则抛物线方程为 ( )A .y 2=±4xB .y 2=±8xC .y 2=4xD .y 2=8x[答案] B[解析] 由抛物线方程知焦点F ⎝⎛⎭⎫a 4,0,∴直线l 方程为y =2⎝⎛⎭⎫x -a 4, 与y 轴交点A ⎝⎛⎭⎫0,-a 2.∴S △OAF =12·|OA |·|OF |=12·⎪⎪⎪⎪-a 2·⎪⎪⎪⎪a 4=a 216=4. ∴a 2=64,a =±8.故y 2=±8x .故选B.5.(文)已知点P 为抛物线y 2=2x 上的动点,点P 在y 轴上的射影是M ,点A 的坐标是A (72,4),则|P A |+|PM |的最小值是 ( ) A.112 B .4 C.92 D .5 [答案] C[解析] 如图,焦点F (12,0),当P 、A 、F 三点共线时|P A |+|PM |才有最小值,此时|P A |+|PM |=|P A |+|PF |-12,即|P A |+|PM |的最小值为|F A |-12=(72-12)2+42-12=5-12=92,故选C.(理)(08·辽宁)已知点P 是抛物线y 2=2x 上的一个动点,则点P 到点(0,2)的距离与点P 到该抛物线准线的距离之和的最小值为 ( )A.172B .3C. 5D.92[答案] A[解析] 记抛物线y 2=2x 的焦点为F ⎝⎛⎭⎫12,0,准线是l ,由抛物线的定义知点P 到焦点F 的距离等于它到准线l 的距离,因此要求点P 到点(0,2)的距离与点P 到抛物线的准线的距离之和的最小值,可以转化为求点P 到点(0,2)的距离与点P 到焦点F 的距离之和的最小值,结合图形不难得知相应的最小值就等于焦点F 与点(0,2)的距离,因此所求的最小值等于⎝⎛⎭⎫122+22=172,选A. 6.(文)对于任意n ∈N *,抛物线y =(n 2+n )x 2-(2n +1)x +1与x 轴交于A n 、B n 两点,以|A n B n |表示该两点的距离,则|A 1B 1|+|A 2B 2|+…+|A 2011B 2011|的值是 ( )A.20102011B.20112012C.20092010D.20092008 [答案] B[解析] 设A n (x n,0),B n (x ′n,0), 则x n +x ′n =2n +1n 2+n ,x n x ′n =1n 2+n ,|A n B n |=|x n -x ′n |=(x n +x ′n )2-4x n x ′n=⎝ ⎛⎭⎪⎫2n +1n 2+n 2-4n 2+n =1n 2+n=1n (n +1)=1n -1n +1,∴|A 1B 1|+|A 2B 2|+…+|A n B n |=⎝⎛⎭⎫1-12+⎝⎛⎭⎫12-13+…+⎝ ⎛⎭⎪⎫1n -1n +1=1-1n +1=nn +1,∴当n =2011时,结果为20112012.[点评] 由条件知A n 、B n 的横坐标x 1、x 2是方程(n 2+n )x 2-(2n +1)x +1=0的两根,∴x 1=1n +1,x 2=1n ,∴|x 1-x 2|=1n -1n +1.(理)已知点M 是抛物线y 2=2px (p >0)上的一点,F 为抛物线的焦点,若以|MF |为直径作圆,则这个圆与y 轴的关系是 ( )A .相交B .相切C .相离D .以上三种情形都有可能 [答案] B[解析] 如图,由MF 的中点A 作准线l 的垂线AE ,交直线l 于点E ,交y 轴于点B ;由点M 作准线l 的垂线MD ,垂足为D ,交y 轴于点C ,则MD =MF ,ON =OF , ∴AB =OF +CM 2=ON +CM2=DM 2=MF 2,∴此圆与y 轴相切. 7.(文)设抛物线y 2=8x 的准线与x 轴交于点Q ,若过点Q 的直线L 与抛物线有公共点,则直线L 的斜率的取值范围是 ( )A.⎣⎡⎦⎤-12,12 B .[-2,2] C .[-1,1]D .[-4,4][答案] C[解析] 由⎩⎪⎨⎪⎧y =k (x +2)y 2=8x,得k 2x 2+(4k 2-8)x +4k 2=4,由Δ=0得,k =±1,结合图形知选C.(理)定点N (1,0),动点A 、B 分别在图中抛物线y 2=4x 及椭圆x 24+y 23=1的实线部分上运动,且AB ∥x 轴,则△NAB 的周长l 的取值范围是 ( )A.⎝⎛⎭⎫23,2B.⎝⎛⎭⎫103,4C.⎝⎛⎭⎫5116,4 D .(2,4)[答案] B[解析] 易知N 为抛物线和椭圆的焦点,设A (x 1,y 1 ),B (x 2,y 2),由抛物线及椭圆的定义知,焦半径|AN |=x 1+1,|BN |=12(4-x 2),又|AB |=x 2-x 1,∴周长l =|AB |+|AN |+|BN |=3+12x 2,由⎩⎪⎨⎪⎧y 2=4x x 24+y 23=1得交点的横坐标为23,∴23<x 2<2.∴103<l <4. 8.(09·全国Ⅰ)设双曲线x 2a 2-y 2b2=1(a >0,b >0)的渐近线与抛物线y =x 2+1相切,则该双曲线的离心率等于 ( )A. 3 B .2 C. 5 D. 6 [答案] C[解析] 双曲线的渐近线方程为y =±b a x ,与抛物线方程联立得x 2±ba x +1=0,Δ=⎝⎛⎭⎫±b a 2-4=0⇒b 2=4a 2,∴c 2-a 2=4a 2,∴c 2=5a 2,e =5,故选C.9.(福建厦门)已知抛物线y 2=4x 的焦点为F ,准线与x 轴的交点为M ,N 为抛物线上的一点,且|NF |=32|MN |,则∠NMF = ( )A.π6B.π4C.π3D.5π12 [答案] A[解析] 如图,过点N 向准线引垂线,垂足为P ,由抛物线的定义知|NP |=|NF |=32·|MN |.在Rt △NMP 中,sin ∠NMP =|NP ||NM |=32⇒∠NMP =π3⇒∠NMF =π6,故选A.10.(北京崇文)已知点M (1,0),直线l :x =-1,点B 是l 上的动点,过点B 垂直于y 轴的直线与线段BM 的垂直平分线交于点P ,则点P 的轨迹是 ( )A .抛物线B .椭圆C .双曲线的一支D .直线 [答案] A[解析] P 在BM 的垂直平分线上,故|PB |=|PM |.又PB ⊥l ,因而点P 到直线l 的距离等于P 到M 的距离,所以点P 的轨迹是抛物线. 二、填空题11.(文)设坐标原点为O ,抛物线y 2=2x 与过焦点的直线交于A ,B 两点,则OA →·OB →=________.[答案] -34[解析] 设直线AB :x =my +12,代入y 2=2x 中,设A (x 1,y 1),B (x 2,y 2),则OA →·OB →=x 1x 2+y 1y 2=-34.(理)已知点A (2,0)、B (4,0),动点P 在抛物线y 2=-4x 上运动,则AP →·BP →取得最小值时的点P 的坐标是______.[答案] (0,0)[解析] 设P ⎝ ⎛⎭⎪⎫-y 24,y ,则AP →=⎝⎛⎭⎫-y 24-2,y ,BP →=⎝⎛⎭⎫-y 24-4,y ,AP →·BP →=⎝⎛⎭⎫-y 24-2⎝⎛⎭⎫-y 24-4+y 2=y 416+52y 2+8≥8,当且仅当y =0时取等号,此时点P 的坐标为(0,0). 12.圆心在第一象限,且半径为1的圆与抛物线y 2=2x 的准线和双曲线x 216-y 29=1的渐近线都相切,则圆心的坐标是________.[答案] ⎝⎛⎭⎫12,138或⎝⎛⎭⎫12,78 [解析] 设圆心为(a ,b ),则a >0,b >0.∵y 2=2x 的准线方程为x =-12,x 216-y29=1的渐近线方程为3x ±4y =0. 由题意知a +12=1,则a =12,|3a ±4b |5=1,解得b =138或b =78, ∴圆心坐标为⎝⎛⎭⎫12,138或⎝⎛⎫12,78.13.已知抛物线y 2=2px (p >0),过(2p,0)作直线交抛物线于A 、B 两点,给出下列结论:①OA ⊥OB ;②△ABO 重心必是抛物线焦点;③△ABO 面积最小值为4p 2.其中正确的结论是________. [答案] ①③[解析] 由⎩⎪⎨⎪⎧x =my +2py 2=2px得:y 2-2pmy -4p 2=0,∴y 1y 2=-4p 2,y 1+y 2=2pm ,x 1x 2=4p 2, k OA ·k OB =-1,S =p |y 1-y 2|=p ·(2pm )2-16p 2≥4p 2.14.已知当抛物线型拱桥的顶点距水面2米时,量得水面宽8米,当水面升高1米后,水面宽度是________米.[答案] 4 2[解析] 设抛物线拱桥的方程为x 2=-2py ,当顶点距水面2米时,量得水面宽8米, 即抛物线过点(4,-2)代入方程得16=4p ∴p =4,则抛物线方程是x 2=-8y , 水面升高1米时,即y =-1时,x =±2 2. 则水面宽为42米.三、解答题15.(文)已知P (x ,y )为平面上的动点且x ≥0,若P 到y 轴的距离比到点(1,0)的距离小1.(1)求点P 的轨迹C 的方程;(2)设过点M (m,0)的直线交曲线C 于A 、B 两点,问是否存在这样的实数m ,使得以线段AB 为直径的圆恒过原点.[解析] (1)由题意得:(x -1)2+y 2-x =1,化简得:y 2=4x (x ≥0).∴点P 的轨迹方程为y 2=4x (x ≥0).(2)设直线AB 为y =k (x -m ),A (x 1,y 1),B (x 2,y 2),由⎩⎪⎨⎪⎧y =k (x -m )y 2=4x,得ky 2-4y -4km =0,∴y 1+y 2=4k ,y 1·y 2=-4m .∴x 1·x 2=m 2,∵以线段AB 为直径的圆恒过原点, ∴OA ⊥OB ,∴x 1·x 2+y 1·y 2=0.即m 2-4m =0⇒m =0或4.当k 不存在时,m =0或4. ∴存在m =0或4,使得以线段AB 为直径的圆恒过原点. [点评] (1)点P 到定点F (1,0)的距离比到y 轴的距离大1,即点P 到定点F (1,0)的距离与到定直线l :x =-1的距离相等.∴P 点轨迹是以F 为焦点,l 为准线的抛物线,∴p =2,∴方程为y 2=4x .(理)如图,O 为坐标原点,直线l 在x 轴和y 轴上的截距分别是a 和b (a >0,b ≠0),且交抛物线y 2=2px (p >0)于M (x 1,y 1),N (x 2,y 2)两点.(1)写出直线l 的方程;(2)证明:1y 1+1y 2=1b;(3)当a =2p 时,求∠MON 的大小.[解析] (1)直线l 的截距式方程为x a +yb=1.①(2)证明:由①及y 2=2px 消去x 可得 by 2+2pay -2pab =0②点M 、N 的纵坐标y 1、y 2为②的两个根,故 y 1+y 2=-2pab ,y 1y 2=-2pa .所以1y 1+1y 2=y 1+y 2y 1y 2=-2pa b -2pa =1b.(3)设直线OM 、ON 的斜率分别为k 1、k 2,则k 1=y 1x 1,k 2=y 2x 2.当a =2p 时,由(2)知,y 1y 2=-2pa =-4p 2,由y 21=2px 1,y 22=2px 2相乘得(y 1y 2)2=4p 2x 1x 2,x 1x 2=(y 1y 2)24p 2=4p 2,因此k 1k 2=y 1y 2x 1x 2=-4p 24p 2=-1, 所以OM ⊥ON ,即∠MON =90°.16.已知抛物线y 2=4x ,过点(0,-2)的直线交抛物线于A 、B 两点,O 为坐标原点.(1)若OA →·OB →=4,求直线AB 的方程.(2)若线段AB 的垂直平分线交x 轴于点(n,0),求n 的取值范围.[解析] (1)设直线AB 的方程为y =kx -2 (k ≠0),代入y 2=4x 中得,k 2x 2-(4k +4)x +4=0①设A (x 1,y 1),B (x 2,y 2),则x 1+x 2=4k +4k 2,x 1x 2=4k2.y 1y 2=(kx 1-2)·(kx 2-2)=k 2x 1x 2-2k (x 1+x 2)+4=-8k.∵OA →·OB →=(x 1,y 1)·(x 2,y 2)=x 1x 2+y 1y 2=4k 2-8k=4,∴k 2+2k -1=0,解得k =-1±2.又由方程①的判别式Δ=(4k +4)2-16k 2=32k +16>0得k >-12,∴k =-1+2,∴直线AB 的方程为y =(2-1)x -2.(2)设线段AB 的中点的坐标为(x 0,y 0),则由(1)知x 0=x 1+x 22=2k +2k 2,y 0=kx 0-2=2k ,∴线段AB 的垂直平分线的方程是 y -2k =-1k ⎝ ⎛⎭⎪⎫x -2k +2k 2. 令y =0,得n =2+2k +2k 2=2k 2+2k+2=2⎝⎛⎭⎫1k +122+32.又由k >-12且k ≠0得1k <-2,或1k >0,∴n >2⎝⎛⎭⎫0+122+32=2.∴n 的取值范围为(2,+∞). 17.(文)设A (x 1,y 1)、B (x 2,y 2)两点在抛物线y =2x 2上,l 是AB 的垂直平分线. (1)当且仅当x 1+x 2取何值时,直线l 经过抛物线的焦点F? (2)当直线l 的斜率为2时,求l 在y 轴上的截距的取值范围.[解析] (1)∵抛物线的准线是x 轴的平行线,y 1≥0,y 2≥0,依题意y 1、y 2不同时为0,x 1≠x 2,∴F ∈l ⇔|F A |=|FB |⇔A 、B 两点到抛物线的准线的距离相等.⇔y 1=y 2⇔x 21=x 22⇔x 1+x 2=0.即当且仅当x 1+x 2=0时,l 经过抛物线的焦点F . (2)设l 在y 轴上的截距为b ,∴l 的方程为y =2x +b ;过点A 、B 的直线方程可设为y =-12x +m ,所以x 1、x 2满足方程2x 2+12x -m =0,∴x 1+x 2=-14;A 、B 为抛物线上不同的两点等价于上述方程的判别式Δ=14+8m >0,即m >-132.设AB 的中点N 的坐标为(x 0,y 0),则 x 0=12(x 1+x 2)=-18,y 0=-12x 0+m =116+m .由N ∈l ,得116+m =-14+b ,于是b =516+m >516-132=932,即得l 在y 轴上截距的取值范围为⎝⎛⎭⎫932,+∞.(理)如图,过点F (1,0)的直线l 与抛物线C :y 2=4x 交于A 、B 两点.(1)若|AB |=8,求直线AB 的方程;(2)记抛物线C 的准线为l ′,设直线OA 、OB 分别交l ′于点M 、N ,求OM →·ON →的值. [解析] (1)设A (x 1,y 1),B (x 2,y 2),|AB |=8,即x 1+x 2+p =8, ∴x 1+x 2=6.∵|AB |>2p ,∴直线l 的斜率存在, 设其方程为y =k (x -1).由方程组⎩⎪⎨⎪⎧y 2=4xy =k (x -1)消去y 得,k 2x 2-(2k 2+4)x +k 2=0,∴x 1+x 2=2k 2+4k 2,即2k 2+4k 2=6,得k =±1.∴直线AB 的方程是x -y -1=0或x +y -1=0. (2)①当直线l 的斜率不存在时,OM →·ON →=OA →·OB →=x 1x 2+y 1y 2=1-4=-3. 当直线l 的斜率存在时,由(1)知, x 1x 2=1,y 1y 2=-16x 1x 2=-4, 设M (-1,y 3),N (-1,y 4), B ,O ,M 三点共线, ∴y 3-1=y 2x 2⇒y 3=-y 2x 2,同理可得y 4=-y 1x 1. ∴OM →·ON →=(-1,y 3)·(-1,y 4)=1+y 3y 4=1+y 1y 2x 1x 2=-3.。
