2.5平行四边形的面积(2)练习题及答案
(完整版)平行四边形练习题及答案(DOC)

20.1平行四边形的判断一、选择题1 .四边形A BCD,从( 1)AB∥CD;( 2)AB=CD;( 3)BC∥AD;( 4) BC=AD这四个条件中任选两个,此中能使四边形ABCD是平行四边形的选法有()A .3种B.4种C.5种D.6种2.四边形的四条边长分别是a, b, c,d,此中 a,b 为一组对边边长, c,d?为另一组对边边长且知足a2+b2+c2+d2=2ab+2cd,则这个四边形是()A .随意四边形B.平行四边形C.对角线相等的四边形 D .对角线垂直的四边形3.以下说法正确的选项是()A.若一个四边形的一条对角线均分另一条对角线,则这个四边形是平行四边形B.对角线相互均分的四边形必定是平行四边形C.一组对边相等的四边形是平行四边形D.有两个角相等的四边形是平行四边形二、填空题4 .在□ ABCD中,点 E, F 分别是线段A D, BC上的两动点,点 E 从点 A 向 D 运动,点F从 C?向 B 运动,点 E 的速度边形.m与点F 的速度n 知足 _______关系时,四边形BFDE为平行四5.如图 1 所示,平行四边形ABCD中, E, F 分别为AD,BC边上的一点,连结EF,若再增添一个条件_______,就能够推出BE=DF.图1图26 .如图 2 所示, AO=OC,BD=16cm,则当 OB=_____cm时,四边形ABCD是平行四边形.三、解答题7.以下图,四边形 ABCD中,对角线 BD=4,一边长 AB=5,其他各边长用含有未知数 x 的代数式表示,且 AD⊥BD于点 D,BD⊥BC 于点 B.问:四边形 ABCD?是平行四边形吗?为什么?四、思虑题8.以下图,在□ABCD中, E,F 是对角线 AC上的两点,且 AF=CE,?则线段 DE?与 BF的长度相等吗?参照答案一、 1. B 点拨:可选择条件(1)(3)或(2)( 4)或( 1)( 2)或( 3)(4).故有 4 种选法.2. B 点拨: a2+b 2+c2+d2=2ab+2cd 即( a-b)2+( c-d )2=0,即( a-b )2=0 且( c-d )2=0.所以 a=b, c=d,即两组对边分别相等,所以四边形为平行四边形.3. B 点拨:娴熟掌握平行四边形的判断定理是解答这种题目的重点.二、 4.相等点拨:利用“一组对边平行且相等的四边形是平行四边形”来确立.5 .AE=CF 点拨:此题答案不唯一,只需增添的条件能使四边形EBFD?是平行四边形即可.6. 8 点拨:依据对角线相互均分的四边形为平行四边形来进行鉴别.三、 7.解:以下图,四边形ABCD是平行四边形.原因以下:在 Rt△BCD中,依据勾股定理,得BC2+BD 2=DC 2,即( x-5 )2+42=( x-3 )2,解得 x=8.所以 AD=11-8=3, BC=x-5=3, DC=x-3=8-3=5 ,所以 AD=BC, AB=DC.所以四边形ABCD是平行四边形.点拨:此题主要告诉的是线段的长度,故只需说明AD=BC, AB=DC即可,此题也可在Rt△ABD中求 x 的值.四、 8.解:线段DE与BF 的长度相等;连结BD交AC于O点,连结DF, BE,以下图.在ABCD中, DO=OB, AO=OC,又因为 AF=EC,所以 AF-AO=CE-OC,即 OF=OE,所以四边形 DEBF是平行四边形,所以DE=BF.点拨:此题若用三角形全等,也能够解答,但过程复杂,学了平行四边形性质后,要学会应用.20.2矩形的判断一、选择题1.矩形拥有而一般平行四边形不拥有的性质是()A.对角相等 B .对边相等 C .对角线相等 D .对角线相互垂直2.以下表达中能判断四边形是矩形的个数是()①对角线相互均分的四边形;②对角线相等的四边形;③对角线相等的平行四边形;④对角线相互均分且相等的四边形.A . 1B. 2C. 3D. 43.以下命题中,正确的选项是()A.有一个角是直角的四边形是矩形B.三个角是直角的多边形是矩形C.两条对角线相互垂直且相等的四边形是矩形 D .有三个角是直角的四边形是矩形二、填空题4.如图 1 所示,矩形 ABCD中的两条对角线订交于点O,∠ AOD=120°, AB=4cm,则矩形的对角线的长为 _____.D E CF OA B图 1图 25.若四边形 ABCD的对角线 AC, BD相等,且相互均分于点 O,则四边形 ABCD?是_____ 形,若∠ AOB=60°,那么AB:AC=______.6.如图 2 所示,已知矩形ABCD周长为 24cm,对角线交于点O,OE⊥DC 于点 E,于点 F, OF-OE=2cm,则 AB=______, BC=______.三、解答题7.以下图,□ABCD的四个内角的均分线分别订交于E, F, G,H 两点,试说明四边形 EFGH是矩形.四、思虑题8.以下图,△ABC中, CE, CF分别均分∠ACB和它的邻补角∠ACD.AE⊥CE于 E,AF⊥CF 于F,直线EF分别交AB, AC于 M, N 两点,则四边形AECF是矩形吗?为何?参照答案一、 1. C点拨:A与B都是平行四边形的性质,而D是一般矩形与平行四边形都不具有的性质.2 .B点拨:③是矩形的判断定理;④中对角线相互均分的四边形是平行四边形,对角线相等的平行四边形是矩形,故④能判断矩形,应选B.3. D 点拨:选项 D 是矩形的判断定理.二、 4. 8cm5.矩; 1: 2 点拨:利用对角线相互均分来判断此四边形是平行四边形,再依据对角线相等来判断此平行四边形是矩形.由矩形的对角线相等且相互均分,?可知△ AOB 是等腰三角形,又因为∠ AOB=60°,所以AB=AO=1AC.26 . 8cm; 4cm三、 7.解:在□ABCD中,因为AD∥BC,所以∠ DAB+∠CBA=180°,又因为∠ HAB= 1∠DAB,∠ HBA=1∠CBA.22所以∠ HAB+∠HBA=90°,所以∠ H=90°.所以四边形EFGH是矩形.点拨:因为“两直线平行,同旁内角的均分线相互垂直”,所以很简单求出四边形EFGH 的四个角都是直角,从而求得四边形EFGH是矩形.四、 8.解:四边形AECF是矩形.原因:因为CE均分∠ ACB, ?CF?均分∠ ACD, ?所以∠ ACE=1∠ACB,∠ ACF=1∠ACD.所以∠ ECF=1(∠ ACB+∠ACD)=90°.222又因为 AE⊥CE,AF⊥CF, ?所以∠ AEC=∠AFC=90°,所以四边形AECF是矩形.点拨: ?此题是经过证四边形中三个角为直角得出结论.还能够经过证其为平行四边形,再证有一个角为直角得出结论.20.3菱形的判断一、选择题1.以下四边形中不必定为菱形的是()A .对角线相等的平行四边形B.每条对角线均分一组对角的四边形C.对角线相互垂直的平行四边形D.用两个全等的等边三角形拼成的四边形2.四个点 A, B, C,D 在同一平面内,从① AB∥CD;② AB=CD;③ AC⊥BD;④ AD=BC;5 个条件中任选三个,能使四边形ABCD是菱形的选法有().A .1种B.2种C.3种D.4种3 .菱形的周长为32cm,一个内角的度数是60°,则两条对角线的长分别是()A.8cm和 4 3 cm B.4cm和83 cm C.8cm和83 cm D.4cm和43 cm二、填空题4.如图 1 所示,已知□ABCD,AC,BD订交于点O,?增添一个条件使平行四边形为菱形,增添的条件为 ________.(只写出切合要求的一个即可)图1图25.如图 2 所示, D, E,F 分别是△ ABC 的边 BC, CA,AB 上的点,且 DE∥AB,DF∥CA,要使四边形 AFDE是菱形,则要增添的条件是 ________.(只写出切合要求的一个即可)6 .菱形 ABCD的周长为48cm,∠ BAD:∠ ABC=1:?2,?则 BD=?_____,?菱形的面积是______.7.在菱形ABCD中, AB=4, AB 边上的高DE垂直均分边AB,则 BD=_____,AC=_____.三、解答题8.以下图,在四边形ABCD中, AB∥CD, AB=CD=BC,四边形 ABCD是菱形吗? ?说明理由.四、思虑题9.如图,矩形 ABCD的对角线订交于点 O,PD∥AC,PC∥BD, PD,PC订交于点 P,四边形 PCOD是菱形吗?试说明原因.参照答案一、 1. A点拨:此题用清除法作答.2. D 点拨:依据菱形的判断方法判断,注意不要漏解.3. C点拨:以下图,若∠ ABC=60°,则△ ABC为等边三角形,?所以 AC=AB=1×32=8( cm), AO=1AC=4cm.42因为 AC⊥BD,在 Rt△AOB中,由勾股定理,得OB=2222AB OA8 4 =43(cm ?),所以 BD=2OB=8 3 cm.二、 4. AB=BC 点拨:还可增添AC⊥BD 或∠ ABD=∠CBD等.5.点 D 在∠ BAC的均分线上(或 AE=AF)26. 12cm; 723 cm点拨:以下图,过 D 作 DE⊥AB 于 E,因为 AD∥BC, ?所以∠ BAD+∠ABC=180°.又因为∠ BAD:∠A BC=1:2,所以∠ BAD=60°,因为 AB=AD,所以△ ABD 是等边三角形,所以BD=AD=12cm.所以 AE=6cm.在 Rt△AED 中,由勾股定理,得 AE 2+ED 2=AD 2, 62+ED 2=12 2,所以 ED 2=108 ,所以 ED=6 3 cm,所以S菱形ABCD=12×63=72 3 (cm2).7. 4;4 3点拨:以下图,因为DE垂直均分 AB,又因为 DA=AB,所以 DA=DB=4.所以△ ABD 是等边三角形,所以∠ BAD=60°,由已知可得AE=2.在 Rt△AED中,2222222?AE +DE=AD,即 2 +DE=4,所以 DE=12,所以 DE=2 3 ,因为1AC·BD=AB·DE,即1AC·4=4×2 3 ,所以AC=4 3 .22三、 8.解:四边形ABCD是菱形,因为四边形ABCD中, AB∥CD,且AB=CD,所以四边形ABCD是平行四边形,又因为AB=BC,所以Y ABCD是菱形.点拨:依据已知条件,不难得出四边形ABCD为平行四边形,又AB=BC,即一组邻边相等,由菱形的定义能够鉴别该四边形为菱形.四、 9.解:四边形PCOD是菱形.原因以下:因为 PD∥OC,PC∥OD, ?所以四边形P COD是平行四边形.又因为四边形ABCD是矩形,所以OC=OD,所以平行四边形PCOD是菱形.20.4正方形的判断一、选择题1.以下命题正确的选项是()A.两条对角线相互均分且相等的四边形是菱形B.两条对角线相互均分且垂直的四边形是矩形C.两条对角线相互垂直,均分且相等的四边形是正方形D.一组邻边相等的平行四边形是正方形2.矩形四条内角均分线能围成一个()A.平行四边形B.矩形C.菱形 D .正方形二、填空题3.已知点 D, E,F 分别是△ ABC 的边 AB, BC, CA的中点,连结 DE, EF, ?要使四边形ADEF是正方形,还需要增添条件_______.4.如图 1 所示,直线L 过正方形ABCD的极点 B,点 A, C 到直线 L?的距离分别是 1 和2,则正方形ABCD的边长是 _______.图1图2图35.如图 2 所示,四边形 ABCD是正方形,点 E 在 BC的延伸线上, BE=BD且 AB=2cm,则∠E的度数是 ______, BE 的长度为 ____.6.如图 3 所示,正方形 ABCD的边长为 4,E 为 BC上一点, BE=1,F?为 AB?上一点, AF=2,P 为 AC上一动点,则当 PF+PE取最小值时, PF+PE=______.三、解答题7.以下图,在 Rt△ABC中, CF为∠ ACB的均分线, FD⊥AC 于 D,FE⊥BC于点 E,试说明四边形 CDFE是正方形.BEF四、思虑题8.已知以下图,在正方形 ABCD中, E,F 分别是(1) AF 与 DE相等吗?为何?(2) AF 与 DE能否垂直?说明你的原因.C D A AB,BC边上的点,且 AE=BF,?请问:参照答案一、 1. C点拨:对角线相互均分的四边形是平行四边形,?对角线相互垂直的平行四边形是菱形,对角线相等的平行四边形是矩形,既是菱形又是矩形的四边形必定是正方形,应选 C.2. D 点拨:由题意画出图形后,利用“一组邻边相等的矩形是正方形”来判断.二、 3.△ ABC是等腰直角三角形且∠ BAC=90°点拨:还可增添△ ABC 是等腰三角形且四边形ADEF是矩形或∠ BAC=90°且四边形ADEF 是菱形等条件.4.5点拨:察看图形易得两直角三角形全等,由全等三角形的性质和勾股定理得正方形的边长为 2212=5.5. 67. 5°; 2 2 cm点拨:因为BD是正方形ABCD的对角线,所以∠ DBC=45°, AD=?AB=2cm.在 Rt△BAD中,由勾股定理得 AD 2+AB 2=BD 2,即 22+22=BD 2,所以 BD=2 2 cm,所以 BE=BD=2 2( cm),又因为BE=BD,所以∠ E=∠EDB= 1(180°- 45°)=67. 5°.26.17点拨:以下图,作 F 对于AC的对称点G.连结EG交AC于P,则 PF+?PE=PG+PE=GE为最短.过 E 作 EH⊥AD.在 Rt△GHE中,HE=4,HG=AG-AH=AF-BE=1,所以 GE= 4212 = 17,?即 PF+PE= 17.三、 7.解:因为∠ FDC=∠FEC=∠BCD=90°,所以四边形CDFE是矩形,因为 CF?均分∠ ACB,FE⊥BC,FD⊥AC,所以FE=FD,所以矩形CDFE是正方形.点拨:此题先说明四边形是矩形,再求出有一组邻边相等,?还能够先说明其为菱形,再求其一个内角为90°.四、 8.解:( 1)相等.原因:在△ ADE 与△ BAF 中, AD=AB,∠ DAE=∠ABF=90°, AE=BF,所以△ ADE≌△ BAF( S. A. S.),所以 DE=AF.( 2) AF 与 DE垂直.原因:如图,设DE与 AF 订交于点O.因为△ ADE≌△ BAF, ?所以∠ AED=∠BFA.又因为∠ BFA+∠EAF=90°,所以∠ AEO+∠EAO=90°,所以∠ EOA=90°,所以DE⊥AF.20.5等腰梯形的判断1 A C 一、选择题.以下结论中,正确的选项是(.等腰梯形的两个底角相等.一组对边平行的四边形是梯形)BD.两个底角相等的梯形是等腰梯形.两条腰相等的梯形是等腰梯形2.以下图,等腰梯形ABCD的对角线 AC,BD订交于点O,则图中全等三角形有()A.2对B.3对C.4对D.5对3.课外活动课上, ?老师让同学们制作了一个对角线相互垂直的等腰梯形形状的风筝,其面积为450cm,则两条对角线所用的竹条长度之和起码为()A. 30 2 cm B.30cm C.60cm D.60 2 cm二、填空题4.等腰梯形上底,下底和腰分别为 4,?10,?5,?则梯形的高为 _____,?对角线为 ______.5.一个等腰梯形的上底长为5cm,下底长为 12cm,一个底角为 60°,则它的腰长为____cm,周长为 ______cm.6.在四边形 ABCD中, AD∥BC,但 AD≠BC,若使它成为等腰梯形,则需要增添的条件是__________ (填一个正确的条件即可).三、解答题7.以下图,AD是∠ BAC的均分线, DE∥AB, DE=AC,AD≠EC.求证: ?四边形 ADCE是等腰梯形.四、思虑题8.以下图,四边形ABCD中,有 AB=DC,∠ B=∠C,且AD<BC,四边形 ABCD是等腰梯形吗?为何?参照答案一、 1. D点拨:梯形的底角分为上底上的角和下底上的角,?所以在等腰梯形的性质和鉴别方法中一定重申同一底上的两个内角(?指上底上的两个内角或下底上的两个内角),不然就会出现错误,所以A, B 选项都不正确,而 C 选项中遗漏了限制条件此外一组对边不平行,若平行该四边形就形成了平行四边形了,所以应选D.2. B点拨:因为△ ABC≌△ DCB,△ BAD≌△ CDA,△ AOB≌△ DOC,所以共有 3 对全等的三角形.3. C点拨:设该等腰梯形对角线长为Lcm,因为两条对角线相互垂直,?所以梯形面积为122L =450,解得 L=30,所以所用竹条长度之和起码为2L=2× 30=60(cm).二、 4. 4:65点拨:以下图,连结BD,过 A,D 分别作 AE⊥BC,DF⊥BC,垂足分别为E, F.易知△ BAE≌△ CDF,在四边形 AEFD为矩形,所以BE=CF=3, AD=EF=4.在 Rt△CDF 中, FC2+DF 2=CD 2,即 32+DF 2=52,所以 DF=4 ,在 Rt △BFD 中, BF2+DF 2=BD 2,即 72+42=BD 2,所以 BD=65 .5. 7;31点拨:以下图,过点D作 DE∥AB 交 BC于 E.因为ABED是平行四边形.所以 BE=AD=5(cm), AB=DE.又因为 AB=CD,所以 DE=?DC,又因为∠ C=60°,所以△ DEC 是等边三角形,所以 DE=DC=EC=7( cm),所以周长为5+?12+7+7=31(cm).6. AB=CD(或∠ A=∠D,或∠ B=∠C,或 AC=BD,或∠ A+∠C=180°,或∠B+∠D=180°)三、 7.证明:因为 AB∥ED,所以∠ BAD=∠ADE.又因为 AD是∠ BAC的均分线,所以∠ BAD=∠CAD,所以∠ CAD=∠ADE,所以 OA=OD.又因为AC=DE,所以 AC-OA=DE-OD即 OC=OE, ?所以∠ OCE=∠OEC,又因为∠ AOD=∠COE,所以∠ CAD=∠OCE.所以AD∥CE,而 AD≠CE,故四边形ADCE是梯形.又因为∠ CAD=∠ADE, AD=DA, AC=DE,所以△ DAC≌△ ADE,所以DC=?AE,所以四边形ADCE是等腰梯形.点拨:证明一个四边形是等腰梯形时,应先证其是梯形尔后再证两腰相等或同一底上的两个角相等.四、 8.解:四边形ABCD是等腰梯形.原因:延伸BA, CD,订交于点 E,以下图,由∠ B=∠C,可得EB=EC.又 AB=DC,所以 EB-AB=EC-DC,即 AE=DE,所以∠ EAD=∠EDA.因为∠ E+∠EAD+∠EDA=180°,∠ E+∠B+∠C=180°,所以∠ EAD=∠B.故 AD∥BC. ?又 AD<BC,所以四边形 ABCD是梯形.又 AB=DC,所以四边形 ABCD是等腰梯形.点拨:由题意可知,只需推出AD∥BC,再由AD<BC便可知四边形ABCD为梯形,再由AB=DC,即可求得此四边形是等腰梯形,由∠ B=∠C联想到延伸 BA,CD,即可获得等腰三角形,从而使 AD∥BC.华东师大版数学八年级(下)第 20 章平行四边形的判断测试(答卷时间: 90 分钟,全卷满分: 100 分)姓名得分 ____________一、认认真真选,沉稳应战!(每题 3 分,共 30 分)1. 正方形拥有菱形不必定拥有的性质是()(A )对角线相互垂直(B)对角线相互均分(C)对角线相等(D)对角线均分一组对角2.如图 (1),EF 过矩形 ABCD 对角线的交点 O,且分别交 AB 、CD 于 E、 F,那么暗影部分的面积是矩形ABCD 的面积的()(A )A 111( D )3A5(B )( C)1043D E FFEB C D HB C(1)(2)(3)3.在梯形ABCD 中, AD ∥ BC ,那么 A : B : C : D 能够等于()( A)4:5:6:3(B)6:5:4:3(C)6:4:5:3(D)3:4:5:64.如图 (2) ,平行四边形ABCD 中,DE ⊥ AB 于 E,DF⊥ BC 于 F,若Y ABCD的周长为48,DE = 5, DF= 10,则Y ABCD的面积等于 ()( A)87.5(B)80(C)75(D)72.55. A 、 B、 C、 D 在同一平面内,从① AB∥CD;② AB=CD;③ BC∥AD;④ BC=AD这四个条件中任选两个,能使四边形ABCD 是平行四边形的选法有()( A)3种(B)4种(C)5种(D)6种6.如图 (3) ,D、E、F分别是VABC各边的中点,AH 是高,假如 ED5cm ,那么 HF的长为()( A ) 5cm(B)6cm(C)4cm(D)不可以确立7.如图( 4):E 是边长为 1 的正方形 ABCD 的对角线 BD 上一点,且 BE = BC, P 为 CE 上随意一点, PQ⊥BC 于点 Q, PR⊥ BE 于点 R,则 PQ+PR 的值是()2132( A )2(B)2(C)2(D)38.如图( 5),在梯形ABCD 中, AD ∥ BC , AB CD , C 60 ,BD均分ABC ,假如这个梯形的周长为30,则AB的长()( A)4( B)5(C)6( D)7A DA DERPB C( 5)B(4)Q C9.右图是一个利用四边形的不稳固性制作的菱形晾衣架.A B C 已知此中每个菱形的边长为20cm,墙上悬挂晾衣架的两个铁钉 A 、 B 之间的距离为20 3 cm,则∠1等于()1)( A)90°(B) 60°(C) 45°(D) 30°10.某校数学课外活动研究小组,在老师的指引下进一步研究了完整平方公式.联合实数的性质发现以下规律:对于随意正数a、 b,都有 a+b ≥ 2ab 建立.某同学在做一个面积为3600cm2,对角线相互垂直的四边形风筝时,运用上述规律,求得用来做对角线用的竹条至少需要准备xcm.则 x 的值是()(A) 1202(B) 602(C) 120(D) 60二、仔认真细填,记录自信!( 每题 2 分,共20 分)11.一个四边形四条边按序是a、b、c、d,且a2 b 2 c 2 d 22ac 2bd,则这个四边形是 _______________ .12.在四边形ABCD中,对角线AC、BD交于点O,从(1)AB CD ;(2) AB∥CD ;(3)OA OC;(4)OB OD ;(5) AC ⊥ BD ;(6) AC 均分 BAD 这六个条件中,选用三个推出四边形ABCD是菱形.如( 1)( 2)( 5)ABCD 是菱形,再写出切合要求的两个:ABCD 是菱形;ABCD 是菱形.13. 如图,已知直线l 把 Y ABCD 分红两部分,要使这两部分的面积相等,直线l 所在地点需知足的条件是____________________. (只需填上一个你以为适合的条件)lA DB C(第 13 题)(第 16 题)14.梯形的上底长为 6cm ,过上底的一极点引一腰的平行线,与下底订交,所构成的三角形周长为 21cm ,那么梯形的周长为_________ cm。
多边形面积练习题及答案

多边形面积练习题及答案练习题一:矩形的面积计算1. 已知一个矩形的长度为12cm,宽度为8cm,求其面积。
解答:矩形的面积等于长度乘以宽度。
根据题目给出的数据,我们可以计算矩形的面积:面积 = 长度 ×宽度 = 12cm × 8cm = 96cm²练习题二:三角形的面积计算2. 已知一个三角形的底边长为5cm,高为6cm,求其面积。
解答:三角形的面积等于底边乘以高再除以2。
根据题目给出的数据,我们可以计算三角形的面积:面积 = 1/2 ×底边 ×高 = 1/2 × 5cm × 6cm = 15cm²练习题三:平行四边形的面积计算3. 已知一个平行四边形的底边长为9cm,高为4cm,求其面积。
解答:平行四边形的面积等于底边乘以高。
根据题目给出的数据,我们可以计算平行四边形的面积:面积 = 底边 ×高 = 9cm × 4cm = 36cm²练习题四:梯形的面积计算4. 已知一个梯形的上底长为6cm,下底长为10cm,高为8cm,求其面积。
解答:梯形的面积等于上底加下底再乘以高再除以2。
根据题目给出的数据,我们可以计算梯形的面积:面积 = 1/2 × (上底 + 下底) ×高 = 1/2 × (6cm + 10cm) × 8cm = 64cm²练习题五:菱形的面积计算5. 已知一个菱形的对角线1长为7cm,对角线2长为4cm,求其面积。
解答:菱形的面积等于对角线1乘以对角线2再除以2。
根据题目给出的数据,我们可以计算菱形的面积:面积 = 1/2 ×对角线1 ×对角线2 = 1/2 × 7cm × 4cm = 14cm²练习题六:不规则多边形的面积计算6. 已知一个不规则四边形的边长依次为5cm、6cm、8cm和7cm,求其面积。
五年级数学 平行四边形的面积 练习题(含答案)

人教版数学五年级上册6.1 平行四边形面积练习卷一、选择题1.将一个长方形拉成平行四边形,它的面积().A.不变B.变大C.变小2.下列说法正确的是()。
A.平行四边形是特殊的长方形B.平行四边形易变形C.梯形两组对边分别平行3.如图,已知“4,7,20,35”(单位:厘米)是一个平行四边形的两条底和两条高的长度,这个平行四边形的面积是()平方厘米。
A.245B.140C.80D.284.把一个长方形拉成一个平行四边形(如图),拉成后的平行四边形与长方形相比,它的周长(),面积()。
A.变小;变小B.变大;变大C.不变;变小二、图形计算5.求图中阴影部分的面积(单位:cm)三、填空题6.一块平行四边形草地,底是3.6米,对应的高是2米,它的面积是( )平方米。
7.如图,M、N分别是平行四边形ABCD两边上的中点,三角形AMN的面积是7.2平方厘米,平行四边形ABCD的面积是平方厘米.8.一个平行四边形相邻的两条边分别是4厘米和6厘米,如果较长边上的高是2厘米,那么这个平行四边形的面积是( ).9.如图,正方形ABCD的边长为4厘米,EF和BC平行,ECH的面积是7平方厘米,EG的长为( )。
10.把一个木条做成的长方形框架沿着对角拉成一个平行四边形,拉成后的平行四边形与原长方形比较,周长( )。
11.一个边长5厘米的正方形木框,拉成一个平行四边形后,面积减少了5平方厘米.拉成的平行四边形的高是厘米.四、判断题12.在平行四边形内画一个最大的三角形,三角形的面积一定等于平行四边形面积的一半。
( )13.两个平行四边形的面积相等,这两个平行四边形的形状也一定相同._____.(判断对错)14.计算组合图形面积时,常用的方法有分割法和添补法..15.一个平行四边形的高和底都扩大到原数的4倍,那么这个平行四边形的面积也要扩大到原数的4倍。
( )16.把平行四边形割补成一个长方形后,面积变小。
( )五、解答题17.植物园里有一个平行四边形的玫瑰园,玫瑰园的底是120m,高是60m,如果每平方米种8株玫瑰,这个玫瑰园一共能种多少株玫瑰?18.河西村有一块平行四边形的实验田,底长600米,高250米.平均每公顷收稻谷1.2吨,这块田可收稻谷多少吨?19.一个平行四边形,若底增加2厘米,高不变,则面积增加6平方厘米;若高增加1厘米,底不变,则面积增加4平方厘米,原平行四边形的面积是多少?参考答案:1.C【详解】2.B(1)平行四边形的两组对边平行且相等,长方形不仅两组对边平行且相等,四个角均为直角。
(完整版)平行四边形的性质练习题及答案

(完整版)平⾏四边形的性质练习题及答案平⾏四边形的性质、课中强化(10分钟训练)1?如图3,在平⾏四边形 ABCD 中,下列各式不⼀定正确的是()A. / 1 + Z 2=180 °B. / 2+ / 3=180 °C. / 3+Z 4=180的周长为()3. 如图5,」ABCD 中,EF 过对⾓线的交点 O,如果AB=4 cm,AD=3 cm,OF=1 cm,则四边形 BCFE 的周长为 ____________________ .4. 如图6,已知在平⾏四边形 ABCD 中,AB=4 cm , AD=7 cm , / ABC 的平分线交 AD 于点E ,5. 如图7,在平⾏四边形 ABCD 中,点E 、F 在对⾓线6. 如图 8,在 ABCD 中,AE 丄BC 于 E,AF 丄 CD 于 F,BE=2 cm,DF=3 cm, / EAF=60° ,试求 CF 的长.D. /2+ /4=180O , OE 丄AC 交AD 于丘,则⼛DCEA.4 cmB.6 cmC.8 cmD.10 cm交CD 的延长线于点 F ,贝U DF= _____________cm.BD 上,且 BE=DF ,求证:AE=CF.图32?如图4,⼆ABCD 的周长为图5图6图7图8三、课后巩固(30分钟训练)1?⼆ABCD中,/A⽐/ B⼤20。
,则/ C的度数为()A.60 °B.80 °C.100 °D.120 2?以A、B、C三点为平⾏四边形的三个顶点,作形状不同的平⾏四边形,⼀共可以作(A.0个或3个B.2个C.3个D.4个3?如图9 所⽰,在—ABCD 中,对⾓线AC、BD交于点0,下列式⼦中⼀定成⽴的是()A.AC 丄BDB.OA=OCC.AC=BDD.AO=OD4?如图10,平⾏四边形ABCD中,对⾓线AC、BD相交于点O ,将⼛AOD平移⾄△ BEC的位置,则图中与OA相等的其他线段有()A.1条B.2条C.3条D.4条5?如图11,在平⾏四边形ABCD中,EF // AB , GH // AD , EF与GH交于点O,则该图中的平⾏四边形的个数共有()6?如图12,平⾏四边形ABCD中,AE丄BD , CF丄BD,垂⾜分别为E、F,求证:/ BAE= / DCF.7、如图13所⽰,已知平⾏四边形ABCD中,E、F分别是BC和AD上的点,且BE=DF.求证:△ ABE CDF.A.7个B.8个C.9个D.11 个图12图138?如图14,已知四边形ABCD是平⾏四边形,/ BCD的平分线CF交边AB于F,/ ADC的平分线DG交边AB于G.⑴求证:AF=GB ;(2)请你在已知条件的基础上再添加⼀个条件,使得△EFG是等腰直⾓三⾓形,并说明理由?19.1.2平⾏四边形的判定⼆、课中强化(10分钟训练)1?如图3,在ABCD中,对⾓线AC、BD相交于点O,E、F是对⾓线AC上的两点,当E、F满⾜下列哪个条件时,四边形DEBF不⼀定是平⾏四边形()A.AE=CFC.Z ADE= / CBFD. / AED= / CFB,使四边形AECF是平⾏四边形.4. 如图6,AD=BC,要使四边形ABCD是平⾏四边形,还需补充的⼀个条件是:__________________5. 如图,在,ABCD中,已知M和N分别是边AB、DC的中点,试说明四边形BMDN也是平⾏四边形.2.如图4,AB 喪DC ,DC=EF=10 ,DE=CF=8,则图中的平⾏四边形有,理由分别是图4 图53.如图5,E、F是平⾏四边形ABCD对⾓线BD上的两点,B.DE=BF图14三、课后巩固(30分钟训练)1?以不在同⼀直线上的三个点为顶点作平⾏四边形最多能作()是平⾏四边形的是()4?已知四边形 ABCD 的对⾓线 AC 、BD 相交于点② OA=OC :③ AB=CD ;④/ BAD= / DCB :⑤ AD // BC.(1)从以上5个条件中任意选取 2个条件,能推出四边形 ABCD 是平⾏四边形的有(⽤序号表⽰): _____________________________ :(2)对由以上5个条件中任意选取 2个条件,不能推出四边形请选取⼀种情形举出反例说明平⾏四边形?6?如图,E 、F 是四边形ABCD 的对⾓线 AC 上的两点,AF=CE , DF=BE , DF // BE. 求证:⑴△AFD ◎△ CEB;(2)四边形ABCD 是平⾏四边形A.4个B.3个C.2个D.1个2?下⾯给出了四边形 ABCD 中/A 、/ B 、/ C 、/ D 的度数之⽐,其中能判定四边形 ABCDA.1 : 2 : 3 : 4B. 2 : 2 : 3 : 3C. 2 : 3 : 3 : 2D. 2 : 3 : 2 : 33?九根⽕柴棒排成如右图形状,图中 ____ 个平⾏四边形 ,你判断的根据是O ,给出下列 5个条件:①AB // CD ;5?若三条线段的长分别为20 cm,14 cm,16 cm,以其中两条为对⾓线 ABCD 是平⾏四边形的,,另17?如图,已知DC // AB,且DC= — AB , E为AB的中点.2(1) 求证:△ AED ◎△ EBC ;(2) 观察图形,在不添加辅助线的情况下,除△EBC⼣⼘,请再写出两个与△ AED的⾯积相等的三⾓形(直接写出结果,不要求证明): ___________________________8?如图,已知⼆ABCD中DE丄AC,BF丄AC,证明四边形DEBF为平⾏四边形9?如图,已知■ ABCD中,E、F分别是AB、CD的中点?求证:(1) △ AFD ◎△ CEB;(2) 四边形AECF是平⾏四边形?⼆、课中强化(10 分钟训练)1 答案:D2. 解析:因为四边形ABCD 是平⾏四边形,所以OA=OC. ⼜0E丄AC , 所以EA=EC.贝U △ DCE 的周长=CD+DE+CE=CD+DE+EA=CD+AD. 在平⾏四边形ABCD 中,AB=CD ,AD=BC ,且AB+BC+CD+AD=16 cm ,所以CD+AD=8 cm.答案:C3?解析:0E=0F=1,其周长=BE+BC+CF+EF=CD+BC+EF=AD+AB+2DF=8(cm).答案:8 cm4?解析:由平⾏四边形的性质AB // DC,知/ ABE= / F,结合⾓平分线的性质/ ABE= / EBC,得/ EBC= / F,再根据等⾓对等边得到BC=CF=7 ,再由AB=CD=4 , AD=BC=7 得到DF=DE=AD-AE=3.答案:35?答案:证明:四边形ABCD是平⾏四边形,AB // CD , AB=CD./ ABE= / CDF.AB CD,在⼛ABE和⼛CDF中,ABE CDF ,BE DF .△ ABE ◎△ CDF.AE=CF.6. 解:/ EAF=60°AE 丄BC,AF 丄CD, C=120°. B=60°「./ BAE=30° .AB=2BE=4(cm). CD=4(cm). CF=1(cm).三、课后巩固(30 分钟训练)1 答案:C2. 解析:分两种情况,A、B、C三点共线时,可作0个当点A、B、C不在同⼀直线上时,可作3 个. 答案:A3. 解析:平⾏四边形对⾓线互相平分,所以OA=OC. 答案:B4. 解析:由平⾏四边形的对⾓线互相平分知OA=OC;再由平移的性质:经过平移,对应线段平⾏且相等可得OA=BE.答案:B5?解析:本题借助于平⾏四边形的定义,按照从左到右,从⼩到⼤的顺序,可找到下列的平⾏四边形:DEOH,.HOFC,. DEFC, EAGO,OGBF,EABF,■ DAGH,■ HGBC,⼆ABCD.答案:C6?答案:证明:四边形ABCD是平⾏四边形,AB // CD , AB=CD. /-Z ABE= / CDF ?/ AE 丄BD , CF 丄BD ,「./ AEB= / CFD=90 .△ABE ◎△ CDF. /.Z BAE= Z DCF.7、答案:证明:四边形ABCD是平⾏四边形,AB=CD, Z B= Z D.在⼛ABE和⼛CDF中,AB CD,B D, ?/△ ABE 也⼛CDF.BE DF.8?答案:(1)证明:四边形ABCD是平⾏四边形,? AB // CD. AGD= Z CDG.vZ ADG= Z CDG,/?/ ADG= Z AGD. ? AD=AG ?同理,BC=BF.⼜四边形ABCD 是平⾏四边形,? AD=BC,AG=BF. ? AG-GF=BF-GF ,即AF=GB.(2)解:添加条件EF=EG.理由如下:1 1由(1)证明易知Z AGD= Z ADG= Z ADC , Z BFC= Z BCF= Z BCD.2 2/ AD // BC,/?/ ADC+ Z BCD=180 ./Z AGD+ Z BFC=90 ./Z GEF=90 .⼜v EF=EG ,?△ EFG为等腰直⾓三⾓形.⼆、课中强化(10分钟训练)1. 解析:当E、F满⾜AE=CF时,由平⾏四边形的对⾓线相等知OB=OD,OA=OC , 故OE=OF.可知四边形DEBF是平⾏四边形.当E、F满⾜Z ADE= Z CBF 时,因为AD // BC,所以Z DAE= Z BCF.⼜AD=BC,可证出⼛ADE ◎△ CBF,所以DE=BF , Z DEA= Z BFC.故Z DEF= Z BFE.因此DE // BF,可知四边形DEBF是平⾏四边形.类似地可说明D也可以.。
2019-2020年五年级数学上册 平行四边形面积的计算及答案(二)教案 苏教版

2019-2020年五年级数学上册平行四边形面积的计算及答案(二)教案苏教版一、求下面平行四边形的面积。
二、求下面平行四边形的周长(单位:分米)三、在两条平行线间画出两个平行四边形(如下图),试判断甲和乙谁的面积大?四、一个平行四边形,若底增加2厘米,高不变,则面积增加6平方厘米;若高增加1厘米,底不变,则面积增加4平方厘米,原平行四边形的面积是多少?参考答案一、解答:(平方厘米)答:这个平行四边形的面积是24平方厘米。
二、已知平行四边形的一组底和高分别是12分米和7分米,可以求出它的面积是(平方分米),通过“平行四边形面积=底×高”,可以逆推出:底=平行四边形面积÷高,已知面积是84平方分米,高是6分米,可以求出和6分米相对应的底,用分米),平行四边形对边相等,已知平行四边形相邻的两条边分别是12分米和14分米,就可以求出它的周长。
解答:(分米)。
答:这个平行四边形的周长是52分米。
三、平行四边形ABCD和BCEF是画在两条平行线之间,那么这两个平行四边形的高相等,因为两条平行线间的距离处处相等。
这两个平行四边形都是以BC为底,所以说这两个平行四边形的底也相等的,底和高都分别相等,那么底和高的乘积(面积)也相等,从两个面积相等的平行四边形中减去同样的一个三角形,剩下的面积也相等,所以甲和乙的面积是一样大的。
四、根据第一组条件,增加部分是一个底是2厘米,面积是6平方厘米的平行四边形,根据平行四边形的面积公式可以求出这个平行四边形的高,即求出原平行四边形的高。
根据第二组条件,,增加部分是一个高为1厘米,面积为4平方厘米的平行四边形,由此可以求出增加部分的底,即求出原平行四边形的底。
解答:(平方厘米)答:原平行四边形的面积是12平方厘米。
Iu附送:2019-2020年五年级数学上册梯形的特征 1教案青岛版教学目标:1.知识目标:使学生掌握梯形的特征和各部分名称,沟通梯形与其它平面图形的联系。
平行四边形面积练习题及答案

平行四边形面积练习题及答案练题1. 已知平行四边形ABCD,其中底边BC的长度为8cm,高线的长度为10cm。
求平行四边形ABCD的面积。
2. 平行四边形EFGH的底边长为12cm,高线的长度为6cm。
若平行四边形EFGH与平行四边形ABCD的面积比为2:3,求平行四边形ABCD的面积。
3. 平行四边形IJKL的底边长为15cm,高线的长度为9cm。
现在将平行四边形IJKL的底边和高线均拉长了2倍,求新平行四边形的面积。
答案1. 平行四边形ABCD的面积可以通过底边长乘以高线长度来计算。
所以,面积等于8cm × 10cm = 80cm²。
2. 若平行四边形EFGH与平行四边形ABCD的面积比为2:3,设平行四边形ABCD的面积为3x。
根据比例关系,平行四边形EFGH的面积为2x。
已知平行四边形EFGH的底边长为12cm,高线的长度为6cm,可以通过平行四边形的面积公式计算平行四边形EFGH的面积:面积 = 底边长 ×高线长度 = 12cm × 6cm = 72cm²根据比例关系,平行四边形ABCD的面积为:3x = 2x × (72cm² / 题目中给出的比例)x = (72cm² / 题目中给出的比例)平行四边形ABCD的面积 = 3x = 3 × (72cm² / 题目中给出的比例)3. 平行四边形IJKL的底边拉长2倍后为30cm,高线拉长2倍后为18cm。
那么新平行四边形的面积可以通过新底边长乘以新高线长度来计算。
所以,新平行四边形的面积为:面积 = 新底边长 ×新高线长度 = 30cm × 18cm = 540cm²以上就是平行四边形面积练习题及答案的文档内容,希望能对你的练习有所帮助!。
人教版小学五年级数学上册 平行四边形的面积练习题及答案

平行四边形的面积1.平行四边形的底和高(1)如图,AE是高,对应的底是边______;以这条边为底,还可以画出______条高.(2)如图,AE是高,对应的底是边______;以这条边为底,还可以画出______条高.(3)如图,AB是底,对应的高是线段______;BC为底,对应的高是线段______.(4)如图,AB是底,对应的高是线段______;BC为底,对应的高是线段______.(5)如图,AB是底,对应的高是线段______;BC为底,对应的高是线段______.(6)如图,BC是底,对应的高是线段______;CD为底,对应的高是线段______.2.求平行四边形的面积(1)下图平行四边形的面积是______平方厘米。
(2)右图中,平行四边形的面积是______平方厘米(3)一个平行四边形的底是18厘米,这个底对应的高是14厘米,它的面积是______平方厘米。
(4)一个平行四边形的一条边长13分米,这条边上的高是9分米,它的面积是______平方分米。
(5)如图,一个平行四边形的周长是72cm,以CD为底时,它的高是18cm,已知BC是21cm,它的面积是______平方厘米。
(6)右图平行四边形ABCD的面积是______平方分米。
(7)下图平行四边形的面积是______平方厘米。
(8)下图平行四边形的面积是______平方厘米。
3.已知平行四边形的面积求底或高(1)如图,已知平行四边形ABCD的面积为306平方厘米,底BC为18厘米,高BE是______厘米。
(2)计算下面平行四边形中的未知量:h=______cm(3)已知平行四边形面积为928平方米,高为8米,这条高所对应的底是______米。
(4)计算右面平行四边形中的未知量:h=______dm(5)已知平行四边形的面积为686平方米,底为98米,这条底所对应的高是______米。
(6)计算右面平行四边形中的未知量:a=______dm4.平行四边形面积未知求底或高(1)如图,图中问号处平行四边形的高是______厘米。
平行四边形练习题及答案

平行四边形练习题及答案一、选择题:1. 平行四边形的特点是()A. 两组对边相等B. 两组对边互相垂直C. 对角线相等D. 没有特定的特点2. 若平行四边形的一组对边长为3cm和6cm,另一组对边长为4cm 和8cm,该平行四边形的周长为()A. 21cmB. 28cmC. 35cmD. 42cm3. 若平行四边形的一组对边长为12cm和8cm,且高为4cm,求该平行四边形的面积。
A. 24cm²B. 32cm²C. 48cm²D. 64cm²二、填空题:1. 平行四边形ABCD中,∠BAD的补角为______。
2. 如果一条直线与一组平行线相交,那么它与另一组平行线的关系是______。
3. 若平行四边形的一组对边长为10cm和6cm,且高为5cm,那么其面积为______。
三、解答题:1. 证明:平行四边形的对角线互相等长。
四、综合题:1. 已知平行四边形ABCD的周长为48cm,其中AB的长为12cm,CD的长为8cm。
求其面积。
2. 已知平行四边形ABCD中,对角线AC的长为5cm,对角线BD 的长为12cm。
求该平行四边形的周长和面积。
答案:一、选择题:1. A2. B3. B二、填空题:1. ∠CAD2. 平行3. 30cm²三、解答题:1. 证明:设平行四边形ABCD的一组对边为AB和CD,对角线AC和BD相交于点O。
∵ AB ∥ CD (已知)∴∠ABC = ∠CDA (同位角)同理可得∠BAC = ∠CDB∵∠ABC = ∠CDA,∠BAC = ∠CDB∴△ABC ≌△CDA (ASA准则)∴ AB = CD (对应边相等)同理可证 AC = BD∴平行四边形ABCD的对角线互相等长。
四、综合题:1. 设平行四边形ABCD的高为h。
∵ AB + BC + CD + DA = 48cm (周长)∴ 12 + BC + 8 + DA = 48∴ BC + DA = 48 - 20∴ BC + DA = 28∵ AB ∥ CD,AD ┴ CD∴高h = AD = BC∴ 2h + 4 + 2h = 28∴ 4h = 24∴ h = 6∴面积 = 底 ×高 = (BC + DA) × h = 28 × 6 = 168cm²所以,平行四边形ABCD的面积为168cm²。
数学五年级上册平行四边形的面积解决问题练习题(含答案)

6.1平行四边形的面积1.一个平行四边形果园,底长150米,高40米.如果这个果园一共种了1000棵果树,那么每棵果树平均占地多少平方米?2.一块平行四边形形稻田,底是90米,高60米,如果每平方米施肥0.2千克,这块稻田需施肥多少千克?3.一个平行四边形的面积是90平方厘米.它的底是15厘米,高是多少厘米?(列方程解)4.有一块平行四边形的菜地,底和高都是12米,它的面积是多少平方米?如果每平方米种10颗白菜,那么这块菜地一共可以种多少棵白菜?5.李大伯家有一块平行四边形的稻田,底是110m,是高的0.25倍.他今年计划每公顷稻田需施肥45kg,那么这块稻田共要施肥多少千克?6.有一块平行四边形的瓜地,底是6.8m,是高的2倍,如果每平方米栽瓜苗5棵,大约可栽多少棵瓜苗?7.如图,红星广告公司要将一块平行四边形的铁板的一面刷上油漆,如果每千克油漆能刷1.2平方米,这块铁板共需多少千克油漆?8.(如图)请回忆老师引导你推导平行四边形面积公式进的情境,给(1)、(2)填空;(3)计算.(1)以将平行四边形转化为长方形来推导平行四边形的面积公式.把平行四边形转化成长方形采用的方法是:(2)观察转化前的平行四边形与转化后的长方形,你发现了什么?(请写在下面的横线上,至少写三条)(3)计算上面平行四边形的面积.(先动手在图中量出计算时需要的数据,再算出它的面积)9.自己测量需要的数据,并求出图中草地的总面积.(测量数据以厘米为单位四舍五入到整数)10.张大爷有一块平行四边形的地,底长175米,高80米,今年共收绿豆2856千克,平均每公顷收绿豆多少千克?这块平行四边形的面积是多少平方米?合多少公顷呢?11.一块底长1.5米,高1.2米的平行四边形铁板.现在要油漆它的两面,每平方米用油漆0.3千克,一共要油漆多少千克?12.学校要制作一块平行四边形宣传牌,底长4米,高2米,如果广告公司制作广告牌每平方米收费30元,那么学校应支付给这个广告公司多少元?13.一块平行四边形的地,底边长250m,高84m,在这块地里种小麦,共收小麦14.7吨,平均每公顷收小麦多少吨?14.在一块底50m,高30m的平行四边形地里栽桃树,平均每6m2栽一棵,这块地能栽多少棵桃树?如果每棵收4.5kg桃子,这块土地共收桃子多少千克?15.有一块平行四边形的菜地,底长48米,高是底的一半,这块地的面积是多少平方米?16.画出下面图形的高,并量出有用的数据标在图上,再计算图形的面积.17.有一块平行四边形的麦田,底225米,高60米,共收小麦10.8吨,这块麦田有多少公顷?平均每公顷收小麦多少吨?18.一块平行四边形的花生地,底长45米,高18米,每平方米种花生6棵,每棵花生的产量约是0.8千克,这块花生地共收花生多少千克?19.一块平行四边形的地共收油菜籽3400kg,它的底长250m,高68m.平均每公顷收油菜籽多少千克?20.某乡镇中学开垦了一块平行四边形荒地种油菜,这块平行四边形地的底是32米,高是35米.如果平均每平方米收油菜1.5千克.这块地一共收油菜多少千克?21.如图,一块长方形草地,长方形的长是16米,宽是10米,中间铺了一条石子路.那么草地部分面积有多大?22.如图是一块长方形草地,长是20米,宽是12米,中间有两条石子路,一条是底是2米的平行四边形,一条是2米的长方形.求草地的面积.23.一块平行四边形钢板,底是3.8m,高是1.5m,求它的面积.这块钢板每平方米重39kg,整块钢板重多少千克?24.一个平行四边形的底边长6分米,高40厘米,面积是多少?25.某工人师傅要将两根长15厘米的钢条都按3:2的长度折弯,然后摆成一个首尾相连的平行四边形,这个平行四边形的面积能不能是36平方厘米?如果能那么平行四边形的高是多少?如果不能,为什么?参考答案1.150×40÷1000=6000÷1000,=6(平方米),答:每棵果树平均占地6平方米.2.2×(90×60)=0.2×5400,=1080(千克);答:这块稻田需施肥1080千克.3.设高为x厘米,15x=90,x=90÷15,x=6.答:高是6厘米.4.平行四边形的面:12×12=144(平方米);一共种多少棵白菜:10×144=1440(棵).答:它的面积是144平方米这块菜地一共可以种1440棵白菜.5.110÷0.25×110,=440×110,=48400(平方米),=4.84(公顷); 4.84×45=217.8(千克);答:这块稻田共要施肥217.8千克.6.平行四边形的高是:6.8÷2=3.4(米),6.8×3.4×5,=23.12×5,≈116(棵);答:大约可载116棵瓜苗.7.(4.2×3.5)÷1.2,=14.7÷1.2,=12.25(千克);答:这块铁板共需12.25千克油漆.8.(1)从左边沿平行四边形的高剪下一个直角三角形,拼到平行四边形的右侧,就形成了一个长方形,把平行四边形转化成长方形采用的方法是:剪拼法;(2)观察转化前的平行四边形与转化后的长方形,发现:长方形的长就是平行四边形的底、长方形的高就是平行四边形的高、长方形的面积等于平行四边形的面积;(3)平行四边形的底是2厘米,高是1厘米,平行四边形的面积=2×1=2(平方厘米);答:平行四边形的面积是2平方厘米.故答案为剪拼法、长方形的长就是平行四边形的底、长方形的高就是平行四边形的高、长方形的面积等于平行四边形的面积.9.经测量知:平行四边形的底是3厘米,高是2.5≈3厘米,通道的长就等于平行四边形的高,宽为0.5≈1厘米,则草地的面积:3×3﹣3×1,=9﹣3,=6(平方厘米);答:草地的总面积是6平方厘米.10.175×80=14000(平方米)=1.4(公顷);2856÷1.4=2040(千克);答:平均每公顷收绿豆2040千克,这块平行四边形的面积是14000平方米,合1.4公顷.11.5×1.2×0.3,=1.8×0.3,=0.54(千克);答:一共要油漆0.54千克.12.4×2×30=8×30=240(元)答:学校应支付给这个广告公司240元.13.250×84=21000(平方米)=2.1(公顷); 14.7÷2.1=7(吨);答:平均每公顷收小麦7吨.14.(1)50×30÷6,=1500÷6,=250(棵),(2)250×4.5=1125(千克),答:这块地能栽250棵桃树;这块土地共收桃子1125千克.15.48×(48÷2),=48×24,=1152(平方米);答:这块地的面积是1152平方米.16.6×2.5,=15(平方分米).答:平行四边形的面积是15平方分米.17.225×60=13500(平方米)=1.35(公顷); 10.8÷1.35=8(吨);答:这块麦田有135公顷,平均每公顷收小麦8吨.18.(45×18)×6×0.8,=810×6×0.8,=3888(千克);答:这块花生地共收花生3888千克.19.400×68÷10000,=27200÷1000,=2.72(公倾);3400÷2.72=1250(千克);答:平均每公顷收油菜籽1250千克.20.32×35×1.5,=1120×1.5,=1680(千克);答:这块地一共收油菜1680千克.21.16×10-16×2=16×(10-2)=16×8=128(平方米)答:草地面积有128平方米.22.解:(20﹣2)×(12﹣2),=18×10,=180(平方米).答:草地的面积是180平方米.23.解:3.8×1.5=5.7(平方米),5.7×39=222.3(千克);答:它的面积是5.7平方米,整块钢板重222.3千克.24.6分米=60厘米,60×40=2400(平方厘米);答:它的面积是2400平方厘米.25.按照3:2折可得到一条边为9厘米,另一条边为6厘米,折成直角时的面积为:9×6=54(平方厘米),如果继续拉,几乎成为直线,那么此时的面积最小,几乎为0,36平方厘米的面积在0到54之间,所以能折成36平方厘米的平行四边形,高为:36÷9=4(厘米);答:能折成面积为36平方厘米的平行四边形,高为4厘米.。
中考数学总复习《平行四边形的性质》练习题及答案

中考数学总复习《平行四边形的性质》练习题及答案班级:___________姓名:___________考号:_____________一、单选题1.如图,在▱ABCD中,E为BC的中点,DE、AC交于点F,则EFDF的值为()A.1B.13C.23D.122.在□ ABCD中,∠A=70∘,则∠B度数为()A.110∘B.100∘C.70∘D.20∘3.如图,在□ABCD中,对角线AC,BD交于点O,下列结论一定成立的是()A.AC⊥BD B.AO=OD C.AC=BD D.OA=OC4.如图,▱ABCD中,CE平分∠BCD,交AB于点E,AE=3,BE=5,DE=4,则CE的长为()A.4√5B.5√5C.5√2D.6√25.如图,在平行四边形ABCD中,⊥A=130°,在AD上取DE=DC,则⊥ECB的度数是()A.65°B.50°C.60°D.75°6.已知▱ABCD中,∠A+∠C=70°,则∠B的度数为()A.125°B.135°C.145°D.155°7.在平行四边形ABCD中,若⊥A+⊥C=80°,则⊥B的度数是()A.140°B.100°C.40°D.120°8.如图,在▱ABCD中,点F是线段CD上一点,点A作▱BFGE,当点F从点C向点D运动过程中,四边形BFGE的面积的变化情况是()A.保持不变B.一直减小C.一直增大D.先增大后减小9.如图,在平行四边形ABCD中,⊥BAD的平分线交BC于点E,⊥ABC的平分线交AD于点F,若BF=12,AB=10,则AE的长为()A.13B.14C.15D.1610.如图,在⊥ABCD中,点E是DC边上一点,连接AE,BE,若AE,BE分别是⊥DAB,⊥CBA的角平分线,且AB=4,则⊥ABCD的周长为()A.10B.8 C.5 D.1211.如图,▱ABCD的对角线AC,BD交于点O,EF和GH过点O,且点E,H在边DC上,点G,F 在边AB上,若▱ABCD的面积为10,则阴影部分的面积为()A.6B.4C.3D.5212.如图,平行四边形ABFC的对角线x∈(1,e)相交于点E,点O为AC的中点,连接BO并延长,交FC的延长线于点D,交AF于点G,连接AD、OE,若平行四边形ABFC的面积为48,则SΔEOG的面积为()A.4B.5C.2D.3二、填空题13.如图,E是⊥ABCD边BC上一点,且AB=BE,连结AE,并延长AE与DC的延长线交于点F,⊥F=70°,则⊥D=度.14.如图,将平行四边形ABCD沿对角线BD折叠,使点A落在点处.若∠1=∠2=50∘,则为.15.平行四边形ABCD的周长为20cm,对角线AC、BD相交于点O,若⊥BOC的周长比⊥AOB的周长大2cm,则CD=cm.16.在平行四边形ABCD中,⊥BAD的平分线AE交BC于点E,且BE=3,若平行四边形ABCD的周长是16,则EC等于.17.如图,已知⊥ABC的三个顶点的坐标分别为A(﹣2,0),B(﹣1,2),C(2,0).请直接写出以A,B,C为顶点的平行四边形的第四个顶点D的坐标18.如图,E、F分别是⊥ABCD的边AB、CD上的点,AF与DE相交于点P,BF与CE相交于点Q,若S⊥APD=10cm2,S⊥BQC=20cm2,则阴影部分的面积为cm2.三、综合题19.如图,▱ABCD中,以A为圆心,DA的长为半径画弧,交BA于点F,作⊥DAB的角平分线,交CD于点E,连接EF.(1)求证:四边形AFED是菱形;(2)若AD=4,⊥DAB=60°,求四边形AFED的面积.20.如图,在平行四边形ABCD中,对角线AC、BD相交于点O,点E在BD的延长线上,且△EAC 是等边三角形.(1)求证:四边形ABCD是菱形.(2)若AC=8,AB=5,求ED的长.21.如图,在▱ABCD中AE⊥BC于E,AF⊥CD于F,且CE=CF.(1)求证:AE=AF;(2)求证:四边形ABCD是菱形.22.如图,四边形ABCD是平行四边形,点E在BC的延长线上,且CE=BC,AE=AB,AE、DC相交于点O,连接DE.(1)求证:四边形ACED是矩形;(2)若⊥AOD=120°,AC=4,求对角线CD的长.23.图1,图2都是8×8的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1,在每个正方形网格中标注了6个格点,这6个格点简称为标注点.(1)请在图1,图2中,以4个标注点为顶点,各画一个平行四边形(两个平行四边形不全等);(2)图2中所画的平行四边形的面积为.24.如图,在平行四边形ABCD中,AB≠BC,连接AC,AE是⊥BAD的平分线,交边DC的延长线于点F.(1)证明:CE=CF;(2)若⊥B=60°,BC=2AB,试判断四边形ABFC的形状,并说明理由.(如图2所示)参考答案1.【答案】D2.【答案】A3.【答案】D4.【答案】A5.【答案】A6.【答案】C7.【答案】A8.【答案】A9.【答案】D10.【答案】D11.【答案】D12.【答案】C13.【答案】4014.【答案】105°15.【答案】416.【答案】217.【答案】(3,2),(﹣5,2),(1,﹣2)18.【答案】3019.【答案】(1)证明:∵AE为⊥DAB的角平分线∴⊥DAE=⊥EAF∵AB//CD∴⊥DEA=⊥EAF∴⊥DAE=⊥DEA∴AD=DE∵AD=AF∴DE=AF∵DE//AF∴四边形AFED为平行四边形∵AD=DE∴四边形AFED是菱形.(2)解:连接DF交AE于点O,如图所示:∵⊥DAB=60°,DA=AF ∴⊥DAF为等边三角形∵AD=4∴DF=4,DO=2∴AO= 2√3,AE= 4√3∴S四边形AFED= 12×4×4√3= 8√3.20.【答案】(1)证明:∵四边形ABCD是平行四边形∴AO=CO∵⊥EAC是等边三角形∴EA=EC∴EO⊥AC∴四边形ABCD是菱形(2)解:∵四边形ABCD是菱形,AC=8∴AO=CO=4,DO=BO在Rt⊥ABO中,BO=√AB2−AO2=3∴DO=BO=3在Rt⊥EAO中,EO=√EA2−AO2=4√3∴ED=EO-DO=4√3-3.21.【答案】(1)证明:∵AE⊥BC于E,AF⊥CD于F.∴△ACE与△ACF为直角三角形∵CE=CF,AC=AC∴Rt△ACE≌Rt△ACF(HL)∴AE=AF;(2)证明:∵在▱ABCD中,AE⊥BC于E,AF⊥CD于F ∴∠B=∠D∵AE=AF(已证)∴△ABE≌△ADF(AAS)∴AB=AD∴▱ABCD为菱形.22.【答案】(1)证明:四边形ABCD是平行四边形AD⊥BC,AD=BC,AB=DCCE=BCAD=CE,AD⊥CE四边形ACED是平行四边形AB=DC,AE=ABAE=DC四边形ACED是矩形;(2)解:四边形ACED是矩形,OA= 12AE,OC=12CD,AE=CD,OA=OC⊥AOC=180°-⊥AOD=180°-120°=60°⊥AOC是等边三角形OC=AC=4CD=8.23.【答案】(1)解:如图1,如图2;(2)624.【答案】(1)证明:如图(1)∵AE 是⊥BAD 的平分线 ∴⊥BAF=⊥DAF∵在平行四边形ABCD 中 ∴AB⊥DF ,AD⊥BC ∴⊥BAF=⊥F ,⊥DAF=⊥CEF ∴⊥F=⊥DAF=⊥CEF ∴CE=FC(2)解:四边形ABFC 是矩形 理由:如图(2)∵⊥B=60°,AD⊥BC ∴⊥BAD=120° ∵⊥BAF=⊥DAF ∴⊥BAF=60°则⊥ABE 是等边三角形可得AB=BE=AE ,⊥BEA=⊥AFC=60° ∵BC=2AB ∴AE=BE=EC∴⊥ABC 是直角三角形,⊥BAC=90° 在⊥ABE 和⊥FCE 中 ∵{∠ABE =∠FCE BE =EC ∠BEA =∠CEF ∴⊥ABE⊥⊥FCE (ASA ) ∴AB=FC 又∵AB⊥FC∴四边形ABFC 是平行四边形 再由⊥BAC=90°故四边形ABFC 是矩形.。
2022年五年级数学上册试题 51《平行四边形的面积》综合练习2 西师大版(含答案)
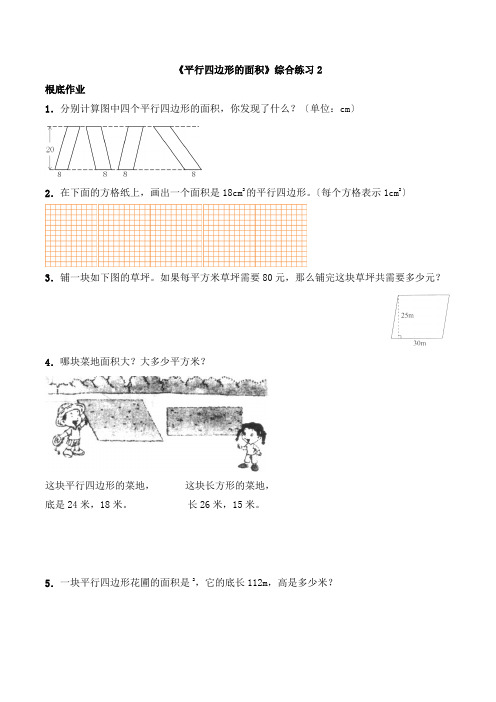
《平行四边形的面积》综合练习2根底作业1.分别计算图中四个平行四边形的面积,你发现了什么?〔单位:cm〕2.在下面的方格纸上,画出一个面积是18cm2的平行四边形。
〔每个方格表示1cm2〕3.铺一块如下图的草坪。
如果每平方米草坪需要80元,那么铺完这块草坪共需要多少元?4.哪块菜地面积大?大多少平方米?这块平行四边形的菜地,这块长方形的菜地,底是24米,18米。
长26米,15米。
5.一块平行四边形花圃的面积是2,它的底长112m,高是多少米?6.一块平行四边形的果园,高是60m,底是高的7倍,如果每棵果树占地4.5 m2,这个果园最多可种果树多少棵?7.小明用两块同样的三角形积木拼成如图的平行四边形。
〔l〕拼成的平行四边形重多少克?〔2〕每块三角一形积木的面积是多少平方厘米?培优作业8.如果要用铁丝围成下面这样的一个平行四边形,至少要用多长的铁丝?参考答案:1.8×20=160〔cm2〕四个平行四边形面积相等,都是160cm2。
发现:平行四边形的面积大小只与平行四边形的底和高有关系,与平行四边形的形状没有关系。
2.画图略。
3.30×25=750〔m2〕 80×750=60000〔元〕4.平行四边形:24×18=432〔平方米〕长方形:26×15=390〔平方米〕432-390=42〔平方米〕平行四边形菜地面积大,大42平方米。
5.85.2÷12=〔m〕6.60×7=420〔m〕 420×60=25200〔m2〕 25200÷=5600〔棵〕7.〔1〕15×l0=150〔cm2〕 150÷100×=〔g〕〔2〕150÷2=75〔cm2〕8.12×6÷9=8〔cm〕〔12+8〕×2=40〔cm〕第二课时图形的放大或缩小一、单项选择题1.一个角是60°,画在1:3的图上,应画〔〕A. 20°B. 60°C. 180°D. 无法确定2.如图,把三角形A按1∶2缩小后,得到三角形B.三角形B三条边的长分别是〔〕A. 14cm、10cm、8cmB. 3.5cm、2.5cm、4cmC. 3.5cm、2.5cm、2cm3.图形的各边按相同的比例放大或缩小后,所得到的图形〔〕不变.A. 面积B. 体积C. 周长D. 形状4.把一个长4厘米、宽2厘米的长方形,画在纸上,( )与原图形相似.A. 长4厘米,宽1厘米B. 长2厘米,宽2厘米C. 长8厘米,宽4厘米5.一个长4cm,宽2cm的长方形按2:1放大,得到的图形的面积是〔〕cm2.A. 2B. 16C. 32D. 64二、判断题6.把一个长方形按3:1放大后,它的面积是原来的3倍。
平行四边形练习题及答案

平行四边形练习题及答案一、解答题1.如图,在矩形ABCD 中,点E 是AD 上的一点(不与点A ,D 重合),ABE ∆沿BE 折叠,得BEF ,点A 的对称点为点F .(1)当AB AD =时,点F 会落在CE 上吗?请说明理由.(2)设()01AB m m AD=<<,且点F 恰好落在CE 上. ①求证:CF DE =.②若AE n AD=,用等式表示m n ,的关系. 2.如图1所示,把一个含45°角的直角三角板ECF 和一个正方形ABCD 摆放在一起,使三角板的直角顶点和正方形的顶点C 重合,点E ,F 分别在正方形的边CB ,CD 上,连接AE 、AF .(1)求证:AE =AF ;(2)取AF 的中点M ,EF 的中点N ,连接MD ,MN .则MD ,MN 的数量关系是 ,MD 、MN 的位置关系是(3)将图2中的直角三角板ECF ,绕点C 旋转180°,如图3所示,其他条件不变,则(2)中的两个结论还成立吗?若成立,请加以证明;若不成立,请说明理由.3.如图,在正方形ABCD 中,E 是边AB 上的一动点(不与点A 、B 重合),连接DE ,点A 关于直线DE 的对称点为F ,连接EF 并延长交BC 于点G ,连接DG ,过点E 作EH DE ⊥交DG 的延长线于点H ,连接BH .(1)求证:GF GC =;(2)用等式表示线段BH 与AE 的数量关系,并证明.4.如图,点P 是正方形ABCD 内的一点,连接,CP 将线段CP 绕点C 顺时针旋转90,︒得到线段,CQ 连接,BP DQ .()1如图甲,求证:CBP CDQ ∠=∠;()2如图乙,延长BP 交直线DQ 于点E .求证:BE DQ ⊥;()3如图丙,若BCP 为等边三角形,探索线段,PD PE 之间的数量关系,并说明理由.5.如图.正方形ABCD的边长为4,点E从点A出发,以每秒1个单位长度的速度沿射线AD运动,运动时间为t秒(t>0),以AE为一条边,在正方形ABCD左侧作正方形AEFG,连接BF.(1)当t=1时,求BF的长度;(2)在点E运动的过程中,求D、F两点之间距离的最小值;(3)连接AF、DF,当△ADF是等腰三角形时,求t的值.6.已知正方形ABCD与正方形(点C、E、F、G按顺时针排列),是的中点,连接,.(1)如图1,点E在上,点在的延长线上,求证:DM=ME,DM⊥.ME简析:由是的中点,AD∥EF,不妨延长EM交AD于点N,从而构造出一对全等的三角形,即≌ .由全等三角形性质,易证△DNE是三角形,进而得出结论.(2)如图2,在DC的延长线上,点在上,(1)中结论是否成立?若成立,请证明你的结论;若不成立,请说明理由.(3)当AB=5,CE=3时,正方形的顶点C 、E 、F 、G 按顺时针排列.若点E 在直线CD 上,则DM= ;若点E 在直线BC 上,则DM= .7.如图,在四边形OABC 是边长为4的正方形点P 为OA 边上任意一点(与点O A 、不重合),连接CP ,过点P 作PM CP ⊥,且PM CP =,过点M 作MN AO ∥,交BO 于点,N 联结BM CN 、,设OP x =.(1)当1x =时,点M 的坐标为( , )(2)设CNMB S y =四形边,求出y 与x 的函数关系式,写出函数的自变量的取值范围.(3)在x 轴正半轴上存在点Q ,使得QMN 是等腰三角形,请直接写出不少于4个符合条件的点Q 的坐标(用x 的式子表示)8.如图,四边形ABCD 为矩形,C 点在x 轴上,A 点在y 轴上,D(0,0),B(3,4),矩形ABCD 沿直线EF 折叠,点B 落在AD 边上的G 处,E 、F 分别在BC 、AB 边上且F(1,4).(1)求G 点坐标(2)求直线EF 解析式(3)点N 在坐标轴上,直线EF 上是否存在点M ,使以M 、N 、F 、G 为顶点的四边形是平行四边形?若存在,直接写出M 点坐标;若不存在,请说明理由9.如图,在平行四边形 ABCD 中,AD=30 ,CD=10,F 是BC 的中点,P 以每秒1 个单位长度的速度从 A 向 D 运动,到D 点后停止运动;Q 沿着A B C D →→→ 路径以每秒3个单位长度的速度运动,到D 点后停止运动.已知动点 P ,Q 同时出发,当其中一点停止后,另一点也停止运动. 设运动时间为 t 秒,问:(1)经过几秒,以 A ,Q ,F ,P 为顶点的四边形是平行四边形(2)经过几秒,以A ,Q ,F , P 为顶点的四边形的面积是平行四边形 ABCD 面积的一半?10.已知三角形纸片ABC 的面积为48,BC 的长为8.按下列步骤将三角形纸片ABC 进行裁剪和拼图:第一步:如图1,沿三角形ABC 的中位线DE 将纸片剪成两部分.在线段DE 上任意..取一点F ,在线段BC 上任意..取一点H ,沿FH 将四边形纸片DBCE 剪成两部分; 第二步:如图2,将FH 左侧纸片绕点D 旋转180°,使线段DB 与DA 重合;将FH 右侧纸片绕点E 旋转180°,使线段EC 与EA 重合,再与三角形纸片ADE 拼成一个与三角形纸片ABC 面积相等的四边形纸片.图1 图2(1)当点F ,H 在如图2所示的位置时,请按照第二步的要求,在图2中补全拼接成的四边形;(2)在按以上步骤拼成的所有四边形纸片中,其周长的最小值为_________.【参考答案】***试卷处理标记,请不要删除一、解答题1.(1)不会,理由见解析;(2)①见解析;②²²20m n n =+-【分析】(1)根据BEF BEA ≅得到BF BA =,根据三角形的三边关系得到BC BF BA >=,与已知矛盾;(2)①根据90BFC BFE ∠=∠=︒、DEC FCB ∠=∠和BF=CD ,利用AAS 证得BCF CED ≅,根据全等三角形的性质即可证明;②设1AD =,则可表示出AE 和AB ,然后根据等角对等边证得CE=CB ,然后在Rt CDE ∆中应用勾股定理即可求解.【详解】(1) 由折叠知BEF BEA ≅ ,所以90BF BA BFE A =∠=∠=︒, .若点F 在CE 上,则90BFC ∠=︒,BC BF BA >=,与AB AD =矛盾,所以点F 不会落在CE 上.(2)①因为()01AB m m AD=<<,则AB AD < , 因为点F 落在CE 上,所以90BFC BFE ∠=∠=︒ ,所以BF BA CD == .因为//AD BC ,所以DEC FCB ∠=∠ ,所以BCF CED ≅ ,所以CF DE =.②若AE n AD=,则AE nAD =. 设1AD =,则AE n AB m ==,.因为//AD BC ,所以BEA EBC ∠=∠ .因为BEF BEA ∠=∠ ,所以EBC BEC ∠=∠ ,所以1CE CB AD === .在Rt CDE ∆中,11DE n CE CD m ===一,, ,所以22211()n m -+= ,所以²²20m n n =+-.故答案为(1)不会,理由见解析;(2)①见解析;②²²20m n n =+-.【点睛】本题考查了三角形全等的性质和判定,和等边对等角,此题属于矩形的折叠问题类综合题,熟练掌握三角形全等的性质,和做出示意图是本题的关键.2.(1)见解析;(2)相等,垂直;(3)成立,理由见解析【分析】(1)由等腰直角△ECF 得到CE=CF ,再由正方形ABCD 进一步得到BE=DF ,最后证明△ABE ≌△ADF 即可求解;(2)MN是△AEF的中位线,得到AE=2MN,又M是直角三角形ADF斜边上的中点,得到AF=2MD,再由(1)中的AE=AF即可得到MN=MD;由∠DMF=∠DAF+∠ADM,∠FMN=∠FAE,∠DAF=∠BAE,∠ADM=∠DAF=∠BAE,由此得到∠DMN=∠BAD=90°;(3)连接AE,同(1)中方法证明△ABE≌△ADF,进而得到AE=AF,此时MN是△AEF中位线,MD是直角△ADF斜边上的中线,证明方法等同(2)中即可求解.【详解】解:(1)证明:如图1中,∵四边形ABCD是正方形∴AB=AD=BC=CD,∠B=∠ADF=90°,∵△CEF是等腰直角三角形,∠C=90°,∴CE=CF,∴BC﹣CE=CD﹣CF,即BE=DF,∴△ABE≌△ADF(SAS),∴AE=AF.(2)如图2中,MD,MN的数量关系是相等,MD、MN的位置关系是垂直,理由如下:∵在Rt△ADF中DM是斜边AF的中线,∴AF=2DM,∵MN是△AEF的中位线,∴AE=2MN,由(1)知:AE=AF,∴DM=MN;∵∠DMF=∠DAF+∠ADM,AM=MD,∵∠FMN=∠FAE,∠DAF=∠BAE,∴∠ADM=∠DAF=∠BAE,∴∠DMN=∠BAD=90°,∴DM⊥MN,故答案为:相等,垂直;(3)如图3中,(2)中的两个结论还成立,理由如下:连接AE,交MD于点G,如下图所示,∵点M为AF的中点,点N为EF的中点,∴MN∥AE,MN=1AE,2由(1)同理可证,AB=AD=BC=CD,∠B=∠ADF,CE=CF,又∵BC+CE=CD+CF,即BE=DF,∴△ABE≌△ADF(SAS),∴AE=AF,在Rt△ADF中,∵点M为AF的中点,∴DM=1AF,2∴DM=MN,∵△ABE≌△ADF,∴∠1=∠2,∵AB∥DF,∴∠1=∠3,同理可证:∠2=∠4,∴∠3=∠4,∵DM=AM,∴∠MAD=∠5,∴∠DGE=∠5+∠4=∠MAD+∠3=90°,∵MN∥AE,∴∠DMN=∠DGE=90°,∴DM⊥MN.故答案为:仍成立.【点睛】本题考查了正方形的性质、三角形的中位线、直角三角形斜边上的中线等于斜边的一半,三角形全等几何知识,熟练掌握各图形的性质是解决本题的关键.3.(1)详见解析;(2)2BH AE,理由详见解析【分析】1)如图1,连接DF,根据对称得:△ADE≌△FDE,再由HL证明Rt△DFG≌Rt△DCG,可得结论;(2)如图2,作辅助线,构建AM=AE,先证明∠EDG=45°,得DE=EH,证明△DME≌△EBH,则EM=BH,根据等腰直角△AEM得:2=,得结论;EM AE【详解】证明:(1)如图1,连接DF ,∵四边形ABCD 是正方形,∴DA DC =,90A C ∠=∠=︒,∵点A 关于直线DE 的对称点为F ,∴ADE ∆≌FDE ∆,∴DA DF DC ==,90DFE A ∠=∠=︒,∴90DFG ∠=︒,在Rt DFG ∆和Rt DCG ∆中,∵DF DC DG DG =⎧⎨=⎩∴Rt DFG ∆≌Rt DCG ∆(HL ),∴GF GC =;(2)2BH AE =,理由是:如图2,在线段AD 上截取AM ,使AM AE =,∵AD AB =,∴DM BE =,由(1)知:12∠=∠,34∠=∠,∵90ADC ∠=︒,∴123490∠+∠+∠+∠=︒,∴222390∠+∠=︒,∴2345∠+∠=︒,即45EDG ∠=︒,∵EH DE ⊥,∴90DEH ∠=︒,DEH ∆是等腰直角三角形,∴190AED BEH AED ∠+∠=∠+∠=︒,DE EH =,∴1BEH ∠=∠,在DME ∆和EBH ∆中,1DM BE BEH DE EH =⎧⎪∠=∠⎨⎪=⎩∴DME ∆≌EBH ∆∴EM BH =,Rt AEM ∆中,90A ∠=︒,AM AE =,∴EM =,∴BH ; 【点睛】本题考查了正方形的性质,全等三角形的判定定理和性质定理,对称的性质,等腰直角三角形的性质等知识,解决本题的关键是利用正方形的性质得到相等的边和相等的角,证明三角形全等,作出辅助线也是解决本题的关键.4.(1)证明见试题解析;(2)证明见试题解析;(3)△DEP 为等腰直角三角形,理由见试题解析.【分析】(1)根据正方形性质得出BC =DC ,根据旋转图形的性质得出CP =CQ 以及∠PCB =∠QCD ,从而得出三角形全等来得出结论;(2)由(1)知∠PBC =∠QBC ,BE 和CD 交点为F ,根据对顶角得出∠DFE =∠BFC ,从而说明BE ⊥QD ;(3)根据等边三角形的性质得出PB =PC =BC ,∠PBC =∠BPC =∠PCB =60°,则∠PCD =30°,根据BC =DC ,CP =CQ 得出△PCD 为等腰三角形,然后根据△DCQ 为等边三角形,从而得出∠DEP =90°,从而得出答案.【详解】(1)证明∵四边形ABCD 是正方形,∴BC =DC ,又∵将线段CP 绕点C 顺时针旋90°得到线段CQ ,∴CP =CQ ,∠PCQ =90°,∴∠PCD +∠QCD =90°,又∵∠PCB +∠PCD =90°,∴∠PCB =∠QCD在△BCP 和△DCQ 中,BC =DC ,CP =CQ ,∠PCB =∠QCD ,∴△BCP ≌△DCQ ,∴∠CBP=∠CDQ;(2)证明:∵△BCP≌△DCQ,∴∠PBC=∠QDC,∴∠DFE=∠BFC,∠FED=∠FCB=90°,∴BE⊥QD;(3)△DEP为等腰直角三角形,理由如下:∵△BPC为等边三角形,∴PB=PC=BC,∠PBC=∠BPC=∠PCB=60°,∴∠PCD=90°-60°=30°,∴∠DCQ=90°-30°=60°,又∵BC=DC,CP=CQ,∴PC=DC,DC=CQ,∴△PCD是等腰三角形,△DCQ是等边三角形,∴∠CPD=∠CDP=75°,∠CDQ=60°,∴∠EPD=180°-75°-60°=45°,∠EDP=180°-75°-60°=45°,∴∠EPD=∠EDP,PE=DE,∴∠DEP=180°-45°-45°=90°,∴△DEP是等腰直角三形.【点睛】本题考查了正方形的性质、三角形全等的判定和性质以及旋转的性质,掌握正方形的四条边相等、四个角都是直角,旋转的性质证明三角形全等是解题的关键.5.(1(2)(3)2或4【分析】(1)由勾股定理可求出答案;(2)延长AF,过点D作射线AF的垂线,垂足为H,设AH=DH=x,在Rt△AHD中,得出x2+x2=42,解方程求出x即可得出答案;(3)分AF=DF,AF=AD,AD=DF三种情况,由正方形的性质及直角三角形的性质可得出答案.【详解】解:(1)当t=1时,AE=1,∵四边形AEFG是正方形,∴AG=FG=AE=1,∠G=90°,∴BF,(2)如图1,延长AF,过点D作射线AF的垂线,垂足为H,∵四边形AGFE 是正方形,∴AE =EF ,∠AEF =90°,∴∠EAF =45°,∵DH ⊥AH ,∴∠AHD =90°,∠ADH =45°=∠EAF ,∴AH =DH ,设AH =DH =x ,∵在Rt △AHD 中,∠AHD =90°,∴x 2+x 2=42,解得x 1=﹣22(舍去),x 2=22,∴D 、F 两点之间的最小距离为22;(3)当AF =DF 时,由(2)知,点F 与点H 重合,过H 作HK ⊥AD 于K ,如图2,∵AH =DH ,HK ⊥AD ,∴AK =2AD =2, ∴t =2.当AF =AD =4时,设AE =EF =x , ∵在Rt △AEF 中,∠AEF =90°,∴x 2+x 2=42,解得x 1=﹣2(舍去),x 2=2,∴AE =2,即t =2.当AD =DF =4时,点E 与D 重合,t =4,综上所述,t 为2或22或4.【点睛】本题是四边形综合题,考查了勾股定理,正方形的性质,等腰三角形的性质等知识,解题的关键是熟练掌握正方形的性质,学会用分类讨论的思想思考问题.6.(1)等腰直角;(2)结论仍成立,见解析;(3)2或42,17.【分析】(1)结论:DM ⊥EM ,DM=EM .只要证明△AMH ≌△FME ,推出MH=ME ,AH=EF=EC ,推出DH=DE ,因为∠EDH=90°,可得DM ⊥EM ,DM=ME ;(2)结论不变,证明方法类似;(3)分两种情形画出图形,理由勾股定理以及等腰直角三角形的性质解决问题即可;【详解】解:(1) △AMN ≌ △FME ,等腰直角.如图1中,延长EM 交AD 于H .∵四边形ABCD 是正方形,四边形EFGC 是正方形,∴0ADE DEF 90∠=∠=,AD CD =,∴//AD EF ,∴MAH MFE ∠=∠,∵AM MF =,AMH FME ∠=∠,∴△AMH ≌△FME ,∴MH ME =,AH EF EC ==,∴DH DE =,∵0EDH 90∠=,∴DM ⊥EM ,DM=ME .(2)结论仍成立.如图,延长EM 交DA 的延长线于点H,∵四边形ABCD 与四边形CEFG 都是正方形,∴0ADE DEF 90∠=∠=,AD CD =,∴AD ∥EF,∴MAH MFE ∠=∠.∵AM FM =,AMH FME ∠=∠,∴△AMF ≌△FME(ASA), …∴MH ME =,AH FE=CE =,∴DH DE =.在△DHE 中,DH DE =,0EDH 90∠=,MH ME =,∴=DM EM ,DM ⊥EM.(3)①当E 点在CD 边上,如图1所示,由(1)的结论可得三角形DME 为等腰直角三角形,则DM 的长为2DE 2,此时DE EC DC 532=-=-=,所以2DM = ②当E 点在CD 的延长线上时,如图2所示,由(2)的结论可得三角形DME 为等腰直角三角形,则DM 2,此时DE DC CE 538=+=+= ,所以42DM = ; ③当E 点在BC 上是,如图三所示,同(1)、(2)理可得到三角形DME 为等腰直角三角形,证明如下:∵四边形ABCD 与四边形CEFG 都是正方形, 且点E 在BC 上∴AB//EF ,∴HAM EFM ∠=∠,∵M 为AF 中点,∴AM=MF∵在三角形AHM 与三角形EFM 中:HAM EFM AM MFAMH EMF ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△AMH ≌△FME(ASA),∴MH ME =,AH FE=CE =,∴DH DE =.∵在三角形AHD 与三角形DCE 中:090AD DC DAH DCE AH EF =⎧⎪∠=∠=⎨⎪=⎩, ∴△AHD ≌△DCE(SAS),∴ADH CDE ∠=∠,∵∠ADC=∠ADH+∠HDC=90°,∴∠HDE=∠CDE+∠HDC=90°,∵在△DHE 中,DH DE =,0EDH 90∠=,MH ME =,∴三角形DME 为等腰直角三角形,则DM 的长为2DE 2,此时在直角三角形DCE 中2222DE DC CE 5334=+=+= ,所以DM=17【点睛】本题考查的是正方形的性质、全等三角形的判定定理和性质定理以及直角三角形的性质,灵活运用相关的定理、正确作出辅助线是解题的关键.7.(1)点M 的坐标为(51),;(2)()44y x =-()04x <<;(3)()224160Q x x +-, ()234160Q x x +- ,()24160Q x x -,()25160(224)Q x x x -<< 【分析】(1)过点M 作ME OA ⊥,由“AAS ”可证COP PEM ∆≅∆,可得4CO PE ==,1OP ME ==,即可求点M 坐标;(2)由(1)可知COP PEM ∆≅∆,设OP=x ,则可得M 点坐标为(4+x ,x ),由直线OB 解析式可得N (x ,x ),即可知MN=4,由一组对边平行而且相等的四边形是平行四边形即可证明四边形BCNM 是平行四边形,进而可求y 与x 的函数关系式;(3)首先画出符合要求的点Q 的图形,共分三种情况,第一种情况:当MN 为底边时,第二种情况:当M 为顶点MN 为腰时,第三种情况:当N 为顶点MN 为腰时,然后根据图形特征结合勾股定理求出各种情况点的坐标即可解答.【详解】解:(1)如图,过点M 作ME OA ⊥,CP PM ⊥90CPO MPE ∴∠+∠=︒,且90CPO PCO ∠+∠=︒PCO MPE ∴∠=∠,且CP PM =,90COP PEM ∠=∠=︒()COP PEM AAS ∴∆≅∆4CO PE ∴==,1OP ME ==5OE ∴=∴点M 坐标为(5,1)故答案为(5,1)(2)由(1)可知COP PEM ∆≅∆4CO PE ∴==,OP ME x ==∴点M 坐标为(4,)x x +四边形OABC 是边长为4的正方形,∴点(4,4)B∴直线BO 的解析式为:y x =//MN AO ,交BO 于点N ,∴点N 坐标为(,)x x4MN BC ∴==,且//BC MN∴四边形BCNM 是平行四边形4(4)y x ∴=- (04)x <<(3)在x 轴正半轴上存在点Q ,使得QMN ∆是等腰三角形,此时点Q 的坐标为:1(2,0)Q x +,22(416Q x x +-,0),23(416Q x x ++-,240)(16Q x x +-250)(16Q x x -,0)其中(04)x <<,理由:当(2)可知,(04)OP x x =<<,4MN PE ==,//MN x 轴,所以共分为以下几种请:第一种情况:当MN 为底边时,作MN 的垂直平分线,与x 轴的交点为1Q ,如图2所示111222PQ PE MN ===, 12OQ x ∴=+,1(2,0)Q x ∴+第二种情况:如图3所示,当M 为顶点MN 为腰时,以M 为圆心,MN 的长为半径画弧交x 轴于点2Q 、3Q ,连接2MQ 、3MQ ,则234MQ MQ ==,2222Q E MQ ME ∴=-222416OQ OE Q E x x ∴=-=+-,22(416Q x x ∴+-0),32Q E Q E =,233416OQ OE Q E x x =+=+-23(416Q x x ∴++-0);第三种情况,当以N 为顶点、MN 为腰时,以N 为圆心,MN 长为半径画圆弧交x 轴正半轴于点4Q ,当022x <<4所示,则2224416PQ NQ NP x =-=-,24416OQ OP PQ x x ∴=+=+-,即24(16Q x x +-,0).当22x =时,则4ON =,此时Q 点与O 点重合,舍去;当224x <<时,如图5,以N 为圆心,MN 为半径画弧,与x 轴的交点为4Q ,5Q .4Q 的坐标为:24(16Q x x -0).2516OQ x x =-25(16Q x x ∴-0)所以,综上所述,1(2,0)Q x +,22(416Q x x +-,0),23(416Q x x ++-,240)(16Q x x +-250)(16Q x x -,0)使QMN ∆是等腰三角形.【点睛】本题考查四边形综合题,解题的关键是明确题意,画出相应的图象,找出所求问题需要的条件,利用数形结合的思想解答问题.8.(1)G (0,32)343y x =-++3)234434366433,,3,(1,423),3333M M M ⎛⎛⎛---+ ⎝⎝⎝. 【解析】【分析】1(1)由F(1,4),B(3,4),得出AF=1,BF=2,根据折叠的性质得到GF=BF=2,在Rt△AGF中,利用勾股定理求出AG=,那么OG=OA-AG=4-,于是G(0,);(2)先在Rt△AGF中,由tan1AGAFGAF∠===,得出∠AFG=60°,再由折叠的性质得出∠GFE=∠BFE=60°,解Rt△BFE,求出BE=BF tan60°,那么CE=4-2E(3,.设直线EF的表达式为y=kx+b,将E(3,F(1,4)代入,利用待定系数法即可求出直线EF的解析.(3)因为M、N均为动点,只有F、G已经确定,所以可从此入手,结合图形,按照FG为一边,N点在x轴上;FG为一边,N点在y轴上;FG为对角线的思路,顺序探究可能的平行四边形的形状.确定平行四边形的位置与形状之后,利用平行四边形及平移的性质求得M点的坐标.【详解】解:(1)∵F(1,4),B(3,4),∴AF=1,BF=2,由折叠的性质得:GF=BF=2,在Rt△AGF中,由勾股定理得,AG==∵B(3,4),∴OA=4,∴∴G(0,(2)在Rt△AGF中,∵tan1AGAFGAF∠===,∴∠AFG=60°,由折叠的性质得知:∠GFE=∠BFE=60°,在Rt△BFE中,∵BE=BF tan60°,.E(3,).设直线EF的表达式为y=kx+b,∵E(3,F(1,4),∴344k bk b⎧+=-⎪⎨+=⎪⎩解得4kb⎧=⎪⎨=+⎪⎩∴4y=++;(3)若以M 、N 、F 、G 为顶点的四边形是平行四边形,则分如下四种情况: ①FG 为平行四边形的一边,N 点在x 轴上,GFMN 为平行四边形,如图1所示. 过点G 作EF 的平行线,交x 轴于点N 1,再过点N :作GF 的平行线,交EF 于点M ,得平行四边形GFM 1N 1.∵GN 1∥EF ,直线EF 的解析式为343,(0,43)y x G =-++- ∴直线GN 1的解析式为34-3y x =-+,当y=0时,1433433,,033x N ⎛⎫--= ⎪ ⎪⎝⎭. ∵GFM 1N 1是平行四边形,且G (0,4-3),F (1,4),N 1(4333- ,0), ∴M ,(433,3);②FG 为平行四边形的一边,N 点在x 轴上,GFNM 为平行四边形,如图2所示. ∵GFN 2M 2为平行四边形,∴GN ₂与FM 2互相平分.∴G (0,3N2点纵坐标为0∴GN :中点的纵坐标为32-, 设GN ₂中点的坐标为(x ,32.∵GN2中点与FM2中点重合,∴3 34322 x-++=-∴x=4396+∵.GN2的中点的坐标为(4393,262+-),.∴N2点的坐标为(4393+,0).∵GFN2M2为平行四边形,且G(0,4-3),F(1,4),N2(4393+,0),∴M2(436,33+-);③FG为平行四边形的一边,N点在y轴上,GFNM为平行四边形,如图3所示.∵GFN3M3为平行四边形,.∴GN3与FM3互相平分.∵G(0,3N2点横坐标为0,.∴GN3中点的横坐标为0,∴F与M3的横坐标互为相反数,∴M3的横坐标为-1,当x=-1时,y=3(1)4343-+=+∴M3(-1,3④FG 为平行四边形的对角线,GMFN 为平行四边形,如图4所示.过点G 作EF 的平行线,交x 轴于点N 4,连结N 4与GF 的中点并延长,交EF 于点M 。
小学四五年级数学《平行四边形的面积》经典看图做题练习题及参考答案

平行四边形面积练习题+答案
1.画出下列图形底边的高。
2.求下面平行四边形的面积。
3.已知正方形的边长是6厘米,平行四边形的面积是多少?
4.完成下表。
5.爷爷种了一块平行四边形菜地,每平方米收获15千克西红柿,这块地能收获多少千克西红柿?
6.下面平行四边形的面积是
7.5×6=45(cm)。
对吗?为什么?
7.一个平行四边形,高2.8米,比底边短0.5米,它的面积是多少平方米?
8.一块平行四边形草地,底长20米,高是底的一半,如果每平方米的草可供4头小羊吃一天,这块草地可供多少只羊吃一天?参考答案:1、略 2、250m 180dm 30cm 3、36cm
4、36.4c㎡ 12dm 25m (从上往下)
5、11250千克
6、不对,应该是底乘以与它对应的高,7.5×4=30(c㎡)
7、9.24平方米
8、800只。
小学数学认识平行四边形练习题及答案

小学数学认识平行四边形练习题及答案平行四边形是小学数学中的一个重要概念,它在几何学中具有丰富的性质和应用。
通过练习题的方式,可以帮助小学生更好地理解和掌握平行四边形的特点和运用方法。
本文将针对小学数学认识平行四边形的练习题及答案进行详细介绍。
练习题一:1. 填写下列图形中相等的角度:(1) ∠ABC = ______ ∠CDA = ______(2) ∠BAD = ______ ∠ADC = ______2. 判断下列图形是否为平行四边形:(1)AB || CDAD || BCAB ≠ AC(2)PQ || RSPS || QRPS = QR3. 在下列图形中连接相对的顶点,判断是否形成平行四边形:(1)O——A\ /B——C(2)I——J\ \K——L练习题二:1. 在平行四边形ABCD中,若∠A = 40°,请计算:(1) ∠C = ______(2) ∠B = ______(3) ∠D = ______2. 在平行四边形WXYZ中,若∠Z = 90°,请计算:(1) ∠Y = ______(2) ∠X = ______(3) ∠W = ______3. 已知平行四边形EFGH中,EF = 6 cm,EG = 8 cm,计算其面积。
答案及解析:练习题一:1.(1) ∠ABC = ∠CDA(2) ∠BAD = ∠ADC2.(1) 是平行四边形,因为根据定义,AB || CD,AD || BC,并且AB ≠ AC。
(2) 不是平行四边形,因为虽然PQ || RS,PS || QR,但是PS ≠ QR,无法满足平行四边形的定义。
3.(1) 形成平行四边形,因为OB || AC,OA || BC。
(2) 不是平行四边形,因为IK和JL不平行。
练习题二:1.(1) ∠C = ∠A = 40°,根据平行四边形的性质,相对角相等。
(2) ∠B = ∠D = 180° - ∠A = 180° - 40° = 140°,根据角的性质,相邻补角和为180°。
第六单元平行四边形面积的实际应用“拓展型”专项练习-五年级数学(解析版)人教版

2023-2024学年五年级数学上册典型例题系列第六单元:平行四边形面积的实际应用“拓展型”专项练习1.下图中两个平行四边形的面积相等吗?它们的面积各是多少?【答案】相等;4.2平方厘米【分析】观察图形可知,两个平行四边形的底都是2.8厘米,高都是1.5厘米,根据平行四边形的面积公式:S=ah,据此代入数值进行计算即可。
【详解】2.8×1.5=4.2(平方厘米)答:图中两个平行四边形的面积相等,它们的面积都是4.2平方厘米。
【点睛】本题考查平行四边形的面积,熟记公式是解题的关键。
2.下面4个平行四边形的面积一样大吗,你发现了什么规律?(单位:cm)【答案】一样大不管平行四边形的形状如何,只要底和高分别相等,面积就相等。
【分析】观察题图可知,4个平行四边形在一组平行线内,说明它们的高相等;它们的底都是1cm,说明底也相等。
平行四边形的面积=底×高,它们四个等底等高,所以面积相等,与它们的形状无关。
【详解】4个平行四边形的面积一样大。
发现:不管平行四边形的形状如何,只要底和高分别相等,面积就相等。
【点睛】明确4个平行四边形等底等高是解答本题的关键。
3.李伯伯积极响应社会主义新农村建设的号召,准备将一块周长为480米的直角梯土地分割成一块三角形和一块平行四边形菜地,计划利用平行四边形菜地种植花菜,请你帮李伯伯在图上分一分,并计算出花菜的种植面积。
【答案】作图见详解;7200平方米【分析】是在同一个平面内,由两组平行线段组成的闭合图形是平行四边形;由三条线段首尾相连围成的封闭图形是三角形,据此将梯形分割成一个三角形和一个平行四边形;梯形周长减去已知的3条边的长度是梯形的高,即平行四边形的高,平行四边形的底=梯形的上底,根据平行四边形面积=底×高,列式解答即可。
【详解】120×(480-120-100-200)=120×60=7200(平方米)答:花菜的种植面积是7200平方米。
数学五年级上册《平行四边形的面积》练习题(含答案)

【同步专练A 】6.1 平行四边形的面积(基础应用篇)一、单选题(共10题)1.两个完全一样的梯形可以拼成一个平行四边形,这个平行四边形的底等于( ).A . 梯形的上底B . 梯形的下底C . 梯形的高D . 梯形的上、下底之和2.一个平行四边形与一个三角形等底且面积相等,如果三角形的高是9厘米,那么平行四边形的高是()厘米.A . 4.5B . 9C . 18D .223.平行四边形的底不变,高扩大2倍,它的面积().A . 扩大2倍B . 缩小2倍C . 无法确定D .扩大10倍4.一个三角形和一个平行四边形的底和面积都相等,那么三角形的高()A . 和平行四边形的高相等B . 是平行四边形高的一半C . 是平行四边形高的2倍D . 是平行四边形高的4倍5.三角形和平行四边形的底相等,面积也相等.已知平行四边形的高是4厘米,三角形的高是()厘米.A . 16B . 8C . 4D .156.如果三角形与平行四边形的面积与底都相等,已知平行四边形的高是8厘米,那么三角形的高应该是()厘米.A . 4B . 8C . 16D . 无法确定7.一个平行四边形的底不变,高扩大到原来的4倍,它的面积( ).A . 扩大到原来的4倍B . 扩大到原来的2倍C . 不变D . 缩小到原来的8.有两个完全一样的梯形,它们的面积都是28平方厘米,把它们拼成一个平行四边形后,平行四边形的底是14厘米,高是()厘米.A . 3B . 4C . 8D .119.如图,平行四边形的面积是()平方厘米.A . 32B . 24C . 48D . 以上答案都不对10.一个平行四边形木框,拉成长方形后,面积().A . 变小B . 变大C . 不变D . 无法确定二、填空题(共10题)11.一个三角形的面积是25C m2 , 和它等底等高的平行四边形的面积是________.12.一个平行四边形的面积是156平方米,底是12米,高是________.13.一个三角形的底边长25厘米,高15厘米,这个三角形的面积是________平方厘米,和它等底等高的平行四边形的面积是________平方厘米.14.一个三角形的底是2.5m,高是2.8m,它的面积是________ m2 , 和它等底等高的平行四边形的面积是________ m2.15.一个三角形与一个平行四边形等底等高,如果三角形的面积是3.6平方分米,那么平行四边形的面积是________平方分米.16.一个平行四边形的面积是56平方分米,高4分米,底是________分米.17.一个正方形的周长是32C m,那么它的边长是________C m,面积是________ C m² .18.把一个长方形框架拉成平行四边形,这个平行四边形与原来的长方形相比,它的周长________,面积________.A 、比原来大B 、比原来小C 、与原来一样大D .无法比较19.一个三角形与一个平行四边形面积相等,底也相等.如果三角形的高是14厘米,那么平行四边形的高是________厘米.20.一个平行四边形的面积是30C m2 , 与它等底等高的三角形的面积是________.三、判断题(共10题)21.三角形的面积总是平行四边形面积的一半.()22.平行四边形的面积大于梯形面积. ()23.两个完全一样的梯形能拼成一个长方形.()24.平行四边形的两组对边不但平行,而且相等. ()25.平行四边形的面积等于三角形面积的2倍.()26.面积相等的两个平行四边形,它们的底和高不一定相等. ()27.把一个长方形木框拉成平行四边形,它的周长和面积都不变.28.周长相等的长方形和平行四边形,面积不一定相等.()29.把一个木条钉成的长方形拉成一个平行四边形,它的面积不变.30.一个平行四边形的底扩大4倍,面积就扩大4倍.()四、计算题(共2题)31.计算下面图形的面积.(1)(2)(3)32.计算如图各图形的面积.五、解决问题(共6题)33.一块占地3.9公顷的平行四边形地,高80米,底是多少米?34. 一块近似平行四边形的苗圃,在苗圃中有一条小路(如图),请你求出苗圃的实际面积是多少平方米?35.有一块平行四边形的荔枝地,它的底是50米,高是24米.36.李大叔要在一块底是93m,高是15m的平行四边形的土地上栽果树,如果每棵果树占地4.5m2 , 这块土地一共能栽多少棵果树?37.一个平行四边形的钢板,底是2.4 m,高是0.5 m.如果每平方米钢板重39 kg,这块钢板大约重多少千克?(得数保留整数)38.用木条做成一个长方形框,如果把它拉成一个平行四边形,发生了怎样的变化?请判断并说明理由.参考答案一、单选题1. D2. A3. A4. C5. B6. C7. A8. B9. B10. B二、填空题11. 50平方厘米12. 13米13. 187.5;37514. 3.5;715. 7.216. 1417. 8;6418. C ;B19. 720. 15平方厘米三、判断题21. ×22. ×23. ×24. √25. ×26. √27. ×28. √29. ×30. ×四、计算题31.(1)解:19×13=247平方米(2)解:26×14=364平方分米(3)解:27.5×13=357.5平方厘米32.解:①3.5×2÷2=3.5(平方厘米)答:三角形的面积是3.5平方厘米.②3×2=6(平方厘米)答:平行四边形的面积是6平方厘米.③(2.5+4)×2÷2=6.5×2÷2=6.5(平方厘米)答:梯形的面积是6.5平方厘米五、解决问题33.解:3.9公顷=39000平方米,39000÷80=487.5(米)答:底是487.5米.34.解: 48×24-48×2=48×(24-2)=48×22=1056(平方米)答:苗圃的实际面积是1056平方米.35. 解:50×24÷3=1200÷3=400(棵)答:这块地可以种400棵荔枝树.36. 解:93×15÷4.5=1395÷4.5=310(棵)答:这块土地一共能栽310棵果树.37. 解:2.4×0.5×39=1.2×39≈47(千克)答:这块钢板大约重47千克.38. 解:面积变小了.理由:长方形的面积等于长乘宽,长方形拉成四边形,长和底相等,但是平行四边形的高比长方形的宽短.。
平行四边形练习题及答案

平行四边形练习题及答案一、解答题1.在四边形ABCD中,AD∥BC,AB=8cm,AD=16cm,BC=22cm,∠ABC=90°.点P从点A 出发,以1cm/s的速度向点D运动,点Q从点C同时出发,以3cm/s的速度向点B运动,其中一个动点到达端点时,另一个动点也随之停止运动,设运动时间为t秒.(1)当t= 时,四边形ABQP成为矩形?(2)当t= 时,以点P、Q与点A、B、C、D中的任意两个点为顶点的四边形为平行四边形?(3)四边形PBQD是否能成为菱形?若能,求出t的值;若不能,请说明理由,并探究如何改变Q点的速度(匀速运动),使四边形PBQD在某一时刻为菱形,求点Q的速度.2.正方形ABCD中,对角线AC与BD交于点O,点P是正方形ABCD对角线BD上的一个动点(点P不与点B,O,D重合),连接CP并延长,分别过点D,B向射线作垂线,垂足分别为点M,N.(1)补全图形,并求证:DM=CN;(2)连接OM,ON,判断OMN的形状并证明.3.如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.(1)求证:四边形BCEF是平行四边形;(2)若∠DEF=90°,DE=8,EF=6,当AF为时,四边形BCEF是菱形.4.在矩形ABCD中,连结AC,点E从点B出发,以每秒1个单位的速度沿着B A 的路径运动,运动时间为t(秒).以BE为边在矩形ABCD的内部作正方形BEHG.(1)如图,当ABCD 为正方形且点H 在ABC ∆的内部,连结,AH CH ,求证:AH CH =;(2)经过点E 且把矩形ABCD 面积平分的直线有______条;(3)当9,12AB BC ==时,若直线AH 将矩形ABCD 的面积分成1:3两部分,求t 的值.5.已知:在ABC 中,∠BAC=90°,AB=AC ,点D 为直线BC 上一动点(点D 不与B 、C 重合).以AD 为边作正方形ADEF ,连接CF .(1)如图1,当点D 在线段BC 上时,BD 与CF 的位置关系为__________;CF 、BC 、CD 三条线段之间的数量关系____________________.(2)如图2,当点D 在线段BC 的延长线上时,其它条件不变,请你写出CF 、BC 、CD 三条线段之间的数量关系并加以证明;(3)如图3,当点D 在线段BC 的反向延长线上时,且点A 、F 分别在直线BC 的两侧,其它条件不变:①请直接写出CF 、BC 、CD 三条线段之间的关系.②若连接正方形对角线AE 、DF ,交点为O ,连接OC ,探究AOC △的形状,并说明理由.6.如图,在平面直角坐标系中,已知▱OABC 的顶点A (10,0)、C (2,4),点D 是OA 的中点,点P 在BC 上由点B 向点C 运动.(1)求点B 的坐标;(2)若点P 运动速度为每秒2个单位长度,点P 运动的时间为t 秒,当四边形PCDA 是平行四边形时,求t 的值;(3)当△ODP 是等腰三角形时,直接写出点P 的坐标.7.感知:如图①,在正方形ABCD 中,E 是AB 一点,F 是AD 延长线上一点,且DF BE =,求证:CE CF =;拓展:在图①中,若G 在AD ,且45GCE ∠︒=,则GE BE GD +=成立吗?为什么? 运用:如图②在四边形ABCD 中,()//AD BC BC AD >,90A B ∠∠︒==,16AB BC ==,E 是AB 上一点,且45DCE ∠︒=,4BE =,求DE 的长.8.如图,点A 的坐标为(6,6)-,AB x ⊥轴,垂足为B ,AC y ⊥轴,垂足为C ,点,D E 分别是射线BO 、OC 上的动点,且点D 不与点B 、O 重合,45DAE ︒∠=.(1)如图1,当点D 在线段BO 上时,求DOE ∆的周长;(2)如图2,当点D 在线段BO 的延长线上时,设ADE ∆的面积为1S ,DOE ∆的面积为2S ,请猜想1S 与2S 之间的等量关系,并证明你的猜想.9.如图①,在ABC 中,AB AC =,过AB 上一点D 作//DE AC 交BC 于点E ,以E 为顶点,ED 为一边,作DEF A ∠=∠,另一边EF 交AC 于点F .(1)求证:四边形ADEF 为平行四边形;(2)当点D 为AB 中点时,ADEF 的形状为 ;(3)延长图①中的DE 到点,G 使,EG DE =连接,,,AE AG FG 得到图②,若,AD AG =判断四边形AEGF 的形状,并说明理由.10.如图,已知正方形ABCD 与正方形CEFG 如图放置,连接AG ,AE .(1)求证:AG AE =(2)过点F 作FP AE ⊥于P ,交AB 、AD 于M 、N ,交AE 、AG 于P 、Q ,交BC 于H ,.求证:NH =FM【参考答案】***试卷处理标记,请不要删除一、解答题1.(1)112;(2)112或4;(3)四边形PBQD 不能成为菱形 【分析】 (1)由∠B=90°,AP ∥BQ ,由矩形的判定可知当AP=BQ 时,四边形ABQP 成为矩形; (2)由(1)可求得点P 、Q 与点A 、B 为顶点的四边形为平行四边形;然后由当PD=CQ 时,CDPQ 是平行四边形,求得t 的值;(3)由PD ∥BQ ,当PD=BQ=BP 时,四边形PBQD 能成为菱形,先由PD=BQ 求出运动时间t 的值,再代入求BP ,发现BP≠PD ,判断此时四边形PBQD 不能成为菱形;设Q 点的速度改变为vcm/s 时,四边形PBQD 在时刻t 为菱形,根据PD=BQ=BP 列出关于v 、t 的方程组,解方程组即可求出点Q 的速度.【详解】(1)如图1,∵∠B=90°,AP ∥BQ ,∴当AP=BQ 时,四边形ABQP 成为矩形,此时有t=22﹣3t ,解得t=112. ∴当t=112时,四边形ABQP 成为矩形; 故答案为112; (2)如图1,当t=112时,四边形ABQP 成为矩形, 如图2,当PD=CQ 时,四边形CDPQ 是平行四边形,则16﹣t=3t ,解得:t=4, ∴当t=112或4时,以点P 、Q 与点A 、B 、C 、D 中的任意两个点为顶点的四边形为平行四边形; 故答案为112或4; (3)四边形PBQD 不能成为菱形.理由如下:∵PD ∥BQ ,∴当PD=BQ=BP 时,四边形PBQD 能成为菱形.由PD=BQ ,得16﹣t=22﹣3t ,解得:t=3,当t=3时,PD=BQ=13,BP=22AB AP + =228t +=2283+=73≠13,∴四边形PBQD 不能成为菱形;如果Q 点的速度改变为vcm/s 时,能够使四边形PBQD 在时刻ts 为菱形,由题意,得221622168t vtt t-=-⎧⎪⎨-=+⎪⎩,解得62t v =⎧⎨=⎩. 故点Q 的速度为2cm/s 时,能够使四边形PBQD 在某一时刻为菱形.【点睛】此题属于四边形的综合题.考查了矩形的判定、菱形的判定以及勾股定理等知识.注意掌握分类讨论思想与方程思想的应用是解此题的关键.2.(1)见解析;(2)MON 为等腰直角三角形,见解析【分析】(1)如图1,由正方形的性质得CB =CD ,∠BCD =90°,再证明∠BCN =∠CDM ,然后根据“AAS”证明△CDM ≌△CBN ,从而得到DM =CN ;(2)如图2,利用正方形的性质得OD =OC ,∠ODC =∠OCB =45°,∠DOC =90°,再利用∠BCN =∠CDM 得到∠OCN =∠ODM ,则根据“SAS”可判断△OCN ≌△ODM ,从而得到ON =OM ,∠CON =∠DOM ,所以∠MON =∠DOC =90°,于是可判断△MON 为等腰直角三角形.【详解】(1)证明:如图1,∵四边形ABCD 为正方形,∴CB =CD ,∠BCD =90°,∵DM ⊥CP ,BN ⊥CP ,∴∠DMC =90°,∠BNC =90°,∵∠CDM+∠DCM =90°,∠BCN+∠DCM =90°,∴∠BCN =∠CDM ,在△CDM 和△CBN 中DMC CNB CD CBCDM BCN ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△CDM ≌△CBN ,∴DM =CN ;(2)解:△OMN 为等腰直角三角形.理由如下:如图2,∵四边形ABCD 为正方形,∴OD =OC ,∠ODC =∠OCB =45°,∠DOC =90°,∵∠BCN =∠CDM ,∴∠BCN ﹣45°=∠CDM ﹣45°,即∠OCN =∠ODM ,在△OCN 和△ODM 中CN DM OCN ODM OC OD =⎧⎪∠=∠⎨⎪=⎩, ∴△OCN ≌△ODM ,∴ON =OM ,∠CON =∠DOM ,∴∠MON =∠DOC =90°, ∴MON 为等腰直角三角形.【点睛】本题考查正方形的性质:正方形的四条边都相等,四个角都是直角;正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角;正方形具有四边形、平行四边形、矩形、菱形的一切性质;两条对角线将正方形分成四个全等的等腰直角三角形,同时,正方形又是轴对称图形,有四条对称轴.也考查全等三角形的判定与性质.3.(1)详见解析;(2)145. 【分析】(1)由AB =DE ,∠A =∠D ,AF =DC ,易证得△ABC ≌DEF (SAS ),即可得BC =EF ,且BC ∥EF ,即可判定四边形BCEF 是平行四边形;(2)由四边形BCEF 是平行四边形,可得当BE ⊥CF 时,四边形BCEF 是菱形,所以连接BE ,交CF 与点G ,由三角形DEF 的面积求出EG 的长,根据勾股定理求出FG 的长,则可求出答案.【详解】(1)证明:∵AF =DC ,∴AC =DF ,在△ABC 和△DEF 中,AB DE A D AC DF =⎧⎪∠=∠⎨⎪=⎩,∴△ABC ≌△DEF (SAS ),∴BC =EF ,∠ACB =∠DFE ,∴BC ∥EF ,∴四边形BCEF 是平行四边形;(2)如图,连接BE ,交CF 于点G ,∵四边形BCEF 是平行四边形,∴当BE ⊥CF 时,四边形BCEF 是菱形,∵∠DEF =90°,DE =8,EF =6,∴DF 222286DE EF +=+10,∴S △DEF 1122EG DF EF DE =⋅=⋅, ∴EG 6824105⨯==, ∴FG =CG 22222418655EF EG ⎛⎫=-=-= ⎪⎝⎭, ∴AF =CD =DF ﹣2FG =10﹣365=145. 故答案为:145. 【点睛】本题考查了全等三角形的判定与性质、平行四边形的判定与性质、菱形的判定与性质以及勾股定理等知识.熟练掌握平行四边形的判定与性质是解题的关键.4.(1)见解析;(2)1条;(3)7211t =或185t = 【分析】(1)证△AEH ≌△CGH (SAS ),即可得出AH=CH ;(2)连接BD 交AC 于O ,作直线OE 即可;(3)分两种情况:①连接AH 交BC 于M ,证出BM=CM=12BC=6,由题意得BE=BG=EH=GH=t ,则AE=9-t ,GM=6-t ,由三角形面积关系得出方程,解方程即可;②连接AH 交CD 于M ,交BC 的延长线于K ,证出DM=CM=12CD ,证△KCM ≌△ADM 得CK=DA=12,则BK=BC+CK=24,且BE=BG=EH=GH=t ,则AE=9-t ,GK=24-t ,由三角形面积关系得出方程,解方程即可.【详解】解:(1)四边形BEHG 是正方形, BE BG ∴=,90BEH BGH ∠=∠=︒,90AEH CGH ∠=∠=︒, 又AB BC =,AE CG ∴=,又EH HG =,()AEH CGH SAS ∴∆≅∆,AH CH ∴=.(2)解:连接BD 交AC 于O ,如图1所示:作直线OE ,则直线OE 矩形ABCD 面积平分,即经过点E 且把矩形ABCD 面积平分的直线有1条,故答案为:1;(3) 解:分两种情况:①如图2所示:连接AH 交BC 于M ,∵四边形ABCD 是矩形,∴△ABC 的面积=△ADC 的面积,∵直线AH 将矩形ABCD 的面积分成1:3两部分,∴△ABM 的面积=△ACM 的面积,∴BM=CM=12CD=6, 由题意得:BE=BG=EH=GH=t ,则AE=9-t ,GM=6-t ,∵△ABM 的面积=△AEH 的面积+正方形BEHG 的面积+△GHM 的面积,∴12×6×9=12t (9-t )+t ²+12t (6-t ),解得:185t=;②如图3所示:连接AH交CD于M,交BC的延长线于K,∵四边形ABCD是矩形,∴∠MCK=∠B=∠D=∠BCD=90°,AD=BC=12,CD=AB=9,△ABC的面积=△ADC的面积,∵直线AH将矩形ABCD的面积分成1:3两部分,∴△ADM的面积=△ACM的面积,∴DM=CM=12CD=92,在△KCM和△ADM中,∠=∠⎧⎪=⎨⎪∠=∠⎩D MCKDM CMAMD KMC,∴△KCM≌△ADM(ASA),∴CK=DA=12,∴BK=BC+CK=24,由题意得:BE=BG=EH=GH=t,则AE=9-t,GK=24-t,∵△ABK的面积=△AEH的面积+正方形BEHG的面积+△GHK的面积,∴12×24×9=12t(9-t)+t²+12t(24-t),解得:7211t=,综上所述,7211t=或185t=,故答案为:7211t=或185t=.【点睛】本题是四边形综合题目,考查了正方形的性质、矩形的性质、全等三角形的判定与性质、三角形面积以及分类讨论等知识;本题综合性强,熟练掌握正方形的性质和矩形的性质,证明三角形全等是解题的关键.5.(1)BD⊥CF,CF=BC-CD;(2)CF=BC+CD,见解析;(3)①CF=CD−BC,②等腰三角形,见解析【分析】(1)先说明△ABC是等腰直角三角形,利用SAS即可证明△BAD≌△CAF,从而证得CF⊥BD、CF=BD,又 BD+CD=BC, CF=BC-CD;(2)先利用SAS即可证得△BAD≌△CAF,从而证得BD=CF,即可得到CF-CD=BC;(3)①与(2)同理可得BD=CF,然后结合图形可得CF=CD-BC;②先根据等腰直角三角形的性质得到∠ABC=∠ACB=45°,再根据邻补角的定义求出∠ABD=135°,再根据同角的余角相等求出∠BAD=∠CAF,然后利用“边角边”证明△BAD≌△CAF,得∠ACF=∠ABD,求出∠FCD=90°,然后根据直角三角形斜边上的中线等于斜边的一半求出OC=12DF,再根据正方形的对角线相等求出OC=OA,从而得到△AOC是等腰三角形.【详解】(1)解:∵∠B4C=90°,AB=AC∴∠ABC=∠ACB=45°∵四边形ADEF是正方形∴AD=AF,∠DAF=90°∵∠BAC=∠BAD+∠DAC=90°,∠DAF=∠CAF+∠DAC=90°∴∠BAD=∠CAF在△BAD和△CAF中,AB=AC,∠BAD=∠CAF,AD=AF,∴△BAD≌△CAF(SAS),∴BD=CF,∠ABD=∠ACF=45°∴∠FCB=∠ACF+ ∠ACB=90°,即CF⊥BC∵BD+CD=BC∴CF+CD=BC;故答案为:BD⊥CF,CF=BC-CD;(2)证明:∵∠BAC=90°,AB=AC,∴∠ABC=∠ACB=45°,∵四边形ADEF是正方形,∴AD=AF,∠DAF=90°,∵∠BAD=∠BAC+∠DAC,∠CAF=∠DAF+∠DAC,∴∠BAD=∠CAF,在△BAD和△CAF中,AB=AC,∠BAD=∠CAF,AD=AF,∴△BAD≌△CAF(SAS),∴BD=CF,∵BD=BC+CD,∴CF=BC+CD;(3)①与(2)同理可得,BD=CF,所以,CF=CD−BC;②∵∠BAC=90°,AB=AC,∴∠ABC=∠ACB=45°,则∠ABD=180∘−45°=135°,∵四边形ADEF 是正方形,∴AD=AF ,∠DAF=90°,∵∠BAC=∠BAF+∠CAF=90°,∠DAF=∠BAD+∠BAF=90°,∴∠BAD=∠CAF ,在△BAD 和△CAF 中,AB=AC ,∠BAD=∠CAF ,AD=AF ,∴△BAD ≌△CAF(SAS),∴∠ACF=∠ABD=180°−45°=135°,∴∠FCD=∠ACF−∠ACB=90°,则△FCD 为直角三角形,∵正方形ADEF 中,O 为DF 中点,∴OC=12DF , ∵在正方形ADEF 中,OA=12AE ,AE=DF , ∴OC=OA ,∴△AOC 是等腰三角形.【点睛】本题考查了四边形的综合题,正方形的性质、全等三角形的判定与性质、等腰直角三角形的性质、等腰三角形的判定以及同角的余角相等的性质,在(1)证明三角形全等得到思路并推广到(2)(3)是解答本题的关键.6.(1)B (12,4);(2)52t s =;(3)58,4,3,4,2,4,,42 【分析】(1)由四边形OABC 是平行四边形,得到OA BC =,//OA BC ,于是得到 10OA =,2OE AF ,可求出点B 的坐标; (2)根据四边形PCDA 是平行四边形,得到PC AD =,即1025t -=,解方程即可得到结论;(3)如图2,可分三种情况:①当5PD OD 时,②当5PO OD 时,③当 PD OP =时分别讨论计算即可.【详解】解:如图1,过C 作CE OA ⊥于E ,过B 作BF OA ⊥于 F ,四边形OABC 是平行四边形,OA BC ,//OA BC , A ,C 的坐标分别为(10,0), (2,4), 10OA ∴=,2OE AF , 10BC ∴=,(12,4)B ;(2)设点P 运动t 秒时,四边形PCDA 是平行四边形,由题意得:102PC t =-,点D 是OA 的中点, 152OD BC AD OA ,四边形PCDA 是平行四边形,PC AD ,即1025t -=,52t ∴=, ∴当52t =秒时,四边形PCDA 是平行四边形; (3)如图2,①当5PDOD 时,过1P 作1PE OA 于 E ,则14PE ,3DE ∴=,1(8,4)P ,又D ,C 的坐标分别为()5,0,(2,4),∴225245CD ,即有,当点P 与点C 重合时,5PD OD ,2,4P ;②当5PO OD 时,过2P 作2P G OA 于 G , 则24P G ,3OG ∴=,2(3,4)P ;③当PD OP =时,过3P 作3P F OA 于 F , 则34P F ,52OF =, 35(2P ,4); 综上所述:当ODP ∆是等腰三角形时,点P 的坐标为(8,4), 5(2,4),(3,4),(2,4). 【点睛】本题是四边形综合题,考查了平行四边形的性质,等腰三角形的性质,勾股定理,熟练掌握平行四边形的性质和等腰三角形的性质是解题的关键.7.(1)见解析;(2)GE=BE+GD 成立,理由见解析;(3)685【分析】(1)利用已知条件,可证出△BCE ≌△DCF (SAS ),即可得到CE=CF ;(2)借助(1)的结论得出∠BCE =∠DCF ,再通过角的计算得出∠GCF =∠GCE ,由SAS 可得△ECG ≌△FCG ,则EG=GF ,从而得出GE=DF+GD=BE+GD ;(3)过C 作CG ⊥AD ,交AD 延长线于G ,先证四边形ABCG 是正方形(有一组邻边相等的矩形是正方形),再设DE =x ,利用(1)、(2)的结论,在Rt △AED 中利用勾股定理构造方程即可求出DE .【详解】(1)证明:如图①,在正方形ABCD 中,BC=CD ,∠B =∠ADC =90°,∴∠CDF=90°,即∠B =∠CDF =90°,在△BCE 和△DCF 中, BC DC B CDF BE DF =⎧⎪∠=∠⎨⎪=⎩,∴△BCE ≌△DCF (SAS ),∴CE=CF ;(2)解:如图①,GE=BE+GD 成立,理由如下:由(1)得△BCE ≌△DCF ,∴∠BCE=∠DCF ,∴∠ECD +∠ECB=∠ECD +∠FCD ,即∠ECF =∠BCD =90°,又∵∠GCE =45°,∴∠GCF =∠ECF −∠ECG =45°,则∠GCF=∠GCE ,在△GEC 和△GFC 中,CE CF GCE GCF GC GC =⎧⎪∠=∠⎨⎪=⎩,∴△GEC ≌△GFC (SAS ),∴EG=GF ,∴GE=DF+GD=BE+GD ;(3)解:如图②,过C 作CG ⊥AD 于G ,∴∠CGA=90°,在四边形ABCD 中,AD ∥BC ,∠A =∠B =90°,∴四边形ABCG 为矩形,又∵AB=BC ,∴四边形ABCG 为正方形,∴AG =BC=AB =16,∵∠DCE =45°,由(1)和(2)的结论可得:ED=BE+DG ,设DE=x ,∵4BE =,∴AE =12,DG=x −4,∴AD =AG −DG =20−x在Rt △AED 中,由勾股定理得:DE 2=AD 2+AE 2,即x 2=(20−x )2+122 解得:685=x , 即685=DE . 【点睛】本题是一道几何综合题,内容主要涉及全等三角形的判定与性质和勾股定理的应用,重点考查学生的数学学习能力,是一道好题.8.(1)12;(2)2S 1=36 +S 2.【分析】(1)根据已知条件证得四边形ABOC 是正方形,在点B 左侧取点G ,连接AG ,使AG=AE ,利用HL 证得Rt △ABG ≌Rt △ACE ,得到∠GAB=∠EAC,GB=CE ,再利用45DAE ︒∠=证得△GAD ≌△EAD ,得到DE=GB+BD ,由此求得DOE ∆的周长;(2) 在OB 上取点F ,使AF=AE ,根据HL 证明Rt △ABF ≌Rt △ACE ,得到∠FAE=∠ABC=90︒,再证明△ADE ≌△ADF ,利用面积相加关系得到四边形AEDF 的面积=S △ACE +S 四边形ACOF +S △ODE ,根据三角形全等的性质得到2S △ADE =S 正方形ABOC +S △OD E ,即可得到2S △ADE =36 +S △ODE .【详解】(1)∵点A 的坐标为(6,6)-,AB x ⊥轴,AC y ⊥轴,∴AB=BO=AC=OC=6,∴四边形ABOC 是菱形,∵∠BOC=90︒,∴四边形ABOC 是正方形,在点B 左侧取点G ,连接AG ,使AG=AE ,∵四边形ABOC 是正方形,∴AB=AC ,∠ABG=∠ACE=90︒,∴Rt △ABG ≌Rt △ACE ,∴∠GAB=∠EAC,GB=CE ,∵∠BAE+∠EAC=90︒,∴∠GAB+∠BAE=90︒,即∠GAE=90︒,∵45DAE ︒∠=∴∠GAD=45DAE ︒∠=,又∵AD=AD,AG=AE ,∴△GAD ≌△EAD ,∴DE=GD=GB+BD,∴DOE ∆的周长=DE+OD+OE=GB+BD+OD+OE=OB+OC=6+6=12(2) 2S 1=36 +S 2,理由如下:在OB 上取点F ,使AF=AE ,∵AB=AC ,∠ABF=∠ACE=90︒,∴Rt △ABF ≌Rt △ACE ,∴∠BAF=∠CAE,∴∠FAE=∠ABC=90︒,∵∠DAE=45︒,∴∠DAF=∠DAE=45︒,∵AD=AD ,∴△ADE ≌△ADF ,∵四边形AEDF 的面积=S △ACE +S 四边形ACOF +S △ODE ,∴2S △ADE =S 正方形ABOC +S △OD E ,∴2S △ADE =36 +S △ODE.即:2S 1=36 +S 2【点睛】此题考查三角形全等的判定及性质,根据题中的已知条件证得三角形全等,即可利用性质得到边长相等,面积相等的关系,(2)中需根据面积的加减关系进行推导,这是此题的难点.9.(1)证明见解析;(2)菱形;(3)四边形AEGF 是矩形,理由见解析.【分析】(1)根据平行线的性质得到BDE A ∠=∠,根据题意得到DEFBDE ∠=∠,根据平行线的判定定理得到//AD EF ,根据平行四边形的判定定理证明;(2)根据三角形中位线定理得到12DE AC =,得到AD DE =,根据菱形的判定定理证明;(3)根据等腰三角形的性质得到AE EG ⊥,根据有一个角是直角的平行四边形是矩形证明.【详解】 (1)证明://DE AC ,BDE A ∴∠=∠,DEF A ∠=∠,DEF BDE ∴∠=∠,//AD EF ∴,又//DE AC ,∴四边形ADEF 为平行四边形;(2)解:ADEF 的形状为菱形, 理由如下:点D 为AB 中点, 12AD AB ∴=, //DE AC ,点D 为AB 中点,12DE AC ∴=, AB AC =,AD DE ∴=,∴平行四边形ADEF 为菱形,故答案为:菱形;(3)四边形AEGF 是矩形,理由如下:由(1)得,四边形ADEF 为平行四边形,//AF DE ∴,AF DE =,EG DE ,//AF DE ∴,AF GE =,∴四边形AEGF 是平行四边形,AD AG ,EG DE =,AE EG ∴⊥,∴四边形AEGF 是矩形.【点睛】本题考查的是平行四边形、矩形、菱形的判定,掌握它们的判定定理是解题的关键.10.(1)证明见解析;(2)证明见解析.【分析】(1)根据正方形的性质证得BG=DE ,利用SAS 可证明ABG ≌ADE ,再利用全等的性质即可得到结论;(2)过M 作MK ⊥BC 于K ,延长EF 交AB 于T ,根据ASA 可证明MHK △≌AED ,得到AE=MH ,再利用AAS 证明TNF △≌DAE △,得到NF=AE ,从而证得MH=NF ,即可得到结论.【详解】证明:(1)∵四边形ABCD 与四边形CEFG 均为正方形,∴AB=AD=BC=CD ,CG=CE ,∠ABG=∠ADE=90°,∴BC -GC=CD -EC ,即BG=DE ,∴ABG ≌ADE ,∴AG=AE ;(2)过M 作MK ⊥BC 于K ,则四边形MKCD 为矩形,∴∠MKH=∠ADE=90°,MK=CD ,∠AMK=90°,∴MK=AD ,∠AMP+∠HMK=90°,又∵FP AE ,∴∠EAD+∠AMP=90°,∴∠HMK=∠EAD ,∴MHK △≌AED ,∴MH=AE ,延长EF 交AB 于T ,则四边形TBGF 为矩形,∴FT=BG ,∠FTN=∠ADE=90°,∵ABG ≌ADE ,∴DE=BG ,∴FT=DE ,∵FP ⊥AE ,∠DAB=90°,∴∠N+∠NAP=∠DAE+∠NAP=90°,∴∠N=∠DAE ,∴TNF △≌DAE △,∴FN=AE ,∴FN=MH ,∴FN -FH=MH -FH ,∴NH=FM .【点睛】本题考查了正方形的性质,矩形的判定与性质,及全等三角形的判定与性质,熟练掌握各性质、判定定理是解题的关键.。
平行四边形的面积(2)练习题及答案

第5课时平行四边形的面积(2)基础作业不夯实基础,难建成高楼。
1. 判断对错。
(1)平行四边形的面积与长方形的面积相等。
()(2)平行四边形的底越长,它的面积就越大。
()(3)等底等高的平行四边形,面积一定相等。
()(4)两个面积相等的平行四边形,底和高也分别相等。
()2.计算下列平行四边形的面积。
(1)(2)3. 一个平行四边形的底为3.6 cm,是高的3倍。
求这个平行四边形的面积。
综合提升重点难点,一网打尽。
4. 下面图中两个平行四边形的面积相等吗?它们的面积各是多少?5. 测量下图中平行四边形一条边的长和它对应的高,并计算出它们的面积。
6. 一块近似平行四边形的草坪,中间有一条石子路(如下图),如果铺 1 m2草坪需要12元,那么铺这块草坪大约需要多少钱?拓展探究举一反三,应用创新,方能一显身手。
7. 用细木条钉成一个长为12 cm,宽为7 cm的长方形框,它的周长和面积各是多少?如果把它拉成一个平行四边形,它的周长和面积有没有变化?为什么?8. 图中大平行四边形的面积是48 cm2。
点A、B分别是上、下两边的中点,你能求出图中小的平行四边形(阴影部分)的面积吗?第5课时1. (1)×(2)×(3)√(4)×2. (1)945 cm2 (2)162 cm23.3.6×(3.6÷3)=4.32(cm2)4. 相等,等底等高的平行四边形,面积相等。
都为12×10=120(cm2)5. 根据实际测量的数计算。
6. 40×15-1.2×15=582(m2)12×582=6984(元)7. 周长:38cm 面积:84cm2周长不变,面积减小,理由略。
8. 24 cm2。
北师大版小学数学五年级上册第四单元《平行四边形的面积》(第2课时)同步练习带答案

《探索活动:平行四边形的面积》第2课时同步习题1.直接写出得数。
5.8×0.4= 14.56-4.65= 72.06÷0.6=6.42+4.2= 12.8÷0.08= 0.09÷3= 3.2×1.1= 3.5÷0.5= 2.计算下面平行四边形的面积。
3.一张平行四边形彩纸的面积是4.4 dm2,底是2.2 dm。
这条底边对应的高是多少分米?4.算一算。
5.计算下面平行四边形的面积,看看你能发现什么?图A的面积是();图B的面积是();图C的面积是();图D的面积是()。
观察上图我发现:图A的面积等于图()的面积,因为();图A的面积还等于图()的面积,因为();图D的面积是图B的()倍,因为();图D的面积是图C的()倍,因为()。
6.填一填。
(1)面积是3.6 m2的平行四边形,高是A m,底是()m。
(2)一个平行四边形的底不变,高扩大到原来的3倍,它的面积()。
(3)一个平行四边形的底扩大到原来的2倍,要使面积不变,高应该()。
7.列式计算。
(1)一个面积为156 cm2的平行四边形,底是12 cm,高是多少?(2)要裁一块面积为22 m2的平行四边形纸板,高度为4 m,底要裁成多少米?8.一块平行四边形草坪的中间有两条宽1m的小路,如下图,求草坪的面积。
参考答案1. 2.32 9.91 120.1 10.62 160 0.03 3.52 72.(1)3×5=15(cm2)(2)22×15=330(m2)3.(1)底×高面积÷底4.4÷2.2=2(dm)(2)解:设这条底边对应的高为x dm。
2.2x=4.4x=2答:这条底边对应的高为2dm。
4.(1)253÷11=23(cm)(2)4×5.5÷5=4.4(dm)5. 24 cm2 24 cm2 24 cm2 48 cm2B 图A和图B的底和高分别相等C 图A的底是图C的一半,图A的高是图C的高的2倍2 图D的高和图B的高相等,但图D的底是图B的底的2倍2 图D的底和图C的底相等,但图D的高是图C的高的2倍6.(1)3.6÷A(2)扩大到原来的3倍(3)缩小到原来的1 27.(1)156÷12=13(cm)(2)22÷4=5.5(m)8.(30-1)×(10-1)=261(m2)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第5课时平行四边形的面积(2)
基础作业
不夯实基础,难建成高楼。
1. 判断对错。
(1)平行四边形的面积与长方形的面积相等。
()
(2)平行四边形的底越长,它的面积就越大。
()
(3)等底等高的平行四边形,面积一定相等。
()X|k |B | 1 . c|O |m (4)两个面积相等的平行四边形,底和高也分别相等。
()
2.计算下列平行四边形的面积。
(1)
(2)
3. 一个平行四边形的底为3.6 cm,是高的3倍。
求这个平行四边形的面积。
综合提升
重点难点,一网打尽。
4. 下面图中两个平行四边形的面积相等吗?它们的面积各是多少?xKb 1.Co m
5. 测量下图中平行四边形一条边的长和它对应的高,并计算出它们的面积。
6. 一块近似平行四边形的草坪,中间有一条石子路(如下图),如果铺1 m2草坪需要12元,那么铺这块草坪大约需要多少钱?
拓展探究
举一反三,应用创新,方能一显身手。
7. 用细木条钉成一个长为12 cm,宽为7 cm的长方形框,它的周长和面积各是多少?如果把它拉成一个平行四边形,它的周长和面积有没有变化?为什么?X K b1.C om
8. 图中大平行四边形的面积是48 cm2。
点A、B分别是上、下两边的中点,你能求出图中小的平行四边形(阴影部分)的面积吗?
第5课时
1. (1)×(2)×(3)√(4)×
2. (1)945 cm2 (2)162 cm2
3.3.6×(3.6÷3)=
4.32(cm2)
4. 相等,等底等高的平行四边形,面积相等。
都为12×10=120(cm2)
5. 根据实际测量的数计算。
6. 40×15-1.2×15=582(m2) X k B 1 . c o m
12×582=6984(元)
7. 周长:38cm 面积:84cm2周长不变,面积减小,理由略。
8. 24 cm2
系列资料。
