2015-2016学年宁夏银川一中高一(上)期末数学试卷

合集下载

2015-2016学年宁夏银川市六盘山高中高一(上)期末数学试卷

2015-2016学年宁夏银川市六盘山高中高一（上）期末数学试卷一、选择题（每小题5分，共60分）1. 给出下列命题中正确的是()A.底面是矩形的平行六面体是长方体B.棱柱被平面分成的两部分可以都是棱柱C.棱柱的底面一定是平行四边形D.棱锥的底面一定是三角形2. 利用斜二测画法得到的：①三角形的直观图是三角形；②平行四边形的直观图是平行四边形；③正方形的直观图是正方形；④菱形的直观图是菱形．以上结论，正确的是()A.①B.①②C.③④D.①②③④3. 正方体ABCD−A1B1C1D1中，与对角线AC1异面的棱有()条.A.6B.8C.3D.44. 如图，直线l1，l2，l3的斜率分别为k1，k2，k3，则必有()A.k3<k1<k2B.k1<k3<k2C.k3<k2<k1D.k1<k2<k35. 圆C1：(x−m)2+(y+2)2=9与圆C2：(x+1)2+(y−m)2=4外切，则m的值为()A.−5B.2C.不确定D.2或−56. 若ac>0且bc<0，直线ax+by+c=0不通过()A.第二象限B.第一象限C.第四象限D.第三象限7. 若圆C的半径为1，圆心在第一象限，且与直线4x−3y=0和x轴都相切，则该圆的标准方程是（）A.(x−2)2+(y+1)2=1B.(x−2)2+(y−1)2=1C.(x+2)2+(y−1)2=1D.(x−3)2+(y−1)2=18. 设m，n是两条不同的直线，α，β是两个不同的平面．考查下列命题，其中正确的命题是()A.α // β，m⊥α，n // β⇒m⊥nB.m⊥α，n⊂β，m⊥n⇒α⊥βC.α⊥β，m⊥α，n // β⇒m⊥nD.α⊥β，α∩β=m，n⊥m⇒n⊥β9. 圆x2+y2−4x−4y−10=0上的点到直线x+y−14=0的最大距离与最小距离的差是()A.18B.36C.5√2D.6√210. 空间四边形ABCD中，若AB=AD=AC=CB=CD=BD，则AC与BD所成角为()A.45∘B.30∘C.60∘D.90∘11. 一个空间几何体的三视图及部分数据如图所示，则这个几何体的体积是()A.52B.3C.32D.212. 已知各顶点都在一个球面上的正四棱柱高为4，体积为16，则这个球的表面积是( )A.20πB.16πC.32πD.24π二、填空题（每小题5分，共20分）在空间直角坐标系中，点A(3, 4, −5)关于x轴的对称点的坐标是________．直线x+2y+3=0与直线2x+4y+5=0的距离等于________．已知直线y=ax−2和y=(a+2)x+1互相垂直，则实数a等于________．直线l将圆x2+y2−2x−4y=0平分，且与直线x+2y=0垂直，则直线l的方程为________．三、解答题（本大题共6题，其中17题10分，其余各题每题12分，共70分．请写出文字说明、演算步骤或证明过程．）求经过两条直线l1:x+y−4=0和l2:x−y+2=0的交点，且分别与直线2x−y−1=0(1)平行的直线方程；(2)垂直的直线方程．求经过原点，且过(−2, 3)，(−4, 1)两点的圆的方程．过原点O作圆x2+y2−8x=0的弦OA，求弦OA中点M的轨迹方程．如图，四棱锥P−ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点．(1)证明：PA // 平面EDB；(2)求直线PB与平面ABCD所成角的正弦值．已知圆C:x2+(y−1)2=5，直线l:mx−y+1−m=0．(1)求证：对m∈R，直线l与圆C总有两个不同的交点；(2)设l与圆C交于A，B两点，若|AB|=√17，求l的倾斜角．如图，PA⊥平面ABC，AE⊥PB，AB⊥BC，AF⊥PC，PA=AB=BC=2. (1)求证：平面AEF⊥平面PBC；(2)求二面角P−BC−A的大小；(3)求三棱锥P−AEF的体积．参考答案与试题解析2015-2016学年宁夏银川市六盘山高中高一（上）期末数学试卷一、选择题（每小题5分，共60分）1.【答案】此题暂无答案【考点】构成因丙几何手的透本元素【解析】此题暂无解析【解答】此题暂无解答2.【答案】此题暂无答案【考点】斜二测来法画兴观图【解析】此题暂无解析【解答】此题暂无解答3.【答案】此题暂无答案【考点】异面体线土判定【解析】此题暂无解析【解答】此题暂无解答4.【答案】此题暂无答案【考点】直线的使象特征原倾回角通斜率的关系【解析】此题暂无解析【解答】此题暂无解答5.【答案】此题暂无答案【考点】圆与来的位德米系及米判定【解析】此题暂无解析【解答】此题暂无解答6.【答案】此题暂无答案【考点】直线的使象特征原倾回角通斜率的关系确明直织填置基几何要素【解析】此题暂无解析【解答】此题暂无解答7.【答案】此题暂无答案【考点】直线与都连位置关系圆的射纳方程点到直使的距离之式【解析】此题暂无解析【解答】此题暂无解答8.【答案】此题暂无答案【考点】空间使如得与平度之间的位置关系【解析】此题暂无解析【解答】此题暂无解答9.【答案】此题暂无答案【考点】圆的常准方簧与坐般客程的转化直线与三相交的要质圆的射纳方程点到直使的距离之式【解析】此题暂无解析【解答】此题暂无解答10.【答案】此题暂无答案【考点】异面直线表烧所成的角【解析】此题暂无解析【解答】此题暂无解答11.【答案】此题暂无答案【考点】由三都问求体积【解析】此题暂无解析【解答】此题暂无解答12.【答案】此题暂无答案【考点】球的表体积决体积【解析】此题暂无解析【解答】此题暂无解答二、填空题（每小题5分，共20分）【答案】此题暂无答案【考点】空间中水三的坐标【解析】此题暂无解析【解答】此题暂无解答【答案】此题暂无答案【考点】两条平行射线间面距离【解析】此题暂无解析【解答】此题暂无解答【答案】此题暂无答案【考点】两条直因垂直滤倾斜汉措斜率的关系【解析】此题暂无解析【解答】此题暂无解答【答案】此题暂无答案【考点】直线和圆体方硫的应用两条直因垂直滤倾斜汉措斜率的关系【解析】此题暂无解析【解答】此题暂无解答三、解答题（本大题共6题，其中17题10分，其余各题每题12分，共70分．请写出文字说明、演算步骤或证明过程．）【答案】此题暂无答案【考点】直线的较般式划程皮直校的垂直关系直线的水根式方务式直线的平行关系【解析】此题暂无解析【解答】此题暂无解答【答案】此题暂无答案【考点】圆的正且方程【解析】此题暂无解析【解答】此题暂无解答【答案】此题暂无答案【考点】轨表方擦【解析】此题暂无解析【解答】此题暂无解答【答案】此题暂无答案【考点】直线与正键所成的角直线与平三平行定判定【解析】此题暂无解析【解答】此题暂无解答【答案】此题暂无答案【考点】直线与三相交的要质直线于倾斜落【解析】此题暂无解析【解答】此题暂无解答【答案】此题暂无答案【考点】二面角的使面角及爱法平面与平明垂钾的判定柱体三锥州、台到的体建计算【解析】此题暂无解析【解答】此题暂无解答。

2016-2017学年宁夏高一上学期期末考试数学word版含答案

2016-2017学年宁夏高一上学期期末考试数学本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共4页。

注意事项：1. 答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。

2．选择题必须使用2B 铅笔填涂；非选择题必须使用0.5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。

3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。

4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。

5. 保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

第Ⅰ卷一、选择题：本题共12小题，每小题5分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.210sin 的值为（） A ．21 B. 23 C. 21- D. 23- 2. 18sin 27cos 18cos 27sin +的值为（）A ．22 B. 23 C. 21 D. 1 3. 已知集合}821|{<<=x x A ，集合}1log 0|{2<<=x x B ，则A B = （）A ．}31|{<<x x B. }21|{<<x x C. }32|{<<x x D. }20|{<<x x4. 已知 80sin =a ，1)21(-=b ，3log 21=c ，则（） A ．c b a >> B. c a b >> C. b a c >> D. a c b >>5. 一扇形的圆心角为60，所在圆的半径为6 ，则它的面积是（）A ．π6 B. π3 C. π12 D. π9 6. 若),0(,πβα∈且 31tan ,21tan ==βα，则=+βα（） A ．4π B. 43π C. 45π D. 47π 7. )32sin(3π-=x y 的一条对称轴是（）A ．32π=x B. 2π=x C. 3π-=x D. 38π=x 8. 要得到)32cos(3π-=x y 的图象，只需将x y 2cos 3=的图象（） A ．右移3π B. 左移3π C. 右移6π D. 左移6π 9. 函数1)2sin(2--=x y π的定义域为（）A ．},65262|{Z k k x k x ∈+≤≤+ππππ B.},656|{Z k k x k x ∈+≤≤+ππππ C. },32232|{Z k k x k x ∈+≤≤+ππππ D. },12512|{Z k k x k x ∈+≤≤+ππππ 10. 函数x x y cos sin +=的值域是（）A ．]2,2[- B. ]1,1[- C. ]2,2[- D. ]2,0[11. 下列函数中既是偶函数，最小正周期又是π的是（）A ．x y 2sin = B. x y cos = C. x y tan = D. |tan |x y =12. 函数1ln )(2-++=a x x x f 有唯一的零点在区间),1(e 内，则实数a 的取值范围是（）A ．)0,(2e - B. )1,(2e - C. ),1(e D. ),1(2e第Ⅱ卷二、填空题：本题共4小题，每小题5分。

【全国百强校】宁夏回族自治区银川一中2015-2016学年高一上学期期末考试化学试题(原卷版)

宁夏回族自治区银川一中2015-2016学年高一上学期期末考试化学试题可能用到的相对原子质量：H-1 C-12 O-16 N-14 Na-23 Mg-24 Al-27 Si-28S-32 Fe-56 Cu-64 Zn-65 Ag-108一、选择题．（共25小题，每小题2分，共50分．每小题只有一个选项符合题意）1.下列对某些问题的认识正确的是A．漂白粉和明矾都常用于自来水的处理，二者的作用原理是相同的B．Na的金属性比Cu强，故可用Na与CuSO4溶液反应制取CuC．不能用带玻璃塞的玻璃瓶盛放碱液D．玻璃、水泥、陶瓷、水晶都是重要的硅酸盐材料2.化学与环境、科学、技术密切相关。

下列有关说法中正确的是A．可使用填埋法处理未经分类的生活垃圾B．光化学烟雾的形成与汽车尾气中的氮氧化物有关C．光导纤维都是有机高分子化合物D．“鸟巢”使用钒氮合金钢，该合金熔点、硬度和强度均比纯铁高3.下列有关说法正确的是：A．在酒精灯加热条件下，Na2CO3、NaHCO3固体都容易发生分解B．Fe(OH)3胶体无色、透明，能发生丁达尔现象C．H2、SO2、CO2三种气体都可用浓硫酸干燥D．SiO2既能和氢氧化钠溶液反应又能和氢氟酸反应，所以是两性氧化物4.如图是同学们经常使用的某品牌修正液包装标签．小明仔细阅读后，结合自己的生活经验和所学知识得出了修正液的某些性质，小明的推测中合理的是（）．A．修正液的成分对纸张具有强腐蚀性B．修正液中不含有化学物质C．修正液是一种胶体，均一、稳定D．修正液的溶剂易挥发、易燃5.在下列溶液中，能大量共存的离子组是A．在强碱性溶液中能大量存在：Na+、K+、Cl-、HCO3﹣B．加入金属铝后溶液中有大量气泡产生的溶液中：Fe2+、Mg2+、NO3﹣、Cl-C．含有大量Fe3+的溶液中：SCN-、I-、K+、Br-D．溶液通入足量氨气后各离子还能大量存在：K+Na+AlO2-、CO32﹣6.取两份铝片，第一份与足量稀硫酸反应，第二份与足量NaOH溶液反应，同温同压下放出相同体积的气体，则两份铝片的质量之比为A．2：3 B．1：1 C．3：2 D．1：37.只用一种试剂可以区别NH4Cl、MgCl2、FeSO4、AlCl3、FeCl3五种溶液，这种试剂是A．稀硫酸B．氨水C．AgNO3溶液D．NaOH溶液8.将等物质的量的Na2O和Na2O2分别投入到足量且等质量的水中，得到溶质的物质的量浓度分别为C1和C2的两种溶液，则C1和C2的关系是A．C1=C2B．C1＞C2C．C1＜C2 D．无法确定9.下列离子方程式书写正确的是A．漂白粉溶液中通入过量的CO2：Ca2++2ClO-+ CO2+ H2O = CaCO3↓+2HClOB．氯气与水的反应：Cl2+H2O2H++Cl-+ClO—C．NaHCO3溶液中加足量Ba(OH)2溶液：HCO3—＋Ba2＋＋OH－=BaCO3↓＋H2OD．钠和冷水反应：Na＋2H2O＝Na+＋2OH ＋H2↑10.由锌、铁、铝、镁四种金属中的两种组成的混合物11.5克，与足量的盐酸反应产生的氢气标准状况下为11.2升，则两种金属组成的混合物是A．锌与镁B．铁与锌C．铝与铁D．镁与铁11.下列装置所示的实验中，能达到实验目的是( )A．分离碘和酒精B．较长时间观察Fe(OH)2白色沉淀C．验证NaHCO3和Na2CO3的热稳定性D除去Cl2中HCl12.下列化合物能用相应元素的单质直接化合生成的是①CuS②FeS③Al2S3④Fe2S3⑤Cu2S⑥FeCl2 ⑦H2S⑧FeCl3A．②③⑤⑦⑧B．①④⑥⑦C．①②③⑤⑦D．④⑥⑦⑧13.设N A为阿伏加德罗常数，下列说法正确的是A．一定条件下，6.4 g铜与过量的硫反应，转移电子数目为0.2N AB．3mol单质Fe完全转变为Fe3O4，失去8N A个电子C．标准状况下，11.2L SO3中含有2N A个原子D ．用石灰乳完全吸收1 mol Cl 2时，转移电子的数目是2N A14.下列实验操作正确且能达到相应实验目的的是15.某同学在实验室中用KMnO 4代替MnO 2制备Cl 2，反应原理为2KMnO 4+16HCl(浓)=2KCl+2MnCl 2+5Cl 2↑+8H 2O 。

宁夏回族自治区银川一中高一上学期期末考试试题(8科8份)(宁夏回族自治区银川一中高一上学期期末考试语

银川一中2015/2016学年度(上)高一期末考试语文试卷一、选择题（每小题2分，共14分）1．下列词语中加点字的注音，没有错误的一组是A．激湍．（tuān）愀．然（qiǎo）山川相缪．（liào）流觞．曲水（shāng）B．庐冢．（zhǒng）肄．业（sì）游目骋．怀（chěng）义愤填膺．（yīng）C．猗．（yī）郁仆．（pū）碑熨．（yùn）帖妖童媛．女（yuán）D．敛裾．（jū）守拙．（zhuō）混．水摸鱼（hún）青青子衿．（jīn）2．下列词语中没有错别字的一组是A．拾掇树巅万户侯坚如磐石 B．弥谤颓废俱乐部急不瑕择C．趣舍贻误笑咪咪夙兴夜寐 D．倩影枕藉鸿门宴大相背弛3．下列各句中，加点的成语使用恰当的一句是A．项羽被困垓下，兵少食尽，外面汉兵层层包围，其处境之危险真是如履薄冰．．．．，想起“西楚霸王”之威名，让人不禁感慨万千。

B．读诺贝尔文学奖获得者莫言的作品，你会随着作品一起愤怒、忧伤、欢喜，时而陷入沉思，时而掩卷失笑，叹为观止．．．．。

C．刚刚还是烈日当头照，一转眼，老天爷的脸一沉，狂风怒吼，大街上尘土飞扬，整个城市瓦．釜雷鸣．．．，紧接着瓢泼大雨倾泻下来。

D．听说这家媒体和当地电信部门将联合举办高校招生大型电话咨询会，请有关专家答疑解惑，考生和家长都喜出望外．．．．。

4．下列关于文学常识和文化常识的表述，不正确的一项是A．《采薇》和《离骚》分别选自《诗经》和《楚辞》。

这两部作品分别是我国现实主义文学和浪漫主义文学的代表作。

《诗经》原称《诗》，是我国最早的诗歌总集，共收录从西周初年到春秋中叶的诗歌305篇，分为“风”“雅”“颂”三大类，艺术手法上常用“赋”“比”“兴”。

B．《巴黎圣母院》的作者是法国19世纪伟大的浪漫主义作家维克多·雨果，这部小说创作于他的青年时期，是他所有小说中浪漫色彩最浓的一部，其中的女主人公是珂赛特。

2015-2016学年宁夏银川市六盘山高中高一(上)数学期末试卷及解析

2015-2016学年宁夏银川市六盘山高中高一（上）期末数学试卷一、选择题（每小题5分，共60分）1．（5.00分）给出下列命题中正确的是（）A．棱柱被平面分成的两部分可以都是棱柱B．底面是矩形的平行六面体是长方体C．棱柱的底面一定是平行四边形D．棱锥的底面一定是三角形2．（5.00分）利用斜二测画法得到的：①三角形的直观图是三角形；②平行四边形的直观图是平行四边形；③正方形的直观图是正方形；④菱形的直观图是菱形．以上结论，正确的是（）A．①②B．①C．③④D．①②③④3．（5.00分）正方体ABCD﹣A1B1C1D1中，与对角线AC1异面的棱有（）条．A．8 B．6 C．4 D．34．（5.00分）如图，直线l1、l2、l3的斜率分别为k1、k2、k3，则必有（）A．k1＜k3＜k2B．k3＜k1＜k2C．k1＜k2＜k3D．k3＜k2＜k15．（5.00分）圆C1：（x﹣m）2+（y+2）2=9与圆C2：（x+1）2+（y﹣m）2=4外切，则m的值为（）A．2 B．﹣5 C．2或﹣5 D．不确定6．（5.00分）若ac＞0且bc＜0，直线ax+by+c=0不通过（）A．第一象限B．第二象限C．第三象限D．第四象限7．（5.00分）若圆C的半径为1，圆心在第一象限，且与直线4x﹣3y=0和x轴都相切，则该圆的标准方程是（）A．（x﹣2）2+（y﹣1）2=1 B．（x﹣2）2+（y+1）2=1 C．（x+2）2+（y﹣1）2=1 D．（x﹣3）2+（y﹣1）2=18．（5.00分）设m、n是两条不同的直线，α、β是两个不同的平面．考查下列命题，其中正确的命题是（）A．m⊥α，n⊂β，m⊥n⇒α⊥βB．α∥β，m⊥α，n∥β⇒m⊥nC．α⊥β，m⊥α，n∥β⇒m⊥n D．α⊥β，α∩β=m，n⊥m⇒n⊥β9．（5.00分）圆x2+y2﹣4x﹣4y﹣10=0上的点到直线x+y﹣14=0的最大距离与最小距离的差是（）A．36 B．18 C．D．10．（5.00分）空间四边形ABCD中，若AB=AD=AC=CB=CD=BD，则AC与BD所成角为（）A．30°B．45°C．60°D．90°11．（5.00分）一个空间几何体的三视图及部分数据如图所示，则这个几何体的体积是（）A．3 B．C．2 D．12．（5.00分）已知各顶点都在一个球面上的正四棱柱高为4，体积为16，则这个球的表面积是（）A．16πB．20πC．24πD．32π二、填空题（每小题5分，共20分）13．（5.00分）在空间直角坐标系中，点A（3，4，﹣5）关于x轴的对称点的坐标是．14．（5.00分）直线x+2y+3=0与直线2x+4y+5=0的距离等于．15．（5.00分）已知直线y=ax﹣2和y=（a+2）x+1互相垂直，则实数a等于．16．（5.00分）直线l将圆x2+y2﹣2x﹣4y=0平分，且与直线x+2y=0垂直，则直线l的方程为．三、解答题（本大题共6题，其中17题10分，其余各题每题12分，共70分．请写出文字说明、演算步骤或证明过程．）17．（10.00分）求经过两条直线l1：x+y﹣4=0和l2：x﹣y+2=0的交点，且分别与直线2x﹣y﹣1=0（1）平行的直线方程；（2）垂直的直线方程．18．（12.00分）求经过原点，且过（﹣2，3），（﹣4，1）两点的圆的方程．19．（12.00分）过原点O作圆x2+y2﹣8x=0的弦OA，求弦OA中点M的轨迹方程．20．（12.00分）如图，四棱锥P﹣ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点．（1）证明：PA∥平面EDB；（2）求直线PB与平面ABCD所成角的正弦值．21．（12.00分）已知圆C：x2+（y﹣1）2=5，直线l：mx﹣y+1﹣m=0．（1）求证：对m∈R，直线l与圆C总有两个不同的交点；（2）设l与圆C交于A、B两点，若|AB|=，求l的倾斜角．22．（12.00分）如图，PA⊥平面ABC，AE⊥PB，AB⊥BC，AF⊥PC，PA=AB=BC=2（1）求证：平面AEF⊥平面PBC；（2）求二面角P﹣BC﹣A的大小；（3）求三棱锥P﹣AEF的体积．2015-2016学年宁夏银川市六盘山高中高一（上）期末数学试卷参考答案与试题解析一、选择题（每小题5分，共60分）1．（5.00分）给出下列命题中正确的是（）A．棱柱被平面分成的两部分可以都是棱柱B．底面是矩形的平行六面体是长方体C．棱柱的底面一定是平行四边形D．棱锥的底面一定是三角形【解答】解：平行于棱柱底面的平面可以把棱柱分成两个棱柱，故A正确；三棱柱的底面是三角形，故C错误；底面是矩形的平行六面体的侧面不一定是矩形，故它也不一定是长方体，故B 错误；四棱锥的底面是四边形，故D错误．故选：A．2．（5.00分）利用斜二测画法得到的：①三角形的直观图是三角形；②平行四边形的直观图是平行四边形；③正方形的直观图是正方形；④菱形的直观图是菱形．以上结论，正确的是（）A．①②B．①C．③④D．①②③④【解答】解：由斜二测画法规则知：①正确；平行性不变，故②正确；正方形的直观图是平行四边形，③错误；因为平行于y′轴的线段长减半，平行于x′轴的线段长不变，故④错误．故选：A．3．（5.00分）正方体ABCD﹣A1B1C1D1中，与对角线AC1异面的棱有（）条．A．8 B．6 C．4 D．3【解答】解：如图：与对角线AC1异面的棱有A1D1、A1B1、DD1、BB1、BC、CD 共6条，故选：B．4．（5.00分）如图，直线l1、l2、l3的斜率分别为k1、k2、k3，则必有（）A．k1＜k3＜k2B．k3＜k1＜k2C．k1＜k2＜k3D．k3＜k2＜k1【解答】解：设直线l1、l2、l3的倾斜角分别为α1，α2，α3．由已知为α1为钝角，α2＞α3，且均为锐角．由于正切函数y=tanx在（0，）上单调递增，且函数值为正，所以tanα2＞tanα3＞0，即k2＞k3＞0．当α为钝角时，tanα为负，所以k1=tanα1＜0．综上k1＜k3＜k2，故选：A．5．（5.00分）圆C1：（x﹣m）2+（y+2）2=9与圆C2：（x+1）2+（y﹣m）2=4外切，则m的值为（）A．2 B．﹣5 C．2或﹣5 D．不确定【解答】解：由圆的方程得C1（m，﹣2），C2（﹣1，m），半径分别为3和2，两圆相外切，∴=3+2，化简得（m+5）（m﹣2）=0，∴m=﹣5，或m=2，故选：C．6．（5.00分）若ac＞0且bc＜0，直线ax+by+c=0不通过（）A．第一象限B．第二象限C．第三象限D．第四象限【解答】解：直线ax+by+c=0 即y=﹣﹣，若ac＞0且bc＜0，则ab＜0，则斜率﹣＞0，﹣＞0，即直线的倾斜角为锐角，在y轴上的截距大于0，故直线不经过第四象限，故选：D．7．（5.00分）若圆C的半径为1，圆心在第一象限，且与直线4x﹣3y=0和x轴都相切，则该圆的标准方程是（）A．（x﹣2）2+（y﹣1）2=1 B．（x﹣2）2+（y+1）2=1 C．（x+2）2+（y﹣1）2=1 D．（x﹣3）2+（y﹣1）2=1【解答】解：设圆心坐标为（a，b）（a＞0，b＞0），由圆与直线4x﹣3y=0相切，可得圆心到直线的距离d==r=1，化简得：|4a﹣3b|=5①，又圆与x轴相切，可得|b|=r=1，解得b=1或b=﹣1（舍去），把b=1代入①得：4a﹣3=5或4a﹣3=﹣5，解得a=2或a=﹣（舍去），∴圆心坐标为（2，1），则圆的标准方程为：（x﹣2）2+（y﹣1）2=1．故选：A．8．（5.00分）设m、n是两条不同的直线，α、β是两个不同的平面．考查下列命题，其中正确的命题是（）A．m⊥α，n⊂β，m⊥n⇒α⊥βB．α∥β，m⊥α，n∥β⇒m⊥nC．α⊥β，m⊥α，n∥β⇒m⊥n D．α⊥β，α∩β=m，n⊥m⇒n⊥β【解答】解：设m、n是两条不同的直线，α、β是两个不同的平面，则：m⊥α，n⊂β，m⊥n时，α、β可能平行，也可能相交，不一定垂直，故A不正确α∥β，m⊥α，n∥β时，m与n一定垂直，故B正确α⊥β，m⊥α，n∥β时，m与n可能平行、相交或异面，不一定垂直，故C错误α⊥β，α∩β=m时，若n⊥m，n⊂α，则n⊥β，但题目中无条件n⊂α，故D也不一定成立，故选：B．9．（5.00分）圆x2+y2﹣4x﹣4y﹣10=0上的点到直线x+y﹣14=0的最大距离与最小距离的差是（）A．36 B．18 C．D．【解答】解：圆x2+y2﹣4x﹣4y﹣10=0的圆心为（2，2），半径为3，圆心到到直线x+y﹣14=0的距离为＞3，圆上的点到直线的最大距离与最小距离的差是2R=6，故选：D．10．（5.00分）空间四边形ABCD中，若AB=AD=AC=CB=CD=BD，则AC与BD所成角为（）A．30°B．45°C．60°D．90°【解答】解：取AC中点E，连接BE，DE因为：AB=AD=AC=CB=CD=BD那么AC垂直于BE，也垂直于DE所以AC垂直于平面BDE，因此AC垂直于BD故选：D．11．（5.00分）一个空间几何体的三视图及部分数据如图所示，则这个几何体的体积是（）A．3 B．C．2 D．【解答】解：由三视图得空间几何体为倒放着的直三棱柱，底面为直角三角形，两直角边长分别等于1和，棱柱高等于，故几何体的体积V=×1××=．故选：D．12．（5.00分）已知各顶点都在一个球面上的正四棱柱高为4，体积为16，则这个球的表面积是（）A．16πB．20πC．24πD．32π【解答】解：正四棱柱高为4，体积为16，底面积为4，正方形边长为2，正四棱柱的对角线长即球的直径为2，∴球的半径为，球的表面积是24π，故选：C．二、填空题（每小题5分，共20分）13．（5.00分）在空间直角坐标系中，点A（3，4，﹣5）关于x轴的对称点的坐标是（3，﹣4，5）．【解答】解：∵在空间直角坐标系中，点（x，y，z）关于x轴的对称点的坐标为：（x，﹣y，﹣z），∴点（3，4，﹣5）关于x轴的对称点的坐标为：（3，﹣4，5）．故答案为：（3，﹣4，5）14．（5.00分）直线x+2y+3=0与直线2x+4y+5=0的距离等于．【解答】解：∵直线x+2y+3=0等价于2x+4y+6=0，∴直线x+2y+3=0与直线2x+4y+5=0的距离：d==．故答案为：．15．（5.00分）已知直线y=ax﹣2和y=（a+2）x+1互相垂直，则实数a等于﹣1．【解答】解：∵直线y=ax﹣2和y=（a+2）x+1互相垂直，∴他们的斜率之积等于﹣1，即a×（a+2）=﹣1，∴a=﹣1，故答案为：﹣1．16．（5.00分）直线l将圆x2+y2﹣2x﹣4y=0平分，且与直线x+2y=0垂直，则直线l的方程为y=2x．【解答】解：设与直线l：x+2y=0垂直的直线方程：2x﹣y+b=0，圆C：x2+y2﹣2x﹣4y=0化为（x﹣1）2+（y﹣2）2=5，圆心坐标（1，2）．因为直线平分圆，圆心在直线2x﹣y+b=0上，所以2×1﹣1×2+b=0，解得b=0，故所求直线方程为y=2x．故答案为：y=2x．三、解答题（本大题共6题，其中17题10分，其余各题每题12分，共70分．请写出文字说明、演算步骤或证明过程．）17．（10.00分）求经过两条直线l1：x+y﹣4=0和l2：x﹣y+2=0的交点，且分别与直线2x﹣y﹣1=0（1）平行的直线方程；（2）垂直的直线方程．【解答】解：联立，解得，（1）由平行关系设所求直线的方程为2x﹣y+c=0代入点（1，3）可得2×1﹣3+c=0，解得c=1故所求直线方程为2x﹣y+1=0（2）由垂直关系设所求直线的方程为x+2y+d=0代入点（1，3）可得1+2×3+d=0，解得d=﹣7故所求直线方程为x+2y﹣7=0．18．（12.00分）求经过原点，且过（﹣2，3），（﹣4，1）两点的圆的方程．【解答】解：设圆的一般方程为：x2+y2+Dx+Ey+F=0，将三点代入方程得：解得：，所以圆的方程为．19．（12.00分）过原点O作圆x2+y2﹣8x=0的弦OA，求弦OA中点M的轨迹方程．【解答】解：设M点坐标为（x，y），那么A点坐标是（2x，2y），A点坐标满足圆x2+y2﹣8x=0的方程，所以（2x）2+（2y）2﹣16x=0所以M点轨迹方程为x2+y2﹣4x=020．（12.00分）如图，四棱锥P﹣ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点．（1）证明：PA∥平面EDB；（2）求直线PB与平面ABCD所成角的正弦值．【解答】证明：（1）如图，连接AC交BD于O．连接EO．∵底面ABCD是正方形，∴点O是AC的中点，在△PAC中，∵E是PC的中点，∴EO是中位线，∴PA∥EO．而EO⊂平面EDB，且PA⊄平面EDB．所以PA∥平面EDB．（6分）解：（2）∵四棱锥P﹣ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，∴由题意PD⊥底面ABCD，∴∠PBD为直线PB与平面ABCD所成角，（8分）设PD=DC=1，在Rt△PBD中，BD==，PB=，∴sin∠PBD===，∴直线PB与平面ABCD所成角的正弦值为．（12分）21．（12.00分）已知圆C：x2+（y﹣1）2=5，直线l：mx﹣y+1﹣m=0．（1）求证：对m∈R，直线l与圆C总有两个不同的交点；（2）设l与圆C交于A、B两点，若|AB|=，求l的倾斜角．【解答】解：（1）圆C的圆心坐标为（0，1），半径为，∵圆心C到直线l的距离（m∈R），即，∴直线l与圆C相交，则对m∈R，直线l与圆C总有两个不同的交点；（2）∵R=，d=，|AB|=，∴根据垂径定理及勾股定理得：，即，整理得：m2=3，解得：，∴直线l的方程为=0或，则直线l的倾斜角为：60°或120°．22．（12.00分）如图，PA⊥平面ABC，AE⊥PB，AB⊥BC，AF⊥PC，PA=AB=BC=2（1）求证：平面AEF⊥平面PBC；（2）求二面角P﹣BC﹣A的大小；（3）求三棱锥P﹣AEF的体积．【解答】解：（1）∵PA⊥平面ABC，BC⊂平面ABC，∴PA⊥BC，∵AB⊥BC，PA∩AB=A，∴BC⊥平面PAB，∵AE⊂平面PAB，∴AE⊥BC，∵AE⊥PB，PB∩BC=B，∴AE⊥平面PBC，∵AE⊂平面AEF，∴平面AEF⊥平面PBC；（2）∵BC⊥平面PAB，PB⊂平面PAB，∴BC⊥PB，结合AB⊥BC，可得∠PBA是二面角P﹣BC﹣A的平面角，∵Rt△PAB中，PA=AB=2，∴∠PBA=45°，由此可得二面角P﹣BC﹣A的大小为45°；（3）由（1）AE⊥平面PBC又∵AF⊥PC∴EF⊥PC（三垂线定理逆定理）∴△PEF∽△PCB∴=，∴S△PEF =S△PBC=，∴V P﹣AEF=V A﹣PEF=××=．。

宁夏回族自治区银川一中1516学年度高一上学期期末考试——数学(数学)

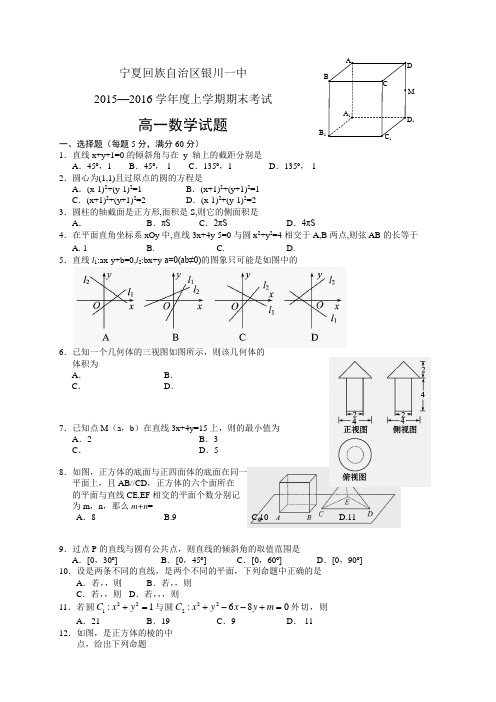
宁夏回族自治区银川一中2015—2016学年度上学期期末考试高一数学试题一、选择题（每题5分，满分60分）1．直线x+y+1=0的倾斜角与在 y 轴上的截距分别是A ．45º，1B ．45º，-1C ．135º，1D ．135º，-12．圆心为(1,1)且过原点的圆的方程是A ．(x-1)2+(y-1)2=1B ．(x+1)2+(y+1)2=1C ．(x+1)2+(y+1)2=2D ．(x-1)2+(y-1)2=23．圆柱的轴截面是正方形,面积是S,则它的侧面积是A ．B ．πSC ．2πSD ．4πS4．在平面直角坐标系xOy 中,直线3x+4y-5=0与圆x 2+y 2=4相交于A,B 两点,则弦AB 的长等于A. 1B.C.D.5．直线l 1:ax-y+b=0,l 2:bx+y-a=0(ab≠0)的图象只可能是如图中的6．已知一个几何体的三视图如图所示，则该几何体的体积为A ．B ．C ．D ．7．已知点M （a ，b ）在直线3x+4y=15上，则的最小值为A ．2B ．3C ．D ．58．如图，正方体的底面与正四面体的底面在同一平面上，且AB//CD ，正方体的六个面所在的平面与直线CE,EF 相交的平面个数分别记为m ，n ，那么m+n =A ．8 B.9 C.10 D.119．过点P 的直线与圆有公共点，则直线的倾斜角的取值范围是A ．[0，30º]B ．[0，45º]C ．[0，60º]D ．[0，90º]10．设是两条不同的直线，是两个不同的平面，下列命题中正确的是A ．若，，则B ．若，，则C ．若，，则D ．若，，，则11．若圆221:1C x y +=与圆222:680C x y x y m +--+=外切，则A ．21B ．19C ．9D ．-1112．如图，是正方体的棱的中点，给出下列命题1BA B C O M V ①过点有且只有一条直线与直线，都相交；②过点有且只有一条直线与直线，都垂直；③过点有且只有一个平面与直线，都相交；④过点有且只有一个平面与直线，都平行.其中真命题是：A ．①②③B ．①②④C ．①③④D ．②③④二．填空题（每题5分，满分20分）13．过l 1:2x-3y+2=0与l 2:3x-4y+2=0的交点且与直线4x+y-4=0平行的直线方程为 .14．若圆C 的半径为1,其圆心与点(1,0)关于直线y=x 对称,则圆C 的标准方程为 .15．若圆锥的表面积是15π,侧面展开图的圆心角是60°,求圆锥的体积________________.16．圆柱形容器内盛有高度为8 cm 的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是 cm.三．解答题17．（本题满分10分）已知正方形ABCD 的中心M(-1,0)和一边CD 所在的直线方程为x+3y-5=0,求其他三边所在的直线方程.18．（本题满分12分）如图,长方体ABCD-A 1B 1C 1D 1中,AB=16,BC=10,AA 1=8,点E,F 分别在A 1B 1,D 1C 1上,A 1E=D 1F=4,过点E,F 的平面α与此长方体的面相交,交线围成一个正方形.(1)在图中画出这个正方形(不必说明画法与理由).(2)求平面α把该长方体分成的两部分体积的比值.19．（本题满分12分）已知圆C 与两平行直线 x-y-8=0和x-y+4=0相切，圆心在直线2x+y-10=0上.（1）求圆C 的方程。

银川一中高一上数学期末试卷及答案

一、选择题（每小题4分，共48分） 1．不共面的四点可以确定平面的个数为( )A ． 2个B ． 3个C ． 4个D ．无法确定 2．利用斜二测画法得到的①三角形的直观图一定是三角形； ②正方形的直观图一定是菱形； ③等腰梯形的直观图可以是平行四边形； ④菱形的直观图一定是菱形. 以上结论正确的是( )A ．①②B ． ①C ．③④D ． ①②③④3．设l ，m 是两条不同的直线，α是一个平面，则下列命题正确的是( ) A. 若l m ⊥，m α⊂，则l α⊥ B. 若l α⊥，l m //，则m α⊥ C. 若l α//，m α⊂，则l m // D. 若l α//，m α//，则l m // 4. 直线10x y ++=的倾斜角与其在y 轴上的截距分别是( )A ．1,135 B.1,45- C.1,45 D.1,135- 5．如果0>AB ，0>BC ，那么直线0=--C By Ax 不经过的象限是 ( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限6．已知直线a x y l 2:1+-=与直线2)2(:22+-=x a y l 平行，则a 的值为 ( )A ．3± B. 1± C. 1 D. 1- 7. 如图在三棱锥BCD A -中,E ､F 是棱AD 上互异的两点,G ､H 是棱BC 上互异的两点,由图可知①AB 与CD 互为异面直线;②FH 分别与DC ､DB 互为异面直线; ③EG 与FH 互为异面直线;④EG 与AB 互为异面直线. 其中叙述正确的是( )A.①③B.②④C.①②④D.①②③④8．在长方体1111D C B A ABCD -中，AD AB ==23，1CC =2，则二面角1C BD C -- 的大小是( )A. 300B. 450C. 600D. 9009. 把3个半径为R 的铁球熔化铸成一个底面半径为R 的圆柱（不计损耗），则圆柱的高为( )A ．R 2B ．R 3C ．R 4D ．R 29 10．半径为r 的球在一个圆锥内部，它的轴截面是一个正三角形与其内切圆，则圆锥的全面积与球面面积的比是 ( )A ．2∶3B ．3∶2C ．4∶9D ．9∶4 11. 已知b a , 满足12=+b a ，则直线03=++b y ax 必过定点( )A ．⎪⎭⎫ ⎝⎛21 ，61 －B ．⎪⎭⎫ ⎝⎛61 ，21C ．⎪⎭⎫ ⎝⎛61- ，21D ．⎪⎭⎫ ⎝⎛21 －，6115．直线0=+ky x ，0832=++y x 和01=--y x 交于一点，则k 的值是 . 16. 两平行直线l 1，l 2分别过点P （－1，3），Q （2，－1），它们分别绕P 、Q 旋转，但始终保持平行，则l 1，l 2之间的距离的取值范围是 .三、解答题17．（本小题满分10分）求与直线0322=-+y x 垂直,并且与原点的距离是5的直线的方程. 18．（本小题满分10分）如图所示是一个半圆柱1OO 与三棱柱111C B A ABC -的组合体，其中，圆柱1OO 的轴截面11A ACC 是边长为4的正方形，∆ABC 为等腰直角三角形，BC AB ⊥.试在给出的坐标纸上画出此组合体的三视图.BCD EF AQ PoB Ay x21．（本小题满分12分）如图直线l 与x 轴、y 轴的正半轴分别交于A （8，0）、B （0，6）两点，P 为直线l 上异于A 、B 两点之间的一动点. 且PQ ∥OA 交OB 于点Q ．（1）若Q P B ∆和四边形OQPA 的面积满足PBQ OQPA S S ∆=3四时，请你确定P 点在AB 上的位置，并求出线段PQ 的长；（2）在x 轴上是否存在点M ，使△MPQ 为等腰直角三角形，若存在，求出点M 与P 的坐标；若不存在，说明理由.银川一中高一期末数学试卷参考答案一、选择题（每小题4分，共48分）1.C;2.B;3.B;4.D;5.B;6.D;7.A;8.A;9.C; 10.D; 11.C; 12.A. 二、填空题（第小题4分，共16分） 13.36; 14.635; 15.21-; 16.]5,0（.三、解答题（2）∵AB CG ⊥又⊥EA 平面ABC ，知CG EA ⊥∴⊥CG 平面ABE 由（1）知⊥DF 平面ABE∴a CD DF 3==--------------------------------------------------8分又2221a AE AB S ABE =⋅=∆ ∴333231a DF S V V ABFE ABE D ABD E =⋅==--∆--------------------12分 20．解：（1）证明：如图，∵ ABC —A 1B 1C 1 是直三棱柱，∴ A 1C 1 ＝B 1C 1 ＝1，且∠A 1C 1B 1 ＝90°．又 D 是A 1B 1 的中点，∴ C 1D ⊥A 1B 1 ．-------------3分 ∵ AA 1 ⊥平面A 1B 1C 1 ，C 1D ⊂平面A 1B 1C 1 ， ∴ AA 1 ⊥C 1D ，∴ C 1D ⊥平面AA 1B 1B ．∴C 1D ⊥AB 1-----------------------------------6分（2）解：作DF ⊥AB 1 交AB 1 于E ，DF 交BB 1 于F ，连结C 1F ，又由（1）C 1D ⊥AB 1则AB 1 ⊥平面C 1DF ，点F 即为所求．---------------------9分连B A 1∵ 2111==AA B A 即四边形11A ABB 为正方形. ∴11AB B A ⊥∴B A 1∥DF 又D 是A 1B 1 的中点，点F 为1BB 的中点.------------12分③当∠PMQ =90°，由PQ ∥OA ，|PM |=|MQ | 且|OM |=|OQ |=21|PQ | 设Q （0，a ,）则M （a ，0）点P 坐标为(2a ,a )代入(*)式得a =512. ∴点M 、P 的坐标分别为（512，0），（512,524）----------------------12分。

宁夏银川市2015-2016学年高一数学上册期末试题

2015-2016学年宁夏银川市育才中学高一（上）期末数学试卷一、选择题（每小题4分，共48分）1．若空间两条直线a和b没有公共点，则a与b的位置关系是（）A．共面B．平行C．异面D．平行或异面2．空间四边形的两条对角线相互垂直，顺次连接四边中点的四边形一定是（）A．空间四边形B．矩形C．菱形D．正方形3．过点M（﹣2，a）和N（a，4）的直线的斜率为1，则实数a的值为（）A．1 B．2 C．1或4 D．1或24．正方体ABCD﹣A1B1C1D1中，与侧棱AB异面且垂直的棱有（）A．8条B．6条C．4条D．3条5．已知圆锥的母线长为5，底面周长为6π，则它的体积为（）A．10πB．12πC．15πD．36π6．直线x+y+2=0的倾斜角为（）A．30°B．60°C．120°D．150°7．过点（1，2）且与原点距离最大的直线方程是（）A．x+2y﹣5=0 B．2x+y﹣4=0 C．x+3y﹣7=0 D．3x+y﹣5=08．平面α与平面β平行的条件可以是（）A．α内有无穷多条直线都与β平行B．直线a∥α，a∥β，且直线a不在α内，也不在β内C．α内的任何直线都与β平行D．直线a在α，直线b在β内，且a∥β，b∥α9．圆x2+y2﹣4=0与圆x2+y2+2x=0的位置关系是（）A．相离B．相切C．相交D．内含10．三视图如图的几何体的全面积是（）A．B．C．D．11．若圆x2+y2﹣2x﹣4y=0的圆心到直线x﹣y+a=0的距离为，则a的值为（）A．﹣2或2 B．或C．2或0 D．﹣2或012．在平面直角坐标系xoy中，圆C的方程为x2+y2﹣8x+15=0，若直线y=kx﹣2上至少存在一点，使得以该点为圆心，1为半径的圆与圆C有公共点，则实数k的最大值为（）A．0 B．C．D．3二、填空题（每小题4分，共16分）13．棱长为2的正方体的顶点在同一个球上，则该球的表面积为．14．过点A（2，1），且在两坐标轴上的截距相等的直线方程是．15．两平行直线x+3y﹣4=0与2x+6y﹣9=0的距离是．16．一个正方体纸盒展开后如图所示，在原正方体纸盒中有如下结论：①AB⊥EF；②AB与CM所成的角为60°；③EF与MN是异面直线；④MN∥CD．以上四个命题中，正确命题的序号是．三、解答题（共56分，解答应写出文字说明，证明过程或演算步骤）17．求满足下列条件的直线方程．（1）直线l1经过点A（4，﹣2），B（﹣1，8）；（2）直线l2过点C（﹣2，1），且与y轴平行．18．如图所示的一块木料中，棱BC平行于面A′C′．（Ⅰ）要经过面A′C′内的一点P和棱BC将木料锯开，应怎样画线？（Ⅱ）所画的线与平面AC是什么位置关系？并证明你的结论．19．设直线x+2y+4=0和圆x2+y2﹣2x﹣15=0相交于点A，B．（1）求弦AB的垂直平分线方程；（2）求弦AB的长．20．如图，PA⊥平面ABC，PA=，AB=1，BC=，AC=2，D是PC的中点．（1）求二面角B﹣PA﹣C的大小；（2）求直线BD与平面ABC所成角的正切值．21．已知直线l1：2x﹣y=0，直线l2：x﹣y+2=0和直线3：3x+5y﹣7=0．（1）求直线l1和直线l2交点C的坐标；（2）求以C点为圆心，且与直线l3相切的圆C的标准方程．22．如图，在四棱锥P﹣ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点，作EF⊥PB交PB于点F．（1）证明平面PAC⊥平面PBD；（2）证明PB⊥平面EFD．2015-2016学年宁夏银川市育才中学高一（上）期末数学试卷参考答案与试题解析一、选择题（每小题4分，共48分）1．若空间两条直线a和b没有公共点，则a与b的位置关系是（）A．共面B．平行C．异面D．平行或异面【考点】空间中直线与直线之间的位置关系．【专题】证明题．【分析】由两条直线的位置特点再结合两条直线平行的定义与两条直线异面的定义可得直线a与直线b平行或异面．【解答】解：当直线a与直线b共面时，由两条直线平行的定义得a∥b．当直线a与直线b不共面时，由异面直线的定义得直线a与直线b异面．故选D．【点评】解决此类问题的关键是熟练掌握两条直线在空间的位置关系与两条直线平行、异面的定义．2．空间四边形的两条对角线相互垂直，顺次连接四边中点的四边形一定是（）A．空间四边形B．矩形C．菱形D．正方形【考点】平面的基本性质及推论．【专题】计算题；数形结合；数形结合法；空间位置关系与距离．【分析】空间四边形ABCD中，由AC⊥BD，E、F、G、H分别是AB、BC、CD、AD的中点，推导出EHGF，EFHG，EH⊥EF，由此能证明四边形EFGH是矩形．【解答】解：如图，空间四边形ABCD中，∵AC⊥BD，E、F、G、H分别是AB、BC、CD、AD的中点，∴EH∥BD，且EH=BD，GF∥BD，且GF=，EF∥AC，且EF=AC，HG∥AC，且HG=AC，∴EHGF，EFHG，EH⊥EF，∴四边形EFGH是矩形．故选：B．【点评】本题考查四边形形状的判断，是基础题，解题时要认真审题，注意三角形中位线定理的合理运用．3．过点M（﹣2，a）和N（a，4）的直线的斜率为1，则实数a的值为（）A．1 B．2 C．1或4 D．1或2【考点】直线的斜率．【专题】计算题．【分析】利用直线的斜率公式可得，解方程求得a的值．【解答】解：由于过点M（﹣2，a）和N（a，4）的直线的斜率为1，∴∴a=1故选：A．【点评】本题考查直线的斜率公式的应用，是一道基础题．4．正方体ABCD﹣A1B1C1D1中，与侧棱AB异面且垂直的棱有（）A．8条B．6条C．4条D．3条【考点】空间中直线与直线之间的位置关系．【专题】计算题；数形结合；数形结合法；空间位置关系与距离．【分析】作出正方体ABCD﹣A1B1C1D1中，数结合列举出与侧棱AB异面且垂直的棱，由此能求出结果．【解答】解：如图，正方体ABCD﹣A1B1C1D1中，与侧棱AB异面且垂直的棱有：CC1，DD1，A1D1，B1C1，共4条．故选：C．【点评】本题考查正方体中与侧棱异面且垂直的棱的条数的求法，是基础题，解题时要认真审题，注意数形结合思想的合理运用．5．已知圆锥的母线长为5，底面周长为6π，则它的体积为（）A．10πB．12πC．15πD．36π【考点】旋转体（圆柱、圆锥、圆台）．【专题】计算题；转化思想；空间位置关系与距离；立体几何．【分析】圆锥的底面周长，求出底面半径，然后求出圆锥的高，即可求出圆锥的体积．【解答】解：∵圆锥的底面周长为6π，∴圆锥的底面半径r=3；又∵圆锥的母线长l=5，∴圆锥的高h=4，所以圆锥的体积为V=×π•32×4=12π，故选：B．【点评】本题是基础题，考查计算能力，圆锥的高的求法，底面半径的求法，是必得分的题目6．直线x+y+2=0的倾斜角为（）A．30°B．60°C．120°D．150°【考点】直线的一般式方程．【专题】直线与圆．【分析】由直线的方程可得直线的斜率，由倾斜角和斜率的关系可得答案．【解答】解：直线x+y+2=0可化为y=﹣x﹣，∴直线的斜率为﹣，设直线的倾斜角为α，可得tanα=﹣，∴α=150°故选：D【点评】本题考查直线的一般式方程，涉及直线的倾斜角和斜率的关系，属基础题．7．过点（1，2）且与原点距离最大的直线方程是（）A．x+2y﹣5=0 B．2x+y﹣4=0 C．x+3y﹣7=0 D．3x+y﹣5=0【考点】两条直线垂直与倾斜角、斜率的关系．【专题】计算题．【分析】先根据垂直关系求出所求直线的斜率，由点斜式求直线方程，并化为一般式．【解答】解：设A（1，2），则OA的斜率等于2，故所求直线的斜率等于﹣，由点斜式求得所求直线的方程为【点评】本题考查用点斜式求直线方程的方法，求出所求直线的斜率，是解题的关键．8．平面α与平面β平行的条件可以是（）A．α内有无穷多条直线都与β平行B．直线a∥α，a∥β，且直线a不在α内，也不在β内C．α内的任何直线都与β平行D．直线a在α，直线b在β内，且a∥β，b∥α【考点】平面与平面平行的判定．【专题】计算题；转化思想；综合法；空间位置关系与距离．【分析】在A、B、D中，α与β相交或平行；在C中，由面面平行的判定定理得α∥β．【解答】解：在A中，α内有无穷多条直线都与β平行，α与β有可能相交，故A错误；在B中：直线a∥α，a∥β，且直线a不在α内，也不在β内，则α与β相交或平行，故B错误；在C中：α内的任何直线都与β平行，由面面平行的判定定理得α∥β，故C正确；在D中：直线a在α，直线b在β内，且a∥β，b∥α，则α与β相交或平行，故D错误．故选：C．【点评】本题考查面面平行的判断，是基础题，解题时要认真审题，注意空间中线线、线面、面面间的关系的合理运用．9．圆x2+y2﹣4=0与圆x2+y2+2x=0的位置关系是（）A．相离B．相切C．相交D．内含【考点】圆与圆的位置关系及其判定．【专题】转化思想；综合法；圆锥曲线的定义、性质与方程．【分析】把圆的方程化为标准形式，求出圆心坐标和圆的半径，再根据这两个圆的圆心距为d=R﹣r，可得两圆相内切．【解答】解：圆x2+y2﹣4=0即x2+y2=4，表示以原点O为圆心、半径等于2的圆，圆x2+y2+2x=0，即（x+1）2+y2 =1，表示以C（﹣1，0）为圆心、半径等于1的圆．由于这两个圆的圆心距为d=OC==2﹣1=R﹣r，故两圆相内切，故选：B．【点评】本题主要考查圆和圆的位置关系的判断方法，两点间的距离公式，属于基础题．10．三视图如图的几何体的全面积是（）A．B．C．D．【考点】由三视图求面积、体积．【专题】计算题．【分析】由三视图知几何体是一个四棱锥，四棱锥的底面是一个边长为1的正方形，一条侧棱与底面垂直，且侧棱的长是1，另外两条侧棱长，得到表面积．【解答】解：由三视图知几何体是一个四棱锥，四棱锥的底面是一个边长为1的正方形，一条侧棱与底面垂直，且侧棱的长是1，∴四棱锥的表面积是1×+2×=2+故选A．【点评】本题考查由三视图还原几何体，本题解题的关键是看出几何体的各个部分的长度，本题是一个基础题．A．﹣2或2 B．或C．2或0 D．﹣2或0【考点】点到直线的距离公式．【专题】计算题．【分析】把圆的方程化为标准方程后，找出圆心坐标，利用点到直线的距离公式表示出圆心到已知直线的距离，根据此距离等于列出关于a的方程，求出方程的解即可得到a的值．【解答】解：把圆x2+y2﹣2x﹣4y=0化为标准方程为：（x﹣1）2+（y﹣2）2=5，所以圆心坐标为（1，2），∵圆心（1，2）到直线x﹣y+a=0的距离为，∴，即|a﹣1|=1，可化为a﹣1=1或a﹣1=﹣1，∴解得a=2或0．故选C．【点评】此题考查学生会将圆的一般式方程化为圆的标准方程并会从标准方程中找出圆心坐标，灵活运用点到直线的距离公式化简求值，是一道中档题．12．在平面直角坐标系xoy中，圆C的方程为x2+y2﹣8x+15=0，若直线y=kx﹣2上至少存在一点，使得以该点为圆心，1为半径的圆与圆C有公共点，则实数k的最大值为（）A．0 B．C．D．3【考点】直线与圆的位置关系．【专题】直线与圆．【分析】圆C的方程为x2+y2﹣8x+15=0，即（x﹣4）2+y2=1，表示以C（4，0）为圆心，半径等于1的圆．由题意可得，直线y=kx﹣2和圆C′：即（x﹣4）2+y2=4 有公共点，由点C′到直线y=kx﹣2的距离为d=≤2，求得实数k的最大值．【解答】解：圆C的方程为x2+y2﹣8x+15=0，即（x﹣4）2+y2=1，表示以C（4，0）为圆心，半径等于1的圆．要使直线y=kx﹣2上至少存在一点，使得以该点为圆心，1为半径的圆与圆C有交点，只要直线y=kx﹣2和圆C′：即（x﹣4）2+y2=4 有公共点即可，由点C′到直线y=kx﹣2的距离为d=≤2，3k2﹣4k≤0，解得0≤k≤，故k的最大值为，故选B．【点评】本题主要考查直线和圆的位置关系，点到直线的距离公式，体现了等价转化的数学思想，属于中档题．二、填空题（每小题4分，共16分）13．棱长为2的正方体的顶点在同一个球上，则该球的表面积为12π．【考点】球内接多面体；球的体积和表面积．【专题】空间位置关系与距离．【分析】由棱长为2的正方体的八个顶点都在同一个球面上，知球半径R=，由此能求出球的表面积．【解答】解：∵棱长为2的正方体的八个顶点都在同一个球面上，∴球半径R==，∴球的表面积S=4π（）2=12π．故答案为：12π．【点评】本题考查球的表面积的求法，解题时要认真审题，注意等价转化思想的合理运用．14．过点A（2，1），且在两坐标轴上的截距相等的直线方程是x﹣2y=0，或x+y﹣3=0．【考点】直线的截距式方程．【专题】分类讨论；直线与圆．【分析】当直线过原点时，用点斜式求得直线方程．当直线不过原点时，设直线的方程为x+y=k，把点A（2，1）代入直线的方程可得k值，从而求得所求的直线方程，综合可得结论．【解答】解：当直线过原点时，方程为y=x，即x﹣2y=0．当直线不过原点时，设直线的方程为x+y=k，把点A（2，1）代入直线的方程可得k=3，故直线方程是x+y﹣3=0．综上，所求的直线方程为x﹣2y=0，或x+y﹣3=0，故答案为x﹣2y=0，或x+y﹣3=0．【点评】本题考查用待定系数法求直线方程，体现了分类讨论的数学思想，注意当直线过原点时的情况，这是解题的易错点，属于基础题．15．两平行直线x+3y﹣4=0与2x+6y﹣9=0的距离是．【考点】两条平行直线间的距离．【专题】计算题．【分析】在一条直线上任取一点，求出这点到另一条直线的距离即为两平行线的距离．【解答】解：由直线x+3y﹣4=0取一点A，令y=0得到x=4，即A（4，0），则两平行直线的距离等于A到直线2x+6y﹣9=0的距离d===．故答案为：【点评】此题是一道基础题，要求学生理解两条平行线的距离的定义．会灵活运用点到直线的距离公式化简求值．16．一个正方体纸盒展开后如图所示，在原正方体纸盒中有如下结论：①AB⊥EF；②AB与CM所成的角为60°；③EF与MN是异面直线；④MN∥CD．以上四个命题中，正确命题的序号是①③．【考点】异面直线及其所成的角；异面直线的判定．【专题】阅读型．【分析】先把正方体的平面展开图还原成原来的正方体，再根据所给结论进行逐一判定即可．【解答】解：把正方体的平面展开图还原成原来的正方体如图所示，则AB⊥EF，EF与MN为异面直线，AB∥CM，MN⊥CD，只有①③正确．故答案为①③【点评】本题主要考查了异面直线及其所成的角，直线与直线的位置关系，考查空间想象能力、运算能力和推理论证能力，属于基础题．三、解答题（共56分，解答应写出文字说明，证明过程或演算步骤）17．求满足下列条件的直线方程．（1）直线l1经过点A（4，﹣2），B（﹣1，8）；（2）直线l2过点C（﹣2，1），且与y轴平行．【考点】待定系数法求直线方程．【专题】计算题；方程思想；综合法；直线与圆．（2）根据直线l2过点C（﹣2，1），且与y轴平行，可得结论．【解答】解：（1）由两点式方程知，直线l1的方程为，化简有2x+y﹣6=0…（2）由题意知直线l2的方程为x=﹣2…【点评】本题考查直线方程，考查学生的计算能力，比较基础．18．如图所示的一块木料中，棱BC平行于面A′C′．（Ⅰ）要经过面A′C′内的一点P和棱BC将木料锯开，应怎样画线？（Ⅱ）所画的线与平面AC是什么位置关系？并证明你的结论．【考点】棱柱的结构特征．【专题】空间位置关系与距离．【分析】（Ⅰ）注意到棱BC平行于面A′C′，故过点P作B′C′的平行线，交A′B′、C′D′于点E，F，连结BE，CF；（Ⅱ）易知BE，CF与平面AC的相交，可证EF∥平面AC．【解答】解：（Ⅰ）过点P作B′C′的平行线，交A′B′、C′D′于点E，F，连结BE，CF；作图如下：（Ⅱ）EF∥平面AC．理由如下：易知BE，CF与平面AC的相交，∵BC∥平面A′C′，又∵平面B′C′CB∩平面A′C′=B′C′，∴BC∥B′C′，∴EF∥BC，又∵EF⊄平面AC，BC⊂平面AC，∴EF∥平面AC．【点评】本题考查了学生的作图能力及线面位置关系的判断，属于中档题．19．设直线x+2y+4=0和圆x2+y2﹣2x﹣15=0相交于点A，B．（1）求弦AB的垂直平分线方程；（2）求弦AB的长．【考点】直线与圆的位置关系；直线的一般式方程与直线的垂直关系．【专题】计算题；直线与圆．【分析】（1）求出圆的圆心为C（1，0），半径r=4．根据垂径定理，弦AB的垂直平分线经过圆心C，由此加以计算即可得出AB的垂直平分线方程；（2）利用点到直线的距离公式，算出圆心C（1，0）到直线x+2y+4=0的距离，再根据垂径定理加以计算，可得弦AB的长．【解答】解：（1）∵圆x2+y2﹣2x﹣15=0化成标准方程得（x﹣1）2+y2=16，∴圆心为C（1，0），半径r=4．∵直线x+2y+4=0和圆x2+y2﹣2x﹣15=0相交于点A、B，∴设弦AB的垂直平分线为l：2x﹣y+m=0，由垂径定理，可知点C（1，0）在l上，得2×1﹣0+m=0，解之得m=﹣2．因此，弦AB的垂直平分线方程为2x﹣y﹣2=0；（2）圆心C（1，0）到直线x+2y+4=0的距离为：根据垂径定理，得|AB|=2=2，即弦AB的长等于2．【点评】本题给出直线与圆相交，求弦的中垂线方程并求弦的长度．着重考查了圆的标准方程、点到直线的距离公式和直线与圆的位置关系等知识，属于中档题．20．如图，PA⊥平面ABC，PA=，AB=1，BC=，AC=2，D是PC的中点．（1）求二面角B﹣PA﹣C的大小；（2）求直线BD与平面ABC所成角的正切值．【考点】直线与平面所成的角；二面角的平面角及求法．【专题】计算题；转化思想；综合法；空间角．【分析】（1）推导出BA⊥PA，CA⊥PA，从而∠BAC为二面角B﹣PA﹣C的平面角，由此能求出二面角B﹣PA ﹣C的大小．（2）过点D作DE⊥AC，垂足为E，连接AE，直线BD与平面ABC所成的角为∠DBE，由此能求出直线BD 与平面ABC所成角的正切值．【解答】解：（1）∵PA⊥平面ABC，AC⊂平面ABC，AB⊂平面ABC，∴BA⊥PA，CA⊥PA，∴∠BAC为二面角B﹣PA﹣C的平面角．在△ABC中，∵，∴AB2+BC2=AC2，∴AB⊥BC，∴△ABC为直角三角形，sin∠BAC==，∴∠BAC=60°，故二面角B﹣PA﹣C的大小为60°…（2）过点D作DE⊥AC，垂足为E，连接AE，从而结合题意知DE⊥平面ABC，∴直线BD与平面ABC所成的角为∠DBE，且．又D是PC的中点，∴，，∴=．∴直线BD与平面ABC所成角的正切值为．…【点评】本题考查三面角的大小的求法，考查线面角的正切值的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．21．已知直线l1：2x﹣y=0，直线l2：x﹣y+2=0和直线3：3x+5y﹣7=0．（1）求直线l1和直线l2交点C的坐标；（2）求以C点为圆心，且与直线l3相切的圆C的标准方程．【考点】圆的切线方程；两条直线的交点坐标．【专题】转化思想；综合法；直线与圆．【分析】（1）把直线l1和直线l2的方程联立方程组，求得直线l1和直线l2交点坐标．（2）根据圆C与直线l3相切，利用点到直线的距离公式求得圆的半径r，从而求得圆C的标准方程．【解答】解：（1）由，求得．所以直线l1和直线l2的交点C的坐标为（2，4）．（2）因为圆C与直线l3相切，所以圆的半径r===，所以圆C的标准方程为（x﹣2）2+（y﹣4）2=．【点评】本题主要考查求两条直线的交点，直线和圆相切的性质，点到直线的距离公式的应用，体现了转化22．如图，在四棱锥P﹣ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点，作EF⊥PB交PB于点F．（1）证明平面PAC⊥平面PBD；（2）证明PB⊥平面EFD．【考点】平面与平面垂直的判定；直线与平面垂直的判定．【专题】计算题；方程思想；综合法；空间位置关系与距离．【分析】（1）推导出AC⊥BD，AC⊥PD，从而AC⊥平面PBD，由此能证明平面PAC⊥平面PBD．（2）推导出DE⊥PC，BC⊥DC，BC⊥PD，从而DE⊥平面PBC由此能证明PB⊥平面EFD．【解答】证明：（1）∵在四棱锥P﹣ABCD中，底面ABCD是正方形，∴AC⊥BD，∵侧棱PD⊥底面ABCD，AC⊂平面ABCD，∴AC⊥PD．又∵BD∩PD=D，∴AC⊥平面PBD．又∵AC⊂平面PAC，∴由平面与平面垂直的判定定理知，平面PAC⊥平面PBD…（2）在△PDC中，由PD=DC，E是PC的中点，知DE⊥PC．由底面ABCD是正方形，知BC⊥DC，由侧棱PD⊥底面ABCD，BC⊂底面ABCD，知BC⊥PD，又DC∩PD=D，故BC⊥平面PCD．而DE⊂平面PCD，所以DE⊥BC．由DE⊥PC，DE⊥BC及PC∩BC=C，知DE⊥平面PBC．又PB⊂平面PBC，故DE⊥PB．又已知EF⊥PB，且EF∩DE=E，∴PB⊥平面EFD．…【点评】本题考查面面垂直、线面垂直的证明，是中档题，解题时要认真审题，注意空间思维能力的培养．薄雾浓云愁永昼，瑞脑消金兽。

宁夏回族自治区银川一中高一上学期期末考试数学试题

一、选择题（每题4分，共计48分） 1．在直角坐标系中，直线的倾斜角是( ) A ．30°B ．60°C ． 120°D ．150°2．在空间给出下面四个命题（其中为不同的两条直线，为不同的两个平面） ①n m n m ⊥⇒⊥αα∥, ②αα∥∥，∥m n n m ⇒ ③βααβ⊥⇒⊥∥，，∥m n n m④βαβαβα∥∥，∥，∥，∥，⇒=⋂n n m m A n m 其中正确的命题个数有( )Ａ.1 个Ｂ.2个Ｃ.3个Ｄ.4个 3．已知直线：与：平行，则k 的值是( ) A ．B ．C ．D ．4．如图所示，在正方体ABCD —A1B 1C 1D 1中，M 、N 分别是BB 1、BC 的中点．则图中阴影部分在平面ADD 1A 1上的正投影为( )5．圆过点的切线方程是( ) A ． B ．C ．D ．6. 如图，正方体ABCD －中，E ，F 分别为棱AB ，的中点，在平面内且与平面平行的直线( )A ．不存在B ．有1条C ．有2条D ．有无数条 7．过点(2,1)的直线中，被圆截得的最长弦所在的直线方程为（）A ．B ． C. D.8．若用半径为R 的半圆卷成一个圆锥，则它的体积为（） A. B. C. D.9．点P 在正方形ABCD 所在平面外，PD ⊥平面ABCD ，PD=AD ，则PA 与BD 所成角的度数（） A ． B. C ． D.10．已知三棱锥S －ABC 的所有顶点都在球O 的球面上，SA ⊥平面ABC ， AB ⊥BC 且AB=BC=1，SA=，则球O 的表面积是（） A.B.C.D.11．如图，边长为的等边三角形ABC 的中线AF 与中位线DE 交于点G ，PABC DEF 已知△是△ADE 绕DE 旋转过程中的一个图形，则下列结论中正确的是( )①动点在平面ABC 上的射影在线段AF 上； ②BC ∥平面；③三棱锥的体积有最大值．A ．①B ．①②C ．①②③D ．②③12．曲线y ＝1＋4－x 2与直线y ＝k (x －2)＋4有两个交点，则实数k 的取值范围是( )A ．(0，512)B ．(512，＋∞)C ．(13，34]D ．(512，34]二、填空题（每小题4分，共计16分）13．点P(2,7)关于直线的对称点的坐标为 .14．设某几何体的三视图如下(尺寸的长度单位为m)．则该几何体的体积为______m 3．15．在空间直角坐标系中，已知点A(1,0,2)，B(1,-3,1)，点M 在y 轴上，且|MA|=|MB|，则M 的坐标是 .16．在平面直角坐标系中，圆C 的方程为，若直线上至少存在一点，使得以该点为圆心，2为半径的圆与圆C 有公共点，则k 的取值范围是 . 三、解答题(本大题共计56分） 17．（本题满分8分）已知在平面直角坐标系中，△三个顶点坐标分别为(1,3),(5,1),(1A B C -- （I ）求边的中线所在的直线方程；（II ）求边的高所在的直线方程18．（本题满分8分）已知圆和圆，直线与圆相切于点（1,1）；圆的圆心在射线上，圆过原点，且被直线截得的弦长为。

宁夏银川一中—学年高一上学期期末考试（数学）

宁夏银川⼀中—学年⾼⼀上学期期末考试（数学）x y Ox y Ox y OxyO银川⼀中2010—2011学年度⾼⼀上学期期末考试数学试题命题教师：康淑霞⼀、选择题：本⼤题共12⼩题，每⼩题5分，共60分，在每⼩题给出的四个选项中，只有⼀项是符合题⽬要求的．1．若⽅程22(62)(352)10a a x a a y a --+-++-=表⽰平⾏于x 轴的直线，则a 的值是（）A ．23B ．12-C ．23， 12-Ｄ．12．在同⼀直⾓坐标系中，表⽰直线y ax =与y x a =+正确的是（）．A ．B ．C ．D ．3. 与直线2360x y +-=关于点(11)-，对称的直线⽅程是（）Ａ．3220x y -+=Ｂ．2370x y ++= Ｃ．32120x y --=Ｄ．2380x y ++=4. 已知⼀个铜质的五棱柱的底⾯积为16cm 2,⾼为4cm ，现将它熔化后铸成⼀个正⽅体的铜块（不计损耗），那么铸成的铜块的棱长是（） A. 2cm; B.cm 34A ．如果α⊥β，那么α内⼀定存在直线平⾏于平⾯β；B ．如果α⊥β，那么α内所有直线都垂直于平⾯β；C ．如果平⾯α不垂直平⾯β，那么α内⼀定不存在直线垂直于平⾯β；D ．如果α⊥γ，β⊥γ，α∩β＝l,那么l ⊥γ.6. 三个球的半径之⽐是1:2:3 则最⼤球的体积是其余两个球的体积之和的（）A . 4倍B . 3倍C . 2倍D . 1倍7. 如图，⼀个空间⼏何体的主视图和左视图都是边长为1⽅形，俯视图是⼀个圆，那么这个⼏何体的侧⾯积．．．为（ A. 4πB . 54π左视图PDC OBASC . π D.32π 8. 点P 是等腰三⾓形ABC 所在平⾯外⼀点,PA ⊥平⾯ABC,PA=8,在三⾓形ABC 中,底边BC=6,AB=5,则P 到BC 的距离为( ) A.45 B.3 C. 33 D. 239. 设直线L 经过点(-1.1),则当点(2.-1)与直线L 的距离最远时,直线L 的⽅程是 ( ) A. 3x-2y+5=0 B. 2x-3y-5=0 C. x-2y-5=0 D. 2x-y+5=010. 直线x-2y-3=0与圆(x-2)2+(y+3)2=9交于E 、F 两点,则△EOF （O 是原点）的⾯积为（）． A ．52 B ．43 C ．23 D ．556 11. 若直线y=kx+4+2k 与曲线24x y -=有两个交点，则k 的取值范围是（）．A ．[1,+∞)C ． (43,1] D ．(-∞,-1] 12.过圆2x +2y －4x=0外⼀点P(m,n)作圆的两条切线，当这两条切线互相垂直时，m,n 应满⾜的关系式为（）A.()22-m + 2n =4 B.2)2(+m +2n =4 C.()22-m + 2n =8 D.2)2(+m +2n =8⼆、填空题：本⼤题共4⼩题，每⼩题5分，共20分，把答案填写在题中横线上． 13. 经过点(41)，且在两坐标轴上的截距相等的直线⽅程是。

2015-2016学年宁夏银川市育才中学高一(上)期末数学试卷

2015-2016学年宁夏银川市育才中学高一（上）期末数学试卷一、选择题（每小题4分，共48分）1. 若空间两条直线a和b没有公共点，则a与b的位置关系是（）A.平行B.共面C.异面D.平行或异面2. 空间四边形的两条对角线相互垂直，顺次连接四边中点的四边形一定是（）A.矩形B.空间四边形C.菱形D.正方形3. 过点M(−2, a)和N(a, 4)的直线的斜率为1，则实数a的值为（）A.2B.1C.1或4D.1或24. 正方体ABCD−A1B1C1D1中，与侧棱AB异面且垂直的棱有（）A.6条B.8条C.4条D.3条5. 已知圆锥的母线长为5，底面周长为6π，则它的体积为（）A.12πB.10πC.36πD.15π6. 直线x+√3y+2=0的倾斜角为（）A.60∘B.30∘C.150∘D.120∘7. 过点(1, 2)，且与原点距离最大的直线方程是( )A.2x+y−4=0B.x+2y−5=0C.x+3y−7=0D.x−2y+3=08. 平面α与平面β平行的条件可以是( )A.直线a // α，a // β，且直线a不在α内，也不在β内B.α内有无数条直线都与β平行C.α内的任何直线都与β平行D.直线a在α内，直线b在β内，且a // β，b // α9. 圆x2+y2−4=0与圆x2+y2+2x=0的位置关系是()A.相切B.相离C.相交D.内含10. 三视图如图的几何体的全面积是（）A.1+√2B.2+√2C.2+√3D.1+√311. 若圆x2+y2−2x−4y=0的圆心到直线x−y+a=0的距离为√22，则a的值为()A.12或32B.−2或2C.2或0D.−2或012. 在平面直角坐标系xoy中，圆C的方程为x2+y2−8x+15=0，若直线y=kx−2上至少存在一点，使得以该点为圆心，1为半径的圆与圆C有公共点，则实数k的最大值为（）A.43B.0C.32D.3二、填空题（每小题4分，共16分）棱长为2的正方体的顶点在同一个球上，则该球的表面积为________．过点A(2, 1)，且在两坐标轴上的截距相等的直线方程是________．两平行直线x+3y−4=0与2x+6y−9=0的距离是________．一个正方体纸盒展开后如图所示，在原正方体纸盒中有如下结论：①AB⊥EF；②AB与CM所成的角为60∘；③EF与MN是异面直线；④MN // CD．以上四个命题中，正确命题的序号是________．三、解答题（共56分，解答应写出文字说明，证明过程或演算步骤）求满足下列条件的直线方程．（1）直线l1经过点A(4, −2)，B(−1, 8)；（2）直线l2过点C(−2, 1)，且与y轴平行．如图所示的一块木料中，棱BC平行于面A′C′．（1）要经过面A′C′内的一点P和棱BC将木料锯开，应怎样画线？（2）所画的线与平面AC是什么位置关系？并证明你的结论．设直线x+2y+4=0和圆x2+y2−2x−15=0相交于点A，B．（1）求弦AB的垂直平分线方程；（2）求弦AB的长．如图，PA⊥平面ABC，PA=√2，AB=1，BC=√3，AC=2，D是PC的中点．（1）求二面角B−PA−C的大小；（2）求直线BD与平面ABC所成角的正切值．已知直线l1:2x−y=0，直线l2:x−y+2=0和直线3:3x+5y−7=0．（1）求直线l1和直线l2交点C的坐标；（2）求以C点为圆心，且与直线l3相切的圆C的标准方程．如图，在四棱锥P−ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点，作EF⊥PB交PB于点F．（1）证明平面PAC⊥平面PBD；（2）证明PB⊥平面EFD．参考答案与试题解析2015-2016学年宁夏银川市育才中学高一（上）期末数学试卷一、选择题（每小题4分，共48分）1.【答案】此题暂无答案【考点】空间表直线擦直英之说的位置关系【解析】此题暂无解析【解答】此题暂无解答2.【答案】此题暂无答案【考点】平面的基使性质及钡论【解析】此题暂无解析【解答】此题暂无解答3.【答案】此题暂无答案【考点】直体的氯率【解析】此题暂无解析【解答】此题暂无解答4.【答案】此题暂无答案【考点】空间表直线擦直英之说的位置关系【解析】此题暂无解析【解答】此题暂无解答5.【答案】此题暂无答案【考点】旋转验（圆柱立圆锥碳藏台）【解析】此题暂无解析【解答】此题暂无解答6.【答案】此题暂无答案【考点】直线的三般式方疫【解析】此题暂无解析【解答】此题暂无解答7.【答案】此题暂无答案【考点】直线的都特式方程两条直因垂直滤倾斜汉措斜率的关系【解析】此题暂无解析【解答】此题暂无解答8.【答案】此题暂无答案【考点】平面与平三平行腔判定直线与平三平行定判定【解析】此题暂无解析【解答】此题暂无解答9.【答案】此题暂无答案【考点】圆与来的位德米系及米判定圆的正且方程【解析】此题暂无解析【解答】此题暂无解答10.【答案】此题暂无答案【考点】由三都问求体积【解析】此题暂无解析【解答】此题暂无解答11.【答案】此题暂无答案【考点】圆的正且方程点到直使的距离之式【解析】此题暂无解析【解答】此题暂无解答12.【答案】此题暂无答案【考点】直线与都连位置关系【解析】此题暂无解析【解答】此题暂无解答二、填空题（每小题4分，共16分）【答案】此题暂无答案【考点】球内较多面绕球的表体积决体积【解析】此题暂无解析【解答】此题暂无解答【答案】此题暂无答案【考点】直线的都特式方程【解析】此题暂无解析【解答】此题暂无解答【答案】此题暂无答案【考点】两条平行射线间面距离【解析】此题暂无解析【解答】此题暂无解答【答案】此题暂无答案【考点】异面体线土判定异面直线表烧所成的角【解析】此题暂无解析【解答】此题暂无解答三、解答题（共56分，解答应写出文字说明，证明过程或演算步骤）【答案】此题暂无答案【考点】待定系数因求滤线方程【解析】此题暂无解析【解答】此题暂无解答【答案】此题暂无答案【考点】棱柱三实构特征【解析】此题暂无解析【解答】此题暂无解答【答案】此题暂无答案【考点】直线与都连位置关系直线的较般式划程皮直校的垂直关系【解析】此题暂无解析【解答】此题暂无解答【答案】此题暂无答案【考点】直线与正键所成的角二面角的使面角及爱法【解析】此题暂无解析【解答】此题暂无解答【答案】此题暂无答案【考点】圆的水射方程两条直验立交点坐标【解析】此题暂无解析【解答】此题暂无解答【答案】此题暂无答案【考点】平面与平明垂钾的判定直线与平正垂直的判然【解析】此题暂无解析【解答】此题暂无解答。

银川一中高一数学期末试卷及答案

(上)高一期末考试数学试卷一、选择题（125'⨯=60分）1．分别在两个平面内的两条直线的位置关系是A ．异面B ．平行C ．相交D ．以上都有可能 2．已知一个几何体的三视图如图所示，则此几何体的组成方式为 A. 上面为圆台，下面为圆柱 B. 上面为圆台，下面为棱柱 C. 上面为棱台，下面为棱柱 D. 上面为棱台，下面为圆柱 3．下列说法中正确的是A ．经过不同的三点有且只有一个平面B ．没有公共点的两条直线一定平行C ．垂直于同一平面的两直线是平行直线D ．垂直于同一平面的两平面是平行平面4．若一个底面是正三角形的三棱柱的正视图如图所示，则其侧面积等于A ． 6 +23B ．2C ．23D ．65．过点M (－2，m )，N (m,4)的直线的斜率等于1，则m 的值为 A ．1B ．4C ．1或3D ． 1或46．函数121()()2xf x x =-的零点个数为A ．0B ．1C ．2D ．3 7．如图,在正四棱柱ABCD —A 1B 1C 1D 1中，E 、F 分别是AB 1、BC 1的中点，则下列说法中错误的是 A ．EF 与BB 1垂直 B ．EF 与BD 垂直 C ．EF 与CD 异面 D ．EF 与A 1C 1异面8．经过圆0222=++y x x 的圆心C ，且与直线0=+y x 垂直的直线方程是 A ．01=++y xB ．01=-+y x111C ．01=+-y xD ．01=--y x9．如右图，某几何体的正视图与侧视图都是边长为1的正方形，且体积为12．则该几何体的俯视图可以是10．若圆C 的半径为1，圆心在第一象限，且与直线4x-3y=0和x 轴都相切，则该圆的标准方程是A ．()137322=⎪⎭⎫ ⎝⎛-+-y xB ．()()11222=-+-y xC ．()()13122=-+-y xD ．()112322=-+⎪⎭⎫ ⎝⎛-y x11．如图，在正三棱柱ABC -A 1B 1C 1中，已知AB =1，D 在棱BB 1上，且BD =1，则AD 与平面AA 1C 1C 所成角的正弦值为A ．64 B. 34 C. 63 D. 3312．如图，动点P 在正方体1111D C B A -ABCD 的对角线1BD 上，过点P 作垂直于平面D D BB 11的直线，与正方体表面相交于N.M,设x,BP =y,M =N 则函数()x f y =的图象大致是二、填空题（45'⨯=20 分）13．已知直线l 1：2(1)40x m y +++=，直线l 2：340mx y ++=，若l 1 //l 2，则实数m ＝________. 14. 若圆锥的侧面积为2π，底面积为π，则该圆锥的体积为 .15. 已知点A (1，1)，B (－2，2)，直线l 过点P (-1,-1)且与线段AB 始终有交点，则直线l 的斜率k的取值范围为 .16．高为2的四棱锥S ABCD -的底面是边长为1的正方形，点S ，A ，B ，C ，D 均在半径为1的同一球面上，则底面ABCD 的中心与顶点S 之间的距离为.A ．B ．C ．D ．11 正视图11 侧视图MN三、解答题（共70分） 17. （本题满分10分）已知直线1l ：3x ＋2y －1＝0 ，直线2l ：5x ＋2y ＋1＝0，直线3l ：3x －5y ＋6＝0，直线L 经过直线1l 与直线2l 的交点，且垂直于直线3l ，求直线L 的一般式方程． 18. （本题满分12分）如图所示，从左到右依次为：一个长方体截去一个角所得多面体的直观图，该多面体的正视图，该多面体的侧视图（单位：cm ）（1）按照给出的尺寸，求该多面体的体积；（2）在所给直观图中连结C B '，证明：C B '//平面EFG ．19. （本题满分12分）求圆心在直线4y x =-上，且与直线:10l x y +-=相切于点()3,2P -的圆的标准方程.20. （本题满分12分）已知点P (2，－1)．(1)若一条直线经过点P ，且原点到直线的距离为2，求该直线的一般式方程； (2)求过点P 且与原点距离最大的直线的一般式方程，并求出最大距离是多少？ 21.（本题满分12分）如图，在正方体1111ABCD A B C D -中，,M N 分别是,AB BC 的中点．(1)求证：平面1B MN ⊥平面11BB D D ；(2)在棱1DD 上是否存在一点P ，使得1BD ∥平面PMN ，若存在，求1:D P PD 的比值；若不存在，说明理由.22.（本小题满分12分）如图，正方形ABCD 所在平面与四边形ABEF 所在平面互相垂直，ABE △是等腰直角三角形，AB AE =，FA FE =，45AEF ∠=°．（1）求证：EF ⊥平面BCE ；EBCDA FPM（2）设线段CD、AE的中点分别为P、M，求PM与BC所成角的正弦值；--的平面角的正切值．（3）求二面角F BD A高一上学期期末考试----数学（参考答案）一.选择题（ 125'⨯=60分）1 2 3 4 5 6 7 8 9 10 11 12 DACDABDCCBAB二.填空题（ 45'⨯=20 分） 13. m ＝－3； 14.33π； 15. 3,k ≤-或1k ≥； 16.10.2三.解答题（共70分. 第17题----10分；第18—第22题，每题12分） 17. （本题满分10分）答案：1l 、2l 的交点 (－1,2) ； l 的一般式方程为： 5x ＋3y －1＝0. 18. （本题满分12分）解析：（1）所求多面体体积=3284()3cm （2）证明：在长方体中，连结，则．因为分别为，中点，所以，从而．又平面，所以面．19. （本题满分12分）答案：()()22148x y -++= 20. （本题满分12分）解:①当l 的斜率k 不存在时， l 的方程为x ＝2；②当l 的斜率k 存在时，设l ：y ＋1＝k (x －2)，即kx －y －2k －1＝0. 由点到直线距离公式得22121k k--=+，得l ：3x －4y －10＝0.故所求l 的方程为： x ＝2 或 3x －4y －10＝0.(2)作图可得过P 点与原点O 距离最大的直线是过P 点且与PO 垂直的直线，由l ⊥OP ，得k l k OP＝－1， k l＝12opk -=，由直线方程的点斜式得y ＋1＝2(x －2)，即2x －y －5＝0.即直线2x －y －5＝0是过P 点且与原点O 距离最大的直线，最大距离为 555-=.21. （本题满分12分）(1)证明：连接AC ，则AC ⊥BD ，又M ，N 分别是AB ，BC 的中点， ∴MN ∥AC ，∴MN ⊥BD. ∵ABCD-A 1B 1C 1D 1是正方体，∴BB 1⊥平面ABCD ， ∵MN ⊂平面ABCD ， ∴BB 1⊥MN ，∵BD∩BB 1=B ， ∴MN ⊥平面BB 1D 1D ，∵MN ⊂平面B 1MN ，∴平面B 1MN ⊥平面BB 1D 1D.(2)设MN 与BD 的交点是Q ，连接PQ ，∵BD 1∥平面PMN ，BD 1⊂平面BB 1D 1D ，平面BB 1D 1D∩平面PMN=PQ ，∴BD 1∥PQ ， PD 1∶DP =1:322.（本小题满分12分）解: （1）因为平面ABEF ⊥平面ABCD ，BC ⊂平面ABCD ，BC AB ⊥，平面ABEF平面ABCD AB =，所以BC ⊥平面ABEF ．所以BC EF ⊥．因为ABE △为等腰直角三角形，AB AE =，所以45AEB ∠=°又因为45AEF ∠=°，所以454590FEB ∠=+=°°°，即EF BE ⊥．因为BC ⊂平面BCE BE ⊂，平面BCE ，BC BE B =，所以EF ⊥平面BCE ．（2）取BE 的中点N ，连结CN MN ，，则12MN AB PC∥∥，所以PMNC 为平行四边形，所以PM CN ∥．所以CN 与BC 所成角NCB ∠即为所求, 在直角三角形NBC 中,3sin .3NCB ∠= (另解：也可平移BC 至点P 处；或者通过构造直角三角形，设值计算可得). （3）由EA AB ⊥，平面ABEF ⊥平面ABCD ，易知，EA ⊥平面ABCD ．作FG AB ⊥，交BA 的延长线于G ，则FG EA ∥．从而，FG ⊥平面ABCD ．作GH BD ⊥于H ，连结FH ，则由三垂线定理知，BD FH ⊥．因此，FHG ∠为二面角F BD A --的平面角．因为45FA FE AEF =∠=，°，所以9045AFE FAG ∠=∠=°，°．EBC DA F PM G NH设1AB =，则1AE =，22AF =． 1sin 2FG AF FAG ==．在Rt BGH △中，45GBH ∠=°，13122BG AB AG =+=+=， 3232sin 224GH BG GBH ===．在Rt FGH △中，2tan 3FG FHG GH ==．故二面角F BD A --的平面角的正切值为2tan 3FG FHG GH ==.。

2015-2016学年高一第一学期数学期末考试试卷(含答案)

10011高一第一学期期末考试试卷本试卷分第I 卷（选择题）和第n 卷（非选择题）两部分.第I 卷 1至2页.第n 卷3至4页，共150分.考试时间120分钟. 注息事项：1•本试卷分第I 卷（选择题）和第n 卷（非选择题）两部分。

答卷前，考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上。

2•问答第I 卷时。

选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动•用橡皮擦干净后，再选涂其它答案标号。

写在本试卷上无效3.回答第n 卷时。

将答案写在答题卡上.写在本试卷上无效•4•考试结束后.将本试卷和答且卡一并交回。

第I 卷一、选择题：本大题共 12小题，每小题5分，在每小题给同的四个选项中，只有一项是符合题目要求的。

1.已知全集 U=R 集合 A |3 Ex <7届=<x |x 2 — 7x +10 ，则 C R （A C B ）=C. ( Y ,3][5,：：)2^a 习a '©'a 的分数指数幕表示为（）A. e ° =1与 In 1=0 B .1C. log 3 9 = 2与92 =3D. 4. 下列函数f(x)中，满足"对任意的x 1,x^ (一叫0)，当x 1 ：: x 2时，总有f (xj• f(x 2) ”的是A. -(5,：：) B. -::,3 一. [5,：：)33A. a 23B. aC.D.都不对log 7 7 = 1 与7— 73.下列指数式与对数式互化不正确的一组是（1001121 xA. f(x) =(x 1) B . f(x)=l n(x-1) C . f (x)D . f (x)二 ex15. 已知函数y = f(x)是奇函数，当x 0时，f(x)=lgx,则f(f( ))的值等于()B.lg2lg2C . lg2D . - lg 26.对于任意的a 0且a=1，函数f x =a x~ 3的图象必经过点（）A. 5,2B. 2,5C.7. 设a= log o.7 0.8 , b= log 1.1 0.9 , c= 1.1A. a<b<cB. b<a<cC.8. 下列函数中哪个是幕函数9.函数y屮g（x-1）|的图象是（）210.已知函数y - -x -2x 3在区间［a, 2］上的最大值为A —- B. - C. —-2 2 211..函数f （x）二e x-丄的零点所在的区间是（）x1 1 3 3A.（0,；）B. （加）C. （1二）D. （；,2）2 2 2 212.在一个倒置的正三棱锥容器内放入一个钢球，钢球恰与棱锥的四个面都接触，过棱锥的一条侧棱和高作截面，正确的截面图形是（4,1 D. 1,4，那么（）a<c<b D. c<a<b（）C. y = . 2xD. y = - 2x则a等于（）D.—-或一-2 2第口卷本卷包括必考题和选考题两部分。

2015-2016学年宁夏银川一中高一上学期期末数学试卷

2015-2016学年宁夏银川一中高一上学期期末数学试卷一、选择题1.直线x+y+1=0的倾斜角与在y轴上的截距分别是（）A. 135°，1B. 45°，﹣1C. 45°，1D. 135°，﹣12.圆心为（1，1）且过原点的圆的方程是（）A. （x﹣1）2+（y﹣1）2=1B. （x+1）2+（y+1）2=1C. （x+1）2+（y+1）2=2D. （x﹣1）2+（y﹣1）2=23.圆柱的轴截面是正方形，且轴截面面积是S，则它的侧面积是（）A. B. πS C. 2Πs D. 4πS4.在平面直角坐标系xOy中，直线3x+4y﹣5=0与圆x2+y2=4相交于A、B两点，则弦AB的长等于（）A. 3B. 2C.D. 15.直线l1：ax﹣y+b=0，l2：bx+y﹣a=0（ab≠0）的图象只可能是图中的（）A. B. C. D.6.已知一个几何体的三视图如图所示，则该几何体的体积为（）A. 12πB. 8πC.D.7.已知点M（a，b）在直线3x+4y=15上，则的最小值为（）A. 2B. 3C.D. 58.如图，正方体的底面与正四面体的底面在同一平面α上，且AB∥CD，正方体的六个面所在的平面与直线CE，EF相交的平面个数分别记为m，n，那么m+n=（）A. 8B. 9C. 10D. 119.过点P（﹣，﹣1）的直线l与圆x2+y2=1有公共点，则直线l的倾斜角的取值范围是（）A. [0，30°]B. [0，45°]C. [0，60°]D. [0，90°]10.设m，n是两条不同的直线，α，β是两个不同的平面，下列命题中正确的是（）A. 若α⊥β，m⊂α，n⊂β，则m⊥nB. 若α∥β，m⊂α，n⊂β，则m∥nC. 若m⊥n，m⊂α，n⊂β，则α⊥βD. 若m⊥α，m∥n，n∥β，则α⊥β11.若圆C1：x2+y2=1与圆C2：x2+y2﹣6x﹣8y+m=0外切，则m=（）A. 21B. 19C. 9D. ﹣1112.如图，M是正方体ABCD﹣A1B1C1D1的棱DD1的中点，给出下列命题①过M点有且只有一条直线与直线AB、B1C1都相交；②过M点有且只有一条直线与直线AB、B1C1都垂直；③过M点有且只有一个平面与直线AB、B1C1都相交；④过M点有且只有一个平面与直线AB、B1C1都平行．其中真命题是（）A. ②③④B. ①③④C. ①②④D. ①②③二、填空题13.过l1：2x﹣3y+2=0与l2：3x﹣4y+2=0的交点且与直线4x+y﹣4=0平行的直线方程为________．14.若圆C的半径为1，其圆心与点（1，0）关于直线y=x对称，则圆C的标准方程为________．15.若圆锥的表面积是15π，侧面展开图的圆心角是60°，则圆锥的体积是________．16.圆柱形容器内部盛有高度为8cm的水，若放入三个相同的球（球的半径与圆柱的底面半径相同）后，水恰好淹没最上面的球（如图所示），则球的半径是________ cm．三、解答题17.如图，已知正方形ABCD的中心为E（﹣1，0），一边AB所在的直线方程为x+3y﹣5=0，求其它三边所在的直线方程．18.如图，长方体ABCD﹣A1B1C1D1中，AB=16，BC=10，AA1=8，点E，F分别在A1B1，D1C1上，A1E=D1F=4．过E，F的平面α与此长方体的面相交，交线围成一个正方形（1）在图中画出这个正方形（不必说出画法和理由）（2）求平面α把该长方体分成的两部分体积的比值．19.已知圆C与两平行直线x﹣y﹣8=0和x﹣y+4=0相切，圆心在直线2x+y﹣10=0上．（1）求圆C的方程．（2）过原点O做一条直线，交圆C于M，N两点，求OM*ON的值．20.如图，在三棱锥V﹣ABC中，平面VAB⊥平面ABC，△VAB为等边三角形，AC⊥BC且AC=BC= ，O，M分别为AB，VA的中点．（1）求证：VB∥平面MOC．（2）求证：平面MOC⊥平面VAB．（3）求二面角C﹣VB﹣A的平面角的余弦值．21.如图，已知二面角α﹣MN﹣β的大小为60°，菱形ABCD在面β内，A、B两点在棱MN上，∠BAD=60°，E是AB的中点，DO⊥面α，垂足为O．（1）证明：AB⊥平面ODE；（2）求异面直线BC与OD所成角的余弦值．22.如图，在平面直角坐标系xOy中，点A（0，3），直线l：y=2x﹣4．设圆C的半径为1，圆心在l上．（1）若圆心C也在直线y=x﹣1上，过点A作圆C的切线，求切线的方程；（2）若圆C上存在点M，使MA=2MO，求圆心C的横坐标a的取值范围．答案解析部分一、选择题1.【答案】D2.【答案】D3.【答案】B4.【答案】B5.【答案】A6.【答案】D7.【答案】B8.【答案】A9.【答案】C10.【答案】D11.【答案】C12.【答案】C二、填空题13.【答案】4x+y﹣10=014.【答案】x2+（y﹣1）2=115.【答案】16.【答案】4三、解答题17.【答案】解：E到直线x+3y﹣5=0距离是= ，所以E到另三边距离也是有一条边CD与AB：x+3y﹣5=0平行，设为x+3y+a=0，则，即|a﹣1|=6∴a=﹣5，a=7 其中a=﹣5就是已知的∴CD方程为：x+3y+7=0另两条和他们垂直，所以斜率为3，设为：3x﹣y+b=0则，即|b﹣3|=6∴b=9，b=﹣3∴AD的方程：3x﹣y﹣3=0；BC的方程：3x﹣y+9=018.【答案】（1）解：交线围成的正方形EFGH如图所示；（2）解：作EM⊥AB，垂足为M，则AM=A1E=4，EB1=12，EM=AA1=8．因为EFGH为正方形，所以EH=EF=BC=10，于是MH= =6，AH=10，HB=6．因为长方体被平面α分成两个高为10的直棱柱，所以其体积的比值为．19.【答案】（1）解：设所求圆的方程是（x﹣a）2+（y﹣b）2=r2．由题意知，两平行线间距离d= =6 ，又到两平行直线距离相等的直线方程为：x﹣y﹣2=0所以由，得．即圆心坐标为（4，2）．所以圆C的方程为：（x﹣4）2+（y﹣2）2=18\（2）解：设OT是圆的切线，切点为T，则OT= = = ，则由切割线定理可得：OM*ON=OT2=220.【答案】（1）证明：因为O，M分别为AB，VA的中点，所以OM∥VB．又因为OM⊂平面MOC，VB⊄平面MOC，所以VB∥平面MOC．（2）证明：因为AC=BC，O为AB中点，所以OC⊥AB．因为平面VAB⊥平面ABC，平面VAB∩平面ABC=AB，OC⊂平面ABC，所以OC⊥平面VAB．因为OC⊂平面MOC，所以平面MOC⊥平面VAB（3）解：由（2）知OC⊥面VAB，过O作OE⊥VB交VB于点E，连结CE，因为OC⊥面VAB，所以OC⊥VB，则∠OEB即为二面角C﹣VB﹣A的平面角．在直角三角形COE中，OE= ，OC=1，CE= ，所以cos∠OEB= ．故二面角C﹣VB﹣A的平面角的余弦值为21.【答案】（1）证明：如图∵DO⊥面α，AB⊂α，∴DO⊥AB，连接BD，由题设知，△ABD是正三角形，又E是AB的中点，∴DE⊥AB，又DO∩DE=D，∴AB⊥平面ODE；（2）解：∵BC∥AD，∴BC与OD所成的角等于AD与OD所成的角，即∠ADO是BC与OD所成的角，由（1）知，AB⊥平面ODE，∴AB⊥OE，又DE⊥AB，于是∠DEO是二面角α﹣MN﹣β的平面角，从而∠DEO=60°，不妨设AB=2，则AD=2，易知DE= ，在Rt△DOE中，DO=DEsin60°= ，连AO，在Rt△AOD中，cos∠ADO= = ，故异面直线BC与OD所成角的余弦值为．22.【答案】（1）解：联立得：，解得：，∴圆心C（3，2）．若k不存在，不合题意；若k存在，设切线为：y=kx+3，可得圆心到切线的距离d=r，即=1，解得：k=0或k=﹣，则所求切线为y=3或y=﹣x+3（2）解：设点M（x，y），由MA=2MO，知：=2 ，化简得：x2+（y+1）2=4，∴点M的轨迹为以（0，﹣1）为圆心，2为半径的圆，可记为圆D，又∵点M在圆C上，C（a，2a﹣4），∴圆C与圆D的关系为相交或相切，∴1≤|CD|≤3，其中|CD|= ，∴1≤ ≤3，解得：0≤a≤。

宁夏回族自治区银川一中高一上学期期末考试试题(8科8

银川一中2015/2016学年度(上)高一期末考试政治试卷(时间：90分钟)第Ⅰ卷（选择题共60分）说明：本大题共40小题，每小题1.5分，共计60分。

在每小题给出的四个选项中，只有一个选项是最符合题意的,请选出最佳答案涂在答题卡上.1．作为消费者总是希望“质优价廉”；作为经营者则强调“优质优价”。

尽管两者关注点有所不同，但都说明商品A．是用于交换的劳动产品B．是使用价值与价值的统一体C．使用价值比价值更重要D．只有通过交换才有使用价值2．2014年10月10日，中国人民银行发行2015中国乙未（羊）年金银纪念币一套。

该套纪念币共16枚，其中金币9枚，银币7枚，均为中华人民共和国法定货币。

该套纪念币①相当于一般等价物，其本质是商品②具有收藏价值。

也可以充当商品交换的媒介③其购买力是由国家规定的④能表现其他一切商品的价值A．②④B．③④C．①④D．①②3．今年中秋国庆小长假，小陈一家选择了标价为3680元/人的云南双飞七日游，小陈在丽江的一个小店花100元买了几件富有少数民族特色的小饰品，她父母则在昆明的商场用刷信用卡消费的方式购买了8000元的玉镯。

在这里涉及到的货币职能依次是A．价值尺度、支付手段、流通手段B．支付手段、流通手段、支付手段C．价值尺度、流通手段、流通手段D．价值尺度、流通手段、支付手段4．2015年是我国人民币汇率形成机制改革十周年。

十年来，人民币对美元总体呈现“小碎步”升值态势。

人民币对美元升值说明①同样多的人民币可以兑换更多的美元②同样多的美元可以兑换更多的人民币③美元汇率升高④人民币汇率升高A．①②B．②③C．①④D．②④5．第二届中国西部名牌产品博览会于2014年10月24日至26日在西安隆重举办。

市场上的名牌产品，一般来说，价格都比较高，根本原因是A．名牌产品质量好，名气大B．名牌产品可以满足人们高层次的需求C．名牌产品耗费的劳动量大D．生产名牌产品的社会劳动生产率高6．价格是市场的信号灯，价格变化给人们的生活和生产带来重要影响，在其他因素不变的情况下，价格与需求、价格与供给的关系可以用下图来表示。

宁夏银川一中2015-2016学年高一数学下学期期末考试试题

银川一中2015/2016学年度(下)高一期末考试数学试卷一、选择题（每小题5分，共60分） 1．计算()sin 600-的值是（）A ．12 B ．2 C ．2- D ．12-2．若0tan <α，且ααcos sin >，则α在( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限 3．设向量(2,4)a =与向量(,6)b x =共线，则实数x =（）A ．2B ．3C ．4D ．6 4．函数2sin cos 44+-=x x y 的最小周期是（） A ．πB ．π2C ．2πD ．4π5．为了得到函数3sin 26y x π⎛⎫=- ⎪⎝⎭的图象，只需把函数3sin 6y x π⎛⎫=-⎪⎝⎭的图象上所有的点的（）A ．横坐标伸长到原来的2倍，纵坐标不变B ．横坐标缩短到原来的12倍，纵坐标不变 C ．纵坐标伸长到原来的2倍，横坐标不变 D ．纵坐标缩短到原来的12倍，横坐标不变6．在ABC ∆中,已知2AB =,1BC =,AC =，则AB BC BC CA CA AB ⋅+⋅+⋅=( )A ．-4B ．-2C ．0D ．47．若)0(137cos sin πααα<<=+，则=αtan ( ) A ．31-B ．512 C ．512-D ．318．已知角θ的顶点与原点重合，始边与x 轴正半轴重合，终边在直线x y 2=上，则)42sin(πθ+的值为（） A ．1027-B ．1027 C ．102- D ．1029．下列四个函数中，以π为最小正周期，且在区间,2ππ⎛⎫⎪⎝⎭上单调递减函数的是（） A ．sin 2y x = B ．2cos y x = C ．cos 2xy = D ．()tan y x =-10．函数)23cos(x y --=π的单调递增区间是（）A ．)(322,342Z k k k ∈⎥⎦⎤⎢⎣⎡+-ππππ B. )(324,344Z k k k ∈⎥⎦⎤⎢⎣⎡+-ππππ C ．)(382,322Z k k k ∈⎥⎦⎤⎢⎣⎡++ππππ D. )(384,324Z k k k ∈⎥⎦⎤⎢⎣⎡++ππππ 11．定义运算bc ad db ca -=.若71cos =α，1433cos sin cos sin =ββαα，20παβ<<<，则β=( )A ．12π B ．6π C ．4πD ．3π12．设函数())sin(2)(||)2f x x x πϕϕϕ=+++<,且其图象关于直线0x =对称,则( )A ．()y f x =的最小正周期为π,且在(0,)2π上为增函数B ．()y f x =的最小正周期为π,且在(0,)2π上为减函数C ．()y f x =的最小正周期为2π,且在(0,)4π上为增函数 D ．()y f x =的最小正周期为2π,且在(0,)4π上为减函数二、填空题（每题5分，共20分）13．已知a 与b 为两个不共线的单位向量，k 为实数，若向量a +b 与向量k a -b 垂直，则k =_______.14．如果函数3cos(2)y x ϕ=+的图象关于点4(,0)3π中心对称，那么||ϕ的最小值为 .15．如图所示，在四边形ABCD 中，AC 和BD 相交于点O ,设AD=,a AB b =,若2AB DC =,则AO = .16．已知1tan()42πα+=,则2sin 2cos 1cos 2ααα-+的值为 . 三、解答题(共70分) 17．（本小题满分10分）求值：（1）18sin 45sin 27cos 18sin 45cos 27sin -+ （2） 80sin 2)]10tan 31(10sin 50sin 2[2++18．（本小题满分12分）在平面直角坐标系中，已知向量22=(,),(sin ,cos ),(0,).222m n x x x π-=∈ （1）若m n ⊥，求tan x 的值；（2）若m n 与的夹角为3π，求x 的值.19．（本小题满分12分）已知函数)0,0,0( ) sin()(πϕωϕω<<>>+=A x A x f 的部分图象，如图所示．（1）求函数解析式；（2）若方程()f x m =在]1213,12[ππ-有两个不同的实根，求m 的取值范围．20．（本小题满分12分）已知函数)0(23cos 3cos sin )(2>++-⋅=a b a x a x x a x f （1）写出函数的单调递减区间；ABCDO（2）设]2,0[π∈x ，)(x f 的最小值是2-，最大值是3，求实数b a ,的值.21．（本小题满分12分）设关于x 的函数22221f (x )cos x a cos x (a )=--+的最小值为g(a ). （1）试用a 写出g(a )的表达式；（2）试求12g(a )=时a 的值，并求此时f (x )的最大值.22. （本小题满分12分）已知向量)2,2cos (x a -=，)2sin 32,2(x b -=，函数4)(-⋅=b a x f . （1）若]2,0[π∈x ，求)(x f 的最大值并求出相应x 的值；（2）若将)(x f 图象上的所有点的纵坐标缩小到原来的21倍，横坐标伸长到原来的2倍，再向左平移3π个单位得到)(x g 图象，求)(x g 的最小正周期和对称中心；（3）若1)(-=αf ，)2,4(ππα∈，求α2sin 的值.高一第二学期期末考试数学试卷——参考答案二、解答题（每小题5分，共20分） 13. 1 14. 6π 15. 2133a b + 16. 56- 17.（本小题10分）解：（1）原式sin(4518)cos 45sin18sin 45cos18tan 451cos(4518)sin 45sin18cos 45cos18-+====--（2）18. （本小题12分）解：（1）由已知得sin cos 0,tan 122x x x -==得（2）由已知得||1,||1,m n ==221sin cos ||||cos 2232m n x x m n π∴⋅=-== 15sin(),(0,),,,422444612x x x x x πππππππ∴-=∈∴-<<∴-==又 19. （本小题12分）解: (1) 由图可知A=1，T 52=,22632T πππππωω-=∴===得由2225()sin()1,033333f ππϕϕπππϕπ=+=-<<<+<得 235+==326πϕπϕπ∴，， 5()sin(2)6f x x π=+ (2)由（1）及图知，5135()[,][,],]12361236f x ππππππ-在及上递减，在[上递增。

(全优试卷)宁夏银川一中高一上学期期末考试数学试题Word含答案

银川一中2017/2018学年度(上)高一期末考试数学试卷命题人：一、选择题（每题5分，共计60分）1．已知过两点A(-3，m),B(m,5)的直线与直线3x+y-1=0平行，则m的值是（）A．3 B．7 C． -7 D．-92．则下列命题中正确的是（）ABCD3．利用斜二测画法画平面内一个△ABC面积与△ABC的面积的比是（）A B C D.4m的值( )A B．-2 C．-2或2 D-25．已知圆C C的方程为（）A BC D6则这个圆锥的体积为（）A BC D7．某几何体的三视图如图所示,则该几何体的表面积等于()A B C D81的角为（）A. C. D.9．BCD，三角形BCD是边长为3的等边三角形，若AB=4）A C D10．的取值范围是（）A B．C D11．若圆（x-a)2+(y-a)2=4上总存在两点到原点的距离为1，则实数a的取值范围是( )12．）B AB C D二、填空题（每小题5分，共计20分）13．过点（2,3）且在两坐标轴上的截距互为相反数的直线方程是____________________. 14．长方体的长、宽、高分别为3,2,1，________. 15．（2,6）_____________．16．在平面直角坐标系中，A,B分别是x轴和y轴上的动点，若以AB为直径的圆C与直线2x+y-4=0相切，则圆C面积的最小值为_____________．三、简答题（共计70分）17．（本小题满分10分）已知圆C（1C相切.（2C相交于A、B两点，且AB.18（1（2（319．（本小题满分12分）P(-1，2)（1（220.如图，直四棱柱ABCD –A 1B 1C 1D 1中，AB //CD ，AD ⊥AB ，AB =2， ADAA 1=3，E 为CD 上一点，DE =1，EC =3. （1）证明：BE ⊥平面BB 1C 1C ; （2）求点B 1到平面EA 1C 1的距离.21(1)(2)22．（本小题满分12分）三棱锥被平行于底面ABC的平面所截得的几何体如图所示，截面为A1B1C1，∠BAC=90°，A1A⊥平面ABC，A1A AB AC=2，A1C1=1（1）证明：1D；（2）求二面角A-CC1-B的余弦值．2017高一上学期期末考试----数学（参考答案）一、选择题（每题5分，共计60分）13.3x-2y=0，或x-y+1=0；；15.三、解答题（共70分. 第17题----10分；第18—第22题，每题12分）17.【解析】（1）把圆C半再求圆心到直距解得…………………5分（2分18…………………4分…………………8分………12分19x+y-1=0．………………………………………12分………12分20.(1)证明：过点B作CD的垂线交CD于点F，则，FC=2.在中，中，ABCD BB1∩BC=B,故BE⊥平面BB1C1C. ………………………6分(2)111A B CS11A C ES=d，则三棱锥B1-EA1C111A C ES=故点B1 到平面EA1C1分21………………6分………………10分………………12分22DBA ∴△∽△AD A = 又A 1⊥A1D. …………………6分AB┴CC1，又CC ∴CC 1┴平面AEB, ∴CC 1┴BE,∴…………………12分。