123高一数学必修3试卷

合集下载

人教A版高中数学必修三试卷高一年级期中考参考答案.docx

高中数学学习材料唐玲出品高一年级数学期中考参考答案一、选择题（每题3分，共10题，合计30分）题号 1 2 3 4 5 6 7 8 9 10 答案BACCBDAAAC二、填空题（每题3分，共7题，合计21分）11．12 12．3 13 ．4π14．22 15．202海里/小时 16．272 17．34三、解答题：本大题共5小题，共49分） 18．23k =-或113k =或3132k ±= ……..7分19．解：（1）213()2cos 1cos()cos cos sin 2322xf x x x x x ωπωωωω=-++=+- 332cos sin 3sin 223x x x πωωω⎛⎫=-=+ ⎪⎝⎭,………..3分由T AB 21==π，得22T ππω==，则1ω=……………..4分（2）由（1）得33)32sin(3)(=+=πx x f ，则31)32sin(=+πx .由⎪⎭⎫⎝⎛∈2,0πx ，得322)32cos(-=+πx ，……………..6分 =-+=∴)3232sin(sin ππx x 32cos )32sin(ππ+x 32sin)32cos(ππ+-x616223)322()21(31-=⨯---⨯=………………10分 20．解:(I)由已知⎩⎨⎧=-+=+5)1(222232d b q d ∴0322=-+d d 得1=d 或23-=d又012>+=d q ∴1=d ⇒2=q ∴1+=n a n , 212+=n n b (6)分(Ⅱ)集合A 与集合B 的相同元素和为:302222432=+++ ……10分21．解(1)由已知得: cos 3sin cos cos c B b C a c B b C ⋅+==+ 3sin cos b C b C ∴=3tan 3C ∴=6C π∴= … …3分（2）由正弦定理得2sin sin sin a b c A B C === 2sin ,2sin 2sin()6a Ab B A π∴===+ 22224sin sin ()423sin(2)63a b A A A ππ⎡⎤∴+=++==+-⎢⎥⎣⎦… …7分由于三角形为锐角三角形 32A ππ∴<<3sin(2)123A π∴<-≤ 227423a b ∴<+≤+… …10分22．解：（1）令1n =，则32111+2a S S =，即32111+2a a a =，所以12a =或11a =-或10a =又因为数列{}n a 的各项都是正数，所以12a =令2n =，则3321222+2a a S S +=，即332121212()2()a a a a a a +=+++解得13a =或12a =-或10a = 又数列{}n a 的各项都是正数，所以23a =… …2分（2）33332123+2(1)n n na a a a S S ++++=33332123111+2(2)(2)n n n a a a a S S n ---∴++++=≥ 由(1)(2)-得32211(+2)(+2)n n n n n a S S S S --=-化简得到212(3)n n n a S S -=++ 21122(3)(4)n n n a S S n ---∴=++≥由(3)(4)-得221112(2)(2)n n n n n n a a S S S S -----=++-++化简得到2211n n n n a a a a ---=+，即11(3)n n a a n --=≥… …6分当2121n a a =-=时，，所以11(2)n n a a n --=≥ 所以数列{}n a 是一个以2为首项，1为公差的等差数列1(1)2(1)1n a a n d n n ∴=+-=+-=+… …8分（3）113(1)2n n n n b λ-+=+-⋅因为对任意的*n N ∈，都有1n n b b +>恒成立，即有12113(1)23(1)2n n n n n n λλ++-++-⋅>+-⋅ 化简得113(1)()32n nλ--<⋅ … …10分当n 为奇数时，13()32n λ<⋅恒成立，113()32λ<⋅，即12λ<当n 为偶数时，13()32n λ>-⋅恒成立，213()32λ>-⋅，即34λ>-3142λ∴-<< … …12分附加题(本大题共10分,每小题5分)1． (0,3⎤⎦2． 372。

新人教版高中数学必修3全册同步测试题及解析答案.doc

新人教版高中数学必修3 全册同步测试题及解析答案篇一:高一数学必修3全册各章节课堂同步习题（详解答案）第一章算法初步1.1算法与程序框图1.1.1算法的概念班次姓名［自我认知］:1.下面的结论正确的是（）.A.一个程序的算法步骤是可逆的B. 一个算法可以无止境地运算下去的C.完成一件事情的算法有且只有一种D. 设计算法要本着简单方便的原则2.下面对算法描述正确的一项是（）. A.算法只能用自然语言来描述B.算法只能用图形方式来表示C.同一问题可以有不同的算法D.同一问题的算法不同，结果必然不同3.下面哪个不是算法的特征（）A.抽象性B.精确性C. 有穷性D.唯一性4.算法的有穷性是指（）A.算法必须包含输出B.算法中每个操作步骤都是可执行的C.算法的步骤必须有限D.以上说法均不正确5.早上从起床到出门需要洗脸刷牙(5min)、刷水壶(2min)、烧水(8min)、泡面(3min)、吃饭(lOmin)、听广播(8min)几个步骤，从下列选项中选最好的一种算法()A.S1洗脸刷牙、S2 刷水壶、S3烧水、S4泡面、S5吃饭、S6听广播 B.S1刷水壶、S2烧水同时洗脸刷牙、S3泡面、S4吃饭、S5听广播 C. S1刷水壶、S2烧水同时洗脸刷牙、S3泡面、S4吃饭同时听广播D.S1吃饭同时听广播、S2泡面；S3烧水同时洗脸刷牙；S4刷水壶6.看下面的四段话，其中不是解决问题的算法是()A.从济南到北京旅游，先坐火车,再坐飞机抵达B.解一元一次方程的步骤是去分母、去括号、移项、合并同类项、系数化为1C.方程x2?l?0有两个实根D.求1+2+3+4+5的值，先计算1+2=3,再计算3+3=6,6+4=10,10+5=15,最终结果为15 7.已知直角三角形两直角边长为a,b,求斜边长c的一个算法分下列三步：①计算c?a,b的值；③输出斜边长c的值，其中正确的顺序是()A.①②③B.②③①C.①③②D.②①③［课后练习］:8.若f?x?在区间?a,b?内单调，且f?a??f?b??O,则f?x?在区间?a,b?内()A.至多有一个根B.至少有一个根C.恰好有一个根D.不确定9.已知一个学生的语文成绩为89,数学成绩为96,外语成绩为99.求他的总分和平均成绩的一个算法为：第一步：取A=89 ,B=96 ,C=99；第二步：①；第三步：②;第四步：输出计算的结果.10.写出求1+2+3+4+5+6+7+100的一个算法.可运用公式l+2+3+?+n= 第一步①；第二步②;第三步输出计算的结果.11.写出Ix2x3x4x5x6的一个算法.12.写出按从小到大的顺序重新排列x,y,z三个数值的算法. n（n?l）直接计算.21.1. 2程序框图［自我认知］:1 •算法的三种基本结构是（）A.顺序结构、条件结构、循环结构B.顺序结构、流程结构、循环结构C.顺序结构、分支结构、流程结构D .流程结构、循环结构、分支结构2 .程序框图中表示判断框的是（）A.矩形框B.菱形框D.圆形框D.椭圆形框3.如图⑴、（2）,它们都表示的是输出所有立方小于1000的正整数的程序框图，那么应分别补充的条件为（）（1）33(2)3A.⑴n>1000 ? (2)n<1000 ?B.⑴n<1000 ?⑵n>1000 ?C.(Dn<1000?⑵n>1000 ?D. (l)n<1000 ?(2)n<1000?4.算法共有三种逻辑结构，即顺序逻辑结构,条件逻辑结构和循环逻辑结构，下列说法正确的是()A.—个算法只能含有一种逻辑结构B.一个算法最多可以包含两种逻辑结构C. 一个算法必须含有上述三种逻辑结构D.—个算法可以含有上述三种逻辑结构的任意组合［课后练习］:5.给出以下一个算法的程序框图(如下图所示)，该程序框图的功能是()A.求输出a,b,c三数的最大数B.求输出a,b,c三数的最小数3333C.将a,b,c按从小到大排列D.将a,b,c按从大到小排列第5题图第6题图6.右边的程序框图（如上图所示），能判断任意输入的数x 的奇偶性：其中判断框内的条件是A.m?O?B.x?O ?C.x?l ?D.m?l?7.在算法的逻辑结构中，要求进行逻辑判断，并根据结果进行不同处理的是哪种结构（）A.顺序结构B.条件结构和循环结构C.顺序结构和条件结构D.没有任何结构?x2?l（x?0）8.已知函数f?x???，设计一个求函数值的算法，并画出其程序框图（x?0）?2x?l1.1.2程序框图（第二课时）［课后练习］:班次姓名1 . 如图⑴的算法的功能是.输出结果i=,i+2=.2.如图⑵程序框图箭头a指向①处时，输出s=.箭头a指向②处时，输出s=.3.如图⑷所示程序的输出结果为s=132,则判断中应填A、i>10? B、i>ll? C、i<ll?D、i>12? 4.如图⑶程序框图箭头b指向①处时，输出s=.箭头b指向②处时, 输出S= _________5、如图⑸是为求1-1000的所有偶数的和而设计的一个程序空白框图，将空白处补上。

人教版高中数学高一A数学必修3测试卷(一)

高中同步测试卷(一)单元检测算法与程序框图 (时间：120分钟，满分：150分)一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．下列关于程序框图的说法正确的是( ) A ．程序框图是描述算法的图形语言B ．在程序框图中，一个判断框最多只能有两个退出点C ．程序框图虽可以描述算法，但不如用自然语言描述算法直观D ．程序框图和流程图不是一个概念 2．已知如图是算法程序框图的一部分其中含条件结构的是( )A ．①②B ．①③C ．②③D ．①②③3．在如图所示的程序框图中，若输入m ＝4，n ＝10，则输出a ，i 的值别是( ) A ．12，4 B ．16，5 C ．20，5 D ．24，6第3题图第5题图4．下列问题中，可以只用顺序结构就能解决的是( ) A ．求关于x 的方程ax 2＋bx ＋c ＝0的根B ．求函数f (x )＝⎩⎪⎨⎪⎧x 2（x ≥0）x （x <0）的值C ．求1＋4＋7＋10＋13的值D ．求一个数x 的绝对值5．按照如图所示的程序框图运行，已知输入x 的值为1＋log 23，则输出y 的值为( ) A.112 B.38 C.712 D.1124 6．如果执行如图所示的程序框图，那么输出的S 等于( ) A ．2 550 B ．－2 550 C ．2 548 D ．－2 552第6题图第7题图7．如图所示，若f (x )＝x 2，g (x )＝log 2x ，输入x ＝0.25，则输出h (x )＝( ) A ．0.25 B ．2 C ．－2 D ．－0.258．如图所示是计算12＋14＋16＋…＋120的值的一个程序框图，其中在判断框内应填入的条件是( )A ．i ≤10B ．i >10C ．i <20D ．i >20第8题图第9题图 9．执行如图所示的程序框图，输出的S 值为( ) A ．1 B ．3 C ．7 D ．1510．阅读如下程序框图，如果输出i ＝5，那么在空白矩形框中应填入的语句为( )A ．S ＝2i －2B ．S ＝2i －1C ．S ＝2iD ．S ＝2i ＋411．若如图所示的框图所给的程序运行结果为S ＝35，那么判断框中应填入的关于k 的条件是( )A ．k ＝7?B ．k ≤6?C ．k <6?D ．k >6?第11题图第12题图12．若执行如图所示的程序框图，输出S的值为4，则判断框中应填入的条件是() A．k<14? B．k<15? C．k<16? D．k<17?题号123456789101112答案二、填空题(本大题共4小题，每小题5分，共20分．把答案填在题中横线上)13．若某程序框图如图所示，则该程序运行后输出的k的值是________．14．如图所示的程序框图是变换两个变量的值并输出，则图中①处应为________．第13题图第14题图第15题图第16题图15．阅读如图所示的程序框图，若输出S＝30，则在判断框内应填入________．16．如图所示，该程序框图运行后输出的结果为________．三、解答题(本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤)17．(本小题满分10分)阅读如图所示的程序框图，若输出y的值为0，则输入的x值是多少？18．(本小题满分12分)设计求经过任意两点P1(x1，y1)，P2(x2，y2)的直线的斜率的算法，并画出相对应的程序框图．19.(本小题满分12分)阅读右边的程序框图，运行相应的程序，试求输出i的值．20.(本小题满分12分)给出50个数1，2，4，7，11，…，其规律是：第1个数是1，第2个数比第1个数大1，第3个数比第2个数大2，第4个数比第3个数大3，…，以此类推，要求计算这50个数的和，请画出程序框图．21．(本小题满分12分)画出求满足1×3×5×7×…×n>10 000的最小自然数n的程序框图．22．(本小题满分12分)某小区每月向居民收取卫生费，计费方法是：3人和3人以下的住户，每户收取5元；超过3人的住户，每超出1人加收1.2元．设计一个算法，根据输入的人数，计算应收取的卫生费，并画出程序框图．参考答案与解析1．[导学号10390001] 解析：选A.由于存在一种多分支判断，所以一个判断框可能有多个退出点，所以B 选项是错误的；相对于自然语言，用程序框图描述算法的优点主要就是直观、形象，容易理解，在步骤表达上简单了许多，所以C 选项是错误的；程序框图就是流程图，所以D 选项也是错误的．A 选项正确．2．解析：选C.①只含顺序结构，②③均有判断框，都含有条件结构．3．解析：选C.输入m ＝4，n ＝10，i ＝1；a ＝4×1＝4，10不能整除4，i ＝1＋1＝2；a ＝4×2＝8，10不能整除8，i ＝2＋1＝3；a ＝4×3＝12，10不能整除12，i ＝3＋1＝4；a ＝4×4＝16，10不能整除16，i ＝4＋1＝5；a ＝4×5＝20，10能整除20；输出20，5，结束．故选C.4．解析：选C.A 、B 、D 项还需用到条件结构．5．[导学号10390002] 解析：选A.因为x ＝1＋log 23＜4，所以x ＝x ＋1＝2＋log 23，所以y ＝⎝⎛⎭⎫122＋log 23＝14×13＝112. 6．解析：选C.这个程序是计算－2＋0＋2＋4＋…＋100的算法，结果为2 548.故选C. 7．[导学号10390003] 解析：选C.h (x )取f (x )与g (x )中的较小值，即h (0.25)＝min{f (0.25)，g (0.25)}，g (0.25)＝log 20.25＝－2，f (0.25)＝(14)2＝116，故选C.8．解析：选A.计算的值是10个数的和．当i ≤10时成立继续循环，当i ＝11时跳出循环体，此时输出的S 就是这10个数的和． 9．解析：选C.程序框图运行如下：k ＝0<3，S ＝0＋20＝1，k ＝1<3；S ＝1＋21＝3，k ＝2<3；S ＝3＋22＝7，k ＝3.输出S ＝7. 10．解析：选C.当i ＝2时，S ＝2×2＋1＝5<10；当i ＝3时，仍然循环，排除D ；当i ＝4时，S ＝2×4＋1＝9<10；当i ＝5时，不满足S <10，即此时S ≥10，输出i ＝5.此时A 项中，S ＝2×5－2＝8，B 项中，S ＝2×5－1＝9，C 项中，S ＝2×5＝10，故C 正确．11．[导学号10390004] 解析：选D.初始值：k ＝10，S ＝1，判断条件成立； S ＝1＋10＝11，k ＝10－1＝9，判断条件成立； S ＝11＋9＝20，k ＝9－1＝8，判断条件成立； S ＝20＋8＝28，k ＝8－1＝7，判断条件成立；S ＝28＋7＝35，k ＝7－1＝6，判断条件不成立，输出S ＝35，结束算法．由此可得判断框中应填k >6？，故选D.12．解析：选C.初始条件S ＝1，k ＝2；运行第一次，S ＝1·log 23＝log 23，k ＝k ＋1＝3；运行第二次，S ＝log 23·log 34，k ＝k ＋1＝4；运行第三次，S ＝log 23·log 34·log 45，k ＝k ＋1＝5；运行第四次，S ＝log 23·log 34·log 45·log 56，k ＝k ＋1＝6；运行第五次，S ＝log 23·log 34·log 45·log 56·log 67，k ＝k ＋1＝7；…；运行第十四次，S ＝log 23·log 34·log 45·log 56·log 67…log 1516＝4，k ＝k ＋1＝16.不满足条件，停止运行，输出的S ＝4，所以判断框中应填入的条件是k <16？，故选C.13．解析：初始值：k ＝2，执行“k ＝k ＋1”得k ＝3，a ＝43＝64，b ＝34＝81，a >b 不成立； k ＝4，a ＝44＝256，b ＝44＝256，a >b 不成立；k ＝5，a ＝45＝1 024，b ＝54＝625，a >b 成立，此时输出k ＝5. 答案：514．解析：交换两个变量的值，需引入第三个量，将其中一个量的值赋给第三个量后，将第二个量的值赋给第一个量，再将第三个量的值赋给第二个量．答案：x ＝y15．[导学号10390005] 解析：由框图可知，算法结构为直到型循环结构，因为30＝12＋22＋32＋42，所以条件应为“i >4？”(或i ≥5？)．答案：i >4？(或i ≥5？)16．解析：当a ＝4时，退出循环，b ＝23＝8. 答案：817．解：由题意，⎩⎪⎨⎪⎧x >1x 2－4x ＋4＝0或⎩⎪⎨⎪⎧x <1，x ＝0，解得x ＝2或0. 18．解：算法设计如下：第一步，输入x 1，y 1，x 2，y 2.第二步，如果x 1＝x 2，输出“斜率不存在”，结束算法；否则，执行第三步．第三步，k ＝y 2－y 1x 2－x 1.第四步，输出k . 程序框图如下：19．[导学号10390006] 解：第一次循环：i ＝1，a ＝2，第二次循环：i ＝2，a ＝5，第三次循环：i ＝3，a ＝16，第四次循环：i ＝4，a ＝65>50，循环结束．所以输出i 的值为4.20．解：程序框图如图所示：21．解：程序框图如图所示：22．[导学号10390007]解：程序框图如下：。

高中数学必修三试卷

高中数学必修三试卷第一部分：选择题（共50分）1. 解方程：2x + 5 = 13.2. 设函数 f(x) = x^2 + 2x + 1, 求 f(-2) 的值.3. 若 A 是方阵，AB = I, 则 B = ?4. 已知函数 f(x) = 2^x ，求 f(3) 的值.5. 正方体 ABCDEFGH，A(-1,2,3)，B(2,5,3)，C(2,2,6)和 E 为对角线BF 的中点，求 BE 的坐标.第二部分：填空题（共30分）1.已知 2x + 5 = 7, 则 x = _____2. 已知sin α = 0.6, 则α 的值应在 _____ 和 _____ 之间.3. 高中四年学期数学平均成绩为 85 ，若前三年的平均成绩为 80 ，四年共有多少门课？4. 画出函数 y = 2x^2 + 3x - 1 的图像，并标明顶点和切线斜率.5. 三角形 ABC 中，已知∠A = 30°，BC = 6，AC = 10，求 AB 的值.第三部分：计算题（共40分）1. 计算 2^3 × 3^2 + 1.2. 计算 1 + 3 + 5 + 7 + 9 + ... + 99.3. 计算 C(7, 3) 的值.4. 一购物车内共有 20 个苹果和 15 个橘子，从中任取一个水果，求取到的是橘子的概率.5. 计算 sin 60° × cos 30°.第四部分：证明题（共80分）1. 证明：对于任意实数 a 和 b，(a + b)^2 = a^2 + 2ab + b^2.2. 证明：若 a + b = 0，则 a = -b.3. 证明：对于任意正整数 n, n^2 + 1 > 2n.4. 证明：在直角三角形 ABC 中，斜边 c 满足 c^2 = a^2 + b^2.5. 证明：若 a × b = 0，则 a = 0 或 b = 0.第五部分：解答题（共100分）1. 用配方法解方程：2x^2 + 4x - 6 = 0.2. 求函数 y = x^2 - 2x 的定义域和值域.3. 在坐标系中，已知 A(2,1)，B(4,5)，C(6,3)，D(5,1)，连接线段 AB 和 BA，线段 CD 和 DC，判断是否互相垂直.4. 在平面直角坐标系中，画出椭圆的图像：(x-3)^2/9 + (y-2)^2/4 = 15. 设 P 是等边三角形 ABC 的内部任意一点，分别连接 PA，PB 和PC，证明：PA + PB + PC 恒等于定值.结束语：本试卷共 300 分。

高一数学必修三试卷及答案

高一数学必修三试卷及答案一．选择题（共12题，每题3分，共36分）1.程序框图中表示判断的是( )A B C D 2.下列说法错误的是( )A 在统计里，把所需考察对象的全体叫作总体B 一组数据的平均数一定大于这组数据中的每个数据C 平均数、众数与中位数从不同的角度描述了一组数据的集中趋势D 一组数据的方差越大，说明这组数据的波动越大3.条件语句的一般形式是“IF A THEN B ELSE C”，其中B表示的是( )A 满足条件时执行的内容B 条件语句C 条件D 不满足条件时执行的内容4.从一个不透明的口袋中摸出红球的概率为1/5，已知袋中红球有3个，则袋*有除红色外完全相同的球的个数为( )．A 5个B 8个C 10个D 12个5．下列给出的赋值语句中正确的是：A、3=AB、M= —MC、B=A=2D、x+y=06. 抛掷一枚质地均匀的硬币，如果连续抛掷1000次，那么第999次出现正面朝上的概率是（）A. 1 999B. 1 1000C. 999 1000D. 1 27．某公司在甲、乙、丙、丁四个地区分别有150个、120个、180个、150个销售点，公司为了调查产品销售的情况，需从这600个销售点中抽取一个容量为100的样本，记这项调查为(1)；在丙地区中有20个特大型销售点，要从中抽取7个调查其销售收入和售后服务情况，记这项调查为(2)。

则完成(1)、(2)这两项调查宜采用的抽样方法依次是( )A．分层抽样法，系统抽样法B．分层抽样法，简单随机抽样法C．系统抽样法，分层抽样法D．简单随机抽样法，分层抽样法8.下列说法正确的是（）A. 任何事件的概率总是在（0，1）之间B. 频率是客观存在的，与试验次数无关C. 随着试验次数的增加，频率一般会越来越接近概率D. 概率是随机的，在试验前不能确定9．从一批产品中取出三件产品，设A=“三件产品全不是次品”，B=“三件产品全是次品”，C=“三件产品至少有一件是次品”，则下列结论正确的是（）A．A与C互斥B．任何两个均互斥C．B与C互斥D．任何两个均不互斥10．如右图,是某算法流程图的一部分，其算法的逻辑结构为（）A. 顺序结构B. 判断结构C. 条件结构D. 循环结构11．从一箱产品中随机地抽取一件，设事件A=｛抽到一等品｝，事件B =｛抽到二等品｝，事件C =｛抽到三等品｝，且已知P（A）= 0.65 ,P(B)=0.2 ,P(C)=0.1。

【试卷】高中数学必修3综合测试题及答案

高一数学（必修3）试题一、选择题（本题共12小题，每小题5分，共60分）1. 在下列各图中，每个图的两个变量具有相关关系的图是（）（1）（2）（3）（4）A．（1）（2） B．（1）（3） C．（2）（4） D．（2）（3）2.在简单随机抽样中，某一个个体被抽中的可能性（）A.与第几次抽样无关，第一次抽中的可能性要大些B.与第几次抽样无关，每次抽中的可能性相等C.与第几次抽样有关，最后一次抽中的可能性大些D.与第几次抽样无关，每次都是等可能的抽取，但各次抽取的可能性不一样3.把18个人平均分成两组，每组任意指定正副组长各1人，则甲被指定为正组长的概率为（）A.181 B.91 C.61 D.314. 下面为一个求20个数的平均数的程序,在横线上应填充的语句为（）A. i>20B. i<20C. i>=20D. i<=205.袋内分别有红、白、黑球3，2，1个，从中任取2个，则互斥而不对立的两个事件是（）A.至少有一个白球；都是白球B.至少有一个白球；至少有一个红球C.恰有一个白球；一个白球一个黑球D.至少有一个白球；红、黑球各一个6. 在区域⎩⎨⎧≤≤≤≤11yx，内任意取一点),(yxP，则122<+yx的概率是（）A．0 B．214-π C．4π D．41π-7. 在右面的程序框图表示的算法中，输入三个实数c b a ,,，要求输出的x是这三个数中最大的数，那么在空白的判断框中，应该填入（） A ．x c > B ．c x > C ．c b > D ．c a >8. 用随机数表法从100名学生（男生25人）中抽选20人进行评教，某男生被抽到的机率是（）A 、1001B 、251C 、51D 、419. 在等腰直角三角形ABC 中，在ACB ∠内部任意作一条射线CM ，与线段AB 交于点M ，则AC AM <的概率（） A 、22 B 、12 C 、34D 、41 10.以集合A={2,4,6,7,8,11,12,13}中的任意两个元素分别为分子与分母构成分数，则这种分数是可约分数的概率是（） A.135 B.285 C.143 D.14511.对某班学生一次英语测试的成绩分析，各分数段的分布如下图（分数取整数），由此，估计这次测验的优秀率（不小于80分）为（）A.92%B.24%C.56%D.76% 12.由小到大排列的一组数据x 1,x 2,x 3,x 4,x 5,其中每个数据都小于-1，则样本1，x 1,-x 2,x 3,-x 4,x 5的中位数可以表示为（） A.212x + B. 212xx - C. 215x + D.243x x - 二、填空题(本题共4小题，每小题5分，共20分)13.投掷一枚均匀的骰子，则落地时，向上的点数是2的倍数的概率是_________，落地时，向上的点数为奇数的概率是________.14.在抽查某产品的尺寸过程中，将其尺寸分成若干个组，［a,b ］是其中一组，抽查出的个体数在该组上的频率为m ，该组上的直方图的高度为h ，则|a-b|=________.15.某人午觉醒来，发现表停了，他打开收音机想听电台报时，则他等待的时间不多于6分钟的概率是_________. 16. 在区间上随机取一个数x ，则的概率为 .三、解答题（本题共6题，共70分，解答应写出文字说明）17. (本题满分10分)如右图求++⨯+⨯+⨯ 431321211100991⨯的算法的程序框图。

高一数学必修三测试题含答案

宜阳县艺术学校2015-2016学年第二学期高一月考数学试题一、选择题（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中只有一个是符合题目要求的)1．算法共有三种逻辑结构，即顺序结构、条件结构和循环结构．下列说法中，正确的是( )A ．一个算法只能含有一种逻辑结果B ．一个算法最多可以包含两种逻辑结构C ．一个算法必须含有上述三种逻辑结构D ．一个算法可以含有上述三种逻辑结构的任意组合 [答案] D2．下列赋值语句错误的是( )A ．i ＝i －1B ．m ＝m 2＋1C ．k ＝－1kD ．x*y ＝a[答案] D[解析] 执行i ＝i －1后，i 的值比原来小1，则A 正确；执行m ＝m 2＋1后，m 的值等于原来m 的平方再加1，则B 正确；执行k ＝－1k 后，k 的值是原来的负倒数，则C 正确；赋值号的左边只能是一个变量，则D 错误． 3．计算机执行右边的程序段后，输出的结果是( ) A ．1,3 B ．4,1 C ．4，-2 D ．6,0[答案] B[解析] 把1赋给变量a ，把3赋给变量b ，由语句“a ＝a ＋b ”得a ＝4，即把4赋给定量a ，由语句“b ＝a －b ”得b ＝1，即把1赋给变量b ，输出a ，b ，即输出4,1.4．执行下图的程序框图，若输入的a ，b ，k 分别为1,2,3，则输出的M ＝( )学校班级姓名考号************************密**********************封***********************线**********************密************************封**A.203 B ．165 C.72 D ．158 [答案] D[解析] 输入a ＝1，b ＝2，k ＝3，n ＝1时， M ＝1＋12＝32，a ＝2，b ＝32；n ＝2时；M ＝2＋23＝83，a ＝32，b ＝83；n ＝3时；M ＝32＋38＝158，a ＝83，b ＝158；n ＝4时；输出M ＝158，选D.5．(2014全国高考重庆卷)执行如图所示的程序框图，若输出k 的值为6，则判断框内可填入的条件是( )A ．21>S B ．57>SC ．107>SD ．54>S[答案] C[解析] ∵10787981091=⨯⨯⨯=S ，∴选C.6．下列各进位制数中，最大的数是( )A ．11111(2)B ．1221(3)C ．312(4)D ．56(8)[答案] C[解析] 11111(2)＝1×24＋1×23＋1×22＋1×21＋1＝31, 1221(3)＝1×33＋2×32＋2×3＋1＝52, 312(4)＝3×42＋1×4＋2＝54, 56(8)＝5×8＋6＝46，故选C.7．用秦九韶算法求多项式f (x )＝4x 5－x 2＋2当x ＝3时的值时，需要________次乘法运算和________次加法(或减法)运算．( )A ．4,2B ．5,3C ．5,2D ．6,2 [答案] C[解析] f (x )＝4x 5－x 2＋2＝(((4x )x )x －1)x )x ＋2，所以需要5次乘法程算和2次加法(或减法)运算．8．利用秦九韶算法计算f (x )＝x 5＋2x 4＋3x 3＋4x 2＋5x ＋6在x ＝5时的值为( ) A ．4881 B ．220 C ．975 D ．4818 [答案] A[解析] 依据秦九韶算法，把多项式改写为f (x )＝((((x ＋2)x ＋3)x ＋4)x ＋5)x ＋6. 按照从内到外的顺序，依次计算x ＝5时的值： v 0＝1；v 1＝1×5＋2＝7； v 2＝7×5＋3＝38； v 3＝38×5＋4＝194； v 4＝194×5＋5＝975；v 5＝975×5＋6＝4881. 故f (5)＝4881.9．从2007名学生中选取50名参加全国数学联赛，若采用下面的方法选取：先用简单随机抽样从2007人中剔除7人，剩下的2000人再按系统抽样的方法抽取，则每人入选的可能性( )A ．不全相等B ．均不相等C ．都相等，且为502007D ．都相等，且为140[答案] C10．(2013～2014·山东淄博一模)某程序框图如图所示，现输入如下四个函数：f (x )＝x 2，f (x )＝1x ，f (x )＝e x ，f (x )＝x 3，则可以输出的函数是( ) A ．f (x )＝x 2B ．f (x )＝1xC ．f (x )＝e xD ．f (x )＝x 3[答案] D[解析] 由程序框图知，输出的函数应该即是奇函数，又存在零点．故选D.11．甲、乙两名运动员在某项测试中的6次成绩的茎叶图如图所示，x 1，x 2分别表示甲、乙两名运动员这项测试成绩的平均数，2221s s 、分别表示甲、乙两名运动员这项测试成绩的方差，则有( )A ．222121,s s x x <> 222121,s s x x >= C ．222121,s s x x == D ．222121,s s x x <=[答案] D[解析] 本题主要考查茎叶图中均值和方差的计算．根据题意，由甲、乙两名运动员在某项测试中的6次成绩的茎叶图，知x 1＝9＋14＋15＋15＋16＋216＝15， x 2＝8＋13＋15＋15＋17＋226＝15，s 21＝16[(－6)2＋(－1)2＋02＋02＋12＋62]＝373， s 22＝16[(－7)2＋(－2)2＋02＋02＋22＋72]＝533，所以s 21＜s 22，故选D.12．如图1是某高三学生进入高中－二年来的数学考试成绩茎叶图，第1次到第14次的考试成绩依次记为A 1，A 2，…，A 14.如图2是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图．那么算法流程图输出的结果是( )A ．7B ．8C ．9D ．10 [答案] D[解析] 本题考查循环结构以及茎叶图．解决此类问题的关键是弄清算法流程图的含义，分析程序中各变量、各语句的作用．根据流程图所示的顺序，可知该程序的作用是累计14次考试成绩超过90分的次数．根据茎叶图可得超过90分的次数为10，二、填空题(本大题共4小题，每小题5分，共20分．)13．217与155的最大公约数是________． [答案] 31[解析]217＝155×1＋62,155＝62×2＋31,62＝31×2，∴217与155的最大公约数为31. 14．用秦九韶算法计算多项式f(x)＝x6－12x5＋60x4－160x3＋240x2－192x＋64当x＝2时的值时，v4的值为________．[答案]80[解析]v0＝1，v1＝v0x＋a5＝1×2－12＝－10，v2＝v1x＋a4＝－10×2＋60＝40，v3＝v2x＋a3＝40×2－160＝－80，v4＝v3x＋a2＝－80×2＋240＝80.15．某工厂要对某批次产品进行质量抽检，现将从800件产品中抽取60件，在利用随机数表抽取样本时，将800件产品按000,001，…，799进行编号，如果从随机数表第8行第7列的数开始向右读，请你依次写出最先检验的5件产品的编号是________(下面摘取了随机数表的第7行至第9行)．84 42 17 53 3157 24 55 06 8877 04 74 47 67217633 50 2583 92 12 06 7663 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 8673 58 0744 39 52 38 7933 2112 34 2978 64 56 07 8252 42 07 44 3815 5100 13 4299 66 02 79 54[答案]785,567,199,507,17516．某企业五月中旬生产A，B，C三种产品共3 000件，根据分层抽样的结果，企业统计员制作了如下的统计表格：产品类别 A B C产品数量(件) 1 300样本容量130容量比C产品的样本容量多10，请你根据以上信息补全表格中的数据：______，______，______，_____.(按左上、右上、左下、右下的顺序依次填入)[答案]9008009080[解析]由产品B的数据可知该分层抽样的抽样比k＝1301 300＝110，设产品C的样本容量为x，则产品A的样本容量为(x＋10)，x＋10＋130＋x＝3 000×110，解之得x＝80，∴产品A的样本容量为90，产品A的数量为90÷110＝900，产品C的数量为80÷110＝800.三、解答题(本大题共6个大题，共70分，解答应写出文字说明，证明过程或演算步骤)17．(本小题满分10分)设计一个算法，求表面积为16π的球的体积（请写出算法步骤）。

高一数学必修三测试卷

2. 从学号为 0～50 的高一某班 50 名学生中随机选取 5 名同学参加数学测试,采用系统抽样的 B. 5,16,27,38,49
9. 右图给出的是计算断框内应填入的条件是（ A． i 21 C． i 21
2
1 1 1 1 的值的一个流程图，其中判 2 4 6 20
）. B． i 11 D． i 11
3. 在如图所示的“茎叶图”表示的数据中，众数和中位数分别（
， 10.函数 f ( x) x x 2，x 5 5 ，在定义域内任取一点 x0 ，使
f ( x0 ) ≤ 0 的概率是（
Ａ．）.
1 10
Ｂ．
2 3
Ｃ．
3 10
Ｄ．
4 5
11．从一批产品中取出三件产品，设 A=“三件产品全不是次品”，B=“三件产品全是次品”C=“三件产品至少有一件是次品”，则下列结论正确的是（ A. A 与 C 互斥如下表：
1．下面对算法描述正确的一项是：（ A．算法只能用自然语言来描述 C．同一问题可以有不同的算法方法,则所选 5 名学生的学号可能是 ( A. 1,2,3,4,5 Ａ．23 与 26 B．31 与 26 C．24 与 30 D．26 与 30 4．下列事件:①连续两次抛掷同一个骰子，两次都出现 2 点； ② 明天下雨； ③某人买彩票中奖；）. ④ 从集合{1,2,3}中任取两个元素,它们的和大于 2; ⑤在标准大气压下，水加热到 90℃时会沸腾。其中是随机事件的个数有（ A. 1 B． 2 Ｃ．3 D. 4 频率组距 5.200 辆汽车通过某一段公路时，时速的频率分布直方图如右图所示，则时速在[50，70)的汽车大约有（）. Ａ．60 辆Ｃ．70 辆则输入 x 的值应该是（ INPUT x IF x<0 THEN y=(x+1)(x+1) ELSE y=(x-1)(x-1) END IF PRINT y END Ａ．3 或-3 B． -5 Ｃ．-5 或 5 Ｄ．5 或-3

人教A版高中数学必修3测试试题【含答案解析】

数学必修3测试试题本试卷分选择题和非选择题两部分，共4页．满分为150分．考试用时120分钟．第一部分选择题（共50分）一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．在用样本频率估计总体分布的过程中，下列说法正确的是Ａ．总体容量越大，估计越精确Ｂ．总体容量越小，估计越精确Ｃ．样本容量越大，估计越精确Ｄ．样本容量越小，估计越精确 2．刻画数据的离散程度的度量，下列说法正确的是（1）应充分利用所得的数据，以便提供更确切的信息；（2）可以用多个数值来刻画数据的离散程度；（3）对于不同的数据集,其离散程度大时，该数值应越小。

A ．(1)和(3)B ．(2)和(3)C ． (1)和(2)D ．都正确３．数据5，7，7，8，10，11的标准差是A ．8B ．4C ．2D ．1４．某公司现有职员160人，中级管理人员30人，高级管理人员10人，要从其中抽取20个人进行身体健康检查，如果采用分层抽样的方法，则职员、中级管理人员和高级管理人员各应该抽取多少人A ．8，15，7B ．16，2，2C ．16，3，1D ．12，3，55．阅读右面的流程图，若输入的a 、b 、c 分别是21、32、75，则输出的a 、b 、c 分别是： A ．75、21、32 B ．21、32、75C ．32、21、75D ．75、32、21 6．已知两组样本数据}{n x x x ,......,21的平均数为h ，}{m y y y ,......,21的平均数为k, 则把两组数据合并成一组以后，这组样本的平均数为A ．2k h+ B ．n m mknh ++ C ．n m nh mk ++ D ．nm kh ++ 7．条件语句的一般形式如右所示，其中B 表示的是 A ．条件 B ．条件语句 C ．满足条件时执行的内容 D ．不满足条件时执行的内容 8．从一批产品中取出三件，设A =“三件产品全不是次品”，B =“三件产品全是次品”，C =“三件产品不全是次品”，则下列结论正确的是A ．A 与C 互斥B ．B 与C 互斥 C ．任两个均互斥D ．任两个均不互斥开始输入a ，b ，cx:=aa:=cc:=b b:=x 输出a ，b ，c结束if A then B else C（1）（2）（3）（4） A ．（1）（2） B ．（1）（3） C ．（2）（4） D ．（2）（3） 10．同时抛掷两枚质地均匀的硬币，则出现两个正面朝上的概率是 A ．21 B ．41 C ．31 D ．81第二部分非选择题（共100分）二、填空题：本大题共4小题，每小题5分，共20分．将最简答案填在题后横线上。

人教A版高中数学必修三试卷高一年级数学月考试卷 .docx

马鸣风萧萧高中数学学习材料马鸣风萧萧*整理制作高一年级数学数学必修三月考试卷高一数学考试时间60分，满分100题号一二三总分得分总分人一、选择题(本大题共12小题，每小题5分，共60分)1．在输入语句中，若同时输入多个变量，则变量之间的分隔符号是（） A.逗号 B.空格 C.分号 D.顿号 2. 二进制数10111转化为五进制（） A.41 B.25 C.21 D.43 3.用秦九韶算法在计算()43223246f x x x x x =+-+-时,要用到的乘法和加法次数分别为（） A.4,3 B.6,4 C.4,4 D.3,44.将232x x y y++表示成计算机程序表达式为了（） A.()^32/2x y x y **++ B.^3*2*/2x y x y ++C.^32/2x y x y ++ D.()^322x y x y +÷+5. 3a = 4b = a b = b a = PRINT ,a b END以上程序输出的结果是（） A.3,4 B. 4,4 C.3,3 D.4,36.三位七进制的数表示的最大的十进制的数是（） A.322 B.332 C.342 D.3527.INPUT a\10/10b a a a =-+ MOD 10 PRINT b END若45a =,则以上程序运行后的结果是（） A.0.5 B.3 C.1.5 D.4.5 8．下列给出的输入语句、输出语句和赋值语句⑴输出语句INPUT a ;b ;c (2)输入语句INPUT x =3 (3)赋值语句3=B (4)赋值语句A=B=2则其中正确的个数是， ( )A ．0个 B. 1个 C. 2个 D. 3个9.下边程序执行后输出的结果是 ( ) 5n =0s =WHILE 15s < s s n =+ 1n n =- WENDPRINT n ENDA. -1B. 0C. 1D. 210.当2x =时,下面的程序段结果是 ( )1i = 0s = WHILE 4i <=*1s s x =+ 1i i =+ WEND评卷人得分座位号马鸣风萧萧PRINT s ENDA. 3B. 7C. 15D. 1711.下面为一个求20个数的平均数的程序,在横线上应填充的语句为 ( ) 0S = 1i = DOINPUT x S S x =+ 1i i =+LOOP UNTIL ___________ /20a S = PRINT a ENDA.20i >B.20i <C. 20i >=D.20i <=12.下列各数中最小的数是 ( ) A.()2111111 B.()6210 C.()41000 D.()981二、填空题（共3小题，每题5分，共15分）13．如图程序框图箭头a 指向①处时，输出 s=__________.箭头a 指向②处时，输出 s=__________.14.用二分法求方程的近似根,精确度为d,则循环结构中止的条件是_________________. 15．2183 和1947的最大公约数是___________________.评卷人得分开始i=1s=0s=s+ii=i+1i ≤6Y① ② aN结束13题输出s马鸣风萧萧三、解答题（共25分）16.用秦九韶算法计算函数()432354f x x x x =++-在2=x 时的函数值.17.某次考试,满分100分,按规定80x ≥者为良好,6080x ≤<者为及格,小于60者不及格,画出当输入一个同学的成绩x 时,输出这个同学属于良好、及格还是不及格的程序框图，并编写程序.18.设计求23631222...2+++++的值的程序框图，并编写程序.评卷人得分。

人教A版高中数学必修三试卷高一年级数学学科试题.docx

高中数学学习材料马鸣风萧萧*整理制作七校联考高一年级数学学科试题一．选择题(共12小题，每小题4分，共48分)1．330sin 的值为（） A ．21-B ．21C ．23-D ．232．下列四式不能化简为AD 的是（）A ．；）＋＋（BC CD AB B ．）；＋）＋（＋（CM BC MB AD C ．；－＋BM AD MB D ．；＋－CD OA OC3．把函数sin y x =（x R ∈）的图象上所有点向左平行移动3π个单位长度，再把所得图象上所有点的横坐标缩短到原来的12倍（纵坐标不变），得到的图象所表示的函数是( ) A ．sin(2)3y x π=-，x R ∈ B.sin()26x y π=+，x R ∈C.sin(2)3y x π=+，x R ∈D.sin(2)32y x π=+，x R ∈ 4．已知)sin ,(cos αα=a ，)sin ,(cos ββ=b ，且()0cos =-βα，那么=+b a （）A ．2B ．22C ．2D ．3 5.已知α是第二象限角，其终边上一点P (x ，5)，且cos α＝24x ，则sin ⎝⎛⎭⎫α＋π2＝( )． A ．－104 B ．－64 C ．64 D ．1046．已知船A 在灯塔C 北偏东85且到C 的距离为km 2，船B 在灯塔C 西偏北25且到C 的距离为km 3，则A ，B 两船的距离为( )A ．km 32B ．km 23 C.．km 15 D ．km 13 7．函数)(x f y =的图象如图所示，则)(x f y =的解析式为( )A ．22sin -=x yB ．13cos 2-=x yC ．1)52sin(--=πx yD ． )52sin(1π--=x y8．在△ABC 中，若22tan tan ba B A =，则△ABC 的形状是( ) A ．直角三角形 B ．等腰或直角三角形 C ．不能确定 D ．等腰三角形9．==-αααα2cos 则,55cos sin 是第一象限角，已知( ) A. 53-B. 53±C.54D.54± 10．已知ABC ∆的重心为G ，内角A ，B ，C 的对边分别为c b a ,,，若033=++GC c GB b GA a ，则角A 为( ) A ．4π B ．6π C ．3π D ．2π11．在△ABC 中，23,4(0)a m b m m ==>，如果三角形有解，则A 的取值范围是（）A ．060A ︒<≤︒B ．030A ︒<<︒10π 207πo xy21 ABCMC ．090A ︒<<︒D ．3060A ︒<<︒12. 如图，O 为△ABC 的外心，BAC AC AB ∠==,2,4为钝角，M 是边BC 的中点，则AO AM ⋅的值( )A ． 4 B.．6 C ．7 D ． 5二．填空题（本大题共6小题，单空题每小题4分,多空题每小题6分每空3分，共28分，将答案填在答题卷的相应位置）13．一扇形的周长等于4cm ，面积等于12cm ，则该扇形的半径为，圆心角为．14．化简()()=+-⎪⎭⎫ ⎝⎛---+αππααπαπs i n 32s i n c os )2c o s (3 ，=++ 35tan 25tan 335tan 25tan ．15．已知向量a 与b 的夹角为120°,且|a |=2, |b |=5,则(2a -b )·a =16．在△ABC 中，角A 、B 、C 的对边分别为a 、b 、c ，若a+b+c=20，三角形面积为310，且角60=A ，则边a = ________17．在ABC ∆中，90=C ，3=CB ,点M 是 AB 上的动点（包含端点），则CB MC ⋅的取值范围为． 18．函数π()3sin 23f x x ⎛⎫=- ⎪⎝⎭的图象为C ，则如下结论中不正确的序号是_________________ ①、图象C 关于直线11π12x =对称； ②、图象C 关于点2π03⎛⎫⎪⎝⎭，对称；③、函数()f x 在区间π5π1212⎛⎫-⎪⎝⎭，内是增函数； ④、由3sin 2y x =的图像向右平移π3个单位长度可以得到图象C三．解答题（本大题有4小题，前2题每题10分，后2题每题12分，共44分．解答应写出文字说明，证明过程或验算步骤.） 19．（本题10分）已知a 、b 、c 是同一平面内的三个向量，其中a =（1，－2）. （1）若|c |52=，且a c //，求c 的坐标；（2）若|b |=1，且a b +与2a b -垂直，求a 与b 的夹角θ的余弦值.20．（本题10分）已知A,B,C 的坐标分别为)sin 3,cos 3(),4,0(),0,4(ααC B A . (1)若)0,(πα-∈且||||BC AC =，求α的值；(2)若0=⋅BC AC ，求αααtan 12sin sin 22++21．（本题12分）已知函数1cos sin 3cos )(2+-=x x x x f ．（1）求函数)(x f 的最小正周期和单调递增区间；（2）若65)(=θf ，)3π23π(，∈θ，求θ2sin 的值．22．（本小题满分12分）在ABC ∆中，角C B A ,,的对边分别为c b a ,,，若()()()C A c B A b a sin sin sin sin -=-+. (1)求角B 的大小；(2)设BC 中点为D ，且3=AD ，求c a 2+的最大值．2015学年第二学期期中杭州地区七校联考高一年级数学学科参考答案一．选择题 1 2 3 4 5 6 7 8 9 10 11 12 ACCCBDDBABAD二．填空题13． 1 ， 2 14． 1-，315． 13 16． 717． []09，- 18． ④ 三．解答题19. 解：（1）设),(y x c =，由a c //和52||=c 可得： ⎩⎨⎧2212020y x x y ⋅+⋅=+= ， ……………….. 2分 ∴ ⎩⎨⎧24x y =-= 或 ⎩⎨⎧24x y ==- ………………..4分 ∴(2,4)c =-，或(2,4)c =- ………………… 5分（2）()(2),a b a b +⊥-∴()(2)0a b a b +⋅-= ……… 7分即2220,a a b b -⋅-=∴22||2||0a a b b -⋅-=，∴ 520a b -⋅-=，所以3a b ⋅=， ………….8分 ∴35cos 5||||a b a b θ⋅==⋅ …………10分 20.解：（1）由已知：)sin 3,4cos 3αα-=（AC ，)4sin 3,cos 3(-=ααBC …………..1分BCAC =()()()()4sin 3cos 3sin 34cos 32222--+=+∴αααα化简得：1tan ,cos sin ==ααα即………………..3分)0,(πα-∈ 43πα-=∴……………………5分（2）0=⋅BC AC 0)4sin 3(sin 3)4sin 3(cos 3=-+-∴αααα43cos sin =+αα ………….7分两边平方得：167cos sin 2-=αα ………………..8分又αααtan 12sin sin 22++=ααααααcos cos sin cos sin 22sin 2++=167cos sin 2-=αα………………….10分 21. 解：（1）1cos sin 3cos )(2+-=x x x x f12sin 2322co 1+-+=x x s ....................2分 23)32cos(++=πx ． ……………..4分函数最小正周期T=π ……………..5分由ππππk x k 2322≤+≤-，得632ππππ-≤≤-k x k （Z k ∈）． ∴函数)(x f 的单调递增区间是]6,32[ππππ--k k （Z k ∈）．…………………………………………….7分（2）∵65)(=θf ，∴6523)32cos(=++πx ，32)32cos(-=+πθ．∵⎪⎭⎫⎝⎛∈323ππθ，，∴)35,(32πππθ∈+，35)32(cos 1)32(sin 2-=+--=+πθπθ． ………………….9分 ∴)32cos(23)32sin(21)332sin(2sin πθπθππθθ+-+=-+=6532-=…………………………………12分 22．解：（1）()()()C A c B A b a sin sin sin sin -=-+ 所以由正弦定理可得()()()c a c b a b a -=-+ ，即ac b c a =-+222，…………………2分由余弦定理可知212cos 222=-+=ac b c a B ，…………………………4分因为()π,0∈B ，所以3π=B …………………………5分(2)设θ=∠BAD ，则在ABD ∆中，由3π=B 可知⎪⎭⎫ ⎝⎛∈32,0πθ，由正弦定理及3=AD 可得23sin32sin sin ==⎪⎭⎫⎝⎛-=πθπθADAB BD，………………………7分所以θsin 2=BD ，θθθπsin cos 332sin 2+=⎪⎭⎫⎝⎛-=AB ，…………………………8分所以⎪⎭⎫⎝⎛+=+=+6sin 34sin 6cos 322πθθθc a ，…………………………10分由⎪⎭⎫⎝⎛∈32,0πθ可知⎪⎭⎫⎝⎛∈+65,66πππθ，所以当26ππθ=+，即3πθ=时，c a 2+的最大值为34.…………………………12分。

人教A版高中数学必修三试卷高一年级数学学科试题.docx

七校联考高一年级数学学科试题一．选择题(共12小题，每小题4分，共48分)1．330sin 的值为（） A ．21-B ．21C ．23-D ．232．下列四式不能化简为AD 的是（）A ．；）＋＋（BC CD AB B ．）；＋）＋（＋（CM BC MB AD C ．；－＋BM AD MB D ．；＋－CD OA OC3．把函数sin y x =（x R ∈）的图象上所有点向左平行移动3π个单位长度，再把所得图象上所有点的横坐标缩短到原来的12倍（纵坐标不变），得到的图象所表示的函数是( ) A ．sin(2)3y x π=-，x R ∈ B.sin()26x y π=+，x R ∈C.sin(2)3y x π=+，x R ∈D.sin(2)32y x π=+，x R ∈4．已知)sin ,(cos αα=a ，)sin ,(cos ββ=b ，且()0cos =-βα，那么=+b a （）A ．2B ．22C ．2D ．3 5.已知α是第二象限角，其终边上一点P (x ，5)，且cos α＝24x ，则sin ⎝⎛⎭⎫α＋π2＝( )． A ．－104 B ．－64 C ．64 D ．1046．已知船A 在灯塔C 北偏东85且到C 的距离为km 2，船B 在灯塔C 西偏北25且到C 的距离为km 3，则A ，B 两船的距离为( )A ．km 32B ．km 23 C.．km 15 D ．km 13 7．函数)(x f y =的图象如图所示，则)(x f y =的解析式为( )A ．22sin -=x yB ．13cos 2-=x yC ．1)52sin(--=πx yD ． )52sin(1π--=x y8．在△ABC 中，若22tan tan b a B A =，则△ABC 的形状是( ) A ．直角三角形 B ．等腰或直角三角形 C ．不能确定 D ．等腰三角形9．==-αααα2cos 则,55cos sin 是第一象限角，已知( ) A. 53-B. 53±C.54D.54± 10．已知ABC ∆的重心为G ，内角A ，B ，C 的对边分别为c b a ,,，若033=++GC c GB b GA a ，则角A 为( ) A ．4π B ．6π C ．3π D ．2π11．在△ABC 中，23,4(0)a m b m m ==>，如果三角形有解，则A 的取值范围是（）A ．060A ︒<≤︒B ．030A ︒<<︒10π 207πo xy21 ABCMC ．090A ︒<<︒D ．3060A ︒<<︒12. 如图，O 为△ABC 的外心，BAC AC AB ∠==,2,4为钝角，M 是边BC 的中点，则AO AM ⋅的值( )A ． 4 B.．6 C ．7 D ． 5二．填空题（本大题共6小题，单空题每小题4分,多空题每小题6分每空3分，共28分，将答案填在答题卷的相应位置）13．一扇形的周长等于4cm ，面积等于12cm ，则该扇形的半径为，圆心角为．14．化简()()=+-⎪⎭⎫ ⎝⎛---+αππααπαπs i n 32s i n c os )2c o s (3 ，=++ 35tan 25tan 335tan 25tan ．15．已知向量a 与b 的夹角为120°,且|a |=2, |b |=5,则(2a -b )·a =16．在△ABC 中，角A 、B 、C 的对边分别为a 、b 、c ，若a+b+c=20，三角形面积为310，且角60=A ，则边a = ________17．在ABC ∆中，90=C ，3=CB ,点M 是 AB 上的动点（包含端点），则CB MC ⋅的取值范围为． 18．函数π()3sin 23f x x ⎛⎫=- ⎪⎝⎭的图象为C ，则如下结论中不正确的序号是_________________ ①、图象C 关于直线11π12x =对称； ②、图象C 关于点2π03⎛⎫⎪⎝⎭，对称；③、函数()f x 在区间π5π1212⎛⎫-⎪⎝⎭，内是增函数； ④、由3sin 2y x =的图像向右平移π3个单位长度可以得到图象C三．解答题（本大题有4小题，前2题每题10分，后2题每题12分，共44分．解答应写出文字说明，证明过程或验算步骤.） 19．（本题10分）已知a 、b 、c 是同一平面内的三个向量，其中a =（1，－2）. （1）若|c |52=，且a c //，求c 的坐标；（2）若|b |=1，且a b +与2a b -垂直，求a 与b 的夹角θ的余弦值.20．（本题10分）已知A,B,C 的坐标分别为)sin 3,cos 3(),4,0(),0,4(ααC B A . (1)若)0,(πα-∈且||||BC AC =，求α的值；(2)若0=⋅BC AC ，求αααtan 12sin sin 22++21．（本题12分）已知函数1cos sin 3cos )(2+-=x x x x f ．（1）求函数)(x f 的最小正周期和单调递增区间；（2）若65)(=θf ，)3π23π(，∈θ，求θ2sin 的值．22．（本小题满分12分）在ABC ∆中，角C B A ,,的对边分别为c b a ,,，若()()()C A c B A b a sin sin sin sin -=-+. (1)求角B 的大小；(2)设BC 中点为D ，且3=AD ，求c a 2+的最大值．2015学年第二学期期中杭州地区七校联考高一年级数学学科参考答案一．选择题 1 2 3 4 5 6 7 8 9 10 11 12 ACCCBDDBABAD二．填空题13． 1 ， 2 14． 1-，315． 13 16． 717． []09，- 18． ④ 三．解答题19. 解：（1）设),(y x c =，由a c //和52||=c 可得：⎩⎨⎧2212020y x x y ⋅+⋅=+= ， ……………….. 2分 ∴ ⎩⎨⎧24x y =-= 或 ⎩⎨⎧24x y ==- ………………..4分∴(2,4)c =-，或(2,4)c =- ………………… 5分（2）()(2),a b a b +⊥-∴()(2)0a b a b +⋅-= ……… 7分即2220,a a b b -⋅-=∴22||2||0a a b b -⋅-=，∴ 520a b -⋅-=，所以3a b ⋅=， ………….8分 ∴35cos 5||||a b a b θ⋅==⋅ …………10分 20.解：（1）由已知：)sin 3,4cos 3αα-=（AC ，)4sin 3,cos 3(-=ααBC …………..1分BCAC =()()()()4sin 3cos 3sin 34cos 32222--+=+∴αααα化简得：1tan ,cos sin ==ααα即………………..3分)0,(πα-∈ 43πα-=∴……………………5分（2）0=⋅BC AC 0)4sin 3(sin 3)4sin 3(cos 3=-+-∴αααα43cos sin =+αα ………….7分两边平方得：167cos sin 2-=αα ………………..8分又αααtan 12sin sin 22++=ααααααcos cos sin cos sin 22sin 2++=167cos sin 2-=αα………………….10分 21. 解：（1）1cos sin 3cos )(2+-=x x x x f12sin 2322co 1+-+=x x s ....................2分 23)32cos(++=πx ． ……………..4分函数最小正周期T=π ……………..5分由ππππk x k 2322≤+≤-，得632ππππ-≤≤-k x k （Z k ∈）． ∴函数)(x f 的单调递增区间是]6,32[ππππ--k k （Z k ∈）．…………………………………………….7分（2）∵65)(=θf ，∴6523)32cos(=++πx ，32)32cos(-=+πθ．∵⎪⎭⎫⎝⎛∈323ππθ，，∴)35,(32πππθ∈+，35)32(cos 1)32(sin 2-=+--=+πθπθ． ………………….9分 ∴)32cos(23)32sin(21)332sin(2sin πθπθππθθ+-+=-+=6532-=…………………………………12分 22．解：（1）()()()C A c B A b a sin sin sin sin -=-+ 所以由正弦定理可得()()()c a c b a b a -=-+ ，即ac b c a =-+222，…………………2分由余弦定理可知212cos 222=-+=ac b c a B ，…………………………4分因为()π,0∈B ，所以3π=B …………………………5分(2)设θ=∠BAD ，则在ABD ∆中，由3π=B 可知⎪⎭⎫ ⎝⎛∈32,0πθ，由正弦定理及3=AD 可得23sin32sin sin ==⎪⎭⎫⎝⎛-=πθπθADAB BD，………………………7分所以θsin 2=BD ，θθθπsin cos 332sin 2+=⎪⎭⎫⎝⎛-=AB ，…………………………8分所以⎪⎭⎫⎝⎛+=+=+6sin 34sin 6cos 322πθθθc a ，…………………………10分由⎪⎭⎫ ⎝⎛∈32,0πθ可知⎪⎭⎫ ⎝⎛∈+65,66πππθ，所以当26ππθ=+，即3πθ=时，c a 2+的最大值为34.…………………………12分。

高一数学必修3测试题及答案

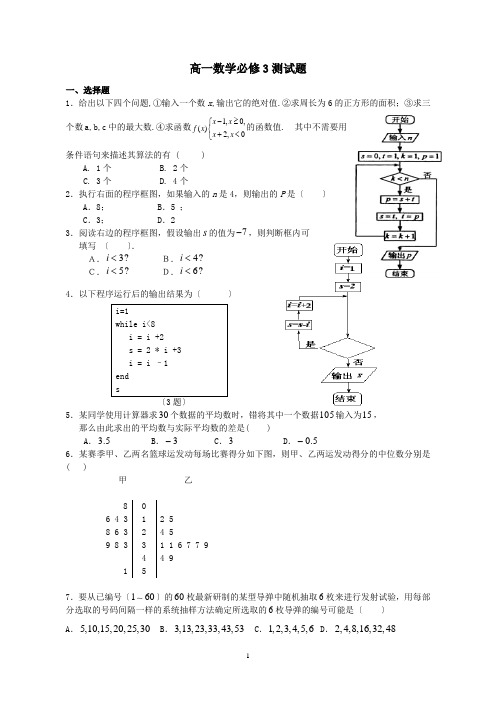
高一数学必修3测试题一、选择题1．给出以下四个问题,①输入一个数x ,输出它的绝对值.②求周长为6的正方形的面积；③求三个数a,b,c 中的最大数.④求函数1,0,()2,0x x f x x x -≥⎧⎨+<⎩的函数值. 其中不需要用条件语句来描述其算法的有 ( )A. 1个B. 2个C. 3个D. 4个2．执行右面的程序框图，如果输入的n 是4，则输出的P 是〔〕 A ．8； B ．5 ； C ．3； D ．23．阅读右边的程序框图，假设输出s 的值为7-，则判断框内可填写〔〕．Ａ．3?i < Ｂ．4?i < Ｃ．5?i < Ｄ．6?i < 4．以下程序运行后的输出结果为〔〕i=1while i<8 i = i +2 s = 2 * i +3 i = i –1 end s〔3题〕5．某同学使用计算器求30个数据的平均数时，错将其中一个数据105输入为15，那么由此求出的平均数与实际平均数的差是( )A ．3.5B ．3-C ．3D ．5.0-6．某赛季甲、乙两名篮球运发动每场比赛得分如下图，则甲、乙两运发动得分的中位数分别是( )甲乙8 6 4 3 8 6 3 9 8 3 1 0 1 2 3 4 5 2 5 4 51 1 6 7 7 94 97．要从已编号〔160〕的60枚最新研制的某型导弹中随机抽取6枚来进行发射试验，用每部分选取的号码间隔一样的系统抽样方法确定所选取的6枚导弹的编号可能是〔〕 A ．5,10,15,20,25,30 B ．3,13,23,33,43,53 C ．1,2,3,4,5,6 D ．2,4,8,16,32,488组号 1 2 3 4 5 6 7 8 频数1013x141513129第三组的频数和频率分别是 ( )A ．14和0.14B ．0.14和14C ．141和0.14 D ． 31和1419．某初级中学有学生270人，其中一年级108人，二、三年级各81人，现要利用抽样方法取10人参加某项调查，考虑选用简单随机抽样、分层抽样和系统抽样三种方案，使用简单随机抽样和分层抽样时，将学生按一、二、三年级依次统一编号为1,2, ……,270；使用系统抽样时，将学生统一随机编号1,2, ……,270，并将整个编号依次分为10段如果抽得号码有以下四种情况： ①7，34，61，88，115，142，169，196，223，250； ②5，9，100，107，111，121，180，195，200，265； ③11，38，65，92，119，146，173，200，227，254； ④30，57，84，111，138，165，192，219，246，270；关于上述样本的以下结论中，正确的选项是〔〕 A ②、③都不能为系统抽样 B ②、④都不能为分层抽样 C ①、④都可能为系统抽样 D ①、③都可能为分层抽样10．假设以连续掷两次骰子分别得到的点数m ，n 作为点P 的坐标，求点P 落在圆x 2＋y 2＝16外部的概率是( ). A ．95 B ．32C ．97D ．98 11．用秦九韶算法计算多项式876532)(2356+++++=x x x x x x f 在2=x 时，2v 的值为〔〕12．假设一组数据n x x x x ,,,,321 的平均数为2，方差为3，则,521+x ,522+x ,,523 +x ,52+n x 的平均数和方差分别是〔〕A.9, 11B.4, 11C.9, 12D.4, 17 二、填空题：13、执行左图所示流程框图，假设输入4x =，则输出y 的值为____________________．14、三个数72,120,168的最大公约数是_________________15．某奶茶店的日销售收入y 〔单位：百元〕与当天平均气温x 〔单位：℃〕之间的关系如下：通过上面的五组数据得到了x 与y 之间的线性回归方程：8.2+-=∧x y ；但现在丧失了一个数据,该数据应为___________.x -2 -1 0 1 2 y522116．设[)10,0∈a 且1≠a ，则函数x x f a log )(=在()+∞,0增函数且xa x g 2)(-=在()+∞,0内也是为增函数的概率为 . 三、解答题：17、为了了解一个小水库中养殖的鱼有关情况，从这个水库中多个不同位置捕捞出100条鱼，称得每条鱼的质量〔单位：千克〕，并将所得数据分组，画出频率分布直方图〔如下图〕〔Ⅰ〕在答题卡上的表格中填写相应的频率；〔Ⅱ〕数据落在〔1.15,1.30〕中的频率为多少；〔Ⅲ〕将上面捕捞的100条鱼分别作一记号后再放回水库，几天后再从水库的多处不同位置捕捞出120条鱼，其中带有记号的鱼有6条，请根据这一情况来估计该水库中鱼的总条数。

123高一数学必修3试卷

人教A版高中数学必修三试卷高一年级期中考参考答案.docx

新人教版高中数学必修3全册同步测试题及解析答案.doc

人教版高中数学高一A数学必修3测试卷(一)

高中数学必修三试卷

高一数学必修三试卷及答案

【试卷】高中数学必修3综合测试题及答案

高一数学必修三测试题含答案

高一数学必修三测试卷

人教A版高中数学必修3测试试题【含答案解析】

人教A版高中数学必修三试卷高一年级数学月考试卷 .docx

人教A版高中数学必修三试卷高一年级 数学学科 试 题.docx

人教A版高中数学必修三试卷高一年级 数学学科 试 题.docx

高一数学必修3测试题及答案

人教A版高中数学必修三试卷高一年级数学学科试题.docx

人教A版高中数学必修三试卷高一年级数学学科试题.docx