热学4
热力学4大定律

热力学4大定律
热力学是研究物质热现象和能量转化的学科,其基础是热力学定律。
其中,热力学的4大定律是热力学的基石,下面一一介绍:第一定律:能量守恒定律
能量无法被创造或毁灭,只能被转化形式。
在系统内,能量的增加等于吸收的热量与对外做功的代数和。
这就是热力学第一定律,也被称为能量守恒定律。
第二定律:熵增定律
热能总是从高温物体流向低温物体,不可能自行流动反向。
这是热力学第二定律,也被称为熵增定律。
熵是一个系统的无序程度,它总是在不断增加。
热力学第二定律告诉我们,任何封闭系统中,熵不可能减少,只能增加或保持不变。
第三定律:绝对零度定律
绝对零度是温度的最低限度,等于绝对零度时,物质的分子运动完全停止。
热力学第三定律规定,任何物体都无法达到绝对零度,但可以接近于零度。
第四定律:热力学定量关系定律
热力学第四定律描述了热力学量之间的定量关系,例如温度、熵、热容等。
这些关系可以用来预测系统中的热力学性质和行为。
这些热力学定律是理解能量和热力学系统运作的基础。
了解这些定律可以帮助我们更好地理解自然规律和技术应用。
- 1 -。
《热学》第四章和第五章复习

第四章 热力学第一定律 基本要求一、 可逆和不可逆过程 (1)准静态过程(2)理解什么是可逆过程,什么是不可逆过程.知道只有无耗散的准静态过程才是可逆过程。
二、 功和热量 (1)明确功是在力学相互作用过程中能量转移,热量是在热学相互作用过程中的能量的转移,它们都是过程量,它们都是过程量。
知道“作功”是通过物体宏观位移来完成;而“热传递”是通过分子之间的相互作用来完成。
(2)知道功有正负,熟练掌握从体积膨胀功微分表达式pdV W d -=出发计算体积膨胀功。
从几何上理解功的大小等于p-V 图上热力学过程曲线下面的面积。
三、热力学第一定律(1)知道能量守恒与转化定律应用到热学中就是热力学第一定律。
明确热力学第一定律是把内能、功和热量这三个具有能量量纲的物理量结合在一个方程中:即 W Q U +=∆; (2)一微小过程中热力学第一定律表示为:W d Q d dU +=;对于准静态过程热力学第一定律表示为:pdV Q d dU -=(3)内能是态函数,内能一般应是温度和体积的函数。
内能应当包含分子的热运动动能和分子之间的相互作用势能,也应包括分子内部的能量;在热学中的内能一般不包括系统做整体运动的机械能。
四、热容和焓(1)知道热容的定义、热容是过程量、热容与物体的量有关。
(2)知道焓的定义pV U H +=;知道焓的物理意义。
五、热力学第一定律对理想气体的应用(1)知道焦耳定律;即理想气体的内能仅是温度的函数;知道理想气体的焓也只是温度的函数。
内能和焓的微分可分别表示为:dT C dU m V ,ν=;dT C dH m p ,ν=;这两个公式适用于理想气体任何过程。
(2)理想气体的准静态过程的热力学第一定律可表示为pdV dT C dQ m V +=,ν;利用上式可得迈耶公式:R C C m V m p =-,,ν;(3)会熟练利用热力学第一定律处理一些常见热力学过程。
(4)会推导准静态绝热过程方程,熟记并会熟练利用绝热过程方程,同时应知道绝热过程方程的适用条件。
传热学第四版第一章

第一章1-1夏天的早晨,一个大学生离开宿舍时的温度为20℃。
他希望晚上回到房间时的温度能够低一些,于是早上离开时紧闭门窗,并打开了一个功率为15W 的电风扇,该房间的长、宽、高分别为5m 、3m 、2.5m 。
如果该大学生10h 以后回来,试估算房间的平均温度是多少? 解:因关闭门窗户后,相当于隔绝了房间内外的热交换,但是电风扇要在房间内做工产生热量:为全部被房间的空气吸收而升温,空气在20℃时的比热为:1.005KJ/Kg.K,密度为1.205Kg/m 3,所以当他回来时房间的温度近似为32℃。
1-2理发吹风器的结构示意图如附图所示,风道的流通面积,进入吹风器的空气压力,温度℃。
要求吹风器出口的空气温度℃,试确定流过吹风器的空气的质量流量以及吹风器出口的空气平均速度。
电加热器的功率为1500W 。
解:1-3淋浴器的喷头正常工作时的供水量一般为每分钟。
冷水通过电热器从15℃被加热到43℃。
试问电热器的加热功率是多少?为了节省能源,有人提出可以将用过后的热水(温度为38℃)送入一个换热器去加热进入淋浴器的冷水。
如果该换热器能将冷水加热到27℃,试计算采用余热回收换热器后洗澡15min 可以节省多少能源? 解:1-4对于附图所示的两种水平夹层,试分析冷、热表面间热量交换的方式有何不同?如果要通过实验来测定夹层中流体的导热系数,应采用哪一种布置?解:(a )中热量交换的方式主要为热传导。
(b )热量交换的方式主要有热传导和自然对流。
所以如果要通过实验来测定夹层中流体的导热系数,应采用(a )布置。
1-5 一个内部发热的圆球悬挂于室内,对于附图所示的三种情况,试分析:(1)圆球表面散热的方式;(2)圆球表面与空气之间的换热方式。
解:(2)圆球为表面传热方式散热。
(1)换热方式:(a )自然对流换热;(b )自然对流与强制对流换热相当的过渡流传热;(c )强制对流换热;1-6 一宇宙飞船的外形示于附图中,其中外遮光罩是凸出于飞船体之外的一个光学窗口,其表面的温度状态直接影响到飞船的光学遥感器。
热力学第4定律

热力学第4定律
热力学第四定律是指熵的增加趋势。
在热力学中,熵是描述系统无序程度的物理量,也是一个衡量能量转化不可逆性的指标。
熵的增加意味着系统的无序程度增加,能量转化更难逆转,系统变得更加难以控制和预测。
在热力学的前三个定律中,我们学习了能量守恒定律、熵的不减定律和温度的零点定律。
这些定律告诉我们能量是守恒的,热量自然会向熵增加的方向流动,并且温度是有物理意义的。
然而,热力学第四定律则探讨了熵增加的趋势。
根据第四定律,自然界中系统的熵总是趋向于增加。
这可以理解为一个系统的无序程度总是增加的,热量总是朝着更高熵的方向传递。
为什么会有熵增加的趋势呢这是由于熵的定义和热力学过程的不可逆性。
熵的定义是系统的无序程度,而不可逆过程是指无法回到初始状态的过程。
热力学中的大部分过程都是不可逆的,例如摩擦、能量转化等。
由于不可逆过程的存在,能量的转化会导致系统的无序程度增加,即熵增加。
这是因为在能量转化过程中,有一部分能量会以废热的形式
散失,无法完全转化为有用的能量。
这就导致了熵的增加。
热力学第四定律的重要性在于提醒我们,自然界中系统总是朝着更高熵的方向发展。
这意味着无论我们如何努力,总会有一部分能量会以废热的形式散失,无法完全利用。
这也限制了热力学系统的能量转化效率。
总结起来,热力学第四定律是指熵的增加趋势,即系统的无序程度总是增加的。
这是由于不可逆过程导致能量转化的不完全性,部分能量以废热的形式散失。
熵的增加限制了能量转化的效率,也提醒我们能量守恒并不意味着能量利用的完全性。
传热学第4章对流换热(Convective Heat Transfer)

第一节:概述 工程应用背景
第四章 对流换热(Convective Heat Transfer)
第一节:概述
热对流 对流换热:
计算关系式
Φ hAtw tf
Φ hAtf tw
本章的主要任务:确定 h 的具体表达式
——请千万小心,步步都是富贵险中求。殊不知多少江湖英豪;名门侠女都 曾栽在这块看似山青湖静,实则风阴涛涌的领域!
第二节:对流换热问题的数学描写—对流换热微分方程组
二维、常物性、不可压、稳态
u v 0 x y
u
u x
v
u y
Fx
1
p x
2u x 2
2u y 2
u
v x
v
v y
Fy
1
p y
2v x 2
2v y 2
u
t x
v
t y
a
2t x 2
2t y 2
t
h tw t y w
第四章 对流换热(Convective Heat Transfer)
第一节:概述 求h主要有以下基本途径:
Φ h At w t f
h
第四章 对流换热(Convective Heat Transfer)
第一节:概述
影响对流换热的基本因素: 流动因素、几何因素和物性参数 流动因素 a 流动起因 自然对流(Natural Convection)—— 强迫对流(Forced Convection)—— b 流动状态 层流(Laminar Flow)—— 紊流(Turbulent Flow)—— c 流体有无相变(Phase Change) 凝结换热(Condensation Heat Transfer) 沸腾换热(Boiling Heat Transfer)
新版热学(秦允豪编)习题解答第四章热力学第一定律-新版.pdf

CV T0 2
CV (
R 2R
1
1
27 3 2
T2 T0
T0
(2)由( 1)式:
8
3
1.5 )
(3)左侧初态亦为 P0 T 0 V 0 ,终态为 P1V1T1
27
P1 P2
P0
∵ 活塞可移动,
8 ,由 PV
RT
RT 2
P0 V 0 T 2
V2
P2
T0
P2
14
V 1 2V 0 V 2
V0
9
P0V 0
3 T0
19
23
q 2 1 .60 10
6 .02 10 C
( q 2N Ae )
两极间电压为 , A q
19
A 1 .229 2 1 .60 10
6 .02
Q'
5
2. 858 10
23
10
82 . 84 %
4.4.7 设 1mol 固 体状 态 方程 为: v v 0 aT bP , 内 能 表示 为: u CT
Py L y S
P0 LS
其中 P0
gh 0
Py P0 可改写为
L Ly
1 P0
对微小振动 y L
Py P0
y 1
L
y
1 P0
1
1 P0
L
y P0
L
h0 gy
L
由功能关系:
m gy
1 mv 2 2
m max gy max
AP
式中 A P 是由于右端空气压强 P y 与左端空气压强 P0 对水银柱作功之和,且
2
T0
27 P0
8
《传热学》第四版_名词解释和简答的总结

1、傅里叶定律P35:在导热的过程中,单位时间内通过给定截面的导热量,正比于垂直该截面方向上的变化率和截面面积,而热量传递的方向则与温度升高的方向相反。
2、热导率(导热系数)P6、P37:表征材料导热性能优劣的参数,即是一种热物性参数,单位W/(m·k)。
数值上,其定义为单位温度梯度(在1m长度内温度降低1K)在单位时间内经单位导热面所传递的热量。
3、绝对黑体P9:简称黑体,是指能吸收投入到其表面上的所有热辐射能量的物体。
4、传热系数P13:数值上,它等于冷、热流体间温差△t=1°C、传热面积A=1m²时热流量的值,是表征传热过程强烈程度的标尺。
5、热扩散率P45:定义式为a=λ/ρc,它表示物体在加热或冷却中,温度趋于均匀一致的能力。
这个综合物性参数对稳态导热没有影响,但是在非稳态导热过程中,它是一个非常重要的参数。
6、接触热阻P67:在未接触的界面之间的间隙常常充满了空气,与两个固体便面完全接触相比,增加了附加的传递阻力,称为接触热阻。
7、肋效率P62:表征肋片散热的有效程度。
肋片的实际散热量与其整个肋片都处于肋基温度下得散热量之比。
8、第一类边界条件P44:规定了边界上的温度值,称为第一类边界条件。
9、第二类边界条件P44:规定了边界上的热流密度值,称为第二类边界条件。
10、第三类边界条件P44:规定了边界上的物体与周围流体间的表面传热系数h及周围流体的温度t f,称为第三类边界条件。
11、集中参数法P117:当固体内部的导热热阻小于其表面的换热热阻时,固体内部的温度趋于一致,近似认为固体内部的温度t仅是时间τ的一元函数而与空间坐标无关,这种忽略物体内部导热热阻的简化方法称为集总参数法。
12、当量直径P?:定义:把水利半径相等的圆管直径定义为非圆管的当量直径。
13、混合对流P273:当0.1≤Gr/Re2≤10时称混合对流。
14、定性温度P?:定性温度为流体的平均温度。
工程热力学4理想气体热力过程及气体压缩g

• 二、过程初,终状态参数间的关系p65
气态方程:
pv RT
过程方程 p1v1 p2v2 p1v1v1 1 p2v2v2 1
T1v1 1 T2v2 1
T1
p 1 1
T2
p2
1
p2 ( v1 )k (4-5) p1 v2
T2 ( v1 )k 1 4-6 T1 v2
研究热力学过程的依据
1) 第一定律: q du w dh wt
稳流:
q
h
1 2
c2
gz
ws
2) 理想气体: pv RT cp cv R u f (T ) h f (T )
k cp cv
3)可逆过程:
w pdv
wt vdp
2) ds δq T
s12
2
ds
1
2 δq ? 0
1T
上述两种结论哪一个对?为什么? 既然 δq 0 q 0 为什么熵会增加?(不可逆)
结论: 1)
ds δq TR
必须可逆
2)熵是状态参数,故用可逆方法推出的熵变 △s 公式也可用于不可逆过程。
3)不可逆绝热过程的熵变大于零。
pv RgT
p T
Rg v
2
s 1 ds
2
1 cV
dT T
Rg
ln
v2 v1
2
1 cp
dT T
Rg
ln
p2 p1
2
1 cp
dv v
2
1 cV
dp p
热学学 第四章 热力学第一定律.
植物,通过氧化把化学能转化为热和机械能。
16
亥姆霍兹 德国 物理学家(1821~1894) 《力之守恒》 化学、力学、电磁学、热学
17
• 2 内能
内能:在热学参考系下,所有分子的无规则运动的能量之和。
热学参考系:使系统宏观静止的参考系
用的能量,在过程中保持为常数,因此可以省略。
• 内能具体包含哪些能量---普遍
分子的动能(包括平动、转动、振动)
+分子内部的振动势能
+分子间的势能
18
---原子核内的能量,不能被运用,省略。 ---系统整体运动的能量,不是内能,排除。 (系统的整体平动、转动的动能) ---对于理想气体,分子间势能在任何过程中始终保持为常数, 可以省略。 • 例子:单原子分子理想气体的内能。 每个分子的动能之和。---热学坐标系。 • 例子:刚性双(多)原子分子理想气体的内能。 每个分子的平动动能之和,每个分子的转动动能之和。 • 例子:非刚性双(多)原子分子理想气体的内能。 每个分子的平动动能之和,每个分子的转动动能之和。每个分 子的振动动能之和,每个分子的振动势能之和。 • 例子:前面的例子都为非理想气体时。 都要包含分子间的势能之和。
系统和外界在非功过程交换的能量,称为热量
注意:1)热量过程量。
2)系统和外界必须有温度差,才能交换热量。
3)系统和外界交换能量的方式只有两种:功,热量。
§4.3 热力学第一定律
本质:能量转化和守恒定律在热学系统的表现。
1 历史
14
焦耳(1818-1889),英国。 热功当量
w电=I 2Rt=JQ w重力=JQ Q cmT
热力学四个基本公式

热力学四个基本公式
1. 第一定律:能量守恒定律
这一定律也被称为能量守恒定律,反映了能量在物质变化过程中的不灭性和不可创性。
简而言之,能量不会凭空消失,也不会从虚无中突然出现,而是在各种物质变化的过程中被转化和传递。
数学表达式:ΔU = Q - W
其中,ΔU表示系统内部的能量变化,Q表示系统从外界吸收
的热能,W表示系统对外界做功。
2. 第二定律:熵增加定律
熵是描述一个系统的无序度量,且在热力学中有着极其重要的作用。
熵增加定律是指在自然界中,任何一个孤立系统的熵都不可能相等或减少,而只能增加。
简而言之,自然界中的任何过程都趋向于更加无序和混乱。
数学表达式:ΔS ≥ Q/T
其中,ΔS表示系统的熵变,Q表示系统从外界吸收的热能,T 表示系统的温度。
3. 第三定律:绝对零度不能达到定律
绝对零度是指温度为零开尔文的状态,也是绝对零度热力学温标的起点。
根据第三定律,无论如何降低温度,都无法达到绝对零度的状态。
简而言之,绝对零度是物质世界中的温度极限。
数学表达式:k → 0时,S → 0
其中,k表示系统的热容量比值,S表示系统的熵。
4. 能量-熵互化定律
能量和熵在热力学中占据着同等重要的地位,而且还存在着一种关系:能量和熵可以在一定条件下互相转化。
简而言之,能量和熵之间不存在一种绝对隔离的关系。
数学表达式:ΔG = ΔH - TΔS
其中,ΔG表示系统的自由能变化,ΔH表示系统内部的焓变化,ΔS表示系统的熵变。
热学第四章

(3) Q p =v C p∆ T ∆T = Qp v Cp = 2× 500 = 8.6K 7× 8.31 2 p∆ V = R∆ T v
T = T0 +∆ T = 8.60C
v R∆ T V 2 = V 1 +∆ V = V 1 + p 2×0.082×8.6 = 44.8 + 1 = 0.046m3 = 46.2(升)
例4.4:理想气体从 ( P1 V1 ) 绝热自由膨胀到状 : 态 ( P2 2V1 ) ,试求末态压强 P2 。 解:绝热过程:Q = 0 绝热过程: 自由膨胀过程: 自由膨胀过程:W=0 由热力学第一定律:Q = U2 - U1 +W ,得 由热力学第一定律: U2 = U1 即:内能不变 因理想气体内能只决定于温度, 因理想气体内能只决定于温度,故 T2 =T1 理想气体的状态方程: 理想气体的状态方程:P2V2 /T2 = P1V1 /T1 已知 V2 = 2V1 T2 = T1 ,得 P2 = P1 / 2
p1 = p0 =1.013×105 Pa 解:
V1 = 44.8×10−3 m3 , T = 273 K 1
CV = 5R / 2
CP = 7R / 2
−3 3
先等压加热到 V2 = 2V1 = 89.6×10 m 则此时温度
V2 T2 = ( )T = 546Κ 1 V 1
在此过程吸收热量: 在此过程吸收热量:
V3 = V2 = 89.6×10−3 m
(四)理想气体的绝热压缩与绝热膨胀
[例4.3〕气体在气 缸中运动速度很快,而热量传递很 例 〕 缸中运动速度很快, 若近似认为这是一绝热过程。试问要把300K、 慢,若近似认为这是一绝热过程。试问要把 、 1atm 下的空气分别压缩到 下的空气分别压缩到10atm及100atm,则末态 及 , 温度分别有多高? 温度分别有多高 〔解〕
高等工程热力学第4章

即
x 1 ( )z y y ( )z x
上式称为倒数关系。
第四章 热力学一般关系式及 应用
如取 dz 0、 dx 0 ,则
x y x ( )z ( )x ( ) y 0 y z z
即
x y z ( ) z ( )x ( ) y 1 y z x
第四章 热力学一般关系式及应用
第一节 基本关联式
1.全微分方程
z f ቤተ መጻሕፍቲ ባይዱ x, y)
dz dz dz ( ) y dx ( ) x dy dx dy
dz dz M ( ) N ( )x 即 记 y , dx dy M N ( )x ( ) y y x
简单系统具有两个独立参数,如选定的两
(30)
上述三个热系数可以由实验直接测定。有 了热系数,积分后可以得出状态方程,是从 实验得到状态方程的基本方法。 绝热压缩系数 ,定义为: s
1 v s ( )s v p 1 p s 。 a 恒为正。
(31)
的单位是 s
第四章 热力学一般关系式及应用
由循环关系式
( p T v )v ( ) p ( )T 1 T v p
( a) (b)
第四章 热力学一般关系式及 应用
将(b)式代入(a)式可得
x y x x y dx ( ) ( ) dz ( ) y ( ) ( ) z d y y z
又有
x x dx ( ) dz ( ) z d z
对定容变化, qv du ,因而 v
u cv ( ) v T
对于定压变化δqp=dhp , 因而
(33)
传热学-第4章-非稳态导热的计算与分析

‹# ›
4.2.2 平壁内温度分布的分析解
Q0 cV t0 t
这是该非稳态导热过程所吸收的总热量 从初始时刻起到某一时刻τ的这段时间内,平壁所吸
收的热量为:
Q V c t x, t0 dV
35
‹# ›
4.2.3 Fo数和Bi数对非稳态过程的影响
• 平壁内温度分布表达式中含有Fo数和Bi数,这说明非稳 态导热的物理过程和特征要受到这两个无量纲量的影响 • 传热学中,通常将表示某一物理现象或物理过程特征的 量纲一的量,称为特征数或准则数
22
‹# ›
4.2.2 平壁内温度分布的分析解
• 为了定量计算平壁内的温度场, 需要建立描述平壁内温度分布 的数学模型 • 由于平壁两侧受流体对称加热, 中心面为对称面
23
‹# ›
4.2.2 平壁内温度分布的分析解
• 由于温度场对称,只需研究 厚为δ的半块平壁即可 • 将坐标原点置于平壁中心面, 建立如图所示的坐标系
到达某个预定温度所需经历的时间,或者在预定时间内可以达到 的温度,或者物体的温度对时间的变化速率。 ——确定非稳态过程的热流量或热量:确定物体在某一瞬间每一位 置处的热流密度、从某一时刻起经过一段时间后的总传热量。
7
‹# ›
4.1 概述
关键:确定温度场t=f(x,y,z,t) 非稳态导热问题的温度场不仅与空间坐标有关,而且还随 时间τ变化,使物体内任位置处的热流量和热流密度也随 时间变化 非稳态导热问题的分析和研究过程更复杂
37
‹# ›
4.2.3 Fo数和Bi数对非稳态过程的影响
将Fo数的定义式改写为:
Fo a 2 2 a
式中,τ和δ2/a都具有时间的量纲 ——分子τ表示:边界上发生热扰动时刻算起到计算时刻 为止的时间 ——分母δ2/a表示:热扰动经过一定厚度的固体层传播到 面积δ2上所需要的时间
传热学第四版完整版答案

第一章思考题1. 试用简练的语言说明导热、对流换热及辐射换热三种热传递方式之间的联系和区别。
答:导热和对流的区别在于:物体内部依靠微观粒子的热运动而产生的热量传递现象,称为导热;对流则是流体各部分之间发生宏观相对位移及冷热流体的相互掺混。
联系是:在发生对流换热的同时必然伴生有导热。
导热、对流这两种热量传递方式,只有在物质存在的条件下才能实现,而辐射可以在真空中传播,辐射换热时不仅有能量的转移还伴有能量形式的转换。
2. 以热流密度表示的傅立叶定律、牛顿冷却公式及斯忒藩-玻耳兹曼定律是应当熟记的传热学公式。
试写出这三个公式并说明其中每一个符号及其意义。
答:① 傅立叶定律:dx dtq λ-=,其中,q -热流密度;λ-导热系数;dx dt -沿x 方向的温度变化率,“-”表示热量传递的方向是沿着温度降低的方向。
② 牛顿冷却公式:)(f w t t h q -=,其中,q -热流密度;h -表面传热系数;w t -固体表面温度;ft -流体的温度。
③ 斯忒藩-玻耳兹曼定律:4T q σ=,其中,q -热流密度;σ-斯忒藩-玻耳兹曼常数;T -辐射物体的热力学温度。
3. 导热系数、表面传热系数及传热系数的单位各是什么?哪些是物性参数,哪些与过程有关?答:① 导热系数的单位是:W/(m.K);② 表面传热系数的单位是:W/(m 2.K);③ 传热系数的单位是:W/(m 2.K)。
这三个参数中,只有导热系数是物性参数,其它均与过程有关。
4. 当热量从壁面一侧的流体穿过壁面传给另一侧的流体时,冷、热流体之间的换热量可以通过其中任何一个环节来计算(过程是稳态的),但本章中又引入了传热方程式,并说它是“换热器热工计算的基本公式”。
试分析引入传热方程式的工程实用意义。
答:因为在许多工业换热设备中,进行热量交换的冷、热流体也常处于固体壁面的两侧,是工程技术中经常遇到的一种典型热量传递过程。
5. 用铝制的水壶烧开水时,尽管炉火很旺,但水壶仍然安然无恙。
黄淑清热学教程第四
关于每个分子力学性质的假设
(1)质点 (分子线度<<分子间平均距离) (2)遵从牛顿力学规律,分子间、分子与器壁间
的碰撞—弹性碰撞
( 3 ) 除碰撞瞬间,分子间、分子与器壁间无相
互作用力。
关于分子集体运动的统计假设
(1)无外场时,平衡态分子按位置均匀分布
n dN N dV V
(2)平衡态分子速度取向各方向等概率
微观大: 标准状态下空气 19 -3 n 2.7 10 cm 10 dN n dV 2.7 10 涨落0
i dt
ix t
§4.4 温度的微观实质
由理想气体状态方程
pV RT
NA R R p T T p nkT V NA V
N A —分子数密度 n
求统计平均值:
ni 2 2 P m ni nm ix nm x n i i
2 ix
2 x 1 2
3
2 P n平 3
1 平 m 2 —平动动能的统计平均值 2
如何取小体元 dV ixdtdA ? 宏观小 微观大
宏观小:
dA
x
例如 dV 109 cm3
W ( ) f ( ) d
0
f ( ) d
§4-6
麦克斯韦速率分布律
一. 麦克斯韦速率分布律 温度为 T 的平衡态下,气体分子速率分布的 3/ 2 概率密度为 m
f ( )
f ( ) 4 2 kT
dN N
e
2
m 2 / 2 kT
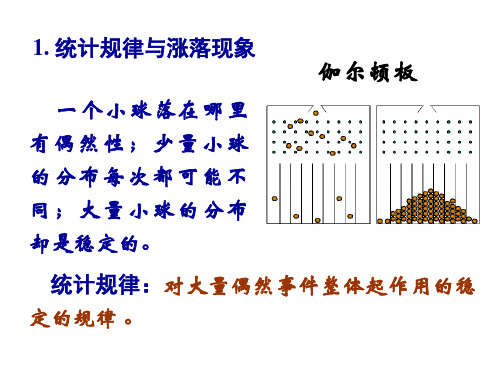
1. 统计规律与涨落现象
伽尔顿板
一个小球落在哪里 有偶然性;少量小球 的分布每次都可能不 同;大量小球的分布 却是稳定的。
物理化学热力学四

热力学四试卷一、选择题( 共17题34分)1. 2 分(0070)苯在一个刚性的绝热容器中燃烧,则:C6H6(l) + (15/2)O2(g) 6CO2+ 3H2O(g)(A) ΔU = 0 , ΔH < 0 , Q = 0(B) ΔU = 0 , ΔH > 0 , W = 0(C) ΔU = 0 , ΔH = 0 , Q = 0(D) ΔU≠0 , ΔH≠0 , Q = 02. 2 分(0746)恒温恒压条件下,某化学反应若在电池中可逆进行时吸热,据此可以判断下列热力学量中何者一定大于零?()(A) ΔU (B) ΔH(C) ΔS(D) ΔG3. 2 分(1232)关于偏摩尔量,下面的叙述中不正确的是:(A) 偏摩尔量的数值可以是正数、负数和零(B) 溶液中每一种广度性质都有偏摩尔量,而且都不等于其摩尔量(C) 除偏摩尔吉布斯自由能外,其他偏摩尔量都不等于化学势(D) 溶液中各组分的偏摩尔量之间符合吉布斯-杜亥姆关系式4. 2 分(0149)在非等压过程中加热某体系, 使其温度从T1升至T2, 吸热Q, 则此过程的焓增量ΔH为:()(A) ΔH=Q(B) ΔH=0(C) ΔH=U+(pV) (D) ΔH等于别的值5. 2 分(0894)1 mol Ag(s)在等容下由273.15 K加热到303.15 K,已知在该温度区间内Ag(s)的C V, m/J·K-1·mol-1=24.48,则其熵变为:( )(A) 2.531 J·K-1(B) 5.622 J·K-1(C) 25.31 J·K-1(D) 56.22 J·K-16. 2 分(0392)某化学反应在恒压、绝热和只作体积功的条件下进行,体系的温度由T1升高到T2,则此过程的焓变ΔH:( )(A) 小于零(B) 等于零(C) 大于零(D) 不能确定7. 2 分(0977)25℃时,1 mol 理想气体等温膨胀,压力从10p∃变到p∃,体系吉布斯自由能变化多少?( )(A) 0.04 kJ (B) -12.4 kJ(C) 1.24 kJ (D) -5.70 kJ8. 2 分(0161)将某理想气体从温度T1加热到T2。
热力学四个基本方程的适用条件

热力学四个基本方程的适用条件
1、热力学第零定律——如果两个热力学系统中的每一个都与第三个热力学系统处于热平衡(温度相同),则它们彼此也必定处于热平衡。
2、热力学第一定律——能量守恒定律在热学形式的表现。
3、热力学第二定律——力学能可全部转换成热能,但是热能却不能以有限次的实验操作全部转换成功(热机不可得)。
推论公式S=Q/T。
4、热力学第三定律——绝对零度不可达到但可以无限趋近。
S=KlnQ。
扩展资料:
热力学第一定律的能量方程式就是系统变化过程中的能量平衡方程式,是分析状态变化过程的根本方程式。
它可以从系统在状态变化过程中各项能量的变化和它们的总量守恒这一原则推出。
把热力学第一定律的原则应用于系统中的能量变化时可写成如下形式:
进入系统的能量- 离开系统的能量= 系统中储存能量的增加
上式是系统能量平衡的基本表达式,任何系统、任何过程均可据此原则建立其平衡式。
对于闭口系统,进入和离开系统的能量只包括热量和作功两项;对于开口系统,因有物质进出分界面,所以进入系统的能量和离开系统的能量除以上两项外,还有随同物质带进、带出系统的能量。
