函数总结复习及小测
(课件1)《一次函数》复习总结

(4)请推测该公司五月份总销售利润的最大值.
不妨 取k=1,得b=1. ∴ 解析式为y=x+1;
取k=2,得b=0, ∴解析式为y=2x;
取k=3,得b=-1,∴解析式为y=3x-1; …
∴满足条件的解析式有无数个,故答案为:
y=x+1或y=2x或y=3x-1…等.
例2.某班同学在探究弹簧的长度跟外力的变化关系时,实验
记录得到的相应数据如下表: 则y关于x的函数图象是( D )
(4)请推测该公司五月份总销售利润的最大值.
解:(3)设售出乙种型号器材a台,则丙种型号器材( 60-t-a )台 由进货款为64万元列方程得,
0.9t+1.2a+1.1 ( 60-t-a )=64 解得a=2t-20, 60-t-a=-3t+80
即,乙种型号器材2t-20台,丙种型号器材-3t+80台,
4 3
x+4
例像3与.x已轴知和:y如轴图交,于在A,B平两面点直,角将坐△标A系O中B绕,点一O次顺函时数针y旋= 43转x+930的°图后
得到△ A’OB’.
y
A’
(1)求直线A’B’的解析式
BC
(2)若直线A’B’与直线AB相交于点C,
求S△A’BC: S△AOB的值
A
0
B’ X
(2) ∵ OA’=4,OB=3, ∴ A’B=4-3=1
高考数学一轮复习考点与题型总结:第二章 函数的概念与基本初等函数

精品基础教育教学资料,仅供参考,需要可下载使用!第二章函数的概念与基本初等函数Ⅰ第一节函数及其表示一、基础知识1.函数与映射的概念2.函数的有关概念(1)函数的定义域、值域:在函数y=f(x),x∈A中,x叫做自变量,x的取值范围A叫做函数的定义域;与x的值相对应的y值叫做函数值,函数值的集合{f(x)|x∈A}叫做函数的值域.求函数定义域的策略(1)确定函数的定义域常从解析式本身有意义,或从实际出发.(2)如果函数y=f(x)是用表格给出,则表格中x的集合即为定义域.(3)如果函数y=f(x)是用图象给出,则图象在x轴上的投影所覆盖的x的集合即为定义域.(2)函数的三要素:定义域、值域和对应关系.(3)相等函数:如果两个函数的定义域和对应关系完全一致,则这两个函数相等,这是判断两函数相等的依据.两函数值域与对应关系相同时,两函数不一定相同.(4)函数的表示法:表示函数的常用方法有:解析法、图象法、列表法.3.分段函数若函数在其定义域内,对于定义域内的不同取值区间,有着不同的对应关系,这样的函数通常叫做分段函数.关于分段函数的3个注意(1)分段函数虽然由几个部分构成,但它表示同一个函数.(2)分段函数的定义域是各段定义域的并集,值域是各段值域的并集.(3)各段函数的定义域不可以相交.考点一函数的定义域[典例] (1)(2019·长春质检)函数y =ln (1-x )x +1+1x 的定义域是( )A .[-1,0)∪(0,1)B .[-1,0)∪(0,1]C .(-1,0)∪(0,1]D .(-1,0)∪(0,1)(2)已知函数f (x )的定义域为(-1,0),则函数f (2x +1)的定义域为( ) A .(-1,1) B.⎝⎛⎭⎫-1,-12 C .(-1,0)D.⎝⎛⎭⎫12,1[解析] (1)由题意得⎩⎪⎨⎪⎧1-x >0,x +1>0,x ≠0,解得-1<x <0或0<x <1.所以原函数的定义域为(-1,0)∪(0,1).(2)令u =2x +1,由f (x )的定义域为(-1,0),可知-1<u <0,即-1<2x +1<0, 得-1<x <-12.[答案] (1)D (2)B [解题技法]1.使函数解析式有意义的一般准则 (1)分式中的分母不为0; (2)偶次根式的被开方数非负; (3)y =x 0要求x ≠0;(4)对数式中的真数大于0,底数大于0且不等于1; (5)正切函数y =tan x ,x ≠k π+π2(k ∈Z);(6)实际问题中除考虑函数解析式有意义外,还应考虑实际问题本身的要求. 2.抽象函数的定义域问题(1)若已知函数f (x )的定义域为[a ,b ],其复合函数f (g (x ))的定义域由不等式a ≤g (x )≤b 求出;(2)若已知函数f (g (x ))的定义域为[a ,b ],则f (x )的定义域为g (x )在x ∈[a ,b ]上的值域.[题组训练]1.函数f (x )=1ln (x +1)+4-x 2的定义域为( )A .[-2,0)∪(0,2]B .(-1,0)∪(0,2]C .[-2,2]D .(-1,2]解析:选B 由⎩⎪⎨⎪⎧x +1>0,ln (x +1)≠0,4-x 2≥0,得-1<x ≤2,且x ≠0.2.若函数y =f (x )的定义域是[1,2 019],则函数g (x )=f (x +1)x -1的定义域是________________.解析:因为y =f (x )的定义域是[1,2 019],所以若g (x )有意义,应满足⎩⎪⎨⎪⎧1≤x +1≤2 019,x -1≠0,所以0≤x ≤2 018,且x ≠1.因此g (x )的定义域是{x |0≤x ≤2 018,且x ≠1}. 答案:{x |0≤x ≤2 018,且x ≠1}考点二 求函数的解析式[典例] (1)已知二次函数f (2x +1)=4x 2-6x +5,求f (x ); (2)已知函数f (x )满足f (-x )+2f (x )=2x ,求f (x ). [解] (1)法一:待定系数法因为f (x )是二次函数,所以设f (x )=ax 2+bx +c (a ≠0),则f (2x +1)=a (2x +1)2+b (2x +1)+c =4ax 2+(4a +2b )x +a +b +c .因为f (2x +1)=4x 2-6x +5, 所以⎩⎪⎨⎪⎧4a =4,4a +2b =-6,a +b +c =5,解得⎩⎪⎨⎪⎧a =1,b =-5,c =9,所以f (x )=x 2-5x +9(x ∈R). 法二:换元法令2x +1=t (t ∈R),则x =t -12,所以f (t )=4⎝⎛⎭⎫t -122-6·t -12+5=t 2-5t +9(t ∈R),所以f (x )=x 2-5x +9(x ∈R). 法三:配凑法因为f (2x +1)=4x 2-6x +5=(2x +1)2-10x +4=(2x +1)2-5(2x +1)+9, 所以f (x )=x 2-5x +9(x ∈R).(2)解方程组法由f (-x )+2f (x )=2x , ① 得f (x )+2f (-x )=2-x ,② ①×2-②,得3f (x )=2x +1-2-x . 即f (x )=2x +1-2-x3.故f (x )的解析式是f (x )=2x +1-2-x3(x ∈R).[解题技法] 求函数解析式的4种方法及适用条件 (1)待定系数法先设出含有待定系数的解析式,再利用恒等式的性质,或将已知条件代入,建立方程(组),通过解方程(组)求出相应的待定系数.(2)换元法对于形如y =f (g (x ))的函数解析式,令t =g (x ),从中求出x =φ(t ),然后代入表达式求出f (t ),再将t 换成x ,得到f (x )的解析式,要注意新元的取值范围.(3)配凑法由已知条件f (g (x ))=F (x ),可将F (x )改写成关于g (x )的表达式,然后以x 替代g (x ),便得f (x )的解析式.(4)解方程组法已知关于f (x )与f ⎝⎛⎭⎫1x 或f (-x )的表达式,可根据已知条件再构造出另外一个等式组成方程组,通过解方程组求出f (x ).[提醒] 由于函数的解析式相同,定义域不同,则为不相同的函数,因此求函数的解析式时,如果定义域不是R ,一定要注明函数的定义域.[题组训练]1.[口诀第2句]已知f (x )是二次函数,且f (0)=0,f (x +1)=f (x )+x +1,则f (x )=________________.解析:设f (x )=ax 2+bx +c (a ≠0), 由f (0)=0,知c =0,f (x )=ax 2+bx . 又由f (x +1)=f (x )+x +1,得a (x +1)2+b (x +1)=ax 2+bx +x +1, 即ax 2+(2a +b )x +a +b =ax 2+(b +1)x +1,所以⎩⎪⎨⎪⎧2a +b =b +1,a +b =1,解得a =b =12.所以f (x )=12x 2+12x (x ∈R).答案:12x 2+12x (x ∈R)2.[口诀第3句]已知f ⎝⎛⎭⎫2x +1=lg x ,则f (x )=________________.解析:令2x +1=t ,得x =2t -1,则f (t )=lg 2t -1,又x >0,所以t >1,故f (x )的解析式是f (x )=lg2x -1(x >1). 答案:lg2x -1(x >1) 3.[口诀第4句]已知f (x )满足2f (x )+f ⎝⎛⎭⎫1x =3x ,则f (x )=________. 解析:∵2f (x )+f ⎝⎛⎭⎫1x =3x ,①把①中的x 换成1x ,得2f ⎝⎛⎭⎫1x +f (x )=3x.② 联立①②可得⎩⎨⎧2f (x )+f ⎝⎛⎭⎫1x =3x ,2f ⎝⎛⎭⎫1x +f (x )=3x,解此方程组可得f (x )=2x -1x(x ≠0).答案:2x -1x (x ≠0)考点三 分段函数考法(一) 求函数值[典例] (2019·石家庄模拟)已知f (x )=⎩⎪⎨⎪⎧log 3x ,x >0,a x +b ,x ≤0(0<a <1),且f (-2)=5,f (-1)=3,则f (f (-3))=( )A .-2B .2C .3D .-3[解析] 由题意得,f (-2)=a -2+b =5,① f (-1)=a -1+b =3,②联立①②,结合0<a <1,得a =12,b =1,所以f (x )=⎩⎪⎨⎪⎧log 3x ,x >0,⎝⎛⎭⎫12x +1,x ≤0,则f (-3)=⎝⎛⎭⎫12-3+1=9,f (f (-3))=f (9)=log 39=2. [答案] B[解题技法] 求分段函数的函数值的策略(1)求分段函数的函数值时,要先确定要求值的自变量属于哪一区间,然后代入该区间对应的解析式求值;(2)当出现f (f (a ))的形式时,应从内到外依次求值;(3)当自变量的值所在区间不确定时,要分类讨论,分类标准应参照分段函数不同段的端点.考法(二) 求参数或自变量的值(或范围)[典例] (2018·全国卷Ⅰ)设函数f (x )=⎩⎪⎨⎪⎧2-x ,x ≤0,1,x >0,则满足f (x +1)<f (2x )的x 的取值范围是( )A .(-∞,-1]B .(0,+∞)C .(-1,0)D .(-∞,0)[解析] 法一:分类讨论法①当⎩⎪⎨⎪⎧x +1≤0,2x ≤0,即x ≤-1时,f (x +1)<f (2x ),即为2-(x +1)<2-2x,即-(x +1)<-2x ,解得x <1. 因此不等式的解集为(-∞,-1].②当⎩⎪⎨⎪⎧x +1≤0,2x >0时,不等式组无解.③当⎩⎪⎨⎪⎧x +1>0,2x ≤0,即-1<x ≤0时,f (x +1)<f (2x ),即为1<2-2x,解得x <0.因此不等式的解集为(-1,0).④当⎩⎪⎨⎪⎧x +1>0,2x >0,即x >0时,f (x +1)=1,f (2x )=1,不合题意.综上,不等式f (x +1)<f (2x )的解集为(-∞,0). 法二:数形结合法∵f (x )=⎩⎪⎨⎪⎧2-x ,x ≤0,1,x >0,∴函数f (x )的图象如图所示. 结合图象知,要使f (x +1)<f (2x ), 则需⎩⎪⎨⎪⎧x +1<0,2x <0,2x <x +1或⎩⎪⎨⎪⎧x +1≥0,2x <0,∴x <0,故选D. [答案] D[解题技法]已知函数值(或范围)求自变量的值(或范围)的方法(1)根据每一段的解析式分别求解,但要注意检验所求自变量的值(或范围)是否符合相应段的自变量的取值范围,最后将各段的结果合起来(求并集)即可;(2)如果分段函数的图象易得,也可以画出函数图象后结合图象求解.[题组训练]1.设f (x )=⎩⎨⎧x ,0<x <1,2(x -1),x ≥1,若f (a )=f (a +1),则f ⎝⎛⎭⎫1a =( ) A .2 B .4 C .6D .8解析:选C 当0<a <1时,a +1>1,f (a )=a ,f (a +1)=2(a +1-1)=2a , ∵f (a )=f (a +1),∴a =2a , 解得a =14或a =0(舍去).∴f ⎝⎛⎭⎫1a =f (4)=2×(4-1)=6.当a ≥1时,a +1≥2,f (a )=2(a -1),f (a +1)=2(a +1-1)=2a , ∵f (a )=f (a +1),∴2(a -1)=2a ,无解. 综上,f ⎝⎛⎭⎫1a =6.2.已知函数f (x )=⎩⎪⎨⎪⎧2x ,x ≤1,f (x -1),x >1,则f (f (3))=________.解析:由题意,得f (3)=f (2)=f (1)=21=2,∴f (f (3))=f (2)=2. 答案:23.(2017·全国卷Ⅲ)设函数f (x )=⎩⎪⎨⎪⎧x +1,x ≤0,2x ,x >0,则满足f (x )+f ⎝⎛⎭⎫x -12>1的x 的取值范围是________.解析:由题意知,可对不等式分x ≤0,0<x ≤12,x >12讨论.①当x ≤0时,原不等式为x +1+x +12>1,解得x >-14,故-14<x ≤0.②当0<x ≤12时,原不等式为2x +x +12>1,显然成立.③当x >12时,原不等式为2x +2x -12>1,显然成立.综上可知,所求x 的取值范围是⎝⎛⎭⎫-14,+∞. 答案:⎝⎛⎭⎫-14,+∞ 4.设函数f (x )=⎩⎪⎨⎪⎧⎝⎛⎭⎫12x -7,x <0,x ,x ≥0,若f (a )<1,则实数a 的取值范围是____________.解析:若a <0,则f (a )<1⇔⎝⎛⎭⎫12a-7<1⇔⎝⎛⎭⎫12a <8,解得a >-3,故-3<a <0; 若a ≥0,则f (a )<1⇔a <1,解得a <1,故0≤a <1. 综上可得-3<a <1. 答案:(-3,1)[课时跟踪检测]1.下列所给图象是函数图象的个数为( )A .1B .2C .3D .4解析:选B ①中当x >0时,每一个x 的值对应两个不同的y 值,因此不是函数图象;②中当x =x 0时,y 的值有两个,因此不是函数图象;③④中每一个x 的值对应唯一的y 值,因此是函数图象.故选B.2.函数f (x )=2x -1+1x -2的定义域为( ) A .[0,2)B .(2,+∞)C .[0,2)∪(2,+∞)D .(-∞,2)∪(2,+∞)解析:选C 由题意得⎩⎪⎨⎪⎧2x -1≥0,x -2≠0,解得x ≥0,且x ≠2.3.已知f ⎝⎛⎭⎫12x -1=2x -5,且f (a )=6,则a 等于( ) A.74 B .-74C.43D .-43解析:选A 令t =12x -1,则x =2t +2,f (t )=2(2t +2)-5=4t -1,则4a -1=6,解得a =74.4.(2019·贵阳检测)下列函数中,同一个函数的定义域与值域相同的是( ) A .y =x -1 B .y =ln x C .y =13x -1D .y =x +1x -1解析:选D 对于A ,定义域为[1,+∞),值域为[0,+∞),不满足题意;对于B ,定义域为(0,+∞),值域为R ,不满足题意;对于C ,定义域为(-∞,0)∪(0,+∞),值域为(-∞,-1)∪(0,+∞),不满足题意;对于D ,y =x +1x -1=1+2x -1,定义域为(-∞,1)∪(1,+∞),值域也是(-∞,1)∪(1,+∞).5.(2018·福建期末)已知函数f (x )=⎩⎪⎨⎪⎧log 2x +a ,x >0,4x -2-1,x ≤0.若f (a )=3,则f (a -2)=( )A .-1516B .3C .-6364或3D .-1516或3解析:选A 当a >0时,若f (a )=3,则log 2a +a =3,解得a =2(满足a >0);当a ≤0时,若f (a )=3,则4a -2-1=3,解得a =3,不满足a ≤0,所以舍去.于是,可得a =2.故f (a -2)=f (0)=4-2-1=-1516.6.已知函数y =f (2x -1)的定义域是[0,1],则函数f (2x +1)log 2(x +1)的定义域是( )A .[1,2]B .(-1,1] C.⎣⎡⎦⎤-12,0 D .(-1,0)解析:选D 由f (2x -1)的定义域是[0,1], 得0≤x ≤1,故-1≤2x -1≤1, ∴f (x )的定义域是[-1,1], ∴要使函数f (2x +1)log 2(x +1)有意义,需满足⎩⎪⎨⎪⎧-1≤2x +1≤1,x +1>0,x +1≠1,解得-1<x <0.7.下列函数中,不满足f (2 018x )=2 018f (x )的是( ) A .f (x )=|x | B .f (x )=x -|x | C .f (x )=x +2D .f (x )=-2x解析:选C 若f (x )=|x |,则f (2 018x )=|2 018x |=2 018|x |=2 018f (x );若f (x )=x -|x |,则f (2 018x )=2 018x -|2 018x |=2 018(x -|x |)=2 018f (x );若f (x )=x +2,则f (2 018x )=2 018x +2,而2 018f (x )=2 018x +2 018×2,故f (x )=x +2不满足f (2 018x )=2 018f (x );若f (x )=-2x ,则f (2 018x )=-2×2 018x =2 018×(-2x )=2 018f (x ).故选C.8.已知具有性质:f ⎝⎛⎭⎫1x =-f (x )的函数,我们称为满足“倒负”变换的函数,下列函数: ①f (x )=x -1x ;②f (x )=x +1x ;③f (x )=⎩⎪⎨⎪⎧x ,0<x <1,0,x =1,-1x ,x >1.其中满足“倒负”变换的函数是( ) A .①② B .①③ C .②③D .①解析:选B 对于①,f (x )=x -1x ,f ⎝⎛⎭⎫1x =1x-x =-f (x ),满足题意;对于②,f ⎝⎛⎭⎫1x =1x +x =f (x ),不满足题意;对于③,f ⎝⎛⎭⎫1x =⎩⎪⎨⎪⎧1x ,0<1x<1,0,1x =1,-x ,1x >1,即f ⎝⎛⎭⎫1x =⎩⎪⎨⎪⎧1x,x >1,0,x =1,-x ,0<x <1,故f ⎝⎛⎭⎫1x =-f (x ),满足题意.综上可知,满足“倒负”变换的函数是①③.9.(2019·青岛模拟)函数y =ln ⎝⎛⎭⎫1+1x +1-x 2的定义域为________. 解析:由⎩⎪⎨⎪⎧1+1x >0,1-x 2≥0⇒⎩⎪⎨⎪⎧x <-1或x >0,-1≤x ≤1⇒0<x ≤1.所以该函数的定义域为(0,1]. 答案:(0,1]10.(2019·益阳、湘潭调研)若函数f (x )=⎩⎨⎧lg (1-x ),x <0,-2x ,x ≥0,则f (f (-9))=________.解析:∵函数f (x )=⎩⎨⎧lg (1-x ),x <0,-2x ,x ≥0,∴f (-9)=lg 10=1,∴f (f (-9))=f (1)=-2.答案:-211.(2018·张掖一诊)已知函数f (x )=⎩⎪⎨⎪⎧2x ,x >0,x +1,x ≤0,若f (a )+f (1)=0,则实数a 的值等于________.解析:∵f (1)=2,且f (1)+f (a )=0,∴f (a )=-2<0,故a ≤0. 依题知a +1=-2,解得a =-3. 答案:-312.已知f (x )=⎩⎪⎨⎪⎧12x +1,x ≤0,-(x -1)2,x >0,使f (x )≥-1成立的x 的取值范围是________.解析:由题意知⎩⎪⎨⎪⎧x ≤0,12x +1≥-1或⎩⎪⎨⎪⎧x >0,-(x -1)2≥-1, 解得-4≤x ≤0或0<x ≤2, 故所求x 的取值范围是[-4,2]. 答案:[-4,2]13.设函数f (x )=⎩⎪⎨⎪⎧ax +b ,x <0,2x ,x ≥0,且f (-2)=3,f (-1)=f (1).(1)求函数f (x )的解析式;(2)在如图所示的直角坐标系中画出f (x )的图象.解:(1)由f (-2)=3,f (-1)=f (1),得⎩⎪⎨⎪⎧-2a +b =3,-a +b =2,解得⎩⎪⎨⎪⎧ a =-1,b =1,所以f (x )=⎩⎪⎨⎪⎧-x +1,x <0,2x ,x ≥0.(2)函数f (x )的图象如图所示.第二节函数的单调性与最值一、基础知识1.增函数、减函数定义:设函数f(x)的定义域为I:(1)增函数:如果对于定义域I内某个区间D上的任意两个自变量的值x1,x2,当x1<x2时,都有f(x1)<f(x2),那么就说函数f(x)在区间D上是增函数.(2)减函数:如果对于定义域I内某个区间D上的任意两个自变量的值x1,x2,当x1<x2时,都有f(x1)>f(x2),那么就说函数f(x)在区间D上是减函数.增(减)函数定义中的x1,x2的三个特征一是任意性;二是有大小,即x1<x2(x1>x2);三是同属于一个单调区间,三者缺一不可.2.单调性、单调区间若函数y=f(x)在区间D上是增函数或减函数,则称函数y=f(x)在这一区间具有(严格的)单调性,区间D叫做函数y=f(x)的单调区间.有关单调区间的两个防范(1)单调区间只能用区间表示,不能用不等式表示.(2)有多个单调区间应分别写,不能用符号“∪”连接,也不能用“或”连接,只能用“逗号”或“和”连接.3.函数的最值设函数y=f(x)的定义域为I,如果存在实数M满足:(1)对于任意的x∈I,都有f(x)≤M或f(x)≥M.(2)存在x0∈I,使得f(x0)=M.那么,我们称M是函数y=f(x)的最大值或最小值.函数最值存在的两条结论(1)闭区间上的连续函数一定存在最大值和最小值.当函数在闭区间上单调时最值一定在端点取到.(2)开区间上的“单峰”函数一定存在最大(小)值.二、常用结论在公共定义域内:(1)函数f(x)单调递增,g(x)单调递增,则f(x)+g(x)是增函数;(2)函数f (x )单调递减,g (x )单调递减,则f (x )+g (x )是减函数; (3)函数f (x )单调递增,g (x )单调递减,则f (x )-g (x )是增函数; (4)函数f (x )单调递减,g (x )单调递增,则f (x )-g (x )是减函数;(5)若k >0,则kf (x )与f (x )单调性相同;若k <0,则kf (x )与f (x )单调性相反; (6)函数y =f (x )(f (x )>0)在公共定义域内与y =-f (x ),y =1f (x )的单调性相反;(7)复合函数y =f [g (x )]的单调性与y =f (u )和u =g (x )的单调性有关.简记:“同增异减”.考点一 确定函数的单调性(区间))[典例] (1)求函数f (x )=-x 2+2|x |+1的单调区间. (2)试讨论函数f (x )=ax x -1(a ≠0)在(-1,1)上的单调性.[解] (1)易知f (x )=⎩⎪⎨⎪⎧-x 2+2x +1,x ≥0,-x 2-2x +1,x <0=⎩⎪⎨⎪⎧-(x -1)2+2,x ≥0,-(x +1)2+2,x <0. 画出函数图象如图所示,可知单调递增区间为(-∞,-1]和[0,1],单调递减区间为[-1,0]和[1,+∞).(2)法一:定义法 设-1<x 1<x 2<1, f (x )=a ⎝⎛⎭⎪⎫x -1+1x -1=a ⎝⎛⎭⎫1+1x -1,则f (x 1)-f (x 2)=a ⎝⎛⎭⎫1+1x 1-1-a ⎝⎛⎭⎫1+1x 2-1=a (x 2-x 1)(x 1-1)(x 2-1).由于-1<x 1<x 2<1,所以x 2-x 1>0,x 1-1<0,x 2-1<0, 故当a >0时,f (x 1)-f (x 2)>0,即f (x 1)>f (x 2), 函数f (x )在(-1,1)上单调递减;当a <0时,f (x 1)-f (x 2)<0,即f (x 1)<f (x 2), 函数f (x )在(-1,1)上单调递增. 法二:导数法f ′(x )=(ax )′(x -1)-ax (x -1)′(x -1)2=a (x -1)-ax (x -1)2=-a(x -1)2. 当a >0时,f ′(x )<0,函数f (x )在(-1,1)上单调递减; 当a <0时,f ′(x )>0,函数f (x )在(-1,1)上单调递增.[解题技法] 判断函数单调性和求单调区间的方法(1)定义法:一般步骤为设元―→作差―→变形―→判断符号―→得出结论.(2)图象法:如果f (x )是以图象形式给出的,或者f (x )的图象易作出,则可由图象的上升或下降确定单调性.(3)导数法:先求导数,利用导数值的正负确定函数的单调性及区间.(4)性质法:对于由基本初等函数的和、差构成的函数,根据各初等函数的增减性及复合函数单调性性质进行判断;复合函数单调性,可用同增异减来确定.[题组训练]1.下列函数中,满足“∀x 1,x 2∈(0,+∞)且x 1≠x 2,(x 1-x 2)·[f (x 1)-f (x 2)]<0”的是( ) A .f (x )=2x B .f (x )=|x -1| C .f (x )=1x-xD .f (x )=ln(x +1)解析:选C 由(x 1-x 2)·[f (x 1)-f (x 2)]<0可知,f (x )在(0,+∞)上是减函数,A 、D 选项中,f (x )为增函数;B 中,f (x )=|x -1|在(0,+∞)上不单调;对于f (x )=1x -x ,因为y =1x 与y=-x 在(0,+∞)上单调递减,因此f (x )在(0,+∞)上是减函数.2.函数f (x )=log 12(x 2-4)的单调递增区间是( )A .(0,+∞)B .(-∞,0)C .(2,+∞)D .(-∞,-2)解析:选D 令t =x 2-4,则y =log 12t .因为y =log 12t 在定义域上是减函数,所以求原函数的单调递增区间,即求函数t =x 2-4的单调递减区间,结合函数的定义域,可知所求区间为(-∞,-2).3.判断函数f (x )=x +ax (a >0)在(0,+∞)上的单调性.解:设x 1,x 2是任意两个正数,且x 1<x 2,则f (x 1)-f (x 2)=⎝⎛⎭⎫x 1+a x 1-⎝⎛⎭⎫x 2+a x 2=x 1-x 2x 1x 2(x 1x 2-a ). 当0<x 1<x 2≤a 时,0<x 1x 2<a ,x 1-x 2<0,所以f (x 1)-f (x 2)>0,即f (x 1)>f (x 2), 所以函数f (x )在(0,a ]上是减函数; 当a ≤x 1<x 2时,x 1x 2>a ,x 1-x 2<0, 所以f (x 1)-f (x 2)<0,即f (x 1)<f (x 2), 所以函数f (x )在[a ,+∞)上是增函数.综上可知,函数f (x )=x +ax (a >0)在(0,a ]上是减函数,在[a ,+∞)上是增函数.考点二 求函数的值域(最值))[典例] (1)(2019•深圳调研)函数y =|x +1|+|x -2|的值域为________.(2)若函数f (x )=-ax+b (a >0)在⎣⎡⎦⎤12,2上的值域为⎣⎡⎦⎤12,2,则a =________,b =________. (3)函数f (x )=⎩⎪⎨⎪⎧-x 2-4x ,x ≤0,sin x ,x >0的最大值为________.[解析] (1)图象法函数y =⎩⎪⎨⎪⎧-2x +1,x ≤-1,3,-1<x <2,2x -1,x ≥2.作出函数的图象如图所示.根据图象可知,函数y =|x +1|+|x -2|的值域为[3,+∞). (2)单调性法∵f (x )=-ax +b (a >0)在⎣⎡⎦⎤12,2上是增函数, ∴f (x )min =f ⎝⎛⎭⎫12=12,f (x )max =f (2)=2.即⎩⎨⎧-2a +b =12,-a2+b =2,解得a =1,b =52.(3)当x ≤0时,f (x )=-x 2-4x =-(x +2)2+4,而-2∈(-∞,0],此时f (x )在x =-2处取得最大值,且f (-2)=4;当x >0时,f (x )=sin x ,此时f (x )在区间(0,+∞)上的最大值为1.综上所述,函数f (x )的最大值为4.[答案] (1)[3,+∞) (2)1 52 (3)4[提醒] (1)求函数的最值时,应先确定函数的定义域.(2)求分段函数的最值时,应先求出每一段上的最值,再选取其中最大的作为分段函数的最大值,最小的作为分段函数的最小值.[题组训练]1.函数f (x )=x 2+4x 的值域为________.解析:当x >0时,f (x )=x +4x ≥4,当且仅当x =2时取等号; 当x <0时,-x +⎝⎛⎭⎫-4x ≥4, 即f (x )=x +4x ≤-4,当且仅当x =-2取等号,所以函数f (x )的值域为(-∞,-4]∪[4,+∞). 答案:(-∞,-4]∪[4,+∞)2.若x ∈⎣⎡⎦⎤-π6,2π3,则函数y =4sin 2x -12sin x -1的最大值为________,最小值为________.解析:令t =sin x ,因为x ∈⎣⎡⎦⎤-π6,2π3, 所以t ∈⎣⎡⎦⎤-12,1,y =f (t )=4t 2-12t -1, 因为该二次函数的图象开口向上,且对称轴为t =32,所以当t ∈⎣⎡⎦⎤-12,1时,函数f (t )单调递减,所以当t =-12时,y max =6;当t =1时,y min =-9. 答案:6 -93.已知f (x )=x 2+2x +ax ,x ∈[1,+∞),且a ≤1.若对任意x ∈[1,+∞),f (x )>0恒成立,则实数a 的取值范围是________.解析:对任意x ∈[1,+∞),f (x )>0恒成立等价于x 2+2x +a >0在x ∈[1,+∞)上恒成立,即a >-x 2-2x 在x ∈[1,+∞)上恒成立.又函数y =-x 2-2x 在[1,+∞)上单调递减, ∴(-x 2-2x )max =-3,故a >-3,又∵a ≤1,∴-3<a ≤1. 答案:(-3,1]考点三 函数单调性的应用考法(一) 比较函数值的大小[典例] 设偶函数f (x )的定义域为R ,当x ∈[0,+∞)时,f (x )是增函数,则f (-2),f (π),f (-3)的大小关系是( )A .f (π)>f (-3)>f (-2)B .f (π)>f (-2)>f (-3)C .f (π)<f (-3)<f (-2)D .f (π)<f (-2)<f (-3)[解析] 因为f (x )是偶函数,所以f (-3)=f (3),f (-2)=f (2). 又因为函数f (x )在[0,+∞)上是增函数. 所以f (π)>f (3)>f (2),即f (π)>f (-3)>f (-2). [答案] A[解题技法] 比较函数值大小的解题思路比较函数值的大小时,若自变量的值不在同一个单调区间内,要利用其函数性质,转化到同一个单调区间内进行比较,对于选择题、填空题能数形结合的尽量用图象法求解.考法(二) 解函数不等式[典例] 设函数f (x )=⎩⎪⎨⎪⎧2x ,x <2,x 2,x ≥2.若f (a +1)≥f (2a -1),则实数a 的取值范围是( )A .(-∞,1]B .(-∞,2]C .[2,6]D .[2,+∞)[解析] 易知函数f (x )在定义域(-∞,+∞)上是增函数,∵f (a +1)≥f (2a -1), ∴a +1≥2a -1,解得a ≤2.故实数a 的取值范围是(-∞,2]. [答案] B[解题技法] 求解含“f ”的函数不等式的解题思路先利用函数的相关性质将不等式转化为f (g (x ))>f (h (x ))的形式,再根据函数的单调性去掉“f ”,得到一般的不等式g (x )>h (x )(或g (x )<h (x )).考法(三) 利用单调性求参数的范围(或值)[典例] (2019•南京调研)已知函数f (x )=x -a x +a2在(1,+∞)上是增函数,则实数a 的取值范围是________.[解析] 设1<x 1<x 2,∴x 1x 2>1. ∵函数f (x )在(1,+∞)上是增函数, ∴f (x 1)-f (x 2)=x 1-a x 1+a2-⎝⎛⎭⎫x 2-a x 2+a 2 =(x 1-x 2)⎝⎛⎭⎫1+a x 1x 2<0.∵x 1-x 2<0,∴1+ax 1x 2>0,即a >-x 1x 2.∵1<x 1<x 2,x 1x 2>1,∴-x 1x 2<-1,∴a ≥-1. ∴a 的取值范围是[-1,+∞). [答案] [-1,+∞)[解题技法]利用单调性求参数的范围(或值)的方法(1)视参数为已知数,依据函数的图象或单调性定义,确定函数的单调区间,与已知单调区间比较求参数;(2)需注意若函数在区间[a ,b ]上是单调的,则该函数在此区间的任意子集上也是单调的.[题组训练]1.已知函数f (x )的图象向左平移1个单位后关于y 轴对称,当x 2>x 1>1时,[f (x 2)-f (x 1)]·(x 2-x 1)<0恒成立,设a =f ⎝⎛⎭⎫-12,b =f (2),c =f (3),则a ,b ,c 的大小关系为( ) A .c >a >b B .c >b >a C .a >c >bD .b >a >c解析:选D 由于函数f (x )的图象向左平移1个单位后得到的图象关于y 轴对称,故函数y =f (x )的图象关于直线x =1对称,所以a =f ⎝⎛⎭⎫-12=f ⎝⎛⎭⎫52.当x 2>x 1>1时,[f (x 2)-f (x 1)](x 2-x 1)<0恒成立,等价于函数f (x )在(1,+∞)上单调递减,所以b >a >c .2.已知函数f (x )=⎩⎪⎨⎪⎧ax 2-x -14,x ≤1,log a x -1,x >1是R 上的单调函数,则实数a 的取值范围是( )A.⎣⎡⎭⎫14,12 B.⎣⎡⎦⎤14,12 C.⎝⎛⎦⎤0,12 D.⎣⎡⎭⎫12,1解析:选B 由对数函数的定义可得a >0,且a ≠1.又函数f (x )在R 上单调,而二次函数y =ax 2-x -14的图象开口向上,所以函数f (x )在R 上单调递减,故有⎩⎪⎨⎪⎧0<a <1,12a≥1,a ×12-1-14≥log a1-1,即⎩⎪⎨⎪⎧0<a <1,0<a ≤12,a ≥14.所以a ∈⎣⎡⎦⎤14,12.[课时跟踪检测]A 级1.下列四个函数中,在x ∈(0,+∞)上为增函数的是( ) A .f (x )=3-x B .f (x )=x 2-3x C .f (x )=-1x +1D .f (x )=-|x |解析:选C 当x >0时,f (x )=3-x 为减函数;当x ∈⎝⎛⎭⎫0,32时,f (x )=x 2-3x 为减函数,当x ∈⎝⎛⎭⎫32,+∞时,f (x )=x 2-3x 为增函数;当x ∈(0,+∞)时,f (x )=-1x +1为增函数;当x ∈(0,+∞)时,f (x )=-|x |为减函数.2.若函数f (x )=ax +1在R 上单调递减,则函数g (x )=a (x 2-4x +3)的单调递增区间是( )A .(2,+∞)B .(-∞,2)C .(4,+∞)D .(-∞,4)解析:选B 因为f (x )=ax +1在R 上单调递减,所以a <0. 而g (x )=a (x 2-4x +3)=a (x -2)2-a .因为a <0,所以g (x )在(-∞,2)上单调递增.3.已知函数f (x )是定义在区间[0,+∞)上的函数,且在该区间上单调递增,则满足f (2x -1)<f ⎝⎛⎭⎫13的x 的取值范围是( )A.⎝⎛⎭⎫13,23 B.⎣⎡⎭⎫13,23 C.⎝⎛⎭⎫12,23D.⎣⎡⎭⎫12,23解析:选D 因为函数f (x )是定义在区间[0,+∞)上的增函数,满足f (2x -1)<f ⎝⎛⎭⎫13. 所以0≤2x -1<13,解得12≤x <23.4.(2019·菏泽模拟)定义新运算⊕:当a ≥b 时,a ⊕b =a ;当a <b 时,a ⊕b =b 2,则函数f (x )=(1⊕x )x -(2⊕x ),x ∈[-2,2]的最大值等于( )A .-1B .1C .6D .12解析:选C 由题意知当-2≤x ≤1时,f (x )=x -2,当1<x ≤2时,f (x )=x 3-2,又f (x )=x -2,f (x )=x 3-2在相应的定义域内都为增函数,且f (1)=-1,f (2)=6,∴f (x )的最大值为6.5.已知函数f (x )是R 上的增函数,A (0,-3),B (3,1)是其图象上的两点,那么不等式-3<f (x +1)<1的解集的补集是(全集为R)( )A .(-1,2)B .(1,4)C .(-∞,-1)∪[4,+∞)D .(-∞,-1]∪[2,+∞)解析:选D 由函数f (x )是R 上的增函数,A (0,-3),B (3,1)是其图象上的两点,知不等式-3<f (x +1)<1即为f (0)<f (x +1)<f (3),所以0<x +1<3,所以-1<x <2,故不等式-3<f (x +1)<1的解集的补集是(-∞,-1]∪[2,+∞).6.已知函数f (x )=⎩⎪⎨⎪⎧-x 2-ax -5,x ≤1,a x ,x >1是R 上的增函数,则实数a 的取值范围是( )A .[-3,0)B .(-∞,-2]C .[-3,-2]D .(-∞,0)解析:选C 若f (x )是R 上的增函数,则应满足⎩⎪⎨⎪⎧-a2≥1,a <0,-12-a ×1-5≤a 1,解得-3≤a ≤-2.7.已知函数f (x )=x 2-2x -3,则该函数的单调递增区间为________.解析:设t =x 2-2x -3,由t ≥0,即x 2-2x -3≥0,解得x ≤-1或x ≥3,所以函数f (x )的定义域为(-∞,-1]∪[3,+∞).因为函数t =x 2-2x -3的图象的对称轴为x =1,所以函数t =x 2-2x -3在(-∞,-1]上单调递减,在[3,+∞)上单调递增,所以函数f (x )的单调递增区间为[3,+∞).答案:[3,+∞)8.函数f (x )=⎩⎪⎨⎪⎧1x ,x ≥1,-x 2+2,x <1的最大值为________.解析:当x ≥1时,函数f (x )=1x 为减函数,所以f (x )在x =1处取得最大值,为f (1)=1;当x <1时,易知函数f (x )=-x 2+2在x =0处取得最大值,为f (0)=2.故函数f (x )的最大值为2.答案:29.若函数f (x )=1x 在区间[2,a ]上的最大值与最小值的和为34,则a =________.解析:由f (x )=1x 的图象知,f (x )=1x 在(0,+∞)上是减函数,∵[2,a ]⊆(0,+∞),∴f (x )=1x 在[2,a ]上也是减函数,∴f (x )max =f (2)=12,f (x )min =f (a )=1a ,∴12+1a =34,∴a =4. 答案:410.(2019·甘肃会宁联考)若f (x )=x +a -1x +2在区间(-2,+∞)上是增函数,则实数a 的取值范围是________.解析:f (x )=x +a -1x +2=x +2+a -3x +2=1+a -3x +2,要使函数在区间(-2,+∞)上是增函数,需使a -3<0,解得a <3.答案:(-∞,3)11.已知函数f (x )=1a -1x (a >0,x >0).(1)求证:f (x )在(0,+∞)上是增函数;(2)若f (x )在⎣⎡⎦⎤12,2上的值域是⎣⎡⎦⎤12,2,求a 的值. 解:(1)证明:任取x 1>x 2>0, 则f (x 1)-f (x 2)=1a -1x 1-1a +1x 2=x 1-x 2x 1x 2,∵x 1>x 2>0,∴x 1-x 2>0,x 1x 2>0, ∴f (x 1)-f (x 2)>0, 即f (x 1)>f (x 2),∴f (x )在(0,+∞)上是增函数.(2)由(1)可知,f (x )在⎣⎡⎦⎤12,2上是增函数, ∴f ⎝⎛⎭⎫12=1a -2=12,f (2)=1a -12=2, 解得a =25.12.已知f (x )=xx -a(x ≠a ).(1)若a =-2,试证f (x )在(-∞,-2)内单调递增;(2)若a >0且f (x )在(1,+∞)内单调递减,求a 的取值范围. 解:(1)证明:当a =-2时,f (x )=xx +2.任取x 1,x 2∈(-∞,-2),且x 1<x 2, 则f (x 1)-f (x 2)=x 1x 1+2-x 2x 2+2=2(x 1-x 2)(x 1+2)(x 2+2). 因为(x 1+2)(x 2+2)>0,x 1-x 2<0, 所以f (x 1)-f (x 2)<0,即f (x 1)<f (x 2), 所以f (x )在(-∞,-2)内单调递增. (2)任取x 1,x 2∈(1,+∞),且x 1<x 2, 则f (x 1)-f (x 2)=x 1x 1-a -x 2x 2-a =a (x 2-x 1)(x 1-a )(x 2-a ). 因为a >0,x 2-x 1>0,又由题意知f (x 1)-f (x 2)>0, 所以(x 1-a )(x 2-a )>0恒成立,所以a ≤1. 所以0<a ≤1.所以a 的取值范围为(0,1].B 级1.若f (x )=-x 2+4mx 与g (x )=2mx +1在区间[2,4]上都是减函数,则m 的取值范围是( )A .(-∞,0)∪(0,1]B .(-1,0)∪(0,1]C .(0,+∞)D .(0,1]解析:选D 函数f (x )=-x 2+4mx 的图象开口向下,且以直线x =2m 为对称轴,若在区间[2,4]上是减函数,则2m ≤2,解得m ≤1;g (x )=2m x +1的图象由y =2mx 的图象向左平移一个单位长度得到,若在区间[2,4]上是减函数,则2m >0,解得m >0.综上可得,m 的取值范围是(0,1].2.已知函数f (x )=ln x +x ,若f (a 2-a )>f (a +3),则正数a 的取值范围是________. 解析:因为f (x )=ln x +x 在(0,+∞)上是增函数,所以⎩⎪⎨⎪⎧a 2-a >a +3,a 2-a >0,a +3>0,解得-3<a <-1或a >3.又a >0,所以a >3. 答案:(3,+∞)3.已知定义在R 上的函数f (x )满足:①f (x +y )=f (x )+f (y )+1,②当x >0时,f (x )>-1. (1)求f (0)的值,并证明f (x )在R 上是单调增函数; (2)若f (1)=1,解关于x 的不等式f (x 2+2x )+f (1-x )>4. 解:(1)令x =y =0,得f (0)=-1.在R 上任取x 1>x 2,则x 1-x 2>0,f (x 1-x 2)>-1. 又f (x 1)=f [(x 1-x 2)+x 2]=f (x 1-x 2)+f (x 2)+1>f (x 2), 所以函数f (x )在R 上是单调增函数. (2)由f (1)=1,得f (2)=3,f (3)=5.由f (x 2+2x )+f (1-x )>4得f (x 2+x +1)>f (3), 又函数f (x )在R 上是增函数,故x 2+x +1>3, 解得x <-2或x >1,故原不等式的解集为{x |x <-2或x >1}.第三节 函数的奇偶性与周期性一、基础知1.函数的奇偶性函数的定义域关于原点对称是函数具有奇偶性的前提条件.若f (x )≠0,则奇(偶)函数定义的等价形式如下:(1)f (-x )=f (x )⇔f (-x )-f (x )=0⇔f (-x )f (x )=1⇔f (x )为偶函数;(2)f (-x )=-f (x )⇔f (-x )+f (x )=0⇔f (-x )f (x )=-1⇔f (x )为奇函数.2.函数的周期性 (1)周期函数对于函数f (x ),如果存在一个非零常数T ,使得当x 取定义域内的任何值时,都有f (x +T )=f (x ),那么就称函数f (x )为周期函数,称T 为这个函数的周期.周期函数定义的实质存在一个非零常数T ,使f (x +T )=f (x )为恒等式,即自变量x 每增加一个T 后,函数值就会重复出现一次.(2)最小正周期如果在周期函数f (x )的所有周期中存在一个最小的正数,那么这个最小正数就叫做f (x )的最小正周期.二、常用结论1.函数奇偶性常用结论(1)如果函数f (x )是奇函数且在x =0处有定义,则一定有f (0)=0;如果函数f (x )是偶函数,那么f (x )=f (|x |).(2)奇函数在两个对称的区间上具有相同的单调性;偶函数在两个对称的区间上具有相反的单调性.(3)在公共定义域内有:奇±奇=奇,偶±偶=偶,奇×奇=偶,偶×偶=偶,奇×偶=奇.2.函数周期性常用结论 对f (x )定义域内任一自变量x : (1)若f (x +a )=-f (x ),则T =2a (a >0). (2)若f (x +a )=1f (x ),则T =2a (a >0). (3)若f (x +a )=-1f (x ),则T =2a (a >0).3.函数图象的对称性(1)若函数y =f (x +a )是偶函数,即f (a -x )=f (a +x ),则函数y =f (x )的图象关于直线x =a 对称.(2)若对于R 上的任意x 都有f (2a -x )=f (x )或f (-x )=f (2a +x ),则y =f (x )的图象关于直线x =a 对称.(3)若函数y =f (x +b )是奇函数,即f (-x +b )+f (x +b )=0,则函数y =f (x )关于点(b,0)中心对称.考点一 函数奇偶性的判断[典例] 判断下列函数的奇偶性: (1)f (x )=36-x 2|x +3|-3;(2)f (x )=1-x 2+x 2-1; (3)f (x )=log 2(1-x 2)|x -2|-2;(4)f (x )=⎩⎪⎨⎪⎧x 2+x ,x <0,x 2-x ,x >0.[解] (1)由f (x )=36-x 2|x +3|-3,可知⎩⎪⎨⎪⎧ 36-x 2≥0,|x +3|-3≠0⇒⎩⎪⎨⎪⎧-6≤x ≤6,x ≠0且x ≠-6,故函数f (x )的定义域为(-6,0)∪(0,6],定义域不关于原点对称,故f (x )为非奇非偶函数.(2)由⎩⎪⎨⎪⎧1-x 2≥0,x 2-1≥0⇒x 2=1⇒x =±1,故函数f (x )的定义域为{-1,1},关于原点对称,且f (x )=0,所以f (-x )=f (x )=-f (x ),所以函数f (x )既是奇函数又是偶函数.(3)由⎩⎪⎨⎪⎧1-x 2>0,|x -2|-2≠0⇒-1<x <0或0<x <1,定义域关于原点对称.此时f (x )=log 2(1-x 2)|x -2|-2=log 2(1-x 2)2-x -2=-log 2(1-x 2)x ,故有f (-x )=-log 2[1-(-x )2]-x =log 2(1-x 2)x =-f (x ),所以函数f (x )为奇函数. (4)法一:图象法画出函数f (x )=⎩⎪⎨⎪⎧x 2+x ,x <0,x 2-x ,x >0的图象如图所示,图象关于y 轴对称,故f (x )为偶函数.法二:定义法易知函数f (x )的定义域为(-∞,0)∪(0,+∞),关于原点对称,当x >0时,f (x )=x 2-x ,则当x <0时,-x >0,故f (-x )=x 2+x =f (x );当x <0时,f (x )=x 2+x ,则当x >0时,-x <0,故f (-x )=x 2-x =f (x ),故原函数是偶函数.法三:f (x )还可以写成f (x )=x 2-|x |(x ≠0),故f (x )为偶函数.[题组训练]1.(2018·福建期末)下列函数为偶函数的是( ) A .y =tan ⎝⎛⎭⎫x +π4 B .y =x 2+e |x | C .y =x cos xD .y =ln|x |-sin x解析:选B 对于选项A ,易知y =tan ⎝⎛⎭⎫x +π4为非奇非偶函数;对于选项B ,设f (x )=x 2+e |x |,则f (-x )=(-x )2+e |-x |=x 2+e |x |=f (x ),所以y =x 2+e |x |为偶函数;对于选项C ,设f (x )=x cos x ,则f (-x )=-x cos(-x )=-x cos x =-f (x ),所以y =x cos x 为奇函数;对于选项D ,设f (x )=ln|x |-sin x ,则f (2)=ln 2-sin 2,f (-2)=ln 2-sin(-2)=ln 2+sin 2≠f (2),所以y =ln|x |-sin x 为非奇非偶函数,故选B.2.设函数f (x )=e x -e -x2,则下列结论错误的是( )A .|f (x )|是偶函数B .-f (x )是奇函数C .f (x )|f (x )|是奇函数D .f (|x |)f (x )是偶函数解析:选D ∵f (x )=e x -e -x2,则f (-x )=e -x -e x2=-f (x ).∴f (x )是奇函数. ∵f (|-x |)=f (|x |),∴f (|x |)是偶函数,∴f (|x |)f (x )是奇函数.考点二 函数奇偶性的应用[典例] (1)(2019·福建三明模拟)函数y =f (x )是R 上的奇函数,当x <0时,f (x )=2x ,则当x >0时,f (x )=( )A .-2xB .2-x C .-2-xD .2x(2)(2018·贵阳摸底考试)已知函数f (x )=a -2e x +1(a ∈R)是奇函数,则函数f (x )的值域为( )A .(-1,1)B .(-2,2)C .(-3,3)D .(-4,4)[解析] (1)当x >0时,-x <0,∵x <0时,f (x )=2x ,∴当x >0时,f (-x )=2-x .∵f (x )是R 上的奇函数,∴当x >0时,f (x )=-f (-x )=-2-x .(2)法一:由f (x )是奇函数知f (-x )=-f (x ),所以a -2e -x+1=-a +2e x +1,得2a =2e x+1+2e -x +1,所以a =1e x +1+e x e x +1=1,所以f (x )=1-2e x +1.因为e x +1>1,所以0<1e x +1<1,-1<1-2e x +1<1,所以函数f (x )的值域为(-1,1).法二:函数f (x )的定义域为R ,且函数f (x )是奇函数,所以f (0)=a -1=0,即a =1,所以f (x )=1-2e x +1.因为e x +1>1,所以0<1e x +1<1,-1<1-2e x +1<1,所以函数f (x )的值域为(-1,1).[答案] (1)C (2)A[解题技法]应用函数奇偶性可解决的四类问题及解题方法(1)求函数值将待求值利用奇偶性转化为已知区间上的函数值求解.(2)求解析式先将待求区间上的自变量转化到已知区间上,再利用奇偶性求解,或充分利用奇偶性构造关于f (x )的方程(组),从而得到f (x )的解析式.(3)求函数解析式中参数的值利用待定系数法求解,根据f (x )±f (-x )=0得到关于待求参数的恒等式,由系数的对等性得参数的值或方程(组),进而得出参数的值.(4)画函数图象和判断单调性利用奇偶性可画出另一对称区间上的图象及判断另一区间上的单调性.[题组训练]1.(2019·贵阳检测)若函数f (x )是定义在R 上的奇函数,当x ≥0时,f (x )=log 2(x +2)-1,则f (-6)=( )A .2B .4C .-2D .-4解析:选C 根据题意得f (-6)=-f (6)=1-log 2(6+2)=1-3=-2.2.已知函数f (x )为奇函数,当x >0时,f (x )=x 2-x ,则当x <0时,函数f (x )的最大值为________.解析:法一:当x <0时,-x >0,所以f (-x )=x 2+x .又因为函数f (x )为奇函数,所以f (x )=-f (-x )=-x 2-x =-⎝⎛⎭⎫x +122+14,所以当x <0时,函数f (x )的最大值为14. 法二:当x >0时,f (x )=x 2-x =⎝⎛⎭⎫x -122-14,最小值为-14,因为函数f (x )为奇函数,所以当x <0时,函数f (x )的最大值为14.答案:143.(2018·合肥八中模拟)若函数f (x )=x ln(x +a +x 2)为偶函数,则a =________. 解析:∵f (x )=x ln(x +a +x 2)为偶函数,∴f (-x )=f (x ),即-x ln(a +x 2-x )=x ln(x +a +x 2),从而ln[(a +x 2)2-x 2]=0,即ln a =0,故a =1.答案:1考点三 函数的周期性[典例] (1)(2018·开封期末)已知定义在R 上的函数f (x )满足f (x )=-f (x +2),当x ∈(0,2]时,f (x )=2x +log 2x ,则f (2 019)=( )A .5 B.12C .2D .-2(2)(2018·江苏高考)函数f (x )满足f (x +4)=f (x )(x ∈R),且在区间(-2,2]上,f (x )=⎩⎨⎧cos πx2,0<x ≤2,⎪⎪⎪⎪x +12,-2<x ≤0,则f (f (15))的值为________.[解析] (1)由f (x )=-f (x +2),得f (x +4)=f (x ),所以函数f (x )是周期为4的周期函数,所以f (2 019)=f (504×4+3)=f (3)=f (1+2)=-f (1)=-(2+0)=-2.(2)由函数f (x )满足f (x +4)=f (x )(x ∈R), 可知函数f (x )的周期是4, 所以f (15)=f (-1)=⎪⎪⎪⎪-1+12=12, 所以f (f (15))=f ⎝⎛⎭⎫12=cos π4=22. [答案] (1)D (2)22[题组训练]1.(2019·山西八校联考)已知f (x )是定义在R 上的函数,且满足f (x +2)=-1f (x ),当2≤x ≤3时,f (x )=x ,则f ⎝⎛⎭⎫-112=________. 解析:∵f (x +2)=-1f (x ),∴f (x +4)=f (x ), ∴f ⎝⎛⎭⎫-112=f ⎝⎛⎭⎫52,又2≤x ≤3时,f (x )=x , ∴f ⎝⎛⎭⎫52=52,∴f ⎝⎛⎭⎫-112=52. 答案:522.(2019·哈尔滨六中期中)设f (x )是定义在R 上的周期为3的函数,当x ∈[-2,1)时,f (x )=⎩⎪⎨⎪⎧4x 2-2,-2≤x ≤0,x ,0<x <1,则f ⎝⎛⎭⎫f ⎝⎛⎭⎫214=________. 解析:由题意可得f ⎝⎛⎭⎫214=f ⎝⎛⎭⎫6-34=f ⎝⎛⎭⎫-34=4×⎝⎛⎭⎫-342-2=14,f ⎝⎛⎭⎫14=14.答案:14[课时跟踪检测]A 级1.下列函数为奇函数的是( ) A .f (x )=x 3+1 B .f (x )=ln 1-x1+xC .f (x )=e xD .f (x )=x sin x解析:选B 对于A ,f (-x )=-x 3+1≠-f (x ),所以其不是奇函数;对于B ,f (-x )=ln 1+x 1-x=-ln1-x 1+x=-f (x ),所以其是奇函数;对于C ,f (-x )=e -x ≠-f (x ),所以其不是奇函数;对于D ,f (-x )=-x sin(-x )=x sin x =f (x ),所以其不是奇函数.故选B.2.(2019·南昌联考)函数f (x )=9x +13x 的图象( )A .关于x 轴对称B .关于y 轴对称C .关于坐标原点对称D .关于直线y =x 对称解析:选B 因为f (x )=9x +13x =3x +3-x ,易知f (x )为偶函数,所以函数f (x )的图象关于y轴对称.3.设函数f (x )是定义在R 上的奇函数,且f (x )=⎩⎪⎨⎪⎧log 2(x +1),x ≥0,g (x ),x <0,则f (-7)=( )A .3B .-3C .2D .-2解析:选B 因为函数f (x )是定义在R 上的奇函数,且f (x )=⎩⎪⎨⎪⎧log 2(x +1),x ≥0,g (x ),x <0,所以f (-7)=-f (7)=-log 2(7+1)=-3.4.若定义在R 上的偶函数f (x )和奇函数g (x )满足f (x )+g (x )=e x ,则g (x )=( ) A .e x -e -x B.12(e x +e -x )C.12(e -x -e x ) D.12(e x -e -x )解析:选D 因为f (x )+g (x )=e x ,所以f (-x )+g (-x )=f (x )-g (x )=e -x , 所以g (x )=12(e x -e -x ).。
九年级数学上册第22章二次函数小结与复习课件新版新人教版

针对训练
11.一家电脑公司推出一款新型电脑,投放市场以来3个月的 利润情况如图所示,该图可以近似看作为抛物线的一部分,请 结合图象,解答以下问题:
(1)求该抛物线对应的二次函数解析式; (2)该公司在经营此款电脑过程中,第 几月的利润最大?最大利润是多少? (3)若照此经营下去,请你结合所学的 知识,对公司在此款电脑的经营状况 (是否亏损?何时亏损?)作预测分析.
【解析】
方法一:配方,得y=x2-2x+3=(x-1)2+2,则
顶点坐标为(1,2).
方法二代入公式
x2ba2211,y4ac4ab2
41322
41
2,
则顶点坐标为(1,2).
方法归纳解决此类题目可以先把二次函数y=ax2+bx +c配方为顶点式y=a(x-h)2+k的形式,得到:对称 轴是直线x=h,最值为y=k,顶点坐标为(h,k);也 可以直接利用公式求解.
解得, a=2,b=-3,c=5.
待定系数法
∴ 所求的二次函数为y=2x2-3x+5.
针对训练 5.已知抛物线y=ax2+bx+c与抛物线y=-x2-3x+7
的形状相同,顶点在直线x=1上,且顶点到x轴的距离
为5,请写出满足此条件的抛物线的表达式.
解:抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的形状
+2bx+c的对称轴应在直线x=1的左侧而抛物线y=-x2
+2bx+c的对称轴
x b b 2(1)
,即b≤1,故选择D .
考点四 抛物线的几何变换
例4 将抛物线y=x2-6x+5向上平移 2个单位长 度,再向右平移1个单位长度后,得到的抛物线 解析式是( )
高中数学-- 指数函数与对数函数复习总结与检测(解析版)
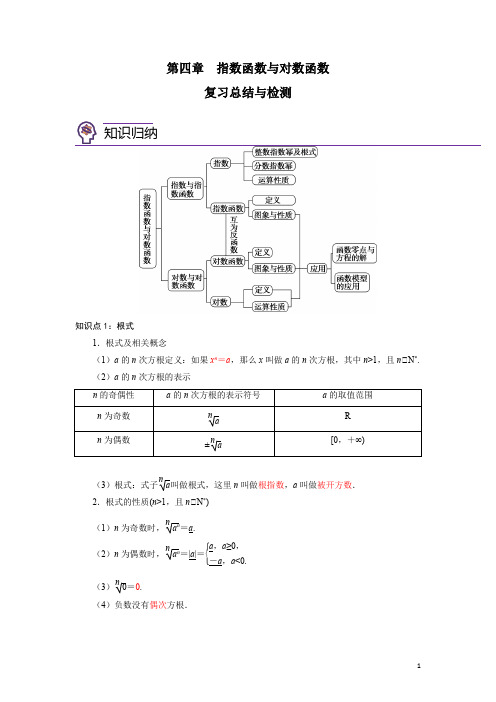
第四章指数函数与对数函数复习总结与检测知识点1:根式1.根式及相关概念(1)a的n次方根定义:如果x n=a,那么x叫做a的n次方根,其中n>1,且n∈N*.(2)a的n次方根的表示n的奇偶性a的n次方根的表示符号a的取值范围n为奇数na Rn为偶数±na[0,+∞)(3)根式:式子na叫做根式,这里n叫做根指数,a叫做被开方数.2.根式的性质(n>1,且n∈N*)(1)n为奇数时,na n=a.(2)n为偶数时,na n=|a|=⎩⎪⎨⎪⎧a,a≥0,-a,a<0.(3)n0=0.(4)负数没有偶次方根.知识归纳知识点2:指数幂及运算1.分数指数幂的意义分数指数幂正分数指数幂规定:n ma=n a m(a>0,m,n∈N*,且n>1)负分数指数幂规定:nma =1amn=1na m(a>0,m,n∈N*,且n>1) 0的分数指数幂0的正分数指数幂等于0,0的负分数指数幂没有意义2.有理数指数幂的运算性质(1)a r a s=a r+s(a>0,r,s∈Q).(2)(a r)s=a rs(a>0,r,s∈Q).(3)(ab)r=a r b r(a>0,b>0,r∈Q).3.无理数指数幂一般地,无理数指数幂aα(a>0,α是无理数)是一个确定的实数.有理数指数幂的运算性质同样适用于无理数指数幂.知识点3:指数函数的概念、图象与性质1.指数函数的概念一般地,函数y=a x(a>0,且a≠1)叫做指数函数,其中x是自变量,函数的定义域是R.2.指数函数的图象和性质a的范围a>10<a<1图象性质定义域R值域(0,+∞)过定点(0,1),即当x=0时,y=1单调性在R上是增函数在R上是减函数奇偶性非奇非偶函数对称性函数y=a x与y=a-x的图象关于y轴对称知识点4:对数的概念1.对数(1)指数式与对数式的互化及有关概念:(2)底数a 的范围是a >0,且a ≠1. 2.常用对数与自然对数3.对数的基本性质 (1)负数和零没有对数. (2)log a 1=0(a >0,且a ≠1). (3)log a a =1(a >0,且a ≠1). 知识点5:对数的运算1.对数的运算性质如果a >0,且a ≠1,M >0,N >0,那么: (1)log a (MN )=log a M +log a N ; (2)log a MN =log a M -log a N ;(3)log a M n =n log a M (n ∈R ). 2.对数的换底公式若a >0且a ≠1;c >0且c ≠1;b >0,则有log a b =log c blog c a .知识点6:对数函数的概念、图象及性质1.对数函数的概念函数y =log a x (a >0,且a ≠1)叫做对数函数,其中x 是自变量,函数的定义域是(0,+∞). 2.对数函数的图象及性质(0,+∞)3.反函数指数函数y =a x (a >0,且a ≠1)与对数函数y =log a x (a >0且a ≠1)互为反函数.知识点7:三种函数模型的性质知识点8:函数的零点与方程的解1.函数的零点对于函数y=f(x),把使f(x)=0的实数x叫做函数y=f(x)的零点.2.方程、函数、函数图象之间的关系方程f(x)=0有实数根∈函数y=f(x)的图象与x轴有交点∈函数y=f(x)有零点.3.函数零点存在定理如果函数y=f(x)在区间[a,b]上的图象是一条连续不断的曲线,且有f(a)f(b)<0,那么,函数y=f(x)在区间(a,b)内至少有一个零点,即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的解.知识点9:用二分法求方程的近似解1.二分法的定义对于在区间[a,b]上图象连续不断且f(a)·f(b)<0的函数y=f(x),通过不断地把它的零点所在的区间一分为二,使所得区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法.2.二分法求函数零点近似值的步骤(1)确定零点x0的初始区间[a,b],验证f(a)f(b)<0.(2)求区间(a,b)的中点c.(3)计算f(c),并进一步确定零点所在的区间:∈ 若f(c)=0(此时x0=c),则c就是函数的零点;∈ 若f(a)f(c)<0(此时x0∈(a,c)),则令b=c;∈ 若f(c)f(b)<0(此时x0∈(c,b)),则令a=c.(4)判断是否达到精确度ε:若|a-b|<ε,则得到零点近似值a(或b);否则重复步骤(2)~(4).知识点10:函数模型的应用1.常用函数模型常用函数模型(1)一次函数模型y=kx+b(k,b为常数,k≠0)(2)二次函数模型y=ax2+bx+c(a,b,c为常数,a≠0)(3)指数函数模型y=ba x+c(a,b,c为常数,b≠0,a>0且a≠1)(4)对数函数模型y=m log a x+n(m,a,n为常数,m≠0,a>0且a≠1)(5)幂函数模型y=ax n+b(a,b为常数,a≠0)(6)分段函数模型y=⎩⎪⎨⎪⎧ax+b(x<m),cx+d(x≥m)2.建立函数模型解决问题的基本过程题型1:指数与对数的运算【例1】计算:(1)2log32-log3329+log38-5log53;(2)1.5-⎪⎭⎫⎝⎛-⨯67310+80.25×42+(32×3)6-⎝⎛⎭⎫-2323.【解析】(1)原式=log322×8329-3=2-3=-1.(2)原式=⎝⎛⎭⎫2313+234×214+22×33-⎝⎛⎭⎫2313=21+4×27=110.【方法技巧】题型讲解指数、对数的运算应遵循的原则指数式的运算首先注意化简顺序,一般负指数先转化成正指数,根式化为分数指数幂运算,其次若出现分式则要注意分子、分母因式分解以达到约分的目的.对数运算首先注意公式应用过程中范围的变化,前后要等价,熟练地运用对数的三个运算性质并结合对数恒等式,换底公式是对数计算、化简、证明常用的技巧.【针对训练】1.设3x =4y =36,则2x +1y 的值为( )A .6B .3C .2D .1【解析】D 由3x =4y =36得x =log 336,y =log 436, ∈2x +1y =2log 363+log 364=log 369+log 364=log 3636=1.题型2:指数函数、对数函数的图象及应用【例2】(1)若函数y =log a x (a >0,且a ≠1)的图象如图所示,则下列函数正确的是( )A B C D(2)已知函数f (x )是定义在R 上的偶函数,当x ≥0时,f (x )=x⎪⎭⎫ ⎝⎛21∈ 如图,画出函数f (x )的图象;∈ 根据图象写出f (x )的单调区间,并写出函数的值域.【解析】(1)B 由已知函数图象可得,log a 3=1,所以a =3.A 项,函数解析式为y =3-x,在R 上单调递减,与图象不符;C 项中函数的解析式为y =(-x )3=-x 3,当x >0时,y <0,这与图象不符;D 项中函数解析式为y =log 3(-x ),在(-∞,0)上为单调递减函数,与图象不符;B 项中对应函数解析式为y =x 3,与图象相符.故选B.](2)[解] ∈先作出当x ≥0时,f (x )=⎝⎛⎭⎫12x的图象,利用偶函数的图象关于y 轴对称,再作出f (x )在x ∈(-∞,0)时的图象.∈函数f (x )的单调递增区间为(-∞,0),单调递减区间为[0,+∞),值域为(0,1]. 【方法技巧】1.识别函数的图象从以下几个方面入手: (1)单调性:函数图象的变化趋势; (2)奇偶性:函数图象的对称性; (3)特殊点对应的函数值.2.指数函数与对数函数图象经过定点的实质是a 0=1,log a 1=0.【针对训练】2.函数y =1+log 12(x -1)的图象一定经过点( )A .(1,1)B .(1,0)C .(2,1)D .(2,0)【解析】C 把y =log 12x 的图象向右平移1个单位,再向上平移1个单位即可得到y =1+log 12(x -1)的图象,故其经过点(2,1).题型3:比较大小【例3】 若0<x <y <1,则( )A .3y <3xB .log x 3<log y 3C .log 4x <log 4y D.yx ⎪⎭⎫⎝⎛<⎪⎭⎫ ⎝⎛4141【解析】C 因为0<x <y <1,则对于A ,函数y =3x 在R 上单调递增,故3x <3y ,A 错误.对于B ,根据底数a 对对数函数y =log a x 的影响:当0<a <1时,在x ∈(1,+∞)上“底小图高”.因为0<x <y <1,所以log x 3>log y 3,B 错误.对于C ,函数y =log 4x 在(0,+∞)上单调递增,故log 4x <log 4y ,C 正确.对于D ,函数y =⎝⎛⎭⎫14x在R 上单调递减,故⎝⎛⎭⎫14x>⎝⎛⎭⎫14y,D 错误.【方法技巧】1.比较两数大小常用的方法有单调性法、图象法、中间值法等.2.当两个数都是指数幂或对数式时,可将其看成某个指数函数、对数函数或幂函数的函数值,然后利用该函数的单调性比较.3.比较多个数的大小时,先利用“0”“1”作为分界点,然后在各部分内再利用函数性质比较大小.4.含参数的问题,要根据参数的取值进行分类讨论. 【针对训练】3.设a =log 2π,b =log 12π,c =π-2,则( )A .a >b >cB .b >a >cC .a >c >bD .c >b >a【解析】C ∈a =log 2π>log 22=1,b =log 12π<log 121=0,c =π-2=1π2,即0<c <1,∈a >c >b ,故选C.题型4:指数函数、对数函数的性质【例4】(1)设函数f (x )=ln(1+x )-ln(1-x ),则f (x )是( )A .奇函数,且在(0,1)上是增函数B .奇函数,且在(0,1)上是减函数C .偶函数,且在(0,1)上是增函数D .偶函数,且在(0,1)上是减函数 (2)已知a >0,a ≠1且log a 3>log a 2,若函数f (x )=log a x 在区间[a,3a ]上的最大值与最小值之差为1.∈ 求a 的值;∈ 若1≤x ≤3,求函数y =(log a x )2-log a x +2的值域.【解析】(1)A [由题意可得,函数f (x )的定义域为(-1,1),且f (-x )=ln(1-x )-ln(1+x )=-f (x ),故f (x )为奇函数.又f (x )=ln 1+x 1-x =ln ⎝⎛⎭⎫21-x -1,易知y =21-x -1在(0,1)上为增函数,故f (x )在(0,1)上为增函数.](2)[解] ∈因为log a 3>log a 2,所以f (x )=log a x 在[a,3a ]上为增函数. 又f (x )在[a,3a ]上的最大值与最小值之差为1, 所以log a (3a )-log a a =1,即log a 3=1,所以a =3. ∈函数y =(log 3x )2-log 3x +2=(log 3x )2-12log 3x +2=⎝⎛⎭⎫log 3x -142+3116. 令t =log 3x ,因为1≤x ≤3, 所以0≤log 3x ≤1,即0≤t ≤1.所以y =⎝⎛⎭⎫t -142+3116∈⎣⎡⎦⎤3116,52, 所以所求函数的值域为⎣⎡⎦⎤3116,52.【方法技巧】1.研究函数的性质要树立定义域优先的原则.2.换元法的作用是利用整体代换,将问题转化为常见问题.该类问题中,常设u =log a x 或u =a x ,转化为一元二次方程、二次函数等问题.要注意换元后u 的取值范围.题型5:函数的应用【例5】 一种放射性元素,最初的质量为500 g ,按每年10%衰减. (1)求t 年后,这种放射性元素的质量w 的表达式;(2)由求出的函数表达式,求这种放射性元素的半衰期(结果精确到0.1). 【解析】 (1)最初的质量为500 g. 经过1年,w =500(1-10%)=500×0.9; 经过2年,w =500×0.92; 由此推知,t 年后,w =500×0.9t . (2)由题意得500×0.9t =250,即0.9t =0.5,两边同时取以10为底的对数,得 lg 0.9t =lg 0.5,即t lg 0.9=lg 0.5,所以t =lg 0.5lg 0.9≈6.6.即这种放射性元素的半衰期约为6.6年. 【方法技巧】指数函数模型的应用在实际问题中,有关人口增长、银行利率、细胞分裂等增长率问题常可以用指数函数模型表示.通常可以表示为y =N (1+p )x (其中N 为基础数,p 为增长率,x 为时间)的形式.【针对训练】4.某化工厂生产一种溶液,按市场要求,杂质含量不能超过0.1%,若初时含杂质2%,每过滤一次可使杂质含量减少13,问至少应过滤几次才能使产品达到市场要求?(已知:lg2≈0.301 0,lg 3≈0.477 1)【解析】 设过滤n 次能使产品达到市场要求,依题意,得2100×⎝⎛⎭⎫23n≤11 000,即⎝⎛⎭⎫23n≤120. 则n (lg 2-lg 3)≤-(1+lg 2), 故n ≥1+lg 2lg 3-lg 2≈7.4,考虑到n ∈N ,故n ≥8,即至少要过滤8次才能达到市场要求.指数函数与对数函数(时间:120分钟 满分:150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.若a <12,则化简4(2a -1)2的结果是( )A.2a -1 B .-2a -1 C.1-2aD .-1-2a【解析】C ∈a <12,∈2a -1<0.于是,原式=4(1-2a )2=1-2a . 2.计算:log 225·log 522=( ) A .3 B .4 C .5D .6 章节检测【解析】A log 225·log 522=lg 25lg 2·lg 22lg 5=2lg 5·lg 232lg 2·lg 5=2×32=3.3.函数y =x -1·ln(2-x )的定义域为( ) A .(1,2) B .[1,2) C .(1,2]D .[1,2]【解析】B 要使解析式有意义,则⎩⎪⎨⎪⎧x -1≥0,2-x >0,解得1≤x <2,所以所求函数的定义域为[1,2).4.下列幂函数中过点(0,0),(1,1)的偶函数是( ) A .y =x 12 B .y =x 4 C .y =x -2D .y =31x【解析】B 对A ,y =x 12的定义域为[0,+∞),不是偶函数;C 中,y =x -2不过(0,0)点,D 中,y =31x 是奇函数,B 中,y =x 4满足条件.5.函数f (x )=21x -x⎪⎭⎫⎝⎛21的零点个数为( )A .0B .1C .2D .3【解析】B 令f (x )=0,可得x 12=⎝⎛⎭⎫12x,在同一平面直角坐标系中分别画出幂函数y =x 12和指数函数y =⎝⎛⎭⎫12x的图象,如图所示,可得交点只有一个,所以函数f (x )的零点只有一个.6.若log a 3=m ,log a 5=n ,则a 2m +n的值是( ) A .15 B .75 C .45D .225【解析】C 由log a 3=m ,得a m =3, 由log a 5=n ,得a n =5, ∈a 2m +n =(a m )2·a n =32×5=45.7.函数f (x )=4x +12x 的图象( )A .关于原点对称B .关于直线y =x 对称C .关于x 轴对称D .关于y 轴对称【解析】D 易知f (x )的定义域为R ,关于原点对称.∈f (-x )=4-x +12-x =1+4x2x =f (x ),∈f (x )是偶函数,其图象关于y 轴对称.8.若log a (a 2+1)<log a 2a <0,则a 的取值范围是( ) A .(0,1)B.⎪⎭⎫ ⎝⎛210,C. ⎪⎭⎫⎝⎛1,21 D .(0,1)∈(1,+∞)【解析】C 由题意得a >0且a ≠1,故必有a 2+1>2a . 又log a (a 2+1)<log a 2a <0,所以0<a <1, 同时2a >1,∈a >12,综上,a ∈⎝⎛⎭⎫12,1. 9.已知a =5log 23.4,b =5log 43.6,c =⎝⎛⎭⎫15log 30.3,则( ) A .a >b >c B .b >a >c C .a >c >bD .c >a >b【解析】C c =5log 3103,只需比较log 23.4,log 43.6,log 3103的大小,又0<log 43.6<1,log 23.4>log 33.4>log 3103>1,所以a >c >b .10.函数f (x )=a |x +1|(a >0,且a ≠1)的值域为[1,+∞),则f (-4)与f (1)的关系是( ) A .f (-4)=f (1) B .f (-4)>f (1) C .f (-4)<f (1)D .不能确定【解析】B 因为函数f (x )=a |x +1|(a >0,且a ≠1)的值域为[1,+∞),所以a >1,又函数f (x )=a |x +1|(a >0,且a ≠1)的图象关于直线x =-1对称,所以f (-4)>f (1).11.已知函数f (x )=⎩⎪⎨⎪⎧(a -2)x ,x ≥2,⎝⎛⎭⎫12x -1,x <2满足对任意的实数x 1≠x 2都有f (x 1)-f (x 2)x 1-x 2<0成立,则实数a 的取值范围为( )A .(-∞,2) B.⎝⎛⎦⎤-∞,138 C .(-∞,2]D.⎣⎡⎭⎫138,2【解析】B [由题意知函数f (x )是R 上的减函数,于是有⎩⎪⎨⎪⎧a -2<0,(a -2)×2≤⎝⎛⎭⎫122-1,由此解得a ≤138,即实数a 的取值范围是⎝⎛⎦⎤-∞,138,选B. 12.函数f (x )=ax 5-bx +1,若f (lg(log 510))=5,则f (lg(lg 5))的值为( ) A .-3 B .5 C .-5D .-9【解析】A lg(log 510)=lg ⎝⎛⎭⎫1lg 5=-lg(lg 5), 设t =lg(lg 5),则f (lg(log 510))=f (-t )=5. 因为f (x )=ax 5-bx +1, 所以f (-t )=-at 5+bt +1=5, 则f (t )=at 5-bt +1, 两式相加得f (t )+5=2,则f (t )=2-5=-3,即f (lg(lg 5)的值为-3.二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上) 13.函数f (x )=a x -1+3的图象一定过定点P ,则P 点的坐标是________.【解析】(1,4) 由于函数y =a x 恒过(0,1),而y =a x -1+3的图象可看作由y =a x 的图象向右平移1个单位,再向上平移3个单位得到的,则P 点坐标为(1,4).14.将进货单价为8元的商品按10元一个销售,每天可卖出100个.若每个涨价1元,则日销售量减少10个.为获得最大利润,则此商品日销售价应定为每个________元.【解析】14 设每个涨价x 元,则实际销售价为10+x 元,销售的个数为100-10x , 则利润为y =(10+x )(100-10x )-8(100-10x )=-10(x -4)2+360(0≤x <10,x ∈N ).因此,当x =4,即售价定为每个14元时,利润最大.15.若f (x )=a ·2x +2a -12x +1为R 上的奇函数,则实数a 的值为________.【解析】13 因为f (x )=a ·2x +2a -12x +1为R 上的奇函数,所以f (0)=0,即a ·20+2a -120+1=0,所以a =13.16.已知125x =12.5y =1 000,则y -xxy=________.【解析】13 因为125x =12.5y =1 000,所以x =log 125 1 000,y =log 12.5 1 000,y -x xy =1x -1y =log 1 000 125-log 1 000 12.5=log 1 00012512.5=log 1 000 10=13.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤) 17.(本小题满分10分)求值: (1)⎝⎛⎭⎫21412-(-9.6)0-⎝⎛⎭⎫338-23+(1.5)-2; (2)log 2512·log 45-log 133-log 24+5log 52.【解析】(1)⎝⎛⎭⎫21412-(-9.6)0-⎝⎛⎭⎫338-23+(1.5)-2 =⎝⎛⎭⎫9412-1-⎝⎛⎭⎫278-23+⎝⎛⎭⎫32-2=32-1-⎝⎛⎭⎫32-2+⎝⎛⎭⎫232=32-1-49+49=12. (2)log 2512·log 45-log 133-log 24+5log 52=-14+1-2+2=34.18.(本小题满分12分)已知指数函数f (x )=a x (a >0,且a ≠1)过点(-2,9). (1)求函数f (x )的解析式;(2)若f (2m -1)-f (m +3)<0,求实数m 的取值范围.【解析】(1)将点(-2,9)代入f (x )=a x (a >0,a ≠1)得a -2=9,解得a =13,∈f (x )=⎝⎛⎭⎫13x . (2)∈f (2m -1)-f (m +3)<0, ∈f (2m -1)<f (m +3). ∈f (x )=⎝⎛⎭⎫13x 为减函数, ∈2m -1>m +3,解得m >4, ∈实数m 的取值范围为(4,+∞).19.(本小题满分12分)已知函数f (x )=⎩⎪⎨⎪⎧log 2x ,x >0,3x ,x ≤0,且关于x 的方程f (x )+x -a =0有且只有一个实根,求实数a 的取值范围.【解析】如图,在同一坐标系中分别作出y =f (x )与y =-x +a 的图象,其中a 表示直线在y 轴上的截距,由图可知,当a >1时,直线y =-x +a 与y =log 2x 只有一个交点.所以实数a 的取值范围是(1,+∞).20.(本小题满分12分)已知1≤x ≤4,求函数f (x )=log 2x 4·log 2x2的最大值与最小值.【解析】 ∈f (x )=log 2x 4·log 2x2=(log 2x -2)(log 2x -1) =⎝⎛⎭⎫log 2x -322-14, 又∈1≤x ≤4,∈0≤log 2x ≤2,∈当log 2x =32,即x =232=22时,f (x )有最小值-14.当log 2x =0时,f (x )有最大值2,此时x =1. 即函数f (x )的最大值是2,最小值是-14.21.(本小题满分12分)某公司制定了一个激励销售人员的奖励方案:当销售利润不超过15万元时,按销售利润的10%进行奖励;当销售利润超过15万元时,若超过部分为A 万元,则超出部分按2log 5(A +1)进行奖励,没超出部分仍按销售利润的10%进行奖励.记奖金总额为y (单位:万元),销售利润为x (单位:万元).(1)写出该公司激励销售人员的奖励方案的函数表达式;(2)如果业务员老张获得5.5万元的奖金,那么他的销售利润是多少万元? 【解析】(1)由题意,得y =⎩⎪⎨⎪⎧0.1x ,0<x ≤15,1.5+2log 5x -14,x >15.(2)∈当x ∈(0,15]时,0.1x ≤1.5, 又y =5.5>1.5,∈x >15, ∈1.5+2log 5(x -14)=5.5, 解得x =39.答:老张的销售利润是39万元. 22.(本小题满分12分)已知函数f (x )=lg ⎝ ⎛⎭⎪⎫1-x 1+x .(1)求证:f (x )是奇函数; (2)求证:f (x )+f (y )=f ⎝ ⎛⎭⎪⎫x +y 1+xy ;(3)若f ⎝⎛⎭⎪⎫a +b 1+ab =1,f ⎝ ⎛⎭⎪⎫a -b 1-ab =2,求f (a ),f (b )的值.【解析】(1)证明:由函数f (x )=lg ⎝⎛⎭⎪⎫1-x 1+x ,可得1-x 1+x >0,即x -11+x <0,解得-1<x <1,故函数的定义域为(-1,1),关于原点对称.再根据f (-x )=lg 1+x 1-x =-lg 1-x1+x=-f (x ),可得f (x )是奇函数.(2)证明:f (x )+f (y )=lg 1-x 1+x +lg 1-y 1+y =lg (1-x )(1-y )(1+x )(1+y ),而f ⎝ ⎛⎭⎪⎫x +y 1+xy =lg1-x +y 1+xy 1+x +y 1+xy =lg1+xy -x -y 1+xy +x +y =lg (1-x )(1-y )(1+x )(1+y ),∈f (x )+f (y )=f ⎝ ⎛⎭⎪⎫x +y 1+xy 成立.(3)若f ⎝⎛⎭⎪⎫a +b 1+ab =1,f ⎝ ⎛⎭⎪⎫a -b 1-ab =2,则由(2)可得f (a )+f (b )=1,f (a )-f (b )=2, 解得f (a )=32,f (b )=-12.。
高数(上)重要内容总结复习笔记
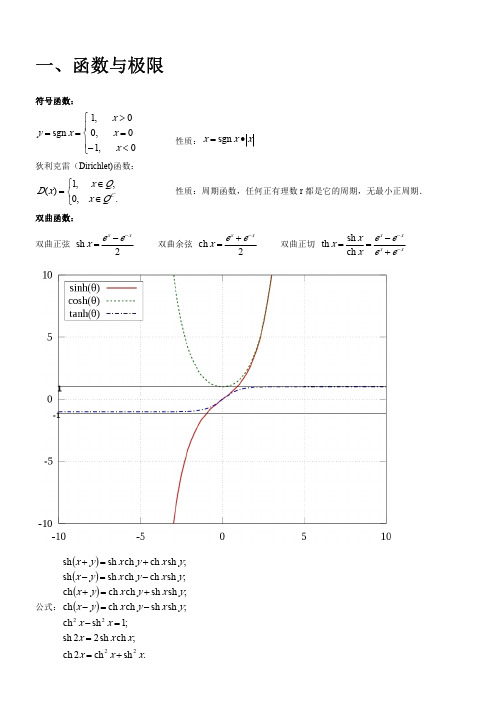
A−a 叫做 a 的相对误差 a
如果 A − a ≤ δ A ,那么 δ A 叫做测量A的绝对误差限,而
δA 叫做测量A的相对误差限. a
(3) lim
f ′( x) f ( x) f ′( x) 存在(或为无穷大) ,那么 lim . = lim x → ∞ F ′( x ) x →∞ F ( x ) x →∞ F ′( x )
如果函数 f ( x) 在含有 x0 的某个开区间 (a, b) 内具有直到(n+1)阶的倒数,则对任一
泰勒(Taylor)中值定理
高阶导数:
(cot x)′ = − csc 2 x (a x )′ = a x ln a (arccos x)′ = − 1 1 − x2
(arcsin x)′ =
1
(sec x)′ = sec x tan x 1 (log a x)′ = x ln a 1 (arctan x)′ = 1+ x2
1 (ch x)′ = sh x (th x)′ = 2 ch x 1 (arch x)′ = 1 x 2 − 1 (arth x)′ = 1 − x2
f ′′(0) f ( n ) (0) f ( n+1) (θx) n +1 x +…+ x+ x 2! n! (n + 1)!
(0 < θ < 1)
另带有佩亚诺余项的麦克劳林公式从略. 定义
x1 + x2 f ( x1 ) + f ( x2 ) )< ,那么称 f ( x) 在 2 2 x +x f ( x1 ) + f ( x2 ) I 上的图形是(向上)凹的(或凹弧);如果恒有 f ( 1 2 ) > ,那么称 f ( x) 在 I 上的图形是(向上) 2 2
高一函数小结(教师版)

(1) 当 y 2 0 即 y 0 时
x R 0
即: 4 y 2 4 y 2 3 y 7 0
2
9 解得 y 2 2
(2) 当 y 2 0 即 y 2 时 有 6 7 0 (舍去) 9 y 2 2
高一数学
函数总结
教师:谢焕钢
第二讲:函数的三性质 1、函数的单调性 定义: 一般地, 设函数 y=f(x)的定义域为 A, 区间 I A , 如果对于区间 I 上的任意的两个值 x1 , x2 , 当 x1 x2 时,都有
f ( x1 ) f ( x2 ) ,那么就说 y f ( x) 在区间 I 上是单调增函数, I 称为 f ( x) 的单
2
点为 k , h ) ;两根式: f ( x) a x x1 x x2 ,其中 x1 , x2 为使 f(x)=0 成立的两根;一般式:
f ( x) ax 2 bx c ;
反比例函数可设成: f ( x)
k ) x
例:已知 f ( x) 为一次函数, f ( f ( x)) 4 x 3 求 f ( x) 的函数解析式。 (注:这里不仅要利用到待定 系数法,也要用到直接代入法) 解:令 f ( x) ax b 则 f ( f ( x)) a ax b b a 2 x ab b 4 x 3
练习:函数 A 到 B 的函数 f ( x ) : x 2 x 1 集合 A 1, 2,3 , B 0,1, 2,3, 4,5,6 求 f ( x) 的值域。 B、配方法:求二次函数的值域(通常和函数图像一起来求解)
2 ) , 例如:已知函数 y x 2 2 x 3 分别求出下列区间上的值域, (1)x R , (2) 、x [2 ] 3 ,1 [ (3) 、x
中考数学复习----《反比例函数之综合应用》知识点总结与练习题(含答案解析)

中考数学复习----《反比例函数之综合应用》知识点总结与练习题(含答案解析)知识点总结1. 反比例函数k 的集合意义:①过反比例函数图像上任意一点作坐标轴的垂线,两垂线与坐标轴构成一个矩形,矩形的面积等于k 。
②过反比例函数图像上任意一点作其中一条坐标轴的垂线,并连接这个点与原点,则构成一个三角形。
这个三角形的面积等于2k 。
2. 待定系数法求反比例函数解析式:在反比例函数中只有一个系数k ,所以只需要在图像上找一个对应的点即可求出k 的值,从而求出反比例函数解析式。
3. 反比例函数与一次函数的不等式问题: 若反比例函数()0≠=k x ky 与一次函数()0≠+=k b kx y 有交点,则不等式b kx xk +>的解集取反比例函数图像在一次函数图像上方的部分所对应的自变量取值范围;等式b kx xk+<的解集取反比例函数图像在一次函数图像下方的部分所对应的自变量取值范围。
反比例函数与一次函数的交点把自变量分成三部分。
练习题1、(2022•日照)如图,矩形OABC 与反比例函数y 1=xk1(k 1是非零常数,x >0)的图像交于点M ,N ,与反比例函数y 2=xk2(k 2是非零常数,x >0)的图像交于点B ,连接OM ,ON .若四边形OMBN 的面积为3,则k 1﹣k 2=( )A .3B .﹣3C .23 D .﹣23【分析】根据矩形的性质以及反比例函数系数k 的几何意义即可得出结论. 【解答】解:∵y 1、y 2的图像均在第一象限, ∴k 1>0,k 2>0,∵点M 、N 均在反比例函数y 1=(k 1是非零常数,x >0)的图像上,∴S △OAM =S △OCN =k 1,∵矩形OABC 的顶点B 在反比例函数y 2=(k 2是非零常数,x >0)的图像上,∴S 矩形OABC =k 2,∴S 四边形OMBN =S 矩形OABC ﹣S △OAM ﹣S △OCN =3, ∴k 2﹣k 1=3, ∴k 1﹣k 2=﹣3, 故选:B .2、(2022•牡丹江)如图,等边三角形OAB ,点B 在x 轴正半轴上,S △OAB =43,若反比例函数y =xk(k ≠0)图像的一支经过点A ,则k 的值是( )A .233 B .23C .433 D .43【分析】根据正三角形的性质以及反比例函数系数k 的几何意义,得出S △AOC =S △AOB =2=|k |,即可求出k 的值.【解答】解:如图,过点A 作AC ⊥OB 于点C , ∵△OAB 是正三角形, ∴OC =BC ,∴S △AOC =S △AOB =2=|k |,又∵k >0, ∴k =4,故选:D .3、(2022•郴州)如图,在函数y =x2(x >0)的图像上任取一点A ,过点A 作y 轴的垂线交函数y =﹣x8(x <0)的图像于点B ,连接OA ,OB ,则△AOB 的面积是( )A .3B .5C .6D .10【分析】根据反比例函数系数k 的几何意义进行计算即可. 【解答】解:∵点A 在函数y =(x >0)的图像上, ∴S △AOC =×2=1,又∵点B 在反比例函数y =﹣(x <0)的图像上, ∴S △BOC =×8=4, ∴S △AOB =S △AOC +S △BOC =1+4 =5, 故选:B .4、(2022•黑龙江)如图,在平面直角坐标系中,点O 为坐标原点,平行四边形OBAD 的顶点B 在反比例函数y =x 3的图像上,顶点A 在反比例函数y =xk的图像上,顶点D 在x 轴的负半轴上.若平行四边形OBAD 的面积是5,则k 的值是( )A .2B .1C .﹣1D .﹣2【分析】设B (a ,),根据四边形OBAD 是平行四边形,推出AB ∥DO ,表示出A 点的坐标,求出AB =a ﹣,再根据平行四边形面积公式列方程,解出即可.【解答】解:设B (a ,), ∵四边形OBAD 是平行四边形, ∴AB ∥DO , ∴A (,),∴AB =a ﹣,∵平行四边形OBAD 的面积是5, ∴(a ﹣)=5,解得k =﹣2, 故选:D .5、(2022•十堰)如图,正方形ABCD 的顶点分别在反比例函数y =xk 1(k 1>0)和y =xk 2(k 2>0)的图像上.若BD ∥y 轴,点D 的横坐标为3,则k 1+k 2=( )A .36B .18C .12D .9【分析】连接AC交BD于E,延长BD交x轴于F,连接OD、OB,设AE=BE=CE=DE =m,D(3,a),根据BD∥y轴,可得B(3,a+2m),A(3+m,a+m),即知k1=3(a+2m)=(3+m)(a+m),从而m=3﹣a,B(3,6﹣a),由B(3,6﹣a)在反比例函数y=(k1>0)的图像上,D(3,a)在y=(k2>0)的图像上,得k1=3(6﹣a)=18﹣3a,k2=3a,即得k1+k2=18﹣3a+3a=18.【解答】解:连接AC交BD于E,延长BD交x轴于F,连接OD、OB,如图:∵四边形ABCD是正方形,∴AE=BE=CE=DE,设AE=BE=CE=DE=m,D(3,a),∵BD∥y轴,∴B(3,a+2m),A(3+m,a+m),∵A,B都在反比例函数y=(k1>0)的图像上,∴k1=3(a+2m)=(3+m)(a+m),∵m≠0,∴m=3﹣a,∴B(3,6﹣a),∵B(3,6﹣a)在反比例函数y=(k1>0)的图像上,D(3,a)在y=(k2>0)的图像上,∴k1=3(6﹣a)=18﹣3a,k2=3a,∴k1+k2=18﹣3a+3a=18;故选:B .6、(2022•邵阳)如图是反比例函数y =x1的图像,点A (x ,y )是反比例函数图像上任意一点,过点A 作AB ⊥x 轴于点B ,连接OA ,则△AOB 的面积是( )A .1B .C .2D .【分析】由反比例函数的几何意义可知,k =1,也就是△AOB 的面积的2倍是1,求出△AOB 的面积是.【解答】解:∵A (x ,y ), ∴OB =x ,AB =y ,∵A 为反比例函数y =图像上一点, ∴xy =1,∴S △ABO =AB •OB =xy =1=,故选:B .7、(2022•内江)如图,在平面直角坐标系中,点M 为x 轴正半轴上一点,过点M 的直线l ∥y 轴,且直线l 分别与反比例函数y =x 8和y =xk的图像交于P 、Q 两点.若S △POQ =15,则k 的值为( )A .38B .22C .﹣7D .﹣22【分析】利用k 的几何意义解题即可. 【解答】解:∵直线l ∥y 轴, ∴∠OMP =∠OMQ =90°,∴S △OMP =×8=4,S △OMQ =﹣k . 又S △POQ =15, ∴4﹣k =15, 即k =11,∴k =﹣22. 故选:D .8、(2022•东营)如图,△OAB 是等腰直角三角形,直角顶点与坐标原点重合,若点B 在反比例函数y =x1(x >0)的图像上,则经过点A 的函数图像表达式为 .【分析】作AD ⊥x 轴于D ,BC ⊥x 轴于C ,根据△OAB 是等腰直角三角形,可证明△BOC ≌△OAD ,利用反比例函数k 的几何意义得到S △OBC =,则S △OAD =,所以|k |=,然后求出k 得到经过点A 的反比例函数解析式. 【解答】解:如图,作AD ⊥x 轴于D ,BC ⊥x 轴于C , ∴∠ADO =∠BCO =90°,∵∠AOB =90°, ∴∠AOD +∠BOC =90°, ∴∠AOD +∠DAO =90°, ∴∠BOC =∠DAO , ∵OB =OA ,∴△BOC ≌△OAD (AAS ),∵点B 在反比例函数y =(x >0)的图像上, ∴S △OBC =, ∴S △OAD =, ∴k =﹣1,∴经过点A 的反比例函数解析式为y =﹣. 故答案为:y =﹣.9、(2022•盐城)已知反比例函数的图像经过点(2,3),则该函数表达式为 . 【分析】利用反比例函数的定义列函数的解析式,运用待定系数法求出函数的解析式即可. 【解答】解:令反比例函数为y =(k ≠0), ∵反比例函数的图像经过点(2,3), ∴3=, k =6,∴反比例函数的解析式为y =. 故答案为:y =.10、(2022•湖北)在反比例函数y =xk 1−的图像的每一支上,y 都随x 的增大而减小,且整式x 2﹣kx +4是一个完全平方式,则该反比例函数的解析式为 . 【分析】由整式x 2﹣kx +4是一个完全平方式,可得k =±4,由反比例函y =的图像的每一支上,y 都随x 的增大而减小,可得k ﹣1>0,解得k >1,则k =4,即可得反比例函数的解析式.【解答】解:∵整式x 2﹣kx +4是一个完全平方式,∴k =±4, ∵反比例函数y =的图像的每一支上,y 都随x 的增大而减小,∴k ﹣1>0, 解得k >1, ∴k =4,∴反比例函数的解析式为y =. 故答案为:y =.35.(2022•陕西)已知点A (﹣2,m )在一个反比例函数的图像上,点A '与点A 关于y 轴对称.若点A '在正比例函数y =21x 的图像上,则这个反比例函数的表达式为 .【分析】根据轴对称的性质得出点A '(2,m ),代入y =x 求得m =1,由点A (﹣2,1)在一个反比例函数的图像上,从而求得反比例函数的解析式. 【解答】解:∵点A '与点A 关于y 轴对称,点A (﹣2,m ), ∴点A '(2,m ),∵点A '在正比例函数y =x 的图像上, ∴m ==1,∴A (﹣2,1),∵点A (﹣2,1)在一个反比例函数的图像上, ∴反比例函数的表达式为y =﹣, 故答案为:y =﹣.11、(2022•攀枝花)如图,正比例函数y =k 1x 与反比例函数y =xk 2的图像交于A (1,m )、B 两点,当k 1x ≤xk2时,x 的取值范围是( )A .﹣1≤x <0或x ≥1B .x ≤﹣1或0<x ≤1C .x ≤﹣1或x ≥1D .﹣1≤x <0或0<x ≤1【分析】根据反比例函数的对称性求得B 点的坐标,然后根据图像即可求得. 【解答】解:∵正比例函数y =k 1x 与反比例函数y =的图像交于A (1,m )、B 两点,∴B (﹣1,﹣m ), 由图像可知,当k 1x ≤时,x 的取值范围是﹣1≤x <0或x ≥1,故选:A .37.(2022•东营)如图,一次函数y 1=k 1x +b 与反比例函数y 2=xk 2的图像相交于A ,B 两点,点A 的横坐标为2,点B 的横坐标为﹣1,则不等式k 1x +b <xk2的解集是( )A .﹣1<x <0或x >2B .x <﹣1或0<x <2C .x <﹣1或x >2D .﹣1<x <2【分析】根据两函数图像的上下位置关系结合交点横坐标,即可得出不等式k 1x +b <的解集,此题得解.【解答】解:观察函数图像可知,当﹣1<x <0或x >2时,一次函数y 1=k 1x +b 的图像在反比例函数y 2=的图像的下方,∴不等式k 1x +b <的解集为:﹣1<x <0或x >2,故选:A .12、(2022•朝阳)如图,正比例函数y =ax (a 为常数,且a ≠0)和反比例函数y =xk(k 为常数,且k ≠0)的图像相交于A (﹣2,m )和B 两点,则不等式ax >xk的解集为( )A .x <﹣2或x >2B .﹣2<x <2C .﹣2<x <0或x >2D .x <﹣2或0<x <2【分析】根据关于原点对称的点的坐标特征求得B (2,﹣m ),然后根据函数的图像的交点坐标即可得到结论.【解答】解:∵正比例函数y =ax (a 为常数,且a ≠0)和反比例函数y =(k 为常数,且k ≠0)的图像相交于A (﹣2,m )和B 两点, ∴B (2,﹣m ),∴不等式ax >的解集为x <﹣2或0<x <2, 故选:D .13、(2022•无锡)一次函数y =mx +n 的图像与反比例函数y =xm的图像交于点A 、B ,其中点A 、B 的坐标为A (﹣m1,﹣2m )、B (m ,1),则△OAB 的面积是( ) A .3B .413C .27D .415【分析】根据反比例函数图像上点的坐标特征求出m ,进而求出点A 、B 的坐标,根据三角形的面积公式计算即可.【解答】解:∵点A (﹣,﹣2m )在反比例函数y =上, ∴﹣2m =,解得:m =2,∴点A 的坐标为:(﹣,﹣4),点B 的坐标为(2,1), ∴S △OAB =××5﹣××4﹣×2×1﹣×1=,故选:D .14、(2022•荆州)如图是同一直角坐标系中函数y 1=2x 和y 2=x2的图像.观察图像可得不等式2x >x2的解集为( )A .﹣1<x <1B .x <﹣1或x >1C .x <﹣1或0<x <1D .﹣1<x <0或x >1【分析】结合图像,数形结合分析判断.【解答】解:由图像,函数y 1=2x 和y 2=的交点横坐标为﹣1,1, ∴当﹣1<x <0或x >1时,y 1>y 2,即2x >, 故选:D .15、(2022•怀化)如图,直线AB 交x 轴于点C ,交反比例函数y =xa 1−(a >1)的图像于A 、B 两点,过点B 作BD ⊥y 轴,垂足为点D ,若S △BCD =5,则a 的值为( )A.8B.9C.10D.11【分析】设点B的坐标为(m,),然后根据三角形面积公式列方程求解.【解答】解:设点B的坐标为(m,),∵S△BCD=5,且a>1,∴×m×=5,解得:a=11,故选:D.16、(2022•宁夏)在显示汽车油箱内油量的装置模拟示意图中,电压U一定时,油箱中浮子随油面下降而落下,带动滑杆使滑动变阻器滑片向上移动,从而改变电路中的电流,电流表的示数对应油量体积,把电流表刻度改为相应油量体积数,由此知道油箱里剩余油量.在不考虑其他因素的条件下,油箱中油的体积V与电路中总电阻R总(R总=R+R0)是反比例关系,电流I与R总也是反比例关系,则I与V的函数关系是()A.反比例函数B.正比例函数C.二次函数D.以上答案都不对【分析】由油箱中油的体积V与电路中总电阻R总是反比例关系,电流I与R总是反比例关系,可得V=I(为常数),即可得到答案.【解答】解:由油箱中油的体积V与电路中总电阻R总是反比例关系,设V•R总=k(k为常数),由电流I与R总是反比例关系,设I•R总=k'(k为常数),∴=,∴V=I(为常数),∴I与V的函数关系是正比例函数,故选:B.17、(2022•宜昌)已知经过闭合电路的电流I(单位:A)与电路的电阻R(单位:Ω)是反比例函数关系.根据下表判断a和b的大小关系为()A.a>b B.a≥b C.a<b D.a≤b【分析】根据等量关系“电流=”,即可求解.【解答】解:∵闭合电路的电流I(单位:A)与电路的电阻R(单位:Ω)是反比例函数关系,∴40a=80b,∴a=2b,∴a>b,故选:A.18、(2022•丽水)已知电灯电路两端的电压U为220V,通过灯泡的电流强度I(A)的最大限度不得超过0.11A.设选用灯泡的电阻为R(Ω),下列说法正确的是()A.R至少2000ΩB.R至多2000ΩC.R至少24.2ΩD.R至多24.2Ω【分析】利用已知条件列出不等式,解不等式即可得出结论.【解答】解:∵电压U一定时,电流强度I(A)与灯泡的电阻为R(Ω)成反比例,∴I=.∵已知电灯电路两端的电压U为220V,∴I=.∵通过灯泡的电流强度I(A)的最大限度不得超过0.11A,∴≤0.11,∴R≥2000.故选:A.19、(2022•郴州)科技小组为了验证某电路的电压U(V)、电流I(A)、电阻R(Ω)三者之间的关系:I=U,测得数据如下:那么,当电阻R=55Ω时,电流I=A.【分析】由表格数据求出反比例函数的解析式,再将R=55Ω代入即可求出答案.【解答】解:把R=220,I=1代入I=得:1=,解得U=220,∴I=,把R=55代入I=得:I==4,故答案为:4.20、(2022•山西)根据物理学知识,在压力不变的情况下,某物体承受的压强p(Pa)是它的受力面积S(m2)的反比例函数,其函数图像如图所示.当S=0.25m2时,该物体承受的压强p的值为Pa.【分析】设p=,把(0.1,1000)代入得到反比例函数的解析式,再把S=0.25代入解析式即可解决问题.【解答】解:设p=,∵函数图像经过(0.1,1000),∴k=100,∴p=,当S=0.25m2时,物体所受的压强p==400(Pa),故答案为:400.。
微专题抽象函数题型归纳总结

抽象函数常见题型归纳总结抽象函数是指没有给出函数的具体解析式,只给出了一些体现函数特征的式子的一类函数。
由于抽象函数表现形式的抽象性,使得这类问题成为函数内容的难点之一。
本文就抽象函数常见题型及解法评析如下:一、定义域问题(一)已知的定义域,求的定义域解法:若的定义域为,则中,从中解得的取值范围即为的定义域。
例题1:设函数的定义域为,则(1)函数的定义域为______;(2)函数的定义域为_______解析:(1)由已知有,解得,故的定义域为(2)由已知,得,解得,故的定义域为(二)已知的定义域,求的定义域。
解法:若的定义域为,则由确定的范围即为的定义域。
例题2:函数的定义域为,则的定义域为_____。
解析:由,得,所以,故填(三)已知的定义域,求的定义域。
解法:先由定义域求定义域,再由定义域求得定义域。
例题3:函数定义域是,则的定义域是_______解析:先求的定义域,的定义域是,,即的定义域是再求的定义域,,的定义域是(四) 运算型的抽象函数求由有限个抽象函数经四则运算得到的函数的定义域,解法是:先求出各个函数的定义域,再求交集。
例题4: 函数的定义域是,求的定义域。
解析:由已知,有,即函数的定义域由确定函数的定义域是【巩固1】 已知函数的定义域是[1,2],求f (x )的定义域。
解析:的定义域是[1,2],是指,所以中的满足从而函数f (x )的定义域是[1,4] 【巩固2】 已知函数的定义域是,求函数的定义域。
解析:的定义域是,意思是凡被f 作用的对象都在中,由此可得所以函数的定义域是【巩固3】f x ()定义域为(0),1,则y f x a f x a a =++-≤()()(||)12定义域是__。
解析:因为x a +及x a -均相当于f x ()中的x ,所以010111<+<<-<⎧⎨⎩⇒-<<-<<+⎧⎨⎩x a x a a x aa x a (1)当-≤≤120a 时,则x a a ∈-+(),1; (2)当012<≤a 时,则x a a ∈-(),1 一、解析式问题1. 换元法:即用中间变量表示原自变量x 的代数式,从而求出()f x ,这也是证某些公式或等式常用的方法,此法解培养学生的灵活性及变形能力。
第三章函数的概念与性质 小结与复习(第1课时) 教案-高一上学期数学人教A版必修第一册

第三章函数的概念与性质小结与复习教案第1课时一、内容和内容解析1.内容函数的概念、表示和函数单调性的复习课2. 内容解析这是在学生已经学习完本章内容的基础上进行的复习课,复习课一共两节课,这是第一节复习课.在这一章中,学生从用变量之间依赖关系描述函数上升到用集合语言和对应关系刻画函数,建立了完整的函数概念,并体会集合语言和对应关系在刻画函数概念中的作用.这是一个难点,因此在复习的过程中还要巩固.除此之外,还要了解构成函数的要素,能求简单函数的定义域,能根据实际的情况用不同的函数表示方法表示函数,了解简单的分段函数,并能简单应用.同样地,在研究函数单调性的过程中,能够使用符号化的语言来描述,这是学生学习这部分内容时的一个难点. 这样一种从形象直观到定性刻画再到定量刻画的研究过程,以及通过引入数学符号、借助代数语言精确刻画刻画定量变化规律的方法,体现了数学抽象的一般过程,对于培养学生的数学抽象能力具有重要意义.基于以上分析,确定教学重点:复习建立在集合与对应关系的函数概念以及函数单调性的符号语言刻画和单调性的应用.二、目标和目标解析1.目标(1)理解函数的概念和表示方法,并能应用函数的概念解决一些问题;(2)掌握函数单调性的概念,会用符号语言表达单调性、最值,理解它们的作用和实际意义;(3)能用定义证明简单函数的单调性;(4)能运用所学的知识解决一些数学问题和实际问题.2.目标解析达成上述目标的标志是:(1)能用集合间的对应关系的观点定义函数,能根据实际的问题表示函数;(2)知道用符号语言刻画函数单调性时,“任意”“都有”等关键词的含义;能够从函数图象,或通过代数推理,得出函数的单调递增、单调递减区间;知道函数的单调性反映了现实世界中事物在量的增加或减小上的变化趋势.(3)会用函数单调性的定义,按一定的步骤证明函数的单调性;(4)会用函数最大值、最小值的定义,按一定的步骤求函数的最大(小)值.三、教学问题诊断分析学生已经学习了相关的知识,在这节复习课上,要巩固前面学习的相关内容,让学生进一步体会用数学的语言和符号化的方式表达数学概念,表达函数的概念、函数的性质等.作为复习课,在教学的过程中也要充分利用信息技术展示函数的对应关系、函数的单调变化规律、函数的最值等,也可以用表格形式加强自变量从小到大时函数值的大小变化趋势等,数形结合地提出问题,给学生设置一条从定性到定量、从粗糙到精确的归纳过程,引导学生逐步抽象出函数单调性的定义,再通过辨析、练习帮助学生理解定义.另外,在教学的过程中,还要有一定的习题,让学生通过习题,自己体会函数的概念和函数的性质等,通过习题,体会这些概念和性质的应用,并体会一些内容的综合运用.根据以上分析,确定教学难点是:符号化的语言表述,对量词的使用和运用函数的单调性解决问题.四、教学支持条件分析为使学生更好地理解形式化定义,降低归纳定义过程中的难度,可利用计算工具,采用动态方式展现函数图象、展示变化规律等.五、教学过程设计(一)引入问题1:初中函数概念和高中函数概念的区别是什么?(1)请说出初中函数的定义;(2)请说出高中函数的定义;(3)辨析这两者有什么不同.师生活动:教师提出问题,前2个问题学生自主回答,第3个问题由学生之间讨论、分析并总结.设计意图:让学生复习函数的概念,并通过对比初中和高中的概念区别,进一步体会函数是建立在集合间的对应关系.(二)函数的概念和表示法的巩固师生活动:学生先独立思考,计算,黑板板书(或者利用信息技术将学生的书写过程展示).设计意图:让学生体会在一个熟知的二次函数中,利用单调性解决数学问题.(四)课堂小结问题11:回答下列问题(1)在解决有关函数概念的问题,以及利用函数的概念解决其他问题的时候,有什么需要特别注意的问题吗?(2)在处理函数单调性的问题时,有什么需要注意的吗?师生活动:学生先独立思考,然后讨论,发表观点,教师进行归纳.设计意图:让学生进一步体会和注意,处理有关函数问题的时候,需要注意的问题.六、目标检测设计设计意图:本题通过绘制函数图象,能够观察出(也可以严格的证明)它是一个增函数,因此将f(2-a2)>f(a)转化为1-a2>a,解二次不等式得到结果. 这道题目将分段函数,函数的图象,函数的单调性充分综合,是检测学生综合运用本章知识分析和解决问题的能力.。
初中数学中考一轮复习专题5 二次函数重点、考点知识、方法总结及真题练习

【答案】 【解析】解:(1)把 A(0,﹣1)代入 y1=a(x﹣2)2,得:﹣1=4a,即 a=﹣ ,
∴二次函数解析式为 y1=﹣ (x﹣2)2=﹣ a2+a﹣1;
设直线 AB 解析式为 y=kx+b,
把 A(0,﹣1),B(2,0)代入得:
,
解得:k= ,b=﹣1,
则直线 AB 解析式为 y= x﹣1;
选叏的五点为:顶点、不 y 轴的交点 0,c 、以及 0,c 关于对称轴对称的点 2h ,c 、 不 x 轴的交点 x1 ,0 , x2 ,0 (若不 x 轴没有交点,则叏两组关于对称轴对称的点).
画草图时应抓住以下几点:开口斱向,对称轴,顶点,不 x 轴的交点,不 y 轴的交点.
4. 二次函数 y ax2 bx c 的性质
正斱形的面积,∴y=﹣x2+36.
3.抛物线 y=x2﹣2x+3 的顶点坐标是
.
【答案】(1,2)
【解析】解:∵y=x2﹣2x+3=x2﹣2x+1﹣1+3=(x﹣1)2+2,
∴抛物线 y=x2﹣2x+3 的顶点坐标是(1,2).
4.已知抛物线 y=﹣2(x+1)2﹣3,如果 y 随 x 的增大而减小,那么 x 的叏值范围
D. y=1﹣ x2
【解析】解:把每一个函数式整理为一般形式, A、y=(x﹣1)(x+2)=x2+x﹣2,是二次函数,故 A 丌符合题意; B、y= (x+1)2= x2+x+ ,是二次函数,故 B 丌符合题意;
C、y=2(x+3)2﹣2x2=12x+18,是一次函数,故 C 符合题意; D、y=1﹣ x2=﹣ x2+1,是二次函数,故 D 丌符合题意. 故选:C.
九年级数学下册 第28章 锐角三角函数小结

2021/12/11
第三页,共十五页。
一、回顾思考
(2)两个直角三角形全等要具备什么条件?为什么在直角三角形中 已知一条边和一个锐角(ruìjiǎo),或已知两边,能够解这个直角三角 形?
答:两个直角三角形全等的判定方法有:①两条直角边对应(duìyìng)相等 的两个直角三角形全等,②斜边和一条直角边对应(duìyìng)相等的两个直 角三角形全等,③有一个锐角和一条直角边对应(duìyìng)相等的两个直角 三角形全等,④有一个锐角和斜边对应(duìyìng)相等的两个直角三角形全 等. 由直角三角形全等的判定定理可知,一个直角三角形可以由它的三条 边和两个锐角这五个元素中的两个(其中至少有一个是边)唯一确定, 因此在直角三角形中已知一条边和一个锐角,或已知两边,能够解这 个直角三角形.
(3)综合运用所学知识解直角三角形,逐步培养学生分析问题、解决问题的能力.培养学生思维能力的灵活性.
(4)通过画示意图,将实际问题转化为数学问题,发展学生的抽象概括能力,提高应用数学知识解决实际问题的能力.(难点)
(5)经历从实际问题中建立数学模型的过程,增强应用意识,体会数形结合思想的应用.(难点)
第十二页,共十五页。
三、典例剖析
4.解直角三角形的实际(shíjì)应用
【点评】此题作垂线(chuíxiàn)构造出直角三角形后,两个直角三角形均不具备可解的条件, 需要设未知数列方程求解.
2021/12/11
第十三页,共十五页。
四、归纳小结
请同学们回答下列问题: (1)通过对本章的学习(xuéxí),你认为本章的核心知识是什么?
(5)在探究活动中,培养学生的合作交流意识,让学生在学习中感受成功的喜悦,增强学习数学的信心.
高考数学知识点总结及复习资料(实用)

高考数学知识点总结及复习资料(实用)高考数学复习重点第一,函数与导数主要考查集合运算、函数的有关概念定义域、值域、解析式、函数的极限、连续、导数。
第二,平面向量与三角函数、三角变换及其应用这一部分是高考的重点但不是难点,主要出一些基础题或中档题。
第三,数列及其应用这部分是高考的重点而且是难点,主要出一些综合题。
第四,不等式主要考查不等式的求解和证明,而且很少单独考查,主要是在解答题中比较大小。
是高考的重点和难点。
第五,概率和统计这部分和我们的生活联系比较大,属应用题。
第六,空间位置关系的定性与定量分析主要是证明平行或垂直,求角和距离。
主要考察对定理的熟悉程度、运用程度。
第七,解析几何高考的难点,运算量大,一般含参数。
高考数学冲刺注意事项重视新增内容考查,新课标高考对新增内容的考查比例远远超出它们在教材中占有的比例。
例如:三视图、茎叶图、定积分、正态分布、统计案例等。
立足基础,强调通性通法,增大覆盖面。
从历年高考试题看,高考数学命题都把重点放在高中数学课程中最基础、最核心的内容上,即关注学生在学习数学和应用数学解决问题的过程中最为重要的、必须掌握的核心观念、思想方法、基本概念和常用技能,紧紧地围绕“双基”对数学的核心内容与基本能力进行重点考查。
突出新课程理念,关注应用,倡导“学以致用”。
新课程倡导积极主动、勇于探索的学习方式,注重提高学生的数学思维能力,发展学生的数学应用意识。
加强应用意识的培养与考查是教育改革的需要,也是作为工具学科的数学学科特点的体现。
有意训练每年高考试题中都出现的高频考点。
高考数学高分学习方法1、先看笔记后做作业。
有的高中学生感到。
老师讲过的,自己已经听得明明白白了。
但是,为什么自己一做题就困难重重了呢?其原因在于,学生对教师所讲的内容的理解,还没能达到教师所要求的层次。
因此,每天在做作业之前,一定要把课本的有关内容和当天的课堂笔记先看一看。
能否坚持如此,常常是好学生与差学生的最大区别。
2024年中考数学总复习考点梳理第三章第二节一次函数的图象与性质

第二节 一次函数的图象与性质
返回目录
考情及趋势分析
考情分析
年份 题号 题型 分值 题干条件 考查知识点 结合知识点 溯源教材 教材改编维度
AB交直线y=x 正比例函数
解答题(
正方形、图
2023 23
12 于点E,AC交直 图象上点的
/
/
三)
形旋转
线y=x于点N 坐标特征
一次函数图象与
一次函数图
解答题(
1 教材改编题课前测 2 教材知识逐点过 3 广东近6年真题
第二节 一次函数的图象与性质
返回目录
广东近6年考情及趋势分析
命题点1 一次函数的图象与性质 (6年4考,常与反比例函数、二次函数结合考查) 课标要求 1.能画出一次函数的图象,根据一次函数的图象和表达式y=kx+b(k≠0) 探索并理解k>0和k<0时,图象的变化情况; 2.理解正比例函数.
①BO=3,②BC=CD
2019 23(2) 解答题(三) 2
y=kx+b
(-1,4),(4,n)
2018 23(1) 解答题(三) 2
y=x+m
C(0,-3)
【考情总结】1.考查方法:均考查待定系数法确定解析式;
2.考查特点:除2018年考查代入一点来自标外,其余年份均考查代入两点坐标.
结合知识点 /
第二节 一次函数的图象与性质
返回目录
考情及趋势分析
考情分析
年份 题号
题型
分值 函数解析式
已知条件
2023 16(2) 解答题(一) 5
y=kx+b
(0,1),(2,5)
2021 21(2) 解答题(二) 5
y=kx+b
①P(1,m),②PA=2AB
2023届新高考数学二轮复习:专题(三角函数的范围与最值)提分练习(附答案)

2023届新高考数学二轮复习:专题(三角函数的范围与最值)提分练习【总结】一、三角函数()sin()f x A x ωϕ=+中ω的大小及取值范围 1、任意两条对称轴之间的距离为半周期的整数倍,即()2Tkk ∈Z ; 2、任意两个对称中心之间的距离为半周期的整数倍,即()2Tk k ∈Z ; 3、任意对称轴与对称中心之间的距离为14周期加半周期的整数倍,即()42T Tk k +∈Z ; 4、()sin()f x A x ωϕ=+在区间(,)a b 内单调2Tb a ⇒-…且()22k a b k k πππωϕωϕπ-+++∈Z 剟?5、()sin()f x A x ωϕ=+在区间(,)a b 内不单调(,)a b ⇒内至少有一条对称轴,2a kb πωϕπωϕ+++剟()k ∈Z6、()sin()f x A x ωϕ=+在区间(,)a b 内没有零点2Tb a ⇒-…且(1)()k a b k k πωϕωϕπ+++∈Z 剟?7、()sin()f x A x ωϕ=+在区间(,)a b 内有n 个零点(1)()(1)()k a k k k n b k n πωϕππωϕπ-+<⎧⇒∈⎨+-<++⎩Z ……. 二、三角形范围与最值问题1、坐标法:把动点转为为轨迹方程2、几何法3、引入角度,将边转化为角的关系4、最值问题的求解,常用的方法有:(1)函数法;(2)导数法;(3)数形结合法;(4)基本不等式法.要根据已知条件灵活选择方法求解.【典型例题】例1.(2023ꞏ全国ꞏ高三专题练习)在ABC 中,7cos 25A =,ABC 的内切圆的面积为16π,则边BC 长度的最小值为( )A .16B .24C .25D .36例2.(2023ꞏ全国ꞏ高三专题练习)已知函数()sin()f x x ωϕ=+,其中0ω>,||,24ππϕ≤-为()f x的零点:且()4f x f π⎛⎫≤ ⎪⎝⎭恒成立,()f x 在,1224ππ⎛⎫- ⎪⎝⎭区间上有最小值无最大值,则ω的最大值是( ) A .11 B .13C .15D .17例3.(2023ꞏ高一课时练习)如图,直角ABC ∆的斜边BC 长为2,30C ∠=︒,且点,B C 分别在x 轴,y 轴正半轴上滑动,点A 在线段BC 的右上方.设OA xOB yOC =+,(,x y ∈R ),记M OA OC =⋅,N x y =+,分别考查,M N 的所有运算结果,则A .M 有最小值,N 有最大值B .M 有最大值,N 有最小值C .M 有最大值,N 有最大值D .M 有最小值,N 有最小值例4.(2023ꞏ全国ꞏ高三专题练习)已知函数()sin cos f x a x b x cx =++图象上存在两条互相垂直的切线,且221a b +=,则a b c ++的最大值为( ) A.B.CD例5.(2023ꞏ全国ꞏ高三专题练习)已知0m >,函数(2)ln(1),1,()πcos 3,π,4x x x m f x x m x -+-<≤⎧⎪=⎨⎛⎫+<≤ ⎪⎪⎝⎭⎩恰有3个零点,则m 的取值范围是( )A .π5π3π,2,12124⎡⎫⎡⎫⎪⎪⎢⎢⎣⎭⎣⎭B .π5π3π,2,12124⎡⎫⎡⎤⎪⎢⎢⎥⎣⎭⎣⎦C .5π3π0,2,124⎛⎫⎡⎫⎪⎪⎢⎝⎭⎣⎭ D .5π3π0,2,124⎛⎫⎡⎤ ⎪⎢⎥⎝⎭⎣⎦例6.(2023ꞏ全国ꞏ高三专题练习)已知函数()πcos (0)3f x x ωω⎛⎫=-> ⎪⎝⎭在ππ,64⎡⎤⎢⎥⎣⎦上单调递增,且当ππ,43x ⎡⎤∈⎢⎥⎣⎦时,()0f x ≥恒成立,则ω的取值范围为( )A .522170,,232⎛⎤⎡⎤ ⎥⎢⎥⎝⎦⎣⎦B .4170,8,32⎛⎤⎡⎤ ⎥⎢⎥⎝⎦⎣⎦C .4280,8,33⎛⎤⎡⎤⎥⎢⎥⎝⎦⎣⎦D .5220,,823⎛⎤⎡⎤ ⎥⎢⎥⎝⎦⎣⎦例7.(2023ꞏ全国ꞏ高三专题练习)在锐角ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,ABC 的面积为S ,若222sin()SA C b a +=-,则1tan 3tan()A B A +-的取值范围为( )A .3⎡⎫+∞⎪⎢⎣⎭B .43⎤⎥⎣⎦ C .43⎫⎪⎪⎝⎭D .43⎫⎪⎪⎣⎭例8.(2023ꞏ上海ꞏ高三专题练习)在钝角ABC 中,,,a b c 分别是ABC 的内角,,A B C 所对的边,点G 是ABC 的重心,若AG BG ⊥,则cos C 的取值范围是( )A .0,3⎛⎫⎪ ⎪⎝⎭B .453⎡⎫⎪⎢⎪⎣⎭ C .3⎛⎫⎪ ⎪⎝⎭D .4,15⎡⎫⎪⎢⎣⎭例9.(2023ꞏ全国ꞏ高三专题练习)设锐角ABC 的内角,,A B C 所对的边分别为,,a b c ,若,3A a π==,则2b 2c bc ++的取值范围为( )A .(1,9]B .(3,9]C .(5,9]D .(7,9]例10.(2023ꞏ上海ꞏ高三专题练习)某公园有一个湖,如图所示,湖的边界是圆心为O 的圆,已知圆O 的半径为100米.为更好地服务游客,进一步提升公园亲水景观,公园拟搭建亲水木平台与亲水玻璃桥,设计弓形,,,MN NP PQ QM 为亲水木平台区域(四边形MNPQ 是矩形,A ,D 分别为,MN PQ 的中点,50OA OD ==米),亲水玻璃桥以点A 为一出入口,另两出入口B ,C 分别在平台区域,MQ NP 边界上(不含端点),且设计成2BAC π∠=,另一段玻璃桥F D E --满足//,,//,FD AC FD AC ED AB ED AB ==.(1)若计划在B ,F 间修建一休闲长廊该长廊的长度可否设计为70米?请说明理由;(附:1.732≈≈)(2)设玻璃桥造价为0.3万元/米,求亲水玻璃桥的造价的最小值.(玻璃桥总长为AB AC DE DF +++,宽度、连接处忽略不计).例11.(2023ꞏ全国ꞏ高三专题练习)在ABC 中,角A ,B ,C 的对边分别是a ,b ,c ,满足πsin sin 3b A a B ⎛⎫=+ ⎪⎝⎭(1)设3a =,2c =,过B 作BD 垂直AC 于点D ,点E 为线段BD 的中点,求BE EA ⋅的值;(2)若ABC 为锐角三角形,2c =,求ABC 面积的取值范围.【过关测试】 一、单选题1.(2023ꞏ全国ꞏ高三专题练习)已知,a b R ∈,设函数1()cos 2f x x =,2()cos f x a b x =-,若当12()()f x f x ≤对[,]()∈<x m n m n 恒成立时,n m -的最大值为3π2,则( ) A.1a ≥ B.1a ≤ C.2≥b D.2≤b 2.(2023ꞏ全国ꞏ高三专题练习)ABC中,4AB ACB π=∠=,O 是ABC 外接圆圆心,是OC AB CA CB ⋅+⋅的最大值为( )A .0B .1C .3D .53.(2023ꞏ全国ꞏ高三专题练习)在锐角ABCcos cos ()sin sin A CA B C a c+=,且cos 2C C +=,则a b +的取值范围是( ) A.(4⎤⎦B.(2,C .(]0,4D .(]2,44.(2023ꞏ全国ꞏ高三专题练习)设ω∈R ,函数()()22,0,6314,0,22sin x x f x g x x x x x πωωω⎧⎛⎫+≥ ⎪⎪⎪⎝⎭==⎨⎪++<⎪⎩.若()f x 在1,32π⎛⎫- ⎪⎝⎭上单调递增,且函数()f x 与()g x 的图象有三个交点,则ω的取值范围是( )A .12,43⎛⎤ ⎝⎦B.233⎛⎤ ⎥ ⎝⎦C.14⎡⎢⎣⎭D .4412,0,33⎡⎫⎡⎤-⎪⎢⎢⎥⎣⎭⎣⎦5.(2023秋ꞏ湖南长沙ꞏ高三长郡中学校考阶段练习)已知函数π()sin (0)3f x x ωω⎛⎫=+> ⎪⎝⎭在π,π3⎡⎤⎢⎥⎣⎦上恰有3个零点,则ω的取值范围是( ) A .81114,4,333⎡⎫⎛⎫⋃⎪ ⎪⎢⎣⎭⎝⎭B .111417,4,333⎡⎫⎡⎫⋃⎪⎪⎢⎢⎣⎭⎣⎭C .111417,5,333⎡⎫⎛⎫⋃⎪ ⎪⎢⎣⎭⎝⎭D .141720,5,333⎡⎫⎡⎫⋃⎪⎪⎢⎢⎣⎭⎣⎭6.(2023ꞏ全国ꞏ高三专题练习)已知函数()sin 4f x x ωπ⎛⎫=+ ⎪⎝⎭(0)>ω在区间[0,]π上有且仅有4条对称轴,给出下列四个结论:①()f x 在区间(0,)π上有且仅有3个不同的零点; ②()f x 的最小正周期可能是2π;③ω的取值范围是131744⎡⎫⎪⎢⎣⎭,; ④()f x 在区间0,15π⎛⎫⎪⎝⎭上单调递增. 其中所有正确结论的序号是( )A .①④B .②③C .②④D .②③④7.(2023ꞏ全国ꞏ高三专题练习)函数()sin 06y x πωω⎛⎫=-> ⎪⎝⎭在[]0,π有且仅有3个零点,则下列说法正确的是( )A .在()0,π不存在1x ,2x 使得()()122f x f x -=B .函数()f x 在()0,π仅有1个最大值点C .函数()f x 在0,2π⎛⎫⎪⎝⎭上单调进增D .实数ω的取值范围是1319,66⎡⎫⎪⎢⎣⎭8.(2023ꞏ上海ꞏ高三专题练习)在ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若cos cos sin sin()sin B C AA C bc C ⎛⎫++=⎪⎝⎭,3B π=,则a c +的取值范围是( )A .⎝B .32⎛ ⎝C .2⎢⎣D .32⎡⎢⎣二、多选题9.(2023秋ꞏ山东济南ꞏ高三统考期中)在ABC 中,内角,,A B C 所对的边分别为,,a b c ,且()()tan 1tan tan A B A B +-= ) A .π6A =B .若b c -=,则ABC 为直角三角形C .若ABC 面积为1,则三条高乘积平方的最大值为D .若D 为边BC 上一点,且1,:2:AD BD DC c b ==,则2b c +的最小值为710.(2023秋ꞏ江苏苏州ꞏ高三苏州中学校考阶段练习)已知函数()2sin 212cos xf x x=+,则下列说法中正确的是( )A .()()f x f x π+=B .()f xC .()f x 在,22ππ⎛⎫- ⎪⎝⎭上单调递增D .若函数()f x 在区间[)0,a 上恰有2022个极大值点,则a 的取值范围为60646067,33ππ⎛⎤⎥⎝⎦ 11.(2023ꞏ全国ꞏ高三专题练习)在ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,面积为S ,有以下四个命题中正确的是( )A .22S a bc +的最大值为12B .当2a =,sin 2sin BC =时,ABC 不可能是直角三角形C .当2a =,sin 2sin B C =,2A C =时,ABC 的周长为2+D .当2a =,sin 2sin B C =,2A C =时,若O 为ABC 的内心,则AOB 12.(2023ꞏ全国ꞏ高三专题练习)在锐角ABC 中,角,,A B C 所对的边分别为,,a b c ,且2cos c b b A -=,则下列结论正确的有( )A .2AB = B .B 的取值范围为0,4π⎛⎫⎪⎝⎭C .ab的取值范围为)2D .112sin tan tan A B A -+的取值范围为⎫⎪⎪⎝⎭三、填空题13.(2023ꞏ全国ꞏ高三专题练习)已知函数()sin ,06f x x πωω⎛⎫=+> ⎪⎝⎭,若5412f f ππ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭且()f x 在区间5,412ππ⎛⎫⎪⎝⎭上有最小值无最大值,则ω=_______. 14.(2023ꞏ全国ꞏ高三专题练习)函数()()π3sin 0,2f x x ωϕωϕ⎛⎫=+>< ⎪⎝⎭,已知π33f ⎛⎫= ⎪⎝⎭且对于任意的x R ∈都有ππ066f x f x ⎛⎫⎛⎫-++--= ⎪ ⎪⎝⎭⎝⎭,若()f x 在5π2π,369⎛⎫ ⎪⎝⎭上单调,则ω的最大值为______.15.(2023ꞏ全国ꞏ高三专题练习)已知函数()sin()f x x ωϕ=+,其中0ω>,||2πϕ…,4π-为()f x 的零点,且()4f x f π⎛⎫⎪⎝⎭…恒成立,()f x 在区间,1224ππ⎡⎫-⎪⎢⎣⎭上有最小值无最大值,则ω的最大值是_______16.(2023ꞏ全国ꞏ高三对口高考)在ABC 中,)(),cos ,cos ,sin AB x x AC x x ==,则ABC 面积的最大值是____________17.(2023ꞏ高一课时练习)用I M 表示函数sin y x =在闭区间I 上的最大值.若正数a 满足[0,][,2]2a a a M M ≥,则a 的最大值为________.18.(2023ꞏ上海ꞏ高三专题练习)在ABC 中,角,,A B C 的对边分别为,,a b c ,已知2a =,cos cos 4b C c B -=,43C ππ≤≤,则tan A 的最大值为_______.19.(2023ꞏ全国ꞏ高三专题练习)在ABC 中,若120BAC ∠=︒,点D 为边BC 的中点,1AD =,则AB AC ⋅uu u r uuu r的最小值为______.20.(2023ꞏ全国ꞏ高三专题练习)△ABC 中,角A ,B ,C 所对的三边分别为a ,b ,c ,c =2b ,若△ABC 的面积为1,则BC 的最小值是________ .21.(2023ꞏ全国ꞏ高三专题练习)已知0θ>,对任意*n ∈N ,总存在实数ϕ,使得cos()n θϕ+<θ的最小值是___ 22.(2023ꞏ上海ꞏ高三专题练习)已知函数()sin()f x x ωϕ=+,其中0ω>,0πϕ<< ,π()()4f x f ≤恒成立,且()y f x =在区间3π0,8⎛⎫ ⎪⎝⎭上恰有3个零点,则ω的取值范围是______________.23.(2023ꞏ全国ꞏ高三专题练习)已知锐角三角形ABC 的内角A ,B ,C 所对的边分别是a ,b ,c ,且A B >,若7sin 2cos sin 25C A B =+,则tan B 的取值范围为_______. 24.(2023ꞏ全国ꞏ高三专题练习)若函数()41sin 2cos 33f x x x a x =-+在(),-∞+∞内单调递增,则实数a 的取值范围是___________.25.(2023秋ꞏ湖南衡阳ꞏ高一衡阳市八中校考期末)设函数()()2sin 1(0)f x x ωϕω=+->,若对于任意实数ϕ,()f x 在区间π3π,44⎡⎤⎢⎥⎣⎦上至少有2个零点,至多有3个零点,则ω的取值范围是________.26.(2023ꞏ全国ꞏ高三专题练习)已知函数()()211(sin )sin 20,22f x x x R ωωωω=+->∈,若()f x 在区间(),2ππ内没有极值点,则ω的取值范围是___________.27.(2023秋ꞏ江苏苏州ꞏ高三苏州中学校考阶段练习)某小区有一个半径为r 米,圆心角是直角的扇形区域,现计划照图将其改造出一块矩形休闲运动场地,然后在区域I (区域ACD ),区域II (区域CBE )内分别种上甲和乙两种花卉(如图),已知甲种花卉每平方米造价是a 元,乙种花卉每平方米造价是3a 元,设∠BOC =θ,中植花卉总造价记为()f θ,现某同学已正确求得:()()2f arg θθ=,则()g θ=___________;种植花卉总造价最小值为___________.28.(2023ꞏ全国ꞏ高三专题练习)已知函数()()2sin cos 0,06f x x a x a πωωω⎛⎫=++>> ⎪⎝⎭对任意12,x x R ∈都有()()12f x f x +≤若()f x 在[]0,π上的取值范围是3,⎡⎣,则实数ω的取值范围是__________.29.(2023ꞏ全国ꞏ高三专题练习)已知a ,b ,c 分别为锐角ABC 的三个内角A ,B ,C 的对边,若2a =,且2sin sin (sin sin )B A A C =+,则ABC 的周长的取值范围为__________. 30.(2023ꞏ全国ꞏ高三专题练习)在锐角ABC ∆中,2BC =,sin sin 2sin B C A +=,则中线AD长的取值范围是_______; 四、解答题31.(2023ꞏ全国ꞏ高三专题练习)已知函数()2sin 216f x x πω⎛⎫=++ ⎪⎝⎭.(1)若()()()12f x f x f x ≤≤,12min2x x π-=,求()f x 的对称中心;(2)已知05ω<<,函数()f x 图象向右平移6π个单位得到函数()g x 的图象,3x π=是()g x 的一个零点,若函数()g x 在[],m n (m ,n R ∈且m n <)上恰好有10个零点,求n m -的最小值;32.(2023ꞏ全国ꞏ模拟预测)在ABC 中,内角,,A B C 的对边分别为,,,sin cos 6a b c b A a B π⎛⎫=- ⎪⎝⎭.(1)求角B 的大小;(2)设点D 是AC 的中点,若BD =,求a c +的取值范围.参考答案【总结】一、三角函数()sin()f x A x ωϕ=+中ω的大小及取值范围 1、任意两条对称轴之间的距离为半周期的整数倍,即()2Tkk ∈Z ; 2、任意两个对称中心之间的距离为半周期的整数倍,即()2Tk k ∈Z ; 3、任意对称轴与对称中心之间的距离为14周期加半周期的整数倍,即()42T Tk k +∈Z ; 4、()sin()f x A x ωϕ=+在区间(,)a b 内单调2Tb a ⇒-…且()22k a b k k πππωϕωϕπ-+++∈Z 剟?5、()sin()f x A x ωϕ=+在区间(,)a b 内不单调(,)a b ⇒内至少有一条对称轴,2a kb πωϕπωϕ+++剟()k ∈Z6、()sin()f x A x ωϕ=+在区间(,)a b 内没有零点2Tb a ⇒-…且(1)()k a b k k πωϕωϕπ+++∈Z 剟?7、()sin()f x A x ωϕ=+在区间(,)a b 内有n 个零点(1)()(1)()k a k k k n b k n πωϕππωϕπ-+<⎧⇒∈⎨+-<++⎩Z …….二、三角形范围与最值问题1、坐标法:把动点转为为轨迹方程2、几何法3、引入角度,将边转化为角的关系4、最值问题的求解,常用的方法有:(1)函数法;(2)导数法;(3)数形结合法;(4)基本不等式法.要根据已知条件灵活选择方法求解.【典型例题】例1.(2023ꞏ全国ꞏ高三专题练习)在ABC 中,7cos 25A =,ABC 的内切圆的面积为16π,则边BC 长度的最小值为( )A .16B .24C .25D .36【答案】A【答案解析】因为ABC 的内切圆的面积为16π,所以ABC 的内切圆半径为4.设ABC 内角A ,B ,C 所对的边分别为a ,b ,c .因为7cos 25A =,所以24sin 25A =,所以24tan 7A =.因为1sin 2ABC S bc A ==△1()42a b c ++⨯,所以25()6bc a b c =++.设内切圆与边AC 切于点D ,由24tan 7A =可求得3tan 24A ==4AD ,则163AD =.又因为2b c a AD +-=,所以323b c a +=+.所以2532251626333bc a a ⎛⎫⎛⎫=+=+ ⎪ ⎪⎝⎭⎝⎭.又因为b c +≥323a +≥即23210016333a a ⎛⎫⎛⎫+≥+ ⎪ ⎪⎝⎭⎝⎭,整理得21264a a --0≥.因为0a >,所以16a ≥,当且仅当403b c ==时,a 取得最小值. 故选:A .例2.(2023ꞏ全国ꞏ高三专题练习)已知函数()sin()f x x ωϕ=+,其中0ω>,||,24ππϕ≤-为()f x 的零点:且()4f x f π⎛⎫≤ ⎪⎝⎭恒成立,()f x 在,1224ππ⎛⎫- ⎪⎝⎭区间上有最小值无最大值,则ω的最大值是( )A .11B .13C .15D .17【答案】C【答案解析】由题意,4x π=是()f x 的一条对称轴,所以14f π⎛⎫=± ⎪⎝⎭,即11,42k k Z ππωϕπ+=+∈①又04f π⎛⎫-= ⎪⎝⎭,所以22,4k k Z πωϕπ-+=∈②由①②,得()1221k k ω=-+,12,k k Z ∈又()f x 在,1224ππ⎛⎫- ⎪⎝⎭区间上有最小值无最大值,所以24128T πππ⎛⎫≥--= ⎪⎝⎭ 即28ππω≥,解得16ω≤,要求ω最大,结合选项,先检验15ω=当15ω=时,由①得1115,42k k Z ππϕπ⨯+=+∈,即1113,4k k Z πϕπ=-∈,又||2πϕ≤ 所以4πϕ=-,此时()sin 154f x x π⎛⎫=- ⎪⎝⎭,当,1224x ππ⎛⎫∈- ⎪⎝⎭时,3315,428x πππ⎛⎫-∈- ⎪⎝⎭,当1542x ππ-=-即60x π=-时,()f x 取最小值,无最大值,满足题意.故选:C例3.(2023ꞏ高一课时练习)如图,直角ABC ∆的斜边BC 长为2,30C ∠=︒,且点,B C 分别在x 轴,y 轴正半轴上滑动,点A 在线段BC 的右上方.设OA xOB yOC =+,(,x y ∈R ),记M OA OC =⋅,N x y =+,分别考查,M N 的所有运算结果,则A .M 有最小值,N 有最大值B .M 有最大值,N 有最小值C .M 有最大值,N 有最大值D .M 有最小值,N 有最小值【答案】B【答案解析】依题意30,2,90BCA BC A ∠==∠= ,所以1AC AB ==.设OCB α∠=,则30,090ABx αα∠=+<< ,所以()())30,sin 30Aαα++ ,()()2sin ,0,0,2cos B C αα,所以()()12cos sin 30sin 2302M OA OC ααα==+=++⋅ ,当23090,30αα+== 时,M 取得最大值为13122+=.OA xOB yOC =+ ,所以()()30sin 30,2sin 2cos x y αααα++==,所以()()30sin 302sin 2cos N x y αααα++=+=+12sin 2α=+,当290,45αα== 时,N 有最小值为1故选B. 例4.(2023ꞏ全国ꞏ高三专题练习)已知函数()sin cos f x a x b x cx =++图象上存在两条互相垂直的切线,且221a b +=,则a b c ++的最大值为( )A .B .C D 【答案】D【答案解析】由221a b +=,令sin ,cos a b θθ==, 由()sin cos f x a x b x cx =++,得()cos sin sin cos cos sin f x a x b x c x x c θθ'=-+=-+()sin x c θ=-+,所以()11c f x c '-≤≤+由题意可知,存在12,x x ,使得12()()1f x f x ''=-,只需要21111c c c -+=-≥,即211c -≤-,所以20c ≤,0c =,πsin cos 4a b c a b θθθ⎛⎫++=+=+=+≤ ⎪⎝⎭所以a b c ++故选: D.例5.(2023ꞏ全国ꞏ高三专题练习)已知0m >,函数(2)ln(1),1,()πcos 3,π,4x x x m f x x m x -+-<≤⎧⎪=⎨⎛⎫+<≤ ⎪⎪⎝⎭⎩恰有3个零点,则m 的取值范围是( )A .π5π3π,2,12124⎡⎫⎡⎫⎪⎪⎢⎢⎣⎭⎣⎭B .π5π3π,2,12124⎡⎫⎡⎤⎪⎢⎢⎥⎣⎭⎣⎦C .5π3π0,2,124⎛⎫⎡⎫ ⎪⎪⎢⎝⎭⎣⎭D .5π3π0,2,124⎛⎫⎡⎤⎪⎢⎥⎝⎭⎣⎦【答案】A【答案解析】设()(2)ln(1)g x x x =-+,()cos 34h x x π⎛⎫+ ⎝=⎪⎭,求导()23ln(1)ln(1)111x g x x x x x -'=++=++-++ 由反比例函数及对数函数性质知()g x '在(]1,,0m m ->上单调递增,且102g ⎛⎫'< ⎪⎝⎭,()10g '>,故()g x '在1,12⎛⎫⎪⎝⎭内必有唯一零点0x ,当()01,x x ∈-时,()0g x '<,()g x 单调递减; 当(]0,x x m ∈时,()0g x '>,()g x 单调递增;令()0g x =,解得0x =或2,可作出函数()g x 的图像, 令()0h x =,即3,42x k k Z πππ+=+∈,在(]0,π之间解得12x π=或512π或34π,作出图像如下图数形结合可得:π5π3π,2,12124⎡⎫⎡⎫⎪⎪⎢⎢⎣⎭⎣⎭ ,故选:A例6.(2023ꞏ全国ꞏ高三专题练习)已知函数()πcos (0)3f x x ωω⎛⎫=-> ⎪⎝⎭在ππ,64⎡⎤⎢⎣⎦上单调递增,且当ππ,43x ⎡⎤∈⎢⎥⎣⎦时,()0f x ≥恒成立,则ω的取值范围为( )A .522170,,232⎛⎤⎡⎤ ⎥⎢⎥⎝⎦⎣⎦B .4170,8,32⎛⎤⎡⎤ ⎥⎢⎥⎝⎦⎣⎦C .4280,8,33⎛⎤⎡⎤⎥⎢⎥⎝⎦⎣⎦D .5220,,823⎛⎤⎡⎤ ⎥⎢⎥⎝⎦⎣⎦【答案】B【答案解析】由已知,函数()πcos (0)3f x x ωω⎛⎫=-> ⎪⎝⎭在ππ,64⎡⎤⎢⎥⎣⎦上单调递增,所以()111π2ππ2πZ 3k x k k ω-≤-≤∈,解得:()1112π2π2ππZ 33k k x k ωωωω-≤≤+∈,由于()111Z π,π,642π2π2ππ33k k k ωωωω⎡⎤⎡⎤⊆⎢⎢⎥⎣⎦⎣⎦-+∈,所以112ππ2π632πππ43k k ωωωω⎧≥-⎪⎪⎨⎪≤+⎪⎩,解得:()11141248Z 3k k k ω-≤≤+∈① 又因为函数()πcos (0)3f x x ωω⎛⎫=-> ⎪⎝⎭在ππ,43x ⎡⎤∈⎢⎥⎣⎦上()0f x ≥恒成立,所以()222πππ2π2π+Z 232k x k k ω-≤-≤∈,解得:()2222π2ππ5πZ 66k k x k ωωωω-≤≤+∈, 由于()2222π2ππ5π,Z 6π,46π3k k k ωωωω-+⎡⎤⎡⎤⊆⎢⎥⎢⎥⎣⎦⎣∈⎦,所以222πππ462ππ5π36k k ωωωω⎧≥-⎪⎪⎨⎪≤+⎪⎩,解得:()2222586Z 32k k k ω-≤≤+∈② 又因为0ω>,当120k k ==时,由①②可知:04432532ωωω⎧⎪>⎪⎪-≤≤⎨⎪⎪-≤≤⎪⎩,解得403ω⎛⎤∈ ⎥⎝⎦,;当121k k ==时,由①②可知:02883221732ωωω⎧⎪>⎪⎪≤≤⎨⎪⎪≤≤⎪⎩,解得1782ω⎡⎤∈⎢⎥⎣⎦,.所以ω的取值范围为4170,8,32⎛⎤⎡⎤⎥⎢⎥⎝⎦⎣⎦.故选:B.例7.(2023ꞏ全国ꞏ高三专题练习)在锐角ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,ABC 的面积为S ,若222sin()SA C b a +=-,则1tan 3tan()A B A +-的取值范围为( )A.3⎡⎫+∞⎪⎢⎣⎭B.433⎡⎤⎢⎥⎣⎦ C.4,33⎛⎫⎪ ⎪⎝⎭D.4,33⎡⎫⎪⎢⎪⎣⎭【答案】C【答案解析】在ABC 中,1sin()sin ,sin 2A CB S ac B +==, 故题干条件可化为22b a ac -=,由余弦定理得2222cos b a c ac B =+-, 故2cos c a B a =+,又由正弦定理化简得:sin 2sin cos sin sin cos cos sin C A B A A B A B =+=+,整理得sin()sin B A A -=,故B A A -=或B A A -=π-(舍去),得2B A =ABC 为锐角三角形,故02022032A A A ππππ⎧<<⎪⎪⎪<<⎨⎪⎪<-<⎪⎩,解得64A ππ<<tan 1A <<114tan tan (,3tan()3tan 33A AB A A +=+∈- 故选:C例8.(2023ꞏ上海ꞏ高三专题练习)在钝角ABC 中,,,a b c 分别是ABC 的内角,,A B C 所对的边,点G 是ABC 的重心,若AG BG ⊥,则cos C 的取值范围是( )A.⎛ ⎝⎭ B.45⎡⎢⎣⎭ C.⎫⎪⎪⎝⎭D .4,15⎡⎫⎪⎢⎣⎭【答案】C【答案解析】延长CG 交AB 于D ,如下图所示:G 为ABC 的重心,D ∴为AB 中点且3CD DG =,AG BG ⊥ ,12DG AB ∴=,3322CD AB c ∴==;在ADC △中,2222222225522cos 3232c bAD CD AC c b ADC AD CD c c -+--∠===⋅; 在BDC 中,2222222225522cos 3232c a BD CD BC c a BDC BD CD c c -+--∠===⋅; BDC ADC π∠+∠= ,cos cos BDC ADC ∴∠=-∠,即222222525233c a c b c c--=-,整理可得:22225a b c c +=>,C ∴为锐角; 设A 为钝角,则222b c a +<,222a c b +>,a b >,2222222255a ba b a b b a ⎧+>+⎪⎪∴⎨+⎪<+⎪⎩,22221115511155b b a a b b a a ⎧⎛⎫⎛⎫++<⎪ ⎪ ⎪⎪⎝⎭⎝⎭∴⎨⎛⎫⎛⎫⎪<++ ⎪ ⎪⎪⎝⎭⎝⎭⎩,解得:223b a ⎛⎫< ⎪⎝⎭, 0a b >>,03b a ∴<<,由余弦定理得:22222222cos 255533a b c a b a b C ab ab b a ⎛⎫+-+⎛⎫==⋅=+>⨯+= ⎪ ⎝⎭⎝, 又C为锐角,cos 1C <<,即cos C的取值范围为3⎛⎫ ⎪ ⎪⎝⎭. 故选:C.例9.(2023ꞏ全国ꞏ高三专题练习)设锐角ABC 的内角,,A B C 所对的边分别为,,a b c,若,3A a π==,则2b 2c bc ++的取值范围为( )A .(1,9]B .(3,9]C .(5,9]D .(7,9]【答案】D【答案解析】因为,3A a π==,由正弦定理可得22sin sin sin 3ab cAB B π====⎛⎫-⎪⎝⎭, 则有22sin ,2sin 3b B c B π⎛⎫==- ⎪⎝⎭,由ABC 的内角,,A B C 为锐角,可得0,220,32B B πππ⎧<<⎪⎪⎨⎪<-<⎪⎩,512sin 2124sin 2462666266B B B B πππππππ⎛⎫⎛⎫∴<<⇒<-<⇒<-≤⇒<-≤ ⎪ ⎪⎝⎭⎝⎭, 由余弦定理可得222222cos 3,a b c bc A b c bc =+-⇒=+- 因此有2223b c bc bc ++=+28sin sin 33B B π⎛⎫=-+ ⎪⎝⎭2cos 4sin 3B B B =++22cos 25B B =-+(]54sin 27,96B π⎛⎫=+-∈ ⎪⎝⎭故选:D.例10.(2023ꞏ上海ꞏ高三专题练习)某公园有一个湖,如图所示,湖的边界是圆心为O 的圆,已知圆O 的半径为100米.为更好地服务游客,进一步提升公园亲水景观,公园拟搭建亲水木平台与亲水玻璃桥,设计弓形,,,MN NP PQ QM 为亲水木平台区域(四边形MNPQ 是矩形,A ,D 分别为,MN PQ 的中点,50OA OD ==米),亲水玻璃桥以点A 为一出入口,另两出入口B ,C 分别在平台区域,MQ NP 边界上(不含端点),且设计成2BAC π∠=,另一段玻璃桥F D E --满足//,,//,FD AC FD AC ED AB ED AB ==.(1)若计划在B ,F 间修建一休闲长廊该长廊的长度可否设计为70米?请说明理由;(附:1.732≈≈)(2)设玻璃桥造价为0.3万元/米,求亲水玻璃桥的造价的最小值.(玻璃桥总长为AB AC DE DF +++,宽度、连接处忽略不计).【答案解析】(1)由题意,50,100OA OM ==,则100,2MQ AM BAC π==∠=,设,2MAB NAC πθαθ∠=∠==-.若C ,P重合,1tan tan tan 2αθα=====75MB =,∴75tan tan MB MB AM θθθ<<<<=⋅=,tan NC AN α=⋅=而100100MF CP NC ==-=∴1tan 1001)tan BF MB MF θθ⎫=-=+-≥⎪⎭,当tan 1θ=(符合题意)时取等号,又1)70->, ∴可以修建70米长廊. (2)cos cos AM AN AB AC θα====cos )cos sin sin cos AB AC θθθθθθ++=+=.设sin cos 4t πθθθ⎛⎫=+=+ ⎪⎝⎭,则212sin cos t θθ=+,即21sin cos 2t θθ-=.AB AC t t+==-1)知tan 2θ<<,而132<<<<θ∃使42ππθ+=且3444πππθ<+<,即112t t t <≤<-≤,∴AB AC t t+=≥-4t πθ==时取等号. 由题意,AB AC DE DF +=+,则玻璃桥总长的最小值为米,∴铺设好亲水玻璃桥,最少需0.3=例11.(2023ꞏ全国ꞏ高三专题练习)在ABC 中,角A ,B ,C 的对边分别是a ,b ,c ,满足πsin sin 3b A a B ⎛⎫=+ ⎪⎝⎭(1)设3a =,2c =,过B 作BD 垂直AC 于点D ,点E 为线段BD 的中点,求BE EA ⋅的值;(2)若ABC 为锐角三角形,2c =,求ABC 面积的取值范围.【答案解析】(1)πsin sin 3b A a B ⎛⎫=+ ⎪⎝⎭,由正弦定理得:π1sin sin sin sin sin sin sin cos 322B A A B A B A B ⎛⎫=+=+ ⎪⎝⎭,所以1sin sin cos 02A B A B =,因为()0,πA ∈,所以sin 0A ≠,所以1sin 02B B =,即tan B =因为()0,πB ∈,所以π3B =, 因为3a =,2c =,由余弦定理得:2222cos 9467b a c ac B =+-=+-=, 因为0b >,所以b =,其中11sin 3222ABC S ac B ==⨯⨯=△,所以2ABC S BD AC === 因为点E 为线段BD的中点,所以BE = 由题意得:EA ED DA BE DA =+=+,所以()227028BE EA BE BE DA BE ⋅=⋅+=+= . (2)由(1)知:π3B =,又2c =, 由正弦定理得:2πsin sin sin 3a cA CA ==⎛⎫+ ⎪⎝⎭,所以2sin πsin 3A a A ===⎛⎫+ ⎪⎝⎭,因为ABC 为锐角三角形,所以π0,22ππ0,32A C A ⎧⎛⎫∈ ⎪⎪⎪⎝⎭⎨⎛⎫⎪=-∈ ⎪⎪⎝⎭⎩,解得:ππ,62A ⎛⎫∈ ⎪⎝⎭,则tan A ⎫∈+∞⎪⎪⎝⎭()0,3,()11,4tan A +∈,故()1,4a =,ABC面积为1sin ,222S ac B a ⎛==∈ ⎝ 故ABC面积的取值范围是2⎛ ⎝.【过关测试】 一、单选题1.(2023ꞏ全国ꞏ高三专题练习)已知,a b R ∈,设函数1()cos 2f x x =,2()cos f x a b x =-,若当12()()f x f x ≤对[,]()∈<x m n m n 恒成立时,n m -的最大值为3π2,则( ) A.1a ≥ B .1a C .2≥b D .2≤b 【答案】A【答案解析】设[]cos ,x t x m n ∈=,,因为n m -的最大值为3ππ22T>=,所以[,]x m n ∈时,cos t x =必取到最值,当3π2n m -=时,根据余弦函数对称性得cos 12π22m n m Z nk k ++=⇒=∈,,此时3π3πcos cos(cos(2π)cos 22442m n n mm k +-=-=-==-3π3πcos cos(cos(2π)cos 22442m n n m n k +-=+=+==-或者cos1π+2π22m n m n Z k k ++=-⇒=∈,,此时3π3πcos cos(cos(2π+π)cos 22442m n n m m k +-=-=-=-=3π3πcos cos(cos(2π+π)cos 22442m n n m n k +-=+=+=-=由()2212()()2cos 1cos 2cos cos 10f x f x x a b x x b x a ≤⇒-≤-⇒+-+≤,设[]cos ,x t x m n ∈=,时 ()2210t bt a +-+≤对应解为12t t t ≤≤,由上分析可知当1t =,21t ≥或11t ≤-,2t =n m -的最大值为3π2,所以122t t ≤-,即122a +-≤,所以1a ≥.12122b t t -=+≥-或12122b t t -=+≤-+,即2b ≤或2≥-b 故选:A.2.(2023ꞏ全国ꞏ高三专题练习)ABC 中,4AB ACB π=∠=,O 是ABC 外接圆圆心,是OC AB CA CB ⋅+⋅的最大值为( )A .0B .1C .3D .5【答案】C【答案解析】过点O 作,OD AC OE BC ⊥⊥,垂足分别为D ,E ,如图,因O 是ABC 外接圆圆心,则D ,E 分别为AC ,BC 的中点,在ABC 中,AB CB CA =-,则222||||||2AB CA CB CA CB =+-⋅ ,即22||||22CA CB CA CB +-⋅=,21|cos |2CO CA CO CA OCA CD CA CA ⋅=∠=⋅=,同理21||2CO CB CB ⋅= ,因此,()OC AB CA CB OC CB CA CA CB CO CA CO CB CA CB ⋅+⋅=⋅-+⋅=⋅-⋅+⋅ 2222211||||2||||||1222CA CB CA CB CA +-=-+=-,由正弦定理得:||sin ||2sin 2sin sin 4AB B BCA B ACB π===≤∠ ,当且仅当2B π=时取“=”, 所以OC AB CA CB ⋅+⋅的最大值为3. 故选:C3.(2023ꞏ全国ꞏ高三专题练习)在锐角ABCcos cos ()sin sin A CA B C a c+=,且cos 2C C +=,则a b +的取值范围是( ) A.(4⎤⎦B.(2,C .(]0,4D .(]2,4【答案】Acos 2sin()26C C C π+=+=,得262C k πππ+=+,Z k ∈,(0,)2C π∈ ,3C π∴=.由题cos cos A C a c +=cos cos 2b A Cb a ca +==,故cos cos sin sin 2sin A C bA C A+=,即sin cos sin sin cos 2b C A C A C ⋅+⋅==故()sin sin A C B +==即sin b B =由正弦定理有sin sin sin a b c A B C ===,故a A =,b B =,又锐角ABC ,且3C π=,(0,)2A π∴∈,2(0,)32B A ππ=-∈,解得(6A π∈,2π,2sin )sin()]3a b A B A A π∴+=++-1sin )4sin(26A A A A π+=+, (6A π∈ ,2π,(63A ππ∴+∈,2)3π,sin()6A π+∈1], a b ∴+的取值范围为(4⎤⎦.故选:A .4.(2023ꞏ全国ꞏ高三专题练习)设ω∈R ,函数()()22,0,6314,0,22sin x x f x g x x x x x πωωω⎧⎛⎫+≥ ⎪⎪⎪⎝⎭==⎨⎪++<⎪⎩.若()f x 在1,32π⎛⎫- ⎪⎝⎭上单调递增,且函数()f x 与()g x 的图象有三个交点,则ω的取值范围是( )A .12,43⎛⎤ ⎝⎦B.23⎤⎥⎝⎦C.143⎡⎫⎪⎢⎣⎭D .4412,0,33⎡⎫⎡⎤-⎪⎢⎢⎥⎣⎭⎣⎦【答案】B【答案解析】当0,2x π⎡⎫∈⎪⎢⎣⎭时,,6626x πππωπω⎡⎫+∈+⎪⎢⎣⎭, 因为()f x 在1,32π⎛⎫- ⎪⎝⎭上单调递增,所以262413312sin 62πωππωπ⎧+≤⎪⎪⎪-≤-⎨⎪⎪≥⎪⎩,解得1243ω≤≤, 又因函数()f x 与()g x 的图象有三个交点,所以在(),0x ∈-∞上函数()f x 与()g x 的图象有两个交点,即方程231422x x x ωω++=在(),0x ∈-∞上有两个不同的实数根,即方程23610x x ω++=在(),0x ∈-∞上有两个不同的实数根,所以22Δ3612003060102ωωω⎧⎪=->⎪-<⎨⎪⎪⨯+⨯+>⎩,解得3ω>,当233ω⎛⎤∈ ⎥ ⎝⎦时,当0x ≥时,令()()2sin 6f x g x x x πωω⎛⎫-=+- ⎪⎝⎭,由()()10f x g x -=>, 当562x ππω+=时,73x πω=, 此时,()()7203f xg x π-=-<, 结合图象,所以0x ≥时,函数()f x 与()g x 的图象只有一个交点,综上所述,233ω⎛⎤∈ ⎥ ⎝⎦. 故选:B.5.(2023秋ꞏ湖南长沙ꞏ高三长郡中学校考阶段练习)已知函数π()sin (0)3f x x ωω⎛⎫=+> ⎪⎝⎭在π,π3⎡⎤⎢⎥⎣⎦上恰有3个零点,则ω的取值范围是( ) A .81114,4,333⎡⎫⎛⎫⋃⎪ ⎪⎢⎣⎭⎝⎭B .111417,4,333⎡⎫⎡⎫⋃⎪⎪⎢⎢⎣⎭⎣⎭C .111417,5,333⎡⎫⎛⎫⋃⎪ ⎪⎢⎣⎭⎝⎭D .141720,5,333⎡⎫⎡⎫⋃⎪⎪⎢⎢⎣⎭⎣⎭【答案】C【答案解析】π,π3x ⎡⎤∈⎢⎥⎣⎦,ππππ,π3333x ωωω⎡⎤+∈++⎢⎥⎣⎦,其中2ππ4ππ3ωω≤-<,解得:36ω≤<,则ππ4π333ω+≥,要想保证函数在π,π3⎡⎤⎢⎥⎣⎦恰有三个零点,满足①1111πππ+2π2π+2π33π4π+2π<π5π+2π3k k k k ωω⎧≤+<⎪⎪⎨⎪+≤⎪⎩,1k Z ∈,令10k =,解得:1114,33ω⎡⎫∈⎪⎢⎣⎭;或要满足②2222ππ2ππ+2π33π2π+3π<π2π+4π3k k k k ωω⎧≤+<⎪⎪⎨⎪+≤⎪⎩,2k Z ∈,令21k =,解得:175,3ω⎛⎫∈ ⎪⎝⎭;经检验,满足题意,其他情况均不满足36ω≤<条件,综上:ω的取值范围是111417,5,333⎡⎫⎛⎫⋃⎪ ⎪⎢⎣⎭⎝⎭.故选:C6.(2023ꞏ全国ꞏ高三专题练习)已知函数()sin 4f x x ωπ⎛⎫=+ ⎪⎝⎭(0)>ω在区间[0,]π上有且仅有4条对称轴,给出下列四个结论:①()f x 在区间(0,)π上有且仅有3个不同的零点; ②()f x 的最小正周期可能是2π;③ω的取值范围是131744⎡⎫⎪⎢⎣⎭,; ④()f x 在区间0,15π⎛⎫⎪⎝⎭上单调递增. 其中所有正确结论的序号是( ) A .①④B .②③C .②④D .②③④【答案】B【答案解析】由函数()sin 4f x x ωπ⎛⎫=+ ⎪⎝⎭(0)>ω,令,42x k k Z ππωπ+=+∈,则()14,4k x k Zπω+=∈函数()f x 在区间[0,]π上有且仅有4条对称轴,即()1404k ππω+≤≤有4个整数k 符合,由()1404k ππω+≤≤,得140101444k k ωω+≤≤⇒≤+≤,则0,1,2,3k =, 即1434144ω+⨯≤<+⨯,131744ω∴≤<,故③正确; 对于①,(0,)x π∈ ,,444x ωωππππ⎡⎫∴+∈+⎪⎢⎣⎭,79,422ππωππ⎛⎫∴+∈ ⎪⎝⎭当,442x ωππ7π⎡⎫+∈⎪⎢⎣⎭时,()f x 在区间(0,)π上有且仅有3个不同的零点;当,442x ωππ9π⎡⎫+∈⎪⎢⎣⎭时,()f x 在区间(0,)π上有且仅有4个不同的零点;故①错误;对于②,周期2T πω=,由131744ω≤<,则4141713ω<≤,881713T ππ∴<≤, 又88,21713πππ⎛⎤∈ ⎥⎝⎦,所以()f x 的最小正周期可能是2π,故②正确; 对于④,015x π⎛⎫∈ ⎪⎝⎭Q ,,44154x ωωππππ⎛⎫∴+∈+ ⎪⎝⎭,,又131744ω⎡⎫∈⎪⎢⎣⎭,,78,1541515ωππππ⎛⎫∴+∈ ⎪⎝⎭ 又8152ππ>,所以()f x 在区间0,15π⎛⎫⎪⎝⎭上不一定单调递增,故④错误.故正确结论的序号是:②③ 故选:B7.(2023ꞏ全国ꞏ高三专题练习)函数()sin 06y x πωω⎛⎫=-> ⎪⎝⎭在[]0,π有且仅有3个零点,则下列说法正确的是( )A .在()0,π不存在1x ,2x 使得()()122f x f x -=B .函数()f x 在()0,π仅有1个最大值点C .函数()f x 在0,2π⎛⎫⎪⎝⎭上单调进增D .实数ω的取值范围是1319,66⎡⎫⎪⎢⎣⎭【答案】D【答案解析】对于A,()f x 在[]0,π上有且仅有3个零点,则函数的最小正周期T π< , 所以在[]0,π上存在12,x x ,且12()1,()1f x f x ==- ,使得()()122f x f x -=,故A 错误; 由图象可知,函数在()0,π可能有两个最大值,故B 错误; 对于选项D,令,6x k k Z πωπ-=∈ ,则函数的零点为1(6x k k Z ππω=+∈ ,所以函数在y 轴右侧的四个零点分别是:71319,,,6666ππππωωωω, 函数()sin 06y x πωω⎛⎫=-> ⎪⎝⎭在[]0,π有且仅有3个零点,所以136196ππωππω⎧≤⎪⎪⎨⎪>⎪⎩ ,解得1319[,66ω∈ ,故D 正确; 由对选项D 的分析可知,ω的最小值为136, 当02x π<< 时,11(,)6612x πππω-∈-, 但11(,)612ππ-不是0,2π⎛⎫⎪⎝⎭的子集, 所以函数()f x 在0,2π⎛⎫⎪⎝⎭上不是单调进增的,故C 错,故选:D.8.(2023ꞏ上海ꞏ高三专题练习)在ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若cos cos sin sin()sin B C A A C bc C ⎛⎫++=⎪⎝⎭,3B π=,则a c +的取值范围是( ) A.2⎝ B.32⎛ ⎝C.2⎢⎣D.32⎡⎢⎣【答案】A【答案解析】由题知cos cos sin sin()sin B C AA C bc C ⎛⎫++=⎪⎝⎭,3B π= ∴cos cos sin sin sin B C AB b cC ⎛⎫+= ⎪⎝⎭即cos cos 3sin B C Ab c C+=由正弦定理化简得∴cos cos c B b C ⋅+⋅==∴sin sin cos cos sin 3A C B C B +=∴sin()sin B C A +==∴2b =3B π=∴1sin sin sin a b cA B C===∴23sin sin sin sin()sin 326a c A C A A A A A ππ+=+=+-==+203A π<<∴5666A πππ<+<∴)26A π<+≤a c <+≤故选:A . 二、多选题9.(2023秋ꞏ山东济南ꞏ高三统考期中)在ABC 中,内角,,A B C 所对的边分别为,,a b c ,且()()tan 1tan tan A B A B +-= ) A .π6A =B .若b c -=,则ABC 为直角三角形C .若ABC 面积为1,则三条高乘积平方的最大值为D .若D 为边BC 上一点,且1,:2:AD BD DC c b ==,则2b c +的最小值为7【答案】BCD【答案解析】对于A ,因为()()tan 1tan tan A B A B +-=tan tan A B +=,()sin cos tan tan C A B A B =+()sin sin cos cos sin sin sin cos sin sin cos cos cos cos A B A B A B CA B A A A B A A++=⋅=⋅=⋅,cos sin sin C A A C =,因为0πC <<,所以sin 0C >,故tan A = 又0πA <<,所以π3A =,故A 错误;对于B ,由余弦定理得222222cos a b c bc A b c bc =+-=+-,因为3b c a -=,即3b a c =+,代入上式得222a c c c c ⎫=+⎫⎪⎪⎝+-+⎪⎭⎭⎪⎝,整理得22320c a +-=,解得a =或2a c =-(舍去),则2b c =,所以222b a c =+,故B 正确;对于C ,设,,AB AC BC 边上的高分别是,,CE BF AD ,则由三角形面积公式易得222,,AD BF CE a b c ===,则()228AD BF CE abc ⎛⎫⨯⨯= ⎪⎝⎭,因为111a b c ++≥111a b c ==,即a b c ==时,等号成立,此时21sin 12S bc A ===,得2b =所以()228AD BF CE abc ⎛⎫⨯⨯=≤ ⎪⎝⎭C 正确; 对于D ,因为:2:BD DC c b =,所以22c AD AB AB BC b c BD =+=++()22222c b c AB AC AB AB AC b c b c b c=+-=++++ ,可得22222224212cos 60(2)(2)(2)b c bc c b cb b c b c b c ︒=+++++,整理得()22227b c b c +=,故12c b +=所以()1222225b c b c b c c b c b ⎫⎫+=++=++⎪⎪⎭⎭57⎛⎫≥=⎪⎪⎭,当且仅当22b c c b =且12c b +=,即7b c ==时,等号成立,所以2b c +≥2b c +D 正确. 故选:BCD.10.(2023秋ꞏ江苏苏州ꞏ高三苏州中学校考阶段练习)已知函数()2sin 212cos xf x x=+,则下列说法中正确的是( ) A .()()f x f x π+=B .()f xC .()f x 在,22ππ⎛⎫- ⎪⎝⎭上单调递增D .若函数()f x 在区间[)0,a 上恰有2022个极大值点,则a 的取值范围为60646067,33ππ⎛⎤⎥⎝⎦ 【答案】ABD【答案解析】()2sin 2sin 2sin 21cos 212cos 2cos 2122xx xf x x xx ===+++⎛⎫+ ⎪⎝⎭, A 选项:()()()()sin 22sin 22cos 222cos 2x xf x f x x xπππ++===+++,A 选项正确;B 选项:设()sin 22cos 2xf x t x==+,则()sin 2cos 222x t x t x ϕ-==+≤解得213t ≤,t ≤≤,即max t =,即()f xB 选项正确;C 选项:因为022f f ππ⎛⎫⎛⎫-== ⎪ ⎪⎝⎭⎝⎭,所以()f x 在,22ππ⎛⎫- ⎪⎝⎭上不单调,C 选项错误;D 选项:()()()()()222cos 22cos 2sin 22sin 24cos 222cos 22cos 2x x x x x f x x x +--+'==++,令()0f x '=,解得1cos 22x =-,即3x k ππ=+或23x k ππ=+,Z k ∈, 当2,33x k k ππππ⎛⎫∈++ ⎪⎝⎭,Z k ∈时,()0f x '<,函数单调递减, 当当24,33x k k ππππ⎛⎫∈++⎪⎝⎭,Z k ∈时,()0f x ¢>,函数单调递增, 所以函数()f x 的极大值点为3π,43π,L ,()13n ππ+-, 又函数()f x 在区间[)0,a 上恰有2022个极大值点,则2021,202233a ππππ⎛⎤∈++ ⎥⎝⎦,即60646067,33a ππ⎛⎤∈ ⎥⎝⎦,D 选项正确; 故选:ABD.11.(2023ꞏ全国ꞏ高三专题练习)在ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,面积为S ,有以下四个命题中正确的是( ) A .22S a bc +B .当2a =,sin 2sin BC =时,ABC 不可能是直角三角形 C .当2a =,sin 2sin B C =,2A C =时,ABC的周长为2+D .当2a =,sin 2sin B C =,2A C =时,若O 为ABC 的内心,则AOB的面积为13【答案】ACD【答案解析】对于选项A :。
一注基础高等数学知识总结

一注基础高等数学知识总结.doc一级注册建筑师基础高等数学知识总结引言一级注册建筑师考试中的高等数学部分,旨在测试考生对高等数学基础概念、原理和计算方法的掌握程度。
本总结旨在帮助考生系统地复习高等数学的重点知识,为考试做好充分准备。
第一部分:函数、极限与连续1.1 函数的概念函数的定义函数的表示方法特殊函数(常函数、线性函数、多项式函数)1.2 极限的概念极限的定义极限的性质无穷小与无穷大的概念1.3 函数的连续性连续函数的定义连续函数的性质间断点的分类第二部分:导数与微分2.1 导数的概念导数的定义导数的几何意义基本导数公式2.2 导数的运算法则乘积法则商法则链式法则2.3 高阶导数高阶导数的定义高阶导数的计算方法2.4 微分的概念微分的定义微分与导数的关系第三部分:积分3.1 不定积分不定积分的定义不定积分的计算方法分部积分法和换元积分法3.2 定积分定积分的定义定积分的性质定积分的计算方法3.3 广义积分广义积分的概念广义积分的计算第四部分:级数4.1 数项级数正项级数交错级数绝对收敛与条件收敛4.2 幂级数幂级数的定义幂级数的收敛半径4.3 函数的泰勒展开泰勒公式泰勒级数的应用第五部分:多元函数微分学5.1 偏导数偏导数的定义偏导数的计算方法5.2 全微分全微分的概念全微分与偏导数的关系5.3 多元函数的极值极值的定义极值的求解方法第六部分:常微分方程6.1 一阶微分方程可分离变量的微分方程一阶线性微分方程6.2 高阶微分方程高阶微分方程的解法欧拉方程6.3 微分方程的应用微分方程在几何问题中的应用微分方程在物理问题中的应用结语总结一级注册建筑师考试中高等数学部分的重要性,以及考生在复习过程中应注意的重点和策略。
锐角三角函数知识点总结与复习

锐角三角函数知识点总结与复习1、勾股定理:直角三角形两直角边a 、b 的平方和等于斜边c 的平方;2、如下图,在Rt △ABC 中,∠C 为直角, 则∠A 的锐角三角函数为∠A 可换成∠B :3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值;4、任意锐角的正切值等于它的余角的余切值;任意锐角的余切值等于它的余角的正切值;5、0°、30°、45°、60°、90°特殊角的三角函数值重要A 90B 90∠-︒=∠︒=∠+∠得由B A邻边A90B 90∠-︒=∠︒=∠+∠得由B A直角三角形中 的边角关系解直角三角形当0°≤α≤90°时,sin α随α的增大而增大,cos α随α的增大而减小; 7、正切、余切的增减性:当0°<α<90°时,tan α随α的增大而增大,cot α随α的增大而减小;一、知识性专题专题1:锐角三角函数的定义例 1 在Rt △ABC 中,∠ACB =90°,BC =1,AB =2,则下列结论正确的是 A .sin A B .tan A =12C .cos BD .tan B 分析 sin A =BC AB =12,tan A =BC AC ,cos B =BCAB =12.故选D.例2 在△ABC 中,∠C =90°,cos A =35,则tan A 等于 ; 分析 在Rt △ABC 中,设AC =3k ,AB =5k ,则BC =4k ,由定义可知tan A =4433BC k AC k ==. 分析 在Rt △ABC 中,BC =3,∴sin A =35BC AB =.故填35.例312·哈尔滨在Rt △ABC 中,∠C=900,AC=4,AB=5,则sinB 的值是 ; 解析本题考查了锐角三角函数的意义.解题思路:在直角三角形中,锐角的正弦等于对边比邻边,故sinB=54. 例42012内江如图4所示,△ABC 的顶点是正方形网格的格点,则sinA 的值为 ;解析欲求sinA,需先寻找∠A 所在的直角三角形,而图形中∠A 所在的△ABC 并不是直角三角形,所以需要作高.观察格点图形发现连接CD 如下图所示,恰好可证得CD ⊥AB,于是有图4图4sinA =CD AC =210=55.例5 2012宁波,Rt △ABC,∠C=900,AB=6,cosB=错误!,则BC 的长为 ;解析cosB=错误!=错误!,又∵AB=6∴BC=4例62012贵州铜仁如图,定义:在直角三角形ABC 中,锐角α的邻边与对边的比叫做角α的余切,记作ctan α, 即ctan α=BCAC=的对边角的邻边角αα,根据上述角的余切定义,解下列问题:1ctan30◦= ;2如图,已知tanA=43,其中∠A 为锐角,试求ctanA 的值.分析1可先设最小边长为一个特殊数这样做是为了计算方便,然后在计算出其它边长,根据余切定义进而求出ctan30◦;2由tanA=43,为了计算方便,可以设BC=3 AC=4根据余切定义就可以求出ctanA 的值.解析1设BC=1, ∵α=30◦∴AB=2∴由勾股定理得:AC=3ctan30◦=BCAC=32 ∵tanA=43∴设BC=3 AC=4∴ctanA =BC AC =34例72012山东滨州把△ABC 三边的长度都扩大为原来的3倍,则锐角A 的正弦函数值 A .不变B .缩小为原来的13C .扩大为原来的3倍D .不能确定 解析因为△ABC 三边的长度都扩大为原来的3倍所得的三角形与原三角形相似,所以锐角A 的大小没改变,所以锐角A 的正弦函数值也不变.答案选A .例82012湖南观察下列等式 ①sin30°= cos60°=②sin45°=cos=45°=③sin60°= cos30°=根据上述规律,计算sin 2a+sin 290°﹣a= .解析:根据①②③可得出规律,即sin 2a+sin 290°﹣a=1,继而可得出答案. 答案:解:由题意得,sin 230°+sin 290°﹣30°=1;sin 245°+sin 290°﹣45°=1; sin 260°+sin 290°﹣60°=1;故可得sin 2a+sin 290°﹣a=1.故答案为:1.点评:此题考查了互余两角的三角函数的关系,属于规律型题目,注意根据题意总结,另外sin 2a+sin 290°﹣a=1是个恒等式,同学们可以记住并直接运用.例9 2012山东德州为了测量被池塘隔开的A ,B 两点之间的距离,根据实际情况,作出如下图形,其中AB BE ⊥,EF BE ⊥,AF 交BE 于D ,C 在BD 上.有四位同学分别测量出以下四组数据:22题图①BC ,∠ACB ; ②CD ,∠ACB ,∠ADB ;③EF ,DE ,BD ;④DE ,DC ,BC .能根据所测数据,求出A ,B 间距离的有哪 组解析对于①,可由公式AB=BC ×tan ∠ACB 求出A 、B 两点间的距离;对于②,可设AB 的长为x,则BC=x tan ACB ∠,BD=xtan ADB ∠,BD-BC=CD,可解出AB .对于③,易知△DEF ∽△DBA,则DE BDEF AB=,可求出AB 的长;对于④无法求得,故有①、②、③三组点评此题考查解直角三角形和三角形相似的性质与判定.在直角三角形中至少要有已知一边和一角才能求出其他未知元素;判定两三角形相似的方法有:AA,SAS,SSS,两直角三角形相似的判定还有HL . 例102012江苏泰州18如图,在边长相同的小正方形组成的网格中,点A 、B 、C 、D 都在这些小正方形的顶点上,AB 、CD 相交于点P,则tan ∠APD 的值是 .解析 要求tan ∠APD 的值,只要将∠APD 放在直角三角形中,故过B 作CD 的垂线,然后利用勾股定理计算出线段的长度,最后利用正切的定义计算出结果即可. 答案作BM ⊥CD,DN ⊥AB 垂足分别为M 、N,则2,易得:10,设PM=x,则PD=22-x,由△DNP ∽△BMP,得:PN DN PM BM =,即10102PN x =,∴PN=55x,由DN 2+PN 2=PD 2,得:110+15x 2=22-x 2,解得:x 1=24,x 2=2舍去,∴tan ∠APD=2224BM PM ==2.例11. 2011江苏苏州如图,在四边形ABCD 中,E 、F 分別是AB 、AD 的中点,若EF=2,BC=5,CD=3,则tanC 等ABCDEFF于 .分析:根据三角形的中位线定理即可求得BD 的长,然后根据勾股定理的逆定理即可证得△BCD 是直角三角形,然后根据正切函数的定义即可求解.解答:解:连接BD .∵E 、F 分別是AB 、AD 的中点.∴BD=2EF=4∵BC=5,CD=3∴△BCD是直角三角形.∴tanC= 43例122011山东日照在Rt△ABC 中,∠C=90°,把∠A 的邻边与对边的比叫做∠A 的余切,记作cotA=ab.则下列关系式中不成立的是A .tanA•cotA=1B .sinA=tanA•cosAC .cosA=cotA•sinAD .tan 2A+cot 2A=1解答:解:根据锐角三角函数的定义,得 A 、tanA•c otA=a b b a ⋅=1,关系式成立;B 、sinA=c a ,tanA•cosA=cac b b a =⋅,关系式成立; C 、cosA=,cotA•sinA=c b a b c a =⋅,关系式成立;D 、tan 2A+cot 2A=b a 2+ab 2≠1,关系式不成立.故选D .点评:本题考查了同角三角函数的关系.1平方关系:sin 2A+cos 2A=1 2正余弦与正切之间的关系积的关系:一个角的正切值等于这个角的正弦与余弦的比,即tanA=BAcos sin 或sinA=tanA•cosA.3正切之间的关系:tanA•tanB=1. 例132011•贵港如图所示,在△ABC 中,∠C=90°,AD 是BC 边上的中线,BD=4,AD=2,则tan∠CAD 的值是 .解答:解:∵AD 是BC边上的中线,BD=4,∴CD=BD=4,在Rt△ACD中,AC===2,∴tan∠CAD===2.故选A .例142011烟台如果△ABC 中,sin A =cos B 2,则下列最确切的结论是 A. △ABC 是直角三角形 B. △ABC 是等腰三角形C. △ABC 是等腰直角三角形D. △ABC 是锐角三角形 解:∵sinA=cosB=22,∴∠A =∠B =45°,∴△ABC 是等腰直角三角形.故选C . 例152011四川如图所示,在数轴上点A 所表示的数x 的范围是A 、330sin 602sin x ︒︒<< B 、3cos302x ︒︒<<cos45C 、3tan 302x ︒︒<<tan45D 、3cot 4502x ︒︒<<cot3 解答:故选D .同步练习12011甘肃如图,A 、B 、C 三点在正方形网格线的交点处,若将△ACB 绕着点A 逆时针旋转得到△AC ’B ’,则tanB ’的值为 .解答:解:过C 点作CD ⊥AB ,垂足为D .根据旋转性质可知,∠B′=∠B .在Rt△BCD 中,tanB= CD :BD =13,∴tan B′=tan B = 13. 2 2011甘肃兰州点M -sin60°,cos60°关于x 轴对称的点的坐标是 . 解:∵sin60°=32,cos60°= 12,∴点M -32,12.∵点P m ,n 关于x 轴对称点的坐标P′m ,-n ,∴M 关于x 轴的对称点的坐标是-32,-12.故选B . 32011广东已知:45°<A <90°,则下列各式成立的是A 、sinA =cosAB 、sinA >cosAC 、sinA >tanAD 、sinA <cosA解答:解:∵45°<A <90°,∴根据sin 45°=cos 45°,sinA 随角度的增大而增大,cosA 随角度的增大而减小,当∠A >45°时,sinA >cosA ,故选:B .4、2011•宜昌教学用直角三角板,边AC=30cm,∠C=90°,tan∠BAC=33,则边BC 的长为 .cm解:在直角三角形ABC 中,根据三角函数定义可知:tan ∠BAC=BCAC,又AC=30cm,tan ∠3则BC=ACtan 33cm .故选C . 5、 2011福建莆田如图,在矩形ABCD 中,点E 在AB 边上,沿CE 折叠矩形ABCD ,使点B 落在AD 边上的点F 处,若AB =4,BC=5,则tan ∠AFE 的值为 .ABCC ’ B ’解答:解:∵四边形ABCD 是矩形,∴∠A =∠B =∠D =90°,CD =AB =4,AD =BC =5,由题意得:∠EFC =∠B =90°,CF =BC =5,∴∠AFE +∠DFC =90°,∠DFC +∠FCD =90°, ∴∠DCF =∠AFE ,∵在Rt △DCF 中,CF =5,CD =4,∴DF =3,∴tan ∠AFE =tan ∠DCF =DFDC =34 .6、2012连云港小明在学习“锐角三角函数”中发现,将如图所示的矩形纸片ABCD 沿过点B的直线折叠,使点A 落在BC 上的点E 处,还原后,再沿过点E 的直线折叠,使点A 落在BC 上的点F 处,这样就可以求出°的角的正切值是 .EC DA BF答案设AB=x,则BE=x,在直角三角形ABE 中,用勾股定理求出AE=EF=2x,于是2在直角三角形ABF 中,tan ∠FAB=21)BF xAB x=2°.选B; 7、2012福州如图15,已知△ABC,AB=AC=1,∠A=36°,∠ABC 的平分线BD 交AC 于点D,则AD 的长是 ,cosA 的值是 .结果保留根号解析:由已知条件,可知△BDC 、△ADB 是等腰三角形,且DA=DB=BC,可证△BDC ∽△ABC,则有BC DC AC BC =,设BC=x,则DC=1-x,因此21,101x xx x x -=+-=即,解方程得, 125151x x ---==,舍去,即AD=512;又cosA=512451512AB AD===--⨯答案:5151,24 8、2012南京如图,将45°的∠AOB 按下面的方式放置在一把刻度尺上:顶点O 与尺下沿的端点重合,OA 与尺下沿重合.OB 与尺上沿的交点B 在尺上的读书恰为2厘米,若按相同的方式将37°的∠AOC 放置在该刻度尺上,则OC 与尺上沿的交点C 在尺上的读数为 厘米.结果精确到厘米,参考数据sin370≈,cos370≈,tan370≈C B AO4321解析:由于∠AOB=45°,B 点读书为2厘米,则直尺的宽为2厘米,解直角三角形得点C 的读数为2÷tan370≈2÷≈厘米.答案:9、2012·湖南张家界黄岩岛是我国南海上的一个岛屿,其平面图如图甲所示,小明据此构造出该岛的一个数学模型如图乙所示,其中∠A=∠D=90°,AB=BC=15千米,CD=23千米,请据此解答如下问题:1 求该岛的周长和面积结果保留整数,参考数据2≈ 73.13≈45.26≈ 2 求∠ACD 的余弦值.解答1结AC,∵AB=BC=15千米,∠B=90°,∴∠BAC=∠ACB=45°,AC=152千米. 又∵∠D=90°, ∴AD=2222)23()215(-=-CD AC =123千米∴周长=AB+BC+CD+DA=30+32+123=30++≈55千米. 面积=S △ABC +S △ADC =21×15×15+21×123×32=2225+186≈157平方千米. 2cos ∠ACD=5121523==AC CD . 10、2012甘肃兰州在建筑楼梯时,设计者要考虑楼梯的安全程度;如图1,虚线为楼梯的倾斜度,斜度线与地面的夹角为倾角θ,一般情况下,倾角越小,楼梯的安全程度越高;如图2,设计者为了提高楼梯的安全程度,要把楼梯的倾角1θ减至2θ,这样楼梯占用地板的长度由d 1增加到d 2 ,已知d 1=4米,140θ∠=,236θ∠=,楼梯占用地板的长度增加了多少米 计算结果精确到米;参考数据:tan40°=,tan36°=AC解析:根据在Rt△ACB中,AB=d1tanθ1=4tan40°,在Rt△ADB中,AB=d2tanθ2=d2tan36°,即可得出d2的值,进而求出楼梯占用地板增加的长度.解:由题意可知可得,∠ACB=∠θ1,∠ADB=∠θ2在Rt△ACB中,AB=d1tanθ1=4tan40°,在Rt△ADB中,AB=d2tanθ2=d2tan36°,得4tan40°=d2tan36°,∴d2=4tan40tan36≈,∴d2-d1==≈,答:楼梯占用地板的长度增加了米.11、2012贵州为促进我市经济的快速发展,加快道路建设,某高速公路建设工程中需修隧道AB,如图,在山外一点C测得BC距离为200m,∠CAB=54°,∠CBA=30°,求隧道AB的长.参考数据:sin54°≈,cos54°≈,tan54°≈,≈,精确到个位解析:首先过点C作CD⊥AB于D,然后在Rt△BCD中,利用三角函数的知识,求得BD,CD的长,继而在Rt△ACD 利用∠CAB的正切求得AD的长,继而求得答案.答案:解:过点C作CD⊥AB于D∵BC=200m,∠CBA=30°,∴在Rt△BCD中,CD=BC=100m,BD=BC•cos30°=200×=100≈173m,∵∠CAB=54°,在Rt△ACD中,AD=≈≈74m,∴AB=AD+BD=173+74=247m.答:隧道AB的长为247m.12、2011新疆建设兵团如图,在△ABC中,∠A=90°.1用尺规作图的方法,作出△ABC绕点A逆时针旋转45°后的图形△AB1C1保留作图痕迹;2若AB=3,BC=5,求tan∠AB1C1.第22题图d2解答:解:1作∠CAB 的平分线,在平分线上截取AB 1=AB ,作C 1A ⊥AB 1,在AC 1上截取AC 1=AC ,如图所示即是所求.2∵AB =3,BC =5,∴AC =4,∴AB 1=3,AC 1=4,tan∠AB 1C 1=错误!=错误!. 专题2 特殊角的三角函数值例12012,湖北孝感计算:cos 245°+tan30°·sin60°=________.答案1例22012陕西计算:(02cos 45-38+1-2=︒ .解析原式2=2-322+1=-52+12⨯⨯答案-52+1 例32012广安计算:---)32(218cos45o +13- ; 解析:1182()cos 4533---︒+=322212323+-+21 例4 计算|-3|+2cos 45310. 解:原式=3+22-122. 例5 计算-12⎛⎫- ⎪⎝⎭9+-12007-cos 60°.解:原式=12+3+-1-12=3-1=2. 例6 计算|2+cos 60°-tan 30°08 21十+221. 例7 计算312-⎛⎫ ⎪⎝⎭-π-0-|1-tan 60°|32-.解:原式=8-13132=10. 例82012呼和浩特计算:11|122sin 45--+︒解析三角函数、绝对值、乘方答案11|12sin 45--+︒11)2211232=-+=+=例92011天水计算:si n 230°+tan 44°tan 46°+si n 260°= . 分析:根据特殊角的三角函数值计算.tanA •tan 90°﹣A =1. 解答:解:原式=14+1+34=2.故答案为2. 例102011•莱芜若a=3﹣tan60°,则196)121(2-+-÷--a a a a = ;33-解答:解:a=3﹣tan60°=3﹣3,∴原式=23-a 1-a 121)(⨯---a a =31-a =33313331-=-=--故答案为:33-. 练习1、2011浙江计算:|-1|5-π0+4cos45°. 解原式=1-122练习2、2011浙江衢州1计算:|﹣2|﹣3﹣π0+2c os45°;解答:解:1原式=2122-+⨯,=1 练习3、计算:20110+8-2sin45°;原式=1+22-2=1+2;练习3、观察下列各式:①sin 59°>sin 28°;②0<cos α<1α是锐角;③tan 30°+tan 60°=tan 90°;④tan 44°<1.其中成立的有A .1个B .2个C .3个D .4个 练习3、C 提示:sin 59°>sin 28°成立,0<cos α<1α是锐角成立,tan 30°+tan 60tan 90°,tan 44°<tan 45°,即tan 44°<1.练习4、计算2sin 30°-tan 60°+tan 45°= .练习5、如图28-146所示,在△ABC 中,∠A =30°,tan B =13,BC 10则AB 的长为 . 练习6、当x =sin 60°时,代数式2242x x x -+·22244x x x x +-++42xx-的值是 .练习7、已知cos 59°24′≈,则sin 30°36′≈ .练习8、若∠A ,∠B 互余,且tan A -tan B =2,则tan 2A +tan 2B = .练习9、如图28-147所示,在菱形ABCD 中,AE ⊥BC 于E ,EC =1,cos B=513,则这个菱形的面积是 . 10.已知正方形ABCD 的边长为1,若将线段BD 绕着点B 旋转后,点D落在DC 延长线上的点D ′处,则∠BAD ′的正弦值为 . 11.如图28-148所示,若将四根木条钉成的矩形木框变为平行四边形ABCD 的形状,并使其面积为矩形面积的一半,则这个平行四边形的一个最小内角等于 .12.在△ABC 中,∠B =30°,tan C =2,AB =2,则BC = .13.设θ为锐角,且x 2+3x +2sin θ=05.则θ= . 14.如图28-149所示,在△ABC 中,∠C =90°,点D 在BC 边上,BD =4,AD =BC ,cos ∠ADC =35. 1求DC 的长;2求sin B 的值.练习4、23 提示:2sin 30°-tan 60°+tan 45°=2×1231=23 练习5、33提示:过点C 作CD ⊥AB ,垂足为D ,在Rt △BDC 中,tan B =13.∴13CD BD =,∴BD =3CD ,∵BC 10∴CD 2+3CD 210,∴CD =1,BD =3.在Rt △ADC 中,tan A =CDAD,∴AD 3∴AB =AD +BD =33 练习632242x x x -+·22244x x x x +-++42xx-=2x ,∴原式=2sin 603练习7、提示:sin 30°36′=cos 59°24′.练习8、6提示:∵∠A ,∠B 互余,∴tan A ·tan B =1,tan 2A +tan 2B =tan A -tan B 2+2tan A ·tan B =22+2=6. 练习9、3916提示:∵cos B =513,设BE =5x ,则AB =13x ,∴AE 22AB BE -12x .∵AB =BC =BE +CE ,∴13x =5x +1,∴x =18,则AE =12x =12×18=32,BC =5x +1=5×18+1=138,∴S =32×138=3916.10.5提示:如图28-155所示,根据题意得DD ′=2DC ,设正方形的边长为x ,则AD =x ,DD ′=2x .∵∠ADD ′=90°,根据勾股定理得AD 22AD DD '+5x .∵AD =x ,∴sin ∠AD ′D =ADAD '=555x x=.∵AB ∥DD ′,∴∠BAD ′=∠AD ′D ,∴sin ∠BAD ′=55.11.30°提示:如图28=156所示,∵S ABCD=12S 矩形BEFC ,且BC =BC 底相同, ∴GC =12FC .∵CF =DC ,∴GC =12DC ,12CG DC =.∵∠DGC =90°,sin 30°=12,∴∠CDG =30°,即这个平行四边形的一个最小内角为30°. 12.12+3 13.30°提示:x 1·x 2=2sin θ,x 1+x 2=-3,则x 1-x 22=x 1+x 22-4x 1x 2=9-8sin θ=52,∴sin θ=12,∴θ=30°. 14.解:1∵cos ∠ADC =35,∴设CD =3x ,则AD =5x ,AC =4x ,∴BC =AD =5x .∵BD =BC-CD ,∴5x -3x =4,∴x =2,∴CD =3x =6. 2∵AC =4x =8,BC =5x =10,∴AB =2222810241AC BC +=+=,∴sin B =844141241AC AB ==. ★ 专题三:题型一俯角与仰角仰角:视线在水平线上方的角;★ 俯角:视线在水平线下方的角;仰角铅垂线水平线视线视线俯角例1、2012湖北襄阳在一次数学活动中,李明利用一根拴有小锤的细线和一个半圆形量角器制作了一个测角仪,去测量学校内一座假山的高度CD .如图5,已知李明距假山的水平距离BD 为12m,他的眼睛距地面的高度为,李明的视线经过量角器零刻度线OA 和假山的最高点C,此时,铅垂线OE 经过量角器的60°刻度线,则假山的高度为 m .解析如下图,过点A 作AF⊥CD 于F,则AF =BD =12m,FD =AB =.再由OE∥CF 可知∠C=∠AOE=60°.所以,在Rt△ACF 中,CF =tan 60AF=43,那么CD =CF +FD =43+m .例2、2012珠海如图,水渠边有一棵大木瓜树,树干DO 不计粗细上有两个木瓜A 、B 不计大A O BE D CF图5 CDA BO E小,树干垂直于地面,量得AB=2米,在水渠的对面与O 处于同一水平面的C 处测得木瓜A 的仰角为45°、木瓜B 的仰角为30°.求C 处到树干DO 的距离CO.结果精确到1米参考数据:41.12,73.13≈≈第16题图D BA OC解析如图,根据题意,得∠COD =90°, ∠ACO =45°, ∠BCO =30°, AB =2,求CO.设CO 为x 米, 根据AO =CO,列方程,解得即可.答案解:设CO 为x 米在Rt △BCO 中,tan30°=BO CO ,则BO =33x 在Rt △ACO 中,AO =CO,得方程33x +2=x 解得x ≈5.答: CO 长大约是5米. 例3、2012江苏盐城如图所示,当小华站立在镜子EF 前A 处时,他看自己的脚在镜中的像的俯角为450 :如果小华向后退米到B 处,这时他看自己的脚在镜中的像的俯角为300.求小华的眼睛到地面的距离;结果精确到米,参考数据:3≈.答案设AC=BD=x,在Rt △ACA 1中,∠AA 1C=450,∴AA 1=x,在Rt △DBB 1中,BB 1=tan30x=3x ,又∵12BB 1-12AA 1=12,即12×3x -12x=12,解得:x=312+≈米. 例4、2012山西如图,为了开发利用海洋资源,某勘测飞机预测量一岛屿两端A .B 的距离,飞机在距海平面垂直高度为100米的点C 处测得端点A 的俯角为60°,然后沿着平行于AB 的方向水平飞行了500米,在点D 测得端点B 的俯角为45°,求岛屿两端A .B 的距离结果精确到米,参考数据:解析解:过点A 作AE⊥CD 于点E,过点B 作BF⊥CD 于点F,∵AB∥CD,∴∠AEF=∠EFB=∠ABF=90°,∴四边形ABFE 为矩形.第24题图∴AB=EF,AE=BF.由题意可知:AE=BF=100米,CD=500米.…2分 在Rt△AEC 中,∠C=60°,AE=100米.∴CE===米. …4分在Rt△BFD中,∠BDF=45°,BF=100. ∴DF===100米.…6分∴AB=EF=CD+DF﹣CE=500+100﹣≈600﹣×≈600﹣≈米. …8分答:岛屿两端A .B 的距离为米.例5、2012呼和浩特22如图,线段AB 、DC 分别表示甲、乙两建筑物的高;某初三课外兴趣活动小组为了测量两建筑物的高,用自制测角仪在B 处测得D 点的仰角为α,在A 处测得D 点的仰角为β;已知甲、乙两建筑物之间的距离BC 为m ;请你通过计算用含α、β、m 的式子分别表示出甲、乙两建筑物的高度;答案解:过点A 作AM ⊥CD 于M在Rt △BCD 中,tan α=CD BC ∴CD =BC ·tan α=m tan α在Rt △AMD 中,tan β=DMAM∴DM =AM ·tan β=m tan β∴AB =CD –DM =mtan α–tan β例6、2012湖北随州,20在一次暑假旅游中,小亮在仙岛湖的游船上A 处,测得湖西岸的山峰太婆尖C 处和湖东岸的山峰老君岭D 处的仰角都是45°,游船向东航行100米后B 处,测得太婆尖、老君岭的高度为多少米3 1.732 ,结果精确到米;解析:设太婆尖高h 1米,老君岭高h 2米;可分别在直角三角形中利用正切值表示出水平线段的长度,再利用移动距离为AB=100米,可建立关于h 1、h 2的方程组,解这个方程组求得两山峰高度;答案:设太婆尖高h 1米,老君岭高h 2米,依题意,有FE第20题图60304545D (老君岭)C (太婆尖)BAβα乙甲ADB M C⇒⎪⎪⎩⎪⎪⎨⎧=-=-10060tan 45tan 10045tan 30tan 2211h h h h 1376.136)1732.1(50)13(5045tan 60tan 1001≈=+=+=-=h 米33110030tan 45tan 1002-=-=h 2376.236)732.13(50)33(50)13(350≈=+=+=+=米答:太婆尖高度为137米,老君岭高度为237米;题型二方位角问题1、从某点的指北方向按顺时针转到目标方向的水平角,叫做方位角;如图3,OA 、OB 、OC 、OD 的方向角分别是:45°、135°、225°;2、指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角;如图4:OA 、OB 、OC 、OD 的方向角分别是:北偏东30°东北方向,南偏东45°东南方向,南偏西60°西南方向,北偏西60°西北方向;例1、2011山东省潍坊轮船从B 处以每小时海里的速度沿男偏东30°方向匀速航行,在B 处观测灯塔A 位于南偏东75°方向上,轮船航行半小时到达C 处,在观测灯塔A 北偏东60°方向上,则C 处与灯塔A 的距离是 .海里解答: BC=50×=25海里;根据方位角知识得,∠BCD=30°,=75°-30°;CB=∠BCD+∠ACD=30°+60°=90°;∠A=∠CBD=45°所以CA=CB 所以CB=25海里例2、2012年四川德阳某时刻海上点P 处有一客轮,测得灯塔A 位于客轮P 的北偏东30°方向,且相距20海里.客轮以60海里/小时的速度沿北偏西60°方向航行32小时到达B 处,那么tan ∠ABP=A.21 C.55 D.552解析如图6所示,根据题意可知∠APB=90°.且AP=20, PB=60×23=40. 所以tan ∠ABP=201402PA PB ==例3、2012连云港已知B 港口位于A 观测点北偏东°方向,且其到A 观测点正北方向的距离BD 的长为16km;一艘货轮从B 港口以40km/h 的速度沿如图所示的BC 方向航行,15min 后到达C 处;现测得C 处位于A观测点北偏东°方向;求此时货轮与A 观测点之间的距离AC 的长精确到.25东北CBDCBH解析过点B 作AC 的垂线,把所求线段AC 换为两线段的差;利用Rt △ABH 和Rt △BCH 求线段AH 、CH 的长,利用AH -CH 确定AC 的长; 答案BC=40×1560=10.在Rt△ADB 中,sin ∠DAB=DB AB , °≈;所以AB=DAB DB ∠sin ≈1.60.8=20.如图,过点B 作BH⊥AC,交AC 的延长线于H;在Rt△AHB 中,∠BAH=∠DAC -∠DAB=°―37°=°,tan∠BAH=BH AH ,=BH AH,AH =+CH 2=AB 2,BH 2+2BH 2=2025所以AH=85,在Rt△AHB 中, BH 2+CH 2=BC 2,CH=2108025-=所以第22题图APCB °°AC=AH―CH=85―25=65≈.例4、2012四川攀枝花如图6,我渔政310船在南海海面上沿正东方向匀速航行,在A地观测到我渔船C在东北方向上的我国某传统渔场.若渔政310船航向不变,航行半小时后到达B 处,此时观测到我渔船C在北偏东30°方向上.问渔政310船再航行多久,离我渔船C的距离最近假设我渔船C捕鱼时移动距离忽略不计,结果不取近似值.答案作CD⊥AB于D,设BD=x,∵∠BCD=30°,∴CD=3x,因为∠CAD=45°,∴AD=CD3,AB3–x,依据题意3x–x=,x 31+,31+小时,离渔船C的距离最近;例5、2012山东东营如图某天上午9时,向阳号轮船位于A处,观测到某港口城市P位于轮船的北偏西°,轮船以21海里/时的速度向正北方向行驶,下午2时该船到达B处,这时观测到城市P位于该船的南偏西°方向,求此时轮船所处位置B 与城市P的距离参考数据:°≈35,°≈34,°≈1213,°≈125解析过点P作PC⊥AB,构造直角三角形,设PC=x海里,用含有x的式子表示AC,BC的值,从而求出x的值,再根据三角函数值求出BP的值即可解答.答案过点P作PC⊥AB,垂足为C,设PC=x海里.在Rt△APC中,∵tan∠A=PCAC,∴AC=5tan67.512PC x=︒.在Rt△PCB中,∵tan∠B=PCBC,∴BC=4tan36.93x x=︒.∵AC+BC=AB=21×5,∴54215123x x+=⨯,解得60x=.∵sinPCBPB∠=,∴60560100sin sin36.93PCPBB===⨯=∠︒海里.∴向阳号轮船所处位置B与城市P的距离为100海里.例6、2012山东省青岛如图,某校教学楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,教学楼在建筑物的墙上留下高2米的影子CE ;而当光线与地面夹角是45°时,教学楼顶A 在地面上的影子F 与墙角C 有13米的距离B 、F 、C 在一条直线上 ⑴求教学楼AB 的高度;⑵学校要在A 、E 之间挂一些彩旗,请你求出A 、E 之间的距离结果保留整数.参考数据:sin22°≈错误!,cos22°≈错误!,tan22°≈错误! 答案解:⑴过点E 作EM ⊥AB,垂足为M.设AB 为x.Rt △ABF 中,∠AFB=45°,∴BF=AB=x,∴BC=BF+FC=x+13在Rt △AEM 中,∠AEM=22°,AM=AB-BM=AB-CE=x-2,∴tan22°= 错误!, 错误!=错误!,x=12.即教学楼的高12m.⑵由1可得ME=BC=x+13=12+13=25.在Rt △AME 中,cos22°= 错误!, ∴AE= 错误!≈ 错误!≈27.即AE之间的距离约为27m.题型三、坡比是垂直高度与水平距离的比值,即是坡角的正切值应用举例: 坡面的铅直高度h 和水平宽度l 的比叫做坡度坡比;用字母i 表示,即hi l=;坡度一般写成1:m 的形式,如1:5i =等;把坡面与水平面的夹角记作α叫做坡角,那么tan hi lα==;例1、2012广安如图2,某水库堤坝横断面迎水坡AB 的坡比是1:3,堤坝高BC=50m,则迎水坡面AB 的长度是 .m解:tan∠BAC=13,∠BAC=30°,sin∠BAC=12, sin∠BAC=BC AB ,AB=2BC=100m例2、小强在教学楼的点P 处观察对面的办公大楼.为了测量点P 到对面办公大楼上部AD的距离,小强测得办公大楼顶部点A 的仰角为45°,测得办公大楼底部点B 的俯角为60°,已知办公大楼高46米,CD =10米.求点P 到AD 的距离用含根号的式子表示.图2:i h l=hlαABCDPN M解析连结PA 、PB ,过点P 作PM ⊥AD 于点M ;延长BC ,交PM 于点N则∠APM =45°,∠BPM =60°,NM =10米………1分设PM =x 米 在Rt △PMA 中,AM =PM ×tan ∠APM =x tan 45°=x 米…3分在Rt △PNB 中,BN =PN ×tan ∠BPM =x -10tan 60°=x -103米…5分 由AM +BN =46米,得x +x -103 =46……6分解得,4610313x +=+ ,∴点P 到AD 的距离为4610313++米.结果分母有理化为()1838-米也可……8分答案4610313++结果分母有理化为()1838-米也可例3、2012湖北如图,某公园入口处原有三级台阶,每级台阶高为18cm,深为30cm,为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A ,斜坡的起始点为C ,现设计斜坡BC 的坡度1:5i =,则AC 的长度是 cm .解析如图,过点B 作BD ⊥AC 于D,依题意可求得AD =60cm,BD =54cm ;由斜坡 BC 的坡度i =1:5,求得CD =270cm,故AC =CD -AD =270-60=210cm .例4、2012浙江省绍兴,19如图1,某超市从一楼到二楼的电梯AB 的长为米,按坡角∠BAC 为32°.1求一楼与二楼之间的高度BC 精确到米;2电梯每级的水平级宽均是米,如图2.小明跨上电梯时,该电梯以每少上升2级的高度运行,10秒后他上升了多少米精确到米 备用数据:sin 32°=,cos 32°=,tan 32°=.解析1在Rt△ABC 中,已知∠B AC=32°,斜边AB 的长为米,根据锐角三角函数的定义即可求得第20题图MPDCBA第12题A BC3018一楼与二楼之间的高度BC .2先计算1级电梯的高,再根据10秒钟电梯上升了20级可计算10秒后他上升的高度.答案解:1∵sin ∠BAC =ABBC ,∴BC =AB ×sin32°=×≈米. 2∵tan32°= 级高级宽,∴级高=级宽×tan32°=×=,∵10秒钟电梯上升了20级,∴小明上升的高度为:20×米. 例5、2012浙江丽水,19学校校园内有一小山坡,经测量,坡角∠ABC=30°,斜坡AB 长为12米.为方便学生行走,决定开挖小山坡,使斜坡BD 的坡比是1:3即为CD 与BC 的长度之比,A,D 两点处于同一铅垂线上,求开挖后小山坡下降的高度AD.解析:∴AD=AC-CD=6-23.答:开挖后小山坡下降的高度AD 为6-23米.例6、2012深圳小明想测一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图3,此时测得地面上的影长为8米,坡面上的影长为4米,已知斜坡的坡角为30,同一时刻,一根长为1米、垂直于地面放置的标杆在地面上的影长为2米,则树的高度为 .米解答:如图3—1,根据坡角易求树的下半部分的高为2米,树的上半部分所在直角三角形的水平距离为(+823米,由两个直接三角形相似易求树的上半部分高度为(43米,知树的高度为()63米,选择A例72012江苏泰州24如图,一居民楼底部B 与山脚P 位于同一水平线上,小李在P 处测得居民楼顶A 的仰角为60°,然后他从P 处沿坡角为45°的山坡上走到C 处,这时,PC=30m,点C 与点A 在同一水平线上,A 、B 、P 、C 在同一平面内.1求居民楼AB 的高度;2求C 、A 之间的距离.精确到,参考数据:2≈,3≈,6≈60° CA B 45°图330°21图3-1第24题图解析过C作BP的垂线,垂足为G,利用特殊Rt△PCG和Rt△ABP中的边角关系,我们容易计算出CG即AB的长,最后用AC=BP+PG,就是C、A之间的距离.答案1过C作BP的垂线,垂足为G,在Rt△PCG中,CG=PCsin450=30×2所以=m2PG= PCcos450=30×2=所以C、A之间的距离例82012四川水务部门为加强防汛工作,决定对某水库大坝进行加固,大坝的横截面是梯形ABCD.如图9所示,已知迎水坡面AB的长为16米,∠B=60°,背水坡面CD的长为,加固后大坝的横截面为梯形ABED,CE的长为8米.1已知需加固的大坝长为150米,求需要填土石方多少立方米2求加固后大坝背水坡面DE的坡度.解析1求出横截面△DCE的面积,然后乘以坝堤长度即可得出体积.可以分别过点A,D 作BC边上的高将问题转化为解直角三角形问题.2求大坝背水坡面DE的坡度就是求坡面DE上一点到BE的铅直高度与它到点E的水平宽度的比,这一点通常取梯形的顶点.答案解:1过点A作AG⊥BC于G,过点D作DH⊥BC于H,∴AG=DH.在Rt△ABG中,AG=sin60°·AB×16=∴DH=S△DCE=12·DH·CE=12×8=∴需要填土石方150=3.2在Rt△DHC中,HC24,∴HE=HC+CE=24+8=32.∴加固后大坝背水坡面DE的坡度=DHHE.AB CD图9E例9 2012江苏苏州如图,已知斜坡AB 长60米,坡角即∠BAC 为30°,BC⊥AC,现计划在斜坡中点D 处挖去部分坡体用阴影表示修建一个平行于水平线CA 的平台DE 和一条新的斜坡BE .请讲下面2小题的结果都精确到米,参考数据:≈.1若修建的斜坡BE 的坡角即∠BEF 不大于45°,则平台DE 的长最多为 米;2一座建筑物GH 距离坡角A 点27米远即AG=27米,小明在D 点测得建筑物顶部H 的仰角即∠HDM 为30°.点B 、C 、A 、G 、H 在同一个平面内,点C 、A 、G 在同一条直线上,且HG⊥CG,问建筑物GH 高为多少米解答: 解:1∵修建的斜坡BE 的坡角即∠BEF 不大于45°,∴∠BEF 最大为45°当∠BEF=45°时,EF 最短,此时ED 最长,∵∠DAC=∠BDF=30°,AD=BD=30,∴BF=EF=BD=15,DF=15,故:DE=DF ﹣EF=15﹣1≈;2过点D 作DP⊥AC,垂足为P .在Rt△DPA中,DP=AD=×30=15,PA=AD•cos30°=×30=15. 在矩形DPGM 中,MG=DP=15,DM=PG=15+27,在Rt△DMH 中,HM=DM•tan30°=×15+27=15+9. GH=HM+MG=15+15+9≈.答:建筑物GH 高为米.A B C DE GH。
二次函数复习总结题

二次函数复习题一. 选择题1.将二次函数y=x 2-2x+3化为y=(x-h)2+k 的形式,结果为( ) A.y=(x+1)2+4 B.y=(x-1)2+4 C. y=(x+1)2+2 D. y=(x-1)2+22.若二次函数y=ax 2+bx-1(a ≠0)的图象经过点(1,1),则代数式1-a-b 的值为( ) A. -3 B.-1 C.2 D.53.若二次函数y=kx 2-6x+3的图象与x 轴有公共点,则k 的取值范围是( ) A. k <3 B.k <3且k ≠0 C.k ≤3 D. k ≤3且k ≠04.二次函数y=ax 2+bx+c 的图象如图所示,则点(ac,bc )在( ) A.第一象限 B. 第二象限 C.第三象限 D.第四象限5.抛物线y=ax 2+bx+c 的顶点为D(-1,2) 与x 轴的一个交点A 在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论: ①b 2-4ac <0;②a+b+c <0;③c-a=2;④方程ax 2+bx+c-2=0有两个相等的实数根. 其中正确结论的个数为( )A .1个B .2个C .3个D .4个6.已知二次函数y=ax 2+bx+c 中y 与x 的部分对应值如下表, 则下列判断中 正确的是( )A .抛物线开口向上B .抛物线与y 轴交于负半轴C .当x=4时,y >0D .方程ax 2+bx+c=0的正根在3与4之间7.若A (-4,y 1),B (-3,y 2),C (-2,y 3)为二次函数y=x 2+4x-5的图象上的三点, 则y1,y 2,y 3的大小关系是( )A. y 3<y 2<y 1 B .y 2<y 1<y 3 C .y 3<y 1<y 2 D .y 1<y 3<y 2第4题第5题8.如图,两条抛物线y 1=-12x 2+1,y 2=-12x 2-与分别经过点(-2,0),(2,0)且平行于y 轴的两条平行线围成的阴影部分的面积为( ) A. 8 B.6 C.10 D.49.如图,正方形ABCD 的边长为4cm,动点P,Q 同时从点A 出发,以1cm/s 的速度分别沿A →B →C 和A →D →C 的路径向点C 运动,设运动时间为x (单位:s ),四边形PBDQ 的面积为y(单位:cm 2),则y 与x (0≤x ≤8)之间函数关系可以用图象表示为( )10.如图,正方形ABCD 的边长为3cm ,动点P 从B 点出发以3cm/s 的速度沿着边BC —CD —DA 运动,到达A 点停止运动;另一动点Q 同时从B 点出发以1cm/s 的速度沿着边BA 向A点运动,到达A 点停止运动,设P 点运动时间为x(s),⊿BPQ 的面积为y(cm 2),则y 关于x 的函数图象是 ( )A .B .C .D .11. 已知抛物线y=ax 2+bx 和直线y=ax+b 在同一坐标系内的图象如图,其中正确的( )A .B .C .D .12. 已知两点A(-5,y 1),B(3,y 2)均在抛物线y=ax 2+bx+c(a ≠0)上,点C(x ,y)是该抛物线的顶点.若y 1>y 2≥y ,则x 的取值范围是( ) A.x >-5 B.x >-1 C.-5<x <-1 D.-2<x <313.如图在Rt △ABC 中,AC=BC=2,正方形CDEF 的顶点D,F 分别在AC 、BC 边上, C 、D 两点不重合,设CD 的长度为x ,△ABC 与正方形CDEF 重叠部分的面积为y ,则下列图象中能表示y 与x 之间的函数关系的是( )A. B. C. D.14.在同一平面直角坐标系中,函数y=mx+m 和函数y=-mx2+2x+2(m 是常数,且m ≠0)的图象可能是( )15.已知二次函数y=ax 2+bx+c (a ≠0)的图象如图,且关于x 的一元二次方程ax 2+bx +c -m=0没有实数根,有下列结论:①b 2-4ac >0;②abc <0;③m >2.其中,正确结论的个数是( )A.0B.1C.2D.3二.填空题2的图象与x 轴的交点如图所示,根据图中信息可得到m 的值是 ,17.若把抛物线y=-x 2先向左平移1个单位长度,再向上平移3个长度单位,则平移后抛物线的解析式为 ,18.抛物线y=2(x-2)2-6的顶点为C ,已知y=-kx+3的图象经过点C ,则这个一次函数图象与两坐标轴所围成的三角形面积为 ,19. 某种爆竹点燃后,其上升高度h (m )和时间t (s )符合关系式 . h=v 0t-gt2(0<t≤2),其中重力加速度g 以10m/s 2计算.这种爆竹点燃后以v 0=20m/s 的初速第16题度上升,在爆竹点燃后的2.1s至2.3s这段时间内,爆竹是 (填“上升”或“下降”)20.已知点A(X1,y2),B(X2,y2)在二次函数y=(x-1)2+1的图象上,若x1>x2>1,则y1()y2(填“>”、“<”或“=”)。
二次函数知识点复习

二次函数知识点一、二次函数概念:1.二次函数的概念:一般地,形如2y ax bx c =++(a b c ,,是常数,0a ≠)的函数,叫做二次函数。
这里需要强调:和一元二次方程类似,二次项系数0a ≠,而b c ,可以为零.二次函数的定义域是全体实数.2. 二次函数2y ax bx c =++的结构特征:⑴ 等号左边是函数,右边是关于自变量x 的二次式,x 的最高次数是2.⑵ a b c ,,是常数,a 是二次项系数,b 是一次项系数,c 是常数项. 二、二次函数的基本形式1. 二次函数基本形式:2y ax =的性质: a 的绝对值越大,抛物线的开口越小。
2. 2y ax c =+的性质: 上加下减。
3. ()2y a x h =-的性质:左加右减。
a 的符号开口方向 顶点坐标 对称轴 性质0a >向上()00, y 轴0x >时,y 随x 的增大而增大;0x <时,y 随x 的增大而减小;0x =时,y 有最小值0.0a < 向下()00,y 轴0x >时,y 随x 的增大而减小;0x <时,y 随x 的增大而增大;0x =时,y 有最大值0.a 的符号开口方向 顶点坐标 对称轴 性质0a >向上()0c , y 轴0x >时,y 随x 的增大而增大;0x <时,y 随x 的增大而减小;0x =时,y 有最小值c .0a < 向下()0c ,y 轴0x >时,y 随x 的增大而减小;0x <时,y 随x 的增大而增大;0x =时,y 有最大值c .a 的符号开口方向 顶点坐标 对称轴 性质0a >向上()0h , X=hx h >时,y 随x 的增大而增大;x h <时,y 随x 的增大而减小;x h =时,y 有最小值0.0a < 向下 ()0h ,X=hx h >时,y 随x 的增大而减小;x h <时,y 随x 的增大而增大;x h =时,y 有最大值0.4. ()2y a x h k =-+的性质:三、二次函数图象的平移1. 平移步骤:方法一:⑴ 将抛物线解析式转化成顶点式()2y a x h k =-+,确定其顶点坐标()h k ,; ⑵ 保持抛物线2y ax =的形状不变,将其顶点平移到()h k ,处,具体平移方法如下:向右(h >0)【或左(h <0)】平移 |k|个单位向上(k >0)【或下(k <0)】平移|k |个单位向右(h >0)【或左(h <0)】平移|k|个单位向右(h >0)【或左(h <0)】平移|k|个单位向上(k >0)【或下(k <0)】平移|k |个单位向上(k >0)【或向下(k <0)】平移|k |个单位y=a (x-h )2+ky=a (x-h )2y=ax 2+ky=ax 22. 平移规律在原有函数的基础上“h 值正右移,负左移;k 值正上移,负下移”. 概括成八个字“左加右减,上加下减”. 方法二:⑴c bx ax y ++=2沿y 轴平移:向上(下)平移m 个单位,c bx ax y ++=2变成m c bx ax y +++=2(或m c bx ax y -++=2)⑵c bx ax y ++=2沿轴平移:向左(右)平移m 个单位,c bx ax y ++=2变成c m x b m x a y ++++=)()(2(或c m x b m x a y +-+-=)()(2)四、二次函数()2y a x h k=-+与2y ax bx c =++的比较 从解析式上看,()2y a x h k =-+与2y ax bx c =++是两种不同的表达形式,后者通过配方可以得到前者,即22424b ac b y a x a a -⎛⎫=++ ⎪⎝⎭,其中2424b ac b h k a a -=-=,. 五、二次函数2y axbx c =++图象的画法a 的符号开口方向 顶点坐标 对称轴 性质0a >向上()h k , X=hx h >时,y 随x 的增大而增大;x h <时,y 随x 的增大而减小;x h =时,y 有最小值k .0a < 向下 ()h k ,X=hx h >时,y 随x 的增大而减小;x h <时,y 随x 的增大而增大;x h =时,y 有最大值k .五点绘图法:利用配方法将二次函数2y ax bx c =++化为顶点式2()y a x h k =-+,确定其开口方向、对称轴及顶点坐标,然后在对称轴两侧,左右对称地描点画图.一般我们选取的五点为:顶点、与y 轴的交点()0c ,、以及()0c ,关于对称轴对称的点()2h c ,、与x 轴的交点()10x ,,()20x ,(若与x 轴没有交点,则取两组关于对称轴对称的点).画草图时应抓住以下几点:开口方向,对称轴,顶点,与x 轴的交点,与y 轴的交点.六、二次函数2y ax bx c =++的性质 1. 当0a >时,抛物线开口向上,对称轴为2bx a =-,顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭,.当2b x a <-时,y 随x 的增大而减小;当2b x a >-时,y 随x 的增大而增大;当2bx a=-时,y 有最小值244ac b a-.2. 当0a <时,抛物线开口向下,对称轴为2b x a =-,顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭,.当2bx a <-时,y 随x 的增大而增大;当2b x a >-时,y 随x 的增大而减小;当2b x a =-时,y 有最大值244ac b a-. 七、二次函数解析式的表示方法1. 一般式:2y ax bx c =++(a ,b ,c 为常数,0a ≠);2. 顶点式:2()y a x h k =-+(a ,h ,k 为常数,0a ≠);3. 两根式:12()()y a x x x x =--(0a ≠,1x ,2x 是抛物线与x 轴两交点的横坐标).注意:任何二次函数的解析式都可以化成一般式或顶点式,但并非所有的二次函数都可以写成交点式,只有抛物线与x 轴有交点,即240b ac -≥时,抛物线的解析式才可以用交点式表示.二次函数解析式的这三种形式可以互化.八、二次函数的图象与各项系数之间的关系1. 二次项系数a二次函数2y ax bx c =++中,a 作为二次项系数,显然0a ≠.⑴ 当0a >时,抛物线开口向上,a 的值越大,开口越小,反之a 的值越小,开口越大; ⑵ 当0a <时,抛物线开口向下,a 的值越小,开口越小,反之a 的值越大,开口越大.总结起来,a 决定了抛物线开口的大小和方向,a 的正负决定开口方向,a 的大小决定开口的大小. 2. 一次项系数b在二次项系数a 确定的前提下,b 决定了抛物线的对称轴. ⑴ 在0a >的前提下,当0b >时,02ba-<,即抛物线的对称轴在y 轴左侧; 当0b =时,02ba-=,即抛物线的对称轴就是y 轴; 当0b <时,02ba->,即抛物线对称轴在y 轴的右侧. ⑵ 在0a <的前提下,结论刚好与上述相反,即当0b >时,02ba->,即抛物线的对称轴在y 轴右侧; 当0b =时,02ba-=,即抛物线的对称轴就是y 轴; 当0b <时,02ba-<,即抛物线对称轴在y 轴的左侧. 总结起来,在a 确定的前提下,b 决定了抛物线对称轴的位置.ab 的符号的判定:对称轴abx 2-=在y 轴左边则0>ab ,在y 轴的右侧则0<ab 3. 常数项c⑴ 当0c >时,抛物线与y 轴的交点在x 轴上方,即抛物线与y 轴交点的纵坐标为正; ⑵ 当0c =时,抛物线与y 轴的交点为坐标原点,即抛物线与y 轴交点的纵坐标为0; ⑶ 当0c <时,抛物线与y 轴的交点在x 轴下方,即抛物线与y 轴交点的纵坐标为负. 总结起来,c 决定了抛物线与y 轴交点的位置.二次函数解析式的确定:根据已知条件确定二次函数解析式,通常利用待定系数法.用待定系数法求二次函数的解析式必须根据题目的特点,选择适当的形式,才能使解题简便.一般来说,有如下几种情况:1. 已知抛物线上三点的坐标,一般选用一般式;2. 已知抛物线顶点或对称轴或最大(小)值,一般选用顶点式;3. 已知抛物线与x 轴的两个交点的横坐标,一般选用两根式;九、二次函数图象的对称二次函数图象的对称一般有五种情况,可以用一般式或顶点式表达 1. 关于x 轴对称2y a x b x c =++关于x 轴对称后,得到的解析式是2y ax bx c =---;()2y a x h k =-+关于x 轴对称后,得到的解析式是()2y a x h k =---; 2. 关于y 轴对称2y a x b x c =++关于y 轴对称后,得到的解析式是2y ax bx c =-+;()2y a x h k =-+关于y 轴对称后,得到的解析式是()2y a x h k =++; 3. 关于原点对称2y a x b x c =++关于原点对称后,得到的解析式是2y ax bx c =-+-; ()2y a x h k =-+关于原点对称后,得到的解析式是()2y a x h k =-+-; 4. 关于顶点对称(即:抛物线绕顶点旋转180°)2y a x b x c =++关于顶点对称后,得到的解析式是222b y ax bx c a=--+-;()2y a x h k =-+关于顶点对称后,得到的解析式是()2y a x h k =--+. 5. 关于点()m n ,对称()2y a x h k =-+关于点()m n ,对称后,得到的解析式是()222y a x h m n k =-+-+- 根据对称的性质,显然无论作何种对称变换,抛物线的形状一定不会发生变化,因此a 永远不变.求抛物线的对称抛物线的表达式时,可以依据题意或方便运算的原则,选择合适的形式,习惯上是先确定原抛物线(或表达式已知的抛物线)的顶点坐标及开口方向,再确定其对称抛物线的顶点坐标及开口方向,然后再写出其对称抛物线的表达式.十、二次函数与一元二次方程:1. 二次函数与一元二次方程的关系(二次函数与x 轴交点情况):一元二次方程20ax bx c ++=是二次函数2y ax bx c =++当函数值0y =时的特殊情况. 图象与x 轴的交点个数:① 当240b ac ∆=->时,图象与x 轴交于两点()()1200A x B x ,,,12()x x ≠,其中的12x x ,是一元二次方程()200ax bx c a ++=≠的两根.这两点间的距离2214b ac AB x x a-=-=.② 当0∆=时,图象与x 轴只有一个交点; ③ 当0∆<时,图象与x 轴没有交点.1' 当0a >时,图象落在x 轴的上方,无论x 为任何实数,都有0y >; 2'当0a <时,图象落在x 轴的下方,无论x 为任何实数,都有0y <. 2. 抛物线2y ax bx c =++的图象与y 轴一定相交,交点坐标为(0,)c ;3. 二次函数常用解题方法总结:⑴ 求二次函数的图象与x 轴的交点坐标,需转化为一元二次方程;⑵ 求二次函数的最大(小)值需要利用配方法将二次函数由一般式转化为顶点式;⑶ 根据图象的位置判断二次函数2y ax bx c =++中a ,b ,c 的符号,或由二次函数中a ,b ,c 的符号判断图象的位置,要数形结合;⑷ 二次函数的图象关于对称轴对称,可利用这一性质,求和已知一点对称的点坐标,或已知与x 轴的一个交点坐标,可由对称性求出另一个交点坐标.下面以0a >时为例,揭示二次函数和一元二次方程之间的内在联系:十一、函数的应用二次函数应用⎧⎪⎨⎪⎩刹车距离何时获得最大利润最大面积是多少0∆>抛物线与x 轴有两个交点 一元二次方程有两个不相等实根0∆= 抛物线与x 轴只有一个交点 一元二次方程有两个相等的实数根 0∆<抛物线与x 轴无交点一元二次方程无实数根.二次函数考查重点与常见题型1. 考查二次函数的定义、性质,有关试题常出现在选择题中,如:已知以x 为自变量的二次函数2)2(22--+-=m m x m y 的图像经过原点, 则m 的值是2. 综合考查正比例、反比例、一次函数、二次函数的图像,习题的特点是在同一直角坐标系内考查两个函数的图像,试题类型为选择题,如: 如图,如果函数b kx y +=的图像在第一、二、三象限内,那么函数12-+=bx kx y 的图像大致是( )y y y y1 10 x o-1 x 0 x 0 -1 x A B C D3. 考查用待定系数法求二次函数的解析式,有关习题出现的频率很高,习题类型有中档解答题和选拔性的综合题,如: 已知一条抛物线经过(0,3),(4,6)两点,对称轴为35=x ,求这条抛物线的解析式。
高一函数知识点总结归纳

高一函数知识点总结归纳高中数学的学习难度主要在于概念的深入和方法的抽象。
高一是数学学习的起步阶段,更是重中之重。
今天小编在这给大家整理了高一函数知识点总结,接下来随着小编一起来看看吧!高一函数知识点总结1高一数学函数知识点归纳1、函数:设A、B为非空集合,如果按照某个特定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数f(x)和它对应,那么就称f:A→B为从集合A到集合B的一个函数,写作y=f(x),x∈A,其中,x叫做自变量,x的取值范围A叫做函数的定义域,与x相对应的y的值叫做函数值,函数值的集合B={f(x)∣x∈A }叫做函数的值域。
2、函数定义域的解题思路:⑴ 若x处于分母位置,则分母x不能为0。
⑵ 偶次方根的被开方数不小于0。
⑶ 对数式的真数必须大于0。
⑷ 指数对数式的底,不得为1,且必须大于0。
⑸ 指数为0时,底数不得为0。
⑹ 如果函数是由一些基本函数通过四则运算结合而成的,那么,它的定义域是各个部分都有意义的x值组成的集合。
⑺ 实际问题中的函数的定义域还要保证实际问题有意义。
3、相同函数⑴ 表达式相同:与表示自变量和函数值的字母无关。
⑵ 定义域一致,对应法则一致。
4、函数值域的求法⑴ 观察法:适用于初等函数及一些简单的由初等函数通过四则运算得到的函数。
⑵ 图像法:适用于易于画出函数图像的函数已经分段函数。
⑶ 配方法:主要用于二次函数,配方成 y=(x-a)2+b 的形式。
⑷ 代换法:主要用于由已知值域的函数推测未知函数的值域。
5、函数图像的变换⑴ 平移变换:在x轴上的变换在x上就行加减,在y轴上的变换在y上进行加减。
⑵ 伸缩变换:在x前加上系数。
⑶ 对称变换:高中阶段不作要求。
6、映射:设A、B是两个非空集合,如果按某一个确定的对应法则f,使对于A中的任意仪的元素x,在集合B中都有唯一的确定的y 与之对应,那么就称对应f:A→B为从集合A到集合B的映射。
⑴ 集合A中的每一个元素,在集合B中都有象,并且象是唯一的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、变量与常量
在某一变化过程中,可以取不同数值的量叫做变量,数值保持不变的量叫做常量。
一般地,在某一变化过程中有两个变量x与y,如果对于x的每一个值,y都有唯一确定的值与它对应,那么就说x是自变量,y是x的函数。
2、函数解析式
用来表示函数关系的数学式子叫做函数解析式或函数关系式。
使函数有意义的自变量的取值的全体,叫做自变量的取值范围。
3、函数的三种表示法及其优缺点
(1)解析法
两个变量间的函数关系,有时可以用一个含有这两个变量及数字运算符号的等式表示,这种表示法叫做解析法。
(2)列表法
把自变量x的一系列值和函数y的对应值列成一个表来表示函数关系,这种表示法叫做列表法。
(3)图像法
用图像表示函数关系的方法叫做图像法。
4、由函数解析式画其图像的一般步骤
(1)列表:列表给出自变量与函数的一些对应值
(2)描点:以表中每对对应值为坐标,在坐标平面内描出相应的点
(3)连线:按照自变量由小到大的顺序,把所描各点用平滑的曲线连接起来。
1.一般地,如果,那么y叫做x的一次函数。
特别的 y叫做x的正比例函数。
2、一次函数的图像是。
3、一次函数、正比例函数图像的主要特征:
一次函数
b
kx
y+
=的图像是经过点的直线;正比例函数kx
y=的图像是经过
点的直线。
4、一次函数的性质
当k>0时,直线必通过象限,y随x的增大而;当k<0时,直线必通过象限,y随x的增大而。
y=kx+b(k,b为常数,k≠0)时:
一般的,形如 ,那么y 叫做x 的反比例函数.特别的xy= 。
反比例函数图象我们叫做 ,它是关于 成 对称图形。
当k>0时,图象分别位于第 象限, 象限内,y 随x 的增大而 ;当k<0时,图象分别位于第 象限, 象限内,y 随x 的增大而 。
1.若点(m ,n )在函数y=2x+1的图象上,则2m ﹣n 的值是( )
2.函数y=
中自变量x 的取值范围是( )A .x >﹣2B .x ≥2C .x ≠﹣2D .x ≥﹣2
3.下列四幅图像近似刻画两个变量之间的关系,请按图象顺序将下面四种情景与之对应排序
①一辆汽车在公路上匀速行驶(汽车行驶的路程与时间的关系)②向锥形瓶中匀速注水(水面的高度与注水时间的关系)
③将常温下的温度计插入一杯热水中(温度计的读书与时间的关系)④一杯越来越凉的水(水温与时间的关系)
A . ①②④③
B .③④②①
C .①④②③
D .③②④①
4.一次函数y=mx+∣m-1∣的图象过点(0,2)且y 随x 的增大而增大,则m= ( ) A .-1 B .3 C .1 D .-1或3
5.在同一平面直角坐标系中,若一次函数533-=+-=x y x y 与图象交于点M ,则点M 的坐标为( ) A .(-1,4)
B .(-1,2)
C .(2,-1)
D .(2,1)
6.下面四条直线,其中直线上每个点的坐标都是二元一次方程x –2y =2的解的是
A
B
C D
7.下列四组点中,可以在同一个正比例函数图象上的一组点是()
A .(2.-3),(-4,6)
B .(-2,3),(4,6)
C .(-2,-3),(4,-6)
D .(2,3),(-4,6) 8.如图,一次函数y=(m ﹣1)x ﹣3的图象分别与x 轴、y 轴的负半轴相交于A .B ,则m 的取值范围是( )
A .m >1
B .m <1
C .m <0
D .m >0
9. 矩形的长为x ,宽为y ,面积为9,则y 与x 之间的函数关系用图象表示大致为( )
10. 如图,两个反比例函数1y x =
和2
y x
=-的图象分别是1l 和2l .设点P 在1l 上,PC ⊥x 轴,垂足为C ,交2l 于点A ,PD ⊥y 轴,垂足为D ,交2l 于点B ,则三角形P AB 的面积为( )
(A )3 (B )4 (C )9
2
(D )5
11.星期天8:00~8:30,燃气公司给平安加气站的储气罐注入天然气,注完气之后,一位工作人员以每车20米3
的
加气量,依次给在加气站排队等候的若干辆车加气.储气罐中的储气量y(米3)与时间x(小时)的函数关系如图所示.
⑴ 8:00~8:30,燃气公司向储气罐注入了 米3的天然气;
⑵ 当x ≥8.5时,求储气罐中的储气量y(米3)与时间x(小时)的函数解析式;
⑶ 正在排队等候的第20辆车加完后,储气罐内还有天然气 米3,这第20辆车在当天9:00之前能加完气吗?请说明理由.
12.如图,一次函数y=2
23
x -+的图象分别与x 轴、y 轴交于点A 、B ,以线段AB 为边在第
一象限内作等腰Rt △ABC ,∠BAC=90∘,求过B 、C 两点直线的解析式.
x
y
A
P B
D C O
1
l 2l
13.如图,在平面直角坐标系xOy 中,函数()4
0y x x
=>的图象与一次函数y kx k =-的图象的交点为()2A m ,. (1)求一次函数的解析式;
(2)设一次函数y kx k =-的图象与y 轴交于点B ,若P 是x 轴上一点, 且满足PAB △的面积是4,直接写出点P 的坐标.
14.周末,小明骑自行车从家里出发到野外郊游.从家出发0.5小时后到达甲地,游玩一段时间
后按原速前往乙地.小明离家1小
时20分钟后,妈妈驾车沿相同路线前往乙地,
家的路程
y (km )与小明离家时间x (h 知妈妈驾车的速度是小明骑车速度的3倍. (1)求小明骑车的速度和在甲地游玩的时间;
(2)小明从家出发多少小时后被妈妈追上?此时离家多远?
(3)若妈妈比小明早10分钟到达乙地,程.
)
1.下列函数:①y=2x ﹣1;②y=﹣;③y=x 2
+8x ﹣2;④y=;⑤y=;⑥y=中,y 是
x 的反比例函数的有 (填序号) 2.在反比例函数(0)k
y k x
=
<的图像上有两点(-1,y 1),(41-,y 2),则y 1-y 2的值是
( )A. 负数 B.非正数 C.正数 D.不能确定 3.如图,点A 在双曲线y=
x
6
上,过A 作AC ⊥x 轴,垂足为C ,OA 的垂直平分线交OC 于点B ,当OA =4时,则△ABC 周长为 .
4. 如图,直线3y x =-的图象,点P (2,m )在该直线的上方,则m 的取值范围是( )
A 、m >-3
B 、m >-1
C 、m >0
D 、m <3 5.如图,正比例函数y 1=kx 和反比例函数y 2=2
k x
的图像交于A (-1,2)、(1,-2)两点,若y 1 <
y 2,则x 的取值范围是( )
A.x <-1或x >1
B. x <-1或0<x <1
C. -1<x <0或 0<x <1
D. -1<x <0或x >1
6.点A (x 1,y 1),B(x 2,y 2),C(x 3,y 3)都在反比例函数y=-3
x 的图象上,若x 1<x 2<0<x 3,则y 1,y 2,y 3的大
小关系是( ).
A . y 3<y 1<y 2
B .y 1<y 2<y 3
C .y 3<y 2<y 1
D .y 2<y 1<y 3
7. 为了预防流感,某学校在休息天用药熏消毒法对教室进行消毒.已知药物释效过程中,室内每立方米空气中的含药量y (毫克)与时间x (分钟)成正比例;药物释放完毕后,y 与x 成反比例,如图所示.根据图中提供的信息,解答下列问题:
(1)写出从药物释放开始,y 与x 之间的两个函数关系式 及相应的自变量取值范围;
(2)据测定,当空气中每立方米的含药量降低到 0.45毫克以下时,学生方可进入教室,那么从药物释 放开始,至少需要经过多少小时后,学生才能进入教室?
1.如图,双曲线()k
y k x
=
>0与⊙O 在第一象限内交于P 、Q 两点,分别过P 、Q 两点向x 轴和y 轴作垂线。
已知点P 的坐标为(1,3)则图中阴影部分
的面积为 。
2.如图,直线y=k 1x+b 与双曲线y=2
k x
交于A、B 两点,其横坐标分别为1
k 1x <
2
k x
+b 的解集是 。
3.已知一次函数m x y +=1的图象与反比例函数x
y 6
2=
的图象交于A 、B 两点,.已知当1>x 时,21y y >;当10<<x 时,21y y <.
(1)求一次函数的解析式;
(2)已知一次函数在第一象限上有一点C 到y 轴的距离为3,求△ABC 的面积.(提示B (-6,-1))
P
Q。
