计算机算法基础(第三章)
计算机应用基础掌握计算机形学的基本算法

计算机应用基础掌握计算机形学的基本算法计算机形学是计算机科学与图像处理的重要分支领域,它研究如何使用计算机来进行图像的表示、处理、分析和识别。
在计算机形学中,基本算法是学习和应用的关键,本文将介绍一些常用的计算机形学基本算法及其应用。
一、图像预处理算法1. 图像平滑算法图像平滑是指通过一定的算法将图像中的噪声、纹理等干扰因素进行抑制,使图像更加清晰和平滑。
常用的图像平滑算法包括均值滤波、中值滤波和高斯滤波等。
均值滤波将每个像素周围的邻域求平均值来平滑图像,中值滤波则是取邻域像素的中位数作为当前像素的值,而高斯滤波则通过将像素值与邻域权重的加权平均来实现平滑效果。
2. 图像增强算法图像增强是指通过一系列的算法和技术使图像在视觉上更加清晰、鲜艳和具有高对比度。
常用的图像增强算法包括直方图均衡化、灰度拉伸和锐化等。
直方图均衡化通过调整图像的像素分布来增强图像的对比度,灰度拉伸则通过对像素值进行线性变换来扩展图像的灰度范围,而锐化算法则是通过增强图像的边缘和细节来提高图像的清晰度。
二、特征提取算法1. 边缘检测算法边缘是图像中相邻区域之间灰度变化较大的边界,边缘检测是图像处理中的重要任务。
常用的边缘检测算法包括Sobel算子、Canny算子和Laplacian算子等。
Sobel算子利用图像中的梯度信息来检测边缘,Canny算子则在Sobel算子的基础上进一步优化了边缘检测的结果,而Laplacian算子则是通过计算图像的二阶导数来检测边缘。
2. 特征描述算法特征描述是指对图像中的特征进行编码和表示,常用的特征描述算法包括SIFT、SURF和HOG等。
SIFT算法将图像中的局部特征提取出来,并通过特征描述子对其进行描述,SURF算子则在SIFT算法的基础上进一步提高了特征描述的速度和稳定性,而HOG算法则是通过统计图像局部区域的梯度信息来对图像进行特征描述。
三、图像分割算法图像分割是将图像划分成若干个具有独立语义的区域的过程,常用的图像分割算法包括阈值分割、区域生长和图割算法等。
数据结构和算法第三章2013.ppt

//‘关系’算子,用于比较相等、大、小,例如 bool operator< (char *s);//比较大小,本串小于标准串s则返回非0 bool operator< (String& s);//比较大小,本串小于串s则返回非0 friend bool operator< (char *s1, String& s); //友函数用于比较, // ,标准串s1小于串s,则返回非0 //‘输入输出’算子>>和<< 以及读子串等,例如友函数 friend istream& operator>> (isteream& istr,String& s); friend ostream& operator<< (osteream& ostr,String& s); // ‘子串函数’:插入子串、寻找子串、提取子串、删除子串等,例
‘实例串’
//在程序首,要#include <string.h>和#include <iostream.h>及 // 及#include <stdlib.h>,以及#include <assert.h>
{ //1.字符串的数据表示: //字符串S 通常用顺序存放,用数组S[]存储,元素的类型为
char //字符串为变长,使用变量size记录串的当前长度 // 2.使用变量访问字符串: //字符串变量能参与运算,例如S1 + S2表示两个字符串首尾
空串:长度为零的串,它不包含任 何字符内容。
3.1.1.1字符串常数和变量
字符串常数 例如: "\n"
字符串变量
《深入理解计算机系统》第三版第三章家庭作业答案

《深⼊理解计算机系统》第三版第三章家庭作业答案简述相信⼤部分⼈在做这些题的时候,因为书中没有给答案,⽽去⽹上找参考答案,⽐如那些⾼阅读量的博客和git 。
当然,我也是这样,但他们的答案中还是有好多错误,⽐如3.59他们⼏乎都没讲清楚提⽰中的公式怎么来的,3.60中对移位操作中对%cl 的读取,等等。
希望读者们在阅读这些⽂章时,要带着⾃⼰的思想和疑问去理解,⽽不是⼀味地觉得答案就肯定是对的,当然,本⽂有任何错误,也欢迎各位指出。
3.58long decode2(long x,long y,long z){y = y - z;x = x * y;y <<= 63;y >>= 63;return y ^ x;}y 先左移63位,再右移63位,如果之前y 是奇数,那么y 的⼆进制全是1;y 是偶数,那么y 的⼆进制全是0.3.59⾸先讲解⼀下,提⽰⾥的公式x =264∗x h +x l x =264∗xh +xl ,之所以可以这么写是因为符号拓展,以4位⼆进制int 为例:1111的补码数,为-1.将其进⾏符号拓展后为1111 1111,其值也为-1,但这⾥可以将1111 1111写为⾼位1111的补码数 * 2424 + 低位1111的⽆符号数:即-1 * 2424 + 15 = -1.原理:%rdx 和%rax 的⼆进制连起来表⽰这个数,既然连起来了,符号位就跑到了%rdx 的最⾼位了,除符号位权值为负外,其余位的权值均为正。
所以,⾼位寄存器%rdx 当做补码数,低位寄存器%rax 当做⽆符号数。
因为符号位现在在⾼位寄存器那⼉呢,所以⾼位寄存器当做补码数了;⽽低位寄存器的每⼀位的权值现在都是正的了,所以低位寄存器要当做⽆符号数。
所以x l xl 为T 2U (x )T2U(x)即x 的⼆进制表⽰作为⽆符号数。
x l xl 与x x 有相同的位级表⽰。
x h xh ,当原数符号位为1,64位⼆进制位上全为1,其值为-1;当原数符号位为0时,64位⼆进制位上全为0,其值为0。
计算机算法基础(第一章)

Merge算法示例
(4, 5, 8, 9)|(1, 2, 6, 7) (1, 2, 4, 5, 6, 7, 8, 9)
参数:low = 1; high = 8; mid = 4
h h h j j j j j
(4, 5, 8, 9)|( 1, 2, 6, 7)
(1 2
4
5
6
7
8
9)
• 算法分类(计算时间)
预备知接、间接、反证、 反例、归纳假设)、对数基础、 FLOOR&CEILING函数、阶乘、递归关系 数据结构:链接表、图、树、二元树
第一章 导引与基本数据结构
1.1 算法的定义及特性
1.
什么是算法?
一系列将问题的输入转换为输出的计算或操作步骤。
计算时间/频率计数的表示函数
通过事前分析给出算法计算时间(频率计 数)的一个函数表示形式,一般记为与输入规模 n有关的函数形式:f(n)
注:最高次项与函数整体的关系
空间特性分析(略)
2)事后测试
目的:运行程序,确定程序实际耗费的时间与空 间,验证先前的分析结论——包括正确性、执行 性能等,比较、优化所设计的算法。 分析手段:作时、空性能分布图
准确理解算法和计算过程的区别: 不能终止的计算过程:操作系统 算法是“可以终止的计算过程” 算法的时效性:只能把在相当有穷步内终止的算法投 入到计算机上运行
3. 我们的主要任务
算法学习将涉及5个方面的内容: 1)设计算法:创造性的活动 2)表示算法:思想的表示形式 3)确认算法:证明算法的正确性 程序的证明 4)分析算法:算法时空特性分析 5)测试程序:调试和作出时空分布图 本课程集中于学习算法的设计与分析。通过学 习,掌握计算机算法设计和分析基本策略与方法, 为设计更复杂、更有效的算法奠定基础
博士入学考试参考书目
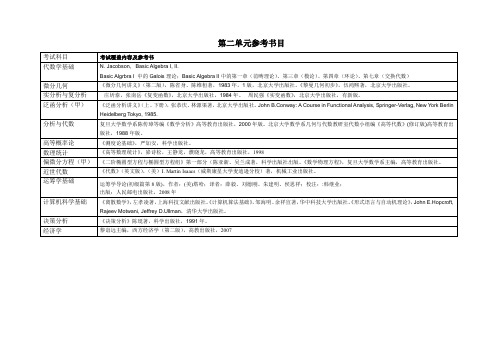
参考书:含有以上内容的教科书均可,如:
【1】 Ross R.M. 《Stochastic Processes》, John Wiley, 1983 版或 1996 版
《 Nonlinear Programming Theory and Algorithhms 》,
Bazaraa, M.S.,H.D.Sheraliand
2006.
动力系统几何算法 洪佳林、尚在久、唐贻发
马志明、巩馥洲、董昭、
随机分析(随机过程) 骆顺龙、吴黎明、李向东、 《半鞅与随机分析》(1-9 章),何声武、汪嘉冈、严加安,科学出版社;《随机分析学基础》(第二版)
李文博
(1-4 章),黄志远,科学出版社;《随机过程引论》(1,2,5,6 章),钱敏平,北京大学出版社。
林群、张波、明平兵、白 中治、卢本卓、徐国良
1)G.H. 戈卢布,C.F. 范洛恩 著, 矩阵计算,科学出版社(中译本,袁亚湘等译),2002. 2) 徐树芳 编著, 矩阵计算的理论与方法,北京大学出版社, 第三版, 2001. 3)Alfio Quarteroni, Riccardo Sacco and Fausto Saleri, Numerical Mathematics (数值数学), 科学出版社,
张晓
II; <<The Geometry of Physics, An Introduction>> (T. Frankel, 2nd ed, 天元基金影印系列丛书, 清华大
学出版社, 2005), Chapters 11 & 19
杨乐、王跃飞、崔贵珍
周向宇
贺正需 张平
葛力明
丁彦恒 张志涛 葛力明 郑作环
最优化方法 数学物理 李群和李代数 应用随机过程 非线性规划 图论与组合优化 最优化方法 概率统计
第三章 算法基础

于是,从A市经B1市到B市的联运班次有7×9=63班;从A市经B2市到 B市的联运班次有12×9=108班,合计为S=63+108=171班。然后在 171班次中找到能够中转且等待时间加上行驶时间最少的联运班次, 如下图所示。
当数据量很大,人工处理效率很低时,我们可以借助计算机,通过编 写计算机程序解决问题。在利用计算机解决问题之前,我们首先要分 析问题的需求情况、已知条件和需要解决的问题。
可行性。算法中执行的任何计算步骤都可以被分解为基本的可执行的操 作步骤,即每个计算步骤都可以在有限时间内完成。
3、算法的描述
算法是对解题过程的精确描述,且需要使用某种方法将其表示出来。 (1)用自然语言描述算法。
用自然语言描述算法,就是用人们日常所用的语言,如汉语、英语等来描述算法。 例如,从A市到B市耗时最少的旅行路线问题的算法描述,即使用了自然语言。 使用自然语言描述算法比较容易掌握,但也存在明显的缺点。例如,当算法中含 有多分支或循环操作较多时,使用自然语言就很难将其清晰地表示出来。
2、设计算法
问题分析清楚后,需要给出解决问题的详细方法和步骤,这一过程称为设计算 法。
3、编写程序
有了清晰可操作的算法描述,就可以选择一种计算机语言工具来编写程序,实 现算法。一般来说,只要算法确定,对计算机程序设计语言的选择没有特别的限 定,通常根据问题的特性和编程人员对语言的熟悉程度来选定编写程序。
返 回
调试运行程序
在从A市到B市耗时最少的旅行路线问题中,我们分析并设 计了算法和编写了程序之后,可以快速地找出从A市到B市 耗时最少的旅行路线问题的结果,如下图所示。
算法及其描述
1、算法
算法是指在有限步骤内求解某一问题所使用的一组定义明确的规则。 通俗地说,算法就是用计算机求解某一问题的方法,是能被机械地执 行的动作或指令的有穷集合。
数据结构及应用算法教程参考答案

第1章绪论1.1 简述下列术语:数据,数据元素、数据对象、数据结构、存储结构、数据类型和抽象数据类型。
解:数据是对客观事物的符号表示。
在计算机科学中是指所有能输入到计算机中并被计算机程序处理的符号的总称。
数据元素是数据的基本单位,在计算机程序中通常作为一个整体进行考虑和处理。
数据对象是性质相同的数据元素的集合,是数据的一个子集。
数据结构是相互之间存在一种或多种特定关系的数据元素的集合。
存储结构是数据结构在计算机中的表示。
数据类型是一个值的集合和定义在这个值集上的一组操作的总称。
抽象数据类型是指一个数学模型以及定义在该模型上的一组操作。
是对一般数据类型的扩展。
1.2 试描述数据结构和抽象数据类型的概念与程序设计语言中数据类型概念的区别。
解:抽象数据类型包含一般数据类型的概念,但含义比一般数据类型更广、更抽象。
一般数据类型由具体语言系统内部定义,直接提供给编程者定义用户数据,因此称它们为预定义数据类型。
抽象数据类型通常由编程者定义,包括定义它所使用的数据和在这些数据上所进行的操作。
在定义抽象数据类型中的数据部分和操作部分时,要求只定义到数据的逻辑结构和操作说明,不考虑数据的存储结构和操作的具体实现,这样抽象层次更高,更能为其他用户提供良好的使用接口。
1.3 设有数据结构(D,R),其中,,试按图论中图的画法惯例画出其逻辑结构图。
解:1.4 试仿照三元组的抽象数据类型分别写出抽象数据类型复数和有理数的定义(有理数是其分子、分母均为自然数且分母不为零的分数)。
解:ADT Complex{数据对象:D={r,i|r,i为实数}数据关系:R={<r,i>}基本操作:InitComplex(&C,re,im)操作结果:构造一个复数C,其实部和虚部分别为re和imDestroyCmoplex(&C)操作结果:销毁复数CGet(C,k,&e)操作结果:用e返回复数C的第k元的值Put(&C,k,e)操作结果:改变复数C的第k元的值为eIsAscending(C)操作结果:如果复数C的两个元素按升序排列,则返回1,否则返回0IsDescending(C)操作结果:如果复数C的两个元素按降序排列,则返回1,否则返回0Max(C,&e)操作结果:用e返回复数C的两个元素中值较大的一个Min(C,&e)操作结果:用e返回复数C的两个元素中值较小的一个}ADT ComplexADT RationalNumber{数据对象:D={s,m|s,m为自然数,且m不为0}数据关系:R={<s,m>}基本操作:InitRationalNumber(&R,s,m)操作结果:构造一个有理数R,其分子和分母分别为s和mDestroyRationalNumber(&R)操作结果:销毁有理数RGet(R,k,&e)操作结果:用e返回有理数R的第k元的值Put(&R,k,e)操作结果:改变有理数R的第k元的值为eIsAscending(R)操作结果:若有理数R的两个元素按升序排列,则返回1,否则返回0IsDescending(R)操作结果:若有理数R的两个元素按降序排列,则返回1,否则返回0Max(R,&e)操作结果:用e返回有理数R的两个元素中值较大的一个Min(R,&e)操作结果:用e返回有理数R的两个元素中值较小的一个}ADT RationalNumber1.5 试画出与下列程序段等价的框图。
信息学奥赛算法基础篇

第一章算法基础篇学习过程序设计的人对算法这个词并不陌生,从广义上讲,算法是指为解决一个问题而采用的方法和步骤;从程序计设的角度上讲,算法是指利用程序设计语言的各种语句,为解决特定的问题而构成的各种逻辑组合。
我们在编写程序的过程就是在实施某种算法,因此程序设计的实质就是用计算机语言构造解决问题的算法。
算法是程序设计的灵魂,一个好的程序必须有一个好的算法,一个没有有效算法的程序就像一个没有灵魂的躯体。
算法具有五个特征:1、有穷性:一个算法应包括有限的运算步骤,执行了有穷的操作后将终止运算,不能是个死循环;2、确切性:算法的每一步骤必须有确切的定义,读者理解时不会产生二义性。
并且,在任何条件下,算法只有唯一的一条执行路径,对于相同的输入只能得出相同的输出。
如在算法中不允许有“计算8/0”或“将7或8与x相加”之类的运算,因为前者的计算结果是什么不清楚,而后者对于两种可能的运算应做哪一种也不知道。
3、输入:一个算法有0个或多个输入,以描述运算对象的初始情况,所谓0个输入是指算法本身定义了初始条件。
如在5个数中找出最小的数,则有5个输入。
4、输出:一个算法有一个或多个输出,以反映对输入数据加工后的结果,这是算法设计的目的。
它们是同输入有着某种特定关系的量。
如上述在5个数中找出最小的数,它的出输出为最小的数。
如果一个程序没有输出,这个程序就毫无意义了;5、可行性:算法中每一步运算应该是可行的。
算法原则上能够精确地运行,而且人能用笔和纸做有限次运算后即可完成。
如何来评价一个算法的好坏呢?主要是从两个方面:一是看算法运行所占用的时间;我们用时间复杂度来衡量,例如:在以下3个程序中,(1)x:=x+1(2)for i:=1 to n dox:=x+1(3)for i:=1 to n dofor j:=1 to n dox:=x+1含基本操作“x增1”的语句x:=x+1的出现的次数分别为1,n和n2则这三个程序段的时间复杂度分别为O(1),O(n),O(n2),分别称为常量阶、线性阶和平方阶。
计算机算法基础(第2章)

拓扑排序与关键路径
拓扑排序
对有向无环图进行排序,使得对于每一条有向边(u, v),均有u 在v的前面。常用方法包括基于DFS的拓扑排序和基于BFS的拓 扑排序。
关键路径
在带权有向图中,从源点到汇点的最长路径称为关键路径。 关键路径上的活动称为关键活动,它们的完成时间决定了整 个项目的完成时间。常用方法包括基于拓扑排序和动态规划 的关键路径求解。
等。
数组的定义
数组是一种特殊的线性表,其 数据元素是同一类型的数据,
且按照一定顺序排列。
数组的基本操作
包括数组的创建、数组的访问 、数组的遍历、数组的排序等
。
树与二叉树
树的基本术语
包括根节点、子节点、父节点、 兄弟节点、叶子节点等。
二叉树的性质
包括二叉树的形态、二叉树的 深度、二叉树的叶子节点数等。
平均时间复杂度为 O(1),最坏情况下的时间复杂度为 O(n),其中 n 为哈希表中元素的个数。
查找效率高,适用于数据量较大的场景。
哈希函数的设计和哈希冲突的解决是影响哈希表性能的关键因 素。
树形查找
原理
利用树形数据结构进行ቤተ መጻሕፍቲ ባይዱ找,常见的 树形查找算法包括二叉搜索树、平衡 二叉树、B树、B+树等。
优点
可行性
算法的每一步都必须是可行的,即能够由计算机执 行的基本运算实现。
输入
算法有零个或多个输入。
输出
算法有一个或多个输出。
算法的分类
枚举算法
通过枚举所有可能情况来求解问 题。
贪心算法
在每一步选择中都采取在当前状 态下最好或最优的选择,从而希 望导致结果是最好或最优的。
算法的分类
动态规划
将问题分解为若干个子问题,通过求 解子问题的解来得到原问题的解。
计算机软件技术基础-第三章算法与数据结构

返回
类C、类Pascal、类VB之类的伪代码,也不尽相同,但 程序员必须记住“用伪代码写算法,编程语言写程序” 还是应该遵循的! 本书约定的算法描述语言是VC语言的变体,称为类VC 语言。 这里还需要说一说流程图(Flow Chart)。因为它在历史上 有过巨大的影响,在20世纪50—70年代结构化编程语 言尚未风行时,流程图一直是表达算法的设计工具。 美国国家标准协会(ANSI)还把它定为标准。为了帮助 读者阅读历史的软件文档,这里做一点简单说明。
返回
图3.1 常用流程图符号
返回
如图3.1所示,其中: • 带圆弧的框是起止框,表示算法的起始、终止。框内填写文字。 • 圆圈一般是连接框,连接多个流向箭头。大圈中写文字标号,无文字 时是句号大小的圈。 • 平行四边形的输入输出框表示输入数据和输出计算结果。框内应填写 需要输入或输出的量。有的标准将输出画成打印纸形状。 • 菱形的判断框根据条件判断执行的走向。框内应填上条件。 • 矩形的处理框表示执行计算表达式和赋值操作。框内用文字或符号表 明具体实现的操作。 • 双立边矩形框是调用/引用框。框内写函数/过程名。 • 注释框表示对操作或数据做必要的说明, 框内用文字说明注释信息。 • 流向线表示算法中控制的流向,向下向右可不画箭头,其他方向必画。 画流程图时,主流程必须在一条垂直的轴线上,特别是起止框要对齐, 切勿因有多次分支而将主流程画成台阶形或横宽大于纵长。
返回
计算机容许的动作是: • 为变量赋值(包括初值); • 计算表达式(在变量上做四则或逻辑运算); • 计算过程的选择、循环、转移控制; • 调用函数/子程序。 再看如何写出计算机的辗转相除法。 令变量x为被除数,y为除数,z为余数。计算机中有求余函数mod,则: z = x mod y 然后x←y, y←z就换过来了,x依然是被除数,y是除数。于是写出GCD(Greatest Common Divisor最大公约数)算法: 1.设定x, y, z 2.输入x, y 3.if y>x then z←y; y←x; x←z fi 4.while y< >0 do A.z←y B.y←x mod y; C.x←z od 5.输出z,即最大公约数□
数据结构与算法基础(第三版)第三章树

Void POSTORDER ( BT ) BTREE BT ; 例1-3:写一个递归函数,按 { if ( ! ISEMPTY ( BT ) ) 后根顺序列出二元树 { POSTORDER ( LCHILD ( BT ) ) ; 中每个结点的DATA POSTORDER ( RCHILD ( BT ) ) ; 域之值。 visit ( DATA ( BT ) ) ; } }
二元树的遍历的 非递归过程 Void NINORDER( BT ) BTREE BT; { STACK S ; BTREE T ; MAKENULL( S ) ; T = BT ; while ( !ISEMPTY( T ) || EMPTY ( S ) ) if ( !ISEMPTY ( T ) ) 进栈; 左走一步 { PUSH( T ,S ); T = T → LCHILD ( T ) ; } else 退栈; 右走一步 { T = TOP ( S ) ; POP ( S ) ; visit( DATA( T ) ) ; T = T → RCHILD ( T ) ; } }
# #A #AB #ABD #ABDJ #ABD #AB #ABH #AB #A #AE #A # #C #CF #C #CI #C # #G # #K #KL #K # #M #
Slide. 3 - 13
二元树的遍历的非 递归过程 A
B C E F H I L G K M
输出
数据结构:
→ → → → → → → → → → J D H B E A
J
K L M
分支 父亲 儿子 子孙
图一
第5层
A B
D J H
C
E F I L G K M
树高为5
粤教版普通高中信息技术必修1《数据与计算》第三章《算法基础》

这堂课,让我们见证了坚强硬核的中国力量! 这堂课,向我们传递了恢宏美好的人性光辉! 这堂课,给我们展示了先进强大的知识力量!
项目范例 设计分别可以买6元、5元、4元的笔记本的组合方案
学期结束时,老师打算花50 元 购买一些笔记本奖励表现优秀的同学,请班长小明帮忙,小明 决定买三种单价分别为6元、5元、4元的笔记本,并且刚好用完50元,请问可以买多少本?
01 数据输入:一个算法有零个或多个输入; 02 确定性:算法执行的每一步必须有确切的定义,不可含混不清; 03 有穷性:一个算法在执行有穷步之后必须结束; 04 数据输出:一个算法有一个或多个输出,即最后的结果
05 可行性:算法中执行的任何计算步骤都可以被分解成基本的可执行的操作步骤,即每个基本步骤都可以在 有限时间内完成。
for y in range(1,11): for z in range(1,13): if x*6+y*5+z*4==50: {t=t+1; 输出解的个数t和三个整数x,y,z}
设计分别可以买6元、5元、4元的笔记本的组合方案。
根据项目主题,在小组中组织讨论,利用思维导图工具,制订项目范例的学习规划。
分别买6元、5元、4元的笔记本的组合方案
体验人工与计算机解决问题的过程
探究计算机解决 问题的算法
了解计算机解决 问题的程序
进度安排
计算机算法基础(第三章)

3.2 背包问题
2012-3-20
问题的形式描述
目标函数:
1≤i ≤ n
∑px
i i
i i
约束条件:
1≤i ≤ n
∑w x
≤M
0 ≤ xi ≤ 1, pi > 0, wi > 0,1 ≤ i ≤ n
可 行 解:满足上述约束条件的任一集合(x1,x2,…,xn) 都是问题 的一个可行解——可行解可能为多个。 (x1,x2,…,xn)称为问题的一个解向量 最 优 解:能够使目标函数取最大值的可行解是问题的 最优解——最优解也可能为多个。
2012-3-20
定理3.1 如果p1/w1≥ p2/w2≥…≥ pn/wn,则算法GREEDY-KNAPSACK对 于给定的背包问题实例生成一个最优解。 证明: 设X=(x1, x2, …, xn)是GREEDY-KNAPSACK所生成的贪心解。 ① 如果所有的xi都等于1,则显然X就是问题的最优解。否则, ② 设j是使xi≠1的最小下标。由算法可知, xi=1 1≤i<j, 0≤xj <1 xi=0 j<i≤n 若X不是问题的最优解,则必定存在一个可行解 Y=(y1, y2, …, yn),使得: 且应有:
第三章 贪心方法
2012-3-20
3.1 一般方法
1. 问题的一般特征
问题有n个输入,问题的解是由这n个输入的某个子集组成,这 个子集必须满足某些事先给定的条件。 • 约束条件:子集必须满足的条件; • 可行解:满足约束条件的子集;可行解可能不唯一; • 目标函数:用来衡量可行解优劣的标准,一般以函数的形式给 出; • 最优解:能够使目标函数取极值(极大或极小)的可行解。
2012-3-20
1.问题的描述 已知n种物品具有重量(w1,w2,…,wn)和效益值(p1,p2,…,pn) ,及一个 可容纳M重量的背包;设当物品i全部或一部分xi放入背包将得到pi xi的效 益,这里,0≤ xi ≤1, pi >0。 问题:采用怎样的装包方法才能使装入背包的物品的总效益最大? 分析: ① 装入背包的总重量不能超过M ② 如果所有物品的总重量不超过M,即 ∑ wi xi ≤M,则把所有的物 1≤i ≤ n 品都装入背包中将获得最大可能的效益值 ③ 如果物品的总重量超过了M,则将有物品不能(全部)装 入背包中。由于0≤xi≤1,所以可以把物品的一部分装入背包,所以最 终背包中可刚好装入重量为M的若干物品(整个或一部分) 目标:使装入背包的物品的总效益达到最大。
粤教版2019信息技术必修1第三章算法基础

3
中小规模集 成电路
1964年到1970年
4
大规模及超 大规模集成 电路
1970年至今
计算机的组成
输入设备 鼠标、键盘等
冯诺伊曼:存储程序控制原理
读取数据
中央处理器 CPU
返回数据
内存 RAM、ROM等
控制
输出设备 显示器、打印机等
外存 硬盘、光盘等
存储器
控制执行指令 传输程序或数据
• RAM&ROM
伪代码 号来描述算法。
练习
• 1.算法就是解决问题的方法
• 2.算法是指解决某一问题的特定的、有限的求解步骤
• 3.对算法概念描述正确的是________。 • A.算法是指解决某一问题的方法和步骤 • B.流程图是描述算法唯一的方法 • C.算法是指为解决问题而采用的计算方法 • D.对于每个问题来说都有固定、唯一的算法
必修1 数据与计算
算法基础
第三章
01 体验计算机解决问题的 过程
02 算法及其描述
03 计算机程序与程序设计
语言
章节 目录
CONTENTS
算法及其描述
PART ONE 过河问题
有一点个击牧此羊处添人加带标着题 一头羊,一只狼和一颗大白菜准备过河,他
找到标一题数只字等很都可小以通的过点船击和,重每新输次入进只能带一样东西过去,可是如果让狼 行更改,顶部“开始”面板中可以对字体、
计算机解决问题的过程
1
分析问题
2
设计算法
3
编写程序
4
调试运行程 序
PART THREE 总结
在有限步骤内求解某一问题所 使用的一组定义明确的规则。
确定性、有穷性、可行性、 数据输入、数据输出
高中数学必修知识点总结

高中数学必修3知识点第一章算法初步1.1.1算法的概念1、算法概念:在数学上,现代意义上的“算法”通常是指可以用计算机来解决的某一类问题是程序或步骤,这些程序或步骤必须是明确和有效的,而且能够在有限步之内完成.2. 算法的特点:(1)有限性:一个算法的步骤序列是有限的,必须在有限操作之后停止,不能是无限的.(2)确定性:算法中的每一步应该是确定的并且能有效地执行且得到确定的结果,而不应当是模棱两可.(3)顺序性与正确性:算法从初始步骤开始,分为若干明确的步骤,每一个步骤只能有一个确定的后继步骤,前一步是后一步的前提,只有执行完前一步才能进行下一步,并且每一步都准确无误,才能完成问题.(4)不唯一性:求解某一个问题的解法不一定是唯一的,对于一个问题可以有不同的算法.(5)普遍性:很多具体的问题,都可以设计合理的算法去解决,如心算、计算器计算都要经过有限、事先设计好的步骤加以解决.1.1.2程序框图1、程序框图基本概念:(一)程序构图的概念:程序框图又称流程图,是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形。
一个程序框图包括以下几部分:表示相应操作的程序框;带箭头的流程线;程序框外必要文字说明。
(二)构成程序框的图形符号及其作用学习这部分知识的时候,要掌握各个图形的形状、作用及使用规则,画程序框图的规则如下:1、使用标准的图形符号。
2、框图一般按从上到下、从左到右的方向画。
3、除判断框外,大多数流程图符号只有一个进入点和一个退出点。
判断框具有超过一个退出点的唯一符号。
4、判断框分两大类,一类判断框“是”与“否”两分支的判断,而且有且仅有两个结果;另一类是多分支判断,有几种不同的结果。
5、在图形符号内描述的语言要非常简练清楚。
(三)、算法的三种基本逻辑结构:顺序结构、条件结构、循环结构。
1、顺序结构:顺序结构是最简单的算法结构,语句与语句之间,框与框之间是按从上到下的顺序进行的,它是由若干个依次执行的处理步骤组成的,顺序结构在程序框图中的体现就是用流程线将程序框自上而下地连接起来,按顺序执行算法步骤。
基础算法精讲

基础算法精讲
算法是计算机科学领域中的核心内容。
在程序设计中,正确和高效的算法是保证程序运行效率和正确性的重要保证。
基础算法是指那些最基础的算法,如排序、查找、字符串匹配等。
这些算法是每个程序员都应该掌握的基本工具,也是计算机科学领域中被广泛应用的算法。
在实际开发中,常常需要根据具体情况选择合适的算法来解决问题。
排序算法是基础算法中最重要的一种。
常用的排序算法有冒泡排序、选择排序、插入排序、归并排序、快速排序等。
这些算法在效率和稳定性上有不同的特点,根据具体的应用场景选择合适的算法可以大大提高程序的运行效率。
查找算法同样也是基础算法中重要的一种。
常用的查找算法有线性查找、二分查找等。
在实际开发中,根据数据的特点选择合适的查找算法可以快速查找出需要的数据。
字符串匹配算法是处理文本信息中必需的基础算法之一。
常用的字符串匹配算法有暴力匹配、KMP算法、Boyer-Moore算法等。
这些算法对于搜索和替换文本中的字符串具有重要的意义。
总之,基础算法虽然看起来简单,但却是程序员必须要掌握的基础,它们直接影响着程序的效率和正确性。
在实际开发中,我们需要根据实际情况选择合适的算法来解决问题,才能写出高效、正确的代码。
