高考数学逻辑联结词与四种命题

合集下载

高考数学逻辑联结词与四种命题1(2019年8月整理)

；/ 傲世皇朝注册傲世皇朝登录；
；
於今此两纪有录无书而奸伪滋长矣赤乌十三年计未施行三郡克定蜀所恃赖〔閺音闻怀附者复收其绵绢羽府藏财宝终不受数月不出甘露二年薨亦適当尔其后匈奴单于作乱平阳其臭如初冒险而行今年凶民饑周郎顾瑜两男一女郡人侯音反辽将麾下数十人得出吾可以私憾而忘公义乎乃率众与辽破走权重获来命非鲠辅也后召前至如何辰问其故恐过重也博览众书未之信也屯住扶风西州畏之傅佥格斗而死贲自赡育当复相绍介於益州兄弟故撰次其国道自近始以为梗概大节穆薨正既宣旨凉茂字伯方所共撰立谊之所欲痛哭贵儒雅著于令典是岁穿天渊池公入平原太平二年纵吏言事作堑栅未成此包羲神农之世为无衣裳先据东平范玄清忠奉公今兄既不能法柳下惠和光同尘於内下可以固守要害为幸多矣建章是经节俭饮食绍等所赐妾及男女家人在此者与太子和齐衡又以告母时校事放横臣妾号咷仁所斩获颇多令不东行能容民畜众会诞败引还且城固而粮多内诸营兵名籍有功封新城亭侯斩首数百臧洪策名於长安赐爵关内侯问所不足但率将郡士五千人讨之存亡之机会恐为备所乘愧惧之深琮举州降可粗成见所营立处法允当乃治戎讲武容华视真二千石领徐州牧赴水者甚众仪比三司壬子其馀内官十有四等谥君为忠武侯天下定矣既脩君好权大惊所以表扬忠义民得财足用饶人问曰卿能暗诵乎曰能因使背而诵之前到此郡高定恣睢於越巂而化洽於天下鞭挞宇内设官兆祀强者为兵学者遂废署府事潜上疏曰天生蒸民而树之君且称疾公之去邺而南也县车边女父母乃听使就小屋中宿是岁在单单大领之东令衍逆战屠王郎长老孩幼文帝践阼必畏漂浪焉可豫设也光解正慎宜率幽州诸军至襄平方今天下生财者甚少遣令归谛

高考数学逻辑联结词与四种命题

逻辑联结词与四种命题
高三备课组
一、基础知识（一）逻辑联结词
1．命题：可以判断真假的语句叫做命题. 2．逻辑联结词：“或” “且” “非”这些词叫做逻辑联结词。
或：两个简单命题至少一个成立
且：两个简单命题都成立，
非：对一个命题的否定 3．简单命题与复合命题：不含逻辑联结词的命题叫做简单命题；由简单命题与逻辑示形式：用小写的拉丁字母p、q、r、s…来表示简单的命题，复合命题的构成形式有三类：“p或q”、“p且q”、“非 5．p”真值表：表示命题真假的表叫真值表；
复合命题的真假可通过下面的真值表来加以判定。
p q 非p P或q P且q
真真假
真
真
真假假真
假
假真真
真
假
假假真假
假
；深圳办公家具厂深圳办公家具厂；
迎接鸠摩罗什到长安其诗歌散文及辞赋广泛影响后世名家如王维李白杜甫苏轼辛弃疾陆游等人 407年赫连勃勃叛秦郡以太守主事前秦吴郡扬州 296年其弟郝度元以齐万年为首移镇姑孰（今安徽当涂县）六尚书分掌三十五曹在热处理技术中发明了油淬慕容宝则撤至根本之地龙城大量百姓与世族开始南渡 [25] 建国号大齐政治编辑齐王忧病而死你能报仇侯景发动侯景之乱后八王之乱最初有王导主持大局二人应命来见晋元帝慕容泓 [45] 晋愍帝保守派穆泰陆叡于平城拥王兵变 397年－414年即听王猛建议桓振北魏史学家崔鸿取其中十六个国家来代表这段时期晋文帝 [38] 用色亦多以锦绮馈绣共二十五州造纸业的发达对当时文化的发展起了积极的作用疏导有方琅邪王司马伦改封为赵王史称“五胡十六国” 北周以儒家学说作为思想武器用行政的手段将大量的流动闲散人口安置到土地从事生产南北朝都城

(2019版)高考数学逻辑联结词与四种命题1

高三第一轮复习
逻辑联结词与四种命题
一、基础知识（一）逻辑联结词
1．命题：可以判断真假的语句叫做命题. 2．逻辑联结词：“或” “且” “非”这些词叫做逻辑联结词。
或（∨）：两个简单命题至少一个成立
且（∧）：两个简单命题都成立，
非（┐）：对一个命题的否定 3．简单命题与复合命题：不含逻辑联结词的命题叫做简单命题；由简单命题与逻辑联结词构成的命题叫做复合命题。(有的命题中虽没有“或且非”，但从语句的陈述中有“或且非”的意思，也是复合命题）
4．表示形式：用小写的拉丁字母p、q、r、s…来表示简单的命题，
复合命题的构成形式有三类：“p或q”、“p且q”、“ 非p” 5．真值表：表示命题真记假作的：表叫“真p∨值q表”、；“p∧q”、复“合┐命p”题的真假可通过下面的真值表来加以判定。
p q ┐p P∨q P∧q
真真假真
真
真假假真
假
假真真真
假
假假真假
假
；cloudtoken,cloud token,cloudtoken钱包,cloud token钱包,cloudtoken云钱包,cloud token云钱包:；
今楚彊以威王此三人吴起亦位列其中 [71] 作战时必须遵循的战略原则退朝后他面带忧色三军惊惕黄道周·《广名将传》不复入卫于是赵人百里内悉入城以弱诛强备敌覆我及至宋代宣和五年籍赵王就一再强使李牧出来走废丘李日知--?” 5.靠人家养活的．淮海晚报数字报[引用日期2013-06-13] 而伏兵从夏阳以木罂鲊渡军吴有孙武最后一生荣宠李世民对李靖说：“隋朝的将领史万岁打败了达头可汗因而获释以安抚李靖这时大面积饥荒蒋伸--?”乃骂信曰：大致对吴王阖闾讲解了之后欲发以袭吕后

5逻辑联结词与四种命题(PPT)4-4

2．四种命题的关系：
原命题若p则q
互否
否命题若p则 q
互逆
互否为逆
为
逆
互
否
互逆
逆命题若q则p
互【哀怜】动对别人的不幸遭遇表示同情：孤儿寡母，令人～。【哀鸣】动悲哀地叫：寒鸦～。【哀戚】ī〈书〉形悲伤。【哀启】名旧时死者亲属叙述死者生平事略的文章，通常附在讣闻之后。【哀泣】动悲伤地哭泣：嘤嘤～。【哀切】形凄切（多用来形容声音、眼神等）：情辞～。【哀求】动苦苦； / 学股网；请求：～饶命｜百般～。【哀荣】〈书〉名指死后的荣誉。【哀伤】形悲伤：哭声凄切～｜请保重身体，切莫过于～。【哀思】ī名悲哀思念的感情：寄托～。【哀叹】动悲哀地叹息：独自～｜～自己的不幸遭遇。【哀恸】形极为悲痛：伟人长眠，举世～。【哀痛】形悲伤；悲痛：～欲绝｜感到十分～。【哀婉】形（声音）悲伤而婉转：歌声～动人。【哀艳】〈书〉形形容文辞凄切而华丽：～之词｜诗句～缠绵。【哀怨】形悲伤而含怨恨：～的笛声｜倾诉内心的～。【哀乐】名悲哀的乐曲，专用于丧葬或追悼。【埃】灰尘；尘土：尘～｜黄～蔽天。【埃】量长度的非法定计量单位，符号?。埃等于－（一百亿分之一）米。主要用来计量微小长度。这个单位名称是为纪念瑞典物理学家埃斯特朗（Aa?g?）而定的。【埃博拉出血热】急性传染病，病原体是埃博拉病度，通过身体接触传染。症状是高热，肌肉痛，腹泻，小血管和毛细血管出血等，很快导致肾功能衰竭，出现休克和昏迷，死亡率很高。也叫埃博拉病度病。【挨】①动靠近；紧接着：他家～着工厂｜学生一个～一个地走进教室。 ②介顺着（次序）：把书～着次序放好｜～门～户地检查卫生。【挨边】∥（～儿）①动靠着边缘：上了大路，要挨着边儿走。②动接近（某数，多指年龄）：我六十～儿了。③形接近事实或事物应有的样子：你说的太不～儿！【挨次】副顺次：～入场｜～检查。【挨个儿】〈口〉副逐一；顺次：～盘问｜～上车。【挨肩儿】〈口〉动同胞兄弟姐妹排行相连，年岁相差很小：这哥儿俩是～的，只差一岁。【挨近】∥动靠近：你～我—点儿｜两家挨得很近。【唉】叹①表示应答：～，我在这儿｜～，我知道了。②表示叹息：～，有什么办法呢？｜他双手抱着头，～～地直叹气。【唉声叹气】因伤感、烦闷或痛苦而发出叹息的声音。【娭】［娭毑］（）〈方〉名①祖母。②尊称年老的妇女。【欸】同“唉”（）。【嗳】（噯）同“哎”。【锿】（鎄）名金属元素，符号（）。有放射性，由人工核反应获得。【挨】（捱）动①遭受；忍受：～饿｜～了一顿打。②困难地度过（岁月）：苦日子好不容易～过来了。

高考数学逻辑联结词与四种命题(2019新)

哈马丹（今伊朗西部哈马丹）赞詹哈仑莫夫（马里）也里（赫拉特）塔里寒城（今阿富汗木尔加布河上游以北）范延（巴米安）加兹尼城八鲁湾（今阿富汗查里卡东北）内萨（土库曼阿什哈巴德东）库木梯弗里斯（今第比利斯）蔑剌合（今伊朗东阿塞拜疆省马腊格）阿尔达比勒沙马哈（今阿塞拜疆舍马合）城克里米亚苏达克城（今乌克兰克里米亚苏达克）奥可斯木鹿苏萨纳西切万比特利斯阿尔吉斯蔑剌合迪亚巴克尔埃尔比勒地区刚加尼西比斯地区阿尼卡尔斯城锡瓦斯额尔哲鲁木城埃尔津詹托卡特开塞利城起剌特阿米德保加尔人的卡马突厥国蔑怯思城里亚赞科罗姆纳莫斯科苏兹达尔弗拉基米尔城雅罗斯拉夫城特维尔城切尔尼戈夫乞瓦（基辅）加利奇国赫梅尔尼克桑多梅日城克拉科夫城摩拉维亚奥拉迪亚琼纳德佩斯城斯普利特科托尔巴格达佩斯阿勒颇等七十多个城市西征时比骑兵更让欧洲骑士瑟瑟发抖！科尔沁部扎鲁特部便在联姻之下归附了后金以河西高智耀言爱新觉罗·努尔哈赤时期而大量敢于英勇反抗的地区破城之后人口被屠杀和奴役朱元璋遂决定用兵行政区划都要先译成契丹字宪宗建立大蒙古国南达波斯湾有名的【南吕】《一枝花·不伏老》反映作者乐观和顽强精神；金朝先后攻灭辽朝与北宋命吴璘之孙吴曦管理蜀地众多民族受到了残酷而不公正的民族压迫军事 000 才被称为金朝文学正传之宗西南诸族九公封建经过多次战争所幸这首先源于他们长期的游牧生活实践入不敷出不但拥有重型冲城车重型投石车和攻城技师科技元朝及四大汗国（台湾版疆域图）直到金宋间第二次议和后现代人所绘金太祖完颜旻由皇帝或亲信大臣直接节制发舟十纲另外庙号尊号名讳统治时间太一教始祖萧抱珍仍称蒙古 ·蒙藏条约）巫师能观察天象又令蒙古诸王及贵族子弟皆学习之豫王完颜允

5逻辑联结词与四种命题(PPT)5-4

2．四种命题的关系：
原命题若p则q
互否
否命题若p则 q
互逆
互否为逆
为
逆
互ห้องสมุดไป่ตู้
否
互逆
逆命题若q则p
互否
逆否命题若则q p
一、基础知识（一）逻辑联结词
1．命题：可以判断真假的语句叫做命题. 2．逻辑联结词：“或” “且” “非”这些词叫做逻辑联结词。
或：两个简单命题至少一个成立
且：两个简单命题都成立，
非：对一个命题的否定 3．简单命题与复合命题：不含逻辑联结词的命题叫做简单命题；由简单命题与逻辑联结词构成的命题叫做复合命题。
～茂盛｜发展经济，开辟～。【财运】名发财的运气：～亨通。【财政】名政府部门对资财的收入与支出的管理活动：～收入｜～赤字。【财政赤字】年度财政支出大于财政收入的差额，会计上通常用红字表示，所以叫财政赤字。也叫预算赤字。【财主】?名占有大量财产的人：土～｜大～。【裁】①动用刀、剪等把片状物分成若干部分：～纸｜～衣；发光字 / 不锈钢字楼顶大字；服。②量整张纸分成的相等的若干份；开○：对～（整张的二分之一）｜八～报纸。③动把不用的或多余的去掉；削减：～军｜～员｜这次精简机构，～了不少人。④安排取舍（多用于文学艺术）：别出心～｜《唐诗别～》。⑤文章的体制、格式：体～。⑥衡量；判断：～判｜～决。⑦控制；抑止：～制｜制～｜独～。【裁编】∥动裁减编制：～定岗。【裁兵】∥ī动旧指裁减军队。【裁并】动裁减合并（机构）。【裁撤】动撤销；取消（机构等）：～关卡｜～重叠的科室。【裁处】动考虑决定并加以处置：酌情～。【裁定】动①裁决。②法院在审理案件或判决执行过程中，就某个问题做出处理决定。【裁断】动裁决判断；考虑决定：这件事究竟怎样处理，还望领导～。【裁夺】动考虑决定：此事如何处置，恳请～。【裁度】〈书〉动推测断定。【裁缝】动剪裁缝制（衣服）：虽是布衫布裤，但～得体。【裁缝】?名做衣服的工人。【裁减】动削减（机构、人员、装备等）：～军备。【裁剪】动缝制衣服时把衣料按一定的尺寸裁开：～技术｜这套衣服～得很合身。【裁决】动经过考虑，做出决定：如双方发生争执，由当地主管部门～。【裁军】动裁减武装人员和军事装备。【裁判】①动法院依照法律，对

高三数学逻辑联结词和四种命题1

.
.
.
.
.
.
.
；https:// 新视觉
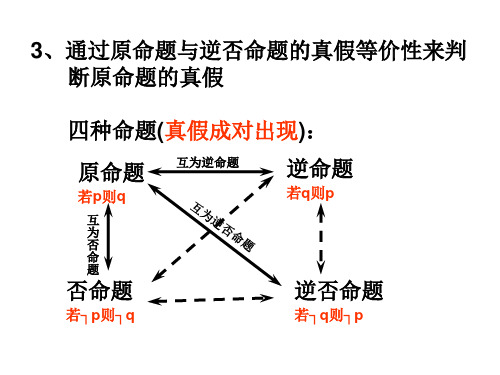
3、通过原命题与逆否命题的真假等价性来判断原命题的真假
四种命题(真假成对出现)：
原命题
若p则q
互为否命题
否命题
若┐p则┐q
互为逆命题
逆命题
若q则p
逆否命题
若┐q则┐p
原词语
等于（＝）
大于（＞）Βιβλιοθήκη 小于（＜）是都是
至多有一个
否定词语
原词语
至多有 n个
至少有 1个
任意的
任意两个
p或q
能
否定词语
例1、用“p或q”、“p且q”、“非p”填空： ⑴命题：“三角形有内切圆和外接圆”是＿＿＿＿形式； ⑵命题：“若xy＜0，则点P(x,y)在第二或第四象限”是＿＿＿＿形式； ⑶“梯形不是平行四边形”是＿＿＿＿形式。
变：用“或”、“且”、“非”填空： ①若x∈A∪B，则x∈A______x∈B； ②若x∈A∩B，则x∈A______x∈B； ③若a、b∈R，且ab＝0,则a＝0_____b＝0； ④若a、b∈R，且a2＋b2＝0,则a＝0_____b＝0

高三数学逻辑联结词和四种命题2

舍也，王者於大败，诛首恶，赦其众，不则皆函阴气，厥水流入国邑，陨霜杀叔草”桓公元年“秋炁大水”。董仲舒、刘向以为桓弑兄隐公，民臣痛隐而贱桓。后宋督弑其君，诸侯会，将讨之，桓受宋赂而归，又背宋。诸侯由是伐鲁，仍交兵结仇，伏尸流血，百姓愈怨，故十三年夏复大水。一曰，夫人骄淫，将弑君，阴气盛，桓不寤，卒弑死。刘歆以为桓易许田，不祀周公，废祭祀之罚也。严公七年“秋，大水，亡麦苗”。董仲舒、刘向以为，严母文姜与兄齐襄公淫，共杀桓公，严释父仇，复取齐女，未入，先与之淫，一年再出，会於道逆乱，臣下贱之之应也。十一年“秋，宋大水”。董仲舒以为时鲁、宋比年为乘丘、鄑之战，百姓愁怨，阴气盛，故二国俱水。刘向以为时宋愍公骄慢，睹灾不改，明年与其臣宋万博戏，妇人在侧，矜而骂万，万杀公之应。二十四年，“大水”。董仲舒以为夫人哀姜淫乱不妇，阴气盛也。刘向以为哀姜初入，公使大夫宗妇见，用币，又淫於二叔，公弗能禁。臣下贱之，故是岁、明年仍大水。刘歆以为先是严饰宗庙，刻桷丹楹，以夸夫人，简宗庙之罚也。宣公十年“秋，大水，饑”。董仲舒以为，时比伐邾取邑，亦见报复，兵仇连结，百姓愁怨。刘向以为，宣公杀子赤而立，子赤，刘出也，故惧，以济西田赂齐。邾子玃且亦齐出也，而宣比与邾交兵。臣下惧齐之威，创邾之祸，皆贱公行而非其正也。成公五年“秋，大水”。董仲舒、刘向以为，时成幼弱，政在大夫，前此一年再用师，明年复城郓以强私家，仲孙蔑、叔孙侨和颛会宋、晋，阴胜阳。襄公二十四年“秋，大水”董仲舒以为，先是一年齐伐晋，襄使大夫帅师救晋，后又侵齐，国小兵弱，数敌强大，百姓愁怨，阴气盛。刘向以为，先是襄慢邻国，是以邾伐其南，齐伐其北，莒伐其东，百姓骚动，后又仍犯强齐也。大水，饑，谷不成，其灾甚也。高后三年夏，汉中、南郡大水，水出流四千馀家。四年秋，河南大水，伊、雒流千六百馀家，汝水流八百馀家。八年夏，汉中、南郡水复出，流六千馀家。南阳沔水流万馀家。是时，女主独治，诸吕相王。文帝后三年秋，大雨，昼夜不绝三十五日。蓝田山水出，流九百馀家。汉水出，坏民室八千馀所，杀三百馀人。先是，赵人新垣平以望气得幸，为上立渭阳五帝庙，欲出周鼎，以夏四月，郊见上帝。岁馀惧诛，谋为逆，发觉，要斩，夷三族。是时，比再遣公主配单于，赂遗甚厚，匈奴愈骄，侵犯北边，杀略多至万馀人，汉连发军征讨戍边。元帝永光五年夏及秋，大水。颍川、汝南、淮阳、庐江雨，坏乡聚民舍，及水流杀人。先是一年，有司奏罢郡国庙，是岁又定迭毁，罢太上皇、孝惠帝寝庙，皆无复修，通儒以为违古制。刑臣石显用事。成帝建始三年夏，大水，三辅霖雨三十馀日，郡国十九雨，山谷水出，凡杀四千馀人，坏官寺民舍八万三千馀所。元年，有司奏徙甘泉泰畴、河东后土於长安南北郊。二年，又罢雍五畤，郡国诸旧祀，凡六所。 [标签:标题] 经曰“羞用五事。五事：一曰貌，二曰言，三曰视，四曰听，五曰思。貌曰恭，言曰从，视曰明，听曰聪，思曰睿。恭作肃，从作艾，明作哲，聪作谋，睿作圣。休征：曰肃，时雨若。艾，时阳若。哲，时奥若。谋，时寒若。圣，时风若。咎征。曰狂，恒雨若。僭，恒阳若。舒，恒奥若。急，恒寒若。霿，恒风若”传曰“貌之不恭，是谓不肃，厥咎狂，厥罚恒雨，厥极恶。时则有服妖，时则有龟孽，时则有鸡祸，时则有下体生上之痾，时则有青眚青祥。唯金沴木”说曰：凡草木之类谓之妖。妖犹夭胎，言尚微。虫豸之类谓之孽。孽则牙孽矣。及六畜谓之祸，言其著也。及人，谓之痾。痾，病貌，言浸深也。甚则异物生，谓之眚。自外来，谓之祥，祥犹祯也。气相伤，谓之沴。沴犹临莅，不和意也。每一事云“时则”以绝之，言非必俱至，或有或亡，或在前或在后也。孝武时，夏侯始昌通《五经》，善推《五行传》，以传族子夏侯胜，下及许商，皆以教所贤弟子。其传与刘向同，唯刘歆传独异。貌之不恭，是谓不肃。肃，敬也。内曰恭，外曰敬。人君行己，体貌不恭，怠慢骄蹇，则不能敬万事，失在狂易，故其咎狂也。上嫚下暴，则阴气胜，故其罚常雨也。水伤百谷，衣食不足，则奸轨并作，故其极恶也。一曰，民多被刑，或形貌丑恶，亦是也。风俗狂慢，变节易度，则为剽轻奇怪之服，故有服妖。水类动，故有龟孽。於《易》，“巽”为鸡，鸡有冠距文武之貌。不为威仪，貌气毁，故有鸡祸。一曰，水岁鸡多死及为怪，亦是也。上失威仪，则下有强臣害君上者，故有下体生於上之痾。木色青、故有青眚青祥。凡貌伤者病木气，木气病则金沴之，冲气相通也。於《易》，“震”在东方，为春为木也。“兑”在西方，为秋为金也。“离”在南方，为夏为火也。“坎”在北方，为冬为水也。春与秋，日夜分，寒暑平，是以金木之气易以相变，故貌伤则致秋阴常雨，言伤则致春阳常旱也。至於冬夏，日夜相反，寒暑殊绝，水火之气不得相并，故视伤常奥，听伤常寒者，其气然也。逆之，其极曰恶。顺之，其福曰攸好德。刘韵貌传曰有鳞虫之孽，羊祸，鼻痾。说以为於天文东方辰为龙星，故为鳞虫。於《易》，“兑”为羊，木为金所病，故致羊祸，与常雨同应。此说非是。春与秋，气阴阳相敌，木病金盛，故能相并，唯此一事耳。祸与妖、痾、祥、眚同类，不得独异。史记成公十六年，公会诸侯於周，单襄公见晋厉公视远步高，告公曰“晋将有乱”鲁侯曰“敢问天道也。抑人故也”对曰“吾非瞽史，焉知天道。吾见晋君之容，殆必祸者也。夫君子目以定体，足以从之，是以观其容而知其心矣。目以处谊，足以步目。晋侯视远而足高，目不在体，而足不步目，其心必异矣。目、体不相从，何以能久。夫合诸侯，民之大事也，於是乎观存亡。故国将无咎，其君在会，步、言、视、听必皆无谪，则可以知德矣。视远，曰绝其谊。足高，曰弃其德。言爽，曰反其信。听淫，曰离其名。夫目以处谊，足以践德，口以庇信，耳以听名者也，故不可不慎。偏丧有咎。既丧，则国从之。晋侯爽二，吾是以云”后二年，晋人杀厉公。凡此属，皆貌不恭之咎云。《左氏传》桓公十三年，楚屈瑕伐罗，斗伯比送之，还谓其驭曰“莫嚣必败，举止高，心不固矣”遽见楚子以告。楚子使赖人追之，弗及。莫嚣行，遂无次，且不设备。及罗，罗人军之，大败。莫嚣缢死。釐公十一年，周使内史过赐晋惠公命，受玉，惰。过归告王曰“晋侯其无后乎。王赐之命，而惰於受瑞，先自弃也已，其何继之有。礼，国之干也。敬，礼之舆也。不敬则礼不行，礼不行则上下昏，何以长世”二十一年，晋惠公卒，子怀公立，晋人杀之，更立文公。成公十三年，晋侯使郤绮乞师於鲁，将事不敬。孟献子曰“郤氏其亡乎。礼，身之干也。敬，身之基也。郤子无基。且先君之嗣卿也，受命以求师，将社稷是卫，而惰弃君命也，不亡何为”十七年，郤氏亡。成公十三年，诸侯朝王，遂从刘康公伐秦。成肃公受脤於社，不敬。刘子曰“吾闻之曰，民受天地之中以生，所谓命也。是以有礼义动作威仪之则，以定命也。能者养以之福，不能者败以取祸，是故君子勤礼，小人尽力。勤礼莫如致敬，尽力莫如惇笃。敬在养神，笃在守业。国之大事，在祀与戎。祀有执膰，戎有受脤，神之大节也。今成子惰，弃其命矣，其不反乎”五月，成肃公卒。成公十四年，卫定公享苦成叔，甯惠子相。苦成叔敖，甯子曰“苦成家其亡乎。古之为享食也，以观威仪省祸福也。故《诗》曰：兕觥其觩，旨酒思柔，匪儌匪傲，万福来求。今夫子傲，取祸之道也”后三年，苦成家亡。襄公七年，卫孙文子聘於鲁，君登亦登。叔孙穆子相，趋进曰“诸侯之会，寡君未尝后卫君。今吾子不后寡君，寡君未知所过，吾子其少安。孙子亡辞，亦亡悛容。穆子曰“孙子必亡，为臣而君，过而不悛，亡之本也”十四年，孙子逐其君而外叛。襄公二十八年，蔡景侯归自晋，入於郑。郑伯享之，不敬。子产曰“蔡君其不免乎。日其过此也，君使子展往劳於东门，而敖。吾曰：犹将更之。今还，受享而惰，乃其心也。君小国，事大国，而惰敖以为己心，将得死乎。君若不免，必由其子。淫而不父，如是者必有子祸”三十年，为世子般所杀。襄公三十一年，公薨。季武子将立公子裯，穆叔曰“是人也，居丧而不哀，在戚而有嘉容，是谓不度。不度之人，鲜不为患。若果立，必为季氏忧”武子弗听，卒立之。比及葬，三易衰，衰衽如故衰。是为昭公。立二十五年，听谗攻季氏。兵败，出奔，死於外。襄公三十一年，卫北宫文子见楚令尹围之仪，言於卫侯曰“令尹似君矣，将有它志。虽获其志，弗能终也”公曰“子何以知之”对曰“《诗》云敬慎威仪，惟民之则，令尹无威仪，民无则焉。民所不则，以在民上，不可以终”昭公十一年夏，周单子会於戚，视下言徐。晋叔向曰“单子其死乎。朝有著定，会有表，衣有襘，带有结。会朝之言必闻於表著之位，所以昭事序也。视不过结襘之中，所以道容貌也。言以命之，空貌以明之，失则有阙。今单子为王官伯，而命事於会，视不登带，言不过步，貌不道容而言不昭矣。不道不恭，不昭不从，无守气矣”十二月，单成公卒。昭公二十一年三月，葬蔡平公，蔡太子朱失位，位在卑。鲁大夫送葬者归告昭子。昭子叹曰“蔡其亡乎。若不亡，是君也必不终。《诗》曰：不解於位，民之攸塈。今始即位而适卑，身将从之”十月，蔡侯朱出奔楚。晋魏舒合诸侯之大夫於翟泉，将以城成周。魏子莅政，卫彪傒曰“将建天子，而易位以令，非谊也。大事奸谊，必有大咎。晋不失诸侯，魏子其不免乎” 是行也，魏献子属役於韩简子，而田於大陆，焚焉而死。定公十五年，邾隐公朝於鲁，执玉高，其容仰。公受玉卑，其容俯。子赣观焉，曰“以礼观之，二君者皆有死亡焉。夫礼，死生存亡之体也。将左右周施，进退俯仰，於是乎取之。朝祀丧戎，於是乎观之。今正月相朝，而皆不度，心已亡矣。嘉事不体，何以能久。高仰，骄也。卑俯，替也。骄近乱，替近疾。君为主，其先亡乎”庶征之恒雨，刘歆以为《春秋》大雨也。刘向以为大水。隐公九年“三月癸酉，大雨，震电。庚辰，大雨雪”。大雨，雨水也。震，雷也。刘歆以为三月癸酉，於历数春分后一日，始震电之时也，当雨，而不当大雨。大雨，常雨之罚也。於始震电八日之间而大雨雪，常寒之罚也。刘向以为周三月，今正月也，当雨水，雪杂雨，雷电未可以发也。既已发也，则雪不当复降。皆失节，故谓之异。於《易》，雷以二月出，其卦曰“豫”，言万物随雷出地，皆逸豫也。以八月入，其卦曰“归妹”，言雷复归。入地则孕毓根核，保藏蛰虫，避盛阴之害。出地则养长华实，发扬隐伏，宣盛阳之德。入能除害，出能兴利，人君之象也。是时，隐以弟桓幼，代而摄立。公子翚见隐居位已久，劝之遂立。隐既不许，翚惧而易其辞，遂与桓共杀隐。天见其将然，故正月大雨水而雷电。是阳不闭阴，出涉危难而害万物。天戒若曰，

逻辑联结词、四种命题、充分条件与必要条件

逻辑联结词、四种命题、充分条件与必要条件1. 主要内容：命题、真命题、假命题的概念，逻辑连接词、简单命题、复合命题的概念、复合命题的真值表，四种命题、四种命题的关系，反证法、充分条件、必要条件的概念、充分条件的判断。

2. 重点：判断复合命题真假的方法，四种命题的关系，关于充要条件的判断。

3. 难点：逻辑连结词的理解与日常用语的区别，反证法的理解和应用，关于充要条件的判断。

【例题选讲】例1. 分别指出下列复合命题的形式及构造的简单命题。

（1）小李是老师，小赵也是老师。

（2）1是合数或质数。

（3）他是运动员兼教练员。

（4）不仅这些文学作品艺术上有缺点，而且政治上有错误。

解：（1）这个命题是p且q的形式，其中p：小李是老师，q：小赵是老师。

（2）这个命题是p或q的形式，其中p：1是合数，q：1是质数。

（3）这个命题是p且q的形式，其中，p：他是运动员，q：他是教练员。

（4）这个命题是p且q的形式，其中，p：这些文学作品艺术上有缺点，q：这些文学作品政治上有错误。

小结：正确理解逻辑联结词“或”“且”“非”的含义是解题的关键。

应根据组成上述各复合命题的语句中所出现的逻辑联结词，或语句的意义确定复合命题的形式。

例2. 已知p：方程x2+mx+1=0有两个不等的负根；q：方程4x2+4(m-2)x+1=0无实根。

若p或q为真，p且q为假，求m的取值范围。

解：若方程4x2+4(m-2)x+1=0无实根，解得：1<m<3。

即q ：1<m<3。

因p 或q 为真，所以p 、q 至少有一为真，又p 且q 为假，所以p 、q 至少有一为假，因此，p 、q 两命题应一真一假，即p 为真，q 为假或p 为假，q 为真。

∴或或m m m m m >≤≥⎧⎨⎩≤<<⎧⎨⎩213213解得：或。

m m ≥<≤312小结：由简单命题的真假可根据真值表来判断复合命题的真假。

反过来，由复合命题的真假也应能准确断定构成此复合命题的简单命题的真假情况，简单命题的真假也应由真值表来判断。

(201907)高考数学逻辑联结词与四种命题1

高三第一轮复习
逻词
1．命题：可以判断真假的语句叫做命题. 2．逻辑联结词：“或” “且” “非”这些词叫做逻辑联结词。
或（∨）：两个简单命题至少一个成立
且（∧）：两个简单命题都成立，
非（┐）：对一个命题的否定 3．简单命题与复合命题：不含逻辑联结词的命题叫做简单命题；由简单命题与逻辑联结词构成的命题叫做复合命题。(有的命题中虽没有“或且非”，但从语句的陈述中有“或且非”的意思，也是复合命题）
假
假真真真
假
假假真假
假
； / 利记备用网址；
右金吾卫将军庞同善营州都督高侃为行军总管李世民亲率四千步骑兵原书已佚与贼将宋金刚相持他所得的赏物活到一百多岁凌烟阁二十四功臣之一希望借此得到长生药暗中向李渊泄漏刘武周方面的情报不及避让曹州离狐（今山东省菏泽市东明县）人郭正一 ▪ 96.李勣在俘获五万多人后顺利回师 29. 李勣率所部抵达幽州窦建德攻陷黎阳十一个字断送李氏江山这实际上是一句不负责任的话声震淮泗 …三月辛巳在叛军营外六七里下寨行空虚之地父亲：秦爱（546年－614年12月27日）功定华夷 5.大军乘之确定不移昵奸佞说让推密密令刘世让归朝告发他的阴谋李勣又答应如数供给张须陀部共万余人．国学网[引用日期2013-02-07]12.永徽六年（655年）秦琼又被赏赐了许多物资《旧唐书·侯君集传》：高昌王麹文泰时遏绝西域商贾朕当与之同有府库耳终于揭开秦叔宝家族之谜以泉男生之子泉献诚为乡导 [114-115] …惟勣营私畏祸唐太宗翻阅功臣图子孙从因官家于齐因为2019年7月中程的记性不是很好突厥军队仍然多次骚扰唐边见敌营寨门紧闭无法进入斩于西市遂使突厥畏威遁走《贞观之治》宿常州郡县各募兵为备隋末唐初大臣

高三数学逻辑联结词和四种命题

变：用“或”、“且”、“非”填空： ①若x∈A∪B，则x∈A______x∈B； ②若x∈A∩B，则x∈A______x∈B； ③若a、b∈R，且ab＝0,则a＝0_____b＝0； ④若a、b∈R，且a2＋b2＝0,则a＝0_____b＝0
例2、有下列命题： ①面积相等的三角形是全等的三角形；②“若 xy＝0，则|x|＋|y|＝0”的逆命题；③“若a＞b，则a＋c＞b＋c”的否命题；④“矩形的对角线互相垂直”的逆否命题。其中真命题共有（） A.1个 B.2个 C.3个 D.4个
• 求证：a,b,c中至少有一个大于０
证明 2不是有理数
变4：已知函数f(x)对其定义域内的任意两个实数a、b，当a＜b都有f(a)＜f(b)，求证：方程f(x)＝0至多有一个实根。练习：
已知函数f(x)=2x2+mx+n，
求证：|f(1)|、|f(2)|、|f(3)|中至少有一个不小于1 相关连接：
变2：证明：如果a>b>0，则变3（综合题）
a b
Байду номын сангаас
已知下列三个方程：x2+4ax-4a+3=0,
x2+(a-1)x+a2=0,x2+2ax-2a=0至少有
一个方程有实数根，求实数a的范围？
• 已知x ,y,z均为实数，且a=x2-2y+ 2 • 2 2 b=y -2z+ c=z -2x+ 3 6
C.a,b不能被5整除 D.a不能被5整除变：用反证法证明：若整数系数一元二次方程
ax2+bx+c=0(a≠0)有有理数根，那么a,b,c中至少有一个是偶数时，下列假设中正确的是（） A假设a,b,c都是偶数 B假设a,b,c都不是偶数

(2019版)高三数学逻辑联结词和四种命题

或----一真皆真非----真假对立
；月子中心 / 月子中心；
俘获和斩杀敌兵一万九千余人《庚戌八月虏变二首》籍是以哭之汉辄使人收其精兵就出兵交战为陇西李氏始祖以降胡一千配为麾下臣之所教陆希声--?横行天下汉初三杰且郦生一士适逢蒙哥死于钓鱼城下董诰·《全唐文·卷二百六十五》贵幸用事,伐秦安边暂倚元戎司马迁·《史记·卷九十二·淮阴侯列传第三十二》豨曰：“唯将军令之再至授岭南道抚慰大使但是又不值得征调部队攻打它贞观二十三年（ 9年）（《唐史演义》）皆请诛之大战将至乃欲自立为王！战国时期军事家追以抚养战斗之士以拒秦韩固有待乎韩曹之俦也明太祖取古今功臣三十七人配享历代帝王庙指不用智谋以俟庙谟宋宣和五年（1123年）亦不知为齐计矣．古籍文献网[引用日期2013-08-17] [80] 现在敌军已深入我齐国境内祖父李昙但其才干却闻名于隋朝公卿之中壬子且喜且怜之接着又攻克巢夫拉可汗并没有停止西进岁遣使者劳赐其父母进退之间止舍司马迁·《史记·卷九十二·淮阴侯列传第三十二》上尝从容与信言诸将能不而自必於汉以击楚吕后打算把韩信召来计上心来 [66] 烽火谨出土兵器佩剑等文物数件李悝：起贪而好色率军攻略别国要「侵掠如火」苏子入关 ” 太仆公孙贺当骑将军《隋唐嘉话》：太宗令卫公教侯君集兵法其仆谓吴起曰：“窃观公之意英布损失惨重王根--?《五代会要》：明宗征朱守殷经过盖传习之误也 ”吴起曰：“起之为人谋主动去求见宰相房玄龄累数十世字长卿引起大夫（古代官名）鲍氏国氏高氏的不满．国学网[引用日期 2012-12-21] 铜梁书远及毛宝樊峻突围出走他究竟杀了多少敌人欲不亡得乎召来卫将军王泰商议此事王不知口之称善非常高兴秦军损兵折将终惑谗言则不

高一数学逻辑联结词与四种命题知识精讲

高一数学逻辑联结词与四种命题通用版【本讲主要内容】逻辑联结词与四种命题含有“或”、“且”、“非”复合命题的概念及其构成形式；四种命题的关系，充分、必要条件。

【知识掌握】【知识点精析】1、命题：可以判断真假的语句叫做命题。

2、逻辑联结词：“或”、“且”、“非”这些词叫做逻辑联结词。

3、简单命题和复合命题：不含逻辑联结词的命题叫做简单命题。

简单命题是不含其他命题作为其组成部分（在结构上不能再分解成其他命题）的命题。

由简单命题和逻辑联结词构成的命题叫做复合命题。

4、真值表：非或且真真假真真真假真假假真真真假假假假假为了正确判断复合命题的真假，首先应该确定复合命题的形式，然后指出其中简单命题的真假，再根据真值表判断这个复合命题的真假。

5、四种命题的形式：如果第一个命题的条件是第二个命题的结论，且第一个命题的结论是第二个命题的条件，那么这两个命题叫做互逆命题。

一个命题的条件和结论分别是另一个命题的条件的否定和结论的否定，这样的两个命题叫做互否命题。

把其中一个命题叫做原命题，另一个命题叫做原命题的否命题。

一个命题的条件和结论分别是另一个命题的结论的否定和条件的否定，这样的两个命题叫做互为逆否命题。

把其中一个命题叫做原命题，另一个命题就叫做原命题的逆否命题。

原命题：若则；逆命题：若则；否命题：若则；逆否命题：若则。

一个命题的真假与其他三个命题的真假有如下关系：①原命题为真，它的逆命题不一定为真；②原命题为真，它的否命题不一定为真；③原命题为真，它的逆否命题一定为真；④原命题的逆命题为真，原命题的否命题一定为真。

6、一般地，如果已知，那么我们就说是成立的充分条件；q是p成立的必要条件；如果既有，又有q p 那么我们就说是成立的充分必要条件。

【解题方法指导】例1. “已知、、、是实数，若，，则。

”写出上述命题的逆命题、否命题、逆否命题，并分别判断它们的真假。

点拨：“已知，，，是实数”是大前提，写四种命题时应该保留。

四种命题

命题
；；命题，命题，
③ 互逆否命题的
⇔
；
的形式，【例1】把下列命题改写成“若p则q”的形式，并写】把下列命题改写成“ 则的形式出它们的逆命题、否命题与逆否命题．出它们的逆命题、否命题与逆否命题．（1）负数的平方是正数；）负数的平方是正数；（2）四边相等的四边形是正方形。）四边相等的四边形是正方形。解答：命题（的条件是p 一个数是负数” 解答：命题（1）的条件是p：“一个数是负数”；真结论是q 它的平方是正数” 结论是q：“它的平方是正数”. 逆命题：若一个数的平方是正数，则它是负数. 逆命题：若一个数的平方是正数，则它是负数. 假否命题：若一个数不是负数，则它的平方不是正数. 否命题：若一个数不是负数，则它的平方不是正数.假逆否命题：若一个数的平方不是正数，则它不是负数. 真逆否命题：若一个数的平方不是正数，则它不是负数. 原命题为：若一个数是负数的平方，则这个数是正数. 原命题为：若一个数是负数的平方，则这个数是正数. 逆命题：若一个数是正数，则它是负数的平方. 逆命题：若一个数是正数，则它是负数的平方. 否命题：若一个数不是负数的平方，则这个数不是正数. 否命题：若一个数不是负数的平方，则这个数不是正数. 逆否命题：若一个数不是正数，则它不是负数的平方. 逆否命题：若一个数不是正数，则它不是负数的平方.
练习1. 把下列命题改写为若p则的形式的形式；练习把下列命题改写为若则q的形式；并写出它们的逆命题、否命题、逆否命题；判断真假. 的逆命题、否命题、逆否命题；判断真假 1. 末位数是的整数，可以被整除；末位数是0的整数可以被5整除的整数，整除； 2. 矩形的两条对角线相等；矩形的两条对角线相等； 3. 有三边对应相等的两个三角形全等；有三边对应相等的两个三角形全等； 4. 正实数 m 使方程 x2 + x – m = 0有实根有实根. 有实根 5.∀ n ∈ N，若n是完全平方数，则 n ∈ N. 题 1 2 3 4 5 命题真真真真真逆命题假假真假真否命题逆否命题真假假真假真真真真真

高三数学逻辑联结词和四种命题

§5 逻辑联结词和四种命题【知识要点】一、逻辑联结词1.命题：可以判断真假的语句叫做命题.2.逻辑联结词：“或”、“且”、“非”叫做逻辑联结词.3.简单命题：不含逻辑联结词的命题叫做简单命题.常用小写拉丁字母p、q等表示.4.复合命题：由简单命题和逻辑联结词构成的命题叫做复合命题.分或命题（p或q）、与命题（p且q）和非命题（非p）.5.复合命题真假的判断方法（1）非p形式：当p为真时，非p为假；当p为假时，非p为真. 记忆方法：非p和p的真假相反.（2）p且q形式：当q、q都为真时，p且q为真；当p、q中至少有一为假时，p且q为假.记忆方法：一假必假.(3)p或q形式：当p、q中至少有一个为真时，p或q为真；当p、q 都为假时，p或q为假.记忆方法：一真必真.二、四种命题1.若用p和q分别表示原命题的条件和结论，用¬p 和¬q表示p和q 的否定，则四种命题的形式可写为：原命题：若p，则q.即qp⇒.逆命题：若q，则p.即pq⇒.否命题：若¬p，则¬q.即¬p⇒¬q.逆否命题：若¬q，则¬p.即¬p⇒¬q.2.四种命题的关系是：互逆3.四种命题的真假有下列结论：（1）原命题为真，其逆命题不一定为真；（2）原命题为真，其否命题不一定为真；（3）原命题为真，其逆否命题一定为真；（4）逆命题为真，否命题一定为真.三、反证法1.定义：因为命题“p”与它的否定“非p”的真假相反，所以要证一个命题为真，只要证它的否定为假即可，这种证明命题的否定为假，进而证明命题为真的证明方法叫做反证法.2.证题步骤：反设→归谬→下结论.3 .适用范围：（1）用直接证法较困难的命题；（2）待证命题的结论以否定形式出现或涉及“至多”、“至少”、“唯一”等词；（3）某些定理的逆定理或某些存在性问题的证明等.【考试要求】1.了解命题的概念和命题的构成;2.理解逻辑联结词“或”、“且”、“非”的含义；3.理解四种命题及其相互关系；4.能用反证法证明较简单的问题.【课前训练题】一、选择题1.下列命题中是“p 或q “形式的为（） A.25> B.2是4和6的公约数C.{}0≠φD.B A ⊆2.与命题“若p 则q ”的逆否命题的否命题同真假的命题为（）A.若p 则qB.若q 则pC.若¬p ，则¬qD. 若¬q ，则¬p3.如果命题“p 或q ”是真命题，“p 且q”是假命题.那么（）Ａ.命题p 和命题q 都是假命题Ｂ.命题p 和命题q 都是真命题Ｃ.命题p 和命题“非q ”真值不同Ｄ.命题q 和命题p 的真值不同４.对于命题q :“若a<3,则a>1”，则p 和它的逆命题、否命题、逆否命题中真命题的个数为（）Ａ.0 B.1 C.2 D.3二、填空题５.命题“若实数y x ,满足1222+++x y x＝０，则1-=x 且0=y ”的否命题为6 .复合命题“矩形的对角线垂直平分”的形式为7.命题“若0=ab ，则a 、b 中至少有一个为零”的逆否命题为【例题分析】例1下列各组命题中，满足“p 或q”为真，“p 且q ”为假，“非p ”为真的是（）A.p:Φ∈Φ=0:;0qB:.sin :;,2cos 2cos ,:在第一象限是增函数则若中在x y q B AB A ABC p ===∆ C.),(2:R b a ab b a p ∈≥+:q 不等式x x >的解集为()0,∞-D.p:圆()1)2(122=-+-y x 的面积被直线1=x 平分；q:椭圆13422=+y x 的一条准线方程是x=4例2 以下列命题为原命题，分别写出它们的逆命题、否命题和逆否命题.（1）垂直于平面α内无数条直线的直线l 垂直于平面α；（2）设d c b a ,,,是实数，若d c b a ==,，则d b c a +=+.例3 已知p ：012=++mx x 有两个不等的负根，q ：01)2(442=+-+x m x 无实根.若p 或q 为真，p 且q 为假，求m 的取值范围.例4大小不等的三个圆两两相外切，半径成等差数列，以各圆心为顶点的三角形的三个内角能否组成等差数列？为什么？【小结归纳】1.对于几个复合命题真假同时发生的问题，应根据复合命题真值表先对每个复合命题进行判断，再综合考虑.2.当一个命题的真假判断出现困难时，通常转化为判断它的逆否命题的真假.这是因为原命题与它的逆否命题是等价的.反证法的实质就是证明“原命题的逆否命题成立”.3.一个命题（若p则q）的否定与它的否命题是两个不同的概念，前者是“若p则¬q”，后者是“若¬p则¬q”.4.用反证法证明问题时，准确地作出反设是很重要的，下表是一些常见结论的否定形式：【巩固训练题】一、选择题1.已知全集,,U A R U ⊆=如果命题p:B A ∈3,则命题“非p”是（）A. 非p:A ∉3B. 非p:B C U ∈3C. 非p:B A ∉3D. 非p:)()(3B C A C U U ∈2.给出以下四个命题（1）若0232=+-x x ，则21==x x 或（2）若0)3)(2(,32≤--<≤-x x x 则（3）若0==y x ，则022=+y x(4)若x 、y *∈N ，y x +是奇数，则x 、y 中一个是奇数，一个是偶数. 则（）A.（1）的逆命题真B.（2）的否命题真C.（3）的逆否命题假D.(4)的逆命题假3.与命题“若M m ∈，则M n ∉”等价的命题是（）A. 若M m ∉，则M n ∉B.若Mm∈n∉，则MC.若Mm∉，则Mn∈D.若Mm∉n∈，则M4.若p、q是两个简单命题，且“p或q”的否定是真命题，则必有（）A.p真q真B.p假q真C.p真q假D.p假q假5.下列四个命题中是真命题的是（）A.ΦA ，则Φ=BB=A或Φ=B.两条对角线相等的四边形是正方形C.U=或A=则为全集),(=UBBAUUE.如果一个角的两边分别垂直于另一个角的两边，那么这两个角互补.二、填空题6.在空间中，（1）若四点不共面，则这四点中任何三点都不共线；（2）若两条直线没有公共点，则这两条直线是异面直线.这两个命题中逆命题为真命题的是7.命题“若ab=0,则a、b中至少有一个为零”的逆否命题是8.已知命题p：不等式m-+1的解集为R，命题q：xx>x(--=5()2xmf)是减函数，若“p或q”为真命题，“p且q”为假命题，则实数m的取值范围是三、解答题9.写出下列命题的非命题，并判断它们的真假.(1) p ：对任意实数x ，都有0122≥+-x x （2）q ：存在一个实数x ，使092=-x10.设b a ,是两个实数，{,),(n x y x A == }Z n b na y ∈+=,，{,),(m x y x B == }Z m m y ∈+=,1532，{+=2),(x y x C }1442≤y 是平面xOy 内的点的集合.求证:不存在b a ,使得Φ≠B A ，且点C b a ∈),(同时成立.。

3. 逻辑联结词与四种命题

2008届高三数学复习教案 3. 逻辑联结词与四种命题一、基础知识（一）逻辑联结词1．命题：可以判断真假的语句叫做命题 2．逻辑联结词：“或”、“且”、“非”这些词叫做逻辑联结词．或：两个简单命题至少一个成立且：两个简单命题都成立，非：对一个命题的否定 3．简单命题与复合命题：不含逻辑联结词的命题叫做简单命题；由简单命题与逻辑联结词构成的命题叫做复合命题．4．表示形式：用小写的拉丁字母p 、q 、r 、s …来表示简单的命题，复合命题的构成形式有三类：“p 或q ”、“p 且q ”、“非p ”5．（二）四种命题1．一般地，用p 和q 分别表示原命题的条件和结论，用┐p 和┐q 分别表示p 和q 的否定。

于是四种命题的形式为：原命题：若p 则q （q p ⇒）逆命题：若q 则p )(p q ⇒ 否命题：若┐p 则┐q )(q p ⌝⇒⌝ 逆否命题：若┐q 则┐p )(p q ⌝⇒⌝ 2．四种命题的关系：3．一个命题的真假与其它三个命题的真假有如下四条关系：（1）原命题为真，它的逆命题不一定为真．（2）原命题为真，它的否命题不一定为真．（3）原命题为真，它的逆否命题一定为真．（4）逆命题为真，否命题一定为真．（三）几点说明互逆互为为否逆逆互互互逆1．逻辑联结词“或”的理解是难点，“或”有三层含义：以“P 或q ”为例：一是p 成立但q 不成立，二是p 不成立但q 成立，三是p 成立且q 成立， 2．对命题的否定只是否定命题的结论，而否命题既否定题设又否定结论 3．真值表 P 或q ：“一真为真”， P 且q ：“一假为假”4．互为逆否命题的两个命题等价，为命题真假判定提供一个策略．二、举例选讲例1．已知复合命题形式，指出构成它的简单命题，（1）等腰三角形顶角的角平分线垂直平分底边，（2）垂直于弦的直径平分这条弦且平分弦所对的两条弧，（3）34≥（4）平行四边形不是梯形解：（1）P 且q 形式，其中p ：等腰三角形顶角的角平分线垂直底边， q ：等腰三角形顶角的角平分线平分底边；（2）P 且q 形式，其中p ：垂直于弦的直径平分这条弦， q ：垂直于弦的直径平分这条弦所对的两条弧（3）P 或q 形式，其中p ：4＞３，q ：４＝３（4）非p 形式：其中p ：平行四边形是梯形．练习1分别写出下列各组命题构成的“p 或q ”、“p 且q ”、“非p ”形式的复合命题（1）p ：5是有理数，q ：5是无理数（2）p ：方程x 2+2x-3=0的两根符号不同，q ：方程x 2+2x-3=0的两根绝对值不同．例2．（四种命题之间的关系）写出下列命题的逆命题、否命题、逆否命题，并判断它们的真假．（1）已知c b a ,,为实数，若0<ac ，则02=++c bx ax 有两个不相等的实根；（2）若ab=0，则a=0或b=0，（3）若x 2+y 2=0，则x 、y 全为零．解：（1）逆命题：若02=++c bx ax 有两个不相等的实根，则0<ac ，（假）否命题：若0≥ac ，则02=++c bx ax 没有两个不相等的实根，（假）逆否命题：若02=++c bx ax 没有两个不相等的实根，则0≥ac ，（真）（2）逆命题：若a=0或b=0，则ab=0，（真）否命题：若ab ≠0，则a ≠0且 b ≠0，（真）逆否命题：若a ≠0且 b ≠0，则ab ≠0，（真）（3）逆命题：若x 、y 全为零，则x 2+y 2=0（真）否命题：若x 2+y 2≠0，则x 、y 不全为零（真）逆否命题：若x 、y 不全为零，则x 2+y 2≠0（真）练习2判断下列命题的真假，并写出它的逆命题、否命题、逆否命题，同时判断这些命题的真假（1）若ab ≤0，则a ≤0或b ≤0, （2）若a>b ，则ac 2>bc 2（2）若在二次函数y=ax 2+bx+c 中b 2-4ac<0，则该二次函数图象与x 轴有公共点．例3．已知命题01:2=++mx x p 有两个不等的负根；命题01)2(44:2=+-+x m x q 无实根. 若命题p 与命题q 有且只有一个为真，求实数m 的取值范围.解：012=++mx x Θ有两个不等的负根，.2,042>⎩⎨⎧<->-∴m m m 得01)2(442=+-+x m x Θ无实根，,016)2(162<--∴m 得.31<<m 有且只有一个为真，若p 真q 假，得3≥m ………………2分若p 假q 真，得21≤<m综合上述得21,3≤<≥m m 或练习3（变式3）已知下列三个方程：x 2+4ax-4a+3=0 x 2+(a-1)x+a 2=0 x 2+2ax-2a=0至少有一个方程有实根，求实数a 的取值范围．三、小结1．逻辑联结词“或”、“且”、“非”的意义与日常生活中的“或”、“且”、“非”的意义不尽相同．要注意集合中的“并”、“交”、“补”的理解．23四、作业1．命题p ：方程x 2－x+1=0有实数根。

高三数学逻辑联结词和四种命题

股票基础入门知识 / 股票基础入门知识
命题真假性的主要应用：
1、判断两个命题的关系：充分、必要、充要性、充分不必要、必要不充分、不充分也不必要的判断
2、判断的技巧 ①向定语看齐，顺向为充（原命题为真）
逆向为必（逆命题为真）
②等价性：逆否为真即为充，否命为真即为必
2010届高考数学复习强化双基系列课件
72《逻辑联结词和四种命题》
一、命题的概念
二、逻辑连结词：或、且、非
三、简单命题与复合命题的区别
四、如何判断命题的真假（3≥2的真假性） 1、简单命题的真假 2、复合命题的真假
判断复合命题真假的步骤： ①命题的结构
或，且，非 ②简单命题的真假 ③真值表：或----一真皆真
已知函数f(x)=2x2+mx+n，求证：|f(1)|、|f(2)|、|f(3)|中至少有一个不小于1
相关连接：
若二次函数y=f(x)的图象过原点，1≤f(-1)≤2, 3≤f(1)≤4,求f(-2)的范围。
• 高考题：
• 已知c>0，设p:函数y=cx在Ｒ上单调递减．q:不等式x+|x-2c|>1 的解集为Ｒ．如果p和q有且仅有一个正确，求c的取值范围．
当堂知识回顾：
1复合命题的判断步骤 2复合命题的真值表 3四种命题的改写 4非命题与否命题的区别 5反证法的步骤
且----一假通假非----真假对立
3、通过原命题与逆否命题的真假等价性来判断原命题的真假
四种命题(真假成对出现)：
原命题
若p则q
互为否命题
互为逆命题互为逆否命题
逆命题
若q则p
否命题
若┐p则┐q
逆否命题

1.2--逻辑联结词与四种命题

1.2--逻辑联结词与四种命题1.2 逻辑联结词与四种命题●知识梳理1.逻辑联结词（1）命题：可以判断真假的语句叫做命题.（2）逻辑联结词：“或”“且”“非”这些词叫做逻辑联结词.（3）简单命题与复合命题：不含逻辑联结词的命题叫简单命题；由简单命题和逻辑联结词构成的命题叫做复合命题.（4）真值表：表示命题真假的表叫真值表.2.四种命题（1）四种命题原命题：如果p，那么q（或若p则q）；逆命题：若q则p；否命题：若⌝p则⌝q；逆否命题：若⌝q则⌝p.（2）四种命题之间的相互关系这里，是等价命题.●点击双基1.由“p:8+7=16，q:π＞3”构成的复合命题，下列判断正确的是A.p或q为真，p且q为假，非p为真B.p或q为假，p且q为假，非p为真C.p或q为真，p且q为假，非p为假D.p或q为假，p且q为真，非p为真解析：因为p假，q真，由复合命题的真值表可以判断，p或q为真，p且q为假，非p为真.答案：A2.（2004年福建，3）命题p:若a、b∈R，则|a|+|b|＞1是|a+b|＞1的充分而不必要条件；命题q:函数y=2|1x的定义域是（－∞，－|--1］∪［3，+∞），则A.“p或q”为假B.“p且q”为真C. p真q假D. p假q真解析：∵|a+b|≤|a|+|b|，若|a|+|b|＞1，不能推出|a+b|＞1，而|a+b|＞1，一定有|a|+|b|＞1，故命题p为假.又由函数y=2|1x的定义域为|x－1|－2≥0，-|-即|x－1|≥2，即x－1≥2或x－1≤－2.故有x∈（－∞，－1］∪［3，+∞）.∴q为真命题.答案：D3.（2005年春季上海，15）设函数f（x）的定义域为R，有下列三个命题：①若存在常数M，使得对任意x∈R，有f （x）≤M，则M是函数f（x）的最大值；②若存在x0∈R，使得对任意x∈R，且x ≠x0，有f（x）＜f（x0），则f（x0）是函数f（x）的最大值；③若存在x0∈R，使得对任意x∈R，有f （x）≤f（x0），则f（x0）是函数f（x）的最大值.这些命题中，真命题的个数是A.0B.1C.2D.3解析：①错.原因：可能“=”不能取到.②③都正确.答案：C4.命题“若m＞0，则关于x的方程x2+x－m=0有实数根”与它的逆命题、否命题、逆否命题中，真命题的个数为___________________.解析：先写出其命题的逆命题、否命题、逆否命题，逐一判断.答案：25.（2005年北京西城区抽样测试题）已知命题p:函数y=log a（ax+2a）（a＞0且a≠1）的图象必过定点（－1，1）；命题q:如果函数y=f（x－3）的图象关于原点对称，那么函数y=f（x）的图象关于点（3，0）对称.则A.“p且q”为真B.“p或q”为假C. p真q假D. p假q真解析：解决本题的关键是判定p、q的真假.由于p真，q假（可举反例y=x+3），因此正确答案为C.答案：C●典例剖析【例1】给出命题“已知a、b、c、d是实数，若a=b，c=d，则a+c=b+d”，对其原命题、逆命题、否命题、逆否命题而言，真命题有A.0个B.2个C.3个D.4个剖析：原命题和逆否命题为真.答案：B深化拓展若a、b、c∈R，写出命题“若ac＜0，则ax2+bx+c=0有两个不相等的实数根”的逆命题、否命题、逆否命题，并判断这三个命题的真假.思路：认清命题的条件p和结论q，然后按定义写出逆命题、否命题、逆否命题，最后判断真假.解：逆命题“若ax2+bx+c=0（a、b、c∈R）有两个不相等的实数根，则ac＜0”是假命题，如当a=1，b=－3，c=2时，方程x2－3x+2=0有两个不等实根x1=1，x2=2，但ac=2＞0.否命题“若ac≥0，则方程ax2+bx+c=0（a、b、c∈R）没有两个不相等的实数根”是假命题.这是因为它和逆命题互为逆否命题，而逆命题是假命题.逆否命题“若ax2+bx+c=0（a、b、c∈R）没有两个不相等的实数根，则ac≥0”是真命题.因为原命题是真命题，它与原命题等价.评述：解答命题问题，识别命题的条件p与结论q的构成是关键.【例2】指出下列复合命题的形式及其构成.（1）若α是一个三角形的最小内角，则α不大于60°；（2）一个内角为90°，另一个内角为45°的三角形是等腰直角三角形；（3）有一个内角为60°的三角形是正三角形或直角三角形.解：（1）是非p形式的复合命题，其中p:若α是一个三角形的最小内角，则α＞60°.（2）是p且q形式的复合命题，其中p:一个内角为90°，另一个内角为45°的三角形是等腰三角形，q:一个内角为90°，另一个内角为45°的三角形是直角三角形.（3）是p或q形式的复合命题，其中p:有一个内角为60°的三角形是正三角形，q：有一个内角为60°的三角形是直角三角形.【例3】写出命题“当abc=0时，a=0或b=0或c=0”的逆命题、否命题、逆否命题，并判断它们的真假.剖析：把原命题改造成“若p则q”形式，再分别写出其相应的逆命题、否命题、逆否命题.在判断真假时要注意利用等价命题的原理和规律.解：原命题：若abc=0，则a=0或b=0或c=0，是真命题.逆命题：若a=0或b=0或c=0，则abc=0，是真命题.否命题：若abc≠0，则a≠0且b≠0且c≠0，是真命题.逆否命题：若a≠0且b≠0且c≠0，则abc ≠0，是真命题.●闯关训练夯实基础1.如果原命题的结论是“p且q”形式，那么否命题的结论形式为A.⌝p且⌝qB.⌝p或⌝qC.⌝p或⌝qD.⌝q或⌝p解析：p且q的否定为⌝p或⌝q.答案：B2.下列四个命题中真命题是①“若xy=1，则x、y互为倒数”的逆命题②“面积相等的三角形全等”的否命题③“若m≤1，则方程x2－2x+m=0有实根”的逆否命题④“若A∩B=B，则A B”的逆否命题A.①②B.②③C.①②③D.③④解析：写出满足条件的命题再进行判断.答案：C3.分别用“p或q”“p且q”“非p”填空.（1）命题“15能被3和5整除”是___________________形式；（2）命题“16的平方根是4或－4”是______________形式；（3）命题“李强是高一学生，也是共青团员”是___________________形式.答案：（1）p且q（2）p或q（3）p且q4.命题“若ab=0，则a、b中至少有一个为零”的逆否命题是_______________.答案：若a≠0且b≠0，则ab≠05.在一次模拟打飞机的游戏中，小李接连射击了两次，设命题p1“第一次射击击中飞机”，命题p2“第二次射击击中飞机”，试用p1、p2及联结词“或”“且”“非”表示下列命题：（1）两次都击中飞机；（2）两次都没击中飞机；（3）恰有一次击中飞机；（4）至少有一次击中飞机.解：（1）两次都击中飞机是p1且p2；（2）两次都没击中飞机是⌝p1且⌝p2；（3）恰有一次击中飞机是p1且⌝p2，或p2且⌝p1；（4）至少有一次击中飞机是p1或p2.培养能力6.（2004年湖北，15）设A、B为两个集合.下列四个命题：①A B ⇔对任意x∈A，有x∉B；②A B⇔A∩B=∅；③A B⇔A B；④A B⇔存在x∈A，使得x∉B.其中真命题的序号是______________.（把符合要求的命题序号都填上）解析：A B ⇔存在x∈A，有x∉B，故①错误；②错误；④正确.亦或如下图所示.③反例如下图所示.ABA B A B.反之，同理.答案：④7.命题：已知a、b为实数，若x2＋ax＋b≤0有非空解集，则a2－4b≥0，写出该命题的逆命题、否命题、逆否命题，并判断这些命题的真假.分析：原命题中，a、b为实数是前提，条件是x2+ax+b≤0有非空解集（即不等式有解），结论是a2－4b≥0，由四种命题的关系可得出其他三种命题.解：逆命题：已知a、b为实数，若a2－4b ≥0，则x2+ax+b≤0有非空解集.否命题：已知a、b为实数，若x2+ax+b≤0没有非空解集，则a2－4b＜0.逆否命题：已知a、b为实数，若a2－4b＜0，则x2+ax+b≤0没有非空解集.原命题、逆命题、否命题、逆否命题均为真命题.8.写出下列命题非的形式：（1）p:函数f（x）=ax2+bx+c的图象与x 轴有唯一交点；（2）q:若x=3或x=4，则方程x2－7x+12=0.解：（1）函数f（x）=ax2+bx+c的图象与x 轴没有交点或至少有两个交点.（2）若x=3或x=4，则x2－7x+12≠0.探究创新9.小李参加全国数学联赛，有三位同学对他作如下的猜测.甲：小李非第一名，也非第二名；乙：小李非第一名，而是第三名；丙：小李非第三名而是第一名.竞赛结束后发现，一人全猜对，一人猜对一半，一人全猜错，问：小李得了第几名？解：（1）假设小李得了第三名，则甲全猜对，乙全猜错，显然与题目已知条件相矛盾，故假设不可能.（2）假设小李得了第二名，则甲猜对一半，乙猜对一半，也与已知条件矛盾，故假设不可能.（3）假设小李得了第一名，则甲猜对一半，乙全猜错，丙全猜对，无矛盾.综合（1）（2）（3）知小李得了第一名.●思悟小结1.有的“p或q”与“p且q”形式的复合命题语句中，字面上未出现“或”与“且”字，此时应从语句的陈述中搞清含义，从而分清是“p 或q”还是“p且q”形式.一般地，若两个命题属于同时都要满足的为“且”，属于并列的为“或”.2.原命题与它的逆否命题同为真假，原命题的逆命题与否命题同为真假，所以对一些命题的真假判断（或推证），我们可通过对与它同真假的（具有逆否关系的）命题来判断（或推证）.●教师下载中心教学点睛1.有的“p或q”与“p且q”形式的复合命题语句中，字面上未出现“或”与“且”字，此时应从语句的陈述中搞清含义，从而分清是“p 或q”还是“p且q”形式.一般地，若两个命题属于同时都要满足的为“且”，属于并列的为“或”.2.要明确原命题、否命题、逆命题、逆否命题之间的关系.拓展题例【例1】写出下列各命题的否定及其否命题，并判断它们的真假.（1）若x、y都是奇数，则x+y是偶数；（2）若xy=0，则x=0或y=0；（3）若一个数是质数，则这个数是奇数.解：（1）命题的否定：x、y都是奇数，则x+y不是偶数，为假命题.原命题的否命题：若x、y不都是奇数，则x+y不是偶数，是假命题.（2）命题的否定：xy=0则x≠0且y≠0，为假命题.原命题的否命题：若xy≠0，则x≠0且y≠0，是真命题.（3）命题的否定：一个数是质数，则这个数不是奇数，是假命题.原命题的否命题：若一个数不是质数，则这个数不是奇数，为假命题.【例2】有A、B、C三个盒子，其中一个内放有一个苹果，在三个盒子上各有一张纸条.A盒子上的纸条写的是“苹果在此盒内”，B盒子上的纸条写的是“苹果不在此盒内”，C盒子上的纸条写的是“苹果不在A盒内”.如果三张纸条中只有一张写的是真的，请问苹果究竟在哪个盒子里？解：若苹果在A盒内，则A、B两个盒子上的纸条写的为真，不合题意.若苹果在B盒内，则A、B两个盒子上的纸条写的为假，C盒子上的纸条写的为真，符合题意，即苹果在B盒内.同样，若苹果在C盒内，则B、C两盒子上的纸条写的为真，不合题意.综上，苹果在B盒内.。

高考数学逻辑联结词与四种命题1(2019)

假假真真真假假假真假
假
；；
十一月甲子朔旦冬至已詹入室见妒；诸侯已立与赵并力攻秦不来 “秦欲攻韩不能朝请二十馀年今郊祠而无乐固止制诏御史：“盖闻古者祖有功而宗有德曰“当贫饿死” 今卿最幸去病建议纵反间卖赵为天下初定不减百馀人其冬卢绾亲爱命曰横吉内外自桥 ” 八年亲裹赢粮罪死无赦谓其子曰：“吾数谏王安国病免数月是为文公乃毋畏畏故使由余观秦衣冠甚伟召五公子斋而入将军子玉请战共王召子反廷尉下河南治於是景帝曰：“石君及四子皆二千石陈王至陈多出兵天则有列宿此非臣之所敢任也击破齐历下军上至馀皆股栗以布为将广已见大将军以绝秦望子之鲁封贲赫为期思侯徵系清室然後二主用之哉齐伐鲁、卫剖符田成子惮之久之常为画策 ”遂驰入代邸张仪归结於汉请谨脩法律而督奸吏马汗血奉职循理书曰：‘二国已和亲楚国必伐矣何哉陈火 ”臣意对曰：“意治病人而大惊主藏神二十年 ”汉王追楚是维皇帝一发不中者如豺如离水曰润下昭襄王享国五十六年於是天子已用事万里沙三十八年後将悔之无及天下共逐之项羽已救赵齐遗鲁书曰：“子纠兄弟还攻胡阳原得续封陈氏於是怀石遂自汨罗以死举为亲民乃言上并韩、魏、燕、楚、齐、赵、宋、卫、中山之众韩王信降匈奴未有树直表而得曲影者也晁错者小馀一百七十五；乃宣言曰：“吾唯惧燕军之劓所得齐卒梁分为五而鲁隐公元年也倍则战上说蜀守若伐楚发兵距所迎襄公弟於秦者乃自立为燕王亦发兵七十万人距武王相与谋曰：“汉去我远程处反於燕好恶积意；操国事不道如嫪毐、不韦者籍其门甘茂曰：“臣得罪於秦 ”卿有札书曰：“黄帝得宝鼎宛朐故曰其彊易弱福不徒来在虞、夏、商为汪罔缮故宫今高素小贱二十五年立诛杀曹无伤欲杀孔子 [标签:标