最新人教版高中数学必修1第二章《指数函数的概念及性质》同步训练(第1课时)
人教版数学高一必修一同步训练 指数函数(一)

3.1.2 指数函数(一)一、基础过关1.下列以x 为自变量的函数中,是指数函数的是 ( )A .y =(-4)xB .y =πxC .y =-4xD .y =a x +2(a >0且a ≠1)2.函数f (x )=(a 2-3a +3)a x 是指数函数,则有( )A .a =1或a =2B .a =1C .a =2D .a >0且a ≠1 3.函数y =21x 的值域是( )A .(0,+∞)B .(0,1)C .(0,1)∪(1,+∞)D .(1,+∞)4.如果某林区森林木材蓄积量每年平均比上一年增长11.3%,经过x 年可以增长到原来的y 倍,则函数y =f (x )的图象大致为( )5.函数f (x )=a x 的图象经过点(2,4),则f (-3)的值为____________. 6.函数y =8-23-x (x ≥0)的值域是________. 7.比较下列各组数中两个值的大小: (1)0.2-1.5和0.2-1.7;(2)(14)13和(14)23; (3)2-1.5和30.2.8.判断下列函数在(-∞,+∞)内是增函数,还是减函数.(1)y =4x ;(2)y =⎝⎛⎭⎫14x ;(3)y =2x3. 二、能力提升9.设函数f (x )=⎩⎪⎨⎪⎧2x , x <0,g (x ), x >0. 若f (x )是奇函数,则g (2)的值是( )A .-14B .-4C.14 D .4 10.函数y =a |x |(a >1)的图象是( )11.若f (x )=⎩⎪⎨⎪⎧a x(x >1),(4-a2)x +2 (x ≤1),是R 上的单调递增函数,则实数a 的取值范围为 ________.12.求函数y =⎝⎛⎭⎫12x 2-2x +2(0≤x ≤3)的值域. 三、探究与拓展13.当a >1时,判断函数y =a x +1a x -1是奇函数.答案1.B 2.C 3.C 4.D 5.186.4,8)12.解 令t =x 2-2x +2,则y =⎝⎛⎭⎫12t, 又t =x 2-2x +2=(x -1)2+1, ∵0≤x ≤3,∴当x =1时,t min =1; 当x =3时,t max =5. 故1≤t ≤5, ∴⎝⎛⎭⎫125≤y ≤⎝⎛⎭⎫121, 故所求函数的值域为⎣⎡⎦⎤132,12.13.证明 由a x -1≠0,得x ≠0,故函数定义域为{x |x ≠0},易判断其定义域关于原点对称. 又f (-x )=a -x +1a -x -1=(a -x +1)a x (a -x -1)a x =1+a x 1-a x =-f (x ),∴f (-x )=-f (x ),∴函数y =a x +1a x -1是奇函数.。
最新人教版高中数学必修1第二章《指数函数》同步训练

3.1.2 指数函数5分钟训练1.下列关于自变量x 的函数中,是指数函数的是( )A.y=(a+1)x (a >-1且a≠0)B.y=(-3)xC.y=-(-3)xD.y=3x+1答案:A解析:∵a >-1且a≠0,∴a+1>0且a+1≠1,∴y=(a+1)x (a >-1且a≠0)为指数函数.2.函数y=a |x|(a >1)的图象是( )答案:B解析:函数f(|x|)是偶函数,应先画出x ≥0时f(x)的图象,然后沿y 轴翻折过去,得到x <0时函数的图象.当x≥0时,y=a |x|=a x 的图象过(0,1)点,在第一象限,图象下凸,是增函数,故选B.3.已知f (x )=3-a x+1的图象恒过定点P ,则点P 的坐标为( )A.(0,3)B.(-1,2)C.(-1,3)D.(3,-1)答案:B解析:由y=a x 的图象恒过(0,1)点,可知当本题中的x+1=0即x=-1时,y=2,与a 的取值无关.由x=-1时,y=3-a 0=2得定点P(-1,2),故选B.4.函数y=2x 的图象与函数y=0.5x 的图象关于____________对称;函数y=2x 的图象与函数y=-2x 的图象关于____________对称.答案:y 轴 x 轴10分钟训练1.已知镭经过100年剩留原来质量的95.76%,设质量为1的镭经过x 年后剩余量为y ,则x 、y 之间的函数关系式是( )A.y=0.957 6xB.y=0.957 6x-1C.y=1009576.0xD.y=x 1009576.0答案:C解析:依题意有:100年后质量为1的镭剩余量y 1=1×95.76%,200年后质量为1的镭剩余量为y 2=1×95.76%×95.76%,…,∴x 年后,y=1009576.0x,故选C.2.函数f(x)=a x-b 的图象如图所示,其中a 、b 为常数,则下列结论正确的是( )A.a >1,b <0B.a >1,b >0C.0<a <1,b >0D.0<a <1,b <0答案:D解析:由题图可知,函数f(x)=a x-b 是单调递减的,∴0<a <1.又由于函数图象与y 轴的交点在点(0,1)的下方,即函数f(x)=a x-b 的图象是由函数f(x)=a x 的图象向左平移得到的,∴-b >0,即b <0.3.函数y=x 31-的定义域是( )A.[0,+∞)B.(-∞,0]C.[1,+∞)D.(-∞,+∞)答案:B解析:要使函数有意义,必须1-3x ≥0,即3x ≤1,3x ≤30,∴x≤0,∴函数的定义域是(-∞,0].4.(2007山东日照实验高中《函数》过关测试,12)下列说法不正确的是( )A.函数y=2xx a a --(a >0,a≠1)是奇函数 B.函数f(x)=1)1(-+x x a x a (a >0,a≠1)是偶函数 C.若f(x)=3x ,则f(x+y)=f(x)f(y)D.若f(x)=a x (a >0,a≠1),且x 1≠x 2,则21[f(x 1)+f(x 2)]<f(221x x +) 答案:D解析:由函数的凹凸性可知D 不成立.5.已知函数y=a 2x +2a x -1(a >0,a≠1)在区间[-1,1]上的最大值是14,则a 的值为____________. 答案:3或31 解析:y=a 2x +2a x -1=(a x +1)2-2,∵函数y=a 2x +2a x -1在[-1,1]上的最大值是14,∴(a x +1)2的最大值为16.当a >1,x=1时,(a+1)2=16,得a=3;当0<a <1,x=-1时,(a 1+1)2=16,得a=31. 6.求下列函数的单调区间和值域.(1)y=x x --23;(2)y=a 2x -2a x -1(a >0,a≠1).解:(1)设y=3u ,u=-x 2-x.则y 随u 的增大而增大,随u 的减小而减小,u 的增区间即是y 的增区间,u 的减区间即为y 的减区间.u=-x 2-x=-(x+21)2+41在(-∞,21-]上递增,在(21-,+∞)上递减. ∴y=x x --23的增区间为(-∞,21-],减区间为(21-,+∞). ∵u=-x 2-x≤41, ∴0<y=x x --23≤413,即函数y=xx --23的值域为(0,43]. (2)y=(a x -1)2-2(a >0,a≠1),设u=a x .∵y=(u-1)2-2在u ∈[1,+∞)时是关于u 的增函数,在u ∈(-∞,1)时是关于u 的减函数,∴当a x ≥1时,原函数的单调性与u=a x 的单调性相同;当a x <1时,原函数的单调性与u=a x 的单调性相反.若a >1,a x ≥1⇔x≥0,a x <1⇔x <0,∴在[0,+∞)上,函数y=a 2x -2a x -1是增函数;在(-∞,0)上,函数y=a 2x -2a x -1是减函数.∵a x >0,∴函数值域是[-2,+∞).30分钟训练1.已知21<(21)b <(21)a <1,则( ) A.a >b >1 B.0<b <a <1C.b >a >1D.0<a <b <1答案:D解析:不等式21<(21)b <(21)a <1即为21<(21)b <(21)a <(21)0,根据指数函数的单调性即可得指数a 、b 、0、1的大小关系.根据指数函数y=(21)x 在R 上是减函数,得0<a <b <1.选D.2.若函数y=a x -(b+1)(a >0,a≠1)的图象在第一、三、四象限,则有( )A.a >1且b <1B.a >1且b >0C.0<a <1且b >0D.0<a <1且b <0答案:B解析:指数函数y=a x 的图象如图所示.由图象可以看出a >1,-(b+1)<-1(向下平移一个单位),即b >0.故选B.3.(2007广东韶关高三摸底,3)函数y=||x xa x(0<a <1)的图象的大致形状是()答案:D解析:y=⎪⎩⎪⎨⎧<->.0,,0,x a x a x x 4.一种单细胞生物以一分为二的方式进行繁殖,每三分钟分裂一次,假设将一个这种细胞放在一个盛有营养液的容器中,恰好一小时这种细胞充满容器,假设开始将两个细胞放入容器,同样充满容器时间是( )A.27分钟B.30分钟C.45分钟D.57分钟 答案:D解析:设要经过时间为x,由2×32x =220,得x=57.5.(2007江苏第二次大联考,11)若函数f(x)=⎪⎩⎪⎨⎧≤+->1,2)24(,1,x x a x a x 是R 上的单调递增函数,则实数a 的取值范围是( )A.(1,+∞)B.(1,8)C.(4,8)D.[4,8)答案:D解析:由f(x)在R 上是单调递增函数知a >1,4-2a >0,a 1≥4-2a +2同时成立,解不等式组得a ∈[4,8).6.(探究题)指数函数①f(x)=m x ,②g(x)=n x 满足不等式0<m <n <1,则它们的图象是( )答案:C解析:令x=1,①②对应的函数值分别为m 和n,由0<m <n <1,可知应选C.7.(2007上海春招,9)若x 1、x 2为方程2x =11)21(+-x 的两个实数解,则x 1+x 2=_______________. 答案:-1解析:由题意得2x =112-x ,即x=11-x,化简得x 2+x-1=0. 由韦达定理可知x 1+x 2=-1.8.(2007山东日照实验高中一轮测试,15)已知集合A n ={x|2n <x <2n+1,且x=7m+1,m 、n ∈N *},则A 6中各元素之和为_______________.答案:891解析:当n=6时,64<x <128,A 6中的各元素为:71,78,85,92,99,106,113,120,127,其和为891.9.(创新题)已知f(x)=x(121-x +21). (1)求函数的定义域;(2)判断函数f(x)的奇偶性;(3)求证:f(x)>0.答案:(1)解:由2x -1≠0,得x≠0,∴函数定义域为{x|x ∈R ,且x≠0}.(2)解:在定义域内任取x,则-x 在定义域内,则有 f(-x)=x x x x x )21212())(21121(+--=-+-- =x x x x x x ∙-+=∙-+-)12(212)21(221, 而f(x)=x x x x x ∙-+=+-)12(212)21121(, ∴f(-x)=f(x).∴函数f(x)为偶函数.(3)证明:当x <0时,由指数函数的性质知0<2x <1,-1<2x -1<0.∴121-x <-1.∴2121121-<+-x . 又x <0,∴f(x)=(121-x +21)x >0. 由f(x)为偶函数,当x >0时,f(x)>0.总之,x ∈R 且x≠0时,函数f(x)>0.10.设函数f (x )是定义在R 上的增函数,且f (x )≠0,对于任意x 1、x 2∈R ,都有f (x 1+x 2)=f (x 1)·f (x 2).(1)求证:f (x 1-x 2)=)()(21x f x f ; (2)若f (1)=2,解不等式f (3x )>4f (x ).答案:(1)证明:∵f(x 1)=f(x 1-x 2+x 2)=f(x 1-x 2)·f(x 2),又f(x)≠0,∴f(x 1-x 2)=)()(21x f x f . (2)解:∵f(1)=2,∴2f(x)=f(1)·f(x)=f(1+x),4f(x)=2·2f(x)=f(1)·f(1+x)=f(2+x).那么f(3x)>4f(x)可化为f(3x)>f(2+x),又因为函数f(x)是定义在R 上的增函数,由f(3x)>f(2+x)得3x>2+x ,即x>1.故不等式f(3x)>4f(x)的解集是{x|x>1}.。
高中数学必修一第二章2.1.2指数函数及其性质习题(含答案)
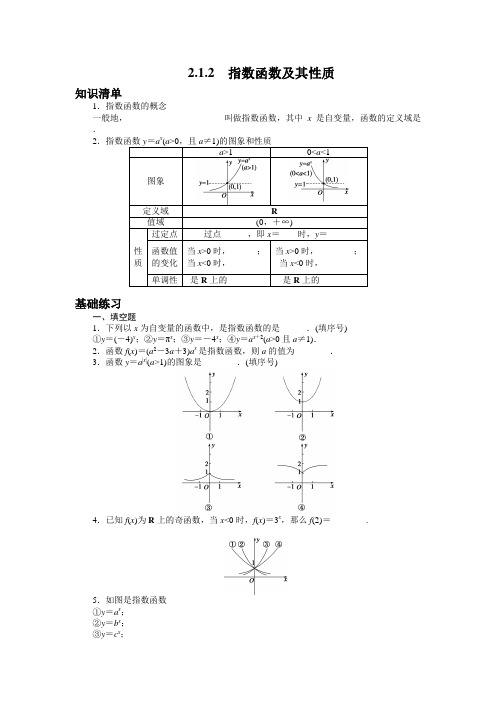
2.1.2 指数函数及其性质知识清单1.指数函数的概念一般地,______________________叫做指数函数,其中x 是自变量,函数的定义域是____.2.指数函数y =a x (a >0,且a ≠1)的图象和性质a >1 0<a<1图象定义域 R 值域 (0,+∞)性 质 过定点过点______,即x =____时,y =____函数值 的变化 当x >0时,______; 当x <0时,________ 当x >0时,________; 当x <0时,________单调性是R 上的________是R 上的________基础练习一、填空题1.下列以x 为自变量的函数中,是指数函数的是______.(填序号)①y =(-4)x ;②y =πx ;③y =-4x ;④y =a x +2(a >0且a ≠1). 2.函数f (x )=(a 2-3a +3)a x 是指数函数,则a 的值为________. 3.函数y =a |x |(a >1)的图象是________.(填序号)4.已知f (x )为R 上的奇函数,当x <0时,f (x )=3x,那么f (2)=________.5.如图是指数函数 ①y =a x ; ②y =b x ; ③y =c x ;④y =d x 的图象,则a 、b 、c 、d 与1的大小关系是________.6.函数y =(12)x -2的图象必过第________象限.7.函数f (x )=a x 的图象经过点(2,4),则f (-3)的值为____.8.若函数y =a x -(b -1)(a >0,a ≠1)的图象不经过第二象限,则a ,b 需满足的条件为________.9.函数y =8-23-x (x ≥0)的值域是________. 二、解答题10.比较下列各组数中两个值的大小:(1)0.2-1.5和0.2-1.7; (2)1314⎛⎫⎪⎝⎭和2314⎛⎫⎪⎝⎭; (3)2-1.5和30.2.11.2000年10月18日,美国某城市的日报以醒目标题刊登了一条消息:“市政委员会今天宣布:本市垃圾的体积达到50 000 m 3”,副标题是:“垃圾的体积每三年增加一倍”.如果把3年作为垃圾体积加倍的周期,请你完成下面关于垃圾的体积V (m 3)与垃圾体积的加倍的周期.(1) (2)根据报纸所述的信息,你估计3年前垃圾的体积是多少? (3)如果n =-2,这时的n ,V 表示什么信息?(4)写出n 与V 的函数关系式,并画出函数图象(横轴取n 轴). (5)曲线可能与横轴相交吗?为什么?12.定义运算a ⊕b =⎩⎪⎨⎪⎧a (a ≤b )b (a >b ),则函数f (x )=1⊕2x 的图象是________.(填序号)13.定义在区间(0,+∞)上的函数f (x )满足对任意的实数x ,y 都有f (x y )=yf (x ). (1)求f (1)的值;(2)若f (12)>0,解不等式f (ax )>0.(其中字母a 为常数).能力提升一、填空题1.设P ={y |y =x 2,x ∈R },Q ={y |y =2x ,x ∈R },则P 、Q 的关系为________. 2.函数y =16-4x 的值域是________.3.函数y =a 在[0,1]上的最大值与最小值的和为3,则函数y =2ax -1在[0,1]上的最大值是________.4.若函数f (x )=3x +3-x 与g (x )=3x -3-x 的定义域均为R ,则下列命题正确的是________.(填序号)①f (x )与g (x )均为偶函数;②f (x )为偶函数,g (x )为奇函数; ③f (x )与g (x )均为奇函数;④f (x )为奇函数,g (x )为偶函数.5.函数y =f (x )的图象与函数g (x )=e x +2的图象关于原点对称,则f (x )的解析式为________. 6.已知a =1335-⎛⎫ ⎪⎝⎭,b =1235-⎛⎫⎪⎝⎭,c =1243-⎛⎫ ⎪⎝⎭,则a ,b ,c 三个数的大小关系是________.7.春天来了,某池塘中的荷花枝繁叶茂,已知每一天新长出荷叶覆盖水面面积是前一天的2倍,若荷叶20天可以完全长满池塘水面,当荷叶刚好覆盖水面面积一半时,荷叶已生长了________天.8.已知函数f (x )是定义在R 上的奇函数,当x >0时,f (x )=1-2-x ,则不等式f (x )<-12的解集是________.9.函数y =2212x x-+⎛⎫ ⎪⎝⎭的单调递增区间是________.二、解答题10.(1)设f (x )=2u ,u =g (x ),g (x )是R 上的单调增函数,试判断f (x )的单调性; (2)求函数y =2212x x --的单调区间.11.函数f (x )=4x -2x +1+3的定义域为[-12,12].(1)设t =2x ,求t 的取值范围; (2)求函数f (x )的值域.12.函数y =2x -x 2的图象大致是________.(填序号)13.已知函数f (x )=2x-12x +1.(1)求f [f (0)+4]的值;(2)求证:f (x )在R 上是增函数;(3)解不等式:0<f (x -2)<1517.知识清单1.函数y =a x (a >0,且a ≠1) R 2.(0,1) 0 1 y >1 0<y <1 0<y <1 y >1 增函数 减函数 基础练习 1.②解析 ①中-4<0,不满足指数函数底数的要求,③中因有负号,也不是指数函数,④中的函数可化为y =a 2·a x ,a x 的系数不是1,故也不是指数函数. 2.2解析 由题意得⎩⎪⎨⎪⎧a 2-3a +3=1,a >0且a ≠1,解得a =2. 3.②解析 该函数是偶函数.可先画出x ≥0时,y =a x 的图象,然后沿y 轴翻折过去,便得到x <0时的函数图象.4.-19解析 当x >0时,-x <0,∴f (-x )=3-x ,即-f (x )=(13)x ,∴f (x )=-(13)x .因此有f (2)=-(13)2=-19.5.b <a <1<d <c解析 作直线x =1与四个指数函数图象交点的坐标分别为(1,a )、(1,b )、(1,c )、(1,d ),由图象可知纵坐标的大小关系. 6.二、三、四解析 函数y =(12)x 的图象上所有的点向下平移2个单位,就得到函数y =(12)x -2的图象,所以观察y =(12)x -2的图象可知.7.18解析 由题意a 2=4,∴a =2.f (-3)=2-3=18.8.a >1,b ≥2解析 函数y =a x -(b -1)的图象可以看作由函数y =a x 的图象沿y 轴平移|b -1|个单位得到.若0<a <1,不管y =a x 的图象沿y 轴怎样平移,得到的图象始终经过第二象限;当a >1时,由于y =a x 的图象必过定点(0,1),当y =a x 的图象沿y 轴向下平移1个单位后,得到的图象不经过第二象限.由b -1≥1,得b ≥2.因此,a ,b 必满足条件a >1,b ≥2. 9.[0,8)解析 y =8-23-x =8-23·2-x =8-8·(12)x=8[1-(12)x ].∵x ≥0,∴0<(12)x ≤1,∴-1≤-(12)x <0,从而有0≤1-(12)x <1,因此0≤y <8.10.解 (1)考察函数y =0.2x . 因为0<0.2<1,所以函数y =0.2x 在实数集R 上是单调减函数.又因为-1.5>-1.7,所以0.2-1.5<0.2-1.7.(2)考察函数y =(14)x .因为0<14<1,所以函数y =(14)x 在实数集R 上是单调减函数.又因为13<23,所以1314⎛⎫ ⎪⎝⎭>2314⎛⎫ ⎪⎝⎭1.(3)2-1.5<20,即2-1.5<1;30<30.2,即1<30.2,所以2-1.5<30.2.11.解 (1)由于垃圾的体积每3年增加1倍,24年后即8个周期后,该市垃圾的体积是50 000×28=12 800 000(m 3).(2)根据报纸所述的信息,估计3年前垃圾的体积是50 000×2-1=25 000(m 3).(3)如果n =-2,这时的n 表示6年前,V 表示6年前垃圾的体积. (4)n 与V 的函数关系式是V =50 000×2n ,图象如图所示.(5)因为对任意的整数n,2n >0,所以V =50 000×2n >0,因此曲线不可能与横轴相交. 12.①解析 由题意f (x )=1⊕2x=⎩⎪⎨⎪⎧1, x ≥0;2x , x <0.13.解 (1)令x =1,y =2,可知f (1)=2f (1),故f (1)=0.(2)设0<x 1<x 2,∴存在s ,t 使得x 1=(12)s ,x 2=(12)t ,且s >t ,又f (12)>0,∴f (x 1)-f (x 2)=f [(12)s ]-f [(12)t ]=sf (12)-tf (12)=(s -t )f (12)>0,∴f (x 1)>f (x 2).故f (x )在(0,+∞)上是减函数. 又∵f (ax )>0,x >0,f (1)=0, ∴0<ax <1,当a =0时,x ∈∅,当a >0时,0<x <1a ,当a <0时,1a<x <0,不合题意.故x ∈∅.综上:a ≤0时,x ∈∅;a >0时,不等式解集为{x |0<x <1a}.能力提升 1.Q P解析 因为P ={y |y ≥0},Q ={y |y >0},所以Q P . 2.[0,4)解析 ∵4x >0,∴0≤16-4x <16, ∴16-4x ∈[0,4). 3.3解析 函数y =a x 在[0,1]上是单调的,最大值与最小值都在端点处取到,故有a 0+a 1=3,解得a =2,因此函数y =2ax -1=4x -1在[0,1]上是单调递增函数,当x =1时,y max =3. 4.②解析 f (-x )=3-x +3x =f (x ),g (-x )=3-x -3x =-g (x ).5.f (x )=-e -x -2解析 ∵y =f (x )的图象与g (x )=e x +2的图象关于原点对称,∴f (x )=-g (-x )=-(e -x +2)=-e -x -2. 6.c <a <b解析 ∵y =(35)x 是减函数,-13>-12,∴b >a >1.又0<c <1,∴c <a <b . 7.19解析 假设第一天荷叶覆盖水面面积为1,则荷叶覆盖水面面积y 与生长时间的函数关系为y =2x -1,当x =20时,长满水面,所以生长19天时,荷叶布满水面一半. 8.(-∞,-1)解析 ∵f (x )是定义在R 上的奇函数, ∴f (0)=0.当x <0时,f (x )=-f (-x )=-(1-2x )=2x -1.当x >0时,由1-2-x <-12,(12)x >32,得x ∈∅;当x =0时,f (0)=0<-12不成立;当x <0时,由2x -1<-12,2x <2-1,得x <-1.综上可知x ∈(-∞,-1). 9.[1,+∞)解析 利用复合函数同增异减的判断方法去判断.令u =-x 2+2x ,则y =(12)u 在u ∈R 上为减函数,问题转化为求u =-x 2+2x 的单调递减区间,即为x ∈[1,+∞).10.解 (1)设x 1<x 2,则g (x 1)<g (x 2).又由y =2u 的增减性得()12g x<()22g x ,即f (x 1)<f (x 2), 所以f (x )为R 上的增函数.(2)令u =x 2-2x -1=(x -1)2-2, 则u 在区间[1,+∞)上为增函数.根据(1)可知y =2212x x --在[1,+∞)上为增函数. 同理可得函数y 在(-∞,1]上为单调减函数.即函数y 的增区间为[1,+∞),减区间为(-∞,1].11.解 (1)∵t =2x 在x ∈[-12,12]上单调递增,∴t ∈[22,2].(2)函数可化为:f (x )=g (t )=t 2-2t +3,g (t )在[22,1]上递减,在[1,2]上递增,比较得g (22)<g (2). ∴f (x )min =g (1)=2, f (x )max =g (2)=5-2 2.∴函数的值域为[2,5-22]. 12.①解析 当x →-∞时,2x →0,所以y =2x -x 2→-∞, 所以排除③、④.当x =3时,y =-1,所以排除②.13.(1)解 ∵f (0)=20-120+1=0,∴f [f (0)+4]=f (0+4)=f (4)=24-124+1=1517.(2)证明 设x 1,x 2∈R 且x 1<x 2, 则22x>12x>0,22x-12x>0,∴f (x 2)-f (x 1)=212121212121x x x x ---++ =()()()21212222121x x x x -++>0,即f (x 1)<f (x 2),所以f (x )在R 上是增函数.(3)解 由0<f (x -2)<1517得f (0)<f (x -2)<f (4),又f (x )在R 上是增函数,∴0<x -2<4,即2<x <6,所以不等式的解集是{x |2<x <6}.。
(人教a版)数学必修一课时训练:2.1.2(第1课时)指数函数的图象及性质(含答案)

温馨提示:此套题为Word版,请按住Ctrl,滑动鼠标滚轴,调节合适的观看比例,答案解析附后。
课时提升卷(十六)指数函数的图象及性质(45分钟 100分)一、选择题(每小题6分,共30分)1.若函数y=(2a-3)x是指数函数,则a的取值范围是( )A.a>B.a>,且a≠2C.a<D.a≠22.指数函数y=f(x)的图象经过点(-2,),那么f(4)·f(2)等于( )A.8B.16C.32D.643.(2013·黄冈高一检测)已知集合M={y|y=-x2+2,x∈R},集合N={y|y=2x,0≤x≤2},则(ðM)∩N=( )RA.[1,2]B.(2,4]C.[1,2)D.[2,4)4.当x>0时,指数函数f(x)=(a-1)x<1恒成立,则实数a的取值范围是( )A.a>2B.1<a<2C.a>1D.a∈R5.(2012·四川高考)函数y=a x-(a>0,a≠1)的图象可能是( )二、填空题(每小题8分,共24分)6.已知函数f(x)=则f(2)+f(-2)= .7.(2012·山东高考改编)若函数f(x)=a x(a>0,a≠1)在[-1,2]上的最大值为4,最小值为m,且函数g(x)=(1-4m)x2在[0,+∞)上是增函数,则a= .8.(2013·长沙高一检测)关于下列说法:(1)若函数y=2x的定义域是{x|x≤0},则它的值域是{y|y≤1}.(2)若函数y=的定义域是{x|x≥2},则它的值域是{y|y≤}.(3)若函数y=2x的值域是{y|0<y≤4},则它的定义域一定是{x|0<x≤2}.其中不正确的说法的序号是.三、解答题(9题,10题14分,11题18分)9.已知函数f(x)=a x+b(a>0,且a≠1).若f(x)的图象如图所示,求a,b 的值.10.(2013·长春高一检测)已知函数f(x)=a x-1(x≥0)的图象经过点(2,),其中a>0且a≠1.(1)求a的值.(2)求函数y=f(x)(x≥0)的值域.11.(能力挑战题)已知函数y=a x(a>0且a≠1)在[1,2]上的最大值与最小值之和为20,记f(x)=.(1)求a的值.(2)证明f(x)+f(1-x)=1.(3)求f()+f()+f()+…+f()的值.答案解析1.【解析】选B.由题意得2a-3>0,且2a-3≠1,所以a>,且a≠2.2.【解析】选D.设f(x)=a x(a>0且a≠1),由已知得=a-2,a2=4,所以a=2,于是f(x)=2x,所以f(4)·f(2)=24·22=26=64.3.【解析】选B.由题可知M=(-∞,2],N=[1,4],∴ðM=(2,+∞),(RðM)∩N=(2,4].R【变式备选】若集合M={y|y=2-x},P={y|y=},则M∩P等于( )A.{y|y>1}B.{y|y≥1}C.{y|y>0}D.{y|y≥0}【解析】选C.y=2-x的值域为{y|y>0},y=的值域为{y|y≥0},因此,其交集为{y|y>0}.故选C.4.【解题指南】结合指数函数的图象,若x>0时,(a-1)x<1恒成立,则必有0<a-1<1,进而求解.【解析】选B.∵x>0时,(a-1)x<1恒成立,∴0<a-1<1,∴1<a<2.5.【解析】选D.当a>1时,y=a x-在R上为增函数,且与y轴的交点为(0,1-),又0<1-<1,故排除A,B.当0<a<1时,y=a x-在R上为减函数,且与y轴的交点为(0,1-),又1-<0,故选D.6.【解析】f(2)+f(-2)=22+3-2=.答案:【举一反三】若对于本题中的函数f(x),有f(a)=16,试求a的值. 【解析】当a≤1时,f(a)=3a≤3<16,故a>1,此时有f(a)=2a=16,所以a=4.7.【解析】当a>1时,有a2=4,a-1=m,此时a=2,m=,此时g(x)=-x2在[0,+∞)上是减函数,不合题意.若0<a<1,则a-1=4,a2=m,故a=,m=,检验知符合题意.答案:8.【解题指南】解答本题一方面要注意利用函数的单调性由定义域求值域,由值域求定义域;另一方面要注意结合函数的图象,弄清楚函数值与自变量的关系.【解析】(1)不正确.由x≤0得0<2x≤20=1,值域是{y|0<y≤1}.(2)不正确.由x≥2得0<≤,值域是{y|0<y≤}.(3)不正确.由2x≤4=22得x≤2,所以若函数y=2x的值域是{y|0<y≤4},则它的定义域一定是{x|x≤2}.答案:(1)(2)(3)9.【解析】由图象得,点(2,0),(0,-2)在函数f(x)的图象上,所以解得10.【解析】(1)∵函数f(x)=a x-1(x≥0)的图象经过点(2,),∴=a2-1,∴a=.(2)由(1)知f(x)=()x-1=2·()x,∵x≥0,∴0<()x≤()0=1,∴0<2·()x≤2,∴函数y=f(x)(x≥0)的值域为(0,2].11.【解析】(1)函数y=a x(a>0且a≠1)在[1,2]上的最大值与最小值之和为20,∴a+a2=20,得a=4或a=-5(舍去).(2)由(1)知f(x)=,∴f(x)+f(1-x)=+=+=+=+=1.(3)由(2)知f()+f()=1,f()+f()=1,…,f()+f()=1,∴f()+f()+f()+…+f()=++…+=1+1+…+1=1 006.。
最新人教版高中数学必修1第二章《指数函数及其性质》(第1课时)1

数学人教A 必修1第二章2.1.2 指数函数及其性质第1课时1.理解指数函数的概念,能画出指数函数图象的草图,会判断指数函数. 2.初步掌握指数函数的性质,并能解决与指数函数有关的问题.1.指数函数的定义一般地,函数y =______(a >0,且a ≠1)叫做指数函数,其中x 是______.指数函数y =a x (a >0,且a ≠1)的结构特征: (1)底数:大于零且不等于1的常数; (2)指数:仅有自变量x ; (3)系数:a x 的系数是1.【做一做1】 已知f (x )=9x ,则f ⎝⎛⎭⎫12等于( ).A.12 B .2 C .3 D .9 2.指数函数的图象和性质指数函数的图象和性质如下表所示:指数函数的性质可用如下口诀来记忆: 指数增减要看清,抓住底数不放松; 反正底数大于0,不等于1已表明; 底数若是大于1,图象从下往上增; 底数0到1之间,图象从上往下减; 无论函数增和减,图象都过(0,1)点.【做一做2-1】 y =⎝⎛⎭⎫34x的图象可能是( ).【做一做2-2】 y =(3)x 的值域是( ). A .R B .[0,+) C .(-,0) D .(0,+) 【做一做2-3】 函数y =(a -2)x 在R 上是增函数,则实数a 的取值范围是__________.答案:1.a x 自变量【做一做1】 C f ⎝⎛⎭⎫12=129=9=3.2.R (0,+∞) (0,1) 增函数 减函数 【做一做2-1】 C 【做一做2-2】 D【做一做2-3】 (3,+∞) 由a -2>1,得a >3.1.对指数函数中底数取值范围的理解剖析:①若a <0,则对于x 的某些数值,可使a x 无意义.如(-2)x ,当x =12时无意义.②若a =0,则当x >0时,a x =0;当x ≤0时,a x 无意义.③若a =1,则对于任何x R ,a x 是一个常量1,没有研究的必要性.为了避免上述各种情况,所以规定a >0,且a ≠1,这样对于任何x R ,a x 都有意义. 2.指数函数y =a x (a >0,且a ≠1)中底数a 对函数图象的影响剖析:设y =f (x )=a x ,则f (1)=a ,即直线x =1与指数函数f (x )=a x 图象交点的纵坐标是底数a .如图(1)所示.(1) (2)指数函数y =a x ,y =b x ,y =c x ,y =d x 的图象如图(2)所示,则有a >b >1>c >d >0.从图中可以看出:在y 轴右侧,图象从上到下相应的底数由大变小,在y 轴左侧,图象从下到上相应的底数由大变小.指数函数y =a x 与y =⎝⎛⎭⎫1a x (或y =a -x)的图象关于y 轴对称.题型一 判断指数函数【例1】 下列函数中,哪些是指数函数? (1)y =(-8)x ;(2)y =212x -;(3)y =(2a -1)x ⎝⎛a >12,且a ≠1 );(4)y =2·3x . 分析:依据指数函数解析式满足的三个特征来判断.反思:判断一个函数是否为指数函数只需判定其解析式是否符合y =a x (a >0,且a ≠1)这一结构,其具备的特点如下:题型二 求定义域、值域【例2】 求下列函数的定义域与值域. (1)142x y -=;(2)23xy -⎛⎫= ⎪⎝⎭.分析:由于指数函数y =a x (a >0,且a ≠1)的定义域是R ,所以函数y =a f (x )(a >0,且a ≠1)与函数f (x )的定义域相同,在定义域内可利用指数函数的单调性来求值域.反思:对于y =a f (x )(a >0,且a ≠1)这类函数: (1)定义域是使f (x )有意义的x 的取值范围; (2)值域问题,应分以下两步求解: ①由定义域求出u =f (x )的值域;②利用指数函数y =a u 的单调性求得此函数的值域. 题型三 定点问题【例3】 若函数f (x )=a x -1+3(a >0,且a ≠1)的图象恒过定点P ,试求点P 的坐标. 分析:利用指数函数y =a x 的图象过定点(0,1)来确定.反思:函数f (x )=ka g (x )+b (k ,a ,b 均为常数,且k ≠0,a >0,且a ≠1).若g (m )=0,则f (x )的图象过定点(m ,k +b ).题型四 易混易错题易错点 利用换元法时,忽视中间变量的取值范围【例4】 求函数y =⎝⎛⎭⎫14x +⎝⎛⎭⎫12x+1的值域.反思:求形如f (a x )的函数的值域时,常利用换元法,设a x =t ,根据f (a x )的定义域求得t 的范围,再转化为求f (t )的值域.答案:【例1】 解:(1)中底数-8<0,故不是指数函数. (2)中指数不是自变量x ,故不是指数函数.(3)中,∵a >12,且a ≠1,∴2a -1>0,且2a -1≠1.∴y =(2a -1)x 是指数函数.(4)中3x 前的系数是2,而不是1,故不是指数函数.综上所述,仅有(3)是指数函数.【例2】 解:(1)由x -4≠0,得x ≠4, ∴定义域为{x |x ∈R ,且x ≠4}. ∵1x -4≠0,∴142x -≠1. ∴y =142x -的值域为{y |y >0,且y ≠1}.(2)定义域为R . ∵|x |≥0,∴0233322xx y -⎛⎫⎛⎫⎛⎫==≥ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭=1. 故23xy -⎛⎫= ⎪⎝⎭的值域为{y |y ≥1}.【例3】 解:令x -1=0,解得x =1,此时f (1)=a 0+3=4,即f (x )的图象恒过定点P 的坐标为(1,4).【例4】 错解:令t =⎝⎛⎭⎫12x ,则原函数可化为y =t 2+t +1=⎝⎛⎭⎫t +122+34≥34,即当t =-12时,y min =34,即原函数的值域是⎣⎡⎭⎫34,+∞. 错因分析:原函数的自变量x 的取值范围是R ,换元后t =⎝⎛⎭⎫12x>0,而不是t ∈R ,错解中,把t 的取值范围当成了实数集R .正解:令t =⎝⎛⎭⎫12x ,t ∈(0,+∞),则原函数可化为y =t 2+t +1=⎝⎛⎭⎫t +122+34.因为函数y =⎝⎛⎭⎫t +122+34在(0,+∞)上是增函数,所以y >1,即原函数的值域是(1,+∞).1若y =(a -3)·(a -2)x是指数函数,则a =______.2函数f (x )=a 3-x -1(a >0,且a ≠1)的图象恒过定点的坐标是__________. 3函数y =4x +2x -3的值域为__________.4已知指数函数f (x )的图象过点(3,8),则f (6)=__________. 5求下列函数的值域:(1)12xy -=;(2)y =答案:1. 4 由题意,得31,20,21,a a a -=⎧⎪->⎨⎪-≠⎩解得a =4.2. (3,0) 令3-x =0,解得x =3,则f (3)=a 0-1=0,即过定点(3,0). 3. (-3,+∞) 函数的定义域是R .设2x =t ,则t >0.∴y =t 2+t -3=211324t ⎛⎫+- ⎪⎝⎭在(0,+)上为增函数,∴y >11344-=-3,∴函数的值域为(-3,+).4. 64 设f (x )=a x (a >0,且a ≠1).∵函数f (x )的图象过点(3,8),∴8=a 3,a =2. ∴f (x )=2x .∴f (6)=26=64.5.解:(1)∵1x-≠0,∴y =12x -≠1.∴y >0且y ≠1,∴值域是(0,1)(1,+).(2)0,∴y =50=1.∴值域是[1,+).。
最新人教版高中数学必修1第二章《指数函数》课后训练

课后训练基础巩固1.若集合A={y|y=2x,x∈R},B={y|y=x2,x∈R},则() A.A⊆B B.A BC.A=B D.A∩B=2.若12=0.5a,13=0.5b,14=0.5c,则a,b,c的大小关系是()A.a>b>c B.a<b<cC.a<c<b D.b<c<a3.函数y=2x+1的图象是()4.对任意实数a(a>0,且a≠1),函数f(x)=a x-1+3的图象必经过点()A.(5,2) B.(2,5)C.(4,1) D.(1,4)5.函数y=2-|x|的单调递增区间是()A.(-∞,+∞) B.(-∞,0)C.(0,+∞) D.不存在6.已知函数f(x)=(x-a)(x-b)(其中a>b),若f(x)的图象如图所示,则函数g(x)=a x+b的图象是()7.函数y=a x-3+5(a>0,且a≠1)的图象恒过定点______.8.函数y=a x在[0,1]上的最大值与最小值之和为3,则a=________. 9.已知-1≤x≤2,求函数f(x)=3+2×3x+1-9x的值域.能力提升10.写出满足条件f(x1)·f(x2)=f(x1+x2)的一个函数f(x)=________.11.设4 ()=42xxf x+.(1)若0<a<1,求f(a)+f(1-a)的值;(2)求121000100110011001f f f⎛⎫⎛⎫⎛⎫+++⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭L.12.已知函数f(x)=3x,且f(a+2)=18,g(x)=3ax-4x的定义域为[0,1].(1)求g(x)的解析式;(2)求g(x)的单调区间,确定其增减性并试用定义证明;(3)求g(x)的值域.13.已知函数f(x)=a x(a>0,a≠1),x∈R.若x1,x2∈R,且x1≠x2.(1)试判断12[f(x1)+f(x2)]与122x xf+⎛⎫⎪⎝⎭的大小关系;(2)若已知函数f(x)=3x,试判断12332x x+与122x xf+⎛⎫⎪⎝⎭的大小关系.参考答案1.A 点拨:∵A ={y |y =2x ,x ∈R }={y |y >0}, B ={y |y =x 2,x ∈R }={y |y ≥0},∴A ⊆B . 2.B 点拨:∵函数y =0.5x 是减函数, 又∵111>>234,∴a <b <c . 3.B 点拨:将函数y =2x 的图象向左平移1个单位长度即可得到y =2x +1的图象,结合图象知,选B.4.D 点拨: 令x -1=0,得x =1,所以y =1+3=4,故函数f (x )的图象过定点(1,4).5.B 点拨:画出函数y =2-|x |图象,如图.由图象可知其递增区间为(-∞,0).6.A 点拨:由f (x )的图象可知,0<a <1,且b <-1,故当x =0时g (x )<0,可排除B ,C.又∵0<a <1时,函数g (x )为减函数,因此选A.7.(3,6) 点拨:∵函数y =a x 的图象过定点(0,1),∴函数y =a x -3的图象过定点(3,1),∴函数y =a x -3+5的图象过定点(3,6).8.2 点拨:由于函数y =a x 在[0,1]上为单调函数,故其最大、最小值在x =0,x =1处取得,所以a 1+a 0=3,即a =2.9.解:∵f (x )=3+2×3x +1-9x =-(3x )2+6×3x +3,令t =3x ,又x ∈[-1,2],则t ∈1,93⎡⎤⎢⎥⎣⎦,则y =-t 2+6t +3=-(t -3)2+12,∴当t =3,即x =1时,y 有最大值12;当t =9,即x =2时,y 有最小值-24. ∴函数f (x )的值域为[-24,12].10.2x (答案不唯一) 点拨:本题答案不唯一,一般地,指数函数y =a x (a >0,且a ≠1),都满足f (x 1)·f (x 2)=f (x 1+x 2).11.解:(1)f (a )+f (1-a )=11444442===142424242442a a a a aa a aa --+++++++⋅+. (2)121000100110011001f f f ⎛⎫⎛⎫⎛⎫+++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭L111000299910001=2100110011001100110011001f f f f f f ⎧⎫⎡⎤⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫++++++⎨⎬ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦⎣⎦⎩⎭L=12×1×1 000=500.12.解:(1)∵f(x)=3x,∴f(a+2)=3a+2=18.∴3a=2.∴g(x)=3ax-4x=(3a)x-4x.∴g(x)=2x-4x.(2)令t=2x.∵x∈[0,1],且函数t=2x在区间[0,1]上单调递增,∴t∈[1,2].则y=t-t2=-(t2-t)=21124t⎛⎫--+⎪⎝⎭,t∈[1,2].∵函数t=2x在区间[0,1]上单调递增,函数y=t-t2在[1,2]上单调递减,∴函数g(x)的单调递减区间为[0,1].下面给出证明:任取x1,x2∈[0,1],且x1<x2,则g(x2)-g(x1)=22112424x x x x--+=211212(22)(22)(22)x x x x x x-++-=2112(22)(122)x x x x---,∵0≤x1<x2≤1,∴212>2x x,且1≤12x<2,1<22x≤2.∴2<1222x x+<4.∴-3<12122x x--<-1.∴2112(22)(122)<0x x x x---.∴g(x2)-g(x1)<0.∴函数g(x)在区间[0,1]上是减函数.(3)∵g(x)在[0,1]上是减函数,∴g(1)≤g(x)≤g(0).∴g(1)=21-41=-2,g(0)=20-40=0.∴-2≤g(x)≤0,∴函数g(x)的值域为[-2,0].13.解:(1)12[f(x1)+f(x2)]-121212()()22=22x xf x f x fx xf+⎛⎫+- ⎪+⎛⎫⎝⎭⎪⎝⎭.由题意知1212()()22x xf x f x f+⎛⎫+- ⎪⎝⎭=12121222222=()x x x xx xa a a a a++--.因为x1≠x2,所以12220x xa a-≠.所以12222()>0x xa a-.所以f(x1)+f(x2)-1222x xf+⎛⎫⎪⎝⎭>0,即12[f(x1)+f(x2)]>122x xf+⎛⎫⎪⎝⎭.(2)由(1)易知121212331=[()()]>222x x x xf x f x f++⎛⎫+ ⎪⎝⎭.。
【人教A版】高中数学必修1同步教学案必修1第二章《指数函数的图象及其性质》练习题(含答案)

第二章基本初等函数(Ⅰ)2.1 指数函数2.1.2 指数函数及其性质第1课时指数函数的图象及其性质A级基础巩固一、选择题1.以x为自变量的四个函数中,是指数函数的为()A.y=(e-1)x B.y=(1-e)xC.y=3x+1D.y=x22.函数y=2x-8的定义域为()A.(-∞,3) B.(-∞,3]C.(3,+∞) D.[3,+∞)3.函数y=a x+1(a>0且a≠1)的图象必经过点()A.(0,1) B.(1,0) C.(2,1) D.(0,2)4.函数y=16-4x的值域是()A.[0,+∞) B.[0,4]C.[0,4) D.(0,4)5.函数y=a x,y=x+a在同一坐标系中的图象可能是()二、填空题6.已知集合A={x|1≤2x<16},B={x|0≤x<3,x∈N},则A∩B =________.7.已知函数f (x )满足f (x )=⎩⎪⎨⎪⎧f (x +2),x <0,2x ,x ≥0,则f (-7.5)的值为________.8.函数y =a x (-2≤x ≤3)的最大值为2,则a =________.三、解答题9.求不等式a 4x +5>a 2x -1(a >0,且a ≠1)中x 的取值范围.10.若0≤x ≤2,求函数y =4x -12-3·2x +5的最大值和最小值.B 级 能力提升1.若f (x )=-x 2+2ax 与g (x )=(a +1)1-x 在区间[1,2]上都是减函数,则a 的取值范围是( )A.⎝ ⎛⎦⎥⎤12,1B.⎝⎛⎦⎥⎤0,12 C .[0,1] D .(0,1]2.已知f (x )=a x +b 的图象如图所示,则f (3)=________.3.已知f (x )是定义在[-1,1]上的奇函数,当x ∈[-1,0]时,函数的解析式为f (x )=14x -a 2x (a ∈R). (1)试求a 的值;(2)写出f (x )在[0,1]上的解析式;(3)求f (x )在[0,1]上的最大值.参考答案第二章基本初等函数(Ⅰ)2.1 指数函数2.1.2 指数函数及其性质第1课时指数函数的图象及其性质A级基础巩固一、选择题1.以x为自变量的四个函数中,是指数函数的为()A.y=(e-1)x B.y=(1-e)xC.y=3x+1D.y=x2解析:由指数函数的定义可知选A.答案:A2.函数y=2x-8的定义域为()A.(-∞,3) B.(-∞,3]C.(3,+∞) D.[3,+∞)解析:由题意得2x-8≥0,所以2x≥23,解得x≥3,所以函数y =2x-8的定义域为[3,+∞).答案:D3.函数y=a x+1(a>0且a≠1)的图象必经过点()A.(0,1) B.(1,0) C.(2,1) D.(0,2)解析:因为y=a x的图象一定经过点(0,1),将y=a x的图象向上平移1个单位得到函数y=a x+1的图象,所以,函数y=a x+1的图象经过点(0,2).答案:D4.函数y=16-4x的值域是()A.[0,+∞) B.[0,4]C.[0,4) D.(0,4)解析:由题意知0≤16-4x<16,所以0≤16-4x<4.所以函数y=16-4x的值域为[0,4).答案:C5.函数y=a x,y=x+a在同一坐标系中的图象可能是()解析:函数y=x+a单调递增.由题意知a>0且a≠1.当0<a<1时,y=a x单调递减,直线y=x+a在y轴上的截距大于0且小于1;当a>1时,y=a x单调递增,直线y=x+a在y轴上的截距大于1.故选D.答案:D二、填空题6.已知集合A={x|1≤2x<16},B={x|0≤x<3,x∈N},则A∩B =________.解析:由1≤2x <16得0≤x <4,即A ={x |0≤x <4},又B ={x |0≤x <3,x ∈N},所以A ∩B ={0,1,2}.答案:{0,1,2}7.已知函数f (x )满足f (x )=⎩⎪⎨⎪⎧f (x +2),x <0,2x ,x ≥0,则f (-7.5)的值为________.解析:由题意,得f (-7.5)=f (-5.5)=f (-3.5)=f (-1.5)=f (0.5)=20.5= 2. 答案:28.函数y =a x (-2≤x ≤3)的最大值为2,则a =________. 解析:当0<a <1时,y =a x 在[-2,3]上是减函数,所以y max =a -2=2,得a =22; 当a >1时,y =a x 在[-2,3]上是增函数,所以y max =a 3=2,解得a =32.综上知a =22或32. 答案:22或32 三、解答题9.求不等式a 4x +5>a 2x -1(a >0,且a ≠1)中x 的取值范围. 解:对于a 4x +5>a 2x -1(a >0,且a ≠1),当a >1时,有4x +5>2x -1,解得x >-3;当0<a <1时,有4x +5<2x -1, 解得x <-3.故当a >1时,x 的取值范围为{x |x >-3};当0<a <1时,x 的取值范围为{x |x <-3}.10.若0≤x ≤2,求函数y =4x -12-3·2x +5的最大值和最小值. 解:y =4x -12-3·2x +5=12(2x )2-3·2x +5. 令2x=t ,则1≤t ≤4,y =12(t -3)2+12, 所以当t =3时,y min =12;当t =1时,y max =52. 故该函数的最大值为y max =52,最小值为y min =12. B 级 能力提升1.若f (x )=-x 2+2ax 与g (x )=(a +1)1-x 在区间[1,2]上都是减函数,则a 的取值范围是( )A.⎝ ⎛⎦⎥⎤12,1B.⎝ ⎛⎦⎥⎤0,12 C .[0,1] D .(0,1]解析:依题意-2a 2×(-1)≤1且a +1>1, 解得0<a ≤1.答案:D2.已知f (x )=a x +b 的图象如图所示,则f (3)=________.解析:因为f (x )的图象过(0,-2),(2,0)且a >1,所以⎩⎨⎧-2=a 0+b ,0=a 2+b ,所以a =3,b =-3,所以f (x )=(3)x -3,f (3)=(3)3-3=33-3.答案:33-33.已知f (x )是定义在[-1,1]上的奇函数,当x ∈[-1,0]时,函数的解析式为f (x )=14x -a 2x (a ∈R). (1)试求a 的值;(2)写出f (x )在[0,1]上的解析式;(3)求f (x )在[0,1]上的最大值.解:(1)因为f (x )是定义在[-1,1]上的奇函数,所以f (0)=1-a =0,所以a =1.(2)设x ∈[0,1],则-x ∈[-1,0],所以f (x )=-f (-x )=-⎝ ⎛⎭⎪⎪⎫14-x -12-x =2x -4x . 即当x ∈[0,1]时,f (x )=2x -4x .(3)f (x )=2x -4x=-⎝ ⎛⎭⎪⎫2x -122+14, 其中2x ∈[1,2],所以当2x =1时,f (x )max =0.。
高中数学2.1.2指数函数及其性质(1)同步讲练新人教版必修1

课题:指数函数及其性质(1)精讲部分学习目标展示(1)理解指数函数的概念(2)掌握指数函数的图象(3)掌握指数函数当底数变化时,函 数图象的变化规律(4)会求指数形式的函数的定义域 衔接性知识1. 分数指数幕如何定义的?m答: a n n a m (a 0 , m , n N , n1 1-^= (a 0 , m ,n N,n 1),n. m a答:函数y x 2的指数为定值 2,而底数是自变量 x ;函数y 2x 的底数是2,而指数是自变量x . 基础知识工具箱m(1) 0n 0(a0,m, n N , n 1)m(2) 0 n (aN ,n 1)无意义2.比较函数 yx 2与y2x 在形式上的不同?1),a特征底不(1)y a x与ya(a0且a1)的图象关于y轴对称同xy 11y a的/两/b x个几个不同的指数函数的图象规律:图在第一象限内,按逆时针方向,底数从少到象0y c.x 大排列,即a b 1 c d 0的r d0X关系典例精讲剖析例1.下列函数中,哪些是指数函数?(1)y 4x ;(2) y X4;(3) y 4x ;(4) y ( 4)x ;(5) y x ;(6) y 4x2;1⑺ y x X; (8) y (2a 1)x (a - , a 1)2[解析](1)、(5)、(8)为指数函数;(2)中底数x不是常数,而4不是变数;(3)是—1与指数函数4x的乘积;(4)中底数一4<0,二不是指数函数;(6)中指数不是自变量X,而是x 的函数;(7)中底数x不是常数•它们都不符合指数函数的定义例2•求列函数的定义域:(1) f(x) 3^ ⑵f(x)(1),2(3) f(x)解:(1)使函数有意义,得3x 2 0,2x 3,所以f (x)的定义域为[2 ,);3(2)使函数有意义,得0,所以f (x)的定义域为(,0) U (0 ,);(3 )使函数有意义,得12x 0 , 2x 1,由y 2x的图象,可知,x 0,所以f(x) 的定义域为(,0).例 3. (1) 指数函数y1f (x)的图象经过点(2,—),求f (21), f(3)的值;(2)若y 2(k 3) (2 k 1)x是指数函数,求实数解:(1 )设 f (x) a x (a 0,且a 1),则Q指数函数y f (x)的图象经过点(2,丄)2 a2丄,即a2子,所以f(x)(曰[答案]Ba >0,故f (x ) = ax 的图象经过一、 三象限,••• A 、D 不正确.若g (x ) = a x 为增函数,则 a >1,与y = ax 的斜率小于1矛盾,故C 不正确.B 中0<a <1,故B正确.2.指数函数y f (x)的图象过点(1,{),则f [ f (2)]f( 1)f(3)(2)由指数函数的定义,得k 22k 2k例4. (1)下图分别是函数①y = a x ;②y = b x ;③y = c x :④y = d x 的图象,a 、b 、c 、d4 3 1分别是下列四数::'2、丁乔、中的一个,则相应的a 、b 、c 、d 应是下列哪一组* 3 10 54 13 , 4 3 1 31,4 A. 3, -,2,5,10 B. 2,3,10,5 C. 10,5, 2,3 D. 10 4, J 2(2)无论a 取何值(a >0且a * 1),函数y 2 a x 3的图象恒过定点 解:(1)法一、指数函数 y = a x 的图象从第一象限看,逆时针方向底数大,故选C.解法二:直线x =1与函数的图象相交,4 3 1从上到下依次为 c >d >a >b ,而.'2>3>10>5,故选C. (2)由指函数 y = a x ( a >0且a *1)过定点(0,1)知,•此函数图象过定点(一3,3).精练部分g (x ) = a 的图象可能是( )[解析]由指数函数的定义知 3a 依次从小变A 类试题(普通班用)1.在同一平面直角坐标系中,函数f (x ) = ax 与指数函数[答案]16[解析]设 f (x) a x(a 0 ,且a 1), T f (x)图象过点(1,1), • a 2 , • f(x) 2x , 22• f[f (2)] f(2 ) f(4)24 163.函数 f (x)(3a 2)3x 4b (a2,a1)的图象过定点 (x ° ,3),3则 X 。
人教A版高中数学必修1第二章2.1.2《指数函数及其性质》同步测试(一)

《指数函数及其性质》同步测试题(一)---主要涉及概念、定义域、值域一.选择题(在每小题给出的四个选项中,只有一项是符合题目要求的) 1.若函数()()21xf x a a a =--是指数函数,则( )A .1a =B .2a =C .1a =或2a =D .0a >且1a ≠2.下列函数中指数函数的个数是( )①23x y =⋅ ①13x y += ①3x y = ①()21xy a =-(a 为常数,12a >,1a ≠)①3y x = ①4x y =- ①()4xy =- A .1B .2C .3D .43.已知指数函数y =(a +2)x ,则实数a 的取值范围是( ). A .(-2,+∞) B .[-2,+∞)C .(-2,-1)(-1,+∞)D .(1,2)∪(2,+∞)4.函数y = )A .()0,+∞B .(),0-∞C .[)0,+∞D .(],0-∞5.函数()f x = ) A .(,0)-∞B .(,0]-∞C .(0,)+∞D .[0,)+∞6.已知函数f (x )的定义域是(1,2),则函数f (2x )的定义域是( ) A .(0,1) B .(2,4) C .(12,1) D .(1,2)7.若221124x x -+⎛⎫≤ ⎪⎝⎭的解集是函数2xy =的定义域,则函数2xy =的值域是( )A .1,28⎡⎫⎪⎢⎭⎣B .128⎡⎤⎢⎥⎣⎦,C .1,8⎛⎤-∞ ⎥⎦⎝D .)2,⎡+∞⎣8.函数[]12,0,1xy x =-∈的值域是( )A .[]0,1B .[]1,0-C .10,2⎡⎤⎢⎥⎣⎦D .1,02⎡⎤-⎢⎥⎣⎦9.函数()1423xx y x R -=++∈的值域为( )A .[)2,+∞B .()3,+∞C .13,3⎛⎫+∞⎪⎝⎭D .[)9,+∞10.设函数()()121xf x x R =∈+,则它的值域为( ) A .(0,1)B .(0,2)C .(1,+∞)D .(2,+∞)11.函数()1212xxf x -=+的值域为( ) A .()1,1- B .(),1-∞C .()1,+∞D .()0,112.函数()26512x x f x -+⎛⎫= ⎪⎝⎭的值域为( )A .(]0,16B .[)16,+∞C .10,16⎛⎤ ⎥⎝⎦D .1,16⎡⎫+∞⎪⎢⎣⎭二.填空题13.函数()1f x x =-的定义域为__________. 14.已知f (x )R ,则实数a 的取值范围是______.15.函数211()3x y -=的值域是___16.函数1()41(0)2xx f x x -⎛⎫=++≥ ⎪⎝⎭的值域是___________. 三.解答题(解答应写出文字说明、证明过程或演算步骤)17.已知函数2()(0,1,0)x f x a a a x -=>≠≥且的图像经过点(3,0.5), (1)求a 值; (2)求函数2()(0)x f x a x -=≥的值域;18.求下列函数的定义域: (1)y =(2)y =19.已知a R ∈,函数1()21x f x a =-+. (1)用函数单调性定义证明:()f x 在(),-∞+∞上单调递增; (2)若()f x 为奇函数,求: ①a 的值; ②()f x 的值域.20.已知()16245x x f x =-⨯+,[]1,2x ∈-. (1)设4x t =,[]1,2x ∈-,求t 的最大值与最小值; (2)求()f x 的最大值与最小值.21.已知函数2()221=+-+x x f x a a a ,其中0a >且1a ≠,满足(1)5f =. (1)求实数a 的值;(2)当[0,3]x ∈,求()f x 的值域;(3)若关于x 的方程()f x m =在区间[0,3]上无解,求实数m 的取值范围.22.已知函数()x f x a b =+(a >0,a ≠1)的图象过点(0,﹣2),(2,0) (1)求a 与b 的值;(2)求x ∈[﹣1,2]时,求f (x )的最大值与最小值. (3)求使()0f x >成立的x 范围.参考答案一.选择题(在每小题给出的四个选项中,只有一项是符合题目要求的)二.填空题 13.(2,1)- 14.[-1,0]15.(]03,16.(1,3]三.解答题(解答应写出文字说明、证明过程或演算步骤) 17.【解析】(1)函数()2x f x a-=的图像经过点()3,0.5320.5a -∴=,12a ∴=(2)由(1)可知()()2102x f x x -⎛⎫=≥ ⎪⎝⎭1012<< ()f x ∴在[0,+∞)上单调递减,则()f x 在0x =时有最大值 ()()21042maxf x f f -⎛⎫∴=== ⎪⎝⎭,又()0f x >∴函数()f x 的值域为0,4](18.【解析】(1)由题意可得210x -≥,即022x ≥, 又指数函数()2xf x =单调递增,得0x ≥.所以函数y =[)0,+∞;(2)由题意,得31903120x x +⎧⎛⎫-≥⎪ ⎪⎨⎝⎭⎪-≠⎩,得230113322x x -+⎧⎛⎫⎛⎫≥⎪ ⎪ ⎪⎨⎝⎭⎝⎭⎪≠⎩,又指数函数()13xg x ⎛⎫= ⎪⎝⎭单调递减,2x ∴≤-且3x ≠-.所以函数y =()(],33,2-∞-⋃--. 19.【解析】(1)设12x x <,则()()()()12121212112*********x x x x x x f x f x a a -⎛⎫⎛⎫-=---= ⎪ ⎪++++⎝⎭⎝⎭, 1212210,210,220x x x x +>+>-<,()()120f x f x ∴-<,()()12f x f x ∴<.故()f x 在(),-∞+∞上单调递增(2)①若()f x 为奇函数,则()1002f a =-=, 解得:12a =.经检验成立 ②11()221x f x =-+, 211x+>,10121x∴<<+,故()1122f x -<<, 故函数的值域为:11,22⎛⎫-⎪⎝⎭. 20.【解析】(1) 因为4x t =在[]1,2-上是增函数,故有1164t ≤≤, 即t 的最小值为14,t 的最大值为16; (2) 设4x t =,[]1,2x ∈-,则22()25(1)4f t t t t =-+=-+,1[,16]4t ∈,max min ()(16)229,()(1)4f t f f t f ====;21.【解析】(1)由2(1)2215f a a a =+-+=,解得2a =±,因为0a >,所以2a =. (2)由(1)知2()2223,x x f x =+⋅-[0,3]x ∈令2x t =,则223,18y t t t =+-≤≤,由223y tt =+-在[1,8]上单调递增,所以当1t =时,min 0y =,此时0x =, 当8t =时,max 77y =,此时3x =,所以()f x 的值域为[0,77].(3)因为()f x m =在区间[0,3]上无解,所以77>m 或0m <; 实数m 的取值范围为(,0)(77,)-∞⋃+∞.22.【解析】(1)因为函数图象过点()0,2-和点()2,0,所以将点()0,2-和点()2,0代入()f x ,得022a b a b ⎧+=-⎨+=⎩,解得3a b ⎧=⎪⎨=-⎪⎩a ,故ab =﹣3;(2)因为()3xf x =-1,所以,该函数在定义域内单调递增,即当[]1,2x ∈-时,()f x 单调递增,所以,()()min 133f x f =-=-,()()max 20f x f ==(3)由()0f x >可得30x->,即23x>=,因为xy =是单调递增函数,所以解得2x >。
必修一同步2.1.2第1课时指数函数及其性质

第二章 2.1 2.1.2 第一课时指数函数及其性质基础巩固一、选择题 1.下列函数,①y =x 2;②y =(-2)x ;③y =2x +1;④y =(a -1)x(a >1,且a ≠2).其中,指数函数的个数是( ) A .1 B .2 C .3 D .4[答案] A2.函数y =1-3x的定义域是( ) A .[0,+∞) B .(-∞,0] C .[1,+∞) D .(-∞,+∞)[答案] B[解析] 1-3x≥0,3x ≤1,∴x ≤0,故选B. 3.函数f (x )=3x -3(1<x ≤5)的值域是( )A .(0,+∞)B .(0,9)C .(19,9]D .(13,27)[答案] C[解析] 因为1<x ≤5,所以-2<x -3≤2.而函数f (x )=3x是单调递增的,于是有19<f (x )≤32=9,即所求函数的值域为(19,9],故选C.4.若点(a,9)在函数y =3x的图象上,则tan a ·180°6的值为( )A .0 B.33C .1 D. 3[答案] D[解析] ∵3a=9,∴a =2,∴tana ·180°6=tan60°=3,故选D.5.函数y =xa x|x |(0<a <1)的图象的大致形状是( )[答案] D[解析] 当x >0时,y =a x(0<a <1),故可排除A 、B 项;当x <0时,y =-a x与y =a x (0<a <1,x <0)的图象关于x 轴对称,故选D.6.(2015·山东梁山一中高一期中质量检测)函数y =a x在[0,1]上的最大值与最小值的和为3,则a 等于( )A.12 B .2 C .4 D.14[答案] B[解析] 当a >1时,y min =a 0=1;y max =a 1=a , 由1+a =3,所以a =2.当0<a <1时,y max =a 0=1,y min =a 1=a .由1+a =3,所以a =2矛盾,综上所述,有a =2. 二、填空题7.函数y =a x-1(a >0,且a ≠1)的定义域是(-∞,0],则实数a 的取值范围为________.[答案] (0,1)[解析] 由a x-1≥0,得a x≥1.∵函数的定义域是(-∞,0],∴a x≥1的解集为(-∞,0],∴0<a <1.8.已知函数f (x )=⎩⎪⎨⎪⎧2x,x >0,x +1,x ≤0.若f (a )+f (1)=0,则实数a 的值等于________.[答案] -3[解析] 由已知,得f (1)=2;又当x >0时,f (x )=2x>1,而f (a )+f (1)=0,∴f (a )=-2,且a <0, ∴a +1=-2,解得a =-3. 三、解答题9.求下列函数的值域: (1)y =2-1x;(2)y =51-x.[解析] (1)∵-1x ≠0,∴y =2-1x≠1.∴y >0且y ≠1,∴所求函数的值域是(0,1)∪(1,+∞). (2)∵1-x ≥0,∴y =51-x≥50=1.∴所求函数的值域是[1,+∞).10.函数f (x )=k ·a -x(k ,a 为常数,a >0且a ≠1)的图象过点A (0,1),B (3,8). (1)求函数f (x )的解析式; (2)若函数g (x )=f x -1f x +1,试判断函数g (x )的奇偶性,并给出证明.[解析] (1)由已知得⎩⎪⎨⎪⎧k =1,k ·a -3=8,∴k =1,a =12,∴f (x )=2x.(2)函数g (x )为奇函数.证明:g (x )=2x-12x +1,其定义域为R ,又g (x )=2-x-12-x +1=1-2x 1+2x =-2x-12x+1=-g (x ), ∴函数g (x )为奇函数.能力提升一、选择题1.若函数y =(1-2a )x是实数集R 上的增函数,则实数a 的取值范围为( ) A .(12,+∞)B .(-∞,0)C .(-∞,12)D .(-12,12)[答案] B2.指数函数y =a x(a ∈{13,12,2,3})的图象如下图,则分别对应于图象①②③④的a的值为( )A.13,12,2,3 B.12,13,3,2 C .3,2,12,13D .2,3,13,12[答案] B3.(2015·河北衡水中学期中)若函数f (x )=a -22x +1是奇函数,则a 的值为( )A .0B .-1C .1D .2[答案] C[解析] ∵f (0)=a -220+1=a -1=0,∴a =1,故选C.4.(2015·湖北教学合作体期末)已知函数f (x )=(x -a )(x -b )(其中a >b )的图象如图下图所示,则函数g (x )=a x+b 的图象是( )[答案] A[解析] 由题图可知0<a <1,b <-1,则g (x )是一个减函数,可排除C ,D ,再根据g (0)=1+b <0,可排除B ,故选A.二、填空题5.指数函数y =f (x )的图象经过点(2,4),那么f (2)·f (4)=________ [答案] 64[解析] 由已知函数图象过(2,4),令y =a x,得a 2=4,∴a =2,∴f (2)·f (4)=22×24=64.6.(2015·云南玉溪一中期中)已知函数f (x )=⎩⎪⎨⎪⎧2a -1 x +7a -2 x <1 ,a xx ≥1在(-∞,+∞)上单调递减,则实数a 的取值范围是________.[答案] [38,12)[解析] 由题意知⎩⎪⎨⎪⎧2a -1<0,0<a <1,9a -3≥a ,解得38≤a <12.三、解答题7.(2015·长春高一检测)已知函数f (x )=a x -1(x ≥0)的图象经过点(2,12),其中a >0且a ≠1.(1)求a 的值;(2)求函数y =f (x )(x ≥0)的值域. [解析] (1)∵函数f (x )=ax -1(x ≥0)的图象经过点(2,12),∴12=a 2-1,∴a =12.(2)由(1)知f (x )=(12)x -1=2·(12)x,∵x ≥0,∴0<(12)x ≤(12)0=1,∴0<2·(12)x≤2,∴函数y =f (x )(x ≥0)的值域为(0,2].8.(能力挑战题)已知函数y =a x(a >0且a ≠1)在[1,2]上的最大值与最小值之和为20,记f (x )=a xa x +2.(1)求a 的值;(2)证明f (x )+f (1-x )=1;(3)求f (12015)+f (22015)+f (32015)+…+f (20142015)的值.[解析] (1)函数y =a x(a >0且a ≠1)在[1,2]上的最大值与最小值之和为20, ∴a +a 2=20,得a =4或a =-5(舍去). (2)由(1)知f (x )=4x4x +2,∴f (x )+f (1-x )=4x 4x +2+41-x 41-x +2=4x4x +2+44x 44x +2=4x 4x +2+42·4x+4=4x4x +2+24x +2=1.(3)由(2)知f (12015)+f (20142015)=1,f (22015)+f (20142015)=1,…, f (10072015)+f (10082015)=1, ∴f (12015)+f (22015)+f (32015)+…+f (20142015)=[f (12015)+f (20142015)]+[f (22015)+f (20132015)]+…+[f (10072015)+f (10082015)]=1+1+…+1=1007.。
高一数学必修1(人教版)同步练习第二章第一节指数函数

2011-2012学年高一数学必修1(人教版)同步练习第二章第一节指数函数一、学习目标:1. 了解基本初等函数(一次函数、二次函数、指数函数、对数函数、幂函数)的实际背景。
了解实数指数幂的意义及对数的作用、了解指数函数与对数函数互为反函数的性质。
2. 理解指数、对数的概念及其运算性质,理解指数函数、对数函数,一次函数、二次函数、幂函数的图象与性质。
3. 掌握幂的运算、对数运算及指数函数、对数函数、一次函数、二次函数性质的应用二、重点、难点:重点:(1)指数幂、对数的运算(2)对一次函数、二次函数、指数函数、对数函数的图象与性质的理解。
难点:一次函数、二次函数、指数函数、对数函数的图象与性质的应用三、考点分析:函数这部分内容是高考中的重点与难点,基本的初等函数是高考函数基础知识考查的重点,因此第一轮的复习重点是把握基本函数的基础知识及其简单的应用,这部分知识点是高考命题的“黄金”知识点,命题的题型有选择题、填空题、中等类型的大题等。
知识梳理注:(1)二次函数的解析式的确定方法有三种形式①一般式:若已知二次函数经过A ,B ,C 三点,可设解析式为c bx ax x f ++=2)(,把三点坐标代入求出a ,b ,c 的值。
②零点式:若已知二次函数图象与x 轴有两个交点)0,(),0,(21x B x A ,可设解析式为:))(()(21x x x x a x f --=,再根据其余的条件确定a 的值。
③顶点式:若已知二次函数的顶点坐标(h ,k ),则可设函数解析式为:k h x a x f +-=2)()(的形式,再根据另外的条件确定a 的值。
(2)二次函数的最值的确定(i )若R x ∈,a >0,当a b x 2-=时,函数取得最小值a b ac x f 44)(2min -=;若R x ∈,a<0,当a bx 2-=时,函数取得最大值a b ac x f 44)(2m ax -=。
最新人教A版数学必修1练习:第二章 2.1 2.1.2 第1课时 指数函数图象及其性质 Word版含解析

[课时作业][A 组 基础巩固]1.下列以x 为自变量的函数中,是指数函数的是( )A .y =(-4)xB.y =λx (λ>1) C .y =-4x D .y =a x +2(a >0且a ≠1)解析:A 中底数不满足大于0且不等于1;C 中系数不是1;D 中指数不是独立的x ;只有选项B 满足指数函数定义.答案:B2.函数f (x )=a x -b 的图象如图所示,其中a ,b 为常数,则下列结论正确的是( )A .a >1,b <0B .a >1,b >0C . 0<a <1,b >0D .0<a <1,b <0解析:从曲线的变化趋势,可以得到函数f (x )为减函数,从而有0<a <1;从曲线位置看,是由函数y =a x (0<a <1)的图象向左平移|-b |个单位而得,所以-b >0,即b <0.故选D.答案:D3.下列关系中正确的是( )A.⎝ ⎛⎭⎪⎫1223 <223<⎝ ⎛⎭⎪⎫1213 B.⎝ ⎛⎭⎪⎫12 23<⎝ ⎛⎭⎪⎫1213<223 C .223<⎝ ⎛⎭⎪⎫1213<⎝ ⎛⎭⎪⎫1223 D .223<⎝ ⎛⎭⎪⎫1223<⎝ ⎛⎭⎪⎫1213 解析:223=⎝ ⎛⎭⎪⎫1223-,∵y =⎝ ⎛⎭⎪⎫12x 是R 上的减函数, ∴⎝ ⎛⎭⎪⎫1223->⎝ ⎛⎭⎪⎫1213>⎝ ⎛⎭⎪⎫1223,即223>⎝ ⎛⎭⎪⎫1213>⎝ ⎛⎭⎪⎫1223. 答案:B4.函数y =2-|x |的值域是( )A .(0,1)B.(0,1] C .(0,+∞) D .R解析:设t =-|x |,则t ≤0,作出y =2t (t ≤0)的简图,由图象知0<2t ≤1.答案:B5.若⎝ ⎛⎭⎪⎫122a +1<⎝ ⎛⎭⎪⎫123-2a ,则实数a 的取值范围是( ) A .(1,+∞)B.⎝ ⎛⎭⎪⎫12,+∞ C .(-∞,1) D .⎝ ⎛⎭⎪⎫-∞,12 解析:∵y =(12)x 是减函数,∴原不等式等价于2a +1>3-2a ,即4a >2,∴a >12.答案:B6.设函数f (x )=⎩⎪⎨⎪⎧ x ,x ≥⎝ ⎛⎭⎪⎫12x ,x <0,则f [f (-4)]=________.解析:依题意,知f (-4)=⎝ ⎛⎭⎪⎫12-4=16, f (16)=16=4,∴f [f (-4)]=f (16)=4.答案:47.已知(a 2+a +2)x >(a 2+a +2)1-x ,则x 的取值范围是________.解析:∵a 2+a +2=(a +12)2+74>1,∴y =(a 2+a +2)x 为R 上的增函数.∴x >1-x .即x >12.答案:⎝ ⎛⎭⎪⎫12,+∞ 8.已知函数f (x )=a x 在x ∈[-2,2]上恒有f (x )<2,则实数a 的取值范围为________.解析:当a >1时,f (x )=a x 在[-2,2]上的最大值为a 2,由a 2<2得,1<a < 2.当0<a <1时,f (x )=a x 在[-2,2]上的最大值为a -2,由a -2<2得a >12. 答案:⎝ ⎛⎭⎪⎫22,1∪(1,2) 9.(1)已知3x ≥30.5,求实数x 的取值范围;(2)已知0.2x <25,求实数x 的取值范围.解析:(1)因为3>1,所以指数函数f (x )=3x 在R 上是增函数.由3x ≥30.5,可得x ≥0.5,即x 的取值范围为[0.5,+∞).(2)因为0<0.2<1,所以指数函数f (x )=0.2x 在R 上是减函数.因为25=⎝ ⎛⎭⎪⎫15-2=0.2-2,所以0.2x <0.2-2. 由此可得x >-2,即x 的取值范围为(-2,+∞).10.比较下列各组数中两个值的大小:(1)0.2-1.5和0.2-1.7; (2)⎝ ⎛⎭⎪⎫1413和⎝ ⎛⎭⎪⎫1423; (3)2-1.5和30.2.解析:(1)考查函数y =0.2x .因为0<0.2<1,所以函数y =0.2x 在实数集R 上是单调减函数.又因为-1.5>-1.7,所以0.2-1.5<0.2-1.7.(2)考查函数y =⎝ ⎛⎭⎪⎫14x .因为0<14<1,所以函数y =⎝ ⎛⎭⎪⎫14x 在实数集R 上是单调减函数.又因为13<23,所以⎝ ⎛⎭⎪⎫1413>⎝ ⎛⎭⎪⎫1423. (3)2-1.5<20,即2-1.5<1;30<30.2,即1<30.2,所以2-1.5<30.2.[B 组 能力提升]1.下列函数中,值域为(0,+∞)的是( )A .y =31xB.y =31-x C .y =3x -1D .y =1-3x 解析:y =31x 的值域为{y |y >0且y ≠1};y =31-x 的值域为{y |y >0};y =3x -1的值域为[0,+∞);y =1-3x 的值域为[0,1).答案:B答案:A3.若函数f (x )=a x -1(a >0且a ≠1)的定义域值域都是[0,2],则实数a 的值为________.解析:当a >1时,函数f (x )=a x -1在[0,2]上是增函数,由题意可知,⎩⎨⎧ a 0-1=a 2-1=2,解得a = 3.当0<a <1时,函数f (x )=a x -1在[0,2]上是减函数,由题意可知,⎩⎨⎧ a 0-1=a 2-1=0,此时a 无解.综上所述,a = 3. 答案: 34.若f (x )=⎩⎪⎨⎪⎧a x ,x >1,⎝ ⎛⎭⎪⎫4-a 2x +2,x ≤1是R 上的单调递增函数,则实数a 的取值范围为________.解析:因为f (x )是R 上的增函数, 所以⎩⎪⎨⎪⎧ a >1,4-a 2>0,4-a 2+2≤a .解得4≤a <8.答案:[4,8) 5.设f (x )=2x -12x +1,求f (x )的值域. 解析:令y =2x -12x +1,(2x +1)y =2x -1,2x (y -1)=-1-y,2x =1+y 1-y, ∵2x >0,∴1+y 1-y >0,∴⎩⎨⎧ 1+y >0,1-y >0,或⎩⎨⎧ 1+y <0,1-y <0,解得-1<y <1.故值域为{y |-1<y <1},即f (x )∈(-1,1).6.已知函数y =a 233x x -+ (a >0且a ≠1),当x ∈[1,3]时有最小值8,求a 的值.解析:令y =a t ,t =x 2-3x +3,x ∈[1,3],对称轴为t =32,x ∈⎣⎢⎡⎦⎥⎤1,32时,t 单调递减;x ∈⎣⎢⎡⎦⎥⎤32,3时,t 单调递增,即x =32时,t min =34. ①当a >1时,y =a t 为增函数,则x ∈⎣⎢⎡⎦⎥⎤1,32时,y =ax 2-3x +3为减函数;x ∈⎣⎢⎡⎦⎥⎤32,3时,y =a 233x x -+为增函数.显然当x =32时,y min =a 34=8,a =16.②当0<a <1时,y =a t为减函数,则x ∈⎣⎢⎡⎦⎥⎤1,32时,y =ax 2-3x +3为增函数,x ∈⎣⎢⎡⎦⎥⎤32,3时,y =a 233x x -+为减函数,这时y min 是x =1或x =3时,对应函数值中最小的一个,f (1)=a ,f (3)=a 3,若a =8,与0<a <1矛盾.若a 3=8,a =38>1与0<a <1矛盾.故舍掉.综上所述,a 的值为16.。
人教新课标版数学高一-数学必修12.1.2指数函数及其性质(第1课时)

第二章 2.1 2.1.2 第一课时一、选择题1.下列各函数中,是指数函数的是( ) A .y =(-3)x B .y =-3x C .y =3x -1 D .y =3x[答案] D2.已知函数y =(a 2-3a +3)a x 是指数函数,则a 的值为( ) A .1 B .2 C .1或2 D .任意值[答案] B[解析] ∵y =(a 2-3a +3)a x 是指数函数.∴⎩⎪⎨⎪⎧a 2-3a +3=1a >0且a ≠1 ∴a =2.3.函数y =4-2x 的定义域是( ) A .(0,2] B .(-∞,2] C .(2,+∞) D .[1,+∞)[答案] B[解析] ∵4-2x ≥0,2x ≤4=22,∴x ≤2. 4.函数y =a |x |(0<a <1)的图象是( )[答案] C[解析] y =⎩⎪⎨⎪⎧a x (x ≥0)⎝⎛⎭⎫1a x (x <0),∵0<a <1,∴在[0,+∞)上单减,在(-∞,0)上单增,且y ≤1,故选C.[点评] 可取a =12画图判断.5.(2013~2014山东梁山一中高一期中质量检测)函数y =a x 在[0,1]上的最大值与最小值的和为3,则a 等于( )A .12B .2C .4D .14[答案] B[解析] 当a >1时,y min =a 0=1;y max =a 1=a , 由1+a =3,所以a =2.当0<a <1时,y max =a 0=1,y min =a 1=a .由1+a =3,所以a =2矛盾,综上所述,有a =2.6.函数①y =3x ;②y =2x ;③y =(12)x ;④y =(13)x .的图象对应正确的为( )A .①-a ②-b ③-c ④-dB .①-c ②-d ③-a ④-bC .①-c ②-d ③-b ④-aD .①-d ②-c ③-a ④-b [答案] B 二、填空题7.已知函数f (x )=⎩⎪⎨⎪⎧2x ,x >1,3x ,x ≤1,则f (2)+f (-2)=________.[答案]379[解析] f (x )=22=4,f (-2)=3-2=19,∴f (2)+f (-2)=3798.指数函数y =f (x )的图象经过点(2,4),那么f (2)·f (4)=________ [答案] 64[解析] 由已知函数图象过(2,4),令y =a x ,得a 2=4,∴a =2,∴f (2)·f (4)=22×24=64. 9.(2013~2014重庆市南开中学期中试题)函数f (x )=2-|x |的值域是________.[答案] (0,1][解析] ∵|x |≥0,∴-|x |≤0,∴0<2-|x |≤1,∴函数y =2-|x |值域为(0,1]. 三、解答题10.已知函数f (x )=a x +b (a >0,且a ≠1),若f (x )的图象如图所示,求a ,b 的值.[解析] 由图象得,点(2,0),(0,-2)在函数f (x )的图象上,所以⎩⎪⎨⎪⎧a 2+b =0,a 0+b =-2,解得⎩⎪⎨⎪⎧a =3,b =-3.11.(2013~2014长春高一检测)已知函数f (x )=a x -1(x ≥0)的图象经过点(2,12),其中a>0且a ≠1.(1)求a 的值;(2)求函数y =f (x )(x ≥0)的值域.[解析] (1)∵函数f (x )=a x -1(x ≥0)的图象经过点(2,12),∴12=a 2-1,∴a =12. (2)由(1)知f (x )=(12)x -1=2·(12)x ,∵x ≥0,∴0<(12)x ≤(12)0=1,∴0<2·(12)x ≤2,∴函数y =f (x )(x ≥0)的值域为(0,2].12.(能力挑战题)已知函数y =a x (a >0且a ≠1)在[1,2]上的最大值与最小值之和为20,记f (x )=a xa x +2.(1)求a 的值;(2)证明f (x )+f (1-x )=1;(3)求f (12013)+f (22013)+f (32013)+…+f (20122013)的值.[解析] (1)函数y =a x (a >0且a ≠1)在[1,2]上的最大值与最小值之和为20, ∴a +a 2=20,得a =4或a =-5(舍去). (2)由(1)知f (x )=4x4x +2,∴f (x )+f (1-x )=4x 4x +2+41-x41-x +2=4x 4x +2+44x44x +2=4x 4x +2+42·4x +4=4x 4x +2+24x +2=1.(3)由(2)知f (12013)+f (20122013)=1,f (22013)+f (20112013)=1,…, f (10062013)+f (10072013)=1, ∴f (12013)+f (22013)+f (32013)+…+f (20122013)=[f (12013)+f (20122013)]+[f (22013)+f (20112013)]+…+[f (10062013)+f (10072013)]=1+1+…+1=1006.。
高中数学(人教A版)必修1同步练习题:第2章2.1.2第1课时指数函数的图象及性质

精品 "正版〞资料系列 ,由本公司独创 .旨在将 "人教版〞、〞苏教版 "、〞北师 大版 "、〞华师大版 "等涵盖几乎所有版本的教材教案、课件、导学案及同步练习和 检测题分享给需要的朋友 .本资源创作于2021年8月 ,是当前最||新版本的教材资源 .包含本课对应 内容 ,是您备课、上课、课后练习以及寒暑假预习的最||正确选择 .学业分层测评(十三)(建议用时:45分钟)[学业达标]一、选择题1.函数y =(a 2-4a +4)a x 是指数函数 ,那么a 的值是( ) A .4 B .1或3 C .3D .1【解析】由题意得⎩⎨⎧a >0a ≠1a 2-4a +4=1得a =3 ,应选C.【答案】 C2.以下各函数中 ,是指数函数的是( ) A .y =(-3)x B .y =-3x C .y =3x -1D .y =【解析】 根据指数函数的定义y =a x (a >0且a ≠1) ,可知只有D 项正确.应选D.【答案】 D3.函数f (x )=2|x |-1在区间[-1,2]上的值域是( ) A .[1,4]B.⎣⎢⎢⎡⎦⎥⎥⎤12 2 C .[1,2] D.⎣⎢⎢⎡⎦⎥⎥⎤12 1 【解析】函数f (x )=2t-1在R 上是增函数 ,∵-1≤x≤2 ,∴0≤|x|≤2 ,∴t∈[0,2] ,∴f(0)≤f(t)≤f(2) ,即12≤f(t)≤2 ,∴函数的值域是⎣⎢⎢⎡⎦⎥⎥⎤122,应选B.【答案】 B4.函数y=a|x|(a>1)的图象是()【解析】当x≥0时,y=a|x|的图象与指数函数y=a x(a>1)的图象相同,当x<0时,y=a|x|与y=a-x的图象相同,由此判断B正确.【答案】B5.如图2-1-1是指数函数①y=a x,②y=b x,③y=c x,④y=d x的图象,那么a ,b ,c ,d与1的大小关系是()图2-1-1A.a<b<1<c<d B.b<a<1<d<cC.1<a<b<c<d D.a<b<1<d<c【解析】法一当指数函数底数大于1时,图象上升,且当底数越大,图象向上越靠近于y轴;当底数大于0小于1时,图象下降,底数越小,图象向右越靠近于x轴,得b<a<1<d<c.法二令x=1 ,由题图知c1>d1>a1>b1 ,∴b<a<1<d<c.【答案】 B二、填空题6.指数函数f(x)=a x+1的图象恒过定点________.【解析】由函数y=a x恒过(0,1)点,可得当x+1=0 ,即x=-1时,y=1恒成立 ,故函数恒过点(-1,1).【答案】 (-1,1)7.函数f (x )=3x -1的定义域为________.【解析】 由x -1≥0得x ≥1 ,所以函数f (x )=3x -1的定义域为[1 ,+∞). 【答案】 [1 ,+∞)8.函数f (x )=3x -3(1<x ≤5)的值域为________.【解析】 因为1<x ≤5 ,所以-2<x -3≤2 ,而函数f (x )=3x 是单调递增的 ,于是有19<f (x )≤32=9 ,即值域为⎝ ⎛⎦⎥⎥⎤19 9. 【答案】 ⎝ ⎛⎦⎥⎥⎤19 9 三、解答题9.函数f (x )=a x -1(x ≥0)的图象经过点⎝ ⎛⎭⎪⎪⎫2 12 ,其中a >0且a ≠1. (1)求a 的值;(2)求函数y =f (x )(x ≥0)的值域. 【解】 (1)因为函数图象过点⎝ ⎛⎭⎪⎪⎫2 12 , 所以a 2-1=12 ,那么a =12. (2)由(1)得f (x )=⎝ ⎛⎭⎪⎫12x -1(x ≥0) ,由x ≥0 ,得x -1≥-1 ,于是0<⎝ ⎛⎭⎪⎫12x -1≤⎝ ⎛⎭⎪⎫12-1=2.所以所求函数的值域为(0,2]. 10.f (x )=9x -2×3x +4 ,x ∈[-1,2].(1)设t =3x ,x ∈[-1,2] ,求t 的最||大值与最||小值; (2)求f (x )的最||大值与最||小值.【解】 (1)设t =3x ,∵x ∈[-1,2] ,函数t =3x 在[-1,2]上是增函数 ,故有13≤t≤9 ,故t的最||大值为9 ,t的最||小值为1 3.(2)由f(x)=9x-2×3x+4=t2-2t+4=(t-1)2+3 ,可得此二次函数的对称轴为t=1 ,且13≤t≤9 ,故当t=1时,函数f(x)有最||小值为3 ,当t=9时,函数f(x)有最||大值为67.[能力提升]1.假设a>1 ,-1<b<0 ,那么函数y=a x+b的图象一定在()A.第|一、二、三象限B.第|一、三、四象限C.第二、三、四象限D.第|一、二、四象限【解析】∵a>1 ,且-1<b<0 ,故其图象如下列图.【答案】 A2.函数y=xa x|x|(0<a<1)的图象的大致形状是()【解析】由函数式可知当x>0时,y=a x(0<a<1) ,当x<0时,y=-a x(0<a<1) ,由函数的图象可知,函数的大致形状是D选项.【答案】 D3.函数f(x)=3x3x+1的值域是________.【解析】 函数y =f (x )=3x3x +1 ,即有3x =-y y -1 ,由于3x >0 ,那么-y y -1>0 ,解得0<y <1 ,值域为(0,1). 【答案】 (0,1)4.函数f (x )=b ·a x (其中a ,b 为常数且a >0 ,a ≠1)的图象经过点A (1,8) ,B (3,32).(1)求f (x )的解析式;(2)假设不等式+1-2m ≥0在x ∈(-∞ ,1]上恒成立 ,求实数m 的取值范围.【解】 (1)把点A (1,8) ,B (3,32)代入函数f (x )=b ·a x,可得⎩⎪⎨⎪⎧a b =8b·a 3=32 得⎩⎪⎨⎪⎧a =2b =4∴f (x )=4·2x . (2)不等式+1-2m ≥0在x ∈(-∞ ,1]上恒成立 ,即m ≤12·⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫12x 2+12·⎝ ⎛⎭⎪⎫12x +12在x ∈(-∞ ,1]上恒成立. 令t =⎝ ⎛⎭⎪⎫12x ,那么m ≤12·t 2+12t +12.记g(t)=12·t 2+12t +12=12·⎝ ⎛⎭⎪⎫t +122+38 , 由x ∈(-∞ ,1] ,可得t ≥12.故当t =12时 ,函数g(t)取得最||小值为78.由题意可得 ,m ≤g(t)min ,∴m ≤78.精品 "正版〞资料系列 ,由本公司独创 .旨在将 "人教版〞、〞苏教版 "、〞北师 大版 "、〞华师大版 "等涵盖几乎所有版本的教材教案、课件、导学案及同步练习和 检测题分享给需要的朋友 .本资源创作于2021年8月 ,是当前最||新版本的教材资源 .包含本课对应 内容 ,是您备课、上课、课后练习以及寒暑假预习的最||正确选择 .。
人教版高一数学必修一2.1.2指数函数及其性质(一)

2.1.2指数函数及其性质(一)班级______________座号_________学生_______________一、选择题1.若函数y =(1-3a )x 是实数集R 上的增函数,则实数a 的取值范围为 ( )A .(13,+∞)B .(-∞,13)C .(-∞,0)D .(-13,13) 2.设a =22.5,b =2.50,c =(12)2.5,则a ,b ,c 的大小关系是 ( )A .a >c >bB .c >a >bC .a >b >cD .b >a >c3.函数f (x )=3-a x -1的图象必经过点 ( )A .(0,1)B .(1,2)C .(2,3)D .(2,4)4.函数y =xa x |x|(0<a <1)的图像的大致形状是 ( )二、填空题5.函数y =2212x x -⎛⎫ ⎪⎝⎭的值域是________.6.若函数f (x )=a x -1(a >0,a ≠1)的定义域和值域都是[0,2],则实数a 等于________.7.已知f (x ),g (x )都是定义在R 上的函数,且满足以下条件①f (x )=a x ·g (x )(a >0,a ≠1);②g (x )≠0;若f (1)g (1)+f (-1)g (-1)=52,则a 等于________.三、解答题8.已知函数f(x)=a x-2(x≥0)的图象经过点(3,4),其中a>0,且a≠1(1)求a的值;(2)求函数f(x)的值域.9.设a>0且a≠1,函数y=a2x+2a x-1在[-1,1]上的最大值是14,求a的值.10.已知函数f(x)=2a·4x-2x-1.(1)当a=1时,求函数f(x)在x∈[-3,0]的值域.(2)若关于x的方程f(x)=0有解,求a的取值范围.2.1.2指数函数及其性质(一)参考答案1.B 【解析】由题意知,此函数为指数函数,且为实数集R 上的增函数,所以底数1-3a >1,解得a <0.2.C 【解析】b =2.50=1,c =(12)2.5=2-2.5,则2-2.5<1<22.5,即c <b <a .【方法技巧】比较指数幂大小的技巧(1)比较两个指数幂大小时,尽量化同底或同指,当底数相同,指数不同时,构造同一指数函数,然后比较大小.(2)当指数相同,底数不同时,构造两个指数函数,利用图像比较大小.3.B 【解析】因为f (1)=3-a 1-1=2,所以的图象必经过点(1,2)4.D 【解析】因为y =xa x |x |=⎩⎨⎧a x (x >0)-a x (x <0),且0<a <1,所以结合选项知,选D . 5. [12,+∞) 【解析】∵2x -x 2=-(x -1)2+1≤1, ∴2212x x -⎛⎫ ⎪⎝⎭≥12.答案:[12,+∞) 6.3【解析】由题意知⎩⎨⎧ 0<a <1a 2-1=0a 0-1=2无解或⎩⎨⎧ a >1a 0-1=0a 2-1=2⇒a = 3.答案: 37. 2或12【解析】由f (x )=a x ·g (x )得f (x )g (x )=a x ,所以由f (1)g (1)+f (-1)g (-1)=52⇒a +a -1=52,解得a =2或12.答案:2或128.解:(1)∵函数f (x )=a x -2(x ≥0)的图象经过点(3,4),∴4=a 3-2,∴a =4.(2)由(1)得f (x )=4x -2(x ≥0),它在定义域上为增函数,且f (0)=116, ∴f (x )=4x -2(x ≥0)的值域为[116,+∞). 9. 解:令t =a x (a >0且a ≠1),则原函数化为y =(t +1)2-2(t >0).(1)当0<a <1时,x ∈[-1,1],t =a x ∈1,a a ⎡⎤⎢⎥⎣⎦,此时f (t )在1,a a ⎡⎤⎢⎥⎣⎦上是增加的. 所以f (t )max =2111f a a ⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭-2=14.所以211a ⎛⎫+ ⎪⎝⎭=16,所以a =-15或a =13. 又因为0<a <1,所以a =13.(2)当a>1时,x∈[-1,1],t=a x∈1,aa⎡⎤⎢⎥⎣⎦,此时f(t)在1,aa⎡⎤⎢⎥⎣⎦上是增加的.所以f(t)max=f(a)=(a+1)2-2=14,解得a=3(a=-5舍去).综上得a=13或3.10.解:(1)当a=1时,f(x)=2·4x-2x-1=2(2x)2-2x-1,令t=2x,x∈[-3,0],则t∈1,1 8⎡⎤⎢⎥⎣⎦.故y=2t2-t-1=2214t⎛⎫-⎪⎝⎭-98,t∈1,18⎡⎤⎢⎥⎣⎦,故值域为9,08⎡⎤-⎢⎥⎣⎦.(2)关于x的方程2a(2x)2-2x-1=0有解,等价于方程2am2-m-1=0在(0,+∞)上有解.记g(m)=2am2-m-1,当a=0时,解为m=-1<0,不成立.当a<0时,开口向下,对称轴m=14a<0,过点(0,-1),不成立.当a>0时,开口向上,对称轴m=14a>0,过点(0,-1),必有一个根为正,所以,a>0.【一题多解】本题还有以下解法:方程2am2-m-1=0可化为a=m+12m2=211122m⎛⎫+⎪⎝⎭-18,所以a的范围即为函数g(m)=211122m⎛⎫+⎪⎝⎭-18在(0,+∞)上的值域,所以a>0.。
人教A版数学必修一§2.1.2(1)指数函数及其性质(课时练).docx

高中数学学习材料唐玲出品§2.1.2(1)指数函数及其性质(课时练)一.选择题:1、函数)1,0(41≠>+=-a a a y x 的图象恒过定点P ,则定点P 的坐标为·················() 、A )5,1( 、B )4,1( 、C )4,0( 、D )0,4(2、函数271312-=-x y 的定义域是················································() 、A ),2(+∞- 、B ),1[+∞- 、C ]1,(--∞ 、D )2,(-∞3、已知1,10-<<<b a ,则函数b a y x +=的图象必定不过····························() 、A 第一象限 、B 第二象限 、C 第三象限 、D 第四象限4、若函数)1,0(1≠>-+=a a b a y x 的图象过第二、三、四象限,则一定有·············() 、A 0,10><<b a 、B 0,1>>b a 、C 0,10<<<b a 、D 0,1<>b a5、设函数⎪⎩⎪⎨⎧≥+<=2,322,2)(x x x x x f x ,若1)(0>xf ,则0x 的取值范围是·····················()、A ),3()2,0(+∞ 、B ),3(+∞ 、C ),2()1,0(+∞ 、D )2,0(二.填空题:6、函数21232x x y --=的定义域为 ;函数2231()2x x y -+=的值域为7、若618.03=a ,Z k k k a ∈+∈],1,[,则k 的值是____________.8、直线a y 2=与函数)1,0(1≠>-=a a a y x 图象有两个公共点,则a 范围是______.三.简答题9、若函数)1,0(122≠>-+=a a a a y x x 在区间]1,1[-上的最大值是14,求实数a 的值. 提示:对实数a 进行分类讨论.10、若函数1212)(---⋅=x x a a x f 为奇函数. (1)求函数的定义域; (2)确定实数a 的值;(3)求函数的值域; (4)讨论函数的单调性.提示:利用x2),0(+∞∈,即可求出函数的值域.§2.1.2(1)指数函数及其性质一、选择题:1.A2.B3.A4.C5.A二、填空题:6. 略7. 略8. 略三、解答题:9.略10. 略。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.1.2 指数函数及其性质
第一课时 指数函数的概念及性质
知识点一:指数函数的概念
1.下列以x 为自变量的函数中,是指数函数的是
A .y =(-4)x
B .y =πx
C .y =-4x
D .y =a x +2(a >0且a ≠1)
2.下列函数中①y =2x 2;②y =4x ;③y =32x ;④y =3×2x ;⑤y =3x +1;⑥y =-3x ,一定是指数函数的个数为
A .0
B .1
C .2
D .3
3.设P ={y|y =x 2,x ∈R },Q ={y|y =2x ,x ∈R },则
A .Q P
B .Q P
C .P ∩Q ={2,4}
D .P ∩Q ={(2,4)}
4.已知a =20.6,b =0.62,则实数a ,b 的大小关系是__________.
5.函数y =(a 2-3a +3)a x 是指数函数,则a 的值为__________.
知识点二:指数函数的定义域和值域
6.当x >0时,函数f(x)=(a 2-1)x 的值总大于1,则实数a 的取值范围是
A .1<|a|< 2
B .|a|<1
C .|a|>1
D .|a|> 2
7.函数f(x)=1-2x 的定义域是
A .(-∞,0)
B .(-∞,0]
C .[0,+∞)
D .(-∞,+∞)
8.集合P ={y|y =k ,k ∈R },Q ={y|y =a x +1,a >0,且a ≠1,x ∈R },若集合P ∩Q 只有一个子集,则k 的取值范围是
A .(-∞,1)
B .(-∞,1]
C .(1,+∞)
D .(-∞,+∞)
9.函数y =(13
)|x|的值域是________. 10.求下列函数的定义域与值域:
(1)y =21
4x ;
(2)y =(23
)-|x|.
能力点一:利用指数函数比较幂和指数值的大小
11.已知集合M ={-1,1},N ={x ∈Z |12
<2x +1<4},则M ∩N 等于 A .{-1,1} B .{-1} C .{0} D .{-1,0}
12.已知a =(35)13-,b =(35)12-,c =(43)12-,则a ,b ,c 三个数的大小关系是 A .c <a <b B .c <b <a C .a <b <c D .b <a <c
13.设3x =17
,则 A .-3<x <-2 B .-2<x <-1
C .-1<x <0
D .0<x <1
14.(2010广东佛山一中期中)若3<(13
)x <27,则 A .-1<x <3 B .x >3或x <-1
C .-3<x <-1
D .1<x <3
15.已知a =0.80.7,b =0.80.9,c =1.20.8,则a ,b ,c 的大小关系是__________.
16.比较下列各题中两个值的大小.
(1)1.72.5,1.73;
(2)0.9-0.1,0.9-0.2;
(3)1.70.3,0.93.1.
能力点二:利用指数函数性质解答综合题
17.函数y =a x 在[0,1]上的最大值与最小值的和为3,则函数y =2ax -1在[0,1]上的最大值是
A .6
B .1
C .3 D.32
18.(2010河南洛阳高一期中)设函数f(x)=⎩⎪⎨⎪⎧
(12)x +2,x ≤0,23x ,x>0,
若f(a)>1,则a 的取值范
围是
A .(-∞,-1)∪(0,+∞)
B .(-∞,-2)∪(0,+∞)
C .(-1,1)
D.(-1,+∞)
19.函数f(x)=a x(a>0且a≠1)在[1,2]上的最大值比最小值大a
2,则a的值为__________.20.如果函数y=a2x+2a x-1(a>0,且a≠1)在区间[-1,1]上的最大值是14,求a的值.
21.求下列函数的定义域与值域:
(1)y=4x+2x+1+1;
(2)y=1-2-x.
22.已知函数y=a2x3x3
-+,当x∈[1,3]时有最小值8,求a的值.
答案与解析
基础巩固
1.B
2.B只有②是指数函数.
3.B因为P={y|y≥0},Q={y|y>0},所以Q P.
4.a >b ∵a =20.6>1,b =0.62<1,∴a >b.
5.2 由y =(a 2-3a +3)a x 是指数函数,
∴⎩⎪⎨⎪⎧ a 2-3a +3=1,a>0且a ≠1.解得⎩⎪⎨⎪⎧
a =1或2,a>0且a ≠1.∴a =2.
6.D 由指数函数的性质,可知f(x)在(0,+∞)上是递增函数,所以a 2-1>1,a 2>2,|a|> 2.
7.B 要使函数有意义,只需1-2x ≥0,2x ≤1,x ≤0.
8.B 由集合P ∩Q 只有一个子集可知,P ∩Q =Ø.由Q ={y|y >1},可知k ≤1.
9.(0,1] ∵|x|≥0,∴0<y ≤1.
10.解:(1)∵x -4≠0,∴x ≠4.
∴定义域是{x ∈R |x ≠4}.
∵1x -4
≠0,∴21
4x -≠1. ∴函数的值域是{y|y >0且y ≠1}.
(2)定义域为R .
∵|x|≥0,
∴y =(23)-|x|=(32)|x|≥(32
)0=1. ∴y =(23
)-|x|的值域是{y|y ≥1}. 能力提升
11.B ∵12
<2x +1<4, ∴2-1<2x +1<22.
∵x ∈Z ,∴x =-1,0.
于是N ={-1,0},M ∩N ={-1}. 12.A ∵y =(35)x 是减函数,-13>-12
,∴b >a >1. 又0<c <1,∴c <a <b.
13.B 3-2<3x =17
<3-1, 即-2<x <-1.
14.C ∵(13)-1<(13)x <(13)-3且函数y =(13
)x 为单调递减函数, ∴-3<x <-1.
15.c >a >b ∵y =0.8x 是减函数,∴0<b <a <1.
又∵c =1.20.8>1,∴c >a >b.
16.解:(1)考察指数函数y =1.7x ,由于底数1.7>1,
∴指数函数y =1.7x 在(-∞,+∞)上是增函数.
∵2.5<3,∴1.72.5<1.73.
(2)考察函数y =0.9x ,由于0<0.9<1,
∴指数函数y =0.9x 在(-∞,+∞)上为减函数.
∵-0.1>-0.2,
∴0.9-0.1<0.9-0.2.
(3)由指数函数的性质得1.70.3>1.70=1,
0.93.1<0.90=1,∴1.70.3>0.93.1.
17.C 函数y =a x 在[0,1]上是单调的,最大值与最小值都在端点处取到,故有a 0+a 1=3,解得a =2,因此函数y =2ax -1=4x -1在[0,1]上是单调递增函数,当x =1时,y max =3.
18.B 当a ≤0时,f(a)>1化为(12
)a +2>1,解得a ∈(-∞,-2); 当a >0时,f(a)>1化为23a >1,解得a ∈(0,+∞),综上可知a 的取值范围是(-∞,-2)∪(0,+∞).
19.12或32 f(x)=a x (a >0,且a ≠1)是单调函数.当a >1时,由a 2-a =a 2
,得a =0(舍去)或a =32;当0<a <1时,由a -a 2=a 2,得a =0(舍去)或a =12
. 20.解:设t =a x ,则y =f(t)=t 2+2t -1=(t +1)2-2.
当a >1时,0<a -1≤t ≤a ,此时y max =a 2+2a -1,由题设a 2+2a -1=14,得a =3或a
=-5,由a >1,知a =3.
当0<a <1时,t ∈[a ,a -1],此时y max =(a -1)2+2a -1-1.
由题设a -2+2a -1-1=14,得a =13或a =-15,由0<a <1,知a =13
. 故所求的a 的值为3或13
. 拓展探究
21.解:(1)定义域是R .
∵y =4x +2x +1+1=(2x )2+2·2x +1=(2x +1)2,
且2x >0,∴y >1.
∴y =4x +2x +1+1的值域是{y|y >1}.
(2)要使函数有意义,必须1-2-x ≥0,即1-(12)x ≥0,也就是(12)x ≤1=(12
)0,得x ≥0,定义域为{x|x ≥0}.
令t =1-(12)x ,当x ≥0时,0<(12)x ≤1,0≤1-(12
)x <1,因此t ∈[0,1),y =t 的值域为[0,1). 22.解:令f(x)=x 2-3x +3,则f(x)=(x -32)2+34
. 当x ∈[1,3]时,f(x)有最小值34
,最大值3. 当a >1时,y =a f(x)≥a 34
=8,此时a =16. 当0<a <1时,y =a f(x)≥a 3=8,此时a =2,与0<a <1矛盾,应舍去.
综上知a =16.。
