2016-2017学年广西南宁八中高一上学期期中数学试卷和解析
广西南宁市高一上学期数学期中考试试卷

广西南宁市高一上学期数学期中考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共12分)1. (1分) (2016高二下·珠海期末) 设,则“,或”是“”的()A . 必要不充分条件B . 充分不必要条件C . 充要条件D . 既不充分也不必要条件2. (1分)函数的定义域为()A .B .C .D .3. (1分) (2016高一上·贵阳期末) 化简÷( b )(a>0,b>0)结果为()A . aB . bC .D .4. (1分)已知函数的图象如右图所示,则的解析式可以是()A .B .C .D .5. (1分) (2017高一上·厦门期末) 下列函数中,是奇函数且在(0,+∞)上单调递减的是()A . y=x﹣1B . y=()xC . y=x3D .6. (1分)已知实数,,则的大小关系为()A .B .C .D .7. (1分) y=ax当x>1(或x<﹣1)时,y>2恒成立,则a的取值范围是()A .B .C . (1,2]D .8. (1分) (2019高一上·盘山期中) 已知函数,则函数零点所在的区间为()A .B .C .D .9. (1分)某品牌电脑投放市场的第一个月销售100台,第二个月销售200台,第三个月销售400台,第四个月销售790台,则下列函数模型中能较好反映销售量y与投放市场月数x之间的关系的是()A . y=100xB . y=50x2﹣50x+100C . y=50×2xD . y=100log2x+10010. (1分) (2019高一上·北京期中) 给出下列四个函数:① ;② ;③ ;④ .其中在区间上是减函数的是()A . ①B . ②C . ③D . ④11. (1分)若函数f(x)在[a,b]上的值域为[,],则称函数f(x)为“和谐函数”.下列函数中:①g(x)=+;②h(x)=;③p(x)=;④q(x)=lnx.“和谐函数”的个数为()A . 1个B . 2个C . 3个D . 4个12. (1分) (2018高二下·科尔沁期末) 函数的零点所在的大致区间是()A . (3,4)B . (2,e)C . (1,2)D . (0,1)二、填空题 (共5题;共5分)13. (1分) (2019高一上·沭阳期中) 某工厂生产某种产品的月产量与月份之间满足关系.现已知该厂今年月份、月份生产该产品分别为万件、万件.则此工厂月份该产品的产量为________万件.14. (1分) (2016高一上·绵阳期末) 计算:lg ﹣lg25=________.15. (1分) (2016高一下·湖北期中) 已知函数f(x)=x2﹣2(a﹣1)x+2在区间(﹣∞,5]上为减函数,则实数a的取值范围为________.16. (1分)若,则a的取值范围为________17. (1分) (2018高一上·黄陵期末) 已知x∈R,集合A中含有三个元素3,x,x2-2x.(1)求元素x满足的条件;(2)若-2∈A,求实数x.三、解答题 (共5题;共9分)18. (2分)设x,y,z∈R+,且3x=4y=6z .(1)求证:;(2)比较3x,4y,6z的大小.19. (2分)某小区现有一块草坪ABCD呈平行四边形形状,AB=3,AD=2,∠BAD=60°,为了改善居民的生活环境,决定将原草坪扩建成三角形PAQ形状,点A,D,P共线,Q,C,P共线,A,B,Q共线,设AP=x,BQ=y.(1)求y关于x的函数关系式;(2)求△APQ面积最小值.20. (2分)某市出租车的收费标准为:乘坐距离3公里以内(含3公里)按起点价10元收费.超过3公里,超出里程每公里按1.5元加收,如果超过15公里,则超出里程按每公里2.1元收费.(1)求收费y(元)与里程x(公里)的函数关系式;(2)若小明乘坐了10公里,应该付费多少?(3)若收费25元,问小明乘坐了多少路程?21. (1分) (2018高一下·淮北期末) 已知,其中 .(1)解关于的不等式;(2)若时,不等式恒成立,求实数的范围.22. (2分) (2019高一上·阜阳月考) 已知函数, .(1)若函数的图像与轴无交点,求的取值范围;(2)若方程在区间上存在实根,求的取值范围;(3)设函数,,当时若对任意的,总存在,使得,求的取值范围.参考答案一、单选题 (共12题;共12分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共5题;共5分)13-1、14-1、15-1、16-1、17-1、17-2、三、解答题 (共5题;共9分) 18-1、18-2、19-1、19-2、20-1、20-2、20-3、21-1、21-2、22-1、22-2、22-3、。
数学---广西南宁八中2016-2017学年高一(上)期末试卷(解析版)

广西南宁八中2016-2017学年高一(上)期末数学试卷一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设全集U={1,2,3,4,5},集合A={1,3,5},集合B={3,4},则(∁U A)∩B=()A.{3} B.{4} C.{3,4} D.{2,3,4}2.点P(1,﹣4)到直线4x+3y﹣2=0的距离为()A.2 B.5 C.7 D.103.已知直线l经过点(0,﹣2),其倾斜角的大小是60°,则直线l与两坐标轴围成三角形的面积S等于()A.B.C.D.4.函数f(x)=x+ln x的零点所在的区间为()A.(﹣1,0)B.(0,1)C.(1,2)D.(1,e)5.已知a=21.2,b=()﹣0.8,c=2log52,则a,b,c的大小关系为()A.c<b<a B.c<a<b C.b<a<c D.b<c<a6.若两平行直线l1:x﹣2y+m=0(m>0)与l2:2x+ny﹣6=0之间的距离是,则m+n=()A.0 B.1 C.﹣2 D.﹣17.如图所示,在正方体ABCD﹣A1B1C1D1中,E,F,G,H分别为AA1,AB,BB1,B1C1的中点.则异面直线EF与GH所成的角等于()A.120°B.90°C.60°D.45°8.设l,m,n是三条不同的直线,α,β是两个不同的平面,下列命题中正确的是()A.若l⊂β且m∥β,则l∥m B.若l⊥m且l⊥n,则m∥nC.若m⊥n且m⊂α,n⊂β,则l∥αD.若m⊥α且m∥n,n∥β,则α⊥β9.若函数f(x)是定义在R上的偶函数,在(﹣∞,0)上是增函数,且f(2)=0,则使f(x)<0的x的取值范围是()A.﹣2<x<2 B.x<﹣2 C.x<﹣2或x>2 D.x>210.若函数y=a x﹣x﹣a有两个零点,则a的取值范围是()A.(1,+∞)B.(0,1)C.(0,+∞)D.∅11.在长方体ABCD﹣A1B1C1D1中,AB=AD=2,CC1=,则二面角C1﹣BD﹣C的大小为()A.30°B.45°C.60°D.90°12.如图,已知一个锥体的正(主)视图,侧(左)视图和俯视图均为直角三角形,且面积分别为3,4,6,则该锥体的体积为()A.24 B.4 C.12 D.2二、填空题:本大题共4小题,每小题5分,共20分.13.f(x)=的定义域是.14.=.15.直线(2k+1)x+(k﹣1)y+(7﹣k)=0(k∈R)经过的定点为.16.已知正三棱锥P﹣ABC,点P,A,B,C都在表面积为12π的球的球面上,若P A,PB,PC两两相互垂直,则球心到截面ABC的距离为.三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.已知函数f(x)=a x+b(a>0,a≠1)的图象过点(0,﹣3),(2,0).(1)求a与b的值;(2)求x∈[﹣2,4]时,f(x)的最大值与最小值.18.已知平面内两点A(8,﹣6),B(2,2).(Ⅰ)求过点P(2,﹣3)且与直线AB平行的直线l的方程;(Ⅱ)求线段AB的垂直平分线方程.19.直三棱柱ABC﹣A1B1C1的三视图如图所示.(1)求三棱柱ABC﹣A1B1C1的体积;(2)若点D为棱AB的中点,求证:AC1∥平面CDB1.20.已知函数.(1)求f(x)的定义域;(2)判断f(x)的奇偶性并证明;(3)若f(a)=3,求f(﹣a)的值.21.如图,在四棱锥P﹣ABCD中,已知P A⊥平面ABCD,∠BAD=90°,AD∥BC,P A=AB=BC=1,AD=2,E为PD的中点.(1)求证:CD⊥平面P AC;(2)求直线EC与平面P AC所成角的正切值.22.已知函数f(x)=log2(2x)•log2(4x),g(t)=﹣3,其中t=log2x(4≤x≤8).(1)求f()的值;(2)求函数g(t)的解析式,判断g(t)的单调性并用单调性定义给予证明;(3)若a≤g(t)恒成立,求实数a的取值范围.参考答案一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的,将其选出后填入答题卷.1.B【解析】因为全集U={1,2,3,4,5},集合A={1,3,5},所以C U A={2,4},又因为集合B={3,4},所以(∁U A)∩B={4},2.A【解析】点P(1,﹣4)到直线4x+3y﹣2=0的距离==2,3.D【解析】因为直线l的倾斜角的大小为60°,故其斜率为,又直线l经过点(0,﹣2),所以其方程为y﹣(﹣2)=x,即x﹣y﹣2=0,由直线l的方程知它在x轴、y轴上的截距分别是、﹣2,所以直线l与两坐标轴围成三角形的面积S==,4.B【解析】令f(x)=x+ln x=0,可得ln x=﹣x,再令g(x)=ln x,h(x)=﹣x,在同一坐标系中画出g(x),h(x)的图象,可知g(x)与h(x)的交点在(0,1),从而函数f(x)的零点在(0,1),5.A【解析】由于函数y=2x在R上是增函数,a=21.2,b=()﹣0.8 =20.8,1.2>0.8>0,∴a>b>20=1.再由c=2log52=log54<log55=1,可得a>b>c,6.C【解析】由题意,解得n=﹣4,即直线l2:x﹣2y﹣3=0,所以两直线之间的距离为d=,解得m=2,所以m+n=﹣2,7.C【解析】如图所示,连接A1B,BC1,A1C1,则EF∥A1B,GH∥BC1,∴∠A1BC1是异面直线EF与GH所成的角,∵△A1BC1是等边三角形,∴∠A1BC1=60°,8.D【解析】由l,m,n是三条不同的直线,α,β是两个不同的平面,知:在A中,若l⊂β且m∥β,则l与m平行或异面,故A错误;在B中,若l⊥m且l⊥n,则m与n相交、平行或异面,故B错误;在C中,若m⊥n且m⊂α,n⊂β,则l与α相交、平行或l⊂α,故C错误;在D中,若m⊥α且m∥n,n∥β,则由面面垂直的判定定理得α⊥β,故D正确.9.C【解析】∵f(x)是R上的偶函数,在(﹣∞,0)上是增函数;∴f(x)在(0,+∞)为减函数;又f(2)=0;∴由f(x)<0得:f(|x|)<f(2);∴|x|>2;∴x<﹣2,或x>2.10.A【解析】①当0<a<1时,易知函数y=a x﹣x﹣a是减函数,故最多有一个零点,故不成立;②当a>1时,y′=ln a•a x﹣1,故当a x<时,y′<0;当a x>时,y′>0;故y=a x﹣x﹣a在R上先减后增,且当x→﹣∞时,y→+∞,当x→+∞时,y→+∞,且当x=0时,y=1﹣0﹣a<0;故函数y=a x﹣x﹣a有两个零点;故成立;11.A【解析】取BD的中点E,连接C1E,CE∵AB=AD=2,∴AC⊥BD,根据三垂线定理可知C1E⊥BD ∴∠C1EC为二面角C1﹣BD﹣C的平面角∴CE=,而CC1=,∴tan∠C1EC==∴二面角C1﹣BD﹣C的大小为30°12.B【解析】由三视图知,几何体是一个三棱锥,根据三棱锥的三视图的面积,设出三棱锥两两垂直的三条侧棱分别是x,y,z∵三视图的面积分别为3,4,6,∴xy=6,xz=8,yz=12,∴y=3,x=2,z=4∴三棱锥的体积是二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卷的横线上.13.(﹣∞,0)∪(0,1]【解析】要使原函数有意义,则,解得:x≤1且x≠0.∴函数f(x)的定义域为:(﹣∞,0)∪(0,1].故答案为:(﹣∞,0)∪(0,1].14.﹣2【解析】原式=lg10﹣﹣1=1﹣2﹣1=﹣2.故答案为:﹣215.(﹣2,5)【解析】∵直线(2k+1)x+(k﹣1)y+(7﹣k)=0(k∈R)经过的定点,∴(2x+y﹣1)k+x﹣y+7=0恒成立,∴,解得x=﹣2,y=5.∴直线(2k+1)x+(k﹣1)y+(7﹣k)=0(k∈R)经过的定点为(﹣2,5).故答案为:(﹣2,5).16.【解析】∵正三棱锥P﹣ABC,P A,PB,PC两两垂直,∴此正三棱锥的外接球即以P A,PB,PC为三边的正方体的外接球O,表面积为12π的球的∵球O的半径为,∴正方体的边长为2,即P A=PB=PC=2,球心到截面ABC的距离即正方体中心到截面ABC的距离,设P到截面ABC的距离为h,则正三棱锥P﹣ABC的体积V=S△ABC×h=S△P AB×PC=××2×2×2=,△ABC为边长为2的正三角形,S△ABC=×(2)2=2,∴h=,∴球心(即正方体中心)O到截面ABC的距离为﹣=.故答案为:.三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.解(1)函数f(x)=a x+b(a>0,a≠1)的图象过点(0,﹣3),(2,0).,解得a=2,b=﹣4;(2)函数f(x)=2x﹣4.函数是增函数,x∈[﹣2,4]时,f(x)的最大值为:24﹣4=12;最小值2﹣2﹣4=﹣.18.解(Ⅰ)因为,…所以由点斜式得直线l的方程4x+3y+1=0…(Ⅱ)因为AB的中点坐标为(5,﹣2),AB的垂直平分线斜率为…所以由点斜式得AB的中垂线方程为3x﹣4y﹣23=0…19.解(1)由直三棱柱的三视图得:,高BB1=4,∴三棱柱ABC﹣A1B1C1的体积V=S△ABC×BB1=3×4=12.证明:(2)连结B1C,BC1,交于点O,连结OD,∵点D为棱AB的中点,∴OD∥AC1,∵OD⊂平面CDB1,AC1⊄平面CDB1.∴AC1∥平面CDB1.20.解(1)由2x﹣1≠0,可得x≠0,∴f(x)的定义域是{x|x≠0};(2)f(﹣x)==﹣f(x),∴f(x)是奇函数;(3)f(﹣a)=﹣f(a)=﹣3.21.证明:(1)连接AC,∵P A⊥平面ABCD,∴P A⊥DC,即DC⊥P A,过C作CC′⊥AD,交AD于C′,则CC′=1,C′D=1,∴CD=2,又AC=2,∴AC2+CD2=2+2=AD2,∴DC⊥AC,∵AC∩P A=A;∴CD⊥平面P AC.解:(2)以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,C(1,1,0),E(0,1,),P(0,0,1),A(0,0,0),D(0,2,0),=(﹣1,1,0),=(1,0,﹣),∵CD⊥平面P AC,∴平面P AC的一个法向量=(﹣1,1,0),设直线EC与平面P AC所成角为θ,则sinθ===,cosθ==,tanθ==,∴直线EC与平面P AC所成角的正切值为.22.解(1)函数f(x)=log2(2x)•log2(4x),可得f()=log2(2)•log2(4)=log22•log22=×=;(2)t=log2x(4≤x≤8),可得2≤t≤3,g(t)=﹣3=﹣3=﹣3==t+,(2≤t≤3).结论:g(t)在[2,3]上递增.理由:设2≤t1<t2≤3,则g(t1)﹣g(t2)=t1+﹣(t2+)=(t1﹣t2)+ =(t1﹣t2)•,由2≤t1<t2≤3,可得t1﹣t2<0,t1t2>4>2,即有g(t1)﹣g(t2)<0,则g(t)在[2,3]上递增.(3)a≤g(t)恒成立,即为a≤g(t)的最小值.由g(t)在[2,3]上递增,可得g(2)取得最小值,且为3.则实数a的取值范围为a≤3.。
高一年级第一学期期中考试数学试卷及其参考答案

高一年级第一学期期中考试数学试卷(基础模块第一章、第二章)一、选择题(每小题5分,共60分)1.下列表示正确的是().A.{ 0 }=∅B.{全体实数}=RC.{ a }∈{a,b,c } D.{ x∈R∣x2+1=0 }=∅2.已知全集U={ 0,1,2,3,4,5},集合A={1,2,5},B={2,3,4},则(U C A)B=().A.{2}B.{0,2,3,4}C.{3,4}D.{1,2,3,4,5}3.已知A={ (x,y) | 2x-y=0 },B={ (x,y) | 3x+2y=7 },则A B=().A.{(2,1)}B.{1,2}C.{(1,2)}D.{x=1,y=2}4.设A={ x | 0< x < 1 },B={ x | x < a } ,若A⊆B,则a的取值范围是().A.[1,+∞) B.(-∞,0]C.[0,+∞)D.(-∞,1]5.已知集合A={ x | x2+14= 0 },若A∩R =∅,则实数m的取值范围是().A.m<1B.m≥1C.0<m<1D.0≤m<16.“A⊆B”是“A B=A”的().A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件7.不等式21-+xx≤0的解集为().A.{ x | x≥2}B.{ x | x≥2或x<-1 }C.{ x|-1<x≤2 }D.{x| x≥2或x≤-1 }8.已知a<b<0,c>0,那么().A.a2<b2B.a b<1C.ca<cb D.ca>cb9.绝对值不等式| 2x-3 |<5的解集是().A.{ x | x<-1或x>4 }B.{ x |-1<x<4 }C.{ x | x<-1 }D.{ x | x>4 }10.与不等式-x2-2x+3>0同解的不等式(组)是().A. x2+2x-3>0B. (x+3)(x-1)<0C.x+3>0x-1D.x+3<0x-1>0⎧⎨⎩a 、b 、c 的大小顺序是( ). A.a>b>c B.c>b>a C.b>a>c D.a>c>b12.若实数0<a <1,则)0>1(a-x)(x-a的解集为( ). A.{ x |1<x<a a } B.{ x | 1<<a x a} C.{ x | 1< >x a 或x a } D.{ x | 1<a >x 或x a}二、填空题(每小题4分,共16分)13.设全集U={ 1,2,3,4,5 },A={ 2,5 },则U C A 的所有子集的个数为 _________. 14.符合条件{a}⊆M {a,c,d}的集合M的个数是 _________.15.设a,b为实数,则“a2=b2”是“a=b”的 _________条件.(填充分或必要)16.不等式2+2m x x+n>0的解集是(11,32-),则不等式2-nx +2x-m >0的解集是 _________.三、解答题(共74分,解答应写出文字说明及演算步骤) 17.已知U={ x |-2<x<7 ,x ∈N },A={ 1,2,4 },B={ 2,3,5}.求: ⑴ A U B ;⑵ A B ;⑶ B C C U U A;⑷ B C C U U A .(12分)18.若集合A={ x | mx 2+2x -1 = 0 , m ∈R , x ∈R }中有且仅有一个元素,那么m 的值是多少?(12分)19.设集合A={ x | x 2-3x +2 = 0 },B = { x | x 2+2(a +1)x +(a 2-5) = 0 },若A B = { 2 },求实数a的值.(12分) 20.解不等式x+23-x≤1.(12分) 21.设全集为R ,A={ x | |x-1|<3 },B={ x | x 2-x -2≥0 },求A B ,A U B ,A CB .(12分)22.已知集合A={ x | x 2-x -12 ≤0 },集合B={ x | m -1≤x ≤2m +3 },若A U B=A ,求实数m 的取值范围.(14分)高一年级第一学期期中考试数学试卷参考答案二、填空题(每小题4分,共16分)13、 8 14、 3 15、 必要 16、 (-2,3)三、解答题:(22题14分,17~21题每题12分,共计74分)17.解:U={ 0,1,2,3,4,5,6 }. ⑴A U B={1,2,3,4,5}.⑵A B={2}.⑶B C C U U A ={ 0,3,5,6 }U { 0,1,4,6 }={ 0,1,3,4,5,6, }. ⑷ B C C U U A={ 0,3,5,6 } { 0,1,4,6 }={ 0,6 }.18. 解:当m=0时, A=12⎧⎫⎨⎬⎩⎭,符合题意.当m ≠0时,要使集合A 中有且仅有一个元素,必须 方程mx 2+2x -1 = 0有两个相等实数根, ∴ 2∆=2+4m =0, 即m=-1,综上所述,m=0或m=-1. 19. 解:A={ 1,2 }∵ A B={ 2 }, ∴ 2 B, ∴ 2是方程x 2+2(a +1)x +(a 2-5) = 0的根,把x=2代入此方程得2a +4a+3=0, ∴ a=-1或a=-3, 当a=-1时,B={ -2,2 }, A B={ 2 },符合题意. 当a=-3时,B={ 2 }, A B={ 2 },符合题意. 综上所述,a 的值为-1或3. 20. 解:原不等式⇔x+2-13-x ≤0⇔x+2-(3-x)3-x ≤0⇔2x-13-x≤0 ⇔2x-1x-3≥00≠⎧⇔⎨⎩x-3(2x-1)(x-3)≥012⇔x ≤或x>3, ∴ 解集为12{x |x ≤或x>3}. 21. 解:解|x-1|<3得-2<x<4, 故A=(-2,4).解x 2-x -2≥0得x ≤-1或x ≥2, 故B=(-∞,-1]∪[2,+∞).∴ A B=(-2,-1]∪[2,4),A U B=R,A C B=(-2,4) (-1,2)=(-1,2).22.解: 解x2-x-12 ≤0得-3≤x≤4, 故A=[-3,4],由A U B=A,知B A,∴⎧⎪⎨⎪⎩m-1≤2m+3,m-1≥-3,2m+3≤4,即12⎧⎪⎪⎨⎪⎪⎩m≥-4,m≥-2,m≤,∴ -2≤m≤12.。
2016-2017年广西南宁八中高一(上)期中数学试卷及参考答案

2016-2017学年广西南宁八中高一(上)期中数学试卷一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的,将其选出后填入答题卷.1.(5.00分)已知集合A={1,2,3},B={2,3},则()A.A=B B.A∩B=∅C.A⊆B D.B⊆A2.(5.00分)已知全集U=R,A={x|x≤0},B={x|x≥1},则集合∁U(A∪B)=()A.{x|x≥0}B.{x|x≤1}C.{x|0≤x≤1}D.{x|0<x<1}3.(5.00分)下列四组函数中,表示同一函数的是()A.y=x﹣1与y=B.y=与y=C.y=lgx﹣2与y=lg D.y=4lgx与y=lgx24.(5.00分)函数f(x)=2x+5x的零点所在大致区间为()A.(0,1) B.(1,2) C.(﹣1,0)D.(﹣2,﹣1)5.(5.00分)函数的图象()A.关于x轴对称B.关于y轴对称C.关于原点对称D.关于直线y=x对称6.(5.00分)函数f(x)=的定义域为()A.(0,2]B.(0,2) C.(﹣2,2)D.[﹣2,2]7.(5.00分)下列函数中,其定义域和值域分别与函数y=10lgx的定义域和值域相同的是()A.y=x B.y=lgx C.y=2x D.y=8.(5.00分)设a=()0.9,b=()﹣0.3,c=log30.7,则有()A.c<a<b B.a<b<c C.c<b<a D.b<a<c9.(5.00分)若幂函数f(x)的图象经过点(3,9),那么函数f(x)的单调增区间是()10.(5.00分)函数f(x)=x2﹣2x零点个数为()A.1 B.2 C.3 D.411.(5.00分)某食品保鲜时间y(单位:小时)与储藏温度x(单位:℃)满足函数关系y=e kx+b(e=2.718…为自然对数的底数,k,b为常数).若该食品在0℃的保鲜时间是192小时,在22℃的保鲜时间是48小时,则该食品在33℃的保鲜时间是()A.16小时B.20小时C.24小时D.28小时12.(5.00分)如果函数f(x)对其定义域内的两个实数x1、x2,都满足不等式,则称函数f(x)在其定义域内具有性质M.给出下列函数:①;②y=x2;③y=2x;④y=log2x.其中具有性质M的是()A.①④B.②③C.③④D.①②③④二、填空题:本大题共4小题,每小题5分,共16分.把答案填在答题卷的横线上.13.(5.00分)设f(x)=,则f(f(3))的值为.14.(5.00分)已知函数y=log a(x﹣3)﹣1的图象恒过定点P,则点P的坐标是.15.(5.00分)若实数α满足log a2>1,则a的取值范围为.16.(5.00分)若函数f(x)为定义在R上的奇函数,且在(0,+∞)为减函数,若f(2)=0,不等式(x﹣1)f(x﹣1)>0的解集为.三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(10.00分)计算下列各式的值(其中,e为自然对数的底数):(1);(2).18.(12.00分)已知全集U=R,集合,B={x|1<x<6}(1)求A∩∁U B;19.(12.00分)已知函数f(x)=lg(3+x)﹣lg(3﹣x)(1)求f(x)的定义域;(2)判断f(x)的奇偶性并证明;(3)若f(a)=4,求f(﹣a)的值.20.(12.00分)随着机构改革工作的深入进行,各单位要减员增效,有一家公司现有职员400人,每人每年可创利10万元.据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年多创利0.05万元,但公司需付下岗职员每人每年2万元的生活费,并且该公司正常运转所需人数不得小于现有职员的,为获得最大的经济效益,该公司应裁员多少人?21.(12.00分)已知函数f(x)=x2+bx+1满足f(1+x)=f(1﹣x),.(1)求函数f(x)的解析式;(2)判断g(x)在[1,2]上的单调性并用定义证明你的结论;(3)求g(x)在[1,2]上的最大值和最小值.22.(12.00分)已知指数函数y=g(x)满足:g(3)=8,定义域为R的函数f(x)=是奇函数.(1)确定y=f(x)和y=g(x)的解析式;(2)若对任意的x∈[1,4],不等式f(2x﹣3)+f(x﹣k)>0恒成立,求k的取值范围.2016-2017学年广西南宁八中高一(上)期中数学试卷参考答案与试题解析一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的,将其选出后填入答题卷.1.(5.00分)已知集合A={1,2,3},B={2,3},则()A.A=B B.A∩B=∅C.A⊆B D.B⊆A【解答】解:因为A={1,2,3},B={2,3},显然,A≠B且B⊆A,根据集合交集的定义得,A∩B={2,3}=A,所以,A∩B≠∅,故选:D.2.(5.00分)已知全集U=R,A={x|x≤0},B={x|x≥1},则集合∁U(A∪B)=()A.{x|x≥0}B.{x|x≤1}C.{x|0≤x≤1}D.{x|0<x<1}【解答】解:A∪B={x|x≥1或x≤0},∴C U(A∪B)={x|0<x<1},故选:D.3.(5.00分)下列四组函数中,表示同一函数的是()A.y=x﹣1与y=B.y=与y=C.y=lgx﹣2与y=lg D.y=4lgx与y=lgx2【解答】解:A.,∴这两函数对应法则不同,不是同一函数;B.的定义域为[1,+∞),的定义域为(1,+∞),∴这两函数定义域不同,不是同一函数;C.,∴这两函数是同一函数;D.y=4lgx的定义域为(0,+∞),y=lgx2的定义域为{x|x≠0},定义域不同,不故选:C.4.(5.00分)函数f(x)=2x+5x的零点所在大致区间为()A.(0,1) B.(1,2) C.(﹣1,0)D.(﹣2,﹣1)【解答】解:∵函数f(x)=2x+5x是单调递增函数,又∵f(﹣1)=2﹣5=﹣3<0,f(0)=1+0=1>0,∴函数f(x)的零点必在区间(﹣1,0)上,故必存在零点的区间是(﹣1,0),故选:C.5.(5.00分)函数的图象()A.关于x轴对称B.关于y轴对称C.关于原点对称D.关于直线y=x对称【解答】解:函数,可得f(﹣x)=(﹣x)2+=x2+=f(x),函数是偶函数,函数图象关于y轴对称.故选:B.6.(5.00分)函数f(x)=的定义域为()A.(0,2]B.(0,2) C.(﹣2,2)D.[﹣2,2]【解答】解:函数f(x)=,由题意得:,解得:0<x<2,故选:B.7.(5.00分)下列函数中,其定义域和值域分别与函数y=10lgx的定义域和值域相同的是()A.y=x B.y=lgx C.y=2x D.y=函数y=x的定义域和值域均为R,不满足要求;函数y=lgx的定义域为(0,+∞),值域为R,不满足要求;函数y=2x的定义域为R,值域为(0,+∞),不满足要求;函数y=的定义域和值域均为(0,+∞),满足要求;故选:D.8.(5.00分)设a=()0.9,b=()﹣0.3,c=log30.7,则有()A.c<a<b B.a<b<c C.c<b<a D.b<a<c【解答】解:∵a=()0.9∈(0,1),b=()﹣0.3>1,c=log30.7<0,则b>a>c.故选:A.9.(5.00分)若幂函数f(x)的图象经过点(3,9),那么函数f(x)的单调增区间是()A.[3,+∞)B.[0,+∞)C.(﹣∞,0]D.(﹣∞,3]【解答】解:设幂函数f(x)=x a,则3a=9,解得a=2,∴f(x)=x2;∴f(x)=x2的单调递增区间是[0,+∞),故选:B.10.(5.00分)函数f(x)=x2﹣2x零点个数为()A.1 B.2 C.3 D.4【解答】解:函数f(x)=x2﹣2x零点个数可化为函数y=x2与y=2x的图象的交点个数,作函数y=x2与y=2x的图象如下,有三个交点,故选:C.11.(5.00分)某食品保鲜时间y(单位:小时)与储藏温度x(单位:℃)满足函数关系y=e kx+b(e=2.718…为自然对数的底数,k,b为常数).若该食品在0℃的保鲜时间是192小时,在22℃的保鲜时间是48小时,则该食品在33℃的保鲜时间是()A.16小时B.20小时C.24小时D.28小时【解答】解:y=e kx+b(e=2.718…为自然对数的底数,k,b为常数).当x=0时,e b=192,当x=22时e22k+b=48,∴e22k==e11k=e b=192当x=33时,e33k+b=(e k)33•(e b)=()3×192=24故选:C.,则称函数f(x)在其定义域内具有性质M.给出下列函数:①;②y=x2;③y=2x;④y=log2x.其中具有性质M的是()A.①④B.②③C.③④D.①②③④【解答】解:函数f(x)对其定义域内的任意两个实数x1,x2都满足不等式,则称函数f(x)在定义域上具有性质M,(为下凸函数).由函数的图象可知:②y=x2;③y=2x.其中具有性质M.故选:B.二、填空题:本大题共4小题,每小题5分,共16分.把答案填在答题卷的横线上.13.(5.00分)设f(x)=,则f(f(3))的值为1.【解答】解:∵f(x)=,∴f(3)=log5(3×3﹣4)=log55=1,f(f(3))=f(1)=2﹣30=1.故答案为:1.14.(5.00分)已知函数y=log a(x﹣3)﹣1的图象恒过定点P,则点P的坐标是(4,﹣1).【解答】解:∵log a1=0,∴x﹣3=1,即x=4时,y=﹣1,∴点P的坐标是P(4,﹣1).故答案为:(4,﹣1).15.(5.00分)若实数α满足log a2>1,则a的取值范围为(1,2).【解答】解:∵log a2>1=log a a,∴或,解得1<a<2或a∈∅.∴a的取值范围为(1,2).故答案为:(1,2).16.(5.00分)若函数f(x)为定义在R上的奇函数,且在(0,+∞)为减函数,若f(2)=0,不等式(x﹣1)f(x﹣1)>0的解集为(﹣∞,﹣1)∪(3,+∞).【解答】解:定义在R上的奇函数,可得f(﹣x)=﹣f(x),在(0,+∞)为减函数,即在R上是减函数,∵f(2)=0,则f(﹣2)=0.令t=x﹣1,不等式(x﹣1)f(x﹣1)>0转化为tf(t)>0.当t>0时,则f(t)<0,可得:t>2,即x﹣1>2,解得:x>3;当t<0时,则f(t)>0,可得:t<﹣2,即x﹣1<﹣2,解得:x<﹣1;综上所得:不等式(x﹣1)f(x﹣1)>0的解集为(﹣∞,﹣1)∪(3,+∞).故答案为:(﹣∞,﹣1)∪(3,+∞).三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(10.00分)计算下列各式的值(其中,e为自然对数的底数):(1);(2).【解答】解:(1)==;(2)=lg25+lg4+ln=lg(25×4)+ln=2+=.18.(12.00分)已知全集U=R,集合,B={x|1<x<6}(1)求A∩∁U B;(2)已知C={x|a≤x≤a+1},若A∩C=C,求实数a的取值范围.【解答】解:(2)∵全集U=R,集合={x|﹣1≤x≤2},B={x|1<x<6}∴∁U B={x|x≤1或x≥6},则A∩∁U B={x|﹣1≤x≤2};(2)∵A∩C=C,∴C⊆A,∴解得:﹣1≤a≤1,则实数a的范围是{a|﹣1≤a≤1}.19.(12.00分)已知函数f(x)=lg(3+x)﹣lg(3﹣x)(1)求f(x)的定义域;(2)判断f(x)的奇偶性并证明;(3)若f(a)=4,求f(﹣a)的值.【解答】解:(1)函数f(x)=lg(3+x)﹣lg(3﹣x)其定义域满足:,解得:﹣3<x<3.故得f(x)的定义域数为{x|﹣3<x<3}.(2)由(1)可得f(x)的定义域数为{x|﹣3<x<3}.设﹣3<x1<x2<3,则f(x1)﹣f(x2)=lg(3+x1)﹣lg(3﹣x1)﹣lg(3+x2)+lg(3﹣x2)=lg=lg因为9+3(x1﹣x2)﹣x1x2>9+(x2﹣x1)﹣x1x2<0,∴<1,即f(x1)﹣f(x2)<0,所以f(x1)<f(x2),即f(x)是(﹣3,3)上的增函数;∴定义域关于原点对称,∵f(﹣x)=lg(3﹣x)+lg(3+x)=f(x),∴函数f(x)是偶函数.∴f(a)=4,则f(﹣a)=f(a)=4.20.(12.00分)随着机构改革工作的深入进行,各单位要减员增效,有一家公司现有职员400人,每人每年可创利10万元.据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年多创利0.05万元,但公司需付下岗职员每人每年2万元的生活费,并且该公司正常运转所需人数不得小于现有职员的,为获得最大的经济效益,该公司应裁员多少人?【解答】解:设裁员x人,可获得的经济效益为y万元,则y=(400﹣x)(10+0.05x)﹣2x=(x﹣80)2+4320依题意400﹣x≥×400=300,∴0<x≤100.∴当x=80时,y取到最大值为4320;综上,为获得最大的经济效益,该公司应裁员80人.21.(12.00分)已知函数f(x)=x2+bx+1满足f(1+x)=f(1﹣x),.(1)求函数f(x)的解析式;(2)判断g(x)在[1,2]上的单调性并用定义证明你的结论;(3)求g(x)在[1,2]上的最大值和最小值.【解答】解:(1)函数f(x)=x2+bx+1满足f(1+x)=f(1﹣x),可知函数的对称轴为:x=1,所以,b=﹣2,函数f(x)的解析式:f(x)=x2﹣2x+1.(2)=x+﹣2,g(x)在[1,2]上的单调性是增函数,证明:设1≤x1<x2≤2,x1﹣x2<0,>0,g(x1)﹣g(x2)=x1﹣x2+=(x1﹣x2)()<0,g(x1)<g(x2),所以函数g(x)在[1,2]上是增函数.(3)由(2)可知,函数是增函数,函数的最小值为:g(1)=0,函数的最大值为:g(2)=.22.(12.00分)已知指数函数y=g(x)满足:g(3)=8,定义域为R的函数f(x)=是奇函数.(1)确定y=f(x)和y=g(x)的解析式;(2)若对任意的x∈[1,4],不等式f(2x﹣3)+f(x﹣k)>0恒成立,求k的取值范围.【解答】解::(1)设g(x)=a x(a>0且a≠1),∵g(3)=8,∴a3=8,解得a=2.∴g(x)=2x.∴f(x)=,∵函数f(x)是定义域为R的奇函数,∴f(0)=0,∴n=1,∴f(x)=,(x∈R);(2)由(Ⅰ)知f(x)=,易知f(x)在R上为减函数,又f(x)是奇函数,∴f(2x﹣3)+f(x﹣k)>0,∴f(2x﹣3)>﹣f(x﹣k)=f (k﹣x),∵f(x)在R上为减函数,由上式得2x﹣3<k﹣x,即对一切x∈(1,4),有3x﹣3<k恒成立,令m(x)=3x﹣3,x∈(1,4),易知m(x)在(1,4)上递增,∴m(x)<3×4﹣3=9,∴k≥9,即实数k的取值范围是[9,+∞).。
广西南宁市宾阳中学2016-2017学年高一上学期期中数学试卷 Word版含解析

2016-2017学年广西南宁市宾阳中学高一(上)期中数学试卷一、选择题:(本大题共12小题,每小题5分,共60分.每小题四个选项中有且只有一个正确.)1.下列各组中的两个集合M和N,表示同一集合的是()A.M={3,6},N={(3,6)}B.M={π},N={3.1415926}C.M={x|1<x<3,x∈R},N={2}D.2.设全集U={﹣2,﹣1,0,1,2},集合M={y|y=2x},N={x|x2﹣x﹣2=0},则(∁U M)∩N═()A.{﹣1}B.{2}C.{﹣1,2}D.{﹣1,﹣2}3.函数的定义域是()A.[﹣1,2)B.(1,2) C.[﹣1,1)∪(1,2)D.(2,+∞)4.()A.(﹣∞,2]B.(0,+∞)C.[2,+∞)D.[0,2]5.用二分法求函数f(x)=x3+x2﹣2x﹣2的一个零点,依次计算得到如表函数值:f(1)=﹣2f(1.5)=0.625f(1.25)=﹣0.984f(1.375)=﹣0.260f(1.438)=0.165f(1.4065)=﹣0.052那么方程x3+x2﹣2x﹣2=0的一个近似根在下列哪两数之间()A.1.25~1.375 B.1.375~1.4065 C.1.4065~1.438 D.1.438~1.56.已知函数,则f(f(5))等于()A.B.5 C.﹣5 D.7.函数f(x)=ln(x+1)﹣的零点所在的大致区间是()A.(0,1) B.(1,2) C.(2,3) D.(3,4)8.设a=log36,b=log612,c=log816,则()A.c>b>a B.b>c>a C.a>c>b D.a>b>c9.定义在R上的偶函数f(x)满足:对任意的x1,x2∈(﹣∞,0](x1≠x2),都有(x2﹣x1)•[f(x2)﹣f(x1)]>0,则()A.f(﹣2)<f(1)<f(3)B.f(1)<f(﹣2)<f(3)C.f(3)<f(﹣2)<f(1)D.f(3)<f(1)<f(﹣2)10.设函数f(x)满足对任意的m,n∈Z+都有f(m+n)=f(m)•f(n)且f(1)=2,则()A.2011 B.2010 C.4020 D.402211.已知函数f(x)=(x﹣a)(x﹣b)(其中a>b)的图象如图所示,则函数g (x)=a x+b的图象是()A.B.C.D.12.设函数y=f(x)在R上有定义,对于任一给定的正数p,定义函数f p(x)=,则称函数f p(x)为f(x)的“p界函数”若给定函数f(x)=x2﹣2x﹣1,p=2,则下列结论不成立的是()A.f p[f(0)]=f[f p(0)]B.f p[f(1)]=f[f p(1)]C.f p[f p(2)]=f[f(2)] D.f p[f(3)]=f[f(3)]二、填空题:(本大题共4小题,每小题5分,共20分,把答案填在答题卡题中横线上)13.已知幂函数f(x)的图象过点(2,),则=.14.函数的递增区间是.15.已知函数f(x)=log0.5(x2﹣ax+4a)在[2,+∞)上单调递减,则a的取值范围是.16.若函数y=f(x)为偶函数,且在(0,+∞)上是减函数,有f(5)=0,的解集为.三、解答题:(本大题共6小题,共70分.解答应写文字说明,证明过程或演算步骤.)17.集合P={x|a+1≤x≤2a+1},Q={x|﹣2≤x≤5}(1)若a=3,求集合(∁R P)∩Q;(2)若P⊆Q,求实数a的取值范围.18.已知函数(1)判断函数在区间[1,+∞)上的单调性,并用定义证明你的结论(2)求该函数在区间[2,4]上的最大值和最小值.19.已知f(x)是定义在R上的偶函数,且.(1)求f(0),f(2);(2)求函数f(x)的解析式.20.已知二次函数f(x)图象过点(0,3),它的图象的对称轴为x=2,且f(x)的两个零点的平方和为10,求f(x)的解析式.21.函数y=lg(3﹣4x+x2)的定义域为M,函数f(x)=4x﹣2x+1(x∈M).(1)求函数f(x)的值域;(2)当x∈M时,关于x方程4x﹣2x+1=b(b∈R)有两不等实数根,求b的取值范围.22.已知函数f(x)是定义在[﹣1,1]上的奇函数,且f(1)=1,若x,y∈[﹣1,1],x+y≠0有(x+y)•[f(x)+f(y)]>0.(1)判断f(x)的单调性,并加以证明;(2)解不等式;(3)若f(x)≤m2﹣2am+1对所有x∈[﹣1,1],a∈[﹣1,1]恒成立.求实数m的取值范围.2016-2017学年广西南宁市宾阳中学高一(上)期中数学试卷参考答案与试题解析一、选择题:(本大题共12小题,每小题5分,共60分.每小题四个选项中有且只有一个正确.)1.下列各组中的两个集合M和N,表示同一集合的是()A.M={3,6},N={(3,6)}B.M={π},N={3.1415926}C.M={x|1<x<3,x∈R},N={2}D.【考点】集合的相等.【分析】利用集合相等的定义即可判断出结论.【解答】解:A.(3,6)表示一个点,因此M≠N.B.∵π是一个无理数,∴M≠N.C.M=(1,3),N={2},因此M≠N.D.由|﹣|=,可得M=N.故选:D.2.设全集U={﹣2,﹣1,0,1,2},集合M={y|y=2x},N={x|x2﹣x﹣2=0},则(∁U M)∩N═()A.{﹣1}B.{2}C.{﹣1,2}D.{﹣1,﹣2}【考点】交、并、补集的混合运算.【分析】化简集合M、N,根据补集与交集的定义写出运算结果即可.【解答】解:全集U={﹣2,﹣1,0,1,2},集合M={y|y=2x}={y|y>0},N={x|x2﹣x﹣2=0}={x|x=﹣1或x=2},则∁U M={x|x≤0},所以(∁U M)∩N═{﹣1}.故选:A.3.函数的定义域是()A.[﹣1,2)B.(1,2) C.[﹣1,1)∪(1,2)D.(2,+∞)【考点】函数的定义域及其求法.【分析】由根式内部的代数式大于等于0,对数式的真数大于0,分式的分母不为0联立不等式组求解.【解答】解:由,解得﹣1≤x<1或1<x<2.∴函数的定义域是[﹣1,1)∪(1,2).故选:C.4.()A.(﹣∞,2]B.(0,+∞)C.[2,+∞)D.[0,2]【考点】函数的值域.【分析】根据函数≥0,而且﹣x2﹣2x+3=﹣(x+1)2+4≤4,从而求得函数的值域.【解答】解:∵函数≥0,而且﹣x2﹣2x+3=﹣(x2+2x﹣3)=﹣(x+1)2+4≤4,∴≤2,∴0≤f(x)≤2,故选D.5.用二分法求函数f(x)=x3+x2﹣2x﹣2的一个零点,依次计算得到如表函数值:f(1)=﹣2f(1.5)=0.625f(1.25)=﹣0.984f(1.375)=﹣0.260f(1.438)=0.165f(1.4065)=﹣0.052那么方程x3+x2﹣2x﹣2=0的一个近似根在下列哪两数之间()A.1.25~1.375 B.1.375~1.4065 C.1.4065~1.438 D.1.438~1.5【考点】二分法求方程的近似解.【分析】由条件利用函数零点的判定定理求得函数f(x)的零点所在的区间,即可得到方程x3+x2﹣2x﹣2=0的一个零点所在的区间.【解答】解:由题意可得函数f(x)=x3+x2﹣2x﹣2为连续函数,且f(1.438)>0,f(1.4065)<0,根据函数零点的判定定理可得函数的零点所在的区间为(1.4065,1.438),即方程x3+x2﹣2x﹣2=0的一个零点所在的区间为(1.4065,1.438),故选:C.6.已知函数,则f(f(5))等于()A.B.5 C.﹣5 D.【考点】函数的值.【分析】先求出f(5)=,从而f(f(5))=f(),由此能求出结果.【解答】解:∵函数,∴f(5)=,f(f(5))=f()==5.故选:B.7.函数f(x)=ln(x+1)﹣的零点所在的大致区间是()A.(0,1) B.(1,2) C.(2,3) D.(3,4)【考点】函数的零点与方程根的关系.【分析】函数f(x)=ln(x+1)﹣的零点所在区间需满足的条件是函数在区间端点的函数值符号相反.【解答】解:∵f(1)=ln(1+1)﹣2=ln2﹣2<0,而f(2)=ln3﹣1>lne﹣1=0,∴函数f(x)=ln(x+1)﹣的零点所在区间是(1,2),故选B.8.设a=log36,b=log612,c=log816,则()A.c>b>a B.b>c>a C.a>c>b D.a>b>c【考点】对数值大小的比较.【分析】利用log a(xy)=log a x+log a y(x、y>0),化简a,b,c然后比较log32,log62,log82大小即可【解答】解:a=log36=1+log32,b=log612=1+log62,c=log816=1+log82,∵y=log2x是增函数,∴log28>log26>log23>log22=1,∴log32>log62>log82,∴a>b>c.故选:D.9.定义在R上的偶函数f(x)满足:对任意的x1,x2∈(﹣∞,0](x1≠x2),都有(x2﹣x1)•[f(x2)﹣f(x1)]>0,则()A.f(﹣2)<f(1)<f(3)B.f(1)<f(﹣2)<f(3)C.f(3)<f(﹣2)<f(1)D.f(3)<f(1)<f(﹣2)【考点】函数单调性的性质;函数单调性的判断与证明.【分析】先根据对任意的x1,x2∈(﹣∞,0](x1≠x2),都有(x2﹣x1)•[f(x2)﹣f(x1)]>0,可得函数f(x)在(﹣∞,0](x1≠x2)单调递增.进而可推断f(x)在[0,+∞)上单调递减,进而可判断出f(3),f(﹣2)和f(1)的大小.【解答】解:∵对任意的x1,x2∈(﹣∞,0](x1≠x2),都有(x2﹣x1)•[f(x2)﹣f(x1)]>0,故f(x)在x1,x2∈(﹣∞,0](x1≠x2)单调递增.又∵f(x)是偶函数,∴f(x)在[0,+∞)上单调递减,且满足n∈N*时,f(﹣2)=f(2),由3>2>1>0,得f(3)<f(﹣2)<f(1),故选:C.10.设函数f(x)满足对任意的m,n∈Z+都有f(m+n)=f(m)•f(n)且f(1)=2,则()A.2011 B.2010 C.4020 D.4022【考点】抽象函数及其应用.【分析】由已知可得=f(1)=2,代入要求的式子化简可得.【解答】解:∵函数f(x)满足对任意的m,n∈Z都有f(m+n)=f(m)•f(n)+且f(1)=2,∴f(m+1)=f(m)•f(1),变形可得=f(1)=2,∴=2010f(1)=4020故选:C11.已知函数f(x)=(x﹣a)(x﹣b)(其中a>b)的图象如图所示,则函数g (x)=a x+b的图象是()A.B.C.D.【考点】函数的图象.【分析】先由函数f(x)的图象判断a,b的范围,再根据指数函数的图象和性质即可得到答案.【解答】解:由函数的图象可知,﹣1<b<0,a>1,则g(x)=a x+b为增函数,当x=0时,y=1+b>0,且过定点(0,1+b),故选:C12.设函数y=f(x)在R上有定义,对于任一给定的正数p,定义函数f p(x)=,则称函数f p(x)为f(x)的“p界函数”若给定函数f(x)=x2﹣2x﹣1,p=2,则下列结论不成立的是()A.f p[f(0)]=f[f p(0)]B.f p[f(1)]=f[f p(1)]C.f p[f p(2)]=f[f(2)] D.f p[f(3)]=f[f(3)]【考点】分段函数的应用.【分析】由于函数f(x)=x2﹣2x﹣1,p=2,求出f2(x)=,再对选项一一加以判断,即可得到答案.【解答】解:∵函数f(x)=x2﹣2x﹣1,p=2,∴f2(x)=,∴A.f p[f(0)]=f2(﹣1)=2,f[f p(0)]=f(﹣1)=1+2﹣1=2,故A成立;B.f p[f(1)]=f2(﹣2)=2,f[f p(1)]=f(﹣2)=4+4﹣1=7,故B不成立;C.f[f(2)]=f(﹣1)=2,f p[f p(2)]=f2(﹣1)=2,故C成立;D.f[f(3)]=f(2)=﹣1,f p[f p(3)]=f2(2)=﹣1,故D成立.故选:B.二、填空题:(本大题共4小题,每小题5分,共20分,把答案填在答题卡题中横线上)13.已知幂函数f(x)的图象过点(2,),则=.【考点】幂函数的概念、解析式、定义域、值域.【分析】利用待定系数法求出函数的解析式,再计算的值.【解答】解:设幂函数f(x)=xα,α∈R;其函数图象过点(2,),∴2α=,解得α=;∴f(x)==,∴==.故答案为:.14.函数的递增区间是(﹣∞,2).【考点】对数函数的图象与性质.【分析】函数的定义域是x<2或x>3,由是减函数,能求出函数的递增区间.【解答】解:∵函数,∴x2﹣5x+6>0,解得x<2或x>3,t=x2﹣5x+6的减区间是(﹣∞,],增区间是[,+∞),∴y=log x是减函数,∴函数的递增区间是(﹣∞,2).故答案为:(﹣∞,2).15.已知函数f(x)=log0.5(x2﹣ax+4a)在[2,+∞)上单调递减,则a的取值范围是(﹣2,4] .【考点】对数函数的图象与性质.【分析】令g(x)=x2﹣ax+4a,则函数g(x)在区间[2,+∞)内单调递增,且恒大于0,可得不等式,从而可求a的取值范围【解答】解:令g(x)=x2﹣ax+3a,∵f(x)=log0.5(x2﹣ax+3a)在[2,+∞)单调递减∴函数g(x)在区间[2,+∞)内单调递增,且恒大于0.a≤2且g(2)>0,∴a≤4且4+2a>0,∴﹣2<a≤4.故答案为:(﹣2,4]16.若函数y=f(x)为偶函数,且在(0,+∞)上是减函数,有f(5)=0,的解集为(﹣5,0)∪(5,+∞).【考点】奇偶性与单调性的综合.【分析】由题意和偶函数的性质判断出:f(x)在(﹣∞,0)上的单调性、图象所过的特殊点,画出f(x)的示意图,将不等式等价转化后,根据图象求出不等式的解集.【解答】解:∵f(x)是偶函数,在(0,+∞)上是减函数,∴f(x)在(﹣∞,0)上是增函数,由f(5)=0得,f(﹣5)=0,作出f(x)的示意图,如图所示:∵等价于,即或,∴由图象得,x>5或﹣5<x<0,∴不等式的解集为:(﹣5,0)∪(5,+∞),故答案为:(﹣5,0)∪(5,+∞).三、解答题:(本大题共6小题,共70分.解答应写文字说明,证明过程或演算步骤.)17.集合P={x|a+1≤x≤2a+1},Q={x|﹣2≤x≤5}(1)若a=3,求集合(∁R P)∩Q;(2)若P⊆Q,求实数a的取值范围.【考点】交、并、补集的混合运算.【分析】(1)将a的值代入集合P中的不等式,确定出P,找出P的补集,求出P补集与Q的交集即可;(2)根据P为Q的子集列出关于a的不等式组,求出不等式组的解集即可得到a的范围.【解答】解:将a=3代入得:P={x|4≤x≤7},可得∁R P={x|x<4或x>7},∵Q={x|﹣2≤x≤5},∴(∁R P)∩Q={x|﹣2≤x<4};(2)由P⊆Q,分两种情况考虑:(ⅰ)当P≠∅时,根据题意得:,解得:0≤a≤2;(ⅱ)当P=∅时,可得2a+1<a+1,解得:a<0,综上:实数a的取值范围为(﹣∞,2].18.已知函数(1)判断函数在区间[1,+∞)上的单调性,并用定义证明你的结论(2)求该函数在区间[2,4]上的最大值和最小值.【考点】函数的最值及其几何意义;函数单调性的判断与证明.【分析】(1)利用函数单调性的定义来证明函数的单调性;(2)根据函数的单调性来求函数在给定区间上的最值问题.【解答】解:(1)f(x)在(﹣1,+∞)上为增函数,证明如下:任取﹣1<x1<x2,则f(x1)﹣f(x2)=﹣=;∵﹣1<x1<x2⇒x1+1>0,x2+1>0,x1﹣x2<0;∴f(x1)﹣f(x2)<0⇒f(x1)<f(x2);所以,f(x)在(﹣1,+∞)上为增函数.(2):由(1)知f(x)[2,4]上单调递增,∴f(x)的最小值为f(2)==,最大值f(4)==.19.已知f(x)是定义在R上的偶函数,且.(1)求f(0),f(2);(2)求函数f(x)的解析式.【考点】对数函数的图象与性质.【分析】(1)直接求解f(0),f(﹣2).(2)根据函数奇偶性的性质即可求函数f(x)的解析式;【解答】解:(1)f(0)=0,f(﹣2)=﹣1(2)当x>0时,则﹣x<0,f(﹣x)=log(x+1)=f(x)f(x)=20.已知二次函数f(x)图象过点(0,3),它的图象的对称轴为x=2,且f(x)的两个零点的平方和为10,求f(x)的解析式.【考点】函数解析式的求解及常用方法;函数的零点与方程根的关系.【分析】由已知中函数f(x)为二次函数,我们可以采用待定系数法求函数的解析式,根据函数f(x)图象过点(0,3),图象的对称轴为x=2,两个零点的平方和为10,结合韦达定理(一元二次方程根与系数的关系),我们可以构造一个关于系数a,b,c的方程组,解方程组求出a,b,c的值后,即可得到f(x)的解析式.【解答】解:设f(x)=ax2+bx+c(a≠0)因为f(x)图象过点(0,3),所以c=3又f(x)对称轴为x=2,∴=2即b=﹣4a所以f(x)=ax2﹣4ax+3(a≠0)设方程ax2﹣4ax+3=0(a≠0)的两个实根为x1,x2,则∴,所以得a=1,b=﹣4所以f(x)=x2﹣4x+321.函数y=lg(3﹣4x+x2)的定义域为M,函数f(x)=4x﹣2x+1(x∈M).(1)求函数f(x)的值域;(2)当x∈M时,关于x方程4x﹣2x+1=b(b∈R)有两不等实数根,求b的取值范围.【考点】对数函数图象与性质的综合应用.【分析】(1)由.3﹣4x+x2>0,求得x的范围可得M={x>3或x<1};令2x=t,则t>8 或0<t<2,故f(x)=g(t)=(t﹣1)2﹣1≥﹣1,可得函数f(x)的值域.(2)由题意可得函数y=t2﹣2t 的图象和直线y=b有2个交点,数形结合可得b 的范围.【解答】解:(1)∵由.3﹣4x+x2>0,解得x>3,或x<1,∴M={x>3或x<1}.∵f(x)=4x﹣2x+1,令2x=t,则t>8 或0<t<2.则f(x)=g(t)=t2﹣2t=(t﹣1)2﹣1,当t>8时,g(t)=(t﹣1)2﹣1>48;当0<t<2时,g(t)=(t﹣1)2﹣1∈[﹣1,0).所以值域为[﹣1,0)∪(48,+∞).(2).∵4x﹣2x+1=b(b∈R)有两不等实数根,∴函数y=t2﹣2t 的图象和直线y=b有2个交点,数形结合可得,﹣1<b<0,即b的范围(﹣1,0).22.已知函数f(x)是定义在[﹣1,1]上的奇函数,且f(1)=1,若x,y∈[﹣1,1],x+y≠0有(x+y)•[f(x)+f(y)]>0.(1)判断f(x)的单调性,并加以证明;(2)解不等式;(3)若f(x)≤m2﹣2am+1对所有x∈[﹣1,1],a∈[﹣1,1]恒成立.求实数m的取值范围.【考点】函数恒成立问题;奇偶性与单调性的综合.【分析】(1)设x1,x2∈[﹣1,1],且x1<x2,则x1﹣x2<0,利用x,y∈[﹣1,1],x+y≠0有(x+y)•[f(x)+f(y)]>0,可得f(x1)+f(﹣x2)<0,根据函数f(x)是定义在[﹣1,1]上的奇函数,即可得函数f(x)在[﹣1,1]上单调增;(2)由(1)知,,解之即可;(3)先确定函数f(x)在[﹣1,1]上的最大值为f(1)=1,将f(x)≤m2﹣2am+1对所有x∈[﹣1,1],a∈[﹣1,1]恒成立转化为:0≤m2﹣2am对所有a∈[﹣1,1]恒成立,从而可求实数m的取值范围.【解答】解:(1)函数f(x)在[﹣1,1]上单调增,证明如下由题意,设x1,x2∈[﹣1,1],且x1<x2则x1﹣x2<0∵x,y∈[﹣1,1],x+y≠0有(x+y)•[f(x)+f(y)]>0.令x=x1,y=﹣x2,∴f(x1)+f(﹣x2)<0∵函数f(x)是定义在[﹣1,1]上的奇函数∴f(x1)﹣f(x2)<0∴函数f(x)在[﹣1,1]上单调增;(2)由(1)知,,解得:(3)由于函数f(x)在[﹣1,1]上单调增,∴函数f(x)在[﹣1,1]上的最大值为f(1)=1∴f(x)≤m2﹣2am+1对所有x∈[﹣1,1],a∈[﹣1,1]恒成立可转化为:0≤m2﹣2am对所有a∈[﹣1,1]恒成立∴,解得m≥2或m≤﹣2或m=02017年2月14日。
广西南宁市第八中学2016_2017学年高一化学上学期期中试题

广西南宁市第八中学2016-2017学年高一化学上学期期中试题可能用到的相对原子质量:H 1 C 12 N 14 O 16 Na 23 Mg 24 Al 27 Cl 35.5 Cu 64第Ⅰ卷选择题部分(共48分)单项选择题(每小题只有一个答案,每题3分,共48分)1.一般检验SO42-的试剂是 ( )A.BaCl2、稀硝酸B.AgNO3、稀硝酸C.稀盐酸、BaCl2D.AgNO3、稀盐酸2.下列有关实验操作错误的是 ( )A.用药匙取用粉末状或小颗粒状固体B. 给盛有2/3体积液体的试管加热C. 用胶头滴管滴加少量液体D.倾倒液体时试剂瓶标签面向手心3.下列各组混合物可用分液漏斗分离的一组是 ( )A. 汽油和水B.碘和四氯化碳C.淀粉溶液和泥沙D.水和酒精4.下列实验操作中错误的是 ( )A. 过滤时,玻璃棒的末端应轻轻靠在三层滤纸上B. 蒸馏时,应使温度计水银球靠近蒸馏烧瓶的支管口处C. 分液时,分液漏斗中下层液体从下口放出,上层液体从上口倒出D. 称氢氧化钠时,不能直接称量,要放在纸片上称量5. 设N A表示阿伏加德罗常数,下列说法中正确的是 ( )A. 1 mol H2O中所含的粒子数目一定是N AB. 1 molNH4+ 所含的质子数是10N AC. 51 g NH3所含原子数为3N AD. 氧气的相对分子质量与2N A个氧原子质量(以g为单位)在数值上相等6. 下列条件下,两瓶气体所含的原子数一定相等的是()①同质量、不同密度的Cl2和CO ②同温度、同体积的H2 和 N2③同体积、同密度的 C2H4和C3H6 两种气体④同压强、同体积的N2O 和 CO2 两种气体A. ①③B. ③C. ③④D. ②④7. 0.5 L AlCl3溶液中含Cl-个数为9.03×1023个,则AlCl3溶液的物质的量浓度 ( )A. 0.1 mol·L-1B. 1 mol·L-1C. 3 mol·L-1D. 1.5 mol·L-18. 将下列各组物质按单质、氧化物、酸、碱分类顺序排列,其中正确的是 ( )A. 氧气、干冰、硫酸、烧碱B. 碘酒、冰、盐酸、烧碱C. 氢气、二氧化硫、硝酸、纯碱D. 铜、硫酸钠、醋酸、石灰水9. 下列电离方程式中,正确的是()A. H2SO4 = H2+ + SO42-B. Ba(OH)2 = Ba2+ + OH –C. NaNO3 = Na + + NO3-D. CuSO4 = Cu+2 + SO4-210. 今有一种固体化合物X,X本身不导电,但熔融状态和溶于水时能够电离,下列关于X的说法中,不正确的是 ( )A. X一定为电解质B. X可能为NaClC. X不能是酸类D. X可以是任何化合物11. 下列叙述正确的是 ( )A. NaCl是电解质,故NaCl晶体能导电B. 浓溶液的导电能力一定强C. NH4NO3电离时产生了NH4+、NO3-,无金属离子,所以NH4NO3不是盐D.熔融状态下 NaHSO4的电离方程式为:NaHSO4 = Na+ + HSO4 -12. 要使溶液中存在K+、Na+、H+、NO3-、SO42- 、Cl-六种离子,则蒸馏水中至少溶解几种物质 ( )A. 两种B. 三种C. 四种D. 五种13. 下列各组微粒,在溶液中能大量共存的是()A. Ca2+、Cl-、CO32-、K+B. Cu2+、Cl-、SO42-、OH -C. K +、Cl-、NO3 -、H+D. H +、Cl-、CO32-、Na+14. 下列离子方程式正确的是 ( )A. 稀硝酸与氢氧化钾溶液反应:H+ + OH- = H2OB. 铝与稀盐酸反应:Al + 2H+ = Al3+ + H2↑C. 三氯化铁溶液与氢氧化钠溶液反应:FeCl3 + 3O H- = Fe(OH)3↓+ 3Cl-D. 足量二氧化碳与澄清石灰水反应:CO2 + 2OH- = CO32- + H2O15. 实验室中需要配制一种仅含四种离子(不包括水电离出的离子)的无色混合溶液,且在混合溶液中四种离子的物质的量浓度均为1 mol·L-1。
广西南宁市数学高一上期中经典测试题(培优练)

一、选择题1.(0分)[ID :11824]已知集合{}{}2|320,,|05,A x x x x R B x x x N =-+=∈=<<∈,则满足条件A C B ⊆⊆的集合C 的个数为( )A .1B .2C .3D .42.(0分)[ID :11811]若35225a b ==,则11a b+=( ) A .12B .14C .1D .23.(0分)[ID :11806]已知函数()25,1,,1,x ax x f x a x x⎧---≤⎪=⎨>⎪⎩是R 上的增函数,则a 的取值范围是( ) A .30a -≤< B .0a < C .2a ≤-D .32a --≤≤4.(0分)[ID :11784]1()xf x e x=-的零点所在的区间是( ) A .1(0,)2B .1(,1)2C .3(1,)2D .3(,2)25.(0分)[ID :11782]设()f x 是定义在R 上的偶函数,且当0x ≥时,()21,0122,1xx x f x x ⎧-+≤<=⎨-≥⎩,若对任意的[],1x m m ∈+,不等式()()1f x f x m -≤+恒成立,则实数m 的最大值是( ) A .1-B .13-C .12-D .136.(0分)[ID :11759]函数()sin lg f x x x =-的零点个数为( ) A .0B .1C .2D .37.(0分)[ID :11753]已知函数224()(log )log (4)1f x x x =++,则函数()f x 的最小值是A .2B .3116C .158D .18.(0分)[ID :11791]已知()201911,02log ,0x x f x x x ⎧+≤⎪=⎨⎪>⎩,若存在三个不同实数a ,b ,c 使得()()()f a f b f c ==,则abc 的取值范围是( ) A .(0,1)B .[-2,0)C .(]2,0-D .(0,1)9.(0分)[ID :11786]若01a b <<<,则b a , a b , log b a , 1log ab 的大小关系为( )A .1log log bab aa b a b >>>B .1log log a bb ab a b a >>>C .1log log b ab aa ab b >>>D .1log log a bb aa b a b >>>10.(0分)[ID :11785]定义在R 上的奇函数()f x 满足()()2f x f x +=-,且当[]0,1x ∈时,()2cos x f x x =-,则下列结论正确的是( )A .()20202019201832f f f ⎛⎫⎛⎫<<⎪ ⎪⎝⎭⎝⎭B .()20202019201832f f f ⎛⎫⎛⎫<< ⎪ ⎪⎝⎭⎝⎭C .()20192020201823f f f ⎛⎫⎛⎫<<⎪ ⎪⎝⎭⎝⎭D .()20192020201823f f f ⎛⎫⎛⎫<<⎪ ⎪⎝⎭⎝⎭11.(0分)[ID :11771]函数2()ln(28)f x x x =--的单调递增区间是 A .(,2)-∞- B .(,1)-∞ C .(1,)+∞D .(4,)+∞12.(0分)[ID :11770]已知定义在R 上的函数()f x 是奇函数且满足,3()(2)32f x f x f ⎛⎫-=-=- ⎪⎝⎭,,数列{}n a 满足11a =-,且2n n S a n =+,(其中n S 为{}n a 的前n 项和).则()()56f a f a +=()A .3B .2-C .3-D .2 13.(0分)[ID :11746]若a >b >0,0<c <1,则A .log a c <log b cB .log c a <log c bC .a c <b cD .c a >c b14.(0分)[ID :11733]设0.60.3a =,0.30.6b =,0.30.3c =,则a ,b ,c 的大小关系为( ) A .b a c <<B .a c b <<C .b c a <<D .c b a << 15.(0分)[ID :11751]三个数20.420.4,log 0.4,2a b c ===之间的大小关系是( )A .a c b <<B .b a c <<C .a b c <<D .b c a <<二、填空题16.(0分)[ID :11924]给出下列四个命题:(1)函数()f x x x bx c =++为奇函数的充要条件是0c ;(2)函数()20xy x -=>的反函数是()2log 01y x x =-<<;(3)若函数()()2lg f x x ax a =+-的值域是R ,则4a ≤-或0a ≥;(4)若函数()1y f x =-是偶函数,则函数()y f x =的图像关于直线0x =对称. 其中所有正确命题的序号是______.17.(0分)[ID :11912]已知函数()(0,1)x f x a b a a =+>≠的定义域和值域都是[]1,0-,则a b += .18.(0分)[ID :11902]设函数()f x 是定义在R 上的偶函数,记2()()g x f x x =-,且函数()g x 在区间[0,)+∞上是增函数,则不等式2(2)(2)4f x f x x +->+的解集为_____ 19.(0分)[ID :11891]某在校大学生提前创业,想开一家服装专卖店,经过预算,店面装修费为10000元,每天需要房租水电等费用100元,受营销方法、经营信誉度等因素的影响,专卖店销售总收入P 与店面经营天数x 的关系是P(x)=21300,0300245000,300x x x x ⎧-≤<⎪⎨⎪≥⎩则总利润最大时店面经营天数是___.20.(0分)[ID :11874]已知f (x )是定义在R 上的偶函数,且f (x +4)=f (x -2).若当x ∈[-3,0]时,f (x )=6-x ,则f (919)=________. 21.(0分)[ID :11868]已知函数()log ,03,40a x x f x x x >⎧=⎨+-≤<⎩,其中0a >且1a ≠,若函数()f x 的图象上有且只有一对点关于y 轴对称,则a 的取值范围是__________.22.(0分)[ID :11859]已知函数()f x 是定义在R 上的偶函数,且当0x ≥时,2()2f x x x =-. 若关于x 的方程()0f x m -=有四个不同的实数解,则实数m 的取值范围是_____.23.(0分)[ID :11858]103383log ()()1255---=__________.24.(0分)[ID :11850]已知函数f(x)=log a (2x −a)在区间[12,23],上恒有f (x )>0则实数a 的取值范围是_____.25.(0分)[ID :11844]有15人进家电超市,其中有9人买了电视,有7人买了电脑,两种均买了的有3人,则这两 种都没买的有 人.三、解答题26.(0分)[ID :11970]设集合222{|40},{|2(1)10}A x x x B x x a x a =+==+++-=,若A ∩B=B ,求a 的取值范围.27.(0分)[ID :11959]已知定义域为R 的函数()122x x bf x a++=+- 是奇函数.(Ⅰ)求a ,b 的值;(Ⅱ)若对任意的t ∈R ,不等式f (t 2-2t )+f (2t 2-2k )<0恒成立,求k 的取值范围. 28.(0分)[ID :11951]如果f (x )是定义在R 上的函数,且对任意的x ∈R ,均有f (-x )≠-f (x ),则称该函数是“X —函数”. (1)分别判断下列函数:①y =211x +;②y =x +1;③y =x 2+2x -3是否为“X —函数”?(直接写出结论)(2)若函数f (x )=x -x 2+a 是“X —函数”,求实数a 的取值范围;(3)设“X —函数”f (x )=21,,x x Ax x B ⎧+∈⎨∈⎩在R 上单调递增,求所有可能的集合A 与B .29.(0分)[ID :11938]设ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c ,tan a b A =,且B 为钝角. (1)证明:2B A π-=; (2)求sin sin A C +的取值范围.30.(0分)[ID :11967]已知函数()f x 是R 上的奇函数,且当0x >时,()f x =1()2x.①求函数()f x 的解析式;②画出函数的图象,根据图象写出函数()f x 的单调区间.【参考答案】2016-2017年度第*次考试试卷 参考答案**科目模拟测试一、选择题 1.D 2.A 3.D 4.B 5.B 6.D 7.B 8.C 9.D 10.C 11.D12.A13.B14.B15.B二、填空题16.(1)(2)(3)【解析】【分析】根据奇函数的定义得到(1)正确根据反函数的求法以及定义域值域得到(2)正确由函数的值域是得出其真数可以取到所有的正数由二次函数判别式大于等于0求解可判断出(3)正确17.【解析】若则在上为增函数所以此方程组无解;若则在上为减函数所以解得所以考点:指数函数的性质18.【解析】【分析】根据题意分析可得为偶函数进而分析可得原不等式转化为结合函数的奇偶性与单调性分析可得解可得的取值范围【详解】根据题意且是定义在上的偶函数则则函数为偶函数又由为增函数且在区间上是增函数则19.200【解析】【分析】根据题意列出总利润L(x)的分段函数然后在各个部分算出最大值比较大小就能确定函数的最大值进而可求出总利润最大时对应的店面经营天数【详解】设总利润为L(x)则L(x)=则L(x)20.6【解析】【分析】先求函数周期再根据周期以及偶函数性质化简再代入求值【详解】由f(x+4)=f(x-2)可知是周期函数且所以【点睛】本题考查函数周期及其应用考查基本求解能力21.【解析】将在轴左侧的图象关于轴对称到右边与在轴右侧的图象有且只有一个交点当时一定满足当时必须解得综上的取值范围是点睛:已知函数有零点求参数取值范围常用的方法和思路(1)直接法:直接根据题设条件构建关22.【解析】【分析】若方程有四个不同的实数解则函数与直线有4个交点作出函数的图象由数形结合法分析即可得答案【详解】因为函数是定义在R上的偶函数且当时所以函数图象关于轴对称作出函数的图象:若方程有四个不同23.【解析】24.(131)【解析】【分析】根据对数函数的图象和性质可得函数f(x)=loga(2x﹣a)在区间1223上恒有f(x)>0即0<a<10<2x-a<1或a>12x-a>1分别解不等式组可得答案【详解】25.【解析】【分析】【详解】试题分析:两种都买的有人所以两种家电至少买一种有人所以两种都没买的有人或根据条件画出韦恩图:(人)考点:元素与集合的关系三、解答题 26. 27. 28. 29. 30.2016-2017年度第*次考试试卷 参考解析【参考解析】**科目模拟测试一、选择题 1.D 解析:D 【解析】 【分析】 【详解】求解一元二次方程,得{}()(){}2|320,|120,A x x x x x x x x =-+=∈=--=∈R R {}1,2=,易知{}{}|05,1,2,3,4B x x x =<<∈=N .因为A C B ⊆⊆,所以根据子集的定义, 集合C 必须含有元素1,2,且可能含有元素3,4, 原题即求集合{}3,4的子集个数,即有224=个,故选D. 【点评】本题考查子集的概念,不等式,解一元二次方程.本题在求集合个数时,也可采用列举法.列出集合C 的所有可能情况,再数个数即可.来年要注意集合的交集运算,考查频度极高.2.A解析:A 【解析】 【分析】由指数式与对数式的转化,结合换底公式和对数的运算,即可求解. 【详解】由题意3225,5225a b==根据指数式与对数式的转化可得35log 225,log 225a b == 由换底公式可得lg 2252lg15lg 2252lg15,lg 3lg 3lg 5lg 5a b ==== 由对数运算化简可得11lg 3lg 52lg152lg15a b +=+ lg3lg52lg15+=lg1512lg152== 故选:A 【点睛】本题考查了指数式与对数式的转化,对数的运算及换底公式的应用,属于中档题.3.D解析:D 【解析】 【分析】根据分段函数的单调性特点,两段函数在各自的定义域内均单调递增,同时要考虑端点处的函数值. 【详解】要使函数在R 上为增函数,须有()f x 在(,1]-∞上递增,在(1,)+∞上递增,所以21,20,115,1a a a a ⎧-≥⎪⎪<⎨⎪⎪--⨯-≤⎩,解得32a --≤≤.故选D. 【点睛】本题考查利用分段函数的单调性求参数的取值范围,考查数形结合思想、函数与方程思想的灵活运用,求解时不漏掉端点处函数值的考虑.4.B解析:B函数f (x )=e x ﹣1x 是(0,+∞)上的增函数,再根据f (12)2<0,f (1)=e ﹣1>0,可得f (12)f (1)<0,∴函数f (x )=e x ﹣1x 的零点所在的区间是(12,1),故选B .点睛:判定函数的零点所在区间,只需计算区间端点处的函数值,并判断是否异号,只要异号,则区间内至少有一个零点存在.5.B解析:B 【解析】 【分析】由题意,函数()f x 在[0,)+∞上单调递减,又由函数()f x 是定义上的偶函数,得到函数()f x 在(,0)-∞单调递增,把不等式(1)()f x f x m -≤+转化为1x x m -≤+,即可求解. 【详解】易知函数()f x 在[)0,+∞上单调递减, 又函数()f x 是定义在R 上的偶函数, 所以函数()f x 在(),0-∞上单调递增, 则由()()1f x f x m -≤+,得1x x m -≥+,即()()221x x m -≥+,即()()22210g x m x m =++-≤在[],1x m m ∈+上恒成立,则()()()()()()3110121310g m m m g m m m ⎧=-+≤⎪⎨+=++≤⎪⎩,解得113m -≤≤-, 即m 的最大值为13-. 【点睛】本题主要考查了函数的基本性质的应用,其中解答中利用函数的基本性质,把不等式转化为1x x m -≤+ 求解是解答的关键,着重考查了分析问题和解答问题的能力,以及推理与运算能力,属于中档试题.6.D解析:D 【解析】画出函数图像,根据函数图像得到答案. 【详解】如图所示:画出函数sin y x =和lg y x =的图像,共有3个交点. 当10x >时,lg 1sin x x >≥,故不存在交点. 故选:D .【点睛】本题考查了函数的零点问题,画出函数图像是解题的关键.7.B解析:B 【解析】 【分析】利用对数的运算法则将函数()()()224log log 41f x x x =++化为()2221log 1log 12x x +++,利用配方法可得结果. 【详解】化简()()()224log log 41f x x x =++()2221log 1log 12x x =+++22211131log log 224161616x x ⎛⎫=++-≥-= ⎪⎝⎭,即()f x 的最小值为3116,故选B.【点睛】本题主要考查对数的运算法则以及二次函数配方法求最值,属于中档题. 求函数最值常见方法有,①配方法:若函数为一元二次函数,常采用配方法求函数求值域,其关键在于正确化成完全平方式,并且一定要先确定其定义域;②换元法;③不等式法;④单调性法;⑤图象法.8.C解析:C【分析】画出函数图像,根据图像得到20a -<≤,1bc =,得到答案. 【详解】()201911,02log ,0x x f x x x ⎧+≤⎪=⎨⎪>⎩,画出函数图像,如图所示:根据图像知:20a -<≤,20192019log log b c -=,故1bc =,故20abc -<≤. 故选:C .【点睛】本题考查了分段函数的零点问题,画出函数图像是解题的关键.9.D解析:D 【解析】因为01a b <<<,所以10a a b b a a >>>>, 因为log log 1b b a b >>,01a <<,所以11a>,1log 0a b <.综上1log log a bb aa b a b >>>;故选D. 10.C解析:C 【解析】 【分析】根据f (x )是奇函数,以及f (x+2)=f (-x )即可得出f (x+4)=f (x ),即得出f (x )的周期为4,从而可得出f (2018)=f (0),2019122f f ⎛⎫⎛⎫=⎪ ⎪⎝⎭⎝⎭,20207312f f ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭然后可根据f (x )在[0,1]上的解析式可判断f (x )在[0,1]上单调递增,从而可得出结果.【详解】∵f(x )是奇函数;∴f(x+2)=f (-x )=-f (x );∴f(x+4)=-f (x+2)=f (x ); ∴f(x )的周期为4;∴f(2018)=f (2+4×504)=f (2)=f (0),2019122f f ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭,20207 312f f ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭∵x∈[0,1]时,f (x )=2x -cosx 单调递增;∴f(0)<12f ⎛⎫⎪⎝⎭ <712f ⎛⎫ ⎪⎝⎭ ∴()20192020201823f f f ⎛⎫⎛⎫<< ⎪ ⎪⎝⎭⎝⎭,故选C. 【点睛】本题考查奇函数,周期函数的定义,指数函数和余弦函数的单调性,以及增函数的定义,属于中档题.11.D解析:D 【解析】由228x x -->0得:x ∈(−∞,−2)∪(4,+∞), 令t =228x x --,则y =ln t ,∵x ∈(−∞,−2)时,t =228x x --为减函数; x ∈(4,+∞)时,t =228x x --为增函数; y =ln t 为增函数,故函数f (x )=ln(228x x --)的单调递增区间是(4,+∞), 故选D.点睛:形如()()y f g x =的函数为()y g x =,()y f x =的复合函数,() y g x =为内层函数,()y f x =为外层函数. 当内层函数()y g x =单增,外层函数()y f x =单增时,函数()()y f g x =也单增; 当内层函数()y g x =单增,外层函数()y f x =单减时,函数()()y f g x =也单减; 当内层函数()y g x =单减,外层函数()y f x =单增时,函数()()y f g x =也单减; 当内层函数()y g x =单减,外层函数()y f x =单减时,函数()()y f g x =也单增.简称为“同增异减”.12.A解析:A 【解析】 由奇函数满足()32f x f x ⎛⎫-=⎪⎝⎭可知该函数是周期为3T =的奇函数, 由递推关系可得:112,21n n n n S a n S a n +-=+=+-, 两式做差有:1221n n n a a a -=--,即()()1121n n a a --=-,即数列{}1n a -构成首项为112a -=-,公比为2q 的等比数列,故:()1122,21n n n n a a --=-⨯∴=-+,综上有:()()()()()552131223f a f f f f =-+=-==--=,()()()()66216300f a f f f =-+=-==,则:()()563f a f a +=. 本题选择A 选项.13.B解析:B 【解析】试题分析:对于选项A ,a b 1gc 1gclog c ,log c lg a lg b==,01c <<,10gc ∴<,而0a b >>,所以lg lg a b >,但不能确定lg lg a b 、的正负,所以它们的大小不能确定;对于选项B ,c lg lg log ,log lg lg c a b a b c c ==,lg lg a b >,两边同乘以一个负数1lg c改变不等号方向,所以选项B 正确;对于选项C ,利用cy x =在第一象限内是增函数即可得到c c a b >,所以C 错误;对于选项D ,利用xy c =在R 上为减函数易得a b c c <,所以D 错误.所以本题选B.【考点】指数函数与对数函数的性质【名师点睛】比较幂或对数值的大小,若幂的底数相同或对数的底数相同,通常利用指数函数或对数函数的单调性进行比较;若底数不同,可考虑利用中间量进行比较.14.B解析:B 【解析】 【分析】根据指数函数的单调性得出0.60.30.30.3<,而根据幂函数的单调性得出0.30.30.30.6<,从而得出a ,b ,c 的大小关系. 【详解】 解:0.3x y =在定义域上单调递减,且0.360.<,0.60.30.30.3∴<,又0.3y x∴=在定义域上单调递增,且0.360.<,0.30.30.30.6∴<, 0.60.30.30.30.30.6∴<<,a cb ∴<<故选:B . 【点睛】考查指数函数和幂函数的单调性,以及增函数和减函数的定义.15.B解析:B 【解析】20.4200.41,log 0.40,21<<,01,0,1,a b c b a c ∴<<∴<<,故选B.二、填空题16.(1)(2)(3)【解析】【分析】根据奇函数的定义得到(1)正确根据反函数的求法以及定义域值域得到(2)正确由函数的值域是得出其真数可以取到所有的正数由二次函数判别式大于等于0求解可判断出(3)正确 解析:(1)(2)(3) 【解析】 【分析】根据奇函数的定义得到(1)正确,根据反函数的求法以及定义域值域得到(2)正确, 由函数()()2lg f x x ax a =+-的值域是R ,得出其真数可以取到所有的正数,由二次函数判别式大于等于0求解,可判断出(3)正确,根据函数图像平移可判断(4)不正确. 【详解】 解:(1)当0c时,()=+f x x x bx ,()()()-=---=-+=-f x x x bx x x bx f x ,当函数为奇函数时()()f x f x -=-,即()++=----+=+-x x bx c x x bx c x x bx c ,解得0c ,所以0c 是函数()f x x x bx c =++为奇函数的充要条件,所以(1)正确;(2)由反函数的定义可知函数()20xy x -=>的反函数是()2log 01y x x =-<<,所以(2)正确;(3)因为函数()()2lg f x x ax a =+-的值域是R ,所以2y x ax a =+-能取遍(0,)+∞的所有实数,所以240a a =+≥△,解得0a ≥或4a ≤-,所以(3)正确; (4)函数()1y f x =-是偶函数,所以()1y f x =-图像关于y 轴对称,函数()y f x =的图像是由()1y f x =-向左平移一个单位得到的,所以函数()y f x =的图像关于直线1x =-对称,故(4)不正确. 故答案为:(1)(2)(3) 【点睛】本题主要考查对函数的理解,涉及到函数的奇偶性、值域、反函数等问题.17.【解析】若则在上为增函数所以此方程组无解;若则在上为减函数所以解得所以考点:指数函数的性质解析:32-【解析】若1a >,则()f x 在[]1,0-上为增函数,所以11{10a b b -+=-+=,此方程组无解;若01a <<,则()f x 在[]1,0-上为减函数,所以10{11a b b -+=+=-,解得1{22a b ==-,所以32a b +=-.考点:指数函数的性质.18.【解析】【分析】根据题意分析可得为偶函数进而分析可得原不等式转化为结合函数的奇偶性与单调性分析可得解可得的取值范围【详解】根据题意且是定义在上的偶函数则则函数为偶函数又由为增函数且在区间上是增函数则 解析:()(),40,-∞-+∞【解析】 【分析】根据题意,分析可得()g x 为偶函数,进而分析可得原不等式转化为()()22g x g +>,结合函数的奇偶性与单调性分析可得22x +>,解可得x 的取值范围. 【详解】根据题意()()2g x f x x =-,且()f x 是定义在R 上的偶函数,则()()()()()22g x f x x f x x g x -=---=-=,则函数()g x 为偶函数,()()()()()()()22224222422f x f x x f x x f g x g +->+⇒+--⇒+>>+,又由()g x 为增函数且在区间[0,)+∞上是增函数,则22x +>, 解可得:4x <-或0x >, 即x 的取值范围为()(),40,-∞-+∞,故答案为()(),40,-∞-+∞;【点睛】本题考查函数的奇偶性与单调性的综合应用,注意分析()g x 的奇偶性与单调性,属于中档题.19.200【解析】【分析】根据题意列出总利润L(x)的分段函数然后在各个部分算出最大值比较大小就能确定函数的最大值进而可求出总利润最大时对应的店面经营天数【详解】设总利润为L(x)则L(x)=则L(x)解析:200【解析】 【分析】根据题意,列出总利润L(x)的分段函数,然后在各个部分算出最大值,比较大小,就能确定函数的最大值,进而可求出总利润最大时对应的店面经营天数. 【详解】 设总利润为L(x),则L(x)=2120010000,0300210035000,300x x x x x ⎧-+-≤<⎪⎨⎪-+≥⎩则L(x)=21(200)10000,0300210035000,300x x x x ⎧--+≤<⎪⎨⎪-+≥⎩当0≤x<300时,L(x)max =10000, 当x ≥300时,L(x)max =5000,所以总利润最大时店面经营天数是200. 【点睛】本题主要考查分段函数的实际应用,准确的写出各个部分的函数关系式是解决本题的关键.20.6【解析】【分析】先求函数周期再根据周期以及偶函数性质化简再代入求值【详解】由f(x+4)=f(x-2)可知是周期函数且所以【点睛】本题考查函数周期及其应用考查基本求解能力解析:6 【解析】 【分析】先求函数周期,再根据周期以及偶函数性质化简()()9191f f =-,再代入求值. 【详解】由f (x +4)=f (x -2)可知,()f x 是周期函数,且6T =,所以()()()919615311f f f =⨯+=()16f =-=.【点睛】本题考查函数周期及其应用,考查基本求解能力.21.【解析】将在轴左侧的图象关于轴对称到右边与在轴右侧的图象有且只有一个交点当时一定满足当时必须解得综上的取值范围是点睛:已知函数有零点求参数取值范围常用的方法和思路(1)直接法:直接根据题设条件构建关解析:(0,1)1,4⋃() 【解析】将()f x 在y 轴左侧的图象关于y 轴对称到右边,与()f x 在y 轴右侧的图象有且只有一个交点.当01a <<时一定满足,当1a >时必须log 41a >,解得4a <.综上a 的取值范围是()0,11,4⋃().点睛:已知函数有零点求参数取值范围常用的方法和思路(1)直接法:直接根据题设条件构建关于参数的不等式,再通过解不等式确定参数范围; (2)分离参数法:先将参数分离,转化成求函数值域问题加以解决;(3)数形结合法:先对解析式变形,在同一平面直角坐标系中,画出函数的图象,然后数形结合求解.22.【解析】【分析】若方程有四个不同的实数解则函数与直线有4个交点作出函数的图象由数形结合法分析即可得答案【详解】因为函数是定义在R 上的偶函数且当时所以函数图象关于轴对称作出函数的图象:若方程有四个不同 解析:(1,0)-【解析】 【分析】若方程()0f x m -=有四个不同的实数解,则函数()y f x =与直线y m =有4个交点,作出函数()f x 的图象,由数形结合法分析即可得答案. 【详解】因为函数()f x 是定义在R 上的偶函数且当0x ≥时,2()2f x x x =-,所以函数()f x 图象关于y 轴对称, 作出函数()f x 的图象:若方程()0f x m -=有四个不同的实数解,则函数()y f x =与直线y m =有4个交点, 由图象可知:10m -<<时,即有4个交点. 故m 的取值范围是(1,0)-,故答案为:(1,0)- 【点睛】本题主要考查了偶函数的性质以及函数的图象,涉及方程的根与函数图象的关系,数形结合,属于中档题.23.【解析】 解析:11【解析】1334383log 27161255-⎛⎫⎛⎫+--+= ⎪ ⎪⎝⎭⎝⎭35181122+-+=24.(131)【解析】【分析】根据对数函数的图象和性质可得函数f (x )=loga (2x ﹣a )在区间1223上恒有f (x )>0即0<a<10<2x-a<1或a>12x-a>1分别解不等式组可得答案【详解】 解析:(13,1)【解析】 【分析】根据对数函数的图象和性质可得,函数f (x )=log a (2x ﹣a )在区间[12,23]上恒有f (x )>0,即{0<a <10<2x −a <1 ,或{a >12x −a >1,分别解不等式组,可得答案.【详解】 若函数f (x )=log a (2x ﹣a )在区间[12,23]上恒有f (x )>0,则{0<a <10<2x −a <1 ,或{a >12x −a >1当{0<a <10<2x −a <1时,解得13<a <1,当{a >12x −a >1时,不等式无解.综上实数a 的取值范围是(13,1) 故答案为(13,1). 【点睛】本题考查的知识点是复合函数的单调性,及不等式的解法,其中根据对数函数的图象和性质构造不等式组是解答的关键,属于中档题.25.【解析】【分析】【详解】试题分析:两种都买的有人所以两种家电至少买一种有人所以两种都没买的有人或根据条件画出韦恩图:(人)考点:元素与集合的关系 解析:【解析】 【分析】 【详解】试题分析:两种都买的有人,所以两种家电至少买一种有人.所以两种都没买的有人.或根据条件画出韦恩图:(人).考点:元素与集合的关系.三、解答题 26.a=1或a≤﹣1 【解析】试题分析:先由题设条件求出集合A ,再由A∩B=B ,导出集合B 的可能结果,然后结合根的判别式确定实数a 的取值范围. 试题解析:根据题意,集合A={x|x 2+4x=0}={0,﹣4},若A∩B=B,则B 是A 的子集, 且B={x|x 2+2(a+1)x+a 2﹣1=0},为方程x 2+2(a+1)x+a 2﹣1=0的解集, 分4种情况讨论:①B=∅,△=[2(a+1)]2﹣4(a 2﹣1)=8a+8<0,即a <﹣1时,方程无解,满足题意; ②B={0},即x 2+2(a+1)x+a 2﹣1=0有两个相等的实根0, 则有a+1=0且a 2﹣1=0,解可得a=﹣1,③B={﹣4},即x 2+2(a+1)x+a 2﹣1=0有两个相等的实根﹣4, 则有a+1=4且a 2﹣1=16,此时无解,④B={0、﹣4},即x 2+2(a+1)x+a 2﹣1=0有两个的实根0或﹣4, 则有a+1=2且a 2﹣1=0,解可得a=1, 综合可得:a=1或a≤﹣1.点睛:A ∩B=B 则B 是A={0,﹣4}的子集,而B={x|x 2+2(a+1)x+a 2﹣1=0}为方程x 2+2(a+1)x+a 2﹣1=0的解集,所以分四种情况进行讨论①B=∅,②B={0},③B={﹣4},④B={0、﹣4},其中①B=∅不要忘记.27.(Ⅰ)2,1a b ==(Ⅱ)16k <- 【解析】 【分析】(Ⅰ)根据()00f =解得1b =,根据()()11f f =--解得2a = (Ⅱ)判断函数为奇函数减函数,将不等式化简为223311()2236k t t t <-=--,求二次函数的最小值得到答案. 【详解】(Ⅰ)定义域为R 的函数()1-22x x bf x a++=+是奇函数则()100,12bf b a-+===+ ()-2114f a +=+,()12-111f a+-=+,根据()()11f f =--,解得2a = ,经检验,满足函数为奇函数(Ⅱ)12111()22221x x xf x +-+==-+++ 易知21x +为增函数,故11()221x f x =-++为减函数 22()(220)2f t t f t k --+<即2222222)()()2(f t t f t k f t k =-<+---即22222t t t k ->-+所以223311()2236k t t t <-=-- 恒成立,即2min3111()2366k t ⎡⎤<--=-⎢⎥⎣⎦ 当13t =时,有最小值16- 故k 的取值范围是16k <- 【点睛】本题考查了函数的单调性,奇偶性,恒成立问题,将恒成立问题通过参数分离转化为二次函数的最值问题是解题的关键.28.(1)①②是“X —函数”,③不是“X —函数”.(2)(0,+∞)(3)A =[0,+∞),B =(-∞,0) 【解析】 【分析】(1)直接利用信息判断结果;(2)利用信息的应用求出参数的取值范围; (3)利用函数的单调性的应用和应用的例证求出结果. 【详解】(1)①②是“X —函数”,③不是“X —函数”; (2)∵f (-x )=-x -x 2+a ,-f (x )=-x +x 2-a ,f (x )=x -x 2+a 是“X —函数”, ∴f (-x )=-f (x )无实数解, 即x 2+a =0无实数解, ∴a >0,∴a 的取值范围为(0,+∞);(3)对任意的x ≠0,若x ∈A 且-x ∈A ,则-x ≠x ,f (-x )=f (x ),与f (x )在R 上单调增矛盾,舍去; 若x ∈B 且-x ∈B ,f (-x )=-f (x ),与f (x )是“X —函数”矛盾,舍去; ∴对任意的x ≠0,x 与-x 恰有一个属于A ,另一个属于B , ∴(0,+∞)⊆A ,(-∞,0)⊆B ,假设0∈B ,则f (-0)=-f (0),与f (x )是“X —函数”矛盾,舍去; ∴0∈A ,经检验,A =[0,+∞),B =(-∞,0)符合题意. 【点睛】本题考查的知识要点:信息题型的应用,反证法的应用,主要考查学生的运算能力和转换能力及思维能力,属于中档题型.29.(1)见解析;(2)29(,]28. 【解析】试题分析:(Ⅰ)运用正弦定理将化简变形,再解三角方程即可获解;(Ⅱ)将角用表示,换元法求函数的值域即可.试题解析:(Ⅰ)由tan a b A =及正弦定理,得sin sin cos sin A a AA b B==,∴sin cos B A =, 即sin sin()2B A π=+,又B 为钝角,因此(,)22A πππ+∈, 故2B A π=+,即2B A π-=;(Ⅱ)由(1)知,()C A B π=-+(2)2022A A πππ-+=->,∴(0,)4A π∈,于是sin sin sin sin(2)2A C A A π+=+-2219sin cos 22sin sin 12(sin )48A A A A A =+=-++=--+,∵04A π<<,∴20sin 2A <<,因此221992(sin )2488A <--+≤,由此可知sin sin A C +的取值范围是29]28. 考点:正弦定理、三角变换,二次函数的有关知识和公式的应用.30.①1)22,(0)()0,(0)(,(0)x x x f x x x ⎧-<⎪⎪==⎨⎪⎪>⎩;②单调递减区间为(,0),(0,)-∞+∞,无单调递增区间. 【解析】【分析】【详解】试题分析:①考察了利用函数的奇偶性求分段函数的解析式,根据求什么设什么所以设,那么,那么,求得的解析式,又因为,即求得函数的解析式;②根据上一问解析式,画出分段函数的图像,观察函数的单调区间.试题解析:解: ①∵函数()f x 是定义在R 上的奇函数,∴(0)0f =.当0x <时,0x ->,1()()()22x x f x f x -=--=-=-.∴函数()f x 的解析式为1)22,(0)()0,(0)(,(0)x x x f x x x ⎧-<⎪⎪==⎨⎪⎪>⎩②函数图象如图所示:由图象可知,函数()f x 的单调递减区间为(,0),(0,)-∞+∞,无单调递增区间. 考点:1.分段函数的解析式;2.函数的图像.。
高一上学期期中考试数学试卷含答案(共3套,新课标版)

高一级第一学期期中调研考试数学考生注意:1.本试卷分选择题和非选择题两部分。
满分150分,考试时间120分钟。
2.考生作答时,请将答案答在答题卡上。
选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;非选择题请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答,超出答题....区域书写的答案无效.........,在试题卷....、草稿纸上作答无效........。
3.本卷命题范围:新人教版必修第一册第一章~第四章。
一、选择题:本题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.若集合{123}A =,,,{}223B x x x =->,则A B =A .{12},B .∅C .{23},D .{1}2.命题“R x ∃∈,||0x ”的否定是A .R x ∀∈,||0x ≥B .R x ∃∈,||0x <C .R x ∀∈,||0x <D .R x ∃∉,||0x <3.若a b >,则下列不等式中成立的是 A .11<a bB .33a b >C .22a b >D .a b >4.函数y =的定义域为 A .(12)-,B .(02),C .[12)-,D .(12]-,5.某企业一个月生产某种商品x 万件时的生产成本为2()410C x x x =++(万元)。
一万件售价是30万元,若商品能全部卖出,则该企业一个月生产该商品的最大利润为 A .139万元B .149万元C .159万元D .169万元6.已知集合2{Z |Z}1A x x =∈∈-,则集合A 的真子集的个数为 A .13B .14C .15D .167.若0.33a =,3log 0.3b =,13log 3c =,则a ,b ,c 的大小关系为 A .b c a <<B .c a b <<C .a b c <<D .b a c <<8.若函数()f x 是奇函数,且在定义域R 上是减函数,(2)3f -=,则满足3(3)3f x -<-<的实数x 的取值范围是 A .(15),B .(24),C .(36),D .(25),二、选择题:本题共4小题,每小题5分,共20分。
2017-2018学年广西南宁市高一上学期期中考试数学试题(解析版12)

高一上学期期中考试数学试题一、单选题1.设集合{}{}1,0,1,|0 A B x R x =-=∈>,则A B ⋂=( )A. {}1,0-B. {}1-C. {}1,0D. {}1 2.如图,阴影部分表示的集合是( ) A. ()U B A ⋂ð B. ()U A B ⋃ð C. ()U A B ⋂ð D. ()U A B ⋃ð3.如图给出的四个对应关系,其中构成映射的是( )A .(1)(2)B .(1)(4)C .(1)(2)(4)D .(3)(4) 4.下列函数中指数函数的个数是( )①y =2x ; ②y =x 2; ③y =2x+1; ④y =x x ; ⑤y =(6a -3)x12,23a a >≠(且).A. 0B. 1C. 2D. 3 5.下列说法:(13±; (2)16的4次方根是2;(3)当n 为大于1的偶数时, 0a ≥时才有意义;(4)当n 为大于1的奇数时,a R ∈有意义.其中正确的个数为 ( )A.4 B .3 C .2 D .16.已知函数()y f x =的定义域为(1,3),则函数()21y f x =+的定义域为( ) A. (1,3) B. (3,7) C. (0,1) D. (-1,1)7.函数()()212log 23f x x x =+-的单调递增区间为( )A. ()3∞-,-B. (),1-∞-C. ()1,-+∞D. ()1,+∞8.已知函数()()22log 2f x x x a =++的定义域为R ,则实数a 的取值范围是 A. ()1,+∞ B. [)1+∞,C. (],1-∞D. ()()11∞⋃+∞-,,9.若函数()221x x a f x -=+是奇函数,则使()13f x >成立的x 的取值范围为( )A. (-∞,-1)B. (-1,0)C. (0,1)D. (1,+∞) 10.函数()x f x a =与g (x )=-x +a 的图象大致是( )A. B.C. D.11.设0.60.50.60.5,0.6,log 0.5a b c ===,则a,b,c 的大小关系是( ) A. c b a << B. c a b << C. a c b << D. a b c << 12.若不等式()()1214lg1lg44x xa x ++-≥-对任意的(],1x ∈-∞恒成立,则实数a 的取值范围是( ) A. (-∞,0] B. (-∞,34] C. [0,+∞) D. [34,+∞)二、填空题13.A ={1,2,3},B ={1,2},定义集合间的运算{}1212|,, A B x x x x x A x B +==+∈∈,则集合A +B 中元素的最大值是________.14.函数()()4log 1(0,1)a f x x a a =+->≠且的图象恒过定点P ,则P 点的坐标是______.15.方程22ln 0x x -=-的根的个数是____________.三、解答题16.已知()f x 是定义域为R 的偶函数,当x ≥0时, ()24f x x x =-,求不等式()25f x +<的解集.17.计算: 422log 30.532314964log 3log 2225627--⎛⎫⎛⎫⎛⎫⋅++ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭-。
广西南宁市八年级上学期数学期中考试试卷

广西南宁市八年级上学期数学期中考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共15题;共30分)1. (2分)如图所示,在△ABC中,AB=AC,BE=CE,则由“SSS”可以判定()A . △ABD≌△ACDB . △BDE≌△CDEC . △ABE≌△ACED . 以上都不对2. (2分)下列说法中不正确的是()A . 线段有1条对称轴B . 等边三角形有3条对称轴C . 角只有1条对称轴D . 底与腰不相等的等腰三角形只有一条对称轴3. (2分)如图,某同学把一块三角形的玻璃打破成了三块,现在他要到玻璃店去配一块完全一样形状的玻璃,那么最省事的办法是带()去配.A . ①B . ②C . ③D . ①和②4. (2分)下列说法不正确的是()A . 如果三角形有一个外角是锐角,那么这个三角形必为钝角三角形B . 三角形的一个外角大于任何一个与它不相邻的内角C . 含盐20%的盐水80克与含盐40%的盐水20克混合后就得到含盐30%的盐水100克D . 方程2x+y=5的正整数解只有2组.5. (2分)(2019·南山模拟) 下列图形既是轴对称图形也是中心对称图形的是()A .B .C .D .6. (2分) (2017八上·满洲里期末) 已知点P(1,a)与Q(b,2)关于x轴成轴对称,则a﹣b的值为()A . ﹣1B . 1C . ﹣3D . 37. (2分) (2015八下·成华期中) 如图,在以BC为底边的等腰△ABC中,∠A=30°,AC=8,则AC边上的高BD的长是()A . 4B . 8C . 2D . 48. (2分)如果等腰三角形的两边长是6cm和3cm,那么它的周长是()A . 6cmB . 12cmC . 15cmD . 12cm或15cm9. (2分) (2019八上·获嘉月考) 如图,D,E分别是△ABC的边AC,BC的中点,那么下列说法中不正确的是()A . DE是△BCD的中线B . BD是△ABC的中线C . AD=DC,BE=ECD . AD=EC,DC=BE10. (2分) (2019八上·榆树期末) 如图,在△ABC中,AB=AC ,∠A=36°,BD , CE分别平分∠ABC ,∠ACB ,若CD=3,则CE等于()A . 2B . 2.5C . 3D . 3.511. (2分) (2016八上·铜山期中) 如图,在△ABC中,BC边上的高为()A . BEB . AEC . BFD . CF12. (2分)如图OP平分∠AOB,PC⊥OA于C,D在OB上,PC=3,则PD的大小关系是()A . PD≥3B . PD=3C . PD≤3D . 不能确定13. (2分) (2018八上·腾冲期中) 如图,将一个三角形纸片沿过点的直线折叠,使点落在边上的点处,折痕为,则下列结论一定正确的是()A .B .C .D .14. (2分)已知:如图,AB,BC,AC是⊙O的三条弦,∠OBC=50°,则∠A=()A . 25°B . 40°C . 80°D . 100°15. (2分) (2018七下·深圳期末) 如图,C为线段AE上一动点(不与A、E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,以下五个结论:①AD=BE;②PQ∥AE;③CP=CQ;④BO=OE;⑤∠AOB=60°,恒成立的结论有()A . ①③⑤B . ①③④⑤C . ①②③⑤D . ①②③④⑤二、解答题 (共9题;共85分)16. (5分) (2019八上·天山期中) 已知一个多边形的内角和与外角和的和为1080°,且这个多边形的各个内角都相等.求这个多边形的每个外角度数.17. (10分) (2019八上·顺德月考) 已知一次函数y=2x﹣4(1)在平面直角坐标系中画出图象;(2)该直线与x轴相交于点A,与y轴相交于点B,线段AB上有点C(1,-2),在y轴上有一动点P,请求出PA+PC的最小值。
广西高一上学期期中数学试卷(重点班)

广西高一上学期期中数学试卷(重点班)姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分) (2016高一上·南充期中) 集合M={x|y= + },N={y|y= • } 则下列结论正确的是()A . M=NB . M∩N={3}C . M∪N={0}D . M∩N=∅2. (2分) (2016高二下·黄骅期中) 已知集合A={X|a+1≤x≤2a﹣1},B={x|﹣2≤x≤5},且A⊆B,则a的取值范围是()A . a<2B . a<3C . 2≤a≤3D . a≤33. (2分) (2019高一上·丹东月考) 下列四组函数中,表示同一函数的是().A . 与B . 与C . 与D . 与4. (2分) (2016高三上·遵义期中) 下列四个函数中,在定义域上不是单调函数的是()A . y=﹣2x+1B . y=C . y=lgxD . y=x35. (2分) (2018高二下·齐齐哈尔月考) 函数(且)的图象恒过定点,若点在直线上,其中,则的最大值为()A .B .C .D .6. (2分) (2018高一上·杭州期中) 设函数,其中表示中的最小者.下列说法错误的()A . 函数为偶函数B . 若时,有C . 若时,D . 若时,7. (2分) (2018高一上·广东期中) 设 ,则()A .B .C .D .8. (2分) (2019高一上·嘉兴期中) 若函数在区间上的最大值是,最小值是,则()A . 与有关,且与有关B . 与无关,但与有关C . 与无关,且与无关D . 与有关,但与无关9. (2分)(2017·山东) 设f(x)= 若f(a)=f(a+1),则f()=()A . 2B . 4C . 6D . 810. (2分)已知函数f(x)=3x+x﹣5,用二分法求方程3x+x﹣5=0在x∈(0,2)内近似解的过程中,取区间中点x0=1,那么下一个有根区间为()A . (0,1)B . (1,2)C . (1,2)或(0,1)都可以D . 不能确定11. (2分)(2020·山东模拟) 已知,则的大小关系为()A .B .C .D .12. (2分) (2017高三上·孝感期末) 下列函数中,既是偶函数又在(0,+∞)上单调递减的函数是()A . y=2x3B . y=|x|+1C . y=﹣x2+4D . y=2|x|二、填空题 (共4题;共4分)13. (1分) (2018高一上·辽宁期中) 满足条件的集合的个数是________14. (1分) (2018高一上·湘东月考) 函数的定义域为________;(用集合或区间表示)15. (1分)函数f(x)=(m2﹣m﹣1)xm是幂函数,且对区间(0,+∞)上任意两个不相等的实数x1 , x2 ,都有x1f(x1)+x2f(x2)>x1f(x2)+x2f(x1)成立,则实数m的值是________ .16. (1分) (2020高二下·铜陵期中) 已知,,若,,则的表达式________.三、解答题. (共6题;共60分)17. (10分) (2019高一上·九台期中) 已知集合,.(1)若,求;(2)若,求的取值范围.18. (5分) (2017高一上·南山期末) 已知函数(其中a为非零实数),且方程有且仅有一个实数根.(Ⅰ)求实数a的值;(Ⅱ)证明:函数f(x)在区间(0,+∞)上单调递减.19. (10分) (2019高一上·蚌埠月考)(1)计算:;(2)计算:20. (10分) (2019高一上·双鸭山月考) 已知函数f(x)对于任意x,y∈R,总有f(x)+f(y)=f(x+y),且当x>0时,f(x)<0,f(1)=- .(1)求证:f(x)在R上是减函数.(2)求f(x)在[-3,3]上的最大值和最小值.21. (15分) (2020高一上·杭州期末) 已知函数具有如下性质:在上是减函数,在上是增函数.(1)若函数的值域为 ,求b的值;(2)已知函数 , ,求函数的单调区间和值域;(3)对于(2)中的函数和函数 ,若对任意 ,总存在 ,使得成立,求实数c的值.22. (10分)(2020·哈尔滨模拟) 已知函数的最大值为3,其中 .(1)求实数m的值;(2)若求证: .。
南宁市高一上学期期中数学试卷C卷

南宁市高一上学期期中数学试卷C卷姓名:________ 班级:________ 成绩:________一、选择题 (共8题;共16分)1. (2分) (2016高一上·宝安期中) 设全集U={x∈Z|﹣5<x<5},集合S={﹣1,1,3},若∁UP⊆S,则这样的集合P的个数共有()A . 3B . 4C . 7D . 82. (2分)设f:x→2x+1是集合A到集合B的映射,若A={﹣2,1,3,m},B={﹣9,n,﹣1,5},则m﹣n 等于()A . ﹣4B . ﹣1C . 0D . 103. (2分)设函数,则是()A . 奇函数,且在上是增函数B . 奇函数,且在上是减函数C . 偶函数,且在上是增函数D . 偶函数,且在上是减函数4. (2分)幂函数f(x)=(m2﹣m﹣1)在(0,+∞)上是减函数,则实数m的值为()A . 2B . 3C . 4D . 55. (2分)在同一坐标系中,函数y=ax+b与y=logax的图象可以是()A .B .C .D .6. (2分) (2018高一上·珠海期末) 某同学用二分法求方程的近似解,该同学已经知道该方程的一个零点在之间,他用二分法操作了7次得到了方程的近似解,那么该近似解的精确度应该为()A . 0.1B . 0.01C . 0.001D . 0.00017. (2分)(2017·泉州模拟) 已知2a+2b=2c ,则a+b﹣2c的最大值等于()A . ﹣2B . ﹣1C .D . ﹣8. (2分)已知函数若均不相等,且,则的取值范围是()A . (1,10)B . (5,6)C . (10,12)D . (20,24)二、填空题 (共7题;共7分)9. (1分) (2017高一上·林口期中) 当x∈[﹣1,1]时,函数f(x)=3x﹣2的值域为________.10. (1分)集合A={x|x2+2x﹣3=0},集合B={x|ax=3},若A∩B=B,则实数a的值组成的集合为________.11. (1分)若f(x)= 是R上的单调减函数,则实数a的取值范围为________.12. (1分) (2016高一上·荆州期中) 已知函数f(x)=4x2﹣kx﹣8在(5,20)上既无最大值也无最小值,则实数k的取值范围是________.13. (1分) (2019高三上·镇江期中) 已知函数的定义城为,对于任意,当时,的最小值为________.14. (1分) (2016高一上·扬州期末) 已知f(x)= ,若对任意θ∈[0, ],不等式f (cos2θ+λsinθ﹣)+ >0恒成立,整数λ的最小值为________.15. (1分) (2017高一上·乌鲁木齐期中) 已知是定义在上的偶函数,在上单调递减,且,若,则的取值范围为 ________ .三、解答题 (共5题;共50分)16. (20分) (2019高一上·纳雍期中) 求下列各式的值(1)(2)(3)(4)17. (5分) (2017高一上·辽源月考) 求:函数 = )的最值及取得最值时的值.18. (5分)已知函数f(x)=﹣x+log2.(1)求的值;(2)当x∈[﹣a,a](其中a∈(0,1)且a是常数)时,f(x)是否存在最小值?如果存在,求出最小值;如果不存在,请说明理由.19. (10分) (2016高一上·万全期中) 已知函数g(x)=ax2﹣2ax+1+b(a>0)在区间[2,4]上的最大值为9,最小值为1,记f(x)=g(|x|).(1)求实数a,b的值;(2)若不等式f(log2k)>f(2)成立,求实数k的取值范围.20. (10分)已知函数f(x)=x+ ﹣1(1)记g(x)=f(x+1),试证明:g(x)图象关于原点对称.(2)若方程f(x)=t(x2﹣2x+3)|x|有三个解,求实数t的取值范围.参考答案一、选择题 (共8题;共16分)1-1、答案:略2-1、答案:略3-1、4-1、5-1、答案:略6-1、答案:略7-1、8-1、二、填空题 (共7题;共7分)9-1、10-1、11-1、12-1、13-1、14-1、15-1、三、解答题 (共5题;共50分) 16-1、答案:略16-2、答案:略16-3、答案:略16-4、答案:略17-1、18-1、19-1、答案:略19-2、答案:略20-1、答案:略20-2、答案:略。
2016年广西南宁市中考数学试卷含答案
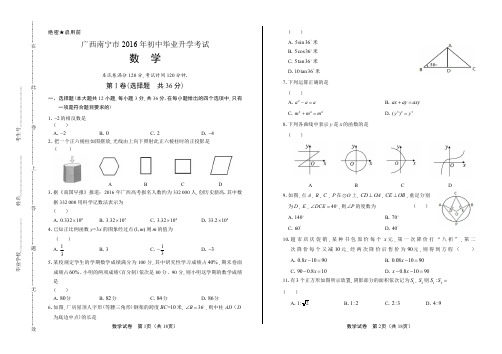
∴ s1 1 , S正方形ABCD 18
∴
S1
1 18
S正方形ABCD
,
∴
S1
1 18
x2
,
∵
S2
1,
S三角形ABC 4
∴
S2
1,
S正方形ABCD 8
∴
S2
1 8
S正方形ABCD
,
∴
S2
1 8
x2
,
∴
S1
:
S2
1 18
x2
:
1 8
x2
4:9
;
故选 D.
【考点】正方形的性质 12.【答案】A 【解析】设 ax2 bx c (0 a 0)的两根为 x1 , x2 ,
数学试卷 第 4页(共 18页)
毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________
------------- -------------------- -------------------- -------------------- -------------------- -------------------- -------------------- -----------------------------------
存在,请说明理由.
广西南宁市 2016 年初中毕业升学考试
数学答案解析
第Ⅰ卷
一、选择题 1.【答案】C 【解析】-2 的相反数是 2,故选 C. 【考点】相反数 2.【答案】A 【解析】把一个正六棱柱如图摆放,光线由上向下照射此正六棱柱时的正投影是正六边 形,故选 A. 【考点】平行投影 3.【答案】B 【解析】将 332000 用科学记数法表示为: 3.2 105 ,故选:B. 【考点】科学记数法—表示较大的数 4.【答案】B 【解析】把点(1,m)代入 y 3x 可得: m 3 ,故选 B
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016-2017学年广西南宁八中高一(上)期中数学试卷一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的,将其选出后填入答题卷.1.(5.00分)已知集合A={1,2,3},B={2,3},则()A.A=B B.A∩B=∅C.A⊆B D.B⊆A2.(5.00分)已知全集U=R,A={x|x≤0},B={x|x≥1},则集合∁U(A∪B)=()A.{x|x≥0}B.{x|x≤1}C.{x|0≤x≤1}D.{x|0<x<1}3.(5.00分)下列四组函数中,表示同一函数的是()A.y=x﹣1与y=B.y=与y=C.y=lgx﹣2与y=lg D.y=4lgx与y=lgx24.(5.00分)函数f(x)=2x+5x的零点所在大致区间为()A.(0,1) B.(1,2) C.(﹣1,0)D.(﹣2,﹣1)5.(5.00分)函数的图象()A.关于x轴对称B.关于y轴对称C.关于原点对称D.关于直线y=x对称6.(5.00分)函数f(x)=的定义域为()A.(0,2]B.(0,2) C.(﹣2,2)D.[﹣2,2]7.(5.00分)下列函数中,其定义域和值域分别与函数y=10lgx的定义域和值域相同的是()A.y=x B.y=lgx C.y=2x D.y=8.(5.00分)设a=()0.9,b=()﹣0.3,c=log30.7,则有()A.c<a<b B.a<b<c C.c<b<a D.b<a<c9.(5.00分)若幂函数f(x)的图象经过点(3,9),那么函数f(x)的单调增区间是()A.[3,+∞)B.[0,+∞)C.(﹣∞,0]D.(﹣∞,3]10.(5.00分)函数f(x)=x2﹣2x零点个数为()A.1 B.2 C.3 D.411.(5.00分)某食品保鲜时间y(单位:小时)与储藏温度x(单位:℃)满足函数关系y=e kx+b(e=2.718…为自然对数的底数,k,b为常数).若该食品在0℃的保鲜时间是192小时,在22℃的保鲜时间是48小时,则该食品在33℃的保鲜时间是()A.16小时B.20小时C.24小时D.28小时12.(5.00分)如果函数f(x)对其定义域内的两个实数x1、x2,都满足不等式,则称函数f(x)在其定义域内具有性质M.给出下列函数:①;②y=x2;③y=2x;④y=log2x.其中具有性质M的是()A.①④B.②③C.③④D.①②③④二、填空题:本大题共4小题,每小题5分,共16分.把答案填在答题卷的横线上.13.(5.00分)设f(x)=,则f(f(3))的值为.14.(5.00分)已知函数y=log a(x﹣3)﹣1的图象恒过定点P,则点P的坐标是.15.(5.00分)若实数α满足log a2>1,则a的取值范围为.16.(5.00分)若函数f(x)为定义在R上的奇函数,且在(0,+∞)为减函数,若f(2)=0,不等式(x﹣1)f(x﹣1)>0的解集为.三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(10.00分)计算下列各式的值(其中,e为自然对数的底数):(1);(2).18.(12.00分)已知全集U=R,集合,B={x|1<x<6}(1)求A∩∁U B;(2)已知C={x|a≤x≤a+1},若A∩C=C,求实数a的取值范围.19.(12.00分)已知函数f(x)=lg(3+x)﹣lg(3﹣x)(1)求f(x)的定义域;(2)判断f(x)的奇偶性并证明;(3)若f(a)=4,求f(﹣a)的值.20.(12.00分)随着机构改革工作的深入进行,各单位要减员增效,有一家公司现有职员400人,每人每年可创利10万元.据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年多创利0.05万元,但公司需付下岗职员每人每年2万元的生活费,并且该公司正常运转所需人数不得小于现有职员的,为获得最大的经济效益,该公司应裁员多少人?21.(12.00分)已知函数f(x)=x2+bx+1满足f(1+x)=f(1﹣x),.(1)求函数f(x)的解析式;(2)判断g(x)在[1,2]上的单调性并用定义证明你的结论;(3)求g(x)在[1,2]上的最大值和最小值.22.(12.00分)已知指数函数y=g(x)满足:g(3)=8,定义域为R的函数f(x)=是奇函数.(1)确定y=f(x)和y=g(x)的解析式;(2)若对任意的x∈[1,4],不等式f(2x﹣3)+f(x﹣k)>0恒成立,求k的取值范围.2016-2017学年广西南宁八中高一(上)期中数学试卷参考答案与试题解析一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的,将其选出后填入答题卷.1.(5.00分)已知集合A={1,2,3},B={2,3},则()A.A=B B.A∩B=∅C.A⊆B D.B⊆A【解答】解:因为A={1,2,3},B={2,3},显然,A≠B且B⊆A,根据集合交集的定义得,A∩B={2,3}=A,所以,A∩B≠∅,故选:D.2.(5.00分)已知全集U=R,A={x|x≤0},B={x|x≥1},则集合∁U(A∪B)=()A.{x|x≥0}B.{x|x≤1}C.{x|0≤x≤1}D.{x|0<x<1}【解答】解:A∪B={x|x≥1或x≤0},∴C U(A∪B)={x|0<x<1},故选:D.3.(5.00分)下列四组函数中,表示同一函数的是()A.y=x﹣1与y=B.y=与y=C.y=lgx﹣2与y=lg D.y=4lgx与y=lgx2【解答】解:A.,∴这两函数对应法则不同,不是同一函数;B.的定义域为[1,+∞),的定义域为(1,+∞),∴这两函数定义域不同,不是同一函数;C.,∴这两函数是同一函数;D.y=4lgx的定义域为(0,+∞),y=lgx2的定义域为{x|x≠0},定义域不同,不是同一函数.故选:C.4.(5.00分)函数f(x)=2x+5x的零点所在大致区间为()A.(0,1) B.(1,2) C.(﹣1,0)D.(﹣2,﹣1)【解答】解:∵函数f(x)=2x+5x是单调递增函数,又∵f(﹣1)=2﹣5=﹣3<0,f(0)=1+0=1>0,∴函数f(x)的零点必在区间(﹣1,0)上,故必存在零点的区间是(﹣1,0),故选:C.5.(5.00分)函数的图象()A.关于x轴对称B.关于y轴对称C.关于原点对称D.关于直线y=x对称【解答】解:函数,可得f(﹣x)=(﹣x)2+=x2+=f(x),函数是偶函数,函数图象关于y轴对称.故选:B.6.(5.00分)函数f(x)=的定义域为()A.(0,2]B.(0,2) C.(﹣2,2)D.[﹣2,2]【解答】解:函数f(x)=,由题意得:,解得:0<x<2,故选:B.7.(5.00分)下列函数中,其定义域和值域分别与函数y=10lgx的定义域和值域相同的是()A.y=x B.y=lgx C.y=2x D.y=【解答】解:函数y=10lgx的定义域和值域均为(0,+∞),函数y=x的定义域和值域均为R,不满足要求;函数y=lgx的定义域为(0,+∞),值域为R,不满足要求;函数y=2x的定义域为R,值域为(0,+∞),不满足要求;函数y=的定义域和值域均为(0,+∞),满足要求;故选:D.8.(5.00分)设a=()0.9,b=()﹣0.3,c=log30.7,则有()A.c<a<b B.a<b<c C.c<b<a D.b<a<c【解答】解:∵a=()0.9∈(0,1),b=()﹣0.3>1,c=log30.7<0,则b>a>c.故选:A.9.(5.00分)若幂函数f(x)的图象经过点(3,9),那么函数f(x)的单调增区间是()A.[3,+∞)B.[0,+∞)C.(﹣∞,0]D.(﹣∞,3]【解答】解:设幂函数f(x)=x a,则3a=9,解得a=2,∴f(x)=x2;∴f(x)=x2的单调递增区间是[0,+∞),故选:B.10.(5.00分)函数f(x)=x2﹣2x零点个数为()A.1 B.2 C.3 D.4【解答】解:函数f(x)=x2﹣2x零点个数可化为函数y=x2与y=2x的图象的交点个数,作函数y=x2与y=2x的图象如下,有三个交点,故选:C.11.(5.00分)某食品保鲜时间y(单位:小时)与储藏温度x(单位:℃)满足函数关系y=e kx+b(e=2.718…为自然对数的底数,k,b为常数).若该食品在0℃的保鲜时间是192小时,在22℃的保鲜时间是48小时,则该食品在33℃的保鲜时间是()A.16小时B.20小时C.24小时D.28小时【解答】解:y=e kx+b(e=2.718…为自然对数的底数,k,b为常数).当x=0时,e b=192,当x=22时e22k+b=48,∴e22k==e11k=e b=192当x=33时,e33k+b=(e k)33•(e b)=()3×192=24故选:C.12.(5.00分)如果函数f(x)对其定义域内的两个实数x1、x2,都满足不等式,则称函数f(x)在其定义域内具有性质M.给出下列函数:①;②y=x2;③y=2x;④y=log2x.其中具有性质M的是()A.①④B.②③C.③④D.①②③④【解答】解:函数f(x)对其定义域内的任意两个实数x1,x2都满足不等式,则称函数f(x)在定义域上具有性质M,(为下凸函数).由函数的图象可知:②y=x2;③y=2x.其中具有性质M.故选:B.二、填空题:本大题共4小题,每小题5分,共16分.把答案填在答题卷的横线上.13.(5.00分)设f(x)=,则f(f(3))的值为1.【解答】解:∵f(x)=,∴f(3)=log5(3×3﹣4)=log55=1,f(f(3))=f(1)=2﹣30=1.故答案为:1.14.(5.00分)已知函数y=log a(x﹣3)﹣1的图象恒过定点P,则点P的坐标是(4,﹣1).【解答】解:∵log a1=0,∴x﹣3=1,即x=4时,y=﹣1,∴点P的坐标是P(4,﹣1).故答案为:(4,﹣1).15.(5.00分)若实数α满足log a2>1,则a的取值范围为(1,2).【解答】解:∵log a2>1=log a a,∴或,解得1<a<2或a∈∅.∴a的取值范围为(1,2).故答案为:(1,2).16.(5.00分)若函数f(x)为定义在R上的奇函数,且在(0,+∞)为减函数,若f(2)=0,不等式(x﹣1)f(x﹣1)>0的解集为(﹣∞,﹣1)∪(3,+∞).【解答】解:定义在R上的奇函数,可得f(﹣x)=﹣f(x),在(0,+∞)为减函数,即在R上是减函数,∵f(2)=0,则f(﹣2)=0.令t=x﹣1,不等式(x﹣1)f(x﹣1)>0转化为tf(t)>0.当t>0时,则f(t)<0,可得:t>2,即x﹣1>2,解得:x>3;当t<0时,则f(t)>0,可得:t<﹣2,即x﹣1<﹣2,解得:x<﹣1;综上所得:不等式(x﹣1)f(x﹣1)>0的解集为(﹣∞,﹣1)∪(3,+∞).故答案为:(﹣∞,﹣1)∪(3,+∞).三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(10.00分)计算下列各式的值(其中,e为自然对数的底数):(1);(2).【解答】解:(1)==;(2)=lg25+lg4+ln=lg(25×4)+ln=2+=.18.(12.00分)已知全集U=R,集合,B={x|1<x<6}(1)求A∩∁U B;(2)已知C={x|a≤x≤a+1},若A∩C=C,求实数a的取值范围.【解答】解:(2)∵全集U=R,集合={x|﹣1≤x≤2},B={x|1<x<6}∴∁U B={x|x≤1或x≥6},则A∩∁U B={x|﹣1≤x≤2};(2)∵A∩C=C,∴C⊆A,∴解得:﹣1≤a≤1,则实数a的范围是{a|﹣1≤a≤1}.19.(12.00分)已知函数f(x)=lg(3+x)﹣lg(3﹣x)(1)求f(x)的定义域;(2)判断f(x)的奇偶性并证明;(3)若f(a)=4,求f(﹣a)的值.【解答】解:(1)函数f(x)=lg(3+x)﹣lg(3﹣x)其定义域满足:,解得:﹣3<x<3.故得f(x)的定义域数为{x|﹣3<x<3}.(2)由(1)可得f(x)的定义域数为{x|﹣3<x<3}.设﹣3<x1<x2<3,则f(x1)﹣f(x2)=lg(3+x1)﹣lg(3﹣x1)﹣lg(3+x2)+lg(3﹣x2)=lg=lg因为9+3(x1﹣x2)﹣x1x2>9+(x2﹣x1)﹣x1x2<0,∴<1,即f(x1)﹣f(x2)<0,所以f(x1)<f(x2),即f(x)是(﹣3,3)上的增函数;(3)∵函数的定义域为(﹣3,3).∴定义域关于原点对称,∵f(﹣x)=lg(3﹣x)+lg(3+x)=f(x),∴函数f(x)是偶函数.∴f(a)=4,则f(﹣a)=f(a)=4.20.(12.00分)随着机构改革工作的深入进行,各单位要减员增效,有一家公司现有职员400人,每人每年可创利10万元.据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年多创利0.05万元,但公司需付下岗职员每人每年2万元的生活费,并且该公司正常运转所需人数不得小于现有职员的,为获得最大的经济效益,该公司应裁员多少人?【解答】解:设裁员x人,可获得的经济效益为y万元,则y=(400﹣x)(10+0.05x)﹣2x=(x﹣80)2+4320依题意400﹣x≥×400=300,∴0<x≤100.∴当x=80时,y取到最大值为4320;综上,为获得最大的经济效益,该公司应裁员80人.21.(12.00分)已知函数f(x)=x2+bx+1满足f(1+x)=f(1﹣x),.(1)求函数f(x)的解析式;(2)判断g(x)在[1,2]上的单调性并用定义证明你的结论;(3)求g(x)在[1,2]上的最大值和最小值.【解答】解:(1)函数f(x)=x2+bx+1满足f(1+x)=f(1﹣x),可知函数的对称轴为:x=1,所以,b=﹣2,函数f(x)的解析式:f(x)=x2﹣2x+1.(2)=x+﹣2,g(x)在[1,2]上的单调性是增函数,证明:设1≤x1<x2≤2,x1﹣x2<0,>0,g(x1)﹣g(x2)=x1﹣x2+=(x1﹣x2)()<0,g(x1)<g(x2),所以函数g(x)在[1,2]上是增函数.(3)由(2)可知,函数是增函数,函数的最小值为:g(1)=0,函数的最大值为:g(2)=.22.(12.00分)已知指数函数y=g(x)满足:g(3)=8,定义域为R的函数f(x)=是奇函数.(1)确定y=f(x)和y=g(x)的解析式;(2)若对任意的x∈[1,4],不等式f(2x﹣3)+f(x﹣k)>0恒成立,求k的取值范围.【解答】解::(1)设g(x)=a x(a>0且a≠1),∵g(3)=8,∴a3=8,解得a=2.∴g(x)=2x.∴f(x)=,∵函数f(x)是定义域为R的奇函数,∴f(0)=0,∴n=1,∴f(x)=,(x∈R);(2)由(Ⅰ)知f(x)=,易知f(x)在R上为减函数,又f(x)是奇函数,∴f(2x﹣3)+f(x﹣k)>0,∴f(2x﹣3)>﹣f(x﹣k)=f (k﹣x),∵f(x)在R上为减函数,由上式得2x﹣3<k﹣x,即对一切x∈(1,4),有3x﹣3<k恒成立,令m(x)=3x﹣3,x∈(1,4),易知m(x)在(1,4)上递增,∴m(x)<3×4﹣3=9,∴k≥9,即实数k的取值范围是[9,+∞).赠送初中数学几何模型【模型五】垂直弦模型:图形特征:运用举例:1.已知A、B、C、D是⊙O上的四个点.(1)如图1,若∠ADC=∠BCD=90°,AD=CD,求证AC⊥BD;(2)如图2,若AC⊥BD,垂足为E,AB=2,DC=4,求⊙O的半径.O DAB CEAOD CB2.如图,已知四边形ABCD内接于⊙O,对角线AC⊥BD于P,设⊙O的半径是2。
