立体几何高考选择填空题
高三数学立体几何专项练习题及答案

高三数学立体几何专项练习题及答案一、选择题1. 下列哪个几何体的所有面都是三角形?A. 正方体B. 圆柱体C. 正六面体D. 球体答案:C2. 一个有8个面的多面体,其中6个面是正方形,另外2个面是等边三角形,它的名字是?A. 正八面体B. 正十二面体C. 正二十面体D. 正二十四面体答案:C3. 空间中任意一点到四个角落连线的垂直距离相等的四棱锥称为?A. 正四棱锥B. 圆锥台C. 四棱锥D. 无法确定答案:C4. 任意多面体的面数与顶点数、棱数的关系是?A. 面数 + 顶点数 = 棱数 + 2B. 面数 + 棱数 = 顶点数 + 2C. 顶点数 + 棱数 = 面数 + 2D. 顶点数 + 面数 = 棱数 + 2答案:A5. 求下列多面体的棱数:(1)正六面体(2)正八面体(3)正十二面体答案:(1)正六面体的棱数为 12(2)正八面体的棱数为 24(3)正十二面体的棱数为 30二、填空题1. 下列说法正确的是:一棱锥没有底面时,它的底面是一个______。
答案:点2. 铅垂线是指从一个多面体的一个顶点到与它相对的棱上所作的垂线,它与该棱垂足的连线相交于该多面体的______上。
答案:中点3. 对正八面体,下列说法不正确的是:_____条对角线与_____两两垂直。
答案:六,相邻面三、计算题1. 一个棱锥的底面是一个边长为6cm的正三角形,其高为8cm。
求棱锥体积。
解答:底面积 S = (1/2) ×底边长 ×高 = (1/2) × 6 × 8 = 24 cm²棱锥体积 V = (1/3) × S ×高 = (1/3) × 24 × 8 = 64 cm³所以,棱锥的体积为64 cm³。
2. 一个正四棱锥的底面是一个边长为10cm的正方形,其高为12cm。
求四棱锥的体积。
解答:底面积 S = 边长² = 10² = 100 cm²四棱锥体积 V = (1/3) × S ×高 = (1/3) × 100 × 12 = 400 cm³所以,四棱锥的体积为400 cm³。
高考数学试题-立体几何选择填空含答案解析

选填训练4答案一、单选题(本大题共8小题,共40.0分。
在每小题列出的选项中,选出符合题目的一项) 1. 如图,在四面体O −ABC 中,G 是底面△ABC 的重心,且OG ⃗⃗⃗⃗⃗⃗ =x OA ⃗⃗⃗⃗⃗ +y OB ⃗⃗⃗⃗⃗⃗ +z OC ⃗⃗⃗⃗⃗ ,则log 3|xyz|等于 ( )A. −3B. −1C. 1D. 3【答案】A 解:连结AG ,OG ⃗⃗⃗⃗⃗⃗ =OA ⃗⃗⃗⃗⃗ +AG ⃗⃗⃗⃗⃗ =OA ⃗⃗⃗⃗⃗ +13(AC ⃗⃗⃗⃗⃗ +AB ⃗⃗⃗⃗⃗ )=OA ⃗⃗⃗⃗⃗ +13(OC ⃗⃗⃗⃗⃗ −OA ⃗⃗⃗⃗⃗ +OB ⃗⃗⃗⃗⃗⃗ −OA ⃗⃗⃗⃗⃗ )=13OA ⃗⃗⃗⃗⃗ +13OB ⃗⃗⃗⃗⃗⃗ +13OC ⃗⃗⃗⃗⃗ =x OA ⃗⃗⃗⃗⃗ +y OB ⃗⃗⃗⃗⃗⃗ +z OC ⃗⃗⃗⃗⃗ ,∴x =y =z =13, 则log 3|xyz|=log 3127=−3.2. 在△ABC 中A =30°,AC =4,BC =a ,若△ABC 仅一个解时,则a 的取值范围是( )A. a ≥4B. a =2C. a ≥4或a =2D. 无法确定【答案】C解:当a =ACsin30°=4×12=2时,以C 为圆心,以a =2为半径画弧,与射线AD 只有唯一交点, 此时符合条件的三角形只有一个,当a ⩾4时,以C 为圆心以a 为半径画弧时,在从垂足到A 点之间得不到交点,交点只能在垂足外侧,三角形也是唯一的, ∴a ≥4或a =2,故选C .3. 设两个向量e 1⃗⃗⃗ ,e 2⃗⃗⃗ 满足|e 1⃗⃗⃗ |=2,|e 2⃗⃗⃗ |=1,e 1⃗⃗⃗ ,e 2⃗⃗⃗ 之间的夹角为60°,若向量2t e 1⃗⃗⃗ +7e 2⃗⃗⃗ 与向量e 1⃗⃗⃗ +t e 2⃗⃗⃗ 的夹角为钝角,则实数t 的取值范围是( )A. (−7,−12)B. (−7,−√142)∪(−√142,−12) C. (−7,−√142)D. (−√142,−12)【答案】B解:由题意知(2t e 1⃗⃗⃗ +7e 2⃗⃗⃗ )·(e 1⃗⃗⃗ +t e 2⃗⃗⃗ )<0,即2t 2+15t +7<0,解得−7<t <−12.又由2t ·t −7≠0,得t ≠±√142,∴t ∈(−7,−√142)∪(−√142,−12). 故选B .4. 已知向量a ⃗ =(1,2),a ⃗ ·b ⃗ =10,|a ⃗ +b ⃗ |=5√2,b ⃗ 方向上的单位向量为e⃗ ,则向量a ⃗ 在 向量b ⃗ 上的投影向量为( ) A. 12e ⃗ B. 2e ⃗ C.125e⃗ D. 52e⃗ 【答案】B解:由a ⃗ =(1,2)可得:|a ⃗ |=√12+22=√5,由|a ⃗ +b|⃗⃗⃗ =5√2两边平方得:|a ⃗ |2+2a ⃗ ·b ⃗ +|b⃗ |2=(5√2)2=50,即:5+2×10+|b⃗ |2=50,解得:|b ⃗ |=5, 设a ⃗ 和b ⃗ 的夹角为θ,则cosθ=a⃗ ·b ⃗|a ⃗ |·|b⃗ |=10√5×5=2√55, 所以向量a ⃗ 在向量b ⃗ 上的投影向量为:|a ⃗ |cosθ·b⃗ |b ⃗ |=√5×2√55e ⃗ =2e ⃗ .故选B .5. 如图所示,在直三棱柱ABC −A 1B 1C 1中,AB ⊥AC ,AB =3,AC =AA 1=4,一只蚂蚁由顶点A 沿棱柱侧面经过棱BB 1爬到顶点C 1,蚂蚁爬行的最短距离为( )A. 4B. 4C.D.+【答案】B解:如图所示,把侧面展开,矩形对角线即为蚂蚁爬行的最短距离,∵AB ⊥AC ,AB =3,AC =AA 1=4,∴BC =√AB 2+AC 2=√32+42=5,由题已知AA 1=CC 1=4,∴蚂蚁爬行的最短距离=√(AB +BC )2+(CC 1)2=√(3+5)2+42=4√5,所以最小值为4√5,故选B .6.在四棱锥P−ABCD中,侧面PAD为正三角形,底面ABCD为正方形,侧面PAD⊥底面ABCD,M为底面ABCD内的一个动点,且满足MP=MC,则点M在正方形ABCD内的轨迹为( )A. B. C. D.【答案】A解:根据题意可知PD=DC,则点D符合“M为底面ABCD内的一个动点,且满足MP=MC”,设AB的中点为N,因为侧面PAD⊥底面ABCD,侧面PAD∩底面ABCD=AD,AB⊥AD,AB⊂底面ABCD,所以AB⊥侧面PAD,又PA⊂侧面PAD,所以AB⊥PA,根据题目条件可知△PAN≌△CBN,∴PN=CN,点N也符合“M为底面ABCD内的一个动点,且满足MP=MC”,故动点M的轨迹肯定过点D和点N,而到点P与到点C的距离相等的点为线段PC 的垂直平分面,线段PC的垂直平分面与平面ABCD的交线是一直线.故选A.7.如图,直角梯形ABCD,AB//CD,∠ABC=90°,CD=2,AB=BC=1,E是边CD中点,△ADE沿AE翻折成四棱锥D′−ABCE,则点C到平面ABD′距离的最大值为( )A. 12B. √3−1 C. √22D. √63【答案】C解:直角梯形ABCD ,AB//CD ,∠ABC =90°,CD =2,AB =BC =1,E 是边CD 中点,△ADE 沿AE 翻折成四棱锥D′−ABCE ,当D′E ⊥CE 时,点C 到平面ABD′距离取最大值,∵D′E ⊥AE ,CE ∩AE =E ,CE ,AE ⊂平面ABCE ,∴D′E ⊥平面ABCE , 以E 为原点,EC 为x 轴,EA 为y 轴,ED′为z 轴,建立空间直角坐标系,则A(0,1,0),C(1,0,0),D′(0,0,1),B(1,1,0), AB ⃗⃗⃗⃗⃗ =(1,0,0),AC ⃗⃗⃗⃗⃗ =(1,−1,0),AD′⃗⃗⃗⃗⃗⃗⃗ =(0,−1,1), 设平面ABD′的法向量n⃗ =(x,y,z),则{n ⃗ ⋅AB ⃗⃗⃗⃗⃗ =x =0n ⃗ ⋅AD′⃗⃗⃗⃗⃗⃗⃗ =−y +z =0,取y =1,得n ⃗ =(0,1,1),∴点C 到平面ABD′距离的最大值为d =|AC ⃗⃗⃗⃗⃗ ⋅n ⃗⃗ ||n ⃗⃗ |=1√2=√22.故选C .8. 在△ABC 中,有正弦定理:asinA =bsinB =csinC =定值,这个定值就是△ABC 的外接圆的直径.如图所示,△DEF 中,已知DE =DF ,点M 在直线EF 上从左到右运动(点M 不与E 、F 重合),对于M 的每一个位置,记△DEM 的外接圆面积与△DMF 的外接圆面积的比值为λ,那么( )A. λ先变小再变大B. 仅当M 为线段EF 的中点时,λ取得最大值C. λ先变大再变小D. λ是一个定值【答案】D解:设△DEM 的外接圆半径为R 1,△DMF 的外接圆半径为R 2,则由题意,πR 12πR 22=λ,点M 在直线EF 上从左到右运动(点M 不与E 、F 重合),对于M 的每一个位置,由正弦定理可得R 1=12×DE sin∠DME,R 2=12×DFsin∠DMF ,又DE =DF ,sin∠DME =sin∠DMF , 可得R 1=R 2,可得λ=1.故选D .二、多选题(本大题共4小题,共20.0分。
【2023高考必备】2013-2022十年全国高考数学真题分类(全国通用):立体几何选填题(解析版)

3 3
时等号成立,故选:C
【题目栏目】立体几何\球的问题\球的其它问题 【题目来源】2022 年全国乙卷理科·第 9 题
5.(2022 年全国乙卷理科·第 7 题) 在正方体 ABCD A1B1C1D1 中,E,F 分别为 A B , B C 的中点,则
()
A.平面 B1 E F 平面 BD D1
乙圆锥的高 h2
l2
1 l2 9
22 3
l
,所以 V甲 V乙
1 3
r12
h1
1 3
r2
2
h2
4l2 5 l 93 1l2 2 2 l 93
10 .
故选:C.
【题目栏目】立体几何\空间几何体的结构特征及其直观图、三视图\空间几何体的展开图问题 【题目来源】2022 年全国甲卷理科·第 9 题
2.(2022 年全国甲卷理科·第 7 题) 在长方体 ABCD A1B1C1D1 中,已知 B1D 与平面 ABCD 和平面 AA1B1B 所成
2013-2022 十年全国高考数学真题分类汇编
专题 16 立体几何选填题
一、选择题 1.(2022 年全国甲卷理科·第 9 题) 甲、乙两个圆锥的母线长相等,侧面展开图的圆心角之和为 2π ,侧面积
分别为
S甲
和
S乙
,体积分别为 V甲
和 V乙
.若
S甲 S乙
=2
,则
V甲 V乙
=
(
)
A. 5 【答案】C
tan BAE c 2 ,所以 BAE 30 ,B 错误; a2
对于 C, AC a2 b2 3c , CB1 b2 c2 2c , AC CB1 ,C 错误;
对于
高考必刷小题 立体几何

11.如图所示,在正方体ABCD-A1B1C1D1中,E是平面ADD1A1的中心,M, N,F分别是B1C1,CC1,AB的中点,则下列说法正确的是 A.MN=12EF
√B.MN≠12EF √C.MN与EF异面
D.MN与EF平行
1 A.4
dm2
C.
3 4
dm2
√B.
2 4
dm2
D.34 2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
根据题意,在平面VAC内,过点P作EF∥AC分别交VA,VC于点F,E, 在平面VBC内,过点E作EQ∥VB交BC于点Q, 在平面VAB内,过点F作FD∥VB交AB于点D,连接DQ,如图所示, 因为EF∥AC, 所以△VEF∽△VCA,设其相似比为k, 则VVAF=VVCE=AECF=k,0<k<1, 因为 VA=VB=VC=1,且两两垂直,所以 AC= 2,
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
因为EF⊂平面VAC, 所以FD⊥EF, 所以四边形 FEQD 是矩形,即 S 矩形 FEQD=
FD·EF=(1-k)· 2k=- 2k-122+ 42,
所以当
k=12时,S
矩形 FEQD
有最大值
2 4.
故该截面面积的最大值是
对于A,如图(1),α∩β=l,m⊥l,n∥l,则满足m∥α,n∥β,m⊥n, 平面α与β不一定垂直,故A错误; 对于B,如图(2),α∩β=l,n∥l,m⊥α,则满足n∥β,m⊥n,平面 α与β不一定垂直,故B错误;
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
立体几何高考选择填空题

1. (2013大纲,10,5分)正四棱锥的顶点都在同一球面上.若该棱锥的高为4,底面边长为2,则该球的表面积为()A. B.16π C.9π D.[解析] 1.易知球心在正四棱锥的高上,设球的半径为R,则(4-R)2+()2=R2,解得R=,所以球的表面积为4π×=π,故选A.2. (2014重庆,7,5分)某几何体的三视图如图所示,则该几何体的体积为()A.12B.18C.24D.30[解析] 2.由三视图可知该几何体是由如图所示的直三棱柱ABC-A1B1C1截掉一个三棱锥D-A1B1C1得到的,其中AC=4,BC=3,AA1=5,AD=2,BC⊥AC,所以该几何体的体积V=·AC·BC·AA1-×·A1C1·B1C1·A1D=×4×3×5-××4×3×3=30-6=24.3. (2014四川,4,5分)某三棱锥的侧视图、俯视图如图所示,则该三棱锥的体积是()A.3B.2C.D.1[解析] 3.由俯视图可知,三棱锥底面是边长为2的等边三角形.由侧视图可知,三棱锥的高为.故该三棱锥的体积V=××2××=1.4. (2014湖北,7,5分)在如图所示的空间直角坐标系O-xyz中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2).给出编号为①、②、③、④的四个图,则该四面体的正视图和俯视图分别为()A.①和②B.③和①C.④和③D.④和②[解析] 4.在空间直角坐标系中构建棱长为2的正方体,设A(0,0,2),B(2,2,0),C(1,2,1),D(2,2,2),则ABCD即为满足条件的四面体,得出正视图和俯视图分别为④和②,故选D.5. (2014湖南,8,5分)一块石材表示的几何体的三视图如图所示,将该石材切削、打磨,加工成球,则能得到的最大球的半径等于()A.1B.2C.3D.4[解析] 5.由三视图可知该几何体是一个直三棱柱,底面为直角三角形,高为12,如图所示,其中AC=6,BC=8,∠ACB=90°,则AB=10.要使该石材加工成的球的半径最大,只需球与直三棱柱的三个侧面都相切,则半径r等于直角三角形ABC的内切圆半径,即r==2,故能得到的最大球的半径为2,故选B.6. (2014安徽,8,5分)一个多面体的三视图如图所示,则该多面体的体积为()A. B. C.6 D.7[解析] 6.由三视图知这个多面体是正方体截去两个全等的三棱锥后剩余的部分,其直观图如图所示,结合题图中尺寸知,正方体的体积为23=8,一个三棱锥的体积为××1×1×1=,因此多面体的体积为8-2×=,故选A.7. (2014浙江,3,5分)某几何体的三视图(单位:cm)如图所示,则该几何体的体积是()A.72 cm3B.90 cm3C.108 cm3D.138 cm3[解析] 7.由三视图可知,该几何体是由一个长方体和一个直三棱柱构成的组合体,如图,其体积为6×4×3+×4×3×3=90 cm3,故选B.8. (2014辽宁,7,5分)某几何体三视图如图所示,则该几何体的体积为()A.8-B.8-C.8-πD.8-2π[解析] 8.由三视图可知,该几何体的体积是一个四棱柱的体积减去半个圆柱的体积,即V=2×2×2-×π×12×2=8-π.故选C.9. (2014课标Ⅱ,6,5分)如图,网格纸上正方形小格的边长为1(表示1 cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3 cm,高为6 cm的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为()A. B. C. D.[解析] 9.该零件是两个圆柱体构成的组合体,其体积为π×22×4+π×32×2=34π cm3,圆柱体毛坯的体积为π×32×6=54π cm3,所以切削掉部分的体积为54π-34π=20π cm3,所以切削掉部分的体积与原来毛坯体积的比值为=,故选C.10. (2014课标Ⅰ,8,5分)如图,网格纸的各小格都是正方形,粗实线画出的是一个几何体的三视图,则这个几何体是()A.三棱锥B.三棱柱C.四棱锥D.四棱柱[解析] 10.由题中三视图可知该几何体的直观图如图所示,则这个几何体是三棱柱,故选B.11.(2011广东, 7, 5分)正五棱柱中, 不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线, 那么一个正五棱柱对角线的条数共有()A. 20B. 15C. 12D. 10[解析] 11.解法一:由题意知从一个顶点可作2条对角线, 故一共有2×5=10条, 故选D.解法二:依题意在一底上选一点共有种选法. 另一底上选符合要求的点有种, 所以共有×=10条对角线.12. (2011重庆, 10, 5分)高为的四棱锥S-ABCD的底面是边长为1的正方形, 点S、A、B、C、D均在半径为1的同一球面上, 则底面ABCD的中心与顶点S之间的距离为()A. B. C. D.[解析] 12. 如图, 连结O1A, SO2, O1O2. 因正方形ABCD的边长为1, 故O1A=,在Rt△OO1A中, OO1===, 图中☉O1和☉O2所在的平面平行, 且O1O2=2OO1=, 因S到面ABCD的距离为, 故S在☉O2上.在Rt△SO2O1中, SO1===, 故选A.13. (2009辽宁, 5, 5分)如果把地球看成一个球体, 则地球上北纬60°纬线长和赤道线长的比值为()A. 0. 8B. 0. 75C. 0. 5D. 0. 25[解析] 13.作出截面图. 由图可知2πr∶2πR=sin 30°=. 故选C.14. (2009四川, 9, 5分)如图, 在半径为3的球面上有A、B、C三点, ∠ABC=90°, BA=BC, 球心O到平面ABC的距离是, 则B、C两点的球面距离是()A. B. π C. π D. 2π[解析] 14.∵∠ABC=90°, AB=BC. 设△ABC外接圆圆心为O1, 则O1在AC中点处. OO1=, OA=3, ∴AO1=, BC=3,∴∠BOC=. ∴B、C两点的球面距离d=×3=π.15. (2009全国Ⅱ, 12, 5分)纸制的正方体的六个面根据其方位分别标记为上、下、东、南、西、北. 现在沿该正方体的一些棱将正方体剪开、外面朝上展平, 得到右侧的平面图形, 则标“△”的面的方位是()A.南B. 北C. 西D. 下[解析] 15. 如图所示.16.(2009湖北, 6, 5分)如图, 在三棱柱ABC-A1B1C1中, ∠ACB=90°, ∠ACC1=60°, ∠BCC1=45°, 侧棱CC1的长为1, 则该三棱柱的高等于()A. B. C. D.[解析] 16.如图, 作C1O⊥底面ABC于点O, 作OE⊥BC于E, 作OF⊥AC于F, 连结C1E、C1F. 可知C1F⊥FC, C1E⊥BC. 根据已知条件可得OE=FC=CC1=.C1E=, ∴高C1O===. 故选A.17. (2009重庆, 9, 5分)在正四棱柱ABCD-A1B1C1D1中, 顶点B1到对角线BD1和到平面A1BCD1的距离分别为h和d, 则下列命题中正确的是()A. 若侧棱的长小于底面的边长, 则的取值范围为(0, 1)B. 若侧棱的长小于底面的边长, 则的取值范围为C. 若侧棱的长大于底面的边长, 则的取值范围为D. 若侧棱的长大于底面的边长, 则的取值范围为[解析] 17.设正四棱柱底面边长为a, 高为b, 如图, B1到平面A1BCD1的距离d==B1E, B1到对角线BD1的距离h=B1F=则====.当a<b即0<<1时, =∈, 选C.18. (2008全国Ⅱ, 12, 5分)已知球的半径为2, 相互垂直的两个平面分别截球面得两个圆. 若两圆的公共弦长为2, 则两圆的圆心距等于()A. 1B.C.D. 2[解析] 18. 如图, 两圆圆心分别为O1、O2, 公共弦为BC, 且BC的中点A, 设O1A=a, 则O1B2=a2+1. 在Rt△OO1B中, O1O2=OB2-O1B2=3-a2.∴O1O2====. 故选C.另解:四边形OO1AO2为矩形, 则O1O2=OA, OA==, ∴选C.19. (2008重庆, 11, 5分)如图, 模块①-⑤均由4个棱长为1的小正方体构成, 模块⑥由15个棱长为1的小正方体构成. 现从模块①-⑤中选出三个放到模块⑥上, 使得模块⑥成为一个棱长为3的大正方体. 则下列选择方案中, 能够完成任务的为()A. 模块①, ②, ⑤B. 模块①, ③, ⑤C. 模块②, ④, ⑤D. 模块③, ④, ⑤[解析] 19. 由四个选择支可以看出一定有模块⑤, 将模块⑤拼上后最上层缺少一个如下图的模块, 显然由①②可组合成, 故选A.20.(2008陕西, 8, 5分)长方体ABCD-A1B1C1D1的各顶点都在半径为1的球面上, 其中AB∶AD∶AA1=2∶1∶, 则A, B两点的球面距离为()A. B. C. D.[解析] 20. 设AB=2x, 则AD=x, AA1=x, 又球直径等于长方体对角线长,∴=2⇒2x=, 即AB=.cos∠AOB==0, 得∠AOB=, 所以所求的球面距离为R=, 故选C.21.(2008湖南, 9, 5分)长方体ABCD-A1B1C1D1的8个顶点在同一个球面上, 且AB=2, AD=, AA1=1, 则顶点A、B间的球面距离是()A. B. C. π D. 2π[解析] 21.长方体对角线交点O即为球心,对角线长l==2, ∴球半径R=.而∠AOB=, ∴A、B两点的球面距离为R=. 故选B.22. (2007安徽, 10, 5分)把边长为的正方形ABCD沿对角线AC折成直二面角, 折成直二面角后, 在A、B、C、D四点所在的球面上, B与D两点之间的球面距离为()A. πB. πC.D.[解析] 22. 如图, 折成直二面角后, AC中点O是A、B、C、D四点所在球的球心,OB=OD=AC=1, ∠BOD=, 所以, B与D两点之间的球面距离为×1=, 故选C.23.(2007陕西, 7, 5分)Rt△ABC的三个顶点在半径为13的球面上, 两直角边的长分别为6和8, 则球心到平面ABC的距离是()A. 5B. 6C. 10D. 12[解析] 23. 由已知:过△ABC三顶点的截面圆半径为r==5, 又球半径R=13,∴ 球心到面ABC距离为d==12. 故选D.24.(2007四川, 6, 5分)设球O的半径是1, A、B、C是球面上三点, 已知A到B、C两点的球面距离都是, 且二面角B-OA-C的大小为, 则从A点沿球面经B、C两点再回到A点的最短距离是()25.A. B. C. D.[解析] 24.由题可知, 最短距离为AB、BC、CA的球面距离之和, 又∠AOB=∠AOC=,∴d min=++=π, 故选C.25.(2007江西, 9, 5分)四面体ABCD的外接球球心在CD上, 且CD=2, AB=, 在外接球面上两点A、B间的球面距离是()A. B. C. D.[解析] 25. 由题意知球的半径R==1, 设AB对应的球心角为θ, 则sin==,∴θ=. ∴AB的球面距离为, 故选C.26. (2011浙江, 7, 5分)若某几何体的三视图如图所示, 则这个几何体的直观图可以是()[解析] 26. 所给选项中, A、C选项的正视图、俯视图不符合, D选项的侧视图不符合, 只有选项B符合, 故选B.27.(2011课标, 8, 5分)在一个几何体的三视图中, 正视图和俯视图如图所示, 则相应的侧视图可以为()[解析] 27. 由几何体的正视图和俯视图可知, 该几何体应为一个半圆锥和一个有一侧面(与半圆锥的轴截面为同一三角形)垂直于底面的三棱锥的组合体, 故其侧视图应为D.28.(2011山东, 11, 5分)右图是长和宽分别相等的两个矩形. 给定下列三个命题:①存在三棱柱, 其正(主)视图、俯视图如图;②存在四棱柱, 其正(主)视图、俯视图如图;③存在圆柱, 其正(主)视图、俯视图如右图. 其中真命题的个数是()A. 3B. 2C. 1D. 0[解析] 28. 如图①②③的正(主)视图和俯视图都与原题相同, 故选A.29. (2011辽宁, 8, 5分)一个正三棱柱的侧棱长和底面边长相等, 体积为2, 它的三视图中的俯视图如图所示, 左视图是一个矩形, 则这个矩形的面积是()A. 4B. 2C. 2D.[解析] 29. 作出直观图(如图所示), 设棱长为a, 由a2·a=2, 解得a=2, 取AB与A1B1的中点分别为D、D1, 则左视图即为矩形CC1D1D, 其中C1D1=, 其面积为2, 故选B.30.(2011江西, 9, 5分)将长方体截去一个四棱锥, 得到的几何体如下图所示, 则该几何体的左视图为()[解析] 30.根据“长对正, 宽相等, 高平齐”原则, 易知选项D符合题意.31.(2010北京, 5, 5分)一个长方体去掉一个小长方体, 所得几何体的正(主)视图与侧(左)视图分别如下图所示, 则该几何体的俯视图为()[解析] 31. 正视图中小长方形在左上方, 对应俯视图应该在左侧, 排除B, D, 侧视图中小长方形在右上方, 排除A, 故选C.32. (2010安徽, 9, 5分)一个几何体的三视图如图, 该几何体的表面积是()A. 372B. 360C. 292D. 280[解析] 32. 该几何体直观图如图所示, 上方长方体长、宽、高分别为6、2、8, 下方长方体长、宽、高分别为8、10、2. 其表面积为两长方体表面积之和再减去如图阴影部分面积的2倍, 即S=S上+S下-2S阴=2×(6×2+2×8+6×8)+2×(8×10+2×8+2×10)-2×6×2=360.33.(2010福建, 3, 5分)若一个底面是正三角形的三棱柱的正视图如图所示, 则其侧面积等于()A. B. 2 C. 2 D. 6[解析] 33.由三棱柱的正视图可知此三棱柱为底面边长为2, 侧棱长为1的正三棱柱, ∴S侧=2×1×3=6, 故选D.34.(2010陕西, 8, 5分)若某空间几何体的三视图如图所示, 则该几何体的体积是()A. 2B. 1C.D.[解析] 34.由三视图知该几何体为倒放着的直三棱柱, 其底面为直角三角形, 两直角边边长分别是1和, 棱柱的高为, 所以该几何体的体积V=×1××=1.35.(2010广东, 9, 5分)如图, △ABC为正三角形, AA'∥BB'∥CC', CC'⊥平面ABC且3AA'=BB'=CC'=AB, 则多面体ABC-A'B'C'的正视图(也称主视图)是()[解析] 35.正视图反映了物体前后的位置关系, 反映物体的高度和宽度, 由给出的选项知, 只有D正确, 故选D36. (2010浙江, 8, 5分)若某几何体的三视图(单位:cm)如图所示, 则此几何体的体积是()A. cm3B. cm3C. cm3D. cm3[解析] 36. 由几何体的三视图可知, 空间几何体为一个长方体与四棱台的组合体. 长方体的长、宽、高分别为4、4、2, 四棱台的上底面为正方形, 其边长为4, 下底面为正方形, 边长为8, 高为2. 因此组合体的体积为V=4×4×2+×(64+16+)×2=32+=, 故选B.37. (2009上海, 16, 4分)如图, 已知三棱锥的底面是直角三角形, 直角边长分别为3和4, 过直角顶点的侧棱长为4, 且垂直于底面, 该三棱锥的主视图是()[解析] 37. 从正面看, 应看到直角边为3的顶点, 而高为4, 故主视图应为B.38. (2009山东, 4, 5分)一空间几何体的三视图如图所示, 则该几何体的体积为()A. 2π+2B. 4π+2C. 2π+D. 4π+[解析] 38. 由几何体的三视图可知, 该几何体是由一个底面直径和高都是2的圆柱和一个底面边长为, 侧棱长为2的正四棱锥叠放而成. 故该几何体的体积V=π ·12·2+·()2·=2π+, 故选C.39.(2009宁夏, 11, 5分)一个棱锥的三视图如图, 则该棱锥的全面积(单位:cm2)为()A. 48+12B. 48+24C. 36+12D. 36+24[解析] 39.如图所示三棱锥.AO⊥底面BCD, O是BD中点, BC=CD=6, BC⊥CD, AO=4, AB=AD.S△BCD=×6×6=18, S△ABD=×6×4=12. 取BC中点E, 连结AE、OE.可得BC⊥AE, AE==5, ∴ S△ABC=S△ACD=×6×5=15,∴ S全=18+12+15+15=48+12.40.(2009福建, 5, 5分)如下图, 某几何体的正视图与侧视图都是边长为1的正方形, 且体积为, 则该几何体的俯视图可以是()[解析] 40. ∵ 体积为, 而高为1, 所以底面为一个直角三角形. 故选C.41.(2008广东, 7, 5分)将正三棱柱截去三个角(如图1所示A, B, C分别是△GHI三边的中点)得到几何体如图2, 则该几何体按图2所示方向的侧视图(或称左视图)为()[解析] 41. 不截去角的侧视图(或左视图)为矩形, 截去三个角之后A依然在, I被截去, F依然在, 则侧视图为故选A.42. (2008山东, 6, 5分)下图是一个几何体的三视图, 根据图中数据, 可得该几何体的表面积是()A. 9πB. 10πC. 11πD. 12π[解析] 42. 由几何体的三视图可知此几何体是圆柱体与球体的组合体. S=4πR2+2πr2+2πr·h, 代入数据得S表=4π·12+2π·12+2π·1·3=12π. 故选D.43.(2007山东, 3, 5分)下列几何体各自的三视图中, 有且仅有两个视图相同的是()A. ①②B. ①③C. ①④D. ②④[解析] 43. 正方体的三视图均为正方形;圆锥的三视图为两个三角形和圆;三棱台的三视图为两个梯形和一个三角形;正四棱锥的三视图为两个三角形和一个正方形, 故选D.44. (2007宁夏, 8, 5分)已知某个几何体的三视图如下, 根据图中标出的尺寸(单位:cm), 可得这个几何体的体积是()A. cm3B. cm3C. 2 000 cm3D. 4 000 cm3[解析] 44. 此几何体的图为S-ABCD, 且平面SCD⊥平面ABCD, ABCD为正方形, 边长为20 cm, S在底面的射影为CD中点E, SE=20 cm, V S-ABCD=S▱ABCD·SE=cm3.故选B.45.(2011北京, 5, 5分)某四棱锥的三视图如图所示, 该四棱锥的表面积是()A. 32B. 16+16C. 48D. 16+32[解析] 45.由三视图知, 四棱锥是底面边长为4, 高为2的正四棱锥,∴四棱锥的表面积是16+4××4×2=16+16, 故选B.46.(2011湖南, 4, 5分)如图是某几何体的三视图, 则该几何体的体积为()A. 9π+42B. 36π+18C. π+12D. π+18[解析] 46. 该几何体是由一个球与一个长方体组成的组合体, 球的直径为3, 长方体的底面是边长为3的正方形, 高为2, 故所求体积为2×32+π=π+18, 故选D.47. (2011陕西, 5, 5分)某几何体的三视图如图所示, 则它的体积为()A. 8-B. 8-C. 8-2πD.[解析] 47. 由给出的三视图可得原几何体为正方体中挖去一圆锥, 且此圆锥以正方体的上底面内切圆为底, 以正方体的棱长为高. 故所求几何体的体积为8-×π×12×2=8-.48. (2011安徽, 8, 5分)一个空间几何体的三视图如图所示, 则该几何体的表面积为()A. 48B. 32+8C. 48+8D. 80[解析] 48.换个视角看问题, 该几何体可以看成是底面为等腰梯形, 高为4的直棱柱, 且等腰梯形的两底分别为2, 4, 高为4, 故腰长为, 所以该几何体的表面积为48+8, 故选C.49.(2011广东, 9, 5分)如图, 某几何体的正视图(主视图), 侧视图(左视图)和俯视图分别是等边三角形, 等腰三角形和菱形, 则该几何体体积为()A. 4B. 4C. 2D. 2[解析] 49. 由三视图可知此几何体为四棱锥, 高为3. 所以V=Sh=××2×2×3=2, 故选C.50. (2011辽宁, 10, 5分)已知球的直径SC=4, A, B是该球球面上的两点, AB=2,∠ASC=∠BSC=45°, 则棱锥S-ABC的体积为()A. B. C. D.[解析] 50. 如图, 设球心为O, 由OS=OA=OC得∠SAC=90°, 又∠ASC=45°, 所以AS=AC=SC, 同理BS=BC=SC, 可得SC⊥面AOB, V S-ABC=S△AOB·SC=××2××4=,故选C.51.(2011全国, 12, 5分)已知平面α截一球面得圆M, 过圆心M且与α成60°二面角的平面β截该球面得圆N. 若该球面的半径为4, 圆M的面积为4π, 则圆N的面积为()A. 7πB. 9πC. 11πD. 13π[解析] 51.设球心为O, 由题意得∠MON=60°, 设圆M与圆N的半径分别为r1、r2, 由π=4π, 得r1=2, 则|OM|==2, |ON|=|OM|·cos 60°=, 所以r2==, 所以圆N 的面积为π=13π, 故选D.52. (2008四川, 8, 5分)设M是球O半径OP的中点, 分别过M、O作垂直于OP的平面, 截球面得两个圆, 则这两个圆的面积比值为()A. B. C. D.[解析] 52.设球的半径为R, 过点M且垂直于OP的圆的半径为r, OM=R. 由r2=R2-OM2=R2, 设过M、O的圆的面积分别是S'、S. S'=πr2=πR2, S=πR2, ∴S'∶S=3∶4. 故选D.53.(2010四川, 12, 5分)半径为R的球O的直径AB垂直于平面α, 垂足为B, △BCD是平面α内边长为R的正三角形, 线段AC、AD分别与球面交于点M、N, 那么M、N两点间的球面距离是()A. RarccosB. RarccosC. πRD. πR[解析] 53. 如图连结MB、NB、OM、ON, 则BM⊥AM, BN⊥AN, ∵AB⊥平面α, BC⊂α,∴AB⊥BC. 又AB=2R, BC=R, ∴AC=R.又AB2=AM·AC, ∴4R2=AM·R, AM=R. 同理AN=R, ∴MN∥CD, =, ∴MN=R. 在△OMN中, 由余弦定理得cos∠MON==, ∴∠MON=arccos,∴M、N两点的球面距离为Rarccos, 故选A.54.(2009全国Ⅰ, 9, 5分)已知三棱柱ABC-A1B1C1的侧棱与底面边长都相等, A1在底面ABC上的射影为BC的中点, 则异面直线AB与CC1所成的角的余弦值为()A. B. C. D.[解析] 54.如图, D为BC的中点, 则由题意得∠A1AD=∠BAD=30°, 由三角余弦公式得cos∠A1AB=, 则异面直线AB与CC1所成的角的余弦值为, 故选D.55. (2009全国Ⅱ, 5, 5分)已知正四棱柱ABCD-A1B1C1D1中, AA1=2AB, E为AA1中点, 则异面直线BE与CD1所成角的余弦值为()A. B. C. D.[解析] 55. 连结A1B, 则有A1B∥CD1,∴∠A1BE就是异面直线BE与CD1所成角, 在△ABE中, 设AB=1, 则有A1E=AE=1, ∴BE=, ∴A1B=. 由余弦定理可知:os∠A1BE==.56.(2007全国Ⅰ, 7, 5分)如图, 正四棱柱ABCD-A1B1C1D1中, AA1=2AB, 则异面直线A1B与AD1所成角的余弦值为()A. B. C. D.[解析] 56.连结CD1, 显然, ∠AD1C即为AD1与A1B所成的角. 设AB=a, 则AD1=CD1=a,AC=a, ∴ cos∠AD1C===. 故选D.57. (2007全国Ⅱ, 7, 5分)已知正三棱柱ABC-A1B1C1的侧棱长与底面边长相等, 则AB1与侧面ACC1A1所成角的正弦值等于()A. B. C. D.[解析] 57. 设正三棱柱棱长均为2a, 过B1作B1H⊥A1C1, 则B1H⊥面ACC1A1, 连AH, 即∠B1AH即为AB1与面ACC1A1所成的角. B1H=a, AB1=2a,∴sin∠B1AH==, ∴选A.58. (2007湖北, 5, 5分)在棱长为1的正方体ABCD-A1B1C1D1中, E、F分别为棱AA1、BB1的中点, G为棱A1B1上的一点, 且A1G=λ(0≤λ≤1), 则点G到平面D1EF的距离为()A. B. C. D.[解析] 58. 由题意知A1B1∥平面D1EF, 所以G到面D1EF的距离, 即A1到面D1EF的距离. ∵ 平面A1D1E⊥平面D1EF, ∴ A1到D1E的距离即为A1到面D1EF的距离=. 故选D.59.(2011全国, 8, 5分)已知直二面角α-l-β, 点A∈α, AC⊥l, C为垂足, 点B∈β, BD⊥l, D为垂足. 若AB=2, AC=BD=1, 则CD=()A. 2B.C.D. 1[解析] 59.由题意得AB2=AC2+CD2+BD2, 即4=1+CD2+1, 解得CD=, 故选C.60. (2009江西, 9, 5分)如图, 在四面体ABCD中, 若截面PQMN是正方形, 则在下列命题中, 错误的为()A. AC⊥BDB. AC∥截面PQMNC. AC=BDD. 异面直线PM与BD所成的角为45°[解析] 60.∵MN∥PQ, ∴MN∥面ABC, ∴MN∥AC. 同理BD∥QM.∵MN⊥QM, ∴AC⊥BD, ∴A是对的;∵AC∥MN, ∴AC∥面PQMN, 故B对;∵BD∥QM, ∴PM与BD所成角即为∠PMQ, ∴PM与BD成45°角, 故D对.在正三棱锥中, AC与BD不一定相等, 而截面正方形PQMN存在. 故AC=BD错, 选C.61.(2012课标全国, 7, 5分) 如图, 网格纸上小正方形的边长为1, 粗线画出的是某几何体的三视图, 则此几何体的体积为()A. 6B. 9C. 12D. 18[解析] 61.由三视图可得, 该几何体为三棱锥S-ABC, 其中底面△ABC为等腰三角形, 底边AC=6, AC边上的高为3, SB⊥底面ABC, 且SB=3, 所以该几何体的体积V=××6×3×3=9.故选B.62.(2012福建, 4, 5分) 一个几何体的三视图形状都相同、大小均相等, 那么这个几何体不可以是()A. 球B. 三棱锥C. 正方体D. 圆柱[解析] 62.A项, 球的三视图为三个全等的圆. 故不选A. B项, 如图所示:正方体内的正四面体的三视图是三个全等的正方形. 故不选B. C项, 正方体的三视图为三个全等的正方形, 故不选C. 故选D.63.(2012浙江, 3, 5分) 已知某三棱锥的三视图(单位: cm) 如图所示, 则该三棱锥的体积是()A. 1 cm3B. 2 cm3C. 3 cm3D. 6 cm3[解析] 63.由三视图可知, 该三棱锥底面为两条直角边分别为1 cm和2 cm的直角三角形, 一条侧棱垂直于底面, 垂足为直角顶点, 且高为3 cm, 所以体积V=××1×2×3=1(cm3) , 故选A.64.(2012湖南, 4, 5分) 某几何体的正视图和侧视图均如图所示, 则该几何体的俯视图不可能是()[解析] 64.A图是两个圆柱的组合体的俯视图; B图是一个四棱柱与一个圆柱的组合体的俯视图; D图是一个底面为直角三角形的三棱柱与一个四棱柱的组合体的俯视图, 采用淘汰法, 故选C.65.(2012江西, 7, 5分) 若一个几何体的三视图如图所示, 则此几何体的体积为()A. B. 5 C. D. 4[解析] 65.由三视图可知该几何体为直六棱柱, 所以V=Sh, 其底面如图所示, 所以V=4, 故选D.66.(2012广东, 7, 5分) 某几何体的三视图如图所示, 它的体积为()A. 72πB. 48πC. 30πD. 24π[解析] 66.由所给三视图可知, 该几何体是一个半球和圆锥的组合体, 其中半球的半径和圆锥的底面半径均为3, 圆锥的高为4, 所以几何体的体积为π×33+π×32×4=30π, 故选C.67.(2012陕西, 8, 5分) 将正方体(如图1所示) 截去两个三棱锥, 得到图2所示的几何体, 则该几何体的左视图为()[解析] 67.由几何体知左视图为正方形且对角线AD1为可视线, CB1看不见, 在视图中画为虚线, 故选B.68.(2012北京, 7, 5分) 某三棱锥的三视图如图所示, 该三棱锥的表面积是()A. 28+6B. 30+6C. 56+12D. 60+12[解析] 68.如图所示: 将三棱锥置于长方体中.此长方体长为5、宽为4、高为4, 三棱锥为P-ABC, P在底面内的射影为P',S P-ABC=S△PAB+S△PBC+S△PAC+S△ABC=×2×6+×4×5+×5×4+×5×4=6+10+10+10 =30+6. 故选B.69.(2012重庆, 9, 5分) 设四面体的六条棱的长分别为1, 1, 1, 1, 和a, 且长为a的棱与长为的棱异面, 则a的取值范围是()A. (0, )B. (0, )C. (1, )D. (1, )[解析] 69.根据题意构造四面体ABCD, AB=a, CD=, AC=AD=BC=BD=1, 取CD中点E, 连结BE, AE, 则AE=BE=. 又∵a<+=,∴0. 故选A.70.(2013大纲,11,5分) 已知正四棱柱ABCD-A1B1C1D1中, AA1=2AB, 则CD与平面BDC1所成角的正弦值等于()A. B. C. D.[解析] 70.∵ABCD-A1B1C1D1为正四棱柱, ∴底面ABCD为正方形, 且侧面与底面垂直.∵AA1=2AB, 设AB=a, 则AA1=2a,∴BC1=a, BD= a. 设C到平面C1DB的距离为h, 则=,∴S△BCD·CC1=·h, ∴h=. 设CD与平面BDC1所成角为θ,则sin θ==. 故选A 71.(2013重庆,8,5分) 某几何体的三视图如图所示, 则该几何体的表面积为()A. 180B. 200C. 220D. 240[解析] 71.由三视图知该几何体是如图所示的四棱柱ABCD-A1B1C1D1.=2×10=20, =(3+2+3) ×10=80,S四边形ABCD==×(2+8) ×4=20, ==10×5=50,∴表面积=20+80+2×20+2×50=240. 故选D72.(2013四川,2,5分) 一个几何体的三视图如图所示, 则该几何体可以是()A. 棱柱B. 棱台C. 圆柱D. 圆台[解析] 72.由正视图和侧视图可知, 该几何体不可能是圆柱, 排除选项C; 又由俯视图可知, 该几何体不可能是棱柱或棱台, 排除选项A、B. 故选D.73.(2013广东,6,5分) 某三棱锥的三视图如图所示, 则该三棱锥的体积是()A. B. C. D. 1[解析] 73.由三视图可知该三棱锥的底面是边长为1的等腰直角三角形, 高为2. 由锥体的体积公式可知V=××1×1×2=. 故选B.74.(2013江西,8,5分) 一几何体的三视图如图所示, 则该几何体的体积为()A. 200+9πB. 200+18πC. 140+9πD. 140+18π[解析] 74.该几何体的直观图是由一个长方体和圆柱的一半所组成的(如图). 其中长方体的长、宽、高分别为10、4、5, 圆柱的底面半径为3, 高为2. 从而该几何体的体积V=10×5×4+π×32×2=200+9π, 故选A.75.(2013湖南,7,5分) 已知正方体的棱长为1, 其俯视图是一个面积为1的正方形, 侧视图是一个面积为的矩形, 则该正方体的正视图的面积等于()A. B. 1 C. D.[解析] 75.由题意可知该正方体的放置如图所示, 侧视图的方向垂直于面BDD1B1, 正视图的方向垂直于面A1C1CA, 且正视图是长为, 宽为1的矩形, 故正视图的面积为, 因此选D.76.(2013浙江,5,5分) 已知某几何体的三视图(单位: cm) 如图所示, 则该几何体的体积是()A. 108 cm3B. 100 cm3C. 92 cm3D. 84 cm3[解析] 76.由三视图可知, 该几何体是一个长方体截去了一个三棱锥, 结合所给数据, 可得其体积为6×6×3-××4×4×3=100(cm3), 故选B77.(2013山东,4,5分) 一个四棱锥的侧棱长都相等, 底面是正方形, 其正(主) 视图如图所示, 则该四棱锥侧面积和体积分别是()A. 4, 8B. 4,C. 4(+1),D. 8,8[解析] 77.由题意知该四棱锥为正四棱锥, 其底面边长为2, 正四棱锥的高为2, 故侧面三角形的高为. 所以该四棱锥的侧面积为4××2×=4, 体积为×22×2=, 故答案为B.78.(2013辽宁,10,5分) 已知直三棱柱ABC-A1B1C1的6个顶点都在球O的球面上. 若AB=3, AC=4, AB⊥AC, AA1=12, 则球O的半径为()A. B. 2 C. D. 3[解析] 78.由题意知, 该三棱柱可以看作是长方体的一部分, 且长方体的三条棱长为3、4、12, 又∵三棱柱的外接球即为长方体的外接球, (2R) 2=32+42+122, ∴R=. 故选C.79.(2013北京,8,5分) 如图, 在正方体ABCD-A1B1C1D1中, P为对角线BD1的三等分点, P 到各顶点的距离的不同取值有()A. 3个B. 4个C. 5个D. 6个[解析] 79.过P作平面A1B1C1D1、ABCD的垂线分别交D1B1、DB于E、F点, 易知P也是EF 的三等分点, 设正方体的棱长为a, 则PA1=PC1=a; PD1=a; PB=a; PB1=a, PA=PC=a;PD=a. 故有4个不同的值. 故选B.80.(2013课标Ⅱ,9,5分) 一个四面体的顶点在空间直角坐标系O-xyz中的坐标分别是(1,0, 1), (1,1, 0), (0,1, 1), (0,0, 0), 画该四面体三视图中的正视图时, 以zOx平面为投影面, 则得到的正视图可以为()[解析] 80.在空间直角坐标系中, 易知O(0,0, 0), A(1,0, 1), B(1,1, 0), C(0,1, 1) 恰为单位正方体的四个顶点. 因此该几何体以zOx平面为投影面所得的正视图为A.81.(2013课标Ⅰ, 11,5分). 某几何体的三视图如图所示, 则该几何体的体积为()A. 16+8πB. 8+8πC. 16+16πD. 8+16π[解析] 81.由所给三视图可知该几何体是一个组合体, 下方是底面为半圆的柱体, 底面半圆的半径为2, 高为4; 上方为长、宽、高分别为4、2、2的长方体. 所以该几何体的体积为π×22×4+4×2×2=16+8π, 故选A.82. (2014江苏,8,5分)设甲、乙两个圆柱的底面积分别为S1、S2,体积分别为V1、V2,若它们的侧面积相等,且=,则的值是________.[解析] 82.设圆柱甲的底面半径为r1,高为h1,圆柱乙的底面半径为r2,高为h2.由题意得==,∴=. 又∵S甲侧=S乙侧,即2πr1h1=2πr2h2,∴==, 故==·=×=.83. (2014山东,13,5分)一个六棱锥的体积为2,其底面是边长为2的正六边形,侧棱长都相等,则该六棱锥的侧面积为________.[解析] 83.设六棱锥的高为h,斜高为h0.因为该六棱锥的底面是边长为2的正六边形,所以底面面积为×2×2×sin 60°×6=6,则×6h=2,得h=1,所以h0==2,所以该六棱锥的侧面积为×2×2×6=12.84. (2014天津,10,5分)一个几何体的三视图如图所示(单位:m),则该几何体的体积为________m3.[解析] 84.由三视图知该几何体是由一个圆锥与一个圆柱构成的组合体,其体积为π×22×2+π×12×4=m3.85. (2014北京,11,5分)某三棱锥的三视图如图所示,则该三棱锥最长棱的棱长为________.[解析] 85.由三视图可知该几何体的直观图如图所示,其中PA⊥面ABC,△ABC为等腰直角三角形,且PA=2,AB=BC=,AC=2,所以PC=2>PB=,故该三棱锥最长棱的棱长为2.86.(2011四川, 15, 4分)如图, 半径为4的球O中有一内接圆柱, 当圆柱的侧面积最大时, 球的表面积与该圆柱的侧面积之差是.[解析] 86.设圆柱的底面半径为r, 则圆柱的高为2, S圆柱侧=2·2πr=4π≤4π·=32π.当r2=16-r2, 即r2=8时, 上式取等号, S圆柱侧=32π,此时, S球=4π·42=64π, 故S球-S圆柱侧=64π-32π=32π.87.(2010全国Ⅱ, 16, 5分)已知球O的半径为4, 圆M与圆N为该球的两个小圆, AB为圆M 与圆N的公共弦, AB=4. 若OM=ON=3, 则两圆圆心的距离MN=.[解析] 87. 由已知得△AOB为正三角形, 其边长为4. 设AB的中点为O1, 则|OO1|=2. 又OM=ON=3, O1M=O1N=. 所以, MN=2×=3.88.(2010湖北, 15, 5分)圆柱形容器内盛有高度为8 cm的水, 若放入三个相同的球(球的半径与圆柱的底面半径相同)后, 水恰好淹没最上面的球(如图所示), 则球的半径是cm.[解析] 88.设球的半径为r cm, 依等体积法知:πr3·3+πr2·8=πr2·6r, ∴2r=8, r=4.89. (2010江西, 16, 5分)长方体ABCD-A1B1C1D1的顶点均在同一个球面上, AB=AA1=1,BC=, 则A, B两点间的球面距离为.[解析] 89.设长方体外接球的球心为O, 半径R==1,。
2022年高考立体几何汇编

2022年高考立体几何汇编一.选择题(共10小题)1.(2021•天津)两个圆锥的底面是一个球的同一截面,顶点均在球面上,若球的体积为,两个圆锥的高之比为1:3,则这两个圆锥的体积之和为()A.3πB.4πC.9πD.12π2.(2021•新高考Ⅱ)北斗三号全球卫星导航系统是我国航天事业的重要成果.在卫星导航系统中,地球静止同步轨道卫星的轨道位于地球赤道所在平面,轨迹高度为36000km(轨道高度是指卫星到地球表面的距离).将地球看作是一个球心为O,半径r为6400km的球,其上点A的纬度是指OA与赤道平面所成角的度数.地球表面上能直接观测到的一颗地球静止同步轨道卫星点的纬度最大值为α,该卫星信号覆盖地球表面的表面积S=2πr2(1﹣cosα)(单位:km2),则S占地球表面积的百分比约为()A.26%B.34%C.42%D.50% 3.(2021•新高考Ⅱ)正四棱台的上、下底面的边长分别为2,4,侧棱长为2,则其体积为()A.20+12B.28C.D.4.(2021•北京)某四面体的三视图如图所示,该四面体的表面积为()A.B.4C.3+D.2 5.(2021•浙江)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是()A.B.3C.D.3 6.(2021•浙江)如图,已知正方体ABCD﹣A1B1C1D1,M,N分别是A1D,D1B的中点,则()A.直线A1D与直线D1B垂直,直线MN∥平面ABCDB.直线A1D与直线D1B平行,直线MN⊥平面BDD1B1C.直线A1D与直线D1B相交,直线MN∥平面ABCDD.直线A1D与直线D1B异面,直线MN⊥平面BDD1B17.(2021•新高考Ⅰ)已知圆锥的底面半径为,其侧面展开图为一个半圆,则该圆锥的母线长为()A.2B.2C.4D.4 8.(2021•甲卷)已知A,B,C是半径为1的球O的球面上的三个点,且AC⊥BC,AC=BC=1,则三棱锥O﹣ABC的体积为()A.B.C.D.9.(2021•甲卷)在一个正方体中,过顶点A的三条棱的中点分别为E,F,G.该正方体截去三棱锥A﹣EFG后,所得多面体的三视图中,正视图如图所示,则相应的侧视图是()A.B.C.D.10.(2021•乙卷)在正方体ABCD﹣A1B1C1D1中,P为B1D1的中点,则直线PB与AD1所成的角为()A.B.C.D.二.多选题(共2小题)11.(2021•新高考Ⅱ)如图,下列正方体中,O为底面的中点,P为所在棱的中点,M,N 为正方体的顶点,则满足MN⊥OP的是()A.B.C.D.12.(2021•新高考Ⅰ)在正三棱柱ABC﹣A1B1C1中,AB=AA1=1,点P满足=λ+μ,其中λ∈[0,1],μ∈[0,1],则()A.当λ=1时,△AB1P的周长为定值B.当μ=1时,三棱锥P﹣A1BC的体积为定值C.当λ=时,有且仅有一个点P,使得A1P⊥BPD.当μ=时,有且仅有一个点P,使得A1B⊥平面AB1P三.填空题(共4小题)13.(2021•上海)已知圆柱的底面圆半径为1,高为2,AB为上底面圆的一条直径,C是下底面圆周上的一个动点,则ABC的面积的取值范围为.14.(2021•甲卷)已知一个圆锥的底面半径为6,其体积为30π,则该圆锥的侧面积为.15.(2021•乙卷)以图①为正视图,在图②③④⑤中选两个分别作为侧视图和俯视图,组成某个三棱锥的三视图,则所选侧视图和俯视图的编号依次为(写出符合要求的一组答案即可).16.(2021•上海)已知圆柱的底面半径为1,高为2,则圆柱的侧面积为.四.解答题(共11小题)17.(2021•天津)如图,在棱长为2的正方体ABCD﹣A1B1C1D1中,E,F分别为棱BC,CD的中点.(1)求证:D1F∥平面A1EC1;(2)求直线AC1与平面A1EC1所成角的正弦值;(3)求二面角A﹣A1C1﹣E的正弦值.18.(2021•新高考Ⅱ)在四棱锥Q﹣ABCD中,底面ABCD是正方形,若AD=2,QD=QA =,QC=3.(Ⅰ)求证:平面QAD⊥平面ABCD;(Ⅱ)求二面角B﹣QD﹣A的平面角的余弦值.19.(2021•上海)如图,在长方体ABCD﹣A1B1C1D1中,已知AB=BC=2,AA1=3.(1)若P是棱A1D1上的动点,求三棱锥C﹣P AD的体积;(2)求直线AB1与平面ACC1A1的夹角大小.20.(2021•北京)已知正方体ABCD﹣A1B1C1D1,点E为A1D1中点,直线B1C1交平面CDE 于点F.(1)求证:点F为B1C1中点;(2)若点M为棱A1B1上一点,且二面角M﹣CF﹣E的余弦值为,求.21.(2021•甲卷)已知直三棱柱ABC﹣A1B1C1中,侧面AA1B1B为正方形,AB=BC=2,E,F分别为AC和CC1的中点,BF⊥A1B1.(1)求三棱锥F﹣EBC的体积;(2)已知D为棱A1B1上的点,证明:BF⊥DE.22.(2021•乙卷)如图,四棱锥P﹣ABCD的底面是矩形,PD⊥底面ABCD,PD=DC=1,M为BC中点,且PB⊥AM.(1)求BC;(2)求二面角A﹣PM﹣B的正弦值.23.(2021•浙江)如图,在四棱锥P﹣ABCD中,底面ABCD是平行四边形,∠ABC=120°,AB=1,BC=4,P A=,M,N分别为BC,PC的中点,PD⊥DC,PM⊥MD.(Ⅰ)证明:AB⊥PM;(Ⅱ)求直线AN与平面PDM所成角的正弦值.24.(2021•甲卷)已知直三棱柱ABC﹣A1B1C1中,侧面AA1B1B为正方形,AB=BC=2,E,F分别为AC和CC1的中点,D为棱A1B1上的点,BF⊥A1B1.(1)证明:BF⊥DE;(2)当B1D为何值时,面BB1C1C与面DFE所成的二面角的正弦值最小?25.(2021•乙卷)如图,四棱锥P﹣ABCD的底面是矩形,PD⊥底面ABCD,M为BC的中点,且PB⊥AM.(1)证明:平面P AM⊥平面PBD;(2)若PD=DC=1,求四棱锥P﹣ABCD的体积.26.(2021•新高考Ⅰ)如图,在三棱锥A﹣BCD中,平面ABD⊥平面BCD,AB=AD,O 为BD的中点.(1)证明:OA⊥CD;(2)若△OCD是边长为1的等边三角形,点E在棱AD上,DE=2EA,且二面角E﹣BC﹣D的大小为45°,求三棱锥A﹣BCD的体积.27.(2021•上海)四棱锥P﹣ABCD,底面为正方形ABCD,边长为4,E为AB中点,PE⊥平面ABCD.(1)若△P AB为等边三角形,求四棱锥P﹣ABCD的体积;(2)若CD的中点为F,PF与平面ABCD所成角为45°,求PC与AD所成角的大小.2021年高考立体几何汇编参考答案与试题解析一.选择题(共10小题)1.(2021•天津)两个圆锥的底面是一个球的同一截面,顶点均在球面上,若球的体积为,两个圆锥的高之比为1:3,则这两个圆锥的体积之和为()A.3πB.4πC.9πD.12π【分析】由题意画出图形,由球的体积求出球的半径,再由直角三角形中的射影定理求得截面圆的半径,代入圆锥体积公式得答案.【解答】解:如图,设球O的半径为R,由题意,,可得R=2,则球O的直径为4,∵两个圆锥的高之比为1:3,∴AO1=1,BO1=3,由直角三角形中的射影定理可得:r2=1×3,即r=.∴这两个圆锥的体积之和为V=.故选:B.【点评】本题考查球内接圆锥体积的求法,考查空间想象能力与思维能力,考查运算求解能力,是中档题.2.(2021•新高考Ⅱ)北斗三号全球卫星导航系统是我国航天事业的重要成果.在卫星导航系统中,地球静止同步轨道卫星的轨道位于地球赤道所在平面,轨迹高度为36000km(轨道高度是指卫星到地球表面的距离).将地球看作是一个球心为O,半径r为6400km的球,其上点A的纬度是指OA与赤道平面所成角的度数.地球表面上能直接观测到的一颗地球静止同步轨道卫星点的纬度最大值为α,该卫星信号覆盖地球表面的表面积S=2πr2(1﹣cosα)(单位:km2),则S占地球表面积的百分比约为()A.26%B.34%C.42%D.50%【分析】由题意,地球静止同步卫星轨道的左右两端的竖直截面图,求解cosα,根据卫星信号覆盖的地球表面面积可得S占地球表面积的百分比.【解答】解:由题意,作出地球静止同步卫星轨道的左右两端的竖直截面图,则OB=36000+6400=424000,那么cosα=;卫星信号覆盖的地球表面面积S=2πr2(1﹣cosα),那么,S占地球表面积的百分比为42%.故选:C.【点评】本题考查了对题目的阅读能力和理解能力,属于基础题.3.(2021•新高考Ⅱ)正四棱台的上、下底面的边长分别为2,4,侧棱长为2,则其体积为()A.20+12B.28C.D.【分析】过A作AE⊥A1B1,得A1E==1,AE==.连接AC,A1C1,过A作AG⊥A1C1,求出A1G=,从而AG==,由此能求出正四棱台的体积.【解答】解:如图ABCD﹣A1B1C1D1为正四棱台,AB=2,A1B1=4,AA1=2.在等腰梯形A1B1BA中,过A作AE⊥A1B1,可得A1E==1,AE===.连接AC,A1C1,AC=,A1C1==4,过A作AG⊥A1C1,A1G==,AG===,∴正四棱台的体积为:V===.故选:D.【点评】本题考查四棱台的体积的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力、推理论证能力,是中档题.4.(2021•北京)某四面体的三视图如图所示,该四面体的表面积为()A.B.4C.3+D.2【分析】由三视图还原原几何体,其中P A⊥底面ABC,AB⊥AC,P A=AB=AC=2,再由三角形面积公式求解.【解答】解:由三视图还原原几何体如图,P A⊥底面ABC,AB⊥AC,P A=AB=AC=1,则△PBC是边长为的等边三角形,则该四面体的表面积为S=.故选:A.【点评】本题考查由三视图求面积、体积,关键是由三视图还原原几何体,是中档题.5.(2021•浙江)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是()A.B.3C.D.3【分析】由三视图还原原几何体,可知该几何体为直四棱柱,底面四边形ABCD为等腰梯形,由已知三视图求得对应的量,再由棱柱体积公式求解.【解答】解:由三视图还原原几何体如图,该几何体为直四棱柱,底面四边形ABCD为等腰梯形,其中AB∥CD,由三视图可知,延长AD与BC后相交于一点,且AD⊥BC,且AB=,CD=,AA1=1,等腰梯形的高为=,则该几何体的体积V==.故选:A.【点评】本题考查由三视图求面积、体积,关键是由三视图还原原几何体,是中档题.6.(2021•浙江)如图,已知正方体ABCD﹣A1B1C1D1,M,N分别是A1D,D1B的中点,则()A.直线A1D与直线D1B垂直,直线MN∥平面ABCDB.直线A1D与直线D1B平行,直线MN⊥平面BDD1B1C.直线A1D与直线D1B相交,直线MN∥平面ABCDD.直线A1D与直线D1B异面,直线MN⊥平面BDD1B1【分析】通过证明直线A1D⊥平面ABD1,MN是△ABD1的中位线,可判断A;根据异面直线的判断可知A1D与直线D1B是异面直线,可判断B;根据异面直线的判断可知直线A1D与直线D1B是异面直线,可判断C;由MN∥AB,可知MN不与平面BDD1B1垂直,可判断D.【解答】解:连接AD1,如图:由正方体可知A1D⊥AD1,A1D⊥AB,∴A1D⊥平面ABD1,∴A1D⊥D1B,由题意知MN为△D1AB的中位线,∴MN∥AB,又∵AB⊂平面ABCD,MN⊄平面ABCD,∴MN∥平面ABCD.∴A对;由正方体可知A1D与平面BDD1相交于点D,D1B⊂平面BDD1,D∉D1B,∴直线A1D与直线D1B是异面直线,∴B、C错;∵MN∥AB,AB不与平面BDD1B1垂直,∴MN不与平面BDD1B1垂直,∴D错.故选:A.【点评】本题考查了线面平行的判定定理和线面垂直的判定定理与性质,考查了逻辑推理核心素养,属于中档题.7.(2021•新高考Ⅰ)已知圆锥的底面半径为,其侧面展开图为一个半圆,则该圆锥的母线长为()A.2B.2C.4D.4【分析】设母线长为l,利用圆锥底面周长即为侧面展开图半圆的弧长,圆锥的母线长即为侧面展开图半圆的半径,列出方程,求解即可.【解答】解:由题意,设母线长为l,因为圆锥底面周长即为侧面展开图半圆的弧长,圆锥的母线长即为侧面展开图半圆的半径,则有,解得,所以该圆锥的母线长为.故选:B.【点评】本题考查了旋转体的理解和应用,解题的关键是掌握圆锥底面周长即为侧面展开图半圆的弧长,圆锥的母线长即为侧面展开图半圆的半径,考查了逻辑推理能力与运算能力和空间思维能力,属于基础题.8.(2021•甲卷)已知A,B,C是半径为1的球O的球面上的三个点,且AC⊥BC,AC=BC=1,则三棱锥O﹣ABC的体积为()A.B.C.D.【分析】先确定△ABC所在的截面圆的圆心O1为斜边AB的中点,然后在Rt△ABC和Rt△AOO1中,利用勾股定理求出OO1,再利用锥体的体积公式求解即可.【解答】解:因为AC⊥BC,AC=BC=1,所以底面ABC为等腰直角三角形,所以△ABC所在的截面圆的圆心O1为斜边AB的中点,所以OO1⊥平面ABC,在Rt△ABC中,AB=,则,在Rt△AOO1中,,故三棱锥O﹣ABC的体积为.故选:A.【点评】本题考查了锥体外接球和锥体体积公式,解题的关键是确定△ABC所在圆的圆心的位置,考查了逻辑推理能力、化简运算能力、空间想象能力,属于中档题.9.(2021•甲卷)在一个正方体中,过顶点A的三条棱的中点分别为E,F,G.该正方体截去三棱锥A﹣EFG后,所得多面体的三视图中,正视图如图所示,则相应的侧视图是()A.B.C.D.【分析】作出正方体,截去三棱锥A﹣EFG,根据正视图,摆放好正方体,即可求解侧视图.【解答】解:由题意,作出正方体,截去三棱锥A﹣EFG,根据正视图,可得A﹣EFG在正方体左侧面,如图,根据三视图的投影,可得相应的侧视图是D图形,故选:D.【点评】本题考查简单空间图形的三视图,属基础题.10.(2021•乙卷)在正方体ABCD﹣A1B1C1D1中,P为B1D1的中点,则直线PB与AD1所成的角为()A.B.C.D.【分析】由AD1∥BC1,得∠PBC1是直线PB与AD1所成的角(或所成角的补角),由此利用余弦定理,求出直线PB与AD1所成的角.【解答】解∵AD1∥BC1,∴∠PBC1是直线PB与AD1所成的角(或所成角的补角),设正方体ABCD﹣A1B1C1D1的棱长为2,则PB1=PC1==,BC1==2,BP==,∴cos∠PBC1===,∴∠PBC1=,∴直线PB与AD1所成的角为.故选:D.【点评】本题考查异面直线所成角和余弦定理,考查运算求解能力,是基础题.二.多选题(共2小题)11.(2021•新高考Ⅱ)如图,下列正方体中,O为底面的中点,P为所在棱的中点,M,N 为正方体的顶点,则满足MN⊥OP的是()A.B.C.D.【分析】对于A,设正方体棱长为2,设MN与OP所成角为θ,求出tanθ=,从而不满足MN⊥OP;对于B,C,D,作出平面直角坐标系,设正方体棱长为2,利用向量法进行判断.【解答】解:对于A,设正方体棱长为2,设MN与OP所成角为θ,则tanθ==,∴不满足MN⊥OP,故A错误;对于B,如图,作出平面直角坐标系,设正方体棱长为2,则N(2,0,0),M(0,0,2),P(2,0,1),O(1,1,0),=(2,0,﹣2),=(1,﹣1,1),=0,∴满足MN⊥OP,故B正确;对于C,如图,作出平面直角坐标系,设正方体棱长为2,则M(2,2,2),N(0,2,0),O(1,1,0),P(0,0,1),=(﹣2,0,﹣2),=(﹣1,﹣1,1),=0,∴满足MN⊥OP,故C正确;对于D,如图,作出平面直角坐标系,设正方体棱长为2,则M(0,2,2),N(0,0,0),P(2,1,2),O(1,1,0),=(0,﹣2,﹣2),=(1,0,2),=﹣4,∴不满足MN⊥OP,故D错误.故选:BC.【点评】本题考查命题真假的判断,考查空间中线线、线面、面面间的位置关系基础知识,考查数学运算、逻辑思维等核心素养,是中档题.12.(2021•新高考Ⅰ)在正三棱柱ABC﹣A1B1C1中,AB=AA1=1,点P满足=λ+μ,其中λ∈[0,1],μ∈[0,1],则()A.当λ=1时,△AB1P的周长为定值B.当μ=1时,三棱锥P﹣A1BC的体积为定值C.当λ=时,有且仅有一个点P,使得A1P⊥BPD.当μ=时,有且仅有一个点P,使得A1B⊥平面AB1P【分析】判断当λ=1时,点P在线段CC1上,分别计算点P为两个特殊点时的周长,即可判断选项A;当μ=1时,点P在线段B1C1上,利用线面平行的性质以及锥体的体积公式,即可判断选项B;当λ=时,取线段BC,B1C1的中点分别为M,M1,连结M1M,则点P在线段M1M上,分别取点P在M1,M处,得到均满足A1P⊥BP,即可判断选项C;当μ=时,取CC1的中点D1,BB1的中点D,则点P在线的DD1上,证明当点P在点D1处时,A1B⊥平面AB1D1,利用过定点A与定直线A1B垂直的平面有且只有一个,即可判断选项D.【解答】解:对于A,当λ=1时,=+μ,即,所以,故点P在线段CC1上,此时△AB1P的周长为AB1+B1P+AP,当点P为CC1的中点时,△AB1P的周长为,当点P在点C1处时,△AB1P的周长为,故周长不为定值,故选项A错误;对于B,当μ=1时,,即,所以,故点P在线段B1C1上,因为B1C1∥平面A1BC,所以直线B1C1上的点到平面A1BC的距离相等,又△A1BC的面积为定值,所以三棱锥P﹣A1BC的体积为定值,故选项B正确;对于C,当λ=时,取线段BC,B1C1的中点分别为M,M1,连结M1M,因为,即,所以,则点P在线段M1M上,当点P在M1处时,A1M1⊥B1C1,A1M1⊥B1B,又B1C1∩B1B=B1,所以A1M1⊥平面BB1C1C,又BM1⊂平面BB1C1C,所以A1M1⊥BM1,即A1P⊥BP,同理,当点P在M处,A1P⊥BP,故选项C错误;对于D,当μ=时,取CC1的中点D1,BB1的中点D,因为,即,所以,则点P在线的DD1上,当点P在点D1处时,取AC的中点E,连结A1E,BE,因为BE⊥平面ACC1A1,又AD1⊂平面ACC1A1,所以AD1⊥BE,在正方形ACC1A1中,AD1⊥A1E,又BE∩A1E=E,BE,A1E⊂平面A1BE,故AD1⊥平面A1BE,又A1B⊂平面A1BE,所以A1B⊥AD1,在正方体形ABB1A1中,A1B⊥AB1,又AD1∩AB1=A,AD1,AB1⊂平面AB1D1,所以A1B⊥平面AB1D1,因为过定点A与定直线A1B垂直的平面有且只有一个,故有且仅有一个点P,使得A1B⊥平面AB1P,故选项D正确.故选:BD.【点评】本题考查了动点轨迹,线面平行与线面垂直的判定,锥体的体积问题等,综合性强,考查了逻辑推理能力与空间想象能力,属于难题.三.填空题(共4小题)13.(2021•上海)已知圆柱的底面圆半径为1,高为2,AB为上底面圆的一条直径,C是下底面圆周上的一个动点,则ABC的面积的取值范围为.【分析】上顶面圆心记为O,下底面圆心记为O',连结OC,过点C作CM⊥AB,垂足为点M,由于AB为定值,则S△ABC的大小随着CM的长短变化而变化,分别求解CM的最大值和最小值,即可得到答案.【解答】解:如图1,上底面圆心记为O,下底面圆心记为O',连结OC,过点C作CM⊥AB,垂足为点M,则,根据题意,AB为定值2,所以S△ABC的大小随着CM的长短变化而变化,如图2所示,当点M与点O重合时,CM=OC=,此时S△ABC取得最大值为;如图3所示,当点M与点B重合,CM取最小值2,此时S△ABC取得最小值为.综上所述,S△ABC的取值范围为.故答案为:.【点评】本题考查了空间中的最值问题,将三角形面积的最值问题转化为求解线段CM 的最值问题进行求解是解题的关键,考查了空间想象能力与逻辑推理能力,属于中档题.14.(2021•甲卷)已知一个圆锥的底面半径为6,其体积为30π,则该圆锥的侧面积为39π.【分析】由题意,设圆锥的高为h,根据圆锥的底面半径为6,其体积为30π求出h,再求得母线的长度,然后确定圆锥的侧面积即可.【解答】解:由圆锥的底面半径为6,其体积为30π,设圆锥的高为h,则,解得,所以圆锥的母线长,所以圆锥的侧面积.故答案为:39π.【点评】本题考查了圆锥的侧面积公式和圆锥的体积公式,考查了方程思想,属于基础题.15.(2021•乙卷)以图①为正视图,在图②③④⑤中选两个分别作为侧视图和俯视图,组成某个三棱锥的三视图,则所选侧视图和俯视图的编号依次为②⑤或③④(写出符合要求的一组答案即可).【分析】通过观察已知条件正视图,确定该正视图的长和高,结合长、高、以及侧视图视图中的实线、虚线来确定俯视图图形.【解答】解:观察正视图,推出正视图的长为2和高1,②③图形的高也为1,即可能为该三棱锥的侧视图,④⑤图形的长为2,即可能为该三棱锥的俯视图,当②为侧视图时,结合侧视图中的直线,可以确定该三棱锥的俯视图为⑤,当③为侧视图时,结合侧视图虚线,虚线所在的位置有立体图形的轮廓线,可以确定该三棱锥的俯视图为④.故答案为:②⑤或③④.【点评】该题考查了三棱锥的三视图,需要学生掌握三视图中各个图形边长的等量关系,以及对于三视图中特殊线条能够还原到原立体图形中,需要较强空间想象,属于中等题.16.(2021•上海)已知圆柱的底面半径为1,高为2,则圆柱的侧面积为4π.【分析】根据圆柱的侧面积公式计算即可.【解答】解:圆柱的底面半径为r=1,高为h=2,所以圆柱的侧面积为S侧=2πrh=2π×1×2=4π.故答案为:4π.【点评】本题考查了圆柱的侧面积公式应用问题,是基础题.四.解答题(共11小题)17.(2021•天津)如图,在棱长为2的正方体ABCD﹣A1B1C1D1中,E,F分别为棱BC,CD的中点.(1)求证:D1F∥平面A1EC1;(2)求直线AC1与平面A1EC1所成角的正弦值;(3)求二面角A﹣A1C1﹣E的正弦值.【分析】(1)建立合适的空间直角坐标系,求出所需点的坐标和向量的坐标,利用待定系数法求出平面A1EC1的法向量,利用直线的方向向量与平面的法向量垂直,即可证明;(2)利用(1)中的结论,由向量的夹角公式求解,即可得到答案;(3)利用待定系数法求出平面AA1C1的法向量,然后利用向量的夹角公式求解即可.【解答】(1)证明:以点A为坐标原点,建立空间直角坐标系如图所示,则A1(0,0,2),E(2,1,0),C1(2,2,2),故,设平面A1EC1的法向量为,则,即,令z=1,则x=2,y=﹣2,故,又F(1,2,0),D1(0,2,2),所以,则,又D1F⊄平面A1EC,故D1F∥平面A1EC1;(2)解:由(1)可知,,则==,故直线AC1与平面A1EC1所成角的正弦值为;(3)解:由(1)可知,,设平面AA1C1的法向量为,则,即,令a=1,则b=﹣1,故,所以==,故二面角A﹣A1C1﹣E的正弦值为=.【点评】本题考查了空间向量在立体几何中的应用,在求解有关空间角问题的时候,一般会建立合适的空间直角坐标系,将空间角问题转化为空间向量问题进行研究,属于中档题.18.(2021•新高考Ⅱ)在四棱锥Q﹣ABCD中,底面ABCD是正方形,若AD=2,QD=QA =,QC=3.(Ⅰ)求证:平面QAD⊥平面ABCD;(Ⅱ)求二面角B﹣QD﹣A的平面角的余弦值.【分析】(Ⅰ)由CD2+QD2=QC2证明CD⊥QD,再由CD⊥AD,证明CD⊥平面QAD,即可证明平面QAD⊥平面ABCD.(Ⅱ)取AD的中点O,在平面ABCD内作Ox⊥AD,以OD为y轴,OQ为z轴,建立空间直角坐标系,求出平面ADQ的一个法向量,平面BDQ的一个法向量,再求cos<,>即可.【解答】(Ⅰ)证明:△QCD中,CD=AD=2,QD=,QC=3,所以CD2+QD2=QC2,所以CD⊥QD;又CD⊥AD,AD∩QD=D,AD⊂平面QAD,QD⊂平面QAD,所以CD⊥平面QAD;又CD⊂平面ABCD,所以平面QAD⊥平面ABCD.(Ⅱ)解:取AD的中点O,在平面ABCD内作Ox⊥AD,以OD为y轴,OQ为z轴,建立空间直角坐标系O﹣xyz,如图所示:则O(0,0,0),B(2,﹣1,0),D(0,1,0),Q(0,0,2),因为Ox⊥平面ADQ,所以平面ADQ的一个法向量为=(1,0,0),设平面BDQ的一个法向量为=(x,y,z),由=(﹣2,2,0),=(0,﹣1,2),得,即,令z=1,得y=2,x=2,所以=(2,2,1);所以cos<,>===,所以二面角B﹣QD﹣A的平面角的余弦值为.【点评】本题考查了空间中的垂直关系应用问题,也考查了利用空间向量求二面角的余弦值应用问题,也可以直接利用二面角的定义求二面角的余弦值,是中档题.19.(2021•上海)如图,在长方体ABCD﹣A1B1C1D1中,已知AB=BC=2,AA1=3.(1)若P是棱A1D1上的动点,求三棱锥C﹣P AD的体积;(2)求直线AB1与平面ACC1A1的夹角大小.【分析】(1)直接由三棱锥的体积公式求解即可;(2)易知直线AB1与平面ACC1A1所成的角为∠OAB1,求出其正弦值,再由反三角表示即可.【解答】解:(1)如图,在长方体ABCD﹣A1B1C1D1中,=;(2)连接A1C1∩B1D1=O,∵AB=BC,∴四边形A1B1C1D1为正方形,则OB1⊥OA1,又AA1⊥OB1,OA1∩AA1=A1,∴OB1⊥平面ACC1A1,∴直线AB1与平面ACC1A1所成的角为∠OAB1,∴.∴直线AB1与平面ACC1A1所成的角为.【点评】本题考查三棱锥体积的求法,考查线面角的求解,考查推理能力及运算能力,属于中档题.20.(2021•北京)已知正方体ABCD﹣A1B1C1D1,点E为A1D1中点,直线B1C1交平面CDE 于点F.(1)求证:点F为B1C1中点;(2)若点M为棱A1B1上一点,且二面角M﹣CF﹣E的余弦值为,求.【分析】(1)连结DE,利用线面平行的判定定理证明CD∥平面A1B1C1D1,从而可证明CD∥EF,即可证明四边形A1B1FE为平行四边形,四边形EFC1D1为平行四边形,可得A1E=B1F,ED1=FC1,即可证明B1F=FC1,故点F为B1C1的中点;(2)建立合适的空间直角坐标系,设点M(m,0,0),且m<0,求出所需点的坐标和向量的坐标,然后利用待定系数法求出平面CMF与CDEF的法向量,由向量的夹角公式列出关于m的关系式,求解即可得到答案.【解答】(1)证明:连结DE,在正方体ABCD﹣A1B1C1D1中,CD∥C1D1,C1D1⊂平面A1B1C1D1,CD⊄平面A1B1C1D1,则CD∥平面A1B1C1D1,因为平面A1B1C1D1∩平面CDEF=EF,所以CD∥EF,则EF∥C1D1,故A1B1∥EF∥C1D1,又因为A1D1∥B1C1,所以四边形A1B1FE为平行四边形,四边形EFC1D1为平行四边形,所以A1E=B1F,ED1=FC1,而点E为A1D1的中点,所以A1E=ED1,故B1F=FC1,则点F为B1C1的中点;(2)解:以点B1为原点,建立空间直角坐标系,如图所示,设正方体边长为2,设点M(m,0,0),且m<0,则C(0,2,﹣2),E(﹣2,1,0),F(0,1,0),故,设平面CMF的法向量为,则,即,所以,b=2,故,设平面CDEF的法向量为,则,即,所以x=0,y=2,故,因为二面角M﹣CF﹣E的余弦值为,则==,解得m=±1,又m<0,所以m=﹣1,故=.【点评】本题考查了立体几何的综合应用,涉及了线面平行的性质定理的应用,二面角的应用,在求解有关空间角问题的时候,一般会建立合适的空间直角坐标系,将空间角问题转化为空间向量问题进行研究,属于中档题.21.(2021•甲卷)已知直三棱柱ABC﹣A1B1C1中,侧面AA1B1B为正方形,AB=BC=2,E,F分别为AC和CC1的中点,BF⊥A1B1.(1)求三棱锥F﹣EBC的体积;(2)已知D为棱A1B1上的点,证明:BF⊥DE.【分析】(1)先证明AB⊥平面BCC1B1,即可得到AB⊥BC,再根据直角三角形的性质可知,最后根据三棱锥的体积公式计算即可;(2)取BC中点G,连接EG,B1G,先证明EG∥AB∥B1D,从而得到E、G、B1、D四点共面,再由(1)及线面垂直的性质定理可得BF⊥EG,通过角的正切值判断出∠CBF=∠BB1G,再通过角的代换可得,BF⊥B1G,再根据线面垂直的判定定理可得BF ⊥平面EGB1D,进而得证.【解答】解:(1)在直三棱柱ABC﹣A1B1C1中,BB1⊥A1B1,又BF⊥A1B1,BB1∩BF=B,BB1,BF⊂平面BCC1B1,∴A1B1⊥平面BCC1B1,∵AB∥A1B1,∴AB⊥平面BCC1B1,∴AB⊥BC,又AB=BC,故,∴,而侧面AA1B1B为正方形,∴,∴,即三棱锥F﹣EBC的体积为;(2)证明:如图,取BC中点G,连接EG,B1G,设B1G∩BF=H,∵点E是AC的中点,点G时BC的中点,∴EG∥AB,∴EG∥AB∥B1D,∴E、G、B1、D四点共面,由(1)可得AB⊥平面BCC1B1,∴EG⊥平面BCC1B1,∴BF⊥EG,∵,且这两个角都是锐角,∴∠CBF=∠BB1G,∴∠BHB1=∠BGB1+∠CBF=∠BGB1+∠BB1G=90°,∴BF⊥B1G,又EG∩B1G=G,EG,B1G⊂平面EGB1D,∴BF⊥平面EGB1D,又DE⊂平面EGB1D,∴BF⊥DE.【点评】本题主要考查三棱锥体积的求法以及线线,线面间的垂直关系,考查运算求解能力及逻辑推理能力,属于中档题.22.(2021•乙卷)如图,四棱锥P﹣ABCD的底面是矩形,PD⊥底面ABCD,PD=DC=1,M为BC中点,且PB⊥AM.(1)求BC;(2)求二面角A﹣PM﹣B的正弦值.【分析】(1)连结BD,利用线面垂直的性质定理证明AM⊥PD,从而可以证明AM⊥平面PBD,得到AM⊥BD,证明Rt△DAB∽Rt△ABM,即可得到BC的长度;(2)建立合适的空间直角坐标系,求出所需点的坐标和向量的坐标,然后利用待定系数法求出平面的法向量,由向量的夹角公式以及同角三角函数关系求解即可.【解答】解:(1)连结BD,因为PD⊥底面ABCD,且AM⊂平面ABCD,则AM⊥PD,又AM⊥PB,PB∩PD=P,PB,PD⊂平面PBD,所以AM⊥平面PBD,又BD⊂平面PBD,则AM⊥BD,所以∠ABD+∠ADB=90°,又∠ABD+∠MAB=90°,则有∠ADB=∠MAB,所以Rt△DAB∽Rt△ABM,则,所以,解得BC=;(2)因为DA,DC,DP两两垂直,故以点D位坐标原点建立空间直角坐标系如图所示,则,P(0,0,1),所以,,设平面AMP的法向量为,则有,即,令,则y=1,z=2,故,设平面BMP的法向量为,则有,即,令q=1,则r=1,故,所以=,设二面角A﹣PM﹣B的平面角为α,则sinα==,所以二面角A﹣PM﹣B的正弦值为.【点评】本题考查了空间中线段长度求解以及二面角的求解,在求解有关空间角问题的时候,一般会建立合适的空间直角坐标系,将空间角问题转化为空间向量问题进行研究,属于中档题.23.(2021•浙江)如图,在四棱锥P﹣ABCD中,底面ABCD是平行四边形,∠ABC=120°,AB=1,BC=4,P A=,M,N分别为BC,PC的中点,PD⊥DC,PM⊥MD.(Ⅰ)证明:AB⊥PM;(Ⅱ)求直线AN与平面PDM所成角的正弦值.【分析】(Ⅰ)由已知求解三角形可得CD⊥DM,结合PD⊥DC,可得CD⊥平面PDM,进一步得到AB⊥PM;(Ⅱ)由(Ⅰ)证明PM⊥平面ABCD,由已知求解三角形可得AM,PM,取AD中点E,连接ME,以M为坐标原点,分别以MD、ME、MP为x、y、z轴建立空间直角坐标系,求出的坐标及平面PDM的一个法向量,由两法向量所成角的余弦值可得直线AN与平面PDM所成角的正弦值.【解答】(Ⅰ)证明:在平行四边形ABCD中,由已知可得,CD=AB=1,CM=BC=2,∠DCM=60°,∴由余弦定理可得,DM2=CD2+CM2﹣2CD×CM×cos60°=,则CD2+DM2=1+3=4=CM2,即CD⊥DM,又PD⊥DC,PD∩DM=D,∴CD⊥平面PDM,而PM⊂平面PDM,∴CD⊥PM,∵CD∥AB,∴AB⊥PM;(Ⅱ)解:由(Ⅰ)知,CD⊥平面PDM,又CD⊂平面ABCD,∴平面ABCD⊥平面PDM,。
高考立体几何试题——选择填空

高考立体几何试题——选择填空1.(安徽文)把边长为2的正方形ABCD 沿对角线AC 折成直二面角,折成直二面角后,在A ,B ,C ,D 四点所在的球面上,B 与D 两点之间的球面距离为(C ) (A)22π(B)π(C)2π (D)3π 2.(北京文)平面α∥平面β的一个充分条件是( ) A.存在一条直线a a ααβ,∥,∥B.存在一条直线a a a αβ⊂,,∥C.存在两条平行直线a b a b a b αββα⊂⊂,,,,∥,∥ D.存在两条异面直线a b a a b αβα⊂,,,∥,∥3.(福建理)已知m n ,为两条不同的直线,αβ,为两个不同的平面,则下列命题中正确的是( D ) A .m n m n ααββαβ⊂⊂⇒,,∥,∥∥ B .m n m n αβαβ⊂⊂⇒∥,,∥ C .m m n n αα⇒⊥,⊥∥ D .n m n m αα⇒∥,⊥⊥4.(福建理)顶点在同一球面上的正四棱柱ABCD A B C D ''''-中,12AB AA '==,,则A C ,两点间的球面距离为( B ) A .π4B .π2C .2π D .2π 5.(湖北理)平面α外有两条直线m 和n ,如果m 和n 在平面α内的射影分别是m '和n ',给出下列四个命题: ①m n m n ''⊥⇒⊥; ②m n m n ''⊥⇒⊥; ③m '与n '相交⇒m 与n 相交或重合; ④m '与n '平行⇒m 与n 平行或重合. 其中不正确的命题个数是( D ) A.1 B.2 C.3 D.4 6.(湖北文)在棱长为1的正方体1111ABCD A B C D -中,E F ,分别为棱11AA BB ,的中点,G 为棱11A B 上的一点,且1(01)A G λλ=≤≤.则点G 到平面1D EF 的距离为( D )A.3B.2C.2λ D.5 7.(湖南理)棱长为1的正方体1111ABCD A B C D -的8个顶点都在球O 的表面上,E F ,分别是棱1AA ,1DD 的中点,则直线EF 被球O 截得的线段长为( D ) A .2B .1C .21+D .28.(湖南文)如图1,在正四棱柱1111ABCD A B C D -中,E F ,分别是1AB ,1BC 的中点,则以下结论中不成立...的是( D )A .EF 与1BB 垂直 B .EF 与BD 垂直C .EF 与CD 异面D .EF 与11A C 异面9.(江苏)已知两条直线m n ,,两个平面αβ,.给出下面四个命题: ①m n ∥,m n αα⇒⊥⊥;②αβ∥,m α⊂,n m n β⊂⇒∥; ③m n ∥,m n αα⇒∥∥;④αβ∥,m n ∥,m n αβ⇒⊥⊥. 其中正确命题的序号是( C ) A.①、③ B.②、④C.①、④ D.②、③10.(江西理)如图,正方体1AC 的棱长为1,过点A 作平面1A BD 的垂线,垂足为点H ,则以下命题中,错误..的命题是( )DA.点H 是1A BD △的垂心 B.AH 垂直平面11CB D C.AH 的延长线经过点1C D.直线AH 和1BB 所成角为45o11.(江西文)四面体ABCD 的外接球球心在CD 上,且2CD =,3AD =,在外接球面上两点A B ,间的球面距离是( C ) A.π6B.π3C.2π3D.5π612.(江西文)如图,正方体1AC 的棱长为1,过点作平面1A BD 的垂线,垂足为点H .有下列四个命题 A.点H 是1A BD △的垂心 B.AH 垂直平面11CB DC.二面角111C B D C --的正切值为2 D.点H 到平面1111A B C D 的距离为3413.(北京理)平面α∥平面β的一个充分条件是( D ) A.存在一条直线a a ααβ,∥,∥B.存在一条直线a a a αβ⊂,,∥C.存在两条平行直线a b a b a b αββα⊂⊂,,,,∥,∥A D1D11A 1B BHCD.存在两条异面直线a b a a b αβα⊂,,,∥,∥14.(辽宁文)若m n ,是两条不同的直线,αβγ,,是三个不同的平面,则下列命题中的真命题...是( B ) A .若m βαβ⊂⊥,,则m α⊥ B .若m β⊥,m α∥,则αβ⊥C .若αγ⊥,αβ⊥,则βγ⊥D .若m αγ=I ,n βγ=I ,m n ∥,则αβ∥15.(全国I 文理)如图,正四棱柱1111ABCD A B C D -中,12AA AB =,则异面直线1A B 与1AD 所成角的余弦值为( D )A .15B .25C .35D .4517.(全国卷Ⅱ理)已知正三棱柱111ABC A B C -的侧棱长与底面边长相等,则1AB 与侧面11ACC A 所成角的正弦值等于( A )A .64B .104C .22D .3218.(全国卷Ⅱ文)已知三棱锥的侧棱长的底面边长的2倍,则侧棱与底面所成角的余弦值等于( ) A .36B .34C .2 D .3219.(陕西理)一个正三棱锥的四个顶点都在半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,则该正三棱锥的体积是( B ) (A )433 (B)33 (C) 43 (D) 12320.(陕西文)Rt △ABC 的三个顶点在半径为13的球面上,两直角边的长分别为6和8,则球心到平面ABC 的距离是( D ) (A )5 (B )6 (C )10 (D )12 21.(陕西文)已知P 为平面a 外一点,直线l ⊂a,点Q ∈l ,记点P 到平面a 的距离为a,点P 到直线l 的距离为b ,点P 、Q 之间的距离为c ,则A (A )c b a ≤≤ (B )c b a ≤≤ (C)b c a ≤≤ (D)a c b ≤≤ 22.(四川文理)如图,ABCD -A 1B 1C 1D 1为正方体,下面结论错误..的是( D ) (A )BD ∥平面CB 1D 1 (B )AC 1⊥BD(C )AC 1⊥平面CB 1D 1 (D )异面直线AD 与CB 1角为60° 23.(四川文理)设球O 的半径是1,A 、B 、C 是球面上三点,已知A 到B 、C 两点的球面距离都是2π,且三面角B -OA -C 的大小为3π,则从A 点沿球面经B 、C 两点再回到A 点的最短距离是C(A )67π (B )45π (C )34π (D )23π24.(四川文理)如图,l 1、l 2、l 3是同一平面内的三条平行直线,l 1与l 2间的距离是1, l 2与l 3间的距离是2,正三角形ABC 的三顶点分别在l 1、l 2、l 3上,则△ABC 的边长是D(A )32(B )364 (C )4173 (D )3212 25.(天津文理)设a b ,为两条直线,αβ,为两个平面,下列四个命题中,正确的命题是( D ) A.若a b ,与α所成的角相等,则a b ∥ B.若a b αβ,∥∥,αβ∥,则a b ∥ C.若a b a b αβ⊂⊂,,∥,则αβ∥ D.若a b αβ⊥⊥,,αβ⊥,则a b ⊥26.(浙江文理)若P 两条异面直线l m ,外的任意一点,则( )B A.过点P 有且仅有一条直线与l m ,都平行 B.过点P 有且仅有一条直线与l m ,都垂直 C.过点P 有且仅有一条直线与l m ,都相交 D.过点P 有且仅有一条直线与l m ,都异面27.(理科数学必修+选修Ⅱ)已知正三棱柱111ABC A B C -的侧棱长与底面边长相等,则1AB 与侧面11ACC A 所成角的正弦值等于( ) A .6B .10 C .2 D .3 28.(文理科数学必修+选修Ⅱ)如图,正四棱柱1111ABCD A B C D -中,12AA AB =,则异面直线1A B 与1AD 所成角的余弦值为( )DA .15B .25C .35D .4530.(重庆文)垂直于同一平面的两条直线( )A A .平行 B .垂直 C .相交 D .异面 31.(重庆理)若三个平面两两相交,且三条交线互相平行,则这三个平面把空间分成( C ) A.5部分 B.6部分 C.7部分 D.8部分 32.(理科数学必修+选修Ⅱ)(16)一个等腰直角三角形的三个顶点分别在正三棱柱的三条侧棱上.已知正三棱柱的底面边长为2,则该三角形的斜边长为 .2333.(浙江文理)已知点O 在二面角AB αβ--的棱上,点P 在α内,且45POB ∠=o.若对于β内异于O 的任意一点Q ,都有45POQ ∠o≥,则二面角AB αβ--的大小是.90o34.(全国I 文)正四棱锥S ABCD -S ,A ,B ,C ,D 都在同一个球面上,则该球的体积为_________.4π335.(文科数学必修+选修1)正四棱锥S ABCD -S ,A ,B ,C ,D 都在同一个球面上,则该球的体积为_________.4π336.(理科数学必修+选修Ⅱ)一个正四棱柱的各个顶点在一个直径为2cm 的球面上.如果正四棱柱的底面边长为1cm ,那么该棱柱的表面积为 cm 2.37.(天津文理)一个长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为1,2,3,则此球的表面积为 .14π38.(安徽理)在四面体O-ABC 中,D c b a ,,,===为BC 的中点,E 为AD 的中点,则= (用a ,b ,c 表示).111244++a b c 39.(安徽理)在正方体上任意选择4个顶点,它们可能是如下各种几何形体的4个顶点,这些几何形体是 (写出所有正确结论的编号..). ①③④⑤ ①矩形;②不是矩形的平行四边形;③有三个面为等腰直角三角形,有一个面为等边三角形的四面体; ④每个面都是等边三角形的四面体; ⑤每个面都是直角三角形的四面体.40.(湖南文)棱长为1的正方体1111ABCD A B C D -的8个顶点都在球O 的表面上,则球O 的表面积是 ;设E F ,分别是该正方体的棱1AA ,1DD 的中点,则直线EF 被球O 截得的线段长为 .3π41.(全国卷Ⅱ文理)一个正四棱柱的各个顶点在一个直径为2cm 的球面上.如果正四棱柱的底面边长为1cm ,那么该棱柱的表面积为 cm 2.2+42.(辽宁文)若一个底面边长为2,棱长为的正六棱柱的所有顶点都在一个球的面上,则此球的体积为 .43.(四川文理)如图,在正三棱柱ABC -A 1B 1C 1中,侧棱长为2,底面三角形的边长为1,则BC 1与侧面ACC 1A 1所成的角是 .6π44.(江苏)正三棱锥P ABC -的高为2,侧棱与底面ABC 成45o角,则点A 到侧面PBC 的距离为_____.545.(全国I 理)一个等腰直角三角形的三个顶点分别在正三棱柱的三条侧棱上.已知正三棱柱的底面边长为2,则该三角形的斜边长为 .46.(上海理)在平面上,两条直线的位置关系有相交、平行、重合三种. 已知αβ,是两个相交平面,空间两条直线12l l ,在α上的射影是直线12s s ,,12l l ,在β上的射影是直线12t t ,.用1s 与2s ,1t 与2t 的位置关系,写出一个总能确定1l 与2l 是异面直线的充分条件: 21//s s ,并且1t 与2t 相交(//1t 2t ,并且1s 与2s 相交)47.(上海文)如图,在直三棱柱111C B A ABC -中,ο90=∠ACB , 21=AA ,1==BC AC ,则异面直线B A 1与AC 所成角的大小是 (结果用反三角函数值表示).66arccos48.广东理12.如果一个凸多面体是n 棱锥,那么这个凸多面体的所有顶点所确定的 直线共有 条.这些直线中共有()f n 对异面直线,则(4)f =49.辽宁理7.若m n ,是两条不同的直线,αβγ,,是三个不同的平面,则下列命题中的真命题是( ) A .若m βαβ⊂⊥,,则m α⊥ B .若m αγ=I n βγ=I ,m n ∥,则αβ∥ C .若m β⊥,m α∥,则αβ⊥D .若αγ⊥,αβ⊥,则βγ⊥50.辽宁理15.若一个底面边长为2,则此球的体积为 .选校网高考频道专业大全历年分数线上万张大学图片大学视频院校库(按ctrl 点击打开)选校网()是为高三同学和家长提供高考选校信息的一个网站。
高考立体几何试题---―选择填空.

高考立体几何试题 选择填空1.(安徽文把边长为仮的正方形ABCD 沿对角线AC 折成直二面角,折成直二面角 后,在A,B,C,D 四点所在的球面上,B 与D 两点之间的球面距离为(C )(A(福建理)已知™ H 为两条不同的直线, S "为两个不同的平面,则下列命题中正确的是( D )me (j> "u jn/f fit H ZZ0 N « B 0 H 川匸 s J 』匸 n n rn"胖也丄* 阿丄uZ/a D . He H 丄a 吕iTi 丄盘n = It 4 B .2 C . 4用与於平行=m 与」,平行或重合.其中不正确的命题个数是(A. 1B. 2C. 3D. 42. (北京文)平面《 "平面"的一个充分条件是(A. 存在一条直线B. 存在一条直线小C Uf ) id"”C. 存在两条平行直线斛 b N 匚《. bu 卩、就"#t b 〃《D. 存在两条异面直线小 b c «1 咼"# t if // ix3. (福建理)顶点在同一球面上的正四棱柱 点间的球面距离为(B )4. ARCD- yTJyrTZ 中 AiJ= L5. (湖北理)平面 卅,给出下列四个命题:外有两条直线 拘和N ,如果也和"在平面^"内的射影分别是fjj"丄ff' = /n 丄川. ②例丄卫 =丄 曲」;③用•与鬥•相交加与力 相交或重合;6. 点, ( (湖北文)在棱长为1的正方体D中,上;F分别为棱4+凹的中G为棱•詔上的一点,且n .则点&•到平面。
厂F的距离为D )Er FA.7.(湖南理)棱长为小,"的中点,1的正方体AFKD "「4的8个顶点都在球Q的表面上,E F分别是棱则直线若F被球Q截得的线段长为(A. -B.】C. 2D .运AEr F分别是m8.(湖南文)如图1,在正四棱柱珂X4 中,的中点,贝U以下结论中不成立的是(D )£尸与砂垂直C.EF与异面9. (江苏)已知两条直线"•给出下面四个命题:也匸a "匸〃=> nr//再.其中正确命题的序号是(A.①、③B.②、④C.①、④D.②、③X 的棱长为I ,过点/I 作平面4妙的垂线,垂足为点川,则以下命DA.点丹是△儿"的垂心C.川丹的延长线经过点「D.直线和月轉所成角为 4511.(江西文)四面体 川吕LD 的外接球球心在LQ 上,且亡Q= r 上两点人 日间的球面距离是九儿詬,在外接球面?C2ii12.(江西文)如图,正方体 L 的棱长为 线,垂足为点丹•有下列四个命题 1,过点作平面人的垂A .点丹是的垂心 B. 0丹垂直平面匚也 C.二面角的正切值为五 D .点丹到平面4XC 的距离为413.(北京理)平面泾"平面"的一个充分条件是( A .存在一条直线S* Z E10 .(江西理)如图,正方体 题中,错误的命题是(.存在一条直线'旳武uS.存在两条平行直线从匕"匸⑺办匸佚MB* "〃疔.存在两条异面直线“bfg14.(辽宁文)若皿刀是两条不同的直线, 则下列命题中的真命题是(B )⑴佚尸是三个不同的平面,"'丄0 贝y冊丄隹B 若"'丄n 序"血贝y M丄"若口丄F W丄",则P丄;“D.若《门r三W , 0 n”二H ,卍"JT ,则"P几4 二 2 Afi(全国I文理)如图,正四棱柱川心中, 则异面直线"与A 口所成角的余弦值为(D )已知正三棱柱皿宀W:的侧棱长与底面边长相等,17.(全国卷n理)则川峙与侧面所成角的正弦值等于(A )18.(全国卷n文)面所成角的余弦值等于已知三棱锥的侧棱长的底面边长的2倍,则侧棱与底(7? 71 7?A . 6B . ^C .-D.19.(陕西 理)一个正 三棱锥的四个顶点都 在半径为1的球面上,其中底 面的三个顶点在该球的一个大圆上,则该正三棱锥的体积是(B )20.(陕西文)分别为6和8,则球心到平面ABC 的距离是(D )(A ) 5 (B ) 6 (C ) 10 (D ) 12 21.(陕西文)已知P 为平面a 外一点,直线i u a,点Q € i ,记点P 到平面a 的距离为a,点P 到直线I 的距离为b 点P 、Q 之间的距离为C ,则A(A) ( B) c ""(四川文理如图,ABCDA 1B 1C 1D 1为正方体,下面结论错误(A ) BD// 平面 CB 1D 1 ( B ) AC 1 丄 BD(C ) AC 1丄平面CE 1D 1 ( D )异面直线 AD 与CB 1角为60°23. (四川文理)设球0的半径是1 , A 、B 、C 是球面上三点,已知A 到B 、C 两点< >r 的球面距离都是-,且三面角E -O/-C 的大小为3,则从A 点沿球面经B C 两点再 回到A点的最短距离是C7厅 5幵4*3.7 (A ) b(B)4(C ) 3(D ) rn24. (四川文理)如图,11、12、13是同一平面内的三条平行直线,11与12间的距 离是1, 12与13间的距离是2,正三角形ABC 的三顶点分别在11、12、13上,贝U △ ABC 的边长是DJ*爲(B 亍(C V (D TTJ —Rt A ABC 的三个顶点在半径为13的球面上,两直角边的长25. (天津文理)设出2、为两条直线,⑴沪为两个平面,下列四个命题中,正确 的命题是(D )A.过点尸有且仅有一条直线与B.过点尸有且仅有一条直线与人C.过点 P 有且仅有一条直线与D.过点P 有且仅有一条直线与27.(理科数学必修+选修n )已知正三棱柱 人月〔=八吗5的侧棱长与底面*1片厂*"』""* ■<边长相等,则''与侧面'',所成角的正弦值等于()4^^ m/TF (B )〒(C ) h (D )A.若 站也与口所成的角相等,贝U '"小B.若 力"”,,则C.若 力 J 0* * # b 则 Ct // fiD.若方丄冷 《丄# 贝ya 丄白26.(浙江文理) 若 尸两条异面直线人E 外的任意一点,则(12 14A .5B .C . 5D .530____ ) AA .平行B .垂直C .相交D .异面31.(重庆理)若三个平面两两相交,且三条交线互相平行,则这三个平面把空间分成 (A. £部分B.占部分C. 7部分D. K 部分32.(理科数学必修+选修n ) (16) 一个等腰直角三角形的三个顶点分别在正三棱柱 的三条侧棱上.已知正三棱柱的底面边长为2,则该三角形的斜边长为_.33.(浙江文理)已知点P 在二面角UB 的棱上,点P 在口内,且 Jpg"".若对于疗内异于P 的任意一点◊,都有A',则二面角口八〃 “的大小是.9F34.(全国I 文)正四棱锥 SP的底面边长和各侧棱长都为血,点S , A ,B ,Tni+选修n )如图,正四棱柱八X4 MS所成角的余弦值为(A JI335.(文科数学必修+选修1)正四棱锥再-川的底面边长和各侧棱长都为 上A JI3C ,D 都在同一个球面上,则该球的体积为 点S ,A , B ,C ,D 都在同一个球面上,则该球的体积为为AD 的中点,贝U f 圧二(用a, b ,c 表示)39.(安徽理在正方体上任意选择4个顶点, 顶点,这些几何形体是 (写出所有正确结论的编号).①③④⑤ ① 矩形;② 不是矩形的平行四边形;③ 有三个面为等腰直角三角形,有一个面为等边三角形的四面体; ④ 每个面都是等边三角形的四面体; ⑤ 每个面都是直角三角形的四面体.40.(湖南文)棱长为1的正方体M3珂X4的8个顶点都在球O 的表面 上,则球◎的表面积是;设疋,F 分别是该正方体的棱 川‘彳,“的中点,则直线 FF 被球。
高考立体几何模型
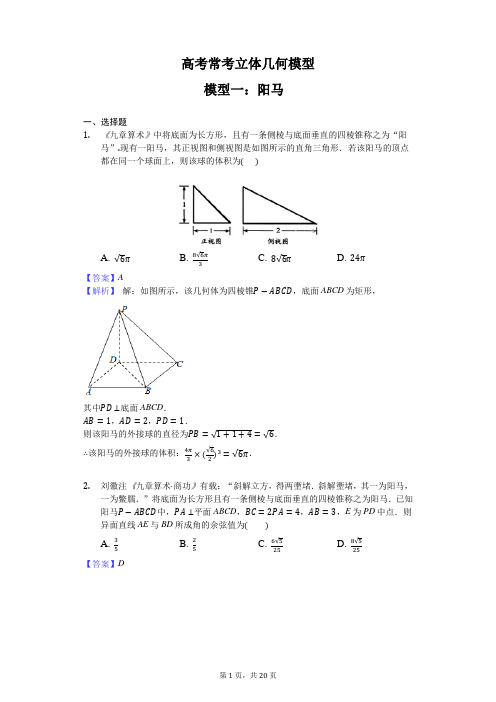
高考常考立体几何模型模型一:阳马一、选择题1.《九章算术》中将底面为长方形,且有一条侧棱与底面垂直的四棱锥称之为“阳马”.现有一阳马,其正视图和侧视图是如图所示的直角三角形.若该阳马的顶点都在同一个球面上,则该球的体积为()A. √6πB. 8√6π3C. 8√6πD. 24π【答案】A【解析】解:如图所示,该几何体为四棱锥P−ABCD,底面ABCD为矩形,其中PD⊥底面ABCD.AB=1,AD=2,PD=1.则该阳马的外接球的直径为PB=√1+1+4=√6.∴该阳马的外接球的体积:4π3×(√62)3=√6π.2.刘徽注《九章算术·商功》有载:“斜解立方,得两壍堵.斜解壍堵,其一为阳马,一为鳖臑.”将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马.已知阳马P−ABCD中,PA⊥平面ABCD,BC=2PA=4,AB=3,E为PD中点.则异面直线AE与BD所成角的余弦值为()A. 35B. 25C. 6√525D. 8√525【答案】D【解析】解:如图,取PB中点为F,连接AF,EF,∵E为PD中点,∴FE//BD,∴∠AEF(或补角)为异面直线AE与BD所成的角.由已知,得AE=12PD=√5,AF=12PB=√132,EF=12BD=52,cos∠AEF=AE2+EF2−AF22AE⋅EF=8√525.即AE与BD所成角的余弦值为8√525.3.《九章算术》中,将底面是长方形且有一条侧棱与底面垂直的四棱锥称为阳马.在阳马P−ABCD中,PC为阳马中最长的棱,AB=1,AD=2,PC=3,若在阳马P−ABCD的外接球内部随机取一点M,则M位于阳马内的概率为()A. 127πB. 427πC. 827πD. 49π【答案】C【解析】根据题意,PC的长等于其外接球的直径,∵PC=√PA2+AB2+AD2,∴3=√PA2+1+4,∴PA=2,又PA垂直平面ABCD,∴V P−ABCD=13×1×2×2=43,,,4.刘徽《九章算术⋅商功》中将底面为长方形,两个三角面与底面垂直的四棱锥称为“阳马”,.某“阳马”的三视图如图所示,则其外接球的体积为()正视图侧视图俯视图A. √3πB. 3πC. √3π2D. 4π【答案】C【解析】解:由题意可知阳马为四棱锥,且四棱锥的底面为长方体的一个底面,四棱锥的高为长方体的一棱长,且阳马的外接球也是长方体的外接球;由三视图可知四棱锥的底面是边长为1的正方形,四棱锥的高为1,∴长方体的一个顶点处的三条棱长分别为1,1,1,∴长方体的对角线为√3,∴外接球的半径为√32,∴外接球的体积为V=4π3⋅(√32)3=√32π.5.《九章算术》中,将底面为矩形,一条侧棱垂直于底面的四棱锥称之为“阳马”.已知某“阳马”的三视图如图所示,其体积为12,则该“阳马”的侧视图中的x=()A. 1B. 2C. 3D. 4【答案】C【解析】解:根据几何体的三视图可知,该几何体是底面长为4,宽为x的矩形,高为3的四棱锥,∵几何体的体积V=13×4×3x=12,解得x=3,6.《九章算术》中将底面为长方形,且有一条侧棱与底面垂直的四棱锥称之为“阳马”.现有一阳马,其正视图和侧视图是如图所示的直角三角形.若该阳马的顶点都在同一个球面上,则该球的体积为()A. √6πB. 8√6π3C. 8√6πD. 24π【答案】A【解析】解:如图所示,该几何体为四棱锥P−ABCD.底面ABCD为矩形,其中PD⊥底面ABCD.AB=1,AD=2,PD=1.则该阳马的外接球的直径为PB=√1+1+4=√6.∴该阳马的外接球的体积:4π3×(√62)3=√6π.7.刘徽注《九章算术·商功》有载:“斜解立方,得两壍堵.斜解壍堵,其一为阳马,一为鳖孺.”将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马.已知阳马P−ABCD中,PA⊥平面ABCD,BC=2PA=4,AB=3,E为PD中点.则异面直线AE与BD所成角的余弦值为A. 35B. 25C. 6√525D. 8√525【答案】D【解析】解:如图,取PB中点为F,连接AF,EF,∵E为PD中点,∴FE//BD,∴∠AEF(或补角)为异面直线AE与BD所成的角.由已知,得AE=12PD=√5,AF=12PB=√132,EF=12BD=52,cos∠AEF=AE2+EF2−AF22AE⋅EF=8√525.即AE与BD所成角的余弦值为8√525.二、填空题8.我国古代数学名著《九章算术》对立体几何也有深入的研究,从其中的一些数学用语可见,譬如“堑堵”意指底面为直角三角形,且侧棱垂直于底面的三棱柱,“阳马”指底面为矩形且有一侧棱垂直于底面的四棱锥.现有一如图所示的“堑堵”即三棱柱ABC−A1B1C1,其中AC⊥BC,若AA1=AB=2,当“阳马”即四棱锥B−A1ACC1体积最大时,“堑堵”即三棱柱ABC−A1B1C1外接球的体积为________.【答案】8√23π【解析】解:设AC=b,BC=a,则a2+b2=AB2=4,所以四棱锥B−A1ACC1=13×BC×AC×AA1=23ab≤2 3×a2+b22=43,当且仅当a=b=√2时取等,此时三棱柱ABC−A1B1C1外接球的球心为A1B的中点,所以外接球的半径R=A1B2=√AA12+AB22=√4+42=√2,所以三棱柱ABC−A1B1C1外接球的体积为43×πR3=43π×2√2=8√23π.故答案为:8√23π.9.我国古代数学名著《九章算术》中将底面为矩形且有一侧棱垂直于底面的四棱锥称为“阳马”,现有一“阳马”如图所示,PA⊥平面ABCD,PA=4,AB=√3,AD=1,则该“阳马”外接球的表面积为________.【答案】【解析】解:如图:因为平面ABCD,PA⊂平面PAD,PA⊂平面PAB,所以平面PAD⊥平面ABCD,交于AD,平面PAB⊥平面ABCD,交于AB,而ABCD是矩形,因此DC⊥平面PAD,BC⊥平面PAB.而PD⊂平面PAD,PB⊂平面PAB,因此DC⊥PD,BC⊥PB.连接AC,因为平面ABCD,AC⊂平面ABCD,所以,因此该“阳马”外接球是以PC为直径的球.又因为PA=4,AB=√3,AD=1,所以PC=√PA2+AB2+AD2=2√5,即外接球的半径为√5,因此该“阳马”外接球的表面积为.故答案为.10.《九章算术》中把底面为直角三角形,且侧棱垂直于底面的三棱柱称为“堑堵”,把底面为矩形且有一侧棱垂直于底面的四棱锥称为“阳马”.现有如图所示的“堑堵”ABC−A1B1C1,其中AC⊥BC,若AA1=1,“堑堵”即三棱柱ABC−A1B1C1π,则“阳马”即四棱锥B−A1ACC1体积的最大值为的外接球的体积为√23_________.【答案】16【解析】解:,设AC=x,则BC=√1−x2,时,取等号.,当且仅当x=√22故四棱锥B−A1ACC1体积的最大值为1.611.我国古代数学名著《九章算术⋅商功》中阐述:“斜解立方,得两壍堵.斜解壍堵,其为阳马,一为鳖臑.阳马居二,鳖臑居一,不易之率也.合两鳖臑三而一,验之以棊,其形露矣.”若称为“阳马”的某几何体的三视图如图所示,图中网格纸上小正方形的边长为1,则对该几何体描述:①四个侧面都是直角三角形;②最长的侧棱长为2√6;③四个侧面中有三个侧面是全等的直角三角形;④外接球的表面积为24π.其中正确的为______________【答案】①②④【解析】解:由题目中的三视图可还原几何体如下:下底面为4宽2的矩形,ED⊥平面ABCD,ED=2,∴①四个侧面都是直角三角形,正确;②最长的侧棱长为EB=2√6,正确;③四个侧面不存在全等的直角三角形,故错误;④外接球的球心为EB中点,半径r=√6,表面积为24π,正确.故正确的描述有①②④,模型二:鳖臑一、选择题12. 在我国古代数学名著《九章算术》中,将四个面都是直角三角形的四面体称为“鳖臑”,在鳖臑A −BCD 中,AB ⊥平面BCD ,BD ⊥CD ,且AB =BD =CD ,M 为AD 的中点,则二面角M −BC −D 的正弦值为A. √22B. √33C. √63D. 1【答案】C【解析】 解:由题意可以C 为原点,CD 为x 轴,CB 为y 轴,过C 作平面BDC 的垂线为z 轴(与AB 平行),建立空间直角坐标系如图所示,设AB =BC =CD =1,则A(0,1,1),B(0,1,0),C(0,0,0),D(1,0,0),M(12,12,12), 则BM ⃗⃗⃗⃗⃗⃗ =(12,−12,12),CD ⃗⃗⃗⃗⃗ =(1,0,0), 设异面直线BM 与CD 夹角为θ,则cosθ=|BM⃗⃗⃗⃗⃗⃗⃗ ⋅CD ⃗⃗⃗⃗⃗ ||BM⃗⃗⃗⃗⃗⃗⃗ |⋅|CD ⃗⃗⃗⃗⃗ |=12√34=√33.∴二面角M −BC −D 的正弦值为√1−cos2θ=(√33)=√63.13. 在我国古代数学名著《九章算术》中,将四个面都是直角三角形的四面体称为“鳖臑”,在鳖臑A—BCD 中,AB ⊥平面BCD ,BD ⊥CD ,且AB =BD =CD ,M 为AD 的中点,则异面直线BM 与CD 所成角的正弦值为A. 0B. √33C. √63D. 1【答案】D【解析】 解:设AB =BD =CD =1,因为BD ⊥CD ,AB ⊥平面BCD ,所以CD ⊥AB ,AB ∩BD =B ,所以CD ⊥面ABD ,CD ⊥AM ,则异面直线BM 与CD 所成角为90° 异面直线BM 与CD 所成角的正弦值为1,14.刘徽注《九章算术·商功》有载:“斜解立方,得两壍堵.斜解壍堵,其一为阳马,一为鳖臑.”将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马.已知阳马P−ABCD中,PA⊥平面ABCD,BC=2PA=4,AB=3,E为PD中点.则异面直线AE与BD所成角的余弦值为A. 35B. 25C. 6√525D. 8√525【答案】D【解析】解:如图,取PB中点为F,连接AF,EF,∵E为PD中点,∴FE//BD,∴∠AEF(或补角)为异面直线AE与BD所成的角.由已知,得AE=12PD=√5,AF=12PB=√132,EF=12BD=52,cos∠AEF=AE2+EF2−AF22AE⋅EF=8√525.即AE与BD所成角的余弦值为8√525.15.在我国古代数学名著《九章算术》中,将四个面都为直角三角形的四面体称为鳖臑,如图,在鳖臑ABCD 中,AB⊥平面BCD,且AB=BC=CD,则异面直线AC 与BD所成角的余弦值为().A. 12B. -12C. √32D. -√32【答案】A【解析】解:如图所示,分别取AB,AD,BC,BD的中点E,F,G,O,则EF//BD,EG//AC,FO⊥OG,∴∠FEG为异面直线AC与BD所成角.设AB=2a,则EG=EF=√2a,FG=√a2+a2=√2a,∴∠FEG=60°,∴异面直线AC与BD所成角的余弦值为12,16.在《九章算术》中,将四个面都为直角三角形的三棱锥称之为鳖臑,已知鳖臑P−ABC的三视图如图所示(单位:cm),则该几何体的外接球的表面积为(单位:cm2)()A. 41πB. 16πC. 25πD. 64π【答案】A【解析】解:由题意将三视图还原几何体,看作是长方体(长4,宽3,高4)截得的三棱锥, 所以球O 的直径,2R =√42+32+42=√41, ∴球O 的半径为√412,∴球O 的表面积为4π⋅(√412)2=41π.17. 刘徽注《九章算术·商功》有载:“斜解立方,得两壍堵.斜解壍堵,其一为阳马,一为鳖臑.”将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马.已知阳马P −ABCD 中,PA ⊥平面ABCD ,BC =2PA =4,AB =3,E 为PD 中点.则异面直线AE 与BD 所成角的余弦值为( )A. 35B. 25C. 6√525D. 8√525【答案】D【解析】 解:如图,取PB 中点为F ,连接AF ,EF ,∵E 为PD 中点,∴FE//BD ,∴∠AEF(或补角)为异面直线AE 与BD 所成的角.由已知,得AE =12PD =√5,AF =12PB =√132,EF =12BD =52,cos ∠AEF =AE 2+EF 2−AF 22AE⋅EF=8√525. 即AE 与BD 所成角的余弦值为8√525.18. 《九章算术》中,将四个面都为直角三角形的三棱锥称之为鳖臑,若三棱锥P -ABC为鳖臑,PA ⊥平面ABC ,PA=3,AB=4,AC=5,三棱锥P -ABC 的四个顶点都在球O 的球面上,则球O 的表面积为( ) A. 17π B. 25π C. 34π D. 50π 【答案】C【解析】解:由题意,PC为球O的直径,∵PC=√PA2+AC2=√9+25=√34,∴球O的半径R=PC2=√342,∴球O的表面积S=4πR2=4π×(√342)2=34π.19.《九章算术》中对一些特殊的几何体有特定的称谓,例如:将底面为直角三角形的直三棱柱称为堑堵,将一堑堵沿其一顶点与相对的棱刨开,得到一个阳马(底面是长方形,且有一条侧棱与底面垂直的四棱锥)和一个鳖臑(四个面均为直角三角形的四面体).在如图所示的堑堵ABC−A1B1C1中,已知AB=3,BC=4,AC=5,若阳马C1−ABB1A1的外接球的表面积等于50π,则鳖臑C1−ABC的所有棱中,最长的棱的棱长为A. 5B. √41C. 5√2D. 8【答案】C【解析】解:由题意知,直三棱柱ABC−A1B1C1中,AA1=AC=5,AB=3,BC=4,四棱锥C1−ABB1A1的外接球即为直三棱柱的外接球,以AB、BC、BB1为共顶点,画出长方体,如图所示,则长方体的最长的棱的棱长为AC1,即外接球的直径,∴外接球的表面积是.∴R=5√2 2∴鳖臑C1−ABC的所有棱中,最长的棱的棱长为AC1=2R=5√2.20.中国古代第一部数学名著《九章算术》中,将一般多面体分为阳马、鳖臑、堑堵三种基本立体图形,其中将四个面都为直角三角形的三棱锥称之为鳖,若三棱锥Q−ABC为鳖臑,QA⊥平面ABC,AB⊥BC,QA=BC=3,AC=5,则三棱锥Q−ABC 外接球的表面积为()A. 16πB. 20πC. 30πD. 34π【答案】D【解析】解:如图,补全为长方体,则2R=√32+42+32=√34,∴R=√342,故外接球得表面积为4πR2=34π,由题意画出图形,补全为长方体,求出长方体的对角线长,可得三棱锥Q−ABC外接球的半径,则答案可求.本题考查多面体外接球的表面积的求法,考查数形结合的解题思想方法,是基础题.二、填空题(本大题共4小题,共20.0分)21.在我国古代的数学专著《九章算术》中,将四个面均为直角三角形的三棱锥称为鳖臑(biēnào),已知鳖臑P−ABC中,PA⊥平面ABC,AB⊥BC,若PA=AB=2√2,BC=2,E,F分别是PB,PC的中点,则三棱锥P−AEF的外接球的表面积为________.【答案】9π【解析】解:PA⊥平面ABC,BC⊂平面ABC,所以PA⊥BC,又因为AB⊥BC,PA∩AB=A,PA,AB⊂面PAB,所以BC⊥面PAB,∵AE⊂面PAB,∴BC⊥AE,∵PA=AB,E为PB的中点,所以AE⊥PB,PB∩BC=B,PB,BC⊂面PBC,所以AE⊥面PBC,∵EF⊂面PBC,所以AE⊥EF,AE⊥PE,又EF//BC,所以EF⊥PE,则EF,PE,AE两两垂直,EF=12BC=1,PE=AE=2,所以三棱锥P−AEF的外接球半径为√1+4+42=32,故球的表面积为4×(94)π=9π,22.《九章算术·商功》中有这样一段话:“斜解立方,得两壍堵.斜解壍堵,其一为阳马,一为鳖臑.”这里所谓的“鳖臑(biēnào)”,就是在对长方体进行分割时所产生的四个面都为直角三角形的三棱锥.已知三棱锥A−BCD是一个“鳖臑”,AB⊥平面BCD,AC⊥CD,且AB=BC=CD=2,则三棱锥A−BCD的外接球的表面积为________.【答案】12π【解析】解:∵三棱锥A−BCD是一个“鳖臑”,AB⊥平面BCD,AC⊥CD,且AB=BC=CD=2,∴三棱锥A−BCD的外接球的半径:R=AD2=√AB2+BC2+CD22=√4+4+42=√3∴三棱锥A−BCD的外接球的表面积为:S=4πR2=12π.故答案为12π.23.《九章算术》中,将四个面都为直角三角形的三棱锥称之为鳖臑.若三棱锥P−ABC为鳖臑,PA⊥平面ABC,PA=AB=2,AC=4,三棱锥P−ABC的四个顶点都在球O的球面上,则球O的表面积为_______ 。
立体几何选择、填空(有难度)

立体几何选择填空问题集班级______姓名________一. 选择题1.定点P 不在△ABC 所在平面内,过P 作平面α,使△ABC 的三个顶点到α的距离相等,这样的平面共有( ) (A)1个 (B)2个 (C)3个 (D)4个2.P 为矩形ABCD 所在平面外一点,且PA ⊥平面ABCD ,P 到B ,C ,D 三点的距离分别是5,17,13,则P 到A 点的距离是( ) (A)1(B)2(C)3(D)43.直角三角形ABC 的斜边AB 在平面α内,直角顶点C 在平面α外,C 在平面α内的射影为C 1,且C 1 AB ,则△C 1AB 为 ( ) (A)锐角三角形(B)直角三角形(C)钝角三角形(D)以上都不对4.已知四点,无三点共线,则可以确定( ) A.1个平面B.4个平面C.1个或4个平面D.无法确定5. 已知球的两个平行截面的面积分别为5π和8π,它们位于球心的同一侧且相距是1,那么这个球的半径是( ) A.4B.3C.2D.56.球面上有3个点,其中任意两点的球面距离都等于大圆周长的61,经过3个点的小圆的周长为4π,那么这个球的半径为( ) A.43 B.23 C.2 D. 37.棱长为1的正方体ABCD -A 1B 1C 1D 1被以A 为球心,AB 为半径的球相截,则被截形体的表面积为( ) A .45π B .87π C .π D .47π 8.某刺猬有2013根刺,当它蜷缩成球时滚到平面上,任意相邻的三根刺都可支撑住身体,且任意四根刺的刺尖不共面,问该刺猬蜷缩成球时,共有( )种不同的支撑身体的方式。
A .2013 B .4022 C .4024 D .4026图-1ESF CB A命题①空间直线a ,b ,c ,若a∥b,b∥c 则a∥c ②非零向量c 、b 、a ,若a ∥b ,b ∥c 则a ∥c ③平面α、β、γ若α⊥β,β⊥γ,则α∥γ ④空间直线a 、b 、c 若有a⊥b,b⊥c,则a∥c⑤直线a 、b 与平面β,若a⊥β,c⊥β,则a∥c 其中所有真命题的序号是( ) A .①②③ B.①③⑤ C.①②⑤ D.②③⑤ 9.在正三棱锥中,相邻两侧面所成二面角的取值范围是( )A 、3ππ(,) B 、23ππ(,) C 、(0,2π) D 、23ππ(,)3 10.以正方体的任意三个顶点为顶点作三角形,从中随机地取出两个三角形,则这两个三角形不共面的概率为 ( ) A .367385 B . 376385 C .192385 D .18385二.填空题11.在三棱锥P —ABC 中,底面是边长为2 cm 的正三角形,PA =PB =3 cm,转动点P 时,三棱锥的最大体积为 .12.P 为ABC ∆所在平面外一点,PA 、PB 、PC 与平面ABC 所的角均相等,又PA 与BC 垂直,那么ABC ∆的形状可以是 。
高考数学-立体几何选择填空

B.若侧棱的长小于底面的变长,则 的取值范围为
C若侧棱的长大于底面的变长,则 的取值范围为
D若侧棱的长大于底面的变长,则 的取值范围为
二、填空题
36、在长方形 中, , , 为 的中点, 为线段 (端点除外)上一动点.现将 沿 折起,使平面 平面 .在平面 内过点 作 , 为垂足.设 ,则 的取值范围是.(1/2,1)
A.πB. 2πC.3πD.
6、如果四棱锥的四条侧棱都相等,就称它为“等腰四棱锥”,四条侧棱称为它的腰,以下4个命题中,假命题是B
A.等腰四棱锥的腰与底面所成的角都相等
B.等腰四棱锥的侧面与底面所成的二面角都相等或互补
C.等腰四锥的底面四边形必存在外接圆D.等腰四棱锥的各顶点必在同一球面上
7、给出下列四个命题:
50、在正方体ABCD-A1B1C1D1中,M,N分别是AB1,BC1上的点,且满足AM=BN,有下列4个结论:①MN⊥AA1;②MN∥AC;③MN∥平面A1B1C1D1;④MN⊥BB1D1D。其中正确的结论的序号是_________
A. B. C. D.
9、过球的一条半径的中点,作垂直于该半径的平面,则所得截面的面积与球的表面积的比为A
(A)(B)(C)(D)
10、如图,平面α⊥平面β,A∈α,B∈β,AB与两平面α、β所成的角分别为和,过A、B分别作两平面交线的垂线,垂足为A′、B′,则AB∶A′B′=A
(A)2∶1(B)3∶1(C)3∶2(D)4∶3
44、已知正三棱柱 的底面边长为1,高为8,一质点自 点出发,沿着三棱柱的侧面绕行两周到达 点的最短路线的长为.
45、若一条直线与一个正四棱柱各个面所成的角都为 ,则 =______√6/3
高考数学-立体几何选择填空

高考立体几何选择填空专练班别:__________ 姓名:_________ 一、选择题:(只有一个选项是正确) 1、表面积为23 的正八面体的各个顶点都在同一个球面上,则此球的体积为AA .23πB .13πC .23π D .223π 2、平面α的斜线AB 交α于点B ,过定点A 的动直线l 与AB 垂直,且交α于点C ,则动点C 的轨迹是A(A )一条直线 (B )一个圆(C )一个椭圆 (D )双曲线的一支3、过平行六面体ABCD-A 1B 1C 1D 1任意两条棱的中点作直线,其中与平面DBB 1D 1平行的直线有DA.4条B.6条C.8条D.12条4、棱长为2的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如图1, 则图中三角形(正四面体的截面)的面积是CA.22B.322 3 5、过半径为2的球O 表面上一点A 作球O 的截面,若OA 与该截面所成的角是60°则该截面的面积是AA .π B. 2π C. 3π D. π326、如果四棱锥的四条侧棱都相等,就称它为“等腰四棱锥”,四条侧棱称为它的腰,以下4个命题中,假命题...是B A .等腰四棱锥的腰与底面所成的角都相等B .等腰四棱锥的侧面与底面所成的二面角都相等或互补C .等腰四棱锥的底面四边形必存在外接圆D .等腰四棱锥的各顶点必在同一球面上7、给出下列四个命题:①垂直于同一直线的两条直线互相平行. ②垂直于同一平面的两个平面互相平行. ③若直线12,l l 与同一平面所成的角相等,则12,l l 互相平行.④若直线12,l l 是异面直线,则与12,l l 都相交的两条直线是异面直线.其中假.命题的个数是D (A)1 (B)2 (C)3 (D)48、已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积是CA .16πB .20πC .24πD .32π9、过球的一条半径的中点,作垂直于该半径的平面,则所得截面的面积与球的表面积的比为A(A )316 (B )916 (C )38 (D )93210、如图,平面α⊥平面β,A ∈α,B ∈β,AB 与两平面α、β所成的角分别为π4和π6,过A 、B 分别作两平面交线的垂线,垂足为A ′、B ′,则AB ∶A ′B ′=A(A )2∶1 (B )3∶1 (C )3∶2 (D )4∶311、已知平面α外不共线的三点A,B,C 到α的距离都相等,则正确的结论是DA.平面ABC 必平行于αB.平面ABC 必与α相交C.平面ABC 必不垂直于αD.存在△ABC 的一条中位线平行于α或在α内12、若空间中有四个点,则“这四个点中有三点在同一直线上”是“这四个点在同一平面上”的 A(A )充分非必要条件;(B )必要非充分条件;(C )充要条件;(D )非充分非必要条件13、已知球O 的半径是1,A 、B 、C 三点都在球面上,A 、B 两点和A 、C 两点的球面距离都是4π,B 、C 两点的球面距离是3π,则二面角B OA C --的大小是C (A )4π B )3π (C )2π (D )23π 14、正四棱锥P ABCD -底面的四个顶点,,,A B C D 在球O 的同一个大圆上,点P 在球面上,如果163P ABCD V -=,则球O 的表面积是D (A )4π (B )8π (C )12π (D )16π15、对于任意的直线l 与平同α , 在平面a 内必有直线m , 使m 与l C(A)平行 (B )相交 (C)垂直 (D)互为异面直线16、正三棱柱ABC -A 1B 1C 1的侧棱长与底面边长相等,则AB 1与面ACC 1A 1所成角的正弦等于A(A) 4 (B)4 (C) 2 (D) 217、已知三棱锥的侧棱长的底面边长的2倍,则侧棱与底面所成角的余弦值等于AA B C .2 D 18、设n m l ,,均为直线,其中n m ,在平面α内,则“l ⊥α”是“l m l n ⊥⊥且”的A (A)充分不必要条件 (B)必要不充分条件(C)充分必要条件(D)既不充分也不必要条件19、把边长为2的正方形ABCD 沿对角线AC 折成直二面角, 折成直二面角后, 在A ,B ,C ,D 四点所在的球面上, B 与D 两点之间的球面距离为 C (A)22π (B)π (C)2π (D)3π 20、半径为1的球面上的四点D C B A ,,,是正四面体的顶点,则A 与B 两点间的球面距离为C(A ))33arccos(- (B ))36arccos(- (C ))31arccos(-(D ))41arccos(- 21、棱长为1的正方体1111ABCD A B C D -的8个顶点都在球O 的表面上,E F ,分别 是棱AA ,1DD 的中点,则直线EF 被球O 截得的线段长为DA .2 B .1 C .12+ D 22、正方体1AC 的棱长为1,过点A 作平面1A BD 的垂线,垂足为H ,则下列命题中错误..的命D A .点H 是1A BD △的垂心 B .AH 垂直平面11CB DC .AH 的延长线经过点1CD .直线AH 和1BB 所成角为4523、四面体ABCD 的外接球球心在CD 上,且2CD =,AB =A B ,间的球面距离是CA .π6B .π3C .2π3D .5π624、在棱长为1的正方体ABCD -A 1B 1C 1D 1中,E 、F 分别为棱AA 1、BB 1的中点,G 为棱A 1B 1上的一点,且A 1G =λ(0≤λ≤1),则点G 到平面D 1EF 的距离为DA.3B.22C.32λ D.5525、一个四棱锥和一个三棱锥恰好可以拼接成一个三棱柱.这个四棱锥的底面为正方形,且底面边长与各侧棱长相等,这个三棱锥的底面边长与各侧棱长也都相等.设四棱锥、三棱锥、三棱柱的高分别为h 1,h 2,h 3,则h 1:h 2:h 3= BA .3:1:1B .3:2:2C .3:2:2D .3:2:326、已知三棱锥S ABC -的各顶点都在一个半径为r 的球面上,球心O 在AB 上,SO ⊥底面ABC ,2AC r =,则球的体积与三棱锥体积之比是DA .πB .2πC .3πD .4π 27、若三个平面两两相交,且三条交线互相平行,则这三个平面把空间分成CA .5部分 B.6部分 C.7部分 D.8部分28、设球O 的半径是1,A 、B 、C 是球面上三点,已知A 到B 、C 两点的球面距离都是2π,且二面角B OA C --的大小是3π,则从A 点沿球面经B 、C 两点再回到A 点的最短距离是C (A )76π (B )54π (C )43π (D )32π 29、一个正三棱锥的四个顶点都在半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,则该正三棱锥的体积是C(A )433 (B)33 (C) 43 (D) 123. 30、已知二面角α-l -β为60 ,动点P 、Q 分别在面α、β内,P 到β3Q 到α的距离为23P 、Q 两点之间距离的最小值为C(A) (B)2 (C) 23 (D)431、在半径为3的球面上有C B A 、、三点,ABC ∠=90°,BC BA =, 球心O 到平面ABC 的距离是223,则C B 、两点的球面距离是B A. 3π B. π C. π34 D.2π 32、正六棱锥P -ABCDEF 中,G 为PB 的中点,则三棱锥D -GAC 与P -GAC 体积之比为C (A )1:1 (B) 1:2 (C) 2:1 (D) 3:2 33、如果把地球看成一个球体,则地球上的北纬060纬线长和赤道长的比值为C(A )0.8 (B )0.75 (C )0.5 (D )0.2534、已知二面角l αβ--的大小为050,P 为空间中任意一点,则过点P 且与平面α和平面β所成的角都是025的直线的条数为BA .2B .3C .4D .535、在正四棱柱1111ABCD A B C D -中,顶点1B 到对角线1BD 和到平面11A BCD 的距离分别为h 和d ,则下列命题中正确的是CA .若侧棱的长小于底面的变长,则h d的取值范围为(0,1) B .若侧棱的长小于底面的变长,则h d的取值范围为223()23 C 若侧棱的长大于底面的变长,则h d 的取值范围为23(2)3 D 若侧棱的长大于底面的变长,则h d 的取值范围为23()3+∞二、填空题36、在长方形ABCD 中,2AB =,1BC =,E 为DC 的中点,F 为线段EC (端点除外)上一动点.现将AFD ∆沿AF 折起,使平面ABD ⊥平面ABC .在平面ABD 内过点D 作DK AB ⊥,K 为垂足.设AK t =,则t 的取值范围是 .(1/2,1)37、直三棱柱111ABC A B C -的各顶点都在同一球面上,若12AB AC AA ===,120BAC ∠=︒,则此球的表面积等于 。
专题10 立体几何选择填空题(解析版)

专题10立体几何选择填空题1.【2019年新课标3文科08】如图,点N 为正方形ABCD 的中心,△ECD 为正三角形,平面ECD ⊥平面ABCD ,M 是线段ED 的中点,则( )A .BM =EN ,且直线BM ,EN 是相交直线B .BM ≠EN ,且直线BM ,EN 是相交直线C .BM =EN ,且直线BM ,EN 是异面直线D .BM ≠EN ,且直线BM ,EN 是异面直线【解答】解:∵点N 为正方形ABCD 的中心,△ECD 为正三角形,平面ECD ⊥平面ABCD ,M 是线段ED的中点,∴BM⊂平面BDE,EN⊂平面BDE,∵BM是△BDE中DE边上的中线,EN是△BDE中BD边上的中线,∴直线BM,EN是相交直线,设DE=a,则BD,BE,∴BM a,EN a,∴BM≠EN,故选:B.2.【2019年新课标2文科07】设α,β为两个平面,则α∥β的充要条件是()A.α内有无数条直线与β平行B.α内有两条相交直线与β平行C.α,β平行于同一条直线D.α,β垂直于同一平面【解答】解:对于A,α内有无数条直线与β平行,α∩β或α∥β;对于B,α内有两条相交直线与β平行,α∥β;对于C,α,β平行于同一条直线,α∩β或α∥β;对于D,α,β垂直于同一平面,α∩β或α∥β.故选:B.3.【2018年新课标2文科09】在正方体ABCD﹣A1B1C1D1中,E为棱CC1的中点,则异面直线AE与CD 所成角的正切值为()A.B.C.D.【解答】解以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,设正方体ABCD﹣A1B1C1D1棱长为2,则A(2,0,0),E(0,2,1),D(0,0,0),C(0,2,0),(﹣2,2,1),(0,﹣2,0),设异面直线AE与CD所成角为θ,则cosθ,sinθ,∴tanθ.∴异面直线AE与CD所成角的正切值为.故选:C.4.【2018年新课标1文科05】已知圆柱的上、下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为()A.12πB.12πC.8πD.10π【解答】解:设圆柱的底面直径为2R,则高为2R,圆柱的上、下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,可得:4R2=8,解得R,则该圆柱的表面积为:12π.故选:B.5.【2018年新课标1文科09】某圆柱的高为2,底面周长为16,其三视图如图.圆柱表面上的点M在正视图上的对应点为A,圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度为()A.2B.2C.3 D.2【解答】解:由题意可知几何体是圆柱,底面周长16,高为:2,直观图以及侧面展开图如图:圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度:2.故选:B.6.【2018年新课标1文科10】在长方体ABCD﹣A1B1C1D1中,AB=BC=2,AC1与平面BB1C1C所成的角为30°,则该长方体的体积为()A.8 B.6C.8D.8【解答】解:长方体ABCD﹣A1B1C1D1中,AB=BC=2,AC1与平面BB1C1C所成的角为30°,即∠AC1B=30°,可得BC12.可得BB12.所以该长方体的体积为:28.故选:C.7.【2018年新课标3文科03】中国古建筑借助榫卯将木构件连接起来.构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是()A.B.C.D.【解答】解:由题意可知,如图摆放的木构件与某一带卯眼的木构件咬合成长方体,小的长方体,是榫头,从图形看出,轮廓是长方形,内含一个长方形,并且一条边重合,另外3边是虚线,所以木构件的俯视图是A.故选:A.8.【2018年新课标3文科12】设A,B,C,D是同一个半径为4的球的球面上四点,△ABC为等边三角形且面积为9,则三棱锥D﹣ABC体积的最大值为()A.12B.18C.24D.54【解答】解:△ABC为等边三角形且面积为9,可得,解得AB=6,球心为O,三角形ABC的外心为O′,显然D在O′O的延长线与球的交点如图:O′C,OO′2,则三棱锥D﹣ABC高的最大值为:6,则三棱锥D﹣ABC体积的最大值为:18.故选:B.9.【2018年北京文科06】某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为()A.1 B.2 C.3 D.4【解答】解:四棱锥的三视图对应的直观图为:P A⊥底面ABCD,AC,CD,PC=3,PD=2,可得三角形PCD不是直角三角形.所以侧面中有3个直角三角形,分别为:△P AB,△PBC,△P AD.故选:C.10.【2017年新课标1文科06】如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不平行的是()A.B.C.D.【解答】解:对于选项B,由于AB∥MQ,结合线面平行判定定理可知B不满足题意;对于选项C,由于AB∥MQ,结合线面平行判定定理可知C不满足题意;对于选项D,由于AB∥NQ,结合线面平行判定定理可知D不满足题意;所以选项A满足题意,故选:A.11.【2017年新课标2文科06】如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为()A.90πB.63πC.42πD.36π【解答】解:由三视图可得,直观图为一个完整的圆柱减去一个高为6的圆柱的一半,V=π•32×10•π•32×6=63π,故选:B.12.【2017年新课标3文科09】已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为()A.πB.C.D.【解答】解:∵圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,∴该圆柱底面圆周半径r,∴该圆柱的体积:V=Sh.故选:B.13.【2017年新课标3文科10】在正方体ABCD﹣A1B1C1D1中,E为棱CD的中点,则()A.A1E⊥DC1B.A1E⊥BD C.A1E⊥BC1D.A1E⊥AC【解答】解:法一:连B1C,由题意得BC1⊥B1C,∵A1B1⊥平面B1BCC1,且BC1⊂平面B1BCC1,∴A1B1⊥BC1,∵A1B1∩B1C=B1,∴BC1⊥平面A1ECB1,∵A1E⊂平面A1ECB1,∴A1E⊥BC1.故选:C.法二:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,设正方体ABCD﹣A1B1C1D1中棱长为2,则A1(2,0,2),E(0,1,0),B(2,2,0),D(0,0,0),C1(0,2,2),A(2,0,0),C(0,2,0),(﹣2,1,﹣2),(0,2,2),(﹣2,﹣2,0),(﹣2,0,2),(﹣2,2,0),∵•2,2,0,6,∴A1E⊥BC1.故选:C.14.【2017年北京文科06】某三棱锥的三视图如图所示,则该三棱锥的体积为()A.60 B.30 C.20 D.10【解答】解:由三视图可知:该几何体为三棱锥,该三棱锥的体积10.故选:D.15.【2019年天津文科12】已知四棱锥的底面是边长为的正方形,侧棱长均为.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆柱的体积为.【解答】解:由题作图可知,四棱锥底面正方形的对角线长为2,且垂直相交平分,由勾股定理得:正四棱锥的高为2,由于圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,有圆柱的上底面直径为底面正方形对角线的一半等于1,即半径等于;由相似比可得圆柱的高为正四棱锥高的一半1,则该圆柱的体积为:v=sh=π()2×1;故答案为:16.【2019年新课标3文科16】学生到工厂劳动实践,利用3D打印技术制作模型.如图,该模型为长方体ABCD﹣A1B1C1D1挖去四棱锥O﹣EFGH后所得的几何体,其中O为长方体的中心,E,F,G,H分别为所在棱的中点,AB=BC=6cm,AA1=4cm.3D打印所用原料密度为0.9g/cm3.不考虑打印损耗,制作该模型所需原料的质量为g.【解答】解:该模型为长方体ABCD﹣A1B1C1D1,挖去四棱锥O﹣EFGH后所得的几何体,其中O为长方体的中心,E,F,G,H,分别为所在棱的中点,AB=BC=6cm,AA1=4cm,∴该模型体积为:V O﹣EFGH=6×6×4=144﹣12=132(cm3),∵3D打印所用原料密度为0.9g/cm3,不考虑打印损耗,∴制作该模型所需原料的质量为:132×0.9=118.8(g).故答案为:118.8.17.【2019年新课标1文科16】已知∠ACB=90°,P为平面ABC外一点,PC=2,点P到∠ACB两边AC,BC的距离均为,那么P到平面ABC的距离为.【解答】解:∠ACB=90°,P为平面ABC外一点,PC=2,点P到∠ACB两边AC,BC的距离均为,过点P作PD⊥AC,交AC于D,作PE⊥BC,交BC于E,过P作PO⊥平面ABC,交平面ABC于O,连结OD,OC,则PD=PE,∴CD=CE=OD=OE1,∴PO.∴P到平面ABC的距离为.故答案为:.18.【2019年北京文科12】某几何体是由一个正方体去掉一个四棱柱所得,其三视图如图所示.如果网格纸上小正方形的边长为l,那么该几何体的体积为.【解答】解:由三视图还原原几何体如图,该几何体是把棱长为4的正方体去掉一个四棱柱,则该几何体的体积V.故答案为:40.19.【2019年北京文科13】已知l,m是平面α外的两条不同直线.给出下列三个论断:①l⊥m;②m∥α;③l⊥α.以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:.【解答】解:由l,m是平面α外的两条不同直线,知:由线面平行的判定定理得:若l⊥α,l⊥m,则m∥α.故答案为:若l⊥α,l⊥m,则m∥α.20.【2018年新课标2文科16】已知圆锥的顶点为S,母线SA,SB互相垂直,SA与圆锥底面所成角为30°.若△SAB的面积为8,则该圆锥的体积为.【解答】解:圆锥的顶点为S,母线SA,SB互相垂直,△SAB的面积为8,可得:,解得SA=4,SA与圆锥底面所成角为30°.可得圆锥的底面半径为:2,圆锥的高为:2,则该圆锥的体积为:V8π.故答案为:8π.21.【2018年天津文科11】如图,已知正方体ABCD﹣A1B1C1D1的棱长为1,则四棱锥A1﹣BB1D1D的体积为.【解答】解:由题意可知四棱锥A1﹣BB1D1D的底面是矩形,边长:1和,四棱锥的高:A1C1.则四棱锥A1﹣BB1D1D的体积为:.故答案为:.22.【2017年新课标2文科15】长方体的长、宽、高分别为3,2,1,其顶点都在球O的球面上,则球O 的表面积为.【解答】解:长方体的长、宽、高分别为3,2,1,其顶点都在球O的球面上,可知长方体的对角线的长就是球的直径,所以球的半径为:.则球O的表面积为:414π.故答案为:14π.23.【2017年新课标1文科16】已知三棱锥S﹣ABC的所有顶点都在球O的球面上,SC是球O的直径.若平面SCA⊥平面SCB,SA=AC,SB=BC,三棱锥S﹣ABC的体积为9,则球O的表面积为.【解答】解:三棱锥S﹣ABC的所有顶点都在球O的球面上,SC是球O的直径,若平面SCA⊥平面SCB,SA=AC,SB=BC,三棱锥S﹣ABC的体积为9,可知三角形SBC与三角形SAC都是等腰直角三角形,设球的半径为r,可得,解得r=3.球O的表面积为:4πr2=36π.故答案为:36π.24.【2017年天津文科11】已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为18,则这个球的体积为.【解答】解:设正方体的棱长为a,∵这个正方体的表面积为18,∴6a2=18,则a2=3,即a,∵一个正方体的所有顶点在一个球面上,∴正方体的体对角线等于球的直径,即a=2R,即R,则球的体积Vπ•()3;故答案为:.1.【2019年湖北省武汉市高考数学(5月份)模拟】已知长方体全部棱长的和为36,表面积为52,则其体对角线的长为( )A .4BC .D .【答案】B 【解析】设长方体的三条棱的长分别为:,,x y z ,则2()524()36xy yz zx x y z ++=⎧⎨++=⎩,===.故选:B .2.【湖北省黄冈中学2019届高三第三次模拟】已知正方体1111ABCD A B C D -的棱长为1,在对角线1A D 上取点M ,在1CD 上取点N ,使得线段MN 平行于对角面11A ACC ,则||MN 的最小值为( )A .1 BC .2D 【答案】D 【解析】作1MM AD ⊥,垂足为1M ,作1NN CD ⊥,垂足为1N ,如下图所示:在正方体1111ABCD A B C D -中,根据面面垂直的性质定理,可得11,MM NN ,都垂直于平面ABCD ,由线面垂直的性质,可知11MM NN ,易知:1111//M M A N N ACC 平面,由面面平行的性质定理可知://11M N AC ,设11DM DN x ==,在直角梯形11MM N N 中,222211)(12)633MN x x x ⎛⎫=+-=-+ ⎪⎝⎭,当13x =时,||MN 故本题选D.3.【广东省2019届高考适应性考试】平面四边形ABCD 中,AD AB ==CD CB ==AD AB ⊥,现将ABD ∆沿对角线BD 翻折成A BD '∆,则在A BD '∆折起至转到平面BCD 的过程中,直线A C '与平面BCD 所成最大角的正切值为( )A .2B .12C D .3【答案】D 【解析】 取BD 的中点O,则,,,A B A D BC CD A O BD CO BD '''==∴⊥⊥即BD ⊥平面A OC ',从而平面BCD ⊥平面A OC ',因此A '在平面BCD 的射影在直线OC 上,即A CO '∠为直线A C '与平面BCD 所成角,因为AD AB ==CD CB ==AD AB ⊥,所以111,2sin sin sin 22A O A O OC A CO OA C OA C OC '''''==∴∠=∠=∠≤,即A CO '∠最大值为π6,因此直线A C '与平面BCD 所成最大角的正切值为πtan 63=,选D.4.【山东省淄博市部分学校2019届高三5月阶段性检测】在正方体1111ABCD A B C D -中,点P 在侧面11BCC B 及其边界上运动,并且保持1AP BD ⊥,则动点P 的轨迹为 ( )A .线段1BC B .线段1BCC .1BB 的中点与1CC 的中点连成的线段D .BC 的中点与11B C 的中点连成的线段 【答案】A 【解析】如图,连接AC ,1AB ,1B C ,在正方体1111ABCD A B C D -中,有1BD ⊥面1ACB , 因为1AP BD ⊥,所以AP ⊂面1ACB , 又点P 在侧面11BCC B 及其边界上运动,∴故点P 的轨迹为面1ACB 与面11BCC B 的交线段1CB .故选:A .5.【四川省名校联盟2019届高考模拟信息卷(一)】已知一个几何体的三视图如图所示,其中俯视图是一个边长为2的正方形,则该几何体的表面积为( )A .223B .20C .20+D .20+【答案】C 【解析】解:该几何体是棱长为2的正方体削去一个角后得到的几何体(如图),其表面积为()122132222222S +⨯=⨯⨯+⨯+⨯⨯1202+⨯=.故选C.6.【山东省淄博市部分学校2019届高三5月阶段性检测】如图,在正方体1111ABCD A B C D -中,点F 是线段1BC 上的动点,则下列说法错误..的是( )A .当点F 移动至1BC 中点时,直线1A F 与平面1BDC 所成角最大且为60B .无论点F 在1BC 上怎么移动,都有11A F BD ⊥C .当点F 移动至1BC 中点时,才有1A F 与1BD 相交于一点,记为点E ,且12A EEF= D .无论点F 在1BC 上怎么移动,异面直线1A F 与CD 所成角都不可能是30 【答案】A 【解析】对于A ,当点F 移动到1BC 的中点时,直线1A F 与平面1BDC 所成角由小到大再到小,如图1所示;且F 为1B C的中点时最大角的余弦值为11132OF A F ==<,最大角大于60︒,所以A 错误; 对于B ,在正方形中,1DB ⊥面11A BC ,又1A F ⊂面11A BC ,所以11A F B D ⊥,因此B 正确; 对于C ,F 为1BC 的中点时,也是1B C 的中点,它们共面于平面11A B CD ,且必相交,设为E ,连1A D 和1B F ,如图2,根据△1A DE ∽△1FB E ,可得1112A E DA EF B F==,所以C 正确;对于D ,当点F 从B 运动到1C 时,异面直线1A F 与CD 所成角由大到小再到大,且F 为1B C 的中点时最小角的正切值为2123=>,最小角大于30°,所以D 正确;故选:A .7.【山东省栖霞市2019届高三高考模拟卷】已知P ,A ,B ,C ,D 是球O 的球面上的五个点,四边形ABCD 为梯形,//AD BC ,2AB DC AD ===,4BC PA ==,PA ⊥面ABCD ,则球O 的体积为( )A .3B .3C .D .16π【答案】A 【解析】取BC 中点E ,连接,,AE DE BD//AD BC 且12AD BC EC == ∴四边形ADCE 为平行四边形 AE DC∴=,又12DC BC = 12D E B C ∴= AE DE BE EC ∴===E ∴为四边形ABCD 的外接圆圆心设O 为外接球的球心,由球的性质可知OE ⊥平面ABCD作OF PA ⊥,垂足为F ∴四边形AEOF 为矩形,2OF AE == 设AF x =,OP OA R ==则()22444x x +-=+,解得:2x = R ∴=∴球O 的体积:343V R π==本题正确选项:A8.【广东省东莞市2019届高三第二学期高考冲刺试题】如图画出的是某几何体的三视图,网格纸上小正方形的边长为1,则该几何体的体积为( )A .253πB .263πC .223πD .233π【答案】A 【解析】由三视图还原原几何体,如图所示,可知原几何体为组合体,是半径为2的球的34与半径为1的球的14, 其球的组合体的体积33341425V 2143433πππ=⨯⨯+⨯⨯= . 故选:A .9.【河南省百校联盟2019届高三考前仿真试卷】阳马,中国古代算数中的一种几何形体,是底面长方形,两个三角面与底面垂直的四棱锥体,在阳马P ABCD -中,PC 为阳马P ABCD -中最长的棱,1,2,3AB AD PC ===,若在阳马P ABCD -的外接球内部随机取一点,则该点位阳马内的概率为( ) A .127πB .427πC .827πD .49π【答案】C 【解析】根据题意,PC 的长等于其外接球的直径,因为PC =3=,∴2PA =,又PA ⊥平面ABCD ,所以314431223332P ABCDV V π-⎛⎫=⨯⨯⨯==⨯ ⎪⎝⎭球,, ∴3483274332P ππ==⎛⎫⨯ ⎪⎝⎭. 10.【湖南省长沙市湖南师范大学附属中学2019届高三高考模拟(二)】已知平面α平面β=直线l ,点A 、C α∈,点B 、D β∈,且A 、B 、C 、D l ∉,点M 、N 分别是线段AB 、CD 的中点,则下列说法正确的是( )A .当2CD AB =时,M 、N 不可能重合B .M 、N 可能重合,但此时直线AC 与l 不可能相交 C .当直线AB 、CD 相交,且//AC l 时,BD 可与l 相交 D .当直线AB 、CD 异面时,MN 可能与l 平行 【答案】B 【解析】A 选项:当2CD AB =时,若,,,A BCD 四点共面且//AC BD 时,则,M N 两点能重合,可知A 错误;B 选项:若,M N 可能重合,则//AC BD ,故//AC l ,此时直线AC 与直线l 不可能相交,可知B 正确;C 选项:当AB 与CD 相交,直线//AC l 时,直线BD 与l 平行,可知C 错误;D 选项:当AB 与CD 是异面直线时,MN 不可能与l 平行,可知D 错误.本题正确选项:B11.【山东省临沂市2019届高三模拟考试(三模)】如图是某几何体的三视图,则过该几何体顶点的所有截面中,最大截面的面积是( )A .2 BC D .1【答案】A 【解析】由三视图可知其对应的几何体是一个半圆锥,且圆锥的底面半径为r =1h =,故俯视图是一个腰长为2,顶角为120的等腰三角形,易知过该几何体顶点的所有截面均为等腰三角形,且腰长为2,顶角的范围为(0,120⎤⎦, 设顶角为θ,则截面的面积:122sin 2sin 2S θθ=⨯⨯⨯=, 当90θ=时,面积取得最大值2. 故选:A .12.【江西省抚州市临川第一中学2019届高三下学期考前模拟】已知如图正方体1111ABCD A B C D -中,P 为棱1CC 上异于其中点的动点,Q 为棱1AA 的中点,设直线m 为平面BDP 与平面11B D P 的交线,以下关系中正确的是( )A .1//m D QB .1m Q B ⊥C .//m 平面11BD Q D .m ⊥平面11ABB A【答案】C 【解析】因为在正方体1111ABCD A B C D -中,11//D B BD ,且11D B ⊄平面BDP ,BD ⊂平面BDP , 所以11//D B 平面BDP ,因为11D B ⊂平面11B D P ,且平面11B D P 平面BDP m =,所以有11//m D B ,而1111D QD B D =,则m 与1D Q 不平行,故选项A 不正确;若1m Q B ⊥,则111B Q D B ⊥,显然1B Q 与11D B 不垂直,矛盾,故选项B 不正确; 若m ⊥平面11ABB A ,则11D B ⊥平面11ABB A ,显然与正方体的性质矛盾,故C 不正确; 而因为11D B ⊂平面11B D P ,m ⊄平面11B D P , 所以有//m 平面11B D P ,所以选项C 正确,.13.【山东省日照市2019届高三5月校际联合考试】如图,三棱锥A BCD -的项点,,,A B C D 都在同一球面上,BD 过球心O ,BD ABC =∆是边长为4的等边三角形,点,P Q 分别为线段BC AO ,上的动点(不含端点),且AP CQ =,则三棱锥P QOC -体积的最大值为______.【答案】23【解析】因为BD 过球心,24=BD ,所以OA OB OC ===,又△ABC 是边长为4等边三角形, 所以AO 2+CO 2=AC 2,AO 2+BO 2=AB 2,所以AO ⊥CO ,AO ⊥BO . 所以AO ⊥平面BCD ,且△BOC 也是等腰直角三角形, 设AP=CQ=x ,则211112sin ))3243323P QCOV x x x x π-⎛⎫=⋅⋅⋅⋅=≤= ⎪ ⎪⎝⎭ 当且紧当2=x 时成立. 故答案为:23. 14.【天津市和平区2018-2019学年度第二学期高三年级第三次质量调查】已知两条不重合的直线m ,n ,两个不重合的平面α,β,有下列四个命题: ①若m n ∥,α⊂m ,则n α∥; ②若n α⊥,m β⊥,且m n ∥,则αβ;③若α⊂m ,n α⊂,β∥m ,n β∥,则αβ;④若αβ⊥,m αβ=,且n β⊂,n m ⊥,则n α⊥.其中所有正确命题的序号为______. 【答案】②④ 【解析】逐一考查所给的命题:①若m n ∥,α⊂m ,有可能n α⊂,不一定有n α∥,题中的命题错误; ②若n α⊥,m β⊥,且m n ∥,由线面垂直的性质定理可得αβ,题中的命题正确;③若α⊂m ,n α⊂,β∥m ,n β∥,若m n ∥,有可能α与β相交,题中的命题错误; ④若αβ⊥,m αβ=,且n β⊂,n m ⊥,由线面垂直的性质定理可得n α⊥,题中的命题正确.综上可得:正确命题的序号为②④.15.【安徽省黄山市2019届高三毕业班第三次质量检测】连接正方体每个面的中心构成一个正八面体,则该八面体的外接球与内切球体积之比为______. 【答案】.【解析】若正八面体的外接球的各个顶点都在同一个球面上,则其中ABCD 四点或AFCE 四点所组成的截面在球的一个大圆面上, 可得,此四点组成的正方形是球的大圆的一个内接正方形, 其对角线的长度即为球的直径,设正八面体边长为2,且每个侧面三角形均为等边三角形,故FE=AC=2,则外接球的半径是,又正方体中心设为O,取AB中点M,则在直角△OME中,斜边ME=,斜边ME上的高即为内切球的半径,大小为,∴外接球与内切球半径之比为,∴外接球与内切球体积之比为故答案为.16.【江苏省七市2019届高三第三次调研】已知直角梯形ABCD中,AB∥CD,AB⊥BC,AB=3 cm,BC=1 cm,CD=2 cm.将此直角梯形绕AB边所在的直线旋转一周,由此形成的几何体的体积为____cm3.【答案】【解析】依据题意,作出如下直角梯形:将此直角梯形绕AB边所在的直线旋转一周,所得几何体体积等于一个圆柱的体积和一个圆锥的体积之和。
高三文科数学立体几何填空选择含答案

空间的角是空间图形的一个要素,在异面直线所成的角、线面角、二面角等知识点上,较好地考查了学生的逻辑推理能力以及化归的数学思想.●锦囊妙计空间角的计算步骤:一作、二证、三算1.异面直线所成的角范围:0°<θ≤90°方法:①平移法;②补形法.2.直线与平面所成的角范围:0°≤θ≤90°方法:关键是作垂线,找射影.3.二面角方法:①定义法;②三垂线定理及其逆定理;③垂面法. 注:二面角的计算也可利用射影面积公式S′=Scosθ来计算命题要点:(1)简单几何体的表面积(′11年3考,′10年3考);(2)简单几何体的体积(′11年5考,′10年4考).A级基础达标演练(时间:40分钟满分:60分)一、选择题(每小题5分,共25分)1.棱长为2的正四面体的表面积是().A. 3 B.4 C.4 3 D.16解析每个面的面积为:12×2×2×32= 3.∴正四面体的表面积为:4 3.答案 C2.把球的表面积扩大到原来的2倍,那么体积扩大到原来的().A.2倍B.22倍 C.2倍 D.32倍解析由题意知球的半径扩大到原来的2倍,则体积V=43πR3,知体积扩大到原来的22倍.答案 B3.(2011·陕西)某几何体的三视图如图所示,则它的体积为( ). A .8-2π3 B .8-π3 C .8-2π D.2π3解析 显然圆锥的底面半径为1,高为2,组合体体积为四棱柱体积减去圆锥体积,即V =22×2-13×π×12×2=8-23π.答案 A4.(2011·温州检测(二))如图所示,一个空间几何体的主视图和左视图都是边长为2的正方形,俯视图是一个直径为2的圆,则这个几何体的全面积为( ).A .2πB .4πC .6πD .8π解析 由三视图知该简单几何体为圆柱,所以其全面积为π×12×2+2π×1×2=6π.答案 C 5.(2012·厦门模拟)已知某几何体的三视图如图,其中主视图中半圆的半径为1,则该几何体的体积为( ).A .24-32π B .24-π3 C .24-π D .24-π2解析 据三视图可得几何体为一长方体内挖去一个半圆柱,其中长方体的棱长分别为:2,3,4,半圆柱的底面半径为1,母线长为3,故其体积V =2×3×4-12×π×12×3=24-3π2.答案 A二、填空题(每小题4分,共12分)6.(2009·全国Ⅱ)设OA 是球O 的半径,M 是OA 的中点,过M 且与OA 成45°角的平面截球O 的表面得到圆C .若圆C 的面积等于7π4,则球O 的表面积等于________.解析设圆C 的半径为r ,有πr 2=7π4.得r 2=74.又设球的半径为R ,如图所示,有OB =R ,OC =R 2·22=24R ,CB =r .在Rt △OCB 中,有OB 2=OC 2+CB 2,即R 2=18R 2+r 2⇒78R 2=74,∴R 2=2,∴S 球=4πR 2=8π.答案 8π7.(2011·天津)一个几何体的三视图如图所示(单位:m),则该几何体的体积为________m 3.解析由三视图知该几何体由两个长方体组成,上面的长方体的长、宽、高分别为1、1、2,下面的长方体的长、宽、高分别为2、1、1.所以该几何体的体积V=1×1×2+2×1×1=4(m3).答案 48.(2012·湖州模拟)如图所示,已知一个多面体的平面展开图由一个边长为1的正方形和4个边长为1的正三角形组成,则该多面体的体积是________.解析由题知该多面体为正四棱锥,底面边长为1,侧棱长为1,斜高为3 2,连接顶点和底面中心即为高,可求得高为22,所以体积V=13×1×1×22=26.答案2 6三、解答题(共23分)9.(11分)某高速公路收费站入口处的安全标识墩如图1所示,墩的上半部分是正四棱锥PEFGH,下半部分是长方体ABCDEFGH.图2、图3分别是该标识墩的主视图和俯视图.(1)请画出该安全标识墩的左视图;(2)求该安全标识墩的体积.解(1)左视图同主视图,如图所示:(2)该安全标识墩的体积为V=V PEFGH+V ABCDEFGH=13×402×60+402×20=64 000(cm3).10.(12分)如图,已知某几何体的三视图如下(单位:cm).(1)画出这个几何体的直观图(不要求写画法);(2)求这个几何体的表面积及体积.解(1)这个几何体的直观图如图所示.(2)这个几何体可看成是正方体AC1及直三棱柱B1C1QA1D1P的组合体.由P A1=PD1=2,A1D1=AD=2,可得P A1⊥PD1.故所求几何体的表面积S=5×22+2×2×2+2×12×(2)2=22+42(cm2),体积V =23+12×(2)2×2=10(cm 3).B 级 综合创新备选(时间:30分钟 满分:40分)一、选择题(每小题5分,共10分) 1.(2011·江门一模)某型号的儿童蛋糕上半部分是半球,下半部分是圆锥,其三视图如图所示,则该型号蛋糕的表面积S =( ).A .115 πB .110 πC .105 πD .100 π解析 由三视图可知,圆锥的母线长为122+52=13,该型号蛋糕的表面积S =2π×52+π×5×13=115 π.答案 A2.(2012·潍坊模拟)如图是一个长方体截去一个角后所得多面体的三视图,则该多面体的体积为( ).A.1423B.2843C.2803D.1403解析根据三视图的知识及特点,可画出多面体的形状,如图所示.这个多面体是由长方体截去一个正三棱锥而得到的,所以所求多面体的体积V=V长方体-V正三棱锥=4×4×6-13×⎝⎛⎭⎪⎫12×2×2×2=2843.答案 B二、填空题(每小题4分,共8分)3.如图所示,半径为2的半球内有一内接正六棱锥P ABCDEF,则此正六棱锥的侧面积是________.解析显然正六棱锥的高为球的半径2,正六棱锥的底面为底面圆的内接正六边形.设O为球心,正六边形中,OA=2,AF=2,由于三角形P AO为直角三角形,得P A=22,从而得侧面等腰三角形的侧高为7,所以正六棱锥的侧面积为6×12×2×7=67.答案674.(2012·南京调研)如图,已知正三棱柱ABCA1B1C1的底面边长为2 cm,高为5 cm,则一质点自点A出发,沿着三棱柱的侧面绕行两周到达点A1的最短路线的长为________cm.解析 根据题意,利用分割法将原三棱柱分割为两个相同的三棱柱,然后将其展开为如图所示的实线部分,则可知所求最短路线的长为52+122=13 (cm).答案 13三、解答题(共22分) 5.(10分)已知某几何体的俯视图是如右图所示的矩形,主视图是一个底边长为8、高为4的等腰三角形,左视图是一个底边长为6、高为4的等腰三角形.(1)求该几何体的体积V ; (2)求该几何体的侧面积S . 解由题设可知,几何体是一个高为4的四棱锥,其底面是长、宽分别为8和6的矩形,正侧面及其相对侧面均为底边长为8,高为h 1的等腰三角形,左、右侧面均为底边长为6,高为h 2的等腰三角形,如右图所示.(1)几何体的体积为:V =13·S 矩形·h =13×6×8×4=64.(2)正侧面及相对侧面底边上的高为:h 1=42+32=5.左、右侧面的底边上的高为:h 2=42+42=4 2.故几何体的侧面面积为:S =2×⎝ ⎛⎭⎪⎫12×8×5+12×6×42=40+24 2.6.(12分)四面体的六条棱中,有五条棱长都等于a . (1)求该四面体的体积的最大值;(2)当四面体的体积最大时,求其表面积.解(1)如图,在四面体ABCD中,设AB=BC=CD=AC=BD=a,AD=x,取AD的中点为P,BC的中点为E,连接BP、EP、CP.得到AD⊥平面BPC,∴V ABCD=V ABPC+V DBPC=13·S△BPC·AP+13S△BPC·PD=13·S△BPC·AD=13·12·a a2-x24-a24·x=a12(3a2-x2)x2≤a12·3a22=18a3(当且仅当x=62a时取等号).∴该四面体的体积的最大值为18a 3.(2)由(1)知,△ABC和△BCD都是边长为a的正三角形,△ABD和△ACD是全等的等腰三角形,其腰长为a,底边长为62a,∴S表=2×34a2+2×12×62a×a2-⎝⎛⎭⎪⎫64a2=32a2+62a×10a4=32a2+15a24=23+154a2.。
高考数学复习总结专题05 立体几何(选择题、填空题) (解析版)

立体几何(选择题、填空题)1.【2020年高考全国Ⅰ卷理数】埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为()515 1 5 1 5 1A. B. C. D.4 2 4 2【答案】C【解析】【分析】1设C D a,PE b,利用P O2 CD PE 得到关于a,b的方程,解方程即可得到答案.22a【详解】如图,设C D a,PE b,则P O PE 2 2 2 ,OE b41 a2 1 b b由题意P O2 ab,即b 2 ab,化简得4() 2 210,2 4 2 a ab1 5解得(负值舍去).a 4故选:C.【点晴】本题主要考查正四棱锥的概念及其有关计算,考查学生的数学计算能力,是一道容易题.2.【2020年高考全国I I卷理数】如图是一个多面体的三视图,这个多面体某条棱的一个端点在正视图中对应的点为M ,在俯视图中对应的点为N ,则该端点在侧视图中对应的点为()A. EB. FC.GD.H【答案】A【解析】【分析】根据三视图,画出多面体立体图形,即可求得M 点在侧视图中对应的点.【详解】根据三视图,画出多面体立体图形,D D B C上的点在俯视图中对应的点为N,3 4上的点在正视图中都对应点M,直线1 4∴在正视图中对应M ,在俯视图中对应N 的点是D4,线段D D,上的所有点在侧试图中都对应E ,∴点3 4D4在侧视图中对应的点为E .故选:A【点睛】本题主要考查了根据三视图判断点的位置,解题关键是掌握三视图的基础知识和根据三视图能还原立体图形的方法,考查了分析能力和空间想象,属于基础题.A, B,C 为球O 的球面上的三个点,⊙O为 A B C的外接圆,若⊙O3. 【2020 年高考全国Ⅰ卷理数】已知11的面积为 4π , AB BC AC OO ,则球O的表面积为()1A. 64πB. 48πC. 36πD. 32π【答案】A 【解析】 【分析】由已知可得等边 AB C 的外接圆半径,进而求出其边长,得出O O的值,根据球的截面性质,求出球的半 1径,即可得出结论. 【详解】设圆O半径为 ,球的半径为 R ,依题意, r 14,r 2 , A B C为等边三角形,得r2由正弦定理可得 AB 2rsin 60 2 3 ,O O AB 2 3 ,根据球的截面性质O O 平面 ABC , 11 O O O A ,R OA O O2 O A 2 OO 1 2 r 4 , 21 1 1 1 O 球2 的表面积 S 4R 64 .故选:A【点睛】本题考查球的表面积,应用球的截面性质是解题的关键,考查计算求解能力,属于基础题. 4. 【2020 年高考全国Ⅲ理数】下图为某几何体的三视图,则该几何体的的表面积是( )A.6+4 2B.4+4 2C.6+2 3D.4+2 3【答案】C【解析】【分析】根据三视图特征,在正方体中截取出符合题意的立体图形,求出每个面的面积,即可求得其表面积.【详解】根据三视图特征,在正方体中截取出符合题意的立体图形1根据立体图形可得:S△ABC S△AD C S△C DB 22 22根据勾股定理可得:AB A D DB 2 2△A DB是边长为22的等边三角形根据三角形面积公式可得:1 1 3S △A D B AB AD s in60(22) 2 2 32 2 2该几何体的表面积是:3223623.故选:C.【点睛】本题主要考查了根据三视图求立体图形的表面积问题,解题关键是掌握根据三视图画出立体图形,考查了分析能力和空间想象能力,属于基础题. 5. 【2020 年高考全国 I I 卷理数】已知△ABC 是面积为若球 O 的表面积为 16π,则 O 到平面 ABC 的距离为( 3 9 34的等边三角形,且其顶点都在球 O 的球面上. )3 A. 3 B.C. 1D.22【答案】C 【解析】 【分析】根据球O 的表面积和 ABC 的面积可求得球O 的半径 R 和 AB C 外接圆半径 ,由球的性质可知所求距r 离 2 2 .d R r 【详解】设球O 的半径为 R ,则 4 R 16 ,解得: R 2 . 2 设 AB C 外接圆半径为 ,边长为 a,r 9 3ABC是面积为 的等边三角形, 41 3 9 32 a 22 9 a 2 ,解得: a 3,r a 2 93 , 2 24 3 4 3 4球心 O 到平面 ABC 2 2 的距离d R r 43 1.故选:C.【点睛】本题考查球的相关问题的求解,涉及到球的表面积公式和三角形面积公式的应用;解题关键是明 确球的性质,即球心和三角形外接圆圆心的连线必垂直于三角形所在平面.6. 【2019 年高考全国Ⅰ卷理数】已知三棱锥 P −AB C 的四个顶点在球 O 的球面上,PA=PB=P C ,△ABC 是边 长为 2 的正三角形,E ,F 分别是 PA ,AB 的中点,∠CEF =90°,则球 O 的体积为A .8 6B . 4 6 D . 6C . 2 6 【答案】D【解析】解法一: PA P B PC, ABC 为边长为 2 的等边三角形,P ABC为正三棱锥,△ PB AC ,又 E , F 分别为 PA , AB 的中点,EF ∥PB ,EF AC ,又 EF CE ,C E AC C,EF 平面 PAC ,∴ PB 平面 PAC ,APB PA PB PC 2 ,P ABC 为正方体的一部分, 2R 2 2 2 6 ,即6 4 4 6 68 R, V R 3 π 6,故选 D . P A, AB 2 3 3解法二:设 PA PB PC 2x ,E, F 分别为 的中点, 1EF ∥PB ,且 EF PB x ,△ABC 为边长为 2 的等边三角形,C F 3 ,21 又 CEF 90,CE 3 x 2, AE PA x , 2 x 243 x 22 x2△AEC 中,由余弦定理可得 cos EAC作 PD AC 于 D ,,A D 1 x 2 4 3 x 4x 21PA PC \ D AC cos EAC , , 为 的中点, ,PA 2x 2x1 2 2x 2 1 2,x 2,x ,PA PB PC 2 ,2 2又 AB=B C=A C=2 , PA , PB , PC 两两垂直,6 2R 2 2 2 6 ,R,24 4 6 68 V R 3 6 ,故选 D. 3 3【名师点睛】本题主要考查学生的空间想象能力,补体法解决外接球问题.可通过线面垂直定理,得到 三棱两两互相垂直关系,快速得到侧棱长,进而补体成正方体解决.7. 【2019 年高考全国Ⅱ卷理数】设α,β为两个平面,则α∥β的充要条件是 A .α内有无数条直线与β平行 C .α,β平行于同一条直线 【答案】BB .α内有两条相交直线与β平行 D .α,β垂直于同一平面【解析】由面面平行的判定定理知: 内两条相交直线都与 平行是∥的充分条件,由面面平行性质定理知,若∥,则必要条件,故选 B .内任意一条直线都与 平行,所以平行是∥内两条相交直线都与的【名师点睛】本题考查了空间两个平面的判定与性质及充要条件,渗透直观想象、逻辑推理素养,利用 面面平行的判定定理与性质定理即可作出判断.面面平行的判定问题要紧扣面面平行判定定理,最容易 犯的错误为定理记不住,凭主观臆断,如:“若 a ,b ,a b ,则 ∥ ∥”此类的错误.8. 【2019 年高考全国Ⅲ卷理数】如图,点 N 为正方形 AB C D 的中心,△EC D 为正三角形,平面 EC D ⊥平 面 ABC D ,M 是线段 E D 的中点,则A .B M =E N ,且直线 B M ,EN 是相交直线 B .B M ≠EN ,且直线 B M ,E N 是相交直线C .B M =E N ,且直线 B M ,E N 是异面直线D .B M ≠EN ,且直线 B M ,EN 是异面直线 【答案】B【解析】如图所示,作 EO C D 于O ,连接O N ,B D ,易得直线 B M ,E N 是三角形 EB D 的中线,是 相交直线.过 M 作 MF OD 于 F ,连接 BF ,AB C D ,E O C D, E O 平面C DE ,EO平面C D E 平面 平面 ABC D , M F 平面 AB C D ,△MFB 与△EO N 均为直角三角 形 . 设 正 方 形 边 长 为 2 , 易 知 E O 3,ON 1,EN 2 ,3 5M F,BF ,BM 7 ,B M EN ,故选 B .2 2【名师点睛】本题考查空间想象能力和计算能力,解答本题的关键是构造直角三角形.解答本题时,先利 用垂直关系,再结合勾股定理进而解决问题.9. 【2018 年高考全国Ⅰ卷理数】某圆柱的高为 2,底面周长为 16,其三视图如图.圆柱表面上的点 M 在正 视图上的对应点为 A ,圆柱表面上的点 N 在左视图上的对应点为 B ,则在此圆柱侧面上,从 M 到 N 的路径中,最短路径的长度为A . 2 17B . 2 5 D .2C .3 【答案】B【解析】根据圆柱的三视图以及其本身的特征,知点 M 在上底面上,点 N 在下底面上,且可以确定点 M 和点 N 分别在以圆柱的高为长方形的宽,圆柱底面圆周长的四分之一为长的长方形的对角线的端点处, 所以所求的最短路径的长度为 ,故选 B .【名师点睛】该题考查的是有关几何体的表面上两点之间的最短距离的求解问题,在解题的过程中,需 要明确两个点在几何体上所处的位置,再利用平面上两点间直线段最短,所以处理方法就是将面切开平 铺,利用平面图形的相关特征求得结果.10. 【2018 年高考全国Ⅰ卷理数】已知正方体的棱长为 1,每条棱所在直线与平面所成的角都相等,则截此正方体所得截面面积的最大值为3 342 3 3 A .C .B .D .3 2 43 2【答案】A【解析】根据相互平行的直线与平面所成的角是相等的,AB C D A B C D 中,1所以在正方体 1 1 1AB D AA , A B , A D 所成的角是相等的,11 11 1平面 与线 1 1AB D 所以平面 与正方体的每条棱所在的直线所成角都是相等的,11 C BD 1同理,平面 也满足与正方体的每条棱所在的直线所成角都是相等的,AB D C BD要求截面面积最大,则截面的位置为夹在两个面与1中间,且过棱的中点的正六边形,且1 12边长为,223 2 3 34所以其面积为S 6,故选A.4 2【名师点睛】该题考查的是有关平面被正方体所截得的截面多边形的面积问题,首要任务是需要先确定截面的位置,之后需要从题的条件中找寻相关的字眼,从而得到其为过六条棱的中点的正六边形,利用六边形的面积的求法,应用相关的公式求得结果.即首先利用正方体的棱是3组每组有互相平行的4条棱,所以与12条棱所成角相等,只需与从同一个顶点出发的三条棱所成角相等即可,从而判断出面的位置,截正方体所得的截面为一个正六边形,且边长是面的对角线的一半,应用面积公式求得结果.11.【2018年高考全国Ⅲ卷理数】中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是【答案】A【解析】本题主要考查空间几何体的三视图.由题意知,俯视图中应有一不可见的长方形,且俯视图应为对称图形.故选A.12.【2018年高考全国Ⅲ卷理数】设A ,,,是同一个半径为的球的球面上四点,△A B C 为等边三B C D 4角形且其面积为A.12 3,则三棱锥D ABC 体积的最大值为9 3B.18 3D.54 3C.24 3【答案】B【解析】如图所示,设点 M 为三角形 ABC 的重心,E 为 AC 中点,当点 D 在平面 ABC 上的射影为 M 时,三棱锥 D ABC 的体积最大,此时,O D OB R 4,3 S △AB CAB 9 3 ,AB 6 ,点 M 为三角形 ABC 的重心,2 4 2B M BE 2 3 ,3 Rt △OB M 中,有O M OB 2 2 2,D M O D O M 4 2 6,B M1V DABCm ax9 36 18 3 ,故选 B. 3【名师点睛】本题主要考查三棱锥的外接球,考查了勾股定理,三角形的面积公式和三棱锥的体积公 式,判断出当点 D 在平面 ABC 上的射影为三角形 AB C 的重心时,三棱锥 DABC 体积最大很关键,2由 M 为三角形 ABC 的重心,计算得到 B M BE 2 3 ,再由勾股定理得到 O M ,进而得到结果, 3属于较难题型.13. 【2018 年高考全国Ⅱ卷理数】在长方体 AB C D A B C D 中,AB BC 1,AA 3 ,则异面直线 A D 与 1 1 1 1 11 D B 所成角的余弦值为1 1 A .5 5 B . D .6 5 2 C .52【答案】C【解析】方法一:用一个与原长方体相同的长方体拼到原长方体的前面,B P ∥A D D B DP= 5B P 2,,则11如图,则 1,连接 DP ,易求得 1 DB P A D DB与所成的角,11是异面直线1 D B2 1 B P 2 DP 25 4 5 5 由余弦定理可得cos DB P 1. 12DB PB 4 5 5 1 1故选 C.方法二:以 D 为坐标原点,DA,D C,D D 所在直线分别为 x ,y ,z 轴建立空间直角坐标系, 1D 0, 0, 0, A 1, 0, 0,B 1, 1, 3,D 0, 0, 3A D1, 0, 3 ,DB 1, 1, 3 ,则 ,所以 1 1 1 1cos AD , DB A D DB A D DB 1 3 2 5 5 1 1因为 , 1 15 1 15 A D DB 所以异面直线 与 所成角的余弦值为 1,故选 C. 15【名师点睛】先建立空间直角坐标系,设立各点坐标,利用向量数量积求向量夹角,再根据向量夹角 与线线角相等或互补关系求结果.利用法向量求解空间线面角的关键在于“四破”:第一,破“建系关”, 构建恰当的空间直角坐标系;第二,破“求坐标关”,准确求解相关点的坐标;第三,破“求法向量关”, 求出直线的方向向量或平面的法向量;第四,破“应用公式关”. ABC A B C 中, ABC 120 BC CC 1,AB 2 ,,113. 【2017 年高考全国Ⅱ卷理数】已知直三棱柱1 1 1 AB BC 所成角的余弦值为1则异面直线 与 13 15 5 A .B .D .2 103 C . 53【答案】CAB C D A B C D ,1【解析】如图所示,补成直四棱柱 1 1 1则所求角为 BC D,BC 2, BD 2 21 221cos 60 3,C D AB 5 ,11 1 1 BC12 5105 易得 C D 12 BD 2BC 12 ,因此cos BC D,故选 C . 1C D1【名师点睛】平移法是求异面直线所成角的常用方法,其基本思路是通过平移直线,把异面问题化归为 共面问题来解决,具体步骤如下:①平移:平移异面直线中的一条或两条,作出异面直线所成的角; ②认定:证明作出的角就是所求异面直线所成的角; ③计算:求该角的值,常利用解三角形;④取舍:由异面直线所成的角的取值范围是(0,],当所作的角为钝角时,应取它的补角作为两条异面2直线所成的角.求异面直线所成的角要特别注意异面直线之间所成角的范围.14.【2017年高考全国Ⅰ卷理数】某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形,这些梯形的面积之和为A.10 B.12D.16C.14【答案】B【解析】由题意该几何体的直观图是由一个三棱锥和三棱柱构成,如下图,则该几何体各面内只有两个相同的梯形,则这些梯形的面积之和为12(24)212,故选.B2【名师点睛】三视图往往与几何体的体积、表面积以及空间线面关系、角、距离等问题相结合,解决此类问题的关键是由三视图准确确定空间几何体的形状及其结构特征并且熟悉常见几何体的三视图.15.【2017年高考全国Ⅱ卷理数】如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为A.90 C.42B.63 D.36【答案】B【解析】由题意,该几何体是一个组合体,下半部分是一个底面半径为3,高为4的圆柱,其体积V 32 436,上半部分是一个底面半径为,高为的圆柱的一半,其体积3 611 V (3 26) 27,故该组合体的体积V V V36 27 63.21 2 2故选 B .【名师点睛】在由三视图还原为空间几何体的实际形状时,要从三个视图综合考虑,根据三视图的规 则,空间几何体的可见轮廓线在三视图中为实线,不可见轮廓线在三视图中为虚线.在还原空间几何 体实际形状时,一般是以正视图和俯视图为主,结合侧视图进行综合考虑.求解以三视图为载体的空 间几何体的体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系,利用 相应体积公式求解.16. 【2017 年高考全国Ⅲ卷理数】已知圆柱的高为 1,它的两个底面的圆周在直径为 2 的同一个球的球面上,则该圆柱的体积为3π π A .C .B .D .4 π π24【答案】B【解析】绘制圆柱的轴截面如图所示:21 1 3 由题意可得: AC 1, AB ,结合勾股定理,底面半径 r 1 2,2 2 223 3由圆柱的体积公式,可得圆柱的体积是V πr 2h π 1 π ,故选 B.2 4【名师点睛】(1)求解空间几何体体积的关键是确定几何体的元素以及线面的位置关系和数量关系, 利用相应体积公式求解;(2)若所给几何体的体积不能直接利用公式得出,则常用等积法、分割法、 补形法等方法进行求解.17. 【2020 年高考全国 I I 卷理数】设有下列四个命题: p :两两相交且不过同一点的三条直线必在同一平面内.1p :过空间中任意三点有且仅有一个平面.2p :若空间两条直线不相交,则这两条直线平行.3p :若直线 l 平面α,直线 m ⊥平面α,则 m ⊥l . 4则下述命题中所有真命题的序号是__________.p p p p p ppp③④122334① ② 1 4【答案】①③④【解析】【分析】p p2利用两交线直线确定一个平面可判断命题的真假;利用三点共线可判断命题的真假;利用异面直线可1p p4判断命题的真假,利用线面垂直的定义可判断命题的真假.再利用复合命题的真假可得出结论.3p1l1l2【详解】对于命题,可设与相交,这两条直线确定的平面为;l l若与相交,则交点A 在平面内,3 1l l同理,与的交点B 也在平面内,3 2所以,AB ,即l3,命题为真命题;p1p2对于命题,若三点共线,则过这三个点的平面有无数个,p命题为假命题;2p对于命题,空间中两条直线相交、平行或异面,3p命题为假命题;3p4,若直线m 平面,对于命题m 垂直于平面则内所有直线,直线l 平面,直线m 直线,lp命题为真命题.4综上可知,,为真命题,,为假命题,p p p p为假命题,1 2为真命题,1 4p p p p为真命题.3 4为真命题,2 3故答案为:①③④.【点睛】本题考查复合命题的真假,同时也考查了空间中线面关系有关命题真假的判断,考查推理能力, 属于中等题.18. 【2020 年高考全国Ⅲ理数】已知圆锥的底面半径为 1,母线长为 3,则该圆锥内半径最大的球的体积为_________. 2 【答案】 3【解析】 【分析】将原问题转化为求解圆锥内切球的问题,然后结合截面确定其半径即可确定体积的值. 【详解】易知半径最大球为圆锥的内切球,球与圆锥内切时的轴截面如图所示,B C 2, AB AC 3 其中 ,且点 M 为 BC 边上的中点,设内切圆的圆心为O ,1由于A M 3 2 1 22 2 ,故 S △ABC2 2 2 2 2 , 2r设内切圆半径为 ,则:1 1 1 S △AB C S △A O B S △BO C S △A O C AB r BC r AC r2 2 21 3 3 2r2 2 ,22 4 2解得: r =,其体积:V r 3 . 2 3 32故答案为:. 3【点睛】与球有关的组合体问题,一种是内切,一种是外接.解题时要认真分析图形,明确切点和接点的 位置,确定有关元素间的数量关系,并作出合适的截面图,如球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径;球外接于正方体,正方体的顶点均在球面上,正方体的体对角线长等于 球的直径.19. 【2019 年高考全国Ⅲ卷理数】学生到工厂劳动实践,利用 3D 打印技术制作模型.如图,该模型为长方体AB C D A B C D 挖去四棱锥 O —EF G H 后所得的几何体,其中 O 为长方体的中心,E ,F ,G ,H 分11 1 1AB = BC = 6 cm, AA = 4 cm 别为所在棱的中点, ,3D 打印所用原料密度为 0.9 g/cm 3,不考虑打印 1损耗,制作该模型所需原料的质量为___________g .【答案】118.81【解析】由题意得, S 46 4 23 12cm 2 ,四边形EF G H2 1∵四棱锥 O −EF G H 的高为 3cm , ∴V O EF G H 123 12cm 3 .3AB C D A B C D V 466 144cm,3又长方体 的体积为 1 1 1 1 2 所以该模型体积为 VV V144 12 132cm 3 ,其质量为 0.9132 118.8g .OEF G H2 【名师点睛】本题考查几何体的体积问题,理解题中信息联系几何体的体积和质量关系,从而利用公式 求解.根据题意可知模型的体积为长方体体积与四棱锥体积之差进而求得模型的体积,再求出模型的质 量即可.20. 【2019 年高考全国Ⅱ卷理数】中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图 1).半正多面体是 由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图 2 是一个棱数为 48 的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为 1.则该半正多面体共 有________个面,其棱长为_________.(本题第一空 2 分,第二空 3 分.)【答案】26,21【解析】由图可知第一层(包括上底面)与第三层(包括下底面)各有9个面,计18个面,第二层共有8个面,所以该半正多面体共有18826个面.x如图,设该半正多面体的棱长为,则AB BE x,延长CB与FE 的延长线交于点G,延长BC交正方体的棱于H ,由半正多面体对称性可知,△BG E 为等腰直角三角形,2 2BG GE C H x,G H 2x x(21)x1,2 21x21,21即该半正多面体的棱长为21.【名师点睛】本题立意新颖,空间想象能力要求高,物体位置还原是关键,遇到新题别慌乱,题目其实很简单,稳中求胜是关键.立体几何平面化,无论多难都不怕,强大空间想象能力,快速还原图形.721.【2018年高考全国I I卷理数】已知圆锥的顶点为S,母线SA,SB 所成角的余弦值为,SA与圆锥8 底面所成角为45°,若△SAB 的面积为515,则该圆锥的侧面积为__________.【答案】402π7 15 8【解析】因为母线 SA , SB 所成角的余弦值为 ,所以母线 SA , SB 所成角的正弦值为,因为 81 15 8 △SAB 的面积为5 15 ,设母线长为l ,所以l 2 25 15 ,l80 , 2π 2因为 SA 与圆锥底面所成角为 45°,所以底面半径为 r l cosl , 4 22 因此圆锥的侧面积为 πr lπl 40 2π. 22【名师点睛】本题考查线面角、圆锥的侧面积、三角形面积等知识点,考查学生空间想象与运算能力. 先根据三角形面积公式求出母线长,再根据母线与底面所成角得底面半径,最后根据圆锥侧面积公式 求结果.22. 【2017 年高考全国 I 卷理数】如图,圆形纸片的圆心为 O ,半径为 5 c m ,该纸片上的等边三角形 ABC 的中心为 O.D ,E ,F 为圆 O 上的点,△DB C ,△ECA ,△FA B 分 别是以 BC ,CA ,AB 为底边的等腰三角形.沿虚线剪开后,分别以 BC ,CA ,AB 为折 痕折起△DB C ,△ECA ,△FAB ,使得 D ,E ,F 重合,得到三棱锥.当△ABC 的边长变 化时,所得三棱锥体积(单位:cm 3)的最大值为 【答案】 4 15.【解析】如下图,连接 DO 交 BC 于点 G ,设 D ,E ,F 重合于 S 点,正三角形的边长为 x(x>0),则 1 3 3O G x x. 3 2 63FG SG 5x , 6223 3x3x, SO h SG2GO2 5 x 556 631 1 3 3 15 3 三棱锥的体积V S △ABC h x2 5 5 x 4 x 5 . 5x3 34 3 1233 5 3 设 n x 5x 4x 5 ,x>0,则 n x 20x 3 x 4, 3 3x 4 n x 0 ,即 4x 30,得 ,易知 n x 在 令 处取得最大值. x 4 3x 4 3 3 15∴V max 48 5 4 4 15 .12【名师点睛】对于三棱锥最值问题,需要用到函数思想进行解决,本题解决的关键是设好未知量,利用图形特征表示出三棱锥体积.当体积中的变量最高次是2次时可以利用二次函数的性质进行解决,当变量是高次时需要用到求导的方式进行解决.。
历届高考数学立体几何选择填空汇总.

考点一:性质定理的判定(2008海南、宁夏文已知平面α⊥平面β,α∩β= l,点A∈α,A l,直线AB∥l,直线AC⊥l,直线m∥α,m∥β,则下列四种位置关系中,不一定成立的是(D)A. AB∥mB. AC⊥mC. AB∥βD. AC⊥β(2008湖南文.已知直线m,n和平面满足,则( D或 D 或(2008湖南理设有直线m、n和平面、.下列四个命题中,正确的是(D.A.若m∥,n∥,则m∥nB.若m,n,m∥,n∥,则∥C.若,m,则mD.若,m,m,则m∥(2008江西文设直线与平面相交但不垂直,则下列说法中正确的是(B)A.在平面内有且只有一条直线与直线垂直B.过直线有且只有一个平面与平面垂直C.与直线垂直的直线不可能与平面平行D.与直线平行的平面不可能与平面垂直(2008辽宁文、理在正方体中,分别为棱,的中点,则在空间中与三条直线,,都相交的直线(D)A.不存在B.有且只有两条C.有且只有三条D.有无数条考点二:空间几何体的表面积和体积1(湖北卷3)用与球心距离为的平面去截球,所得的截面面积为,则球的体积为()A. B. C. D.解:截面面积为截面圆半径为1,又与球心距离为球的半径是,所以根据球的体积公式知,故B 为正确答案.2棱长为a 的正方体的各个顶点都在一个球面上,则这个球的体积是_______32a _____(2008全国Ⅱ卷文正四棱锥的侧棱长为,侧棱与底面所成的角为,则该棱锥的体积为( B )A .3B .6C .9D .18(2008四川文 若三棱柱的一个侧面是边长为2的正方形,另外两个侧面都是有一个内角为的菱形,则该棱柱的体积等于( B(A)(B)(C) (D)【解】:如图在三棱柱中,设,由条件有,作于点,则∴ ∴∴ 故选B( 2008福建文、理若三棱锥的三条侧棱两两垂直,且侧棱长均为,则其外接球的表面积是.(2008海南、宁夏文、理一个六棱柱的底面是正六边形,其侧棱垂直底面。
2020高考—立体几何(选择+填空+答案)

2020年高考——立体几何1.(20全国Ⅰ文3).埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥.以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为A .514-B .512-C .514+D .512+ 2.(20全国Ⅰ文12).已知,,A B C 为球O 的球面上的三个点,⊙1O 为ABC △的外接圆,若⊙1O 的面积为4π,1AB BC AC OO ===,则球O 的表面积为A .64πB .48πC .36πD .32π3.(20全国Ⅱ文11).已知△ABC 是面积为934的等边三角形,且其顶点都在球O 的球面上.若球O 的表面积为16π,则O 到平面ABC 的距离为A .3B .32C .1D .324.(20全国Ⅱ理7).右图是一个多面体的三视图,这个多面体某条棱的一个端点在正视图中对应的点为M ,在俯视图中对应的点为N ,则该端点在侧视图中对应的点为A .EB .FC .GD .H5.(20全国Ⅱ理10).已知△ABC是面积为934的等边三角形,且其顶点都在球O的球面上.若球O的表面积为16π,则O到平面ABC的距离为A.3B.32C.1 D.326.(20全国Ⅲ文9).如图为某几何体的三视图,则该几何体的表面积是A.6+42B.4+42C.6+23D.4+237.(20新高考Ⅰ4).日晷是中国古代用来测定时间的仪器,利用与晷面垂直的晷针投射到晷面的影子来测定时间.把地球看成一个球(球心记为O),地球上一点A的纬度是指OA 与地球赤道所在平面所成角,点A处的水平面是指过点A且与OA垂直的平面.在点A处放置一个日晷,若晷面与赤道所在平面平行,点A处的纬度为北纬40°,则晷针与点A 处的水平面所成角为A.20°B.40°C.50°D.90°8.(20天津5).若棱长为23A.12πB.24πC.36πD.144π9.(20浙江5).某几何体的三视图(单位:cm )如图所示,则该几何体的体积(单位:cm 3)是A .73B .143C .3D .610.(20北京4).某三棱柱的底面为正三角形,其三视图如图所示,该三棱柱的表面积为( ).A .63+B .623+C .123+D .123+11.(20新高考Ⅰ16).已知直四棱柱ABCD –A 1B 1C 1D 1的棱长均为2,∠BAD =60°.以1D 为球5BCC 1B 1的交线长为________.12.(20全国Ⅰ理16).如图,在三棱锥P –ABC 的平面展开图中,AC =1,3AB AD =AB⊥AC ,AB ⊥AD ,∠CAE =30°,则cos ∠FCB = .13.(20全国Ⅱ文16).设有下列四个命题:p 1:两两相交且不过同一点的三条直线必在同一平面内.p 2:过空间中任意三点有且仅有一个平面.p 3:若空间两条直线不相交,则这两条直线平行.p 4:若直线l ⊂平面α,直线m ⊥平面α,则m ⊥l .则下述命题中所有真命题的序号是__________.①14p p ∧ ②12p p ∧ ③23p p ⌝∨ ④34p p ⌝∨⌝ 14.(20全国Ⅲ文16).已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为_________.15.(20天津15).如图,在四边形ABCD 中,60,3B AB ∠=︒=,6BC =,且3,2AD BC AD AB λ=⋅=-,则实数λ的值为_________,若,M N 是线段BC 上的动点,且||1MN =,则DM DN ⋅的最小值为_________.16.(20浙江14).已知圆锥的侧面积(单位:cm 2)为2π,且它的侧面展开图是一个半圆,则这个圆锥的底面半径(单位:cm )是_______.17.(20江苏9).如图,六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的.已知螺帽的底面正六边形边长为2 cm ,高为2 cm ,内孔半轻为0.5 cm ,则此六角螺帽毛坯的体积是 ▲ cm.参考答案:1.C 2.A 3.C 4.A 5.C 6.C 7.B 8.C9.A 10. D 112π12.14-13.①③④215.16;13216.1 17.1232π。
高考立体几何试题——选择填空

高考立体几何试题——选择填空1.(安徽文)把边长为2的正方形ABCD 沿对角线AC 折成直二面角,折成直二面角后,在A ,B ,C ,D 四点所在的球面上,B 与D 两点之间的球面距离为(C ) (A)22π(B)π(C)2π (D)3π 2.(北京文)平面α∥平面β的一个充分条件是( ) A.存在一条直线a a ααβ,∥,∥B.存在一条直线a a a αβ⊂,,∥C.存在两条平行直线a b a b a b αββα⊂⊂,,,,∥,∥ D.存在两条异面直线a b a a b αβα⊂,,,∥,∥3.(福建理)已知m n ,为两条不同的直线,αβ,为两个不同的平面,则下列命题中正确的是( D ) A .m n m n ααββαβ⊂⊂⇒,,∥,∥∥ B .m n m n αβαβ⊂⊂⇒∥,,∥ C .m m n n αα⇒⊥,⊥∥ D .n m n m αα⇒∥,⊥⊥4.(福建理)顶点在同一球面上的正四棱柱ABCD A B C D ''''-中,12AB AA '==,,则A C ,两点间的球面距离为( B ) A .π4B .π2C .24π D .22π 5.(湖北理)平面α外有两条直线m 和n ,如果m 和n 在平面α内的射影分别是m '和n ',给出下列四个命题: ①m n m n ''⊥⇒⊥; ②m n m n ''⊥⇒⊥; ③m '与n '相交⇒m 与n 相交或重合; ④m '与n '平行⇒m 与n 平行或重合. 其中不正确的命题个数是( D ) A.1 B.2 C.3 D.46.(湖北文)在棱长为1的正方体1111ABCD A B C D -中,E F ,分别为棱11AA BB ,的中点,G 为棱11A B 上的一点,且1(01)A G λλ=≤≤.则点G 到平面1D EF 的距离为( D )A.3B.22C.23λ D.557.(湖南理)棱长为1的正方体1111ABCD A B C D -的8个顶点都在球O 的表面上,E F ,分别是棱1AA ,1DD 的中点,则直线EF 被球O 截得的线段长为( D ) A .22B .1C .212+D .28.(湖南文)如图1,在正四棱柱1111ABCD A B C D -中,E F ,分别是1AB ,1BC 的中点,则以下结论中不成立...的是( D ) A .EF 与1BB 垂直B .EF 与BD 垂直C .EF 与CD 异面D .EF 与11A C 异面9.(江苏)已知两条直线m n ,,两个平面αβ,.给出下面四个命题: ①m n ∥,m n αα⇒⊥⊥;②αβ∥,m α⊂,n m n β⊂⇒∥; ③m n ∥,m n αα⇒∥∥;④αβ∥,m n ∥,m n αβ⇒⊥⊥. 其中正确命题的序号是( C ) A.①、③ B.②、④C.①、④ D.②、③10.(江西理)如图,正方体1AC 的棱长为1,过点A 作平面1A BD 的垂线,垂足为点H ,则以下命题中,错误..的命题是( )DA.点H 是1A BD △的垂心 B.AH 垂直平面11CB D C.AH 的延长线经过点1CD.直线AH 和1BB 所成角为4511.(江西文)四面体ABCD 的外接球球心在CD 上,且2CD =,3AD =,在外接球面上两点A B ,间的球面距离是( C ) A.π6B.π3C.2π3D.5π612.(江西文)如图,正方体1AC 的棱长为1,过点作平面1A BD 的垂线,垂足为点H .有下列四个命题 A.点H 是1A BD △的垂心 B.AH 垂直平面11CB DC.二面角111C B D C --的正切值为2 D.点H 到平面1111A B C D 的距离为3413.(北京理)平面α∥平面β的一个充分条件是( D ) A.存在一条直线a a ααβ,∥,∥B.存在一条直线a a a αβ⊂,,∥C.存在两条平行直线a b a b a b αββα⊂⊂,,,,∥,∥ D.存在两条异面直线a b a a b αβα⊂,,,∥,∥14.(辽宁文)若m n ,是两条不同的直线,αβγ,,是三个不同的平面,则下列命题中的真命题...是( B ) A D1D 1C1A 1BBHCA .若m βαβ⊂⊥,,则m α⊥B .若m β⊥,m α∥,则αβ⊥C .若αγ⊥,αβ⊥,则βγ⊥D .若m αγ=,n βγ=,m n ∥,则αβ∥15.(全国I 文理)如图,正四棱柱1111ABCD A B C D -中,12AA AB =,则异面直线1A B 与1AD 所成角的余弦值为( D ) A .15B .25C .35D .4517.(全国卷Ⅱ理)已知正三棱柱111ABC A B C -的侧棱长与底面边长相等,则1AB 与侧面11ACC A 所成角的正弦值等于( A )A .64B .104C .22D .3218.(全国卷Ⅱ文)已知三棱锥的侧棱长的底面边长的2倍,则侧棱与底面所成角的余弦值等于( ) A .36B .34C .22D .3219.(陕西理)一个正三棱锥的四个顶点都在半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,则该正三棱锥的体积是( B ) (A )433 (B)33 (C) 43 (D) 12320.(陕西文)Rt △ABC 的三个顶点在半径为13的球面上,两直角边的长分别为6和8,则球心到平面ABC 的距离是( D ) (A )5 (B )6 (C )10 (D )1221.(陕西文)已知P 为平面a 外一点,直线l ⊂a,点Q ∈l ,记点P 到平面a 的距离为a,点P 到直线l 的距离为b ,点P 、Q 之间的距离为c ,则A (A )c b a ≤≤ (B )c b a ≤≤ (C)b c a ≤≤ (D)a c b ≤≤ 22.(四川文理)如图,ABCD -A 1B 1C 1D 1为正方体,下面结论错误..的是( D ) (A )BD ∥平面CB 1D 1 (B )AC 1⊥BD(C )AC 1⊥平面CB 1D 1 (D )异面直线AD 与CB 1角为60°23.(四川文理)设球O 的半径是1,A 、B 、C 是球面上三点,已知A 到B 、C两点的球面距离都是2π,且三面角B -OA -C 的大小为3π,则从A 点沿球面经B 、C 两点再回到A点的最短距离是C(A )67π (B )45π (C )34π(D )23π 24.(四川文理)如图,l 1、l 2、l 3是同一平面内的三条平行直线,l 1与l 2间的距离是1, l 2与l 3间的距离是2,正三角形ABC 的三顶点分别在l 1、l 2、l 3上,则△ABC的边长是D(A )32(B )364 (C )4173 (D )3212 25.(天津文理)设a b ,为两条直线,αβ,为两个平面,下列四个命题中,正确的命题是( D ) A.若a b ,与α所成的角相等,则a b ∥ B.若a b αβ,∥∥,αβ∥,则a b ∥ C.若a b a b αβ⊂⊂,,∥,则αβ∥ D.若a b αβ⊥⊥,,αβ⊥,则a b ⊥26.(浙江文理)若P 两条异面直线l m ,外的任意一点,则( )B A.过点P 有且仅有一条直线与l m ,都平行 B.过点P 有且仅有一条直线与l m ,都垂直 C.过点P 有且仅有一条直线与l m ,都相交 D.过点P 有且仅有一条直线与l m ,都异面27.(理科数学必修+选修Ⅱ)已知正三棱柱111ABC A B C -的侧棱长与底面边长相等,则1AB 与侧面11ACC A 所成角的正弦值等于( ) A .64B .104C .22D .3228.(文理科数学必修+选修Ⅱ)如图,正四棱柱1111ABCD A B C D -中,12AA AB =,则异面直线1A B 与1AD 所成角的余弦值为( )DA .15B .25C .35D .4530.(重庆文)垂直于同一平面的两条直线( )A A .平行 B .垂直 C .相交 D .异面31.(重庆理)若三个平面两两相交,且三条交线互相平行,则这三个平面把空间分成( C ) A.5部分 B.6部分 C.7部分 D.8部分32.(理科数学必修+选修Ⅱ)(16)一个等腰直角三角形的三个顶点分别在正三棱柱的三条侧棱上.已知正三棱柱的底面边长为2,则该三角形的斜边长为 .2333.(浙江文理)已知点O 在二面角AB αβ--的棱上,点P 在α内,且45POB ∠=.若对于β内异于O 的任意一点Q ,都有45POQ ∠≥,则二面角AB αβ--的大小是.9034.(全国I 文)正四棱锥S ABCD -的底面边长和各侧棱长都为2,点S ,A ,B ,C ,D 都在同一个球面上,则该球的体积为_________.4π335.(文科数学必修+选修1)正四棱锥S ABCD -的底面边长和各侧棱长都为2,点S ,A ,B ,C ,D 都在同一个球面上,则该球的体积为_________.4π336.(理科数学必修+选修Ⅱ)一个正四棱柱的各个顶点在一个直径为2cm 的球面上.如果正四棱柱的底面边长为1cm ,那么该棱柱的表面积为 cm 2.37.(天津文理)一个长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为1,2,3,则此球的表面积为 .14π38.(安徽理)在四面体O-ABC 中,D c OC b OB a AB ,,,===为BC 的中点,E 为AD 的中点,则OE = (用a ,b ,c 表示).111244++a b c 39.(安徽理)在正方体上任意选择4个顶点,它们可能是如下各种几何形体的4个顶点,这些几何形体是 (写出所有正确结论的编号..). ①③④⑤ ①矩形;②不是矩形的平行四边形;③有三个面为等腰直角三角形,有一个面为等边三角形的四面体; ④每个面都是等边三角形的四面体; ⑤每个面都是直角三角形的四面体.40.(湖南文)棱长为1的正方体1111ABCD A B C D -的8个顶点都在球O 的表面上,则球O 的表面积是 ;设E F ,分别是该正方体的棱1AA ,1DD 的中点,则直线EF 被球O 截得的线段长为 .3π,241.(全国卷Ⅱ文理)一个正四棱柱的各个顶点在一个直径为2cm 的球面上.如果正四棱柱的底面边长为1cm ,那么该棱柱的表面积为 cm 2.242+42.(辽宁文)若一个底面边长为62,棱长为6的正六棱柱的所有顶点都在一个球的面上,则此球的体积为 .43π43.(四川文理)如图,在正三棱柱ABC -A 1B 1C 1中,侧棱长为2,底面三角形的边长为1,则BC 1与侧面ACC 1A 1所成的角是 .6π 44.(江苏)正三棱锥P ABC -的高为2,侧棱与底面ABC 成45角,则点A 到侧面PBC 的距离为_____.65545.(全国I 理)一个等腰直角三角形的三个顶点分别在正三棱柱的三条侧棱上.已知正三棱柱的底面边长为2,则该三角形的斜边长为 .2346.(上海理)在平面上,两条直线的位置关系有相交、平行、重合三种. 已知αβ,是两个相交平面,空间两条直线12l l ,在α上的射影是直线12s s ,,12l l ,在β上的射影是直线12t t ,.用1s 与2s ,1t 与2t 的位置关系,写出一个总能确定1l 与2l 是异面直线的充分条件: 21//s s ,并且1t 与2t 相交(//1t 2t ,并且1s 与2s 相交) 47.(上海文)如图,在直三棱柱111C B A ABC -中,90=∠ACB , 21=AA ,1==BC AC ,则异面直线B A 1与AC 所成角的大小是 (结果用反三角函数值表示).66arccos48.广东理12.如果一个凸多面体是n 棱锥,那么这个凸多面体的所有顶点所确定的 直线共有 条.这些直线中共有()f n 对异面直线,则(4)f =49.辽宁理7.若m n ,是两条不同的直线,αβγ,,是三个不同的平面,则下列命题中的真命题是( ) A .若m βαβ⊂⊥,,则m α⊥ B .若m αγ=n βγ=,m n ∥,则αβ∥C .若m β⊥,m α∥,则αβ⊥D .若αγ⊥,αβ⊥,则βγ⊥50.辽宁理15.若一个底面边长为32,棱长为6的正六棱柱的所有顶点都在一个平面上,则此球的体积为 .选校网高考频道专业大全历年分数线上万张大学图片大学视频院校库 (按ctrl 点击打开)选校网()是为高三同学和家长提供高考选校信息的一个网站。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
立体几何
视图 1、将正三棱柱截去三个角(如图1所示A 、B 、C 分别
是GHI ∆三边的中点)得到的几何体如图2,则该几何
体按图2所示方向的侧视图(或称左视图)为( )
2、如题(11)图,模块①-⑤均由4个棱长为1的小
正方体构成,模块⑥由15个棱长为1的小正方体构成.现从模块①-⑤中选出三个放到模块⑥上,使得模块⑥成为一个棱长为3的大正方体.则下列选择方案中,能够完成任务的为( )
(A)模块①,②,⑤ (B)模块①,③,⑤ (C)模块②,④,⑥ (D)模块③,④,⑤
3、右图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( )
A .9π
B .10π
C .11π
D .12π
表面积
4、若一个球的体积
为,则它的表面积为 .
5、设M 是球心O 的半径OP 的中点,分别过,M O 作垂直于OP 的平面,截球面得两个圆,则这两个圆的面积比值为:( ) (A)41 (B)12 (C)23 (D)34
体积
1、若三棱柱的一个侧面是边长为2的正方形,另外两
个侧面都是有一个内角为0
60的菱形,则该棱柱的体积
等于( )
(B)
(C)
D)2、用与球心距离为1的平面去截球,所得的截面面积为π,则球的体积为( ) A. 38π B. 328π
C. π28
D. 332π
3、正四棱锥的侧棱长为32,侧棱与底面所成的角为
︒60,则该棱锥的体积为( ) A .3 B .6 C .9 D .18 4、一个六棱柱的底面是正六边形,其侧棱垂直底面。
已知该六棱柱的顶点都在同一个球面上,且该六棱柱
3,那么这个球的体积为_____
5、已知球O 点面上四点A 、B 、C 、D ,DA ⊥平面ABC , AB ⊥BC ,DA=AB=BC=3,则球O 点体积等于
位置关系 1、已知,m n 是两条不同直线,
,,αβγ是三个不同平面,下列命题中正确的是( ) A .,,αγβγαβ⊥⊥若则‖
B .,,m n m n αα⊥⊥若则‖
C .,,m n m n αα若则‖‖‖
D .,,m m αβαβ若则‖‖‖
2、对两条不相交的空间直线a 和b ,必定存在平面α,
使得( ) (A ),a b αα⊂⊂ (B ),//a b αα⊂
(C ),a b αα⊥⊥ (D ),a b αα⊂⊥ 3、给定空间中的直线l 及平面α.条件“直线l 与平面α内两条相交直线都垂直”是“直线l 与平面α垂直”的( )
A.充分非必要条件 B.必要非充分条件 C .充要条件 D.既非充分又非必要条件 4、已知平面α⊥平面β,α∩β= l ,点A ∈α,A ∉l ,直线AB ∥l ,直线AC ⊥l ,直线m ∥α,m ∥β
,则下
俯视图
正(主)视图 侧(左)视图
列四种位置关系中,不一定...
成立的是( ) A. AB ∥m B. AC ⊥m C. AB ∥β D. AC ⊥β
5、设直线l ⊂平面α,过平面α外一点A 与,l α都成
030角的直线有且只有:( )
(A)1条 (B)2条 (C)3条 (D)4条
6、设直线m 与平面α相交但不.垂直,则下列说法中正确的是( )
A .在平面α内有且只有一条直线与直线m 垂直
B .过直线m 有且只有一个平面与平面α垂直
C .与直线m 垂直的直线不.可能与平面α平行
D .与直线m 平行的平面不.
可能与平面α垂直 7、设a b ,是两条直线,αβ,是两个平面,则a b ⊥的
一个充分条件是( ) A .a b αβαβ⊥⊥,∥, B .a b αβαβ⊥⊥,,∥ C .a b αβαβ⊂⊥,,∥
D .a b αβαβ⊂⊥,∥,
8、如图,l A B A B αβαβαβ⊥=∈∈,,,,,到
l 的距离分别是a 和b ,AB 与αβ,所成的角分别是
θ和ϕ,AB 在αβ,内的射影分别是m 和n ,若
a b >,则( )
A .m n θϕ>>,
B .m n θϕ><,
C .m n θϕ<<,
D .m n θϕ<>,
9、在正方体1111ABCD A BC D -中,E F ,分别为棱1AA ,1CC 的中点,
则在空间中与三条直线11A D ,EF ,CD 都相交的直线( )
A .不存在
B .有且只有两条
C .有且只有三条
D .有无数条 距离 1、已知球的半径为2,相互垂直的两个平面分别截球面得两个圆.若两圆的公共弦长为2,则两圆的圆心距等于( )
A .1
B .2
C .3
D .2
2、长方体1111ABCD A BC D -的各顶点都在半径为1的球面上,
其中1::AB AD AA =,则两,A B 点的
球面距离为( ) A .
4
π
B .
3
π C .
2
π D .
23
π 3、已知点,,,A B C D 在同一个球面,,AB BCD ⊥平面
,BC CD ⊥若6,AB
=AC =8AD =,则,B C
两点间的球面距离是
4、已知菱形ABCD 中,2AB =,120A ∠=,沿对角线BD 将ABD △折起,使二面角A BD C --为
120,则点A 到BCD △所在平面的距离等于 .
5、长方体1111ABCD A BC D -的8个顶点在同一个球面上,且AB=2,AD=3,11=AA ,则顶点A 、B 间的球面距离是( ) A .
42π B .2
2π
C .π2
D .2π2 6、
在体积为的球的表面上有A 、B ,C 三点,AB =1,
BC
A ,C
两点的球面距离为3
,则球心到平面ABC 的距离为_________.
线面成角
1、如图,在长方体ABCD -A 1B 1C 1D 1中,AB=BC =2,AA 1=1,则AC 1与平面A 1B 1C 1D 1所成角的正弦值为( )
A.
3 B.23
C.4
D.13
2、已知三棱柱111ABC A B C -的侧棱与底面边长都相
等,1A 在底面
ABC 内的射影为ABC △的中心,则1AB 与底面ABC 所成角的正弦值等于( ) A .
13
B
.
3
C
.
3
D .
23。
