简单几何体的外接球与内切球问题
专题——几何体的外接球和内切球问题

B.112π
C.1 000π 9
D.5 000 10π 81
※内切球问题 1.正棱锥的内切球.
第一步:先现出内切球的截面图, E, H 分别是两个三角形的外心; 第二步:由 POE 相似于 PDH ,建立等式: OE PO ,解出 r
DH PD
2.任意多面体的内切球:等体积法,
例 3 非直二面角类型
(1)内切球球心到多面体各面的距离均相等,外接球球心到多面体各顶点的距离均相等。
专题——几何体的外接球和内切球问题
※基础知识:
1.常见平面图形:正方形,长方形,正三角形的外接圆和内切圆
长方形(正方形)的外接圆半径为对角线长的一半,正方形的内切圆半径为边长的一半;
正三角形的内切圆半径: 3 a 6
外接圆半径: 3 a 3
面体的外接球的球心。 由定义,给出以下简单多面体外接球的球心的结论。
结论 1:正方体或长方体的外接球的球心就是其体对角线的中点,即其外接球的半径 R 满足:
2R2 a2 b2 c2 ,即 R a2 b2 c2
2 结论 2:正棱柱的外接球的球心是上下底面中心的连线的中点,即正棱柱的外接球的半径 R 为: R h 2 r 2 (其中 h 为正棱柱的侧棱长, r 是底面多边形的外接圆的半径)
(1)已知边长为 2 3 的菱形 ABCD 中,BAD 60 ,沿对角线 BD 折成二面角 A BD C 的大
小为120 的四面体,则该四面体的外接球的表面积为
。
第一步:先求出多面体的表面积和体积; 第二步:解出 r 3V S表
例 1、正方体的内切球与其外接球的体积之比为( )
球。
3.球的截面:
用一平面 去截一个球 O ,设 OO 是平面 的垂线段,O 为垂 足,且 OO d ,所得的截面是以球心在截面内的射影为圆心,以
内切球和外接球常见解法

内切球和外接球常见解法内切球和外接球是在几何学中常用的概念,它们分别指的是一个几何体内切或外接于另一个几何体的球。
在实际问题中,内切球和外接球常常用于优化问题和几何问题的求解,其解法也有多种。
以下将介绍一些常见的解法。
1. 解法一:利用勾股定理求解。
内切球和外接球都可以利用勾股定理求解。
以内切球为例,我们可以考虑任意三角形ABC,设其内切球的半径为r,以I为内切圆心,则:AB + AC = 2r;AC + BC = 2r;AB + BC = 2r。
整理可得:r = [ABC] / (s + a + b + c),其中s为半周长,a、b、c为三角形ABC的三边长,[ABC]为三角形ABC的面积。
而外接球的半径r'则可用公式r'=[ABC] / (4S),其中S为三角形ABC的外接圆半径。
欧拉定理是内切球和外接球求解的另一个重要工具。
欧拉定理有两种形式,分别为:对于任意四面体,其四个顶点、三条棱的中点和六面体质心共九个点在同一球面上。
对于任意三角形ABC,其外接圆心、垂足交点、垂心、重心四点在同一圆上,且圆心为外接球心。
利用欧拉定理可以求得内切球半径:点O为六面体质心,点I为内切圆心,则IO等于内切球半径r。
点O为三角形外心,点H为垂心,点G为重心,则OG等于外接球半径r'。
对于一些优化问题,内切球和外接球也可以通过线性规划求解。
例如,对于一个凸多面体,求其内切球或外接球的半径最大值,可以将问题转化为线性规划问题,即:max rs.t. A_i * x <= b_i, i=1,2,...,mx_i >= 0, i=1,2,...,n其中,A_i是多面体的几何信息,b_i是多面体中某一点到各个面的距离,x是优化变量,r就是所需要求的内切球或外接球半径。
可以使用线性规划求解器求解其最优解。
立体几何中球的内切和外接问题完美版

性质
内切球的球心位于旋转体 的轴线上,且球的半径等 于旋转体半径。
应用
在几何和工程领域中,内 切球常用于研究旋转体的 体积和表面积。
旋转体的外接球
定义
旋转体的外接球是指与旋 转体外侧相切的球。
性质
外接球的球心位于旋转体 外侧,且球的半径等于旋 转体轴线到旋转体外侧的 垂直距离。
应用
在几何ቤተ መጻሕፍቲ ባይዱ工程领域中,外 接球常用于研究旋转体的 空间位置和关系。
立体几何中球的内 切和外接问题完美 版
目 录
• 球与多面体的内切和外接问题 • 球与旋转体的内切和外接问题 • 球与几何体的内切和外接问题实例 • 总结与展望
01
CATALOGUE
球与多面体的内切和外接问题
多面体的内切球
01
02
03
04
多面体的内切球是指与多面 体的所有顶点和面都相切的
球。
内切球半径的求法:设多面体的 每个面为$S_i$,内切球的半径
03
CATALOGUE
球与几何体的内切和外接问题实例
多面体内切球实例
总结词
多面体内切球是指一个球完全内切于一个多面体,且与多面体的每个面都相切 。
详细描述
多面体内切球的问题可以通过几何定理和公式来解决,例如欧拉公式和球内切 定理。例如,一个正方体的内切球就是其中心,半径等于正方体边长的一半。
旋转体外接球实例
外接球的性质:外接球与 多面体的每个顶点都相切 ,且外接球的直径等于多 面体的对角线长度。
外接球的应用:在几何、 物理和工程领域中,外接 球的概念被广泛应用于研 究多面体的性质和计算。
02
CATALOGUE
球与旋转体的内切和外接问题
外接球和内切球问题总结归纳

外接球和内切球问题总结归纳外接球和内切球问题总结归纳在几何学中,外接球和内切球问题是一个重要的概念。
它们不仅在数学领域有着重要的应用,同时也被广泛运用在物理学、工程学以及计算机科学等领域。
本文将对外接球和内切球问题进行深入探讨,从基础概念到应用实例,帮助读者全面理解这一主题。
一、外接球和内切球的定义1. 外接球外接球是指一个球与给定的多边形的所有顶点相切于球面的情况。
在数学中,外接球常常与三角形、四边形等几何图形相关联,其特点是与多边形的各个顶点相切,并且球心通常位于多边形的某个重要位置。
2. 内切球内切球则是指一个球完全被给定的多边形所包围,且球与多边形的边界相切。
在实际应用中,内切球往往能够最大化地利用多边形所包围的空间,因此在工程设计和优化问题中具有重要意义。
二、外接球和内切球的性质1. 外接球的性质外接球的半径通常与多边形的边或者角有着特定的关系。
以三角形为例,外接圆的半径等于三角形三条边的乘积除以其周长的两倍。
这一性质在计算三角形的外接圆时具有重要意义,同时也为几何问题的解决提供了基础。
2. 内切球的性质内切球的半径与多边形的边界有着紧密的联系。
以正方形为例,内切圆的半径等于正方形的边长的一半。
这一性质在优化问题中有着重要的应用,能够帮助设计者最大化地利用空间,提高效率和节约成本。
三、外接球和内切球的应用1. 工程设计外接球和内切球在工程设计中有着广泛的应用。
例如在建筑设计中,内切球可以帮助设计者合理利用建筑空间,提高使用效率;在机械设计中,外接球则可以帮助设计者确定零部件的匹配度和适用性。
2. 计算机科学外接球和内切球也在计算机科学领域有着重要的应用。
例如在计算机图形学中,外接球和内切球经常被用来描述物体的外形和几何特征,同时也可以用于物体的碰撞检测和三维建模。
个人观点和总结外接球和内切球作为一个基础的数学概念,在几何学、工程学和计算机科学等领域有着重要的应用。
通过对外接球和内切球的定义、性质和应用进行深入探讨,我们可以更好地理解其在实际问题中的作用和意义,进一步拓展其在更多领域的应用。
高中数学《简单几何体的外接球与内切球问题》练习题

简单几何体的外接球与内切球问题一、外接球的问题:(一) 由球的定义确定球心在空间,如果一个定点与一个简单多面体的所有顶点的距离都相等,那么这个定点就是该简单多面体的外接球的球心.由上述性质,可以得到确定简单多面体外接球的球心的如下结论.结论1:正方体或长方体的外接球的球心其体对角线的中点.结论2:正棱柱的外接球的球心是上下底面中心的连线的中点.结论3:直三棱柱的外接球的球心是上下底面三角形外心的连线的中点.结论4:正棱锥的外接球的球心在其高上,具体位置可通过计算找到.结论5:若棱锥的顶点可构成共斜边的直角三角形,则公共斜边的中点就是其外接球的球心.例1、一个六棱柱的底面是正六边形,其侧棱垂直于底面,已知该六棱柱的顶点都在同一个球面上,且该六棱柱的体积为98,底面周长为3,则这个球的体积为 . 43π 例2、已知各顶点都在同一个球面上的正四棱柱的高为4,体积为16,则这个球的表面积是 .24π例3、在直三棱柱111C B A ABC -中,4,3,6,41====AA A AC AB π,则直三棱柱111C B A ABC -的外接球的表面积 .1603π例46 (二)构造正方体或长方体确定球心长方体或正方体的外接球的球心是在其体对角线的中点处.以下是常见的、基本的几何体补成正方体或长方体的途径与方法.途径1:正四面体、三条侧棱两两垂直的正三棱锥、四个面都是是直角三角形的三棱锥都分别可构造正方体.途径2:同一个顶点上的三条棱两两垂直的四面体、相对的棱相等的三棱锥都分别可构造长方体和正方体.途径3:若已知棱锥含有线面垂直关系,则可将棱锥补成长方体或正方体.途径4:若三棱锥的三个侧面两两垂直,则可将三棱锥补成长方体或正方体.例6、在三棱锥BCD A -中,BC CD BCD AB ⊥⊥,平面,543===CD BC AB ,,,则三棱锥BCD A -外接球的表面积 . 50π例7、在三棱锥BCD A -中,2,3,4AB CD AD BC AC BD ======,则三棱锥BCD A -外接球的体积 .(三) 由性质确定球心利用球心O 与截面圆圆心1O 的连线垂直于截面圆及球心O 与弦中点的连线垂直于弦的性质,确定球心.例6、正四棱锥S ABCD -S A B C D 、、、、都在同一球面上,则此球的体积为 . 43π 例8、三棱锥S_-ABC 中,SA ⊥面ABC ,SA=2。
简单几何体的外接球和内切球的半径的求法
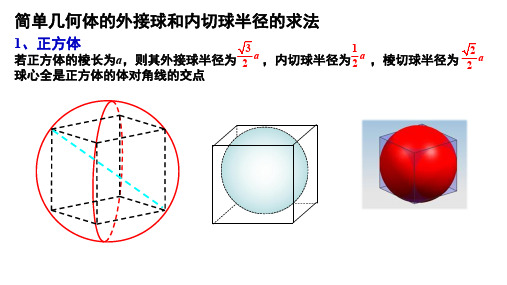
简单几何体的外接球和内切球半径的求法1、正方体若正方体的棱长为a ,则其外接球半径为 ,内切球半径为 ,棱切球半径为 球心全是正方体的体对角线的交点32a 12a 22a例:一个正方体的顶点都在球面上,它的棱长是a cm ,求球的体积.解:该球是正方体的外接球,球心到正方体各顶点的距离相等,因此球心是正方体的体对角线的交点,球的直径是正方体的体对角线长设球的半径为R ,a R a R 2332==得则)(23)23(34343333cm a a R πππ==∴球的体积为若一个多面体的各顶点都在一个球的球面上,则称这个多面体是这个球的内接多面体,这个球是这个多面体的外接球。
外接球的球心到多面体各顶点的距离均相等。
例:将一个棱长为6cm 的正方体铁块磨制成一个球体零件,求可能制作的最大零件的体积。
解:这个最大的球体是正方体的内切球,球心到正方体各个面的距离相等,因此球心是正方体的体对角线的交点,球的直径是正方体的棱长设球的半径为R ,则2R =6,得R =3)(3633434333cm R πππ=⨯=∴最大零件的体积为若一个多面体的各面都与一个球的球面相切, 则称这个多面体是这个球的外切多面体,这个球是这个多面体的内切球。
内切球的球心到多面体各面的距离均相等。
⑴正方体的内切球直径=⑵正方体的外接球直径=⑶与正方体所有棱相切的球直径=探究 若正方体的棱长为a ,则a3a2a右图,红色球是正方体的棱切球棱切球的球心到正方体各条棱的距离相等,因此球心是正方体的体对角线的交点,球的直径是正方体的面对角线的长2、长方体若长方体的长、宽、高分别为a、b、c,则其外接球半径为球心是长方体的体对角线的交点222 1+2a b c例:有一个球与长方体的面相切,这个球的最大直径是多少?长方体的长、宽、高中的最小者例:一个长方体的各顶点均在同一个球的球面上,且一个顶点上的三条棱的长分别为1,2,3,则此球的表面积为____________若一个多面体的各顶点都在一个球的球面上,则称这个多面体是这个球的内接多面体,这个球是这个多面体的外接球。
八个模型全搞定空间几何的外接球和内切球问题(学生版)

1八个模型搞定空间几何体的外接球与内切球一、直棱柱模型1.已知各顶点都在同一球面上的正四棱柱的高为4,体积为16,则这个球的表面积是。
2.一个正六棱柱的底面上正六边形,其侧棱垂直于底面,已知该六棱柱的顶点都在同一个球面上,且该六棱柱的体积为98,底面周长为3,则这个球的体积为。
3.直三棱柱111ABC A B C -的各顶点都在同一球面上,若12AB AC AA ===,120BAC ∠=︒,则此球的表面积等于。
4.在直三棱柱ABC A B C 111中,AB 4,AC 6,,A 3AA 14则直三棱柱ABC A B C 111的外接球的表面积为。
5.若三棱锥S ABC 的三条侧棱两两垂直,且SA 2,SB SC 4,则该三棱锥的外接球半径为。
6.三棱锥S ABC 中,侧棱SA 平面ABC ,底面ABC的正三角形,SA ,则该三棱锥的外接球体积等于。
,则其外接球的表面积是。
8.在四面体S ABC -中,SA ABC 平面,,,,BAC SA AC AB 12021则该四面体的外接球的表面积为。
二、棱锥所有侧棱相等模型1、一个正三棱锥的四个顶点都在半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,则该正三棱锥的体积是。
2.正三棱锥S ABC 中,底面ABC侧棱长为2,则该三棱锥的外接球体积等于。
3、在三棱锥P ABC中,PA PB PC ,侧棱PA 与底面ABC 所成的角为60 ,2则该三棱锥外接球的体积为。
三、侧面与底面垂直模型1.三棱锥P ABC 中,平面PAC 平面ABC ,AC 2,PA PC 3,AB BC ,则三棱锥P ABC 外接球的半径为。
2.三棱锥P ABC 中,平面PAC 平面ABC ,△PAC 边长为2的正三角形,AB BC ,则三棱锥P ABC 外接球的半径为。
3.已知EAB 所在的平面与矩形ABCD 所在的平面互相垂直,,EA EB AD AEB 3260,则多面体E ABCD 的外接球的表面积为。
高中数学解题指导八个无敌模型全搞定空间几何的外接球和内切球问题

高中数学解题指导八个无敌模型全搞定空间几何的外接球和内切球问题八个有趣模型——搞定空间几何体的外接球与内切球类型一、墙角模型墙角模型是指三条线段两两垂直的几何体,通过公式(2R) = a + b + c,即2R = a^2 + b^2 + c^2,可以求出其外接球半径R。
例1:1)已知顶点都在同一球面上的正四棱柱的高为4,体积为16,求该球的表面积。
解:由V = ah = 16,得a = 2,4R = a + a + h = 4 + 4 + 16 = 24,S = 24π,答案为C。
2)若三棱锥的三个侧面两两垂直,且侧棱长均为3,求其外接球的表面积。
解:由2R = a + b + c = 3 + 3 + 3 = 9,得R = 9/4,S =4πR^2 = 9π。
3)在正三棱锥S-ABC中,M、N分别是棱SC、BC的中点,且AM⊥MN,若侧棱SA = 23,求正三棱锥S-ABC外接球的表面积。
解:由墙角模型的特点可知,正三棱锥的对棱互垂直。
连接AB、BC的中点D、E,连接AE、CD,交于H,则H是底面正三角形ABC的中心。
由AM⊥MN,SB//MN,可得AM⊥SB,AC⊥SB,故SB⊥平面SAC,SB⊥SA,SB⊥SC,即SB⊥SA,BC⊥SA,故SA⊥平面SBC,SA⊥SC。
因此,三棱锥S-ABC的三棱条侧棱两两互相垂直,由2R^2 = 23^2 + 23^2 + 23^2 = 36,得R^2 = 9,S = 36π。
类型二、棱台模型棱台模型是指上底面和下底面都是正多边形,且两底面中心连线与侧棱垂直的几何体。
通过勾股定理和相似三角形,可以求出其外接球半径R和内切球半径r。
例2:1)已知棱台的上底面和下底面都是正三角形,上底边长为3,下底边长为6,侧棱长为5,求其外接球半径R和内切球半径r。
解:由勾股定理可得棱台的高为4√3.设外接球半径为R,内切球半径为r,则有R/r = (a + b + c)/(a + b - c) = (3 + 6 +5)/(3 + 6 - 5) = 7,解得R = 7r。
空间几何体的外接球与内切球问题(学生版)

空间几何体的外接球与内切球问题目录一、必备秘籍二、典型题型题型一:内切球等体积法题型二:内切球独立截面法题型三:外接球公式法题型四:外接球补型法题型五:外接球单面定球心法题型六:外接球双面定球心法三、专项训练一、必备秘籍1.球与多面体的接、切定义1;若一个多面体的各顶点都在一个球面上,则称这个多面体是这个球的内接多面体,这个球是多面体的外接球。
定义2;若一个多面体的各面都与一个球的球面相切,则称这个多面体是这个球的外切多面体,这个球是多面体的内切球。
类型一球的内切问题(等体积法)例如:在四棱锥P-ABCD中,内切球为球O,求球半径r.方法如下:V P-ABCD=V O-ABCD+V O-PBC+V O-PCD+V O-PAD+V O-PAB即:V P-ABCD=13S ABCD⋅r+13S PBC⋅r+13S PCD⋅r+13S PAD⋅r+13S PAB⋅r,可求出r.类型二球的外接问题1、公式法正方体或长方体的外接球的球心为其体对角线的中点2、补形法(补长方体或正方体)①墙角模型(三条线两个垂直)题设:三条棱两两垂直(重点考察三视图)②对棱相等模型(补形为长方体)题设:三棱锥(即四面体)中,已知三组对棱分别相等,求外接球半径(AB=CD,AD=BC,AC=BD) 3、单面定球心法(定+算)步骤:①定一个面外接圆圆心:选中一个面如图:在三棱锥P-ABC中,选中底面ΔABC,确定其外接圆圆心O1(正三角形外心就是中心,直角三角形外心在斜边中点上,普通三角形用正弦定理定外心2r=asin A);②过外心O1做(找)底面ΔABC的垂线,如图中PO1⊥面ABC,则球心一定在直线(注意不一定在线段PO1上)PO1上;③计算求半径R:在直线PO1上任取一点O如图:则OP=OA=R,利用公式OA2=O1A2+OO12可计算出球半径R.4、双面定球心法(两次单面定球心)如图:在三棱锥P-ABC中:①选定底面ΔABC,定ΔABC外接圆圆心O1②选定面ΔPAB,定ΔPAB外接圆圆心O2③分别过O1做面ABC的垂线,和O2做面PAB的垂线,两垂线交点即为外接球球心O.二、典型题型题型一:内切球等体积法1(22·23·全国·专题练习)正三棱锥P-ABC的三条棱两两互相垂直,则该正三棱锥的内切球与外接球的半径之比为()A.1:3B.1:3+3C.3+1 :3D.3-1 :32(22·23下·朔州·阶段练习)正四面体的内切球、棱切球(与各条棱均相切的球)及外接球的半径之比为.3(23·24上·萍乡·期末)已知球O 是棱长为1的正四面体的内切球,AB 为球O 的一条直径,点P 为正四面体表面上的一个动点,则PA ⋅PB的取值范围为.4(22·23上·张家口·期中)球O 为正四面体ABCD 的内切球,AB =4,PQ 是球O 的直径,点M 在正四面体ABCD 的表面运动,则MP ⋅MQ的最大值为.5(22·23上·河南·阶段练习)已知正四面体ABCD 的棱长为12,球O 内切于正四面体ABCD ,E ,F 是球O 上关于球心O 对称的两个点,则AE ⋅BF的最大值为.6(22·23上·扬州·期中)中国古代数学名著《九章算术》中将底面为矩形且有一条侧棱垂直于底面的四棱锥称为“阳马”.现有一“阳马”的底面是边长为3的正方形,垂直于底面的侧棱长为4,则该“阳马”的内切球表面积为,内切球的球心和外接球的球心之间的距离为.题型二:内切球独立截面法1(23·24上·淮安·开学考试)球M 是圆锥SO 的内切球,若球M 的半径为1,则圆锥SO 体积的最小值为()A.43π B.423π C.83π D.4π2(22·23下·咸宁·期末)已知球O 内切于圆台(即球与该圆台的上、下底面以及侧面均相切),且圆台的上、下底面半径r 1:r 2=2:3,则圆台的体积与球的体积之比为()A.32B.1912C.2D.1963(22·23·全国·专题练习)若圆锥的内切球(球面与圆锥的侧面以及底面都相切)的半径为1,当该圆锥体积取最小值时,该圆锥体积与其内切球体积比为.4(23·24上·佛山·开学考试)若圆锥的内切球(球面与圆锥的侧面以及底面都相切)的体积为4π3,当该圆锥体积取最小值时,该圆锥的表面积为.5(22·23下·成都·阶段练习)已知圆锥的底面半径为2,高为42,则该圆锥的内切球表面积为.题型三:外接球公式法1(16·17·全国·单元测试)若长方体从一个顶点出发的三条棱长分别为3,4,5,则该长方体的外接球表面积为 ()A.50πB.100πC.150πD.200π2(22·23·全国·专题练习)设球O 是棱长为4的正方体的外接球,过该正方体的棱的中点作球O 的截面,则最小截面的面积为()A.3πB.4πC.5πD.6π3(14·15上·佛山·阶段练习)正方体的外接球(正方体的八个顶点都在球面上)与其内切球(正方体的六个面都与球相切)的体积之比是.题型四:外接球补型法1(23·24上·成都·开学考试)在三棱锥P -ABC 中,PA =PB =PC =2,PA ⊥PB ,PA ⊥PC ,PB ⊥PC ,则该三棱锥的外接球的表面积为()A.43πB.12πC.48πD.323π2(22·23下·揭阳·期中)在三棱锥S -ABC 中,SA =BC =5,SB =AC =41,SC =AB =34,则该三棱锥的外接球表面积是()A.50πB.100πC.150πD.200π3(23·24上·成都·开学考试)已知四面体ABCD 满足AB =CD =3,AD =BC =5,AC =BD =2,且该四面体ABCD 的外接球的表面积是()A.2πB.6πC.6π11D.4π4(22·23下·黔西·阶段练习)正三棱锥P -ABC 的三条棱两两互相垂直,则该正三棱锥的内切球与外接球的半径之比为.5(22·23下·黔西·期中)如图,已知在三棱锥P -ABC 中,PA ⊥PB ,PB ⊥PC ,PC ⊥PA ,且PA =2PB =2PC =2,求该三棱锥外接球的表面积是.题型五:外接球单面定球心法1(23·24上·汉中·模拟预测)如图,在三棱锥P -ABC 中,PA ⊥平面ABC ,PA =6,BC =3,∠CAB =π6,O为△ABC 外接圆的圆心,O 为三棱锥P -ABC 外接球的球心,OQ ⊥PA ,则三棱锥P -ABC 的外接球O 的表面积为.2(23·24上·秦皇岛·开学考试)三棱锥P-ABC中,AB⊥BC,P在底面的射影O为△ABC的内心,若AB=4,BC=3,PO=5,则四面体PABC的外接球表面积为.3(22·23下·石家庄·阶段练习)已知球O是正四面体P-ABC的外接球,E为棱PA的中点,F是棱PB上的一点,且FC=2EF,则球O与四面体P-EFC的体积比为.4(22·23下·淄博·期末)已知四棱锥P-ABCD的底面ABCD是矩形,侧面PAD为等边三角形,平面PAD⊥平面ABCD,其中AD=2,AB=3,则四棱锥P-ABCD的外接球表面积为.题型六:外接球双面定球心法1(22·23上·抚州·期中)已知菱形ABCD的各边长为2,∠D=60°.如图所示,将△ACD沿AC折起,使得点D到达点S的位置,连接SB,得到三棱锥S-ABC,此时SB=3.若E是线段SA的中点,点F在三棱锥S-ABC的外接球上运动,且始终保持EF⊥AC则点F的轨迹的面积为.2(22·23·赣州·模拟预测)如图,正三角形ABC中,D,E分别为边AB,AC的中点,其中AB=4,把△ADE沿着DE翻折至△A DE的位置,得到四棱锥A -BCED,则当四棱锥A -BCED的体积最大时,四棱锥A -BCED外接球的球心到平面A BC的距离为.3(22·23下·湖南·期末)为加强学生对平面图形翻折到空间图形的认识,某数学老师充分利用习题素材开展活动,现有一个求外接球表面积的问题,活动分为三个步骤,第一步认识平面图形:如图(一)所示的四边形PABC中,AB=BC=2,PA=PC,∠ABC=60°,PA⊥PC.第二步:以AC为折痕将△PAC折起,得到三棱锥P-ABC,如图(二).第三步:折成的二面角P-AC-B的大小为120°,则活动结束后计算得到三棱锥P-ABC外接球的表面积为.三、专项训练一、单选题1(22·23下·河南·模拟预测)已知直六棱柱的所有棱长均为2,且其各顶点都在同一球面上,则该球的表面积为( ).A.16πB.20πC.24πD.25π2(22·23下·宁德·期中)正四面体ABCD的外接球的半径为2,过棱AB作该球的截面,则截面面积的最小值为()A.2π3B.4π3C.8π3D.3π3(23·24上·河北·开学考试)长方体的一个顶点上三条棱长是3,4,5,且它的八个顶点都在同一球面上,这个球的体积是()A.12523π B.1252π C.50π D.125π4(22·23下·临夏·期末)已知四棱锥P-ABCD的体积为83,侧棱PA⊥底面ABCD,且四边形ABCD是边长为2的正方形,则该四棱锥的外接球的表面积为()A.12πB.8πC.4πD.2π5(23·24上·广东·阶段练习)如图,在边长为2的正方形ABCD中,E,F分别是AB,BC的中点,将△AED,△BEF,△DCF分别沿DE,EF,DF折起,使得A,B,C三点重合于点A ,若三棱锥A -EFD的所有顶点均在球O的球面上,则球O的表面积为()A.2πB.3πC.6πD.8π6(23·24上·安徽·开学考试)在封闭的等边圆锥(轴截面为等边三角形)内放入一个球,若球的最大半径为1,则该圆锥的体积为()A.3πB.6πC.9πD.12π7(23·24上·莆田·阶段练习)三棱锥P-ABC中,△ABC是边长为23的正三角形,PA=4,PA⊥AB,D为BC中点且PD=5,则该三棱锥外接球的表面积为()A.16πB.32πC.48πD.64π8(22·23·九江·一模)三棱锥A-BCD中,△ABD与△BCD均为边长为2的等边三角形,若平面ABD ⊥平面BCD,则该三棱锥外接球的表面积为()A.8π3B.20π3C.8πD.20π二、填空题9(23·24·柳州·模拟预测)已知圆锥的底面直径为23,轴截面为正三角形,则该圆锥内半径最大的球的体积为.10(22·23·唐山·二模)已知某圆台的上、下底面的圆周在同一球的球面上,且圆台上底面半径为1,下底面半径为2,轴截面的面积为3,则该圆台的外接球的体积为.11(22·23·大同·模拟预测)四个面都为直角三角形的四面体称之为鳌臑.在鳌臑P-ABC中,PA⊥平面ABC,PA=4,AB=BC=2,鳌臑P-ABC的四个顶点都在同一个球面上,则该球的表面积是.12(23·24上·辽宁·阶段练习)已知圆锥的底面半径为2,侧面展开图的面积为8π,则该圆锥的内切球的体积为.13(23·24上·成都·阶段练习)已知三棱锥S-ABC底面ABC是边长为2的等边三角形,平面SAB⊥底面ABC,SA=SB=2,则三棱锥S-ABC的外接球的表面积为.14(23·24上·遂宁·阶段练习)已知正三棱柱ABC-A1B1C1的六个顶点在球O1上,又球O2与此三棱柱的5个面都相切,则球O1与球O2的表面积之比为.15(22·23下·赣州·阶段练习)已知圆锥的内切球半径为1,若圆锥的侧面展开图恰好为一个半圆,则该圆锥的体积为.。
几何体外接球和内切球问题的解答方法

几何体的外接球和内切球问题大家知道,几何体的外接球和内切球问题是近几年的高考热点内容,尤其是几何体的外接球问题,基本上近几年的高考试题中都有出现。
归结起来这类问题主要包括两种类型:①已知几何体的顶点都在同一球面上,几何体满足一定的条件,求球的体积;②已知几何体的顶点都在同一球面上,几何体满足一定的条件,求球的表面积;解答这类问题的基本思路是根据问题给出的条件,求出球的半径,然后再运用球的体积(或表面积)公式进行计算得出结果。
从题型上看是5分小题,可能是选择题,也可能是填空题;从难易程度上看,属于中、低档难度的问题。
那么如何解答这类问题呢?下面通过例题的解析来回答这个问题。
【典例1】解答下列问题:1、已知三棱锥P —ABC 的三个顶点在球O 的球面上,PA=PB=PC ,∆ABC 是边长为2的正三角形,E ,F 分别是PA ,AB 的中点,∠CEF=.90,则球O 的体积为( )(2019全国高考新课标I (理))π π π π2、《九章算术》中将底面为长方形,且有一条侧棱与底面垂直的四棱锥称之为“阳马”,现有一阳马,其正视图和侧 1视图是如图所示的直角三角形,若该阳马的顶点都在同一个 1 2 球面上,则该球的体积为( )(2018成都市高三二诊)A πB πC πD 24π【解析】1、【考点】①正三棱锥的定义与性质;②正三棱锥外接球的定义与性质;③几何体外接球半径的求法;④球的体积计算公式与方法;【解题思路】运用正三角形的性质和正三棱锥外接球的性质求出外接球的半径,再运用球的体积公式进行计算得出结果; P【详细解答】如图,取BC 的中点D ,连接AD ,PD ,设正三角形ABC 外接圆的圆心为1O ,连接P 1O ,设外接 E O 球的球心为O ,连接AO ,∆ABC 是边长为2的正 C 三角形,D ,F 分别BC ,AB 的中点,∴AD=CF=2⨯ A F 1O B⇒A 1O ,PA=PB=PC ,∆ABC 是正三角形,∴P —ABC 是正三棱锥,⇒PB ⊥AC ,E ,F 分别是PA ,AB 的中点,∴EF//PB ,⇒EF ⊥AC ,∠CEF=.90,AC CE=C ,AC ,EC ⊂平面PAC ,∴EF ⊥平面PAC ,⇒PB ⊥平面PAC ,⇒∠APB=.90,⇒⇒PD =1,⇒P 1O 3R ,在Rt ∆AO 1O 中,AO=R ,O 1O =-R ,A 1O =,2AO =21OO +21AO ,∴2R =2)R -+2(3,⇒R=2,∴O V 球=343R π=43⨯4π=π⇒选D 。
空间几何体的外接球内切球问题

P DS CAO空间几何体的外接球、内切球问题外接球问题一.棱锥的外接球三棱锥都有外接球;底面有外接圆的任意棱锥都有外接球。
1.确定棱锥外接球球心的通法先找到棱锥底面的外接圆的圆心D ,过D 作底面的垂线DP交一侧棱的中垂面于O ,点O 即为外接球的球心。
练习:1.三棱锥S-ABC 的各顶点都在同一球面上,若SB ⊥平面ABC ,SB=6,AB=AC=2120BAC ∠=︒,则此球的表面积等于 。
2. 点A 、B 、C 、D 均在同一球面上,其中△ ABC 是正三角形,AD ⊥平面ABC ,AD=2AB=6则该球的体积为 。
3.四面体ABCD 的四个顶点在同一球面上,AB=BC=CD=DA=3,32=AC ,6=BD ,则该球的表面积为 ( )A . π14 B.π15 C.π16 D.π182.补成长方体或正方体,再利用体对角线是外接球直径这一结论求解。
练习:1.三棱锥O ABC -中,,,OA OB OC 两两垂直,且22OA OB OC a ===,则三棱锥O ABC -外接球的表面积为( )A .26a πB .29a πC .212a πD .224a π2.已知,,,S A B C 是球O 表面上的点,SA ABC ⊥平面,AB BC ⊥,1SA AB ==,BC =O 表面积等于(A )4π (B )3π (C )2π (D )π3.,四个顶点在同一个球面上,则此球的表面积为( )A.3πB.4πD.6π4.3.公共边所对的两个角为直角确定球心法 练习1.在矩形ABCD 中,4,3AB BC ==,沿AC 将矩形ABCD 折成一个直二面角B ACD --,则四面体ABCD 的外接球的体积为 A.12512π B.1259π C.1256π D.1253π2.空间四边形ABCD中,1,AB BC AD DC ====ABCD 的外接球的表面积为4.利用轴截面截球为大圆确定球半径正四、六、八棱锥的外接球的一个轴截面为大圆,该圆的半径等于外接球的半径. 练习:1.正四棱锥S ABCD -S A B C D 、、、、都在同一球面上,则此球的体积为 .2.正六棱锥EF S ABCD -的底面边长为1S A B C D 、、、、、E 、F 都在同一球面上,则此球的表面积为 .3.表面积为的正八面体的各个顶点都在同一个球面上,则此球的体积为_ C_ A_ O_ D _ BA.3B.13π C.23π D.3二.棱柱的外接球底面有外接圆的直棱柱才有外接球。
常用几何体的内切外接球

知识回顾 Knowledge Review
Hale Waihona Puke 祝您成功!2.已知棱长为a的正四面体,则此正四面体的表面积S1与其内切球的表 面积S2的比值为多少? 解答
正四面体的表面积为 S1=4·43·a2= 3a2,
其内切球半径 r 为正四面体高的14,即 r=14·36a=126a,
因此内切球表面积为
S2=4πr2=π6a2,则SS12=
π3aa22=6
π
3 .
解答
由题意可知,此正方体的体对角线长即为其外接球的直径,正方体的 棱长即为其内切球的直径. 设该正方体外接球的半径为R,内切球的半径为r. 又正方体的棱长为 4,故其体对角线长为 4 3, 从而 V 外接球=43πR3=43π×(2 3)3=32 3π, V 内切球=43πr3=43π×23=323π.
常见几何体的内切、外接球
①若球为正方体 的外接球 2R 3a
若球为正方体的内切球,则 2R=a
③若球与正方体 的各棱相切,则
2R 2a
知识拓展 1.几个与球有关的切、接常用结论 (1)正方体的棱长为a,球的半径为R,
①若球为正方体的外接球 2R 3a
②若球为正方体的内切球,则 2R=a
③若球与正方体的各棱相切,则 2R 2a
(2)若长方体的同一顶点的三条棱长分别为a,b,c,外接球的半径为R, 则2R= a2+b2+c2 .
(3)正四面体棱长为a,其外接球的半径: 内切球的半径: 球心的位置:
外接球的半径与内切球的半径之比:
引申探究 1.已知棱长为4的正方体,则此正方体外接球和内切球的体积各是多少?
6
3.已知侧棱和底面边长都是3 2 的正四棱锥,则其外接球的半径是多少?
简单几何体的外接球与内切球(1)

的外接球与内切球问题
1、正方体的外接球与内切球问题 若正方体的棱长为a,则 ⑴正方体的内切球直径=
a
若正方体的棱长为a,则
⑴正方体的内切球直径=
⑵正方体的外接球直径=
a
若正方体的棱长为a,则
⑴正方体的内切球直径= a
⑵正方体的外接球直径= 3a ⑶与正方体所有棱相切的球直径= 2a
结论、 若正棱锥的侧棱长为b,高为h,则
b 正棱锥的外接球半径r= 2 h
2
高考题欣赏
A
2018年广东省理科第一次模拟
6:在三棱锥P-ABC中,PA PC,AB BC 且AB= 1,BC= 3,则它外接球的体积为_______
结论五:在三棱锥P-ABC中,如果有两个面是有公共斜边 的直角三角形,那么三棱锥P-ABC的外接球直径就是这条斜边
空间几何体的外接球中的最值问题
高考题欣赏:
4 3
B
2、 若正四棱锥的底面边长为a,侧棱长为b,高为h
则正四棱锥的内切球半径r=
ah a 4h a
2 2
1 2 2 2 a h b 2
8、 直棱柱的外接球与内切球问题
1、直三棱柱的外接球问题
设直棱柱底面边长为分别为a,b,c,高为h,求外接球的半径 解析:设直棱柱外接球的半径为R,
球心到底面ABC的距离为d,ΔABC的外接圆半径为r. 球心在上下底面的外心的连线的中点。
A B O A1 C1 C
O1
B1
8、 直棱柱的外接球与内切球问题
2、直三棱柱的内切球问题
设直棱柱底面边长为分别为a,b,c,高为h,求内切球的半径 解析:设直棱柱内切球的半径为r,
ΔABC的外接圆半径为r.
超全的外接球与内切球问题

第二章:外接球与内切球1.空间几何体的内切球几何体示例图像截面图对应性质圆柱r h 、分别为圆柱的底面圆半径和高,R 为内切球半径.R r =且2h R =;正三棱柱r h 、分别为柱体的底面三角形内切圆半径和高,R 为内切球半径.R r =且2h R =;正棱锥PE 为锥体的斜高,h r 、分别为锥体的高和底面内切圆半径,R 为内切球半径.1POF PEO △∽△可得R OP h R r PE PE -==“钻石”PE 为锥体的斜高,h r 、分别为锥体的高和底面内切圆半径,R 为内切球半径.在Rt POE △中,满足h rR PE⋅=一般三棱锥记R 为内切球半径,三棱锥的四个面面积分别为1234S S S S 、、、,则1234VR S S S S =+++【示例1】1.如图,在圆柱12O O 内有一个球O ,该球与圆柱的上、下底面及母线均相切,记圆柱12O O 的体积为1V ,球O 的体积为2V ,则12V V =__________.【解析】记内切球半径为R ,底面圆半径为r ,圆柱高为h ;则R r =且2h R =;则23122V h s r r r ππ=⋅=⋅=,3324433V R r ππ==;∴1232V V =2.如果一个球的外切圆锥的高是这个球的半径的3倍,则圆锥的侧面面积和球的表面积之比为__________.【解析】轴截面如右图,记h r 、为圆锥的高和底面圆半径,R 为内切球半径;由题意,3h R =,同时由1POF PEO △∽△可得1OP OFPE EO =;即R r==,得r =,则PE =.∴在圆锥1O P 中,2212S PE r R ππ=⋅=侧,2=4S R π球;则:3:1S S =侧球【例1】1.已知正方体的内切球(球与正方体的六个面都相切)的体积是323π,则该正方体的表面积为__________.2.如果一个八面体各个面都是全等的正三角形,如图所示,则这个几何体叫正八面体,则棱长为4的正八面体的内切球半径是__________.3.在封闭的直三棱柱111ABC A B C -内有一个体积为V 的球,若AB BC ⊥,6AB =,8BC =,13AA =,则V 的最大值是__________.4.天津滨海文化中心地处天津滨海新区开发区,是天津乃至京津冀地区的标志性文化工程.其中滨海图书馆建筑独具特色,被称为“滨海之眼”,如图1所示,中心球状建筑引起了小明的注意,为了测量球的半径,小明设计了两个方案,方案甲,构造正三棱柱侧面均与球相切如图2所示,底面边长约为30米,估计此时球的完整表面积为平方米;方案乙,测量球被地面截得的圆的周长约为16π米,地面到球顶部高度约为16米,估计此时球的完整体积为立方米,你认为哪种方案好呢?课堂练习1:1.一个球与一个正三棱柱的三个侧面和两个底面都相切,已知这个球的体积是32,那么3这个球的半径是,三棱柱的体积是.2.正四棱锥的高与底面边长相等且体积为83,(1)以底面中心为球心,经过四棱锥四条侧棱中点的球的表面积为__________;(2)该正四棱锥的内切球体积为__________.3.农历五月初五是端午节,民间有吃粽子的习惯,粽子又称粽籺,俗称“粽子”,古称“角黍”,是端午节大家都会品尝的食品,传说这是为了纪念战国时期楚国大臣、爱国主义诗人屈原.如图,平行四边形形状的纸片是由六个边长为1的正三角形构成的,将它沿虚线折起来,可以得到如图所示粽子形状的六面体,则该六面体的体积为;若该六面体内有一球,则该球体积的最大值为.2.柱体外接球问题概述具备外接球的柱体,一定是“直”的,即侧棱垂直于底面或圆柱体.其球心必在柱体上下底面外接圆圆心连线的中点.此时球心到柱体底面的距离d 等于柱体高h 的一半(即2h d =).示例图像圆柱长方体直三棱柱计算公式222224h R d r r =+=+22224R a b c =++2sin ar A=,222R d r =+问题设计①.先求出柱体高和底面相关信息,再求外接球半径;②.已知外接球半径,求柱体的高或底面相关变量.【示例2】1.如图,长方体1111ABCD A B C D -的底面是面积为2的正方形,该长方体的外接球体积为323π,点E 为棱AB 的中点,则三棱锥1D ACE -的体积是__________.【解析】Ⅰ.确定长方体的高→Ⅱ.求1D ACEV -3432233V R R ππ==→=球,则2222114222AB AD AA R AA AB AD ⎫++=⎪→=⎬==⎪⎭;∴在三棱锥1D ACE -中,122112ACE h AA S AE BC ⎧==⎪⎨=⋅=⎪⎩△;得112233D ACE ACE V h S -=⋅=△2.已知直三棱柱111ABC A B C -的外接球半径为4,同时BA BC ⊥,BA BC =则111ABC A B C -体积的最大值为__________.【解析】Ⅰ.找到侧棱和底面棱长的关系→Ⅱ.函数求最值显然Rt ABC △为等腰直角三角形,则22r AB =;此时212ABC S AB CB r =⋅=△;同时222224h R d r r =+=+可得22164h r =-;则()()23116640844ABCh V h S h h h h ⎛⎫=⋅=⋅-=-<< ⎪⎝⎭△;令()()36408f x x x x =-+<<,则()2364f x x '=-+;令()0f x '=得x =;∴()f x 在⎛ ⎝上递增,在⎫⎪⎭上递减,则()max 9f x f ==,则()max max14V f x ==【例2】1.若一个圆柱的轴截面是面积为4的正方形,则该圆柱的外接球的表面积为__________.2.在正方体1111ABCD A B C D -中,三棱锥11A B CD -的表面积为,则正方体外接球的体积为__________.3.已知直三棱柱的各棱长都相等,三棱柱的所有顶点都在球O 的表面上,若球O 的表面积为28π,则该三棱柱的体积为__________.4.如图,直三棱柱111ABC A B C -的六个顶点都在半径为1的半球面上,AB AC =,侧面11BCC B 是半球底面圆的内接正方形,则侧面11ABB A 的面积为__________.5.“迪拜世博会”于2021年10月1日至2022年3月31日在迪拜举行,中国馆建筑名为“华夏之光”,外观取型中国传统灯笼,寓意希望和光明.它的形状可视为内外两个同轴圆柱,某爱好者制作了一个中国馆的实心模型,已知模型内层底面直径为12cm ,外层底面直径为16cm ,且内外层圆柱的底面圆周都在一个直径为20cm 的球面上.此模型的体积为__________.课堂练习2:1.已知正方体的体积是8,则这个正方体的外接球的体积是__________.2.在正方体1111ABCD A B C D -中,三棱锥11A B CD -的表面积为,则正方体外接球的体积为__________.3.一直三棱柱的每条棱长都是2,且每个顶点都在球O 的表面上,则球O 的表面积为__________.4.已知一个体积为8的正方体内接于半球体,即正方体的上底面的四个顶点在球面上,下底面的四个顶点在半球体的底面圆内.则该半球体的体积为__________.3.侧棱垂直于底面的锥体外接球问题阐述若锥体有一条侧棱PA 满足PA ⊥底面ABC ,则该锥体必可还原成一个直棱柱.即侧棱垂直于底面的棱锥与还原之后的直棱柱具有相同的外接球.示例图像还原至长方体还原至长方体还原至直三棱柱对应条件AP AB AC 、、两两垂直AP AB BC 、、两两垂直PA ⊥面ABC 计算公式22224R AP AB AC =++22224R PA AB BC =++12sin AB r C =⋅且12d h =222R d r =+备注当锥体有三条棱两两垂直时,记这三条棱的棱长分别为a b c 、、,则22224R a b c =++.若锥体的底面不含直角,仅有侧棱垂直于底面时,用222R d r =+求出外接球半径【示例3】在三棱锥P ABC -中,90ACB ∠=︒,8AB =,PC ⊥面ABC 且6PC =,则该三棱锥外接球的表面积为__________.【解析】由题意可知CA CB CP 、、两两垂直;则222222222464410041006R CP CB CA CA CB AB R S R CP ππ⎫=++⎪+==→=→==⎬⎪=⎭【例3】1.在三棱锥A BCD -中,AB AC AD 、、两两垂直,且ACB ACD ABD △、△、△的面积分别为22A BCD -的外接球的表面积为__________.2.在三棱锥P ABC -中,PA ⊥平面ABC ,且ABC △为等边三角形,2AP AB ==,则三棱锥P ABC -的外接球的表面积__________.3.如图,PA ⊥面ABCE ,其中ABCD 为正方形,2AD =,1ED =.若三棱锥P ADE -的外接球的体积为92π.则四棱锥P ABCD -的外接球的表面积为__________.课堂练习3:1.在边长为2的等边三角形ABC 中,点D 是BC 的中点.以AD 为折痕,将ABC △折成直二面角B AD C --,则过A B C D 、、、四点的球的表面积为__________.2.在四面体S ABC -中,SA ⊥平面ABC ,120BAC ∠=︒,1AB =,2AC =,3SA =,则该四面体外接球面积为__________.3.在《九章算术》中,将底面为矩形且有一条侧棱与底面垂直的四棱锥称为阳马.已知四棱锥M ABCD -为阳马,侧棱MA ⊥底面ABCD ,且1MA =,2BC =,3AB =.若该四棱锥的顶在都在同一球面上,则该球的表面积为__________.4.正棱锥和圆锥的外接球补充:问题阐述①.正四面体内嵌于正方体,则两者具有相同的外接球.记正四面体的边长为a ,正方体的边长为b ,外接球半径为R ;②.两个具有相同底面,且顶点(P Q 、)在底面的射影均为底面外接圆圆心的锥体的外接球.记底面外接圆半径为r ,两个锥体的高分别为12h h 、,外接球半径为R示例图像对应计算①.2a b =且2243R b =;②.22342R a =①.122h h R +=且PA QA ⊥(PQ 为球的直径);②.212r h h =⋅(直角三角形内射影定理);【示例4】1.正三棱锥底面边长为3,侧棱与底面成60︒角,则其外接球的体积为__________.【解析】Ⅰ.确定正棱锥的高和底面外接圆半径ABC △是边长为3的等边三角形,则333r AB ==;在Rt POA △中,3360OA r OP h PAO ⎫==⎪→==⎬∠=︒⎪⎭;Ⅱ.求外接圆半径,并求其体积则2231243222633h r R V R h ππ+===→==2.两个圆锥的底面是一个球的同一截面,顶点均在球面上,若球的体积为323π,两个圆锥的高之比为1:3,则这两个圆锥的体积之和为__________.【解析】Ⅰ.求出12R h h r→→、3432233V R R ππ==→=球,显然PQ 是球O 的直径,则PA QA ⊥,则212r h h =⋅;121122243331h h R h r h h h +===⎫⎧→→=⎬⎨==⎭⎩Ⅱ.求锥体的体积则()21211233V h S h h r ππ=⋅=+⋅=【例4】1.若一个四面体的所有棱长均为1,四个顶点在同一个球面上,则此球的表面积为__________.2.如图,半球内有一内接正四棱锥S ABCD -,该四棱锥的体积为3,则该半球的体积为__________.3.已知圆锥的顶点和底面圆周都在球O 的球面上,圆锥的母线长为3,侧面展开图的面积为3π,则球O 的表面积等于__________.4.以ABC 为底的两个正三棱锥P ABC -和Q ABC -内接于同一个球,并且正三棱锥P ABC -的侧面与底面ABC 所成的角为45︒,记正三棱锥P ABC -和正三棱锥Q ABC -的体积分别为1V 和2V ,则12V V =__________.5.《九章算术》是我国古代的数学名著,其中有很多对几何体体积的研究,已知某囤积粮食的容器的下面是一个底面积为32π,高为h 的圆柱,上面是一个底面积为32π,高为h 的圆锥,若该容器有外接球,则外接球的体积为__________.6.已知三棱锥P ABC -的四个顶点在球O 的球面上,PA PB PC ==,ABC △是边长为2的正三角形,E F 、分别是PA AB 、的中点,90CEF ∠=︒,则球O 的体积为__________.课堂练习4:1.正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为__________.2.底面是边长为1的正方形,侧面是等边三角形的四棱锥的外接球的体积为__________.3.已知正方体1111ABCD A B C D -的棱长为2,其各面中心分别为E F G H M N 、、、、、,则连接相邻各面中心构成的几何体的外接球表面积为__________.4.设A ,B ,C ,D 是同一个半径为4的球的球面上四点,ABC ∆为等边三角形且面积为D ABC -体积的最大值为__________.5.在正三棱锥P ABC -中,6AB BC AC ===,点D 是PA 的中点.若PB CD ⊥,则该三棱锥外接球的表面积为__________.5.其他模型问题阐述①.面ABC ⊥面BCD ;②.记12r r 、分别为ABC BCD △、△的外接圆半径,R 为三棱锥A BCD -外接球半径.①.三棱锥D ABC -中,AD 为外接球直径;②.记球面距1OO d =,ABC △的外接圆半径为r ,D ABC -的高为h .示例图像对应性质①.2h d =;②.2222124BC R r r =+-(BC 为交线长);①.AB DB AC DC ⊥⊥、(直径所对圆周角);②.222R d r =+且2h d =;解题步骤①.确定三棱锥A BCD -中的两个垂直平面;②.求出对应的外接圆半径和交线长;③.求外接球的半径;①.确定外接球的直径;②.求出底面三角形外接圆半径r ;③.22D ABC R r d h V --→→→;【示例5】1.将长、宽分别为4和3的长方形ABCD 沿对角线AC 折成直二面角,得到四面体A BCD -,则四面体A BCD -的外接球的表面积为__________.【解析】由题意,面ACD ⊥面ACB 且5AC =而ACD ACB △、△都是直角三角形,则12522AC r r ===;则2222122544AC R r r =+-=;得2425S R ππ==2.已知三棱锥S ABC -的所有顶点都在球O 的表面上,ABC △是边长为1的正三角形,SC 为球O 的直径,且2SC =,则此三棱锥的体积为__________.【解析】在ABC △中,2sin 3AB r C ==;同时112R SC ==,则d ==,则2h d ==∴111sin 33326V hS AB AC C ==⨯⋅⋅=【例5】1.已知三棱维A BCD -中,侧面ABC ⊥底面BCD ,ABC △是边长为6的正三角形,BCD ∆是直角三角形,且2BCD π∠=,4CD =,则此三棱锥外接球的表面积为__________.2.在三棱锥A BCD -中,BA AD ⊥,BC CD ⊥,且AD ==A BCD -外接球的体积为__________.3.已知球的直径4SC =,A ,B 是该球球面上的两点,AB =,30ASC BSC ∠=∠=︒,则棱锥S ABC -的体积为__________.4.已知球的直径4SC =,A ,B 是该球球面上的两点.2AB =,45ASC BSC ∠=∠=︒,则棱锥S ABC -的体积为__________.5.已知三棱锥S ABC -外接球的球心O 在线段SA 上,若ABC △与SBC △均为面积是的等边三角形,则三棱锥S ABC -外接球的体积为__________.6.已知三棱锥S ABC -的所有顶点都在球O 的球面上,SC 是球O 的直径.若平面SCA ⊥平面SCB ,SA AC =,SB BC =,三棱锥S ABC -的体积为9,则球O 的表面积为__________.课后作业:1.已知圆锥的底面圆周及顶点均在球面上,若圆锥的轴截面为正三角形,则圆锥的体积与球的体积之比为__________.2.已知一个圆柱的高是底面半径的2倍,且其上、下底面的圆周均在球面上,若球的体积为323π,则圆柱的体积为__________.3.已知在ABC ∆中,角A B C 、、所对的边分别为a b c 、、,且2a =,6A π=,又点A B C 、、都在球O 的球面上,且点O 到平面ABC ,则球O 的体积为__________.4.一个正三棱锥的底面边长等于一个球的半径,该正三棱锥的高等于这个球的直径,则球的体积与正三棱锥体积的比值为__________.5.正四面体A BCD -的棱长为4,点E 为BC 边上的中点,过点E 做其外接球的截面,则截面圆的面积最小值为__________.6.已知一个正三棱柱所有棱长均为3,若该正三棱柱内接于半球体,即正三棱柱的上底面的三个顶点在球面上,下底面的三个顶点在半球体的底面圆内,则该半球体的体积为__________.7.所有棱长都是3的直三棱柱111ABC A B C -的六个顶点都在同一球面上,则该球的表面积是__________.8.已知圆柱1OO 的两底面圆周上的所有点都在球C 的表面,且圆柱1OO 的底面半径为1,高为,则球C 的表面积为__________.9.已知某圆柱的轴截面为正方形,则此圆柱的表面积与此圆柱外接球的表面积之比为__________.10.已知直三棱柱111ABC A B C -的6个顶点都在球O 的球面上,若1AB =,AC =,AB AC ⊥,14AA =,则球O 的表面积为__________.11.已知正三棱台的高为1,上、下底面边长分别为和,其顶点都在同一球面上,则该球的表面积为__________.12.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为__________.13.正三棱柱111ABC A B C -内接于半径为2的球,若A ,B 两点的球面距离为π,则正三棱柱的体积为__________.14.直三棱柱111ABC A B C -的各顶点都在同一球面上,若12AB AC AA ===,120BAC ∠=︒,则此球的表面积等于__________.15.已知矩形ABCD 的顶点都在半径为2的球O 的球面上,且AB =,BC =,过点D作DE 垂直于平面ABCD ,交球O 于点E ,则棱锥E ABCD -的体积为__________.16.在三棱锥P ABC -中,PA ⊥平面ABC ,AB BC ⊥,3AB =,4BC =,5PA =,则三棱锥P ABC -的外接球的表面积为__________.17.《九章算术》中,将四个面都为直角三角形的三棱锥称之为鳖臑.若三棱锥P ABC-为鳖臑,PA⊥平面ABC,2==,4PA AB-的四个顶点都在球O的球AC=,三棱锥P ABC面上,则球O的表面积为__________.18.已知在半径为2的球面上有A、B、C、D四点,若2==,则四面体ABCD的AB CD体积的最大值为().A B C.D19.已知四棱锥P ABCD=====,且底面ABCD为正方形,则-满足2PA PB PC PD AB该四棱锥的外接球的体积为__________.20.已知三棱锥P ABC -的四个顶点在球O 的球面上,PA PB PC ==,ABC ∆是边长为2的正三角形,PA PC ⊥,则球O 的体积为__________.21.高为1的圆锥内接于半径为1的球,则该圆锥的体积为__________.22.已知正四棱锥P ABCD -的高为2,AB =,过该棱锥高的中点且平行于底面ABCD的平面截该正四棱锥所得截面为1111A B C D ,若底面ABCD 与截面1111A B C D 的顶点在同一球面上,则该球的表面积为__________.23.已知正四棱锥的侧棱长为l ,其各顶点都在同一球面上.若该球的体积为36π,且3l ≤≤,则该正四棱锥体积的取值范围是__________.24.已知球O 的半径为1,四棱锥的顶点为O ,底面的四个顶点均在球O 的球面上,则当该四棱锥的体积最大时,其高为__________.25.已知四棱锥S ABCD -的所有棱长均相等,且底面是边长为的正方形,其5个顶点都在直径为10的球面上,则该四棱锥的体积为__________.26.已知1111ABCD A B C D -是边长为1的正方体,S ABCD -是高为1的正四棱锥,若点1111S A B C D 、、、、在同一球面上,则该球的表面积为__________.27.已知三棱锥S ABC -的底面是以AB 为斜边的等腰直角三角形,2SA SB SC AB ====,设S ,A ,B ,C 四点均在以O 为球心的某个球面上,则O 到平面ABC 的距离为__________.28.现有一副斜边长相等的直角三角板.若将它们的斜边AB 重合,其中一个三角板沿斜边折起形成三棱锥A BCD -,如图所示,已知6DAB π∠=,4BAC π∠=,三棱锥的外接球的表面积为4π,该三棱锥的体积的最大值为().A B C D 29.已知三棱锥A BCD -的四个顶点A ,B ,C ,D 都在球O 的表面上,BC CD ⊥,AC ⊥平面BCD ,且AC =,2BC CD ==,则球O 的表面积为__________.30.已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积是__________.31.已知矩形ABCD的顶点都在半径为2的球O的球面上,且AB=,BC=,过点D 作DE垂直于平面ABCD,交球O于点E,则棱锥E ABCD-的体积为().32.已知圆锥底面圆的直径为3,圆锥的高为,该圆锥的内切球也是棱长为a的正四面2体的外接球,则此正四面体的棱长a为__________.33.设P,A,B,C为球O表面上的四个点,PA,PB,PC两两垂直,且3PB=,PA=,6三棱锥P ABC-的体积为18,则球O的体积为__________.34.已知六棱锥P ABCDEFPA=,PA⊥底面-的七个顶点都在球O的表面上,若2ABCDEF,且六边形ABCDEF是边长为1的正六边形,则球O的体积为__________.35.已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为18,则这个球的体积为__________.36.如图,圆形纸片的圆心为O,半径为5cm,该纸片上的等边三角形ABC的中心为O.D、∆分别是以BC,CA,AB为底边的等腰三E、F为圆O上的点,DBC∆,ECA∆,FAB角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起DBC∆,使得D、∆,FAB∆,ECAcm的最大E、F重合,得到三棱锥.当ABC△的边长变化时,所得三棱锥体积(单位:3)值为__________.37.已知底面边长为1的正四棱柱的各顶点均在同一球面上,则该球的体积为__________.38.已知S ,A ,B ,C 是球O 表面上的点,SA ⊥平面ABC ,AB BC ⊥,1SA AB ==,BC =O 的表面积等于__________.39.已知在半径为2的球面上有A 、B 、C 、D 四点,若2AB CD ==,则四面体ABCD 的体积的最大值为__________.40.已知点P A B C D 、、、、是球O 表面上的点,PA ⊥平面ABCD ,四边形ABCD 是边长为正方形.若PA =,则OAB ∆的面积为__________.41已知四面体P ABC -的外接球的球心O 在AB 上,且OP ⊥面ABC ,2AC =.若32P ABC V -=,则该球的体积为__________.。
立体几何中球的内切和外接问题(完美版)
C 1
注意:①割补法,② V多面体 3 S全 r内切球
变式训练:一个正方体内接于一个球,过球心作一截面,如 图所示,则截面的可能图形是( )
①
②
③
④
• A .①② B.②④ C.①②③ D.②③④
D A
D1 A1
C
B O
C1 B1
球的内接正方体的对角线等于球直径。
变式训练:已知正四面体内接于一个球,某人画出四 个过球心的平面截球与正四面体所得的图形如下,
的动点,当弦 MN 的长度最大时, PM • PN 的取值范围是
.
感谢阅读
• 感谢阅读
• 感谢阅读
• 感谢阅读
• 感谢阅读
2023最新整理收集 do something
球与多面体的内切、外接
球的半径r和正方体 的棱长a有什么关系?
.r
a
一、 球体的体积与表面积
①
②
二、球与多面体的接、切
定义1:若一个多面体的各顶点都在一个球的球面上,
则称这个多面体是这个球的内接多面体,
这个球多是面这体个的外接球
。
定义2:若一个多面体的各面都与一个球的球面相切,
,即 为该四面体的外接球的球心
A
O
C
所以该外接球的体积为
03
破译规律-特别提
醒
2 例题剖析-针对讲 解
04
举一反三-突破提
升
4 举一反三-突破提 升 1、(2015 海淀二模)已知斜三棱柱的三 视图如图所示,该斜三棱柱的体积为 ______.
4 举一反三-突破提 升
2、(2015 郑州三模) 正三角形ABC的2 边3 长
5 正棱锥的外接球的球心是在其 高上
空间几何体外接球与内切球问题解决方法

空间几何体的外接球与内切球问题一、有关定义1.球的定义:空间中到定点的距离等于定长的点的集合(轨迹)叫球面,简称球.2.外接球的定义:若一个多面体的各个顶点都在一个球的球面上,则称这个多面体是这个球的内接多面体,这个球是这个多面体的外接球.3.内切球的定义:若一个多面体的各面都与一个球的球面相切,则称这个多面体是这个球的外切多面体,这个球是这个多面体的内切球.二、外接球的有关知识与方法1.性质:性质1:过球心的平面截球面所得圆是大圆,大圆的半径与球的半径相等;性质2:经过小圆的直径与小圆面垂直的平面必过球心,该平面截球所得圆是大圆;性质3:过球心与小圆圆心的直线垂直于小圆所在的平面(类比:圆的垂径定理);性质4:球心在大圆面和小圆面上的射影是相应圆的圆心;性质5:在同一球中,过两相交圆的圆心垂直于相应的圆面的直线相交,交点是球心(类比:在同圆中,两相交弦的中垂线交点是圆心).2.结论:结论1:长方体的外接球的球心在体对角线的交点处,即长方体的体对角线的中点是球心;结论2:若由长方体切得的多面体的所有顶点是原长方体的顶点,则所得多面体与原长方体的外接球相同;结论3:长方体的外接球直径就是面对角线及与此面垂直的棱构成的直角三角形的外接圆圆心,换言之,就是:底面的一条对角线与一条高(棱)构成的直角三角形的外接圆是大圆;结论4:圆柱体的外接球球心在上下两底面圆的圆心连一段中点处;结论5:圆柱体轴截面矩形的外接圆是大圆,该矩形的对角线(外接圆直径)是球的直径;结论6:直棱柱的外接球与该棱柱外接圆柱体有相同的外接球;结论7:圆锥体的外接球球心在圆锥的高所在的直线上;结论8:圆锥体轴截面等腰三角形的外接圆是大圆,该三角形的外接圆直径是球的直径;结论9:侧棱相等的棱锥的外接球与该棱锥外接圆锥有相同的外接球.3.终极利器:勾股定理、正定理及余弦定理(解三角形求线段长度);三、内切球的有关知识与方法1.若球与平面相切,则切点与球心连线与切面垂直.(与直线切圆的结论有一致性).2.内切球球心到多面体各面的距离均相等,外接球球心到多面体各顶点的距离均相等.(类比:与多边形的内切圆).3.正多面体的内切球和外接球的球心重合.4.正棱锥的内切球和外接球球心都在高线上,但不一定重合.5.基本方法:(1)构造三角形利用相似比和勾股定理;(2)体积分割是求内切球半径的通用做法(等体积法).四、八大模型类型一柱体背景的模型题型1、墙角模型(三条棱两两垂直,不找球心的位置即可求出球半径)方法:找三条两两垂直的线段,直接用公式2222)2(c b a R ++=,即2222c b a R ++=,求出R 例1(1)已知各顶点都在同一球面上的正四棱柱的高为4,体积为16,则这个球的表面积是(C)A.π16B.π20C.π24D.π32解:162==h a V ,2=a ,24164442222=++=++=h a a R ,π24=S ,选C;(2)若三棱锥的三个侧面两两垂直,且侧棱长均为3,则其外接球的表面积是π9解:933342=++=R ,ππ942==R S ;(3)在正三棱锥S ABC -中,M N 、分别是棱SC BC 、的中点,且MN AM ⊥,若侧棱SA =,则正三棱锥ABC S -外接球的表面积是.π36解:引理:正三棱锥的对棱互相垂直.证明如下:如图(3)-1,取BC AB ,中点E D ,,连接CD AE ,,CD AE ,交于H ,连接SH ,则H 是底面正三角形ABC 的中心,∴⊥SH 平面ABC ,∴AB SH ⊥,BC AC =,BD AD =,∴AB CD ⊥,∴⊥AB 平面SCD ,∴SC AB ⊥,同理:SA BC ⊥,SB AC ⊥,即正三棱锥的对棱互垂直,本题图如图(3)-2, MN AM ⊥,MN SB //,∴SB AM ⊥, SB AC ⊥,∴⊥SB 平面SAC ,∴SA SB ⊥,SC SB ⊥, SA SB ⊥,SA BC ⊥,∴⊥SA 平面SBC ,∴SC SA ⊥,故三棱锥ABC S -的三棱条侧棱两两互相垂直,∴36)32()32()32()2(2222=++=R ,即3642=R ,∴正三棱锥ABC S -外接球的表面积是π36.(4)在四面体S ABC -中,ABC SA 平面⊥,,1,2,120====∠︒AB AC SA BAC 则该四面体的外接球的表面积为(D )π11.A π7.B π310.C π340.D 解:在ABC ∆中,7120cos 2222=⋅⋅-+= BC AB AB AC BC ,7=BC ,ABC ∆的外接球直径为372237sin 2==∠=BAC BC r ,∴3404)372()2()2(2222=+=+=SA r R ,340π=S ,选D (5)如果三棱锥的三个侧面两两垂直,它们的面积分别为6、4、3,那么它的外接球的表面积是解:由已知得三条侧棱两两垂直,设三条侧棱长分别为c b a ,,(+∈R c b a ,,),则⎪⎩⎪⎨⎧===6812ac bc ab ,∴24=abc ,∴3=a ,4=b ,2=c ,29)2(2222=++=c b a R ,ππ2942==R S ,(6)已知某几何体的三视图如图所示,三视图是腰长为1的等腰直角三角形和边长为1的正方形,则该几何体外接球的体积为解:3)2(2222=++=c b a R ,432=R ,23=R πππ2383334343=⋅==R V 球,题型2、对棱相等模型(补形为长方体)题设:三棱锥(即四面体)中,已知三组对棱分别相等,求外接球半径(CD AB =,BC AD =,BD AC =)第一步:画出一个长方体,标出三组互为异面直线的对棱;第二步:设出长方体的长宽高分别为c b a ,,,x BC AD ==,y CD AB ==,z BD AC ==,列方程组,⎪⎩⎪⎨⎧=+=+=+222222222za c y cb x b a ⇒2)2(2222222z y xc b a R ++=++=,补充:图2-1中,abc abc abc V BCD A 31461=⨯-=-.第三步:根据墙角模型,22222222z y x c b a R ++=++=,82222z y x R ++=,8222z y x R ++=,求出R .思考:如何求棱长为a 的正四面体体积,如何求其外接球体积?例2(1)如下图所示三棱锥A BCD -,其中5,6,7,AB CD AC BD AD BC ======则该三棱锥外接球的表面积为.解:对棱相等,补形为长方体,如图2-1,设长宽高分别为c b a ,,,110493625)(2222=++=++c b a ,55222=++c b a ,5542=R ,π55=S (2)在三棱锥BCD A -中,2==CD AB ,3==BC AD ,4==BD AC ,则三棱锥BCD A -外接球的表面积为.π229解:如图2-1,设补形为长方体,三个长度为三对面的对角线长,设长宽高分别为c b a ,,,则922=+b a ,422=+c b ,1622=+a c ∴291649)(2222=++=++c b a ,291649)(2222=++=++c b a ,229222=++c b a ,22942=R ,π229=S(3)正四面体的各条棱长都为2,则该正面体外接球的体积为解:正四面体对棱相等的模式,放入正方体中,32=R ,23=R ,ππ2383334=⋅=V (4)棱长为2的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如下图,则图中三角形(正四面体的截面)的面积是.解:如解答图,将正四面体放入正方体中,截面为1PCO ∆,面积是2.题型3、汉堡模型(直棱柱的外接球、圆柱的外接球)题设:如图3-1,图3-2,图3-3,直三棱柱内接于球(同时直棱柱也内接于圆柱,棱柱的上下底面可以是任意三角形)第一步:确定球心O 的位置,1O 是ABC ∆的外心,则⊥1OO 平面ABC ;第二步:算出小圆1O 的半径r AO =1,h AA OO 212111==(h AA =1也是圆柱的高);第三步:勾股定理:21212O O A O OA +=⇒222)2(r hR +=⇒22)2(h r R +=,解出R 例3(1)一个正六棱柱的底面上正六边形,其侧棱垂直于底面,已知该六棱柱的顶点都在同一个球面上,且该六棱柱的体积为89,底面周长为3,则这个球的体积为解:设正六边形边长为a ,正六棱柱的高为h ,底面外接圆的半径为r ,则21=a ,正六棱柱的底面积为833)21(4362=⋅⋅=S ,89833===h Sh V 柱,∴3=h ,4)3(14222=+=R 也可121()23(222=+=R ),1=R ,球的体积为34π=球V ;(2)直三棱柱111ABC A B C -的各顶点都在同一球面上,若12AB AC AA ===,120BAC ∠=︒,则此球的表面积等于.解:32=BC ,4120sin 322==r ,2=r ,5=R ,π20=S ;(3)已知EAB ∆所在的平面与矩形ABCD 所在的平面互相垂直,︒=∠===60,2,3AEB AD EB EA ,则多面体ABCD E -的外接球的表面积为.π16解:折叠型,法一:EAB ∆的外接圆半径为31=r ,11=OO ,231=+=R ;法二:231=M O ,21322==D O r ,4413432=+=R ,2=R ,π16=表S ;法三:补形为直三棱柱,可改变直三棱柱的放置方式为立式,算法可同上,略.换一种方式,通过算圆柱的轴截面的对角线长来求球的直径:162)32()2(222=+=R ,π16=表S ;(4)在直三棱柱111C B A ABC -中,4,3,6,41====AA A AC AB π,则直三棱柱111C B A ABC -的外接球的表面积为.π3160解:法一:282164236162=⋅⋅⋅-+=BC ,72=BC ,37423722==r ,372=r ,3404328)2(2122=+=+=AA r R ,π3160=表S ;法二:求圆柱的轴截面的对角线长得球直径,此略.类型二锥体背景的模型题型4、切瓜模型(两个大小圆面互相垂直且交于小圆直径——正弦定理求大圆直径是通法)1.如图4-1,平面⊥PAC 平面ABC ,且BC AB ⊥(即AC 为小圆的直径),且P 的射影是ABC ∆的外心⇔三棱锥ABC P -的三条侧棱相等⇔三棱ABC P -的底面ABC ∆在圆锥的底上,顶点P 点也是圆锥的顶点.解题步骤:第一步:确定球心O 的位置,取ABC ∆的外心1O ,则1,,O O P 三点共线;第二步:先算出小圆1O 的半径r AO =1,再算出棱锥的高h PO =1(也是圆锥的高);第三步:勾股定理:21212O O A O OA +=⇒222)(r R h R +-=,解出R ;事实上,ACP ∆的外接圆就是大圆,直接用正弦定理也可求解出R .2.如图4-2,平面⊥PAC 平面ABC ,且BC AB ⊥(即AC 为小圆的直径),且AC PA ⊥,则利用勾股定理求三棱锥的外接球半径:①222)2()2(r PA R +=⇔22)2(2r PA R +=;②2122OO r R +=⇔212OO r R +=3.如图4-3,平面⊥PAC 平面ABC ,且BC AB ⊥(即AC 为小圆的直径)21212O O C O OC +=⇔2122O O r R +=⇔2122O O R AC -=4.题设:如图4-4,平面⊥PAC 平面ABC ,且BC AB ⊥(即AC 为小圆的直径)第一步:易知球心O 必是PAC ∆的外心,即PAC ∆的外接圆是大圆,先求出小圆的直径r AC 2=;第二步:在PAC ∆中,可根据正弦定理R CcB b A a 2sin sin sin ===,求出R .例4(1)正四棱锥的顶点都在同一球面上,若该棱锥的高为1,底面边长为32,则该球的表面积为.解:法一:由正弦定理(用大圆求外接球直径);法二:找球心联合勾股定理,72=R ,ππ4942==R S ;(2)正四棱锥ABCD S -的底面边长和各侧棱长都为2,各顶点都在同一球面上,则此球体积为解:方法一:找球心的位置,易知1=r ,1=h ,r h =,故球心在正方形的中心ABCD 处,1=R ,34π=V 方法二:大圆是轴截面所的外接圆,即大圆是SAC ∆的外接圆,此处特殊,SAC Rt ∆的斜边是球半径,22=R ,1=R ,34π=V .(3)一个正三棱锥的四个顶点都在半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,则该正三棱锥的体积是()A.433B.33C.43D.123解:高1==R h ,底面外接圆的半径为1=R ,直径为22=R ,设底面边长为a ,则260sin 2==a R ,3=a ,433432==a S ,三棱锥的体积为4331==Sh V ;(4)在三棱锥ABC P -中,3===PC PB PA ,侧棱PA 与底面ABC 所成的角为 60,则该三棱锥外接球的体积为()A.πB.3π C.4πD.43π解:选D,由线面角的知识,得ABC ∆的顶点C B A ,,在以23=r 为半径的圆上,在圆锥中求解,1=R ;(5)已知三棱锥S ABC -的所有顶点都在球O 的求面上,ABC ∆是边长为1的正三角形,SC 为球O 的直径,且2SC =,则此棱锥的体积为()AA.6B.6C.3D.2解:36)33(12221=-=-=r R OO ,362=h ,62362433131=⋅⋅==Sh V 球题型5、垂面模型(一条直线垂直于一个平面)1.题设:如图5,⊥PA 平面ABC ,求外接球半径.解题步骤:第一步:将ABC ∆画在小圆面上,A 为小圆直径的一个端点,作小圆的直径AD ,连接PD ,则PD 必过球心O ;第二步:1O 为ABC ∆的外心,所以⊥1OO 平面ABC ,算出小圆1O 的半径r D O =1(三角形的外接圆直径算法:利用正弦定理,得r C c B b A a 2sin sin sin ===),PA OO 211=;第三步:利用勾股定理求三棱锥的外接球半径:①222)2()2(r PA R +=⇔22)2(2r PA R +=;②2122OO r R +=⇔212OO r R +=.2.题设:如图5-1至5-8这七个图形,P 的射影是ABC ∆的外心⇔三棱锥ABC P -的三条侧棱相等⇔三棱锥ABC P -的底面ABC ∆在圆锥的底上,顶点P 点也是圆锥的顶点.解题步骤:第一步:确定球心O 的位置,取ABC ∆的外心1O ,则1,,O O P 三点共线;第二步:先算出小圆1O 的半径r AO =1,再算出棱锥的高h PO =1(也是圆锥的高);第三步:勾股定理:21212O O A O OA +=⇒222)(r R h R +-=,解出R 方法二:小圆直径参与构造大圆,用正弦定理求大圆直径得球的直径.例5一个几何体的三视图如图所示,则该几何体外接球的表面积为()A.π3B.π2C.316πD.以上都不对解:选C,法一:(勾股定理)利用球心的位置求球半径,球心在圆锥的高线上,221)3(R R =+-,32=R ,ππ31642==R S ;法二:(大圆法求外接球直径)如图,球心在圆锥的高线上,故圆锥的轴截面三角形PMN 的外接圆是大圆,于是3460sin 22==R ,下略;类型三二面角背景的模型题型6、折叠模型题设:两个全等三角形或等腰三角形拼在一起,或菱形折叠(如图6)第一步:先画出如图6所示的图形,将BCD ∆画在小圆上,找出BCD ∆和BD A '∆的外心1H 和2H ;第二步:过1H 和2H 分别作平面BCD 和平面BD A '的垂线,两垂线的交点即为球心O ,连接OC OE ,;第三步:解1OEH ∆,算出1OH ,在1OCH Rt ∆中,勾股定理:22121OC CH OH =+注:易知21,,,H E H O 四点共面且四点共圆,证略.例6(1)三棱锥ABC P -中,平面⊥PAC 平面ABC ,△PAC 和△ABC 均为边长为2的正三角形,则三棱锥ABC P -外接球的半径为.解:如图,3460sin 22221=== r r ,3221==r r ,312=H O ,35343121222=+=+=r H O R ,315=R ;法二:312=H O ,311=H O ,1=AH ,352121222=++==O O H O AH AO R ,315=R ;(2)在直角梯形ABCD 中,CD AB //, 90=∠A ,45=∠C ,1==AD AB ,沿对角线BD 折成四面体BCD A -',使平面⊥'BD A 平面BCD ,若四面体BCD A -'的顶点在同一个球面上,则该项球的表面积为π4解:如图,易知球心在BC 的中点处,π4=表S ;(3)在四面体ABC S -中,BC AB ⊥,2==BC AB ,二面角B AC S --的余弦值为33-,则四面体ABC S -的外接球表面积为π6解:如图,法一:33)2cos(cos 211-=+∠=∠πO OO B SO ,33sin 21=∠O OO ,36cos 21=∠O OO ,22cos 21211=∠=O OO O O OO ,232112=+=R ,ππ642==R S ;法二:延长1BO 到D 使111r BO DO ==,由余弦定理得6=SB ,2=SD ,大圆直径为62==SB R ;(4)在边长为32的菱形ABCD 中,60=∠BAD ,沿对角线BD 折成二面角C BD A --为120的四面体ABCD ,则此四面体的外接球表面积为π28解:如图,取BD 的中点M ,ABD ∆和CBD ∆的外接圆半径为221==r r ,ABD ∆和CBD ∆的外心21,O O 到弦BD 的距离(弦心距)为121==d d ,法一:四边形21MO OO 的外接圆直径2=OM ,7=R ,π28=S ;法二:31=OO ,7=R ;法三:作出CBD ∆的外接圆直径CE ,则3==CM AM ,4=CE ,1=ME ,7=AE ,33=AC ,72147227167cos -=⋅⋅-+=∠AEC ,7233sin =∠AEC ,72723333sin 2==∠=AEC AC R ,7=R ;(5)在四棱锥ABCD 中,120=∠BDA ,150=∠BDC ,2==BD AD ,3=CD ,二面角C BD A --的平面角的大小为120,则此四面体的外接球的体积为解:如图,过两小圆圆心作相应小圆所在平面的垂线确定球心,32=AB ,22=r ,弦心距32=M O ,13=BC ,131=r ,弦心距321=M O ,∴2121=O O ,72120sin 21==O O OM ,法一:∴292222=+==OM MD OD R ,29=R ,∴329116π=球V ;法二:2522222=-=M O OM OO ,∴29222222=+==OO r OD R ,29=R ,∴329116π=球V .题型7、两直角三角形拼接在一起(斜边相同,也可看作矩形沿对角线折起所得三棱锥)模型题设:如图7,90=∠=∠ACB APB ,求三棱锥ABC P -外接球半径(分析:取公共的斜边的中点O ,连接OC OP ,,则AB OP OC OB OA 21====,∴O 为三棱锥ABC P -外接球球心,然后在OCP 中求出半径),当看作矩形沿对角线折起所得三棱锥时与折起成的二面角大小无关,只要不是平角球半径都为定值.例7(1)在矩形ABCD 中,4=AB ,3=BC ,沿AC 将矩形ABCD 折成一个直二面角D AC B --,则四面体ABCD 的外接球的体积为()A.π12125B.π9125C.π6125D.π3125解:(1)52==AC R ,25=R ,6125812534343πππ=⋅==R V ,选C(2)在矩形ABCD 中,2=AB ,3=BC ,沿BD 将矩形ABCD 折叠,连接AC ,所得三棱锥BCD A -的外接球的表面积为.解:BD 的中点是球心O ,132==BD R ,ππ1342==R S .类型四多面体的内切球问题模型题型8、锥体的内切球问题1.题设:如图8-1,三棱锥ABC P -上正三棱锥,求其内切球的半径.第一步:先现出内切球的截面图,H E ,分别是两个三角形的外心;第二步:求BD DH 31=,r PH PO -=,PD 是侧面ABP ∆的高;第三步:由POE ∆相似于PDH ∆,建立等式:PDPODH OE =,解出r 2.题设:如图8-2,四棱锥ABC P -是正四棱锥,求其内切球的半径第一步:先现出内切球的截面图,H O P ,,三点共线;第二步:求BC FH 21=,r PH PO -=,PF 是侧面PCD ∆的高;第三步:由POG ∆相似于PFH ∆,建立等式:PFPOHF OG =,解出3.题设:三棱锥ABC P -是任意三棱锥,求其的内切球半径方法:等体积法,即内切球球心与四个面构成的四个三棱锥的体积之和相等第一步:先画出四个表面的面积和整个锥体体积;第二步:设内切球的半径为r ,建立等式:PBC O PAC O PAB O ABC O ABC P V V V V V -----+++=⇒rS S S S r S r S r S r S V PBC PAC PAB ABC PBC PAC PAB ABC ABC P ⋅+++=⋅+⋅+⋅+⋅=∆∆∆∆-)(3131313131第三步:解出PBCO PAC O PAB O ABCO ABCP S S S S V r -----+++=3例8(1)棱长为a 的正四面体的内切球表面积是62a π,解:设正四面体内切球的半径为r ,将正四面体放入棱长为2a的正方体中(即补形为正方体),如图,则2622313133a a V V ABCP =⋅==-正方体,又 r a r a Sr V ABC P 223343314314=⋅⋅⋅=⋅=-,∴263332a r a =,62a r =,∴内切球的表面积为6422a r S ππ==表(注:还有别的方法,此略)(2)正四棱锥ABCD S -的底面边长为2,侧棱长为3,则其内切球的半径为2217+解:如图,正四棱锥ABCD S -的高7=h ,正四棱锥ABCD S -的体积为374=-ABCD S V 侧面斜高221=h ,正四棱锥ABCD S -的表面积为284+=表S ,正四棱锥ABCD S -的体积为r r S V ABCD S ⋅+==-328431表,∴3743284=⋅+r ,771427)122(7221728474-=-=+=+=r (3)三棱锥ABC P -中,底面ABC ∆是边长为2的正三角形,⊥PA 底面ABC ,2=PA ,则该三棱锥的内切球半径为47332++解:如图,3=∆ABC S ,2==∆∆ACP ABP S S ,7=∆BCP S ,743++=表S ,三棱锥ABC P -的体积为332=-ABC P V ,另一表达体积的方式是r r S V ABC P ⋅++==-347331表,∴3323473=⋅++r ,∴47332++=r巩固练习:1.若三棱锥ABC S -的三条侧棱两两垂直,且2=SA ,4==SC SB ,则该三棱锥的外接球半径为()A.3B.6C.36D.9解:【A】616164)2(2=++=R ,3=R 【三棱锥有一侧棱垂直于底面,且底面是直角三角形】【共两种】2.三棱锥ABC S -中,侧棱⊥SA 平面ABC ,底面ABC 是边长为3的正三角形,32=SA ,则该三棱锥的外接球体积等于.332π解:260sin 32== r ,16124)2(2=+=R ,42=R ,2=R ,外接球体积332834ππ=⋅【外心法(加中垂线)找球心;正弦定理求球小圆半径】3.正三棱锥ABC S -中,底面ABC 是边长为3的正三角形,侧棱长为2,则该三棱锥的外接球体积等于.解:ABC ∆外接圆的半径为,三棱锥ABC S -的直径为3460sin 22== R ,外接球半径32=R ,或1)3(22+-=R R ,32=R ,外接球体积2733233834343πππ=⋅==R V ,4.三棱锥ABC P -中,平面⊥PAC 平面ABC ,△PAC 边长为2的正三角形,BC AB ⊥,则三棱锥ABC P -外接球的半径为.解:PAC ∆的外接圆是大圆,3460sin 22== R ,32=R ,5.三棱锥ABC P -中,平面⊥PAC 平面ABC ,2=AC ,3==PC PA ,BC AB ⊥,则三棱锥ABC P -外接球的半径为.解:973324992cos 222=⋅⋅-+=⋅-+=∠PC PA AC PC PA P ,8121697(1sin 22⋅=-=∠P ,924sin =∠P ,42922992422===R ,829=R 6.三棱锥ABC P -中,平面⊥PAC 平面ABC ,2=AC ,PC PA ⊥,BC AB ⊥,则三棱锥ABCP -外接球的半径为.解:AC 是公共的斜边,AC 的中点是球心O ,球半径为1=R。
总结常见几何体的外接球和内接球问题的方法

总结常见几何体的外接球和内接球问题的方
法
几何体的外接球和内接球问题是在确定几何体的最大和最小包络体积时遇到的问题。
常见几何体的外接球和内接球问题的方法有以下几种:
1. 立方体:立方体的外接球是一个直径与边长相等的球,内接球是一个与立方体接触的球,球心在立方体的中心点上。
2. 正方体:正方体的外接球和内接球与立方体的情况相同。
3. 圆柱体:圆柱体的外接球是一个与圆柱体的高相等的球,且球心与圆柱体的中心点在同一直线上。
内接球是一个与圆柱体接触的球,且球心与圆柱体的中心点在同一直线上。
4. 圆锥体:圆锥体的外接球是一个与圆锥体的高相等的球,且球心与圆锥体的顶点重合。
内接球是一个与圆锥体接触的球,且球心与圆锥体的顶点重合。
5. 球体:球体的外接球和内接球与球本身相同。
在求解外接球和内接球问题时,可以利用几何体的对称性质进行简化。
例如,可以通过几何体的中心点、顶点、侧面的中点等来确定外接球和内接球的位置。
对于特殊形状的几何体,也可以通过计算几何体上的点到球心的距离来确定外接球和内接球的半径。
立体几何外接圆球及内切圆球问题

立体几何外接圆球及内切圆球问题
立体几何是研究三维空间中的图形和体积的学科。
外接圆球和内切圆球问题是立体几何中常见的一个问题。
外接圆球问题
在立体几何中,外接圆球是指一个球能够刚好与一个多面体的所有顶点相切。
对于不规则多面体来说,外接圆球可能无法通过所有的顶点,但可以通过一部分顶点。
外接圆球的半径通常被称为外接球的半径,是从多面体的中心到多面体顶点的最远距离。
要计算外接球的半径,可以使用多面体的顶点坐标来求得多面体的边长和中心点的坐标,然后使用勾股定理来计算半径的长度。
内切圆球问题
内切圆球是指一个球刚好能够与多面体的所有面相切。
与外接
圆球问题类似,对于不规则多面体来说,内切圆球可能无法与所有
的面相切,但可以与一部分面相切。
内切圆球的半径通常被称为内切球的半径,是从多面体的中心
点到多面体的面的最短距离。
要计算内切球的半径,可以使用多面
体的面的法向量和距离公式来求得。
应用和意义
外接圆球和内切圆球问题在立体几何中具有重要的应用和意义。
它们可以用来解决很多实际问题,如计算多面体的体积、表面积,
以及优化多面体的设计。
外接圆球和内切圆球问题也被广泛应用于计算机图形学和计算
机辅助设计领域。
在三维建模和渲染中,可以使用外接圆球和内切
圆球来估计或近似多面体的几何特征,以便更高效地处理和渲染三
维模型。
结论
立体几何中的外接圆球和内切圆球问题是一个有趣且实用的领域。
通过计算外接球和内切球的半径,可以获得关于多面体的重要信息,并应用于多个领域,包括工程设计和计算机图形学。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
简单几何体的外接球与内切球问题
简单几何体的外接球与内切球问题
定义1:若一个多面体的各顶点都在一个球的球面上,则称这个多面体是这个球的内接多面体,这个球是这个多面体的外接球。
定义2:若一个多面体的各面都与一个球的球面相切, 则称这个多面体是这个球的外切多面体,这个球是这个多面体的内切球。
1、内切球球心到多面体各面的距离均相等,外接球球心到多面体各顶点的距离均相等。
2、正多面体的内切球和外接球的球心重合。
3、正棱锥的内切球和外接球球心都在高线上,但不重合。
4、基本方法:构造三角形利用相似比和勾股定理。
5、体积分割是求内切球半径的通用做法。
一、 直棱柱的外接球 1、
长方体的外接球:
长方体中从一个顶点出发的三条棱长分别为c b a ,,,则体对角线长为222c b a l ++=,几何体的外接球直径R 2为体对
角线长l 即2
2
22c b a R ++=
2、 正方体的外接球:
正方体的棱长为a ,则正方体的体对角线为a 3,其外接球的直径R 2为a 3。
3、
其它直棱柱的外接球:
方法:找出直棱柱的外接圆柱,圆柱的外接球就是所求直棱柱的外接球。
例1、一个六棱柱的底面是正六边形,其侧棱垂直于底面,已知该六棱柱的顶点都在同一个球面上,且该六棱柱的体积为98
,底面周长为3,则这个球的体积为 .
例2、已知各顶点都在同一个球面上的正四棱柱的高为4,体积为16,则这个球的表面积是
A.16π
B.20π
C.24π
D.32π 二、 棱锥的外接球 1、
正棱锥的外接球
方法:球心在正棱锥的高线上,根据球心到各个顶点的距离是球半径,列出关于半径的方程。
例3、正四棱锥S ABCD -2,点S A B C D 、、、、都在同一球面上,则此球的体积
为 .
例5、若正四面体的棱长为4,则正四面体的外接球的表面积为___________。
例6、一个正三棱锥的四个顶点都在半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,则该正三棱锥的体积是:( ) (A )4
33 (B)
3
3
(C)
4
3 (D)
12
3
2、
补体方法的应用
(1)、正四面体(2)、三条侧棱两两垂直的三棱锥 (3)、四个面均为直角三角形的三棱锥
例7、如果三棱锥的三个侧面两两垂直,它们的面积分别为62cm 、42cm 和32cm ,那么它的外接球的体积是 。
例9、在三棱锥BCD A -中,BC CD BCD AB ⊥⊥,平面,543===CD BC AB ,, 则三棱锥BCD A -外接球的表面积__________。
例10、如图为一个几何体的三视图,则该几何体的外接球的表面积为( )
A. 4π
B. 8π
C. 12π
D. 16π
三、圆柱、圆锥的外接球
旋转体的外接球,可以通过研究轴截面求球的半径。
例11、圆柱的底面半径为4,母线为8,求该圆柱的外接球的半径。
例12、圆锥的底面半径为2,母线长为4,求该圆锥的外接球的半径。
四、正方体的内切球
设正方体的棱长为a ,求(1)内切球半径;(2)与棱相切的球半径。
(1)截面图为正方形EFGH 的内切圆,得2
a R =
;(2)与正方体各棱相切的球:球与正方体的各棱相切,切点为各棱的中点,作截面图,圆
O 为正方形EFGH 的外接圆,易得a R 2
2
=。
五、 棱锥的内切球(分割法)
将内切球的球心与棱锥的各个顶点连线,将棱锥分割成以原棱锥的面为底面,内切球的半径为高的小棱锥,根据分割前后的体积相等,列出关于半径R 的方程。
若棱锥的体积为V ,表面积为S ,则内切球的半径为S
V R 3=. 例17、正四棱锥S ABCD -,底面边长为2,侧棱长为3,则内切球的半径是多少?
图1
图2
例18、三棱锥P ABC -中,底面ABC ∆是边长为2的正三角形, PA ⊥底面ABC ,且2PA =,则此三棱锥内切球的半径为( )
六、 圆柱(轴截面为正方形)、圆锥的内切球(截面法)
例19、圆锥的高为4,底面半径为2,求该圆锥内切球与外接球的半径比。
例20、圆柱的底面直径和高都是6,求该圆柱内切球的半径。
巩固训练:
1、一个正三棱柱恰好有一个内切球(球与三棱柱的两个底面和三个侧面都相切)和一个外接球(球经过三棱柱的6个顶点),则此内切球与外接球表面积之比为 。
2、如图,半径为2的半球内有一内接正六棱锥P ABCDEF -,则此正六棱锥的侧面积是
________.
3、棱长为2的正四面体的四个顶点都在同一个 球面上,若过该球球心的一个截面如图,则图中 三角形(正四面体的截面)的面积是 .
A B C P
D
E
F
4、已知三棱锥S ABC -的所有顶点都在球O 的球面上,
ABC ∆是边长为1的正三角形,SC 为球O 的直径,且2SC =;则此棱锥的体积为 ( )
A .
26
B .
36
C .
23
D .
22
5、已知点P,A,B,C,D 是球O 表面上的点,PA ⊥平面ABCD,四边形ABCD 是边长为3.若6,则△OAB 的
面积为______________.。
