人教版八年级数学上册 第十一章 三角形 单元测试题含参考答案
人教版八年级数学上册第十一章三角形单元测试卷-(含答案)

人教版八年级数学上册第十一章三角形单元测试卷一、单选题(共30分,每小题3分)1.能用三角形的稳定性解释的生活现象是()A.B.C.D.2.如图,BE、CF都是ABC的角平分线,且115BDC∠=︒,则A∠=()A.45°B.50°C.65°D.70°3.如果一个多边形的每一个外角都是90︒,那么这个多边形的内角和是()A.180︒B.360︒C.540︒D.720︒4.若一个多边形的每个内角都等于150°,则这个多边形的边数是()A.10B.11C.12D.135.一个多边形截去一个角后,得到的多边形的内角和为1980,那么原来的多边形的边数为().A.12或13取14B.13或14C.12或13D.13或14或15 6.下列命题正确的是()A.三角形的角平分线、中线、高均在三角形内部B.三角形中至少有一个内角不小于60︒C.直角三角形仅有一条高D .直角三角形斜边上的高等于斜边的一半7.下列各组线段,能构成三角形的是( )A .1,3,5cm cm cmB .2,4,6cm cm cmC .4,4,1cm cm cmD .8,8,20cm cm cm8.在三角形的①三条中线;①三条角平分线;①三条高中,一定相交于一点的是( )A .①①①B .①C .①D .①① 9.如图,在①ABC 中,D 是BC 延长线上一点,①B =40°,①ACD =120°,则①A 等于A .60°B .70°C .80°D .90° 10.如图在△ABC 中,BO ,CO 分别平分①ABC ,①ACB ,交于O ,CE 为外角①ACD 的平分线,BO 的延长线交CE 于点E ,记①BAC =①1,①BEC =①2,则以下结论①①1=2①2,①①BOC =3①2,①①BOC =90°+①1,①①BOC =90°+①2正确的是( )A .①①①B .①①①C .①①D .①①①二、填空题(共24分,每小题3分) 11.若一个多边形的内角和是 1980°,则这个多边形的边数为________. 12.等腰三角形一边长为5,另一边长为7,则周长为__________.13.如图,①BCD =145°,则①A +①B +①D 的度数为_____.14.一个多边形的每一个外角都等于60°,则这个多边形的内角和为_____度. 15.如果一个多边形的内角和为1260°,那么从这个多边形的一个顶点可以连___________条对角线.16.小华从点A 出发向前走10m ,向右转36︒然后继续向前走10m ,再向右转36︒,他以样的方法继续走下去,当他走回到点A 时共走_________米.17.如图,在①ABC 中,①CAD =①CDA ,①CAB −①ABC =30°,则①BAD =________︒.18.如图,在ABC 中,12∠=∠,34∠=∠,80A ∠=︒,则x =______.三、解答题(共66分) 19.如图,ABCD 是四根木条钉成的四边形,为了使它不变形,小明加了根木条AE ,小明的做法正确吗?说说你的理由.(共6分)20.如图①A =20°,①B =45°,①C =40°,求①DFE 的度数.(共6分)21.已知,如图,在ABC ∆中,AD 、AE 分别是ABC ∆的高和角平分线,若30ABC ∠=,60ACB ∠=(共8分)(1)求DAE ∠的度数;(2)写出DAE ∠与C B ∠-∠的数量关系 ,并证明你的结论22.若一个多边形的内角和比外角和多540°,求这个多边形的边数.(共8分)23.如图:(共8分)(1)画出△ABC 的BC 边上的高线AD ;(2)画出△ABC 的角平分线CE .24.已知在△ABC 中,∠A :∠B :∠C =2:3:4,CD 是∠ACB 平分线,求∠A 和∠CDB 的度数.(共10分)25.如图,已知:点P 是ABC ∆内一点.(共10分)(1)求证:BPC A ∠>∠;(2)若PB 平分ABC ∠,PC 平分ACB ∠,40A ︒∠=,求P ∠的度数.26.如图,五边形ABCDE的内角都相等,且AB=BC,AC=AD,求①CAD的度数.(共10分)答案第1页,共1页 参考答案:1.C2.B3.B4.C5.A6.B7.C8.D9.C10.C 11.1312.17或1913.145°14.72015.616.10017.1518.13020.小明的做法正确,21.105°22.(1)15°;(2)()12DAE C B ∠=∠-∠, 23.724.略25.∠A =40°,∠CDB =80°.26.(1)略;(2)110°27.①CAD =36°.。
八年级数学上册《第十一章 三角形》单元测试卷及答案(人教版)

八年级数学上册《第十一章三角形》单元测试卷及答案(人教版)学校:___________班级:___________姓名:___________考号:___________一、选择题1.下列长度的三条线段能组成三角形的是()A.3,3,7 B.3,4,8 C.5,6,11 D.5,6,102.如图,一扇窗户打开后,用窗钩BC可将其固定,这里所运用的数学原理是()A.三角形具有稳定性B.两点确定一条直线C.两点之间线段最短D.三角形的两边之和大于第三边3.一个正多边形,它的每一个内角都等于140°,则该正多边形是()A.正六边形B.正七边形C.正八边形D.正九边形4.把一块直角三角板和一把直尺如图放置,若∠1=35°,则∠2的度数等于()A.65°B.55°C.45°D.60°5.如图,AD是△ABC的边BC上的高,若BC=3,AB=6,AD=4则AB边上的高为()A.1 B.2 C.3 D.无法计算6.如图1是我国古建筑墙上采用的八角形空窗,其轮廓是一个正八边形,窗外之境如同镶嵌于一个画框之中.如图2是八角形空窗的示意图,它的一个外角∠1=()A.45°B.60°C.110°D.135°7.如图,在△ABC中,点I到△ABC的三边距离相等,连接AI、BI,若∠ACB=70∘,则∠AIB的大小为()A.160∘B.140∘C.130∘D.125∘8.如图AB∥CD,点E在线段BC上(不与点B,C重合),连接DE,若∠D=40°,∠BED=60°则∠B=()A.10°B.20°C.40°D.60°二、填空题9.一个不等边三角形的两边分别为5cm和7cm,第三边的长度为奇数,则满足条件的三角形共有个.10.正十边形的每个内角是度.11.如图,在△ABC中,AD是BC边上的中线,若S△ABC=12,AC=3则点D到AC的距离为.12.如图,在△ABC中,点O是△ABC角平分线的交点,若∠A=70°,∠BOC=.13.如图,在△ABC中AB=AC,点D、E分别在边BC、AB上AD=DE,如果∠CAD=60°,∠BDE=15°那么∠C=°.14.如图,AB//CD,∠BED=110°,BF平分∠ABE,DF平分∠CDE,则∠BFD=.三、解答题15.AD、BE为△ABC的高,AD、BE相交于H点∠C=50°,求∠BHD.16.如图,△ABC中∠ACB=90°,CD为AB边上的高,BE平分∠ABC,且分别交CD,AC于点F,E求证:CE=CF.17.如图,在△ABC中,BD是∠ABC的平分线,CE是AB边上的高,且∠ACB=60°,∠ADB=100°,求∠A和∠ACE的度数.18.如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E,点F为AC延长线上的一点,连接DF.(1)求∠CBE的度数;(2)若∠F=25°,求证:BE∥DF.19.(本题满分10分)如图AC∥EF,∠1+∠3=180°.(1)求证AF∥CD;(2)若AC平分∠FAB,AC⊥EB于点C,∠4=78°求∠BCD的度数.参考答案1.D2.A3.D4.B5.B6.A7.D8.B9.510.14411.412.125°13.3514.125°15.解:∵AD是△ABC的高∴∠BHD+∠HBD=90°∵BE是△ABC的高∴∠HBD+∠C=90°∴∠BHD=∠C∵∠C=50°∴∠BHD=50°.16.证明:∵∠ACB=90°∴∠ACD+∠BCD=90°∵CD为AB边上的高∴∠ADC=90°∴∠A+∠ACD=90°∴∠A=∠BCD∵BE是∠ABC的平分线∴∠ABE=∠CBE∴∠CFE=∠BCD+∠CBE=∠A+∠ABE∵∠CEF=∠A+∠ABE∴∠CEF=∠CFE∴CE=CF.17.解:∵∠ADB=∠DBC+∠ACB∴∠DBC=∠ADB﹣∠ACB=100°﹣60°=40°.∵BD是角平分线∴∠ABC=80°∴∠A=180°﹣∠ABC﹣∠ACB=40°;∵CE是高∴∠AEC=90°∴∠ACE=90°﹣∠A=50°18.(1)解:∵∠ACB=90°,∠A=40°∴∠CBD=∠A+∠ACB=130°∵BE平分∠CBD∠CBD=65°∴∠CBE=12(2)证明:∵∠ACB=90°∴∠BCE=90°∵∠CBE=65°∴∠BEC=90°-65°=25°∵∠F=25°∴∠F=∠BEC∴BE∥DF19.(1)证明:∵AC∥EF∴∠1+∠2=180°.又∵∠1+∠3=180°∴∠2=∠3.∴AF∥CD.(2)解:∵AC平分∠FAB∴∠2=∠CAD.∵∠2=∠3∴∠CAD=∠3.∵∠4+∠ADC=180°且∠4=78°∴∠ADC=180°−78°=102°.∴∠CAD=∠3=180°−102°2=39°∵AC⊥EB ∴∠ACB=90°.∴∠BCD=90°−∠3=90°−39°=51°.。
人教版数学八年级上第11章三角形全章测试含答案

第11章 三角形 全章测试一、选择题(每题3分,共30分)1. 以下列各组长度的线段为边,能构成三角形的是 ( )A .7,3,4B .5,6,12C .3,4,5D .1,2,3 2. 等腰三角形的一个外角是80°,则其底角是( )A .100°B .100°或40°C .40°D .80 3.一个多边形的每一个外角都等于40°,那么这个多边形的内角和为( )A .1260°B .1080°C .1620°D .360°4.用一批完全相同的多边形地砖铺地面,不能进行镶嵌的是( ) A.正三角形 B.正方形 C.正六边形 D.正八边形5.下列说法正确的是( )A.三角形的角平分线、中线及高都在三角形内B.直角三角形的高只有一条.C.三角形至少有一条高在形内D.钝角三角形的三条高都在形外. 6.一个多边形的内角和比它的外角的和的2倍还大180°,这个多边形的边数是( ) A .5 B .6 C .7 D .8 7.在下图中,正确画出AC 边上高的是( ).EBAC C A BCA BCA BE EE(A ) (B ) (C ) (D ) 8.如图所示,∠A 、∠1、∠2的大小关系是( ) A. ∠A >∠1>∠2 B. ∠2>∠1>∠A C. ∠A >∠2>∠1 D. ∠2>∠A >∠19. 给出下列命题:⑴三角形的一个外角一定大于它的一个内角.⑵若一个三角形的三个内角之比为1:3:4,它肯定是直角三角形 ⑶三角形的最小内角不能大于60°⑷三角形的一个外角等于和它不相邻的两个内角的和 其中真命题的个数是 ( )(A )1个 (B )2个 (C )3个 (D )4个10.如图1,把△ABC 纸片沿DE 折叠,当点A 落在四边形BCDE 内部时,则∠A 与∠1+∠2之间有一种数量关系始终保持不变.请试着找一找这个规律,你发现的规律是( )A .∠A=∠1+∠2B .2∠A=∠1+∠2C .3∠A=2∠1+∠2D .3∠A=2(∠1+∠2)E DA CB二、填空题(每题3分,共30分)11.为了使一扇旧木门不变形,木工师傅在木门的背面加钉了一根木条,这样做的道理是 . 12.已知等腰三角形的两边长是5cm 和11cm ,则它的周长是 _______13.一个等腰三角形的周长为18,已知一边长为5,则其他两边长为 ____________. 14.已知一个三角形的三条边长为2、7、x ,则x 的取值范围是 _______. 15.如图所示,AB∥CD,∠ABE=66°,∠D=54°,则∠E 的度数为 . 16.如图,∠A +∠B +∠C +∠D +∠E +∠F= .17.在△ABC 中,在△ABC 中,∠A-∠B=∠B-∠C =15°则∠A 、∠B 、∠C 分别为 .18.如图,在△ABC 中,两条角平分线BD 和CE 相交于点O ,若∠BOC=116°,那么∠A 的度数是_______。
(完整)新人教版八年级数学上册第十一章三角形单元测试题含答案,推荐文档

初中数学八(上)学习过程评价题 班级: 内容:第11章三角形 姓名: 得分: 一、选择题(30分). 1. 从五边形的一个顶点出发的对角线,把这个五边形分成 A.5B.4C.3 2. 以下列各组线段长为边能组成三角形的是 (). A.lcm , 2cm, 4cm B.2cm , 4cm, 6cm C.4cm ,个三角形. D.24. 一个三角形的三条角平分线的交点在 (). A.三角形内 B.三角形外 C. 三角形的某边上5. 某人到瓷砖商店去买一种多边形形状的瓷砖用来铺设无缝地板, 是()• A.正三角形 B.矩形 C.正六边形6. 能把一个任意三角形分成面积相等的两部分的是 ( A.角平分线 B.中线 C.高 D.以上二种情形都有可能 他购买的瓷砖形状不可以 D. 正八边形 ). D.A7. 一个角的两边与另一个角的两边互相垂直,且这两个角之差为为(). A.70。
和 110° B.80 。
和 120° C.40 。
和 140° 8. 一个三角形三个内角的度数之比为 2:3:7,这个三角形一 A .直角三角形B.等腰三角形 C •锐角三角形 9. ( n+1)边形的内角和比 n 边形的内角和大(). A.180 ° B.360 °C.n • 180° 40 B 、C 都可以,那么这两个角分别 D.100 定是(). D .钝角三角形 和 140°D.n • 360°10.如图,把△ ABC 纸片沿DE 折叠,当点A 落在四边形BCDE 内部时,则/ A 与/ 1 + Z 2之间 有一种数量关系始终保持不变,试着找一找这个规律 .你发现的规律是().C. / A=2 (/ 1 + Z 2)D. 第11题图二、填空题. 11.木工师傅做完房门后,为防止变形,会在门上钉上一条斜拉的木条 是 (每题2分,共16 分)12. 某一个三角形的外角中有一个角是锐角,那么这个三角形是 ____________ 角三角形•13. 一个多边形的内角和是外角和的一半,则它的边数是—14. 如图所示:(1 )在厶ABC中,BC边上的高是_______ ;(2)在厶AEC中,AE边上的高是.15. 如图,正方形ABCD中,截去/ B、/ D后,/ 1、/ 2、/ 3、/ 4的和为16. 若一个等腰三角形的两边长分别是 3 cm和5 cm,则它的周长是cm~17. 三角形的三边长分别为5, 1+2x , 8,则x的取值范围是 ___________ .18. 一个四边形的四个内角中最多有 ________ 个钝角,最多有______ 个锐角?三、解答题(2X 4/=8/).19. 一个多边形的内角和等于它的外角和的6倍,这是一个几边形.20. 已知三角形的两个外角分别是久° , 3°,且满足(a—50)2=—|a +^—200|.求此三角形各角的度数.四、解答题(3X 5/=15/).21. △ ABC中,/ ABC / ACB的平分线相交于点0.(1)若/ ABC = 40 °,/ ACB = 50 °,则/ BOC = __________(2)若/ ABC +/ ACB =116°,则/ BOC = _________ .(3)_______________________________ 若/ A = 76 °,则/ BOC = .(4)_______________________________ 若/ BOC = 120°,则/ A = .22.如图的四边形是某地板厂加工地板时剩下的边角余料嵌吗?请说明理由.,用这种四边形的木板可以进行镶(5)你能找出/ A与/ BOC之间的数量关系吗?23. 已知等腰三角形中,AB= AC, —腰上的中线BD把这个三角形的周长分成15cm和6cm两部分,求这个等腰三角形的底边的长.四、解答题(3X 7/=21/).24. 如图,已知△ ABC D在BC的延长线上,E在CA的延长线上, F在AB上,试比较/ 1与/ 2的大小.25. 已知:如图,AC和BD相交于点0,说明:AC+BD>AB+CD.现测得/ A=145°, / B=75°, / C=85°Z D=55°,就断定这块模板是合格26.如图,它是一个大型模板,设计要求BA与CD相交成20°角, DA与CB相交成40°角, 的,这是为什么?五、解答题((3X 10/=30/)).27. 如图,四边形ABCD中,/ A=Z C= 90°, BE、DF分别是/ B/ D的平分线.(1)/ 1与/ 2大小有何关系,为什么?( 2) BE与DF有何关系?请说明理由C28. 如图1, / ACD>^ ABC的外角,BE平分/ ABC CE平分/ ACD且BE、CE交于点E.求证:⑴/ E= j / A;2(2)若BE、CE是厶ABC两外角的平分线且交于点E,则/ E与/ A又有什么关系?并说明理由29. 如图,/ ECM 90° ,线段AB的端点分别在CE和CF上,BD平分/ CBA并与/ CAB的外角平分线AG所在的直线交于一点 D. (1)Z D与/ C有怎样的数量关系?(2)点A在射线CE上运动(不与点C重合)时,其它条件不变,(1)中结论还成立吗?说说你的理由.参考答案1C ; 2.C ; 3.C ; 4.A ; 5.D ; 6.B ; 7.A ; 8.D ; 9.A ; 10.A ; 11.三角形具有稳定性; 12.钝;13.3 ; 14.AB 、CD 15.540 ° ; 16.11 或 13; 17.1 V x V 6; 18.3、3;22.能进行镶嵌;理由:由镶嵌的条件知,在一个顶点处各个内角的和为 360 °时,就能镶嵌.而任意四边形的内角和是 360 °,只要放在同一顶点的 4个内角和为360 ° 故能进行镶嵌. 23.如图,根据题意得: AB=AC, AD=CD, 设 BC=xcm, AD=CD=ycm 则 AB=AC=2ycm,①若 AB+AD=15cm, BC+CD=6cm 则 2y y 15x y 6解得:x 1 5 y即 AB=AC=10cm, BC=1cm ;②若 AB+AD=6cm , BC+CD=15cm2y 6 则x y 15解得:x 13y 2即 AB=AC=4cm, BC=13cm,19.14;20.13030°、 20°21. /OBC )••• 4+4=8V 13,不能组成三角形,舍去;•••这个等腰三角形的底边的长为1cm.24.根据三角形的外角性质,在△ AEF中,/ BAC >/ 1, 在厶ABC 中,/ 2>Z BAC ,所以,/ 2>Z 1.25.证明:••• AO+BO > AB , DO+CO > CD ,•AO+BO+DO+CO > AB+ CD ,即AC+BD > AB+ CD .26. 解:延长DA、CB,相交于F,•••/ C+Z ADC=85° +55°=140°,•••/ F=180° -140 ° =40 ° ;延长BA、CD相交于E,•/Z C+Z ABC=85° +75°=160°,•Z E=180° -160 °=20 °,故合格.27.(1 )Z 1+ Z 2=90°;•/ BE , DF分别是Z ABC , Z ADC的平分线, • Z 1 = Z ABE , Z 2=Z ADF ,/Z A= Z C=9C° ,• Z ABC+ Z ADC=180 ,••• 2 (/ 1+ / 2) =180° , • BE // DF .28. (1)证明:•••/ ACD= Z A+ /ABC ,1 •••Z2= — (/A+ /ABC )2•••左+ 72= 1 (/A+ ZABC )2•••左+ 1 (/A+ ZACB ) + 1 (/A+ /ABC ) =180。
八年级数学上册《第十一章 三角形》单元测试卷及答案-人教版
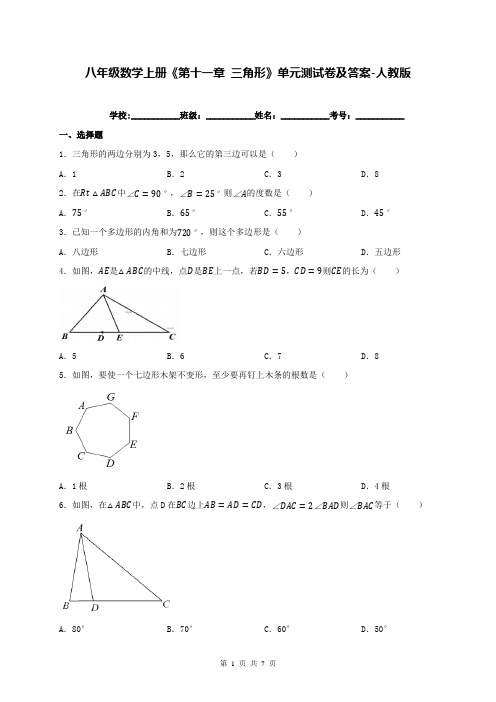
八年级数学上册《第十一章三角形》单元测试卷及答案-人教版学校:___________班级:___________姓名:___________考号:___________一、选择题1.三角形的两边分别为3,5,那么它的第三边可以是()A.1 B.2 C.3 D.82.在Rt△ABC中∠C=90°,∠B=25°则∠A的度数是()A.75°B.65°C.55°D.45°3.已知一个多边形的内角和为720°,则这个多边形是()A.八边形B.七边形C.六边形D.五边形4.如图,AE是△ABC的中线,点D是BE上一点,若BD=5,CD=9则CE的长为()A.5 B.6 C.7 D.85.如图,要使一个七边形木架不变形,至少要再钉上木条的根数是()A.1根B.2根C.3根D.4根6.如图,在△ABC中,点D在BC边上AB=AD=CD,∠DAC=2∠BAD则∠BAC等于()A.80°B.70°C.60°D.50°7.如图,直线a∥b,∠1=85°,∠2=45°则∠3的度数是()A.75°B.40°C.35°D.50°8.如图D、E分别是BC、AC的中点SΔCDE=2,则△ABC的面积为()A.4 B.8 C.10 D.12二、填空题9.一个三角形的两边长分别是3和7,则它的第三边的长为x,则x的范围为.10.如图,已知∠B=20°,∠C=35°,∠D=165°,则∠A的度数为°.11.根据如图所表示的已知角的度数,求出其中∠α的度数为.12.如图,△ABC的三条中线AD,BE,CF交于点O,若△ABC的面积为20,那么阴影部分的面积之和为.13.如图,在△ABC中AB⊥AC,∠C=55°点E为BA延长线上一点,点F为BC边上一点,若∠E=30°,则∠CFE的度数为.三、解答题14.如图∠B=30°,∠CAD=65°,AD平分∠CAE,求∠ACD的度数.15.如图,在△ABC中,AD平分∠BAC交BC于D,DE⊥AC于E,∠B=54°,∠C=40°求∠ADE 的度数.16.如图,AD是△ABC的角平分线,CE是△ABC的高∠BAC=50°,∠BCE=25°求∠ADB的度数.17.在△ABC中AB=8,AC=1.(1)若BC是整数,求BC的长.(2)已知AD是△ABC的中线,若△ACD的周长为10,求三角形ABD的周长.18.如图,在四边形ABCD中AB//CD,点E、F分别在AD、BC边上,连接AC交EF于G,∠1=∠BAC.(1)求证:EF//CD;(2)若∠CAF=15°,∠2=45°,∠3=20°求∠B和∠ACD的度数.参考答案1.C2.B3.C4.C5.D6.C7.B8.B9.4<x<1010.11011.50°12.1013.65°14.解:∵∠CAD=65°,AD平分∠CAE∴∠EAC=2∠CAD=2×65°=130°∴∠BAC=180°−∠EAC=180°−130°=50°∵∠B=30°∴∠ACD=∠B+∠CAB=30°+50°=80°.15.解:∵∠B=54°∴∠BAC=180°−∠B−∠C=86° .∵AD平分∠BAC∠BAC=43° .∴∠DAE=12∵DE⊥AC∴∠AED=90°∴∠ADE=180°−∠DAE−∠AED=47°.16.解:∵AD是△ABC的角平分线,∠BAC=50°∴∠BAD=25°又∵CE是△ABC的高∠BCE=25°∴∠BEC=90°∴∠B=65°∴∠ADB=180°-∠B-∠BAD=180°-65°-25°=90°.17.(1)解:由三角形三边关系可得,在△ABC中AB=8,AC=1则AB−AC<BC<AB+AC即7<BC<9又∵BC是整数∴BC=8(2)解:∵AD是△ABC的中线∴BD=CD由△ACD的周长为10可得AC+CD+AD=10,则CD+AD=10−AC=9三角形ABD的周长=AB+BD+AD=8+9=1718.(1)证明:如下图∵∠1=∠BAC∴AB∥EF又∵AB∥CD∴EF∥CD.(2)解:由(1)可知:AB∥EF∴∠B+∠BFE=180°∵∠BFE=∠2+∠3,∠2=45°,∠3=20°∴∠BFE=65°∴∠B=115°又∵∠1是△AGF的外角,∠CAF=15°∴∠1=∠3+∠GAF=35°∵EF∥CD∴∠ACD=∠1=35°.。
人教版八年级数学第十一章《三角形》单元测试题(含答案)

人教版八年级数学第十一章《三角形》单元测试题(含答案)时间:120分钟满分:120分一、选择题(共10小题,满分30分,每小题3分)1.(3分)若一个多边形的一个内角为144°,则这个图形为正()边形.A.十一B.十C.九D.八2.(3分)下列长度的三条线段中,能组成三角形的是()A.1cm,2cm,3cm B.2cm,3cm,4cmC.4cm,6cm,10cm D.5cm,8cm,14cm3.(3分)某三角形的三边长分别为3,6,x,则x可能是()A.3B.9C.6D.104.(3分)有下列两种图示均表示三角形分类,则正确的是()A.①对,②不对B.②对,①不对C.①、②都不对D.①、②都对5.(3分)一个正六边形的内角和的度数为()A.1080°B.720°C.540°D.360°6.(3分)如图,为估计池塘岸边A、B两点的距离,小明在池塘的一侧选取一点O,测得OA=10米,OB=8米,A、B间的距离不可能是()A.12米B.10米C.20米D.8米7.(3分)如图,窗户打开后,用窗钩AB可将其固定,其所运用的几何原理是()A.两点之间,线段最短B.两点确定一条直线C.垂线段最短D.三角形具有稳定性8.(3分)在△ABC中,且满足∠A+∠B=90°,则△ABC一定是()A.锐角三角形B.直角三角形C.钝角三角形D.不能确定9.(3分)若一个正多边形的每一个外角都等于36°,则它是()A.正九边形B.正十边形C.正十一边形D.正十二边形10.(3分)如图,∠1=40°,则∠C的度数为()A.30°B.40°C.50°D.60°二、填空题(共5小题,满分15分,每小题3分)11.(3分)如图,BD是△ABC的中线,AB=8,BC=5,△ABD和△BCD的周长的差是.12.(3分)在△ABC中,AC=3,BC=4,若∠C是锐角,那么AB长的取值范围是.13.(3分)在一个各内角都相等的多边形中,每一个内角都比相邻外角的3倍还大20°,则这个多边形的内角和为.14.(3分)如图,△ABC中,∠B=40°,∠C=30°,点D为边BC上一点,将△ADC沿直线AD折叠后,点C落到点E处,若∠BAE=50°,则∠DAC的度数为°.15.(3分)如图所示,在△ABC中,∠A=60°,∠B=40°,DE∥BC,则∠AED的度数是.三、解答题(共10小题,满分75分)16.(7分)已知a,b,c是△ABC的三边,a=4,b=6,若三角形的周长是小于18的偶数.(1)求c边的长;(2)判断△ABC的形状.17.(7分)若a、b、c是△ABC的三边,化简:|a﹣b+c|﹣|c﹣a﹣b|+|a+b+c|.18.(7分)如图,五边形ABCDE的每个内角都相等,已知EF⊥BC,求证:EF平分∠AED.19.(7分)如图,四边形ABCD中,AB⊥AC.(1)若AB∥CD,且∠D=60°,求∠1的度数;(2)若∠1+∠B=90°,求证:AD∥BC.20.(7分)如图,∠ABE是四边形ABCD的外角,已知∠ABE=∠D.求证:∠A+∠C=180°.21.(7分)如图,在四边形ABCD中,BE平分∠ABC,交AD于点G,交CD的延长线于点E,F为DC延长线上一点,∠ADE+∠BCF=180°.(1)求证:AD∥BC;(2)若∠DGE=30°,求∠A的度数.22.(7分)如图,在△ABC中,∠B=30°,∠C=65°,AE⊥BC于E,AD平分∠BAC,(1)求∠DAE的度数;(2)如图②,若把“AE⊥BC”变成“点F在DA的延长线上,FE⊥BC”,其它条件不变,求∠DFE的度数.23.(8分)已知:如图,点D、E、F、G都在△ABC的边上,EF∥AC,且∠1+∠2=180°.(1)求证:AE∥DG;(2)若EF平分∠AEB,∠C=35°,求∠BDG的度数.24.(9分)如图,在△ABC中,∠CAE=18°,∠C=42°,∠CBD=27°.(1)求∠AFB的度数;(2)若∠BAF=2∠ABF,求∠BAF的度数.25.(9分)如图,在△ABC中,CD平分∠ACB,AE⊥CD,垂足为F,交BC于点E,若∠BAE=33°,∠B=37°,求∠EAC的度数.参考答案一、选择题(共10小题,满分30分,每小题3分)1.B;2.B;3.C;4.B;5.B;6.C;7.D;8.B;9.B;10.C;二、填空题(共5小题,满分15分,每小题3分)11.3;12.1<AB<5;13.1260°;14.30;15.80°;三、解答题(共10小题,满分75分)16.解:(1)∵a,b,c是△ABC的三边,a=4,b=6,∴2<c<10,∵三角形的周长是小于18的偶数,∴2<c<8,∴c=4或6;(2)当c=4或6时,△ABC的形状都是等腰三角形.17.解:∵a、b、c是△ABC的三边,∴a﹣b+c>0,c﹣a﹣b<0,a+b+c>0,∴原式=a﹣b+c+c﹣a﹣b+a+b+c=a﹣b+3c.18.证明:∵五边形内角和为(5﹣2)×180°=540°且五边形ABCDE的5个内角都相等,∴.∵EF⊥BC,∴∠3=90°.又∵四边形的内角和为360°,∴在四边形ABFE中,∠1=360°﹣(108°+108°+90°)=54°,又∵∠AED=108°,∴∠1=∠2=54°,∴EF平分∠AED.19.(1)解:∵AB⊥AC,∴∠BAC=90°,∵AB∥CD,∴∠BAC=∠ACD=90°,∵∠D=60°,∴∠1=30°;(2)证明:∵∠B+∠BCA=90°,∠1+∠B=90°,∴∠1=∠BCA,∴AD∥BC.20.证明:∵∠ABE=∠D,∠ABE+∠ABC=180°,∴∠ABC+∠D=180°,又∵四边形内角和等于360°,∴∠A+∠C=180°.21.(1)证明:∵∠ADE+∠BCF=180°,∠BCE+∠BCF=180°,∴∠ADE=∠BCE,∴AD∥BC;(2)解:由(1)得,AD∥BC,∴∠AGB=∠EBC,∵∠AGB=∠DGE,∴∠AGB=∠EBC=∠DGE=30°,∵BE平分∠ABC,∴∠AGB=∠EBC,∴∠A=180°﹣30°﹣30°=120°.22.解:(1)∵∠B=30°,∠C=65°,∴∠BAC=85°,∵AD平分∠BAC,∴∠CAD=42.5°,∵AE⊥BC,∴∠CAE=25°,∴∠DAE=∠CAD﹣∠CAE=17.5°;(2)如图,∵∠B=30°,∠C=65°,∴∠BAC=85°,∵AD平分∠BAC,∴∠CAD=42.5°,∴∠F AG=180°﹣∠CAD=137.5°,∵EF⊥BC,∴∠CGE=25°,∴∠AGF=25°,∴∠DFE=180°﹣∠AGF﹣∠F AG=17.5°.23.(1)证明:∵EF∥AC,∴∠1=∠CAE.∵∠1+∠2=180°,∴∠2+∠CAE=180°.∴AE∥DG.(2)解:∵EF∥AC,∠C=35°,∴∠BEF=∠C=35°.∵EF平分∠AEB,∴∠1=∠BEF=35°.∴∠AEB=70°.由(1)知AE∥DG,∴∠BDG=∠AEB=70°.24.解:(1)∵∠AEB=∠C+∠CAE,∠C=42°,∠CAE=18°,∴∠AEB=60°,∵∠CBD=27°,∴∠BFE=180°﹣27°﹣60°=93°,∴∠AFB=180°﹣∠BFE=87°;(2)∵∠BAF=2∠ABF,∠BFE=93°,∴3∠ABF=93°,∴∠ABF=31°,∴∠BAF=62°.25.解:∵AE⊥CD交CD于点F,∴∠AFC=∠EFC=90°,∵CD平分∠ACB,∴∠ACF=∠ECF,∵∠AFC+∠EAC+∠ACF=180°,∠EFC+∠CEA+∠ECF=180°,∴∠EAC=∠CEA,∵∠CEA=∠B+∠BAE,∠B=37°,∠BAE=33°,∴∠CEA=70°,∴∠EAC=70°。
最新人教版八年级数学上册第11章《三角形》单元测试(含答案)(精校版)

第11章三角形一、选择题1.平行四边形的内角和为()A.180°B.270°C.360°D.640°2.如图,正六边形的每一个内角都相等,则其中一个内角α的度数是()A.240°B.120°C.60° D.30°3.五边形的内角和是()A.180°B.360°C.540°D.600°4.如果一个多边形的内角和是720°,那么这个多边形是()A.四边形 B.五边形C.六边形D.七边形5.将一个n边形变成n+1边形,内角和将()A.减少180°B.增加90°C.增加180°D.增加360°6.一个多边形的每个内角均为108°,则这个多边形是()A.七边形 B.六边形C.五边形D.四边形7.若一个多边形的内角和是900°,则这个多边形的边数是()A.5 B.6 C.7 D.88.一个多边形的内角和是900°,这个多边形的边数是()A.10 B.9 C.8 D.79.一个多边形的内角和是360°,这个多边形是()A.三角形 B.四边形C.六边形D.不能确定10.一个多边形的每个外角都等于60°,则这个多边形的边数为()A.8 B.7 C.6 D.511.如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP、CP分别平分∠EDC、∠BCD,则∠P 的度数是()A.60°B.65° C.55° D.50°12.已知正多边形的一个外角等于60°,则该正多边形的边数为()A.3 B.4 C.5 D.613.如果一个多边形的每一个外角都是60°,则这个多边形的边数是()A.3 B.4 C.5 D.614.八边形的内角和等于()A.360°B.1080°C.1440°D.2160°15.一个多边形的内角和是外角和的2倍,则这个多边形是()A.四边形 B.五边形C.六边形D.八边形二、填空题16.若一个正多边形的一个内角等于135°,那么这个多边形是正______边形.17.正多边形一个外角的度数是60°,则该正多边形的边数是______.18.正多边形的一个外角等于20°,则这个正多边形的边数是______.19.n边形的每个外角都等于45°,则n=______.20.一个多边形的内角和比外角和的3倍多180°,则它的边数是______.21.一个正多边形的一个外角等于30°,则这个正多边形的边数为______.22.五边形的内角和为______.23.四边形的内角和是______.24.若正多边形的一个外角为40°,则这个正多边形是______边形.25.内角和与外角和相等的多边形的边数为______.26.若正n边形的一个外角为45°,则n=______.27.四边形的内角和为______.28.如图,一个零件的横截面是六边形,这个六边形的内角和为______.29.某正n边形的一个内角为108°,则n=______.30.正多边形的一个外角是72°,则这个多边形的内角和的度数是______.第11章三角形参考答案一、选择题(共15小题)1.C;2.B;3.C;4.C;5.C;6.C;7.C;8.D;9.B;10.C;11.A;12.D;13.D;14.B;15.C;二、填空题(共15小题)16.八;17.六;18.18;19.8;20.9;21.12;22.540°;23.360°;24.九;25.四;26.8;27.360°;28.720°;29.5;30.540°;。
八年级数学上册《第十一章 三角形》单元测试卷-带答案(人教版)

八年级数学上册《第十一章三角形》单元测试卷-带答案(人教版)一、单选题1.安装空调一般会采用如图的方法固定,其根据的几何原理是()A.三角形的稳定性B.两点之间线段最短C.两点确定一条直线D.垂线段最短2.如图,一束光线与水平面成60°的角度照射地面,现在地面AB上支放一个平面镜CD,使这束光线经过平面镜反射后成水平光线,则平面镜CD与地面AB所成角∠DCB的度数等于()A.30°B.45°C.50°D.60°3.若一个多边形的每个外角都等于36°,则它的内角和是( )A.1 080°B.1 440°C.1 800°D.2 160°4.三角形的下列线段中能将三角形的面积分成相等的两部分的是()A.三角形的中线B.三角形的角平分线C.三角形的高D.以上答案均符合题意5.如图所示,AB∥CD,∠E=37°,∠C=20°,则∠EAB的度数为:()A.57°B.60°C.63°D.123°6.如图,直线AB∥CD,∠A=115°,∠E=80°,则∠CDE的度数为()A.15∘B.20∘C.25∘D.30∘7.如图,F是△ABC的角平分线CD和BE的交点,CG⊥AB于点G.若∠ACG=32°,则∠BFC的度数是()A.119°B.122°C.148°D.150°8.如图,将三角板的直角顶点放在直线a上,a∥b,∠1=55°,∠2=60°,则∠3的大小是()A.55°B.60°C.65°D.75°二、填空题9.在△ABC中,如果∠A=∠B+∠C,那么△ABC是三角形.(填“锐角”、“钝角”或“直角”)10.如果一个正多边形的每个外角是60°,则这个正多边形的对角线共有条.11.如图,△ABC中,点D、E分别是BC、AD的中点,△ABC的面积为6,则阴影部分的面积是.12.把一块直尺与一块直角三角板如图放置,若∠1=40°,则∠2的度数为.13.如图,AB∥CD,EF 分别交AB,CD 于点 J、G.,I为 AB 上一点,连接 FI 交 CD 于点 H,连接GI,若∠EJB=60°,∠IHD=40°,则∠F 的度数为.三、解答题14.一个多边形的内角和比四边形的外角和多540°,并且这个多边形的各内角都相等.这个多边形的每一个内角等于多少度?它是正几边形?15.如图所示,在△ABC中,AC=5,BC=6,BC边上高AD=4,若点P在边AC上(不含端点)移动,求BP最短时的值.16.如图1,一副三角板的两个直角重叠在一起,∠A=30°,∠C=45°△COD固定不动,△AOB绕着O点逆时针旋转α°(0°<α<180°)(1)若△AOB绕着O点旋转图2的位置,若∠BOD=60°,求∠AOC ;(2)若0°<α<90°,在旋转的过程中∠BOD+∠AOC的值会发生变化吗?若不变化,请求出这个定值;(3)若90°<α<180°,问题(2)中的结论还成立吗?说明理由;(4)将△AOB绕点O逆时针旋转α度(0°<α<180°),问当α为多少度时,两个三角形至少有一组边所在直线垂直?(请直接写出所有答案).17.如图,△ABC中,AD、AE分别是边BC上的中线和高,AE=4,S△ABD=10,求BC,CD的长.18.某个零件的的形状如图所示,按规定∠A等于90°,∠B、∠D应分别等于20°和30°,小李量得∠BCD=145°,他断定这个零件不合格,你能说出其中的道理吗?19.在△ABC 中,∠ABC 和∠ACB 的角平分线交于点 M.(1)若∠ABC=40°,∠ACB=60°,求∠BMC 的度数;(2)∠BMC 可能是直角吗?作出判断,并说明理由.参考答案1.A2.A3.B4.A5.A6.A7.A8.C9.直角10.911.3212.130°13.20°14.解:设边数为n,根据题意,得(n﹣2)×180°=360°+540°(n﹣2)×180°=900°n﹣2=5∴n=7.900÷7=9007.答:这个多边形的每一个内角等于9007度、它是正七边形.15.解:根据垂线段最短可知,当BP⊥AC时,BP最短.∵S△ABC=12×BC×AD=12×AC×BP∴6×4=5BP,∴PB=245即BP最短时的值为245.16.解:(1)∵∠BOD=60°,△AOB绕着O点旋转了30°,即∠AOD=30°,∴∠AOC=∠AOD+∠COD=30°+90°=120°;(2)若0°<α<90°,∵∠AOD=α,∠AOC=∠COD+∠AOD,∴∠BOD+∠AOC=(∠BOD+∠AOD)+∠COD=90°+90°=180°,在旋转的过程中∠BOD+∠AOC的值不变化,∠BOD+∠AOC=180°;(3)若90°<α<180°,问题(2)中的结论还成立理由:若90°<α<180°,∵∠AOB=∠COD=90°;又∵∠BOD+∠AOC+∠AOB+∠COD=360°∴∠BOD+∠AOC=360°﹣∠AOD﹣∠COD=360°﹣90°﹣90°=180°;(4)α=90°、60°、45°、105°、150°、135°时,两个三角形至少有一组边所在直线垂直。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、选择题(本大题共 7 小题,每小题 4 分,共 28 分;在每小题列出的四个选项中,只有一项符合题意) 1.如图 1,在△ABC 中,表示 AB 边上的高的图形是( )
图1 2.如图 2,直线 l1∥l2,若∠1=140°,∠2=70°,则∠3 的度数是( )
A.1 种
B.2 种
C.3 种
D.4 种
6.若多边形每一个内角都等于 120°,则从此多边形的一个顶点出发的对角线共有( )
A.2 条
B.3 条
C.6 条
D.9 条
7.如图 4,把△ABC 沿 DE 折叠,当点 A 落在四边形 BCED 内部时,∠A 与∠1+∠2 之间有一种数量关
系始终保持不变,这个关系是( )
2 又∵∠BAC=180°-(∠B+∠C),
∴∠1=1[180°-(∠B+∠C)]=90°-1(∠B+∠C).
2
2பைடு நூலகம்
∴∠EDF=∠B+∠1=∠B+90°-1(∠B+∠C)=90°+1(∠B-∠C).
2
2
又∵EF⊥BC,∴∠EFD=90°,
∴∠DEF=90°-∠EDF=90°-[90°+1(∠B-∠C)]=1(∠C-∠B).
图2
A.70°
B.80°
C.65°
D.60°
3.在△ABC 中,∠A=2∠B=70°,则∠C 的度数为( )
A.35°
B.40°
C.75°
D.105°
4.如图 3,六根木条钉成一个六边形框架 ABCDEF,要使框架稳固且不活动,至少还需要添加木条( )
图3
A.1 根
B.2 根
C.3 根
D.4 根
5.长为 9,6,5,4 的四根木条,选其中三根组成三角形,选法有( )
2
2
图4 A.∠A=∠1+∠2 B.2∠A=∠1+∠2 C.3∠A=2∠1+∠2 D.3∠A=2(∠1+∠2) 二、填空题(本大题共 6 小题,每小题 4 分,共 24 分) 8.如图 5,在△ABC 中,∠A=85°,点 D 在 BC 的延长线上,∠ACD=140°,则∠B=________°.
图5 9.已知三角形的三边长分别为 3,8,x,若 x 为偶数,则 x=________. 10.如图 6,在四边形 ABCD 中,AB∥CD,将四边形 ABCD 沿对角线 AC 折叠,使点 B 落在点 B′ 处.若∠1=∠2=44°,则∠B=________°.
42
2
当腰长是 18 时,则底边长为 18×4=24,此时能构成三角形,且周长为 2×18+24=60. 3
综上可知,此三角形的周长为 45 或 60.
16.解:(1)~(3)如图.
(4)S△ABC=2S△ADC=2×12×AD×CF=15. 17.解:∵∠BAC=∠BAS+∠SAC=45°+30°=75°,∠NBA=∠SAB=45°,∴∠ABC=∠NBC- ∠NBA=60°-45°=15°.∴在△ABC 中,∠C=180°-(75°+15°)=90°. 18.解:设∠C=x°, 则∠ABC=x°,∠ABD=x°-30°. ∵∠ADB 是△DBC 的外角, ∴∠ADB=30°+x°,于是∠A=30°+x°. 在△ABD 中,2(30+x)+(x-30)=180, 解得 x=50.故∠BDC=180°-(30°+50°)=100°. 19.解:(1)∵∠1=∠2,∴∠1=1∠BAC.
3
3
ACE,则∠D 的度数为________.
图9 三、解答题(本大题共 6 小题,共 48 分) 14.(6 分)有一个 n 边形的内角和与外角和之比是 9∶2,求它的边数 n.
15.(8 分)已知等腰三角形的一边长为 18,腰长是底边长的3,试求此三角形的周长. 4
16.(8 分)如图 10,已知△ABC. (1)画 BC 边上的中线 AD; (2)画△ABD 的角平分线 AE; (3)画△ADC 的边 AD 上的高 CF; (4)若 AD=5,CF=3,求△ABC 的面积.
图 10
17.(8 分)如图 11,点 B 在点 A 的南偏西 45°方向,点 C 在点 A 的南偏东 30°方向,点 C 在点 B 的北 偏东 60°方向,求∠C 的度数.
图 11
18.(8 分)已知:如图 12,在△ABC 中,∠ABC=∠C,D 是 AC 边上一点,∠A=∠ADB,∠DBC= 30°.求∠BDC 的度数.
图 13
参考答案
1.D 2.A 3.C 4.C 5.C
6.B 7.B 8.55
9.6,8 或 10
10.114
11.67.5
12.105
13.24°
14.解:依题意得(n-2)180∶360=9∶2.
即 360(n-2)=360×9.解得 n=11.
15.解:当底边长是 18 时,则腰长为 18×3=27,此时能构成三角形,且周长为 2×27+18=45;
图6 11.如图 7,若该图案是由 8 个形状和大小相同的梯形拼成的,则∠1=________°.
图7 12.如图 8,已知 a∥b,若∠1+∠2=75°,则∠3+∠4=________°.
图8
13.如图 9 所示,在△ABC 中,∠A=36°,E 是 BC 延长线上一点,∠DBE=2∠ABE,∠DCE=2∠
图 12
19.(10 分)如图 13①所示,在△ABC 中,∠1=∠2,∠C>∠B,E 为 AD 上一点,且 EF⊥BC 于点 F. (1)试探索∠DEF 与∠B,∠C 之间的数量关系; (2)如图 13②所示,当点 E 在 AD 的延长线上时,其余条件都不变,你在(1)中探索得到的结论是否还成 立?
