正交试验设计表
3因素3水平正交试验设计表

3因素3水平正交试验设计表标题:探寻完美咖啡的秘密引言:咖啡,是许多人每天都离不开的饮品。
它的醇香和浓郁的口感让无数人为之倾倒。
然而,要制作出一杯完美的咖啡并不简单。
为了揭开咖啡的秘密,我们进行了一项以3因素3水平正交试验设计的研究。
本文将带您走进我们的实验室,一起探索制作完美咖啡的奥秘。
正文:一、因素一:咖啡豆的选择咖啡豆是制作咖啡的基础,其种类和烘焙程度直接影响着咖啡的口感。
我们选取了3种不同种类的咖啡豆:阿拉比卡、罗布斯塔和埃塞俄比亚。
这三种咖啡豆分别代表了不同的风味特点。
通过正交试验设计,我们探索了不同咖啡豆的搭配和比例对口感的影响。
二、因素二:研磨度的调整研磨度的调整对咖啡的口感和提取效率有着重要影响。
我们选取了3种不同的研磨度:细研磨、中研磨和粗研磨。
这三种研磨度代表了不同的提取效率和咖啡颗粒大小。
我们通过正交试验设计,研究了不同研磨度对咖啡的醇度和苦味的影响。
三、因素三:冲泡方法的选择冲泡方法是制作咖啡的关键环节,不同的冲泡方法会带来不同的口感体验。
我们选取了3种不同的冲泡方法:滴滤、法压和意式浓缩。
这三种方法代表了不同的萃取方式和时间。
通过正交试验设计,我们研究了不同冲泡方法对咖啡的酸度和香气的影响。
结果与讨论:通过正交试验设计,我们获得了一组数据,可以清楚地看出不同因素和水平对咖啡口感的影响。
我们发现,阿拉比卡咖啡豆搭配中研磨度和法压冲泡方法可以制作出口感平衡、香气浓郁的咖啡。
而罗布斯塔咖啡豆搭配粗研磨度和滴滤冲泡方法则可以制作出苦味浓郁、醇度较高的咖啡。
埃塞俄比亚咖啡豆则适合细研磨度和意式浓缩冲泡方法,以突出其酸度和花香。
结论:本研究通过正交试验设计,探究了咖啡豆的选择、研磨度的调整和冲泡方法的选择对咖啡口感的影响。
我们得出了一些有价值的结论,为制作完美咖啡提供了一定的指导。
然而,咖啡制作的艺术性和个人口味的差异也需要被充分尊重。
希望本研究能为咖啡爱好者们提供一些启发,让每一杯咖啡都成为独一无二的艺术品。
正交试验设计常用正交表

(1) L 4(23)任意两列间的交互作用为另外一列。
(2) L 8(27)L 8(27)二列间的交互作用表1 2 3 1 1 1 1 2 1 2 2 3 2 1 2 4 22112 3 4 5 6 7 1 1 11 1 1 1 12 1 1 1 2 2 2 23 1 2 2 1 1 2 24 1 2 2 2 2 1 15 2 1 2 1 2 1 26 2 1 2 2 1 2 17 2 2 1 1 2 2 1 8221211212 3 4 5 6 7(1) 3 2 6 4 7 6 (2) 1 5 7 4 5 (3) 7 6 5 4 (4) 1 2 3 (5) 3 2 (6) 1(7)列 号 试验 号列号试验 号列号列号L 8(27)表头设计1 2 3 4 5 6 7 3 A B A ×B C A ×C B ×C 4 A B A ×B C ×D C A ×C B ×D B ×C A ×D D 4 A B C ×D A ×B C B ×D A ×C D B ×C A ×D 5 A D ×EB C ×DA ×BC ×EC B ×DA ×CB ×ED A ×E B ×CE A ×D(3) L 8(4×24)L 8(4×24)表头设计1 2 3 4 5 2 A B (A ×B)1 (A ×B)2(A ×B)33 A B C4 A B C D 5ABCDE1 2 3 4 5 1 11 1 1 12 1 2 2 2 23 2 1 1 2 24 2 2 2 1 15 3 1 2 1 26 3 2 1 2 17 4 1 2 2 1 842112列号 因 子 数列号 试验 号列号 因 子 数(4) L 12 (211)(5) L 16 (215)12 3 4 5 6 7 8 9 10 11 1 1 11 1 1 1 1 1 1 1 12 1 1 1 1 1 2 2 2 2 2 23 1 1 2 2 2 1 1 1 2 2 24 1 2 1 2 2 1 2 2 1 1 25 1 2 2 1 2 2 1 2 1 2 16 1 2 2 2 1 2 2 1 2 1 17 2 1 2 2 1 1 2 2 1 2 18 2 1 2 1 2 2 2 1 1 1 29 2 1 1 2 2 2 1 2 2 1 1 10 2 2 2 1 1 1 1 2 2 1 2 11 2 2 1 2 1 2 1 1 1 2 2 122211212122112 3 4 5 6 7 8 9 10 11 12 13 14 15 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 3 1 1 1 2 2 2 2 1 1 1 1 2 2 2 2 4 1 1 1 2 2 2 2 2 2 2 2 1 1 1 1 5 1 2 2 1 1 2 2 1 1 2 2 1 1 2 2 6 1 2 2 1 1 2 2 2 2 1 1 2 2 1 1 7 1 2 2 2 2 1 1 1 1 2 2 2 2 1 1 8 1 2 2 2 2 1 1 2 2 1 1 1 1 2 2 9 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 10 2 1 2 1 2 1 2 2 1 2 1 2 1 2 1 11 2 1 2 2 1 2 1 1 2 1 2 2 1 2 1 12 2 1 2 2 1 2 1 2 1 2 1 1 2 1 2 13 2 2 1 1 2 2 1 1 2 2 1 1 2 2 1 14 2 2 1 1 2 2 1 2 1 1 2 2 1 1 2 15 2 2 1 2 1 1 2 1 2 2 1 2 1 1 2 16221211221121221列号试验 号列号试验 号L16(215)二列间的交互作用表1 2 3 4 5 6 7 8 9 10 11 12 13 14 15(1) 3 2 5 4 7 6 9 8 11 10 13 12 15 14(2) 1 6 4 5 10 11 8 9 14 15 12 13(3) 7 6 5 4 11 10 9 8 15 14 13 12(4) 1 2 3 12 13 14 15 8 9 10 11(5) 3 2 13 12 15 14 9 8 11 10(6) 1 14 15 12 13 10 11 8 9(7) 15 14 13 12 11 10 9 8(8) 1 2 3 4 5 6 7(9) 3 2 5 4 7 6(10) 1 6 7 4 5(11) 7 6 5 4(12) 1 2 3(13) 3 2(14) 1L 16(215)表头设计15EC ×E B ×FC ×E B ×F A ×GC ×E B ×F A ×GD ×H14 A ×EGG13 B ×E F F F 12 C ×D C ×D C ×D A ×FC ×D A ×F A ×GC ×D A ×F A ×GE ×H11 C ×E EEE10 B ×D B ×D B ×D A ×EB ×D A ×EC ×GB ×D A ×EC ×G F ×H9 A ×D A ×D A ×D B ×E C ×FA ×DB ×EC ×F A ×D B ×E C ×FG ×H 8 D D D D D7 D ×E H 6 B ×C B ×C B ×C E ×F B ×C E ×F D ×G B ×C E ×F D ×G A ×H5 A ×C A ×C A ×C D ×F A ×C D ×F E ×G A ×C D ×F E ×G B ×H 4 C C C C C 3A ×B A ×B A ×B D ×E A ×B D ×E F ×G A ×B D ×E F ×GC ×H2 B B BBB1 A A A A A 列号 因子数4 5 6 7 8(6) L 16 (4×212)L 16 (4×212)表头设计1 2 3 4 5 6 7 3 A B (A ×B)1 (A ×B)2 (A ×B)3 C (A ×C)1 4 A B (A ×B)1 C ×D (A ×B)2 (A ×B)3 C (A ×C)1 B ×D 5A B (A ×B)1 C ×D (A ×B)2 C ×E (A ×B)3 C (A ×C)1 B ×D8 9 10 11 12 13 3 (A ×C)2 (A ×C)3 B ×C 4 (A ×C)2 (A ×C)3 B ×C (A ×D)1 D (A ×D)3 (A ×D)2 5 (A ×C)2 B ×E(A ×C)3B ×C (A ×D)1 (A ×E)2D (A ×E)3E (A ×D)3(A ×E)1 (A ×D)2(7) L 16 (42×29)12 3 4 5 6 7 8 9 10 11 12 13 1 1 11 1 1 1 1 1 1 1 1 1 12 1 1 1 1 1 2 2 2 2 2 2 2 23 1 2 2 2 2 1 1 1 1 2 2 2 24 1 2 2 2 2 2 2 2 2 1 1 1 15 2 1 1 2 2 1 1 2 2 1 1 2 26 2 1 1 2 2 2 2 1 1 2 2 1 17 2 2 2 1 1 1 1 2 2 2 2 1 18 2 2 2 1 1 2 2 1 1 1 1 2 29 3 1 2 1 2 1 2 1 2 1 2 1 2 10 3 1 2 1 2 2 1 2 1 2 1 2 1 11 3 2 1 2 1 1 2 1 2 2 1 2 1 12 3 2 1 2 1 2 1 2 1 1 2 1 2 13 4 1 2 2 1 1 2 2 1 1 2 2 1 14 4 1 2 2 1 2 1 1 2 2 1 1 2 15 4 2 1 1 2 1 2 2 1 2 1 1 2 164211221121221列号 试验 号列 号因 子数列号 因 子 数(8) L 16 (43×26)(9) L 16 (44×23)12 3 4 5 6 7 8 9 10 11 1 1 11 1 1 1 1 1 1 1 12 1 2 1 1 1 2 2 2 2 2 23 1 3 2 2 2 1 1 1 2 2 24 1 4 2 2 2 2 2 2 1 1 15 2 1 1 2 2 1 2 2 1 2 26 2 2 1 2 2 2 1 1 2 1 17 2 3 2 1 1 1 2 2 2 1 18 2 4 2 1 1 2 1 1 1 2 29 3 1 2 1 2 2 1 2 2 1 2 10 3 2 2 1 2 1 2 1 1 2 1 11 3 3 1 2 1 2 1 2 1 2 1 12 3 4 1 2 1 1 2 1 2 1 2 13 4 1 2 2 1 2 2 1 2 2 1 14 4 2 2 2 1 1 1 2 1 1 2 15 4 3 1 1 2 2 2 1 1 1 2 164411211222112 3 4 5 6 7 8 9 1 1 11 1 1 1 1 1 12 1 2 2 1 1 2 2 2 23 1 3 3 2 2 1 1 2 24 1 4 4 2 2 2 2 1 15 2 1 2 2 2 1 2 1 26 2 2 1 2 2 2 1 2 17 2 3 4 1 1 1 2 2 18 2 4 3 1 1 2 1 1 29 3 1 3 1 2 2 2 2 1 10 3 2 4 1 2 1 1 1 2 11 3 3 1 2 1 2 2 1 2 12 3 4 2 2 1 1 1 2 1 13 4 1 4 2 1 2 1 2 2 14 4 2 3 2 1 1 2 1 1 15 4 3 2 1 2 2 1 1 1 16441121222列号试验 号列号 试验 号(10) L16 (45)1 2 3 4 5 6 71 1 1 1 1 1 1 12 1 2 2 2 1 2 23 1 3 3 3 2 1 24 1 4 4 4 2 2 15 2 1 2 3 2 2 16 2 2 1 4 2 1 27 2 3 4 1 1 2 28 2 4 3 2 1 1 19 3 1 3 4 1 2 210 3 2 4 3 1 1 111 3 3 1 2 2 2 112 3 4 2 1 2 1 213 4 1 4 2 2 1 214 4 2 3 1 2 2 115 4 3 2 4 1 1 116 4 4 1 3 1 2 21 2 3 4 51 1 1 1 1 12 1 2 2 2 23 1 3 3 3 34 1 4 4 4 45 2 1 2 3 46 2 2 1 4 37 2 3 4 1 28 2 4 3 2 19 3 1 3 4 210 3 2 4 3 111 3 3 1 2 412 3 4 2 1 313 4 1 4 2 314 4 2 3 1 415 4 3 2 4 116 4 4 1 3 2列号试验号列号试验号(11) L 16 (8×28)(12) L 20 (219)12 3 4 5 6 7 8 9 1 1 11 1 1 1 1 1 12 1 2 2 2 2 2 2 2 23 2 1 1 1 1 2 2 2 24 2 2 2 2 2 1 1 1 15 3 1 1 2 2 1 1 2 26 3 2 2 1 1 2 2 1 17 4 1 1 2 2 2 2 1 18 4 2 2 1 1 1 1 2 29 5 1 2 1 2 1 2 1 2 10 5 2 1 2 1 2 1 2 1 11 6 1 2 1 2 2 1 2 1 12 6 2 1 2 1 1 2 1 2 13 7 1 2 2 1 1 2 2 1 14 7 2 1 1 2 2 1 1 2 15 8 1 2 2 1 2 1 1 2 168211212211 2 3 4 56 7 8 9 10 11 12 13 14 15 16 17 18 191 1 1 1 1 1 1 1 1 1 1 1 1 111 1 1 1 12 2 2 1 1 2 2 2 2 1 2 1 2 1 1 1 1 2 2 13 2 1 1 2 2 2 2 1 2 1 2 1 1 1 1 2 2 1 24 1 1 2 2 2 2 1 2 1 2 1 1 1 1 2 2 1 2 25 1 2 2 2 2 1 2 1 2 1 1 1 1 2 2 1 2 2 16 2 2 2 2 1 2 1 2 1 1 1 1 2 2 1 2 2 1 17 2 2 2 1 2 1 2 1 1 1 1 2 2 1 2 2 1 1 28 2 2 1 2 1 2 1 1 1 1 2 2 1 2 2 1 1 2 29 2 1 2 1 2 1 1 1 1 2 2 1 2 2 1 1 2 2 2 10 1 2 1 2 1 1 1 1 2 2 1 2 2 1 1 2 2 2 2 11 2 1 2 1 1 1 1 2 2 1 2 2 1 1 2 2 2 2 1 12 1 2 1 1 1 1 2 2 1 2 2 1 1 2 2 2 2 1 2 13 2 1 1 1 1 2 2 1 2 2 1 1 1 2 2 2 1 2 1 14 1 1 1 1 2 2 1 2 2 1 1 2 2 2 2 1 2 1 2 15 1 1 1 2 2 1 2 2 1 1 2 2 2 2 1 2 1 2 1 16 1 1 2 2 1 2 2 1 1 2 2 2 2 1 2 1 2 1 1 17 1 2 2 1 2 2 1 1 2 2 2 2 1 2 1 2 1 1 1 18 2 2 1 2 2 1 1 2 2 2 2 1 2 1 2 1 1 1 1 19 2 1 2 2 1 1 2 2 2 2 1 2 12 1 1 1 1 2 列号 试验 号列 号 试 验 号(13) L9 (34)(14) L18 (2×37)1 2 3 41 1 1 1 12 1 2 2 23 1 3 3 34 2 1 2 35 2 2 3 16 2 3 1 27 3 1 3 28 3 2 1 39 3 3 2 11 2 3 4 5 6 7 81 1 1 1 1 1 1 1 12 1 1 2 2 2 2 2 23 1 1 3 3 3 3 3 34 1 2 1 1 2 2 3 35 1 2 2 2 3 3 1 16 1 2 3 3 1 1 2 27 1 3 1 2 1 3 2 38 1 3 2 3 2 1 3 19 1 3 3 1 3 2 1 210 2 1 1 3 3 2 2 111 2 1 2 1 1 3 3 212 2 1 3 2 2 1 1 313 2 2 1 2 3 1 3 214 2 2 2 3 1 2 1 315 2 2 3 1 2 3 2 116 2 3 1 3 2 3 1 217 2 3 2 1 3 1 2 318 2 3 3 2 1 2 3 1列号试验号列号试验号(15) L27 (313)L27 (313)表头设计1 2 3 4 5 6 73 A B (A×B)1(A×B)2 C (A×C)1(A×C)24 A B (A×B)1(C×D)2(A×B)2 C(A×C)1(B×D)2(A×C)28 9 10 11 12 13 3 (B×C)1 D (A×D)1(B×C)2(B×D)1(C×D)14(B×C)1(A×D)2(A×D)1(B×C)21 2 3 4 5 6 7 8 9 10 11 12 131 1 1 1 1 1 1 1 1 1 1 1 1 12 1 1 1 1 2 2 2 2 2 2 2 2 23 1 1 1 1 3 3 3 3 3 3 3 3 34 1 2 2 2 1 1 1 2 2 2 3 3 35 1 2 2 2 2 2 2 3 3 3 1 1 16 1 2 2 2 3 3 3 1 1 1 2 2 27 1 3 3 3 1 1 1 3 3 3 2 2 28 1 3 3 3 2 2 2 1 1 1 3 3 39 1 3 3 3 3 3 3 2 2 2 1 1 110 2 1 1 3 1 2 3 1 2 3 1 2 311 2 1 2 3 2 3 1 2 3 1 2 3 112 2 1 3 3 3 1 2 3 1 2 3 1 213 2 2 1 1 1 2 3 2 3 1 3 1 214 2 2 2 1 2 3 1 3 1 2 1 2 315 2 2 3 1 3 1 2 1 2 3 2 3 116 2 3 1 2 1 2 3 3 1 2 2 3 117 2 3 2 2 2 3 1 1 2 3 3 1 218 2 3 3 2 3 1 2 2 3 1 1 2 319 3 1 3 2 1 3 2 1 3 2 1 3 220 3 1 3 2 2 1 3 2 1 3 2 1 321 3 1 3 2 3 2 1 3 2 1 3 2 122 3 2 1 3 1 3 2 2 1 3 3 2 123 3 2 1 3 2 1 3 3 2 1 1 3 224 3 2 1 3 3 2 1 1 3 2 2 1 325 3 3 2 1 1 3 2 3 2 1 2 1 326 3 3 2 1 2 1 3 1 3 2 3 2 127 3 3 2 1 3 2 1 2 1 3 1 3 2列号试验号列号因子数列号因子数L27 (313)二列间的交互作用表1 2 3 4 5 6 7 8 9 10 11 12 13(1)3 2 2 6 5 5 9 8 8 12 11 114 4 3 7 7 6 10 10 9 13 13 12 (2)1 1 8 9 10 5 6 7 5 6 74 3 11 12 13 11 12 13 8 9 10(3)1 9 10 8 7 5 6 6 7 52 13 11 12 12 13 11 10 8 9(4)10 8 9 6 7 5 7 5 612 13 11 13 11 12 9 10 8(5)1 1234 2 4 37 6 11 13 12 8 10 9(6)1 423 3 2 45 13 12 11 10 9 8(7)3 4 2 4 3 212 11 13 9 8 10(8)1 123 410 9 5 7 6(9)1 42 38 7 6 5(10)3 4 26 5 7(11)1 113 12(12)1111 2 3 4 5 61 1 1 1 1 1 12 1 2 2 2 2 23 1 3 3 3 3 34 1 4 4 4 4 45 1 5 5 5 5 56 2 1 2 3 4 57 2 2 3 4 5 18 2 3 4 5 1 29 2 4 5 1 2 3 10 2 5 1 2 3 4 11 3 1 3 5 2 4 12 3 2 4 1 3 5 13 3 3 5 2 4 1 14 3 4 1 3 5 2 15 3 5 2 4 1 3 16 4 1 4 2 5 3 17 4 2 5 3 1 4 18 4 3 1 4 2 5 19 4 4 2 5 3 1 20 4 5 3 1 4 2 21 5 1 5 4 3 2 22 5 2 1 5 4 3 23 5 3 2 1 5 4 24 5 4 3 2 1 5 255 5 4 3 2 1列 号 试验 号31122121122112122130122121122112122129122121121221211228122121121221211227 122112212112211226 1 22112212112211225 1 2 2 112211221122124 1 2 2 1 12211221122123 1 2 1 2 2 1 212121121222 1 2 1 2 2 1 2 12121121221 1 2 1 2 2 1 2 1 1212212120 1 2 1 2 2 1 2 1 1 2 12212119 1 2 1 2 1 2 1 2 2 1 2 1 212118 1 2 1 2 1 2 1 2 2 1 2 1 2 12117 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 16 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 15 1 1 2 2 2 2 1 1 2 2 1 1 1 1 2 2 14 1 1 2 2 2 2 1 1 2 2 1 1 1 1 2 2 13 1 1 2 2 2 2 1 1 1 1 2 2 1 1 2 2 12 1 1 2 2 2 2 1 1 1 1 2 2 1 1 2 2 11 1 1 2 2 1 1 2 2 2 2 1 1 2 2 1 1 10 1122112222112211 9 11221122112211228 1 1 2 2 1 1 2 2 1 1 2 2 1 1 2 2 7 1 1 1 1 2 2 2 2 2 2 2 2 1 1 1 1 6 1 1 1 1 2 2 2 2 2 2 2 2 1 1 1 1 5 1 1 1 1 2 2 2 2 1 1 1 1 2 2 2 2 4 1 1 1 1 2 2 2 2 1 1 1 1 2 2 2 2 3 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 21 1 1 1 1 1 1 12 2 2 2 2 2 2 2完美格式整理版111111111111111 1 1列号试验号12345678910111213141516。
正交试验设计(多指标)

综合平衡法
通过各因素对各指标影响的综合分析,得 出较好的试验方案是: B3 粒度 第3水平:8 C1 碱度 第1水平:1.1 A2 水份 第2水平:9
2) 综合评分法
综合评分法 综合评分法是:先按重要性程度不
同给各个指标赋以权数,再对各试验 计算加权指标,化为单一指标问题。
(1)综合平衡法
例 为了提高某产品质量,要对生产该 产品的原料进行配方试验。要检验3 项指标:抗压强度、落下强度和裂纹 度,前两个指标越大越好,第三个指 标越小越好。根据以往的经验,配方 中有3个重要因素:水份、粒度和碱 度。它们各有3个水平,具体数据如 表所示。试进行试验分析,找出最好 的配方方案。
因素 水平
1 2 3
A水份 % 8
9
7
B粒度 % 4
6
8
C碱度 1.1 1.3 1.5
返回
列号 1
试验号
A
2 3 抗压强度
BC
Kg/个
落下强度 0.5m/次
1
1
1
1
11.5
1.1
2
1
2
2
4.5
3.6
3
1
3
3
11.0
4.6
4
2
1
2
7.0
1.1
5
2
2
3
8.0
1.6
6
2
3
1
18.5
15.1
7
3
1
3
9.0
1.1
8
3
回收率 综合 评分
30.0 100.0 41.2 89.2 60.0 84.0 24.2 56.2 51.0 69.0 58.4 74.4 31.0 65.0 20.5 48.5 73.5 91.5
正交试验设计经典案例

正交试验设计经典案例
一、L9(3^4)正交试验设计
这个实验设计是一个L9(3^4)正交试验设计,用于研究铜锌合金中锌的含量、冶炼时间、冷却速率和成型压力对铜锌合金硬度的影响。
在这个设计中,有四个因素(锌的含量、冶炼时间、冷却速率和成型压力)和三个水平(低、中、高)。
该试验的九个试验条件如下表所示。
2、L16(4^5)正交试验设计
这个实验设计是一个L16(4^5)正交试验设计,用于研究发酵生产中,发酵液pH 值、生物量、发酵温度、曲菌培养基和曲菌翻转次数对干酪根的质量影响。
在这个设计中,有五个因素(发酵液pH值、生物量、发酵温度、曲菌培养基和曲菌翻转次数)和四个水平(低、中低、中高、高)。
该试验的十六个试验条件如下表所示。
3、L16(4^5)正交试验设计
这个实验设计是一个L16(4^5)正交试验设计,用于研究太阳能集热器的建造,包括集热面积、集热器长度、集热器宽度、太阳能采集器的形状和位置对太阳能集热器效率的影响。
在这个设计中,有五个因素(集热面积、集热器长度、集热器宽度、太阳能采集器的形状和位置)和四个水平(低、中低、中高、高)。
该试验的十六个试验条件如下表所示。
以上这些都是经典的正交试验设计案例,这些设计都遵循着统计学中的一些原则和方法,有效地结合了多个因素的影响,将因素控制在一定范围内,从而帮助我们更好地理解问题并提出相应的解决方案。
正交试验设计表-图

选择合适的正交表
根据因素和水平数量,选择合适 的正交表,确保试验具有足够的 代表性和均衡性。
制定试验计划
按照正交表的安排,制定详细的 试验计划,包括试验顺序、条件 控制等。
试验因素与水平的确定
确定关键因素
01
根据研究目的和问题背景,确定对试验结果有显著影响的因素
作为关键因素。
确定因素水平
02
为关键因素选择合适的水平,确保试验结果具有实际意义和应
农业科学中的应用
肥料配比优化
通过正交试验设计,可以找出最佳的肥料配比方案,提高农作物的 产量和品质。
农药喷施方案优化
正交试验设计可用于评估不同农药喷施方案对农作物病虫害防治效 果的影响,从而选择出最佳的喷施方案。
种植技术优化
在农业种植技术中,正交试验设计可用于分析不同种植方式对农作物 生长的影响,从而选择出最佳的种植技术。
科学决策依据
正交试验设计得出的最优 解具有一定的可信度,可 以为科学决策提供有力的 依据。
正交试验设计的步骤与流程
明确试验目的和因素
首先需要明确试验的目的和考察的因素,为 后续的试验设计提供基础。
确定水平
根据实际情况和试验要求,为每个因素选择合 适的水平。
选择合适的正交表
根据因素和水平数量,选择合适的正交表,确保 试验设计的均衡分散和整齐可比。
用价值。
控制其他因素
Байду номын сангаас03
在试验过程中,应尽量控制其他非关键因素的干扰,以提高试
验的准确性和可靠性。
试验数据的收集与分析
记录试验数据
在试验过程中,详细记录每个试验条件下的数据,包括试验结果、 误差等。
数据整理与清洗
正交试验设计表

2 正交试验设计的基本程序
对于多因素试验,正交试验设计是简单常用的一种试验设计方法,其设计基本程序如 图所示。正交试验设计的基本程序包括试验方案设计及试验结果分析两部分。
1.3.2.2 代表性 一方面:(1)任一列的各水平都出现,使得部分试验中包括了所有因素的所有水平;
(2)任两列的所有水平组合都出现,使任意两因素间的试验组合为全面试验。 另一方面:由于正交表的正交性,正交试验的试验点必然均衡地分布在全面试验点中,具有很强的 代表性。因此,部分试验寻找的最优条件与全面试验所找的最优条件,应有一致的趋势。 1.3.2.3 综合可比性 (1)任一列的各水平出现的次数相等; (2)任两列间所有水平组合出现次数相等,使得任一因素各水平的试验条件相同。这就保证了在每 列因素各水平的效果中,最大限度地排除了其他因素的干扰。从而可以综合比较该因素不同水平对 试验指标的影响情况。
表10-1
因素3水平的全面试验水平组合数为34=81 ,5图因1素0-13水平的全面试验水平组合数为 35=243,这在科学试验中是有可能做不到的。
正交设计就是从选优区全面试验点(水平组合)中挑选出有代表性的部分试
验点(水平组合)来进行试验。图10-1中标有试验号的九个“(·)”,就是利用正
交表L9(34)从27个试验点中挑选出来的9个试验点。即:
正交试验设计的基本特点是:用部分试验来代替全面试验,通过对部分试验结果的分析,了解全 面试验的情况。
正因为正交试验是用部分试验来代替全面试验的,它不可能像全面试验那样对各因素效 应、交互作用一一分析;当交互作用存在时,有可能出现交互作用的混杂。虽然正交试验设计有 上述不足,但它能通过部分试验找到最优水平组合 ,因 而 很 受实际工作者青睐。如对于上述 3因素3水平试验,若不考虑交互作用,可利用正交表L9(34)安排,试验方案仅包含9个水平组合, 就能反映试验方案包含27个水平组合的全面试验的情况,找出最佳的生产条件。
正交试验设计

实验一正交实验设计1为了提高某种产品的质量,研究A(温度,℃),B(压力,kg),C(配比,%),D(时间,h)四个因素对质量指标的影响。
每个因素各取3个水平(见表1.1)进行实验。
请根据实验方案选择合适的正交表安排实验,并用直观分析方法寻找最优实验方案。
9实验数据分析表:效应曲线图:结果分析:极差越大,影响越大;虚拟值越大,条件越优对质量指标的影响:温度>压力>时间>配比极值最大为:A3,B2 ,C2 ,D3选取最优方案为:温度470℃,压力20 kg ,配比5% ,时间3h2为了提高铸件的精铸性能指标,确定最优的工艺条件,研究以下5个具有2水平的因素。
见表1.2,且A与B、B与C之间存在交互作用,见表1.3,试用L8(27)设计实验,并做直观分析。
表1.2实验数据分析表:结果分析:极差越大,影响越大;虚拟值越大,条件越优对性能指标的影响:A(硬化剂相对密度)>A×B>E(脱蜡条件)>B(硬化时间)=D(晾干时间)>B×C>C(硬化剂温度)所以,最优工艺条件为:硬化剂密度1.48, 硬化时间2min, 硬化剂温度(根据BC交互判定)25℃,晾干时间15h,脱蜡条件HCl3、试用正交表方差分析方法,确定T8钢的最优热处理工艺方案,因素与水平见表1.4。
表1.4注,其中A与B有交互作用,测试淬火后钢的硬度,硬度越大越好。
选L8(27)设计,实验结果如下:方差分析表1.对T8钢的影响因素大小如下:A×B(或者C)>A>B(或者D)>E>e2.由于测试淬火后钢的硬度,硬度越大越好。
则由实验结果可知:实验2的结果最优!即在淬火温度为800℃,淬火时间为15 min,A×B为1,冷却液为水,e为2,E为2,操作方法为D2时得到的钢是最硬的!。
正交试验设计常用正交表分析-共16页
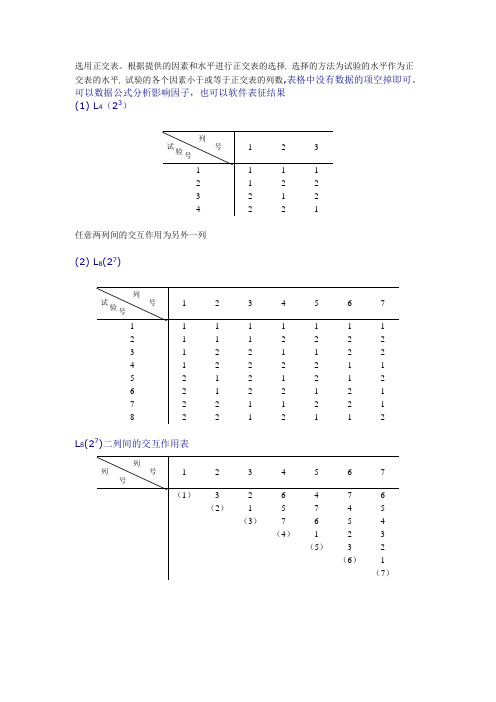
选用正交表。
根据提供的因素和水平进行正交表的选择, 选择的方法为试验的水平作为正 交表的水平, 试验的各个因素小于或等于正交表的列数,表格中没有数据的项空掉即可。
可以数据公式分析影响因子,也可以软件表征结果 (1) L 4(23)任意两列间的交互作用为另外一列(2) L 8(27)L 8(27)二列间的交互作用表1 2 3 1 1 1 1 2 1 2 2 3 2 1 2 4 2211 2 3 4 5 6 7 1 1 1 1 1 1 1 1 2 1 1 1 2 2 2 2 3 1 2 2 1 1 2 2 4 1 2 2 2 2 1 1 5 2 1 2 1 2 1 2 6 2 1 2 2 1 2 1 7 2 2 1 1 2 2 1 822121121 2 3 4 5 6 7 (1) 3 2 6 4 7 6 (2) 1 5 7 4 5 (3) 7 6 5 4 (4) 1 2 3 (5) 3 2 (6) 1(7)列号 试验 号 列号试验 号列号列号L 8(27)表头设计1 2 3 4 5 6 7 3 A B A ×B C A ×C B ×C 4 A B A ×B C ×D C A ×C B ×D B ×C A ×D D 4 A B C ×D A ×B C B ×D A ×C D B ×C A ×D 5 A D ×EB C ×DA ×BC ×EC B ×DA ×CB ×ED A ×E B ×CE A ×D(3) L 8(4×24)L 8(4×24)表头设计1 2 3 4 5 2 A B (A ×B)1 (A ×B)2(A ×B)33 A B C4 A B C D 5ABCDE1 2 3 4 5 1 1 1 1 1 1 2 1 2 2 2 2 3 2 1 1 2 2 4 2 2 2 1 1 5 3 1 2 1 2 6 3 2 1 2 1 7 4 1 2 2 1 842112列号 因 子 数列号试 验号列号因 子数(4) L 12 (211)(5) L 16 (215)1 2 3 4 5 6 7 8 9 10 11 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 2 2 2 2 2 2 3 1 1 2 2 2 1 1 1 2 2 2 4 1 2 1 2 2 1 2 2 1 1 2 5 1 2 2 1 2 2 1 2 1 2 1 6 1 2 2 2 1 2 2 1 2 1 1 7 2 1 2 2 1 1 2 2 1 2 1 8 2 1 2 1 2 2 2 1 1 1 2 9 2 1 1 2 2 2 1 2 2 1 1 10 2 2 2 1 1 1 1 2 2 1 2 11 2 2 1 2 1 2 1 1 1 2 2 12221121212211 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 3 1 1 1 2 2 2 2 1 1 1 1 2 2 2 2 4 1 1 1 2 2 2 2 2 2 2 2 1 1 1 1 5 1 2 2 1 1 2 2 1 1 2 2 1 1 2 2 6 1 2 2 1 1 2 2 2 2 1 1 2 2 1 1 7 1 2 2 2 2 1 1 1 1 2 2 2 2 1 1 8 1 2 2 2 2 1 1 2 2 1 1 1 1 2 2 9 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 10 2 1 2 1 2 1 2 2 1 2 1 2 1 2 1 11 2 1 2 2 1 2 1 1 2 1 2 2 1 2 1 12 2 1 2 2 1 2 1 2 1 2 1 1 2 1 2 13 2 2 1 1 2 2 1 1 2 2 1 1 2 2 1 14 2 2 1 1 2 2 1 2 1 1 2 2 1 1 2 15 2 2 1 2 1 1 2 1 2 2 1 2 1 1 2 16221211221121221列号试 验号 列号试 验 号L16(215)二列间的交互作用表1 2 3 4 5 6 7 8 9 10 11 12 13 14 15(1) 3 2 5 4 7 6 9 8 11 10 13 12 15 14(2) 1 6 4 5 10 11 8 9 14 15 12 13(3) 7 6 5 4 11 10 9 8 15 14 13 12(4) 1 2 3 12 13 14 15 8 9 10 11(5) 3 2 13 12 15 14 9 8 11 10(6) 1 14 15 12 13 10 11 8 9(7) 15 14 13 12 11 10 9 8(8) 1 2 3 4 5 6 7(9) 3 2 5 4 7 6(10) 1 6 7 4 5(11) 7 6 5 4(12) 1 2 3(13) 3 2(14) 1L 16(215)表头设计15EC ×E B ×FC ×E B ×F A ×GC ×E B ×F A ×GD ×H14 A ×EGG13 B ×E F F F 12 C ×D C ×D C ×D A ×FC ×D A ×F A ×GC ×D A ×F A ×GE ×H11 C ×E EEE10 B ×D B ×D B ×D A ×EB ×D A ×EC ×GB ×D A ×EC ×G F ×H9 A ×D A ×D A ×D B ×E C ×FA ×DB ×EC ×F A ×D B ×E C ×FG ×H 8 D D D D D7 D ×E H 6 B ×C B ×C B ×C E ×F B ×C E ×F D ×G B ×C E ×F D ×G A ×H5 A ×C A ×C A ×C D ×F A ×C D ×F E ×G A ×C D ×F E ×G B ×H 4 C C C C C 3A ×B A ×B A ×B D ×E A ×B D ×E F ×G A ×B D ×E F ×GC ×H2 B B BBB1 A A A A A 列号 因子数4 5 6 7 8(6) L 16 (4×212)L 16 (4×212)表头设计1 2 3 4 5 6 7 3 A B (A ×B)1 (A ×B)2 (A ×B)3 C (A ×C)1 4 A B (A ×B)1 C ×D (A ×B)2 (A ×B)3 C (A ×C)1 B ×D 5A B (A ×B)1 C ×D (A ×B)2 C ×E (A ×B)3 C (A ×C)1 B ×D8 9 10 11 12 13 3 (A ×C)2 (A ×C)3 B ×C 4 (A ×C)2 (A ×C)3 B ×C (A ×D)1 D (A ×D)3 (A ×D)2 5 (A ×C)2 B ×E(A ×C)3B ×C (A ×D)1 (A ×E)2D (A ×E)3E (A ×D)3(A ×E)1 (A ×D)2(7) L 16 (42×29)1 2 3 4 5 6 7 8 9 10 11 12 13 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 2 2 2 2 2 2 2 2 3 1 2 2 2 2 1 1 1 1 2 2 2 2 4 1 2 2 2 2 2 2 2 2 1 1 1 1 5 2 1 1 2 2 1 1 2 2 1 1 2 2 6 2 1 1 2 2 2 2 1 1 2 2 1 1 7 2 2 2 1 1 1 1 2 2 2 2 1 1 8 2 2 2 1 1 2 2 1 1 1 1 2 2 9 3 1 2 1 2 1 2 1 2 1 2 1 2 10 3 1 2 1 2 2 1 2 1 2 1 2 1 11 3 2 1 2 1 1 2 1 2 2 1 2 1 12 3 2 1 2 1 2 1 2 1 1 2 1 2 13 4 1 2 2 1 1 2 2 1 1 2 2 1 14 4 1 2 2 1 2 1 1 2 2 1 1 2 15 4 2 1 1 2 1 2 2 1 2 1 1 2 164211221121221列号试 验 号列 号因 子数列号 因 子 数(8) L 16 (43×26)(9) L 16 (44×23)1 2 3 4 5 6 7 8 9 10 11 1 1 1 1 1 1 1 1 1 1 1 1 2 1 2 1 1 1 2 2 2 2 2 2 3 1 3 2 2 2 1 1 1 2 2 2 4 1 4 2 2 2 2 2 2 1 1 1 5 2 1 1 2 2 1 2 2 1 2 2 6 2 2 1 2 2 2 1 1 2 1 1 7 2 3 2 1 1 1 2 2 2 1 1 8 2 4 2 1 1 2 1 1 1 2 2 9 3 1 2 1 2 2 1 2 2 1 2 10 3 2 2 1 2 1 2 1 1 2 1 11 3 3 1 2 1 2 1 2 1 2 1 12 3 4 1 2 1 1 2 1 2 1 2 13 4 1 2 2 1 2 2 1 2 2 1 14 4 2 2 2 1 1 1 2 1 1 2 15 4 3 1 1 2 2 2 1 1 1 2 16441121122211 2 3 4 5 6 7 8 9 1 1 1 1 1 1 1 1 1 1 2 1 2 2 1 1 2 2 2 2 3 1 3 3 2 2 1 1 2 2 4 1 4 4 2 2 2 2 1 1 5 2 1 2 2 2 1 2 1 2 6 2 2 1 2 2 2 1 2 1 7 2 3 4 1 1 1 2 2 1 8 2 4 3 1 1 2 1 1 2 9 3 1 3 1 2 2 2 2 1 10 3 2 4 1 2 1 1 1 2 11 3 3 1 2 1 2 2 1 2 12 3 4 2 2 1 1 1 2 1 13 4 1 4 2 1 2 1 2 2 14 4 2 3 2 1 1 2 1 1 15 4 3 2 1 2 2 1 1 1 16441121222列号试 验号 列号试 验 号(10) L16 (45)1 2 3 4 5 6 71 1 1 1 1 1 1 12 1 2 2 2 1 2 23 1 3 3 3 2 1 24 1 4 4 4 2 2 15 2 1 2 3 2 2 16 2 2 1 4 2 1 27 2 3 4 1 1 2 28 2 4 3 2 1 1 19 3 1 3 4 1 2 210 3 2 4 3 1 1 111 3 3 1 2 2 2 112 3 4 2 1 2 1 213 4 1 4 2 2 1 214 4 2 3 1 2 2 115 4 3 2 4 1 1 116 4 4 1 3 1 2 21 2 3 4 51 1 1 1 1 12 1 2 2 2 23 1 3 3 3 34 1 4 4 4 45 2 1 2 3 46 2 2 1 4 37 2 3 4 1 28 2 4 3 2 19 3 1 3 4 210 3 2 4 3 111 3 3 1 2 412 3 4 2 1 313 4 1 4 2 314 4 2 3 1 415 4 3 2 4 116 4 4 1 3 2列号试验号列号试验号(11) L 16 (8×28)(12) L 20 (219)1 2 3 4 5 6 7 8 9 1 11 1 1 1 1 1 1 12 1 2 2 2 2 2 2 2 23 2 1 1 1 1 2 2 2 24 2 2 2 2 2 1 1 1 15 3 1 1 2 2 1 1 2 26 3 2 2 1 1 2 2 1 17 4 1 1 2 2 2 2 1 18 4 2 2 1 1 1 1 2 29 5 1 2 1 2 1 2 1 2 10 5 2 1 2 1 2 1 2 1 11 6 1 2 1 2 2 1 2 1 12 6 2 1 2 1 1 2 1 2 13 7 1 2 2 1 1 2 2 1 14 7 2 1 1 2 2 1 1 2 15 8 1 2 2 1 2 1 1 2 168211212211 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 1 1 2 2 2 2 1 2 1 2 1 1 1 1 2 2 1 3 2 1 1 2 2 2 2 1 2 1 2 1 1 1 1 2 2 1 2 4 1 1 2 2 2 2 1 2 1 2 1 1 1 1 2 2 1 2 2 5 1 2 2 2 2 1 2 1 2 1 1 1 1 2 2 1 2 2 1 6 2 2 2 2 1 2 1 2 1 1 1 1 2 2 1 2 2 1 1 7 2 2 2 1 2 1 2 1 1 1 1 2 2 1 2 2 1 1 2 8 2 2 1 2 1 2 1 1 1 1 2 2 1 2 2 1 1 2 2 9 2 1 2 1 2 1 1 1 1 2 2 1 2 2 1 1 2 2 2 10 1 2 1 2 1 1 1 1 2 2 1 2 2 1 1 2 2 2 2 11 2 1 2 1 1 1 1 2 2 1 2 2 1 1 2 2 2 2 1 12 1 2 1 1 1 1 2 2 1 2 2 1 1 2 2 2 2 1 2 13 2 1 1 1 1 2 2 1 2 2 1 1 1 2 2 2 1 2 1 14 1 1 1 1 2 2 1 2 2 1 1 2 2 2 2 1 2 1 2 15 1 1 1 2 2 1 2 2 1 1 2 2 2 2 1 2 1 2 1 16 1 1 2 2 1 2 2 1 1 2 2 2 2 1 2 1 2 1 1 17 1 2 2 1 2 2 1 1 2 2 2 2 1 2 1 2 1 1 1 18 2 2 1 2 2 1 1 2 2 2 2 1 2 1 2 1 1 1 1 19 2 1 2 2 1 1 2 2 2 2 1 2 1 2 1 1 1 1 2 201221122221212111122列号 试验 号列 号 试验 号(13) L9 (34)(14) L18 (2×37)1 2 3 41 1 1 1 12 1 2 2 23 1 3 3 34 2 1 2 35 2 2 3 16 2 3 1 27 3 1 3 28 3 2 1 39 3 3 2 11 2 3 4 5 6 7 81 1 1 1 1 1 1 1 12 1 1 2 2 2 2 2 23 1 1 3 3 3 3 3 34 1 2 1 1 2 2 3 35 1 2 2 2 3 3 1 16 1 2 3 3 1 1 2 27 1 3 1 2 1 3 2 38 1 3 2 3 2 1 3 19 1 3 3 1 3 2 1 210 2 1 1 3 3 2 2 111 2 1 2 1 1 3 3 212 2 1 3 2 2 1 1 313 2 2 1 2 3 1 3 214 2 2 2 3 1 2 1 315 2 2 3 1 2 3 2 116 2 3 1 3 2 3 1 217 2 3 2 1 3 1 2 318 2 3 3 2 1 2 3 1列号试验号列号试验号(15) L27 (313)L27 (313)表头设计1 2 3 4 5 6 73 A B (A×B)1(A×B)2 C (A×C)1(A×C)24 A B (A×B)1(C×D)2(A×B)2 C(A×C)1(B×D)2(A×C)28 9 10 11 12 13 3 (B×C)1 D (A×D)1(B×C)2(B×D)1(C×D)14(B×C)1(A×D)2(A×D)1(B×C)21 2 3 4 5 6 7 8 9 10 11 12 131 1 1 1 1 1 1 1 1 1 1 1 1 12 1 1 1 1 2 2 2 2 2 2 2 2 23 1 1 1 1 3 3 3 3 3 3 3 3 34 1 2 2 2 1 1 1 2 2 2 3 3 35 1 2 2 2 2 2 2 3 3 3 1 1 16 1 2 2 2 3 3 3 1 1 1 2 2 27 1 3 3 3 1 1 1 3 3 3 2 2 28 1 3 3 3 2 2 2 1 1 1 3 3 39 1 3 3 3 3 3 3 2 2 2 1 1 110 2 1 1 3 1 2 3 1 2 3 1 2 311 2 1 2 3 2 3 1 2 3 1 2 3 112 2 1 3 3 3 1 2 3 1 2 3 1 213 2 2 1 1 1 2 3 2 3 1 3 1 214 2 2 2 1 2 3 1 3 1 2 1 2 315 2 2 3 1 3 1 2 1 2 3 2 3 116 2 3 1 2 1 2 3 3 1 2 2 3 117 2 3 2 2 2 3 1 1 2 3 3 1 218 2 3 3 2 3 1 2 2 3 1 1 2 319 3 1 3 2 1 3 2 1 3 2 1 3 220 3 1 3 2 2 1 3 2 1 3 2 1 321 3 1 3 2 3 2 1 3 2 1 3 2 122 3 2 1 3 1 3 2 2 1 3 3 2 123 3 2 1 3 2 1 3 3 2 1 1 3 224 3 2 1 3 3 2 1 1 3 2 2 1 325 3 3 2 1 1 3 2 3 2 1 2 1 326 3 3 2 1 2 1 3 1 3 2 3 2 127 3 3 2 1 3 2 1 2 1 3 1 3 2列号试验号列号因子数列号因子数L27 (313)二列间的交互作用表1 2 3 4 5 6 7 8 9 10 11 12 13(1)3 2 2 6 5 5 9 8 8 12 11 114 4 3 7 7 6 10 10 9 13 13 12 (2)1 1 8 9 10 5 6 7 5 6 74 3 11 12 13 11 12 13 8 9 10(3)1 9 10 8 7 5 6 6 7 52 13 11 12 12 13 11 10 8 9(4)10 8 9 6 7 5 7 5 612 13 11 13 11 12 9 10 8(5)1 1234 2 4 37 6 11 13 12 8 10 9(6)1 423 3 2 45 13 12 11 10 9 8(7)3 4 2 4 3 212 11 13 9 8 10(8)1 123 410 9 5 7 6(9)1 42 38 7 6 5(10)3 4 26 5 7(11)1 113 12(12)1111 2 3 4 5 6 1 1 1 1 1 1 1 2 1 2 2 2 2 2 3 1 3 3 3 3 3 4 1 4 4 4 4 4 5 1 5 5 5 5 5 6 2 1 2 3 4 5 7 2 2 3 4 5 1 8 2 3 4 5 1 2 9 2 4 5 1 2 3 10 2 5 1 2 3 4 11 3 1 3 5 2 4 12 3 2 4 1 3 5 13 3 3 5 2 4 1 14 3 4 1 3 5 2 15 3 5 2 4 1 3 16 4 1 4 2 5 3 17 4 2 5 3 1 4 18 4 3 1 4 2 5 19 4 4 2 5 3 1 20 4 5 3 1 4 2 21 5 1 5 4 3 2 22 5 2 1 5 4 3 23 5 3 2 1 5 4 24 5 4 3 2 1 5 25554321列 号 试 验 号31122121122112122130122121122112122129122121121221211228122121121221211227 122112212112211226 1 22112212112211225 1 2 2 112211221122124 1 2 2 1 12211221122123 1 2 1 2 2 1 212121121222 1 2 1 2 2 1 2 12121121221 1 2 1 2 2 1 2 1 1212212120 1 2 1 2 2 1 2 1 1 2 12212119 1 2 1 2 1 2 1 2 2 1 2 1 212118 1 2 1 2 1 2 1 2 2 1 2 1 2 12117 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 16 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 15 1 1 2 2 2 2 1 1 2 2 1 1 1 1 2 2 14 1 1 2 2 2 2 1 1 2 2 1 1 1 1 2 2 13 1 1 2 2 2 2 1 1 1 1 2 2 1 1 2 2 12 1 1 2 2 2 2 1 1 1 1 2 2 1 1 2 2 11 1 1 2 2 1 1 2 2 2 2 1 1 2 2 1 1 10 1122112222112211 9 11221122112211228 1 1 2 2 1 1 2 2 1 1 2 2 1 1 2 2 7 1 1 1 1 2 2 2 2 2 2 2 2 1 1 1 1 6 1 1 1 1 2 2 2 2 2 2 2 2 1 1 1 1 5 1 1 1 1 2 2 2 2 1 1 1 1 2 2 2 2 4 1 1 1 1 2 2 2 2 1 1 1 1 2 2 2 2 3 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 21 1 1 1 1 1 1 12 2 2 2 2 2 2 211111111111111111列号试验号12345678910111213141516。
第五章 正交试验设计

0.18
0.30 0.50 0.80
C A B
优方案
C1A3B1
隶属度计算方法:
指标隶属度 指标值 - 指标最小值 指标最大值- 指标最小值
若两个指标的重要性不一样,取代度和酯化率 的权重分别为0.4和0.6,每号试验的综合分数 =取代度隶属度×0.4+酯化率隶属度×0.6,满 分为1.00。
2
3 4 5
1
1 2 2
2
3 1 2
2
3 2 3
2
3 3 1
2.18
2.45 2.70 2.49
40.36
54.31 41.09 56.29
0.00
0.35 0.67 0.40
0.00
0.55 0.03 0.63
0.00
0.47 0.29 0.54
6
7 8 9 K1 K2 K3 极差R 因素主次
2
3 3 3 1.47 1.01 1.60 0.59
5.1.3 正交试验设计的基本步骤
(1)明确试验目的,确定评价指标
任何一个试验都是为了解决某一个(或某些)问题,或为 了得到某些结论而进行的,所以任何一个正交试验都应该 有一个明确的目的,这是正交试验设计的基础。 挑选的因素不易过多,一般以3~7个为宜; 确定因素的水平数时,一般重要的因素可多取一些水平, 各水平的数值应适当拉开,以利于试验结果的分析。当因 素的水平数相等时,可方便试验数据处理。
第五章 正交试验设计
任课教师:王凤花 现代农业工程学院
第五章 正交试验设计
5.1 概述 5.2 正交试验设计结果的直观分析法 5.3 正交试验设计结果的方差分析法 5.4 本章习题
正交试验设计常用正交表分析
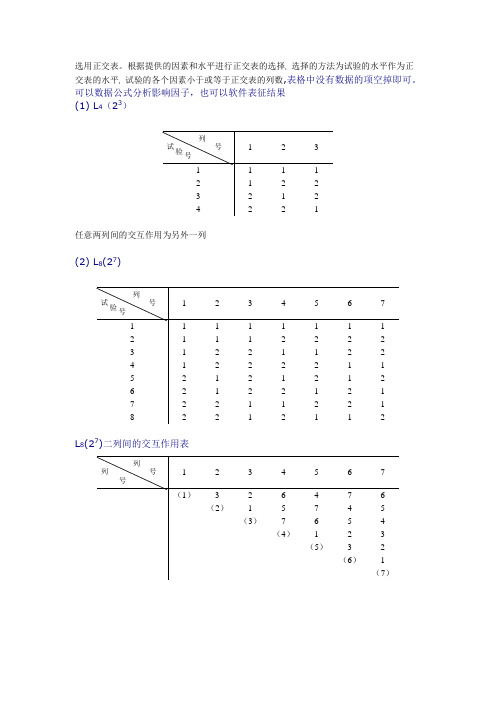
选用正交表。
根据提供的因素和水平进行正交表的选择, 选择的方法为试验的水平作为正 交表的水平, 试验的各个因素小于或等于正交表的列数,表格中没有数据的项空掉即可。
可以数据公式分析影响因子,也可以软件表征结果 (1) L 4(23)任意两列间的交互作用为另外一列(2) L 8(27)L 8(27)二列间的交互作用表1 2 3 1 1 1 1 2 1 2 2 3 2 1 2 4 2211 2 3 4 5 6 7 1 1 1 1 1 1 1 1 2 1 1 1 2 2 2 2 3 1 2 2 1 1 2 2 4 1 2 2 2 2 1 1 5 2 1 2 1 2 1 2 6 2 1 2 2 1 2 1 7 2 2 1 1 2 2 1 822121121 2 3 4 5 6 7 (1) 3 2 6 4 7 6 (2) 1 5 7 4 5 (3) 7 6 5 4 (4) 1 2 3 (5) 3 2 (6) 1(7)列号 试验 号 列号试验 号列号列号L 8(27)表头设计1 2 3 4 5 6 7 3 A B A ×B C A ×C B ×C 4 A B A ×B C ×D C A ×C B ×D B ×C A ×D D 4 A B C ×D A ×B C B ×D A ×C D B ×C A ×D 5 A D ×EB C ×DA ×BC ×EC B ×DA ×CB ×ED A ×E B ×CE A ×D(3) L 8(4×24)L 8(4×24)表头设计1 2 3 4 5 2 A B (A ×B)1 (A ×B)2(A ×B)33 A B C4 A B C D 5ABCDE1 2 3 4 5 1 1 1 1 1 1 2 1 2 2 2 2 3 2 1 1 2 2 4 2 2 2 1 1 5 3 1 2 1 2 6 3 2 1 2 1 7 4 1 2 2 1 842112列号 因 子 数列号试 验号列号因 子数(4) L 12 (211)(5) L 16 (215)1 2 3 4 5 6 7 8 9 10 11 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 2 2 2 2 2 2 3 1 1 2 2 2 1 1 1 2 2 2 4 1 2 1 2 2 1 2 2 1 1 2 5 1 2 2 1 2 2 1 2 1 2 1 6 1 2 2 2 1 2 2 1 2 1 1 7 2 1 2 2 1 1 2 2 1 2 1 8 2 1 2 1 2 2 2 1 1 1 2 9 2 1 1 2 2 2 1 2 2 1 1 10 2 2 2 1 1 1 1 2 2 1 2 11 2 2 1 2 1 2 1 1 1 2 2 12221121212211 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 3 1 1 1 2 2 2 2 1 1 1 1 2 2 2 2 4 1 1 1 2 2 2 2 2 2 2 2 1 1 1 1 5 1 2 2 1 1 2 2 1 1 2 2 1 1 2 2 6 1 2 2 1 1 2 2 2 2 1 1 2 2 1 1 7 1 2 2 2 2 1 1 1 1 2 2 2 2 1 1 8 1 2 2 2 2 1 1 2 2 1 1 1 1 2 2 9 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 10 2 1 2 1 2 1 2 2 1 2 1 2 1 2 1 11 2 1 2 2 1 2 1 1 2 1 2 2 1 2 1 12 2 1 2 2 1 2 1 2 1 2 1 1 2 1 2 13 2 2 1 1 2 2 1 1 2 2 1 1 2 2 1 14 2 2 1 1 2 2 1 2 1 1 2 2 1 1 2 15 2 2 1 2 1 1 2 1 2 2 1 2 1 1 2 16221211221121221列号试 验号 列号试 验 号L16(215)二列间的交互作用表1 2 3 4 5 6 7 8 9 10 11 12 13 14 15(1) 3 2 5 4 7 6 9 8 11 10 13 12 15 14(2) 1 6 4 5 10 11 8 9 14 15 12 13(3) 7 6 5 4 11 10 9 8 15 14 13 12(4) 1 2 3 12 13 14 15 8 9 10 11(5) 3 2 13 12 15 14 9 8 11 10(6) 1 14 15 12 13 10 11 8 9(7) 15 14 13 12 11 10 9 8(8) 1 2 3 4 5 6 7(9) 3 2 5 4 7 6(10) 1 6 7 4 5(11) 7 6 5 4(12) 1 2 3(13) 3 2(14) 1L 16(215)表头设计15EC ×E B ×FC ×E B ×F A ×GC ×E B ×F A ×GD ×H14 A ×EGG13 B ×E F F F 12 C ×D C ×D C ×D A ×FC ×D A ×F A ×GC ×D A ×F A ×GE ×H11 C ×E EEE10 B ×D B ×D B ×D A ×EB ×D A ×EC ×GB ×D A ×EC ×G F ×H9 A ×D A ×D A ×D B ×E C ×FA ×DB ×EC ×F A ×D B ×E C ×FG ×H 8 D D D D D7 D ×E H 6 B ×C B ×C B ×C E ×F B ×C E ×F D ×G B ×C E ×F D ×G A ×H5 A ×C A ×C A ×C D ×F A ×C D ×F E ×G A ×C D ×F E ×G B ×H 4 C C C C C 3A ×B A ×B A ×B D ×E A ×B D ×E F ×G A ×B D ×E F ×GC ×H2 B B BBB1 A A A A A 列号 因子数4 5 6 7 8(6) L 16 (4×212)L 16 (4×212)表头设计1 2 3 4 5 6 7 3 A B (A ×B)1 (A ×B)2 (A ×B)3 C (A ×C)1 4 A B (A ×B)1 C ×D (A ×B)2 (A ×B)3 C (A ×C)1 B ×D 5A B (A ×B)1 C ×D (A ×B)2 C ×E (A ×B)3 C (A ×C)1 B ×D8 9 10 11 12 13 3 (A ×C)2 (A ×C)3 B ×C 4 (A ×C)2 (A ×C)3 B ×C (A ×D)1 D (A ×D)3 (A ×D)2 5 (A ×C)2 B ×E(A ×C)3B ×C (A ×D)1 (A ×E)2D (A ×E)3E (A ×D)3(A ×E)1 (A ×D)2(7) L 16 (42×29)1 2 3 4 5 6 7 8 9 10 11 12 13 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 2 2 2 2 2 2 2 2 3 1 2 2 2 2 1 1 1 1 2 2 2 2 4 1 2 2 2 2 2 2 2 2 1 1 1 1 5 2 1 1 2 2 1 1 2 2 1 1 2 2 6 2 1 1 2 2 2 2 1 1 2 2 1 1 7 2 2 2 1 1 1 1 2 2 2 2 1 1 8 2 2 2 1 1 2 2 1 1 1 1 2 2 9 3 1 2 1 2 1 2 1 2 1 2 1 2 10 3 1 2 1 2 2 1 2 1 2 1 2 1 11 3 2 1 2 1 1 2 1 2 2 1 2 1 12 3 2 1 2 1 2 1 2 1 1 2 1 2 13 4 1 2 2 1 1 2 2 1 1 2 2 1 14 4 1 2 2 1 2 1 1 2 2 1 1 2 15 4 2 1 1 2 1 2 2 1 2 1 1 2 164211221121221列号试 验 号列 号因 子数列号 因 子 数(8) L 16 (43×26)(9) L 16 (44×23)1 2 3 4 5 6 7 8 9 10 11 1 1 1 1 1 1 1 1 1 1 1 1 2 1 2 1 1 1 2 2 2 2 2 2 3 1 3 2 2 2 1 1 1 2 2 2 4 1 4 2 2 2 2 2 2 1 1 1 5 2 1 1 2 2 1 2 2 1 2 2 6 2 2 1 2 2 2 1 1 2 1 1 7 2 3 2 1 1 1 2 2 2 1 1 8 2 4 2 1 1 2 1 1 1 2 2 9 3 1 2 1 2 2 1 2 2 1 2 10 3 2 2 1 2 1 2 1 1 2 1 11 3 3 1 2 1 2 1 2 1 2 1 12 3 4 1 2 1 1 2 1 2 1 2 13 4 1 2 2 1 2 2 1 2 2 1 14 4 2 2 2 1 1 1 2 1 1 2 15 4 3 1 1 2 2 2 1 1 1 2 16441121122211 2 3 4 5 6 7 8 9 1 1 1 1 1 1 1 1 1 1 2 1 2 2 1 1 2 2 2 2 3 1 3 3 2 2 1 1 2 2 4 1 4 4 2 2 2 2 1 1 5 2 1 2 2 2 1 2 1 2 6 2 2 1 2 2 2 1 2 1 7 2 3 4 1 1 1 2 2 1 8 2 4 3 1 1 2 1 1 2 9 3 1 3 1 2 2 2 2 1 10 3 2 4 1 2 1 1 1 2 11 3 3 1 2 1 2 2 1 2 12 3 4 2 2 1 1 1 2 1 13 4 1 4 2 1 2 1 2 2 14 4 2 3 2 1 1 2 1 1 15 4 3 2 1 2 2 1 1 1 16441121222列号试 验号 列号试 验 号(10) L16 (45)1 2 3 4 5 6 71 1 1 1 1 1 1 12 1 2 2 2 1 2 23 1 3 3 3 2 1 24 1 4 4 4 2 2 15 2 1 2 3 2 2 16 2 2 1 4 2 1 27 2 3 4 1 1 2 28 2 4 3 2 1 1 19 3 1 3 4 1 2 210 3 2 4 3 1 1 111 3 3 1 2 2 2 112 3 4 2 1 2 1 213 4 1 4 2 2 1 214 4 2 3 1 2 2 115 4 3 2 4 1 1 116 4 4 1 3 1 2 21 2 3 4 51 1 1 1 1 12 1 2 2 2 23 1 3 3 3 34 1 4 4 4 45 2 1 2 3 46 2 2 1 4 37 2 3 4 1 28 2 4 3 2 19 3 1 3 4 210 3 2 4 3 111 3 3 1 2 412 3 4 2 1 313 4 1 4 2 314 4 2 3 1 415 4 3 2 4 116 4 4 1 3 2列号试验号列号试验号(11) L 16 (8×28)(12) L 20 (219)1 2 3 4 5 6 7 8 9 1 11 1 1 1 1 1 1 12 1 2 2 2 2 2 2 2 23 2 1 1 1 1 2 2 2 24 2 2 2 2 2 1 1 1 15 3 1 1 2 2 1 1 2 26 3 2 2 1 1 2 2 1 17 4 1 1 2 2 2 2 1 18 4 2 2 1 1 1 1 2 29 5 1 2 1 2 1 2 1 2 10 5 2 1 2 1 2 1 2 1 11 6 1 2 1 2 2 1 2 1 12 6 2 1 2 1 1 2 1 2 13 7 1 2 2 1 1 2 2 1 14 7 2 1 1 2 2 1 1 2 15 8 1 2 2 1 2 1 1 2 168211212211 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 1 1 2 2 2 2 1 2 1 2 1 1 1 1 2 2 1 3 2 1 1 2 2 2 2 1 2 1 2 1 1 1 1 2 2 1 2 4 1 1 2 2 2 2 1 2 1 2 1 1 1 1 2 2 1 2 2 5 1 2 2 2 2 1 2 1 2 1 1 1 1 2 2 1 2 2 1 6 2 2 2 2 1 2 1 2 1 1 1 1 2 2 1 2 2 1 1 7 2 2 2 1 2 1 2 1 1 1 1 2 2 1 2 2 1 1 2 8 2 2 1 2 1 2 1 1 1 1 2 2 1 2 2 1 1 2 2 9 2 1 2 1 2 1 1 1 1 2 2 1 2 2 1 1 2 2 2 10 1 2 1 2 1 1 1 1 2 2 1 2 2 1 1 2 2 2 2 11 2 1 2 1 1 1 1 2 2 1 2 2 1 1 2 2 2 2 1 12 1 2 1 1 1 1 2 2 1 2 2 1 1 2 2 2 2 1 2 13 2 1 1 1 1 2 2 1 2 2 1 1 1 2 2 2 1 2 1 14 1 1 1 1 2 2 1 2 2 1 1 2 2 2 2 1 2 1 2 15 1 1 1 2 2 1 2 2 1 1 2 2 2 2 1 2 1 2 1 16 1 1 2 2 1 2 2 1 1 2 2 2 2 1 2 1 2 1 1 17 1 2 2 1 2 2 1 1 2 2 2 2 1 2 1 2 1 1 1 18 2 2 1 2 2 1 1 2 2 2 2 1 2 1 2 1 1 1 1 19 2 1 2 2 1 1 2 2 2 2 1 2 1 2 1 1 1 1 2 201221122221212111122列号 试验 号列 号 试验 号(13) L9 (34)(14) L18 (2×37)1 2 3 41 1 1 1 12 1 2 2 23 1 3 3 34 2 1 2 35 2 2 3 16 2 3 1 27 3 1 3 28 3 2 1 39 3 3 2 11 2 3 4 5 6 7 81 1 1 1 1 1 1 1 12 1 1 2 2 2 2 2 23 1 1 3 3 3 3 3 34 1 2 1 1 2 2 3 35 1 2 2 2 3 3 1 16 1 2 3 3 1 1 2 27 1 3 1 2 1 3 2 38 1 3 2 3 2 1 3 19 1 3 3 1 3 2 1 210 2 1 1 3 3 2 2 111 2 1 2 1 1 3 3 212 2 1 3 2 2 1 1 313 2 2 1 2 3 1 3 214 2 2 2 3 1 2 1 315 2 2 3 1 2 3 2 116 2 3 1 3 2 3 1 217 2 3 2 1 3 1 2 318 2 3 3 2 1 2 3 1列号试验号列号试验号(15) L27 (313)L27 (313)表头设计1 2 3 4 5 6 73 A B (A×B)1(A×B)2 C (A×C)1(A×C)24 A B (A×B)1(C×D)2(A×B)2 C(A×C)1(B×D)2(A×C)28 9 10 11 12 13 3 (B×C)1 D (A×D)1(B×C)2(B×D)1(C×D)14(B×C)1(A×D)2(A×D)1(B×C)21 2 3 4 5 6 7 8 9 10 11 12 131 1 1 1 1 1 1 1 1 1 1 1 1 12 1 1 1 1 2 2 2 2 2 2 2 2 23 1 1 1 1 3 3 3 3 3 3 3 3 34 1 2 2 2 1 1 1 2 2 2 3 3 35 1 2 2 2 2 2 2 3 3 3 1 1 16 1 2 2 2 3 3 3 1 1 1 2 2 27 1 3 3 3 1 1 1 3 3 3 2 2 28 1 3 3 3 2 2 2 1 1 1 3 3 39 1 3 3 3 3 3 3 2 2 2 1 1 110 2 1 1 3 1 2 3 1 2 3 1 2 311 2 1 2 3 2 3 1 2 3 1 2 3 112 2 1 3 3 3 1 2 3 1 2 3 1 213 2 2 1 1 1 2 3 2 3 1 3 1 214 2 2 2 1 2 3 1 3 1 2 1 2 315 2 2 3 1 3 1 2 1 2 3 2 3 116 2 3 1 2 1 2 3 3 1 2 2 3 117 2 3 2 2 2 3 1 1 2 3 3 1 218 2 3 3 2 3 1 2 2 3 1 1 2 319 3 1 3 2 1 3 2 1 3 2 1 3 220 3 1 3 2 2 1 3 2 1 3 2 1 321 3 1 3 2 3 2 1 3 2 1 3 2 122 3 2 1 3 1 3 2 2 1 3 3 2 123 3 2 1 3 2 1 3 3 2 1 1 3 224 3 2 1 3 3 2 1 1 3 2 2 1 325 3 3 2 1 1 3 2 3 2 1 2 1 326 3 3 2 1 2 1 3 1 3 2 3 2 127 3 3 2 1 3 2 1 2 1 3 1 3 2列号试验号列号因子数列号因子数L27 (313)二列间的交互作用表1 2 3 4 5 6 7 8 9 10 11 12 13(1)3 2 2 6 5 5 9 8 8 12 11 114 4 3 7 7 6 10 10 9 13 13 12 (2)1 1 8 9 10 5 6 7 5 6 74 3 11 12 13 11 12 13 8 9 10(3)1 9 10 8 7 5 6 6 7 52 13 11 12 12 13 11 10 8 9(4)10 8 9 6 7 5 7 5 612 13 11 13 11 12 9 10 8(5)1 1234 2 4 37 6 11 13 12 8 10 9(6)1 423 3 2 45 13 12 11 10 9 8(7)3 4 2 4 3 212 11 13 9 8 10(8)1 123 410 9 5 7 6(9)1 42 38 7 6 5(10)3 4 26 5 7(11)1 113 12(12)1111 2 3 4 5 6 1 1 1 1 1 1 1 2 1 2 2 2 2 2 3 1 3 3 3 3 3 4 1 4 4 4 4 4 5 1 5 5 5 5 5 6 2 1 2 3 4 5 7 2 2 3 4 5 1 8 2 3 4 5 1 2 9 2 4 5 1 2 3 10 2 5 1 2 3 4 11 3 1 3 5 2 4 12 3 2 4 1 3 5 13 3 3 5 2 4 1 14 3 4 1 3 5 2 15 3 5 2 4 1 3 16 4 1 4 2 5 3 17 4 2 5 3 1 4 18 4 3 1 4 2 5 19 4 4 2 5 3 1 20 4 5 3 1 4 2 21 5 1 5 4 3 2 22 5 2 1 5 4 3 23 5 3 2 1 5 4 24 5 4 3 2 1 5 25554321列 号 试 验 号31122121122112122130122121122112122129122121121221211228122121121221211227 122112212112211226 1 22112212112211225 1 2 2 112211221122124 1 2 2 1 12211221122123 1 2 1 2 2 1 212121121222 1 2 1 2 2 1 2 12121121221 1 2 1 2 2 1 2 1 1212212120 1 2 1 2 2 1 2 1 1 2 12212119 1 2 1 2 1 2 1 2 2 1 2 1 212118 1 2 1 2 1 2 1 2 2 1 2 1 2 12117 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 16 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 15 1 1 2 2 2 2 1 1 2 2 1 1 1 1 2 2 14 1 1 2 2 2 2 1 1 2 2 1 1 1 1 2 2 13 1 1 2 2 2 2 1 1 1 1 2 2 1 1 2 2 12 1 1 2 2 2 2 1 1 1 1 2 2 1 1 2 2 11 1 1 2 2 1 1 2 2 2 2 1 1 2 2 1 1 10 1122112222112211 9 11221122112211228 1 1 2 2 1 1 2 2 1 1 2 2 1 1 2 2 7 1 1 1 1 2 2 2 2 2 2 2 2 1 1 1 1 6 1 1 1 1 2 2 2 2 2 2 2 2 1 1 1 1 5 1 1 1 1 2 2 2 2 1 1 1 1 2 2 2 2 4 1 1 1 1 2 2 2 2 1 1 1 1 2 2 2 2 3 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 21 1 1 1 1 1 1 12 2 2 2 2 2 2 211111111111111111列号试验号12345678910111213141516。
正交试验设计常用正交表分析

2
2
1
2
2
6
2
2
1
2
2
2
1
1
2
1
1
7
2
3
2
1
1
1
2
2
2
1
1
8
2
4
2
1
1
2
1
1
1
2
2
9
3
1
2
1
2
2
1
2
2
1
2
10
3
2
2
1
2
1
2
1
1
2
1
11
3
3
1
2
1
2
1
2
1
2
1
12
3
4
1
2
1
1
2
1
2
1
2
13
4
1
2
2
1
2
2
1
2
2
1
14
4
2
2
2
1
1
1
2
1
1
2
15
4
3
1
1
2
2
2
1
1
1
2
16
4
4
1
1
2
1
1
2
2
2
1
(8)L16(43×26)
11
8
9
14
15
12
13
(3)
7
6
5
4
11
正交试验设计常用的正交表

16
221211221 1 2 1 2 2 1
精彩文档
实用标准文案
L16(215)二列间的交互作用表
精彩文档
实用标准文案
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
(1) 3 2 5 4 7 6 9 8 11 10 13 12 15 14
(2) 1 6
4 5 10 11 8 9 14 15 12 13
B
(A×B)1 C×D
(A×B)2
(A×B)3
C
(A×C)1 B×D
B
(A×B)1 C×D
(A×B)2 C×E
(A×B)3
C
(A×C)1 B×D
9
10
11
12
13
3
(A×C)2 (A×C)3 B×C
4
(A×C)2
(A×C)3
B×C (A×D)1
D
(A×D)3 (A×D)2
5
(A×C)2 B×E
(A×C)3
1
1111111111111
2
1111122222222
3
1222211112222
4
1222222221111
5
2112211221122
6
2112222112211
7
2221111222211
8
2221122111122
9
3121212121212
10
3121221212121
11
3212112122121
1
2
3
4
5
6
7
列
列
号
号
(1) 3
正交设计表

正交设计高乃群S080660001因素水平溶剂浓度超声时间pH 料液比1 60% 15min 5 1:82 70% 20 6 1:103 80% 25 7 1:12因素实验号溶剂浓度A超声时间BPhC料液比D滴定原花青素值1 1 1 1 12 1 2 2 23 1 3 3 34 2 1 2 35 2 2 3 16 2 3 1 27 3 1 3 28 3 2 1 39 3 3 2 1均值1均值2均值3极差R提取次数趋势平缓,可直接确定为:1次,超声温度无法控制。
设为室温。
提取方法,单因素直接确定为:超声提取。
正交表是一整套规则的设计表格,L 为正交表的代号,n 为试验的次数,t为水平数,c 为列数,也就是可能安排最多的因素个数。
例如L9(34),它表示需作9次实验,最多可观察4 个因素,每个因素均为3 水平。
一个正交表中也可以各列的水平数不相等,我们称它为混合型正交表,如L8(4×24) ,此表的5 列中有1 列为4 水平,4 列为2水平。
根据正交表的数据结构看出,正交表是一个n 行c 列的表,其中第j 列由数码1,2,… Sj 组成,这些数码均各出现N/S 次,例如表11 中,第二列的数码个数为3,S=3 ,即由1、2、3 组成,各数码均出现N/3=9/3=3次。
正交表是一整套规则的设计表格,用。
L为正交表的代号,n为试验的次数,t为水平数,c为列数,也就是可能安排最多的因素个数。
例如L9(34),(表11),它表示需作9次实验,最多可观察4个因素,每个因素均为3水平。
一个正交表中也可以各列的水平数不相等,我们称它为混合型正交表,如L8(4×24) (表12),此表的5列中,有1列为4水平,4列为2水平。
根据正交表的数据结构看出,正交表是一个n行c列的表,其中第j列由数码1,2,… Sj 组成,这些数码均各出现N/S 次,例如表11中,第二列的数码个数为3,S=3 ,即由1、2、3组成,各数码均出现次。
第四章 正交试验设计

6.60 7.67 8.00
1.40
因素主次
优化方案 Ⅰ Ⅱ Ⅲ 葛根总 黄酮含 量/% k1 k2 k3 R 因素主次 优化方案 18.6 20.2 22.3 6.20 6.73 7.43 1.23 19.3 20.7 21.1 6.43 6.90 7.03 0.6
CAB
C3A2B2或C3A2B3 20.0 20.2 20.9 6.67 6.73 6.97 0.3 ACB A 3 C 3B 3 18.5 20.5 22.1 6.17 6.83 7.37 1.20
17
4.2 无交互作用的正交试验设计
Ⅰ Ⅱ Ⅲ 葛根素 含量/% k1 k2 k3 R 7.2 7.4 8.1 2.40 2.47 2.70 0.3 7.3 8.1 7.3 2.43 2.70 2.43 0.27 7.7 7.1 7.9 2.57 2.37 2.63 0.26 6.8 7.8 8.1 2.27 2.60 2.70 0.43
0.78 0.76 0.74 0.72 0.7 0.68 0.66 0.64 0.62 1 2 3 4 5
0.8
0.75
0.7
0.65
0.6
甲
乙
丙
13
4.2 无交互作用的正交试验设计
4.2.3多指标正交试验的结果分析
在多指标试验中,不同指标的重要程度往往不一样, 各因素对不同指标的影响程度也不完全相同,为了兼顾各 个指标、因素的取优,可以采用以下两种结果分析方法: 综合平衡法和综合评分法。
L16 (4 4 23 )
L16 (8 28 )
L18 (2 37 )
4.1.3 正交表的性质——正交性原理
1、分配均匀性:正交表中因素的每一水平出现的次数 相同。 2、搭配均匀性:正交表中两列有序数对(水平搭配) 出现的次数相同。 正是基于正交性原理,正交试验设计可以用少数次 分布十分均匀的试验来很好地代表全部试验。
正交试验常用表

正交试验常用表正交试验是一种常用的试验设计方法,用于研究多个因素对实验结果的影响。
在进行正交试验时,需要使用正交试验表来安排实验方案。
正交试验表是根据正交设计原理编制的一种表格,能够全面、均匀地考察各个因素对结果的影响,从而减少试验次数,提高试验效果。
正交试验表通常由因素列和水平列组成。
因素列是指需要研究的各个因素,如温度、压力、时间等,而水平列则是指每个因素的不同水平,如高、中、低。
通过在因素列和水平列中选择相应的因素和水平,可以建立适合实验的正交试验表。
正交试验表的编制有一定的规则和原则。
首先,正交试验表应该保证各个因素和水平之间的均衡性。
也就是说,每个因素的每个水平应该尽可能地出现在不同的试验中,以避免因素之间的相互影响。
其次,正交试验表应该考虑到可重复性。
也就是说,同一个试验应该能够进行多次,以验证结果的可信度。
最后,正交试验表还需要考虑到实验的实际可行性和经济性。
也就是说,试验的次数和条件应该在可接受范围内,以避免过多的资源浪费。
正交试验表的应用范围非常广泛。
在工业生产中,正交试验表可以用于选择最佳的工艺参数,优化生产工艺,提高产品质量和产量。
在科学研究中,正交试验表可以用于探究各个因素对研究结果的影响,从而提出新的理论或解释现象。
在市场调研中,正交试验表可以用于确定消费者对产品的喜好和需求,为产品开发提供依据。
正交试验表的使用需要注意一些问题。
首先,正交试验表只能用于研究定量因素,而不能用于研究定性因素。
其次,正交试验表只能提供各个因素对结果的主要影响,而不能提供因素之间的相互作用效应。
最后,正交试验表只能作为一种初步的试验设计方法,需要结合实际情况进行调整和改进。
总之,正交试验表是一种非常实用的试验设计工具,能够全面、均衡地考察各个因素对结果的影响。
在进行正交试验时,我们需要根据实际情况选择合适的正交试验表,并注意表格的均衡性、可重复性和可行性。
通过合理地利用正交试验表,我们可以减少试验次数,提高试验效果,从而为工业生产、科学研究和市场调研提供可靠的依据。
正交试验设计表

在这 9 个水平组合中, A 因素各水平下包括 了 B 、 C 因素的 3个水平,虽然搭配方式不同, 但B、C皆处于同等地位,当比较A因素不同水 平时,B因素不同水平的效应相互抵消,C因素 不同水平的效应也相互抵消。所以A因素3个水 平间具有综合可比性。同样, B 、 C 因素 3个水 平间亦具有综合可比性。
10-3 因素水平表
试验因素 水平 加水量 加酶量 (mL/100g) (mL/100g) A B 10 50 90 1 4 7 酶解温度 (℃) C 20 35 50 酶解时间 (h) D 1.5 2.5 3.5
1 2 3
(3) 选择合适的正交表
正交表的选择是正交试验设计的首要问题。确定了 因素及其水平后,根据因素、水平及需要考察的交互作 用的多少来选择合适的正交表。正交表的选择原则是在 能够安排下试验因素和交互作用的前提下,尽可能选用 较小的正交表,以减少试验次数。 一般情况下,试验因素的水平数应等于正交表中的 水平数;因素个数(包括交互作用)应不大于正交表的 列数;各因素及交互作用的自由度之和要小于所选正交
个水平为宜。对主要考察的试验因素,可以多取水平,但不宜过
多(≤6),否则试验次数骤增。因素的水平间距,应根据专业
知识和已有的资料,尽可能把水平值取在理想区域。
上一张 下一张 主 页 退 出
对本试验分析,影响山楂液化率的因素很多, 如山楂品种、山楂果肉的破碎度、果肉加水量、原 料pH 值、果胶酶种类、加酶量、酶解温度、酶解 时间等等。经全面考虑,最后确定果肉加水量、加 酶量、酶解温度和酶解时间为本试验的试验因素, 分别记作A、B、C和D,进行四因素正交试验,各 因素均取三个水平,因素水平表见表10-3所示。
例如,要考察增稠剂用量、pH值和杀菌温度对豆奶稳
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正交表来设计安排试验。
正交试验设计的基本特点是:用部分试验 来代替全面试验,通过对部分试验结果的分析, 了解全面试验的情况。
1.2 正交试验设计的基本原理
在试验安排中 ,每个因素在研究的范围内选几个 水平,就好比在选优区内打上网格 ,如果网上的每个 点都做试验,就是全面试验。如上例中,3个因素的选 优区可以用一个立方体表示(图10-1),3个因素各取 3个水平,把立方体划分成27个格点,反映在 图10-1 上就是立方体内的27个“.”。若27个网格点都试验, 就是全面试验,其试验方案如表10-1所示。
上一张 下一张 主 页 退 出
整齐可比是指每一个因素的各水平间
具有可比性。因为正交表中每一因素的任 一水平下都均衡地包含着另外因素的各个 水平 ,当比较某因素不同水平时,其它 因素的效应都彼此抵消。如在A、B、C 3个因素中,A因素的3个水平 A1、A2、 A3 条件下各有 B 、C 的 3个不同水平, 即:
上一张 下一张 主 页 退 出
1 正交试验设计的概念及原理
1.1 正交试验设计的基本概念
正交试验设计是利用正交表来安排与分 析多因素试验的一种设计方法。它是由试 验因素的全部水平组合中,挑选部分有代
表性的水平组合进行试验的,通过对这部
分试验结果的分析了解全面试验的情况,
找出最优的水平组合。
上一张 下一张 主 页 退 出
1.3.2.3 综合可比性
(1)任一列的各水平出现的次数相等;(2)任 两列间所有水平组合出现次数相等,使得任一因 素各水平的试验条件相同。这就保证了在每列因 素各水平的效果中,最大限度地排除了其他因素 的干扰。从而可以综合比较该因素不同水平对试 验指标的影响情况。
根据以上特性,我们用正交表安排的试验, 具有均衡分散和整齐可比的特点。 所谓均衡分散,是指用正交表挑选出来的 各因素水平组合在全部水平组合中的分布是均 匀的 。 由 图10-1可以看出,在立方体中 ,任 一平面内都包含 3 个“(· )”, 任一直线上都包 含1个“(· )” ,因此 ,这些点代表性强 ,能够 较好地反映全面试验的情况。
组合)来进行试验。图 10-1 中标有试验号的九
个“ (·)”,就是利用正交表 L9(34) 从 27个试验点
中挑选出来的9个试验点。即:
(1)A1B1C1 (2)A2B1C2 (3)A3B1C3
(4)A1B2C2
(7)A1B3C3
(5)A2B2C3
(8)A2B3C1
(6)A3B2C1
(9)A3B3C2
验点;在立方体的每条线上也恰有一个试验点。
9个试验点均衡地分布于整个立方体内 ,有很强
的代表性 , 能 够比较全面地反映选优区内的基本情 况。
上一张 下一张 主 页 退 出
1.3 正交表及其基本性质
1.3.1 正交表
由于正交设计安排试验和分析试验结果都要用正
交表,因此,我们先对正交表作一介绍。
表10-2是一张正交表,记号为L8(27),其中“L”
2、混合水平正交表
各列水平数不完全相同
的正交表称为混合水平正交表。如 L8(4×24)表中有一
列的水平数为 4 ,有 4 列水平数为 2 。也就是说该表可
以安排一个4水平因素和4个2水平因素。再如 L16(44×23),L16(4×212)等都混合水平正交表。
上一张 下一张 主 页 退 出
2
正交试验设计的基本程序
次;L9(34) 中 (1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2,
3), (3, 1), (3, 2), (3, 3)各出现1次。即每个因素的一个 水平与另一因素的各个水平所有可能组合次数相等, 表明任意两列各个数字之间的搭配是均匀的。
上一张 下一张 主 页
素自由度+交互作用自由度+误差自由度。
此 例有 4 个 3 水平因素,可以选用 L9(34) 或
表的总自由度,以便估计试验误差。若各因素及交互作
用的自由度之和等于所选正交表总自由度,则可采用有 重复正交试验来估计试验误差。
等水平正交表 La(bc)
因素个数,列数 正交设计
La(bc)
试验总次数,行数 因素水平数
正交表选择依据:
列:正交表的列数c≥因素所占列数+交
互作用所占列数+空列。
自由度:正交表的总自由度(a-1)≥因
试验结果极差分析
试验结果方差分析
绘 制 因 素 指 标 趋 势 图
计 算 K 值
计 算 k 值
计 算 极 差 R
计算各列偏差平方和、 自由度 列方差分析表, 进行F 检验 分析检验结果, 写出结论
优水平 优组合
因素主次顺序
结 论
实例:为提高山楂原料的利用率,研究酶法液化工艺 制造山楂原汁,拟通过正交试验来寻找酶法液化的最 佳工艺条件。
第十章 正交试验设计
对于单因素或两因素试验,因其因素少 ,试验 的设计 、实施与分析都比较简单 。但在实际 工作中 ,常常需要同时考察 3个或3个以上的 试验因素 ,若进行全面试验 ,则试验的规模 将很大 ,往往因试验条件的限制而难于实施 。 正交试验设计就是安排多因素试验 、寻求最优 水平组合 的一种高效率试验设计方法。
退 出
上一张 下一张 主 页
上述选择 ,保证了A因素的每个水平与B因素、C
因素的各个水平在试验中各搭配一次 。对于A、B、C 3个因素来说 , 是在27个全面试验点中选择9个试验 点 ,仅 是全面试验的 三分之一。 从图10-1中可以看到 ,9个试验点在选优区中分
布是均衡的,在立方体的每个平面上 ,都恰是3个试
上一张 下一张 主 页 退 出
正交表的三个基本性质中,正 交性是核心,是基础,代表性
和综合可比性是正交性的必然 结果
1.4
正交表的类别 1、等水平正交表
各列水平数相同的正交表
称为等水平正交表。如L4(23)、L8(27)、L12(211)等各列 中的水平为 2 ,称为 2 水平正交表; L9(34) 、 L27(313) 等 各列水平为3,称为3水平正交表。
正因为正交试验是用部分试验来代替全面
试验的,它不可能像全面试验那样对各因素效
应、交互作用一一分析;当交互作用存在时,
有可能出现交互作用的混杂。虽然正交试验设
计有上述不足,但它能通过部分试验找到最优
水平组合 ,因 而 很 受实际工作者青睐。
上一张 下一张 主 页 退 出
如对于上述3因素3水平试验,若不考虑交互作用, 可利用正交表 L9(34)安排,试验方案仅包含 9个水平组 合,就能反映试验方案包含 27个水平组合的全面试验 的情况,找出最佳的生产条件。
代表正交表;L右下角的数字“8”表示有8行 ,用这张 正交表安排试验包含8个处理(水平组合) ;括号内的底 数“2” 表示因素的水平数,括号内2的指数“7”表示 有7列 ,用这张正交表最多可以安排7个2水平因素。
上一张 下一张 主 页 退 出
表10-2
上一张 下一张 主 页
退 出
常用的正交表已由数学工作者制定出来,供进行 正交设计时选用。2水平正交表除L8(27)外,还有L4(23)、 L16(215) 等 ; 3 水 平 正 交 表 有 L9(34) 、 L27(213)…… 等 (详见附表14及有关参考书)。 1.3.2 正交表的基本性质
(2) 选因素、定水平,列因素水平表
根据专业知识、以往的研究结论和经验,从影响试验指标的
诸多因素中,通过因果分析筛选出需要考察的试验因素。一般确
定试验因素时,应以对试验指标影响大的因素、尚未考察过的因
素、尚未完全掌握其规律的因素为先。试验因素选定后,根据所
掌握的信息资料和相关知识,确定每个因素的水平,一般以2-4
2.1 试验方案设计
(1) 明确试验目的,确定试验指标
试验设计前必须明确试验目的,即本次试验要 对本试验而言,试验目的是为了提高山楂原料 解决什么问题。试验目的确定后,对试验结果如何衡 的利用率。所以可以以液化率{液化率=[(果肉重量 量,即需要确定出试验指标。试验指标可为定量指标, -液化后残渣重量)/果肉重量]×100%}为试验指 如强度、硬度、产量、出品率、成本等;也可为定性 标,来评价液化工艺条件的好坏。液化率越高,山 指标如颜色、口感、光泽等。一般为了便于试验结果 的分析,定性指标可按相关的标准打分或模糊数学处 楂原料利用率就越高。 理进行数量化,将定性指标定量化。
对于多因素试验,正交试验设计是 简单常用的一种试验设计方法,其设计 基本程序如图所示。正交试验设计的基 本程序包括试验方案设计及试验结果分 析两部分。
试验目的与要求
试验方案设计:
试验指标
选因素、定水平 因素、水平确定 选择合适正交表 表头设计 列试验方案 试验结果分析
试验结果分析:
进行试验,记录试验结果
退 出
1.3.2.2 代表性
一方面: (1)任一列的各水平都出现,使得部 分试验中包括了所有因素的所有水平; (2)任两列的所有水平组合都出现, 使任意两因素间的试验组合为全面试验。 另一方面:由于正交表的正交性,正交试验的试 验点必然均衡地分布在全面试验点中,具有很强 的代表性。因此,部分试验寻找的最优条件与全 面试验所找的最优条件,应有一致的趋势。
在这 9 个水平组合中, A 因素各水平下包括 了 B 、 C 因素的 3个水平,虽然搭配方式不同, 但B、C皆处于同等地位,当比较A因素不同水 平时,B因素不同水平的效应相互抵消,C因素 不同水平的效应也相互抵消。所以A因素3个水 平间具有综合可比性。同样, B 、 C 因素 3个水 平间亦具有综合可比性。
