2013届高考数学一轮复习 第27讲 正、余弦定理及应用精品学案
高三数学一轮复习精品教案1:正弦定理和余弦定理教学设计

4.6正弦定理和余弦定理1.正弦定理a sin A =b sin B =c sin C=2R ,其中R 是三角形外接圆的半径.由正弦定理可以变形: (1)a ∶b ∶c =sin_A ∶sin_B ∶sin_C ; (2)a =2R sin_A ,b =2R sin_B ,c =2R sin_C . 2.余弦定理a 2=b 2+c 2-2bc cos_A ,b 2=a 2+c 2-2ac cos_B ,c 2=a 2+b 2-2ab cos_C .余弦定理可以变形:cos A =b 2+c 2-a 22bc ,cos B =a 2+c 2-b 22ac ,cos C =a 2+b 2-c 22ab.3.三角形中常用的面积公式 (1)S =12ah (h 表示边a 上的高);(2)S =12bc sin A =12ac sin B =12ab sin C ;(3)S =12r (a +b +c )(r 为三角形的内切圆半径).1.由正弦定理解已知三角形的两边和其中一边的对角求另一边的对角时易忽视解的判断.2.在判断三角形形状时,等式两边一般不要约去公因式,应移项提取公因式,以免漏解.『试一试』1.如图,在△ABC 中,D 是边AC 上的点,且AB =AD,2AB =3BD ,BC =2BD ,则sin C 的值为________.『解析』设BD =1,则AB =AD =32,BC =2.在△ABD 中,解得sin A =223,在△ABC 中,由正弦定理AB sin C =BC sin A ,得sin C =66.『答案』662.(2013·扬州三模)如果满足∠ABC =60°,AB =8,AC =k 的△ABC 有两个,那么实数k 的取值范围是________.『解析』由条件得8sin 60°<k <8,从而k 的取值范围是(43,8). 『答案』(43,8)1.把握三角形中的边角关系在三角形中,大角对大边,大边对大角;大角的正弦值也较大,正弦值较大的角也较大,即在△ABC 中,A >B ⇔a >b ⇔sin A >sin B .2.选用正弦定理或余弦定理的原则如果式子中含有角的余弦或边的二次式,要考虑用余弦定理;如果遇到的式子中含有角的正弦或边的一次式时,则考虑用正弦定理;以上特征都不明显时,则要考虑两个定理都有可能用到.『练一练』1.在△ABC 中,a =32,b =23,cos C =13,则△ABC 的面积为________.『答案』432.设△ABC 的内角A ,B ,C 所对边的长分别为a ,b ,c .若b +c =2a ,3sin A =5sin B ,则角C =________.『解析』由3sin A =5sin B 可得3a =5b ,又b +c =2a ,所以可令a =5t (t >0),则b =3t ,c =7t ,可得cos C =a 2+b 2-c 22ab=5t2+3t 2-7t 22×5t ×3t=-12,故C =2π3.『答案』2π3考点一利用正弦、余弦定理解三角形『典例』 (2013·徐州摸底)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,已知a cos C -b cos C =c cos B -c cos A ,且C =120°.(1)求角A ; (2)若a =2,求c .『解析』 (1)由正弦定理及a cos C -b cos C =c cos B -c cos A 得sin A cos C -sin B cos C =sin C cos B -sin C cos A .所以sin(A +C )=sin(B +C ).因为A ,B ,C 是三角形的内角,所以A +C =B +C ,所以A =B . 又因为C =120°,所以A =30°.(2)由(1)知a =b =2,所以c 2=a 2+b 2-2ab cos C =4+4-2×2×2cos 120°=12,所以c =2 3.『备课札记』 『类题通法』1.应熟练掌握正、余弦定理及其变形.解三角形时,有时可用正弦定理,有时也可用余弦定理,应注意用哪一个定理更方便、简捷.2.已知两角和一边,该三角形是确定的,其解是唯一的;已知两边和一边的对角,该三角形具有不唯一性,通常根据三角函数值的有界性和大边对大角定理进行判断.『针对训练』(2013·南京、盐城一模)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c . (1)若cos ⎝⎛⎭⎫A +π6 =sin A ,求A 的值; (2)若cos A =14,4b =c ,求sin B 的值.『解析』(1)因为cos ⎝⎛⎭⎫A +π6=sin A , 即cos A cos π6-sin A sin π6=sin A ,所以32cos A =32sin A . 显然cos A ≠0,否则由cos A =0得sin A =0,与sin 2 A +cos 2 A =1矛盾,所以tan A =33. 因为0<A <π,所以A =π6.(2)因为cos A =14,4b =c ,根据余弦定理得a 2=b 2+c 2-2bc cos A =15b 2,所以a =15b .因为cos A =14,所以sin A =1-cos 2 A =154.由正弦定理得15b sin A =b sin B ,所以sin B =14. 考点二利用正弦、余弦定理判定三角形的形状『典例』 在△ABC 中,a ,b ,c 分别为内角A ,B ,C 的对边,且2a sin A =(2b -c )sin B +(2c -b )sin C .(1)求角A 的大小;(2)若sin B +sin C =3,试判断△ABC 的形状. 『解析』 (1)∵2a sin A =(2b -c )sin B +(2c -b )sin C ,得2a 2=(2b -c )b +(2c -b )c , 即bc =b 2+c 2-a 2, ∴cos A =b 2+c 2-a 22bc =12,∴A =60°.(2)∵A +B +C =180°, ∴B +C =180°-60°=120°. 由sin B +sin C =3, 得sin B +sin(120°-B )=3,∴sin B +sin 120°cos B -cos 120°sin B = 3. ∴32sin B +32cos B =3, 即sin(B +30°)=1.又∵0°<B <120°,30°<B +30°<150°, ∴B +30°=90°, 即B =60°. ∴A =B =C =60°, ∴△ABC 为正三角形.『备课札记』在本例条件下,若sin B ·sin C =sin 2A ,试判断△ABC 的形状. 『解析』由正弦定理,得bc =a 2, 又b 2+c 2=a 2+bc , ∴b 2+c 2=2bc .∴(b -c )2=0.即b =c ,又A =60°, ∴△ABC 是等边三角形. 『类题通法』判定三角形形状的两种常用途径(1)通过正弦定理和余弦定理,化边为角,利用三角变换得出三角形内角之间的关系进行判断.(2)利用正弦定理、余弦定理,化角为边,通过代数恒等变换,求出边与边之间的关系进行判断.提醒:在判断三角形形状时一定要注意解是否唯一,并注重挖掘隐含条件.另外,在变形过程中要注意角A ,B ,C 的范围对三角函数值的影响.『针对训练』(2014·镇江期末)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,满足b cos C +12c =a .(1)求角B ;(2)若a ,b ,c 成等比数列,判断△ABC 的形状.『解析』(1)法一:由正弦定理得sin B cos C +12sin C =sin A .而sin A =sin(B +C )=sin B cos C +cos B sin C . 故cos B sin C =12sin C .在△ABC 中,sin C ≠0,故cos B =12.因为0<B <π,所以B =π3.法二:由余弦定理得b ·a 2+b 2-c 22ab +12c =a .化简得a 2+b 2-c 2+ac =2a 2,即b 2-c 2+ac =a 2, 所以cos B =a 2+c 2-b 22ac =12.因为0<B <π,所以B =π3.(2)由题知b 2=ac .由(1)知b 2=a 2+c 2-ac ,所以a 2+c 2-2ac =0,即a =c , 所以a =b =c ,所以△ABC 是等边三角形.考点三与三角形面积有关的问题『典例』 (2013·苏州暑假调查)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若B =60°且cos(B +C )=-1114.(1)求cos C 的值;(2)若a =5,求△ABC 的面积.『解析』 (1)在△ABC 中,由cos(B +C )=-1114.得sin(B +C )=1-cos 2B +C =1-⎝⎛⎭⎫-11142=5314.又B =60°,所以cos C =cos 『(B +C )-B 』=cos(B +C )cos B +sin(B +C )sin B =-1114×12+5314×32=17.(2)因为cos C =17,C 为△ABC 的内角,sin(B +C )=5314,所以sin C =1-cos 2C = 1-⎝⎛⎭⎫172=437,sin A =sin(B +C )=5314.在△ABC 中,由正弦定理a sin A =c sin C 得55314=c 437, 所以c =8.又a =5,sin B =32, 所以△ABC 的面积为S =12ac sin B =12 ×5×8×32=10 3. 『备课札记』 『类题通法』三角形面积公式的应用原则(1)对于面积公式S =12ab sin C =12ac sin B =12bc sin A ,一般是已知哪一个角就使用哪一个公式.(2)与面积有关的问题,一般要用到正弦定理或余弦定理进行边和角的转化. 『针对训练』(2013·南通一调)在△ABC 中,A ,B ,C 所对的边分别是a ,b ,c ,且b cos B 是a cos C ,c cos A 的等差中项.(1)求B 的大小;(2)若a +c =10,b =2,求△ABC 的面积. 『解析』(1)由题意得a cos C +c cos A =2b cos B .由正弦定理得sin A cos C +sin C cos A =2sin B cos B ,即sin(A +C )=2sin B cos B . 因为A +C =π-B,0<B <π,所以sin(A +C )=sin B ≠0,所以cos B =12,所以B =π3.(2)由B =π3得a 2+c 2-b 22ac =12,即a +c2-2ac -b 22ac=12, 所以ac =2.所以S △ABC =12ac sin B =32.『课堂练通考点』1.在△ABC 中,a =1,c =2,B =60°,则b =________. 『解析』由余弦定理得b =12+22-2×1×2cos 60°= 3. 『答案』32.(2014·无锡调研)在△ABC 中,A =45°,C =105°,BC =2,则AC 的长度为________. 『解析』在△ABC 中,由A =45°,C =105°得B =30°.由正弦定理AC sin B =BC sin A 得AC 12=222,所以AC =1.『答案』13.(2014·镇江质检)在△ABC 中,sin A ∶sin B ∶sin C =2∶3∶4,则cos C =________. 『解析』由正弦定理a sin A =b sin B =csin C, 得sin A ∶sin B ∶sin C =a ∶b ∶c ,令a =2,b =3,c =4, 再利用余弦定理得cos C =-14.『答案』-144.(2013·山东高考改编)△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,若B =2A ,a =1,b =3,则c =________.『解析』由已知及正弦定理得1sin A =3sin B =3sin 2A =32sin A cos A ,所以cos A =32,A =30°.结合余弦定理得12=(3)2+c 2-2c ×3×32,整理得c 2-3c +2=0,解得c =1或c =2. 当c =1时,△ABC 为等腰三角形,A =C =30°,B =2A =60°,不满足内角和定理,故c =2.『答案』25.(2013·南通一调)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,tan C =sin A +sin Bcos A +cos B .(1)求角C 的大小;(2)若△ABC 的外接圆直径为1,求a 2+b 2的取值范围. 『解析』(1)因为tan C =sin A +sin Bcos A +cos B ,即sin C cos C =sin A +sin Bcos A +cos B. 所以sin C cos A +sin C cos B =cos C sin A +cos C sin B , 即sin C cos A -cos C sin A =cos C sin B -sin C cos B , 所以sin(C -A )=sin(B -C ).所以C -A =B -C 或C -A =π-(B -C )(不成立), 即2C =A +B ,所以C =π3.(2)由C =π3,设A =π3+α,B =π3-α,0<A <2π3,0<B <2π3,知-π3<α<π3.因为a =2R sin A =sin A ,b =2R sin B =sin B , 所以a 2+b 2=sin 2A +sin 2 B =1-cos 2A 2+1-cos 2B2=1-12⎣⎡⎦⎤cos ⎝⎛⎭⎫2π3+2α+cos ⎝⎛⎭⎫2π3-2α =1+12cos 2α.由-π3<α<π3知-2π3<2α<2π3,-12<cos 2α≤1,故34<a 2+b 2≤32.。
高三数学一轮复习26正余弦定理学案

高三数学一轮复习 26.正余弦定理学案【学习目标】掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题.预习案1.正弦定理asin A===2R 其中2R为△ABC外接圆直径.变式:a=,b=,c= .a∶b∶c=∶∶ .2.余弦定理a2=;b2=;c2=.变式:cos A=;cos B=;cos C= .sin2A=sin2B+sin2C-2sin B sin C cos A.3.解三角形(1)已知三边a、b、c.运用余弦定理可求三角A、B、C.(2)已知两边a、b及夹角C. 运用余弦定理可求第三边c(3)已知两边a、b及一边对角A. 先用正弦定理,求sin B:sin B=b sin A a.①A为锐角时,若a<b sin A,;若a=b sin A,;若b sin A<a<b,;若a≥b,.②A为直角或钝角时,若a≤b,;若a>b,.4.已知一边a及两角A,B(或B,C)用正弦定理,先求出一边,后求另一边.4.三角形常用面积公式 (1)S=12a·h a(h a表示a边上的高).(2)S=12ab sin C=12ac sin B=12bc sin A=abc4R. (3)S=12r(a+b+c)(r为内切圆半径).【预习自测】1.在锐角△ABC中,角A,B所对的边长分别为a,b.若2a sin B=3b,则角 A 等于( )A.π12B.π6C.π4D.π32.在△ABC中,∠ABC=π4,AB=2,BC=3,则sin∠BAC= ( )A.1010B.105C.31010D.553.在△ABC中,若a=3,b=3,∠A=π3,则∠C的大小为________.4.设△ABC的内角A,B,C所对的边分别为a,b,c.若(a+b-c)(a+b+c)=ab,则角C =________.5.△ABC 中,已知c =102,A =45°,在a 分别为20,102,2033,10和5的情况下,求相应的角C .探 究 案题型一:利用正余弦定理解斜三角形例1.(1)在△ABC 中,已知a =2,b =3,A =45°,求B ,C 及边c .(2)已知sin A ∶sin B ∶sin C =(3+1)∶(3-1)∶10,求最大角.拓展1:(1)在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c .若a sin B cos C +c sin B cos A =12b ,且a >b ,则∠B =________.(2)已知a ,b ,c 分别为△ABC 三个内角A ,B ,C 的对边,a cos C +3a sin C -b -c =0.①求A ; ②若a =2,△ABC 的面积为3,求b ,c .题型二:面积问题例2.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c .已知A =π4,b sin(π4+C )-c sin(π4+B )=a .(1)求证:B -C =π2; (2)若a =2,求△ABC 的面积.拓展2.△ABC的内角,A,B,C的对边分别为a,b,c,已知a=b cos C+c sin B.(1)求B; (2)若b=2,求△ABC面积的最大值.题型三:判断三角形形状例3;(1)设△ABC的内角A,B,C所对的边分别为a,b,c,若b cos C+c cos B=a sin A,则△ABC 的形状为 ( )A.锐角三角形B.直角三角形 C.钝角三角形 D.不确定(2)在△ABC中,已知a cos A=b cos B,则△ABC为 ( )A.等腰三角形 B.直角三角形 C.等腰三角形或直角三角形 D.等腰直角三角形拓展3. (1)在△ABC中,a,b,c分别表示三个内角A,B,C的对边,如果(a2+b2)sin(A-B)=(a2-b2)·sin(A+B),试判断该三角形的形状.(2)在△ABC中,A、B、C是三角形的三个内角,a、b、c是三个内角对应的三边,已知b2+c2=a2+bc. ①求角A的大小;②若sin B sin C=34,试判断△ABC的形状,并说明理由.题型四:解三角形的应用例4.在△ABC中,内角A,B,C所对的边分别为a,b,c,已知sin B(tan A+tan C)=tan A tan C.(1)求证:a,b,c成等比数列; (2)若a=1,c=2,求△ABC的面积S.拓展4. 在△ABC中,角A,B,C所对的边分别为a,b,c,已知cos C+(cos A-3sin A)cos B =0. (1)求角B的大小; (2)若a+c=1,求b的取值范围.我的学习总结:(1)我对知识的总结 . (2)我对数学思想及方法的总结。
高三数学一轮复习学案:正弦定理、余弦定理

高三数学一轮复习学案:正弦定理、余弦定理一、考试要求:了解利用向量知识推导正弦定理和余弦定理;掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题二、知识梳理: 1. 正弦定理: ____________________.强调几个问题:(1)正弦定理适合于任何三角形;(2)可以证明R Aa__sin =(R 为ABC ∆的外接圆半径);(3)每个等式可视为一个方程:知三求一; (4)公式的变形:①2sin ,2sin ,2sin a R A b R B c R C ===;②sin ,sin ,sin 222a b c A B C R R R ===;③sin sin sin ::::A B C a b c =.(5)三角形面积公式:=∆ABC S ____ ____=______ ___=_____ ___. (6)正弦定理的应用范围: ①已知两角和任一边,求其它两边和一角。
②已知两边和其中一边的对角,求另一边的对角。
2. 余弦定理: =2a _____________________;=2b ____________________; =2c _____________________.强调几个问题:(1)熟悉定理的结构,注意“平方”“夹角”“余弦”等;(2)知三求一;(3)当夹角为90 时,即三角形为直角三角形时即为勾股定理(特例);(4)变形:bc a c b A 2cos 222-+= acb c a B 2cos 222-+=ac c b a C 2cos 222-+=.(5)余弦定理的应用范围:①已知三边,求三个角;②已知两边和它们的夹角,求第三边和其他两个角.3. 解斜三角形(1).两角和任意一边,求其它两边和一角;(2).两边和其中一边对角,求另一边的对角,进而可求其它的边和角。
(见图示)已知a, b 和A, 用正弦定理求B 时的各种情况: ①若A 为锐角时:⎪⎪⎩⎪⎪⎨⎧≥<<=<)( b a ) ,( b a bsinA )( bsinA a sin 锐角一解一钝一锐二解直角一解无解A b a已知边a,b 和∠A有两个解仅有一个解无解CH=bsinA<a<b a=CH=bsinA a<CH=bsinA②若A 为直角或钝角时:⎩⎨⎧>≤)( b a 锐角一解无解b a三、基础检测:1. 在 中, ,则 等于( )A .B .C .D .2. 若 是 ( )A .等边三角形B .有一内角是30°C .等腰直角三角形D .有一内角是30°的等腰三角形 3. 在,面积,则BC 长为( )A .B .75C .51D .494.在 中,已知角 则角A 的值是( )A .15°B .75°C .105°D .75°或15°5. 中,sinB=23sin ,21=C ,则a :b :c 为( )A.1:3:2B.1:1:3C.1:2:3D.2:1:3或1:1:36. 如图,在△ABC 中,D 是边AC 上的点,且,2,2AB CD AB BC BD ===,则sin C 的值为A .3B .6C .3D .67.若的三个内角成等差数列,且最大边为最小边的2倍,则三内角之比为________。
高三数学一轮复习27正余弦定理应用举例学案
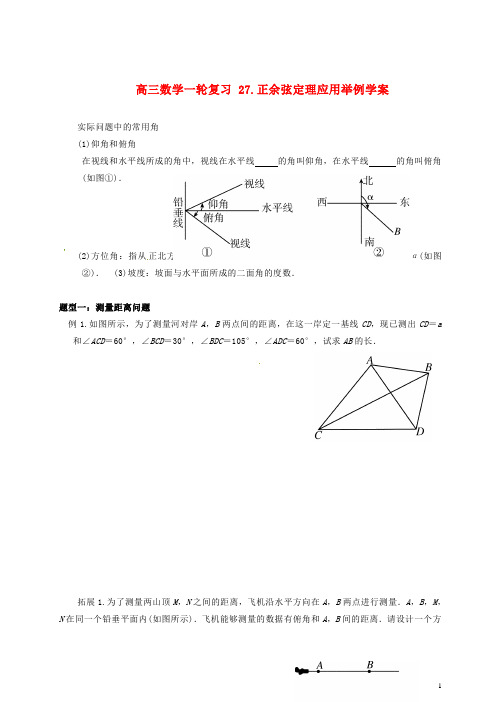
高三数学一轮复习 27.正余弦定理应用举例学案实际问题中的常用角(1)仰角和俯角在视线和水平线所成的角中,视线在水平线的角叫仰角,在水平线的角叫俯角(如图①).(2)方位角:指从正北方向顺时针转到目标方向线的水平角,如B点的方位角为α(如图②). (3)坡度:坡面与水平面所成的二面角的度数.题型一:测量距离问题例1.如图所示,为了测量河对岸A,B两点间的距离,在这一岸定一基线CD,现已测出CD=a 和∠ACD=60°,∠BCD=30°,∠BDC=105°,∠ADC=60°,试求AB的长.拓展1.为了测量两山顶M,N之间的距离,飞机沿水平方向在A,B两点进行测量.A,B,M,N在同一个铅垂平面内(如图所示).飞机能够测量的数据有俯角和A,B间的距离.请设计一个方案,包括:①指出需要测量的数据(用字母表示,并在图中标出);②用文字和公式写出计算M,N间的距离的步骤.题型二:测量高度问题例2. 某人在塔的正东沿着南偏西60°的方向前进40米后,望见塔在东北方向,若沿途测得塔顶的最大仰角为30°,求塔高.拓展2. 要测底部不能到达的电视塔AB的高度,在C点测得塔顶A的仰角是45°,在D点测得塔顶A的仰角是30°,并测得水平面上的∠BCD=120°,CD=40 m,求电视塔的高度.题型三:测量角度问题例3. 如图所示,A,B是海面上位于东西方向相距5(3+3) 海里的两个观测点.现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B 点相距20 3 海里的C点的救援船立即前往营救,其航行速度为30 海里/小时,该救援船到达D 点需要多长时间?拓展3. 如图所示,中国渔民在中国南海黄岩岛附近捕鱼作业,中国海监船在A地侦察发现,在南偏东60°方向的B地,有一艘某国军舰正以每小时13海里的速度向正西方向的C地行驶,企图抓捕正在C地捕鱼的中国渔民.此时,C地位于中国海监船的南偏东45°方向的10海里处,中国海监船以每小时30海里的速度赶往C地救援我国渔民,能不能及时赶到?(2≈1.41,3≈1.73,6≈2.45)我的学习总结:(1)我对知识的总结 . (2)我对数学思想及方法的总结。
高考数学一轮复习:正弦、余弦定理与解三角形

角,该三角形具有不唯一性,通常根据三角函数值的“有界性”和“大边对大
角”进行判断.
对点训练1(1)(2020福建福州三模,理15)在△ABC中,内角A,B,C的对边分别
为a,b,c,若2sin2A+cos B=1,则 − 的取值范围为
又因为 0<A<π,所以
π
A=3.
由余弦定理可得a2=b2+c2-bc,
因为sin A,sin B,sin C成等差数列,
所以2sin B=sin A+sin C,即2b=a+c,
即(2b-c)2=b2+c2-bc,可得b=c.
所以△ABC为等边三角形.
方案二:选条件②.
由 4S=√3(b2+c2-a2),可得 2bcsin A=2√3bccos A,所以 tan A=√3.
(1)利用正弦定理、余弦定理把已知条件转化为边边关系,通过因式分解、
配方等得出边的相应关系,从而判断三角形的形状.
(2)利用正弦定理、余弦定理把已知条件转化为内角的三角函数之间的关
系,通过三角恒等变换,得出内角的关系,从而判断出三角形的形状,此时要
注意应用A+B+C=π这个结论.
对点训练2设△ABC的内角A,B,C所对的边分别为a,b,c,若bcos C+ccos
1
(3)S=2r(a+b+c)(r
为内切圆半径).
A= .
4
2.正弦定理和余弦定理
在△ABC中,若角A,B,C所对的边分别是a,b,c,则
正弦定理
余弦定理
语言
2013高考数学教案和学案有答案

2013高考数学教案和学案(有答案)--第1章学案1第1章集合与常用逻辑用语学案1 集合的概念与运算导学目标: 1.能用自然语言、图形语言、集合语言(列举法或描述法)描述不同的具体问题.2.理解集合之间包含与相等的含义,能识别给定集合的子集.3.理解两个集合的并集与交集的含义,会求两个简单集合的并集与交集.4.理解在给定集合中一个子集的补集的含义,会求给定子集的补集.5.能使用Venn图表达集合的关系及运算.自主梳理12?表示. 3.集合的表示法:列举法、描述法、图示法、区间法. 4.集合间的基本关系对任意的x∈A,都有x∈B,则A?B(或B?A).若A?B,且在B中至少有一个元素x∈B,但x?A,则 A B(或B A).若A?B且B?A,则A=B. 5.集合的运算及性质设集合A,B,则A∩B={x|x∈A且x∈B},A∪B={x|x∈A 或x∈B}.设全集为S,则?SAA∩?=?,A∩B?AA∩B=A?A?B.A∪?=A,A∪B?A,A∪B?B, A∪B=B.A∩?UA=?;A∪?UA=U. 自我检测 1.(2011·无锡高三检测)下列集合表示同一集合的是________(填序号).①M={(3,2)},N={(2,3)};②M={(x,y)|x+y=1},N={y|x+y=1};③M={4,5},N={5,4};④M={1,2},N={(1,2)}.答案③ 2.(2009·辽宁改编)已知集合M={x|-3<x≤5},N={x|-5<x<5},则M∩N=________. 答案{x|-3<x<5}解析画数轴,找出两个区间的公共部分即得M∩N={x|-3<x<5}. 3.(2010·湖南)已知集合A={1,2,3},B={2,m,4},A∩B={2,3},则m=________. 答案 3解析∵A∩B={2,3},∴3∈B,∴m=3.224.(2010·常州五校联考)集合M={y|y=x-1,x∈R},集合N={x|y=-x,x∈R},则M∩N=________. 答案 [-1,3]解析∵y=x2-1≥-1,∴M=[-1,+∞).又∵y=9-x2,∴9-x2≥0.∴N=[-3,3].∴M∩N=[-1,3].5.已知集合A={1,3,a},B={1,a2-a+1},且B?A,则a=________. 答案-1或2解析由a2-a+1=3,∴a=-1或a=2,经检验符合.由a2-a+1=a,得a=1,但集合中有相同元素,舍去,故a=-1或2.探究点一集合的基本概念b例1 若a,b∈R,集合{1,a+b,a}={0,b},求b-a的值.a解题导引解决该类问题的基本方法为:利用集合中元素的特点,列出方程组求解,但解出后应注意检验,看所得结果是否符合元素的互异性.b解由{1,a+b,a}={0,b}可知a≠0,则只能a+b=0,则有以下对应法则:aa+b=0,a+b=0,??b?a=a,??b=1由①得???b=a,①或?b??a1.②??a=-1,?b=1,? 符合题意;②无解.∴b-a=2.变式迁移1 设集合A={1,a,b},B={a,a2,ab},且A =B,求实数a,b. 解由元素的互异性知,a≠1,b≠1,a≠0,又由A=B,22???a=1,?a=b,得?或?解得a=-1,b=0. ?ab=b,?ab =1,??探究点二集合间的关系例2 设集合M={x|x=5-4a+a2,a∈R},N={y|y=4b2+4b+2,b∈R},则M与N之间有什么关系?解题导引一般地,对于较为复杂的两个或两个以上的集合,要判断它们之间的关系,应先确定集合中元素的形式是数还是点或其他,属性如何.然后将所给集合化简整理,弄清每个集合中的元素个数或范围,再判断它们之间的关系.解集合M={x|x=5-4a+a2,a∈R}={x|x=(a-2)2+1,a∈R}={x|x≥1}, N={y|y=4b2+4b+2,b∈R}={y|y=(2b+1)2+1,b∈R}={y|y≥1}.∴M=N.2变式迁移2 设集合P={m|-1<m<0},Q={m|mx+4mx -4<0对任意实数x恒成立,且m∈R},则集合P与Q之间的关系为________.答案 P Q解析 P={m|-1<m<0},??m<0,Q:?或m=0.∴-1<m≤0. 2?Δ=16m+16m<0,?∴Q={m|-1<m≤0}.∴P Q.探究点三集合的运算例3 设全集是实数集R,A={x|2x2-7x+3≤0},B={x|x2+a<0}.(1)当a=-4时,求A∩B和A∪B;(2)若(?RA)∩B=B,求实数a的取值范围.解题导引解决含参数问题的集合运算,首先要理清题目要求,看清集合间存在的相互关系,注意分类讨论、数形结合思想的应用以及空集的特殊性.1解 (1)A={x≤x≤3}.2当a=-4时,B={x|-2<x<2},1∴A∩B={x≤x<2},2A∪B={x|-2<x≤3}.1(2)?RA={x|x<或x>3}.2当(?RA)∩B=B时,B??RA,即A∩B=?.①当B=?,即a≥0时,满足B??RA;②当B≠?,即a<0时,B={x|-a<x<a},11要使B??RA-a≤a<0.241综上可得,a的取值范围为a≥.4变式迁移 3 已知A={x||x-a|<4},B={x||x-2|>3}. (1)若a=1,求A∩B;(2)若A∪B=R,求实数a的取值范围.解 (1)当a=1时,A={x|-3<x<5}, B={x|x<-1或x>5}.∴A∩B={x|-3<x<-1}.(2)∵A={x|a-4<x<a+4},B={x|x<-1或x>5},且A∪B=R, ??a-4<-1∴??1<a<3. ?a+4>5?∴实数a的取值范围是(1,3).分类讨论思想在集合中的应用2例 (14分)(1)若集合P={x|x+x-6=0},S={x|ax+1=0},且S?P,求由a的可取值组成的集合;(2)若集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1},且B?A,求由m的可取值组成的集合.【答题模板】解 (1)P={-3,2}.当a=0时,S=?,满足S?P;[2分]1当a≠0时,方程ax+1=0的解为x,[4分]a11为满足S?P3=2,aa11即a=a.[6分]3211故所求集合为{0,}.[7分]32(2)当m+1>2m-1,即m<2时,B=?,满足B?A;[9分] 若B≠?,且满足B?A,如图所示,∴2≤m≤3.[13分]?m+1≤2m-1,?则?m+1≥-2,??2m-1≤5,?m≥2,?即?m≥-3,??m≤3,故m<2或2≤m≤3,即所求集合为{m|m≤3}.[14分]【突破思维障碍】在解决两个数集关系问题时,避免出错的一个有效手段即是合理运用数轴帮助分析与求解,另外,在解含有参数的不等式(或方程)时,要对参数进行讨论,分类时要遵循“不重不漏”的分类原则,然后对于每一类情况都要给出问题的解答.【易错点剖析】(1)容易忽略a=0时,S=?这种情况.(2)想当然认为m+1<2m-1忽略“>”或“=”两种情况.解答集合问题时应注意五点:1.注意集合中元素的性质——互异性的应用,解答时注意检验.2.注意描述法给出的集合的元素.如{y|y=2x},{x|y=2x},{(x,y)|y=2x}表示不同的集合.3.注意?的特殊性.在利用A?B解题时,应对A是否为?进行讨论. 4.注意数形结合思想的应用.在进行集合运算时要尽可能借助Venn图和数轴使抽象问题直观化,一般地,集合元素离散时用Venn图表示,元素连续时用数轴表示,同时注意端点的取舍.5.注意补集思想的应用.在解决A∩B≠?时,可以利用补集思想,先研究A∩B=?.的情况,然后取补集.(满分:90分)一、填空题(每小题6分,共48分) 1.(2010·北京改编)集合P={x∈Z|0≤x<3},M={x∈Z|x2≤9},则P∩M=________. 答案 {0,1,2}解析由题意知:P={0,1,2},M={-3,-2,-1,0,1,2,3},∴P∩M={0,1,2}. 2.(2011·南京模拟)设P、Q为两个非空集合,定义集合P+Q={a+b|a∈P,b∈Q}.若P={0,2,5},Q={1,2,6},则P+Q=________________. 答案{1,2,3,4,6,7,8,11}解析 P+Q={1,2,3,4,6,7,8,11}.3.满足{1}A?{1,2,3}的集合A的个数是________.答案 3解析 A={1}∪B,其中B为{2,3}的子集,且B非空,显然这样的集合A有3个,即A={1,2}或{1,3}或{1,2,3}. 4.(2010·天津改编)设集合A={x||x-a|<1,x∈R},B={x|1<x<5,x∈R}.若A∩B=?,则实数a 的取值范围是______________.答案 a≤0或a≥6解析由|x-a|<1得-1<x-a<1,即a-1<x<a+1.由图可知a+1≤1或a-1≥5,所以a≤0或a≥6. 5.设全集U是实数集R,2M={x|x2>4},N={x|≥1},则如图中阴影部分所表示的集合是________.x-1答案 {x|1<x≤2}解析题图中阴影部分可表示为(?UM)∩N,集合M为{x|x>2或x<-2},集合N为 {x|1<x≤3},由集合的运算,知(?UM)∩N={x|1<x≤2}. 6.(2011·泰州模拟)设集合A={1,2},则满足A∪B={1,2,3}的集合B的个数为________.答案 4解析由题意知B的元素至少含有3,因此集合B可能为{3}、{1,3}、{2,3}、{1,2,3}.*7.(2009·天津)设全集U=A∪B={x∈N|lg x<1},若A ∩(?UB)={m|m=2n+1,n=0,1,2,3,4},则集合B=______________. 答案 {2,4,6,8}*解析 A∪B={x∈N|lg x<1}={1,2,3,4,5,6,7,8,9},A ∩(?UB)={1,3,5,7,9},∴B={2,4,6,8}.28.(2010·江苏)设集合A={-1,1,3},B={a+2,a+4},A∩B={3},则实数a=____. 答案 12解析∵3∈B,由于a+4≥4,∴a+2=3,即a=1. 二、解答题(共42分)229.(14分)集合A={x|x+5x-6≤0},B={x|x+3x>0},求A∪B和A∩B. 解∵A={x|x2+5x-6≤0} ={x|-6≤x ≤1}.(3分)B={x|x2+3x>0}={x|x<-3或x>0}.(6分)如图所示,∴A∪B={x|-6≤x≤1}∪{x|x<-3或x>0}=R.(10分) A∩B={x|-6≤x≤1}∩{x|x<-3或x>0} ={x|-6≤x<-3,或0<x≤1}.(14分)110.(14分)(2011·南通模拟)已知集合A={x|0<ax+1≤5},集合B={x|<x≤2}.若2B?A,求实数a的取值范围.解当a=0时,显然B?A;(2分)当a<0时,若B?A,如图,41-,a2则(6分)1-,a???a≥-8,??1∴?∴-a<0;(8分) 12?a>-2.?当a>0时,如图,若B?A,1-,?-1a2则?4?a2, (11分)??a≤2,∴?∴0<a≤2.(13分) ?a≤2.?1综上知,当B?A时,-a≤2.(14分) 2x-5211.(14分)已知集合A={x|≤0},B={x|x-2x-m<0}, x+1(1)当m=3时,求A∩(?RB);(2)若A∩B={x|-1<x<4},求实数m的值.x-5解由≤0, x+1所以-1<x≤5,所以A={x|-1<x≤5}.(3分)(1)当m=3时,B={x|-1<x<3},则?RB={x|x≤-1或x≥3},(6分)所以A∩(?RB)={x|3≤x≤5}.(10分)(2)因为A={x|-1<x≤5},A∩B={x|-1<x<4},(12分)所以有42-2×4-m=0,解得m=8.此时B={x|-2<x<4},符合题意,故实数m的值为8.(14分)荐小学数学教案[1000字] 荐初二数学教案(800字) 荐生活中的数学教案[1000字] 荐人教版初一上数学教案(全册) [1500字]荐工程数学教案 (500字)。
第一轮复习单元讲座(人教版)--第27讲 正、余弦定理及应用

普通高中课程标准实验教科书—数学 [人教版]高三新数学第一轮复习教案(讲座27)—正、余弦定理及应用一.课标要求:(1)通过对任意三角形边长和角度关系的探索,掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题;(2)能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题。
二.命题走向对本讲内容的考察主要涉及三角形的边角转化、三角形形状的判断、三角形内三角函数的求值以及三角恒等式的证明问题,立体几何体的空间角以及解析几何中的有关角等问题。
今后高考的命题会以正弦定理、余弦定理为知识框架,以三角形为主要依托,结合实际应用问题考察正弦定理、余弦定理及应用。
题型一般为选择题、填空题,也可能是中、难度的解答题。
三.要点精讲1.直角三角形中各元素间的关系:如图,在△ABC 中,C =90°,AB =c ,AC =b ,BC =a 。
(1)三边之间的关系:a 2+b 2=c 2。
(勾股定理) (2)锐角之间的关系:A +B =90°; (3)边角之间的关系:(锐角三角函数定义)sin A =cos B =c a ,cos A =sin B =c b ,tan A =ba。
2.斜三角形中各元素间的关系:如图6-29,在△ABC 中,A 、B 、C 为其内角,a 、b 、c 分别表示A 、B 、C 的对边。
(1)三角形内角和:A +B +C =π。
(2)正弦定理:在一个三角形中,各边和它所对角的正弦的比相等。
R CcB b A a 2sin sin sin ===。
(R 为外接圆半径)(3)余弦定理:三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。
a 2=b 2+c 2-2bc cos A ;b 2=c 2+a 2-2ca cos B ;c 2=a 2+b 2-2ab cos C 。
3.三角形的面积公式:(1)△=21ah a =21bh b =21ch c (h a 、h b 、h c 分别表示a 、b 、c 上的高); (2)△=21ab sin C =21bc sin A =21ac sin B ;(3)△=)sin(2sin sin 2C B C B a +=)sin(2sin sin 2A C A C b +=)sin(2sin sin 2B A BA c +;(4)△=2R 2sin A sin B sin C 。
正弦定理和余弦定理 学案-高三数学一轮复习

正弦定理和余弦定理【考情分析】以利用正弦、余弦定理解三角形为主,常与三角函数的图象和性质、三角恒等变换、三角形中的几何计算交汇考查,加强数形结合思想的应用意识.题型多样,中档难度.【复习目标】1、能准确表达并会证明正弦定理、余弦定理.2、能正确选择正弦定理或余弦定理,求有关三角形的边和角的问题.3、能够应用定理及定理的变形,解决一些与三角形的计算有关的度量问题.【再现型题组】1、表达并证明正弦定理(可采用多种方法)2、表达并证明余弦定理(可采用多种方法)3、在△ABC 中. 3,4,2ππ===B A a ,那么b=________. 4、在△ABC 中. 10,2,3===BC AC AB 那么A cos =_______,=S 面积 . 【总结归纳】【稳固型题组】()角形唯一确定下列那些条件能使的三中,在变式,30,2: ==∆A b ABC (多项选择) 2.在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,假设cos cos a A b B =,请判断△ABC 的形状.4.如图,设B C 、两点在河的两岸,一测量者在B 所在的同侧河岸边选定一点A ,测出AB 的距离为100m ,105ABC ∠=︒,45CAB ∠=︒后,就可以计算出B C 、两点的距离为( )A. m C. m D. m【总结归纳】【提高型题组】例.设△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,且b sin A =3a cos B .〔1〕求角B 的大小;〔2〕假设b =3,sin C =2sin A ,求a ,c 的值.【总结归纳】【反应型题组】1.在ABC ∆中,假设2sin sin cos a A B b A +=,那么b a= 2.在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,ABC ∆的面积为4222c b a -+,那么c =〔〕3.在ABC ∆中,12,cos ,3sin 2sin 4a c A B ==-=,那么c =4.在ABC ∆中,内角,,A B C 的对边分别为,,a b c ,cos 2cos 2cos A C c a B b--=, 〔1〕求sin sin C A 的值; 〔2〕假设1cos ,24B b ==,求ABC ∆的面积S .5.在∆ABC 中,222+=a c b .〔1〕求B ∠ 的大小;〔2〕cos cos A C + 的最大值. 【课堂小结。
正弦定理和余弦定理知识点总结(学案)

求:(1)A 处与 D 处之间的距离; (2)灯塔 C 与 D 处之间的距离.
1.如图,从气球 A 上测得其正前下方的河流两岸 B,C 的俯角分别为 75°,30°,此时气
球的高度 AD 是 60 m,则河流的宽度 BC 是( )
A.240( 3-1)m
B.180( 2-1) m
C.120( 3-1) m
(3)若 sin B=bsian A<1,则满足条件的三角形的个数为 1 或 2.
显然由 0<sin
B=bsian
A <1
可得
B
有两个值,一个为钝角,一个为锐角,考虑到“大角对
大边”、“三角形内角和等于 180°”等,此时需进行讨论.
判断三角形解的个数也可由“三角形中大边对大角”来判定.设 A 为锐角,若 a≥b,则
cos A=b2+2cb2c-a2; cos B=c2+2aa2c-b2; cos C=a2+2ba2b-c2
正弦定理可以用来解决两类解三角形的问题:
1.已知两角和任意一边,求另两边和另一角;
2.已知两边和其中一边的对角,求其他的边和角.
第一类问题有唯一解,当三角形的两角和任一边确定时,三角形就被唯一确定.
30280052如图在海岸a处发现北偏东45方向距离a为1nmile的b处有一艘走私船在a处北偏西75方向距离a为2nmile的c处有一艘缉私艇奉命以10v3nmileh的速度追截走私船此时走私船正以10nmileh的速度从b处向北偏东30方向逃窜问缉私艇沿什么方向行驶才能最快追上走私船并求出所需时间
14.在△ABC 中,角 A,B,C 的对边分别为 a,b,c,且 bcosC=3acosB-ccosB. (1)求 cosB 的值. (2)若错误!未找到引用源。·错误!未找到引用源。=2,且 b=2 错误!未找到引用源。,求 a 和 c
高三数学一轮复习:正、余弦定理及其应用(一)(教案)

第四课时 正、余弦定理及其应用(一)(教案)【复习目标】1.掌握正弦定理、余弦定理及三角形面积公式;2.能用正、余弦定理进行边角关系的转换,熟练进行边角计算; 3.会求三角形的未知元素,能解决有关三角形的求值、化简和证明问题.【知识梳理】1. 三角形内角和定理①利用π=++C B A ,有)s i n (s i n C B A +=,)cos(cos C B A +-=,tan tan()A B C =-+等;②利用2222π=++C B A ,有2cos 2sin C B A +=等; 2.正弦定理2()sin sin sin sin sin a b c a b c R R ABC A B C sinA B C++====∆++是的外接圆的半径 ::sin :sin :sin a b c A B C =利用正弦定理解决:①已知两角和其中一边;②已知两边和其中一边的对角. (先求另一边的对角,要注意两解,一解或无解情况) 3.余弦定理2222222cos cos 2b c a b c bc A A bc a+=+-=⇔-2222222cos cos 2a c b a c ac B B acb+=+-=⇔-2222222cos cos 2a b c a b ab C C abc=+-=⇔+-.利用余弦定理解决:①已知三边;②已知两边及两边的夹角. 4.常用三角形的面积公式111sin sin sin 222S ab C bc A ca B∆===221sin sin sin 2sin sin sin 22sin()4a B C abcS ab C R A B C B C R====+=2a b c s ++=)5.判断三角形的形状判断三角形的形状时,一般把等式中的边化为角或角化为边,然后再完成恒等变换.注意:齐次等式或齐次式比值中的正弦等价转化. 如:2sin sin 2sin a b c A B C +=⇔+=,CBA c b a sin sin sin +=+. 6.解斜三角形问题:按已知条件得不同,可以分为以下四个类型: ① 已知两角一边;② 已知两边夹角; 解唯一 ③ 已知三边;④ 已知两边一对角; 解不唯一,要讨论;如已知:边,a b ,角A(1)A 为锐角A b a sin < A b a sin = A b a b sin >> b a > 无解 一解 二解 一解 (2)A 为钝角b a ≤ b a > 无解 一解 7.对于解斜三角形的实际应用问题,要理解题意,分清已知与所求,根据题意画出示意图,抽象或构造出三角形,明确先用哪个公式或定理,先求哪些量,确定解三角形的方法.在演算过程中,要算法简练、算式工整、计算正确,还要注意近似计算的要求.对于实际应用问题中的有关名词、术语,要理解清楚,如坡角、俯角、仰角、视角、方向角、方位角等. 【基础练习】 1.在△ABC 中,若CcB b A a cos cos cos ==,则△ABC 是(B )A .直角三角形B .等边三角形A b CA b C Ab C C A b aA Cb CA baC .钝角三角形D .等腰直角三角形 2.△ABC 中,::4:1:1A B C =,则::a b c 为(D )A .3∶1∶1B .2∶1∶1C1∶1 D1∶13.若,,A B C 是△ABC 的三个内角,且A B C <<(C ≠2π),则下列结论中正确的是(A )A .sin sin A C < B .cot cot A C < C .tan tan A C < D .cos cos A C < 4.不等边△ABC 中,,,a b c 分别对角,,A B C ,且最大边a 满足条件222a b c <+,则A ∠的取值区间是(C )A .,2ππ⎛⎫⎪⎝⎭B .,63ππ⎛⎫⎪⎝⎭ C .,32ππ⎛⎫ ⎪⎝⎭ D .,42ππ⎛⎫ ⎪⎝⎭5.满足条件4,45a b A ===︒的三角形ABC 的个数是(B )A .一个B .两个C .无数个D .不存在6.在△ABC 中,222a cb ab -+=,则C ∠=(A )A .60︒B .45︒或135︒C .120︒D .30︒7.在△ABC 中,已知5cos 13A =,3sin 5B =,则cosC 的值为(A ) A.1665 B.5665 C.1665或5665 D.1665- 8.在△ABC 中,A B >是sin sin A B >的(C )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件9.在△ABC中,AC =,45A ∠=,75C ∠=,则BC10.在ABC ∆中,若︒=120A ,5,7AB BC ==,则AB C ∆的面积S =3415. 【典型例题】【例1】解答下列各题: (1)在ABC ∆中,若30A =︒, 2a b ==,求角B ; (2)在ABC ∆中,已知:2,15a b C === ,求角B .解:(1)由正弦定理,得sin sin a bA B=, 即sinsin b A B a =,得 sin B ==∵a b <,∴30B A >=︒,B 为锐角或钝角.即45B =︒或135︒;(2)由余弦定理,得2222cos 4822cos15c a b ab C =+-=+-⨯⨯︒,因为cos151)︒==,所以21248c =-=-所以c ==所以222cos 2b c a A bc +-===,所以30A =︒,135B =︒. 【例2】在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,且31cos =A . (1)求A CB 2cos 2sin2++的值; (2)若3=a ,求bc 的最大值.解:(1)A C B 2cos 2sin2++=)1cos 2()]cos(1[212-++-A C B=)1cos 2()cos 1(212-++A A =)192()311(21-++= 91-;(2)∵31cos 2222==-+A bc a c b ∴2222232a bc a cb bc -≥-+=,又∵3=a ,∴49≤bc ,当且仅当23==c b 时bc 取最大值是49. 【例3】在ABC ∆中,已知AB 边的长4c =,AC 边的长7b =,且BC 边的中线长72AD =,求解这一三角形.解:设x DC BD ==,∵ADB ADC π∠=-∠, ∴cos cos ADB ADC ∠=-∠,由余弦定理,得x x x x ⋅⨯-+-=⋅⨯-+2727)27(2724)27(222222, 解得29=x ,∴9a =,∴72472947cos 222-=⨯⨯-+=A ,∴72arccos -=πA ,又32492749cos 222=⨯⨯-+=B ,∴32arccos =B ,同理可得 2119arccos =C .【例4】已知,,a b c ABC ∆是的三边,S ABC ∆是面积,求使不等式2224c a b ab pS --+≥恒成立的实数p 取值范围.解:∵2222cos ,c a b ab C =+-∴142cos sin,84cos sin2ab ab C p ab C C p C -≥⋅-≥84cos,(0,),sinCp CC π-≤∈又84cossinCC-的最小值为,(,p∴∈-∞说明:由不等式的结构特征,联想到余弦定理与三角形面积公式,把关于p 的不等式转化为只含参数角C的不等式,本题恒成立的问题就变为求84cossinCC-在(0,)Cπ∈时的最小值问题.【备用例题】1.已知ABC∆的三条边长分别为cba、、;(1)若cba、、依次成等差数列,求B∠的取值范围;(2)若cba、、依次成等比数列,证明ABC∆中至少有两个内角不超过60 .思考:两题的结论可以互换吗?答:可以解:(1)依题意,cab+=2,2122123221)(4324)(2cos22222222=-≥-+=+-+=-+=acacacacaccaaccacaacbcaB而π<<B0,Bcos单调递减,∴B的取值范围是]30(π,;(2)已知acb=2,由正弦定理,得2222221cos2222a cb ac ac ac acBac ac ac+-+--==≥=,∴060≤B,又由acb=2知ca、中必有一数不大于b,不妨设bc≤,则060≤≤BC,证毕.2.已知cba、、是ABC∆中∠A、∠B、∠C的对边,S是ABC∆的面积.若4,5,a b S===c的长度.解:∵1sin2S ab C=,∴sin2C=,于是60C∠= 或120C∠= ;又∵2222cosc a b ab C=+-,当60C∠= 时,222c a b ab=+-,c当120C∠= 时,222c a b ab=++,c=∴c的长度为21或61.【巩固练习】1.在ABC ∆中,设命题,sin sin sin :AcC b B a p ==命题q :ABC ∆是等边三角形,那么命题p 是命题q 的(C ) A .充分不必要条件 B .必要不充分条件C .充分必要条件D .既不充分又不必要条件 2.已知锐角三角形的边长分别为2、3、x ,则x 的取值范围是(B )A .15x <<Bx <<C.1x <<D5x <<3.已知ABC ∆中,1,30a b B ==︒,则ABC ∆或. 4.在ABC ∆中,4:3:2sin :sin :sin =C B A ,则ABC ∠=1611arccos (用反三角函数值表示).5.在ABC ∆中,已知():():()4:5:6b c c a a b +++=,给出下列结论: ①由已知条件这一三角形被唯一确定; ②ABC ∆一定是一个钝角三角形;③sin :sin :sin 7:5:3A B C =;④若8=+c b ,则ABC ∆的面积是2315.其中正确结论的序号是_______②③____________ .6.在ABC ∆中,已知:2,15a b C === ,求:角,B A 和边c .答案:30,135A B c === .7.已知在ABC ∆中, , 4,c a b C π=>=tan tan 6A B ⋅=,试求,a b 以及此三角形的面积. 解:∵tan tan tan()(1tan tan )A B A B A B +=+-tan (1tan tan )tan(16)54C A B π=--=--=又∵tan tan 6A B ⋅=,且a b >,则ta n t a n A B >,∴tan 3,tan 2A B ==.而0, 022A B ππ<<<<,∴sin , sin 105A B ==利用正弦定理,可得sin sin c A a C ===sinsin5c BbC===1124∴sin225525.ABCS ab C∆==⨯⨯⨯=8.在ABC∆中,已知4442222a b c c a b++=+(),求角C.提示:4442222222222222()2,a b c c a b a b c a b a b c++=++-=∴+-=(),得答案:0045135或9.如图,水平飞行的飞机的航线和山顶在同一铅直平面内,已知飞机高度为海拔8000米,速度为600千米/时,飞行员在A处先看到山顶M的俯角︒=50α,经10秒后在B处看到山顶M的俯角︒=70β,求山顶M 的海拔高度.(精确到1米)答案:4492米10.三角形两边分别为3,1,第三边上的中线长为1,则三角形的外接圆半径为__1__.11.ABC∆中,若22tan sin tan sinA B B A⋅=⋅,则ABC∆一定是等腰三角形或直角三角形.12.若ABC∆的三条边为,,a b c满足()()3a b c a b c ab++⋅+-=,则C=60︒.13.设ABC∆的内角,,A B C的对边长分别为,,a b c,3cos()cos2A C B-+=,2b ac=,求B.解:由3cos()cos2A C B-+=及()B A Cπ=-+得3cos()cos()2A C A C---=,3cos cos sin sin(cos cos sin sin)2A C A C A C A C+--=,3sin sin4A C=.又由2b ac=及正弦定理得2sin sin sinB A C=,故23sin4B=,sin B=或sin B=(舍去),于是3B π=或23B π=. 又由2b ac =知b a b c ≤≤或,所以3B π=.14.ABC ∆中,角,,A B C 对边的边长分别是,,a b c ,且(c o s c o s )a B C b c+=+.(1)求证:2A π=;(2)若ABC ∆外接圆半径为1,求ABC ∆周长的取值范围.解:(1)证明:∵(cos cos )a B C b c +=+ ∴由余弦定理得22222222a c a b acabbca abc +-+-⋅+⋅=+,∴整理得222()()0a b b c c +--=. ∵0b c +>,∴222a b c =+.故2A π=.(2)∵ABC ∆外接圆半径为1,2A π=,∴2a =.∴2(sin cos ))4b c B B B π+=+=+.∵02B π<<,∴3444B πππ<+<,∴2b c <+≤∴42a b c <++≤+故ABC ∆周长的取值范围是(4,2+.15.在ABC ∆中,设,,BC a CA b AB c ===, 若22299190a b c +-=,则B AC co t co t co t += 95解:B A C cot cot cot +=C C B A 2sin cos sin sin =2c ab •2222a b c ab+-=95。
高三数学一轮复习 正弦定理与余弦定理综合应用教学案

正弦定理与余弦定理的应用一、考纲要求正弦定理与余弦定理的应用(B 级要求).二、复习目标 能运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题.三、重点难点利用两个定理工具解决一些与测量和几何计算有关的实际问题.四、要点梳理1.仰角与俯角:与目标视线在同一铅垂平面内的水平视线和目标视线的夹角.目标视线在水平视线上方时叫____________,目标视线在水平视线下方时叫____________.2.方位角:从正________方向沿顺时针到目标方向线的水平角叫方位角.五、基础自测1.如图,为了测量河的宽度,在一岸边选定两点A ,B 望对岸的标记物C ,测得∠CAB=30°,∠CBA =75°,AB =120 m ,这条河的宽度为________2.已知向量a,b,c ,且a +b +c =0,a 与b 的夹角为135,c 与b 的夹角为120,2=c ,则+=a b ________.3.甲乙两楼相距20 m ,从乙楼楼底望甲楼楼顶的仰角为60°,从 甲楼楼顶望乙楼楼顶的俯角为30°,则甲、乙两楼的高分别是______.4、在ABC ∆中,120A =,c=5,a =7,则sin sin B C的值为________. 5.一船向正北航行,看见正西方向有相距10海里的两个灯塔恰好与它在一条直线上,继续航行半小时后,看见一灯塔在船的南偏西60°,另一灯塔在船的南偏西75°,则这艘船的速度是每小时__________海里6.如图,在四边形ABCD 中,已知AD⊥CD,AD =10,AB =14,∠BDA=60°,∠BCD=135°,则BC 的长为________.六、典例精讲例1、如图所示,在平面四边形ABCD 中,DA ⊥AB ,DE =1,EC =7,EA =2,∠ADC =2π3,∠BEC =π3. (1)求sin∠CED 的值;(2)求BE 的长.例2、在海岸A 处,发现北偏东45方向,距离A 1n mile 的B 处有一艘走私船,在A 处北偏西75方向,距离A 为2 n mile 的C 处有一艘缉私艇奉命以的速度追截走私船,此时,走私船正以10 n mile / h 的速度从B 处向北偏东30方向逃窜,问缉私艇沿什么方向行驶才能最快追上走私船?并求出所需时间例3.如图,某市拟在长为8km的道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数y=Asinωx(A>0, ω>0) x∈[0,4]的图象,且图象的最高点为S(3,;赛道的后一部分为折线段MNP,为保证参赛运动员的安全,限定∠MNP=120o(1)求A , ω的值和M,P两点间的距离;(2)应如何设计,才能使折线段赛道MNP最长?例4、某兴趣小组测量电视塔AE的高度H(单位:m),如示意图,垂直放置的标杆BC的高度h=4m,仰角∠ABE=α,∠ADE=β.(1)该小组已经测得一组α、β的值,tanα=1.24,t anβ=1.20,请据此算出H的值;(2)该小组分析若干测得的数据后,认为适当调整标杆到电视塔的距离d(单位:m),使α与β之差较大,可以提高测量精确度.若电视塔的实际高度为125m,试问d为多少时,α-β最大?七、反思感悟正弦定理与余弦定理的应用课时练习1.在△ABC 中,内角A,B,C 的对边分别是a,b,c,若22a b -=,sin C B =,则A=________2.已知△ABC 中,AB a =,AC b =,0a b ⋅<,154ABC S ∆=,3,5a b ==,则BAC ∠=________ 3.某人朝正东方向走3km 后,向右转150︒然后朝新方向走kmx ,结果他离出发点恰好,那么x 的值为_________4.在ABC ∆中,设BC =a ,CA =b ,AB =c ,已知a 与b 的夹角为135︒,b 与c 的夹角为120︒,2||=c .则ABC ∆的最长的边的长为5.已知在海岛A 上有一座海拔1千米的山,山顶上有一个观察站P ,上午11时,测得一轮船在岛的北偏东30°,俯角30°的B 处,到11时10分又测得该船在岛的北偏西60°,俯角60°的C 处,则轮船航行速度是 千米/小时6.在塔底的水平面上某点测得塔顶的仰角为θ沿直线走30 m ,测得 塔顶的仰角为2θ,再向前走则测得塔顶的仰角为4θ,则塔高是 .7.如图,为测量山高MN ,选择A 和另一座山的山顶C 测量观测点.从A 点测得M 点的仰角∠MAN =60°,C 的仰角∠CAB =45°,以及∠MAC =75°,从C 点测得∠MCA =60°已知山高BC =100 m ,则山高MN =_____m 8.如图,某同学在教学楼五楼P 处(P 点高出地面20m),测得楼前广场地面上正南方向甲同学所在A 处,俯角为30︒乙同学在地面上南偏西30︒方向的B 处,俯角为45︒,求甲乙两同学之间的距离.9.如图所示,甲船由A 岛出发向北偏东45°的方向作匀速直线航行,速度为152海里/小时,在甲船从A 岛出发的同时,乙船从A 岛正南40海里处的B 岛出发,朝北偏东θ(tan θ=12)的方向作匀速直线航行,速度为105海里/小时.(1)求出发后3小时两船相距多少海里?A C(2)求两船出发后多长时间距离最近?最近距离为多少海里?(3)两船在航行中能否相遇,试说明理由.10.如图,游客从某旅游景区的景点A 处下山至C 处有两种路径.一种是从A 沿直线步行到C ,另一种是先从A 沿索道乘缆车到B ,然后从B 沿直线步行到C .现有甲、乙两位游客从A 处下山,甲沿AC 匀速步行,速度为min /50m .在甲出发min 2后,乙从A 乘缆车到B ,在B 处停留min 1后,再从匀速步行到C .假设缆车匀速直线运动的速度为min /130m ,山路AC 长为m 1260,经测量,1312cos =A ,53cos =C . (1)求索道AB 的长; (2)问乙出发多少分钟后,乙在缆车上与甲的距离最短? (3)为使两位游客在C 处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内?C BA。
1.2正余弦定理应用举例学案

四平市第一高级中学 2013级高一年级数学学科学案学案类型: 新课 材料序号: 3编稿教师: 刘强 审稿教师: 朱立梅 课题:1.2应用举例一、学习目标:1、加深对正弦定理、余弦定理的理解,提高熟练程度。
2、加深正弦定理、余弦定理在实际中的应用:①测量距离;②测量高度;③测量角度。
二、学习重、难点:教学重点:综合运用正弦定理、余弦定理等知识和方法解决一些实际问题。
教学难点:综合运用正弦定理、余弦定理等知识和方法解决一些实际问题。
三、知识导学:1、实际问题中常用的角(1)仰角和俯角:在视线和水平线所成角中,视线在水平线________的角叫做仰角,视线在水平线______的角叫做俯角。
(2)方位角:从正北方向_____转到目标方向线的水平角,如B 点的方位角为α。
2、坡角与坡度(1)坡角坡面与水平面的夹角,即图中的角β。
(2)坡度坡度是指路线纵断面上同一坡段两点间的高度差与其水平距离的比值,即坡角的正切值,lh ==βtan 坡度。
四、典型例题:1、测量距离的问题【例1】为了测量河对岸两个建筑物B A 、之间的距离,在河岸边取点D C 、,︒=∠45BCD ,︒=∠75ACB ,︒=∠30ADC ,︒=∠45ADB ,3=CD 千米,已知D C B A 、、、在同一平面内,试求B A 、之间的距离。
水平线 视线 视线 仰角 俯角 铅垂线αB 西 南 东北βh l2、测量高度【例2】如图,在山顶铁塔上B 处测得地面上一点A 的仰角︒=60α,在 塔底C 处测得A 处的俯角︒=45β。
已知铁塔BC 部分的高为m 30,求出山高CD 。
3、测量角度【例3】一艘渔船在我海域遇险,且最多只能坚持45分钟,我海军舰艇在A 处获悉后,立即测出该渔船在方位角为︒45、距离为10海里的C 处,并测得渔船以9海里/时的速度沿方位角为︒105的方向航行,我海军舰艇立即以21海里/时的速度前去营救。
求舰艇赶上遇险渔船所需的最短时间,能否营救成功?4、三角恒等式证明【例4】在△ABC 中,求证:)cos cos cos (2222C ab B ca A bc c b a ++=++。
(优质课)正、余弦定理及其应用

BD2 + CD2 - CB2 202 + 212 - 312 1 cosβ = = =- , 2BD·CD 2×20×21 7
返回目录
∴sinβ=
4 3 . 7
而sinα=sin(β-60°)=sinβcos60°-sin60°cosβ ° ° °
4 3 1 3 1 5 3 = × + × = , 7 2 2 7 14 21 AD 在△ACD中, 中 = o sin60 sinα
考点三
应用问题
某观测站C在城 的南偏西 由城A出发的一 某观测站 在城A的南偏西 °的方向 由城 出发的一 在城 的南偏西20°的方向,由城 条公路,走向是南偏东 ° 在 处测得公路上 处测得公路上B处有一 条公路 走向是南偏东40°,在C处测得公路上 处有一 走向是南偏东 千米,正沿公路向 城走去,走了 人,距C为31千米 正沿公路向 城走去 走了 千米后到 距 为 千米 正沿公路向A城走去 走了20千米后到 此时CD间的距离为 千米,问 这人还要走多少 达D处,此时 间的距离为 千米 问:这人还要走多少 处 此时 间的距离为21千米 千米才能到达A城 千米才能到达 城?
3. 2
∵a>b,∴A=60°或A=120°. ∴ ° ° ①当A=60°时,C=180°- 45°- 60°=75°, ° ° ° ° °
bsinC 6 + 2 = . ∴c= sinB 2
②∵当A=120°时,C=180°- 45°- 120°=15°, ° ° ° ° °
bsinC 6 − 2 = . ∴c= sinB 2
正弦定理、 正弦定理、余弦 定理及应用
a = 1.正弦定理 sinA 正弦定理: 正弦定理
b sinB
《正弦定理、余弦定理的应用》教学案

1.3《正弦定理、余弦定理的应用》教学案•三维目标1. 知识与技能( 1)能把一些简单的实际问题转化为数学问题,并能应用正弦定理、余弦定理及相关的三角公式解决这些问题;( 2)体会数学建模的基本思想,掌握应用解三角形知识解决实际问题的一般步骤;( 3)了解常用的测量相关术语 ( 如:仰角、俯角、方位角、视角及坡度、经纬度等有关名词和术语的确切含义 ) ,综合运用正弦定理、余弦定理等知识和方法解决与测量学、航海问题等有关的实际问题;( 4)能够从阅读理解、信息迁移、数学化方法、创造性思维等方面,多角度培养学生分析问题和解决问题的能力;( 5)规范学生的演算过程:逻辑严谨,表述准确,算法简练,书写工整,示意图清晰.2. 过程与方法(1)本节课是解三角形应用举例的延伸,利用正弦定理、余弦定理等知识和方法解决一些几何和物理上的问题;( 2)让学生进一步巩固所学的知识,加深对所学定理的理解,提高创新能力;进一步培养学生学习数学、应用数学的意识及观察、归纳、类比、概括的能力.3.情感、态度与价值观( 1)激发学生学习数学的兴趣,并体会数学的应用价值;( 2)培养学生提出问题、正确分析问题、独立解决问题的能力,并在教学过程中激发学生的探索精神;(3) 培养学生运用图形、数学符号表达题意和应用转化思想解决数学问题的能力. •重点、难点重点: (1) 综合运用正弦定理、余弦定理等知识和方法解决一些实际问题;( 2)掌握求解实际问题的一般步骤;难点:根据题意建立数学模型,画出示意图.体验将实际问题转化为数学问题的过程与思想,认识研究实际问题的方法,是本节教学的重中之重,而突破这一重难点的关键在于引导学生对实际问题进行分析,抽象出数学问题,再利用解三角形的知识加以解决.教学方案设计( 教师用书独具 )•教学建议在学生回忆正弦定理、余弦定理以及它们可以解决哪些类型的三角形的基础上,让学生尝试绘制知识纲目图. 生活中错综复杂的问题本源仍然是我们学过的定理,因此系统掌握前一节内容是学好本节课的基础. 解有关三角形的应用题有固定的解题思路,引导学生寻求实际问题的本质和规律,从一般规律到生活的具体运用,这方面需要多琢磨和多体会.测量的主要内容是求角和距离,教学中要注意让学生分清仰角、俯角、张角、视角和方位角及坡度、经纬度等概念,将实际问题转化为解三角形问题. 解决有关测量、航海等问题时,首先要搞清题中有关术语的准确含义,再用数学语言(符号语言、图形语言)表示已知条件、未知条件及其关系,最后用正弦定理、余弦定理予以解决.能否灵活求解问题的关键是正弦定理和余弦定理的选用,有些题目只选用其一,或两者混用,这当中有很大的灵活性,需要对原来所学知识进行深入的整理、加工,鼓励一题多解,训练发散思维.借助计算机等多媒体工具来进行演示,利用动态效果能使学生更好地明辨是非、掌握方法.引导学生总结解斜三角形应用题的一般步骤:(1)分析:理解题意,分清已知与未知,画出示意图;(2)建模:根据已知条件与求解目标,把已知量与求解量尽量集中在有关的三角形中,建立一个解斜三角形的数学模型;(3)求解:利用正弦定理或余弦定理有序地解出三角形,求得数学模型的解;(4)检验:检验上述所求的解是否符合实际意义,从而得出实际问题的解.•教学流程课前自主导学【问题导思】小明出家门向南前进200米,再向东前进200米,至U达学校上课. 1•小明的学校在家的哪个方向?【提示】东南方向.2•能否用角度确定学校的方位?【提示】能.课堂互动探究例1如图1-3—1图1—3—1在山顶C测得塔顶A的俯角为45°已知塔高AB为20 m,求山高CD(精确到0. 1 m)【思路探究】D(可放到厶BCD中,要求CD已知/ DBC= 60° / CDB= 90°所以只需求BD 或CB在厶AB(中,AB勺长度已知,三个内角都可以求出,所以可求得CB则Cd CB-s in 60°【自主解答】由条件知/ DBC= 60° / ECA= 45°•••/ ABC 90° —60°= 30° / ACB 60°—45°= 15° ,/ CA= 180° —( / ABQ-Z ACB = 135°BC AB在^ ABC中,由正弦定理得sin 135 ° = sin 15 ° ,AB- sin 135 °20x 2 40二B C= sin 15 °= 1 = 3— 1.4乐-衣7在Rt △ BC中,40 \/3CD^ BC- sin / CB=书—〔x 2 ~ 47. 3(m).•山高C哟为47.3 m.规律方法1.本例是典型的测量高度问题,抽象出平面图形,并且将相应数据聚化到相应三角形中,十分关键.2.测量高度的有关问题,大部分都是转化为同一铅垂面上的解三角形问题,但也有转化为立体图形的问题.变式训练如图1-3-2所示,空中有一气球 C,图1-3—2在它的正西方A点测得它的仰角为45°同时在它的南偏东60°的B点,测得它的仰角为3 0° A, B两点间的距离为266米,这两个测点均离地1米,则气球离地多少米?【解】设0C= x,则OA= x, OB= x • tan 60°= 3x.在厶AO中,/ A0= 90° + 60°= 150° AB= 266,所以A^= OA+ OB - 2OA OBi os / AOB=x2+ 3x2— 2x •3x • (—) = 7x2,所以x= TAB= T X 266= 38 7(米),所以气球离地(38,7 + 1)米.例2甲船在A处遇险,在甲船西南10海里B处的乙船收到甲船的报警后,测得甲船是沿着东偏北105°的方向,以每小时9海里的速度向某岛靠近,如果乙船要在40分钟内追上甲船, 问乙船至少应以什么速度、向何方向航行?【思路探究】画图T分析三角形满足条件T选择定理列方程T求相关量T作答【自主解答】如图所示:设乙船速度为v海里/小时,在C处追上甲船,/ BAC= 45°180° —105° = 120°在厶AB(中,由余弦定理得,BC= AC+ A8— 2AC・ AB- cos / BA(2 2 2(3v) 2= ( 3 x 9)2+ 102— 2 x 3X 9x 10x cos 120°,整理得v= 21.BC AC又由正弦定理可知 sin Z BAC= sin B,2AC- sin Z BAC 3x9坐sin B= BC = 2 x sin 120° = 14 ,3x 21■ B^ 2147'.即B应以每小时21海里的速度,按东偏北 45。
【方法】高考数学一轮复习第五章三角函数解三角形第27课正弦定理和余弦定理教师用书

【关键字】方法第27课正弦定理和余弦定理[最新考纲](1)S=a·ha(ha表示边a上的高);(2)S=absin C=acsin B=bcsin A.(3)S=r(a+b+c)(r为内切圆半径).1.(思考辨析)判断下列结论的正误.(正确的打“√”,错误的打“×”)(1)在△ABC中,若A>B,则必有sin A>sin B.( )(2)在△ABC中,若b2+c2>a2,则△ABC为锐角三角形.( )(3)在△ABC中,若A=60°,a=4,b=4,则B=45°或135°.( )(4)在△ABC中,=.( )[解析] (1)正确.A>B⇔a>b⇔sin A>sin B.(2)错误.由cos A=>0知,A为锐角,但△ABC不一定是锐角三角形.(3)错误.由b<a知,B<A.(4)正确.利用a=2Rsin A,b=2Rsin B,c=2Rsin C,可知结论正确.[答案] (1)√(2)×(3)×(4)√2.(教材改编)在△ABC中,若sin+sin2B<sin,则△ABC的形状是________.钝角三角形[由正弦定理,得=sin A,=sin B,=sin C,代入得到a2+b2<c2,由余弦定理得cos C=<0,所以C为钝角,所以该三角形为钝角三角形.] 3.(2016·全国卷Ⅰ改编)△ABC的内角A,B,C的对边分别为a,b,c,已知a=,c =2,cos A=,则b=________.3 [由余弦定理得5=b2+4-2×b×2×,解得b=3或b=-(舍去).]4.在△ABC中,角A,B,C所对的边分别为a,b,c,已知A=,a=1,b=,则B=________.或[由正弦定理=,代入可求得sin B=,故B=或B=.]5.在△ABC中,A=60°,AC=4,BC=2,则△ABC的面积等于________.2 [由题意及余弦定理得cos A===,解得c=2,所以S=bcsin A=×4×2×sin 60°=2.]. 【导学号:】[解] 设△ABC的内角∠BAC,B,C所对边的长分别是a,b,c,由余弦定理得a2=b2+c2-2bccos∠BAC=(3)2+62-2×3×6×cos=18+36-(-36)=90,所以a=3.又由正弦定理得sin B===,由题设知0<B<,所以cos B===.在△ABD中,因为AD=BD,所以∠ABD=∠BAD,所以∠ADB=π-2B,故由正弦定理得AD====.[规律方法] 1.正弦定理是一个连比等式,只要知道其比值或等量关系就可以运用正弦定理通过约分达到解决问题的目的.2.(1)运用余弦定理时,要注意整体思想的运用.(2)在已知三角形两边及其中一边的对角,求该三角形的其它边角的问题时,首先必须判断是否有解,如果有解,是一解还是两解,注意“大边对大角”在判定中的应用.[变式训练1] (1)已知a,b,c分别为△ABC三个内角A,B,C的对边,且(b-c)(sinB +sin C)=(a -c)sin A ,则角B 的大小为________.(2)(2016·全国卷Ⅱ)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,若cos A =,cos C =,a =1,则b =________.(1)30° (2) [(1)由正弦定理==及(b -c)·(sin B +sin C)=(a -c)sin A 得(b -c)(b +c)=(a -c)a ,即b2-c2=a2-ac ,∴a2+c2-b2=ac.又∵cos B =,∴cos B =,∴B =30°.(2)在△ABC 中,∵cos A =,cos C =,∴sin A =,sin C =,∴sin B =sin(A +C)=sin Acos C +cos Asin C =×+×=. 又∵=,∴b ===.](1)在△ABC bcos B ,则△ABC 的形状为________.(2)(2017·镇江期中)在△ABC 中,若cos A =,sin B +sin C =2sin A ,则△ABC 的形状为________.(1)等腰三角形或直角三角形 (2)等边三角形 [(1)∵acos A =bcos B ,由正弦定理得sin Acos A =sin Bcos B ,即sin =sin 2B ,∴=2B 或+2B =π,即A =B 或A +B =,∴△ABC 为等腰三角形或直角三角形.(2)∵sin B +sin C =2sin A ,∴b +c =, 又cos A =,∴=, ∴b 2+c 2-a 2=bc ,又b +c =2a ,则(b +c )2-a 2=3bc =3a 2, ∴a 2=bc =⎝⎛⎭⎪⎫b +c 22,∴(b -c )2=0,即b =c ,∴b =c =a ,∴△ABC 为等边三角形.][规律方法] 1.判定三角形形状的途径:(1)化边为角,通过三角变换找出角之间的关系.(2)化角为边,通过代数变形找出边之间的关系,正(余)弦定理是转化的桥梁.2.无论使用哪种方法,都不要随意约掉公因式;要移项提取公因式,否则会有漏掉一种形状的可能.[变式训练2] (1)设角A ,B ,C 是△ABC 的三个内角,则“A +B <C ”是“△ABC 是钝角三角形”的________条件.(2)设△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,若2sin A cos B =sin C ,那么△ABC 一定是________三角形. 【导学号:】(1)充分不必要 (2)等腰 [(1)由A +B +C =π,A +B <C ,可得C >π2,故三角形ABC为钝角三角形,反之不成立.(2)法一:由已知得2sin A cos B =sin C =sin(A +B )=sin A cos B +cos A sin B ,即sin(A -B )=0,因为-π<A -B <π,所以A =B .法二:由正弦定理得2a cos B =c ,再由余弦定理得2a ·a 2+c 2-b 22ac=c ⇒a 2=b 2⇒a =b .]与三角形面积有关的问题已知a ,b ,c 分别为△ABC 内角A ,B ,C 的对边,sin 2B =2sin A sinC .(1)若a =b ,求cos B ;(2)设B =90°,且a =2,求△ABC 的面积. [解] (1)由题设及正弦定理可得b 2=2ac . 又a =b ,可得b =2c ,a =2c .由余弦定理可得cos B =a 2+c 2-b 22ac =14.(2)由(1)知b 2=2ac .因为B =90°,由勾股定理得a 2+c 2=b 2, 故a 2+c 2=2ac ,进而可得c =a = 2. 所以△ABC 的面积为12×2×2=1.[规律方法] 三角形面积公式的应用方法:(1)对于面积公式S =12ab sin C =12ac sin B =12bc sin A ,一般是已知哪一个角就使用哪一个公式.(2)与面积有关的问题,一般要用到正弦定理或余弦定理进行边和角的转化. [变式训练3] (2016·全国卷Ⅰ)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知2cos C (a cos B +b cos A )=c .(1)求C ;(2)若c =7,△ABC 的面积为332,求△ABC 的周长.[解] (1)由已知及正弦定理得2cos C (sin A cos B +sin B cos A )=sin C , 即2cos C sin(A +B )=sin C , 故2sin C cos C =sin C . 可得cos C =12,所以C =π3.(2)由已知得12ab sin C =332.又C =π3,所以ab =6.由已知及余弦定理得a 2+b 2-2ab cos C =7, 故a 2+b 2=13,从而(a +b )2=25. 所以△ABC 的周长为5+7. [思想与方法]1.在解三角形时,应熟练运用内角和定理:A +B +C =π,A 2+B 2+C 2=π2中互补和互余的情况,结合诱导公式可以减少角的种数.2.判定三角形的形状,主要有两种途径:(1)化边为角;(2)化角为边,并常用正弦(余弦)定理实施边、角转换.3.在△ABC 中,A >B ⇔a >b ⇔sin A >sin B . [易错与防范]1.已知两边及一边的对角,利用正弦定理求其它边或角.可能有一解、两解、无解. 在△ABC 中,已知a ,b 和A 时,解的情况如下:2.课时分层训练(二十七)A 组 基础达标 (建议用时:30分钟)一、填空题1.在△ABC 中,a =15,b =10,A =60°,则cos B =__________.63 [由正弦定理可得1532=10sin B,所以sin B =33,再由b <a ,可得B 为锐角, 所以cos B =1-sin 2B =63.] 2.(2016·天津高考改编)在△ABC 中,若AB =13,BC =3,∠C =120°,则AC =________.1 [由余弦定理得AB 2=AC 2+BC 2-2AC ·BC ·cos C ,即13=AC 2+9-2AC ×3×cos 120°,化简得AC 2+3AC -4=0,解得AC =1或AC =-4(舍去).]3.在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,且a 2+b 2-c 2=ab =3,则△ABC 的面积为________.34 [依题意得cos C =a 2+b 2-c 22ab =12,C =60°,因此△ABC 的面积等于12ab sin C =12×3×32=34.] 4.在△ABC 中,已知b =40,c =20,C =60°,则此三角形的解的情况是________(填“一解”“二解”“不存在”).不存在 [∵b sin c =40×sin 60°=203,c =20, ∴b sin c >c , ∴△ABC 不存在.]5.(2016·全国卷Ⅲ改编)在△ABC 中,B =π4,BC 边上的高等于13BC ,则sin A =________.31010 [过A 作AD ⊥BC 于D ,设BC =a ,由已知得AD =a 3.∵B =π4,∴AD =BD ,∴BD =AD =a3,DC =23a ,∴AC =⎝ ⎛⎭⎪⎫a 32+⎝ ⎛⎭⎪⎫23a 2=53a ,在△ABC 中,由正弦定理得a sin ∠BAC =53a sin 45°,∴sin ∠BAC =31010.]6.若a cos(π-A )+b sin ⎝ ⎛⎭⎪⎫π2+B =0,内角A ,B 的对边分别为a ,b ,则三角形ABC 的形状为________.等腰三角形或直角三角形 [因为a cos(π-A )+b sin ⎝ ⎛⎭⎪⎫π2+B =0,所以-a cos A +b cos B =0,所以-sin A cos A +sin B cos B =0,所以sin 2A =sin 2B ,所以A =B 或A +B =π2,所以三角形ABC 的形状为等腰三角形或直角三角形.]7.已知△ABC 中,AB =3,BC =1,sin C =3cos C ,则△ABC 的面积为________. 【导学号:】32 [由sin C =3cos C 得tan C =3>0,所以C =π3.根据正弦定理可得BC sin A =AB sin C ,即1sin A =332=2,所以sin A =12.因为AB >BC ,所以A <C ,所以A =π6,所以B =π2,即三角形为直角三角形,故S △ABC =12×3×1=32.]8.(2017·镇江期中)在△ABC 中,如果sin A ∶sin B ∶sin C =2∶3∶4,那么tan C =________.-15 [∵sin A ∶sin B ∶sin C =a ∶b ∶c , ∴a ∶b ∶c =2∶3∶4, 设a =2x ,则b =3x ,c =4x , ∴cos C =4x 2+9x 2-16x 22×2x ×3x =-14.又c ∈(0,π),∴sin c =154, ∴tan C =sin Ccos C=-15.]9.(2017·盐城模拟)在锐角△ABC 中,AB =2,BC =3,△ABC 的面积为332,则AC 的长为________.7 [∵S △ABC =12AB ·BC ·sin B =12×2×3sin B =332,∴sin B =32. 又△ABC 为锐角三角形,故cos B =12.在△ABC 中,由余弦定理得AC 2=4+9-2×2×3cos B =13-12×12=7.∴AC =7.]10.(2017·苏州期中)在△ABC 中,角A ,B ,C 的对边分别是a ,b ,c ,若tan A =2tanB ,a 2-b 2=13c ,则c =________.1 [∵tan A =2tan B ,∴sin A cos A =2sin Bcos B,∴a cos B =2b cos A ,∴a 2+c 2-b 22c =b 2+c 2-a 2c,∴3a 2-3b 2=c 2, 又a 2-b 2=13c ,∴c 2-c =0,即c =1,或c =0(舍去).] 二、解答题11.(2017·南通一模)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,(a +b -c )(a +b +c )=ab .(1)求角C 的大小;(2)若c =2a cos B ,b =2,求△ABC 的面积. 【导学号:】[解] (1)在△ABC 中,由(a +b -c )(a +b +c )=ab ,得a 2+b 2-c 22ab =-12,即cos C =-12. 因为0<C <π,所以C =2π3.(2)法一:因为c =2a cos B ,由正弦定理,得 sin C =2sin A cos B ,因为A +B +C =π,所以sin C =sin(A +B ),所以sin(A +B )=2sin A cos B ,即sin A cos B -cos A sin B =0,即sin(A -B )=0, 又-π3<A -B <π3,所以A -B =0,即A =B ,所以a =b =2.所以△ABC 的面积为S △ABC =12ab sin C =12×2×2×sin 2π3= 3.法二:由c =2a cos B 及余弦定理,得c =2a ×a 2+c 2-b 22ac,化简得a =b ,所以,△ABC 的面积为S △ABC =12ab sin C =12×2×2×sin 2π3= 3.12.(2016·苏北四市期末)在锐角三角形ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,已知sin A =35,tan(A -B )=-12.(1)求tan B 的值;(2)若b =5,求c . 【导学号:】[解] (1)在锐角三角形ABC 中,由sin A =35,得cos A =1-sin 2A =45,所以tan A =sin A cos A =34.由tan(A -B )=tan A -tan B 1+tan A ·tan B =-12,得tan B =2.(2)在锐角三角形ABC 中,由tan B =2,得sin B =255,cos B =55,所以sin C =sin(A +B )=sin A cos B +cos A sin B =11525, 由正弦定理b sin B =c sin C ,得c =b sin C sin B =112.B 组 能力提升 (建议用时:15分钟)1.在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,若△ABC 的面积为S ,且2S =(a +b )2-c 2,则tan C =________.-43[因为2S =(a +b )2-c 2=a 2+b 2-c 2+2ab ,则结合面积公式与余弦定理,得ab sin C =2ab cos C +2ab ,即sin C -2cos C =2, 所以(sin C -2cos C )2=4, sin 2C -4sin C cos C +4cos 2Csin 2C +cos 2C =4, 所以tan 2C -4tan C +4tan 2C +1=4, 解得tan C =-43或tan C =0(舍去).]2.在△ABC 中,tanA +B2=2sin C ,若AB =1,则12AC +BC 的最大值为________. 213 [因为tan A +B2=2sin C , 所以sinA +B 2cosA +B 2=2sin C ,2sinA +B2·cos A +B22⎝⎛⎭⎪⎫cosA +B 22=2sin C ,sin A +B1+cos A +B=2sin C .因为A +B +C =π,所以A +B =π-C , 所以sin(A +B )=sin C ,cos(A +B )=-cos C , 所以sin C 1-cos C=2sin C .又sin C ≠0,所以cos C =12,sin C =32,C =π3.因为BC sin A =AC sin B =AB sin C =233,所以12AC +BC =33sin B +233sin A=33sin ⎝ ⎛⎭⎪⎫2π3-A +233sin A=33⎝ ⎛⎭⎪⎫32cos A +12sin A +2sin A =213sin(A +φ), 其中0<φ<π2,tan φ=35,当sin(A +φ)=1时,12AC +BC 取得最大值213.]3.(2017·南京模拟)在△ABC 中,三个内角A ,B ,C 所对的边分别为a ,b ,c ,且满足a cos B +b cos Ac=2cos C .(1)求角C 的大小;(2)若△ABC 的面积为23,a +b =6,求边c 的长.[解] (1)由余弦定理知a cos B +b cos A =a ·a 2+c 2-b 22ac +b ·b 2+c 2-a 22bc =2c 22c=c ,∴a cos B +b cos Ac =1,∴cos C =12,又C ∈(0,π),C =π3.(2)∵S △ABC =12ab sin C =23,∴ab =8.又∵a +b =6,∴c 2=a 2+b 2-2ab cos C =(a +b )2-3ab =12, ∴c =2 3.文档来源为:从网络收集整理.word 版本可编辑.欢迎下载支持.11文档来源为:从网络收集整理.word 版本可编辑. 4.(2016·苏北四市摸底)在锐角△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,b =4,c =6,且a sin B =2 3.(1)求角A 的大小;(2)若D 为BC 的中点,求线段AD 的长.[解] (1)由正弦定理,得a sin B =b sin A ,因为b =4,a sin B =23,所以sin A =32, 又0<A <π2,所以A =π3. (2)由已知得b =4,c =6,cos A =12,由余弦定理得 a 2=b 2+c 2-2bc cos A =16+36-2×24×12=28,所以a =27.又因为a sin B =23,所以sin B =217,从而cos B =277 因为D 为BC 的中点,所以BD =DC =7.在△ABD 由余弦定理,得AD 2=AB 2+BD 2-2AB ·BD ·cos B ,即AD 2=36+7-2×6×7×277=19, 所以,AD =19.此文档是由网络收集并进行重新排版整理.word 可编辑版本!。
2013届高考数学总复习教学案:正弦定理和余弦定理

第七节正弦定理和余弦定理[知识能否忆起]1.正弦定理2.余弦定理3.三角形中常用的面积公式 (1)S =12ah (h 表示边a 上的高);(2)S =12bc sin A =12ac sin B =12ab sin C ;(3)S =12r (a +b +c )(r 为三角形的内切圆半径).[小题能否全取]1.(2012·广东高考)在△ABC 中,若∠A =60°,∠B =45°,BC =32,则AC =( ) A .43 B .2 3 C. 3D.32解析:选B 由正弦定理得:BC sin A =AC sin B ,即32sin 60°=AC sin 45°,所以AC =3232×22=2 3.2.在△ABC 中,a =3,b =1,c =2,则A 等于( ) A .30° B .45° C .60°D .75°解析:选C ∵cos A =b 2+c 2-a 22bc =1+4-32×1×2=12,又∵0°<A <180°,∴A =60°.3.(教材习题改编)在△ABC 中,若a =18,b =24,A =45°,则此三角形有( ) A .无解 B .两解C .一解D .解的个数不确定解析:选B ∵a sin A =bsin B ,∴sin B =b a sin A =2418sin 45°,∴sin B =223.又∵a <b ,∴B 有两个.4.(2012·陕西高考)在△ABC 中,角A ,B ,C 所对边的长分别为a ,b ,c .若a =2,B =π6,c =23,则b =________. 解析:由余弦定理得b 2=a 2+c 2-2ac cos B =4+12-2×2×23×32=4,所以b =2. 答案:25.△ABC 中,B =120°,AC =7,AB =5,则△ABC 的面积为________. 解析:设BC =x ,由余弦定理得49=25+x 2-10x cos 120°, 整理得x 2+5x -24=0,即x =3.因此S △ABC =12AB ×BC ×sin B =12×3×5×32=1534.答案:1534(1)在三角形中,大角对大边,大边对大角;大角的正弦值也较大,正弦值较大的角也较大,即在△ABC 中,A >B ⇔a >b ⇔sin A >sin B .(2)在△ABC 中,已知a 、b 和A 时,解的情况如下:典题导入[例1] (2012·浙江高考)在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,且b sin A =3a cos B .(1)求角B 的大小;(2)若b =3,sin C =2sin A ,求a ,c 的值. [自主解答] (1)由b sin A =3a cos B 及正弦定理 a sin A =bsin B,得sin B =3cos B , 所以tan B =3,所以B =π3.(2)由sin C =2sin A 及a sin A =csin C ,得c =2a .由b =3及余弦定理b 2=a 2+c 2-2ac cos B , 得9=a 2+c 2-ac . 所以a =3,c =2 3.在本例(2)的条件下,试求角A 的大小.解:∵a sin A =b sin B, ∴sin A =a sin Bb =3·sinπ33=12.∴A =π6.由题悟法1.应熟练掌握正、余弦定理及其变形.解三角形时,有时可用正弦定理,有时也可用余弦定理,应注意用哪一个定理更方便、简捷.2.已知两角和一边,该三角形是确定的,其解是唯一的;已知两边和一边的对角,该三角形具有不唯一性,通常根据三角函数值的有界性和大边对大角定理进行判断.以题试法1.△ABC 的三个内角A ,B ,C 所对的边分别为a ,b ,c ,a sin A sin B +b cos 2A =2a . (1)求b a;(2)若c 2=b 2+3a 2,求B . 解:(1)由正弦定理得,sin 2A sin B +sin B cos 2A = 2sin A ,即 sin B (sin 2A +cos 2A )=2sin A . 故sin B = 2sin A ,所以ba= 2.(2)由余弦定理和c 2=b 2+3a 2,得cos B =(1+3)a2c .由(1)知b 2=2a 2,故c 2=(2+3)a 2.可得cos 2B =12,又cos B >0,故cos B =22,所以B =45°.典题导入[例2] 在△ABC 中a ,b ,c 分别为内角A ,B ,C 的对边,且2a sin A =(2b +c )sin B +(2c +b )sin C .(1)求A 的大小;(2)若sin B +sin C =1,试判断△ABC 的形状.[自主解答] (1)由已知,根据正弦定理得2a 2=(2b +c )·b +(2c +b )c ,即a 2=b 2+c 2+bc . 由余弦定理得a 2=b 2+c 2-2bc cos A , 故cos A =-12,∵0<A <180°,∴A =120°.(2)由(1)得sin 2A =sin 2B +sin 2C +sin B sin C =34.又sin B +sin C =1, 解得sin B =sin C =12.∵0°<B <60°,0°<C <60°,故B =C , ∴△ABC 是等腰的钝角三角形.由题悟法依据已知条件中的边角关系判断三角形的形状时,主要有如下两种方法:(1)利用正、余弦定理把已知条件转化为边边关系,通过因式分解、配方等得出边的相应关系,从而判断三角形的形状;(2)利用正、余弦定理把已知条件转化为内角的三角函数间的关系,通过三角函数恒等变形,得出内角的关系,从而判断出三角形的形状,此时要注意应用A +B +C =π这个结论.[注意] 在上述两种方法的等式变形中,一般两边不要约去公因式,应移项提取公因式,以免漏解.以题试法2.(2012·安徽名校模拟)已知△ABC 的三个内角A ,B ,C 所对的边分别为a ,b ,c ,向量m =(4,-1),n =⎝⎛⎭⎫cos 2A 2,cos 2A ,且m ·n =72. (1)求角A 的大小;(2)若b +c =2a =23,试判断△ABC 的形状. 解:(1)∵m =(4,-1),n =⎝⎛⎭⎫cos 2A2,cos 2A , ∴m ·n =4cos 2A2-cos 2A =4·1+cos A 2-(2cos 2A -1)=-2cos 2A +2cos A +3.又∵m ·n =72,∴-2cos 2A +2cos A +3=72,解得cos A =12.∵0<A <π,∴A =π3.(2)在△ABC 中,a 2=b 2+c 2-2bc cos A ,且a =3, ∴(3)2=b 2+c 2-2bc ·12=b 2+c 2-bc .①又∵b +c =23,∴b =23-c ,代入①式整理得c 2-23c +3=0,解得c =3,∴b = 3,于是a =b =c = 3,即△ABC 为等边三角形.典题导入[例3] (2012·新课标全国卷)已知a ,b ,c 分别为△ABC 三个内角A ,B ,C 的对边,a cos C +3a sin C -b -c =0.(1)求A ;(2)若a =2,△ABC 的面积为3,求b ,c .[自主解答] (1)由a cos C +3a sin C -b -c =0及正弦定理得sin A cos C +3sin A sin C -sin B -sin C =0.因为B =π-A -C ,所以3sin A sin C -cos A sin C -sin C =0. 由于sin C ≠0,所以sin ⎝⎛⎭⎫A -π6=12. 又0<A <π,故A =π3.(2)△ABC 的面积S =12bc sin A =3,故bc =4.而a 2=b 2+c 2-2bc cos A ,故b 2+c 2=8. 解得b =c =2.由题悟法1.正弦定理和余弦定理并不是孤立的.解题时要根据具体题目合理选用,有时还需要交替使用.2.在解决三角形问题中,面积公式S =12ab sin C =12bc sin A =12ac sin B 最常用,因为公式中既有边也有角,容易和正弦定理、余弦定理结合应用.以题试法3.(2012·江西重点中学联考)在△ABC 中,12cos 2A =cos 2A -cos A .(1)求角A 的大小;(2)若a =3,sin B =2sin C ,求S △ABC .解:(1)由已知得12(2cos 2A -1)=cos 2A -cos A ,则cos A =12.因为0<A <π,所以A =π3.(2)由b sin B =c sin C ,可得sin B sin C =b c=2, 即b =2c .所以cos A =b 2+c 2-a 22bc =4c 2+c 2-94c 2=12,解得c =3,b =23,所以S △ABC =12bc sin A =12×23×3×32=332.1.在△ABC 中,a 、b 分别是角A 、B 所对的边,条件“a <b ”是使“cos A >cos B ”成立的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件解析:选C a <b ⇔A <B ⇔cos A >cos B .2.(2012·泉州模拟)在△ABC 中,a ,b ,c 分别是角A ,B ,C 所对的边.若A =π3,b =1,△ABC 的面积为32,则a 的值为( ) A .1 B .2 C.32D. 3解析:选D 由已知得12bc sin A =12×1×c ×sin π3=32,解得c =2,则由余弦定理可得a 2=4+1-2×2×1×cos π3=3⇒a = 3.3.(2013·“江南十校”联考)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,已知a =23,c =22,1+tan A tan B =2c b,则C =( )A .30°B .45°C .45°或135°D .60°解析:选B 由1+tan A tan B =2c b 和正弦定理得cos A sin B +sin A cos B =2sin C cos A , 即sin C =2sin C cos A , 所以cos A =12,则A =60°.由正弦定理得23sin A =22sin C ,则sin C =22, 又c <a ,则C <60°,故C =45°.4.(2012·陕西高考)在△ABC 中 ,角A ,B ,C 所对边的长分别为a ,b ,c ,若a 2+b 2=2c 2,则cos C 的最小值为( )A.32B.22C.12D .-12解析:选C 由余弦定理得a 2+b 2-c 2=2ab cos C ,又c 2=12(a 2+b 2),得2ab cos C =12(a 2+b 2),即cos C =a 2+b 24ab ≥2ab 4ab =12.5.(2012·上海高考)在△ABC 中,若sin 2 A +sin 2B <sin 2C ,则△ABC 的形状是( ) A .锐角三角形 B .直角三角形 C .钝角三角形D .不能确定解析:选C 由正弦定理得a 2+b 2<c 2,所以cos C =a 2+b 2-c 22ab <0,所以C 是钝角,故△ABC 是钝角三角形.6.在△ABC 中,角A 、B 、C 所对的边分别是a 、b 、c .若b =2a sin B ,则角A 的大小为________.解析:由正弦定理得sin B =2sin A sin B ,∵sin B ≠0, ∴sin A =12,∴A =30°或A =150°.答案:30°或150°7.在△ABC 中,若a =3,b =3,A =π3,则C 的大小为________.解析:由正弦定理可知sin B =b sin Aa=3sin π33=12,所以B =π6或5π6(舍去),所以C =π-A -B =π-π3-π6=π2.答案:π28.(2012·北京西城期末)在△ABC 中,三个内角A ,B ,C 的对边分别为a ,b ,c .若b =25,B =π4,sin C =55,则c =________;a =________.解析:根据正弦定理得b sin B =c sin C ,则c =b sin Csin B=22,再由余弦定理得b 2=a 2+c 2-2ac cos B ,即a 2-4a -12=0,(a +2)(a -6)=0,解得a =6或a =-2(舍去).答案:22 69.(2012·北京高考)在△ABC 中,若a =2,b +c =7,cos B =-14,则b =________.解析:根据余弦定理代入b 2=4+(7-b )2-2×2×(7-b )×⎝⎛⎭⎫-14,解得b =4. 答案:410.△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,a sin A +c sin C -2a sin C =b sin B . (1)求B ;(2)若A =75°,b =2,求a ,c .解:(1)由正弦定理得a 2+c 2-2ac =b 2. 由余弦定理得b 2=a 2+c 2-2ac cos B . 故cos B =22,因此B =45°. (2)sin A =sin(30°+45°)=sin 30°cos 45°+cos 30°sin 45°=2+64. 故a =b ×sin A sin B =2+62=1+3,c =b ×sin C sin B =2×sin 60°sin 45°= 6.11.(2013·北京朝阳统考)在锐角三角形ABC 中,a ,b ,c 分别为内角A ,B ,C 所对的边,且满足3a -2b sin A =0.(1)求角B 的大小;(2)若a +c =5,且a >c ,b =7,求AB ·AC 的值. 解:(1)因为3a -2b sin A =0, 所以 3sin A -2sin B sin A =0, 因为sin A ≠0,所以sin B =32.又B 为锐角,所以B =π3.(2)由(1)可知,B =π3.因为b = 7.根据余弦定理,得7=a 2+c 2-2ac cos π3,整理,得(a +c )2-3ac =7. 由已知a +c =5,得ac =6. 又a >c ,故a =3,c =2.于是cos A =b 2+c 2-a 22bc =7+4-947=714,所以AB ·AC =|AB |·|AC |cos A =cb cos A =2×7×714=1. 12.(2012·山东高考)在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,已知sin B (tan A +tan C )=tan A tan C .(1)求证:a ,b ,c 成等比数列; (2)若a =1,c =2,求△ABC 的面积S .解:(1)证明:在△ABC 中,由于sin B (tan A +tan C )= tan A tan C ,所以sin B ⎝⎛⎭⎫sin A cos A +sin C cos C =sin A cos A ·sin C cos C , 因此sin B (sin A cos C +cos A sin C )=sin A sin C , 所以sin B sin(A +C )=sin A sin C . 又A +B +C =π, 所以sin(A +C )=sin B , 因此sin 2B =sin A sin C . 由正弦定理得b 2=ac , 即a ,b ,c 成等比数列.(2)因为a =1,c =2,所以b =2,由余弦定理得cos B =a 2+c 2-b 22ac =12+22-22×1×2=34,因为0<B <π,所以sin B =1-cos 2B =74, 故△ABC 的面积S =12ac sin B =12×1×2×74=74.1.(2012·湖北高考)设△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c .若三边的长为连续的三个正整数,且A >B >C ,3b =20a cos A ,则sin A ∶sin B ∶sin C 为( )A .4∶3∶2B .5∶6∶7C .5∶4∶3D .6∶5∶4解析:选D 由题意可得a >b >c ,且为连续正整数,设c =n ,b =n +1,a =n +2(n >1,且n ∈N *),则由余弦定理可得3(n +1)=20(n +2)·(n +1)2+n 2-(n +2)22n (n +1),化简得7n 2-13n -60=0,n ∈N *,解得n =4,由正弦定理可得sin A ∶sin B ∶sin C =a ∶b ∶c =6∶5∶4.2.(2012·长春调研)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,已知4sin 2A +B 2-cos 2C =72,且a +b =5,c =7,则△ABC 的面积为________. 解析:因为4sin 2A +B 2-cos 2C =72, 所以2[1-cos(A +B )]-2cos 2C +1=72, 2+2cos C -2cos 2C +1=72,cos 2C -cos C +14=0, 解得cos C =12.根据余弦定理有cos C =12=a 2+b 2-72ab , ab =a 2+b 2-7,3ab =a 2+b 2+2ab -7=(a +b )2-7=25-7=18,ab =6,所以△ABC 的面积S △ABC =12ab sin C =12×6×32=332. 答案:3323.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且满足(2b -c )cos A -a cos C =0.(1)求角A 的大小;(2)若a =3,S △ABC =334,试判断△ABC 的形状,并说明理由. 解:(1)法一:由(2b -c )cos A -a cos C =0及正弦定理,得(2sin B -sin C )cos A -sin A cos C =0,∴2sin B cos A -sin(A +C )=0,sin B (2cos A -1)=0.∵0<B <π,∴sin B ≠0, ∴cos A =12. ∵0<A <π,∴A =π3. 法二:由(2b -c )cos A -a cos C =0,及余弦定理,得(2b -c )·b 2+c 2-a 22bc -a ·a 2+b 2-c 22ab=0, 整理,得b 2+c 2-a 2=bc ,∴cos A =b 2+c 2-a 22bc =12, ∵0<A <π,∴A =π3. (2)∵S △ABC =12bc sin A =334, 即12bc sin π3=334, ∴bc =3,①∵a 2=b 2+c 2-2bc cos A ,a =3,A =π3, ∴b 2+c 2=6,② 由①②得b =c =3,∴△ABC 为等边三角形.1.已知a ,b ,c 分别是△ABC 的三个内角A ,B ,C 所对的边.若a =1,b =3,A +C =2B ,则sin C =________.解析:在△ABC 中,A +C =2B ,∴B =60°.又∵sin A =a sin Bb =12,∴A =30°或150°(舍),∴C =90°,∴sin C =1.答案:12.在△ABC 中,a =2b cos C ,则这个三角形一定是( )A .等腰三角形B .直角三角形C .等腰直角三角形D .等腰或直角三角形 解析:选A 法一:(化边为角)由正弦定理知:sin A =2sin B cos C ,又A =π-(B +C ),∴sin A =sin(B +C )=2sin B cos C .∴sin B cos C +cos B sin C =2sin B cos C ,∴sin B cos C -cos B sin C =0,∴sin(B -C )=0.又∵B 、C 为三角形内角,∴B =C .法二:(化角为边)由余弦定理知cos C =a 2+b 2-c 22ab, ∴a =2b ·a 2+b 2-c 22ab =a 2+b 2-c 2a,∴a 2=a 2+b 2-c 2,∴b 2=c 2,∴b =c .3.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,已知cos 2C =-14. (1)求sin C 的值;(2)当a =2,2sin A =sin C 时,求b 及c 的长.解:(1)因为cos 2C =1-2sin 2C =-14,且0<C <π, 所以sin C =104. (2)当a =2,2sin A =sin C 时,由正弦定理a sin A =c sin C ,得c =4.由cos 2C =2cos 2C -1=-14,及0<C <π得cos C =±64. 由余弦定理c 2=a 2+b 2-2ab cos C ,得b 2±6b -12=0,解得b =6或26,所以⎩⎨⎧ b =6,c =4或⎩⎨⎧b =26,c =4.4.设△ABC 的内角A ,B ,C 所对的边长分别为a ,b ,c ,且cos B =45,b =2. (1)当A =30°时,求a 的值;(2)当△ABC 的面积为3时,求a +c 的值.解:(1)因为cos B =45,所以sin B =35. 由正弦定理a sin A =b sin B ,可得a sin 30°=103,所以a =53. (2)因为△ABC 的面积S =12ac ·sin B ,sin B =35, 所以310ac =3,ac =10. 由余弦定理得b 2=a 2+c 2-2ac cos B ,得4=a 2+c 2-85ac =a 2+c 2-16, 即a 2+c 2=20.所以(a +c )2-2ac =20,(a +c )2=40.所以a +c =210.。
高考数学一轮复习 4.5 正弦定理和余弦定理精品教学案(教师版)新人教版

2013年高考数学一轮复习精品教学案4.5 正弦定理和余弦定理(新课标人教版,教师版)【考纲解读】1.掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题.2.能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题. 【考点预测】高考对此部分内容考查的热点与命题趋势为:1.解三角形是历年来高考重点内容之一,正余弦定理的考查,选择题、填空题与解答题都有可能出现,在考查正余弦定理知识的同时,又考查函数思想、转化思想等解决问题的能力.2.2013年的高考将会继续保持稳定,坚持考查正余弦定理及变形公式,命题形式会更加灵活.【要点梳理】 1.正弦定理:2sin sin sin a b cR A B C===(R 为ABC ∆的外接圆半径), 即三角形的各边长与它所对角的正弦的比相等,等于该三角形的外接圆直径. 2.正弦定理的变形公式:(1)2sin ,2sin ,2sin a R A b R B c R C ===;(2)sin ,2R a A =sin ,2R b B =sin 2R cC =;(3)::sin :sin :sinC a b c A B =; (4)sin sin sin sin sin a b a b c A B A B C +++=+++2sin aR A==.3.余弦定理:在∆ABC 中, 2222cos c a b ab C =+-;2222cos b a c ac B =+-; 2222cos a b c bc A =+-即三角形任何一边的平方等于其它两边的平方和减去这两边与它们夹角的余弦的积的两倍. 4.余弦定理的变形公式:222cos 2b c a A bc +-=;222cos 2a c b B ac+-=;222cos 2a b c C ab +-=.5.解三角形的类型:(1)已知两角一边,解三角形,用------定理,有解时,只有一解.(2)已知两边及其一边的对角,解三角形,用-----------定理,有解的情况可分别为几种情况.在∆ABC 中,已知a 、b 和解A 、B,解的情况如下:A为锐角A为钝角或直角图形关系式a=bsinA bsinA<a<b a≥b a≥b解个数一解两解一解一解上图中A为锐角时,若a<bsinA,无解;A为钝角或直角时,若a=b,a<b,均无解.(3)已知三边,解三角形,用余弦定理,有解时,只有一解.(4)已知两边及夹角,解三角形,用余弦定理,必有一解.5.三角形的面积公式:(1)111sin sin sin222ABCS ab C bc A ac B∆===(经常用);(2)1()2ABCS a b c r∆=++⋅ (其中r是ABC∆的内切圆半径).【例题精析】考点一解三角形例1.(2012年高考北京卷文科11)在△ABC中,若a=3,b=3,∠A=3π,则∠C的大小为_________.【变式训练】1.(2012年高考陕西卷理科9)在ABC∆中,角,,A B C所对边的长分别为,,a b c,若2222a b c+=,则cos C的最小值为()(A )32 (B ) 22 (C ) 12 (D ) 12- 【答案】C【解析】2122cos 2222222=+-≥-+=ba c c abc b a C ,故选C. 考点二 判断三角形的形状例2. (2012年高考上海卷文科17)在△ABC 中,若222sin sin sin A B C +<,则△ABC 的形状是( )A .钝角三角形B 、.直角三角形 C.锐角三角形 D.不能确定【变式训练】2.在△ABC 中,若cos cos ,a A b B =试判断这个三角形的形状.考点三 正余弦定理的综合应用例3.(2012年高考山东卷文科17) 在△ABC 中,内角,,A B C 所对的边分别为,,a b c ,已知sin (tan tan )tan tan B A C A C +=.(Ⅰ)求证:,,a b c 成等比数列; (Ⅱ)若1,2a c ==,求△ABC 的面积S . 【解析】(I)由已知得:sin (sin cos cos sin )sin sin B A C A C A C +=, sin sin()sin sin B A C A C +=,【变式训练】3. (2011年高考山东卷文科17)在V ABC 中,内角A ,B ,C 的对边分别为a ,b ,c.已知cos A-2cosC 2c-a=cos B b. (I ) 求sin sin CA的值;(II ) 若cosB=14,5b ABC V 的周长为,求的长.【易错专区】 问题:解三角形例.在ABC ∆中,若30,23,2B AB AC ===o,求ABC ∆的面积.【课时作业】1. (2012年高考天津卷理科6)在△ABC 中,内角A ,B ,C 所对的边分别是,,a b c ,已知8=5b c ,=2C B ,则cosC=( )(A )725(B)725- (C)725± (D)24252.(2011年高考浙江卷文科5)在ABC ∆中,角,,A B C 所对的边分,,a b c .若cos sin a A b B =,则2sin cos cos A A B +=( )(A)-12 (B) 12(C) -1 (D) 13.(湖北省襄阳市2012年3月高三调研文理科)如图,设A 、B 两点在河的两岸,一测量者在A 的同侧,在所在的河岸边洗定一点C ,测出AC 的距离为50m ,45ACB ∠=︒, 105CAB ∠=︒后,就可以计算出A 、B 两点的距离为 ( )A .502mB .503mC .252mD .2522m 【答案】 A【解析】由图可容易计算出A 、B 两点的距离为502m ,故选A.4. (2011年高考四川卷文科8)在△ABC 中,sin 2A ≤ sin 2B+ sin 2C-sinBsinC,则A 的取值范围是( )(A )(0,]6π (B )[,)6ππ (C) (0,]3π(D )[,)3ππ5. (2011年高考福建卷文科14)若△ABC 的面积为3,BC =2,C=︒60,则边AB 的长度等于_____________.6.(湖北省荆门、天门等八市2012年3月高三联考理科)如图:已知树顶A 离地面212米,树上另一点B 离地面112米,某人在离地面32米的C 处看此树,则该人离此树 米时,看A 、B 的视角最大.7. (2011年高考江西卷文科17)在ABC ∆中,C B A ,,的对边分别是c b a ,,,已知C b B c A a cos cos cos 3+=.(1)求A cos 的值; (2)若332cos cos ,1=+=C B a ,求边c 的值.【考题回放】1. (2012年高考广东卷文科6)在△ABC中,若∠A=60°,∠B=45°,BC=32,则AC =( )3A. 43B. 23C. 3D.2. (2012年高考湖北卷文科8)设△ABC的内角A,B,C所对的边分别为a,b,c,若三边的长为连续的三个正整数,且A>B>C,3b=20acosA,则s inA∶sinB∶sinC为( ) A.4∶3∶2 B.5∶6∶7 C.5∶4∶3 D.6∶5∶43. (2012年高考湖南卷文科8)在△ABC中,7,BC=2,B =60°,则BC边上的高等于A .32 B.332 C.362+ D.3394+4.(2012年高考重庆卷文科13)设△ABC 的内角A B C 、、 的对边分别为a b c 、、,且1cos 4a b C ==1,=2,,则sin B = 【答案】155. (2012年高考湖北卷理科11)设△ABC 的内角A ,B ,C ,所对的边分别是a ,b ,c.若(a+b-c )(a+b+c )=ab ,则角C=______________.6.(2012年高考福建卷文科13)在△ABC 中,已知∠BAC=60°,∠ABC=45°,,则AC=_______。
2013年普通高考数学科一轮复习精品学案第27讲正、余弦定理及应用

2013年普通高考数学科一轮复习精品学案第27讲 正、余弦定理及应用一.课标要求:(1)通过对任意三角形边长和角度关系的探索,掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题;(2)能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题。
二.命题走向对本讲内容的考察主要涉及三角形的边角转化、三角形形状的判断、三角形内三角函数的求值以及三角恒等式的证明问题,立体几何体的空间角以及解析几何中的有关角等问题。
今后高考的命题会以正弦定理、余弦定理为知识框架,以三角形为主要依托,结合实际应用问题考察正弦定理、余弦定理及应用。
题型一般为选择题、填空题,也可能是中、难度的解答题。
三.要点精讲1.直角三角形中各元素间的关系:如图,在△ABC 中,C =90°,AB =c ,AC =b ,BC =a 。
(1)三边之间的关系:a 2+b 2=c 2。
(勾股定理) (2)锐角之间的关系:A +B =90°; (3)边角之间的关系:(锐角三角函数定义) sin A =cos B =c a ,cos A =sin B =c b ,tan A =ba。
2.斜三角形中各元素间的关系:如图6-29,在△ABC 中,A 、B 、C 为其内角,a 、b 、c 分别表示A 、B 、C 的对边。
(1)三角形内角和:A +B +C =π。
(2)正弦定理:在一个三角形中,各边和它所对角的正弦的比相等。
R Cc B b A a 2sin sin sin ===。
(R 为外接圆半径)(3)余弦定理:三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。
a 2=b 2+c 2-2bc cos A ;b 2=c 2+a 2-2ca cos B ;c 2=a 2+b 2-2ab cos C 。
3.三角形的面积公式:(1)△=21ah a =21bh b =21ch c (h a 、h b 、h c 分别表示a 、b 、c 上的高); (2)△=21ab sin C =21bc sin A =21ac sin B ;(3)△=)sin(2sin sin 2C B C B a +=)sin(2sin sin 2A C A C b +=)sin(2sin sin 2B A BA c +;(4)△=2R 2sin A sin B sin C 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013年普通高考数学科一轮复习精品学案第27讲 正、余弦定理及应用一.课标要求:(1)通过对任意三角形边长和角度关系的探索,掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题;(2)能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题。
二.命题走向对本讲内容的考察主要涉及三角形的边角转化、三角形形状的判断、三角形内三角函数的求值以及三角恒等式的证明问题,立体几何体的空间角以及解析几何中的有关角等问题。
今后高考的命题会以正弦定理、余弦定理为知识框架,以三角形为主要依托,结合实际应用问题考察正弦定理、余弦定理及应用。
题型一般为选择题、填空题,也可能是中、难度的解答题。
三.要点精讲1.直角三角形中各元素间的关系:如图,在△ABC 中,C =90°,AB =c ,AC =b ,BC =a 。
(1)三边之间的关系:a 2+b 2=c 2。
(勾股定理) (2)锐角之间的关系:A +B =90°; (3)边角之间的关系:(锐角三角函数定义) sin A =cos B =c a ,cos A =sin B =c b ,tan A =ba。
2.斜三角形中各元素间的关系:如图6-29,在△ABC 中,A 、B 、C 为其内角,a 、b 、c 分别表示A 、B 、C 的对边。
(1)三角形内角和:A +B +C =π。
(2)正弦定理:在一个三角形中,各边和它所对角的正弦的比相等。
R CcB b A a 2sin sin sin ===。
(R 为外接圆半径)(3)余弦定理:三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。
a 2=b 2+c 2-2bc cos A ;b 2=c 2+a 2-2ca cos B ;c 2=a 2+b 2-2ab cos C 。
3.三角形的面积公式:(1)△=21ah a =21bh b =21ch c (h a 、h b 、h c 分别表示a 、b 、c 上的高); (2)△=21ab sin C =21bc sin A =21ac sin B ;(3)△=)sin(2sin sin 2C B C B a +=)sin(2sin sin 2A C A C b +=)sin(2sin sin 2B A BA c +;(4)△=2R 2sin A sin B sin C 。
(R 为外接圆半径) (5)△=Rabc 4; (6)△=))()((c s b s a s s ---;⎪⎭⎫ ⎝⎛++=)(21c b a s ; (7)△=r ·s 。
4.解三角形:由三角形的六个元素(即三条边和三个内角)中的三个元素(其中至少有一个是边)求其他未知元素的问题叫做解三角形.广义地,这里所说的元素还可以包括三角形的高、中线、角平分线以及内切圆半径、外接圆半径、面积等等.解三角形的问题一般可分为下面两种情形:若给出的三角形是直角三角形,则称为解直角三角形;若给出的三角形是斜三角形,则称为解斜三角形。
解斜三角形的主要依据是:设△ABC 的三边为a 、b 、c ,对应的三个角为A 、B 、C 。
(1)角与角关系:A +B +C = π;(2)边与边关系:a + b > c ,b + c > a ,c + a > b ,a -b < c ,b -c < a ,c -a >b ;(3)边与角关系: 正弦定理R CcB b A a 2sin sin sin ===(R 为外接圆半径); 余弦定理 c 2= a 2+b 2-2bc cos C ,b 2= a 2+c 2-2ac cos B ,a 2= b 2+c 2-2bc cos A ;它们的变形形式有:a = 2R sin A ,baB A =sin sin ,bc a c b A 2cos 222-+=。
5.三角形中的三角变换三角形中的三角变换,除了应用上述公式和上述变换方法外,还要注意三角形自身的特点。
(1)角的变换因为在△ABC 中,A+B+C=π,所以sin(A+B)=sinC ;cos(A+B)=-cosC ;tan(A+B)=-tanC 。
2sin 2cos ,2cos 2sinCB AC B A =+=+; (2)三角形边、角关系定理及面积公式,正弦定理,余弦定理。
r 为三角形内切圆半径,p 为周长之半。
(3)在△ABC 中,熟记并会证明:∠A,∠B,∠C 成等差数列的充分必要条件是∠B=60°;△ABC 是正三角形的充分必要条件是∠A,∠B,∠C 成等差数列且a ,b ,c 成等比数列。
四.典例解析 题型1:正、余弦定理例1.(1)在∆ABC 中,已知032.0=A ,081.8=B ,42.9=a cm ,解三角形; (2)在∆ABC 中,已知20=a cm ,28=b cm ,040=A ,解三角形(角度精确到01,边长精确到1cm )。
解析:(1)根据三角形内角和定理,0180()=-+C A B 000180(32.081.8)=-+066.2=;根据正弦定理,00sin 42.9sin81.880.1()sin sin32.0==≈a B b cm A ;根据正弦定理,00sin 42.9sin66.274.1().sin sin32.0==≈a C c cm A(2)根据正弦定理,0sin 28sin40sin 0.8999.20==≈b A B a因为00<B <0180,所以064≈B ,或0116.≈B①当064≈B 时, 00000180()180(4064)76=-+≈-+=C A B ,sin 20sin7630().sin sin40==≈a C c cm A②当0116≈B 时,180()180(40116)24=-+≈-+=C A B ,0sin 20sin2413().sin40==≈a C c cm 点评:应用正弦定理时(1)应注意已知两边和其中一边的对角解三角形时,可能有两解的情形;(2)对于解三角形中的复杂运算可使用计算器。
例2.(1)在∆ABC 中,已知=a c 060=B ,求b 及A ; (2)在∆ABC 中,已知134.6=a cm ,87.8=b cm ,161.7=c cm ,解三角形 解析:(1)∵2222cos =+-b a c ac B=222+-⋅cos 045=2121)+- =8∴=b求A 可以利用余弦定理,也可以利用正弦定理:解法一:∵cos 2222221,22+-=b c a A bc ∴060.=A解法二:∵sin 0sin sin45,=a A B b2.4 1.43.8,+=2 1.8 3.6,⨯=∴a <c ,即00<A <090, ∴060.=A(2)由余弦定理的推论得:cos 2222+-=b c a A bc 22287.8161.7134.6287.8161.7+-=⨯⨯0.5543,≈ 05620'≈A ;cos 2222+-=c a b B ca 222134.6161.787.82134.6161.7+-=⨯⨯ 0.8398,≈ 03253'≈B ;0000180()180(56203253)''=-+≈-+C A B 09047.'= 点评:应用余弦定理时解法二应注意确定A 的取值范围。
题型2:三角形面积例3.在∆ABC 中,sin cos A A +=22,AC =2,AB =3,求A t an 的值和∆ABC的面积。
解法一:先解三角方程,求出角A 的值。
.21)45cos(,22)45cos(2cos sin =-∴=-=+ A A A A又0180<<A , 4560,105.A A ∴-==tan tan(4560)2A ∴=+==- .46260sin 45cos 60cos 45sin )6045sin(105sin sin +=+=+== A S AC AB A ABC ∆=⨯=⨯⨯⨯+=+1212232643426sin ()。
解法二:由sin cos A A +计算它的对偶关系式sin cos A A +的值。
sin cos A A +=22 ① .0cos ,0sin ,180021cos sin 221)cos (sin 2<>∴<<-=∴=+∴A A A A A A A23cos sin 21)cos (sin 2=-=-A A A A , ∴-=sin cos A A 62② ① + ② 得 s i n A=+264。
① - ② 得 c o s A=-264。
从而sin tan 2cos A A A ===- 以下解法略去。
点评:本小题主要考查三角恒等变形、三角形面积公式等基本知识,着重数学考查运算能力,是一道三角的基础试题。
两种解法比较起来,你认为哪一种解法比较简单呢?例4.已知ΔABC 的三个内角A 、B .C 成等差数列,其外接圆半径为1,且有22)cos(22sin sin =-+-C A C A 。
(1)求A 、B .C 的大小;(2)求ΔABC 的的面积。
解析:∵A+B+C=180°且2B=A+C ,∴B=60°,A+C=120°,C=120°-A 。
∵22)cos(22sin sin =-+-C A C A , ∴)]60(sin 21[22cos 23sin 2102--+-A A A =22, .22)60sin(0)60sin(,0)]60sin(21)[60sin(0000=-=-∴=---∴A A A A 或 又∵0°<A<180°,∴A=60°或A=105°,当A=60°时,B=60°,C=60°,;43360sin 421sin 21 032=⨯==∆R B ac S 此时 当A=105°时,B=60°,C=15°,.4360sin 15sin 105sin 421sin 21 0002=⨯==∆R B ac S 此时 点评:要善于借助三角形内的部分变形条件,同时兼顾三角形的面积公式求得结果。
题型3:与三角形边角相关的问题例5.(1)△ABC 中,,3,3A BC π==则△ABC 的周长为( )A .)33B π++ B .)36B π++ C .6sin()33B π++ D .6sin()36B π++(2)在45,ABC B AC C ∆∠=︒==中,,求(1)?BC =(2)若点D AB 是的中点,求中线CD 的长度。
