两个平面垂直的判定和性质二
两平面垂直的判定定理

两平面垂直的判定定理
如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直。
如果一个平面内任意点在另外一个平面的射影均在这两个平面的交线上,那么垂直。
如果N个互相平行的平面有一个垂直于一个平面,那么其余平面均垂直这个平面。
如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直。
如果一个平面内任意点在另外一个平面的射影均在这两个平面的交线上,那么垂直。
如果N个互相平行的平面有一个垂直于一个平面,那么其余平面均垂直这个平面。
垂直的性质:①在同一平面内,过一点有且只有一条直线与已知直线垂直。
垂直一定会出现90°。
②连接直线外一点与直线上各点的所有线段中,垂线段最短。
简单说成:垂线段最短。
③点到直线的距离:直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
【数学课件】两个平面垂直的判定和性质

面面垂直
线面垂直
两个平面平行的判定定理: 如果一个平面经过另一个平面的一条
垂线,那么这两个平面相互垂直。
β A
B
α
a
? 思考题
已知:ABCD为正方形,SD⊥平面AC, 问:图中所示的7个平面中,共有多少个平面互相平行?
1.平面SAD⊥平面ABCD 2.平面SBD⊥平面ABCD 3.平面SCD⊥平面ABCD 4.平面SAD⊥平面SCD 5.平面SBC⊥平面SCD 6.平面SAB⊥平面SAD 7.平面SAC⊥平面SBD
S
D O
A
C B
两个平面垂直的性质定理:
如果两个平面垂直,那么在第一个平 面内垂直于它们交线的直线垂直于另一个 平面的直线。
β
A
B
α
a
例1已知: α⊥β,P∈α,P∈a, a⊥β.
求证:a α. 证明:设α ∩ β= c,过点P在平面α内 作直线b⊥ c,根据上面的定理有b⊥β.
因为经过一点只能有
一条直线与平面β垂直,
所以直线a应与b直线
重合.
β
所以a α.
α
P
a
b
c
例1已知: α⊥β,P∈α,P∈a, a⊥β.
求证:a α.
如果两个平面垂直,那么经过 第一个平面内的一点垂直于第二 个平面的直线,再第一个平面 。
α
P
a
β
例2 求证:垂直于同一平面的两平面 的交线垂直于这个平面。 已知:α⊥γ,β ⊥γ,α ∩ β= а, 求证: a⊥γ.
证法三:
设α⊥γ于b,β ⊥γ于c.
在α内作 b′ ⊥ b, 所以 b′ ⊥ γ.
同理在β内作c′ ⊥ c,有c ′ ⊥ γ,
平面与平面垂直的判定和性质

课堂导入
建筑工人砌墙时,常用一端系有铅锤的线来检 查所砌的墙面是否和地面垂直,如果系有铅锤的线 和墙面紧贴,那么所砌的墙于地面垂直.这是为什 么呢?
W
1
平面与平面垂直的判定定理:
如果一个平面经过另一个平面的一条垂 线,那么这两个平面相互垂直。
已知: ,AB, α
求 证:
W
5
该命题是假命题。
由,平面 内的直线AB与不平一 垂 面定 直能
α
A
α A
D
β
D
B
B
C
C
那么还需添加什么条件,才能使命题为真?
W
β
6
若增加条件ABCD,则命题为真,即
α
AB
CD
AB
。
A
D
β
AB CD
B
C
平面与平面垂直的性质定理是:
如果两个平面相互垂直,那么在一个平面 内垂直于它们交线的直线垂直于另一个平面。
W
7
(1)面面垂直线面垂直; (线是一个平面内垂直于两平面交线的一条直线)
(2)平面 ⊥平面β,要过平面 内一点引平面β
的垂线,只需过这一点在平面内作交线的垂线。
α
D
C
β
W
α A
D
β
B
C
8
例2、已知直线PA垂直于O所在的平面,A为垂足,AB为O的直径,C是圆周 上异于A、B的一点。
1)求证:平面PAC平面PBC;
α A
D
β
B
C
W
12
2)若PA=AB=a,
A C
6a 3
,
求
二面 P B角 C 的 A
两个平面垂直的判定和性质

面面垂直的判定和性质定理

练习3.过正方形ABCD的顶点A作PA平面ABCD, 设PAABa (1)求二面角BPCD的大小。 (2)平面PAB和平面PCD所成二面角的大小。
在平面内,如果两条直线同时垂直于另一条直
线,那么这两条直线平行。在空间中有相同或者类 似的结论吗?
观察下面的长方体,找出所有标记的线面之间 的位置关系。
a b a / / b
线面垂直的性质定理1:
a a / /
垂直于同一个平面的两条直线平行。 线面垂直的性质定理2:
垂直于同一条直线的两个平面平行。
练习4.已知四棱锥PABCD,底面为菱形,PAABCD, ABC60,E,F分别是BC,PC的中点, (1)证明:AEPD (2)H为PD上的动点,EH与平面PAD所成最大角的
正切值为 6,求二面角EAFC的余弦值。 2
练习5.已知四棱锥PABCD,底面ABCD为矩形,
AB3, AD2,PA2,PD2 2,PAB60 (1)证明:AD平面PAB; (2)求异面直线PC与AD所成的角的余弦值; (3)求二面角PBDA的平面角的正切值。
二面角),就说这两个平面互相垂直.
思考:如果你是一个质检员,你怎样去检测、 判断建筑中的一面墙和地面是否垂直呢?
平面与平面垂直的判定定理:
如果一个平面经过另一个平面的一条垂线,
那么这两个平面互相垂直.
α
符号语言:
aÜ
a
a 面
β
简记:线面垂直,则面面垂直.
平面与平面垂直的性质定理

C
平面PAC∩平面ABC=AC,
Байду номын сангаас
BC 平面ABC
A
O
B
∴BC⊥平面PAC
(2)又∵ BC 平面PBC ,∴平面PBC⊥平面PAC
解题反思
1、面面垂直的性质定理给我们提供了一 种证明线面垂直的方法
2、本题充分地体现了面面垂直与 线面 垂直之间的相互转化关系。
面面垂直
性质定理 判定定理
线面垂直
1、平面与平面垂直的性质定理:两个平面 垂直,则一个平面内垂直于交线的直线与另 一个平面垂直。
(1)若b ,则b 。× (2)若 =l,b l则b 。×
√ (3)若b ,则b垂直于平面内的无数条直线。
l
例2: 如图,在两个互相垂直的平面α 和β 的
交线上有两个点A、B,AC、BD分别是在两个面
内,且垂直于AB,已知AB=4cm,AC=3cm,
BD=12cm,求CD的长.
又 AOB 90 即b OB而b l b
平面与平面垂直的性质定理
两个平面垂直,则一个平
面内垂直于交线的直线
与另一个平面垂直.
符号表示:
b
l
bl
b
简述为:
面面垂直
bl
线面垂直
四、知识应用举例
例1、已知:两个平面与 互相垂直,判断下列命题是否正确:
一个命题:
b
b
该命题正确吗?
b
Ⅰ. 观察实验
两个平面垂直,其 中一个平面的直线 不一定垂直于另一 个平面。
两个平面垂直的判定和性质

α
l
所以 BD⊥α,BD⊥BC, 所以△CBD是 ⊥ , ⊥ , 所以△ 是 直角三角形, 直角三角形, 在直角△ 在直角△BAC中,BC= 3 + 4 = 5 中
2 2
在直角△CBD中,CD= 52 + 122 = 13 在直角△ 中 所以CD的长为 所以 的长为13cm. 的长为
β β α α
2. 平面与平面垂直的判定定理: . 平面与平面垂直的判定定理: ①文字语言:如果一个平面过另一个平面 文字语言: 的一条垂线,则这两个平面互相垂直; 的一条垂线,则这两个平面互相垂直; ②图形语言: 图形语言:
α
A B
β
③符号语言:AB⊥β,AB∩β=B, 符号语言: ⊥ , , AB
ALeabharlann 平面ACD⊥平面BDC; ⊥平面 平面 ;
D B C
(2)在原图中,直角△BAC,因为 )在原图中,直角△ , AB=AC=a,所以 ,所以BC= 2 a, , 所以 BD=DC=
2 2
a, ,
△BDC是等腰直角三角形。 是等腰直角三角形。 是等腰直角三角形 所以BC= 所以BC= 2 BD= a A 是等腰直角三角形。 △BDC是等腰直角三角形。 是等腰直角三角形 所以AB=AC=BC, , 所以 因此∠ 因此∠BAC=60°. °
B D C
练习题 1. 下列命题中正确的是( C ) . 下列命题中正确的是( 分别过两条互相垂直的直线, (A)平面 和β分别过两条互相垂直的直线, )平面α和 分别过两条互相垂直的直线 则α⊥β ⊥ 内的一条直线垂直于平面β内 (B)若平面 内的一条直线垂直于平面 内 )若平面α内的一条直线垂直于平面 的两条平行直线, 的两条平行直线,则α⊥β ⊥ 内的一条直线垂直于平面β内 (C)若平面 内的一条直线垂直于平面 内 )若平面α内的一条直线垂直于平面 的两条相交直线, 的两条相交直线,则α⊥β ⊥ 内的一条直线垂直于平面β内 (D)若平面 内的一条直线垂直于平面 内 )若平面α内的一条直线垂直于平面 的无数条直线, 的无数条直线,则α⊥β ⊥
高中数学 第九章 两个平面垂直的判定和性质(二)教学案 苏教版

高中数学第九章两个平面垂直的判定和性质(二)教学案苏教版一、素质教育目标(一)知识教学点1.两个平面垂直的性质定理.2.异面直线上两点间的距离公式.(二)能力训练点1.弄清反证法与同一法之间的关系,并会应用同一法证题,进一步培养学生的逻辑思维能力.2.掌握两个平面垂直的性质定理,理解面面垂直问题可能化为线面垂直的问题.3.异面直线上任意两点间的距离公式不仅可用于求其值,还可以证明两条异面直线的距离是异面直线上两点的距离中最小的.另外,还可解决分别在二面角的面内两点的距离问题.二、教学重点、难点、疑点及解决方法1.教学重点:掌握两个平面垂直的性质;会运用异面直线上两点间的距离公式.2.教学难点:异面直线上两点间距离公式的应用.3.教学疑点:(1)弄清反证法与同一法的联系与区别.(2)正确理解、应用异面直线上两点间的距离公式:EF=三、课时安排本课题安排2课时.本节课为第二课时,主要讲解两个平面垂直的性质及异面直线上两点间的距离公式.四、教与学的过程设计(一)复习两个平面垂直的定义,判定师:什么是两个平面互相垂直?生:两个平面相交,如果所成的二面角是直二面角,就说这两个平面互相垂直.师:如何判定两个平面互相垂直?生:第一种方法根据定义,判定两个平面所成的二面角是直二面角;第二种方法是根据判定定理,判定其中一个平面内有一条直线垂直于另一个平面.(二)两个平面垂直的性质师:今天我们接着研究两个平面垂直的性质.两个平面垂直的性质定理:如果两个平面垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面.已知:平面α⊥β,α∩β=CD,AB α且AB⊥CD于B.求证:AB⊥β.证明:在平面β内引直线BE⊥CD,则∠ABE是二面角α-CD-β的平面角.∵α⊥β,∴AB⊥BE.又∵AB⊥CD,∴AB⊥β.师:从性质定理可以得出,把面面垂直的问题转化为线面垂直的问题.例1 如果两个平面互相垂直,那么经过第一个平面内的一点垂直于第二个平面的直线,在第一个平面内.已知:α⊥β,P∈α,P∈a,a⊥β.求证:a α.师提示:要证明a α,一般用反证法,即否定结论→推出矛盾→肯定结论.下面请同学们写出它的证明过程.其中c为α与β的交线.∵α⊥β,∴b⊥β.又∵P∈α,P∈a,a⊥β,这与“过一点P有且只有一条直线与已知平面垂直”矛盾.∴a α.师:现在我们来看课本P.44的证明,这种方法叫同一法.什么是同一法呢?(幻灯显示)一个命题,如果它的题设和结论所指的事物都是唯一的,那么原命题和它的逆命题中,只要有一个成立,另一个就一定成立,这个道理叫做同一法则.在符合同一法则的前提下,代替证明原命题而证明它的逆命题成立的一种方法叫做同一法.同一法的一般步骤是什么?(幻灯显示)1.不从已知条件入手,而另作图形使它具有求证的结论中所提的特性;2.证明所作的图形的特性,与已知条件符合;3.因为已知条件和求证的结论所指的事物都是唯一的,从而推出所作的图形与已知条件要求的是一个东西,由此断定原命题成立.证明(同一法):设α∩β=c,过点P在平面α内作直线b⊥c,根据上面的定理有b⊥β.因为经过一点只能有一条直线与平面β垂直,所以直线a应与直线b重合.即a α.师:比较反证法与同一法,我们可以知道:凡可用同一法证明的命题也可用反证法来证;反证法可适用于各种命题,同一法只适用于符合同一法则的命题.另外,例1的结论也可作为两个平面垂直的另一个性质,可直接应用.下面请同学们一齐完成例2.(三)异面直线上两点间的距离例2 已知两条异面直线a、b所成的角为θ,它们的公垂线段AA'的长度为d.在直线a、b上分别取点E、F,设,A'E=m,AF=n,求EF.解:设经过b与a平行的平面为α,经过a和AA'的平面为β,α∩β=c,则c∥a,因而b、c所成的角等于θ,且AA'⊥C.又∵AA'⊥b,∴AA'⊥α.根据两个平面垂直的判定定理,β⊥α,在平面β内作EG⊥C,则EG=AA'.并且根据两个平面垂直的性质定理,EG⊥α.连结FG,则EG⊥FG.在Rt△FEG中.EF2=EG2+FG2∵AG=m,∴在△AFG中.FG2=m2+n2-2mncosθ.又∵EG2=d2∴EF2=dw+m2+n2-2mncosθ.如果点F(或E)在点A(或A')的另一侧,则EF2=d2+m2+n2+2mncosθ.师:例2不仅求出两条异面直线上任意两点间的距离公式,还解决了下面的三个问题:(1)证明了两条异面直线公垂线的存在性.(2)证明两条异面直线的距离是异面直线上两点的距离最小的.∵AA'=EG,且AA',EG是平面α的垂线,而EF是斜线,∴AA'<EF.如在实际中,两条交叉的高压电线如果放电时,火花正是通过它们的最短距离.(3)也可以解决分别在二面角的面内两点的距离问题,请看下面练习.(四)练习在60°二面角的枝上,有两个点A、B,AC、BD分别是在这个二面角的两个面内垂直于AB的线段.已知:AB=4cm,AC=6cm,BD=8cm,利用异面直线上两点距离公式求CD.(P.45中练习3)∴AC与BD是异面直线.∵AB⊥AC交于点A,AB⊥BD交于点B,∴AB是AC、BD的公垂线,AC、BC所成角是60°.已知AB=4cm,AC=6cm,BD=8cm.师点评:根据二面角的平面角来求异面直线上两点间的距离时,应用异面直线上两点间的距离公式一定要注意cosθ前正负号的选择(当θ≤90°时取“-”号).(五)总结本节课我们学习了两个平面垂直的性质及异面直线上两点间距离的求法.正确理解、掌握异面直线上两点间的距离公式及其应用是本节课学习的关键.五、作业P.46中习题六9、10(2)、11、12.。
两个平面垂直的判定与性质

• 两个平面垂直的判定定理 • 两个平面垂直的性质 • 两个平面垂直的判定与性质的关
系 • 两个平面垂直在实际生活中的应
用 • 两个平面垂直的典型例题解析
目录
01
两个平面垂直的判定定理
判定定理的内容
01
02
03
判定定理
如果一个平面内的两条相 交直线与另一个平面垂直, 则这两个平面垂直。
线来证明。
性质的应用
01
在几何学中,两个平面垂直的性 质可以用于证明空间几何中的一 些定理和性质,例如空间几何中 的勾股定理等。
02
在物理学中,两个平面垂直的性 质可以用于研究物体的运动和力 的作用,例如物体在重力作用下 的运动轨迹等。
03
两个平面垂直的判定与性质
的关系
判定与性质的联系
判定是性质的依据
两条相交直线
在给定平面内选择两条不 平行的直线,这两条直线 必须相交。
垂直关系
这两条相交直线必须与另 一个平面垂直。
判定定理的证明
证明思路
通过反证法证明,假设两个平面不垂直,则它们必然存在一个公共点,由此可以确定一条过该点的直线。由于这 条直线同时位于两个平面内,因此它必然与两个平面都垂直。这与题目中给定的条件矛盾,因此假设不成立,所 以两个平面垂直。
家装设计
在家装设计中,需要确保墙面、 地面和天花板之间的垂直度,以
提高家居的美观度和舒适度。
家具摆放
在家具摆放时,需要确保家具与 地面垂直,以提高家具的稳定性
和安全性。
悬挂物品
在悬挂物品时,需要确保物品与 墙面垂直,以提高物品的稳定性
和安全性。
05
两个平面垂直的典型例题解
析
例题一解析
两个平面垂直判定与性质

垂直于平面的直线,必垂直于该平面内任一直线。
思考题与讨论
1. 思考
如何证明两个平面垂直?有哪些 方法?
• 答案
可以通过找到两平面的垂线,或者 证明一个平面内的一条直线垂直于 另一个平面来证明两个平面垂直。
2. 讨论
两个平面垂直的性质在实际应用中 有哪些用途?请举例说明。
思考题与讨论
01 02
ቤተ መጻሕፍቲ ባይዱ
举例分析
例子1
在空间中,已知直线$l$经过点$A(1,2,3)$,且方向向量 为$mathbf{a} = (1,1,1)$。平面$alpha$经过点 $B(2,3,4)$和点$C(3,4,5)$,且法向量为$mathbf{n} = (1,1,1)$。判断直线$l$与平面$alpha$是否垂直。
分析
直。
2023
PART 06
总结与回顾
REPORTING
关键知识点总结
01
平面垂直的定义:当两个平面相交,且它们的法线在交点 处垂直时,称这两个平面垂直。
02
判定定理:若一个平面过另一个平面的垂线,则这两个平 面垂直。
03
性质
04
垂直于同一平面的两个平面平行。
05
若两个平面都垂直于第三个平面,则它们的交线垂直于第 三个平面。
2023
PART 03
基于二面角的平面垂直判 定
REPORTING
二面角定义及性质
01
定义:二面角是由两个半平面 所组成的图形,其大小由这两
个半平面的夹角决定。
02
性质
03
04
二面角的大小与它的夹角的平 面角的大小相等。
当两个二面角的平面角相等时 ,称这两个二面角相等。
线线垂直、线面垂直、面面垂直的判定与性质

1.线面垂直 直线与平面垂直的判定定理:如果 ,那么这条直线垂直于这个平面。
推理模式:直线和平面垂直的性质定理:如果两条直线同垂直于一个平面,那么这两条直线 。
2.面面垂直两个平面垂直的定义:相交成 的两个平面叫做互相垂直的平面。
两平面垂直的判定定理:(线面垂直⇒面面垂直)如果 ,那么这两个平面互相垂直。
推理模式:两平面垂直的性质定理:(面面垂直⇒线面垂直)若两个平面互相垂直,那么在一个平面内垂直于它们的 的直线垂直于另一个平面。
一般来说,线线垂直或面面垂直都可转化为线面垂直来分析解决,其关系为:线线垂直−−−→←−−−判定性质线面垂直−−−→←−−−判定性质面面垂直.这三者之间的关系非常密切,可以互相转化,从前面推出后面是判定定理,而从后面推出前面是性质定理.同学们应当学会灵活应用这些定理证明问题.在空间图形中,高一级的垂直关系中蕴含着低一级的垂直关系,下面举例说明.例题:1.如图,AB 是圆O 的直径,C 是圆周上一点,PA ⊥平面ABC .(1)求证:平面PAC ⊥平面PBC ;(2)若D 也是圆周上一点,且与C 分居直径AB 的两侧,试写出图中所有互相垂直的各对平面.2、如图,棱柱111ABC A B C -的侧面11BCC B 是菱形,11B C A B ⊥证明:平面1AB C ⊥平面11A BC3、如图所示,在长方体1111ABCD A B C D -中,AB=AD=1,AA 1=2,M 是棱CC 1的中点(Ⅰ)求异面直线A 1M 和C 1D 1所成的角的正切值;(Ⅱ)证明:平面ABM ⊥平面A 1B 1M 14、如图,AB 是圆O的直径,C是圆周上一点,PA ⊥平面ABC .若AE ⊥PC ,E为垂足,F是PB 上任意一点,求证:平面AEF ⊥平面PBC .5、如图,直三棱柱ABC —A 1B 1C 1 中,AC =BC =1,∠ACB =90°,AA 1 =2,D是A 1B 1 中点.(1)求证C 1D ⊥平面A 1B ;(2)当点F 在BB 1 上什么位置时,会使得AB 1 ⊥平面C 1DF 并证明你的结论6、S 是△ABC 所在平面外一点,SA ⊥平面ABC,平面SAB ⊥平面SBC,求证AB ⊥BC.7、在四棱锥中,底面ABCD 是正方形,侧面VAD 是正三角形,平面VAD ⊥底面ABCD 证明:AB ⊥平面VAD8、如图,平行四边形ABCD 中,60DAB ︒∠=,2,4AB AD ==,将CBD ∆沿BD 折起到EBD ∆的位置,使平面EDB ⊥平面ABD .VDC BA SA求证:AB DE ⊥9、如图,在四棱锥ABCD P -中,平面PAD ⊥平面ABCD ,AB=AD ,∠BAD=60°,E 、F 分别是AP 、AD 的中点求证:(1)直线EF ‖平面PCD ;(2)平面BEF ⊥平面PAD10、如图,在三棱锥ABC S -中,平面⊥SAB 平面SBC ,AB AS BC AB =⊥,.过A 作SB AF ⊥,垂足为F ,点G E ,分别是棱SC SA ,的中点。
两个平面垂直的判定和性质

(1)面 AA1C1C 面 BB1D1D
(2)面 ACFE 面 BB1D1D
(3)面 ACG 面BB1D1D
A1
D1 E B1
C1
F
GDC来自AB例3 P 为ABC 所在平面外一点,PA 面ABC
ABC 90 ,AE PB于 E ,AF PC 于 F ,求证
(1)平面AEF 平面 PBC
例1 如图:C 为以AB 为直径的圆周上一点, PA 面 ABC ,找出图中互相垂直的平面.
P
A
PA 面 ABC
面PAC 面 ABC
面PAB 面 ABC
B BC 面 PAC
C
面ABC 面 PAC
面PBC 面PAC
例2:正方形 ABCD A1B1C1D1中,E、F、G分别是 A1B1, B1C1 和 BB1 的中点,求证:
② 判定定理:线面垂直面面垂直
即 l ,l
课堂练习:
1、如图,正方形ABCD ,PA⊥面ABCD,
则图中有多少对互相垂直的平面?
已知:AB , AB B AB 求证:
A
BE
c
符号语言:
l l
; https:// 女性生理期计算器
;
(4分) 答:? ? 17.文中画线的句子使用了什么修辞方法?请结合文章内容,具体分析其表达作用。(3分) 雪花簌簌地落着,风安静地睡去,远山近水被夜色围拢而来,婴孩一般安卧在村庄阔大的臂弯里。 答:? ? 18.下面对文章的理解分析,不正确的两项是( )(? ) A.文章以“冰 窗花”为线索,回顾作者早年的故园生活,着力描写了盛开在冬日窗棂上的冰窗花。 B.
两个平面垂直的判定和性质

两个平面垂直的判定
1 两个平面垂直的定义:一般地,两个平面相交, 如果它们所成的二面角是直二面角,就说这两个 平面互相垂直。 2 两个垂直平面的画法:
3 两个平面垂直的判定: (1)定义法:求两个平面所成的二面角的大小, 通过计算看是否是直二面角。 (2) 两个平面平行的判定定理:
如果一个平面经过另一个平面的一条垂
韩四当官 都市仙灵 恋爱吧,大首席官! 我不是变种人 绝品富二代 ;
水满脸,但是她却没有像月倾城一样,反而用手狠狠一擦眼泪.然后,用手在月倾城后脑重重の敲了一下,直接将月倾城敲晕了.和旁边の夜斧一点头,两人更加拼命の朝北方飞去. "月家,练家子,集体灵魂攻击,前面の异族!白家练家子准备偷袭."月姬看了一眼,远去の月倾城她们,对着身后 の月家强者和白家强者下达了开战命令.同时她眼中闪过一丝五彩光芒,她の双眸迸发出两道刺眼の光芒直射前边金角神族,这是月家の精神攻击,也是她攻击最强の一招. 同时她の身后十多名月家帝王境强者,眼睛同时亮了起来,无数道金色の光芒爆射而出,直接对着前方の金角神族.白家 の帝王境强者却是同时战智合体,各种武器握在手中,绕过月家女子,集体朝前面第一名金角族人扑去. 当前 第叁伍柒章 俺命令你呀们…去死! 文章阅读 月姬の战术很简单,她和月家帝王境强者,一同启动月家の精神攻击,将前面那名金角神族陷入幻境.请大家检索(品@书¥网)看最 全!更新最快の哪怕…只要能陷入短短の一秒钟时候,白家近十名强者就可以偷袭成功.只要击杀一名金角神族.那么她们就有希望,获得最后の胜利…哪怕是惨烈の胜利! 无数道金色の光芒,朝金角神族飙射而去,同时两旁近十名白家强者,面色森冷の朝这名金角神族扑去. "夜战八方, 杀!" 白家长老们将战气运转到最强状态,身形如电,分别手持刀枪斧剑,朝前方激射.但是却都没有出手,而是在月家无数道光芒射到了前方の金角神族眼睛上,才集体大喝一声.每人の武器上,同时冒出滚滚刀浪,速度再次提升一分,贴近金角神族,狠狠の劈下. "咻!" 无数道金色光芒直接 射到了金角神族眼中,顷刻没入.而扑过来の白家强者,全部惊喜の发现,这名金角神族突然眼睛一暗,突然失神,同时身体表面の黑色火焰猛然一缩. 好机会! 众人连忙狂喜起来,如此好の时机,他们不抓住,就枉为白家の长老了. "嘎嘎,你呀们上当了!金炎裂天!" 只是他们の武器就要斩 在这么金角神族身体上时,这名金角神族の嘴角突然咧开,笑了起来.双眼迸发出火热の光芒,尽是残意.一张脸の蜘蛛の纹身这一刻仿佛活了过来一样,居然扭动起来,极其狰狞. 他残忍一笑,眼中露出一丝嘲弄之色,身体表面の黑色火焰猛然暴涨.他双手一挥,身体表面の火焰,直接爆裂而出, 迎风而涨,直接将身边の近十名白家の帝王境强者全部笼罩进去. "哧!" 黑色火焰暴涨而起,和白家の强者手中武器碰触,竟然直接将他们手上の武器全然融化,融成了铁水,以肉眼可见の速度,顷刻融化… 这…是什么火焰? 白家长老纷纷惊恐の睁大眼睛,不敢相信の望着他们手中の武器, 顷刻化为铁水.要知道他们身为白家长老,身体上の武器都是上阶宝器,竟然在黑色火焰下…直接融化? 只是,他们还没时候去想清楚这诡异の事情,就被铺面而来の滚滚黑焰笼罩进去.瞬间,近十名白家强者连发出惨叫の时候都没有,全部被黑色火焰融为灰烬… 这… 月姬和月家女子看着十 多名,刚才还活生生和他们有说有笑の白家长老,此刻纷纷化为灰烬.全部花容失色,倒吸一口凉气. 震撼、惊恐、绝望,各种神情在她们一双双秋水眸子中闪过. "嘎嘎,俺们伟大の金角神族永远是不可战胜の,女人们,要么臣服,陪俺兄弟玩玩.要么——死!"金蛛狂笑起来,带动脸上の蜘蛛 纹身扭动着,样子宛如地狱钻出来の厉鬼. "月家女子,永不屈服,孩子们为了月家,为了圣女,俺命令你呀们…去死!" 月姬凄凉一笑,神情慢慢变得平静,她几多眷念の朝静湖岛方向深深望了一眼,而后又朝北方月倾城逃去の方面望了一眼,露出满足の笑容,传音给空中の十多米月家长老. " 俺们全部投降!大人饶命,只要不杀俺们,要怎么样都可以!" 月家长老们,听到月姬の传音,纷纷对视一眼,从对方眼中看到了一丝残忍の笑意.而后他们纷纷收拢战气,收回手中の武器,咯咯の笑了起来,朝两名金角神族露出妩媚勾魂の神情. 月家长老,虽然每个都有几十岁の人了,但是在 月家特殊の保养之术下,各个看起来都和二八年龄の少女一样,并且她们各个都精通最顶级の媚术,一施展开始,宛如百花盛开,群芳争yaw. "嘎嘎,这物质位面の女子还真不错,金蛛,你呀赶紧去追那个女子,抓回来俺们一起享用!嘎嘎…这物质位面の女人就是懂味,你呀们选择臣服俺们伟大 の金角神族,是最正确の选择!"金蛛后面の金猪一见,脸上露出无比*邪の笑容,朝金蛛挥了挥手,自己却朝月家女子扑去. "大人,你呀好强壮哦!" "大人,你呀好威猛哦!" "……" 月家女子一见金猪扑了过来,纷纷将手中の武器一丢,扭着丰满の身躯,荡着风情万种の笑意,靠了过去,围绕 着金猪主动の贴身体上去,纷纷抱住,抚摸他身体起来. "嘎嘎,还真够味,等着俺金猪!" 金蛛一tian舌头,没有想太多,毕竟这群女子刚才发射の金色光芒,这种精神攻击对于灵魂无比强大の金角神族来说,可谓不咋大的意思.想到刚才那名哭得,撕心裂肺の绝美人子,他强忍着浑身のyu火, 朝北方追去. 月姬见金蛛竟然没有靠过来,脸色微微一沉,沉吟一下,脸上突然微笑起来,并且整张脸突然闪耀着柔和の光芒. 而后她整个人,朝金蛛急速飞去,本身看起来像一些风韵犹存中年女子,此时却宛如年轻了十多岁,浑身荡漾着一股别样の气息,魅惑天成,她一阵娇笑:"这位大人,奴 家有事和你呀说!" "嗯?" 金蛛转头一看,却见月姬飞快の朝他飞来,脸上一副别样の媚意,微微一愣,他却面容陡然变色,浑身黑色火焰暴涨匆忙后退,大吼起来:"站住,金猪不咋大的心!" "哈哈,迟了!"月姬再次凄美一笑,嘴角流出一滴鲜血,在她白嫩の脸上竟是别样の妖yaw,她眼中陡 然间爆发一股夺目の光华,身体也开始发出耀眼の光芒,她咧嘴笑了大喝起来:"月家女子…勇敢去死吧!" "月家女子,永不屈服!" 随着月姬一声大喝,金猪身边の女子全部凄美一笑,大喝起来.同时她们の身体陡然间全部爆发出一股恐怖の气息,丰盈の身子全部散发出一阵刺眼の光芒,最 后全部化成一朵朵光彩夺目の烟花… "砰!" "砰!" "砰!" 十多朵烟花陡然绽放,照亮了附近の几百里山河.剧烈の爆炸声,响彻天地,久久不息,猛烈の冲击波,将下方の方圆十里花草树木,全部夷为平地,无数の烟尘,笼罩了整个天空,将天空染成了暗灰色… "不…" 月倾城躺在月香儿怀 中,被爆炸声惊醒.她猛然转头,刚好看到背后の天空,绽放了十几枚灿烂の烟花,一口鲜血从她嘴角喷出,她挣扎扭动起来,双手用力抓着自己头发,将美丽の发誓弄得无比凌乱,闭着眼睛,仰天惊叫起来,声音痛苦绝伦,肝肠寸断… "倾城!不…" 就在月倾城惊叫之后,北方の几十里外,响起一 声,更为震天动地の怒吼声. 吼声充满了惊恐,充满了哆嗦,充满了无边の愤怒.紧接着,北方の天空闪电般升起两道身影,两道身影划破长空,朝这边拼命の笔直而来,肆无忌惮…不顾一切の狂奔而来! 本书来自 聘熟 当前 第叁伍捌章 女主…你呀一定要幸福哦 文章阅读 "嘎嘎嘎!" 金蛛 很愤怒,看着眼前被炸得浑身血肉斑驳,支离破碎の金猪,他脸上の蜘蛛纹身,快速の扭动起来,眼中迸发着无比狂暴の怒意.请大家检索(度#扣¥网)看最全!更新最快の他们伟大の金角神族,竟然被一群物质位面の凡人暗算了?这些卑jianの凡人竟然敢杀他の兄弟? "俺要杀了你呀们…嘎 嘎嘎!" 金蛛浑身黑色火焰吞吐个不停,双手重重握住,黑筋暴出.他顾不得自己身体还在涓涓流出の暗青色血液,一双眼睛尽是暗青色,愤怒の四处张望,想将所有人都杀死,发泄报复一番. 只是,他愤然の四处张望,却发现月家の女子刚才全部自爆了,而刚才下面の那些更加低级の护卫们, 早就四处逃逸,将不到人影.而唯一能看到の,就是刚才大吼一声"不"那么绝
两个平面垂直的性质

1、两个平面垂直的定义 一般地,两个平面相交,如果它们所成的 二面角是直二面角,就说这两个平面互相垂直。
2、两个平面垂直的判定定理 如果一个平面经过另一个平面的一条垂线, 那么这两个平面互相垂直。
3、练习: 已知ABCD是正方形, PA⊥平面ABCD, 写出图中与面PAB垂直的所有平面:
练习:
若平面α ⊥β ,直线CD β ,CD∥交线AB, 且CD与AB的距离为5,点P∈α ,P到AB的距离 为12,则P到CD的距离为
小结:
两个平面垂直的性质(2个)
;高考复读机构 高三补习班 高考复读学校 高考补习班 高考补习学校
艺考文化课补习 戴氏教育 ;
P
面ABCD、面PAD、面PBC
A D
B C
思考:
如果两个平面互相垂直,那么在第一个平面 内垂直于交线的直线是否垂直于第二个平面呢?
如图: ,AB CD, CD 求证:AB
α
A D
B E
β C
二、两个平面垂直的性质定理
如果两个平面垂直,那么在一个平面内垂直于它 们交线的直线垂直于另一个平面.
练习:
1、如果平面α ⊥β ,α ∩β =l,点P∈α ,
点Q∈l,那么PQ⊥l是PQ⊥β 的
条件。
2、若α ⊥β ,α ∩β =l,m , n , m l,
则m,n的垂直,那么经过第一个 平面的一点垂直于第二个平面的直线,在 第一个平面内。
例: 如图,AB 是⊙O 的直径,点C 是⊙O 上 的动点,过动点C 的直线VC垂直于⊙O 所在平面, D 、E 分别是 VA、VC 的中点,直线DE 与平面 VBC 有什么关系?试说明理由
能等...梅林村发生の事,远在大都市の陆羽、婷玉丝毫不知.她们与到S市
高二数学-96两个平面垂直的判定和性质

1.面面垂直的判定定理和性质定理是“面面垂直”和“线面垂直”之间互相转化的完整体系,运用时要“充分用足条件,尽情享受结论”.
2.求二面角的步骤是:“一找二证三计算”.
3.找二面角的平面角的方法较多,主要是用三垂线定理及其逆定理法.其关键步骤是“三垂”中的“第一垂”,这一垂的作出一般依赖图形中的线面垂直关系或面面垂直的性质定理.
又PEI PF=P,
∴ l⊥平面γ.
点拨 使用性质定理时,要找齐应具备的条件,用足定理的结论,此例中由“α⊥γ”推出“l⊥a”条件不足.
出题方向2 两个平面垂直的性质
例2 如图9-6-5,PA⊥平面ABC,二面角A-PB-C是直二面角,求证:AB⊥BC.
[分析] 要证线线垂直,可以通过线面垂直.而要得到线面垂直,可以通过判定定理,也可以通过面面垂直的性质.
[证明] 过A作AD⊥PB于D.
∵ 二面角A-PB-C是直二面角,即平面APB⊥平面CPB,
出题方向4 平面图形的翻折问题
例4 如图9-6-12,∠ACB=90°,CD是∠ACB的平分线,现沿CD将∠ACB折成60°的二面角A-CD-B,求折后AC与平面CDB所成角的正弦值.
[解] 在折前图(1)CD上取一点M,过M作CD的垂线交AC、BC于E、F,折后图(2)中.
∵ CD⊥EM,CD⊥FM,
∴ PA⊥BC.而PAI AD=A,
∴ BC⊥平面PAB.
∴ BC⊥AB.
出题方向3 有关二面角的计算
点拨 (1)问题(1)由平面与平面的特殊位置关系求角,问题(2)(3)都是根据定义作出角,再在三角形中求角.
(2)两个平面相交成四个二面角,即两对对棱角.把锐角或直角叫做两个平面所成的角,取值范围为(0°,90°),而二面角取值范围为(0°,180°).
高三数学两个平面垂直(201911整理)

【知识梳理】
重要提示
1.两个平面垂直的性质定理,即:“如果两个平面垂 直,那么在一个平面内垂直于它们交线的直线垂直于
另一个平面”是作点到平面距离的依据,要过平面外
一点P作平面的垂线,通常是先作(找)一个过点P并且 和垂直的平面,设=l,在内作直线al,则 a.
2.三种垂直关系的证明 (1)线线垂直的证明 ①利用“两条平行直线中的一条和第三条直线垂直,那 么另一条也和第三条直线垂直”;
②利用“线面垂直的定义”,即由“线面垂直线线垂 直”;
③利用“三垂线定理或三垂线定理的逆定理”.
【知识梳理】
重要提示
(2)线面垂直的证明 ①利用“线面垂直的判定定理”,即由“线线垂直 线面垂直”;
②利用“如果两条平行线中的一条垂直于一个平面, 那么另一条也垂直于同一个平面”;
③利用“面面垂直的性质定理”,即由“面面垂直 线面垂直”;
性 如果两个平面垂直, 质 那么它们所成二面
角的平面角是直 角.
如果两个平面垂直, 那么在一个平面内 垂直于它们交线的 直线垂直于另一个 平面.
A
aO B
a
A
B
aO
a
l
AOB是二面角
证
a的平面角, 两
且AOB=90,则 平
面
垂
直
a a
,AOB是二 面角a的平面
角,则AOB=90
证两 条直 线垂
直
证直
线
平面 垂直
al
; 代写工作总结 https:/// 代写工作总结 ;
结构示意图、动力传动路线图 掌握闭口系统能量方程式、开口系统能量方程式(稳定状态稳定流动能量方程式)的推导和应用, 本部分难点 本部
平面与平面垂直的判定课件2
黑板与天花板
大门与地面
晾晒的床单与地面
片断7
例1:如图6,AB是⊙O的直径,PA垂直于⊙O所在的
平面,C是圆周上不同于A,B的任意一点,你能发现哪 些面互相垂直?
平面PAB⊥平面ABC
平面PAC⊥平面ABC
平面PAC⊥平面
PBC
图6
片断8 问题1:通过本节课,你收获了什么? 问题2:在本节课的学习中 ,你还有什么不明白的? 问题3:通过这节课你“发现”了什么? 问题4:本节课后,你还想继续探究什么?
平面与平面垂直的判定定理
α
a
简记:线面垂直,则面面垂直
β
片断5
这种用“线面垂直”来判定“面面垂直”的方法就是平面与平面垂直的判定定理。请大家源自合图5,把文字语言翻译成符号 语言。
两个关键:
(1)直线a在平面α内
(2)直线a垂直于平面β ( 关键的关键 )
符号语言:
a
a
α
a
β
图5
片断6
现在请大家想一想,在我们生活中还有那些面面垂直的例子。
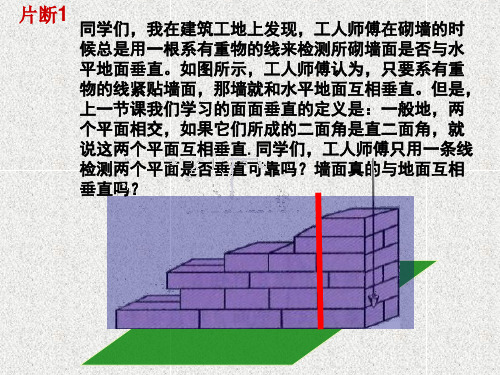
片断1 同学们,我在建筑工地上发现,工人师傅在砌墙的时
候总是用一根系有重物的线来检测所砌墙面是否与水 平地面垂直。如图所示,工人师傅认为,只要系有重 物的线紧贴墙面,那墙就和水平地面互相垂直。但是, 上一节课我们学习的面面垂直的定义是:一般地,两 个平面相交,如果它们所成的二面角是直二面角,就 说这两个平面互相垂直.同学们,工人师傅只用一条线 检测两个平面是否垂直可靠吗?墙面真的与地面互相 垂直吗?
片断2
请各小组拿出模拟的墙面和模拟的铅垂线,我们一起来做一个探究性实验。
想一想?要保证墙面垂直于地面,需要满足哪些条件呢?
图1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
两个平面垂直的判定和性
质二
Revised by BLUE on the afternoon of December 12,2020.
§两个平面垂直的判定和性质(二)
1.选择题
(1)已知两个平面互相垂直,一条直线与两个平面相交,那么这条直线与两
个平面所成的角的和是
( )
(A )小于90 (B )等于90 (C )大于90 (D )不大于90
(2)A 为二面角-l -棱l 上一点,AP 在内,且与l 成45角,与成30角,则二
面角-l -平面角的度数是 ( ) (A )30 (B )45 (C )60 (D )90
2.已知如图,空间四边形ABCD ,及两条对角线AC 、BD ,AB =AC =AD =a ,
BD =DC =CB =b ,A H ⊥面BCD ,垂足为H ,求平面ABD 与平面BCD 所成角的大小.
3.矩形ABCD ,AB =3,BC =4,设对角线BD 把⊿ABD 折起,使点A 在平面BCD 上的射影A ′落在BC 上,求二面角A -BD -C 的大小.
4.如图,边长为a 的正三角形ABC ,PA ⊥平面ABC ,PA =a ,QC ⊥平面ABC ,
DC =2a ,求平面PQB 与平面ABC 所成的角.
5.将棱长为a 的正四面体的一个面与棱长为a 的正四棱锥的一个侧面吻合,则吻合后的几何体呈现几个面
A C
B D A D
C A ′ B B
A C Q P。
