2015届高考数学(新课标 理)一轮复习辅导第13讲 排列、组合及二项式定理、概率与统计新题赏析 精品讲义
35:排列组合和二项式定理高三复习数学知识点总结(全)

排列、组合与二项式定理1.两个计数原理(1)分类计数定理(加法原理):如果完成一件事,有n 类方式,在第1类方式中有1m 种不同的方法,在第2类方式中有2m 种不同的方法,......,在第n 类方式中有n m 种不同的方法,那么完成这件事共有n m m m N +++=...21种不同的方法.(2)分步计数定理(乘法原理):如果完成一件事,需要完成n 个步骤,做第1步有1m 种不同的方法,做第2步有2m 种不同的方法,......,做第n 步有n m 种不同的方法,那么完成这件事共有n m m m N ⨯⨯⨯= 21种不同的方法.(3)两个计数原理的区别分类计数原理与分步计数原理的区别关键在于看事件能否完成,事件完成了就是分类,分类后要将种数相加;事件必须要连续若干步才能完成的则是分步,分步后要将种数相乘.2.排列(1)排列的定义:一般地,从n 个不同元素中取出)(n m m ≤个元素,按照一定的顺序排成一列,叫做从n 个不同元素中取出m 个元素的一个排列.(2)排列数的定义:一般地,从n 个不同元素中取出)(n m m ≤个元素的所有排列的个数,叫做从n 个不同元素中取出m 个元素的排列数,用符号m n A 表示.(3)排列数公式:)1()2)(1()!(!+---=-=m n n n n m n n A m n .特别地:①(全排列).123)2)(1(!⋅⋅--== n n n n A n n ②.1!0=3.组合(1)组合的定义:一般地,从n 个不同元素中取出)(n m m ≤个元素并成一组,叫做从n 个不同元素中取出m 个元素的一个组合.(2)组合数的定义:一般地,从n 个不同元素中取出)(n m m ≤个元素的所有组合的个数,叫做从n 个不同元素中取出m 个元素的组合数,用符号m n C 表示.(3)组合数公式:()()()()121!!!!m m n n m m n n n n m A n C A m m n m ---+===- .特别地:01n C =.(4)组合数的性质:①m n n m n C C -=;②11-++=m n m n m n C C C ;③11--=kn k n nC kC .4.解决排列与组合问题的常用方法通法:先特殊后一般(有限制条件问题),先组合后排列(分组问题),先分类后分步(综合问题).例:某校开设9门课程供学生选修,其中A 、B 、C 三门由于上课时问相同,至多选一门,学校规定,每位同学选修4门,共有多少种不同的选修方案?答:.75461336=+C C C (1)特殊元素、位置优先安排法:对问题中的特殊元素或位置优先考虑排列,然后排列其他一般元素或位置.例4-1:0、2、3、4、5这五个数字,组成没有重复数字的三位数,其中偶数共有几个?答:.3013131224=+C C C A (2)限制条件排除法:先求出不考虑限制条件的个数,然后减去不符合条件的个数.也适用于解决“至多”“至少”的排列组合问题.例4-2:从7名男同学和5名女同学中选出5人,若至少有2名女同学当选,问有多少种情况?答:.596)(471557512=+-C C C C(3)相邻问题“捆绑法”:将必须相邻的元素“捆绑”在一起,当作一个元素进行排列,待整个问题排好之后再考虑它们内部的排列数,它主要用于解决相邻问题.例4-3:5个男生3个女生排成一列,要求女生排一起,共有几种排法?答:6363A A =4320(4)不相邻问题“插空法”:先把无位置要求的元素进行排列,再把规定不相邻的元素插入已排列好的元素形成的“空档”中(注意两端).例4-4:5个男生3个女生排成一列,要求女生不相邻且不可排两头,共有几种排法?答:5354A A (5)元素相同“隔板法”:若把n 个不加区分的相同元素分成m 组,可通过n 个相同元素排成一排,在元素之间插入1-m 块隔板来完成分组,共11--+m m n C 种方法.例4-5:10张参观公园的门票分给5个班,每班至少1张,有几种选法?答:.49C (6)元素不多“列举法”:即把符合条件的一一列举出来.例4-6:将数字1、2、3、4填入标号为1、2、3、4的四个方格内,每个方格填一个,则每个方格的标号与所填的数字均不相同的填法种数有种。
2015高考数学一轮精品课件:10.3 二项式定理

二项式定理
第一页,编辑于星期五:十三点 四分。
第十一章
10.3
二项式定理
考纲要求
梳理自测
探究突破
巩固提升
1.能用计数原理证明二项式定理.
2.会用二项式定理解决与二项展开式有关的简单问题.
第二页,编辑于星期五:十三点 四分。
第十一章
10.3
二项式定理
考纲要求
梳理自测
梳理自测
探究突破
巩固提升
0
10
2
(3)奇数项的二项式系数和为C10
+ C10
+…+C10
=29,
1
3
9
偶数项的二项式系数和为C10
+ C10
+…+C10
=29.
考点一
考点二
考点三
误区警示
第十五页,编辑于星期五:十三点 四分。
10.3
第十一章
二项式定理
考纲要求
探究突破
探究突破
梳理自测
巩固提升
(4)令 x=y=1,得到 a0+a1+a2+…+a10=1,①
探究突破
梳理自测
巩固提升
考点三 二项式定理的应用
【例 3】 设 a∈Z,且 0≤a<13,若 512 012+a 能被 13 整除,则 a=(
A.0
B.1
C.11
D.12
)
关闭
∵52 能被 13 整除,∴512 012 可化为(52-1)2 012,
其二项式系数为 Tr+1=C2 012 522 012-r·(-1)r.
二项展开式的通项为
(新课标)北京市高考数学一轮复习 第13讲 排列、组合及二项式定理、概率与统计新题赏析 理

第13讲 排列、组合及二项式定理、概率与统计新题赏析题一:在333(1)(1(1x +++的展开式中,x 的系数为_________ (用数字作答)题二:若5(1,a a b =+为有理数),则a b +=( ) A .45 B .55 C .70 D .80 题三:已知(124x +)n 的展开式中前三项的二项式系数的和等于37,求展式中二项式系数最大的项的系数.题四:已知在(3x -123x)n 的展开式中,第6项为常数项.(1)求n ;(2)求含x 2的项的系数;(3)求展开式中所有的有理项.题五:把一个正方体各个面都涂上漆,之后分为125个大小相等的小正方体,放入一个不透明的袋子中搅拌均匀,随机从中抽取一个正方体,它是一个各个面都没有涂漆的正方体的概率是( )A.8125 B.36125 C.54125 D.27125题六:一个篮球运动员投篮一次得3分的概率为a ,得2分的概率为b ,不得分的概率为c ,a 、b 、c ∈(0,1),且无其他得分情况,已知他投篮一次得分的数学期望为1,则ab 的最大值为( ) A.148 B.124 C.112 D.16题七:一位国王的铸币大臣在每箱100枚的硬币中各掺入了10枚劣币,国王怀疑大臣作弊,他用在10箱子中各任意抽查的方法来检测,国王能发现至少一枚劣币的概率为 .题八:如图,三行三列的方阵中有九个数a ij (i =1,2,3;j =1 , 2 , 3),从中任取三个数,则至少有两个数位于同行或同列的概率是 ( )111213212223313233a a a a a a a a a ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦A. 37B. 47C. 114D. 1314题九:某饮料公司招聘一名员工,现对其进行一项测试,以便确定工资级别.公司准备了两种不同的饮料共8杯,其颜色完全相同,并且其中4杯为A 饮料,另外4杯为B 饮料,公司要求此员工一一品尝后,从8杯饮料中选出4杯A 饮料.若4杯都选对,则月工资定为3500元;若4杯选对3杯,则月工资定为2800元;否则月工资定为2100元.令X 表示此人选对A 饮料的杯数.假设此人对A 和B 两种饮料没有鉴别能力. (1)求X 的分布列;(2)求此员工月工资的期望.题十:某品牌汽车的4S 店,对最近100位采用分期付款的购车者进行了统计,统计结果如下表所示:已知分3期付款的频率为0.2,且4S 店经销一辆该品牌的汽车,顾客分1期付款,其利润为1万元;分2期或3期付款其利润为1.5万元;分4期或5期付款,其利润为2万元.用η表示经销一辆汽车的利润.(1)3期付款”的概率P ( A );(2)求η的分布列及其数学期望E (η).第13讲 排列、组合及二项式定理、概率与统计新题赏析题一:7.详解:由条件易知333(1),(1,(1x +展开式中x 项的系数分别是123333,,C C C , 即所求系数是3317++=.题二:C. 详解:∵(5123450123455555551CCC CC C=+++++1202041=+++=+由已知,得41a +=+412970a b +=+=.故选C.题三:358. 详解:由01237n n n C C C ++=,得11(1)372n n n ++-=,得8n =. 444458135()(2)48T C x x ==,∴该项的系数最大为358.题四:(1)10;(2)454;(3)210C (-12)2x 2,510C (-12)5,810C (-12)8x —2.详解:(1)通项公式为T r +1=r nC x3n r -·1()2r -x 3r-=1()2rr n C -x23n r-.∵第6项为常数项,∴当r =5时,有n -2r3=0,即n =10.(2)令n -2r 3=2,得r =12(n -6)=12×(10-6)=2,∴所求的系数为22101()2C -=454.(3)根据通项公式和题意得1023010r r r -⎧∈⎪⎪≤≤⎨⎪∈⎪⎩Z Z ,令10-2r 3=k ( k ∈Z),则10-2r =3k ,即r =5-32k . ∵r ∈Z,∴k 应为偶数.∴k 可取2,0,-2,即r 可取2 , 5 , 8.∴第3项,第6项与第9项为有理项,它们分别为 222101()2C x -,55101()2C -,882101()2C x --.题五:D .详解:把一个正方体各个面都涂上漆,之后分为125个大小相等的小正方体,可知只有3×3×3=27个小正方体各个面都没有涂漆,因此随机从袋中抽取一个正方体,它是一个各个面都没有涂漆的正方体的概率27125P =故选D .题六:B详解:依题意得3a +2b +0×c =1,∵a >0,b >0,∴3a +2b ≥26ab ,即26ab ≤1,∴ab ≤ 124.当且仅当3a =2b 即a = 25,b = 35时等式成立.题七:109()10. 详解:从10箱中任抽1枚,抽不到劣币的概率是109()10.那么至少抽到1枚的概率是 109()10,故答案为109()10.题八:D .详解:从九个数中任取三个数的不同取法共有39C =9×8×71×2×3=84 (种),因为取出的三个数分别位于不同的行与列的取法共有111321C C C ⋅⋅=6,所以至少有两个数位于同行或同列的概率为1-684=1314,选D .题九:(1)省略;(2)2280.详解:(1)选对A 饮料的杯数分别为0X =,1X =,2X =,3X =,4X =,其概率分布分别为: ()7010484404==C C C P ,()70161483414==C C C P ,()70362482424==C C C P ,()70163481434==C C C P ,()7014484404==C C C P . (2)()2280210070170167036280070163500701=⨯⎪⎭⎫⎝⎛+++⨯+⨯=E ζ.题十:(1)0.896;(2)η的分布列为:η的数学期望为1.4(万元).详解:(1)由题意可知“购买该品牌汽车的3位顾客中有1位采用分3期付款” 的概率为0.2,所以P (A )=0.83+13C ×0.2×(1-0.2)2=0.896.(2)由a100=0.2得a =20,∵40+20+a +10+b =100,∴b =10. 记分期付款的期数为ξ,依题意得:P (ξ=1)=40100=0.4,P (ξ=2)=20100=0.2,P (ξ=3)=20100=0.2,P (ξ=4)=10100=0.1,P (ξ=5)=10100=0.1.由题意知η的可能取值为:1 , 1.5 , 2 (单位:万元). P (η=1)=P (ξ=1)=0.4,P (η=1.5)=P (ξ=2)+P (ξ=3)=0.4;P (η=2)=P (ξ=4)+P (ξ=5)=0.1+0.1=0.2. ∴η的分布列为:∴η的数学期望E (η)=1×0.4+1.5×0.4+2×0.2=1.4 (万元).。
高三数学一轮复习教学案:排列、组合、二项式定理 学案
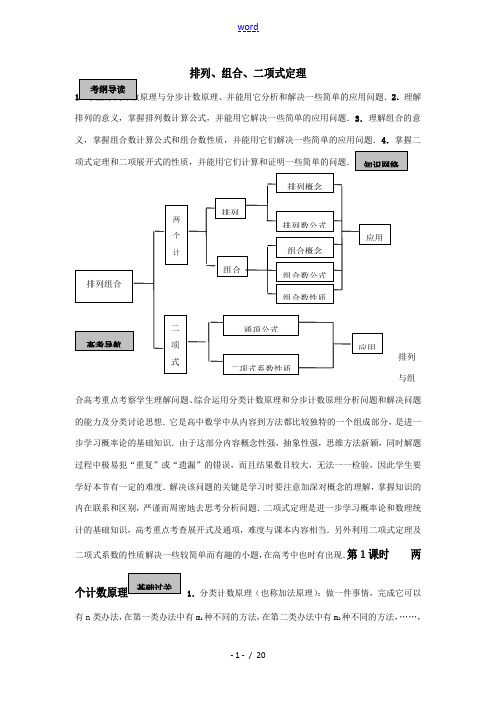
排列、组合、二项式定理2.理解排列的意义,掌握排列数计算公式,并能用它解决一些简单的应用问题.3.理解组合的意义,掌握组合数计算公式和组合数性质,并能用它们解决一些简单的应用问题.4.掌握二排列与组合高考重点考察学生理解问题、综合运用分类计数原理和分步计数原理分析问题和解决问题的能力及分类讨论思想.它是高中数学中从内容到方法都比较独特的一个组成部分,是进一步学习概率论的基础知识.由于这部分内容概念性强,抽象性强,思维方法新颖,同时解题过程中极易犯“重复”或“遗漏”的错误,而且结果数目较大,无法一一检验,因此学生要学好本节有一定的难度.解决该问题的关键是学习时要注意加深对概念的理解,掌握知识的内在联系和区别,严谨而周密地去思考分析问题.二项式定理是进一步学习概率论和数理统计的基础知识,高考重点考查展开式及通项,难度与课本内容相当.另外利用二项式定理及二项式系数的性质解决一些较简单而有趣的小题,在高考中也时有出现.第1课时两1.分类计数原理(也称加法原理):做一件事情,完成它可以有n类办法,在第一类办法中有m1种不同的方法,在第二类办法中有m2种不同的方法,……,在第n 类办法中有m n 种不同的方法,那么完成这件事共有N =种不同的方法.2.分步计数原理(也称乘法原理):做一件事情,完成它需要分成n 个步骤,做第一步有m 1种不同的方法,做第二步有m 2种不同的方法,……,做n 步有m n 种不同的方法,那么完成这件事共有N =种不同的方法.3.解题方法:枚举法、插空法、隔板法.(2)、(3)班分别有学生48,50,52人(1) 从中选1人当学生代表的方法有多少种?(2) 从每班选1人组成演讲队的方法有多少种?(3) 从这150名学生中选4人参加学代会有多少种方法?(4) 从这150名学生中选4人参加数理化四个课外活动小组,共有多少种方法?解:(1)48+50+52=150种 (2)48×50×52=124800种 (3)4150C (4)4150A 变式训练1:在直角坐标x -o -y 平面上,平行直线x=n ,(n=0,1,2,3,4,5),y=n ,(n=0,1,2,3,4,5),组成的图形中,矩形共有( )A 、25个B 、36个C 、100个D 、225个解:在垂直于x 轴的6条直线中任意取2条,在垂直于y 轴的6条直线中任意取2条,这样的4条直线相交便得到一个矩形,所以根据分步记数原理知道:得到的矩形共有22515152626=⨯=⋅C C 个, 故选D 。
2015届高考数学(理)一轮讲义:第13讲 排列、组合及二项式定理、概率与统计新题赏析 精品讲义

排列组合、二项式定理、概率与统计新题赏析主讲教师:陈孟伟 北京八中数学特级教师重难点突破●计数原理 ●二项式定理 ●概率 ● 统计新题赏析题一:从0,2中选一个数字,从1,3,5中选两个数字,组成无重复数字的三位数,其中奇数的个数为( ).A .24B .18C .12D .6题二:6个人排成一行,其中甲、乙两人不相邻的不同排法共有__________种(用数字作答).题三:从3名骨科、4名脑外科和5名内科医生中选派5人组成一个抗震救灾医疗小组,则骨科、脑外科和内科医生都至少有1人的选派方法种数是_________(用数字作答).题四:已知5(1)(1)ax x ++的展开式中2x 的系数为5,则a =( ).A .4-B .3-C .2-D .1-题五:设m 为正整数,2()m x y +展开式的二项式系数的最大值为a ,21()m x y ++展开式的二项式系数的最大值为b ,若137a b =,则m =( ).A .5B .6C .7D .8题六:将一个各面都涂了油漆的正方体,切割成125个同样大小的小正方体。
经过搅拌后,从中随机取出一个小正方体,记它的涂油漆面数为X ,则X 的均值为()E X =( ).A .126125 B .65 C .168125 D .75题七:一位国王的铸币大臣在每箱100枚的硬币中各掺入了一枚劣币,国王怀疑大臣作弊,他用两种方法来检测。
方法一:在10箱子中各任意抽查一枚;方法二:在5箱中各任意抽查两枚。
国王用方法一、二能发现至少一枚劣币的概率分别为1p 和2p , 则( ).A .12p p =B .12p p <C .12p p >D .以上均有可能题八:某人在如图所示的直角边长为4米的三角形地块的每个格点(指纵、横直线的交叉点以及三角形的顶点)处都种了一株相同品种的作物. 根据历年的种植经验,一株该种作物的年收获量Y (单位:kg )与它的“相近”作物株数X 之间的关系如下表所示:这里,两株作物“相近”是指它们之间的直线距离不超过1米.(1)从三角形地块的内部和边界上分别随机选取一株作物,求它们恰好“相近”的概率;(2)从所种作物中随机选取一株,求它的年收获量的分布列与数学期望.排列组合、二项式定理、概率与统计新题赏析新题赏析题一:B 题二:480 题三:590 题四:D题五:B 题六:B 题七:B题八:(1) 2=P ;(2)分布列: X()46=E Y0 1 2 3 4。
排列组合与二项式定理(高考试题)

排列组合与二项式定理一、排列组合1.(2016年四川高考)用数字1,2,3,4,5组成没有重复数字的五位数,其中奇数的个数为( )(A )24 (B )48 (C )60 (D )72【答案】D 【解析】由题意,要组成没有重复的五位奇数,则个位数应该为1、3、5,其他位置共有44A ,所以其中奇数的个数为44372A =,故选D. 2.(2015年四川高考)用数字0,1,2,3,4,5组成没有重复数字的五位数,其中比40000大的偶数共有( )(A )144个 (B )120个 (C )96个 (D )72个【答案】B 【解析】据题意,万位上只能排4、5.若万位上排4,则有342A ⨯个;若万位上排5,则有343A ⨯个.所以共有342A ⨯343524120A +⨯=⨯=个.选B. 3. (2015年广东高考)某高三毕业班有40人,同学之间两两彼此给对方仅写一条毕业留言,那么全班共写了 条毕业留言.(用数字作答)【答案】1560.【解析】依题两两彼此给对方写一条毕业留言相当于从40人中任选两人的排列数,所以全班共写了24040391560A =⨯=条毕业留言,故应填入1560.4.(2014大纲全国,理5)有6名男医生、5名女医生,从中选出2名男医生、1名女医生组成一个医疗小组,则不同的选法共有( ).A .60种B .70种C .75种D .150种答案:C 解析:从6名男医生中选出2名有26C 种选法,从5名女医生中选出1名有15C 种选法,故共有216565C C 57521⨯⋅=⨯=⨯种选法,选C. 5.(2014福建,理10)用a 代表红球,b 代表蓝球,c 代表黑球.由加法原理及乘法原理,从1个红球和1个蓝球中取出若干个球的所有取法可由(1+a )(1+b )的展开式1+a +b +ab 表示出来,如:“1”表示一个球都不取、“a ”表示取出一个红球、而“ab ”则表示把红球和蓝球都取出来.依此类推,下列各式中,其展开式可用来表示从5个无区别的红球、5个无区别的蓝球、5个有区别的黑球中取出若干个球,且所有的蓝球都取出或都不取出的所有取法的是( ).A .(1+a +a 2+a 3+a 4+a 5)(1+b 5)(1+c )5B .(1+a 5)(1+b +b 2+b 3+b 4+b 5)(1+c )5C .(1+a )5(1+b +b 2+b 3+b 4+b 5)(1+c 5)D .(1+a 5)(1+b )5(1+c +c 2+c 3+c 4+c 5)答案:A 解析:本题可分三步:第一步,可取0,1,2,3,4,5个红球,有1+a +a 2+a 3+a 4+a 5种取法;第二步,取0或5个蓝球,有1+b 5种取法;第三步,取5个有区别的黑球,有(1+c )5种取法.所以共有(1+a +a 2+a 3+a 4+a 5)(1+b 5)(1+c )5种取法.故选A.6.(2014辽宁,理6)6把椅子摆成一排,3人随机就座,任何两人不相邻的坐法种数为( ).A .144B .120C .72D .24答案:D 解析:插空法.在已排好的三把椅子产生的4个空档中选出3个插入3人即可.故排法种数为34A =24.故选D.7.(2014四川,理6)六个人从左至右排成一行,最左端只能排甲或乙,最右端不能排甲,则不同的排法共有( ).A .192种B .216种C .240种D .288种答案:B 解析:(1)当最左端排甲的时候,排法的种数为55A ;(2)当最左端排乙的时候,排法种数为1444C A . 因此不同的排法的种数为514544A +C A =120+96=216.8.(2014重庆,理9)某次联欢会要安排3个歌舞类节目、2个小品类节目和1个相声类节目的演出顺序,则同类节目不相邻的排法种数是( ).A .72B .120C .144D .168答案:B 解析:解决该问题分为两类:第一类分两步,先排歌舞类33A ,然后利用插空法将剩余3个节目排入左边或右边3个空,故不同排法有3333A 2A 72⋅=.第二类也分两步,先排歌舞类33A ,然后将剩余3个节目放入中间两空排法有122222C A A ,故不同的排法有32213222A A A C 48=,故共有120种不同排法,故选B. 9.(2014浙江,理14)在8张奖券中有一、二、三等奖各1张,其余5张无奖.将这8张奖券分配给4个人,每人2张,不同的获奖情况有________种(用数字作答).答案:60解析:不同的获奖情况分为两种,一是一人获两张奖券一人获一张奖券,共有2234C A =36种;二是有三人各获得一张奖券,共有34A =24种.因此不同的获奖情况有36+24=60种.10.(2014北京,理13)把5件不同产品摆成一排.若产品A 与产品B 相邻,且产品A 与产品C 不相邻,则不同的摆法有__________种.答案:36解析:产品A ,B 相邻时,不同的摆法有2424A A =48种.而A ,B 相邻,A ,C 也相邻时的摆法为A 在中间,C ,B 在A 的两侧,不同的摆法共有2323A A =12(种).故产品A 与产品B 相邻,且产品A 与产品C 不相邻的不同摆法有48-12=36(种).11.(2013山东,理10)用0,1,…,9十个数字,可以组成有重复数字的三位数的个数为( )A .243B .252C .261D .279B [解析] (排除法)十个数排成不重复数字的三位数求解方法是:第一步,排百位数字,有9种方法(0不能作首位),第二步,排十位数字,有9种方法,第三步,排个位数字,有8种方法,根据乘法原理,共有9×9×8 = 648(个)没有重复数字的三位数.可以组成所有三位数的个数:9×10×10=900,所以可以组成有重复数字的三位数的个数是:900-648=252.12.(2013福建,理5) 满足a ,b ∈{-1,0,1,2},且关于x 的方程ax 2+2x +b =0有实数解的有序数对(a ,b )的个数为( )A .14B .13C .12D .10B [解析] 当a =0时,2x +b =0,∴ x =-b 2,有序数对(0,b )有4个;当a ≠0时,Δ=4-4ab ≥0,∴ ab ≤1,有序数对(-1,b )有4个,(1,b )有3个,(2,b )有2个,综上共有4+4+3+2=13个,故选B.13.(2013大纲全国,理14)6个人排成一行,其中甲、乙两人不相邻的不同排法共有________种.(用数字作答)480 [解析] 先排另外四人,方法数是A 44,再在隔出的五个位置安插甲乙,方法数是A 25,根据乘法原理得不同排法共有A 44A 25=24×20=480种.14.(2013北京,理13) 将序号分别为1,2,3,4,5的5张参观券全部分给4人,每人至少1张,如果分给同一人的2张参观券连号,那么不同的分法种数是________.96 [解析] 5张参观券分为4堆,有2个连号有4种分法,然后每一种全排列有A 44种方法,所以不同的分法种数是4A 44=96.解析:按照要求要把序号分别为1,2,3,4,5的5张参观券分成4组,然后再分配给4人,连号的情况是1和2,2和3,3和4,4和5,故其方法数是4A 44=96.15.(2013浙江,理14) 将A ,B ,C ,D ,E ,F 六个字母排成一排,且A ,B 均在C 的同侧,则不同的排法共有________种(用数字作答).480 [解析一] 先在6个位置找3个位置,有C 36种情况,A ,B 均在C 的同侧,有CAB ,CBA ,ABC ,BAC ,而剩下D ,E ,F 有A 33种情况,故共有4C 36A 33=480种.解析二:本题考查对排列、组合概念的理解,排列数、组合数公式的运用,考查运算求解能力以及利用所学知识解决问题的能力.“小集团”处理,特殊元素优先,C 36C 12A 22A 33=480. 16.(2012·安徽卷)6位同学在毕业聚会活动中进行纪念品的交换,任意两位同学之间最多交换一次,进行交换的两位同学互赠一份纪念品.已知6位同学之间共进行了13次交换,则收到4份纪念品的同学人数为( )A .1或3B .1或4C .2或3D .2或4D [解析] 任意两个同学之间交换纪念品共要交换C 26=15次,如果都完全交换,每个人都要交换5次,也就是得到5份纪念品,现在6个同学总共交换了13次,少交换了2次,这2次如果不涉及同一个人,则收到4份纪念品的同学人数有4人;如果涉及同一个人,则收到4份纪念品的同学人数有2人,答案为D.17.(2012·辽宁卷)一排9个座位坐了3个三口之家.若每家人坐在一起,则不同的坐法种数为( )A .3×3!B .3×(3!)3C .(3!)4D .9!C [解析] 本小题主要考查排列组合知识.解题的突破口为分清是分类还是分步,是排列还是组合问题.由已知,该问题是排列中捆绑法的应用,即先把三个家庭看作三个不同元素进行全排列,而后每个家庭内部进行全排列,即不同坐法种数为A 33·A 33·A 33·A 33=(3!)4.18.(2011北京,理12)用数字2,3组成四位数,且数字2,3至少都出现一次,这样的四位数共有__________个.(用数字作答)【答案】14【解析】个数为42214-=.19.(2010山东,理8)某台小型晚会由6个节目组成,演出顺序有如下要求:节目甲必须排在前两位、节目乙不能排在第一位,节目丙必须排在最后一位,该台晚会节目演出顺序的编排方案共有( )(A )36种 (B )42种 (C)48种 (D )54种【答案】B 【解析】分两类:一类为甲排在第一位共有4424A =种,另一类甲排在第二位共有133318C A =种,故编排方案共有241842+=种,故选B.20.(2009四川卷理)3位男生和3位女生共6位同学站成一排,若男生甲不站两端,3位女生中有且只有两位女生相邻,则不同排法的种数是( )A. 360B. 288C. 216D. 96解析:6位同学站成一排,3位女生中有且只有两位女生相邻的排法有32223342A C A A 432=种,其中男生甲站两端的有1442223232212=A A C A A ,符合条件的排法故共有288解析2:由题意有2221122222322323242A (C A )C C +A (C A )A 288⋅⋅⋅⋅⋅⋅⋅=,选B.21.(2009天津卷理)用数字0,1,2,3,4,5,6组成没有重复数字的四位数,其中个位、十位和百位上的数字之和为偶数的四位数共有 个(用数字作答)解析:个位、十位和百位上的数字为3个偶数的有:901333143323=+C A C A C 种;个位、十位和百位上的数字为1个偶数2个奇数的有:23413332313143323=+C A C C C A C 种,所以共有32423490=+个.22.(2009浙江卷理)甲、乙、丙3人站到共有7级的台阶上,若每级台阶最多站2人,同一级台阶上的人不区分站的位置,则不同的站法种数是 (用数字作答).答案:336 【解析】对于7个台阶上每一个只站一人,则有37A 种;若有一个台阶有2人,另一个是1人,则共有2237C A 种,因此共有不同的站法种数是336种.23.(2009·宁夏、海南,12)7名志愿者中安排6人在周六、周日两天参加社区公益活动.若每天安排3人,则不同的安排方案共有________种(用数字作答).解析:法一:先从7人中任取6人,共有C 67种不同的取法.再把6人分成两部分,每部分3人,共有C 36C 33A 22种分法.最后排在周六和周日两天,有A 22种排法,∴C 67×C 36C 33A 22×A 22=140种.法二:先从7人中选取3人排在周六,共有C 37种排法.再从剩余4人中选取3人排在周日,共有C 34种排法,∴共有C 37×C 34=140种.答案:14024.(2010浙江,10)有4位同学在同一天的上、下午参加“身高与体重”、“立定跳远”、“肺活量”、“握力”、“台阶”五个项目的测试,每位同学上、下午各测试一个项目,且不重复.若上午不测“握力”项目,下午不测“台阶”项目,其余项目上、下午都各测试一人.则不同的安排方式共有________种(用数字作答). 解析:上午测试安排有A 44种方法,下午测试分为:(1)若上午测试“台阶”的同学下午测试“握力”,其余三位同学有2种方法测试;(2)若上午测试“台阶”的同学下午不测试“握力”,则有C 13种方法选择,其余三位同学选1人测试“握力”有C 13种方法,其余两位只有一种方法,则共有C 13·C 13=9种, 因此测试方法共有A 44·(2+9)=264种.答案:264 25.(2009·辽宁,5)从5名男医生、4名女医生中选3名医生组成一个医疗小分队,要求其中男、女医生都有,则不同的组队方案共有( )A .70种B .80种C .100种D .140种解析:分恰有2名男医生和恰有1名男医生两类,从而组队方案共有:C 25×C 14+C 15×C 24=70种.答案:A26.(2013重庆,5)从3名骨科、4名脑外科和5名内科医生中选派5人组成一个抗震救灾医疗小组,则骨科、脑外科和内科医生都至少有1人的选派方法种数是________(用数字作答).解析:本题考查排列组合问题,意在考查考生的思维能力.直接法分类,3名骨科,内科、脑外科各1名;3名脑外科,骨科、内科各1名;3名内科,骨科、脑外科各1名;内科、脑外科各2名,骨科1名;骨科、内科各2名,脑外科1名;骨科、脑外科各2名,内科1名.所以选派种数为C 33·C 14·C 15+C 34·C 13·C 15+C 35·C 13·C 14+C 24·C 25·C 13+C 23·C 25·C 14+C 23·C 24·C 15=590.答案:59027.(2012新课标全国,5)将2名教师,4名学生分成2个小组,分别安排到甲、乙两地参加社会实践活动,每个小组由1名教师和2名学生组成,不同的安排方案共有( )A .12种B .10种C .9种D .8种解析:先安排1名教师和2名学生到甲地,再将剩下的1名教师和2名学生安排到乙地,共有C 12C 24=12种安排方案.答案:A二、二项式定理1、(2016年北京高考)在6(12)x -的展开式中,2x 的系数为__________________.(用数字作答)【答案】60.2、(2016年山东高考)若(a x 2)5的展开式中x 5的系数是—80,则实数a =_______. 【答案】-2 3、(2016年上海高考)在n x x ⎪⎭⎫ ⎝⎛-23的二项式中,所有项的二项式系数之和为256,则常数项等于_________ 【答案】1124、(2016年四川高考)设i 为虚数单位,则6(i)x +的展开式中含x 4的项为( )(A )-15x 4 (B )15x 4 (C )-20i x 4 (D )20i x 4【答案】A5、(2016年天津高考)281()x x -的展开式中x 2的系数为__________.(用数字作答)【答案】56-6、(2016年全国I 高考)5(2x +的展开式中,x 3的系数是 .(用数字填写答案)【答案】10。
2015年高考理数专题复习--排列组合二项式定理(理科)(解析版)

2015年高考理数专题复习--排列组合二项式定理排列、组合、二项定理是高中数学中独立性较强的一部分,也是密切联系实际的一部分,是高考必考内容,每年都有1—2道有关的试题,题型一般为选择题和填空题,考查基础知识、思维能力,多数题难度与教材习题难度相当,但也有个别难度较大。
预测明年仍以考查排列、组合应用题、通项、二项式系数,展开式系数为主,可单独考查本节知识,也可出现与其他章节知识结合的小综合。
复习建议1.排列组合应用题的处理方法和策略⑪使用分类计数原理还是分步计数原理要根据我们完成某件事情时采取的方式而定,分类来完成这件事情时用分类计数原理,分步骤来完成这件事情时用分步计数原理.怎样确定是分类,还是分步骤?“分类”表现为其中任何一类均可独立完成所给事件,而“分步骤”必须把各步骤均完成才能完成所给事情.所以准确理解两个原理的关键在于明确:分类计数原理强调完成一件事情的几类办法互不干扰,彼此之间交集为空集,并集为全集,不论哪一类办法中的哪一种方法都能单独完成事件;分步计数原理强调各步骤缺一不可,需要依次完成所有步骤才能完成事件,步与步之间互不影响,即前一步用什么方法不影响后一步采取什么方法.⑫排列与组合定义相近,它们的区别在于是否与顺序有关.⑬复杂的排列问题常常通过试验、画简图、小数字简化等手段使问题直观化,从而寻求解题途径,由于结果的正确性难以直接检验,因而常需要用不同的方法求解来获得检验.⑭按元素的性质进行分类、按事件发生的连续过程分步,是处理组合问题的基本思想方法,要注意题设中“至少”“至多”等限制词的意义.⑮处理排列组合的综合性问题,一般思想方法是先选元素(组合),后排列,按元素的性质“分类”和按事件发生的连续过程“分步”,始终是处理排列、组合问题的基本方法和原理,通过解题训练要注意积累分类和分步的基本技能.⑯在解决排列组合综合性问题时,必须深刻理解排列与组合的概念,能够熟练确定——问题是排列问题还是组合问题,牢记排列数、组合数计算公式与组合数性质.容易产生的错误是重复和遗漏计数.常见的解题策略有以下几种:①特殊元素优先安排的策略;②合理分类与准确分步的策略;③排列、组合混合问题先选后排的策略;④正难则反、等价转化的策略;⑤相邻问题捆绑处理的策略;⑥不相邻问题插空处理的策略;⑦定序问题除法处理的策略;⑧分排问题直排处理的策略;⑨“小集团”排列问题中先整体后局部的策略;⑩构造模型的策略.2.二项定理问题的处理方法和技巧⑪ 运用二项式定理一定要牢记通项T r+1 =C r n an -r b r,注意(a +b)n 与(b+a)n 虽然相同,但具体到它们展开式的某一项时是不相同的,我们一定要注意顺序问题.另外二项展开式的二项式系数与该项的(字母)系数是两个不同的概念,前者只指C r n ,而后者是字母外的部分.⑫ 对于二项式系数问题,应注意以下几点:①求二项式所有项的系数和,可采用“特殊值取代法”,通常令字母变量的值为1; ②关于组合恒等式的证明,常采用“构造法”——构造函数或构造同一问题的两种算法; ③证明不等式时,应注意运用放缩法.⑬ 求二项展开式中指定的项,通常是先根据已知条件求r ,再求T r+1,有时还需先求n ,再求r ,才能求出T r+1.⑭ 有些三项展开式问题可以变形为二项式问题加以解决;有时也可以通过组合解决,但要注意分类清楚,不重不漏.⑮ 对于二项式系数问题,首先要熟记二项式系数的性质,其次要掌握赋值法,赋值法是解决二项式系数问题的一个重要手段.⑯ 近似计算要首先观察精确度,然后选取展开式中若干项.⑰ 用二项式定理证明整除问题,一般将被除式变为有关除式的二项式的形式再展开,常采用“配凑法”“消去法”配合整除的有关知识来解决. 母题一:641)1)的展开式中x 的系数是( )A .3-B .4-C .4D .4【答案】A【解析】641)1)241)1)]=4(1)(1)x x =+-.其展开式中含x 的项是:00411344(1)1(1)3xC x C x x -+⋅-=-,系数等于3-所以选A 。
2015年高考数学(理)真题分项解析:专题11+排列组合、二项式定理

专题十一 排列组合、二项式定理1.【2015高考陕西,理4】二项式(1)()n x n N ++∈的展开式中2x 的系数为15,则n =( ) A .4 B .5 C .6 D .7 【答案】C【解析】二项式()1nx +的展开式的通项是1C r r r n x +T =,令2r =得2x 的系数是2C n ,因为2x 的系数为15,所以2C 15n =,即2300n n --=,解得:6n =或5n =-,因为n +∈N ,所以6n =,故选C . 【考点定位】二项式定理.【名师点晴】本题主要考查的是二项式定理,属于容易题.解题时一定要抓住重要条件“n +∈N ”,否则很容易出现错误.解本题需要掌握的知识点是二项式定理,即二项式()na b +的展开式的通项是1C k n k kk n a b -+T =.2.【2015高考新课标1,理10】25()x x y ++的展开式中,52x y 的系数为( )(A )10 (B )20 (C )30 (D )60 【答案】C【解析】在25()x x y ++的5个因式中,2个取因式中2x 剩余的3个因式中1个取x ,其余因式取y,故52x y 的系数为212532C C C =30,故选 C.【考点定位】本题主要考查利用排列组合知识计算二项式展开式某一项的系数.【名师点睛】本题利用排列组合求多项展开式式某一项的系数,试题形式新颖,是中档题,求多项展开式式某一项的系数问题,先分析该项的构成,结合所给多项式,分析如何得到该项,再利用排列组知识求解.3.【2015高考四川,理6】用数字0,1,2,3,4,5组成没有重复数字的五位数,其中比40000大的偶数共有( )(A )144个 (B )120个 (C )96个 (D )72个 【答案】B 【解析】据题意,万位上只能排4、5.若万位上排4,则有342A ⨯个;若万位上排5,则有343A ⨯个.所以共有342A ⨯343524120A +⨯=⨯=个.选B.【考点定位】排列组合.【名师点睛】利用排列组合计数时,关键是正确进行分类和分步,分类时要注意不重不漏.在本题中,万位与个位是两个特殊位置,应根据这两个位置的限制条件来进行分类. 4.【2015高考湖北,理3】已知(1)n x +的展开式中第4项与第8项的二项式系数相等,则奇数项的二项式 系数和为( )A.122 B .112 C .102 D .92【答案】D【解析】因为(1)n x +的展开式中第4项与第8项的二项式系数相等,所以73nn C C =,解得10=n ,所以二项式10(1)x +中奇数项的二项式系数和为9102221=⨯. 【考点定位】二项式系数,二项式系数和.【名师点睛】二项式定理中应注意区别二项式系数与展开式系数,各二项式系数和:n n n n n n C C C C 2210=+⋅⋅⋅+++,奇数项的二项式系数和与偶数项的二项式系数和相等=⋅⋅⋅++++420n n n C C C 15312-=⋅⋅⋅++++n n n n C C C .5、【2015高考广东,理12】某高三毕业班有40人,同学之间两两彼此给对方仅写一条毕业留言,那么全班共写了 条毕业留言.(用数字作答) 【答案】1560.【考点定位】排列问题.【名师点睛】本题主要考查排列问题,属于中档题,解答此题关键在于认清40人两两彼此给对方仅写一条毕业留言是个排列问题.6.【2015高考重庆,理12】53x ⎛ ⎝的展开式中8x 的系数是________(用数字作答).【答案】52【解析】二项展开式通项为7153521551()()2k k kk k k k T C x C x --+==,令71582k -=,解得2k =,因此8x 的系数为22515()22C =. 【考点定位】二项式定理【名师点晴】()na b +的展开式的二项式系数与该项的系数是两个不同的概念,前者只是指knC ,它仅是与二项式的幂的指数n 及项数有关的组合数,而与a ,b 的值无关;而后者是指该项除字母外的部分,即各项的系数不仅与各项的二项式系数有关,而且也与a ,b 的系数有关.在求二项展开式特定项的系数时要充分注意这个区别.7.【2015高考广东,理9】在4)1(-x 的展开式中,x 的系数为 . 【答案】6.【解析】由题可知()()44214411r rrrrr r T CC x--+=-=-,令412r-=解得2r =,所以展开式中x 的系数为()22416C -=,故应填入6.【考点定位】二项式定理.【名师点睛】本题主要考查二项式定理和运算求解能力,属于容易题,解答此题关键在于熟记二项展开式的通项即展开式的第1r +项为:()*12,r n r r r n T C a b n N n r N -+=∈≥∈且.8.【2015高考四川,理11】在5(21)x -的展开式中,含2x 的项的系数是 (用数字作答). 【答案】40-. 【解析】55(21)(12)x x -=--,所以2x 的系数为225(2)40C -⨯-=-.【考点定位】二项式定理.【名师点睛】涉及二项式定理的题,一般利用其通项公式求解.9.【2015高考天津,理12】在614x x ⎛⎫- ⎪⎝⎭ 的展开式中,2x 的系数为 .【答案】1516【解析】614x x ⎛⎫- ⎪⎝⎭展开式的通项为6621661144rrr r r r r T C x C x x --+⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭,由622r -=得2r =,所以222236115416T C x x ⎛⎫=-= ⎪⎝⎭,所以该项系数为1516.【考点定位】二项式定理及二项展开式的通项.【名师点睛】本题主要考查二项式定理及二项展开式的通项的应用.应用二项式定理典型式的通项,求出当2r =时的系数,即可求得结果,体现了数学中的方程思想与运算能力相结合的问题.10.【2015高考安徽,理11】371()x x+的展开式中5x 的系数是 .(用数字填写答案) 【答案】35【解析】由题意,二项式371()x x +展开的通项372141771()()r r r r r r T C x C x x--+==,令2145r -=,得4r =,则5x 的系数是4735C =.【考点定位】1.二项式定理的展开式应用.【名师点睛】常规问题直接利用二项式定理求解,其中通项是核心,运算是保证;比较复杂的问题要回到最本质的计数原理去解决,而不是一味利用公式.另外,概念不清,涉及幂的运算出现错误,或者不能从最本质的计数原理出发解决问题,盲目套用公式都是考试中常犯的错误.11.【2015高考福建,理11】()52x + 的展开式中,2x 的系数等于 .(用数字作答) 【答案】80【解析】()52x + 的展开式中2x 项为2325280C x =,所以2x 的系数等于80.【考点定位】二项式定理.【名师点睛】本题考查二项式定理的特定项问题,往往是根据二项展开式的通项和所求项的联系解题,属于基础题,注意运算的准确度.12.【2015高考北京,理9】在()52x +的展开式中,3x 的系数为 .(用数字作答)【答案】40【考点定位】本题考点为二项式定理,利用通项公式,求指定项的系数.【名师点睛】本题考查二项式定理,利用通项公式求出指定项的系数,本题属于基础题,要求正确使用通项公式1r n r r r n T C a b -+=,准确计算指定项的系数.13.【2015高考新课标2,理15】4()(1)a x x ++的展开式中x 的奇数次幂项的系数之和为32,则a =__________. 【答案】3【解析】由已知得4234(1)1464x x x x x +=++++,故4()(1)a x x ++的展开式中x 的奇数次幂项分别为4ax ,34ax ,x ,36x ,5x ,其系数之和为441+6+1=32a a ++,解得3a =. 【考点定位】二项式定理.【名师点睛】本题考查二项式定理,准确写出二项展开式,能正确求出奇数次幂项以及相应的系数和,从而列方程求参数值,属于中档题.【2015高考湖南,理6】已知5的展开式中含32x 的项的系数为30,则a =( )B. C.6 D-6 【答案】D. 【解析】试题分析:r rr r r x a C T -+-=2551)1(,令1=r ,可得6305-=⇒=-a a ,故选D.【考点定位】二项式定理.【名师点睛】本题主要考查了二项式定理的运用,属于容易题,只要掌握nb a )(+的二项展开式的通项第1+r 项为rr n r nr b a C T -+=1,即可建立关于a 的方程,从而求解. 【2015高考上海,理11】在10201511x x ⎛⎫++ ⎪⎝⎭的展开式中,2x 项的系数为 (结果用数值表示). 【答案】45【解析】因为10101019102015201520151111(1)(1)(1)x x x C x x x x ⎛⎫⎛⎫++=++=++++⎪ ⎪⎝⎭⎝⎭,所以2x 项只能在10(1)x +展开式中,即为8210C x ,系数为81045.C = 【考点定位】二项展开式【名师点睛】(1)求二项展开式中的指定项,一般是利用通项公式进行化简通项公式后,令字母的指数符合要求(求常数项时,指数为零;求有理项时,指数为整数等),解出项数r +1,代回通项公式即可.(2)对于三项式问题一般先变形化为二项式再解决.【2015高考上海,理8】在报名的3名男教师和6名女教师中,选取5人参加义务献血,要求男、女教师都有,则不同的选取方式的种数为(结果用数值表示).【答案】120【解析】由题意得,去掉选5名女教师情况即可:55961266120.C C-=-=【考点定位】排列组合【名师点睛】涉及排列与组合问题,区分的关键是看选出的元素是否与顺序有关,排列问题与顺序有关,组合问题与顺序无关.“含”与“不含”的问题:“含”,则先将这些元素取出,再由另外元素补足;“不含”,则先将这些元素剔除,再从剩下的元素中去选取.通常用直接法分类复杂时,考虑逆向思维,用间接法处理.。
高三数学第一轮复习教案讲义排列、组合、二项式定理复习资料

高三新数学第一轮复习教案—排列、组合、二项式定理一.课标要求:1.分类加法计数原理、分步乘法计数原理通过实例,总结出分类加法计数原理、分步乘法计数原理;能根据具体问题的特征,选择分类加法计数原理或分步乘法计数原理解决一些简单的实际问题;2.排列与组合通过实例,理解排列、组合的概念;能利用计数原理推导排列数公式、组合数公式,并能解决简单的实际问题;3.二项式定理能用计数原理证明二项式定理; 会用二项式定理解决与二项展开式有关的简单问题。
二.命题走向本部分内容主要包括分类计数原理、分步计数原理、排列与组合、二项式定理三部分;考查内容:(1)两个原理;(2)排列、组合的概念,排列数和组合数公式,排列和组合的应用;(3)二项式定理,二项展开式的通项公式,二项式系数及二项式系数和。
排列、组合不仅是高中数学的重点内容,而且在实际中有广泛的应用,因此新高考会有题目涉及;二项式定理是高中数学的重点内容,也是高考每年必考内容,新高考会继续考察。
考察形式:单独的考题会以选择题、填空题的形式出现,属于中低难度的题目,排列组合有时与概率结合出现在解答题中难度较小,属于高考题中的中低档题目;预测2007年高考本部分内容一定会有题目涉及,出现选择填空的可能性较大,与概率相结合的解答题出现的可能性较大。
三.要点精讲1.排列、组合、二项式知识相互关系表2.两个基本原理(1)分类计数原理中的分类;(2)分步计数原理中的分步;正确地分类与分步是学好这一章的关键。
3.排列(1)排列定义,排列数(2)排列数公式:系m n A =)!(!m n n =n ·(n -1)…(n -m+1);(3)全排列列:n n A =n!;(4)记住下列几个阶乘数:1!=1,2!=2,3!=6,4!=24,5!=120,6!=720;4.组合(1)组合的定义,排列与组合的区别;(2)组合数公式:C n m =)!(!!m n m n -=12)1(1)m -(n 1)-n (⨯⨯⨯-⨯+ m m n ; (3)组合数的性质①C n m =C n n-m;②r n r n r n C C C 11+-=+;③rC n r =n ·C n-1r-1;④C n 0+C n 1+…+C n n =2n ;⑤C n 0-C n 1+…+(-1)n C n n =0,即 C n 0+C n 2+C n 4+…=C n 1+C n 3+…=2n-1;5.二项式定理(1)二项式展开公式:(a+b)n =C n 0a n +C n 1a n-1b+…+C n k a n-k b k +…+C n n b n ;(2)通项公式:二项式展开式中第k+1项的通项公式是:T k+1=C n k a n-k b k ;6.二项式的应用(1)求某些多项式系数的和;(2)证明一些简单的组合恒等式;(3)证明整除性。
高三数学排列,组合和二项式定理

精品学案:排列,组合和二项式定理高考大纲对排列,组合和二项式定理这一章的考试内容及考试要求为: 1.分类计数和分步计数原理; 2.排列组合公式3.组合组合数公式和组合数的两个性质 4.二项式定理和二项式展开式 考试要求掌握分类计数和分步计数原理,并能用他们解决一些简单的应用问题。
理解排列的意义,掌握排列的计数公式,并能用他解决一些简单的应用问题。
理解组合的意义,掌握组合的计数公式,并能用他解决一些简单的应用问题。
掌握二项式定理和他的展开式的性质,并能用他计算和证明一些简单的应用问题。
要点一计数原理1分类计数原理:做一件事情,完成它可以有n 类办法,在第一类办法中有1m 种不同的方法,在第二类办法中有2m 种不同的方法,……,在第n 类办法中有n m 种不同的方法那么完成这件事共有 12n N m m m =+++种不同的方法2.分步计数原理:做一件事情,完成它需要分成n 个步骤,做第一步有1m 种不同的方法,做第二步有2m 种不同的方法,……,做第n 步有n m 种不同的方法,那么完成这件事有12n N m m m =⨯⨯⨯ 种不同的方法 要点二排列1.排列的概念:从n 个不同元素中,任取m (m n ≤)个元素(这里的被取元素各不相同)按照一定的顺序.....排成一列,叫做从n 个不同元素中取出m 个元素的一个排列....2.排列数的定义:从n 个不同元素中,任取m (m n ≤)个元素的所有排列的个数叫做从n 个元素中取出m 元素的排列数,用符号mn A 表示3.排列数公式:(1)(2)(1)mn A n n n n m =---+(,,m n N m n *∈≤)和m n A =!()!n n m -4阶乘:!n 表示正整数1到n 的连乘积,叫做n 的阶乘规定0!1=.要点三组合1组合的概念:一般地,从n 个不同元素中取出m ()m n ≤个元素并成一组,叫做从n 个不同元素中取出m 个元素的一个组合2.组合数的概念:从n 个不同元素中取出m ()m n ≤个元素的所有组合的个数,叫做从n 个不同元素中取出m 个元素的组合数....用符号mn C 表示. 3.组合数公式:(1)(2)(1)!m m n nm m A n n n n m C A m ---+==或)!(!!m n m n C mn -=,,(n m N m n ≤∈*且4组合数的性质1:m n n m n C C -=.规定:10=n C ;2:m n C 1+=m n C +1-m n C要点四二项式定理1.正确理解二项式展开式中的第r +1项,第r +1项的二项式系数,第r +1项的系数之间的差别.2.二项系数的性质问题求二项式系数最大的项,可直接根据二项式系数的增减性与最大值性质,当为n 奇数时,中间两项的二项式系数最大;当n 为偶数时,中间一项的二项式系数最大,若求系数最大的项,则要根据各项系数的正、负变化情况并采用列不等式组、比较系数法求解.3.二项式的某项系数问题该问题解法多样,既可化归为二项式问题求解,又可从组合角度求解,一般地,三项式(a +b+c)n的展开式中,a p b q c r的系数为4.赋值法在二项展开式中的运用赋值法的模式是:对任意的x∈A,某式子恒成立,那么对A中的特殊值,该式子一定成立.特殊值如何选取?视具体问题而定,没有一成不变的规律,它的灵活性较强,一般x0=0, 1,-1取较多.一般地,多项式f(x)的各项系数和为f(1),奇次项系数和为1[(1)(1)]2f f--,偶次项系数和为1[(1)(1)]2f f+-.如二项式系数性质。
排列、组合与二项式定理(理)

二项式定理的未来发展方向
理论完善
随着数学的发展,二项式定理的理论体系将不断完善,新的证明方 法和技巧将不断涌现。
应用拓展
随着各学科的发展,二项式定理的应用领域将不断拓展,特别是在 大数据处理、人工智能和量子计算等领域。
排列数的计算
01
二项式定理也可以用来计算排列数,特别是当排列数的上标和
下标较大时,使用二项式定理可以简化计算过程。
排列数的性质
02
通过二项式定理,我们可以推导出排列数的性质,如排列数的
增减性等。
排列数的递推关系
03
利用二项式定理,我们可以得到排列数的递推关系,从而更方
便地计算排列数。
利用二项式定理解决实际问题
互异性
有序性
排列中的元素顺序是确定的,不能随 意调换。
排列中的元素没有重复出现的情况。
组合的定义与性质
组合的定义
从n个不同元素中取出m个元素 (0<m≤n),不考虑顺序,称为 从n个不同元素中取出m个元素的
一个组合。
互异性
组合中的元素没有重复出现的情况。
无序性
组合中的元素顺序不影响其组合结 果。
排列与组合的关系
利用组合数的性质,通过数学推导推导出二项式定理的展开式。
利用多项式乘法推导
将$(a+b)^n$展开成多项式,然后利用多项式乘法的性质推导出二 项式定理的展开式。
利用幂的性质推导
利用幂的性质,将$(a+b)^n$展开成幂的形式,然后通过数学推导 推导出二项式定理的展开式。
04 二项式定理的应用举例
利用二项式定理计算组合数
高三一轮复习:排列、组合、二项式定理

排列与组合【知识要点】 一、计数原理:1、乘法原理:如果完成一件事需要n 个步骤,第1步有1m 种不同的方法,第2步有2m 种不同的方法,……,第n 步有n m 种不同的方法,那么完成这件事共有12n N m m m =L 种不同的方法;2、加法原理:如果完成一件事有n 类办法,在第1类办法中有1m 种不同的方法,在第2类办法中有2m 种不同的方法,……,在第n 类办法中有n m 种不同的方法,那么完成这件事共有12n N m m m =+++L 种不同的方法。
二、排列和排列数:1、排列:从n 个不同元素中取出m (m n ≤)个元素,按照一定的次序排成一列,叫做从n 个不同元素中取出m 个元素的一个排列;n 个不同元素全部取出的一个排列,叫做n 个元素的一个全排列;2、排列数:从n 个不同元素中取出m (m n ≤)个元素的所有排列的个数叫做从n 个不同元素中取出m 个元素的排列数,用符号P mn 表示; 3、排列数公式:!P (1)(2)(1)()!mn n n n n n m n m =---+=-L (m n ≤,m 、n ∈N *)。
【注】1°记!P (1)(2)321nn n n n n ==⋅-⋅-⋅⋅⋅⋅L ; 2°规定0!1=。
三、组合和组合数:1、组合:从n 个不同元素中取出m (m n ≤)个元素组成一组,叫做从n 个不同元素中取出m 个元素的一个组合;2、组合数:从n 个不同元素中取出m (m n ≤)个元素的所有组合的个数,叫做从n 个不同元素中取出m 个元素的组合数,用符号C mn 表示; 3、组合数公式:P (1)(2)(1)!C P !!()!m n mnm mn n n n m n m m n m ---+===-L (m n ≤,m 、n ∈N *)【注】规定0C 1n =。
4、组合数的两个性质:(1)C C m n m n n -=; (2)11C C C m m m n n n -++=。
高三第一轮复习——排列、组合、二项式定理

1
3
5
7
9
11
10
是……………………………………( C )
A.4032 B.-4032 C.126 D.-126
一般来说,家居装修有四大块支出:装修部分(包括厨卫设备);家具部分;家电部分;装饰部分。这四大部分在装修总投资 里占有多大的分配比例,现今有很多说法。有的认为装修、厨卫占50%,家具占30%,家用电器及其他占20%;也有的认为 ,装 修与家具、家电配套的投资比例应该在1:1或1:2之间。 ; https:/// 武汉装修公司 lgh91neh 其实这些分配比例都只是相对的 ,当今装修行业并没有一个统一、确定的标准。由于职业、个性、喜好等不同,因此消费者 对装修投资的分配比例也不可能相同。但是,消费者依然可以把大家比较认可的比例,作为预计装修投资,控制装修 总支出 的一个计算依据。
乘法原理
做一件事,完成它可以有n个步骤, 做第一步中有m1种不同的方法, 做第二步中有m2种不同的方法……, 做第n步中有mn种不同的方法, 那么完成这件事共有 N=m1· m2· m3·…·mn 种不同的方法.
定 义 相同点 不同点
做一件事或完成一项工作的方法数
直接(分类)完成
间接(分步骤)完成
1.排列和组合的区别和联系:
练习1
1.书架上层放有6本不同的数学书,下层放有5本不同的语文书, ①从中任取一本,有多少中不同的取法? ②从中任取数学书与语文书各取一本,有多少种不同的取法? 6+5=11
6×5=30
2. 若x、y可以取1,2,3,4,5中的任一个,则点(x,y)的不同个 数有多少?
5×5=25
练习2
1.计算: 4 p ③ 4 24 =
高考第一轮复习——排列组合与二项式定理(理)

年 级 高三 学 科 数学版 本通用版课程标题 高考第一轮复习——排列组合与二项式定理编稿老师 胡居化 一校林卉二校李秀卿审核王百玲一、学习目标:1. 理解排列、组合的有关概念,排列与组合的区别及分步计数原理和分类计数原理的含义。
2. 掌握排列数、组合数的公式及排列与组合的性质,并能进行简单的计算和解决简单的实际问题。
3. 理解二项式定理的内容、其通项公式的概念及其简单的应用。
4. 体会方程的数学思想、等价转化的数学思想、化归与类比的数学思想、分类讨论的数学思想及赋值法、待定系数法等数学思想方法的应用。
二、重点、难点:重点:(1)排列、组合的知识及两个原理的简单应用 (2)二项式定理的简单应用难点:利用排列与组合的知识解决实际问题。
三、考点分析:新课标高考对排列、组合及二项式定理的考查以基础知识为主,应重点理解排列、组合及二项式定理的有关概念、简单的运算。
考查的题型以选择、填空题为主,题目难度较小,易得分。
一、两个原理,排列、组合的有关基础知识: 1. 分类计数原理与分步计数原理:(1)分类计数原理:做一件事情,完成它可以有n 类方法,在第一类办法中有m 1种不同的方法,在第二类办法中有m 2种不同的方法……,在第n 类办法中有m n 种不同的方法,那么完成这件事共有N 种不同的方法,即N=n m m m +++ 21.(2)分步计数原理:做一件事情,完成它需要n 个步骤,做第一步有m 1种不同的方法,做第二步有m 2种不同的方法……,做第n 步有m n 种不同的方法,那么完成这件事共有N 种不同的方法。
即N=n m m m ⨯⨯⨯ 212. 排列的有关基础知识(1)排列的定义:一般地,从n 个不同的元素中取出m ()n m ≤个元素,按照一定的顺序排成一列,叫做从n 个不同元素中取出m 个元素的一个排列。
注:(i )排列的定义中包括两个基本内容:一是取出元素,二是按一定的顺序排列。
(ii )当且仅当元素完全相同,排列顺序完全相同的两个排列是同一排列。
排列组合和二项式定理理

(2011·东北四市联考)计划在4个体育馆举办排球、篮 球、足球3个项目的比赛,每个项目的比赛只能安排在一个
体育馆进行,则在同一个体育馆比赛的项目不超过2项的安 排方案共有( )
A.24种
B.36种
C.42种
D.60种
[答案] D
[解析] 每个项目的比赛安排在任意一个体育馆进行, 共有43=64种安排方案;三个项目都在同一个体育馆比赛, 共有4种安排方案;所以在同一个体育馆比赛的项目不超过 2项的安排方案共有60种,故选D.
由分类计数原理,共有3+8+5=16种选法. (2)分三步选人,第一步选老师,有3种方法;第二步 选男生,有8种方法;第三步选女生,有5种方法. 由分步计数原理,共有3×8×5=120种选法.
(3)可分两类,第一类又分两步:第一类,选一名老师 再选一名男生,有3×8=24种选法;第二类,选一名老师 再选一名女生,有3×5=15种选法.
3.二项式定理 (1)定理:(a+b)n=Can+Can-1·b+…+Can-rbr+…+ Cabn-1+Cbn(n∈N*). 通项(展开式的第r+1项):Tr+1=Can-rbr.其中C(r= 0,1,…,n)叫做二项式系数. (2)二项式系数的性质 ①在二项式展开式中,与首末两端“等距离”的两项的 二项式系数相等,即
A.36种 B.42种 C.48种 D.54种
[答案] B
[解析] 分两类,第一类:甲排在第一位时,丙排在 最后一位;中间4个节目无限制条件,有A种排法;第二类: 甲排在第二位时,从甲、乙、丙之外的3个节目中选1个节 目排在第1位时有C种排法,其他3个节目有A种排法,故有 CA种排法.依分类加法计数原理,知共有A+CA=42(种) 编排方案.
[评析] 本例可看成是一类应用问题——涂色问题,它 也是排列组合的一类综合应用问题.
高三数学 排列、组合、二项式定理

高三数学 排列、组合、二项式定理【考点梳理】 一、考试内容1.分类计数原理与分步计数原理。
2.排列、排列数公式。
3.组合、组合数公式。
4.组合数的两个性质。
5.二项式定理,二项式展开的性质。
二、考试要求1.掌握分类计数原理与分步计数原理,并能用这两个原理分析和解决一些简单的问题。
2.理解排列、组合的意义,掌握排列数、组合数的计算公式和组合数的性质,并能用它解决一些简单的问题。
3.掌握二项式定理和二项式系数的性质,并能用它们计算和论证一些简单问题。
三、考点简析1.排列、组合、二项式知识相互关系表〔1〕分类计数原理中的分类。
〔2〕分步计数原理中的分步。
正确地分类与分步是学好这一章的关键。
〔1〕排列定义,排列数〔2〕排列数公式:系mn A =)!(!m n n -=n ·(n-1)…(n-m+1)〔3〕全排列列:nn A =n!〔4〕记住如下几个阶乘数:1!=1,2!=2,3!=6,4!=24,5!=120,6!=720〔1〕组合的定义,排列与组合的区别 〔2〕组合数公式:m=)!(!!m n m n -=12)1(1)m -(n 1)-n (⨯⨯⨯-⨯+ m m n〔3〕组合数的性质 ①m =n-m②r n r n r n C C C 11+-=+③r r =n ·-1r-1④0+1+…+n=2n⑤0-1+…+(-1)nn=0即0+2+4+…=1+3+…=2n-1〔1〕二项式展开公式(a+b)n=0a n+1a n-1b+…+k a n-k b k+…+n b n〔2〕通项公式:二项式展开式中第k+1项的通项公式是T k+1=k a n-k b k〔1〕求某些多项式系数的和。
〔2〕证明一些简单的组合恒等式。
〔3〕证明整除性。
①求数的末位;②数的整除性与求系数;③简单多项式的整除问题。
〔4〕近似计算。
当|x|充分小时,我们常用如下公式估计近似值:①(1+x)n≈1+nx②(1+x)n≈1+nx+2)1(nnx2〔5〕证明不等式。
排列组合二项式定理知识点以及典型例题总结排列组合二项式定理知识点

排列组合二项式定理知识点以及典型例题总结考纲要求:1.知道分类计数原理与分步计数原理的区别,会用两个原理分析和解决一些简单的问题2.知道排列和组合的区别和联系,记住排列数和组合数公式,能用它们解决一些简单的应3.知道一些组合数性质的应用.4.了解二项式定理及其展开式5.记住二项式展开式的通项公式,并能够运用它求展开式中指定的项6.了解二项式系数的性质,能够利用二项式展开式的通项公式求出展开式中二项式系数最大的项.7.了解二项式的展开式中二项式系数与项的系数的区别知识点一:计数原理1.分类加法计数原理如果完成一件事,有n类办法,在第1类办法中有m1种不同的方法,在第2类办法中有m2种不同的方法,…,在第n类办法中有m n种不同的方法,那么完成这件事共有N=m1+m2+…+m n种不同的方法.两个基本计数原理的区别:分类计数原理——每一类办法都能把事单独完成;分步计数原理——缺少任何一个步骤都无法把事完成.2.分步乘法计数原理如果完成一件事,需分成n个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法,…,做第n步有m n种不同的方法,那么完成这件事共有N=m1·m2·…·m n种不同的方法.知识点二:排列1.排列的定义:一般地,从n个不同的元素中,任取m(m≤n)个元素,按照一定顺序排成一列,叫作从n个不同元素中取出m 个元素的一个排列.如果m <n ,这样的排列叫作选排列.如果m =n ,这样的排列叫作全排列.2. 排列数的定义:从n 个不同元素中取出m (m ≤n )个元素的所有排列的个数,叫作从n 个不同元素中取出m 个元素的排列数,用符号P mn 表示.3. 排列数的公式: (1) P m n =n ·(n -1)·(n -2)·…·(n -m +1);(2) P m n =()!!n n m -; 规定:0!=1.知识点三:组合1.组合的定义:一般地,从n 个不同元素中,任取m (m ≤n )个元素并成一组,叫做从n 个不同元素中取出m 个元素的一个组合.2.组合数的定义:从n 个不同元素中取出m (m ≤n )个元素的所有组合的个数,叫做从n 个不同元素中取出m 个元素的组合数,用符号C mn 表示.3. 组合数公式: (1)()()()121P C P !m mn n m n n n n n m m ---+==(2)()!C !!m n n m n m =-(n ,m ∈N +,且m ≤n ) 4. 组合数性质:(1) C =C m n m n n -;(2) 111C +C C mm m n n n +++=知识点四:二项式定理1. 二项式定理(a +b )n =011222C C C C C n n n m n m nn n n n n n a a b a b a b b ---++++++, n ∈N +其中C m n (m =0,1,2,…,n )叫做二项式系数;T m +1=C m n m m n a b -叫做二项式展开式的通项公式.2. 二项式系数的性质:(1)每一行的两端都是1,其余每一个数都是它“肩上”两个数的和;(2)在二项展开式中,与首末两端“等距离”的两项的二项式系数相等,即C C r n r n n -=(3)如果二项式的幂指数n 是偶数,那么中间一项即第12n +项的系数最大;如果二项式的幂指数n 是奇数,那么中间两项即第12n +项和第32n +项的二项式系数相等且最大; (4)(a +b )n 的二项式系数之和为2n ,即012C C C ++C ++C m n n n n n n ++=2n ; (5)(a +b )n 的二项展开式中,奇数项的二项式系数之和等于偶数项的二项式系数之和,都等12n -,024C C C +n n n ++135C +C C n n n =++12n -=.题型一 分类加法计数原理例1 一个盒子里有4个不同的红球,3个不同的黄球和5个不同的蓝球.从盒子中任取一个球,有多少种不同的取法?分析:盒子中取出一个球就可以完成任务,所以考察分类加法计数原理.解答:从盒子中任取一个球,共有三类方案:第一类方案,从4个不同的红球中任取一球,有4种方法;第二类方案,从3个不同的黄球中任取一球,有3种方法;第三类方案,从5个不同的蓝球中任取一球,有5种方法.所以,选一个班担任升旗任务的方法共有:12+10+10=32(种)题型二分步乘法计数原理例2 一个盒子里有4个不同的红球,7个不同的黄球和5个不同的蓝球.从盒子中取红球、黄球和蓝球各一个,有多少种不同的取法?分析:盒子中各取出一个球需要分三步,所以考察分步乘法计数原理.解答:完成这件事需要分三步.第一步,从4个不同的红球中任取一球,有4种方法;第二步,从3个不同的黄球中任取一球,有3种方法;第三步,从5个不同的蓝球中任取一球,有5种方法.由分步乘法计数原理,从盒子中取红球、黄球和蓝球各一个共有⨯⨯435=60种不同的取法.例3 邮政大厅有4个邮筒,现将三封信逐一投入邮筒,共有多少种投法?分析:三封信逐一投入邮筒分成三个步骤,每个步骤投一封信,分别均有4种方法.解答:应用分步计数原理,投法共有44464⨯⨯=种.题型三分类分步混合运算例4 一个盒子里有4个不同的红球,7个不同的黄球和5个不同的蓝球.从盒子中任取2个颜色不同的球,有多少种不同的取法?分析分类计数原理与分步计数原理混合使用的问题,一般要“先分类,后分步”.解答:可按所选两球的颜色分为如下3类.第1类:红球、黄球各一个,有4×7=28种选法;第2类:红球、蓝球各一个,有4×5=20种选法;第3类:黄球、蓝球各一个,有7×5=35种选法.根据分类计数原理,不同的选法种数为N =28+20+35=83(种).知识点二 排列题型一 排列数公式的运用例5 已知221P P n n +-=10,则n 的值为( ). A .4 B .5 C .6 D .7解答:由221P P n n +-=10,得(n +1)n -n (n -1)=10,解得n =5.故选B .题型二 排列的运用例6 小华准备从7本世界名著中任选3本,分别送给甲、乙、丙3位同学,每人1本,共有多少种选法?分析 选出3本不同的书,分别送给甲乙丙3位同学,书的不同排序,结果是不同的.因此选法的种数是从7个不同元素中取出3个元素的排列数.解答:不同的送法的种数是 37P 765210=⨯⨯=.即共有210种不同送法.题型三 某元素一定在某位置例7 4名男生和3名女生排成一排照相,分别按下列要求,求各有多少种不同的排法.(1)男生甲一定在中间位置;(2)男生甲不在中间位置.分析 本题是有限制条件的排列问题,若有特殊元素优先考虑特殊元素,若有特殊位置,优先考虑特殊位置.(1)分两步完成:第一步,男生站在中间位置,有一种排法;第二步,排其他的元素,共有66P 种排法.所以,男生甲一定在中间位置共有661P 720⨯=种排法.(2)分两步完成:第一步,男生不在中间位置,有5种排法;第二步,排其他的元素,共有66P 种排法.所以,男生甲一定在中间位置共有665P 3600⨯=种排法. 题型四 某几个元素相邻例8 4名男生和3名女生排成一排照相,同学甲、乙相邻有多少种排法?分析:解决“相邻”问题采用的是“捆绑法”解答:第一步,把甲、乙看成一个元素,与其他5人共6个元素进行全排列;第二步,甲、乙二人进行全排列.即6262P P =720×2=1440(种).题型五 某几个元素不相邻例9 4名男生和3名女生排成一排照相,同学甲、乙不相邻有多少种排法?分析:解决“不相邻”问题采用的是“插空法”.解答:第一步,把甲、乙之外的5名同学进行全排列;第二步,在5名同学之间或两端共6个空中插入甲、乙两名同学.即5256P P =120×30=3600(种). 例10 4名男生和3名女生排成一排照相,男女同学相间排列,有多少种排法? 分析:“相间”是特殊的“不相邻”问题解答:第一步,男生全排列,有44P 种排法;第二步,女生全排列,有33P 种排法;第三步,相间插入有2中插入方法.即男女同学相间排列,有4343P P 2576⨯=种种排法.题型六 数字的排列问题例11 用数字0,1,2,3,4组成没有重复数字的三位数,求:(1)组成的三位数的个数;(2)组成的三位数中偶数的个数;分析:对数字进行排列时,如果数字中含有0,应区别对待.因为0作为特殊元素,不能在首位出现.解答:(1)应采用特殊位置优先法.因为0不能为首位(百位),所以首位的排法有14P 种,其他两位是从剩余的4个数字中选2个的一个排列,有24P 种,所以共有1244P P =48(种).(2)由于0的存在,应分两类:第一类个位是0,有24P 个;第二类,个位不是0,先确定个位,从2,4中选一个,有12P 种,再确定首位,有13P 种,剩余的一位是从3个数中选1个,有13P 种.所以共有21114233P P P P +=30(种). 知识点三 组合题型一 组合的应用例12 学校组织一项活动,要从5名男同学,3名女同学中选4名.共有多少种选法? 分析: 从5名男同学,3名女同学中选4名, 选出的4名同学任务是一样的,因此选法的种数是从8个不同元素中取出4个元素的组合数. 解答:不同的选法种数是488765C 704321⨯⨯⨯==⨯⨯⨯种. 题型二 一定包含或一定不包含某元素例13 学校组织一项活动,要从5名男同学,3名女同学中选4名.(1)若甲同学必须去,有多少种选法?(2)若甲同学一定不去,有多少种选法?分析:若甲同学必须去,再从其他7人中选3人即可.解答:(1)共有37765C 321⨯⨯=⨯⨯=35种选法. 分析:若甲同学一定不去,从其他7人中选4人即可.解答:(2)共有47C 35=种选法.题型三 至多、至少问题例14 学校组织一项活动,要从5名男同学,3名女同学中选4名.若男生甲、女生乙至少有一个被选中,有多少种选法?分析:至多、至少问题从正面解,一般情况先分类,再求解.当从正面求解困难时,可从对立面求解.解答:方法一 男生甲、女生乙至少有一个被选中,分成两类:第一类 男生甲、女生乙只有一个人被选中,有1326C C 260120=⨯=种选法; 第二类 男生甲、女生乙都被选中,有2226C C 21530=⨯=种选法.所以,男生甲、女生乙至少有一个被选中,共有120+30=150种不同的选法.题型四 组合数性质的的相关计算例15 若44511C C C n n n --=+,求n .分析:考察组合数的性质111C +C C m m m n nn +++=;C =C m n m n n-. 解答:45511C +C =C ,n n n --∴45C =C ,n n∴n =4+5=9.题型四 排列、组合混合应用例16 从6名男生和5名女生中选出3名男生和2名女生排成一行,有多少种不同排法? 分析:可以首先将男生选出,再将女生选出,然后对选出的5名学生排序.解 不同排法的总数为32565565454C C P 543212400032121⨯⨯⨯⋅⋅=⨯⨯⨯⨯⨯⨯=⨯⨯⨯(种). 知识点四 二项式定理题型一 求二项式展开式的指定项例17 求二项式103x x ⎛⎫- ⎪⎝⎭的展开式中第4项. 分析:.二项式103x x ⎛⎫- ⎪⎝⎭的展开式第4项,则n 的值为10,m 的值为3,可直接用二项式的通项T m +1=C m n m m n a b -求解.解答:T 4=T 3+1=337103C x x ⎛⎫- ⎪⎝⎭=-3240x 4, ∴第4项是-3240x 4.. 例18 求二项式103x x ⎛⎫- ⎪⎝⎭的展开式中含x 6的项. 分析:二项式103x x ⎛⎫- ⎪⎝⎭的展开式中含x 6的项,则n 的值为10,m 的值未知.此类问题应先写出二项式的通项,结合条件“含x 6的项”确定出m 的值.从而求出含x 6的项.解答: ∵T m +1=()1010210103C 3C m m m mm m x x x --⎛⎫-=- ⎪⎝⎭, 令10-2m =6,得m =2.∴含x 6的项为T 3=T 2+1=(-3)2210C x 6=405x 6. 例19 在二项式103x x ⎛⎫- ⎪⎝⎭的展开式,求: (1)常数项;(2)二项式系数最大的项.分析:(1)求常数项,因为不知道m 的值,要根据“常数项”之一条件确定m 的值.所以,与例18过程相似;(2)可计算出第10162+=项为二项式系数最大的项,其实就是求第6项,所以与例17过程相似.解答:(1)∵T m +1=()1010210103C 3C m m m mm m x x x --⎛⎫-=- ⎪⎝⎭, 10-2m =0,即m =5.∴展开式的第6项是常数项,即T 6=T 5+1=5555510103C =(3)C x x ⎛⎫-- ⎪⎝⎭=-61236. (2)∵n =10,∴展开式有11项,中间一项的二项式系数最大,中间一项为第6项. ∴T 6=T 5+1=5555510103C =(3)C x x ⎛⎫-- ⎪⎝⎭=-61236. 题型二 求二项式展开式的某一项系数与某一项的二项式系数.例20 求92)x -(的二项展开式中6x 的系数和该项的二项式系数. 分析:二项展开式中某项的的系数与这一项二项式系数是两个不同的概念. 某项的系数是除字母外的所有数乘积的结果,某项的二项式系数是该项的组合数,和其他无关. 解答: 92)x -(的展开式的通项公式为99199C (2)C (1)2m m m m m m m m T x x --+=-=-⋅⋅ 由9-m =6,得m =3.即二项展开式中含6x 的项为第4项.故这一项的系数是3339987C (1)2(8)672321⨯⨯⨯-⨯=⨯-=-⨯⨯.该项的二项式系数为39987C 84321⨯⨯==⨯⨯. 题型三 二项式各项系数和与二项式系数和例21 在(1-x )5的二项展开式中,各项系数和为____________;所有项的二项式系数之和为____________.分析:在二项式中令式子中的字母为1,可得各项系数和;所有项的二项式系数之和为2n ,即012C C C ++C ++C m n n n n n n ++=2n ,故所有项的二项式系数之和只和n 有关.解答:在(1-x )5中,令x =1,可得各项系数和为0.(1-x )5的二项式系数之和为25=32.。
2015年高考数学第一轮复习课件:10.3二项式定理

辨析感悟
探究一 通项公式及其应用
技能与规律探究 探究二 二项式系数的性质
与各项的系数和 探究三 二项式定理的应用
例1 训练1
例2 训练2
例3 训练3
经典题目再现
第一页,编辑于星期五:十一点 四十六分。
1.二项式定理
二项式 定理
二项展开 式的通项
公式 二项式
系数
(a+b)n= Cn0an+C1nan-1b+…+Crnan-rbr+…+Cnnbn (n∈N*) Tr+1= Crnan-rbr ,它表示第 r+1 项
规律方法
(1)二项式定理的核心是通项公式,求解此类问题可以分两步完成:第一步根 据所给出的条件(特定项)和通项公式,建立方程来确定指数(求解时要注意二
项式系数中n和r的隐含条件,即n,r均为非负整数,且(n≥r),如常数项指 数为零、有理项指数为整数等);第二步是根据所求的指数,再求 所求解的项.
(2)求两个多项式的积的特定项,可先化简或利用分类加法计数原理讨论求 解.
∴Tr+1=Cr8·x8-r·1xr=Cr8·x8-2r,
当 8-2r=-2 时,r=5,∴x12的系数为 C58=C38=56. 答案 (1)B (2)56
第九页,编辑于星期五:十一点 四十六分。
二项式系数的性质与各项的系数和
【例 2】 (1)(2014·青岛模拟)设(1+x)n=a0+a1x+a2x2+…+anxn,若 a1+ a2+…+an=63,则展开式中系数最大的项是( ). A.15x2 B.20x3 C.21x3 D.35x3
项,如(1).
二项式系数与展开式项的系数的异同
一是在 Tr+1=Crnan-rbr 中,Crn是该项的二项 式系数,与该项的(字母)系数是两个不同的 概念,前者只指 Crn,而后者是字母外的部分, 前者只与 n 和 r 有关,恒为正,后者还与 a, b 有关,可正可负,如(2)就是混淆两个概念 的区别. 二是二项式系数的最值与增减性与指数 n 的 奇偶性有关,当 n 为偶数,中间一项的二项 式系数最大,如(6);当 n 为奇数时,中间两 项的二项式系数相等,且同时取得最大值.
高三第一轮复习——排列、组合、二项式定理

0 n
1 n
n
C 15 C C 161700
2 6 97 100 4 6
15
C 56
3 8
2.用排列数表示下列各式:
① ②
10 9 8 7 6
24 23 21 3 2 1
n ( n 1) ( n 2) ( n 3)
n
2 C C C C C C _____ .
1 11 3 11 5 11 7 11 9 11 11 11
10
3.(x-2)9的展开式中,第6项的二项式系数
是……………………………………( C )
A.4032 B.-4032 C.126 D.-126
需要更完整的资源请到 新世纪 教育网 -
m n
P
m n
C
P
m m
m n m m m m 1 Cn Cn Cn C C , 1 n n
全排列:n个不同元素全部取出的一个排列.全排列数公式:所 需要更完整的资源请到 新世纪 n 有全排列的个数,即:Pn 教育网 - n ( n 1) ( n 2) 2 1
两个原理的区别与联系:
名称 内容
加法原理
做一件事,完成它可以有n类办法, 第一类办法中有m1种不同的方法, 第二类办法中有m2种不同的方法…, 第n类办法中有mn种不同的方法, 那么完成这件事共有 N=m1+m2+m3+…mn 种不同的方法
乘法原理
做一件事,完成它可以有n个步骤, 做第一步中有m1种不同的方法, 做第二步中有m2种不同的方法……, 做第n步中有mn种不同的方法, 那么完成这件事共有 N=m1· m2· m3·…·mn 种不同的方法.
2015高考数学一轮精品课件:10.2 排列与组合

有A33 种排法,这样总共有A22 A35 A33 =720 种不同排法.
(4)先排甲、乙和丙 3 人以外的其他 4 人,有A44 种排法;由于甲、乙要相邻,
故再把甲、乙排好,有A22 种排法;最后把甲、乙排好的这个整体与丙分别插入原
先排好的 4 人的空当中有A25 种排法.这样,总共有A44 A22 A25 =960 种不同排法.
梳理自测
梳理自测
探究突破
巩固提升
1.排列与排列数:“排列”与“排列数”是两个不同的概念,“一个排列”是
指“从 n 个不同元素中取出 m(m≤n)个元素,按照一定的顺序排成一列”,它
是一件事情,只有元素与其排列顺序都相同的排列才是同一排列;“排列数”
是指“从 n 个不同元素中取出 m(m≤n)个元素的所有不同排列的个数”,它
行排列,同时要考虑相邻元素的内部是否需要排列,这种方法称为“捆绑法”;
对于不相邻的元素,可先排其他元素,然后将这些要求不相邻的元素插入空
当,这种方法称为“插空法”;对于“在”或者“不在”的排列问题的计算方法
主要有:位置优先法、元素优先法、间接计算法.
考点一
考点二
考点三
第十二页,编辑于星期五:十三点 四分。
4
故选法共有C12
+ C14 ·C73 + C42 ·C72 + C43 ·C17 + C44 =790(种).
答案
答案
考点一
考点二
考点三
第十四页,编辑于星期五:十三点 四分。
第十一章
10.2
排列与组合
考纲要求
梳理自测
探究突破
探究突破
巩固提升
方法提炼
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
排列组合、二项式定理、概率与统计新题赏析
重难点突破
●计数原理
●二项式定理
●概率
●统计
新题赏析
题一:从0,2中选一个数字,从1,3,5中选两个数字,组成无重复数字的三位数,其中奇数的个数为( ).
A.24 B.18 C.12 D.6
题二:6个人排成一行,其中甲、乙两人不相邻的不同排法共有__________种(用数字作答).
题三:从3名骨科、4名脑外科和5名内科医生中选派5人组成一个抗震救灾医疗小组,则骨科、脑外科和内科医生都至少有1人的选派方法种数是_________(用数字作答).
题四:已知5
(1)(1)
ax x
++的展开式中2x的系数为5,则a=( ).
A.4-B.3-C.2-D.1-
题五:设m为正整数,2
()m
x y
+展开式的二项式系数的最大值为a,21
()m
x y+
+展开式的二项式系数的最大值为b,若137
a b
=,则m=( ).
A.5 B.6 C.7 D.8
题六:将一个各面都涂了油漆的正方体,切割成125个同样大小的小正方体。
经过搅拌后,从中随机取出一个小正方体,记它的涂油漆面数为X,则X的均值为()
E X=( ).
A.126
125
B.
6
5
C.
168
125
D.
7
5
题七:一位国王的铸币大臣在每箱100枚的硬币中各掺入了一枚劣币,国王怀疑大臣作弊,他用两种方法来检测。
方法一:在10箱子中各任意抽查一枚;方法二:在5箱中各任意抽
查两枚。
国王用方法一、二能发现至少一枚劣币的概率分别为1p 和2p , 则( ).
A .12p p =
B .12p p <
C .12p p >
D .以上均有可能
题八:某人在如图所示的直角边长为4米的三角形地块的每个格点(指纵、横直线的交叉点以及三角形的顶点)处都种了一株相同品种的作物. 根据历年的种植经验,一株该种作物的年收获量Y (单位:kg )与它的“相近”作物株数X 之间的关系如下表所示:
这里,两株作物“相近”是指它们之间的直线距离不超过1米.
(1)从三角形地块的内部和边界上分别随机选取一株作物,求它们恰好“相近”的概率;
(2)从所种作物中随机选取一株,求它的年收获量的分布列与数学期望.
排列组合、二项式定理、概率与统计新题赏析
新题赏析
题一:B 题二:480 题三:590 题四:D
题五:B 题六:B 题七:B
题八:(1) 2=P ;(2)分布列: X
()46=E Y。
