安徽省蚌埠二中2012届高三上学期期中考试文科
安徽蚌埠二中2012届高三4月质考试文综试题及答案

安徽蚌埠二中2011—2012学年度高三4月质考试文综试题及答案蚌埠二中2011—2012学年度高三4 月质量检测考试文科综合试题(考试时间:150 分钟试卷分值:300 分)注意:本试卷包含Ⅰ、Ⅱ两卷。
第Ⅰ卷为选择题,所有答案必须用2B 铅笔涂在答题卡中相应的位置。
第Ⅱ卷为非选择题,所有答案必须填在答题卷的相应位置。
第Ⅰ卷(选择题共132 )本卷共33小题,每小题4分,共132分。
在每题给出的四个选项中,只有一项是最符合题目要求的。
1.存款储蓄是一种投资方式。
假设某储户有6 万元一年期的定期存款,年利率为3.50%。
一年后物价平均水平上涨了5%,与存款时相比,则该储户的到期后存款收益的实际购买力是A.21OO 元B.2000 元C.1995 元D.2205 元2.依托科研机构进行技术研发的企业要积极开展循环经济技术攻关和适用技术的推广应用,不断研发新产品,只有这样,企业的销售收入与利润才会上升。
这是因为①产品创新增强了企业竞争优势②产研联合实现了双方优势互补③新产品的新功能增大了其价值④科技产品的需求弹性小利润大A.①②B.②③C.③④D.①④3.从2012年春季学期起,安徽省12 个县近140 万名农村义务教育学生将享受到国家实施的营养改善计划试点待遇。
中央财政每年将安排安徽将8 亿多元资金,向这些学生提供每人每天 3 元的营养膳食补助。
这说明财政(来源 教育城)A.是促进社会公平、改善人民生活的物质保障B.具有促进资源合理配收入的作用C.具有促进国民经济平稳运行的作用D.是建立合理的收入分配的制度保证4.民政部2012 年1 月4 日出台并公布《关于促进农民工融入城市社区的意见》,首次从国家层面描绘了农民工参与社区生活的“路线图”,切实保障农民工参与社区自治的权利。
农民工参与社区生活可以享有的权益有①间接选举居委员会成员②参加居委会讨论决定涉及居民切身利益的重要事务③对居委会成员进行监督④参与管理社区的公共事务和公益事业A.①②B. ①③C. ②③D. ③④5.“三公”经费公开是指政府部门人员因公出国(境)经费、公务车购置及运行费、公务招待费向社会公开。
安徽省蚌埠市2012届高三第一次教学质量检查考试语文试题(高清扫描版)

蚌埠市2012届高三年级第一次教学质量检查考试语文试题答案1.D(A项,应是“大体相同的地理条件”。
B项,强加因果。
C项,文中没有依据。
)2.B(印度瑜伽不讲求“长生”。
)3.C4.C(“卒”应为“最终”)5.D(D项都表转折。
A项,来,连词/把,介词。
B用来……的办法/表原因。
C作为,动词/因为,介词。
)6.A(B项“被迫”应为“主动”;C项“预期”错误;D项“只要……就”应为“如果……那么”)7.(10分)(1)他们就各自带着妻子儿女回家了,(临行时),欢呼的声音响遍了街巷。
(得分点:“挈”“彻”及句意各1分)(2)他当时只把救活人命放在心上,即使用尽了他的家产又有什么可顾虑的!(得分点:“但”“活”“虽”及句意各1分,“为”意为“作为”,意译也可。
)(3)懂得了这个道理,他即使承担天下的大事也是做得到的。
(得分点:“义”“任”及句意各1分)8.(4分)答题要点:冰凉镜体之寒;对夫失望及韶华易逝之寒。
(每点2分)9.(4分)答题要点:点题,点出写真寄夫的目的;首尾呼应,遥应首句;直抒胸臆,正面规劝丈夫。
(每点2分,答出两点即可)10.(5分)(1)宠辱僧忘(2)夫庸知其年之先后生于吾乎(3)沧海月明珠有泪(4)塞上风云接地阴(5)而世之奇伟、瑰怪、非常之观(6)栗深林兮惊层巅(7)水随天去秋无际(8)别有幽愁暗恨生11.悬念指:①名人、名街、名店撞在一起,能出得来名著吗?(1分)②即便不受干扰,萨特为什么不在优裕舒适的家里思考、写作而要挤到小小的咖啡室?(1分)悬念落地:①每个人都有自筑的气场,每个气场都是内向、自足的,萨特可严守在自己的工作状态下不关顾别人的存在,因而能写出名著。
(2分)②萨特并非对周围的一切无知无觉,只不过已经把这种知觉泛化,泛化为对热闹人世的领会,对城市神韵的把握,这种泛化的知觉成了池城市文化活动的前提和背景,对他极其重要。
(2分)(摘抄文中浯句或概述大意均可)12.开篇两段通过“我”的观察描写了咖啡馆的环境,为后文写我们对周际环境的敏感作铺垫,(2分)同时与咖啡馆中其他人对我们的视而不见、形若无人形成对比,(2分)从而引出不同地域两种不同的生态悖论。
安徽省蚌埠二中2012届高三年级月考(十月)语文试卷

安徽蚌埠二中2012届高三年级月考(十月)语文试卷第Ⅰ卷(阅读题共66分)一、(9分)阅读下面的文字,完成1~3题。
“敬”的当代价值对于孔子思想的认识,学界一般以“礼”和“仁”为核心,认为孔子继承了周礼,发展出“仁”的思想,因而着重探讨两者的关系及其当代意义。
其实,在“礼”和“仁”之中还有更本质性的精神内涵,这种精神内涵可以用“敬”来概括。
礼最早是祭祀天地神灵的仪式活动。
在那些高高在上的“天”、“神”面前,人自然产生敬畏的心理。
其中的敬是出于内心的崇拜仰慕,而畏则是害怕受到惩罚。
最早的礼活动即内含着这种敬畏的心情。
礼由祭祀的仪式活动发展为社会政治活动的规范形式时,“敬”作为内质也留存下来。
这种“敬”保障了礼的实践可能性,而且其发自内心,即出于天赋,由“敬”而发的礼活动也就合乎天理,具有道德价值了。
因此在国家政治活动中要求“敬”,社会的一切活动和个人的修养也以“敬”为内核。
孔子继承“礼”的同时,自然吸纳了“敬”的精神。
在《论语》中,“敬”出现21次,频率颇高。
这些关于“敬”的阐述,有继承,也有发展。
关于祭祀活动,孔子继承了上古对“天”和“神”的敬仰态度,强调“祭如在,祭神如神在”,“祭思敬”。
即使“敬鬼神而远之”一语,强调实践理性的重要性,也告诫人们对于鬼神要有敬畏的心态。
关于政治活动,孔子也承传了西周以来的敬谨精神,故而回答鲁哀公说:“治礼,敬为大。
”孔子对于“敬”的发展,在于把它扩展为普通人对待事物的敬业精神。
“敬”原本主要表现在人对神、臣民对君王等下对上的关系上,孔子以后则成为所有社会成员为人做事的基本原则。
《论语》中出现的21次“敬”中,关于敬事的即有18次。
而且,由“礼”中发展出来的“仁”也以“敬”为本。
一般认为,“仁”是“礼”的内核,“礼”是“仁”的形式,故而许多学者着重以“仁”为核心建构孔子的思想体系。
其实,“仁”之中也必有“敬”的精神。
没有发自内心的“敬”,也就没有真切的仁爱之情。
2012学年第一学期期中考试高三(文科)数学试卷

2012学年第一学期期中考试高三(文科)数学试卷本试题卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间为120分钟.第 Ⅰ 卷 (选择题 共50分)注意事项:用钢笔或圆珠笔将题目做在答题卷上,做在试题卷上无效.一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合U={1,2,3,4,5},A={1,2,3},B={2,3,4},则)(B A C U ⋂等于 (A){2,3} (B){1,4,5} (C){4,5} (D){1,5} 2. =︒330tan (A)3 (B)3- (C)33 (D)33- 3.函数f (x )=234lg(1)x x x -+++-的定义域是 (A )[-1,4](B )[1,4] (C )(1, 4] (D )(-1, 4]4. 若b a ,为实数,则“1≤+b a ”是“21≤a 且21≤b ”的 (A)必要而不充分条件 (B)充分而不必要条件 (C)充要条件 (D)既不充分也不必要条件5.o2o3-sin70=2-cos 10(A)12(B)22(C) 2(D) 326.函数13y x =的图像是7.在△ABC 中,点M 满足0=++MC MB MA ,若 0=++AM m AC AB ,则实数m 的值是 (A)3 (B)23 (C) 23- (D)3- 8.等差数列{}n a 的前n 项和为n S ,且224,6a S ==,则64n nS a +的最小值是 (A)7 (B)152(C) 8(D)172(A)(B) (C)(D)9. 若实数y x ,满足不等式组⎪⎩⎪⎨⎧≥--≤--≤-+01033022y x y x y x ,则x y +的最小值是(A )0 (B )1-/(C )1 (D )210.函数()M f x 的定义域为R ,且定义如下: 1(),()0(),M x M f x x M ∈⎧=⎨∉⎩(其中M 为非空数集且R M ⊆),在实数集R 上有两个非空真子集A 、B 满足A B =∅,则函数()1()()()1A B A B f x F x f x f x +=++的值域为(A) ∅(B) {12}(C) {1} (D) {12,1} 第Ⅱ卷(非选择题共100分)注意事项:将卷Ⅱ的题目做在答题卷上,做在试题卷上无效.11.公差为1的等差数列{}n a 满足2469a a a ++=,则579a a a ++的值等于▲. 12.已知a 与b 为两个不共线的单位向量,若向量a +b 与向量k a -b 垂直,则实数k =▲.13.若sin α+cos α=12,则sin 2α=▲.14.在直角三角形ABC中,,1,==⊥AC AB AC AB DC BD 21=,则CD AD ⋅的值等于▲.15.函数()sin()f x A x ωϕ=+(A ,ω,ϕ是常数,0A >,0ω>)的部分图象如图所示,则(0)f 的值是▲.16. 类比等差数列求和公式的推导方法,解决下列问题:设()()sin sin 30x f x x =︒-,则()()()()()12293159f f f f f ︒+︒++︒+︒++︒=__ ▲___.17.等比数列{}n a 中,120121,9a a ==,函数122012()()()()2f x x x a x a x a =---+,则曲线()y f x = 在点(0,(0))f 处的切线方程为 __▲__ .三、解答题:本大题共5小题.共72分.解答应写出文字说明、证明过程或演算步骤. 18.(本题满分14分)在ABC ∆中,角C B A ,,所对应的边分别为c b a ,,且满足sin 3cos b A a B =.(Ⅰ)求角B 的值; (Ⅱ)若25cos25A =,求sin C 的值. 19.(本题满分14分) 函数22x y -=和213y x =的图象如图所示,xy O 3π712π2-(第15题图)其中有且只有1x x =、2x 、3x 时,两函数数值相等,且1230x x x <<<,o 为坐标原点. (Ⅰ)请指出图中曲线1C 、2C 分别对应的函数; (Ⅱ)现给下列二个结论: ①当(,1)x ∈-∞-时,22x -<213x ; ②2(1,2)x ∈; 请你判定是否成立,并说明理由.20.(本题满分14分)已知二次函数)0,,,()(2≠∈++=a R c b a c bx ax x f ,0)0()2(==-f f ,)(x f 的最小值为1-.(Ⅰ)求函数)(x f 的解析式;(Ⅱ)设1)()()(+--=x f m x f x g ,若)(x g 在]1,1[-上是减函数,求实数m 的取值范围. 21.(本题满分15分)已知数列}{n a ,}{n b 满足:291=a ,n n n a a 2621⋅=-+, 12+-=n n n ab (*N n ∈).(Ⅰ)证明数列}{n b 为等比数列.并求数列}{n a ,}{n b 的通项公式; (Ⅱ)记数列}{n a ,}{n b 的前n 项和分别为n n T S ,,若对任意的∈n N*都有nn n b mT S ≤, 求实数m 的最小值.22.(本题满分15分)设1x 、)(212x x x ≠是函数)0()(223>-+=a x a bx ax x f 的两个极值点. (Ⅰ)若2,121=-=x x ,求函数)(x f 的解析式;(Ⅱ)若,22||||21=+x x 求实数b 的最大值;(Ⅲ)函数)()()(1x x a x f x g --'=若,,221a x x x x =<<且求函数)(x g 在),(21x x 内的最小值.(用a 表示)高三数学(文科)参考答案一.选择题:本大题共10小题,每小题5分,共50分.二.填空题:本大题共7小题,每小题4分,共28分.请将答案填在答题卡对应的位置上. 三.解答题:本大题共5小题,共72分.解答应写出文字说明、证明过程或演算步骤. 18.在ABC ∆中,角C B A ,,所对应的边分别为c b a ,,且满足sin cos b A B =.第19题图(Ⅰ)求角B 的值; (Ⅱ)若25cos25A =,求sin C 的值. 解:(Ⅰ)由正弦定理BbA a sin sin =及已知条件sin 3cos b A a B =得…………………2分 B A A B cos sin 3sin sin =,………………………………………………………4分又因为0sin ≠A ,所以B B cos 3sin =,即3tan =B ,……………………6分又),0(π∈B ,所以3π=B ;…………………………………………………………7分(Ⅱ)因为25cos25A =,所以5312cos 2cos 2=-=A A ,………………………9分 又),0(π∈A ,所以54sin =A ,由(Ⅰ)知32π=+C A ,………………11分 所以10334sin 32cos cos 32sin )32sin(sin +=-=-=A A A C πππ.…………14分 19.函数22x y -=和213y x =的图象如图所示, 其中有且只有1x x =、2x 、3x 时,两函数数值相等,且1230x x x <<<,o 为坐标原点.(Ⅰ)请指出图中曲线1C 、2C 分别对应的函数; (Ⅱ)现给下列二个结论: ①当(,1)x ∈-∞-时,22x -<213x ; ②2(1,2)x ∈; 请你判定是否成立,并说明理由. 解:(Ⅰ)1C 为213y x =,………3分2C 为22x y -=; ………5分 (Ⅱ)结论①成立,理由如下:函数22x y -=在(,1]-∞-上是增函数,∴(,1)x ∈-∞-时,2121228x ---<=.…7分 又函数213y x =在(,1]-∞-上是减函数,∴(,1)x ∈-∞-时,22111(1)333x >⨯-=而1183<,所以当(,1)x ∈-∞-时,22123x x -<;……………10分结论②成立,理由如下: 构造函数221()23x f x x -=-, 则11(1)0,(2)063f f =>=-<∴()f x 在区间(1,2)内有零点.…14分20.已知二次函数)0,,,()(2≠∈++=a R c b a c bx ax x f ,第19题图0)0()2(==-f f ,)(x f 的最小值为1-.(Ⅰ)求函数)(x f 的解析式;(Ⅱ)设1)()()(+--=x f m x f x g ,若)(x g 在]1,1[-上是减函数,求实数m 的取值范围. 解:(Ⅰ)由题意设)2()(+=x ax x f ,…………………………………………2分 ∵ )(x f 的最小值为1-,∴ 0>a ,且1)1(-=-f ,∴ 1=a ,…………4分∴ x x x f 2)(2+= . ………………………………………………………7分 (Ⅱ)∵ 1)1(2)1()(2++--=x m x m x g ,………………………………8分 ① 当1=m 时,14)(+-=x x g 在[-1, 1]上是减函数,∴1=m 符合题意.……………………………………………………10分 ② 当1≠m 时,对称轴方程为:mmx -+=11, ⅰ)当01>-m ,即 1<m 时,抛物线开口向上,由111≥-+mm, 得 m m -≥+11 , ∴ 10<≤m ;……12分 ⅱ)当01<-m , 即 1>m 时,抛物线开口向下,由111-≤-+mm ,得 m m +-≥+11, ∴1>m .……13分 综上知,实数m 的取值范围为[)∞+,0.………………………14分21.已知数列}{n a ,}{n b 满足:291=a ,n n n a a 2621⋅=-+; 12+-=n n n ab (*N n ∈).(Ⅰ)证明数列}{n b 为等比数列.并求数列}{n a ,}{n b 的通项公式; (Ⅱ)记数列}{n a ,}{n b 的前n 项和分别为n n T S ,,若对任意的∈n N*都有nn n b mT S ≤, 求实数m 的最小值.解:(Ⅰ)由已知得1212)2(2+++-=-n n n n a a ,……………………………………2分所以n n b b 211=+, 因为211=b ,所以}{n b 为等比数列.………………………………………4分 所以n n b )21(=, ……………………………………………6分进而n n n a )21(21+=+. ……………………………………………7分(Ⅱ)1211422121)2121()222(2132+--=++++++++=++n n n n n nn T S 124+⋅=n (10)分则nn n m 21421)124(+=+⋅≥对任意的∈n N*成立. ……………………12分 所以数列}214{n +是递减数列,所以29)214(max =+n所以m 的最小值为29. ……………………………………………………15分22.设1x 、)(212x x x ≠是函数)0()(223>-+=a x a bx ax x f 的两个极值点. (Ⅰ)若2,121=-=x x ,求函数)(x f 的解析式; (Ⅱ)若,22||||21=+x x 求实数b 的最大值;(Ⅲ)函数)()()(1x x a x f x g --'=若,,221a x x x x =<<且求函数)(x g 在),(21x x 内的最小值.(用a 表示)解:).0(23)(22>-+='a a bx ax x f -------------------------------------------------------1分 (1)2,121=-=x x 是函数)(x f 的两个极值点,由⎪⎪⎩⎪⎪⎨⎧-=-=⨯--=+-332132212aa a ab 可得⎩⎨⎧-==9,6b a ------------------------------- ------------3分 x x x x f 3696)(23--=∴ -------------------------------------------------------------------4分(2)∵1x 、)(212x x x ≠是函数)0()(223>-+=a x a bx ax x f 的两个极值点,0)()(21='='∴x f x f ,∴21,x x 是方程02322=-+a bx ax 的两根,∵32124a b +=∆, ∴0>∆对一切R b a ∈>,0恒成立,而3,322121ax x a b x x -=⋅-=+,0>a ,021<⋅∴x x , ,3494)3(4)32(4)(||||||222212212121a a b a a b x x x x x x x x +=---=-+=-=+∴………6分由).6(3,22349422||||222221a a b a ab x x -=∴=+=+得………………7分 .60,0)6(3,022≤<≥-∴≥a a a b ………………………………………… 8分令.369)(),6(3)(22a a a h a a a h +-='-=则)(0)(,40a h a h a ∴>'<<时在(0,4)内是增函数; 0)(,64<'<<a h a 时∴h (a )在(4,6)内是减函数.∴4=a 时,)(a h 有极大值为96,(]6,0)(在a h ∴上的最大值是96,∴b 的最大值是.64…………………………………………………………………10分 (3)∵x 1、x 2是方程0)(='x f 的两根, )0(23)(22>-+='a a bx ax x f,31,,31221-=∴=-=⋅x a x a x x -------------------------------------------------11分∴)()()(1x x a x f x g --'=)31)(31(3)31())(31(3--+=+--+=a x x a x a a x x a ----------12分对称轴为2a x =,0>a ,),(),31(221x x a a =-∈∴ []12)23()312(3)312)(312(3)2()(22min+-=+-=--+==∴a a a a a a a a a g x g .-- ------15分。
安徽省蚌埠市第二中学高三上学期期中考试数学(文)试题Word版含答案

蚌埠二中2017-2018学年度高三第一学期期中考试数学试题(满分150分,考试时间120分钟 )第Ⅰ卷(共60分)所有选择题答案必须用2B 铅笔涂在答题卡中相应的位置,否则,该大题不予计分。
一、选择题(本大题共12小题,每小题5分,共60分) 1.已知集合{}{}21,0,1,2,3,230A B x x x =-=--<,则AB =()A .{}1,0,1,2-B .{}0,1,2C .{}0,1,2,3D .{}1,0,1,2,3-2.若复数满足,则的虚部为( )A. B. C. D.3.若,则cos (π﹣2α)=( )A. B. C . D. 4.从长度分别为,,,,的5条线段中,任意取出3条,3条线段能构成三角形的概率是( ) A. 0.2B. 0.3 C. 0.4 D. 0.55.已知m ,n 是两条不同直线,α,β是两个不同平面,则下列命题正确的是 ( )A. 若α,β垂直于同一平面,则α与β平行B. 若m ,n 平行于同一平面,则m 与n 平行C. 若α,β不平行,则在α内不存在与β平行的直线D. 若m ,n 不平行,则m 与n 不可能垂直于同一平面6.我国古代数学著作《九章算术》有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升.问,米几何?”如图是解决该问题的程序框图,执行该程序框图,若输出的S=1.5(单位:升),则输入k 的值为( ) A .4.5 B .6C .7.5D .97.已知动圆圆心在抛物线上,且动圆恒与直线相切,则此动圆必过定点( )A. B. C. D.8.函数的图像大致是( )A. B.C. D.9.数列满足,且对于任意的都有,则等于 ( )A. B. C. D.10.一个几何体的三视图如图所示,则该几何体外接球的表面积为A. 28π B.32π C. 3128π11.函数)0,20)(2sin()(>≤<+=A x A x f πϕϕ部分图象如图所示,且()()0f a f b ==,对不同的[]12,,x x a b ∈,若()()12f x f x =,有()12f x x +=则( ) A.()f x 在5,1212ππ⎛⎫-⎪⎝⎭上是减函数 B.()f x 在5,1212ππ⎛⎫-⎪⎝⎭上是增函数 C.()f x 在5,36ππ⎛⎫⎪⎝⎭上是减函数 D. ()f x 在5,36ππ⎛⎫⎪⎝⎭上增函数12.已知方程ln|x|﹣ax 2+=0有4个不同的实数根,则实数a 的取值范围是( )A. B. C. D.第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.已知双曲线)0,0(12222>>=-b a by a x 的离心率为3,则该双曲线的渐近线方程为________.14.已知平面向量和的夹角为60°,,,则=__________.15.已知实数x ,y 满足约束条件,若∃x 、y 使得2x ﹣y <m ,则实数m 的取值范围是________.16.已知等差数列{}n a 的公差d 为正数,11a =,12(1)(1)n n n a a tn a ++=+,t 为常数,则n a =________.三、解答题 (本大题共6小题,共70分) 17.在中,角的对边分别为,且acosC,bcosB,ccosA 成等差数列.(1)求的值; (2)求的范围.18.某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100]. (1)求图中a 的值;(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;(3)若这100名学生语文成绩某些分数段的人数(x )与数学成绩相应分数段的人数(y )之比如表所示,求数学成绩在[50,90)之外的人数.19.如图,四棱锥P ABCD -中,底面ABCD 是矩形,平面PAD ⊥底面ABCD ,且PAD ∆是边长为2的等边三角形,PC M =在PC 上,且PA 面MBD . (1)求证:M 是PC 的中点;(2)求多面体PABMD 的体积.20.已知椭圆错误!未找到引用源。
安徽省蚌埠二中2012年届高三文科数学模拟测试一

安徽省蚌埠二中2012年届高三文科数学模拟测试一一、填空题:本大题共14小题,每小题5分,共70分 1.已知集合{}R x x x x A ∈≤-=,02|2,}{a x x B ≥=|,若B B A = ,则实数a 的取值范围是 。
2已知i b iia -=+3,其中Rb a ∈,,i 为虚数单位,则=+b a 。
3某单位从4名应聘者A 、B 、C 、D 中招聘2人,如果这4名应聘者被录用的机会均等,则A ,B 两人中至少有1人被录用的概率是 。
4、某日用品按行业质量标准分成王五个等级,等级系数X 依次为1,2,3,4,5.现从一批该日用品中随机抽取200件,对其等级系数进行统计分析,得到频率f 的分布如下的件数为 。
5已知变量y x ,满足约束条件⎪⎩⎪⎨⎧≤≤-≥+212y y x y x ,则目标函数y x z +-=2的取值范围是6已知双曲线1222=-y ax 的一条渐近线方程为02=-y x ,则该双曲线的离心率=e7已知圆C 的经过直线022=+-y x 与坐标轴的两个交点,又经过抛物线x y 82=的焦点,则圆C 的方程为 。
8设n S 是等差数列{}n a 的前n 项和。
若3173=S S,则=76S S 。
9、已知函数)sin(ϕω+=x A y )2||,0,0(πϕω<>>A 的部分图象如图所示,则ω的值为。
10、在如图所示的流程图中,若输入n 的值为11,则输出A 的值为 。
11、一块边长为10cm 的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形作侧面,以它们的公共顶点P 为顶点,加工成一个如图所示的正四棱锥形容器。
当cm x 6=时,该容器的容积为 3cm 。
12、下列四个命题①“,R x ∈∃112≤+-x x ”的否定;②“若,062≥-+x x 则2>x ”的否命题;(第17题图)(第18题图)ABDl③在ABC ∆中,“”是30>A “21sin >A ”的充分不必要条件; ④“函数)tan()(ϕ+=x x f 为奇函数”的充要条件是“)(z k k ∈=πϕ”。
安徽省蚌埠二中2011-2012学年高三4月质量检测考试语文试题(答案扫描)

安徽省蚌埠二中2011-2012学年高三4月质量检测考试语文本试卷分第Ⅰ卷(阅读题)和第Ⅱ卷(表达题)两部分,全卷满分150 分,考试时间150 分钟。
请考生将单项选择题答案用2B 铅笔填涂在答题卡相应的位置,否则,该大题不予计分。
第11 题双项选择题答案写在答题卷的相应位置。
第Ⅰ卷(阅读题66 分)一、(9 分)阅读下面的文字,完成1~3 题中国文化的内涵季羡林我曾经把文化分为两类:狭义的文化和广义的文化。
狭义指的是哲学、宗教、文学、艺术、政治、经济、伦理、道德等等。
广义指的是包括精神文明和物质文明所创造的一切东西,连汽车、飞机等等当然都包括在内。
周一良先生曾把文化分为三个层次:狭义的、广义的、深义的。
对于深义的文化,周先生有自己的看法。
他说:“在狭义文化的某几个不同领域,或者在狭义和广义文化的某些互不相干的领域中,进一步综合、概括、集中、提炼、抽象、升华,得出一种较普遍地存在于这许多领域中的共同东西。
这种东西可以称为深义的文化,亦即一个民族文化中最为本质或最具特征的东西。
”他举日本文化为例,他认为日本深义的文化的特质是“苦涩”、“闲寂”。
具体表现是简单、质朴、纤细、含蓄、古雅、引而不发、不事雕饰等。
我不想从民族心态上来探索,我想换一个角度,同样也能显示出中华文化的深层结构或者内涵。
中国哲学同外国哲学不同之处极多,其中最主要的差别之一就是,中国哲学喜欢谈论知行问题。
我想按照知和行两个范畴,把中国文化分为两部分:一部分是认识、理解、欣赏等等,这属于知的范畴;一部分是纲纪伦常、社会道德等等,这属于行的范畴。
在这两部分的后面存在着一个最为本质、最具有特征的深义的中华文化。
寅恪先生论中国思想史时指出:“南北朝时,即有儒释道三教之目。
故自晋至今,言中国之思想,可以儒释道三教代表之。
此虽通俗之谈,然稽之旧史之事实,验以今世之人情,则三教之说,要为不易之论。
故两千年来华夏民族所受儒家学说之影响,最深最巨者,实在制度法律公私生活之方面,而关于学说思想之方面,或转有不如佛道二教者。
安徽省蚌埠二中2012年届高三文科数学模拟测试(二)
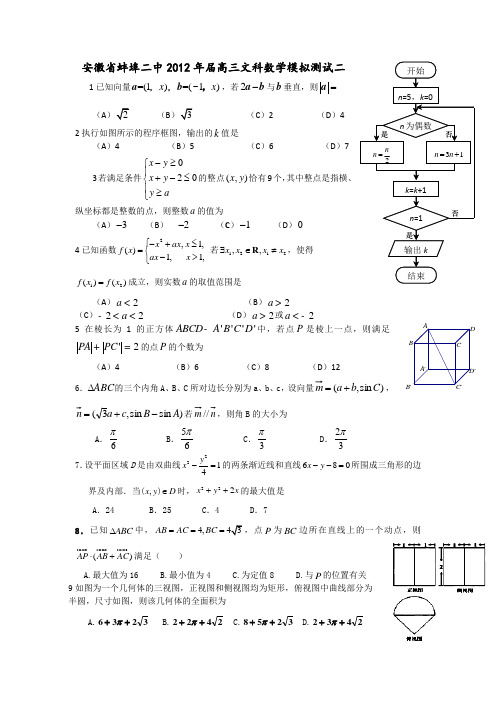
安徽省蚌埠二中2012年届高三文科数学模拟测试二1已知向量=(1)=(1)x x ,a b ,,-,若2-a b 与b 垂直,则=a(A(B(C )2 (D )4 2执行如图所示的程序框图,输出的k 值是(A )4 (B )5 (C )6 (D )73若满足条件020x y x y y a -≥⎧⎪+-≤⎨⎪≥⎩的整点(,)x y 恰有9个,其中整点是指横、纵坐标都是整数的点,则整数a 的值为(A )3- (B ) 2- (C )1- (D )04已知函数2,1,()1,1,x ax x f x ax x ⎧-+≤=⎨->⎩ 若1212,,x x x x ∃∈≠R ,使得12()()f x f x =成立,则实数a 的取值范围是(A )2a < (B )2a >(C )22a -<< (D )2a >或2a <-5在棱长为1的正方体''''ABCD A B C D -中,若点P 是棱上一点,则满足'2PA PC +=的点P 的个数为(A )4(B )6 (C )8 (D )126.ABC ∆的三个内角A 、B 、C 所对边长分别为a 、b 、c ,设向量)sin ,(C b a +=, )sin sin ,3(A B c a -+=若//,则角B 的大小为A .6πB .65π C .3π D .32π 7.设平面区域D 是由双曲线2214y x -=的两条渐近线和直线680x y --=所围成三角形的边界及内部.当,x y D ∈()时,222x y x ++的最大值是A .24B .25C .4D .78.已知ABC ∆中,4,AB AC BC ===,点P 为BC 边所在直线上的一个动点,则()AP AB AC ⋅+满足( )A.最大值为16B.最小值为4C.为定值8D.与P 的位置有关 9如图为一个几何体的三视图,正视图和侧视图均为矩形,俯视图中曲线部分为 半圆,尺寸如图,则该几何体的全面积为A.3236++πB.2422++πC.3258++πD.2432++πA'B'C'D'A BCD10.下列四个命题中,正确的是A .对于命题2:,10p x R x x ∃∈++<使得,则:p x R ⌝∀∈,均有210x x ++>;B .函数()x x f x e e -=-切线斜率的最大值是2;C .已知函数0()sin ,af a xdx =⎰则1cos 1)2(+=⎥⎦⎤⎢⎣⎡πf f D .函数321x y =⋅+的图象可以由函数2x y =的图象仅通过平移变换得到;11. 已知函数()f x 的定义域为(2,2),-导函数为(0)0()2cos ,f f x x ='=+且,则满足2(1)()0f x f x x ++->的实数x 的取值范围为A. (1,1)-B. (11)-,C. (1D. (11 12. 在正三棱锥S-ABC 中,M 、N 分别是SC 、BC 的中点,且AM MN ⊥,若侧棱SA=32,则正三棱锥 S-ABC 外接球的表面积为A .12πB .32πC .36πD .48π13)复数2i1ia +-在复平面内所对应的点在虚轴上,那么实数a = . 14过双曲线221916x y -=的右焦点,且平行于经过一、三象限的渐近线的直线方程是 15若1tan 2α=,则cos(2)απ2+= . 16以抛物线24y x =上的点0(,4)x 为圆心,并过此抛物线焦点的圆的方程是17已知三条侧棱两两垂直的正三棱锥的俯视图如图所示,那么此三棱锥的体积是,左视图的面积是 . 18已知函数1,,()0,.x f x x ìÎïï=íïÎïîR Q Q ð 则()()______f f x = 下面三个命题中,所有真命题的序号是 . ① 函数()f x 是偶函数;② 任取一个不为零的有理数T ,()()f x T f x +=对x ∈R 恒成立;③ 存在三个点112233(,()),(,()),(,()),A x f x B x f x C x f x 使得ABC ∆为等边三角形.俯视图19已知函数()sin sin()3f x x x π=+-.(Ⅰ)求()f x 的单调递增区间; (Ⅱ)在ABC ∆中,角A ,B ,C 的对边分别为,,a b c .已知()f A =a =,试判断ABC ∆的形状.20已知菱形ABCD 中,AB =4, 60BAD ∠=(如图1所示),将菱形ABCD 沿对角线BD 翻折,使点C 翻折到点1C 的位置(如图2所示),点E ,F ,M 分别是AB ,DC 1,BC 1的中点.(Ⅰ)证明:BD //平面EMF ;(Ⅱ)证明:1AC BD ⊥; (Ⅲ)当EF AB ⊥时,求线段AC 1 的长.21已知函数211()ln (0)22f x a x x a a =-+∈≠且R . (Ⅰ)求()f x 的单调区间;(Ⅱ)是否存在实数a ,使得对任意的[)1,x ∈+∞,都有()0f x ≤?若存在,求a 的取值范围;若不存在,请说明理由.AB CD图1M FEABC 1D 图222对于集合M ,定义函数1,,()1,.M x M f x x M -∈⎧=⎨∉⎩对于两个集合M ,N ,定义集合{()()1}M N M N x f x f x ∆=⋅=-. 已知A ={2,4,6,8,10},B ={1,2,4,8,16}.(Ⅰ)写出(1)A f 和(1)B f 的值,并用列举法写出集合A B ∆; (Ⅱ)用Card (M )表示有限集合M 所含元素的个数.(ⅰ)求证:当()()Card X A Card X B ∆+∆取得最小值时, 2X Î; (ⅱ)求()()Card X A Card X B ∆+∆的最小值.23 已知数列{}n a 满足:111,1,22,n n n a n n a a a n n +⎧+⎪==⎨⎪-⎩为奇数为偶数,且*22,n n b a n N =-∈。
安徽省蚌埠二中高三上学期期中考试(语文)

安徽省蚌埠二中高三上学期期中考试语文试题(考试时间:150分钟试卷分值:150分)命题人:刘欣注意:所有选择题的答案必须用2B铅笔涂在答题卡中相应的位置,否则,该题不予记分。
第Ⅰ卷(共66分)一、(9分)阅读下面的文字,完成1~3题。
鼎在中国由来已久。
它最初是古代的烹饪之器,相当于现在的锅,用以炖煮和盛放食品。
鼎有三足圆鼎,也有四足方鼎。
最早的鼎是粘土烧制的陶鼎,后来又发展为用青铜铸造的铜鼎。
传说夏禹曾收九牧之金铸九鼎于荆山之下,以象征九州。
自从有了禹铸九鼎的传说,鼎就从一般的炊器演变为传国的重器了。
国灭则鼎迁,夏朝灭,商朝兴,九鼎迁于商都亳京;商朝灭,周朝兴,九鼎又迁于周都镐京。
从商至周,都把定都或建立王朝称为“定鼎”。
鼎自从被视为传国重器、国家和权力的象征后,“鼎”字也被赋予了显赫、尊贵、盛大等政治引申意义。
譬如一言九鼎、大名鼎鼎、三足鼎立等等。
鼎是我国青铜文化的代表。
它既是文明的见证,又是文化的载体。
根据禹铸九鼎的传说,可以推想,我国早在400前就有了青铜冶炼和铸造技术。
中国历史博物馆收藏的“司母戊”大方鼎就是商代晚期的青铜鼎,它呈长方形、四足,是我国现存最大的商代青铜器。
鼎腹内有“司母戊”三字,是商王为祭祀其母戊而铸造的。
清代出土的大盂鼎、大克鼎等都是西周时期的著名青铜器。
鼎和其它青铜器上的铭文,记载了商周时代的典章制度和册封、祭祀、征伐等史实,而且还把西周时期的大篆文字传给了后世,形成了具有很高审美价值的金文书法艺术,鼎也因此更加身价不凡。
美学家李泽厚认为,中国青铜器以其特有的三足器——鼎为主要代表,器制沉雄厚实,纹饰狞厉神秘,刺镂深重凸出,是我国青铜冶炼和铸造技术最具审美价值的工艺品。
现代汉字中的“鼎”字,虽然经过了甲骨文、金文、小篆、隶书等多次变化,但仍然保留着“鼎”这一事物的风范和形体特点,其物其字几乎融为一体,都有着丰富的文化内涵。
鼎又是旌功记绩的礼器。
周代的国君或王公大臣在重大庆典或接受赏赐时都要铸鼎,以记载盛况。
蚌埠二中2012~2013学年高三12月月考语文试题(word版首发)

蚌埠二中2012~2013学年高三12月月考语文试题(word版首发)蚌埠二中2012~2013学年高三12月月考语文试题(word版首发)程道流的一方蓝天蚌埠二中2012~2013学年高三12月月考语文试题(满分150分,时间150分钟)命题人:彭玲第卷阅读题(66分)一、论述类文本阅读(9分,每小题3分)阅读下面的文字,完成1~3题。
孔孟黄仁宇在儒家的传统中,孔孟总是形影相随。
既有大成至圣,则有亚圣;既有《论语》,则有《孟子》;孔曰“成仁”,孟曰“取义”,他们的宗旨也始终相配合。
《史记》说:“孟子序诗书,述仲尼之意。
”今人冯友兰,也把孔子比做苏格拉底,把孟子比做柏拉图。
但是我们仔细比较他们,却也发现很多不相同的地方。
最明显的,《论语》中所叙述的孔子,有一种轻松愉快的感觉,不如孟子凡事紧张。
所以大成至圣能够以“君子坦荡荡”的风格,避免“小人常戚戚”的态度去保持他的悠闲。
孔子令门人言志,只有曾皙最得他的赞许。
而曾皙所说的,大致等于我们今天的郊游和野餐,“暮春者,春服既成,冠者五六人,童子六七人,浴乎沂,风乎舞雩,咏而归”。
与这种态度截然相对的是孟子“生于忧患,死于安乐”的主张。
孔子还说饭菜不做好,这样不吃那样不吃,衣服也要色彩裁剪都合式。
孟子却毫不忌讳地提出“庖有肥肉,厩有肥马,民有饥色,野有饿莩”,而且“老羸乎沟壑,壮者散之四方”等辞句也经常出现在他的嘴中。
孔子没有直接的提到人之性善或性恶。
《论语》之中,“仁”字出现了66次,没有两个地方解释完全相同。
但是他既说出虽为圣贤,仍要经常警惕才能防范不仁的话,可见他认为性恶来自先天。
他又说“观过,斯知仁矣”,好像这纠正错误,促使自己为善的能力,虽系主动的,但仍要由内外观察而产生。
孟子则没有这样犹疑。
他曾斩钉截铁的说出:“人性之善也,犹水之就下也;人无有不善,水无有不下。
”孔子自己承认,他一生学习,到70岁才能随心所欲不逾矩。
孟子的自信,则可以由他自己所说“我善养吾浩然之气”的一句话里看出。
蚌埠二模 安徽省蚌埠市2012届高三年级第三次教学质量检查考试语文试题

蚌埠市2012届高三年级第三次教学质量检查考试语文本试卷分第1卷(阅读题)和第Ⅱ卷(表达题)两部分,共150分,考试时间150分钟。
所有客观选择题用2B铅笔填涂,所有题目答案请写在答题卷上,考试结束时只需上交答题卷。
第I卷(阅读题65分)一、(9分)阅读下面的文字,完成l一3题中国传统诗词需要创新龙剑宇中国当代社会日新月异,呈现出百花齐放、百家争鸣的局面,什么是万变不离其宗的价值取向?什么是激浊扬清的试金石?以什么来区分真假、善恶和美丑?许许多多的价值观,充斥着这个社会,有人清醒也有人迷茫。
中国应当有它的主流文化,而这个文化应当有它深厚的民族根基,同时又要有新时代的强大生命力。
那么传统的诗词可作为构筑当代人文精神大厦的一根顶梁柱!中国传统诗词风格各异,千变万化,但从内容和形式上看无非是两大主流:婉约与豪放。
在婉约中则有格调向上的(健康的)和消沉悲观的,婉约多见于宋词元曲,前者如李商隐、李清照、辛弃疾、陆游、马致远等人,于低回婉转中见艺术功力亦见真情流露;后者如南唐后主李煜和宋代词人晏珠、晏几道等,一味地悲欢离合儿女情长,虽情深意笃,艺术水平也了得,但读多了不免意志消沉;更有甚者则是那些凄婉的无病呻吟。
豪放派是中国诗词的珍宝,豪放加上婉约则更是极品,历来也是最为人所称道的。
诗经以平实为主,然也有婉约,也有豪放;从楚地的屈原到汉魏的曹操、唐朝的李白、宋朝的苏轼、陆游、辛弃疾等等,均以豪放见称。
以现在眼光观之,诗词既可以是一种休闲的材料或者体闲的过程,但也可以是一种生存状态的记录。
作为休闲的材料,她向人们展示了生活的美或忧愁或理想,因而引起读者的共鸣,浅层次来说可以帮助有闲的人们打发多余的时光或者给忙碌的人们提供短暂的休息;深层次上说,诗词有可能振奋人心,给人力量,或者让读者回顾历史,展望未来。
这就决定了诗词具有指引审美或休闲导向的作用。
一味地婉约,不免让人消沉,而一味地豪放,则不免使人太过紧张,如果豪放与婉约能够适当地配合,诗词就必然成为绝佳的休闲材料或者休闲的过程。
安徽省蚌埠二中11—12学年高三上学期期中考试(语文)

蚌埠二中2011—2012学年第一学期期中考试高三语文试题(试卷分值:150分 考试时间150分钟 ) 命题人:王从好注意:本试卷包含Ⅰ、Ⅱ两卷.第Ⅰ卷为阅读题,第Ⅱ卷为表达题。
所有答案必须答在答题卷及答题卡...............的相应位置.....。
答案写在试卷上均无效..........,不予记分....。
共150分,考试时间150分钟。
第Ⅰ卷(阅读题共66分)所有选择题答案必须用2B 铅笔涂在答题卡中相应的位置,否则,该大题不予记分. 一、阅读下面文字,完成1-3题(9分):对当前“时尚史学"的几点思考(许海云)“时尚史学"是近年来国内史学界出现的一种新现象,具体表现为社会传媒高调推出由各方专家对历史的“大众解读与评说”,同时伴之以大量带有“戏说、恶搞”成分的历史题材影视作品.“时尚史学”缺乏历史的现实价值表达。
众所周知,历史认识的本质在于追求真实,求真是史学研究的一种基本价值导向,因为只有真实的历史,才具备历史的现实价值,才能真正发挥其社会教化功用,这一点早已为史学研究的内在规律所决定。
历史研究的目的于此,历史知识普及的目的也在此,两者在这一点上是空前一致的。
然而,历史学所普遍奉行的这一金科玉律,在“时尚史学”中却遭到质疑,甚至有被扭曲之嫌。
“时尚史学”没有科学、系统的研究方法作为支撑。
“时尚史学”对此所做的解释是,它所面对的社会群体是普通大众以及历史爱好者,它的目标在于历史知识的传播而非学术研究。
“时尚史学”这一凝固的模式,限制了其自身的发展,使之无法形成完整、系统的研究方法。
正因为如此,“时尚史学”似乎总是支离破碎,其兴趣点基本上围绕着一些固定的“热点”话题展开,而这些话题又总是和社会精英、帝王将相联系在一起。
因此,“时尚史学"所讲述的内容几乎只能集中在历史上有限的、可讲的某些“英雄人物",品说他们的丰功伟业、生活逸事、社会趣闻,而对波澜壮阔的社会活动却熟视无睹。
安徽省蚌埠市2012届高三年级第三次教学质量检查考试文科综合试题

安徽省蚌埠市2012届高三年级第三次教学质量检查考试文科综合试题12.安徽地区的先贤们在中华民族精神主体、中国古典文化的构建过程中,都经做出不可磨灭的贡献。
下列表述正确的是①《逍遥游》表达了老子力图在乱世保持独立的人格,追求逍遥无恃的精神自由思想②吴敬梓的《儒林外史》是我国清代一部杰出的现实主义长篇讽刺小说③李鸿章践行了“中体西用”思想,促进了中国近代化的发展④陈独秀的《文学改良刍议》体现了解放思想、探索新知、再造文明的精神A.①②B.①③C.②③D.③④13.1514年,广东布政司参议陈伯献上奏说:“近许官府抽分(注:征收进口税),公为贸易,遂使奸民数千,驾造巨舶,私置兵器,纵横海上”。
据此可知A.陈伯献反对海禁政策B.明政府加强海禁力度C.明代东南沿海遭到西方侵略D.明政府曾经放松海禁14.隋唐时官方对曹操的评价以肯定为主,认为他是大英雄;到了北宋则完全相反,从官方到民间对他的评价都以否定为主。
形成这种变化的主要原因是A.宋代商品经济高度发展促进思想解放B.宋代统治者强化中央集权的需要C.理学发展为官方统治哲学的结果D.宋代市民文学发展的结果15.小周同学在学习了盂德斯鸠的思想后认为,“三权分立”的主张和董仲舒的“天人感应”有一致之处。
这是因为它们A.都主张权力制约B.都强调权力集中C.都主张分权制衡D.都认可君权无限16.当光绪帝把变法的想法通过庆亲王奕勖转告给太后时,太后就曾对光绪皇帝的变法愿望和志向予以赞同。
她表示,“变法乃素志”,“苟可以致富强者,儿自为之,吾不内制也。
”而她的条件是“戒帝毋操之过蹙而已。
”由此可以推断慈禧后来反对变法的原因可能是A.维新派变法措施过于激进B.慈禧顽固守旧,一贯反对改革C.慈禧一向善变,出尔反尔D.维新派保守软弱,改革效果不佳A.17.造成表1中米价变化的主要原因是表1:1946年1月-6月中国几个主要城市的米价(单位:百元/市石)A.抗战胜利,粮食丰收B.自然灾害,粮食减产C.内战在即,通货膨胀D.国共和谈,经济好转18.图2摄于20世纪50年代后期的中国。
5安徽省蚌埠二中高三上学期10月考语文

蚌埠二中2012届高三年级月考(十月)语文试卷(考试时间:150分钟试卷分值:150分)命题人:刘建尧第Ⅰ卷(阅读题共66分)一、(9分)阅读下面的文字,完成1~3题。
“敬”的当代价值对于孔子思想的认识,学界一般以“礼”和“仁”为核心,认为孔子继承了周礼,发展出“仁”的思想,因而着重探讨两者的关系及其当代意义。
其实,在“礼”和“仁”之中还有更本质性的精神内涵,这种精神内涵可以用“敬”来概括。
礼最早是祭祀天地神灵的仪式活动。
在那些高高在上的“天”、“神”面前,人自然产生敬畏的心理。
其中的敬是出于内心的崇拜仰慕,而畏则是害怕受到惩罚。
最早的礼活动即内含着这种敬畏的心情。
礼由祭祀的仪式活动发展为社会政治活动的规范形式时,“敬”作为内质也留存下来。
这种“敬”保障了礼的实践可能性,而且其发自内心,即出于天赋,由“敬”而发的礼活动也就合乎天理,具有道德价值了。
因此在国家政治活动中要求“敬”,社会的一切活动和个人的修养也以“敬”为内核。
孔子继承“礼”的同时,自然吸纳了“敬”的精神。
在《论语》中,“敬”出现21次,频率颇高。
这些关于“敬”的阐述,有继承,也有发展。
关于祭祀活动,孔子继承了上古对“天”和“神”的敬仰态度,强调“祭如在,祭神如神在”,“祭思敬”。
即使“敬鬼神而远之”一语,强调实践理性的重要性,也告诫人们对于鬼神要有敬畏的心态。
关于政治活动,孔子也承传了西周以来的敬谨精神,故而回答鲁哀公说:“治礼,敬为大。
”孔子对于“敬”的发展,在于把它扩展为普通人对待事物的敬业精神。
“敬”原本主要表现在人对神、臣民对君王等下对上的关系上,孔子以后则成为所有社会成员为人做事的基本原则。
《论语》中出现的21次“敬”中,关于敬事的即有18次。
而且,由“礼”中发展出来的“仁”也以“敬”为本。
一般认为,“仁”是“礼”的内核,“礼”是“仁”的形式,故而许多学者着重以“仁”为核心建构孔子的思想体系。
其实,“仁”之中也必有“敬”的精神。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
安徽省蚌埠二中2012届高三上学期期中考试数学(文)试题(试卷分值:150分 考试时间:120分钟 )命题人:耿晓燕注意事项:第Ⅰ卷所有选择题的答案必须用2B 铅笔涂在答题卡中相应的位置、第Ⅱ卷的答案做在答题卷的相应位置上,否则不予计分。
第Ⅰ卷(选择题 共50分)一、选择题(本大题共10小题,每小题5分,共50分)[来源:学科网ZXXK]1.若集合{}0P y y =≥, P Q Q =I ,则集合Q 不可能是 ( )A.{}2,y y x x R =∈ B.{}2,xy y x R =∈C.{}lg ,0y y x x =>D.{}3,0y y xx -=≠2.已知a R ∈,则 “2a >”是“22a a >”的 ( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件 3.设等比数列{}n a 的公比2=q ,前n 项和为n S ,则=24a S ( ) A .B .C .215 D .2174.对于函数()cos f x x x =+,下列命题中正确的是( )[来源:学.科.网Z.X.X.K]A .,()2x R f x ∀∈=B .,()2x R f x ∃∈=C .,()2x R f x ∀∈>D .,()2x R f x ∃∈>5. 已知0cos sin ,54sin <=θθθ则θ2sin 的值为 ( ) A.2524- B.2512- C.54- D. 25246.若O 是ABC ∆所在平面内一点,且满足|2|||OA OC OB OC OB -+=-,则ABC ∆的形状为( )A. 等腰直角三角形B.直角三角形C.等腰三角形D.等边三角形7.若不等式(a -2)x 2+2(a -2)x -4<0对一切x ∈R 恒成立,则a 的取值范围是 ( )A. (-2,2]B. (-∞,2]C. [-2,2]D.(-∞,-2)8.已知函数20122011ln )23()(2-++-=x x x x x f ,则方程()0f x =在下面哪个区间内必有实根( )A.)1,0( B.)2,1( C.)3,2( D.)4,2( 9.定义在R 上的偶函数f (x )在[)+∞,0上是增函数,且0)31(=f ,则不等式0)(log 81>x f 的解集是( )[来源:] A .)0,21(B .),2(+∞C .),2()21,0(+∞YD .),2()1,21(+∞Y10.已知函数|lg |,010()16,102x x f x x x <≤⎧⎪=⎨-+>⎪⎩,若,,a b c 互不相等,且()()()f a f b f c ==,则abc 的取值范围是( )A .(1,10)B .(5,6)C .(10,12)D .(20,24)第Ⅱ卷(非选择题 共100分)二、填空题(本大题共5小题,每小题5分,满分25分) 11.设集合{}1|3,|0,4x A x x B x x -⎧⎫=>=<⎨⎬-⎩⎭则A B =I _____________. 12.已知向量)2,(cos α=,)1,(sin α=且b a //,则=︒-)45tan(α 。
13.已知数列 {}n a ()*∈Nn 中,11=a,121+=+n nn a a a ,则n a = 。
14.若函数32()33(2)1f x x ax a x =++++,既有极大值又有极小值,则的取值范围 是 。
15.关于函数x x x f 2cos 2sin )(-=有下列命题:①函数)(x f y =的周期为; ②直线4π=x 是)(x f y =的一条对称轴;③点)0,8(π是)(x f y =的图象的一个对称中心;④将)(x f y =的图象向左平移4π个单位,可得到x y 2sin 2=的图象.其中真命题的序号是 .(把你认为真命题的序号都写上)三、解答题(本大题6小题,满分75分) 16、(12分) 已知函数2cos 22sin 3)(2++=x x x f(I )求)(x f 的最小正周期与单调递减区间;(II )在△ABC 中,c b a ,,分别是角A 、B 、C 的对边,若,1,4)(==b A f △ABC 的面积为23,求的值.17、(12分)设集合1{|24},{|(1)(21)0}32x A x B x x m x m -==-+--<≤≤. (Ⅰ)求A Z I ;(Ⅱ)若A B ⊇,求的取值范围.18、(12分)如图,在四棱锥ABCD P -中,底面ABCD 是矩形, ⊥PA 平面ABCD ,且AD PA =,点是棱PD 的中点,点在棱CD 上移动. (Ⅰ)当点为CD 的中点时,试判断直线EF 与平面PAC 的关系, 并说明理由;(Ⅱ)求证:AF PE ⊥.19、(13分)数列{}n b ()*∈N n 是递增的等比数列,且4,53131==+b b b b . (1)求数列{}n b 的通项公式;(2)若3log 2+=n n b a ,求证数列{}n a 是等差数列; (3)若11+⋅=n n n a a c ,求数列{}n c 的前项和n S .PAB CD FE20、(13分)已知函数()x f 的定义域为()()∞+⋃∞-,,00,且满足条件:①()()()y f x f y x f +=⋅,②(),12=f ③当()0,1>>x f x 时. (1)求证:函数()x f 为偶函数; (2)讨论函数()x f 的单调性;(3)求不等式()()23≤-+x f x f 的解集21、(13分)设二次函数()2f x mx nx t =++的图像过原点,()33(0)g x ax bx x =+->,(),()f x g x 的导函数为()//,()f x g x ,且()//00,(1)2f f =-=-,()),1(1g f =()//1(1).f g =(1)求函数()f x ,()g x 的解析式; (2)求())()(x g x f x F -=的极小值;(3)是否存在实常数k 和,使得()m kx x f +≥和()?m kx x g +≤若存在,求出k 和的值;若不存在,说明理由。
蚌埠二中2011-2012学年第一学期期中考试高三数学参考答案(文科)一选择题三解答题16. 解:I )2cos 22sin 3)(2++=x x x f 32cos 2sin 3++=x x 3)62sin(2++=πxππ==∴22T )(326)(2326222Z k k x k Z k k x k ∈+≤≤+∴∈+≤+≤+πππππππππ令)](32,6[)(Z k k k x f ∈++∴ππππ的单调减区间为(II )由4)(=A f 得21)62sin(43)62sin(2)(=+∴=++=ππA A A f的内角为又ABC A ∆Θ656267626πππππ=+∴<+<∴A A 3π=∴A。
[来源:] 23sin 211,33=∴==∆A bc b S ABC Θ 2=∴c 32112214cos 2222=⨯⨯⨯-+=-+=∴A bc c b a 3=∴a 17. 解:(Ⅰ)化简可得,集合{}25A x x =-≤≤.则{2,1,0,1,2,3,4,5}A =--Z I .(Ⅱ)集合{(1)(21)0}B x x m x m =-+--<, ① 当2m =-时,B =∅,所以B A ⊆;② 当2m <-时,∵(21)(1)20m m m +--=+<,∴(21,1)B m m =+-.因此,要使B A ⊆,只需21215m m +-⎧⎨-⎩≥≤,解得362m -≤≤,所以值不存在.③ 当2m >-时,(1,21)B m m =-+,要使B A ⊆,只需12215m m --⎧⎨+⎩≥≤,解得12m -≤≤.综上所述,的取值范围是2m =-或12m -≤≤.18. 解:(Ⅰ)当点为CD 的中点时,//EF 平面PAC . 理由如下:点F E ,分别为CD ,PD 的中点, //EF PC . PAC PC 平面⊂,PAC EF 平面⊄,//EF 平面PAC .(Ⅱ) ABCD PA 平面⊥,ABCD CD 平面⊂ ,PA CD ⊥∴.又ABCD 是矩形,AD CD ⊥∴,PA AD A =Q I ,PAD CD 平面⊥∴. PAD AF 平面⊂Θ AF CD ∴⊥. AD PA =Θ,点是PD 的中点, PD AF ⊥∴.又D PD CD =I , PDC AF 平面⊥∴. PDC ,PE 平面⊂Θ AF PE ⊥∴. 19. 解:(Ⅰ)由 ⎩⎨⎧=+=543131b b b b 知31,b b 是方程2540x x -+=的两根,注意到n n b b >+1得 131,4b b ==.43122==b b b 得22=b . 4,2,1321===b b b等比数列.{}n b 的公比为212=b b ,1112--==∴n n n qb b [来源:学|科|网Z|X|X|K] (Ⅱ)122log 3log 2313 2.n n n a b n n -=+=+=-+=+∵()[]11221n n a a n n +-=++-+=⎡⎤⎣⎦数列{}n a 是首相为3,公差为1的等差数列. [来源:Z 。
xx 。
] (Ⅲ))3)(2(1++=n n c n ,)3()2(1541431+⨯+++⨯+⨯=n n S n Λ312151414131+-+++-+-=n n Λ93+=n n 20. 解:(1)在①中令x =y=1, 得f (1)= f (1)+ f (1)⇒ f (1)=0, 令x =y=-1, 得f (1)= f (-1)+ f (-1)⇒ f (-1)=0,再令y=-1, 得f (-x )= f (x )+ f (-1)⇒ f (x ), ∴f (x )为偶函 数; (2)在①中令),()1()1()()1(,1x f xf x f x f f x y -=⇒+==得 先讨论),0()(+∞在x f 上的单调性, 任取x 1http:///x 2,设x 2>x 1>0, ,1),()1()()()(12121212>=+=-∴x x x x f x f x f x f x f Θ由③知:)(12x x f >0,∴f (x 2)>f (x 1), ∴f (x )在(0,+∞)上是增函数, ∵偶函数图象关于y 轴对称 ,∴f (x )在(-∞,0)上是减函数;[来源:Z+xx+] (3)∵f [x (x -3)]= f (x )+ f (x -3)≤2, 由①②得2=1+1= f (2)+ f (2)= f (4)= f (-4), 1)若x (x -3)>0 , ∵f (x )在(0,+∞)上为增函数, 由f [x (x -3)] ≤f (4) 得CABDPEF;430141304)3(0)3(≤<<≤-⇒⎩⎨⎧≤≤-><⇒⎩⎨⎧-≤->-x x x x x x x x x 或或 2)若x (x -3)<0, ∵f (x )在(-∞,0)上为减函数;由f [x (x -3)] ≤f (-4)得 ;30304)3(0)3(<<⇒⎩⎨⎧∈<<⇒⎩⎨⎧-≥-<-x Rx x x x x x∴原不等式的解集为:}.43|{}30|{}01|{≤<⋃<<⋃<≤-x x x x x x 21.解:(1)由已知得()/0,2t f x mx n ==+, 则()//00,(1)22fn f m n ==-=-+=-,从而0,1n m ==,∴2()f x x =,()x x f2/=,()b ax x g +=2/3。
