2010年学而思杯初一数学A卷试题及答案
【学而思培优】初一年级期中冲刺数学100题及答案

18. (白云广雅)一个四边形纸片 ABCD , B D 90 ,把纸片按如图所示折叠,使点 B 落在 AD 边上的点 B 处, AE 是折痕. ⑴试判断 BE 与 DC 的位置关系,并说明理由. ⑵如果 C 130 ,求 AEB 的度数.
| 初一期中复习 Байду номын сангаас00 题 | 第 4 页 共 24 页
)
34. (二中本部) 已知 n 为整数, 而且 4 n 5 , 请写出一个满足条件的 n 的值: ________. 35. (执信)已知 x、y 都是实数,且 y x 2 2 x 4 ,则 y x 的值是________. 36. (中大附中)若 a 满足 2012 a a 2013 a ,那么 a 20122 ________. 37. (侨外)有理数 a、b 满足 5 3a 2b 3 a ,则 a ________, b ________. 38. (七中)化简计算: ⑴
广州学而思培优
初一数学期中考前 冲刺
100 题
广州学而思中考团队荣誉出品
特别感谢:佘鑫 方聪 付春早 赵晶晶 邱佳麟
| 初一期中复习 100 题 | 第 1 页 共 24 页
相交线与平行线
1. (侨外)下列命题中,真命题的个数有( ) ①同一平面内,两条直线一定互相平行; ②有一条公共边的角叫邻补角; ③内错角相等; ④对顶角相等; ⑤从直线外一点到这条直线的垂线段,叫做点到直线的距离. A.0 个 B.1 个 C.2 个 D.3 个 (执信)下列命题是真命题的是( ) A.和为 180 的两个角是邻补角 B.一条直线的垂线有且只有一条 C.点到直线的距离是指这点到直线的垂线段 D.两条直线被第三条直线所截,内错角相等,则同位角必相等 (侨外)一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那 么两次拐弯的角度是( ) A.第一次右拐 50 ,第二次左拐 130 B.第一次左拐 50 ,第二次右拐 50 C.第一次左拐 50 ,第二次左拐 130 D.第一次右拐 50 ,第二次右拐 50 (广外)如图,正方形 P、Q 夹在 ABCD 框架中,正方形 P 下边 一条边与 AB 夹角为 15 ,正方形 P、Q 有两个相邻边夹角为 ) 100 ,则 1 为( A. 15 B. 55 C. 65 D. 75 (广外)如图,有 a、b、c 三户家用电路接入电表,相邻电路的电线 等距排列,则三户所用电线( ) A. a 户最长 B. b 户最长 C. c 户最长 D.一样长
2010 学而思杯 6年级 数学 真题及答案
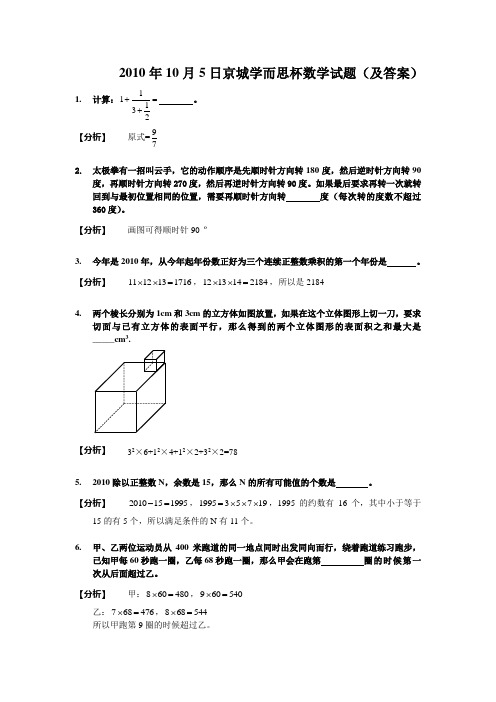
2010年10月5日京城学而思杯数学试题(及答案)1.计算:11132+=+。
【分析】原式=9 72.太极拳有一招叫云手,它的动作顺序是先顺时针方向转180度,然后逆时针方向转90度,再顺时针方向转270度,然后再逆时针方向转90度。
如果最后要求再转一次就转回到与最初位置相同的位置,需要再顺时针方向转度(每次转的度数不超过360度)。
【分析】画图可得顺时针90 º3.今年是2010年,从今年起年份数正好为三个连续正整数乘积的第一个年份是。
【分析】1112131716⨯⨯=,1213142184⨯⨯=,所以是21844.两个棱长分别为1cm和3cm的立方体如图放置,如果在这个立体图形上切一刀,要求切面与已有立方体的表面平行,那么得到的两个立体图形的表面积之和最大是_____cm3.【分析】32×6+12×4+12×2+32×2=785.2010除以正整数N,余数是15,那么N的所有可能值的个数是。
【分析】2010151995-=,199535719=⨯⨯⨯,1995的约数有16个,其中小于等于15的有5个,所以满足条件的N有11个。
6.甲、乙两位运动员从400米跑道的同一地点同时出发同向而行,绕着跑道练习跑步,已知甲每60秒跑一圈,乙每68秒跑一圈,那么甲会在跑第圈的时候第一次从后面超过乙。
【分析】甲:860480⨯=,960540⨯=乙:768476⨯=,868544⨯=所以甲跑第9圈的时候超过乙。
7.将100个5分硬币排成一排,每次操作都从第一个开始。
第一次操作将硬币按顺序1,2,1,2……数,然后将数到2的硬币全部用1角硬币替换;第二次操作将硬币按顺序1,2,3,1,2,3……数,然后将数到3的硬币全部用5角硬币替换;第三次操作将硬币按顺序1,2,3,4,1,2,3,4……数,然后将数到4的硬币全部用1元硬币替换,那么经过上述操作后这100个硬币的总值是元。
2010-2015学而思杯真题(三年级)

(2)第三天买糖果时,如果要想使得他们付完糖果钱后三人互不相欠, 甲、乙、丙 3 人应该各出多少元?(9 分)
④:①~⑤题的答案中,A 最__________,B 最__________(可以并列); A、多;多 B、少;少 C、多;少 D、少;多
⑤:本题的答案是__________. A、A B、B C、C D、D
如果上述①~⑤题的答案可以使得其题干内容正确,互不矛盾,那么这五道题 的答案写成五位数是__________.(1 代表 A,2 代表 B,3 代表 C,4 代表 D.例 如:如果①~⑤题的答案是 ABCDA,则填涂 12341)
3
14. 如图,将一个边长为 50 厘米的正方形分割成一个边长为 10 厘米的小正方形和 四个梯形,而且梯形①的面积是梯形②面积的 2 倍,梯形②的面积是梯形③面 积的 2 倍,那么,梯形④的面积是__________平方厘米.
④
10cm
③
①
②
50cm
15. 将数字 1~9 分成三组,第一组 2 个数,第二组 3 个数,第三组 4 个数,并且满 足:第一组 2 个数的和大于第二组 3 个数的和,第二组 3 个数的和大于第三组 4 个数的和.那么,满足要求的分组方式有__________种.
(2) 21 7 84 14 84 7
六. 解答题(每题 15 分,共 30 分) 19. 在风和日丽的植树节,同学们乘汽车到公园植树: (1)如果每车坐 60 人,则有 15 人没车可坐;如果每车坐 65 人,则空 10 个座 位,那么,共有多少个同学去植树?(5 分)
(2)一班学生比二班学生多种了 16 棵树,而且,一班所种的数量是二班所种 数量的 3 倍.那么,一班种了多少棵树?(5 分)
初一年级第一学期期末考试数学试卷B及答案

北京市西城区2010 — 2011学年度第一学期期末试卷(北区)七年级数学(B 卷)2011.1(时间100分钟,满分100分)题号 一 二 三 四 五 六 七 总分 得分一、选择题(本题共30分,每小题3分)下面各题均有四个选项,其中只有一个..是符合题意的. 1.14-的绝对值是 A .14B .14-C .4D .4-2.2010年11月12日至27日第16届亚运会在广州举行.广州亚运城的建筑面积约为358000平方米,将358000用科学记数法表示应为A .4108.35⨯ B .51058.3⨯ C .610358.0⨯ D .61058.3⨯ 3.如果单项式y x m231和342+n y x 是同类项,那么m 、n 的值分别是( ) A . ⎩⎨⎧-==22n m B .⎩⎨⎧==14n m C . ⎩⎨⎧==12n m D . ⎩⎨⎧-==24n m 4.下列各式中,去括号正确的是A .x +2(y -1)=x +2y -1B .x -2(y -1)=x +2y +2C .x -2(y -1)=x -2y -2D .x -2(y -1)=x -2y +25. M 地是海上观测站,从M 地发现两艘船A 、B 的方位如图所示.下列说法中,正确的是A .船A 在M 的南偏东30°方向B .船A 在M 的南偏西30°方向C .船B 在M 的北偏东40°方向D .船B 在M 的北偏东50°方向6.如图,直角三角尺AOB 的顶点O 在直线CD 上, 若∠AOC =35°,则∠BOD 的度数为( ) A .65° B .55°C .45°D .35° 7.某厂2009年的生产总值为a 万元,2010年的生产总值比2009年增长了10%,那么该厂2010年的生产总值是() A .a %10万元 B .)%10(a +万元 C. a %)101(+万元 D .[]a a %)101(++万元8.有理数a b ,在数轴上的位置如图所示,则下列结论中,错误..的是( ) OAB C D BA南 西东 北30ºM50ºA .b a <<0B . b a >C .b a >- D . b a a b +<-9.延长线段AB 至C ,使得AB BC 21=,反向延长线段AC 至D ,使得AC AD 31=,则线段CD 的长等于 A .AB 21 B .AB 41 C .AB 23D .AB 2 10.小明同学设计了右图所示的正方体形状的包装纸盒,把下面四个表面展开图折叠(不计接缝),和小明同学设计的纸盒完全相同的是二、填空题(本题共16分,每小题2分) 1132的相反数是__ ___. 12若0)3(22=-++y x ,则xy = .13.如图,点B 在射线AE 上,∠D +∠ABC =180°,若∠CBE =80°,则∠D = °.14.若一个角的补角比它的余角的4倍少15°,则这个角的度数为°.15.关于x 的方程0652=-+m x 的解是2m x =,那么m m 1042+的值是 . 16.如图, 线段AB 表示一根对折以后的绳子,现从P 处把绳子剪断,剪断后的各段绳子中最长的一段为40cm ,若AP =12PB ,则这条绳子的原长为 cm . 17.在数学活动课上,李老师要求同学们在边长为1的正方形格纸中,画出一个“风车”图案.小红同学的做法是:如图甲所示,把一个三角形按顺时针方向旋转90°,连续转三次,形成四个叶片的“风车”图案;类似地,把一个梯形按顺时针方向旋转90°,连续转三次,形成图乙所示的四个叶片的“风车”图案.请你仿照小红同学的做法,在备用图中,画一个新的四个叶片的“风车”图案,并使得 “风车”的四个叶片的面积和图乙中四个叶片的面积相同.18.观察按下列顺序排列的等式:3309=+⨯, 13419=+⨯, 23529=+⨯, 33639=+⨯, 43749=+⨯,……猜想:第n 个等式(n 为正整数)应表示为 . 三、解答题(本题共16分,每小题4分)19.计算:431417)539(524----. 解:20.计算:)4()81(1655.2-÷-⨯÷-. 解:ab图乙 图甲 备用图 DACDEABP21.计算: 24)43232812(⨯-+ . 22. 6)8325.0()21()1(3220112⨯---÷-+-.四、解答题(本题共15分,每小题5分) 23.先化简下式,再求值:)45()2(32222ab b a ab b a ---,其中2=a ,1-=b .24.解方程:x x x -=-+7)52(34. 解:25.解方程:12271243xx -=-+. 解:五、按要求作图,并回答问题(本题4分) 26.如图,点B 为射线OA 上一点.①在OA 的上方,画∠AOC =120°,画∠OBD =90°; ②画出∠AOC 的平分线OE ,交射线BD 于点P . 测量点O 、P 之间的距离(精确到1cm ).六、列方程解使用题(本题共8分,每小题4分) 27.某校开展了向贫困山区学生捐书的活动,已知七年级、八年级和九年级学生共捐书1680本,其中九年级学生所捐图书数量比七年级学生所捐图书数量的3倍少270本;八年级学生所捐图书数量比七年级学生所捐图书数量的2倍多150本,在这次活动中,七年级学生捐了多少本书? 解:28.某服装厂接到一批校服的生产加工任务,要求按计划天数加工完成.该厂如果每天加工20套校服,按计划时间交货时,比定货任务少加工100套;如果每天加工23套校服,按规定时间交货时,还能比定货任务多加工20套.这批校服的加工任务是多少套?原计划多少天加工完成? 解:A B O七、解答题(本题共11分,第29小题6分,第30小题5分) 29.如图,O 是直线AB 上一点,∠COD 是直角,OE 是∠BOC 的平分线.(1)如图1,若∠AOC =40°,求∠DOE 的度数;(2)在图1中,若∠AOC =α,直接写出∠DOE 的度数(用含α的代数式表示); (3)将图1中的∠COD 按顺时针方向旋转至图2所示的位置.①探究∠AOC 和∠DOE 之间的数量关系,写出你的结论,并说明理由; ②在∠AOC 的内部有一条射线OF ,满足:2∠AOF +∠BOE =21(∠AOC -∠AOF ), 试确定∠AOF 和∠DOE 的度数之间的数量关系.解:(1)①(2)∠DOE = ; (3)① ②30.如图,已知数轴上点A 表示的数为6, B 是数轴上一点,且AB =10.动点P 从点A 出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t (t >0)秒.(1) ①写出数轴上点B 表示的数 ,点P 表示的数 (用含t 的代数式表示);②M 为AP 的中点,N 为PB 的中点.点P 在运动的过程中,线段MN 的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,并求出线段MN 的长;(2)动点Q 从点A 出发,以每秒1个单位长度的速度沿数轴向左匀速运动;动点R 从点B 出发,以每秒34个单位长度的速度沿数轴向左匀速运动,若P 、Q 、R 三动点同时出发,当点P 遇到点R 时,立即返回向点Q 运动,遇到点Q 后则停止运动.那么点P 从开始运动到停止运动,行驶的路程是多少个单位长度?解:(1)①数轴上点B 表示的数是 , 数轴上点P 表示的数是 (用含t 的代数式表示);②(2)A B C D O图1A B EC DO 图2BO北京市西城区2010 — 2011学年度第一学期期末试卷(北区)七年级数学参考答案及评分标准(B 卷)2011.1一、选择题(本题共30分,每小题3分)题号 1 2 3 4 5 6 7 8 9 10 答案 A B A D C B C D D C二、填空题(本题共16分,每小题2分)11.32- ; 12.6-; 13.80; 14.55; 15. 12;16.60 cm 或120(答对一个结果得1分); 17.举例见右图: (答案不唯一)18.3)1(10)2()1(9+-=++-n n n . 三、解答题(本题共16分,每小题4分) 19.解:431417)539(524----=431417539524--+ ········································································· 1分 =914- ························································································· 3分 =5 ······························································································· 4分20.解:)4()81(1655.2-÷-⨯÷- =)41815165.2(⨯⨯⨯- ·········································································· 2分=41-··························································································· 4分 21.解: 24)43232812(⨯-+=24411243224817⨯-⨯+⨯ ································································· 1分 =661651-+ ················································································· 2分 =1 ····························································································· 4分22.计算:6)8325.0()21()1(3220112⨯---÷-+- 解:6)8325.0()21()1(3220112⨯---÷-+- =681419⨯+⨯-- ············································································· 3分=43419+⨯-- =4112- ··························································································· 4分四、解答题(本题共15分,每小题5分) 23.解:)45()2(32222ab b a ab b a ---=b a 2222························································ 2分 =22ab b a +. ··············································································· 3分当2=a ,1-=b 时,原式=22)1(2)1(2-⨯+-⨯=-2. ······················································· 5分24.解:去括号,得 x x x -=-+71564. ·················································· 2分移项,得 15764+=++x x x . ····················································· 3分 合并同类项,得 2211=x . ·························································· 4分 系数化为1,得 2=x . ································································· 5分25.解:去分母(方程两边同乘以12),得)27(12)43(6x x -=-+. ································································ 1分去括号,得x x 27122418-=-+. ·················································· 2分 移项,得 12247218+-=+x x . ·················································· 3分 合并同类项,得 520-=x . ·························································· 4分 系数化为1,得 41-=x . ···················分 五、按要求作图,并回答问题(本题4分)答:OP = 3cm . 阅卷说明:画∠AOC =120°,∠OBD =90°(各1分); 画∠AOC 的平分线OE ,交射线BD 于点P ; ························································ 3分 量得OP =3cm . ···································· 4六、列方程解使用题(本题共8分,每小题4分)27.解:设在这次活动中,七年级学生捐了x 学生捐书)2703(-x 本. ·························分依题意有:1680)2703()1502(=-+++x x x .分 解得 300=x . ···································分 答:在这次活动中,七年级学生捐了300分 28.解:设这批校服的的加工任务是x 套,原计划20100-x 天加工完成. ················ 1分 CABD PE依题意,得232020100+=-x x . ·························································· 2分 解得 900=x . ··········································································· 3分4020100900=-(天). 答:这批校服的加工任务是900套,原计划40天加工完成. ························ 4分 七、解答题(本题共11分,第29小题6分,第30小题5分) 29.解:(1)①∵ O 是直线AB 上一点(如图1),∴∠AOC +∠BOC =180°.∵∠AOC =40°, ∴∠BOC =140°. ∵OE 平分∠BOC ,∴∠COE =21∠BOC =21×140°=70°. ········································· 1分 ∵∠DOE =∠COD -∠COE ,∠COD =90°,∴∠DOE =20°. ··································································· 2分(2)∠DOE =α21. ······································································· 3分 (3)①答:∠DOE =21∠AOC . 理由如下:∵ O 是直线AB 上一点(如图2), ∴∠AOC +∠BOC =180°. ∴∠BOC =180°-∠AOC . ∵OE 平分∠BOC ,∴∠COE =21∠BOC . =)180(21AOC ∠-︒.∵∠DOE =∠COD -∠COE ,∠COD =90°, ∴∠DOE =)180(2190AOC ∠-︒-︒=AOC ∠21. ∴∠DOE =21∠AOC . ······················································ 4分 ②答:5∠AOF +180°=4∠DOE . ······································· 5分 ∵2∠AOF +∠BOE =21(∠AOC -∠AOF ) ∴5∠AOF +2∠BOE =∠AOC如图3,根据①中的结论:2∠DOE =∠AOC ,ABC D O图1ABECDO图2ABE COF∴5∠AOF +2∠BOE =2∠DOE . ∵OE 平分∠BOC ,∴∠BOE =∠COE =DOE ∠-︒90. ∴5∠AOF +2(DOE ∠-︒90)=2∠DOE . 整理,得5∠AOF +180°=4∠DOE .∴5∠AOF +180°=4∠DOE . ············································· 6分30.(1)-4,t 66-; ··············································································· 2分 (2)分两种情况:①当点P 在A 、B 两点之间运动时(如图1),MN =MP +NP .=21AP +21BP =21AB =5. ·························································· 3分 ②当点P 运动到点B 的左侧时(如图2), MN =MP -NP=21AP -21BP =21AB =5 . ······················································· 4分 综上所述,线段MN 的长度不发生变化,其值为5.(3)设点P 运动x 秒时,在点C 处追上点R (如图3),AC =x 6,BC =x 34. ∵AC -BC =AB , ∴10346=-x x .解得 715=x .设点P 运动y 秒时,P 和点Q 相遇. ∴)(26BC AB y y +=+,∴)7153410(26⨯+=+y y . 解得 49180=y . ∴点P 运动的路程为 491080491806=⨯(单位长度). ∴点P 从开始运动到停止运动行驶的路程为491080个单位长度. ··············· 5分BC图3P B 图2 N BOP M图1。
2010-2015学而思杯真题集(一年级)

yánɡshìdìsānmínɡ měiyánɡyánɡbǐlǎnyánɡyánɡpǎodekuài fâiyánɡyánɡbǐměiyánɡ
羊 是第三 名 ,美 羊 羊 比懒 羊 羊 跑的 快 ,沸 羊 羊 比美 羊
ɡâzuìshěnɡqiándefānɡfǎ liǎnɡrãnzuìshǎohuā
yuánjiùnãnɡquánbùdōu
个 最 省 钱 的 方 法, 两 人 最 少 花
元 就 能 全 部都
cānɡuān
参 观.
4
绝密★启用前
2011 年首届全国学而思综合能力测评(学而思杯)
数学试卷(一年级 A 卷)
5. 甲、乙、丙、丁 4 只小动物站成一排,已知甲在丙左边 5 米处,丁在乙左边 3 米处,丙在丁右边 2 米处,问最左边和最右边的两只小动物之距离米.
…… …○ ……… …○… ……… 外…… …… ○…… ……装 ……… …○… ……… 订… ……… ○…… ……线 ……… …○ ……… … …… …○ ……… …○… ……… 内…… …… ○…… ……装 ……… …○… ……… 订… ……… ○…… ……线 ……… …○ ……… …
1
huǒcháibànɡbǎichãnɡdeshù
5. 火 柴 棒 摆 成 的 数
rúɡuǒzàiɡěinǐ yīɡēnhuǒcháibànɡrànɡnǐtiān
,如 果 再 给 你一 根 火 柴 棒 让 你 添
jiāzài
加在
shànɡ tiānjiāhîudeliǎnɡwâishùzuìdàshì
黄 、蓝 、绿、紫、黑 6 种 不 同 的 颜 色,那么,
学而思杯高中数学竞赛试题

学而思杯高中数学竞赛试题学而思杯高中数学竞赛试题一、选择题(共20小题,每小题4分,满分80分)1. 设函数f(x)=2x^2-3x+5,若f(1)=k, 则k的取值范围是:A. k≥4B. k>4C. k≤4D. k<42. 设函数f(x)=log_2(x+1),则f(3)+f(5)的值是:A. 2B. 3C. 4D. 53. 已知函数f(x)=mx+n的图像过点(1,4),且与x轴交于点(2,0),则m 与n的值分别是:A. m=2,n=2B. m=2,n=-2C. m=-2,n=2D. m=-2,n=-24. 若x满足7^x-4(3^x)=0,则x的值是:A. 0B. 1C. 2D. 35. 设在点A处函数f(x)=3x^2+mx+2与y轴相切,且过B点(2,14),则m的值是:A. -2B. -1C. 0D. 1……二、填空题(共5小题,每小题8分,满分40分)1. 设ΔABC中,∠A=35°,∠B=70°,则∠C的度数是______。
2. 已知函数f(x)=ax^2+2ax+b的图像与x轴相交于点(2,0),则a与b的值分别是______。
3. 若x为正实数,且5^x=25,则x的值是______。
4. 已知α是锐角,sinα=1/2,cosα=√3/2,则tanα的值是______。
5. 设π/4 < θ < π/2,cosθ=√2/2,则sinθ的值是______。
……三、解答题(共3小题,每小题20分,满分60分)1. 已知函数f(x)=ax^2+bx+c的图像过点(1,2),且顶点坐标为(2,3),求a、b、c的值。
2. 已知在平面直角坐标系中,点A(-1,1),点B(2,3),点C(4,-1),求△ABC的周长。
3. 某车站到A、B两地的铁轨长度分别为600 km和800 km。
现有一辆火车同时从A、B两地出发,两地之间的相对速度为100 km/h,问两车相遇需要多少小时?……四、证明题(共2题,每题20分,满分40分)1. 已知△ABC中,∠ABC=∠ACB,点D为BC边的中点,证明△ABD≌△ACD。
2010年学而思杯数学试题-详解

2010年学而思杯数学试题——解题精讲【题目1】a=10.8+10.98+10.998+10.9998+10.99998,a的整数部分是。
解:a=11-0.2+11-0.02+11-0.002+11-0.0002+11-0.00002=55-0.22222所以a的整数部分是54。
【题目2】四个质数2、3、5、7的乘积为,经验证200到220之间仅有一个质数,请问这个质数是。
解:四个质数乘积2*3*5*7=210;200到220的质数,所以偶数不用看,只看奇数201,203,205,207,209,211,213,215,217,219排除能被5整除的205、215排除能被3整除的201,207,213,219剩下203、209、211、217注意210能被7整除,所以和210相差7的203和217都能被7整除剩下209和211,根据能被11整除的特征,209肯定能被11整除所以只能211是质数。
【题目3】如图,棱长分别为1厘米、2厘米、3厘米的三个正方体紧贴在一起,则所得到的立体图形的表面积是平方厘米。
解:把顶面往下补,把最下面的这个正方体补全了,上面两个正方体各剩4个侧面,表面积一共是:3*3*6+2*2*4+1*1*4=54+16+4=74【题目4】12个人围成一圈,从中选出3个人,其中恰有两个人相邻,共有种不同的选法。
解:分两步,第一步:选出两个相邻的人有12种选法第二步:再选一个和他们两个不相邻的,有8种选法根据乘法原理,共有12*8=96种解:由于分子和分母相差7,所以当分子是7的倍数时,改分数就不是最简分数,1到2002中7的倍数的数共有286个,故最简分数有2002-286=1716个。
【题目7】放满一个水池,如果同时打开1,2号阀门,则12分钟可以完成;如果同时打开1,3号阀门,则15分钟可以完成;如果单独打开1号阀门,则20分钟可以完成;那么,如果同时打开1,2,3号阀门,分钟可以完成。
学而思答案

8.
从 0,1 开始的这列数的规律是偶,奇,奇,偶,奇,奇,…,也就是说这列数是按一偶两奇一偶两 奇…的规律排成一行的.因 80 3 26 2 ,所以,题中最右边的一个数是奇数.
9.
要想使 11 只杯子全部向下,需要翻动奇数次,而每次翻 8 只总次数为偶数,所以不可能.
10. 不能. 因为数码都小于 5 所以这两个四位数相加不会产生进位,所以这两个四位数的数码和等于 7356 的数码和,第二个四位数仅仅是第一个四位数的四个数码调换了位置,所以两个四位数的数码
5.
后来乙比甲多 14 16 30 千克油,所以这时甲桶油的重量是: 30 (4 1) 10 (千克),甲桶原来有油
10 16 26 千克.
6.
原来室外、室内活动人数相差 480 人,现把室内的 50 人改为室外活动,这样室外活动人数比室内人 这时室外活动人数正好是室内人数的 5 倍, 现在室内活动人数为 580 4 145 , 数多 480 50 2 580 人, 室内、外人数之和: 145 (5 1) 870 人.
9.
原正方形的边长为 (95 5 5) 5 2 7 厘米,所以面积为 49 平方厘米.
10. 小正方形的边长为 (40 11 4) 1 4 9 厘米, 面积为 81 平方厘米; 大正方形边长为 9 2 11 厘米,
面积为 121 平方厘米.
第二讲
1. 2. 3. 4.
和为偶数,而 7356 的数码和是奇数,所以不成立.
第三讲
1. 2. 3. 4. 5. 6. 7.
原式 3 5 7 (10 9) 105 19 1995
巧算乘法
99 99 99 (100 1) 9900 99 9801 125 792 125 (800 8) 125 800 125 8 1000 100 1000 1000 (100 1) 99000
2010年学而思杯初一数学B卷试题及答案

2012年 初一数学 (B 卷)姓名 得分_______________Ⅰ卷一、选择题:(本题共15小题,每小题4分,共60分)1. 已知a 、b 为实数,且4ab =,设2424a b M a b =+++,1122N a b =+++,则M 、N 的大小关系是M _______N .(填“>”、“<”、“=”其中一个)2. 如图,长方形ABCD 恰好可分成7个形状大小相同的小长方形,如果小长方形的面积是3,则长方形ABCD 的周长是___________.3. 已知a ,b ,c 为整数,且2010a b +=,2009c a -=.若a b <,则a b c ++的最大值为 .4. 观察下列算式:123456782=22=42=82=162=322=642=1282=256,,,,,,,,……通过观察,用你所发现的规律写出118的末位数字是__________.5. 已知0abc ≠,0a b c ++=,则111111()()()a b c b c c a a b+++++的值为_________.6. 如图,正方形的网格中,12∠+∠=_________.7. 三个正方形连成如下图形,求x ∠=____________.8. 若3210x x x +++=,则2010200920081220092010....1...x x x x x x x x ----++++++++++=____.9. 已知2220082007a =-,2220092008b =-,2220102009c =-,则,,a b c 的大小关系为________.10. 已知三角形的三边,,a b c 的长都是整数,且a b c ≤<,如果5b =,则这样的三角形共有________个.11. 某人将2008看成了一个填数游戏式:2□□8,于是他在每个框中各填写了一个两位数ab 与cd ,结果所得到的六位数28abcd 恰是一个完全立方数,则ab cd +=________.12. 已知x y z 、、是三个非负实数,满足325x y z ++=,2x y z +-=,若2S x y z =+-,则S 的最大值与最小值的和为___________.13. 有一种足球是由32块黑白相间的牛皮缝制而成,黑皮为正五边形,白皮为正六边形,且边长都相等(如图),则白皮的块数是__________.14. 设四位数abcd 是一个完全平方数,且21ab cd =+,则这个四位数为________.15. 如果对于不小于8的自然数n ,当31n +是一个完全平方数时,1n +都能表示成k 个完全平方数的和,那么k 的最小值为___________.Ⅱ卷二、解答题(每题10分,共40分)16. 为进一步丰富市民的文化生活,海淀文化局计划把海淀影剧院进行改造.把原来的1000个座位改为现在的2004个座位.改建后的影剧院从第二排起后排都比前一排多一个座位,要求排数大于20.问有几种设计方案,如何设计?17. 将长为2n (n 为自然数且4n ≥)的一根铅丝折成各边的长均为整数的三角形,记(a ,b ,c )为三边长分别是a ,b ,c 且满足a b c <<的一个三角形,就6n =的情况,分别写出所有满足题意的(,,)a b c .18.将正整数1、2、3、4、5、6……按下列规律进行排列:首先将这些数从“1”开始每隔一数取出,形成一列数:1、3、5、7排成一行;然后在剩下的数2、4、6、8……中从第一个数“2”开始每隔一数取出,形成第二列数:2、6、10、……排成第二行;照此下去,第三排的数由剩下的4、8、12、16、……中从第一个数“4”开始每隔一数取出4、12、20、……;如此一直继续下去,我们可以排成一张表如下表所示.(1)问32、42、72分别在表中的第几行?(2)对于表中第3列第n行的数,请你用关于n的代数式表示出来;(3)176在这个表中的第几行第几列.1 3 5 7 ……2 6 10 14 ……4 12 20 28 ……8 24 40 56 ………………………………19.已知五位数abcde满足下列条件:(1)它的各位数字均不为零;(2)它是一个完全平方数;(3)它的万位上的数字a是一个完全平方数,千位和百位上的数字顺次构成的两位数bc以及十位和个位上的数字顺次构成的两位数de也都是完全平方数.试求出满足上述条件的所有五位数.三、附加题(10分)20. 一只青蛙在平面直角坐标系上从点(1,1)开始,可以按照如下两种方式跳跃:①能从任意一点(,)a b ,跳到点(2,)a b 或(,2)a b ;②对于点(,)a b ,如果a b >,则能从(,)a b 跳到(,)a b b -;如果a b <,则能从(,)a b 跳到(,)a b a -. 例如,按照上述跳跃方式,这只青蛙能够到达点(3,1),跳跃的一种路径为:(1,1)(2,1)(4,1)(3,1)→→→.请你思考:这只青蛙按照规定的两种方式跳跃,能到达下列各点吗?如果能,请分别给出从点(1,1)出发到指定点的路径;如果不能,请说明理由.⑴ (3,5); ⑵ (12,60); ⑶ (200,5); ⑷ (200,6).2010年“学而思杯中学生理科能力展示大赛”初一数学 (B 卷答案)Ⅰ卷一、选择题:(本题共15小题,每小题4分,共60分)1. 1124242222a b a b M N a b a ab b ab b a =+=+=+=++++++2. 设每个小长方形的长为x ,宽为y ,则有 23433234x y x x xy =⎧⇒=⇒=⎨=⎩,故32y = 从而ABCD 的周长为19.3. 201020094019a b c a a ++=++=+20102201010051004a b a a a a <=-⇒<⇒<⇒≤故4019401910045023a b c a ++=++=≤ 即其最大值为5023. 4. 11311338(2)2== 33481=⨯+ 故118的末尾数字为2.5. 111111()()()3a c a b b c a b c b c c a a b b c a++++++++=++=-.6. 此题完全是灵感闪现,不难,很巧,左图用在学生版,右图是辅助线,很明显答案为45度. 7. 31x =︒. 8. 1. 1x =-9. 2220082007(20082007)(20082007)20082007a =-=+-=+ 同理,20092008b =+,20102009c =+,故a b c <<.10. 若三边能构成三角形则必有两小边之和大于第三边,即a b c +>.又b c <,则b c a b +<<又c b a b -<≤,故15a <≤,从而2,3,4,5a =. 当2a =时,57c <<,此时,6c =; 当3a =时,58c <<,此时,6,7c =; 当4a =时,59c <<,此时,6,7,8c =; 当5a =时,510c <<,此时,6,7,8,9c =; 故一共有123410+++=个.11. 设328()abcd xy =,则据末位数字特征得2y =,进而确定xy :因360216000=,370343000=,所以6070xy <<,故只有,62xy =,而362238328=,则38ab =,32cd =,70ab cd +=. 12. 由325x y z ++=,2x y z +-=可得,13,41x z y z =-=+.由,,0x y z ≥可知,103z ≤≤.22(13)4133S x y z z z z z =+-=-++-=-,故3S 2≤≤,故应填5.13. 设白皮有x 块,则黑皮有32x -块,则黑皮共有的边为5(32)x - 因为黑皮与白皮有三条边重合,则黑皮共有的边还可以用3x 表示 故5(32)320x x x -=⇒=. 14. 5929.15. 设231n m +=,则231(1)(1)n m m m =-=+-,故1,1m m +-中必有一个是3的倍数 不妨设13m a -=,则231(1)(1)(32)3(32)n m m m a a n a a =-=+-=+⋅⇒=+22221(32)1321(1)n a a a a a a a +=++=++=+++故其最小值为3.Ⅱ卷二、解答题(每题10分,共40分) 16. 设第一排有x 个座位,共有y 排,则(1)....(1)2x x x y +++++-=,即3(21)400823167y x y +-==⨯⨯ 因为,x y 均为正整数,且20y >,故,21y x y +-,奇偶性不同,且21x y y +->,故 2116724x y y +-=⎧⎨=⎩,解得72x =.故满足题意的方案只有一种,即第一排的座位为72个,共24排. 17. 当6n =时, 12a b c ++=由a b c +>可知, 126c c c ->⇒<又a b c <<,故3a b c c ++<,即1234c c <⇒> 故46c <<,从而可知, 5c =.于是7a b +=,又由a b c <<可知, 3a a b c <++,故1243a <=,从而可知, 1,2,3a = 对应的, 6,5,4b =.又a b c <<,故满足题意的(,,)a b c 为(3,4,5).18. (1) 因为5322=,故32在第6行.142221221=⨯=⨯,故42在第2行. 3728929=⨯=⨯,故72在第4行. (2)152n -⨯(3)4176211=⨯,故176必在第5行,第6列. 19. 设2M abcde =,且2a m =(一位数),2bc n =(两位数),2de t =(两位数),则 224221010M m n t =⨯+⨯+,由题意可知,2222422(10)10210M m t m tm t =⨯+=⨯+⨯+ 故22n tm =,从而n 必然是2的倍数,故2n 必然是4的倍数,且是完全平方数. 故216,36,64n =.当216n =时,8mt =,由2t 为两位数可知,4,8t =,此时2,1m = 符合题意的数为11664或41616.当236n =时,18mt =,由2t 为两位数可知,6,9t =,此时3,2m =,符合题意的数 有43681或93636.当264n =时,32mt =,经验证没有符合题意的数. 三、附加题(10分)20. ⑴ 能到达点(3,5)和点(200,6).从(1,1)出发到(3,5)的路径为:(1,1)(2,1)(4,1)(3,1)(3,2)(3,4)(3,8)(3,5)→→→→→→→.从(1,1)出发到(200,6)的路径为:(1,1)(1,2)(1,4)(1,3)(1,6)(2,6)(4,6)(8,6)(16,6)(10,6)(20,6)(40,6)(80,6)(160,6)(320,6)(206)(200,6).→→→→→→→→→→→→→→→→前面的数反复减次⑵ 不能到达点(12,60)和(200,5).理由如下:∵ a 和b 的公共奇约数a =和2b 的公共奇约数2a =和b 的公共奇约数, ∴ 由规则①知,跳跃不改变前后两数的公共奇约数.∵ 如果a b >,a 和b 的最大公约数()a b =-和b 的最大公约数, 如果a b <,a 和b 的最大公约数()b a =-和b 的最大公约数,∴ 由规则②知,跳跃不改变前后两数的最大公约数.从而按规则①和规则②跳跃,均不改变坐标前后两数的公共奇约数.∵ 1和1的公共奇约数为1,12和60的公共奇约数为3,200和5的公共奇约数为5. ∴ 从(1,1)出发不可能到达给定点(12,60)和(200,5).。
2010-2015学而思杯真题集(二年级)

1
2
4
7
8
10
13
… “+1”、“+2”、“+3”循环出现
+1 +2 +3 +1 +2 +3 …
14. 如下图所示,用 1 个大长方形和 6 个完全一样的小长方形拼成了一个大正方 形.如果小长方形的周长是 60 厘米,那么,最上面的大长方形的周长是 __________厘米.
4
15. 甲、乙、丙、丁四人比赛跑步,比赛结束后,他们有如下对话: 甲:“我比乙快,丁比丙慢.” 乙:“我比甲快,甲比丁慢.” 丙:“我比甲快,也比丁快.” 丁:“我比乙慢,丙比甲慢.” 事实表明,只有跑得最快的人所说的两句话都是真话,其余人都是一句真话一 句假话.那么,甲是第__________名,乙是第__________名,丙是第__________ 名,丁是第__________名.
10. 下面左图是 2015 年 4 月的日历,将一个正方体纸盒的六个面展开,刚好盖住了 日历中的 6 个数.右图是覆盖的结果,被盖住的六个数分别是 6、7、14、15、 22、23.那么,盖住 6 的面和盖住__________的面是原来正方体的一组对面.
2015 年 4 月 日一二三四五六
1234 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
2. 贝儿有 20 张积分卡,多多的积分卡数量是贝儿的 2 倍,那么,多多有__________ 张积分卡.
3. 下列四个数字中,只有一个数字不能一笔画出.那么,这个数字是__________.
4. 如图,用火柴棍摆成 74,然后拿走其中 1 根火柴棍,能形成一个新的两位数, 这个两位数是__________.(最下面的图给出了用火柴棍摆数字 0~9 的方法)
2011年“学而思杯”初一数学试卷及答案

2011年“学而思杯”中学生理科能力大赛初 一 数 学 试 卷学校______________ 姓名_________ 准考证号________ 成绩_________一、填空题(本题共60分,每小题5分)1. 计算:()3179111315231220304256⎛⎫-+-+-⨯-= ⎪⎝⎭ _________.2. 如图,MN PQ ∥,A B 、分别在MN PQ 、上,70ABP ∠=︒,BC 平分ABP ∠,且20CAM ∠=︒,则C ∠的度数为______________.3. 当2x =时,代数式31ax bx -+的值等于17-,那么当1x =-时,代数式31235ax bx --的值等于__________.4. 已知关于x 的方程3243a x x x ⎡⎤⎛⎫--= ⎪⎢⎥⎝⎭⎣⎦和3151128x a x +--=有相同的解,那么这个解是x =_______.5. 已知ABC △中,90BAC ∠≠︒,AD BC ⊥,BE AC ⊥,且AD BE 、交于点H ,连接CH , 则ACH BAE ∠+∠=_______.6. a b c 、、三个有理数满足0a b c <<<,且1a b c ++=,b c M a +=,a c N b +=,a bP c+=, 则M N P 、、之间的大小关系是________________.7. 如图,ABC △中,D 在AC 上,E 在AB 上,且BD CE 、相交于O ,OB OD =,2OC OE =,若2BOC S =△,则ABC S =△__________.CBAQP N M OEDCBA8. 平面直角坐标系xOy 中有两个点()44A -,,()62B --,,则AOB △的面积为___________.9. 若关于x 的方程()42a x b bx a -+=-+-有无穷多个解,则323a b +的值为__________.10. 如图,ABC △中,90C ∠=︒,ABC ∠和EAC ∠的平分线交于点D ,ABD ∠和BAD ∠的平分线交于点F ,则AFB ∠的度数为_________.11. 若21234m m --+=,则m 的取值范围是_____________12. 已知ABC △中,AB AC =,D 为BC 边上一点,若ACD △和ABD △都是等腰三角形,则C ∠的度数为_______________.二、解答题(本题共40分,每小题10分)13. 如图,M N 、为四边形ABCD 的边AD BC 、的中点,AN BM 、交于P 点,CM DN 、交于Q 点. 若四边形ABCD 的面积为150,四边形MPNQ 的面积为50,求阴影部分的面积之和.FEDC BA14. 数形结合思想是中学数学解题中常用的数学思想,利用这种思想,可以将代数问题转化为几何问题,也可以将几何问题转化为代数问题。
2010-2015学而思杯真题集(一年级)

而思大 门 口 , 看 到 老 师 手 里举了 这 三
zhānɡshùzì kǎpiàn
qǐnɡwânyînɡzhâsānzhānɡ
张 数 字卡 片 4、7、6,请 问 用 这 三 张
kǎpiànkě yǐ zǔchãnɡ
ɡâ bùtïnɡdesānwâishù zhù qízhōnɡshùzì de kǎ
12. 学 而思 综 合 能 力测 评 , 今 天 早 上 8:00 准 时 开 始 ,8:00-9:
kǎoshùxuã
kǎo yǔ wãn
kǎoyīnɡyǔ xiǎopãnɡyǒumen
00 考 数 学 ,9:20-9:50 考 语 文 ,9:50-10:20 考 英 语, 小 朋 友 们
suànsuànsānkēkǎoshìdeshíjiānɡînɡxū
xiǎopãnɡyǒumenzhǎoyīzhǎoxiàmianliǎnɡfú túzhōnɡdì
bùfenbùtïnɡ
2. 小 朋 友 们 找 一 找 下 面 两 幅 图 中 第___________部 分 不 同 .
yîutúzhōnɡɡînɡyǒu
ɡâsānjiǎoxínɡ
3. 右 图 中 共 有 ___________个 三 角 形 .
普 通 票 加 海 洋 公 园 套 票 40 元 / 人 , 海 洋 公 园 加 熊 猫
ɡuǎntàopiào yuán rãn měirãndōubì xūmǎipǔtōnɡpiào wēiãrbānɡmā māxiǎnɡle yī
馆 套 票 45 元 / 人 .每 人 都 必须 买 普 通 票 ,薇 儿 帮 妈妈 想 了一
黄 、蓝 、绿、紫、黑 6 种 不 同 的 颜 色,那么,
2009秋[1].学而思.入学测试题(初一数学).学生版
![2009秋[1].学而思.入学测试题(初一数学).学生版](https://img.taocdn.com/s3/m/fb679527a5e9856a5612605c.png)
1 ▎入学测试题·学生版 ▎2009年初一秋季班入学测试题提示:60分钟完成12道题.试卷说明:答案完全正确才算对,多解、漏解、错解均为错.题1 计算:()2164845-+++-=-- = .题2 若a,b,c 为整数,且27871a bc a-+-=,试求c a a b b c -+-+-的值。
题3 在钟表中,4点半时,时针与分针的夹角为 .题4 对于正整数a,b 定义一种新运算,a b 等于由a 开始的连续b 个正整数之和,如23=2+3+4=9,(1)试计算3(97)的值(2)若x 5=45,求x题5 如图正方形的边长为4cm ,5cm AE =,DF =_____cm .题6 经过不在同一直线上的四点中的任意两点可以画出_________条直线。
题7 如图是一个33⨯的正方形,则129∠+∠++∠= .987654321FE DCB A2 ▎入学测试题·学生版 ▎题8 关于x 的方程917x kx -=的解为正整数,则整数k 的值为 .题9 一条公路修在湖边时,需拐弯绕湖而过,如果第一次拐的角A ∠是120,第二次拐的角B ∠是150,,第三次拐的角是C ∠,这时的道路恰好和第一次拐弯之前的道路平行,则C ∠是________题10 如图所示,ABC S ∆=1, 若BDE S ∆=DEC S ∆=ACE S ∆,则ADE ∆的面积是多少?题11 某人沿电车路行走,每12分钟有一辆电车从后面追上,每4分钟有一辆电车迎面开来,假定此人和电车都是匀速前进,则电车每隔 分钟从起点开出一辆.题12 设,,,a b x y 满足3ax by +=,227ax by +=,3316ax by += ,4442ax by +=, 55ax by +等于___________。
2011年“学而思杯”初二数学试卷及答案

2011年“学而思杯”中学生理科能力大赛初 二 数 学 试 卷一、填空题(本题共60分,每小题5分)1. 点()1x x --,不可能在第________象限.2. 函数y =x 的取值范围是______________.3. 已知()2x y -+的算术平方根和()21x y +-互为相反数,则3yx-的平方根为___________.4. 如图,在矩形ABCD 中,E 是BC 的中点,30BAE ∠=︒,2AE =, 则矩形ABCD 的面积为___________.5. 已知,函数y kx m =+和y ax b =+的图象交于点P ,则根据图象 可得不等式组0kx m ax b kx m +>⎧⎨+>+⎩的解集为___________.6. 如图,直线1y x =--交两坐标轴于A 、B 两点,平移线段AB 到CD ,使两点都落在反比例函数()0ky x x=>的图象上,DM y ⊥轴于点M ,DN x ⊥轴于点N ,则DM DN -= .EDCBA7. 如果实数a b ,满足2840a a --=,2840b b --=,则b aa b+的值为 .8. 已知x y a 、、都是实数,且1x a =-,()()2211y a a a =---,则31x y a +++的值为________.9. 设实数a b c ,,满足2142a b c +++=,那么ba c-的值为_______.10. 如图,Rt ABC △中,E D F 、、分别在AB BC AC 、、上,且四边形AEDF 是正方形.已知8CD =,12BD =,则阴影部分的面积为_____________.11. 若实数,x y 满足333333331343615456x y x y ⎧+=⎪⎪++⎨⎪+=⎪++⎩,则x y +的值是 _____ .12. 已知正方形ABCD 所在平面内的直线满足:⑴ 正方形四个顶点到这条直线的距离只有两种; ⑵ 两种距离中,较大的是较小的三倍. 那么符合上述条件的直线一共有 条二、解答题(本题共40分,每小题10分)13. 如图,直角梯形ABCD 中,AB CD ∥,90DAB ∠=︒,12CD AB =,2245BC AD =, ⑴ 求证:AD AB =.⑵ AC BD 、交于点E ,AO BD ⊥交BD 于O ,交BC 于F ,求证:CE CF =. ⑶ 作点F 关于点O 的对称点H ,试判断BH 与AE 的关系,并证明你的结论.HFEO DC BA14. 如图1,已知直线12y x m=-+与反比例函数kyx=的图象在第一象限内交于A B、两点(点A在点B的左侧),分别与x y、轴交于点C D、,AE x⊥轴于E.⑴若12OE CE⋅=,求k的值.⑵如图2,作BF y⊥轴于F,求证:EF CD∥.⑶在⑴⑵的条件下,EFAB=P是x轴正半轴上一点,且PAB△是以P为直角顶点的等腰直角三角形,求P点的坐标.15. 如图,D 为ABC △中线AM 的中点,过M 作AB 、AC 边的垂线,垂足分别为P 、Q .过P 、Q分别作DP 、DQ 的垂线交于点N .⑴ 求证:PN QN =; ⑵ 求证:MN BC ⊥.16. 若x y z ,,满足1x y z ++=,2222x y z ++=,3333x y z ++=,求444x y z ++的值.2011年“学而思杯”中学生理科能力大赛初二数学答案一、填空题(每小题5分,答对得5分,答错、不答或答不全均不得分)QP N M DCB A二、解答题(每小题10分,按解题过程分步给分,若只有答案且正确,给2分) 13. ⑴ 过C 点作CM AB ⊥于M ,∵AB CD ∥,90DAB ∠=︒,∴四边形AMCD 是矩形,∴AM CD =………………………………………………………………1分∵12CD AB =,∴AM BM = ∴AC BC =………………………………………………………………2分 ∵在Rt ACD △中,90ADC ∠=︒,∴2222AD CD AC BC +==, ∵2245BC AD =,∴2214CD AD =,即12CD AD =, ∴AD AB =.……………………………………………………………4分 ⑵ 由⑴知:45ADB ABD ∠=∠=︒,又AC BC =,∴CAB CBA ∠=∠,∴CAF CBE ∠=∠,……………………………………………………5分 ∴在ACF △和DCE △中, ACF BCE AC BCCAF CBE ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴()ASA ACF BCE △≌△, ∴CE CF =.……………………………………………………………7分 ⑶ 解法一:延长BH 交AE 于N .由⑵可得:AE BF =,∵F H 、关于点O 对称,∴BH BF =,OBF OBH ∠=∠,∴BH AE =………………………………………………………………8分 ∵CAF CBE ∠=∠,∴OBH CAF ∠=∠,∴90ANH BOH ∠=∠=︒,即BH AE ⊥.……………………………10分 解法二:延长BH 交AE 于N ,∵F H 、关于点O 对称,∴BH BF =,OBF OBH ∠=∠, ∵CAF CBE ∠=∠,∴OBH CAF ∠=∠,∴90ANH BOH ∠=∠=︒,即BH AE ⊥.…………………………9分 ∵AO BD ⊥,∴AO BO =,90AOE BOH ∠=∠=︒, ∴AOE BOH △≌△,∴AE BH =.………………………………………………………10分 14. ⑴ 设OE a =,∴12A a a m ⎛⎫-+ ⎪⎝⎭,,∵点A 在反比例函数图象上,∴12a a m k ⎛⎫-+= ⎪⎝⎭,即212k a am =-+,……2分由一次函数解析式可得()20C m ,,∴2CE m a =-, ∴()22212OE CE a m a a am ⋅=-=-+=,……………………3分∴()211212622k a am =-+=⨯=.……………………………4分 ⑵ 连接AF BE 、,过E F 、分别作FM AB ⊥,EN AB ⊥, ∴FM EN∥.∵AE x ⊥轴,BF y ⊥轴,∴AE BF ⊥N MA BCD OE F H122AEF k S AE OE =⋅=△,122BEF k S BF OF =⋅=△, ∴AEF BEF S S =△△, …………………………………………5分 ∴FM EN =,∴四边形EFMN 是矩形,∴EF CD ∥.………………………………………………7分 ⑶由⑵可知,EF AD BC ==,∴CD =.由直线解析式可得OD m =,2OC m =, ∴4OD =,又EF CD ∥,∴2OE OF =,∴1OF =,2OE =,………………………………………8分 ∴3DF =,∴3AE DF ==,∵AB =AP =∴1EP =,…………………………………………………9分∴()30P ,.………………………………………………10分 15. ⑴ 连接DN ,由已知得APM △和AQM △都是直角三角形,AM 是公共斜边,∵D 是AM 的中点,∴12PD AM QD ==,……………………………………2分 ∵PN PD ⊥,QN QD ⊥,∴DPN DQN ∠=∠,∴Rt Rt DPN DQN △≌△()HL ,∴NP NQ =.……………………………………………………………………4分 ⑵ 取BM 、MC 的中点S 、T ,连结SP 、SN 、TQ 、TN . 1122SP BM MC TQ ===,…………………………………………………………5分9090SPN BPS NPM B DPA ∠=︒-∠-∠=︒-∠-∠ 9090B BAM AMC =︒-∠-∠=︒-∠9090DMQ QMT DQM MQT =︒-∠-∠=︒-∠-∠TQN =∠.………………………………………………7分∴SPN TQN △≌△()SAS .∴SN TN =,……………………………………………8分 ∵SM TM =,∴MN BC ⊥.…………………………10分16. ∵()2222222x y z x y z xy yz zx ++=+++++, ∴()111222xy yz zx ++=-=-,…………………………………2分 ∵()()3332223x y z xyz x y z x y z xy yz zx ++-=++++---, ∴16xyz =.………………………………………………………4分 ()()24442222222222x y z x y z x y y z z x ++=++-++,…………6分又()()22222222111222612x y y z z x xy yz zx xyz x y z ⎛⎫++=++-++=--⨯=- ⎪⎝⎭,……………8分∴444212522126x y z ⎛⎫++=-⨯-= ⎪⎝⎭.…………………………………………………………10分NQ。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2010年“学而思杯中学生理科能力展示大赛”初一数学 (A 卷)姓名 区 学校 准考证号Ⅰ卷一、选择题:(本题共15小题,每小题4分,共60分)1. 已知a 是正数,且21a a-=,则224a a -等于_________.2. 已知223,2x xy xy y +=+=-,则2223x xy y --= .3. 观察按下列规则排成的一列数:11,12,21,13,22,31,14,23,32,41,15,24,33,42,51,16,……在上式中,从左起第个数记为()G m ,当2()2010G m =时,则m 的值为________,这m 个数的积为___________. 4. 若n 满足22(2004)(2005)1n n -+-=,则(2004)(2005)n n --等于_____________.5. 设x 、y 、z 均为正实数,且满足222222z x yx y zy x zx y y z z x++++++<<+++,则x y z 、、三个数的大小关系是_________.6. 将一长方形切去一角后得一边长分别是13、19、20、25和31的五边形(顺序不一定按此).则此五边形的面积为__________.7. 水果市场有甲、乙、丙三种水果,如果买甲2千克,乙1千克,丙4千克,共付钱6元;如果买甲4千克,乙2千克,丙2千克,共付钱4元;今要买甲4千克,乙2 千克,丙5千克,则共应付钱____________.8. 已知,p q 均为质数,且满足27379p q +=,则p = ,q =_________.9. 若干名游客要乘坐汽车,要求每辆汽车坐的人数相等,如果每辆汽车乘坐30人,那么有一人未能上车;如果少一辆汽车,那么,所有游客正好能平均分到各辆汽车上,已知每辆汽车最多容纳40人,则有游客 人.10. 方程2311x y x y --+++=的整数解的个数是 .11. 如图,矩形ABCD 中,点,,,E F G H 分别在边AB ,BC ,CD ,DA 上,点P 在矩形ABCD 内.若4cm AB =,6cm BC =,3cm AE CG ==,4cm BF DH ==,四边形AEPH 的面积为25cm ,则四边形PFCG 的面积为_________2cm .12. 设22211148()34441004A =⨯++--- ,则A 的整数部分是__________.13. 已知2226,12a b c a b c ++=++=,则201020102010a b c -+=_____________.14. 已知:m 为非零实数,且1122x x m -+=,则21x x+=__________.15. 对于一个自然数n ,如果能找到自然数(0)a a >和(0)b b >,使1n a b ab -=++,则称n 为一个“十字相乘数”,例如:411111-=++⨯,则4是一个“十字相乘数”,在1~20这20个自然数中,“十字相乘数”共有_________个.Ⅱ卷二、解答题(每题10分,共40分)16. 观察:2123415⋅⋅⋅+=,22345111⋅⋅⋅+=,23456119⋅⋅⋅+=,………… (1)请写出一个具有普遍性的结论,并给出证明.(2)根据(1),计算20002001200220031⋅⋅⋅+的结果(用一个最简式子表示).17. 若x y m n +=+,且2222x y m n +=+.求证:2010201020102010x y m n +=+.18. 设1232010,,,,x x x x 是整数,且满足下列条件:① 12n x -≤≤,1,2,3,,2010n = ; ②1232010200x x x x ++++= ;③222212320102010x x x x ++++= .求 33331232010x x x x ++++ 的最小值和最大值.19. 小明家电话号码原为六位数,第一次升位是在首位号码和第二位号码之间加上数字8,成为一个七位数的电话号码;第二次升位是在首位号码前加上数字2,成为一个八位数的电话号码.小明发现,他家两次升位后的电话号码的八位数,恰是原来电话号码的六位数的81倍,则小明家原来的电话号码是多少?三、附加题(10分)20.10张卡片上分别写有0到9这10个数,先将它们从左到右排成一排,再采用交换相邻两张卡片位置的方法对它们进行操作,规则如下:当相邻两张卡片左边卡片上的数比右边卡片上的数大时,交换它们的位置,否则不进行交换.若规定将相邻两张卡片交换一次位置称为1次操作,那么无论开始时这10张卡片的排列顺序如何,至多经过次操作,就能将它们按从小到大的顺序排列.2010年“学而思杯中学生理科能力展示大赛”初一数学 (A 卷答案)Ⅰ卷一、选择题:(本题共15小题,每小题4分,共60分) 1. 3.提示:224222()()a a a a aaaa-=+-=+2222()()8189a a a a+=-+=+=故23a a+=,2243a a-=.2. 12.提示:2222232()3()233(2)12x xy y x xy xy y --=+-+=⨯-⨯-=.3. 2021057;12021057.提示:分子分母和为2的数有1个,和为3的数有2,和为4的数有3,依次类推,和为2011的数有2010个,故前面一共有12010123..20102010201110052+++++=⨯=⨯个数,再加上12011,前面一共有 2021056个数,故22010是第2021057个数, 2021057m =,这些数的乘积为121201120102021057⨯=. 4. 0.提示:222(2004)(2005)1(20042005)n n n n -+-==-+-22(2004)(2005)2(2004)(2005)n n n n =-+-+-- 从而可知, (2004)(2005)0n n --=. 5. z x y <<.提示:由222222z x y x y z y x z x y y z z x ++++++<<+++可知,222z x yx y y z z x+<+<++++ 从而可知,z x y x y y z z x <<+++,x y y z z xz x y+++>>,111x y y z z x z x y ++++>+>+,即x y z y z x z x yz x y++++++>>. 故z x y <<.6. 745. 提示:画图可知,符合题意的情况如下:故此五边形的面积为131251257452⨯-⨯⨯=.7. 8.提示:设甲、乙、丙的价格分别为,,x y z ,则2464224x y z x y z ++=⎧⎨++=⎩可设425(24)(422)x y z A x y z B x y z ++=+++++,则有 24412214252A B A A B B A B +=⎧=⎧⎪⎪+=⇒⎨⎨=⎪⎪+=⎩⎩,故425628x y z ++=+=.也可采用消元法,减少一个未知数,不再给出. 8. 2p =,17q =.提示:由奇偶性可知,,p q 中必有一个偶数2,若2p =,则17q =,符合题意; 若2q =,则p 不是整数,不合题意. 9. 961.提示:设汽车有x 辆,则有301(1)x k x +=-,其中40k ≤, 故 301313011x k x x +==+-- 故131x -=或11x -=时满足题意,此时32x =或2x =但2x =时,经检验可知,不合题意,故32x =,游客有30321961⨯+=人. 10. 2组提示:由题意可知,23110x y x y --=⎧⎨++=⎩,23110x y x y --=-⎧⎨++=⎩,23011x y x y --=⎧⎨++=⎩,23011x y x y --=⎧⎨++=-⎩解得整数解为01x y =⎧⎨=-⎩,11x y =⎧⎨=-⎩,故有2组.11. 8.提示:连结EF 、FG 、GH 、HE .易证AEH CGF ∆∆≌,DGH BEF ∆∆≌,四边形EFGH 是 平行四边形.易得平行四边形EFGH 的面积为14,PEH ∆的面积为2,故PFG ∆的面积为5.所以四边形PFCG 的面积为8. 12. 24提示:22211148()34441004A =⨯++--- 11148...(32)(32)(42)(42)(1002)(1002)⎡⎤=⨯+++⎢⎥+-+-+-⎣⎦111111148(...)43232424210021002=⨯⨯-+-++--+-+-+111111112(1...)5263798102=⨯-+-+-++- 111111112(1.........)2398567102=⨯++++----111111112(1)23499100101102=⨯+++---- 111111111264312()2512()9910010110299100101102=+++-⨯+++=-⨯+++ ∵41111401212()1211029910010110299<⨯<⨯+++<⨯< ∴2425A <<.故其整数部分为24. 13. 20102.提示:由6a b c ++=可知,2()36a b c ++=,即22222236a b c ab bc ca +++++= 又22212a b c ++=,故22224ab bc ca ++= 2222()(222)122240a b c ab bc ca ++-++=⨯-= 即222()()()0a b b c c a -+-+-=,故2a b c === 20102010201020102a b c -+=.14. 22m -. 提示:111222222212111()2()22x x x x x m x xx -+=+=+-=+-=-15. 7.提示:由1n a b ab -=++可知,1(1)(1)n a b ab a b =+++=++ 当a b =时,“十字相乘数”可取4,9,16这3个数; 当a b ≠时,不妨设a b >,则若2b =时,则2a >,且2017215333a a +⇒=≤≤,故3,4,5a =,此时“十字相乘数”为12,15,18;若3b =时,则3a >,且20144a a +⇒≤≤,故4a =,此时“十字相乘数”为20;若3b >,不合题意. 故符合题意的“十字相乘数”一共有7个. 二、解答题(每题10分,共40分)16. (1)结论:对于自然数n ,有22(1)(2)(3)1(31)n n n n n n ++++=++…………2分证明:22(1)(2)(3)1(3)(32)1n n n n n n n n ++++=++++ ………………4分 222(3)2(3)1n n n n =++++ ……………………6分22(31)n n =++ ………………………………………8分∴22(1)(2)(3)1(31)n n n n n n ++++=++(2)由(1)得2200020012002200314006001⨯⨯⨯+= …………………………10分17. 由x y m n +=+可得, 222222x y xy m n mn ++=++ …………………………2分又2222x y m n +=+,故22xy mn = ……………………………………………4分 从而222222x y xy m n mn +-=+-,即22()()x y m n -=-…………………………6分 故x y m n -=-或n m - …………………………………………………………8分 再结合x y m n +=+可知, x m y n =⎧⎨=⎩或x ny m =⎧⎨=⎩…………………………………10分于是2010201020102010x y m n +=+成立.18. 设1232010,,,,x x x x 中有r 个1-、s 个1、t 个2,则2200,42010.r s t r s t -++=⎧⎨++=⎩……………………………………………2分 两式相加,得31105s t +=,故0368t ≤≤. ………………………………4分∵ 333123x x x +++…320108x r s t +=-++6200t =+. ……………………………………………5分∴ 3333123201020063682002408x x x x ++++⨯+= ≤≤. ……………………6分当0,1105,905t s r ===时,33331232010x x x x ++++ 取最小值200, …………8分 当368,1,537t s r ===时,33331232010x x x x ++++ 取最大值2408. …………10分 19. 设原来电话号码的六位数为abcdef ,则经过两次升位后电话号码的八位数为28a bcdef .根据题意,有8128abcdef a bcdef ⨯= ……………………………………2分 记43210101010x b c d e f =⨯+⨯+⨯+⨯+………………………………………4分 于是5568110812081010a x a x ⨯⨯+=⨯+⨯+解得1250(20871)x a =⨯-. ………………………………………6分因为5010x ≤<,所以501250(20871)10a ⨯-≤<,故1282087171a <≤. ……8分 因为a 为整数,所以2a =.于是1250(208712)82500x =⨯-⨯=. ……10分 所以,小明家原来的电话号码为282500. 三、附加题(10分)20. 记2n ≥张卡片至多经过n a 次操作后,能将它们按从小到大顺序排列,则232431091;2;3;............9.a a a a a a a ==+=+=+所以10123.....945a =++++=.。
