八年级数学下册17函数及其图象17.2函数的图像17.2.1平面直角坐标系教案新版华东师大版_372
华东师大版八年级下册数学17.2.1平面直角坐标系教案
《平面直角坐标系》教学设计思考2 :由1你发现数轴上的点与实数是什么关系?①数轴上的每个点都对应一个实数(这个实数叫作这个点在数轴上的坐标);②反过来,知道一个数,这个数在数轴上的位置就确定了。
思考3:类似于利用数轴确定直线上点的位置,能不能找到一种方法来确定平面内的点的位置呢?法国数学家笛卡儿最早引入坐标系,用代数方法研究几何图形。
是近代科学的始祖,是欧洲近代哲学的奠基人之一,黑格尔称他为“现代哲学之父”。
在教师的引导下完成思考1,2,3通过思考1和2复习数轴上的点与实数一一对应,以及思考3的提问来引入本节课新知。
二、探究活动一(约10分钟)平面直角坐标系的概念①两条数轴②互相垂直③原点重合构成平面直角坐标系。
水平的数轴称为x轴或横轴,习惯取向右为正方向;竖直的数轴称为y轴或纵轴,取向上方向为正方向,两坐标轴的交点为平面直角坐标系的原点。
练一练:1.你会画吗?在作业纸上试着画一个平面直角坐标系,比一比看谁画得最完整。
你能说一说平面直角坐标系的组成及特征吗?2.下面四个图形中,是平面直角坐标系的是()( A ) ( B )学习平面直角坐标系及相关概念,即平面直角坐标系、x轴、y轴、正方向、原点独立引导学生感受法国数学家笛卡儿的成就,顺利引入平面直角坐标系及相关概念。
利用练一练两道题,培养学生动手操作、观察、归纳和语言表达能力。
C3·2·1·-1·-2·······-2 -1 0 1 2 3 xy·····2 1 0 -1 -2 xy2·1·-1·-2·( C ) ( D ) 完成练一练,然后举手回答三、探究活动二(约8分钟)有了平面直角坐标系,平面内的点就可以用一个有序数对来表示了。
例如,由点A分别向x轴、y轴作垂线,垂足M在x轴上的坐标3,垂足N在y轴上的坐标是4,我们说A点的横坐标是3,纵坐标是4,有序数对(3,4)就叫做A点的坐标,记作A(3,4)。
新华东师大版八年级数学下册《17章 函数及其图象 17.2 函数的图象 平面直角坐标系》课件_21

x 12345
-2
4、两条坐标轴把平面划分为几部分,每一部 分的名称分别是什么?
y
3
第二象限 2
第一象限
1
-4 -3 -2 -1 0 -1
第三象限 -2
x 12345
第四象限
-3
-4
5、在163页的网格纸上画出平面直角坐标系。
三、研究实例,再探新知
问题1、请同学们以教室的第四排为横轴,第五列为纵轴 建立平面直角坐标系,写出属于自己的坐标。
破译密码--男生
6我
小
5
是
4
哥
3
2
1
帅
ABCDE
女生密码: A6 B5 A5 C4 E1 C6 D3 B2
破译密码—女生
6我
小
5 可是
4
爱
3
女
2
生
1
的
ABCDE
达人在我们中间!
讲台
1 2 34 5 6 7 8 1 2 3 4 5 6
你知道吗? 数学家笛卡儿
早在1637年以前,法国数学家、 解析几何的创始人笛卡尔受到了 经纬度的启发,创建了平面直角 坐标系,所以平面直ቤተ መጻሕፍቲ ባይዱ坐标系也 称笛卡尔直角坐标系。
这里得到的结果 告诉我们什么?
在平面直角坐标系中的点和有序实数对是一一对应的.
四、快乐套餐,应用新知
坐标知识竞赛
进入到了今天的总决赛,我给大家带来了5 道不同难度的题目,若答对题目,可给本组获 得相应的积分;若答错不得分。请看题目!
50分
(10分)若点M(a,b)在第四象限,则a, b的取值范围是( C )
细读课本34—35页,认真思考以下问题: 1、什么叫平面直角坐标系? 2、平面直角坐标系有哪些特征? 3、坐标平面上的点可以用什么表示? 4、两条坐标轴把平面划分为几部分,每一部分 的名称分别是什么? 5、在163页的网格纸上画出平面直角坐标系。
新华东师大版八年级数学下册《17章 函数及其图象 17.2 函数的图象 平面直角坐标系》课件_27

-2
到一对有序实数 (-
-3
4,1)称为点p的坐标,
-4
这时点p可记做(-4,1)
纵轴 y 5 4
B(- 4,1)3
2 1
A点在x 轴上的坐标为4 A点在y 轴上的坐标为2 A点在平面直角坐标系中的坐标为(4, 2)
记作:A(4,2)
· A x轴上的坐标 写在前面
-4 -3 -2 -1 0 -1 -2 -3
y
5
4
3
A(3,2)
2
·A
1
-4 -3 -2 -1 o -1 -2
12345
x
点A到x 轴的距离是_____2___,到y 轴的距 离是___3_____,到原点的距离是 __13_ .
纵轴 y
5
•D(0,4)
4
3 2
坐标轴上的点的 坐标有何特点?
• • A(-4,0)
O1 (0,0)B(2,0)
用”列和行”两个量就可以确定平面上点的位置
y y轴或纵轴
6
在平面内画两条原点重合、 5
互相垂直且具有相同单位长 4
度的数轴,这就建立了平面 3
直角坐标系.
2
1原 点
x轴或横轴
x -6-5-4-3 -2 -1-o1 1 2 3 4 5 6
通常把其中水平的数轴叫 -2 做x轴或横轴,取向右为正 -3 方向;铅直的数轴叫做y轴 -4 或纵轴,取向上为正方向;-5 两条数轴的交点O叫做坐标 -6 原点。
在 第一或第三 象限,若xy<0,则
点P在 第二或第四 象限;若 xy=O则点P在 坐标轴 上.
本节课学习了什么知识?
什么是数轴?
是一条规定了原点、正方向、单位长度 的直线就构成了数轴.
第17章《函数及其图象》集体备课文稿

长兴县实验初中教师集体备课文稿一. 授课内容和课时安排授课内容:八年级下册第17章《函数及其图象》§17. 1变量与函数、§17.2函数的图象、§17.3一次函数课时安排:第一课时:变量与函数(1) 第六课时:一次函数的认识 第二课时:变量与函数(2) 第七课时:一次函数的图象(1) 第三课时:平面直角坐标系(1) 第八课时:一次函数的图象(2) 第四课时:平面直角坐标系(2) 第九课时:一次函数的性质第五课时:函数的图象 第十课时:一次函数的图象及性质二.第16章《数的开方》授课存在的主要问题:1.对于平方根和立方根的概念,学生比较容易接受,但在做题时,对于正数的平方根经常出现漏解的情况;2.对于二次根式的三条性质,前两条比较容易接受,在具体的习题中也能很好的利用。
但 对于性质3:a a =2,很多同学经常容易搞错,特别是a 为负数时,2a 应该等于a 的 相反数容易出错,例如:()=-2)6(,有的同学会填-6;也有同学会写±6;3.对于二次根式的化简,部分同学还不过关,有待进一步加强和相关训练;4.在实数范围内的化简、计算以及因式分解、求方程的解等等,很多同学由于多种原因,解题正确率不高;5.刚接触无理数、实数这两个概念,在区分无理数、有理数、整数、分数时,部分学生容易混淆。
三.三节内容的教材分析【教学目标】本章前三节的主要内容是变量与函数的认识,以及函数图象的认识;另外主要是一次函数的图象及性质。
教学目标是:1.通过对实际问题中数量之间相互依存关系的探索,学会用函数思想去进行描述和研究其变化规律;通过结合丰富的实际问题,让学生了解常量和变量、自变量与函数的意义,初步理解对应的思想,逐步学会运用函数的观点观察、分析问题,预测实际问题中变量的变化趋势。
2.认识并会画平面直角坐标系,了解现实生活中数形结合思想的实例,体会平面直角坐标系在函数研究中的地位和作用。
八年级数学下册 17.2 函数的图像 17.2.1 平面直角坐标系教学课件 (新版)华东师大版

纵轴 y
5
4
3 2
平面直角坐标系具有以下特征: ①两条数轴互相垂直 ②原点重合 ③通常取向右、向上为正方向 ④单位长度相同
1
-4 -3 -2 -1 0
-1
原点 -2
-3
12345
x 横轴
-4
横轴、纵轴统称为坐标轴
选择:下面四个图形中,是平面直角坐标系的是( D )
Y
Y
2
-3 -2 -1 O1 2 3
17.2.1 平面直角坐标系
回顾
在直线上规定了原点、正方向、单位长 度就构成了数轴。
A
c
B
-3 -2 -1 0 1 2 3 4 5 6
数轴上的点与实数一一对应。
导入
你能说出下图各个棋子在棋盘中的位置吗?
10 9 8 7 6 5 4 3 2 1
1 2 3 4 56 7 8 9
教学目标:
(1)理解平面直角坐标系的有关概念,能正确画出 直角坐标系。
-1
-2 -3
-4
12345
·E ( 1,- 2 )
x 横轴
(三)由坐标找点
y
2
在平面直角坐标
1
系中找到表示 A(3,-2)的点.
-3 -2 -1 O 1 2 3 x
-1
-2
A
由坐标找点的方法:
-3
先找到表示横坐标与纵坐标的点,
然后过这两点分别作x轴与y轴的垂线,
垂线的交点就是该坐标对应的点。
例2.在平面直角坐标系中描出下列各点, A(5,2) 、B(0,5)、C(2,-3)、 D(-2,-3)、
X
1
X
3 2 1 O -1 -2 -3 -1
初中数学华东师大版八年级下册17.函数的图象课件

学习目标
概念剖析
典型例题
当堂检测
课堂总结
例1.画出函数 y 1 x2 的图象: 2
分析:从函数解析式可以看出,x的取值范围是 全体实数
.
第一步:①列表:从x的取值范围中选取一些简洁的数值, 算出y的对应值,填写在表格里:
4.5 2 0.5 0 0.5 2 4.5
学习目标
概念剖析
典型例题
当堂检测
从丙港(B)返回到出发点甲港(E)用了2个小时.
学习目标
概念剖析
典型例题
当堂检测
课堂总结
(2)轮船从甲港前往乙港的平均行驶速度快,还是轮船返回的平均速度快呢? 轮船从甲港前往乙港的平均行驶速度快.
(3)如果轮船往返的机器速度是一样的,那么从甲港到乙港是顺水还是逆水? 从甲港到乙港是顺水.
学习目标
概念剖析
典型例题
1.函数y=x的图像大致是( A )
当堂检测
课堂总结
A
B
C
D
分析:将函数y=x,按图象的一般步骤画出可大致得出图象,可以通过代入 法求知,当x=1时,y=1,这个点在第一象限,x=-1时,y=-1这个点在第三象 限,因此A正确.
学习目标
概念剖析
典型例题
当堂检测
课堂总结
2.画出下列函数的图象:
课堂总结
②描点:分别以表中对应的 x、y为横纵坐标,在坐标系中
y
·
5 4
·y 1 x2 2
描出对应的点. ③连线:用光滑的曲线把这些
3
·2 · · · · 1
-4 -3 -2 -1 o 1 2 3 4 5 x -1
ቤተ መጻሕፍቲ ባይዱ
点依次连接起来.
吉林省八年级数学下册17函数及其图象17.2函数的图象17.2.2函数的图象教学设计新版华东师大版

吉林省八年级数学下册17函数及其图象17.2函数的图象17.2.2函数的图象教学设计新版华东师大版一. 教材分析吉林省八年级数学下册17函数及其图象,主要介绍了函数的图象。
这部分内容是学生在学习了函数概念和性质的基础上,进一步研究函数图象的特征和规律。
通过本节课的学习,使学生掌握函数图象的基本性质,提高学生分析问题和解决问题的能力。
二. 学情分析学生在学习本节课之前,已经掌握了函数的概念、性质以及简单的函数解析式。
但是,对于函数图象的绘制和分析,部分学生可能还存在一定的困难。
因此,在教学过程中,需要关注学生的个体差异,针对不同层次的学生进行有针对性的教学。
三. 教学目标1.知识与技能:使学生掌握函数图象的基本性质,能够绘制和分析简单的函数图象。
2.过程与方法:培养学生运用数形结合的方法解决问题的能力。
3.情感态度与价值观:激发学生对数学的兴趣,培养学生的团队合作意识和创新精神。
四. 教学重难点1.教学重点:函数图象的基本性质,函数图象的绘制方法。
2.教学难点:函数图象的分析和应用。
五. 教学方法采用问题驱动法、案例分析法、小组合作探究法等,引导学生主动参与课堂,提高学生的动手操作能力和思维能力。
六. 教学准备1.准备相关的函数图象案例,用于分析和讨论。
2.准备多媒体教学设备,用于展示函数图象和分析过程。
3.准备练习题,用于巩固所学知识。
七. 教学过程1.导入(5分钟)通过展示一些生活中的实际问题,引导学生关注函数图象的应用,激发学生的学习兴趣。
例如,分析商品价格与销售量的关系,探讨如何制定合理的商品价格来提高销售量。
2.呈现(10分钟)呈现已经准备好的函数图象案例,引导学生观察和分析函数图象的特征。
例如,分析正比例函数、一次函数、二次函数的图象特征,总结它们之间的异同。
3.操练(10分钟)让学生自己动手绘制一些简单的函数图象,加深对函数图象的理解。
例如,让学生绘制y=2x和y=-3x的图象,并分析它们的特征。
八年级数学下册17_2函数的图像17_2_1平面直角坐标系教案新版华东师大版

平面直角坐标系图18.2.1图18.2.2轴或横轴;铅直向上方向的数轴叫做y轴或纵轴;两条坐标轴的公共原点叫做坐标系的原点.建立了坐标系的平面叫做坐标平面.在坐标平面中,两条坐标轴把坐标平面分成几个部分?点,满足这种条件的点能画出几个?生:动用尝试,交流画图的结果,并回答问题。
明确:在给定点的坐标的情况下,所画出的点是唯一的,说明任给一点的坐标坐标平面内都有唯一的一个点与它相对应。
归纳可知:有序实数对(点的坐标)与平面内的点成一一对应关系。
互动4:师:请阅读教材第31页“试一试”的肉容,并解答问题1和2(如图18.2.3所示)。
生:动手操作,交流结果,举手回答问题。
明确:象限内点的坐标具有的特征是:点在第一象限⇔(+,+);点在第二象限⇔(-,+);点在第三象限⇔(-,-);点在第四象限⇔(+,-);坐标轴上点的坐标的特征:点在横轴上⇔点的纵坐标是0;点在纵轴上⇔点的横坐标是0;坐标系原点⇔(0,0).互动5师:请同学们在直角坐标系中描出点P (-3,-4),再按照下列要求画出它的对称点,然后回答提出的问题.(1)画出点P 关于x 轴的对称点1P ; (2)画出点P 关于Y 轴的对称点2P ;(3)画出点P 关于坐标系原点的对称点3P .观察上述各对称点的坐标特点,你有什么发现?生:动手操作,讨论画图和个人猜想的结果,小组选出代表回答问题。
师:利用多媒体演示幻灯片5,验证同学们的操作结果。
明确:师生共同归纳得:(1)关于x 轴对称的两点⇔其横坐标相同,纵坐标互为相反数;(2)关于Y 轴对称的两点⇔其横坐标互为相反数,纵坐标相同;(3)关于原点对称的两点⇔其横、纵坐标都互为相反数。
三、质疑再探:( 分钟)1.现在,我们已经解决了自探问题。
下面我们再回看一下,开始我们提出的问题还有那些没有解决?2.本节的知识已经学完,对于本节的学习,谁还有什么问题或不明白的地方?请提出来,大家一起来解决.四、运用拓展( 分钟)(一)根据本节学习内容,学生自编习题,交流解答。
八年级数学下册 17.2.1 函数的图象平面直角坐标系课件 (新版)华东师大版

关于(guānyú)原点对称点的坐(标-2,为3)
2)点(3,5)与点(3,-5)关于(guānyXú)________轴对 称.
3)点A关于(guānyú)原点对称点的坐标为(2,3),则
点A
(2,-3)
关于(guānyú) y 轴对称点的坐标为
.
第十三页,共17页。
若点在第一、三象限角平分线上或者(huòzhě)
Y
Y 3
ōng) 练习-3 -2 -1 O 1 2 3 X
2
1
-3 -2 -10 0O1 2 3 X
-1
(A)
-2 (B)
3Y 2 1
3Y
2
1
X
-3 -2 -1-1 O1 2 3 X
-2 -3
(C)
第五页,共17页。
-3 -2 -1-1O1 2 3
-2
-3 (D)教程(jiàochén
A点在x 轴上的坐标(zuòbiāo)为3
❖在第一(dìyī)、三象限角平分线上,它的横坐标等于纵坐标
在第二、四象限角平分线上,
❖在第二、四象限角平分线上,它的横坐标与纵坐标 互为
相它反的数横. 、纵坐标有什么特点?
y
· (-4,4) P
5 4
3
2
·O(4,4)
1
-4
-3
-2
-1
0 -1
12345x
-2 -3
-4
第十四页,共17页。
四、交流反思 1.平面(píngmiàn)直角坐标系的有关概念及画法; 2.在直角坐标系中,根据坐标找出点;由点求出坐标的 方法; 3.在四个象限内的点的坐标特征;两条坐标轴上的点的 坐标特征;第一、三象限角平分线上点的坐标特征;第 二、四象限角平分线上点的坐标特征; 4.分别关于x轴、y轴及原点的对称的两点坐标之间的关 系
八年级数学下册 第17章 函数及其图象17.2 函数的图像 1平面直角坐标系课件 (新版)华东师大版

(打“√”或“×”) (1)平面直角坐标系中,点(0,2),(2,0)的位置相同.( × ) (2)平面直角坐标系中的点和有序实数对是一一对应的.( √ ) (3)点(-3,-4)在第三象限. ( √ )
知识点 1 平面直角坐标系中点的特征及应用
【例1】(1)在平面直角坐标系中,点P(m,m-2)在第一象限内,
0,
解得,
0
1 m 1.
2
3
4.如图,已知棋子“车”的坐标为(-2,3),棋子“马”的坐 标为(1,3),则棋子“炮”的坐标为( )
A.(3,2) C.(2,2)
B.(3,1) D.(-2,2)
【解析】选A.棋子“车”的坐标为(-2,3),棋子“马”的坐 标为(1,3),纵坐标都是3,所以棋子“炮”的纵坐标为2;根 据“车”和“马”的横坐标-2,1,确定棋子“炮”的横坐标 为3.所以“炮”的坐标为(3,2).
(2)点B与点E、点C与点D,它们的横坐标相同,纵坐标互为相 反数. (3)关于x轴对称的点的横坐标相同,纵坐标互为相反数.
【总结提升】对称点的坐标规律 (1)关于x轴对称的点,横坐标相同,纵坐标互为相反数. (2)关于y轴对称的点,纵坐标相同,横坐标互为相反数. (3)关于原点对称的点,横坐标与纵坐标都互为相反数.
5.(1)在平面直角坐标系中,描出下列各点:A(4,3),B(-2, 3),C(-4,-1),D(2,-2). (2)写出图中E,F,G,H,O各点的坐标,你能从中得出什么结 论?
【思路点拨】由平面直角坐标系中点A,B,C,D,E的位置 得点的坐标. 【自主解答】由平面直角坐标系中点的位置可得, A(-2,0),B(0,-2),C(2,-1),D(2,1),E(0,2). (1)∵点A的纵坐标为0,点B和点E的横坐标为0,点C和点D的 横坐标都是2, ∴点A在x轴上,点B和点E在y轴上,且点B和点E、点C与点D 都关于x轴对称.
华东师大版八年级下册数学17.《平面直角坐标系》课件

试一试
1.写出下图中的多边形ABCDEF各个顶点的坐标,并说出各顶点
所在的象限或坐标轴.
【答案】
y 3
F
E
A(-2,0)在x轴上
2
A
1
D
-2 -1 O 1 2 3 4
-1
-2
-3
B
C
B(0,-3)在y轴上 x C(3,-3)在第四象限
D(4,0)在x轴上 E(3,3)在第一象限
F(0,3)在y轴上
时间:5分钟
要求:
1.思考:如何在平面内建立直角坐标系?
2.在课本162页方格图上建立平面直角坐标
系,并指出坐标系各部分的名称(x轴、y轴、原
点及第一、二、三、四象限).
定义: 在平面内画两条互相垂直,并且有公共原点
O的数轴,组成平面直角坐标系
坐标平面
y
6 5 4 3 2 1
纵轴
横轴和纵轴 统称为坐标轴
试一试
2. 在平面直角坐标系中分别描出点P(3,2)、Q(2,3) 、 S(-1,4) 、R(4,-1). 视察:P(3,2)与Q(2,3)是同一个点吗?
S(-1,4)与R(4,-1)是同一个点吗?
平面直角坐标系内的点和有序实数对是一一结对果应这告的里知。得我到们的什 么?
合作探究
写出点A,B,C,D,E,F的坐标.
作业
教材课后练习1、2、3题
我们愈是学习,愈觉得自己的贫乏。 —— 雪莱
【答案】
A(3,3)
B(-5,2)
C(-4,-3)
·F
D(4,-3)
视察各点坐标, 思考: (1)在四个象限内点 的坐标各有什么特征?
(2)两条坐标轴上的 点的坐标各有什么特征?
华师大版八年级数学下册第17章函数及其图象【创新教案】平面直角坐标系

17.2.1 平面直角坐标系课题平面直角坐标系教学目标知识目标:1.理解平面直角坐标系的有关概念,并会正确画出平面直角坐标系.2.能根据点的位置确定点的坐标,能根据点的坐标描点.能力目标:联系数轴知识、统计图知识,经历探索平面直角坐标系的概念的过程;通过学生积极动手画图,达到训练的程度,并充分感受直角坐标系上的点和有序实数对是一一对应的含义.情感目标:培养学生细致、认真的学习习惯.通过介绍笛卡儿创立直角坐标系的背景知识,激励学生敢于探索,勇攀科学高峰.重点能在给定的平面直角坐标系中,由点求出坐标,由坐标描出点难点探索象限内点的特征与坐标轴上点的特征,以及它们特征的简单运用.教学过程创设情境:你知道四川大地震的地理位置吗?北京时间2008年5月12日14时28分,在四川汶川县(北纬31.0度,东经103.4度)发生7.8级地震。
重庆、山西、陕西、湖北等地有震感。
14时35分左右,北京通州发生3.9级地震。
问题1 例如你去过电影院吗?还记得在电影院是怎么找座位的吗?在数学中,我们可以用一对有序实数来确定平面上点的位置.为此,在平面上画两条原点重合、互相垂直且具有相同单位长度的数轴(如图),这就建立了平面直角坐标系(rightangledcoordinates system).通常把其中水平的一条数轴叫做x轴或横轴,取向右为正方向;铅直的数轴叫做y轴或纵轴,取向上为正方向;两数轴的交点O叫做坐标原点.在平面直角坐标系中,任意一点都可以用一对有序实数来表示.例如,图中的点P,从点P分别向x轴和y轴作垂线,垂足分别为M 和N.这时,点M在x轴上对应的数为3,称为点P的横坐标;点N在y轴上对应的数为2,称为点P的纵坐标(ordinate).依次写出点P的横坐标和纵坐标,得到一对有序实数(3,2),称为点P的坐标(coordinates).这时点P可记作P(3,2).在直角坐标系中,两条坐标轴把平面分成如图所示的Ⅰ、Ⅱ、Ⅲ、Ⅳ四个区域,分别称为第一、二、三、四象限.坐标轴上的点不属于任何一个象限.实践应用例1在上图中分别描出坐标是(2,3)、(-2,3)、(3,-2)的点Q、S、R,Q(2,3)与P(3,2)是同一点吗?S(-2,3)与R(3,-2)是同一点吗?例2(教材P35)写出图中的点A、B、C、D、E、F的坐标.观察你所写出的这些点的坐标,回答:(1)在四个象限内的点的坐标各有什么特征?(2)两条坐标轴上的点的坐标各有什么特征?检测反馈1.判断下列说法是否正确:(1)(2,3)和(3,2)表示同一点; (2)点(-4,1)与点(4,-1)关于原点对称;(3)坐标轴上的点的横坐标和纵坐标至少有一个为0;(4)第一象限内的点的横坐标与纵坐标均为正数.2.如图是一个围棋棋盘,我们可以用类似于直角坐标系的方法表示各个棋子的位置.例如,图中右下角的一个棋子可以表示为(12,十三).请至少说出图中四个棋子的“位置”.3.填空: (1)点P(5,-3)关于x轴对称点的坐标是;(2)点P(3,-5)关于y轴对称点的坐标是; (3)点P(-2,-4)关于原点对称点的坐标是交流反思1.平面直角坐标系的有关概念及画法;2.在直角坐标系中,根据坐标找出点;由点求出坐标的方法;3.在四个象限内的点的坐标特征;两条坐标轴上的点的坐标特征;第一、三象限角平分线上点的坐标特征;第二、四象限角平分线上点的坐标特征;4.分别关于x轴、y轴及原点的对称的两点坐标之间的关系.课后作业课后反思板书设计。
吉林省八年级数学下册17函数及其图象17.2函数的图像17.2.2函数的图象教案新版华东师大版_373
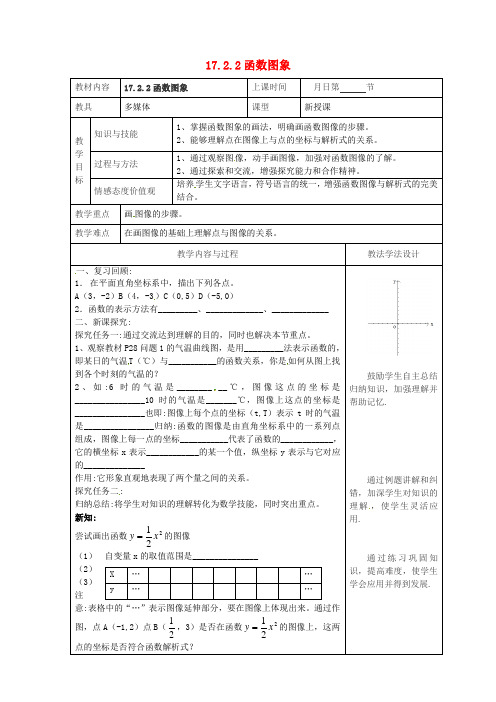
1 x 的函数图像 2 6 1 2、画出函数 y 的 函数图像,并判断点(2,3)点( ,-36)是 x 6
1、 画出函数 y 否在函数图像上?
教 学 反 思
17.2.2 函数图象
教材内容 教具 17.2.2 函数图象 多媒体 知识与技能 过程与方法 情感态度价值观 教学重点 教学难点 上课时间 课型 月日第 新授课 节
教 学 目 标
1、掌握函数图象的画法,明确画函数图像的步骤。 2、能够理解点在图像上与点的坐标与解析式的关系。 1、通过观察图 像,动手画图像,加强对函数图像的了解。 2、通过探索和交流,增强探究能力和合作精神。 培养 学生文字语言,符号语言的统一,增强函数图像与解析式的完美 结合。
1 1 2 ,3)是否在函数 y x 的图像上,这两 2 2
点的坐标是否符合函数解析式?
归纳: (1)点在图像上,该点坐标满足_____________ (2)若某点的坐标满足________________,则这个 点在函数图像上。 或者说图像_________该点。 三、典型例题 例 1:画出函数 y x 2 的图像例 2:画出函数 y 3x 的图像
鼓励学生自主总结 归纳知识,加强理解并 帮助记忆.
通过例题讲解和纠 错,加深学生对知识的 理解 ,使学生灵活应 用.
1 2 x 的图像 2
通过练习巩固知 识,提高难度,使学生 学会应用并得到发展.
(1) 自变量 x 的取值范围是_______________ (2) X … … (3) y … … 注 意:表格中的“…”表示图像延伸部分,要在图像上体现出来。通过作 图,点 A(-1,2)点 B(
1、在函数 y x 1 的图像上的点的坐标是() A.(0,1)B.(2-1)C.(-1,1)D.( 2、 若点 (
八年级数学下册 第十七章 勾股定理 17.2 函数的图象 1.平面直角坐标系课件

12/2/2021
第十页,共十页。
解:A(3,2),B(2,3),C(-2,3),D(-1,-3).
第七页,共十页。
第八页,共十页。
第九页,共十页。
内容(nèiróng)总结
No 17.2 函数的图象。3.象限(xiàngxiàn)及各象限(xiàngxiàn)内点的坐标的符号特征。建立了平面直角坐
标系以后,坐标平面就被两条坐标轴分成四部分,分别叫做。探究点一:坐标平面内点的坐标特征。所以横 坐标应为-3,纵坐标应为4,。坐标平面内点的坐标特征。探究点二:根据点的特征确定点的位置。解:(1)横 坐标与纵坐标相等的点:。2.在平面直角坐标系中,位于第三象限(xiàngxiàn)的点是( )。-5
探究点二:根据点的特征确定点的位置
【例2】 各写出5个满足下列条件的点,并在平面直角坐标系中描出它们:
(1)横坐标与纵坐标相等;
(2)横坐标与纵坐标互为相反数.
【导学探究】
1.在第一、三象限(xiàngxiàn)的
上的点,横坐标与纵坐标相等.
2.第二、四象限的
角平上分的线点的横坐标与纵坐标互为相反数.
①点P(x,y)在第一象限⇔x>0,y>0; ②点P(x,y)在第二象限⇔x<0,y>0;
③点P(x,y)在第三象限⇔x<0,y<0;
④点P(x,y)在第四象限⇔x>0,y<0.
(2)坐标轴上的点有如下特征:
点P(x,y)在x轴上⇔y=0,x为任意数; 点P(x,y)在y轴上⇔x=0,y为任意数.
第四页,共十页。
第一(dì象yī)限、
如图所示.
第二象(d限ì 、èr)
第象三限和
华师大版数学八年级下册《第17章 函数及其图象 17-2 函数的图象 1-平面直角坐标系》教学课件

D -1
C
-2
-3
思考
我们知道,数轴上的点和全体实数是一一对 应的.上面的“试一试”也给我们这样的启发;平 面直角坐标系中的点和有序实数对也是一一对应 的.你能说出这句话的含义吗?
对称点的坐标
P(x, y)关于 x 轴的对称点 P′(x, -y); P(x, y)关于 y 轴的对称点 P′(-x, y); P(x, y)关于原点的对称点 P′(-x, -y);
谢谢 大家
本课件是在Micorsoft PowerPoint的平台上制作的,可以在Windows环境下独立 运行,集文字、符号、图形、图像、动画、声音于一体,交互性强,信息量大,能多路 刺激学生的视觉、听觉等器官,使课堂教育更加直观、形象、生动,提高了学生学习的 主动性与积极性,减轻了学习负担,有力地促进了课堂教育的灵活与高效。
B(-a , b )在第四象限.
(√)
(4)若点 P 的坐标为(a,b),且 a·b =0,
则点 P 一定在坐标原点.
( ×)
2. 点 A(2, 3) 到 x 轴的距离为__3___;点 B(-4, 0) 到 y 轴的距离为__4___;点 C 到 x 轴 的距离为 1,到 y 轴的距离为 3,且在第三象 限,则 C 点坐标是_(_-_3_, _-1_)__.
有序实数来表示.
y
3
P
2
思考 如何确定平面直角
1
-3 -2 -1 O 1 2 3 x
-1
坐标系中点的坐标?
-2
-3
从点 P 分别向 x 轴和 y 轴作垂线,垂足分别为
点 M 和点 N .
点 M 在 x 轴上对应的数 为3,称为点 P 的横坐标.
点 N 在 y 轴上对应的数 为2,称为点 P 的纵坐标.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、内容总结
定义
平面直角坐标系点与坐标的对应关系
特殊点的坐标的特征
2、方法归纳
建 立平面直角坐标系,感受数 形结合思想
五、课后作业:书41页第1、3题;
让学生通过自主探究,发现问题并学会分析解决问题。
鼓励学生自主总结归纳知识,加强理解并帮助记忆.
通过例题讲解和纠错,加深学生对知识的理解,使学生灵活应用.
17.2.1平面直角坐标系
教材内容
17.2.1平面直角坐标系
上课时间
月日第节
教具
多媒体
课型
新授课
教
学
目
标
知识与技能
1、通ቤተ መጻሕፍቲ ባይዱ实例使学生感受和理解平面坐标系等概念,了解平面直角坐标系中点的坐标的特点;
2、能会求点的对称点的坐标;
过程与方法
通过直观感知操作确认的方式探索平面直角坐标系的特征,进一步渗透数形结合的思想。
通过练习巩固知识,提高难度,使学生学会应用并得到发展.
教学反思
问:(1)在四个象限内的点的坐标有什么特征?
(2)两条坐标轴上的点的坐标各有什么特征?
(3)点A和点B,点 A和点C,点A和点D有什么特点?
新知:
(1)象限内点的坐标特征:点在第一象限(+,+),点在第二象限(-,+),点在第三象限(―,―),点在第四象限(+,-)。
(2)坐标轴上点在坐标特征:点在x轴上点的纵坐标是0,点在y轴上点的横坐标是0,坐标原点(0,0)。
情感态度价值观
初步渗透对应思想,知道事物是相互联系的,培养学生的辩证唯物主义观。
教学重点
平面直角坐标系及其相关概念
教学难点
对点的坐标的理解
教学内容与过程
教法学法设计
一、课前准备
【复习】
1、什么是数轴?
2、数轴上的点与实数的关系是什么?
3、各种统计图具有怎样的共 同特征?
二、新课导学
探究任务一:通过交流达到理解目的
探究任务二:
在练习本上建立坐标系,在平面内任取一点P,过点P分别作横轴或纵轴的垂线,分别标出垂足M、N,垂足M、N分别在两条坐标轴上各有几个实数和它相对应。
新知:
在平面内任取一点,总有唯一的有序实数对和它对应。
注:横坐标写在前面,纵坐标写 在后面,例:P(x,y)
探究任务三:
三、典型例题:
例1:在直角坐 标系中,指出A(2,3),B(-2,3),C(2,-3),D(-2,-3 ),E(0,3),F(-2,0)这些点,同时指出各点所在的象限。
(3)关于x轴对称的两点横坐标相同,纵坐标互为相反数。
关于y轴对称的 两点横坐标互为相反数,纵坐标相同。
关于原点对称的两点横、纵坐标都互为相反数。
1、平面直角坐标系中,点P(-5,-3)位于____象限;
2、若点A(a+2,a-1)在y轴上,则a=_____;
3、点A(-3,a)与点 B(b,4)关于y轴对称,则a=____,b=____。
提问:
王敏同学在教室内座位的位置,能否用所在的行和排来确定呢?
如何在平面内建立直角坐标系呢?
新知:
(1)在平面内画两条有公共原点且互相垂直的数轴,水平向右方向的数轴叫x轴或横轴,垂直向上方向的数轴叫y轴或纵轴,两条坐标轴的公共 原点叫坐标系的原点,建立了坐标系的平面叫坐标平面。
(2)坐标轴把坐标平面分成四个部分,如图中Ⅰ、Ⅱ、Ⅲ、Ⅳ依次叫做第一、二、三、四象限。注意:坐标轴不属于任何象限。
