推荐-上海市第2018届“金桥杯”中学生数学知识竞赛试
2018年全国初中数学联合竞赛试题(含解答)

2018年全国初中数学联合竞赛试题(含解答)2018年全国初中数学联合竞赛试题参考答案及评分标准说明:评阅试卷时,请依据本评分标准。
第一试,选择题和填空题只设7分和0分两档;第二试各题,请严格按照本评分标准规定的评分档次给分,不要再增加其他中间档次。
如果考生的解答方法和本解答不同,只要思路合理,步骤正确,在评卷时请参照本评分标准划分的档次,给予相应的分数。
第一试一、选择题(本题满分42分,每小题7分)1.已知$x,y,z$满足$\frac{2355x-y}{y+2z}=\frac{x}{z-z^2}$,则$\frac{y+2z}{3x-y-z}$的值为()A) 1.(B) $\frac{5}{3}$。
(C) $-\frac{1}{3}$。
(D) $-\frac{3}{5}$.答】B.解:由$\frac{2355x-y}{y+2z}=\frac{x}{z-z^2}$,得$5x-3y=3xz-3xz^2$,即$y=\frac{5}{3}x-\frac{3}{3}z+\frac{3}{3}xz^2$,所以$\frac{y+2z}{3x-y-z}=\frac{\frac{5}{3}x+\frac{1}{3}z}{\frac{4}{3}x-\frac{2}{3}z}=\frac{5}{3}$,故选(B)。
注:本题也可用特殊值法来判断。
2.当$x$分别取值$1,\frac{1}{2},\frac{1}{3},\cdots,\frac{1}{2005},\frac{1}{2006}, \frac{1}{2007}$时,计算$\frac{1}{2007}+\frac{x}{21+x^2}$代数式的值,将所得的结果相加,其和等于()A) $-1$。
(B) $1$。
(C) $0$。
(D) $2007$.答】C.解:$\frac{1}{2007}+\frac{x}{21+x^2}=\frac{1}{21}\left(\frac{21}{ 2007}+\frac{21x}{21+x^2}\right)=\frac{1}{21}\left(\frac{1}{1+x ^{-2}}\right)$,所以当$x=1,\frac{1}{2},\frac{1}{3},\cdots,\frac{1}{2005},\frac{1}{200 6},\frac{1}{2007}$时,计算所得的代数式的值之和为$0$,故选(C)。
2018全国初中数学竞赛试题及参考答案

中国教育学会中学数学教学专业委员会“《数学周报》杯”2018年全国初中数学竞赛试题答题时注意:1.用圆珠笔或钢笔作答; 2.解答书写时不要超过装订线; 3.草稿纸不上交.一、选择题<共5小题,每小题7分,共35分. 每道小题均给出了代号为A ,B ,C ,D 的四个选项,其中有且只有一个选项是正确的. 请将正确选项的代号填入题后的括号里,不填、多填或错填都得0分)qfRgF4dw271.设1a =,则代数式32312612a a a +--的值为( >.<A )24 <B )25 <C )10 <D )122.对于任意实数a b c d ,,,,定义有序实数对a b (,)与c d (,)之间的运算“△”为:<a b ,)△<c d ,)=<ac bd ad bc ++,).如果对于任意实数u v ,, 都有<u v ,)△<x y ,)=<u v ,),那么<x y ,)为( >.qfRgF4dw27<A )<0,1) <B )<1,0) <C )<﹣1,0) <D )<0,-1)3.若1x >,0y >,且满足3y y x xy x x y==,,则x y +的值为( >.<A )1 <B )2 <C )92<D )1124.点D E ,分别在△ABC 的边AB AC ,上,BE CD ,相交于点F ,设1234BDF BCF CEF EADF S S S S S S S S ∆∆∆====四边形,,,,则13S S 与24S S 的大小关系为( >.<A )1324S S S S < <B )1324S S S S = <C )1324S S S S > <D )不能确定5.设3333111112399S =++++,则4S 的整数部分等于( >. <A )4 <B )5 <C )6 <D )7 二、填空题<共5小题,每小题7分,共35分)6.若关于x 的方程2(2)(4)0x x x m --+=有三个根,且这三个根恰好可以作为一个三角形的三条边的长,则m 的取值范围是 .7.一枚质地均匀的正方体骰子的六个面上的数字分别是1,2,2,3,3,4;另一枚质地均匀的正方体骰子的六个面上的数字分别是1,3,4,5,6,8. 同时掷这两枚骰子,则其朝上的面两数字之和为奇数的概率是 .NW2GT2oy018.如图,点A B ,为直线y x =上的两点,过A B ,两点分别作y 轴的平行线交双曲线1y x=<x >0)于C D ,两点. 若2BD AC =,则224OC OD - 的值为 .NW2GT2oy019.若112y x x =-+-的最大值为a ,最小值为b ,则22a b +的值为 .10.如图,在Rt △ABC 中,斜边AB 的长为35,正方形CDEF 内接于△ABC ,且其边长为12,则△ABC 的周长为 .NW2GT2oy01三、解答题<共4题,每题20分,共80分)11.已知关于x 的一元二次方程20x cx a ++=的两个整数根恰好比方程20x ax b ++=的两个根都大1,求a b c ++的值.12.如图,点H 为△ABC 的垂心,以AB 为直径的⊙1O 和△BCH 的外接圆⊙2O 相交于点D ,延长AD 交CH 于点P ,求证:点P 为CH 的中点.13.如图,点A 为y 轴正半轴上一点,A B ,两点关于x 轴对称,过点A 任作直线交抛物线<第8题)<第10题)<第12题)223y x =于P ,Q 两点. <1)求证:∠ABP =∠ABQ ;<2)若点A 的坐标为<0,1),且∠PBQ =60º,试求所有满足条件的直线PQ 的函数解读式.14.如图,△ABC 中,60BAC ∠=︒,2AB AC =.点P 在△ABC 内,且352PA PB PC ===,,,求△ABC 的面积.中国教育学会中学数学教学专业委员会“《数学周报》杯”2018年全国初中数学竞赛试题参考答案 一、选择题1.A解:因为71a =-, 17a +=, 262a a =-, 所以322312612362126261261260662126024.a a a a a a a a a a a +--=-+---=--+=---+=()()()2.B解:依定义的运算法则,有ux vy u vx uy v +=⎧⎨+=⎩,,即(1)0(1)0u x vy v x uy -+=⎧⎨-+=⎩,对任何实数u v ,都成立. 由于实数u v ,的任意性,得<x y ,)=<1,0).3.C<第13题)<第14题)解:由题设可知1y y x -=,于是341y y x yx x -==,所以 411y -=, 故12y =,从而4x =.于是92x y +=.4.C解:如图,连接DE ,设1DEF S S ∆'=,则1423S S EF S BF S '==,从而有1324S S S S '=.因为11S S '>,所以1324S S S S >.5.A解:当2 3 99k =,,,时,因为()()()32111112111k k k k k k k ⎡⎤<=-⎢⎥-+-⎣⎦, 所以 3331111115111239922991004S ⎛⎫<=++++<+-< ⎪⨯⎝⎭. 于是有445S <<,故4S 的整数部分等于4.二、填空题 6.3<m ≤4解:易知2x =是方程的一个根,设方程的另外两个根为12 x x ,,则124x x +=,12x x m =.显然1242x x +=>,所以122x x -<, 164m ∆=-≥0,即 ()2121242x x x x +-<,164m ∆=-≥0,所以1642m -<, 164m ∆=-≥0,<第4题)解之得 3<m ≤4.7.19解: 在36对可能出现的结果中,有4对:<1,4),<2,3),<2,3),<4,1)的和为5,所以朝上的面两数字之和为5的概率是41369=.NW2GT2oy01 8.6解:如图,设点C 的坐标为a b (,),点D 的坐标为c d (,),则点A 的坐标为a a (,),点B 的坐标为.c c (,) 因为点C D ,在双曲线1y x=上,所以11ab cd ==,.由于AC a b =-,BD c d =-, 又因为2BD AC =,于是 22222242c d a b c cd d a ab b -=--+=-+,(),所以 22224826a b c d ab cd +-+=-=()(),即224OC OD -=6.9.32解:由1x -≥0,且12x -≥0,得12≤x ≤1.22213113122()2222416y x x x =+-+-=+--+. 由于13124<<,所以当34x =时,2y 取到最大值1,故1a =. 当12x =或1时,2y 取到最小值12,故22b =. 所以,2232a b +=. 10.84解:如图,设BC =a ,AC =b ,则<第8题)22235a b +==1225. ①又Rt △AFE ∽Rt △ACB ,所以FE AF CB AC =,即1212b a b-=,故 12()a b ab +=. ② 由①②得2222122524a b a b ab a b +=++=++()(), 解得a +b =49<另一个解-25舍去),所以493584a b c ++=+=.三、解答题11.解:设方程20x ax b ++=的两个根为αβ,,其中αβ,为整数,且α≤β,则方程20x cx a ++=的两根为11αβ++,,由题意得()()11a a αβαβ+=-++=,,两式相加得 2210αβαβ+++=, 即 (2)(2)3αβ++=,所以 2123αβ+=⎧⎨+=⎩,; 或232 1.αβ+=-⎧⎨+=-⎩,解得 11αβ=-⎧⎨=⎩,; 或53.αβ=-⎧⎨=-⎩,又因为[11]a b c αβαβαβ=-+==-+++(),,()(),所以 012a b c ==-=-,,;或者8156a b c ===,,,故3a b c ++=-,或29.12.证明:如图,延长AP 交⊙2O 于点Q ,连接 AH BD QB QC QH ,,,,. <第10题)因为AB 为⊙1O 的直径, 所以∠ADB =∠BDQ =90°, 故BQ 为⊙2O 的直径. 于是CQ BC BH HQ ⊥⊥,.又因为点H 为△ABC 的垂心,所以.AH BC BH AC ⊥⊥,所以AH ∥CQ ,AC ∥HQ ,四边形ACQH 为平行四边形. 所以点P 为CH 的中点.13.解:<1)如图,分别过点P Q , 作y 轴的垂线,垂足分别为C D , .设点A 的坐标为<0,t ),则点B 的坐标为<0,-t ).设直线PQ 的函数解读式为y kx t =+,并设P Q,的坐标分别为 P P x y (,),Q Q x y (,).由223y kx t y x =+⎧⎪⎨=⎪⎩,, 得 2203x kx t --=,于是 32P Q x x t =-,即 23P Q t x x =-.于是 222323P P Q Qx t y t BC BD y t x t ++==++22222()333.222()333P P Q P P Q P QQ P Q Q Q P x x x x x x x x x x x x x x --===--- 又因为PQx PCQD x =-,所以BC PC BDQD=.因为∠BCP =∠90BDQ =︒,所以△BCP ∽△BDQ , 故∠ABP =∠ABQ .<第12题)<第13题)<2)解法一 设PC a =,DQ b =,不妨设a ≥b >0,由<1)可知∠ABP =∠30ABQ =︒,BC ,BD ,所以AC 2-,AD =2.因为PC ∥DQ ,所以△ACP ∽△ADQ .于是PCACDQAD =,即a b =,所以a b +=.由<1)中32P Q x x t =-,即32ab -=-,所以322ab a b =+=, 于是可求得2a b =将2b =代入223y x =,得到点Q 的坐标,12).再将点Q 的坐标代入1y kx =+,求得3k =-所以直线PQ 的函数解读式为1y x =+.根据对称性知,所求直线PQ 的函数解读式为1y x =+,或1y +. 解法二 设直线PQ 的函数解读式为y kx t =+,其中1t =. 由<1)可知,∠ABP =∠30ABQ =︒,所以2BQ DQ =.故 2Q x = 将223Q Q y x =代入上式,平方并整理得4241590Q Q x x -+=,即22(43)(3)0Q Q x x --=.所以 2Q x =又由 (1>得3322P Q x x t =-=-,32P Q x x k +=.若32Q x =,代入上式得 3P x =-, 从而 23()33P Q k x x =+=-.同理,若3Q x =, 可得32P x =-, 从而 23()33P Q k x x =+=.所以,直线PQ 的函数解读式为313y x =-+,或313y x =+. 14.解:如图,作△ABQ ,使得QAB PAC ABQ ACP ∠=∠∠=∠,,则△ABQ ∽△ACP . 由于2AB AC =,所以相似比为2. 于是22324AQ AP BQ CP ====,.60QAP QAB BAP PAC BAP BAC ∠=∠+∠=∠+∠=∠=︒.由:2:1AQ AP =知,90APQ ∠=︒,于是33PQ AP ==.所以 22225BP BQ PQ ==+,从而90BQP ∠=︒. 于是222()2883AB PQ AP BQ =++=+ .故 213673sin 60282ABC S AB AC AB ∆+=⋅︒==. 申明:所有资料为本人收集整理,仅限个人学习使用,勿做商业用途。
上海市中学生历届数学知识竞赛

上海市首届“金桥杯”中学生数学知识应用竞赛(1991~1992)首届“金桥杯”中学生数学知识应用竞赛初赛于1991年10月举行.决赛于1992年3月举行.【初赛试题】初赛试题共有十五题,其中一~十题,每题满分为10分;十一~十五题,每题满分为16分.满分为180分.一、小明家前面造了一幢高层楼房,小明在自己楼房的A层测得高层楼房CD的仰角为α,俯角为β;小明又在自己楼房的B层测得高层高层楼房与小明楼房之间的距离d.二、筹建中的天然气管道网设计如图3—2所示,A,B,…,L表示压缩机站,流动主向用箭头表示,每个管道旁的数字表示管段长度.现需要求该网络从起点A到终点L的最短通道,并确定沿最优路径相应的压缩机站所处的节点.三、某厂1989年生产产值是1979年生产产值的8倍(即翻三番),那么从1979年到1989年产值平均年增长率为多少?按这样速度发展,到了2000年的产值是1989年产值的几倍?(取整数)四、相距40公里的两个城镇A、B之间有一个圆形湖泊,它的圆心落在AB连线的中点O,半径为10公里,如图3—3所示.现要修建一条连结两城镇的公路,问应如何选择公路的路线,使公路最短,并给出证明.五、有一批1米长的合金钢材,现要截成长为23厘米和13厘米两种规格,用怎样方案截取使材料利用率为最高?并求出材料最高利用率.六、四种小商品A、B、C、D的价格分别为0.13元、0.17元、0.22元、0.35元,现在用2元钱恰好买了10件小商品,问买得小商品A、B、C、D各为多少?七、某工厂生产甲、乙两种产品,生产每一吨产品需要电力、煤、劳动力及相应产值如下表所示:该厂的劳动力满员是200人,根据限额每天用电不得超过160千度,用煤不得超过150吨.问每天生产这两种产品各几吨时,才能创造最大的经济价值?八、用两根绳子牵引重为F1=100kg物体,两根绳子拉力分别为F2、F3,保持平衡,如图3—4所示.如果F2=80kg,F2与F3夹角α=135°,求F3的大小和F3与F1的夹角β值.九、在一边长为9m,一边长为16m的长方形的土地内,任意种植49颗树,试证明其中总有两颗树之间的距离不大于2.5m.十、仓库有一种堆垛方式,如图3—5所示,最高一层2盒,第二层6盒,第三层12盒,第四层20盒,第五层30盒……,当堆垛到第n层时,求出总的盒数.十一、数学竞赛给出了A、B、C三道题目,有30个学生参加,每人至少解出一道题.只解出A题的人数比其余解出A题的人数多3人;在没有解出A题的人中,解出B题人数是解出C题人数的3倍;在只解出一题的人中,解出A题的人数是没有解出A题的人数的一半,求至少解出两题的学生人数.十二、根据下列三视图(如图3—6),画出这个立体的直观图与展开图,并求出它的体积.十三、A、B、C三个工厂,它们之间的距离为AB=13公里、BC=14公里、CA=15公里,要求寻找一个供应站点H,使得它到三个工厂的距离和HA+HB+HC为最短,并且求出这最短距离.十四、某矿石基地A和冶炼厂B在铁路MN的两侧,A距铁路m公里,B距铁路n公里,在铁路上要建造两火车站C、D,A地矿石先用汽车由公路运到火车站C,然后用火车运输到火车站D,再用汽车运到B地,如图3—7所示,且A、B在铁路MN上投影A'B'距离长l公里,若汽车速度每小时u公里,火车速度每小时v公里,这里v>u,要使运输矿石的时间最短,火车站C,D应该建立在什么地方?十五、将一个母线为2a,底面半径为a的圆锥(有底)的铁皮模型,沿着母线剪开摊平作材料做一个圆柱形罐子(有底无盖),试问材料如何剪裁,使做出的圆柱形罐子的体积为最大?(这里圆柱侧面不能用两块材料拼接,且不考虑裁剪损耗.)【决赛试题】决赛试题共五题,其中一~三题,每题满分为32分,四、五题,每题满分为42分,总共满分为180分.一、如图3—8,有一块半径为a的圆铁皮,剪去一个圆心角α,将它卷成一个圆锥(无底),试问:(2)求出这个圆锥的体积最大值.二、A、B、C三厂联营生产同一种产品,产品是哪个厂生产就在产品上盖上那个厂的厂名,如果产品是两个厂或三个厂联合生产,那么产品上就盖上两个厂或三个厂的厂名.今有一批产品,发现盖过A厂、B厂、C厂的厂名的产品分别为18件、24件、30件,同时盖过A、B厂,B、C厂,C、A厂的产品,分别有12件、14件,16件,问这批产品的总数最多有几件?三、某项科学实验显示:实验结果y与实验时的温度t,呈现y=at2+bt(a≠0)关系,由实验条件限制,温度t取值范围为|t|≤c(c>0).试问:当温度t取什么值时,实验结果y达到最小值,并求出其最小值.四、已知某工程中的重点部位计划完工期为14天,预算总费用为63000元(包括每天的管理费1000元).若对某些工序增加一些费用的投入(如加班或技术改造等费用),则它的完工时间可以缩短.一个工序的最短完工时间,我们称为该工序的“极限时间”.另外,如该重点部位的完工期能缩短,则相应的管理费可以节省,有关工序流程图与数据如图3—9所示.注:赶工费用率为工序每提前一天耗用的加班或技术改造等费用.试回答下列两个问题:(1)求这个重点部位工程的最低完工费用,并制定相应的施工方案(包括完工期).(2)求这个重点部位最短完工期,并制定相应的施工方案(包括费用).五、要对几种药品进行试验,每次选择3种药品作试验,要求这样来安排试验方案,使得任意两种药品都至少有一次被安排在同一次试验中,同时为了节省时间与费用,还要求试验次数尽可能少.我们以C(n)表示对n种药品所作符合上述要求的最少试验次数.例如:当n=4,记所要作试验的药品为a1,a2,a3,a4,下面的分组试验方案(a1,a2,a3),(a1,a2,a4),(a2,a3,a4),是符合要求的.这个方案共进行了三次试验,因此,C(4)≤3.问题:(1)证明C(4)<3是不可能的.(2)试确定C(6)的值,并给出证明.(3)试给出C(n)的一个下界.【初赛试题解答要点与参考答案】二、最短通道:A→D→E→G→J→L.4+3+2+1+4=14.三、(1+x)10=8,x=23.11%(平均年增长率).(1+0.2311)21÷8=9.48≈10.(2000年产值是1989年产值的10倍)四、过A、B在AB同侧分别作⊙O的切线AA'、BB',则AA'2),则4×13+2×23=98,即截4段13厘米,2段23厘米,材料利用率为98%.六、设购买A、B、C、D商品数分别为x、y、z、w,则w只可能取0、1、2、3,相应找出z、y、x非负整数值,得到解答列表如下:七、设甲、乙产品分别生产x、y吨,则由题意得:满足上述约束条件的点在下列五条直线2x+8y=160,3x+5y=150,5x+2y=200,x=0,y=0所围成的五边形内(包括边界九、将长方形土地平分成48块相等的小长方形,每块长为2m、宽为1.5m,总有一块小长方形土地有两颗树,它的距离不大于对角线:十一、画出集合图如图3—10,只解出A题x人,只解出B题y人,只解出C题z人,解出A、B题w+t人,解出B题、C题u+t人,解出A 题、C题v+t人,解出A题、B题、C题t人.根据题意可列出方程:所以 u=5,y=13,x=7,z=1.即u+v+w+t=30-x-y-z=9(人)十二、直观图,展开图分别如图3—11,3—12.V=(2a)3÷2=4a3.十三、H点应取∠AHB=∠BHC=∠CHA=120°时,AH+BH+CH为最小,由Fermat-steiner最短线定理可证得(证略).十五、将圆锥侧面展开为半圆,半圆内裁出圆柱侧面,圆锥底改成圆柱底就可以(如图3—13所示).【决赛试题解答要点与参考答案】二、由题意得:m(A)=18,m(B)=24,m(C)=30,m(A∩B)=12,m(B ∩C)=14,m(C∩A)=16.当m(A∩B∩C)≤9或m(A∩B∩C)≥13时,与题意有矛盾,所以10≤m(A∩B∩C)≤12.m(A∪B∪C)=m(A)+m(B)+m(C)-m(A∩B)-m(B∩C)-m(C∩A)+m(A∩B∩C)=30+m(A∩B∩C).当m(A∩B∩C)=12时,m(A∪B∪C)=42(件),故这批产品总数最多为42件.四、从工程网络列表如下:△C1=2400-3000=-600,△C2=2400+500+1000+2800-6000=700.(1)最优费用方案:工序(1,3)减少3天,赶工费增加 2400,间接费用减少3000,总工期减少3天为11天完成.总费用 C=63000+(2400-3000)=62400(元).(2)最优时间方案:工序(1,3)减少3天,(3,6),(5,6)各减少1天,(6,7)减少2天,总工期减少6天共为8天完成.总费用C=63000+(2400+500 + 1000+ 2800- 6000)=63700(元)五、(1)设这4种药品为a1,a2,a3,a4由于每个组包含三种药品,而a1至少与a2,a3,a4相遇一次,因此至少有两个组包含a1,不妨设为{a1a2a3},{a1a2a4},但这里a3、a4没有相遇,因此,至少还应有一组,所以C(4)≥3.(2)设这6种药品为a1,a2,a3,a4,a5,a6,对每一个1≤i≤6,固定i,则包含a i的每次试验,正好还包含两种不同于a i的药品,而每次试验包含3种药品,因此试验总次数不小于6×3÷3=6,即C(6)≥ 6.我们构造一个用6次试验的方案满足条件:{a1a2a3},{a1a4a5},{a1a4a6},{a2a3a4},{a2a5a6},{a3a5a6}因此,C(6)≤6,综合之即得C(6)=6.(3)设n种药品为a1,a2,…,a n,对任意取定a i(1≤i≤n),则i≠j 时,a i与a j至少相遇一次,而每一个包含a i的组正好包含两个不3.2 上海市第二届“金桥杯”中学生数学知识应用竞赛(1993)上海市第二届“金桥杯”中学生数学知识应用竞赛初赛于1993年3月举行,决赛在9月举行.【初赛试题】初赛试题共有十五题,其中一~十题,每题满分为10分;十一~十五题,每题满分为16分.满分为180分.一、为测量建造中的上海东方明珠电视塔已达到的高度.小明在学校操场某一直线上选择三点A、B、C,且AB=BC=60米,分别在A、B、C三点观察塔的最高点,测得仰角为45°,54.2°,60°,小明身高为1.5米,试问建造中的电视塔现在已达到的高度.(结果保留一位小数)二、已知边长为a的正三角形铁皮材料,剪去三个全等的四边形,如图3—14所示,可制成无盖的正三棱柱的盒子.试问如何剪裁才能使正三棱柱的体积最大?并求出体积最大值和此时材料利用率.三、某布店的一页帐簿上沾了墨水,如下图所示:所卖呢料米数看不清楚了,但记得是卖了整数米;金额项目只看到后面三个数码7.28,但前面的三个数码看不清楚了,请您帮助查清这笔帐.四、某出口加工区总公司与下属各子公司进行信息联网,已测得各子公司A、B、C、D、E、F、G、H、J之间与总公司S联网费用如图3—15所示(单位:千元).现拟设计一个联网优化方案,既要求各子公司之间与总公司都能连通,又要使联网费用最省,试问如何联网?费用是多少?五、在下乡劳动中,30个学生,每人拾了一篮稻穗放在田埂旁,每隔5米排成一列,不妨依次叫第1号、第2号、…、第30号,每人将篮中稻穗集中到第n号处(1≤n≤30),放在一起,然后带着空篮走回原处,试求使大家所走路程总和最小的n值.六、一半径R=150mm球形工件,打一斜孔如图3—16(a)所示,为了准确测量斜孔两端半径r1和r2,用两精密量球(半径R2=100mm和R2=80mm)以如图3—16(b)所示方式测量,测得两球外端水平距离L1=651.40mm;再将右端量球换为半径R3=80mm,左端量球不变仍为R2=80mm,又测得L2=610.17mm.(1)求r1和r2(结果保留两位小数);(2)求小孔的斜角α的值(结果保留分).七、A、B两个产地分别生产同一规格产品12千吨、8千吨,而D、E、F三地分别需要8千吨、6千吨、6千吨,每千吨的运价表如下:怎样确定调运方案,使总的运费为最小?八、在机械设计中,已知AB=AC=a,CD⊥BD,∠CAD=θ(图3—17),当θ为何值时,△BDC面积最大,并求出最大值.九、某一信托投资公司,考虑投资1600万元建造一座涉外宾馆,经预测,该宾馆建成后,每年底可获利600万元,试问三年内能否把全部投资收回?假设银行每年复利计息,利率为10%,若需要在三年内收回全部投资,每年至少应收益多少万元?(结果保留一位小数)十、在正方形铁皮上任意划9条直线,如果每一条直线都将正方形分成两部分面积之比为m∶n(m, n∈N),那么这样9条直线中至少有3条直线交于一点,对吗,为什么?十一、五种商品价格如下:现在用60元恰好选购10件商品,试问有哪几种选购方式?十二、根据图3—18所示零件的视图,画出它的直观图、展开图(并要留出做成模型的粘贴处),并求出这个零件的表面积与体积.一个供应站H的位置,使它到四个工厂距离和HA+HB+HC+HD为最小,说明道理,并求出最小值.十四、一个零件模具的底面由甲、乙、丙三个边长均为a的正方形按如下要求叠合而成:甲的一个顶点落在乙的中心上,乙的一个顶点落在丙的中心上,丙的一个顶点落在甲的中心上.求这个模具底面的面积.十五、一煤粉炉球磨机衬板为圆台的侧面,上底半径R1=270 mm,下底半径R2=1147 mm,轴截面母线夹角为154°,这圆台侧面是由18块相同的扇环形钢板焊接而成。
上海市第05届“金桥杯”中学生数学知识应用竞赛决赛试题(Word版,含答案)

上海市第05届“金桥杯”中学生数学知识应用竞赛决赛试题一、在气象台A的正东方向300千米处有一台风中心.该台风中心正以每小时40千米的速度向西北方向移动,离台风中心250千米以内的地方将受其影响.问大约经过多少时间气象台所在地将受到台风影响?影响的持续时间将是多少?二、股票交易的开盘价是这样决定的:每天开盘前由投资者填报某种股票的意向买价或意向卖价以及相应的意向股数.然后由计算机根据这些数据确定适当的价格,使得在该价位上能够成交的股数最多.试根据以下数据,确定该种股票的开盘价以及能即时成交的股数.(注:当卖方意向价低于开盘价以及买方意向价高于开盘价时即可成交)三、水上游乐场的人工瀑布是在离地面10米处建造一段水平的水槽.在水槽的末端设置一个坡度为30°,坡长为60厘米的挑水坎.用水泵把水抽入水槽中,冲上挑水坎,最后在空中下落形成美丽的瀑布(见图3-69).已知槽内水的流速为6米/秒,试分析出槽水流曲线的类型,并计算人工瀑布下端与水槽基底的水平距离S.四、图画挂在墙上,它的下缘在观察者的眼睛上方a米处,而上边缘在b米处,问观察者在离墙多远的地方,才能使视角最大(从而看得最清楚)?五、附表给出五位工人完成五种工作所能取得的效益,试求出分配该五位工人分别担任一项工作的方案,使取得的效益最大.六、如图3-70所示的镀锌铁皮材料ABCD,上沿AD为圆弧,其圆心O在BC上.圆半径为2米,AB、CD均垂直于BC,且BO=CD=1m.现要用这材料裁一个矩形做圆柱的侧面,裁一个圆做圆柱的底,做一个有底无盖的圆柱形桶(这里不考虑拚接、裁剪的损耗).试问怎样落料能使水桶体积最大?并求出材料的利用率.七、一零件的轮廓由边长为a的正三角形ABC的等距曲线构成,等距为r(如图3-71).为了用数控机床加工,要求出轮廓线的精确公式.设坐标原点O与三角形的重心重合,x轴与AB平行.试求曲线的七个工件安排在同一台机床上加工.设各工件的加工时间依次为14,6,24,12,6,18,12(分钟).该机床一次只能加工一个工件,每一工件加工完毕即可运走投入下一工序.(1)试安排一个加工次序,使各工件的加工和等待时间之总和最小并说明理由.(2)若工件6,7必须先于工件2加工,工件1,2,4必须先于工件3加工,工件7必须先于工件4加工,工件3必须先于工件5加工,试找出使各工件的加工和等待时间之总和最短的加工次序.决赛试题解答要点与参考答案一、以气象台A为坐标原点,正东方向为x轴正向建立平面直角坐标系,则台风中心B坐标参数方程为时气象台将受到台风的影响.解此不等式,得即 1.99≤t≤8.61.约经过2小时后,气象台所在地将开始受到台风的影响,持续时间大约7小时.二、可确定开盘价为2.20,可能成交股数为600.三、以挑水坎末端A为坐标原点,以水平方向和垂直方向分别为x 轴和y轴建立平面直角坐标系.水离开A点时的速度Vt可由下式求得.方向沿挑水坎方向.设当时间t=0时,某个水质点D在A处,则当时间为t时,D点坐标满足方程得人工瀑布下端与水槽基底的水平距离S=8.3米.四、由题意,观察者的视角θ=∠BPA=∠BPH-∠APH.显然0<θ<90°,故tgθ=tg(∠BPH-∠APH)五、首先取附表中每一列之最大值,如下页表所示.表中有“*”号的数字为所在列蝗最大值,显然.这些有“*”号的数字和(最后一列有两个带“*”号的数字,求和时取一个)是进行五项工作的最大效益.但不满足每人一项工作的要求.以此表为基础进行调整,使调整后满足每人一项工作的要求,且与上表的差值最小.容易验证下表所示为调整后的最佳方案.即最佳方案为A→4(A做第四项工作),B→2,C→1,D→3,E→5.六、根据经验可按下图所示裁剪矩形与圆.第一种方法:以BE为圆柱底周长进行裁剪.此时应满足可见按第一种方法进行裁剪所得圆柱之体积最大.裁BE=2.07,EG =1.69的矩形.剩下材料裁半径为0.33的圆.得到的圆柱体积为0.58m3.七、弧段LM由直线部分LN与圆弧NM构成.圆弧NM的表示式为八、(1)因为加工和等待时间的总和为T=∑(8-i)Ti ,其中Ti为安排在第i位加工的工件的加工时间.因此使其总和最小的加工顺序应是2→5→4→7→1→6→3其中2和5,4和7的位置可以对调.(2)根据给出的条件可画出下面的网络:据此网络图,可先对工件1,2,4,6,7进行排序.首先,4,2,7,6这四个工件可有以下几种排序法:6→7→4→2,7→6→4→2,7→4→6→2,6→7→2→4,7→6→2→4.由于t6=18>t7=12,6→7→4→2和6→7→2→4两种情况可不考虑.又因t4=12>t2=6,7→6→4→2情况也可不考虑.这样就剩下以下两种情况:7→4→6→2,7→6→2→4.再考虑工件1的位置.对7→4→6→2情况,可有以下几种情形:(a)1→7→4→6→2,(b)7→1→4→6→2,(c)7→4→1→6→2,(d)7→4→6→1→2,(e)7→4→6→2→1.由于t1=14>t7=12,t1=14>t4=12知(b)优于(a),(c)优于(b);又由于t1=14>t2=6,可知(e)优于(d).比较(e)与(c)两种情况下的等待与加工的总耗时:(e)5t7+4t4+3t6+2t2+t1,(c)5t7+4t4+3t1+2t6+t2,可知(e)优于(c)也就是说情形7→4→6→2→1→3→5耗时最少.同理可判定情形7→4→6→2→1→3→5耗时也最少.最少的耗时为T=7t7+6t4+5t6+4t2+3t1+2t3+t5=366(分钟).。
最新-上海市2018初中数学 竞赛试卷 沪科版 精品

2018年(新知杯)上海市初中数学竞赛试卷(2018年12月12日 上午9:00~11:00)解答本试卷可以使用计算器一、填空题(第1~5小题,每题8分,第6~10小题,每题10分,共90分)1. 已知31=+x x ,则=+++10551011x x x x _________。
2. 满足方程()()33222=-+++y x y x 的所有实数对()y x ,为__________。
3. 已知直角三角形ABC 中,3690===∠CA BC C ,,,CD 为C ∠的角平分线,则CD=_________。
4. 若前2018个正整数的乘积201121⨯⨯⨯ 能被k 2010整除,则正整数k 的最大值为________。
5. 如图,平面直角坐标系内,正三角形ABC 的顶点B ,C 的坐标分别为(1,0),(3,0),过坐标原点O 的一条直线分别与边AB ,AC 交于点M ,N ,若OM=MN ,则点M 的坐标为_________。
6. 如图,矩形ABCD 中,AB=5,BC=8,点E ,F ,G ,HOG F EH D C B A分别在边AB ,BC ,CD ,DA 上,使得AE=2,BF=5,DG=3,AH=3,点O 在线段HF 上,使得四边形AEOH 的面积为9,则四边形OFCG 的面积是_________。
7. 整数q p ,满足2010=+q p ,且关于x 的一元二次方程0672=++q px x 的两个根均为正整数,则=p ________。
8. 已知实数c b a ,,满足0=++≥≥c b a c b a ,且0≠a 。
设21x x ,是方程02=++c bx ax 的两个实数根,则平面直线坐标系内两点()()1221x x B x x A ,,,之间的距离的最大值为_______。
9. 如图,设ABCDE 是正五边形,五角星ACEBD (阴影部分)的面积为1,设AC 与BE 的交点为P ,BD 与CE 的交点为Q ,则四边形APQD 的面积等于_______。
2018年上海市初中数学竞赛(第1试 含答案)

2018年上海市初中数学竞赛(第一试)1.已知1.1=a ,9.01.1=b ,1.19.0=c ,则将a 、b 、c 从小到大排列,并用“<”表示是 .2.若16842321321161814121218x x x x x x x a +++++++++=-=-,则a 的值是 . 3.已知a 为无理数,且525102-+-+=b a ab b a b a ,则ba 的值为 . 4.由1-=x y 的图象与2=y 的图象围成的图形的面积是 .5.三角形的三条边a ,b ,c 满足7531≤≤≤≤≤≤c b a ,当此三角形的面积最大时,它的周长是 .6.方程2002111=+y x 的正整数解构成的有序数组(x ,y )共有 组. 7.如图,在△ABC 中,F 、G 是BC 边上两点,使∠B 、∠C 的平分线BE 、CD 分别垂直AG ,AF (E 、D 为垂足).若△ABC 的周长为22,BC 边长为9,则DE 的长为 .8.已知二次函数c bx ax y ++=2(其中a 为正整数)经过点A (1-,4)与点B (2,1),且与x 轴有两个不同的交点,则c b +的最大值为 .9.如图,点P 、Q 在△ABC 的AC 边上,且AP ∶PQ ∶QC=1∶2∶3,点R 在BC 边上,且BR ∶RC=1∶2,AR 与BP 、BQ 分别相交于D 、E ,则S PQED ∶S △ABC = .10.整数x 、y 满足x xy y x 10244522<+++,则y x +的值是 .11.设abc d 是一个四位数,且满足d c ab d c b a ⋅==+++(ab 表示为两位数),则具有上述性质的最大四位数是 .12.已知m 、n 是正整数,且n m ≥.由mn 5个单位正方体组成长、宽、高顺次为m 、n 、5的长方体,将此长方体相交于某一顶点三个面涂色,若恰有一半的单位正方体各面都没有涂到颜色,则有序数组(m ,n )= .13.在△ABC 中,点D 、E 、F 顺次在边AB 、BC 、CA 上,设AB p AD ⋅=,BC q BE ⋅=,CA r CF ⋅=,其中p 、q 、r 是正数,且使32=++r q p ,52222=++r q p ,则S △DEF ∶S △ABC = .14.已知a 、b 、c 都是整数,且对一切实数x ,))((2)2002)((c x b x x a x --=---都成立,则这样的有序数组(a ,b ,c )共有 组.15.如图,I 是Rt △ABC (︒=∠90C )的内心,过I 作直线EF ∥AB ,分别交CA 、CB 于E 、F .已知m EI =,n IF =,则用m 、n 表示S △ABC = .答案:1.c<a<b ;2.8;3.-1;4.7;5.348+;6.81;7.2;8.-4;9.5∶24;10.-5;11.1863;12.(16,3)或(6,4);13.16∶45;14.4;15.)(2)(22222n m n m n m mn ++++.。
最新-上海市2018年“新知杯”初中数学竞赛试卷0181 精品
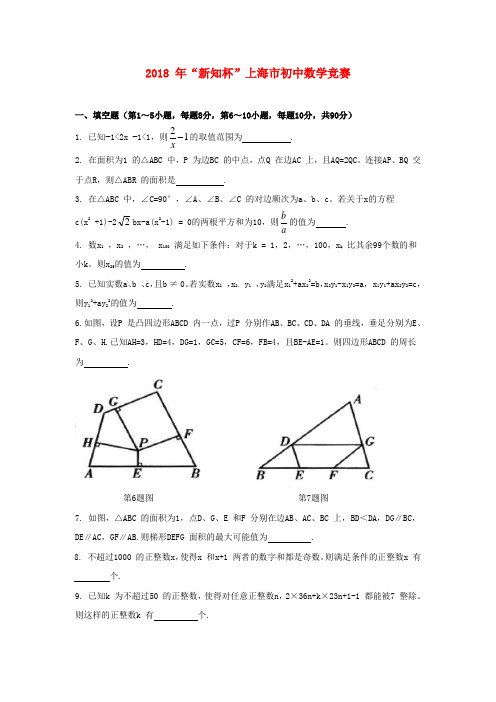
2018 年“新知杯”上海市初中数学竞赛一、填空题(第1~5小题,每题8分,第6~10小题,每题10分,共90分)1. 已知−1<2x −1<1,则12 x的取值范围为 . 2. 在面积为1 的△ABC 中,P 为边BC 的中点,点Q 在边AC 上,且AQ=2QC 。
连接AP 、BQ 交于点R ,则△ABR 的面积是 .3. 在△ABC 中,∠C =90°,∠A 、∠B 、∠C 的对边顺次为a 、b 、c 。
若关于x 的方程 c(x 2 +1)-22bx-a(x 2-1) = 0的两根平方和为10,则ab 的值为 . 4. 数x 1 ,x 2 ,…, x 100 满足如下条件:对于k = 1,2,…,100,x k 比其余99个数的和小k 。
则x 25的值为 .5. 已知实数a 、b 、c ,且b ≠ 0。
若实数x 1 ,x 2, y 1 ,y 2满足x 12+ax 22=b ,x 2y 1-x 1y 2=a , x 1y 1+ax 2y 2=c ,则y 12+ay 22的值为 .6.如图,设P 是凸四边形ABCD 内一点,过P 分别作AB 、BC 、CD 、DA 的垂线,垂足分别为E 、F 、G 、H.已知AH=3,HD=4,DG=1,GC=5,CF=6,FB=4,且BE-AE=1。
则四边形ABCD 的周长为 .第6题图 第7题图7. 如图,△ABC 的面积为1,点D 、G 、E 和F 分别在边AB 、AC 、BC 上,BD <DA ,DG ∥BC , DE ∥AC ,GF ∥AB.则梯形DEFG 面积的最大可能值为 .8. 不超过1000 的正整数x ,使得x 和x+1 两者的数字和都是奇数。
则满足条件的正整数x 有 个.9. 已知k 为不超过50 的正整数,使得对任意正整数n ,2×36n+k ×23n+1-1 都能被7 整除。
则这样的正整数k 有 个.10. 使得22)1(++p p 是完全平方数的所有质数p 为 . 二、(20 分)如图,在 Rt△ABC 中,∠C =90°,BC=2,AC=x ,点F 在边AB 上,点G 、H 在边BC 上,四边形EFGH 是一个边长为y 的正方形,且AE=AC.(1)求y 关于x 的函数解析式.(2)当x 为何值时,y 取到最大值?并求出y 的最大值.三、(20 分)求满足下列条件的正整数 n 的所有可能值:对这样的n ,能找到实数a 、b ,使得函数 b ax x nx f ++=21)(对任意整数x ,f (x )都是整数.四、(20 分)在一个盒子里有红、黄、黑三种颜色的小球共 88 个.已知从中任意取出24 个,就可以保证至少有10个小球是同色的.问在满足上述条件下,无论各种颜色的小球如何分配,至少要从盒子中任意取出多少个小球,才能保证至少有20 个小球是同色的?。
上海市各区2018届九年级中考二模数学试卷精选汇编:几何证明专题

上海市各区2018届九年级中考二模数学试卷精选汇编几何证明专题宝山区、嘉定区23.(本题满分12分,第(1)小题6分,第(2)小题6分)如图6,在正方形ABCD 中,点M 是边BC 上的一点(不与B 、C 重合),点N 在CD 边的延长线上,且满足︒=∠90MAN ,联结MN 、AC ,MN 与边AD 交于点E . (1)求证;AN AM =;(2)如果NAD CAD ∠=∠2,求证:AE AC AM ⋅=2.23.证明:(1)∵四边形ABCD 是正方形∴AD AB =,︒=∠=∠=∠=∠90BCD ADC B BAD ……1分 ∴︒=∠+∠90MAD MAB ∵︒=∠90MAN∴︒=∠+∠90MAD NAD ∴NAD MAB ∠=∠………1分 ∵︒=∠+∠180ADC ADN ∴︒=∠90ADN ……1分 ∴ADN B ∠=∠……………………1分 ∴△ABM ≌△ADN ………………………1分 ∴AN AM = ……………………………1分(2)∵四边形ABCD 是正方形 ∴AC 平分BCD ∠和BAD ∠ ∴︒=∠=∠4521BCD BCA ,︒=∠=∠=∠4521BAD CAD BAC ……1分 ∵NAD CAD ∠=∠2 ∴︒=∠5.22NAD∵NAD MAB ∠=∠ ∴︒=∠5.22MAB ………1分 ∴︒=∠5.22MAC ∴︒=∠=∠5.22NAE MAC ∵AN AM =,︒=∠90MAN ∴︒=∠45ANE图6图6∴ANE ACM ∠=∠…………………1分 ∴△ACM ∽△ANE …………1分 ∴ANACAE AM =……1分 ∵AN AM =∴AE AC AM ⋅=2…………1分长宁区23.(本题满分12分,第(1)小题5分,第(2)小题7分)如图,在四边形ABCD 中,AD //BC ,E 在BC 的延长线,联结AE 分别交BD 、CD 于点 G 、F ,且AG GF BE AD =.(1)求证:AB //CD ;(2)若BD GD BC ⋅=2,BG =GE ,求证:四边形ABCD 是菱形.23.(本题满分12分,第(1)小题5分,第(2)小题7分)证明:(1)∵BC AD // ∴BG DG BE AD = (2分)∵AG GFBE AD =∴AGGF BG DG = (1分) ∴ CD AB // (2分) (2)∵BC AD //,CD AB //∴四边形ABCD 是平行四边形 ∴BC=AD (1分) ∵ BD GD BC ⋅=2∴ BD GD AD ⋅=2即ADGDBD AD =又 ∵BDA ADG ∠=∠ ∴ADG ∆∽BDA ∆ (1分) ∴ABD DAG ∠=∠∵CD AB // ∴BDC ABD ∠=∠ ∵BC AD // ∴E DAG ∠=∠∵BG =GE ∴E DBC ∠=∠ ∴DBC BDC ∠=∠ (3分)ACDEF GB第23题图∴BC=CD (1分) ∵四边形ABCD 是平行四边形 ∴平行四边形ABCD 是菱形. (1分)崇明区23.(本题满分12分,第(1)、(2)小题满分各6分)如图,AM 是ABC △的中线,点D 是线段AM 上一点(不与点A 重合).DE AB ∥交BC 于点K ,CE AM ∥,联结AE .(1)求证:AB CMEK CK=; (2)求证:BD AE =.23.(本题满分12分,每小题6分) (1)证明:∵DE AB ∥∴ ABC EKC =∠∠ ……………………………………………………1分∵CE AM ∥∴ AMB ECK =∠∠ ……………………………………………………1分∴ABM EKC △∽△ ……………………………………………………1分 ∴AB BMEK CK=………………………………………………………1分 ∵ AM 是△ABC 的中线∴BM CM = ………………………………………………………1分∴AB CMEK CK=………………………………………………………1分 (2)证明:∵CE AM ∥ ∴DE CMEK CK=………………………………………………………2分 (第23题图)ABK MCDE又∵AB CMEK CK=∴DE AB = ………………………………………………………2分 又∵DE AB ∥∴四边形ABDE 是平行四边形 …………………………………………1分 ∴BD AE = ………………………………………………………1分奉贤区23.(本题满分12分,每小题满分各6分)已知:如图7,梯形ABCD ,DC ∥AB ,对角线AC 平分∠BCD , 点E 在边CB 的延长线上,EA ⊥AC ,垂足为点A . (1)求证:B 是EC 的中点;(2)分别延长CD 、EA 相交于点F ,若EC DC AC ⋅=2,求证:FC AC AF AD ::=.黄浦区23.(本题满分12分)如图,点E 、F 分别为菱形ABCD 边AD 、CD 的中点. (1)求证:BE =BF ;(2)当△BEF 为等边三角形时,求证:∠D =2∠A .ACD E图7B23. 证:(1)∵四边形ABCD为菱形,∴AB=BC=AD=CD,∠A=∠C,——————————————————(2分)又E、F是边的中点,∴AE=CF,——————————————————————————(1分)∴△ABE≌△CBF———————————————————————(2分)∴BE=BF. ——————————————————————————(1分)(2)联结AC、BD,AC交BE、BD于点G、O. ——————————(1分)∵△BEF是等边三角形,∴EB=EF,又∵E、F是两边中点,∴AO=12AC=EF=BE.——————————————————————(1分)又△ABD中,BE、AO均为中线,则G为△ABD的重心,∴1133OG AO BE GE===,∴AG=BG,——————————————————————————(1分)又∠AGE=∠BGO,∴△AGE≌△BGO,——————————————————————(1分)∴AE=BO,则AD=BD,∴△ABD是等边三角形,———————————————————(1分)所以∠BAD=60°,则∠ADC=120°,即∠ADC=2∠BAD. —————————————————————(1分)金山区23.(本题满分12分,每小题6分)如图7,已知AD 是△ABC 的中线, M 是AD 的中点, 过A 点作AE ∥BC ,CM 的延 长线与AE 相交于点E ,与AB 相交于点F . (1)求证:四边形AEBD 是平行四边形; (2)如果AC =3AF ,求证四边形AEBD 是矩形.23.证明:(1)∵AE //BC ,∴∠AEM =∠DCM ,∠EAM =∠CDM ,……………………(1分)又∵AM=DM ,∴△AME ≌△DMC ,∴AE =CD ,…………………………(1分) ∵BD=CD ,∴AE =BD .……………………………………………………(1分) ∵AE ∥BD ,∴四边形AEBD 是平行四边形.……………………………(2分)(2)∵AE //BC ,∴AF AEFB BC=.…………………………………………………(1分) ∵AE=BD=CD ,∴12AF AE FB BC ==,∴AB=3AF .……………………………(1分)∵AC=3AF ,∴AB=AC ,…………………………………………………………(1分) 又∵AD 是△ABC 的中线,∴AD ⊥BC ,即∠ADB =90°.……………………(1分) ∴四边形AEBD 是矩形.……………………………………………………(1分)静安区23.(本题满分12分,第(1)小题满分6分,第(2)小题满分6分) 已知:如图,在平行四边形ABCD 中, AC 、DB 交于点E , 点F 在BC 的延长线上,联结EF 、DF ,且∠DEF =∠ADC .EAFMD图7CA DE(1)求证:DBABBF EF =; (2)如果DF AD BD ⋅=22,求证:平行四边形ABCD 是矩形.23.(本题满分12分,第(1)小题6分,第(2)小题6分) 证明:(1)∵平行四边形ABCD ,∴AD //BC ,AB //DC∴∠BAD +∠ADC =180°,……………………………………(1分) 又∵∠BEF +∠DEF =180°, ∴∠BAD +∠ADC =∠BEF +∠DEF ……(1分) ∵∠DEF =∠ADC ∴∠BAD =∠BEF , …………………………(1分) ∵AB //DC , ∴∠EBF =∠ADB …………………………(1分)∴△ADB ∽△EBF ∴DB AB BF EF =………………………(2分) (2) ∵△ADB ∽△EBF ,∴BFBEBD AD =, ………………………(1分) 在平行四边形ABCD 中,BE =ED =BD 21∴221BD BE BD BF AD =⋅=⋅∴BF AD BD ⋅=22, ………………………………………(1分) 又∵DF AD BD ⋅=22∴DF BF =,△DBF 是等腰三角形 …………………………(1分) ∵DE BE =∴FE ⊥BD , 即∠DEF =90° …………………………(1分) ∴∠ADC =∠DEF =90° …………………………(1分) ∴平行四边形ABCD 是矩形 …………………………(1分)闵行区23.(本题满分12分,其中第(1)小题5分,第(2)小题7分)如图,已知在△ABC 中,∠BAC =2∠C ,∠BAC 的平分线AE 与∠ABC 的平分线BD 相交于点F ,FG ∥AC ,联结DG .(1)求证:BF BC AB BD ⋅=⋅; (2)求证:四边形ADGF 是菱形.CAB第23题图DE FABCFD23.证明:(1)∵AE 平分∠BAC ,∴∠BAC =2∠BAF =2∠EAC .∵∠BAC =2∠C ,∴∠BAF =∠C =∠EAC .…………………………(1分) 又∵BD 平分∠ABC ,∴∠ABD =∠DBC .……………………………(1分) ∵∠ABF =∠C ,∠ABD =∠DBC ,∴ABF CBD ∆∆∽.…………………………………………………(1分) ∴AB BFBC BD=.………………………………………………………(1分) ∴BF BC AB BD ⋅=⋅.………………………………………………(1分) (2)∵FG ∥AC ,∴∠C =∠FGB ,∴∠FGB =∠FAB .………………(1分)∵∠BAF =∠BGF ,∠ABD =∠GBD ,BF =BF ,∴ABF GBF ∆∆≌.∴AF =FG ,BA =BG .…………………………(1分) ∵BA =BG ,∠ABD =∠GBD ,BD =BD ,∴ABD GBD ∆∆≌.∴∠BAD =∠BGD .……………………………(1分) ∵∠BAD =2∠C ,∴∠BGD =2∠C ,∴∠GDC =∠C ,∴∠GDC =∠EAC ,∴AF ∥DG .……………………………………(1分) 又∵FG ∥AC ,∴四边形ADGF 是平行四边形.……………………(1分) ∴AF =FG .……………………………………………………………(1分) ∴四边形ADGF 是菱形.……………………………………………(1分)普陀区23.(本题满分12分)已知:如图9,梯形ABCD 中,AD ∥BC ,DE ∥AB ,DE 与对角线AC 交于点F ,FG ∥AD ,且FG EF =.(1)求证:四边形ABED 是菱形; (2)联结AE ,又知AC ⊥ED ,求证:212AE EF ED =.ABC DE FG图923.证明:(1)∵ AD ∥BC ,DE ∥AB ,∴四边形ABED 是平行四边形. ··························· (2分)∵FG ∥AD ,∴FG CFAD CA=. ·················································································· (1分) 同理EF CFAB CA = . ··································································································· (1分) 得FG AD =EF AB∵FG EF =,∴AD AB =. ··················································································· (1分) ∴四边形ABED 是菱形. ························································································· (1分) (2)联结BD ,与AE 交于点H .∵四边形ABED 是菱形,∴12EH AE =,BD ⊥AE . ····································· (2分) 得90DHE ∠= .同理90AFE ∠=.∴DHE AFE ∠∠=. ······························································································· (1分) 又∵AED ∠是公共角,∴△DHE ∽△AFE . ··················································· (1分)∴EH DEEF AE =. ········································································································ (1分) ∴212AE EF ED =. ······························································································ (1分) 青浦区23.(本题满分12分,第(1)、(2)小题,每小题6分)如图7,在梯形ABCD 中,AD ∥BC ,对角线AC 、BD 交于点M ,点E 在边 BC 上,且DAE DCB ∠=∠,联结AE ,AE 与BD 交于点F .(1)求证:2DM MF MB =⋅; (2)联结DE ,如果3BF FM =,求证:四边形ABED 是平行四边形.23.证明:(1)∵AD //BC ,∴∠=∠DAE AEB , ····························································· (1分)∵∠=∠DCB DAE ,∴∠=∠DCB AEB , ··········································· (1分)MFE DCBA图7∴AE //DC , ···································································································· (1分)∴=FM AMMD MC. ························································································· (1分) ∵AD //BC ,∴=AM DMMC MB, ····································································· (1分) ∴=FM DM MD MB, ························································································· (1分) 即2=⋅MD MF MB .(2)设=FM a ,则=3BF a ,=4BM a . ························································· (1分)由2=⋅MD MF MB ,得24=⋅MD a a ,∴2=MD a , ································································································ (1分) ∴3==DF BF a . ························································································ (1分) ∵AD //BC ,∴1==AF DFEF BF, ····································································· (1分) ∴=AF EF , ································································································· (1分) ∴四边形ABED 是平行四边形. ······································································ (1分)松江区23.(本题满分12分,第(1)小题满分7分,第(2)小题满分5分)如图,已知梯形ABCD 中,AB ∥CD ,∠D =90°,BE 平分∠ABC ,交CD 于点E , F 是AB 的中点,联结AE 、EF ,且AE ⊥BE .求证:(1)四边形BCEF 是菱形;(2)2BE AE AD BC ⋅=⋅.23.(本题满分12分,第(1)小题满分7分,第(2)小题满分5分) 证明:(1) ∵BE 平分∠ABC ,∴∠ABE =∠CBE …………………………………………………1分 ∵AE ⊥BE(第23题图)FACD EB∴∠AEB =90°∵F 是AB 的中点 ∴12EF BF AB ==………………………………………………1分 ∴∠FEB =∠FBE …………………………………………………1分∴∠FEB =∠CBE …………………………………………………1分∴EF ∥BC …………………………………………………1分∵AB ∥CD∴四边形BCEF 是平行四边形…………………………1分∵EF BF =∴四边形BCEF 是菱形……………………………………1分(2) ∵四边形BCEF 是菱形,∴BC =BF ∵12BF AB = ∴AB =2BC ………………………………………………1分∵ AB ∥CD∴ ∠DEA =∠EAB∵ ∠D =∠AEB∴ △EDA ∽△AEB ………………………………………2分∴AD AE BE AB = …………………………………………1分 ∴ BE ·AE =AD ·AB∴ 2BE AE AD BC ⋅=⋅…………………………………1分徐汇区23. 在梯形ABCD 中,AD ∥BC ,AB CD =,BD BC =,点E 在对角线BD 上,且DCE DBC ∠=∠.(1)求证:AD BE =;(2)延长CE 交AB 于点F ,如果CF AB ⊥,(第23题图)F A C D E B⋅=⋅.求证:4EF FC DE BD杨浦区23、(本题满分12分,第(1)小题6分,第(2)小题6分)已知:如图7,在□ABCD中,点G为对角线AC的中点,过点G的直线EF分别交边AB、CD 于点E、F,过点G的直线MN分别交边AD、BC于点M、N,且∠AGE=∠CGN。
上海市第02届“金桥杯”中学生初中数学知识应用竞赛初赛试题

上海市第02届“金桥杯”中学生数学知识应用竞赛初赛试题上海市第二届“金桥杯”中学生数学知识应用竞赛初赛于1993年3月举行,决赛在9月举行.【初赛试题】初赛试题共有十五题,其中一~十题,每题满分为10分;十一~十五题,每题满分为16分.满分为180分.一、为测量建造中的上海东方明珠电视塔已达到的高度.小明在学校操场某一直线上选择三点A、B、C,且AB=BC=60米,分别在A、B、C三点观察塔的最高点,测得仰角为45°,54.2°,60°,小明身高为1.5米,试问建造中的电视塔现在已达到的高度.(结果保留一位小数)二、已知边长为a的正三角形铁皮材料,剪去三个全等的四边形,如图3—14所示,可制成无盖的正三棱柱的盒子.试问如何剪裁才能使正三棱柱的体积最大?并求出体积最大值和此时材料利用率.三、某布店的一页帐簿上沾了墨水,如下图所示:所卖呢料米数看不清楚了,但记得是卖了整数米;金额项目只看到后面三个数码7.28,但前面的三个数码看不清楚了,请您帮助查清这笔帐.四、某出口加工区总公司与下属各子公司进行信息联网,已测得各子公司A、B、C、D、E、F、G、H、J之间与总公司S联网费用如图3—15所示(单位:千元).现拟设计一个联网优化方案,既要求各子公司之间与总公司都能连通,又要使联网费用最省,试问如何联网?费用是多少?五、在下乡劳动中,30个学生,每人拾了一篮稻穗放在田埂旁,每隔5米排成一列,不妨依次叫第1号、第2号、…、第30号,每人将篮中稻穗集中到第n号处(1≤n≤30),放在一起,然后带着空篮走回原处,试求使大家所走路程总和最小的n值.六、一半径R=150mm球形工件,打一斜孔如图3—16(a)所示,为了准确测量斜孔两端半径r1和r2,用两精密量球(半径R2=100mm和R2=80mm)以如图3—16(b)所示方式测量,测得两球外端水平距离L1=651.40mm;再将右端量球换为半径R3=80mm,左端量球不变仍为R2=80mm,又测得L2=610.17mm.(1)求r1和r2(结果保留两位小数);(2)求小孔的斜角α的值(结果保留分).七、A、B两个产地分别生产同一规格产品12千吨、8千吨,而D、E、F三地分别需要8千吨、6千吨、6千吨,每千吨的运价表如下:怎样确定调运方案,使总的运费为最小?八、在机械设计中,已知AB=AC=a,CD⊥BD,∠CAD=θ(图3—17),当θ为何值时,△BDC面积最大,并求出最大值.九、某一信托投资公司,考虑投资1600万元建造一座涉外宾馆,经预测,该宾馆建成后,每年底可获利600万元,试问三年内能否把全部投资收回?假设银行每年复利计息,利率为10%,若需要在三年内收回全部投资,每年至少应收益多少万元?(结果保留一位小数)十、在正方形铁皮上任意划9条直线,如果每一条直线都将正方形分成两部分面积之比为m∶n(m, n∈N),那么这样9条直线中至少有3条直线交于一点,对吗,为什么?十一、五种商品价格如下:现在用60元恰好选购10件商品,试问有哪几种选购方式?十二、根据图3—18所示零件的视图,画出它的直观图、展开图(并要留出做成模型的粘贴处),并求出这个零件的表面积与体积.一个供应站H的位置,使它到四个工厂距离和HA+HB+HC+HD为最小,说明道理,并求出最小值.十四、一个零件模具的底面由甲、乙、丙三个边长均为a的正方形按如下要求叠合而成:甲的一个顶点落在乙的中心上,乙的一个顶点落在丙的中心上,丙的一个顶点落在甲的中心上.求这个模具底面的面积.=270 mm,下底十五、一煤粉炉球磨机衬板为圆台的侧面,上底半径R1半径R=1147 mm,轴截面母线夹角为154°,这圆台侧面是由18块相同的2扇环形钢板焊接而成。
2018全国初中数学竞赛试题及参考答案

中国教育学会中学数学教学专业委员会 “《数学周报》杯”2018年全国初中数学竞赛试题答题时注意:1.用圆珠笔或钢笔作答; 2.解答书写时不要超过装订线; 3.草稿纸不上交.一、选择题<共5小题,每小题7分,共35分. 每道小题均给出了代号为A ,B ,C ,D 的四个选项,其中有且只有一个选项是正确的. 请将正确选项的代号填入题后的括号里,不填、多填或错填都得0分)1.设1a ,则代数式32312612a a a +--的值为( >.<A )24 <B )25 <C )10 <D )12+2.对于任意实数a b c d ,,,,定义有序实数对a b (,)与c d (,)之间的运算“△”为:<a b ,)△<c d ,)=<ac bd ad bc ++,).如果对于任意实数u v ,, 都有<u v ,)△<x y ,)=<u v ,),那么<x y ,)为( >.<A )<0,1) <B )<1,0) <C )<﹣1,0) <D )<0,-1)3.若1x >,0y >,且满足3y y xxy x x y==,,则x y +的值为( >.<A )1 <B )2 <C )92 <D )1124.点D E ,分别在△ABC 的边AB AC ,上,BE CD ,相交于点F ,设1234BDF BCF CEF EADF S S S S S S S S ∆∆∆====四边形,,,,则13S S 与24S S 的大小关系为( >.<A )1324S S S S < <B )1324S S S S = <C )1324S S S S > <D )不能确定5.设3333111112399S =++++,则4S 的整数部分等于( >. <A )4 <B )5 <C )6 <D )7 二、填空题<共5小题,每小题7分,共35分)6.若关于x 的方程2(2)(4)0x x x m --+=有三个根,且这三个根恰好可 以作为一个三角形的三条边的长,则m 的取值范围是 .7.一枚质地均匀的正方体骰子的六个面上的数字分别是1,2,2,3,3,4;另一枚质地均匀的正方体骰子的六个面上的数字分别是1,3,4,5,6,8. 同时掷这两枚骰子,则其朝上的面两数字之和为奇数的概率是 .8.如图,点A B ,为直线y x =上的两点,过A B ,两点分别作y 轴的平行线交双曲线1y x=<x >0)于C D ,两点. 若2BD AC =,则224OC OD - 的值为 .9.若y a ,最为b ,则22a b +的值为 .小值10.如图,在Rt △ABC 中,斜边AB 的长为35,正方形CDEF 内接于△ABC ,且其边长为12,则△ABC 的周长为 .三、解答题<共4题,每题20分,共80分)11.已知关于x 的一元二次方程20x cx a ++=的两个整数根恰好比方程20x ax b ++=的两个根都大1,求a b c ++的值.12.如图,点H 为△ABC 的垂心,以AB 为直径的⊙1O 和△BCH 的外接圆⊙2O 相交于点D ,延长AD 交CH 于点P ,求证:点P 为CH 的中点.<第12题)13.如图,点A 为y 轴正半轴上一点,A B ,两点关于x 轴对称,过点A 任作直线交抛物线223y x =于P ,Q 两点. <1)求证:∠ABP =∠ABQ ;<2)若点A 的坐标为<0,1),且∠PBQ =60o ,试求所有满足条件的直线PQ 的函数解读式.14.如图,△ABC 中,60BAC ∠=︒,2AB AC =.点P 在△ABC内,且52PA PB PC ===,,求△ABC 的面积.中国教育学会中学数学教学专业委员会“《数学周报》杯”2018年全国初中数学竞赛试题参考答案一、选择题 1.A解:由于1a =-,1a +=, 262a a =-, 所以 2.B解:依定义的运算法则,有ux vy u vx uy v +=⎧⎨+=⎩,,即(1)0(1)0u x vy v x uy -+=⎧⎨-+=⎩,对任何实数u v ,都成立. 由于实数u v ,的任意性,得<x y ,)=<1,0).3.C解:由题设可知1y y x -=,于是341y y x yx x -==,<第13题)<第14题)所以 411y -=, 故12y =,从而4x =.于是92x y +=.4.C解:如图,连接DE ,设1DEF S S ∆'=,则1423S S EF S BF S '==,从而有1324S S S S '=.由于11S S '>,所以1324S S S S >.5.A解:当2 3 99k =,,,时,由于()()()32111112111k k k k k k k ⎡⎤<=-⎢⎥-+-⎣⎦, 所以 3331111115111239922991004S ⎛⎫<=++++<+-< ⎪⨯⎝⎭. 于是有445S <<,故4S 的整数部分等于4.二、填空题 6.3<m ≤4解:易知2x =是方程的一个根,设方程的另外两个根为12 x x ,,则124x x +=,12x x m =.显然1242x x +=>,所以122x x -<, 164m ∆=-≥0,即2<,164m ∆=-≥0,所以2<, 164m ∆=-≥0,解之得 3<m ≤4.7.19解:在36对可能出现的结果中,有4对:<1,4),<2,3),<2,3),<4,1)的和为5,所以朝上的面两数字之和为5的概率是41369=. 8.6解:如图,设点C 的坐标为a b (,),点D 的坐标为c d (,),则点A 的坐标为a a (,),点B 的坐标为.c c (,) 由于点C D ,在双曲线1y x=上,所以11ab cd ==,.由于AC a b =-,BD c d =-, 又由于2BD AC =,于是 所以 22224826a b c d ab cd +-+=-=()(), 即224OC OD -=6.9.32解:由1x -≥0,且12x -≥0,得12≤x ≤1.21122y =+=+ 由于13124<<,所以当34x =时,2y 取到最大值1,故1a =. 当12x =或1时,2y 取到最小值12,故2b =.所以,2232a b +=. 10.84解:如图,设BC =a ,AC =b ,则22235a b +==1225. ①又Rt △AFE ∽Rt △ACB ,所以FE AFCB AC=,即1212b a b-=,故 12()a b ab +=. ② 由①②得2222122524a b a b ab a b +=++=++()(),解得a +b =49<另一个解-25舍去),所以493584a b c ++=+=.三、解答题11.解:设方程20x ax b ++=的两个根为αβ,,其中αβ,为整数,且α≤β,则方程20x cx a ++=的两根为11αβ++,,由题意得()()11a a αβαβ+=-++=,,两式相加得 2210αβαβ+++=, 即 (2)(2)3αβ++=,所以 2123αβ+=⎧⎨+=⎩,; 或232 1.αβ+=-⎧⎨+=-⎩,解得 11αβ=-⎧⎨=⎩,; 或53.αβ=-⎧⎨=-⎩,又由于[11]a b c αβαβαβ=-+==-+++(),,()(),所以 012a b c ==-=-,,;或者8156a b c ===,,,故3a b c ++=-,或29.12.证明:如图,延长AP 交⊙2O 于点Q ,连接 AH BD QB QC QH ,,,,. 由于AB 为⊙1O 的直径, 所以∠ADB =∠BDQ =90°, 故BQ 为⊙2O 的直径.于是CQ BC BH HQ ⊥⊥,. 又由于点H 为△ABC 的垂心,所以.AH BC BH AC ⊥⊥,所以AH ∥CQ ,AC ∥HQ ,四边形ACQH 为平行四边形. 所以点P 为CH 的中点.13.解:<1)如图,分别过点P Q , 作y 轴的垂线,垂足分别为C D , .设点A 的坐标为<0,t ),则点B 的坐标为<0,-t ).设直线PQ 的函数解读式为y kx t =+,并设P Q ,的坐标分别为 P P x y (,),Q Q x y (,).由得 2203x kx t --=, 于是 32P Q x x t =-,即 23P Q t x x =-.于是222323P P Q Qx t y t BC BD y t x t ++==++22222()333.222()333P P Q P P Q P Q Q P Q Q Q P x x x x x x x x x x x x x x --===--- 又由于P Q x PC QD x =-,所以BC PCBD QD=. 由于∠BCP =∠90BDQ =︒,所以△BCP ∽△BDQ , 故∠ABP =∠ABQ .<2)解法一 设PC a =,DQ b =,不妨设a ≥b >0,由<1)可知∠ABP =∠30ABQ =︒,BC,BD,所以 AC2-,AD=2.由于PC ∥DQ ,所以△ACP ∽△ADQ . 于是PC ACDQ AD=,即a b =,所以a b +=.由<1)中32P Q x x t =-,即32ab -=-,所以32ab a b =+=,于是可求得2a b ==将b =代入223y x =,得到点Q 的坐标,12).再将点Q 的坐标代入1y kx =+,求得k = 所以直线PQ的函数解读式为1y =+. 根据对称性知,所求直线PQ的函数解读式为13y x =-+,或13y x =+. 解法二 设直线PQ 的函数解读式为y kx t =+,其中1t =. 由<1)可知,∠ABP =∠30ABQ =︒,所以2BQ DQ =.故2Q x =将223Q Q y x =代入上式,平方并整理得 4241590Q Q x x -+=,即22(43)(3)0Q Q x x --=.所以Q x =又由 (1>得3322P Q x x t =-=-,32P Q x x k +=.若Q x =代入上式得P x = 从而2()3P Q k x x =+=.同理,若Q x =可得P x = 从而2()3P Q k x x =+=.所以,直线PQ的函数解读式为1y =+,或1y +. 14.解:如图,作△ABQ ,使得QAB PAC ABQ ACP ∠=∠∠=∠,,则△ABQ ∽△ACP .由于2AB AC =,所以相似比为2. 于是224AQ AP BQ CP ====.60QAP QAB BAP PAC BAP BAC ∠=∠+∠=∠+∠=∠=︒.由:2:1AQ AP =知,90APQ ∠=︒,于是3PQ ==.所以 22225BP BQ PQ ==+,从而90BQP ∠=︒.于是222()28AB PQ AP BQ =++=+ .故 21sin 602ABC S AB AC AB ∆=⋅︒==. 申明:所有资料为本人收集整理,仅限个人学习使用,勿做商业用途。
2018年初中数学联赛试题参考答案和评分标准word版

2018年初中数学联赛试题参考答案及评分标准说明:评阅试卷时,请依据本评分标准•第一试,选择题和填空题只设7分和0分两档;第二试各题, 请按照本评分标准规定的评分档次给分•如果考生的解答方法和本解答不同,只要思路合理,步骤正确,在评卷时请参照本评分标准划分的档次,给予相应的分数第一试(A)一、选择题:(本题满分42分,每小题7分)21.设二次函数y x 2ax 22a的图象的顶点为A,与x轴的交点为B, C •当△ ABC为等边三角形时,其边长为A. 6 .%【答】C.由题设知A( a, 弩).设B(x ,0) , C(x ,0),二次函数的图象的对称轴与2 1 2x轴的交点为D,则BC | x1 x21X)224x x1 2又AD _3 BC,则|2所以,△ ABC的边长BC 2a22a2.a2a2(舍去)ABCD2.如图,在矩形中, BAD BD的平分线交于点,AB CAE 15 BE,则CJ ,J2 1. D. 1.3【答】D.延长AE交BC于点F,过点由已知得EBH ACB BAF30 .FADE作BC的垂线,垂足为H .AFB HEF 45 , BF ABE-、—AC设BE x,则2 HF HE x , BH W3x .2因为BF BH HF ,所以3x122x,解得x 3 1.所以BE2 3.设p,q均为大于3的素数,则使p25pq 4q为完全平方数的素数对(p, q)的个数为(A.1 . 【答】B. B.2.C.3.D.4.2 2 2设p 5 pq 4q m ( m 为自然数) (m p 2q)(m p 2q) pq .【答】C.0的整数组(x, y, z)的个数为由对称性,同样可得由于p, q 为素数,且 m p 2q p, m p 2q q ,所以 m p 2q 1 , m p 2q pq ,从而 pq 2 p 4q 1 0,即(p 4)(q 2) 9,所以(p, q)(5,11)或(7, 5).所以,满足条件的素数对 (p, q)的个数为 2.4.若实数 a, b 满足a2,2(1 a)2b(1 b)2 4a A.46 .B.64.C.82.D.128.(y @ z) @ x xy z xy yz zx xyz , (z @ x) @ yz xyyz zx xyz .所以,由已知可得x y z xy yz zx xyz0,即(x 1)( y1)(z 1)1.所以,x, y, z 为整数时,只能有以下几种情况:1, x 11, x 11, 1, 或 y11, 或 y11,或1, 1,z 1所以, 1, z 11, z 11, (x, y, z) (2,2,0)或(2,0,2)或(0,2,2)或(0,0,0),故共有4个符合要求的整数组.1,2 ,则(p 2q)2 pq m 2 , 即(1由条件—ba)2(1b)22 22a 2 2b 2 4aba 3b 3 0,2即(a b) 2[(a b)2 4ab] (a2 b)[(a b)23ab]又 a b 2,所以 22[4 4ab] 2[43ab] 0 ,解得 ab1.所以 a 2 b 2 (ab)22ab 6 ,a 3b 3 ( a b)[( a b)23ab] 14, a 5 b 5 (a 22 3 32 2 b 2 )(a3 b 3)a 2b 2(a b) 82.5.对任意的整数x, y ,定义x@ y xxy , 则使得 (x@y) @z(y@z) @x (z@x) @yA.1 . 【答】D.B.2 .C.3 .D.4.(x @ y) @ z (x y xy) @ z (x y xy) (x yxy)z z xyyz zx xyz ,1_£ 2018 2019 B.61 •_£2020C.62•因为 M 2018133,所以 M 1~~201833 61 335.__ 1 ___ 1 __ 1 1345 ■^050 ) -2030 13^050 20 83230 ,1 83230 1185 1 所以M 1345 61 1345,故M 的整数部分为61.、填空题:(本题满分 28分,每小题7 分)1.如图,在平行四边形 ABCD 中,BC 2AB ,CE AB 于E ,F 为AD 的中点,若 AEF48, 则 B ___ •【答】84 .设BC 的中点为G ,连结FG 交CE 于H ,由题设条件知 FGCD 为菱形•由AB // FG // DC 及F 为AD 的中点,知H 为CE 的中点• 又CE AB ,所以CE FG ,所以FH 垂直平分CE ,故 DFC GFC EFG AEF 48 . 所以 B FGC 180 2 48 84 •3 115 k 3孙三k 3 4k15 26•设M A.60 • 【答】B.-,则」的整数部分是 2050 MD.63 •又 M (丽^1^^12030才(203T120324(x y ) 15,则x y 的最大值为2由X 3y 3(x42(X y )( x xy令X y k ,注又因为x 2xy15可得(x y )( X 2152 .14(x y)2xy(X3Xyy 2) 11 X y) 1「即2y )2 43y 214 0,故由①式可得k 3 _3xyk _14 k152,所以xy A FG2.若实数 X, y 满足【答】3.117)x 2于是,x, y可看作关于t的一元二次方程t 2 ktk3 1k 坐(k ) 2 4 ——4 ---------- 2 0 ,3k3 2化简得k 3 k 30 0,即(k 3)(k 2 3k 10) 0,所以0 k 3.故x y的最大值为3.3. __________________________________________________ 没有重复数字且不为5的倍数的五位数的个数为__________________________________________________________ .【答】21504.显然首位数字不能为0,末位不能为0和5.当首位数字不为5时,则首位只能选0,5之外的8个数•相应地个位数只能选除0,5及万位数之外的7 个数,千位上只能选万位和个位之外的8个数,百位上只能选剩下的7个数,十位上只能选剩下的6个数•所以,此时满足条件的五位数的个数为8 7 8 7 6 18816个•当首位数字为5时,则个位有8个数可选,依次千位有8个数可选,百位有7个数可选,十位有6个数可选•所以,此时满足条件的五位数的个数为8 8 7 6 2688个•所以,满足条件的五位数的个数为18816 2688 21504 (个).5.55222 a b c4. 已知实数a,b, c满足a b c 0 ,a be 1 ,则-abc【答】5 .21 2222 13 3 3由已知条件可得ab bc ca 2 [(a b c)2 (a2 b2 c2)] 2,a b3 c 3abc,所以a5 b55,2.2 2、/ 3 .3c (a b c )(a b c3) [a2 (b3c3) .2/3 3、b (ac )2 3 3c (a b )]3abc [a2b2 ( a b) a2 c2 ( a c ) b 2 c2 (b c)] 2 23abc (abc2 2 2 2 a c bb c a)3abc 1 abc(ab bc ca) 3abc 2abc-5c K2 abc5a b c 5所以—abc 2第一试(B)一、选择题:(本题满分42分,每小题7分)2 x21.满足(x x 1) 1的整数x的个数为A.1 .B.2C.3.【答】C.当x 220 且x2.x 1 0 时,x 2.当x2x 1 1时,x 2 或x 1.当x2x 1 1且x 2为偶数时,x 0.所以,满足条件的整数x有3个.2.已知x1,x2,x3( X1X2 x3 )为关于x的方程x 34x1 X12 x22 X32A.5 .B.6C.7 .( ) D.4 .3 X2 ( a 2) x a 0的三个实数根,则( ) D.8 .【答】A.2 方程即(x 1)(x 2x a ) 0,它的一个实数根为 1,另外两个实数根之和为 2,其中必有一根小 于1,另一根大于1,于是x 2 1, x l x 3 2,故 (x 3x )( x 3x ) 2( x x 1 ) 2( x x ) 1 5 . 3 13.已知点E , F 分别在正方ABCD 的边 CD , AD 上, CD 4CE , EFB tan ABF A. 1 . B. 3 . C. & . D. ■ 3 .2 5 2 2【答】B.FBC ,贝U 不妨设CD 4,则CE 1, DE 3.设DF x 」U AF 4 x , EF J x 29 .作BH EF 于H .因为 EFB FB C AFB :, BAF △ BAF ^△BHF ,所以 BH BA 4.由SSS SS 得四边形ABF BEF DE F BCEABCD2 1 42 - 4 2 4 (4 x) 1 2 4 x 2 9 1 2 31x 2 41,解得x 8512AF 3所以AF 4 x 5 ,tan ABF AB 5 .4.方程3 x 3 x 的实数根的个数为 ( )A.0 .B.1 .C.2.D.3.【答】B. 90 BHF , BF 公共,所以FB令y 9 x ,则y 0 ,且x y 2 9,原方程变为它3 y 』y 2 9,解得y6,从而可得x 8或x 27 . 检验可知: x 8是增根,舍去;x 27是原方程的实数根. 所以,原方程只有1个实数根 5.设a, b, c 为三个实数,它们中任何一个数加上其余两数之积的 2017倍都等于2018,则这样的三元数组(a, b, c )的个数为A.4 .B.5.【答】B. C.6 . D.7.由已知得,a 2017bc 2018, b2017ac 2018, c 2017ab2018,两两作差,可得(a b)(12017c) 0 , (b c)(12017a) 0 , (c a)(12017b) 0 .1由(a b)(1 2017c) 0,可得a b 或c~2017 .(1 )当a b c 时,有2017a2 a 2018 0,解得 a 1 或a 20182017(2 )当a b c 时,解得a b ___ L , c 2018 12017 2017(3)当a b时,c 1,此时有:a 1 , b 2018 1,或a 2018 1 , b 12017 2017 2017 2017 2017 故这样的三元数组(a, b, c)共有5个.3 6.已知实数a, b满足a2 33a2 5a 1, b33b25b5,则a b ()A.2 .B.3 .C.4 .D.5【答】A.有已知条件可得(a 1)32(a 1) 2 , (b 1)32(b1)2,两式相加得(a 1) 32( a 1) (b 1) 32(b 1)因式分解得(a b 2)[( a 1) 2 ( a 1)b 1) (b 1) 22] 0 . 因为2(a 1)2 (a 1)(b 1)2(b 1)2 2 [(a 1)1 2(b 1)]23 (b 1)2 2 0 ,2 4所以a b 2 0,因此 a b 2.二、填空题:(本题满分28分,每小题7分)1.已知p, q, r为素数,且pqr 整除pq qr rp 1,则p q r .【答】10 .设k p qr rp 1 1 1 1 1 由题意知k是正整数,又p, q, r 2,所以k 3,从pqr p q r pqr 2而k 1 ,即有pq qr rp 1pqr,于F是可知p, q, r互不相等.当2 p q r 时,pqr pq qr rp 1 3qr,所以q 3,故q 2 .于是2qr qr 2q 2r 1,故(q 2)(r 2) 3,所以q 2 1, r 2 3,即q 3, r 5 ,所以,(p, q, r) (2,3,5).再由p, q, r的对称性知,所有可能的数组(3,5,2),(p, q, r)共有6组,即(2,3,5) , (2,5,3) , (3,2,5), (5,2,3) , (5,3,2).于是p q r 10.2.已知两个正整数的和比它们的积小 1000,若其中较大的数是完全平方数,则较小的数为 _____________ .【答】&2 2 Q Q设这两个数为 m , n (m n),贝U m n mn 1000,即(m 21)( n 1) 1001.又 10011001 1 143 7 91 1177 13,所以(m 21, n 1) = (1001,1)或(143, 7)或(91,11)2 2或(77,13),验证可知只有(m 2 1, n 1) (143,7)满足条件,此时 m 2 144, n 8 .3 .已知D 是厶ABC 内一点,E 是AC 的中点,AB 6 , BC 10 , BAD BCD ,EDC ABD ,贝U DE ________ .【答】4.延长CD 至F ,使DF DC ,贝U DE // AF 且DE 丄AF ,2所以 AFD EDC ABD ,故A, F, B, D 四点共圆,于是整数对(m, n)的个数为【答】16.综合可知:符合条件的正整数对 (m, n)有 8+ 4 + 2+1 + 1 = 16 个.2 2 21)]2 4(m 2 4n 250) 0 ,整理得因为二次函数的图象在 x 轴的上方,所以 514n 49,即(m 1)(2n 1)2 .因为 m, n 为正整数,所以(m 1)(2n 1)25 .2n 1 彳5?,故 n 5. [2(m 2n4mn 2m 1 2,所以 1时, _53, 故亍223,符合条件的正整数对 (m, n)有8 个;2时, 5,故m4,符合条件的正整数对(m, n)有4个;3时, 257 ,m — 187,符合条件的正整数对(m, n)有2 个; 4时, 25 m —179,符合条件的正整数对(m, n)有1 个;5时,1125,故m 1411 ,符合条件的正整数对 (m, n)有1个.BFDBAD BCD ,所以 BF BC 10,且 BD FC ,故 FABFDB 90 .又AB 6,故 AF . 102628,所以DE 丄 AF 4 .24.已知二次函数yx 22(m 2n 1)x(m 2 4n 250)的图象在x 轴的上方,则满足条件的正第二试 (A )、(本题满分 2 20分)设a, b, c, d 为四个不同的实数,若 a, b 为方程x 10cx 11d 0的根,c, d c d 的值. a b 2 为方程x 10ax 11b 0的根,求 解由韦达定理得 10c , 10a ,两式相加得 abed 10(a c). 2 因为a 是方程x 2 10cx 11d0的根, 2 所以a 2 10ac 11d 0 ,又 d 10a c ,所以 2a 2110a 11c10ac10分 2类似可得c 2110c 11a 10ac 0.15分①一②得(a ©(a c 121) 0 .因为a c ,所以ac 121,所以a10(a c) 1210 .20分二、(本题满分25分)如图,在扇形 OAB 中, AOB 4,点D 为OB 的中点,点E 为弧AB 上的动点,OE 与CD 的交点为F . (1 )当四边形 (2)求 CE 90,OA 12,点 C 在 OA 上, AC分别过 由ODODEC 的面积S 最大时,求EF ; 2DE 的最小值. O, E 作CD 的垂线,垂足为 M , N .6, OC 8,得 CD 10.所以OCD S ECD-' CD (OM EN )^2 CD OE _12 10 12 60, 当OEDC 时,S 取得最大值60.此时,EF OE OF12 -(2)延长 OB 至点G,使BG因为ODOE 」, DOE OEOG2所以CE 2DECE EG故CE 2DE 的最小值为& 10.OB 6 8 10 CG36 512,连结 GC,GE .E\ M F :” h” NJ !*____G10分EOG ,所以△ ODE OEG ,所以 DE 1,故 EG 2DE . EG 220分242 82 8 10,当C, E, G 三点共线时等号成立.25分2018年初中数学联赛试题参考答案及评分标准第11页(共10页)三、(本题满分25分)求所有的正整数 m, n ,使得33 2 2m n m n(m n)22 2 2 S (m n)[(m n)3mr] m n (m n)2第二试 (B )、 (本题满分20分)若实数a, b, c 满足(a b (a bc)(1」〕)的值.a bc解 记a bc x , ab bc ca y ,abc111(ab c)(ab 5c b c 5a c a 5b )x[3x 212(a b c)x36(ab bc ca )]c)(11 1 ) -9,求a b 5c b c 5a c a 5b 5z ,则11 1x( x 6ax 6b x 6c ) x (9 x 236》m 3 rh m 2 n 2因为 m, n 为正整数,故可令mnm np, q 为正整数,且 (p, q) 1. S (m n)凹 P 厘(mP 2n)3 pq q 2 2P因为 S 为非负整数,所以2P I q ,又(P, q)1,故 P 1,(m n) | mn .①10分所以mn n是整数,所以(m n) | n 2,故n 22 ,即 n mn .又由m 3 n 3 m 2n 2n 3m 2n 2m 3 所以 由对称性,同理可得mm 2 (n 2 故m m) m 2n , n . 所以20分n 代入①,得2 | m , n 代入②,得2m 34m 4 0,即 m2.所以, 满足条件的正整数m, n 为m25分3 2 x 6(a b c)x 36(ab be ca)x 216abc 5 x 336xy 216Z , ........................... 10分---------------- 是非负整数.(m n)竺£ ( mn )2 .m nm n2018年初中数学联赛试题参考答案及评分标准第10页(共10页)2结合已知条件可得 一x( 9X _361) 9,整理得xy ^Zz .所以 36xy 216z 5 2 5 x 3(a b c)(l a 1) xy z 27 2 20分 二、(本题满分 角形,AB AC , 25分) 如图, DE DC . 点E 在四边形 ABCD 的边AB 上,△ ABC 和厶CDE 都是等腰直角三 ACE 30,求 DP . (1 )由题意知ACB DCE 45 , BC .:2AC , EC 2DC, DCAECAC DC ,所以△ ADC BEC ,故 DAC BC EC45,所以 DAC ACB ,所以 AD // BC .10分 2 )设 AE x , 因为 ACE 30,可得 AC 3x , CE2x , DE 设AC 与DE 交于点P ,如果 (1)证明:AD // BC ;( 2) EBC 解 所以 PE DC 因为 EAP CDP 90 , EPA CPD ,所以△ APE DPC ,故可得 S APE — 12 S DPC •15分EPC S APES ACE —fx 2 , S EPC S DPC S CDE x 2,于是可得S DPCDPCA2S EPC (3 1)x .(2S 20分 25分PESEPC-个四位数,x 的各位数字之和为 m , x 1的各位数字之和为2的素数.求x .n ,并解 设xabcd , 由题设知 m 与n 若d9,则nm 1 ,所以(m, 若c9 ,则n m 1 9 m 8若b 9, 显然a 9, 所以n m13 , m n 26 39 36 ,矛盾. 若b 9 , 则n m 1 9 9 m于是可得x 8899 或 9799.故(m, n) n 的最大公约数 n) 1,矛盾, 1 9 9 三、(本题满分25分)设x 是 且m 与n 的最大公约数是一个大于(m, n)为大于2的素数.(m,8),它不可能是大于 2的素数,矛盾,故 c 9 .9 m 26,17,故 ( m, n) ( m,17) 10分故(m, n) ( m, 26) 13,但此时可得17 ,只可能 n 17, m 34 .15分20分 25分。
上海市第二届“金桥杯”中学生数学知识应用竞赛试题及简解

上海市第二届“金桥杯”中学生数学知识应用竞赛试题及简解余致甫
【期刊名称】《数学教学》
【年(卷),期】1994(000)001
【摘要】由上海市少年科技站、上海市工业与应用数学学会、上海金桥出口加工区联合发展有限公司联合举办的上海市第二届中学生数学知识应用竞赛已于93年9月中旬举行了决赛。
这次竞赛中,大同中学、市西中学、加定一中、华师大二附中、外语附中、华师大一附中等六所学校荣获团体前六名。
【总页数】3页(P31-33)
【作者】余致甫
【作者单位】上海师大数学系
【正文语种】中文
【中图分类】G633.6
【相关文献】
1.2001年上海市第十届中学生数学知识应用竞赛(初赛试题) [J], 唐明元;王镇;陈敢
2.第二届北京市高中学生数学知识应用竞赛初赛试题和解答 [J],
3.上海市第五届“浦东金桥杯”中学生数学知识应用竞赛决赛试题及简解 [J], 丁颂康[1];王镇[2]
4.上海市第六届“浦东金桥杯”——中学生数学知识应用竞赛试题及简解 [J], 蒋
鲁敏[1];王镇[2]
5.上海市第三届“浦东金桥杯”中学生数学知识应用竞赛试题及简解 [J], 余致甫因版权原因,仅展示原文概要,查看原文内容请购买。
最新-2018年上海市高中数学竞赛(杯)试卷 精品

2018年上海市高中数学竞赛(CASIO 杯)试卷(2018年3月27日 星期日 上午8:30~10:30)【说明】解答本试卷不得使用计算器一、填空(前4小题每小题7分,后4小题每小题8分,共60分) 1.计算:0!1!2!100!i +i +i ++i = .(i 表示虚数单位)2.设θ是某三角形的最大内角,且满足sin 8sin 2θθ=,则θ可能值构成的集合是 .(用列举法表示)3.一个九宫格如图,每个小方格内都填一个复数,它的每行、每列及对角线上三个格内的复数和都相等,则x 表示的复数是 .4.如图,正四面体ABCD 的棱长为6cm ,在棱AB 、CD 上各有一点E 、F ,若1AE =cm ,2CF =cm ,则线段EF 的长为 cm .5.若关于x 的方程4(3)250x xa ++⋅+=至少有一个实根在区间[1,2]内,则实数a 的取值范围为 .6.a 、b 、c 、d 、e 是从集合{}1,2,3,4,5中任取的5个元素(允许重复),则abcd e +为奇数的概率为.7.对任意实数x 、y ,函数()f x 满足()()()1f x f y f x y xy +=+--,若(1)1f =,则对负整数n ,()f n 的表达式.8.实数x 、y 、z 满足0x y z ++=,且2221x y z ++=,记m 为2x 、2y 、2z 中最大者,则m 的最小值为 . 二、(本题满分14分)设()f x =a 的值:至少有一个正数b ,使()f x 的定义域和值域相同.i x 1A B FDE三、(本题满分14分)已知双曲线22221x y a b-=(a 、b ∈+R )的半焦距为c ,且2b ac =.,P Q 是双曲线上任意两点,M 为PQ 的中点,当PQ 与OM 的斜率PQ k 、OM k 都存在时,求PQ OM k k ⋅的值. 四、(本题满分16分)设[]x 表示不超过实数x 的最大整数.求集合2|,12004,2005k n n k k ⎧⎫⎡⎤⎪⎪=≤≤∈⎨⎬⎢⎥⎪⎪⎣⎦⎩⎭N 的元素个数.五、(本题满分16分)数列{}n f的通项公式为1122n nn f ⎡⎤⎛⎛⎢⎥=- ⎢⎥⎝⎭⎝⎭⎣⎦,n ∈+Z . 记1212C +C ++C nn n n n n S f f f =,求所有的正整数n ,使得n S 能被8整除.。
年历年上海市初中数学竞赛试卷及答案

2013上海市初中数学竞赛(新知杯)(2013年12月8日 上午9:00~11:00)1.已知721,721-=+=b a ,则.________33=-+-b b a a2.已知43214321//////,//////m m m m l l l l ,._______,20,100===EFGH ILKJ ABCD S S S 则3.已知F E AC AB A 、,,8,690==︒=∠在AB 上且3,2==BF AE 过点E 作AC 的平行线交BC 于D ,FD 的延长线交AC 的延长线于G ,则.__________=GF4.已知凸五边形的边长为)(,,,,,54321x f a a a a a 为二次三项式;当1a x =或者5432a a a a x +++=时,5)(=x f ,当21a a x +=时,,)(p x f =当543a a a x ++=时,q x f =)(,则.________=-q p 5.已知一个三位数是35的倍数且各个数位上数字之和为15,则这个三位数为___________. 6.已知关于x 的一元二次方程0)2)(1(2=++++m m ax x 对于任意的实数a 都有实数根,则m 的取值范围是_________________.7.已知四边形ABCD 的面积为2013,E 为AD 上一点,CDE ABE BCE ∆∆∆,,的重心分别为321,,G G G ,那么321G G G ∆的面积为________________.8.直角三角形斜边AB 上的高3=CD ,延长DC 到P 使得2=CP ,过B 作AP BF ⊥交CD 于E ,交AP 于F ,则._________=DE二、解答题(第9题、第10题15分,第11题、第12题20分) 9.已知︒=∠90BAC ,四边形ADEF 是正方形且边长为1,求CABC AB 111++的最大值. 10.已知a 是不为0的实数,求解方程组:⎪⎪⎩⎪⎪⎨⎧=-=-ax y xy a yxxy 111.已知:,1>n n a a a a ,,,,321Λ为整数且2013321321=⋅⋅⋅⋅=++++n n a a a a a a a a ΛΛ,求n 的最小值.12.已知正整数d c a 、、、b 满足),13(),13(22-=+=d c b d c a 求所有满足条件的d 的值. 答案:1.27102- 3.265 6.12-≤≤-m 7.3671 8.599.CA BC AB 111++4221+≤ 10.经检验原方程组的解为:⎪⎩⎪⎨⎧+=+=1122a y a a x ,⎪⎩⎪⎨⎧+-=+-=1122a y a a x .11.【解析】2013,1,1,554321===-===a a a a a n 当满足题设等式,下证当4≤n 时,不存在满足等式要求的整数,不妨设n a a a a ≤≤≤≤Λ321,(1)当4=n 时,611132013⨯⨯=,当4321,,,a a a a 中有负整数时,必为⎩⎨⎧==+⇒-==20132015,1434321a a a a a a ,若2013,143==a a 不满足条件,当20152671,344343<≤+⇒≤⇒≥a a a a a 无解.不可能,当4321,,,a a a a 中无负整数时,显然20134≠a ,6714≤a ,容易验证等式不可能成立.(2)当3=n 时,当321,,a a a 中有负整数时,必为,121-==a a 显然等式不成立,当321,,a a a 中无负整数时,同上容易验证等式不可能成立.(3)当2=n 时,21,a a 均为正整数,同上易验证等式不可能成立. 综上所述,n 的最小值为5. 12.85=d2013上海新知杯初中数学竞赛答案2012年(新知杯)上海市初中数学竞赛试卷(2012年12月9日 上午9:00~11:00)一、 填空题(每题10分,共80分)1. 已知的边上的高为,与边平行的两条直线将的面积三等分,则直线与之间的距离为_____________。
2018年全国初中数学联赛试题参考答案和评分标准 精品

2018年全国初中数学联赛试题参考答案和评分标准精品2018年全国初中数学联合竞赛试题参考答案及评分标准说明:评阅试卷时,请依据本评分标准。
第一试,选择题和填空题只设7分和0分两档;第二试各题,请按照本评分标准规定的评分档次给分。
如果考生的解答方法和本解答不同,只要思路合理,步骤正确,在评卷时请参照本评分标准划分的档次,给予相应的分数。
第一试一、选择题:(本题满分42分,每小题7分)1.已知$a=1+\frac{1}{2+1}$,$b=3-2$,$c=6-2$,那么$a,b,c$的大小关系是()A。
$a<b<c$B。
$a<c<b$XXX<a<c$D。
$b<c<a$答】C.因为 $\frac{1}{2+1}=\frac{1}{3}$,所以$a=1+\frac{1}{3}=\frac{4}{3}$,$b=1$,$c=4$。
因为 $\frac{1}{3}<1$,所以$a<\frac{4}{3}+1=\frac{7}{3}<c$,所以 $b<a<c$。
2.方程$x^2+2xy+3y^2=34$的整数解$(x,y)$的组数为()A。
3B。
4C。
5D。
6答】B.方程即$(x+y)^2+2y^2=34$,显然$x+y$必须是偶数,所以可设$x+y=2t$,则原方程变为$2t^2+y^2=17$。
因为$2t^2\leq 16$,所以$t=\pm 2$,从而可求得原方程的整数解为$(x,y)=(-7,3),(1,3),(7,-3),(-1,-3)$,共4组。
3.已知正方形ABCD的边长为1,E为BC边的延长线上一点,$CE=1$,连接AE,与CD交于点F,连接BF并延长与线段DE交于点G,则BG的长为()A。
$\frac{65}{26}$B。
$\frac{3}{3}$C。
$\frac{2}{5}$D。
$\frac{9}{4}$答】D.过点C作$CP\parallel BG$,交DE于点P。
上海中学初中数学竞赛

上海中学初中数学竞赛
【原创实用版】
目录
1.上海中学初中数学竞赛简介
2.上海中学初中数学竞赛的历史
3.上海中学初中数学竞赛的参赛对象和报名方式
4.上海中学初中数学竞赛的竞赛形式和内容
5.上海中学初中数学竞赛的奖项设置和意义
正文
【上海中学初中数学竞赛简介】
上海中学初中数学竞赛,是由上海市教委主管、上海中学主办的一项面向全市初中学生的数学竞赛活动。
该竞赛旨在激发初中学生学习数学的兴趣,提高数学应用能力和创新思维,选拔和培养优秀的数学人才。
【上海中学初中数学竞赛的历史】
上海中学初中数学竞赛始于 1990 年,至今已有 30 多年的历史。
在这期间,该竞赛不断发展和完善,逐渐成为上海市初中数学教育的一项重要活动,吸引了越来越多的学校和学生参与。
【上海中学初中数学竞赛的参赛对象和报名方式】
该竞赛的参赛对象为全市初中学生,包括上海市各区县的初中学校和民办初中。
参赛学生可以通过所在学校统一报名,也可以个人自行报名参加。
报名一般分为初赛和复赛两个阶段,初赛通过的学生可以进入复赛。
【上海中学初中数学竞赛的竞赛形式和内容】
竞赛分为初赛和复赛两个阶段。
初赛主要测试学生的基本数学知识和技能,包括选择题、填空题和解答题等。
复赛则更加注重学生的数学应用
能力和创新思维,题目难度相对较高,包括数学建模、数学探究等。
【上海中学初中数学竞赛的奖项设置和意义】
竞赛奖项分为个人奖和团体奖。
个人奖根据学生的竞赛成绩设立一、二、三等奖,团体奖则根据各学校参赛学生的整体表现设立优秀团体奖。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.6 上海市第六届“浦东金桥杯”中学生
数学知识应用竞赛(1997)
上海市第六届“浦东金桥杯”竞赛初赛于1997年5月举行,决赛于1997年9月举行.
【初赛试题】
初赛试题共有十五题,其中一~十题每题满分为10分,十一~十五题每题满分为16分,总共满分为180分.
一、一学校决定举行“庆祝香港回归知识竞赛”,各班派出10名代表参加,为了使人人参与,规定全校同学都作准备,赛前由各班用抽签方式,决定参赛人选.同学们对抽签之事展开讨论,有同学说先抽的人抽到的机会较大,也有同学持不同意见,请你对抽签次序是否影响抽签结果发表自己的意见,说明理由.
二、下了一场大雪后,整座山脉剖面(如图3—75所示)可近似看作三角形.其中L为山高,2l为山脉底面宽,h为山顶雪厚,H为山脚雪厚.假定山脉总长为10km,试求积雪的体积.
三、某一种牌号的彩电,现在的价格为4200元,销售为50万台,市场调查显示,如果价格每降低100元可多销2万台,但如果降到3000元,则厂家销售收入恰抵生产成本,假设每台电视机成本不随产量而变化,问价格应定多少时,可使厂家利润最大?
四、某地区堆着一堆建筑垃圾,影响市容.这堆垃圾长为80步,宽为20步,堆高估计1米,上底长、宽比下底长、宽各少2米,现在要彻底清除垃圾,用4吨卡车装运,约需要装几车?(一步约0.6米,一立方建筑垃圾约1.5吨)
五、A厂、B厂生产的水泥应当分送到1号、2号、3号建筑工地上去.A 厂、B厂每昼夜生产水泥分别为320吨、380吨,而1号、2号、3号建筑工地每夜分别需要水泥为200吨、280吨、220吨,由工厂运送1吨水泥到建筑工地的运费如下表:
要求拟定运费最少的运送水泥的计划,并求运费最小值.
六、某人40足岁时参加养老保险,有2家保险公司推出二种不同的方案.方案1:40足岁起每年交费437元,一直交到59足岁为止;从60足岁起每年领取养老金1200元直至死亡,死亡后保险公司一次性支付给家属10000元.方案2:40足岁起每年交费750元,连续交纳10年;从60足岁起领取养老金,第一年1000元,以后每年递增50元,直至死亡,死亡后保险公司一次性支付给家属10000元.若预期寿命为75岁、银行年利率7.47%,试问哪一种方案对投保人有利.
七、用长为2a,宽为a的矩形薄铁皮作材料,做一个有底的圆锥体模型,问如何落料才能使体积最大?并求出体积最大值.
八、图3—77为山东省威海地区省级公路示意图(图中各边上数字为该路段的公里数),试求出从威海市到文登、荣城、乳山、石岛和成山卫的最短路径和距离.
九、半径为a的半圆材料上,如图3—78截两个正方形ABCD,BEFG,
D、F两点在半圆周上,C、G在半圆内,试求这样两块面积和,并可得出什么结论.
十、用边长为a的正三角形四块、正方形三块、正六边形一块组成封闭八面体作为雕塑底座平台,(1)画出平台的立体图、视图、展开图;(2)求出平台的表面积与体积.
十一、某公司自去年11月份开始月利润如下表:
假定短期内利润增长基本符合对数规律,预测一下今年5月、6月利润是多少?
十二、一个仪表仪器中零件毛坯,尺寸如图3—79所示.现要在长500、宽300的矩形镀锌铁皮上落料,这里不考虑落料工艺要求与损耗,试问怎样落料才能使毛坯最多,可落多少个零件毛坯?画出落料示意图.
十四、为了满足零件自动设计要求,需确定零件轮廓线与扫过的面
上部分为CD圆弧,其圆心在AB中点O.如图3—81所示,M点在BC、CD、DA上移动,设BM=x,OM所扫过面积OBM(或OBCM或OBCDM)为y,试求出y=f(x)函数式,并画出它的图象.
十五、试根据下列工序资料绘出工程网络图,并求出关键路线和总工期、各工序的总时差.(单位:天)
【决赛试题】
(本试题共五题,前三题每题20分,最后二题每题30分,满分120分)
一、某一仪器外壳造型为:上部分是底边长为a,高为a/2的正四棱锥;下部分是边长为a,高为a/2的正四棱柱切去如下的四个相等的四面体所留下的一个台体:四面体的顶点为正四棱柱同一棱上的位于上下底面的两个顶点及下底面上与该棱相邻的两边的中点.
(1)画出仪器外壳的立体图、三视图、展开图;
(2)求出仪器外壳的表面积与体积,用a表示.
二、敌舰于某时刻通过坐标原点,且以不变的速度V0,沿y油正向行驶.位于X轴上坐标(A,0)处的我导弹部队立即发射导弹拦截,已知导弹发射后将沿发射方向直线飞行:先以等加速a加速到速度V后,维持速度V不变.设上述各量的数值如下:V0=k,A=1000k,V=20k,a=4k(其中k为常数).
(1)为使导弹击中敌舰,求导弹发射方向与X轴正向的夹角(精确到小数点后3位).
(2)如果导弹在与敌舰距离不大于50k时即可自动追踪,将敌舰摧毁,求能最早摧毁敌舰的发射角.
三、有一截面为直角梯形的棱柱形液体容器,其尺寸如图3—82所
一条棱旋转一个角度θ(0<θ<π/6)使液面面积最小,试求出θ(要求写出解题过程).
四、某零件的加工需经过A、B、C、D、E、F六道工序,而按工艺的要求,工序B和C必需安排在工序A之后,工序D必需在工序B之后,工序E必需在C之后,工序F必需在工序D、E之后,已知i工序完工后紧接开始J工序的准备时间t ij见下表(单位:分钟).
试问:(a)有几不同的安排加工顺序?列出所有可能的加工顺序.
(b)哪一种方式的准备工作的总时间最省?
五、工厂有50台同一型号的设备,厂方与修理厂协议的维修价格为:每台设备正常维护一次的费用100元,而一台设备发生故障进行应急修理的费用为1000元.设一台设备正常维护后在第K年发生故障的概率为P k,
P1=0.18,P2=0.18,P3=0.1,P4=0.13,P5=0.18.
假设设备经应急修理后在下一次正常维护前不会再发生故障.试为厂方制订定期正常维护的策略,即决定设备定期正常维护的周期K年,使平均年维修费最省(K<5=?。
