雅礼中学2012届高三第七次月考文科数学试题
2024届湖南省长沙雅礼中学高三下学期月考(七)语文试题及答案

雅礼中学2024届高三月考试卷(七)语文注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、现代文阅读(35分)(一)现代文阅读I(本题共5小题,19分)阅读下面的文字,完成1~5题。
乡土文学内涵丰富多彩,既可书写乡土历史,也可关注乡村现实,或写实,或象征,或抒情。
但无论如何,乡土小说在未来要有所突破,更具审美价值,能对中国乡村历史、现实与未来前景作出更具梯度与广度的思考,须摆脱传统叙事范式的限度,“接通”乡村现实的巨变,在多方面进行更新。
一是更新对乡土文明的价值认知。
也就是说,充分尊重乡村的本体地位与独立价值,重构乡土文明的正向价值。
长期以来,由于对现代性的某种迷思,乡土文明通常被预设、框定为传统、落后的文化形态,与现代化构成一种悖论与张力,总是遭到无情的批判与碾压,中国百年来的乡土文学基本上是在此方向上惯性地书写。
事实上,中华文明本质上是一种农耕文明,而乡村则是农耕文明的实体载体与存在空间。
可以说,乡村文化不仅是建构中华民族心理认同感的重要精神源泉,还滋育着中华文明的根脉。
“乡村文明是中华民族文明史的主体,村庄是这种文明的载体,耕读文明是我们的软实力。
”因此,悠久、灿烂的农耕文明支撑了古代中国的生存与繁荣,也为当代中国积淀了文化基因与根脉。
乡土文明有其独立存在的价值,并非仅仅是评判现代性的参照坐标,亦不是城市文明的附庸,它同样有着现代文明的价值指向。
因此现代化并非是完全要抛弃传统,现代化也可以说是植根于传统的一种转型与生长,与传统一脉相承。
未来的乡土小说不必再视乡村为一种话语批判的武器,实有必要以平视的姿态去看待农耕文化中那些悠远的传统元素,通过对乡村固有的风俗、风情、风景的展示,建构乡村自身之美,从而彰显乡村文化的丰盈,赋予乡土以中华民族的文化记忆功能。
湖南省雅礼中学2014届高三第八次月考数学文试题

湖南省雅礼中学2014届高三第八次月考数学文 2014.4.(时量:120分钟 满分:150分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的,请将所选答案填在答题卡对应位置.1.已知集合2{|03},{|540}M x x N x x x =<<=-+≥,则M N =A .{|01}x x <≤B .{|13}x x ≤<C .{|04}x x <≤D .{|0x x <或4}x ≥2.若复数221z i i=++,其中i 是虚数单位,则复数z 的模为A .1BCD .23.运行下面的程序,如果输入的n 是6,那么输出的p 是INPUT “n =”; n k =1 p =1WHILE k<=np =p*kk =k +1WEND PRINT p ENDA .120B .720C .1440D .50404.已知直线01)2(:,02)2(:21=-+-=--+ay x a l y a x l ,则“1-=a ”是“21l l ⊥的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件5.已知y x ,的取值如下表:y x 与线性相关,从散点图可以看出且回归方程为0.95y x a =+,则a =A. 3.2 B .3.0 C. 2.8 D .2.66.一个几何体的三视图如图所示,其中俯视图与左视图均为半径是2的圆,则这个几何体的 表面积是x 0 1 3 4 y2.24.34.86.7A .16πB .14πC .12πD .8π7.已知向量b a ,满足||1,(1,3)a b ==-,且()b a a +⊥,则a 与b 的夹角为A . 60B . 90C . 120D . 1508.已知函数()sin()f x A x x R ωϕ=+∈,(其中0022A ππωϕ>>-<<,,),其部分图像如图所示,将()f x 的图像纵坐标不变,横坐标变成原来的2倍,再向右平移1个单位得到()g x 的图像,则函数()g x 的解析式为A .()sin(1)2g x x π=+B .()sin(1)8g x x π=+C .()sin(1)2g x x π=+D .()sin(1)8g x x π=+9.若函数()xxf x ka a-=-(a >0且1a ≠)在(,-∞+∞)上既是奇函数又是增函数,则()log ()a g x x k =+的图象是正视图 俯视图左视图10.某企业生产甲、乙两种产品,已知生产每吨甲产品要用A 原料3吨、B 原料2吨;生产每吨乙产品要用A 原料1吨、B 原料3吨.销售每吨甲产品可获得利润5万元,每吨乙产品可获得利润3万元,该企业在一个生产周期内消耗A 原料不超过13吨,B 原料不超过18吨,那么该企业可获得最大利润是A. 12万元B. 20万元C. 25万元D. 27万元答案 ABB ADA CBC D二、填空题:本大题共5小题,每小题5分,共25分.把答案填在答题卡中对应题号后的横线上.11.若直线24sin :=⎪⎭⎫ ⎝⎛-πθρl 与曲线()为参数t ty t x C ⎩⎨⎧==2:相交于B A ,两点, 则AB = .12.已知数列121,,,9a a 是等差数列,数列1231,,,,9b b b 是等比数列,则212b a a +的值为_____________.13.已知函数()f x 在()+∞,0内可导,且满足x e e f x x +=)(,则()f x 在点()(1,1)M f 处的切线方程为_____________________14.过椭圆C :()012222>>=+b a by a x 的右顶点作圆222b y x =+的两条切线,切点分别为A ,B ,若120AOB ∠=(O 是坐标原点),则C 的离心率为__________ 15.对于定义域为[]1,0的函数()f x ,如果同时满足以下三个条件: ①对任意的]1,0[∈x ,总有0)(≥x f②1)1(=f③若0,021≥≥x x ,121≤+x x ,都有)()()(2121x f x f x x f +≥+ 成立 则称函数)(x f 为理想函数.(Ⅰ)若函数)(x f 为理想函数,则=)0(f ________;(Ⅱ)下列结论正确的是_________________.(写出所有正确结论的序号) ①函数])1,0[(12)(∈-=x x f x 是理想函数;②若函数)(x f 是理想函数,假定存在]1,0[0∈x ,使得]1,0[)(0∈x f ,且00)]([x x f f =,则00)(x x f =.答案11.23 12.103 13.012=--y x 14. 23 15.(Ⅰ)0(Ⅱ)①②三、解答题:本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤.16. (本小题满分12分)某班50位学生期中考试数学成绩的频率分布直方图如图4所示,其中成绩分组区间 是:[)40,50、[)50,60、[)60,70、[)70,80、[)80,90、[]90,100. (Ⅰ)求图中x 的值及平均成绩;(Ⅱ)从成绩不低于80分的学生中随机选取2人, 求2人成绩都不低于90分的概率.解:(Ⅰ)由()0.00630.010.054101x ⨯+++⨯=,解得0.018x =. 3分 平均成绩为()748518.07554.0651.095554506.0=⨯+⨯+⨯+++⨯. 6分 (Ⅱ)分数在[)80,90、[]90,100的人数分别是500.018109⨯⨯=人、500.006103⨯⨯=人. 从成绩不低于80分的12学生中随机选取2人共有66种取法,从成绩不低于90分的3名学生中随机选取2人共有3种取法,故所求的概率为.221663= 12分17. (本小题满分12分)如图,设D 是直角ABC ∆斜边BC 上一点,且AD AB =,记βα=∠=∠ABC CAD ,. (Ⅰ)证明:02cos sin =+βα; (Ⅱ)若DC AC 3=,求β的值.解(Ⅰ)因为(),22222πββπππα-=--=∠-=BAD 所以.02cos sin ,2cos )22sin(sin =+-=-=βαβπβα即 6分(Ⅱ)()αβββπαsin 3sin ,sin 3sin sin ==-=∆所以中,由正弦定理得在DCAC DC ADC . 由(1)有()1sin 23sin 1sin 22cos sin 22-=-=-=ββββα,所以,即3,20.33sin 23sin ,03sin sin 322πβπβββββ=<<-===--因此又或解得 12分18.(本小题满分12分)如图,在长方体1111ABCD A BC D -中,E AD AA ,21==为CD 中点. (Ⅰ)求证:11B E AD ⊥ ;(Ⅱ)在棱1AA 上是否存在一点P ,使得//DP 平面1B AE ?若存在,求AP 的长;若不存在,说明理由.(Ⅰ)连D A 1,1111111111,,AD A B DA D A A B AD D A AD AA ⊥⊥⊥=所以平面又,所以因为所以D B A AD 111平面⊥,又因为11B A ∥DE ,所以,因此平面D B A E B 111⊂11B E AD ⊥. 6分 (Ⅱ)取棱1AA 的中点P ,则有//DP 平面1B AE ,其中AP 的长为1.证明如下: 取PF B AA PF F AB 的中位线,所以为则的中点111,∆∥,又且111121B A PF B A = ED ∥PF B A ED B A ,所以且111121=∥,且ED PF ED =所以DP ∥EF 又 DP AEB EF AEB DP ,所以平面平面11,⊂⊄∥平面1B AE . 12分19.(本小题满分13分)已知不在x 轴上的动点P 与点()0,2F 的距离是它到直线l :21=x 的距离的2倍. (Ⅰ)求点P 的轨迹E 的方程;(Ⅱ)过点F 的直线交E 于C B ,两点,试判断以线段BC 为直径的圆是否过定点?并说明理由.解:(1)设P (x ,y )12||2x =-化简得x 2-23y =1(y ≠0). 4分(2)由题意可设过点F 的直线的方程为2+=ky x ,代入1322=-y x 得 ()09121322=++-ky y k由题意知3k 2-1≠0且△>0,设()()2211,,,y x C y x B ,则⎩⎨⎧1391312221221-=--=+k y y k k y y 8分设()0,1-A ,因为()()()()()()()()()09133613199313311,1,1222221212212121212211=+---+=++++=+++=+++=++=⋅k k k k y y k y y k y y ky ky y y x x y x y x AC AB AC AB ⊥∴,故以线段BC 为直径的圆过定点()0,1-A . 13分20.(本小题满分13分)对于任意的*n N ∈(n 不超过数列的项数),若数列{}n a 满足:n n a a a a a a ⋅⋅=+++ 2121,则称该数列为K 数列. (Ⅰ)若数列{}n a 是首项12a =的K 数列,求3a 的值; (Ⅱ)若数列1n a ⎧⎫⎨⎬⎩⎭是K 数列. (1)试求1n a +与n a 的递推关系; (2)当时且1031<<≥a n ,试比较na a a 11121+++ 与316的大小.解(Ⅰ)有题意可得.222,2222121==+=+a a a a a a a ,所以即 又,42233321321a a a a a a a a =++=++,即所以343=a . 3分 (Ⅱ)(1)因为数列1n a ⎧⎫⎨⎬⎩⎭是K 数列,所以()11111≥===∑n a a n i i n i i ① 111111+=+==∑n i i n i i a a ②两式相减得()11111111≥⎪⎪⎭⎫ ⎝⎛-==++n a a a n i i n n ③ 则()20111111≥≠⎪⎪⎭⎫ ⎝⎛-=-=n a a a n i in n ④两式相除得()2111111111≥-⎪⎪⎭⎫ ⎝⎛-=++n a a a a a nn n n n ,整理得()2121≥+-=+n a a a n n n 又1221211,1111a a a a a a -=⋅=+所以. 综上所述,1+n a 与递推关n a 系为⎩⎨⎧≥+-=-=+2,11,121n a a n a a n nn n . 8分 (2)()41613161314343,143214311010124223121≥≥>=+-⎪⎭⎫⎝⎛≥<+⎪⎭⎫ ⎝⎛-=≤<-=<<<+n a a a a a a a a n n ,又所以,从而,所以因为又当1111121---=≥+n n n a a a n 时,,所以 当时,3≥n.31611111111111111111111111121132121≥-=--=---+=⎪⎪⎭⎫⎝⎛---++⎪⎪⎭⎫ ⎝⎛---+=+++++++n n n n n n a a a a a a a a a a a a a13分21.(本小题满分13分)已知函数()x a x x f ln 1)(2+-=有两个极值点,,21x x 且.21x x <(Ⅰ)求实数a 的取值范围,并讨论)(x f 的单调性; (Ⅱ)证明:42ln 21)(2->x f . 解(Ⅰ)由题设知,函数)(x f 的定义域为()()()0,22,,02='+-='+∞x f xax x x f 且有两个不同的根,且,即的判别式故21084022,,221<>-=∆=+-a a a x x x x.00.22112211121>>-+=--=a x a x a x ,故又,因此a 的取值范围是⎪⎭⎫⎝⎛210,. 4分()()0;002121<'<<>'><<x f x x x x f x x x x 时,当时,或当.因此()()()上单调递减,上单调递增,在,和,在21210)(x x x x x f ∞+. 6分 (Ⅱ)由(Ⅰ)可知()22212121122,2,1x x x x a ax x x x -====+所以,因此()()()121ln 121ln 1)(2222222222<<-+-=+-=x x x x x x a x x f ,其中. 9分()()()则设),121(ln 1212<<-+-=t t t t t t h()()()()(),0ln 21211ln 21212>-=⎥⎦⎤⎢⎣⎡-+-+-='t t t t t t t t t h所以42ln 21)21()(121)(-=>⎪⎭⎫⎝⎛h t h t h 单调递增,所以,在.即42ln 21)(2->x f . 13分。
2012届长沙市一中、雅礼中学联考数学文科试题word版

湖南省2012届高三·长沙市一中、雅礼中学联考文科数学试卷总分:150分 时量:120分钟 考试时间:2012年3月31日下午2:30~4:30一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的,请将所选答案填在答题卡中对应位置. 1.已知全集U R =,集合{}1,2,3,4,[3,A B ==+∞),则图中阴影部分( ) A. {}1,2 B. {}0,1,2 C. {}1,2,3 D. {}0,1,2,3 2.在复平面内,复数1(1)i i -++对应的点在( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限3.甲乙两名篮球运动员在某几场比赛得分的茎叶图如左下图所示,则甲、乙两人这几场比赛得分的中位数之和是( ) A. 56 B. 57 C. 58 D. 594.某程序框图如右上图所示,则输出S 的值是( )A. 22B. 27C. 31D. 565.设椭圆22221x y a b +=、双曲线22221y x a b-=、抛物线22()y a b x =+(其中0a b >>)的离心率依次为123,,e e e ,则下列判断正确的是( )A. 123e e e >B. 123e e e <C. 123e e e =D.12e e 与3e 的大小不确定 6.设,,αβγ为平面,,,m n l 为直线,则l β⊥的一个充分条件是( ) A.,m l m αβ,αβ⊥=⊥ B. ,,l αγαγβγ=⊥⊥ C. ,,l αγβγα⊥⊥⊥ D. ,,n n l αβα⊥⊥⊥7.已知变量,x y 满足420,0x y x y x y +≤⎧⎪-≤⎨⎪≥≥⎩,若目标函数z mx y =+仅在点(3,1)处取得最大值,则m 的取值范围是( )A. 1m <-B. 1m ≤-C. 1m >D. 1m ≥8.若圆222240x y ax a +++-=关于斜率为k 的直线l 对称,且直线l 与该圆在第一象限内有交点的概率为16,则a 等于( ) A. -1 B. 1 C. 2 D. -1或19.函数()f x 的定义域为D ,若对于任意12,x x D ∈,当12x x <时,都有12()()f x f x ≤,则称函数()f x 在D 上为非减函数,设函数()f x 在[0,1]上为非减函数,且满足以下三个条件,①(0)0f =;②1()()32x f f x =;③(1)1()f x f x -=-,则11()()927f f +等于( ) A. 12 B. 23 C. 34 D. 38二、填空题:本大题共8个小题,考生作答7个小题,每小题5分,共35分,把答案填写在题中的横线上.(一)选做题(请在第10、11两题中任选一题作答,如果全做,则按前一题记分) 10.用0.618法寻找最佳点时,达到精度0.03的要求,至少需 次试验. (参考数据:lg0.6180.209,lg30.4771≈-≈).11.已知曲线1C 的参数方程为1cos (sin x y θθθ=+⎧⎨=⎩为参数),曲线2C 的极坐标方程为()4R θρπ=∈,若曲线2C 与曲线1C 交于点,A B ,则||AB 的值为 .(二)必做题(12〜16题)12.如图是一个几何体的三视图,其正视图与侧视图是边长为2的正三角形,俯视图轮廓为正方形,则这个几何体的侧面积是 . 13.设n S 是等比数列{}n a 的前n 项和,若123421,2a a a a +==,则n n S a += .14.已知函数()y f x =是偶函数,当0x >时,()lg ,f x x =则1(())10f f 的值为 . 15.已知向量OA 与1OA关于y 轴对称,(1,0)i =,则满足不等式210i OA AA +⋅≤ 的点(,)A x y 到直线10x y ++=的距离的最小值为 .16.小明喜欢玩一个蚂蚁跳跃的电子游戏,其游戏规划是:一只蚂蚁在平面直角坐标上从点(1,1)开始按如下规则跳跃:(1)该蚂蚁从任一点(,)m n 跳到点(2,)m n 或(,2)m n ;(2)如果m n >,该蚂蚁能从(,)m n 跳到(,)m n n -,如果m n <,该蚂蚁能从(,)m n 跳到(,)m n m -. 则在①(2,1),②(3,8),③(24,5),④(30,24)四点中,蚂蚁能到达的点是 ;蚂蚁跳到(800,4)至少要跳跃 次.正视图侧视图俯视图三、解答题:本大题共6个小题,共75分,解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分)已知向量(,),(,)m n a c b a c b a =-=+-,且0m n ⋅=,其中A B C 、、是ABC ∆的三内角,a b c 、、分别是角A B C 、、的对边,且c =(Ⅰ)求角C 的大小;(Ⅱ)求ABC ∆周长的取值范围.18.(本小题满分12分)长沙市为增强市民交通安全意识,面向全市征召宣传 志愿者.现从符合条件的志原者中随机抽取100名按年龄 分组:第1组[20,25),第2组[25,30),第3组[30,35),第 4组[35,40),第5组[40,45),得到的频率分布直方图如图所示.(Ⅰ)若从第1,4,5组中用分层抽样的方法抽取7名志愿者参加安全宣讲活动,它从第1,4,5组各抽取多少名志愿者?(Ⅱ)在(Ⅰ)的条件下,该市决定从第4组抽取的志愿者中再选取2名,从第5组抽取的志愿者中再选取1名,共3名志愿者介绍宣传经验,求第4组中志愿者1B 和第5组中志愿者1C 同时被选中的概率.19.(本小题满分12分)如图所示,在平行四边形ABCD 中,24,120,AB BC ABC N ==∠= 为线段AB 中点,E 为线段DN 的中点,将ADN ∆沿直线DN 翻折到1A DN ∆,使二面角1A DN C --的平面角为60 ,M 为线段1AC 的中点. (Ⅰ)求证:BM 平面1A DN ; (Ⅱ)求三棱锥1A DNC -的体积;ADE MA 120.(本小题满分13分)某公司为了激发销售人员开发市场的热情,每建立一处销售网点都要给予奖励.制定了三种奖励方案:第一种,每建立一处销售网点奖励100元;第二种,每建立一处销售网点奖励50元,以后每建立一处都比前面建立的一处多奖励4元;第三种,建立第一处销售网点奖励5元,以后每建立一处都比前面建立的一处奖励翻一番(即增加1倍),且三种方案可任意选择.(Ⅰ)设销售人员建立*(,n n N ∈且12)n ≤处销售网点按三种奖励方案获得的奖金依次为,,n n n A B C ,试求出,,n n n A B C 的表达式;(Ⅱ)在(Ⅰ)的条件下,如果你是该公司的一名销售人员,为了得到最多的奖金,你应如何选择奖励方案?21.(本小题满分13分)已知椭圆1C 中心在原点,焦点在x 轴上,且过点,等轴双曲线2C 的渐近线与直线l 平行,直线l 过双曲线的右焦点F ,且与椭圆1C 相交于A B 、两点. (Ⅰ)求椭圆1C 的标准方程;(Ⅱ)求AOB ∆面积的最大值及此时双曲线2C 的方程.22.(本小题满分13分) 已知函数2()2ln ,()1a axg x ax x h x x x =--=+. (Ⅰ)若2a =,求曲线()g x 在点(2,(2))g 处的切线方程;(Ⅱ)若0a >,求函数()g x 的单调递增区间;(Ⅲ)若[1,]u e ∃∈,使()2g u >成立,同时[1,]v e ∃∈,使()2h v >成立,求实数a 的取值范围.湖南省2012届高三·长沙市一中、雅礼中学联考文科数学参考答案一.选择题10. 9 11. 12. 8 13. 1 14. 0 1 16.(1) ①②③ ,(2) 15 三.解答题17.【解】(Ⅰ)由0m n ⋅=得,()()()0a c a c b b a -++-=,即2220a b c ab +--=………………2分由余弦定理得2221cos 222a b c ab C ab ab +-===………………………………………………3分又因为0C <<π,所以3C π=…………………………………………………………………5分(Ⅱ)(一法)由 (Ⅰ)知,2222122cos60()3c a b ab a b ab ==+-=+- ,…………………………6分即2312()ab a b =-+由于2222()4(a b ab a b ab +≥⇔+≥当且仅当a b =时取等号) ………………………7分所以223312()()4ab a b a b =-+≤+,即2()48a b +≤,…………………………………10分由于0a b c +>=,所以a b <+≤11分也所以a b c <++≤即ABC ∆周长的取值范围为………………12分 (二法)由(Ⅰ)知4sin sin sin a b cA B C===,所以4sin ,sin a A b B ==,……………………7分所以ABC ∆周长4(sin sin )L a b c A B =++=+而22,33A B C B A ππ+=π-==-,代入上式得234[s i n s i n (234s i n c o s )322L a b c A A A A π=++++-+)6A π=+……………………………………………………………………9分又因为203A π<<,所以5666A πππ<+<,所以1sin()126A π<+≤,从而)6A π+≤11分ACD E MHOF A1其中不等式右边当且仅当62A ππ+=,即3A π=时等号. 即ABC ∆周长的取值范围为……………………………………………………12分 18.【解】(Ⅰ)由题知,第1,4,5组中人数分别有:100(0.015)5,100(0.045)20,100(0.025)10⨯⨯=⨯⨯=⨯⨯=…………………………………3分 因为第1,4,5组共有35名志愿者,所以利用分层抽样的方法从中抽取7名,每组的抽取人数分别为77751,204,102353535⨯=⨯=⨯= 所以应从第1,4,5组分别抽取人数为1人,4人,2人. ……………………………………6分(Ⅱ)依题意设第4组中的4名志愿者的编号分别为1234,,,B B B B ;第5组中两名志愿者编号分别为12,C C ,由题得基本事件有:112113114123124134,,,,,C B B C B B C B B C B B C B B C B B ;212213,,C B B C B B 214223224234,,,C B B C B B C B B C B B ,共12种,…………………………………………………10分又事件A ={志愿者1B 和志愿者1C 同时被选中}发生有112113114,,C B B C B B C B B 共3种……11分所以由古典概型知,31()124P A ==,即求……………………………………………………12分 19.【证明】(Ⅰ)〖证法一〗如图取1A D 中点H ,连接MH ,则12MH CD ………………2分又12BN CD ,所以BN HM ,即四边形HMBN 是平行四边形,………………………4分所以BM HN ,……………………………………………………………………………5分 又BM ⊄平面1A DN ,而HN ⊂平面1A DN ,所以BM 平面1A DN .……………………6分 〖证法二〗如图,取CD 中点F ,连接FM FB 、,则易知,112MF A D,又FM ⊄平面1A DN ,而1A D ⊂平面1A DN , 所以FM 平面1A DN ,同理,由BN DF ,可知BF DN ,所以BF 平面1A DN , 又由于FB FM F = ,且,BF FM ⊂平面BFM , 所以平面BFM 平面1A DN ,又BM ⊂平面BFM ,所以BM 平面1A DN .(Ⅱ)由题知,ADN ∆是边长为2的正三角形,所以2DN =,又BNC ∆是顶角为120 ,腰长为2的等腰三角形,由余弦定理知,CN =所以222DN CN CD +=,即90DNC ∠=,DNC S ∆=又延长AE 交CD 于点F ,易知菱形AFND 中AF DN ⊥,也所以1A E DN ⊥ 所以1A EF ∠为1A DN C --的平面角,即160A EF ∠= ,又AE EF =,所以1A EF ∆为正三角形,取FE 中点O ,连接1AO ,则1AO EF ⊥, 又易知1DN AO ⊥,DN EF E = ,所以1AO ⊥平面ABCD .又113sin 602AO A E === ,所以1113A DNC DNC V S AO -∆=⨯⨯=即求. 20.【解】(Ⅰ)由题知,100,n A n =…………………………………………………………………2分25054[504(1)]248n B n n n =++++⨯-=+ ………………………………………4分155252525n n n C -=+⨯++⨯=⨯- ;其中*,n N ∈且12n ≤;……………………6分(Ⅱ)由函数图象可令,n n A B >得,2100248n n n >+,解得026n <<,又因为012n <≤,所以n n A B >恒成立;……………………………………………………8分 又令n n A C >,即1005(21)n n >-,2012n n +>,可得07n <≤……………………………10分 所以当7n ≤时,n A 最大;当812n ≤≤时,n C 最大;…………………………………………12分 综上,如果销售网点未超过7个时,应选择第一种方案;当销售网点超过7个时应选择第三种方案; ………………………………………………13分21.【解】(Ⅰ)由题设椭圆1C 的标准方程为22221(0)x y a b a b+=>>,则a =2分又2c e a ==所以1c =,…………………………………………………………………3分 又2221b a c =-=,所以椭圆1C 的方程为2212x y +=………………………………………4分(Ⅱ)设等轴双曲线2C 的方程为:222(x y λλ-=>则其渐近线方程为y x =±,右焦点,0)F 不妨设直线l 与直线y x =平行,所以直线:l x y =+,设1122(,),(,A x y B x y 则12121|||||2AOB S OF y y y y ∆=⨯-=-=又2222x y x y ⎧=+⎪⎨+=⎪⎩,得2232(1)0y y λ++-=…………8分 由22824(1)0λλ∆=-->得,2302λ<< ……①……………9分且212122(1),33y y y y λ--+==…………………………10分所以AOB S ∆=11分又因为22232322AOBS λλ∆+-≤⨯=…………………………12分 (亦可将根号下视为2λ的二次函数来求解,同样按步骤给分)当且仅当22232λλ=-,即233(0,)42λ=∈时取等号;所以AOB ∆此时双曲线2C 的方程2234x y -=.…………………13分 〖表示法二〗设等轴双曲线的右焦点为(,0)(0)F t t >,则直线:l x y t =+,双曲线方程:2222t x y -=;又设1122(,),(,)A x y B x y ,则12121||||||22AOB t S OF y y y y ∆=⨯-=-=…7分又2222x y tx y =+⎧⎨+=⎩,得223220y ty t ++-=………………………………………………………8分 由22412(2)0t t ∆=-->得,203t << ……①………………………………………………9分且2121222,33t t y y y y --+==…………………………………………………………………10分所以AOBS ∆===………11分 所以当23(0,3)2t =∈时,AOB S ∆………………………………………………12分 所以此时双曲线2C 的方程2234x y -=.………………………………………………………13分〖表示法三〗同表示法二前半部分,但1||2ABO S AB d ∆=,其中d 是点O 直线AB的距离=所以121|2ABO S y y ∆=-=后面同表示法二.22.【解】(Ⅰ)当2a =时,2()22ln (0)g x x x x x =-->,222(2)32ln 2,()2g g x x x'=-=+-……1分所以曲线()g x 在点(2,(2))g 处的切线斜率为3(2)2g '=, 所以切线方程为3(32ln 2)(2)2y x --=-,即32ln 22y x =-……………………………3分 (Ⅱ)当0a >时,22222()a ax x ag x a x x x -+'=+-=…………………………………………………4分由于方程220ax x a -+=的判别式244a ∆=-,所以①当2440a ∆=-≤,即1a ≥时,()0g x '≥,所以函数()g x 的递增区间为(0,)+∞;……………5分②当440a ∆=->,即01a <<时,220ax x a -+=的两根为120x x <<=所以当12(0,)(,)x x x ∈+∞ 时,()0g x '>,即此时函数()g x 的递增区间为)+∞;…………………………………………………………………6分综上,1a ≥时,()g x 的递增区间为(0,)+∞,01a <<时()g x 的递增区间为)+∞;…………………………7分 (Ⅲ)由题知2()21ax h x x =>+在[1,]x e ∈上有解,即12a x x >+有解, 易知函数211(10)y x y x x'=+=-≥在[1,]x e ∈单调递增,所以2y ≥即只须2,42aa >>………①……………………………………………………………………9分同理()2ln 2ag x ax x x=-->在[1,]x e ∈上有解, 〖一法〗即max ()2g x >成立,下面求函数max ()g x由(Ⅱ)知,22222()a ax x ag x a x x x -+'=+-=且由①知,4a >,所以2440a ∆=-<,所以()0g x '>恒成立, ……………………………11分 所以()g x 在[1,]e 上单调递增,所以1max ()()2g x a e e -=-- 也所以1max ()()22g x a e e -=-->,即14a e e ->-,…………………………………………12分 显然有144e e->-, 综上可知4a >时,符合题意; …………………………………………………………………13分〖二法〗即11ln 2a xx x -+>-在1,]x e ∈(上有解(1x =时,原不等式显然不成立); 令11ln ()(1)xh x x e x x -+=<≤-,则22122ln ln ()0()x x x h x x x x ----'=<⋅-………………………………11分 所以()h x 在定义域上单调递减,所以min 12()()h x h e e e -==- 即只须1124,2a a e e e e -->>--,…………………………………………………………………12分 显然有144e e ->-,综上可知4a >时,符合题意; …………………………………………………………………13分。
雅礼中学高三月考试卷(一)数学及答案

雅礼中学高三月考试卷(一)数学一、单项选择题:本大题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项符合题目要求。
1.已知集合A =-2,0 ,B =x x 2-2x =0 ,则以下结论正确的是()A.A =BB.A ∩B =0C.A ∪B =AD.A ⊆B2.已知等比数列a n 满足a 1=1,a 3⋅a 5=4a 4-1 ,则a 7的值为()A.2B.4C.92D.63.已知复数z =a +1 -ai a ∈R ,则a =-1是z =1的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4.已知向量a =cos θ,sin θ ,b =2,-1 ,若a ⊥b ,则cos 2θ+12sin2θ的值为()A.13B.35C.45D.235.如图,在棱长为2的正方体ABCD -A 1B 1C 1D 1中,E ,F 分别是棱AA 1,CC 1的中点,过BE 的平面α与直线A 1F 平行,则平面α截该正方体所得截面的面积为()A.5B.25C.4D.56.某工厂有A ,B 两个生产车间,所生产的同一批产品合格率分别是99%和98%,已知某批产品的60%和40%分别是A ,B 两个车间生产,质量跟踪小组从中随机抽取一件,发现不合格,则该产品是由A 车间生产的概率为()A.34B.47C.12D.377.已知椭圆C :x 2a2+y 2b 2=1(a >b >0)的左、右焦点分别为F 1,F 2,P 为椭圆上一点,且∠F 1PF 2=π3,若F 1关于∠F 1PF 2平分线的对称点在椭圆C 上,则该椭圆的离心率为()A.22B.33C.12D.138.△ABC 中,角A ,B ,C 所对的三边分别为a ,b ,c ,c =2b ,若△ABC 的面积为1,则BC 的最小值是()A.2B.3C.3D.33二、多项选择题:本大题共4个小题,每小题5分,共20分。
2024-2025学年湖南省长沙市雅礼中学高三上学期月考(三)数学试题(含答案)

2024-2025学年湖南省长沙市雅礼中学高三上学期月考(三)数学试题一、单选题:本题共8小题,每小题5分,共40分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.命题“存在x∈Z,x2+2x+m≤0”的否定是( )A. 存在x∈Z,x2+2x+m>0B. 不存在x∈Z,x2+2x+m>0C. 任意x∈Z,x2+2x+m≤0D. 任意x∈Z,x2+2x+m>02.已知集合A={ i , i2 , i3 ,i4 }(i是虚数单位),B={ 1 , −1 },则A∩B=( )A. { −1 }B. { 1 }C. { 1 , −1 }D. ⌀3.已知奇函数f(x)=(2x+m⋅2−x)cos x,则m=( )A. −1B. 0C. 1D. 124.已知m,l是两条不同的直线,α,β是两个不同的平面,则下列可以推出α⊥β的是( )A. m⊥l,m⊂β,l⊥αB. m⊥l,α∩β=l,m⊂αC. m//l,m⊥α,l⊥βD. l⊥α,m//l,m//β5.已知函数f(x)=4cos(ωx+φ)(ω>0)图象的一个最高点与相邻的对称中心之间的距离为5,则f(−6φπ)=( )A. 0B. 2φC. 4D. φ26.已知M是圆C:x2+y2=1上一个动点,且直线l1:mx−ny−3m+n=0与直线l2:nx+my−3m−n=0(m,n∈R,m2+n2≠0)相交于点P,则|PM|的取值范围是( )A. [3−1,23+1]B. [2−1,32+1]C. [2−1,22+1]D. [2−1,33+1]7.P是椭圆C:x2a2+y2b2=1(a>b>0)上一点,F1、F2是C的两个焦点,PF1⋅PF2=0;点Q在∠F1PF2的平分线上,O为原点,OQ//PF1,且|OQ|=b.则C的离心率为( )A. 12B. 33C. 63D. 328.设集合A={(x1,x2,x3,x4,x5)|x i∈{−1,0,1},i=1,2,3,4,5},那么集合A中满足条件“1≤|x1|+|x2|+|x3|+ |x4|+|x5|≤3”的元素个数为( )A. 60B. 90C. 120D. 130二、多选题:本题共3小题,共18分。
湖南省长沙市雅礼中学2024-2025学年高三上学期入学考试数学试题解析版

雅礼中学2025届高三上学期入学考试试卷数 学时量:120分钟 分值:150分一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、 已知集合{}240A x x =-≤,则A =N ( )A .{}0B .{}0,1C .{}0,1,2D .{}1,22、 )A B C D3、 (暑假作业原题)若正数x ,y 满足 ²20x xy -+=,则x y +的最小值是( )A .B .C .4D .6【答案】C【分析】根据已知条件及基本不等式即可求解.4、过椭圆22:1169x yC+=的中心作直线l交椭圆于,P Q两点,F是C的一个焦点,则PFQ△周长的最小值为()A.16 B.14 C.12 D.10所以PFQ△的周长为PF当线段PQ为椭圆短轴时,故选:B5、已知圆C的方程为22(2)x y a+-=,则“2a>”是“函数y x=的图象与圆C有四个公共点”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】B6、 (暑假作业原题)如图是一块高尔顿板的示意图,在一块木板上钉着若干排相互平行但相互错开的圆柱形小木钉,小木钉之间留有适当的空隙作为通道,前面挡有一块玻璃.将小球从顶端放入,小球下落的过程中,每次碰到小木钉后都等可能地向左或向右落下,最后落入底部的格子中.记格子从左到右的编号分别为0,1,2,⋯,10,用X 表示小球最后落入格子的号码,若0()()P X k P X k == ,则0(k = )A .4B .5C .6D .7【分析】小球在下落过程中,共10次等可能向左或向右落下,则小球落入格子的号码X 服从二项分布,且落入格子的号码即向右次数,即1~(10,)2X B ,则10101()()(02kP X k C k ===,1,2...,10),然后由二项式系数对称性即可得解.【解答】解:小球在下落过程中,共10次等可能向左或向右落下, 则小球落入格子的号码X 服从二项分布, 且落入格子的号码即向右次数,即1~(10,2X B ,所以10101010111()()(1()(0222k k k kP X k C C k -==-==,1,2...,10),由二项式系数对称性知,当5k =时,10kC 最大,故05k =. 故选:B .【点评】本题考查了二项分布及二项式系数的性质的应用,属于中档题.7、 (教材原题)以正方体的顶点为顶点的三棱锥的个数是( ) A .70B .64C .60D .58【分析】从8个顶点中选4个,共有48C 种结果,在这些结果中,有四点共面的情况,6个表面有6个四点共面,6个对角面有6个四点共面,用所有的结果减去不合题意的结果,得到结论.【解答】解:首先从8个顶点中选4个,共有48C 种结果,在这些结果中,有四点共面的情况,6个表面有6个四点共面,6个对角面有6个四点共面, ∴满足条件的结果有4488661258C C --=-=.故选:D .【点评】本题是一个排列问题同立体几何问题结合的题目,是一个综合题,这种问题实际上是以排列为载体考查正方体的结构特征.8、 (暑假作业原题)已知定义域为R 的函数()f x ,其导函数为()f x ',且满足()2()0f x f x '-<,(0)1f =,则( )A .2(1)1e f -<B .()21f e >C .1(2f e >D .1(1)(2f ef <【分析】构造函数2()()xf xg x e =,由()2()0f x f x '-<得()0g x '<,进而判断函数()g x 的单调性,判断各选项不等式.【解答】解:2()()x f x g x e=,则22222()2()()2()()()x x x x f x e f x e f x f x g x e e '⋅-'-'==, 因为()2()0f x f x '-<在R 上恒成立,所以()0g x '<在R 上恒成立,故()g x 在R 上单调递减, 所以220(1)(0)(1)(0),(1)1f f g g e f e e --->=->=,故A 不正确; 所以g (1)(0)g <,即20(1)(0)f f e e<,即f (1)22(0)e f e <=,故B 不正确;1()(0)2g g <,即101()(0)21f f e e <=,即1(2f e <,故C 不正确; 1()(1)2g g >,即121()(1)2f f e e >,即1(1)()2f ef <,故D 正确.故选:D .【点评】本题考查了利用导数研究函数的单调性,考查了函数思想,属中档题.二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9、 已知复数12,z z ,下列说法正确的是( )A .若12=z z ,则2212z z =B .1212z z z z =C .1212z z z z -≤+D .1212z z z z +≤+10、 已知函数()ππ)02,22f x x ωϕωϕ⎛⎫=+<≤-<< ⎪⎝⎭,函数()()12g x f x =+的部分图象如图所示,则下列说法中正确的是( )A .()f x 的表达式可以写成()24f x x π⎛⎫=- ⎪⎝⎭B .()f x 的图象向右平移3π8个单位长度后得到的新函数是奇函数 C .()()1h x f x =+的对称中心ππ,182k ⎛⎫-+⎪⎝⎭,Z k ∈ D .若方程()1f x =在()0,m 上有且只有6个根,则5π13π,24m ⎛⎫∈ ⎪⎝⎭11、 如图,过点(C a ,0)(0)a >的直线AB 交抛物线22(0)y px p =>于A ,B 两点,连接AO 、BO ,并延长,分别交直线x a =-于M ,N 两点,则下列结论中一定成立的有( )A .//BM ANB .以AB 为直径的圆与直线x a =-相切C .AOB MON S S ∆∆=D .24MCN ANC BCM S S S ∆∆∆=⋅【分析】设出直线与抛物线联立,利用韦达定理及斜率公式,结合三角形的面积公式及直线与圆的位置关系的判断方法即可求解.【解答】解:对于A ,令直线:AB x my a =+,1(A x ,1)y ,2(B x ,2)y , 联立22x my a y px=+⎧⎨=⎩,消x 可得2220y pmy pa --=,则△2(2)80pm pa =+>,122y y pa =-,122y y pm +=, 则21212()222x x m y y a pm a +=++=+, 则1111,:OA y y k OA y x x x ==则直线,∴11(,)ayM a x --,故12211122212220()BMay pay y x y y y pak x a x a y x a +++====+++, 同理0AN k =,//BM AN ∴,故A 正确; 对于B ,如图,设AB 中点1212(,22x x y y Q ++,即2(Q pm a +,)pa -,则Q 到直线x a =-的距离22d pm a =+, 以AB为直径的圆的半径12||||2AB y y =-=,所以222||(2)(2)4AB d p a a p m -=+-, 当2p a =时相切,当2pa ≠时不相切,故B 错误;对于C ,设x a =-与x 轴交于P ,PON AOC S S ∆∆=,MOP BOC S S ∆∆=, 则PON MOP AOC BOC S S S S ∆∆∆∆+=+,则AOB MON S S ∆∆=,故C 正确; 对于D ,112211(),()22ANC BCM S x a y S x a y ∆∆=+=-+,则1212121211()()(2)(2)44ANC BCM S S x a x a y y my a my a y y ∆∆⋅=-++=-++221212121[2()4]4m y y am y y a y y =-+++22221[(2)2(2)4](2)(2)4m pa am pm a pa pa pm a =--++-=+,而121212||||2MCN MPC NPC S S S a y y a y y ∆∆∆=+=⋅-=-, 所以2222222121212()[()4]4(2)4MCN ANC BCM S a y y a y y y y pa pm a S S ∆∆∆=-=+-=+=⋅,故D 正确.故选:ACD .【点评】本题考查了已知两点求斜率,由斜率判断两条直线平行,判断直线与圆的位置关系,根据韦达定理求参数,属于中档题.三、填空题:本题共3小题,每小题5分,共15分.12、 已知随机变量X 服从正态分布()25,N σ,若(56)0.27P X <≤=,则(4)P X <= .13、 已知向量()sin ,cos a θθ=,()3,1b =,若a b ∥,则2sin sin 2θθ+的值为 .14、 设0k >,若存在正实数x ,使得不等式14log 20kx x k --⋅≥成立,则k 的最大值为 .四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.15、 (13分)平面多边形中,三角形具有稳定性,而四边形不具有这一性质.如图所示,四边形ABCD 的顶点在同一平面上,已知2,AB BC CD AD ====(1)当BD cos A C -是否为一个定值?若是,求出这个定值;若否,说明理由.(2)记ABD △与BCD △的面积分别为1S 和2S ,请求出2212S S +的最大值.【答案】cos A C -为定值,定值为1 (2)14【详解】(1)法一:在ABD △中,由余弦定理222cos 2+-=⋅AD AB BD A AD AB,得cos A =2168BD A -=①,同理,在BCD △中,22222cos 222BD C +-=⨯⨯,即28cos 8BD C -=②,①-②cos 1A C -=,所以当BD cos A C -为定值,定值为1; 法二:在ABD △中,由余弦定理2222cos BD AD AB AD AB A =+-⋅得222222cos BD A =+-⨯⨯,即216BD A =-, 同理,在BCD △中,2222cos 88cos BD CD CB CD CB C C =+-⋅=-,所以1688cos A C -=-1cos A C -=cos 1A C -=,所以当BD cos A C -为定值,定值为1;(2)222222221211sin sin 44S S AB AD A BC CD C +=⋅⋅+⋅⋅ 222212sin 4sin 12sin 44cos A C A C =+=+-2212sin 41)A A =+--224cos 12A A =-++,令()cos ,1,1A t t =∈-,所以2224122414y t t ⎛=-++=-+ ⎝⎭,所以t =cos A = 2212S S +有最大值为14.16、 (15分)(暑假作业原题)函数()e 4sin 2xf x x λλ=-+-的图象在0x =处的切线为3,y ax a a =--∈R .(1)求λ的值;(2)求()f x 在(0,)+∞上零点的个数. 解析【小问1详解】因为()e 4sin 2,()e 4cos x x f x x f x x λλλλ'=-+-=-, 所以(0)4f λ'=-,所以切线斜率为4λ-,即4a λ=-, 所切线方程为()41y x λλ=--+又(0)1f λ=-,所以切点坐标为(0,1)λ-,代入得则11λλ-=-+,解得1λ=.【小问2详解】由(1)得()e 4sin 1,()e 4cos x x f x x f x x '=--=-, 令()()e 4cos xg x f x x ==-',则()e 4sin xg x x =+',当πx ≥时,()e 4cos 0x f x x '=->恒成立,所以()f x 在[)π,+∞上递增, 所以ππ()(π)e 4sin 1e 50f x f x ≥=--≥->, 因此()f x 在[π,)+∞无零点;当0πx <<时,()e 4sin 0xg x x '=+>恒成立,所以()f x '单调递增,又π(0)30,(π)e 40f f ''=-<=+>, 所以()f x '在(0,π)上存在唯一的零点0x , 当()00,,()0,()∈<'x x f x f x 单调递减;当()0,π,()0,()x x f x f x '∈>单调递增;又()0(0)0,(0)0f f x f =<=,π(π)e 10f =->, 因此()f x 在(0,π)上仅有1个零点; 综上,()f x 在(0,)+∞上仅有1个零点.17、 (15分)如图,四面体ABCD 中,,,AD CD AD CD ADB BDC ⊥=∠=∠,E 为AC 的中点.(1)证明:平面BED ⊥平面ACD ;(2)设2,60AB BD ACB ==∠=︒,点F 在BD 上,当AFC △的面积最小时,求CF 与平面ABD 所成的角的正弦值.【详解】(1)因为AD CD =,E 为AC 的中点,所以AC DE ⊥; 在ABD △和CBD △中,因为,,B A C D CD ADB DB DB D ∠=∠==,所以ABD CBD ≌△△,所以AB CB =,又因为E 为AC 的中点,所以AC BE ⊥; 又因为,DE BE ⊂平面BED ,DE BE E ⋂=,所以AC ⊥平面BED , 因为AC 平面ACD ,所以平面BED ⊥平面ACD .(2)连接EF ,由(1)知,AC ⊥平面BED ,因为EF ⊂平面BED , 所以AC EF ⊥,所以1=2AFC S AC EF ⋅△,当EF BD ⊥时,EF 最小,即AFC △的面积最小. 因为ABD CBD ≌△△,所以2CB AB ==,又因为60ACB ∠=︒,所以ABC 是等边三角形,因为E 为AC 的中点,所以1AE EC ==,BE =AD CD ⊥,所以112DE AC ==, 在DEB 中,222DE BE BD +=,所以BE DE ⊥.以E 为坐标原点建立如图所示的空间直角坐标系E xyz -, 则()()()1,0,0,,0,0,1A B D ,所以()()1,0,1,AD AB =-=-,设平面ABD 的一个法向量为(),,n x y z = ,则0n AD x z n AB x ⎧⋅=-+=⎪⎨⋅=-=⎪⎩,取y =()n =,又因为()31,0,0,4C F ⎛⎫- ⎪ ⎪⎝⎭,所以34CF ⎛⎫= ⎪ ⎪⎝⎭ ,所以cos ,n CF n CF n CF⋅===, 设CF 与平面ABD 所成的角的正弦值为02πθθ⎛⎫≤≤ ⎪⎝⎭,所以sin cos ,n CF θ== CF 与平面ABD(1)求C 的方程;(2)记双曲线C 的左右顶点分别为1A ,2A ,直线1A M ,2A N 的斜率分别为1k ,2k ,求12k k 的值. (3)探究圆E :224410x y x y +---=上是否存在点S ,使得过S 作双曲线的两条切线1l ,2l 互相垂直.【答案】(1)22143x y -=; (2)13-; (3)存在.【详解】(1)由对称性知,双曲线C 过点(4,3),则221691b a a b ⎧=⎪⎪⎨⎪-=⎪⎩,解得2a b =⎧⎪⎨=⎪⎩,所以双曲线C 的方程为22143x y -=. (2)由(1)得12(2,0),(2,0)A A -,设()()1122,,,M x y N x y , 显然直线MN 不垂直于y 轴,设直线MN 的方程为4x my =+, 由2243412x my x y =+⎧⎨-=⎩消去x 得220(34)2436m y my -++=, 显然22340,144(4)0m m -≠∆=+>,1212222436,3434m y y y y m m -+==--, 则121223m y y y y +=-,即()121232my y y y =-+, 所以()()()()11212112212222222262y y x y my k x y k x y y my x -++===++-()()1211211221223221236362y y y my y y my y y y y y -+++===-+-++.(3)圆22:4410E x y x y +---=上存在点S ,使得过S 作双曲线的两条切线互相垂直. 若双曲线的两条切线有交点,则两条切线的斜率存在且不为0, 设双曲线的两条切线分别为1122,y k x n y k x n =+=+,将y kx n =+代入22143x y -=消去y 得:22(3484120)k knx n ----=,由0'∆=得()()2222644344120k n k n +-+=,解得2243n k =-,因此2222112243,43n k n k =-=-,设两条切线的交点坐标为()00,x y ,则01010202y k x n y k x n -=⎧⎨-=⎩,即有()22010143y k x k -=-,且()22020243y k x k-=-,即()()2222220100100200204230,4230x k x y k y x k x y k y --++=--++=, 于是12,k k 是方程()22200004230x k x y k y --++=的两根,而121k k =-,则2020314y x +=--,即22001x y +=,从而两条切线们交点的轨迹为圆221x y +=, 而221x y +=的圆心为(0,0)O ,半径为1,圆222:(2)(2)3E x y -+-=的圆心(2,2)E ,半径为3,显然||OE ==,满足31||31OE -<<+,即圆O 与圆E 相交, 所以圆22:4410E x y x y +---=上存在点S ,使得过S 作双曲线的两条切线互相垂直.19、 (17分)对于数列{}n a ,如果存在等差数列{}n b 和等比数列{}n c ,使得()n n n a b c n *=+∈N ,则称数列{}n a 是“优分解”的.(1)证明:如果{}n a 是等差数列,则{}n a 是“优分解”的.(2)记()2*11ΔΔΔΔn n n n n n a a a a a a n ++=-=-∈N ,,证明:如果数列{}n a 是“优分解”的,则()2*Δ0n a n =∈N 或数列{}2Δn a 是等比数列.(3)设数列{}n a 的前n 项和为n S ,如果{}n a 和{}n S 都是“优分解”的,并且123346a a a ===,,,求{}n a 的通项公式.【答案】(1)证明见解析 (2)证明见解析 (3)122n n a -=+【详解】(1){}n a 是等差数列,∴设()()111111n a a n d a n d ⎡⎤=+-=-+-+⎣⎦, 令()111,1n n b a n d c =-+-=,则{}n b 是等差数列,{}n c 是等比数列,所以数列{}n a 是“优分解”的.(2)因为数列{}n a 是“优分解”的,设()*n n n a b c n =+∈N ,其中()()11111,0,0n n n b b n d c c q c q -=+-=≠≠,则()12121111Δ1,ΔΔΔ(1)n n n n n n n n a a a d c q q a a a c q q --++=-=+-=-=-. 当1q =时,()2*Δ0n a n =∈N ;当1q ≠时,{}2Δn a 是首项为21(1)c q -,公比为q 的等比数列. (3)一方面, 数列{}n S 是“优分解”的,设()*n n n S B C n =+∈N ,其中()()11111,0,0n n n B B n D C C Q C Q -=+-=≠≠,由(2)知2121Δ(1)n n S C Q Q -=-因为12122323Δ4,Δ6S S S a S S S a =-===-==,所以2121ΔΔΔ2S S S =-=.{}221(1)2,1,Δn C Q Q S ∴-=∴≠∴是首项为2,公比为()1Q Q ≠的等比数列.另一方面,因为{}n a 是“优分解”的,设()*n n n a b c n =+∈N ,其中()()11111,0,0n n n b b n d c c q c q -=+-=≠≠,()2111211Δ,ΔΔΔ1n n n n n n n n n n S S S a S S S a a d c q q +++++=-==-=-=+- {}2Δn S 是首项为2,公比为()1Q Q ≠的等比数列, 0,1q q ∴≠≠,且()()()2222213ΔΔΔS S S =⋅,()()()223111111d c q q d c q q d c q q ⎡⎤⎡⎤⎡⎤∴+-=+-⋅+-⎣⎦⎣⎦⎣⎦化简得()311111(1)0,0,0,1,0,Δ1n n n n c dq q c q q d a a a c q q -+-=≠≠≠∴=∴=-=- ,即数列{}Δn a 是首项121Δ1a a a =-=,公比为q 的等比数列. 又232Δ2,2a a a q =-=∴= ,又()211Δ2,12,0,2,S d c q q d q =∴+-===∴ 解得11111,312c b a c =∴=-=-=,综上所述,()1111122n n n a b n d c q --=+-+=+.。
2012届高三模拟考试作文试题集萃

2012届高三模拟考试作文试题集萃写作佳苑04-04 06302012届高三模拟考试作文试题集萃湖南省雅礼中学2012届高三第五次月考语文试题七、写作(60分)21.阅读下面的文字,按要求作文。
(60分)关怀,需要及于他人,这不是为了赢取欢心,而是出于对人性的尊重。
读到“他人”,你会想到谁或哪些人?请从材料生发立意,自拟题目,写一篇800字以上的记叙文或议论文,表达你对于“关怀”的真切体验或真诚思索。
话题看起来相对完整,其实还是可以通过“增补词语”的方法使之更清晰、更完整。
A、关怀他人的什么?关怀他人的生命、生活、成长、学习、健康、心理……B、如何关怀他人?用爱心、用真诚、用宽容、用劝慰、用激励、用批评、用能所能及的经济援助……C、关怀他人其实就是善待自己,善待自己的生命、品格、荣誉、名声、工作、事业……5、本话题的写作重心可以从“为什么”、“怎么办”任意一个角度去突破。
【审题结论示例】1、和谐社会需要人与人之间相互关怀,相互关怀是让这世界成为美好人间的基础,只有人人付出,才会有社会和谐;关怀他人,也是尊重他人,尊重他人其实也就尊重了自己,有利于实现社会和谐。
2、“关怀他人”其实也是“善待自己”。
因为在“关怀他人”的同时,我们也在自觉地完善自己的品格;在“关怀他人”的同时,我们也得到他人的回馈与帮助;在“关怀他人”的同时,我们创造的和谐社会会让自己生活更美好。
【典型素材示例】1、“盲人提灯”的故事。
2、蜜蜂采花的故事。
3、地狱人的自私与天堂人的互助的故事。
4、张良与项伯的故事。
5、曹操与关羽的故事。
6、人民的总理爱人民,人民的总理人民爱。
7、赠人玫瑰,手留余香。
8、老吾老以及人之老,幼吾幼以及人之幼.9、谭千秋与范跑跑的区别。
10、特蕾莎修女播洒着自己博大的爱,同时,她也收获着数以万计的穷人的爱戴。
11、城管与走鬼的关系。
浙江宁海城管专门开辟让走鬼经营的“钟点市场”。
12、“王老吉”汶川地震捐款1亿元赢得短短两月销售收入超十亿的佳绩。
湖南省长沙市雅礼中学高三下学期第七次月考生物试题()

雅礼中学2022届高三月考试卷(七)生物注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题2分,共24分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.水和矿质元素对植物的生命活动影响非常巨大。
民间有句谚语“有收无收在于水,收多收少在于肥”。
下列说法正确的是C.冬季,植物体内的自由水相对含量升高,以增强植物的抗寒能力D.少数矿质元素以化合物的形式存在,如Mg存在于叶绿体的各种色素中2.细胞作为生命系统中最基本的层次,可以完成多项生命活动。
下列有关细胞结构和功能的叙述,正确的是A.蛋白质是生命活动的主要承担者,都是由内质网上附着的核糖体合成的B.黑藻和蓝藻都是自养生物,其光合色素都分布在叶绿体的类囊体薄膜上C.真核细胞的生物膜系统保证细胞内能够同时进行多种反应且互不干扰D.内质网膜可与核膜、高尔基体膜、细胞膜直接相连,有利于物质的运输3.细胞可运用不同的方式跨膜转运物质,下列相关叙述错误的是A.物质自由扩散进出细胞的速度与浓度梯度有关,与分子大小无关+的通道蛋白和运出Na+的载体蛋白都具有特异性A.组织细胞的更新涉及细胞分裂、分化等过程D.细胞癌变和细胞凋亡都是基因选择性表达的结果,前者是异常表达,后者是正常表达5.如图为某哺乳动物体内细胞连续进行两次分裂的示意图,有关叙述正确的是A.若细胞甲为卵原细胞,则细胞丙一定是卵细胞B.若两次分裂均出现着丝点分裂,则甲、乙、丙染色体数相同C.若细胞甲为基因型为Mm的精原细胞,M与m的分离一定发生在第一次分裂过程中D.在细胞分裂的过程中,核DNA分子数和染色体数始终保持一致A、IB、i共同决定,其中I A I A、I A i为A型血,I B I B、I B i为B型血,I A I B为AB型血,ii为O型血。
湖南省长沙市雅礼中学2009届高三第六次月考试卷文科数学

湖南省长沙市雅礼中学2009届高三月考试卷数学(文史类)命题:高三数学组 审卷:高三数学组本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分,考试时间120分钟. 参考公式: 正棱锥、圆锥的侧面积公式 如果事件A 、B 互斥,那么 cl S 21=锥侧 P (A+B )=P (A )+P (B )如果事件A 、B 相互独立,那么 其中,c 表示底面周长、l 表示斜高或 P (A ·B )=P (A )·P (B ) 母线长如果事件A 在1次实验中发生的概率是 球的体积公式 P ,那么n 次独立重复实验中恰好发生k 334R V π=球 次的概率k n kk n n P P C k P --=)1()( 其中R 表示球的半径第I 卷(共40分)一.选择题:本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合要求的. 1.已知全集U ={1,2,3,4,5},集合M ={1,2,3},N ={3,4,5},则M ∩(U C N )=A.{1,2} B.{4,5} C.{3} D.{1,2,3,4,5}2.()()811x x -+的展开式中含7x 项的系数是A.-21 B.21 C.28- D.283.已知a ,b ∈R ,且a >b ,则下列不等式中恒成立的是A.a 2>b 2B.ba>1 C.lg(a -b)>0 4:已知⎩⎨⎧>+-≤=0,1)2(0,sin )(x x f x x x f π,则)61()61(--f f 的值为A .2-B .1-C .1D .25.给出下面四个命题:①“直线a 、b 为异面直线”的充分非必要条件是:直线a 、b 不相交; ②“直线l 垂直于平面α内所有直线”的充要条件是:l ⊥平面α; ③“直线a ⊥b ”的充分非必要条件是“a 垂直于b 在平面α内的射影”;④“直线a ∥平面β”的必要非充分条件是“直线a 至少平行于平面β内的一条直线”. 其中正确命题的个数是 A.1个 B.2个C.3个 D.4个6.北京2008年第29届奥运会开幕式上举行升旗仪式,在坡度15°的看台上,同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°, 第一排和最后一排的距离 为610米(如图所示),旗杆底部与第一 排在一个水平面上.已知国歌长度约为50 秒,升旗手匀速升旗的速度为 A.51(米/秒) B.53(米/秒) C.56(米/秒)7.已知P 是椭圆13422=+y x 上的一点,21,F F 是该椭圆的两个焦点,若21F PF ∆的内切圆半径为21,则21PF PF ⋅的值为 A.23C.49- D.08.若二次函数)(4)(2R x c x ax x f ∈+-=的值域为(]0,∞-,则ac c a 44-+-的最小值为 A 4B.C .6D.第II 卷二.填空题:本大题共7小题,每小题5分(第14题第一空2分,第二空3分,第15题第一空3分,第二空2分),共35分.把答案填在答题卡...中对应题号后的横线上. 9.0sin15010.若向量()12,23a λλ=+-与()4,1b =共线,则λ11.已知,x y 满足约束条件50,0,3,x y x y x -+≥⎧⎪+≥⎨⎪≤⎩则y x z +=21213.某商贸公司为了解员工对工资福利的满意度,用分层抽样的方法从销售、财务、人事三个部门的员工中抽取一个容量为20的样本。
2012高考湖南文科数学试题及答案(高清版)

2012年普通高等学校夏季招生全国统一考试数学文史类(湖南卷)一、选择题:本大题共9小题,每小题5分,共45分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合M ={-1,0,1},N ={x |x 2=x },则M ∩N 等于( ) A .{-1,0,1} B .{0,1} C .{1} D .{0}2.复数z =i(i +1)(i 为虚数单位)的共轭复数是( ) A .-1-i B .-1+i C .1-i D .1+i3.命题“若π4α=,则tan α=1”的逆否命题是( ) A .若π4α≠,则tan α≠1 B .若π4α=,则tan α≠1C .若tan α≠1,则π4α≠D .若tan α≠1,则π4α=4.某几何体的正视图和侧视图均如图所示,则该几何体的俯视图不可能是( )5.设某大学的女生体重y (单位:kg)与身高x (单位:cm)具有线性相关关系,根据一组样本数据(x i ,y i )(i =1,2,…,n ),用最小二乘法建立的回归方程为0.8585.71y x =-,则下列结论中不正确的是( )A .y 与x 具有正的线性相关关系B .回归直线过样本点的中心(,)x yC .若该大学某女生身高增加1 cm ,则其体重约增加0.85 kgD .若该大学某女生身高为170 cm ,则可断定其体重必为58.79 kg6.已知双曲线C :22221x y a b-=的焦距为10,点P (2,1)在C 的渐近线上,则C 的方程为( )A .221205x y -= B .221520x y -= C .2218020x y -= D .2212080x y -= 7.设a >b >1,c <0,给出下列三个结论: ①c ca b>;②a c <b c ;③log b (a -c )>log a (b -c ). 其中所有的正确结论的序号是( )A .①B .①②C .②③D .①②③ 8.在△ABC 中,AC =7,BC =2,B =60°,则BC 边上的高等于( )A .32 B .332 C .362+ D .3394+9.设定义在R 上的函数f (x )是最小正周期为2π的偶函数,f ′(x )是f (x )的导函数.当x ∈[0,π]时,0<f (x )<1;当x ∈(0,π)且π2x ≠时,(x -π2)f ′(x )>0,则函数y =f (x )-sin x 在[-2π,2π]上的零点个数为( )A .2B .4C .5D .8二、填空题:本大题共7小题,考生作答6小题,每小题5分,共30分.把答案填在答题卡中对应题号后的横线上.(一)选做题(请考生在第9,10,11三题中任选两题作答,如果全做,则按前两题记分) 10.在极坐标系中,曲线C 1:ρ(2cos θ+sin θ)=1与曲线C 2:ρ=a (a >0)的一个交点在极轴上,则a =________.11.某制药企业为了对某种药用液体进行生物测定,需要优选培养温度,试验范围定为29~63℃,精确度要求±1℃,用分数法进行优选时,能保证找到最佳培养温度需要的最少试验次数为________.(二)必做题(12~16题)12.不等式x 2-5x +6≤0的解集为________. 13.如图是某学校一名篮球运动员在五场比赛中所得分数的茎叶图,则该运动员在这五场比赛中得分的方差为________.(注:方差()()()2222121[]n s x x x x x x n=-+-++-…,其中x 为x 1,x 2,…,x n 的平均数)14.如果执行如图所示的程序框图,输入x =4.5,则输出的数i =________.15.如图,在平行四边形ABCD 中,AP ⊥BD ,垂足为P ,且AP =3,则AP AC ⋅=________.16.对于n ∈N *,将n 表示为n =a k ×2k+a k -1×2k -1+…+a 1×21+a 0×20,当i =k 时,a i =1,当0≤i ≤k -1时,a i 为0或1.定义b n 如下:在n 的上述表示中,当a 0,a 1,a 2,…,a k 中等于1的个数为奇数时,b n =1;否则b n =0.(1)b 2+b 4+b 6+b 8=________;(2)记c m 为数列{b n }中第m 个为0的项与第m +1个为0的项之间的项数,则c m 的最大值是________.三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤. 17.某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的100位顾客的相关数据,如下表所示.一次购 物量 1至4件 5至8件 9至 12件 13至 16件 17件 及以上 顾客数(人) x 30 25 y 10结算时间(分钟/人)1 1.52 2.5 3已知这100位顾客中一次购物量超过8件的顾客占55%.(1))确定x ,y 的值,并估计顾客一次购物的结算时间的平均值; (2)求一位顾客一次购物的结算时间不超过2分钟的概率. (注:将频率视为概率)18.已知函数f (x )=A sin(ωx +φ)(x ∈R ,ω>0,π02<<)的部分图象如图所示.(1)求函数f (x )的解析式; (2)求函数g (x )=f (x -π12)-f (x +π12)的单调递增区间. 19.如图,在四棱锥P -ABCD 中,P A ⊥平面ABCD ,底面ABCD 是等腰梯形,AD ∥BC ,AC ⊥BD .(1)证明:BD ⊥PC ;(2)若AD =4,BC =2,直线PD 与平面P AC 所成的角为30°,求四棱锥P -ABCD 的体积.20.某公司一下属企业从事某种高科技产品的生产,该企业第一年年初有资金2 000万元,将其投入生产,到当年年底资金增长了50%.预计以后每年资金年增长率与第一年的相同.公司要求企业从第一年开始,每年年底上缴资金d 万元,并将剩余资金全部投入下一年生产,设第n 年年底企业上缴资金后的剩余资金为a n 万元.(1)用d 表示a 1,a 2,并写出a n +1与a n 的关系式;(2)若公司希望经过m (m ≥3)年使企业的剩余资金为4 000万元,试确定企业每年上缴资金d 的值(用m 表示).21.在直角坐标系xOy 中,已知中心在原点,离心率为12的椭圆E 的一个焦点为圆C :x 2+y 2-4x +2=0的圆心.(1)求椭圆E 的方程;(2)设P 是椭圆E 上一点,过P 作两条斜率之积为12的直线l 1,l 2,当直线l 1,l 2都与圆C 相切时,求P 的坐标.22.已知函数f (x )=e x -ax 1,其中a >0.(1)若对一切x ∈R ,f (x )≥1恒成立,求a 的取值集合;(2)在函数f (x )的图象上取定两点A (x 1,f (x 1)),B (x 2,f (x 2))(x 1<x 2),记直线AB 的斜率为k ,证明:存在x 0∈(x 1,x 2),使f ′(x 0)=k 成立.1. B 由N ={x |x 2=x },知x =0或x =1.又∵M ={-1,0,1},∴M ∩N ={0,1}.2.A z =i(i +1)=i 2+i =-1+i ,∴1i z =--. 3. C 命题“若π4α=,则tan α=1”的逆否命题是“若tan α≠1,则π4α≠”. 4. D 若为D 项,则主视图如图所示,故不可能是D 项.5. D D 项中,若该大学某女生身高为170 cm ,则其体重约为:0.85×170-85.71= 58.79(kg).故D 项不正确. 6. A 由2c =10,得c =5, ∵点P (2,1)在直线by x a=上, ∴21ba=.又∵a 2+b 2=25,∴a 2=20,b 2=5. 故C 的方程为221205x y -=. 7. D ①()c c c b a a b ab--=,∵a >b >1,c <0,∴()0c b a ab->. 即0c ca b->.故①正确. ②考察函数y =x c (c <0),可知为单调减函数. 又∵a >b >1,∴a c <b c .故②正确.③∵a >b >1,c <0,∴log b (a -c )>0,log a (b -c )>0,∴log ()lg()lg log ()lg lg()b a a c a c ab c b b c --=--. ∵lg()1lg()a c b c ->-,lg 1lg ab >, ∴lg()lg 1lg lg()a c ab bc ->-,故③正确. 8. B 在△ABC 中,由余弦定理可知:AC 2=AB 2+BC 2-2AB ·BC cos B , 即7=AB 2+4-2×2×AB ×12.整理得AB 2-2AB -3=0. 解得AB =-1(舍去)或AB =3.故BC 边上的高AD =AB ·sin B =3×sin60°=332. 9. B 由x ∈(0,π)且π2x ≠时,(x -π2)f ′(x )>0可知: 当x ∈(0,π2)时,f ′(x )<0,f (x )单调递减; 当x ∈(π2,π)时,f ′(x )>0,f (x )单调递增. 又∵x ∈[0,π]时,f (x )∈(0,1),且f (x )是最小正周期为2π的偶函数,可画出f (x )的草图为:对于y =f (x )-sin x 的零点,可在同一坐标系中再作出y =sin x 的图象,可知在[-2π,2π]上零点个数为4.10.答案:22解析:把曲线C 1:ρ(2cos θ+sin θ)=1化成直角坐标方程,得2x +y =1; 把曲线C 2:ρ=a (a >0)化成直角坐标方程,得x 2+y 2=a 2. ∵C 1与C 2的一个交点在极轴上, ∴2x +y =1与x 轴交点(22,0)在C 2上, 即(22)2+0=a 2. 又∵a >0,∴22a =. 11.答案:7解析:由分数法计算可知最少实数次数为7. 12.答案:{x |2≤x ≤3}解析:∵x 2-5x +6≤0,∴(x -2)(x -3)≤0.∴2≤x ≤3. 13.答案:6.8解析:∵89101315115x ++++==,∴222222(811)(911)(1011)(1311)(1511) 6.85s -+-+-+-+-==. 14.答案:4解析:i =1时,x =4.5-1=3.5;i =1+1=2时,x =3.5-1=2.5; i =2+1=3时,x =2.5-1=1.5; i =3+1=4时,x =1.5-1=0.5; 0.5<1,输出i =4. 15.答案:18解析:∵过C 作BD 的平行线,延长AP 交该平行线于点Q , 则AQ =2AP =6.故||||cos ,||||3618AP AC AP AC AP AC AP AQ ⋅=⋅=⋅=⨯=.16.答案:(1)3 (2)2解析:(1)由题意知2=1×2,b 2=1;4=1×22,b 4=1;6=1×22+1×2,b 6=0;8=1×23,b 8=1,所以b 2+b 4+b 6+b 8=3.(2)①若n 为偶数,且b n =0,则n =a k ×2k +a k -1×2k -1+…+a 1×21+a 0×20中a 0=0,且a k ,a k -1,…a 1中有偶数个1,n +1=a k ×2k +a k -1×2k -1+…+a 1×21+1×20,b n +1=1 n +2=a m ′ ×2m +a m -1′×2m -1+…+a 1′ ×21+0×20, 若b n +2=0,此时c m =1;若b n +2=1,则n +3=a m ′×2m +a m -1′×2m -1+…+a 1′ ×21+1×20, 则b n +3=0,此时c m =2.②若n 为奇数,n =a k ×2k +…+1×20,且b n =0, 则n +1=a m ′ ×2m +…+a 1′ ×21+0×20, 若b n +1=0,此时c m =0.若b n +1=1,则n +2=a m ′×2m +…+a 1′ ×21+1×20,b n +2=0. 此时,c m =1.综上所述,c m 的最大值为2.(注:也可列举连续的几项,作出猜测)17.解:(1)由已知得25+y +10=55,x +30=45, 所以x =15,y =20.该超市所有顾客一次购物的结算时间组成一个总体,所收集的100位顾客一次购物的结算时间可视为总体的一个容量为100的简单随机样本,顾客一次购物的结算时间的平均值可用样本平均数估计,其估计值为115 1.530225 2.5203101.9100⨯+⨯+⨯+⨯+⨯=(分钟).(2)记A 为事件“一位顾客一次购物的结算时间不超过2分钟”,A 1,A 2,A 3分别表示事件“该顾客一次购物的结算时间为1分钟”“该顾客一次购物的结算时间为1.5分钟”“该顾客一次购物的结算时间为2分钟”,将频率视为概率得1153()10020P A ==,2303()10010P A ==,3251()1004P A ==. 因为A =A 1∪A 2∪A 3,且A 1,A 2,A 3是互斥事件, 所以P (A )=P (A 1∪A 2∪A 3) =P (A 1)+P (A 2)+P (A 3) =33172010410++=. 故一位顾客一次购物的结算时间不超过2分钟的概率为710. 18.解:(1)由题设图象知,周期11π5π2()π1212T =-=, 所以2π2T ω==, 因为点(5π12,0)在函数图象上,所以A sin(2×5π12+φ)=0,即sin(5π6+φ)=0.又因为0<φ<π2,所以5π5π4π663ϕ<+<,从而5π6+φ=π,即π6ϕ=.又点(0,1)在函数图象上, 所以πsin16A =,得A =2. 故函数f (x )的解析式为f (x )=2sin(2x +π6). (2)ππππ()2sin[2()]2sin[2()]126126g x x x =-+-++ =2sin2x -2sin(2x +π3)=132sin22(sin2cos2)22x x x -+=sin2x -3cos2x=2sin(2x -π3).由πππ2π22π232k x k -≤-≤+,得π5πππ1212k x k -≤≤+,k ∈Z , 所以函数g (x )的单调递增区间是π5ππ,π1212k k ⎡⎤-+⎢⎥⎣⎦,k ∈Z . 19.解:(1)证明:因为P A ⊥平面ABCD ,BD 平面ABCD , 所以P A ⊥BD .又AC ⊥BD ,P A ,AC 是平面P AC 内的两条相交直线,所以BD ⊥平面P AC , 而PC 平面P AC ,所以BD ⊥PC .(2)设AC 和BD 相交于点O ,连结PO ,由(1)知,BD ⊥平面P AC , 所以∠DPO 是直线PD 和平面P AC 所成的角, 从而∠DPO =30°.由BD ⊥平面P AC ,PO 平面P AC 知,BD ⊥PO . 在Rt △POD 中,由∠DPO =30°得PD =2OD .因为四边形ABCD 为等腰梯形,AC ⊥BD , 所以△AOD ,△BOC 均为等腰直角三角形,从而梯形ABCD 的高为12AD +12BC =12×(4+2)=3, 于是梯形ABCD 的面积S =12×(4+2)×3=9.在等腰直角三角形AOD 中,2222OD AD ==,所以PD =2OD =42,224PA PD AD =-=.故四棱锥P -ABCD 的体积为 V =13×S ×P A =13×9×4=12. 20.解:(1)由题意得a 1=2 000(1+50%)-d =3 000-d ,a 2=a 1(1+50%)-d =32a 1-d =4 500-52d . a n +1=a n (1+50%)-d =32a n -d .(2)由(1)得a n =32a n -1-d =32(32a n -2-d )-d=(32)2a n -2-32d -d =…=(32)n -1a 1-d [1+32+(32)2+…+(32)n -2].整理得a n =(32)n -1(3 000-d )-2d [(32)n -1-1]=(32)n -1(3 000-3d )+2d .由题意,a m =4 000,即(32)m -1(3 000-3d )+2d =4 000. 解得13[()2]10001000(32)2332()12m m m m mm d +-⨯-==--, 故该企业每年上缴资金d 的值为11000(32)32m m m m+--时,经过m (m ≥3)年企业的剩余资金为4 000万元.21.解:(1)由x 2+y 2-4x +2=0得(x -2)2+y 2=2, 故圆C 的圆心为点(2,0).从而可设椭圆E 的方程为22221x y a b+=(a >b >0),其焦距为2c . 由题设知c =2,12c e a ==, 所以a =2c =4,b 2=a 2-c 2=12.故椭圆E 的方程为2211612x y +=. (2)设点P 的坐标为(x 0,y 0),l 1,l 2的斜率分别为k 1,k 2.则l 1,l 2的方程分别为l 1:y -y 0=k 1(x -x 0),l 2:y -y 0=k 2(x -x 0),且1212k k =. 由l 1与圆C :(x -2)2+y 2=2相切得101021|2|21k y k x k +-=+,即[(2-x 0)2-2]k 12+2(2-x 0)y 0k 1+y 02-2=0. 同理可得[(2-x 0)2-2]k 22+2(2-x 0)y 0k 2+y 02-2=0.从而k 1,k 2是方程[(2-x 0)2-2]k 2+2(2-x 0)y 0k +y 02-2=0的两个实根.于是20(2)20,0,x ⎧--≠⎨∆>⎩①且20122021(2)22y k k x -==--. 由220020201,161221(2)22x y y x ⎧+=⎪⎪⎨-⎪=⎪--⎩ 得5x 02-8x 0-36=0,解得x 0=-2或0185x =. 由x 0=-2得y 0=±3;由0185x =得0575y =±,它们均满足①式,故点P 的坐标为(-2,3),故(-2,-3),或1857(,)55,或1857(,)55-. 22.解:(1)f ′(x )=e x -a .令f ′(x )=0得x =ln a . 当x <ln a 时,f ′(x )<0,f (x )单调递减; 当x >ln a 时,f ′(x )>0,f (x )单调递增.故当x =ln a 时,f (x )取最小值f (ln a )=a -a ln a ,于是对一切x ∈R ,f (x )≥1恒成立,当且仅当a -a ln a ≥1.①令g (t )=t -t ln t ,则g ′(t )=-ln t .当0<t <1时,g ′(t )>0,g (t )单调递增;当t >1时,g ′(t )<0,g (t )单调递减. 故当t =1时,g (t )取最大值g (1)=1. 因此,当且仅当a =1时,①式成立. 综上所述,a 的取值集合为{1}.(2)由题意知,21212121()()e e x x f x f x k a x x x x --==---.令φ(x )=f ′(x )-k =e x -2121e ex x x x --,则φ(x 1)=121e x x x --[e x 2-x 1-(x 2-x 1)-1],φ(x 2)=221e x x x -[e x 1-x 2-(x 1-x 2)-1],令F (t )=e t -t -1,则F ′(t )=e t -1. 当t <0时,F ′(t )<0,F (t )单调递减; 当t >0时,F ′(t )>0,F (t )单调递增.故当t ≠0时,F (t )>F (0)=0,即e t -t -1>0.从而e x 2-x 1-(x 2-x 1)-1>0,e x 1-x 2-(x 1-x 2)-1>0.又121e 0x x x >-,221e 0x x x >-, 所以φ(x 1)<0,φ(x 2)>0. 因为函数y =φ(x )在区间[x 1,x 2]上的图象是连续不断的一条曲线,所以存在x 0∈(x 1,x 2),使φ(x 0)=0,即f ′(x 0)=k 成立.。
2024-2025学年湖南省长沙市雅礼中学高三(上)月考数学试卷(一)(含答案)

2024-2025学年湖南省长沙市雅礼中学高三(上)月考数学试卷(一)一、单选题:本题共8小题,每小题5分,共40分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合A ={x |log 2x >1},B ={x |0<x <4},则A ∩B =( )A. {x |2<x <4}B. {x |2⩽x <4}C. {x |0<x⩽2}D. {x |x⩽2}2.已知复数z 满足(1―i )z =2i ,且z +ai (a ∈R )为实数,则a =( )A. 1B. 2C. ―1D. ―23.设向量a =(1,0),b =(12,12),则下列结论中正确的是( )A. |a |=|b | B. a ⋅b = 22 C. a ―b 与b 垂直 D. a //b4.已知a 是函数f (x )=2x ―log 12x 的零点,若0<x 0<a ,则f (x 0)的值满足( )A. f (x 0)=0B. f (x 0)>0C. f (x 0)<0D. f (x 0)的符号不确定5.若sinx +cosx =13,x ∈(0,π),则sinx ―cosx 的值为( )A. ± 173 B. ― 173 C. 13 D. 1736.用数字1,2,3,4,5组成的无重复数字的四位偶数的个数为( )A. 8B. 24C. 48D. 1207.函数y =f (x )的图象如图①所示,则如图②所示的函数图象所对应的函数解析式可能为( )A. y =f (1―12x )B. y =―f (1―12x )C. y =f (4―2x )D. y =―f (4―2x )8.刍曹是我国传统建筑造型之一,蕴含着丰富的数学元素.安装灯带可以勾勒出建筑轮廓,展现造型之美.如图,某屋顶可视为五面体ABCDEF ,四边形ABFE 和CDEF 是全等的等腰梯形,△ADE 和△BCF 是全等的等腰三角形.若AB =25m ,BC =AD =10m ,且等腰梯形所在的面、等腰三角形所在的面与底面夹角的正切值均为145.为这个模型的轮廓安装灯带(不计损耗),则所需灯带的长度为( )A. 102mB. 112mC. 117mD. 125m二、多选题:本题共3小题,共18分。
湖南省长沙市雅礼中学2024-2025学年高三上学期月考(三)数学试题(含解析)

雅礼中学2025届高三月考试卷(三)数学命题人:审题人:得分:________本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共8页.时量120分钟,满分150分.第Ⅰ卷一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.命题“存在,”的否定是A.存在,B.不存在,C.任意,D.任意,2.若集合(i 是虚数单位),,则等于A. B. C. D.3.已知奇函数,则A.-1B.0C.1D.4.已知,是两条不同的直线,,是两个不同的平面,则下列可以推出的是A.,, B.,,C.,, D.,,5.已知函数图象的一个最高点与相邻的对称中心之间的距离为5,则A.0B. C.4D.x ∈Z 220x x m ++…x ∈Z 220x x m ++>x ∈Z 220x x m ++>x ∈Z 220x x m ++…x ∈Z 220x x m ++>{}2341,i ,i ,i A ={}1,1B =-A B ⋂{}1-{}1{}1,1-∅()()22cos x x f x m x -=+⋅m =12m l αβαβ⊥m l ⊥m β⊂l α⊥m l ⊥l αβ⋂=m α⊂m l m α⊥l β⊥l α⊥m l m β()()4cos (0)f x x ωϕω=+>6f ϕπ⎛⎫-=⎪⎝⎭2ϕ2ϕ6.已知是圆上一个动点,且直线与直线(,,)相交于点,则的取值范围为A. B.C. D.7.是椭圆上一点,,是的两个焦点,,点在的角平分线上,为原点,,且.则的离心率为A.8.设集合,那么集合中满足条件“”的元素个数为A.60B.90C.120D.130二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分.9.如图为某地2014年至2023年的粮食年产量折线图,则下列说法正确的是A.这10年粮食年产量的极差为16B.这10年粮食年产量的第70百分位数为35C.这10年粮食年产量的平均数为33.7D.前5年的粮食年产量的方差小于后5年粮食年产量的方差10.已知函数满足,,并且当时,,则下列关于函数说法正确的是M 22:1C x y +=1:30l mx ny m n --+=2:30l nx my m n +--=m n ∈R 220m n +≠P PM 1,1⎤-+⎦1⎤-⎦1,1⎤-+⎦1⎤+⎦P 2222:1(0)x y C a b a b+=>>1F 2F C 120PF PF ⋅= Q 12F PF ∠O 1OQPF OQ b =C 12(){}{}{}12345,,,,|1,0,1,1,2,3,4,5iAx x x x x x i ∈-=A 1234513x x x x x ++++……()f x ()()22f x f x ππ+=-()()0fx f x ππ++-=()0,x π∈()cos f x x =()f xA. B.最小正周期C.的图象关于直线对称D.的图象关于对称11.若双曲线,,分别为左、右焦点,设点是在双曲线上且在第一象限的动点,点为的内心,,则下列说法不正确的是A.双曲线的渐近线方程为B.点的运动轨迹为双曲线的一部分C.若,,则D.不存在点,使得取得最小值答题卡题号1234567891011得分答案第Ⅱ卷三、填空题:本题共3小题,每小题5分,共15分.12.的展开式中的系数为________.13.各角的对应边分别为,,,满足,则角的取值范围为________.14.对任意的,不等式(其中e 是自然对数的底)恒成立,则的最大值为________.四、解答题:本题共5小题,共77分.请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤.15.(本小题满分13分)设为正项等比数列的前项和,,.(1)求数列的通项公式;(2)数列满足,,求数列的前项和.302f π⎛⎫=⎪⎝⎭2T π=()f x x π=()f x (),0π-22:145x y C -=1F 2F P I12PF F △()0,4A C 045x y±=I 122PF PF =12PI xPF yPF =+ 29y x -=P 1PA PF +523x x ⎛⎫+ ⎪⎝⎭4x ABC △a b c 1b ca c a b+++…A *n ∈N 11e 1nan n n ⎛⎫⎛⎫+⋅ ⎪ ⎪+⎝⎭⎝⎭…a n S {}n a n 21332S a a =+416a ={}n a {}n b 11b =1222log log n nn n b a b a ++={}n b n n T16.(本小题满分15分)如图,在四棱锥,,,,点在上,且,.(1)若为线段的中点,求证:平面;(2)若平面,求平面与平面所成夹角的余弦值.17.(本小题满分15分)已知函数有两个极值点为,,.(1)当时,求的值;(2)若(e 为自然对数的底数),求的最大值.18.(本小题满分17分)已知抛物线的焦点为,为上任意一点,且的最小值为1.(1)求抛物线的方程;(2)已知为平面上一动点,且过能向作两条切线,切点为,,记直线,,的斜率分别为,,,且满足.①求点的轨迹方程;②试探究:是否存在一个圆心为,半径为1的圆,使得过可以作圆的两条切线,,切线,分别交抛物线于不同的两点,和点,,且为定值?若存在,求圆的方程,不存在,说明理由.19.(本小题满分17分)对于一组向量,,,…,(且),令,如果存在,使得,那么称是该向量组的“长向量”.(1)设,且,若是向量组,,的“长向量”,求实数的取值范P ABCD -BCAD 1AB BC ==3AD =E AD PE AD ⊥2DE PE ==F PE BFPCD AB ⊥PAD PAB PCD ()21ln 2f x x x ax =+-1x ()212x x x <a ∈R 52a =()()21f x f x -21e x x …()()21f x f x -2:2(0)E x py p =>F H E HF E P P E M N PM PN PF 1k 2k 3k 123112k k k +=P ()0,(0)Q λλ>P Q 1l 2l 1l 2l E ()11,A s t ()22,B s t ()33,C s t ()44,D s t 1234s s s s Q 1a 2a 3a n a N n ∈3n …123n n S a a a a =++++{}()1,2,3,,p a p n ∈ p n p a S a - …p a(),2n a n x n =+n ∈N 0n >3a 1a 2a 3ax围;(2)若,且,向量组,,,…,是否存在“长向量”?给出你的结论并说明理由;(3)已知,,均是向量组,,的“长向量”,其中,.设在平面直角坐标系中有一点列,,,…,,满足为坐标原点,为的位置向量的终点,且与关于点对称,与(且)关于点对称,求的最小值.sin,cos 22n n n a ππ⎛⎫= ⎪⎝⎭n ∈N 0n >1a 2a 3a 7a 1a 2a 3a 1a2a3a()1sin ,cos a x x =()22cos ,2sin a x x = 1P 2P 3P n P 1P 2P 3a 21k P +2k P 1P 22k P +21k P +k ∈N 0k >2P10151016P P参考答案一、二、选择题题号1234567891011答案DCADCBCDACDADABD1.D2.C 【解析】集合,,.故选C.3.A【解析】是奇函数,,,,,.故选A.4.D 【解析】有可能出现,平行这种情况,故A 错误;会出现平面,相交但不垂直的情况,故B 错误;,,,故C 错误;,,又由,故D 正确.故选D.5.C 【解析】设的最小正周期为,函数图象的一个最高点与相邻的对称中心之间的距离为5,则有,得,则有,解得,所以,所以.故选C.6.B 【解析】依题意,直线恒过定点,直线恒过定点,显然直线,因此,直线与交点的轨迹是以线段为直径的圆,其方程为:,圆心,半径,而圆的圆心,半径,如图:,两圆外离,由圆的几何性质得:,{}i,1,1,i A =--{}1,1B =-{}1,1A B ⋂=-()f x ()()22cos x x f x m x -=+⋅()()()2222x x x xf x f x m --⎡⎤∴+-=+++⎣⎦cos 0x =()()122cos 0x x m x -∴++=10m ∴+=1m =-αβαβm l m α⊥l βαβ⊥⇒ l α⊥m l m α⇒⊥ m βαβ⇒⊥ ()f x T 224254T ⎛⎫+= ⎪⎝⎭12T =212πω=6πω=()4cos 6f x x πϕ⎛⎫=+ ⎪⎝⎭664cos 4cos046f ϕϕπϕππ⎛⎫⎛⎫-=-⨯+== ⎪ ⎪⎝⎭⎝⎭()()1:310l m x n y ---=()3,1A ()()2:130l n x m y -+-=()1,3B 12l l ⊥1l 2l P AB 22(2)(2)2x y -+-=()2,2N 2r =C ()0,0C 11r =12NC r r =>+12min1PMNC r r =--=-,所以的取值范围为.故选B.7.C 【解析】如图,设,,延长交于点,由题意知,为的中点,故为中点,又,即,则,又由点在的角平分线上得,则是等腰直角三角形,故有化简得即代入得,即,又,所以,所以,.故选C.8.D 【解析】因为或,所以若,则在中至少有一个,且不多于3个.所以可根据中含0的个数进行分类讨论.①五个数中有2个0,则另外3个从1,-1中取,共有方法数为,②五个数中有3个0,则另外2个从1,-1中取,共有方法数为,③五个数中有4个0,则另外1个从1,-1中取,共有方法数为,所以共有种.故选D.9.ACD 【解析】将样本数据从小到大排列为26,28,30,32,32,35,35,38,39,42,这10年的粮食年产量极差为,故A 正确;,结合A 选项可知第70百分位数为第7个数和第812max1PMNC r r =++=+PM 1⎤-+⎦1PF m =2PF n =OQ 2PF A 1OQ PF O 12F F A 2PF 120PF PF ⋅= 12PF PF ⊥2QAP π∠=Q 12F PF ∠4QPA π∠=AQP △2222,4,11,22m n a m n c b n m ⎧⎪+=⎪+=⎨⎪⎪+=⎩2,2,m n b m n a -=⎧⎨+=⎩,,m a b n a b =+⎧⎨=-⎩2224m n c +=222()()4a b a b c ++-=2222a b c +=222b a c =-2223a c =223e =e =0i x =1i x =1234513x x x x x ++++……()1,2,3,4,5i x i =1i x =i x 2315C 2N =⋅3225C 2N =⋅435C 2N =⋅23324555C 2C 2C 2130N =⋅+⋅+⋅=422616-=1070%7⨯=个数的平均数,即,故B 不正确;这10年粮食年产量的平均数为,故C 正确;结合图形可知,前5年的粮食年产量的波动小于后5年的粮食产量波动,所以前5年的粮食年产量的方差小于后5年的粮食年产量的方差,故D 正确.故选ACD.10.AD 【解析】由于时,,并且满足,则函数的图象关于直线对称.由于,所以,故,故,故函数的最小正周期为,根据,知函数的图象关于对称.由于时,,,故A 正确,由于函数的最小正周期为,故B 错误;由函数的图象关于对称,易知的图象不关于直线对称,故C 错误;根据函数图象关于点对称,且函数图象关于直线对称,知函数图象关于点对称,又函数的最小正周期为,则函数图象一定关于点对称,故D 正确.故选AD.11.ABD 【解析】双曲线,可知其渐近线方程为,A 错误;设,,的内切圆与,,分别切于点,,,可得,,,由双曲线的定义可得:,即,又,解得,则点的横坐标为,由点与点的横坐标相同,即点的横坐标为,故在定直线上运动,B 错误;由,且,解得,,,,则,同理可得:,设直线,直线,联立方程得,设的内切圆的半径为,则,解得,即,353836.52+=()13232302835384239263533.710⨯+++++++++=()0,x π∈()cos f x x =()()22f x f x ππ+=-()f x 2x π=()()0fx f x ππ++-=()()fx f x ππ+=--()()()()()22f xf x f x f x ππππ--+=+=--=-()()()24f x f x f x ππ=-+=+4π()()0fx f x ππ++-=()f x (),0π()0,x π∈()cos f x x =3cos 022222f f ff πππππππ⎛⎫⎛⎫⎛⎫⎛⎫=+=--=-=-=⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭4π()f x (),0π()f x x π=(),0π2x π=()3,0π4π(),0π-22:145x y C -=02x =1PF m =2PF n =12PF F △1PF 2PF 12F F S K T PS PK =11F S FT =22F T F K =2m n a -=12122F S F K FT F T a -=-=122FT F T c +=2F T c a =-T a I T I 2a =I 2x =122PF PF =1224PF PF a -==18PF =24PF =1226F F c ==126436167cos 2868PF F ∠+-∴==⨯⨯12sin PF F ∠==12tan PF F ∠∴=21tan PF F ∠=)1:3PF y x =+)2:3PF y x =-(P 12PF F △r ()12118684622PF F S r =⨯⨯=⨯++⋅△r =I ⎛ ⎝,,,由,可得解得,,故,C 正确;,,当且仅当,,三点共线取等号,易知,故存在使得取最小值,D 错误.故选ABD.三、填空题:本题共3小题,每小题5分,共15分.12.90 【解析】展开式的通项公式为,令,解得,所以展开式中的系数为.13. 【解析】从所给条件入手,进行不等式化简,观察到余弦定理公式特征,进而利用余弦定理表示,由可得,可得.14. 【解析】对任意的,不等式(其中e 是自然对数的底)恒成立,只需恒成立,只需恒成立,只需恒成立,2,PI ⎛∴=- ⎝ (17,PF =- (21,PF =- 12PI xPF yPF =+ 27,,x y -=--⎧⎪⎨=⎪⎩29x =49y =29y x -=1224PF PF a -== 12244PA PF PA PF AF ∴+=+++…A P 2F ()1min549PA PF +=+=P 1PA PF +523x x ⎛⎫+ ⎪⎝⎭()()521031553C C 3rr rrr r r T x x x --+⎛⎫=⋅⋅=⋅⋅ ⎪⎝⎭1034r -=2r =4x 225C 310990⋅=⨯=0,3π⎛⎤⎥⎝⎦()()1b c b a b c a c a c a b+⇒+++++……()()222a c a b b c a bc ++⇒++…cos A 222b c a ac +-…2221cos 22b c a A bc +-=…0,3A π⎛⎤∈ ⎥⎝⎦11ln2-*n ∈N 11e 1n an n n ⎛⎫⎛⎫+⋅ ⎪ ⎪+⎝⎭⎝⎭…11e n an +⎛⎫+ ⎪⎝⎭…()1ln 11n a n ⎛⎫++ ⎪⎝⎭…11ln 1a n n -⎛⎫+ ⎪⎝⎭…构造,,,.下证,再构造函数,,,,设,,,令,,,,在时,,单调递减,,即,所以递减,,即,所以递减,并且,所以有,,所以,所以在上递减,所以的最小值为.,即的最大值为.四、解答题:本题共5小题,共77分.请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤.15.【解析】(1)因为是正项等比数列,所以,公比,因为,所以,即,则,解得(舍去)或,∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙(3分)又因为,所以,所以数列的通项公式为.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙(6分)(2)依题意得,∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙(7分)当时,,所以,因为,所以,当时,符合上式,所以数列的通项公式为.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙(10分)()()11ln 1m x x x =-+(]0,1x ∈()()()()()22221ln 11ln 1x x x m x x x x ++-=++'(]0,1x ∈()(]22ln 1,0,11x x x x+<∈+()()22ln 11x h x x x =+-+(]0,1x ∈()()()2221ln 12(1)x x x xh x x ++-'-=+(]0,1x ∈()()()221ln 12F x x x x x =++--()()2ln 12F x x x =+-'(]0,1x ∈()()2ln 12G x x x =+-(]0,1x ∈()21xG x x=-+'(]0,1x ∈(]0,1x ∈()0G x '<()G x ()()00G x G <=()0F x '<()F x ()()00F x F <=()0h x '<()h x ()00h =()22ln 11x x x+<+(]0,1x ∈()0m x '<()m x (]0,1x ∈()m x ()111ln2m =-11ln2a ∴-…a 11ln2-{}n a 10a >0q >21332S a a =+()121332a a a a +=+21112320a q a q a --=22320q q --=12q =-2q =3411816a a q a ===12a ={}n a 2n n a =1222222log log 2log log 22n n n n n n b a nb a n +++===+2n …()324123112311234511n n b b b b n b b b b n n n --⨯⋅⋅⋅=⨯⨯⨯⨯=++ ()121n b b n n =+11b =()21n b n n =+1n =1n b ={}n b ()21n b n n =+因为,所以.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙(13分)16.【解析】(1)设为的中点,连接,,因为是中点,所以,且,因为,,,,所以四边形为平行四边形,,且,所以,且,即四边形为平行四边形,所以,因为平面平面,所以平面.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙(6分)(2)因为平面,所以平面,又,所以,,相互垂直,∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙(7分)以为坐标原点,建立如图所示的空间直角坐标系,则,,,,,所以,,,,∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙(9分)设平面的一个法向量为,则取,则,∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙(11分)设平面的一个法向量为,()211211n b n n n n ⎛⎫==- ⎪++⎝⎭1111112212221223111n n T n n n n ⎛⎫⎛⎫⎛⎫⎛⎫=-+-++-=-=⎪ ⎪ ⎪ ⎪+++⎝⎭⎝⎭⎝⎭⎝⎭M PD FM CM F PE FMED 12FM ED =AD BC 1AB BC ==3AD =2DE PE ==ABCE BC ED 12BC ED =FM BC FM BC =BCMF BFCM BF ⊄,PCD CM ⊂PCD BF PCD AB ⊥PAD CE ⊥PAD PE AD ⊥EP ED EC E ()0,0,2P ()0,1,0A -()1,1,0B -()1,0,0C ()0,2,0D ()1,0,0AB = ()0,1,2AP = ()1,0,2PC =- ()1,2,0CD =-PAB ()111,,m x y z =1110,20,m AB x m AP y z ⎧⋅==⎪⎨⋅=+=⎪⎩ 11z =-()0,2,1m =- PCD ()222,,n x y z =则取,则,∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙(13分)设平面与平面所成夹角为,则∙∙∙∙∙∙∙∙∙∙∙(15分)17.【解析】(1)函数的定义域为,则,当时,可得,,∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙(2分)当或时,;当时,;所以在区间,上单调递增,在区间上单调递减;∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙(4分)所以和是函数的两个极值点,又,所以,;所以,即当时,.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙(6分)(2)易知,又,所以,是方程的两个实数根,则且,,所以,∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙(9分)所以,∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙(11分)设,由,可得,令,,∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙(13分)则,所以在区间上单调递减,222220,20,n PC x z n CD x y ⎧⋅=-=⎪⎨⋅=-+=⎪⎩ 21z =()2,1,1n = PAB PCD θcos θ=()21ln 2f x x x ax =+-()0,+∞()211x ax f x x a x x -+=+-='52a =()()2152122x x x x f x x x'⎛⎫---+ ⎪⎝⎭==10,2x ⎛⎫∈ ⎪⎝⎭()2,x ∈+∞()0f x '>1,22x ⎛⎫∈ ⎪⎝⎭()0f x '<()f x 10,2⎛⎫ ⎪⎝⎭()2,+∞1,22⎛⎫ ⎪⎝⎭12x =2x =()f x 12x x <112x =22x =()()()211115152ln225ln 2ln222848f x f x f f ⎛⎫⎛⎫-=-=+--+-=- ⎪ ⎪⎝⎭⎝⎭52a =()()21152ln28f x f x -=-()()()()22221212111ln2x f x f x x x a x x x -=+---()21x ax f x x-+='1x 2x 210x ax -+=2Δ40a =->120x x a +=>121x x =2a >()()()()()()()2222222121212112211111lnln 22x x f x f x x x a x x x x x x x x x x -=+---=+--+-()()222222221212111121121111lnln ln 222x x x x x x x x x x x x x x x x ⎛⎫=--=-⋅-=-- ⎪⎝⎭21x t x =21e x x (21)e x t x =…()11ln 2g t t t t ⎛⎫=-- ⎪⎝⎭e t …()222111(1)1022t g t t t t-⎛⎫=-+=-< ⎪⎝⎭'()g t [)e,+∞得,故的最大值为.∙∙∙∙∙∙∙∙∙∙∙∙∙∙(15分)18.【解析】(1)设抛物线的准线为,过点作直线于点,由抛物线的定义得,所以当点与原点重合时,,所以,所以抛物线的方程为.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙(4分)(2)①设,过点且斜率存在的直线,联立消去,整理得:,由题可知,即,所以,是该方程的两个不等实根,由韦达定理可得∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙(6分)又因为,所以,,由,有,所以,因为,,,所以点的轨迹方程为.②由①知,设,,且,∙∙∙∙∙∙∙∙∙(9分)联立消去,整理得,又,,,,由韦达定理可得,同理可得,所以,∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙(11分)又因为和以圆心为,半径为1的圆相切,,即.同理,所以,是方程的两个不等实根,()()11e 1e 1e 12e 22eg t g ⎛⎫=--=-+ ⎪⎝⎭…()()21f x f x -e 1122e -+E l 2py =-H 1HH ⊥l 1H 1HF HH =H O 1min 12pHH ==2p =E 24x y =(),P m n P ():l y k x m n =-+()24,,x y y k x m n ⎧=⎪⎨=-+⎪⎩y 24440x kx km n -+-=()2Δ164440k km n =--=20k mk n -+=1k 2k 1212,,k k m k k n +=⎧⎨=⎩()0,1F 31n k m -=0m ≠123112k k k +=121232k k k k k +=21m m n n =-0m ≠12n n -=1n ∴=-P ()10y x =-≠(),1P m -()14:1l y k x m =--()25:1l y k x m =--1m ≠±0m ≠()244,1,x y y k x m ⎧=⎪⎨=--⎪⎩y 2444440x k x k m -++=()11,A s t ()22,B s t ()33,C s t ()44,D s t 12444s s k m =+34544s s k m =+()()()212344515454444161616s s s s k m k m k k m m k k =++=+++1l ()0,(0)Q λλ>1()()2224412120m k m k λλλ-++++=()()2225512120m k m k λλλ-++++=4k 5k ()()22212120m k m k λλλ-++++=所以由韦达定理可得∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙(14分)所以,若为定值,则,又因为,所以,∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙(16分)所以圆的方程为.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙(17分)19.【解析】(1)由题意可得:,解得.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙(3分)(2)存在“长向量”,且“长向量”为,,∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙(5分)理由如下:由题意可得,若存在“长向量”,只需使,又,故只需使,即,即,当或6时,符合要求,故存在“长向量”,且“长向量”为,.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙(8分)(3)由题意,得,,即,即,同理,,∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙(10分)三式相加并化简,得,即,,所以,设,由得∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙(12分)设,则依题意得:∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙(13分)()452245221,12,1m k k m k k m λλλ⎧++=-⎪⎪-⎨+⎪=⎪-⎩()()()22222123445452216161616162221621611m m s s s s k k m m k k m m λλλλ=+++=+--+=-+--1234s s s s 220λ-=0λ>λ=Q 22(1x y +=312a a a +…40x -……2a 6a1n a ==p a1n p S a - …()()712371010101,01010100,1S a a a a =++++=+-+++--+++-+=-71p S a -=== 022cos12p π+ (1)1cos 22p π--……2p =2a 6a123a a a + (2)2123a a a + …()22123a a a +...222123232a a a a a ++⋅ (2)22213132a a a a a ++⋅ …222312122a a a a a ++⋅…2221231213230222a a a a a a a a a +++⋅+⋅+⋅…()21230a a a ++…1230a a a ++ …1230a a a ++=()3,a u v = 1220a a a ++= sin 2cos ,cos 2sin ,u x x v x x =--⎧⎨=--⎩(),n n n P x y ()()()()()()212111222222222121,2,,,,2,,,k k k k k k k k x y x y x y x y x y x y ++++++⎧=-⎪⎨=-⎪⎩得,故,,所以,,当且仅当时等号成立,∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙(16分)故.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙(17分)()()()()2222221122,2,,,k k k k x y x y x y x y ++⎡⎤=-+⎣⎦()()()()2222221122,2,,,k k x y k x y x y x y ++⎡⎤=-+⎣⎦()()()()2121221122,2,,,k k x y k x y x y x y ++⎡⎤=--+⎣⎦()()()212222212221221112,4,,4k k k k k k P P x x y y k x y x y k PP ++++++⎡⎤=--=-=⎣⎦22212(sin 2cos )(cos 2sin )58sin cos 54sin21PP x x x x x x x =--+--=+=+ …()4x t t ππ=-∈Z 10151016min1014420282P P =⨯=。
湖南省长沙市雅礼中学2014届高三第七次月考试题 文综历史 Word版含答案

雅礼中学高三第七次月考试题历史试卷24.历史材料:一、“丧礼,君与父母、妻、后子死,三年丧服……或以不丧之间,诵《诗》三百,弦《诗》三百,歌《诗》三百,舞《诗》三百。
”二、“厚葬久丧,重为棺椁,多为衣衾,送死若徙,三年哭泣,扶后起,杖后行,耳无闻,目无见,此足以丧天下。
”据此判断以下符合材料的观点为A.两种观点分别为儒家和法家思想B.两种观点都反映的是下层民众的立场C.两种观点都主张厚葬久葬D.两种观点都着眼于“礼”的社会功能[答案]D25.古希腊喜剧《骑士》中,一位将军试图劝服一个卖香肠的人去夺取民主派领袖的职位时说:“要做政客,惟一的麻烦就在于你什么都知道。
适于做人民领袖的不是那些有学问的人,或诚实的人,而是那些无知而卑微的人。
你可千万别错过这个绝好的机会。
”这段话A.道出了民主政治的真谛B.体现了古希腊的平等思想C.表达了对民主制度的不满D.成为雅典政客的最好描述[答案]C26.(清)赵翼说:“(唐)开元以来,诸王皆居京师,而支庶得自奋于功名。
如宗室为宰相者,至有十余人。
其出仕于外,嗣虢王巨、嗣吴王牛,当国家寇乱时,俱能守郡掌兵,为国宣力。
此法之最善者也。
”由此可知当时A.相权不断削弱,皇权得以强化B.利用宗法分封制加强中央对地方的控制C.科举考试成为宗室子弟控制政权的工具D.严格防止宗室诸王发展成地方割据势力[答案]D27.观察下图, 分析表中数据能得到的合理结论是图1太湖地区东晋至清各代水旱比较示意图A.经济发展水平与水旱灾害次数成正比B.隋唐政治制度完善导致水旱灾害较少C.农耕经济发展致使生态环境遭到破坏D.两宋时期水旱灾害较多导致经济倒退[答案]C28.18世纪,以“纤细、轻盈和繁琐的装饰,爱好清淡柔和、精美雅致的色彩”为特征的洛可可艺术流行欧洲。
欧洲学者认为,这种艺术风格深受物化形态的中国文化影响。
此中国文化的主要载体应是A.宋明文人画B.程朱理学与心学C.瓷器与丝绸D.明清小说与京剧[答案]C29.某条约签订后,清廷希望再开谈判,以免除关税为代价,换取外族放弃公使驻京、江河通路、内地游历和归还广东省城。
湖南省长沙市雅礼中学2014届高三第三次月考试题(11月) 数学(文) Word版含答案

高三月考试卷(文科数学)(3)(时量:120分钟 满分:150分)一、选择题:本大题共9小题,每小题5分,共45分.在每小题给出的四个选项中,只有一项是符合题目要求的,请将所选答案填在答题卡对应位置.1.下列函数中,在其定义域内既是奇函数又是减函数的是A .e x y =B .3y x =-C .sin 2y x =D .x y ln -=2.下列命题中,假命题为( ) A .∀x ∈R,012>++x x B .存在四边相等的四边形不.是正方形 C .若x ,y ∈R ,且x +y >2,则x ,y 至少有一个大于1D .a +b =0的充要条件是ab=-13.执行下面的框图,若输出结果为3,则可输入的实数x 值的个数为A .1B .2C .3D .44.如图,的等腰直角三角形,则该三棱锥的四个面的面 积中最大的是A .1B C .2D .5.已知某生产厂家的年利润y (单位:万元)与年产量x (单位:万件)的函数关系式为31812343y x x =-+-,则使该生产厂家获得最大年利润的年产量为A.9万件B.11万件C.12万件D.13万件 6.下面关于复数21z i=-+的四个结论,正确的是 ①2=z ②i z 22= ③i z +1的共轭复数为 ④1-的虚部为z A .①② B .②③C .②④D .③④7.若直线1:+=kx y l 被圆032:22=--+x y x C 截得的弦最短,则直线l 的方程是 A.0=x B.1=y C.01=-+y x D.01=+-y x8.已知非负实数b a ,满足1≤+b a ,则关于x 的一元二次方程022=++b ax x 有实根的概 率是A.31 B.21 C.61 D.32 9.已知ABC ∆是边长为2的正三角形,B 为线段EF 的中点,且3=EF ,则AF AC AE AB ⋅+⋅的取值范围是A.[]3,0B. []6,3C. []9,6D. []9,3BDCBACDAD二、填空题:本大题共6小题,每小题5分,共30分.把答案填在答题卡中对应题号后的横线上.10.为了研究性别不同的高中学生是否爱好某项运动,运用22⨯列联表进行独立性检验,经计算8.72=K ,则所得到的统计学结论是:有______的把握认为“爱好该项运动与性别 有关”. 附:11.在直角坐标系xOy 中,以原点O 为极点,x 轴的正半轴为极轴建立极坐标系.曲线1C 的参数方程为1x y t ⎧=⎪⎨=+⎪⎩t 为参数),曲线2C 的极坐标方程为34sin 2=⎪⎭⎫ ⎝⎛-πθρ,则1C 与2C 交点在直角坐标系中的坐标为___________.12.在ABC ∆中,若2,60,a B b =∠=︒=,则BC 边上的高等于 .13.已知双曲线22214x y m m -=+的右焦点到其渐进线的距离为22,则此双曲线的离心率为__________.14.设集合(){}(){}≠+-≤=-≥=B A a x y y x B x y y x A ,|,,1|,¢. (Ⅰ)实数a 的取值范围是 ; (Ⅱ)当3=a 时,若()x y A B ∈,,则y x +2的最大值是 .15已知集合{}n a a a A ,,,21 =,其中)(),2,1(A l n n i R a i >≤≤∈表示和)1(n j i a a j i ≤<≤+中所有不同值的个数.(Ⅰ)若集合{}16,8,4,2=A ,则________)(=A l ; (Ⅱ)当108=n 时,)(A l 的最小值为____________.10.99﹪11.()5,25 14.(Ⅰ)[)+∞,1(Ⅱ)5 15.(Ⅰ)6(Ⅱ)213.三、解答题:本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤.16. (本小题满分12分) 已知函数()0,016sin )(>>+⎪⎭⎫⎝⎛-=ωπωA x A x f 的最大值为3,其图像相邻两条对称轴之间的距离为2π.(Ⅰ)求函数)(x f 的解析式; (Ⅱ)设5112,2,0=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛∈απαf ,求αcos 的值.解:(1)∵函数f(x)的最大值为3,∴A +1=3,即A =2,∵函数图像的相邻两条对称轴之间的距离为π2,∴最小正周期T =π,∴ω=2,故函数f(x)的解析式为y =2sin(2x -π6)+1. 6分(2)∵f ⎝⎛⎭⎫α2=2sin ⎝⎛⎭⎫α-π6+1=511,即sin ⎝⎛⎭⎫α-π6=53, ∵0<α<π2,∴-π6<α-π6<π3,∴1033466cos cos ,546cos -=⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛-==⎪⎭⎫⎝⎛-ππααπα所以. 12分中华人民共和国《道路交通安全法》中将饮酒后违法驾驶机动车的行为分成两个档次:“酒 后驾车”和“醉酒驾车”,其检测标准是驾驶人员血液中的酒精含量Q (简称血酒含量,单 位是毫克/100毫升),当8020≤≤Q 时,为“酒后驾车”;当80>Q 时,为“醉酒驾车”. 某市公安局交通管理部门于2013年11月的某天晚上8点至11点在该市区解放路某处设点 进行一次拦查行动,共依法查出了60名饮酒后违法驾驶机动车者,如图为这60名驾驶员抽 血检测后所得结果画出的频率分布直方图(其中140≥Q 的人数计入140120<≤Q 人数之 内).(Ⅰ)求此次拦查中“醉酒驾车”的人数;(Ⅱ)从违法驾车的60人中按“酒后驾车”和“醉酒驾车”利用分层抽样抽取8人做样本进行研究,再从抽取的8人中任取2人,求2人中其中1人为“酒后驾车”另1人为“醉酒驾车”的概率.高 考 资 源 网 解:(Ⅰ) (0.0032+0.0043+0.0050)×20=0.25,0.25×60=15,所以此次拦查中“醉酒驾车”的人数为15人. 6分 (Ⅱ)由分层抽样方法可知抽取的8人中“酒后驾车”的有6人,记为)6,,2,1( =i A i , “醉酒驾车”的有2人,记为)2,1(=j B j . 9分 所以从8人中任取2人共有()() 3121,A A A A 等281234567=++++++种,2人中其 中1人为“酒后驾车”另1人为“醉酒驾车”共有()()() 122111,,,B A B A B A 等1226=⨯种, 因此所求的概率为732826=⨯=P 12分已知在直三棱柱ABC -A 1B 1C 1中,AB =4,AC =BC =3,D 为AB 的中点. (Ⅰ)求异面直线CC 1和AB 的距离;(Ⅱ)若AB 1⊥A 1C ,求二面角A 1-CD -B 1的平面角的余弦值.解:(1)因AC =BC ,D 为AB 的中点,故CD ⊥AB .又直三棱柱中,CC 1⊥面ABC ,故CC 1⊥CD ,所以异面直线CC 1和AB 的距离为CD =BC 2-BD 2= 5. 5分(2)由CD ⊥AB ,CD ⊥BB 1,故CD ⊥面A 1ABB 1,从而CD ⊥DA 1,CD ⊥DB 1,故∠A 1DB 1为所求的二面角A 1-CD -B 1的平面角. 8分又CD ⊥1AB ,AB 1⊥A 1C ,所以AB 1⊥平面D A AB DC A 111, 从而,从而∠A 1AB 1,∠A 1DA 都与∠B 1AB 互余,因此∠A 1AB 1=∠A 1DA ,所以Rt △A 1AD ∽Rt △B 1A 1A ,因此AA 1AD=A 1B 1AA 1,得AA 21=AD ·A 1B 1=8.从而A 1D =AA 21+AD 2=23,B 1D =A 1D =23, 所以在△A 1DB 1中,由余弦定理得cos ∠A 1DB 1=A 1D 2+DB 21-A 1B 212·A 1D ·DB 1=13. 12分19.(本小题满分13分)设n S 为数列{}n a 的前n 项和,且有,4,3,2,3,211==+=-n n S S a S n n(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)若数列{}n a 是单调递增数列,求a 的取值范围.解(Ⅰ)当2≥n 时,由已知213n n S S n -+= … ① 于是213(1)n n S S n ++=+ …② 由②-①得163n n a a n ++=+ …… ③ 于是2169n n a a n +++=+ …… ④ 由④-③得26n n a a +-= …… ⑤上式表明:数列2{}k a 和21{}k a +分别是以2a ,3a 为首项,6为公差的等差数列. 4分 又由①有2112S S +=,所以2122a a =-,由③有3215a a +=,4321a a +=,所以332a a =+,4182a a =-. 所以226(1)k a a k =+-()()*∈-+-=Nk k a 16212,,1a a =2136(1)k a a k +=+-()()*∈-++=N k k a 1623. 8分(Ⅱ)数列{}n a 是单调递增数列12a a ⇔<且22122k k k a a a ++<<对任意的k ∈N*成立.12a a ⇔<且2346(1)6(1)6(1)a k a k a k +-<+-<+- 1234a a a a ⇔<<<9151223218244a a a a a ⇔<-<+<-⇔<<. 所以a 的取值范围是.41549<<a 13分20.(本小题满分13分)已知R a ∈,函数()a x x x f -=)(.(Ⅰ)求函数)(x f 的单调区间;(Ⅱ)求函数)(x f 在区间[]2,1上的最小值. 解(Ⅰ)函数的定义域为),0[+∞.xa x x xa x x f 232)(-=+-='①当0≤a 时,)0(0)(≠>'x x f ,所以.),0[)(上为增函数在+∞x f②当0>a 时,当0)(,3;0)(,30>'><'<≤x f ax x f a x 时当时. 故上为增函数在上为减函数在),3[,)3,0[)(+∞aa x f . 6分(Ⅱ)(1)当0≤a 时,由(Ⅰ)知 a f f x f -==1)1(,,]2,1[)(min 所以上为增函数在;(2) 当0>a 时, ①当6≥a 时,32a≤, 由(Ⅰ)知 ()a f f x f -==22)2(,,]2,1[)(min 所以上为减函数在;②当63<<a 时,231<<a, 由(Ⅰ)知 ,,]2,3(,)3,1[)(所以上为增函数在上为减函数在aa x f 32)3(min a a a f f -== ③当30≤<a 时,13≤a, 由(Ⅰ)知 a f f x f -==1)1(,,]2,1[)(min 所以上为增函数在; 综上所述,()⎪⎪⎩⎪⎪⎨⎧≥-<<-≤-=时当时当时当6,2263,323,1mina a a a a a a f 13分21.(本小题满分13分)已知曲线1C 上任意一点M 到直线4:=x l 的距离是它到点()0,1F 距离的2倍;曲线2C 是以原点为顶点,F 为焦点的抛物线. (Ⅰ)求1C ,2C 的方程;(Ⅱ)过F 作两条互相垂直的直线21,l l ,其中1l 与1C 相交于点B A ,,2l 与2C 相交于点D C ,,求四边形ACBD 面积的取值范围.解(Ⅰ)设),(y x M ,则由题意有()41222-=+-x y x ,化简得:13422=+y x .故1C 的方程为13422=+y x ,易知2C 的方程为x y 42=. 4分(Ⅱ)由题意可设2l 的方程为1+=ky x ,代入x y 42=得0442=--ky y , 设()()2211,,,y x D y x C ,则k y y 421=+,所以)1(44)(1122121+=++=+++=+=k y y k x x DF CF CD . 7分因为21l l ⊥,故可设1l 的方程为)1(--=x k y ,代入13422=+y x 得()01248342222=-+-+k x k x k ,设()()4433,,,y x B y x A ,则3482243+=+k k x x , 所以()()()()34112214421421224343++=+-=-+-=+=k k x x x x BF AF AB . 10分 故四边形ACBD 的面积为()⎪⎭⎫⎝⎛++=⎪⎭⎫ ⎝⎛+-+-=-=++=⋅=212321411423142434124212222s s t t t t k k CD AB S (314,112≥-=≥+=t s k t 其中)设[)单调递增,在,故则∞+>-=-='≥+=3)(0111)(),3(1)(222s f s s s s f s s s s f ,因此 82313232123=⎪⎭⎫⎝⎛++≥⎪⎭⎫ ⎝⎛++=s s S ,当且仅当3=s 即0=k 等号成立. 故四边形ACBD 面积的取值范围为[)+∞,8. 13分。
湖南省长沙市雅礼中学2014届高三上学期第二次月考试题(10月) 数学(文) Word版含答案
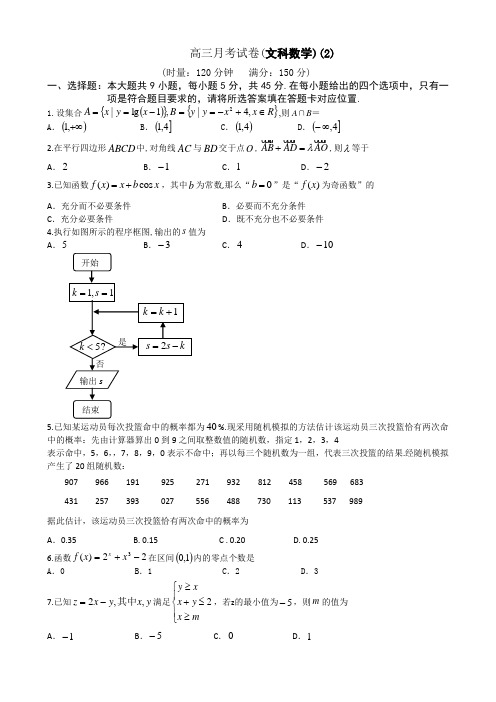
高三月考试卷(文科数学)(2)(时量:120分钟 满分:150分)一、选择题:本大题共9小题,每小题5分,共45分.在每小题给出的四个选项中,只有一项是符合题目要求的,请将所选答案填在答题卡对应位置.1.设集合(){}{}R x x y y B x y x A ∈+-==-==,4|,1lg |2,则A ∩B =A .()+∞,1B .(]4,1C .()4,1D .(]4,∞-2.在平行四边形ABCD 中,对角线AC 与BD 交于点O ,AB AD AO λ+=,则λ等于 A .2B .1-C .1D .2-3.已知函数()cos f x x b x =+,其中b 为常数,那么“0b =”是“()f x 为奇函数”的A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件4.执行如图所示的程序框图,输出的s 值为A .5B .3-C .4D .10-5.已知某运动员每次投篮命中的概率都为40%.现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器算出0到9之间取整数值的随机数,指定1,2,3,4 表示命中,5,6,,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了20组随机数:907 966 191 925 271 932 812 458 569 683 431 257 393 027 556 488 730 113 537 989 据此估计,该运动员三次投篮恰有两次命中的概率为A .0.35 B. 0.15 C . 0.20 D. 0.25 6.函数22)(3-+=x x f x在区间()1,0内的零点个数是A .0B .1C .2D .37.已知y x y x z ,,2其中-=满足2y x x y x m ≥⎧⎪+≤⎨⎪≥⎩,若z 的最小值为5-,则m 的值为A .1-B .5-C .0D .18.已知复数()πθθθ<≤+=0sin cos i z ,则使12-=z 的θ的值为A. 0B.4π C. 2π D. 43π9.已知点(1,0),(1,0),(0,1)A B C -,直线(0)y ax b a =+>与N M BC AC ,,分别交于点, 且将△ABC 分割为面积相等的两部分,则b 的取值范围是A.1(1]3B .11[,)32 C.1(1)2D . (0,1)BACDDBACA二、填空题:本大题共6小题,每小题5分,共30分.把答案填在答题卡中对应题号后的横线上.10.在直角坐标系xOy 中,以原点O 为极点,x 轴的正半轴为极轴建立极坐标系.已知圆的极坐标方程为θρsin 8=,则该圆的圆心到直线⎩⎨⎧-==t y tx 2(t 为参数)的距离是_________.11.图2是美职篮某新秀在五场篮球比赛中所得分数的茎叶图,则该新秀在这五场比赛中得分的方差为_________.08910352图 (注:方差2222121()()()n s x x x x x x n⎡⎤=-+-++-⎣⎦,其中x 为n x x x ,,,21 的平均数)12.一个几何体的三视图如下图所示,13.已知{}n a 是等差数列,11a =,公差0d ≠,n S 为其前n 项和,若125,,a a a 成等比数列,则.________=n S14.抛物线()022>=p px y 的焦点为F ,其准线与双曲线1222=-y x 相交于,A B 两点, 若ABF ∆为等边三角形,则=p _______. 15. 已知实数)2,,,3,2,1,1(144,,,2121>∈=≥=+++*n N n n i a a a a a a a i n n 且其中满足(Ⅰ)当3=n 时,若21a a =,且321,,a a a 是ABC ∆的三条边长,则3a 的取值范围是______; (Ⅱ)如果这n 个数中任意三个数都不能构成一个三角形的三条边长,则n 的最大值是____.10.2 11.8.6 12.38 13. 2n 14.32 15.(Ⅰ)[)72,1,(Ⅱ)10.三、解答题:本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤.16. (本小题满分12分)设向量()()A C c a ⊥-==且,sin ,cos ,,,其中,,a b c 分别是ABC ∆中角,,A B C 所对的边.高 考 资 源 网(I )求角C 的大小; (IIcos()4A B π-+的最大值,并求取得最大值时角,A B 的大小.解:(I )由0sin cos ,0,=-=⋅⊥A c C a 即得,再由正弦定理得sin sin sin cos .C A A C =因为0,A π<<所以sin 0.sin cos .cos 0,tan 1,4A C C C C C π>=≠==从而又所以则 6分(II )由(I )知3.4B A π=-于是cos()cos()4cos 2sin().63110,,,,46612623A B A A A A A A A A A ππππππππππ-+=--=+=+<<∴<+<+==从而当即时 2sin()6A π+取最大值2.cos()4A B π-+的最大值为2,此时5,.312A B ππ==12分17. (本小题满分12分)后检查存货,若发现存货少于2件,则当天进货补充..至3件,否则不进货...,将频率视为概率.(Ⅰ)设每销售一件该商品获利1000元,某天销售该商品获利情况如下表,完成下表,并求试销期间日(Ⅱ)求第二天开始营业时该商品的件数为3件的概率.解(I )日获利分别为0元,1000元,2000元,3000元的频率分别为41,52,103,201;试销期间日平均获利数为1850元 . 6分 (Ⅱ)P P =(“当天商品销售量为0件”)P +(“当天商品销售量为2件”)P +(“当天商品销售量为3件”).107205208201=++=12分18.(本小题满分12分)如图所示,CE ABC PA ACB BC AC ,,90,1平面⊥=∠== ∥22,==CE PA PA . (Ⅰ)求三棱锥PAB E -的体积;(Ⅱ)在棱PB 上是否存在一点F ,使得EF ∥平面ABC ?证明你的结论.解:(Ⅰ) .311122131=⨯⎪⎭⎫⎝⎛⨯⨯⨯==--EPA B PAB E V V 6分(Ⅱ)取棱PB 的中点为F ,则有EF ∥平面ABC .证明如下: 取棱PB 的中点为F ,FG GC FG EF G AB 则有连的中点为,,,, ∥EC PA FG PA ,又且121,==∥PA FG CE ,所以且1=∥EC FG CE =且,,因此四边形EF EFGC 为平行四边形,所以∥ABC CG ABC EF CG 平面平面又⊂⊄,,,所以 EF ∥平面ABC . 12分19.(本小题满分13分)某调酒师把浓度分别为a 和b ()b a >的两瓶均为300毫升的酒(分别记为A 瓶液体、B 瓶液体)进行混合.先把100毫升的A 瓶液体倒入B 瓶进行充分混合,然后再把100毫升的B 瓶液体倒入A 瓶进行充分混合,这样称为一次操作,依此类推.(Ⅰ)设经过n 次操作后, A 瓶液体与B 瓶液体的浓度之差为n c ,试写出,,21c c 及数列{}n c 的通项公式; (Ⅱ)当70=a %,10=b %时,需经过多少次操作后才能使两瓶酒的浓度之差小于1%?解(Ⅰ)设,n n a b 分别为A 瓶液体、B 瓶液体经过n 次操作后的浓度.则0a =a ,0b =b ,且()()11111003001002001312, 1003004410020033n n n n n n n n n n a b b a b a b a b a ++++++==+=+++=.(*) P由(*)可得:()()1111112221313333442n n n n n n n n n n n n a b b a b a b a a b a b +++++⎡⎤⎛⎫⎛⎫-=+-=-=-+=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,即n n c c 211=+ ∴数列{}n c 是以b a b a -=-00为首项,以12为公比的等比数列. ∴()nn b a c ⎪⎭⎫⎝⎛⨯-=21.其中()()b a c b a c -=-=41,2121 . 9分(Ⅱ) 设经过n 次操作后才能使两瓶酒的浓度之差小于1%,则有())0,,1.0,7.0(01.021≥∈==<⎪⎭⎫⎝⎛-n N n b a b a n其中得60121<⎪⎭⎫⎝⎛n.所以5>n .即经过6次操作后才能使两瓶酒的浓度之差小于1%. 13分20.(本小题满分13分)已知椭圆()012222>>=+b a by a x 的左、右焦点分别为1F 、2F ,离心率为22,过1F 的直线1l 交椭圆于A 、B 两点,且2ABF ∆的周长为24.(Ⅰ)求椭圆的方程;(Ⅱ)过2F 且与1l 垂直的直线2l 交椭圆于C 、D 两点,求证:CDAB 11+为定值.解(Ⅰ)由题意,112244,22=====b c a a a c 从而,得,故所求的椭圆的方程为 1222=+y x . 4分 (Ⅱ)由题意直线1l ,2l 中至少有一条存在斜率,不妨设1l 的斜率为k ,又1l 过()0,11-F ,故1l 的方程为)1(+=x k y ,代入02222=-+y x 得()022*******=-+++k x k x k ,设()()2211,,,y x B y x A ,则222122212122,214k k x x k k x x +-=+-=+,所以()()222122122112241k k x x x x k AB ++=-+⋅+=. 8分(1)当0≠k 时,因为21l l ⊥,所以2l 的斜率为k1-,同上可推得 ()222221221211122k k k k CD ++=⎪⎭⎫⎝⎛-+⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-+== 故CD AB 11+=423)1(222)1(22212222=+++++k k k k . 11分 (2)当0=k 时,容易求得,2,22==CD AB 同样有CDAB 11+=423. 综合(1),(2)即知CDAB 11+为定值. 13分21.(本小题满分13分)已知函数()0ln )(2≠--=a bx ax x x f .(Ⅰ) 当1=b 时,若函数)(x f 存在单调递减区间,求a 的取值范围;(Ⅱ)当1-=b 时,如果)(x f 的图像与x 轴交于()()()2,0,,0,2102121x x x x x x B x A +=<记.试问: )(x f 的图像在点())(,00x f x C 处的切线是否平行于x 轴?证明你的结论.解:(Ⅰ)函数()f x 的定义域为()+∞,0.由题意()0121212<-+-=--='xx ax ax x x f 有解.故a 的取值范围是()+∞⋃⎪⎭⎫⎝⎛-,00,81. 5分 (Ⅱ)假设)(x f 的图像在点())(,00x f x C 处的切线平行于x 轴,则有()()0121212121000=++-+=+-='x x a x x ax x x f ,从而()122121-+=+x x a x x ① 又0ln )(12111=+-=x ax x x f ② 0ln )(22222=+-=x ax x x f ③②-③得()()()()1ln,0ln 21212121212121-+=-=-+-+-x x a x x x x x x x x x x a x x 从而 ④由①④得()1122ln ,2ln 2121212121212121+⎪⎪⎭⎫⎝⎛-=+-=+=-x x x x x x x x x x x x x x x x 即 令()()112ln ,1021+-=<<=t t t t t x x 得 ⑤ 10分 令()()()()()()011141,10112ln )(222>+-=+-='<<+--=t t t t t t h t t t t t h 则,所以)(t h 在()1,0上单调递增,从而有()112ln ,0)1()(+-<=<t t t h t h 即,这与⑤式矛盾,故)(x f 的图像在点())(,00x f x C 处的切线不平行于x 轴. 13分。
湖南省长沙市雅礼中学2023届高三月考试卷(二)数学试题含答案

雅礼中学2023届高三月考试卷(二)数学本试卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,时量120分钟,满分150分.第I 卷一、选择题:本题共8小题 ,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合{}220,{2}M x x x N =--=<∣, 则M N ⋂= A. (0,2) B. [0,2] C. [-1,4) D. [-1,2]2. 在平面直角坐标系xOy 中, 以点(0,1)为圆心且与直线10x y --=相切的圆的标准方程为A. 22(1)2x y +-=B. 22(1)1x y -+=C. 22(1)x y +-=D. 22(1)4x y -+=3.Logistic 模型是常用数学模型之一,可应用于流行病学领域,有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数()I t (t 的单位:天)的Logistic 模型:-0.23(-53)()1t K I t e=+,其中K 为最大确诊病例数.当()*0.95I t K =时,标志着已初步遏制疫情,则*t 约为(ln193)≈ A .60B .63C .66D .694.在某种信息传输过程中,用6个数字的一个排列(数字允许重复)表示一个信息,不同排列表示不同信息,若所用数字只有0和1,例如001100就是一个信息.在所有信息中随机取一信息,则该信息恰有2个1的概率是 A .516B .1132 C .1532D .15165. 已知圆锥的母线长为 2 , 轴截面顶角的正弦值是12, 过圆锥的母线作截面,则截面面积的最大值是A. 1 C. 1 或 2 D. 2 6. 设函数2()(,,)f x ax bx c a b c =++∈R , 若1x =-为函数()()x g x e f x =的一个极值点, 则下列图象不可能为()y f x =的图象的是7. 已知12,F F 分别是双曲线22:221(0,0)x y C a b a b-=>>的左、右焦点, 过2F 的直线与双曲线C 的左支相交于P 、Q 两点, 且1PQ PF ⊥. 若1||PQ PF =, 则双曲线C 的离心率为 63522- 522+ D.122+8. 在棱长为 6 的正方体1111ABCD A B C D -中,M 是BC 的中点, 点P 是面11DCC D 内的动点, 且满足 APD MPC ∠=∠, 则三棱锥D PBC -体积的最大值是A. 3B. 24C. 3D. 36 二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,有选错的得0分,部分选对的得2分. 9.关于统计数据的分析,有以下几个结论,其中正确的是A.利用残差进行回归分析时,若残差点比较均匀地落在宽度较窄的水平带状区域内,则说明线性回归模型的拟合精度较高B.将一组数据中的每个数据都减去同一个数后, 期望与方差均没有变化C.调查剧院中观众观后感时,从50排(每排人数相同)中任意抽取一排的人进行调查是分层抽样法D.样本数据9,3,5,7,12,13,1,8,10,18的第80百分位数是12.510.1748年,瑞士数学家欧拉发现了复指数函数和三角函数的关系,并写下公式i e cos isin x x x =+(,i x ∈R 为虚数单位),这个公式在复变函数中有非常重要的地位,被誉为“数学中的天桥”,据此公式,则有 A .e 10i π+=B .20221312⎛⎫+= ⎪ ⎪⎝⎭C .i -i e e 2x x+≤D .i -i 2e e 2x x -≤-≤11. 已知函数()sin(cos )cos(sin )f x x x =+, 则下列结论正确的是A. ()f x 是偶函数B. ()f x 在区间0,2π⎛⎫⎪⎝⎭单调递㖪C. ()f x 的周期是πD. ()f x 的最大值为 212. 下列不等关系正确的是A. 33e 3e π<<B. 3e e e ππ<<C. 3e e πππ≤<D.333e ππ<<第Ⅱ卷三、填空题: 本题共 4 小题,每小题 5 分,共 20 分. 13. 已知||2||=b a 且()0⋅-=b a a , 则,b a 的夹角是_____.14. 已知函数()x x f x e ae -=+(a 为常数)为奇函数, 且()()g x f x mx =-为增函数, 则实数m 的取值范围是_____.15. 已知抛物线2:4E y x =, 直线:(1)l y k x =-与E 相交于,A B 两点, 若(1,1)M -使90AMB ︒∠=, 则 k =_____. 16. 已知三角形数表:现把数表按从上到下、从左到右的顺序展开为数列{}n a ,记此数列的前n 项和为n S .若()277tm S t m m =∈∈>Z N ,且,则m 的最小值是_____.四、解答题:本题共6小题,共70分.请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤. 17. (本小题满分10分)已知*n ∈N ,抛物线2y x n =-+与x 轴正半轴相交于点A .设n a 为该拋物线在点A 处的切线在y 轴上的截距. (1)求数列{}n a 的通项公式;(2) 设2n n na b =, 求证: 1211112n b b b n +++<-(*n ∈N 且2n ).18.(本小题满分 12 分)在ABC 中, 角,,A B C 的对边分别为,,a b c , 若2A C B +.(1) 求证: B 3π;(2) 对*n ∈N , 请你给出一个n 的值, 使不等式2n n n a c b +成立或不成立,并证明你的结论.19. (本小题满分 12 分)如图 1, 在ABC 中,2,90,30,AC ACB ABC P ︒︒=∠=∠=是AB 边的中点. 现把ACP 沿CP 折成如图 2所示的三棱锥A BCP -, 使得10AB =(1)求证: 平面ACP ⊥平面BCP ; (2)求二面角B AC P --的余弦值.20. (本小题满分 12 分)品酒师需定期接受酒味鉴别功能测试,一种通常采用的测试方法如下:拿出n 瓶外观相同但品质不同的酒让其品尝,要求其按品质优劣为它们排序;经过一段时间,等其记忆淡忘之后,再让其品尝这n 瓶酒,并重新按品质优劣为它们排序,这称为一轮测试.根据一轮测试中的两次排序的偏离程度的高低为其评级.现设4n =,分别以1234,,,a a a a 表示第一次排序时被排为1,2,3,4的四种酒在第二次排序时的序号,并令12341234X a a a a =-+-+-+-, 则X 是对两次排序的偏离程度的一种描述.(1)假设1234,,,a a a a 等可能地为1,2,3,4的各种排列,写出X 的可能值集合,并求X 的分布列;(2)某品酒师在相继进行的三轮测试中,都有2X ≤,①试按(1)中的结果,计算出现这种现象的概率(假定各轮测试相互独立); ②你认为该品酒师的酒味鉴别功能如何?说明理由. 21. (本小题满分 12 分)已知(1,0),A B -是圆22:2150F x x y -+-=上的任意一点, 线段AB 的垂直平分线交BF 于点P .(1) 求动点P 的轨迹C 的方程;(2) 设,PA PF 交轨迹C 于另两点,D E . 记PAF 和PDE 的面积分别为12,S S . 求12SS 的取值范围. 22. (本小题满分 12 分)已知函数11()t tttf x x x x +=+- (0, x t >为正有理数). (1) 求函数()f x 的单调区间;(2) 证明: 当2x 时,()0f x .雅礼中学2023届高三月考试卷(二)数学参考答案题号 1 2 3 4 5 6 7 8 9 101112 答案B ACD C D B A ADABC ABABD13.3π 14.(],2-∞ 15. 2 16. 95四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.【解析】(1) 抛物线在点,0)A n 处的切线方程为2()y n x n =--, 所以它在y 轴上的截距 2n a n =.(2)222121*********12121223(1)n b b b n n n n +++=++⋅<++++=-⨯⨯-. 18.【解析】(1) 由A B C π++=且2A C B +得23B B B ππ-⇒.(2) 当2n =时, 不等式成立, 即有2222a c b +. 证明如下: 由余弦定理有()()()2222222222cos b a c a c ac B a c -+=++--224cos 24cos 2(12cos )a c ac B ac ac B ac B =+--=-由 (1) 知1,cos cos 12cos 0332B B B πππ<∴=⇒-, 所以()22220b a c -+, 即2222a c b +.或当1n =时, 不等式成立, 即有2a c b +. 证明如下: 由正弦定理有2()2[2sin (sin sin )]24sin cos 2sin cos 2222B B A C A C b a c R B A C R +-⎛⎫-+=-+=- ⎪⎝⎭4cos 2sin cos 222B B A C R -⎛⎫=- ⎪⎝⎭ (其中R 是ABC 外接圆的半径)由 (1) 知1,sin sin 2sin 136222622B B BB πππππ<∴<⇒=⇒. 而cos 12AC -, 所以2sin cos 022B A C --, 又cos 02B>, 所以2()0b a c -+, 即2a c b +.或222()(2)a c b a c b +⇔+,而由余弦定理 ()()222222(2)()42cos 2b a c a c ac B a c ac-+=+--+-()2238cos 268cos 24(12cos )a c ac B ac ac ac B ac ac B =+----=- 由 (1) 知1,cos cos12cos 0332B B B πππ<∴=⇒-, 所以22(2)()0b a c -+, 即2a c b +.或当5n =时, 不等式不成立, 即5552a c b +不成立. 证明如下:取,23A B ππ==, 则有555sin 2sin 3a A b B ⎛⎫⎛⎫=> ⎪ ⎪⎭⎝⎭=⎝, 所以552a c b b ⎛⎫⎛⎫+> ⎪ ⎪⎝⎭⎝⎭, 即5552a c b +>.说明此时5552a c b +≤不成立19.【解析】(1)在图1中,取CP 的中点O ,连接AO 交CB 于E ,则AE CP ⊥.在图2中,取CP 的中点O,连接AO,OB, 因为2AC AP CP ===, 所以AO CP ⊥且 3AO =在OCB 中, 由余弦定理有2221(23)21237OB ︒=+-⨯⨯=, 所以22210AO OB AB +==, 所以AO OB ⊥, 又,AO CP CP OB O ⊥⋂=, 所以AO ⊥面PCB , 又AO ⊂面ACP , 所以平面ACP ⊥平面CPB .(2)因为AO ⊥面PCB 且OC OE ⊥,故可建立如图2空间直角坐标系, 则(0,0,0),(1,0,0),(0,0,3),(1,0,0),(3,0)O C A P B --(2,3,3),(1,0,3)AB AC =--=.设平面ABC 的法向量为(,,)x y z =m , 则由0,0,AB AC ⎧⋅=⎪⎨⋅=⎪⎩m m 得(3,3,1)=m又平面ACP 的法向量为(0,1,0)=n .所以313cos ||||13131θ⋅===⋅⨯m n m n . 因此, 二面角B AC P --的余弦值为1313.20.【解析】(1) X 的可能取值集合为{0,2,4,6,8},在1,2,3,4中奇数与偶数各有两个, 所以24,a a 中奇数个数等于13,a a 中偶数个数, 因此1313a a -+-与2424a a -+-的奇偶性相同, 从而X 必为偶数.X 的值非负, 且易知其值不大于 8 .容易举出使得X 的值等于0,2,4,6,8各值的排列的例子.可以用列表或者树状图列出1、2、3、4的一共24种排列,计算每种排列下的X 的值,在等可能的假定下, 得到X 的分布列为X 0 2 4 6 8P124 324 724924 424(2)①首先(2)(0)(2)246P X P X P X ≤==+=== 将三轮测试都有X ≤2的概率记做P ,有上述结果和独立性假设得311P 6216⎛⎫==⎪⎝⎭ ②由于15P 2161000=<是一个很小的概率, 这表明仅凭随机猜测得到三轮测试都有X ≤2的结果的可能性很小, 所以我们认为该品酒师确实有良好的鉴别功能,不是靠随机猜测.21.【解析】(1) 由题意可知||||||||||42||PA PF PB PF FB AF +=+==>=, 所以动点P 的轨迹是以A 、F 为焦点且长轴长为 4 的椭圆, 因此C 方程为22143x y += 设||(13),PA x x PAF θ=<<∠=, 则在PAF 中, 由余弦定理得32cos x θ=-,则有3cos 2xθ=-. 同理33||2cos()2cos AD πθθ==--+.所以22212124||||||4cos 43342x PD PA AD x x θ=+===--⎛⎫-- ⎪⎝⎭. 设||PF y =, 则4x y +=. 同理可得24||43y PE y =-所以12||(43)(43)391||||1616S PA PF x y S PD PE xy xy ⋅--===-⋅∣. 易知(4)(3,4]xy x x =-∈,所以12S S 的取值范围是325,1664⎛⎤ ⎥⎝⎦.22.【解析】(1) 函数的定义域为(0,)+∞.()111111111111()11t t t t t t t t f x txx t x tx x x x t t t-+--'--⎛⎫⎛⎫=+-+=-+- ⎪ ⎪⎝⎭⎝⎭. 当01x <<时, ()0f x '>; 当1x >时, ()0f x '<. 所以函数()f x 的单调区间为(0,1),(1,)+∞且()f x 在(0,1)上单调递增, 在(1,)+∞上单调递减. (2) 因为()f x 在[2,)+∞单调递减, 所以11()(2)222t tttf x f +=+-.记11(0)()222t tttg t t +=+>-,因此要证()0f x ≤,只要证()0g t ≤即可而1()g t g t ⎛⎫= ⎪⎝⎭且(1)0g =,因此只要证明: 当1t 时,()0g t .而1111()2222221t t tt tt ttg t +-⎛⎫=+--+ ⎪⎝⎭=.令122)1(1)(t t t h t t -+=-≥1121()2(ln 2)12t t t h t t -'⎛⎫=+- ⎪⎝⎭, 令1m t =, 则01m <. 令2()12(01)m F m m m =++<,2()22ln 2,()22ln 2(01),()22(ln 2)0m m m F m m G m m m G x ''=-=-<=->令, 所以()G m 在(0,1]上单调递增, 又(0)ln 20,(1)22ln 20G G =-<=->, 又()G m 在(0,1]上连续, 故存在0(0,1]x ∈, 使得()00,x x ∈时,(]0()0,,1G m x x <∈时, $G(m)>0$. 所以()F m 在()00,x 上单调递减, 在(]0,1x 单调递增. 又(0)(1)0F F ==, 所以()0F m .即()0h t ', 所以()h t 在[1,)+∞单调递减, 所以()(1)0h t h =, 即()0g t . 综上所述, 当2x 时,()0f x .。
2023-2024学年湖南省长沙市雅礼中学高三上学期月考试卷(二)数学试卷及答案

大联考雅礼中学2024届高三月考试卷(二)数学得分:___________本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共8页.时量120分钟,满分150分.第Ⅰ卷一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 若12z i =+,则()1z z +⋅=( )A. 24i-- B. 24i-+ C. 62i- D. 62i+2. 全集U =R ,集合{2,3,5,7,9}A =,{4,5,6,8}B =,则阴影部分表示的集合是( )A. {2,3,5,7,9}B. {2,3,4,5,6,7,8,9}C. {4,6,8}D. {5}3. 函数()2log 22x x xx f x -=+部分图象大致是( )A. B.C. D.4. 在边长为3的正方形ABCD 中,点E 满足2CE EB = ,则AC DE ⋅=( )A. 3B. 3- C. 4- D. 45. 某校科技社利用3D 打印技术制作实心模型.如图,该模型的上部分是半球,下部分是圆台.其中半球的的体积为3144πcm ,圆台的上底面半径及高均是下底面半径的一半.打印所用原料密度为31.5g/cm ,不考虑打印损耗,制作该模型所需原料的质量约为( )(1.5 4.7π≈)A. 3045.6gB. 1565.1gC. 972.9gD. 296.1g6. 已知数列{}n a 为等比数列,其前n 项和为n S ,10a >,则“公比0q >”是“对于任意*n ∈N ,0n S >”的( )A. 充分而不必要条件B. 必要而不充分条件C. 充分必要条件D. 既不充分也不必要条件7. 若存在实数a ,对任意的x ∈[0,m ],都有(sin x -a )·(cos x -a )≤0恒成立,则实数m 的最大值为( )A.4πB. 2πC.34π D.54π8. 已知函数()f x 定义域为R ,()()()()2,24f x f x f f +=--=-,且()f x 在[)1,+∞上递增,则()10xf x ->的解集为( )A. ()()2,04,∞-⋃+B. ()(),15,∞∞--⋃+C. ()(),24,-∞-+∞ D. ()()1,05,∞-⋃+二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分.9. 对于实数a ,b ,c ,下列选项正确的是( )A. 若a b >,则2a ba b +>> B. 若0a b >>,则a b>>C. 若11a b>,则0a >,0b < D. 若0a b >>,0c >,则b c ba c a+>+10. 已知函数()2sin cos f x x x x =+,则下列说法正确的是( )A ()πsin 23f x x ⎛⎫=-⎪⎝⎭的.B. 函数()f x 的最小正周期为πC. 函数()f x 的对称轴方程为()5πZ 12x k k π=+∈D. 函数()f x 的图象可由sin 2y x =的图象向右平移π3个单位长度得到11. 设n S 是公差为d (0d ≠)的无穷等差数列{}n a 的前n 项和,则下列命题正确的是( )A. 若0d <,则1S 是数列{}n S 的最大项B. 若数列{}n S 有最小项,则0d >C. 若数列{}n S 是递减数列,则对任意的:*N n ∈,均有0nS <D. 若对任意的*N n ∈,均有0n S >,则数列{}n S 是递增数列12. 如图所示,在棱长为2的正方体1111ABCD A B C D -中,点M ,N 分别为棱11B C ,CD 上的动点(包含端点),则下列说法正确的是( )A. 四面体11A D MN 的体积为定值B. 当M ,N 分别为棱11B C ,CD 的中点时,则在正方体中存在棱与平面1A MN 平行C. 直线MN 与平面ABCDD. 当M ,N 分别为棱11B C ,CD 的中点时,则过1A ,M ,N 三点作正方体的截面,所得截面为五边形第Ⅱ卷三、填空题:本题共4小题,每小题5分,共20分.13. 若函数()ln f x x a x =-的图象在1x =处的切线斜率为3,则=a __________.14. 在平面直角坐标系xOy 中,圆O 与x 轴正半轴交于点A ,点B ,C 在圆O 上,若射线OB 平分的AOC ∠,34,55B ⎛⎫ ⎪⎝⎭,则点C 的坐标为__________.15. 已知函数()f x 的定义域为R ,()e xy f x =+是偶函数,()3e x y f x =-是奇函数,则()f x 的最小值为_____________.16. 已知菱形ABCD中,对角线BD =,将ABD △沿着BD 折叠,使得二面角A BD C --为120°,AC =,则三棱锥A BCD -的外接球的表面积为________.四、解答题:本题共6小题,共70分.请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤.17. 已知正项数列{}n a 的前n 项和为n S ,且满足22n n n S a a =+.(1)求数列{}n a 的通项公式;(2)设24n n n b a a +=,数列{}n b 的前n 项和为n T ,证明:3n T <.18. 在ABC 中,角A 、B 、C 所对的边分别为a 、b 、c)sin a C C =-.(1)求A ;(2)若8a =,ABCABC 的周长.19. 如图,在三棱柱111ABC A B C -中,11BC B C O = ,12BC BB ==,1AO =,160B BC ∠=︒,且AO ⊥平面11BB C C .(1)求证:1AB B C ⊥;(2)求二面角111A B C A --的正弦值.20. 如图,已知椭圆2222:1(0)x y C a b a b+=>>上一点A ,右焦点为(c,0)F ,直线AF交椭圆于B 点,且满足||2||AF FB =,||AB =.(1)求椭圆C 的方程;(2)若直线(0)y kx k =>与椭圆相交于,C D 两点,求四边形ACBD 面积的最大值.21. 如图所示,A BCP -是圆锥的一部分(A 为圆锥的顶点),O 是底面圆的圆心,23BOC π∠=,P 是弧BC 上一动点(不与B 、C 重合),满足COP θ∠=.M 是AB 的中点,22OA OB ==.(1)若//MP 平面AOC ,求sin θ的值;(2)若四棱锥M OCPB -体积大于14,求三棱锥A MPC -体积的取值范围.22. 混管病毒检测是应对单管病毒检测效率低下的问题,出现的一个创新病毒检测策略,混管检测结果为阴性,则参与该混管检测的所有人均为阴性,混管检测结果为阳性,则参与该混管检测的人中至少有一人为阳性.假设一组样本有N 个人,每个人患病毒的概率相互独立且均为()01p p <<.目前,我们采用K 人混管病毒检测,定义成本函数()Nf X KX K=+,这里X 指该组样本N 个人中患病毒的人数.(1)证明:()E f X N ≥⎡⎤⎣⎦;(2)若4010p -<<,1020K ≤≤.证明:某混管检测结果为阳性,则参与该混管检测的人中大概率恰有一人为阳性.的大联考雅礼中学2024届高三月考试卷(二)数学得分:___________本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共8页.时量120分钟,满分150分.第Ⅰ卷一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 若12z i =+,则()1z z +⋅=( )A. 24i --B. 24i-+ C. 62i- D. 62i+【答案】C 【解析】【分析】根据复数的乘法运算和共轭复数的定义求解.【详解】()()()122i 12i 244i 2i 62i z z +⋅=+-=+-+=-.故选:C .2. 全集U =R ,集合{2,3,5,7,9}A =,{4,5,6,8}B =,则阴影部分表示的集合是( )A. {2,3,5,7,9}B. {2,3,4,5,6,7,8,9}C. {4,6,8}D. {5}【答案】C 【解析】【分析】根据给定的条件利用韦恩图反应的集合运算直接计算作答.【详解】韦恩图的阴影部分表示的集合为()U A B ð,而全集U =R ,集合{2,3,5,7,9}A =,{4,5,6,8}B =,所以(){4,6,8}U A B ⋂=ð.故选:C 3. 函数()2log 22x xxx f x -=+的部分图象大致是( )A. B.C. D.【答案】A 【解析】【分析】利用函数的奇偶性和特殊点即得.【详解】易知()2log 22x xxx f x -=+的定义域为{}0x x ≠,因为()()22log log 2222x x x xx x x f x x f x-----==-=-++,所以()f x 为奇函数,排除答案B ,D ;又()2202222f -=>+,排除选项C .故选:A .4. 在边长为3的正方形ABCD 中,点E 满足2CE EB = ,则AC DE ⋅=( )A. 3 B. 3- C. 4- D. 4【答案】A 【解析】【分析】建立直角坐标系,写出相关点的坐标,得到AC ,DE,利用数量积的坐标运算计算即可.【详解】以B 为原点,BC ,BA 所在直线分别为x ,y 轴,建立如图所示直角坐标系,由题意得()()()()0,3,1,0,3,0,3,3A E C D ,所以()3,3AC =- ,()2,3DE =--,所以()()()32333AC DE ⋅=⨯-+-⨯-=.故选:A.5. 某校科技社利用3D 打印技术制作实心模型.如图,该模型的上部分是半球,下部分是圆台.其中半球的体积为3144πcm ,圆台的上底面半径及高均是下底面半径的一半.打印所用原料密度为31.5g/cm ,不考虑打印损耗,制作该模型所需原料的质量约为( )(1.5 4.7π≈)A. 3045.6gB. 1565.1gC. 972.9gD. 296.1g【答案】C 【解析】【分析】由题意可知所需要材料的体积即为半球体积与圆台体积之和,先求出圆台的体积,再利用组合体的体积乘以打印所用原料密度可得结果.【详解】设半球的半径为R ,因为332π144πcm 3V R ==半球,所以6R =,由题意圆台的上底面半径及高均是3,下底面半径为6,所以((223113π6π363πcm 33V S S h =+=⋅+⋅+⨯=下上圆台,所以该实心模型的体积为3144π63π207πcm V V V =+=+=半球圆台,所以制作该模型所需原料的质量为207π 1.5207 4.7972.9g ⨯≈⨯=故选:C6. 已知数列{}n a 为等比数列,其前n 项和为n S ,10a >,则“公比0q >”是“对于任意*n ∈N ,0n S >”的( )A. 充分而不必要条件B. 必要而不充分条件C. 充分必要条件D. 既不充分也不必要条件【答案】A 【解析】【分析】根据等比数列的通项公式以及前n 项和公式,分别验证充分性以及必要性即可得到结果.详解】若10a >,且公比0q >,则110n n a a q -=>,所以对于任意*n ∈N ,0n S >成立,故充分性成立;若10a >,且12q =-,则()111112212111101323212n n nn n a S a a ⎡⎤⎛⎫--⎢⎥ ⎪⎡⎤⎡⎤⎝⎭⎢⎥⎛⎫⎛⎫⎣⎦==-=--⨯>⎢⎥⎢⎥ ⎪ ⎪⎛⎫⎝⎭⎝⎭⎢⎥⎢⎥⎣⎦⎣⎦-- ⎪⎝⎭,所以由对于任意*n ∈N ,0n S >,推不出0q >,故必要性不成立;所以“公比0q >”是“对于任意*n ∈N ,0n S >”的充分不必要条件.故选:A7. 若存在实数a ,对任意的x ∈[0,m ],都有(sin x -a )·(cos x -a )≤0恒成立,则实数m 的最大值为( )A.4πB. 2πC.34π D.54π【答案】C 【解析】【分析】根据已知不等式得到,要求y =sin x 和y =cos x 图象不在y =a的同一侧,利用正弦函数、余弦函数图象的性质进行解答即可.【详解】在同一坐标系中,作出y =sin x 和y =cos x 的图象,【的当m =4π时,要使不等式恒成立,只有a ,当m >4π时,在x ∈[0,m ]上,必须要求y =sin x 和y =cos x 的图象不在y =a 的同一侧.∴由图可知m 的最大值是34π.故选:C.8. 已知函数()f x 的定义域为R ,()()()()2,24f x f x f f +=--=-,且()f x 在[)1,+∞上递增,则()10xf x ->的解集为( )A. ()()2,04,∞-⋃+B. ()(),15,∞∞--⋃+C. ()(),24,-∞-+∞D. ()()1,05,∞-⋃+【答案】D 【解析】【分析】根据()()2f x f x +=-可得()f x 关于直线1x =对称,根据()()24f f -=-可得()()240f f -==,结合函数()f x 的单调性可得函数图象,根据图象列不等式求解集即可.【详解】解:函数()f x ,满足()()2f x f x +=-,则()f x 关于直线1x =对称,所以()()()244f f f -==-,即()()240f f -==,又()f x 在[)1,+∞上递增,所以()f x 在(),1-∞上递减,则可得函数()f x 的大致图象,如下图:所以由不等式()10xf x ->可得,20210x x -<<⎧⎨-<-<⎩或414x x >⎧⎨->⎩,解得10x -<<或5x >,故不等式()10xf x ->的解集为()()1,05,∞-⋃+.故选:D.二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分.9. 对于实数a ,b ,c ,下列选项正确的是( )A. 若a b >,则2a ba b +>> B. 若0a b >>,则a b>>C. 若11a b>,则0a >,0b < D. 若0a b >>,0c >,则b c ba c a+>+【答案】ABD 【解析】【分析】利用比较法、特例法逐一判断即可.【详解】对选项A ,因为a b >,所以022a b a b a +--=>,022a b a bb +--=>,所以2a ba b +>>,故A 正确;对选项B ,0a b >>1=>,所以a >,1=>b >,即a b >>,故B 正确;对选项C ,令2a =,3b =1b>,不满足0a >,0b <,故C 错误;对选项D ,因为0a b >>,0c >,所以()()()()()0a b c b a c c a b b c b a c a a a c a a c +-+-+-==>+++,故D 正确.故选:ABD .10. 已知函数()2sin cos f x x x x =+,则下列说法正确的是( )A. ()πsin 23f x x ⎛⎫=-⎪⎝⎭B. 函数()f x 的最小正周期为πC. 函数()f x 的对称轴方程为()5πZ 12x k k π=+∈D. 函数()f x 图象可由sin 2y x =的图象向右平移π3个单位长度得到【答案】AB的【解析】【分析】利用二倍角公式及辅助角公式化简函数,再结合正弦函数的图像性质逐项判断.【详解】()211cos 21πsin cos sin 2sin 22sin 22223x f x x x x x x x x +⎛⎫=-+==-=- ⎪⎝⎭,所以A 正确;对于B ,函数()f x 的最小正周期为2ππ2=,所以B 正确;对于C ,由ππ2π32x k -=+,k ∈Z ,得5ππ122k x =+,Z k ∈,所以函数()f x 的对称轴方程为5ππ122k x =+,Z k ∈,所以C 不正确;对于D ,sin 2y x =的图象向右平移π6个单位长度,得ππsin 2sin 263y x x ⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭,所以函数()f x 的图象可由sin 2y x =的图象向右平移π6个单位长度得到,所以D 不正确.故选:AB .11. 设n S 是公差为d (0d ≠)的无穷等差数列{}n a 的前n 项和,则下列命题正确的是( )A. 若0d <,则1S 是数列{}n S 的最大项B. 若数列{}n S 有最小项,则0d >C. 若数列{}n S 是递减数列,则对任意的:*N n ∈,均有0nS <D. 若对任意的*N n ∈,均有0n S >,则数列{}n S 是递增数列【答案】BD 【解析】【分析】取特殊数列判断A ;由等差数列前n 项和的函数特性判断B ;取特殊数列结合数列的单调性判断C ;讨论数列{}n S 是递减数列的情况,从而证明D.【详解】对于A :取数列{}n a 为首项为4,公差为2-的等差数列,2146S S =<=,故A 错误;对于B :等差数列{}n a 中,公差0d ≠,211(1)(222n n n d dS na d n a n -=+=+-,n S 是关于n 的二次函数.当数列{}n S 有最小项,即n S 有最小值,n S 对应的二次函数有最小值,对应的函数图象开口向上,0d >,B 正确;对于C :取数列{}n a 为首项为1,公差为2-的等差数列,22n S n n =-+,122(1)2(1)(2)210n n S n n n n S n =-+++-+---=+<+,即1n n S S <+恒成立,此时数列{}n S 是递减数列,而110S =>,故C 错误;对于D :若数列{}n S 是递减数列,则10(2)n n n a S S n -=-<≥,一定存在实数k ,当n k >时,之后所有项都为负数,不能保证对任意*N n ∈,均有0n S >.故若对任意*N n ∈,均有0n S >,有数列{}n S 是递增数列,故D 正确.故选:BD12. 如图所示,在棱长为2的正方体1111ABCD A B C D -中,点M ,N 分别为棱11B C ,CD 上的动点(包含端点),则下列说法正确的是( )A. 四面体11A D MN 的体积为定值B. 当M ,N 分别为棱11B C ,CD 的中点时,则在正方体中存在棱与平面1A MN 平行C. 直线MN 与平面ABCDD. 当M ,N 分别为棱11B C ,CD 的中点时,则过1A ,M ,N 三点作正方体的截面,所得截面为五边形【答案】ACD 【解析】【分析】求出四面体的体积判断A ;把正方体的棱分成3类,再判断各类中的一条即可判断B ;作出线面角,并求出其正切表达式判断C ;利用线线、线面平行的性质作出截面判断D.【详解】点M ,N 在棱11B C ,CD 上运动时,M 到11A D 距离始终为2,N 到平面11A D M 的距离始终为2,所以四面体11A D MN 的体积11114222323N A MD V -=⨯⨯⨯⨯=恒为定值,A 正确;在正方体1111ABCD A B C D -中,棱可分为三类,分别是1111,,A A A B A D ,及分别与它们平行的棱,又1111,,A A A B A D 不与平面1A MN 平行,则在正方体1111ABCD A B C D -中,不存在棱与平面1A MN 平行,B 错误;正方体棱长为2,如图1,过M 作1MM BC ⊥于1M ,则有1MM ⊥平面ABCD ,于是MN 与平面ABCD 所成角即为1MNM ∠,于是11112tan MM MNM M N M N∠==,又1M N长度的最大值为MN 与平面ABCD,C 正确;如图2,取BC 中点M ',连接,AM MM '',有11////MM BB AA ',且11MM BB AA '==,则四边形1AA MM '是平行四边形,有1//AM A M ',过N 作AM '的平行线交AD 于点E ,此时14DE DA =,则1//EN A M ,即EN 为过1A ,M ,N 三点的平面与平面ABCD 的交线,连接1A E ,在BC 上取点F ,使得14CF CB =,同证1//AM A M '的方法得11//A E B F ,在棱1CC 上取点G ,使113CG CC =,连接MG 并延长交直线BC 于H ,则112CH C M CF ==,即11FH C M B M ==,而1//FH B M ,于是四边形1FHMB 是平行四边形,有11////MG B F A E ,则MG 为过1A ,M ,N 三点的平面与平面11BCC B 的交线,连接NG ,则可得五边形1A MGNE 即为正方体中过1A ,M ,N 三点的截面,D 正确.故选:ABD【点睛】方法点睛:作截面的常用三种方法:直接法,截面的定点在几何体的棱上;平行线法,截面与几何体的两个平行平面相交,或者截面上有一条直线与几何体的某个面平行;延长交线得交点,截面上的点中至少有两个点在几何体的同一平面上.第Ⅱ卷三、填空题:本题共4小题,每小题5分,共20分.13. 若函数()ln f x x a x =-的图象在1x =处的切线斜率为3,则=a __________.【答案】2-【解析】【分析】求导,利用()13f '=求解即可.【详解】解:因为()ln f x x a x =-,所以()1a f x x'=-,又函数()ln f x x a x =-的图象在1x =处的切线斜率为3,则()1131af '=-=,所以2a =-.故答案为:2-14. 在平面直角坐标系xOy 中,圆O 与x 轴的正半轴交于点A ,点B ,C 在圆O 上,若射线OB 平分AOC ∠,34,55B ⎛⎫⎪⎝⎭,则点C 的坐标为__________.【答案】2425⎛⎫⎪⎝⎭【解析】【详解】由题意可知圆O 1=,设AOB BOC α∠=∠=,由题意可知4sin 5α=,3cos 5α=,则点C 的横坐标为271cos 212sin 25αα⨯=-=-,点C 的纵坐标为241sin 22sin cos 25ααα⨯==.故答案为:724,2525⎛⎫-⎪⎝⎭.15. 已知函数()f x 的定义域为R ,()e xy f x =+是偶函数,()3e x y f x =-是奇函数,则()f x 的最小值为_____________.【答案】【解析】【分析】由题意可得()e 2e xxf x -=+,再结合基本不等式即可得答案.【详解】解:因为函数()e xy f x =+为偶函数,则()()e e x x f x f x --+=+,即()()ee xx f x f x ---=-,①又因为函数()3e xy f x =-为奇函数,则()()3e 3e xx f x f x ---=-+,即()()3e 3ex xf x f x -+-=+,②联立①②可得()e 2e xxf x -=+,由基本不等式可得()e 2e x x f x -=+≥=,当且仅当e 2e x x -=时,即当1ln 22x =时,等号成立,故函数()f x 的最小值为故答案为:16. 已知菱形ABCD 中,对角线BD =,将ABD △沿着BD 折叠,使得二面角A BD C --为120°,AC =,则三棱锥A BCD -的外接球的表面积为________.【答案】28π【解析】【分析】将ABD 沿BD 折起后,取BD 中点为E ,连接AE ,CE ,得到120AEC ∠=︒,在AEC △中由余弦定理求出AE 的长,进一步求出AB 的长,分别记三角形ABD △与BCD △的重心为G 、F ,记该几何体ABCD 的外接球球心为O ,连接OF ,OG ,证明Rt OGE △与Rt OFE 全等,求出OE ,再推出BD OE ⊥,连接OB ,由勾股定理求出OB ,即可得出外接球的表面积.【详解】将ABD 沿BD 折起后,取BD 中点为E ,连接AE ,CE ,则AE BD ⊥,CE BD ⊥,所以AEC ∠即为二面角A BD C --的平面角,所以120AEC ∠=︒;设AE a =,则AE CE a ==,在AEC △中2222cos120AC AE EC AE CE =+-⋅⋅︒,即2127222a a a ⎛⎫=-⨯⨯⨯- ⎪⎝⎭解得3a =,即3AE =,所以AB ==所以ABD △与BCD △是边长为.分别记三角形ABD △与BCD △的重心为G 、F ,则113EG AE ==,113EF CE ==;即EF EG =;因为ABD △与BCD △都是边长为所以点G 是ABD △的外心,点F 是BCD △的外心;记该几何体ABCD 的外接球球心为O ,连接OF ,OG ,根据球的性质,可得OF ⊥平面BCD ,OG ⊥平面ABD ,所以 OGE 与OFE △都是直角三角形,且OE 为公共边,所以Rt OGE △与Rt OFE 全等,因此1602OEG OEF AEC ∠=∠=∠=︒,所以2cos 60EFOE ==︒;因为AE BD ⊥,CE BD ⊥,AE CE E =I ,且AE ⊂平面AEC ,CE ⊂平面AEC ,所以BD ⊥平面AEC ;又OE ⊂平面AEC ,所以BD OE ⊥,连接OB ,则外接球半径为OB ===,所以外接球表面积为2428S ππ=⨯=.故答案为:28π【点睛】思路点睛:求解几何体外接球体积或表面积问题时,一般需要结合几何体结构特征,确定球心位置,求出球的半径,即可求解;在确定球心位置时,通常需要先确定底面外接圆的圆心,根据球心和截面外接圆的圆心连线垂直于截面,即可确定球心位置;有时也可将几何体补型成特殊的几何体(如长方体),根据特殊几何体的外接球,求出球的半径.四、解答题:本题共6小题,共70分.请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤.17. 已知正项数列{}n a 的前n 项和为n S ,且满足22n n n S a a =+.(1)求数列{}n a 的通项公式;(2)设24n n n b a a +=,数列{}n b 的前n 项和为n T ,证明:3n T <.【答案】(1)n a n =; (2)证明见解析.【解析】【分析】(1)利用,n n a S 的关系,结合已知条件以及等差数列的通项公式即可求得结果;(2)根据(1)中所求,利用裂项求和法求得n T ,即可证明.【小问1详解】依题意可得,当1n =时,2111122S a a a ==+,0n a >,则11a =;当2n ≥时,22n n n S a a =+,21112n n n S a a ---=+,两式相减,整理可得()()1110n n n n a a a a --+--=,又{}n a 为正项数列,故可得11n n a a --=,所以数列{}n a 是以11a =为首项,1d =为公差的等差数列,所以n a n =.【小问2详解】证明:由(1)可知n a n =,所以()42222n b n n n n ==-++,()44441324352n T n n =+++⋅⋅⋅+⨯⨯⨯+22222222222222132435462112n n n n n n =-+-+-+-⋅⋅⋅+-+-+---++2221312n n =+--<++,所以3n T <成立18. 在ABC 中,角A 、B 、C 所对的边分别为a 、b 、c)sin a C C =-.(1)求A ;(2)若8a =,ABCABC 的周长.【答案】(1)2π3(2)18.【解析】【分析】(1)由正弦定理结合两角和的正弦公式化简可得出tan A的值,结合角A的取值范围可求得角A 的值;(2)利用三角形的面积公式可得出182b c bc++=,结合余弦定理可求得b c+的值,即可求得ABC的周长.【小问1详解】)sina C C=-,)sin sinB AC C=-,①因为πA B C++=,所以()sin sin sin cos cos sinB AC A C A C=+=+,sin sin sinA C A C=-,又因为A、()0,πC∈,sin0C≠sin0A A=-<,所以tan A=,又因为()0,πA∈,解得2π3A=.【小问2详解】解:由(1)知,2π3A=,因为ABC所以()1sin2ABCS a b c A=++=⋅△,即()8b c++=,所以,182b c bc++=②,由余弦定理2222π2cos3a b c bc=+-⋅得2264b c bc++=,所以()264b c bc+-=③,联立②③,得()()22864b c b c+-++=,解得10b c+=,所以ABC的周长为18a b c++=.19. 如图,在三棱柱111ABC A B C-中,11BC B C O=,12BC BB==,1AO=,160B BC∠=︒,且AO⊥平面11BB C C.(1)求证:1AB B C ⊥;(2)求二面角111A B C A --的正弦值.【答案】(1)证明见解析 (2【解析】【分析】(1)根据线面垂直的性质和判断定理可得1B C ⊥平面1ABC ,从而即可证明1AB B C ⊥;(2)建立以O 为原点,分别以OB ,1OB ,OA 所在直线为x ,y ,z 轴的空间坐标系,利用空间向量求解即可.【小问1详解】证明:因AO ⊥平面11BB C C ,1B C ⊂平面11BB C C ,所以1AO B C ⊥,因为1BC BB =,四边形11BB C C 是平行四边形,所以四边形11BB C C 是菱形,所以11BC B C ⊥.又因为1AO BC O ⋂=,AO ⊂平面1ABC ,1BC ⊂平面1ABC ,所以1B C ⊥平面1ABC ,因为AB ⊂平面1ABC ,所以1AB B C ⊥.【小问2详解】解:以O 为原点,分别以OB ,1OB ,OA 所在直线为x ,y ,z 轴建立如图所示的空间直角坐标系,如图所示,则)B,()10,1,0B ,()0,0,1A,()1C ,所以()10,1,1AB =-,)11C B =,)110,1A B AB ==-,为设平面11AB C 的一个法向量为()1111,,n x y z = ,则11111111100n AB y z n C B y ⎧⋅=-=⎪⎨⋅=+=⎪⎩ ,取11x =,可得1y =1z =,所以(11,n =u r,设平面111B C A 的一个法向量为()2222,,n x y z = ,则211221112200n A B z n C B y ⎧⋅=-=⎪⎨⋅=+=⎪⎩ ,取21x =,可得2y =2z =,所以(21,n = ,设二面角111A B C A --的大小为θ,因为1212121cos ,7n n n n n n ⋅〈〉===⋅ ,所以sin θ==,所以二面角111A B C A --.20. 如图,已知椭圆2222:1(0)x y C a b a b+=>>上一点A ,右焦点为(c,0)F ,直线AF 交椭圆于B 点,且满足||2||AF FB =, ||AB =.(1)求椭圆C 的方程;(2)若直线(0)y kx k =>与椭圆相交于,C D 两点,求四边形ACBD 面积的最大值.【答案】(1)22132x y +=;(2).【解析】【分析】(1)由已知得b =,由||2||AF FB =且||AB =,知||AF a ==,即可求出椭圆C 的标准方程;(2)直线AF0y +=,与椭圆联立求出3(,2B ,求出点,A B 到直线(0)y kx k =>的距离为1d =,2d =,联立直线y kx =与椭圆方程结合弦长公式求出CD ,求出四边形ACBD 的面积121()2S CD d d =+,整理化简利用二次函数求出最值.【详解】(1)A Q 为椭圆C上一点,b ∴=又 ||2||AF FB =,||AB =可得,||AF =,即a =所以椭圆C 的标准方程是22132x y +=.(2)由(1)知(1,0)F,A ,∴直线AF0y +-=,联立221320x y y ⎧+=⎪⎨+-= ,整理得:22462(3)0x x x x -=-=,解得:1230,2x x ==,∴3(,2B设点A,3(,2B 到直线(0)y kx k =>的距离为1d 和2d ,则1d =,2d = 直线(0)y kx k =>与椭圆相交于,C D 两点,联立22132x y y kx ⎧+=⎪⎨⎪=⎩,整理得:22(32)6k x +=,解得:34x x ==4CD x ∴=-=∴设四边形ACBD 面积为S,则121()2S CD d d =+=(0)k =>.设)t k =+∞,则k t =S ∴====≤当1t =,即t k ===k =ACBD面积有最大值【点睛】思路点睛:解决直线与椭圆的综合问题时,要注意:(1)注意观察应用题设中的每一个条件,明确确定直线、椭圆的条件;(2)强化有关直线与椭圆联立得出一元二次方程后的运算能力,重视根与系数之间的关系、弦长、斜率、三角形的面积等问题.21. 如图所示,A BCP -是圆锥的一部分(A 为圆锥的顶点),O 是底面圆的圆心,23BOC π∠=,P 是弧BC 上一动点(不与B 、C 重合),满足COP θ∠=.M 是AB 的中点,22OA OB ==.(1)若//MP 平面AOC ,求sin θ的值;(2)若四棱锥M OCPB -的体积大于14,求三棱锥A MPC -体积的取值范围.【答案】(1(2)【解析】【分析】(1)取OB 的中点N ,连接MN ,证明出//NP OC ,可得出3ONP π∠=,OPN θ∠=,然后在ONP △中利用正弦定理可求得sin θ的值;(2)计算得出四边形OCPB的面积364S πθ⎛⎫=+> ⎪⎝⎭,结合20,3πθ⎛⎫∈ ⎪⎝⎭可求得θ的取值范围,设三棱锥A MPC -的体积为2V ,三棱锥A BPC -的体积为3V,计算得出2361123V V πθ⎛⎫==+ ⎪⎝⎭,结合正弦型函数的基本性质可求得结果.【小问1详解】解:取OB 的中点N ,连接MN ,M 为AB 的中点,则//MN OA ,MN ⊄ 平面AOC ,AO ⊂平面AOC ,则//MN 平面AOC ,由题设,当//MP 平面AOC 时,因为MP MN M ⋂=,所以,平面//MNP 平面AOC ,NP ⊂ 平面MNP ,则//NP 平面AOC ,因为NP ⊂平面OBPC ,平面OBPC 平面AOC OC =,则//NP OC ,所以,3ONP BOC ππ∠=-∠=,OPN COP θ∠=∠=,在OPN 中,由正弦定理可得sin sin 3ON OP πθ=,故sin 3sin ON OP πθ==.【小问2详解】解:四棱锥M OCPB -的体积1111323V OA S S =⋅⋅=,其中S 表示四边形OCPB 的面积,则112111sin sin sin sin 223222S OP OC OP OB πθθθθθ⎫⎛⎫=⋅+⋅-=++⎪ ⎪⎪⎝⎭⎭3sin 46πθθθ⎛⎫=+=+ ⎪⎝⎭,所以,111364V S πθ⎛⎫==+> ⎪⎝⎭,可得sin 6πθ⎛⎫+> ⎪⎝⎭203πθ<< ,则5666πππθ<+<,故2363πππθ<+<,解得,62ππθ⎛⎫∈ ⎪⎝⎭.设三棱锥A MPC -的体积为2V ,三棱锥A BPC -的体积为3V ,由于M 是AB 的中点,则231112sin 2623V V OA S OB OC π⎛⎫==⋅-⋅ ⎪⎝⎭136πθ⎛⎫=+∈ ⎪⎝⎭.22. 混管病毒检测是应对单管病毒检测效率低下的问题,出现的一个创新病毒检测策略,混管检测结果为阴性,则参与该混管检测的所有人均为阴性,混管检测结果为阳性,则参与该混管检测的人中至少有一人为阳性.假设一组样本有N 个人,每个人患病毒的概率相互独立且均为()01p p <<.目前,我们采用K 人混管病毒检测,定义成本函数()N f X KX K=+,这里X 指该组样本N 个人中患病毒的人数.(1)证明:()E f X N ≥⎡⎤⎣⎦;(2)若4010p -<<,1020K ≤≤.证明:某混管检测结果为阳性,则参与该混管检测的人中大概率恰有一人为阳性.【答案】(1)证明见解析(2)证明见解析【解析】【分析】(1)由均值的性质及基本不等式即可证明.(2)由二项分布的概率及条件概率化简即可证明.【小问1详解】由题意可得X 满足二项分布(),X B N p ,由()()E aX b aE X b +=+知,()()N NE f X K X E pN N K K K =+=+⋅≥⎡⎤⎣⋅⎦,当且仅当1Kp K=时取等号;【小问2详解】记P P =(混管中恰有1例阳性|混管检测结果为阳性),i P P =(混管中恰有i 例阳性)=()C 1K i ii K p p --,0,1,,i K = ,令()e 1xh x x =--,33210210x ---⨯<<⨯,则()e 1xh x '=-,当()3021,0x -⨯∈-时,()0h x '<,()h x 为单调递减,当()300,21x -∈⨯时,()0h x '>,()h x 为单调递增,所以()()00h x h ≥=,且()()332103210e 21010h ---⨯--⨯=--⨯-≈,()()332103210e 21010h --⨯-⨯=-⨯-≈,所以当33210210x ---⨯<<⨯,e 10x x --≈即e 1x x ≈+,两边取自然对数可得()ln 1x x ≈+,所以当4010p -<<,1020K ≤≤时,所以()()ln 11e e K K p Kp p Kp ---=≈≈-,则()()()()110111111111K K Kp K p Kp p P P K p P Kp p ---⎡⎤-⎣⎦==≈=--≈---.故某混管检测结果为阳性,则参与该混管检测的人中大概率恰有一人为阳性.。
湖南省长沙市雅礼中学2022届高三下学期月考(七)数学试题(解析版)

C. 或 D. 或
【8题答案】
【答案】C
【解析】
【分析】函数 的零点个数为5等价于 与 的图像交点的个数为5,然后作出函数图象,数形结合即可得出结果.
【详解】∵偶函数 , , 是奇函数,得 ,即
, ,得 , ,即 与 的图像交点的个数,因为 ,即为 与 的图像交点的个数,因为
的图像为半圆,故由图像可知斜率 应该在 与 之间或为 ,
雅礼中学2022届高三月考试卷(七)
数学
一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合 , ,则 ()
A. B. C. D.
【1题答案】
【答案】C
【解析】
【分析】首先解一元二次不等式与指数不等式得到集合 、 ,再根据交集的定义计算可得;
【详解】解:由 可得 , 可得 ,所以集合 , ,所以 .
故选:C.
2. 已知复数 ,则 ( )
A.5B. C. D.2
【2题答案】
【答案】C
【解析】
【分析】
先求出 ,再根据复数模的求法即可求得结果
【详解】由复数 ,得 ,
所以 .
故选:C.
3. 函数 的图像可能是( )
A. B.
C. D.
【3题答案】
【详解】延长 与直线 相交于F,连接 ,
则平面 与平面 的交线为 ,
又∵
∴ 为平面 与平面 的交线与直线 所成角,
∵ 是棱 的中点,且 ∥ ,
∴ ,∴ .
故选:A.
6. 现行普通高中学生在高一时面临着选科的问题,学校抽取了部分男、女学生意愿的一份样本,制作出如下两个等高堆积条形图:
湖南省长沙市雅礼中学2025届高三上学期月考(二)数学试题

湖南省长沙市雅礼中学2025届高三上学期月考(二)数学试题一、单选题1.已知集合{}21,A x x k k ==-∈N ,{}1,0,1,2,3B =-,则A B =I ( ) A .{}1,3B .{}0,1,3C .{}1,1,3-D .{}1,0,1,2,3-2.若复数()21i 68iz -=+,则z z +=( )A B .25C .35D .453.设a r ,b r 是单位向量,则()2a ba b +-⋅r rr r 的最小值是( )A .1-B .0C .34D .14.已知()2cos 23cos 0αββ+-=,则()tan tan ααβ+=( ) A .5B .15C .-5D .15-5.巴黎奥运会期间,旅客人数(万人)为随机变量X ,且()2~30,2X N .记一天中旅客人数不少于26万人的概率为0p ,则0p 的值约为( )(参考数据:若()2~,X N μσ,有()0.683P X μσμσ-<≤+≈,()220.954P X μσμσ-<≤+≈,()330.997P X μσμσ-<≤+≈) A .0.977B .0.9725C .0.954D .0.6836.已知抛物线C :24x y =的焦点为F ,过点F 的直线与C 相交于M ,N 两点,则122MF NF +的最小值为( ) A .92B .4C .72D .37.若x ,0y ≥,1x y += )A .⎡⎣B .[]1,2C .2⎤⎦D .12⎡⎢⎣8.从重量分别为1,2,3,4,…,10克的砝码(每种砝码各2个)中选出若干个,使其总重量恰为9克的方法总数为m ,下列各式的展开式中9x 的系数为m 的选项是( )A .()()()()23101111x x x x ++++LB .()()()()11213110x x x x ++++LC .()()()()()222222341011111x x x x x +++++LD .()()()()22222232101111x x x x x x x x x ++++++++++L L二、多选题9.(多选)下列选项中,正确的是( )A .不等式220x x +->的解集为{|2x x <-或1}x >B .不等式2112x x +≤-的解集为{|32}x x -≤< C .不等式21x -≥的解集为{|13}x x ≤≤ D .设R x ∈,则“11x -<”是“405x x +<-”的充分不必要条件 10.如图,透明塑料制成的长方体容器1111ABCD A B C D -内灌进一些水,固定容器一边AB 于地面上,再将容器倾斜,随着倾斜度的不同,有下面几个结论,其中正确的命题有( )A .没有水的部分始终呈棱柱形B .水面EFGH 所在四边形的面积为定值C .随着容器倾斜度的不同,11AC 始终与水面所在平面平行D .当容器倾斜如图(3)所示时,AE AH ⋅为定值11.已知奇函数()f x 在R 上单调递增,()()f x g x '=,()()g x f x '=,若()()()22f x f x g x =,则( )A .()g x 的图象关于直线0x =对称B .()()()222g x gx f x =+C .()00g =或1D .()()221gx f x -=三、填空题12.从14,13,12,2,3,4,6,9中任取两个不同的数,分别记为m ,n ,记A =“log 0m n <”,则()P A =.13.如图,ABC V 中,6AB =,2AC BC =,D 为AB 中点,则tan BDC ∠的取值范围为.14.小军和小方两人先后在装有若干黑球的黑盒子与装有若干白球的白盒子(黑球数少于白球数)轮流取球,规定每次取球可以从某一盒子中取出任意多颗(至少取1颗),或者在两个盒子中取出相同颗数的球(至少各取1颗),最后不能按规则取的人输.已知两盒中共有11个球,且两人掷硬币后决定由小军先手取球.小方看了眼黑盒中的球,对小军说:“你输了!”若已知小方有必胜策略,则黑盒中球数为.四、解答题15.记ABC V 的内角,,A B C 的对边分别为,,a b c .已知2a b -=,()sin sin sin 2A BA B +-=. (1)求c ;(2)若ABC V 的内切圆在AB 上的切点为D ,求AD .16.已知动圆P 过点()2,0A -且与圆B :()22236x y -+=内切.(1)求动圆圆心P 的轨迹E 的方程;(2)设动圆1C :2221x y t +=,1C 与E 相交于,,,A B C D 四点,动圆2C :()222212x y t t t +=≠与E相交于,,,A B C D ''''四点.若矩形ABCD 与矩形A B C D ''''的面积相等,求2212t t +的值.17.为提高我国公民整体健康水平,2022年1月,由国家卫生健康委疾控局指导、中国疾病预防控制中心和国家体育总局体育科学研究所牵头组织编制的《中国人群身体活动指南(2021)》(以下简称《指南》)正式发布,《指南》建议18~64岁的成年人每周进行150~300分钟中等强度或75~150分钟高强度的有氧运动(以下简称为“达标成年人”),经过两年的宣传,某体育健康机构为制作一期《达标成年人》的纪录片,采取街头采访的方式进行拍摄,当采访到第二位“达标成年人”时,停止当天采访.记采访的18~64岁的市民数为随机变量X (2X ≥),且该市随机抽取的18~64岁的市民是达标成年人的概率为13,抽查结果相互独立.(1)求某天采访刚好到第五位可停止当天采访的概率;(2)若抽取的18~64岁的市民数X 不超过n 的概率大于13,求整数n 的最小值.18.已知函数()12ex xf x x λ-=-.(1)当1λ=时,求()f x 的图象在点 1,f 1 处的切线方程; (2)若1x ≥时,()0f x ≤,求λ的取值范围; (3)求证:()1111111232124e 2e*n n n n nnn +++++-+++->∈N L .19.高斯-博内公式是大范围微分几何学的一个经典的公式,是关于曲面的图形(由曲率表征)和拓扑(由欧拉示性数表征)间联系的一项重要表述,建立了空间的局部性质和整体性质之间的联系.其特例是球面三角形总曲率x 与球面三角形内角和θ满足:πx θα=+,其中α为常数,(如图,把球面上的三个点用三个大圆(以球心为半径的圆)的圆弧联结起来,所围成的图形叫做球面三角形,每个大圆弧叫做球面三角形的一条边,两条边所在的半平面构成的二面角叫做球面三角形的一个角.球面三角形的总曲率等于2SR,S 为球面三角形面积,R 为球的半径).(1)若单位球面有一个球面三角形,三条边长均为π2,求此球面三角形内角和;(2)求α的值;(3)把多面体的任何一个面伸展成平面,如果所有其他各面都在这个平面的同侧,这样的多面体叫做凸多面体.设凸多面体Ω顶点数为V ,棱数为E ,面数为F ,试证明凸多面体欧拉示性数()ΩV E F χ=-+为定值,并求出()Ωχ.。
