几何动点+函数图像+ 运动图像 --2019中考真题汇编(教师版)
2019中考数学动点的函数图像(含详细答案)

2019年中考数学总复习专题题型复习题型一几何问题中的函数图象针对演练1.(青海)如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG动点P从点A出发,沿A T »— I B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ ABP勺面积S随着时间t变化的函数图象大致为2.(资阳)如图,AD BC是O O的两条互相垂直的直径,点P从点O出发,沿C T C T D TO的路线匀速运动,设/ APB= y(单位:度),那么y与P运动的时间x(单位:秒)的关系图是()第2越图3.如图,正方形l : x = t , (0 <积为S,则函数S与ABC啲顶点A(0, #), B(#, 0),顶点C, D位于第t < 2)将正方形ABC酚成两部分,设位于直线l左侧部分(阴影部分)的面)),B(f)第3题0S4.(泰安)如图,正△ ABC的边长为4,点P为BC边上的任意一点(不与点B C重合),BD= y,则y关于x的函数图象大致是ABC哒长为1, E、F、G H分别为y, AN x,则y关于x的函数图象大致是(5.如图,正方形=BF= CG DH设小正方形EFG啲面积为AB BC CD DA边上的点,且AE)C第§题増6.如图,等边△ ABC的边长为2 cm,点P从点A出发,以同时点Q从点A出发,以1 cm/s的速度沿A T B-C的方向向点2 21 cm/s的速度向点C移动,若△ APQ的面积为S(cm),则下列最能反映S(cm)与移动时间t (s)之间函数关系的大致图象是((点C不与点A7.如图,点C是以点0为圆心,AB为直径的半圆上的动点AB= 4.设弦AC的长为x, △ ABD的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是()第丁題圈8.(鄂州)如图,O是边长为4 cm的正方形ABCD勺中心,开始沿折线A—B—M方向匀速运动,到M时停止运动,速度为为t(s),点P的运动路径与OA OP所围成的图形面积为S (cm2),则描述面积S(cm2)与时间t(s)的关系的图象可以是()M是BC的中点,动点P由A1 cm/s,设P点的运动时间K(II S(t tkl I6F /rm'J1/厲P薛*題国9.(莆田)如图,在矩形ABCDK6rh)CAB= 2,点E在边AD上,/ ABE= 45°,It接BD点P在线段DE上,过点P作PQ/ BD交BE于点Q 连接QD设PD= x, 积为y,则能表示y与x函数关系的图象大致是()6i(n)DBB DE 连△ PQD勺面410.(钦州)如图,△ ABC中, AB= 6, BC= 8, tan / B= 3•点D是边BC上的一个动点(点D与点B不重合),过点D作DEL AB垂足为E,点F是AD的中点,连接EF.设厶AEF的面积为y ,点D从点B沿BC运动到点C的过程中,D与B的距离为x,则能表示y与x的函数关系的图象大致是()12. 如图,在?ABCD 中,/ A = 60°, 发,点P 沿A R B^C R D 方向以2 cm/s 的速度前进,点Q 沿A —D 方向以1 cm/s 的速度前进, 当Q 到达点D 时,两个点随之停止运动.设运动时间为 x s ,P 、Q 经过的路径与线段 PQ 围 成的图形的面积为 y (单位:cn i ),贝U y 与x 的函数图象大致是()11.如图,两个等腰 Rt △ ABC Rt △ DEF 的斜边都为4羽cm ,点 D M 分别是 AB AC 边上的中点,DE 与AQ 或BC 交于点P,当点P 从点M 出发以1 cm/s 的速度沿M R C 运动至 点C 后又立即沿C R B 运动至点B 结束•若运动时间为t (单位:s ) , Rt △ ABC 和Rt △ DEF 重 叠部分的面积为y (单位:cm ),贝U y 关于t 的图象大致是( ) 蒸11駆图AB= 6 cm , BC= 12 cm ,点P 、Q 同时从顶点 A 出BC 位于同一条直线I 上,开始时,点 C 与B 重合,△ ABC 固定不动, 自左向右沿直线I 平移,移出△ ABC^(点B'与C 重合)停止,设厶A 然后把△ A B' C' B' C 平移的距离为【答案】1. B【解析】当点P在AD上时,△ ABP的底边AB不变,高增大,所以△ ABP的面积S 随着时间t的增大而增大;当点P在DE上时,△ ABP勺底边AB不变,高不变,所以△ ABP 的面积S不变;当点P在EF上时,△ ABP的底边AB不变,高减小,所以△ ABP的面积S随着时间t的增大而减小;当点P在FG上时,△ ABP的底边AB不变,高不变,所以△ ABP的面积S不变;当点P在GB上时,△ ABP的底边AB不变,高减小,所以△ ABP的面积S随着时间t的增大而减小.故选 B.2. B【解析】当点P在点0处时,/ APB=Z AOB= 90°,当点P沿OC运动到点C时,1 1/ APB=㊁/AOB= 45°;当点P在CDk运动时,/ APB=訂AOB= 45° ;当点P沿DO运动到点O 时,/ APB从45°增大到90° .结合选项可知B选项符合.3. C【解析】根据图形知道,当直线I : x = t在BD的左侧时,S= t2,当直线I : x =t在BD右侧时,S=- (t —2)2+ 1,结合选项,只有选项C符合.4. C 【解析I:/ APC是厶ABP 的外角,•••/ AP&/ PABF Z B,同理/ BDP=Z PAB+ Z APD 又I / B=/ APD •/ APC^Z BDP B=/ C= 60°,BD x y 1 2丸即4=4—x,整理得,y= — 4 x+ x,故选C.15. C【解析】依题意,得y= S正方形ABCD— & AEH— & BEF—S^CFG一 & DGF F12 22x —2x + 1,即y = 2x —2x + 1(0 < x< 1),抛物线开口向上,对称轴为x=?,故选C.6. C【解析】当0W t W2时,S= 1 - t - sin60 ° - t =jt2,此函数抛物线开口向上,且函数图象为抛物线右侧的一部分;当2 v t <4时,S= 2 X 2・sin60 ° (4 —t) 一 + 举,此函数图象是直线的一部分,且S随t的增大而减小•所以符合题意的函数图象只有 C.7. B【解析】•/ AB= 4,AC= x, • BC=p AB—AC =p16—x2, • S AABC= *ACBC=抑16-x2, •••此函数不是二次函数,也不是一次函数,•排除A、C, •/ AB为定值,当OCL AB时,△ABC 面积最大,此时A(= 2 2,即当x= 2 2时,y最大,故排除D,选B.1 AD 1 48. A【解析】根据题意,当0 v t <4时,S= ^X AP X = -X t X 2= t,面积S随时间1 1t的增大而增大;当4v t <6时,S= S四边形ABM—S A(2 + 4) X 2—- X (6 —t) X 2= t , 因此S始终是t的正比例函数,故选 A.9. C【解析】T/ ABE= 45°,/ A= 90°,「・A ABE是等腰直角三角形,• AE= AB=2,「. BE=^AB= 2农,T BE= DE PD= x,「・PE= DE- PD= 2羽-x,:PQ// BD BE= DE• QE= PE= 2 2 —x,又•••△ ABE是等腰直角三角形,.••点Q到AD的距离为2(2 2 —x) = 2,• y= 2x(2 —~22x) =—"^(x2— 2.2x + 2) +彳=—¥(x —2)2+#,结合选项,只有C选项符合.4 3 410. B 【解析】•••BD= x, DEI AB tan / B= ,•••在Rt △BED中, BE= x, DE= x,3 5 53 - 、「“亠- 1 11T AA6,「. AE= 6 —孑,又•••点F 为AD的中点,•• &AEF=2&ADE= q X-AE- DE •- y= AEF1 3 4 32 6=4X (6 —&x) X 5X,化简得y = —25X + 5x(0 v x< 8), • y与x的函数关系式为开口向下的二次函数,且自变量x的取值范围为0v x w 8,结合题中给出的选项,只有选项B符合.11 C【解析】如解图,连接DM过点D作DH L BC于点H,记DF与BC相交于点N, •.•点D1 1M分别是AB AC边的中点,• DM= 2BC= 2 cm , MC= g AO 2 cm , • DM= MC •四边形DMCH 为正方形,•DHh DM 又I/ NDHF Z/ PD= 90°, •••/ ND=Z PDM第11题解图•••△ DNH^A DPMI①当点P从点M出发,沿M-C运动时,即0w t v 2时,y = S^N卄S四2 __ ” ”边形DHC = S A DP M+ S 四边形DHC= S正方形DMC= 4 cm ;②当点P运动至点C时,即t = 2时,y = S\DBC= 4 2; 1 1 cnf③当点P从点C出发沿C-B运动至B处时,即2v t <6时,y= S A DBP=寸 BP- DHh?(6 —t) X2= 6—t,可知y是t的一次函数,故选C.12. A【解析】当点P在AB上时,即0< x<3时,P、Q经过的路径与线段PQ围成的图形的面积=2x X 3x = 多2;当点P在BC上时,即3v x<9时,P、Q经过的路径与线段PQ围成的图形的面积=2X 3X 3 , 3 + g(2x — 6 + x—3) X3 •. 3 = —9 3, y随x的增大而增大;当点P在CD上时,即9v x< 12时,P Q经过的路径与线段PQ围成的图形的面积= 12X3 3 —1(12 —x)(12 3 —3x) = 一fx2* 12 3x—36 3.综上,选项 A 符合题意.13. B 【解析】由题意知:在厶A B C移动的过程中,阴影部分总为等边三角形. 当1 \[3 \[320<x<1时,重合部分边长为x,此时y = ^XX-^X = -^x ;当1 v x<2时,重合部分为△ A B' C',此时y = 1X仃石3 =-43;当2v x<3时,重合部分边长为 3 —x,此时y= 2(3—x) X "2^(3 —x) = -4-(3 —x)2.由以上分析可知,这个分段函数的图象左边为开口向上的抛物线的一部分,中间为直线y =〒的一部分,右边为开口向上的抛物线的一部分,且顶点为(3 , 0),最高点为(2 ,〒),结合选项中的图象可知,选项B符合.。
函数与动点综合问题(函数)-全国各地2019中考数学压轴题函数大题题型分类汇编(解析版)

2019全国各地中考数学压轴大题函数综合十一、函数与动点综合问题1.(2019•丹东)如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c与x轴交于B,C两点,与y轴交于点A,直线y=﹣x+2经过A,C两点,抛物线的对称轴与x轴交于点D,直线MN与对称轴交于点G,与抛物线交于M,N两点(点N在对称轴右侧),且MN∥x轴,MN=7.(1)求此抛物线的解析式.(2)求点N的坐标.(3)过点A的直线与抛物线交于点F,当tan∠F AC=时,求点F的坐标.(4)过点D作直线AC的垂线,交AC于点H,交y轴于点K,连接CN,△AHK沿射线AC以每秒1个单位长度的速度移动,移动过程中△AHK与四边形DGNC产生重叠,设重叠面积为S,移动时间为t (0≤t≤),请直接写出S与t的函数关系式.解:(1)直线y=﹣x+2经过A,C两点,则点A、C的坐标分别为(0,2)、(4,0),则c=2,抛物线表达式为:y=﹣x2+bx+2,将点C坐标代入上式并解得:b=,故抛物线的表达式为:y=﹣x2+x+2…①;(2)抛物线的对称轴为:x=,点N的横坐标为:+=5,故点N的坐标为(5,﹣3);(3)∵tan∠ACO==tan∠F AC=,即∠ACO=∠F AC,①当点F在直线AC下方时,设直线AF交x轴于点R,∵∠ACO=∠F AC,则AR=CR,设点R(r,0),则r2+4=(r﹣4)2,解得:r=,即点R的坐标为:(,0),将点R、A的坐标代入一次函数表达式:y=mx+n得:,解得:,故直线AR的表达式为:y=﹣x+2…②,联立①②并解得:x=,故点F(,﹣);②当点F在直线AC的上方时,∵∠ACO=∠F′AC,∴AF′∥x轴,则点F′(3,2);综上,点F的坐标为:(3,2)或(,﹣);(4)如图2,设∠ACO=α,则tanα==,则sinα=,cosα=;①当0≤t≤时(左侧图),设△AHK移动到△A′H′K′的位置时,直线H′K′分别交x轴于点T、交抛物线对称轴于点S,则∠DST=∠ACO=α,过点T作TL⊥KH,则LT=HH′=t,∠LTD=∠ACO=α,则DT====t,DS=,S=S△DST=DT×DS=t2;②当<t≤时(右侧图),同理可得:S=S梯形DGS′T′=×DG×(GS′+DT′)=3+(+﹣)=t﹣;③当<t≤时,同理可得:S=t+;综上,S=.2.(2019•葫芦岛)如图,直线y=﹣x+4与x轴交于点B,与y轴交于点C,抛物线y=﹣x2+bx+c经过B,C两点,与x轴另一交点为A.点P以每秒个单位长度的速度在线段BC上由点B向点C运动(点P 不与点B和点C重合),设运动时间为t秒,过点P作x轴垂线交x轴于点E,交抛物线于点M.(1)求抛物线的解析式;(2)如图①,过点P作y轴垂线交y轴于点N,连接MN交BC于点Q,当时,求t的值;(3)如图②,连接AM交BC于点D,当△PDM是等腰三角形时,直接写出t的值.解:(1)直线y=﹣x+4中,当x=0时,y=4 ∴C(0,4)当y=﹣x+4=0时,解得:x=4∴B(4,0)∵抛物线y=﹣x2+bx+c经过B,C两点∴解得:∴抛物线解析式为y=﹣x2+3x+4(2)∵B(4,0),C(0,4),∠BOC=90°∴OB=OC∴∠OBC=∠OCB=45°∵ME⊥x轴于点E,PB t∴∠BEP=90°∴Rt△BEP中,sin∠PBE∴BE=PE PB=t∴x M=x P=OE=OB﹣BE=4﹣t,y P=PE=t ∵点M在抛物线上∴y M=﹣(4﹣t)2+3(4﹣t)+4=﹣t2+5t∴MP=y M﹣y P=﹣t2+4t∵PN⊥y轴于点N∴∠PNO=∠NOE=∠PEO=90°∴四边形ONPE是矩形∴NC=OC﹣ON=4﹣t∵MP∥CN∴△MPQ∽△NCQ∴∴解得:t1,t2=4(点P不与点C重合,故舍去)∴t的值为(3)∵∠PEB=90°,BE=PE∴∠BPE=∠PBE=45°∴∠MPD=∠BPE=45°①若MD=MP,则∠MDP=∠MPD=45°∴∠DMP=90°,即DM∥x轴,与题意矛盾②若DM=DP,则∠DMP=∠MPD=45°∵∠AEM=90°∴AE=ME∵y=﹣x2+3x+4=0时,解得:x1=﹣1,x2=4∴A(﹣1,0)∵由(2)得,x M=4﹣t,ME=y M=﹣t2+5t∴AE=4﹣t﹣(﹣1)=5﹣t∴5﹣t=﹣t2+5t解得:t1=1,t2=5(0<t<4,舍去)③若MP=DP,则∠PMD=∠PDM如图,记AM与y轴交点为F,过点D作DG⊥y轴于点G ∴∠CFD=∠PMD=∠PDM=∠CDF∵A(﹣1,0),M(4﹣t,﹣t2+5t),设直线AM解析式为y=ax+m∴解得:∴直线AM:y=tx+t∴F(0,t)∴CF=OC﹣OF=4﹣t∵tx+t=﹣x+4,解得:x∴DG=x D∵∠CGD=90°,∠DCG=45°∴CD DG∴4﹣t解得:t 1综上所述,当△PDM是等腰三角形时,t=1或t1.3.(2019•辽阳)如图,在平面直角坐标系中,Rt△ABC的边BC在x轴上,∠ABC=90°,以A为顶点的抛物线y=﹣x2+bx+c经过点C(3,0),交y轴于点E(0,3),动点P在对称轴上.(1)求抛物线解析式;(2)若点P从A点出发,沿A→B方向以1个单位/秒的速度匀速运动到点B停止,设运动时间为t秒,过点P作PD⊥AB交AC于点D,过点D平行于y轴的直线l交抛物线于点Q,连接AQ,CQ,当t为何值时,△ACQ的面积最大?最大值是多少?(3)若点M是平面内的任意一点,在x轴上方是否存在点P,使得以点P,M,E,C为顶点的四边形是菱形,若存在,请直接写出符合条件的M点坐标;若不存在,请说明理由.解:(1)将点C、E的坐标代入二次函数表达式得:,解得:,故抛物线的解析式为:y=﹣x2+2x+3,则点A(1,4);(2)将点A、C的坐标代入一次函数表达式并解得:直线AC的表达式为:y=﹣2x+6,点P(1,4﹣t),则点D(,4﹣t),设点Q(,4),S△ACQ DQ×BC t2+t,∵0,故S△ACQ有最大值,当t=2时,其最大值为1;(3)设点P(1,m),点M(x,y),①当EC是菱形一条边时,当点M在点P右方时,点E向右平移3个单位、向下平移3个单位得到C,则点P向右平移3个单位、向下平移3个单位得到M,则1+3=x,m﹣3=y,而MP=EP得:1+(m﹣3)2=(x﹣1)2+(y﹣m)2,解得:y=m﹣3,故点M(4,);当点M在点P左方时,同理可得:点M(﹣2,3);②当EC是菱形一对角线时,则EC中点即为PM中点,则x+1=3,y+m=3,而PE=PC,即1+(m﹣3)2=4+m2,解得:m=1,故x=2,y=3﹣m=3﹣1=2,故点M(2,2);综上,点M(4,)或(﹣2,3)或M(2,2).4.(2019•烟台)如图,顶点为M的抛物线y=ax2+bx+3与x轴交于A(﹣1,0),B两点,与y轴交于点C,过点C作CD⊥y轴交抛物线于另一点D,作DE⊥x轴,垂足为点E,双曲线y(x>0)经过点D,连接MD,BD.(1)求抛物线的表达式;(2)点N,F分别是x轴,y轴上的两点,当以M,D,N,F为顶点的四边形周长最小时,求出点N,F的坐标;(3)动点P从点O出发,以每秒1个单位长度的速度沿OC方向运动,运动时间为t秒,当t为何值时,∠BPD的度数最大?(请直接写出结果)解:(1)C(0,3)∵CD⊥y,∴D点纵坐标是3,∵D在y上,∴D(2,3),将点A(﹣1,0)和D(2,3)代入y=ax2+bx+3,∴a=﹣1,b=2,∴y=﹣x2+2x+3;(2)M(1,4),B(3,0),作M关于y轴的对称点M',作D关于x轴的对称点D',连接M'D'与x轴、y轴分别交于点N、F,则以M,D,N,F为顶点的四边形周长最小即为M'D'+MD的长;∴M'(﹣1,4),D'(2,﹣3),∴M'D'直线的解析式为y x∴N(,0),F(0,);(3)设P(0,t),N(r,t),作△PBD的外接圆N,当⊙N与y轴相切时此时圆心N到BD的距离最小,圆心角∠DNB最大,则,∠BPD 的度数最大;∴PN=ND,∴r,∴t2﹣6t﹣4r+13=0,易求BD的中点为(,),直线BD的解析式为y=﹣3x+9,∴BD的中垂线解析式y x,N在中垂线上,∴t r,∴t2﹣18t+21=0,∴t=9+2或t=9﹣2,∵圆N与y轴相切,∴圆心N在D点下方,∴0<t<3,∴t=9﹣2.5.(2019•桂林)如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣2,0)和B(1,0),与y轴交于点C.(1)求抛物线的表达式;(2)作射线AC,将射线AC绕点A顺时针旋转90°交抛物线于另一点D,在射线AD上是否存在一点H,使△CHB的周长最小.若存在,求出点H的坐标;若不存在,请说明理由;(3)在(2)的条件下,点Q为抛物线的顶点,点P为射线AD上的一个动点,且点P的横坐标为t,过点P作x轴的垂线l,垂足为E,点P从点A出发沿AD方向运动,直线l随之运动,当﹣2<t<1时,直线l将四边形ABCQ分割成左右两部分,设在直线l左侧部分的面积为S,求S关于t的函数表达式.解:(1)抛物线与x轴交于点A(﹣2,0)和B(1,0)∴交点式为y=﹣(x+2)(x﹣1)=﹣(x2+x﹣2)∴抛物线的表示式为y=﹣x2﹣x+2(2)在射线AD上存在一点H,使△CHB的周长最小.如图1,延长CA到C',使AC'=AC,连接BC',BC'与AD交点即为满足条件的点H ∵x=0时,y=﹣x2﹣x+2=2∴C(0,2)∴OA=OC=2∴∠CAO=45°,直线AC解析式为y=x+2∵射线AC绕点A顺时针旋转90°得射线AD∴∠CAD=90°∴∠OAD=∠CAD﹣∠CAO=45°∴直线AD解析式为y=﹣x﹣2∵AC'=AC,AD⊥CC'∴C'(﹣4,﹣2),AD垂直平分CC'∴CH=C'H∴当C'、H、B在同一直线上时,C△CHB=CH+BH+BC=C'H+BH+BC=BC'+BC最小设直线BC'解析式为y=kx+a∴解得:∴直线BC':y=x﹣∵解得:∴点H坐标为(﹣,﹣)(3)∵y=﹣x2﹣x+2=﹣(x+)2+∴抛物线顶点Q(﹣,)①当﹣2<t≤﹣时,如图2,直线l与线段AQ相交于点F设直线AQ解析式为y=mx+n∴解得:∴直线AQ:y=x+3∵点P横坐标为t,PF⊥x轴于点E∴F(t,t+3)∴AE=t﹣(﹣2)=t+2,FE=t+3∴S=S△AEF=AE•EF=(t+2)(t+3)=t2+3t+3②当﹣<t≤0时,如图3,直线l与线段QC相交于点G,过点Q作QM⊥x轴于M ∴AM=﹣﹣(﹣2)=,QM=∴S△AQM=AM•QM=设直线CQ解析式为y=qx+2把点Q代入:﹣q+2=,解得:q=﹣∴直线CQ:y=﹣x+2∴G(t,﹣t+2)∴EM=t﹣(﹣)=t+,GE=﹣t+2∴S梯形MEGQ=(QM+GE)•ME=(﹣t+2)(t+)=﹣t2+2t+∴S=S△AQM+S梯形MEGQ=+(﹣t2+2t+)=﹣t2+2t+③当0<t<1时,如图4,直线l与线段BC相交于点N设直线BC解析式为y=rx+2把点B代入:r+2=0,解得:r=﹣2∴直线BC:y=﹣2x+2∴N(t,﹣2t+2)∴BE=1﹣t,NE=﹣2t+2∴S△BEN=BE•NE=(1﹣t)(﹣2t+2)=t2﹣2t+1∵S梯形MOCQ=(QM+CO)•OM=×(+2)×=,S△BOC=BO•CO=×1×2=1∴S=S△AQM+S梯形MOCQ+S△BOC﹣S△BEN=++1﹣(t2﹣2t+1)=﹣t2+2t+综上所述,S=6.(2019•天门)如图,在平面直角坐标系中,四边形OABC的顶点坐标分别为O(0,0),A(12,0),B(8,6),C(0,6).动点P从点O出发,以每秒3个单位长度的速度沿边OA向终点A运动;动点Q 从点B同时出发,以每秒2个单位长度的速度沿边BC向终点C运动.设运动的时间为t秒,PQ2=y.(1)直接写出y关于t的函数解析式及t的取值范围:y=25t2﹣80t+100(0≤t≤4);(2)当PQ=3时,求t的值;(3)连接OB交PQ于点D,若双曲线y=(k≠0)经过点D,问k的值是否变化?若不变化,请求出k的值;若变化,请说明理由.解:(1)过点P作PE⊥BC于点E,如图1所示.当运动时间为t秒时(0≤t≤4)时,点P的坐标为(3t,0),点Q的坐标为(8﹣2t,6),∴PE=6,EQ=|8﹣2t﹣3t|=|8﹣5t|,∴PQ2=PE2+EQ2=62+|8﹣5t|2=25t2﹣80t+100,∴y=25t2﹣80t+100(0≤t≤4).故答案为:y=25t2﹣80t+100(0≤t≤4).(2)当PQ=3时,25t2﹣80t+100=(3)2,整理,得:5t2﹣16t+11=0,解得:t1=1,t2=.(3)经过点D的双曲线y=(k≠0)的k值不变.连接OB,交PQ于点D,过点D作DF⊥OA于点F,如图2所示.∵OC=6,BC=8,∴OB==10.∵BQ∥OP,∴△BDQ∽△ODP,∴===,∴OD=6.∵CB∥OA,∴∠DOF=∠OBC.在Rt△OBC中,sin∠OBC===,cos∠OBC===,∴OF=OD•cos∠OBC=6×=,DF=OD•sin∠OBC=6×=,∴点D的坐标为(,),∴经过点D的双曲线y=(k≠0)的k值为×=.7.(2019•黄冈)如图①,在平面直角坐标系xOy中,已知A(﹣2,2),B(﹣2,0),C(0,2),D(2,0)四点,动点M以每秒个单位长度的速度沿B→C→D运动(M不与点B、点D重合),设运动时间为t(秒).(1)求经过A、C、D三点的抛物线的解析式;(2)点P在(1)中的抛物线上,当M为BC的中点时,若△P AM≌△PBM,求点P的坐标;(3)当M在CD上运动时,如图②.过点M作MF⊥x轴,垂足为F,ME⊥AB,垂足为E.设矩形MEBF 与△BCD重叠部分的面积为S,求S与t的函数关系式,并求出S的最大值;(4)点Q为x轴上一点,直线AQ与直线BC交于点H,与y轴交于点K.是否存在点Q,使得△HOK 为等腰三角形?若存在,直接写出符合条件的所有Q点的坐标;若不存在,请说明理由.解:(1)设函数解析式为y=ax2+bx+c,将点A(﹣2,2),C(0,2),D(2,0)代入解析式可得,∴,∴y=﹣﹣x+2;(2)∵△P AM≌△PBM,∴P A=PB,MA=MB,∴点P为AB的垂直平分线与抛物线的交点,∵AB=2,∴点P的纵坐标是1,∴1=﹣﹣x+2,∴x=﹣1+或x=﹣1﹣,∴P(﹣1﹣,1)或P(﹣1+,1);(3)CM=t﹣2,MG=CM=2t﹣4,MD=4﹣(BC+CM)=4﹣(2+t﹣2)=4﹣t,MF=MD=4﹣t,∴BF=4﹣4+t=t,∴S=(GM+BF)×MF=(2t﹣4+t)×(4﹣t)=﹣+8t﹣8=﹣(t﹣)2+;当t=时,S最大值为;(4)设点Q(m,0),直线BC的解析式y=﹣x+2,直线AQ的解析式y=﹣(x+2)+2,∴K(0,),H(,),∴OK2=,OH2=+,HK2=+,①当OK=OH时,=+,∴m2﹣4m﹣8=0,∴m=2+2或m=2﹣2;②当OH=HK时,+=+,∴m2﹣8=0,∴m=2或m=﹣2;③当OK=HK时,=+,不成立;综上所述:Q(2+2,0)或Q(2﹣2,0)或Q(2,0)或Q(﹣2,0);8.(2019•巴中)如图,抛物线y=ax2+bx﹣5(a≠0)经过x轴上的点A(1,0)和点B及y轴上的点C,经过B、C两点的直线为y=x+n.①求抛物线的解析式.②点P从A出发,在线段AB上以每秒1个单位的速度向B运动,同时点E从B出发,在线段BC上以每秒2个单位的速度向C运动.当其中一个点到达终点时,另一点也停止运动.设运动时间为t秒,求t为何值时,△PBE的面积最大并求出最大值.③过点A作AM⊥BC于点M,过抛物线上一动点N(不与点B、C重合)作直线AM的平行线交直线BC于点Q.若点A、M、N、Q为顶点的四边形是平行四边形,求点N的横坐标.解:①∵点B、C在直线为y=x+n上,∴B(﹣n,0)、C(0,n),∵点A(1,0)在抛物线上,∴,∴a=﹣1,b=6,∴抛物线解析式:y=﹣x2+6x﹣5;②由题意,得,PB=4﹣t,BE=2t,由①知,∠OBC=45°,∴点P到BC的高h为BP sin45°=(4﹣t),∴S△PBE=BE•h==,当t=2时,△PBE的面积最大,最大值为2;③由①知,BC所在直线为:y=x﹣5,∴点A到直线BC的距离d=2,过点N作x轴的垂线交直线BC于点P,交x轴于点H.设N(m,﹣m2+6m﹣5),则H(m,0)、P(m,m﹣5),易证△PQN为等腰直角三角形,即NQ=PQ=2,∴PN=4,Ⅰ.NH+HP=4,∴﹣m2+6m﹣5﹣(m﹣5)=4解得m1=1,m2=4,∵点A、M、N、Q为顶点的四边形是平行四边形,∴m=4;Ⅱ.NH+HP=4,∴m﹣5﹣(﹣m2+6m﹣5)=4解得m1=,m2=,∵点A、M、N、Q为顶点的四边形是平行四边形,m>5,∴m=,Ⅲ.NH﹣HP=4,∴﹣(﹣m2+6m﹣5)﹣[﹣(m﹣5)]=4,解得m1=,m2=,∵点A、M、N、Q为顶点的四边形是平行四边形,m<0,∴m=,综上所述,若点A、M、N、Q为顶点的四边形是平行四边形,点N的横坐标为:4或或.。
中考数学复习----《动点问题的函数图像》压轴真题练习(含答案解析)

中考数学复习----《动点问题的函数图像》压轴真题练习(含答案解析)1.(2021•益阳)如图,已知▱ABCD的面积为4,点P在AB边上从左向右运动(不含端点),设△APD的面积为x,△BPC的面积为y,则y关于x的函数图象大致是()A.B.C.D.【答案】B【解答】解:∵▱ABCD的面积为4,x+y是平行四边形面积的一半,∴x+y=2,∴y=2﹣x,∴y是x的一次函数,且当x=0时,y=2;x=2时,y=0;故只有选项B符合题意.2.(2021•河南)如图1,矩形ABCD中,点E为BC的中点,点P沿BC从点B运动到点C,设B,P两点间的距离为x,PA﹣PE=y,图2是点P运动时y随x变化的关系图象,则BC的长为()A.4B.5C.6D.7【答案】C【解答】解:由函数图象知:当x=0,即P在B点时,BA﹣BE=1.利用三角形两边之差小于第三边,得到PA﹣PE≤AE.∴y的最大值为AE,∴AE=5.在Rt△ABE中,由勾股定理得:BA2+BE2=AE2=25,设BE的长度为t,则BA=t+1,∴(t+1)2+t2=25,即:t2+t﹣12=0,∴(t+4)(t﹣3)=0,由于t>0,∴t+4>0,∴t﹣3=0,∴BC=2BE=2t=2×3=6.故选:C.3.(2022•鞍山)如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=4cm,CD⊥AB,垂足为点D,动点M从点A出发沿AB方向以cm/s的速度匀速运动到点B,同时动点N从点C出发沿射线DC方向以1cm/s的速度匀速运动.当点M停止运动时,点N也随之停止,连接MN.设运动时间为ts,△MND的面积为Scm2,则下列图象能大致反映S与t之间函数关系的是()A.B.C.D.【答案】B【解答】解:∵∠ACB=90°,∠A=30°,AB=4,∴∠B=60°,BC=AB=2,AC=BC=6,∵CD⊥AB,∴CD=AC=3,AD=CD=3,BD=BC=,∴当M在AD上时,0≤t≤3,MD=AD﹣AM=3﹣t,DN=DC+CN=3+t,∴S=MD•DN=(3﹣t)(3+t)=﹣t2+,当M在BD上时,3<t≤4,MD=AM﹣AD=t﹣3,∴S=MD•DN=(t﹣3)(3+t)=t2﹣,故选:B.4.(2022•菏泽)如图,等腰Rt△ABC与矩形DEFG在同一水平线上,AB=DE =2,DG=3,现将等腰Rt△ABC沿箭头所指方向水平平移,平移距离x是自点C到达DE之时开始计算,至AB离开GF为止.等腰Rt△ABC与矩形DEFG的重合部分面积记为y,则能大致反映y与x的函数关系的图象为()A.B.C.D.【答案】B【解答】解:如图,作CH⊥AB于点H,∵AB=2,△ABC是等腰直角三角形,∴CH=1,当0≤x≤1时,y=×2x•x=x2,当1<x≤3时,y==1,当3<x≤4时,y=1﹣=﹣(x﹣3)2+1,故选:B.5.(2022•鄂尔多斯)如图①,在正方形ABCD中,点M是AB的中点,点N 是对角线BD上一动点,设DN=x,AN+MN=y,已知y与x之间的函数图象如图②所示,点E(a,2)是图象的最低点,那么a的值为()A.B.2C.D.【答案】 A【解答】解:如图,连接AC交BD于点O,连接NC,连接MC交BD于点N′.∵四边形ABCD是正方形,∴O是BD的中点,∵点M是AB的中点,∴N′是△ABC的重心,∴N′O=BO,∴N′D=BD,∵A、C关于BD对称,∴NA=NC,∴AN+MN=NC+MN,∵当M、N、C共线时,y的值最小,∴y的值最小就是MC的长,∴MC=2,设正方形的边长为m,则BM=m,在Rt△BCM中,由勾股定理得:MC2=BC2+MB2,∴20=m2+(m)2,∴m=4,∴BD=4,∴a=N′D=BD=×4=,故选:A.6.(2021•鞍山)如图,△ABC是等边三角形,AB=6cm,点M从点C出发沿CB方向以1cm/s的速度匀速运动到点B,同时点N从点C出发沿射线CA 方向以2cm/s的速度匀速运动,当点M停止运动时,点N也随之停止.过点M作MP∥CA交AB于点P,连接MN,NP,作△MNP关于直线MP对称的△MN′P,设运动时间为ts,△MN′P与△BMP重叠部分的面积为Scm2,则能表示S与t之间函数关系的大致图象为()A.B.C.D.【答案】A【解答】解:如图1中,当点N′落在AB上时,取CN的中点T,连接MT.∵CM=t(cm),CN=2t(cm),CT=TN,∴CT=TN=t(cm),∵△ABC是等边三角形,∴∠C=∠A=60°,∴△MCT是等边三角形,∴TM=TC=TN,∴∠CMN=90°,∵MP∥AC,∴∠BPM=∠A=∠MPN=60°,∠BMP=∠C=60°,∠C+∠CMP=180°,∴∠CMP=120°,△BMP是等边三角形,∴BM=MP,∵∠CMP+∠MPN=180°,∴CM∥PN,∵MP∥CN,∴四边形CMPN是平行四边形,∴PM=CN=BM=2t,∴3t=6,∴t=2,如图2中,当0<t≤2时,过点M作MK⊥AC于K,则MK=CM•sin60°=t,∴S=•(6﹣t)•t=﹣t2+t.如图3中,当2<t≤6时,S=•MQ•PQ=×(6﹣t)×(6﹣t)=×(6﹣t)2,观察图象可知,选项A符合题意,故选:A.7.(2021•威海)如图,在菱形ABCD中,AB=2cm,∠D=60°,点P,Q同时从点A出发,点P以1cm/s的速度沿A﹣C﹣D的方向运动,点Q以2cm/s 的速度沿A﹣B﹣C﹣D的方向运动,当其中一点到达D点时,两点停止运动.设运动时间为x(s),△APQ的面积为y(cm2),则下列图象中能大致反映y与x之间函数关系的是()A.B.C.D.【答案】A【解答】解:∵四边形ABCD为菱形,∴AB=BC=CD=DA=2cm,∠B=∠D=60°.∴△ABC、△ACD都是等边三角形,∴∠CAB=∠ACB=∠ACD=60°.如图1所示,当0≤x≤1时,AQ=2xcm,AP=xcm,作PE⊥AB于E,∴PE=sin∠PAE×AP=(cm),∴y=AQ•PE=×2x×=,故D选项不正确;如图2,当1<x≤2时,AP=xcm,CQ=(4﹣2x)cm,作QF⊥AC于点F,∴QF=sin∠ACB•CQ=(cm),∴y===,故B选项不正确;如图3,当2<x≤3时,CQ=(2x﹣4)cm,CP=(x﹣2)cm,∴PQ=CQ﹣CP=2x﹣4﹣x+2=(x﹣2)cm,作AG⊥DC于点G,∴AG=sin∠ACD•AC=×2=(cm),∴y===.故C选项不正确,故选:A.8.(2021•日照)如图,平面图形ABD由直角边长为1的等腰直角△AOD和扇形BOD组成,点P在线段AB上,PQ⊥AB,且PQ交AD或交于点Q.设AP=x(0<x<2),图中阴影部分表示的平面图形APQ(或APQD)的面积为y,则函数y关于x的大致图象是()A.B.C.D.【答案】D【解答】解:当Q在AD上时,即点P在AO上时,有0<x≤1,此时阴影部分为等腰直角三角形,∴y=,该函数是二次函数,且开口向上,排除B,C选项;当点Q在弧BD上时,补全图形如图所示,阴影部分的面积等于等腰直角△AOD的面积加上扇形BOD的面积,再减去平面图形PBQ的面积即减去弓形QBF的面积,设∠QOB=θ,则∠QOF=2θ,∴,S弓形QBF=﹣S△QOF,当θ=45°时,AP=x=1+≈1.7,S弓形QBF=﹣=﹣,y=+﹣(﹣)=≈1.14,当θ=30°时,AP=x≈1.87,S弓形QBF=﹣=﹣,y=+﹣(﹣)=≈1.24,当θ=60°时,AP=x≈1.5,y≈0.98,在A,D选项中分别找到这两个特殊值,对比发现,选项D符合题意.故选:D.法二、当1<x<2时,即P在OB之间时,设∠QOD=θ,则θ∈(0,),则PQ=cosθ,OP=sinθ,则弧QD的长为θπ,此时S阴影=+θπ+sinθcosθ=+θ+sin2θ,∴y随x的增大而增大,而且增加的速度越来越慢,分析四个选项中的图象,只有选项D符合.故选:D.9.(2021•辽宁)如图,在矩形ABCD中,AB=6,AD=4,E是CD的中点,射线AE与BC的延长线相交于点F,点M从A出发,沿A→B→F的路线匀速运动到点F停止.过点M作MN⊥AF于点N.设AN的长为x,△AMN 的面积为S,则能大致反映S与x之间函数关系的图象是()A.B.C.D.【答案】B【解答】解:如图,∵E是CD的中点,∴CE=DE,∵四边形ABCD是矩形,∴∠D=∠DCF=90°,AD=BC=4,在△ADE与△FCE中,,∴△ADE≌△FCE(SAS),∴CF=AD=4,∴BF=CF+BC=8,∴AF=,当点M在AB上时,在Rt△AMN和Rt△AFB中,tan∠NAM=,∴NM=x=x,∴△AMN的面积S=×x×x=x2,∴当点M在AB上时,函数图象是开口向上、经过原点的抛物线的一部分;当点M在BF上时,如图,AN=x,NF=10﹣x,在Rt△FMN和Rt△FBA中,tan∠F=,∴=﹣,∴△AMN的面积S==﹣,∴当点M在BF上时,函数图象是开口向下的抛物线的一部分;故选:B.10.(2021•苏州)如图,线段AB=10,点C、D在AB上,AC=BD=1.已知点P从点C出发,以每秒1个单位长度的速度沿着AB向点D移动,到达点D后停止移动.在点P移动过程中作如下操作:先以点P为圆心,PA、PB的长为半径分别作两个圆心角均为60°的扇形,再将两个扇形分别围成两个圆锥的侧面,设点P的移动时间为t(秒),两个圆锥的底面面积之和为S,则S关于t的函数图象大致是()A.B.C.D.【答案】D【解答】解:∵AB=10,AC=BD=1,∴CD=10﹣1﹣1=8,∵PC=t,∴AP=t+1,PB=8﹣t+1=9﹣t,设围成的两个圆锥底面圆半径分别为r和R则:2πr=;.解得:r=,R=,∴两个圆锥的底面面积之和为S===,根据函数关系式可以发现该函数图象是一个开口向上的二次函数.故选:D.11.(2021•甘肃)如图1,在△ABC中,AB=BC,BD⊥AC于点D(AD>BD).动点M从A点出发,沿折线AB→BC方向运动,运动到点C停止.设点M的运动路程为x,△AMD的面积为y,y与x的函数图象如图2,则AC的长为()A.3B.6C.8D.9【答案】B【解答】解:由图2知,AB+BC=2,∵AB=BC,∴AB=,∵AB=BC,BD⊥AC,∴AC=2AD,∠ADB=90°,在Rt△ABD中,AD²+BD²=AB²=13①,设点M到AC的距离为h,∴S△ADM=AD•h,∵动点M从A点出发,沿折线AB→BC方向运动,∴当点M运动到点B时,△ADM的面积最大,即h=BD,由图2知,△ADM的面积最大为3,∴AD•BD=3,∴AD•BD=6②,①+2×②得,AD²+BD²+2AD•BD=13+2×6=25,∴(AD+BD)²=25,∴AD+BD=5(负值舍去),∴BD=5﹣AD③,将③代入②得,AD(5﹣AD)=6,∴AD=3或AD=2,∵AD>BD,∴AD=3,∴AC=2AD=6,故选:B.12.(2021•百色)如图,矩形ABCD各边中点分别是E、F、G、H,AB=2,BC=2,M为AB上一动点,过点M作直线l⊥AB,若点M从点A开始沿着AB方向移动到点B即停(直线l随点M移动),直线l扫过矩形内部和四边形EFGH外部的面积之和记为S.设AM=x,则S关于x的函数图象大致是()A.B.C.D.【答案】D【解答】解:①当M点运动在AE段,此时S=S△HAE+S△GHD﹣S△EOM﹣S△GPS,∵四边形ABCD是矩形,直线l⊥AB,H、E、F、G为AD、AB、BC、CD的中点,∴AH=AD==1,AE=AB=,S△HAE=S△GHD,S△EOM=S△GPS,∴S=2S△HAE﹣2S△EOM,∴S△HAE=AE•AH=;∵直线l⊥AB,∴∠OME=∠A=90°,∠HEA=∠OEM,∴△HAE∽△OME,∴,∴OM=,又∵ME=AE﹣AM=﹣x,∴OM=ME=,∴S△EOM=,∴S=2S△HAE﹣2S△EOM=,此时,对应抛物线开口向下;②当M点运动到在BE段,此时,S=S△HAE+S△GHD+S△EO1M1+S△GP1S1,即S=2S△HAE+2S△EO1M1,与①同理,O1M1=,又∵M1E=AM1﹣AE=x﹣,∴O1M1=M1E=,∴S△EO1M1=,∴S=2S△HAE+2S△EO1M1=,此时,对应抛物线开口向上,故选:D.13.(2021•鄂尔多斯)如图①,在矩形ABCD中,H为CD边上的一点,点M 从点A出发沿折线AH﹣HC﹣CB运动到点B停止,点N从点A出发沿AB 运动到点B停止,它们的运动速度都是1cm/s,若点M、N同时开始运动,设运动时间为t(s),△AMN的面积为S(cm2),已知S与t之间函数图象如图②所示,则下列结论正确的是()①当0<t≤6时,△AMN是等边三角形.②在运动过程中,使得△ADM为等腰三角形的点M一共有3个.③当0<t≤6时,S=.④当t=9+时,△ADH∽△ABM.⑤当9<t<9+3时,S=﹣3t+9+3.A.①③④B.①③⑤C.①②④D.③④⑤【答案】A【解答】解:由图②可知:点M、N两点经过6秒时,S最大,此时点M在点H处,点N在点B处并停止不动,如图,①∵点M、N两点的运动速度为1cm/s,∴AH=AB=6cm,∵四边形ABCD是矩形,∴CD=AB=6 cm.∵当t=6s时,S=9cm2,∴×AB×BC=9.∴BC=3cm.∵当6≤t≤9时,S=且保持不变,∴点N在B处不动,点M在线段HC上运动,运动时间为(9﹣6)秒,∴HC=3 cm,即点H为CD的中点.∴BH=cm.∴AB=AH=BH=6cm,∴△ABM为等边三角形.∴∠HAB=60°.∵点M、N同时开始运动,速度均为1cm/s,∴AM=AN,∴当0<t≤6时,△AMN为等边三角形.故①正确;②如图,当点M在AD的垂直平分线上时,△ADM为等腰三角形:此时有两个符合条件的点;当AD=AM时,△ADM为等腰三角形,如图:当DA=DM时,△ADM为等腰三角形,如图:综上所述,在运动过程中,使得△ADM为等腰三角形的点M一共有4个.∴②不正确;③过点M作ME⊥AB于点E,如图,由题意:AM=AN=t,由①知:∠HAB=60°.在Rt△AME中,∵sin∠MAE=,∴ME=AM•sin60°=tcm,∴S=AN×ME=cm2.∴③正确;④当t=9+时,CM=cm,如图,由①知:BC=3cm,∴MB=BC﹣CM=2cm.∵AB=6cm,∴tan∠MAB=,∴∠MAB=30°.∵∠HAB=60°,∴∠DAH=90°﹣60°=30°.∴∠DAH=∠BAM.∵∠D=∠B=90°,∴△ADH∽△ABM.∴④正确;⑤当9<t<9+3时,此时点M在边BC上,如图,此时MB=9+3﹣t,∴S=×AB×MB=×6×(9+3﹣t)=27+9﹣3t.∴⑤不正确;综上,结论正确的有:①③④.故选:A.14.(2021•通辽)如图,在矩形ABCD中,AB=4,BC=3,动点P,Q同时从点A出发,点P沿A→B→C的路径运动,点Q沿A→D→C的路径运动,点P,Q的运动速度相同,当点P到达点C时,点Q也随之停止运动,连接PQ.设点P的运动路程为x,PQ2为y,则y关于x的函数图象大致是()A.B.C.D.【答案】C【解答】解:当0≤x≤3时,在Rt△APQ中,∠QAP=90°,AP=AQ=x,∴PQ2=2x2.∴y=PQ2=2x2;当3≤x≤4时,DQ=x﹣3,AP=x,∴y=PQ2=32+32=18;当4≤x≤7时,CP=7﹣x,CQ=7﹣x,∴y=PQ2=CP2+CQ2=2x2﹣28x+98.故选:C.15.(2021•湖北)如图,AC为矩形ABCD的对角线,已知AD=3,CD=4,点P沿折线C﹣A﹣D以每秒1个单位长度的速度运动(运动到D点停止),过点P作PE⊥BC于点E,则△CPE的面积y与点P运动的路程x间的函数图象大致是()A.B.C.D.【答案】D【解答】解:∵BC∥AD,∴∠ACB=∠DAC,∵∠PEC=∠D=90°,∴△PCE∽△CAD,∴==,∵AD=3,CD=4,∴AC==5,∴当P在CA上时,即当0<x≤5时,PE==x,CE==x,∴y=PE•CE==x2,当P在AD上运动时,即当5<x≤8时,PE=CD=4,CE=8﹣x,∴y=PE•CE=×4×(8﹣x)=16﹣2x,综上,当0<x≤5时,函数图象为二次函数图象,且y随x增大而增大,当5<x≤8时,函数图象为一次函数图象,且y随x增大而减小,故选:D.16.(2021•衡阳)如图1,菱形ABCD的对角线AC与BD相交于点O,P、Q 两点同时从O点出发,以1厘米/秒的速度在菱形的对角线及边上运动.点P 的运动路线为O﹣A﹣D﹣O,点Q的运动路线为O﹣C﹣B﹣O.设运动的时间为x秒,P、Q间的距离为y厘米,y与x的函数关系的图象大致如图2所示,当点P在A﹣D段上运动且P、Q两点间的距离最短时,P、Q两点的运动路程之和为厘米.【答案】(2+3)【解答】解:由图分析易知:当点P从O→A运动时,点Q从O→C运动时,y不断增大,当点P运动到A点,点Q运动到C点时,由图象知此时y=PQ=2cm,∴AC=2cm,∵四边形ABCD为菱形,∴AC⊥BD,OA=OC==cm,当点P运动到D点,Q运动到B点,结合图象,易知此时,y=BD=2cm,∴OD=OB=BD=1cm,在Rt△ADO中,AD===2(cm),∴AD=AB=BC=DC=2cm,如图,当点P在A﹣D段上运动,点P运动到点E处,点Q在C﹣B段上运动,点Q运动到点F处时,P、Q两点的距离最短,此时,OE=OF==,AE=CF===,∴当点P在A﹣D段上运动且P、Q两点间的距离最短时,P、Q两点的运动路程之和为:(cm),故答案为:(2+3).17.(2021•武汉)如图(1),在△ABC中,AB=AC,∠BAC=90°,边AB上的点D从顶点A出发,向顶点B运动,同时,边BC上的点E从顶点B出发,向顶点C运动,D,E两点运动速度的大小相等,设x=AD,y=AE+CD,y 关于x的函数图象如图(2),图象过点(0,2),则图象最低点的横坐标是.【答案】﹣1【解答】解:∵图象过点(0,2),即当x=AD=BE=0时,点D与A重合,点E与B重合,此时y=AE+CD=AB+AC=2,∵△ABC为等腰直角三角形,∴AB=AC=1,过点A作AF⊥BC于点F,过点B作NB⊥BC,并使得BN=AC,如图所示:∵AD=BE,∠NBE=∠CAD,∴△NBE≌△CAD(SAS),∴NE=CD,又∵y=AE+CD,∴y=AE+CD=AE+NE,当A、E、N三点共线时,y取得最小值,如图所示,此时:AD=BE=x,AC=BN=1,∴AF=AC•sin45°=,\又∵∠BEN=∠FEA,∠=∠AFE∴△NBE∽△AFE∴,即,解得:x=,∴图象最低点的横坐标为:﹣1.故答案为:.18.(2022•营口)如图1,在四边形ABCD中,BC∥AD,∠D=90°,∠A=45°,动点P,Q同时从点A出发,点P以cm/s的速度沿AB向点B运动(运动到B点即停止),点Q以2cm/s的速度沿折线AD→DC向终点C运动,设点Q的运动时间为x(s),△APQ的面积为y(cm2),若y与x之间的函数关系的图象如图2所示,当x=(s)时,则y=cm2.【答案】【解答】解:过点D作DE⊥AB,垂足为E,在Rt△ADE中,∵∠AED=90°,∠EAD=45°,∴,∵点P的速度为cm/s,点Q的速度为2cm/s,∴AP=x,AQ=2x,∴,在△APQ和△AED中,=,∠A=45°,∴△AED∽△APQ,∴点Q在AD上运动时,△APQ为等腰直角三角形,∴AP=PQ=x,∴当点Q在AD上运动时,y=AP•AQ=×x×x=x2,由图像可知,当y=9此时面积最大,x=3或﹣3(负值舍去),∴AD=2x=6cm,当3<x≤4时,过点P作PF⊥AD于点F,如图:此时S△APQ=S△APF+S四边形PQDF﹣S△ADQ,在Rt△APF中,AP=x,∠PAF=45°,∴AF=PF=x,FD=6﹣x,QD=2x﹣6,∴S△APQ=x2+(x+2x﹣6)•(6﹣x)﹣×6×(2x﹣6),即y=﹣x2+6x,当x=时,y=﹣()2+6×=,故答案为:.。
九年级中考 专题01 动点与分段函数解析式题型讲义(教师版)

动点与分段函数解析式一、典例解析例1.【2020·辽宁本溪】如图,在Rt △ABC 中,∠ACB =90°,AC =BC =2√2,CD ⊥AB 于点D .点P 从点A 出发,沿A →D →C 的路径运动,运动到点C 停止,过点P 作PE ⊥AC 于点E ,作PF ⊥BC 于点F .设点P 运动的路程为x ,四边形CEPF 的面积为y ,则能反映y 与x 之间函数关系的图象是( )A .B .C .D .【答案】A. 【解析】解:当点P 在AD 上运动时,0≤x ≤2时,y=PE ·CE=2x ·(2x )=2x -12x 2, 当点P 在DC 上运动时,2<x ≤4时,S= PE ·4-x )(4-x )=12(x -4)2,结合函数解析式判断选项A 符合要求. 故答案为:A.例2. 【2020·山东淄博】如图1,点P 从△ABC 的顶点B 出发,沿B →C →A 匀速运动到点A ,图2是点P 运动时,线段BP 的长度y 随时间x 变化的关系图象,其中M 是曲线部分的最低点,则△ABC 的面积是( )A.12B.24C.36D.48【答案】D.【解析】解:由图2知,AB=BC=10,当BP⊥AC时,y的值最小,即△ABC中,BC边上的高为8(即此时BP=8),当y=8时,PC=√BC2−BP2=√102−82=6,△ABC的面积=12×AC×BP=12×8×12=48,故答案为:D.例3. 【2020·辽阳】如图,在Rt△ABC中,∠ACB=90°,AC=BC=2√2,CD⊥AB于点D.点P从点A 出发,沿A→D→C的路径运动,运动到点C停止,过点P作PE⊥AC于点E,作PF⊥BC于点F.设点P 运动的路程为x,四边形CEPF的面积为y,则能反映y与x之间函数关系的图象是()A.B.C.D.【答案】A.【解析】解:∵在Rt△ABC中,∠ACB=90°,AC=BC=2√2,∴AB=4,∠A=45°,∵CD⊥AB于点D,∴AD=BD=2,∵PE⊥AC,PF⊥BC,∴四边形CEPF是矩形,∴CE=PF,PE=CF,∵点P运动的路程为x,∴AP=x,则AE=PE=x•sin45°=√22x,∴CE=AC﹣AE=2√2−√22x,∵四边形CEPF的面积为y,∴当点P从点A出发,沿A→D路径运动时,即0<x<2时,y=PE•CE=√22x(2√2−√22x)=−12(x﹣2)2+2,∴当0<x<2时,抛物线开口向下;当点P沿D→C路径运动时,即2≤x<4时,∵CD是∠ACB的平分线,∴PE=PF,∴四边形CEPF是正方形,∵AD=2,PD=x﹣2,∴CP=4﹣x,y=12(4﹣x)2=12(x﹣4)2.∴当2≤x<4时,抛物线开口向上,综上所述:能反映y与x之间函数关系的图象是:A.故答案为:A.例4. 【2020·上海】小明从家步行到学校需走的路程为1800米,图中的折线反映了小明从家步行到学校所走的路程s (米)与时间t (分钟)的函数关系,根据图像提供的信息,当小明从家出发去学校步行15 分钟时,到学校还需步行 米.【答案】350.【解析】解:由题意知:线段AB 的解析式为:S=70t+400(8≤t≤20)当t=15时,S=1450,还需要步行1800-1450=350米.故答案为:350.例5. 【2020·重庆A 卷】A ,B 两地相距240 km ,甲货车从A 地以40km/h 的速度匀速前往B 地,到达B 地后停止,在甲出发的同时,乙货车从B 地沿同一公路匀速前往A 地,到达A 地后停止,两车之间的路程y (km )与甲货车出发时间x (h )之间的函数关系如图中的折线CD DE EF --所示.其中点C 的坐标是()0240,,点D 的坐标是()2.40,,则点E 的坐标是 .【答案】(4,160).【解析】解: 由题意知,乙车的速度为:240÷2.4-40=60 km/h ,乙车从B 到A 需要的时间为:240÷60= 4 h ,当乙车到达A 地时,甲车行驶的路程为:40×4=160 km ,点E 坐标为(4,160)故答案为(4,160).例6.【2020·北京】有一个装有水的容器,如图所示,容器内的水面高度是10cm ,现向容器内注水,并同时开始计时,在注水过程中,水面高度以每秒0.2cm 的速度匀速增加,则容器注满水之前,容器内的水面高度与对应的注水时间满足的函数关系是( )A.正比例函数关系B.一次函数关系C.二次函数关系D.反比例函数关系【答案】B.【解析】解:设容器内的水面高度为h,注水时间为t,根据题意得:h=0.2t+10,∴容器注满水之前,容器内的水面高度与对应的注水时间满足的函数关系是一次函数关系.故答案为:B.二、刻意练习1.【2020·湖北恩施州】甲乙两车从A城出发前往B城,在整个行程中,汽车离开A城的距离y与时刻t的对应关系如图所示,则下列结论错误的是()A.甲车的平均速度为60km/h B.乙车的平均速度为100km/hC.乙车比甲车先到B城D.乙车比甲车先出发1h【答案】D.【解析】解:由图象知:A.甲车的平均速度为30010−5=60km/h,故A选项不合题意;B.乙车的平均速度为3009−6=100km/h,故B选项不合题意;C.甲10时到达B城,乙9时到达B城,所以乙比甲先到B城,故C选项不合题意;D.甲5时出发,乙6时出发,所以乙比甲晚出发1h,故此选项错误,故答案为:D .2.【2020·湖北武汉】一个容器有进水管和出水管,每分钟的进水量和出水量是两个常数.从某时刻开始4min 内只进水不出水,从第4min 到第24min 内既进水又出水,从第24min 开始只出水不进水,容器内水量y (单位:L )与时间x (单位:min )之间的关系如图所示,则图中a 的值是( )A .32B .34C .36D .38【答案】C. 【解析】解:由图象可知,进水的速度为:20÷4=5(L /min ),出水的速度为:5﹣(35﹣20)÷(16﹣4)=3.75(L /min ),第24分钟时的水量为:20+(5﹣3.75)×(24﹣4)=45(L ),a =24+45÷3.75=36.故答案为:C .3.【2020·江苏连云港】快车从甲地驶往乙地,慢车从乙地驶往甲地,两车同时出发并且在同一条公路上匀速行驶.图中折线表示快、慢两车之间的路程与它们的行驶时间之间的函数关系.小欣同学结合图象得出如下结论:①快车途中停留了;②快车速度比慢车速度多;③图中;④快车先到达目的地. 其中正确的是A .①③B .②③C .②④D .①④【答案】B.【解析】解:根据题意可知,两车的速度和为:,()y km ()x h 0.5h 20/km h 340a =()3602180(/)km h ÷=相遇后慢车停留了,快车停留了,此时两车距离为,故①结论错误;慢车的速度为:,则快车的速度为,所以快车速度比慢车速度多;故②结论正确;,所以图中,故③结论正确;,,所以慢车先到达目的地,故④结论错误.所以正确的是②③.故答案为:B .4.【2020·重庆B 】周末,自行车骑行爱好者甲、乙两人相约沿同一路线从A 地出发前往B 地进行骑行训练,甲、乙分别以不同的速度匀速骑行,乙比甲早出发5分钟.乙骑行25分钟后,甲以原速的85继续骑行,经过一段时间,甲先到达B 地,乙一直保持原速前往B 地.在此过程中,甲、乙两人相距的路程y (单位:米)与乙骑行的时间x (单位:分钟)之间的关系如图所示,则乙比甲晚 分钟到达B 地.【答案】12.【解析】解:由题意乙的速度为1500÷5=300(米/分),设甲的速度为x 米/分.则有:7500﹣20x =2500,解得x =250,25分钟后甲的速度为250×85=400(米/分).由题意总里程=250×20+61×400=29400(米),86分钟乙的路程为86×300=25800(米),∴29400−25800300=12(分钟).故答案为:12.0.5h 1.6h 88km 88(3.6 2.5)80(/)km h ÷-=100/km h 20/km h 88180(5 3.6)340()km +⨯-=340a =(360280)80 2.5()h -⨯÷=5 2.5 2.5()h -=5.【2020·浙江台州】如图1,小球从左侧的斜坡滚下,到达底端后又沿着右侧斜坡向上滚,在这个过程中,小球的运动速度v(m/s)与运动时间t(s)的函数图象如图2,则该小球的运动路程y(m)与运动时间t 之间的函数图象大致是()图1 图2A B C D【答案】C.【解析】解:由图2知,小球的是先匀加速再匀减速运动,选项C符合题意.6.【2020·贵州铜仁】如图,在矩形ABCD中,AB=3,BC=4,动点P沿折线BCD从点B开始运动到点D,设点P运动的路程为x,△ADP的面积为y,那么y与x之间的函数关系的图象大致是()A.B.C.D.【答案】D.【解析】解:由题意,当0≤x ≤4时,y =12×AD ×AB =12×3×4=6,当4<x <7时,y =12×PD ×AD =12×(7﹣x )×4=14﹣2x .故答案为:D .7.【2020·安徽】如图,△ABC 和△DEF 都是边长为2的等边三角形,它们的边BC ,EF 在同一条直线l 上,点C ,E 重合,现将△ABC 沿着直线l 向右移动,直至点B 与F 重合时停止移动. 在此过程中,设点C 移动的距离为x ,两个三角形重叠部分的面积为y ,则y 随x 变化的函数图象大致为( )【答案】A.【解析】解:当0≤x ≤2时,重叠部分为边长为x 的等边三角形,y=2 当2<x ≤4时,重叠部分为边长为(4-x )的等边三角形,y=)24x - 故答案为:A.8.【2020·甘肃金昌】如图①,正方形ABCD中,AC,BD相交于点O,E是OD的中点.动点P从点E出发,沿着E→O→B→A的路径以每秒1个单位长度的速度运动到点A,在此过程中线段AP的长度y随着运动时间x的函数关系如图②所示,则AB的长为()A.4√2B.4C.3√3D.2√2【答案】A.【解析】解:如图,连接AE.∵四边形ABCD是正方形,∴AC⊥BD,OA=OC=OD=OB,由题意DE=OE,设DE=OE=x,则OA=OD=2x,∵AE=2√5,∴x2+(2x)2=(2√5)2,解得x=2或﹣2(不合题意舍弃),∴OA=OD=4,∴AB=AD=4√2,故答案为:A.9.【2020·黑龙江大兴安岭】李强同学去登山,先匀速登上山顶,原地休息一段时间后,又匀速下山,上山的速度小于下山的速度.在登山过程中,他行走的路程S随时间t的变化规律的大致图象是()A.B.C.D.【答案】B.【解析】解:因为登山过程可知:先匀速登上山顶,原地休息一段时间后,又匀速下山,上山的速度小于下山的速度.所以在登山过程中,他行走的路程S随时间t的变化规律的大致图象是B.故答案为:B.10.【2020·湖北黄冈】2020年初以来,红星消毒液公司生产的消毒液在库存量为m吨的情况下,日销售量与产量持平.自1月底抗击“新冠病毒”以来,消毒液需求量猛增,该厂在生产能力不变的情况下,消毒液一度脱销,下面表示2020年初至脱销期间,该厂库存量y(吨)与时间t(天)之间函数关系的大致图象是()A.B.C.D.【答案】D.【解析】解:根据题意:时间t与库存量y之间函数关系的图象为先平,再逐渐减小,最后为0.故答案为:D.11.【2020·湖北随州】小明从家出发步行至学校,停留一段时间后乘车返回,则下列函数图象最能体现他离家的距离(s)与出发时间(t)之间的对应关系的是()A.B.C.D.【答案】B.【解析】解:①从家出发步行至学校时,为一次函数图象,是一条从原点开始的线段;②停留一段时间时,离家的距离不变,③乘车返回时,离家的距离减小至零,纵观各选项,只有B选项符合.故答案为:B.12.【2020·湖北孝感】如图,在四边形ABCD中,AD∥BC,∠D=90°,AB=4,BC=6,∠BAD=30°.动点P沿路径A→B→C→D从点A出发,以每秒1个单位长度的速度向点D运动.过点P作PH⊥AD,垂足为H.设点P运动的时间为x(单位:s),△APH的面积为y,则y关于x的函数图象大致是()A.B.C.D.【答案】D.【解析】解:①当点P在AB上运动时,y=12AH×PH=12×AP sin A×AP cos A=12×x2×√34=√38x2,图象为二次函数;②当点P在BC上运动时,如下图,由①知,BH′=AB sin A=4×12=2,同理AH′=2√3,则y=12×AH×PH=12(2√3+x﹣4)×2=2√3−4+x,为一次函数;③当点P在CD上运动时,同理可得:y=12×(2√3+6)×(4+6+2﹣x)=(3+√3)(12﹣x),为一次函数;故答案为:D.13.【2020·湖南衡阳】如图1,在平面直角坐标系中,▱ABCD在第一象限,且BC∥x轴.直线y=x从原点O出发沿x轴正方向平移,在平移过程中,直线被▱ABCD截得的线段长度n与直线在x轴上平移的距离m的函数图象如图2所示.那么四边形ABCD的面积为()A.3B.3√2C.6D.6√2【答案】B.【解析】解:过B作BM⊥AD于点M,分别过B,D作直线y=x的平行线,交AD于E,AE =6﹣4=2,DE =7﹣6=1,BE =2,∴AB =2+1=3,∵直线BE 平行直线y =x ,∴BM =EM =√2, ∴平行四边形ABCD 的面积是:AD •BM =3×√2=3√2.故答案为:B .14.【2020·内蒙古通辽】如图①,在△ABC 中,AB =AC ,∠BAC =120°,点E 是边AB 的中点,点P 是边BC 上一动点,设PC =x ,P A +PE =y .图②是y 关于x 的函数图象,其中H 是图象上的最低点.那么a +b 的值为 .【答案】7.【解析】解:将△ABC 沿BC 折叠得到△A ′BC ,则四边形ABA ′C 为菱形,菱形的对角线交于点O ,由图②知,当点P 与点B 重合时,y =P A +PE =AB +BE =AB +12AB =3√3,解得:AB =2√3,即:菱形的边长为2√3,则该菱形的高为√32AB =3, 点A 关于BC 的对称点为点A ′,连接A ′E 交BC 于点P ,此时y 最小,∵AB =AC ,∠BAC =120°,则∠BAA ′=60°,故AA ′B 为等边三角形,∵E 是AB 的中点,故A ′E ⊥AB ,而AB ∥A ′C ,故∠P A ′C 为直角,A ′C =AB =2√3,则PC =A′C cos∠BCA′=√3√32=4, 此时b =PC ,a =A ′E =3(菱形的高),则a +b =3+4=7.故答案为7.15.【2020·青海】将一盛有部分水的圆柱形小水杯放入事先没有水的大圆柱形容器内,现用一个注水管沿大容器内壁匀速注水,如图所示,则小水杯水面的高度h (cm )与注水时间t (min )的函数图象大致为图中的( )A .B .C .D .【答案】B. 【解析】解:将一盛有部分水的圆柱形小玻璃杯放入事先没有水的大圆柱形容器内,小玻璃杯内的水原来的高度一定大于0,则可以判断A 、D 一定错误;用一注水管沿大容器内壁匀速注水,水开始时不会流入小玻璃杯,因而这段时间h 不变,当大杯中的水面与小杯水平时,开始向小杯中流水,h 随t 的增大而增大,当水注满小杯后,小杯内水面的高度h 不再变化. 故答案为:B .16.【2020·四川攀枝花】甲、乙两地之间是一条直路,在全民健身活动中,赵明阳跑步从甲地往乙地,王浩月骑自行车从乙地往甲地,两人同时出发,王浩月先到达目的地,两人之间的距离与运动时间的函数关系大致如图所示,下列说法中错误的是( )()s km ()t hA .两人出发1小时后相遇B .赵明阳跑步的速度为C .王浩月到达目的地时两人相距D .王浩月比赵明阳提前到目的地 【答案】C.【解析】解:由图象可知,两人出发1小时后相遇,故答案为项A 正确;赵明阳跑步的速度为,故答案为项B 正确; 王皓月的速度为:,王皓月从开始到到达目的地用的时间为:,故王浩月到达目的地时两人相距,故答案为项C 错误; 王浩月比赵明阳提前到目的地,故答案为项D 正确; 故答案为:C .8/km h 10km 1.5h 2438(/)km h ÷=241816(/)km h ÷-=2416 1.5()h ÷=8 1.512()km ⨯=3 1.5 1.5h -=。
函数图像--2019中考真题汇编
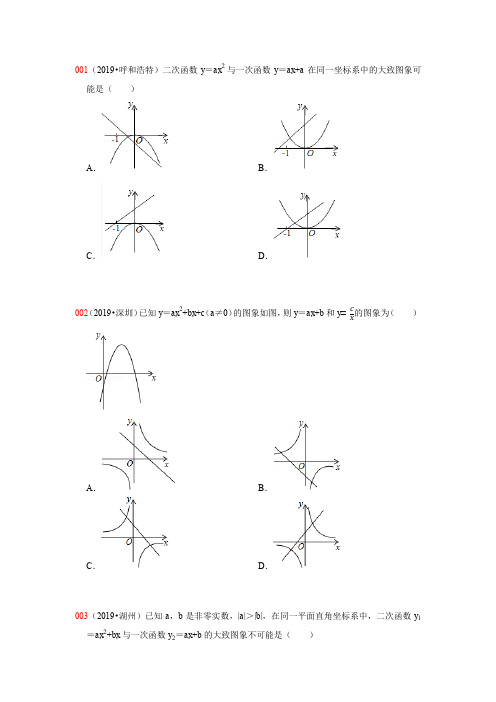
001(2019•呼和浩特)二次函数y=ax2与一次函数y=ax+a在同一坐标系中的大致图象可能是()A.B.C.D.002(2019•深圳)已知y=ax2+bx+c(a≠0)的图象如图,则y=ax+b和y的图象为()A.B.C.D.003(2019•湖州)已知a,b是非零实数,|a|>|b|,在同一平面直角坐标系中,二次函数y1=ax2+bx与一次函数y2=ax+b的大致图象不可能是()A.B.C.D.004(2019•德州)若函数y与y=ax2+bx+c的图象如图所示,则函数y=kx+b的大致图象为()A.B.C.D.005(2019•青岛)已知反比例函数y的图象如图所示,则二次函数y=ax2﹣2x和一次函数y=bx+a在同一平面直角坐标系中的图象可能是()A.B.C.D.006(2019•攀枝花)在同一坐标系中,二次函数y=ax2+bx与一次函数y=bx﹣a的图象可能是()A.B.C.D.007(2019•自贡)一次函数y=ax+b与反比列函数y的图象如图所示,则二次函数y=ax2+bx+c的大致图象是()A.B.C.D.008(2019•宁夏)函数y和y=kx+2(k≠0)在同一直角坐标系中的大致图象是()A.B.C.D.009(2019•通辽)关于x、y的二元一次方程组的解满足x<y,则直线y=kx﹣k﹣1与双曲线y在同一平面直角坐标系中大致图象是()A.B.C.D.010(2019•贺州)已知ab<0,一次函数y=ax﹣b与反比例函数y在同一直角坐标系中的图象可能()A.B.C.D.011(2019•鄂州)在同一平面直角坐标系中,函数y=﹣x+k与y(k为常数,且k≠0)的图象大致是()A.B.C.D.012(2019•大庆)正比例函数y=kx(k≠0)的函数值y随着x增大而减小,则一次函数y =x+k的图象大致是()A.B.C.D.013(2019•辽阳)若ab<0且a>b,则函数y=ax+b的图象可能是()A.B.C.D.014(2019浙江杭州)(2019•杭州)已知一次函数y1=ax+b和y2=bx+a(a≠b),函数y1和y2的图象可能是()A.B.C.D.015(2019•河池)如图,抛物线y=ax2+bx+c的对称轴为直线x=1,则下列结论中,错误的是()A.ac<0 B.b2﹣4ac>0 C.2a﹣b=0 D.a﹣b+c=0016(2019•梧州)已知m>0,关于x的一元二次方程(x+1)(x﹣2)﹣m=0的解为x1,x2(x1<x2),则下列结论正确的是()A.x1<﹣1<2<x2B.﹣1<x1<2<x2C.﹣1<x1<x2<2 D.x1<﹣1<x2<2017(2019•沈阳)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论正确的是()A.abc<0 B.b2﹣4ac<0 C.a﹣b+c<0 D.2a+b=0018(2019•临沂)从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.下列结论:①小球在空中经过的路程是40m;②小球抛出3秒后,速度越来越快;③小球抛出3秒时速度为0;④小球的高度h=30m时,t=1.5s.其中正确的是()A.①④B.①②C.②③④D.②③019(2019•成都)如图,二次函数y=ax2+bx+c的图象经过点A(1,0),B(5,0),下列说法正确的是()A.c<0B.b2﹣4ac<0C.a﹣b+c<0D.图象的对称轴是直线x=3020(2019•广元)如图,抛物线y=ax2+bx+c(a≠0)过点(﹣1,0),(0,2),且顶点在第一象限,设M=4a+2b+c,则M的取值范围是.021二次函数y=x2﹣ax+b的图象如图所示,对称轴为直线x=2,下列结论不正确的是()A.a=4B.当b=﹣4时,顶点的坐标为(2,﹣8)C.当x=﹣1时,b>﹣5D.当x>3时,y随x的增大而增大022(2019•资阳)如图是函数y=x2﹣2x﹣3(0≤x≤4)的图象,直线l∥x轴且过点(0,m),将该函数在直线l上方的图象沿直线l向下翻折,在直线1下方的图象保持不变,得到一个新图象.若新图象对应的函数的最大值与最小值之差不大于5,则m的取值范围是()A.m≥1 B.m≤0 C.0≤m≤1 D.m≥1或m≤0。
2019年中考真题几何最值分类汇编(PDF版含解析)

(2)设 AD 的中点为 M,连接 OM、MC,当四边形 OMCD 的面积为 时,求 OA 的长;
2
(3)当点 A 移动到某一位置时,点 C 到点 O 的距离有最大值,请直接写出最大值,并求此时 cos∠OAD 的值.
第 26 题图
第 26 题备用图
【解题过程】(1)如图 1,过点 C 作 CE⊥y 轴,垂足为 E.
(3)过点 P 作 PG∥CQ 交 AC 于点 G,则△APG 是等边三角形.∵BP⊥PQ,∴EG= 1 AG.∵PG∥CQ,∴∠ 2
PGD=∠QCD,∵∠PDG=∠QDC,PG=PA=CG=t,∴△PGD≌△QCD.∴GD= 1 GC.∴DE= 1 AC=3.
2
2
(4)连接 AM,∵△ABC 为等边三角形,点 M 是 BC 的中点,∴BM=3.由勾股定理,得 AM=3 3 . 由折叠,
∴OD= 1 AD=3.∴点 C 的坐标为(2, 3 2 3 ). 2
(2)∵M 为 AD 的中点,
∴DM=3, S△DCM
6 .又∵ S四边形OMCD
21 2
,∴
S△ODM
9 2
,∴
Sห้องสมุดไป่ตู้OAD
9.
设
OA=x,OD=y,则
x
2
1 2
xy
y2 9
36
,∴
x2
y2
7
2019 中考试题分类汇编
以同样的速度沿 BC 延长线方向匀速运动.当点 P 到达点 B 时,点 P、Q 同时停止运动.设运动时间为 t(s).过 点 P 作 PE⊥AC 于 E,连接 PQ 交 AC 边于 D.以 CQ、CE 为边作平行四边形 CQFE. (1)当 t 为何值时,△BPQ 为直角三角形; (2)是否存在某一时刻 t,使点 F 在∠ABC 的平分线上?若存在,求出 t 的值,若不存在,请说明理由;
函数图像--2019中考真题汇编(教师版)
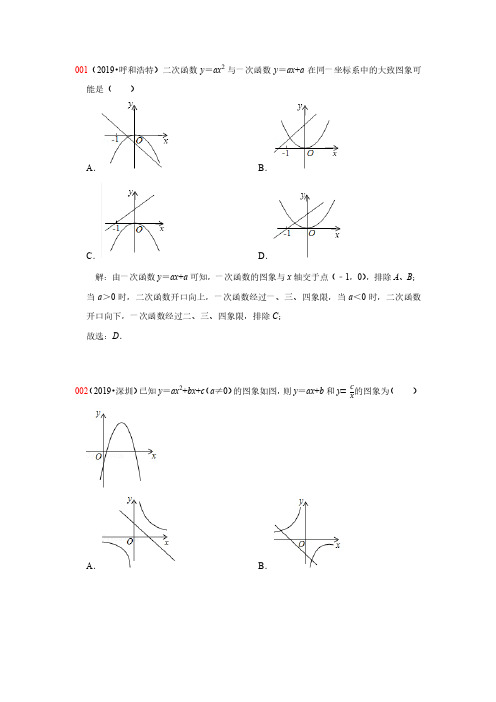
001(2019•呼和浩特)二次函数y=ax2与一次函数y=ax+a在同一坐标系中的大致图象可能是()A.B.C.D.解:由一次函数y=ax+a可知,一次函数的图象与x轴交于点(﹣1,0),排除A、B;当a>0时,二次函数开口向上,一次函数经过一、三、四象限,当a<0时,二次函数开口向下,一次函数经过二、三、四象限,排除C;故选:D.002(2019•深圳)已知y=ax2+bx+c(a≠0)的图象如图,则y=ax+b和y=c的图象为()xA.B.C .D .解:根据二次函数y =ax 2+bx +c (a ≠0)的图象, 可得a <0,b >0,c <0, ∴y =ax +b 过一、二、四象限, 双曲线y =cx 在二、四象限, ∴C 是正确的. 故选:C .003(2019•湖州)已知a ,b 是非零实数,|a |>|b |,在同一平面直角坐标系中,二次函数y 1=ax 2+bx 与一次函数y 2=ax +b 的大致图象不可能是( )A .B .C .D .解:{y =ax 2+bx y =ax +b 解得{x =−ba y =0或{x =1y =a +b .故二次函数y =ax 2+bx 与一次函数y =ax +b (a ≠0)在同一平面直角坐标系中的交点在x 轴上为(−ba ,0)或点(1,a +b ).在A 中,由一次函数图象可知a >0,b >0,二次函数图象可知,a >0,b >0,−ba <0,a +b >0,故选项A 错误;在B中,由一次函数图象可知a>0,b<0,二次函数图象可知,a>0,b<0,由|a|>|b|,则a+b>0,故选项B错误;在C中,由一次函数图象可知a<0,b<0,二次函数图象可知,a<0,b<0,a+b<0,故选项C错误;在D中,由一次函数图象可知a<0,b>0,二次函数图象可知,a<0,b>0,由|a|>|b|,则a+b<0,故选项D正确;故选:D.004(2019•德州)若函数y=k与y=ax2+bx+c的图象如图所示,则函数y=kx+b的大致图象x为()A.B.C.D.解:根据反比例函数的图象位于二、四象限知k<0,根据二次函数的图象确知a>0,b<0,∴函数y=kx+b的大致图象经过二、三、四象限,故选:C.005(2019•青岛)已知反比例函数y=ab的图象如图所示,则二次函数y=ax2﹣2x和一次函x数y=bx+a在同一平面直角坐标系中的图象可能是()A.B.C.D.解:∵当x=0时,y=ax2﹣2x=0,即抛物线y=ax2﹣2x经过原点,故A错误;∵反比例函数y=abx的图象在第一、三象限,∴ab>0,即a、b同号,当a<0时,抛物线y=ax2﹣2x的对称轴x=1a<0,对称轴在y轴左边,故D错误;当a>0时,b>0,直线y=bx+a经过第一、二、三象限,故B错误,C正确.故选:C.006(2019•攀枝花)在同一坐标系中,二次函数y=ax2+bx与一次函数y=bx﹣a的图象可能是()A.B.C.D.解:由方程组{y =ax 2+bxy =bx −a 得ax 2=﹣a ,∵a ≠0∴x 2=﹣1,该方程无实数根,故二次函数与一次函数图象无交点,排除B .A :二次函数开口向上,说明a >0,对称轴在y 轴右侧,则b <0;但是一次函数b 为一次项系数,图象显示从左向右上升,b >0,两者矛盾,故A 错;C :二次函数开口向上,说明a >0,对称轴在y 轴右侧,则b <0;b 为一次函数的一次项系数,图象显示从左向右下降,b <0,两者相符,故C 正确;D :二次函数的图象应过原点,此选项不符,故D 错. 故选:C .007(2019•自贡)一次函数y =ax +b 与反比列函数y =c x的图象如图所示,则二次函数y =ax 2+bx +c 的大致图象是( )A .B .C .D .解:∵一次函数y 1=ax +b 图象过第一、二、四象限, ∴a <0,b >0, ∴−b2a >0,∴二次函数y 3=ax 2+bx +c 开口向下,二次函数y 3=ax 2+bx +c 对称轴在y 轴右侧; ∵反比例函数y 2=cx 的图象在第一、三象限, ∴c >0,∴与y 轴交点在x 轴上方.满足上述条件的函数图象只有选项A . 故选:A .008(2019•宁夏)函数y =kx 和y =kx +2(k ≠0)在同一直角坐标系中的大致图象是( )A .B .C .D .解:在函数y =k x和y =kx +2(k ≠0)中,当k >0时,函数y =k x的图象在第一、三象限,函数y =kx +2的图象在第一、二、三象限,故选项A 、D 错误,选项B 正确,当k <0时,函数y =k x 的图象在第二、四象限,函数y =kx +2的图象在第一、二、四象限,故选项C 错误, 故选:B .009(2019•通辽)关于x 、y 的二元一次方程组{x −2y =k 2x −3y =−4k 的解满足x <y ,则直线y =kx ﹣k ﹣1与双曲线y =k x 在同一平面直角坐标系中大致图象是( )A .B .C .D .解:二元一次方程组{x −2y =k2x −3y =−4k 中第二个方程减去第一个方程得:x ﹣y =﹣5k ,∵关于x 、y 的二元一次方程组{x −2y =k2x −3y =−4k 的解满足x <y ,∴x ﹣y <0, ∴﹣5k <0, 即:k >0,∴y =kx ﹣k ﹣1经过一三四象限,双曲线y =kx 的两个分支位于一三象限,B 选项符合, 故选:B .010(2019•贺州)已知ab <0,一次函数y =ax ﹣b 与反比例函数y =ax 在同一直角坐标系中的图象可能( )A .B .C .D .解:若反比例函数y=ax经过第一、三象限,则a>0.所以b<0.则一次函数y=ax﹣b的图象应该经过第一、二、三象限;若反比例函数y=ax经过第二、四象限,则a<0.所以b>0.则一次函数y=ax﹣b的图象应该经过第二、三、四象限.故选项A正确;故选:A.011(2019•鄂州)在同一平面直角坐标系中,函数y=﹣x+k与y=kx(k为常数,且k≠0)的图象大致是()A.B.C.D.解:∵函数y=﹣x+k与y=kx(k为常数,且k≠0),∴当k>0时,y=﹣x+k经过第一、二、四象限,y=kx经过第一、三象限,故选项A、B错误,当k<0时,y=﹣x+k经过第二、三、四象限,y=kx经过第二、四象限,故选项C正确,选项D错误,故选:C.012(2019•大庆)正比例函数y=kx(k≠0)的函数值y随着x增大而减小,则一次函数y=x+k的图象大致是()A.B.C.D.解:∵正比例函数y=kx(k≠0)的函数值y随x的增大而减小,∴k<0,∵一次函数y=x+k的一次项系数大于0,常数项小于0,∴一次函数y=x+k的图象经过第一、三象限,且与y轴的负半轴相交.故选:A.013(2019•辽阳)若ab<0且a>b,则函数y=ax+b的图象可能是()A.B.C.D.解:∵ab<0,且a>b,∴a>0,b<0,∴函数y=ax+b的图象经过第一、三、四象限.故选:A.014(2019浙江杭州)(2019•杭州)已知一次函数y1=ax+b和y2=bx+a(a≠b),函数y1和y2的图象可能是()A.B.C.D.解:A、由①可知:a>0,b>0.∴直线②经过一、二、三象限,故A正确;B、由①可知:a<0,b>0.∴直线②经过一、二、三象限,故B错误;C、由①可知:a<0,b>0.∴直线②经过一、二、四象限,交点不对,故C错误;D、由①可知:a<0,b<0,∴直线②经过二、三、四象限,故D错误.故选:A.015(2019•河池)如图,抛物线y=ax2+bx+c的对称轴为直线x=1,则下列结论中,错误的是()A.ac<0B.b2﹣4ac>0C.2a﹣b=0D.a﹣b+c=0解:A、由抛物线的开口向下知a<0,与y轴的交点在y轴的正半轴上,可得c>0,因此ac<0,故本选项正确,不符合题意;B、由抛物线与x轴有两个交点,可得b2﹣4ac>0,故本选项正确,不符合题意;C、由对称轴为x=−b=1,得2a=﹣b,即2a+b=0,故本选项错误,符合题意;2aD、由对称轴为x=1及抛物线过(3,0),可得抛物线与x轴的另外一个交点是(﹣1,0),所以a﹣b+c=0,故本选项正确,不符合题意.故选:C.016(2019•梧州)已知m>0,关于x的一元二次方程(x+1)(x﹣2)﹣m=0的解为x1,x2(x1<x2),则下列结论正确的是()A.x1<﹣1<2<x2B.﹣1<x1<2<x2C.﹣1<x1<x2<2D.x1<﹣1<x2<2解:关于x的一元二次方程(x+1)(x﹣2)﹣m=0的解为x1,x2,可以看作二次函数m=(x+1)(x﹣2)与x轴交点的横坐标,∵二次函数m=(x+1)(x﹣2)与x轴交点坐标为(﹣1,0),(2,0),如图:当m>0时,就是抛物线位于x轴上方的部分,此时x<﹣1,或x>2;又∵x1<x2∴x1=﹣1,x2=2;∴x1<﹣1<2<x2,故选:A.017(2019•沈阳)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论正确的是()A.abc<0B.b2﹣4ac<0C.a﹣b+c<0D.2a+b=0解:由图可知a>0,与y轴的交点c<0,对称轴x=1,∴b=﹣2a<0;∴abc>0,A错误;由图象可知,函数与x轴有两个不同的交点,∴△>0,B错误;当x=﹣1时,y>0,∴a﹣b+c>0,C错误;∵b=﹣2a,D正确;故选:D.018(2019•临沂)从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.下列结论:①小球在空中经过的路程是40m;②小球抛出3秒后,速度越来越快;③小球抛出3秒时速度为0;④小球的高度h=30m时,t=1.5s.其中正确的是()A.①④B.①②C.②③④D.②③解:①由图象知小球在空中达到的最大高度是40m;故①错误;②小球抛出3秒后,速度越来越快;故②正确;③小球抛出3秒时达到最高点即速度为0;故③正确;④设函数解析式为:h=a(t﹣3)2+40,把O(0,0)代入得0=a(0﹣3)2+40,解得a=−409,∴函数解析式为h=−409(t﹣3)2+40,把h=30代入解析式得,30=−409(t﹣3)2+40,解得:t=4.5或t=1.5,∴小球的高度h=30m时,t=1.5s或4.5s,故④错误;故选:D.019(2019•成都)如图,二次函数y=ax2+bx+c的图象经过点A(1,0),B(5,0),下列说法正确的是()A.c<0B.b2﹣4ac<0C.a﹣b+c<0D.图象的对称轴是直线x=3解:A.由于二次函数y=ax2+bx+c的图象与y轴交于正半轴,所以c>0,故A错误;B.二次函数y=ax2+bx+c的图象与x轴由2个交点,所以b2﹣4ac>0,故B错误;C.当x=﹣1时,y<0,即a﹣b+c<0,故C错误;D.因为A(1,0),B(5,0),所以对称轴为直线x=1+52=3,故D正确.故选:D.020(2019•广元)如图,抛物线y=ax2+bx+c(a≠0)过点(﹣1,0),(0,2),且顶点在第一象限,设M=4a+2b+c,则M的取值范围是﹣6<M<6.解:将(﹣1,0)与(0,2)代入y=ax2+bx+c,∴0=a﹣b+c,2=c,∴b=a+2,∵−b2a>0,a<0,∴b>0,∴a>﹣2,∴﹣2<a<0,∴M=4a+2(a+2)+2=6a+6=6(a+1)∴﹣6<M<6,故答案为:﹣6<M<6;021二次函数y=x2﹣ax+b的图象如图所示,对称轴为直线x=2,下列结论不正确的是()A.a=4B.当b=﹣4时,顶点的坐标为(2,﹣8)C.当x=﹣1时,b>﹣5D.当x>3时,y随x的增大而增大解:∵二次函数y=x2﹣ax+b∴对称轴为直线x=a2=2∴a=4,故A选项正确;当b=﹣4时,y=x2﹣4x﹣4=(x﹣2)2﹣8∴顶点的坐标为(2,﹣8),故B选项正确;当x=﹣1时,由图象知此时y<0即1+4+b<0∴b<﹣5,故C选项不正确;∵对称轴为直线x=2且图象开口向上∴当x>3时,y随x的增大而增大,故D选项正确;故选:C.022(2019•资阳)如图是函数y=x2﹣2x﹣3(0≤x≤4)的图象,直线l∥x轴且过点(0,m),将该函数在直线l上方的图象沿直线l向下翻折,在直线1下方的图象保持不变,得到一个新图象.若新图象对应的函数的最大值与最小值之差不大于5,则m的取值范围是()A.m≥1B.m≤0C.0≤m≤1D.m≥1或m≤0解:如图1所示,当t等于0时,∵y=(x﹣1)2﹣4,∴顶点坐标为(1,﹣4),当x=0时,y=﹣3,∴A(0,﹣3),当x=4时,y=5,∴C(4,5),∴当m=0时,D(4,﹣5),∴此时最大值为0,最小值为﹣5;如图2所示,当m=1时,此时最小值为﹣4,最大值为1.综上所述:0≤m≤1,故选:C.。
中考专题08 几何图形初步-2019年中考真题数学试题分项汇编(解析版)
专题08 几何图形初步1.(2019•玉林)若α=29°45′,则α的余角等于A.60°55′B.60°15′C.150°55′D.150°15′【答案】B【解析】∵α=29°45′,∴α的余角等于:90°–29°45′=60°15′.故选B.【名师点睛】本题考查了互为余角的定义:如果两个角的和为90°,那么这两个角互为余角.2.(2019•广西)如图,将下面的平面图形绕直线l旋转一周,得到的立体图形是A.B.C.D.【答案】D【解析】面动成体,直角三角形绕直角边旋转一周可得圆锥,长方形绕一边旋转一周可得圆柱,那么所求的图形是下面是圆锥,上面是圆柱的组合图形.故选D.【名师点睛】此题考查点、线、面、体的问题,解决本题的关键是得到所给出的平面图形是得到几何体的主视图的被纵向分成的一半.3.(2019•深圳)下列哪个图形是正方体的展开图A.B.C.D.【答案】B【解析】根据正方体展开图的特征,选项A、C、D不是正方体展开图;选项B是正方体展开图.故选B.【名师点睛】此题主要考查了正方体的展开图,正方体展开图有11种特征,分四种类型,即:第一种:“1–4–1”结构,即第一行放1个,第二行放4个,第三行放1个;第二种:“2–2–2”结构,即每一行放2个正方形,此种结构只有一种展开图;第三种:“3–3”结构,即每一行放3个正方形,只有一种展开图;第四种:“1–3–2”结构,即第一行放1个正方形,第二行放3个正方形,第三行放2个正方形.4.(2019•山西)某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与“点”字所在面相对面上的汉字是A.青B.春C.梦D.想【答案】B【解析】展开图中“点”与“春”是对面,“亮”与“想”是对面,“青”与“梦”是对面;故选B.【名师点睛】本题考查正方体的展开图;熟练掌握正方体展开图找对面的方法是解题的关键.5.(2019•吉林)曲桥是我国古代经典建筑之一,它的修建增加了游人在桥上行走的路程,有利于游人更好地观赏风光.如图,A、B两地间修建曲桥与修建直的桥相比,增加了桥的长度,其中蕴含的数学道理是A.两点之间,线段最短B.平行于同一条直线的两条直线平行C.垂线段最短D.两点确定一条直线【答案】A【解析】这样做增加了游人在桥上行走的路程,其中蕴含的数学道理是:利用两点之间线段最短,可得出曲折迂回的曲桥增加了游人在桥上行走的路程.故选A.【名师点睛】此题主要考查了两点之间线段最短,正确将实际问题转化为数学知识是解题关键.6.(2019•深圳)如图,已知l1∥AB,AC为角平分线,下列说法错误的是A.∠1=∠4 B.∠1=∠5 C.∠2=∠3 D.∠1=∠3【答案】B【解析】∵l1∥AB,∴∠2=∠4,∠3=∠2,∠5=∠1+∠2,∵AC为角平分线,∴∠1=∠2=∠4=∠3,∠5=2∠1.故选B.【名师点睛】本题考查了平行线的性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.7.(2019•河南)如图,AB∥CD,∠B=75°,∠E=27°,则∠D的度数为A.45°B.48°C.50°D.58°【答案】B【解析】如图,∵AB∥CD,∴∠B=∠1,∵∠1=∠D+∠E,∴∠D=∠B–∠E=75°–27°=48°,故选B.【名师点睛】此题考查平行线的性质,关键是根据平行线的性质解答.8.(2019•海南)如图,直线l1∥l2,点A在直线l1上,以点A为圆心,适当长度为半径画弧,分别交直线l1、l2于B、C两点,连接AC、BC.若∠ABC=70°,则∠1的大小为A.20°B.35°C.40°D.70°【答案】C【解析】∵点A为圆心,适当长度为半径画弧,分别交直线l1、l2于B、C,∴AC=AB,∴∠CBA=∠BCA=70°,∵l1∥l2,∴∠CBA+∠BCA+∠1=180°,∴∠1=180°–70°–70°=40°,故选C.【名师点睛】此题考查平行线的性质,关键是根据平行线的性质解答.9.(2019•河北)下面是投影屏上出示的抢答题,需要回答横线上符号代表的内容则回答正确的是A.◎代表∠FEC B.@代表同位角C.▲代表∠EFC D.※代表AB【答案】C【解析】延长BE交CD于点F,则∠BEC=∠EFC+∠C(三角形的外角等于与它不相邻两个内角之和).又∠BEC=∠B+∠C,得∠B=∠EFC.故AB∥CD(内错角相等,两直线平行).综上可得※代表CD,◎代表∠EFC,▲代表∠EFC,@代表内错角.故选C.【名师点睛】本题考查了平行线的判定,三角形外角的性质,比较简单.10.(2019•新疆)如图,AB∥CD,∠A=50°,则∠1的度数是A.40°B.50°C.130°D.150°【答案】C【解析】如图,∵AB∥CD,∴∠2=∠A=50°,∴∠1=180°–∠2=180°–50°=130°,故选C.【名师点睛】此题考查平行线的性质,关键是根据平行线的性质解答.11.(2019•兰州)如图,直线a,b被直线c所截,a∥b,∠1=80°,则∠2=A.130°B.120°C.110°D.100°【答案】D【解析】如图,∵∠1=80°,∴∠3=80°,∵a∥b,∴∠2+∠3=180°,∴∠2=180°–80°=100°.故选D.【名师点睛】本题考查了平行线的性质,要熟记平行线的有关性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.12.(2019•甘肃)如图,将一块含有30°的直角三角板的顶点放在直尺的一边上,若∠1=48°,那么∠2的度数是A.48°B.78°C.92°D.102°【答案】D【解析】∵将一块含有30°的直角三角板的顶点放在直尺的一边上,∠1=48°,∴∠2=∠3=180°–48°–30°=102°.故选D.【名师点睛】此题主要考查了平行线的性质,正确得出∠3的度数是解题关键.13.(2019•随州)如图,直线l l∥l2,直角三角板的直角顶点C在直线l1上,一锐角顶点B在直线l2上,若∠1=35°,则∠2的度数是A.65°B.55°C.45°D.35°【答案】B【解析】如图,∵∠1+∠3=90°,∠1=35°,∴∠3=55°.又∵直线l l∥l2,∴∠2=∠3=55°.故选B.【名师点睛】本题考查了平行线的性质,余角的定义,熟记性质并准确识图是解题的关键.14.(2019•长沙)如图,平行线AB,CD被直线AE所截,∠1=80°,则∠2的度数是A.80°B.90°C.100°D.110°【答案】C【解析】∵∠1=80°,∴∠3=100°,∵AB∥CD,∴∠2=∠3=100°.故选C.【名师点睛】此题主要考查了平行线的性质以及邻补角的定义,正确掌握平行线的性质是解题关键.15.(2019•常州)如果∠α=35°,那么∠α的余角等于__________°.【答案】55【解析】∵∠α=35°,∴∠α的余角等于90°﹣35°=55°,故答案为:55.【名师点睛】本题考查的两角互余的基本概念,题目属于基础概念题,比较简单.16.(2019•广州)一副三角板如图放置,将三角板ADE绕点A逆时针旋转α(0°<α<90°),使得三角板ADE的一边所在的直线与BC垂直,则α的度数为__________.【答案】【解析】分情况讨论:①当DE⊥BC时,∠BAD=75°,∴α=90°﹣∠BAD=15°;②当AD⊥BC时,∠BAD=45°,即α=45°.故答案为:15°或45°.【名师点睛】本题主要考查了垂直的定义,旋转的定义以及一副三角板的各个角的度数,理清定义是解答本题的关键.17.(2019•吉林)如图,E为△ABC边CA延长线上一点,过点E作ED ∥BC.若∠BAC=70°,∠CED=50°,则∠B=__________°.【答案】60【解析】∵ED∥BC,∴∠CED=∠C=50°,又∵∠BAC=70°,∴△ABC 中,∠B=180°﹣50°﹣70°=60°,故答案为:60.【名师点睛】本题主要考查了平行线的性质和三角形的内角和,解题时注意运用两直线平行,内错角相等.18.(2019•广州)如图,点A,B,C在直线l上,PB⊥l,PA=6cm,PB=5cm,PC=7cm,则点P到直线l的距离是__________cm.【答案】5【解析】∵PB⊥l,PB=5cm,∴点P到直线l的距离是垂线段PB的长度,即为5cm,故答案为:5.【名师点睛】本题考查了点到直线的距离,点到直线的距离是直线外的点到这条直线的垂线段的长度.19.(2019•广东)如图,已知a∥b,∠1=75°,则∠2=__________.【答案】105°【解析】∵直线c与直线a,b相交,且a∥b,∠1=75°,∴∠3=∠1=75°,∴∠2=180°﹣∠3=180°﹣75°=105°.故答案为:105°.【名师点睛】此题考查平行线的性质,解题关键为:两直线平行,同旁内角互补,对顶角相等.20.(2019•南京)结合图,用符号语言表达定理“同旁内角互补,两直线平行”的推理形式:∵__________,∴a∥b.【答案】∠1+∠3=180°【解析】∵∠1+∠3=180°,∴a∥b(同旁内角互补,两直线平行).故答案为:∠1+∠3=180°.【名师点睛】本题主要考查了平行线的判定,两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.21.(2019•青岛)如图,一个正方体由27个大小相同的小立方块搭成,现从中取走若干个小立方块,得到一个新的几何体.若新几何体与原正方体的表面积相等,则最多可以取走__________个小立方块.【答案】16【解析】若新几何体与原正方体的表面积相等,最多可以取走16个小正方体,只需留11个,分别是正中心的3个和四角上各2个,如图所示:故答案为:16.【名师点睛】本题主要考查了几何体的表面积.22.(2019•武汉)如图,点A、B、C、D在一条直线上,CE与BF交于点G,∠A=∠1,CE∥DF,求证:∠E=∠F.【答案】见解析【解析】∵CE∥DF,∴∠ACE=∠D,∵∠A=∠1,∴180°﹣∠ACE﹣∠A=180°﹣∠D﹣∠1,又∵∠E=180°﹣∠ACE﹣∠A,∠F=180°﹣∠D﹣∠1,∴∠E=∠F.【名师点睛】本题考查了平行线的性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.也考查了三角形内角和定理.。
2019年全国中考数学真题汇编-专题08几何图形初步

角的和等于 180°,就说这两个角互为补角.
4.(2019•湖南怀化)与 30°的角互为余角的角的度数是
A.30°
B.60°
C.70°
D.90°
【答案】B
【解析】与 30°的角互为余角的角的度数是:60°.故选 B.
【名师点睛】此题主要考查了互为余角的定义,正确把握互为余角的定义是解题关键.
5.(2019▪贵州毕节)如图,△ABC 中,CD 是 AB 边上的高,CM 是 AB 边上的中线,点 C 到边 AB 所在直线
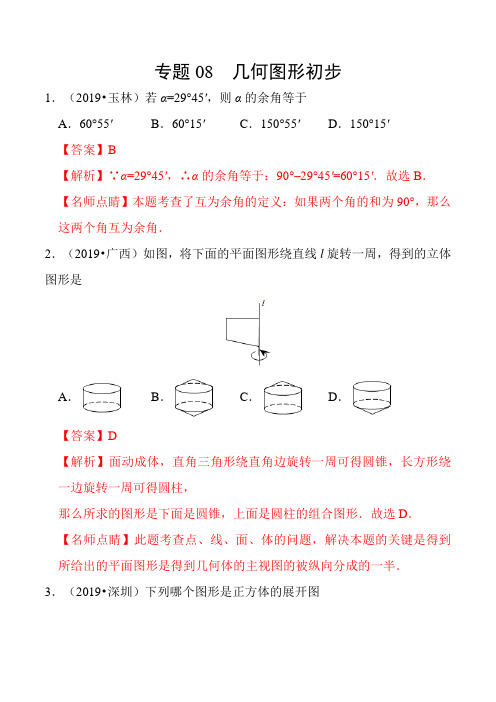
专题 08 几何图形初步
1.(2019•甘肃武威)下列四个几何体中,是三棱柱的为
A.
B.
C.
D.
【答案】C
【解析】A.该几何体为四棱柱,不符合题意;
B.该几何体为四棱锥,不符合题意;
C.该几何体为三棱柱,符合题意;
D.该几何体为圆柱,不符合题意.
故选 C.
【名师点睛】考查了认识立体图形的知识,解题的关键是能够认识各个几何体,难度不大.
A.105°
B.100°
C.75°
D.60°
【答案】A
【解析】由题意知∠E=45°,∠B=30°,
∵DE∥CB,∴∠BCF=∠E=45°,
在△CFB 中,∠BFC=180°﹣∠B﹣∠BCF=180°﹣30°﹣45°=105°,
故选 A.
【名师点睛】本题考查了特殊直角三角形的性质,平行线的性质,三角形内角和定理等,解题关键是
A.45° 【答案】B 【解析】如图,
B.55°
C.65°
D.75°
作 EF∥AB∥CD, ∴∠2=∠AEF=35°,∠1=∠FEC, ∵∠AEC=90°,∴∠1=90°﹣35°=55°, 故选 B. 【名师点睛】此题考查平行线的性质,关键是根据平行线的性质得出∠2=∠AEF=35°,∠1=∠FEC. 18.(2019 湖北仙桃)如图,CD∥AB,点 O 在 AB 上,OE 平分∠BOD,OF⊥OE,∠D=110°,则∠AOF 的 度数是
中考数学专题复习《动点函数图像(面积类)》测试卷-附带答案

中考数学专题复习《动点函数图像(面积类)》测试卷-附带答案学校:___________班级:___________姓名:___________考号:___________一.1.如图,在矩形ABCD中,AB=8cm,AD=6cm.点P从点A出发,以2cm/s的速度在矩形的边上沿A→B→C→D运动,点P与点D重合时停止运动.设运动的时间为t(单位:s),△APD的面积为S(单位:cm2),则S随t变化的函数图象大致为()A. B.C. D.2.如图,矩形ABCD中,AB=8cm,BC=6cm,点P从点A出发,以1cm/s的速度沿A→D→C 方向匀速运动,同时点Q从点A出发,以2cm/s的速度沿A→B→C方向匀速运动,当一个点到达点C时,另一个点也随之停止.设运动时间为t(s),△APQ的面积为S(cm2),下列能大致反映S与t之间函数关系的图象是()A B C D3.如图,在边长为3的菱形ABCD中,点P从A点出发,沿A→B→C→D运动,速度为每秒3个单位;点Q同时从A点出发,沿A→D运动,速度为每秒1个单位,则△APQ的面积S关于时间t的函数图象大致为()A B C D4.如图,Rt△ABC中,∠C=90°,AB=5cm,AC=4cm,点P从点A出发,以1cm/s的速度沿A→C向点C运动,同时点Q从点A出发,以2cm/s的速度沿A→B→C向点C运动,直到它们都到达点C为止.若△APQ的面积为S(cm2),点P的运动时间为t(s),则S与t的函数图象是()A B C D5.在边长为2的正方形ABCD中,对角线AC与BD相交于点O,P是BD上一动点,过P作EF∥AC,分别交正方形的两条边于点E,F.设BP=x,△BEF的面积为y,则能反映y与x之间关系的图象为()A B C D6.如图,Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,动点P沿折线CA﹣AB运动,到点B停止,动点Q沿BA﹣AC运动到点C停止,点P运动速度为2cm/s,点Q的运动速度为2.5cm/s,设运动时间为t(s),△APQ的面积为S,则S与t(0≤t≤4.5)对应关系的图象大致是()A B C D7.如图,△ABC为等边三角形,AB=6cm,直线l经过点B,且l⊥BC于点B;将直线l从点B处开始,沿BC方向以1cm/s的速度向点C运动,移动过程中与AB或AC交于点M,与BC交于点N,当直线运动到点C时停止.若直线运动的时间是t(s),移动过程中△BMN的面积为S (cm2),则S与t之间函数关系的图象大致是()A B C D二.1.如图,矩形ABCD中,AB=4,BC=3,动点E从BC的中点出发,沿矩形的边逆时针运动至边AD的中点时停止.设点E运动的路程为x,△ABE的面积为y,则y与x的函数关系用图象表示正确的是()A B C D2.如图,在长方形ABCD中,点E为AB上一点,且CD=5,AD=2,AE=3,动点P从点E出发,沿路径E﹣B﹣C﹣﹣D运动,则△DPE的面积y与点P运动的路径长x之间的关系用图象表示大致为()A.B.C.D.3.如图,边长为4的正方形ABCD的边上一动点P,沿A→B→C→D→A的路径匀速移动,设P点经过的路径长为x,三角形APB的面积是y,则变量y与变量x的关系图象正确的是()A B C D三.1.如图,△ABC中,∠C=90°,BC=6cm,AC=8cm.点P,Q同时从点A出发,点P以4cm/s的速度沿AC向点C运动,点Q以5cm/s的速度沿AB向点B运动,当其中一个点到达终点时,另一个点也随之停止运动.作▱APDQ,设运动时间为ts,▱APDQ与△ABC重合部分的面积为Scm2,则下列图象中能大致反映S与t的函数关系的是()A B C D2.如图,在△ABC中,AC=BC,∠ACB=90°,S△ABC=4cm2.正方形CDEF的顶点D,F分别在AC,BC边上,设CD=CF=x,△ABC与正方形CDEF重叠部分的面积为y,则下列图象中能表示y与x之间的函数关系的是()A B C D答案及解析一.答案:DADCCBC总结:此类题正常的方法就是把每一段的解析式求出来,然后根据解析式判断图像,但是,很多时候解析式并不好求,所以急需简便方法。
初中数学中考二轮复习重难突破专题03 动点函数图象(含答案)

1.点P(x,y)在x轴上,y=0如图①中,点点出发沿运动到点的运动路程为,的面积为,与的函数图像如图②所示,则AB的长为(A. 10B. 12C. 14D. 16【答案】A【解析】由函数图像可知:当时,,面积最大时,可以求出,最后由勾股定理求出AB的值.【详解】当时,,面积最大时,∴,∴,解得或,∴,故选A.【点拨】本题考查函数图像与几何动点问题,需要分析清楚函数图像各个拐点的意义是解题关键.2.如图①,在矩形ABCD中,AB>AD,对角线A C.B D相交于点O,动点P由点A出发,沿AB→BC→CD向点D运动,设点P的运动路径为x,△AOP的面积为y,图②是y关于x的函数关系图象,则AB边的长为( )A. 3B. 4C. 5D. 6【答案】B【解析】根据图形,分情况分析:当P点在AB上运动时,△AOP面积逐渐增大,当P点到达B点时,△AOP面积最大为3,推出AB•BC=12;当P点在BC上运动时,△AOP面积逐渐减小,当P点到达C点时,△AOP面积为0,此时结合图象可知P点运动路径长为7,可推出A B.【详解】解:当P点在AB上运动时,△AOP面积逐渐增大,当P点到达B点时,△AOP面积最大为3.∴AB•BC=3,即AB•BC=12.当P点在BC上运动时,△AOP面积逐渐减小,当P点到达C点时,△AOP面积为0,此时结合图象可知P点运动路径长为7,∴AB+BC=7.则BC=7﹣AB,代入AB•BC=12,得AB2﹣7AB+12=0,解得AB=4或3,因为AB>BC,所以AB=4.故选B.【点拨】本题主要考查动点问题的函数图象,解题的关键是分析三角形面积随动点运动的变化过程,找到分界点极值,结合图象得到相关线段的具体数值.3.如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1 cm/s的速度匀速运动到点B,图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为( )A. 2B.C.D.【答案】B【解析】通过分析图象,点F从点A到D用a s,此时,△FBC的面积为a,依此可求菱形的高DE,再由图象可知,B D=,应用两次勾股定理分别求B E和a.【详解】过点D作D E⊥B C于点E由图象可知,点F由点A到点D用时为a s,△F BC的面积为a cm2.∴A D=a∴D E•A D=a∴D E=2当点F从D到B时,用s∴BD=Rt△D BE中,B E=∵A BCD是菱形∴E C=a-1,D C=aRt△D EC中,a2=22+(a-1)2解得a=故选B.【点拨】本题综合考查了菱形性质和一次函数图象性质,解答过程中要注意函数图象变化与动点位置之间的关系.4.如图甲所示,A,B是半径为2的⊙O上两点,且OA⊥OB,点P从点A出发,在⊙O以每秒一个单位长度度速度匀速运动,回到点A运动结束,设P点的运动时间为x(单位:s),弦BP的长为y,那么在图乙中可能表示y与x函数关系的是( )A. ①B. ②C. ②或④D. ①或③【答案】D【解析】分两种情形讨论当点顺时针旋转时,图象是③,当点逆时针旋转时,图象是①,由此即可解决问题.【详解】解:当点顺时针旋转,到达⊙O顶点时,运动过程中BP逐渐增大,从增大到4,据此可以判断,y与x函数图象是③,当点逆时针旋转,到达B点时,运动过程中BP逐渐减小,从减小到0,据此可以判断,y与x函数图象是①,故①③正确,故选:D.【点拨】本题考查动点问题函数图象、圆的有关知识,解题的关键理解题意,学会用分类讨论的思想思考问题.5. 如图1,四边形是轴对称图形,对角线,所在直线都是其对称轴,且,相交于点E.动点P从四边形的某个顶点出发,沿图1中的线段匀速运动.设点P运动的时间为x,线段的长为y,图2是y与x的函数关系的大致图象,则点P的运动路径可能是()A. B.C. D.【答案】D【解析】根据图像,以及点的运动变化情况,前两段是y关于x的一次函数图像,判断y随x的增减变化趋势,第一段的最高值与第二段的最高值不相等,即可排除A,B,C选项.【详解】根据图像,前端段是y关于x的一次函数图像,∴应在A C,B D两段活动,故A,B错误,第一段y随x的增大而减小,第二段y随x增大而增大,第一段的最高值与第二段的最高值不相等,∵A E=E C∴C错误故选:D【点拨】本题考查函数的图像,比较抽象,解题的关键是根据图像判断函数值随自变量的值的增减变化情况,以及理解分段函数的最值是解题的关键.6.如图,菱形ABCD的边长为5 cm,s in A=,点P从点A出发,以1 cm/s的速度沿折线AB﹣BC﹣CD运动,到达点D停止;点Q同时从点A出发,以1 cm/s的速度沿AD运动,到达点D停止设点P运动x(s)时,△APQ的面积为y(cm2),则能够反映y与x之间函数关系的图象是( )A. B.C. D.【答案】C【解析】根据题意可以分别得到各段y与x的函数解析式,从而可以解答本题.【详解】解:∵菱形ABCD的边长为5 cm,P,Q的速度都是1 cm/s,当时,,点都在运动,, 故选项A、\D错误,当时,点停止,点运动,高不变,,当时,点停止,点运动,,故选项B错误,选项C正确,故选:C.【点拨】本题考察了三角函数,菱形性质等知识点,讨论动点在不同边的情况,求出对应函数关系式,再去判断是解题关键.7.李叔叔开车上班,最初以某一速度匀速行驶,中途停车加油耽误了几分钟,为了按时到单位,李叔叔在不违反交通规则的前提下加快了速度,仍保持匀速行驶,则汽车行驶的路程y(千米)与行驶的时间t(小时)的函数关系的大致图象是()A. B. C. D.【答案】B【解析】根据“路程速度时间”可得与之间的函数关系式,再根据加完油后,加快了速度可得后面的一次函数的一次项系数更大,图象更陡,由此即可得.【详解】解:设最初的速度为千米/小时,加快了速度后的速度为千米/小时,则,由题意得:最初以某一速度匀速行驶时,,加油几分钟时,保持不变,加完油后,,,函数的图象比函数的图象更陡,观察四个选项可知,只有选项B符合,故选:B.【点拨】本题考查了一次函数的图象,熟练掌握一次函数图象的特征是解题关键.8..如图,在中,,,点从点沿边,匀速运动到点,过点作交于点,线段,,,则能够反映与之间函数关系的图象大致是()A. B. C. D.【答案】D【解析】分两种情况:①当P点在OA上时,即0≤x≤2时;②当P点在A B上时,即2<x≤4时,求出这两种情况下的P C长,则y=P C•OC的函数式可用x表示出来,对照选项即可判断.【详解】解:∵△AOB是等腰直角三角形,A B=,∴O B=4.①当P点在OA上时,即0≤x≤2时,P C=O C=x,S△P OC=y=PC•OC=x2,是开口向上的抛物线,当x=2时,y=2;O C=x,则B C=4-x,P C=B C=4-x,S△P OC=y=PC•OC=x(4-x)=-x2+2x,是开口向下的抛物线,当x=4时,y=0.综上所述,D答案符合运动过程中y与x的函数关系式.故选:D.【点拨】本题主要考查了动点问题的函数图象,解决这类问题要先进行全面分析,根据图形变化特征或动点运动的背景变化进行分类讨论,然后动中找静,写出对应的函数式.。
2019年全国中考试题汇编知识点48 几何最值(通用版全解全析)

2019年全国中考试题汇编知识点48 几何最值(通用版全解全析)一、选择题12.(2019·长沙)如图,△ABC中,AB=AC=10,tanA=2,BE⊥AC于点E,D是线段BE上的一个动点,则CD+5 BD的最小值是【】A.25B.45C.53D.10【答案】B2.3.二、填空题16.(2019·黄冈)如图,AC,BD在AB的同侧,AC=2,BD=8,AB=8.点M为AB的中点.若∠CMD=120°,则CD的最大值是.【答案】14【解析】将△CAM沿CM翻折到△CA′M,将△DBM沿DM翻折至△DB′M,则A′M=B′M,∠AMC=∠A′MC,∠DMB=∠DMB′,∵∠CMD=120°,∴∠AMC+∠DMB=∠A′MC+∠DMB′=60°,∴∠A′MB′=180°-(∠AMC+∠DMB+∠A′MC+∠DMB′)=60°,∴△A′MB′是等边三角形,又∵AC=2,BD=8,AB=8.点M为AB的中点,∴A′B′=A′M=B′M=AM=12AB=4,CA′=AC=2,DB′=DB=8,又CD≤CA′+A′B′+DB′=2+4+8=14.三、解答题24.(2019山东威海,24,12分)如图,在正方形ABCD中,AB=10cm,E为对角线BD上一动点,连接AE,CE,过E点作EF⊥AE,交直线BC于点F.E点从B点出发,沿着BD方向以每秒2cm的速度运动,当点E与点D重合时,运动停止,设△BEF的面积为ycm2,E点的运动时间为x秒.(1)求证:CE=EF;(2)求y与x之间关系的函数表达式,并写出自变量x的取值范围;(3)求△BEF面积的最大值.【解题过程】(1)证明:过E作MN∥AB,交AD于M,交BC于N,∵四边形ABCD是正方形,∴AD∥BC,AB⊥AD,∴MN⊥AD,MN⊥BC,∴∠AME=∠FNE=90°=∠NFE+∠FEN,∵AE⊥EF,∴∠AEF=∠AEM+∠FEN=90°,∴∠AEM=∠NFE,∵∠DBC=45°,∠BNE=90°,∴BN=EN=AM.∴△AEM≌△EFN(AAS).∴AE=EF.∵四边形ABCD是正方形,∴AD=CD,∠ADE=∠CDE,∵DE=DE,∴△ADE≌△CDE(SAS),∴AE=CE=EF.(2)在Rt△BCD中,由勾股定理得:BD=,∴0≤x≤.由题意,得BE=2x,∴BN=EN x.由(1)知:△AEM≌△EFN,∴ME=FN,∵AB=MN=10,∴ME=FN=10x,如图(1),当0≤x时,∴BF=FN-BN=10x x=10-x.∴y=12BF·EN=1(102-=-2x2+(0≤x≤2);如图(2),当2<x≤ ∴BF =BN -FN-(10x)=-10, ∴y =12BF ·EN=12-=2x 2-(2≤x≤.∴222(0);22(2x x y x x ⎧-+≤≤⎪⎪=⎨⎪-<≤⎪⎩(1) (2) (3)y =-2x 2+5x =-2(x-524)2+254,∵-2<0, ∴当x =524时,y 有最大值是;即△BEF 面积的最大值是;当2<x ≤ y =2x 2-=22(4x --254, 此时2>0,开口向上,对称轴为直线x =4, ∵对称轴右侧,y 随x 的增大而增大, ∴当x =y 最大值=50.∴当x =BEF 面积的最大值是50.【知识点】四边形综合运用,二次函数的解析式,二次函数的最值问题,三角形全等的判定. 25.(2019山东省威海市,题号25,分值12) (1)方法选择如图①,四边形ABCD 是OO 的内接四边形,连接AC ,BD .AB =BC =AC .求证:BD =AD +CD .小颖认为可用截长法证明:在DB 上截取DM =AD ,连接AM ..…… 小军认为可用补短法证明:延长CD 至点N ,使得DN =AD …… 请你选择一种方法证明.(2)类比探究【探究1】如图②,四边形ABCD 是⊙O 的内接四边形,连接AC ,BD .BC 是⊙O 的直径,AB =AC .试用等式表示线段AD ,BD ,CD 之间的数量关系,并证明你的结论. 【探究2】如图③,四边形ABCD 是⊙O 的内接四边形,连接AC ,BD .若BC 是⊙O 的直径,∠ABC =30°,则线段AD ,BD ,CD 之间的等量关系式是. (3)拓展猜想如图④,四边形ABCD 是⊙O 的内接四边形,连接AC ,BD .若BC 是O 0的直径,BC :AC :AB =a :b :c ,则线段AD ,BD ,CD 之间的等量关系式是.【思路分析】(1)选小颖的截长法,如图①,在DB 上截取DM =AD ,连接AM ,由旋转全等得BM =CD ,∴BD =MD +BM =AD +CD(2)【探究1】数量关系为:BDAD +CD如图②,在DB 上截取AD =AN ,连接AN ,可得△AND 为等腰直角三角形,∴NDAD ,由旋转全等得BN =CD ,∴BD =ND +BNAD +CD 【探究2】数量关系为:BD =2ADCD如图③,在DB 上截取2AD =PD ,连接AP ,可得△APD 为30°的直角三角形,图①图②B图③BC 图④BC由旋转相似得BP,∴BD =PD +BP =2AD(3)拓展猜想数量关系为:BD =a bAD +c b CD如图④,过A 作AQ ⊥AD 交BD 于Q ,连接AQ ,由旋转相似得=BQ AB c CD AC b =,=DQ BC aAD AC b=, ∴BQ =c b CD ,BQ =a b AD ,∴BD =PD +BP =a bAD +c b CD【解题过程】(1)选小颖的截长法,如图①,在DB 上截取DM =AD ,连接AM ,可得△AMD 为等边三角形,可证△BAM ≌△CAD (SAS )得BM =CD ,∴BD =MD +BM =AD +CD(2)【探究1】数量关系为:BDAD +CD如图②,在DB 上截取AD =AN ,连接AN ,可得△AND 为等腰直角三角形,∴NDAD ,∠BAN =∠CAD ,可证△BAN ≌△CAD (SAS )得BN =CD ,∴BD =ND +BNAD +CD【探究2】数量关系为:BD =2ADCD如图③,在DB 上截取2AD =PD ,连接AP ,可得△APD 为30°的直角三角形,∴=tan 30AP ABAD AC=︒,∠BAP =∠CAD ,可证△BAP ∽△CAD 得BPCD ,∴BD =PD +BP =2ADCD答案图①答案图②B(3)拓展猜想数量关系为:BD =a bAD +c b CD如图④,过A 作AQ ⊥AD 交BD 于Q ,连接AQ ,可得∠BAQ =∠CAD ,∠ABQ =∠ACD ,∠ADQ =∠ACB ,∠BAC =∠QAD ∴△BAP ∽△CAD ,△ADQ ∽△ACB ∴=BQ AB c CD AC b =,=DQ BC aAD AC b=, ∴BQ =c b CD ,BQ =a b AD ,∴BD =PD +BP =a bAD +cb CD26.(2019·益阳)如图,在半面直角坐标系xOy 中,矩形ABCD 的边AB=4,BC=6.若不改变矩形ABCD 的形状和大小,当形顶点A 在x 轴的正半轴上左右移动时,矩形的另一个顶点D 始终在y 轴的正半上随之上下移动. (1)当∠OAD=30°时,求点C 的坐标;(2)设AD 的中点为M ,连接OM 、MC ,当四边形 OMCD 的面积为221时,求OA 的长; (3)当点A 移动到某一位置时,点C 到点O 的距离有最大值,请直接写出最大值,并求此时cos ∠OAD 的值.第26题图 第26题备用图【解题过程】(1)如图1,过点C 作CE ⊥y 轴,垂足为E.答案图③B答案图④BC第26题答图1∵矩形ABCD 中,CD ⊥AD , ∴∠CDE+∠ADO=90°, 又∵∠OAD+∠ADO=90°, ∴∠CDE=∠OAD=30°. 在Rt △CED 中,CE=21CD=2, ∴DE=32242222=-=-CE CD ; 在Rt △OAD 中,∠OAD=30°, ∴OD=21AD=3. ∴点C 的坐标为(2,323+). (2)∵M 为AD 的中点, ∴DM=3,6=DCM S △. 又∵221=OMCD S 四边形, ∴29=ODM S △, ∴9=OAD S △. 设OA=x ,OD=y ,则⎪⎩⎪⎨⎧==+9213622xy y x , ∴xy y x 222=+, 即0)(2=-y x ,∴x=y.将x=y 代入3622=+y x 得182=x , 解得23=x (23-不合题意,舍去), ∴OA 的长为23.(3)OC 的最大值为8.理由如下: 如图2,第26题答图2 ∵M 为AD 的中点,∴OM=3,522=+=DM CD CM .∴OC ≤OM+CM=8,当O 、M 、C 三点在同一直线时,OC 有最大值8.连接OC ,则此时OC 与AD 的交点为M ,过点O 作ON ⊥AD ,垂足为N. ∵∠CDM=∠ONM=90°,∠CMD=∠OMN , ∴△CMD ∽△OMN , ∴OM CMMN DM ON CD ==, 即3534==MN ON , 解得59=MN ,512=ON , ∴56=-=MN AM AN . 在Rt △OAN 中, ∵55622=+=AN ON OA , ∴55cos ==∠OA AN OAD .26.(2019·衡阳)如图,在等边△ABC中,AB=6cm,动点P从点A出发以cm/s的速度沿AB匀速运动.动点Q同时从点C出发以同样的速度沿BC延长线方向匀速运动.当点P到达点B时,点P、Q同时停止运动.设运动时间为t(s).过点P作PE⊥AC于E,连接PQ交AC边于D.以CQ、CE为边作平行四边形CQFE.(1)当t为何值时,△BPQ为直角三角形;(2)是否存在某一时刻t,使点F在∠ABC的平分线上?若存在,求出t的值,若不存在,请说明理由;(3)求DE的长;(4)取线段BC的中点M,连接PM,将△BPM沿直线PM翻折,得△B′PM,连接AB′,当t为何值时,AB′的值最小?并求出最小值.解:(1)∵△ABC为等边三角形,∴∠B=60°,∵BP⊥PQ,∴2BP=BQ即2(6-t)=6+t,解得t=2.∴当t为2时,△BPQ为直角三角形;(2)存在.作射线BF,∵PE⊥AC,∴AE=0.5t.∵四边形CQFE是平行四边形,∴FQ=EC=6-0.5t,∵BF 平分∠ABC,∴∠FBQ+∠BQF=90°.∵BQ=2FQ,BQ=6+t,∴6+t=2(6-0.5t),解得t=3.(3)过点P作PG∥CQ交AC于点G,则△APG是等边三角形.∵BP⊥PQ,∴EG=12AG.∵PG∥CQ,∴∠PGD=∠QCD,∵∠PDG=∠QDC,PG=PA=CG=t,∴△PGD≌△QCD.∴GD=12GC.∴DE=12AC=3.(4)连接AM,∵△ABC为等边三角形,点M是BC的中点,∴BM=3.由勾股定理,得AM=.由折叠,得BM′=3.当A 、B′、M在同一直线上时,AB′的值最小,此时AB′=3.过点B′作B′H⊥AP于点H,则cos30°=AHAB',t,解得t=9-∴t为9-AB′的值最小,最小值为-3.MMM QB C1.(2019·重庆A 卷)如图,在平面在角坐标系中,抛物线y =x 2-2x -3与x 轴交与点A ,B (点A 在点B 的左侧)交y 轴于点C ,点D 为抛物线的顶点,对称轴与x 轴交于点E .(1)连结BD ,点M 是线段BD 上一动点(点M 不与端点B ,D 重合),过点M 作MN ⊥BD 交抛物线于点N (点N 在对称轴的右侧),过点N 作NH ⊥x 轴,垂足为H ,交BD 于点F ,点P 是线段OC 上一动点,当MN 取得最大值时,求HF +FP +13PC 的最小值;(2)在(1)中,当MN 取得最大值,HF +FP +13PC 取得小值时,把点P单位得到点Q ,连结AQ ,把△AOQ 绕点O 顺时针旋转一定的角度α(0°<α<360°),得到△A OQ '',其中边A Q ''交坐标轴于点G ,在旋转过程中,是否存在一点G ,使得OG Q Q ''∠=∠?若存在,请直接写出所有满足条件的点Q '的坐标;若不存在,请说明理由.解:(1)由题意得A (-1,0),B (3,0),C (0,-3),D (1,-4),直线BD :y =2x -6. 如答图1,连接DN 、BN ,则S △BDN =12BD •MN ,而BD 为定值,故当MN 最大时,S △BDN 取最大值.此时由S △BDN =S △DFN +S △BFN =12EH •FN +12BH •FN =12BE •FN =FN ,从而S △BDN 取最大值时,即为FN 有最大值.令N (m ,m 2-2m -3),则F (m ,2m -6),从而FN =(2m -6)-(m 2-2m -3)=-m 2+4m -3=-(m -2)2+1,此时,当且仅当m =2,FN 有最大值为1,于是N (2,-3),F (2,-2),H (2,0). 在直角三角形中,设最小的直角边为a ,斜边为3a ,较长直角边为3,即可求出a=4,于是在x 轴上取点M BK (0),连接KC ,易求直线KC :y =-x -3.如答图1,过点F 作FR ⊥CK 于点R ,交OC 于点P ,作FT ⊥OC ,交CK 于点T ,则∠OCK =∠TFR ,于是,由△PCR ∽△ACO ∽△TFR ,得133PR OK a PC KC a ===,从而PR =13PC ,因此由FH 为定值,再由定点F 到直线的垂直线最短,可知MN 取得最大值时,HF +FP+13PC 最小值=HF +FR .在y =-x -3中,当y =-2,x =-4,于是FT =2+4.在Rt △FTR中,由3FR FT =,得FR =3FT =3(2+4)=133+,故HF +FP +13PC 最小值=2+13+=.(2)(,(,,. 2.(2019·重庆B 卷)在平面直角坐标系中,抛物线2y =++与x 轴交于A ,B 两点(点A 在点B 左侧),与y 轴交于点C ,顶点为D ,对称轴与x 轴交于点Q .(1)如图1,连接AC ,BC .若点P 为直线BC 上方抛物线上一动点,过点P 作PE ∥y 轴交BC 于点E ,作PF⊥BC 于点F ,过点B 作BG ∥AC 交y 轴于点G .点H ,K 分别在对称轴和y 轴上运动,连接PH ,HK .当△PEF 的周长最大时,求PH +HKKG 的最小值及点H 的坐标. (2)如图2,将抛物线沿射线AC 方向平移,当抛物线经过原点O 时停止平移,此时抛物线顶点记作D ’,N 为直线DQ 上一点,连接点D ’,C ,N ,△D ’CN 能否构成等腰三角形?若能,直接写出满足条件的点N 的坐标;若不能,请说明理由.解:(1)∵2y x =+与x 轴交于A ,B 两点, ∴当y=0时,即20=+,∴122,4x x =-=,即A (-2,0),B (4,0), 设直线BC 的解析式为y =kx +b ,∵C (0,,B (4,0),∴40b k b ⎧=⎪⎨+=⎪⎩,∴b k ⎧=⎪⎨=⎪⎩,∴直线BC的解析式为y =+设点2(,4),P m m +<< ∵PE ∥y 轴且点E 在直线BC上,∴(,E m +∠PEF =∠OCE ,∴2(04),PE m =<< ∵PF ⊥BC ,∴∠PFE =∠COB =90°,∴△PEF ∽△BCO ,设△PEF 的周长为1l ,△BCO 的周长为2l , 则12l PEl BC=,∵B (4,0),C (0,,∴BC=24l =+ 备用图图1图2∴21)(04),l m =+<< ∴当m=2时,1l此时点P 的坐标为(2,, ∵A (-2,0),C (0,,∴∠ACO =30°,∠CAO =60°, ∵BG ∥AC ,∴.∠BGD =30°,∠OBG =60°,∴G (0,-, 直线BG解析式为y -PM解析式为y =,过点G 作GN ⊥BG ,过点P 作PM ⊥GN 于点M ,如图1,此时,点H 为PM 与对称轴的交点,K 为PM 与y 轴的交点,点K 与点O 重合, 则KM=OMKG ,PH +HKKG 的最小值为线段PM 的长.(此问题是胡不归问题).解法一:(作一线三直角利用相似求解)如图2,过点P 作PQ ∥x 轴交对称轴于点T , 过点M 作MQ ⊥y 轴交PT 于点Q ,过点G 作GJ ⊥MQ 交MQ 于点J.设点Q (n,,∴J (n,-,∴PQ =2-n ,2-n ), ∵GJ =-n ,∴MJ=,∴MQ +MJ =CG=(--=2-n )+()=n =-3,∴Q (-3,,∴PQ =5, ∴PM =2PQ =10,∴PH +HKKG 的最小值为10, ∵∠OGM =60°,∠PHT=30°,∠HPT=60°,∴PT =1,∴HTH (1.图1N解法二:由上面的解法可知MG ⊥BG ,直线MG的解析式为:y =- 如图3,过点P 作PR ⊥x 轴交MG 于点R ,∴R (2,, 由第一种解法可知∠PRG =60°,∴PMP R()=10, ∴PH +HKKG 的最小值为10,同理可求H (1.(2)这样的N 点存在.当△'CD N 为等腰三角形时,这样的N有:1N,2N,3N,4N,5N .【提示】由(1)可知∠ACO=30°,∠OAC=60°,又∵221)y x =++=-D (1, ∵抛物线按射线AC的方向平移,设平移后顶点'(D a +,平移后的抛物线解析式为21)y x a =--++ 图2NN该抛物线经过原点,则201)a =--+∴2280a a --=,∴a =4或a =-2(舍去),即D .设点N (1,b )'CD =CN ='ND 如图4,当△'CD N 为等腰三角形时,分三种情况:①当'CD CN ==,可得1N ,2N ;②当''CD D N ==3N ,4N ,③当'CN D N ==可得5N ,∴当△'CD N 为等腰三角形时,这样的N 有:1N ,2N ,3N ,4N ,5N .3.(2019·天津)已知抛物线y=x 2-bx+c(b,c 为常数,b>0)经过点A (-1,0),点M(m,0)是x 轴正半轴上的动点, (1)当b=2时,求抛物线的顶点坐标;(2)点D(b,y D )在抛物线上,当AM=AD,m=5时,求b 的值; (3)点Q(1b ,2+y Q )2QM +的最小值为4时,求b 的值. 解:(1)∵抛物线y=x 2-bx+c 经过点A (-1,0), ∴1+b+c=0,∴c=-1-b 当b=2时,c=-3,∴抛物线的解析式为y=x 2-2x-3, ∴顶点坐标为(1,-4) (2)由(1)知,c=-1-b , ∵点D(b,y D )在抛物线上, ∴y D =-b-1,∵b>0,∴b 02b >>,-b-1<0,∴D(b,-b-1)在第四象限,且在抛物线对称轴2bx =的右侧.如图,过点D作DE⊥x轴于E,则E(b,0),∴AE=b+1=DE,所以1) b+,∵m=5,∴AM=5-(-1)=6,∴1) b+∴b=(3)∵点Q(1b,2+y Q)在抛物线上,∴yQ=2113)()12224bb b b b+-+--=--(,∴点Q(1b,2+3-24b-)在第四象限,且在直线x=b的右侧,2QM+的最小值为4,A(-1,0)∴取点N(0,1),如图,过点Q作QH⊥x轴于H,作QG⊥AN于G,QG与x轴交于点M,则H(1b,2+0),∠GAM=45°,∴GM= AM,∵M(m,0),∴AM=m+1,MH=1b2m+-,QH=324b+,∵MH=QH,∴1b 2m +-=324b +, ∴m=1-24b , ∴AM=13-12424b b +=+,3)24b =+2QM +33)2())24244b b +++=,∴b=4. 4.(2019·自贡)如图,已知直线AB 与抛物线:y =ax 2+2x +c 相交于点A (-1,0)和点B (2,3)两点. (1)求抛物线C 函数解析式;(2)若点M 是位于直线AB 上方抛物线上的一动点,以MA 、MB 为相邻的两边作平行四边形MANB ,当平行四边形MANB 的面积最大时,求此时平行四边形MANB 的面积S 及点M 的坐标; (3)在抛物线C 的对称轴上是否存在顶点F ,使抛物线C 上任意一点P 到F 的距离等于到直线y =174的距离,若存在,求出定点F 的坐标;若不存在,请说明理由.解:(1)将A (-1,0)和B (2,3)代入抛物线解析式得{a −2+c =04a +4+c =3解得,{a =−1c =3∴抛物线解析式为y =-x 2+2x +3.(2)过M 作MH ∥y 轴,交AB 于H ,设直线AB 为y =kx +b ,将A ,B 坐标代入得,{−k +b =02k +b =3解得,{k =1b =1.∴直线AB 的解析式为y =x +1.设M 为(m ,-m 2+2m +3),则H (m ,m +1) ∴MH =y M -Y H =(-m 2+2m +3)-( m +1)=-m 2+m +2. ∴S △ABM =S △AMH +S △BMH =12·MH ·(x B -x A )=12·(-m 2+m +2)·(2+1) =-32(m 2-m )+3=-32(m -12)2+278.∵四边形MANB 是以MA 、MB 为相邻的两边的平行四边形, ∴△ABM ≌△BAN .∴S 四边形MANB =2 S △ABM =-3(m -12)2+274,∵a =-3<0且开口向下,∴当m =12时,S 四边形MANB 的最大值为274. 此时,M 坐标为(12,154). (3)存在,理由如下:过P 作直线y =174的垂线,垂足为T ,∵抛物线为y =-x 2+2x +3=-(x -1)2+4.∴抛物线的对称轴为直线x =1,顶点坐标为(1,4). 当P 为顶点,即P (1.4)时, 设F 点坐标为(1,t ), 此时PF =4-t ,PT =174-4=14.∵P 到F 的距离等于到直线y =174的距离, ∴4-t =14, 即t =154.∴F 为(1,154)设P 点为(a ,-a 2+2a +3),由勾股定理,PF 2=(a -1)2+(-a 2+2a +3-154)2 =a 4-4a 3+132a 2-5a +2516.又∵PT 2=[174-(-a 2+2a +3)]2= a 4-4a 3+132a 2-5a +2516. ∴PF 2=PT 2,即PF =PT .∴当F 为(1,154)时,抛物线C 上任意一点P 到F 的距离等于到直线y =174的距离 .27.(2019·淮安)如图①,在△ABC 中,AB=AC=3,∠BAC=100°,D 是BC 的中点.小明对图①进行了如下探究:在线段AD 上任取一点P ,连接PB.将线段PB 绕点P 按逆时针方向旋转80°,点B 的对应点是点E ,连接BE ,得到△BPE.小明发现,随着点P 在线段AD 上位置的变化,点E 的位置也在变化,点E 可能在直线AD 的左侧,也可能在直线AD 上,还可能在直线AD 的右侧. 请你帮助小明继续探究,并解答下列问题: (1)当点E 在直线AD 上时,如图②所示. ①∠BEP=°;②连接CE ,直线CE 与直线AB 的位置关系是.(2)请在图③中画出△BPE ,使点E 在直线AD 的右侧,连接CE.试判断直线CE 与直线AB 的位置关系,并说明理由.(3)当点P 在线段AD 上运动时,求AE 的最小值.【解题过程】(1)①由题意得,PE=PB ,∠BPE=80°,∴∠BEP=︒=︒-︒50280180; ②如图所示,∵AB=AC ,D 是BC 的中点,∠BAC=100°,∴∠ABC=︒=︒-︒402100180,∵∠BEP=50°,∴∠BCE=∠CBE=40°, ∴∠ABC=∠BCE , ∴CE ∥AB.答案:①50°;②平行(2)在DA 延长线上取点F ,使∠BFA=∠CFA=40°,总有△BPE ∽△BFC. 又∵△BPF ∽△BEC , ∴∠BCE=∠BFP=40°, ∴∠BCE=∠ABC=40°, ∴CE ∥AB.(3)当点P 在线段AD 上运动时,由题意得PB=PE=PC , ∴点B 、E 、C 在以P 为圆心、PB 为半径的圆上, 如图所示:∴AE 的最小值为AC=3.5.(2019·凉山州)如图,抛物线y = ax 2+bx +c 的图象过点A (-1,0)、B (3,0)、C (0,3). (1)求抛物线的解析式;(2)在抛物线的对称轴上是否存在一点P ,使得△P AC 的周长最小,若存在,请求出点 P 的坐标及△P AC 的周长;若不存在,请说明理由;(3)在(2)的条件下,在x 轴上方的抛物线上是否存在点M (不与C 点重合),使得 S △P AM =S △P AC ,若存在,请求出点M 的坐标;若不存在,请说明理由.解:(1)由题知⎪⎩⎪⎨⎧==++=+-30390c c b a c b a ,解得⎪⎩⎪⎨⎧==-=321c b a ,∴抛物线的解析式为y = -x 2+2x +3;(2)存在.连接BC 交抛物线对称轴于点P ,此时△P AC 的周长最小.设BC :y =kx +3,则3k +3=0,解得k =-1,∴BC :y =-x +3.由抛物线的轴对称性可得其对称轴为直线x =1,当x =1时,y =-x +3=2,∴P (1,2).在Rt △OAC 中,AC =2231+=10;在Rt △OBC 中,BC =2233+=32.∵点P 在线段AB 的垂直平分线上,∴P A =PB ,∴△P AC 的周长=AC +PC +P A = AC +PC +PB =AC +BC =10+32.综上,存在符合条件的点P ,其坐标为(1,2),此时△P AC 的周长为10+32;(3)存在.由题知AB =4,∴S △P AC =S △ABC -S △P AB =21×4×3-21×4×2=2.设:AP :y =mx +n ,则⎩⎨⎧=+=+-20n m n m ,解得⎩⎨⎧==11n m ,∴AP :y =x +1. ①过点C 作AP 的平行线交x 轴上方的抛物线于M ,易得CM :y =x +3,由⎩⎨⎧++-=+=3232x x y x y 解得⎩⎨⎧==3011y x ,⎩⎨⎧==4122y x ,∴M (1,4);②设抛物线对称轴交x 轴于点E (1,0),则S △P AC =21×2×2=2=S △P AC .过点E 作AP 的平行线交x 轴上方的抛物线于M ,设EM :y =x +t ,则1+t =0,∴t =-1,∴EM :y =x -1. 由⎩⎨⎧++-=-=3212x x y x y 解得⎪⎪⎩⎪⎪⎨⎧--=-=2171217111y x (舍),⎪⎪⎩⎪⎪⎨⎧+-=+=2171217122y x ,∴M (2171+,2171+-). 综上,存在符合条件的点M ,其坐标为(1,4)或(2171+,2171+-).27.(2019·苏州,26,10)已知矩形ABCD中,AB=5cm,点P为对角线AC上的一点,且AP=.如图①,动点M从点A出发,在矩形边上沿着A→B→C的方向匀速运动(不包含点C).设动点M的运动时间为t(s),△APM的面积为S(cm2),S与t的函数关系如图②所示.(1)直接写出动点M的运动速度为cm/s,BC的长度为cm;(2)如图③,动点M重新从点A出发,在矩形边上按原来的速度和方向匀速运动,同时,另一个动点N从点D出发,在矩形边上沿着D→C→B的方向匀速运动,设动点N的运动速度为v(cm/s).已知两动点M,N 经过时间x(s)在线段BC上相遇(不包含点C),动点M,N相遇后立即同时停止运动,记此时△APM与△DPN的面积分别为S1(cm2),S2(cm2)①求动点N运动速度v(cm/s)的取值范围;②试探究S1•S2是否存在最大值,若存在,求出S1•S2的最大值并确定运动时间x的值;若不存在,请说明理由.图①图②图③(第27题)【解题过程】解:(1)∵t=2.5s时,函数图象发生改变,∴t=2.5s时,M运动到点B处,∴动点M的运动速度为52.52cm/s,∵t=7.5s时,S=0,∴t=7.5s时,M运动到点C处,∴BC=(7.5﹣2.5)×2=10(cm),故答案为2,10;(2)①∵两动点M ,N 在线段BC 上相遇(不包含点C ),∴当在点C 相遇时,v 527.53==(cm/s ),当在点B 相遇时,v 5102.5+==6(cm/s ),∴动点N 运动速度v (cm/s )的取值范围为23cm/s <v ≤6cm/s ; ②过P 作EF ⊥AB 于F ,交CD 于E ,如图所示:则EF ∥BC ,EF =BC =10,∴AF APAB AC=,∵AC==∴5AF =解得AF =2,∴DE =AF =2,CE =BF =3,PF ==4, ∴EP =EF ﹣PF =6,∴S 1=S △APM =S △APF +S 梯形PFBM ﹣S △ABM 12=⨯4×212+(4+2x ﹣5)×312-⨯5×(2x ﹣5)=﹣2x +15,S 2=S △DPM =S △DEP +S 梯形EPMC ﹣S △DCM 12=⨯2×612+(6+15﹣2x )×312-⨯5×(15﹣2x )=2x ,∴S 1•S 2=(﹣2x +15)×2x =﹣4x 2+30x =﹣4(x 154-)22254+,∵2.5154<<7.5,在BC 边上可取,∴当x 154=时,S 1•S 2的最大值为2254.第27题答图6.(2019·巴中)如图,抛物线y =ax 2+bx -5(a ≠0)经过x 轴上的点A(1,0)和点B 及y 轴上的点C,经过B,C 两点的直线为y =x+n.①求抛物线的解析式;②点P 从A 出发,在线段AB 上以每秒1个单位的速度向B 运动,同时点E 从B 出发,在线段BC 上以每秒2个单位的速度向C 运动.当其中一个点到达终点时,另一点也停止运动.设运动时间为t 描,求t 为何值时,△PBE 的面积最大,并求出最大值.③过点A 作AM ⊥BC 与点M,过抛物线上一动点N(不与点B,C 重合)作直线AM 的平行线交直线BC 于点Q,若点A,M,N,Q 为顶点的四边形是平行四边形.求点N 的横坐标.第26题图分析:①由点A 和直线y =x+n 可得方程组,解出系数,求得二次函数的解析式;②根据题意表示出三角形面积,利用二次函数最值进行求解;③分析得到AM 平行且等于NQ,设出坐标,利用坐标关系列方程进行求解,并检验.解:①因为点B,C 在y =x+n 上,所以B(-n,0),C(0,n),因为点A(1,0)在抛物线上,所以250505a b an bn n ì+-=ïï--=íï=-ïî,解得,a =-1,b =6,所以抛物线的解析式为:y =-x 2+6x -5.②由题意得:PB =4-t,,BE =2t ,由①可知:∠OBC =45°,点P 到BC 上的高h =BPsin45(4-t), 所以S △PBE =12BE h 鬃=)22t --+当t =2时,S取得最大值为③因为l BC :y =x -5,所以B(5,0), 因为A(1,0),所以AB =4,在Rt △ABM 中,∠ABM =45°,AMAB=M(3,-3), 过点N 作x 轴的垂线交直线BC 于点P 交x 轴于点H, 设N(m,-m 2+6m -5),则H(m,0),P(m,m -5),易证△PQN 为等腰直角三角形,即NQ =PQ=所以PN =4.当NH+HP =4时,即-m 2+6m -5-(m -5)=4, 解之得,m 1=1,m 2=4.当m 1=1时,点N 与点A 重合,故舍去;当NH+HP =4时,即m -5-(-m 2+6m -5)=4, 解得,m 12因为m>5,所以m当NH -HP =4,即-(-m 2+6m -5)-[-(m -5)]=4,解得,m 12因为m<0,所以m综上所述,要使点A,M,N,Q 为顶点的四边形是平行四边形,点N 的横坐标为:4第26题答图7.(2019·淄博)如图,顶点为M 的抛物线y =ax 2+bx +3与x 轴交于A (3,0),B (-1,0)两点,与y 轴交于点C .(1)求这条抛物线对应的函数表达式;(2)问在y 轴上是否存在点P ,使得△P AM 为直角三角形?若存在,求出点P 的坐标;若不存在,说明理由. (3)若在第一象限的抛物线下方有一动点D ,满足DA =OA ,过D 作DG ⊥x 轴于点G ,设△ADG 的内心为I ,试求CI 的最小值.解:(1)将A 、B 两点坐标代入抛物线表达式,得933030a b a b ++=⎧⎨-+=⎩,解得12a b =-⎧⎨=⎩.∴y =-x 2+2x +3.(2)假设存在点P ,使△P AM 是直角三角形.当点M 为直角顶点,过M 作CD ⊥y 轴,过A 作AD ⊥x 轴,交CD 于D ,CD 交y 轴于C ,∵∠AMP =90°, ∴∠CMP +∠AMD =90,∴∠CMP =∠MAD ,又∵∠DM =∠PCM ,∴△CPM ∽△DMA ,∴CM AD =PCMD, ∴14=2PC ,∴PC =12,∴P 1(0,72); 当点A 为直角顶点,过A 作CD ⊥x 轴,过M 作MD ⊥y 轴交AD 于D ,过P 作PC ⊥y 轴交CD 于C ,同上△CP A∽△DAM ,∴PC AD =AC MD ,∴34=2AC ,∴AC =32,∴P 2(0,-32); 当点P 为直角顶点,过M 作CM ⊥y 轴于C ,∴△CPM ∽△OAP ,∴PC AO =CM PO ,∴3PC =14-PC,∴PC =1或3,∴P 3(0,3),P 4(0,1).综上所述,使△P AM 是直角三角形的点P 的是P 1(0,72),P 2(0,-32),P 3(0,3),P 4(0,1).(3)(方法1)由(1)得DA =OA =3,设D (x ,y ),△ADG 的内切圆半径为r ,则△ADG 的内心I 为(x +r ,r ), ∴DG =y ,AG =3-x由两点距离公式可得()2222339DA x y =-+==①图(2)答图1由等面积法得r =()33+22y x DG AG DA +---==2y x-② ∴()()2223CI x r r =++-③由①②③得(2229123124CI x y -⎡⎤⎡⎤⎛⎫=-+-+ ⎪⎢⎥⎢⎥⎝⎭⎣⎦⎣⎦,2CI 在3335=512105x y =--,最小,此时CI 也最小,()()min 912253=10-242CI -=(方法2)简解:如图,由内心易知:∠DIA =135°,∠DAI =∠OAI ,△DAI ≌△OAI (SAS ),∴∠DIA =∠OIA =135°,则I 在圆周角∠OIA =135°⊙T 的圆周上运动,且半径R =322,圆心T 为(32,32),∴CI =3102在△CIA 中,CI ≥CT -IT =()310-22,当C 、I 、T 三点一线时,()min 3=10-22CI .8.(2019·枣庄)已知抛物线y =ax 2+32x+4的对称轴是直线x =3,与x 轴相交于A 、B 两点(点B 在点A 的右侧),与y 轴交于点C.(1)求抛物线的解析式和A 、B 两点的坐标;(2)如图1,若点P 是抛物线上B 、C 两点之间的一个动点(不与B 、C 重合),是否存在点P ,使四边形PBOC 的面积最大?若存在,求点P 的坐标及四边形PBOC 面积的最大值;若不存在,请说明理由.(3)如图2,若点M 是抛物线上任意一点,过点M 作y 轴的平行线,交直线BC 于点N ,当MN =3时,求点M 的坐标.Iy 12解:(1)抛物线y=ax2+32x+4的对称轴为:x=332224ba a a-=-=-=3,∴a=14-,∴抛物线的解析式为:y=14-x2+32x+4,令y=0,得14-x2+32x+4=0,解之,得,x1=-2,x2=8,∵点B在点A的右侧,∴A(-2,0),B(8,0);(2)连接BC,在抛物线y=14-x2+32x+4中,令x=0,得y=4,∴C(0,4),∴OC=4,OB=8,∴S△OBC=16,∵B(8,0),C(0,4),设l BC:y=kx+b,得0=8k+b,4=b,∴k=12-,b=4,l BC:y=12-x+4,∴过点P作PD∥y轴交BC于点D,过点C作CE垂直PD于点E,过点B作BF⊥PD于点F,则S△PBC=S△PCD+S△PBD=12PD×CE+12PD×BF=12PD×(CE+BF)=12PD×(x B-x C)=12PD×8=4PD,∵点P在抛物线上,设点P(x,14-x2+32x+4),∵PD∥y轴,点D在直线BC上,∴D(x,12-x+4),∵点P在B,C间的抛物线上运动,∴PD=y P-y D=14-x2+32x+4-(12-x+4)=14-x2+2x,S△PBC=4PD=4(14-x2+2x)=-x2+8x=-(x-4)2+16,∴当x=4时,S△PBC取最大值16,∴此时S四边形OBPC=S△OBC+S△PBC=32;第25题答图(3)∵MN∥y轴,∴设M,N的横坐标为m,∵点M在抛物线上,设点M(m,n),其中n=14-m2+32m+4,点N在直线BC上,∴N(m,12-m+4),∵点M是抛物线上任意一点,∴点M和点N的上下位置关系不确定,∴MN=|14-m2+32m+4-(12-m+4)|=|14-x2+2x|,∵MN=3,∴|14-x2+2x|=3,即14-x2+2x=3或14-x2+2x=-3,解这两个方程,得m1=2,m2=6, m3=4+4=4-∴n1=6, n2=4, n3-1, n4-1,∴M1(2,6), M2(6,4), M3(4+-1), M4(4-1).9.(2019·聊城)如图,在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于点A(-2,0),点B(4,0),与y轴交于点C(0,8),连接BC,又已知位于y轴右侧且垂直于x轴的动直线l,沿x轴正方向从O运动到B(不含O点和B点),且分别交抛物线,线段BC以及x轴于点P,D,E.(1)求抛物线的表达式;(2)连接AC,AP,当直线l运动时,求使得△PEA和△AOC相似的点P的坐标;(3)作PF⊥BC,垂足为F,当直线l运动时,求Rt△PFD面积的最大值.第25题图解:(1)由已知,将C(0,8)代入y =ax 2+bx+c,∴c =8,将点A(-2,0)和B(4,0)代人y =ax 2+bx+8,得428016480a b a b -+=⎧⎨++=⎩,解得12a b =-⎧⎨=⎩,∴抛物线的表达式为y =-x 2+2x+8; (2)∵A(-2,0),C(0,8),∴OA =2,OC =8,∵l ⊥x 轴,∠PEA =∠AOC =90°,∵∠PAE ≠∠CAO,只有当∠PAE =∠ACO 时,△PEA ∽△AOC.此时AE PECO AO=,∴AE =4PE.设点P 的纵坐标为k,则PE =k,AE =4k,∴OE =4k -2,P 点的坐标为(4k -2,k),将P(4k -2,k)代入y =-x 2+2x+8,得-(4k -2)2+2(4k -2)+8=k,解得k 1=0(舍去),k 2=2316,当k =2316时,4k -2=154,∴P 点的坐标为(154,2316). (3)在Rt △PFD 中,∠PFD =∠COB =90°,∵l ∥y 轴,∴∠PDF =∠OCB,∴Rt △PFD ∽Rt △BOC,∴2PFD=S PD S BC ⎛⎫ ⎪⎝⎭△△BOC,∴S △PFD =2PD S BC ⎛⎫⋅ ⎪⎝⎭△BOC ,由B(4,0)知OB =4,又∵OC =8,∴BC 又S △BOC =12OB OC ⋅=16,∴S △PFD =215PD ,∴当PD 最大时,S △PFD 最大.由B(4,0),C(0,8)可解得BC 所在直线的表达式为y =-2x+8,设P(m,-m 2+2m+8),则D(m,-2m+8),∴PD =-(m -2)2+4,当m =2时,PD 取得最大值4,∴当PD =4时,S △PFD =165,为最大值.10.(2019·济宁)如图1,在矩形ABCD 中,AB =8,AD =10,E 是CD 边上一点,连接AE ,将矩形ABCD 沿AE 折叠,顶点D 恰好落在BC 边上点F 处,延长AE 交BC 的延长线于点G . (1)求线段CE 的长;(2)如图2,M ,N 分别是线段AG ,DG 上的动点(与端点不重合),且∠DMN =∠DAM ,设AM =x ,DN =y . ①写出y 关于x 的函数解析式,并求出y 的最小值;②是否存在这样的点M ,使△DMN 是等腰三角形?若存在,请求出x 的值;若不存在,请说明理由.解:(1)由折叠可得AF=AD=10,EF=ED,矩形ABCD中,∠B=90°,∴AB2+BF2=AF2,∴6, BF===∴CF=BC-BF=AD-BF=10-6=4.设CE=x,则EF=DE=CD-CE=AB-CE=8-x,∵EF2=CE2+CF2.∴(8-x)2=x2+42.∴x=3,∴CE=3.(2)①∵矩形ABCD中,AD∥BC,∴∠DAG=∠AGF,∵∠DAG=∠F AG, ∠DAG=∠AGF,∴∠F AG=∠AGF,∴AF=FG=10,∴BG=BF+FG=6+10=16.∵矩形ABCD中∠B=90°,∴AB2+BG2=AG2,∴AG==∵AD=FG,AD∥FG,∴四边形AFGE是平行四边形,又∵AD=AF,∴平行四边形AFGE是菱形,∴DG=DA=10,∴∠DAG=∠DGA,∵∠DMG=∠DMN+∠NAG=∠DAM+∠ADM, ∠DMN=∠DAM,∴∠NMG=∠ADM.在△ADM和△MNG中,∠ADM=∠NMG, ∠DAG=∠DGA,∴△ADM∽△GMN.∴AD AMMG NG=10xy=-,∴211010y x x=+,∵110>0,∴当51210x=-=⨯时,y有最小值为214101021410⎛⨯⨯-⎝⎭=⨯.∴y关于x的函数解析式是:211010y x x=-+,当x=y有最小值为2.②在△DMN和△DMG中,∠DMN=∠DGM,∠MDG=∠MDG,∴△DMN和△DMG是相似三角形.当△DMG是等腰三角形时,△DMN也是等腰三角形.∵M 不与A 重合,∴DM ≠DG ,∴△DMG 是等腰三角形只有GM =GD 或DM =GM 两种情况:(1)如图3,当△DMG 中GM =GD =10时,△DMN 也是等腰三角形,即x =AG -MG =10;(2)如图4,当△DMG 中DM =GM 时,△DMN 也是等腰三角形,∴∠MDG =∠DGM ,∴∠DAG =∠MDG =∠MDG ,∴△ADG ∽△DMG ,∴AD AGMG DG =,=x综上:当x 的值为2△DMN 是等腰三角形. 11.(2019·滨州)如图①,抛物线y =-x 2+x +4与y 轴交于点A ,与x 轴交于点B ,C ,将直线AB 绕点A 逆时针旋转90°,所得直线与x 轴交于点D .(1)求直线AD 的函数解析式;(2)如图②,若点P 是直线AD 上方抛物线上的一个动点①当点P 到直线AD 的距离最大时,求点P 的坐标和最大距离;②当点P 到直线AD 的距离为时,求sin ∠P AD 的值.解:(1)当x =0时,y =4,则点A 的坐标为(0,4),………………………………………1分当y =0时,0=-x 2+x +4,解得x 1=-4,x 2=8,则点B 的坐标为(-4,0),点C 的坐标为(8,0),∴OA =OB =4,∴∠OBA =∠OAB =45°.∵将直线AB绕点A逆时针旋转90°得到直线AD,∴∠BAD=90°,∴OAD=45°,∴∠ODA=45°,∴OA=OD,∴点D的坐标为(4,0).………………………………………………………………………2分设直线AD的函数解析式为y=kx+b,,得,即直线AD的函数解析式为y=-x+4.……………………………………………………………4分(2)作PN⊥x轴交直线AD于点N,如右图①所示,设点P的坐标为(t,-t2+t+4),则点N的坐标为(t,-t+4),∴PN=(-t2+t+4)-(-t+4)=-t2+t,………………………………………………6分∴PN⊥x轴,∴PN∥y轴,∴∠OAD=∠PNH=45°.作PH⊥AD于点H,则∠PHN=90°,∴PH==(-t2+t)=t=-(t-6)2+,∴当t=6时,PH取得最大值,此时点P的坐标为(6,),………………………………8分即当点P到直线AD的距离最大时,点P的坐标是(6,),最大距离是.………………9分②当点P到直线AD的距离为时,如右图②所示,则t=,解得t1=2,t2=10,………………………………………………………………………10分则P1的坐标为(2,),P2的坐标为(10,-).当P1的坐标为(2,),则P1A==,∴sin∠P1AD==;…………………………………………………………12分当P2的坐标为(10,-),则P2A==,∴sin∠P2AD==;由上可得,sin∠P AD的值是或.……………………………………………14分。
线段最值+几何小题--2019中考真题汇编(教师版)

001(2019•安徽)如图,在正方形ABCD中,点E,F将对角线AC三等分,且AC=12,点P在正方形的边上,则满足PE+PF=9的点P的个数是()A.0B.4C.6D.8解:作点F关于BC的对称点M,连接FM交BC于点N,连接EM,交BC于点H,可得点H到点E和点F的距离之和最小,可求最小值,即可求解.如图,作点F关于BC的对称点M,连接FM交BC于点N,连接EM,交BC于点H∵点E,F将对角线AC三等分,且AC=12,∴EC=8,FC=4=AE,∵点M与点F关于BC对称∴CF=CM=4,∠ACB=∠BCM=45°∴∠ACM=90°∴EM==4则在线段BC存在点H到点E和点F的距离之和最小为4<9在点H右侧,当点P与点C重合时,则PE+PF=12∴点P在CH上时,4<PE+PF≤12在点H左侧,当点P与点B重合时,BF==2∵AB=BC,CF=AE,∠BAE=∠BCF∴△ABE≌△CBF(SAS)∴BE=BF=2∴PE+PF=4∴点P在BH上时,4<PE+PF<4∴在线段BC上点H的左右两边各有一个点P使PE+PF=9,同理在线段AB,AD,CD上都存在两个点使PE+PF=9.即共有8个点P满足PE+PF=9,故选:D.002(2019•陕西)如图,在正方形ABCD中,AB=8,AC与BD交于点O,N是AO的中点,点M在BC边上,且BM=6.P为对角线BD上一点,则PM﹣PN的最大值为2.解:作以BD为对称轴作N的对称点N',连接PN',MN',依据PM﹣PN=PM﹣PN'≤MN',可得当P,M,N'三点共线时,取“=”,再求得,即可得出PM∥AB∥CD,∠CMN'=90°,再根据△N'CM为等腰直角三角形,即可得到CM=MN'=2.如图所示,作以BD为对称轴作N的对称点N',连接PN',MN',根据轴对称性质可知,PN=PN',∴PM﹣PN=PM﹣PN'≤MN',当P,M,N'三点共线时,取“=”,∵正方形边长为8,∴AC AB,∵O为AC中点,∴AO=OC,∵N为OA中点,∴ON,∴ON'=CN',∴AN',∵BM=6,∴CM=AB﹣BM=8﹣6=2,∴∴PM∥AB∥CD,∠CMN'=90°,∵∠N'CM=45°,∴△N'CM为等腰直角三角形,∴CM=MN'=2,即PM﹣PN的最大值为2,故答案为:2.003(2019•安顺)如图,在Rt△ABC中,∠BAC=90°,且BA=3,AC=4,点D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连接MN,则线段MN的最小值为.解:由勾股定理求出BC的长,再证明四边形DMAN是矩形,可得MN=AD,根据垂线段最短和三角形面积即可解决问题.∵∠BAC=90°,且BA=3,AC=4,∴BC5,∵DM⊥AB,DN⊥AC,∴∠DMA=∠DNA=∠BAC=90°,∴四边形DMAN是矩形,∴MN=AD,∴当AD⊥BC时,AD的值最小,此时,△ABC的面积AB×AC BC×AD,∴AD,∴MN的最小值为;故答案为:.004(2019•包头)如图,在平面直角坐标系中,已知A(﹣3,﹣2),B(0,﹣2),C(﹣3,0),M是线段AB上的一个动点,连接CM,过点M作MN⊥MC交y轴于点N,若点M、N在直线y=kx+b上,则b的最大值是()A.B.C.﹣1 D.0解:当点M在AB上运动时,MN⊥MC交y轴于点N,此时点N在y轴的负半轴移动,定有△AMC∽△NBM;只要求出ON的最小值,也就是BN最大值时,就能确定点N的坐标,而直线y=kx+b与y轴交于点N(0,b),此时b的值最大,因此根据相似三角形的对应边成比例,设未知数构造二次函数,通过求二次函数的最值得以解决.连接AC,则四边形ABOC是矩形,∴∠A=∠ABO=90°,又∵MN⊥MC,∴∠CMN=90°,∴∠AMC=∠MNB,∴△AMC∽△NBM,∴,设BN=y,AM=x.则MB=3﹣x,ON=2﹣y,∴,即:y x2x∴当x时,y最大()2,∵直线y=kx+b与y轴交于N(0,b)当BN最大,此时ON最小,点N(0,b)越往上,b的值最大,∴ON=OB﹣BN=2,此时,N(0,)b的最大值为.故选:A.005(2019•通辽)如图,在边长为3的菱形ABCD中,∠A=60°,M是AD边上的一点,且AM AD,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C.则A′C长度的最小值是1.解:过点M作MH⊥CD,由勾股定理可求MC的长,由题意可得点A'在以M为圆心,AM为半径的圆上,则当点A'在线段MC上时,A'C长度有最小值.过点M作MH⊥CD交CD延长线于点H,连接CM,∵AM AD,AD=CD=3∴AM=1,MD=2∵CD∥AB,∴∠HDM=∠A=60°∴HD MD=1,HM HD∴CH=4∴MC∵将△AMN沿MN所在直线翻折得到△A′MN,∴AM=A'M=1,∴点A'在以M为圆心,AM为半径的圆上,∴当点A'在线段MC上时,A'C长度有最小值∴A'C长度的最小值=MC﹣MA' 1故答案为: 1006(2019•玉林)如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,点O是AB的三等分点,半圆O与AC相切,M,N分别是BC与半圆弧上的动点,则MN的最小值和最大值之和是()A.5 B.6 C.7 D.8解:设⊙O与AC相切于点D,连接OD,作OP⊥BC垂足为P交⊙O于F,此时垂线段OP最短,MN最小值为OP﹣OF,当N在AB边上时,M与B重合时,MN最大值1,由此不难解决问题.如图,设⊙O与AC相切于点D,连接OD,作OP⊥BC垂足为P交⊙O于F,此时垂线段OP最短,PF最小值为OP﹣OF,∵AC=4,BC=3,∴AB=5∵∠OPB=90°,∴OP∥AC∵点O是AB的三等分点,∴OB5,,∴OP,∵⊙O与AC相切于点D,∴OD⊥AC,∴OD∥BC,∴,∴OD=1,∴MN最小值为OP﹣OF1,如图,当N在AB边上时,M与B重合时,MN经过圆心,经过圆心的弦最长,MN最大值1,∴MN长的最大值与最小值的和是6.故选:B.007(2019•鸡西)如图,矩形ABCD中,AB=4,BC=6,点P是矩形ABCD内一动点,且S△P AB=S△PCD,则PC+PD的最小值为2.解:由于S△P AB=S△PCD,这两个三角形等底同高,可得点P在线段AD的垂直平分线上,根据最短路径问题,可得PC+PD=AC此时最小,有勾股定理可求结果.∵ABCD为矩形,∴AB=DC又∵S△P AB=S△PCD∴点P到AB的距离与到CD的距离相等,即点P线段AD垂直平分线MN上,连接AC,交MN与点P,此时PC+PD的值最小,且PC+PD=AC故答案为:2008(2019•鄂州)如图,在平面直角坐标系中,已知C(3,4),以点C为圆心的圆与y轴相切.点A、B在x轴上,且OA=OB.点P为⊙C上的动点,∠APB=90°,则AB长度的最大值为16.解:连接OC并延长,交⊙C上一点P,以O为圆心,以OP为半径作⊙O,交x轴于A、B,此时AB的长度最大,根据勾股定理和题意求得OP=8,则AB的最大长度为16.连接OC并延长,交⊙C上一点P,以O为圆心,以OP为半径作⊙O,交x轴于A、B,此时AB的长度最大,∵C(3,4),∴OC5,∵以点C为圆心的圆与y轴相切.∴⊙C的半径为3,∴OP=OA=OB=8,∵AB是直径,∴∠APB=90°,∴AB长度的最大值为16,故答案为16.009(2019•黄冈)如图,AC,BD在AB的同侧,AC=2,BD=8,AB=8,点M为AB的中点,若∠CMD=120°,则CD的最大值是14.解:如图,作点A关于CM的对称点A′,点B关于DM的对称点B′,证明△A′MB′为等边三角形,即可解决问题.如图,作点A关于CM的对称点A′,点B关于DM的对称点B′.∵∠CMD=120°,∴∠AMC+∠DMB=60°,∴∠CMA′+∠DMB′=60°,∴∠A′MB′=60°,∵MA′=MB′,∴△A′MB′为等边三角形∵CD≤CA′+A′B′+B′D=CA+AM+BD=2+4+8=14,∴CD的最大值为14,故答案为14.010(2019•黄石)如图,矩形ABCD中,AC与BD相交于点E,AD:AB:1,将△ABD 沿BD折叠,点A的对应点为F,连接AF交BC于点G,且BG=2,在AD边上有一点H,使得BH+EH的值最小,此时()A.B.C.D.解:设BD与AF交于点M.设AB=a,AD a,根据矩形的性质可得△ABE、△CDE 都是等边三角形,利用折叠的性质得到BM垂直平分AF,BF=AB=a,DF=DA a.解直角△BGM,求出BM,再表示DM,由△ADM∽△GBM,求出a=2,再证明CF=CD=2.作B点关于AD的对称点B′,连接B′E,设B′E与AD交于点H,则此时BH+EH=B′E,值最小.建立平面直角坐标系,得出B(3,2),B′(3,﹣2),E(0,),利用待定系数法求出直线B′E的解析式,得到H(1,0),然后利用两点间的距离公式求出BH=4,进而求出.如图,设BD与AF交于点M.设AB=a,AD a,∵四边形ABCD是矩形,∴∠DAB=90°,tan∠ABD,∴BD=AC2a,∠ABD=60°,∴△ABE、△CDE都是等边三角形,∴BE=DE=AE=CE=AB=CD=a.∵将△ABD沿BD折叠,点A的对应点为F,∴BM垂直平分AF,BF=AB=a,DF=DA a.在△BGM中,∵∠BMG=90°,∠GBM=30°,BG=2,∴GM BG=1,BM GM,∴DM=BD﹣BM=2a.∵矩形ABCD中,BC∥AD,∴△ADM∽△GBM,∴,即,∴a=2,∴BE=DE=AE=CE=AB=CD=2,AD=BC=6,BD=AC=4.易证∠BAF=∠F AC=∠CAD=∠ADB=∠BDF=∠CDF=30°,∴△ADF是等边三角形,∵AC平分∠DAF,∴AC垂直平分DF,∴CF=CD=2.作B点关于AD的对称点B′,连接B′E,设B′E与AD交于点H,则此时BH+EH=B′E,值最小.如图,建立平面直角坐标系,则A(3,0),B(3,2),B′(3,﹣2),E(0,),易求直线B′E的解析式为y x,∴H(1,0),∴BH4,∴.故选:B.011(2019•十堰)如图,正方形ABCD和Rt△AEF,AB=5,AE=AF=4,连接BF,DE.若△AEF绕点A旋转,当∠ABF最大时,S△ADE=6.解:作DH⊥AE于H,如图,由于AF=4,则△AEF绕点A旋转时,点F在以A为圆心,4为半径的圆上,当BF为此圆的切线时,∠ABF最大,即BF⊥AF,利用勾股定理计算出BF=3,接着证明△ADH≌△ABF得到DH=BF=3,然后根据三角形面积公式求解.作DH⊥AE于H,如图,∵AF=4,当△AEF绕点A旋转时,点F在以A为圆心,4为半径的圆上,∴当BF为此圆的切线时,∠ABF最大,即BF⊥AF,在Rt△ABF中,BF3,∵∠EAF=90°,∴∠BAF+∠BAH=90°,∵∠DAH+∠BAH=90°,∴∠DAH=∠BAF,在△ADH和△ABF中,∴△ADH≌△ABF(AAS),∴DH=BF=3,∴S△ADE AE•DH3×4=6.故答案为6.012(2019•武汉)问题背景:如图1,将△ABC绕点A逆时针旋转60°得到△ADE,DE与BC交于点P,可推出结论:P A+PC=PE.问题解决:如图2,在△MNG中,MN=6,∠M=75°,MG.点O是△MNG内一点,则点O到△MNG三个顶点的距离和的最小值是2.(1)在BC上截取BG=PD,通过三角形求得证得AG=AP,得出△AGP是等边三角形,得出∠AGC=60°=∠APG,即可求得∠APE=60°,连接EC,延长BC到F,使CF=P A,连接EF,证得△ACE是等边三角形,得出AE=EC=AC,然后通过证得△APE≌△ECF(SAS),得出PE=PF,即可证得结论;(2)以MG为边作等边三角形△MGD,以OM为边作等边△OME.连接ND,可证△GMO≌△DME,可得GO=DE,则MO+NO+GO=NO+OE+DE,即当D、E、O、N四点共线时,MO+NO+GO值最小,最小值为ND的长度,根据勾股定理先求得MF、DF,然后求ND的长度,即可求MO+NO+GO的最小值.(1)证明:如图1,在BC上截取BG=PD,在△ABG和△ADP中,∴△ABG≌△ADP(SAS),∴AG=AP,∠BAG=∠DAP,∵∠GAP=∠BAD=60°,∴△AGP是等边三角形,∴∠AGC=60°=∠APG,∴∠APE=60°,∴∠EPC=60°,连接EC,延长BC到F,使CF=P A,连接EF,∵将△ABC绕点A逆时针旋转60°得到△ADE,∴∠EAC=60°,∠EPC=60°,∵AE=AC,∴△ACE是等边三角形,∴AE=EC=AC,∵∠P AE+∠APE+∠AEP=180°,∠ECF+∠ACE+∠ACB=180°,∠ACE=∠APE=60°,∠AED=∠ACB,∴∠P AE=∠ECF,在△APE和△ECF中∴△APE≌△ECF(SAS),∴PE=PF,∴P A+PC=PE;(2)解:如图2:以MG为边作等边三角形△MGD,以OM为边作等边△OME.连接ND,作DF⊥NM,交NM的延长线于F.∵△MGD和△OME是等边三角形∴OE=OM=ME,∠DMG=∠OME=60°,MG=MD,∴∠GMO=∠DME在△GMO和△DME中∴△GMO≌△DME(SAS),∴OG=DE∴NO+GO+MO=DE+OE+NO∴当D、E、O、M四点共线时,NO+GO+MO值最小,∵∠NMG=75°,∠GMD=60°,∴∠NMD=135°,∴∠DMF=45°,∵MG.∴MF=DF=4,∴NF=MN+MF=6+4=10,∴ND2,∴MO+NO+GO最小值为2,故答案为2,013(2019•长沙)如图,△ABC中,AB=AC=10,tan A=2,BE⊥AC于点E,D是线段BE 上的一个动点,则CD BD的最小值是()A.2B.4C.5D.10解:如图,作DH⊥AB于H,CM⊥AB于M.由tan A2,设AE=a,BE=2a,利用勾股定理构建方程求出a,再证明DH BD,推出CD BD=CD+DH,由垂线段最短即可解决问题.如图,作DH⊥AB于H,CM⊥AB于M.∵BE⊥AC,∴∠AEB=90°,∵tan A2,设AE=a,BE=2a,则有:100=a2+4a2,∴a2=20,∴a=2或﹣2(舍弃),∴BE=2a=4,∵AB=AC,BE⊥AC,CM⊥AB,∴CM=BE=4(等腰三角形两腰上的高相等))∵∠DBH=∠ABE,∠BHD=∠BEA,∴sin∠DBH,∴DH BD,∴CD BD=CD+DH,∴CD+DH≥CM,∴CD BD≥4,∴CD BD的最小值为4.故选:B.014(2019•连云港)如图,在矩形ABCD中,AB=4,AD=3,以点C为圆心作⊙C与直线BD相切,点P是⊙C上一个动点,连接AP交BD于点T,则的最大值是3.方法1、过点A作BD的垂线AG,AG为定值;过点P作BD的垂线PE,只要PE最大即可,进而求出PE最大,即可得出结论;方法2、先判断出最大时,BE最大,再用相似三角形的性质求出BG,HG,CH,进而判断出HM最大时,BE最大,而点M在⊙C上时,HM最大,即可HP',即可得出结论.方法1、解:如图,过点A作AG⊥BD于G,∵BD是矩形的对角线,∴∠BAD=90°,∴BD5,∵AB•AD BD•AG,∴AG,∵BD是⊙C的切线,∴⊙C的半径为过点P作PE⊥BD于E,∴∠AGT=∠PET,∵∠ATG=∠PTE,∴△AGT∽△PET,∴,∴PE∵1,要最大,则PE最大,∵点P是⊙C上的动点,BD是⊙C的切线,∴PE最大为⊙C的直径,即:PE最大,∴最大值为13,故答案为3.方法2、解:如图,过点P作PE∥BD交AB的延长线于E,∴∠AEP=∠ABD,△APE∽△ATB,∴,∵AB=4,∴AE=AB+BE=4+BE,∴,∴BE最大时,最大,∵四边形ABCD是矩形,∴BC=AD=3,CD=AB=4,过点C作CH⊥BD于H,交PE于M,并延长交AB于G,∵BD是⊙C的切线,∴∠GME=90°,在Rt△BCD中,BD5,∵∠BHC=∠BCD=90°,∠CBH=∠DBC,∴△BHC∽△BCD,∴,∴,∴BH,CH,∵∠BHG=∠BAD=90°,∠GBH=∠DBA,∴△BHG∽△BAD,∴,∴,∴HG,BG,在Rt△GME中,GM=EG•sin∠AEP=EG EG,而BE=GE﹣BG=GE,∴GE最大时,BE最大,∴GM最大时,BE最大,∵GM=HG+HM HM,即:HM最大时,BE最大,延长MC交⊙C于P',此时,HM最大=HP'=2CH,∴GP'=HP'+HG,过点P'作P'F∥BD交AB的延长线于F,∴BE最大时,点E落在点F处,即:BE最大=BF,在Rt△GP'F中,FG,∴BF=FG﹣BG=8,∴最大值为13,故答案为:3.015(2019•无锡)如图,在△ABC中,AB=AC=5,BC=4,D为边AB上一动点(B点除外),以CD为一边作正方形CDEF,连接BE,则△BDE面积的最大值为8.解:过点C作CG⊥BA于点G,作EH⊥AB于点H,作AM⊥BC于点M.由AB=AC=5,BC=4,得到BM=CM=2,易证△AMB∽△CGB,求得GB=8,设BD=x,则DG=8﹣x,易证△EDH≌△DCG,EH=DG=8﹣x,所以S△BDE,当x=4时,△BDE面积的最大值为8.过点C作CG⊥BA于点G,作EH⊥AB于点H,作AM⊥BC于点M.∵AB=AC=5,BC=4,∴BM=CM=2,易证△AMB∽△CGB,∴,即∴GB=8,设BD=x,则DG=8﹣x,易证△EDH≌△DCG(AAS),∴EH=DG=8﹣x,∴S△BDE,当x=4时,△BDE面积的最大值为8.故答案为8.016(2019•宿迁)如图,正方形ABCD的边长为4,E为BC上一点,且BE=1,F为AB 边上的一个动点,连接EF,以EF为边向右侧作等边△EFG,连接CG,则CG的最小值为.解:由题意分析可知,点F为主动点,G为从动点,所以以点E为旋转中心构造全等关系,得到点G的运动轨迹,之后通过垂线段最短构造直角三角形获得CG最小值.由题意可知,点F是主动点,点G是从动点,点F在线段上运动,点G也一定在直线轨迹上运动将△EFB绕点E旋转60°,使EF与EG重合,得到△EFB≌△EHG从而可知△EBH为等边三角形,点G在垂直于HE的直线HN上作CM⊥HN,则CM即为CG的最小值作EP⊥CM,可知四边形HEPM为矩形,则CM=MP+CP=HE EC=1故答案为.017(2019•镇江)已知抛物线y=ax2+4ax+4a+1(a≠0)过点A(m,3),B(n,3)两点,若线段AB的长不大于4,则代数式a2+a+1的最小值是.解:根据题意得4a+1≥3,解不等式求得a,把x代入代数式即可求得.∵抛物线y=ax2+4ax+4a+1(a≠0)过点A(m,3),B(n,3)两点,∴ 2∵线段AB的长不大于4,∴4a+1≥3∴a∴a2+a+1的最小值为:()21;故答案为.018(2019•镇江)如图,菱形ABCD的顶点B、C在x轴上(B在C的左侧),顶点A、D 在x轴上方,对角线BD的长是,点E(﹣2,0)为BC的中点,点P在菱形ABCD的边上运动.当点F(0,6)到EP所在直线的距离取得最大值时,点P恰好落在AB的中点处,则菱形ABCD的边长等于()A.B.C.D.3解:如图1中,当点P是AB的中点时,作FG⊥PE于G,连接EF.首先说明点G与点F重合时,FG的值最大,如图2中,当点G与点E重合时,连接AC交BD于H,PE 交BD于J.设BC=2a.利用相似三角形的性质构建方程求解即可.如图1中,当点P是AB的中点时,作FG⊥PE于G,连接EF.∵E(﹣2,0),F(0,6),∴OE=2,OF=6,∴EF2,∵∠FGE=90°,∴FG≤EF,∴当点G与E重合时,FG的值最大.如图2中,当点G与点E重合时,连接AC交BD于H,PE交BD于J.设BC=2a.∵P A=PB,BE=EC=a,∴PE∥AC,BJ=JH,∵四边形ABCD是菱形,∴AC⊥BD,BH=DH,BJ,∴PE⊥BD,∵∠BJE=∠EOF=∠PEF=90°,∴∠EBJ=∠FEO,∴△BJE∽△EOF,∴,∴,∴a,∴BC=2a,故选:A.019(2019•东营)如图所示是一个几何体的三视图,如果一只蚂蚁从这个几何体的点B出发,沿表面爬到AC的中点D处,则最短路线长为()A.3B.C.3 D.3解:将圆锥的侧面展开,设顶点为B',连接BB',AE.线段AC与BB'的交点为F,线段BF是最短路程.如图将圆锥侧面展开,得到扇形ABB′,则线段BF为所求的最短路程.设∠BAB′=n°.∵4π,∴n=120即∠BAB′=120°.∵E为弧BB′中点,∴∠AFB=90°,∠BAF=60°,∴BF=AB•sin∠BAF=63,∴最短路线长为3.故选:D.020(2019•东营)如图,AC是⊙O的弦,AC=5,点B是⊙O上的一个动点,且∠ABC=45°,若点M、N分别是AC、BC的中点,则MN的最大值是.解:根据中位线定理得到MN的长最大时,AB最大,当AB最大时是直径,从而求得直径后就可以求得最大值.∵点M,N分别是BC,AC的中点,∴MN AB,∴当AB取得最大值时,MN就取得最大值,当AB是直径时,AB最大,连接AO并延长交⊙O于点B′,连接CB′,∵AB′是⊙O的直径,∴∠ACB′=90°.∵∠ABC=45°,AC=5,∴∠AB′C=45°,∴AB′5,∴MN最大.故答案为:.021(2019•聊城)如图,在Rt△ABO中,∠OBA=90°,A(4,4),点C在边AB上,且,点D为OB的中点,点P为边OA上的动点,当点P在OA上移动时,使四边形PDBC 周长最小的点P的坐标为()A.(2,2)B.(,)C.(,)D.(3,3)解:根据已知条件得到AB=OB=4,∠AOB=45°,求得BC=3,OD=BD=2,得到D (0,2),C(4,3),作D关于直线OA的对称点E,连接EC交OA于P,则此时,四边形PDBC周长最小,E(0,2),求得直线EC的解析式为y x+2,解方程组即可得到结论.∵在Rt△ABO中,∠OBA=90°,A(4,4),∴AB=OB=4,∠AOB=45°,∵,点D为OB的中点,∴BC=3,OD=BD=2,∴D(0,2),C(4,3),作D关于直线OA的对称点E,连接EC交OA于P,则此时,四边形PDBC周长最小,E(0,2),∵直线OA的解析式为y=x,设直线EC的解析式为y=kx+b,∴,解得:,∴直线EC的解析式为y x+2,解得,,∴P(,),故选:C.022(2019•泰安)如图,矩形ABCD中,AB=4,AD=2,E为AB的中点,F为EC上一动点,P为DF中点,连接PB,则PB的最小值是()A.2 B.4 C.D.解:根据中位线定理可得出点点P的运动轨迹是线段P1P2,再根据垂线段最短可得当BP ⊥P1P2时,PB取得最小值;由矩形的性质以及已知的数据即可知BP1⊥P1P2,故BP的最小值为BP1的长,由勾股定理求解即可.如图:当点F与点C重合时,点P在P1处,CP1=DP1,当点F与点E重合时,点P在P2处,EP2=DP2,∴P1P2∥CE且P1P2CE当点F在EC上除点C、E的位置处时,有DP=FP由中位线定理可知:P1P∥CE且P1P CF∴点P的运动轨迹是线段P1P2,∴当BP⊥P1P2时,PB取得最小值∵矩形ABCD中,AB=4,AD=2,E为AB的中点,∴△CBE、△ADE、△BCP1为等腰直角三角形,CP1=2∴∠ADE=∠CDE=∠CP1B=45°,∠DEC=90°∴∠DP2P1=90°∴∠DP1P2=45°∴∠P2P1B=90°,即BP1⊥P1P2,∴BP的最小值为BP1的长在等腰直角BCP1中,CP1=BC=2∴BP1=2∴PB的最小值是2故选:D.023(2019•威海)如图,在平面直角坐标系中,点A,B在反比例函数y(k≠0)的图象上运动,且始终保持线段AB=4的长度不变.M为线段AB的中点,连接OM.则线段OM长度的最小值是(用含k的代数式表示).解:如图,当OM⊥AB时,线段OM长度的最小.首先证明点A与点B关于直线y=x 对称,因为点A,B在反比例函数y(k≠0)的图象上,AB=4,所以可以假设A(m,),则B(m+4,4),则有,解得k=m2+4m,推出A(m,m+4),B(m+4,m),可得M(m+2,m+2),求出OM即可解决问题.如图,当OM⊥AB时,线段OM长度的最小,∵M为线段AB的中点,∴OA=OB,∵点A,B在反比例函数y(k≠0)的图象上,∴点A与点B关于直线y=x对称,∵AB=4,∴可以假设A(m,),则B(m+4,4),∴,解得k=m2+4m,∴A(m,m+4),B(m+4,m),∴M(m+2,m+2),∴OM,∴OM的最小值为.故答案为.024(2019•潍坊)如图,直线y=x+1与抛物线y=x2﹣4x+5交于A,B两点,点P是y轴上的一个动点,当△P AB的周长最小时,S△P AB=.解:根据轴对称,可以求得使得△P AB的周长最小时点P的坐标,然后求出点P到直线AB的距离和AB的长度,即可求得△P AB的面积,本题得以解决.,解得,或,∴点A的坐标为(1,2),点B的坐标为(4,5),∴AB3,作点A关于y轴的对称点A′,连接A′B与y轴的交于P,则此时△P AB的周长最小,点A′的坐标为(﹣1,2),点B的坐标为(4,5),设直线A′B的函数解析式为y=kx+b,,得,∴直线A′B的函数解析式为y x,当x=0时,y,即点P的坐标为(0,),将x=0代入直线y=x+1中,得y=1,∵直线y=x+1与y轴的夹角是45°,∴点P到直线AB的距离是:(1)×sin45°,∴△P AB的面积是:,故答案为:.025(2019•成都)如图,在边长为1的菱形ABCD中,∠ABC=60°,将△ABD沿射线BD 的方向平移得到△A'B'D',分别连接A'C,A'D,B'C,则A'C+B'C的最小值为.解:根据菱形的性质得到AB=1,∠ABD=30°,根据平移的性质得到A′B′=AB=1,∠A′B′D=30°,当B′C⊥A′B′时,A'C+B'C的值最小,推出四边形A′B′CD是矩形,∠B′A′C=30°,解直角三角形即可得到结论.∵在边长为1的菱形ABCD中,∠ABC=60°,∴AB=1,∠ABD=30°,∵将△ABD沿射线BD的方向平移得到△A'B'D',∴A′B′=AB=1,∠A′B′D=30°,当B′C⊥A′B′时,A'C+B'C的值最小,∵AB∥A′B′,AB=A′B′,AB=CD,AB∥CD,∴A′B′=CD,A′B′∥CD,∴四边形A′B′CD是矩形,∠B′A′C=30°,∴B′C,A′C,∴A'C+B'C的最小值为,故答案为:.026(2019•广元)如图,△ABC是⊙O的内接三角形,且AB是⊙O的直径,点P为⊙O上的动点,且∠BPC=60°,⊙O的半径为6,则点P到AC距离的最大值是6+3.解:过O作OM⊥AC于M,延长MO交⊙O于P,则此时,点P到AC距离的最大,且点P到AC距离的最大值=PM,解直角三角形即可得到结论.过O作OM⊥AC于M,延长MO交⊙O于P,则此时,点P到AC距离的最大,且点P到AC距离的最大值=PM,∵OM⊥AC,∠A=∠BPC=60°,⊙O的半径为6,∴OP=OA=6,∴OM OA6=3,∴PM=OP+OM=6+3,∴则点P到AC距离的最大值是6+3,故答案为:6+3.027(2019•乐山)如图,抛物线y x2﹣4与x轴交于A、B两点,P是以点C(0,3)为圆心,2为半径的圆上的动点,Q是线段P A的中点,连结OQ.则线段OQ的最大值是()A.3 B.C.D.4解:连接BP,如图,先解方程x2﹣4=0得A(﹣4,0),B(4,0),再判断OQ为△ABP 的中位线得到OQ BP,利用点与圆的位置关系,BP过圆心C时,PB最大,如图,点P运动到P′位置时,BP最大,然后计算出BP′即可得到线段OQ的最大值.连接BP,如图,当y=0时,x2﹣4=0,解得x1=4,x2=﹣4,则A(﹣4,0),B(4,0),∵Q是线段P A的中点,∴OQ为△ABP的中位线,∴OQ BP,当BP最大时,OQ最大,而BP过圆心C时,PB最大,如图,点P运动到P′位置时,BP最大,∵BC5,∴BP′=5+2=7,∴线段OQ的最大值是.故选:C.028(2019•凉山州)如图,正方形ABCD中,AB=12,AE AB,点P在BC上运动(不与B、C重合),过点P作PQ⊥EP,交CD于点Q,则CQ的最大值为4.解:先证明△BPE∽△CQP,得到与CQ有关的比例式,设CQ=y,BP=x,则CP=12﹣x,代入解析式,得到y与x的二次函数式,根据二次函数的性质可求最值.∵∠BEP+∠BPE=90°,∠QPC+∠BPE=90°,∴∠BEP=∠CPQ.又∠B=∠C=90°,∴△BPE∽△CQP.∴.设CQ=y,BP=x,则CP=12﹣x.∴,化简得y(x2﹣12x),整理得y(x﹣6)2+4,所以当x=6时,y有最大值为4.故答案为4.029(2019•眉山)如图,在Rt△AOB中,OA=OB=4.⊙O的半径为2,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则线段PQ长的最小值为2.解:首先连接OQ,根据勾股定理知PQ2=OP2﹣OQ2,可得当OP⊥AB时,即线段PQ 最短,然后由勾股定理即可求得答案.连接OQ.∵PQ是⊙O的切线,∴OQ⊥PQ;根据勾股定理知PQ2=OP2﹣OQ2,∴当PO⊥AB时,线段PQ最短,∵在Rt△AOB中,OA=OB=4,∴AB OA=8,∴OP4,∴PQ2.故答案为2.030(2019•内江)若x、y、z为实数,且,则代数式x2﹣3y2+z2的最大值是26.解:解三元一次方程组,用z表示出x、y,根利用配方法计算即可.,①﹣②得,y=1+z,把y=1+z代入①得,x=2﹣z,则x2﹣3y2+z2=(2﹣z)2﹣3(1+z)2+z2=﹣z2﹣10z+1=﹣(z+5)2+26,当z=﹣5时,x2﹣3y2+z2的最大值是26,故答案为:26.031(2019•自贡)如图,已知A、B两点的坐标分别为(8,0)、(0,8),点C、F分别是直线x=﹣5和x轴上的动点,CF=10,点D是线段CF的中点,连接AD交y轴于点E,当△ABE面积取得最小值时,tan∠BAD的值是()A.B.C.D.解:如图,设直线x=﹣5交x轴于K.由题意KD CF=5,推出点D的运动轨迹是以K为圆心,5为半径的圆,推出当直线AD与⊙K相切时,△ABE的面积最小,作EH⊥AB于H.求出EH,AH即可解决问题.如图,设直线x=﹣5交x轴于K.由题意KD CF=5,∴点D的运动轨迹是以K为圆心,5为半径的圆,∴当直线AD与⊙K相切时,△ABE的面积最小,∵AD是切线,点D是切点,∴AD⊥KD,∵AK=13,DK=5,∴AD=12,∵tan∠EAO,∴,∴OE,∴AE,作EH⊥AB于H.∵S△ABE•AB•EH=S△AOB﹣S△AOE,∴EH,∴AH,∴tan∠BAD,故选:B.。
动点的函数图象问题(压轴题专项讲练)—2024-2025学年九年级数学上册压轴题专项(沪科版原卷版)

动点的函数图象问题数形结合思想:所谓数形结合,就是根据数与形之间的对应关系,通过数与形的相互转化来解决数学问题的思想,实现数形结合,常与以下内容有关:(1)实数与数轴上的点的对应关系;(2)函数与图象的对应关系;(3所给的等式或代数式的结构含有明显的几何意义。
【典例1】如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD=2,CD⊥AB于点D,点E、F、G分别是边CD、CA、AD的中点,连接EF、FG,动点M从点B出发,以每秒2个单位长度的速度向点A方向运动(点M运动到AB的中点时停止);过点M作直线MP∥BC与线段AC交于点P,以PM为斜边作Rt△PMN,点N在AB 上,设运动的时间为t(s),Rt△PMN与矩形DEFG重叠部分的面积为S,则S与t之间的函数关系图象大致为()A.B.C.D.本题考查几何动点问题的函数图象,正确分段并分析是解题的关键.根据题意先分段,分为0≤t≤0.5,0.5<t≤1,1<t≤2三段,分别列出三段的函数解析式便可解决,本题也可只列出0≤t≤0.5,1<t≤2两段,用排除法解决.解:分析平移过程,①从开始出发至PM与点E重合,由题意可知0≤t≤0.5,如图,则BM=2t,过点M作MT⊥BC于点T,∵∠B=60°,CD⊥AB,∴BC=2BD=4,CD==BT=12BM=t,∵∠ACB=90°,MP∥BC,∴∠ACB=∠MPA=90°,∴四边形CTMP为矩形,∴PM=CT=BC―BT=4―t,∵∠PMN=∠B=60°,PN⊥AB,∴MN=PM2=4―t2,∴DN=MN―MD=MN―BD+BM=3t2,∵E为CD中点,∴DE=CD2=∴S=DE⋅DN=∴S与t的函数关系是正比例函数;②当0.5<t≤1,即从PM与E重合至点M与点D重合,如图,由①可得QN=ED=DM=2―2t,DN=32t,S矩形EDNQ=∵∠PMN=∠B=60°,CD⊥AB,∴SD==,∴ES=ED―SD=∴ER ==2t ―1,∴S =S 矩形EDNQ ―S △ERS =12(2―2t ―1)=―2+此函数图象是开口向下的二次函数;③当1<t ≤2,即从点M 与点D 重合至点M 到达终点,如图,由①可得DN =32t ,MN =4―t 2,∵AD ==6, DG =12AD =3,∴NG =DG ―DN =3―32t ,∴QF =NG =3―32t ,∴PQ==,∴HQ ==1―12t ,∴S =(HQ+MN )×QN 2==―∴S 与t 的函数关系是一次函数,综上,只有选项A 的图象符合,故选:A .1.(2024·四川广元·二模)如图,在矩形ABCD 中,AB =4cm ,AD =2cm ,动点M 自点A 出发沿AB 方向以每秒1cm 的速度向点 B 运动,同时动点N 自点A 出发沿折线AD -DC -CB 以每秒2cm 的速度运动,到达点B 时运动同时停止.设△AMN的面积为y (cm2),运动时间为x (秒),则下列图象中能大致反映y 与x 之间的函数关系的是( )A .B .C .D .2.(22-23九年级上·安徽合肥·期中)如图,在△ABC 中,∠C =135°,AC =BC =P 为BC 边上一动点,PQ∥AB 交AC 于点Q ,连接BQ ,设PB =x ,S △BPQ =y ,则能表示y 与x 之间的函数关系的图象大致是( )A .B .C .D .3.(2024·河北石家庄·二模)如图所示,△ABC 和△DEF 均为边长为4的等边三角形,点A 从点D 运动到点E 的过程中,AB 和DF 相交于点G ,AC 和EF 相交于点H ,(S △BGF +S △FCH )为纵坐标y ,点A 移动的距离为横坐标x ,则y 与x 关系的图象大致为( )A.B.C.D.4.(2023·辽宁铁岭·模拟预测)如图,矩形ABCD中,AB=8cm,AD=12cm,AC与BD交于点O,M是BC 的中点.P、Q两点沿着B→C→D方向分别从点B、点M同时出发,并都以1cm/s的速度运动,当点Q到达D点时,两点同时停止运动.在P、Q△OPQ的面积随时间t变化的图象最接近的是()A.B.C.D.5.(2023·江苏南通·模拟预测)如图,在矩形ABCD中,AB=4,BC=6,E为AB中点,动点P从点B开始沿BC方向运动到点C停止,动点Q从点C开始沿CD→DA方向运动,与点P同时出发,同时停止;这两点的运动速度均为每秒1个单位;若设他们的运动时间为x(s),△EPQ的面积为y,则y与x之间的函数关系的图像大致是()A.B.C.D.6.(2024·河南开封·一模)如图1,在△ABC中,∠B=60°,点D从点B出发,沿BC运动,速度为1cm/s.点P在折线BAC上,且PD⊥BC于点D.点D运动2s时,点P与点A重合.△PBD的面积S(cm2)与运动时间t(s)的函数关系图象如图2所示,E是函数图象的最高点.当S(cm2)取最大值时,PD的长为()A.B.(1+cm C.(1+cm D.(2+cm7.(2024·安徽·一模)如图,在四边形ABCD中,∠A=60°,CD⊥AD,∠BCD=90°,AB=BC=4,动点P,Q同时从A点出发,点Q以每秒2个单位长度沿折线A―B―C向终点C运动;点P以每秒1个单位长度沿线段AD向终点D运动,当其中一点运动至终点时,另一点随之停止运动.设运动时间为x秒,△APQ的面积为y 个平方单位,则y随x变化的函数图象大致为()A.B.C.D.8.(23-24九年级上·浙江温州·期末)某兴趣小组开展综合实践活动:在Rt△ABC中,∠C=90°,CD=,D为AC上一点,动点P以每秒1个单位的速度从C点出发,在三角形边上沿C→B→A匀速运动,到达点A时停止,以DP为边作正方形DPEF,设点P的运动时间为t s,正方形DPEF的面积为S,当点P由点C运动到点A 时,经探究发现S是关于t的二次函数,并绘制成如图2所示的图象,若存在3个时刻t1,t2,t3(t1<t2<t3)对应的正方形DPEF的面积均相等,当t3=5t1时,则正方形DPEF的面积为()C.4D.5A.3B.3499.(22-23九年级上·浙江嘉兴·期中)如图,在Rt △ABC 中,∠C =90°,∠ABC =60°,BC =6,点O 为AC 中点,点D 为线段AB 上的动点,连接OD ,设BD =x ,OD 2=y ,则y 与x 之间的函数关系图像大致为( )A .B .C .D .10.(2024·广东深圳·三模)如图,在Rt △ABC 中,∠C =90°,AC =12,BC =8,点D 和点E 分别是AB 和AC 的中点,点M 和点N 分别从点A 出发,沿着A→C→B 方向运动,运动速度都是1个单位/秒,当点N 到达点B 时,两点间时停止运动.设△DMN 的面积为S ,运动时间为t ,则S 与t 之间的函数图象大致为( )A .B .C.D.11.(2024·河南南阳·二模)如图是一种轨道示意图,其中A、B、C、D分别是菱形的四个顶点,∠A=60°.现有两个机器人(看成点)分别从A,C两点同时出发,沿着轨道以相同的速度匀速移动,其路线分别为A→B→C和C→D→A.若移动时间为t,两个机器人之间距离为d.则d²与t之间的函数关系用图象表示大致为()A.B.C.D.12.(2024·山东聊城·二模)如图,等边△ABC与矩形DEFG在同一直角坐标系中,现将等边△ABC按箭头所指的方向水平移动,平移距离为x,点C到达点F为止,等边△ABC与矩形DEFG重合部分的面积记为S,则S关于x的函数图象大致为()A.B.C.D.13.(2024·河南·模拟预测)如图,在等腰直角三角形ABC中,∠ABC=90°,BD是AC边上的中线,将△BCD 沿射线BA方向匀速平移,平移后的三角形记为△B1C1D1,设△B1C1D1与△ABD重叠部分的面积为y,平移距离为x,当点B1与点A重合时,△B1C1D1停止运动,则下列图象最符合y与x之间函数关系的是()A.B.C.D.14.(23-24九年级上·安徽滁州·期末)如图,菱形ABCD的边长为3cm,∠B=60°,动点P从点B出发以3cm/ s的速度沿着边BC―CD―DA运动,到达点A后停止运动;同时动点Q从点B出发,以1cm/s的速度沿着边BA 向A点运动,到达点A后停止运动.设点P的运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象为()A.B.C.D.15.(2023·辽宁盘锦·中考真题)如图,在平面直角坐标系中,菱形ABCD的顶点A在y轴的正半轴上,顶点B、C在x轴的正半轴上,D,P(―1,―1).点M在菱形的边AD和DC上运动(不与点A,C重合),过点M作MN∥y轴,与菱形的另一边交于点N,连接PM,PN,设点M的横坐标为x,△PMN的面积为y,则下列图象能正确反映y与x之间函数关系的是()A.B.C.D.16.(22-23九年级上·安徽蚌埠·期末)如图,在平面直角坐标系中,点A(2,0),点B,点C(―,点P从点O出发沿O→A→B路线以每秒1个单位的速度运动,点Q从点O出发沿O→C→B的速度运动,当一个点到达终点时另一个点随之停止运动,设y=PQ2,运动时间为t秒,则正确表达y与t的关系图象是()A.B.C.D.17.(2022·辽宁·中考真题)如图,在等边三角形ABC中,BC=4,在Rt△DEF中,∠EDF=90°,∠F=30°,DE=4,点B,C,D,E在一条直线上,点C,D重合,△ABC沿射线DE方向运动,当点B与点E 重合时停止运动.设△ABC运动的路程为x,△ABC与Rt△DEF重叠部分的面积为S,则能反映S与x之间函数关系的图象是( )A.B.C.D.18.(2023·山东聊城·三模)如图(1)所示,E 为矩形ABCD 的边AD 上一点,动点P ,Q 同时从点B 出发,点P 沿折线BE ―ED ―DC 运动到点C 时停止,点Q 沿BC 运动到点C 时停止,它们运动的速度都是1cm/秒,设P ,Q 同时出发t 秒时,△BPQ 的面积为y cm 2.已知y 与t 的函数关系图像如图(2)(曲线OM 为抛物线的一部分),则下列结论不正确的是( )A .AB:AD =4:5B .当t =2.5秒时,PQ =C .当t =294时,BQ PQ =53D .当△BPQ 的面积为4cm 2时,t 或475秒19.(2023·辽宁·中考真题)如图,∠MAN =60°,在射线AM ,AN 上分别截取AC =AB =6,连接BC ,∠MAN 的平分线交BC 于点D ,点E 为线段AB 上的动点,作EF ⊥AM 交AM 于点F ,作EG∥AM 交射线AD 于点G ,过点G 作GH ⊥AM 于点H ,点E 沿E 与点B 重合时停止运动.设点E 运动的路程为x ,四边形EFHG 与△ABC 重叠部分的面积为S ,则能大致反映S 与x 之间函数关系的图象是( )A .B .C .D .20.(22-23九年级上·安徽滁州·期末)如图,在平面直角坐标系中,菱形ABCD的边长为4,且点A与原点O 重合,边AD在x轴上,点B的横坐标为―2,现将菱形ABCD沿x轴以每秒1个单位长度的速度向右平移,设平移时间为t(秒),菱形ABCD位于y轴右侧部分的面积为S,则S关于t的函数图像大致为()A.B.C.D.。
专题05 几何图形初步(广东专版)-2019年中考真题数学试题分项汇编(解析版)

专题05 几何图形初步1.(2019•深圳)如图,已知l1∥AB,AC为角平分线,下列说法错误的是A.∠1=∠4 B.∠1=∠5C.∠2=∠3 D.∠1=∠3【答案】B【解析】∵l1∥AB,∴∠2=∠4,∠3=∠2,∠5=∠1+∠2,∵AC为角平分线,∴∠1=∠2=∠4=∠3,∠5=2∠1.故选B.【名师点睛】本题考查了平行线的性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.2.(2019年广东省湛江市霞山区中考数学一模试卷)如果一个角的余角是50°,那么这个角的度数是A.30°B.40°C.50°D.130°【答案】B【解析】设这个角为x°,由题意得:90-x=50,解得:x=40,故选B.【名师点睛】此题考查了余角的定义,难度不大.3.(广东省汕头市金平区三区2018-2019届九年级中考模拟考试数学试题)如图,直角三角板的直角顶点A在直线上,则∠1与∠2A.一定相等B.一定互余C.一定互补D.始终相差10°【答案】B【解析】如图,三角板的直角顶点在直线l上,则∠1+∠2=180°-90°=90°.故选B.【名师点睛】此题考查了余角和补角的性质,难度不大.4.(广东省湛江市四校2019届中考模拟二数学试题)已知∠α=140°-5m,∠β=5m-50°,∠α和∠β关系一定成立的是A.互余B.互补C.∠α=∠βD.∠α=2∠β【答案】A【解析】∵∠α=140°-5m,∠β=5m-50°,140°-5m+5m-50°=90°,∴∠α,∠β的关系是互余.故选A.【名师点睛】本题考查了互余角的数量关系.熟记互为余角的两个角的和为90°是解题的关键.5.(2019年广东省深圳市福田区中考数学三模试卷)如图,直线l1∥l2,且分别与直线l交于C、D两点,把一块含30°角的三角尺按如图所示的位置摆放,若∠1=53°,则∠2的度数是A .93°B .97°C .103°D .107°【答案】B【解析】如图,∵l 1∥l 2,∴∠1=∠3=53°,又∵∠4=30°,∴∠2=180°-∠3-∠4=180°-53°-30°=97°, 故选B .【名师点睛】此题主要考查了平行线的性质,三角板的特征,角度的计算,熟练掌握是解题的关键. 6.(广东省中山市第一中学2019届九年级5月质量调研检测数学试题)如图,直线a b ∥,点B 在直线b 上,且AB BC ⊥,155∠=︒,则2∠的度数为A .35︒B .45︒C .55︒D .65︒【答案】A【解析】如图,∵AB⊥BC,∴∠ABC=90°,∵直线a∥b,∠1=55°,∴∠3=∠1=55°,∴∠2=180°-90°-55°=35°,故选A.【名师点睛】此题考查平行线的性质,难度不大.7.(2019年广东省佛山市顺德区中考数学三模试卷)如图,直线a∥b,∠2=35°,∠3=40°,则∠1的度数是A.75°B.105°C.140°D.145°【答案】B【解析】如图,∵a∥b,∴∠1=∠4,又∵∠2=35°,∠3=40°,∴∠4=180°-35°-40°=105°,∴∠1=105°,故选B.【名师点睛】本题考查了平行线的性质和三角形内角和定理,熟练掌握性质定理是解题的关键.8.(2019·广东华南师大附中初一中考模拟)如图,点E在BC的延长线上,则下列条件中,能判定AD平行于BC的是A.∠1=∠2 B.∠3=∠4C.∠D+∠DAB=180°D.∠B=∠DCE【答案】B【解析】∵∠3=∠4(已知),∴AD∥BC(内错角相等,两直线平行).故选B.【名师点睛】此题考查了平行线的判定,平行线的判定方法有:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.9.(2019·广东华南师大附中初一中考模拟)如图,下列说法错误的是A.∠A与∠B是同旁内角B.∠1与∠3是同位角C.∠2与∠A是同位角D.∠2与∠3是内错角【答案】B【解析】由图可知:∠1与∠3是同旁内角,故B说法错误,故选B.【名师点睛】本题考查了同旁内角、同位角、内错角,根据同位角、内错角、同旁内角的意义是解题关键.10.(2019年广东省深圳市二十三校联考中考数学模拟试卷)如图,直线a∥b.将一直角三角形的直角顶点置于直线b上,若∠1=28°,则∠2的度数是A.108°B.118°C.128°D.152°【答案】B【解析】如图,∵AB∥CD,∠CBE=90°,∴∠2=∠ABC=∠1+∠CBE=28°+90°=118°,故选B.【名师点睛】掌握平行线的性质是解题的关键.11.(2019年广东省深圳市福田区中考数学一模试卷)如图,已知a∥b,点A在直线a上,点B、C在直线b上,∠1=120°,∠2=50°,则∠3为A.70°B.60°C.45°D.30°【答案】A【解析】∵a∥b,∠1=120°,∴∠ACD=120°,∵∠2=50°,∴∠3=120°-50°=70°,故选A.【名师点睛】本题考查平行线的性质,三角形的外角等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.12.(2019年广东省汕头市潮南区两英镇中考数学模拟试卷)如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠2=42°,则∠1=A.48°B.42°C.40°D.45°【答案】A【解析】如图,∵∠2=42°,∴∠3=90°-∠2=48°,∴∠1=48°.故选A.【名师点睛】考查了平行线的性质.两直线平行,同位角相等的应用是解此题的关键.13.(2019•广东)如图,已知a∥b,∠1=75°,则∠2=__________.【答案】105°【解析】∵直线L直线a,b相交,且a∥b,∠1=75°,∴∠3=∠1=75°,∴∠2=180°-∠3=180°-75°=105°.故答案为:105°.【名师点睛】本题考查了邻补角的定义,平行线的性质,熟练掌握两直线平行,内错角相等是解本题的关键.14.(2019•广州)如图,点A,B,C在直线l上,PB⊥l,PA=6 cm,PB=5 cm,PC=7 cm,则点P到直线l的距离是__________cm.【答案】5【解析】∵PB⊥l,PB=5 cm,∴P到l的距离是垂线段PB的长度5 cm,故答案为:5.【名师点睛】本题考查了点到直线的距离,点到直线的距离是直线外的点到这条直线的垂线段的长度.15.(2019年广东省佛山市顺德区中考数学三模试卷)计算:18°30′=__________°.【答案】18.5【解析】18°30′=18.5°,故答案为:18.5.【名师点睛】本题考查了度分秒的换算,掌握1°=60′,1′=60″是解题的关键.16.(广东省广州市白云区2019年初中毕业班综合测试一初三数学试题)已知∠1=23°,则∠1的余角是__________°.【答案】67【解析】根据定义可知,∠1的余角=90°-23°=67°.故答案为:67.【名师点睛】本题考查角互余的概念:和为90度的两个角互为余角,属于基础题,较简单.17.(2019年广东省汕头市澄海区中考数学一模试卷)如图,已知直线AB∥CD,∠1=60°,∠2=45°,则∠CBD的度数为__________.【答案】75°【解析】如图,∵AB∥CD,∴∠1=∠3=60°,∠2=∠4=45°,∴∠CBD=180°-60°-45°=75°,故答案为:75°.【名师点睛】本题考查平行线的性质,平角的定义等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.18.(2019·广东华南师大附中初一中考模拟)如图,E点为DF上的点,B为AC上的点,∠1=∠2,DF∥AC,求证:∠C=∠D.【解析】∵∠1=∠2,又∵∠1=∠3,∴∠2=∠3,∴BD∥CE,∴∠DBA=∠C,∵DF∥AC,∴∠D=∠DBA,∴∠C=∠D.【名师点睛】此题考查平行线的性质和判定,正确掌握平行线的性质及判定定理是解题关键.。
新疆维吾尔自治区2019年中考数学试题研究几何图形的动点问题题库

几何图形的动点问题1. 如图①,在平行四边形ABCD 中,∠ABC =120°,动点P 从点B 从发,沿着B →C →D →A 方向运动至点A 处停止,设点P 运动的路程为x ,△ABP 的面积为y ,如果y 关于x 的函数图象如图②所示,则下列说法不正确的是( )第1题图A. 当x =2时,y =43B. 平行四边形ABCD 的面积是24 3C. 当x =10时,y =123D. 当y =83时,x =4D 【解析】由题意知∠ABC =120°,由题图②可知:BC =AD =6,CD =8.当x =2时,点P 在BC 上,y =12AB ·BP ×32=43,A 选项正确;平行四边形ABCD 的面积为AB ·BC ×32=243,B 选项正确;当x =10时,点P 在CD 上,y =12AB ·BC ×32=123,C 选项正确;当y =83时,点P 在BC 或AD 上,∴x =4或x =16,D 选项错误.2. 如图,在Rt △ABC 中,AB =AC =4 cm ,∠A =90°,点O 是BC 的中点.动点D 从点B 出发沿BA 方向向A 匀速运动,运动速度为1 cm/s ,连接DO ,过点O 作OE ⊥DO ,交AC 于点E ,连接DE .设运动时间为x ,△DOE 的面积为y ,则y (cm)关于x (s)的函数图象大致是( )第2题图D 【解析】如解图,连接OA ,在Rt △ABC 中,∠BAC =90°,AB =AC =4,∠C =45°,∵O 是BC 的中点,∴AO =CO ,AO ⊥BC ,∠DAO =∠C =45°,∵DO ⊥OE ,∴∠DOA +∠AOE =∠AOE +∠EOC ,∴∠DOA =∠EOC ,∴△DAO ≌△ECO (ASA),∴AD =CE =4-x ,S 四边形ADOE =S △AOC =12S △ABC =12×12×4×4=4,∵AB =AC ,∴AE =BD =x ,∴S △ADE =12AD ·AE =12×(4-x )x =-12x 2+2x ,∴y =4-S △ADE =4-(-12x 2+2x )=12x 2-2x +4,是对称轴为直线x =2,开口向上的抛物线,且当x =2时取最小值2,故选D.第2题解图3. 如图①,在等边△ABC 中,动点P 从点A 出发,沿三角形的边以每秒1个单位长度的速度沿A →C →B 匀速运动,设点P 运动的时间为x ,△ABP 的面积为y ,把y 看作x 的函数,函数的图象如图②所示,则t =6 s 时,△ABP 的面积为( )第3题图 A. 2 3 B. 4 3 C. 4 D. 8A 【解析】由题图②可知等边△ABC 的边长为4,如解图,过点A 作AD ⊥BC 于点D ,∵AC =4,∠C =60°,∴sin60°=AD AC ,即AD =AC ·sin60°=4×32=23,∴S △ABC =12BC ·AD =12×4×23=4 3.由题图①可知,t =6 s 时,点P 运动到BC 的中点,此时S △ABP =12S △ABC =2 3.第3题解图4. 如图,在Rt △ABC 中,∠ACB =90°,点P 以2 cm/s 的速度从点A 出发,沿折线AC →CB 运动,到点B 停止.过点P 作PD ⊥AB ,垂足为D ,若AC =6 cm ,BC =8 cm.当点P 运动5 s 时,线段PD 的长为________cm.第4题图2.4 【解析】∵P 以2 cm/s 的速度从点A 出发,AC =6 cm ,BC =8 cm ,在Rt △ABC中,∠ACB =90°,∴AB =AC 2+BC 2=62+82=10 cm ,∴sin B =AC AB =610=35,∵当点P 运动5 s 时,BP =2×7-2×5=4 cm ,∴PD =4·sin B =4×35=2.4 cm. 5. 如图,矩形ABCD 的对角线AC 、BD 交于点O ,点P 是边AD 上的一个动点,PE ⊥AC 于E ,PF ⊥BD 于F ,AC =10,则PE +PF 的最大值为________.第5题图102 【解析】如解图,连接OP ,∵AC 、BD 是矩形ABCD 的对角线,∴OD =OA =12AC =102,∵S △AOP +S △DOP =S △AOD ,∴12PE ·OA +12PF ·OD =12OA ·OD ·sin ∠COD ,即12(PE +PF )·OA = 12OA 2·sin ∠COD ,∴PE +PF 的最大值为OA ·sin ∠COD 的最大值,当∠COD =90°时,OA ·sin ∠COD =102.∴PE +PF 的最大值为102.第5题解图6. 如图,在矩形ABCD 中,AD =6,AE ⊥BD ,垂足为E ,ED =3BE ,点P 、Q 分别在BD 、AD 上,则AP +PQ 的最小值为________.第6题图3 3 【解析】如解图,延长AE 到点F ,使得EF =EA ,过点F 作FQ ⊥AD 于点Q ,交BD 于点P ,连接AP ,此时AP +PQ =FP +PQ =FQ 是AP +PQ 的最小值.∵四边形ABCD 是矩形,∴AB ∥PF ,∴∠BAE =∠PFE ,∠ABE =∠FPE ,∵AE =EF ,∴△AEB ≌△FEP (AAS),∴BE =PE ,PF =AB .∵DE =3BE ,∴DP =BP ,∴AP =BP =AB ,∴△APB 是等边三角形,∴∠ABP =60°.∵AD=6,∴AB =AD tan ∠ABD =23,∴PF =AP =AB =23,∴PQ =12AP =12AB =3,∴FQ =PF +PQ =33,即AP +PQ 的最小值为3 3.错误!第6题解图7. 如图,正方形ABCD的边长为2,点E为边BC的中点,点P在对角线BD上移动,则PE+PC的最小值是________.第7题图5 【解析】如解图,由正方形的性质可知E点关于线段BD的对称点为线段AB的中点F,即BE=BF=1,易得PF=PE,∴PE+PC=PF+PC,又∵PF+PC≥CF,由两点之间线段最短可知PE+PC的最小值为CF的长度,CF=BF2+BC2=1+4= 5.第7题解图8. 如图,边长为23的菱形ABCD中,AE⊥BC于点E,且点E是BC的中点.连接BD,交AE于点F,点M是AD上的一个动点,连接MF,MC,则MF+MC的最小值是________.第8题图27 【解析】如解图,作点F关于AD的对称点N,连接CN,交AD于点M,则CN即为MF+MC的最小值,∵AE⊥BC,点E是BC的中点,四边形ABCD为菱形,∴BE=3,AE=3,∠EBF=30°,∴EF=1,AF=2=AN,∴EN=5.在Rt△CEN中,CN=CE2+EN2=27.第8题解图9. 如图,O为矩形ABCD对角线AC、BD的交点,AB=6,M、N是BC边上的动点,且MN =2,则OM+ON的最小值是________.第9题图 210 【解析】作点O 关于BC 的对称点P ,连接PM ,将MP 沿着MN 的方向平移至点M 与点N 重合,得到NQ ,连接PQ ,则四边形MNQP 是平行四边形,∴MN =PQ =2,PM =NQ =MQ ,∴OM +ON =QN +ON .当O 、N 、Q 在同一直线时,OM +ON 的最小值等于OQ 的长,连接PO ,交BC 于点E ,由轴对称的性质可得BC 垂直平分OP ,又∵矩形ABCD 中,OB =OC ,∴E 是BC 的中点,∴OE 是△ABC 的中位线,∴OE =12AB =3,∴OP =2×3=6,又∵PQ ∥MN ,∴PQ ⊥OP ,∴在Rt △OPQ 中,OQ =OP 2+PQ 2=62+22=210.∴OM +ON 的最小值是210.第9题解图10. 如图,等腰△ABC 的底边BC 的长为4 cm ,面积是12 cm 2,腰AB 的垂直平分线EF交AC 于点F ,若D 为BC 上的中点,M 为线段EF 上一动点,则△BDM 周长的最小值为________cm.第10题图8 【解析】如解图,连接AD ,∵△ABC 是等腰三角形,点D 是BC 边的中点,∴AD ⊥BC ,∴S △ABC =12BC +AD =12×4×AD =12 cm 2,解得AD =6 cm ,∵EF 是线段AB 的垂直平分线,∴点B 关于直线EF 的对称点为点A ,∴AD 的长为BM +MD 的最小值,∴△BDM 周长的最小值=(BM +MD )+BD =AD +12BC =6+12×4=6+2=8 cm.第10题解图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
001(2019•天水)已知点P为某个封闭图形边界上一定点,动点M从点P出发,沿其边界顺时针匀速运动一周,设点M的运动时间为x,线段PM的长度为y,表示y与x的函数图象大致如图所示,则该封闭图形可能是()A.B.C.D.解:y与x的函数图象分三个部分,而B选项和C选项中的封闭图形都有4条线段,其图象要分四个部分,所以B、C选项不正确;A选项中的封闭图形为圆,开始y随x的增大而增大,然后y随x的减小而减小,所以A 选项不正确;D选项为三角形,M点在三边上运动对应三段图象,且M点在P点的对边上运动时,PM 的长有最小值.故选:D.002(2019•白银)如图①,在矩形ABCD中,AB<AD,对角线AC,BD相交于点O,动点P由点A出发,沿AB→BC→CD向点D运动.设点P的运动路程为x,△AOP的面积为y,y与x的函数关系图象如图②所示,则AD边的长为()A.3 B.4 C.5 D.6解:当P点在AB上运动时,△AOP面积逐渐增大,当P点到达B点时,△AOP面积最大为3.∴AB•BC=3,即AB•BC=12.当P点在BC上运动时,△AOP面积逐渐减小,当P点到达C点时,△AOP面积为0,此时结合图象可知P点运动路径长为7,∴AB+BC=7.则BC=7﹣AB,代入AB•BC=12,得AB2﹣7AB+12=0,解得AB=4或3,因为AB<AD,即AB<BC,所以AB=3,BC=4.故选:B.003(2019•铜仁市)如图,平行四边形ABCD中,对角线AC、BD相交于点O,且AC=6,BD=8,P是对角线BD上任意一点,过点P作EF∥AC,与平行四边形的两条边分别交于点E、F.设BP=x,EF=y,则能大致表示y与x之间关系的图象为()A.B.C.D.解:当0≤x≤4时,∵BO为△ABC的中线,EF∥AC,∴BP为△BEF的中线,△BEF∽△BAC,∴,即,解得y,同理可得,当4<x≤8时,y(8﹣x).故选:D.004(2019•赤峰)如图是九年级某考生做的水滴入一个玻璃容器的示意图(滴水速度保持不变),能正确反映容器中水的高度(h)与时间(t)之间对应关系的大致图象是()A.B.C.D.解:由于容器的形状是下宽上窄,所以水的深度上升是先慢后快.表现出的函数图形为先缓,后陡.故选:D.005(2019•河池)如图,△ABC为等边三角形,点P从A出发,沿A→B→C→A作匀速运动,则线段AP的长度y与运动时间x之间的函数关系大致是()A.B.C.D.解:根据题意得,点P从点A运动到点B时以及从点C运动到点A时是一条线段,故选项C与选项D不合题意;点P从点B运动到点C时,y是x的二次函数,并且有最小值,∴选项B符合题意,选项A不合题意.故选:B.006(2019•齐齐哈尔)“六一”儿童节前夕,某部队战士到福利院慰问儿童.战士们从营地出发,匀速步行前往文具店选购礼物,停留一段时间后,继续按原速步行到达福利院(营地、文具店、福利院三地依次在同一直线上).到达后因接到紧急任务,立即按原路匀速跑步返回营地(赠送礼物的时间忽略不计),下列图象能大致反映战士们离营地的距离S 与时间t之间函数关系的是()A.B.C.D.解:由题意可得,战士们从营地出发到文具店这段过程中,S随t的增加而增大,故选项A错误,战士们在文具店选购文具的过程中,S随着t的增加不变,战士们从文具店去福利院的过程中,S随着t的增加而增大,故选项C错误,战士们从福利院跑回营地的过程中,S随着t的增大而减小,且在单位时间内距离的变化比战士们从营地出发到文具店这段过程中快,故选项B正确,选项D错误,故选:B.007(2019•本溪)如图,点P是以AB为直径的半圆上的动点,CA⊥AB,PD⊥AC于点D,连接AP,设AP=x,P A﹣PD=y,则下列函数图象能反映y与x之间关系的是()A. B.C. D.解:设:圆的半径为R,连接PB,则sin∠ABP,∵CA⊥AB,即AC是圆的切线,则∠PDA=∠PBA=α,则PD=AP sinα=x x2,则y=P A﹣PD x2+x,图象为开口向下的抛物线,故选:C.008(2019•衢州)如图,正方形ABCD的边长为4,点E是AB的中点,点P从点E出发,沿E→A→D→C移动至终点C.设P点经过的路径长为x,△CPE的面积为y,则下列图象能大致反映y与x函数关系的是()A.B.C.D.解:通过已知条件可知,当点P与点E重合时,△CPE的面积为0;当点P在EA上运动时,△CPE的高BC不变,则其面积是x的一次函数,面积随x增大而增大,当x=2时有最大面积为4,当P在AD边上运动时,△CPE的底边EC不变,则其面积是x的一次函数,面积随x 增大而增大,当x=6时,有最大面积为8,当点P在DC边上运动时,△CPE的底边EC不变,则其面积是x的一次函数,面积随x增大而减小,最小面积为0;故选:C.009(2019•武汉)“漏壶”是一种古代计时器,在它内部盛一定量的水,不考虑水量变化对压力的影响,水从壶底小孔均匀漏出,壶内壁有刻度.人们根据壶中水面的位置计算时间,用t表示漏水时间,y表示壶底到水面的高度,下列图象适合表示y与x的对应关系的是()A.B.C.D.解:∵不考虑水量变化对压力的影响,水从壶底小孔均匀漏出,t表示漏水时间,y表示壶底到水面的高度,∴y随t的增大而减小,符合一次函数图象,故选:A.010(2019•孝感)一个装有进水管和出水管的空容器,从某时刻开始4min内只进水不出水,容器内存水8L;在随后的8min内既进水又出水,容器内存水12L;接着关闭进水管直到容器内的水放完.若每分钟进水量和出水量是两个常数,容器内的水量y(单位:L)与时间x(单位:min)之间的函数关系的图象大致的是()A.B.C.D.解:∵从某时刻开始4min内只进水不出水,容器内存水8L;∴此时容器内的水量随时间的增加而增加,∵随后的8min内既进水又出水,容器内存水12L,∴此时水量继续增加,只是增速放缓,∵接着关闭进水管直到容器内的水放完,∴水量逐渐减少为0,综上,A选项符合,故选:A.011(2019•衡阳)如图,在直角三角形ABC中,∠C=90°,AC=BC,E是AB的中点,过点E作AC和BC的垂线,垂足分别为点D和点F,四边形CDEF沿着CA方向匀速运动,点C与点A重合时停止运动,设运动时间为t,运动过程中四边形CDEF与△ABC 的重叠部分面积为S.则S关于t的函数图象大致为()A.B.C.D.解:∵在直角三角形ABC中,∠C=90°,AC=BC,∴△ABC是等腰直角三角形,∵EF⊥BC,ED⊥AC,∴四边形EFCD是矩形,∵E是AB的中点,∴EF AC,DE BC,∴EF=ED,∴四边形EFCD是正方形,设正方形的边长为a,如图1当移动的距离<a时,S=正方形的面积﹣△EE′H的面积=a2t2;当移动的距离>a时,如图2,S=S△AC′H(2a﹣t)2t2﹣2at+2a2,∴S关于t的函数图象大致为C选项,故选:C.012(2019•常州)随着时代的进步,人们对PM2.5(空气中直径小于等于2.5微米的颗粒)的关注日益密切.某市一天中PM2.5的值y1(ug/m3)随时间t(h)的变化如图所示,设y2表示0时到t时PM2.5的值的极差(即0时到t时PM2.5的最大值与最小值的差),则y2与t的函数关系大致是()A.B.C.D.解:当t=0时,极差y2=85﹣85=0,当0<t≤10时,极差y2随t的增大而增大,最大值为43;当10<t≤20时,极差y2随t的增大保持43不变;当20<t≤24时,极差y2随t的增大而增大,最大值为98;故选:B.013(2019•淮安)当矩形面积一定时,下列图象中能表示它的长y和宽x之间函数关系的是()A.B.C.D.解:∵根据题意xy=矩形面积(定值),∴y是x的反比例函数,(x>0,y>0).故选:B.014(2019•菏泽)如图,正方形ABCD的边长为2cm,动点P,Q同时从点A出发,在正方形的边上,分别按A→D→C,A→B→C的方向,都以1cm/s的速度运动,到达点C运动终止,连接PQ,设运动时间为xs,△APQ的面积为ycm2,则下列图象中能大致表示y 与x的函数关系的是()A.B.C.D.解:①当0≤x≤2时,∵正方形的边长为2cm,∴y=S△APQ AQ•AP x2;②当2≤x≤4时,y=S△APQ=S正方形ABCD﹣S△CP′Q′﹣S△ABQ′﹣S△AP′D,=2×2(4﹣x)22×(x﹣2)2×(x﹣2)x2+2x所以,y与x之间的函数关系可以用两段二次函数图象表示,纵观各选项,只有A选项图象符合.故选:A.015(2019•潍坊)如图,在矩形ABCD中,AB=2,BC=3,动点P沿折线BCD从点B开始运动到点D.设运动的路程为x,△ADP的面积为y,那么y与x之间的函数关系的图象大致是()A.B.C.D.解:由题意当0≤x≤3时,y=3,当3<x<5时,y3×(5﹣x)x.故选:D.016(2019•淄博)从某容器口以均匀地速度注入酒精,若液面高度h随时间t的变化情况如图所示,则对应容器的形状为()A.B.C.D.解:根据图象可知,容器大致为:容器底部比较粗,然后逐渐变细,然后又逐渐变粗,最后又变得细小,并且最后非常细,推断可能是C容器.故选:C.017(2019•达州)如图,边长都为4的正方形ABCD和正三角形EFG如图放置,AB与EF 在一条直线上,点A与点F重合.现将△EFG沿AB方向以每秒1个单位的速度匀速运动,当点F与B重合时停止.在这个运动过程中,正方形ABCD和△EFG重叠部分的面积S与运动时间t的函数图象大致是()A.B.C.D.解:当0≤t≤2时,S,即S与t是二次函数关系,有最小值(0,0),开口向上,当2<t≤4时,S,即S与t 是二次函数关系,开口向下,由上可得,选项C符合题意,故选:C.018(2019•广元)如图,点P是菱形ABCD边上的动点,它从点A出发沿A→B→C→D路径匀速运动到点D,设△P AD的面积为y,P点的运动时间为x,则y关于x的函数图象大致为()A.B.C.D.解:分三种情况:①当P在AB边上时,如图1,设菱形的高为h,y AP•h,∵AP随x的增大而增大,h不变,∴y随x的增大而增大,故选项C和D不正确;②当P在边BC上时,如图2,y AD•h,AD和h都不变,∴在这个过程中,y不变,故选项B不正确;③当P在边CD上时,如图3,y PD•h,∵PD随x的增大而减小,h不变,∴y随x的增大而减小,∵P点从点A出发沿在A→B→C→D路径匀速运动到点D,∴P在三条线段上运动的时间相同,故选项A正确;故选:A.019(2019•自贡)均匀的向一个容器内注水,在注满水的过程中,水面的高度h与时间t的函数关系如图所示,则该容器是下列四个中的()A.B.C.D.解:相比较而言,前一个阶段,用时较少,高度增加较快,那么下面的物体应较细.由图可得上面圆柱的底面半径应大于下面圆柱的底面半径.故选:D.。
