成都市2008届高中毕业班第三次诊断性检测数学(理科)
2008年四川省成都市高中阶段教育学校统一招生考试数学试卷及答案(word)

某某市二00八年高中阶段教育学校统一招生考试试卷(含某某市初三毕业会考)数学全卷分A 卷和B 卷,A 卷满分100分,B 卷满分50分;考试时间120分钟。
A 卷分第Ⅰ卷和第Ⅱ卷,第Ⅰ卷为选择题,第Ⅱ为其它类型的题。
第Ⅰ卷(选择题,共30分)注意事项:1. 第Ⅰ卷共2页。
答第Ⅰ卷前,考生务必将自己的某某、某某号、考试科目涂写在试卷和答题卡上。
考试结束,监考人员将试卷和答题卡一并收回。
2. 第Ⅰ卷全是选择题。
各题均有四个选项,只有一项符合题目要求。
每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动骼橡皮摖干净后,再先涂其他答案,选择题的答案不能答在试卷上。
请注意机读答题卡的横竖格式。
A 卷(共100分)一、选择题。
(每小题3分,共30分)1.2cos45°的值等于(A )22(B )2(C )42(D )22 2.化简(-3x 2)·2x 3的结果是(A )-6x 5(B )-3x 5(C )2x 5(D )6x 53.奥运会火炬传递以“和谐之旅”为主题,以“点燃激情 传递梦想”为口号进行,其传递总路程约为1370000千米,这个路程用科学记数法表示为×104千米×105千米×105千米×106千米4.用若干个大小相同,棱长为1的小正方体搭成一个几何体模型,其三视图如图所示,则搭成这个几何体模型所用的小正方体的个数是(A)4 (B)5 (C)6 (D)75.下列事件是必然事件的是(A)打开电视机,任选一个频道,屏幕上正在播放天气预报(B)到电影院任意买一X电影票,座位号是奇数(C)在地球上,抛出去的篮球会下落(D)掷一枚均匀的骰子,骰子停止转动后偶数点朝上x 中,自变量x的取值X围是6.在函数y=3(A)x≥- 3 (B)x≤- 3 (C)x≥3 (D )x≤ 37.如图,在△ABC与△DEF中,已有条件AB=DE,还需添加两个条件才能使△ABC≌△DEF,不能添加的一组条件是(A)∠B=∠E,BC=EF (B)BC=EF,AC=DF(C)∠A=∠D,∠B=∠E (D)∠A=∠D,BC=EF8.一交通管理人员星期天在市中心的某十字路口,对闯红灯的人次进行统计,根据上午7∶00 ~ 12∶00中各时间段(以1小时为一个时间段)闯红灯的人次,制作了如图所示的条形统计图,则各时间段闯红灯人次的众数和中位数分别为(A)15,15 (B)10,15 (C)15,20 (D)10,209. 如图,小红同学要用纸板制作一个高4cm ,底面周长是6πcm 的圆锥形漏斗模型,若不计接缝和损耗,则她所需纸板的面积是(A )12πcm 2 (B )15πcm 2 (C )18πcm 2 (D )24πcm 210. 有下列函数:①y = - 3x ;②y = x – 1:③y = - x1 (x < 0);④y = x2 + 2x + 1.其中当x 在各自的自变量取值X 围内取值时,y 随着x 的增大而增大的函数有(A )①② (B )①④ (C )②③ (D )③④第Ⅱ卷(非选择题,共70分)注意事项:1. A 卷的第Ⅱ卷和B 卷共10页,用蓝、黑钢笔或圆珠笔直接答在试卷上。
修改版2008届高三调研考试数学试题(理科)答案及评分标准校对版
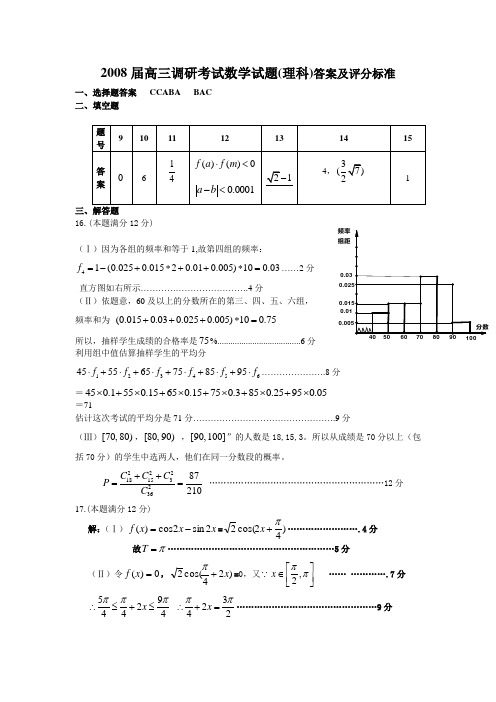
0.030.01频率组距2008届高三调研考试数学试题(理科)答案及评分标准一、选择题答案 CCABA BAC 二、填空题三、解答题16.(本题满分12分)(Ⅰ)因为各组的频率和等于1,故第四组的频率:41(0.0250.01520.010.005)100.03f =-+*++*=……2分直方图如右所示……………………………….4分(Ⅱ)依题意,60及以上的分数所在的第三、四、五、六组, 频率和为 (0.0150.030.0250.005)100.75+++*=所以,抽样学生成绩的合格率是75%......................................6分 利用组中值估算抽样学生的平均分123456455565758595f f f f f f ⋅+⋅+⋅+⋅+⋅+⋅………………….8分=450.1550.15650.15750.3850.25950.05⨯+⨯+⨯+⨯+⨯+⨯ =71估计这次考试的平均分是71分………………………………………….9分(Ⅲ)[70,80),[80,90) ,[90,100]”的人数是18,15,3。
所以从成绩是70分以上(包括70分)的学生中选两人,他们在同一分数段的概率。
22218153236C C C P C ++==87210 ……………………………………………………12分 17.(本题满分12分)解:(Ⅰ)x x x f 2sin 2cos )(-==)42cos(2π+x …………………….4分故π=T …………………………………………………5分 (Ⅱ)令0)(=x f ,)24cos(2x +π=0,又 ,2x ππ⎡⎤∈⎢⎥⎣⎦…… ………….7分 592444x πππ∴≤+≤ 3242x ππ∴+=…………………………………………9分故58x π=函数)(x f 的零点是58x π= ……………. 12分 18.(本题满分12分)证(Ⅰ)因为AB ⊥侧面11BB C C ,故1AB BC ⊥ 在1BC C 中,1111,2,3BC CC BB BCCπ===∠=由余弦定理有1BC == 故有 222111BC BC CC C B BC += ∴⊥而 BC AB B = 且,AB BC ⊂平面ABC∴1C B ABC ⊥平面(Ⅱ)由11,,,,EA EB AB EB ABAE A AB AE ABE ⊥⊥=⊂平面从而1B E ABE ⊥平面 且BE ABE ⊂平面 故1BE B E ⊥不妨设 CE x =,则12C E x =-,则221BE x x =+-又1123B C C π∠= 则2211B E x x =++在1Rt BEB 中有 22114x x x x +++-+= 从而1x =±(舍负)故E 为1CC 的中点时,1EA EB ⊥法二:以B 为原点1,,BC BC BA 为,,x y z 轴,设CE x =,则11(0,0,0),(1),(2B E x B A -- 由1EA EB ⊥得 10EA EB ⋅=即11(1,2)(,0)2211(1)(2)022x x x x x x x --=⎫--=⎪⎪⎭化简整理得 2320x x -+= 1x = 或 x = 当2x =时E 与1C 重合不满足题意EC 1B 1A 1CBA111当1x =时E 为1CC 的中点 故E 为1CC 的中点使1EA EB ⊥(Ⅲ)取1EB 的中点D ,1A E 的中点F ,1BB 的中点N ,1AB 的中点M 连DF 则11//DF A B ,连DN 则//DN BE ,连MN 则11//MN A B 连MF 则//MF BE ,且MNDF 为矩形,//MD AE 又1111,A B EB BE EB ⊥⊥ 故MDF ∠为所求二面角的平面角在Rt DFM 中,111(22DF A B BCE==∆为正三角形)111222MF BE CE === 1tan 2MDF ∴∠== 法二:由已知1111,EA EB B A EB ⊥⊥, 所以二面角11A EB A --的平面角θ的大小为向量11B A与EA 的夹角因为11B A BA ==1(2EA=-- 故 11112cos tan 3EA B A EA B A θθ⋅==⇒=⋅.19. (本题满分14分)解:(Ⅰ)依题意知,直线l 的方程为:1x =-.点R 是线段FP 的中点,且RQ ⊥FP ,∴RQ 是线段FP 的垂直平分线.…………………….2分∴PQ 是点Q 到直线l 的距离.∵点Q 在线段FP 的垂直平分线,∴PQ QF =.…………4分 故动点Q 的轨迹E 是以F 为焦点,l 为准线的抛物线,其方程为:24(0)y x x =>.…………………………………………………….7分(Ⅱ) 设()()B B A A y x B y x A ,,,,()()N N M M y x N y x M ,,,,直线AB 的方程为)1(-=x k y…………………………………………………….8分则⎪⎩⎪⎨⎧==)2(4)1(422BB AA x y x y(1)—(2)得k y y B A 4=+,即ky M 2=,……………………………………9分代入方程)1(-=x k y ,解得122+=kx M .所以点M的坐标为222(1,)k k+.……………………………………10分同理可得:N 的坐标为2(21,2)k k +-.直线MN 的斜率为21kkx x y y k N M N M MN -=--=,方程为 )12(1222---=+k x kkk y ,整理得)3()1(2-=-x k k y ,………………12分 显然,不论k 为何值,(3,0)均满足方程,所以直线MN 恒过定点R (3,0). (14)20. (本题满分14分) .解:11n na kn a +=+ 故2211a a k a ==+,.……………………………………1分 又因为()211111,,2n n n n n a a a a a a n N n +--+==+∈≥则3121a a a a =22a +,即3322221,21,2a aa k a k a a =+=+∴=又.………………………3分 所以212,1k a k k +==∴=, ……………………………………4 (2)11,n na n a +=+ 121121n n n n n a a a a a a a a ---=⋅⋅⋅⋅⋅⋅⋅⋅=()1...21!n n n ⋅-⋅⋅⋅= ……………………………………6 因为()()11!n n a x g x n -=-=1n nx -所以,当1x =时,()()()11123 (2)n n f x f n +==++++=.................................7 当1x ≠时,()21123...n f x x x nx -=++++. (1)()1x ⋅得()()23123...1n n xf x x x x n x nx -=++++-+……(2) ()()()()2112:11...n n x f x x x x nx ---=++++-=11nn x nx x--- ()()2111nn x nx f x xx -∴=--- ……………………………9 综上所述:2(1),12()1,1(1)1n nn n x f x x nx x x x+⎧=⎪⎪=⎨-⎪-≠⎪--⎩ ……………………………10 (3)因为()()()212221211212nnn n f n -∴=-=-+-- 又()333n g n=,易验证当1,2n =,3时不等式不成立; ……………………………11 假设()3n k k =≥,不等式成立,即()3121kkk >-+ 两边乘以3得:()()111331232131222k k k k k k k k k +++>-+=⋅++--+又因为()()()131222233223220k k k k k k k k k +--⋅+=--+=-+>所以()11113213122221k k k k k k k k k ++++>⋅++--+>⋅+即1n k =+时不等式成立.故不等式恒成立. (14)21. (本题满分14分) 解:(Ⅰ)()ln(1)(1),x f x a e a x =+-+(1)()(1)011x xx xae a e f x a e e-+-'∴=-+=<++恒成立,………………………… 所以函数()f x 在(,)-∞+∞上是单调减函数. …………………………4分(Ⅱ) 证明:据题意1,12233(()),(,()),(,())A x f x B x f x C x f x 且x 1<x 2<x 3,由(Ⅰ)知f (x 1)>f (x 2)>f (x 3), x 2=231x x +…………………………6分 12123232(,()()),(,()()BA x x f x f x BC x x f x f x ∴=--=--12321232()()[()()][()()]BA BC x x x x f x f x f x f x ∴⋅=--+--…………………8分123212320,0,()()0,()()0x x x x f x f x f x f x -<->->-<0,(,)2BA BC B ππ∴⋅<∴∠∈即⊿ABC 是钝角三角形……………………………………..9分(Ⅲ)假设⊿ABC 为等腰三角形,则只能是BA BC =即2132()()()f x f x f x =+3212132ln(1)2(1)[ln(1)(1)(1)()x x x a e a x a e e a x x ⇔+-+=++-++ 321222ln(1)2(1)[ln(1)(1)2(1)x x x a e a x a e e a x ⇔+-+=++-+3212ln(1)ln(1)(1)x x x e e e ⇔+=++31332122122(1)(1)(1)2x x x x x x x x x e e e e e e e e +⇔+=++⇔+=++3212x x x e e e ⇔=+ ① …………………………………………..12分而事实上, 3122xx x e e e +≥= ②由于31xxe e <,故(2)式等号不成立.这与(1)式矛盾. 所以⊿ABC 不可能为等腰三角形..14分222212123232()[()()]()[()()]x x f x f x x x f x f x -+-=-+-即:2221321232[()()][()()]x x x x f x f x f x f x -=-∴-=-。
2008届成都高中毕业班第三次诊断性检测

How does the man feel about his driving to work? A . It takes him too much time. B . The distance is a little long. C . He feels satisfied with it.What do the girls have in common according to the dialogue?How much wil1 the lady pay for the shirt if she buys one?选项中选出最佳选项, 并标在试卷的相应位置。
听每段对话或独白前, 你将有时间阅读各个 小题,每小题 5 秒钟;听完后,每小题将给出 5 秒钟的作答时间。
每段对话或独白读两遍。
听第 6 段材料,回答第 6 至 8 题。
2008届四川省成都市高中毕业班第三次诊断性检测英语试题考试时间 120 分钟,满分 150 分)第 I 卷(共 115 分) 第一部分:听力(共两节,满分 30 分) 做题时, 先将答案划在试卷上。
录音内容结束后, 你将有两分钟的时间将试卷上的答案 转涂到答题卡上。
第一节 (共 5 小题;每小题 1.5 分,满分 7.5分) 听下面 5 段对话。
每段对话后有一个小题,从题中所给的 A 、 B 、C 三个选项中选出最 佳选项,并标在答题卷的相应位置。
听完每段对话后,你都有 10 秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. Where did the woman probably go? A . To the cinema. B .To the schoo1.C .To the park.2.3. A . They like sports.B .They like shopping.C . They like soap operas.4.5. A . 180 dollars.B .200 dollars.C . 220 dollars.What can we 1earn from the conversation?A . The man will probably take the sleeping pil1.B .The man didn 't sleep well 1ast week. C . The woman will buy some sleeping pills. 第二节共 15 小题;每题 1.5 分,满分 22.5 分)听下面 5 段对话或独白。
四川省绵阳市高2008级第三次诊断性考试(数学理)

四川省绵阳市高2008级第三次诊断性考试数 学(理工类)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷,全卷150分。
第Ⅰ卷1至2页,第Ⅱ卷3至10页,考试结束后,将第Ⅱ卷和答题卡两部分一并交回。
第Ⅰ卷(选择题,共60分)注意事项:1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目用4B 或5B 铅笔涂写在答题卡上。
2.每小题选出答案后,用4B 或5B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试题卷上。
参考公式:如果事件A 、B 互斥,那么P(A+B)=P(A)+P(B);如果事件A 、B 相互独立,那么)()()(B P A P B A P ∙=∙;如果事件A 在一次试验中发生的概率为P ,那么n 次独立重复试验中恰好发生k 次的概率:kn k k n n P P C k P --∙∙=)1()(;正棱锥、圆锥的侧面积公式cl S 21=锥侧,其中c 表示底面周长,l 表示斜高与母线长;球的体积公式334R V π=球,其中R 表示球的半径。
一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的,把它选出来填涂在答题卡上。
1.复数212⎪⎭⎫⎝⎛+i i 的虚部为( B )A .-2B .2C .-2iD .2i2.下列各选项中,与︒2008sin 最接近的是( A )A .-21 B .21 C .22-D .223.对平面α和异面直线l 1,l 2,下面四个命题中正确的是( D )A .若α⊂1l ,则l 2与α相交B .若α⊂1l ,则l 2一定不垂直于αC .若直线l 1’,l 2’是l 1,l 2在α内的射影,则l 1’,l 2’是相交直线D .若21l l ⊥,且l 1与α成︒45的角,则l 2与α所成的最大角是︒45 4.已知a,b 是非零向量,且3),(π=b a ,则向量||||b b a a p +=的模为( B )A .2B .3C .2D .35.设实数a,b 满足a<b,b+b<0,ab>0,则下列不等式一定成立的是( C )A .ba ab > B .2211ba>C .ba a->11 D .ba ab2211>6.若对于任意实数x ,有x 3=a 0+a 1(3-x)+a 2(3-x)2+a 3(3-x)3,则a 0+a 2=( D )A .36B .18C .10D .47.已知:集合⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎩⎨⎧≥+≤-=u y x y x y x G 2),(,集合}2|),{(22=+=y x y x H ,“命题:G y x ∈),(”是“命题:H y x ∈),(”的必须而不充分条件,则u 的取值范围是( A )A .2≤u B .2-≤u C .2≤u D .2-≤u8.已知lga<0,则函数f(x)=a |logax|的图象是( D)9.直三棱柱ABCD-A 1B 1C 1的底面是︒=∠90BAC 的等腰三角形,M AA AB ,21==是CC 1的中点,设三棱柱的外接球球心为O ,则点O 到面A 1B 1M 的距离等于(A )A .55 B .105 C .510 D .101010.设F 1,F 2分别是椭圆)0(12222>>=+b a by ax 的左、右焦点,与直线y=b 相切的⊙F 2交椭圆于点E ,E 恰好是直线EF 1与⊙F 2的明点,则椭圆的离心率为( C )A .23 B .33 C .45 D .3511.定义f(M)=(m,n,p),其中M 是ABC ∆内一点,m 、n 、p 分别是MBC ∆、MCA ∆、MAB ∆的面积已知ABC ∆中,),,21()(,30,32y x N f BAC AC AB =︒=∠=∙,则yx41+的最小值是( D )A .8B .9C .16D .18 12.若*221,555N n a a a nn ∈+++=λ,且a 1、a 2、…、}4,0{∈n a ,则λ一定不属于...( C ) A .)1,0[ B .]1,0( C .⎪⎭⎫⎢⎣⎡54,51 D .⎥⎦⎤ ⎝⎛54,51 第Ⅱ卷(共90分)二、填空题:本大题共4小题,每小题4分,共16分。
四川省成都市高三第三次诊断考试数学(理)试题

成都市2013级高中毕业班第三次诊断性检测数学(理工类)第Ⅰ卷(选择题,共50分)一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知田径队有男运动员56人,女运动员42人,若按男女比例用分层抽样的方法,从全体运动员中抽出14人参加比赛,则抽到女运动员的人数为A. 2B. 4C. 6D. 82.命题()()"1,,ln 1"x x x ∀∈-+∞+<的否定是A. ()()1,,ln 1x x x ∀∉-+∞+<B. ()()0001,,ln 1x x x ∀∉-+∞+<C. ()()1,,ln 1x x x ∀∈-+∞+≥D. ()()0001,,ln 1x x x ∃∈-+∞+≥3.已知复数(其中为虚数单位),则A. 3B.C. 2D. 14.已知是空间中两个不同的平面,为平面内的一条直线,则是的A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件5.已知向量满足,则在方向上的投影为A. B. C. D.6. 某工厂用A,B 两种配件生产甲乙两种产品,每生产一件甲产品需用4个A 配件耗时1h ,每生产一件乙产品需用4个B 配件耗时2h ,该厂每天最多可从配件厂获得24个A 配件和16个B 配件,每天生产总耗时不超过8h.若生产一件甲产品获利3万元,生产一件乙产品获利4万元,则通过恰当的生产安排,该工厂每天可获得的最大利润为A. 24万元B.22万元C. 18万元D. 16万元7.执行如图所示的程序框图,若依次输入1122210.6,0.6,3m n p -⎛⎫=== ⎪⎝⎭,则输出的结果为 A. 1213⎛⎫ ⎪⎝⎭ B. C. D.8.某学校食堂早餐只有花卷、包子、面条和蛋炒饭四种主食可供食用,有5名同学前去就餐,每人只选择其中一种,且每种主食都至少有一名同学选择.已知包子数量不足仅够一人食用,甲同学肠胃不好不会选择蛋炒饭,则这5名同学不同的主食选择方案种数为A.144B. 132C. 96D.489. 定义在上的函数同时满足:①对任意的恒有 成立;②当时,记函数()()()1g x f x k x =--,若函数恰好有两个零点,则实数的取值范围是A. B. C. D.10. 已知O 为坐标原点,双曲线()2222:10,0x y C a b a b-=>>的左焦点为,以OF 为直径的圆交双曲线C 的渐近线于A,B ,O 三点,且.关于的方程的两个实数根分别为和,则以为边长的三角形的形状是A. 钝角三角形B. 直角三角形C. 锐角三角形D. 等腰直角三角形第Ⅱ卷(非选择题,共100分)二、填空题:(大题共5小题,每小题5分,共25分.11.计算:sin 65cos35sin 25sin35-= .12. 一块边长为8cm 的正方形铁板按如图所示的阴 影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥(底面是正方形,从顶点向底面作垂线,垂足为底面中心的四棱锥)形容器,O 为底面ABCD 的中心,则侧棱SC 与底面ABCD 所成角的余弦值为13. 已知椭圆()22:101616x y C n n+=<<的两个焦点分别为,过的直线交椭圆C 于A,B 两点,若的最大值为10,则的值为 .14. 若直线()2101,0ax by a b +-=>->经过曲线()cos 101y x x π=+<<的对称中心,则的最小值为 .15.函数()()0,0b f x a b x a=>>-,因其图象像“囧”字,被称为“囧函数”.我们把函数的图像与轴的交点关于原点对称的点称为函数的“囧点”;以函数的“囧点”为圆心,与函数的图象有公共点的圆,皆称为函数的“囧圆”.当时,有以下命题:①对任意,都有成立;②存在,使得成立;③函数的“囧点”与函数图象上的点的最短距离为;④函数的所有“囧圆”中其周长的最小值为.其中正确的命题序号有 .(写出所有正确命题的序号)三、解答题:本大题共6小题,满分70分.解答应写出文字说明、证明过程或演算步骤.16.(本小题满分10分)已知函数()22sin cos 44f x x x x ππ⎛⎫⎛⎫=+++ ⎪ ⎪⎝⎭⎝⎭ (1)求函数的单调递增区间;(2)在中,内角A,B,C 的对边分别为,角A 满足,若,求的值.17.(本小题满分12分)如图,在三棱台中,已知底面ABC 是以AB 为斜边的直角三角形,FC 底面ABC ,AB=2DE,G,H 分别为AC,BC 的中点.(1)求证:平面ABED//平面GHF;(2))若BC=CF=AB=1,求二面角A-DE-F 的余弦值.18.(本小题满分12分)某高校一专业在一次自主招生中,对20名已经选拔入围的学生进行语言表达能力和逻辑思维能力测试,结果如下表:由于部分数据丢失,只知道从这20名参加测试的学生中随机抽取一人,抽到语言表达能力优秀或逻辑思维能力优秀的学生的概率为(1) 从参加测试的语言表达能力良好的学生中任意抽取2名,求其中至少有一名逻辑思维能力优秀的学生的概率;(2))从参加测试的20名学生中任意抽取2名,设语言表达能力优秀或逻辑思维能力优秀的学生人数为,求随机变量的分布列及其均值.19.(本小题满分12分)已知数列的前项和为,且330,.n n S a n N *+-=∈(1)求数列的通项公式;(2)设数列满足,求12231111n n n T b b b b b b +=+++,求使成立的的最小值.20.(本小题满分13分)已知一动圆经过点,且在轴上截得的弦长为4,设动圆圆心的轨迹为曲线C.(1)求曲线C 的方程;(2)过点任意作相互垂直的两条直线,分别交曲线C 于不同的两点A,B 和不同的两点D,E.设线段AB,DE 的中点分别为P,Q.①求证:直线PQ 过定点R ,并求出定点R 的坐标;②求的最小值;21.(本小题满分14分)已知函数,其中为自然对数的底数.(1)设函数()()()223,.g x x ax a f x a R =+--∈试讨论函数的单调性; (2)设函数()()2,.h x f x mx x m R =--∈,若对任意,且都有()()()21121221x h x x h x x x x x ->-成立,求实数的取值范围.。
成都七中08级高三数学三诊模拟((理)

2008年成都七中08级三诊模拟((理)第I 卷(选择题 共60分)一、选择题(共60分,每题5分,将答案涂到机读卡上)1.设i 为虚数单位,则集合*{}n i n N ∈的元素个数是 A.3 B.4 C.5 D.62.已知函数()f x 的定义域是(0,)+∞,若不等式()0f x >的解集是(1,)+∞,则不等式()0f x ≤的解集是A.(,1)-∞B.(,1]-∞C.(0,1)D.(0,1]3.设,a b R ∈且0ab ≠,则a b >的一个充分条件是A.22a b >B.33a b >C.a b >D.11a b< 4.白雪公主之所以能一次又一次地躲过敌人的追杀,除运气较好、命不该绝外,还得益于她具有很强的应用数学知识解决实际问题的意识和能力.4月1日这天,她用年轻时学过的数学知识为7个小矮人测量了身高,其中6人的身高分别为(单位:厘米)69; 78; 81; 72; 84; 75.若7个小矮人的身高的平均数是78,则第7人的身高是A.66B.76.5C.78D.875.关于方程22tan (,)sin cos 2x y k k Z πθθθθ+=≠∈,下列说法中不正确...的是 A.可表示椭圆 B.可表示双曲线 C.可表示直线 D.可表示圆 6.100(1)x -的展开式的第40项的系数是A.39100C -B.39100CC.40100C -D.40100C7.空间四边形ABCD 中,点,,,E F G H 分别 在边,,,BC CD DA AB 上,满足////EF BD HG ,则下 列说法中正确的是A.直线EH 与直线FG 不可能相交B.直线EH 与直线FG 不可能平行C.直线EH 与直线FG 不可能异面D.直线EH 与直线FG 不可能垂直8.两个非零向量,a b 满足a b a b ==+,则a b -与a 所成的角是A.030B.060C.0120D.01509.已知22222()(1)2f x x a b x a ab b =++-++-是偶函数,则()y f x =的图象与y 轴交点的纵坐标的最大值是B.2C. D.410.2008年初某岛有陆地10002km ,每年填海新增陆地是前一年陆地的10%,同时由于气候恶化,每年被海水侵蚀的陆地是b 2km ,为使2010年末该岛陆地面积不少于10002km ,b 的最大值是A.1102kmB.1002kmC.902km C.852km11.设点P 在平面区域22021020x y x y x y -+≥⎧⎪-+≤⎨⎪+-≤⎩上,点Q 在22(2)1x y ++=上,则PQ 的最小值为1B.1C.1112.设0a >且1a ≠,()log a f x x =,设01m <<,过点(,0)P m 作曲线()y f x =的两切线,切点分别为,M N ,则下列结论中正确的是 A.直线MN 与x 轴的交点是点P B.直线MN 与x 轴的交点在点P 右侧 C.直线MN 与x 轴的交点在点P 左侧D.直线MN 与x 轴不相交第II 卷(非选择题 共90分)二、填空题(共16分,每题4分,将答案填到下页指定位置) 13.抛物线24y x =的准线方程是___________.14.已知关于x 的1kx =+无实数解,则k 的范围是_______. 15.某校所有学生的身高(单位cm )近似服从正态分布(160,25)N .已知所有学生中身高在153cm 以下的人数为202人,则该校学生总人数约为________人(用整16.一个数列有30项,满足213230293331a a a a a a -=-==-=且1303a a =,则此数列所有项的和为_________.成都七中08级三诊模拟(理科数学)答卷 分数________二、填空题(共16分,每题4分)11._____________; 12.________; 13_________________________; 14______.三、解答题(共74分)17.(12分)已知0ω>,函数()2sin()sin()3f x x x πωω=+的最小正周期为π.(1)求ω的值.(2)设A 为三角形内角,求()f A 的单调递增区间.18.(12分)QQ 先生的鱼缸中有7条鱼,其中6条青鱼和1条黑鱼,计划从当天开始,每天中午从该鱼缸中抓出1条鱼(每条鱼被抓到的概率相同)并吃掉.若黑鱼未被抓出,则它每晚要吃掉1条青鱼(规定青鱼不吃鱼).(1)求这7条鱼中至少有5条被QQ 先生吃掉的概率.(2)以ξ表示这7条鱼中被QQ 先生吃掉的鱼的条数,求E ξ.19.(12分)四面体ABCD 中,AB AC ==2,1,BC BD DA DC ===又O 为BC中点.(1)求证:AO BD ⊥.(2)求异面直线OD 与AC 所成的角.(3)求点B 到平面ACD 的距离.20.(12分)设a 为常数,)1()1ln()(+-+=x a x x x f .(1)若()0f x '>对[1,)x ∈+∞恒成立,求a 的取值范围.(2)求1)()(+-'=x axx f x g 有极值的条件及相应的极值.22.(12分)已知数列{}n a 满足:113a =,2*122()1nn na a n N a +=∈+.(1)计算2a 的值并证明{}n a 单调递减.(2)证明当2n ≥时,有123n n na a a +≤+.(3)证明1123n n a +≤-对*n N ∈恒成立..22.(14分)坐标平面内两点P 和Q 满足y y OP e OQ e ⋅=⋅,其中y e 是y 轴正方 向的单位向量,O 是原点,直线PQ 交y 轴于点M ,且32MP MQ =.(1)当点Q 在圆229x y +=上运动时,求点P 的轨迹Γ的方程.(2)设直线l 过点(0,)D m 且与Γ交于,A B 两点且B 在.y 轴下方...,点A 关于y 轴的对称点为1A ,又(0,2)E ,使1,,B E A 共线,求m 的值.(3)对(2)中的,D E 和,A B ,记BOC AOD θ=∠-∠,其中C 为D 关 于原点的对称点,求tan θ的取值范围.参考解答一、选择题(共60分,每题5分) BDBD CACA ABA B二、填空题(共16分,每题4分) 13.116y =-; 14.(,1)(1,)-∞-⋃+∞; 15.2500; 16.292-. 三、解答题(共74分)17.(12分)已知0ω>,函数()2sin()sin()3f x x x πωω=+的最小正周期为π.(1)求ω的值.(2)设A 为三角形内角,求()f A 的单调递增区间. 17.解.(1)先化为1()cos(2)23f x x πω=-+或者1()sin(2)26f x x πω=+-(随便用什么方法),由22ππω=得1ω=.(6分) (2)由(1)知1()cos(2)23f A A π=-+,又(0,)A π∈,故2(,2)333A ππππ+∈+,显然()f A 的增区间就是cos(2)3y A π=+的减区间.令2(,][2,2)333A ππππππ+∈⋃+,解得5(0,][,)36A πππ∈⋃,从而()f A 有增区间(0,]3π和5[,)6ππ.(6分)18.(12分)QQ 先生的鱼缸中有7条鱼,其中6条青鱼和1条黑鱼,计划从当天开始,每天中午从该鱼缸中抓出1条鱼(每条鱼被抓到的概率相同)并吃掉.若黑鱼未被抓出,则它每晚要吃掉1条青鱼(规定青鱼不吃鱼).(1)求这7条鱼中至少有5条被QQ 先生吃掉的概率.(2)以ξ表示这7条鱼中被QQ 先生吃掉的鱼的条数,求E ξ.18.解.(1)QQ 先生能吃到的鱼的条数ξ可取4,5,6,7,最坏的情况是只能吃到4条鱼:前3天各吃掉1条青鱼,其余3条青鱼被黑鱼吃掉,第4天QQ 先生吃掉黑鱼,其概率为 64216(4)75335P ξ==⨯⨯= 故QQ 先生至少吃掉5条鱼的概率是19(5)1(4)35P P ξξ≥=-==.(6分) (2)与(1)相仿地可得,641861615(5),(6),(7)753357535735P P P ξξξ==⨯⨯===⨯====故416586675535353535E ξ⨯⨯⨯⨯=+++=,故所求期望值为5.(6分)19.(12分)四面体ABCD 中,AB AC ==2,1,BC BD DA DC ===又O 为BC中点.(1)求证:AO BD ⊥.(2)求异面直线OD 与AC所成的角.(3)求点B 到平面ACD 的距离.19.解.(1)由222AB BD AD +=,得BD AB ⊥,又222BC BD CD +=,故BD BC ⊥,于是BD ⊥平 面ABC ,从而AO BD ⊥.(4分)(2)随便用什么办法,比如建立以O 为原点,OC ,OA 分别为y 轴和z 轴的空间直角坐标系,或用所求角的余弦等于cos cos ACO BOD ∠∠等均可求出异面直线OD 与AC 所成的角为060.(4分)(3)随便用什么方法可得所求距离为3(4分) 注.若(1)未证对,但(2),(3)解对,后两小题仍给满分.20.(12分)设a 为常数,)1()1ln()(+-+=x a x x x f .(1)若()0f x '>对[1,)x ∈+∞恒成立,求a 的取值范围.(2)求1)()(+-'=x axx f x g 有极值的条件及相应的极值. 20.解.(1)易得()ln(1)01x f x x a x '=++->+,故原条件化为ln(1)1xa x x<+++对[1,)x ∈+∞恒成立.令()ln(1)1x h x x x =+++,则211()1(1)h x x x '=+++,当[1,)x ∈+∞时显然有()0h x '>,故),1[)(+∞在x h 上单调递增,从而1(1)ln 22a h <=+. 故所求a 的取值范围是)2ln 21,(+-∞.(6分) (2)2(1)2()ln(1),(1,),()1(1)a x x ag x x a x g x x x -+-'=++-∈-+∞=++. ①若1a >,则(1,2)x a ∈--时()0g x '<,即()g x 在(1,2]a --单减;(2,)x a ∈-+∞时,()0g x '>,即()g x 在[2,)a -+∞单增,从而()g x 有极小值(2)2ln(1)g a a -=+--2a②若1a ≤,则(1,)x ∈-+∞时()0g x '>,即()g x 在其定义域上是增函数,从而无极值. 综上所述,当且仅当1a >时()g x 有极小值2ln(1)a +-.21.(12分)已知数列{}n a 满足:113a =,2*122()1nn na a n N a +=∈+.(1)计算2a 的值并证明{}n a 单调递减.(2)证明当2n ≥时,有123n n na a a +≤+.(3)证明1123n n a +≤-对*n N ∈恒成立.21.解.(1)易得215a =,且{}n a 各项恒正.又212n n a a +≥,故22122212n n n n n na a a a a a +=≤=+,且其中取等条件是1n a =,由1n n a a +≤及11a <知等号不能取到,故1n n a a +<对*n N ∈恒成立,即{}n a 单调递减.(3分)(2)须证当2n ≥时,222222461451123n n n n n n n n na a a a a a a a a ≤⇔+≤+⇔+≤++,但由(1)知2n ≥时215n a a ≤=,从而21145451525n n a a +≤⋅+⋅=,故结论成立.(3分)(3)当1n =及2n =时,易验证1123n n a +≤-成立.由(2),当2n ≥时,有123nn na a a +≤+,即1111121133222n n n n n n n a a a a ++++≥+⇒≥+,从而当3n ≥时有 323434132431113113113,,,222222222n n nn n a a a a a a ---≥-≥-≥ 将这2n -个不等式相解得23321131131(1)(2)2282282n n n n a a ---≥+++=-,故3n ≥时有233211315313(2)(2)222824822n n n nn a a --≥+-=+-=-,从而结论成立.(6分) 方注.学生可能有不同解法,阅卷老师应认真对待.若有较好解法,请设法转告我.22.(14分)坐标平面内两点P 和Q 满足y y OP e OQ e ⋅=⋅,其中y e 是y 轴正方向的单位向量,O 是原点,直线PQ 交y 轴于点M ,且32MP MQ =.(1)当点Q 在圆229x y +=上运动时,求点P 的轨迹Γ的方程.(2)设直线l 过点(0,)D m 且与Γ交于,A B 两点且B 在y 轴下方,点A 关于y 轴的对称点为1A ,又(0,2)E ,使1,,B E A 共线,求m 的值.(3)对(2)中的,D E 和,A B ,记BOC AOD θ=∠-∠,其中C 为D 关于原点的对称点,求tan θ的取值范围.22.解.(1)由y y OP e OQ e ⋅=⋅知0y PQ e ⋅=即0y MP e ⋅=,从而,P Q 的纵坐标相同,再由32MP MQ =知32Q P x x =,故若设(,)P x y ,则3(,)2Q x y ,由Q 在圆229x y +=上知有223()92x y +=,故P 的轨迹Γ的方程为22149x y +=.(3分) (2)l 重合于y 轴的情形不必考虑.设l :y kx m =+,代入Γ的方程并整理得222(94)84360k x kmx m +++-= ①令0∆>,得22224(9)(49)0k m m k --+>,即2249k m >- ②设1122(,),(,)A x y B x y ,则111(,)A x y -且12,x x 是①的根,从而122849km x x k -+=+, 212243649m x x k -=+ ③又11122(,2),(,2)EA x y EB x y =--=-, 故1,,B E A 共线等价于1//EA EB ,等价于12211221(2)(2)(2)(2)x y x y x kx m x kx m --=-⇔-+-=+-12122(2)()0kx x m x x ⇔+-+=再由③知其等价于22(436)(2)(8)0k m m km -+--=,再由0k ≠可解得92m =.(6分) (3)当92m =时,③化为1223649k x x k -+=+,1224549x x k =+, 由对称性知只须考虑0k >的情形,由B 在.y 轴下方...知,A B 分别在二、三象限,故94k >,且BOC∠和AOD∠都是锐角,且2211221122tan ,tan 2929x x x x BOC AOD y kx y kx --∠==∠==++,于是 1221211212212121212(418)(418)818()tan (29)(29)44(1)18()81kx x x kx x x kx x x x kx kx x x k x x k x x θ+++++==++--+++ 22284518(36)324(1)4518(36)81(49)1661k k kk k k k k ⋅+⋅-==-⋅+⋅-++- 显然当94k >时6116k k -为k 的增函数且恒正,故232tan 1661k k θ=-为k 的减函数,从而 7218tan 81615θ<=-且当k →+∞时tan 0θ→,故tan θ的取值范围是18(0,)5.(5分)注.(3)直接用几何方法得答案者给2分.。
成都市2008届高中毕业班第三次诊断性检测

成都市2008届高中毕业班第三次诊断性检测语文说明:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷,第Ⅰ卷1至4页,第Ⅱ卷5至12页。
共150分。
考试时间150分钟。
2.答第Ⅰ卷前,考生务必将自己的姓名、考号、考试科目涂写在答题卡上。
3.答第Ⅰ卷时,每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案,不能答在试卷上。
答第Ⅱ卷时,用蓝黑钢笔或圆珠笔将答案直接写在试卷上;答卷前将密封线内的项目填写清楚。
4.考试结束,监考人员将第Ⅱ卷和答题卡一并收回。
第Ⅰ卷(选择题,共30分)一、(12分,每小题3分)1.下列各组词语中加点字读音完全相同的一组是A.矍铄诡谲角逐咬文嚼字B.犄角跻身畸形有案可稽C.莅临旖旎瓦砾风声鹤唳D.桎梏对峙炽热栉风沐雨2.下列各组词语中.没有错别字的一项是A.厄运发祥地大事渲染放之四海而皆准B.蝉联发牢骚以老卖老有过之而无不及C.名分副食品行迹可疑男儿有泪不轻谈D.欠收肇事者因噎废食解铃还须系铃人3.下列各句中,加点的成语使用恰当的一句是A.一些食品生产商在生产过程中违规添加对人体健康有害的保鲜剂,却在广告中宣称绝对是“纯天然绿色产品”,这是用掩耳盗铃式的手段欺骗广大消费者。
B.教育部日前宣布,将在10个省份开展京剧进课堂试点。
一石激起千层浪,社会各界对此意见分歧,一时争论不已。
C.巴以双方发表联合声明,力争于2008年底前达成协议,为建立独立的巴勒斯坦国铺平道路,这种姿态是大势所趋,众望所归,受到国际社会的欢迎.D.香港教育界的传奇夫妻钟期荣、胡鸿烈。
抛家舍业,悬壶济世,自筹资金创办树仁学院,为香港社会培养了数以万计的人才。
4.依次填入下面一段文字中横线处的语句。
与上下句衔接最恰当的一组是以苏东坡之才,治国经邦都会有独特的建树,他任杭州太守期间的政绩就是明证。
可是,他毕竟太富于诗人气质了,禁不住______.结果总是得罪人。
他的诗名冠绝一时,流芳百世,但他的五尺之躯______,______,他都照例不受欢迎。
四川省成都市高中毕业班第三次诊断性检测数学(理科)试题(解析版)

四川省成都市高中毕业班第三次诊断性检测数学(理科)试题本试卷分选择题和非选择题两部分。
第Ⅰ卷(选择题,第Ⅱ卷(非选择题),满分150分,考试时间120分钟。
注意事项:1.答题前,务必将自己的姓名、考籍号填写在答题卡规定的位置上。
2.答选择题时,必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦擦干净后,再选涂其它答案标号。
3.答非选择题时,必须使用0.5毫米黑色签字笔,将答案书写在答题卡规定的位置上。
4.所有题目必须在答题卡上作答,在试题卷上答题无效。
5.考试结束后,只将答题卡交回。
第Ⅰ卷(选择题,共60分)一、选择题:本大题共12小题,每小题5分,满分60分. 在每小题给出的四个选项中,只有一项符合题目要求.1.设全集{}=0123U ,,,,集合()(){}130A x x x =∈--≤N ,则集合UA 中元素的个数是( )A .1B .2C .3D .4 2.若复数i1ia z +=-(i 是虚数单位)为纯虚数,则实数a 的值为( ) A .2- B .1- C .1 D .23.命题“()1,x ∀∈+∞,1ln x x -≥”的否定是( )A .()1,x ∀∈+∞,1ln x x -≤B .()1,x ∀∈+∞,1ln x x -<C .()01,x ∃∈+∞,001ln x x -≥D .()01,x ∃∈+∞,001ln x x -<4.定义符号函数1,0,sgn 0,0,1,0,x x x x >⎧⎪==⎨⎪-<⎩则函数()sin sgn f x x x =⋅的图象大致是( )5.已知实数ln 22a =,22ln 2b =+,()2ln 2c =,则,,a b c 的大小关系是( )A .c a b <<B .c b a <<C .b a c <<D .a c b <<6.当,2απ⎛⎫∈π⎪⎝⎭时,若()()sin cos 3ααπ--π+=,则sin cos αα-的值为( )A .3 B .3- C .43 D .43-7.已知甲袋中有1个黄球和1个红球,乙袋中有2个黄球和2个红球.现随机地从甲袋中出1个球放入乙袋中,再从乙袋中随机取出1个球,则从乙袋中取出红球的概率为( )A .13 B .12 C .59 D .298.某企业可生产,A B 两种产品.投资生产A 产品时,每生产100吨需要资金200万元,场地200平方米;投资生产B 产品时,每生产100吨需要资金300万元,场地100平方米.若该企业现可使用资金1400万元,场地900平方米投资生产,A B 两种产品,则两种产品的量之和的最大值是( )A .467吨B .450吨C .575吨D .600吨9.在正三棱柱111ABC A B C - (底面是正三角形,侧棱垂直于底面的棱柱)中,所有棱长之和为定值a .若正三棱柱111ABC A B C -的顶点都在球O 的表面上,则当正三棱柱侧面积取得最大值24时,该球的表面积为( )A .B .323π C .12π D .643π10.已知P 为ABC △所在平面内一点,AB PB PC ++=0,2PC PB AB ===,则PBC △的面积等于( )A B . C . D .11.已知,A B 是椭圆C :221259x y +=上关于坐标原点O 对称的两个点,,,P M N 是椭圆C 异于,A B 的点,且AP ∥OM ,BP ∥ON ,则MON △的面积为( )A .2 B .32 C .152 D .25212.在关于x 的不等式()2222e e 4ee4e 0x xx a x a -+++> (其中e 2.71828=为自然对数的底数)的解集中,有且仅有两个大于2的整数,则实数a 的取值范围为( )A .4161,5e 2e ⎛⎤⎥⎝⎦ B .391,4e 2e ⎡⎫⎪⎢⎣⎭ C .42164,5e 3e ⎛⎤ ⎥⎝⎦ D .3294,4e 3e ⎡⎫⎪⎢⎣⎭第Ⅱ卷(非选择题,共90分)二、填空题:本大题共5小题,每小题5分,共25分.请将答案填在题后横线上.13.51x x ⎛⎫- ⎪⎝⎭的展开式中各项系数之和为 .14.如图,在正方体1111ABCD A B C D -中,E 是棱1DD 的中点,则异面直线AE 与1BD 所成角的余弦值为 .15.在ABC △中,内角,,A B C 所对的边分别为,,a b c ,已知66a c b -=,sin 6sin B C =.则cos 26A π⎛⎫-= ⎪⎝⎭ . 16.已知集合{}1,2,3,4,5,6,7,8,9M =的所有3个元素的子集记为123,,,,k A A A A ,*k ∈N .记i a 为集合i A (1,2,3,,i k =)中的最大元素,则12k a a a +++= .三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.17.(本小题满分12分)已知n S 为等比数列{}n a 的前n 项和,243,,S S S 成等差数列,且23438a a a ++=-. (I )求数列{}n a 的通项公式;(Ⅱ)设n n b n a =,求数列{}n b 的前n 项和n T .18.(本小题满分12分)某企业统计自2011年到2017年的产品研发费x 和销售额y 的数据如下表:根据上表中的数据作出散点图,得知产品研发费的自然对数值z (精确到小数点后第二位)和销售额y 具有线性相关关系.(I )求销售额y 关于产品研发费x 的回归方程ˆˆˆln yb x a =+ (ˆˆ,a b 的计算结果精确到小数点后第二位);(Ⅱ)根据(I )的结果预则:若2018年的销售额要达到70万元,则产品研发费大约需要多少万元?19.(本小题满分12分)如图①,在等腰梯形ABCD 中,已知AB ∥CD ,60ABC ∠=,2CD =,4AB =,点E 为AB 的中点;现将三角形BEC 沿线段EC 折起,形成直二面角P EC A --,如图②,连接,PA PD 得四棱锥P AECD -,如图③.(I )求证:PD EC ⊥;(Ⅱ)求平面PEC 与平面PAD 所成的锐二面角的余弦值.20.(本小题满分12分)在平面直角坐标系xOy 中,动点M 与定点()1,0F 的距离和它到直线4x =的距离的比是1:2.记动点M 的轨迹为曲线C ,直线l :()0y kx m m =+≠与曲线C 相交于不同的两点,P Q .(I )求曲线C 的方程; (Ⅱ)求OPQ △面积的最大值.21.(本小题满分12分)已知函数()()1ln 1f x k x k x k =--+-,其中,0k k ∈≠R . (I )讨论函数()f x 的单调性;(Ⅱ)设函数()f x 的导函数为()g x .若函数()f x 恰有两个零点()1212,x x x x <,证明:12203x x g +⎛⎫> ⎪⎝⎭.请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分.作答时,用2B 铅笔在答题卡上把所选题目对应的标号涂黑. 22.(本小题满分10分)选修4-4:极坐标与参数方程在极坐标系中,曲线C 的极坐标方程是4cos ρθ=,直线l sin 14θπ⎛⎫+= ⎪⎝⎭,点,2Q ρπ⎛⎫⎪⎝⎭在直线l 上.以极点为坐标原点O ,极轴为x 轴的正半轴,建立平面直角坐标系xOy ,且两坐标系取相同的单位长度.(I )求曲线C 及直线l 的直角坐标方程;(Ⅱ)若直线l 与曲线C 相交于不同的两点,A B ,求QA QB +的值. 23.(本小题满分10分)选修4-5:不等式选讲已知函数()21f x x x a =++-,a ∈R . (I )当2a =时,解不等式()4f x ≤;(Ⅱ)若不等式()1f x <的解集为非空集合,求a 的取值范围.试题答案第Ⅰ卷(选择题,共60分)一、选择题:本大题共12小题,每小题5分,满分60分. 在每小题给出的四个选项中,只有一项符合题目要求.1.设全集{}=0123U ,,,,集合()(){}130A x x x =∈--≤N ,则集合UA 中元素的个数是( )A .1B .2C .3D .4 【答案】 A【解析】由题意得{}1,2,3A =,所以{}0UA =,故选A.考点:集合的基本运算. 2.若复数i1ia z +=-(i 是虚数单位)为纯虚数,则实数a 的值为( ) A .2- B .1- C .1 D .2【答案】 C 【解析】因为()()()i 1i 11ii 1i 22a a a a z ++-+++===-是纯虚数,所以10a -=,即1a =,故选C. 考点:1、复数的运算,2、纯虚数的概念.3.命题“()1,x ∀∈+∞,1ln x x -≥”的否定是( )A .()1,x ∀∈+∞,1ln x x -≤B .()1,x ∀∈+∞,1ln x x -<C .()01,x ∃∈+∞,001ln x x -≥D .()01,x ∃∈+∞,001ln x x -< 【答案】 D【解析】“()1,x ∀∈+∞,1ln x x -≥”的否定是“()01,x ∃∈+∞,001ln x x -<”,故选D. 考点:含一个量词的命题否定.4.定义符号函数1,0,sgn 0,0,1,0,x x x x >⎧⎪==⎨⎪-<⎩则函数()sin sgn f x x x =⋅的图象大致是( )【答案】 B【解析】用排除法,易知()f x 是偶函数,故排除A 选项;当0x <<π时,()0f x >,故排除D 选项;当2x π<<π时,()0f x <,故排除C 选项.故选B. 考点:函数的图象. 5.已知实数ln 22a =,22ln 2b =+,()2ln 2c =,则,,a b c 的大小关系是( )A .c a b <<B .c b a <<C .b a c <<D .a c b << 【答案】A 【解析】易知ln 2122<<,22ln22+>,()20ln 21<<,所以c a b <<.故选A.考点:指数与对数运算及单调性. 6.当,2απ⎛⎫∈π⎪⎝⎭时,若()()2sin cos 3ααπ--π+=,则sin cos αα-的值为( )A .23 B .23- C .43 D .43-【答案】C【解析】由诱导公式得()()2sin cos sin cos ααααπ--π+=+=,所以72sin cos 9αα=-,()()2216sin cos sin cos 4sin cos 9αααααα-=+-=,又,2απ⎛⎫∈π ⎪⎝⎭,所以sin cos 0αα->所以4sin cos 3αα-=.故选C.考点:1、诱导公式;2、同角基本关系求值.7.已知甲袋中有1个黄球和1个红球,乙袋中有2个黄球和2个红球.现随机地从甲袋中出1个球放入乙袋中,再从乙袋中随机取出1个球,则从乙袋中取出红球的概率为( )A .13 B .12 C .59 D .29【答案】B【解析】先从甲袋中取出1个球放入乙袋,再从乙袋出1个球的总数为112510C C =,取出红球的总数为111113125C C C C +=,所以乙袋中取出红球的概率为51102P ==.故选B. 考点:古典概型.8.某企业可生产,A B 两种产品.投资生产A 产品时,每生产100吨需要资金200万元,场地200平方米;投资生产B 产品时,每生产100吨需要资金300万元,场地100平方米.若该企业现可使用资金1400万元,场地900平方米投资生产,A B 两种产品,则两种产品的量之和的最大值是( ) A .467吨 B .450吨 C .575吨 D .600吨 【答案】C【解析】设生产,A B 产品的产量分别为,x y (单位:100吨),由题意得约束条件2003001400,200100900,0,0,x y x y x y +≤⎧⎪+≤⎪⎨≥⎪⎪≥⎩求目标函数z x y =+的最大值.由约束条件得可行区域(如图),其中()4.5,0A ,()3.25,2.5B ,140,3C ⎛⎫⎪⎝⎭.由可行区域可得目标函数z x y =+经过()3.25,2.5B 时,z 取最大值,故max 5.75z =(100吨). 故选C. 考点:线性规划问题.9.在正三棱柱111ABC A B C - (底面是正三角形,侧棱垂直于底面的棱柱)中,所有棱长之和为定值a .若正三棱柱111ABC A B C -的顶点都在球O 的表面上,则当正三棱柱侧面积取得最大值24时,该球的表面积为( )A .3πB .323π C .12π D .643π【答案】D【解析】设正三棱柱111ABC A B C -底面边长为x ,侧棱为y ,则63x y a +=,三棱柱111ABC A B C -侧面积3S xy =.所以2216336224x y a S xy +⎛⎫=≤= ⎪⎝⎭,当且仅当632a x y ==,即,126a a x y ==时,等号成立,所以24a =,2x =,4y =.所以正三棱柱111ABC A B C -的外接球的球心O 到顶点A 的距离为4=,所以该球的表面积为643π.故选D. 考点:1、简单几何体;2、基本不等式.10.已知P 为ABC △所在平面内一点,AB PB PC ++=0,2PC PB AB ===,则PBC △的面积等于( )A B . C . D . 【答案】A【解析】分别取边BC ,AC 的中点,D E ,则2PB PC PD +=,2AB ED =, 因为AB PB PC ++=0,所以ED PD =-,所以,,E D P 三点共线,且1ED PD ==.又2PC PB ==,所以PD BC ⊥,所以23BC =,所以PBC △的面积112S =⨯=故选A.考点:平面向量线性运算.11.已知,A B 是椭圆C :221259x y +=上关于坐标原点O 对称的两个点,,,P M N 是椭圆C 异于,A B 的点,且AP ∥OM ,BP ∥ON ,则MON △的面积为( )A .2 B .32 C .152 D .252【答案】C【解析】方法一:特殊值法,取,A B 为短轴的端点,即()0,3A ,()0,3B -,点P 为左顶点()5,0P -,则直线OM ,ON 的方程分别为35y x =,35y x =-,所以M ,N ,所以152MON S =△.故选A.方法二:若,PA PB 与坐标轴平行或垂直时,可得点,M N 为椭圆C 长轴和短轴的一个端点,所以1155322MON S =⨯⨯=△;若,PA PB 与坐标轴不平行或不垂直时,则925PA PB k k ⋅=-,设直线OM ,ON 的方程分别为1y k x =,2y k x =,则12925k k ⋅=-.联立2211,259,x y y k x ⎧+=⎪⎨⎪=⎩解得M ⎛⎫,同理可得N ⎛⎫,所以MON S =△()121222515.2152k k k k ==-==- 故选A.考点:直线与椭圆的位置关系.12.在关于x 的不等式()2222e e 4e e 4e 0x x x a x a -+++> (其中e 2.71828=为自然对数的底数)的解集中,有且仅有两个大于2的整数,则实数a 的取值范围为( )A .4161,5e 2e ⎛⎤⎥⎝⎦ B .391,4e 2e ⎡⎫⎪⎢⎣⎭ C .42164,5e 3e ⎛⎤ ⎥⎝⎦ D .3294,4e 3e ⎡⎫⎪⎢⎣⎭ 【答案】D【解析】易得()2222e e 4e e4e 0x xx a x a -+++>⇔()()22e 21e x x a x ->-.设()()22e2f x x =-,()()1e xg x a x =-,则原不等式等价与()()f x g x >.若0a ≤,则当2x >时,()0f x >,()0g x <,所以原不等式的解集中有无数个大于2的整数,所以0a >. 因为()20f =,()22e 0g a =>,所以()()22f g <.当()()33f g ≤,即12ea ≥时,设()()()()4h x f x g x x =-≥, 则()()()22e 2e 2e 2e 22exxx h x x ax x '=--≤--.设()()()2e 2e 242exx x x x ϕ=--≥,则()()()21e 2e 302e xx x ϕϕ+''=-≤=,所以()x ϕ在[)4,+∞上为减函数,所以()()()242e 2e 0x ϕϕ≤=-<, 所以当4x ≥时,()0h x '<,所以()h x 在[)4,+∞上为减函数,所以()()324223e 3e 44e 3e 4e e 4022h x h a ⎛⎫≤=-≤-=-< ⎪⎝⎭, 所以当4x ≥时,不等式()()f x g x <恒成立,所以原不等式的解集中没有大于2的整数.所以要使原不等式的解集中有且仅有两个大于2的整数,则()()()()()()33,44,55,f g f g f g >⎧⎪>⎨⎪≤⎩所以232425e 2e ,4e 3e ,9e 4e ,a a a ⎧>⎪>⎨⎪≤⎩解得32944e 3ea ≤<.故选D.考点:利用导数研究函数的性质解决不等式成立问题.第Ⅱ卷(非选择题,共90分)二、填空题:本大题共5小题,每小题5分,共25分.请将答案填在题后横线上.13.51x x ⎛⎫- ⎪⎝⎭的展开式中各项系数之和为 .【答案】0【解析】令1x =,得展开式中各项系数之和为()5110-=. 考点:二项式定理.14.如图,在正方体1111ABCD A B C D -中,E 是棱1DD 的中点,则异面直线AE 与1BD 所成角的余弦值为 .【答案】155【解析】以点D 原点,1,,DA DB DD 分别为,,x y z 轴建立空间直角坐标系,设棱长为2,则()2,0,0A ,()0,0,1E ,()2,2,0B ,()10,0,2D ,所以()2,0,1AE =-,()12,2,2BD =--,所以11115cos ,5AE BD AE BD AE BD ⋅==,所以异面直线AE 与1BD 所成角的余弦值为155.考点:空间角.15.在ABC △中,内角,,A B C 所对的边分别为,,a b c ,已知66a cb -=,sin 6sin B C =.则cos 26A π⎛⎫-= ⎪⎝⎭ .【答案】8【解析】因为sin B C =,所以b =,又6a c -=,所以2a c =,由余弦定理得2222cos 24b c a A bc +-===,所以sin 4A =,所以sin 2A =1cos 24A =-.所以cos 2cos 2cos sin 2sin 666A A A πππ⎛⎫-=+= ⎪⎝⎭ 考点:1、正余弦定理;2、三角恒等变换.16.已知集合{}1,2,3,4,5,6,7,8,9M =的所有3个元素的子集记为123,,,,k A A A A ,*k ∈N .记i a 为集合i A (1,2,3,,i k =)中的最大元素,则12k a a a +++= .【答案】630【解析】集合M 含有3个元素的子集共有3984C =,所以84k =.在集合i A (1,2,3,,i k =)中:最大元素为3的集合有221C =个;最大元素为4的集合有233C =;最大元素为5的集合有246C =;最大元素为6的集合有2510C =;最大元素为7的集合有2615C =;最大元素为8的集合有2721C =;最大元素为9的集合有2828C =.所以12314356610715821928630k a a a +++=⨯+⨯+⨯+⨯+⨯+⨯+⨯=.考点:1、集合间的基本关系;2、组合.三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤. 17.(本小题满分12分)已知n S 为等比数列{}n a 的前n 项和,243,,S S S 成等差数列,且23438a a a ++=-. (I )求数列{}n a 的通项公式;(Ⅱ)设n n b n a =,求数列{}n b 的前n 项和n T .【答案】(I)112n n a -⎛⎫=- ⎪⎝⎭;(Ⅱ)1242n n n T -+=-. 【解析】考点:1、等比数列;2、错位相减法. 18.(本小题满分12分)某企业统计自2011年到2017年的产品研发费x 和销售额y 的数据如下表:根据上表中的数据作出散点图,得知产品研发费的自然对数值z (精确到小数点后第二位)和销售额y 具有线性相关关系.(I )求销售额y 关于产品研发费x 的回归方程ˆˆˆln yb x a =+ (ˆˆ,a b 的计算结果精确到小数点后第二位);(Ⅱ)根据(I )的结果预则:若2018年的销售额要达到70万元,则产品研发费大约需要多少万元?【答案】(I)ˆ11.99ln 21.86y x =+;(Ⅱ)55.5.【解析】考点:1、用线性回归方程系数公式求线性方程;2、用样本估计总体解决简单实际问题.19.(本小题满分12分)如图①,在等腰梯形ABCD 中,已知AB ∥CD ,60ABC ∠=,2CD =,4AB =,点E 为AB 的中点;现将三角形BEC 沿线段EC 折起,形成直二面角P EC A --,如图②,连接,PA PD 得四棱锥P AECD -,如图③.(I )求证:PD EC ⊥;(Ⅱ)求平面PEC 与平面PAD 所成的锐二面角的余弦值. 【答案】(I)见解析;(Ⅱ)22. 【解析】考点:1、点线面间的垂直关系;2、向量方法求面面的夹角. 20.(本小题满分12分)在平面直角坐标系xOy 中,动点M 与定点()1,0F 的距离和它到直线4x =的距离的比是1:2.记动点M 的轨迹为曲线C ,直线l :()0y kx m m =+≠与曲线C 相交于不同的两点,P Q .(I )求曲线C 的方程; (Ⅱ)求OPQ △面积的最大值.【答案】(I)22143x y +=;(Ⅱ)3. 【解析】考点:1、椭圆的方程;2、直线与椭圆的位置关系. 21.(本小题满分12分)已知函数()()1ln 1f x k x k x k =--+-,其中,0k k ∈≠R . (I )讨论函数()f x 的单调性;(Ⅱ)设函数()f x 的导函数为()g x .若函数()f x 恰有两个零点()1212,x x x x <,证明:12203x x g +⎛⎫>⎪⎝⎭. 【答案】(I)22143x y +=;(Ⅱ)3. 【解析】考点:导数在研究函数的单调性中的应用.请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分.作答时,用2B 铅笔在答题卡上把所选题目对应的标号涂黑.22.(本小题满分10分)选修4-4:极坐标与参数方程在极坐标系中,曲线C 的极坐标方程是4cos ρθ=,直线l 的极坐标方程是2sin 14ρθπ⎛⎫+= ⎪⎝⎭,点,2Q ρπ⎛⎫ ⎪⎝⎭在直线l 上.以极点为坐标原点O ,极轴为x 轴的正半轴,建立平面直角坐标系xOy ,且两坐标系取相同的单位长度.(I )求曲线C 及直线l 的直角坐标方程;(Ⅱ)若直线l 与曲线C 相交于不同的两点,A B ,求QA QB +的值.【答案】(I)()2224x y -+=,10x y +-=;(Ⅱ)32. 【解析】考点:1、极坐标和直角坐标的互化;2、参数的意义.23.(本小题满分10分)选修4-5:不等式选讲已知函数()21f x x x a =++-,a ∈R .(I )当2a =时,解不等式()4f x ≤;(Ⅱ)若不等式()1f x <的解集为非空集合,求a 的取值范围.【答案】(I)[]1,1-;(Ⅱ)31,22⎛⎫-⎪⎝⎭. 【解析】考点:解含绝对值的不等式.。
四川省成都市届高中班第三次诊断性检测数学试题理科

四川省成都市届高中班第三次诊断性检测数学试题理科四川省成都市2009届高中毕业班第三次诊断性检测数学试题(理科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,考试结束后,将本试卷和答题卡一并交回。
全卷满分150分。
完成时间为120分钟。
第Ⅰ卷注意事项:1.答第Ⅰ卷前,考生务必将自己的姓名、考号、考试科目涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试卷上。
3.本卷共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
参考公式:如果事件A 、B 互斥,那么球的表积公式:P (A+B )=P (A )+P (B ) 24R S π=如果事件A 、B 相互独立,那么 其中R 表示球的半径P (A ·B )=P (A )·P (B ) 球的体积公式如果事件A 在一次试验中发生的概率是P ,334R V π= 那么n 次独立重复试验中恰好发生k 次的概率 其中R 表示球的半径一、选择题: 1.3cos 的值( )A .小于0B .大于0C .等于0D .无法确定 2.已知集合a N M a N a M 则若},4{},1,2{},,1{2=⋂-==等于( ) A .4 B .0或4 C .0或2 D .23.已知)tan()(),,,()1(b ax x f i R b a i i bi a +=∈-=+则函数为虚数单位的最小正周期是( ) A .π2B .πC .2π D .14.已知等差数列5332*:,2:5:),(}{S S a a N n S n a nn则若项和为的前=∉等于( )A .3:2B .3:5C .2:5D .2:3 5.在标准正态总体N (0,1)中,已知9762.0)98.1(=φ,则标准正态总体在区间)98.1,98.1(-内取值的概率为( )A .0.9672B .0.9706C .0.9412D .0.9524 6.已知点O 为坐标原点,点P 满足2||=,则点P 到直线023=--y x 的最短距离为( ) A .5B .3C .1D .237.若A 、B 为一对对立事件,其概率分别为y x yB P x A P +==则,1)(,4)(的最小值为( )A .9B .10C .6D .88.从0、1、4、5、8这5个数字中任选四个数字组成没有重复数字的四位数,在这些四位数中,不大于5104的四位数的总个数是 ( ) A .56 B .55C .54D .529.已知)()(),(1x f x f x f分别是函数'-的反函数和导函数,若2ln )1()1(,log )(121f f x x f '+-=-则的值等于( )A .2ln 21+ B .2 C .1D .2ln 3+10.有下列命题:①在空间中,若B O A AOB B O OB A O OA '''∠=∠'''则,//,//;②直角梯形是平面图形;③{正四棱柱}⊆{直平行六面体}⊆{长方体};④在四面体P —ABC 中,AC PB BC PA ⊥⊥,,则点A 在平面PBC 内的射影恰为PBC ∆的垂心,其中逆否命题为真命题的个数是 ( ) A .1 B .2C .3D .411.设D 是由⎩⎨⎧≥≥+-0))((y y x y x 所确定的平面区域,记“平面区域D 被夹在直线])1,1[(1-∈=-=t t x x 和之间的部分的面积”为S ,则函数)(t f S =的大致图象为 ( )12.已知曲线E 的参数方程为)(cos 2sin 12为参数θθθ⎩⎨⎧=-=y x ,则下列说法正确的是 ( )A .过点(1,0)并与曲线E 相交所得弦长为8的直线存在且有两条B .0)3(0=-+=y m x m 是直线与曲线E 相切的充分不必要条件C .若),(y x P 为曲线E 上的点,则22x y -的最大值为3D .与曲线E 相交所得弦的中点为Q (2,2)的直线存在且其方程为0=-y x第Ⅱ卷注意事项:1.用钢笔或圆珠笔直接答在试题卷中。
08届高三第三次联考数学试卷

08届高三第三次联考数学试卷08届高三第三次联考数学试卷本试卷分选择题和非选择题两部分,共4页,满分150,考试时间120分钟,答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的班级.姓名.座位号填写在答题卷的密封线内.所有题目必须用黑色字迹的钢笔或签字笔答在答题卷上,否则答案无效.一.选择题:(本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项).1.设集合,集合,那么下列结论正确的是: ( )A.B. C. D.2.设,则对任意实数,是的( )A. 充分必要条件B. 充分而不必要条件C. 必要而不充分条件D. 既不充分也不必要条件3.方程一定有解,则的取值范围是( )A.B.C.D.以上都不对4.如果执行下面的程序框图,那么输出的( ).A.2450 B.2500 C.2550 D.26525.将函数的图象先向左平移,然后将所得图象上所有的点的横坐标变为原来的倍(纵坐标不变),则所得到的图象对应的函数解析式为( ).A.B.C.D.6.等差数列{an}.{bn}的前n项和分别为Sn.Tn,且,则使得为整数的正整数n的个数是()A.3 B.4 C.5 D.67.右图是一个正方体,它的展开图可能是下面四个展开图中的( )A.B.C.D.8. 如图,设P.Q为△ABC内的两点,且, =+,则△ABP的面积与△ABQ的面积之比为( )A. B.C.D.第8题第Ⅱ卷(非选择题,共100分)二.填空题:(本大题共6小题,每小题5分,满分30分).9.化简: .10. 一物体在力F(_)=4_+2(力的单位:N)的作用下,沿着与力F相同的方向,从_=0处运动到_=5处(单位:m),则力F(_)所作的功___________11.已知点的坐标满足条件,点为坐标原点,那么的最大值等于_______,最小值等于____________.12.从装有个球(其中个白球,1个黑球)的口袋中取出个球,共有种取法.在这种取法中,可以分成两类:一类是取出的个球全部为白球,共有,即有等式:成立.试根据上述思想化简下列式子:..▲选做题:以下三小题请选做其中两题,若三小题都做的,只计前两小题得分.13.如图,在△ABC中,AB=AC,∠C=720,⊙O过A.B两点且与BC相切于点B,与AC交于点D,连结BD,若BC=,则AC=.14.极坐标方程化为直角坐标方程是,它表示的图形是 __15.设_,y均为正实数,且,则_y的最小值为三.解答题:(本大题共6小题,共80分,解答应写出文字说明,证明过程或演算步骤).16.(本小题满分12分)已知函数(Ⅰ)求函数的最小正周期和单调递减区间;(Ⅱ)在所给坐标系中画出函数在区间的图象(只作图不写过程).17.(本小题满分14分)将一颗骰子先后抛掷2次,观察向上的点数,问:(1)两数之和为8的概率;(2)两数之和是3的倍数的概率;(3)两数之积是6的倍数的概率.(4)以第一次向上点数为横坐标_,第二次向上的点数为纵坐标y的点(_,y)在圆_2+y2=25的内部的概率.18.(本小题满分14分)已知函数图像上的点处的切线方程为.(1)若函数在时有极值,求的表达式;19.(本题满分14分)如图,在矩形中,是的中点,以为折痕将向上折起,使为,且平面平面.(Ⅰ)求证:;(Ⅱ)求直线与平面所成角的正弦值.20. (本小题满分14分)如图,矩形的两条对角线相交于点,边所在直线的方程为, 点在边所在直线上.(I)求边所在直线的方程;(II)求矩形外接圆的方程;20题(III)若动圆过点,且与矩形的外接圆外切,求动圆的圆心的方程.21.(本小题满分14分)已知(m为常数,m_gt;0且)设是首项为4,公差为2的等差数列.(Ⅰ)求证:数列{an}是等比数列;(Ⅱ)若bn=an·,且数列{bn}的前n项和Sn,当时,求Sn;(Ⅲ)若cn=,问是否存在m,使得{cn}中每一项恒小于它后面的项?若存在,求出m 的范围;若不存在,说明理由.(2)函数在区间上单调递增,求实数的取值范围.参考答案一:选择题题号12345678答案代号CAACCBAB二.填空题: 9 . 2 10. 11. ,12 . 6013. 2 14.(或) , 两条直线15. 161.C; ,2.A; 显然为奇函数,且单调递增.于是若,则,有,即,从而有.反之,若,则,推出,即.故选A.3.A; 由 , 知 ;4.C; 05.C;6.B;, ;7.A 把握住4,6,8三个面有一个共同的顶点这一个特点8.B; 如下图,设,,则.由平行四边形法则,知NP∥AB,所以=,同理可得.故,选B.9.2(略)10.60; 力F(_)所作的功为11. 从图中看出 ,所以选A12.;根据题中的信息,可以把左边的式子归纳为从个球(n个白球,k个黑球)中取出m个球,可分为:没有黑球,一个黑球,……,k个黑球等类,故有种取法.13.2; 由已知得, ,解得14.;两条直线;由 ,得 , ,,;两条直线15.16;由可化为_y =8+_+y,_,y均为正实数_y =8+_+y(当且仅当_=y等号成立)即_y-2-8可解得,即_y16故_y的最小值为16.三.解答题:16.(本小题满分12分)解:………………3分(Ⅰ)函数的最小正周期,………………5分令,∴函数的单调递减区间为…………7分(Ⅱ)---------------12分17.(本小题满分14分)解: 将一颗骰子先后抛掷2次,此问题中含有36个等可能基本事件-----------1分(1)记〝两数之和为8〞为事件A,则事件A中含有5个基本事件,所以P(A)=;答:两数之和为6的概率为.--------------------------------------- 4分(2)记〝两数之和是3的倍数〞为事件B,则事件B中含有12个基本事件,所以P(B)=;答:两数之和是3的倍数的概率为.-------------------------------7分(2)记〝向上的两数之积是6的倍数〞为事件C,则事件C中含有其中的15个等可能基本事件,所以P(C)=,答:两数之积是6的倍数的概率为.-------------------------------10分(3)基本事件总数为36,点(_,y),在圆_2+y2=25的内部记为事件D,则D包含13个事件,所以P(D)=.答:点(_,y)在圆_2+y2=25的内部的概率.----------------------14分18.(本小题满分13分)解:, -----------------2分因为函数在处的切线斜率为-3,所以,即,------------------------3分又得.------------------------4分(1)函数在时有极值,所以,-------5分解得,------------------------------------------7分所以.------------------------------------8分(2)因为函数在区间上单调递增,所以导函数在区间上的值恒大于或等于零,------------------------------------10分则得,所以实数的取值范围为.----------------------------------13分19.(本小题满分13分)解(Ⅰ)在中,,在中,,∵,∴.---------------------------2分∵平面平面,且交线为,∴平面.∵平面,∴.------------------------------------5分(Ⅱ)设与相交于点,由(Ⅰ)知,∵,∴平面,∵平面,∴平面平面,且交线为,---------7分如图19-2,作,垂足为,则平面,连结,则是直线与平面所成的角.-------------------9分由平面几何的知识可知,∴.--------------11分在中,,在中,,可求得.∴.------------------------------------------------------------------------13分20.(本题满分14分)【解析】(I)因为边所在直线的方程为,且与垂直,所以直线的斜率为.又因为点在直线上,所以边所在直线的方程为..-----------------3分(II)由解得点的坐标为,------------4分因为矩形两条对角线的交点为.所以为矩形外接圆的圆心.-----------------6分又.从而矩形外接圆的方程为.----------------------9分(III)因为动圆过点,所以是该圆的半径,又因为动圆与圆外切, 所以,即.------------------------11分故点的轨迹是以为焦点,实轴长为的双曲线的左支.因为实半轴长,半焦距.所以虚半轴长.从而动圆的圆心的轨迹方程为.-----------------14分21.(本小题满分14分)解:(Ⅰ)由题意即∴……………………2分∴∵m_gt;0且,∴m2为非零常数,∴数列{an}是以m4为首项,m2为公比的等比数列…………4分(Ⅱ)由题意,当∴①…………6分①式两端同乘以2,得②…………7分②-①并整理,得=-----------------------------------------------10分(Ⅲ)由题意要使对一切成立,即对一切成立,①当m_gt;1时, 成立;…………12分②当0_lt;m_lt;1时,∴对一切成立,只需,解得, 考虑到0_lt;m_lt;1, ∴0_lt;m_lt;综上,当0_lt;m_lt;或m_gt;1时,数列{cn }中每一项恒小于它后面的项. ----------14分。
2008届成都高中毕业班第三次诊断性检测

2008届四川省成都市高中毕业班第三次诊断性检测英语试题(考试时间120分钟,满分150分)第I卷(共115分)第一部分:听力(共两节,满分30分)做题时,先将答案划在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在答题卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1.Where did the woman probably go?A.To the cinema. B.To the schoo1. C.To the park.2.How does the man feel about his driving to work?A.It takes him too much time.B.The distance is a little long.C.He feels satisfied with it.3.What do the girls have in common according to the dialogue?A.They like sports. B.They like shopping. C.They like soap operas. 4.How much wil1 the lady pay for the shirt if she buys one?A.180 dollars. B.200 dollars. C.220 dollars.5.What can we 1earn from the conversation?A.The man will probably take the sleeping pil1.B.The man didn’t sleep well 1ast week.C.The woman will buy some sleeping pills.第二节(共15小题;每题1.5分,满分22.5分)听下面5段对话或独白。
成都市2008届高中毕业班第三次诊断性检测数学(理科)

成都市2008届高中毕业班第三次诊断性检测数学(理科)注意事项:本试卷分为第I 卷(选择题)和第II 卷(非选择题)两部分。
第1卷l 至2页,第II 卷3至8页。
全卷满分为150分,完成时间为120分钟. 参考公式: 如果事件A 、B 互斥,那么 球的表面积公式 P (A+B )=P (A )+P (B )S=4πR 2如果事件A 、B 相互独立.那么其中R 表示球的半径P (A·B )=P (A )·P (B )球的体积公式如果事件A 在一次试验中发生的概率足P , 343V R π=那么n 次独立重复试验中恰好发生女次的概率其中R 表示球的半径()(1)k kn k n n P k C P P -=-(数学社区 正在录入)第I 卷(选择题,共60分)注意事项:1.答第I 卷前,考生务必将自己的姓名、考号、考试科目涂写往答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,不能答在试题卷上。
一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项足符合题目要求的,把正确选项的代号涂在机读卡的相应位置上。
1.计算212sin8π-的值为(A )1 (B )12(C )2(D )22.已知a 、b R ∈,i 为虚数单位,若21ia bi i=++,则a b +的值为 (A )0(B )1(C )2(D )33.设{|01}A x x =<<,{|||1}B x x =<,则“x A ∈”是“x B ∈”的 (A )充分而不必要的条件(B )必要而不充分的条件(C )充要条件 (D )既不充分也不必要的条件4.12lim 12n n n +→∞+ (n N *∈)的结果为(A )1 (B )2 (C )3 (D )不存在5.已知61()ax x-的二项展开式中常数项为160-,则实数a 的值为(A (B )(C )2-(D )26.若非零向量AB 与AC满足||||AB AC BC += ,则△ABC 的形状是(A )等边三角形 (B )等腰三角形 (C )直角三角形 (D )等腰直角三角形7.若函数()y g x =与21y x =+(x ≤0)互为反函数,则函数()y g x =-的大致图象为(A )(B )(C )(D )8.如图,已知二面角的大小为,点为棱上一点,,,则点到平面的距离为(A )若12a =,1b =-,则函数f (x )为R 上的增函数 (B )若12a =,1b =-,则函数f (x )为R 上的减函数(C )若函数f (x )为定义在R 上的偶函数,则1b =± (D )若函数f (x )为定义在R 上的奇函数,则1b =9.某炮兵旅接到上级命令,要派出4个连队急赴某市遭受冻雪灾情较重的、、三地执行抢险救灾任务(每地至少派1个连队),则恰有2个连队被派往受灾最重的地的概率为 (A )12 (B )13 (C )14 (D )1610.设随机变量服从正态分布,若,则的值为 (A ) (B )(C ) (D )11.设计一个计算机自动运算程序:,,,,则的输出结果为(A )2008 (B )2017 (C )2013(D )200812.已知是抛物线上的一个动点,是椭圆上的一个动点,定点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
成都市2008届高中毕业班第三次诊断性检测数学(理科)
注意事项:本试卷分为第I 卷(选择题)和第II 卷(非选择题)两部分。
第1卷l 至2页,第II 卷3至8页。
全卷满分为150分,完成时间为120分钟. 参考公式: 如果事件A 、B 互斥,那么 球的表面积公式 P (A+B )=P (A )+P (B )
S=4πR 2
如果事件A 、B 相互独立.那么
其中R 表示球的半径
P (A·B )=P (A )·P (B )
球的体积公式
如果事件A 在一次试验中发生的概率足P , 34
3
V R π=
那么n 次独立重复试验中恰好发生女次的概率
其中R 表示球的半径
()(1)k k
n k n n P k C P P -=-(数学社区 正在录入)
第I 卷(选择题,共60分)
注意事项:
1.答第I 卷前,考生务必将自己的姓名、考号、考试科目涂写往答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,不能答在试题卷上。
一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项足符合题目要求的,把正确选项的代号涂在机读卡的相应位置上。
1.计算2
12sin
8
π
-的值为
(A )1 (B )
1
2
(C )
2
(D )
2
2.已知a 、b R ∈,i 为虚数单位,若21i
a bi i
=++,则a b +的值为 (A )0
(B )1
(C )2
(D )3
3.设{|01}A x x =<<,{|||1}B x x =<,则“x A ∈”是“x B ∈”的 (A )充分而不必要的条件
(B )必要而不充分的条件
(C )充要条件 (D )既不充分也不必要的条件
4.12lim 12
n n n +→∞+ (n N *
∈)的结果为
(A )1 (B )2 (C )3 (D )不存在
5.已知61()ax x
-的二项展开式中常数项为160-,则实数a 的值为
(A (B )
(C )2-
(D )2
6.若非零向量AB 与AC
满足||||AB AC BC += ,则△ABC 的形状是
(A )等边三角形 (B )等腰三角形 (C )直角三角形 (D )等腰直角三角形
7.若函数()y g x =与2
1y x =+(x ≤0)互为反函数,则函数()y g x =-的大致图象为
(A )
(B )
(C )
(D )
8.如图,已知二面角的大小为,点为棱上一点,,,则点到平面的距离为
(A )若1
2a =
,1b =-,则函数f (x )为R 上的增函数 (B )若1
2
a =,1
b =-,则函数f (x )为R 上的减函数
(C )若函数f (x )为定义在R 上的偶函数,则1b =± (D )若函数f (x )为定义在R 上的奇函数,则1b =
9.某炮兵旅接到上级命令,要派出4个连队急赴某市遭受冻雪灾情较重的、、三地执行抢险救灾任务(每地至少派1个连队),则恰有2个连队被派往受灾最重的地的概率为 (A )
12 (B )13 (C )14 (D )16
10.设随机变量服从正态分布,若,则的值为 (A ) (B )(C ) (D )
11.设计一个计算机自动运算程序:,,,,则的输出结果为
(A )2008 (B )2017 (C )2013
(D )2008
12.已知是抛物线上的一个动点,是椭圆上的一个动点,定点。
若轴,且,则的周长的取值范围是
(A )70
(B )30
(C )180
(D )150
第II卷(非选择题,共90分)
注意事项:1.第II卷共6页,用钢笔或盼圆珠笔直接答在试卷上。
2.答卷前将密封线内的项目填写清楚。
二、填空题:(本大题共4小题,每小题4分,共16分)
把答案填在题中横线上。
13.已知数列的通项公式为,其前项的和为,则当取最大值时,。
14.已知函数的图象上相邻最高点与最低点之间的距离为,则函数的最小正周期为。
15.已知圆以双曲线的右焦点为圆心,并经过双曲线的左准线与渐近线的交点,则圆的标准方程为。
16.已知平行六面体中,,,为的中点,给出下列四个命题:①为异面直线所成的角;
②三棱锥是正三棱锥;③平面;④;⑤。
其中正确的命题有。
(写出所有正确命题的序号)
三、解答题:(本大题共6小题,共74分)
解答应写出文字说明.证明过程或演算步骤.
17.(本小题满分12分)
已知中,角所对边的长分别为、、,若直线:与:互相平行。
(I)求角的大小;
(II)若,,当向量与向量垂直时,求实数的值。
18.(本小题满分12分)
如图1,在平行四边行中,,,是上的一个动点,现将该平行四边行沿对角线折成直二面角,如图2所示。
(I)若分别是的中点,且平面,求证:平面;
(II)当图1中最小时,求图2中二面角的大小。
19.(本小题满分12分)
某中学开展“创建文明城市知识竞赛”活动,竞赛题由20道选择题构成,每道选择题有4个选项,其中有且只有一个是正确的,要求学生在规定时间内通过笔试完成,且每道题必须选出一个选项(不得多选和不选),每道题选择正确得6分,已知学生甲对任一道题选
择正确的概率是3
4
;学生乙由于未作准备,因此只能从每道题中4个选项中随机地选择1
个。
(I)若选错得0分,比较甲得66分的概率与乙得54分的概率的大小;
(II)为防止个别学生像乙那样随机地作出选择,学校决定对每道题选择错误的倒扣若干分,但倒扣太多对学生不公平,倒扣太少又达不到杜绝乱选的目的,倒扣的分数,应该恰到好处,使乱选一通的学生一无所获。
换句话说,如果学生每道题都随机选择,那么20道题所得总分的数学期望应该是0。
问:对每道题选择错误应倒扣多少分较合适?
20.(本小题满分12分)
已知定义在上的奇函数的导函数为,且在点处取得极值。
(I)求函数的解析式;
(II)若函数在区间上是增函数,求实数所有取值的集合;
(III)当时,求的最大值。
21.(本小题满分1 2分)
已知为坐标原点,点的坐标分别为、,点满足,,过点且垂直于的直线交线段于点,设点的轨迹为。
(I)求轨迹的方程;
(II)若轨迹上存在两点和关于直线:对称,求的取值范围;
(III)在(II)的条件下,设直线与轨迹交于不同的两点、,对点和向量,求取最大值时直线的方程。
22.(本小题满分14分)
已知各项均为正数的数列满足:
(I)求、、,猜测的表达式并证明;
(II)求证:;
(III)设数列的前项和为,求证:。
