2011-2012高数B(下)A卷试题
11-12(下)高数B参考答案及评分标准

高数期末试题B 参考答案及评分标准一、判断题二、填空题(本大题共10小题,每小题2分,共20分)(6) 2 (7)x z y 522=+(8) -1 (9)9122≤+<y x (10)2ln 162(11) 6 (12)yPx Q ∂∂=∂∂ (13) 右手 (14)⎰20)2sin(21πdt t (15) 偶(16)求曲面42222=++z y x 在点(1,1,1)处的切平面方程,并求过原点与该切平面垂直的直线方程。
()())2(112)3(042111)2()2,2,4(|),,(11142),,()1,1,1(222分直的直线方程为:通过原点与该切平面垂分点处的切平面方程为,,曲面在分点处的法向量,,则曲面在解:记 zy x z y x F F F z y x z y x F z y x ===-++∴==-++=(17)设函数),(y x z z =由方程23222320x z y z x y +-+=所确定,求全微分dz 。
)1(43344322)3(4334)3(43222),,(222222223222222223322232分分分则解:记 dy zy z x y yz dx z y z x x xz dz zy z x y yz F F y z zy z x xxz F F x z y x z y z x z y x F z y z x ++-+--=∴++-=-=∂∂+--=-=∂∂+-+=(18)计算Ω⎰⎰⎰,其中Ω是由0,1z z ==和222x y x +=围成的区域。
)1(9163238cos 38cos 34)1(21)2(21)1(21)2()1)1(D (203223cos 202222221222212222分分分分分:其中解: =⋅=====+=+=≤+-+=+⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰--Ωπππθππθθθθρρθθρρd d d d d d dxdy y x zdz dxdy y x y x dz y x z dxdy dv y x z DDDD(19)计算,)536()24(L⎰+++-+dy y x dx y x 其中L 为三角形(3,0),(3,2),(0,0)的正向边界。
2011高等数学下试卷及答案

华南农业大学期末考试试卷(A 卷)2010--2011学年第2学期 考试科目: 高等数学A Ⅱ 考试类型:(闭卷)考试 考试时间: 120 分钟 学号 姓名 年级专业一、单项选择题(本大题共5小题,每小题3分,共15分)1.与三坐标轴夹角均相等的单位向量为 ( )A.(1,1,1) B.111(,,)333 C. D.111(,,)333--- 2.设lnxz y=,则11x y dz ===( )A.dy dx - B.dx dy - C.dx dy + D.03.下列级数中收敛的是 ( )A.1n ∞= B.1n ∞= C.113n n ∞=∑ D.113n n∞=∑4.当||1x <时,级数11(1)n n n x ∞-=-∑是 ( )A.绝对收敛 B.条件收敛 C.发散 D.敛散性不确定 5.设函数()p x ,()q x ,()f x 都连续,()f x 不恒为零,1y ,2y ,3y 都是()()()y p x y q x y f x '''++=的解,则它必定有解是( )(今年不作要求)A.123y y y ++ B.123y y y +- C.123y y y -- D.123y y y ---二、填空题(本大题共5小题,每小题3分,共15分)1.微分方程''6'90y y y -+=的通解为_____.(今年不作要求) 2.设有向量(4,3,1)a →=,(1,2,2)b →=-,则2a b →→-=_________. 3.过点(1,1,0)-且与平面32130x y z +--=垂直的直线方程是______. 4.设2cos()z xy =,则zy∂∂=_______. 5.设L 为曲线2y x =上从点(0,0)到点(1,1)的一线段,则32(2)Lx y dx +⎰___.三、计算题(本大题共7小题,每小题6分,共42分) 1.求微分方程2(12)(1)0x y dx x dy +++=的通解.2.设22()xyz x y =+,求z x ∂∂及2z x y∂∂∂.3.判断级数23112123!10101010nn ⋅⋅⋅+++++的敛散性.4.设一矩形的周长为2,现让它绕其一边旋转,求所得圆柱体体积为最大时矩形的面积及圆柱体的体积.5.将函数2()x f x xe -=展开成x 的幂级数,并确定其收敛域. 6.设(,)z z x y =是由方程2z x y z e +-=确定的隐函数,求全微分dz. 7.计算二重积分cos Dydxdy y⎰⎰,其中D 是由y y x =围成的区域.四、解答题(本大题共4小题,每小题7分,共28分) 1.计算曲线积分22(2)()Lxy x dx x y dy -++⎰,其中L 是由曲线2y x =和2y x =所围成的区域的正向边界曲线. 2.计算二重积分Dσ⎰⎰,其中区域D 由221x y +≤,0x ≥及0y ≥所确定.3.设()u f xyz =,(0)0f =,(1)1f '=,且3222()ux y z f xyz x y z ∂'''=∂∂∂,试求u 的表达式.(今年不作要求)4.计算曲面积分)I xdydz ydzdx zdxdy ∑=++,其中∑为上半球面z =(今年不作要求)参考答案一、选择题(本大题共5小题,每小题3分,共15分) 1.C 2.B 3.C 4.A 5.B 二、填空题(本大题共5小题,每小题3分,共15分) 1.312()x y C C x e =+ 2.(7,8,0) 3.11321x y z+-==- 4.22sin()xy xy - 5.710三、计算题(本大题共7小题,每小题6分,共42分) 1.求微分方程2(12)(1)0x y dx x dy +++=的通解. 解:21112x dx dy x y =-++⎰⎰..........(1分) 221111(1)(12)21212d x d y x y+=-+++⎰⎰.........(5分) 2ln(1)ln |12|ln x y C +=-++,即2(1)(12)x y C ++=......(6分) 2.设22()xyz x y =+,求z x ∂∂及2zx y∂∂∂.解:设v z u =,22u x y =+,v xy =..........(1分)22222222()(ln())xy z z u z v x y x y y x y x u x v x x y∂∂∂∂∂=+=+++∂∂∂∂∂+..........(3分)243342222222222(2)()[(21ln())ln()]()xy z x x y y x y xy xy x y x y x y x y ∂++=++++++∂∂+.(6分) 3.判断级数23112123!10101010n n ⋅⋅⋅+++++的敛散性.解:11(1)!10lim lim !10n n n n n nu n u n ρ++→∞→∞+==..........(3分) 1lim10n n →∞+==∞...........(5分)所以级数发散........(6分)4.设一矩形的周长为2,现让它绕其一边旋转,求所得圆柱体体积为最大时矩形的面积及圆柱体的体积.解:设矩形两边长分别为,x y .则1x y +=,假设绕长度为y 的一边旋转,则圆柱体体积为2V x y π=............(2分)作拉氏函数2(,,)(1)F x y x y x y λπλ=++-........(3分) 解方程组22001xy x x y πλπλ+=⎧⎪+=⎨⎪+=⎩................(4分) 得可能的极值点21(,)33..............(5分)由题意知道其一定是所求的最值点,所以最大体积为427π,对应面积为29..........(6分) 5.将函数2()x f x xe -=展开成x 的幂级数,并确定其收敛域.解:因为212!!n xx x e x n =+++++ .......(1分)所以2221(1)222!2!xnnn x x x en -=-+++-+⋅⋅ ..........(3分)23112211()(1)(1)222!2!2(1)!x n nnn n n n x x x x f x xex n n +∞---===-+++-+=-⋅⋅⋅-∑(5分)收敛域为(,)-∞+∞..................(6分)6.设(,)z z x y =是由方程2z x y z e +-=确定的隐函数,求全微分dz . 解:2(,,)z F x y z x y z e =+--........(1分) 1,2,1z x y z F F y F e ===--...........(3分) 所以12,11y x z z z z F F z z y x F e y F e ∂∂=-==-=∂+∂+.........(5分) 故1(2)1zz z dz dx dy dx ydy x y e ∂∂=+=+∂∂+..........(6分) 7.计算二重积分cos Dydxdy y ⎰⎰,其中D 是由y =及y x =围成的区域. 解:积分区域为:2{(,)|01,}D x y y y x y =≤≤≤≤........(1分)210cos cos y y Dyy dxdy dy dx y y =⎰⎰⎰⎰..........(3分) 1(1)cos y ydy =-⎰............(5分) 1cos1=-.........(6分)四、解答题(本大题共4小题,每小题7分,共28分) 1.计算曲线积分22(2)()Lxy x dx x y dy -++⎰,其中L 是由曲线2y x =和2y x =所围成的区域的正向边界曲线. 解:22(2)()(12)LDxy x dx x y dy x d σ-++=-⎰⎰⎰......(2分) 212)xdx x dy =-⎰........(4分) 1312322(22)x x x x dx =--+⎰........(6分)130=......(7分) 2.计算二重积分Dσ⎰⎰,其中区域D 由221x y +≤,0x ≥及0y ≥所确定. 解:'DD σθ=..........(2分)120d πθ=⎰⎰............(4分) 224d ππθ-=⎰......(6分)=(2)8ππ-=.........(7分)3.设()u f xyz =,(0)0f =,'(1)1f =,且3222()ux y z f xyz x y z ∂'''=∂∂∂,试求u 的表达式.解:22(),()()u u yzf xyz zf xyz xyz f xyz x x y∂∂''''==+∂∂∂3222()3()()uf xyz xyzf xyz x y z f xyz x y z∂''''''=++∂∂∂........(2分) 因为3222()u x y z f xyz x y z∂'''=∂∂∂,所以()3()0f xyz xyzf xyz '''+=令xyz t =,得3()()0tf t f t '''+=......(4分)解之得113311(),(1)1,1,()由得所以f t C t f C f t t --'''====.....(5分)解得22332233(),(0)0,0,()22由得所以f t t C f C f t t =+===.....(6分)即233()()2u f xyz xyz ==.......(7分)4.计算曲面积分)I xdydz ydzdx zdxdy ∑=++,其中∑为上半球面z = 解:因为在曲面∑a ,所以()I a xdydz ydzdx zdxdy ∑=++⎰⎰..........(1分)补曲面2221{(,,)|0,}x y z z x y a ∑==+≤,1∑取下侧..........(2分) 由高斯公式得1()I a xdydz ydzdx zdxdy ∑+∑=++⎰⎰=342(111)323a dv a a a ππΩ++=⨯=⎰⎰⎰..(4分) 而111()00a xdydz ydzdx zdxdy azdxdy dxdy ∑∑∑++===⎰⎰⎰⎰⎰⎰.....(6分)故)I xdydz ydzdx zdxdy ∑=++=114()()2a xdydz ydzdx zdxdy a π∑+∑∑-++=⎰⎰⎰⎰.......(7分)。
2011-12高数三(下)期末试题参考答案

2011-2012学年第二学期全校经管类等专业《高等数学三(下)》期末试卷一、基本题(共6个小题,每小题6分,共36分) 1. 设 0lim =∞→n n a ,求级数∑∞=+-11)(n n na a的部分和n S 、和S .12n n S u u u =+++= 12231n n a a a a a a +=-+-++- 11n a a +=-111lim lim n n n n S S a a a +→∞→∞==-=2. 设 10055++=x y x x ,求差分x y ∆、x y 2∆.=-=∆+x x x y y y 1155(1)100(55100)435x x x x x ++++-++=⨯+=∆∆=∆)(x x y y 21455(455)165x x x +⨯+-⨯+=⨯3. 判断正项级数∑∞=-⋅⋅1!)12(531n n n 的敛散性. 正项级数比值审敛法,121limlim 211n n n nu n u n ρ+→∞→∞+===>+,所以发散4. 改变二次积分⎰⎰210),(xdy y x f dx 的积分次序.D 是X 型区域且012x x y ≤≤⎧⎨≤≤⎩ Y 型区域表示为12D D +,1D :010y x y ≤≤⎧⎨≤≤⎩ 2D 1201y x ≤≤⎧⎨≤≤⎩120(,)xdx f x y dy =⎰⎰100(,)ydy f x y dx ⎰⎰+2110(,)dy f x y dx ⎰⎰ 5. 求微分方程232y xdx dy =满足条件1)0(=y 的特解. 分离变量得到232y dy xdx = 两端积分得 32y x C =+ 这就是原方程的通解由条件1)0(=y 得到 1C =,故321y x =+是满足条件的特解6. 求差分方程9101=-+x x y y 的通解.原方程对应的齐次方程 1100x x y y +-= 齐次方程的通解为10xY C =因为101a =-≠-,所以设特解ya = ,代入 原方程 对比系数可以得到1a =- 因此 原方程的通解为101xy Y yC =+=-二、(共4个小题,每小题9分,共36分)1. 求过点)1,2,1(-M 且与直线 ⎪⎩⎪⎨⎧=+-+=+-+012012z y x z y x 垂直的平面方程.最主要是求出平面的法向量n ,即直线的方向向量s,常用方法:直线通过两个已知平面,方向向量s,12,n s n s ⊥⊥,所以取12112{3,1,1}121i j ks n n =⨯=-=--所以平面方程为3(1)(2)(1)0x y z +--+-= 整理得340x y z -++=2. 设函数 ),(y x e e xy f z +=,其中f 具有连续一阶偏导数,求x z ∂∂,yz ∂∂,与dz . 12x z yf e f x ∂''=+∂,12y zxf e f y∂''=+∂, 则z zdz dx dy x y∂∂=+=∂∂12()x yf e f dx ''++12()y xf e f dy ''+ 3. 设 )sin(22y x z +=,求x z ∂∂,y z ∂∂,与y x z∂∂∂2. x z ∂∂222cos()x x y =+ yz∂∂222cos()y x y =+ yx z∂∂∂2()zx y∂∂∂=∂224sin()xy x y =-+ 4. 设有A 和B 两种商品,其单价分别为10元和50元 ,某消费者消费x 单位A 商品和y 单位B 商品所获得的效用为 )ln ln (21),(y x y x u +=,求该消费者在这两种商品的预算消费支出为2000元时所获得的最大效用,以及各商品的消费数量.已知条件 10502000x y +=,即105020000x y +-= 目标函数:)ln ln (21),(y x y x u +=求目标函数在已知条件下的最大值问题,利用拉格朗日乘数法: 设(,,)ln ln (10502000)F x y x y x y λλ=+++-求解方程组11001500105020000x y F x F y F x y λλλ⎧=+=⎪⎪⎪=+=⎨⎪⎪=+-=⎪⎩求解得到5100,x y == 即当100,20x y ==时,总效用达到最大。
山西忻州市2011-2012学年第二学期高一联考试题数学B类

学校 姓名 准考证号忻州市2011-2012学年第二学期高中联考试题高一数学(B 类)注意事项:1.答题前,考生务必用0.5mm 黑色中性笔,将学校名称、姓名、班级、准考证号填写在试题和答题卡上。
2.请把答案做在答题卡上,交卷时只交答题卡,不交试题,答案写在试题上无效。
3.满分150分,考试时间120分钟。
一.选择题(本大题共12个小题,每小题5分,共60分,在每个小题给出的四个选项中,只有一项是符合题目要求的) 1.tan300°的值为A .3B .33 C .-33 D .-3 2.三个正数a 、b 、c 成等比数列,则lga 、 lgb 、 lgc 是A .等比数列B .既是等差又是等比数列C .等差数列D .既不是等差又不是等比数列3.已知函数⎩⎨⎧>≤-=1,ln 1,1)(x x x e x f x ,那么)2(ln f 的值是A .0B .1C .)2ln(lnD .24.在四边形ABCD 中,若AB →·CD →=-|AB →|·|CD →|,且BC →·AD →=|AD →|·|BC →|,则该四边形一定是A .平行四边形B .矩形C .菱形D .正方形5.某校500名学生中,O 型血有200人,A 型血有125人,B 型血有125人,AB 型血有50人,为了研究血型与色弱的关系,需从中抽取一个容量为20的样本.按照分层抽样方法抽取样本,则从O 型血、A 型血、B 型血、AB 型血的人中分别抽( )人A .2,5,5,8B .2,4,5,8C .8,5,5,2D .4,5,5,26.已知a ,b ∈R ,下列不等式不.成立的是 A .a +b ≥2ab B .a 2+b 2≥2abC .ab ≤(a +b 2)2D .|a |+|b |≥2|ab |7.执行如图所示的程序框图,其输出的结果是A .1B .21-C .45-D .813-8.已知|a →|=5,a →与b →的夹角为60º,a →在b →方向上的投影是A .25B .3C .-25D .-3 (7题图) 9.将函数f (x )=sin (ωx +φ)的图象向左平移π2个单位.若所得图象与原图象重合,则ω的值不可能等于A .4B .6C .8D .1210.数列{a n }满足a 1=1,a 2=2, 2a n +1=a n +a n +2,则数列{a n }的前5项和等于 A .25 B .20 C .15 D .1011.设等差数列{}n a 的公差d 不为0,19a d = 若k a 是1a 与2k a 的等比中项,则k = A .4 B .2 C .6 D .812.设向量a →=(cos 55°,sin 55°),b →=(cos 25°,sin 25°),若t 是实数,则|a →-t b →|的最小值为A . 2B .1C .22 D . 12二.填空题(本大题共4小题,每小题5分,共20分,把答案填在答卷纸的相应位置上) 13.已知ABC ∆的三个内角,,A B C 所对的边分别是,,a b c ,且30,45,2A B a ===,则b = .14.等比数列{a n }中,a 2=2,a 5=16,那么数列{a n }的前6项和S 6=________.15.函数f (x )=)32(221--⎪⎭⎫ ⎝⎛x x 的单调递增区间是__________.16.函数f (x )=cos x +2|cos x |,x ∈[0,2π]的图像与直线y =m 有且仅有2个交点,则实数m 的取值范围__________.三.解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤,并把解答写在答卷纸的相应位置上) 17.(本题满分10分)一个盒子中有2个红球和1个白球,每次取一个,每次取出后放回,连续取两次, 记A=“取出两球都是红球”,B=“第一次取出红球,第二次取出白球”,求概率P(A),P(B).18.(本题满分12分)已知不等式x 2-2x -3<0的解集为A ,不等式x 2+4x -5<0的解集为B . (1)求A B ;(2)若不等式x 2+ax +b <0的解集是A B ,求ax 2+x +b ≥0的解集.19.(本题满分12分)是否存在实数a [)0,1-∈,使函数f (x )=x 2-2ax +a 的定义域为[-1,1]时,值域为 [-2,2]?若存在,求a 的值;若不存在,说明理由.20.(本题满分12分)已知函数f (x )=cos 2 2xsin (π4+x )cos (π4+x )(1)求f (-512π)的值;(2)当x ∈ [0,π4) (π4,π2]时,求g (x )=12f (x )+sin 2x 的最大值和最小值.21.(本题满分12分)已知ABC ∆的三个内角,,A B C 所对的边分别是,,a b c , 它的周长为2+1, 且a +b =2c . (1)求边c 的长;(2)若△ABC 的面积为16sin C ,求cos C 的值.22.(本题满分12分)在等差数列}{n a 中,21=a ,12321=++a a a . (1) 求数列}{n a 的通项公式;(2) 令n n n a b 3⋅=,求数列}{n b 的前n 项和n S .忻州市2011−2012学年第二学期高中联考 高一数学(B 类)参考答案及评分标准一.选择题(每小题5分,共60分) DCBAC ACABC AD二.填空题(每小题5分,共20分)13.22 14.63 15.(-∞,1) 16.m =0或1<m ≤3三.解答题(本大题共6小题,共70分)17.解:取出后放回,连续取两次,两个红球分别记为红1和红2,列树状图如下:红1⎪⎩⎪⎨⎧21红红白 红2⎪⎩⎪⎨⎧21红红白白⎪⎩⎪⎨⎧21红红白 即共有9种,其中“取出两球都是红球”有4种,“第一次取出红球,第二次取出白球”有2种, 所以P (A )=94. ………………5分 P (B )=92. ………………10分18.解:(1)解不等式x 2-2x -3<0,得A ={x |-1<x <3}. ………………2分 解不等式x 2+4x -5<0,得B ={x |-5<x <1}, ………………4分∴A ∪B ={x |-5<x <3}. ………………6分 (2)由x 2+ax +b <0的解集是(-5,3),∴⎩⎪⎨⎪⎧ 25-5a +b =0 9+3a +b =0,解得⎩⎪⎨⎪⎧a =2b =-15. ……………9分 ∴2x 2+x -15≥0,求得解集为{x |x ≥52或x ≤-3}. ……12分19.解:f (x )=(x -a )2+a -a 2 . ………………4分-1≤a <0时,⎩⎪⎨⎪⎧f (a )=a -a 2=-2,f (1)=1-a =2 ………………8分a =-1. ………………12分20.解:(1)f (x )=cos 2 2xsin (π4+x )cos (π4+x )=2cos 2 2xsin (π2+2x )=2cos 2 2x cos 2x =2cos 2x . .………………4分 f (-5π12)=2cos (-5π6)=2cos 5π6=-2cos π6=-3. .………………6分(2)g (x )=cos 2x +sin 2x =2sin (2x +π4),………………8分x ∈[0,π4)∪(π4,π2]⇒2x +π4∈[π4,5π4]且2x +π4≠3π4, ………………10分∴x =π8时,g (x )max =2;x =π2时,g (x )min =-1. . ………………12分21.解:(1)a+b+c =2+1,a+b =2c ,两式相减,得c =1. ………………5分 (2)由△ABC 的面积12a ·b ·sin C =16sin C ,得a ·b =13, ………………8分由余弦定理得cos C =b 2+a 2-c 22b ·a ………………10分=(b +a)2-2b ·a -c 22b ·a =12. ………………12分22.解:(1)设数列}{n a 的公差为d ∵,12321=++a a a ∴3122=a ∴42=a ∴d=221=-a a …………4分; ∴n a n 2=.……6分 (2)∴n n n b 32⋅=∴n n n S 3236343232⋅+⋅⋅⋅+⨯+⨯+⨯=……①∴132323)1(234323+⋅+⋅-+⋅⋅⋅+⨯+⨯=n n n n n S ……② ………8分 ①-②得:13232323232322+⋅-⨯+⋅⋅⋅+⨯+⨯+⨯=-n n n n S =n n n 322)13(32⋅--⋅…………10分∴233)12(1+⋅-=+n n n S . ………………12分说明:各题如有其它解法可参照给分.高一数学(B类)双向细目表。
2012级高数(下)试题及答案解析

南昌大学 2012~2013学年第二学期期末考试试卷 一、填空题(每空 3 分,共 15 分) 1. 设:020202x y z Ω≤≤≤≤≤≤,,,则三重积分xyzdV Ω=⎰⎰⎰ _____.2. 交换二次积分的顺序2 22 0(,)yy dy f x y dx ⎰⎰= _________.3. 函数22(,)4()f x y x y x y =---的极大值为_______.4. 将1()6f x x =-展开成x 的幂级数为________.5. 点(2,1,0)到平面3450x y z ++=的距离为__________.二、单项选择题 (每小题3分,共15分)1. 函数xy x yz +=arcsin 的定义域是( )(A ){}0,|),(≠≤x y x y x ;(B ){}0,|),(≠≥x y x y x ;(C ){}(,)|0,0x y x y x ≥≥≠{}0,0|),(≠≤≤x y x y x ; (D ){}{}0,0|),(0,0|),(<<>>y x y x y x y x .2.设∑为由曲面22y x z +=及平面1=z所围成的立体的表面,则曲面积分22()x y dS ∑+⎰⎰= ( )(A )π22; (B )π221+; (C )2π; (D )0.3.级数∑∞=+111n p n 发散,则( )(A )0≤p ;(B )0>p ;(C )1≤p ;(D )1<p .4.设函数222222,0(,)0,0xyx y x y f x y x y ⎧+≠⎪+=⎨⎪+=⎩,则在点(0,0)处 ( )(A )连续且偏导数存在; (B )连续但偏导数不存在; (C )不连续但偏导数存在; (D )不连续且偏导数不存在。
5.设123,,y y y 是常系数线性非齐次方程()y py qy f x '''++=的三个线性无关的解,则0y py qy '''++=的通解为 ( )(A )1122C y C y +; (B )1223C y C y +;(C )1122C y C y +33C y +;(D )1122C y C y +123()C C y -+.三、计算题(共24分,每小题8分)1、设arctan x yz x y +=-,求z x ∂∂和2z x y ∂∂∂.2、判断级数1313n n n ∞=-∑的敛散性.3、求微分方程71212y y y x '''-+=的通解 四、解答题(一)(共24分,每小题8分) 1、设方程(,)0f xz yz =可确定z 是,x y 的函数,且(,)f u v 具有连续偏导数,求dz .2、计算曲线积分22(sin 2)()L x y dx x y dy --+⎰,其中L 为由点(0,2)A 到(0,0)O 的左半圆周222x y y +=.3、求级数12nn n x n ∞=⋅∑的收敛域与和函数.五、解答题(二)(共16分,每小题8分)1、求椭球面2222349x y z ++=上点(1,1,1 ) 处的切平面方程和法线方程.2、利用高斯公式计算曲面积分()()()x y dydz y z dzdx z x dxdy ∑+++++⎰⎰,其中∑为平面0,0,0,1,1,1x y z x y z ====== 所围成的立体的表面的外侧.六、证明题(本题满分6分)设数列{}n a 单调减少,0n a >(1,2,n =)且1(1)nn n a ∞=-∑发散,证明11()1nn n a ∞=+∑收敛.南昌大学 2012~2013学年第二学期期末考试试卷及答案一、填空题(每空 3 分,共 15 分) 1. 设:020202x y z Ω≤≤≤≤≤≤,,,则三重积分xyzdV Ω=⎰⎰⎰8.2. 交换二次积分的顺序2 22 0(,)yy dy f x y dx ⎰⎰=()402,dx f x y dy ⎰⎰.3. 函数22(,)4()f x y x y x y =---的极大值为8.4. 将1()6f x x =-展开成x 的幂级数为()10666n n n x x ∞+=-<<∑.5. 点(2,1,0)到平面3450x y z ++=的距离为.二、单项选择题 (每小题3分,共15分)1. 函数xy x yz +=arcsin 的定义域是( C )(A ){}0,|),(≠≤x y x y x ;(B ){}0,|),(≠≥x y x y x ;(C ){}(,)|0,0x y x y x ≥≥≠{}0,0|),(≠≤≤x y x y x ; (D ){}{}0,0|),(0,0|),(<<>>y x y x y x y x .2.设∑为由曲面22y x z +=及平面1=z所围成的立体的表面,则曲面积分22()x y dS ∑+⎰⎰= ( B ) (A )π22; (B )π221+; (C )2π; (D )0.3.级数∑∞=+111n p n 发散,则(A )(A )0≤p ;(B )0>p ;(C )1≤p ;(D )1<p .4.设函数222222,0(,)0,0xyx y x y f x y x y ⎧+≠⎪+=⎨⎪+=⎩,则在点(0,0)处 ( C )(A )连续且偏导数存在; (B )连续但偏导数不存在; (C )不连续但偏导数存在; (D )不连续且偏导数不存在。
2011年高等数学BⅡ考题

华南农业大学期末考试试卷(A 卷)2011~2012学年第二学期 考试科目: 高等数学B Ⅱ 考试类型:(闭卷)考试 考试时间: 120 分钟 学号 姓名 年级专业一、填空题(本大题共5小题,每小题3 分,共15分)1. 设向量(3,2,1)=a ,向量4(2,,)3k =b ,若⊥a b ,则k = ;若//a b ,则k = .22.(1,2)d _____________z x y z ==函数在点处的全微分是 .3.已知D 是长方形区域{(,)|,01}x y a x b y ≤≤≤≤,又已知()d d 1Dyf x x y =⎰⎰,则()d baf x x =⎰____ .4. 幂级数()()0+121nn x n ∞=+∑的收敛域为 .5. 微分方程+=0xy y '满足初始条件(1)=2y 的特解为 .二、选择题(本大题共5小题,每小题3分,共15分)1.直线11211x yz -+==-与平面1x y z -+=的位置关系是( ). (A )垂直 (B ) 平行 (C ) 夹角为π4 (D ) 夹角为π4- 2. 000000(,),(,)(,)x y f x y f x y x y 偏导数存在是函数在点处可微的( ).(A) 充分条件 (B ) 必要条件 (C )充要条件 (D )无关条件3. 将极坐标系下的二次积分:π2sin 00d (cos ,sin )d I rf r r r θθθθ=⎰⎰化为直角坐标系下的二次积分,则I =( ).(A ) 1111d (,)d I y f x y x -=⎰⎰(B ) 2d (,)d I x f x y y =⎰(C )11d (,)d I y f x y x -=⎰ (D )1111d (,)d I x f x y y -=⎰⎰4.交错级数1111(1)3n n n ∞--=-∑ ( ). (A) 绝对收敛 (B)条件收敛 (C)发散 (D)敛散性无法确定5.差分方程t t t t y y 2221⋅=-+的特解形式为( ).(A)t t kt y 22⋅= (B) ()22tt y at bt c =++⋅(C) ()322tt y at bt ct =++⋅ (D) 以上都不对三、计算题(本题六个小题,每小题7分,满分42分)1. 2232(,)e 0,,zz zz f x y x y xyz x y ∂∂=++-=∂∂设是由所确定的隐函数求.2.设,y x z f x y ⎛⎫= ⎪⎝⎭,求 z zx y x y ∂∂+∂∂ .3. 判别级数 n 12!n n n n∞=∑的敛散性.4. 计算二重积分2Dxdxdy y⎰⎰,其中D 为1,xy y x ==及2y =所围成的闭区域.5.求伯努利方程 42323y y x y x'+= 的通解.21(),32f x x x x =++6.用间接展开法把展开成的幂级数并写出其收敛区间.四、(本题两个小题,任意选做一题,多选不多得分,满分8分)1. 求微分方程()3y y y ''''=+满足初始条件()()00,01y y '==的特解. 2. 求微分方程323e -'''++=x y y y x 的通解.五、应用题(本题三个小题,任意选做二题,多选不多得分,满分16分)1.设有连结点O(0,0)和(1,1)A 的一段向上凸的曲线弧OA ,对于OA 上任一点(,)P x y ,曲线弧OP 与直线段OP 所围成图形的面积为2x ,求曲线弧OA 的方程. 2 . 某公司生产产品A (x 件),产品B (y 件)的收益函数和成本函数分别为: ()22(,)109,(,)400230.0133R x y x y C x y x y x xy y =+=+++++, 试求获得最大利润的产量水平及最大利润.3.求由球面zz六、证明题(本题满分4分)211:,n n n n u u ∞∞==∑∑证明如果正项级数收敛则也收敛.。
11-12-2高等数学下(通信电子本科)A卷及答案

2011-2012学年第二学期期末考试《高等数学(下)》试卷(A)答卷说明:1、本试卷共6页,四个大题,满分100分,120分钟完卷。
2、闭卷考试。
3、适用班级:11级通信系、电子系本科各班.评阅人:_____________ 总分人:______________一、单项选择题(共10小题,每小题3分,共30分)。
【A 】设有直线L :12121x y z --==-及平面π:21x y +=,则直线L (A)平行于π (B)在π内 (C)垂直于π (D)与π斜交【D 】2.锥面z =与柱面22z x =所围立体在xoy 面的投影为(A)22(1)1x y -+= (B)22(1)1x y -+≤ (C)220,(1)1z x y =-+= (D)220,(1)1z x y =-+≤ 【C】3.设函数),(y x z z =由方程ze e xyz =+确定,则)1,0,1(yz ∂∂的值为(A)1e -- (B)e (C)1e - (D)1【A 】4.函数),(y x f z =,则函数在该点(A)必连续 (B)偏导数必存在且连续 (C)必有极值 (D)偏导数不一定存在__________________系__________专业___________班级 姓名_______________ 学号_______________………………………………(密)………………………………(封)………………………………(线)………………………………【C 】5.将二次积分11(,)xdx f x y dy ⎰⎰转化成先对x ,后对y 的二次积分为(A)⎰⎰110),(ydx y x f dy (B)⎰⎰xdx y x f dy 010),((C)⎰⎰y dx y x f dy 010),( (D)⎰⎰110),(dx y x f dy【D 】6.设L 为圆周221x y +=(逆时针方向),则()(32)Lx y dx y x dy ++-=⎰(A)3π (B)2π (C)4π (D)3π- 【D 】7.下列级数中,收敛的级数是(A)n ∞= (B)1(3)2n n n ∞=-∑ (C)2111n nn ∞=++∑ (D)1(1)1n n n ∞=-+∑ 【B 】8.幂级数1(1)3nnn x n ∞=-∑的收敛域为 (A)(2,4)- (B)[2,4)- (C)[2,4]- (D)(2,4]- 【C 】9.微分方程0y y '-=满足初始条件0|2x y ==的特解为(A)1xy e =+ (B)2x y e =+ (C)2x y e = (D)xy e =【B 】10.具有特解xx xey e y --==21,的二阶常系数齐次线性微分方程是(A)02=+'-''y y y (B)02=+'+''y y y (C)02=-'+''y y y (D)02=+'-''y y y二、填空题(共5小题,每小题3分,共15分)1.设两点(1,2,1)A 及)3,1,2(B ,则=||||6AB =向量与z 轴的夹角为γ,则方向余弦=γcos_______.cos γ=2.设xz y =,则dz =_1ln xx dz y ydx xy dy -=+.3.函数22(,)f x y x y y =-在点(1,1)P 处方向导数的最大值为4.设L 是连接(1,0)及(0,1)两点的直线段,则()Lx y ds +=⎰___________.5.函数13x +展开成x 的幂级数为____10(1),333n n n n x x ∞+=--<<∑三、计算题(共7小题,每小题6分,共42分)1.已知曲面222z x y =+-上一点(2,1,3)M ,(1)求曲面在M 点处的一个法向量;(2)求曲面在M 点处的切平面及法线方程.2.求函数22(,)2()f x y x y x y =---的极值.3.平面薄片的面密度为22(,)1x y x y μ=++,所占的闭区域D 为圆周221x y +=及坐标轴所围成的第一象限部分,求该平面薄片的质量.4.利用高斯公式计算曲面积分232(3)(2)(3)z x dydz y xz dxdz x z dxdy ∑+-+⎰⎰,其中∑为上半球面z =0z =所围立体的整个边界曲面的外侧.5.设曲线通过原点,且曲线上任一点),(y x M 处的切线斜率等于x y -,求该曲线的方程.6.求微分方程xe y y y =+'-''23的通解.7.判断级数113(1)4n nn n∞-=-∑是否收敛?如果收敛,是绝对收敛还是条件收敛?四、综合应用题(共2小题,共13分,其中第1题6分,第2题7分).1.(6分)要用钢板造一个体积为4(3m ) 长方体无盖容器,应如何选择容器的尺寸,使得用料最省?2.(7分)设在xoy 平面有一变力→→→-++=j xy i y x y x F )82()(),(2构成力场,(1)证明质点在此力场中移动时,场力所作的功与路径无关;(2)计算质点从点)0,1(A 移动到点)1,2(B 时场力所作的功.一.选择题(每小题3分,共30分).二.填空题(每小题3分,共15分).(1)||6AB =;cos 3γ=(2)1ln x x dz y ydx xy dy -=+ (3)(5)10(1),333n nn n x x ∞+=--<<∑三.计算题(每小题6分,共42分).1.(6分)(1)由222z x y =+-得,2,2x y z x z y ==, 曲面在点(2,1,3)M 处的一个法向量为(n →=-(或(4,2,1)n →=--) ………………………………………………………………(2分)(2)在点(2,1,3)M 的切平面方程为4(2)2(1)(3)0x y z -+---= 即4270x y z +--= ……………………………………………………………………………(2分) 法线方程为213421x y z ---==- …………………………………………………………………(2分) 2.(6分)22,22x y f x f y=-=--,令0,0,x y f f =⎧⎪⎨=⎪⎩,得驻点(1,- …………………………………(2分) 2,0,2xx xy yy f f f =-==-,有(1,1)2,(1,1)0,(1,1)2,xx xy yy A f B f C f =-=-=-==-=-则240,0AC B A -=><, ……………………………………………………………………………(2分) 所以(1-为极大值点,极大值为(1,1)2f -= ……………………………………………………(2分)3.(6分)平面薄片的质量22(,)(1)DDM x y dxdy x y dxdy μ==++⎰⎰⎰⎰ ……………………(2分)1220(1)d d πθρρρ=+⎰⎰ ……………………………………(2分)4210113[]2428πρρπ=+= …………………………………(2分) 4.(6分)所围空间区域{(,,)|0x y z z Ω=≤≤由高斯公式,有原式⎰⎰⎰Ω∂∂+∂∂+∂∂=dv zRy Q x P )(222(333)z y x dv Ω=++⎰⎰⎰ …………………………(2分)222203sin ad d r r dr ππθϕϕ=⋅⎰⎰⎰ ……………………(2分)552001632[cos ][]55a r a ππϕπ=⋅⋅-⋅= ……………………(2分)5.(6分)设所求曲线为)(x y y =,由题意得,y x y '=-,0)0(=y , 该方程为一阶线性微分方程y y x'+=,其中()1,P x Q x x== ………………………………(2分) 故通解为()()[()][]P x dx P x dx dx dx y e e Q x dx C e xe dx C --⎰⎰⎰⎰=+=+⎰⎰[]()1x x x x x x e xe dx C e xe e C Ce x ---=+=-+=+-⎰ …………………………(2分) 由)0(=y ,得1C =,从而所求曲线为1xy e x -=+- ……………………………………(2分)6.(6分)对应的齐次方程023=+'-''y y y 的特征方程为0232=+-r r , 得特征根11=r ,22=r则对应的齐次方程的通解为x x e C e C y 221+= ……………………………………………………(2分)对于非齐次方程xe y y y =+'-''23,1=λ为0232=+-r r 的单根,1)(=x P ,设其特解为xe x Q y )(*=,其中ax x Q =)(,a 为待定系数,)(x Q 满足)()()2()(x P x Q p x Q ='++''λ,即1))(312(0=-⋅+a ,所以1-=a , …………………………(2分)从而x x Q -=)(,特解xxe y -=*, 故原方程的通解为x x x xe e C e C y -+=221. ………………………………………………………(2分)7.(6分) 由于11133(1)44n n n n n n n ∞∞-==-=∑∑, 而111lim lim 44n n n nu n u n +→∞→∞+==,则113(1)4n nn n∞-=-∑收敛,………………………………………………(3分) 从而113(1)4n n n n∞-=-∑也收敛,且为绝对收敛. ……………………………………………………(3分)四、综合应用题(共2小题,共13分,其中第1题6分,第2题7分).1.(6分)设该容器的长,宽,高为z y x ,,,由题意知4xyz =,则4z xy=,容器的表面积488222()A xy yz xz xy x y xy xy x y=++=++=++,0,0>>y x ……………(3分)令228080x y A y x A x y ⎧=-=⎪⎪⎨⎪=-=⎪⎩, 解得驻点2x y == ……………………………………………………(2分)因实际问题存在最小值,且驻点唯一,所以当2()x y m ==,1()z m =时,容器的表面积最小,从而用料最省. ……………………………………………………………………………………………(1分)2.(7分)证明: (1)2),(y x y x P +=,82),(-=xy y x Q , 由于在xoy 面内,x Q y y P ∂∂==∂∂2恒成立,且,P Q y x∂∂∂∂连续, 故质点在该力场中移动时场力所作的功与路径无关. ………………………………………………(4分)(2)质点从点)0,1(A 移动到点)1,2(B 时场力所作的功(与路径无关) ,路径L 可取折线段B C C A →→,,其中点)0,2(C ,从而(2,1)(2,1)(1,0)(1,0)W F dr Pdx Qdy =⋅=+⎰⎰⎰-++=)0,2()0,1(2)82()(dyxy dx y x +⎰-++)1,2()0,2(2)82()(dy xy dx y x29)84(1021-=-+=⎰⎰dy y xdx …………………………………(3分)。
高数B(二)期末卷(2011)--A卷

高数B(二)期末卷(2011)--A卷上海海洋大学试卷姓名: 学号: 专业班名: 任课教师:____________一 .用图解法解下列线性规划问题(要求:画图时,必要的点要标清,否则不给分):1212121212min 2..0,2,33,,0.x x s t x x x x x x x x +-≥+≤+≥≥二. 试通过求基本可行解来确定下列线性规划问题的最优解.12123124min 25..216,212,0,1,2,,4.j x x s t x x x x x x x j +++=++=≥=L三. 用单纯形法解下列线性规划问题:12312312123min 3..22,24,246,0,1,2,3.j x x x s t x x x x x x x x x j -++-+≤-+≤-++≤≥=四. 分别用两步法、大M 法求解下列线性规划问题:1231231212min3..28,2,210,0,1,2,3.j x x x s t x x x x x x x x j -+-+=+≥+≤≥=五. 写出下列线性规划的对偶规划:12312312313(1)min 435..3215,273,1,0,1,2,3.j x x x s t x x x x x x x x x j -+++≤-+-≥+=≥=1234123412341234124(2)min 457..21,2633,4325,,,0.x x x x s t x x x x x x x x x x x x x x x ---+++-≥-++≤-+++=-≥六. 给定下列线性规划问题:1231323min 4618..33,25,0,1,2,3.j x x x s t x x x x x j +++≥+≥≥=(1)用对偶单纯形法求解;(2)若右端向量35b ⎛⎫= ⎪⎝⎭改为24b ⎛⎫'= ⎪⎝⎭,原来的最优基是否还为最优基?利用原来的最优表求新问题的最优解.七. 利用最小元素法求下面运输问题的一个基本可行解(直接填在表内即可): A .必要而非充分条件 B .充分而非必要条件 C.充分必要条件D .既非充分又非必要条件 2.柱面 20x z +=的母线平行于( )A .y 轴B .x 轴C .z 轴D .xoz 面3. 方程y x ''=经过点(0,1)且在此点与直线112y x =+相切的积分曲线为( )A .3116y x x =++ B .31216y x c x c =++C .311162y x x =++ D .212y c xc x=+4.下列命题正确的是 ( ) A .若lim 0nn u→∞=,则级数1n n u ∞=∑收敛 B .若lim 0nn u→∞≠,则级数1n n u ∞=∑发散C .若级数1n n u ∞=∑发散,则lim 0nn u→∞≠ D .若级数1n n u ∞=∑发散,则必有lim nn u→∞=∞5.已知微分方程2xy y y e '''+-=的一个特解为*xy xe =,则它的通解是( )A .212xc x c xxe ++ B .212xx xc ec e xe -++C .212xc x c xe ++ D .12x x xc ec e xe -++二、填空题(5153'=⨯'): 1.过点(2,4,0)且与直线210320x z y z +-=⎧⎨--=⎩ 垂直的平面方程为____________________。
2011-2012高等数学期末考试1B(B卷)
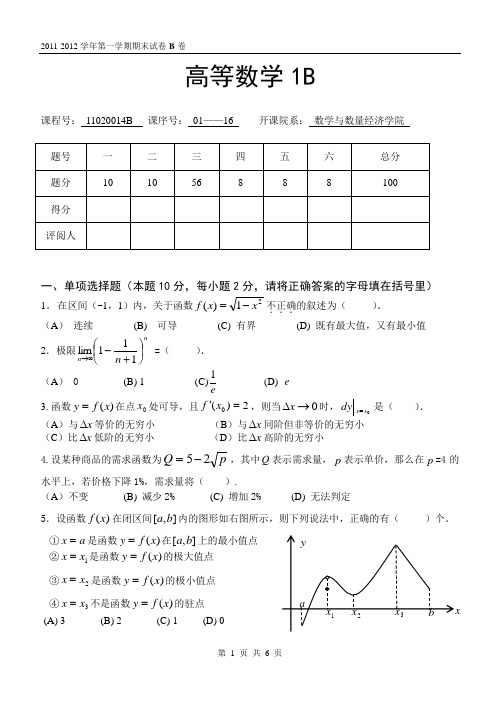
2011-2012学年第一学期期末试卷-B 卷高等数学1B课程号: 11020014B 课序号: 01——16 开课院系: 数学与数量经济学院一、单项选择题(本题10分,每小题2分,请将正确答案的字母填在括号里)1.在区间(-1,1)内,关于函数21)(x x f -=不正确...的叙述为( ). (A ) 连续 (B) 可导 (C) 有界 (D) 既有最大值,又有最小值2.极限nn n ⎪⎭⎫ ⎝⎛+-∞→111lim =( ). (A ) 0 (B) 1 (C)e1(D) e3.函数)(x f y =在点0x 处可导,且2)(0='x f ,则当0→∆x 时,0x x dy=是( ).(A )与x ∆等价的无穷小 (B )与x ∆同阶但非等价的无穷小(C )比x ∆低阶的无穷小(D )比x ∆高阶的无穷小 4.设某种商品的需求函数为p Q25-=,其中Q 表示需求量,p 表示单价,那么在p =4的水平上,若价格下降1%,需求量将( ).(A )不变 (B) 减少2% (C) 增加2% (D) 无法判定5.设函数)(x f 在闭区间],[b a 内的图形如右图所示,则下列说法中,正确的有( )个. ①a x =是函数)(x f y =在],[b a 上的最小值点 ②1x x =是函数)(x f y =的极大值点 ③2x x =是函数)(x f y =的极小值点 ④3x x =不是函数)(x f y =的驻点 (A) 3 (B) 2 (C) 1 (D) 0二、填空题(本题10分,每小题2分,请将正确答案写在横线上)1.函数22)(2---=x x x x f 的可去间断点为 .2.曲线12+-=x x y 的所有渐近线共有 条.3.已知C xdx x x f +='⎰21)(ln ,且1)0(=f ,则=)(x f . 4.曲线32x y =在点)0,0(处的切线方程为 .5.设)(2x f y =,其中)(x f 有二阶导数,则22dxyd = .三、计算题(本题56分,每小题7分)1.求极限()()()32tan 11212cos 1lim2x ex x x x ⋅--+⋅-→2.求极限 ⎥⎦⎤⎢⎣⎡+-→20)1ln(1lim x x x x3. 求极限ex e x e x -→⎪⎭⎫ ⎝⎛1sin sin lim2011-2012学年第一学期期末试卷-B 卷4.设函数⎩⎨⎧<<--+≤<-+=10,1101),1ln()(x x x x x x f ,求)(x f '的表达式.5. 设函数3232x y f x -⎛⎫= ⎪+⎝⎭,且2()arcsin f x x '=,求0x dy dx =6.已知由方程e xy e y=+确定了y 是x 的函数,求=x dxdy及022=x dx y d7.求不定积分()dx xx⎰+3118.求不定积分dx x x x ⎰3sin cos四、(本题8分)已知函数21x y +=,计算后填写下表:2011-2012学年第一学期期末试卷-B 卷五、(本题8分)某工厂生产一种产品的总成本函数为Q Q C 21200)(+=,价格与需求量之间的函数关系为QP 100=,其中Q 为产量,P 为价格,求(1)边际成本函数、边际收益函数、边际利润函数;(2)生产该产品的产量为多少时能获得最大利润,最大利润是多少?六、证明题(本题8分)1.证明:当0>x 时,3!31sin x x x ->2.设函数)(x f 在]1,0[上连续,在)1,0(内可导, 且0)1(=f .求证:至少存在一点)1,0(∈ξ, 使得 3'()()0f f ξξξ+=。
2012年高数(下学期)试卷及参考答案(已更正20140622)(1)

华南农业大学期末考试试卷(A 卷)2011~2012学年第2 学期 考试科目:高等数学A Ⅱ 考试类型:(闭卷)考试 考试时间: 120 分钟 学号 姓名 年级专业一、填空题(本大题共5小题,每小题3分,共15分)1.设有向量(1,2,2)a =- ,(2,1,2)b =- ,则数量积()()a b a b -⋅+。
2.曲面22z x xy y =++在点(1,1,3)M 处的切平面方程是 。
3.设u =(1,1,1)u =grad 。
4.幂级数0()3n n x∞=∑的收敛半径R = 。
5.微分方程430y y y '''-+=的通解是 。
二、单项选择题(本大题共5小题,每小题3分,共15分)1.已知(1,1,1)A ,(2,2,1)B ,(2,1,2)C ,则AB 与AC的夹角θ是(B )A .4π B .3π C .6π D .2π 2.函数2z xy =在点(1,2)处的全微分是 ( D )A .8B .4dx dy +C .22y dx xydy +D .4()dx dy +3.设L 为圆周222x y a +=,取逆时针方向,则2222()Lx ydx x xy dy ++=⎰ ( B )A .2a πB .42a π C .2πD .04.下列级数中收敛的是 ( C )A.1n ∞= B.1n ∞= C .114n n ∞=∑ D .114n n∞=∑5.微分方程12x y e-'=的通解是 ( C )A .12x y eC -=+ B .12x y e C =+ C .122x y e C -=-+ D .12x y Ce-=三、计算题(本大题共7小题,每小题7分,共49分) 1.设2,,xs f x xyz y⎛⎫= ⎪⎝⎭,且f 具有一阶连续偏导数,求s x ∂∂,s y ∂∂,s z∂∂. 2. 设由方程22240x y z z +++=确定隐函数(,)z z x y =,求全微分dz 。
2011-2012学年第二学期高等数学IB期末考试 试卷A

2011-2012学年第二学期高等数学IB 期末考试 试卷A参考答案 试卷号:A20120625一、单项选择题(每题3分,共15分)1、微分方程20=-'+''y y y 的通解是( ) (A )212+xxy C e C e -=; (B )212+x xy C e C e -=;(C )212+x x y C e C e -=; (D) x xe C eC y 221+=-.2、改变10(,)dy f x y dx ⎰⎰的积分次序,则下列结果正确的是( )(A )110(,)dx f x y dy -⎰⎰ ; (B )10(,)dx f x y dy ⎰⎰;(C )11(,)dx f x y dy -⎰⎰; (D )10(,)dx f x y dy ⎰⎰.3、函数),(y x f 在点),(y x P 处可微的充分条件是( )(A )),(y x f 的全部一阶偏导数存在; (B )),(y x f 连续; (C )),(y x f 的全部一阶偏导数连续; (D )),(y x f 连续且yf x f ∂∂∂∂,均存在. 4、设L 是从(1,2)A -到(1,0)B 的直线段,则曲线积分()Lx y ds +=⎰( )(A); (B) (C) 2; (D) 0.5、若级数∑∞=1n na收敛,∑∞=1n nb发散,则级数( )(A)∑∞=1)(n nn ba 收敛; (B)∑∞=1)(n nn b a 发散 ;(C)∑∞=+1)(n n nb a收敛; (D)∑∞=+1)(n n nb a发散.二、填空题(每题3分,共15分)1、设∑是球面2222a z y x =++的外侧,则曲面积分⎰⎰∑zdxdy =_______.2、已知级数∑∞=1n nu的前n 项和1+=n ns n ,则该级数的通项n u =__________.3、比较积分的大小:⎰⎰+Dd y x σ)ln(_____⎰⎰+Dd y x σ2)][ln((填>、=或<),其中区域D 是三角形闭区域,三顶点各为(1,0),(1,1,),(2,0).4、定积分2()f x dx =⎰_________, 其中,01()2,12x x f x x x ≤≤⎧=⎨-<≤⎩.5、 函数(,,)zf x y z xy y=+的全微分(,,)df x y z = ________________,梯度 (2,1,1)(,,)|grad f x y z =u u u u u v___________. 三、解答题(每题6分,共30分)1、计算定积分1cos x xdx ⋅⎰.2、求微分方程'''0xy y +=的通解.3、计算二重积分3()Dx y yd σ+⎰⎰,其中{(,)|11,01}D x y x y =-≤≤≤≤. 4、求幂级数231(1)23n n x x x x n--+++-+L L 的收敛半径及收敛域. 5、计算曲面积分2y dS ∑⎰⎰,其中{(,,)|1,0,0,0}x y z x y z x y z ∑=++=≥≥≥. 四、(本题满分8分) 计算三重积分22()I x y dv Ω=+⎰⎰⎰,其中Ω由抛物面22z x y =+与平面1z =围成闭区域. 五、(本题满分10分)已知L 是第一象限中从点(0,0)沿圆周222x y x +=到点(2,0),再沿圆周224x y +=到点(0,2)的曲线段,计算曲线积分233(2)LI x ydx x x y dy =++-⎰.(利用格林公式计算) 六、(本题满分8分)设(,)f u v 具有连续的偏导数, (,)w f xy yz =,证明: w w wxz y x z y∂∂∂+=∂∂∂.七、(本题满分14分)(1)已知三个正数之和为a,试问这三个正数分别为何值时,它们的倒数之积最小.(2)判断级数13nn n∞=∑的敛散性,若收敛,求级数的和.。
华农-11-12年第二学期高等数学下试题及参考答案

华南农业大学期末考试试卷(A 卷)2011~2012学年第2 学期 考试科目:高等数学A Ⅱ 考试类型:(闭卷)考试 考试时间: 120 分钟学号 姓名 年级专业一、填空题(本大题共5小题,每小题3分,共15分)1.设有向量(1,2,2)a =-,(2,1,2)b =-,则数量积()()a b a b -⋅+ 。
2.曲面22z x xy y =++在点(1,1,3)M 处的切平面方程是 。
3.设u =,则(1,1,1)u =grad 。
4.幂级数0()3n n x∞=∑的收敛半径R = 。
35.(此题新大纲不做要求,已删除)二、单项选择题(本大题共5小题,每小题3分,共15分)1.已知(1,1,1)A ,(2,2,1)B ,(2,1,2)C ,则AB 与AC 的夹角θ是(B )A .4π B .3π C .6π D .2π2.函数2z xy =在点(1,2)处的全微分是 ( D )A .8B .4dx dy +C .22y dx xydy +D .4()dx dy + 3.设L 为圆周222x y a +=,取逆时针方向,则2222()Lx ydx x xy dy ++=⎰( B )A .2a πB .42a π C .2πD .04.下列级数中收敛的是 ( C )A.n ∞= B.1n ∞= C .114n n ∞=∑ D .114n n∞=∑5.微分方程12x y e-'=的通解是 ( C )A .12x y eC -=+ B .12x y e C =+C .122x y e C -=-+ D .12x y Ce -=三、计算题(本大题共7小题,每小题7分,共49分) 1.设2,,xs f x xyz y⎛⎫= ⎪⎝⎭,且f 具有一阶连续偏导数,求s x ∂∂,s y ∂∂,s z∂∂. 2. 设由方程22240x y z z +++=确定隐函数(,)z z x y =,求全微分dz 。
11-12高数文C2A卷参考答案

高等数学C2A 卷参考答案及评分标准2011~2012第二学期二、填空题(每空3分,共15分)11、4122<+<y x 。
12、41。
13、zy x zy x 322++--。
14、)3,2,1(--。
15、 ln2 。
三、解答题(共6题,每小题9分,总分54分)16、(1))3cos()3sin(y x x y x x z -+-=∂∂ , )3cos(3y x x yz --=∂∂; dy y x x dx y x x dx y x dz )3cos(3)3cos()3sin(---+-=(……5分)(2))3sin(922y x x y z --=∂∂,)3sin(3)3cos(32y x x y x yx z -+--=∂∂∂(……4分)17、(1)方程为:12'-=y y ,满足初始条件:10==x y (……4分) (2)通解为:212+=xCe y ,特解为21212+=x e y (……5分) 18、解:令x t =,原式⎰=22dt te t(……3分)22222220+=-=⎰e dt e te t t (……6分)19、解:(1) 2=a 时,n n a a 111<+,而级数∑∞=01n n a 收敛,故级数∑∞=+-01)1(n n na 绝对收敛(……6分) (2) 5.0=a 时,0111lim ≠=++∞→n n a ,故此时级数∑∞=+-01)1(n n na 发散(……3分)20、解:(1) 2222)12()12(lim x x n x n n n n =-+-+∞→,当12<x 时,级数绝对收敛; 而当1±=x 时,级数均为∑∞=+1)12(n n 发散。
故收敛半径为1,收敛域为)1,1(-(……4分)(2))'1()'()'()12(2311211212x x xxxn n n n n n n-===+∑∑∑∞=+∞=+∞=故)1,1(,)1(3)12(224212-∈--=+∑∞=x x x x x n n n(……5分)21.解:⎰⎰+y ydx x y dy 110=⎰⎰+x x dy x y dx 2110(……3分)=241)(211032=-⎰dx x x (……6分)四、证明题(共2题,总分11分)22. 本题满分6分 证:)('222y x xf x z +=∂∂,)('222y x yf yz+=∂∂(……4分) 则0'2'2=-=∂∂-∂∂xyf xyf yzx x z y,得证(……2分) 23. 本题满分5分证:对左边,令2x t =,则⎰⎰⎰==22023)(21)(21)(a a a dx x xf dt t tf dx x f x (……5分)。
东北财经大学 高等数学2A 期末试卷 11-12学年 A卷

2011-2012学年第一学期期末试卷-A 卷高等数学A2一、填空题(共8道题,每题3分,共24分)1. 函数(),arcsin f x y y = 2. 2020ln(1)lim sin x x t dt x x →+=⎰3.积分1+∞⎰的敛散性为: 4. 22121(1)n n n n ∞=+=+∑ 5. 交换累次积分的次序:100(,)x dx f x y dy =⎰⎰6.函数ln(1)y x x =+在0x =处的Maclaurin 级数为7.微分方程0y y '-=的通解为8.已知函数2z x y =,则(1,1)|dz =二、 单项选择题(共8道题,每题2分,共16分。
)1.设函数()f x 在闭区间[0,2]上连续,若令变量2t x =,则定积分10(2)f x dx ⎰化为2112000011) () ) () ) 2() ) 2()22A f t dt B f t dt C f t dt D f t dt ⎰⎰⎰⎰ 2.设函数()f x 在(,)-∞+∞内为奇函数且可导,则下列函数中为奇函数的为A ) sin '()f xB )0(sin )()x x f t dt ⎰ C ) 0sin ()x f t dt ⎰ D) 0(())x t f t dt +⎰ 3.对函数2(,)2f x y y xy =+,点M(0,0)A ) 不是驻点B )是驻点却不是极值点C ) 是极大值点 D) 是极小值点4.函数(,)z f x y =在00(,)M x y 点偏导数存在,则在该点处A ) 二重极限存在B )连续C ) 可微 D) 以上都不成立5.若级数1n n a∞=∑收敛,1n n b ∞=∑发散,则1n n n a b ∞=∑ A ) 收敛 B )发散 C ) 条件收敛 D) 敛散性不定6.幂级数11n n x n∞=∑的收敛域为 ) (1,1) ) [1,1] ) [1,1) ) (1,1]A B C D ----7.微分方程20xdy ydx +=的通解是A ) y cx =B )2y cx =C ) c y x = D) 2c y x= 8.微分方程0y y '+=满足初值条件0|3x y ==的特解为A ) 3x y e -=B )3x y e =C ) 3x y e -=+ D) 3x y e =+三、 计算题:(共8道题,每题5分,共40分)1) 计算:120ln(1)x dx +⎰2) 已知函数()2,ln(),y f x y x x=+求(,)df x y3) 设(,)z f xy y =,其中f 具有二阶连续偏导数,求2z x y∂∂∂2011-2012学年第一学期期末试卷-A 卷.4) 计算:2sin Dy I d y σ=⎰⎰,其中D由20,y x y x ==所围成的封闭区域5)计算:D I σ=,其中:22:{(,)|14}D x y x y ≤+≤6)判断级数1(1)ln(1n n ∞=-∑的敛散性 ,若收敛,问是绝对收敛还是条件收敛7) 求幂级数21121n n x n -∞=-∑的和函数,并求级数11(21)2n n n ∞=-∑的和8) 设可微函数()f x ,满足:2()22()x xf x x f t dt =++⎰,求()f x四、 概念题(每题6分,共6分) 已知函数()22222222ln(), 0,40, 0x y x y x y f x y x y ⎧+++≠⎪=⎨⎪+=⎩求2(,)(0,0)(,)x y f x y x y =∂∂∂2011-2012学年第一学期期末试卷-A 卷五、 应用题:(每题10分,共10分) 某企业生产某产品的产量3144(,)80Q x y x y =,其中x 为劳动力人数,y 为设备台数,该企业投入40万元生产该产品,设招聘一个劳动力需要600元,购买一台设备需要2000元,试求该企业最佳资金投入分配方案。
2012级郑州大学高等数学(下)(A)卷及其参考答案

2012~2013年第二学期《微积分》期末考试试卷(A 卷)及其参考答案(985)一、解答题(每题5分,共 301.设xyez arctan=,求dz2.求曲面22y x z +=在点()5,2,1处的切平面方程.3.设金属板上电压分布为22450y x V --=,问在点()2,1-处(1)沿哪个方向电压升高最快?速率是多少?(2)沿哪个方向电压降低最快?速率是多少?(3)沿哪个方向电压变化率为零? 4.求二重积分dxdy xxD⎰⎰sin ,其中D 是由直线x y =和抛物线2x y =所围成的区域. 5.有某物质分布在圆锥螺线()π20,sin ,cos ≤≤===t t z t t y t t x 上,其分布密度为()z z y x =,,μ,求这种物质的总质量. .6.计算⎰Γ++xdz zdy ydx ,其中Γ为曲线()π20,sin ,cos ≤≤===t bt z t a y t a x上按t 1.()()ny mx y x nm++≈++1112.设 (),y x F ()1,0的某邻域内是否都存在唯一的函数()x y y =)00y =.3.求三重积分Ω由球面4222=++z y x 的上半球面与抛物面z y x 322=+围成的区域. 4.计算曲面积分()d S z y x⎰⎰∑++222,其中∑是球面z z y x 2222=++围成的区域5.计算()dydz x S⎰⎰+12,其中S 是由xoy 平面上的曲线x y =()10≤≤x 绕x 轴一周所得曲面的外侧.三、解答题(每题7分,共21分)1.已知制造商的生产函数(生产量)是()4143100,y x y x f =,其中x 表示劳动力数量,y 为资本数量(y 个单位资本).每个劳动力与每单位资本的成本分别为150元及250元.该制造商的总预算是50000元.问他该如何分配这笔钱雇佣劳力与资本,以使生产量最大? 2.积分⎰+-Ly x xdy ydx 22是否在任何区域内都与积分路径无关?求⎰+-=L yx xdyydx I 22,其中L 沿曲线x y cos =上从点⎪⎭⎫ ⎝⎛0,2πA 到点⎪⎭⎫⎝⎛-0,2πB 的曲线段.3.(1)将()ππ≤≤-x x x 0632展成余弦级数; (2)求下面级数之和:()...1 (31)2112122+-+-+--n n(3四、(每题满分9分)设()t x u ,22222xu a t u ∂∂=∂∂(1)作代换,证明弦振动方程22222x u a t u ∂∂=∂∂可以化为 (2来.五、(每题满分10分)设V 为空间中的有界闭区域,其边界曲面S 为光滑曲面,{}γβαcos ,cos ,cos =为S 的单位外法线向量,()z y x u u ,,=在V 内有二阶连续偏导数,在V 上连续,并且满足0222222=∂∂+∂∂+∂∂zuy u x u ① (1;(2)证明 dV z u y u x u dS n V S ⎰⎰⎰⎰⎰⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛∂∂+⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂=∂222; (3)若()z y x u u ,,=在S 上恒为零,证明()z y x u u ,,=在V 内也恒为零.答案 一1、解:xyxye y x y x y x y exz arctan 2222arctan 11+-=⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛+=∂∂ xyxye y x x x x y e yz arctan 222arctan 111+=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛+=∂∂所以 dy y z dx x z dz ∂∂+∂∂=.22arctan ⎥⎦⎤⎢⎣⎡+-=∂∂y x ydx xdy e x z xy2、【解】令()22,,y x z z y x F --=.则{}(){}(){}1,4,21,2,2,,||5,2,1`5,2,1--=--='''=y x F F F z y x .(.2--x ,即 0542=++--z y x3、【解】(1}y x 8,2-,(){}16,2|2,1-=-gradV ,所以沿{}16,2-=()26016222=+-;(2)沿=()26016222=-+;(3)沿与()|2,1-gradV 垂直的方向,即沿{}2,16±方向的电压变化率为零.4、解dy x x dx dxdy x x x x D⎰⎰⎰⎰=103sin sin ()⎰-=102sin dx x x x x ⎰=10sin xdx ⎰-10sin xdx x 1sin 1-=5、解:()()()1,cos sin ,sin cos ='+='-='t z t t t t y t t t t x ()()()dt t dt t z t y t x ds 22222+='+'+'=所以()()220220222212,,t d t dt t t ds z y x M ++=+==⎰⎰⎰Γππμ()()⎥⎦⎤⎢⎣⎡-+=+=22423123123220232|ππt6、解:()()()[]dt b t a t a bt t a t a xdz zdy ydx ⎰⎰++-=++Γπ20.cos cos .sin .sin .2πa -=二、1、【证明】令()()()nmy x y x f ++=11,. 则()()()nm x y x m y x f ++='-11,1;()()()111,-++='n m y y x n y x f()y x f x ,'及()y x f y ,'在点()0,0处都是y x ,的二元连续函数,故()y x f ,在点()0,0处可微分,于是,当x 和y 都很小时,有()()()()y f x f f y x f y x 0,00,00,00,0'+'≈-++,即()()ny mx y x n m ++≈++111.2、【解】因为()x y x F x 2,=',()y y x F y 2,='是连续的,且在点()1,0处()0,≠'y x F y .所以在点()1,0的邻域内存在唯一的()x y y =,使得 ()()0,≡x y x F ,且()10=y ,表达式为y 邻域内不存在唯一的()x y y =,使得()()0,≡x y x F 3、z 得 Ω向xoy 面上的投影区域为 3:22≤+y x D xy .所以 ⎰⎰⎰Ω=zdxdydz I 【柱面坐标】⎰⎰⎰-=2243203r r zdz dr r d πθ⎰⎥⎦⎤⎢⎣⎡=-3432|32212r r z r π⎰⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛--=304294dr r r r .41354423|0642ππ=⎥⎦⎤⎢⎣⎡--=r r r【解法二】⎰⎰⎰Ω=zdxdydz I 【切片法】()⎰⎰⎰⎰⎰⎰⎪⎭⎫ ⎝⎛-≤+≤++=222222242113z y x zy x dxdy zdzdxdy zdz().4134243||21421121322πππππ=⎪⎪⎭⎫ ⎝⎛-+=-+=⎰⎰z z z dz z z dz z 4、解】记22111:y x z --+=∑(上半球面),22211:y x z ---=∑(下半球面).1∑和2∑向xoy 坐标面上的投影区域都是1:22≤+y x D xy .并且对1∑和2∑都有d x d yyx d x d y z z dS y x 2222111--='+'+=. 于是(x⎰⎰∑2==+=.8π5、.记S 与1S 1⎰⎰⎰Ω=dxdydz 2【切片法】⎰⎰⎰=xD dydz dx 21()ππ=⎥⎦⎤⎢⎣⎡=⎰1022dx x .所以 ()()d y d z x d y d zx S S⎰⎰⎰⎰+-=+11212π. 又1:1=x S (前侧)向yoz 坐标面上的投影区域为1:22≤+z y D yz ,故()dydz x S ⎰⎰+112()π41121=+=⎰⎰dydz yz D .所以,().3412πππ-=-=+⎰⎰dydz x S【解法二】旋转曲面的方程为22:z y x S +=,其向yoz 坐标面上的投影区域为1:22≤+z y D yz .()()⎰⎰⎰⎰++-=+yzD Sdydz z ydydz x 221212dz dy yzD ⎰⎰-=2()dz dy z y yzD ⎰⎰+-222⎰⎰-=--=ππθπ2012222r d r r d 三、1、【解法一】这是一个条件极值问题.41y 与函数()y x y x f ln 41ln 4310ln 2,ln ++=()y x f ,ln 在条件050000250150=-+y x 下的极值.令 ()ln 1ln 310ln 2,,+++=y x y x L λ则由((⎪⎪⎪⎩⎪⎪⎪⎨⎧=''',,L y x L y x L yxλ .50,250==y x 个,其余的钱用于资本,可使生产量最大.此时,(1671950,250≈f .【解法二】问题等价为求函数()y x f ,4在条件100053=+y x ①下的极值.()()[]y x x x y x y x f5 (105)110,8384⨯==【均值不等式】4845.1051⎥⎦⎤⎢⎣⎡+++⨯≤y x x x 48453.1051⎥⎦⎤⎢⎣⎡+⨯=y x 【由①】 =⎥⎦⎤⎢⎣⎡⨯=4841000.1051.10451204⨯⨯ 因此有()1617910451,54≈⨯⨯≤y x f . ② 由均值不等式中等号成立的条件知,②中等号成立的条件是 y x 5=. ③将③代入①解得 .50,250==y x所以,当50,250==y x 时,生产量最大,即应该雇佣劳动力250个,其余的钱用于资本,可使生产量最大.此时,()1671950,250=f . 2、【解】(一)显然2222y x y y yx xx ⎪⎪⎭⎫ ⎝⎛+∂∂=⎪⎪⎭⎫ ⎝⎛+-∂∂()0,0O 外处成立.因此当区域D 不通过也不包围原点D 内与路径无关;而当区域D 通过或包围原点()0,0O . (二)因为含在某个不通过也不包围原点()0,0O 的区域D 内,故⎰改选取沿上半圆周2222:⎪⎭⎫ ⎝⎛=+'πy x L ()0≥y .⎰+Ly x 22⎰'+-=L y x x d y x 22⎰'⎪⎭⎫ ⎝⎛-=L x d yy d x 22π ⎰'-=L x d y y d x 24π.又L '的参数方程为πππ~0:,s i n 2,c o s 2:t t y t x L ⎪⎪⎩⎪⎪⎨⎧=='.所以dt t t t t y x xdy ydx L⎰⎰⎥⎦⎤⎢⎣⎡-⎪⎭⎫ ⎝⎛-=+-ππππππ222cos 2.cos 2sin 2.sin 24ππππ-=⎥⎦⎤⎢⎣⎡-=⎰dt 02244. 3、【解】(1)对()()ππ≤≤-=x x x x f 0632进行偶延拓及周期延拓.,...)2,1(0==n b n ;()()()2023204326322|πππππππππ-=-=-==⎰⎰x x dx x x dx x f a ;()()⎰⎰-==πππππ02cos 632cos 2nxdx x x nxdx x f a n()()⎰-=πππ02sin 632nx d x x n ()()⎥⎦⎤⎢⎣⎡---=⎰πππππ002sin 66|sin 632nxdx x nx x x n ()()⎰-=πππ02cos 12nx d x n ()⎥⎦⎤⎢⎣⎡--=⎰ππππ002cos cos 12|nxdx nx x n212n=,...)2,1(=n所以,()ππ≤≤-x x x 0632的余弦级数为nx3,()π≤≤x 0. ① (2 )π- 即∑∞=-=-122112n nnπ()∑∞=---=121112n n n所以有()...1 (31)2112122+-+-+--n n ().1212121π=-=∑∞=-n n n (2)(3)从②式可见,第二问的结果可以用来求π的近似值.四【解】(1)因为ηξηξηηξξ∂∂+∂∂=∂∂+∂∂=∂∂∂∂+∂∂∂∂=∂∂uu u u x u x u x u 1.1...;()⎪⎪⎭⎫ ⎝⎛∂∂-∂∂=-∂∂+∂∂=∂∂∂∂+∂∂∂∂=∂∂ηξηξηηξξu u a a ua u t u t u t u ..... 故有⎪⎪⎭⎫⎝⎛∂∂∂∂+∂∂∂∂∂+⎪⎪⎭⎫ ⎝⎛∂∂∂∂∂+∂∂∂∂='⎪⎪⎭⎫⎝⎛∂∂+'⎪⎪⎭⎫ ⎝⎛∂∂=∂∂x u x u x u x u u u x u xx ηηξξηηηξξξηξ....22222222 222222ηηξξ∂∂+∂∂∂+∂∂=uu u . ② ⎥⎦⎤⎢⎣⎡'⎪⎪⎭⎫ ⎝⎛∂∂-'⎪⎪⎭⎫ ⎝⎛∂∂=∂∂t t u u a t uηξ22⎢⎣⎡-⎪⎪⎭⎫ ⎝⎛∂∂∂∂∂+∂∂∂∂=t u t u a ηηξξξ..222 ()⎢⎣⎡ ⎝⎛∂∂∂-⎪⎪⎭⎫ ⎝⎛-∂∂∂+∂∂=a u a u a u a ...2222ξηηξξ⎪⎪⎭⎫⎝⎛∂∂+∂∂∂-∂∂=2222222ηηξξu u u a . ③⎪⎪⎭⎫ ⎝⎛∂∂+∂∂∂+∂∂2222222ηηξξu u u a . ④ ⑤(2 02=∂∂∂ηξu故得到()⎰⎰==∂∂∂=∂∂ξϕηηηξξd d uu 02. ⑥其中()ξϕ为任意函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、填空题(每小题3分,共15分)1、向量(4,3,4)a=-在向量(2,2,1)b=上的投影为________.2、函数xyz e=在点(2,1)处的全微分为________.3、若积分区域D为{}22(,)|14x y x y≤+≤,则二重积分(,)Df x y dσ⎰⎰化为极坐标形式的二次积分为。
4、设积分曲线L为圆周122=+yx,则曲线积分2(+)Lx x ds=⎰________.5、若级数1n∞=收敛,则p的取值范围是________.二、选择题(每小题3分,共15分)1、在曲线23,,x t y t z t==-=的所有切线中,与平面x+24y z+=平行的切线())A只有两条)B只有一条)C至少有3条)D不存在2、二次积分100(,)xdx f x y dy⎰⎰交换积分次序后为())A100(,)ydy f x y dx⎰⎰)B11(,)ydy f x y dx⎰⎰)C101(,)ydy f x y dx⎰⎰)D1100(,)dy f x y dx⎰⎰3、已知(32)(4)x ay dx x y dy+++为某一函数的全微分,则a=())A3)B1)C2)D44、设)(xf为周期为2π的函数,它在区间[)ππ-,上定义为,0()0,0x xf xxππ-≤<⎧=⎨≤<⎩,则)(xf的傅立叶级数在xπ=处收敛())A 0 )B32π )C 2π )D 2π- 5、方程///2322y y y x -+=的一个特解应具有形式( ))A 2ax ; )B 2ax bx c ++; )C )(2c bx ax x ++; )D )(22c bx ax x ++.三、(共21分)1、(7分)设()22,z f xy x y =,f 具有二阶连续偏导数,求2zx y∂∂∂。
2、(7分)计算二重积分22()Dx y x dxdy +-⎰⎰,其中D 是由直线2,y y x ==及2y x =所围成的闭区域3、(7分)利用高斯公式计算曲面积分222xz dydz yx dzdx zy dxdy ∑++⎰⎰,其中∑是柱体{}22=(,,)|4,03x y z x y z Ω+≤≤≤的整个边界曲面的外侧。
四、(共21分)1、(7分)利用格林公式计算()()x yLI e y dx e x dy =+-+⎰,其中L是在圆周y = 上由点(2,0)-到点(2,0)的上半圆弧。
2、(7分)求微分方程()0ln ln =-+dx x y xdy x 的通解。
3、(7分)设函数232u xy z xyz =+-,求 (1)u 在点(1,1,2)A 处的梯度;(2)u 在点(1,1,2)A 处沿着从点(1,1,2)A 到点(2,2,3)B 的方向的方向导数。
五、(共16分)1、(8分)求幂级数2121nn x n ∞=+∑的收敛域及和函数。
2、(8分)设曲面22z x y =+在点A 处的切平面平行于平面240x y z +-=,求该曲面在点A 处的切平面及法线的方程。
六、(共12分) 1、(6分)设常数0,λ> 若级数21n n a ∞=∑收敛,证明级数11nn ∞=∑(-收敛。
2、(6分)设函数2()ny z x f x =,f 可导.证明2.z zx y nz x y∂∂+=∂∂(答案要注明各个要点的评分标准)一、 填空题:(每小题3分,共15分)1. 2;2. 222e dx e dy +;3. 221(cos ,sin )d f r r rdr πθθθ⎰⎰ ;4.π; 5. 43p > 。
二、选择题:(每小题3分,共15分)1).A 2).B 3).C 4).D 5).B三、(共21分)1、解22121222zf y f xy y f xyf x∂''''=⋅+⋅=+∂ -------------------------------------------2分 ()()221122222z yf y f xf xy f x y y y∂∂∂''''=+++∂∂∂∂ -----------------------------------4分()()222111122212222222yf y f xy f x xf xy f xy f x ''''''''''=+⋅+⋅++⋅+⋅32231112221225222xy f x y f x yf yf xf ''''''''=++++。
-------------------------------7分2、解:222222()=()yy Dx y x dxdy dy x y x dx +-+-⎰⎰⎰⎰ -----------------------------------4分232193()248y y dy =-⎰13.6=- ---------------------------------------7分3.解:由高斯公式得222xz dydz yx dzdx zy dxdy ∑++⎰⎰=222()z x y dv Ω++⎰⎰⎰ 223220()d d z dz πθρρρ=+⎰⎰⎰ …………………………………4分2202(39)60d πρρρπ=+=⎰ …………………………………7分四、(共21分)1、解 设沿x 轴从(-2,0)到(2,0)的直线段为L 1,则L 1:y =0,x 从-2到2。
记L 与1L 所围成区域为D ,则由Green 公式知1()()(11)-x y L L De y dx e x dy dxdy π-++-+=--=⎰⎰⎰, --------------------------4分又122221()()x yx L e y dx e x dy e dx e e -+-+==-⎰⎰, -------------------------5分 故221+I e eπ=-。
-------------------------7分 2、解 原方程可化为xy x x y 1ln 1=+'------------------------------------2分 这是一阶非齐次线性微分方程,可用公式法。
设()()xx Q x x x P 1,ln 1== 原方程通解为()()()⎥⎦⎤⎢⎣⎡+⎰⎰=⎰-C dx e x Q e y dx x P dx x P ---------------------------------4分⎪⎪⎭⎫ ⎝⎛+⎰⎰=⎰-C dx e x e dx x x dx x x ln 1ln 11⎪⎭⎫ ⎝⎛+=C x x 2ln 21ln 1- -----------------------------------7分 3、解(1)22(,,)(2,22,32)u u ugradu y yz xy xz z xy x y z∂∂∂==---∂∂∂ ----------------2分 (1,1,2)(3,2,10)gradu =--- ---------------- 3分(2) (1,1,1)l AB ==,cos cos cos 3αβγ===--------------------------5分(1,1,2)|3210u l ∂=--=-∂ -------------------------7分 五、(共16分)1、解:级数的收敛域为(1,1)-; 显然(0)0,s =对(1,0)(0,1),x ∀∈-⋃212011111()21x n n n n s x x x dx x n x ∞∞+====+∑∑⎰ ………………………………………3分2011x nn x dx x ∞==∑⎰ ………………………………………5分 220111(ln )1121x x x dx x x x x+==---⎰ ………………………………………8分2、解、解: 设22(,,)F x y z x y z =+- -------------------------------1分则2,2,1F F Fx y x y z∂∂∂===-∂∂∂ ------------------------------4分 则曲面在点000,,)A x y z (处切平面法向量为00(2,2,1)n x y =- -----------------------------6分因240x y z +-=的法向量为 (2,4,1)- , 故0000022,24,1, 2.x y x y ====即此时z =5。
切平面方程为:2(1)4(2)(5)0x y z -+---=整理得 2450x y z +--= -----------------------------7分法线方程为125241x y z ---==- ------------------------------8分 六、(共12分)1、证明:证明:设11nn U ∞==∑(-则22211(),2nn a U a n n=<≤+ --------------------2分 由级数21n n a ∞=∑收敛且211n n ∞=∑收敛,知原级数绝对收敛,故原级数收敛。
--------------------5分( 2、证明:'+'=∂∂2122yf xf x z ,'+'-=∂∂2122xf yf yz ----------2分 "+"+"+'=∂∂222211121224842f y xyf f x f xz --------------------3分 "+"-"+'-=∂∂222121121224842f x xyf f y f yz --------------------4分所以,"-"+"+"+=∂∂+∂∂1221221122222288))(44(xyf xyf f f y x yz x z -------5分因为函数f 二阶偏导连续,故"="1221f f 又已知条件02211="+"f f ,所以02222=∂∂+∂∂yzx z ,结论得证。
--------------6分。
